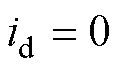 的磁场定向控制条件下,PMLSM电磁推力
的磁场定向控制条件下,PMLSM电磁推力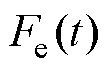 为
为摘要 针对永磁直线同步电机(PMLSM)在跟踪不同参考轨迹运动时,易受参数变化、外部扰动以及摩擦力等不确定因素影响而降低伺服性能的问题,提出一种基于自适应模糊神经网络时变滑模控制器(AFNNTSMC)的精密位置跟踪方法。首先,在PMLSM数学模型的基础上,将时变滑模面引入到传统滑模控制器(SMC)中设计时变滑模控制器(TSMC)。通过调整时变滑模面的斜率,可以在保证鲁棒性的前提下,有效缩短系统状态到达滑动模态的时间,提高系统的响应速度。其次,由于TSMC中斜率值较难获得,因此将其与模糊神经网络相结合设计AFNNTSMC方法。通过采用Lyapounov函数设计自适应律,对时变滑模面的斜率值实时估计并在线调整,保证系统达到最佳伺服性能。最后,在参数变化和外部扰动两种实验条件下,验证所提方法的有效性。实验结果表明,AFNNTSMC可以有效提高系统的响应速度和位置跟踪精度,对不确定性因素具有较强的鲁棒性。
关键词:永磁直线同步电机 时变滑模控制 自适应模糊神经网络 鲁棒性
随着新兴电力电子技术和稀土永磁材料的发展,永磁直线同步电机(Permanent Magnet Linear Synchronous Motor, PMLSM)被广泛应用到数控机床、机器人、激光切割平台等领域[1]。PMLSM采用直接驱动方式,在结构上削减了齿轮、链条等传动环节,具有大推力、高精度和高可靠性等优点。然而,由于PMLSM中参数变化以及负载阻力等因素的存在,也使直线电机易受干扰,导致无法精准跟踪给定位置,从而降低系统的伺服性能[2-3]。
尽管PID控制等传统方法在工业上有大量的应用,但是在一些要求高精度高速度的场合,传统方法无法保证PMLSM对以上不确定性因素的克服能力[4]。相比传统控制策略,近年来,自适应控制[5]、反推控制[6]、滑模变结构控制[7]等现代控制策略,越来越多地应用到直线伺服系统的控制中,保证了系统的鲁棒性能和跟踪性能。此外,模糊控制[8]、神经网络控制[9]等具有强学习能力的智能控制方法也逐步应用到PMLSM的控制中,此类方法无需系统精准的数学模型,可以对系统不确定性进行在线辨识。因此,为保证系统在受到干扰时仍然能够准确地跟踪给定位置,需要结合现代控制理论和智能控制算法,设计出复合有效的控制器。
针对PMLSM伺服系统中存在的问题,需要所设计的控制器对不确定性具有极强的鲁棒性。由于滑模控制器(Sliding Mode Controller, SMC)设计简单,对匹配不确定性具有完全的鲁棒性,在伺服电机的控制中应用广泛,但其趋近速度与抖振之间存在的矛盾问题仍亟待解决[10]。文献[11]设计了超螺旋滑模轮廓控制方法,并利用最优控制算法优化位置控制器,提高了系统的轮廓加工精度。文献[12]将SMC与自适应区间二型模糊控制相结合,利用模糊控制逼近滑模控制增益,有效地削弱了抖振,并提高了系统的鲁棒性。文献[13]将SMC与迭代学习控制相结合,抑制直线电机的重复性干扰。文献[14]设计了时滞自适应积分滑模,改善了系统的跟踪精度和鲁棒性。此外,离散分数阶SMC[15]方法和自适应递归终端SMC[16]方法也应用于直线伺服系统中,不但保证了跟踪误差在有限时间内收敛到零,削弱了抖振,还提高了系统的抗干扰能力。
本文设计了自适应模糊神经网络时变滑模控制器(Adaptive Fuzzy Neural Network Time-varying Sliding Mode Controller, AFNNTSMC),并将其应用于PMLSM伺服系统中,以确保系统具有良好的伺服性能。设计时变滑模控制器(Time-varying Sliding Mode Control, TSMC)提高系统响应速度,引入自适应模糊神经网络进一步提高跟踪精度。为验证所提方法的有效性,采用SMC、TSMC和AFNNTSMC三种方法进行对比实验,结果表明,将AFNNTSMC应用于PMLSM伺服系统中,可以保证系统在存在参数变化、外部扰动等不确定性时,具有高精度、快响应和强鲁棒的优点。
在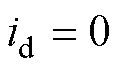 的磁场定向控制条件下,PMLSM电磁推力
的磁场定向控制条件下,PMLSM电磁推力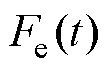 为
为
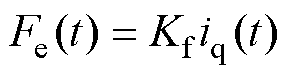 (1)
(1)式中,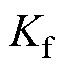 为电磁推力系数;
为电磁推力系数;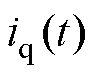 为q轴电流。
为q轴电流。
PMLSM的非线性模型表示为
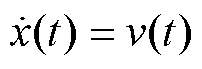 (2)
(2)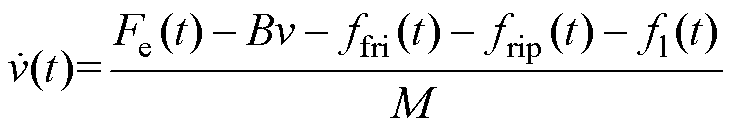 (3)
(3)
式中,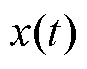 为电机动子位置;
为电机动子位置;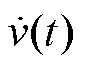 为加速度;
为加速度;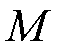 为动子质量;
为动子质量;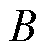 为粘滞摩擦因数;
为粘滞摩擦因数;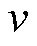 为电机速度;
为电机速度;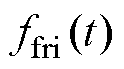
为摩擦力;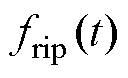 为推力波动;
为推力波动;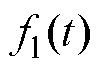 为系统扰动,包括参数变化、负载扰动等。
为系统扰动,包括参数变化、负载扰动等。
系统中存在的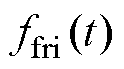 模型可以表示为
模型可以表示为
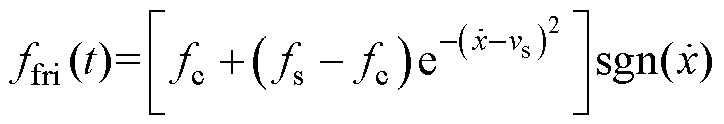 (4)
(4)式中, 为静摩擦力;
为静摩擦力;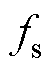 为库仑摩擦力;
为库仑摩擦力;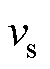 为速度系数;
为速度系数;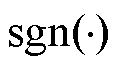 为符号函数。
为符号函数。
系统中存在的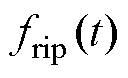 模型可以表示为
模型可以表示为
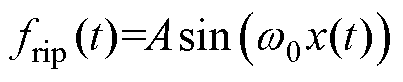 (5)
(5)式中,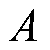 为
为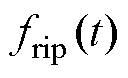 的幅值;
的幅值; 为角速度。
为角速度。
为便于控制器的设计,结合式(2)和式(3),将PMLSM伺服系统表示为

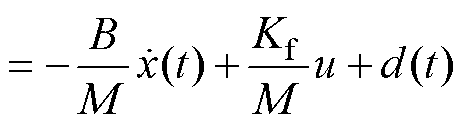 (6)
(6)
式中,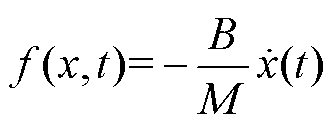 和
和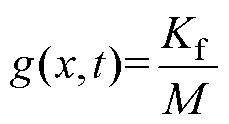 为系统函数;
为系统函数;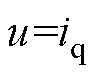 为控制量;
为控制量;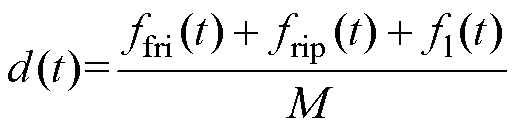 为系统总不确定性。
为系统总不确定性。
由式(6)可知,PMLSM是典型的非线性时变系统,不确定性的存在会严重影响电机的跟踪控制精度。为此,需设计具有强鲁棒性的控制器保证系统伺服性能。
PMLSM伺服系统的控制目标是使系统在存在参数变化、外部扰动等不确定性因素时,PMLSM的动子仍然可以准确地跟踪不同的给定位置参考轨迹。因此,本文设计了AFNNTSMC方法保证系统的位置跟踪性能。首先设计TSMC抑制不确定性对系统的影响,通过设计时变滑模面,可以有效减小系统状态点到达滑模面的时间,提高系统的响应速度。其次引入自适应模糊神经网络对时变滑模面的斜率值进行在线调整,进一步提高系统的鲁棒性和位置跟踪精度。基于AFNNTSMC的PMLSM伺服系统总体框图如图1所示。
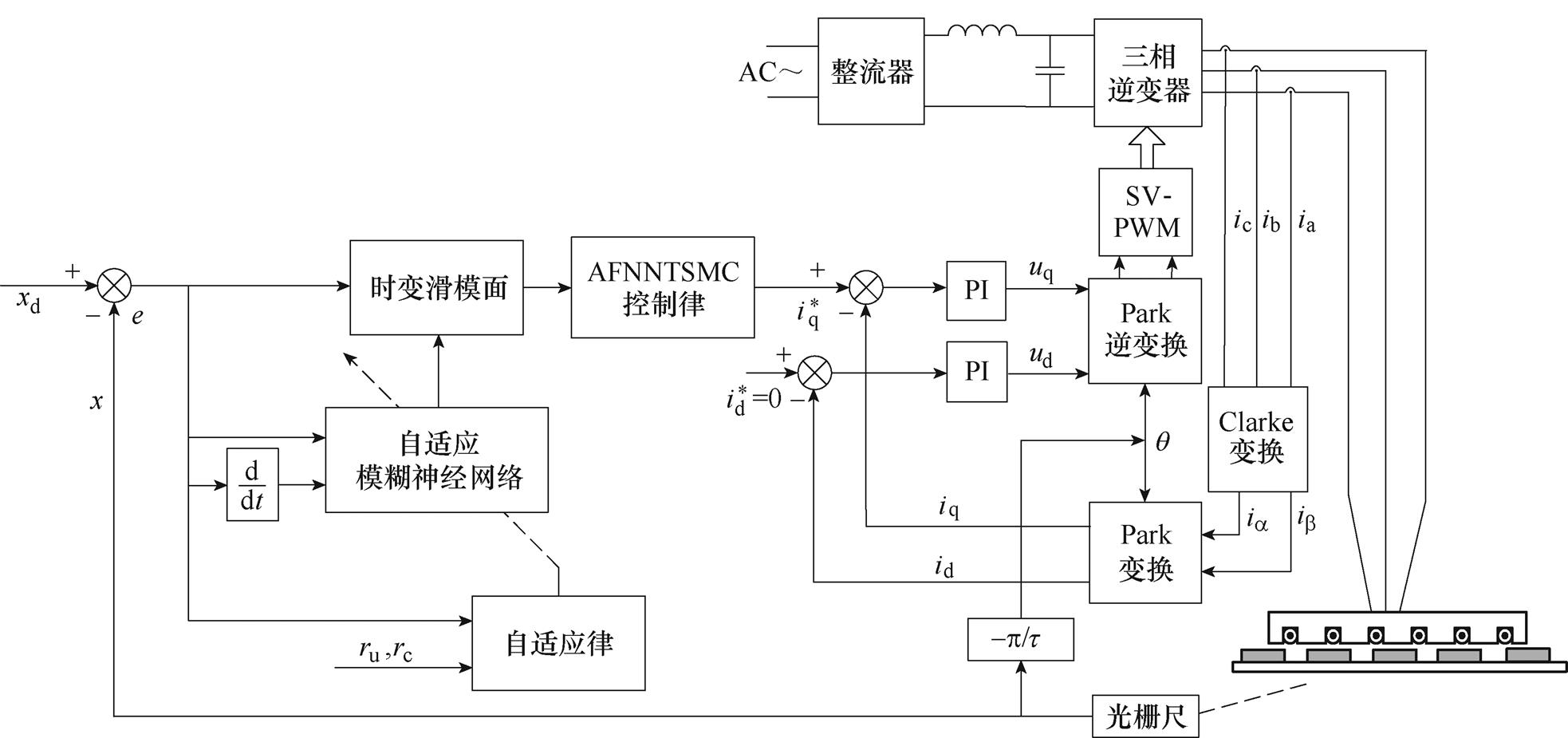
图1 基于AFNNTSMC的PMLSM伺服系统框图
Fig.1 Block diagram of PMLSM servo system based on AFNNTSMC
定义位置跟踪误差为
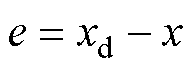 (7)
(7)式中,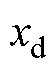 为参考位置;e为位置跟踪误差。设计滑模面为
为参考位置;e为位置跟踪误差。设计滑模面为
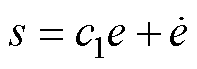 (8)
(8)
式中,c1为给定正常数。
对式(8)的滑模面求导可得
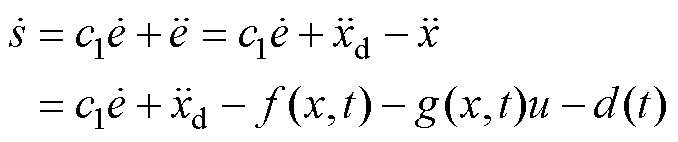 (9)
(9)根据式(9),在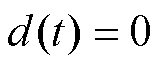 条件下,可求出SMC的等效控制律
条件下,可求出SMC的等效控制律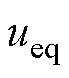 为
为
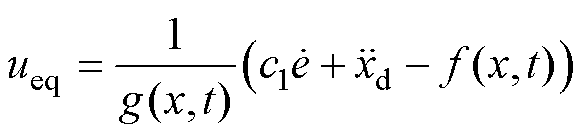 (10)
(10)
在实际应用中,需要考虑不确定性的存在,为此,针对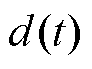 设计切换控制律
设计切换控制律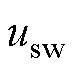 为
为
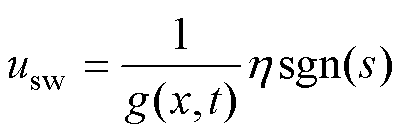 (11)
(11)结合式(10)和式(11),得到SMC控制律为
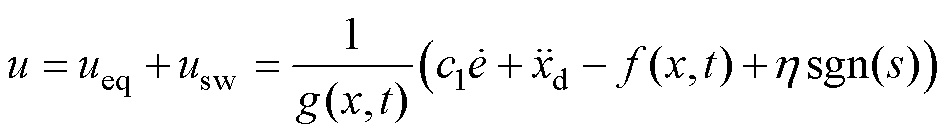 (12)
(12)
式中,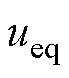 为等效控制律;
为等效控制律;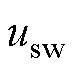 为切换控制律,可以保证系统状态停留到滑模面;
为切换控制律,可以保证系统状态停留到滑模面;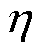 为正常数,且
为正常数,且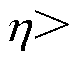
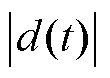 。
。
为证明系统稳定性,定义Lyapunov函数为
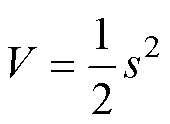 (13)
(13)结合式(9)对式(13)求导可得
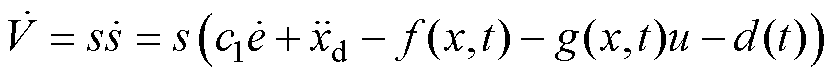 (14)
(14)
将式(12)代入式(14)中得
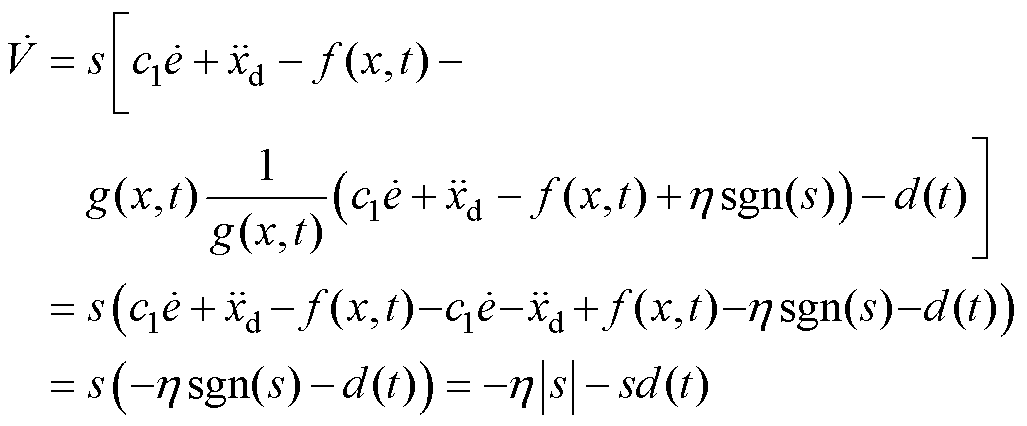
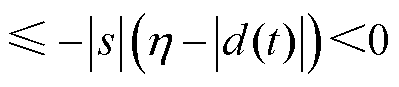 (15)
(15)
因此,满足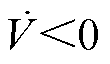 ,满足Lyapounov稳定性,可从理论上保证系统状态点收敛到零。
,满足Lyapounov稳定性,可从理论上保证系统状态点收敛到零。
2.1节所设计的SMC中,由于参数变化、外部扰动等不确定性的存在,会使系统状态点到滑模面的时间较长,从而影响系统的响应速度。因此,为降低到达时间,设计了TSMC,通过引入时变滑模面的概念,缩短到达时间。
设计时变滑模面为
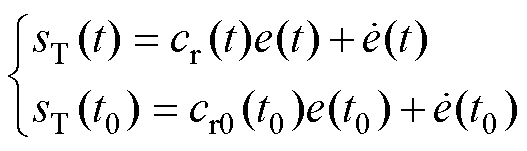 (16)
(16)式中,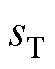 为时变滑模面;
为时变滑模面;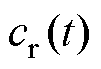 为时变滑模面的斜率,
为时变滑模面的斜率,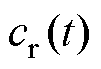 随时间变化趋势如图2所示;
随时间变化趋势如图2所示;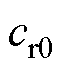 为初始斜率。
为初始斜率。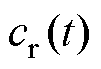 调整旋转方式如图3所示,变化的旋转平面
调整旋转方式如图3所示,变化的旋转平面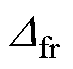 为
为
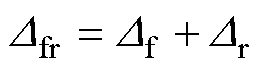 (17)
(17)
式中, 为滑模面非理想特性,如时间延迟等;
为滑模面非理想特性,如时间延迟等;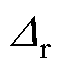 为自修正参数。
为自修正参数。
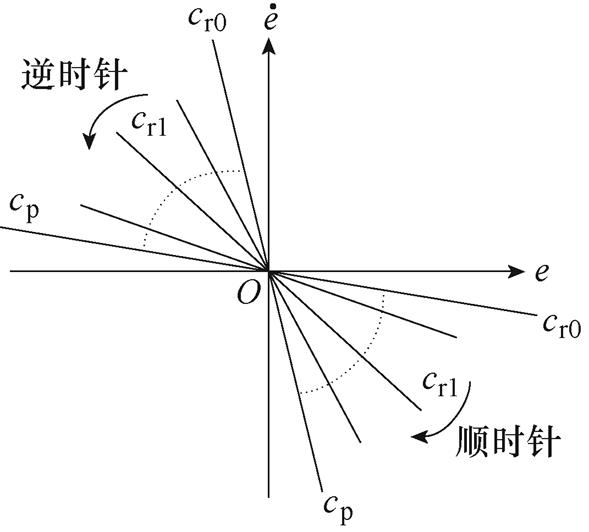
图2 时变滑模面斜率变化
Fig.2 Slope change diagram of time-varying sliding surface
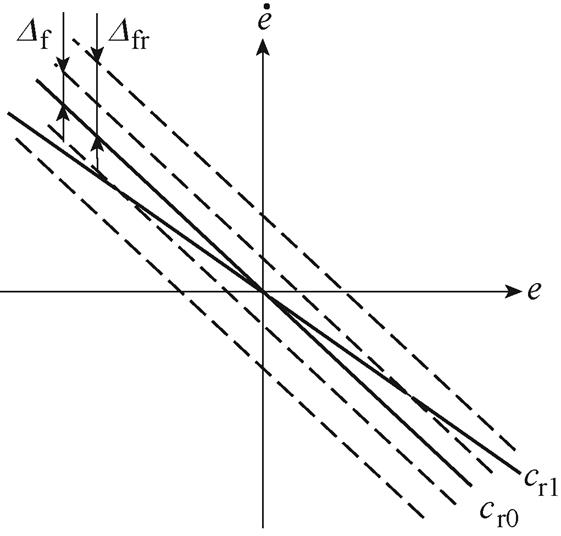
图3 时变滑模面斜率调整旋转方式
Fig.3 Rotation mode diagram for slope adjustment of time-varying sliding surface
为方便理解,将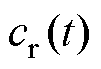 随时间的改变趋势表示为流程图,如图4所示。可以看出,时变滑动平面的斜率变化的具体步骤如下。
随时间的改变趋势表示为流程图,如图4所示。可以看出,时变滑动平面的斜率变化的具体步骤如下。
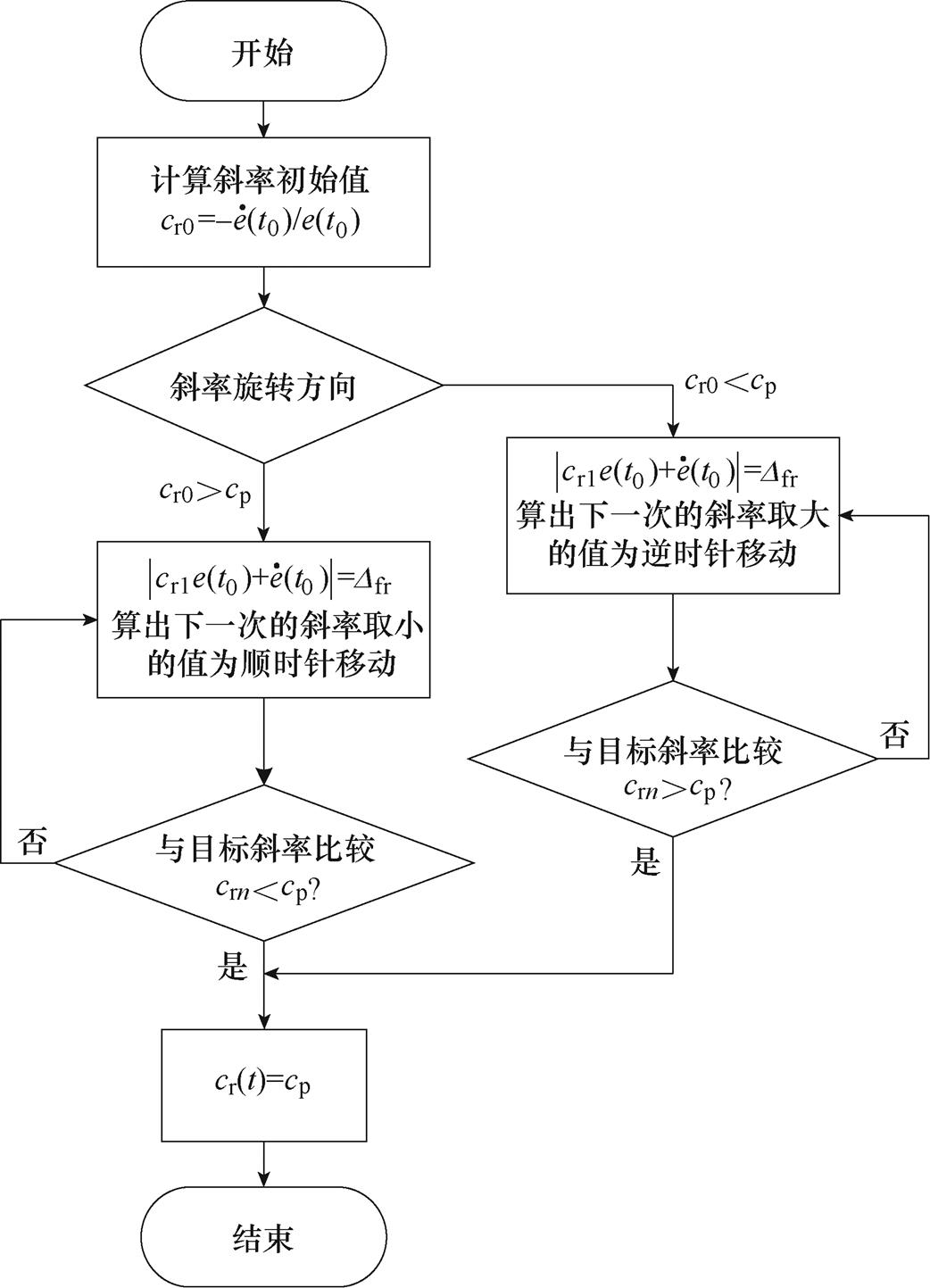
图4 时变滑模面的斜率改变流程
Fig.4 Flow chart of slope change of time-varying sliding surface
(1)确定适当的常数 、
、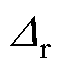 ,并定义式(17)所示的旋转平面
,并定义式(17)所示的旋转平面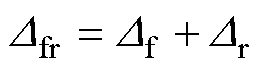 。
。
(2)令式(16)中的 ,满足滑模面条件,则可以计算初始时刻的斜率
,满足滑模面条件,则可以计算初始时刻的斜率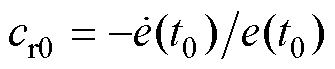 。
。
(3)判断平面旋转的方向,通过比较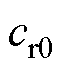 与最后斜率
与最后斜率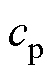 的大小来决定旋转方向。如果
的大小来决定旋转方向。如果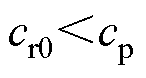 ,则旋转方向为逆时针;如果
,则旋转方向为逆时针;如果 ,则旋转方向为顺时针。
,则旋转方向为顺时针。
(4)如图2所示,当平面旋转到下一平面时会产生一个新的斜率 ,通过
,通过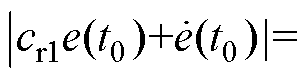
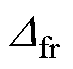 计算,计算
计算,计算 的解会有两个,比较大的值作为逆时针旋转后的斜率,比较小的值作为顺时针旋转后的斜率。在经过极短的时间
的解会有两个,比较大的值作为逆时针旋转后的斜率,比较小的值作为顺时针旋转后的斜率。在经过极短的时间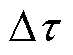 后,通过
后,通过
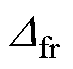 计算出
计算出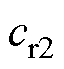 ,所用的时间则为
,所用的时间则为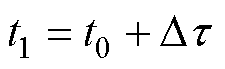 。
。
(5)经过系统判断一段时间后,在下列的条件下做停止动作:逆时针时,如果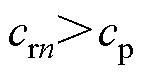 ,斜率
,斜率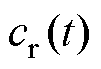 就选择为
就选择为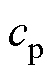 ;相反,在顺时针时,如果
;相反,在顺时针时,如果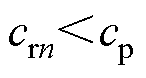 ,斜率
,斜率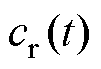 就固定为
就固定为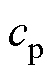 。斜率
。斜率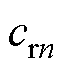 通过
通过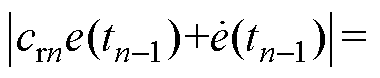
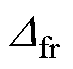 来计算,且
来计算,且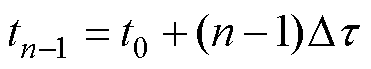 。
。
因此,通过设计斜率可变的时变滑模面,可缩短系统到达滑模模态的时间,但该方法必须先提前知道旋转到最后的斜率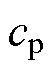 ,这就是通过判断方式调整斜率最大的缺点。因此,为改善上述问题,引入自适应模糊逻辑的概念来调整滑动平面。
,这就是通过判断方式调整斜率最大的缺点。因此,为改善上述问题,引入自适应模糊逻辑的概念来调整滑动平面。
由于旋转到最后的斜率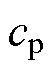 无法提前预知,使TSMC方法的应用存在一定的困难,因此,采用自适应模糊神经网络控制算法求出系统当下状态所适合的斜率
无法提前预知,使TSMC方法的应用存在一定的困难,因此,采用自适应模糊神经网络控制算法求出系统当下状态所适合的斜率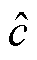 。
。
模糊神经网络结构如图5所示,具体介绍如下。
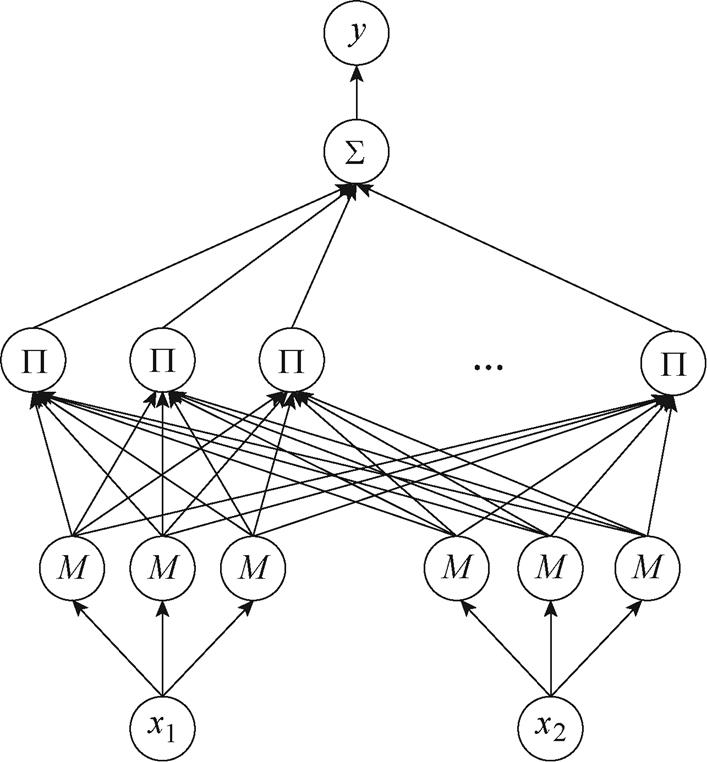
图5 模糊神经网络结构
Fig.5 Structure diagram of fuzzy neural network
输入层: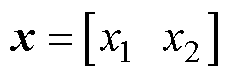 为模糊输入状态变量。定义
为模糊输入状态变量。定义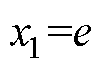 ,
, 。
。
隶属函数层:通过高斯隶属函数得出状态变量 各自的隶属度
各自的隶属度 ,将两者相乘,作为隶属函数的输出。
,将两者相乘,作为隶属函数的输出。
规则层:包含模糊规则和模糊推论两部分,规则层中节点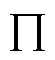 为一个模糊规则,表示为
为一个模糊规则,表示为
 (18)
(18)式中, 为变量
为变量 的隶属函数值;
的隶属函数值;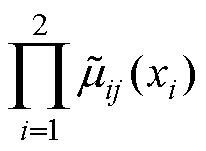 为模糊规则输出。
为模糊规则输出。
输出层:输出层的节点采用重心平均法进行解模糊化,模糊输出表示为
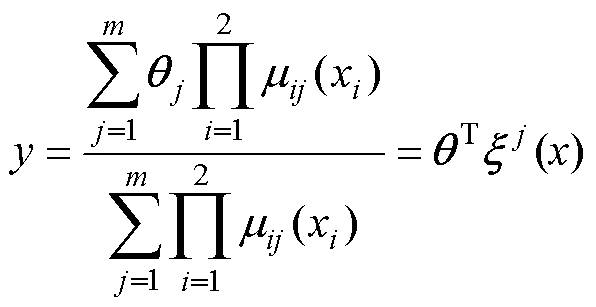 (19)
(19)式中,m为模糊规则;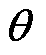 为m个模糊规则的权重;
为m个模糊规则的权重;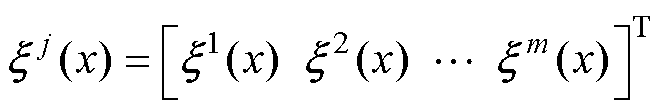 为模糊基本函数向量,表示为
为模糊基本函数向量,表示为
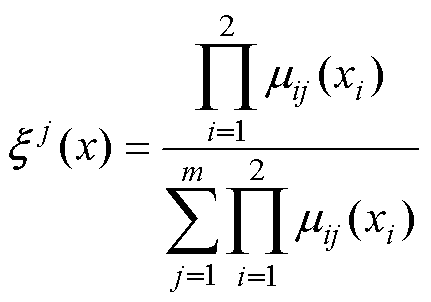 (20)
(20)
在设计AFNNTSMC时,采用Lyapounov函数推导出自适应律调整斜率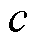 ,由于需要调整的斜率
,由于需要调整的斜率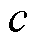 仅存在于等效控制律中,因此根据式(19),可将式(10)的等效控制律解模糊化为
仅存在于等效控制律中,因此根据式(19),可将式(10)的等效控制律解模糊化为
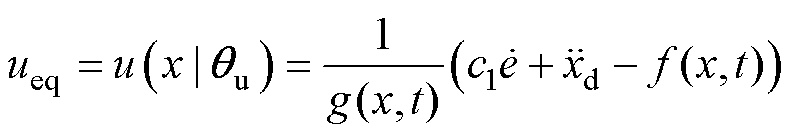 (21)
(21)结合式(21),将式(12)代入式(9)可得
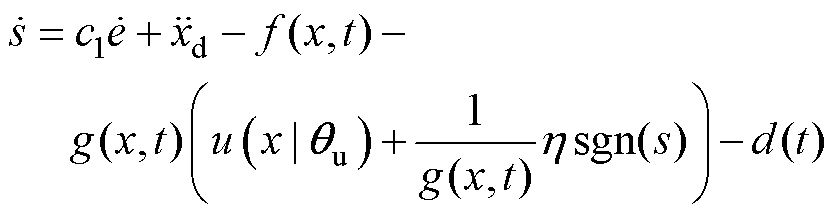 (22)
(22)
由于采用自适应律估计斜率c,估计误差是一定存在的,定义估计误差为
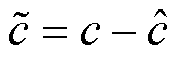 (23)
(23)式中,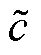 为斜率估计误差;
为斜率估计误差;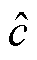 为模糊神经网络控制算法输出的系统当下状态所适合的斜率。
为模糊神经网络控制算法输出的系统当下状态所适合的斜率。
为得到自适应律调整斜率的估计误差,将式(22)改写为
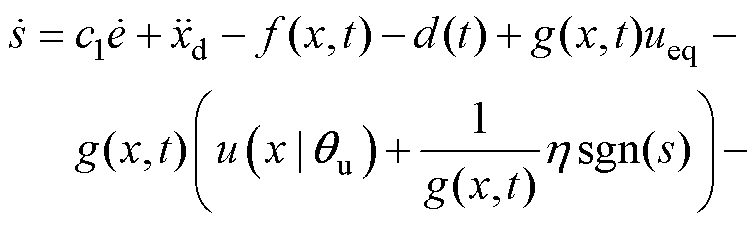
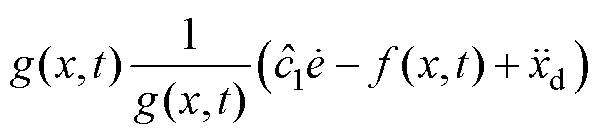 (24)
(24)
结合式(23),可将式(24)改写为
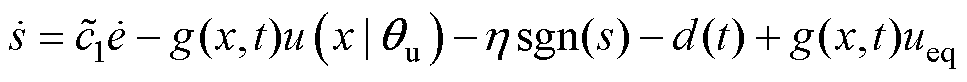 (25)
(25)定义 为估计模糊逻辑系统的最佳值,定义
为估计模糊逻辑系统的最佳值,定义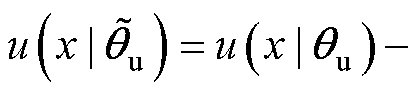
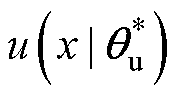 为误差,最小近似误差为
为误差,最小近似误差为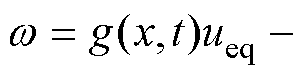
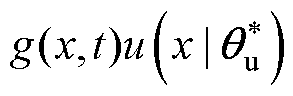 ,
,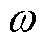 为非常小的值可忽略不计,则式(25)可表示为
为非常小的值可忽略不计,则式(25)可表示为
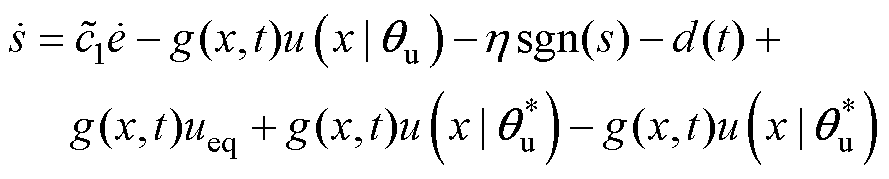 (26)
(26)
定义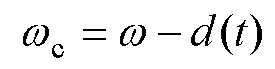 ,可得
,可得
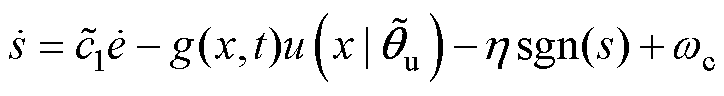 (27)
(27)将模糊化后的系统解模糊化可得
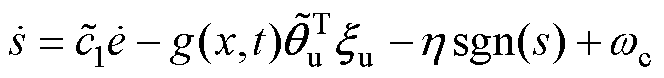 (28)
(28)
为验证系统的稳定性并求取自适应律,定义Lyapounov函数为
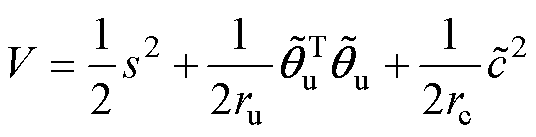 (29)
(29)式中,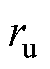 和
和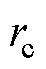 为学习律。
为学习律。
对式(29)求导可得
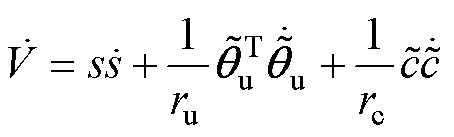 (30)
(30)将式(28)代入式(30)可得
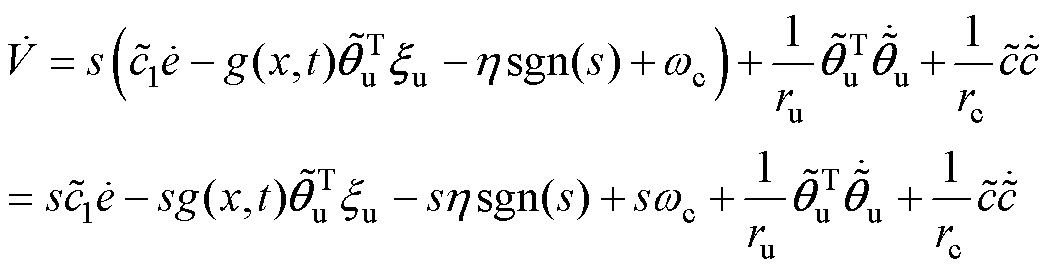
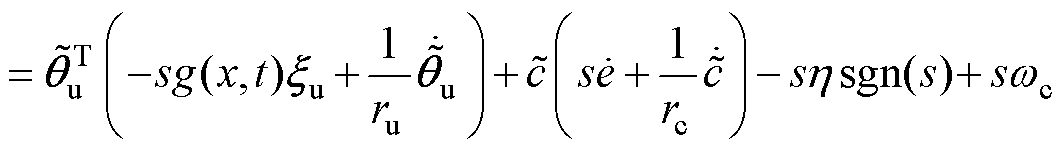
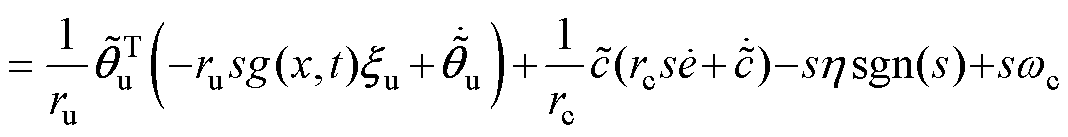 (31)
(31)
为保证AFNNTSMC系统的稳定,需满足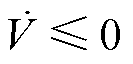 。由于s有正值负值变化,所以不确定式(31)的正负
。由于s有正值负值变化,所以不确定式(31)的正负
值。令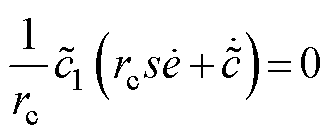 和
和 ,设计自适应律为
,设计自适应律为
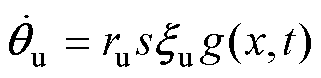 (32)
(32)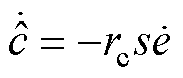 (33)
(33)
可得
 (34)
(34)由于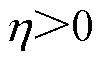 ,因此,
,因此,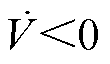 ,满足Lyapounov稳定性理论,系统是稳定的。
,满足Lyapounov稳定性理论,系统是稳定的。
实验系统由上位机+运动控制箱+PMLSM构成,上位机基于软件PeWin32Pro2编写相应的运动控制程序,实验系统结构如图6所示。此外,选用MicroE公司的MercuryII6000系列金属直线光栅尺,分辨率0.05~5mm范围可调,最大精度±1mm。选用PMLSM的主要参数见表1。
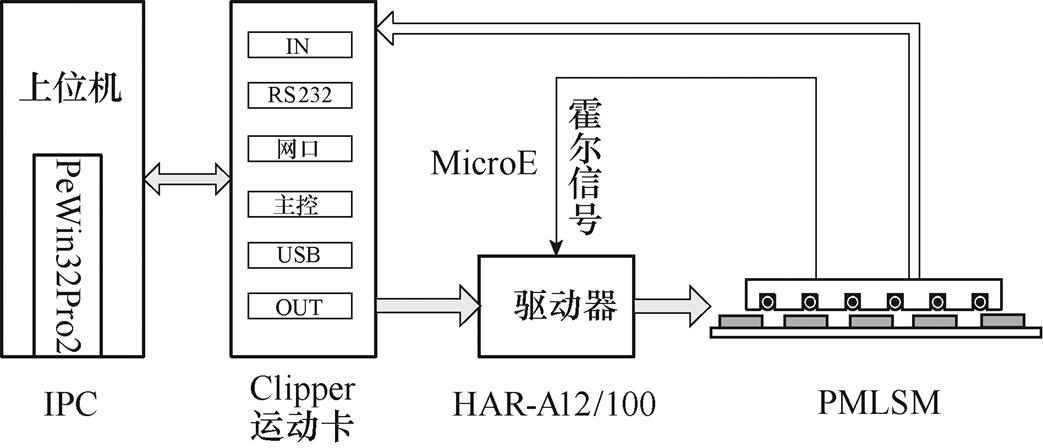
图6 实验系统结构
Fig.6 Structure diagram of experimental system
表1 PMLSM参数
Tab.1 Parameters of PMLSM

参 数数 值 电阻Rs/W2.1 电感Ld, Lq/mH41.4 动子质量M/kg10 推力系数Kf/(N/A)33.7 持续推力Fc/N63 峰值推力Fp/N188 峰值电流Ip/A7.1 持续电流Ic/A1.8
实验中,在正弦和梯形两种位置参考轨迹下将SMC、TSMC和AFNNTSMC三种控制方法应用于PMLSM伺服系统中进行对比。SMC中参数为:初始斜率c=3,h =3。TSMC中参数为:最终斜率cp=7,c=6。AFNNTSMC中参数为:初始斜率cr0=4,学习律ru=rc=0.01,采用高斯函数为隶属函数。
实验一中对系统给定幅值为50mm,频率为p rad/sec的正弦参考轨迹,运行时间设为5s,同时施加突变负载,负载变化曲线如图7所示。在SMC、TSMC和AFNNTSMC三种方法控制下的位置响应曲线、跟踪误差曲线分别如图8和图9所示。从图8可以看出,三种方法下的位置相应曲线均可以较好地跟踪给定信号。对比图9所示的误差曲线可看出,在负载发生突变时,即1s、3s和4s时,位置误差曲线均出现明显波动,但采用AFNNTSMC的系统误差最小,在1s时约为3.7mm,稳态误差约为0.8mm。此外,通过对比图9中误差曲线的响应初期波形以及负载突变瞬间波形可以看出,采用FTSMC和AFNNTSMC方法的系统具有较快的响应速度,明显小于SMC方法的响应时间。这是由于时变滑模面可以确保系统状态轨迹于短时间内收敛到滑动模态,从而减小系统响应时间,提高运行效率。因此,在负载扰动情况下,AFNNTSMC可以在较短的时间内克服扰动变化,使系统具有较高的跟踪精度和较快的响应速度。
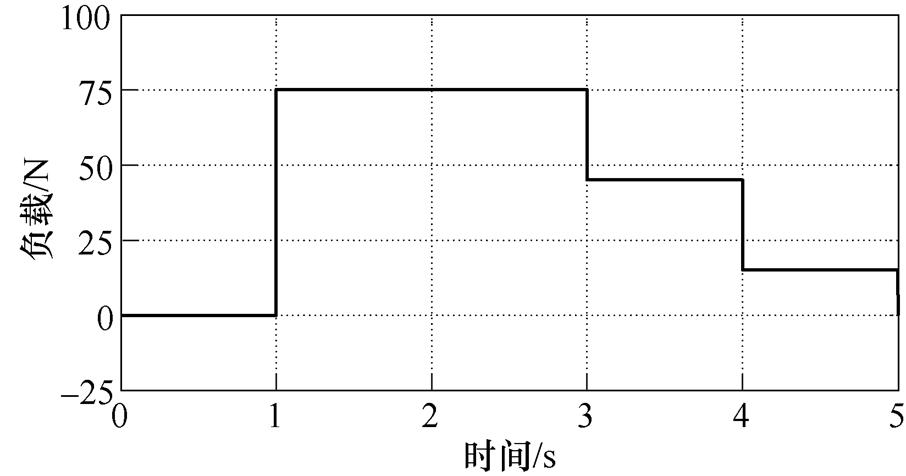
图7 负载变化曲线
Fig.7 Curve of load variation
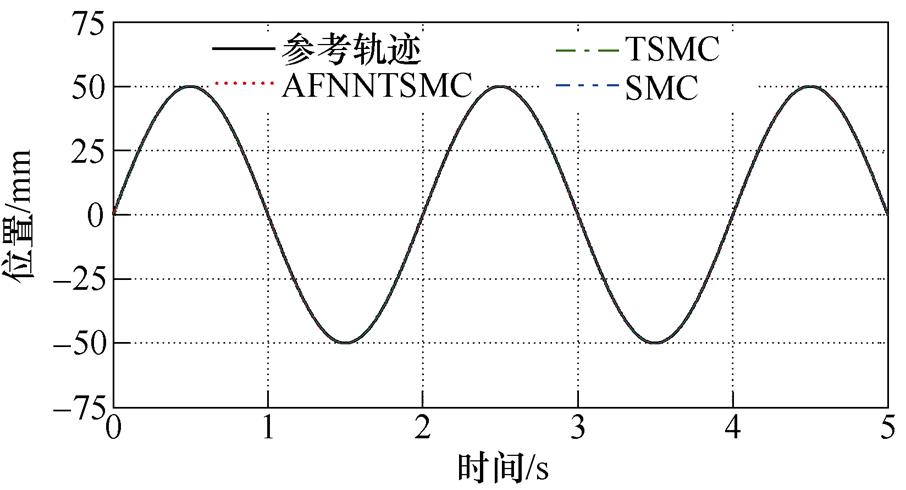
图8 位置响应曲线(正弦参考轨迹)
Fig.8 Curves of position response (sinusoidal reference trajectory)
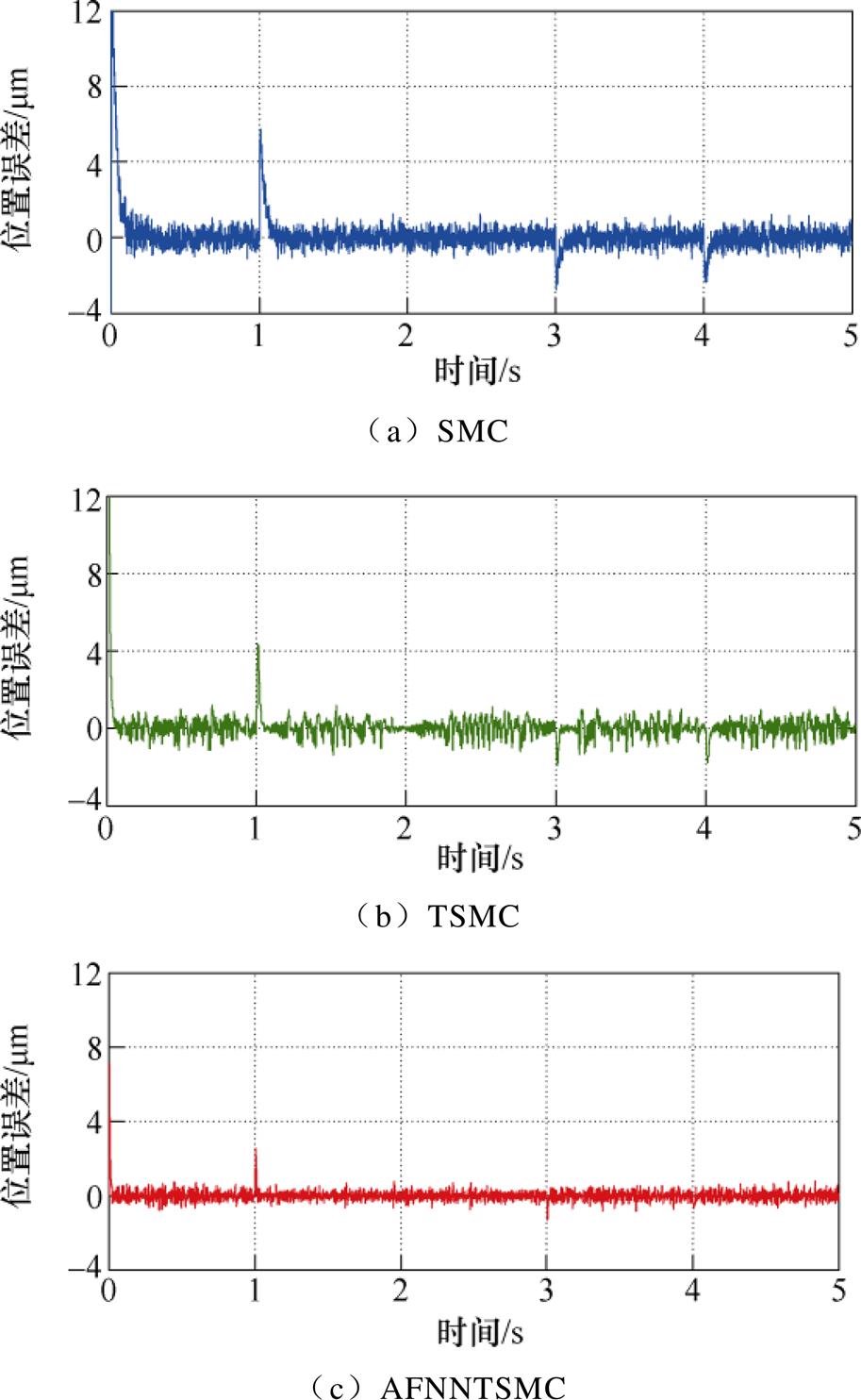
图9 位置跟踪误差曲线(正弦参考轨迹)
Fig.9 Curves of position tracking error (sinusoidal reference trajectory)
实验二中对系统给定变化的梯形参考轨迹,并调整实际电阻为2Rs,实际电感为1.8Ld, 1.8Lq。在参数变化条件下,基于SMC、TSMC和AFNNTSMC的系统位置响应曲线如图10所示。为更清晰地对比实验结果,给出跟踪误差曲线如图11所示。从图11可以看出,同SMC和TSMC方法相比,采用AFNNTSMC方法的位置跟踪误差曲线具有更小的波动,且在梯形波拐点处的波动最小,这证明了AFNNTSMC方法对于参数变化这一不确定性具有很好的抑制能力,可以保证系统强鲁棒性。
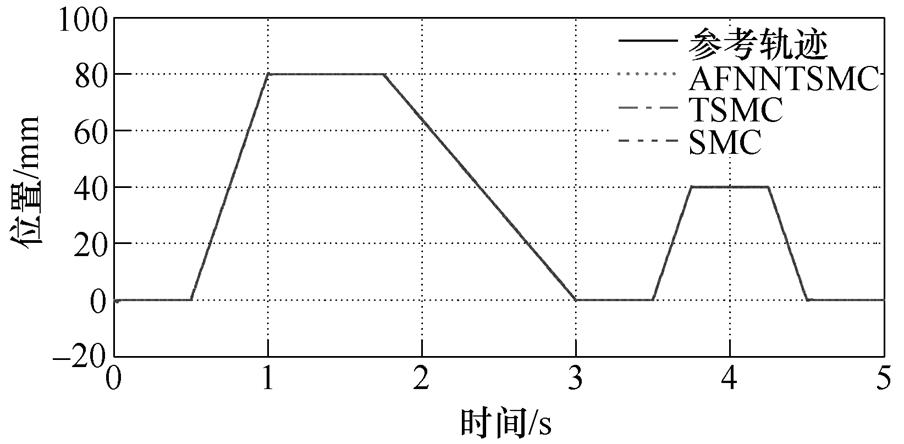
图10 位置响应曲线(梯形参考轨迹)
Fig.10 Curves of position response (trapezoidal reference trajectory)
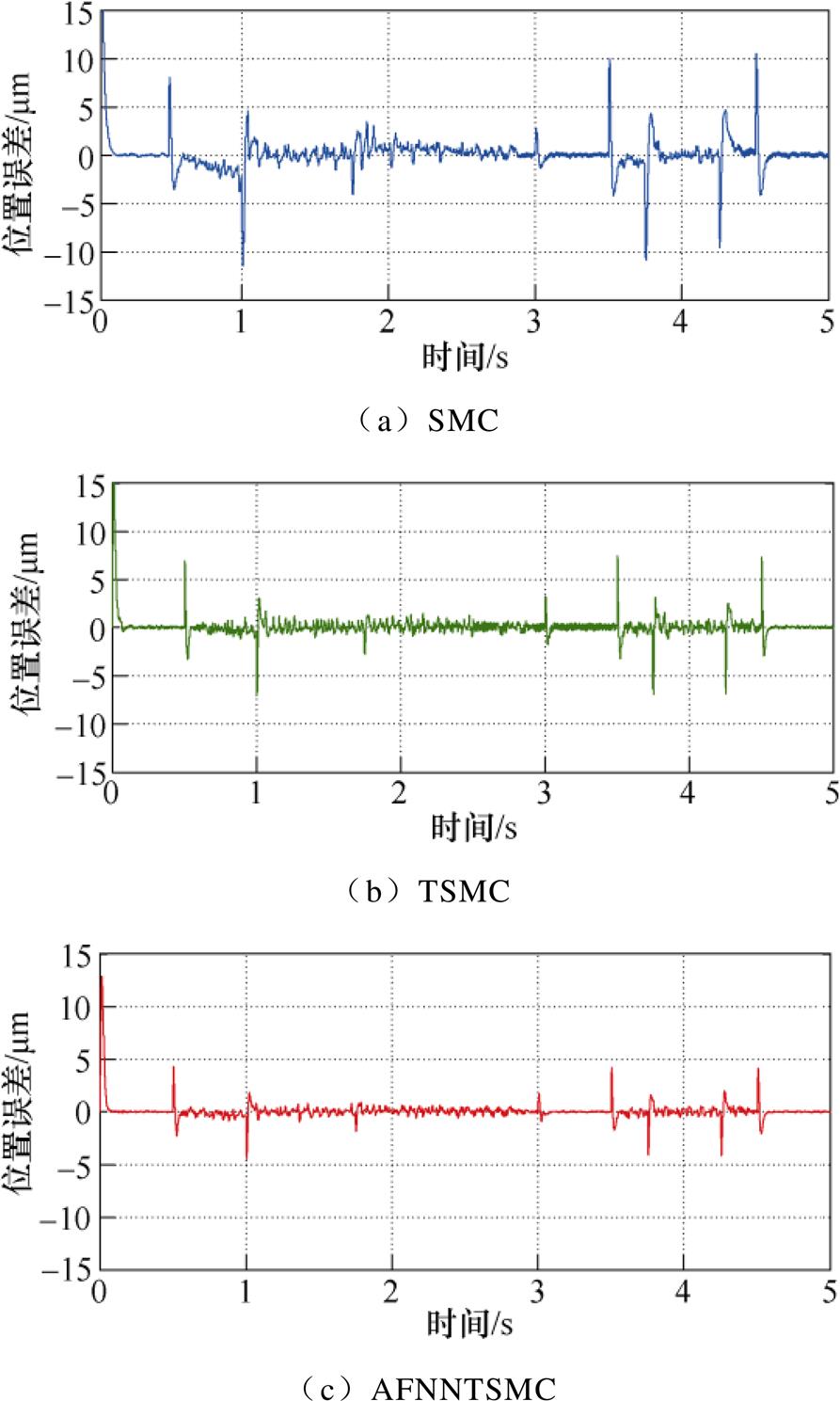
图11 位置跟踪误差曲线(梯形参考轨迹)
Fig.11 Curves of position tracking error (trapezoidal reference trajectory)
为更便于对比且清晰明了,给出两种实验条件下跟踪误差的平均值、最大值以及稳态值来评估AFNNTSMC方法的有效性,误差对比见表2。可以看出,无论是在参数变化还是外部扰动条件下,所提出的AFNNTSMC方法控制性能均优于SMC和TSMC,可以克服系统不确定性,保证系统的跟踪精度满足要求。
表2 误差对比
Tab.2 Comparison of errors (单位: mm)

实验控制器误差指标 平均值最大值稳态值 实验一:正弦参考轨迹SMC2.455.931.79 TSMC1.984.171.39 AFNNTSMC1.223.520.95 实验二:梯形参考轨迹SMC4.879.891.74 TSMC3.567.861.37 AFNNTSMC2.234.520.93
为解决PMLSM在运行过程中易受不确定性干扰而影响伺服性能的问题,设计了基于AFNNTSMC的位置跟踪方法。通过引入自适应模糊神经网络实时调整时变滑模面,AFNNTSMC可以在保证系统鲁棒性的前提下,使系统状态轨迹在较短的时间内收敛到滑动模态上,从而提高系统响应速度。实验结果表明,AFNNTSMC在参数变化和外部扰动等不确定因素存在时,仍然可以保证系统高精度快响应运行。
参考文献
[1] 张春雷, 张辉, 叶佩青, 等. 两相圆筒型永磁同步直线电机无传感算法[J]. 电工技术学报, 2019, 34(23): 4901-4908.
Zhang Chunlei, Zhang Hui, Ye Peiqing, et al. Research on sensorless algorithm of two-phase tubular permanent magnet synchronous linear motor[J]. Transactions of China Electrotechnical Society, 2019, 34(23): 4901-4908.
[2] Wang Ze, Hu Chuxiong, Zhu Yu, et al. Newton-ILC contouring error estimation and coordinated motion control for precision multi-axis systems with comparative experiments[J]. IEEE Transactions on Industrial Electronics, 2017, 65(2): 1470-1480.
[3] 陈晓, 赵文祥, 吉敬华, 等. 考虑边端效应的双边直线永磁游标电机模型预测电流控制[J]. 电工技术学报, 2019, 34(1): 49-57.
Chen Xiao, Zhao Wenxiang, Ji Jinghua, et al. Model predictive current control of double-side linear vernier permanent magnet machines considering end effect[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 49-57.
[4] Lin F J, Chou P H, Hung Y C, et al. Field- programmable gate array-based functional link radial basis function network control for permanent magnet linear synchronous motor servo drive system[J]. IET Electric Power Applications, 2010, 4(5): 357-372.
[5] 姬相超, 赵希梅. 永磁直线同步电动机的自适应时滞控制[J]. 电工技术学报, 2020, 35(6): 83-90.
Ji Xiangchao, Zhao Ximei. Adaptive time delay control of permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 83-90.
[6] 赵希梅, 金洋洋, 王丽梅. PMLSM伺服系统的自适应RBFNN反推控制[J]. 电机与控制学报, 2020, 24(4): 149-157.
Zhao Ximei, Jin Yangyang, Wang Limei. Adaptive RBFNN backstepping control for PMLSM servo system[J]. Electric Machines and Control, 2020, 24(4): 149-157.
[7] 刘宇博, 王旭东, 周凯. 基于滑模观测器的永磁同步电机电流偏差解耦控制[J]. 电工技术学报, 2020, 35(8): 44-54.
Liu Yubo, Wang Xudong, Zhou Kai. Current deviation decoupling control with a sliding mode observer for permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 44-54.
[8] Ting Chensheng, Lieu J F, Liu Chunshan, et al. An adaptive FNN control design of PMLSM in stationary reference frame[J]. Journal of Control Automation & Electrical Systems, 2016, 27(4): 391-405.
[9] 王硕, 康劲松. 一种基于自适应线性神经网络算法的永磁同步电机电流谐波提取和抑制方法[J]. 电工技术学报, 2019, 34(4): 654-663.
Wang Shuo, Kang Jinsong. Harmonic extraction and suppression method of permanent magnet syn- chronous motor based on adaptive linear neural network[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 654-663.
[10] Li Jin, Du Haibo, Cheng Yingying, et al. Position tracking control for permanent magnet linear motor via fast nonsingular terminal sliding mode control[J]. Nonlinear Dynamics, 2019, 97(4): 2595-2605.
[11] 武志涛, 朱连成. 基于滑模轮廓控制器的直线电机精密运动平台轨迹跟踪控制[J]. 中国电机工程学报, 2015, 35(23): 6188-6193.
Wu Zhitao, Zhu Liancheng. Trajectory tracking control for the motion table driven by linear motors based on sliding mode contour tracking con- trollers[J]. Proceedings of the CSEE, 2015, 35(23): 6188-6193.
[12] 孙宜标, 王亚朋, 刘春芳. 永磁直线电机自适应区间二型模糊滑模控制[J]. 沈阳工业大学学报, 2017, 39(6): 601-606.
Sun Yibiao, Wang Yapeng, Liu Chunfang. Adaptive interval type-2 fuzzy sliding mode control for permanent magnet linear motor[J]. Journal of Shenyang University of Technology, 2017, 39(6): 601-606.
[13] 严乐阳, 叶佩青, 张辉, 等. 基于多周期迭代滑模控制的直线电机干扰抑制[J]. 电机与控制学报, 2017, 21(1): 8-13.
Yan Leyang, Ye Peiqing, Zhang Hui, et al. Dis- turbance rejection for linear motor based on multi- periodic learning variable structure control[J]. Elec- tric Machines and Control, 2017, 21(1): 8-13.
[14] 赵希梅, 姬相超, 王浩林. 永磁直线同步电动机的时滞自适应积分滑模控制[J]. 电机与控制学报, 2020, 24(8): 44-50.
Zhao Ximei, Ji Xiangchao, Wang Haolin. Time delay adaptive integral sliding mode control for permanent magnet linear synchronous motor[J]. Electric Machines and Control, 2020, 24(8): 44-50.
[15] Sun Guanghui, Ma Zhiqiang, Yu Jinyong. Discrete- time fractional order terminal sliding mode tracking control for linear motor[J]. IEEE Transactions on Industrial Electronics, 2018, 65(4): 3386-3394.
[16] Shao Ke, Zheng Jinchuan, Huang Kang, et al. Finite- time control of a linear motor positioner using adaptive recursive terminal sliding mode[J]. IEEE Transactions on Industrial Electronics, 2020, 67(8): 6659-6668.
Adaptive Fuzzy Neural Network Time-Varying Sliding Mode Control for Permanent Magnet Linear Synchronous Motor
Abstract Aiming at the problem that the servo performance of permanent magnet linear synchronous motor (PMLSM) tracking different reference trajectories is easily affected by parameter changes, external disturbances, friction and other uncertain factors, a precise position tracking method based on adaptive fuzzy neural network time-varying sliding mode controller (AFNNTSMC) is proposed. Firstly, based on the PMLSM mathematical model, the time-varying sliding mode controller (TSMC) is designed by introducing the time-varying sliding surface into the sliding mode controller (SMC). By adjusting the slope of the time-varying sliding surface, the time for the system state to reach the sliding mode can be effectively shortened and the response speed of the system can be improved on the premise of robustness. Besides, because the slope value of TSMC is difficult to obtain, it is combined with the fuzzy neural network to design the AFNNTSMC method. Using the Lyapunov function to design adaptive law, the slope value is estimated in real time and adjusted online to ensure the optimal servo performance of the system. Finally, the effectiveness of the proposed method is verified under two experimental conditions of parameter variation and external disturbance. The experimental results show that AFNNTSMC can effectively improve the response speed and position tracking accuracy of the system, and has strong robustness to uncertainties.
keywords:Permanent magnet linear synchronous motor, time-varying sliding mode control, adaptive fuzzy neural network, robustness
DOI: 10.19595/j.cnki.1000-6753.tces.210641
中图分类号:TM351
魏惠芳 女,1986年生,博士研究生,讲师,研究方向为驱动控制与精密伺服技术。E-mail: weihuifang088@163.com
王丽梅 女,1969年生,教授,博士生导师,研究方向为交流伺服驱动技术。E-mail: wanglm@sut.edu.cn(通信作者)
收稿日期 2021-05-07
改稿日期 2021-07-28
国家自然科学基金资助项目(51875366)。
(编辑 崔文静)