Tab.1 Parameters of prototype motor
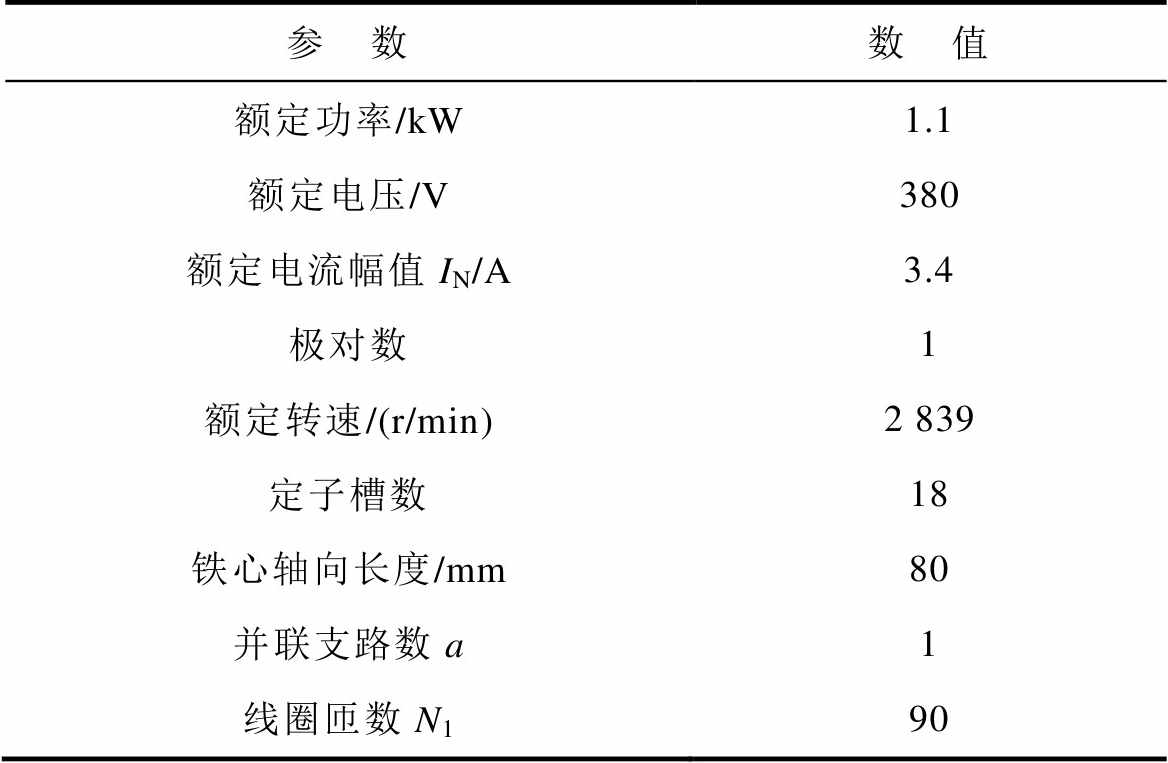
参 数数 值 额定功率/kW1.1 额定电压/V380 额定电流幅值IN/A3.4 极对数1 额定转速/(r/min)2 839 定子槽数18 铁心轴向长度/mm80 并联支路数a1 线圈匝数N190
摘要 通常中小型电机多应用感应电机，通过转子斜槽的结构达到抑制寄生转矩、电磁振动和噪声等目的，同时斜槽结构会增加转子导条间的横向电流，影响感应电机的起动性能以及电机效率。因此，该文主要研究横向电流对单斜槽感应电机性能的影响，通过总结单斜槽感应电机中横向电流在转子表面的分布规律，提出一种能计及横向电流的2D多截面有限元模型，相比已有计算横向漏电流时的3D模型，有效减少了仿真时间。通过在转子内建立过渡层的方式，利用多截面有限元的方法等效斜槽感应电机，在2D有限元仿真中考虑横向漏电流，利用此模型预测三相感应电机中横向漏电流对电机性能的影响，通过对Y802-2感应电机内横向漏电流损耗进行仿真，并与三维有限元的损耗值进行对比，验证模型的可行性与有效性，同时利用此模型分析横向电阻值对电机的起动转矩特性的影响。
关键词：感应电机 斜槽 横向电流 损耗 转矩
感应电机作为传统电机发展多年，因其具有众多优势应用于工业发展各领域。在电机设计中，为降低谐波损耗、抑制寄生转矩与噪声等，感应电机多采用斜槽方式，但采用斜槽（定子或转子）技术后，斜槽结构使得气隙主磁场扭斜，造成基波电流降低、轴向力不平衡，同时产生横向漏电流损耗[1]。横向漏电流损耗隶属于感应电机杂散损耗，文献[2]提到，横向漏电流损耗占电机杂散损耗的1/3，研究横向漏电流对减小单斜槽感应电机杂散损耗以及响应国家能源战略号召具有重要意义。
感应电机转子多为浇铸笼型结构，在电机性能分析中，假定导条与铁心绝缘性能良好，未考虑横向漏电流的产生。在电机实验中，由于转子导条扭斜的结构，使同一根导条处于不同的基波磁场下，导条两侧感生出切向电动势差，由于转子导条与铁心之间非绝缘特性，使得在相邻导条间有电流产生，称为横向漏电流。横向漏电流的产生使得转子电流沿轴向分布不均匀、电机发热不均，特别在堵转情况下，横向漏电流现象尤为显著，严重时烧毁铁心叠片间绝缘[3-4]。为提高感应电机运行效率，横向漏电流对感应电机性能影响问题亟需关注。在电机设计中，忽略斜槽电机横向漏电流影响，使得电机仿真与实验结果呈现一定误差[5-7]，为研究人员预估电机性能带来很大挑战，同时对电机内故障时诊断的特征量带来误差[8-9]。故越来越多的研究学者开始关注感应电机的横向漏电流损耗问题。本文总结已有文献成果并对横向漏电流的影响做进一步探究。
根据横向漏电流产生回路，国外学者A. M. Odock最先提出横向漏电流的概念，其在文献[10]中假设已知气隙各次谐波，且导条与铁心均匀接触的前提下，建立斜槽感应电机转子解析模型并提出横向漏电流解析方程，同时提出完整笼型转子方法间接测量横向电阻值。1960年，翟加涅克提出切除端环法，对切除端环后的转子测量转子各导条对转子铁心的电压降，破坏转子结构的同时提高横向电阻的测量精度。丁梵林等在文献[11-12]中总结已有测量方法并提出一种能提高完整笼型转子方法测量精度的措施，并通过测量69个笼型转子的横向电阻进行验证。文献[13-14]通过在相邻导条间建立横向电阻回路，对横向漏电流做进一步研究，并对横向漏电流转子解析方程中的参数进行修正，根据在不同参数下转矩与电流二次方的比值变化曲线与实验测量曲线对比，最终得到结论：在通常情况下（即非特殊结构转子，端环阻抗远小于横向漏电流阻抗），横向漏电流的产生路径中，导条与铁心间的接触电阻占主要部分，只考虑接触电阻时计算结果与实验测量结果相差不大。文献[15]建立斜槽电机的等效模型，沿轴向将其分成两部分直槽电机，并通过集总参数建立横向漏电流通路，计算横向漏电流损耗。文献[16]将其扩展到多段级联电路，通过采用多段级联方法分析横向漏电流损耗问题，更进一步提出采用高斯分布沿轴向对电机分段，提高模型的准确度[17]。
在解析计算较为成熟的前提下，在电机仿真中考虑横向漏电流损耗成为难点。斜槽电机的气隙磁场是随时间变化的三维时变场，采用三维有限元方法分析横向漏电流是最直接、有效的方法，要准确计入时间谐波和空间谐波的电磁影响，特别是齿槽效应对横向漏电流分布的影响，需要能够反映转子转动过程的三维时步有限元模型[18-19]，但三维仿真的时间太长。文献[20-21]通过二维与三维有限元耦合计算横向漏电流损耗，将二维有限元仿真得到的转子铁心磁导率代入到电流激励的三维模型中，在保证精度的同时大幅缩短仿真时间。文献[22]利用二维与三维有限元结合的方法，通过二维多截面有限元取得定子损耗以及气隙磁通密度，在三维场频域内求解横向漏电流损耗。文献[23]提出在二维涡流场内求解横向漏电流损耗，并将求解域缩减到一个齿距，缩减计算时间。横向漏电流对电机转矩影响的分析中，文献[24]通过在三维场内计算电机等效参数，得到计及横向漏电阻的等效电路，再利用等效参数计算电机转矩。文献[25]在考虑横向漏电阻的影响后修正感应电机等效电路，改进感应电机中转子回路，考虑横向电阻后再对感应电机的性能进行分析。文献[26-27]修正转子等效电路，利用Flux多截面有限元模型，通过对比直槽、无横向漏电流斜槽和计及横向漏电流斜槽三种情况下转矩-转速曲线，得到横向漏电流对转矩的影响，特别是对起动过程中转矩的影响。
本文针对二维场内难以计及横向漏电流影响问题，依据转子横向损耗解析计算方程提出一种斜槽感应电机模型，在磁场仿真中考虑转子横向电阻回路，通过在二维场内添加过渡层（位于转子导条与铁心之间），将实验测量得到的横向漏电阻值转化为过渡层电导率，通过此电机模型利用2D多截面有限元的方法等效斜槽，在二维场内计算感应电机横向漏电流损耗，将其损耗值与三维模型仿真值相对比证明模型的可行性，最后利用此模型对转子内横向漏电流影响做进一步分析，探究横向电阻值对电机起动转矩的影响。
本文针对一台单斜槽1.1kW两极感应电机，通过完整笼型转子测量方法实验测量其转子横向电阻，并将横向电阻值代入仿真模型中，计算稳态时转子横向漏电流损耗值，计算过程中忽略定子侧各次谐波对转子的影响，电机模型参数见表1。
表1 样机参数
Tab.1 Parameters of prototype motor
参 数数 值 额定功率/kW1.1 额定电压/V380 额定电流幅值IN/A3.4 极对数1 额定转速/(r/min)2 839 定子槽数18 铁心轴向长度/mm80 并联支路数a1 线圈匝数N190
本文通过等效转子结构进行解析分析，其等效转子解析模型如图1所示，电路元件可划分为转子导条和横向电阻两类。将电机沿轴向分段，分成若干段，每一段认为是单元电机。在单元电机中，除包含转子端环的单元电机外，其余单元电机转子端环为横向电阻，单元电机损耗求解过程中计入横向电阻。计算横向漏电流损耗时，对单元电机的横向损耗沿轴向积分，解得单斜槽感应电机横向漏电流损耗。
为便于分析，作如下基本假设[10]：①忽略端环阻抗；②导条与铁心间的阻抗为纯阻性；③转子导条间横向漏电阻沿轴向分布均匀。
图1 等效转子解析模型
Fig.1 Equivalent rotor analytical model
根据转子模型于节点ABCD列写回路方程[28]为
（1）
式中，
为第n个单元电机中第r根导条内电流；
为第n个单元电机中第r+1根导条内电流；
为第n个单元电机中第r个端环的端环电流；
为第n+1个单元电机中第r个端环的端环电流；
为第n-1个单元电机中第r个端环的端环电流；
为第n个单元电机中第r根导条电压；
为第n个单元电机中第r+1根导条电压；
为单位轴向长度下导条电抗；
为单位轴向长度；
为单元电机中端环阻抗。
对单元电机中相邻导条电流关系为
（2）相邻单元电机的电流关系为
（3）
单元电机端环电流有
（4）式中，p为极对数；
为导条扭斜角度的正切值；
为转子半径；
为相邻导条间的电角度。
将式（2）～式（4）代入式（1）中并化简方 程，有
（5）式中，
为围绕导条一半周长单位轴向长度的接触电阻率。假定横向电阻沿导条轴向分布均匀，若接触电阻小，在满足上述条件式（5）时，认为相邻导条间的端环电压近似为零，不考虑边界值。单元电机中，横向电流指流经转子表面的相邻单元电机端环电流的差值，而横向电流损耗近似为横向电流流经单元电机端环所产生的损耗[28]，即
（6）
式中，
为第n个单元电机中流经端环电流；
为完整电机转子中横向漏电流损耗；
为转子轴向长度；
为转子导条数；
为单位长度导条电压；
为导条斜过的总距离。
关于抑制横向漏电流损耗问题。横向损耗与横向电阻呈非线性关系，横向损耗存在理论极大值点，可通过解析公式寻找理论极值点。基于这一前提，本文进一步提出一种能减少横向损耗的措施：将电机转子硅钢片分两部分，槽型附近硅钢片单独为一部分，将横向损耗极值点处的电导率叠加到槽型附近硅钢片的电导率内，借此增加横向电流回路电阻值，使得横向电阻值稳定越过极大损耗值点，在保留横向电流正面影响的前提下减小横向漏电流损 耗值。
计入横向漏电流影响的感应电机模型中，2D有限元仿真无法直接考虑横向漏电流损耗问题，通常采用3D斜槽感应电机模型计算[18]，但计及横向漏电流影响的三维有限元仿真需要在原有基础上对电机转子进行更为细致的剖分，计算占用大量时间，难以快速预估电机性能。本文根据转子横向漏电流损耗解析计算思想，将单位轴向长度电机认定为单元电机，依据解析计算时单元电机中横向漏电流回路的分析，在场计算同时考虑转子横向电流路径，修改并建立2D有限元模型，同时采用2D多截面有限元方式等效斜槽转子。针对在电机性能预估中难以计及横向漏电流影响问题，本文依据单元电机概念修改电机模型并在二维有限元仿真中考虑横向漏电流损耗，与三维模型计算横向漏电流损耗值相对比，在保证一定准确度的基础上大幅减少计算时间，有利于快速预估横向漏电流损耗值，可用于重复性仿真探究横向漏电流对电机性能影响问题，并利用此模型探究横向漏电流对电机性能的影响。横向接触电阻主要是制作工艺的体现，在电机理论中并未考虑到导条与铁心间接触问题，即忽略横向漏电流回路问题，为仿真模型更贴近于实际，故而在转子导条与铁心间添加过渡层，过渡层厚度为0.5mm[18]，过渡层电阻率值取决于制作（铝铸或者焊接）时产生的额外电阻值。
通过对Y802-2电机转子实验测量横向电阻，将实验测量得到的横向电阻转化为过渡层电阻率，有
（7）式中，
为单根导条过渡层截面积；
为实验测量的横向电阻；
为过渡层电阻率，为单位轴向长度的接触电阻率。
感应电机运行过程中，横向漏电流由导条切向流出，经过接触电阻、转子铁心，流向相邻导条，而在电机仿真中，通常假定导条与铁心接触良好，未能充分考虑横向漏电流对电机性能产生的影响，忽略横向漏电流，使得在对电机杂散损耗计算结果中，仿真值与实验测量值存在误差。为进一步探究电机各项参数如转矩、损耗与横向电阻的关系，本文在模型中增加过渡层，仿真中通过控制过渡层电导率的方式探究横向电阻的变化对电机各项参数的影响。Y802-2电机模型的横截面如图2所示。
图2 Y802-2电机模型
Fig.2 Y802-2 motor model
为探究添加过渡层后对电机参数的影响，围绕感应电机转子槽型建立过渡层，对比添加过渡层前后电机稳态运行下的气隙磁通密度，如图3所示，添加过渡层后，对稳态运行下气隙主磁通影响不大。对稳态电机气隙磁通密度进行傅里叶分解，对比添加过渡层前后各次谐波幅值，如图4所示，添加过渡层后，气隙中各次谐波幅值相较于正常转子时略有增长，且对稳态时的基波磁通密度影响微小，但对17次谐波磁通密度幅值有较大抑制作用[29]。
图3 添加过渡层前后气隙磁通密度对比
Fig.3 Comparison of air gap magnetic density before and after adding the transition layer
图4 稳态运行时气隙磁通密度谐波分析
Fig.4 Harmonic analysis of air-gap flux density during steady state
横向漏电流位于转子表面，流通于相邻导条间，感应电机稳态运行时，导条内感生电流频率较低，约为2～3Hz，故而在实验测量横向漏电阻时采用直流电源近似代替实际工况，而文献[14]通过实验证明了此近似在电流源频率小于1 200Hz时具有准确性，并表明横向漏电流回路阻抗呈现电阻性。在实际中难以直接测量横向电阻数值，而间接的测量方法主要包括完整笼型转子测量法与切除端环法两种，其中广泛使用的方法是完整笼型转子测量法。由于漏电阻回路中转子与铁心的接触电阻占整个回路电阻的主要部分，故间接测量实验是将导条与铁心间的接触电阻近似为横向电阻。
测量横向接触电阻的两种方法中，切除端环法的测量精度较高，但需要切除笼型转子端环，属于破坏性实验，不能重复测量；完整笼型转子测量方法虽在测量精度上有所下降，但其测量方法简便，更容易实现，且测量精度可随着输入电流源幅值的增大而提升。故本文选择通过完整笼型转子测量方法实验测量转子导条与铁心间的接触电阻。
间接测量横向电阻基于下列条件：
（1）转子横向电抗和横向接触电阻相比数值很小，可以忽略，因此可用直流代替交流来进行测定。
（2）横向电阻值沿导条轴向分布均匀或相差不大。
（3）导条与端环的电阻同横向接触电阻相比可以忽略。于是在直流情况下，整个转子笼型结构可看成是一个等位体。
实验时均匀选中转子四根导条，沿轴向在每根导条上均匀取15个点，以转子左端为正极，转子右端为负极，距离正极起始点标号为1，其余点沿轴向依次标记；在正极（左侧）端环处均匀选中四根导条且利用导线并联，确保直流电流均匀流入端环内，实验平台位于绝缘板上，减少其余因素对测量数值的影响。横向电阻实验测量如图5所示，图中，①为100A可调直流电流源，②为KEITHLEY万用表，③为被测转子、绝缘板以及导线若干。
图5 实验测量
Fig.5 Experimental measurement
实验前，先对转子转轴两端通电，测量转子转轴两端电压，记录转轴实验数据；实验过程中将直流电流源正极通入转子端环，通过四根并联导条均匀流入笼型转子，电流经端环流入导条—铁心—转轴回到电流源内。由万用表测量四根导条共60个点的电压值，以夹钳笔为参考点，沿轴向移动针头笔测量标记点电压，考虑到转轴温升对测量结果影响问题将实验分为四部分，每次只测量单根导条15个数值，重复测量实验间隔30min等待转轴冷却，且每次实验后测量正极（转子左侧）端环到另一侧转轴电压值并记录；根据测量导条电压计算横向接触电阻及横向接触电阻率，后者是沿转子轴向单位长度、围绕导条一半周长单位面积的接触电阻率。
在实验中采用幅值为100A直流电流源，使用量程为200mV的万用表测量直流电压数值。测试中，转子导条长80mm，间隔5mm取一个点，每根导条取15个测量电压点，选取四根导条共60个测量电压点。忽略铝铸导条上产生的压降，测得导条到铁心电压，可近似认为是接触电阻上的电压降。用这些测量点电压的平均值和电流源电流计算接触电阻。
由实验数据可知，导条测量点电压由电流源正极附近沿轴向逐次下降，且数值下降具有一定规律。由于横向电阻的数量级为10-7，为确保测量结果的真实准确，本文采用两种不同的测量仪器（FLUKE与KEITHLEY）对比。导条沿轴向不同位置测量点电压结果如图6所示，由图6b可知，KEITHLEY测量结果较为集中，相邻导条测量电压波动小，测量数据更为稳定，故选取KEITHLEY得到的实验数据作为横向电阻测量结果，并将其代入式（8）计算横向电阻。
图6 沿轴向位置导条电压
Fig.6 Voltage of bar in axial position
通过对KEITHLEY测量数据进行整理，得到实验测量中各导条至铁心电压降如图7所示，通过测量整根导条电压降求得整个笼型转子结构对转子铁心电压降数值，即横向接触电阻上产生的电压降，可近似为转子横向电阻产生压降，由此电压与直流电源比值得到Y802-2电机转子导条间接触电阻值，实验测量数据计算公式为
（8） 式中，
为直流电流源幅值；
为单根导条上所取点的个数；
为第
根导条上采集点电压；
为导条到铁心电压降的平均值。
图7 各根导条电压降
Fig.7 Voltage drop of each bar
数据分析时，由于横向电阻的阻值沿导条轴向分布不均匀，例如，铝铸过程中气泡的随机分布、焊接工艺时导条与转子铁心的不完全接触。为减小工艺过程所造成的影响，将导条电压降平均值作为计算量。将实验数据代入式（8）计算横向电阻值与电阻率，将电阻率代入式（6），计算1.1kW感应电机转子横向电流损耗，所测实验数据见表2。
表2 实验数据分析
Tab.2 Analysis of experimental data
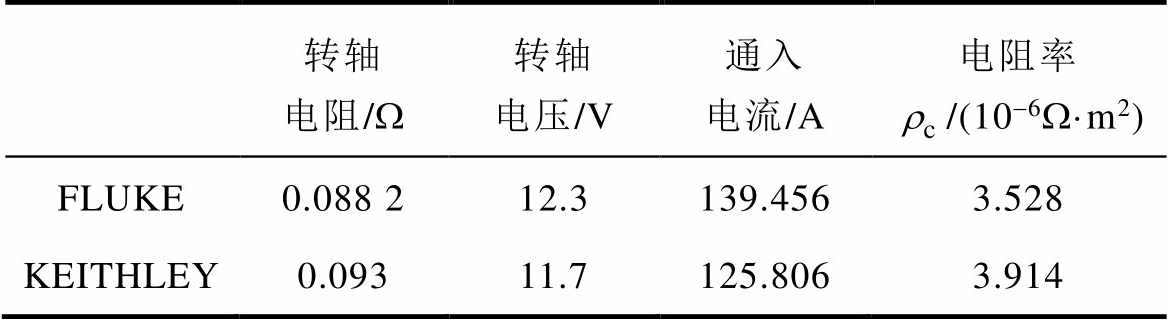
转轴电阻/W转轴电压/V通入电流/A电阻率/(10-6W·m2) FLUKE0.088 212.3139.4563.528 KEITHLEY0.09311.7125.8063.914
对特定电机而言，其横向电阻值与导条数目、铁心长度及转子工艺相关，需要针对转子情况进行实验测量。在工业应用中考虑横向电阻值时，为便于研究人员快速研究横向电阻值影响，忽略气泡、氧化等工艺因素，对于槽数不多、轴向长度不长且无特殊结构的感应电机而言[28]，可估算横向电阻为
（9）式中，
为工业应用中估算横向电阻；
为单位轴向长度单位面积的接触电阻率，可近似取0.01W·m2；
为槽型周长。
在估算电阻时，只考虑不同介质间的接触电阻，忽略电机型号与工艺制作，假定导条与槽型周围铁心接触良好且均匀，依据式（9）对文中感应电机横向电阻进行估算，并与两种测量仪器下的测量电阻作出对比，对比结果见表3。
表3 横向电阻数据对比
Tab.3 Comparison of inter-bar resistance
FLUKEKEITHLEY(选定)公式估算 横向电阻/(10-6W)2.2052.4442.379
针对完整笼型转子测量法实验测量误差问题。本文利用实验前转子转轴测量电阻、实验后对端环至转轴测量电阻和转子横向接触电阻构建虚拟电路，分析各电阻对导条电压降灵敏度。其中，转轴电阻为公共回路，端环至转轴电阻与横向接触电阻串联，对整个转子回路而言，转子横向接触电阻构成强关联环形桶状网络。针对同一根导条横向电阻存在电阻分布不均匀情况时，对导条测量点电压降影响不大，由虚拟电路灵敏度分析可知，强关联性桶状网络，单条支路开断不会影响导条测量点电压数值，故而在解析计算时可忽略横向电阻不均匀分布情况，而转轴电阻作为公共回路，其变化对电压降数值有较大影响，故而需要在采用两种测量仪器的同时还考虑温升问题。
利用2D多截面有限元计算横向漏电流损耗，可有效缩短仿真时间。快速预估电机损耗，为验证改进模型计算的准确性，本文利用3D模型仿真结果对比，并进行了相应的仿真分析，其结论有较好的工程应用价值。计及横向漏电流的3D模型如图8所示，仿真时主要考虑感应电机在稳态运行情况下，定子旋转磁场对转子的影响，计及转子涡流效应且忽略横向电流所产生磁场对一次侧定子绕组影响，相比于二维多截面有限元计算考虑笼型转子端环影响，故而认为三维计算在考虑横向接触电阻后更接近于实际工况。在对模型整体剖分时，对定子剖分较为粗糙，对转子剖分更为细致，主要是对过渡层部分的剖分，转子剖分如图9所示。
图8 带过渡层的3D模型
Fig.8 3D with transition layer
图9 3D模型转子剖分
Fig.9 3D model rotor split drawing
通过2D多截面仿真结果与3D仿真磁通密度对比验证模型可行性，即此模型能够计及横向漏电流影响。单斜槽感应电机3D转子表面磁通密度沿轴向分布如图10所示，从图中可以看出，考虑横向漏电流后，横向漏电流加剧转子轴向磁通密度的不均匀分布，而靠近端环附近最为明显。与本文多截面仿真对比，采用2D有限元分析时，转子磁通密度分布如图11所示，图11a中未考虑横向电阻情况指过渡层电阻率为转子铁心的电阻率，此时电机转子铁心虽分为两部分，但其电阻率相同，与传统电机仿真相同；图11b中考虑横向电阻情况指过渡层电阻率由铁心自身电阻率与实验测量的横向电阻共同决定。可以看出，在考虑横向电阻后对转子槽型周围的磁通密度有较大影响，与3D结果相吻合，也与解析计算结果相对应。解析计算中横向漏电流幅值由轴向中间至两端逐渐增加，在靠近端环附近横向电流最为明显，故而在带中环的斜槽感应电机中，中环能起到汇集横向电流的作用，使横向电流沿轴向分布更均匀，减小电机振动[30]。
图10 3D转子磁通密度分布
Fig.10 3D rotor magnetic density map
图11 2D多截面中磁通密度对比
Fig.11 Magnetic density comparison in 2D multi-sliced
针对2D有限元仿真误差问题。横向漏电流损耗是指相邻导条间流过电流所产生的损耗，在2D模型中计算横向电流损耗，实际是以转子解析计算方程中单元电机为依据，建立单元电机的二维模型，在单位轴向长度的单元电机模型中加入横向电阻，在磁场分析中计入转子横向电阻回路。考虑到转子模型杂散损耗问题，为精确定位横向漏电流损耗，通过对比考虑横向电阻和未考虑横向电阻两种情况时的电机杂散损耗，对两种情况下的杂散损耗做差计算横向漏电流损耗，模型作差的方式消除了仿真时设置铁心参数带来的误差，但在利用模型做差的同时，损失了部分横向漏电流损耗。表4中显示2D仿真结果与3D仿真结果对比。2D模型计算思路来源于解析计算中单元电机概念，考虑到在损耗解析计算时所简化的条件，忽略转子端环阻抗的影响，同时在模型作差方式下减小部分横向漏电流损耗，所以2D模型计算横向漏电流损耗数值比3D计算值稍小，其误差分为两部分：一是端环损耗，其损耗会随着模型轴向增加而减小；二是模型作差损失的部分，随着模型功率的增加所占比例逐渐减小。故其误差百分比会随着电机模型轴向长度的增加呈减小趋势。本文提供一种能在二维有限元中考虑横向漏电流影响的模型，并通过计算横向漏电流损耗与3D模型作对比证明其可行性，可用于快速预估横向漏电流损耗问题，降低对硬件需求的同时大幅缩短仿真时间，可用于重复性仿真探究横向漏电流对电机性能影响问题。
表4 横向损耗数据对比
Tab.4 Comparison of inter-bar loss
方法横向损耗值/W额定转矩/(N·m) 2D多截面仿真16.763.81 3D仿真20.203.74
横向电流的产生使得导条电流回路增加，导条电流不仅仅通过端环联接。由转子解析模型可知，部分电流通过笼型转子端环汇聚，少部分电流通过横向电阻流经相邻导条，最终汇聚至端环，转子表面电流分布的变化使得感应电机转子等效电路发生改变[31]，因此对电机转矩有显著影响。通常转子导条在旋转磁场中切割磁场产生电流，认为导条电流经端环与其余导条相连，得到感应电机转子等效电路，进而通过等效电路计算电机转矩[32-33]，图12a所示为等效电路计算与改进模型后2D多截面仿真两条转矩曲线对比，传统等效电路转矩计算本身未考虑横向电流，2D模型仿真时设定过渡层为绝缘计算转速-转矩曲线，两者计算结果相符，证明在未考虑横向电流时模型的准确性。考虑横向漏电流产生后，电机转子的等效电路已经改变，仿真时通过改变导条与铁心间过渡层电导率等效横向电阻变化，探究横向电阻对感应电机转速-转矩曲线的影响，图12b所示为不同过渡层电导率时电机转速-转矩曲线，将不同横向漏电阻情况等效为过渡层电导率数值变化，在过渡层电导率分别为1×102S/m、1×104S/m、1×106S/m、1× 107S/m情况时2D多截面计算的电机转速-转矩曲线。
图12 转矩-转速曲线对比
Fig.12 Comparison of torque-speed curves
在电机稳定运行过程中，稳态平均转矩主要与转子基波相关，横向电阻为谐波性质，对电机平均转矩的影响微小[34]。如图13所示为稳态运行且考虑横向电流情况时，轴向不同位置对平均转矩的贡献，即设定导条与铁心间过渡层电导率为2.79× 107S/m时，通过2D多截面有限元将斜槽转子沿轴向分成五段，由文献[35-36]可知，增加轴向分段数能提高仿真精度，但每段之间相互错开1/4斜槽度时，等效已具有足够的计算精度，在额定转速条件下时，各分段转子对电机平均转矩的贡献。采用多截面等效斜槽时，由图13中所示可知，考虑横向电阻后，稳态时转子轴向各位置对电机平均转矩的贡献程度不同，但以转子轴向中心为起点，两侧转矩贡献相互对称甚至互补，整体所表现的转矩特性波动微小，故而证明横向漏电流对稳态运行情况下的电机转矩影响微小，呈谐波性质。
图13 轴向不同位置对电机转矩的贡献
Fig.13 Contribution of different axial positions to motor torque
由于横向漏电流主要为谐波性质，故而转子横向电阻的变化对电机起动过程转矩影响显著，尤其是堵转情况下横向电阻的变化对电机转矩影响较大，如图14所示为堵转时，横向电导率对起动转矩的影响，图中横坐标表示对过渡层电导率S取对数。在转子模型等效结构中，由导条电流路径可知，横向电阻与端环为并联关系，端环电导率约为108S/m，在横向电阻远大于端环电阻的情况下，即过渡层电导率较小时（图左侧），导条内感生电流更多流经端环电阻而非横向电阻，电机起动转矩为正，且在电导率小于某一阈值后，电导率对转矩影响到稳定阶段；同样在横向电阻远小于端环电阻的情况下，即过渡层电导率较大时（图右侧），横向电阻对转矩起抑制作用，且在增大到一定程度后，对电机转矩的影响达到稳定阶段，而在横向电阻位于端环电阻附近时，起动转矩对横向电阻的变化尤为敏感。
图14 横向电导率对转矩的影响
Fig.14 Effect of inter-bar conductivity on torque
本文针对感应电机横向漏电流损耗进行研究，由转子横向漏电流损耗解析模型，提出一种能计及横向漏电流影响的2D有限元模型，并借此提出一种能减小横向漏电流损耗的措施。随后，对有限元模型进行磁场分析，并通过与3D模型仿真损耗做对比，证明模型的可行性。最后，利用此模型计算速度快的优点，分析了横向电阻对电机转速-转矩曲线的影响，并进一步探究了横向电阻对电机起动转矩的影响，同时考虑到横向电流的热效应与磁效应，横向电流对电机内部的温升贡献及电机轴向振动的影响有待后续探究。
由横向漏电流的探究，得出主要结论如下：
1）在笼型感应电机稳态运行时，由转差率可知，转子切割主磁场速度较慢，在转子导条内感生电流频率很低，故转子中横向漏电流回路阻抗在电机额定条件下稳定运行时呈现电阻性。
2）斜槽电机运行时横向漏电流的产生加剧了转子磁通密度分布的不对称性，横向漏电流分布沿轴向由中间向两端逐渐增加，靠近端环附近横向漏电流最为明显，同时横向漏电流损耗随着横向电阻的增加呈现先增加后减小的趋势。
3）横向漏电流主要表现为谐波性质，其值同转子转差率与横向电阻相关，特别是在电机起动过程中对电机转矩有显著影响，而对电机稳态运行时的平均转矩影响不大。
4）横向漏电流沿轴向分布不均匀，对电机内沿轴向不同位置温升的贡献不同，对电机内部温升影响有待后续研究；同时在转子断条故障情况下，回路的改变与转差率的变化均会加剧横向漏电流，在电机主磁场作用下对电机轴向振动的影响有待 探究。
参考文献
[1] Dorrell D G, Holik P J, Rasmussen C B. Analysis and effects of inter-bar current and skew on a long skewed-rotor induction motor for pump appli- cations[J]. IEEE Transactions on Magnetics, 2007, 43(6): 2534-2536.
[2] Nishizawa H, Itomi K, Hibino S, et al. Study on reliable reduction of stray load losses in three-phase induction motor for mass production[J]. IEEE Power Engineering Review, 1987, 7(9): 51-52.
[3] 邓东, 孙玉田, 谭国伟, 等. 飞来峡水电站发电机的运行故障分析[J]. 大电机技术, 2003, 33(6): 13-17.
Deng Dong, Sun Yutian, Tan Guowei, et al. Analysis on operating faults of generator in Feilaixia hydropower station[J]. Large Electric Machine and Hydraulic Turbine, 2003, 33(6): 13-17.
[4] 詹阳, 孔伉伉, 许国瑞, 等. 交流电机转子导条间横向漏电流研究综述与展望[J]. 中国电机工程学报, 2018, 38(7): 2132-2143.
Zhan Yang, Kong Kangkang, Xu Guorui, et al. Review and prospect of the research on rotor inter-bar currents in AC machines[J]. Proceedings of the CSEE, 2018, 38(7): 2132-2143.
[5] 杨淑英, 杨澍, 李筱筠, 等. 一种基于铁损模型的异步电机矢量控制策略[J]. 电机与控制学报, 2020, 24(2): 36-45.
Yang Shuying, Yang Shu, Li Xiaojun, et al. Vector control strategy of induction motor based on iron loss model[J]. Electric Machines and Control, 2020, 24(2): 36-45.
[6] 谢颖, 黎志伟, 郭金鹏. 电动汽车用高功率密度感应电机的设计与研究[J]. 电机与控制学报, 2020, 24(2): 49-57.
Xie Ying, Li Zhiwei, Guo Jinpeng. Design and research on high power denity induction motor in electric vehicle[J]. Electric Machines and Control, 2020, 24(2): 49-57.
[7] Zhang Zhenyang, Liu Huijuan, Song Tengfei, et al. Performance evaluation of a 60kW IPM motor for medium commercial EV traction application[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(2), 195-203.
[8] 李永刚, 王罗, 李俊卿, 等. 基于多源信息融合的同步发电机转子绕组匝间短路故障识别[J]. 电力系统自动化, 2019, 43(16): 162-170.
Li Yonggang, Wang Luo, Li Junqing, et al. Identi- fication of inter-turn short-circuit fault in rotor windings of identification of inter-turn short-circuit fault in rotor[J]. Automation of Electric Power Systems, 2019, 43(16): 162-170.
[9] 魏书荣, 吴锐, 符杨, 等. 海上双馈感应发电机定子绕组匝间短路容错技术可行性分析[J]. 电力系统自动化, 2019, 43(5): 400-410.
Wei Shurong, Wu Rui, Fu Yang, et al. Feasibility analysis of fault tolerant technology for offshore double-fed induction generator stator windings[J]. Automation of Electric Power Systems, 2019, 43(5): 400-410.
[10] Odok A M. Stray-load losses and stray torques in induction machines[J]. IEEE Transactions on Power Apparatus and Systems, 1958, 77(3): 43-53.
[11] 丁梵林, 孙自强, 董伯祥. 鼠笼转子横向接触电阻的测试[J]. 电工技术杂志, 1985, 6(12): 3-6.
Ding Fanlin, Sun Ziqiang, Dong Boxiang. Measure- ment of transverse contact resistances in cage rotors[J]. Electrotechnical Journal, 1985, 6(12): 3-6.
[12] 丁梵林. 提高鼠笼转子横向接触电阻测试精度的方法[J]. 西安交通大学学报, 1986, 20(1): 121-122, 103.
Ding Fanlin. A method for precise measurement of cage rotor transverse contact resistance[J]. Journal of Xi’an Jiaotong University, 1986, 20(1): 121-122, 103.
[13] Williamson S, Poh C Y. Inter-bar currents in cage induction motors[J]. IEE Proceedings-Electric Power Applications, 2005, 152(5): 1106-1112.
[14] Williamson S, Smith A C. Equivalent circuits for cage induction motors with inter-bar currents[J]. IEE Proceedings-Electric Power Applications, 2002, 149(3): 173-183.
[15] Rao V S, Butler O. Stray losses of poly-phase cage- induction motors with particular reference to the condition of imperfect rotor-bar-iron insulation[J]. Proceedings of the Institution of Electrical Engineers, 1969, 116(5): 737-751.
[16] Dorrell D G, Miller T J E, Rasmussen C B. Inter-bar currents in induction machines[J]. IEEE Transactions on Industry Applications, 2003, 39(3): 677-684.
[17] Dorrell D G, Holik P J, Thougaard H J, et al. Modelling axial variations in induction motors with rotor using multi-sliced 2D finite element analysis[C]// IET International Conference on Power Electronics, Ireland, 2007: 686-690.
[18] Gudelhofer J, Gottkehaskamp R, Mockel A. 3D FEM approach to study the physics of inter-bar currents in induction machines[C]//IEEE 2016 XXII International Conference on Electrical Machines (ICEM), Switzerland, 2016: 18-24.
[19] Yamada K, Takahashi Y, Fujiwara K. Simplified 3D modeling for skewed rotor slots with end-ring of cage induction motors[J]. IEEE Transactions on Magnetics, 2016, 52(3): 1-4.
[20] Ho S L, Fu W N, Wong H C. Estimation of stray losses of skewed rotor induction motors using coupled 2-D and 3-D time stepping finite element methods[J]. IEEE Transactions on Magnetics, 1998, 34(5): 3102- 3105.
[21] 张文, 郑晓钦, 吴新振. 多相感应电机三维电磁分析与损耗计算[J]. 电工技术学报, 2018, 33(增刊2): 81-87.
Zhang Wen, Zheng Xiaoqin, Wu Xinzhen. Three- dimensional electromagnetic analysis and loss calcu- lation of multiphase induction motors[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 81-87.
[22] Yamazaki K, Watanabe Y. Inter-bar current analysis of induction motors using 3-D finite-element method considering lamination of rotor core[J]. IEEE Transactions on Magnetics, 2006, 42(4): 1287-1290.
[23] 张小宁, 王泽忠. 异步电动机斜槽横向电流二维场计算[J]. 华北电力学院学报, 1992, 19(4): 21-26.
Zhang Xiaoning, Wang Zezhong. Calculation of 2D field of skew slot inter-bar currents in asynchronous motor[J]. Journal of North China Institute of Electric Power, 1992, 19(4): 21-26.
[24] 鲍晓华, 方金龙, 徐威, 等. 考虑横向电流和饱和轴向变化的双斜槽转子感应电机起动转矩分析[J]. 电工技术学报, 2019, 34(4): 14-21.
Bao Xiaohua, Fang Jinlong, Xu Wei, et al. Starting torque analysis of doubly skewed rotor induction motor considering inter-bar currents and axial variations in saturation[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 14-21.
[25] Williamson S, Poh C Y. Inter-bar currents in cage induction motors[J]. IEE Proceedings-Electric Power Applications, 2005, 152(5): 1106-1112.
[26] Holik P J, Dorrell D G, Lombard P, et al. A multi-sliced finite element model for induction machines incorporating inter-bar current[C]//IEEE IAS Meeting, Tampa, FL, USA, 2006: 819-826.
[27] Stening A, Sadarangani C. Starting performance of induction motors with cast aluminium and copper rotors including the effects of saturation and inter- bar currents[C]//IEEE International Conference on Electrical Machines & Systems, Tokyo, Japan, 2010: 1-5.
[28] 海勒尔. 异步电机中谐波磁场的作用[M]. 北京: 机械工业出版社, 1980.
[29] Müller G H, Landy C F. A novel method to direct broken rotor bars in squirrel cage induction motors when interbar currents are present[J]. IEEE Transa- ctions on Energy Conversion, 2003,18(1): 71-79.
[30] 莫会成, 励鹤鸣. 鼠笼异步电动机的横向电流和设置中环的感应电机[J]. 微电机, 1988, 17(4): 16-21.
Mo Huicheng, Li Heming. Squirrel-cage asynchronous motors transverse current and induction machine with interring[J]. Micromotors, 1988, 17(4): 16-21.
[31] Akihito N, Satoshi K, Kazuo N, et al. High-frequency inter-bar current losses in cage induction motors under no-load condition[J]. IEEE Transactions on Energy Conversion, 2014, 29(3): 698-705.
[32] 凌在汛, 周理兵, 张毅, 等. 笼型实心转子屏蔽感应电机电磁场及参数研究(三): 实用等效电路及其参数的推导[J]. 电工技术学报, 2018, 31(19): 4496- 4507.
Ling Zaixun, Zhou Libing, Zhang Yi, et al. Parameters determination and electromagnetic field analysis of canned solid-rotor induction motor (3): practical equivalent circuit and its parameter analysis[J]. Transactions of China Electrotechnical Society, 2018, 31(19): 4496-4507.
[33] 凌在汛, 周理兵, 张毅, 等. 笼型实心转子屏蔽感应电机电磁场及参数研究(四): 等效电路参数有限元计算法及验证[J]. 电工技术学报, 2018, 33(21): 91-101.
Ling Zaixun, Zhou Libing, Zhang Yi, et al. Parameters determination and electromagnetic field analysis of canned solid-rotor induction motor (4): practical equivalent circuit and its parameter analysis[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 91-101.
[34] Carlson R, Silva C A D, Sadowski N, et al. Analysis of the effect of inter-bar currents on the performance of polyphase cage-induction motors[J]. IEEE Transa- ctions on Industry Applications, 2003, 39(6): 1674- 1680.
[35] 梁文毅, 陆天雄, 张翔. 基于分段斜槽技术的电机斜槽特性分析[J]. 电工技术学报, 2011, 26(11): 139-144.
Liang Wenyi, Lu Tianxiong, Zhang Xiang. Skew effect simulation based on multi-slices model[J]. Transactions of China Electrotechnical Society, 2011, 26(11): 139-144.
[36] 胡小飞, 刘超, 王毅, 等. 单相无刷有槽有限转角电机的分析与优化[J]. 电工技术学报, 2019, 34(13): 2744-2751.
Hu Xiaofei, Liu Chao, Wang Yi, et al. Analysis and optimization of single phase brushless slotted limited- angle torque motor[J]. Transactions of China Electro- technical Society, 2019, 34(13): 2744-2751.
Analysison Lossand Torque of Induction Motor Considering Inter-Bar Current in Two-Dimensional Field
Abstract In general, small and medium-sized induction motors (IM) are mostly used for induction motors. The skewed rotor structure can suppress parasitic torque, electromagnetic vibration and noise, but it will increase the inter-bar current between the rotor bars, affecting the starting characteristics and efficiency of the IM. Hence, the influence of inter-bar current on the performance of skewed rotor IM was studied in this paper. By summarizing the distribution of inter-bar current on the rotor in the IM with skewed rotor, a two-dimensional multi-section finite element model that can take into account the inter-bar current was proposed. The model effectively reduces the simulation time compared with the three-dimensional finite element model considering inter-bar current. Moreover, this model takes into account the influence of the inter-bar current on the skewed rotor motor in the two-dimensional finite element through establishing the transition layer in the rotor, which can be used to predict the influence of the inter-bar current on the motor performance. The inter-bar current loss in the Y802-2 IM was simulated and compared with the loss value of the three-dimensional finite element simulation. The feasibility and effectiveness of the model were verified, and this model was used to analyze the effect of different inter-bar current resistance values on the starting torque characteristics of the IM.
keywords：Induction motor, skewed rotor, inter-bar current, loss, torque
DOI: 10.19595/j.cnki.1000-6753.tces.201086
中图分类号：TM343
谢 颖 女，1974年生，教授，博士生导师，研究方向为电机内电磁场、温度场、振动噪声计算及感应电机故障诊断及检测。E-mail: xieying_1975@163.com（通信作者）
毛 攀 男，1993年生，硕士研究生，研究方向为电机内电磁场与损耗分析。E-mail: 15736707637@163.com
收稿日期 2020-08-25
改稿日期 2020-09-218
国家自然科学基金资助项目（51977052）。
（编辑 崔文静）