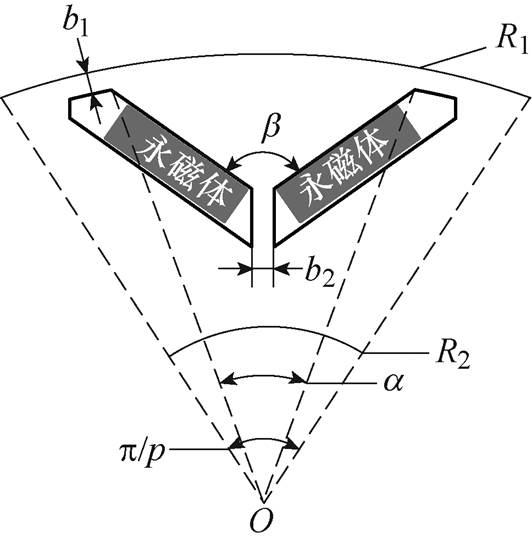
图1 转子结构示意图
Fig.1 Schematic diagram of rotor structure
摘要 对于变频器驱动的内置式永磁同步电机,大多数研究集中于变频器共模电压对轴承电压的影响,忽略了磁路不平衡导致的轴电压。针对内置式永磁同步电机动态偏心故障下的轴电压,首先,运用解析法推导轴电压的表达式,分析轴电压的特征频率;其次,研究改变转子磁极的极弧系数削弱偏心轴电压的方法;最后,建立4极6槽、2极9槽、4极9槽、8极9槽在内的4台内置式永磁同步电机偏心轴电压模型,进行有限元验证。仿真结果表明,通过削弱固有轴电压分量可以削弱偏心轴电压,40%偏心度下4台电机削弱效果分别为59.05%、26.90%、43.31%、 22.60%。
关键词:内置式永磁同步电机 动态偏心 特征频率 轴电压
由于具有功率密度高、效率高等优点[1-6],内置式永磁同步电机广泛应用于风力发电、医疗器械、电动汽车、航空航天等场合[7-8]。在这些应用场合中,内置式永磁同步电机需长期稳定运行,必须具有高可靠性。轴承是电机系统重要的零部件,也是脆弱、易损坏的部件[9]。据统计,超过40%的电机故障是由于轴承失效引起的[10]。其中,轴电压是导致轴承过早失效的关键因素。分数槽永磁电机由于极槽配合的原因可能存在固有轴电压,影响电机系统的可靠性[11]。同时,变频器驱动的电机系统由于共模电压、共模电流和快速开关频率等原因也会产生轴电压、轴电流[12-15]。另外,转子偏心故障导致的电机磁路不平衡也会在电机转轴两端感应出轴电压。当轴电压超过轴承油膜的击穿阈值电压,轴承内部产生电火花放电电流,流过轴承滚动体、轴承内圈和外圈。电流释放的热量对轴承造成损伤,降低润滑剂的化学性质,从而导致轴承过早失效,严重降低了电机系统的可靠性[16-17]。因此,轴电压的削弱研究对于提高电机工作的可靠性和稳定性具有重要的意义。
文献[18]列举了轴电压、轴电流抑制方案,包括:①共模电压滤波器、dv/dt滤波器等;②屏蔽电缆;③接地电刷、绝缘轴承、混合轴承和含导电油脂的轴承。文献[19]研究了一种新型电磁屏蔽感应电机,在感应电机气隙中插入一个法拉第屏蔽来阻断定子与转子间的电容耦合,测试实验表明,电磁屏蔽感应电机可以有效削弱逆变器引起的电机轴电压。文献[20]研究了RSPWM、NSPWM、AZSPWM1、AZSPWM3四种无零矢量脉宽调制技术的调制策略,与传统的空间矢量脉宽调制策略进行仿真对比,验证了无零矢量技术抑制共模电压的有效性。文献[21]推导了固有轴电压的解析表达式,研究了改变极弧系数来削弱表贴式分数槽永磁电机的固有轴电压,并通过有限元仿真分析验证了其有效性。文献[22]提出改变永磁同步电机内部耦合电容值来削弱电机轴电压的方法,实验验证了改变定子绕组形状减小定子绕组与转子之间的耦合电容值可以有效地抑制轴电压,同时对电机的转矩特性影响较小。
文献[23]研究了偏心对异步电机轴电压的影响,在定子绕组串联和并联两种情况下对电机进行了实验。实验表明,静态偏心度越大,轴电压越高;定子绕组并联可以降低轴电压。文献[24]研究了转子偏心对轴承电压和轴电压的影响,研究表明,偏心会使轴承电压减小、轴电压增大,并通过仿真验证了其有效性。文献[25]仿真分析了转子偏心对12/ 10极磁通切换永磁电机固有轴电压的影响,得到转子偏心对其固有轴电压影响较小的结论。文献[26]运用磁动势磁导法,分析了汽轮发电机典型故障下的轴电压,总结了静态偏心和励磁绕组匝间短路故障下的轴电压特征频率,并通过实验验证了其准确性。
对于内置式永磁同步电机,本文运用解析法,首先推导了不偏心时空载固有轴电压表达式,接着推导了动态偏心故障下的轴电压表达式,分析了轴电压的特征频率,研究了偏心轴电压的削弱措施。
本文以具有V型转子磁路结构的内置式永磁同步电机为例,分析其空载固有轴电压特性,转子结构示意图如图1所示。图中,R1为转子外径,R2为转轴半径,b 为永磁体夹角,a 为永磁体槽对应的圆心角,b1为主隔磁桥宽度,b2为辅助隔磁桥宽度。

图1 转子结构示意图
Fig.1 Schematic diagram of rotor structure
为简化分析,假设:定转子铁心的磁导率无穷大,不计铁心饱和的影响。永磁体磁动势沿气隙圆周的分布如图2所示,q=0位于相邻两个永磁体的中心线上。图中,ap为磁极的极弧系数,p为极对数,F为磁动势的幅值。
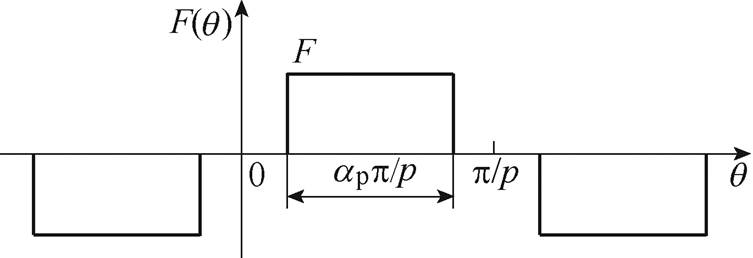
图2 永磁体磁动势沿气隙圆周的分布
Fig.2 Distribution of permanent magnet magnetomotive force along the circumference of air gap
永磁体磁动势的傅里叶展开式为
 (1)
(1)式中,F2n-1为永磁体磁动势的第2n-1次谐波幅值;qr为转子沿气隙圆周的位置角。傅里叶系数F2n-1可以表示为
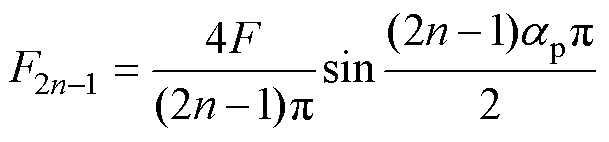 (2)
(2)
气隙磁导函数表达式为
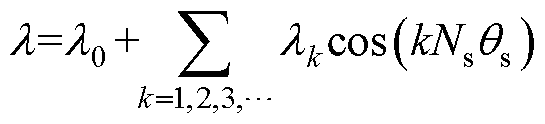 (3)
(3)式中,l0为气隙磁导的不变分量;lk为气隙磁导的k阶谐波分量;Ns为定子槽数;qs为定子沿气隙圆周的位置角。
基于磁路分析法,内置式永磁同步电机的径向气隙磁通密度表达式为
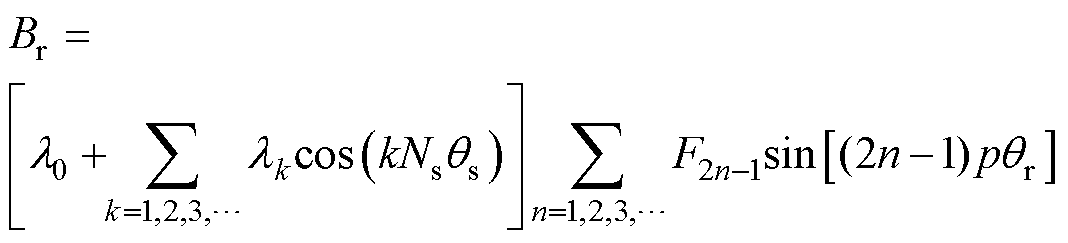 (4)
(4)定、转子沿气隙圆周位置角的关系可以表示为
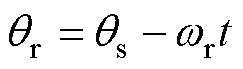 (5)
(5)
式中,wr为转子机械角速度;t为时间。
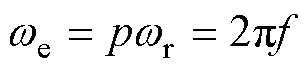 (6)
(6)式中,we为电角速度;f为定子槽内的导体感应电动势频率,也为同步转速频率。
把式(5)代入式(4)中,径向气隙磁通密度可以表示为
 (7)
(7)其中
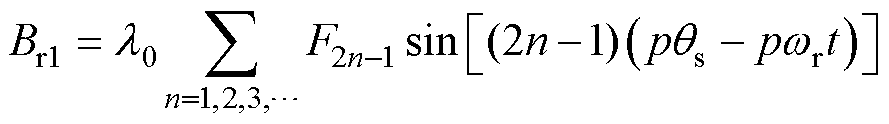 (8)
(8)

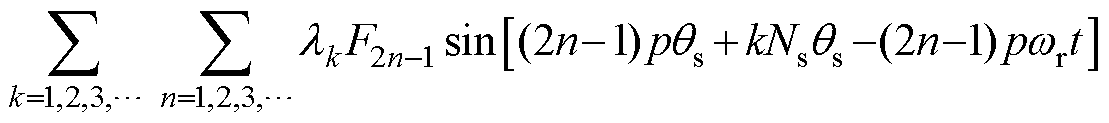 (9)
(9)
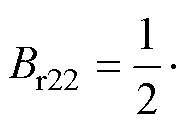
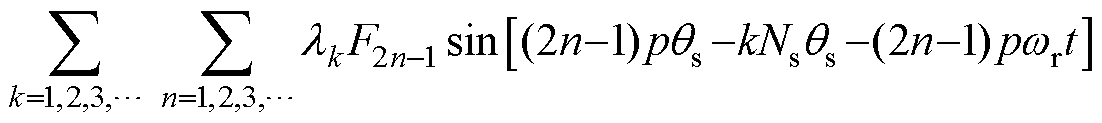 (10)
(10)如果电机的定子槽数Ns和极对数p有最大公约数GCD(Ns, p),即
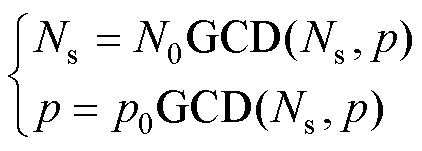 (11)
(11)式中,N0为单元电机定子槽数;p0为单元电机极对数。
对于三相对称绕组内置式永磁同步电机[27],有
 (12)
(12)当c=1, 3, 5,…时,N0为奇数,满足
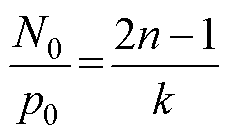 (13)
(13)
利用三角函数族的正交性,Br1、Br21、Br22沿气隙圆周[0, 2p]的积分表达式分别为
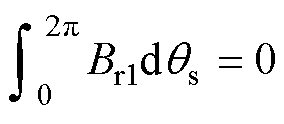 (14)
(14)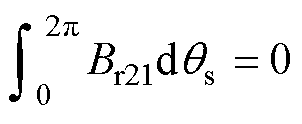 (15)
(15)
 (16)
(16)
由式(16)可知,电机内部磁路不平衡。因此,电机会产生环绕转轴的随时间变化的气隙磁通jshaft,有
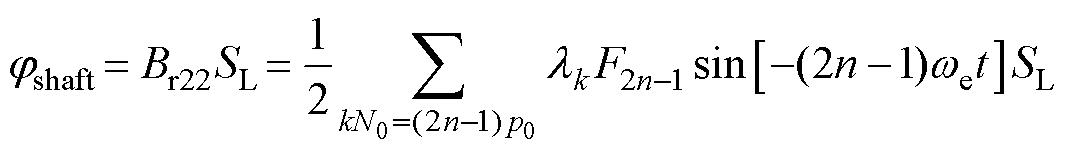 (17)
(17)式中,SL为环绕转轴的气隙磁通面积。
当c=2, 4, 6,…时,N0为偶数,不满足式(13)。利用三角函数族的正交性,Br1、Br21、Br22沿气隙圆周[0, 2p]的积分值均为零,电机不存在环绕转轴的气隙磁通。
因此,N0为奇数时,内置式永磁同步电机会产生环绕转轴的气隙磁通。根据法拉第电磁感应定律,转轴两端会感应出电压差,即内置式永磁同步电机的固有轴电压Vshaft,有
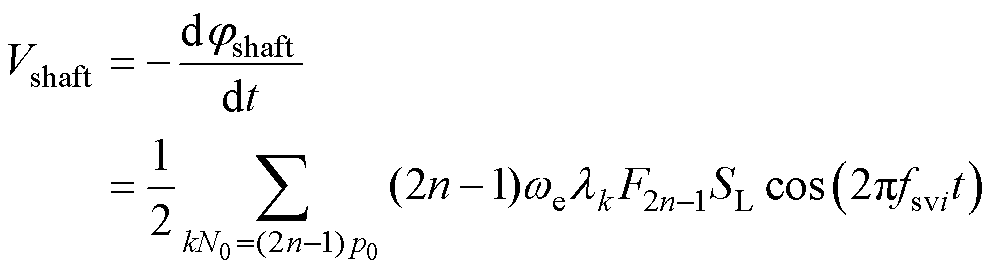 (18)
(18)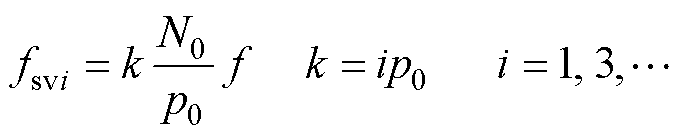 (19)
(19)
式中,fsvi为固有轴电压频率。
电机发生动态偏心故障时,定转子位置如图3所示。图中,O0为定子中心,O1为旋转中心,O2为转子中心,e为偏心距,g 为初始位置偏心角,定子中心与旋转中心重合。动态偏心度可以表示为
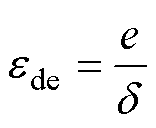 (20)
(20) 式中,d 为不偏心时均匀气隙长度。
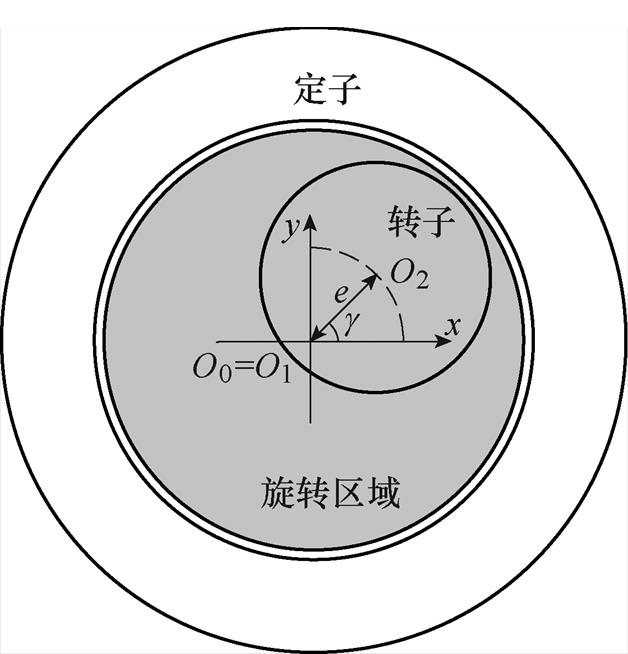
图3 定转子位置
Fig.3 Position of stator and rotor
内置式永磁同步电机的气隙最小位置随着电机的旋转而改变,因此,气隙磁导函数也发生变化。由于偏心导致的电机内部磁路不平衡,会产生环绕转轴的气隙磁通,从而在转轴两端感应出电压。
考虑到定子侧的齿槽效应,采用磁导修正系数法[28-29],动态偏心故障下的气隙磁通密度表达式相当于不偏心的气隙磁通密度表达式乘以动态偏心气隙磁导修正系数。偏心气隙磁导修正系数可表示为
 (21)
(21)式中,rde0为偏心气隙磁导修正系数的不变分量;rdev为偏心气隙磁导修正系数的ν阶谐波分量。
因此,动态偏心故障下的内置式永磁同步电机的气隙磁通密度表达式为
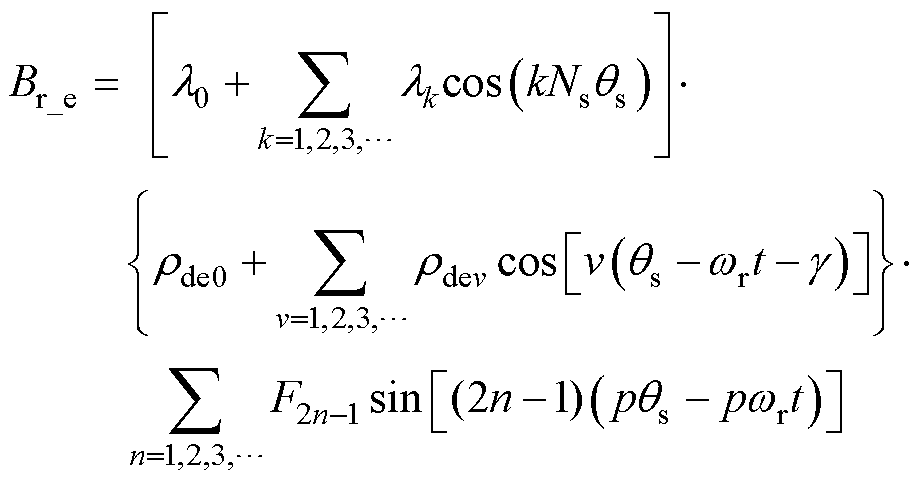 (22)
(22)式(22)可以进一步整理为
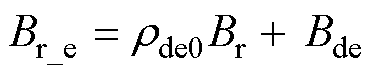 (23)
(23)
式中,Bde为动态偏心时引入的气隙磁通密度。
Bde的表达式为
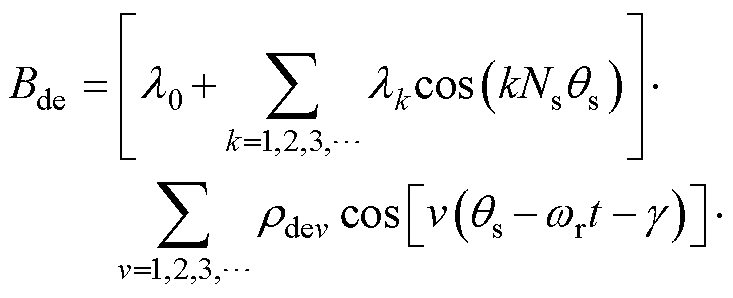
 (24)
(24)
式(24)进行三角函数积化和差化为
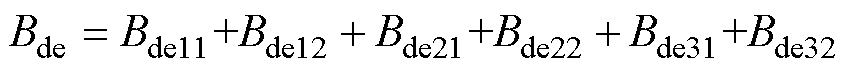 (25)
(25)其中
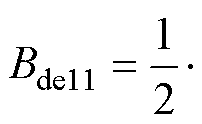
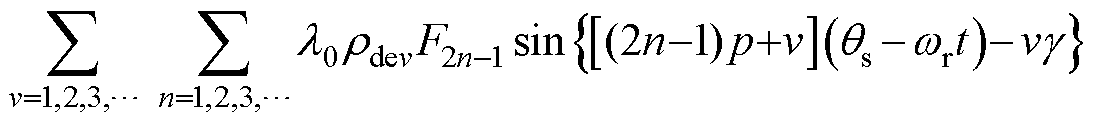 (26)
(26)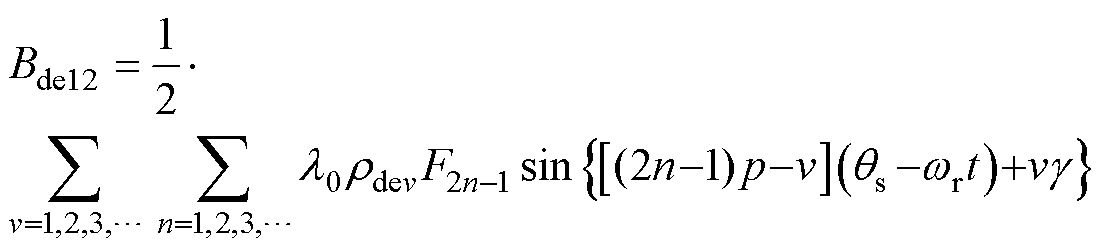 (27)
(27)
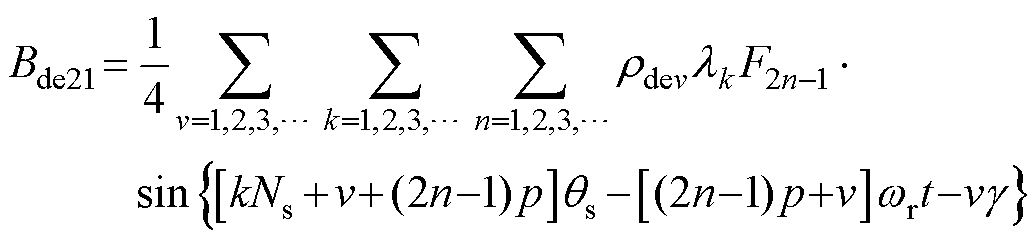 (28)
(28)
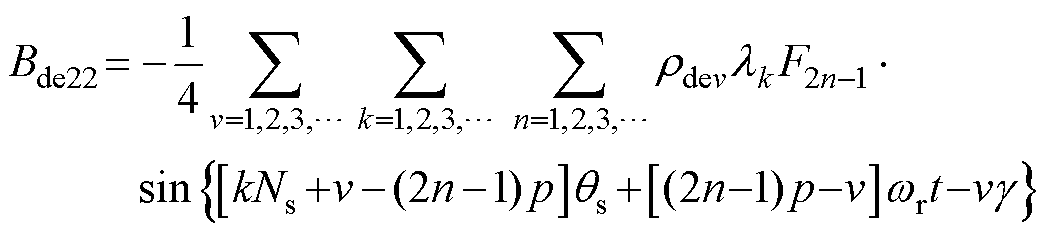 (29)
(29) (30)
(30)
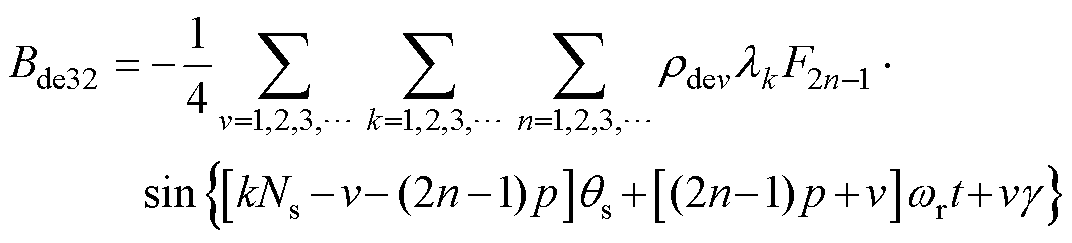 (31)
(31)
基于三角函数族的正交性,可知式(26)、式(28)在[0, 2p]的积分为零,不会产生环绕转轴的磁通。
对于Bde12,当满足
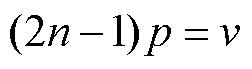 (32)
(32) (33)
(33)
产生环绕转轴的气隙磁通为
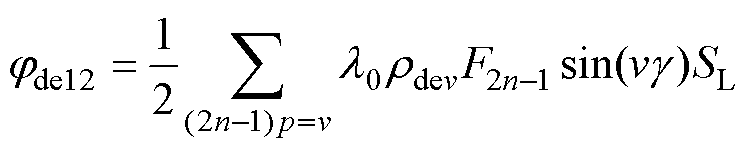 (34)
(34)对于Bde22,当满足
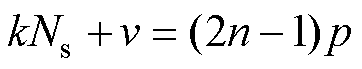 (35)
(35)
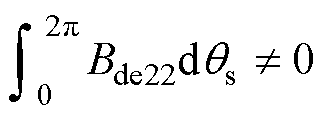 (36)
(36)产生环绕转轴的气隙磁通为
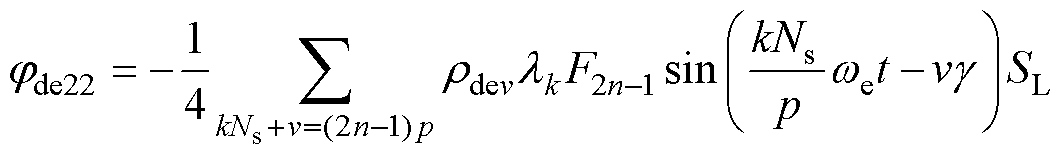 (37)
(37)
对于Bde31,当满足
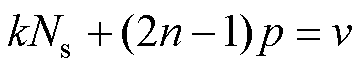 (38)
(38) (39)
(39)
产生环绕转轴的气隙磁通为
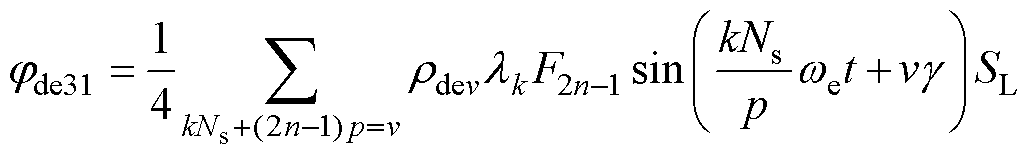 (40)
(40)对于Bde32,当满足
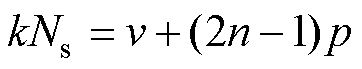 (41)
(41)
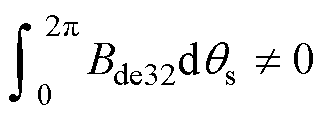 (42)
(42)产生环绕转轴的气隙磁通为
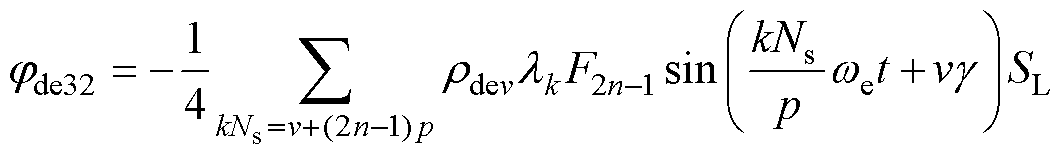 (43)
(43)
因此,动态偏心故障下的轴电压表达式为
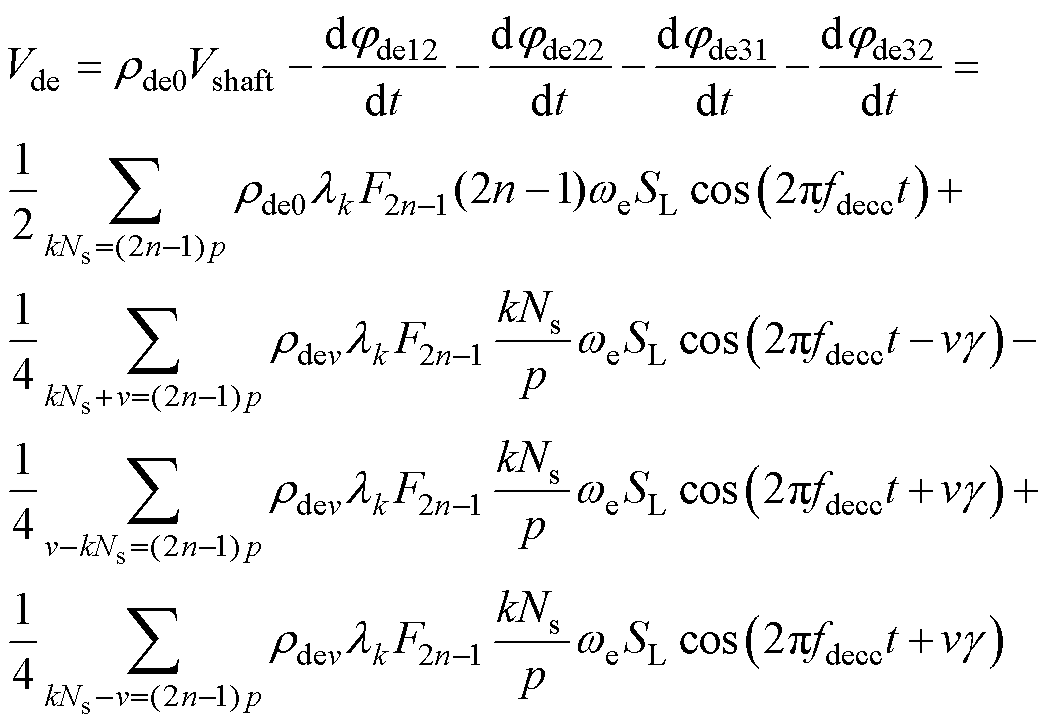 (44)
(44) (45)
(45)
式中,fdecc为动态偏心故障下的轴电压特征频率。
根据式(44)、式(45),动态偏心故障下的轴电压特征频率见表1。
表1 动态偏心故障下的轴电压特征频率
Tab.1 Characteristic frequency of shaft voltage under dynamic eccentricity fault

性质固有轴电压分量偏心轴电压分量 条件kNs=(2n-1)pkNs±ν=(2n-1)pν-kNs=(2n-1)p 特征频率kNs f/pkNs f/pkNs f/p
基于上述解析推导与表1,内置式永磁同步电机发生动态偏心故障后,轴电压特征频率为kNs f/p (k=1, 2,…)。对于单元电机定子槽数为奇数的电机,轴电压频谱中kNs f/p(k=ip0,i=1, 3,…)为固有轴电压分量对应的频率,频谱中其他频率为偏心轴电压分量对应的频率;对于单元电机定子槽数为偶数的电机,轴电压频谱中频率均为偏心轴电压分量对应的频率。因此,可以根据电机的极槽配合和轴电压频谱图,快速诊断内置式永磁同步电机发生动态偏心故障。
基于第2节的分析,根据式(44),使与偏心轴电压表达式相关的磁动势傅里叶系数F2n-1值为零,削弱内置式永磁同步电机的偏心轴电压组成分量,进而达到削弱偏心轴电压的目的。
单元电机定子槽数为奇数的内置式永磁同步电机发生动态偏心故障时,轴电压包括固有轴电压分量和由偏心引起的轴电压分量。由表1可知,固有轴电压是内置式永磁同步电机的空载固有属性,与轴电压相关的磁动势傅里叶系数可以通过极槽配合唯一确定;而与由偏心引起的轴电压分量磁动势傅里叶系数不能唯一确定。以4极9槽内置式永磁同步电机为例,偏心轴电压分析见表2(特征频率列举到18f)。可知,某一特征频率轴电压分量,对应有不同的v值、2n-1值(表2仅列出部分)。当v值不同时,特征频率对应的轴电压分量幅值占比以低阶偏心气隙磁导对应的轴电压幅值为主,如表2中*所示。当v值相同时,与偏心轴电压分量幅值占比为主的相关的磁动势傅里叶系数需要通过有限元仿真来确定,如表2中△所示。另外,在偏心度较小时,固有轴电压基波数值较大,而由偏心引起的轴电压分量数值较小。偏心轴电压中固有轴电压基波幅值占比大。
表2 偏心轴电压分析
Tab.2 Analysis of shaft voltage under eccentricity
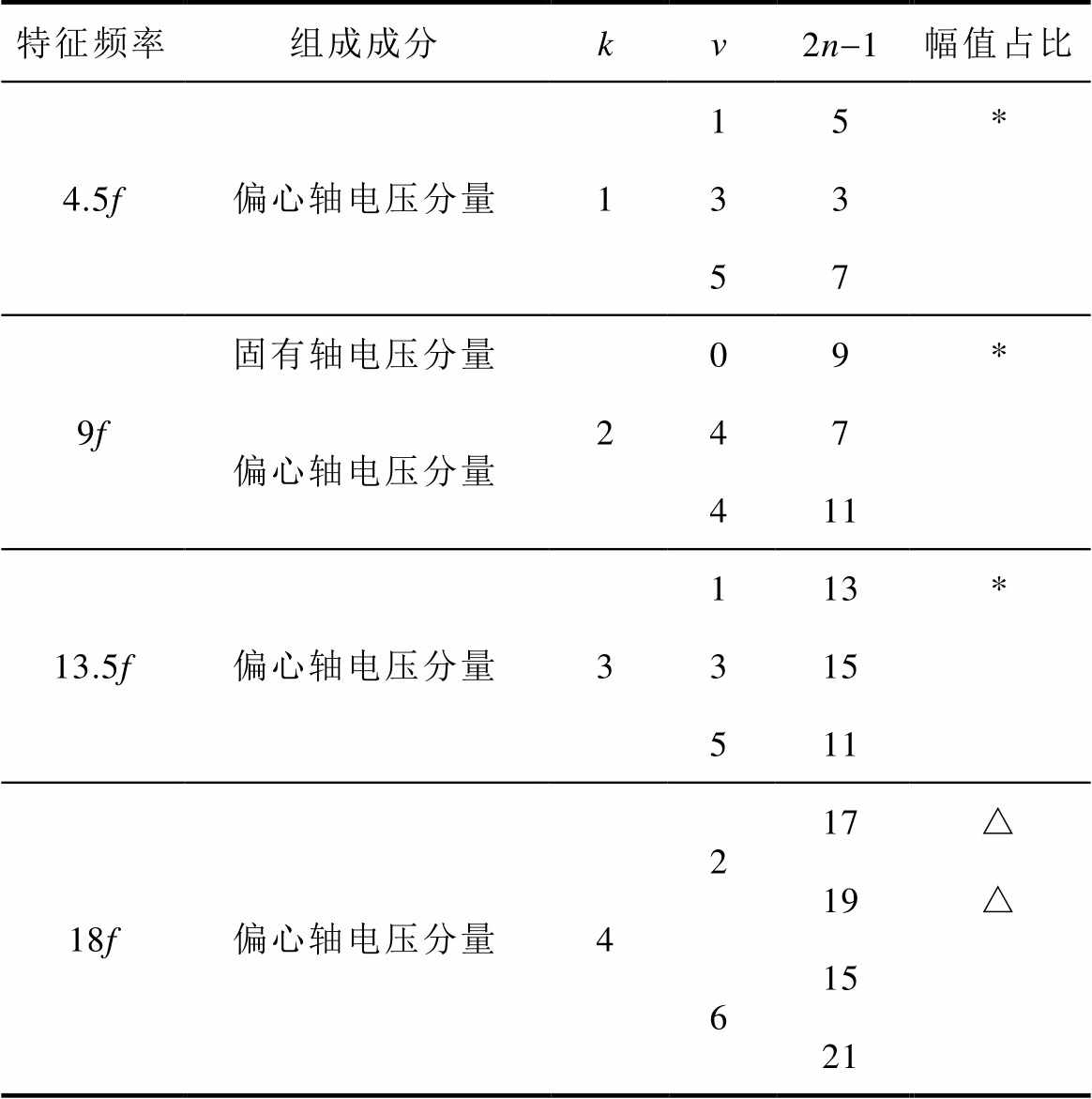
特征频率组成成分kν2n-1幅值占比 4.5f偏心轴电压分量115* 33 57 9f固有轴电压分量209* 偏心轴电压分量47 411 13.5f偏心轴电压分量3113* 315 511 18f偏心轴电压分量4217△ 19△ 615 21
单元电机定子槽数为偶数的内置式永磁同步电机发生动态偏心故障时,轴电压仅由偏心引起的轴电压分量组成。与轴电压分量相关的磁动势傅里叶系数分析与上面相同。例如,4极24槽内置式永磁同步电机,偏心轴电压特征频率为k×12f(k=1, 2,…)等。当k=1,频率=12f,相对应的v=2,2n-1=11、13;v=6,2n-1=9、15等。
因此,本文通过削弱固有轴电压基波分量,来削弱动态偏心后的轴电压。
内置式永磁同步电机的极弧系数可以表示为
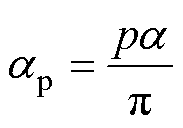 (46)
(46)通过改变V型永磁体的夹角,可以改变电机的极弧系数,使与偏心轴电压相关的磁动势的傅里叶系数F2n-1值为零。
根据式(2),令F2n-1=0,可得
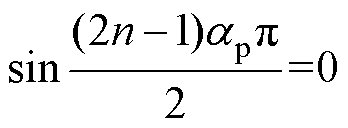 (47)
(47)极弧系数的解析计算值表达式为
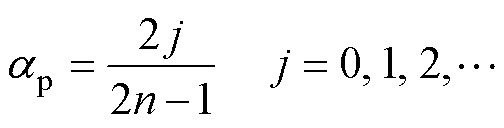 (48)
(48)
约束条件为
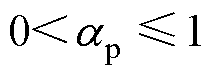 (49)
(49)本文以4极6槽、2极9槽、4极9槽、8极9槽4台内置式永磁同步电机为例,利用Maxwell 2D有限元软件,建立内置式永磁同步电机动态偏心轴电压有限元仿真模型,电机主要参数见表3。
表3 电机主要参数
Tab.3 Main parameters of motors
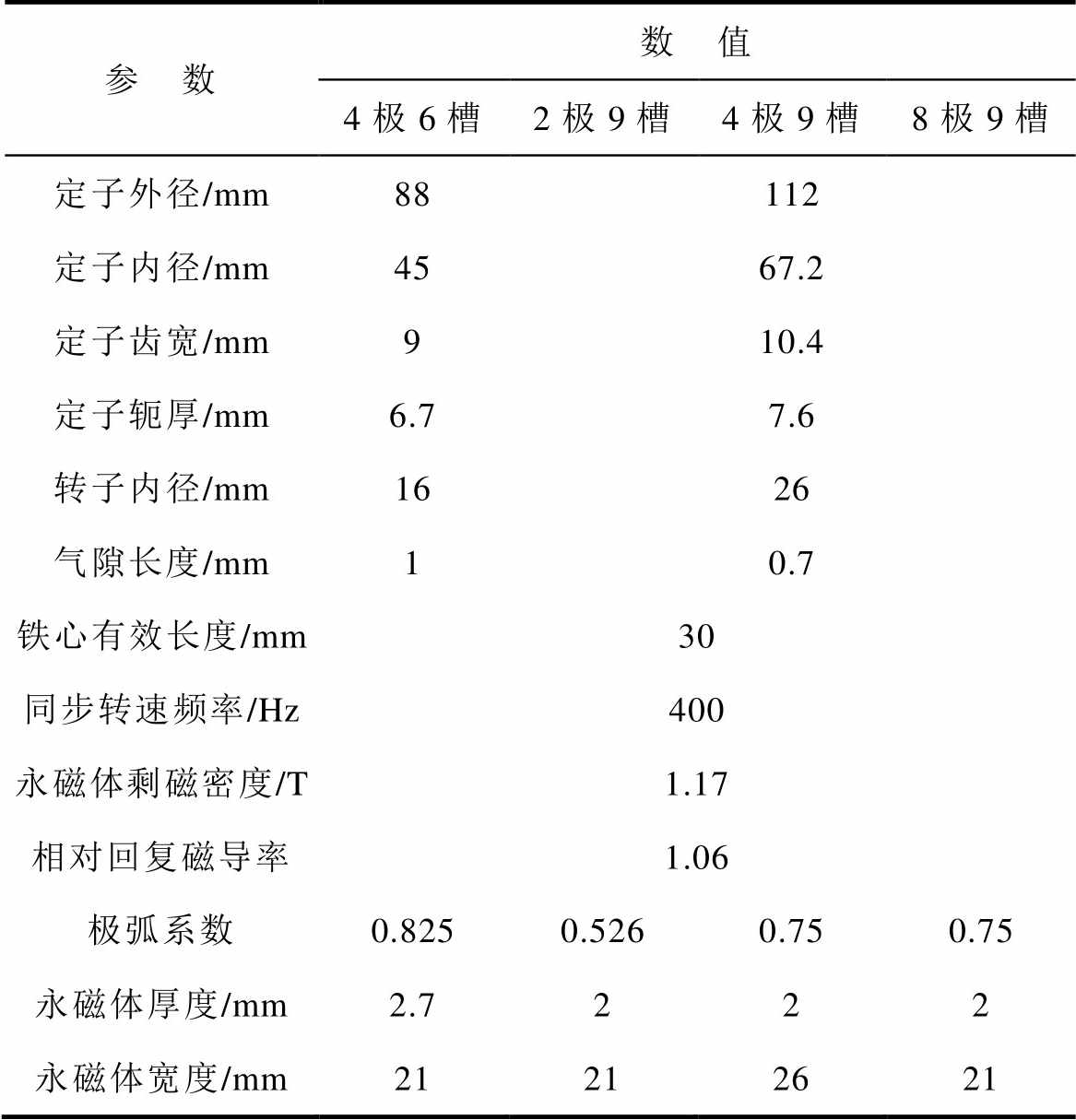
参 数数 值 4极6槽2极9槽4极9槽8极9槽 定子外径/mm88112 定子内径/mm4567.2 定子齿宽/mm910.4 定子轭厚/mm6.77.6 转子内径/mm1626 气隙长度/mm10.7 铁心有效长度/mm30 同步转速频率/Hz400 永磁体剩磁密度/T1.17 相对回复磁导率1.06 极弧系数0.8250.5260.750.75 永磁体厚度/mm2.7222 永磁体宽度/mm21212621
对于上述4台电机,经过解析计算,削弱固有轴电压基波的解析极弧系数见表4。
表4 削弱固有轴电压基波的解析极弧系数
Tab.4 Analytical pole-arc coefficient of weakening the fundamental wave of inherent shaft voltage
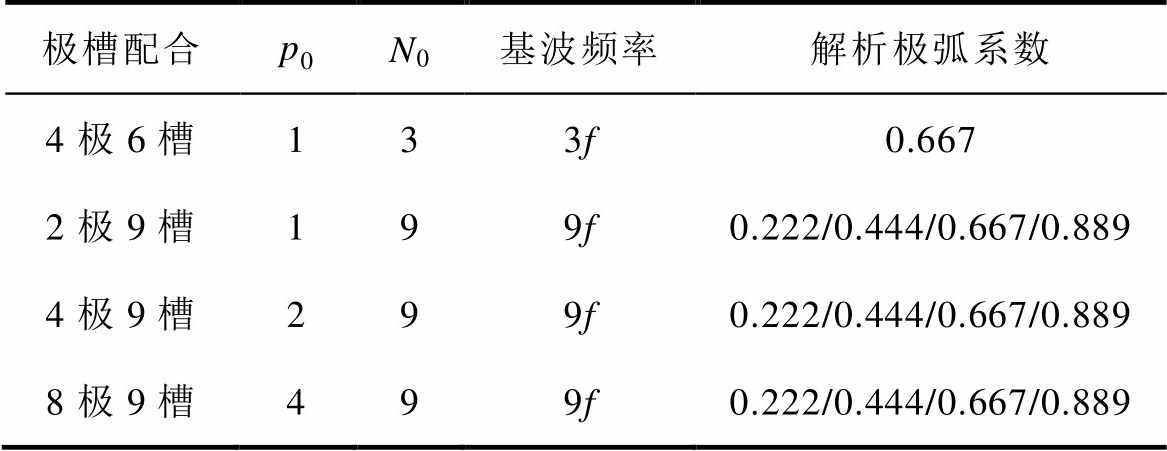
极槽配合p0N0基波频率解析极弧系数 4极6槽133f0.667 2极9槽199f0.222/0.444/0.667/0.889 4极9槽299f0.222/0.444/0.667/0.889 8极9槽499f0.222/0.444/0.667/0.889
不偏心状态下,以4极6槽、4极9槽内置式永磁同步电机为例,通过改变永磁体的夹角,在极弧系数区间[0.55, 0.9],仿真计算了两台电机的空载固有轴电压。固有轴电压基波幅值随极弧系数变化曲线如图4所示。4极6槽内置式永磁同步电机永磁体受到转子尺寸限制,有限元仿真模型极弧系数最大仿真值为0.85。
从图4可以看出,4极6槽、4极9槽电机的轴电压基波幅值在表4所示的解析计算值附近存在拐点。极弧系数解析计算值与有限元优化值比较见 表5。
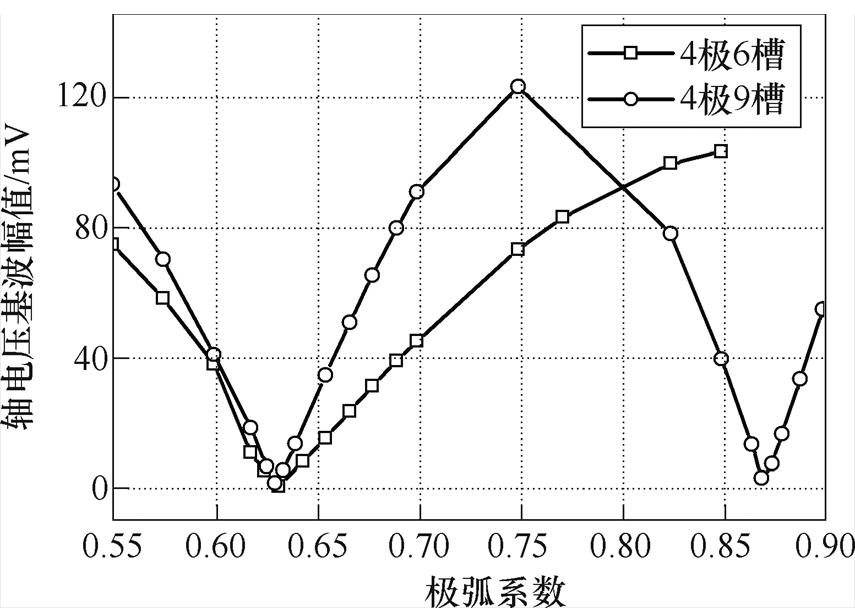
图4 轴电压基波幅值与极弧系数的关系
Fig.4 The relationship between the fundamental amplitude of shaft voltage and pole-arc coefficient
表5 极弧系数解析计算值与有限元优化值比较
Tab.5 Comparison between the calculated values and the finite element optimization values of pole-arc coefficient
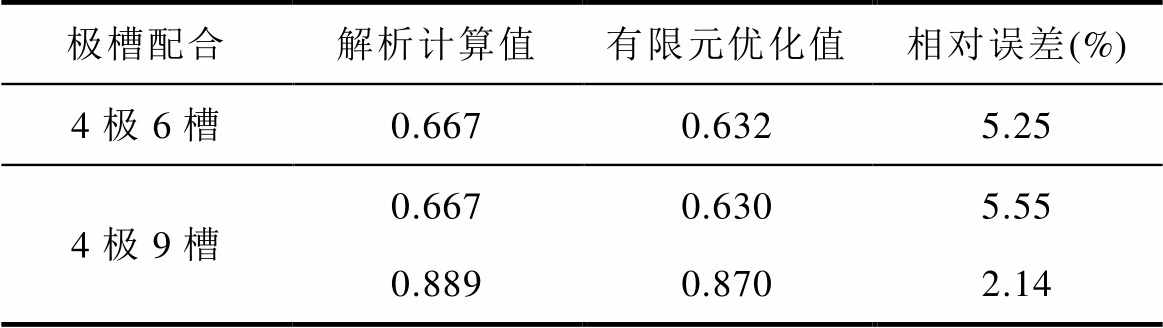
极槽配合解析计算值有限元优化值相对误差(%) 4极6槽0.6670.6325.25 4极9槽0.6670.6305.55 0.8890.8702.14
由表5可知,极弧系数的解析计算值与有限元优化值相对误差在6%以内。需要注意的是,内置式永磁同步电机隔磁桥饱和、定子齿尖局部饱和、定子槽口宽度、永磁体槽底部到转轴表面高度等均会影响有限元优化值。
电机不偏心时,转子初始位置一个磁极的中心线位于x轴正半轴。在Maxwell 2D有限元软件中,将转子沿着不同的偏心角进行偏移,建立偏心轴电压模型,分析初始位置偏心角对轴电压的影响。在偏心度为40%时,4极9槽内置式永磁同步电机不同初始位置偏心角下的轴电压曲线、轴电压频谱分别如图5和图6所示。
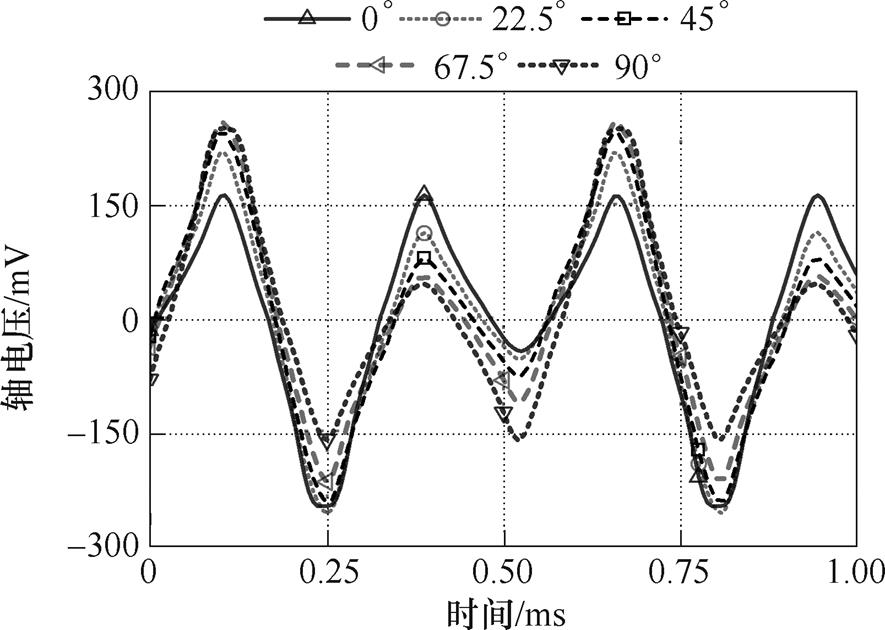
图5 不同初始位置偏心角下的轴电压曲线
Fig.5 Shaft voltage curves under different eccentric angles of initial position
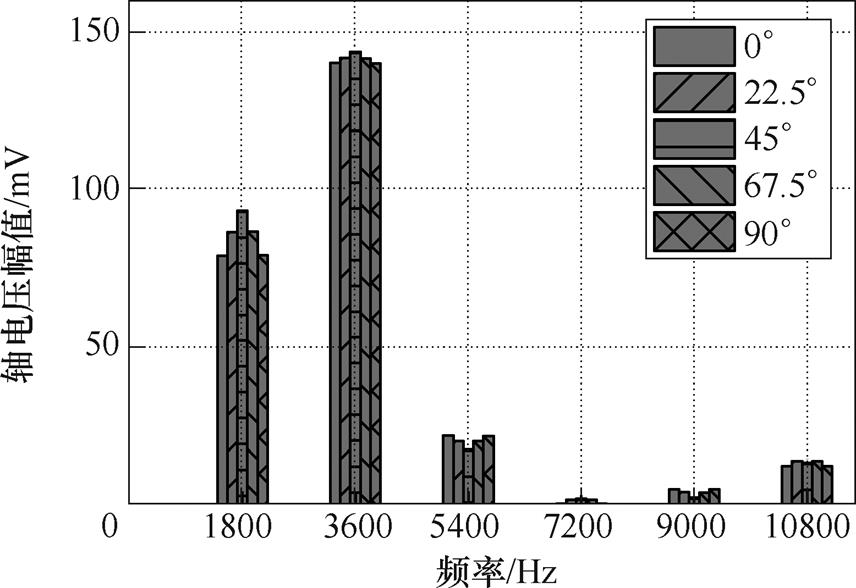
图6 不同初始位置偏心角下的轴电压频谱
Fig.6 Shaft voltage spectrum under different eccentric angles of initial position
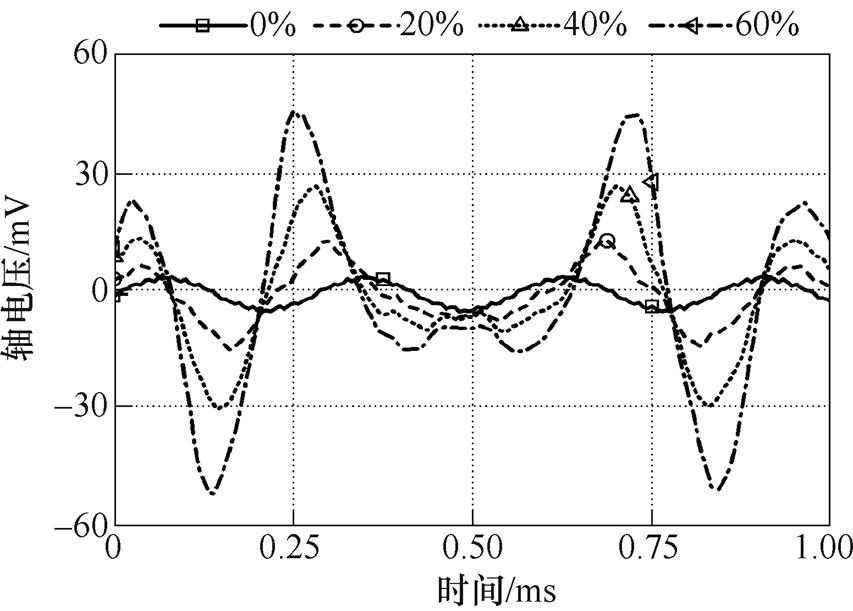
从图5可知,不同初始位置偏心角下,轴电压曲线波形不相同。初始位置偏心角为0°时,轴电压曲线最大值为161.88mV,最小值为-249.25mV;初始位置偏心度为90°时,轴电压曲线最大值为249.01mV,最小值为-161.91mV;初始位置偏心角为22.5°时,轴电压曲线最大值为218.15mV,最小值为-257.76mV;初始位置偏心角为67.5°时,轴电压曲线最大值为257.52mV,最小值为-218.02mV;初始位置偏心角为45°时,轴电压曲线最大值为244.36mV,最小值为-244.51mV。初始位置偏心角为0°、90°时,初始位置分别沿着永磁体不同极性磁极中心线偏移,因此,两个曲线最大值与最小值刚好相反。电机旋转时,由于一个极性的永磁体距离定子位置始终最小,因此,轴电压曲线最大值与最小值不相等。初始位置偏心角为45°时,初始位置沿着相邻的两个不同极性永磁体的中心线偏移。电机旋转时,不同极性的永磁体距离定子最小位置相等。因此,轴电压曲线最大值与最小值相等。
由图6可知,不同初始位置偏心角下的轴电压谐波幅值不相同,但是特征频率是相同的,分别为4.5f、9f、13.5f、18f等。因此,建立偏心轴电压的仿真模型时,不同初始位置偏心角对轴电压谐波幅值有影响。根据表1、表2,解析计算的特征频率为4.5f(k=1)、9f(k=2)、13.5f(k=3)、18f(k=4)等,与有限元仿真结果一致。因此,根据轴电压频谱图中的频率kNs f/p(k=1, 2,…),可以快速诊断电机发生动态偏心故障。
为了验证削弱固有轴电压分量来削弱偏心轴电压的可行性,以转子初始位置偏心角为0°,建立20%、40%、60%偏心度下的4极6槽(p0=1)、2极9槽(p0=1)、4极9槽(p0=2)、8极9槽(p0=4)内置式永磁同步电机偏心轴电压模型。4台电机优化模型的极弧系数分别为0.667、0.444、0.889、0.667。图7~图14分别为4极6槽、2极9槽、4极9槽、8极9槽内置式永磁同步电机不同偏心度下的轴电压曲线、轴电压频谱。
对于4极6槽内置式永磁同步电机,由图7可知,不偏心时,原模型轴电压曲线幅值为148.07mV,优化模型轴电压曲线幅值为37.68mV,削弱74.55%;20%偏心度时,原模型轴电压曲线幅值为157.82mV,优化模型轴电压曲线幅值为48.51mV,削弱69.26%;40%偏心度时,原模型轴电压曲线幅值为175.52mV,优化模型轴电压曲线幅值为71.87mV,削弱59.05%;60%偏心度时,原模型轴电压曲线幅值为243.92mV,优化模型轴电压曲线幅值为97.61mV,削弱59.98%。
对于2极9槽内置式永磁同步电机,由图9可知,不偏心时,原模型轴电压曲线幅值为114.92mV,优化模型轴电压曲线幅值为77.14mV,削弱32.88%;20%偏心度时,原模型轴电压曲线幅值为116.43mV,优化模型轴电压曲线幅值为83.80mV,削弱28.03%;40%偏心度时,原模型轴电压曲线幅值为128.44mV,优化模型轴电压曲线幅值为93.89mV,削弱26.90%;60%偏心度时,原模型轴电压曲线幅值为141.86mV,优化模型轴电压曲线幅值为103.63mV,削弱26.95%。

图7 不同偏心度下4极6槽电机轴电压曲线
Fig.7 Shaft voltage curves of 4p6s motor under different eccentric degree
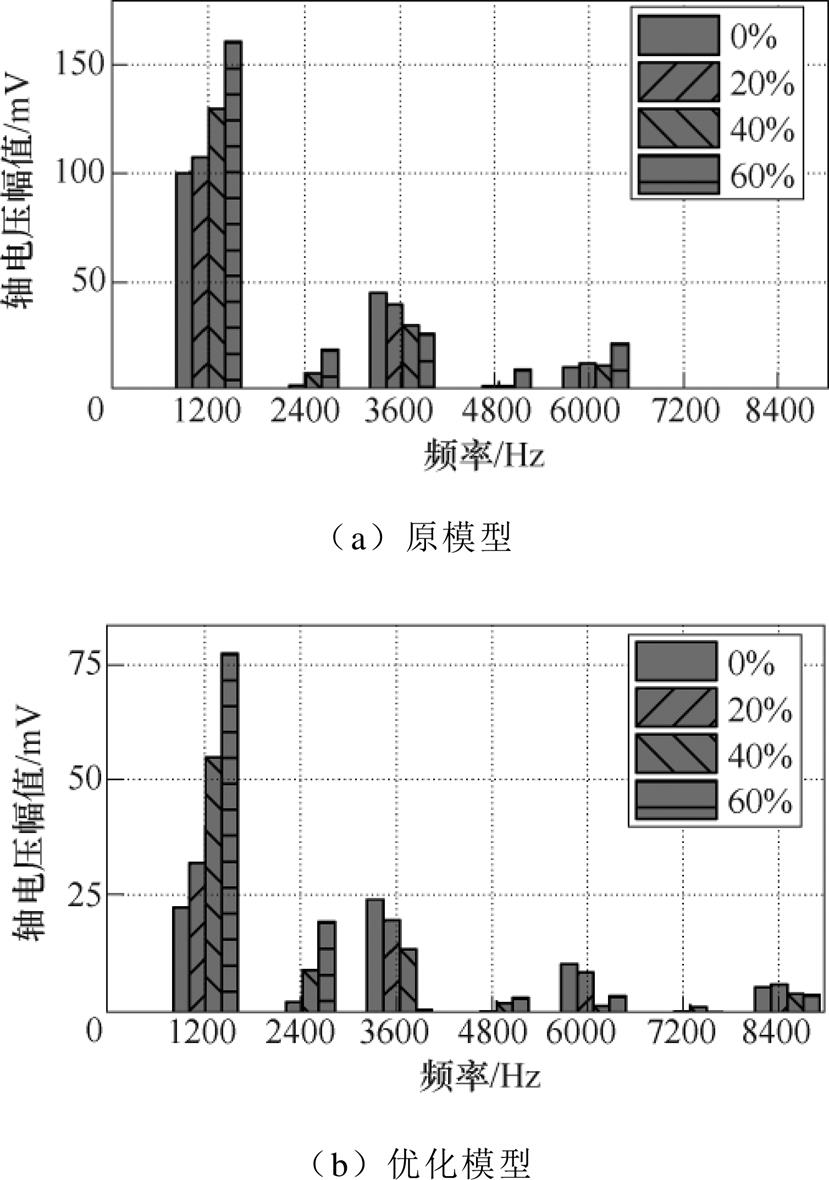
图8 不同偏心度下4极6槽电机轴电压频谱
Fig.8 Shaft voltage spectrum of 4p6s motor under different eccentric degree
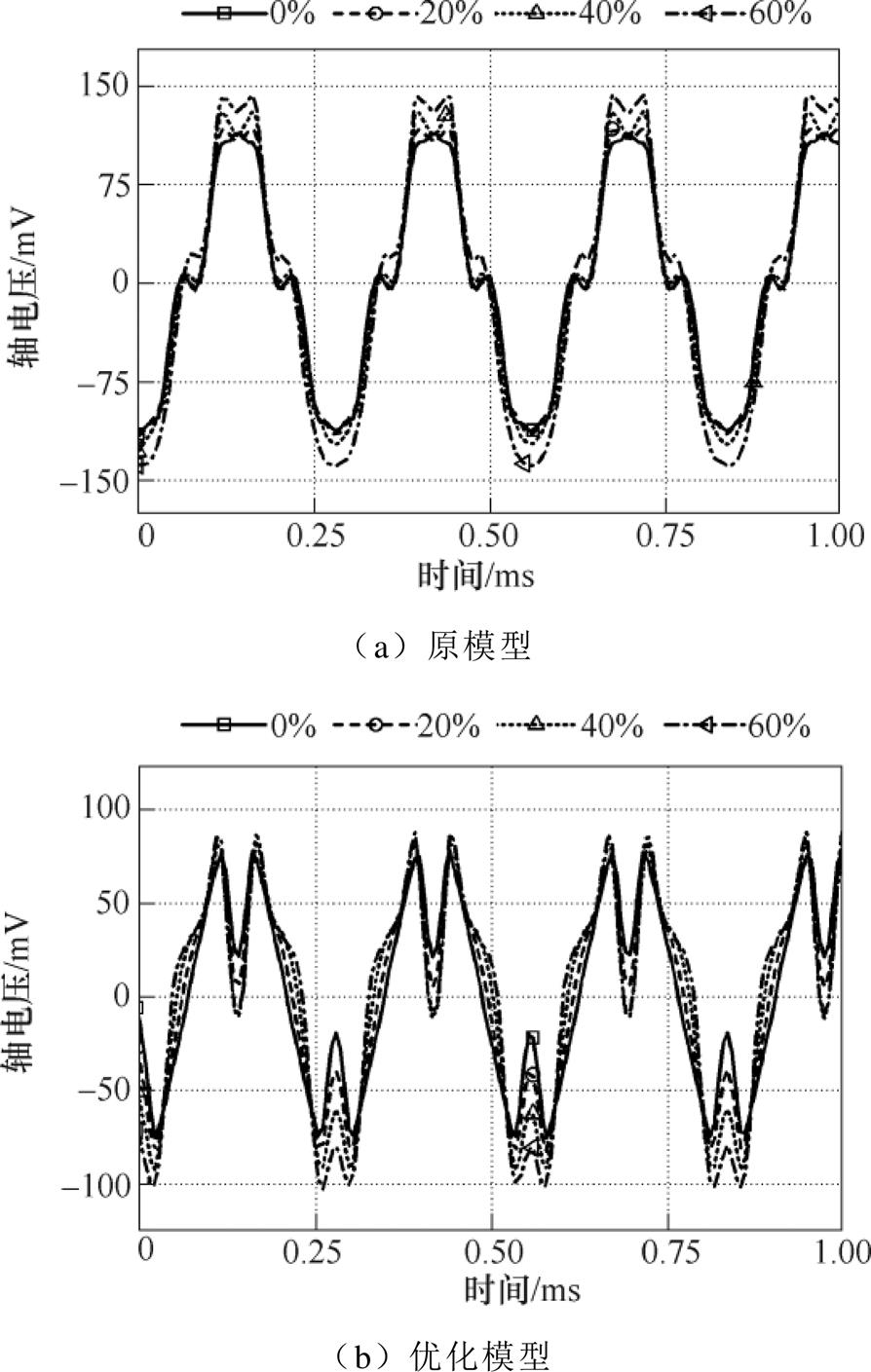
图9 不同偏心度下2极9槽电机轴电压曲线
Fig.9 Shaft voltage curves of 2p9s motor under different eccentric degree
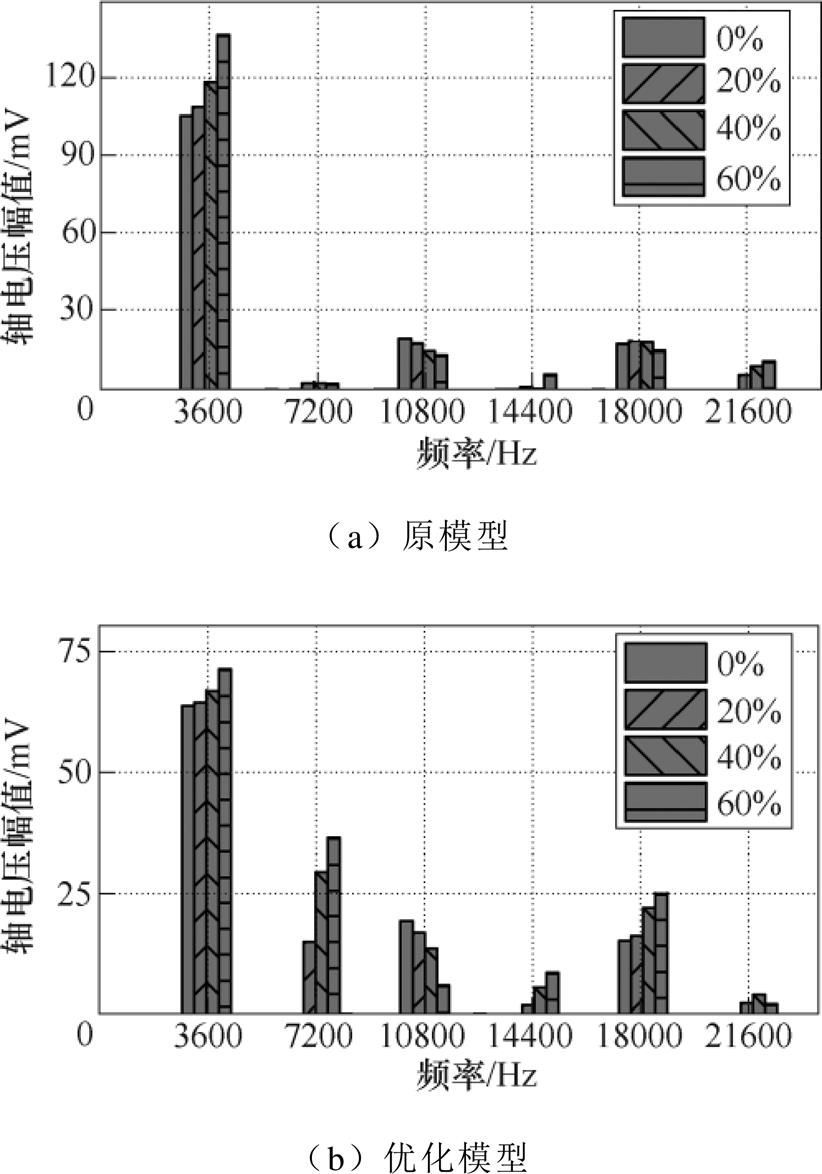
图10 不同偏心度下2极9槽电机轴电压频谱
Fig.10 Shaft voltage spectrum of 2p9s under different eccentric degree
观察图8、图10,对于原模型和优化模型,在不同偏心度下,固有轴电压基波幅值占比最大,偏心轴电压分量幅值较小。优化模型固有轴电压基波分量小于原模型轴电压基波分量,因此,偏心轴电压得到削弱。
对于4极9槽内置式永磁同步电机,由图11可知,不偏心时,原模型轴电压曲线幅值为141.80mV,优化模型轴电压曲线幅值为35.89mV,削弱74.69%;20%偏心度时,原模型轴电压曲线幅值为200.56mV,优化模型轴电压曲线幅值为84.25mV,削弱57.99%;40%偏心度时,原模型轴电压曲线幅值为249.25mV,优化模型轴电压曲线幅值为141.29mV,削弱43.31%;60%偏心度时,原模型轴电压曲线幅值为335.85mV,优化模型轴电压曲线幅值为217.54mV,削弱35.23%。随着偏心度的增大,轴电压削弱效果在减小。观察图12,随着偏心度的增大,优化模型频率值为1 800Hz的偏心轴电压分量占比增大,且其幅值超过原模型对应的轴电压谐波幅值。由于优化模型固有轴电压基波分量得到大幅度削弱,因此,偏心轴电压得到削弱。
对于8极9槽内置式永磁同步电机,由图13可知,不偏心时,原模型轴电压曲线幅值为22.62mV,优化模型轴电压曲线幅值为4.48mV,削弱80.19%;20%偏心度时,原模型轴电压曲线幅值为28.51mV,优化模型轴电压曲线幅值为14.38mV,削弱49.56%;40%偏心度时,原模型轴电压曲线幅值为38.71mV,优化模型轴电压曲线幅值为29.96mV,削弱22.60%;60%偏心度时,原模型轴电压曲线幅值为54.57mV,优化模型轴电压曲线幅值为51.93mV,削弱4.84%。随着偏心度的增大,轴电压削弱效果在快速减小。观察图14,对于原模型和优化模型,随着偏心度的增大,频率值为2 700Hz、4 500Hz的偏心轴电压分量幅值增大。对比原模型与优化模型,优化模型的固有轴电压基波分量得到了大幅度削弱,但是由于偏心轴电压分量的影响,60%偏心度时,优化模型的轴电压依然较大。需要注意的是,在通过削弱固有轴电压来削弱偏心轴电压时,需要考虑到偏心轴电压分量的影响。
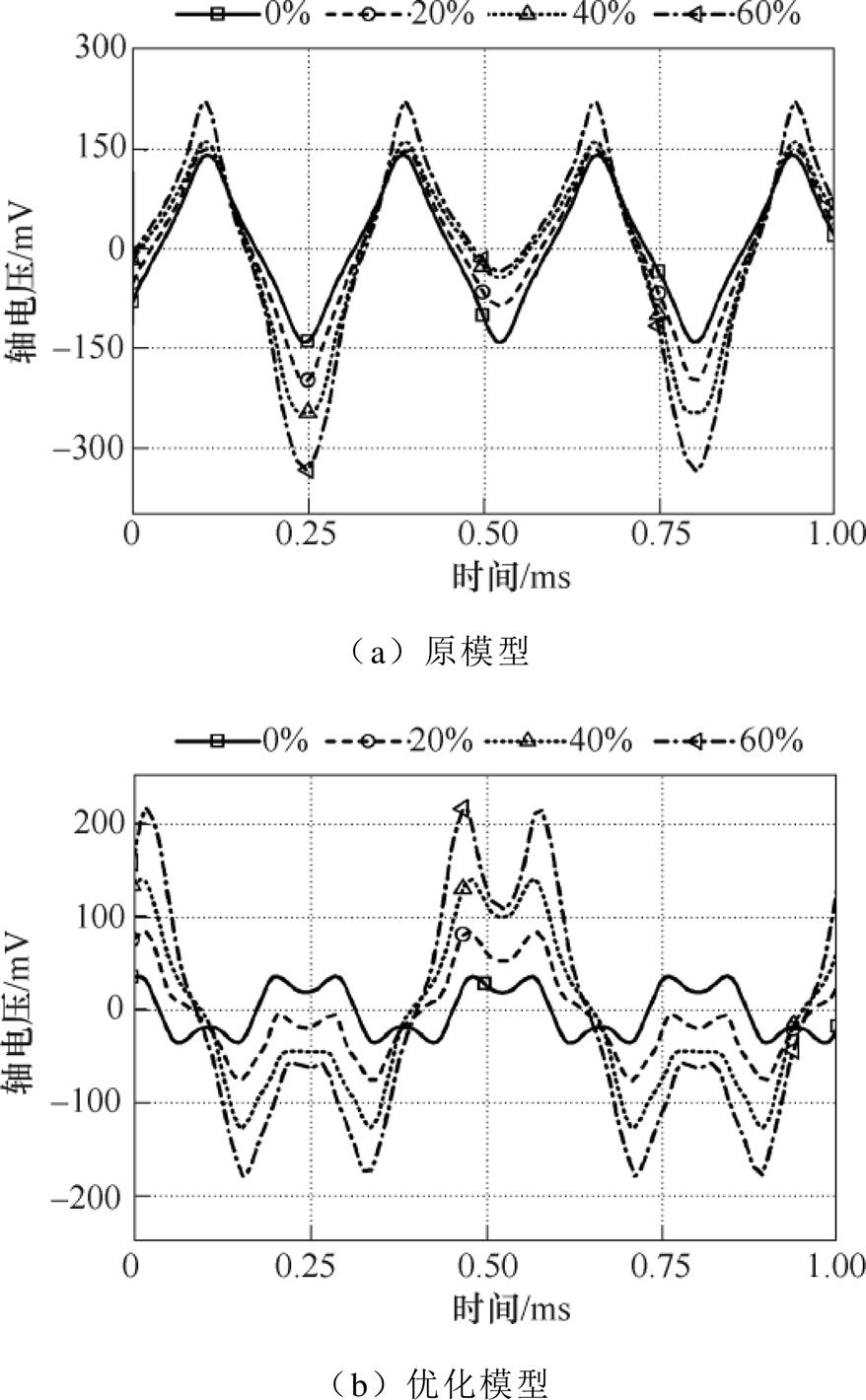
图11 不同偏心度下4极9槽电机轴电压曲线
Fig.11 Shaft voltage curves of 4p9s motor under different eccentric degree
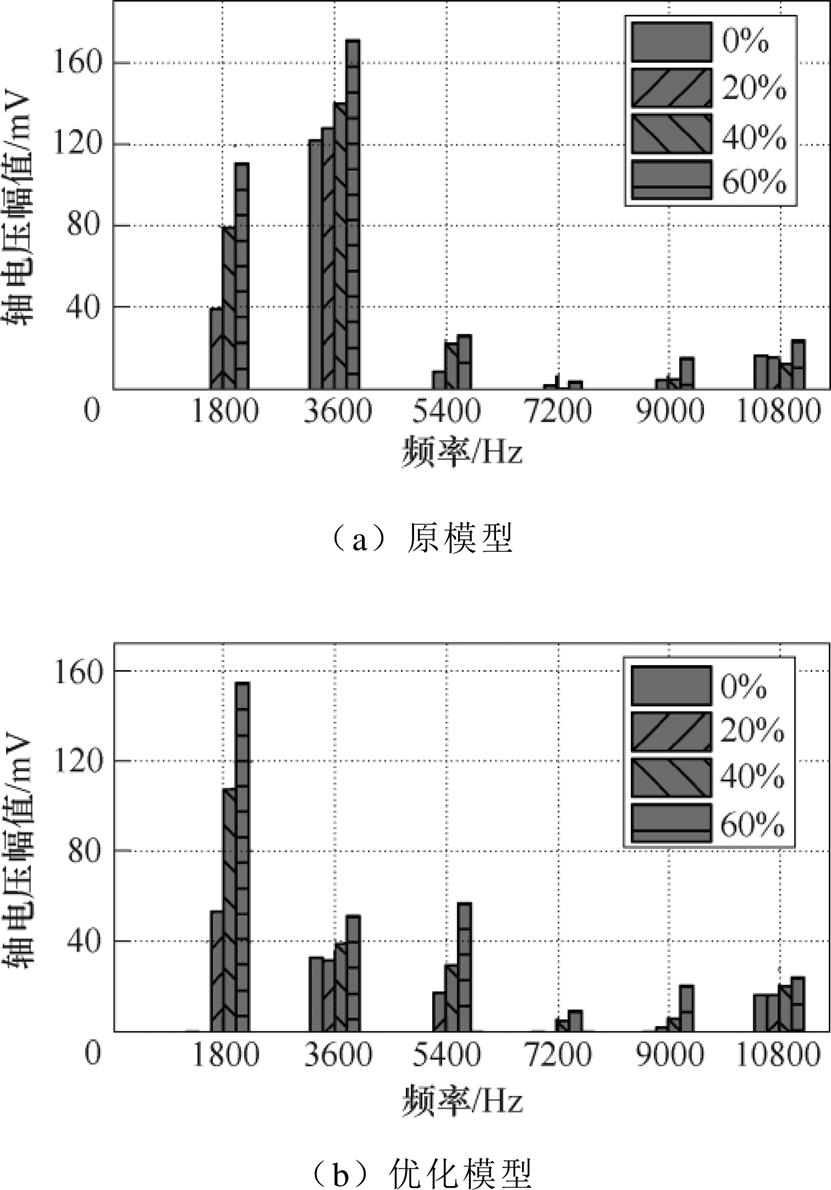
图12 不同偏心度下4极9槽电机轴电压频谱
Fig.12 Shaft voltage spectrum of 4p9s motor under different eccentric degree

(a)原模型
(b)优化模型
图13 不同偏心度下8极9槽电机轴电压曲线
Fig.13 Shaft voltage curves of 8p9s motor under different eccentric degree
本文运用解析法推导出内置式永磁同步电机动态偏心故障下的轴电压表达式,分析了轴电压的特征频率,研究了通过削弱固有轴电压分量来削弱偏心轴电压的方法,主要得到以下结论:

(a)原模型

(b)优化模型
图14 不同偏心度下8极9槽电机轴电压频谱
Fig.14 Shaft voltage spectrum of 8p9s motor under different eccentric degree
1)根据电机的极槽配合和轴电压频谱图中的特征频率kNs f/p(k=1, 2,…),可以快速诊断电机发生动态偏心故障。不同转子初始位置偏心角会影响偏心轴电压的波形及其谐波幅值。
2)对于4极6槽、2极9槽、4极9槽、8极9槽内置式永磁同步电机,选择合适的极弧系数可以削弱偏心轴电压。
3)相比p0=1的电机,动态偏心对p0≠1的电机轴电压影响更大。对于4极9槽、8极9槽内置式永磁同步电机,随着偏心度的增大,偏心轴电压分量幅值逐渐增大,占偏心轴电压主要成分。
参考文献
[1] 王秀和. 永磁电机[M]. 北京: 中国电力出版社, 2007.
[2] 井立兵, 龚俊, 章跃进, 等. Halbach阵列磁力变速永磁无刷电机解析计算与设计[J]. 电工技术学报, 2020, 35(5): 954-962.
Jing Libing, Gong Jun, Zhang Yuejin, et al. Analy- tical calculation and design of magnetic variable speed permanent magnet brushless machine with Halbach arrays[J]. Transactions of China Electro- technical Society, 2020, 35(5): 954-962.
[3] 蒋钱, 卢琴芬, 李焱鑫. 双三相永磁直线同步电机的推力波动及抑制[J]. 电工技术学报, 2021, 36(5): 883-892.
Jiang Qian, Lu Qinfen, Li Yanxin. Thrust ripple and depression method of dual three-phase permanent magnet linear synchronous motors[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 883-892.
[4] 王明杰, 徐伟, 杨存祥, 等. 基于精确子域模型的永磁直线同步电机空载磁场解析计算[J]. 电工技术学报, 2020, 35(5): 942-953.
Wang Mingjie, Xu Wei, Yang Cunxiang, et al. Analytical calculation of no-load magnetic field in permanent magnet linear synchronous motors based on an accurate subdomain model[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 942-953.
[5] 高峰阳, 李晓峰, 齐晓东, 等. 非对称V型磁极偏移内置式永磁同步电机转矩脉动分析[J]. 电机与控制学报, 2021, 25(9): 112-120.
Gao Fengyang, Li Xiaofeng, Qi Xiaodong, et al. Analysis of torque ripple of the interior permanent magnet synchronous motor with asymmetric V-pole offset[J]. Electric Machines and Control, 2021, 25(9): 112-120.
[6] 石玉君, 程子活, 蹇林旎. 两种典型的场调制型永磁电机的对比分析[J]. 电工技术学报, 2021, 36(1): 120-130.
Shi Yujun, Cheng Zihuo, Jian Linni. Comparative analysis of two typical field modulated permanent- magnet machines[J]. Transactions of China Electro- technical Society, 2021, 36(1): 120-130.
[7] Zheng Junqiang, Zhao Wenxiang, Lee C H, et al. Improvement torque performances of interior permanent- magnet machines[J]. China Electrotechnical Society Transactions on Electrical Machines and Systems, 2019, 3(1): 12-18.
[8] Tian Le, Wu Lijian, Huang Xiaoyan, et al. Driving range parametric analysis of electric vehicles driven by interior permanent magnet motors considering driving cycles[J]. China Electrotechnical Society Transactions on Electrical Machines and Systems, 2019, 3(4): 377-381.
[9] He Feng, Xie Guoxin, Luo Jianbin. Electrical bearing failures in electric vehicles[J]. Friction, 2020, 8(1): 4-28.
[10] Zhang Pinjia, Du Yi, Habetler T G, et al. A survey of condition monitoring and protection methods for medium-voltage induction motors[J]. IEEE Transa- ctions on Industry Applications, 2011, 47(1): 34-46.
[11] Peng Bo, Wang Xiuhe, Zhao Wengliang, et al. Study on shaft voltage in fractional slot permanent magnet machine with different pole and slot number com- binations[J]. IEEE Transactions on Magnetics, 2019, 55(6): 1-5.
[12] Chen Shaotang, Lipo T A, Fitzgerald D. Source of induction motor bearing currents caused by PWM inverters[J]. IEEE Transactions on Energy Con- version, 1996, 11(1): 25-32.
[13] Erdman J M, Kerkman R J, Schlegel D W, et al. Effect of PWM inverters on AC motor bearing currents and shaft voltages[J]. IEEE Transactions on Industry Applications, 1996, 32(2): 250-259.
[14] Shami U T, Akagi H. Identification and discussion of the origin of a shaft end-to-end voltage in an inverter-driven motor[J]. IEEE Transactions on Power Electronics, 2010, 25(6): 1615-1625.
[15] 刘瑞芳, 任雪娇, 陈嘉垚. 双馈异步风力发电机的轴电流分析[J]. 电工技术学报, 2018, 33(19): 4517-4525.
Liu Ruifang, Ren Xuejiao, Chen Jiayao. Analysis of bearing currents in doubly-fed induction wind turbines[J]. Transactions of China Electrotechnical Society, 2018, 33(19): 4517-4525.
[16] 白保东, 刘威峰, 王禹, 等. PWM驱动感应电机轴电压轴承电流[J]. 电工技术学报, 2013, 28(增刊2): 434-440.
Bai Baodong, Liu Weifeng, Wang Yu, et al. Research on shaft voltage and bearing current of induction motor driven by PWM inverter[J]. Transactions of China Electrotechnical Society, 2013, 28(S2): 434-440.
[17] 才家刚, 王勇. 电机轴承应用技术[M]. 北京: 机械工业出版社, 2020.
[18] Hadden T, Jiang J W, Bilgin B, et al. A review of shaft voltages and bearing currents in EV and HEV motors[C]//IECON 2016-42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, 2016: 1578-1583.
[19] Busse D, Erdman J, Kerkman R J, et al. An evaluation of the electrostatic shielded induction motor: a solution for rotor shaft voltage buildup and bearing current[J]. IEEE Transactions on Industry Appli- cations, 1997, 33(6): 1563-1570.
[20] 章勇高, 邝光健, 龙立中. 三相逆变器的无零矢量共模电压抑制技术研究[J]. 电力系统保护与控制, 2013, 41(2): 138-143.
Zhang Yonggao, Kuang Guangjian, Long Lizhong. Research of reduced commom-mode voltage tech- nique with nonzero vector pulse width modulation for three-phase inverters[J]. Power System Protection and Control, 2013, 41(2): 138-143.
[21] Peng Bo, Zhao Wengliang, Wang Xiuhe. The method for reducing intrinsic shaft voltage by suitable selection of pole-arc coefficient in fractional-slot permanent-magnet synchronous machines[J]. IEEE Transactions on Magnetics, 2018, 54(11): 1-5.
[22] Park J K, Wellawatta T R, Choi S, et al. Mitigation method of the shaft voltage according to parasitic capacitance of the PMSM[J]. IEEE Transactions on Industry Applications, 2017, 53(5): 4441-4449.
[23] Hsu J S, Stein J. Effects of eccentricities on shaft signals studied through windingless rotors[J]. IEEE Transactions on Energy Conversion, 1994, 9(3): 564-571.
[24] Park J, Jeong C, Bianchi N, et al. Frame-to-shaft voltage and end-to-end shaft voltage analysis accor- ding to eccentricity in IPMSMs[C]//IEEE Energy Conversion Congress and Exposition, Portland, 2018: 3255-3262.
[25] 李伟, 程明, 朱洒. 磁通切换永磁电机固有轴电压分析[J]. 电工技术学报, 2017, 32(15): 1-9.
Li Wei, Cheng Ming, Zhu Sa. Analysis of inherent shaft voltage in flux-switching permanent magnet machine[J]. Transactions of China Electrotechnical Society, 2017, 32(15): 1-9.
[26] Wu Yucai, Li Yonggang, Li Heming. Diagnosis of turbine generator typical faults by shaft voltage[C]// 2012 IEEE Industry Applications Society Annual Meeting, Las Vegas, 2012: 1-6.
[27] 谭建成. 永磁无刷直流电机技术[M]. 北京: 机械工业出版社, 2011.
[28] Zhu Ziqiang, Wu Lijian, Mohd Jamil M L. Influence of pole and slot number combinations on cogging torque in permanent-magnet machines with static and rotating eccentricities[J]. IEEE Transactions on Industry Applications, 2014, 50(5): 3265-3277.
[29] 李全峰, 黄厚佳, 黄苏融, 等. 表贴式永磁电机转子偏心故障快速诊断研究[J]. 电机与控制学报, 2019, 23(12): 48-58.
Li Quanfeng, Huang Houjia, Huang Surong, et al. Research on fast diagnosis of rotor eccentricity fault for surface-mounted permanent magnet motor[J]. Electric Machines and Control, 2019, 23(12): 48-58.
Analysis and Reduction of Shaft Voltage in Interior Permanent Magnet Synchronous Motors under Dynamic Eccentricity Fault
Abstract For interior permanent magnet synchronous motors driven by inverters, most studies focus on the effect of the common mode voltage on the bearing voltage, ignoring the shaft voltage caused by asymmetric magnetic fields. Regarding the shaft voltage under dynamic eccentricity fault, the expression is deduced by the analytical method, and the characteristic frequency is analyzed. Then, the method of reducing the eccentric shaft voltage is studied by changing the pole-arc coefficient of rotor poles. Finally, four eccentric shaft voltage models with different pole-slot combinations including 4p6s, 2p9s, 4p9s and 8p9s are established. The effectiveness of analytical analysis is verified by the finite element method. The simulation results show that the eccentric shaft voltage can be weakened by reducing the inherent shaft voltage. And the eccentric shaft voltage at 40% eccentric degree is reduced by 59.05%, 26.90%, 43.31%, 22.60%, respectively.
keywords:Interior permanent magnet synchronous motor, dynamic eccentricity, characteristic frequency, shaft voltage
DOI: 10.19595/j.cnki.1000-6753.tces.200915
中图分类号:TM351
赵方伟 男,1995 年生,硕士研究生,研究方向为永磁电机。E-mail: summer_fwz@163.com
王秀和 男,1967年生,教授,博士生导师,研究方向为永磁 电机。E-mail: wangxh@sdu.edu.cn(通信作者)
收稿日期 2020-07-24
改稿日期 2021-01-29
国家自然科学基金资助项目(52077122, 51737008)。
(编辑 崔文静)