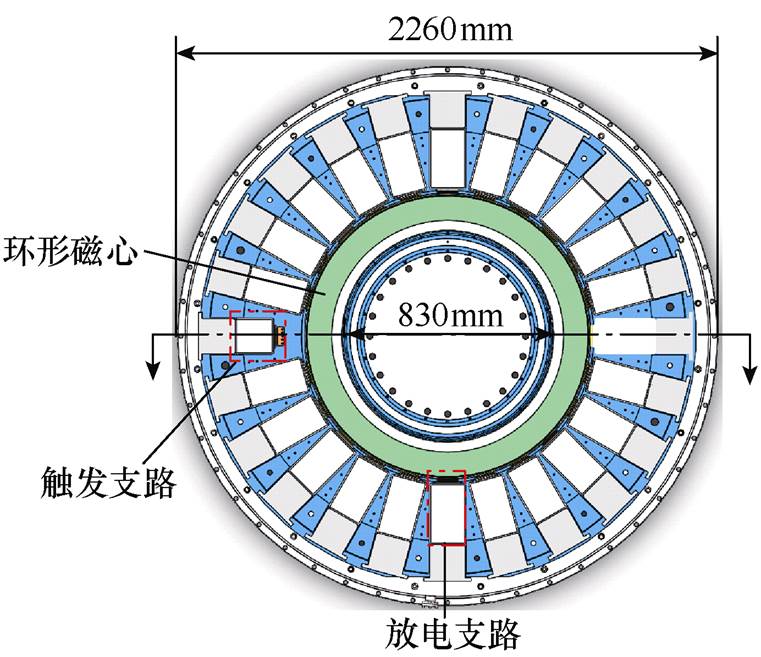
图1 4级串联FLTD的工程模型顶视图
Fig.1 Top view of the CAD model of the 4-stage FLTD
摘要 快脉冲直线型变压器驱动源(FLTD)感应腔内部结构和媒质分布复杂,支路放电时快速上升沿脉冲将使空间离散更为繁密,导致计算量剧增。该文利用时域有限积分理论首次研究4级串联共用、独立腔体结构MA级FLTD在支路放电时的电磁场分布规律。使用场路耦合将电路中电容元件的放电电流作为激励耦合至三维场模型,使用非均匀网格对FLTD初级感应腔内的关键部件剖分网格进行加密处理,使用表面阻抗边界条件描述良导体以降低求解自由度数量,使用基于等效原理的区域分解算法将4级串联FLTD划分为24个不同的求解子区域。结果表明,时域有限积分技术可有效分析FLTD初级腔体内脉冲放电瞬态过程,两种感应腔结构的输出性能和电磁场分布基本一致,4级串联共用腔体结构FLTD设计方案可行。
关键词:直线型变压器驱动源 有限积分技术 瞬态电磁场 场路耦合 区域分解算法
传统的脉冲功率装置一般基于Marx发生器多级(2~4级)脉冲压缩结构,其主要缺点为能量传输效率低、部件耐受电压高、开关寿命短[1]。快脉冲直线型变压器驱动源(Fast Linear Transformer Driver, FLTD)是近十几年来获得广泛关注的一种新型脉冲功率源技术,可直接产生百纳秒前沿、兆安培级幅值的高功率脉冲电流[2],在Z箍缩、X射线闪光照相、高能量密度物理等国防和工业领域具有重要的应用前景,是下一代脉冲功率驱动源最有前景的技术路线[3]。目前,美国圣迪亚国家实验室、俄罗斯强电流电子研究所、中国工程物理研究院和中国西北核技术研究院等科研机构已开展FLTD技术研究及装置研制[1-2]。
在FLTD的设计和研发过程中,运用数值计算技术,准确分析其电磁性能是十分必要的,国内外对于FLTD和Z箍缩装置的仿真分析主要采用等效电路法[4-7]、时域有限差分法[7-8]、有限元法[9]和部分单元等效电路法[10]。等效电路模型具有计算量小、速度快的优点,但难以描述FLTD感应腔内场分布的细节。时域有限差分(Finite Difference Time Domain, FDTD)法的计算简单,可有效地处理电磁波问题,但计算精度受到Yee元胞阶梯近似和数值色散的限制[11]。有限元法(Finite Element Method, FEM)适合处理具有复杂结构和媒质分布的情况,但计算速度较慢、资源消耗较高[12]。部分单元等效电路法可将多导体系统的瞬态电磁模型直接嵌入电路中,但对于磁性材料的建模较为困难[13]。
有限积分技术(Finite Integration Technique, FIT)由德国达姆施塔特工业大学的T. Weiland 教授提出,并成为MAFIA代码的理论基础[14]。FIT从积分形式的Maxwell方程组出发,且将场量在相应网格棱边或面元上的积分量定义为求解的自由度,可直接在求解区域内得到离散的矩阵方程[15]。FIT的时域表达式在Yee元胞中与FDTD法是完全等效的,但与自由度是微分量的FDTD法和FEM不同,以积分量作为状态变量的FIT适应于媒质分布突变的界面上。文献[16]使用基于共形网格和并行计算的时域有限积分技术,可降低仿真无线传播和衰减问题的内存消耗和计算时间。为了设计高功率微波设备,文献[17]采用场路耦合方法将非线性的电路元件和经过FIT空间离散的场模型耦合至系统方程并求解。文献[18-21]利用基于有限积分理论的CST Studio Suite软件,分别针对静电放电发生器、考虑频变参数的接地网、电力变压器和单级FLTD进行仿真分析,并验证了数值模型的准确性。
在之前的研究中,分别使用时域FIT(Time Domain FIT, TD-FIT)和时步FEM(Time-Stepping FEM, TS-FEM),针对单级共用、独立腔体结构FLTD进行计算,结果表明,TD-FIT在分析单级FLTD脉冲放电瞬态问题上具有较高的计算精度和计算效率[21-23]。在此基础上,本文采用TD-FIT计算4级串联共用、独立腔体结构FLTD的电磁特性。
考虑到4级串联FLTD不满足旋转对称性,需建立其三维数值模型。4级串联FLTD的工程模型顶视图和4级串联共用、独立腔体结构FLTD数值模型剖面分别如图1和图2所示,仿真模型主要包括由两个薄膜电容和一个气体开关串联组成的放电支路、非晶合金磁心、磁心环氧外壳、绝缘板、水介质变阻抗传输线(以下简称水线)、不锈钢腔体、回流板、分立柱以及假负载。与单级FLTD相比,多级串联FLTD中用回流板代替了相邻级间的接地盖板且次级水线逐级叠加初级脉冲能量[24]。
FLTD感应腔体中复杂结构多、空间尺度差异大、媒质分布复杂、脉冲上升沿快(约100ns),为保证计算顺利进行,需适当简化或忽略工程模型中一些对场分布影响较小或不关注的因素[8-10, 18-20]:

图1 4级串联FLTD的工程模型顶视图
Fig.1 Top view of the CAD model of the 4-stage FLTD
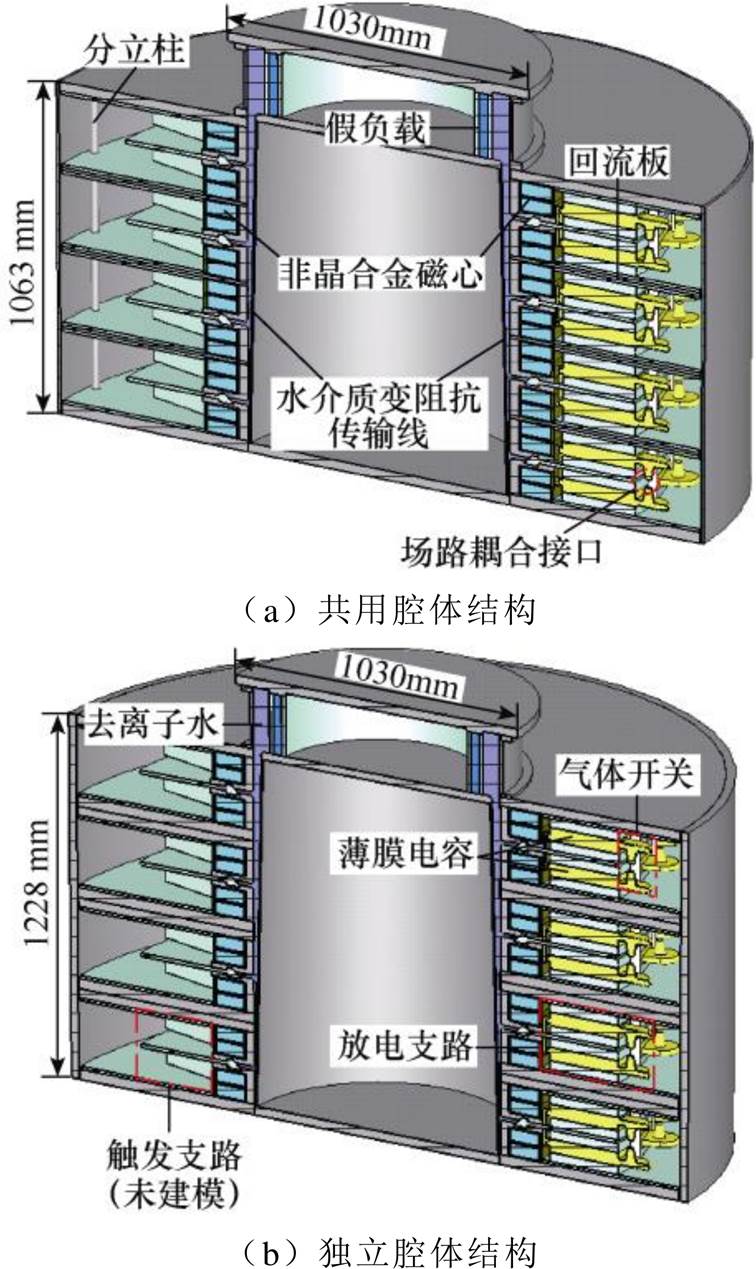
图2 4级串联共用、独立腔体结构FLTD数值模型剖面
Fig.2 Cross-sectional view of the numerical model of the 4-stage FLTD with common/independent induction cavity
(1)忽略螺钉开孔等不影响计算结果的细节。
(2)忽略薄膜电容内部的精细结构,仅模拟其等效电容、等效电感和等效电阻[22]。
(3)忽略气体开关导通时的动态电阻和电感,将开关导通路径等效为具有恒定感值的良导体。
(4)忽略非晶合金磁心的卷绕结构,等效为实心导体[22],忽略磁心的非线性磁滞特性。
(5)忽略感应腔内的触发支路,假设其已将触发信号传递至同级腔体所有放电支路的气体开关。
(6)忽略放电支路气体开关动作的延迟和抖动,假设同一级腔体中所有放电支路都是同时导通。
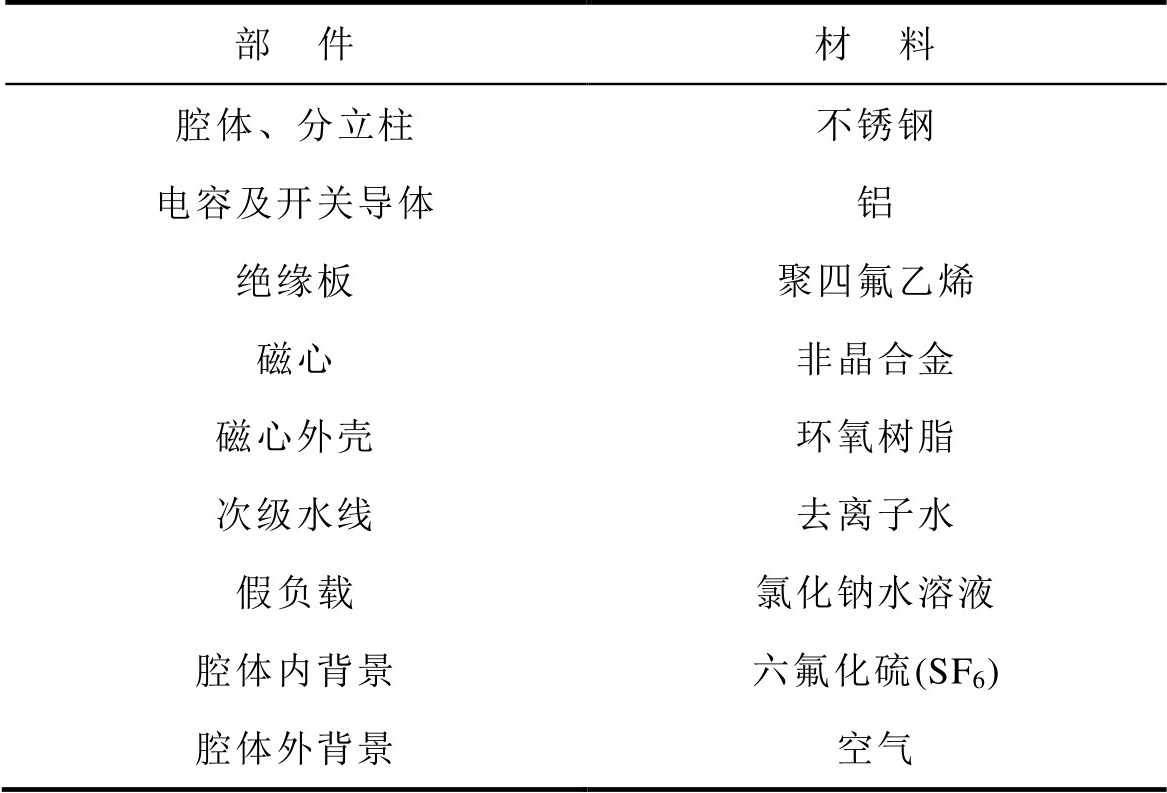
仿真计算时FLTD各组成部件的媒质种类见 表1,媒质属性的参数设置可参考文献[22]。
表1 FLTD各组成部件的媒质种类
Tab.1 Materials of the key components in the FLTD
部 件材 料 腔体、分立柱不锈钢 电容及开关导体铝 绝缘板聚四氟乙烯 磁心非晶合金 磁心外壳环氧树脂 次级水线去离子水 假负载氯化钠水溶液 腔体内背景六氟化硫(SF6) 腔体外背景空气
多级串联FLTD的脉冲放电能量是通过电磁感应逐级依次叠加至次级水线。次级水线一般为圆锥形结构,对于4级串联FLTD,因其内筒半径变化较小,可将水线近似等效为同轴传输线。由于水线内筒半径、外筒半径以及电磁波最小波长满足同轴传输线的单模传输条件,在正常工况(无开关自放电等)下,水线中仅存在TEM模电磁波。根据阻抗匹配原则,去离子水的相对磁导率mr=1.0、相对介电常数er=80.0时,每级腔体中次级水线末端的特征阻抗和内筒半径应满足
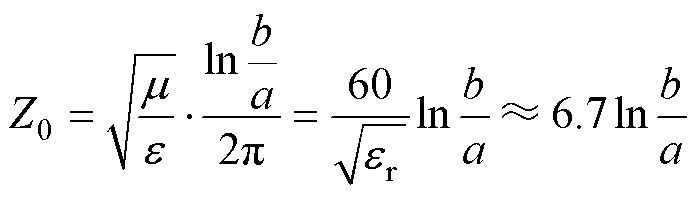 (1)
(1)式中,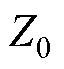 为每级水线特征阻抗
为每级水线特征阻抗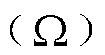 ;
;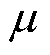 为磁导率(H/m);
为磁导率(H/m);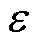 为介电常数(F/m);
为介电常数(F/m); 为外筒半径,
为外筒半径, =450mm;
=450mm; 为内筒半径(mm)。
为内筒半径(mm)。
根据有限积分理论,可得到Maxwell网格方程以及材料本构方程[14, 22]为
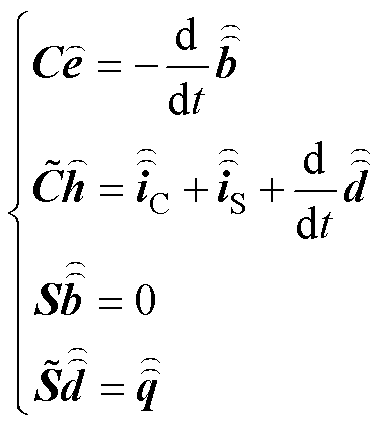 (2)
(2)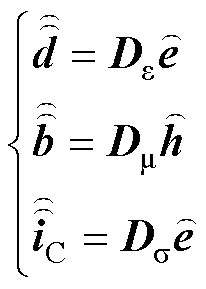 (3)
(3)
式中,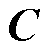 和
和 分别为主网格和对偶网格的离散旋度矩阵;
分别为主网格和对偶网格的离散旋度矩阵;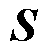 和
和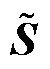 分别为主网格和对偶网格的离散散度矩阵;
分别为主网格和对偶网格的离散散度矩阵; 和
和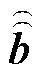 分别为主网格中沿棱边的电压量和通过面元的磁通量;
分别为主网格中沿棱边的电压量和通过面元的磁通量;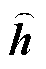 为对偶网格中沿棱边的磁压量;
为对偶网格中沿棱边的磁压量; 、
、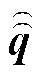 、
、 和
和 分别为对偶网格中通过面元的电通量、电荷量、损耗电流量和外加电流量;
分别为对偶网格中通过面元的电通量、电荷量、损耗电流量和外加电流量;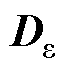 、
、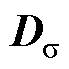 和
和 分别为介电常数、电导率和磁导率的对角矩阵。
分别为介电常数、电导率和磁导率的对角矩阵。
对式(2)中两个旋度方程的时间导数项采用中心差分离散以及蛙跳策略,则显式时域递推方程为
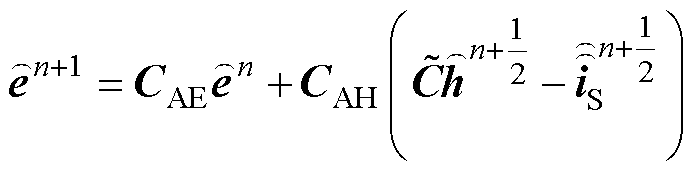 (4)
(4) (5)
(5)
其中,系数矩阵CAE和CAH为
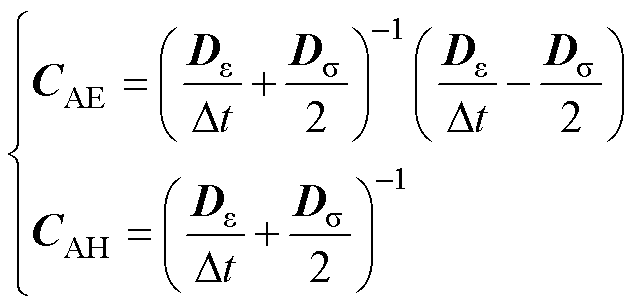 (6)
(6)式中,外加电流量为0。
根据式(4)~式(6),可计算瞬态电磁过程。但应注意的是,时间步长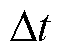 须满足稳定性条件的限制。对于4级串联FLTD,由于其求解自由度数接近1亿,需利用场路耦合、非均匀网格、表面阻抗边界条件以及区域分解算法来提高求解速度。
须满足稳定性条件的限制。对于4级串联FLTD,由于其求解自由度数接近1亿,需利用场路耦合、非均匀网格、表面阻抗边界条件以及区域分解算法来提高求解速度。
考虑到电容内部结构过于复杂而无法在三维场模型中直接表征,故将放电支路的等效电容通过外部电路的集总电容元件与场模型相连接,并给定电容元件的初始充电电压值。在电路中的开关导通时,电容放电产生激励电流,三维场模型中的电容元件仅表征其等效串联电感和电阻。如图2a中所示,开关导通时正负电极间的放电通路为三维场模型和电路模型的耦合接口。为实现场路耦合,需在安培定律右端增加电流量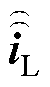 项表示集总元件电流[17],即
项表示集总元件电流[17],即
 (7)
(7)对于复杂模型,为了确保计算的精度,须采用尺寸较小网格,以保证有效模拟数值模型的精细结构,但这会使得网格总数增加和TD-FIT显式递推时间步长减小,导致计算所需的资源和时间剧增。使用非均匀网格或亚网格技术可解决此问题[25],即仅在求解区域内电磁场变化剧烈的区域采用小尺寸细网格,而在其余区域采用大尺寸粗网格,从而获得计算精度和计算效率的良好平衡。
图3所示为4级串联共用腔体结构FLTD中第3级和第4级腔体网格划分的剖面。由图可知,细网格主要分布于FLTD腔体内的开关、磁心和绝缘板等部件,在均匀细网格和均匀粗网格间的过渡区,非均匀网格尺寸应按比例逐步变化以减小电磁波反射和数值色散。此外,采用共形网格技术对曲面(如开关端子)进行离散,以消除阶梯近似误差。

图3 第3级和第4级腔体的网格划分剖面图
Fig.3 Cross sectional view of primal grid of the 3rd- and 4th-stage of the 4-stage FLTD sharing common cavity shell
考虑到在快放电脉冲作用下,FLTD中良导体的趋肤深度很小,且需要精细的网格来适应剧烈变化的场。使用表面阻抗边界条件(Surface Impedance Boundary Condition, SIBC)可以在不计算媒质内部场分布和较粗网格划分的前提下,直接求得其表面电磁场分布[25]。因此,在本文TD-FIT的计算中引入一阶SIBC可有效降低自由度数量。
由于SIBC是在频域中定义的,为了在时域中处理SIBC,采用矢量拟合技术和一阶有理函数近似来处理频域转换至时域的卷积运算。与集总元件类似,一阶SIBC所产生的表面等效电流量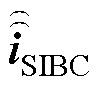 需加至安培定律右端,作为附加电流源项[22],即
需加至安培定律右端,作为附加电流源项[22],即
 (8)
(8)
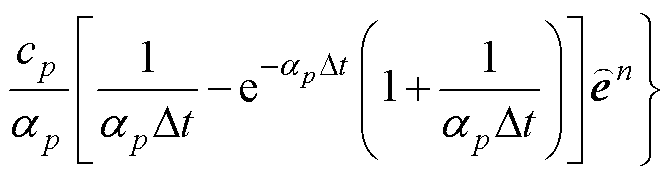 (9)
(9)
式中,P为有理函数近似的总项数;c0和cp为有理函数的系数;ap为有理函数的极点。
由式(7)~式(9)可知,使用场路耦合、非均匀网格和一阶SIBC后,仅改变相应网格中待求变量的递推系数,TD-FIT方程仍满足显式递推格式。
在处理电大尺寸和空间多尺度设备时,区域分解算法(Domain Decomposition Method, DDM)根据几何特性或媒质属性将原始问题分解为若干个子区域进行求解,并利用适当的传输条件来保证子区域间场和电流的连续性[26]。DDM可分为重叠型DDM、非重叠型DDM和基于等效原理的DDM[27]。前两类较多应用在基于有限元法的计算中,本文采用基于等效原理的DDM,其基本思想是将原模型转化为子区域间虚拟面上的等效电流及磁流问题[28]。
由式(4)~式(9),系统矩阵方程可整理为
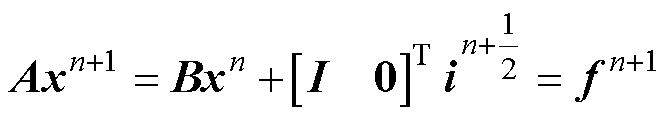 (10)
(10)其中
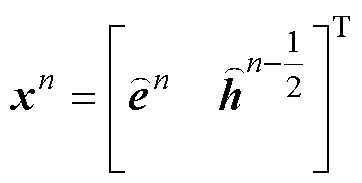
式中,A和B均为系数矩阵;I为单位矩阵;i为等效电流源;f为右端项。
假设将计算空间分解为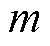 个子区域,则在某个时间步
个子区域,则在某个时间步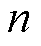 内,其原始系统方程式(10)表示为
内,其原始系统方程式(10)表示为
 (11)
(11)式中,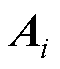 为子区域
为子区域 的系统矩阵;
的系统矩阵;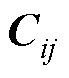 为子区域
为子区域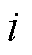 和
和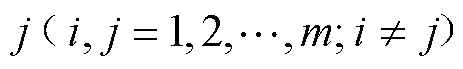 间的耦合矩阵;
间的耦合矩阵;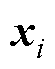 为子区域
为子区域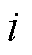 中的未知量;
中的未知量;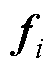 为子区域
为子区域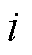 的激励项。
的激励项。
根据场的等效原理,等效系统方程[29]表示为
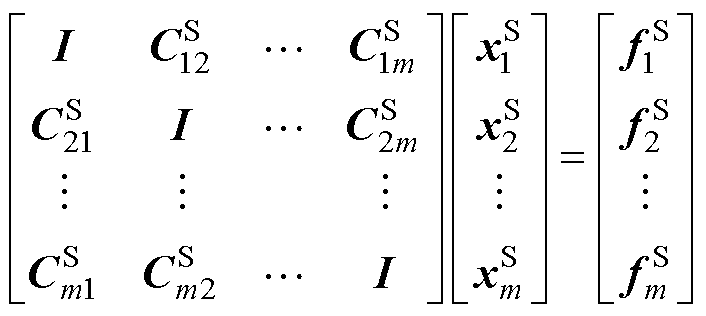 (12)
(12)式中,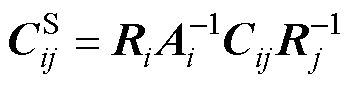 为子区域
为子区域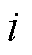 和
和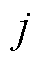 间的表面耦合矩阵,其中,
间的表面耦合矩阵,其中,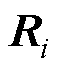 为将子区域
为将子区域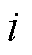 中未知量转化为虚拟面上未知量的限制矩阵;
中未知量转化为虚拟面上未知量的限制矩阵; 为子区域
为子区域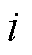 的表面未知量;
的表面未知量;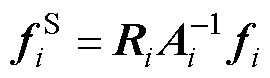 为子区域
为子区域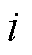 的表面电流源和磁流源激励。
的表面电流源和磁流源激励。
在式(12)中,未知量是虚拟面上的电压量和磁压量,降低了待求解的变量总数。在计算出某个子区域的表面未知量后,根据唯一性定理,即可求出该子区域内部的所有电磁场量[28]。因式(12)左端的系统刚度矩阵一般是不对称的,可采用广义极小残量迭代算法来求解此类非对称线性方程组[30]。在计算4级串联FLTD时,因不同级模块间具有相似的结构,可将同一级模块划分为6个子区域,则整个求解区域共划分为24个子区域,如图4所示。图中,Si(i=1, 2,…, 24)为子域编号,沿圆周方向展开仿真模型。在单台工作站(2颗Xeon E5-2680 CPU, 32 GB RAM)上采用多核心并行计算的方式,每个子区域分别使用一个独立核心,实现对单个任务的加速计算。
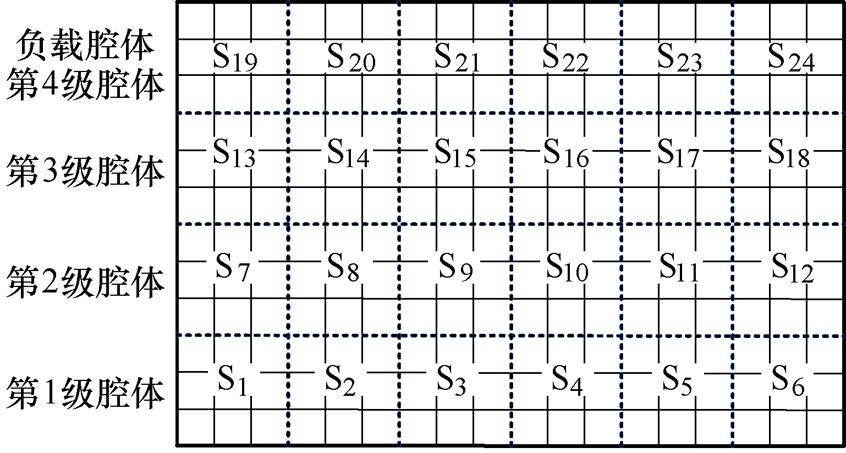
图4 将4级串联FLTD划分为24个子区域示意图
Fig.4 Schematic of the 24 subdomains of the 4-stage FLTD
计算时,单个放电支路的等效电容值为50nF,电容充电电压为±80kV或±100kV,气体开关导通后电容放电产生脉冲电流。每级FLTD腔体的次级水线按阻抗匹配原则设计,水线末端假负载的电阻值设定为0.4W。独立腔体结构每级模块轴向高度为277mm,共用腔体结构每级模块轴向高度为257mm,因此电脉冲在每级水线中的传输时间分别为8.18ns和7.59ns。为实现多级串联FLTD按理想感应电压叠加器(Induction Voltage Adder, IVA)时序触发,则应使气体开关的触发延迟时间与感应电脉冲在次级水线的传输时间相同。仿真中使用Matlab和CST Studio Suite进行脚本编写以及计算。最大网格长度设置为1个波长的1/30(模型区域)和1/10(背景区域),则4级串联共用和独立腔体结构FLTD的六面体主网格数量分别为25 498 720和21 096 120。考虑到仿真模型沿剖面具有对称性,使用理想磁导体对称边界。计算区域的外边界采用卷积完美匹配层吸收边界条件,且在每个方向上均包含8层网格。最终,可得到如图5所示的整体计算流程。

图5 使用TD-FIT计算4级串联FLTD的流程
Fig.5 Flow chart of the calculation of four-stage series-connected FLTD based on the TD-FIT
图6为4级串联共用腔体结构FLTD负载电流和电压波形(电容充电电压±80kV)。由图可知,数值模型能够较好地模拟实际工程模型,仿真得到的负载电流和电压波形与实验结果比较接近。共用、独立腔体结构单次时域仿真的耗时分别为11h39min和10h22min。因此,采用场路耦合的TD-FIT计算4级串联FLTD的瞬态放电过程是合理有效的。
图7为4级串联共用、独立腔体结构FLTD的负载电流仿真波形(电容充电电压±100kV)。由图可知,两种感应腔体结构的输出性能基本一致。图8和图9分别为4级串联共用和独立腔体结构FLTD在电压峰值时刻电场分布和电流峰值时刻磁场分布的幅值和矢量。由图可知,两种腔体结构具有相似的电磁场分布规律。电场强度、磁场强度较高的区域均为次级水线、中间绝缘板以及初次级界面;电场在初级区域主要沿轴向分布,在次级区域沿径向分布,而磁场在初级和次级区域均沿圆周方向分布。
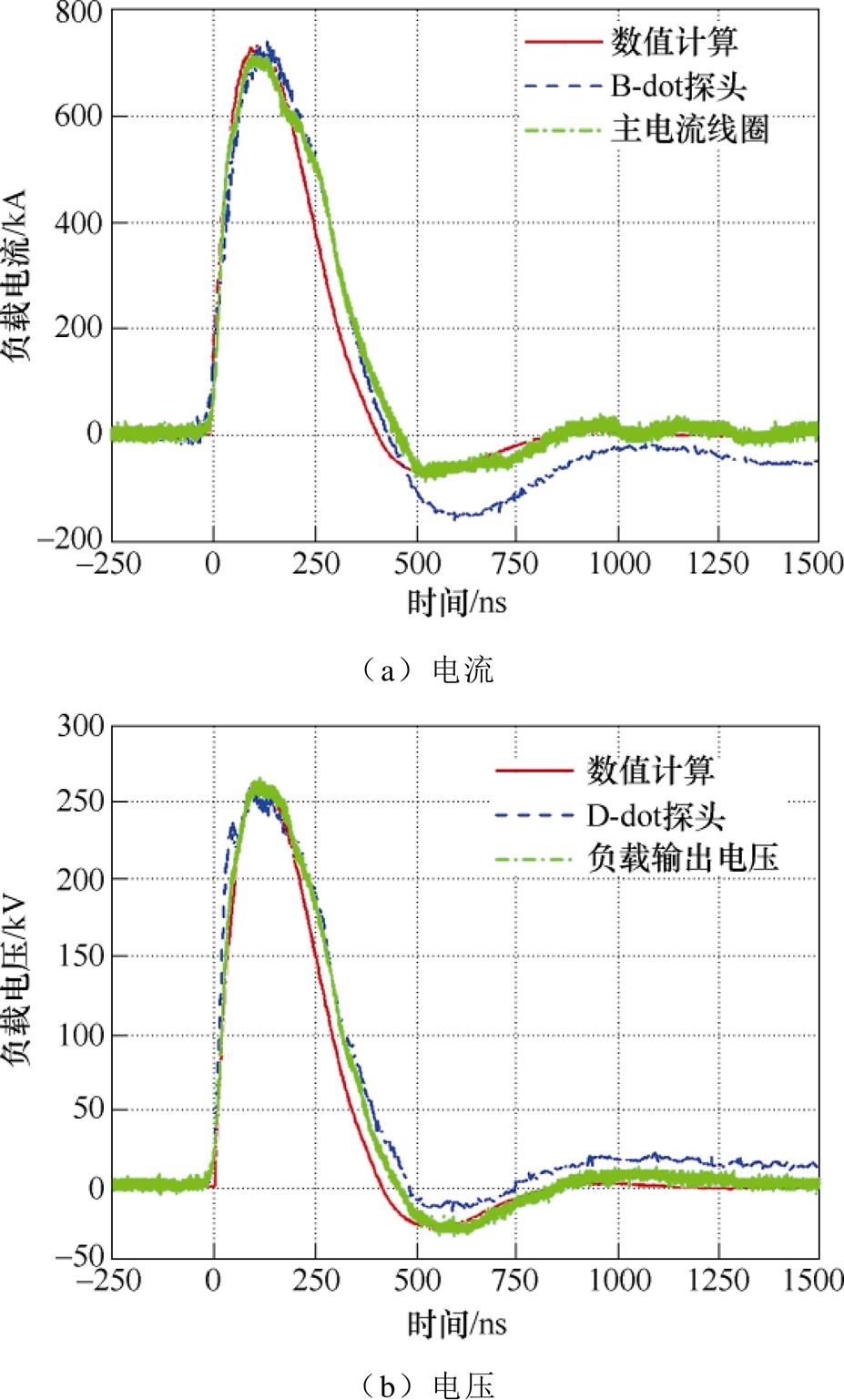
图6 共用腔体结构FLTD负载电流和电压波形
Fig.6 Load current and voltage waveforms of the four-stage FLTD sharing common cavity shell
因此,根据仿真计算和实验测试结果,多级串联共用腔体结构FLTD设计方案是可行的。在腔体电气性能和电磁特性相接近的前提下,共用腔体结构FLTD具有比独立腔体结构FLTD更高的功率密度(4级腔体轴向高度由1 228mm降至1 063mm)、更简单的触发系统和更好的维护性。

图7 共用、独立腔体结构FLTD的负载电流仿真波形
Fig.7 Simulated load current waveforms of the four-stage FLTD with common and independent induction cavity
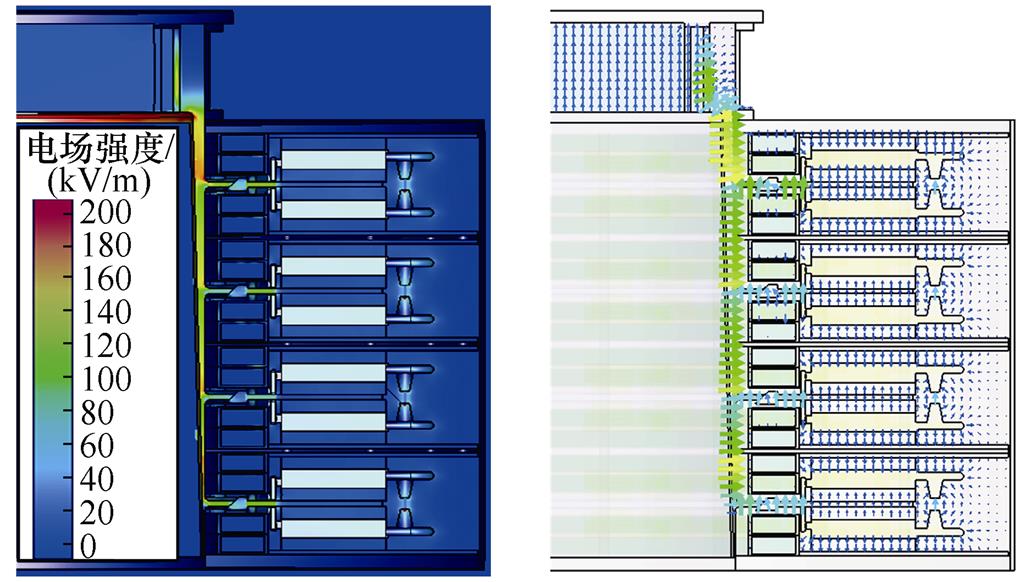
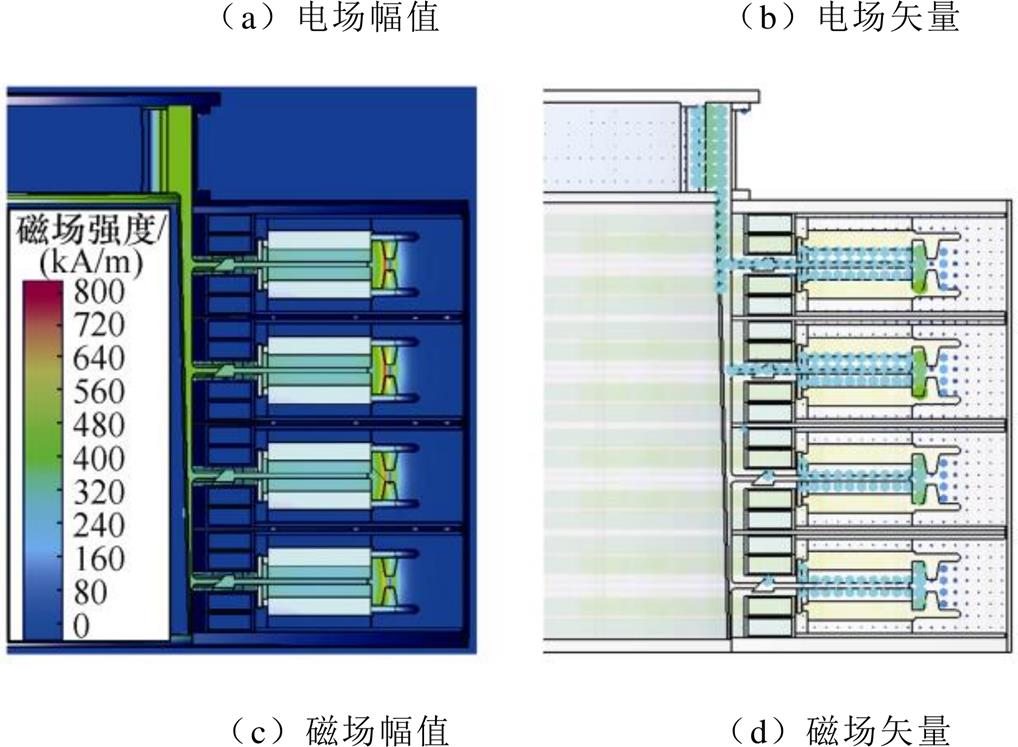
图8 共用腔体结构FLTD的电、磁场分布幅值和矢量
Fig.8 Amplitude and vector diagram of electric and magnetic field intensity for the FLTD sharing common cavity shell
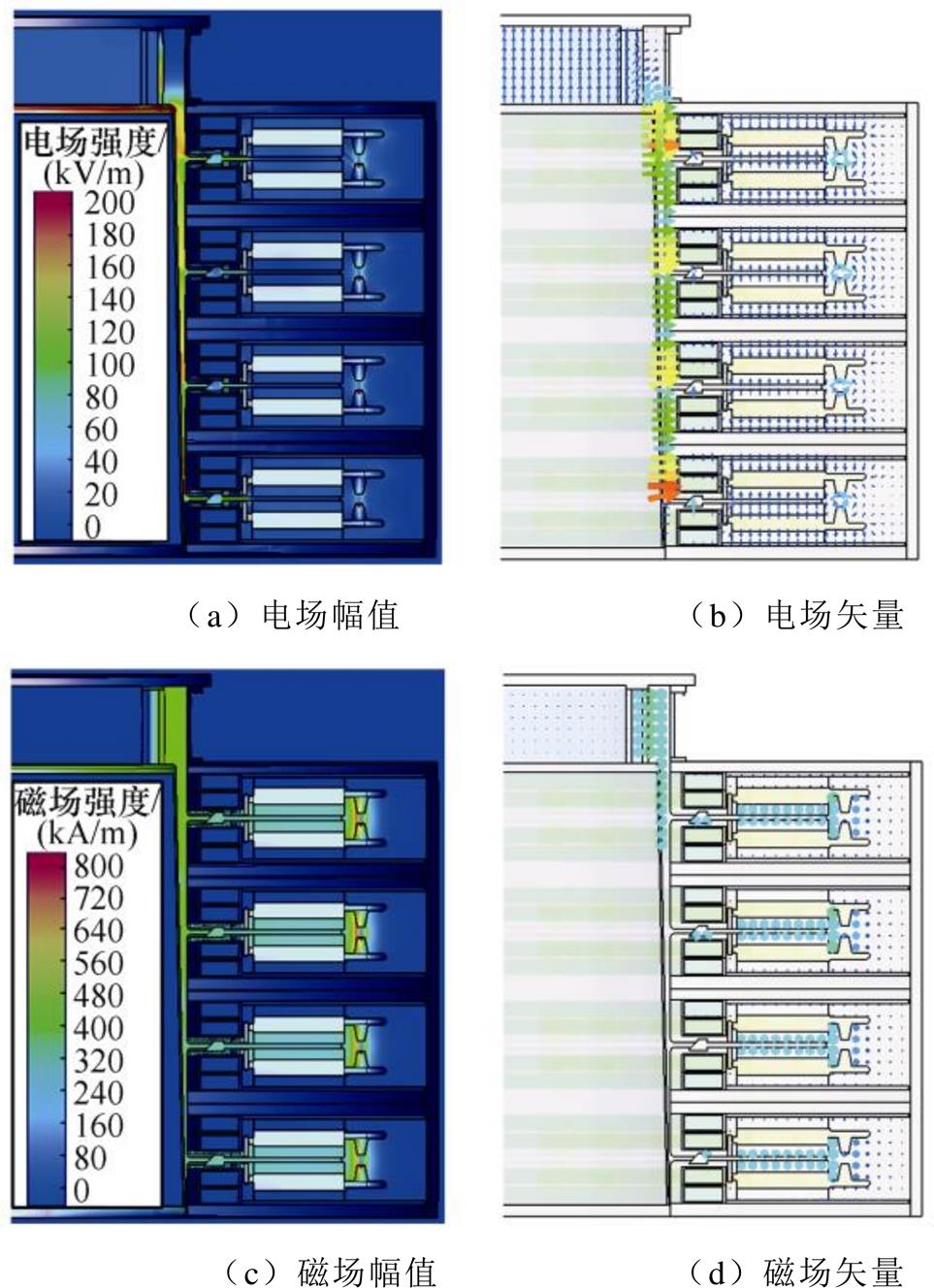
图9 独立腔体结构FLTD的电、磁场分布幅值和矢量
Fig.9 Amplitude and vector diagram of electric and magnetic field intensity for the FLTD with independent cavity
在共用腔体结构FLTD中,不同级模块之间仅有回流板隔离,且回流板与外腔体之间存在5mm间隙以满足工程安装的需要,形成了典型的孔缝结构。本小节分析两种感应腔体结构在仅第1级模块的支路直接短路放电时,第2~4级模块中的电磁干扰情况。图10为分析共用腔体结构中电磁泄漏的仿真模型,独立腔体结构具有完全相同的放电支路短路和电磁场探头布置。图11为4级串联共用、独立腔体结构FLTD中第2~4级中接收到的电场强度幅值变化曲线。由图可知,在支路脉冲放电时,共用腔体结构FLTD中后级模块的干扰电场强度大于独立腔体结构FLTD中的干扰电场强度。

图10 分析共用腔体结构中电磁泄漏的仿真模型
Fig.10 Simulation model for analysing electromagnetic leakage in the FLTD sharing common cavity shell
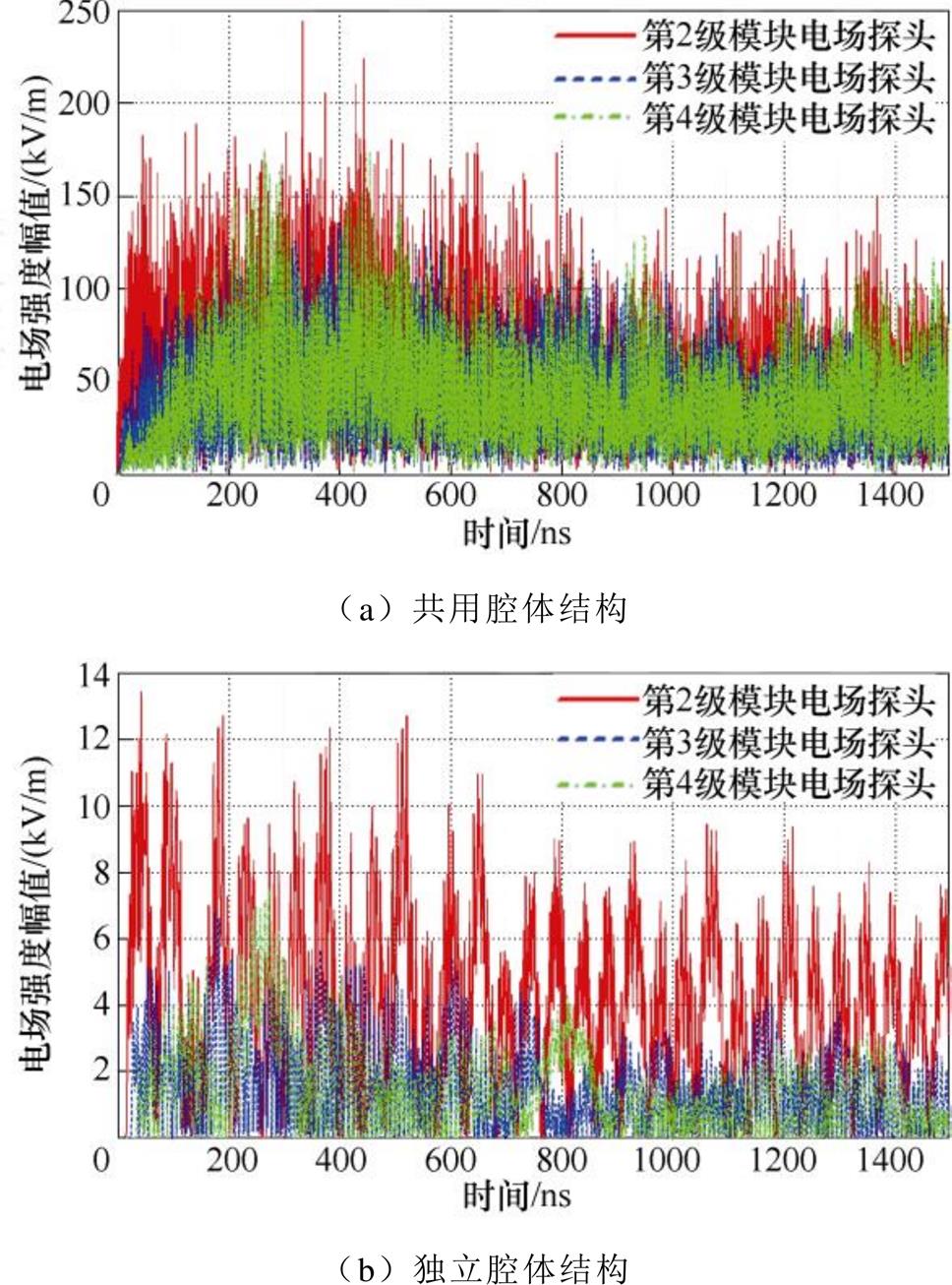
图11 共用、独立腔体结构后级模块干扰电场强度幅值
Fig.11 Magnitude of interference electric field of the 2nd to 4th module for the common and independent induction cavity
对于4级串联共用腔体结构FLTD,本节在计算时分别使用圆锥状、阶梯状和直筒状三种结构的次级水线,其中前两种结构每级水线的特征阻抗分别为0.1W、0.2W、0.3W 和0.4W,第三种结构每级水线的特征阻抗均为0.4W。三种不同结构的次级水线如图12所示。

图12 三种不同结构的次级水线
Fig.12 Three different kinds of secondary side water insulated transmission-line impedance transformer
图13对比了不同结构次级水线的负载电流波形,由图可知,不同结构次级水线对于4级串联FLTD输出性能的影响较小。其中,圆锥状和阶梯状次级水线的输出电流波形基本一致,直筒状次级水线因仅第4级满足阻抗匹配,前3级处于阻抗过匹配状态,输出电流峰值降低、上升时间增加。
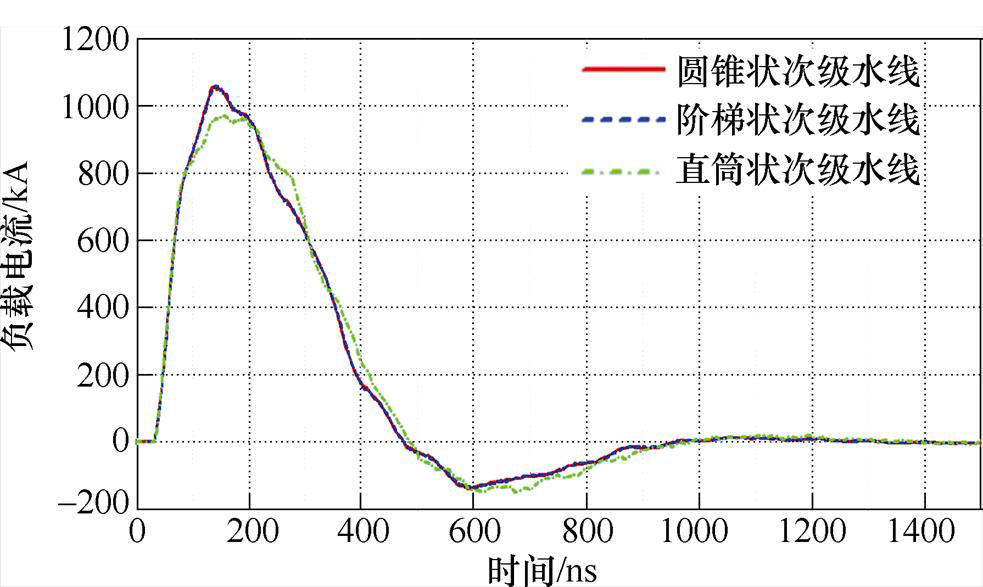
图13 不同结构次级水线的负载电流波形
Fig.13 Load currents waveforms of different kinds of secondary side water insulated transmission-line impedance transformer
上述4级串联FLTD的计算都是基于理想IVA时序触发,本节讨论不同支路开关触发时序对FLTD输出性能的影响。以4级串联共用腔体结构FLTD为例,次级水线为圆锥状结构。
为了方便描述,定义次级阻抗系数k和开关闭合时序系数a, k为某级模块的次级阻抗与包括该级模块之前的多级串联模块初级等效阻抗之比,a 为相邻FLTD模块的开关闭合延迟时间与电脉冲在相邻模块之间的传输时间之比[31],有
 (13)
(13)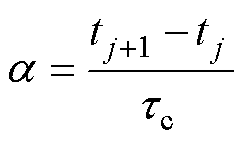 (14)
(14)
式中,Zj为第j级模块次级水线阻抗;Zdr为第j级模块之前(包括第j级模块)的多级串联FLTD初级腔体等效阻抗;Zq为末端水线阻抗;LS和CS分别为模块初级腔体等效电感和电容;q为总的串联模块数量;c为一个时间常数,表示触发脉冲沿触发电缆在两相邻串联模块间传播所需时间;tj为脉冲电压沿次级水线传播至第j级模块的时间。
显然,当次级阻抗系数 时,次级水线阻抗匹配;当开关闭合时序系数
时,次级水线阻抗匹配;当开关闭合时序系数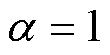 时,触发时序为理想IVA时序。假设次级水线阻抗匹配,即
时,触发时序为理想IVA时序。假设次级水线阻抗匹配,即 保持不变,改变a,使其分别等于1、0、1、1.2和1.5,计算4级串联FLTD的输出特性和电磁场分布,可得到如图14所示的负载电流波形。
保持不变,改变a,使其分别等于1、0、1、1.2和1.5,计算4级串联FLTD的输出特性和电磁场分布,可得到如图14所示的负载电流波形。

图14 不同a 下的4级串联FLTD负载电流波形
Fig.14 Load current waveforms for different a values of the four-stage series-connected FLTD
由图14可知,4级串联FLTD的开关触发闭合时序对负载电流有重要的影响。当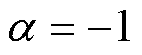 时,负载电流峰值最大;当
时,负载电流峰值最大;当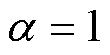 时,负载电流前沿最陡;当a 为1.2和1.5时,电流波形基本一致。因此,在理想IVA触发时序下,负载电流具有较大的峰值电流和最短的脉冲前沿。对于多级(如8~12级)串联共用腔体FLTD中开关触发闭合时序变化对输出电流和电磁场分布的影响,有待更进一步的研究。
时,负载电流前沿最陡;当a 为1.2和1.5时,电流波形基本一致。因此,在理想IVA触发时序下,负载电流具有较大的峰值电流和最短的脉冲前沿。对于多级(如8~12级)串联共用腔体FLTD中开关触发闭合时序变化对输出电流和电磁场分布的影响,有待更进一步的研究。
本文采用时域有限积分技术建立了4级串联共用、独立腔体结构快脉冲直线型变压器驱动源的数值计算模型,并得到以下结论:
1)利用场路耦合的时域有限积分技术,结合非均匀网格、表面阻抗边界条件和区域分解算法等加速方法计算了4级串联共用、独立腔体结构FLTD的电磁特性。在支路电容充电电压±80kV下,4级串联FLTD输出电流峰值约720kA,上升时间约120ns,仿真和实验负载电流、电压波形基本一致,验证了该算法应用于快放电脉冲瞬态的有效性。
2)共用、独立腔体结构的输出性能和电磁场分布的一致性较好,共用腔体结构具有功率密度更高、触发系统更简单和维护方便的优点,验证了共用腔体结构4级串联FLTD设计方案的可行性。
3)通过分析共用腔体结构FLTD内部的电磁干扰问题,以及次级水线结构和开关闭合触发时序对FLTD输出性能和电磁场分布的影响,为FLTD腔体的结构优化提供必要的参考。
后续研究需要定量分析共用腔体结构对多级串联FLTD电磁兼容性能的影响,并在数值模型中考虑气体开关的延迟和抖动以及支路自放电等不确定性因素对FLTD电磁特性的影响。
参考文献
[1] 孙凤举, 邱爱慈, 魏浩, 等. 快Z箍缩百太瓦级脉冲驱动源概念设计的发展[J]. 现代应用物理, 2017, 8(2): 13-24.
Sun Fengju, Qiu Aici, Wei Hao, et al. Development of conceptual design on fast Z-pinch pulsed power driver with hundreds of Terawatt[J]. Modern Applied Physics, 2017, 8(2): 13-24.
[2] McBride R D, Stygar W A, Cuneo M E, et al. A primer on pulsed power and linear transformer drivers for high energy density physics applications[J]. IEEE Transactions on Plasma Science, 2018, 46(11): 3928- 3967.
[3] 董守龙, 王艺麟, 曾伟荣, 等. 一种全固态多匝直线型变压器驱动源的研制[J]. 电工技术学报, 2020, 35(7): 1584-1591.
Dong Shoulong, Wang Yilin, Zeng Weirong, et al. The development of all solid-state multi-turn linear transformer driver[J]. Transactions of China Electro- technical Society, 2020, 35(7): 1584-1591.
[4] 董守龙, 王艺麟, 余亮, 等. 一种基于感应隔离的双极性脉冲发生器[J]. 电工技术学报, 2020, 35(24): 5050-5056.
Dong Shoulong, Wang Yilin, Yu Liang, et al. A bipolar pulse generator based on inductive isolation[J]. Transactions of China Electrotechnical Society, 2020, 35(24): 5050-5056.
[5] Chen Lin, Zou Wenkang, Zhou Liangji, et al. Development of a fusion-oriented pulsed power module[J]. Physical Review Accelerators and Beams, 2019, 22(3): 030401.
[6] Wei Zhenyu, Rao Xuni, He Xu, et al. Circuit simulation with nonlinear magnetic core of a new linear transformer driver stage[J]. IEEE Transactions on Plasma Science, 2019, 47(8): 4084-4090.
[7] 孙凤举, 姜晓峰, 魏浩, 等. 一种多级串联共用外腔体新结构LTD[J]. 强激光与粒子束, 2017, 29(2): 61-66.
Sun Fengju, Jiang Xiaofeng, Wei Hao, et al. Novel configuration linear transformer driver with multi- stages in series sharing common cavity shell[J]. High Power Laser and Particle Beams, 2017, 29(2): 61- 66.
[8] Rose D V, Miller C L, Welch D R, et al. Circuit models and three-dimensional electromagnetic simu- lations of a 1MA linear transformer driver stage[J]. Physical Review Special Topics Accelerators & Beams, 2010, 13(9): 90401.
[9] Flisgen T, Gjonaj E, Glock H, et al. Generalization of coupled S-parameter calculation to compute beam impedances in particle accelerators[J]. Physical Review Accelerators and Beams, 2020, 23(3): 034601.
[10] Yan Jiaqi, Wang Guiji, Chen Xuemiao, et al. Modeling and experimental study on multi-brick parallel discharge driver based on PEEC method[J]. IEEE Transactions on Plasma Science, 2018, 46(10): 3364-3373.
[11] 胡亚楠, 包家立, 朱金俊, 等. 纳秒电脉冲对肝脏组织不可逆电穿孔消融区分布的时域有限差分法仿真[J]. 电工技术学报, 2021, 36(18): 3841-3850.
Hu Yanan, Bao Jiali, Zhu Jinjun, et al. The finite difference time domain simulation of the distribution of irreversible electroporation ablation area in liver tissue by nanosecond electrical pulse[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3841-3850.
[12] 程显, 陈硕, 吕彦鹏, 等. 纳秒脉冲作用下核孔复合体影响细胞核膜电穿孔变化的仿真研究[J]. 电工技术学报, 2021, 36(18): 3821-3828.
Cheng Xian, Chen Shuo, Lü Yanpeng, et al. Simu- lation study on the effect of nuclear pore complexes on cell electroporation under nanosecond pulse[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3821-3828.
[13] 刘欣, 王利桐, 梁贵书, 等. 压装组件中圆柱形母线的部分电感计算方法[J]. 电工技术学报, 2020, 35(增刊1): 1-9.
Liu Xin, Wang Litong, Liang Guishu, et al. Com- puting method for partial inductance of cylindrical busbar conductor[J]. Transactions of China Elec- trotechnical Society, 2020, 35(S1): 1-9.
[14] Weiland T. Time domain electromagnetic field computation with finite difference methods[J]. Inter- national Journal of Numerical Modelling: Electronic Networks, Devices and Fields, 1996, 9(4): 295-319.
[15] Weiland T. Electromagnetic simulators-status and future directions[J]. IET Science, Measurement & Technology, 2017, 11(6): 681-686.
[16] You Jianwei, Cui Tiejun. Efficient approach to accurately analyze wireless propagation and fading in time domain[J]. IEEE Antennas and Wireless Pro- pagation Letters, 2016, 15(2): 1767-1770.
[17] You Jianwei, Zhang Jianfeng, Gu Weihui, et al. Numerical analysis of passive intermodulation arisen from nonlinear contacts in HPMW devices[J]. IEEE Transactions on Electromagnetic Compatibility, 2018, 60(5): 1470-1480.
[18] Yousaf J, Park M, Lee H, et al. Efficient circuit and an EM model of an electrostatic discharge gener- ator[J]. IEEE Transactions on Electromagnetic Compatibility, 2018, 60(4): 1078-1086.
[19] Razi-Kazemi A A, Hajian M. Probabilistic assessment of ground potential rise using finite integration technique[J]. IEEE Transactions on Power Delivery, 2018, 33(5): 2452-2461.
[20] Samimi M H, Hillenbrand P, Tenbohlen S, et al. Investigating the applicability of the finite integration technique for studying the frequency response of the transformer winding[J]. International Journal of Electrical Power & Energy Systems, 2019, 110(3): 411-418.
[21] Qiu Hao, Wang Shuhong, Sun Fengju, et al. Transient electromagnetic field analysis for the single-stage fast linear transformer driver with two different con- figurations using the finite-element method and finite integration technique[J]. IEEE Transactions on Magnetics, 2020, 56(4): 7515805.
[22] Qiu Hao, Wang Shuhong, Zhang Naming, et al. Numerical analysis of a single-stage fast linear trans- former driver using field-circuit coupled time-domain finite integration theory[J]. Applied Sciences, 2020, 10(22): 8301.
[23] Qiu Hao, Wang Shuhong, Zhang Naming, et al. Field- circuit coupling and electromagnetic-thermal-mechanical coupling analysis of the single-stage fast linear trans- former driver using time-domain finite integration technique[J]. IEEE Transactions on Magnetics, 2021, 57(6): 8401205.
[24] Qiu Hao, Wang Shuhong, Sun Fengju, et al. Com- putational investigations on the four-stage MA-class fast linear transformer driver with sharing cavity shell[J]. IEEE Transactions on Plasma Science, 2021, 49(8): 2364-2372.
[25] 毛云龙. 基于表面阻抗的时域有限差分方法边界条件研究[D]. 哈尔滨: 哈尔滨工程大学, 2018.
[26] 王明杰, 徐伟, 杨存祥, 等. 基于精确子域模型的永磁直线同步电机空载磁场解析计算[J]. 电工技术学报, 2020, 35(5): 942-953.
Wang Mingjie, Xu Wei, Yang Cunxiang, et al. Analytical calculation of no-load magnetic field in permanent magnet linear synchronous motors based on an accurate subdomain model[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 942-953.
[27] 江明, 胡俊, 陈涌频, 等. 基于积分方程区域分解算法的研究进展[J]. 电波科学学报, 2020, 35(2): 169-177.
Jiang Ming, Hu Jun, Chen Yongpin, et al. The progress of domain decomposition method based on integral equation[J]. Chinese Journal of Radio Science, 2020, 35(2): 169-177.
[28] 杨旗, 杨帆, 高兵, 等. 基于惠更斯原理的电气设备局部放电电磁传播计算方法[J]. 电工技术学报, 2019, 34(21): 4419-4427.
Yang Qi, Yang Fan, Gao Bing, et al. Research on electromagnetic propagation of partial discharge for electrical equipment using Huygens principle[J]. Transactions of China Electrotechnical Society, 2019, 34(21): 4419-4427.
[29] Muth F, Euler T. Investigating an equivalence principle based stopping criterion for a black box framework for domain decomposition[C]//The 19th International Conference on Electromagnetics in Advanced Applications, Verona, 2017: 715-717.
[30] 陶瑞祥, 王泽忠. 基于有限元的电场区域分解法的广义极小残量迭代算法[J]. 电工技术学报, 2018, 33(2): 225-231.
Tao Ruixiang, Wang Zezhong. Generalized minimal residual iteration method for finite element based on domain decomposition technique for electric field problem[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 225-231.
[31] Liu Peng, Sun Fengju, Yin Jiahui, et al. Numerical analysis of the output-pulse shaping capability of linear transformer drivers[J]. Plasma Science and Technology, 2011, 13(2): 246-251.
The Electromagnetic Characteristics of the Four-Stage Series-Connected Fast Linear Transformer Driver Based on Time-Domain Finite Integration Technique
Abstract The material distribution and internal structure of the fast linear transformer driver (FLTD) induction cavity are complex, and the short rise time of the discharging current will make the spatial discretization more dense, leading to a sharp increase in the computational expenditure. In this paper, the electromagnetic field distributions of the 4-stage MA-class FLTD during brick discharge is studied using the time-domain finite integration technique (TD-FIT). The discharge currents of capacitors in the circuit model are coupled to the 3-D field model as excitations. The grid length of the important parts in the FLTD cavity is refined by the nonuniform grid. To reduce the number of degrees of freedom, the surface impedance boundary condition is adopted to model good conductors. The FLTD is divided into 24-different subdomains by the domain decomposition method based on the equivalence principle theorem. The results demonstrate that the TD-FIT can effectively analyse the pulsed transients in the FLTD cavity, the output performance and electromagnetic field characteristics of the two induction cavities are in good agreement, and the design of the four-stage FLTD sharing common cavity shell is practicable.
keywords:Linear transformer driver, finite integration technique, electromagnetic transients, field-circuit coupling, domain decomposition method
DOI: 10.19595/j.cnki.1000-6753.tces.L90321
中图分类号:TM15; TM832
邱 浩 男,1986年生,博士,研究方向为电磁场数值计算。E-mail: haoqiu@stu.xjtu.edu.cn
王曙鸿 男,1968年生,教授,博士生导师,研究方向为电路、电磁场及多物理场的理论、数值分析方法和软件技术,先进电工材料(超导材料、磁性材料等)的电磁特性建模和仿真。E-mail: shwang@mail.xjtu.edu.cn(通信作者)
收稿日期 2020-07-09
改稿日期 2020-12-07
国家自然科学基金重大资助项目(51790521)。
(编辑 崔文静)