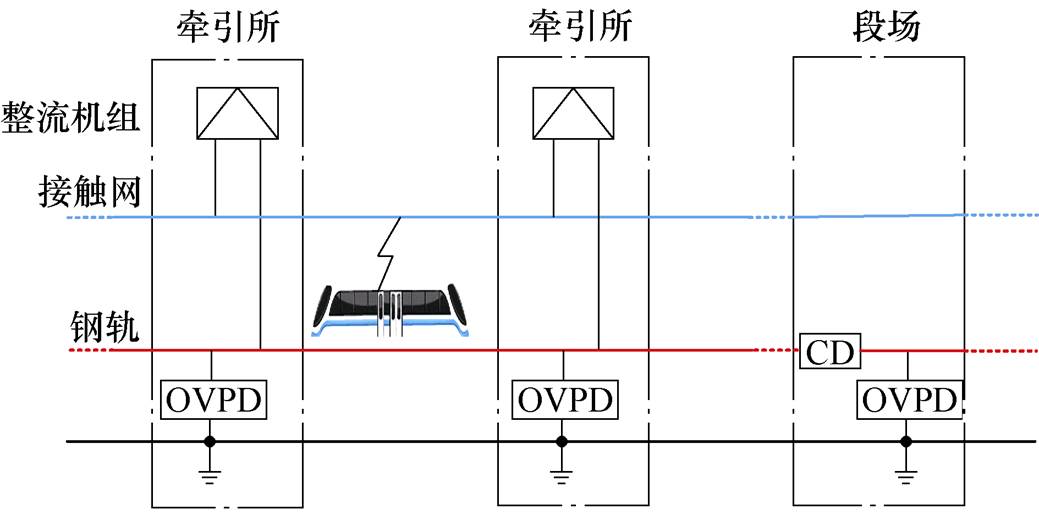
图1 城市轨道交通供电系统
Fig.1 Urban rail transit power supply system
摘要 为控制杂散电流与钢轨电位,钢轨电位限制装置(OVPD)、连接装置(CD)等设备广泛运用于轨道交通运营线路,直流牵引供电系统中的钢轨电位异常问题越来越引起重视。回流系统设备的状态切换会造成钢轨电位动态分布发生显著变化。建立回流系统等效电路模型时不应只考虑正线,也应当考虑段场以及回流设备的行为过程。为此,该文建立OVPD和段场等效电路的通用模型,并提出计及回流设备行为过程的直流牵引供电计算方法。以某实际地铁工程为例,对运营线路进行仿真,采用该文算法的计算结果与实际工程中的钢轨电位变化过程更加吻合。在此基础上,讨论分析正线与段场之间的相互影响,结果表明,段场单向导通装置(UCD)的设置无法避免正线与段场之间的相互影响;段场钢轨直接接地更易恶化正线钢轨电位,相较于正线与段场之间采用阻断式连接装置(BCD)的情况下,正线钢轨电位Umax和Umin分别提高34.46%和降低33.97%。
关键词: 直流牵引供电系统 连接装置 钢轨电位 杂散电流
国内的直流牵引供电系统主要采用750V或1 500V供电,列车通过受电弓由接触网取电,钢轨回流。钢轨虽然通过扣件绝缘安装在混凝土道床上,但是由于受到运营环境、技术条件等因素限制,钢轨与道床结构之间往往无法做到完全绝缘,钢轨总会泄漏部分电流至大地,形成杂散电流[1-3]。列车在正常行驶过程中,牵引电流可达到数千安,由于钢轨自身存在阻抗且受杂散电流影响,钢轨与大地之间不可避免地存在钢轨电位问题[4-5]。而目前国内地铁运营时的钢轨电位经常达到120V甚至更高,对地铁运营造成严重影响。
为了减少杂散电流和钢轨电位,国内外学者做了大量研究。文献[6]提出应结合潮流计算方法分析直流牵引供电系统杂散电流,并研究了在正常运行以及线路短路情况下沿线钢轨对地电压空间分布。文献[7]基于CDEGS软件建立地铁供电系统杂散电流仿真模型,研究了过渡电阻对地铁杂散电流分布影响,并在此基础上估算了钢轨和排流网的年腐蚀量。文献[8]利用建立的三层网络模型,研究了不均匀过渡电阻对杂散电流的影响,结果表明,不均匀过渡电阻虽然不会影响钢轨上的电压降,但是会改变钢轨对地电位分布。文献[9]对比分析了不同电流跨区间传输情况下的钢轨电位变化,指出有效避免跨区间授流,可大大降低线路钢轨电位幅值。
GB 50157-2013《地铁设计规范》中规定,在正常双边供电运行时,站台处走行轨对地电位不应大于120V,车辆基地库线走行轨对地电位不应大于60V[10]。为防止钢轨电位过高对人体造成危害,在各个车站都安装钢轨电位限制器(Over-Voltage Protection Device, OVPD),用以监测钢轨与大地之间的电压[11]。实际上,当某车站OVPD合闸后,该车站的钢轨电位会被钳制到地电位,邻近车站的钢轨电位将升高或降低,从而造成钢轨电位问题在线路上的传播。文献[12]为准确评估动态牵引网络的钢轨电位与杂散电流,建立了考虑OVPD和排流装置行为机理的仿真模型。仿真结果表明,在多个列车运行过程中,钢轨电位和杂散电流很大程度上受OVPD和排流装置的运行影响,并且可以通过调整OVPD动作后的接地电阻值,降低钢轨电位和杂散电流。文献[13]仿真结果表明,单处的钢轨电位控制过程会导致全线钢轨电位分布的动态改变,从而引起其他位置OVPD的联锁动作。目前,段场钢轨主要存在两种接地形式:①直接接地;②采用OVPD悬浮接地。段场与正线之间的钢轨接地方式不完全相同,单向导通装置(Unidirectional Connection Device, UCD)为杂散电流提供路径的同时,使得正线和段场的钢轨电位互相影响。
综合国内外研究文献来看,影响杂散电流与钢轨电位的因素众多。直流牵引供电系统中,回流设备的状态切换会引起系统参数发生变化,却少有文献关注OVPD和正线与段场连接装置(Connection Device, CD)的行为过程以及段场钢轨接地方式对钢轨电位动态分布造成的影响。因此,本文考虑了OVPD和CD的行为过程以及正线和段场的不同接地方式,提出一种计及回流设备行为过程的直流牵引供电计算方法,在迭代过程中对回流系统参数进行修正。并针对某地铁运营线路,对比实测与仿真的钢轨电位变化过程,验证了算法的有效性,讨论分析了正线与段场之间的相互影响。
城市轨道交通供电系统主要包括整流机组、接触网、牵引网、OVPD和CD等,城市轨道交通供电系统如图1所示。
城市轨道交通的24脉波整流机组可采用理想电压源串联电阻的戴维南等效电路或理想电流源并联电阻的诺顿等效电路对其进行建模[14]。
列车是轨道交通的主要负荷,当列车处于牵引工况时,从牵引网吸收功率,当其处于制动工况时,向牵引网回馈功率。考虑到列车功率受网压波动较小,采用恒功率源对其进行等效建模。仿真过程中,每个仿真时刻t的列车功率保持不变,接触网授流在迭代过程中根据牵引网压实时修正。

图1 城市轨道交通供电系统
Fig.1 Urban rail transit power supply system
在对牵引网进行建模时,采用“接触网、钢轨、大地”的三层网络模型,钢轨与大地存在过渡电阻,为模拟钢轨电位与杂散电流情况,通过p 型单元电路纵向连接。
以下为本文对直流牵引供电系统回流系统主要设备的行为过程进行建模。
忽略OVPD分合闸的中间过程,其工作状态可分为分闸和合闸状态。由OVPD的控制特性可知,只有当OVPD合闸时,钢轨直接接地,t时刻OVPD所在位置处的钢轨对地电阻为
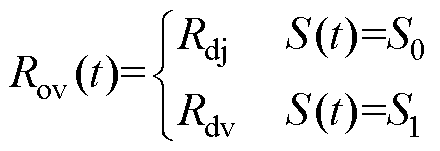 (1)
(1)式中,S(t)为t时刻OVPD的状态;S0为OVPD处于分闸状态;S1为OVPD处于合闸状态;Rdj为OVPD处于分闸状态时的钢轨对地电阻;Rdv为OVPD处于合闸状态时的钢轨对地电阻。
影响OVPD工作状态的参数主要为OVPD的m段动作整定值Um、Um的对应动作延时tm、动作后的复归时间tre以及其所在位置处的钢轨对地电压u(x,t)。目前,常见的OVPD整定值方案多为Ⅲ段整定值方案。为避免OVPD装置动作后复归产生的操作过电压导致装置误动作的情况,也提出了多段整定值方案。据此,OVPD的状态切换策略如图2所示。图中,DT0为u(x, t)≥Um的持续时间,DT1为OVPD处于合闸状态的持续时间。
对于OVPD的合闸过程而言,不仅要满足当前时刻u(x, t)≥Um,还要满足其持续时间DT0≥tm的条件;而当OVPD处于S1时,只要满足DT1≥tre的条件,OVPD即可实现分闸。
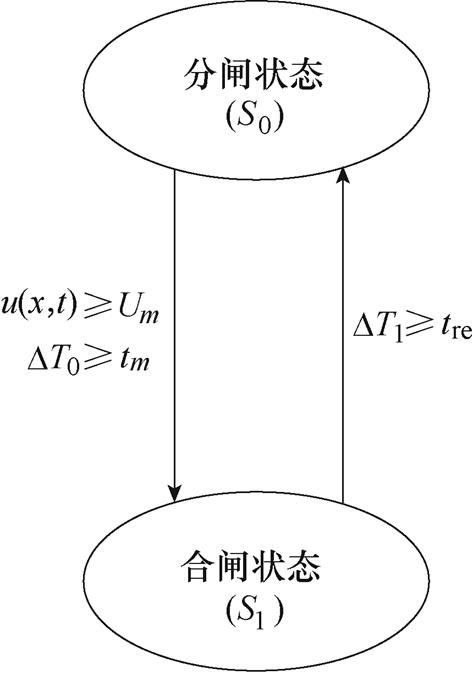
图2 OVPD状态切换策略
Fig.2 Switching strategy of OVPD’s state
在地铁正线和车辆段、停车场之间一般设置钢轨绝缘节,段场分布情况如图3所示。钢轨绝缘节的部位通常并联CD,以避免列车经过绝缘节时出现打火现象。因此,建立段场的通用等效电路模型时必须考虑CD的控制特性。
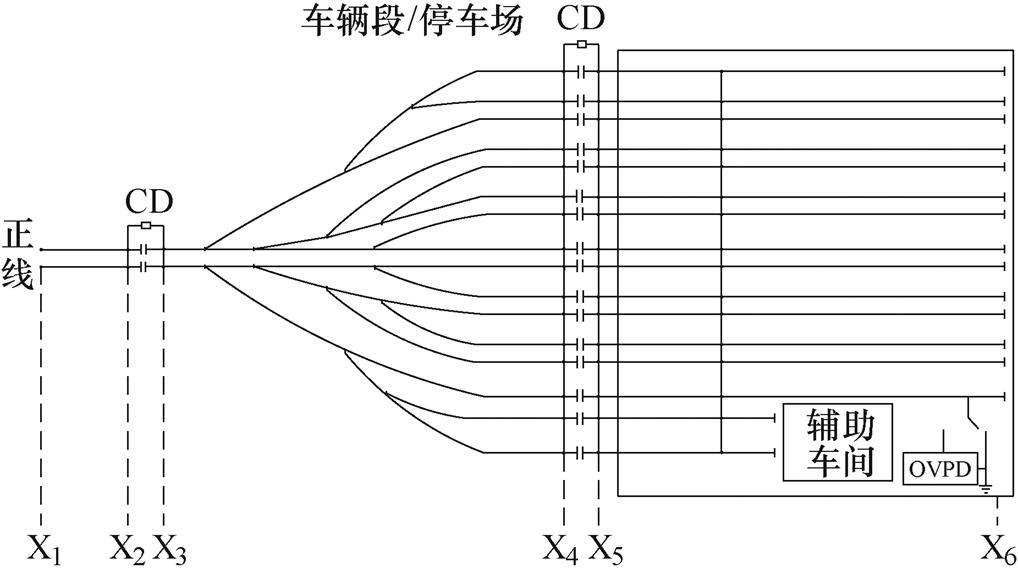
图3 段场分布情况
Fig.3 Distribution of a parking lot and depot
现有CD主要分三种类型:①UCD,由反并联的二极管与晶闸管消弧支路组成,通过钢轨电位控制晶闸管的工作状态;②阻断式连接装置(Blocking Connection Device, BCD),通过列车信号控制,当有列车经过时,BCD导通闭合,无列车经过时,保证正线与段场之间电气分隔;③贯通式连接装置(Through Connection Device, TCD),正线与段场之间完全电气连通。综合考虑段场CD的控制特性和钢轨的接地方式后,段场的等效电路模型如图4所示。图中,R1为X1~X2之间的钢轨电阻;Rz为X2~X3和X4~X5之间的等效电阻,如式(2)所示;R2为X3~X4之间的钢轨电阻;R3为X5~X6之间的钢轨电阻;Rd1~Rd5为相应区段的钢轨对地过渡电阻;Rk为X6处采用不同钢轨接地方式下的钢轨对地电阻,如式(3)所示。
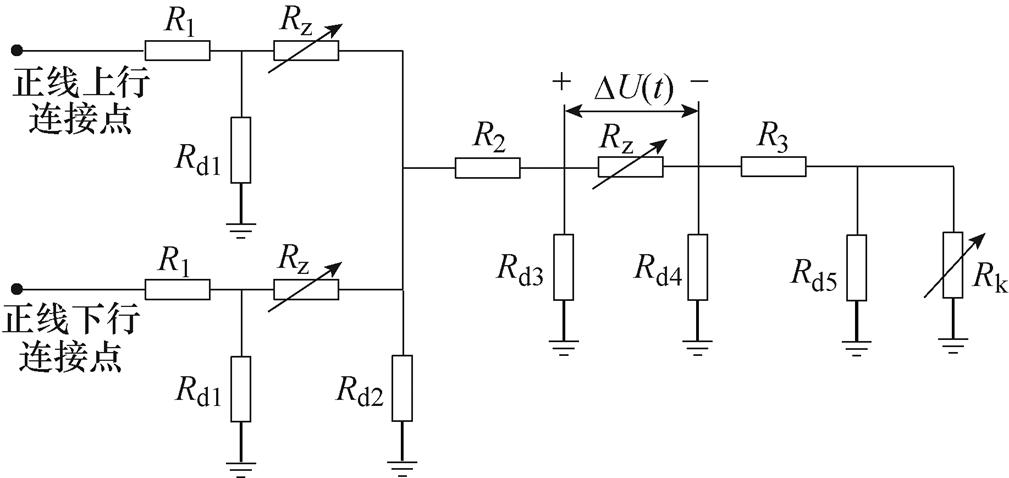
图4 段场的等效电路模型
Fig.4 Equivalent circuit model of parking lot and depot
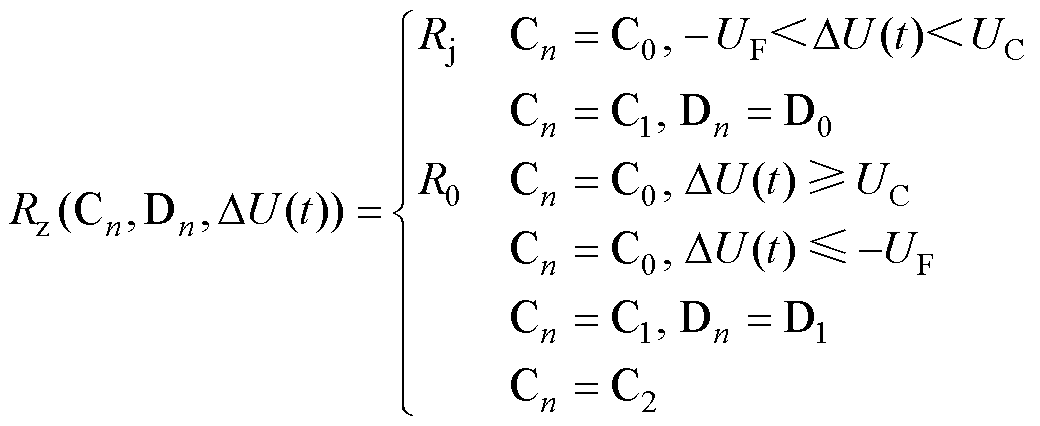 (2)
(2)式中,Cn为CD类型;C0、C1、C2为段场分别采用UCD、BCD和TCD;UF为UCD二极管的正向导通电压降;UC为装置消弧支路的触发电压;DU(t)为t时刻CD两侧的电压差;Rj为钢轨绝缘节电阻;R0为CD导通后的电阻;Dn为列车通过信号,D0为未检测到列车通过,D1为检测到列车通过。
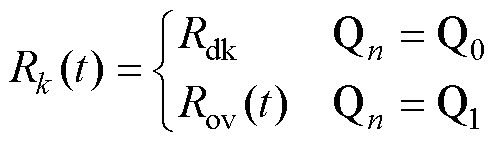 (3)
(3)
式中,Qn为段场钢轨的接地方式;Q0为直接接地;Q1为通过OVPD悬浮接地;Rdk为钢轨直接接地电阻。
计及回流设备行为过程的直流牵引供电计算方法主要由内外两层循环组成,外层循环包括整流机组、段场、OVPD的计算模型调整;内层循环用于供电系统网络的单次求解计算。其步骤如下:
(1)扫描列车运行图。通过读取牵引计算结果,获得当前时刻t的列车信息,确定列车的位置和功率以及接触网授流情况。
(2)初始化系统参数。任意牵引所初始工作状态为整流状态(REC),全线OVPD设置为S0,电压收敛精度为e。
(3)扫描全线元件。根据各元件(整流机组、段场、OVPD、CD等)t时刻状态,更新节点-支路导纳矩阵信息。
(4)对形成的直流牵引供电系统节点-支路导纳矩阵进行求解计算。
(5)根据求解得到的各节点电压、支路信息等,判断电压是否满足收敛条件。若不满足,返回步骤(3);若满足,则继续。
(6)判断列车节点电压是否达到车载制动电阻起动电压Uon。若达到,起动车载制动电阻,返回步骤(3);否则,继续。
(7)判断牵引所的状态是否合理。若不合理,则调整牵引所状态,返回步骤(3);若合理,则继续。
(8)根据式(2)判断CD的Rz阻值是否需要修改。若是,则调整支路信息,并返回步骤(3);否则,继续。
(9)判断OVPD状态S(t)是否满足切换条件。若满足,则根据式(1)调整支路信息,返回步骤(3);否则,继续。
(10)判断是否达到仿真结束时刻。若是,仿真结束;否则,t=t+1,返回步骤(3)。
计及回流设备行为过程的供电计算算法流程如图5所示。
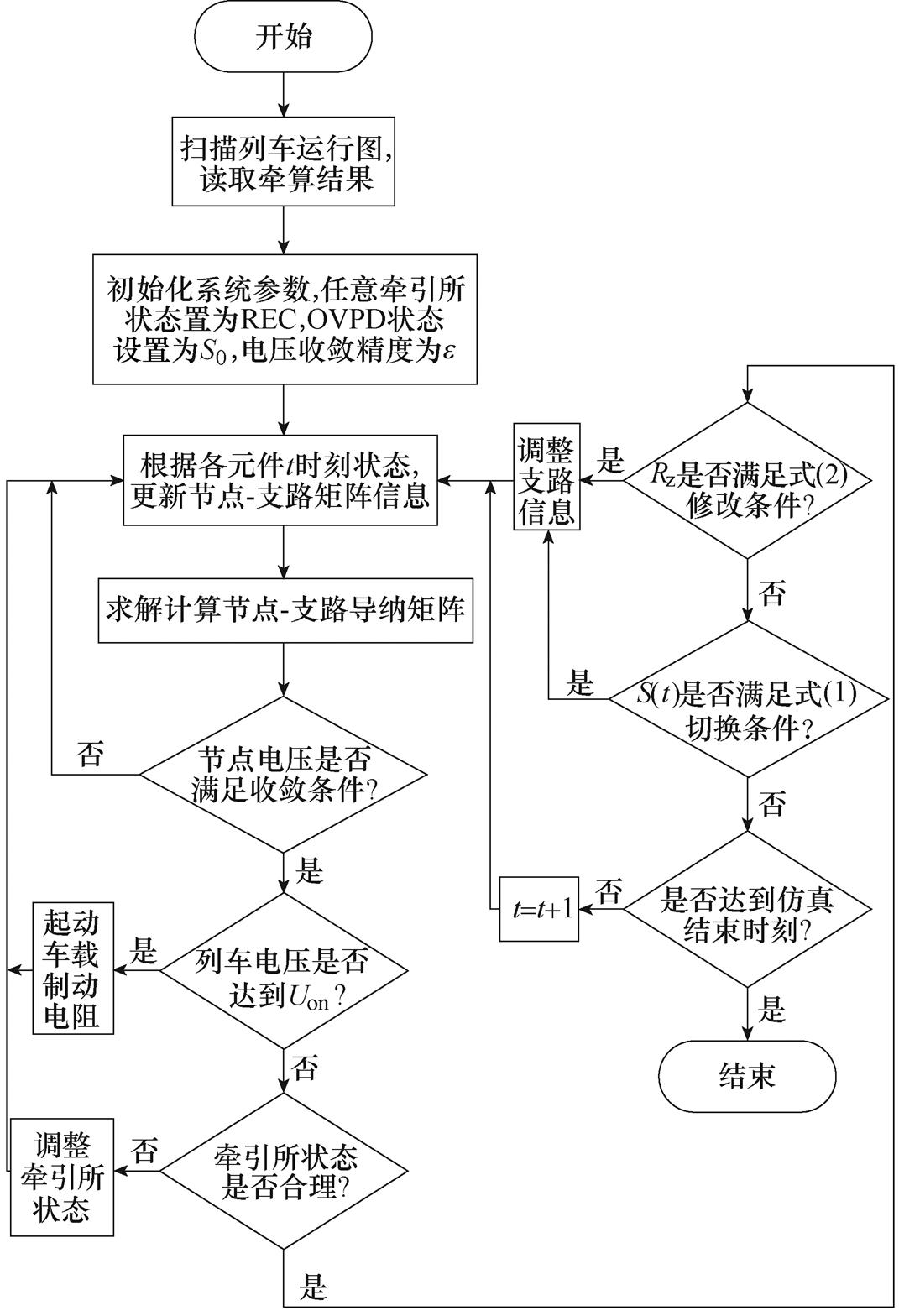
图5 计及回流设备行为过程的供电计算算法流程
Fig.5 Considering the equipment behavior process of recirculation system in algorithm flow
为验证算法的有效性,对某地铁运营线路进行供电计算,结合实测进行对比分析。
该线路全长为58.35km,采用直流1 500V接触轨授流,钢轨回流。全线共设置22个车站,1段1场,牵引所18个,其中3个区间所,该地铁工程系统如图6所示,各牵混所的位置分布见表1。其中,停车场A位于车站6和车站7之间,与正线交界处为7.44km处,车辆段B位于车站22号和车站23号之间,与正线交界在50.78km处。段场的CD类型为C0,OVPD及UCD详细设备参数见表2,表中,括号内表示段场的OVPD整定值。接触轨电阻为0.010 6W/km,钢轨电阻为0.02W/km。环境条件对钢轨对地过渡电阻影响较大,而该运营线路正线分为地下段和地上段。同时,对该运营线路的不同环境区段进行了钢轨对地过渡电阻检测,仿真时采用真实测量值,设置地下段钢轨对地过渡电阻Rdx=1.816W·km,地上段钢轨对地过渡电阻Rds= 19.119W·km,段场与正线的钢轨对地过渡电阻保持一致。
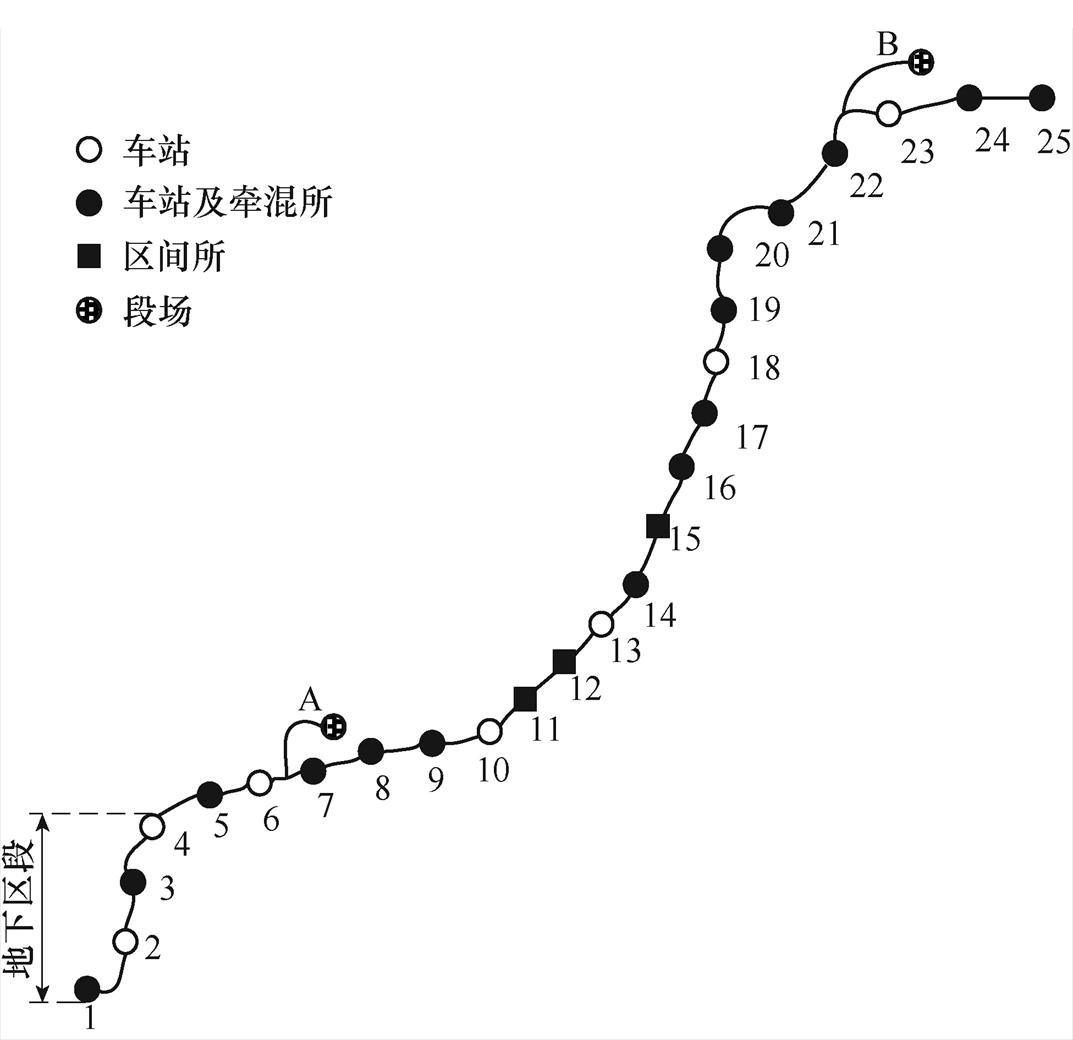
图6 某地铁工程系统
Fig.6 Power supply system of one subway project
线路的车辆参数见表3,全天采取大、小交路发车,大交路为牵混所1~25号,发车间隔890s;小交路为牵混所1~20号,发车间隔425s。牵引计算模拟得到的上下行列车速度-位置曲线和功率-位置曲线如图7所示。仿真总时长890s,列车在正线 运行。
表1 某地铁工程牵混所分布
Tab.1 Location distribution of traction mixed substations for certain subway project

牵混所编号位置/km牵混所编号位置/km 10.2841532.150 32.2551634.250 55.7451737.121 78.5931941.135 811.3392044.249 915.1362146.956 1119.7442249.862 1224.2302454.655 1428.6572557.97
表2 设备参数
Tab.2 Device parameters

设备整定值参数数 值 OVPDU1/V120(60) U2/V200 U3/V600 t1/s1 t2/s0.1 t3/s0 Rd/W0.004 tre/s5 Rjd/W1×107 UCDUF/V1 UC/V30 Rj/W1×107 R0/W0.02
表3 车辆参数
Tab.3 Train parameters

参 数数 值 编组4B 车重/t196.68 结构速度/(km/h)120 最大加速度/(m/s2)1 最大减速度/(m/s2)1.2
最靠近段场的正线车站的钢轨电位变化情况更能直接反映段场对正线的影响。为此,选取该线路车站22号以及车辆段B的钢轨对地电位进行同步监测。测量时,不同位置的设备检测信号通过GPS同步授时,监测点的详细布置方案如图8所示。
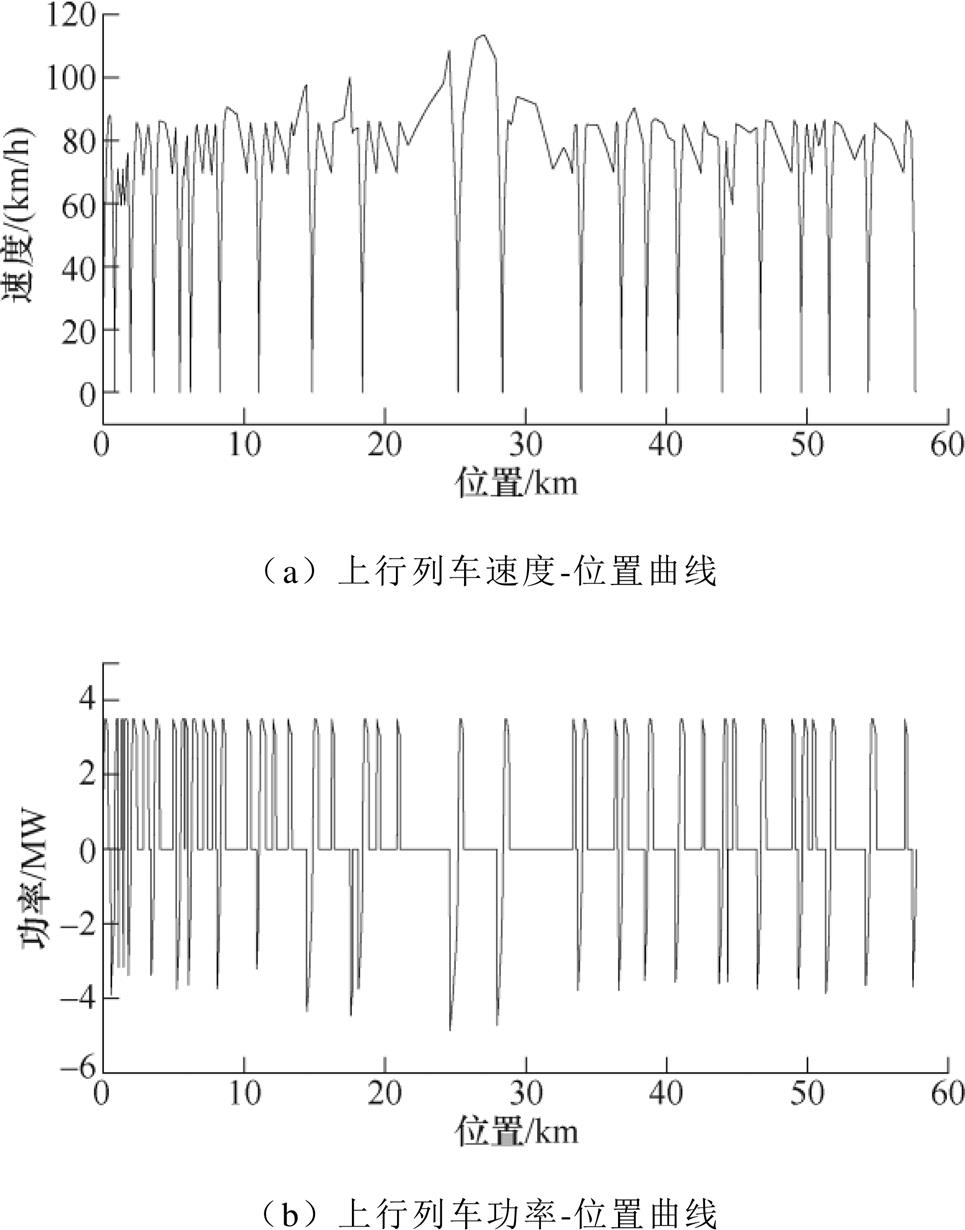
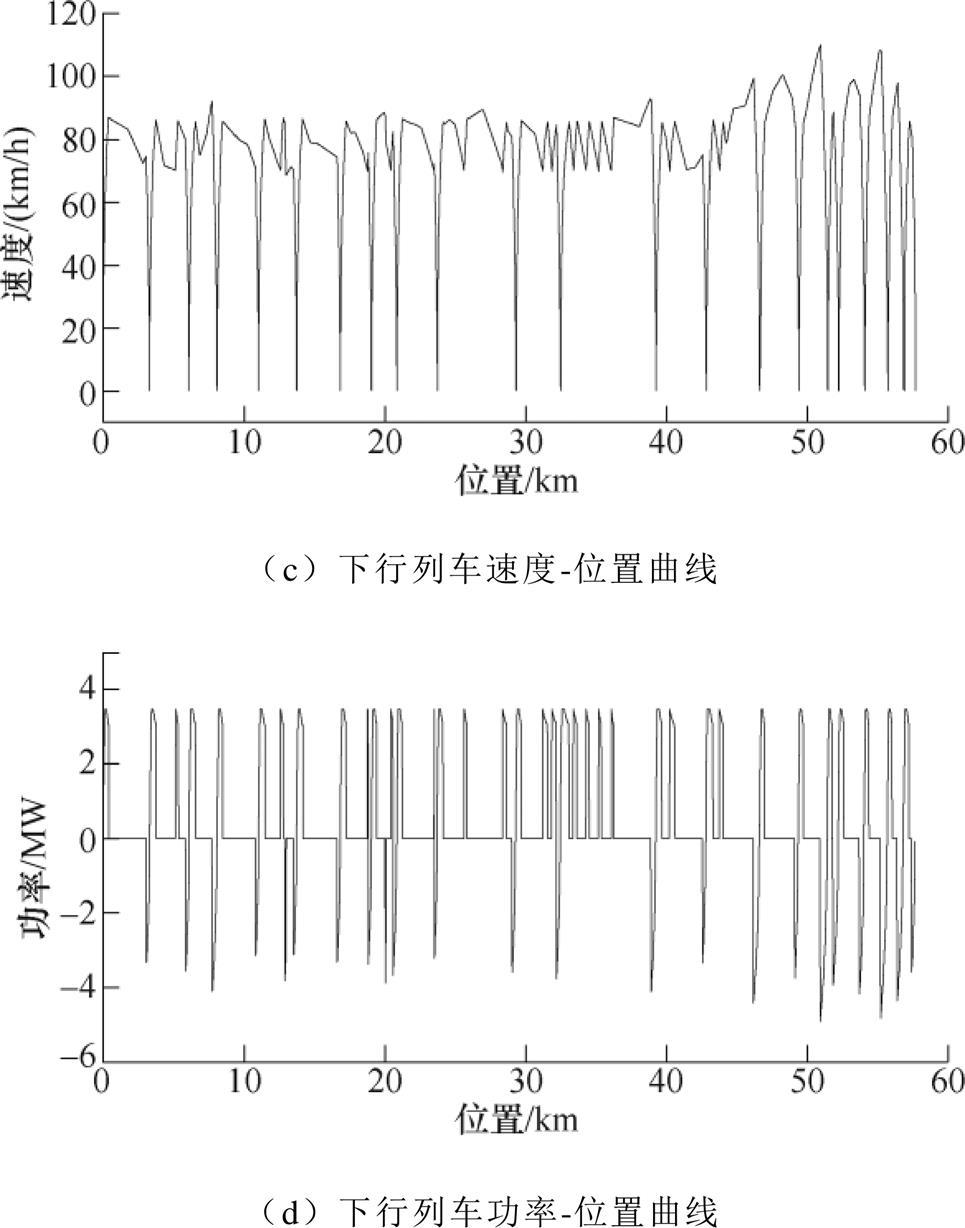
图7 上下行列车运行曲线
Fig.7 Operation curves of up and down train
同时,对该运营线路的钢轨电位进行仿真,并与实测钢轨电位进行比较,车辆段B的OVPD动作前后钢轨电位如图9所示。图9a为车辆段B的钢轨电位变化过程,图9b为车站22号的钢轨电位变化过程,T1和T2分别为车辆段B的OVPD动作与复归时刻。
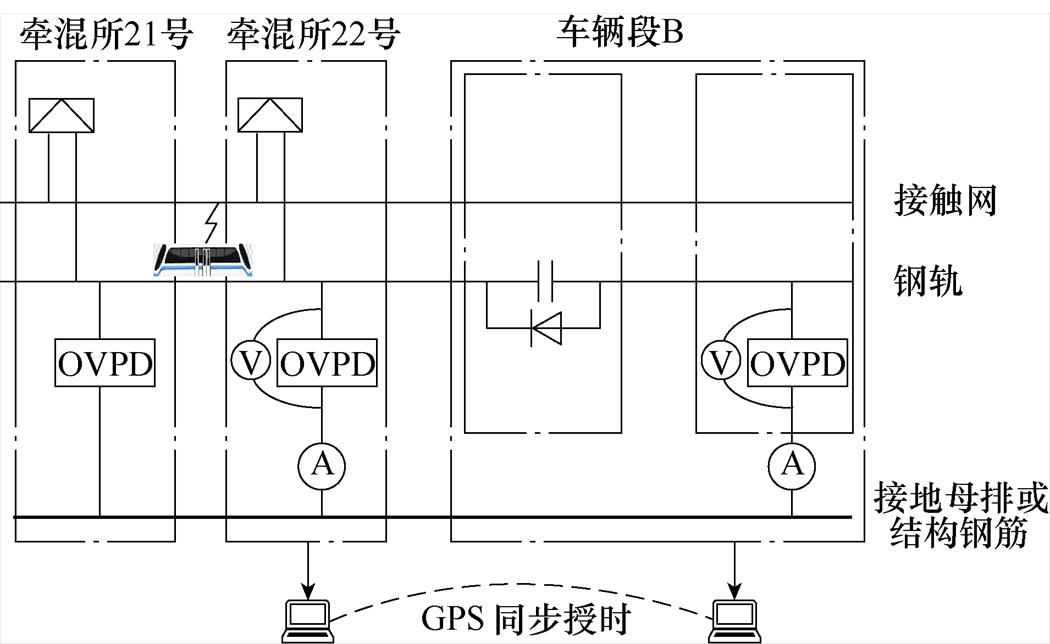
图8 监测点位置分布
Fig.8 Schematic diagram of monitoring installation point
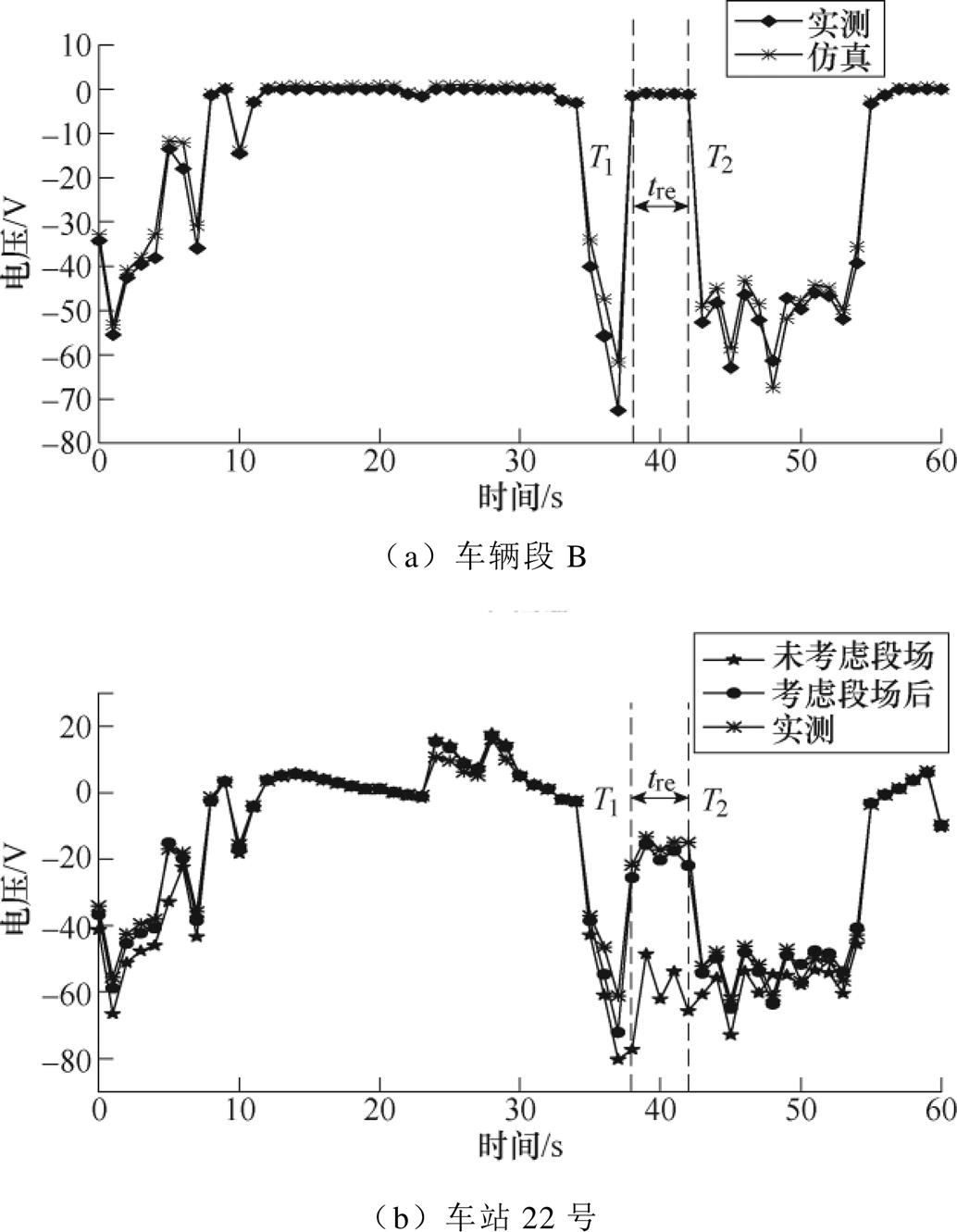
图9 车辆段B的OVPD动作前后钢轨电位
Fig.9 Rail potential before and after OVPD action in depot B
当靠近车辆段B的正线钢轨电位为负时,UCD的二极管环节导通,钢轨电位通过UCD传递至车辆段B内。由于段场内OVPD的整定值为60V,在T1时刻动作,钢轨直接接地,钳制正线的钢轨电位。因此,供电计算中如果不考虑CD和段场内OVPD的行为过程,如车站22号所示,正线和段场的钢轨电位过程仿真差别较大。因仿真条件设置与实际过程中的接触轨授流情况和全线钢轨对地过渡电阻情况不完全一致,仿真与实测结果之间虽然存在一定差异,但在误差允许范围内。其中,考虑段场后的车站22号的钢轨电位仿真结果与实测钢轨电位的Pearson相关系数达到0.99,绝对误差的平均值为1.29V。
为进一步探究不同条件下正线与段场之间的关系,改变仿真条件设置见表4。表中,Qn(U1/V)为段场钢轨采用OVPD悬浮接地时,OVPD的I段整定值,Q0(/)表示段场内钢轨直接接地。
表4 仿真条件设置
Tab.4 Simulation condition setting
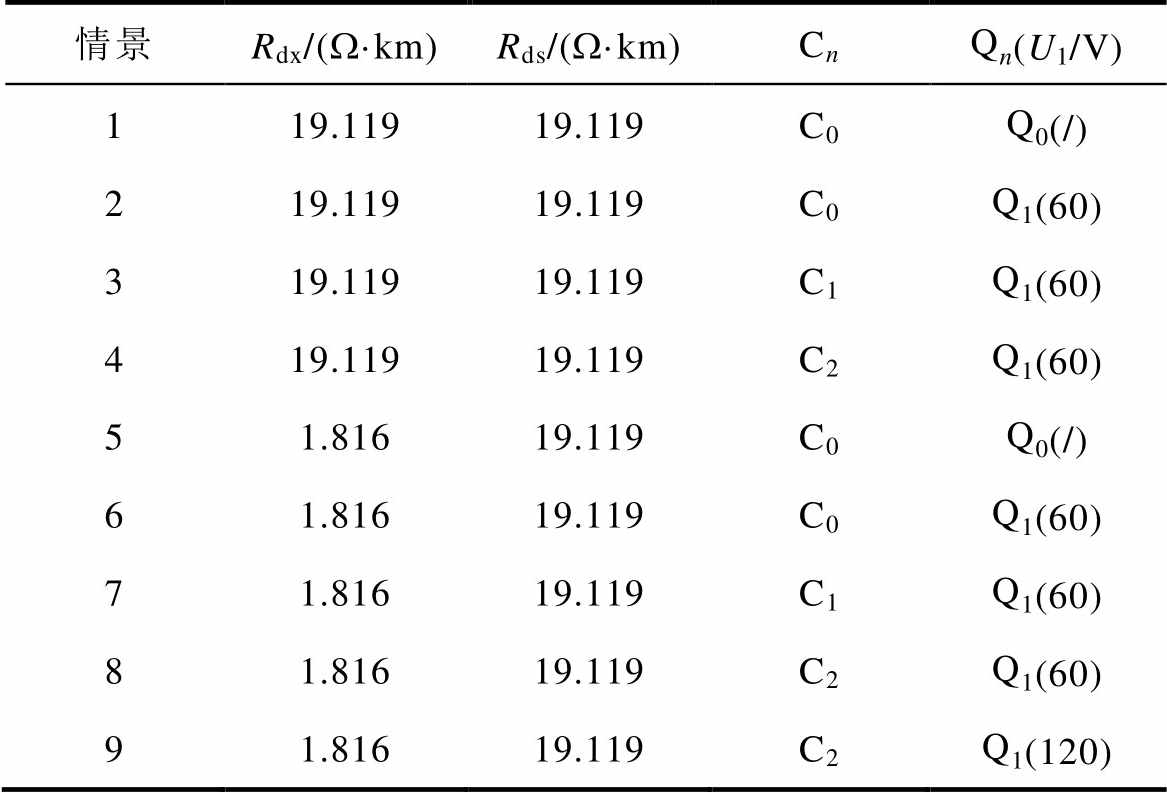
情景Rdx/(W·km)Rds/(W·km)CnQn(U1/V) 119.11919.119C0Q0(/) 219.11919.119C0Q1(60) 319.11919.119C1Q1(60) 419.11919.119C2Q1(60) 51.81619.119C0Q0(/) 61.81619.119C0Q1(60) 71.81619.119C1Q1(60) 81.81619.119C2Q1(60) 91.81619.119C2Q1(120)
对仿真期间890s内段场OVPD动作次数进行统计,动作次数见表5。
表5 段场OVPD动作次数统计
Tab.5 Statistics of OVPD closing times in the parking lot and depot

案例(Case)停车场A车辆段B 1—— 241 300 431 5—— 606 700 806 900
Case2、Case4、Case6和Case8,段场OVPD均多次动作。其中,Case6和Case8中仅车辆段B的OVPD动作。原因是Rdx不达标,钢轨电位普遍偏低,而停车场A距离地下段较近,正线传递至停车场A的钢轨电位未满足OVPD的状态切换条件。而线路首端钢轨对地过渡电阻低,导致线路末端的钢轨电位普遍上升,车辆段B受正线钢轨电位的影响,更加频繁动作。
CD为C0或C2时,仅Case9仿真过程中段场的OVPD没有动作,其原因是Case9中段场OVPD的整定值设定与正线保持一致。正线与段场OVPD的设置均是为了保障人身安全,保持正线和段场OVPD整定值一致,既能兼顾人生安全,又能够有效避免段场OVPD频繁动作。
图10为停车场A钢轨接地支路电流。段场CD为C0或C2,且钢轨直接接地时,大量的杂散电流通过停车场A泄漏或收集,附近的管道及其他金属结构也将受到极其严重的腐蚀。当段场采用OVPD悬浮接地时,只有正线通过CD传递至段场内的钢轨电位满足OVPD的状态切换条件时,OVPD才会动作。OVPD动作后,段场收集或泄漏杂散电流与钢轨直接接地情况基本保持一致。段场采用OVPD悬浮接地能够有效抑制其收集或泄漏的杂散电流。

图10 停车场A钢轨接地支路电流分布情况
Fig.10 Dynamic distribution of stray current of rail grounding branch in depot A
段场CD类型以及钢轨接地方式不同,导致段场对正线造成影响程度也不同。选取Case2车辆段B的OVPD动作前一仿真时刻进行分析,如图11所示,L1、L2分别为表示停车场A、车辆段B与正线钢轨的交界。Case1正线钢轨电位分布与其他仿真条件下的钢轨电位分布有明显差异,Case2、Case4与Case3有略微差异。其原因在于,供电计算时,UCD达到导通条件,而Case1中段场钢轨直接接地,正线钢轨电位立刻被钳制;Case2、Case4中段场钢轨采用OVPD悬浮接地,故仿真得到的钢轨电位基本保持一致。
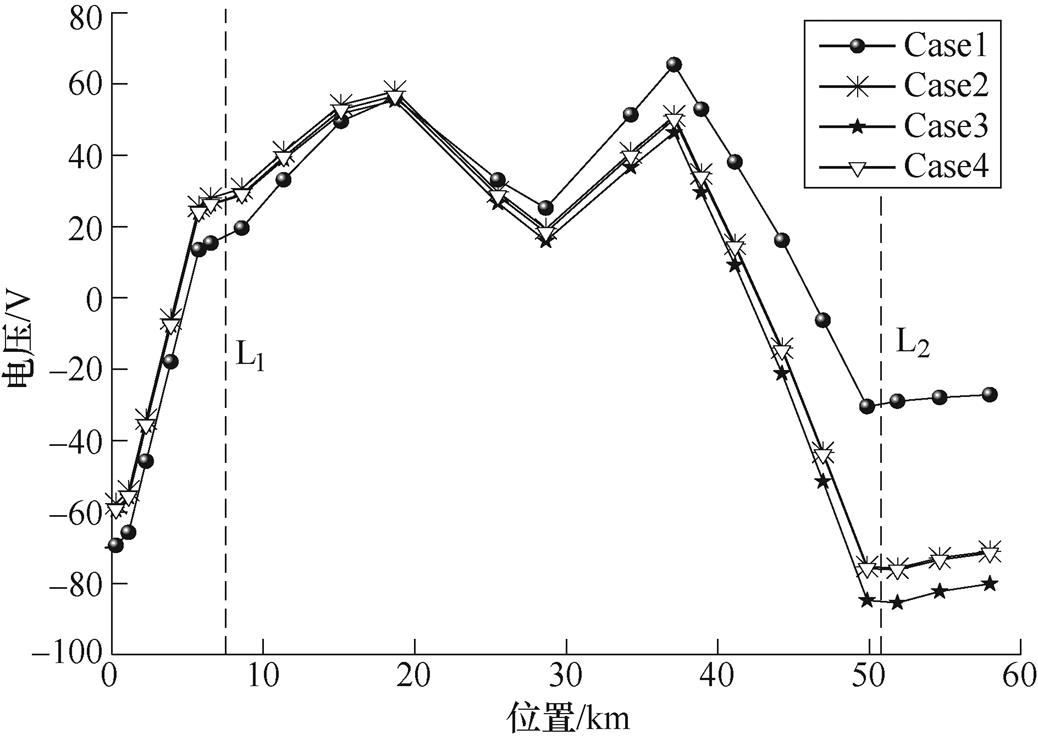
图11 正线钢轨电位分布情况
Fig.11 Simulation of the rail potential distribution in main line
图12为仿真时间段内的正线钢轨电位最值分布情况。Case2、Case3和Case4的正线钢轨电位最值基本保持一致,而Case1差别较大。段场钢轨直接接地会恶化距离段场较远处的正线钢轨电位。其中,车站10号的钢轨电位恶化程度最严重,Umax= 138.101V,Umin=-117.288V,相较于Case3分别提高34.46%和降低33.97%。
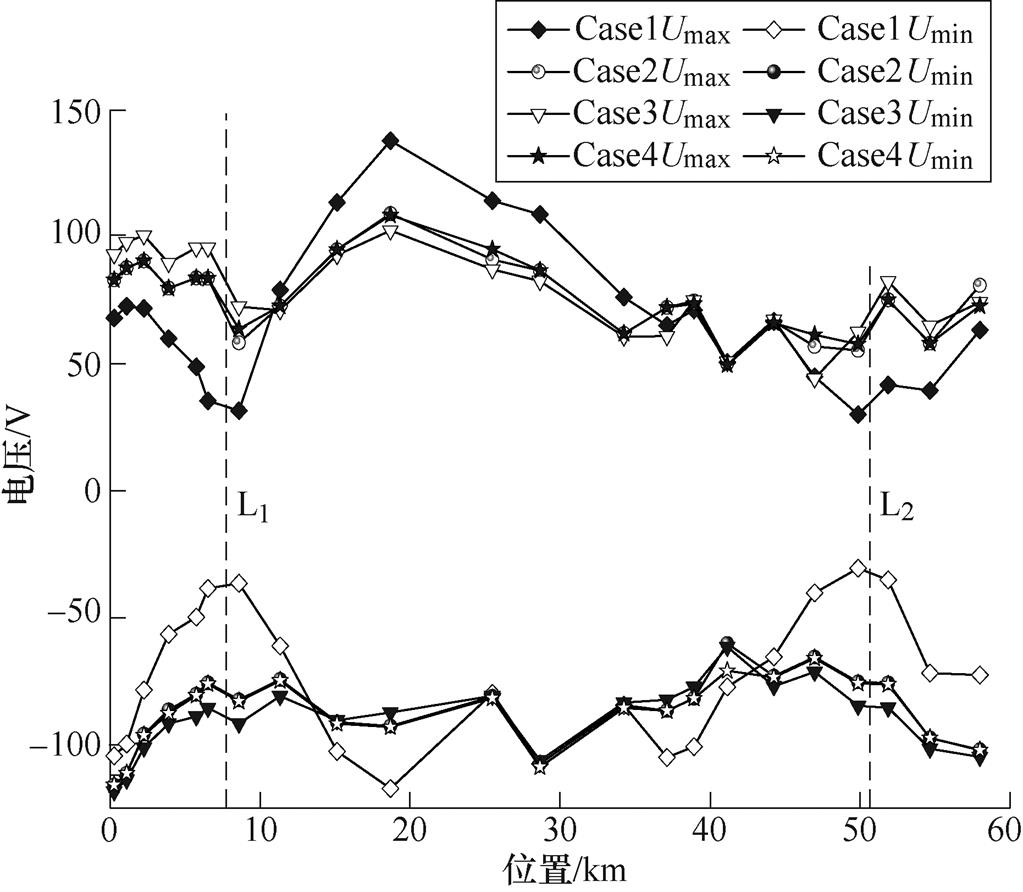
图12 正线钢轨电位最值分布情况
Fig.12 The distribution of maximum and minimum value of rail potential in main line
Case5仿真过程中,车站10号的OVPD在第3s时动作,对比分析OVPD动作前一仿真时刻至复归后的钢轨电位,图13~图15分别为Case5、Case6和Case7正线钢轨电位的动态变化过程。Case6与Case7中钢轨电位基本一致,Case5差别较大。在第2s时(OVPD动作前1s),该站在Case7中钢轨电位达到119.4V,而在Case5中达到127.6V。正线钢轨对地过渡电阻部分区段不达标,易恶化钢轨对地过渡电阻较高区段的钢轨电位至限值附近。Case5和Case6段场均设置UCD,仿真期间仅Case5中正线OVPD动作,段场钢轨直接接地对正线钢轨电位影响程度最大。
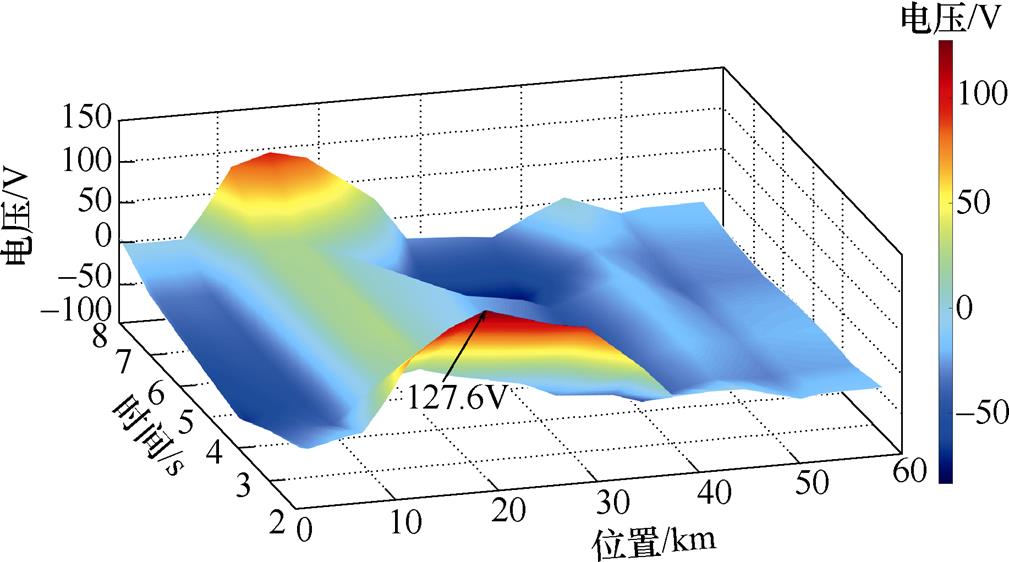
图13 Case5正线钢轨电位动态变化过程
Fig.13 The dynamic change process of main line potential in Case5
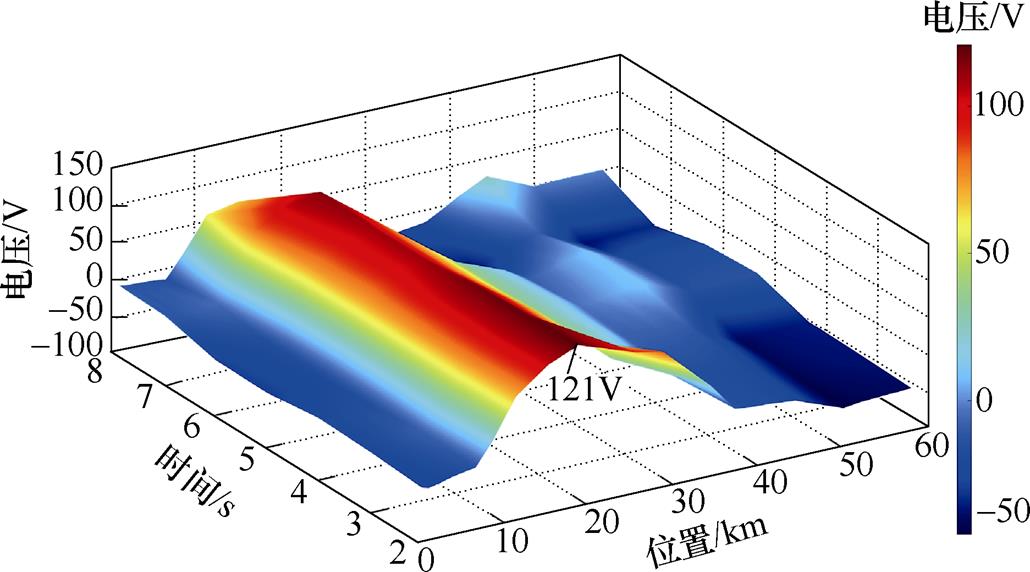
图14 Case6正线轨电位动态变化过程
Fig.14 The dynamic change process of main line potential in Case6
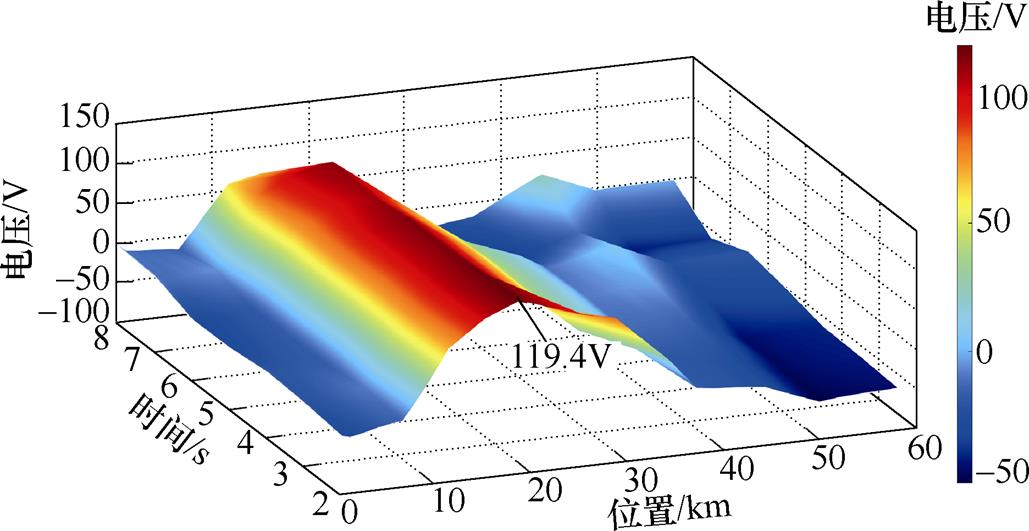
图15 Case7正线轨电位动态变化过程
Fig.15 The dynamic change process of main line potential in Case7
正线OVPD动作后,钢轨直接接地,当有列车在附近牵引时,会有大量电流直接注入大地,图16为该车站OVPD动作前一仿真时刻至复归后的杂散电流泄漏情况。Case5中该车站OVPD动作后,注入电流最高达到1 884.75A。
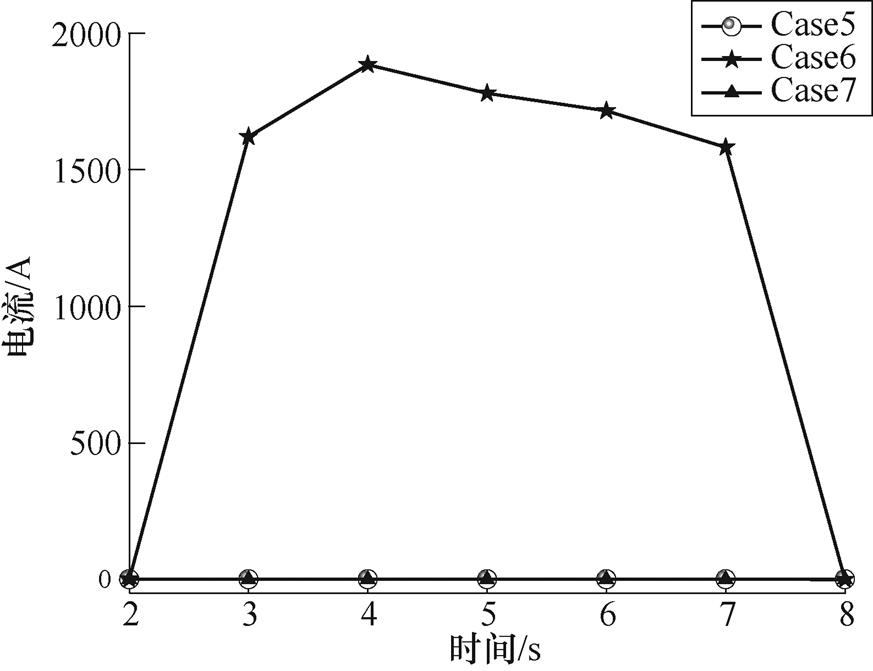
图16 车站10杂散电流泄漏情况
Fig.16 Stray current leakage of station 10 in main line
本文建立了考虑OVPD、CD行为过程和段场接地方式的直流牵引供电系统仿真模型,并通过实测验证了仿真模型在钢轨电位动态计算方面的有效性。主要结论如下:
1)段场钢轨采用直接接地的方式:①会导致段场直接收集正线泄漏的杂散电流,严重腐蚀段场附近的管线等金属结构;②通过UCD的传导,恶化正线的钢轨电位,相较于采用BCD情况,钢轨电位Umax和Umin分别提高了34.46%和降低33.97%。
2)段场采用UCD方案时,当正线钢轨电位为负,钢轨电位传入段场,是段场内OVPD负电位频繁动作的主要原因。段场OVPD频繁动作,反过来又会恶化正线钢轨电位和杂散电流。
3)正线钢轨过渡电阻局部不达标,会恶化其他区段的钢轨电位,传递至段场内,导致段场的OVPD更加频繁动作。在保证人身安全的前提下,提高段场的钢轨电位限值能够减少段场的OVPD动作次数,进而避免段场钢轨频繁接地对正线钢轨电位造成影响。
参考文献
[1] 杨晓峰, 薛皓, 郑琼林. 基于双向可变电阻模块的杂散电流与轨道电位动态模拟系统[J]. 电工技术学报, 2019, 34(13): 2793-2805.
Yang Xiaofeng, Xue Hao, Trillion Q. Zheng. Stray current and rail potential dynamic simulation system based on bidirectional variable resistance module[J]. Transactions of China Electrotechnical Society, 2019, 34(13): 2793-2805.
[2] 李国欣. 直流牵引回流系统分析及轨电位相关问题研究[D]. 徐州: 中国矿业大学, 2010.
[3] Dolara A, Foiadelli F, Leva S. Stray current effects mitigation in subway tunnels[J]. IEEE Transactions on Power Delivery, 2012, 27(4): 2304-2311.
[4] Xu Yishao, Li Wei, Wang Yuqiao. Effects of vehicle running mode on rail potential and stray current in DC mass transit systems[J]. IEEE Transactions on Vehicular Technology, 2013, 62(8): 3569-3580.
[5] Zaboli A, Vahidi B, Yousefi S, et al. Evaluation and control of stray current in DC-electrified railway systems[J]. IEEE Transactions on Vehicular Techno- logy, 2017, 66(2): 974-980.
[6] Rodriguez J V, Feito J S. Calculation of remote effects of stray currents on rail voltages in DC railways systems[J]. IET Electrical Systems in Transportation, 2013, 3(2): 31-40.
[7] 蔡力, 王建国, 樊亚东, 等. 地铁走行轨对地过渡电阻杂散电流分布的影响[J]. 高电压技术, 2015, 41(11): 3604-3610.
Cai Li, Wang Jianguo, Fan Yadong, et al. Influence of the track-to-earth resistance of subway on stray current distribution[J]. High Voltage Engineering, 2015, 41(11): 3604-3610.
[8] 朱峰, 李嘉成, 曾海波, 等. 城市轨道交通轨地过渡电阻对杂散电流分布特性的影响[J]. 高电压技术, 2018, 44(8): 2738-2745.
Zhu Feng, Li Jiacheng, Zeng Haibo, et al. Influence of rail-to-ground resistance of urban transit systems on distribution characteristics of stray current[J]. High Voltage Engineering, 2018, 44(8): 2738-2745.
[9] 杜贵府, 张栋梁, 王崇林, 等. 直流牵引供电系统电流跨区间传输对钢轨电位影响[J]. 电工技术学报, 2016, 31(11): 129-139.
Du Guifu, Zhang Dongliang, Wang Chonglin, et al. Effect of traction current transmission among power sections on rail potential in DC mass transit system[J]. Transactions of China Electrotechnical Society, 2016, 31(11): 129-139.
[10] 地铁设计规范: GB 50157-2013[S]. 北京: 中国建筑工业出版社, 2013.
[11] 陈民武, 赵鑫, 丁大鹏, 等. 城市轨道交通供电系统钢轨电位限制装置操作过电压研究[J]. 中国铁道科学, 2017, 38(6): 94-99.
Chen Minwu, Zhao Xin, Ding Dapeng, et al. Research on switching surge of rail over-voltage protection device in power supply system for urban rail transit[J]. China Railway Science, 2017, 38(6): 94-99.
[12] Du Guifu, Wang Jun, Jiang Xingxing, et al. Evalu- ation of rail potential and stray current with dynamic traction networks in multitrain subway systems[J]. IEEE Transactions on Transportation Electrification, 2020, 6(2): 784-796.
[13] 黄蕾, 杜贵府, 王俊, 等. 城轨回流系统动态排流与钢轨电位控制仿真研究[J]. 铁道标准设计, 2019, 63(10): 152-158.
Huang Lei, Du Guifu, Wang Jun, et al. Simulation of dynamic drainage and rail potential control in urban rail power supply system[J]. Railway Standard Design, 2019, 63(10): 152-158.
[14] 刘炜, 吴拓剑, 禹皓元, 等. 直流牵引供电系统地面储能装置建模与仿真分析[J]. 电工技术学报, 2020, 35(19): 4207-4215.
Liu Wei, Wu Tuojian, Yu Haoyuan, et al. Modeling and simulation of way-side energy storage devices in DC traction power supply system[J]. Transactions of China Electrotechnical Society, 2020, 35(19): 4207- 4215.
Dynamic Simulation of Rail Potential Considering the Equipment Behavior Process of Recirculation System
Abstract The abnormal rail potential in the DC traction power supply system has attracted more and more attention. In order to control the stray current and rail potential, the rail potential limiter over-voltage protection device (OVPD), the connection device connection device (CD) and other equipment are widely used in operating lines. The dynamic distribution of rail potential will be significantly changed with the state switching of the equipment. When establishing the equivalent circuit model of the recirculation system, not only the main line should be considered, but also the parking lot/depot and the behavior of recirculation equipment. To this end, this paper established a general model of parking lot/depot equivalent circuit and OVPD. And a DC traction power supply calculation method is proposed considering the behavior of the recirculation devices. Taking an actual subway project as a simulation example, the calculation results with the proposed algorithm are more consistent with the rail potential change process in the actual project. On this basis, the interaction between the main line and the parking lot/depot was discussed and analyzed. The results show that the setting of the unidirectional connection device (UCD) of the parking lot/depot cannot avoid the interaction between the main line and the parking lot/depot, and the direct grounding of rail in parking lot/depot is more likely to deteriorate the rail potential of the main line. Compared with the case of a blocking connection device (BCD) between the main line and parking lot/depot, the rail potential Umax and Umin in main increased by 34.46% and decreased by 33.97%, respectively.
keywords:DC traction power supply system, connection device, rail potential, stray current
DOI: 10.19595/j.cnki.1000-6753.tces.210024
中图分类号:TM922.3
刘 炜 男,1982年生,副教授,研究方向为牵引供电系统理论与仿真、杂散电流与钢轨电位和再生制动能量利用。E-mail: liuwei_8208@swjtu.cn(通信作者)
杨 龙 男,1997年生,硕士研究生,研究方向为杂散电流与钢轨电位。E-mail: 572841475@qq.com
收稿日期 2021-01-07
改稿日期 2021-03-03
国家重点研发计划子课题:基于车-地-轨耦合的杂散电流评估与控制技术资助项目(2017YFB1201103-05)。
(编辑 陈 诚)