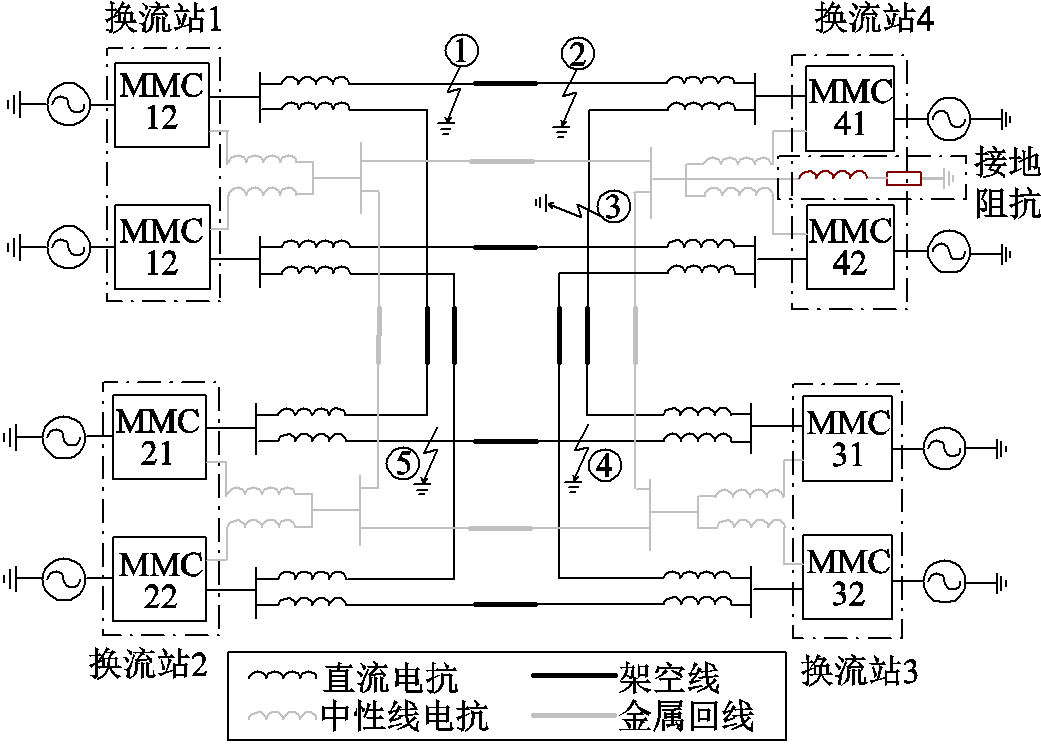
图1 四端MMC-HVDC电网
Fig.1 Four-terminal MMC-HVDC grid
摘要 对于采用架空线的基于模块化多电平换流器的高压直流(MMC-HVDC)电网,直流侧接地短路故障发生率高,严重危害电网安全。在各类影响因素中,接地方式对故障电流演化影响明显。该文从系统的宏观能量转移与耗散的角度提出了基于暂态能量流(TEF)分析的接地参数优化方法,对接地电阻、电抗参数及接地点位置等因素对MMC-HVDC电网直流短路故障电流的演化影响进行了分析。该方法以TEF抑制率和抑制效率为优化目标,以直流电网中接地阻抗参数取值、接地点为优化变量,同时考虑了中性线电抗和故障点的影响。该文选取四端双极MMC-HVDC电网中的直流单极接地故障(PTGF)算例,基于PSCAD/EMTDC搭建了仿真模型进行分析和优化。仿真结果表明该参数优化方法能有效地指导接地参数的设计,抑制直流故障电流和健全极过电压。
关键词:基于模块化多电平换流器的高压直流电网 暂态能量流 接地参数优化 限流效果
模块化多电平变换器(Modular Multilevel Converter, MMC)自21世纪初问世以来,以其低损耗、波形质量高、制造难度低和阶跃电压低[1-3]等明显优势在近年来获得快速发展。预计其在新能源并网方面具有良好的应用前景,有望成为未来构建高压直流(High Voltage Direct Current, HVDC)电网的关键技术[4-6]。其中,采用半桥子模块(Half Bridge Sub Module, HBSM)的基于模块化多电平变换器的高压直流(MMC-HVDC)电网以其成本优势成为目前应用的主流,如,典型应用案例张北示范工程。然而,这种子模块拓扑下的换流器不具备故障自清除能力,因此必须依靠其他保护设备——直流断路器(DC Circuit Breakers, DCCB),切断故障线路实现故障清除与恢复[7-9]。
依据现有的HVDC电网结构,主要分为对称单极接线与双极接线两种形式。其接地方式可分为交流侧接地和直流侧接地两种类型[10]。交流侧接地包括联接变压器阀侧经星形连接电抗器串联电阻接地,联接变压器中性点串电阻或大电抗接地,主要用于对称单极系统;直流侧接地包括中性点经钳位电容或电阻接地,主要用于双极结构。现有文献对不同接地方式下的故障机理进行了充分分析[11]。文献[12]针对基于电压源换相的高压直流输电(Voltage Source Converter based HVDC, VSC-HVDC)系统,对不同接地方式下的电网谐波特性、交流母线故障特性及直流线路故障特性进行了仿真研究,分析得出滤波器中性点与直流电容中点相连并通过高阻接地对于提高VSC-HVDC系统的性能更加有利。文献[13]以基于MMC的海上风电外送电网模型对交流侧接地方式下多种故障情况进行了仿真分析,认为在过电压特性方面,变压器阀侧三种接地方式最大过电压水平相似,均可作为海上风电柔直系统的接地方式。
以上研究主要针对称单极接线方式、单极对地故障(Pole-to-Ground Short Circuit Fault, PTGF)对系统性能做了多方面的分析。与单极接线方式系统不同,双极HVDC电网,由于接线形式的差异,通常采用直流侧中性点直接接地,或经金属回线接电阻或电抗接地。相比单极电网,双极电网可以提高可靠性并减少单极大地大负荷运行时对环境的影响[14],如张北工程即采用金属回线接15Ω电阻接地[15]。文献[16]对比了两种接地方式,结果显示金属回线能保证换流站直流中性点电压相同,且系统出现接地故障时大地仅存一个故障通路,可减小故障电流对人和电气设备的潜在危害,更适用于多端柔性直流电网。文献[17]分析了对张北工程发生PTGF时健全极过电压机理,认为产生健全极过电压的主要原因是金属回线中故障电流的流通导致的中性点电位的抬升,并得出接地极电阻和中性线电抗对中性点电位影响较大的结论。这些文献充分分析论证了合适的接地方式在双极MMC-HVDC电网中的重要作用,但多停留在机理分析阶段,多关于金属回线问题,电网系统内接地阻抗、接地地点的具体设置的优化方面鲜有涉及。因此分析接地位置对MMC-HVDC电网PTGF的影响,并对其规划提出合理性建议具有重要的意义。
直流侧短路故障打破了原有的系统能量平衡状态,使得系统电容和电感之间存在大量的能量交换,并伴随着电流和电压的剧烈变化。因此,如果能够从抑制元件或支路注入/吸收的电磁暂态能量出发,分析接地方式及参数对MMC-HVDC电网故障电流时空演化的规律,则更能把握问题的本质。为此,本文提出了暂态能量流(Transient Energy Flow, TEF)的分析指标,并基于TEF分析了直流侧PTGF条件下,接地方式对直流故障演化的影响。相对于传统的以故障电流为主的分析方法,TEF具有以下几个优点:①TEF可由暂态功率计算得到。因此,在对短路故障进行优化分析时,相较于故障电流和电压,TEF能够从能量的角度统一、综合地反映电压和电流故障特征的时空分布演化。这样,可以将不同因素对故障电流演化的影响采用统一的指标来进行量化评价。②TEF是功率在一段时间内的积分,反映了故障电流、电压的持续作用产生的累积影响。这种累积影响在实际工程中一直被关注,例如在对断路器进行设计时,不仅需要满足故障电流峰值的要求,还要满足所提供的总能量的要求。
本文针对半桥子模块型的MMC-HVDC电网,详细分析了变换器交流侧注入、子模块电容及相邻线路三部分的TEF抑制率与抑制效率,并基于此形成对应的TEF综合目标函数,以接地点及接地阻抗参数为优化变量,同时考虑故障位置与中性线电抗的影响,从而构建完整的优化模型。通过建立四端双极MMC-HVDC电网PTGF的PSCAD/EMTDC模型,对所提出的模型的有效性进行了验证。
考虑到柔性直流电网的建设成本及检修问题,架空线路更为广泛地被接受。但是架空线路故障率更高,其主要是PTGF和双极短路故障,而双极短路故障的故障回路中并不包括接地阻抗。对于换流器而言,又以其出口处发生金属性PTGF最严重。因此,本文主要研究双极系统中PTGF条件下接地参数(R或L)、中性线电抗设计与接地点设置优化问题。
对于直流电网,其主要通过增加故障回路阻抗来达到限制故障电流的目的。接地阻抗和中性线电抗均处在故障后的电流放电回路中。但由于稳态时接地极不存在电流,则其不会影响系统的稳态运行。
四端双极MMC-HVDC电网结构如图1所示[18],此结构采用金属回线作为接地极。目前,换流站子模块多采用半桥型结构,发生直流侧故障后,无法通过闭锁子模块来清除故障电流。

图1 四端MMC-HVDC电网
Fig.1 Four-terminal MMC-HVDC grid
直流电网发生PTGF时,对于交流侧,相当于三相短路,对于直流侧,忽略交流影响的条件下,主要表现为子模块电容放电的二阶电路。双极MMC-HVDC电网故障两端等效结构相同,只是存在电网结构参数带来的故障回路阻抗的差异。
不同接地方式下换流站出口处发生单极接地故障的故障极电流及健全极电压波形如图2所示,各接地方式的参数见表1。
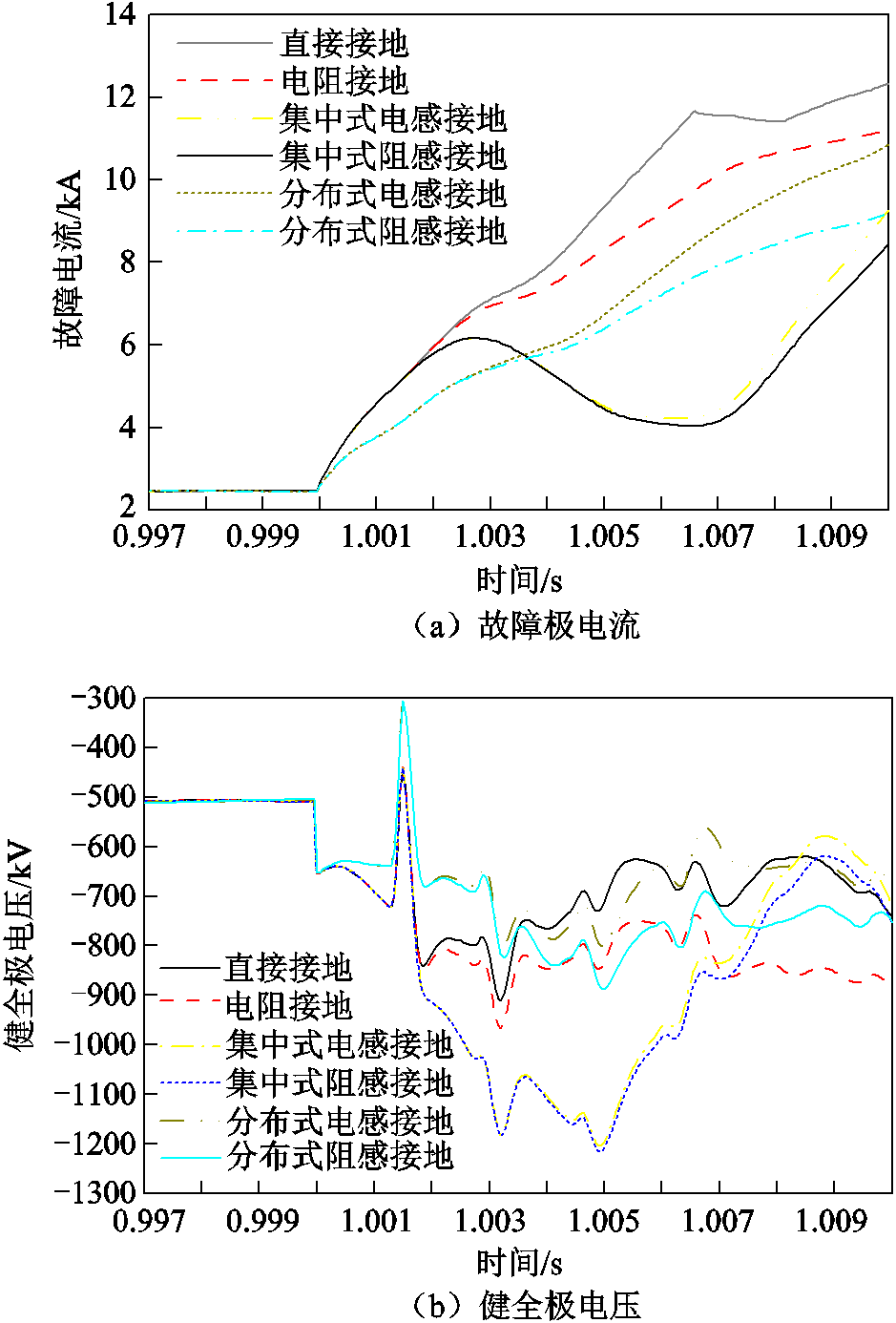
图2 不同接地方式故障电流和健全极电压
Fig.2 Fault current and sound pole voltage of different grounding modes
表1 不同接地方式的接地参数值
Tab.1 Grounding parameter values of different grounding modes
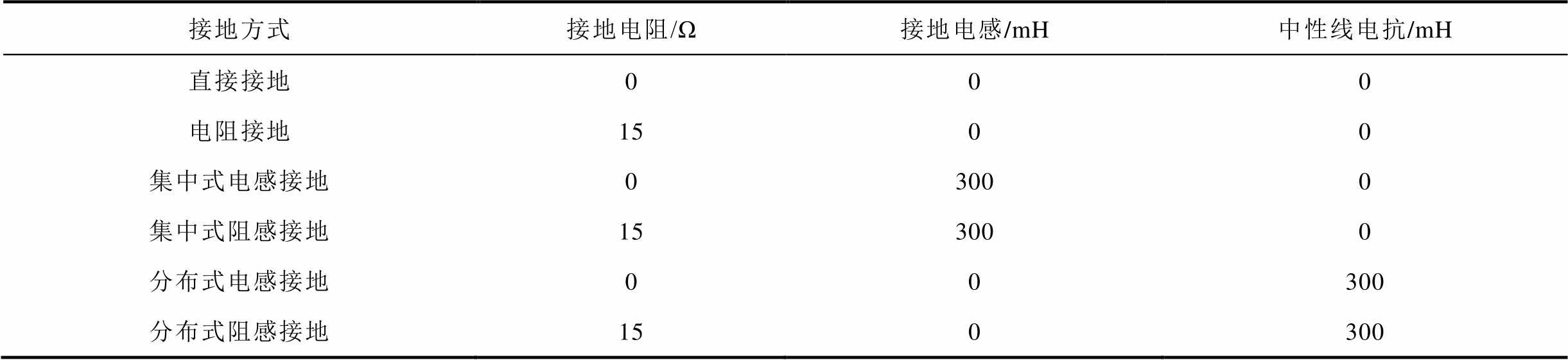
接地方式接地电阻/Ω接地电感/mH中性线电抗/mH 直接接地000 电阻接地1500 集中式电感接地03000 集中式阻感接地153000 分布式电感接地00300 分布式阻感接地150300
从图2a可以看出,故障发生后3ms内分布式接地对故障电流峰值和上升率的抑制效果最佳,而故障发生后6ms内集中式接地对故障电流峰值和上升率的抑制效果更佳。由图2b可以看出,集中式接地的健全极过电压水平最高,分布式接地的过电压水平最低。因此,本文后续仅针对分布式和集中式接地涉及的接地电阻、接地电感和中性线电抗进行优化。
对于MMC-HVDC电网,本文采用的TEF是指元件在故障后的电磁暂态过程中吸收或释放的瞬时能量,或者某一支路流入或流出的瞬时能量[19],整体上包括换流站交流系统能量、直流侧能量及换流站内部能量三部分。
具体电感、电容和电阻的TEF为
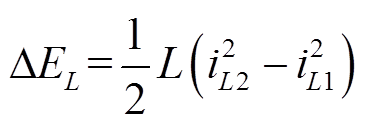 (1)
(1)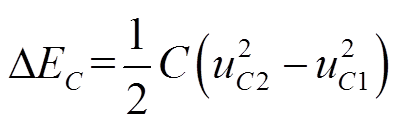 (2)
(2)
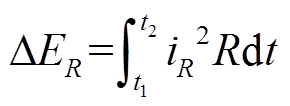 (3)
(3)
式中,ΔEL、ΔEC、ΔER分别为电感、电容和电阻在时间区间[t1,t2]内的TEF;iL、iC和uL、uC分别为电感、电容的电流和电压;iR为电阻电流。相应的TEF变化率为
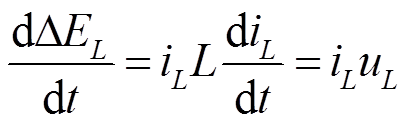 (4)
(4)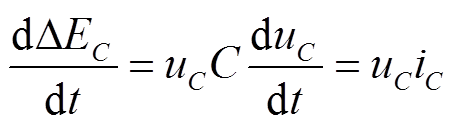 (5)
(5)
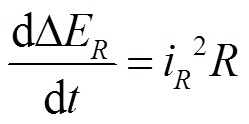 (6)
(6)
由此可见,各元件TEF的变化率就是自身的瞬时功率。
对于直流侧和线路TEF,计算公式为
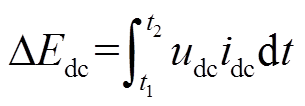 (7)
(7)式中,idc和udc分别为直流出口处或者架空线路上的电流和对地电压。其变化量为
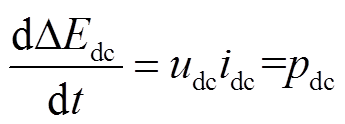 (8)
(8)
式中,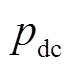 为换流站出口处直流侧功率或线路功率。类似地,基于瞬时功率理论,交流侧输入系统的瞬时功率(即暂态能量流变化率)
为换流站出口处直流侧功率或线路功率。类似地,基于瞬时功率理论,交流侧输入系统的瞬时功率(即暂态能量流变化率)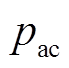 为
为
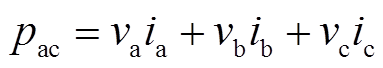 (9)
(9)式中,vj和ij分别为交流侧瞬时三相电压和电流,j=a,b,c。其交流侧TEF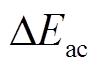 为
为
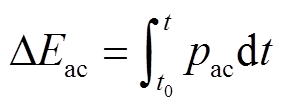 (10)
(10)
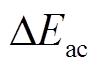 变化率即为
变化率即为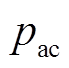 。依据以上公式,交流侧TEF正、负分别代表积分时间段内交流能量的输出或吸收,其余TEF的正、负分别代表积分时间段内能量的吸收(或消耗)与释放。TEF绝对值越大表明元件或区域的能量增加(或减少)越快,反之越慢。
。依据以上公式,交流侧TEF正、负分别代表积分时间段内交流能量的输出或吸收,其余TEF的正、负分别代表积分时间段内能量的吸收(或消耗)与释放。TEF绝对值越大表明元件或区域的能量增加(或减少)越快,反之越慢。
从式(1)~式(10)可看出, TEF的变化率本质上是各元件或区域的瞬时功率。在实际计算过程中,元件或区域TEF可通过电磁暂态仿真数据直接量测或简单的电压电流乘积计算获得,不需要建立复杂的能量模型。通过这种数据驱动的方式,可以分析电感、电容和电阻等元件参数的摄动影响。
为定量评价接地阻抗对故障电流的抑制效果,本文提出了TEF抑制率与抑制效率的概念。
基于能量守恒定律,对电网一端换流站有
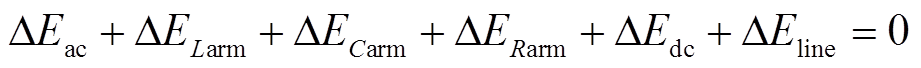 (11)
(11)式中,ΔEdc为直流侧(包括直流限流电抗器)TEF;ΔEac、ΔELarm、ΔECarm、ΔERarm、ΔEline分别为交流侧、桥臂电感、桥臂电容、桥臂电阻及故障点一端换流站相邻线路TEF。
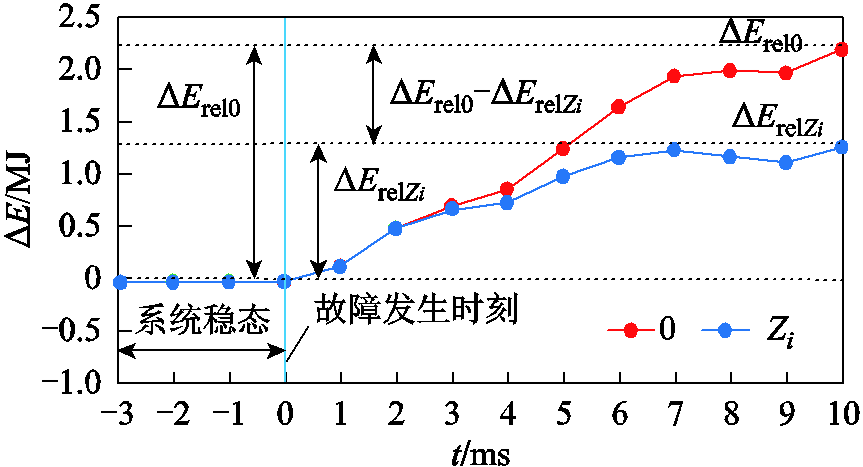
对于多端MMC-HVDC电网的整流侧换流站,其能量流包括式(11)中的六个部分。稳态条件下,能量释放的主要来源是交流系统;PTGF暂态条件下,直流电网保护要求故障电流被抑制到IGBT闭锁电流值以下,保证半桥子模块的IGBT不因过电流而闭锁。因此,MMC-HVDC电网中,故障点一侧的能量主要释放源是交流系统、桥臂电容及相邻线路馈入能量。而对于能量的吸收(或消耗)部分,构成则较为复杂,包括换流器桥臂电感、桥臂电阻、直流侧限流电感、线路及直流侧等效负荷等。对于逆变侧换流站,不同的是,交流侧从能量吸收转变为能量释放,但故障后TEF峰值阶段能量传递特性与整流侧相同。因此,为了方便分析,基于式(11),将各暂态能量源的TEFΔErel(代指交流侧,桥臂电容或相邻线路TEF)作为研究对象,通过研究ΔErel消涨来分析接地参数的限流效果。对于电网系统,TEF的波动越小表明系统能量传输越稳定,在故障初始能量相同的条件下,TEF越小表明能量释放越缓慢,即故障发展越缓慢。据此,本文提出TEF抑制率及TEF抑制效率的概念,考虑到直流断路器保护要求在故障发生后10ms内完成故障清除,以直接接地时故障发生后10ms内ΔErel的峰值为基准值,记为ΔErel0,则不同接地方式及接地参数下能量释放侧TEF抑制率λZi定义为
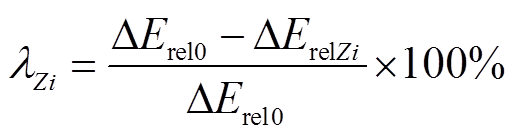 (12)
(12)式中,ΔErel0为直接接地即接地阻抗为0时,从故障开始时刻至故障发生后10ms内元件或区域TEF峰值,即元件或区域暂态能量波动值的峰值;ΔErelZi为接地阻抗为Zi时,从故障开始时刻至故障发生后10ms内元件或区域TEF的峰值。
因此,式(12)中,分母表示采用直接接地措施即接地阻抗值为0时,故障发生后的10ms内TEF的峰值,分子表示故障发生后的10ms内接地阻抗为0时TEF与接地阻抗为Zi时TEF差值,其含义为,接地参数变化引起的TEF的变化量。式(12)体现了接地参数变化时相对于接地参数为0时其抑制元件或区域暂态能量波动的能力。ΔErel0、ΔErelZi含义如附图1所示。于是,相应的TEF抑制效率kλZi可以表示为
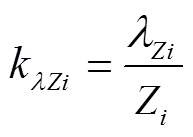 (13)
(13)式(13)的含义为,接地阻抗元件每mH或每Ω抑制TEF释放的能力,体现了接地阻抗元件抑制暂态能量的经济性。Zi=0的情况表示接地阻抗值为0即直接接地时的情况,这种情况在优化变量的取值中被排除在外,在后续的抑制效率计算中Zi不会取为0。Zi=0的情况只提取其TEF,作为不同接地阻抗值Zi下的抑制率的计算基准。
利用式(12)可以获得有接地阻抗下与直接接地时TEF的抑制比例。正值代表TEF减小,能量增长放缓,数值越大,增速下降越大;负值代表TEF增大,能量增长加速,绝对值越大,增速增长越大。对于故障条件下,希望TEF抑制率为正且越大越好。式(13)进一步计算了单位电阻或电抗的抑制率,从而定量评价不同参数接地阻抗的抑制效率的高低,体现接地参数配置的经济性。
本文将以抑制率和抑制效率为目标对接地阻抗值、中性线电抗值及直流电网的接地地点三个因素进行优化配置,优化模型为
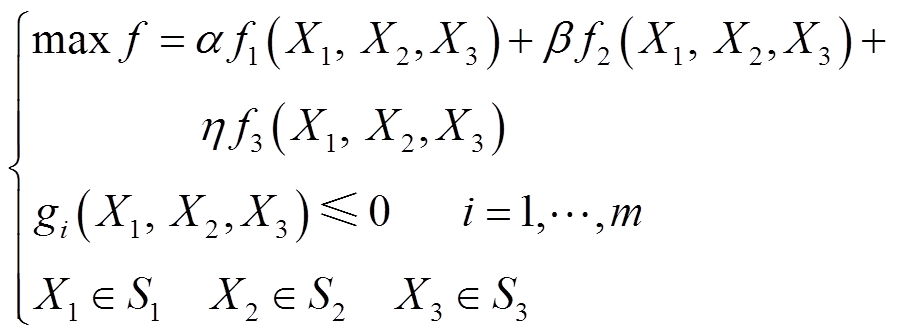 (14)
(14)式中,f为优化目标函数;α、β和η为权重;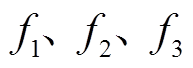 为子目标函数;
为子目标函数;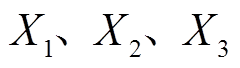 为待优化的变量;
为待优化的变量;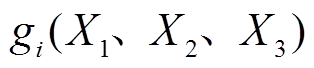 为约束函数;m为约束条件的数量;
为约束函数;m为约束条件的数量; 分别为
分别为 的取值范围。
的取值范围。
2.2.1 目标函数
基于2.1节定义的抑制率与抑制效率,将二者结合形成评价不同接地方式对故障的抑制效果的函数。为此,对二者进行了标幺化处理。能量释放侧的交流侧、桥臂电容或相邻线路TEF的三部分子目标函数f1、f2、f3定义为
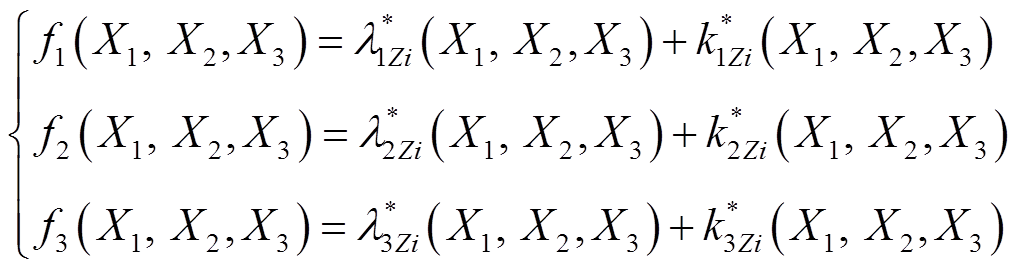 (15)
(15)式中,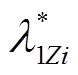 和
和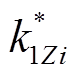 分别为交流侧TEF抑制率与抑制效率的标幺值;
分别为交流侧TEF抑制率与抑制效率的标幺值;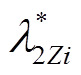 和
和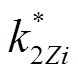 分别为桥臂电容TEF抑制率与抑制效率的标幺值;
分别为桥臂电容TEF抑制率与抑制效率的标幺值;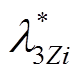 和
和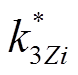 分别为相邻线路TEF抑制率与抑制效率的标幺值。
分别为相邻线路TEF抑制率与抑制效率的标幺值。
2.2.2 优化变量
连续变量X1和X2代表接地电阻和接地电抗,整数变量X3代表接地点位置,即
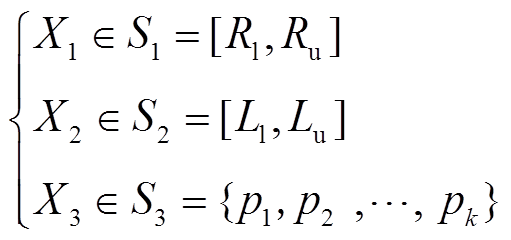 (16)
(16)式中,Rl和Ll分别为接地电阻值和接地电抗值的下限;Ru和Lu分别为接地电阻值和接地电抗值的上限;pk为接地点位置;k为不同的换流站。
2.2.3 约束条件
对于采用金属回线的直流电网,在直流故障电流的作用下,非故障极线路电压在故障后迅速抬升,而接地阻抗的存在会加剧这一过程。过大的过电压水平会对各部分作为保护用的避雷器提出更高的要求,从而提高了建设成本。因此需要对其过电压水平进行限制,以将绝缘压力降低到一定水平,可表示为
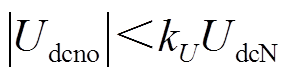 (17)
(17)式中,Udcno为非故障极直流电压;kU为非故障极电压的过电压系数;UdcN为直流额定电压。文献[20]推荐,双极MMC-HVDC电网直流侧接地故障时过电压水平应不大于2.0(pu),则此处取2.0(pu)。
2.2.4 优化方法
由于优化变量取值范围有限,本文采用枚举法对中性线电抗、接地阻抗参数及接地点位置进行优化,简单而有效。目标函数所需数据均可以通过PSCAD仿真获得,这为枚举法的应用带来方便。
以张北柔性直流电网工程为基础,在PSCAD/EMTDC中搭建四端双极MMC-HVDC电网。图1所示的直流电网中,换流站1和2是送端,换流站3和4是受端。各换流站中性点通过金属回线连接,在定电压控制的换流站4处接地。其中,MMCx1和MMCx2分别代表换流站x(x=1,2,3,4)的正负换流阀。直流电网的具体参数见附表1。本文以工程上典型的接地参数值作为优化的基础。
假设系统初始运行于稳态,在t=1s时,换流站出口处发生PTGF(故障接地电阻0.01Ω)。考虑到直流电网要求必须在故障发生后10ms内实现故障清除,这里采用故障发生后10ms,即1~1.01s内的数据进行分析。直流故障发展是ms级的,TEF计算采用的积分步长Δt=t-t0=1ms。本文所搭建的仿真系统中采样步长为50ms,在利用式(1)~式(10)计算暂态能量流时,是对每1ms时间段内20个采样点求取平均值后,用平均值乘以时间1ms作为其1ms的TEF值,可以有效抑制高频分量的干扰。其中,接地电阻值设置为0~50Ω,参数间隔5Ω,接地电感值设置为0~500mH,参数间隔50mH,即各次试验均为11组。同时考虑不同故障点的影响,设置5个不同的出口处PTGF如图1所示。同时考虑接地点的影响,在四个换流站依次接地。
在3.1节实验数据基础上,对实验中各部分的TEF进行了定量分析,同时计算目标函数值并进行比较。MMC1能量释放侧TEF如图3所示。
图3a是换流站4接地,中性线电抗300mH,故障点1发生PTGF,分别采用0Ω、15Ω、30Ω电阻接地时故障发生后10ms内,MMC1交流侧TEF、桥臂电容TEF和相邻线路TEF占三者之和ΔEsumZi的比例随时间的变化,通过式(18)计算获得。
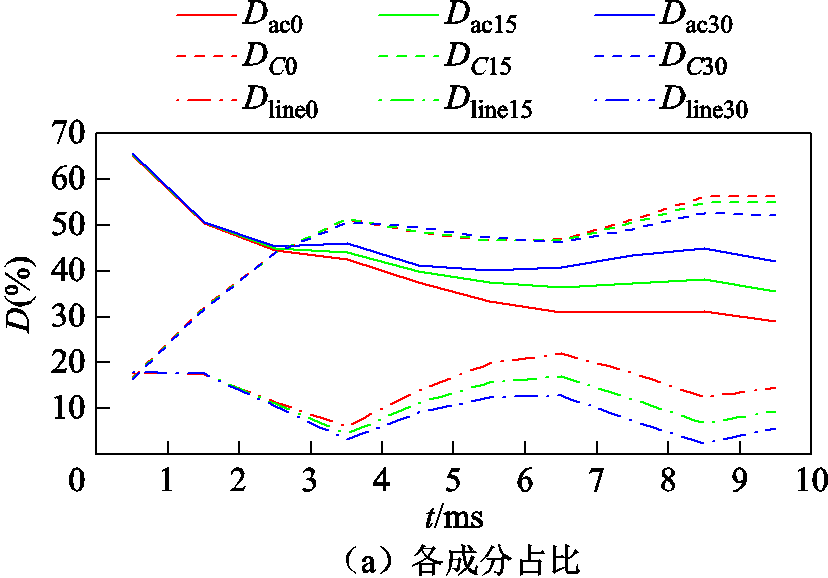
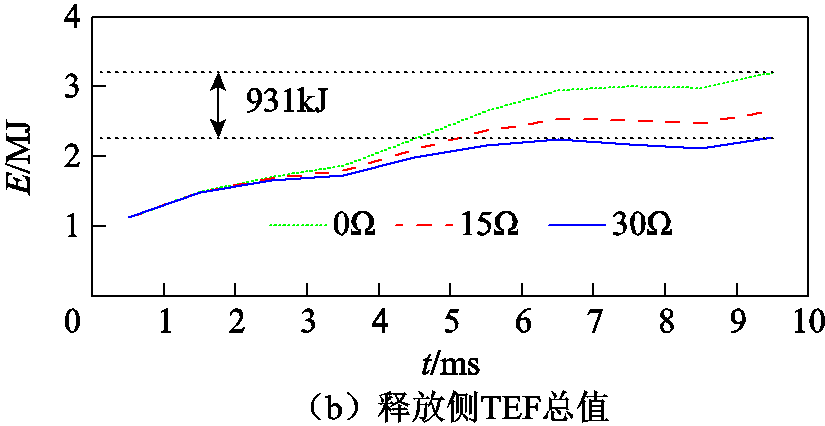
图3 MMC1能量释放侧TEF
Fig.3 TEF at MMC1 energy release side
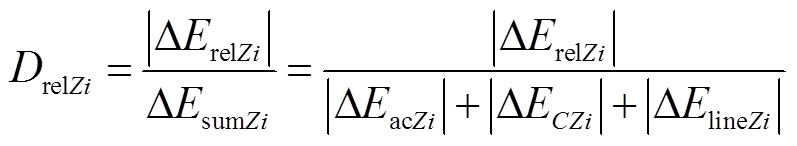 (18)
(18)式中,DrelZi为阻抗Zi时,交流TEF、桥臂电容TEF及相邻线路TEF分别在三者之和中所占的比例;ΔEacZi、ΔECZi和ΔElineZi分别为阻抗Zi时,交流TEF、桥臂电容TEF和相邻线路TEF的占比。
从图3a可以看出,故障发生后4ms内,无接地电阻时,电容TEF占比从故障初期较低值上升到50%成为能量释放的主要来源,同时交流侧TEF占比则是从65%降到约30%,而相邻线路的比例在20%左右波动。同时,接地电阻的变化主要改变交流侧和相邻线路TEF,据此,式(14)中,权重因子α、β和η分别取值0.3、0.5和0.2。
图3b是能量释放侧的总TEF随时间的变化情况,可见能量的释放速度不断攀升。故障发生后3ms内,接地电阻对能量的影响非常有限,之后,接地电阻的增加能明显抑制能量的释放速度,故障发生后7ms时采用30Ω电阻时最大降幅达931kJ,近30%。
以下先分析中性线电抗300mH、换流站4接地条件下,阻感接地参数的优化。
3.2.1 换流站4接地故障点①
考虑最严重的故障,故障点均设置在换流站出口处,正、负极对称,则正极故障点对电网的故障特性有较大的代表性,因此,设置如图1所示的直流电网故障点①。
换流站4电阻接地,点①发生故障时,各部分TEF抑制率和抑制效率随电阻变化的趋势如图4所示。
图4a中交流侧TEF抑制率与抑制效率在任一电阻下均为负值,表明接地电阻会促进交流侧向故障点馈入能量。图4b和图4c中电容和相邻线路的TEF抑制率与抑制效率趋势基本一致,TEF抑制率随电阻增加而增大,在40Ω后基本不变,而TEF抑制效率则是在不断下降中,抑制率与抑制效率变化趋势相反。相比之下,桥臂电容的TEF抑制率最后稳定在45%,相邻线路的TEF抑制率则维持在90%。同样,桥臂电容TEF抑制效率从1.4%/Ω降到0.9%/Ω,而相邻线路的TEF抑制效率从4%/Ω降到1.8%/Ω。
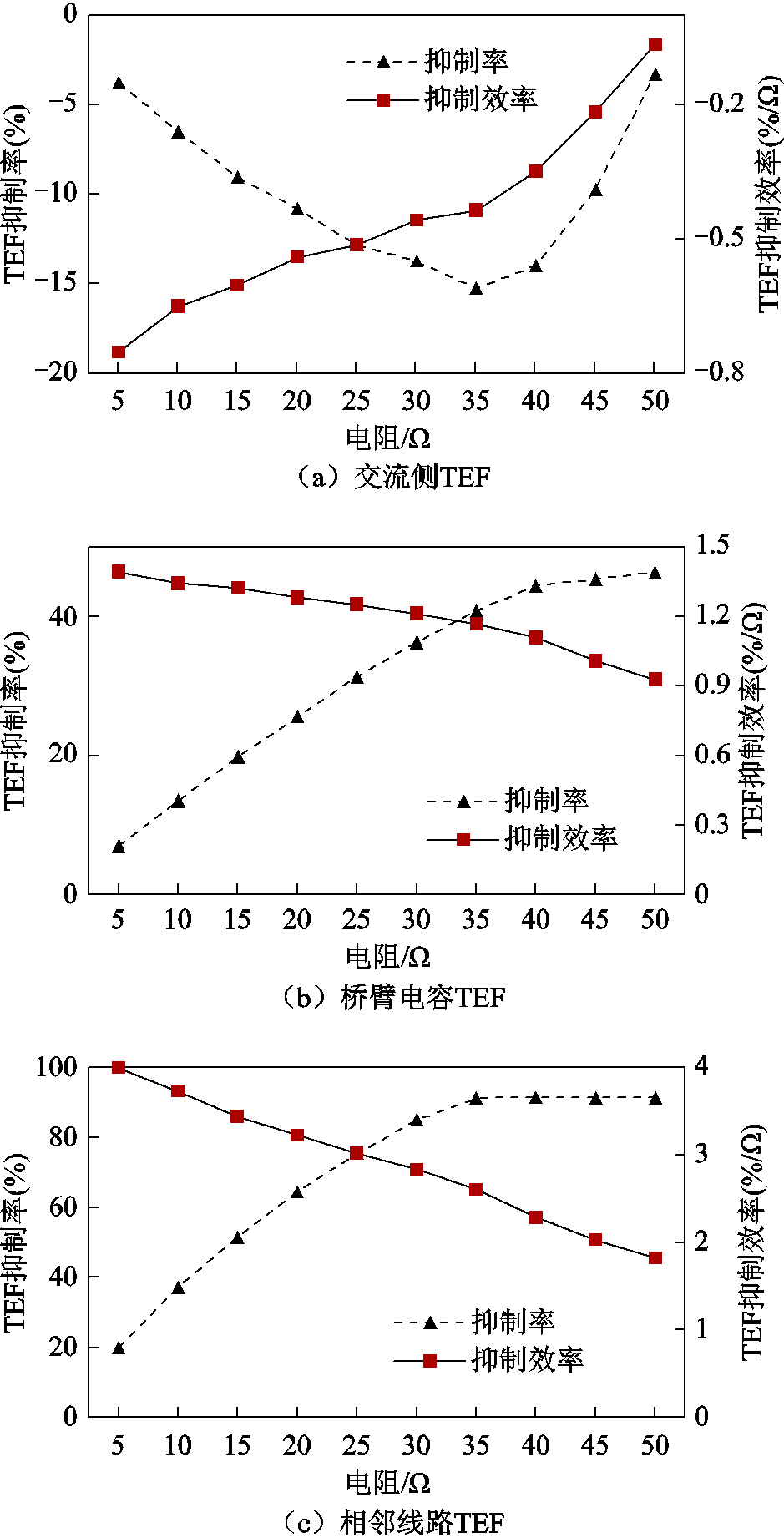
图4 不同接地电阻TEF抑制效果
Fig.4 Suppress effect of TEF under different grounding resistance
TEF抑制率与抑制效率的矛盾,在目标函数中得到很好的诠释,综合了三者的关系,计算结果表明在电阻取30Ω时,整体TEF的抑制效果最好,取得最大值4.85。
换流站4电感接地,点①发生故障时,各部分TEF抑制率和抑制效率随电感变化的趋势如图5所示。
相较于接地电阻,图5a中接地电抗对交流侧TEF具有明显的抑制效果,随电抗增加,TEF抑制率不断上升,至400mH达到64%并基本维持,抑制效率则在0.15~0.16%/mH之间波动。图5b和图5c中桥臂电容TEF和相邻线路TEF的抑制率均随电感增加而上升,分别在350mH和300mH达到60%和91%并维持。桥臂电容TEF抑制效率在0.17~0.2%/mH之间波动,相邻线路TEF抑制效率从0.7%/mH迅速下降至0.2%/mH。
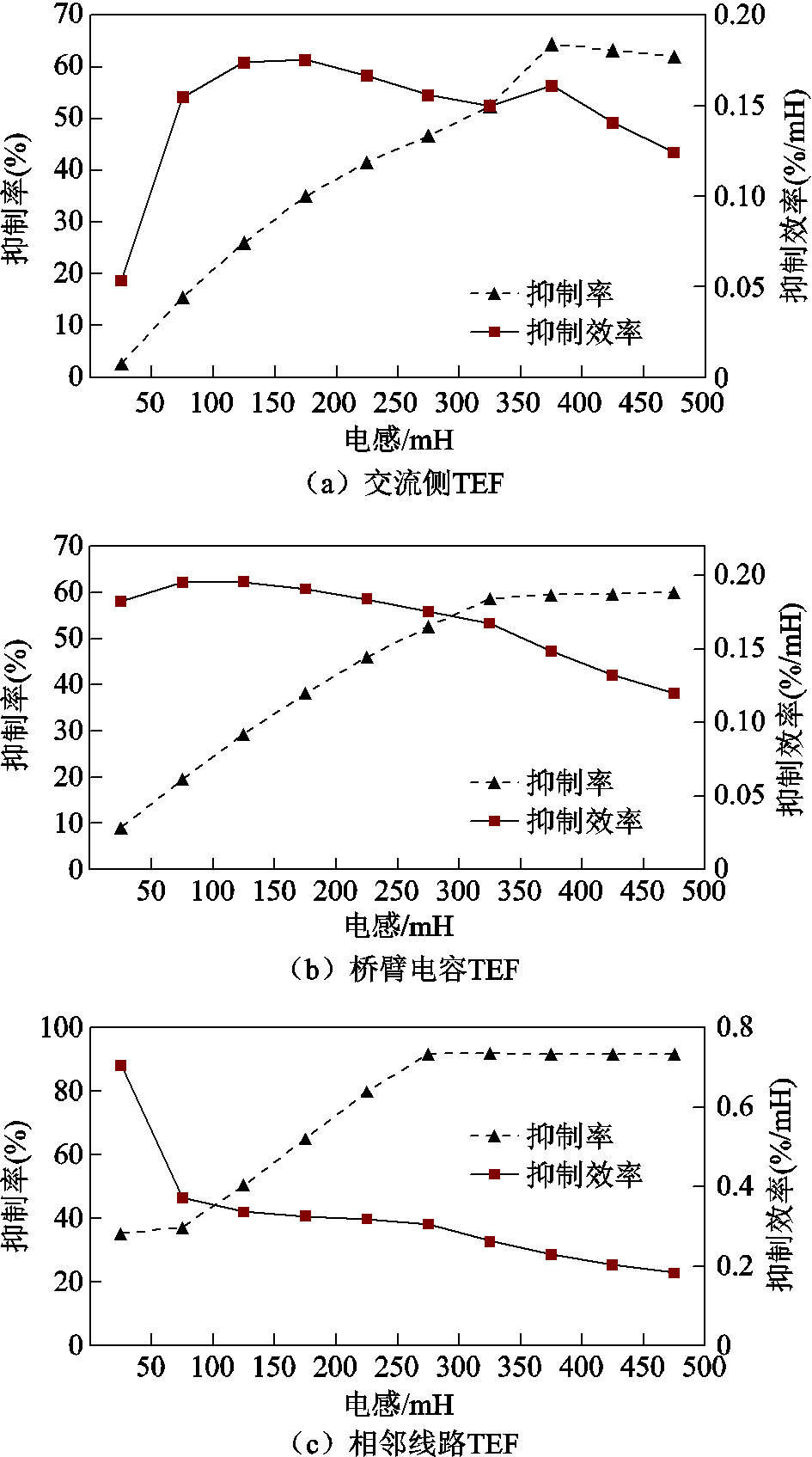
图5 不同接地电抗TEF抑制效果
Fig.5 Suppress effect of TEF under Different grounding reactance
从各部分TEF抑制率的数值上可以看出,接地电抗要优于电阻,但是接地电抗的使用存在严重的健全极过电压的情况,因此电抗取值被限制在100mH以内,制约了其使用,其目标函数值仅为1.45,远小于接地电阻的目标值。
3.2.2 换流站1~3接地故障点①
前面详细分析了换流站4接地,故障发生在点①时的接地参数抑制效果,在此基础上,考虑接地点对接地参数抑制效果的影响。对于四端电网,可在任一换流站接地,也可以在多地同时接地,由于接地点的建设成本较高,且就故障抑制而言效果并不是很明显[21],这里暂不考虑多地接地的情况。
采用相同的方法对换流站1~3分别采用电阻和电抗接地的情况进行分析,并计算目标函数值。在不考虑约束条件的情况下,不同接地点目标函数值随阻抗变化的情况如图6所示。
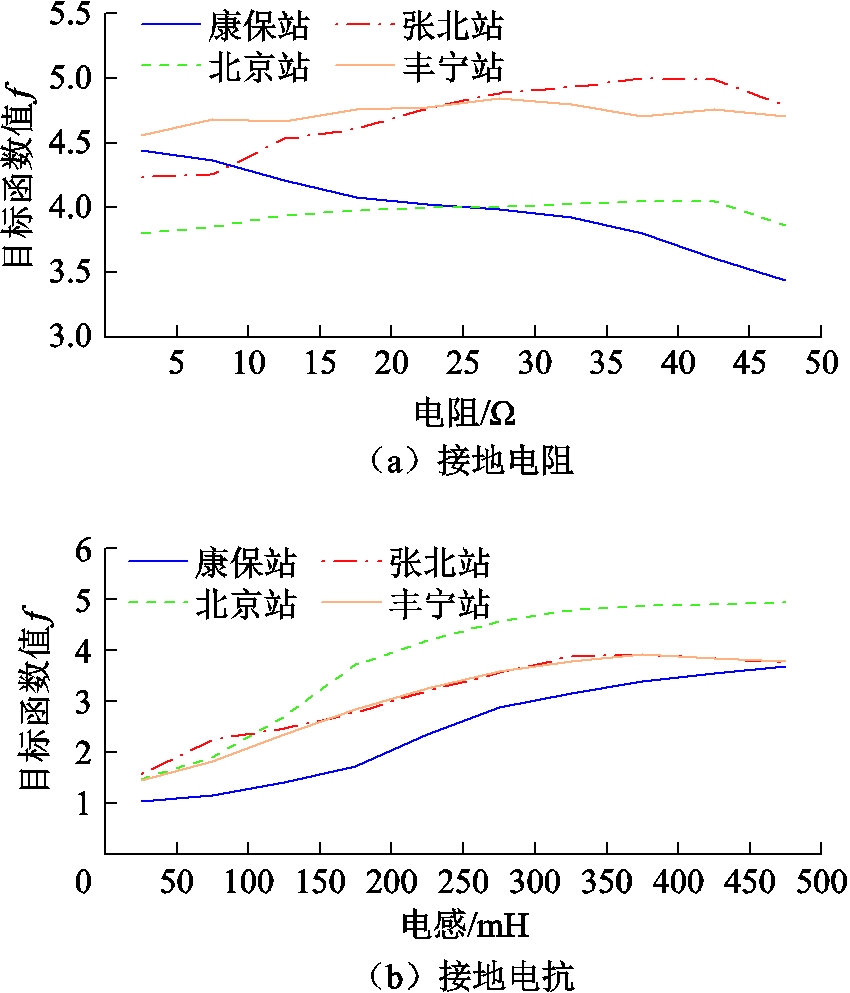
图6 不同接地点目标函数值
Fig.6 Objective function values for different grounding point
图6a中采用接地电阻时,目标函数均在3~5之间,不同接地点函数值随电阻变化的趋势不同。相比之下,采用接地电抗时函数值呈现明显的上升趋势,峰值与接地电阻持平。由于金属回线的存在,接地点不同,使得同一故障点故障后的回路也会产生一定差异,影响TEF抑制率与抑制效率计算的基础值,从而不能直接以目标函数值决定最优取值。因此,采用式(19)来标准化目标值。
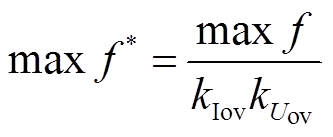 (19)
(19)式中,kIov和kUov分别为无接地阻抗时,各直流电网的故障线路电流的过电流倍数和健全极电压过电压倍数。不同接地点,接地电抗和接地电阻的优化结果见表2。
从表2可以看出,受到健全极过电压的约束,接地电抗的目标值远低于接地电阻。标准化后,不同电阻取值下,受端换流站2和换流站4的目标值相当,送端换流站1和换流站3的目标值相当,但前者高于后者。由此可见,在受端换流站接地要优于送端换流站。最后,在换流站4采用30Ω电阻接地被认为是最优的选择。
表2 接地点与接地参数优化结果
Tab.2 Theoptimization results of grounding point and grounding parameters
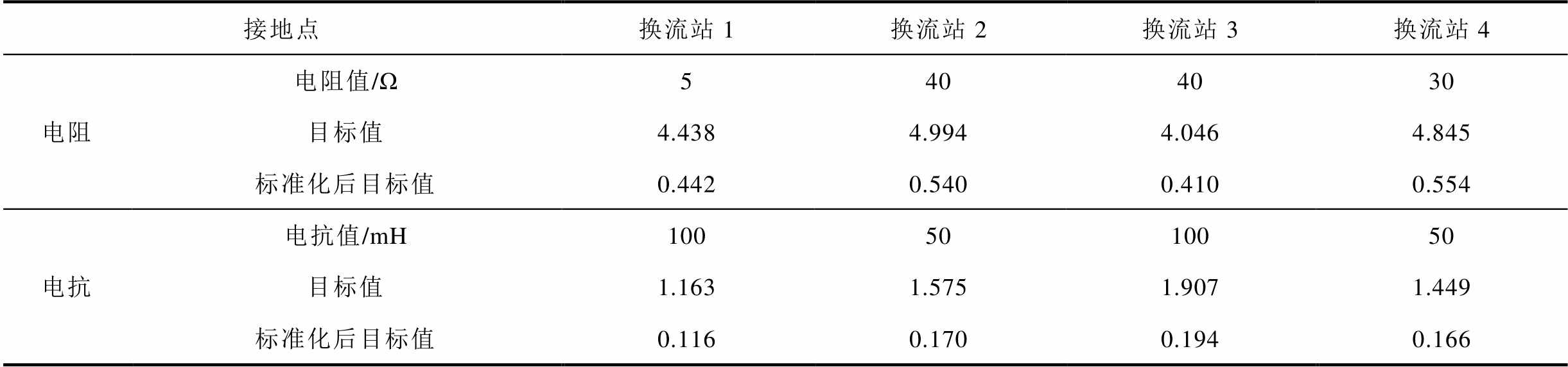
接地点换流站1换流站2换流站3换流站4 电阻电阻值/Ω5404030 目标值4.4384.9944.0464.845 标准化后目标值0.4420.5400.4100.554 电抗电抗值/mH1005010050 目标值1.1631.5751.9071.449 标准化后目标值0.1160.1700.1940.166
3.2.3 换流站4接地故障点2~5
前面考虑了直流电网直流侧接地点对接地参数优化的影响,下面继续研究故障点对其影响。对于架空线发生故障可能在任意地点,通过典型的5个故障点对比分析,研究接地参数对不同故障抑制能力的一致性。由于接地电抗效果要差于电阻,这里不考虑采用接地电抗的情况。
在不考虑约束条件的情况下,不同故障点目标函数值随阻抗变化如图7所示。图7中,除故障点3,其余四个故障点下函数值均小范围波动,其中,故障点3和4下的函数值明显较其他故障点小。对于接近接地点的故障2和3,采用5Ω接地电阻就有很好的抑制效果,且函数值波动相对更大,而较远的其他故障点最优的接地电阻相对更大,达20~30Ω。从直流电网的角度,故障大概率发生在远离接地点的位置,更多故障点加入考量,使得最优值为30Ω更具有合理性。
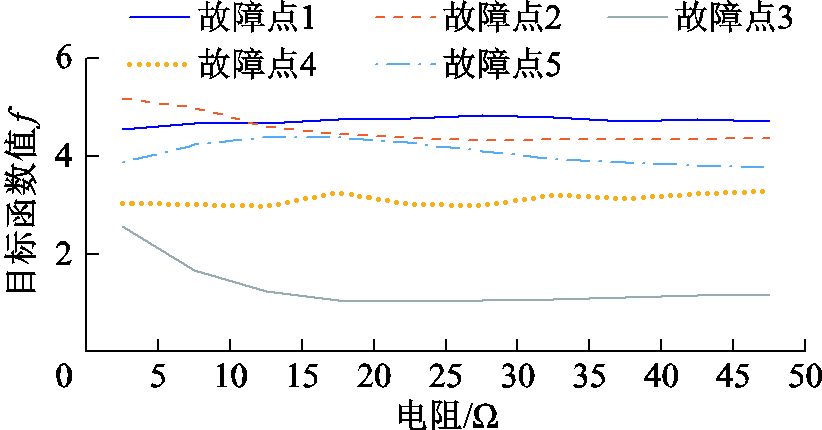
图7 不同故障点目标函数值
Fig.7 Objective function value at different fault points
中性线电抗位于换流站内部换流阀之间的连接处,正常运行时,其通过稳态直流电流,故障条件下处于故障回路中,能够抑制故障电流的发展,其作用与直流限流电抗类似。中性线电抗处于直流电流回路中,其数值选取可能影响电网对控制系统的响应速度,从而增加电网的稳态波动,带来一定损耗与运行风险。因此,考虑中性线电抗取值时,需增加以下约束条件。
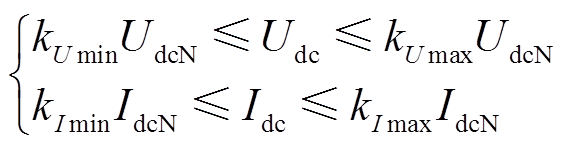 (20)
(20)式中,Udc、Idc分别为直流稳态电压、电流;UdcN,IdcN分别为直流额定电压、电流;kUmax、kUmin、kImax、kImin分别为电压、电流的最大、最小允许偏移系数。
对于中性线电抗,选取0mH、200mH及400mH和前文的300mH做对比分析,采用换流站4接地,故障点①进行分析,采取3.2.2节方法对不同中性线电抗下的目标值进行处理,结果见表3,其中400mH中性线电抗不满足约束式(20)。
表3 中性线电抗与接地电阻优化结果
Tab.3 Theoptimization results of neutral line reactance and grounding resistance

中性线电抗值/mH0100300400 电阻/Ω1053035 目标值5.9785.1914.8455.049 标准化后目标值0.4860.4870.5540.638
从表3可以看出,随着中性线电抗的增加,标准化后的目标值不断增大,可见从对故障后总体的能量释放的抑制来看,中性线电抗越大越好,相应的接地电阻也随之增大,而中性线电抗过大将严重制约电网对控制的响应,400mH时,已不能满足系统要求。据此,中性线电抗选择300mH是合适的。
通过前文的优化分析,得出在换流站4采用30Ω电阻接地,同时中性线电抗采用300mH时为最佳选择。为了展示优化结果,这里采用换流站4接地,300mH中性线电抗下0Ω、20Ω接地电阻与50mH接地电抗;换流站4接地,100mH中性线电抗下30Ω接地电阻及换流站1接地,300mH中性线电抗下30Ω接地电阻作为对比对象,观察其直流故障电流和健全极电压,如图8所示。
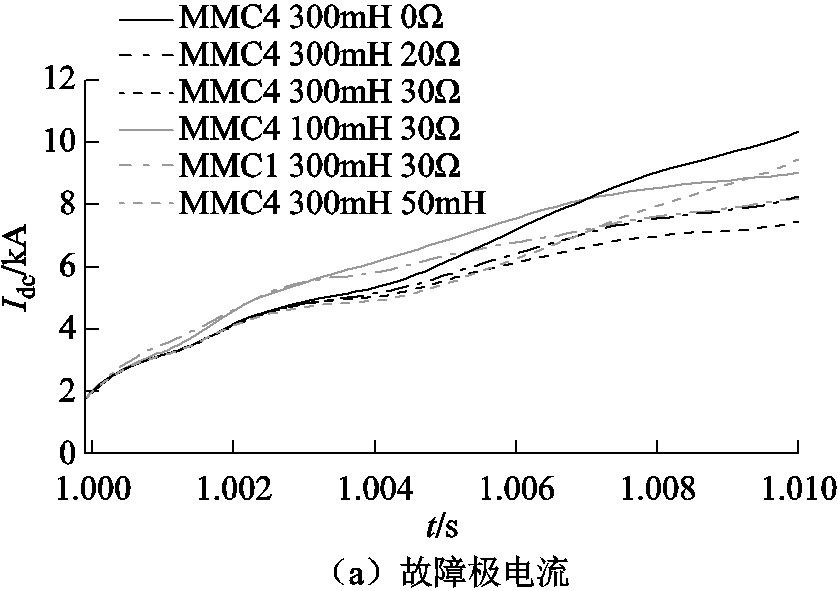
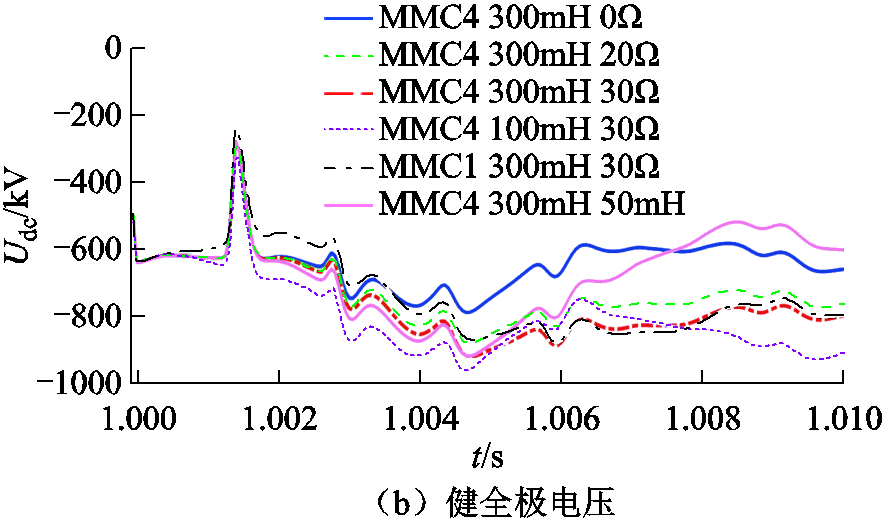
图8 优化结果对比
Fig.8 Comparison of optimization results
从图8可以看出,选择换流站4接地、300mH中性线电抗及30Ω接地电阻的方案,其对应的故障电流峰值最小为7.44kA,其健全极过电压峰值931kV,1.86(pu),在各组中处于合理水平,因为金属回线导致的第一组直接接地时过电压就达到1.6(pu)的水平了。从图8中故障电流和健全极电压的对比可以看出,优化选择的30Ω接地电阻是综合考量的结果。这印证了本文观点的正确性,即可以从宏观的能量平衡与波动的角度对故障进行有效地综合分析。
本文基于直流电网故障后能量释放侧的交流侧、桥臂电容或线路三部分的TEF,提出利用TEF抑制率与TEF抑制效率作为指标建立优化模型,对接地参数和接地点位置及中性线电抗参数进行优化。通过四端双极MMC-HVDC电网接地优化的算例分析,得出如下结论:
1)基于暂态能量流抑制率和抑制效率的接地优化计算表明,最优接地配置与网架结构密切相关。在暂态能量流的抑制效果上,接地电感要优于接地电阻,但与此同时接地电感会引起严重的健全极过电压;接地位置位于功率接受端对故障电流的抑制效果要优于接地位置位于功率输送端时的限流效果。因此,综合考量本文的优化结果为在换流站4采用30Ω电阻接地。
2)若同时考虑故障点位置的影响,并将中性线电抗增加为优化对象,从TEF抑制效果上看,电抗越大越好,而受制于控制性能的要求,300mH中性线电抗被认为是较好的选择。
3)需要注意的是,本文针对四端双极MMC-HVDC电网的接地方式优化结果,是综合考虑接地点、接地电抗、接地电阻和中性线电抗,以及兼顾故障电流和健全极电压两个方面约束得到的优化方案,对工程实际的接地设置具有一定的参考价值。如果相应的条件改变或网架结构及其他参数的改变,所得变量具体优化值亦可能改变。但本文提出的优化建模方法具有通用性,只需根据故障线路的并联数适当修改目标函数即可推广至复杂MMC-HVDC电网接地方式的优化。
附表1 四端MMC-HVDC电网参数
App.Tab.1 The parameter of the four-terminal MMC-HVDC grid
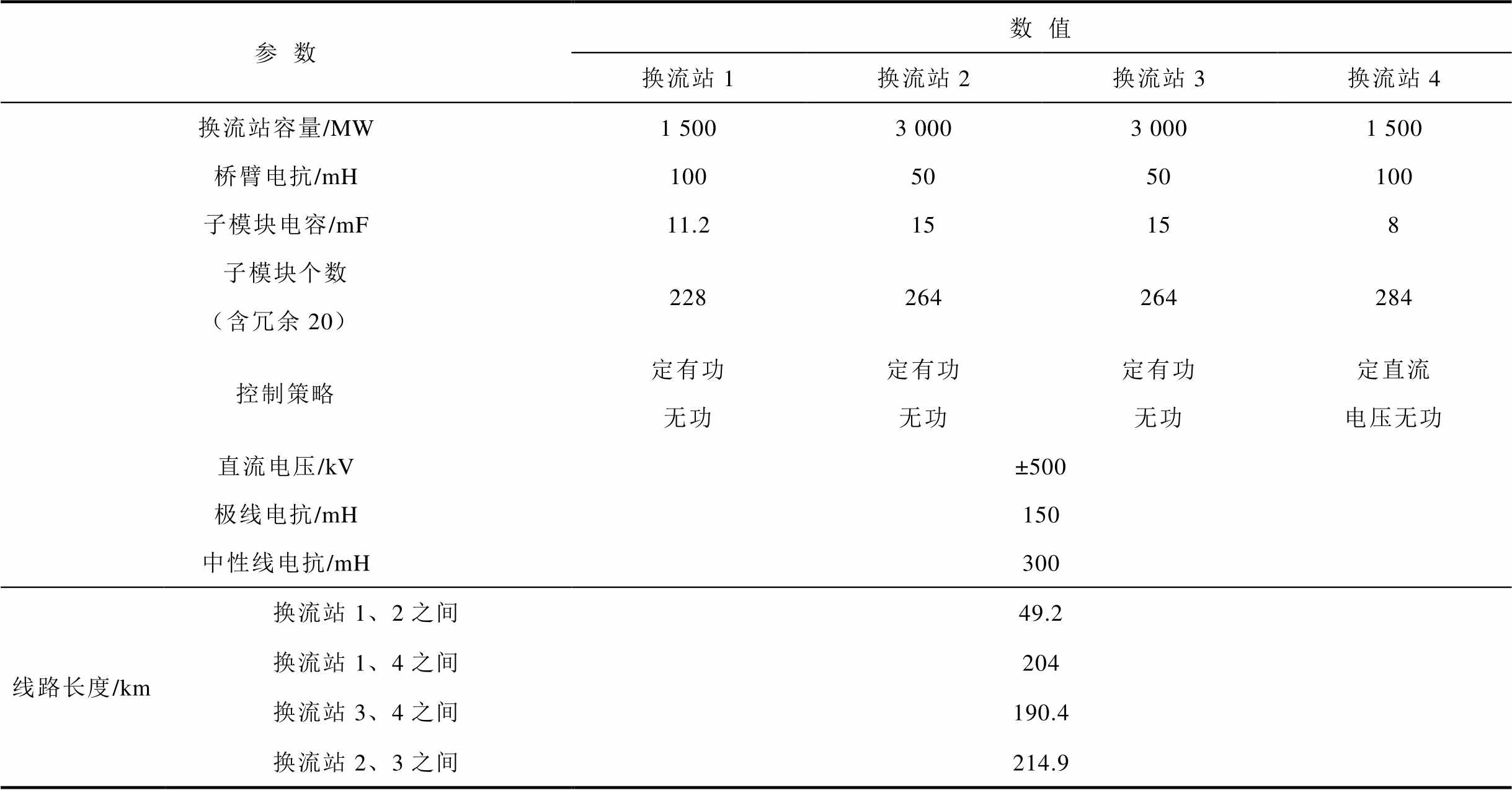
参数数值 换流站1换流站2换流站3换流站4 换流站容量/MW1 5003 0003 0001 500 桥臂电抗/mH1005050100 子模块电容/mF11.215158 子模块个数(含冗余20)228264264284 控制策略定有功无功定有功无功定有功无功定直流电压无功 直流电压/kV±500 极线电抗/mH150 中性线电抗/mH300 线路长度/km换流站1、2之间49.2 换流站1、4之间204 换流站3、4之间190.4 换流站2、3之间214.9
附图1 TEF抑制率
App.Fig.1 Diagram of significance of TEF suppression rate
参考文献
[1] 徐政. 柔性直流输电系统[M]. 北京: 机械工业出版社, 2017.
[2] 杜东冶, 郭春义, 贾秀芳, 等. 基于附加带阻滤波器的模块化多电平换流器高频谐振抑制策略[J]. 电工技术学报, 2021, 36(7): 1516-1525.
Du Dongye, Guo Chunyi, Jia Xiufang, et al. Suppression strategy for high frequency resonance of modular multilevel converter based on additional band-stop filter[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1516-1525.
[3] 王浩翔, 赵冬梅, 陶然, 等. 基于分解的多目标进化算法的含MMC-HVDC交直流混合系统最优潮流研究[J]. 电工技术学报, 2020, 35(17): 3691-3702.
Wang Haoxiang, Zhao Dongmei, Tao Ran, et al. Research on optimal power flow of MMC-HVDC ACDC hybrid system based on decomposition-based multi-objective evolutionary algorithm[J]. Transactions of China Electrotechnical Society, 2020, 35(17): 3691-3702.
[4] 汤广福, 罗湘, 魏晓光. 多端直流输电与直流电网技术[J]. 中国电机工程学报, 2013, 33(10): 8-17, 24.
Tang Guangfu, Luo Xiang, Wei Xiaoguang. Multi-terminal HVDC and DC-grid technology[J]. Proceedings of the CSEE, 2013, 33(10): 8-17, 24.
[5] Li Yan, Liu Hongzhi, Fan Xiaojie, et al.Engineering practices for the integration of large-scale renewable energy VSC-HVDC systems[J]. Global Energy Interconnection, 2020, 3(2): 149-157.
[6] 贺之渊, 陆晶晶, 刘天琪等. 柔性直流电网故障电流抑制关键技术与展望[J]. 电力系统自动化, 2021, 45(2): 73-183.
He Zhiyuan, Lu Jingjing, Liu Tianqi, et al. Key technology and prospect of fault current suppression in flexible DC grid[J]. Automation of Electric Power Systems, 2021, 45(2): 173-183.
[7] 汤广福, 王高勇, 贺之渊, 等. 张北500 kV直流电网关键技术与设备研究[J]. 高电压技术, 2018, 44(7): 2097-2106.
Tang GuTang Guangfu, Wang Gaoyong, et al. Research on key technology and equipment for Zhangbei 500 kV DC grid[J]. High Voltage Engineering, 2018, 44(7): 2097-2106.
[8] 韩乃峥, 樊强, 贾秀芳, 等. 一种具备限流能力的多端口直流断路器[J]. 中国电机工程学报, 2019, 39(17): 5172-5181, 5298.
Han Naizheng, Fan Qiang, Jia Xiufang, et al. A multi-port DC circuit breaker with current limiting capability[J]. Proceedings of the CSEE, 2019, 39(17): 5172-5181, 5298.
[9] 苏见燊, 郭敬东, 金涛. 柔性直流电网中直流故障特性分析及线路故障重启策略[J]. 电工技术学报, 2019, 34(增刊1): 352-359.
Su Jianshen, Guo Jingdong, Jin Tao. DC fault characteristics and line fault recovery strategy in flexible DC power network[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 352-359.
[10] 国家市场监督管理总局、中国国家标准化管理委员会.GB/T 37012—2018 柔性直流输电接地设备技术规范[S]. 北京: 中国标准出版社,2018.
[11] 梅念, 苑宾, 乐波, 等. 对称单极接线柔直系统联结变阀侧单相接地故障分析及保护[J]. 电力系统自动化, 2020, 44(21): 116-127.
Mei Nian, Yuan Bin, Yue Bo, et al. Analysis and protection of single-phase-to-ground fault on valve side of interface transformer in VSC-HVDC system with symmetrical monopolar configuration[J]. Automation of Electric Power Systems, 2020, 44(21): 116-127.
[12] 杨杰, 郑健超, 汤广福, 等. 电压源换相高压直流输电系统接地方式设计[J]. 中国电机工程学报, 2010, 30(19): 14-19.
Yang Jie, Zheng Jianchao, Tang Guangfu, et al. Grounding design analysis of VSC-HVDC system[J]. Proceedings of the CSEE, 2010, 30(19): 14-19.
[13] 傅春翔, 汪天呈, 郦洪柯, 等. 用于海上风电并网的柔性直流系统接地方式研究[J]. 电力系统保护与控制, 2019, 47(20): 119-126.
Fu Chunxiang, Wang Tiancheng, Li Hongke, et al. Study on grounding methods of VSC-HVDC for off-shore wind farm integration[J]. Power System Protection and Control, 2019, 47(20): 119-126.
[14] 张义, 梁艺, 汪步云. 特高压直流输电单极大地金属回线转换过程分析[J]. 电力设备管理, 2020(11): 61-63.
Zhang Yi, Liang Yi, Wang Buyun. Analysis of conversion process of monopole earth metallic return in UHVDC transmission[J]. Power Equipment Management, 2020(11): 61-63.
[15] 郭铭群, 梅念, 李探, 等. ±500kV 张北柔性直流电网工程系统设计[J]. 电网技术, 2021, 45(10): 4194-4204.
Guo Mingqun, Mei Nian, Li Tan, et al. System design of ±500kV Zhangbei VSC-based DC grid project[J]. Power System Technology, 2021, 45(10): 4194-4204.
[16] 薛士敏, 范勃旸, 刘冲, 等. 双极柔性直流输电系统换流站交流三相接地故障分析及保护[J]. 高电压技术, 2019, 45(1): 21-30.
Xue Shimin, Fan Boyang, Liu Chong, et al. Fault analysis and protection scheme for converter AC three-phase grounding of bipolar HVDC systems[J]. High Voltage Engineering, 2019, 45(1): 21-30.
[17] 赵翠宇, 齐磊, 陈宁, 等. ±500 kV张北柔性直流电网单极接地故障健全极母线过电压产生机理[J]. 电网技术, 2019, 43(2): 530-536.
Zhao Cuiyu, Qi Lei, Chen Ning, et al. Research on producing mechanism of healthy pole bus overvoltage for monopolar grounding fault in ±500kV Zhangbei flexible DC power grid[J]. Power System Technology, 2019, 43(2): 530-536.
[18] 何莉萍, 高仕林, 叶华. 不对称双极多端柔性直流电网短路电流特性分析[J]. 电力系统自动化, 2020, 44(12): 101-107.
He Liping, Gao Shilin, Ye Hua. Characteristic analysis on short-circuit current for asymmetric bipolar modular multilevel converter based multi-terminal direct current grid[J]. Automation of Electric Power Systems, 2020, 44(12): 101-107.
[19] Mao Meiqin, Cheng Dejian, Chang Liuchen. Investigation on the pattern of transient energy flow under DC fault of MMC-HVDC grid[C]//2019 4th IEEE Workshop on the Electronic Grid (eGRID), Xiamen, China, 2019: 1-5.
[20] 国家市场监督管理总局、中国国家标准化管理委员会. GB/T 37015.2—2018 柔性直流输电系统性能第2部分:暂态[S]. 北京: 中国标准出版社,2018.
[21] 赵翠宇. 张北±500kV柔性直流电网直流侧短路故障过电压仿真研究[D]. 北京: 华北电力大学, 2019.
Optimal Allocation of Grounding System in High Voltage Direct Current Grid with Modular Multi-Level Converters Based on Transient Energy Flow
Abstract For modular multi-level converter based high voltage direct current (MMC-HVDC) grid using overhead lines, the incidence of DC side grounding short circuit fault is high, which seriously endangers the safety of the power grid. Among all kinds of influencing factors, the grounding mode has an obvious influence on the evolution of fault current. In this paper, an optimization method of grounding parameters based on transient energy flow (TEF) analysis is proposed from the point of view of perspective of macroscopic energy transfer and dissipation of the system. The effects of grounding resistance, reactance parameters and grounding location on the evolution of DC short circuit fault current in MMC-HVDC grid are analyzed. In this method, the TEF suppression rate and suppression efficiency are taken as the optimization objectives, the grounding impedance parameters and the grounding location in the DC grid are taken as the optimization variables. Meanwhile, the influence of neutral line reactance and fault point are considered. In this paper, an example of four-terminal bipolar MMC-HVDC grid under DC pole-to-ground fault (PTGF) condition is selected and a simulation model is built based on PSCAD/EMTDC for analysis and optimization. The simulation results show that the parameter optimization method can effectively guide the design of grounding parameters, restrain DC fault current and overvoltage of healthy pole.
keywords:Modular multi-level converter based high voltage direct current(MMC-HVDC)grid, transient energy flow(TEF), grounding parameters optimization, current limiting effect
DOI:10.19595/j.cnki.1000-6753.tces.210208
中图分类号:TM721.1
国家重点研发计划(2018YFB0904600)和高等学校学科创新引智计划(BP0719039)资助项目。
收稿日期 2021-02-19
改稿日期 2021-05-30
茆美琴 女,1961年生,博士,教授,研究方向为电力电子技术在可再生能源发电系统中的应用、微电网系统。E-mail:mmqmail@163.com(通信作者)
程德健 男,1996年生,硕士研究生,研究方向为柔性直流输电技术。E-mail:chengdejian1996@qq.com
(编辑 赫蕾)