图1 高压进线的四端口PET拓扑结构
Fig.1 Topology of a four port PET with HV input
摘要 多端口电力电子变压器是面向未来智能配电网的关键设备，正示范应用于新能源发电、交直流混合电网和数据中心供电系统中。当多台电力电子变压器集群运行时，能够提供互联、共享、互补、优化的能力，但需要互联端口模式切换控制的支撑。该文依托电力电子变压器集群示范工程，提出一种基于占空比同步的交流端口模式切换控制，能够不依赖端口控制策略的同构性，而有效减小切换过程的暂态冲击。该文通过谐波线性化方法分析了并联逆变器系统阻抗特性，对切换过程中出现的振荡问题进行了分析，提出基于改进阻尼和分步同步切换策略，提高了切换过程的稳定性。在两台MA·A级电力电子变压器互联系统上，实验验证了所提控制的有效性。
关键词：电力电子变压器 并联逆变器 主从式结构 平滑切换
多端口电力电子变压器（Power Electronics Transformer，PET）或电能路由器（Electric Energy Router）是面向未来智能配电网的关键设备[1]，正示范应用于新能源发电、交直流混合电网和数据中心供电系统中[2]。
以图1所示的某数据中心示范工程的电力电子变压器为例：每个PET分别具有10kV高压交流、750V低压直流、10kV高压直流和380V低压交流四类端口，针对该结构的PET的研究可以参见文献[3-6]。示范工程中，四台PET同类型端口互联运行，按主从式结构运行，系统结构如图2所示，其中主机表示该端口采取恒压模式运行，从机则表示端口采取恒功率模式运行。由于数据中心供电高效率和高可靠性的要求，当主机故障需要一台从机变为主机保证端口电压和功率稳定，或者效率寻优算法判断某一台机器工作于主机模式时效率更高，则需要主机和一台从机配合完成模式切换，而交流端口的模式切换相对直流端口更为复杂，本文主要研究电力电子变压器系统低压交流端口的模式切换控制。
针对逆变器的形态切换研究主要面向应用场景为单台或多台逆变器构成的交流微网在孤岛运行模式和并网运行模式之间的平滑切换[7-16]。目前针对这一应用场景已有大量研究，主要思路有基于主从结构的平滑切换方法[7-8]、基于下垂控制的切换方法[9-13]、主从控制和对等控制结合[14]方法、基于虚拟同步发电机的逆变器控制和模式切换[15-16]。基于PQ和V/f的主从切换策略虽然可以实现双模式的平滑切换，但是受限于主从同构的稳态结构设计；常规下垂控制效果受到线路阻抗影响，当供电设备和负载短距离就近连接时，下垂控制策略较为复杂，增大了设计难度，虚拟同步控制也有控制参数设计复杂的问题。文献[17]将控制器的切换扩展到了常规PQ控制和下垂控制间的切换，但是没有对切换过程的稳定性进行分析。
图1 高压进线的四端口PET拓扑结构
Fig.1 Topology of a four port PET with HV input
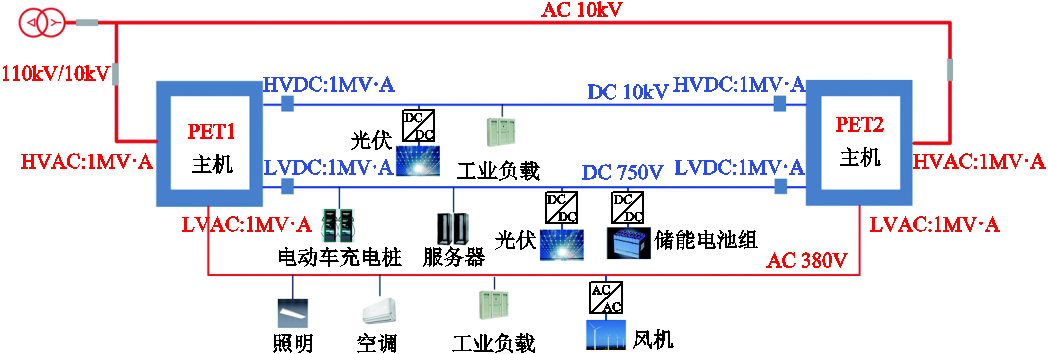
图2 数据中心两台四端口PET系统结构
Fig.2 Topology of two four-port PETs for data center
面向逆变器并离网所提出切换方法主要是针对单台逆变器的行为，而面向数据中心的供电解决方案，高压进线[18]后通过固态变压器转换输出低压交流的站用电具有较高的供电效率，因此站用380V交流电一般由电网构建型变换器支撑，不与传统交流电网直接相连。在此情景下，低压交流端口的模式切换要求两个控制器几乎同时交换工作模式，保障数据中心设备的稳定运行。相比于并离网只对主控逆变器进行控制，同步切换对实时性和并联逆变器的稳定性要求更高。文献[19]介绍了舰载逆变器和同步发电机之间的协调控制和模式切换，文中提到了同步发电机和逆变器的阻抗匹配是切换的关键影响因素。
本文主要针对主从式逆变器系统构建电网运行时，主从控制结构具有较大差异情况下的平滑过渡问题进行研究。首先介绍了主从逆变器的控制策略，提出了一种基于占空比同步的切换控制，解决了双模式异构控制器切换问题；在对两台并联逆变器的切换过程稳定性问题分析基础上，提出了一种分步同步的切换控制方法，避免了切换过程中逆变器阻抗不匹配导致暂态振荡甚至失稳的情况。
PET低压交流端口并联运行结构如图3所示，单个交流端口的结构为三相四桥臂，滤波器为LC滤波器，第四桥臂输出经滤波器后接地，且通过50%占空比控制保证中性点电压平衡。设1号PET低压交流端口采用主控制结构，2号PET低压交流端口采用从控制结构，分别控制公共点交流电压和端口功率分配。
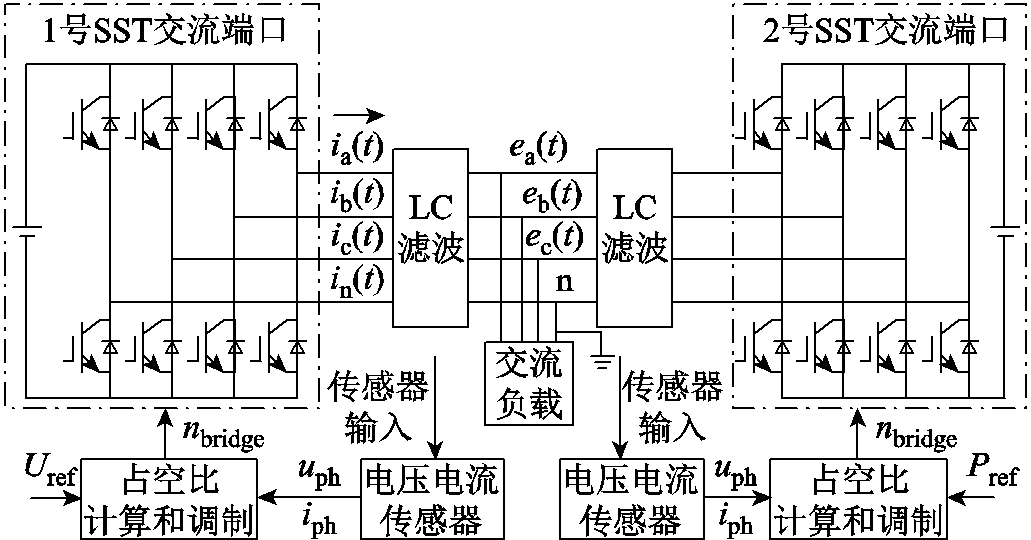
图3 PET低压交流端口主从式结构
Fig.3 Structureof the master-slave controlled PET LVAC units
从机控制器选取为基于旋转坐标系的电流PI控制方法，其理论基础是三相对称逆变器在旋转坐标系下的电路模型，即
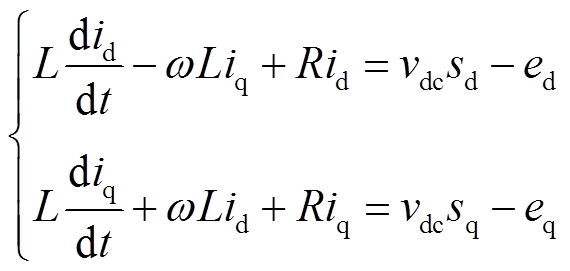（1）式中，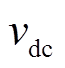
为直流侧电容电压、L和R为滤波电感的电感和电阻参数；
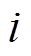为电感电流；
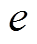为逆变器输出节点的电动势；
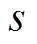为逆变桥臂的开关函数；下标d和q对应旋转坐标系的d轴和q轴。
式（1）给出的控制方法可以表示为图4所示的控制框图，其中UC为滤波电容电压、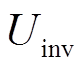
为逆变桥滤波前的电压、UL为滤波电感电压。由于从机算法不承担不对称负载，因此从机的第四桥臂保持闭锁。
图4 从控制器结构
Fig.4 Structure of slave controller
主模式控制选取四桥臂分相独立的谐振控制方法，该方法相比于旋转坐标系的优势在于：①每一相电压单独控制，因此三相负载不对称工况下，主机仍能确保三相电压对称；②省去了电压电流的Park变换和控制器输出时的Park反变换，极大地减少了控制器计算量；③谐振控制器的特点使得该算法的谐波增益很低，同时省略了不对称工况下的正、负、零序控制，具有简单的控制结构。
主机控制的结构框图如图5所示，分相独立的谐振控制方法的核心是电压外环的准PR调节器，该控制器在连续系统中的传递函数为
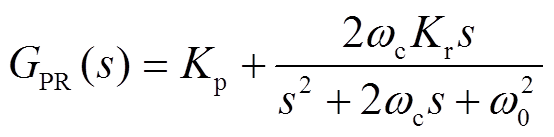（2）式中，
为PR。
该调节器在谐振频率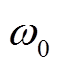
处有最大的幅值增益和0相位偏移，在频率远离谐振频率时幅值增益迅速衰减。因此当电压外环输入为工频50Hz参考值时，系统具有接近无穷大的开环增益，从而保证逆变器输出电压对于参考信号的跟踪。
图5 主控制器结构
Fig.5 Structure of master controller
对比主从双模式的控制结构，可以发现两结构既没有共同的电流内环，电压电流等物理量的坐标系也不同，对于这种主从结构差异较大（后续称为异构）的情况常规的主从切换方法无法适用。
数据中心示范工程中的PET多端口连接采取了模块化多有源桥（Modular Multi-Active Bridge, MMAB）的结构[4-5]，具体结构如图1所示。低压交流端口到高压交流之间的电能变换，包含高压交流侧整流控制、MMAB级的电压控制以及逆变器控制。由于系统结构较为复杂，本文只对逆变级影响较大的MMAB电压控制进行说明和分析。
根据文献[3]中提出的基于交叉前馈解耦的MMAB多端口协同控制策略，可以将低压交流端口直流侧的电压控制简化为以HVAC为一次侧、LVAC为二次侧的DAB电压控制策略，如图6所示。
图6 等效DAB控制器结构
Fig.6 Structure of equivalent DAB controller
由图6的控制框图，可以得到逆变前级的电压控制的开环传递函数为
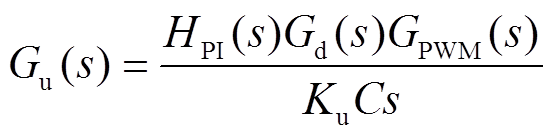（3）式中，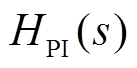
为电压调节器的传递函数；
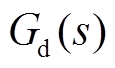为采样部分的延迟环节；
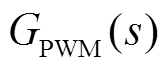为驱动部分等效的采样保持环节；
为电压和模块并联数相关的常数；
为直流侧的滤波电容。取额定电压代入开环传递函数，可得开环传递函数Bode图如图7所示。结果显示电压传递函数的截止频率在6kHz左右，该结果表明等效的DAB电压控制具有较快的动态响应，因此对逆变级的影响较小。为了简化分析，在后续的逆变侧阻抗计算中，将忽略直流电容电压的动态。
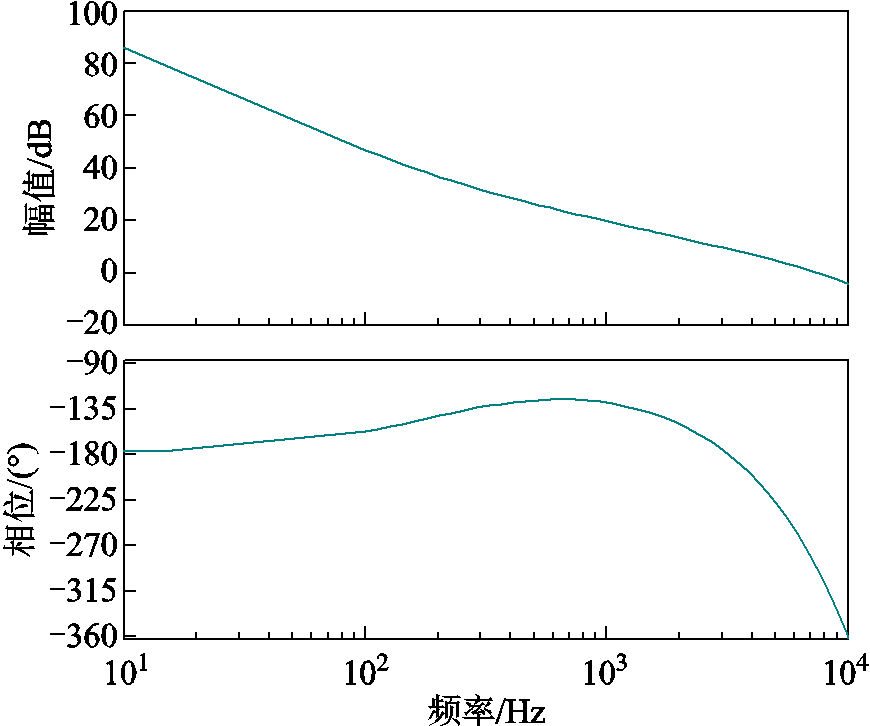
图7 等效DAB电压开环传递函数伯德图
Fig.7 Bode diagram of equivalent DAB voltage open-loop transfer function
针对异构情况下形态切换的需求，本文提出了一种基于占空比预同步的切换控制，如图8所示，其中Dm和Ds分别表示主模式和从模式控制器输出占空比。图中切换开关S=1时表示控制器工作于主机模式，S=0时表示控制器工作于从机模式。当控制器工作于从机模式时，主模式控制器的输入为主模式控制器的输出占空比和从模式控制器的输出占空比，考虑到从机输出的占空比信号基波为50Hz工频信号，主模式控制器的谐振特性使得主模式的输出可以跟随从模式输出变化。切换瞬间，输出到驱动的信号由从模式输出改变为主模式输出，同时将主模式控制器输入改变为电压参考值和电压采样值。
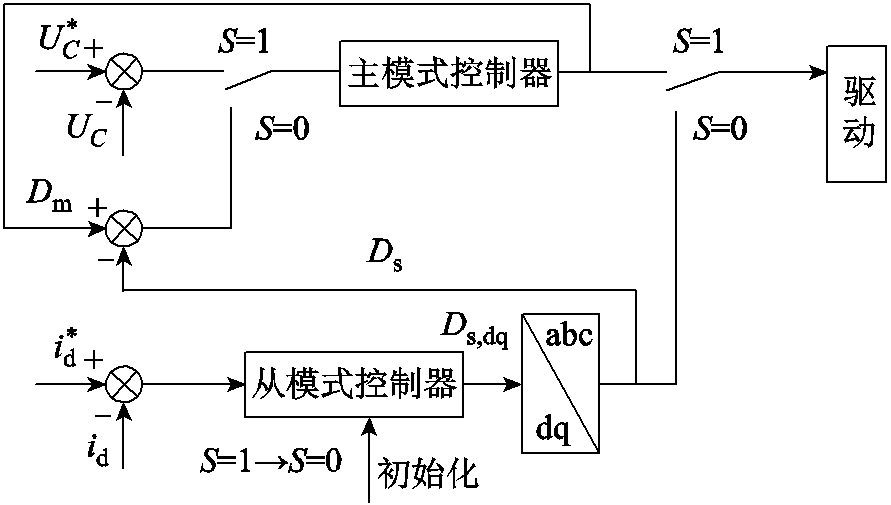
图8 基于占空比同步的平滑切换算法
Fig.8 Block diagram of smooth control method based on duty cycle synchronization
当变换器需要由主机切换为从机时，对应图8中开关S=1变为S=0，从机控制器投入运行，这个过程中需要对从模式控制器内置积分器进行赋值，以保证控制器输出和稳态结果尽量一致。期望的控制器输出对应于逆变器滤波前的输出电压，该期望值可以通过公共点电压和滤波电感上的压降在dq坐标系下计算得到。
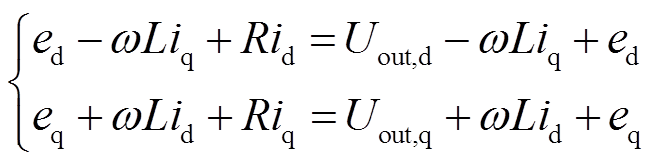（4）式中，“=”左边为期望的逆变器输出电压，右边为控制器输出的实际电压，对比发现稳态下PI输出（
, 
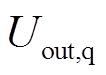）为0时输出的实际电压约等于期望的逆变器输出电压。因此在变换器由主机切换为从机的瞬间，只要将控制器的积分器置零，而比例环节的输出很小，所以可以满足输出电压接近期望的逆变器输出电压。
前2.1和2.2小节的分析均基于参数无偏差且忽略采样和控制下发等环节延迟的理想情况，由于本文所研究的模式形态切换涉及两台变换器的相互配合，控制器需要通过相互通信确保切换的同步执行，而实际系统中不可避免地存在通信延迟，此外电压电流的纹波无法完全消除，切换时系统扰动仍然存在。考虑到互联通信受到电磁干扰，可能出现通信错误的情况，项目实施中为避免意外的通信错误导致切换失败，通信的一帧数据中只包含3位有效数据，用于表示切换状态和切换类型，其余均为校验位。当校验位错误时，控制器保持原有模式继续运行几个控制周期，直到接收到正确的数据或者超时保护。在延迟时间内系统会逐渐偏离工作点。在系统稳定性良好且通信正常的情况下，上述扰动造成的影响很小，但是如果因为参数设计、通信错误等原因，并联逆变器系统的稳定裕度较小或者通信延迟较大、通信出现错误时，系统偏离正常工作状况较远，可能导致电压电流出现振荡。
在数据中心示范工程PET实际运行过程中，发现即使采用预同步和切换重置结合的方法，系统在切换时仍有可能出现暂态振荡，一方面原因是非理想因素导致切换瞬间引入了扰动，另一方面是并联系统本身的稳定裕度不足，在切换过程扰动大的情况下容易振荡。本节针对切换过程中的振荡问题，首先分析了并联系统稳定性，并以此为基础提出了改进阻尼的分布切换方法，解决了切换过程中的暂态振荡。
并联系统的稳定性分析方法主要有状态空间方程特征值分析法、阻抗分析法和非线性分叉理论[20-26]等。本文选取物理意义明确，且可以更为直观地展现阻抗与频率关系的阻抗分析法对并联逆变器系统的稳定性进行分析。
并联逆变器系统阻抗分析法是将系统根据电网构建型和跟随型的特点，分别等效为一个戴维南支路和诺顿支路，当各自电压源和电流源稳定的前提下，两并联变换器交换电流可以写作
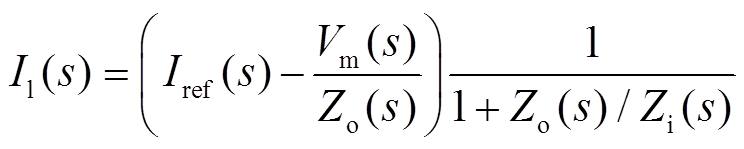（5）式中，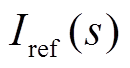
为诺顿支路的理想电流源；
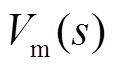为戴维南支路的理想电压源。式（5）表明系统的稳定性取决于电网构建型变换器的输出阻抗Zo(s)和并网变换器输入阻抗Zi(s)之比。
为了使系统具有较高的阻抗比裕度，一般要求系统阻抗比满足
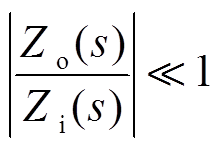（6）从开环传递函数的角度理解，式（6）使得并联变换器系统具有较大的幅值裕度。从电网构建型变换器和并网型变换器的角度出发，当电网构建型变换器具有较小的输出阻抗，或者并网型变换器具有较高的输入阻抗时，系统具有更好的稳定性。
主机的输出阻抗的物理含义是当有一个小信号的电流扰动
注入主机端口时，主机输出电压改变化量为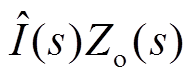
。由图5给出的电压模式控制框图，输出电压可以写成电压参考和输入电流的组合，即
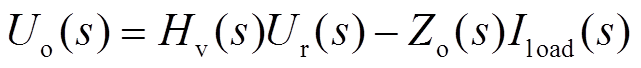（7）根据Mason公式可以写出输出阻抗的表达式为
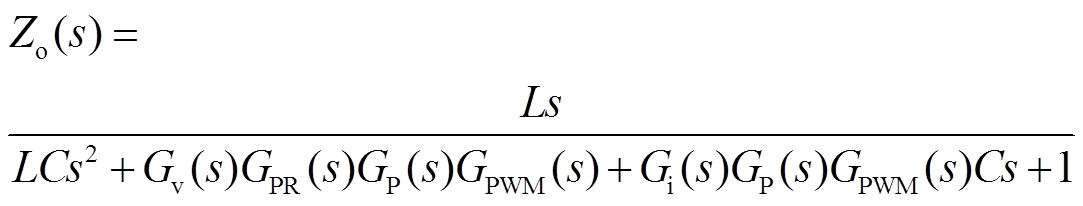（8）式中，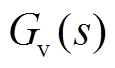
、
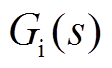分别为电压电流采样环节对应的传递函数；
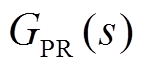为PR调节器的传递函数；
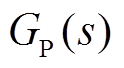为电流内环比例调节器的传递函数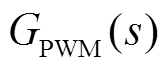；为计算结果到实际执行过程延迟环节对应的传递函数。选取实际系统中使用的控制参数得到输出阻抗的频率特性如图9所示。频率特性表明，主机的输出阻抗在工频段很小，且呈现出感性特征，但是在800Hz左右的LC滤波器谐振点阻抗值较大，呈现出电容特性。
图9 主机输出阻尼伯德图
Fig.9 Bode diagram of grid-forming converter output impedance
电网跟随型逆变器的外环控制带宽一般远小于电流内环，因此在分析输入阻抗时可以忽略功率外环的动态，认为电流内环具有固定的参考值。文献[23]给出了单电感滤波的从机系统序阻抗的求解方法。推导过程考虑了延迟环节、采样环节、锁相环等因素的影响。由于本文双模式的形态切换面临的问题是较高频率的振荡，因此忽略锁相环和功率外环等低带宽环节的影响，推导出单电感滤波的输入阻抗为
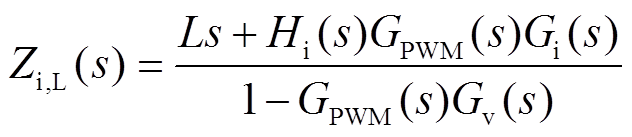（9）对于正序阻抗，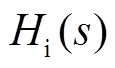
可以表示为
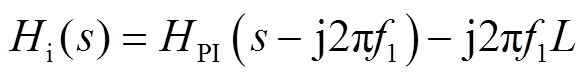（10）式中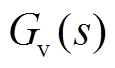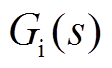，、分别为电压、电流的采样环节等效传递函数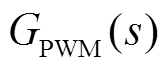；为执行环节的等效传递函数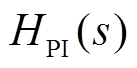；为电流调节器的传递函数。
以上结果为针对单电感控制器的输入阻抗传递函数，本文研究面向的电力电子变压器逆变模块输出级含有滤波电容，由于图4所示的控制环路中电容电流不参与控制环路调节，因此输入阻抗可以看作电容和单电感逆变器输出阻抗的并联结果，即
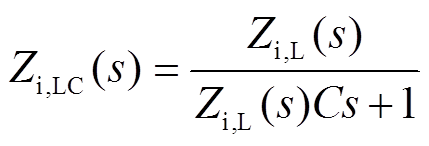（11）由式（10）得到的LC滤波的逆变器输入阻抗表达式，结合表1中控制器参数和电路参数，得到LC滤波的从机输出阻尼Bode图如图10所示。输入阻抗的频率特性表明该系统在低频段的幅值远大于电网构建型逆变器的输出阻抗，但是在较高频段，特别是谐振频率800Hz附近，输入阻抗和输出阻抗具有接近的幅值，且主机输出阻抗相位响应随频率快速变化，阻抗比很有可能包含(-1，j0)点，导致互联逆变器高频稳定性不足。
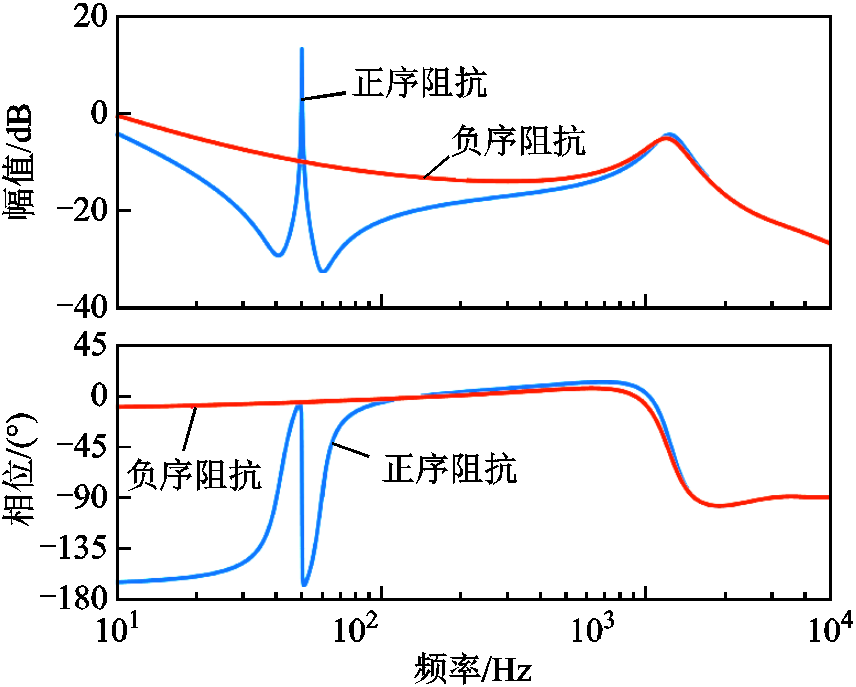
图10 LC滤波的从机输出阻尼伯德图
Fig.10 Bode diagram of grid-following converter input impedance with LC filter
分析已知互联逆变器系统具有较小的高频稳定裕度，且切换过程容易引入高频扰动，因此系统在切换时刻可能出现高频振荡，导致切换性能下降甚至切换失败停机。由于从机的阻尼在高频段主要由延迟环节和滤波器参数决定，调节的范围有限，并且高频阻尼幅值裕度低的主要原因是主机阻尼在谐振频率附近迅速增大，因此本文选择对切换过程中主机阻尼特性进行改良。最为简单的一种改善高频阻尼特性的方法是使变换器运行于半开环模式，该模式没有电压闭环，通过前一时刻的电压电流计算得到控制器输出占空比的幅值和初始相位，该方法的好处是同时改善了阻尼特性和戴维南支路电压源稳定性，缺点是存在稳态误差，且谐波控制能力差。该模式下变换器的输出阻尼近似为变换器的滤波电抗，其频率特性如图11所示，改进后的阻尼特性牺牲了低频阻尼特性，获得了更小的高频阻尼，从而保证切换动态不会出现高频振荡。
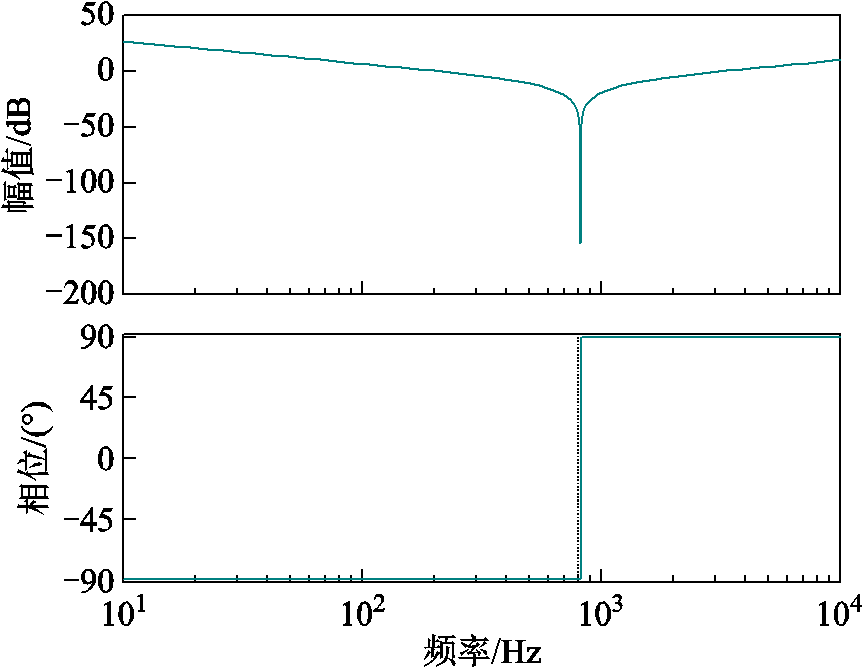
图11 改进主机输出阻尼伯德图
Fig.11 Bode diagram of improved grid-forming converter output impedance
为了提升系统在模式切换时刻的稳定性，同时不影响原有控制系统的稳态性能，本文采用一种分步切换的控制方法。该方法的切换过程如图12所示。初始时刻1号机工作于恒压模式，2号机工作于功率模式，①1号机从恒压模式转为功率控制，这一步通过2.2节中提到的控制器初始化方法实现；②2号机切换为主机，先运行改进阻尼的电压模式，保证并联系统不会因切换扰动而发生高频振荡，由于过渡电压控制不含调节器和电压闭环，因此只需获取初始参考电压相位；③2号机再从改进阻尼的电压模式转换为常规电压模式，这一步按照2.1节介绍的同步方法，用常规电压模式控制器跟随改进阻尼的电压模式控制器输出。
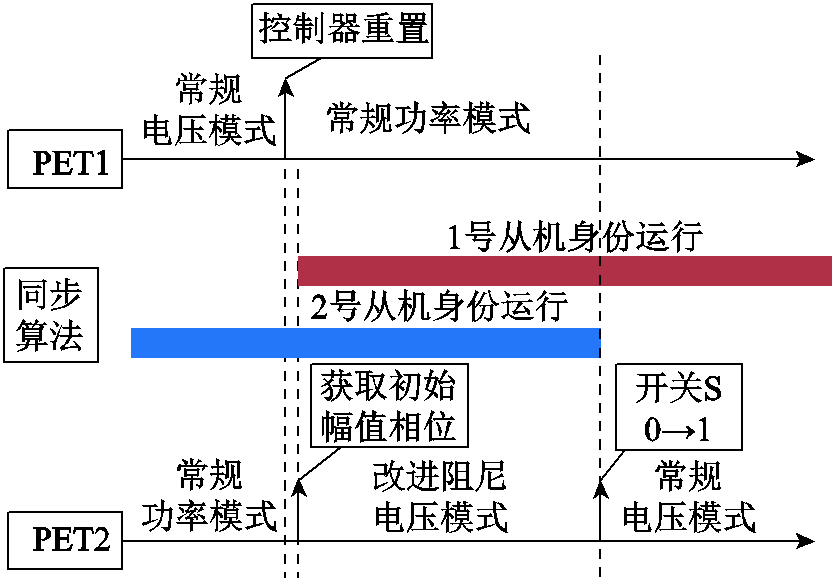
图12 分步切换时序图
Fig.12 Sequence diagram of multi-step mode transition
分步切换方法实质上是将主从形态切换分解为两步，第一步双机主从模式开始互换，因为前面提到的非理想因素，这一步具有较大的扰动，常规切换时主从并联系统阻尼特性容易受该扰动引起高频振荡，因此采样改进主机阻尼特性来提升系统抗扰动能力；第二步再将主机从过渡模式转为常规运行模式，该步不受通信延迟因素影响，扰动很小，因此具有良好的动态性能。
本文以数据中心示范工程两台1MV∙A的PET低压交流端口为原型，搭建了逆变级的仿真平台，通过小扰动分析方法仿真计算出100～2 000Hz频段的阻抗特性，仿真与理论分析的对比结果如图13和图14所示。
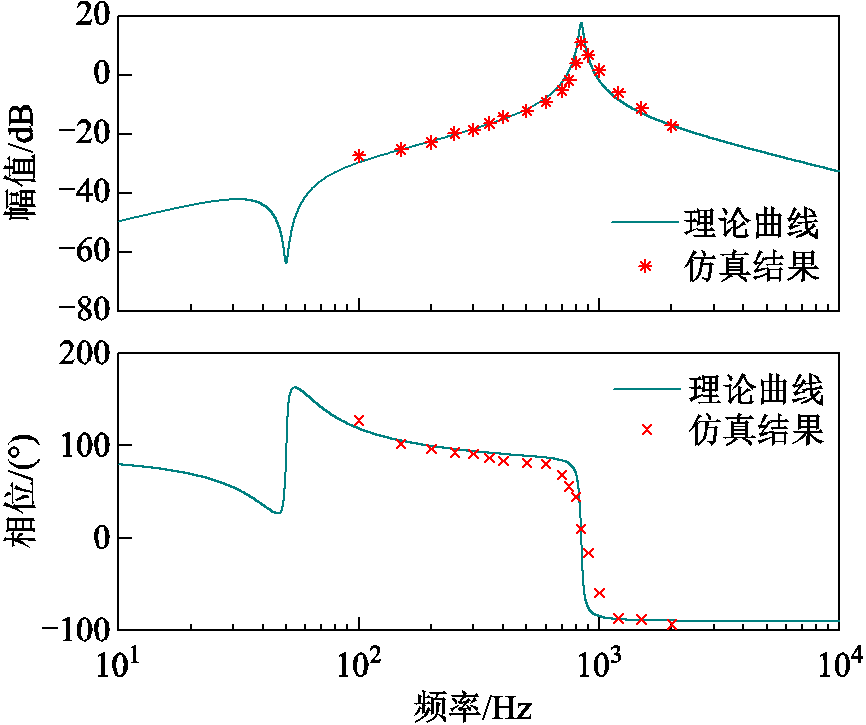
图13 主机输出阻尼理论曲线与仿真结果
Fig.13 The oretical curves and simulation results of grid-forming converter output impedance
图14 从机输入阻尼理论曲线与仿真结果
Fig.14 The oretical curves and simulation results of grid-following converter input impedance
仿真结果和理论分析给出的数值在中高频段吻合较好，结合第3节的分析说明了原并联逆变器系统在800Hz附近的稳定性较差。
本文以应用于数据中心的电力电子变压器进行了逆变端口的主从切换实验验证，实验平台如图15所示。
图15 数据中心MV·A级PET示意图
Fig.15 Schematic diagram of MV·A PET in the DC
实验工况为整机四端口并联运行，高压交流接10kV电网，功率在并联端口间分配。通过手动下发指令或者故障检测指令生成切换信号，主机检测到切换信号后进行模式切换，同时通过光纤通信给从机发出模式切换指令。电路参数见表1。
表1 并联逆变器系统参数
Tab.1 The parameters of parallel inverter system
参数数值 滤波电感/mH54 滤波电容/mF700 直流侧电压/V680 LVAC端口额定容量/kW750 逆变器控制频率/kHz5 采样滤波截止频率/kHz20
通过录波仪记录公共连接点（Point of Common Coupling, PCC）三相电压和一号机单相电流。图16为无同步算法实验结果，切换瞬间电压、电流出现剧烈波动，系统迅速失稳触发保护；图17和图18分别为含同步算法的单步失败和成功的切换结果，同步算法在一定情况下减小了切换振荡，但是由于系统抗高频扰动能力差，所以单步切换仍存在失败情况；图19为双步切换结果，主机采用了3个工频周期的过渡算法，也即改进阻尼的电压控制方法。
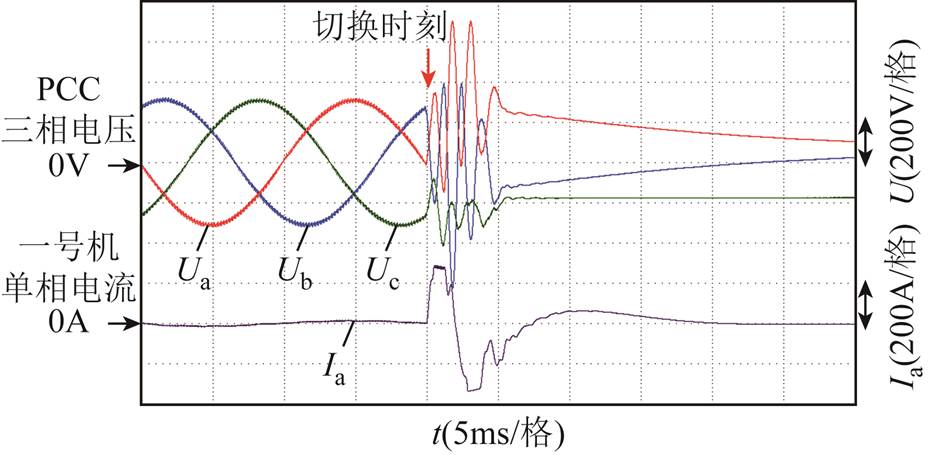
图16 无同步算法情况下主从形态切换失败波形
Fig.16 Mode transition failed waveforms with non-synchronization scheme
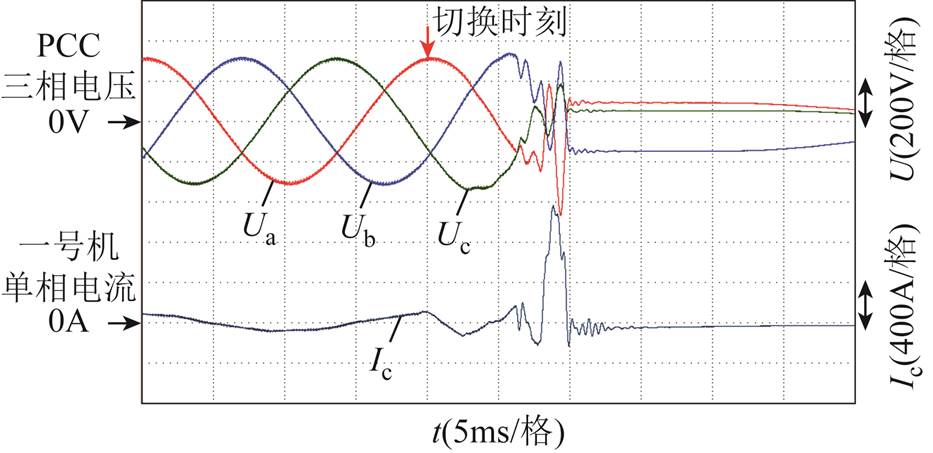
图17 含同步算法的单步形态切换失败波形
Fig.17 Single-step mode transition failed waveforms with synchronization scheme
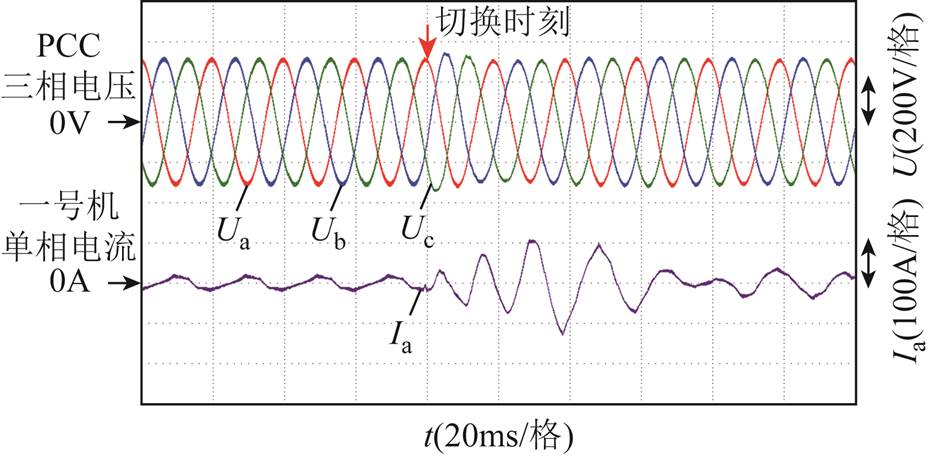
图18 含同步算法的单步形态切换成功波形
Fig.18 Single-step mode transition success waveforms with synchronization scheme
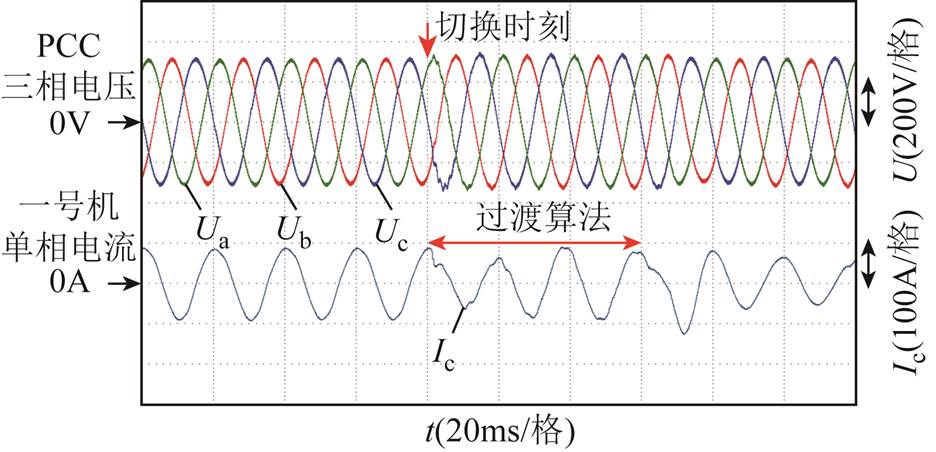
图19 含同步算法的分步形态切换波形
Fig.19 Multi-step mode transition waveforms with synchronization scheme
对比四种不同的实验结果，可以总结出以下结论：
（1）无同步算法的情况下进行形态切换时，控制器参数突变，导致公共点电压电流波形快速振荡，系统迅速失稳，结果如图16所示。
（2）有同步算法但阻尼不匹配的情况下，当切换延迟较高或负载功率增大时，切换容易出现失败，结果如图17所示。
（3）有同步算法但阻尼不匹配的情况下，当通信延迟小且负载功率小的情况下主从机可以成功切换，结果如图18所示。
（4）过渡电压模式使得系统具有更好的鲁棒性，可以保证主从机稳定切换，但过渡电压模式的稳态控制性能较差，结果如图19过渡算法开始瞬间电压电流波形。
（5）同步算法保证过渡电压模式和常规电压模式间相对平滑过渡，结果如图19过渡算法结束瞬间电压电流波形。
本文提出的基于占空比同步的模式切换控制可以实现主从异构情况下互联逆变器系统的平滑模式切换。基于谐振原理的占空比跟随算法和基于逆变器dq坐标系数学模型的控制器重置方法可以保证切换瞬间控制器状态的连续。针对数据中心电力电子变压器的阻抗特性分析表明，主从机在LC滤波器谐振频率附近的阻抗比可能越过了稳定边界，因此在切换扰动情况下系统的稳定性难以保证。本文提出的过渡电压控制方法可以提升系统模式切换过程中的鲁棒性，分步切换则在保证稳定性的同时不影响并联系统的稳态性能。
本文通过在两台1MV·A的电力电子变压器低压交流端口上进行实验对本文所提出的方法进行了验证。
参考文献
[1] 赵争鸣, 冯高辉, 袁立强,等. 电能路由器的发展及其关键技术[J]. 中国电机工程学报, 2017, 37(13): 3823-3834.
Zhao Zhengming, Feng Gaohui, Yuan Liqiang, et al. The development and key technologies of electric energy router[J]. Proceedings of the CSEE, 2017, 37(13): 3823-3834.
[2] 李凯, 赵争鸣, 袁立强, 等. 面向交直流混合配电系统的多端口电力电子变压器研究综述[J]. 高电压技术, 2021, 47(4): 1233-1250.
LI Kai, Zhao Zhengming, Yuan Liqiang, et al. Overview on research of multi-port power electronic transformer oriented for AC/DC hybrid distribution grid[J]. High Voltage Engineering, 2021, 47(4): 1233-1250.
[3] 文武松, 赵争鸣, 莫昕, 等. 基于高频汇集母线的电能路由器能量自循环系统及功率协同控制策略[J]. 电工技术学报, 2020, 35(11): 2328-2338.
Wen Wusong, Zhao Zhengming, Mo Xin, et al. Energy self-circulation scheme and power coordinated control of high-frequency-bus based electric energy router[J]. Transactions of China Electrotechnical Society, 2020, 35(11): 2328-2338.
[4] 文武松, 赵争鸣, 袁立强, 等. 电能路由器公共高频母线超瞬态过程机理及抑制措施[J]. 中国电机工程学报, 2021, 41(15): 5283-5294.
Wen Wusong, Zhao Zhengming, Yuan Liqiang, et al. Mechanism and suppression strategy of the ultra-transient behavior of high-frequency-bus in electric energy router[J]. Proceedings of the CSEE, 2021, 41(15): 5283-5294.
[5] 蔡伟谦, 沈瑜, 李凯, 等. 共高频交流母线的电能路由器直流端口控制策略[J]. 电网技术, 2020, 44(12): 4600-4607.
CaiWeiqian, Shen Yu, Li Kai, et al. DC port control strategy for electric energy router with high frequency AC link[J]. Power System Technology, 2020, 44(12): 4600-4607.
[6] Zhao Zhengming, Tan Dong, Shi Bochen, et al. A breakthrough in design verification of megawatt power electronic systems[J]. IEEE Power Electronics Magazine, 2020, 7(3): 36-43.
[7] 陈新, 姬秋华, 刘飞. 基于微网主从结构的平滑切换控制策略[J]. 电工技术学报, 2014, 29(2): 163-170.
Chen Xin, Ji Qiuhua, Liu Fei. Smooth transferring control method of microgrids based on master-slave configuration[J]. Transactions of China Electrotechnical Society, 2014, 29(2): 163-170.
[8] 郑竞宏, 王燕廷, 李兴旺, 等. 微电网平滑切换控制方法及策略[J].电力系统自动化, 2011, 35(18): 17-24.
Zheng Jinghong, Wang Yanting, Li Xingwang, et al. Control methods and strategies of microgrid smooth switchover[J]. Automation of Electric Power Systems, 2011, 35(18): 17-24.
[9] 李鑫卓. 基于主从控制的微电网平滑切换控制[J].电气自动化, 2019, 41(4): 27-29.
Li Xinzhuo. Smooth switching control of microgrids based on master-slave control[J]. Electrical Automation, 2019, 41(4): 27-29.
[10] 王明玥, 罗安, 陈燕东, 等. 三相逆变器的双模式及其平滑切换控制方法[J]. 电工技术学报, 2016, 31(16): 124-134.
Wang Mingyue, Luo An, Chen Yandong, et al. The dual-mode control and seamless transfer control method of three-phase inverter[J]. Transactions of China Electrotechnical Society, 2016, 31(16): 124-134.
[11] 梁建钢, 金新民, 吴学智, 等. 微电网逆变器VCS模式与CCS模式的切换技术[J]. 电网技术, 2014, 38(4): 830-837.
Liang Jiangang, Jin Xinmin, Wu Xuezhi, et al. Switching technology between VCS mode and CCS mode of inverters in microgrids[J]. Power System Technology, 2014, 38(4): 830-837.
[12] Wang Jing, Chang N C P, Feng Xiaowei. Design of a generalized control algorithm for parallel inverters for smooth microgrid transition operation[J]. IEEE Transactions on Industrial Electronics, 2015, 62(8): 4900-4914.
[13] Micallef A, Apap M, Spiteri-Staines C, et al. Single-phase microgrid with seamless transition capabilities between modes of operation[J]. IEEE Transactions on Smart Grid, 2015, 6(6): 2736-2745.
[14] 杨彦杰, 杨康, 邵永明, 等. 微电网的并离网平滑切换控制策略研究[J]. 可再生能源, 2018, 36(1): 36-42.
Yang Yanjie, Yang Kang, Shao Yongming, et al. Control strategy for smooth switching between island operation mode and grid-connection operation mode of microgrid[J]. Renewable Energy Resources, 2018, 36(1): 36-42.
[15] 杨向真. 微网逆变器及其协调控制策略研究[D]. 合肥: 合肥工业大学,2011.
[16] Ramezani M, Li S, Musavi F, et al. Seamless transition of synchronous inverters using synchronizing virtual torque and flux linkage[J]. IEEE Transactions on Industrial Electronics, 2020, 67(1): 319-328.
[17] 梁建钢. 微电网变流器并网运行及并网和孤岛切换技术研究[D]. 北京: 北京交通大学, 2015.
[18] 王大获. 数据中心电源系统节能方案设计[D]. 广州: 华南理工大学, 2017.
[19] 杨荣峰, 于雁南, 俞万能, 等. 新能源船舶并网逆变器电网支撑协调控制[J]. 电工技术学报, 2019, 34(10): 2141-2154.
Yang Rongfeng, Yu Yannan, Yu Wanneng, et al. New energy ship grid-connected inverter grid support and cooperative control[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2141-2154.
[20] 姜齐荣, 王玉芝. 电力电子设备高占比电力系统电磁振荡分析与抑制综述[J]. 中国电机工程学报, 2020, 40(22): 7185-7201.
Jiang Qirong, Wang Yuzhi. Overview of the analysis and mitigation methods of electromagnetic oscillations in power systems with high proportion of power electronic equipment[J]. Proceedings of the CSEE, 2020, 40(22): 7185-7201.
[21] 谢志为, 陈燕东, 伍文华, 等. 弱电网下多逆变器并网系统的全局高频振荡抑制方法[J]. 电工技术学报, 2020, 35(4): 885-895.
XieZhiwei, Chen Yandong, Wu Wenhua, et al．A global high-frequency oscillation suppression method for multi-inverter grid-connected system in weak grid[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 885-895.
[22] Shah S, Parsa L. Impedance modeling of three-phase voltage source converters in dq, sequence, and phasor domains[J]. IEEE Transactions on Energy Conversion, 2017, 32(3): 1139-1150．
[23] Cespedes M, Sun J. Impedance modeling and analysis of grid-connected voltage-source converters[J]. IEEE Transactions on Power Electronics, 2013, 29(3): 1254-1261.
[24] 姚骏, 谭义, 杜红彪, 等. 孤岛模式下逆变器并联系统的谐振特性分析及其抑制策略研究[J]. 电工技术学报, 2016, 31(23): 199-210.
YaoJun, Tan Yi, Du Hongbiao, et al. Analysis of resonant characteristics and resonance suppression strategy of inverter parallel system in islanding mode[J]. Transactions of China Electrotechnical Society, 2016, 31(23): 199-210.
[25] Zong Haoxiang, Lu Jing, Cai Xu, et al．Analysis of bifurcation behaviors in MMC connected to a weak grid[C]// IECON 2018-44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 2018, DOI: 10.1109/IECON. 2018. 8592728.
[26] 张旸, 陈新, 王昀, 等. 弱电网下并网逆变器的阻抗相角动态控制方法[J]. 电工技术学报, 2017, 32(1): 97-106.
Zhang Yang, Chen Xin, Wang Yun, et al. Impedance-phased dynamic control method of grid-connected inverters under weak grid condition[J]. Transactions of China Electrotechnical Society, 2017, 32(1): 97-106.
Mode Transition for Low Voltage AC Port of Power Electronic Transformers Based on Duty Cycle Synchronization
Abstract Multi-port power electronic transformer(PET) is the critical equipment in the future smart grid and is applied to new energy generation, hybrid AC-DC grid and DC(data center) power supply system. When multiple PETs are running in cluster, function of interconnection, information sharing, complementation and optimization is provided. Thus, mode transition which is the base of the cluster running is significant for the PETs. A duty cycle synchronization based mode transition method was proposed for a PET cluster demonstration system. The proposed method can effectively reduce the mode transition impact while the similar control scheme is not required for master and slave inverter. The impedance characteristics of the parallel inverter system were analyzed by the harmonic linearization method, which explained the reason of system oscillation during mode transition.Thus, the multi-step switchover method was applied to improve the stability of the mode transition. Finally, the proposed method was verified by mode transition experiments on two parallel MV·A PETs system.
keywords：Power electronics transformer(PET), parallel inverters, master-slave structure, seamless mode transition
DOI:10.19595/j.cnki.1000-6753.tces.210915
中图分类号：TM464
国家重点研发计划资助项目（2017YFB0903203）。
收稿日期 2021-06-21
改稿日期 2021-07-14
袁立强 男，1976年生，博士，研究员，研究方向为电力电子变压器、电能路由器等。E-mail：ylq@tsinghua.edu.cn
高 深 男，1997年生，硕士研究生，研究方向为电力电子变压器、电能路由器等。E-mail：gaos19@mails.tsinghua.edu.cn（通信作者）
（编辑 郭丽军）