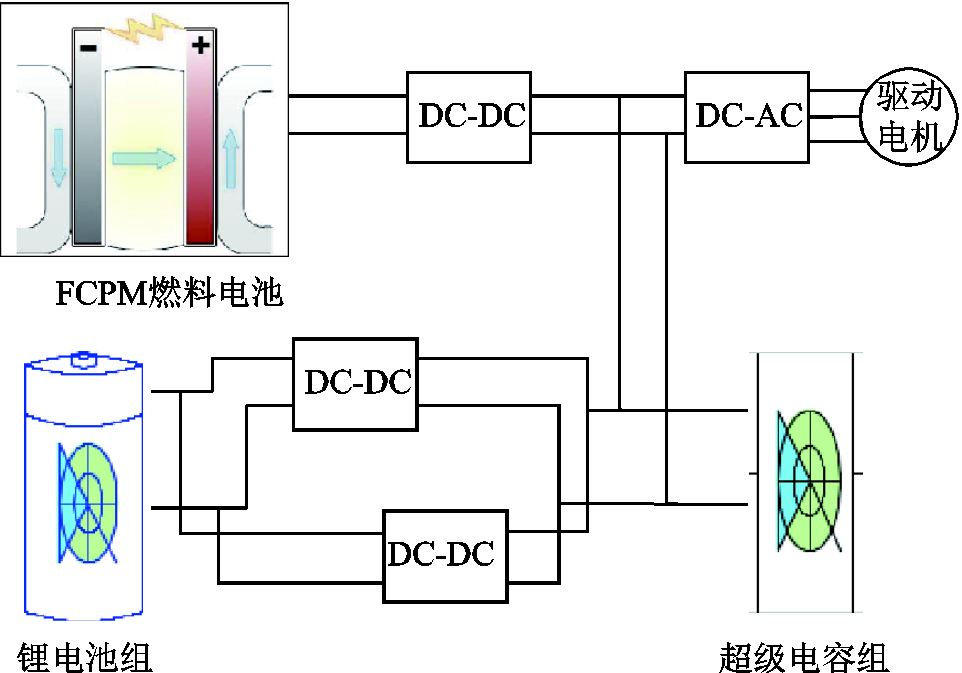
图1 有轨电车复合供电系统拓扑结构
Fig.1 Basic structure of tram power supply system
摘要 针对燃料电池/超级电容/锂电池混合储能有轨电车能量管理中存在的等效能耗受负载随机性影响较大,无法保证全局功率分配最优的问题,同时为进一步提升燃料经济性,提出一种基于外部能耗的运行优化策略。首先,将负载能量需求分为内部能源燃料电池的实时燃料消耗和外部电源锂电池/超级电容的电能消耗两部分;其次,旨在通过将等效能耗最小化策略的目标函数改写为最大化外部电源出力,以分担燃料电池的高功率负载压力,使其不需要评估等效能耗,从而达到增强对负载变载的鲁棒性,同时最小化实时氢耗的目的;最后,将所提优化策略与等效能耗最小化及状态机和功率解耦策略进行对比分析。结果表明:在整个循环工况中,所提方法相较于等效能耗最小化策略燃料电池氢气消耗降低17.68g,峰值电流降低21.81A;相较于状态机和功率解耦策略氢气消耗降低39.04g,峰值电流降低56.9A,且母线电压偏移范围和各能量源应力均有显著改善。
关键词:混合储能有轨电车 燃料电池 能量管理 功率分配 外部能耗
燃料电池具有绿色节能、高能量转换率及噪声小等突出优点,是目前全世界公认的未来最佳车载能源[1]。结合锂电池和超级电容作为辅助电源所具有的优势,构建以燃料电池为主电源的新型有轨电车混合动力系统,不仅可实现无燃料电池状态下的紧急供电,亦可在电车制动阶段实现能量回收[2],同时还兼具节约成本、改善能源结构及无污染等特点,已发展成为有轨电车无电弓受流系统的一种理想解决方案[3]。但多种储能单元的组合也使能量管理策略趋于复杂。
混合储能系统能量管理优化是节能、降低成本、达到整体高效率和增强动态性能的关键。现有混合储能有轨电车领域主流的能量管理策略可分为基于规则和基于优化的两类。基于规则的策略是以根据专家经验或离线规则得到的负载功率需求占比为原则分配给不同储能单元,其优点包括实时性好及易于求解和实现。应用较为广泛的方法主要有逻辑门限值[4]、模糊逻辑控制[5]、功率解耦控制[6]等。逻辑门限值即阈值法最早出现在有轨电车混合动力系统控制策略的研究中。文献[7]依据有轨电车的进站停车、无网运行、首末站充电三种工作状态的周期性变化,设定各自阈值,从而划分各能量源需承担的功率,虽然简单实用,但并未定量描述优化目标,无法实现全局最优。模糊逻辑控制解决了复合电源这一复杂时变非线性强耦合系统的建模问题。文献[8]通过划分未来时间窗格内的能量消耗,并结合有轨电车运行状态制定模糊规则,虽然相较于阈值法具有更低的能耗,但也存在隶属度函数与模糊规则权重过度依赖专家经验的缺陷,且当输入量较多时,模糊规则也趋于复杂。功率解耦控制策略也是较为经典的方法之一,其主要思路是对负载功率需求作分频处理,以实现对主电源的保护,延长其使用寿命。文献[9]在令燃料电池承担低频功率、由锂电池/超级电容供电单元承担高频功率的基础上,引入状态机进行能量再分配与管理,有效地减少了燃料电池的高频波动。但在城市轨道交通领域,特别是无接触网受流情况下,高频含量相对较少,其适应性并不如其他基于规则的策略。
相较于基于规则的策略,基于优化策略的优点在于能够通过目标或成本函数将能量管理问题转换为数学优化问题进行定量求解。研究较为成熟的智能算法主要包含多目标优化算法[10]、模型预测控制[11]、动态规划[12]等。文献[13]以混合动力系统全寿命周期成本最低、容量配置最优为目标函数获取Pareto前沿,有效降低了整车服役周期成本,但求解复杂,易于陷入维数灾难。文献[14]以降低混合储能系统总损耗及稳定母线电压为主要目标,结合模型预测控制实现了离线优化的在线运行,但对于模型精度要求高、实时性差。文献[15]在传统动态规划的基础上调整了状态转移方程,通过只对混合储能系统状态量进行离散,解决了插值计算导致的误差累积问题,但仍然无法实现对在线运行参数的实时计算。
在车载燃料电池混合储能系统领域,大多数基于优化策略的核心思想都是降低等效能耗,而传统方法中等效因子无法适应负载变载动态情况。为解决这一问题,文献[16]提出用未来负载电力需求时间序列代替等效因子。文献[17]提出用根据负载曲线确定的充放电信号代替等效因子。文献[18]提出用电池荷电状态(State of Charge, SOC)和SOC平衡系数的经验表达式在线调节等效因子的大小。这些方法虽然显著提高了能量管理的性能,但代价是提高了控制复杂度。
为综合考虑能量管理系统的抗干扰能力、整体效率、能量源应力及能耗,本文提出一种外部能耗最大化策略。旨在通过在任一给定时刻,在保证不过充过放的条件下令锂电池平均功率和超级电容峰值功率出力最大化,以分担燃料电池的运行压力,从而使目标函数中不涉及任何取决于负载变化的参数,改善系统的工况适应性及最大限度地降低氢气消耗量,并通过仿真实验对比证明所提策略的有效性和优越性。
混合动力电源箱采用模块化设计原则,编组方案为两动一拖的结构,每个混合动力系统包含一个双向DC-DC电源电池箱和一个超级电容箱共两个箱体,对称布置于两个Mc(Mc指安装动力转向架和驾驶室的动车模块)车车顶中部,便于车辆布线和质量管理。两套燃料电池系统布置于T(T指安装拖车转向架和燃料电池系统的拖车模块)车车顶,对称布置于散热器两端,便于对供电和供氢进行设计。储氢系统布置于T车(中间车)车顶。
建立有轨电车车载混合储能系统的主动式拓扑结构,如图1所示。为了便于对燃料电池和锂电池能量进行控制,分别经单向和双向DC-DC变换器连接到直流母线上。由于超级电容在该系统中的作用主要是“削峰填谷”,所以采用未经变换器直接并联于直流侧母线端的结构。能量管理控制器跟踪检测各能量源的能量状态,以调控各变换器的开关状态,使三者匹配工作,有轨电车主要技术参数见表1。

图1 有轨电车复合供电系统拓扑结构
Fig.1 Basic structure of tram power supply system
表1 有轨电车主要技术参数
Tab.1 Main technical parameters of tram

参数 数值 变流器/VDC750(500~900) 驱动电机/kW 轴重/t12 列车自重/t47 列车车体长度/mm31 075 续驶里程/km>40 最高运行速度/(km/h)60
FCPM(fuel cell power module)质子交换膜燃料电池以其满足从怠速到满负荷快速启动的优点,成为新能源有轨电车中应用最为广泛的燃料电池[19]。在Matlab中使用SimPowerSystems(SPS)工具箱搭建了燃料电池堆动态参数模型,如图2所示,E为仅考虑活化损失(由于电极表面缓慢的化学反应造成的损失)的堆电压。

图2 燃料电池堆动态参数模型
Fig.2 Dynamic parameter model of fuel cell stack
该模型反映了当燃料和空气的流量、配比、压力及温度等参数动态变化时,对塔菲尔斜率A、燃料电池交换电流i0,以及开路电压Eoc的影响,如式(1)~式(3)所示。
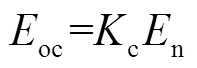 (1)
(1)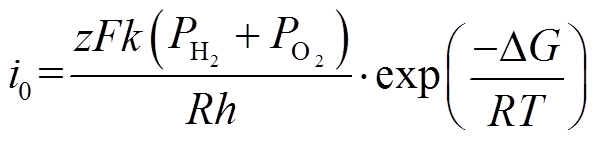 (2)
(2)
 (3)
(3)
式中,Kc为额定工作条件下的电压常数;En为能斯特电压;z为移动电子数(等于2);F为常数,F=96 485A·s/mol;k为玻耳兹曼常数;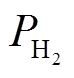 和
和 分别为燃料电池堆内氢气和氧气的供给压力;R为常数,R=8.314 5J/(mol·K);h为普朗克常数;
分别为燃料电池堆内氢气和氧气的供给压力;R为常数,R=8.314 5J/(mol·K);h为普朗克常数; 为电荷转移系数;
为电荷转移系数;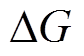 为活化能垒;T为工作温度。
为活化能垒;T为工作温度。
该模型设置了A、B和C三个计算模块实时更新A、i0及Eoc的值。首先采用第一个模块A计算燃料电池对氢气和氧气的利用率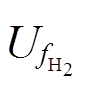 和
和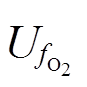 ,如式(4)和式(5)所示。
,如式(4)和式(5)所示。
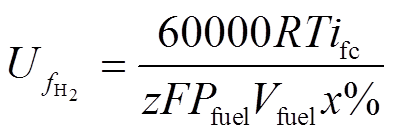 (4)
(4)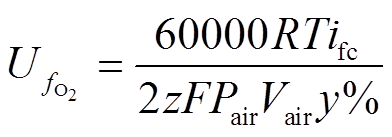 (5)
(5)
式中,Pfuel与Pair分别为燃料和空气的绝对供给压力;Vfuel和Vair分别为燃料和空气的流量;x%和y%分别为燃料中氢气和氧气的配比;ifc为燃料电池电流。
采用模块B确定各气体的绝对供给压力以及能斯特电压,如式(6)~式(9)所示。
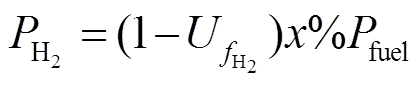 (6)
(6)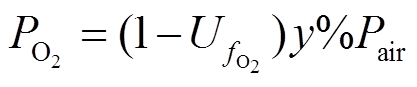 (7)
(7)
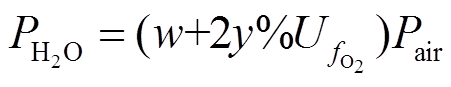 (8)
(8)
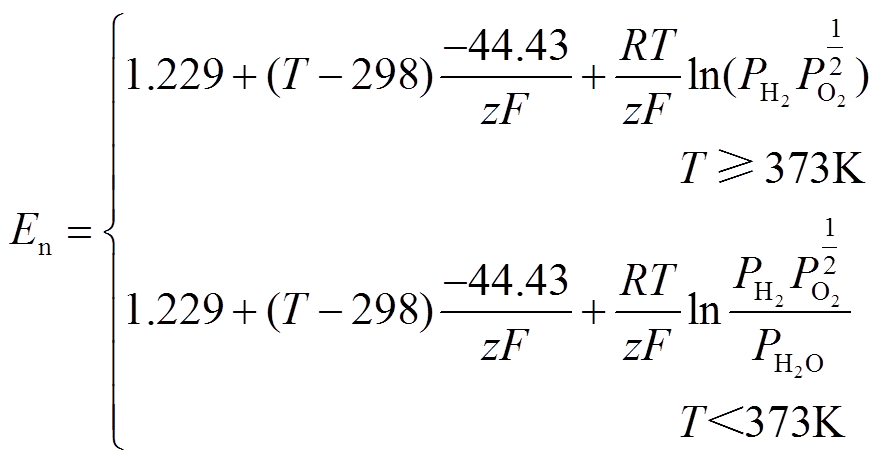 (9)
(9)式中,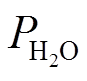 和w分别为水蒸气的绝对供给压力和在氧化剂中的占比。采用式(1)和式(2)更新Eoc和i0;采用模块C,即式(3)更新A的值。
和w分别为水蒸气的绝对供给压力和在氧化剂中的占比。采用式(1)和式(2)更新Eoc和i0;采用模块C,即式(3)更新A的值。
模型所需运行参数由FCPM燃料电池单体的极化测试得到,通过直接连接到可编程负载,测试从空载启动到逐渐增大的阶跃放电电流下的电压和功率,拟合出的极化曲线如图3所示。
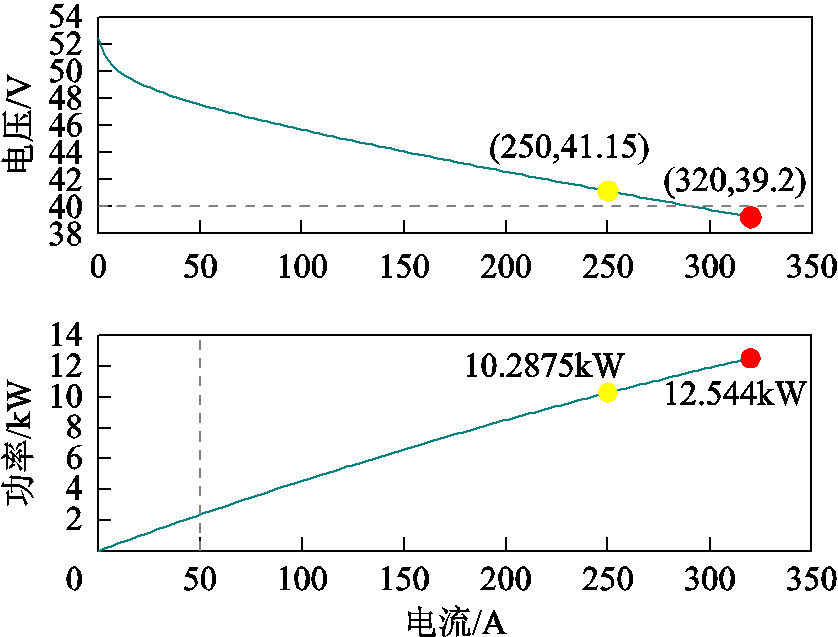
图3 燃料电池单体极化测试拟合曲线
Fig.3 Fitting curve of fuel cell unit polarization test
在额定条件(Pfuel=0.116MPa,Pair=0.1MPa,T=45℃)下对该模型进行阶跃放电电流仿真测试,同一条件下电压曲线与Hydrogenics公司提供的单体实际放电数据的对比如图4a所示,随时间变化的电压实时误差如图4b所示。从图4中可以看出:瞬态误差最大为-0.4V,稳态误差在±0.1V以内,表明该模型具有较高的精度,能正确地描述燃料电池在实际运行过程中的电压行为。
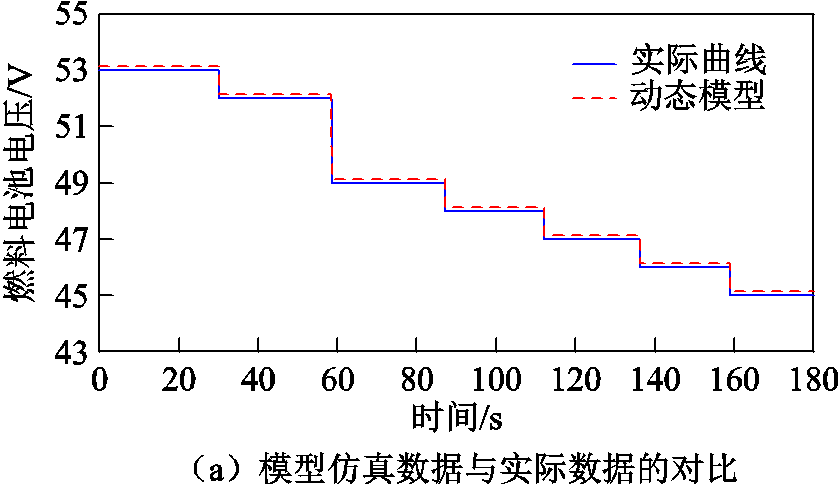

图4 燃料电池动态参数模型精度验证
Fig.4 Accuracy verification of model of fuel cell
锂电池采用如图5所示改进Shepherd模型,为降低代数环和仿真的不稳定性,去除了原本模型受控电压源中随电流幅值和实际充电量变化的非线性电压项。该模型中受控源只受实际电池电量控制,当电池完全放电时,端电压将降为零,从而更为准确地模拟电池端电压行为。假设充放电过程具有相同的特性,受控源电压和端电压表达式分别为
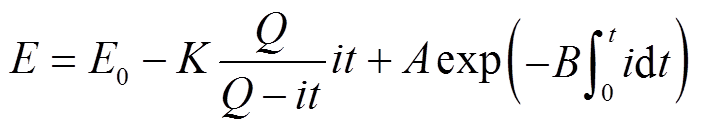 (10)
(10)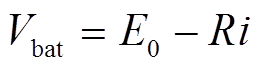 (11)
(11)
式中,E、E0、K和Q分别为受控源电压、锂电池额定电压、极化电压及额定容量;A为充满电时的电池电压;B为额定放电电流倍率;Vbat为锂电池端电压;R为电池内阻;i为电池电流。
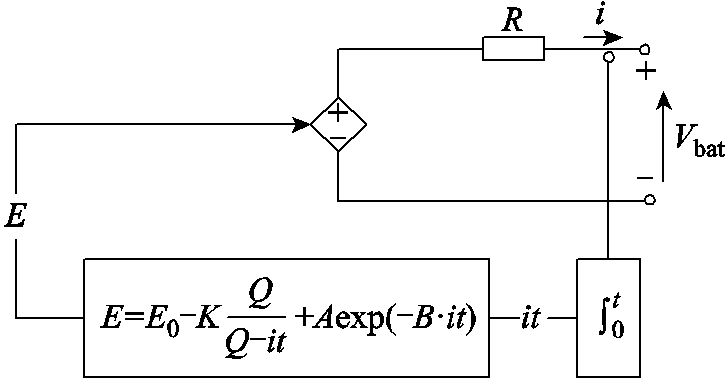
图5 改进Shepher锂电池模型
Fig.5 Improved shepher lithium battery mode
通过选取适当的参数,对锂电池单体分别在额定放电电流倍率,即0.434 78C(17.391 3A)、20A、80A下进行脉冲放电仿真测试,得到的放电曲线如图6所示。该曲线与苏州星恒公司提供的特性曲线基本吻合,说明选用的电池模型是恰当、可靠的。
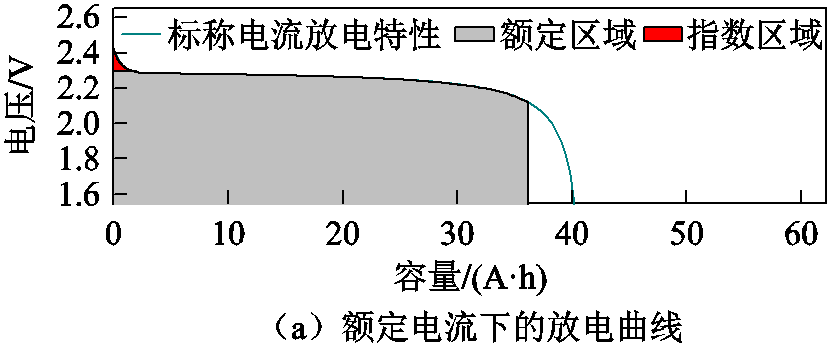
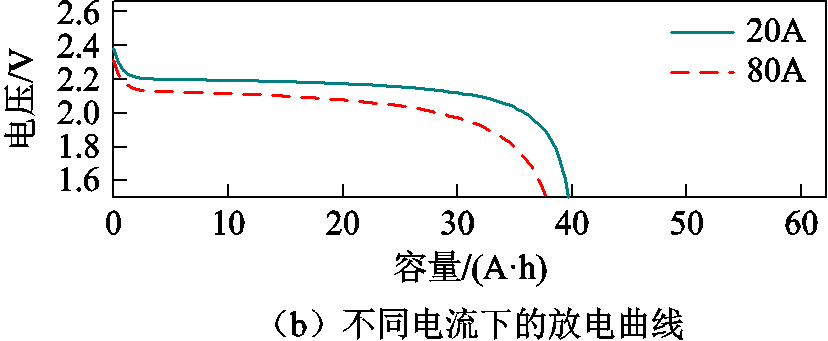
图6 放电特性仿真曲线
Fig.6 Simulation curve of discharge characteristics
超级电容器的动态行为与所用电解液的离子迁移率和多孔电极的孔隙率效应密切相关[20]。由于存在离子惯性,电容和阻抗的实部随充放电频率的增加而减小。传统模型只关注高频下的动态行为,且存在无法模拟自放电现象,以及在低频下精度很低的问题。为此,本文在传统模型的基础上提出一种全频段超级电容模型,如图7所示。该模型由三个支路并联组成:支路1描述各充放电频率域下的超级电容等效阻抗ZP;支路2用串联RC支路表征超级电容快速充放电后的恢复现象;支路3是考虑自放电现象的漏电电阻Rleak。其中等效阻抗ZP为

式中,Ri为频率趋近于无穷时第i条支路等效电阻;Li为第i条支路的漏感;V为图7中的端电压;τ为时间的维度;Rp为各充放电频率域下等效电阻。漏感通常为几十纳赫兹,在此可以忽略不计。
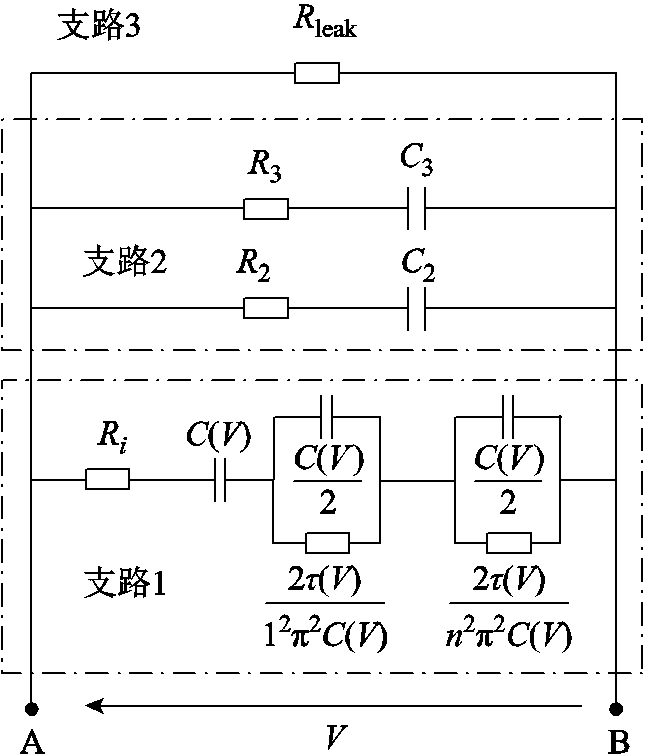
图7 全频段超级电容模型
Fig.7 Full-frequency-range supercapacitor model
对该模型表征的超级电容单体分别在10A、20A、100A及500A的电流下进行了脉冲电流充电测试,得到的充电曲线如图8所示。
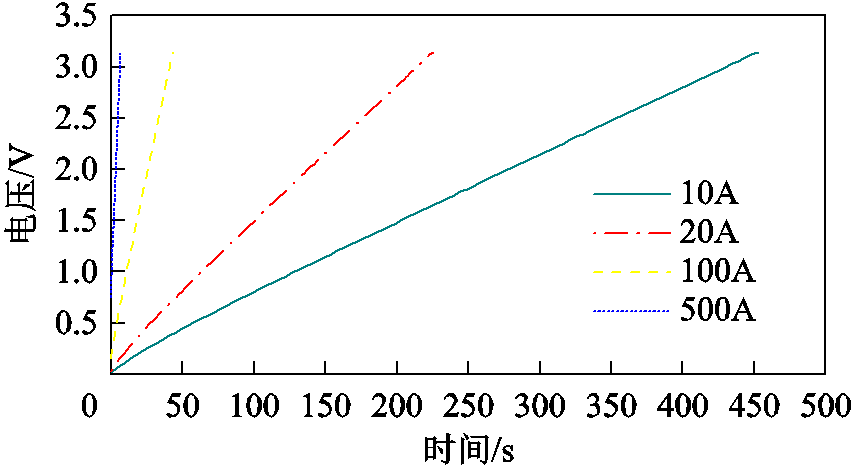
图8 不同充电电流下的超级电容单体端电压曲线
Fig.8 Voltage curve of supercapacitor under different charging current
燃料电池混合动力能量管理系统旨在通过优化管理策略调整各能量源的功率响应,在保证负载功率需求的同时达到降低燃料电池氢能耗、提高系统整体效率、压缩电池和超级电容SOC变化范围及延长循环使用寿命的目的。由于超级电容未经DC-DC变换器直接并联于母线直流侧,不同能量管理策略之间的区别主要在于燃料电池参考功率的确定方法。基于此系统要求,本文针对传统等效氢能耗优化策略(Equivalent Consumption Minimization Strategy, ECMS)的缺陷做出改进,提出一种更适用于优化成本函数的外部能耗最大化能量管理策略(External Energy Maximization Strategy, EEMS)。
ECMS是一种在车载复合电源领域应用广泛的优化瞬时成本函数的方法[21]。通过降低整个循环工况中燃料电池内部燃料消耗和维持锂电池/超级电容SOC变化范围所需的等效能耗,从而实现总体能耗最小化,而超级电容等效能耗主要作用是补偿系统的峰值功率,因此在稳态情况下可忽略不计。ECMS的管理性能取决于等效能耗的计算精度,而等效能耗与锂电池的能量等效因子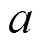 成正比,其表达式为
成正比,其表达式为
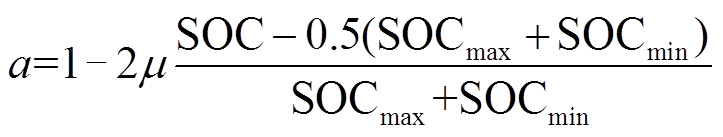 (13)
(13)式中,SOCmin和SOCmax分别为电池SOC的下、上限值;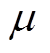 为电池SOC的平衡系数(取0.65,根据经验确定,以限制电池SOC波动)。当电池SOC低于下限值时,等效因子趋近于最大值,此时优化算法控制燃料电池输出更多能量给锂电池充电。
为电池SOC的平衡系数(取0.65,根据经验确定,以限制电池SOC波动)。当电池SOC低于下限值时,等效因子趋近于最大值,此时优化算法控制燃料电池输出更多能量给锂电池充电。
ECMS优化算法的目标函数为燃料电池内部能耗与锂电池等效能耗之和的总能量E最小化,即
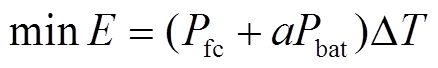 (14)
(14)约束条件为
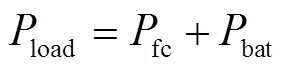 (15)
(15)
边界条件为
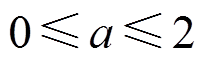 (16)
(16)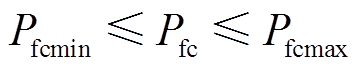 (17)
(17)
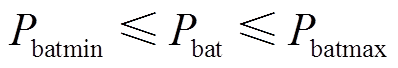 (18)
(18)
式中,Pfc、Pbat、Pload分别为燃料电池、锂电池和负载功率;ΔT为采样时间;Pfcmax和Pfcmin分别为燃料电池功率的上、下限值;Pbatmax和Pbatmin分别为锂电池功率的上、下限。
ECMS整体的示意图如图9所示,通过负载功率Pload和锂电池SOC确定燃料电池参考功率,再除以燃料电池电压Vfc和其DC-DC变换器效率h的乘积得到燃料电池的参考电流值。混合动力系统直流母线电压受稳压调节器控制,该调节器用于确定锂电池双向DC-DC变换器的参考电流值。由于系统输入量含有随机性较强的负载功率,考虑改进优化算法,使其输入量更加稳定可控。

图9 ECMS整体示意图
Fig.9 Overall schematic diagram of ECMS strategy
为增强能量管理策略的工况适应性,旨在通过在SOC约束范围内最大化超级电容和锂电池的能量输出,即外部电源出力,间接地降低燃料电池高负载压力。该方法的优点主要在于不需要评估受负载变化影响很大的等效能耗,使目标函数中无取决于负载功率的变量。目标函数为
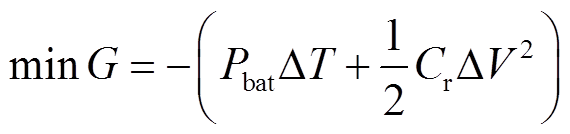 (19)
(19)约束条件为
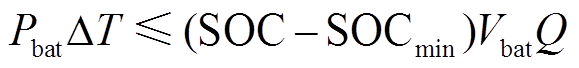 (20)
(20)
边界条件为
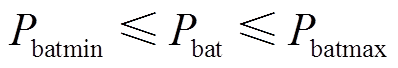 (21)
(21)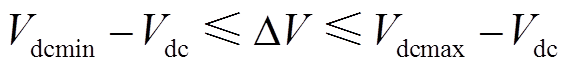 (22)
(22)
式中,G为一个采样周期内的最大外部电源输出电能;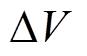 为超级电容的充放电电压;Cr为超级电容的额定电容;Vdcmax和Vdcmin分别为母线电压的上、下限值;Vbat和Q分别为锂电池额定电压和额定容量;SOCmin是初始值的90%。
为超级电容的充放电电压;Cr为超级电容的额定电容;Vdcmax和Vdcmin分别为母线电压的上、下限值;Vbat和Q分别为锂电池额定电压和额定容量;SOCmin是初始值的90%。
EEMS整体的示意图如图10所示,通过EEMS优化算法确定锂电池参考功率和超级电容充放电电压,再根据式(15)确定燃料电池参考功率。并采用超级电容电压相对母线电压的偏移量决定超级电容的充放电能量,母线电压通过锂电池DC-DC转换器占空比控制。
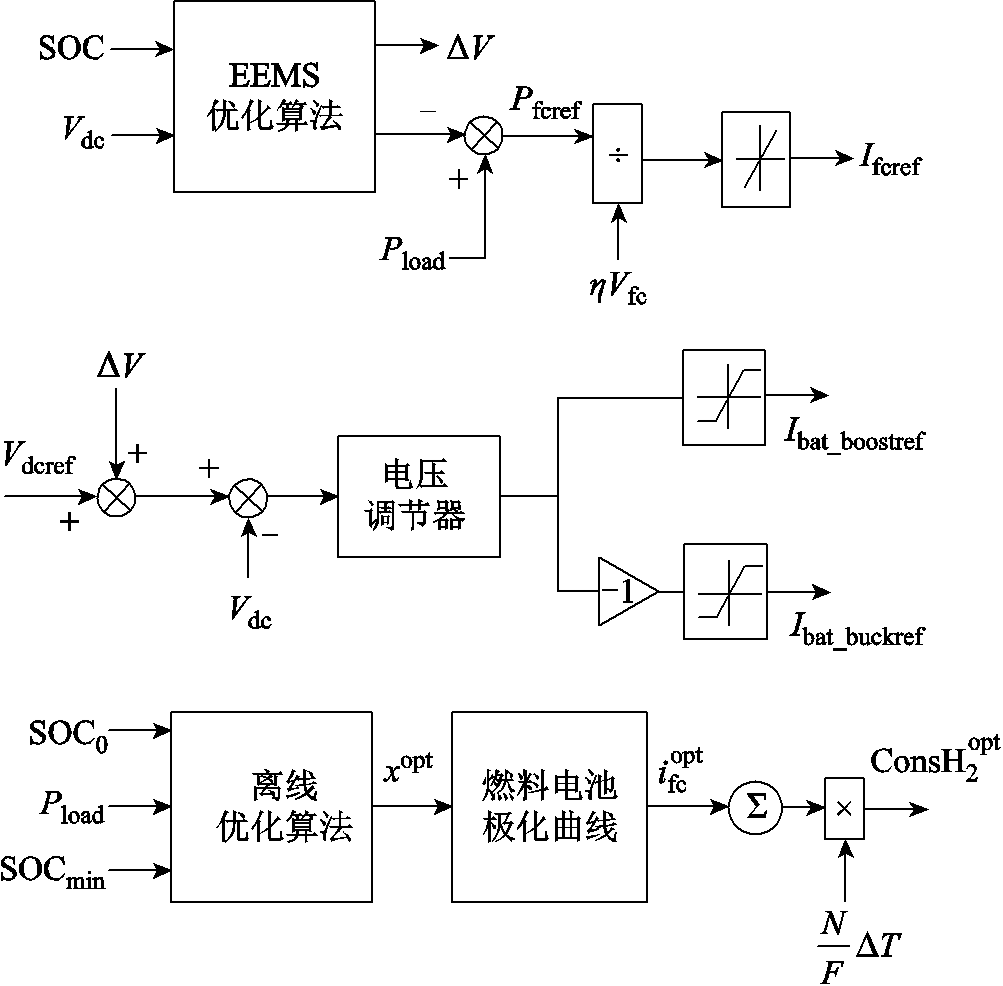
图10 EEMS整体示意图
Fig.10 Overall schematic diagram of EEMS strategy
燃料经济性方面,通过离线优化算法在给定时间和SOC限制范围内计算燃料电池最低输出能量进行评估,通过对负载功率的实时采样,以满足负载功率需求和锂电池不过放的条件,求取燃料电池瞬时输出功率的个体最优解;通过对n次采样后的燃料电池净输出能量进行整合,以总能量最低为目标判断是否为全局最优的氢气消耗量。该离线优化算法以负载功率Pload、锂电池荷电状态初始值SOC0及下限值作为输入,目标函数为
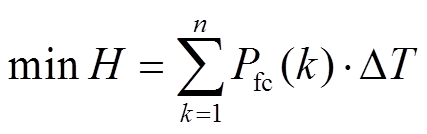 (23)
(23)约束条件为
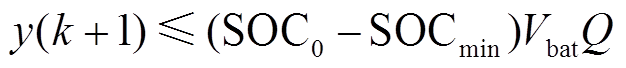 (24)
(24)
 (25)
(25)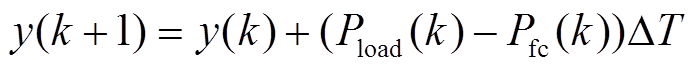 (26)
(26)
边界条件为
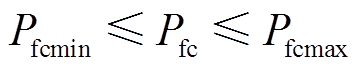 (27)
(27)式中,n为采样次数;y(k)为k次采样以后的锂电池能量;H为整个循环工况中燃料电池输出给负载的能量;min H为最小化燃料电池的净输出能量。
最佳氢气消耗量ConsHopt 2为
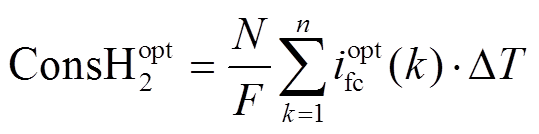 (28)
(28)式中,F为法拉第常数;N为电堆单节单体数量。如图10所示,通过所提离线优化算法得到最优燃料电池功率xopt,再通过图3所示的燃料电池极化曲线拟合得到最优燃料电池电流iopt fc。
为了验证所提策略的有效性和优越性,使用Matlab/Simulink中的SPS工具箱中搭建了燃料电池为主电源,锂电池和超级电容为辅助电源的有轨电车车载混合储能系统仿真模型,仿真参数见表2,在负载波动性较强的循环工况中,对比研究不同能量管理策略的性能。为了与储能系统实际运行情况相匹配,锂电池SOC初始值设置为65%;为了模拟实际工况,仿真时间与所采用工况运行时间一致,设置为270s。
表2 车载复合电源仿真参数
Tab.2 Simulation parameters of vehicle hybrid power supply
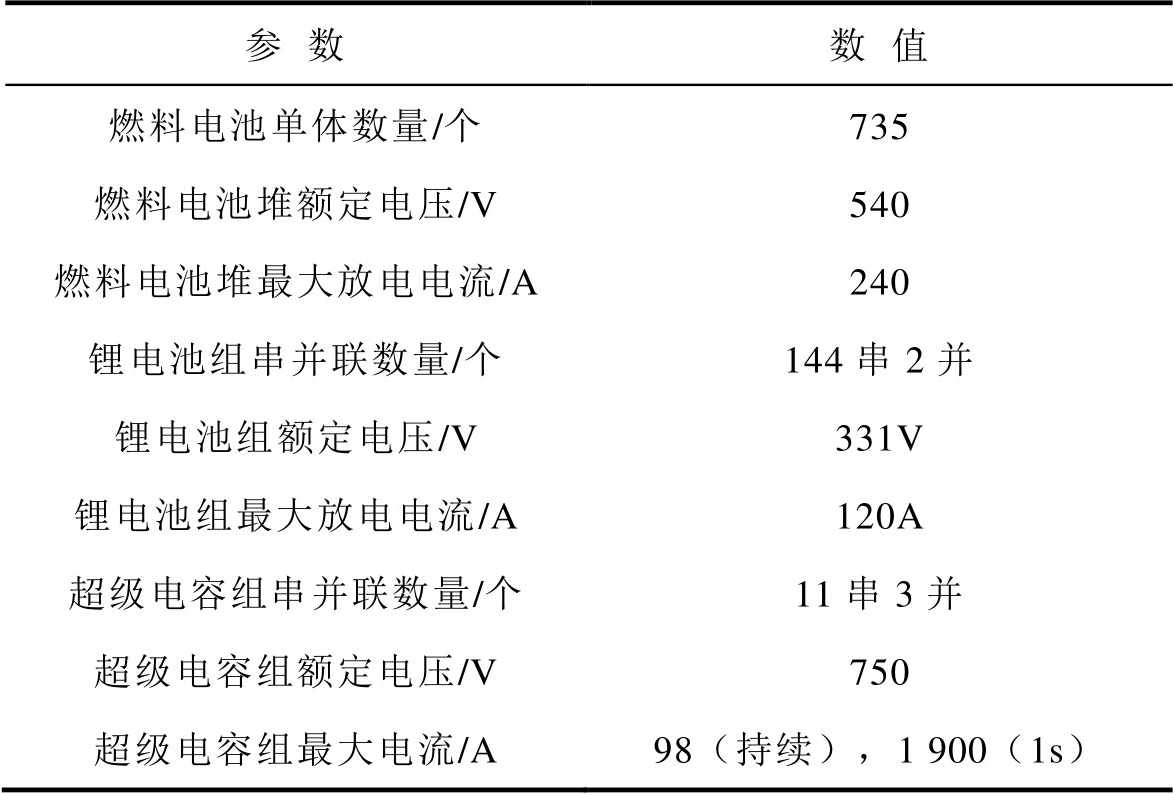
参数数值 燃料电池单体数量/个735 燃料电池堆额定电压/V540 燃料电池堆最大放电电流/A240 锂电池组串并联数量/个144串2并 锂电池组额定电压/V331V 锂电池组最大放电电流/A120A 超级电容组串并联数量/个11串3并 超级电容组额定电压/V750 超级电容组最大电流/A98(持续),1 900(1s)
为综合考虑城市轨道交通车辆载重的时变性以及坡度信息对车辆运行特性的影响,选取实测的美国有轨电车负载工况条件,如图11a所示。对EEMS、ECMS及状态机和功率解耦能量管理策略的功率分配结果进行了对比,如图11b、图11c、图11d所示。在0~10s时,列车未启动负载功率为零,燃料电池输出功率为辅助电源系统充电,为列车启动做准备;10s时列车启动,经过一个短暂的加速过程后,在25~40s时进入第一个低功率平稳运行时期;40~60s时,列车进入第一个进站制动减速阶段,这一时期的再生制动能量由锂电池和超级电容吸收;60~75s时,为第一个进站停车时间;75~170s和170~270s分别为第二个和第三个站间运行阶段,由于地形坡度较大,这一阶段的负载功率存在高峰值特征。
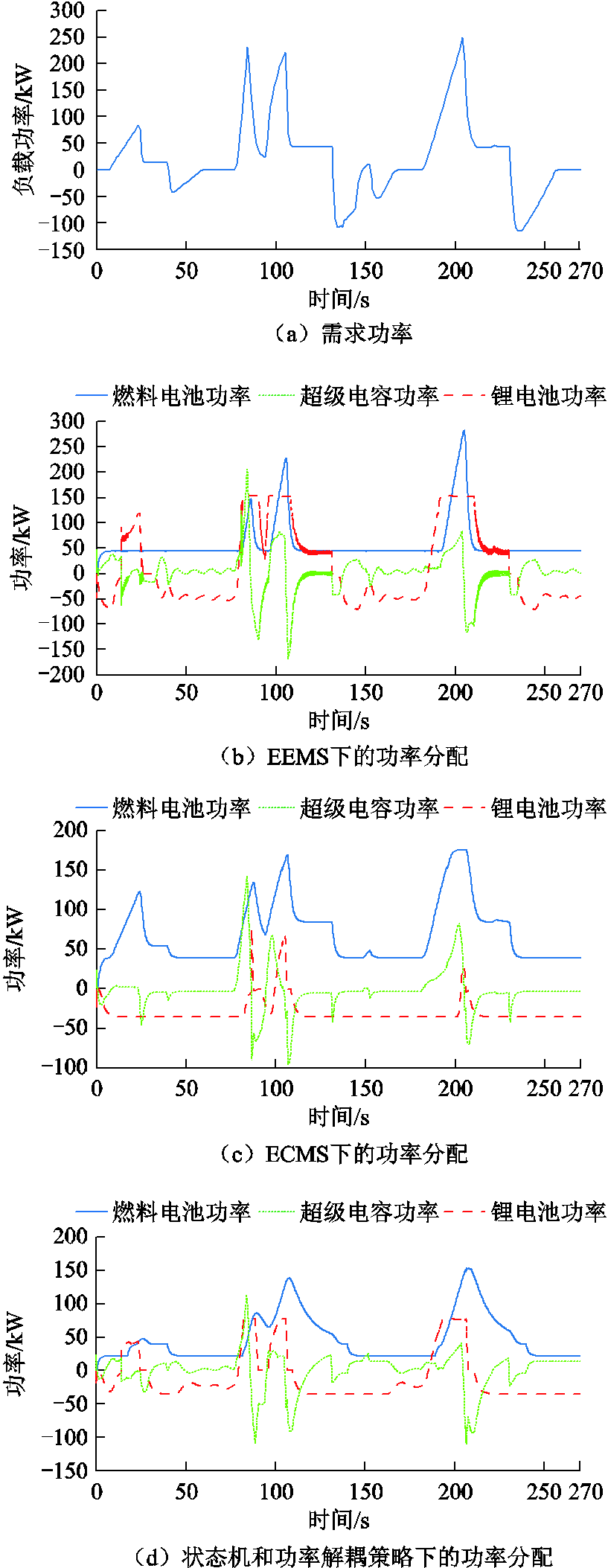
图11 三种策略下的功率分配对比
Fig.11 Comparison of power allocation under three
图11b中锂电池和超级电容分别作为补偿平均功率和峰值功率的辅助电源,在负载功率较低时,可以吸收燃料电池输出功率中过剩的部分,使得燃料电池功率曲线更为平滑,波动更小;在负载功率峰值较高时,锂电池可以输出较高的功率,超级电容可以吸收较高的再生制动功率。图11c中虽然锂电池功率波动更为平缓与稳定,但平均功率出力较小,导致燃料电池功率在高功率需求时期急剧波动。图11d中虽然锂电池输出功率较大,但超级电容吸收和输出的峰值功率较小,弱化了其“削峰填谷”的能力。综上所述,采用EEMS策略可以在保证需求功率的同时,使锂电池和超级电容供电单元最大限度地发挥作用,从而有效分担燃料电池的负载功率压力。
图12a和图12b分别为在相同条件下,整个循环工况过程中的燃料电池氢气消耗量和锂电池SOC的变化范围。燃料经济性方面,从图12a可以看到:EEMS氢气消耗量全过程均低于其他两种策略,在运行结束,即270s时,EEMS、ECMS与状态机和功率解耦策略分别消耗氢气24.92g、42.60g、63.96g。由于状态机和功率解耦策略是基于经验规则的方法,无法保证全局最优,所以导致其燃料消耗远高于其他两种策略。而ECMS策略具有最小化锂电池和超级电容等效能耗的特点,导致辅助电源出力不足,不能给予燃料电池足够的支持,因此燃料电池内部能耗较大。综上所述,采用EEMS能量管理策略可以大幅降低氢气消耗量,燃料经济性可以实现实时和全局最优。
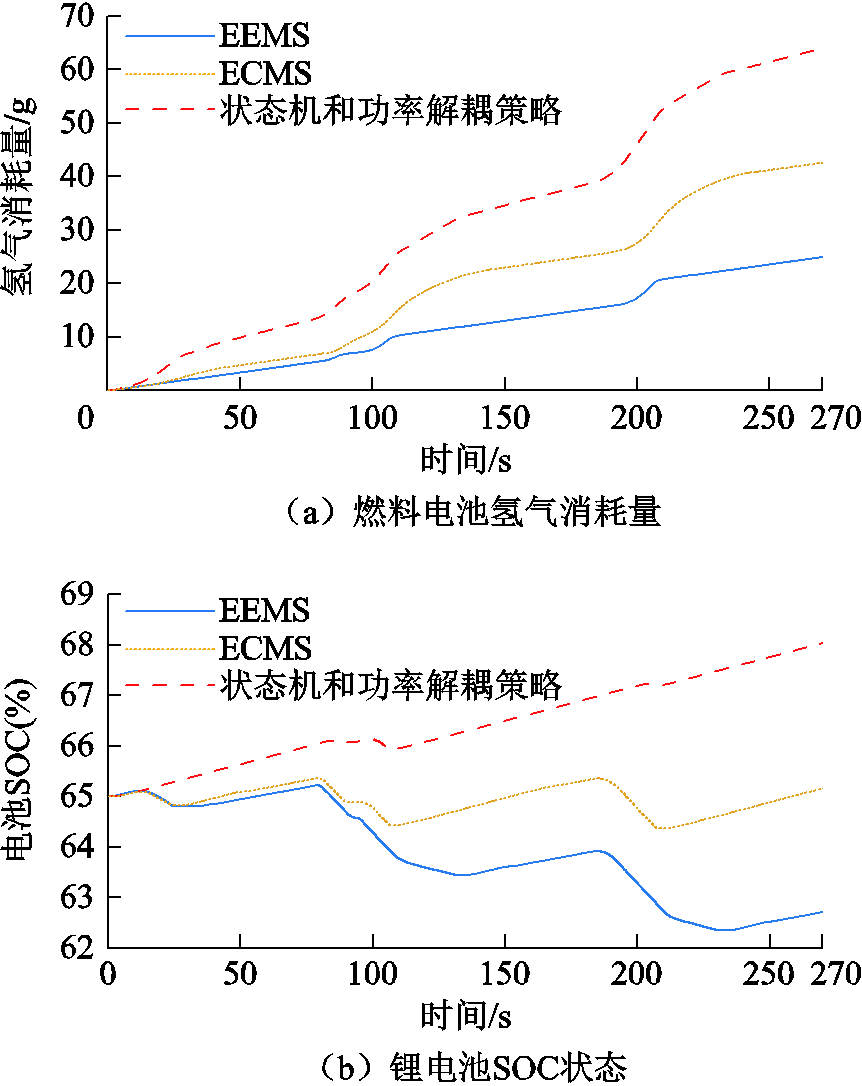
图12 三种策略下的氢气消耗量和锂电池SOC对比
Fig.12 Comparison of hydrogen consumption and SOC of lithium battery under three strategies
锂电池SOC方面,从图12b可以看到:状态机和功率解耦策略全程呈上升趋势,最终达到68.04%;ECMS策略波形较为稳定,全程均在65%左右小幅变化,最终上升到65.17%;EEMS策略先是上升到65.11%,最终跌落到62.71%,这是因为在列车高功率需求时,锂电池需要起到最大辅助供电的作用,承担一部分负载功率,确保满足负载功率需求,导致EEMS策略SOC波动相对其他两种策略较大,最大偏移量为2.29%,对照2.2节中定义的SOCmin,属于合理水平之内。因此,采用EEMS策略可以更加有效地利用锂电池能量。
图13a和图13b分别为在整个循环工况中直流侧母线电压和燃料电池的变化情况。母线电压方面,从图13a可以看到:EEMS母线电压偏移范围在±0.4%以内,ECMS在±0.86%以内,状态机和功率解耦策略在±1.47%以内,均符合供电要求。三种策略下运行结束时的母线电压之所以都有不同程度的上升,是因为最后一个制动过程中超级电容吸收能量较多,导致母线电压有所上升。因此采用EEMS策略可以有效平抑母线电压波动,明显改善混合储能系统的运行稳定性。
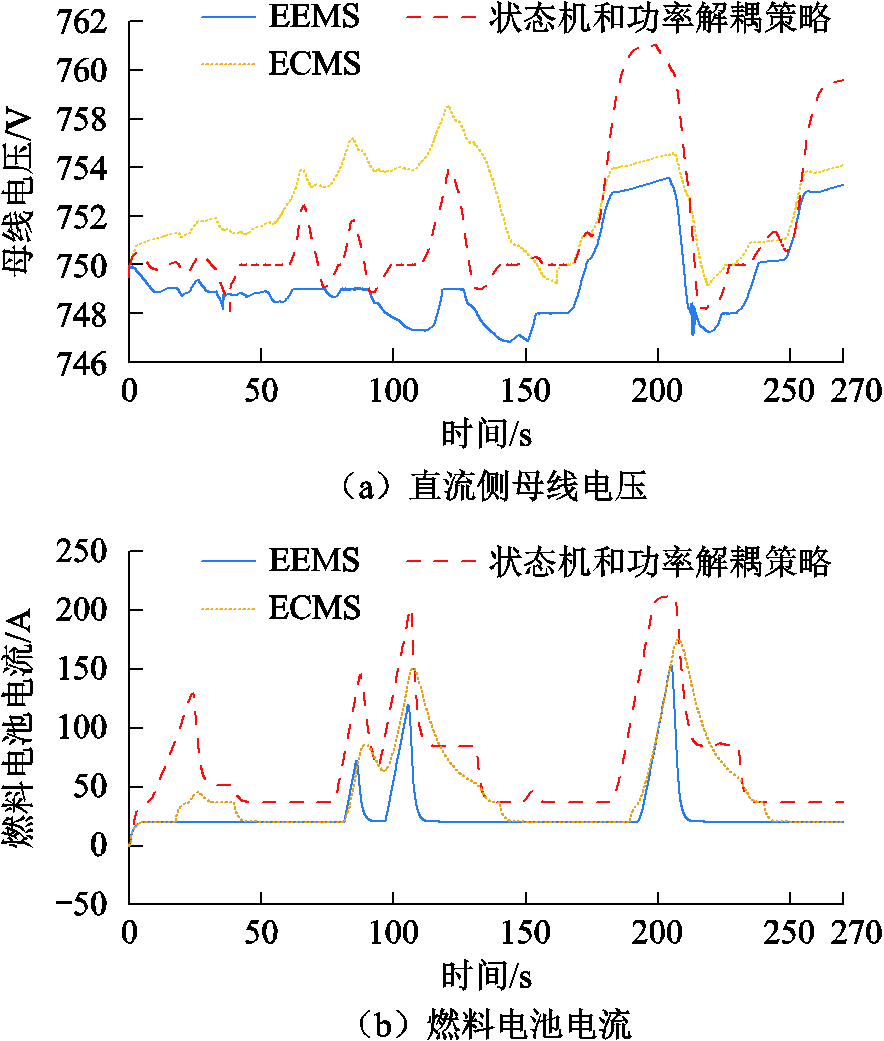
图13 直流侧母线电压和燃料电池电流对比
Fig.13 Comparison of DC bus voltage and fuel cell current
燃料电池电流方面,从图13b可以看到:EEMS的最高峰值电流为154.67A;ECMS的最高峰值电流为176.48A;状态机和功率解耦策略最高峰值电流为211.57A。因此EEMS策略能降低大电流放电对于燃料电池的冲击,从而延长循环使用寿命。
混合储能系统的能量源应力指的是在整个循环工况中各能量源输出功率的频率,频率越小代表能量源被利用的循环充放电次数越少,也就意味着剩余可使用寿命越长[22]。为了表征这一指标,采用基于Harr小波基的五级小波变换分别将各能量源的瞬时功率分解成高频分量和低频分量,将高频分量的标准差等效成能量源应力,其数值见表3。燃料电池、锂电池和超级电容瞬时功率的第五级高频分量对比如图14所示。在图中可以看出各能量源应力中采用EEMS分量占比最小,且数值也很小,因此采用EEMS可以大幅度降低各能量源运行压力,延长列车一次充氢后的可运行里程。
表3 能量源应力和系统整体效率对比
Tab.3 Comparison of energy source stress and overall system efficiency

指标EEMSECMS状态机和功率解耦策略 燃料电池应力12.0417.9523.42 锂电池应力21.912224.44 超级电容应力34.735.9238.64 整体效率(%)80.5580.4779.32
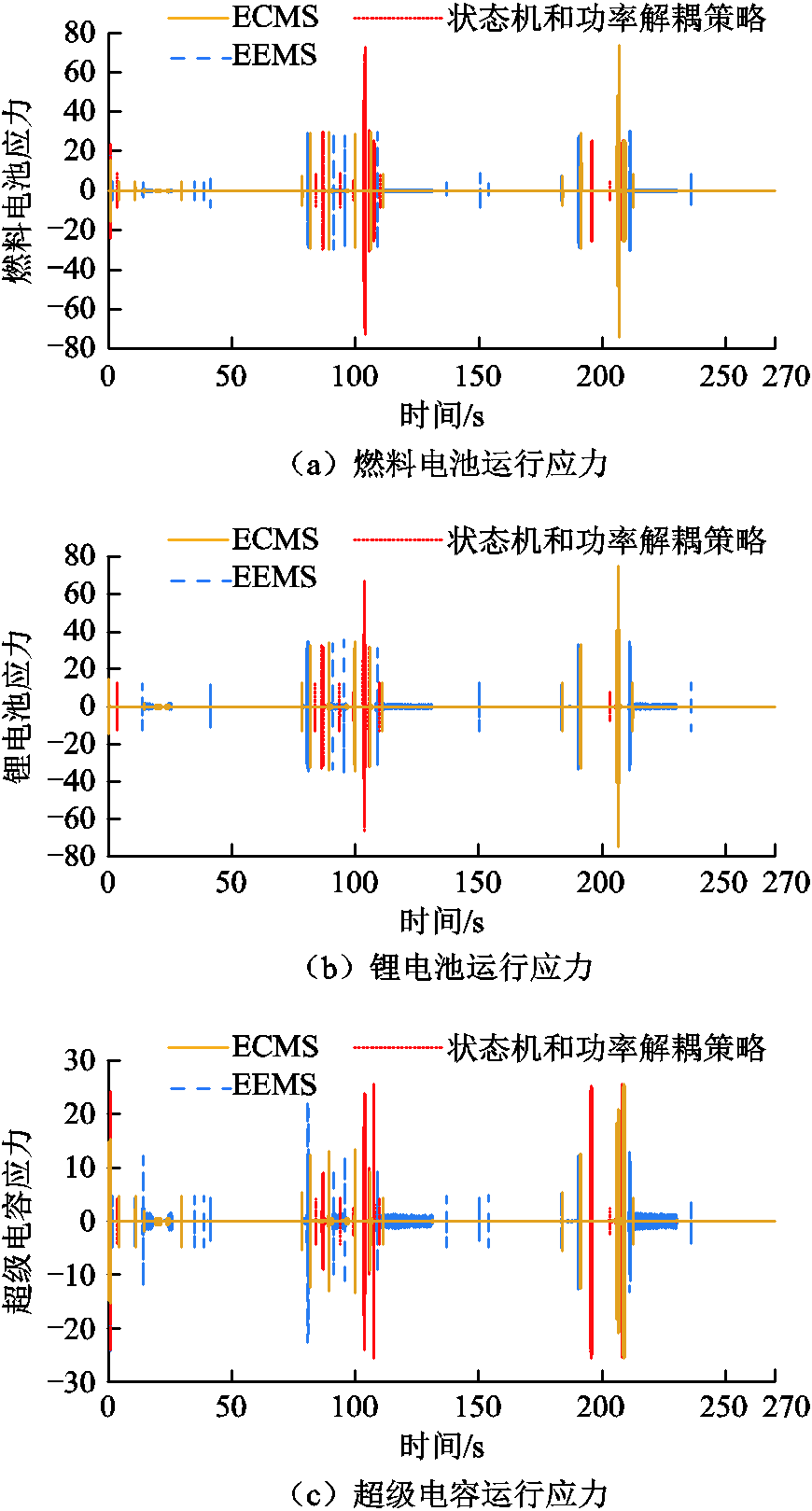
图14 能量源瞬时功率高频分量对比
Fig.14 Comparison of high frequency components of instantaneous power of energy sources
系统整体效率方面,采用功率转换度的思想,将其定义为
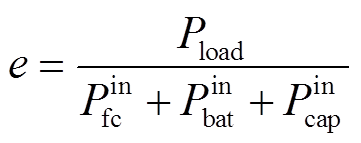 (29)
(29)式中,Pin fc、Pin bat和Pin cap分别为输入到燃料电池、锂电池DC-DC变换器的功率及超级电容的功率。整体效率的数值对比见表3,所提出的EEMS策略整体效率最高。
1)与传统的等效氢能耗最小化策略相比,通过最大化外部电源出力,可以使优化过程的算法和控制结构更为简单,对负载的鲁棒性更强。
2)EEMS相对于其他两种策略,在大幅降低氢气消耗量、燃料电池峰值电流、母线电压波动范围及能量源应力的同时,可实现混合储能系统的总体高效运行。
3)由于高负载功率的需求,所研究的混合储能系统采用储能元件单体数量过多,应用到工程实际上不能很好地满足空间和成本的要求。
后续研究应在考虑容量配置与能量管理策略耦合关系的基础之上进行联合优化。
参考文献
[1] 陈维荣, 钱清泉, 李奇. 燃料电池混合动力列车的研究现状与发展趋势[J]. 西南交通大学学报, 2009, 44(1): 1-6.
Chen Weirong, Qian Qingquan, Li Qi. Investigation status and development trend of hybrid power train based on fuel cell[J]. Journal of Southwest Jiaotong University, 2009, 44(1): 1-6.
[2] 陈维荣, 张国瑞, 孟翔, 等. 燃料电池混合动力有轨电车动力性分析与设计[J]. 西南交通大学学报, 2017, 52(1): 1-8.
Chen Weirong, Zhang Guorui, Meng Xiang, et al. Dynamic performance analysis and design of fuel cell hybrid locomotive[J]. Journal of Southwest Jiaotong University, 2017, 52(1): 1-8.
[3] Hu Xiaosong, Murgovski N, Johannesson L M, et al. Comparison of three electrochemical energy buffers applied to a hybrid bus power train with simultaneous optimal sizing and energy management[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(3): 1193-1205.
[4] Talla J, Streit L, Peroutka Z, et al. Position-based T-S fuzzy power management for tram with energy storage system[J]. IEEE Transactions on Industrial Electronics, 2015, 62(5): 3061-3071.
[5] 郭伟, 赵洪山. 基于改进分布式一致性算法的电池储能阵列分组控制策略[J]. 电工技术学报, 2019, 34(23): 4991-5000.
Guo Wei, Zhao Hongshan. Grouping control strategy of battery energy storage array based on improved distributed consistency algorithm[J]. Transactions of China Electrotechnical Society, 2019, 34(23): 4991-5000.
[6] Shen Junyi, Dusmez S, Khaligh A. Optimization of sizing and battery cycle life in battery/ultracapacitor hybrid energy storage systems for electric vehicle applications[J]. IEEE Transactions on Industrial Informatics, 2014, 10(4): 2112-2121.
[7] 陈亚爱, 林演康, 王赛, 等. 基于滤波分配法的混合储能优化控制策略[J]. 电工技术学报, 2020, 35(19): 4009-4018.
Chen Yaai, Lin Yankang, Wang Sai, et al. Hybrid energy storage optimal control strategy based on filter distribution method[J]. Transactions of China Electrotechnical Society, 2020, 35(19): 4009-4018.
[8] Mesbahi T, Khenfri F, Rizoug N, et al. Combined optimal sizing and control of Li-ion battery/ supercapacitor embedded power supply using hybrid particle swarm-nelder-mead algorithm[J]. IEEE Transactions on Sustainable Energy, 2017, 8(1): 59-73.
[9] Herrera V, Milo A, Gazta Aga H, et al. Adaptive energy management strategy and optimal sizing applied on a battery-supercapacitor based tramway[J]. Applied Energy, 2016, 169(1): 831-845.
[10] Wang Yu, Yang Zhongping, Fei Lei. Optimization of energy management strategy and sizing in hybrid storage system for tram[J]. Energies, 2018, 11(4): 752-769.
[11] Hu Xiaosong, Murgovski N, Johannesson L M, et al. Optimal dimensioning and power management of a fuel cell/battery hybrid bus via convex programming[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20(1): 457-468.
[12] 周美兰, 冯继峰, 张宇, 等. 纯电动客车复合储能系统功率分配控制策略研究[J]. 电工技术学报, 2019, 34(23): 5001-5013.
Zhou Meilan, Feng Jifeng, Zhang Yu, et al. Study on power distribution control strategy of hybrid energy storage system for pure electric bus[J]. Transactions of China Electrotechnical Society, 2019, 34(23): 5001-5013.
[13] 安星锟, 杨中平, 王玙, 等. 基于改进型凸优化算法的有轨电车混合储能系统容量配置帕累托解集[J].电工技术学报, 2020, 35(14): 3116-3125.
An Xingkun, Yang Zhongping, Wang Yu, et al. Pareto solution set of capacity allocation for hybrid energy storage system of tram based on improved convex optimization algorithm[J]. Transactions of China Electrotechnical Society, 2020, 35(14): 3116-3125.
[14] 林泓涛, 姜久春, 贾志东, 等. 权重系数自适应调整的混合储能系统多目标模型预测控制[J]. 中国电机工程学报, 2018, 38(18): 5538-5547.
Lin Hongtao, Jiang Jiuchun, Jia Zhidong, et al. Multi objective model predictive control of hybrid energy storage system with adaptive weight coefficient[J]. Proceedings of the CSEE, 2018, 38 (18): 5538-5547.
[15] 陈维荣, 胡斌彬, 李奇, 等. 基于动态规划的混合动力有轨电车能量管理方法[J]. 西南交通大学学报, 2020, 55(5): 903-911.
Chen Weirong, Hu Binbin, Li Qi, et al. Energy mana- gement method for hybrid electric tram based on dyn- amic programming algorithm[J]. Journal of Southwest Jiaotong University, 2020, 55(5): 903-911.
[16] 石岩, 高锋阳, 张国恒, 等. 一种城轨列车的混合动力能量优化控制[J]. 铁道标准设计, 2019, 63(11): 155-159, 164.
Shi Yan, Gao Fengyang, Zhang Guoheng, et al. Hybrid power energy optimization control of urban rail train[J]. Railway standard design, 2019, 63(11): 155-159, 164.
[17] Zhang Shuo, Xiong Rui, Cao Jiayi. Battery durability and longevity based power management for plug-in hybrid electric vehicle with hybrid energy storage system[J]. Applied Energy, 2016, 179(1): 316-328.
[18] 高锋阳, 张国恒, 石岩, 等. 新型城轨电车混合动力系统能量管理策略[J]. 铁道学报, 2019, 41(4): 48-54.
Gao Fengyang, Zhang Guoheng, Shi Yan, et al. Energy management strategy of hybrid power system of new urban rail transit[J]. Railway Transaction, 2019, 41(4): 48-54.
[19] 王玙, 杨中平, 李峰, 等. 有轨电车混合动力系统能量交互型管理策略与容量配置协同优化研究[J].电工技术学报, 2019, 34(8): 226-234.
Wang Yu, Yang Zhongping, Li Feng, et al. Study on collaborative optimization of energy interactive man- ement strategy and capacity allocation of tram hybrid system[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 226-234.
[20] 陈维荣, 燕雨, 李奇. 基于状态机的燃料电池混合动力系统控制策略[J]. 西南交通大学学报, 2019, 54(4): 663-670.
Chen Weirong, Yan Yu, Li Qi. Control strategy based on state machine for fuel cell hybrid power system[J]. Journal of Southwest Jiaotong University, 2019, 54(4): 663-670.
[21] 韦绍远, 姜久春, 程龙, 等. 储能式有轨电车车地一体化配置模型[J]. 电工技术学报, 2019, 34(2): 427-436.
Wei Shaoyuan, Jiang Jiuchun, Cheng Long, et al. Vehicle ground integrated configuration model of energy storage tram[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 427-436.
[22] 李奇, 王晓锋, 孟翔, 等. 基于在线辨识和极小值原理的PEMFC混合动力系统综合能量管理方法[J]. 中国电机工程学报, 2020, 40(21): 242-253.
Li Qi, Wang Xiaofeng, Meng Xiang, et al. Integrated energy management method for PEMFC hybrid system based on online identification and minimum principle[J]. Proceedings of the CSEE, 2020, 40(21): 242-253.
Energy Saving Operation Optimization of Hybrid Energy Storage System for Hydrogen Fuel Cell Tram
Abstract Aiming at the problem that the equivalent energy consumption in the energy management of fuel cell/super capacitor/lithium battery hybrid energy storage trams is greatly affected by load randomness so it cannot guarantee the optimal global power distribution, and to further enhance the fuel economy. An operation optimization strategy is proposed based on external energy consumption. Firstly, the load energy demand is divided into two parts: the real-time fuel consumption of the internal energy fuel cell and the power consumption of the external power lithium battery/super capacitor; secondly, in order to share the high power load pressure of the fuel cell, the objective function is rewritten from the equivalent energy consumption minimization strategy to maximization of the external power output, thus, there is no need to evaluate equivalent energy consumption, so as to achieve the purpose of enhancing the robustness for load change and minimizing real-time hydrogen consumption; finally, the proposed optimization strategy is compared with the equivalent energy consumption minimization and the state machine and power decoupling strategy. The results show that, in the whole cycle conditions, comparing with the equivalent energy minimization strategy, the proposed method reduces the hydrogen consumption by 17.68g and the peak current by 21.81A; comparing with the state machine and power decoupling strategy, it reduces the hydrogen consumption by 39.04g and the peak current by 56.9A; moreover, the bus voltage deviation range and the stress of each energy source are significantly improved as well.
keywords: Hybrid energy storage tram, fuel cell, energy management, power distribution, external energy consumption
DOI:10.19595/j.cnki.1000-6753.tces.201645
中图分类号:TM92
国家重点研究发展计划资助项目(2017YFB1201003-020)。
收稿日期 2020-12-16
改稿日期 2021-02-16
高锋阳 男,1970年生,教授级高工,研究方向为城轨列车的车载储能及故障诊断技术等。E-mail:ljdgaofy@mail.lzjtu.cn
张浩然 男,1996年生,硕士研究生,研究方向为城轨列车的车载储能技术。E-mail:1021235110@qq.com(通信作者)
(编辑 赫蕾)