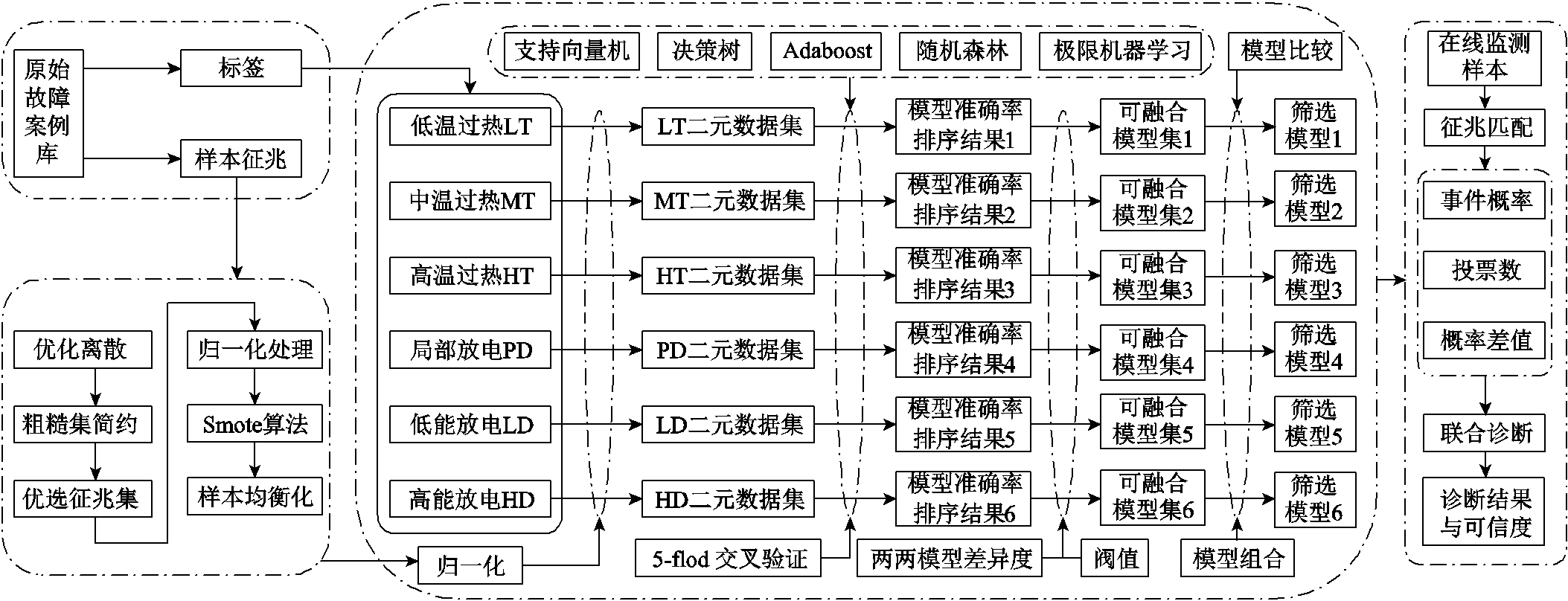
图1 数据信息挖掘流程
Fig.1 Data information mining framework
摘要 电力变压器作为电力系统的核心设备，其安全稳定运行对于电力系统具有重要意义。电力变压器在线故障诊断是实现电力变压器实时状态分析的重要方法，油中溶解气体分析是最常用的电力变压器在线故障诊断方法。目前变压器故障诊断征兆优选多采用基于启发式算法的策略，虽然相较于遍历型算法简化了筛选流程，但仍需消耗大量算力。电力变压器融合故障诊断方面的研究多注重于整体诊断效果的提升，未关注单个样本诊断结果可靠性方面的分析。为解决上述问题，该文提出一种结合数据分布的征兆自主离散及征兆自主降维优选、单事件多模型融合分析的变压器状态分析方法。经实例验证，该方法可以有效分析各征兆数据分布，进行征兆优选，可以从单个事件的角度给出变压器运行状态及可信度。
关键词：优化离散 征兆选择 可信度 辅助分析
电力变压器是电力系统电能变换及电力传输的关键设备，为保证其安全稳定运行，多种电力变压器故障诊断技术及状态分析方法被提出。
为提高电力变压器故障诊断与状态分析结果的准确性，油中溶解气体[1-2]、油温[3]、电气实验数据[4]、油实验数据[5]等被作为特征量用于变压器状态分析。基于这些征兆及人工智能算法，多种智能诊断策略被提出。相较于传统气体比值方法，其诊断效果有了很大程度的提升。为进一步提升诊断效果，融合策略也被用于变压器故障诊断。文献[6]使用改进三比值法（Improved Three Ratio Method, ITR)、Dornenburg气体比值法（Doernenburg Ratio Method, DRM)、大卫三角法（Duval Triangle Method, DTR)及HAE诊断方法的特征量分别作为自适应网络模糊推理系统（Adaptive Network-based Fuzzy Inference System, ANFIS）的输入，再通过融合策略进行变压器故障诊断。文献[7]以变压器漏感参数为特征量，使用支持向量（Support Vector Machine, SVM）及有限元分析法实现对变压器绕组的状态分类识别，诊断效果良好。文献[8]以油色谱数据相对含量、征兆比值、电气试验数据为征兆，分别训练SVM模型，再通过证据融合理论（Dempster-Shafer envidence theory, DS）进行最后决策。这些方法将不同渠道获得的信息进行融合决策，诊断效果好于单独诊断方法。
随着变压器故障诊断征兆的丰富，不同征兆之间存在冗余性，需要对征兆进行优选。文献[9]使用遗传算法结合多个征兆重要度排序算法对油中溶解气体衍生出的故障征兆进行优选。这种征兆优选方法属于启发式算法，相较于遍历型算法可以减少对算力的消耗，但是只能得到征兆组合的较优解，难以得到唯一的最优解，且依然需要进行多次迭代。如何降低征兆优选所需的算力，使样本更新时征兆的优选可以重新快速完成是一个有待解决的问题。目前，电力数据信息辅助决策主要体现在系统状态评估和故障诊断两个方面，可分为能体现建模过程及物理意义的“白箱”方法和可进行大量历史数据学习的“黑箱”方法。“白箱”方法虽然能更好地体现各物理量的现实联系，但多用于电力设备事件的事后分析，难以实现在线设备状态评估及事件分析。“黑箱”方法中的单个决策模型虽然整体决策效果良好，但仍然存在单个样本决策错误的情况。而单个样本的决策结果是否可靠决定了辅助系统给出意见时应对策略的可执行程度，提高决策结果的可信度对于辅助意见的“落地”具有重要意义。决策结果的可信度应包含决策结果可信与不可信两个方面。因此，如何避免诊断模型给出的决策结果过于绝对，解决常用诊断结果没有不确定度的问题是另外一个值得思考的方面。
为解决上述问题，本文中采用离散化方法对征兆进行数据标准化，实现对数据密集区的详细划分及稀疏区的粗略划分，降低征兆优选对于算力的需求。使用多个诊断模型得出单个事件的分析结果，并从多个角度分析诊断结果的可信度，为诊断结果是否采纳提供依据，进而实现电力变压器状态分析从传统的物理模型向“物理模型+辅助决策”方式转变。
电力变压器辅助分析模型的构建流程如图1所示，辅助决策的目的：①对于新监测的样本数据给出明确的诊断结论；②通过分析诊断过程中多个诊断模型的过程数据给出诊断结论可靠程度。
图1 数据信息挖掘流程
Fig.1 Data information mining framework
在对电力数据进行挖掘时，首先按照数据类别将其分成两类：一类数据是可用于分析变压器运行状态的监测数据；另一类数据是表述变压器状态的标识量。然后对征兆数据进行规范化处理，文中采用优化离散方法对各征兆进行预处理，这种方法可以在较小数据区间内对数据分布特点进行分析，并确定离散边界，进而区分相近故障类别间数据分布的细微差别。基于离散化样本数据，采用无监督属性选择算法进行征兆优选，以此加快数据分析及建模过程，并简化事件辅助模型，减少过度拟合。
在得到优选征兆集后，使用样本按照故障类型单独训练诊断模型。通过预测算法库可以得到多个每种故障类别的二元分类预测模型。文中算法库包括SVM[10]、决策树算法[11]（Decision Tree, DT）、Adaboost算法、随机森林算法（Random Forests, RF）[12]、极限机器学习算法（Extreme Learning Machine, ELM）[13]。对每个故障类型，分析模型诊断结果的差异，选择可以互补的模型进行融合，以减少单个模型的误判。结合每个模型的诊断结果及概率值，计算融合模型的诊断结果和可信度，再通过分析单个样本在不同融合模型上的诊断结果和可信度得到样本的最终诊断结果。
以上变压器状态分析方法可以对单个样本进行更加综合的分析。从增加单个故障类别诊断信息源、融合多个模型诊断结果、分析不同融合模型诊断结果及可信度三个方面评估单个样本诊断结果及可信度，避免了单个诊断模型总体诊断效果好，单个样本诊断结果可靠性难以分析的问题。
各征兆监测数据的数量级和量纲差异往往很大，当某个征兆的历史监测数据存在一个较大异常值时，会导致在较小区间内正常分布的密集数据被严重压缩，导致较大数据信息吞噬小数据信息的情况。为避免这种问题，本文采用优化离散方法进行数据预处理。优化离散通过分析数据分布实现数据预处理，以实现密集数据间的多区间划分及稀疏数据间的简略划分，进而保留数据的主要信息，避免极端数据影响。本文采用基于卡方检验的优化离散方法进行数据规范化，该方法是监督数据离散方法，可以实现离散边界的自主确定，离散边界的确定方法如下：
卡方检验可以统计样本实际出现的次数与理论计算出现次数之间的偏离程度，卡方值越大，说明偏离越明显，可用于分析两个相邻数据区间的样本类别分布差异，区间i与其右侧相邻区间的故障类别j卡方值为
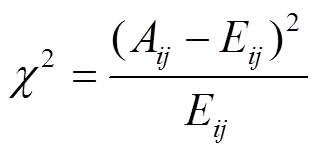（1）式中，Aij为第i个区间上，状态类别j实际出现的次数，称为实际频数；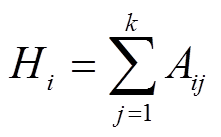
，表示在第i个区间上，所有状态类别出现的总频数，k为状态类别个数，本文对每种故障类别分别建模，故k为2；
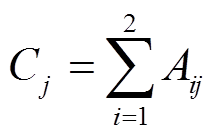，表示第j个状态在区间i及其右侧相邻区间上出现的总频数；
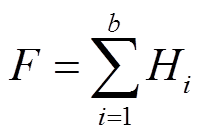，表示所有状态类别区间i及其右侧相邻区间上的总频数，本文比较的是两个相邻区间统计意义上是否相同，故b为2；
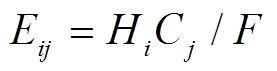，为第i个区间中，状态j期望出现的频数，也称理论频数。
首先得到某个征兆所有样本数据的升序排列及其对应的标签，标签值作为该样本征兆数值及其右侧相邻样本征兆数值所构成区间的类别分布，如[xi，xi+1]构成第i个区间。然后将具有相同类别的相邻区间合并，再统计相邻两个区间上状态类别实际频度，例如两个相邻区间i与i+1上S个类别标签出现的次数分别为[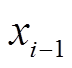
,
]：{
,
,
,
,,
,
}；[,
]：{
,
,,
,,
,
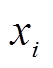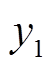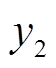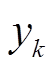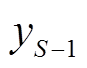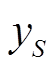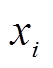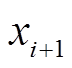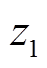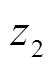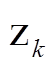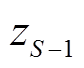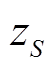}。可得第i个区间与其右侧相邻区间的故障类别j的理论频数为
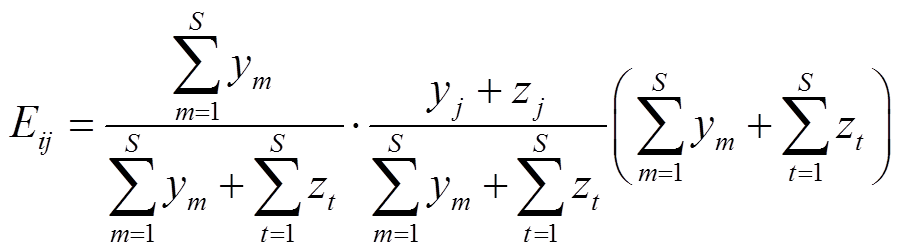（2）再利用式（1）计算其对应的卡方值，将第i个区间与其左右相邻区间所得到的卡方值进行比较，将卡方值小的两个区间合并。然后重新计算各区间的卡方值，逐渐减少区间数，直到区间个数满足设定阈值，将区间边界值作为离散划分点。通过参考电力设备事件预警等级等划分方法，本文对连续性信息数据的离散区间个数设置为5。
征兆数据预处理之后，对数据进行建模以实现监测数据的信息挖掘，用实时监测运行数据与变压器运行状态间的映射模型实现电力变压器运行状态的辅助分析，下文将详细阐述本文提出的电力变压器运行状态辅助决策模型构建方法。
（1）D5000作为新一代的智能电网调度技术支持系统基础平台，集合了设备运行数据、监测数据和气象数据等多种信息，为调度计划和决策提供了重要信息源。通过D5000系统输变电在线监测与分析应用模块等数据共享与管理平台收集变压器历史故障监测数据及其对应的事件标签。设本文收集到的变压器故障事件及对应监测数据类别总数为N，记全数据集为{X1, X2, X3, 
, Xi-1, Xi, Xi+1, , XN-2, XN-1, XN}。
（2）将全数据集按照数据性质分为征兆型和事件型。将所有征兆型数据放到一个集合作为征兆集，记为{R1, R2, R3, , Ri, Ri+1, , RT-2, RT-1, RT}，T为变压器故障时所检测的数据种类个数，T＜N。将所有事件型数据放到一个集合作为事件集，记为{D1, D2, D3, , Di-1, Di, Di+1, , DS-2, DS-1, DS}，S为从监测系统中收集到的变压器状态种类个数，即样本标签类别数，S＜N。
（3）使用2.1节中的方法对征兆集进行数据优化离散，然后进行征兆优选，剔除冗余征兆。目前，所有的征兆优选方法中，只有遍历所有征兆集的子集筛选出的征兆才是最优的，但这会消耗大量算力，尤其是当征兆集征兆个数较多时，耗时会急剧增加，不利于实际应用。本文采用粗糙集方法进行征兆优选，粗糙集[14-15]算法是无监督算法，它通过建立最小决策表分析征兆间的冗余性，进而达到约简征兆集的目的。基于离散化数据，约简后的征兆集称为优选征兆集，记为{G1, G2, G3,Gi-1, Gi, Gi+1, , Gr-2, Gr-1, Gr}，r为约减后的征兆个数，r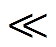
T。
（4）将事件集中Di的标签标为1，其余标签标为0，形成二元标签。使用预测算法库中的现有算法对事件Di的二元标签和优选征兆集{G1, G2, G3, , Gi-1, Gi, Gi+1, , Gr-2, Gr-1, Gr}的历史数据进行学习。为保证样本的均衡性，将二元标签中为1的样本数量使用Smote算法扩充至二元标签中为0的数量。
假设预测算法库有k个预测算法，那么使用k个预测算法分别在训练数据集上训练，得到k个预测模型，记为{M1, M2, M3, , Mi-1, Mi, Mi+1, , Mk-2, Mk-1, Mk}。
（5）为增加单个样本诊断信息源，尽可能地避免单个诊断模型在单个样本上的诊断错误，有必要进行多模型融合。基于模型差异度与融合诊断效果的综合分析策略是常用的模型选择性融合方法，但这种方式通常是基于启发式的遍历性策略[16]，期间需要训练多个融合模型进行比对，对于算力消耗极大。为简化这一过程，本文将差异性分析与融合模型诊断环节分开，首先分析模型间差异度，差异度在0.5以上的模型纳入融合范围，其他模型不进行融合。差异化度量方法的具体原理参见文献[17]。
（6）根据入选融合范围模型，按照子集组合的方式训练多个融合，基于同一个验证集，一次性分析融合模型的优劣。根据预测准确率，从事件类别中选取一个模型。这样得到对于S个事件的S个诊断模型。
（7）对于新采样的样本，每个事件模型Mi诊断后可以得出是否属于该事件的诊断结果及可信度PMi，其计算方法如式（3）所示。若使用事件模型计算出某样本的可信度PMi值大于0.5，则认为属于该事件。
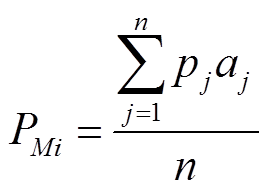（3）式中，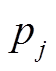
为模型Mi中第j个单独模型预判新采样样本属于该事件的概率；
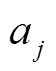为模型Mi中第j个单独模型在验证集的整体诊断准确率；n为事件模型所融合的单独模型个数。
比较每个事件模型的可信度，选取可信度值最高的事件模型所代表的事件作为诊断结果。除可信度外，为进一步丰富诊断结果的可信度评价信息，将可信度最高的事件模型投票数（事件模型所融合的单独模型中，若单独模型对样本属于该故障类型的诊断概率大于0.5，则记一票，票数记为U1）、不同事件模型对某样本给出的可信度值中最大值与第二大值的差值纳入诊断结果评价范围（差异越小说明不同事件模型的诊断结果可能过于接近，容易出现错误，差值记为U2）。按照表1中的原则判定诊断结果可信度，用于分析单事件诊断结果的可信度。
表1 联合评价方法
Tab.1 Joint evaluation method
联合评价信息诊断结果 U1≥n/2U2≥0.2 是是可信度高 是否可信度一般 否是可信度低 否否结果易出错
为验证本文提出方法的可行性与正确性，下文给出变压器事件辅助决策建模构建实例并进行分析。为符合实际应用分析情况，本文从国网某省电力数据监控平台收集到已知故障类型的变压器历史数据983组。根据IEC 60599—2015及GB/T 7252—2001导则，收集到的数据可划分为六种故障类型。将收集到的全数据集按照2.2节步骤（1）的原则划分为表2中的征兆集和表3中的事件集。表2中TH表示总烃（CH4、C2H6、C2H4与C2H6之和）。
表2 征兆集
Tab.2 Features set
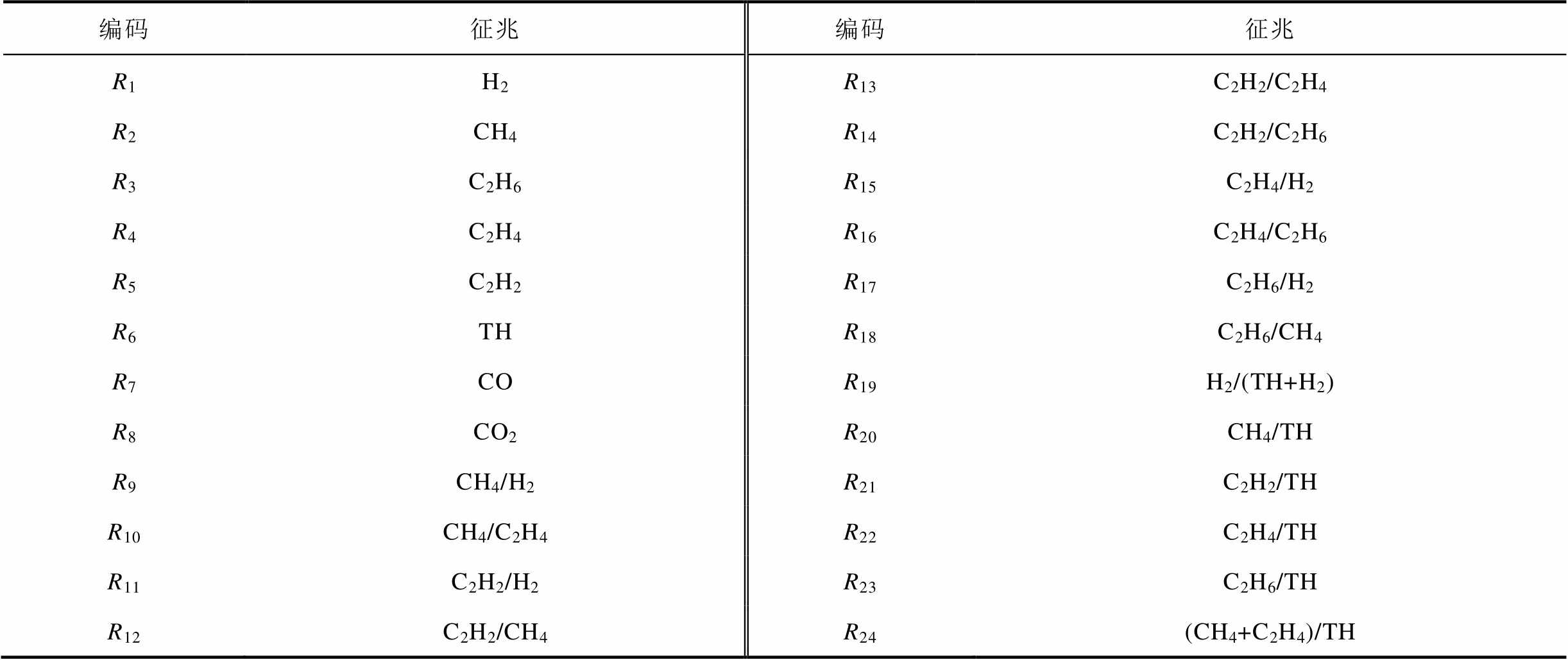
编码征兆编码征兆 R1H2R13C2H2/C2H4 R2CH4R14C2H2/C2H6 R3C2H6R15C2H4/H2 R4C2H4R16C2H4/C2H6 R5C2H2R17C2H6/H2 R6THR18C2H6/CH4 R7COR19H2/(TH+H2) R8CO2R20CH4/TH R9CH4/H2R21C2H2/TH R10CH4/C2H4R22C2H4/TH R11C2H2/H2R23C2H6/TH R12C2H2/CH4R24(CH4+C2H4)/TH
表3 事件集
Tab.3 Fault event set
编码故障类型数量编码故障类型数量 D1低温过热102D4局部放电119 D2中温过热107D5低能放电176 D3高温过热243D6高能放电236
首先对样本进行数据预处理，按照2.1节中的离散优化方法对数据进行离散，获得的各征兆离散边界见表4，将样本按照表3中的故障类型形成6个二元标签集。
表4 征兆离散边界
Tab.4 Features set
编码边界1边界2边界3边界4 R10.192 900.958 04.900 056 R20.290 038.400 0316391 R30.100 07.570 035.700 0142 R40.100 011.600 052.980 0177 R50.010 00.040 00.350 01.074 0
（续）
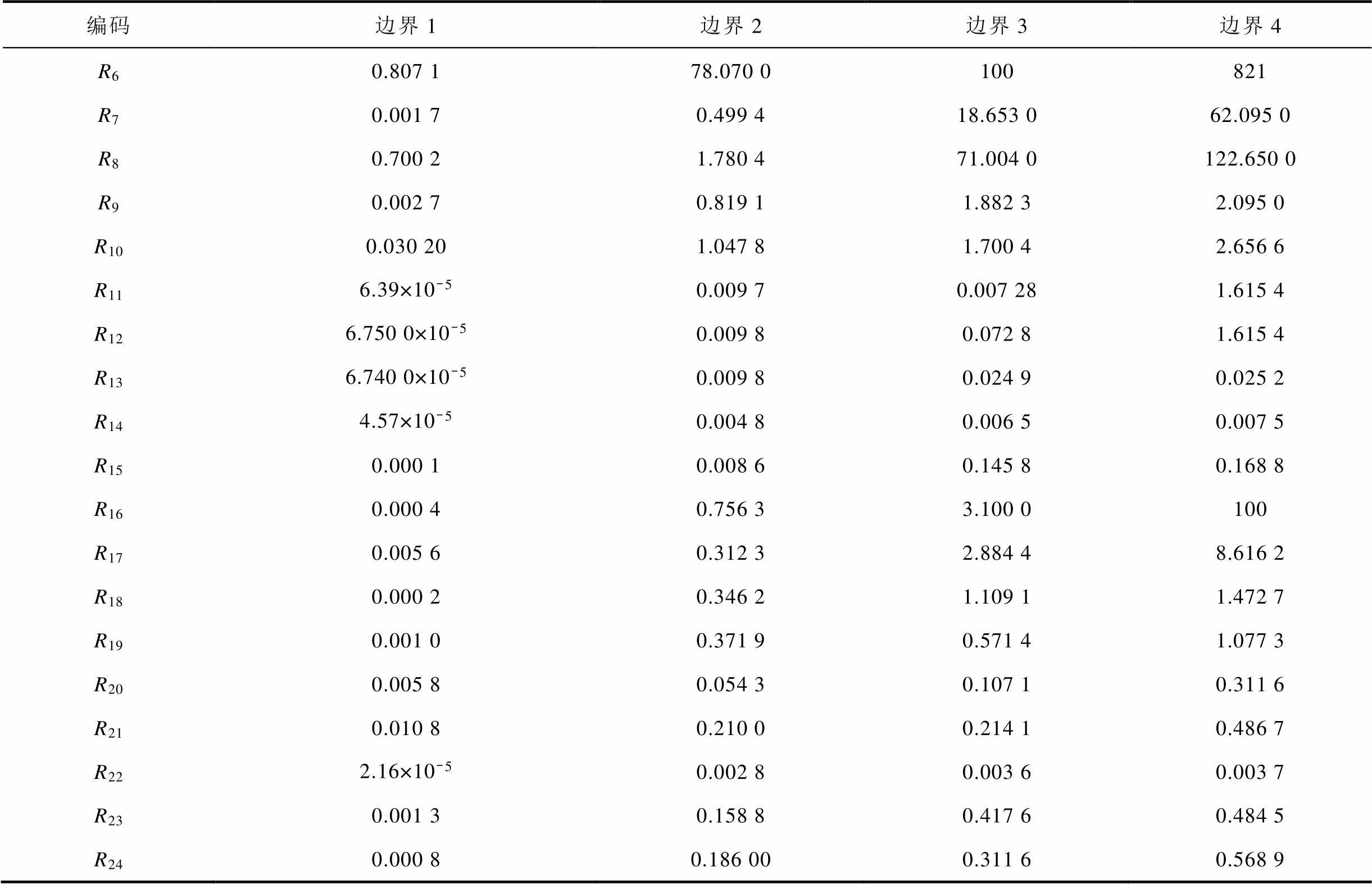
编码边界1边界2边界3边界4 R60.807 178.070 0100821 R70.001 70.499 418.653 062.095 0 R80.700 21.780 471.004 0122.650 0 R90.002 70.819 11.882 32.095 0 R100.030 201.047 81.700 42.656 6 R116.39×10-50.009 70.007 281.615 4 R126.750 0×10-50.009 80.072 81.615 4 R136.740 0×10-50.009 80.024 90.025 2 R144.57×10-50.004 80.006 50.007 5 R150.000 10.008 60.145 80.168 8 R160.000 40.756 33.100 0100 R170.005 60.312 32.884 48.616 2 R180.000 20.346 21.109 11.472 7 R190.001 00.371 90.571 41.077 3 R200.005 80.054 30.107 10.311 6 R210.010 80.210 00.214 10.486 7 R222.16×10-50.002 80.003 60.003 7 R230.001 30.158 80.417 60.484 5 R240.000 80.186 000.311 60.568 9
在获得离散样本之后，使用粗糙集算法进行征兆简约，简约后的优选征兆集见表5。经过征兆优选后，故障征兆减少至11个。故障征兆集征兆个数的缩减，减少了建模复杂度及训练耗时。
表5 粗糙集简约结果
Tab.5 Optimal features result of rough set algorithm
简约结果 优化离散R6、R9、R12、R14、R15、R16、R18、R20、R21、R22、R24
以局部放电故障为例阐述本文2.2节步骤（4）～步骤（6）的执行过程，使用预测算法库中五种算法对事件D4构成的二元标签及表5中优选征兆的归一化数据进行模型的融合与筛选。筛选过程采用5次交叉验证方式，每次抽取4/5的样本组成训练集，其余样本组成验证集。基于训练集数据得到五个预测模型。SVM算法、决策树算法、Adaboost算法、随机森林算法、ELM算法训练得到的模型分别表示为MSVM、MDT、MAdaboost、MRF、MELM。然后使用这五个预测模型分别在验证集上进行样本故障预判。
将五个预测模型在验证集的预测结果与实际标签进行对比，若样本预测结果正确则记为1，否则记为0。这样五个预测模型可以在验证集上得出其对应的二元编码，并可以计算出各诊断模型在验证集上的准确率，以5次交叉验证的平均准确率作为最终整体准确率。五个预测模型在事件D4的8个验证集样本的诊断结果正误见表6。从表6可知预测模型{MSVM, MDT, MRF}诊断正误结果相同，预测模型{MAdaboost, MELM}相同，预测模型{MSVM, MDT, MRF}与预测模型{MAdaboost, MELM}的诊断正误结果存在差异性。
表6 验证集样本预测结果正误
Tab.6 The diagnostic result of examples in validation set
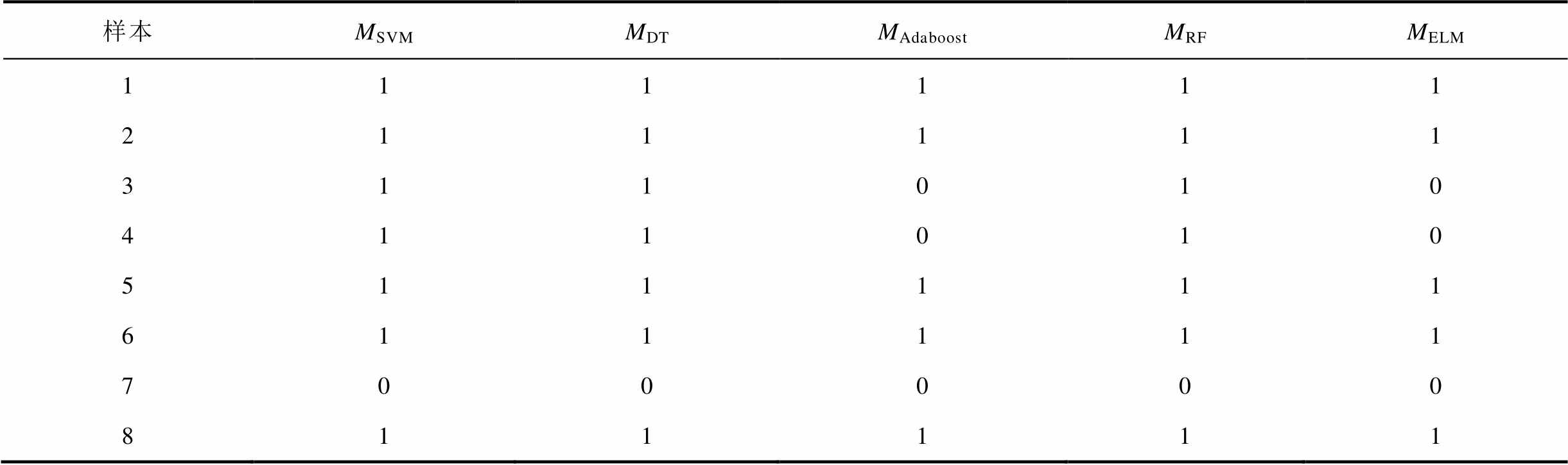
样本MSVMMDTMAdaboostMRFMELM 111111 211111 311010 411010 511111 611111 700000 811111
按照各模型验证集准确率大小从高到低排列，MRF、MELM、MDT、MSVM、MAdaboost在D4样本集的整体诊断准确率分别为0.914 3、0.901 2、0.899 7、0.856 1、0.831 0。按照步骤（5）中的方法计算各模型间的差异度值，两两模型间的差异度值如图2所示。
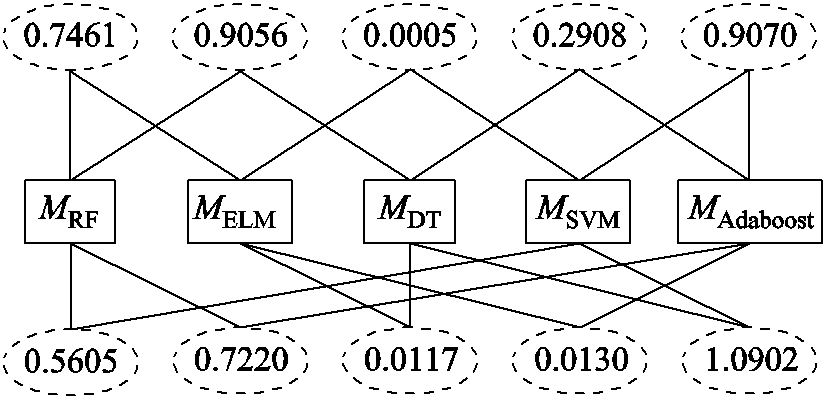
图2 预测模型的差异度
Fig.2 The difference value of five prediction models
从MRF开始逐步寻找差异度较大的模型，用于融合的模型寻找的基本原则是：选择诊断准确率高、差异度大的模型进行融合，以尽可能避免诊断效果差的模型在单个样本上的诊断错误。寻找的过程是：按准确率高低分析两两相邻模型间的差异度，若差异度值大于0.5，则将模型纳入融合选择范围，若小于0.5就停止对于模型的寻找。
从图2可知，MRF作为初始模型纳入融合选择范围，MRF和MELM的差异度值为0.746 1，故将MELM也纳入考虑范围，因为MELM和MDT的的差异度值小于0.5，故停止寻找。则事件D4筛选的用于融合的模型全集为{MRF, MELM}，通过对比其子集{MRF}、{MELM}、{MRF, MELM}的诊断效果选出事件模型。同样对{MRF, MELM}组成的融合模型使用5次交叉原则，采用5次平均准确率作为诊断效果。诊断结果见表7。
表7 事件模型D4筛选
Tab.7 Event model D4 selection
模型MRFMELMMRF&MELM 平均准确率0.914 30.901 20.925 2
从表7中可知，MRF&MELM的诊断效果最好，故将该模型作为D4的事件模型。表6中第3组样本的不同模型诊断正误存在差异，表8给出了MRF、MELM模型诊断该样本为局部放电事件的概率及整体准确率。按照步骤（7）中的原则可以计算出事件模型D4诊断该样本是否属于局部放电故障的概率。从表8中可知，属于局部放电故障的概率大于不属于的概率，故诊断结果为属于该事件，这一结论的可信度为0.538 8。
表8 各模型的局部放电故障概率
Tab.8 The probability of different models for PD fault
诊断模型局部放电故障整体准确率 是否 MRF0.826 30.173 70.914 3 MELM0.357 40.642 60.901 2 MRF&MELM0.538 80.368 9—
按照上述原则及过程可以计算出低温过热故障、中温过热故障、高温过热故障、低能放电故障和高能放电故障类别的事件模型见表9。
表9 事件模型
Tab.9 Event models
编码事件模型编码事件模型 D1MRF&MSVMD4MRF&MELM D2MRF&MDTD5MRF D3MRF&MELM&MDTD6MRF&MDT
按照步骤（7）中的原则计算表9中的6个事件模型在表6中第3组样本的U1和U2值，结果见表10。从表10中可知，该样本的最终联合诊断结论为局部放电故障，该结论的可信度一般。
表10 事件模型
Tab.10 Event models
事件模型PMiU1U1≥n/2U2U2≥0.2 MRF&MSVM0.001 40—0.079 4否 MRF&MDT0.073 20— MRF&MELM&MDT0.021 50— MRF&MELM0.538 81是 MRF0.459 41— MRF&MDT0.125 30—
使用粗糙集算法进行征兆简约可以在很大程度上节省算力，但是样本的离散方式对于征兆的简约效果存在很大影响。为分析本文优化离散方式的优劣，分别采用等距划分和等幅划分方式对样本进行离散。等距划分是将各样本征兆数据从小到大排列，按照样本数量等间距确定离散边界。等幅划分是统计各样本某征兆数据的最大、最小值，在这两个值之间等间距确定离散边界。将离散区间个数选为5，使用粗糙集算法分别对这两种方法的离散结果进行征兆优选，优选结果见表11。
表11 基于不同离散方式的征兆简约结果
Tab.11 Optimal features result of different discrete models
离散方式优选征兆 等距划分R3、R5、R10、R11、R13、R14、R15、R16、R18、R19、R21、R22、R24 等幅划分R1、R3、R6、R8、R9、R10、R13、R14、R16、R17、R18、R19、R21、R23、R24
基于表5和表11中的优选征兆集，使用本文收集的样本采用10-flod交叉验证方法进行结果比较，每次实验训练集和测试集的样本数量比例为9:1，以测试集的平均诊断准确率作为最终结果，诊断算法选用决策树、随机森林[18]和SVM[19-21]，诊断结果见表12。此处，决策树算法采用Weka及Matlab Weka Interface工具包中的C4.5算法实现，算法参数使用默认参数；随机森林算法使用Matlab的统计和机器学习工具箱来实现，经反复试验，本文算法中决策树个数（NumTrees）设置为100；SVM使用LibSVM实现，参数选择参考文献[22]。
表12 基于不同离散方式的诊断效果
Tab.12 Diagnosis result of different discrete models
诊断算法等距划分等幅划分优化离散 决策树0.809 40.876 30.881 1 随机森林0.817 60.891 30.903 2 SVM0.803 70.887 50.890 3
从表12中可知，本文基于优化离散的征兆优选策略诊断效果好于等距划分方法和等幅划分方法，说明优化离散方法可以更好地展现数据分布特点。
为分析本文方法的整体诊断效果，采用与4.1节相同的训练集和测试集样本分配策略，在交叉验证结束后，分类别统计各故障样本的诊断结果并计算各类别样本及整体样本的诊断准确率。诊断算法同样选用决策树、随机森林和SVM，诊断结果见表13。
表13 基于不同诊断算法的诊断效果
Tab.13 Diagnosis result of different diagnosis algorithm
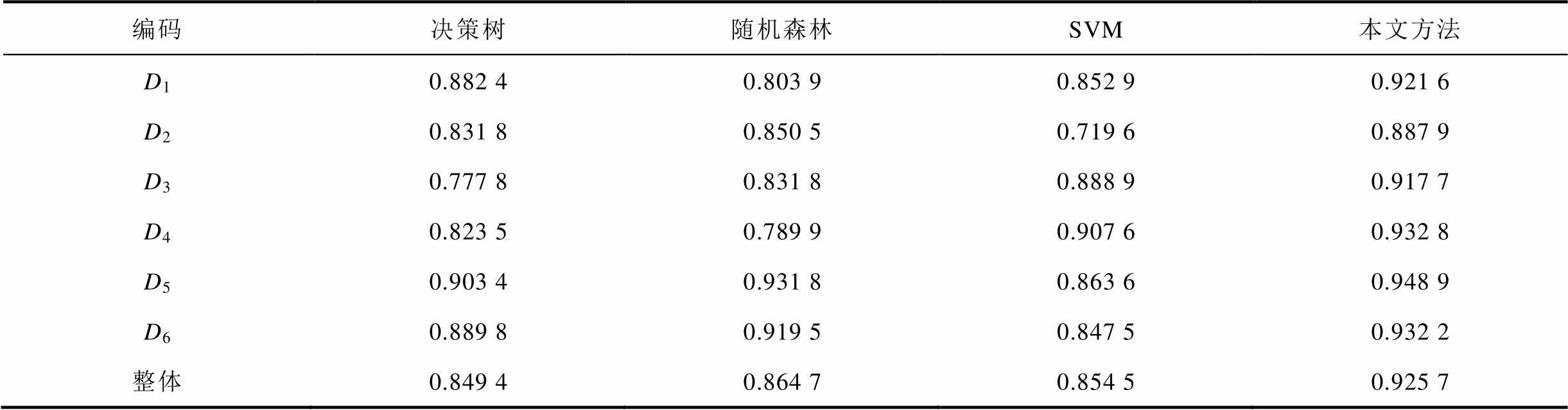
编码决策树随机森林SVM本文方法 D10.882 40.803 90.852 90.921 6 D20.831 80.850 50.719 60.887 9 D30.777 80.831 80.888 90.917 7 D40.823 50.789 90.907 60.932 8 D50.903 40.931 80.863 60.948 9 D60.889 80.919 50.847 50.932 2 整体0.849 40.864 70.854 50.925 7
从表13可知，本文方法的诊断准确率好于基于决策树、随机森林和SVM算法的诊断策略，而且各个故障类别的诊断效果更加均衡。
针对新采集的样本，在目前诊断方法无法保证诊断结果完全可靠的情况下，给出诊断结果适当的评价信息有助于模型诊断方法的落地应用。表14中给出了4.2节实验所有样本诊断结果的联合评价信息分布。如果将表1中表述为“可信度高”和“可信度一般”的评价信息认同为样本诊断结果正确，“可信度低”和“结果易出错”认同为样本诊断结果错误，则评价信息的准确率可达0.960 3，见表14中加粗部分所示，所以本文结果评价方法对单个样本的诊断结果应用有帮助。
表14 基于不同诊断算法的诊断效果
Tab.14 Diagnosis result of different diagnosis algorithm
诊断结果正误联合评价信息样本数量 U1≥n/2U2≥0.2 正确是是675 正确是否201 正确否是0 正确否否34 错误是是0 错误是否5 错误否是27 错误否否41
本文通过构建事件辅助决策模型实现征兆数据离散边界的自主确定、事件关联征兆的自主优选、事件模型的简化与融合；通过构建单个样本诊断结果的可信度评价体系有助于分析结果可信度，避免诊断结果的绝对性，使辅助决策更实用。研究结果表明，融合诊断有助于提高诊断结果的可靠性，综合分析融合过程中各单一模型诊断结果的可信度有助于分析诊断结果是否可靠。通过提升融合模型诊断准确率和判断单个样本诊断结果是否可信的准确性，可以进一步促进智能诊断方法的落地应用，有助于解决整体样本诊断效果良好但单个样本诊断结果无法确信的问题。下一步研究将继续完善联合评价体系，提高可信度评价精准度。
参考文献
[1] 李恩文, 王力农, 宋斌, 等. 基于混沌序列的变压器油色谱数据并行聚类分析[J]. 电工技术学报, 2019, 34(24): 5104-5114.
Li Enwen, Wang Linong, Song Bin, et al. Parallel clustering analysis of dissolved gas analysis data based on chaotic seduences[J]. Transactions of China Electrotechnical Society, 2019, 34(24): 5104-5114.
[2] 李赢, 舒乃秋. 基于模糊聚类和完全二叉树支持向量机的变压器故障诊断[J]. 电工技术学报, 2016, 31(4): 64-70.
Li Ying, Shu Naiqiu. Transformer fault diagnosis based on fuzzy clustering and complete binary tree support vector machine[J]. Transactions of China Electrotechnical Society, 2016, 31(4): 64-70.
[3] Susa D, Palola J, Lehtonen, et al. Temperature rises in an OFAF transformer at OFAN cooling mode in service[J]. IEEE transactions on Power Delivery, 2005, 20(4): 2517-2525.
[4] 刘云鹏, 付浩川, 许自强, 等. 基于AdaBoost-RBF算法与DSmT的变压器故障诊断技术[J]. 电力自动化设备, 2019, 39(6): 166-172.
Liu Yunpeng, Fu Haochuan, Xu Ziqiang, et al. Transformer fault diagnosis technology based on AdaBoost-RBF algorithm and DSmT[J]. Electric Power Automation Equipment, 2019, 39(6): 166-172.
[5] 赵文清, 祝玲玉, 高树国, 等. 基于多源信息融合的电力变压器故障诊断方法研究[J]. 电力信息与通信技术, 2018, 16(10): 25-30.
Zhao Wenqing, Zhu Lingyu, Gao Shuguo, et al. Research on fault diagnosis method of power transformer based on multi-source information fusion[J]. Electric Power Information and Communication Technology, 2018, 16(10): 25-30.
[6] Kari T, Gao Wensheng, Zhao Dongbo, et al. An integrated method of ANFIS and dempster-shafer theory for fault diagnosis of power transformer[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2018, 25(1): 360-371.
[7] 邓祥力, 谢海远, 熊小伏, 等. 基于支持向量机和有限元分析的变压器绕组变形分类方法[J]. 中国电机工程学报, 2015, 35(22): 5778-5786.
Deng Xiangli, Xie Haiyuan, Xiong Xiaofu, et al. Classification method of transformer winding deformation based on SVM and finite element analysis[J]. Proceedings of the CSEE, 2015, 35(22): 5778-5786.
[8] 司马莉萍, 舒乃秋, 李自品, 等. 基于SVM和D-S证据理论的电力变压器内部故障部位识别[J]. 电力自动化设备, 2012, 32(11): 72-77.
Sima Liping, Shu Naiqiu, Li Zipin, et al. Identification of interior fault position based on SVM and D-S evidence theory for electric transformer[J]. Electric Power Automation Equipment, 2012, 32(11): 72-77.
[9] Kari T, Gao Wensheng, Zhao Dongbo, et al. Hybrid feature selection approach for power transformer fault diagnosis based on support vector machine and genetic algorithm[J]. IET Generation, Transmission & Distribution, 2018, 12(21): 5672-5680.
[10] 朱永利, 申涛, 李强. 基于支持向量机和DGA的变压器状态评估方法[J]. 电力系统及其自动化学报, 2008, 20(6): 111-115.
Zhu Yongli, Shen Tao, Li Qiang. Transformer condition assessment based on support verctor machine and DGA[J]. Proceedings of the CSU-EPSA, 2008, 20(6): 111-115.
[11] Wu X, Kumar V, Quinlan J R, et al. Top 10 algorithms in data mining [J]. Knowledge and Information System, 2008, 14(1): 1-37.
[12] 胡青, 孙才新, 杜林, 等. 核主成分分析与随机森林相结合的变压器故障诊断方法[J]. 高电压技术, 2010, 36(7): 1725-1729.
Hu Qing, Sun Caixin, Du Lin, et al. Transformer fault diagnosis method using random froests and kernel principle component analysis[J]. High Voltage Engineering, 2010, 36(7): 1725-1729.
[13] 吴杰康, 覃炜梅, 梁浩浩, 等. 基于自适应极限学习机的变压器故障识别方法[J]. 电力自动化设备, 2019, 39(10): 181-186.
Wu Jiekang, Qin Weimei, Liang Haohao, et al. Transformer fault identification method based on self-adaptive extreme learning machine[J]. Electric Power Automation Equipment, 2019, 39(10): 181-186.
[14] 李春茂, 周妺末, 袁海满, 等. 基于DGA的粗糙集与决策信息融合变压器故障诊断[J]. 电工电能新技术, 2018, 37(1): 84-90.
Li Chunmao, Zhou Momo, Yuan Haiman, et al. Fault diagnosis of transformer based on rough set theory and decision information fusion[J]. Advanced Technology of Electrical Engineering and Energy, 2018, 37(1): 84-90.
[15] 张景明, 肖倩华, 王时胜. 融合粗糙集和神经网络的变压器故障诊断[J]. 高电压技术, 2007, 33(8): 122-125.
Zhang Jingming, XiaoQianhua, Wang Shisheng. Transformer fault diagnosis by combination of rough set and neural network[J]. High Voltage Engineering, 2007, 33(8): 122-125.
[16] 张育杰, 李典阳, 冯健, 等. 基于多模型选择性融合的变压器在线故障诊断[J]. 电力系统自动化, 2021, 45(13): 95-101.
Zhang Yujie, Li Dianyang, Feng Jian, et al. Transformer online fault diagnosis based on selective hybrid of multiple models[J]. Automation of Electric Power Systems, 2021, 45(13): 95-101.
[17] Zhou Zhihua. Ensemble methods: foundations and algorithms[M]. Florida: Chapman and Hall/CRC, 2012.
[18] 王雪, 韩韬. 基于贝叶斯优化随机森林的变压器故障诊断[J]. 电测与仪表, 2021, 58(6): 167-173.
Wang Xue, Han Tao. Transformer fault diagnosis based on Bayesian optimized random forest[J]. Electrical Measurement & Instrumentation, 2021, 58(6): 167-173.
[19] 张婷婷, 于明, 李宾, 等. 基于Wavelet降噪和支持向量机的锂离子电池容量预测研究[J]. 电工技术学报, 2020, 35(14): 3126-3136.
Zhang Tingting, Yu Ming, Li Bin, et al. Capacity prediction of lithium-ion batteries based on wavelet noise reduction and support vector machine[J]. Transactions of China Electrotechnical Society, 2020, 35(14): 3126-3136.
[20] 徐心愿, 王云冲, 沈建新. 基于最大转矩电流比的同步磁阻电机DTC-SVM控制策略[J]. 电工技术学报, 2020, 35(2): 246-254.
Xu Xinyuan, Wang Yunchong, Shen Jianxin. Direct torque control-Space vector modulation control Strategy of synchronous reluctance motor based on maximum torque per-ampere[J]. Transactions of China Electrotechnical Society, 2020, 35(2): 246-254.
[21] 范贤浩, 刘捷丰, 张镱议, 等. 融合频域介电谱及支持向量机的变压器油浸纸绝缘老化状态评估[J]. 电工技术学报, 2021, 36(10): 2161-2168.
Fan Xianhao, Liu Jiefeng, Zhang Yiyi, et al. Aging evaluation of transformer oil-immersed insulation combining frequency domain spectroscopy and support vector machine[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2161-2168.
[22] 汪可, 李金忠, 张书琦, 等. 变压器故障诊断用油中溶解气体新特征参量[J]. 中国电机工程学报, 2016, 36(23): 6570-6578, 6625.
Wang Ke, Li Jinzhong, Zhang Shuqi, et al. New features derived from dissolved gas analysis for fault diagnosis of power transformers[J]. Proceedings of the CSEE, 2016, 36(23): 6570-6578, 6625.
Multi-Dimensional Diagnosis of Transformer Fault Sample and Credibility Analysis
Abstract Power transformer is the core equipment of power system, and its safe and stable operation is of great significance to power system. Online fault diagnosis of power transformers is an important method to realize real-time status analysis of power transformers. At present, the selection of features subset for transformer fault diagnosis mainly adopts heuristic-based method, which simplifies the selection process compared to traversal algorithms, but it still consumes a lot of computing power. Moreover, the research of hybrid fault diagnosis motheds for power transformer focuses on the improvement of the diagnosis effect in all samples, and does not pay attention to the credibility analysis of the diagnosis results in single sample. In order to solve this problem, this paper proposed a transformer state analysis method that combines autonomous discretization and optimization of data distribution signs, and single-event multi-model fusion analysis. Proved by examples, this method can effectively analyze the data distribution of each feature, perform feature optimization, and can get the operating status and reliability of the transformer from the perspective of a single event.
keywords：Optimized discrete, feature selection, result credibility, auxiliary analysis
DOI:10.19595/j.cnki.1000-6753.tces.210070
中图分类号：TM41
国家自然科学基金资助项目（61673093）。
收稿日期 2021-01-15
改稿日期 2021-04-07
李典阳 男，1987年生，博士研究生，研究方向为电网运行及电力调度控制技术与应用。E-mail：2824804703@qq. com
张育杰 男，1996年生，硕士研究生，研究方向为电力设备故障诊断与状态预判。E-mail：zyj_neu@163. com（通信作者）
（编辑 赫蕾）