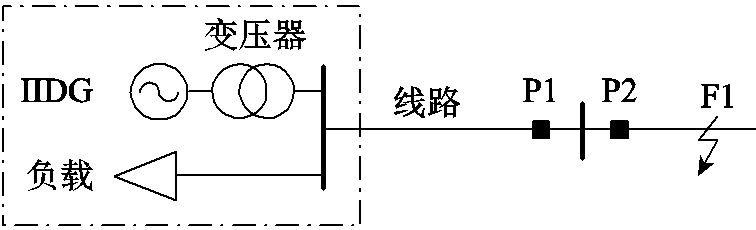
图1 并网运行微电网的局部区域
Fig.1 A partial area of the grid-connected microgrid
摘要 微电网具有双向故障电流，其保护的一个关键问题是如何准确判别故障方向。对微电网正序故障附加网络的分析表明，逆变型分布式电源（IIDG）正序故障分量阻抗角所在象限决定了正序故障分量方向元件在并网运行微电网中的适用性。然而，IIDG功率输出策略的多样性和故障后IIDG并网点电压变化的不确定性导致IIDG正序故障分量阻抗角所在象限无法确定。对此，该文提出一种多阶段的IIDG故障控制方法，通过改变IIDG在特定时间窗口内的故障响应特性将其正序故障分量阻抗角控制为给定值，从而在微电网中构造出不依赖于IIDG功率输出策略的正序故障分量特征。基于Simulink的仿真结果验证了采用所提出IIDG故障控制方法时微电网故障方向识别的准确性。
关键词：并网运行微电网 故障方向 逆变型分布式电源 正序故障分量
微电网是一个由分布式电源、负载、储能及监控保护设备组成的小型发配电系统[1-3]。大多数分布式电源都必须经“逆变器”或者“整流器-逆变器”将电能转换成适当形式后才能接入微电网[4-5]，这类分布式电源称为逆变型分布式电源（Inverter Interfaced Distributed Generator, IIDG）。IEEE 1547.4标准要求IIDG具备即插即用功能，这导致IIDG的接入位置在网络中具有不确定性。当微电网线路发生故障时，故障点两侧可能都有电流流过。为了实现最小范围切除故障线路，微电网保护系统应正确判断故障点方向。
分布式电源接入电网后，将在一定程度上改变电网故障特征，从而影响传统方向元件的工作准确性。文献[6]基于风电系统故障特征，分析了传统选相及方向元件在风电接入系统中的适应性。文献[7]建立了IIDG在恒功率控制策略下的等效模型，在此基础上分析了基于正序电流故障分量幅值和相位比较的保护原理在微电网中的适用性。文献[8]推导了送出线路光伏电站侧故障电流相量表达式，深入分析了有功、无功参考值、控制目标、电压不平衡度等因素对序故障分量方向元件和相量故障分量方向元件动作性能的影响。文献[9]通过分析双馈风机等效序突变量阻抗的相位变化特征，揭示了双馈风机对故障分量方向元件的影响机理。文献[10]对逆变型电源等效正、负序突变量阻抗解析表达式进行推导，揭示了逆变型电源对各类故障分量方向元件的影响机理。虽然不同文献所研究的分布式电源类型及功率控制策略不同，但大多数结论都认为传统方向元件的性能出现了下降，甚至存在误判的可能。
对此，部分学者提出了改进的故障方向判别方法。例如，文献[11]提出一种具有低电压穿越能力的光伏电源接入配电网方向元件的新判据，在光伏电源采用无功支撑策略时具有良好的实用性。文献[12]对采用低电压穿越策略的IIDG在微电网高阻故障和低阻故障下的故障响应特性进行了分析，提出了一种基于正序故障分量的故障方向判别方法。文献[13]提出一种具有新型逻辑结构的方向元件，该元件在IIDG采用纯正序电流输出与同步电机模拟这两类故障穿越策略时具有良好的表现。
针对具体的IIDG控制策略改进故障方向判据是目前采用较广泛的一种思路，但考虑到IIDG在故障情况下可采用的功率输出策略非常灵活多样[14-16]，上述改进方法在应用于其他场景时难以保证其适用性。借鉴国内学者提出的控制-保护协同概念[17-19]，本文提出一种多阶段的IIDG故障控制方法，通过改变IIDG在特定时间窗口内的故障响应特性构造出恒定的微电网正序故障分量特征，从而可实现不依赖IIDG功率输出策略的故障方向判别。
本文首先分析了IIDG正序故障分量阻抗角对并网运行微电网故障方向判别的影响；然后研究了不同功率优先输出策略下，IIDG正序故障分量阻抗角随并网点电压幅值、相角变化之间的规律；最后，详细介绍了所设计的IIDG故障电流参考信号生成方法，并基于Simulink进行了仿真验证。
基于正序故障分量的继电保护检测原理具有无需判断故障类型、不受故障点过渡电阻及负荷电流影响的突出优点，正序故障分量阻抗角常用于判断故障方向[20]。然而，IIDG的故障特性不同于传统电源，在微电网中应用正序故障分量方向元件时，必须考虑IIDG对微电网正序故障分量特征的影响。
图1所示为并网微电网的一个局部区域，点画线框为微电网的基本组成单元，包括连接在同一母线上的IIDG、变压器及负载等。P1和P2是方向元件，其正方向定义为从母线指向所在线路。
图1 并网运行微电网的局部区域
Fig.1 A partial area of the grid-connected microgrid
当F1处发生故障时，图1所示区域的正序故障分量附加网络如图2所示。其中，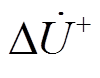
、
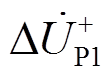和
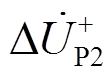分别表示IIDG并网点、P1、P2处的正序电压故障分量，
、
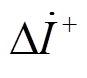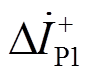和
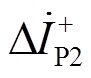分别表示IIDG并网点、P1、P2处的正序电流故障分量。
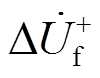表示故障点的正序电压故障分量。ZLine表示线路阻抗，ZLoad表示负载阻抗，ZT表示变压器阻抗。
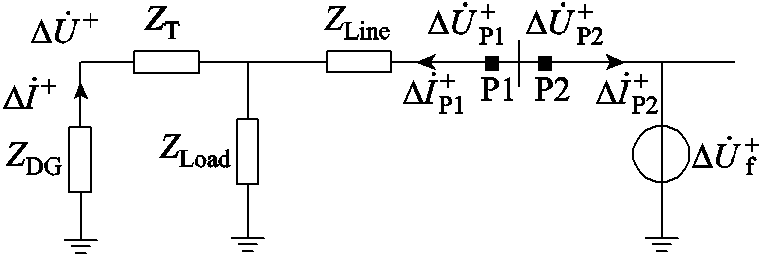
图2 并网运行微电网局部区域的故障分量附加网络
Fig.2 The positive sequence fault additional network of the partial area of grid-connected microgrid
根据图2，P1和P2处的正序故障分量阻抗ZP1、ZP2可分别表示为
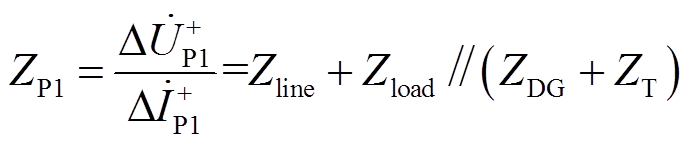（1）
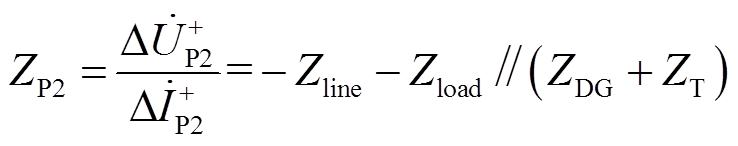（2）
式中，ZDG为IIDG的正序故障分量阻抗，其定义为
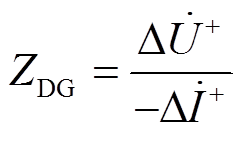（3）当故障点位于方向元件的反方向时，方向元件的正方向是一个只包含ZDG、ZLine、ZT及ZLoad的纯阻抗网络，此时ZP（如图2中的P1）可用“ZDG⊕ZLine⊕ZT⊕ZLoad”的形式来表示，⊕表示串联或并联。当故障点位于方向元件正方向时，阻抗网络出现在方向元件的反方向一侧，此时ZP（如图2中的P2）具有“–( ZDG⊕ZLine⊕ZT⊕ZLoad)”的形式。
ZLine、ZT和ZLoad通常为阻-感性，其阻抗角位于第一象限。若ZDG为阻-感类型，则根据阻抗元件的串联、并联理论，易知ZP1的阻抗角在第一象限，而ZP2的阻抗角在第三象限。类似地，当ZDG为负阻-感类型或者阻-容类型时，ZDG与ZLine、ZT、ZLoad存在部分相同的阻抗属性（例如，共同含有电感部分或者电阻部分），此时也可推断出ZP1与ZP2阻抗角所在的象限，结果见表1。但是，当ZDG为负阻-容类型时，ZDG与ZLine、ZT、ZLoad的阻抗属性完全不同，此时ZP1与ZP2的阻抗角所在象限与ZDG、ZLine、ZT、ZLoad的具体数值及其连接关系有关，在微电网复杂多变的运行情况下无法预先确定。
表1 ZP1和ZP2阻抗角所在象限
Tab.1 Quadrants of the impedance angels of ZP1 and ZP2
ZDG类型argZDGargZP1argZP2 阻-感第一象限第一象限第三象限 负阻-感第二象限第一、二象限第三、四象限 负阻-容第三象限不确定不确定 阻-容第四象限第一、四象限第二、三象限
根据表1可知，当ZDG阻抗角位于第一、第二或第四象限时，ZP1和ZP2阻抗角能够确定所在象限，且不存在重叠区域，此时方向元件可根据正序故障分量阻抗角判断故障方向。当ZDG阻抗角位于第三象限时，ZP1和ZP2阻抗角所在象限无法确定，不能用于判断故障方向。值得注意的是，当微电网基本组成单元中包含更多的IIDG与负载，或者考虑更多的基本组成单元时，容易分析得出，方向元件处的正序故障分量阻抗仍然是ZDG、ZLine、ZT和ZLoad的串联、并联组合，以上结论同样是成立的。因此，ZDG的阻抗角所在象限决定了正序故障分量方向元件在并网运行微电网中的适用性。
电网发生故障后，系统电压将出现幅值跌落和相位跳变[21-23]。若IIDG并网点的正序电压降低至故障前的k(0＜k＜1)倍，相位跳变为φ，则IIDG并网点电压的正序故障分量为
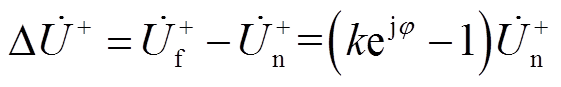（4）式中，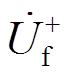
为故障后的IIDG并网点正序电压；
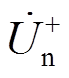为故障前IIDG并网点正序电压。对于其他变量，本文同样用下标f和n分别指代故障后和故障前。
在并网运行的微电网中，IIDG以功率跟踪为目标[24-26]，假设只从正相序输出功率，则其输出电流为
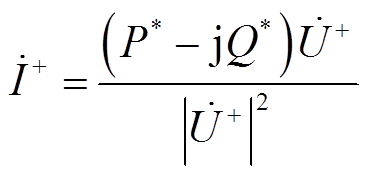（5）式中，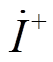
为IIDG输出电流；
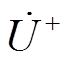为IIDG并网点的正序电压；P*为IIDG的有功功率参考值；Q*为IIDG的无功功率参考值；
表示取模值。对于其他变量，本文同样用上标“*”表示其参考值。IIDG的正序电流故障分量为
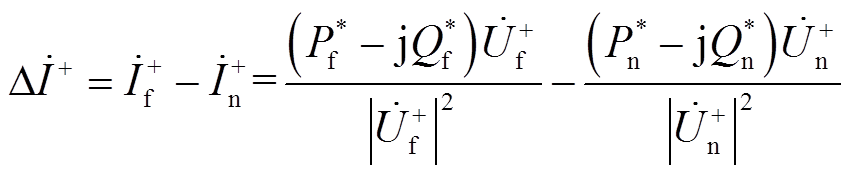（6）
综合式（5）和式（6），可推导出IIDG的正序故障分量阻抗为
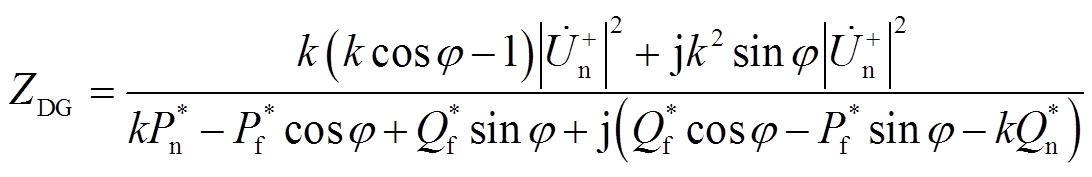（7）显然，ZDG阻抗角与IIDG并网点正序电压的幅值跌落程度、相位跳变及IIDG在故障前后的有功/无功功率参考值有关。根据IIDG并网点电压跌落程度及功率输出优先级的不同，IIDG功率参考值存在三种可能的变化。
1）电压跌落程度较轻。此时IIDG仍能完成故障前的功率跟踪目标，故障前后IIDG的功率参考值基本保持不变。
2）电压跌落严重且IIDG采用有功功率优先策略。当IIDG并网点电压跌落较严重时，由于IIDG的最大输出电流一般不超过其额定电流的1.2～2倍，IIDG输出功率的能力将远小于其额定容量。此时无功功率参考值首先被削减，当无功功率输出降为零，有功功率参考值也有可能被削减。
3）电压跌落严重且IIDG采用无功功率优先策略。有功功率参考值将首先被削减，当有功功率输出减为零，无功功率参考值也有可能被削减。
用Cmax表示IIDG的最大过电流倍数，则IIDG在微电网故障后可输出功率的最大值为
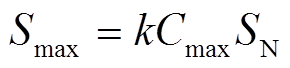（8）式中，SN为IIDG的额定视在功率。
当采用有功功率优先输出策略时，IIDG的功率参考值为
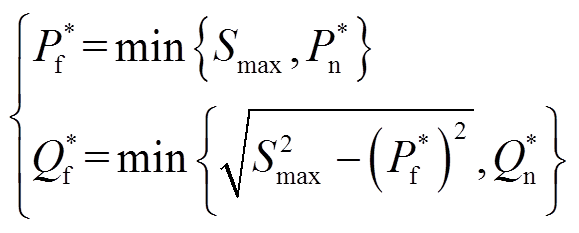（9）根据式（7）～式（9），对有功功率优先策略下ZDG阻抗角随k与φ的变化规律进行分析，得到图3所示的结果（以
=0.8pu，
=0.2pu，Cmax=1.5为例）。
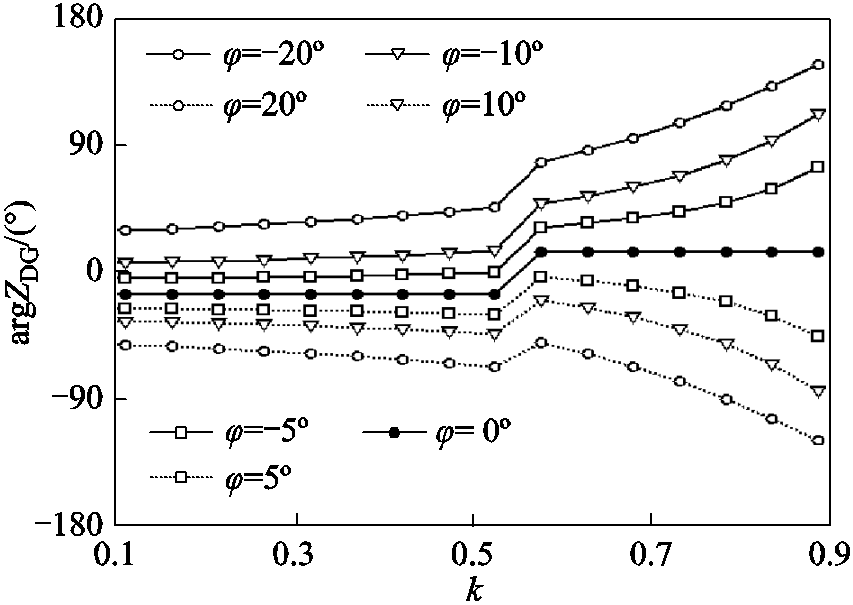
图3 ZDG阻抗角随k与φ的变化规律（有功优先情形）
Fig.3 Variation of impedance angle of ZDG with k and φ（cases where active power has higher priority）
当采用无功功率优先输出策略时，IIDG的功率参考值为
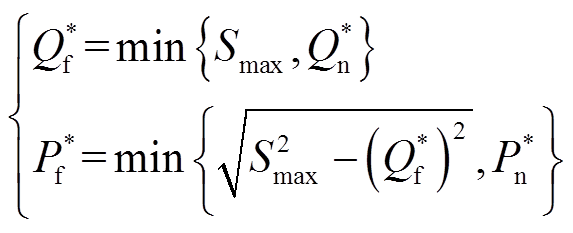（10）根据式（7）、式（8）和式（10），对无功优先策略下ZDG阻抗角随k与φ的变化规律进行分析，结果如图4所示（以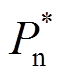=0.8pu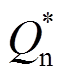，=0.2pu，Cmax=1.5为例）。
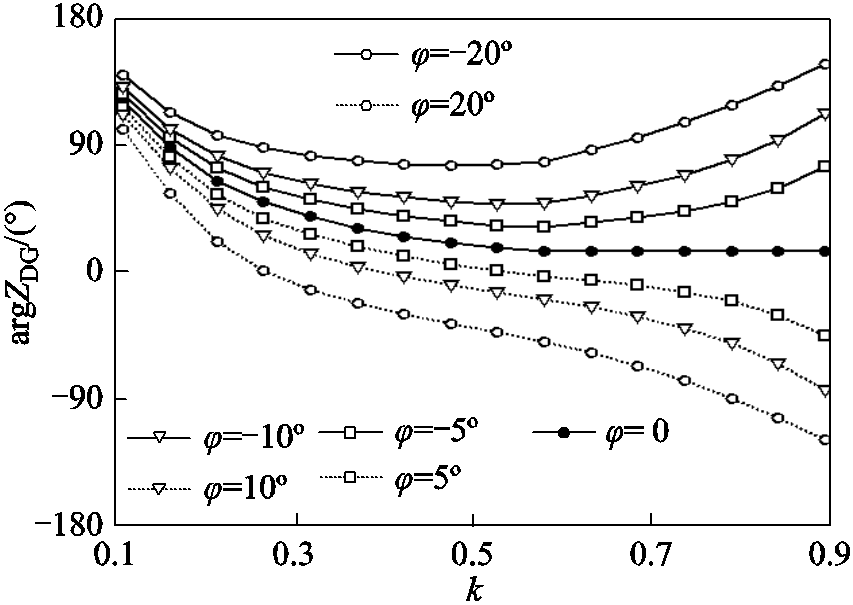
图4 ZDG阻抗角随k与φ的变化规律（无功优先情形）
Fig.4 Variation of impedance angle of ZDG with k and φ（cases where reactive power has higher priority）
根据图3和图4可知，无论采用哪种功率优先输出策略，当k与φ变化时，ZDG阻抗角不会固定在某一个象限，而是会跨越多个象限，使故障方向判别特征复杂化。若φ取较大的正值，则ZDG阻抗角有可能进入第三象限，导致正序故障分量方向元件无法判断故障方向。
方向元件提取正序故障分量时只需利用故障后较短时间内的故障信息，在这段时间内，若通过控制手段将ZDG的阻抗角限制在某一固定象限，则可为简化微电网故障方向判断提供有利条件。根据式（3）可知，ZDG阻抗角由IIDG并网点的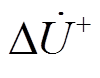和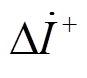共同决定，虽然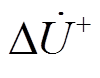不可控，但可通过控制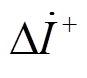对ZDG阻抗角进行调节。若arg ZDG∈[0，90º]，则IIDG在正序故障附加网络中可等效为电阻RDG与电感LDG的并联，如图5所示。
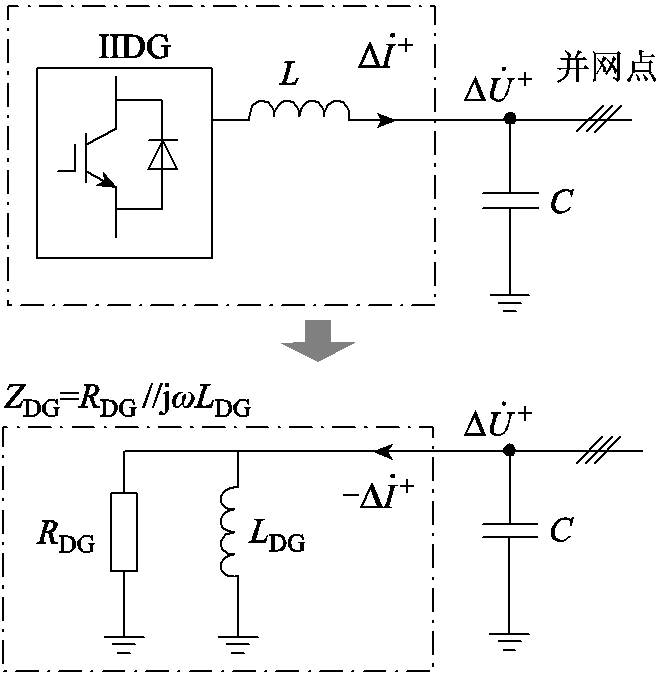
图5 IIDG在正序故障附加网络中的等效形式
Fig.5 Equivalent form of IIDG in positive sequence fault additional network
此时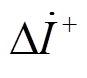可表示
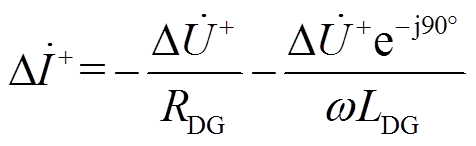（11）假设IIDG输出电流可以快速准确地跟踪其参考信号，则有
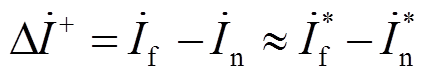（12）
根据式（11）和式（12），IIDG的电流参考信号应设置为
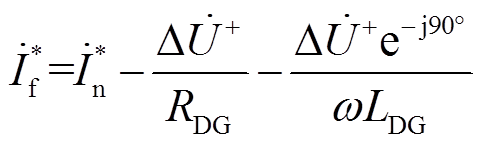（13）式（13）所示的参考电流只在故障后存在较短时间，随后将被切换为以功率跟踪为目标的参考电流。具体来说，本文将IIDG的故障控制过程划分为惯性保持阶段、过渡阶段与功率跟踪阶段。在惯性保持阶段，IIDG的参考电流由式（13）给定；在功率跟踪阶段，IIDG的参考电流根据具体的功率输出策略确定；过渡阶段位于惯性保持与故障穿越阶段之间，用于实现IIDG参考电流的平滑切换。综上，IIDG电流参考信号可表述为
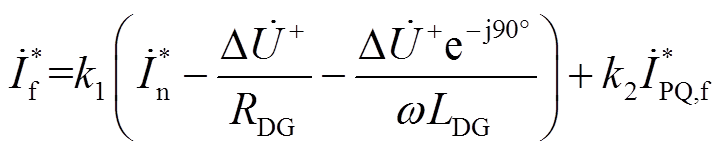（14）
式中，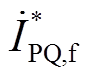
为IIDG根据故障后的功率参考值
、
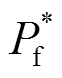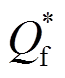计算出的参考电流；k1和k2为随时间变化的系数，其取值规律如图6所示。
在式（13）和式（14）中，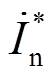
是正弦稳态信号，因此只要提取的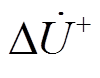达到稳态，就可以认为
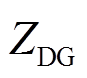具有稳定的阻抗角。本文使用双二阶广义积分器锁频环（Dual Second Order Generalized Integrator Frequency Locked Loop, DSOGI-FLL）提取并网点电压的正序分量，与同步参考坐标系锁相环（Synchronous Reference Frame Phase Locked Loop, SRF-PLL）相比，DSOGI-FLL 更有助于并网系统的稳定运行[27]。DSOGI-FLL的调节时间与电压频率有关，其参数采用文献[28]给出的推荐值（
，
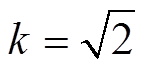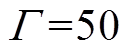），适用于频率为50Hz且频率波动范围较小的电压信号，可确保在动态响应速度与超调量之间达到较好的平衡。对于50Hz的工频电压跌落，DSOGI-FLL能够在22.5ms后准确地检测出跌落电压的幅值和相位，误差不超过5%。在故障后的第2个周期，即可认为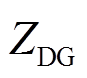基本达到稳态。因此，本文将惯性保持阶段设定为40ms。
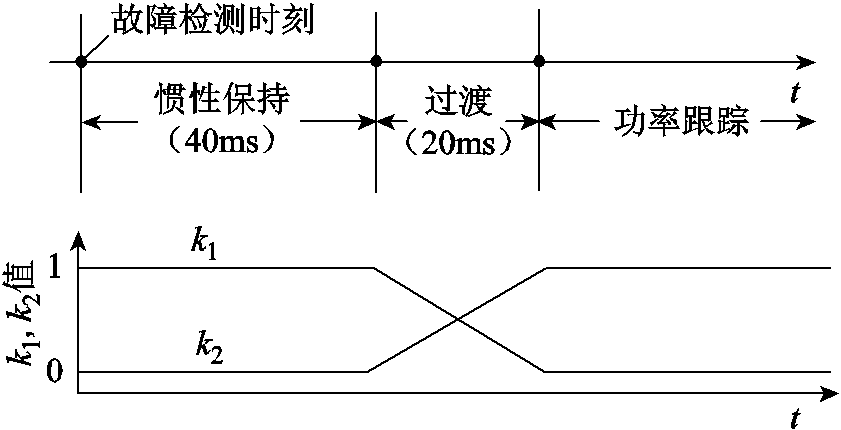
图6 IIDG的多阶段控制方案
Fig.6 Multi-stage control scheme of IIDG
参照国家标准GB/T 37408—2019《光伏发电并网逆变器技术要求》，自逆变器交流侧电压异常时刻起，动态无功电流的响应时间不大于60ms，该响应时间对应于本文提出的惯性保持阶段与过渡阶段时长之和，因此过渡阶段设定为20ms。采用这一设定方式之后，本文所提出的IIDG多阶段控制方案不会对微电网的故障穿越效果造成显著影响。
IIDG参考电流信号计算逻辑如图7所示。图中，i和u分别表示IIDG输出电流矢量和并网点电压矢量。
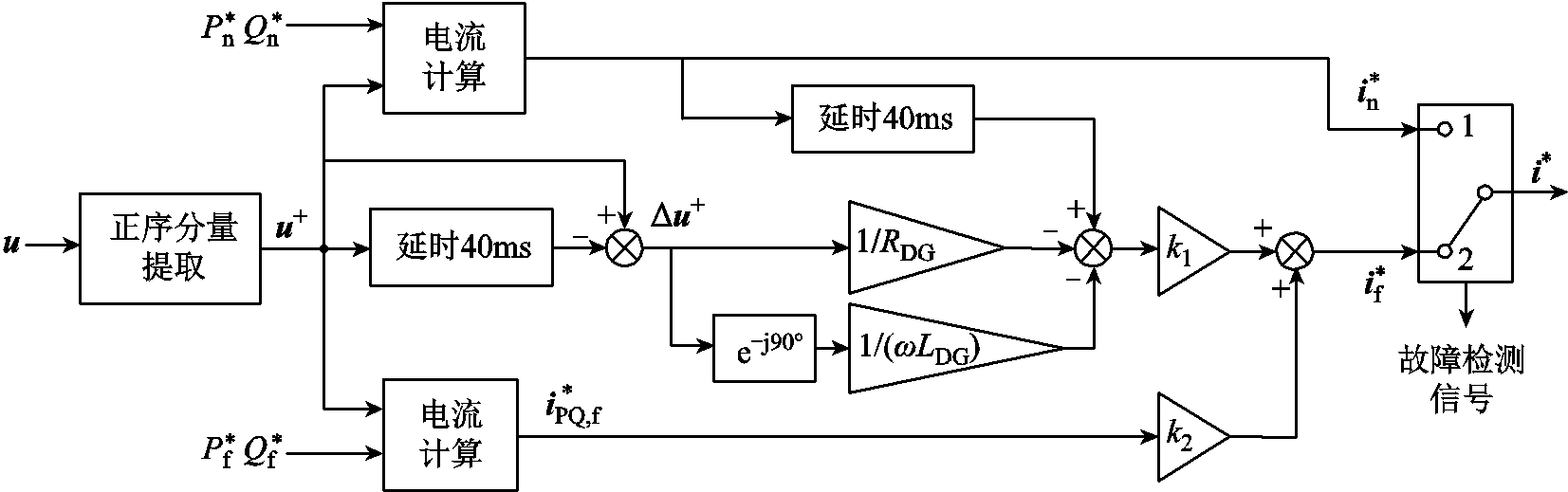
图7 IIDG参考电流信号计算逻辑
Fig.7 Generation method of the output current reference of IIDG
当检测到故障发生时，IIDG电流参考信号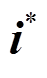
立即从
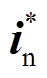切换至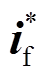
。根据式（14），故障后参考电流的计算需要以故障前的参考电流为基础，因此在图7引入缓存模块对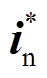进行延时。IIDG利用并网点三相电压uA、uB、uC突变量超过给定阈值作为故障检测信号，如式（15）所示。
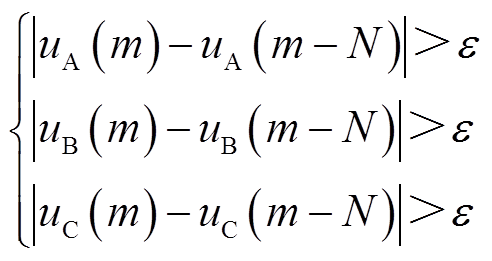（15）式中，m为IIDG并网点三相电压的采样点序号；N为每周期的采样点数；ε可取0.2倍额定电压。
将ZDG阻抗角的设定值记为θ，则RDG与LDG应满足
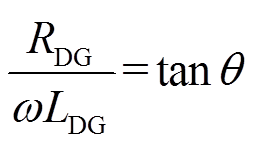（16）此外，还应确保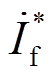
的幅值不超过IIDG的电流允许范围，即
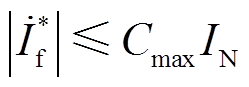（17）
式中，IN为IIDG的相电流额定值。将IIDG的相电压额定值记为UN，考虑到存在关系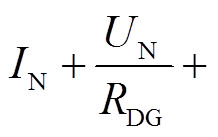
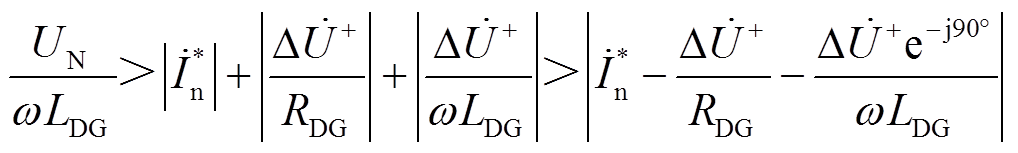易知当RDG与LDG满足式（18）所示条件时，式（17）必然成立。
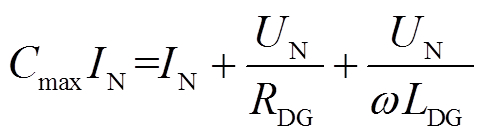（18）联立式（16）和式（18），即可计算出RDG与LDG。
采用图7所示的IIDG参考电流计算策略后，ZDG阻抗角被控制在第一象限。此时，方向元件能够根据正序故障分量阻抗角argZP判断故障方向，且argZP与故障方向有如下规律：
1）故障发生在方向元件的正方向时，argZP∈ [-180º, -90º]。
2）故障发生在方向元件的反方向时，argZP∈[0, 90º]。
在故障后的第2个周期，ZDG基本达到稳态，方向元件对ZP的检测值也达到稳态。因此，若以故障检测时刻作为时间起点t=0，则方向元件采用t=20～40ms时间窗口内的采样数据可确保测量结果稳定，从而准确地给出故障方向判别结果。
最后，需要说明的是，本文所提出的阻抗角控制主要是通过对IIDG逆变器设置特定的电流参考信号来实现，虽然光伏、直驱式风力发电与储能电池在故障下的动态特性存在差异，但只要能够维持其逆变器直流侧电压稳定，就可以实施本文提出的逆变器控制方法。由于惯性保持阶段只需维持40ms，而各分布式电源逆变器直流侧通常会配置一定容量的电容或储能设备，可确保直流侧电压在该阶段内维持稳定，因此本文所提出的IIDG故障控制方案具有较广泛的适用性。
在Simulink中建立图8所示的并网微电网系统。其中，配电网电压等级为10kV，系统阻抗为1.2+j7.2Ω；点画线框内部分为微电网，采用放射型馈线结构[29-30]。额定电压下负载1消耗的功率为17kW+6kvar，负载2消耗的功率为16kW+5kvar；IIDG1和IIDG2的额定电压均为380V，额定容量均为30kV·A，最大过电流倍数均为1.5；IIDG1故障前的功率参考值为21kW+5kvar，IIDG2故障前的功率参考值为15kW+6kvar；变压器T1和T2的额定容量均为30kV·A，电压比均为10kV/0.4kV，联结组别号分别为Yy0和Dy11；线路1位于母线N和母线M之间，其长度为2km（单位长度阻抗为0.161+j0.19Ω/km）。
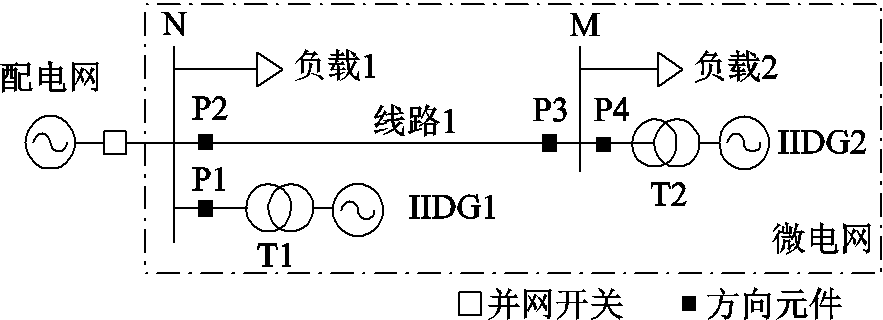
图8 并网微电网系统
Fig.8 A grid-connected microgrid system
算例1：t=0.12s时，变压器T2的高压侧出口位置发生AB两相短路故障，过渡电阻为1Ω。假设IIDG在故障穿越阶段优先输出无功功率，且全部从正相序输出功率。在惯性保持阶段，IIDG的正序故障分量阻抗角设置为45º。IIDG1和IIDG2的输出电流和输出功率分别如图9和图10所示。
在图9a和图10a中，水平虚线表示IIDG的最大允许电流。可以看出，当微电网发生故障后，IIDG1和IIDG2的输出电流始终保持在允许范围内。此外，从惯性保持阶段到功率跟踪阶段的过渡过程中，IIDG输出电流和输出功率具有平滑切换的特性，未出现明显的振荡过程。
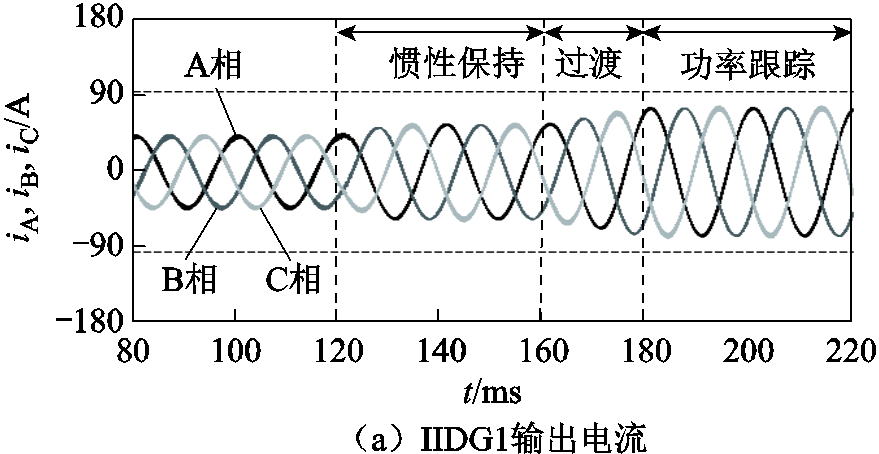
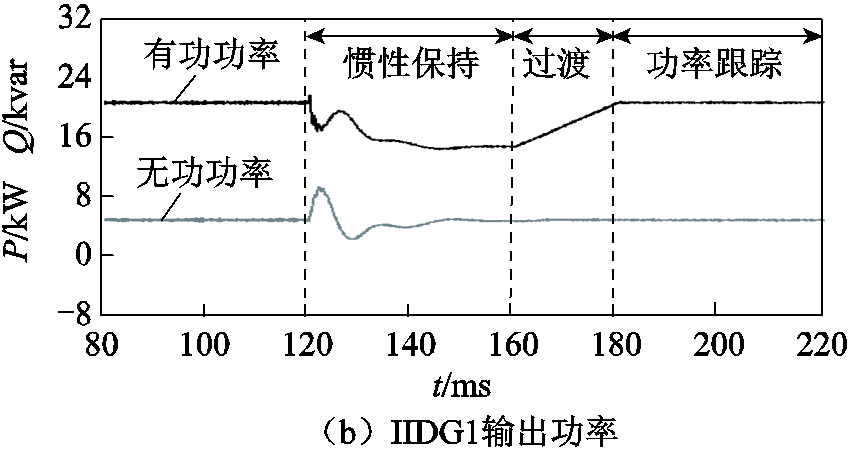
图9 IIDG1的输出电流和输出功率（算例1）
Fig.9 Currents and powers of IIDG1（case 1）
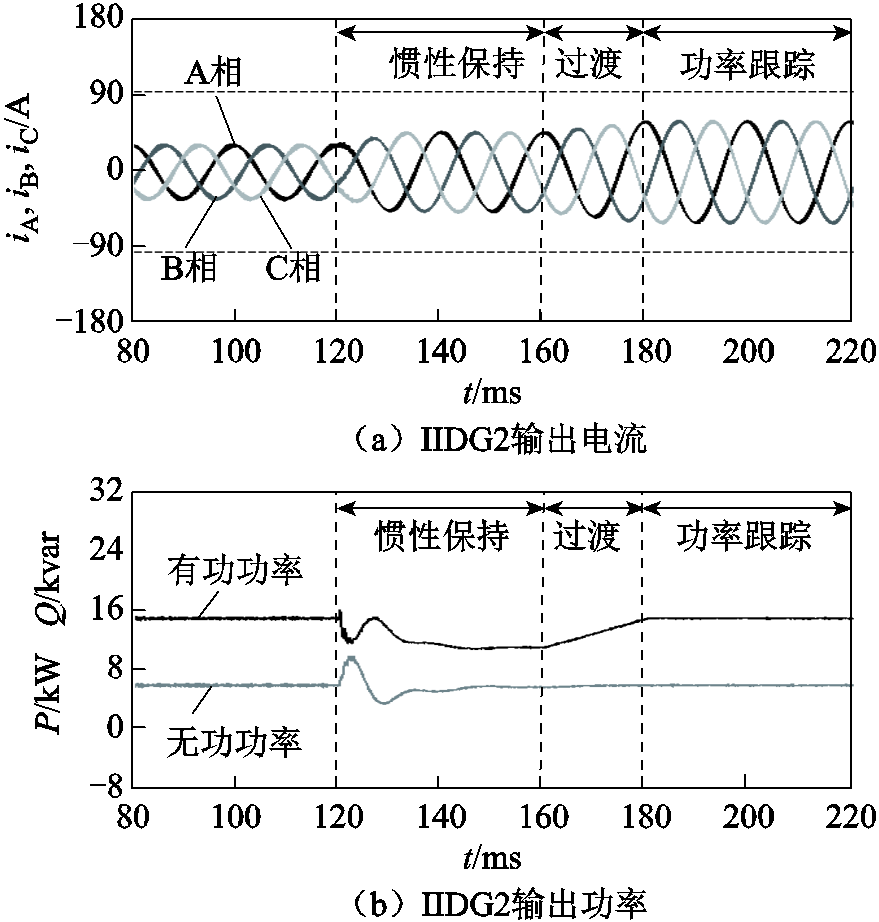
图10 IIDG2的输出电流和输出功率（算例1）
Fig.10 Currents and powers of IIDG2 （case 1）
方向元件P1～P4对其安装处的电压和电流进行采样，得到电压故障分量和电流故障分量如图11所示（已进行归一化处理）。提取其中的正序分量即可计算得到各方向元件处的正序故障分量阻抗，计算结果与故障方向判别结果见表2。
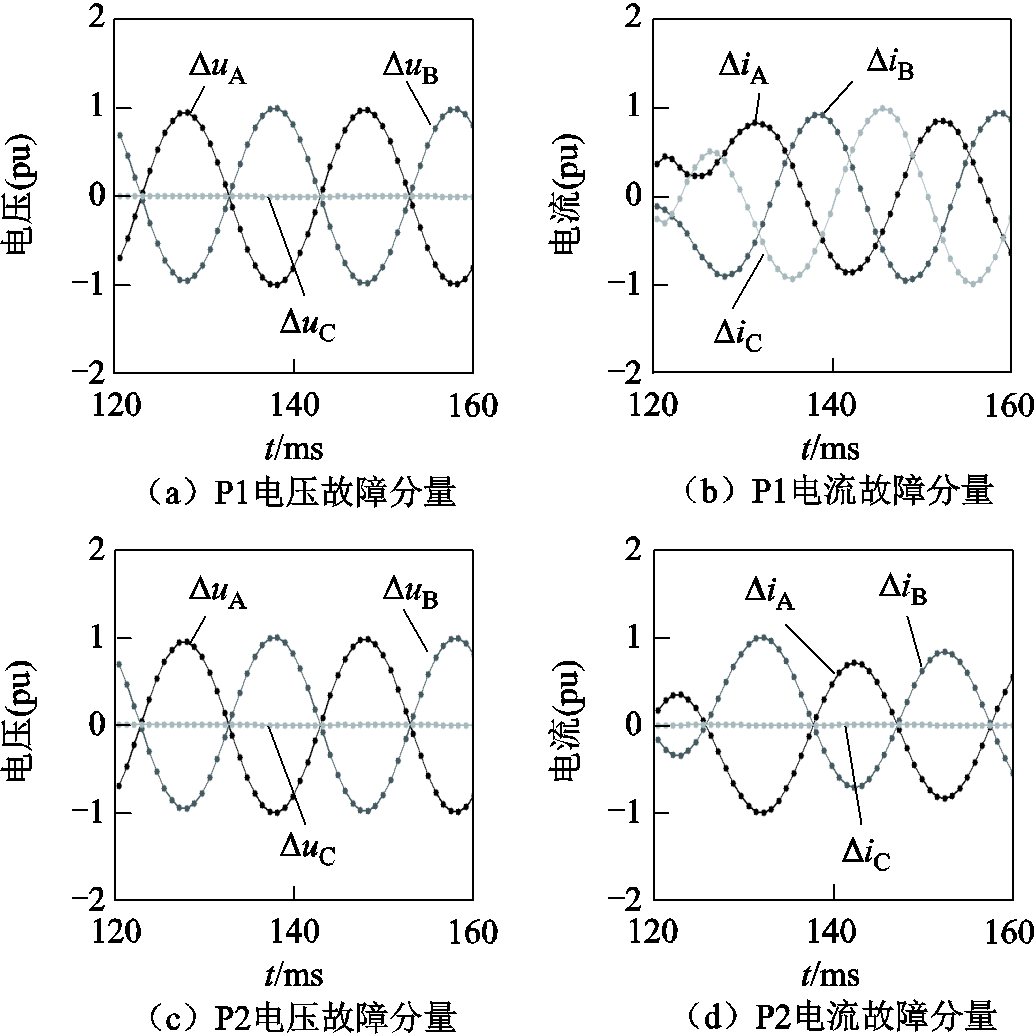
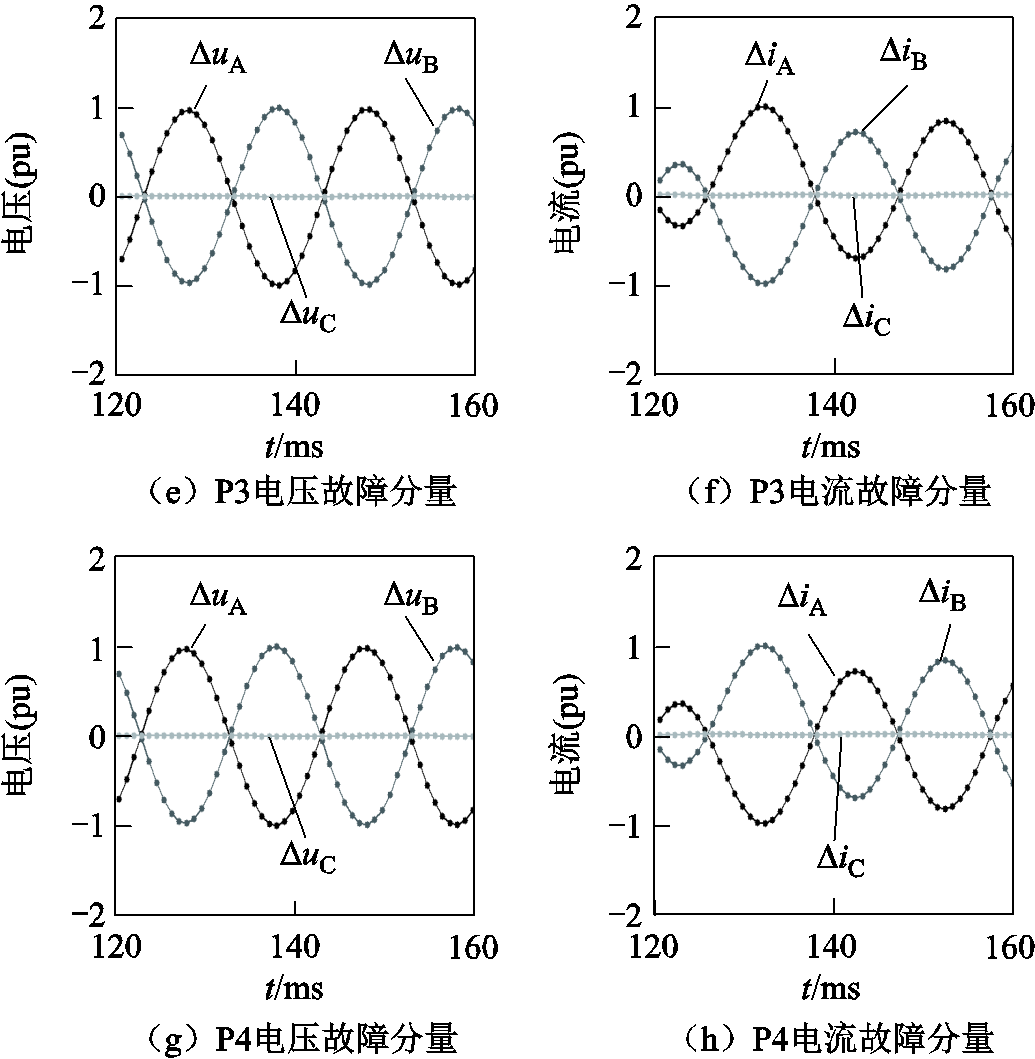
图11 方向元件处的故障分量（算例1）
Fig.11 Fault components at direction elements （case 1）
表2 方向元件阻抗计算及故障方向判断结果（算例1）
Tab.2 Impedance computation results and fault direction results of direction elements （case 1）
方向元件正序故障分量阻抗/W故障方向判断结果 P16 488.1∠46.17º反方向 P27.5∠-100.88º正方向 P37.9∠77.29º反方向 P47.9∠-102.78º正方向
根据图8可知，P1测量、计算得到的阻抗角实质上就是IIDG1的阻抗角（变压器短路阻抗远小于IIDG的正序故障分量阻抗），方向元件P1的正序故障分量阻抗角为46.17º，与设定值45º基本相符。根据正序故障分量阻抗角与故障方向之间的关系，P1和P3判断故障点位于反方向，P2和P4判断故障点位于正方向，这与故障点的实际位置是相符的。
算例2：t=0.12s时，线路1中点发生三相对称短路故障，过渡电阻为2Ω。IIDG1和IIDG2的输出电流和输出功率分别如图12和图13所示。
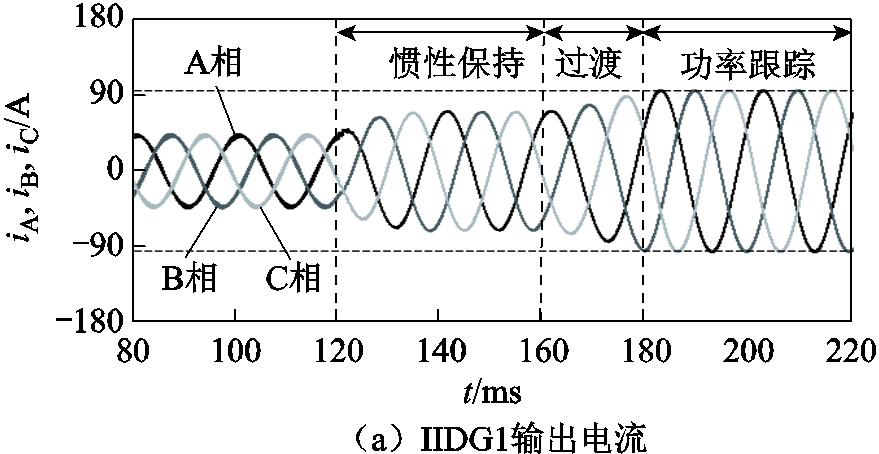
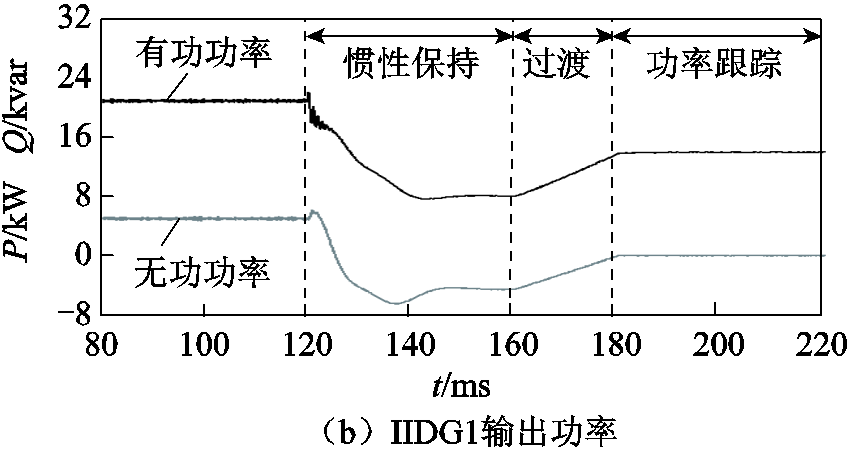
图12 IIDG1的输出电流和输出功率（算例2）
Fig.12 Currents and powers of IIDG1 （case 2）
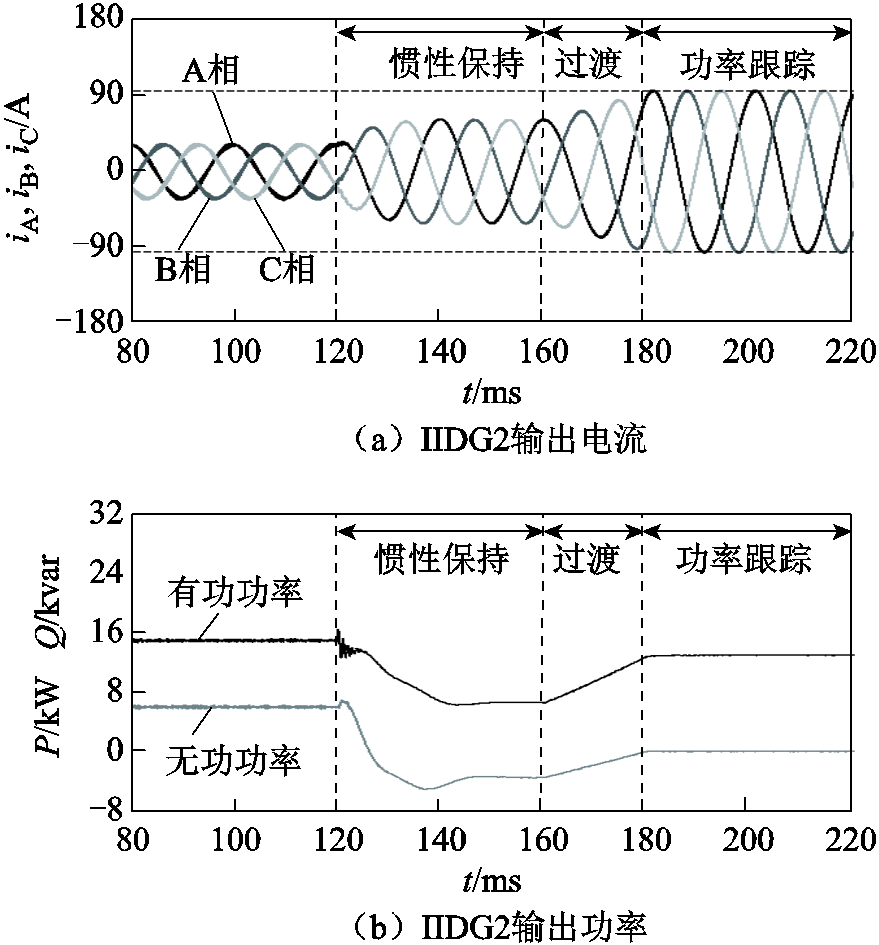
图13 IIDG2的输出电流和输出功率（算例2）
Fig.13 Currents and powers of IIDG2（case 2）
从图12和图13可以看出，从惯性保持阶段到功率跟踪阶段的切换过程中，IIDG输出电流始终保持在允许范围内，且电流和功率变化也具备平滑过渡的特点。方向元件P1～P4处的电压故障分量和电流故障分量如图14所示。同样，利用电压、电流故障分量计算得到各方向元件处的正序故障分量阻抗及故障方向判别结果见表3。
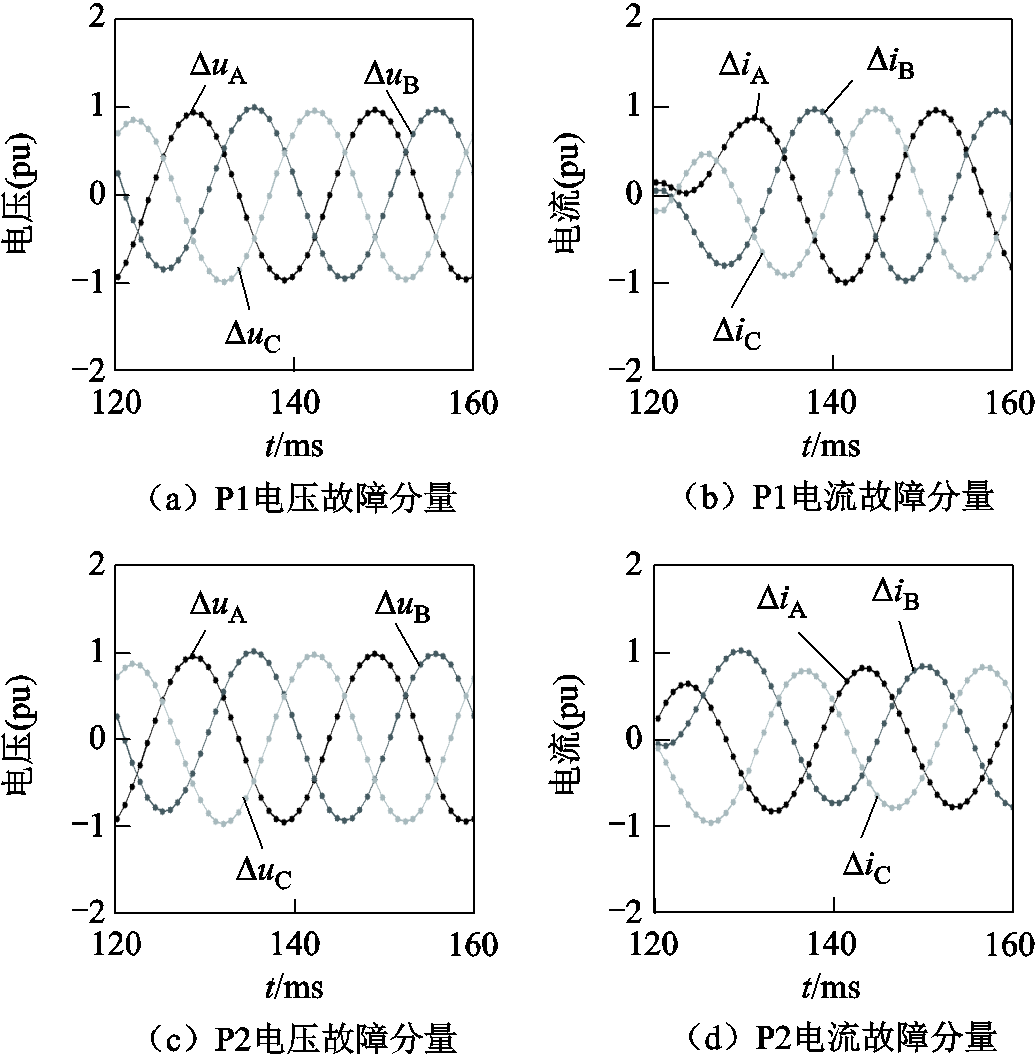
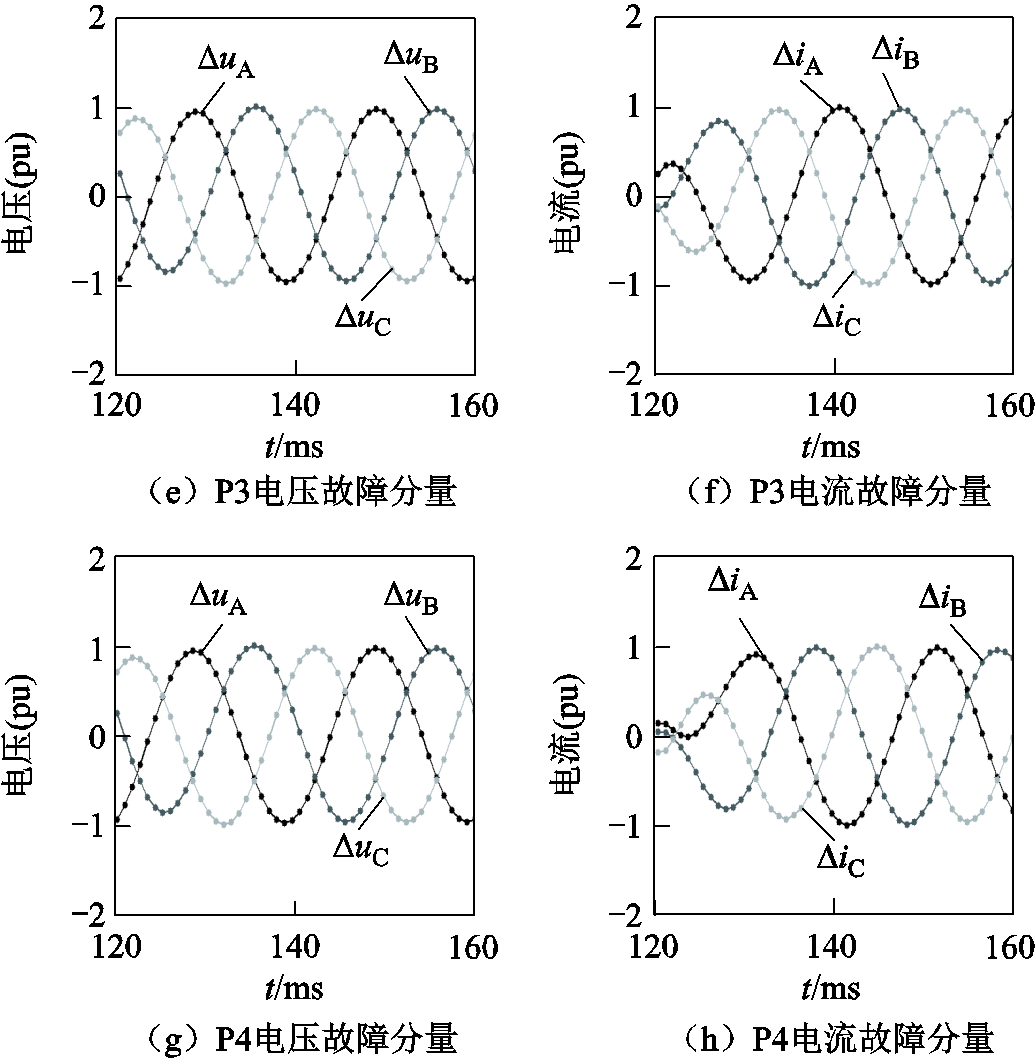
图14 方向元件处的故障分量（算例2）
Fig.14 Fault components of direction elements（case 2）
表3 方向元件阻抗计算及故障方向判断结果（算例2）
Tab.3 Impedance computation results and fault direction results of direction elements （case 2）
方向元件正序故障分量阻抗/W故障方向判断结果 P16 537.6∠46.07º反方向 P27.3∠-100.03º正方向 P33 208.9∠-148.88º正方向 P46 493.7∠46.07º反方向
方向元件P1和P4处的正序故障分量阻抗角均为46.07º，表明在三相短路情形下，IIDG的阻抗角同样与其设置值基本相符。P1～P4的故障判别结果也与故障点的实际位置相符。
算例1和算例2的结果表明，采用所提出IIDG故障控制方法时，ZDG阻抗角能够被控制为设定值，微电网中将出现与故障方向相关联的正序故障分量阻抗角特征，方向元件利用该特征能够准确识别故障方向。
本文根据IIDG对微电网正序故障分量特征的作用规律，提出了一种考虑并网运行微电网故障方向判别的IIIDG故障控制方法，并得出以下结论：
1）当IIDG的正序故障分量阻抗角位于第一、第二或第四象限时，利用方向元件处的正序故障分量阻抗角能够区分微电网故障方向。
2）由于故障后IIDG并网点电压变化的不确定性及IIDG本身功率控制策略的多样性，IIDG的正序故障分量阻抗角所在象限无法唯一确定。
3）采用本文所提出的IIDG多阶段故障控制方案，可以在特定时间窗口内将IIDG正序故障分量阻抗角控制为设定值，并网运行微电网中将出现与故障方向相关联的正序故障分量阻抗角特征，方向元件利用该特征能够准确识别故障方向。
参考文献
[1] 王萧博, 黄文焘, 邰能灵, 等. 一种源-荷-储协同的电热微网联络线功率平滑策略[J]. 电工技术学报, 2020, 35(13): 2817-2829.
Wang Xiaobo, Huang Wentao, Tai Nengling, et al. A tie-line power smoothing strategy for microgrid with heat and power system using source-load-storage coordination control[J]. Transactions of China Elecrotechnical Society, 2020, 35(13): 2817-2829.
[2] 赵卓立, 杨苹, 郑成立, 等. 微电网动态稳定性研究述评[J]. 电工技术学报, 2017, 32(10): 111-122.
Zhao Zhuoli, Yang Ping, Zheng Chengli, et al. Review on dynamic stability research of microgrid[J]. Transactions of China Elecrotechnical Society, 2017, 32(10): 111-122.
[3] 杨海柱, 岳刚伟, 康乐. 微网分段动态自适应下垂控制策略研究[J]. 电力系统保护与控制, 2019, 47(8): 86-93.
Yang Haizhu, Yue Gangwei, Kang Le. Research on piecewise dynamic adaptive droop control strategy for microgrid[J]. Power System Protection and Control, 2019, 47(8): 86-93.
[4] 李玉齐, 张健. 关于微网的新型配电系统研究概述与思考[J]. 电气技术, 2020, 21(5): 1-5.
Li Yuqi, Zhang Jian. Summary and thinking on the research of new distribution system of microgrid[J]. Electrical Engineering, 2020, 21(5): 1-5.
[5] 杨荣峰, 于雁南, 俞万能, 等. 新能源船舶并网逆变器电网支撑协调控制[J]. 电工技术学报, 2019, 34(10): 2141-2154.
Yang Rongfeng, Yu Yannan, Yu Wanneng, et al. New energy ship grid-connected inverter grid support and cooperative control[J]. Transactions of China Elecrotechnical Society, 2019, 34(10): 2141-2154.
[6] 王晨清, 宋国兵, 汤海雁, 等. 选相及方向元件在风电接入系统中的适应性分析[J]. 电力系统自动化, 2016, 40(1): 89-95.
Wang Chenqing, Song Guobing, Tang Haiyan, et al. Adaptability analysis of phase selectors and direction relays in power systems integrated with wind farms[J]. Automation of Electric Power Systems, 2016, 40(1): 89-95.
[7] 韩海娟, 牟龙华, 郭文明. 基于故障分量的微电网保护适用性[J]. 电力系统自动化, 2016, 40(3): 96-102.
Han Haijuan, Mu Longhua, Guo Wenming. Adaptability of microgrid protection based on fault components[J]. Automation of Electric Power Systems, 2016, 40(3): 96-102.
[8] 许冠军, 梁营玉, 查雯婷, 等. 方向元件在光伏电站送出线路中的适应性分析[J]. 电网技术, 2019, 43(5): 1632-1639.
Xu Juanjun, Liang Yingyu, Zha Wenting, et al. Adaptability analysis of directional relay for transmission line out-sending from photovoltaic power plant[J]. Power System Technology, 2019, 43(5): 1632-1639.
[9] 黄涛, 陆于平, 蔡超. DFIG等效序突变量阻抗相角特征对故障分量方向元件的影响分析[J]. 中国电机工程学报, 2016, 36(14): 3929-3939.
Huang Tao, Lu Yuping, Cai Chao. Analysis of phase angle characteristics of DFIG equivalent sequence superimposed impedances and its impact on fault components based direction relay[J]. Proceedings of the CSEE, 2016, 36(14): 3929-3939.
[10] 李彦宾, 贾科, 毕天姝, 等. 逆变型电源对故障分量方向元件的影响机理研究[J]. 电网技术, 2017, 41(10): 3230-3236.
Li Yanbin, Jia Ke, Bi Tianshu, et al. Influence mechanism of inverter-interfaced renewable energy generators on fault component based directional relay[J]. Power System Technology, 2017, 41(10): 3230-3236.
[11] 张惠智, 李永丽, 陈晓龙, 等. 具有低电压穿越能力的光伏电源接入配电网方向元件新判据[J]. 电力系统自动化, 2015, 39(12): 106-112.
Zhang Huizhi, Li Yongli, Chen Xiaolong, et al. New criteria of directional component in distribution network with photovoltaic generator of low voltage ride through capability[J]. Automation of Electric Power Systems, 2015, 39(12): 106-112.
[12] Zhang F, Mu L. A fault detection method of microgrids with grid-connected inverter interfaced distributed generators based on the PQ control strategy[J]. IEEE Transactions on Smart Grid, 2019, 10(5): 4816-4826.
[13] Hooshyar A, Iravani R. A new directional element for microgrid protection[J]. IEEE Transactions on Smart Grid, 2018, 9(6): 6862-6876.
[14] 孟建辉, 彭嘉琳, 王毅, 等. 多约束下光储系统的灵活虚拟惯性控制方法[J]. 电工技术学报, 2019, 34(14): 3046-3058.
Meng Jianhui, Peng Jialin, Wang Yi, et al. Multi-constrained flexible virtual inertial control method for photovoltaic energy storage system. Transactions of China Electrotechnical Society, 2019, 34(14): 3046-3058.
[15] Camacho A, Castilla M, Miret J, et al. Positive and negative sequence control strategies to maximize the voltage support in resistive-inductive grids during grid faults[J]. IEEE Transactions on Power Electronics, 2018, 33(6): 5362 - 5373.
[16] 杨超颖, 王金浩, 杨赟磊, 等. 不对称故障条件下并网光伏逆变器峰值电流抑制策略[J]. 电力系统保护与控制, 2018, 46(16): 103-111.
Yang Chaoying, Wang Jinhao, YangYunlei, et al. Control strategy to suppress peak current for grid-connected photovoltaic inverter under unbalanced voltage sags[J]. Power System Protection and Control, 2018, 46(16): 103-111.
[17] 宋国兵, 王婷, 张保会, 等. 利用电力电子装置的探测式故障识别技术分析与展望[J]. 电力系统自动化, 2020, 44(20): 173-183.
Song Guobing, Wang Ting, Zhang Baohui, et al. Analysis and prospect of detective fault identification technologies using power electronic device[J]. Automation of Electric Power Systems, 2020, 44(20): 173-183.
[18] 王守相, 刘琪, 薛士敏, 等. 直流配电系统控制与保护协同关键技术及展望[J]. 电力系统自动化, 2019, 43(23): 23-30.
Wang Shouxiang, Liu Qi, Xue Shimin, et al. Key technologies and prospect for coordinated control and protection in DC distribution system[J]. Automation of Electric Power Systems, 2019, 43(23): 23-30.
[19] 贾科, 宣振文, 朱正轩, 等. 光伏直流升压接入系统故障穿越协同控保方法[J]. 电网技术, 2018, 42(10): 3249-3258.
Jia Ke, Xuan Zhenwen, Zhu Zhengxuan, et al. A coordinated control and active protection for PV DC boosting integration system during FRT[J]. Power System Technology, 2018, 42(10): 3249-3258.
[20] 安艳秋，高厚磊. 正序故障分量及其在继电保护中的应用[J]. 电力系统及其自动化学报, 2003, 15(4): 76-78.
An Yanqiu, Gao Houlei. Positive sequence fault components and its application in protective relaying[J]. Proceedings of the CSU-EPSA, 2003, 15(4): 76-78.
[21] 潘舒扬, 李勇, 贺悝, 等. 考虑微电网参与的主动配电网分区自动电压控制策略[J]. 电工技术学报, 2019, 34(21): 4580-4589.
Pan Shuyang, Li Yong, He Li, et al. Automatic voltage control strategy based on zone-division for active distribution network with microgrids[J]. Transactions of China Elecrotechnical Society, 2019, 34(21): 4580-4589.
[22] Taul M G, Wang Xiongfei, Davari P, et al. Robust fault ride-through of converter-based generation during severe faults with phase jumps[J]. IEEE Transactions on Industry Applications, 2020, 56(1): 570-583.
[23] Zhang Dongdong, Liu Tianhao. Effects of voltage sag on the performance of induction motor based on a new transient sequence component method[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(3): 316-324.
[24] 郑晨玲, 朱革兰, 兰金晨, 等. 逆变型分布式电源接入对电压时间型馈线自动化的影响分析[J]. 电力系统保护与控制, 2020, 48(1): 112-116.
Zheng Chenling, Zhu Gelan, Lan Jinchen, et al. Research on the effect of inverter interfaced distributed generation on voltage-time feeder automation[J]. Power System Protection and Control, 2020, 48(1): 112-116.
[25] 颜湘武, 宋子君, 崔森, 等. 基于变功率点跟踪和超级电容器储能协调控制的双馈风电机组一次调频策略[J]. 电工技术学报, 2020, 35(3): 82-93.
Yan Xiangwu, Song Zijun, Cui Sen, et al. Primary frequency regulation strategy of doubly-fed wind turbine based on variable power point tracking and supercapacitor energy storage[J]. Transactions of China Elecrotechnical Society, 2020, 35(3): 82-93.
[26] 商立群, 朱伟伟. 基于全局学习自适应细菌觅食算法的光伏系统全局最大功率点跟踪方法[J]. 电工技术学报, 2019, 34(12): 2606-2614.
Shang Liqun, Zhu Weiwei. Photovoltaic system global maximum power point tracking method based on the global learning adaptive Bacteria Foraging algorithm[J]. Transactions of China Elecrotechnical Society, 2019, 34(12): 2606-2614.
[27] 王赟程, 陈新, 张旸, 等. 三相并网逆变器锁相环频率特性分析及其稳定性研究[J]. 中国电机工程学报, 2017, 37(13): 3843-3853.
Wang Yuncheng, Chen Xin, Zhang Yang, et al. Frequency characteristics analysis and stability research of phase locked loop for three-phase grid-connected inverters[J]. Proceedings of the CSEE, 2017, 37(13): 3843-3853.
[28] Rodríguez P, Luna A, Muñoz-Aguilar R S, et al. A stationary reference frame grid synchronization system for three-phase grid-connected power converters under adverse grid conditions[J]. IEEE Transactions on Power Electronics, 2011, 27(1): 99-112.
[29] 鲁宗相, 王彩霞, 闵勇, 等. 微电网研究综述[J]. 电力系统自动化, 2007, 31(19): 100-107.
Lu Zongxiang, Wang Caixia, Min Yong, et al. Overview on microgrid research[J]. Automation of Electric Power Systems, 2007, 31(19): 100-107.
[30] 黄文焘, 邰能灵, 范春菊, 等. 微电网结构特性分析与设计[J]. 电力系统保护与控制, 2012, 40(18): 149-155.
Huang Wentao, Tai Nengling, Fan Chunju, et al. Study on structure characteristics and designing of microgrid[J]. Power System Protection and Control, 2012, 40(18): 149-155.
Fault Control of Inverter Interfaced Distributed Generator Considering Fault Direction Identification of the Grid-Connected Microgrid
Abstract The microgrid fault current is bidirectional, and a key issue of its protection is how to determine the fault direction. The analysis of positive-sequence additional network of microgrid shows that the applicability of the positive-sequence fault component (PFSC) based directional element in gird-connected microgrid is decided by the quadrant of the PSFC impedance angle of inverter interfaced distributed generator (IIDG). However, due to the diversity of IIDG power output strategy and the uncertainty of voltage variation at the IIDG coupling point, the quadrant of PSFC impedance angle of IIDG cannot be determined. In this regard, this paper proposed a multi-stage IIDG fault control method. By manipulating the fault response characteristic of IIDG in a specific time window, the PSFC impedance angle was controlled to a given value, so as to construct a PSFC feature independent of IIDG power output strategy in microgrid. The Simulink simulation results verified the accuracy of the microgrid fault direction identification by adopting the proposed IIDG fault control method.
keywords：Grid-connected microgrid, fault direction, inverter interfaced distributed generator, positive-sequence fault component
DOI:10.19595/j.cnki.1000-6753.tces.201672
中图分类号：TM77
中央高校基本科研业务费用专项（22120210164）和国家电网公司总部科技项目（5216A019000R）资助。
收稿日期 2020-12-23
改稿日期 2021-04-22
朱吉然 男，1985年生，博士研究生，高级工程师，研究方向为配电自动化、信息化和智能配电网设备。E-mail：zhujiran040356@163.com
牟龙华 男，1963年生，教授，博士生导师，研究方向为电力系统保护与控制。E-mail：lhmu@tongji.edu.cn（通信作者）
（编辑 赫蕾）