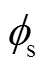(x,t)和液相电势
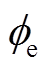(x,t)的分布，并由描述固液界面电化学反应的Butler-Volmer方程更新x轴上各处的净电流密度jLi(x,t)。其中，任意时刻的电池端电压U(t)和输出电流I(t)与电池内部微观量满足关系摘要 高倍率磷酸铁锂电池的机理建模对电池设计与应用管理具有重要意义。针对当前机理模型存在全阶形式复杂度高、简化形式在高倍率下难拟合的问题，将简化的准二维（P2D）电化学模型与双状态热模型结合，建立电化学-热耦合简化机理模型，并通过参数辨识实现了模型在10～40C高倍率、宽范围下的实际放电曲线拟合。基于辨识后的模型，分析了电池高倍率放电下外部曲线变化趋势所反映的内部演化机理，发现高倍率放电初期电池端电压秒级的大幅度下降与液相锂离子浓度分布的不均匀性有关，放电中期的端电压回升来源于温度上升导致的电池内部各材料活性的不断增强。
关键词：高倍率 磷酸铁锂电池 机理模型 液相扩散 端电压回升
以磷酸铁锂为正极材料的锂离子电池以其优异的电化学稳定性和长寿命等优点，广泛应用于国防、航天、乘用车等领域各类对安全性、稳定性要求较高的场合[1-4]。近年来针对电磁发射等特殊应用工况设计的高倍率磷酸铁锂电池，其额定放电倍率可达数十倍C[5]，相比传统5C以下的磷酸铁锂电池有很大的倍率性能差异。目前对于这类电池的模型及放电特性的研究较少，不利于该类电池的优化设计、应用和成组管理。
针对锂离子电池的建模方法主要分为等效电路模型、数据驱动模型和电化学机理模型三类[6]。其中等效电路模型[7]利用电路元件的串并联来模拟电池的外特性，具有模型简单、计算量小的优点，广泛应用于各类电池管理系统中；数据驱动模型[8]利用机器学习方法构建各外部量之间的映射函数，灵活性好，可方便拟合电池的外特性曲线；区别于这两类侧重于电池外部特性的模型，电化学机理模型通过一系列偏微分方程描述电池充放电过程中的电化学行为，可精确表征电池的内部微观量和外部宏观量，是进行电池机理研究的必要途径，其简化模型也是未来电池应用研究的重要手段。目前，已有学者利用等效电路模型[9]和数据驱动模型[10-12]对高倍率磷酸铁锂电池进行了建模，但仍缺少从机理角度出发的建模研究和特性分析。
由J. Newman、M. Doyle等[13-14]提出的锂电池准二维（Pseudo-two-Dimensions, P2D）电化学模型作为锂离子电池机理仿真的经典模型，具有很高的计算精度，但其涉及大量相互耦合的偏微分方程和材料参数，模型求解和参数辨识均具有相当大的难度，难以在电池实时管理和数字孪生等领域推广应用。S. Santhanagopalan等[15]通过“单粒子”简化，使P2D模型可在小于1C的低倍率下快速计算，但简化模型无法匹配电池高倍率的放电特性。进一步，一些学者[16-17]通过将界面反应净电流密度简化为均匀分布，成功拟合5C以下锂离子电池的放电曲线，但还缺乏更高倍率下的简化机理建模。
本文针对高倍率磷酸铁锂电池的简化机理建模需求，建立了电化学-热耦合简化机理模型，通过参数辨识实现了模型在10～40C高倍率、宽范围下的实际放电曲线拟合，并基于辨识后的模型分析了电池端电压在40C高倍率放电初期秒级大幅度下降和中期回升的内部机理。
标准的P2D模型基于多孔电极理论，所建立的锂离子电池内部结构如图1所示，模型的具体内容见附录，相关的参数及符号含义见表1。P2D模型将电池正负极各处均视为固相球形颗粒电极材料和液相电解液的叠加，多孔隔膜区域充满电解液，且只允许离子通过。正负极区域中，沿负极指向正极的x方向上布满固相球形颗粒，由固相扩散方程来描述各颗粒内部的固相Li+浓度cs,a/c(x,r,t)沿半径r方向的分布；电解液充满整个负极集流体到正极集流体之间的区域，由液相扩散方程来描述液相Li+浓度ce(x,t)沿x方向的分布；基于Li+固、液相浓度分布，通过固相电势方程和液相电势方程可求解固相电势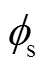(x,t)和液相电势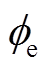(x,t)的分布，并由描述固液界面电化学反应的Butler-Volmer方程更新x轴上各处的净电流密度jLi(x,t)。其中，任意时刻的电池端电压U(t)和输出电流I(t)与电池内部微观量满足关系
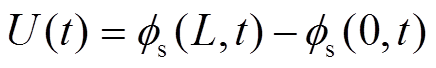（1）
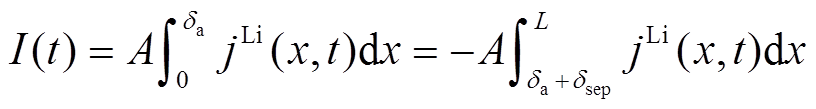（2）
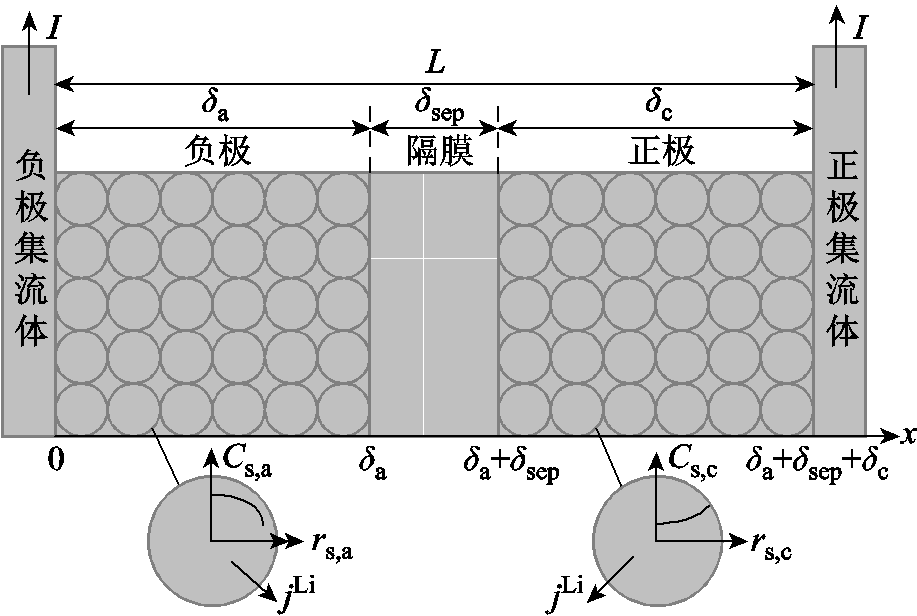
图1 锂离子电池P2D模型结构示意图
Fig.1 Schematic diagram of Li-ion battery P2D model
表1 锂离子电池电化学模型参数及符号含义
Tab.1 Li-ion battery electrochemical model parameters and symbolic meanings
参数含义单位 A电极面积m2 as,a/c负极/正极材料的比表面积m2/m3 BruggBruggman系数— cs,a/c负极/正极区域固相Li+浓度mol/m3 cs,a/c,0负极/正极区域固相Li+初始浓度mol/m3 cs,a/c,max负极/正极区域固相Li+最大浓度mol/m3 cs,a/c,surf负极/正极区域固相Li+表面浓度mol/m3 ce液相Li+浓度mol/m3 ce,0液相Li+初始浓度mol/m3
（续）
参数含义单位 Ds,a/c负极/正极材料Li+固相扩散系数m2/s De液相Li+扩散系数m2/s 负极/隔膜/正极区域Li+液相有效扩散系数m2/s F法拉第常数C/mol I电池输出电流A i0界面反应交换电流密度A/m2 jLi界面反应净电流密度A/m3 ka/c负极/正极界面反应常数m2.5/(mol0.5∙s) L正负极集流体间距m R气体常数J/(mol∙K) Rs,a/c负极/正极区域固相球形颗粒半径m RSEI,a/c负极/正极SEI膜内阻Ω∙m2 t+Li+迁移数— Ua/c负极/正极开路电动势V δa/sep/c负极/隔膜/正极区域厚度m ɛs,a/c负极/正极材料固相体积分数— ɛe,a/sep/c负极/隔膜/正极材料液相体积分数— 固相/液相电势V η界面反应过电势V σa/c负极/正极材料固相电导率S/m 负极/正极区域固相有效电导率S/m κ电解液电导率S/m 负极/隔膜/正极区域液相有效电导率S/m 负极/隔膜/正极区域液相有效扩散电导率S/m θa/c负极/正极嵌锂百分数—
注：下标s表示固相（solid phase），下标e表示液相（electrolyte phase），下标a表示负极（anode），下标sep表示隔膜（separator），下标c表示正极（cathode）。
为避免P2D全阶模型沿x轴各位置处的Li+固、液相扩散方程需耦合计算，简化电化学模型[16-17]将界面反应净电流密度jLi沿x轴的分布降阶为如图2所示的均匀分布，从而将Li+固相扩散与液相扩散解耦。根据式（2）可得到负极区域的净电流密度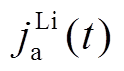
与正极区域的净电流密度
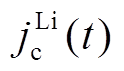满足
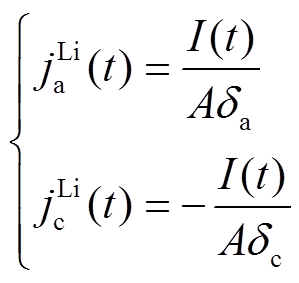（3）
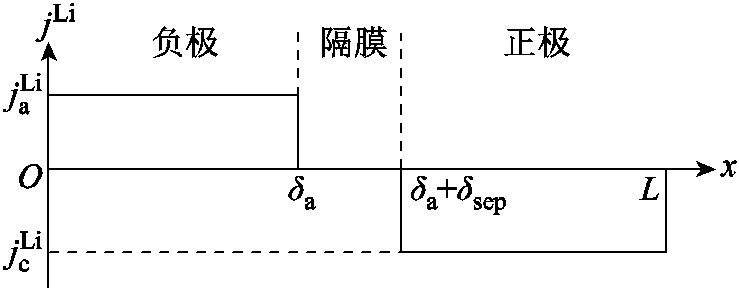
图2 简化的净电流密度分布
Fig.2 Simplified form of net current density
将式（3）代入式（A1）和式（A2），可得到排除x坐标影响的固相扩散方程为
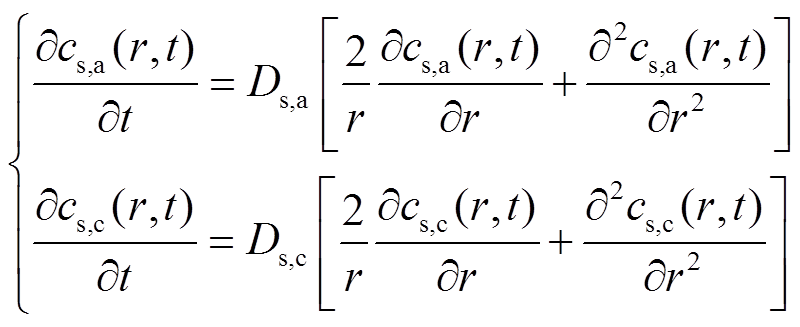（4）其边界条件为
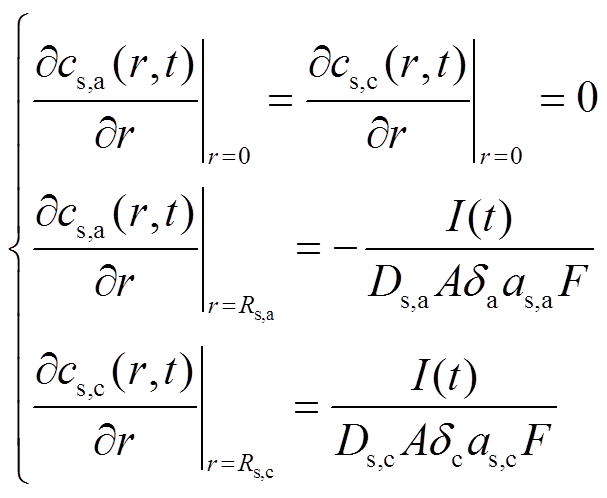（5）将式（3）代入式（A4）和式（A5），可得到解耦后的液相扩散方程为
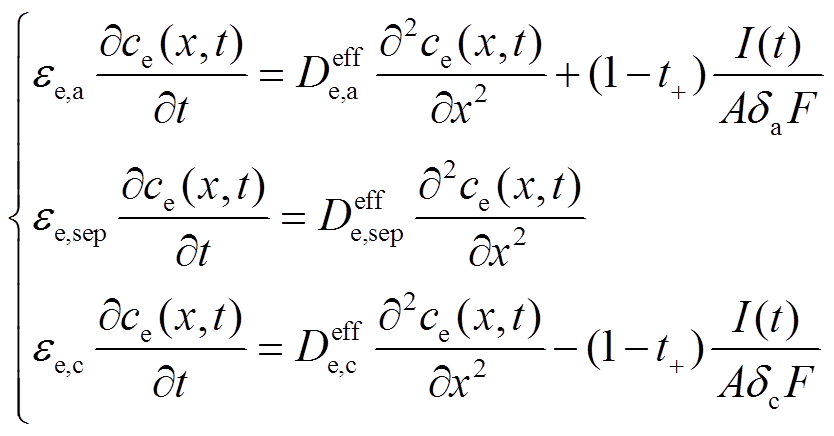（6）其边界条件为
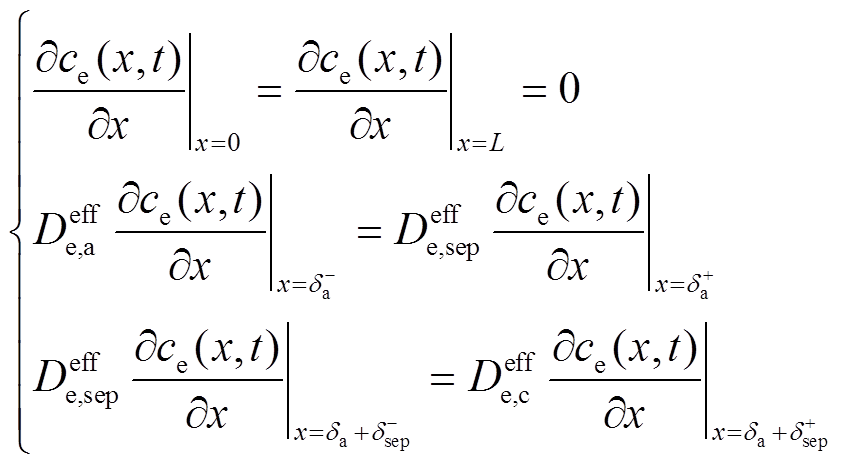（7）将式（3）代入式（A14），可得到x方向两端靠近集流体位置处的固相电势为
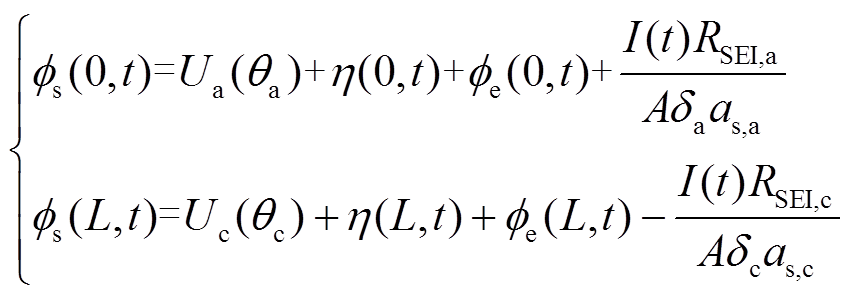（8）将式（3）代入式（A10）并沿x方向积分，可得到两端靠近集流体处的液相电势之差为[16]
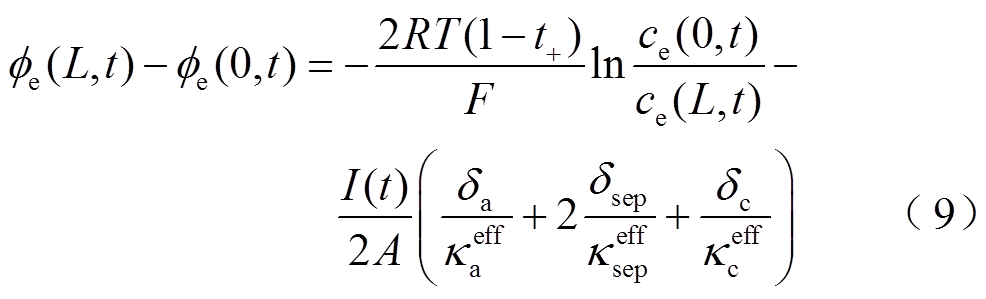
将式（3）代入式（A13），可得到两端靠近集流体处的界面反应过电势为
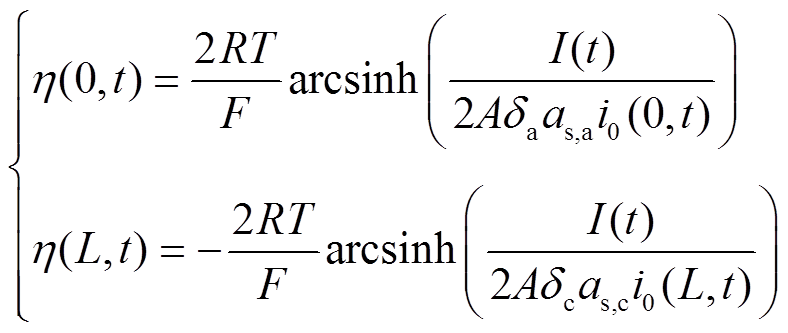（10）整理式（1）、式（8）～式（10），得到电池的端电压
从式（11）可看出，电池的端电压由五部分组成，分别对应开路电压Uocv、负极电化学极化过电势Up,a、正极电化学极化过电势Up,c、液相浓差极化过电势Ud以及欧姆电压降RohmI，因此定义如下参数。
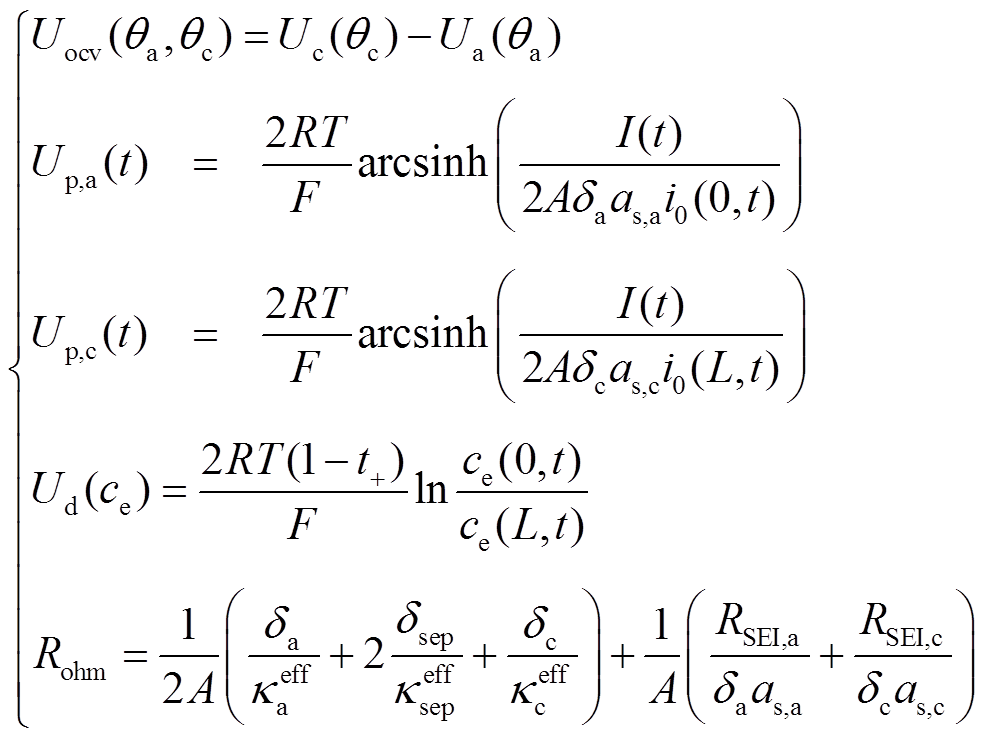（12）则式（11）可改写为
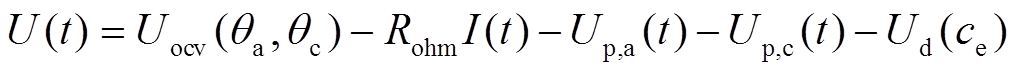（13）式（13）即为简化后的模型端电压表达式，计算端电压前需要先得到Li+固、液相分布，再计算电池开路电压与极化情况。
双状态热模型基于电芯平均温度T(t)和电池壳体温度To(t)两个集中参数状态来表征测量的壳体温度与内部电芯温度的差别[6]，模型结构如图3所示，相关的参数及符号含义见表2。
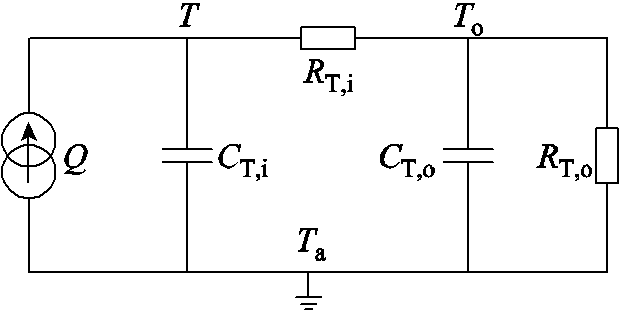
图3 双状态热模型结构示意图
Fig.3 Schematic diagram of two-state thermal model
表2 锂离子电池热模型参数及符号含义
Tab.2 Li-ion battery thermal model parameters and symbolic meanings
参数含义单位 CT,i电芯热容J/K CT,o壳体热容J/K Q电池产热功率W RT,i电芯与壳体间的传导热阻K/W RT,o壳体与外界环境间的对流热阻（K/W）K/W T电芯平均温度K To壳体温度)K Ta环境温度K
根据图3可列写传热方程[18]为
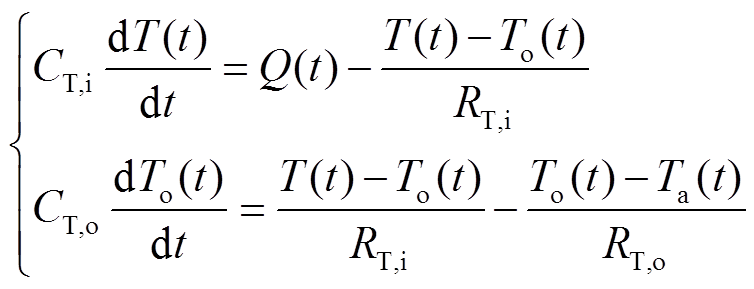（14）其中，电池放电过程中的产热功率Q(t)可根据电模型输出结果进行计算，即
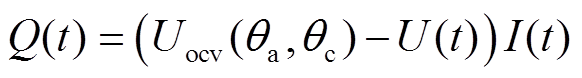（15）电芯温度对电化学参数Ds,a/c、De、ka/c、Rohm的影响可通过Arrhenius公式来修正[19]，即
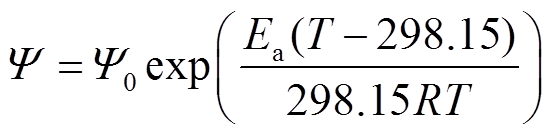（16）式中，Ψ0为各电化学参数Ψ在25℃下的取值；Ea为各电化学参数Ψ随温度变化的活化能。
基于以上方程，整理简化机理模型电化学-热耦合计算流程如图4所示。
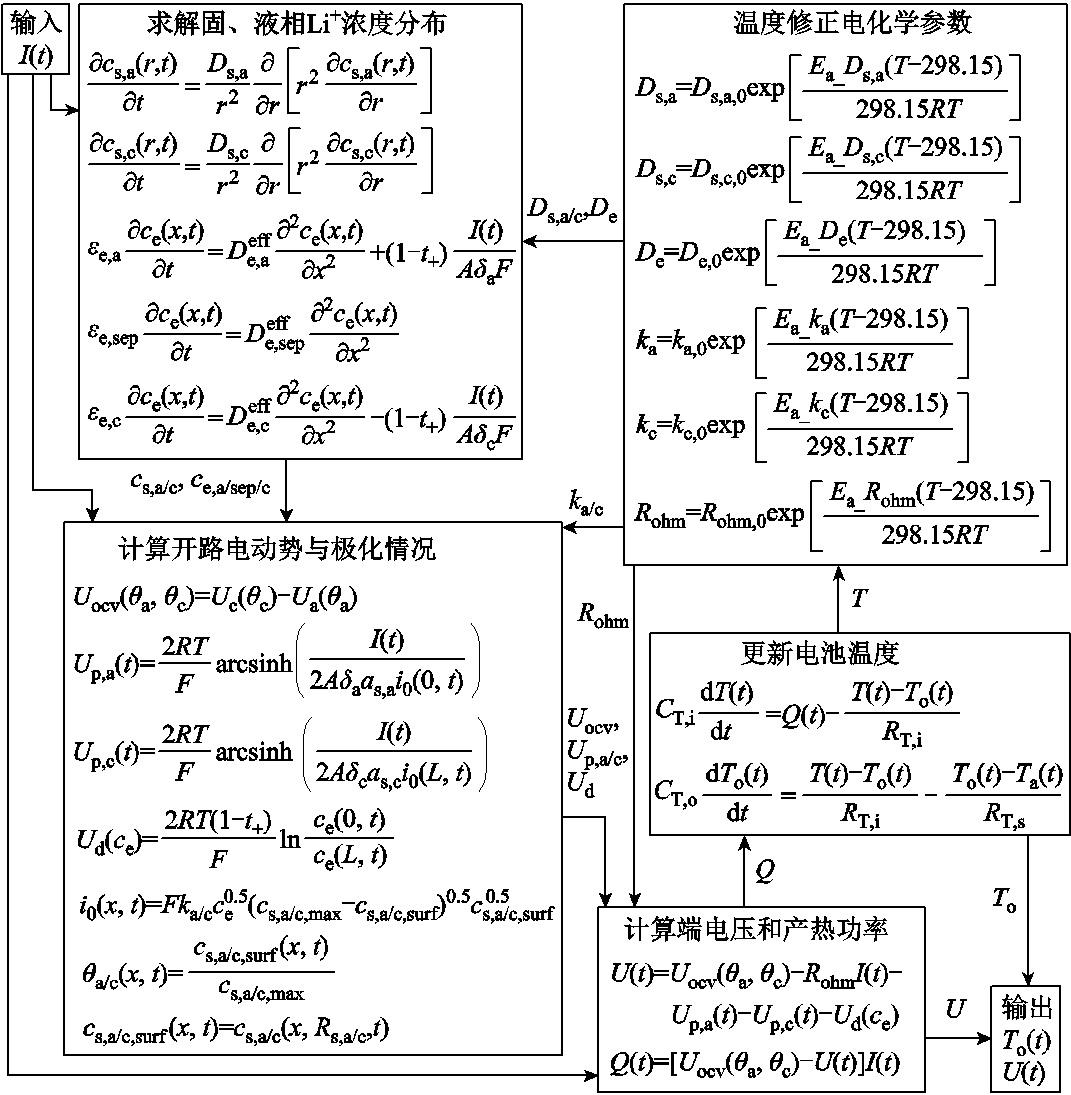
图4 简化机理模型计算流程
Fig.4 Calculation process of simplified mechanism model
简化机理模型的参数可分为常数、电池设计参数和材料性能参数三类，其中常数、电池设计参数和部分材料参数可作为已知参数，取值列于表3。
表3 简化机理模型已知参数取值
Tab.3 Known parameters of simplified mechanism model
参数单位负极隔膜正极来源 RJ/(mol∙K)8.314 38.314 38.314 3常数 FC/mol96 485.3396 485.3396 485.33常数 Brugg—1.51.51.5常数 Am21.361.361.36实测 δm55×10-618×10-673×10-6实测 Rsm4×10-6—80×10-9实测 ɛs—0.56—0.43实测 ɛe—0.280.400.36实测 ce,0mol/m31.35×1031.35×1031.35×103实测 cs,maxmol/m331 370—22 806[20] t+—0.3630.3630.363[21]
石墨负极和磷酸铁锂正极的开路电动势Ua/c与嵌锂百分数θa/c的关系可表示为[20]
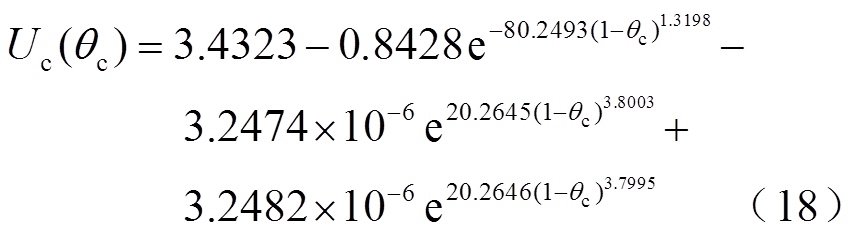
式（4）、式（6）所对应的Li+固、液相扩散方程为偏微分方程，本文采用有限差分法（Finite Difference Method，FDM）对其进行离散化处理[22]。
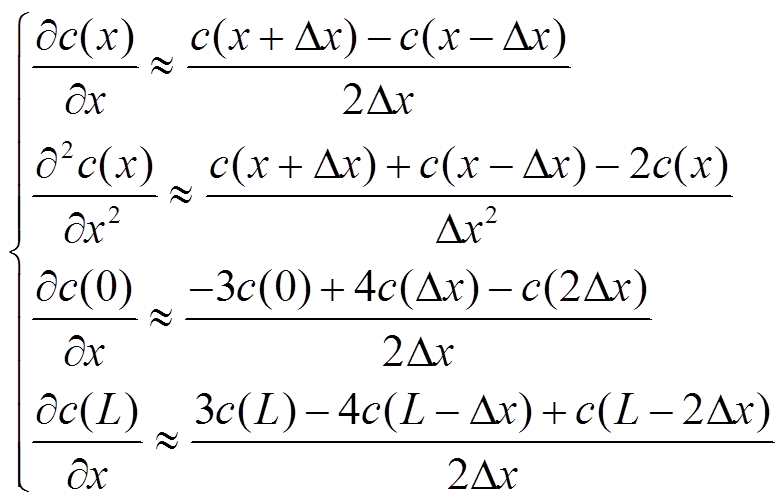（19）由于机理模型涉及较多难以直接获取材料的性能参数，可采用遗传算法[23]、粒子群算法[24]等智能搜索算法进行参数辨识，这要求模型的单次运算时间不能过长。图5展示了不同等距节点数下的负极固相与正极固相Li+浓度沿r方向的分布，可以看出当节点数较少时，随着计算节点的增加，固相Li+浓度分布有较为明显的变化。较多节点可更为精确地描述Li+浓度分布，但也会增加模型单次运算时间，因此，选取负极固相计算节点数Ns,a=20，正极固相计算节点数Ns,c=25。图6为不同节点数下的液相Li+浓度沿x方向的分布，其中负极、隔膜与正极区域的节点数相同，节点在各区域内为等距分布，可以看出计算节点数的变化对各节点处的液相Li+浓度影响较小，因此可在运行搜索算法时选取液相计算节点数Ne=3×3，在需要更为细致地观察液相Li+浓度分布时再增加节点数量。
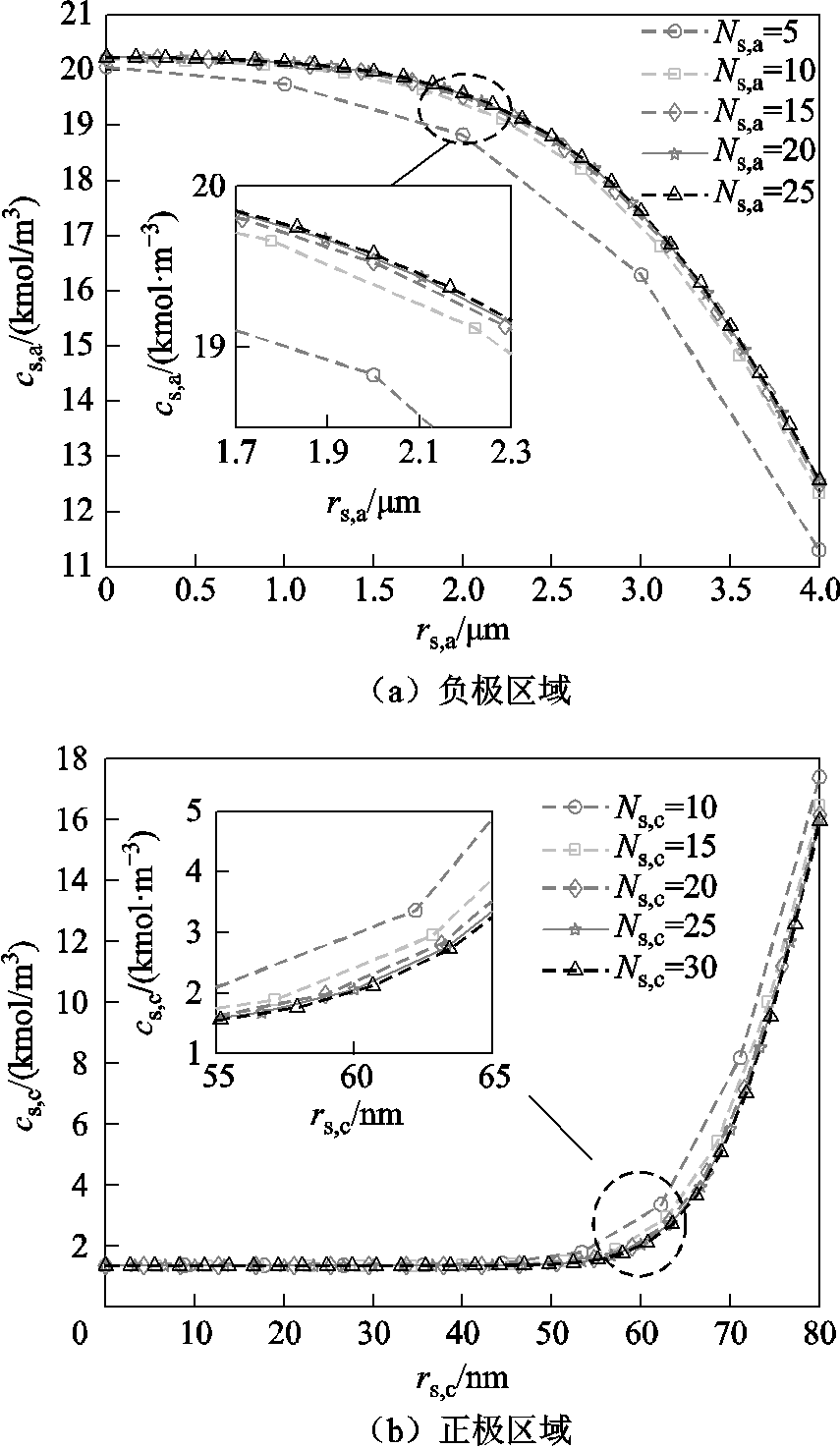
图5 不同节点数下沿r方向的固相Li+浓度分布
Fig.5 Solid phase Li+ concentration along r-direction with various number of nodes
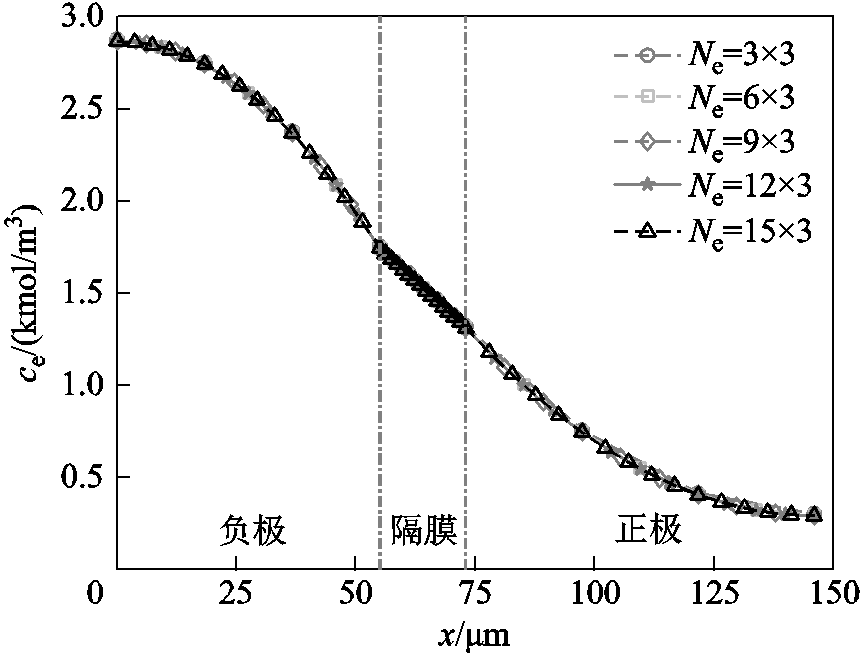
图6 不同节点数下沿x方向的液相Li+浓度分布
Fig.6 Electrolyte phase Li+ concentration along x-direction with various number of nodes
采用粒子群（Particle Swarm Optimization, PSO）算法对未知参数进行辨识[25-26]，所采用的适应度函数为
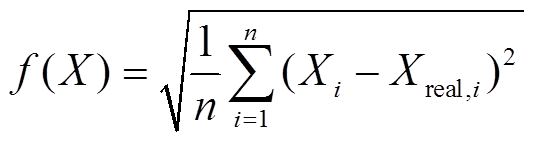（20）式中，Xi为模型仿真输出值；Xreal,i为实际测量值；PSO算法辨识以f(X)取值最小为目标。
由于简化机理模型的输出量中包含电池端电压U与壳体温度To两个可与实际测量值匹配的物理量，且考虑到辨识的参数需要适应不同放电倍率下的结果，因此采用如图7所示的辨识方法，即先以f(To,40C)最小作为目标，以实际测量的OCV-SOC曲线及40C放电倍率下的电池端电压U40C,real、输出电流I40C,real、壳体温度To,40C,real作为输入，对热模型的参数进行初步辨识；将辨识的热模型参数代入简化机理模型中，再以f(U40C)最小作为目标，以U40C,real、I40C,real作为输入，对所有未知参数进行辨识；最后以10C放电倍率下的f(U10C)最小作为目标，以U10C,real、I10C,real作为输入，对已辨识的参数进行低倍率的修正。
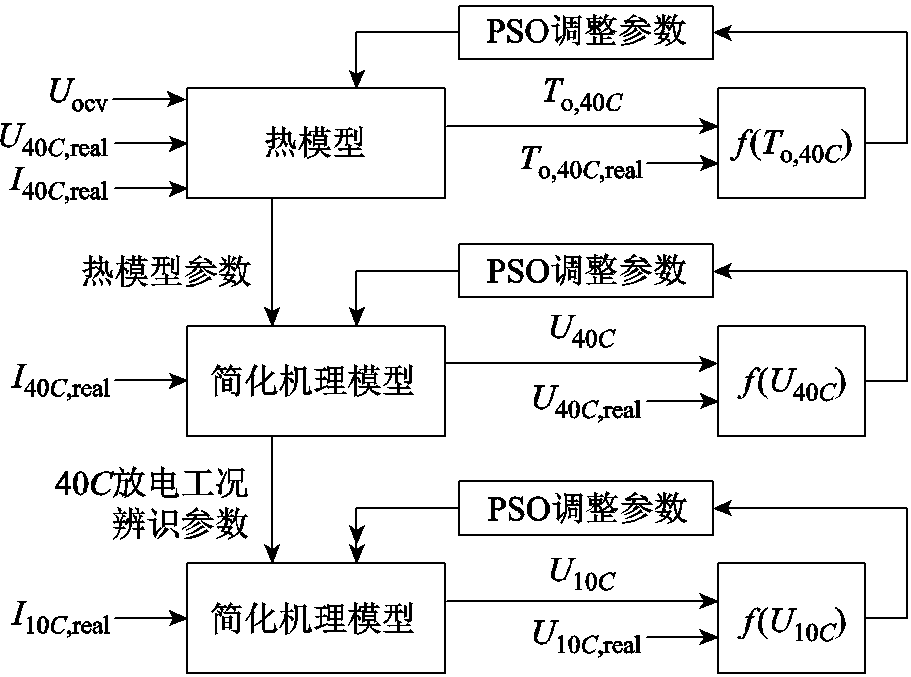
图7 PSO辨识参数流程
Fig.7 Process of PSO parameter identification
表4为采用PSO算法进行辨识的各参数的取值范围、辨识结果与敏感度，敏感度根据各参数在取值范围内变动时对适应度f(X)的影响来确定，具体方法为：保持其他参数恒定，在第k个参数的取值范围内等距取m个值，计算每个值对应的适应度fk,i(X)以及标准偏差Std(k)为
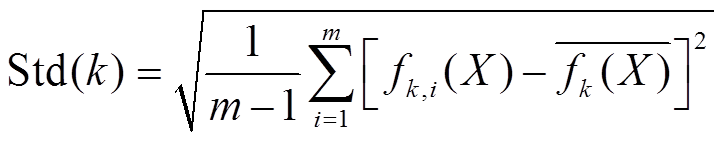（21）其中，热模型参数CT,i、CT,o、RT,i、RT,o根据壳体温度敏感度来评判，Std(k)＞1K定义为“高敏感”，在0.1～1K之间的定义为“敏感”；其他未知参数根据端电压敏感度来评判，Std(k)＞10mV定义为“高敏感”，在1～10mV之间的定义为“敏感”，小于1mV的参数定义为“低敏感”[27]。
表4 PSO辨识参数的取值范围、结果及敏感度
Tab.4 Parameter ranges, results and sensitivities of PSO identification
参数单位取值范围辨识结果敏感度 CT,iJ/K[600,1 400]1 062*** CT,oJ/K[10, 300]54*** RT,iK/W[0.1, 1]0.408*** RT,oK/W[1, 60]56** cs,a,0mol/m3[18 000, 25 000]20 280*** cs,c,0mol/m3[100, 3 000]1 363*** Ds,a,0m2/s[10-15, 10-13]3.58×10-14*** Ds,c,0m2/s[10-19, 10-17]2.46×10-18*** De,0m2/s[10-10, 10-9]5.77×10-10*** ka,0m2.5/(mol0.5∙s)[10-10, 10-8]8.21×10-9* kc,0m2.5/(mol0.5∙s)[10-13, 10-11]8.07×10-13*** Rohm,0Ω[2×10-4, 4×10-4]2.52×10-4***
（续）
参数单位取值范围辨识结果敏感度 Ea_Ds,aJ/mol[3×104, 105]3.52×104*** Ea_Ds,cJ/mol[3×104, 105]9.96×104*** Ea_DeJ/mol[5×103, 4×104]2.14×104** Ea_kaJ/mol[5×103, 4×104]1.32×104* Ea_kcJ/mol[5×103, 4×104]1.23×104** Ea_RohmJ/mol[-4×104, -5×103]-2.31×104**
注：“***”代表“高敏感”，“**”代表“敏感”，“*”代表“低敏感”。
采用高倍率磷酸铁锂电池10～40C的实际放电曲线验证简化机理模型的有效性，所使用的锂电池测试系统的电流控制精度为±0.1%，电压检测误差小于1mV，采样频率100Hz；温度检测误差小于0.1℃，采样频率1Hz，实验时的环境温度为23.1℃。电池从满电开始放电，直至端电压降为2.5V后停止，图8为10～40C放电的仿真与实测曲线。
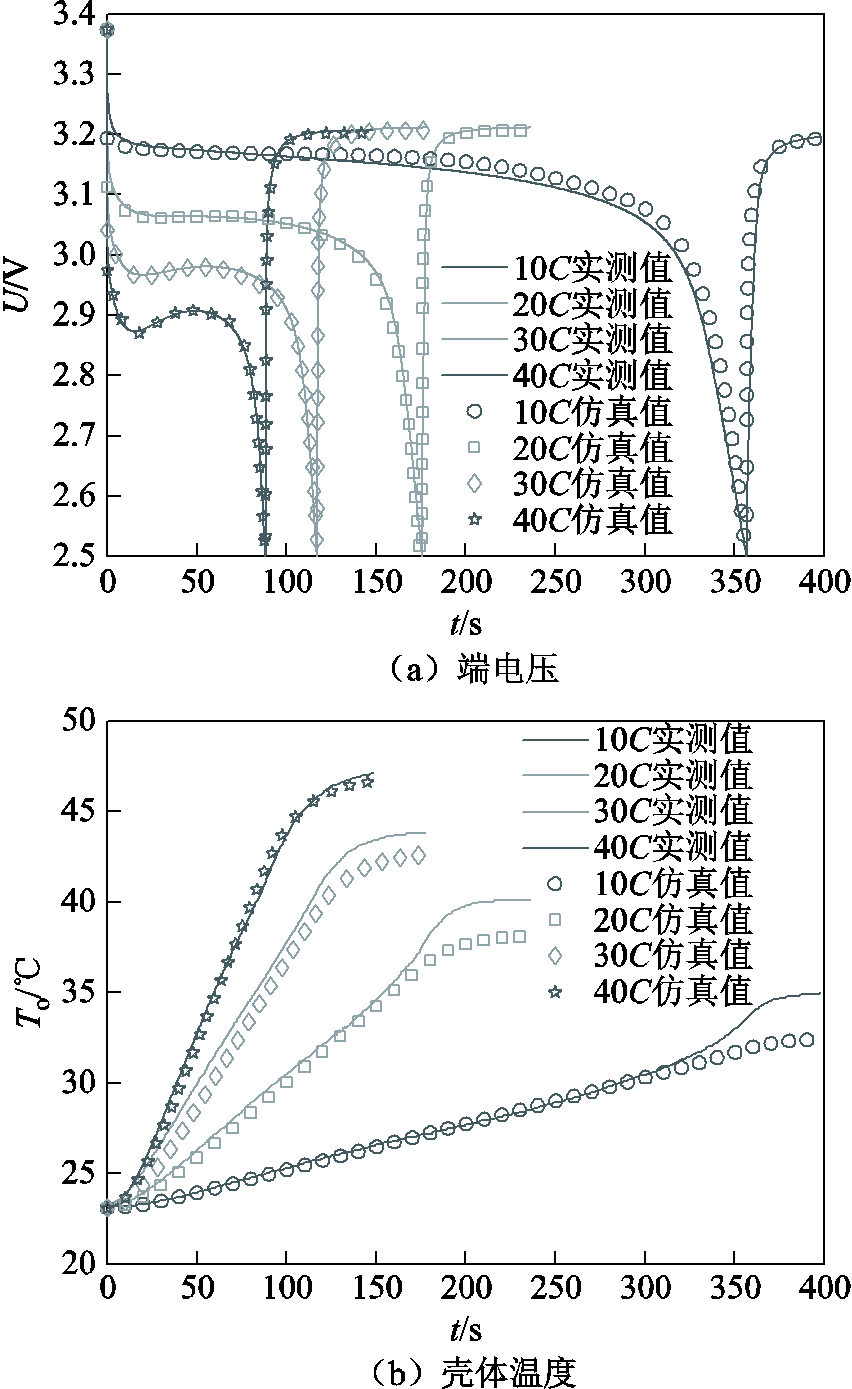
图8 仿真与实测曲线
Fig.8 Simulation and measured curves
从图8中可看出不同放电倍率下的模型仿真结果与实测结果基本吻合。由于模型参数在辨识训练时主要依靠40C高倍率的放电数据，因此高倍率下的拟合效果优于低倍率下，各倍率下的模型平均误差情况见表5。
表5 不同放电倍率下的模型平均误差
Tab.5 Model average errors at various discharge rates
参数端电压/mV壳体温度/℃ 10C17.50.39 20C6.90.80 30C5.41.09 40C3.80.35
尽管简化机理模型无法达到全阶模型描述电化学现象的细致程度，但由于其所用公式基于电化学原理推导，且模型参数经过了实际数据的辨识，因此仍具有一定的电化学分析意义，可基于简化机理模型进行高倍率磷酸铁锂电池放电特性的研究。
观察图8a可发现，排除放电末期因电量较低而导致的端电压快速下降，高倍率磷酸铁锂电池的端电压在10C、20C低倍率放电时整体较为平缓，但在30C、40C高倍率放电时呈现出明显的先下降后回升的现象。为分析此现象所对应的电池内部机理，通过式（12）、式（13）分解出10C与40C放电时除开路电压外可能对电池端电压造成影响的各极化项成分，如图9所示，可看出40C放电时的各极化项相比10C放电时均有明显的上升，且极化过电压主要由欧姆电压降RohmI、正极电化学极化过电势Up,c以及液相浓差极化过电势Ud构成，负极电化学极化对端电压的影响似乎很微弱，从表4在25℃下的负极界面反应常数ka,0及其活化能Ea_ka两个参数较低的端电压敏感度中也可印证这一猜测，但不排除这是由于ka,0取值范围的局限性造成的。
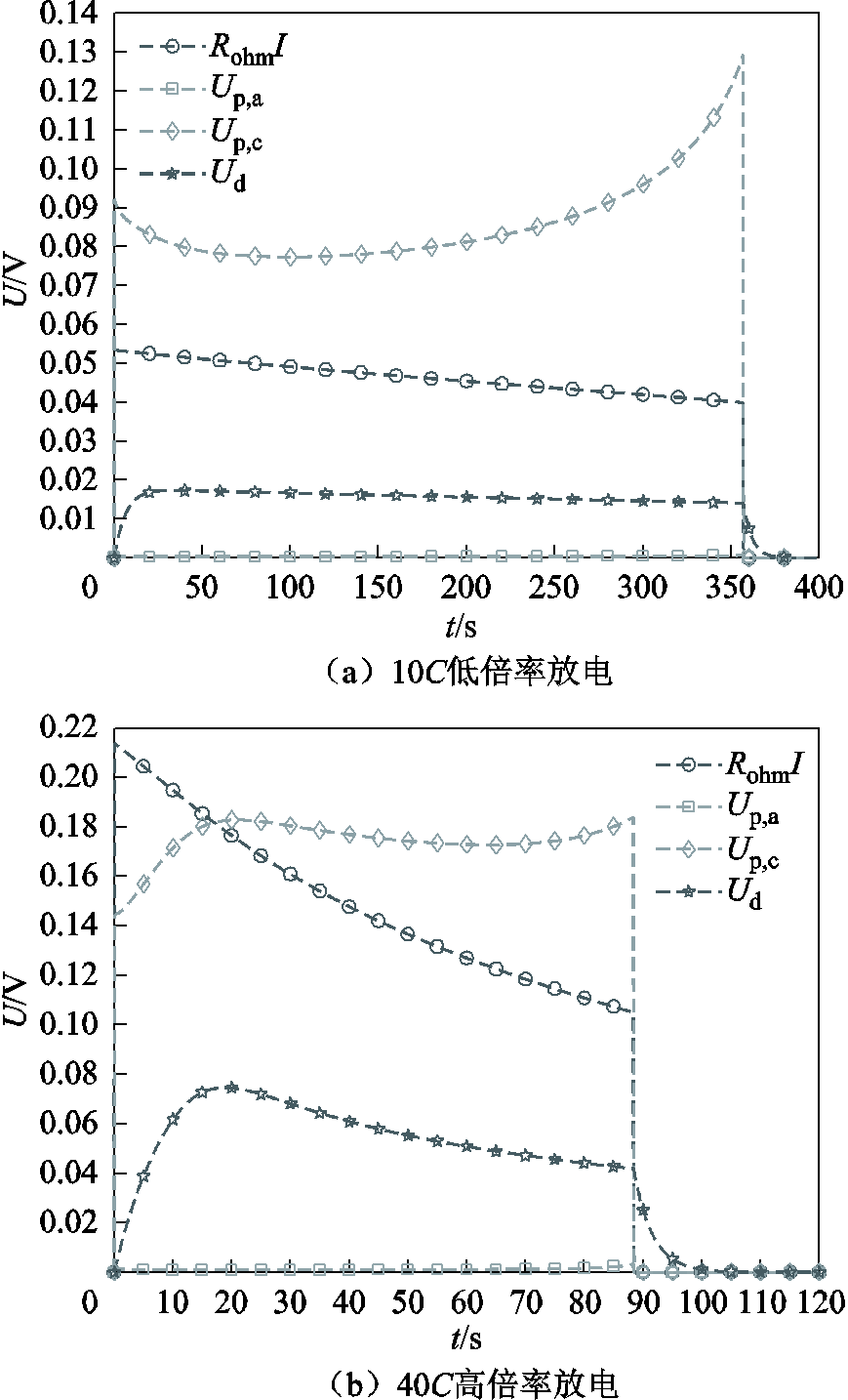
图9 不同倍率放电时的电池极化情况
Fig.9 Battery polarization at various discharge rates
从图9b中可看出，40C放电时电池端电压初期的下降主要与Ud和Up,c的增加有关，其中Ud的增加来自高倍率放电下不均匀的液相Li+浓度分布，放电初期Li+的液相电迁移与浓差扩散无法及时补充正极反应带来的Li+损失与消耗负极反应带来的Li+生成，直至20s左右形成动态平衡，如图10所示，从而造成显著的液相浓差极化过电势Ud。正极电化学极化过电势Up,c在10C与40C放电初期呈现出不同的变化趋势，这与正极处的固/液相Li+浓度有关。低倍率放电时，由于液相Li+浓度的变化较小，因此Up,c主要受正极固相Li+浓度的影响，随着固相Li+浓度的增长，正极固液界面反应逐渐活跃，交换电流密度i0随之增长，带来放电初期Up,c的逐渐下降；高倍率放电时，正极液相Li+浓度明显降低，引起i0的降低，从而导致Up,c的不断上升，直至液相Li+的消耗与补充达到平衡。
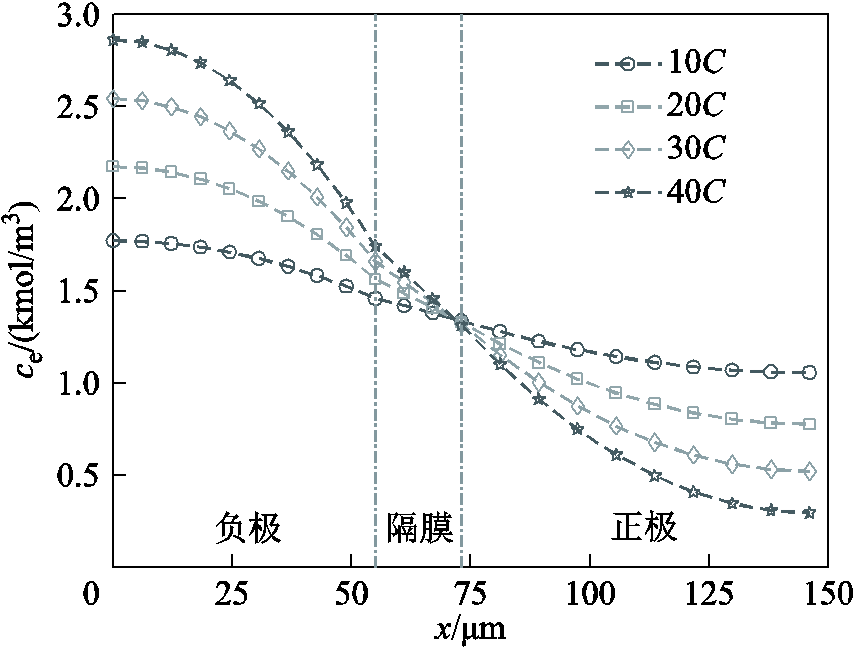
图10 不同倍率下放电20s时的液相Li+浓度分布
Fig.10 Electrolyte phase Li+ concentration at various C-rates discharge for 20s
对于高倍率放电中期的端电压回升，从图9b中可看出主要与RohmI和Ud的下降有关。高倍率放电的中后期，电池温升较大，造成各热耦合电化学参数Ds,a/c、De、ka/c、Rohm有较为明显的变化，如图11所示，也即Li+的固/液相分布趋向均匀、正/负极界面反应更加容易进行、电流路径上各处的材料导电性增强，从而造成影响端电压的各极化项均有不同程度的减弱，其中，Up,c虽然在放电中期有下降趋势，但受正极固相Li+浓度趋于饱和的影响，下降幅度较小，且在末期出现小幅回升。
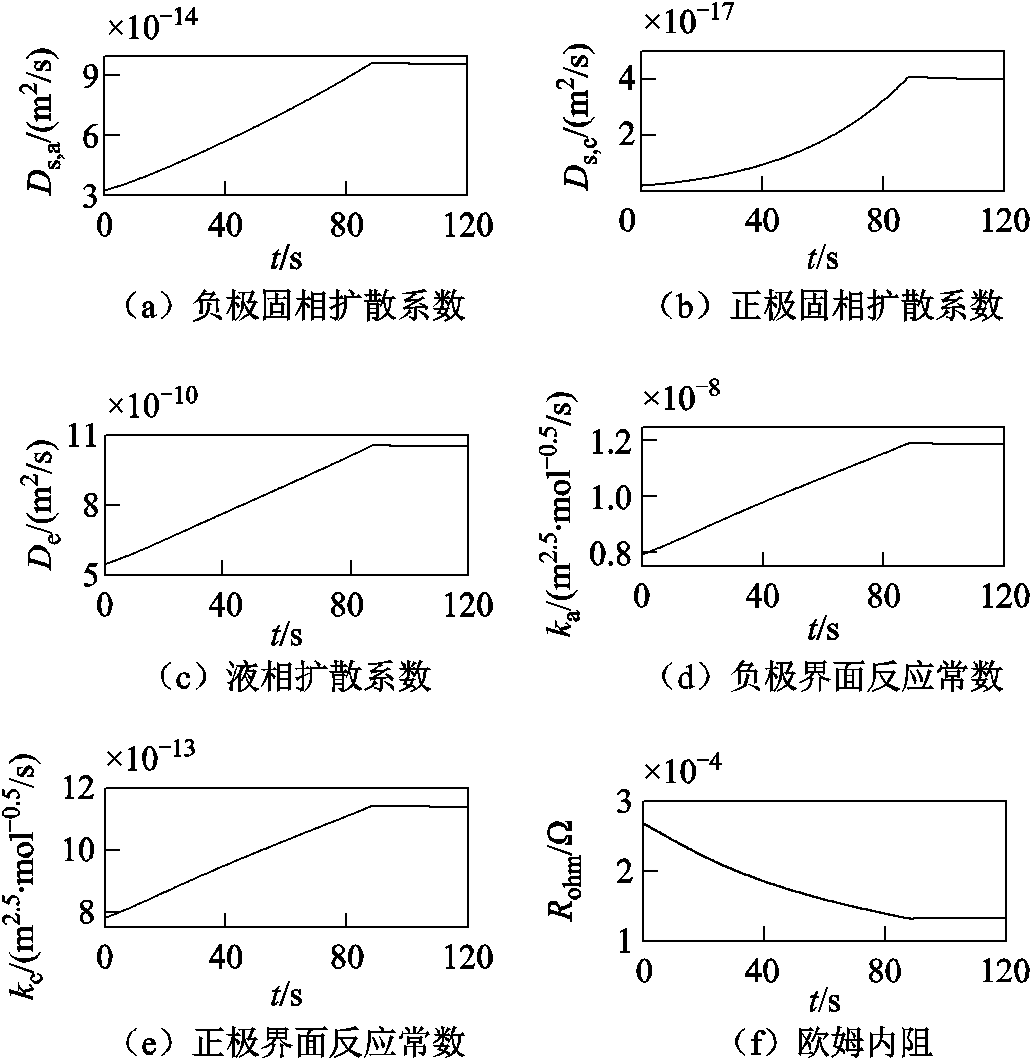
图11 40C放电时各热耦合电化学参数的变化情况
Fig.11 Thermal coupled electrochemical parameters at 40C-rate discharge
本文对高倍率磷酸铁锂电池进行了简化机理建模，利用实验曲线验证了模型的有效性，并基于模型简要分析了电池高倍率下的放电特性，得出以下两点结论：
1）高倍率放电初期电池端电压秒级的大幅度下降主要与液相Li+浓度分布的不均匀性有关，电池优化设计时应对该方面加强关注，机理模型简化时不可忽略Li+的液相电迁移与浓差扩散作用。
2）高倍率放电中期的电池端电压回升与温度的快速上升有关，针对高倍率电池的放电过程建模时需要考虑温度对电池放电特性的影响。
下一步将从机理模型的角度进一步研究高倍率磷酸铁锂电池的充放电特性和循环寿命特性，并探索更适合该类电池及实际应用工况的机理模型简化方法。
标准的P2D模型由以下五部分组成。
1）固相扩散方程
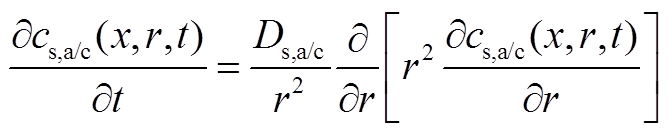（A1）边界条件满足
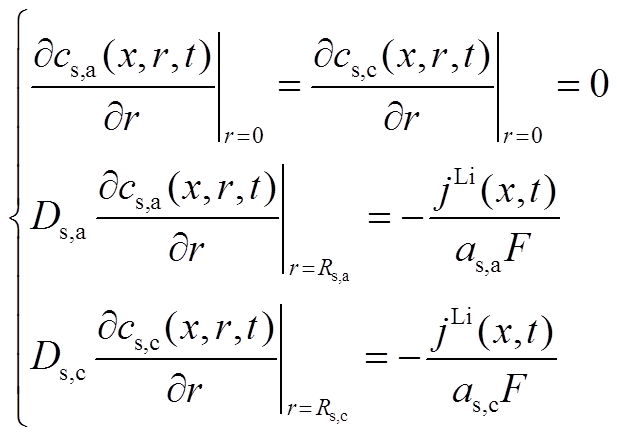（A2）其中
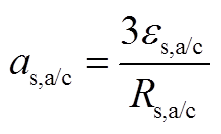（A3）2）液相扩散方程
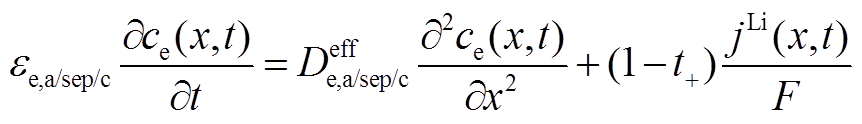（A4）边界条件满足
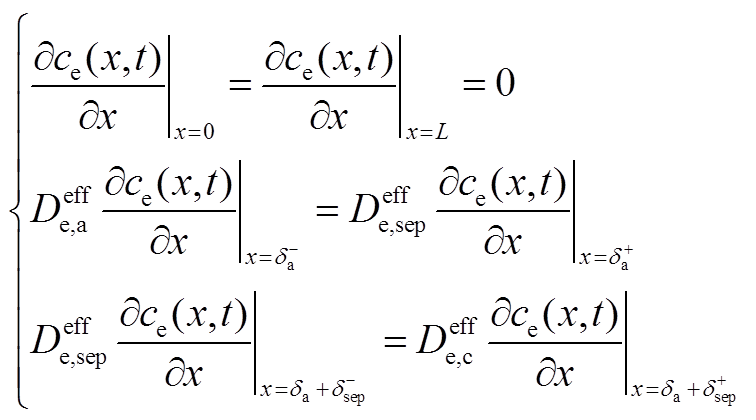（A5）其中
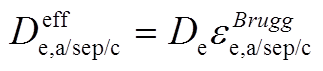（A6）3）固相电势方程
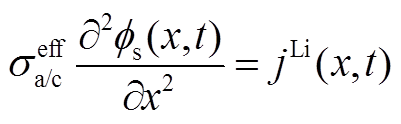（A7）边界条件满足
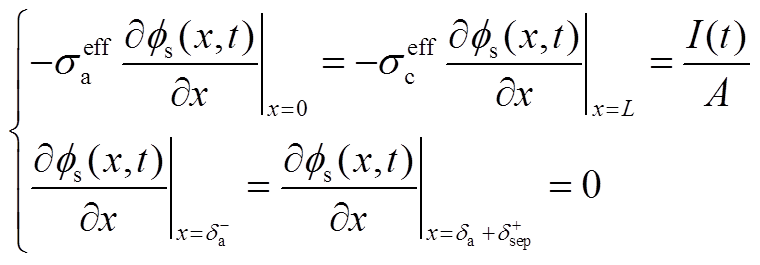（A8）其中
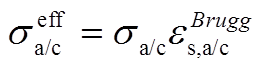（A9）4）液相电势方程
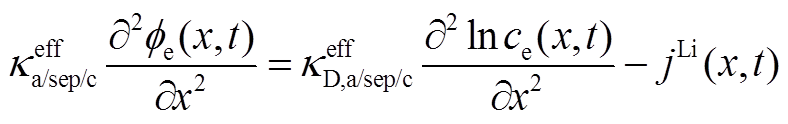（A10）边界条件满足
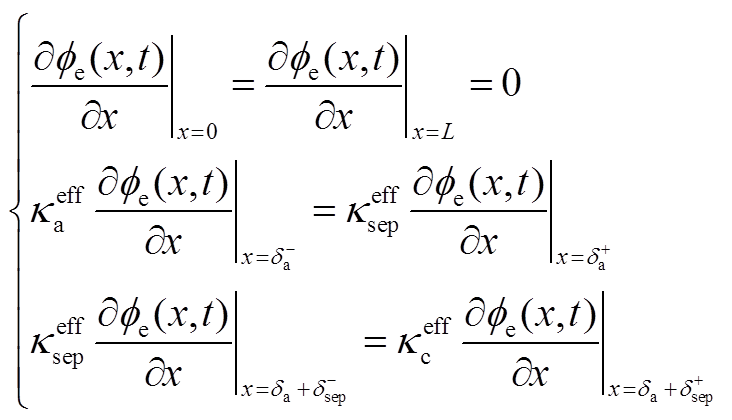（A11）其中
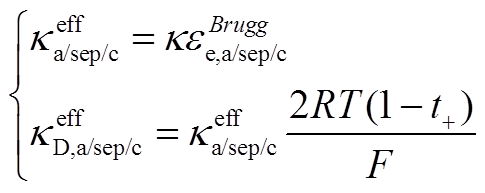（A12）5）Butler-Volmer方程
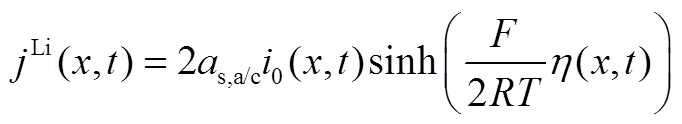（A13）其中
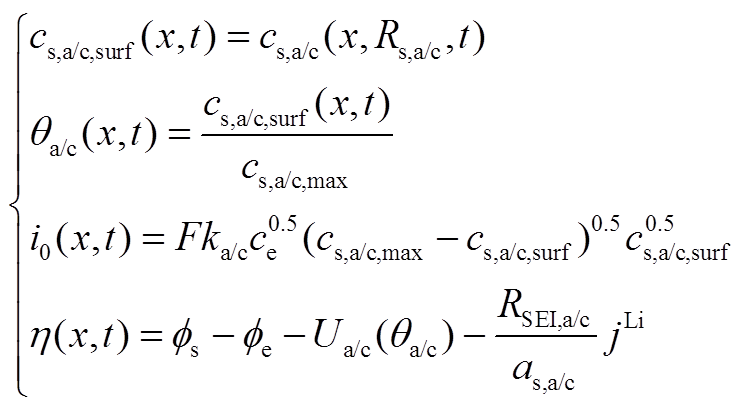（A14）参考文献
[1] 龙鑫林, 鲁军勇, 魏静波, 等. 锂电池储能在电磁发射中的应用[J]. 国防科技大学学报, 2019, 41(4): 66-72.
Long Xinlin, Lu Junyong, Wei Jingbo, et al. Application on lithium batteries for electromagnetic launch[J]. Journal of National University of Defense Technology, 2019, 41(4): 66-72.
[2] 王榘, 熊瑞, 穆浩. 温度和老化意识融合驱动的电动车辆锂离子动力电池电量和容量协同估计[J]. 电工技术学报, 2020, 35(23): 4980-4987.
Wang Ju, Xiong Rui, Mu Hao. Co-estimation of lithium-ion battery state-of-charge and capacity through the temperature and aging awareness model for electric vehicles[J]. Transactions of China Electrotechnical Society, 2020, 35(23): 4980-4987.
[3] 焦东升, 王海云, 朱洁, 等. 基于离散Fréchet距离的电动汽车电池健康状态诊断方法[J]. 电力系统保护与控制, 2016, 44(12): 68-74.
Jiao Dongsheng, Wang Haiyun, Zhu Jie, et al. EV battery SOH diagnosis method based on discrete Fréchet distance[J]. Power System Protection and Control, 2016, 44(12): 68-74.
[4] 连湛伟, 石欣, 克潇, 等. 电动汽车充换电站动力电池全寿命周期在线检测管理系统[J]. 电力系统保护与控制, 2014, 42(12): 137-142.
Lian Zhanwei, Shi Xin, Ke Xiao, et al. The whole life cycle on-line detection and management system of power battery in the electric vehicle charging and exchanging station[J]. Power System Protection and Control, 2014, 42(12): 137-142.
[5] Long Xinlin, Lu Junyong, Wu Yiting, et al. Research on high rate lithium-ion batteries for electromagnetic launcher[C]//2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, IEEE, 2019: 1671-1675.
[6] 胡晓松, 唐小林. 电动车辆锂离子动力电池建模方法综述[J]. 机械工程学报, 2017, 53(16): 20-31.
Hu Xiaosong, Tang Xiaolin. Review of modeling techniques for lithium-ion traction batteries in electric vehicles[J]. Journal of Mechanical Engineering, 2017, 53(16): 20-31.
[7] 宫明辉, 乌江, 焦朝勇. 基于模糊自适应扩展卡尔曼滤波器的锂电池SOC估算方法[J]. 电工技术学报, 2020, 35(18): 3972-3978.
Gong Minghui, Wu Jiang, Jiao Chaoyong. SOC estimation method of lithium battery based on fuzzy adaptive extended Kalman filter[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3972- 3978.
[8] 刘晓程, 王建明, 王武. 基于数据驱动的锂电池随机动态系统建模[J]. 电气技术, 2015, 16(5): 17-21. Liu Xiaocheng, Wang Jianming, Wang Wu. Modeling of lithium-ion battery stochastic dynamic system based on data-driven[J]. Electrical Engineering, 2015, 16(5): 17-21.
[9] 张振宇, 汪光森, 聂世雄, 等. 脉冲大倍率放电条件下磷酸铁锂电池荷电状态估计[J]. 电工技术学报, 2019, 34(8): 1769-1779.
Zhang Zhenyu, Wang Guangsen, Nie Shixiong, et al. State of charge estimation of LiFePO4 battery under the condition of high rate pulsed discharge[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1769-1779.
[10] 李超然, 肖飞, 樊亚翔, 等. 基于卷积神经网络的锂离子电池SOH估算[J]. 电工技术学报, 2020, 35(19): 4106-4119.
Li Chaoran, Xiao Fei, Fan Yaxiang, et al. An approach to lithium-ion battery SOH estimation based on convolutional neural network[J]. Transactions of China Electrotechnical Society, 2020, 35(19): 4106-4119.
[11] 李超然, 肖飞, 樊亚翔, 等. 基于门控循环单元神经网络和Huber-M估计鲁棒卡尔曼滤波融合方法的锂离子电池荷电状态估算方法[J]. 电工技术学报, 2020, 35(9): 2051-2062.
Li Chaoran, Xiao Fei, Fan Yaxiang, et al. A hybrid approach to lithium-ion battery SOC estimation based on recurrent neural network with gated recurrent unit and Huber-M robust Kalman filter[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 2051- 2062.
[12] 李超然, 肖飞, 樊亚翔, 等. 一种基于LSTM-RNN的脉冲大倍率工况下锂离子电池仿真建模方法[J]. 中国电机工程学报, 2020, 40(9): 3031-3042.
Li Chaoran, Xiao Fei, Fan Yaxiang, et al. An approach to lithium-ion battery simulation modeling under pulsed high rate condition based on LSTM-RNN[J]. Proceedings of the CSEE, 2020, 40(9): 3031-3042.
[13] Doyle Marc, Fuller Thomas F, Newman John. Modeling of galvanostatic charge and discharge of the lithium/polymer/insertion cell[J]. Journal of the Electrochemical Society, 1993, 140(6): 1526-1533.
[14] Doyle Marc, Newman John. Comparison of modeling predictions with experimental data from plastic lithium ion cells[J]. Journal of the Electrochemical Society, 1996, 143(6): 1890-1903.
[15] Santhanagopalan Shriram, White Ralph E. Online estimation of the state of charge of a lithium ion cell[J]. Journal of Power Sources, 2006, 161(2): 1346-1355.
[16] Prada E, Domenico D Di, Creff Y, et al. Simplified electrochemical and thermal model of LiFePO4 -graphite Li-ion batteries for fast charge applications[J]. Journal of the Electrochemical Society, 2012, 159(9): A1508-A1519.
[17] 庞辉. 基于电化学模型的锂离子电池多尺度建模及其简化方法[J]. 物理学报, 2017, 66(23): 312-322.
Pang Hui. Multi-scale modeling and its simplification method of Li-ion battery based on electrochemical model[J]. Acta Physica Sinica, 2017, 66(23): 312-322.
[18] Lin Xinfan, Perez Hector E, Mohan Shankar, et al. A lumped-parameter electro-thermal model for cylindrical batteries[J]. Journal of Power Sources, 2014, 257(1): 1-11.
[19] Mao Jing, Tiedemann William, Newman John. Simulation of temperature rise in Li-ion cells at very high currents[J]. Journal of Power Sources, 2014, 271(20): 444-454.
[20] Safari M, Delacourt C. Modeling of a commercial graphite/LiFePO4 cell[J]. Journal of the Electrochemical Society, 2011, 158(5): A562-A571.
[21] Valøen, Lars Ole, Reimers Jan N. Transport properties of LiPF6-based Li-ion battery electrolytes[J]. Journal of the Electrochemical Society, 2005, 152(5): A882-A891.
[22] Diwakar Vinten D. Towards efficient models for lithium ion batteries[D]. Cookeville, USA: Tennessee Technological University, 2009.
[23] Forman Joel C, Moura Scott J, Stein Jeffrey L, et al. Genetic identification and fisher identifiability analysis of the Doyle-Fuller-Newman model from experimental cycling of a LiFePO4 cell[J]. Journal of Power Sources, 2012, 210(15): 263-275.
[24] Rahman Md Ashiqur, Anwar Sohel, Izadian Afshin. Electrochemical model parameter identification of a lithium-ion battery using particle swarm optimization method[J]. Journal of Power Sources, 2016, 307(1): 86-97.
[25] Wu Jiangling, Sun Xiaodong, Zhu Jianguo. Accurate torque modeling with PSO-based recursive robust LSSVR for a segmented-rotor switched reluctance motor[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(2): 96-104.
[26] 徐正清, 肖艳炜, 李群山, 等. 基于灵敏度及粒子群算法的输电断面功率越限控制方法对比研究[J]. 电力系统保护与控制, 2020, 48(15): 177-186.
Xu Zhengqing, Xiao Yanwei, Li Qunshan, et al. Comparative study based on sensitivity and particle swarm optimization algorithm for power flow over-limit control method of transmission section[J]. Power System Protection and Control, 2020, 48(15): 177-186.
[27] Zhang Liqiang, Lü Chao, Hinds Gareth, et al. Parameter sensitivity analysis of cylindrical LiFePO4 battery performance using multi-physics modeling[J]. Journal of the Electrochemical Society, 2014, 161(5): A762-A776.
Simplified Mechanism Modeling and Discharge Characteristic Analysis of High C-Rate LiFePO4 Battery
Abstract Mechanism modeling of high C-rate LiFePO4 battery is very important to guide the design and application of battery. However, the full order mechanism model has high complexity, and the simplified form fits bad in high C-rate currently. To solve these problems, a simplified electrochemical thermal coupling mechanism model was established by combining the simplified pseudo-two-dimensions (P2D) electrochemical model with the two-state thermal model. Through parameter identification, the model can well fit the actual battery discharge curves in a wide range of 10～40C high rate. Based on the identified model, the internal evolution mechanism corresponding to the trend of external curves under high C-rate discharge was analyzed. The results show that: the seconds level sharp decrease of battery terminal voltage in the high C-rate discharge initial period is related to the heterogeneity of Li+ concentration distribution in the electrolyte phase, and the recovery of the terminal voltage in the intermediate period is due to the increasing activity of internal materials caused by the temperature rise.
keywords：High C-rate, LiFePO4 battery, mechanism model, electrolyte phase diffusion, terminal voltage recovery
DOI:10.19595/j.cnki.1000-6753.tces.201206
中图分类号：TM912
国家自然科学基金（51925704, 51877214, 51907203）、湖北省自然科学基金（2019CFB371, 2019CFB373, 2020CFB341）和中国博士后特别资助基金（2019T120972）资助项目。
收稿日期 2020-09-12
改稿日期 2021-04-20
严康为 男，1996年生，博士研究生，研究方向为电磁发射技术。E-mail：yan_kangwei@163.com
龙鑫林 男，1982年生，副研究员，硕士生导师，研究方向为电磁发射技术及蓄电池储能技术。E-mail：longxinlin1982@163.com（通信作者）
（编辑 郭丽军）