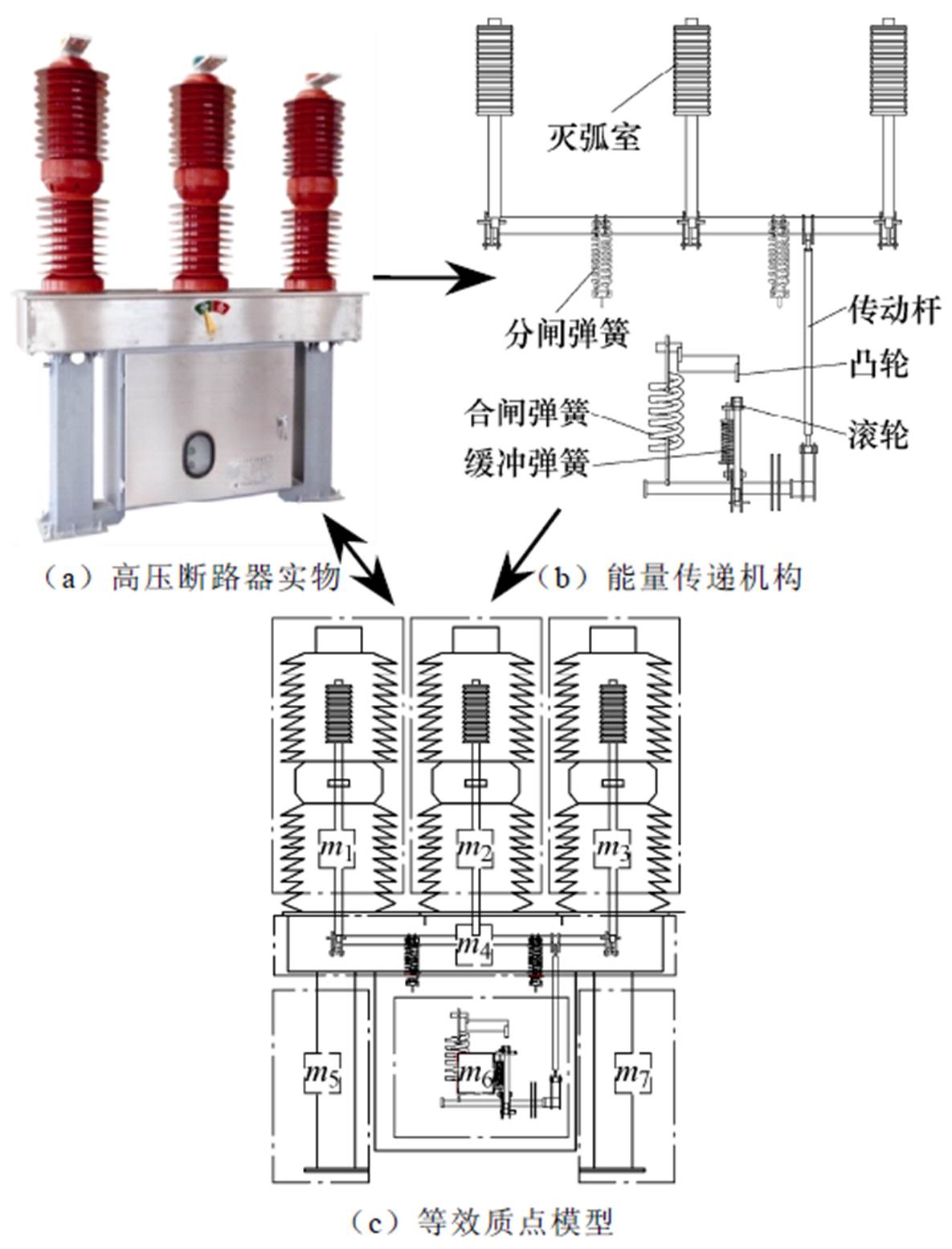
图1 高压断路器质点模型
Fig.1 High voltage circuit breaker mass point model
摘要 针对在运高压断路器时有发生弹簧疲劳故障且传统方法无法在线检测的问题,该文提出一种基于振动信号的高压断路器弹簧疲劳程度检测方法。首先,根据高压断路器的工作原理,对其运动过程能量传递机理进行分析,并将整体进行了质点简化;然后,对振动信号进行滤波处理,结合简化的质点模型,构建不同测点动能的函数关系式,换算得到各个质点的等效能量分布;最后,采用非线性最小二乘法构建出高压断路器能量传递函数,并推算出了弹簧储能值。实验结果表明,利用所提方法计算得到的弹簧储能值检测误差在2.2%以内,验证了所提方法的有效性和准确性,为高压断路器弹簧疲劳程度在线检测提供了一种新的思路。
关键词:高压断路器 弹簧疲劳 振动信号 非线性最小二乘法
高压断路器在电力系统中起着重要的保护与控制作用[1-2],其分合闸性能的稳定性对于选相合闸控制、故障情况下及时断开线路均具有重要意义[3-5]。国网和南网运行多年的高压断路器时常出现因弹簧疲劳导致的合闸不到位或分闸时间长燃弧爆炸的事故,且随投运年数的增长,弹簧疲劳故障发生率越高,及时检测出弹簧疲劳并采取相应的措施避免安全事故,对于提高供电可靠性以及电力系统的安全稳定运行具有重要意义[6-8],而如何有效检测出弹簧疲劳的问题成为摆在运维人员面前的难题,亟待解决。
针对高压断路器弹簧疲劳机理,部分学者对高压断路器发生弹簧疲劳后其动特性的变化开展相关研究,杨秋玉等利用机械系统动力学自动分析(Automatic Dynamic Analysis of Mechanical Systems, ADAMS)软件对高压断路器弹簧机构进行仿真研究,建立了相应的动力学模型,对分合闸弹簧故障进行了仿真分析,揭示了弹簧疲劳故障下其特性参数的动态变化规律[9]。文献[10]分析了弹簧储能和负载之间的关系,得出完成合闸动作最小储能值,分析得到长期处于压缩状态下合闸弹簧的静态应力变化,建立了合闸弹簧的储能寿命和疲劳寿命模型,实现了高压断路器合闸弹簧寿命预测。文献[11]对合闸弹簧疲劳后高压断路器动触头的行程曲线变化进行了研究,提出了将振动信号中包含的振动事件时间节点用来评估弹簧疲劳特性,取得了一定的成效。但上述研究更多的是从理论层面对弹簧疲劳后高压断路器性能展开分析,可对高压断路器的设计、制造和组装等环节提供指导,在推广到实际在运高压断路器弹簧疲劳故障检测方面还有一定的应用壁垒。
对于高压断路器的故障诊断,国内外学者开展了大量相关研究[12-18]。其中,Zhang Guogang等开展了弹簧应力松弛研究,建立了预测弹簧疲劳的线性回归方程,分析总结出高压断路器在不同疲劳情况下其特性参数的变化规律,尝试将多种模式识别算法应用在弹簧操动机构的力学状态识别和预测中,取得了一定的效果[19]。刘宝稳团队提出了基于S变换D-SVM AlexNet模型的气体绝缘组合电器(Gas Insulated Switchgear, GIS)机械故障诊断方法,通过搭建合闸驱动弹簧疲劳松动故障模拟系统,从模式识别的角度对S变换图像进行处理,取得了较好的时频图像分类效果[20]。王继锋针对弹簧疲劳故障进行了大量模拟实验,采用小波包对振动信号进行处理,提取各频带的小波包能量作为特征向量,结合Kolmogorov-Smirnov检验法实现降维处理,利用支持向量机准确诊断出弹簧疲劳故障[21]。武建文团队探索了利用多个传感器诊断高压断路器弹簧疲劳等机械故障问题,提出了一种改进的多传感器证据组合规则,对不同传感器收集起来的特征进行了优化,实验测试表明,所提方法具有良好的优越性[22]。
总体而言,目前学者们更多的是从模式识别的角度来对弹簧疲劳等机械故障进行定性诊断[23-28],然而高压断路器在实际运行中由于长期处于拉伸或压缩的状态其疲劳演变是逐渐发生的,直至分合闸时间等特性参数超过核定的阈值时认为高压断路器达到退役标准,如何针对弹簧的疲劳程度进行定量的在线监测,实现高压断路器弹簧状态的实时感知和故障的及时诊断具有重要意义,也是目前工程领域亟须攻关解决的瓶颈问题之一。
作为探索和改进,本文以高压断路器分闸过程振动信号作为研究对象,提出了一种基于振动信号的高压断路器弹簧疲劳程度检测方法。利用不同测点的振动信号反推高压断路器能量变化规律,构建不同测点动能的函数关系式,探寻能量变化敏感测点,推导不同测点能量和系统总能量的映射关系。利用非线性最小二乘法推导出弹簧储能的计算公式,基于多个测点的振动信号分析来实现对弹簧的疲劳程度在线检测。
配备弹簧操动机构的高压断路器分合闸过程,本质上是将弹簧储存的操作功转化为机构零件的运动的过程,以实现动触头的上下移动完成分合闸动作,下面结合高压断路器的机械结构,对其分合闸过程中能量传递机理进行解释说明。
高压断路器质点模型如图1所示,高压断路器弹簧操动机构能量传递机理如下:
(1)合闸过程。合闸电磁铁通电后,触发合闸挚子脱扣,在合闸弹簧的作用下,凸轮开始转动挤压滚轮向下运动,滚轮带动转轴转动,转轴带动传动杆和动触头向上运动,同时压缩缓冲弹簧、拉伸分闸弹簧,直至完成合闸动作系统回到静止状态。弹簧储能克服摩擦力后,部分转化为缓冲弹簧和分闸弹簧的弹性势能,部分转化为运动部件动能,经零件冲击碰撞后转化为高压断路器本体振动。

图1 高压断路器质点模型
Fig.1 High voltage circuit breaker mass point model
(2)分闸过程。分闸电磁铁通电后,触发分闸挚子脱扣,在分闸弹簧和缓冲弹簧的作用下,带动三相连杆转动,使得动触头向下运动,动触头和运动部件从静止到加速运动再到碰撞停止的过程,缓冲弹簧和分闸弹簧释放的能量转化为高压断路器本体的振动。
如图1c所示,考虑高压断路器的机械结构组成,将高压断路器整体简化为7个质点,各个点的质量分别定义为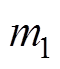 ~
~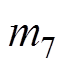 。根据高压断路器的三维尺寸及零件材料计算得出各个质点的质量,具体明细见表1。
。根据高压断路器的三维尺寸及零件材料计算得出各个质点的质量,具体明细见表1。
表1 高压断路器各个质点质量
Tab.1 Particle mass of high voltage circuit breaker (单位: kg)

质点质量 m191.6 m291.6 m391.6 m484.3 m549.2 m6109.3 m749.2
根据高压断路器能量传递机理分析,结合能量守恒定律,在分闸过程中,弹簧储存能量最终转化为7个质点的振动能量,尝试根据各个质点的振动能量评估弹簧储能情况。
以某开关厂生产的ZW57-40.5型高压断路器和LW42A-40.5型高压断路器为研究对象,二者均配备弹簧操动机构,探索其分闸过程中不同测点振动信号的变化,并构建能量计算模型,推导换算公式。
高压断路器平常处于静止状态,在接收到分合闸指令后会在极短时间内完成动作,一般只有几十毫秒。考虑到断路器工作环境特殊,在采集到的振动信号中,难免会受到电磁等噪声的干扰,本文利用变分模态分解对信号进行分解,变分模态分解(Variational Mode Decomposition, VMD)是K. Dragomiretskiy等提出的一种信号处理新方法,其核心思想是变分问题。该方法在获取本征模态分量(Intrinsic Mode Function, IMF)时不同于经验模态分解和局部均值分解算法所使用的循环筛分剥离的信号处理方式,而是将信号分解过程转移到变分框架内,通过迭代搜寻变分模型最优解来确定每个分量的频率中心及带宽,从而能够自适应地实现信号的频域剖分及各分量的有效分离,突出了数据的局部特征,表现出更好的噪声鲁棒性,且具有良好的采样效应,算法详见文献[29]。
针对分解得到的各个模态分量,提出利用波形匹配方差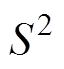 来评估各阶模态分量所包含的冲击与原始信号的匹配性程度,
来评估各阶模态分量所包含的冲击与原始信号的匹配性程度,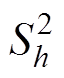 越小,第h阶模态分量与原始信号波形的匹配性越好,故提取与原始信号匹配方差较小的信号分量进行重构,实现振动信号的滤波处理。匹配方差计算公式为
越小,第h阶模态分量与原始信号波形的匹配性越好,故提取与原始信号匹配方差较小的信号分量进行重构,实现振动信号的滤波处理。匹配方差计算公式为
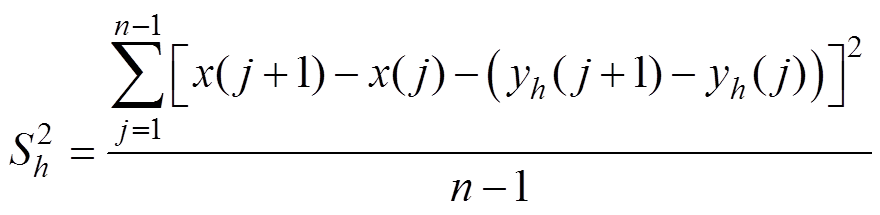 (1)
(1)
式中,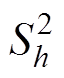 为第h阶模态分量与原始信号波形的匹配方差;
为第h阶模态分量与原始信号波形的匹配方差;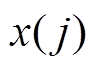 为原始信号第
为原始信号第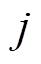 个数据;
个数据;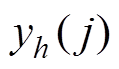 为第h阶模态分量的第
为第h阶模态分量的第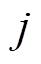 个数据;
个数据;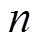 为采样点数。
为采样点数。
动静触头碰撞和零部件的冲击引起各个质点的振动,尝试根据加速度传感器测量得到的信号,换算出质点振动能量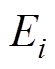 的大小,以操动机构处振动信号为例进行能量计算,有
的大小,以操动机构处振动信号为例进行能量计算,有
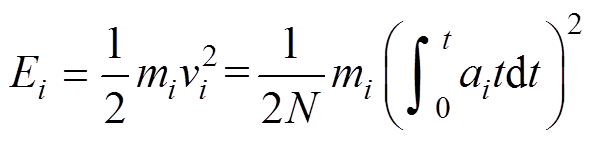 (2)
(2)
式中,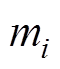 为各个质点的等效质量;
为各个质点的等效质量;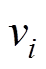 为各个质点的速度;
为各个质点的速度;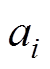 为各质点的加速度;
为各质点的加速度;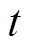 为采样时间;N为采样点数。
为采样时间;N为采样点数。
研究各个质点振动信号能量和弹簧储能的对应关系,尝试根据各个质点的能量变化推导弹簧储存能量变化,结合上述构建的7个质点的能量公式,推导弹簧储能公式系数。
结合高压断路器能量传递机理,根据能量守恒定律,分析得出高压断路器能量传递函数为
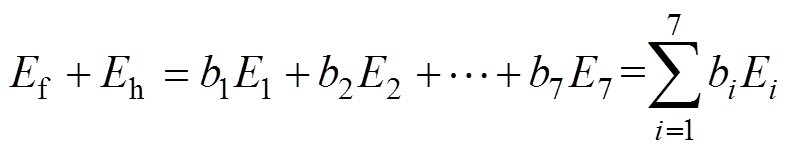 (3)
(3)
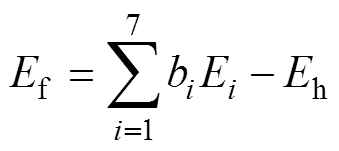 (4)
(4)
式中,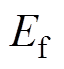 为分闸弹簧储存能量;
为分闸弹簧储存能量;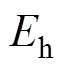 为缓冲弹簧储存能量;
为缓冲弹簧储存能量;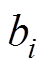 为各个质点能量的权重系数。
为各个质点能量的权重系数。
式(4)可以转化为
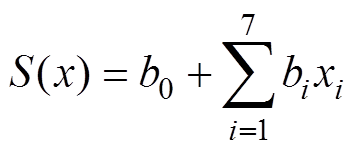 (5)
(5)
式中,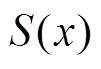 为分闸弹簧储存能量;
为分闸弹簧储存能量;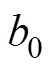 为初始值,
为初始值,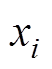 为各个质点能量。
为各个质点能量。
通过查阅相关资料,可计算出分闸弹簧和缓冲弹簧储能参数的大小,上述公式求解转换为求出各个质点能量权重系数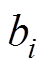 大小的问题。单纯的依据高压断路器结构和储能参数很难直接推导出
大小的问题。单纯的依据高压断路器结构和储能参数很难直接推导出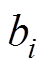 ,引入一个近似的多项式函数
,引入一个近似的多项式函数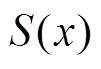 ,使这些离散点的拟合值接近实际值。系数寻优准则为使得累计误差二次方和最小,定义累计误差二次方和
,使这些离散点的拟合值接近实际值。系数寻优准则为使得累计误差二次方和最小,定义累计误差二次方和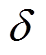 为
为
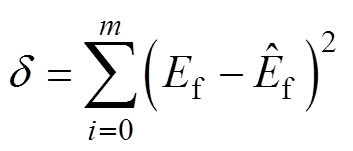 (6)
(6)
式中,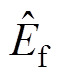 为分闸弹簧储存能量真实值;
为分闸弹簧储存能量真实值;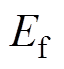 为分闸弹簧储存能量计算值;
为分闸弹簧储存能量计算值;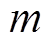 为测量次数。
为测量次数。
利用多组测量得到的数据,构建弹簧疲劳推导公式,采用非线性最小二乘(Nonlinear Least Square, NLS)法对权重系数进行推导求解。
假设取函数定义域内的线性无关函数1, 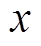 ,
, 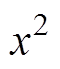 ,
, ,
, 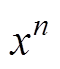 ,具有以下函数关系
,具有以下函数关系
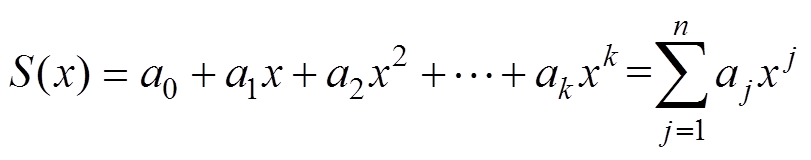 (7)
(7)
求解式(7)中各项系数值,需寻找到函数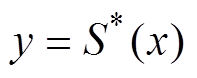 ,使得式(7)中误差二次方和最小,为了使得目标函数达到最优,函数
,使得式(7)中误差二次方和最小,为了使得目标函数达到最优,函数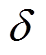 对每个系数
对每个系数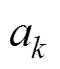 求其偏导数为0,即
求其偏导数为0,即
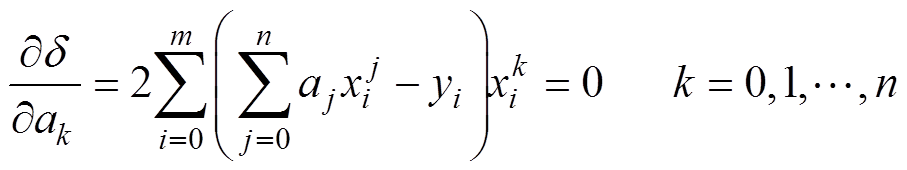 (8)
(8)
式(8)变换可得
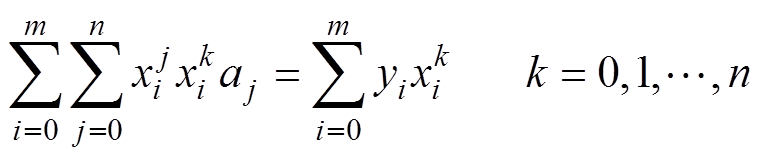 (9)
(9)
式(9)是一个关于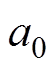 ,
, 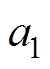 ,
, ,
, 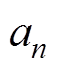 的线性方程组,求解式(9)即可得出最小二乘法的拟合函数
的线性方程组,求解式(9)即可得出最小二乘法的拟合函数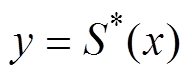 。
。
非线性最小二乘法需采用复杂的优化算法求解,常用的包括搜索算法和迭代算法,本文采用迭代算法求解。
通过获取高压断路器在不同储能状态下的振动信号,并对振动信号进行滤波处理,换算得到各个质点的能量,结合拟合得到的弹簧储能与测点能量的映射函数,实现了高压断路器弹簧储能的检测。具体来说,高压断路器弹簧储能检测流程如图2所示。

图2 弹簧疲劳检测流程
Fig.2 Flow chart of spring fatigue detection
高压断路器实验如图3所示。利用加速度传感器分别选取7个测点对高压断路器各部分振动进行测量(图3标号代表各个测点),包括ABC三相灭弧室的振动、横梁振动、操动机构振动和支架的振动,分别检测触头冲击、缓冲振动以及零件碰撞能量。

图3 高压断路器实验
Fig.3 Experiment of high voltage circuit breaker
高压断路器分闸时,系统是按照起动、加速、冲击(缓冲)和停止的过程完成分闸动作,弹簧储存的弹性势能首先转化为零件的动能,然后零件的动能转化为动触头和缓冲零件的冲击碰撞,进而引起局部和整体的振动。因零件冲击形成振源位置的差异性,造成不同测点的振动信号能量及变化存在一定的差异,测点1~3可直接检测到ABC三相动触头的振动情况,测点4可对三相连杆以及缓冲能量引起的振动进行准确检测,测点6可准确反映弹簧操动机构在一系列的冲击、碰撞等连续动作下振动能量变化,测点5、7能反映断路器整体阻尼衰减情况,故不同的检测位置对应不同冲击源,相应的对其冲击力(能量)的变化等更敏感,构建的测点体系有利于全方位评估断路器各部分能量变化。
实验采用东华1A115E型号的加速度传感器,量程为1 000g,采集仪型号为东华动态信号测试分析系统5 922N,采样频率设置为10K,采样时间设置为200ms,利用开口型霍尔传感器夹持到分闸线圈的控制线上,当检测到线圈电流时触发采集仪开始信号采集,7个测点采集到的信号如图4所示。
从图4中可以发现,ABC三相绝缘子处振动冲击非常敏感,形成了多个明显的振动冲击;另外,横梁和操动机构处的振动冲击也较为明显,两侧支柱的振动冲击相对于其他测点并不明显。
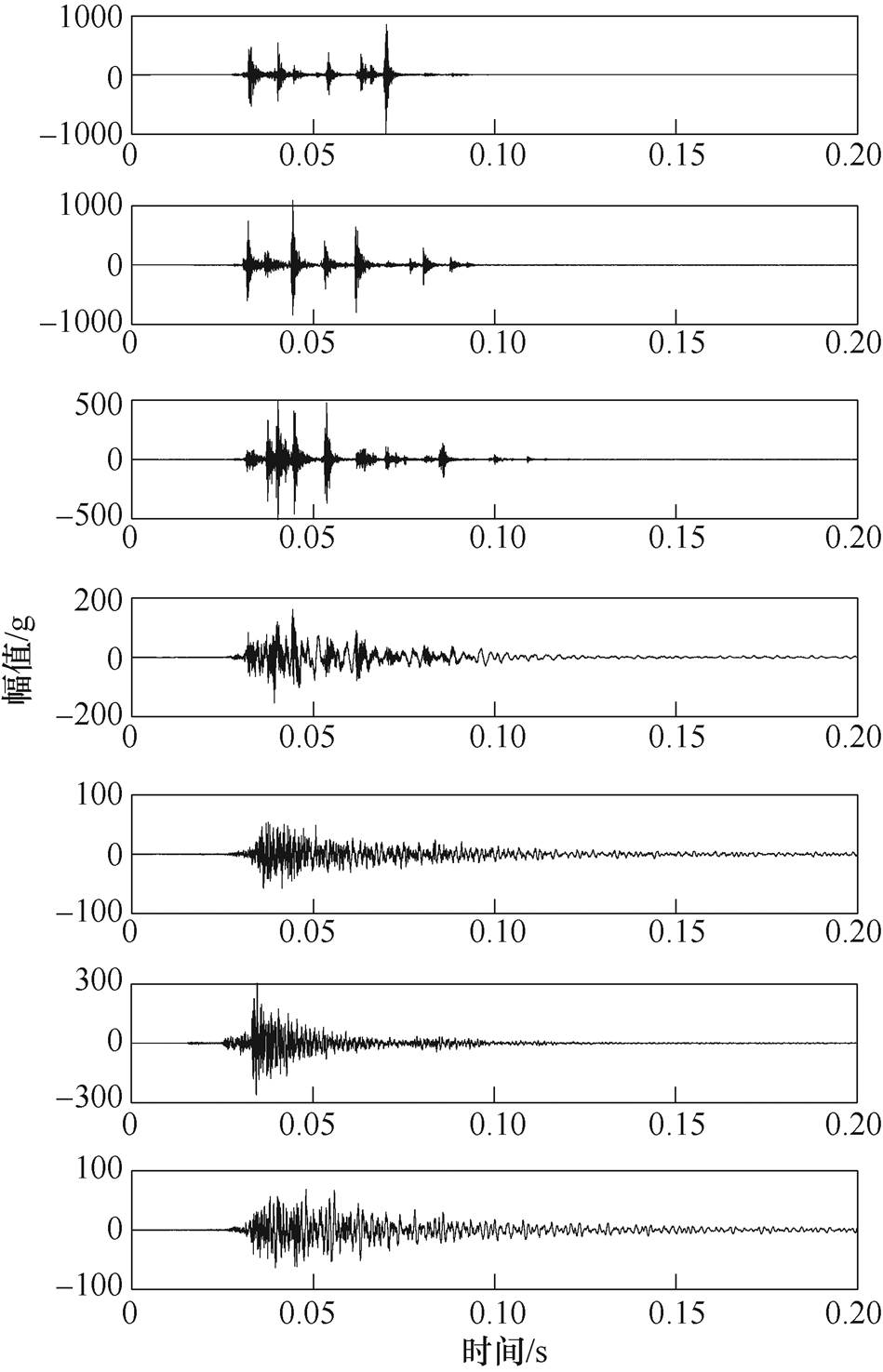
图4 高压断路器振动信号
Fig.4 Vibration signal of high voltage circuit breaker
高压断路器分闸弹簧由4根型号一样的弹簧构成,分闸弹簧基本参数见表2。缓冲弹簧的刚度系数为19.8N/mm,分闸动作位移为45mm,预紧力为100N,计算得出储能值为24.55J;通过调节分闸弹簧紧固螺栓改变预紧力大小的方式模拟分闸弹簧疲劳故障,分别模拟分闸弹簧在正常状态、轻微疲劳(预紧力退化19.20%)、一般疲劳(预紧力退化37.55%)和严重疲劳(预紧力退化75.15%)共四种工况下的高压断路器分闸动作,不同疲劳程度下分闸弹簧储能计算结果见表3。每种工况各动作10次,测量得到不同疲劳程度下各个测点的振动信号。
表2 分闸弹簧基本参数
Tab.2 The basic parameters of opening spring
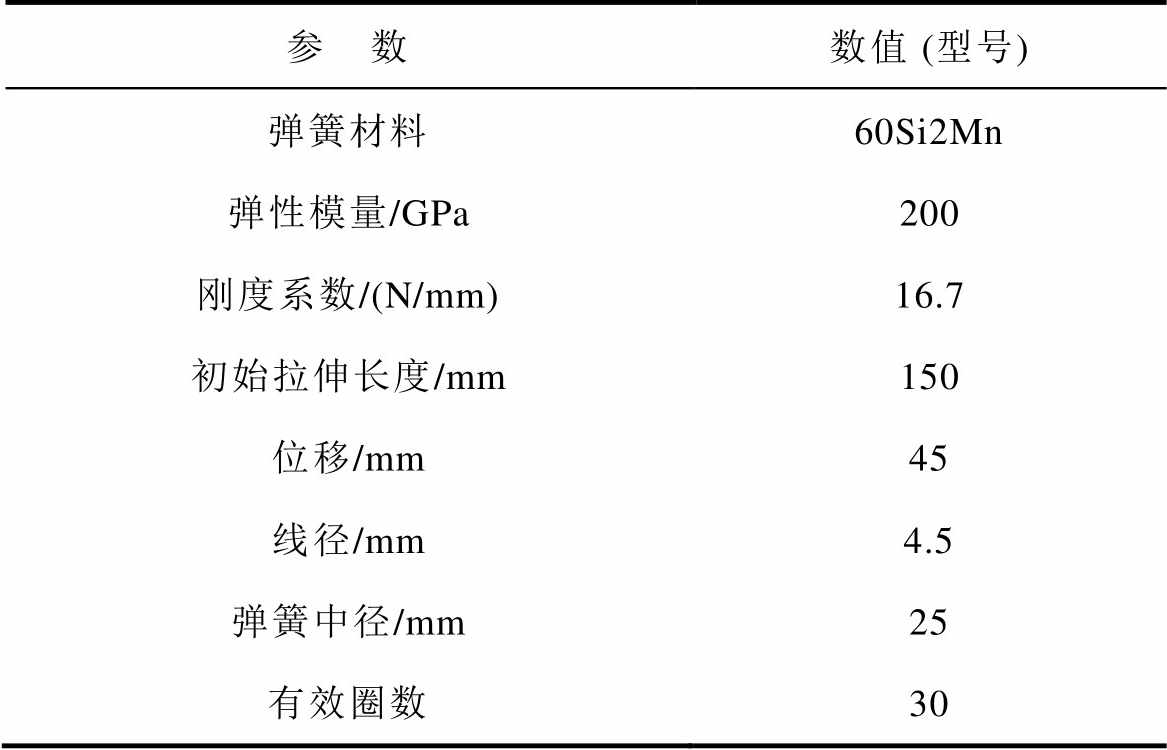
参 数数值 (型号) 弹簧材料60Si2Mn 弹性模量/GPa200 刚度系数/(N/mm)16.7 初始拉伸长度/mm150 位移/mm45 线径/mm4.5 弹簧中径/mm25 有效圈数30
表3 分闸弹簧储能结果
Tab.3 The energy storage results of opening spring
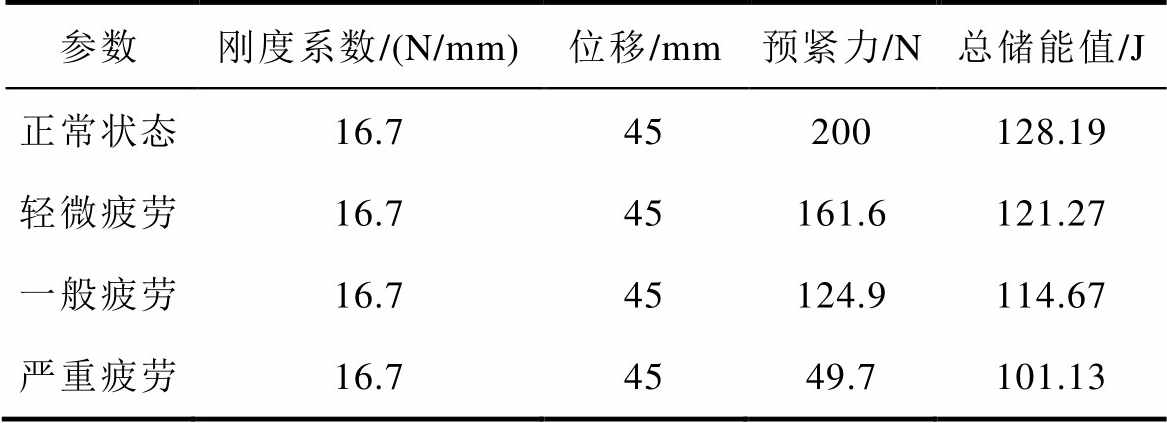
参数刚度系数/(N/mm)位移/mm预紧力/N总储能值/J 正常状态16.745200128.19 轻微疲劳16.745161.6121.27 一般疲劳16.745124.9114.67 严重疲劳16.74549.7101.13
进一步研究,通过对比不同弹簧疲劳程度下各个测点的时域信号,不能直观地观测出各路信号的明显变化,无法简单地根据多个测点的时域信号评估弹簧储能状态,需对信号内有效信息进一步提取。
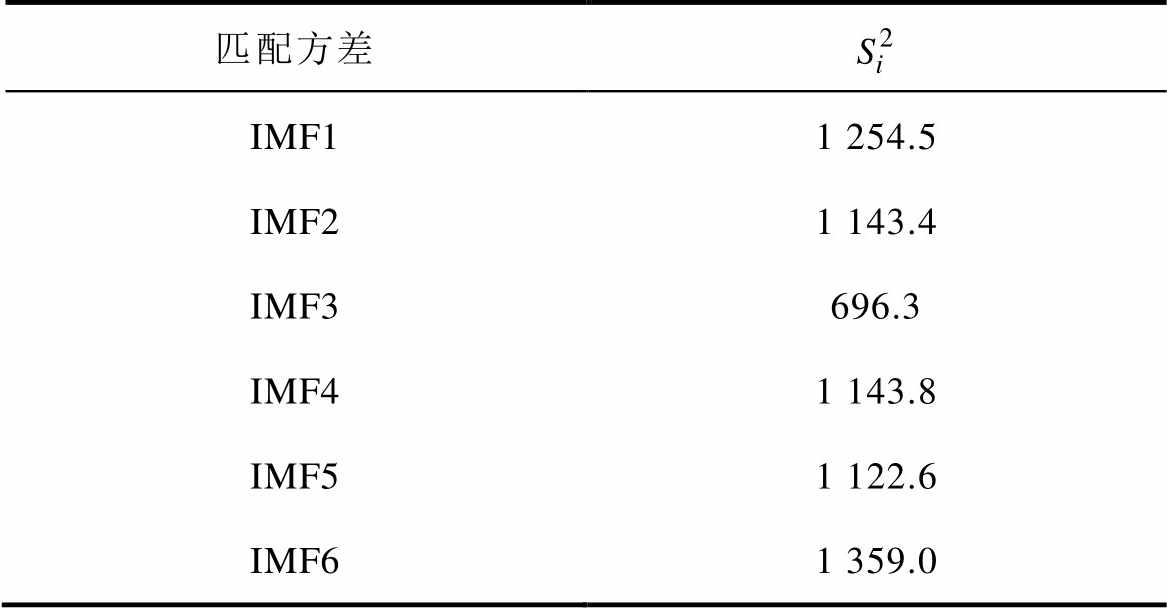
对采集到的多路信号进行滤波处理,进一步增强信号中有效信息。首先利用VMD对振动信号进行分解,根据各模态分量中心频率是否接近确定分解分量K的个数,实验表明,当分量个数K设置为7的时候中心频率出现了相近的情况,所以设置K为6。提取与原始信号匹配方差较小的模态分量进行重构,达到去噪的目的。以采集到的A相灭弧室的振动信号为例,对其进行VMD分解,结果如图5所示。然后求取各模态分量与原始信号的匹配方差,见表4。
根据各分量与原始信号的匹配方差,参考分解结果时域信号的关键时刻点,选取匹配方差较小的5个分量重构断路器分闸过程A相灭弧室振动信号,A相灭弧室振动信号重构信号如图6所示。
通过图6和原始信号的对比可以看出,原始信号中的噪声得到有效滤除,振动事件的冲击得到进一步的强化,有效抑制了干扰信号。
如3.1节所述,对采集到的四种工况(正常状态和三种疲劳故障)下的振动信号进行滤波处理后,得到40组数据,每种工况10组数据,取每种工况7组数据共28组数据作为训练数据,用来构建弹簧储能推导公式,拟采用非线性最小二乘法对权重系数进行推导求解。
部分训练数据各个简化质点的动能按照式(2)计算得到的结果见表5。
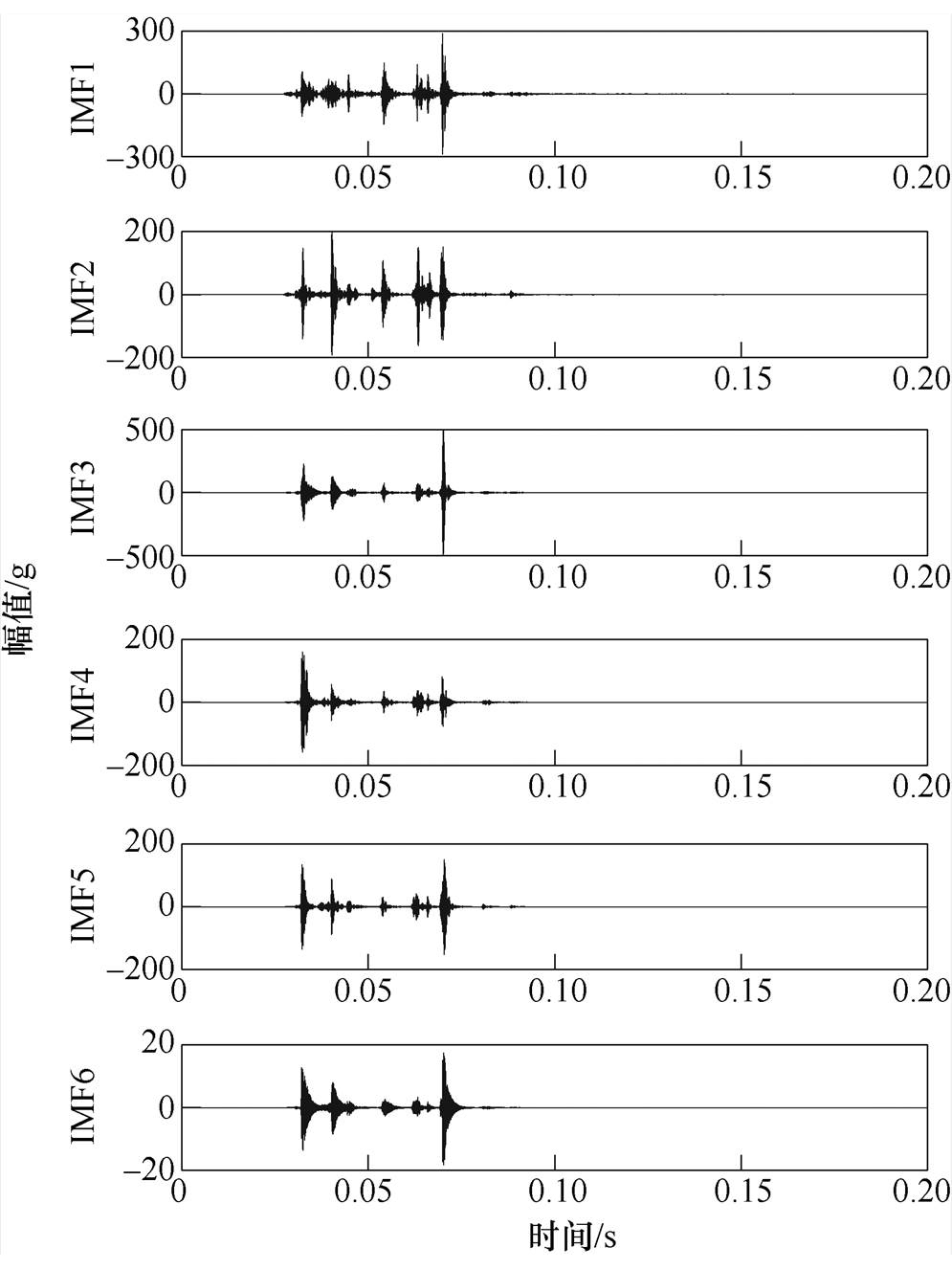
图5 VMD分解结果
Fig.5 Results of VMD decomposition
表4 各模态分量与原始信号匹配方差
Tab.4 The matching variance of IMFs and the original signal
匹配方差 IMF11 254.5 IMF21 143.4 IMF3696.3 IMF41 143.8 IMF51 122.6 IMF61 359.0
图6 重构信号
Fig.6 Reconstructed signal
采用非线性最小二乘法对权重系数进行推导求解,得到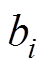 ,最终拟合得出的分闸弹簧储能公式为
,最终拟合得出的分闸弹簧储能公式为
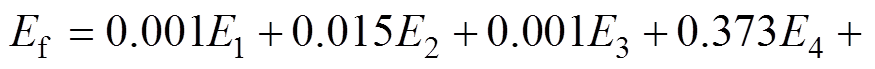
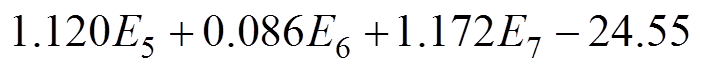 (10)
(10)
表5 各个质点动能计算结果
Tab.5 The calculation results of each particle kinetic energy(单位: J)
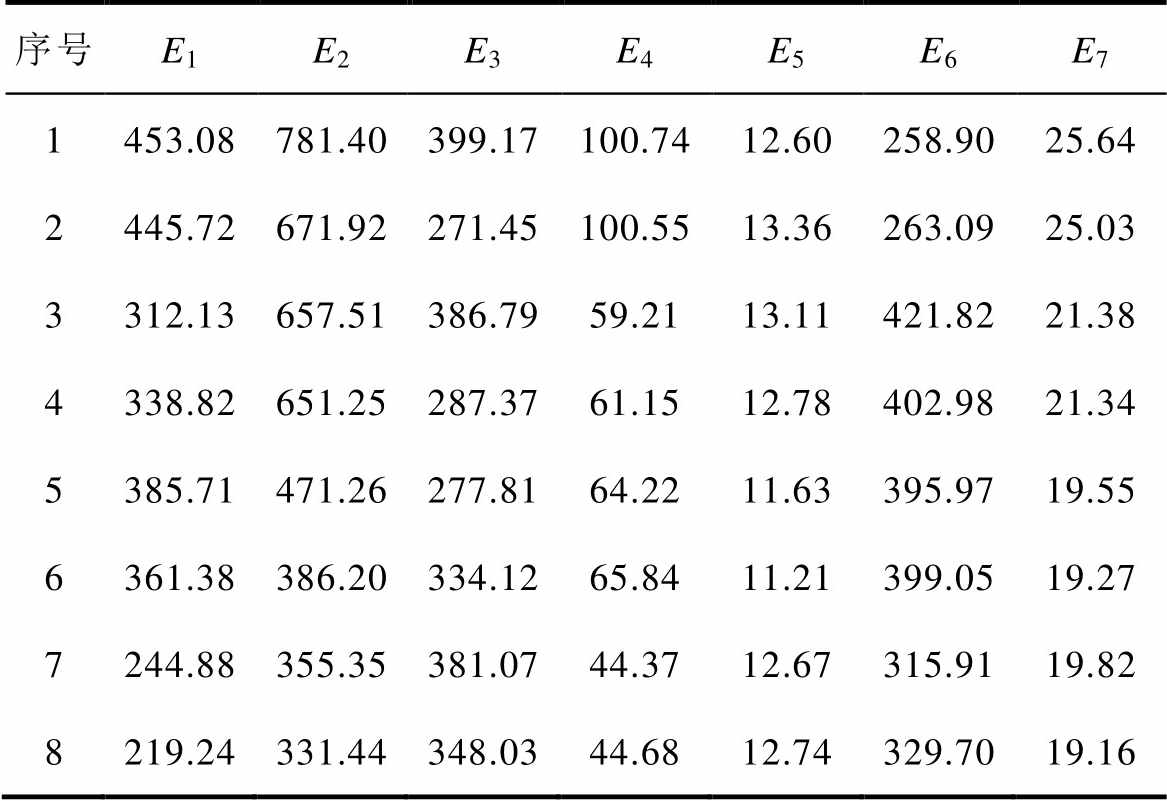
序号E1E2E3E4E5E6E7 1453.08781.40399.17100.7412.60258.9025.64 2445.72671.92271.45100.5513.36263.0925.03 3312.13657.51386.7959.2113.11421.8221.38 4338.82651.25287.3761.1512.78402.9821.34 5385.71471.26277.8164.2211.63395.9719.55 6361.38386.20334.1265.8411.21399.0519.27 7244.88355.35381.0744.3712.67315.9119.82 8219.24331.44348.0344.6812.74329.7019.16
为了探究本文所提方法的普适性,除ZW57-40.5型高压断路器外,还探索了LW42A-40.5型高压断路器的测试应用效果,分别模拟高压断路器分闸弹簧不同疲劳状态,并测量得到各个测点的振动信号,采用上述方法对测量得到的信号进行处理,实验过程及拟合得到各个测点的等效能量 如图7所示。
如图7所示。
分析图7可发现,对于同一类型的断路器,不同质点的等效能量相差较大,其中横梁、操动机构本体以及支架处能量相对较大。虽然不同质点的等效能量大小不一,但随着弹簧疲劳程度的加深,各个质点的等效能量总体呈现逐步下降的趋势,变化趋势基本一致,可评估各测点能量变化敏感性,据此为弹簧疲劳测点的选择提供参考。
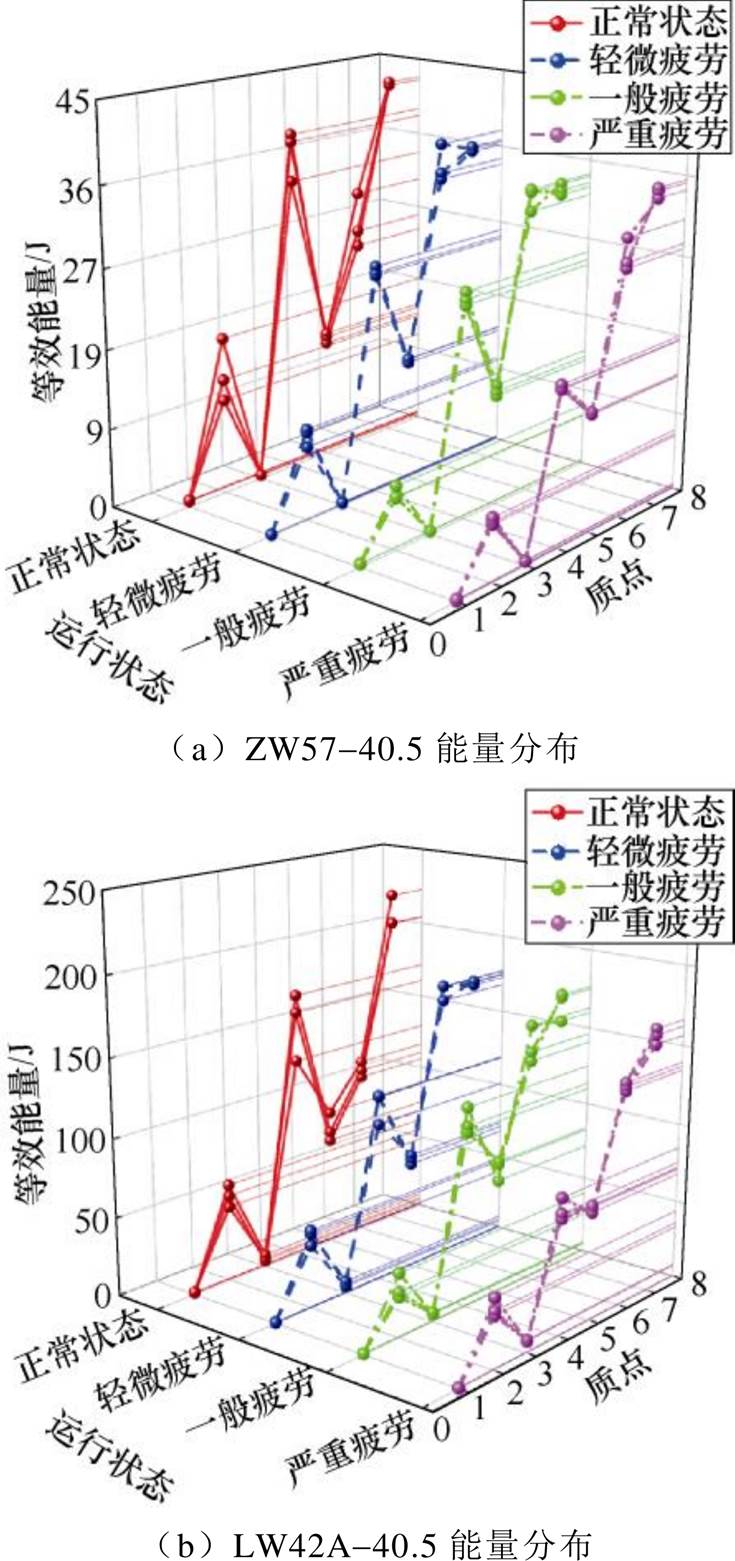

图7 各个质点等效能量
Fig.7 The equivalent energy of each particle
图7a与图7b对比可发现,两种断路器因结构、型号的差异性,质点等效能量大小存在一定的差异性,但各个质点的等效能量变化趋势一致,随着弹簧疲劳程度的加深,各个质点的等效能量总体呈逐步下降的趋势,表明了所提方法的有效性。
为了对比非线性最小二乘(Nonlinear Least Square, NLS)法的处理效果,同时运用了非线性回归(Nonlinear Regression, NR)法和多元线性回归(Multiple Linear Regression, MLR)法对ZW57-40.5型高压断路器信号进行处理,求解得出的权重系数见表6,利用不同方法拟合得到的弹簧储能值如图8所示。
表6 不同方法求解得到的权重系数
Tab.6 The weight coefficient obtained by different methods
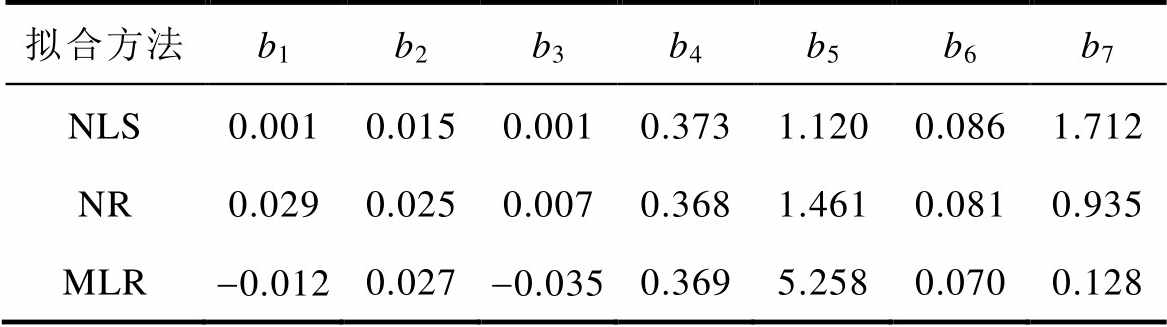
拟合方法b1b2b3b4b5b6b7 NLS0.0010.0150.0010.3731.1200.0861.712 NR0.0290.0250.0070.3681.4610.0810.935 MLR-0.0120.027-0.0350.3695.2580.0700.128
通过分析表6可以发现,不同质点的能量权重系数相差较大,但横梁和两个支架处振动信号权重系数相对于其他测点的权重系数较大,且不同方法求解结果相一致,说明这3个测点处能量和分闸弹簧储能更相关,能较好地反映分闸弹簧释放能量的变化。
图8中,圆点实线为弹簧储能理论真实值,拟合值越接近圆点实线代表拟合效果越好。通过分析对比可发现,不同拟合方法的整体变化趋势一致,随着弹簧疲劳程度的加深,能量呈现逐步下降的趋势,且均在理论储能值附近上下波动,验证了所提方法理论的可行性。通过三种拟合方法对比可以看出,采用非线性最小二乘法拟合得到的弹簧储能结果和理论储能值大小更接近,误差相对于其他算法更小,相对于其他算法拟合效果更好。
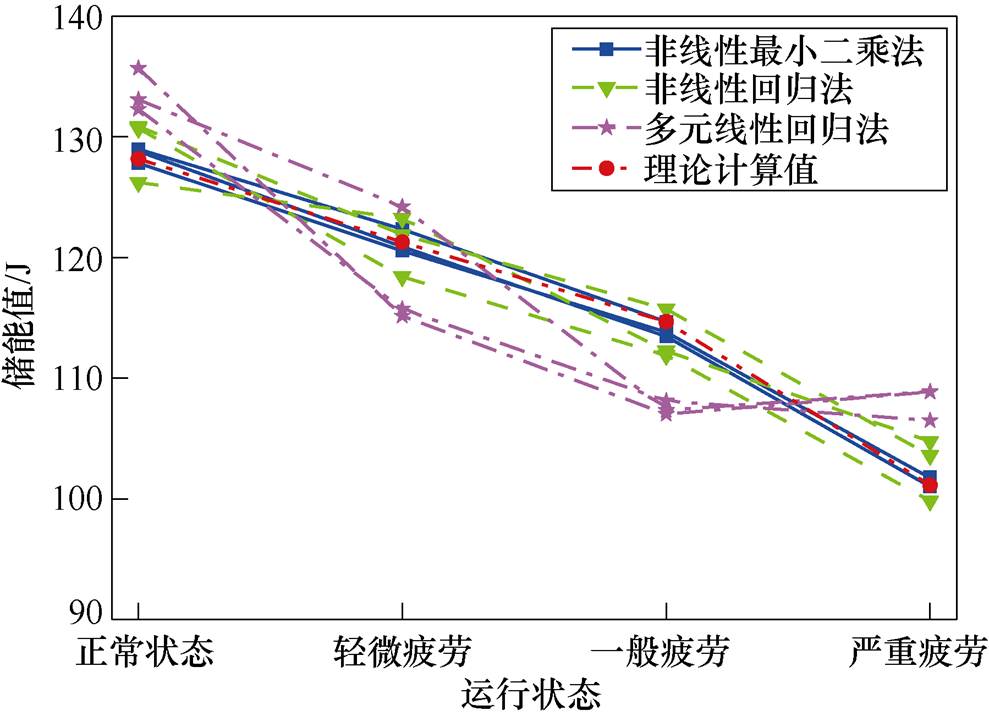
图8 不同拟合方法结果对比
Fig.8 Comparison of different fitting methods
利用本文所提出的VMD和NLS相结合(VMD- NLS)的方法评估高压断路器分闸弹簧性能,为了对比VMD去噪效果,同时利用NLS处理原始振动信号构建出拟合公式。测量弹簧在正常和不同疲劳程度共四种状态下7个测点的振动信号,每种状态测量3次数据,分别利用上述方法求解弹簧储能检测结果,不同疲劳状态下检测结果见表7。
表7 分闸弹簧储能检测结果对比
Tab.7 Comparison of opening spring energy
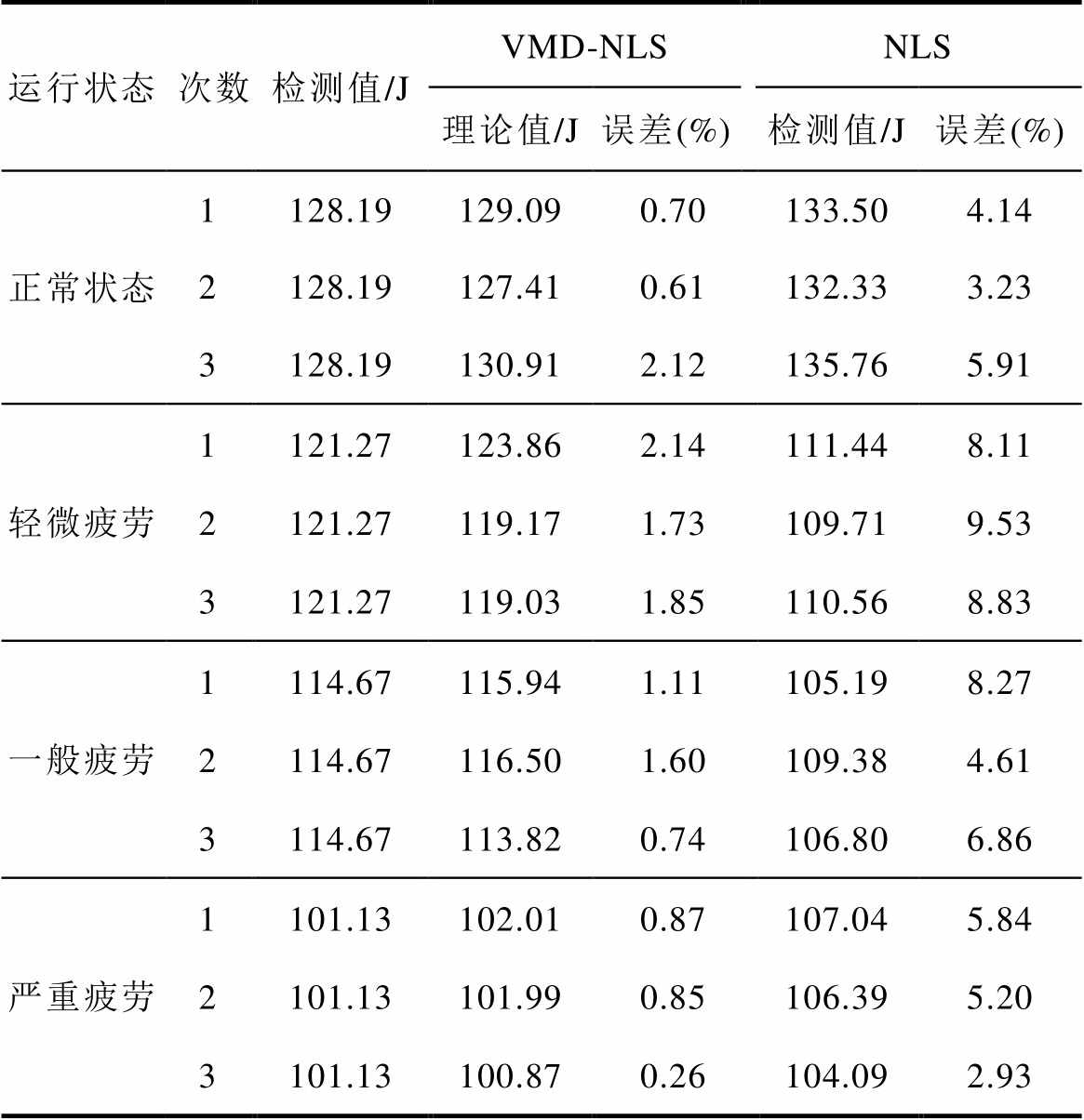
运行状态次数检测值/JVMD-NLSNLS 理论值/J误差(%)检测值/J误差(%) 正常状态1128.19129.090.70133.504.14 2128.19127.410.61132.333.23 3128.19130.912.12135.765.91 轻微疲劳1121.27123.862.14111.448.11 2121.27119.171.73109.719.53 3121.27119.031.85110.568.83 一般疲劳1114.67115.941.11105.198.27 2114.67116.501.60109.384.61 3114.67113.820.74106.806.86 严重疲劳1101.13102.010.87107.045.84 2101.13101.990.85106.395.20 3101.13100.870.26104.092.93
从表7中可以看出,利用VMD-NLS处理测量得到的信号,对于同一运行状态下,拟合得到的储能值和理论储能值基本一致,多次测量误差相对较小;对于不同运行状态下,利用振动信号拟合得出的储能值存在明显的大小层次,且基本接近理论储能值。与此同时,利用NLS直接处理原始信号拟合得到的结果对比发现,虽然不同运行状态下拟合得到的储能值呈现阶梯式下降趋势,但对于同一运行状态下拟合得到的储能值与理论储能值误差较大,因信号中噪声成分的干扰降低了拟合效果,实验结果表明,所提VMD-NLS检测方法相对于NLS可更为精准计算出弹簧储能值。
为了对比非线性最小二乘法的处理效果,同时运用非线性回归法和多元线性回归法处理得到的权重系数对振动信号能量进行拟合,对拟合结果与理论储能值求取误差平均值,对比结果如图9所示。
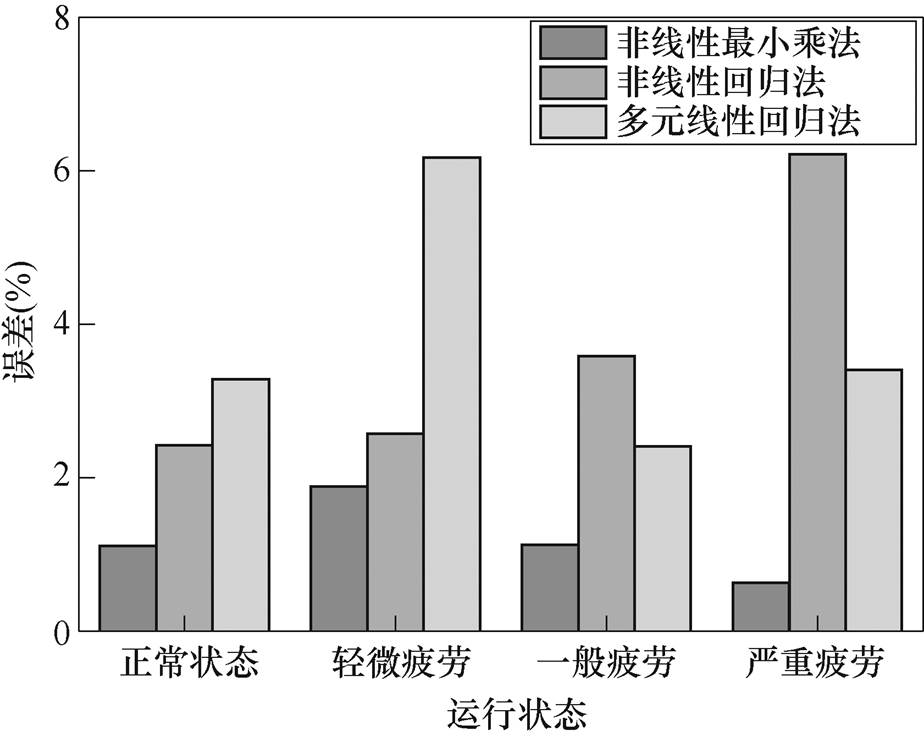
图9 不同方法拟合误差
Fig.9 The fitting error of different methods
从图9中可以看出,无论是在同一运行状态还是不同运行状态下,采用非线性最小二乘法的拟合得到的数值与理论储能值对比,误差都最小;非线性回归法和多元线性回归法拟合误差在不同程度上均大于非线性最小二乘法的误差。通过不同算法的对比,有效验证了非线性最小二乘拟合算法的优越性。本文所提方法对于高压断路器分闸弹簧储能值检测误差均控制在2.2%以内,从实验角度验证了所提方法的准确性。
本文以高压断路器分闸过程振动信号作为研究对象,提出了一种利用振动信号评估弹簧疲劳程度的检测方法。首先采用变分模态分解处理各个测点振动信号,选择与原始信号匹配方差较小的成分分量进行重构,实现信号滤波;然后分析各个测点的等效能量变化规律;最后利用非线性最小二乘法推导出弹簧储能和测点响应能量的映射关系,构建出弹簧储能的计算公式,实现了高压断路器弹簧疲劳程度的检测。通过本文研究得出以下结论:
1)首次提出了利用多个测点振动信号实现高压断路器弹簧疲劳程度的检测方法,解决了传统测量方法需停电检修、无法在线测试的问题。
2)提出了基于质点简化的高压断路器能量分布分析方法,总结了质点能量随弹簧疲劳程度变化规律,对高压断路器振动测点的选择提供有益参考。
3)利用变分模态分解与非线性最小二乘法相结合的方法处理断路器振动信号,构建了弹簧储能的计算公式,可准确检测弹簧储存能量值。
4)通过对配备弹簧操动机构的高压断路器开展分闸弹簧疲劳模拟实验,验证所提方法的有效性和准确性,与理论储能值对比表明检测精度较好,检测误差可收敛在2.2%以内。本文研究为高压断路器弹簧储能在线检测提供了一种新的思路。
参考文献
[1] 温伟杰, 李鹏宇, 李斌, 等. 多端口机械式直流断路器的动作策略与参数优化[J]. 电力系统自动化, 2021, 45(11): 86-94.
Wen Weijie, Li Pengyu, Li Bin, et al. Operation strategy and parameter optimization of multi-port mechanical DC circuit breaker[J]. Automation of Electric Power Systems, 2021, 45(11): 86-94.
[2] 王灿, 杜船, 徐杰雄. 中高压直流断路器拓扑综述[J]. 电力系统自动化, 2020, 44(9): 187-199.
Wang Can, Du Chuan, Xu Jiexiong. Review of topologies for medium-and high-voltage DC circuit breaker[J]. Automation of Electric Power Systems, 2020, 44(9): 187-199.
[3] Polycarpou A A, Soom A, Swarnakar V, et al. Event timing and shape analysis of vibration bursts from power circuit breakers[J]. IEEE Transactions on Power Delivery, 1996, 11(2): 848-857.
[4] Lee D W, Sohn J H, Yoo W S. Mass effect analysis of a coil spring for the performance evaluation of a gas insulated circuit breaker[J]. International Journal of Precision Engineering and Manufacturing, 2014, 15(12): 2543-2548.
[5] Rudsari F N, Razi-Kazemi A A, Shoorehdeli M A. Fault analysis of high-voltage circuit breakers based on coil current and contact travel waveforms through modified SVM classifier[J]. IEEE Transactions on Power Delivery, 2019, 34(4): 1608-1618.
[6] 林莘, 王飞鸣, 刘卫东, 等. 高压SF6断路器冷态介质恢复特性试验研究[J]. 中国电机工程学报, 2016, 36(14): 3973-3981.
Lin Xin, Wang Feiming, Liu Weidong, et al. Experi- ment researches on cold state dielectric recovery characteristics in high voltage SF6 circuit breakers[J]. Proceedings of the CSEE, 2016, 36(14): 3973- 3981.
[7] Runde M, Ottesen G E, Skyberg B, et al. Vibration analysis for diagnostic testing of circuit-breakers[J]. IEEE Transactions on Power Delivery, 1996, 11(4): 1816-1823.
[8] 李鹏飞, 周文俊, 曾国, 等. 高压断路器合闸弹簧动态特性及储能状态检测方法[J]. 电工技术学报, 2016, 31(3): 104-112.
Li Pengfei, Zhou Wenjun, Zeng Guo, et al. The dynamic characteristics and energy storage state detection method of high-voltage circuit breaker closing spring[J]. Transactions of China Electro- technical Society, 2016, 31(3): 104-112.
[9] 杨秋玉, 彭彦卿, 庄志坚. 基于ADAMS的高压断路器弹簧机构动力学仿真与故障分析[J]. 高压电器, 2018, 54(6): 67-73, 80.
Yang Qiuyu, Peng Yanqing, Zhuang Zhijian. Dynamic simulation and failure analysis of spring mechanism of high-voltage circuit breaker based on ADAMS[J]. High Voltage Apparatus, 2018, 54(6): 67-73, 80.
[10] Su Yi, Lu Yufeng, Xie Zhibiao, et al. Study on closing spring fatigue characteristics of high voltage circuit breaker[J]. IOP Conference Series: Earth and Environmental Science, 2020, 508(1): 012174.
[11] Dou Longjiang, Wan Shuting. Characteristic para- meter change of circuit breaker under closing spring fatigue[J]. Transactions of the Canadian Society for Mechanical Engineering, 2019, 43(2): 189-198.
[12] 程显, 袁晓东, 葛国伟, 等. 真空开关高动作稳定性的永磁操动机构控制系统[J]. 电工技术学报, 2021, 36(21): 4617-4626.
Cheng Xian, Yuan Xiaodong, Ge Guowei, et al. Permanent magnet mechanism control system with high operation stability of vacuum switch[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(21): 4617-4626.
[13] 万书亭, 豆龙江, 李聪, 等. 基于振动信号的高压断路器合闸特性参数在线检测方法研究[J]. 振动工程学报, 2019, 32(2): 359-367.
Wan Shuting, Dou Longjiang, Li Cong, et al. Study on on-line detection of high voltage circuit breaker closing characteristic parameters based on vibration signal[J]. Journal of Vibration Engineering, 2019, 32(2): 359-367.
[14] 杨秋玉, 王栋, 阮江军, 等. 基于振动信号的断路器机械零部件故障程度识别[J]. 电工技术学报, 2021, 36(13): 2880-2892.
Yang Qiuyu, Wang Dong, Ruan Jiangjun, et al. Fault severity estimation method for mechanical parts in circuit breakers based on vibration analysis[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2880-2892.
[15] 孙曙光, 张伟, 王景芹, 等. 基于动作过程振动检测的低压断路器机械寿命预测[J]. 仪器仪表学报, 2020, 41(12): 146-157.
Sun Shuguang, Zhang Wei, Wang Jingqin, et al. Mechanical life prediction of low-voltage circuit breaker based on vibration detection during operation[J]. Chinese Journal of Scientific Instrument, 2020, 41(12): 146-157.
[16] 杨秋玉, 阮江军, 张灿, 等. 基于定量递归分析的高压断路器机械缺陷辨识及应用[J]. 电工技术学报, 2020, 35(18): 3848-3859.
Yang Qiuyu, Ruan Jiangjun, Zhang Can, et al. Study and application of mechanical defect identification for high-voltage circuit breakers using recurrence quanti- fication analysis[J]. Transactions of China Elec- trotechnical Society, 2020, 35(18): 3848-3859.
[17] 杨元威, 关永刚, 陈士刚, 等. 基于声音信号的高压断路器机械故障诊断方法[J]. 中国电机工程学报, 2018, 38(22): 6730-6737.
Yang Yuanwei, Guan Yonggang, Chen Shigang, et al. Mechanical fault diagnosis method of high voltage circuit breaker based on sound signal[J]. Proceedings of the CSEE, 2018, 38(22): 6730-6737.
[18] 孙曙光, 李勤, 杜太行, 等. 基于一维卷积神经网络的低压万能式断路器附件故障诊断[J]. 电工技术学报, 2020, 35(12): 2562-2573.
Sun Shuguang, Li Qin, Du Taihang, et al. Fault diagnosis of accessories for the low voltage con- ventional circuit breaker based on one-dimensional convolutional neural network[J]. Transactions of China Electrotechnical Society, 2020, 35(12): 2562- 2573.
[19] Liu Yakui, Zhang Guogang, Zhao Chenchen, et al. Mechanical condition identification and prediction of spring operating mechanism of high voltage circuit breaker[J]. IEEE Access, 8: 210328-210338.
[20] 刘宝稳, 汤容川, 马钲洲, 等. 基于S变换D-SVM AlexNet模型的GIS机械故障诊断与试验分析[J]. 高电压技术, 2021, 47(7): 2526-2538.
Liu Baowen, Tang Rongchuan, Ma Zhengzhou, et al. GIS mechanical fault diagnosis and test analysis based on S transform D-SVM AlexNet model[J]. High Voltage Engineering, 2021, 47(7): 2526-2538.
[21] 王继锋. 基于信号多维特征值提取的弹簧操动机构断路器故障诊断方法研究[D]. 广州: 华南理工大学, 2016.
[22] Ma Suliang, Yuan Yang, Wu Jianwen, et al. Multi- sensor decision approach for HVCB fault detection based on the vibration information[J]. IEEE Sensors Journal, 2021, 21(2): 985-994.
[23] Zhao Shutao, Ma Li, Wang Kedeng, et al. Research on optimal identification method of circuit breaker defect type based on phase space reconstruction and SVM[J]. IEEJ Transactions on Electrical and Electronic Engineering, 2019, 14(10): 1471-1477.
[24] Zhang Yingjie, Jiang Yuan, Chen Yan, et al. Fault diagnosis of high voltage circuit breaker based on multi-classification relevance vector machine[J]. Journal of Electrical Engineering & Technology, 2020, 15(1): 413-420.
[25] Zhang Hongye, Xie Yanzhao, Yi Tongqiang, et al. Fault detection for high-voltage circuit breakers based on time-frequency analysis of switching transient E-fields[J]. IEEE Transactions on Instrumentation and Measurement, 2020, 69(4): 1620-1631.
[26] Yao Yu, Wang Nan. Fault diagnosis model of adaptive miniature circuit breaker based on fractal theory and probabilistic neural network[J]. Mechani- cal Systems and Signal Processing, 2020, 142: 106772.
[27] Liu Mingliang, Li Bing, Zhang Jianfeng, et al. An application of ensemble empirical mode decom- position and correlation dimension for the HV circuit breaker diagnosis[J]. Automatika, 2019, 60(1): 105- 112.
[28] 赵书涛, 许文杰, 李云鹏, 等. 基于优选泛特征的真空断路器弹簧机构储能状态辨识方法[J]. 高电压技术, 2021, 47(11): 3777-3784.
Zhao Shutao, Xu Wenjie, Li Yunpeng, et al. Identification method for energy storage state of spring mechanism of vacuum circuit breaker based on optimal multi-characteristics[J]. High Voltage Engin- eering, 2021, 47(11): 3777-3784.
[29] Dragomiretskiy K, Zosso D. Variational mode decomposition[J]. IEEE Transactions on Signal Pro- cessing, 2014, 62(3): 531-544.
Detecting Method of High Voltage Circuit Breaker Spring Fatigue Based on Vibration Signal
Abstract Spring fatigue is a typical fault that frequently occurs in high-voltage circuit breakers. However, most traditional test methods cannot detect online. Therefore, a way to detect the spring fatigue fault based on vibration signals is proposed. Firstly, according to the working principle of the high-voltage circuit breaker, the energy transfer mechanism in the operation process is analyzed, and the whole structure is simplified into particle points. Then, after filtering the noise in the vibration signal, the equivalent energy distribution is calculated by constructing the kinetic energy function of each particle point. Finally, the energy transfer function of the high voltage circuit breaker is constructed by the nonlinear least square method to calculate the spring energy. The experimental results show that the detection error of the spring energy is within 2.2%, which verifies the effectiveness and accuracy of the proposed method. This method can provide a new way to detect spring fatigue in high-voltage circuit breakers.
keywords:High voltage circuit breaker, spring fatigue, vibration signal, nonlinear least square method
DOI: 10.19595/j.cnki.1000-6753.tces.212014
中图分类号:TM561
国家自然科学基金(51777075, 51777074)、中央高校基本科研业务资金(2020MS110)、河北省自然科学基金(E2020502031)、保定市科技计划基础研究专项基金(2172P010)和河北省青年拔尖人才支持计划([2018]-27)资助项目。
收稿日期 2021-12-10
改稿日期 2022-01-05
豆龙江 男,1988年生,博士,讲师,研究方向为电站设备在线监测与故障诊断。E-mail: doulongjiang@126.com
何玉灵 男,1984年生,副教授,博士生导师,研究方向为复杂机电系统建模。E-mail: heyuling1@ncepu.edu.cn(通信作者)
(编辑 崔文静)