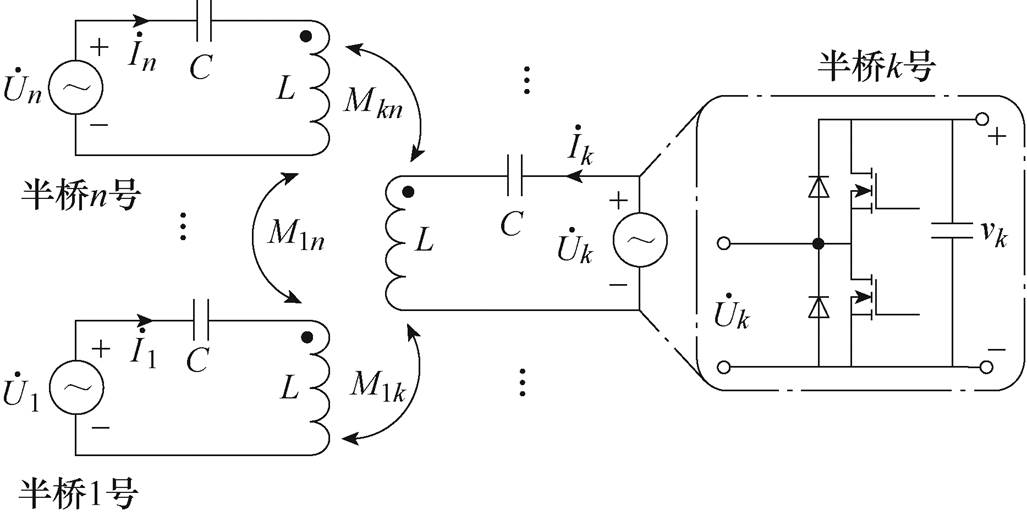
图1 MWiDC的等效电路
Fig.1 Equivalent circuit of the MWiDC
摘要 多端口无线电能DC-DC变换器(MWiDC)具备实现可灵活扩展的高效率多端口功率变换的潜力,但其系统建模与功率流控制缺乏一般性理论。为扩充相关理论,该文提出一种模块化MWiDC架构。首先,建立MWiDC的一般性数学模型。在此基础上,提出一种电压功率混合解耦控制策略,并给出该策略下闭环系统直流增益、高频特性和稳定性的数学证明。作为比较,该文对不解耦直接控制策略也进行理论分析,此时闭环系统过于复杂,其稳定性有待证明。最后,以一台三端口原型机为例进行硬件实验及仿真分析。实验结果表明,在不同输入/输出配置或线圈偏移工况下,原型机能实现零电压开关,系统效率可达91%。仿真结果表明,两种控制策略都能实现电压功率混合控制,但解耦控制策略具有更强的抗干扰性。
关键词:多端口DC-DC变换器 无线电能传输 解耦控制 多向功率流
多端口DC-DC变换器(Multiport DC-DC Con- verter, MDC)具有高集成度、高效率和多向功率流管理能力,已被广泛应用在新能源接入的直流微电网与用电系统、“光-储-充”一体化的电动汽车充电站、储能系统电池均衡等重要领域中[1]。
MDC一般可分为共直流母线型[2-3]和多端口变压器型[4-6]两大类型。共直流母线型MDC结构简单,但存在开关损耗高、缺乏可靠隔离、主动器件数量多、控制复杂等缺点[7]。引入多个隔离型DC-DC变换器虽能提高可靠性,但功率变换级数增加,效率和经济性随之降低。基于多端口变压器的MDC虽然有更小的开关损耗,但多端口变压器体积较大且设计制作复杂,变压器端口数量固定难以灵活扩展。上述两类MDC不仅难以兼顾效率、隔离和功率密度,还存在定制化程度高、可重构性差、功率流方向受限、制作工艺要求高等问题。
得益于非接触且无需闭合磁路的耦合机构,基于磁感应耦合式的无线电能传输(Wireless Power Transfer, WPT)具备实现可灵活扩展的多端口功率变换的潜力。由于无需提供完美闭合磁路的铁心,在传统单发射与单接收无线电能传输线圈间插入额外耦合线圈即可通过无线功率连接扩展功率变换的端口数量,实现端口可灵活扩展与重构的多端口功率变换系统,即多端口无线电能DC-DC变换器(Multiport Wireless DC-DC Converter, MWiDC)。而现有磁感应耦合式WPT研究主要以2~4端口系统[8-10]为主,缺少一般性的n端口MWiDC的系统建模、补偿设计以及多端口功率流控制等理论研究。
在电路建模方面,由于拓扑的相似性,部分文献如文献[11-12]尝试采用多有源桥(Multi-Active Bridge, MAB)的功率流模型。其成立的前提,是线圈之间紧贴无漏磁。但在绝大多数WPT系统中,线圈漏磁不可忽略,MAB的功率流模型不能直接应用。
在电路控制方面,谐振DC-DC变换器一般采用移相控制。但MWiDC各端口间存在复杂的耦合:其他端口输入(移相角)会影响本端口输出(电压/功率),即前向耦合;其他端口输出也影响本端口输出,即反向耦合。交叉耦合大大增加了控制难度,故MWiDC解耦控制的一般性研究目前较少。
文献[8, 13-14]均采用不解耦的直接控制策略。这些文献虽然在实验中实现了定电压或定功率控制,但并没有对不解耦控制器能控制耦合系统这一反常现象进行解释,更没有其普遍可行性的理论证明。文献[15-17]提出了MAB解耦控制策略,对MWiDC的控制有参考价值,但只考虑了前向耦合,未讨论反向耦合。另外,由于忽略漏磁的问题,MAB的结论并不能移植到MWiDC中。
针对MWiDC缺乏一般性电路模型和解耦控制理论的问题,本文提出了一种模块化多端口无线电能DC-DC变换器(Modular MWiDC, MMWiDC),建立了n端口MWiDC的一般性数学模型,并在此基础上提出了一种电压功率混合解耦控制(Power- Voltage Hybrid Decoupling Control, PVHDC)策略。解耦控制下闭环系统的稳定性、直流增益和高频特性得到理论证明。作为比较,本文也对非解耦控制策略进行了频域建模,但非解耦闭环系统的传递函数矩阵(下文简称“闭环传函矩阵”)表达式繁琐,其稳定性等尚待证明。
为验证所提MWiDC及其解耦控制策略,本文搭建了一台三端口原型机,并对其进行硬件实验和仿真分析。实验表明,该三端口原型机能够在弱耦合条件下,在双输入单输出(Dual-Input Single-Output, DISO)、单输入双输出(Single-Input Dual-Output, SIDO)、单输入单输出(Single-Input Single-Output, SISO)及线圈偏移状态下实现端口定电压、定功率、电压功率混合控制,且能够实现零电压软开关(Zero Voltage Switching, ZVS),系统效率可达91%。最后本文对比了多端口解耦与非解耦控制,两种控制策略都能实现电压功率混合控制,但PVHDC比非解耦直接控制策略具有更强的抗干扰性。
n端口MWiDC的等效电路如图1所示。该系统由n个完全相同的模块构成,一个模块由单相半桥、谐振电容和线圈组成。所有线圈自感均为L,谐振电容容值均为C,两者满足串联谐振关系,谐振频率约为系统工作频率f1,令w1=2pf1。

图1 MWiDC的等效电路
Fig.1 Equivalent circuit of the MWiDC
模块k半桥直流侧电压为vk。若忽略死区,半桥上管的开关信号可视为占空比50%、正弦初相位为jk的方波。因此,模块k交流侧电压uk(t)是占空比50%、电平为0和vk的方波。由于L和C构成串联谐振,整个电路可采用基波分析法求解。因此,模块k交流侧电压、电流可用正弦基波有效值相量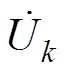 和
和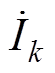 表示。其中电压相量为
表示。其中电压相量为
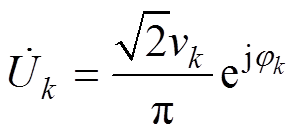 (1)
(1)
定义由相量组成的n维列向量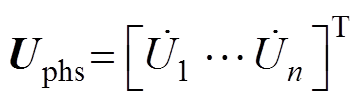 、
、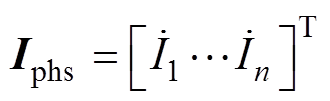 ,则图1的网孔电流方程为
,则图1的网孔电流方程为
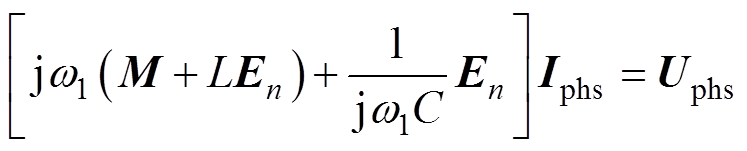 (2)
(2)
式中,M为线圈之间的互感矩阵;En为n阶单位阵。由式(2)可解得Iphs,进而模块k直流侧吸收功率为
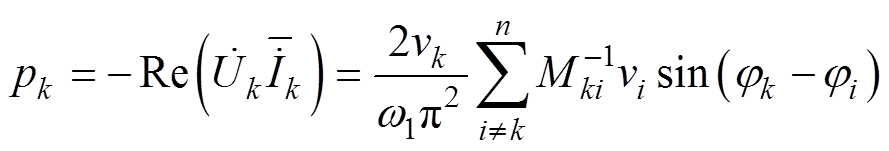 (3)
(3)
从而流入直流侧的直流电流为
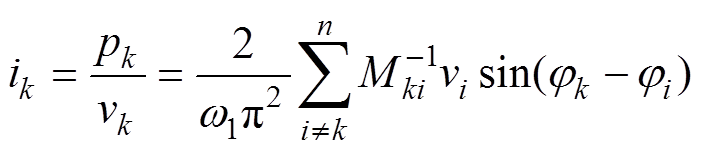 (4)
(4)
式中,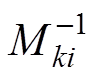 为
为 的第k行第i列元素。由于L和C近似满足串联谐振条件,式(3)、式(4)中的C被消去。
的第k行第i列元素。由于L和C近似满足串联谐振条件,式(3)、式(4)中的C被消去。
式(3)表明任意两个模块间的传输功率,正比于两者开关信号相位差的正弦。因此,MWiDC应采用移相控制。
在实际工程中,DC-DC变换器一般有定电压输出和定功率输出两种工作模式。本文所提出的MWiDC与普通MDC相比,各端口功率方向和工作模式都可任意指定。n端口MWiDC的一般形式如图2所示,涉及的向量定义见表1。
为方便后续运算,不妨设MWiDC的输出端口号为1~m,其余皆为输入端口。输入端口k连接直流电压源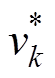 ;输出端口i连接等效负载电阻Ri、并联电容Ci。在输出端口中,又规定前l个端口为定电压输出,剩余m−l个端口为定功率输出。这种指定并不失一般性。
;输出端口i连接等效负载电阻Ri、并联电容Ci。在输出端口中,又规定前l个端口为定电压输出,剩余m−l个端口为定功率输出。这种指定并不失一般性。
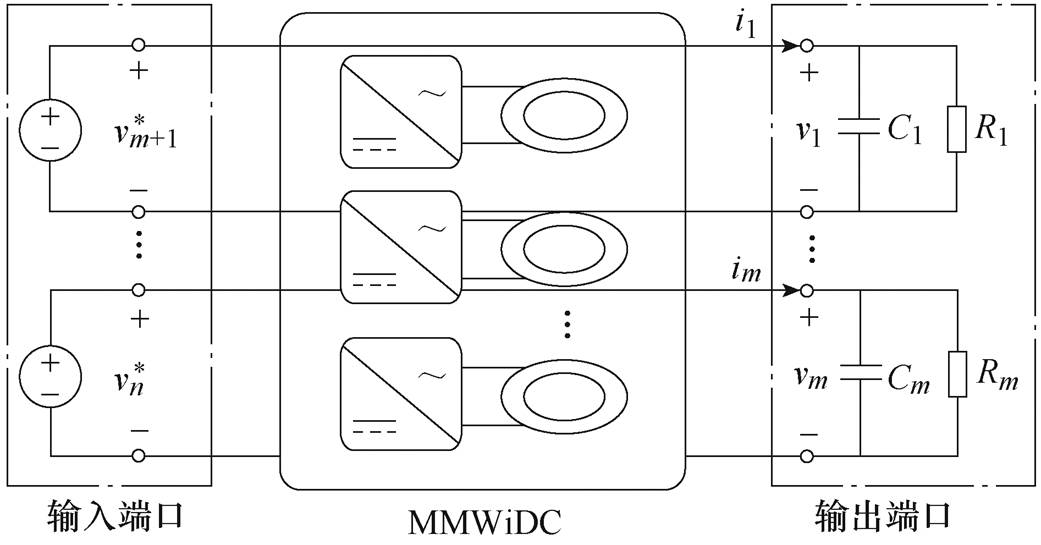
图2 MWiDC的一般形式
Fig.2 General form of the MWiDC
表1 向量定义
Tab.1 Vector definitions
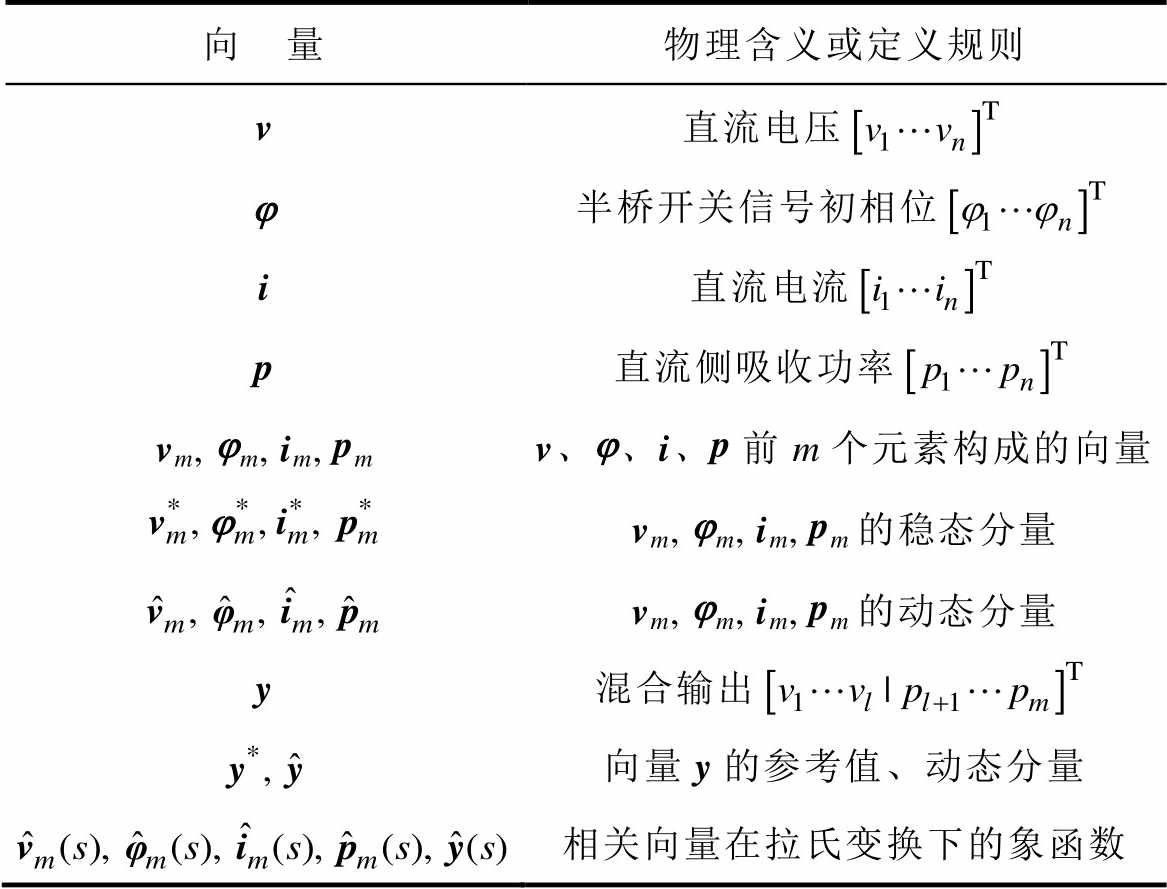
向 量物理含义或定义规则 v直流电压 j半桥开关信号初相位 i直流电流 p直流侧吸收功率 vm, jm, im, pmv、j、i、p前m个元素构成的向量 vm, jm, im, pm的稳态分量 vm, jm, im, pm的动态分量 y混合输出 向量y的参考值、动态分量 相关向量在拉氏变换下的象函数
输入端口k由于连接独立电压源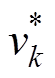 ,相当于电力系统中的平衡节点,故规定输入端口k对应的开关信号初相角始终保持稳态值
,相当于电力系统中的平衡节点,故规定输入端口k对应的开关信号初相角始终保持稳态值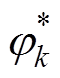 。因此,小信号建模只需针对m个输出端口。
。因此,小信号建模只需针对m个输出端口。
对MWiDC进行大信号动态建模时,会大大增加系统阶数和控制器的复杂程度。由于各直流端口电气量以直流分量为主,且控制器带宽远小于f1,可在MWiDC的静态工作点(v*, j*)处直接对式(4)进行小信号线性化,可得到
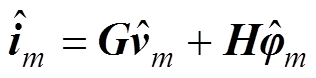 (5)
(5)
式中,m阶方阵G、H的第k行第i列元素分别为
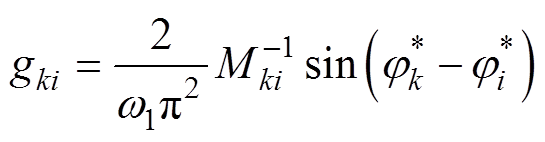 (6)
(6)
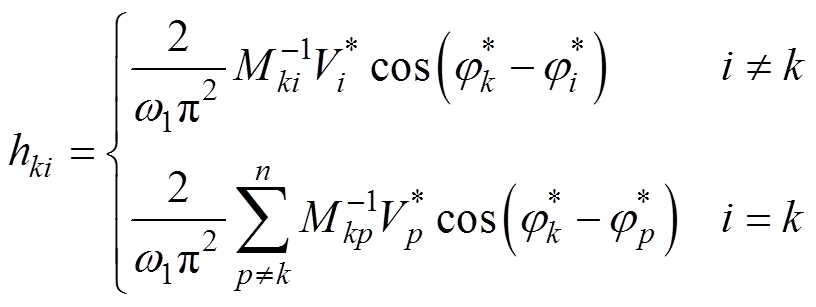 (7)
(7)
设模块k直流侧阻抗为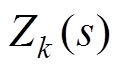 ,并定义直流阻抗矩阵
,并定义直流阻抗矩阵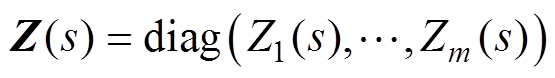 。由欧姆定律得
。由欧姆定律得
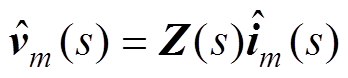 (8)
(8)
对于定功率控制的端口k,功率动态分量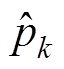 和电压动态分量
和电压动态分量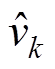 成正比,比例系数Jk定义为
成正比,比例系数Jk定义为
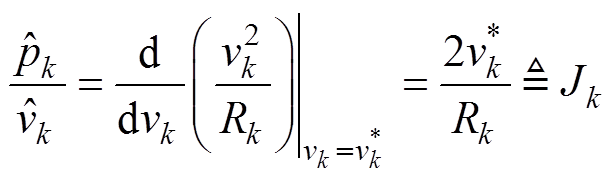 (9)
(9)
式中,Rk为端口k的负载电阻。定义二进制量sk表示输出端口k的控制方式:0为定电压控制,1为定功率控制。由式(9)知,混合输出向量y的动态分量为
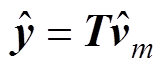 (10)
(10)
式中,T=(J−Em)S+Em,Em为m阶单位阵,对角阵J=diag(J1,…,Jm),控制模式矩阵S=diag(S1,…,Sm)。式(5)、式(8)、式(10)构成系统的小信号模型,如图3所示。
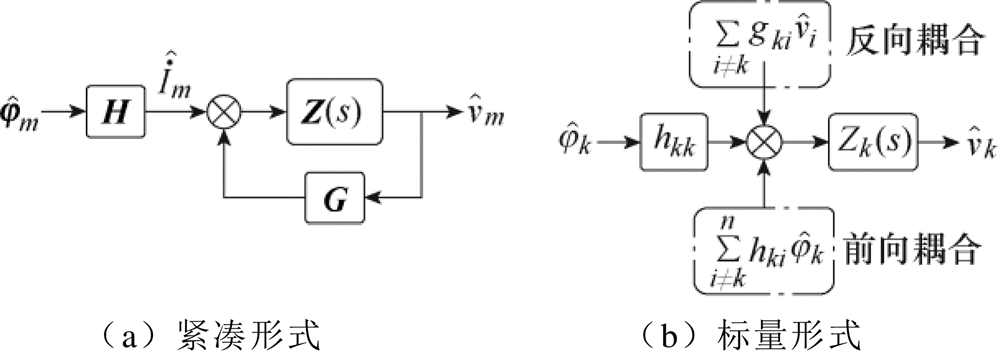
图3 MWiDC系统小信号模型
Fig.3 Small signal model of the MWiDC
根据功率流模型式(3)、式(4),已知参考值,控制输出端口1~m的电压或功率,等价于求出对应的j,最终归结于求解稳态分量j*和动态分量 。其中,稳态分量j*可根据各端口电压或功率参考值,使用文献[18]中的方法求解,此处不再赘述。
。其中,稳态分量j*可根据各端口电压或功率参考值,使用文献[18]中的方法求解,此处不再赘述。
动态分量 可利用比例积分(Proportional Integral, PI)调节器构成输出电压或功率负反馈进行调整。当m≥2时,各输出端口之间存在前向耦合(H的非对角元)和反向耦合(G的元素)。在系统闭环传递函数矩阵中,分别称其对角元、非对角元为前向传递函数、耦合传递函数。为使耦合传递函数尽量接近0,需要进行解耦控制。
可利用比例积分(Proportional Integral, PI)调节器构成输出电压或功率负反馈进行调整。当m≥2时,各输出端口之间存在前向耦合(H的非对角元)和反向耦合(G的元素)。在系统闭环传递函数矩阵中,分别称其对角元、非对角元为前向传递函数、耦合传递函数。为使耦合传递函数尽量接近0,需要进行解耦控制。
解耦控制器及闭环系统如图4所示。引入图4a的解耦控制器后,小信号闭环系统如图4b所示。显然,反向耦合项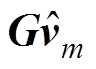 和前向耦合增益矩阵H在整个环路中被抵消,余下的PI环节、直流阻抗Z(s)和变换矩阵T均为对角阵,系统实现了解耦。注意到常数矩阵G和H均只和输出参考向量y*有关,故其求逆等运算容易实现。
和前向耦合增益矩阵H在整个环路中被抵消,余下的PI环节、直流阻抗Z(s)和变换矩阵T均为对角阵,系统实现了解耦。注意到常数矩阵G和H均只和输出参考向量y*有关,故其求逆等运算容易实现。
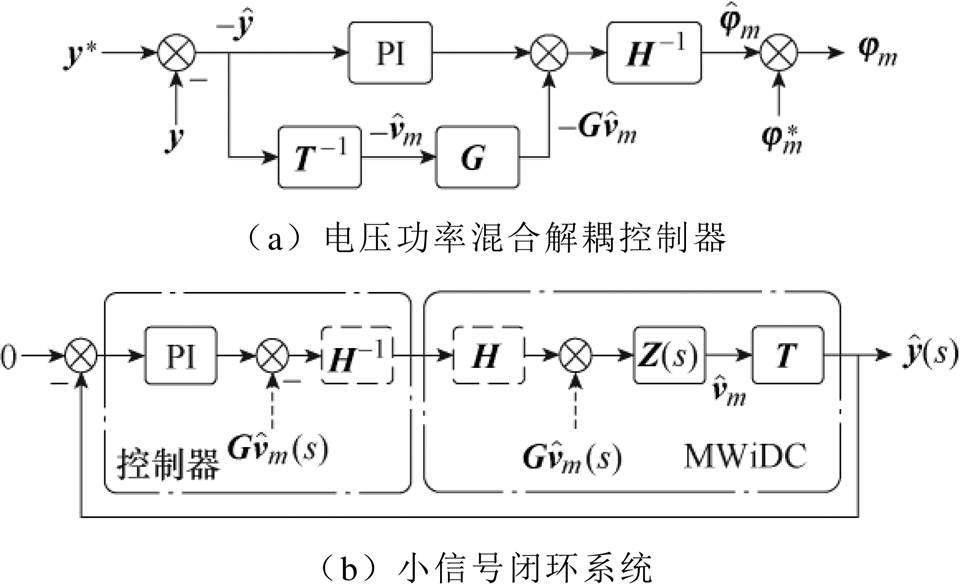
图4 解耦控制器及闭环系统
Fig.4 Decoupling controller and close-loop system
由图4b可知,全系统的小信号开环、闭环传递函数矩阵分别为
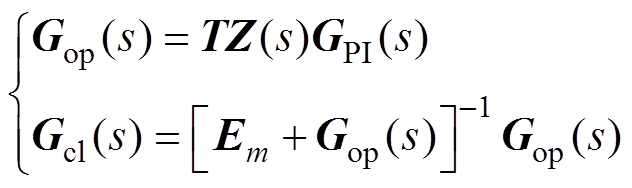 (11)
(11)
式(11)的标量形式为
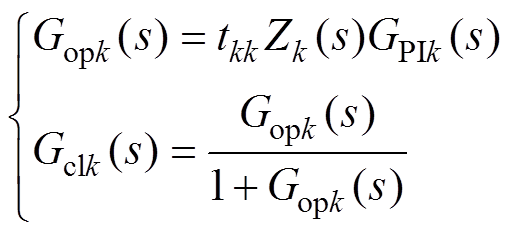 (12)
(12)
式中,tkk=(Jk−1)sk+1为矩阵T的第k行第k列元素,直流阻抗和PI调节器的传递函数Zk(s)、GPIk(s)分别为
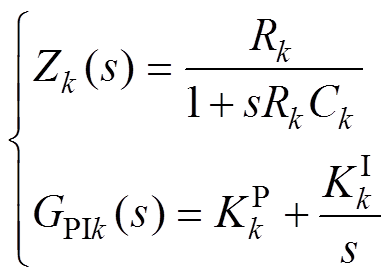 (13)
(13)
式中,Ck为端口k的直流侧电容;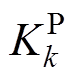 、
、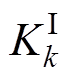 为控制器PI参数。由附录(定理1)可得,闭环系统直流增益为1,在高频段近似为一阶惯性环节,且闭环系统稳定。
为控制器PI参数。由附录(定理1)可得,闭环系统直流增益为1,在高频段近似为一阶惯性环节,且闭环系统稳定。
文献[8, 13-14]不加分析地给出了不解耦直接控制策略,如图5所示。为与图4保持相同的PI参数,控制器中引入了H对角部分的逆矩阵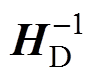 。
。
直接控制策略没有实现解耦,此时系统开环、闭环传函矩阵分别为
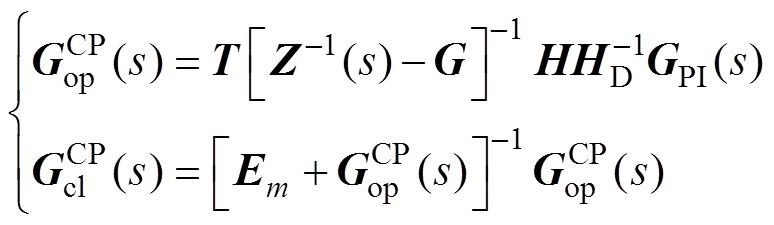 (14)
(14)
由附录(定理2),输入参考值为纯直流量时,直接控制下闭环系统耦合传递函数可忽略不计。由于变换器正常工作时,电压或功率参考值是常数,故文献[8, 13-14]无需解耦也能得到预期的实验结果。上述文献并没有解释直接控制器能够控制耦合系统的原因,而本文给出了数学证明。
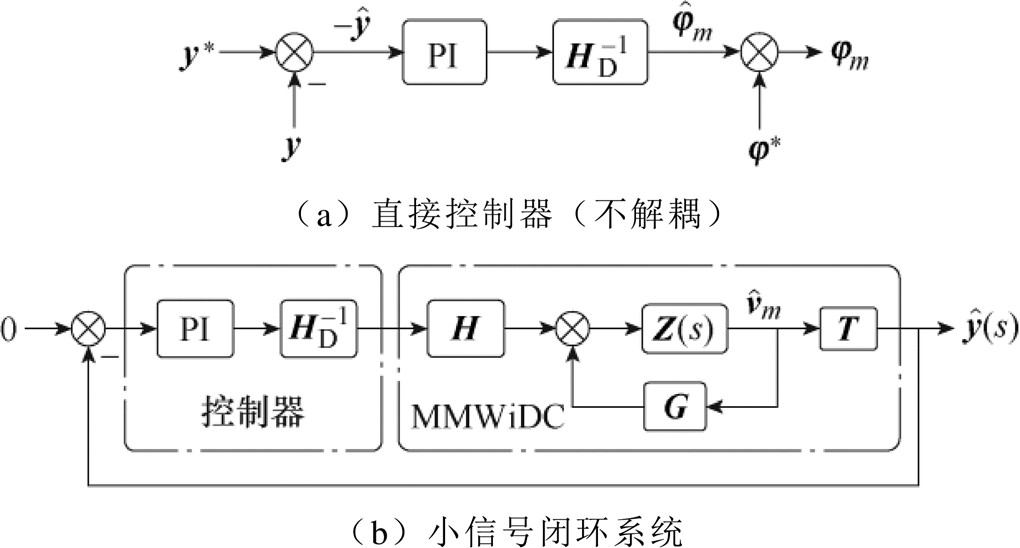
图5 不解耦直接控制器
Fig.5 Direct controller without decoupling
然而在直接控制策略下,一旦某端口输出电压/功率有交流分量扰动,该扰动将耦合到其他端口,降低电能质量。另外,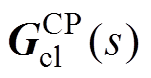 阶数高、表达式繁琐,闭环系统的幅频特性、稳定性、带宽等具体性质难以进行一般性分析。因此直接控制策略的一般性理论尚待补充。
阶数高、表达式繁琐,闭环系统的幅频特性、稳定性、带宽等具体性质难以进行一般性分析。因此直接控制策略的一般性理论尚待补充。
为验证MWiDC的电压、功率控制的能控性和运行效率,本文搭建了如图6所示的三端口MWiDC原型机。原型机参数见表2。

图6 三端口MWiDC原型机
Fig.6 A three-port MWiDC prototype
在三端口样机中,任一端口k都可连接直流电源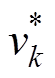 或电阻Rk。给定j 后,v和p随之确定。当
或电阻Rk。给定j 后,v和p随之确定。当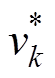 或Rk(端口配置)改变后,若改变j 能够使输出端口的电压或功率与端口配置变化前保持一致,则能证明该系统具有电压或功率控制的可控性。
或Rk(端口配置)改变后,若改变j 能够使输出端口的电压或功率与端口配置变化前保持一致,则能证明该系统具有电压或功率控制的可控性。
表2 原型机参数
Tab.2 Prototype parameters
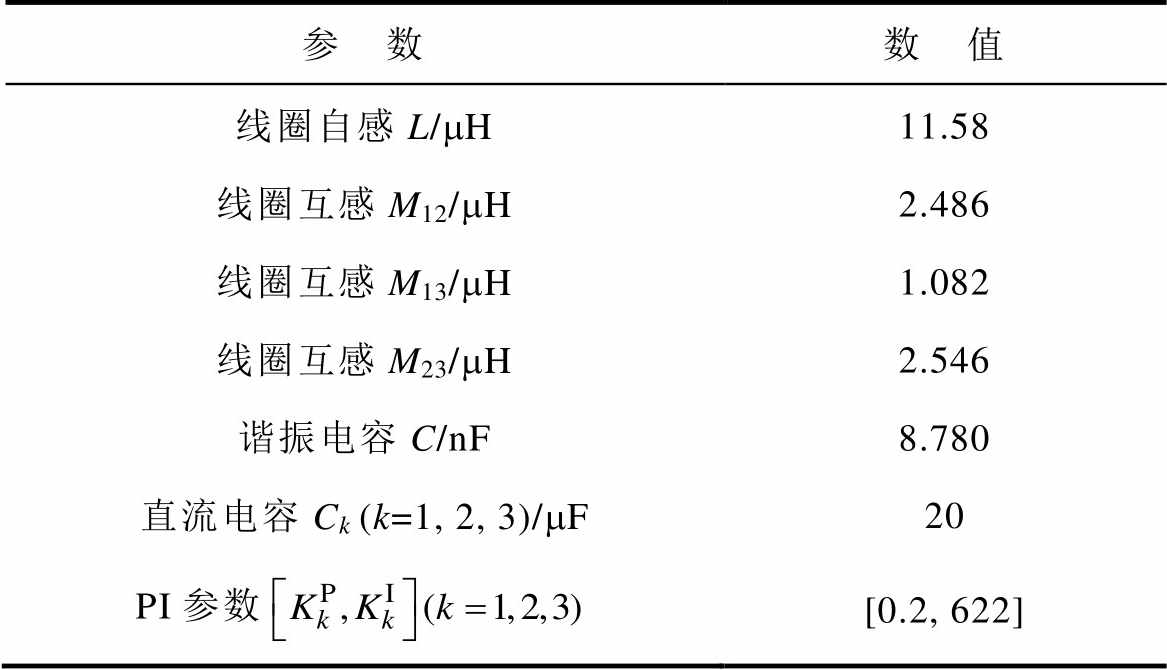
参 数数 值 线圈自感L/mH11.58 线圈互感M12/mH2.486 线圈互感M13/mH1.082 线圈互感M23/mH2.546 谐振电容C/nF8.780 直流电容Ck (k=1, 2, 3)/mF20 PI参数[0.2, 622]
3.2.1 双输入单输出模式(DISO)
在DISO模式下,不妨设端口Ⅰ为输出,端口Ⅱ和Ⅲ为输入,则系统的端口配置可表示为三元组(R1, 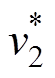 ,
, 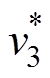 )。规定
)。规定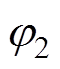 恒为0,则开关信号初相位可用二元组(j1, j3)表示。为验证输出端口Ⅰ的可控性,利用原型机设计的三组实验见表3。
恒为0,则开关信号初相位可用二元组(j1, j3)表示。为验证输出端口Ⅰ的可控性,利用原型机设计的三组实验见表3。
表3 DISO模式下可控性验证
Tab.3 Controllability test under DISO mode
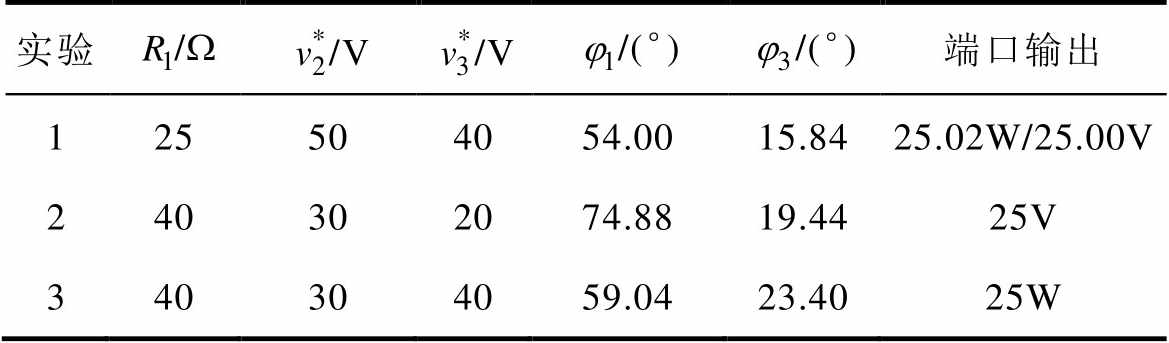
实验/W/V/V/(°)/(°)端口输出 125504054.0015.8425.02W/25.00V 240302074.8819.4425V 340304059.0423.4025W
实验1为初始状态,此时端口Ⅰ输出电压和功率分别为25V和25.02W。改变端口配置为实验2中数值后,(j1, j3)变化为(74.88°, 19.44°)时,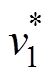 仍为25V(与实验1一致)。
仍为25V(与实验1一致)。
对比实验1、实验2可知,当端口配置变化时,可通过改变j 来稳定输出电压,即验证了系统输出电压的可控性。类似地,实验1、3验证了系统输出功率的可控性。
3.2.2 单输入双输出模式(SIDO)
在SIDO模式下,令端口Ⅱ为输入、端口Ⅰ和Ⅲ为输出。则端口配置可表示为(R1, 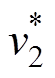 , R3),开关信号初相位表示方法同3.2.1节。SIDO模式下需验证电压功率混合、定电压和定功率三种方式的可控性,实验设计思路与3.2.1节类似,见表4。
, R3),开关信号初相位表示方法同3.2.1节。SIDO模式下需验证电压功率混合、定电压和定功率三种方式的可控性,实验设计思路与3.2.1节类似,见表4。
在初始状态(实验4)下,端口Ⅰ、Ⅲ输出均为20V/10W。表4实验5~7对应“端口输出”列的数据结构分别为(v1, p3)、(v1, v3)和(p1, p3)。将实验5、6、7分别与实验4对比,能验证混合控制、定电压控制和定功率控制的可控性。
表4 SIDO模式下可控性验证
Tab.4 Controllability test under SIDO mode

组别R1/W/VR3/Wj1/(°)j3/(°)端口输出 440504055.8055.8010.04W/19.96V 550503074.8819.44(20.00V, 10.05W) 650503059.0423.40(19.95V, 20.21V) 740604050.4059.00(9.97W, 10.00W)
3.2.3 异常工况
为验证MWiDC在异常工况下的鲁棒性,设计如下两个实验:一个模块(因故障等因素)被移除后,三端口原型机可以退化为普通的双端WPT系统,记为实验8;移动图6中线圈Ⅰ,令线圈Ⅰ、Ⅱ间隔加倍,同时水平方向移动一个线圈半径的距离,记为实验9。
以上九组实验中,线圈电压和半桥下管开关波形如附图1所示。附图1中,Vcoil、Vds和Vgs分别为线圈电压、下管漏源电压和下管栅源电压。下管Vds的下降沿略超前于Vgs的上升沿,因此系统能实现零电压开关。
上述九组实验中原型机效率如图7所示。各组效率均超过84%。在异常工况下,系统效率仍可达到91%。

图7 各组实验中原型机效率
Fig.7 Prototype efficiency in each experiment group
为了更全面地分析验证直接控制策略和解耦控制策略,本节以3.2.2节实验4下的三端口原型机为例进行分析,且控制方式设置为端口Ⅰ定电压控制、端口Ⅲ定功率控制。由式(12)、式(14)可知,解耦控制和直接控制下闭环系统为
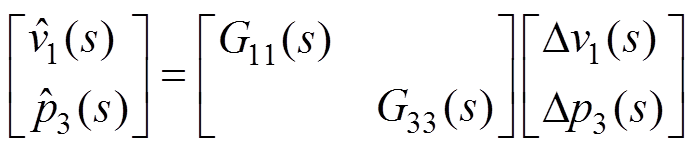 (15)
(15)
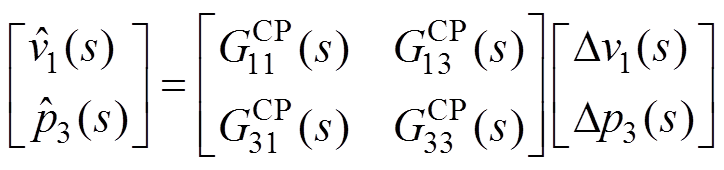 (16)
(16)
在直接控制策略下,v1的扰动会以增益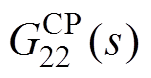 影响p3,p3的扰动也影响v1。
影响p3,p3的扰动也影响v1。
图8以伯德图形式对比了模块Ⅲ的前向、耦合传递函数。从图中可以看出,G33(s)和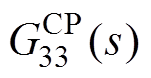 的幅频特性基本相同,近似为一阶惯性环节。而
的幅频特性基本相同,近似为一阶惯性环节。而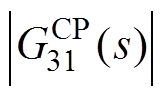 始终不超过-7.91dB,具有“全阻”特性。G11(s)、
始终不超过-7.91dB,具有“全阻”特性。G11(s)、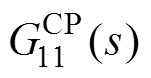 和
和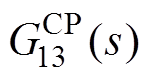 的关系与图8类似,不再赘述。
的关系与图8类似,不再赘述。
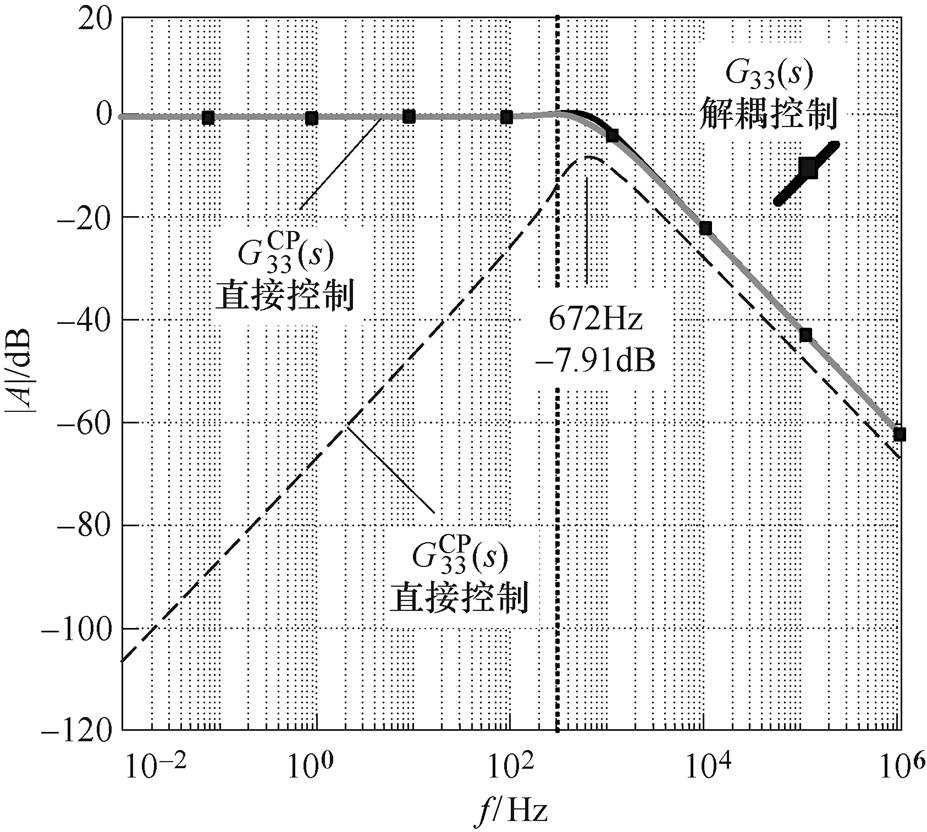
图8 闭环系统伯德图(幅频特性)
Fig.8 Magnitude-phase Bode diagram of closed-loop system
因此,在该算例中,直接控制策略下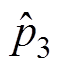 的动态特性与解耦控制系统基本相同,且交叉耦合本身也会被大大抑制,并不影响整体控制效果。
的动态特性与解耦控制系统基本相同,且交叉耦合本身也会被大大抑制,并不影响整体控制效果。
然而正如2.2节所述,在本算例中控制是否解耦对控制效果影响不大,并不代表直接控制策略具有普遍可行性。
在正常控制状态下,MWiDC各端口的电压或功率参考值均为常数,即频率为0。此时,从图8可知,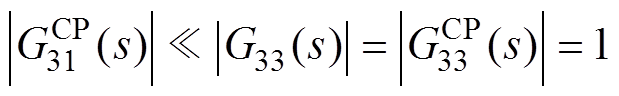 ,解耦控制和直接控制几乎无区别。这与附录的理论证明结果一致。图8可看作对文献[8, 13-14]实验结果的图形解释。
,解耦控制和直接控制几乎无区别。这与附录的理论证明结果一致。图8可看作对文献[8, 13-14]实验结果的图形解释。
为突出端口Ⅰ和端口Ⅲ之间的耦合,端口Ⅰ电压参考值在20V的基础上,叠加一峰峰值为2V、频率为200Hz的锯齿波扰动Dv1。端口Ⅲ功率参考值仍为纯直流分量10W。此时,Dv1为锯齿波,Dp3恒为0。在直接控制下,锯齿波Dv1会传递到端口Ⅲ,引起p3的波动;而在解耦控制下,p3的波动应该显著降低。图9和图10恰好证明了这一点。

图9 端口Ⅰ电压波形
Fig.9 Waveforms of v1
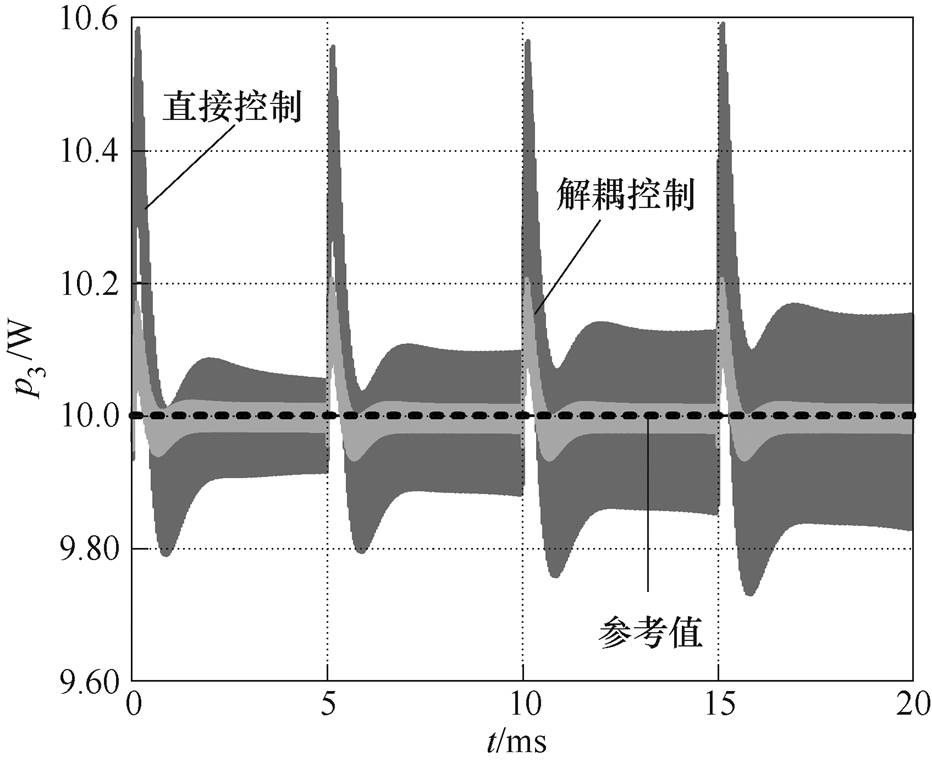
图10 端口Ⅲ功率波形
Fig.10 Waveforms of p3
端口Ⅰ电压波形如图9所示,端口Ⅲ功率波形如图10所示。两种控制策略下v1虽都能跟随锯齿形参考值,但直接控制的跟踪误差明显更大。在图10中,若系统采用直接控制策略,Dv1传递到端口Ⅲ,引起p3的波动。由于本文的工程实用小信号模型并非完全精确,解耦控制并不能完美地消除扰动。但即便如此,在解耦控制下,v1的跟踪误差更小,p3的波动也显著低于直接控制。
本节从阶跃响应的角度对两种控制策略进行比较。端口Ⅰ电压阶跃响应和端口Ⅲ功率阶跃响应分别如图11和图12所示。参考值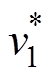 和
和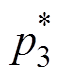 都在5ms发生阶跃,如图11、图12黑色虚线所示。两种控制策略下系统的阶跃响应基本相同,这与频域分析结果一致。
都在5ms发生阶跃,如图11、图12黑色虚线所示。两种控制策略下系统的阶跃响应基本相同,这与频域分析结果一致。
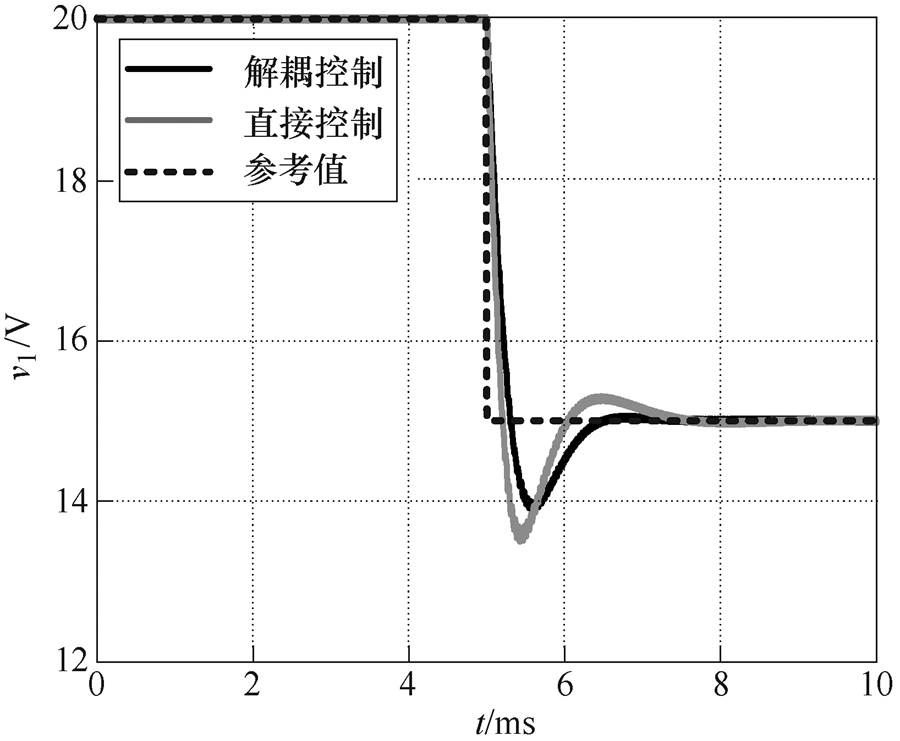
图11 端口Ⅰ电压阶跃响应
Fig.11 Step response of v1
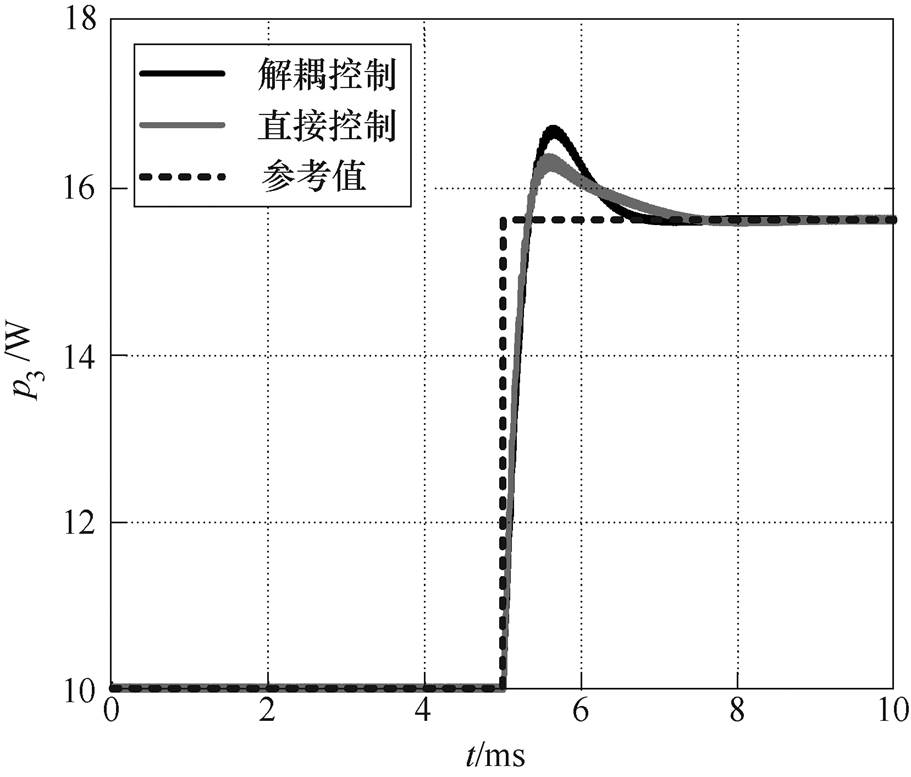
图12 端口Ⅲ功率阶跃响应
Fig.12 Step response of p3
本文提出了一种模块化MWiDC架构。和传统MDC相比,MWiDC具有更高的灵活性、可重构性和鲁棒性。首先,本文建立了MWiDC的数学模型,并提出了电压功率混合解耦控制策略。作为比较,本文也对直接控制策略进行了建模,并指出其抗干扰性差和稳定性缺乏一般性证明的问题。
为验证MWiDC及其控制策略,本文搭建了三端口原型机。硬件实验表明,原型机能灵活工作在DISO、SIDO和SISO三种模式,在线圈移位时仍能保持高效率。仿真表明,直接控制策略也能实现电压功率混合控制,但本文所提策略的抗干扰性更强。
定理1:PVHDC下各端口闭环系统均稳定,其直流增益为1,在高频段近似为一阶惯性环节。
证明:由式(12)、式(13)可得式(A1)。在式(A1)中令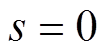 知直流增益为Gclk(0)=1。
知直流增益为Gclk(0)=1。
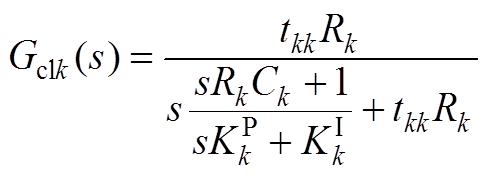 (A1)
(A1)
在高频段,|s|充分大,则
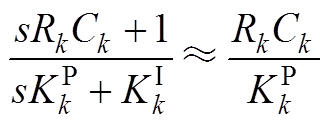 (A2)
(A2)
联立式(A1)、式(A2)可知
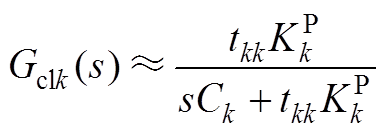 (A3)
(A3)
因此闭环系统在高频特性近似为一阶惯性环节。
根据式(A1),Gcl(s)的特征多项式为
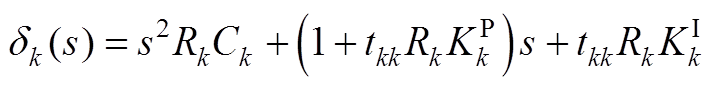 (A4)
(A4)
由劳斯判据易知闭环系统稳定。
定理2:在直接控制策略下,闭环系统直流增益矩阵为单位阵,高频段增益矩阵收敛于零矩阵。
证明:引入电阻矩阵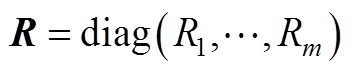 ,电容矩阵
,电容矩阵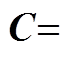
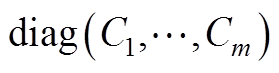 。对于所有PI调节器,引入比例系数矩阵
。对于所有PI调节器,引入比例系数矩阵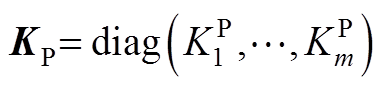 和积分系数矩阵
和积分系数矩阵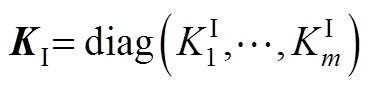 。于是
。于是
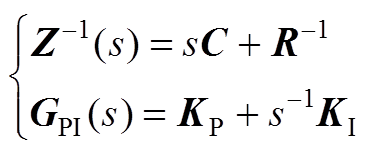 (A5)
(A5)
将式(A5)代入式(14)得
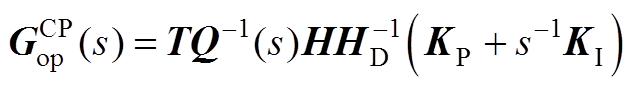 (A6)
(A6)
式中,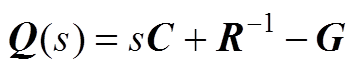 ,其行列式为m次多项式。
,其行列式为m次多项式。
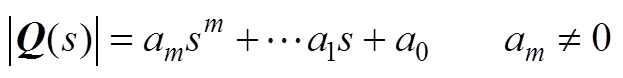 (A7)
(A7)
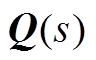 的伴随矩阵的各元素均为m-1次多项式。
的伴随矩阵的各元素均为m-1次多项式。
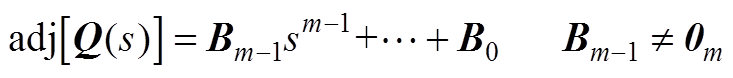 (A8)
(A8)
式中,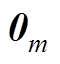 为m阶零矩阵。联立式(A7)、式(A8)可得
为m阶零矩阵。联立式(A7)、式(A8)可得
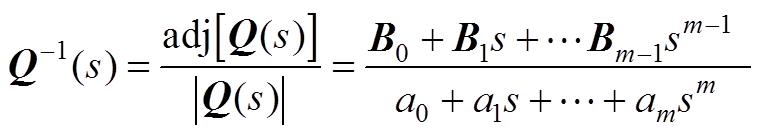 (A9)
(A9)
对式(A9)求极限有
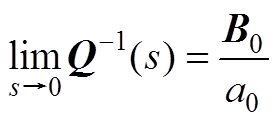 (A10)
(A10)
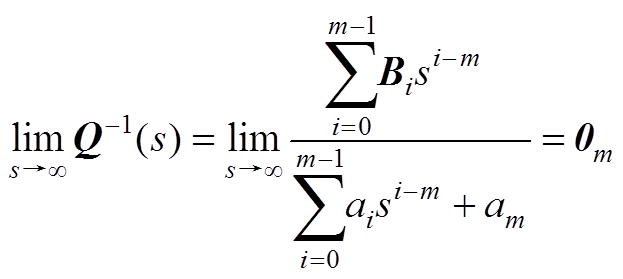 (A11)
(A11)
记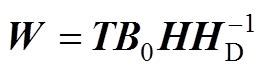 ,则有以下矩阵极限
,则有以下矩阵极限
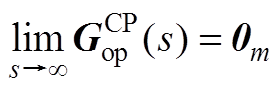 (A12)
(A12)
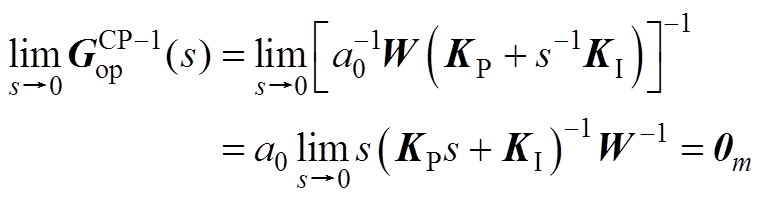 (A13)
(A13)
联立式(A12)、式(A13)和式(14)可知
 (A14)
(A14)
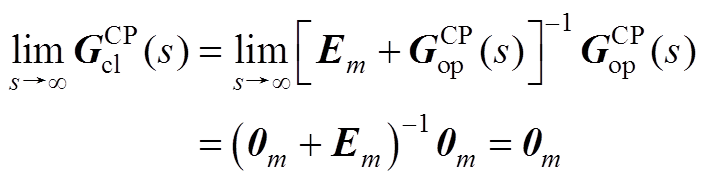 (A15)
(A15)
附图1为实验1~实验9中,线圈电压波形和半桥下管开关波形(以模块Ⅲ为例)。Vcoil、Vds和Vgs分别为线圈电压、下管漏源电压和栅源电压。


附图1 零电压开关波形(以模块Ⅲ为例)
Fig.App.1 Switching waveforms of ZVS (module Ⅲ)
参考文献
[1] 张辉, 梁誉馨, 孙凯, 等. 直流微电网中多端口隔离型DC-DC变换器的改进虚拟电容控制策略[J]. 电工技术学报, 2021, 36(2): 292-304.
Zhang Hui, Liang Yuxin, Sun Kai, et al. Improved virtual capacitor control strategy of multi-port isolated DC-DC converter in DC microgrid[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 292-304.
[2] 刘计龙, 朱志超, 肖飞, 等. 一种面向舰船综合电力系统的模块化三端口直流变换器[J]. 电工技术学报, 2020, 35(19): 4085-4096.
Liu Jilong, Zhu Zhichao, Xiao Fei, et al. A modular three-port DC-DC converter for vessel integrated power system[J]. Transactions of China Electro- technical Society, 2020, 35(19): 4085-4096.
[3] Alshareef M, Lin Zhengyu, Li Fulong, et al. A grid interface current control strategy for DC micro- grids[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(3): 249-256.
[4] 孙孝峰, 刘飞龙, 熊亮亮, 等. 双Buck/Boost集成双有源桥三端口DC-DC变换器[J]. 电工技术学报, 2016, 31(22): 73-82.
Sun Xiaofeng, Liu Feilong, Xiong Liangliang, et al. Dual Buck/Boost integrated dual active bridge three- port DC-DC converter[J]. Transactions of China Electrotechnical Society, 2016, 31(22): 73-82.
[5] 刘贝, 帅智康, 肖凡, 等. 三有源桥变换器简化分析模型及优化控制策略[J]. 电工技术学报, 2021, 36(11): 2394-2407.
Liu Bei, Shuai Zhikang, Xiao Fan, et al. Simplified analysis model and optimal control strategy of triple active bridge converter[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2394-2407.
[6] El Shafei A, Ozdemir S, Altin N, et al. Development of a medium voltage, high power, high frequency four-port solid state transformer[J]. CES Transactions on Electrical Machines and Systems, 2022, 6(1): 95-104.
[7] 宫金武, 查晓明, 王盼, 等. 大容量多端口变换器拓扑研究综述[J]. 电源学报, 2017, 15(5): 1-9.
Gong Jinwu, Zha Xiaoming, Wang Pan, et al. Review of topology research on high-power multi ports converter[J]. Journal of Power Supply, 2017, 15(5): 1-9.
[8] Zhang Xin, Liu Fuxin, Lei Kelin, et al. Three-port magnetically coupling resonant wireless energy router and its zero-power-flow control scheme[C]//IECON 2020 The 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 2020: 3936- 3941.
[9] Liu Xiaobo, Rong Cancan, Tao Xiong, et al. Multi- DoF wireless power transfer systems based on magnetic dipole coils with multiple receivers[J]. Journal of Power Electronics, 2022, 22(3): 534-546.
[10] Shi Liming, Yin Zhenggang, Jiang Longbin, et al. Advances in inductively coupled power transfer technology for rail transit[J]. CES Transactions on Electrical Machines and Systems, 2017, 1(4): 383- 396.
[11] Liu Ming, Wang Ping, Guan Yueshi, et al. A 13.56MHz multiport-wireless-coupled (MWC) battery balancer with high frequency online electrochemical impedance spectroscopy[C]//2019 IEEE Energy Con- version Congress and Exposition (ECCE), Baltimore, USA, 2019: 537-544.
[12] Liu Ming, Chen Yenan, Elasser Y, et al. Dual frequency hierarchical modular multilayer battery balancer architecture[J]. IEEE Transactions on Power Electronics, 2021, 36(3): 3099-3110.
[13] Wang Ping, Chen Yenan, Kushima P, et al. A 99.7% efficient 300W hard disk drive storage server with multiport AC-coupled differential power processing (MAC-DPP) architecture[C]//2019 IEEE Energy Con- version Congress and Exposition (ECCE), Baltimore, USA, 2019: 5124-5131.
[14] Chen Yenan, Wang Ping, Elasser Y, et al. Multicell reconfigurable multi-input multi-output energy router architecture[J]. IEEE Transactions on Power Elec- tronics, 2020, 35(12): 13210-13224.
[15] Zhao Chuanhong, Kolar J W. A novel three-phase three-port UPS employing a single high-frequency isolation trans-former[C]//(IEEE Cat. No. 04CH37551), Aachen, Germany, 2004, 6: 4135-4141.
[16] Falcones S, Ayyanar R, Mao Xiaolin. A DC-DC multiport-converter-based solid-state transformer integrating distributed generation and storage[J]. IEEE Transactions on Power Electronics, 2013, 28(5): 2192-2203.
[17] Repecho V, Olm J M, Griñó R, et al. Modelling and nonlinear control of a magnetically coupled multi- port DC-DC converter for automotive applications[J]. IEEE Access, 2021,9: 63345-63355.
[18] Wang Ping, Chen Minjie. Towards power FPGA: architecture, modeling and control of multiport power converters[C]//2018 IEEE 19th Workshop on Control and Modeling for Power Electronics (COMPEL), Padova, Italy, 2018: 1-8.
Modular Multiport Wireless DC-DC Converter with Multidirectional Power Flow and Its Decoupling Control Strategy
Abstract Multiport wireless DC-DC converter (MWiDC) has the potential to realize efficient multiport power conversion with high-level flexibility and expansibility. However, its system modeling and power flow management need more general theory. Therefore, this paper proposes a modular MWiDC. Firstly, a model of an arbitrary MWiDC is established, and a power-voltage hybrid decoupling control (PVHDC) strategy is designed. The closed-loop DC gain, high-frequency characteristic, and stability under the PVHDC strategy are demonstrated. This paper also analyzes the direct control strategy (DCS) without decoupling for comparison. However, the closed-loop stability of the DCS still needs to be proved due to the system’s complexity. Finally, the experiment and simulations are carried out on a three-port prototype. The experimental results show that the prototype can realize zero voltage switching with an efficiency of 91%. The simulation indicates that both PVHDC and DCS can realize voltage-power hybrid control, but PVHDC has a stronger anti-disturbance.
keywords:Multiport DC-DC converter (MDC), wireless power transfer (WPT), decoupling control, multidirectional power flow (MPF)
DOI: 10.19595/j.cnki.1000-6753.tces.220977
中图分类号:TM724
上海市自然科学基金项目(21ZR1431100)和台达电力电子科教发展基金项目资助。
收稿日期 2022-05-31
改稿日期 2022-08-15
宋 钊 男,1998年生,硕士研究生,研究方向为多端口无线能量传输系统。E-mail: szh-98@sjtu.edu.cn
刘 明 男,1985年生,副教授、博士生导师,研究方向为兆赫兹无线能量传输、高频电力电子。E-mail: mingliu@sjtu.edu.cn(通信作者)
(编辑 陈 诚)