1，fs为变换器的开关频率，Ts为变换器的开关周期，fr为谐振腔的串联谐振频率，其可表示为摘要 该文提出一种基于脉宽调制的电流断续型谐振变换器，并对其进行深入研究。该变换器采用定频脉冲宽度调制控制，其在一次侧桥臂增加了辅助电感和辅助电容，通过调节一次侧桥臂驱动信号的占空比可以改变桥臂中点之间的电压幅值，继而可以调节变换器的电压增益。通过合理的参数设计，变换器的谐振电流工作在断续模式，因此不存在无功电流。同时，该变换器的所有开关管皆可实现软开关，减小了开关损耗。该文首先对变换器的工作原理及开关模态进行分析；然后结合变换器的工作特性，推导变换器的电压转换增益、软开关条件以及断续工作的条件，并且提出一种参数设计方法；最后研制了一台1 000W的样机来验证变换器的可行性与理论分析的正确性。
关键词：电流断续模式 脉冲宽度调制 谐振变换器 软开关
近年来，随着新能源产业的快速发展，电力电子变换装置遇到了更高的挑战，越来越多的研究工作者开展了大量的研究以追求变换器的高功率、高转换效率以及高功率密度。而直流变换器作为电能变换中重要的环节也成为了研究的重点[1-3]。
直流变换器可分为脉冲宽度调制（Pulse Width Modulation, PWM）型变换器和谐振型变换器。PWM型直流变换器有常见的Buck、Boost、正激、反激和推挽等形式，其通过PWM信号以实现电压增益的控制[4-5]。但这些变换器通常难以实现软开关，因而影响其转换效率。常见的谐振型变换器有LC和LLC形式等[6]，由于LLC谐振变换器能够实现全负载范围零电压开通（Zero Voltage Switching, ZVS）和零电流关断（Zero Current Switching, ZCS），并且具有较高的转换效率，因而得到了广泛的应用[7]。
传统LLC谐振变换器通常采用变频率调制（Pulse Frequency Modulation, PFM）来实现电压增益的调整[8]。同时，为了满足LLC谐振变换器较宽的增益范围，通常变压器会设计较小的励磁电感，但这将导致变换器在运行时具有较大的环流，从而影响其转换效率[9]，并且变频率控制会增大变换器磁性元器件的设计难度，增加磁心的损耗。为此，亦有研究工作者将移相控制应用于LLC变换器，通过调整变换器一次侧逆变桥臂的内移相角度来控制变换器的电压增益[10]。但是，当变换器运行在较大的移相角度时，ZVS较难实现。为此可以添加一些辅助元器件来帮助变换器实现ZVS。如在一次侧桥臂中点连接辅助电感，以便于在死区时间内注入额外的电流对开关管的结电容进行充放电[11]。但是此方法不仅给变换器带来了额外的损耗，同时也增加了磁性元器件的数量。
为了提高谐振变换器的性能，研究工作者亦从拓扑结构改进的角度来解决目前所面临的问题。两级式结构的组合变换器具有结构简单和控制灵活的优点，文献[12-13]将Buck变换器与LLC谐振变换器进行组合。其中LLC变换器工作在谐振工作点，以实现电气隔离以及高效率电能变换，并且采用Buck变换器进行调压，但是两级式结构导致系统转换效率偏低。文献[14-16]采用并联组合式结构以实现变换器调压功能，其中LLC变换器工作在谐振点，并且传递变换器的大部分功率。而通过对另一个变换器进行增益调节来改变变换器总的输出电压。但是该结构增加了器件数量与成本。文献[17]在LLC变换器的基础上为变压器增加了一个调压绕组，通过控制调压电路的增益来实现变换器输出电压的调整。对于文献[14-17]所提出的调压方法，其皆在LLC变换器的基础上增加了额外的开关电路来辅助调节总电压增益，对此不仅增加了拓扑结构的复杂度，也提高了变换器的成本。
本文提出了一种基于脉宽调制的电流断续型谐振变换器。该变换器采用定频PWM控制，并在一次侧桥臂上增加了辅助电感La与辅助电容Ca。通过调节一次侧开关管的驱动信号的占空比可以改变一次侧桥臂中点之间的电压幅值，继而可以调节变换器电压增益。由于变换器的谐振电流工作在断续模式，因此谐振腔中不存在无功电流。同时，变换器的所有开关管皆可实现软开关，有助于减小开关损耗。本文首先分析了变换器的拓扑结构及其工作原理；然后从变换器增益、软开关条件和断续运行条件三个方面进行分析，并给出了变换器参数设计步骤；最后通过建立实验平台对所提拓扑的可行性进行验证。
本文所提出的基于脉宽调制的电流断续型谐振变换器如图1所示。图1中，Vin为输入电压，Vo为输出电压，ir为变压器一次电流，is为变压器二次电流，开关管S1～S4组成变换器的一次侧逆变桥，S5～S8组成同步整流桥，La为辅助电感，Ca为辅助电容，La连接在S1和S2组成的桥臂中点A与开关管S4的源极之间，Ca连接在S2与S4的源极之间，Cb为隔直电容，其与变压器一次侧串联连接在A点与B点之间，Cr与Lr组成变换器的谐振腔，其与变压器二次侧串联连接在二次侧桥臂中点C与D之间，Cf为变换器的输出直流电容，R为输出负载。
变换器的参数定义如下：变压器一次侧与二次侧的电压比定义为n1，fs为变换器的开关频率，Ts为变换器的开关周期，fr为谐振腔的串联谐振频率，其可表示为
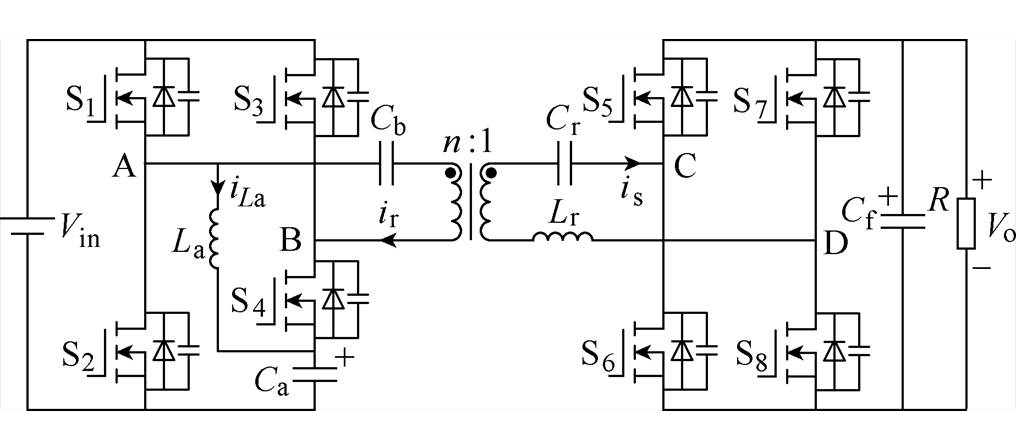
图1 基于脉宽调制的电流断续型谐振变换器
Fig.1 Discontinuous current mode resonant converter with pulse width modulation control
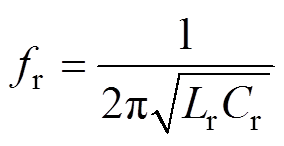（1）
变换器工作在恒定的开关频率，使用PWM来调节变换器增益，其主要的工作波形如图2所示。图2中，开关管S1与S4、S2与S3；S5与S8、S6与S7同时开通和关断。S2与S3的导通时间与开关周期的比例定义为占空比D。一次侧输入电源Vin通过开关管S1与S2和辅助电感La将能量传递至Ca。当变换器的占空比D改变时，辅助电容Ca上的电压VCa也会随之改变。继而改变一次侧逆变桥中点电压vAB的电压幅值，同时变换器增益也随之改变。因此，该变换器的一部分能量通过辅助电感La进行传递，而另一部分能量直接通过逆变桥进行传递。
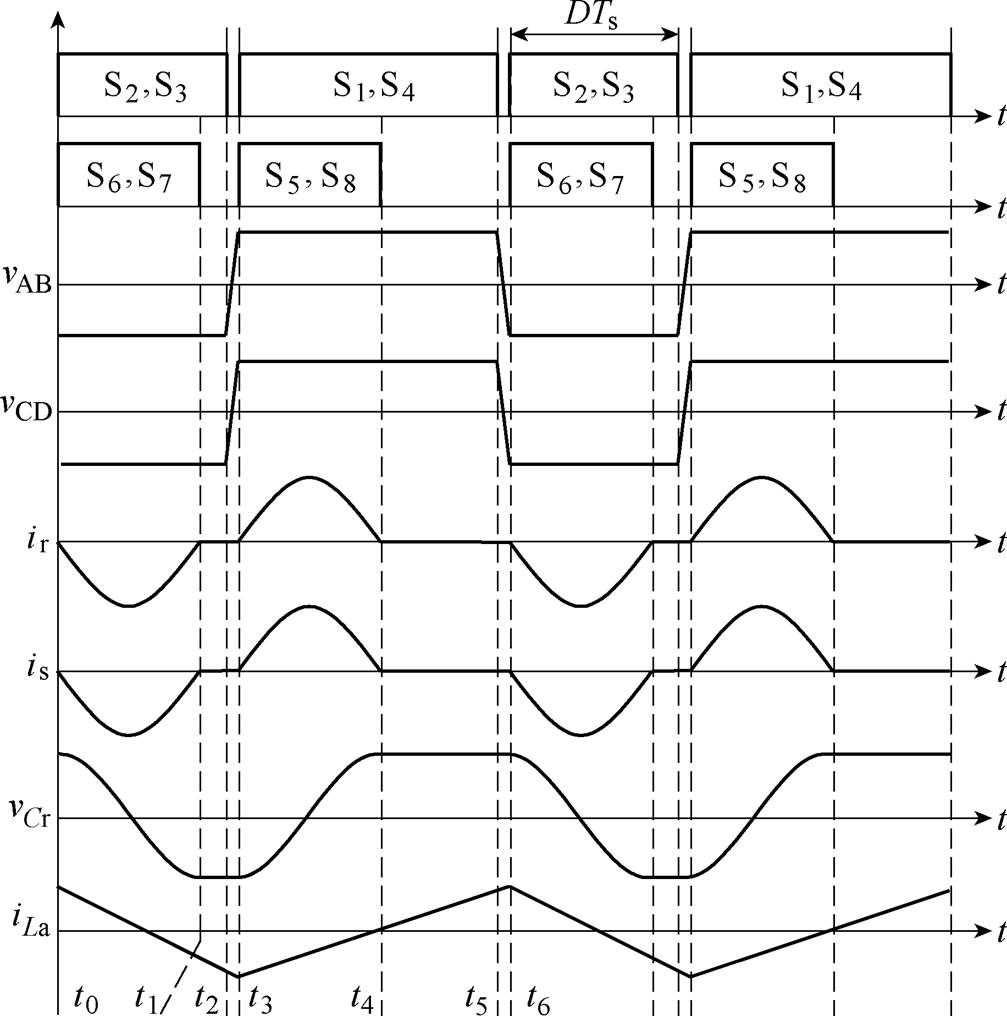
图2 变换器主要工作波形
Fig.2 The key operating waveforms of the propsoed converter
为了简化分析，作如下假设：
（1）除了考虑开关管的结电容外，电路中的开关管与本体二极管均为理想器件。
（2）输出滤波电容Cf足够大，同时忽略输入输出电压纹波。
（3）变压器的励磁电感远大于谐振电感，因此在分析时，不考虑励磁电感。
（4）隔直电容Cb足够大，不影响谐振频率。
变换器在各个阶段的等效运行电路如图3所示。其具体描述如下。
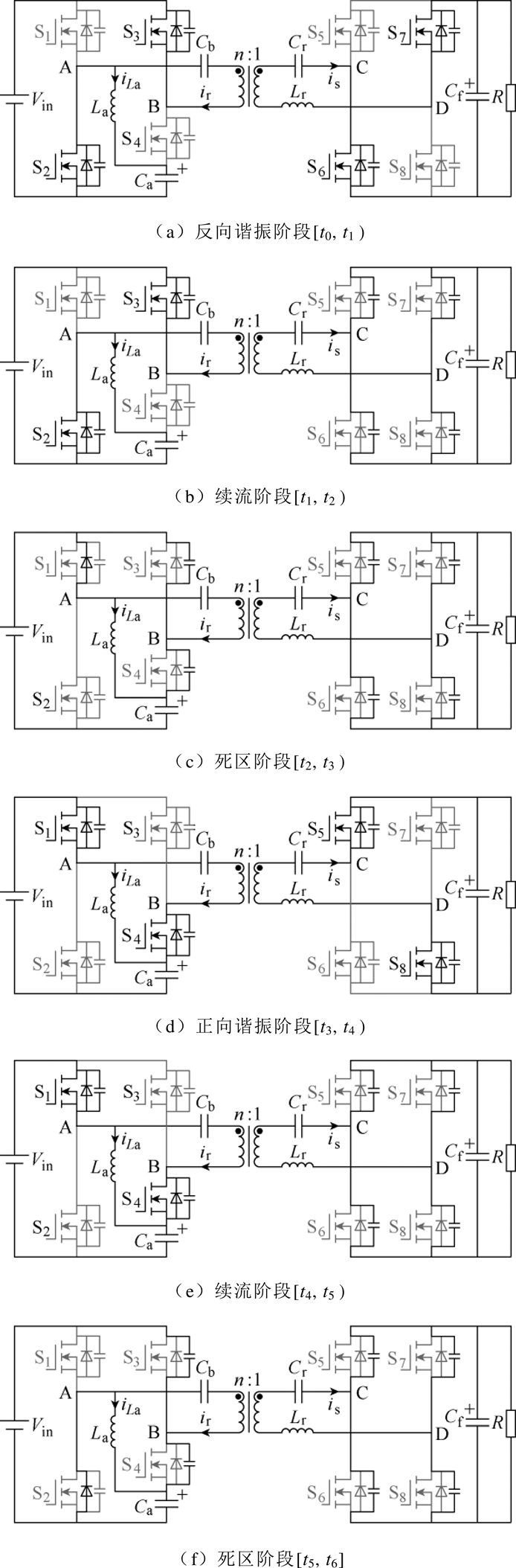
图3 变换器各阶段等效电路
Fig.3 Equivalent circuits of the converter in each interval
反向谐振阶段[t0, t1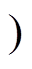
：如图3a所示，在t0时刻，开关管S2零电压开通，S3零电流开通。辅助电感电流iLa线性下降。同时，谐振电感Lr与谐振电容Cr开始谐振，谐振电流ir从零开始反向谐振变化。然后，S6和S7作为同步整流管开通。在t1时刻，谐振电流ir谐振至零时，该阶段结束，同时，同步整流管S6和S7零电流关断。在这个阶段，谐振电流可以表示为
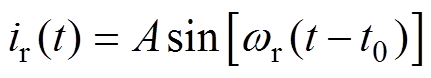（2）
式中，A为谐振电流峰值；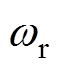
为串联谐振角频率，
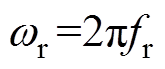。辅助电感电流iLa可表示为
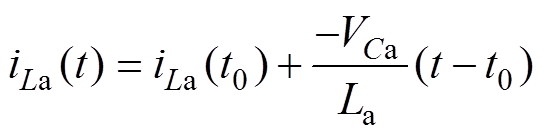（3）
式中，iLa(t0)为在t0时刻辅助电感电流初值；VCa为辅助电容Ca两端的电压。
续流阶段[t1, t2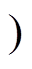：如图3b所示，在t1时刻，同步整流管S6和S7零电流关断。由于开关管S2未关断，辅助电感电流iLa继续线性下降。在这个阶段中，谐振电流恒定为零，变换器不传递能量。t2时刻，开关管S2和S3关断，该阶段内谐振电流ir和辅助电感电流iLa可以分别表示为
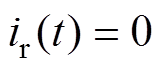（4）
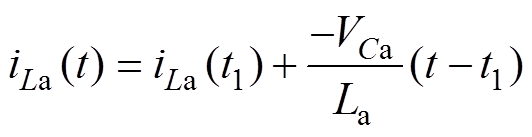（5）
死区阶段[t2, t3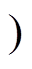：如图3c所示，在t2时刻，开关管S2和S3关断。由于此时辅助电感电流极性为负，所以在死区时间内辅助电感电流将通过开关管S1的本体二极管进行续流，为下一时刻S1零电压开通做好准备。
该变换器后半个周期的工作原理与前半个周期类似，因此不做详细的介绍。
变换器工作在断续谐振模式，通过调节PWM信号的占空比来改变变换器增益。根据图2所示的变换器工作波形，可以列出变换器的输入功率表达式为
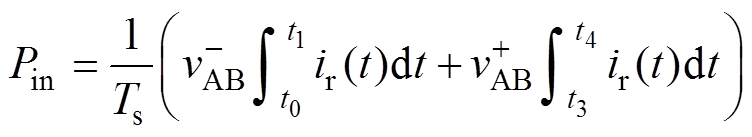（6）
式中，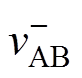
为vAB在t0～t1时刻的值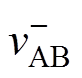，=-Vin；
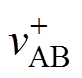为vAB在t3～t4时刻的值，可表示为
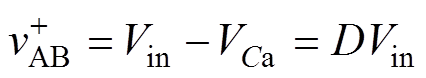（7）
由于变换器的正负半周的谐振电流对称，有
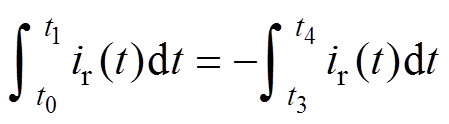（8）
继而变换器的输入功率可以化简为
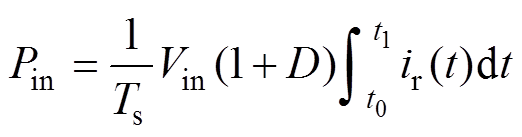（9）
根据相同的方法，变换器的输出功率可表示为
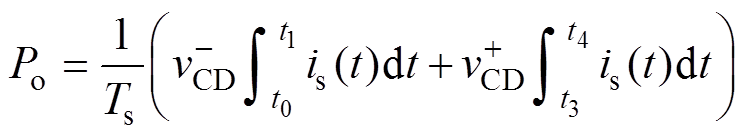（10）
式中，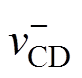
为vCD在t0～t1时刻的值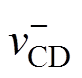，=-Vo；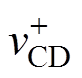
为vCD在t3～t4时刻的值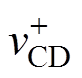，=Vo。由于is=nir，因此变换器输出功率可以化简为
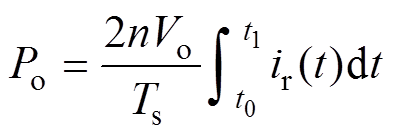（11）
根据功率守恒原理，变换器的输入功率等于输出功率。因此可以求得变换器的电压增益为
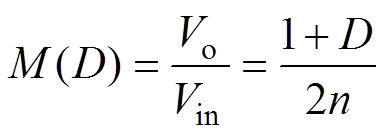（12）
根据式（12）可知，所提出的变换器理论上可实现2倍的电压增益范围。但是由于变换器运行的最小占空比需要大于零，因此，变换器的电压增益范围在实际运行中会小于2倍。通过联立式（2）和式（11），变换器的输出功率可以化简为
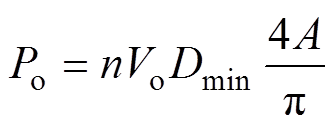（13）
式中，Dmin为变换器的最小运行占空比，Dmin=fs/(2 fr)。通过分析式（13）可知，在相同的输出功率下，最小运行占空比Dmin越小，谐振电流峰值A越大，继而开关管所承受的电流应力越大。因此，在对变换器参数设计时需要在电压增益范围与谐振电流峰值之间做出折中。
根据图2所示的变换器主要工作波形分析可知，一次侧开关管S3与S4可实现零电流开通与关断。二次侧开关S5～S8作为同步整流管，可以实现零电流开通与零电流关断。通过对辅助电感La合理的设计，开关管S1与S2可以实现零电压开通。
为实现开关管S1与S2的零电压开通，在死区时间内，辅助电感需要存储充足的能量以对开关管的结电容进行充放电。因此，可以得到
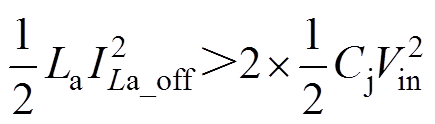（14）
式中，ILa_off为开关管关断时辅助电感的电流；Cj为开关管的结电容。
分析图1所示的电路拓扑可知，流过辅助电感La的电流平均值与开关管S4的平均电流互为相反数，可以表示为
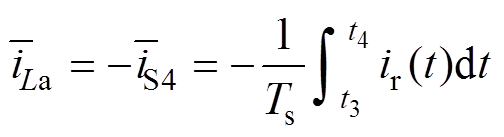（15）
继而可以求得iLa在t0时刻和t3时刻的值分别为
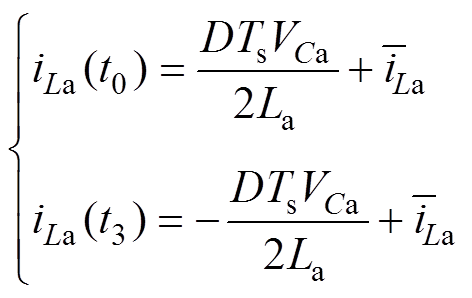（16）
从式（16）可知，iLa在t0时刻的峰值小于在t3时刻的峰值，因此只要开关管在t0时刻能实现零电压开通，在t3时刻时便能实现零电压开通。根据式（14）、式（16）可得开关管S1与S2的零电压开通条件为
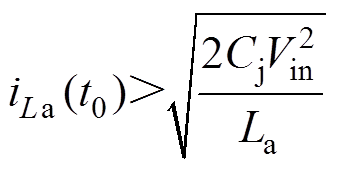（17）
根据图2所示的变换器主要工作波形可知，变换器的谐振电流工作在断续模式。为了维持谐振电流断续的状态，在续流阶段，谐振电流应维持为零，避免电流反谐振。
图4所示为变换器的等效电路。为保持断续模式，在续流阶段内，谐振电容上的电压应小于vAB、vCD和隔直电容上的电压之和。根据此关系可以列出
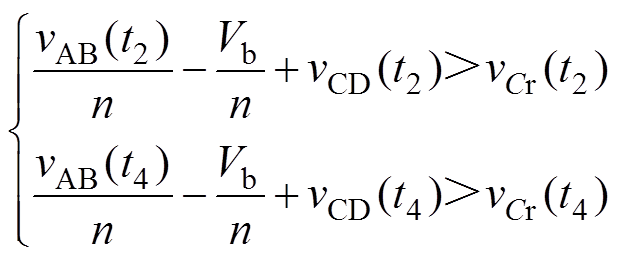（18）
式中，Vb为隔直电容上的电压，其值为vAB的平均值，可表示为
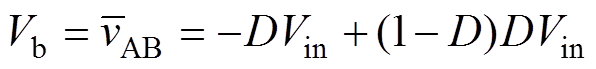（19）
谐振电容两端电压在t2和t4时刻可分别表示为
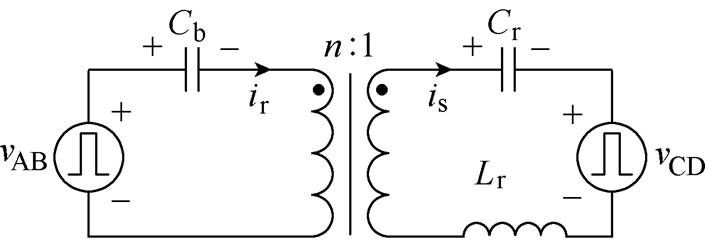
图4 变换器等效电路
Fig.4 Equivalent circuit of the proposed converter
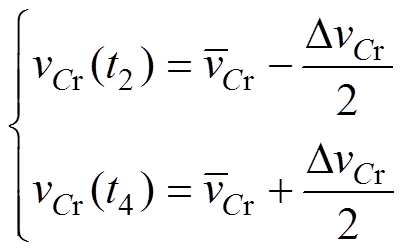（20）
式中，谐振电容电压的平均值等于vCD的平均值，可表示为
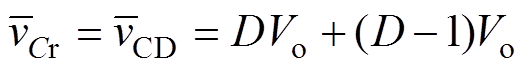（21）
DvCr为谐振电容电压的峰峰值，其可以计算为
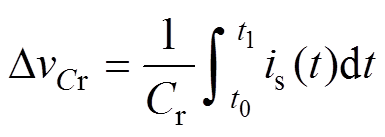（22）
根据输出功率表达式（11）、式（21）可化简为
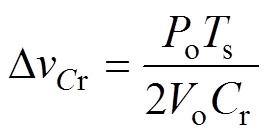（23）
由式（23）可知，谐振电容两端电压的峰峰值随着功率的增大而增大。为了保持变换器工作在断续模式，DvCr不应太大。因此需要根据功率需求合理地设计谐振电容Cr的大小。
变压器的电压比n可以根据变换器的增益表达式（12）进行设计。图5所示为变换器的归一化电压增益与占空比D的曲线。如图5所示，变换器理论上可达到2倍电压增益。倘若变换器工作在较小的占空比，会导致较大的谐振电流峰值。因此，在实际应用中，变换器需小于2倍的电压增益。
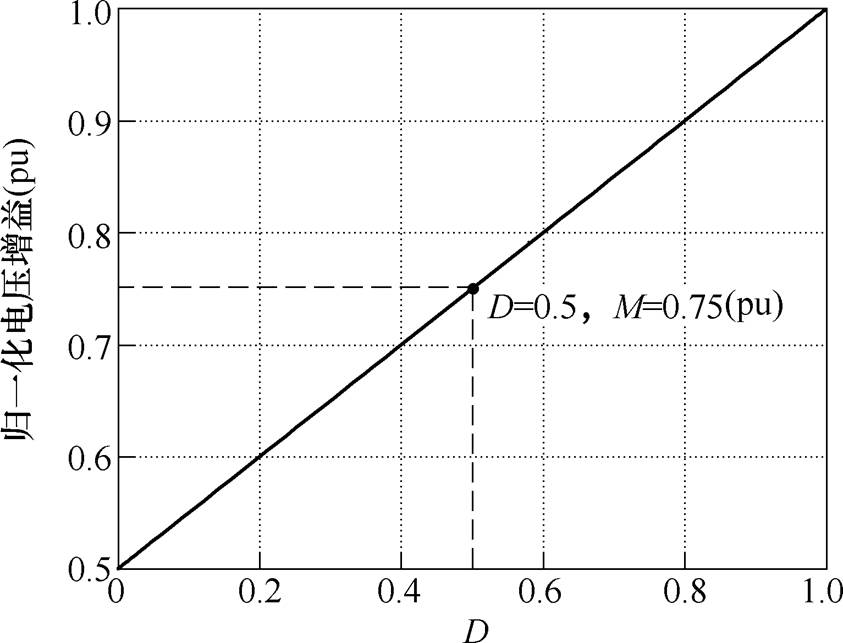
图5 变换器电压增益标幺值
Fig.5 The normalized voltage gain of the converter
根据电压增益表达式（12），则与变压器电压比关系可表示为
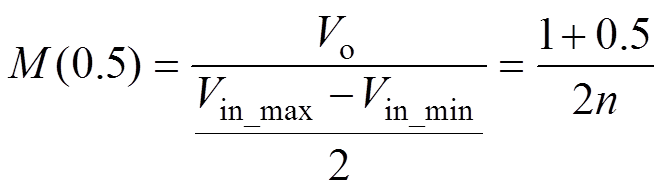（24）
式中，Vin_max和Vin_min分别为输入电压的最大值与最小值。
LC谐振腔参数可以根据谐振频率和最大传递功率进行设计。为了满足断续运行条件，变换器开关管最小导通时间需大于半个谐振周期，因此谐振频率可以计算为
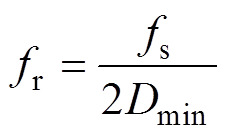（25）
式中，Dmin为最小占空比，其可根据输入电压范围确定。谐振电容Cr的大小可以根据电流断续条件进行设计，表示为
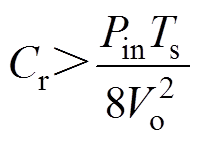（26）
从式（26）可以看出，谐振电容的大小与变换器输入功率成正比。谐振电感可以根据式（1）进行设计，表示为
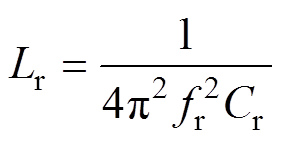（27）
根据式（25）～式（27），谐振电感的范围可计算为
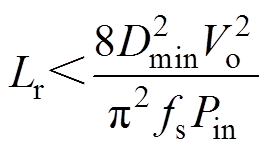（28）
辅助电感La的设计需要考虑开关管S1与S2的零电压开通条件。通过联立式（15）～式（17）可以得到
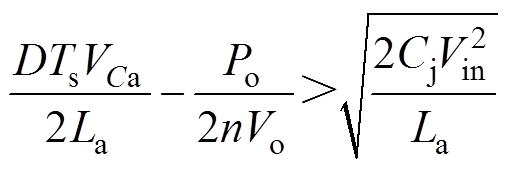（29）
根据式（29）可以计算出辅助电感La的大小。
根据对变换器的工作特性分析可以得到，流过辅助电感La的电流平均值与开关管S4的平均电流互为相反数。通过化简式（15）可以得到电感电流平均值的表达式为
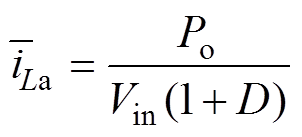（30）
从式（30）可知，辅助电感La的电流应力与变换器的运行占空比D有关，当运行占空比D最小时，电流应力最大。
对于辅助电容Ca，其电压可计算为
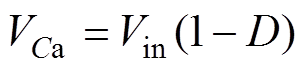（31）
从式（31）可知，当变换器运行占空比最小时，辅助电容承受的应力最大，其值为输入电压Vin。
为了验证所提出拓扑的可行性以及理论分析的正确性，根据第3节的设计方法，设计了一台输入电压范围100～125V，输出电压400V，最大输出功率1 000W的实验样机如图6所示，变换器实验样机参数见表1。根据式（28）和变换器样机的参数，可以计算得谐振电感应小于116mH。由于实验样机变压器的自身漏感为8mH，其值满足变换器断续运行的条件，因此实验样机可以使用变压器的自身漏感作为谐振电感，而无需增加外置谐振电感。
图6 实验样机
Fig.6 The prototype of the proposed converter
表1 变换器实验样机参数
Tab.1 The prototype parameters of the proposed converter
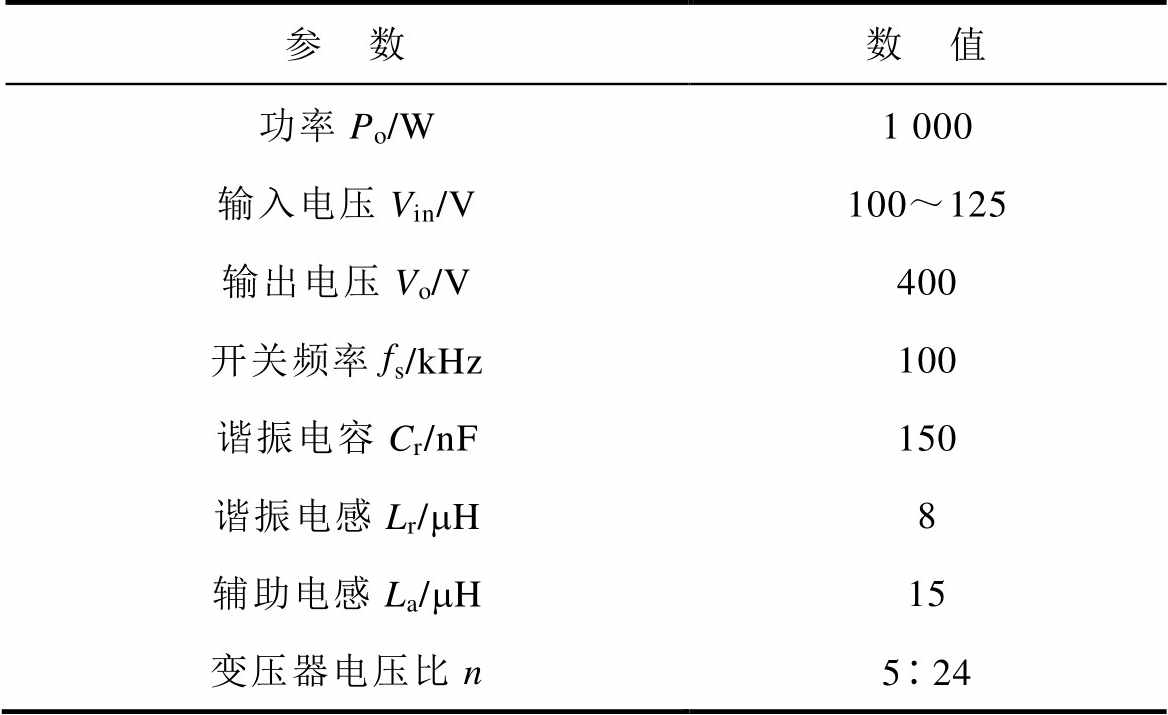
参 数数 值 功率Po/W1 000 输入电压Vin/V100～125 输出电压Vo/V400 开关频率fs/kHz100 谐振电容Cr/nF150 谐振电感Lr/mH8 辅助电感La/mH15 变压器电压比n524
对于传统变频式谐振变换器，在其设计变换器的增益曲线时，需要对漏感和励磁电感的比例进行设计。因此，传统的变频式谐振变换器需要添加和设计额外的漏感。不同于传统方案，所提出变换器的电压增益不受谐振电感大小的影响。因此，在所提出拓扑的实验样机中，变换器的谐振电感采用变压器的自身漏感。在实验样机中，所提出变换器包含两个磁性元件（辅助电感和变压器），其数量与传统变频式谐振变换器相同。因此，以元器件数量角度对比于传统方案，所提出的拓扑仅增加了辅助电容和隔直电容。在实验样机中，辅助电容和隔直电容采用了陶瓷式贴片电容，其体积与质量只占整体装置较小的一部分。此外，对比于传统变频式谐振变换器，所提出拓扑采用定频PWM控制策略能够降低磁性元件损耗。最后，虽然辅助电容和隔直电容的引入使得装置体积有所增加，但其简化了拓扑控制和降低了磁性元件损耗。
图7所示为变换器在不同输入电压下的满载稳态工作波形，图中，vgs1和vgs5分别为开关管S1和S5的驱动电压，is为二次侧谐振电流，vo为输出电压。变换器工作在电流断续的模式，因此开关管S3～S8可以实现零电流开通和零电流关断。在不同输入电压下时，vgs1的占空比不同。变换器可以通过调节占空比来改变电压增益。
图8所示为变换器在不同输入电压下的零电压开通波形，图中，vgs2为开关管S2的驱动电压，vds2为开关管S2的漏源极电压，vAB为变换器桥臂中点A与B之间的电压，iLa为辅助电感La的电流。在不同输入电压下，开关管S2可实现零电压开通。
图7 变换器在不同输入电压下的满载稳态波形
Fig.7 The steady-state waveforms of the converter with different input voltages at reated power
图8 变换器在不同输入电压下零电压开关波形
Fig.8 ZVS waveforms of the converter with different input voltages
图9所示为变换器在不同输入电压下从轻载切换至满载的动态波形，io为输出电流。由图9可知，变换器在切换负载时能够正常闭环工作。同时，在不同输入电压下，变换器切载的动态调节时间基本一致。
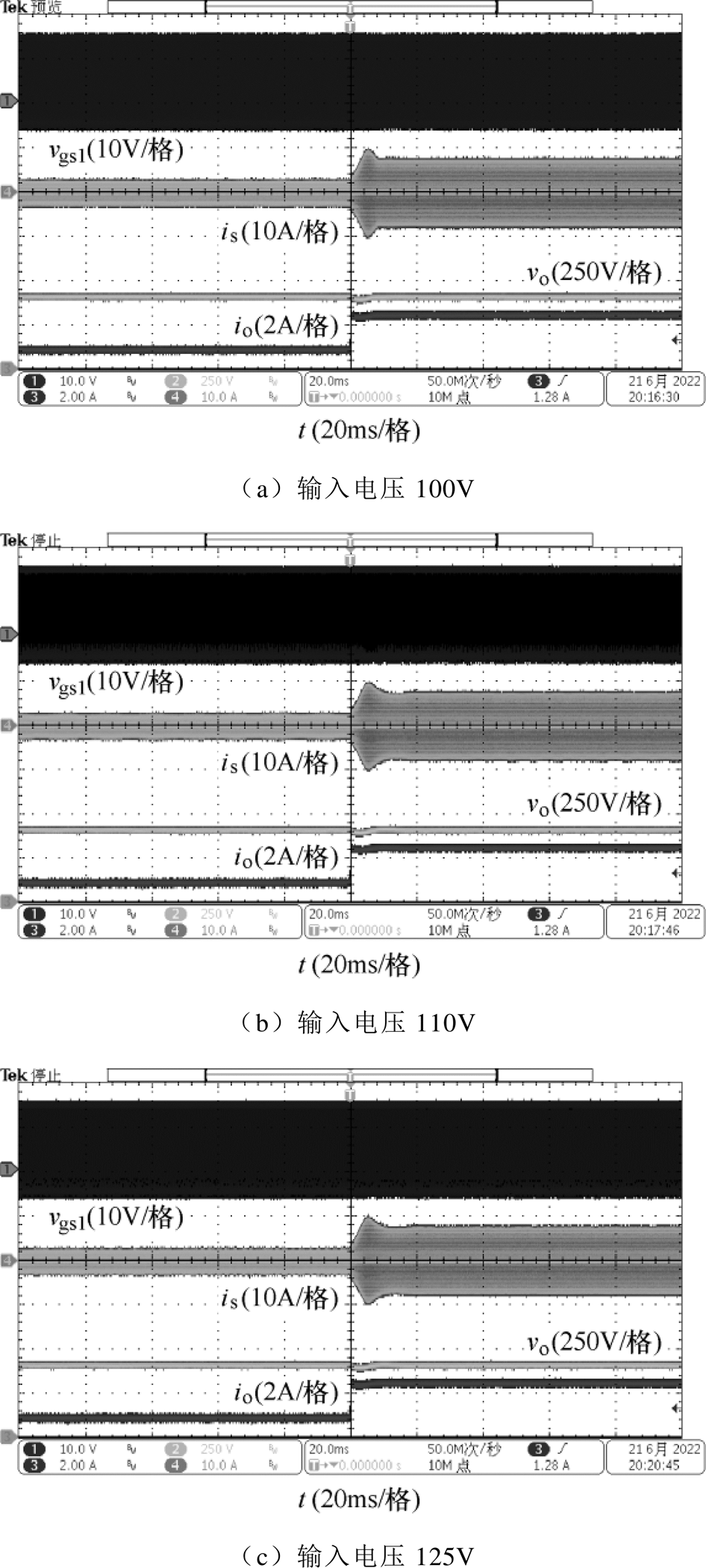
图9 变换器在不同输入电压下的切载动态波形
Fig.9 Dynamic waveforms of the load step change for the converter with different input voltages
图10为变换器在输入电压变化时的动态波形，vin为变换器的输入电压。图10中，变换器在输入电压变化时，其输出电压基本保持不变。因此，变换器具有良好的闭环控制性能。
图11给出了变换器在不同输入电压和输出功率下的效率对比曲线。图11中，变换器在不同输入电压下的转换效率接近。在输入电压为125V时，其效率会略低于变换器在100V与110V的效率。变换器工作在输出功率为460W附近时效率最高，其峰值效率约为95%，变换器的满载效率约为93%。
图10 变换器在输入电压变化时的动态波形
Fig.10 Dynamic waveforms of the input voltage change for the converter
图11 变换器在不同输入电压与输出功率下的效率曲线
Fig.11 The efficiency of the converter with different input voltages and different output power
本文提出了一种基于脉宽调制的电流断续型谐振变换器，并对其工作原理进行了深入研究。该变换器在一次侧桥臂增加了辅助元件La与Ca，通过调节一次侧桥臂的驱动信号占空比可以改变桥臂中点A与B之间的电压幅值，继而可以调节变换器的电压增益。结合变换器的工作特性，本文对变换器的电压增益、软开关条件和谐振电流断续条件进行了分析，同时提出了一种变换器的参数设计方法。最后，通过设计一台1 000W的实验样机来验证理论分析的可行性。该变换器的主要优点可总结如下：
1）谐振电流工作在断续模式，因此谐振腔中不包含无功电流。同时，断续的电流有助于开关管实现零电流开通与关断。
2）采用定频PWM，只需要改变占空比即可调节变换器的电压增益，易于控制与实现。
3）不需要增加额外的开关管，只要增加无源元件La与Ca。同时，辅助电感La有助于实现部分开关的零电压开通。
参考文献
[1] 王议锋, 陈博, 吕雯, 等. 拓扑变换型LLC-C谐振软开关直流变换器[J]. 电工技术学报, 2019, 34(18): 3810-3820.
Wang Yifeng, Chen Bo, Lü Wen, et al. A topology morphing LLC-C resonant soft-switching DC-DC converter[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3810-3820.
[2] 倪梦涵, 杨晓峰, 王淼, 等. 多电平均压型直流变换器输入电流纹波抑制策略[J]. 电工技术学报, 2021, 36(16): 3354-3364.
Ni Menghan, Yang Xiaofeng, Wang Miao, et al. Input current ripple suppression strategy of multilevel voltage-balancing DC-DC converter[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3354-3364.
[3] 赵子先, 康龙云, 于玮, 等. 基于简化时域模型的CLLC直流变换器参数设计[J]. 电工技术学报, 2022, 37(5): 1262-1274.
Zhao Zixian, Kang Longyun, Yu Wei, et al. Parameter design method of CLLC DC-DC converter based on simplified time domain model[J]. Transactions of China Electrotechnical Society, 2022, 37(5): 1262- 1274.
[4] 杨晨, 谢少军, 毛玲, 等. 高输入电压双管Buck- Boost变换器控制策略研究[J]. 电工技术学报, 2014, 29(4): 70-78.
Yang Chen, Xie Shaojun, Mao Ling, et al. Research on control strategy of two-switch Buck-Boost con- verter for high voltage application[J]. Transactions of China Electrotechnical Society, 2014, 29(4): 70-78.
[5] 张海亮, 刘树林, 王航杰, 等. 一种新型二次侧自复位正激变换器研究[J/OL]. 电工技术学报: 1-7 [2022-05-26]. DOI: 10.19595/j.cnki.1000-6753.tces. 191581.
Zhang Hailiang, Liu Shulin, Wang Hangjie, et al. Research on a new forward converter with self- magnetically reset on the secondary side[J/OL]. Transactions of China Electrotechnical Society, 1-7 [2022-05-26]. DOI: 10.19595/j.cnki.1000-6753.tces. 191581.
[6] 赵进. 高频谐振变换器的设计和控制关键技术研究[D]. 南京: 东南大学, 2021.
[7] 王泽景, 王颖, 龚春英. 高降压比LLC谐振型直流变压器[J]. 电工技术学报, 2015, 30(14): 193-200.
Wang Zejing, Wang Ying, Gong Chunying. High step-down LLC resonant DC-DC transformer[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 193-200.
[8] 丁超, 李勇, 姜利, 等. 电动汽车直流充电系统LLC谐振变换器软开关电压边界分析[J]. 电工技术学报, 2022, 37(1): 3-11.
Ding Chao, Li Yong, Jiang Li, et al. Analysis of soft switching voltage boundary of LLC resonant con- verter for EV DC charging system[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 3-11.
[9] Li Bin, Li Qiang, Lee F C. High-frequency PCB winding transformer with integrated inductors for a bi-directional resonant converter[J]. IEEE Transa- ctions on Power Electronics, 2019, 34(7): 6123-6135.
[10] 刘博林, 张晓冬, 李越, 等. 应用于电动汽车充电的变频-移相控制方法LLC谐振变换器[J]. 电源学报, 2020, 18(5): 43-52.
Liu Bolin, Zhang Xiaodong, Li Yue, et al. Variable frequency-phase shift control method for LLC reso- nant converter applied to electric vehicle charging[J]. Journal of Power Supply, 2020, 18(5): 43-52.
[11] 李小双, 田钦元, 王正仕. 基于变频与副边移相控制的双向LLC谐振变换器[J]. 电工技术, 2021(21): 83-86, 96.
Li Xiaoshuang, Tian Qinyuan, Wang Zhengshi. Bidirectional LLC resonant converter based on frequency conversion and secondary-side phase shift control[J]. Electric Engineering, 2021(21): 83-86, 96.
[12] 石健将, 章江铭, 龙江涛, 等. 高频变压器一次侧串联LLC+输出端并联Buck级联直流变换器[J]. 电工技术学报, 2015, 30(24): 93-102.
Shi Jianjiang, Zhang Jiangming, Long Jiangtao, et al. A cascaded DC converter with primary series trans- former LLC and output interleaved Buck[J]. Transa- ctions of China Electrotechnical Society, 2015, 30(24): 93-102.
[13] 孙孝峰, 仇江峰, 栗晓华, 等. 一种具有宽输入电压范围的集成Buck-Boost LLC级联变换器[J]. 中国电机工程学报, 2016, 36(6): 1667-1673.
Sun Xiaofeng, Qiu Jiangfeng, Li Xiaohua, et al. An integrated Buck-Boost LLC cascaded converter with wide input voltage range[J]. Proceedings of the CSEE, 2016, 36(6): 1667-1673.
[14] Ahmed M H, Fei Chao, Lee F C, et al. Single-stage high-efficiency 48/1V sigma converter with inte- grated magnetics[J]. IEEE Transactions on Industrial Electronics, 2020, 67(1): 192-202.
[15] Wu Zongheng, Wang Zhiwei, Zhang Yi, et al. A high efficiency and high power density DC transformer topology with output regulation capability[J]. IEEE Transactions on Power Electronics, 2022, 37(7): 8232-8247.
[16] Liao Yuefeng, Xu Guo, Peng Tao, et al. An LLC- DAB bidirectional DCX converter with wide load range ZVS and reduced switch count[J]. IEEE Transa- ctions on Power Electronics, 2022, 37(2): 2250-2263.
[17] Liu Tianji, Wu Xinke, Yang Shu. 1MHz 48-12V regulated DCX with single transformer[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(1): 38-47.
Discontinuous Current Mode Resonant Converter with Pulse Width Modulation Control
Abstract This paper proposes a discontinuous current mode resonant converter with pulse width modulation (PWM) control. The fixed-frequency PWM control is employed, and an auxiliary inductor and an auxiliary capacitor are added to the primary side switch network. By adjusting the duty cycle of the drive signal of the primary side switch, the voltage amplitude between the midpoints of the bridge arm can be changed, and then the voltage gain of the converter can be adjusted. The resonant current works in discontinuous mode through a suitable parameter design for the converter, so there is no reactive current. Meanwhile, all switches can realize soft-switching, which reduces the switching loss. This paper first analyzes the working principle and operating modes of the converter. Then, the characteristics of the converter, including the voltage gain, soft-switching conditions, and discontinuous current mode conditions, are deduced, and a parameter design method is proposed. Finally, a 1 000W prototype is built to verify the feasibility of the converter and the correctness of the theoretical analysis.
keywords：Discontinuous current mode, pulse width modulation, resonant converter, soft- switching
DOI: 10.19595/j.cnki.1000-6753.tces.220959
中图分类号：TM46
中央高校基本科研业务费专项（2021zzts0187）、国家自然科学基金青年科学基金（51907206）和电力系统及大型发电设备安全控制和仿真国家重点实验室开放课题（SKLD21KM06）资助项目。
收稿日期 2022-05-30
改稿日期 2022-06-28
陈孝莺 男，1995年生，博士，主要研究方向为电力电子变换器及其控制。E-mail: chenxiaoying01@csu.edu.cn
许 国 男，1990年生，副教授，主要研究方向为功率变换器拓扑及控制。E-mail: xuguocsu@csu.edu.cn（通信作者）
（编辑 陈 诚）