模块化多电平谐振变换器多自由度调压控制及子模块电容均压方法
盛 景1 陈 聪1 向 鑫1 李楚杉1,2 李武华1
(1. 浙江大学电气工程学院 杭州 310027 2. 浙江大学伊利诺伊大学厄巴纳香槟校区联合学院 海宁 314400)
摘要 模块化多电平谐振变换器(MMRC)因具备模块化多电平拓扑和谐振电路的共同优点而在中压领域得到广泛研究,但在宽范围输入下的配用电场合,针对该拓扑的高效调控方法仍缺少相关深入探究。为此,该文提出一种适用于中压宽范围输入的模块化多电平谐振变换器多自由度调压控制方法。首先,分析开关频率和调制比应用于电压增益调节的效果和特点。接着,结合调频和调制比两种控制自由度提出多自由度组合的宽范围调压方法,并且揭示变调制比控制引发的子模块电容电压波动大的问题,针对性地提出一种监督式电容均压算法以降低纹波。最后,基于输入电压8~16kV、输出功率60kW的实验样机验证所提调控方法的有效性,并实现了全输入电压范围满载效率大于96%,子模块电容电压纹波幅值降低60%。
关键词:模块化多电平谐振变换器 宽范围中压 多自由度调控 电容电压纹波抑制
0 引言
随着新能源发电、电气化轨道交通和大型数据中心的迅速发展,中压直流(Medium Voltage DC, MVDC)配电系统以其高效率、高电能质量和高稳定性的优势得到广泛关注[1-3]。在MVDC系统中,DC-DC变换器,亦称直流变换器,是连接不同电压等级电网或将中压直流转换为低压直流(Low Voltage DC, LVDC)为设备供电的关键角色[4-5],因此成为中压直流系统研究重点之一。
通常单个功率器件可以满足低压变换领域电压和电流要求。然而,目前在中压应用中,器件、模块或变换器的串并联是不可避免的实现方式[6-7]。早期MVDC到LVDC转换的解决方案是采用输入串联输出并联(Input-Series-Output-Parallel, ISOP)拓扑,由于其模块化结构和易于控制的优点,该结构已得到广泛使用[8-9]。但是隔离式ISOP结构中有众多分立的高频变压器,在10kV中压下,每个变压器的一次侧和二次侧均需承受数十kV的绝缘耐压。此时,单个模块体积急剧增加,功率密度提升严重受限[10]。该缺点限制了ISOP结构在更高电压、功率等级应用中的推广。
近年来,模块化多电平变换器(Modular Multi- level Converter, MMC)结构凭借其模块化和灵活性高、易于拓展电压和功率等级的优势为中压变换提供了一种可行的解决方案。与ISOP众多分布式低功率变压器相比,集中式变压器具有绝缘设计简单、功率密度高和生产制造容易的优点[10]。大量文献提出了适用于中高压直流变换的MMC DC拓扑结构,如双有源桥结构和谐振型结构[11-13]。在MMC级联子模块中,由于可采用特性良好的低压功率器件,开关频率可达数kHz甚至更高,因此,电容、电感和变压器等无源元器件的体积将显著减小[11-12]。此外,MMC DC拓扑子模块开关器件可以实现零电压开关[14-15],从而降低高频下开关损耗。
在某些MVDC到LVDC供电场合,需要满足宽范围输入需求[16]。例如,在海底观测网系统中,陆上中压直流电源通过单极海底电缆为百千km外的海底观测仪器供电。由于海底电缆的绝缘和制造成本限制,寄生电阻远大于陆地上的架空线。一般15kV等级海缆每1km寄生电阻约为1W。当供电电流为0~10A变化时,在500km的电缆上会有0~5kV的压降。因此,为大型海底观测网络设计具有宽电压增益范围的中压直流变换器可以延拓观测网范围,允许铺设更多的大功率仪器,对于长期、不间断的海洋探索具有重要意义[17]。
鉴于MMC结构的灵活性,一些控制自由度(Degree of Freedom, DOF)可用于调节MMC DC- DC变换器的电压增益,如开关频率、移相角、子模块占空比等。目前,大多数现有文献倾向于以不同方式调节移相角。文献[15, 18]讨论了通过增加子模块间投入切除移相角实现梯形波、三角波调制,以改变MMC输出电压的基波分量。该方法可以实现电压增益在0.81~1.27之间连续调节。另外,一些控制策略调节MMC相单元之间或变压器一次侧和二次侧之间的移相角[19]。显然,相间移相或一次侧与二次侧间移相控制会增加MMC内部环流和无功功率。
文献[21-22]提出了结合MMC和LLC结构的模块化多电平谐振直流变换器(Moduar Multilevel Resonant Converter, MMRC)。为了实现宽范围调压,文献[21]根据输入电压调节所需投入子模块个数,减小LLC单元工作频率范围。然而,该方法投入子模块个数和开关频率范围的选取标准没有进行优化设计,这将导致MMRC继承LLC在轻载下的开关频率非常高的问题[23]。此外,现有文献尚未深入研究开关频率和改变投切子模块个数对中压MMRC的影响。
针对上述不足,本文提出了一种优化的多自由度组合的调压控制策略及其设计方法。首先,基于对不同开关频率下MMRC工作模态的分析,揭示了当开关频率大于LLC主谐振频率时,桥臂电感和变压器会承受输入电压10kV级别的高电压应力和高dv/dt问题。接着,提出了一种新的多自由度调控准则来设计MMC调制比和开关频率。将全输入电压、全负载工况下的开关频率限制在一个狭窄的范围,降低LLC单元和变压器设计难度。同时该控制策略也避免了桥臂电感和变压器的高电压应力。最后,针对变调制比控制下子模块电容电压纹波大的问题,提出了一种监督式子模块电容均压算法,大幅度降低了子模块电容纹波,从而降低了子模块电容设计需求。
本文首先介绍了MMRC的工作原理及其调制方式。其次对MMRC开关频率和调制比两个自由度的进行探讨,重点研究基于变调制比和调频控制的多自由度电压调控策略以适应宽范围输入。接着针对变调制比控制引发的电容电压纹波大的问题,提出了一种有监督的均压算法。最后基于所提方法搭建仿真模型并研制8~16kV输入,375V/60kW输出的实验样机,并给出了仿真和实验结果,验证了本文所提方法的可行性与有效性。
1 运行原理与调制方法
1.1 运行原理
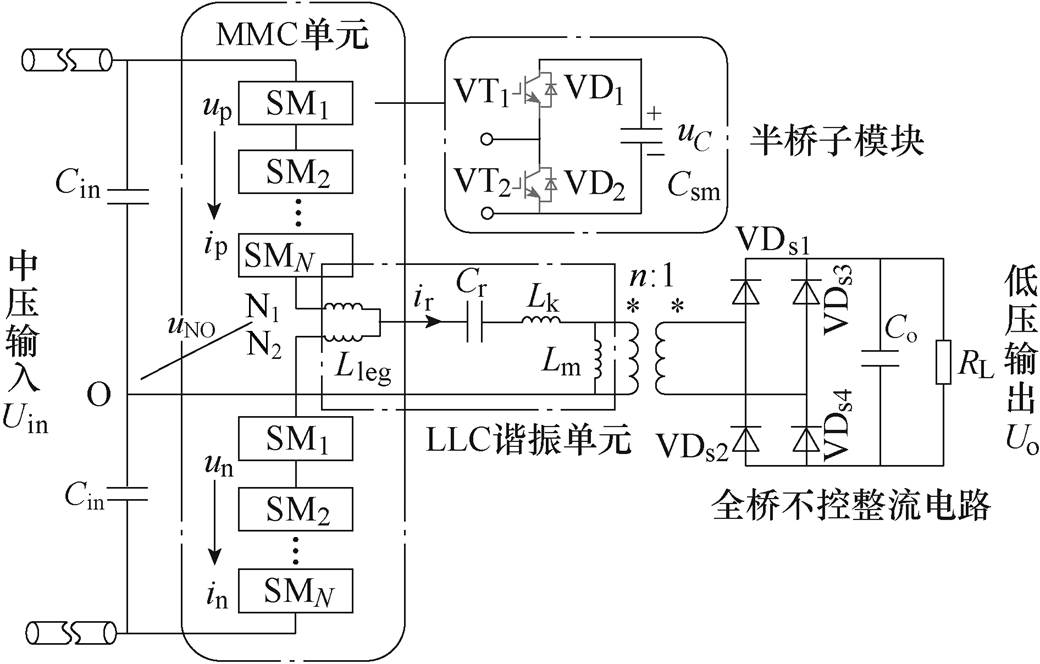
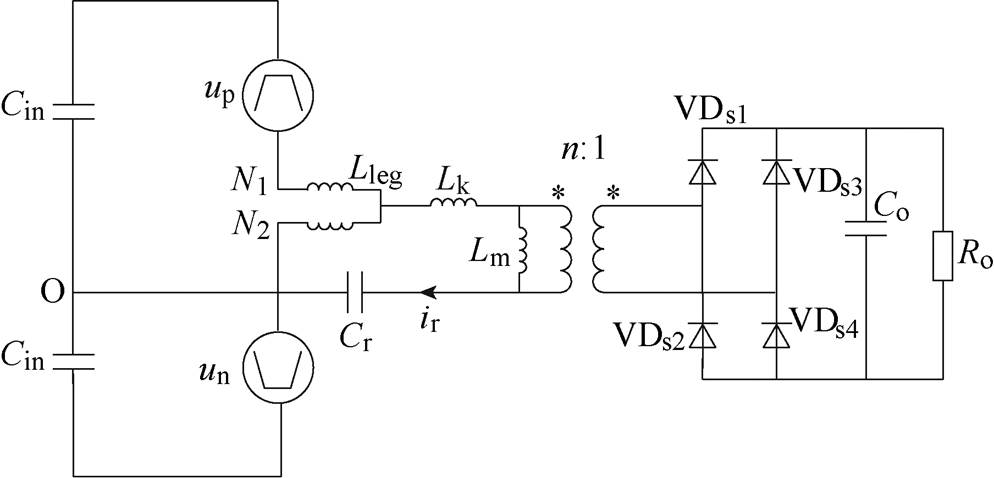
将传统低压半桥LLC谐振电路的开关器件替换为模块化多电平电路的级联子模块,可得到最简易的模块化多电平谐振变换器拓扑如图1所示。图1中,Uin为中压输入电压,Uo为低压输出电压,上下桥臂级联子模块SM1~SMN均采用半桥子模块结构,其中VT1、VT2、VD1、VD2为半桥子模块的下管IGBT和二极管,半桥子模块电容电压记作uC,uC=Csm。中压输入侧电容Cin为输入端提供中性点,消除谐振电容的直流电压偏置,同时吸收LLC谐振电流的交流成分。MMC单元上下桥臂分别由N个半桥子模块和一个桥臂电感组成。此处的桥臂电感有三个作用:①降低子模块投入和切除过程中的电流冲击;②抑制桥臂二倍频环流,减小直流输入电流脉动;③在交流输出侧等效为LLC谐振电感的一部分。因此,LLC谐振单元由变压器励磁电感Lm、谐振电容Cr和谐振电感Lr组成,其中LLC谐振单元的谐振电感Lr由MMC桥臂电感Lleg和变压器漏感Lk共同组成,可表示为
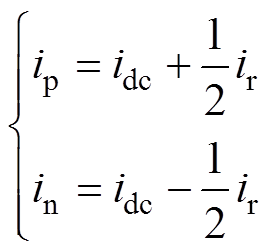 (3)
(3)
隔离变压器电压比为n 1以匹配输入输出电压,变压器二次侧接VDs1~VDs4构成的全桥不控整流电路,并经过输出电容Co给等效负载RL供电。
1以匹配输入输出电压,变压器二次侧接VDs1~VDs4构成的全桥不控整流电路,并经过输出电容Co给等效负载RL供电。
模块化多电平谐振变换器的典型运行波形如图2所示,图中,Ts为基波周期。LLC谐振运行模式下,MMC功率器件可以实现宽范围软开关。根据图2a和图2b,子模块软开关状态取决于投入切除时刻桥臂电流的方向,这一特性与传统半桥LLC有所区别。当桥臂电流中的直流分量idc小于变压器励磁分量幅值im/2,子模块由投入状态切换为切除状态时桥臂电流为负,子模块由切除状态切换为投入状态时桥臂电流为正,此工况可以实现子模块上下管IGBT(VT1和VT2)的零电压软开关开通(Zero Voltage Switching on, ZVS on)和反并二极管(VD1和VD2)的零电流软开关关断(Zero Current Switching off, ZCS off)。当桥臂电流中的直流分量idc大于变压器励磁分量幅值im/2,子模块在投切时桥臂电流始终为正,此时VD1和VT2的软开关丢失,但VT1同时实现了ZVS on和ZCS off。最后将子模块的软开关状态总结见表1。此外,由于谐振电流自然谐振到0,输出侧二极管可以实现零电流关断。
表1 子模块软开关状态
Tab.1 Switching states of MMC submodule devices
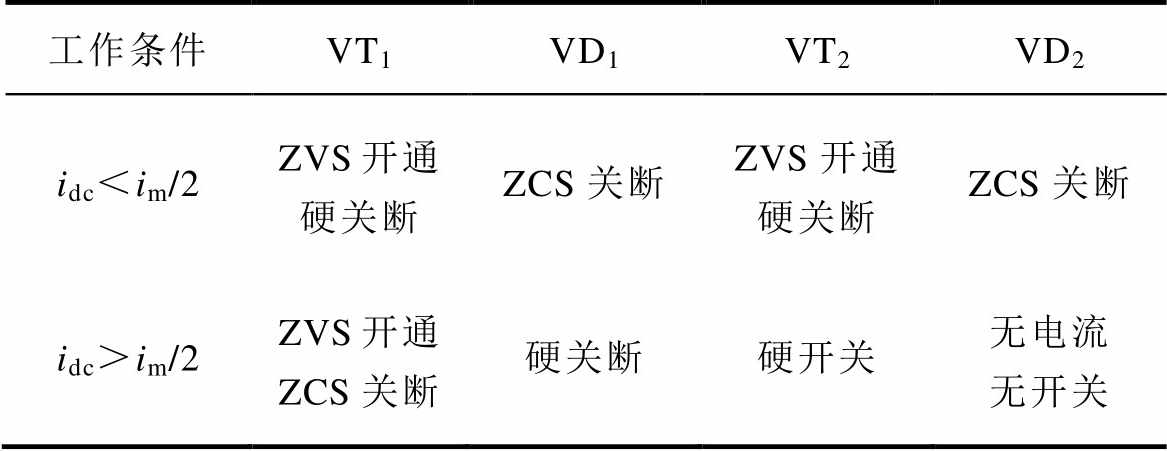
工作条件VT1VD1VT2VD2 idc<im/2ZVS开通硬关断ZCS关断ZVS开通硬关断ZCS关断 idc>im/2ZVS开通ZCS关断硬关断硬开关无电流无开关
1.2 调制方法
对于MMRC,MMC交流输出只是中间环节,无须采用低谐波的正弦调制。为了提高直流电压利用率同时降低dv/dt,MMC单元通常采用准方波(Quasi-Square Wave, QSW)调制策略,上、下桥臂互补输出准方波,模块化多电平谐振变换器准方波调制方式如图3所示。有两种方式可以生成准方波:①采用等占空比调制,如图3a所示,每个子模块均采用50%占空比方波驱动,但模块间存在微小延时;②变占空比调制,如图3b所示,每个模块占空比不等,但平均占空比为50%。
两种调制方式均容易在数字控制器中实现,但在电容充放电效果方面迥异。例如,轻载下两种调制方法对子模块电容充放电能力对比如图4所示,在轻载工况下,MMC桥臂电流仅存在励磁电流。等占空比调制方式的每个驱动信号对电容充放电能力均不同,移相角为0的驱动信号充电能力最强,而最大移相角的驱动信号放电能力最强,因此均压算法可通过排序分配驱动信号实现动态均压。而变占空比调制方式的每个驱动信号对电容充放电能力均近似为零,一旦电容电压发生不均,重新分配驱动信号无法回归均衡。因此,等占空比调制被广泛采用,并提出了诸多电容均压算法[20-21, 24-25]。
2 多自由度宽范围调压方法
2.1 调频调压与变调制比调压
LLC谐振运行模式不仅可以实现子模块功率器件软开关,而且可以通过改变开关频率调节增益。忽略MMC输出准方波的斜坡区间,LLC单元的电压增益特性与半桥LLC相同。当负载增加时,同样调频范围下的增益区间迅速缩减,而且在轻载下,当开关频率大于主谐振频率时,几乎丧失调频调压能力[26]。另外,当开关频率大于LLC主谐振频率时,LLC将会退化为LC谐振模式。该工作模式下,MMRC简化等效电路如图5所示,谐振电流是连续的,变压器二次电压被输出电压钳位。因此,变压器一次绕组电压是一个完整的方波电压,准方波调制策略将失去意义。此外,在MMC子模块短暂投切期间,由于变压器一次和二次电压被输出电容钳位,且回路中电容电压无法突变,MMC桥臂阶梯电压将会直接施加在桥臂电感两端,无疑会增加绝缘要求。综上所述,如果将LLC调频调压直接应用于宽范围输入MMRC拓扑,将难以避免调频范围宽、电压应力高、变换效率低的问题。
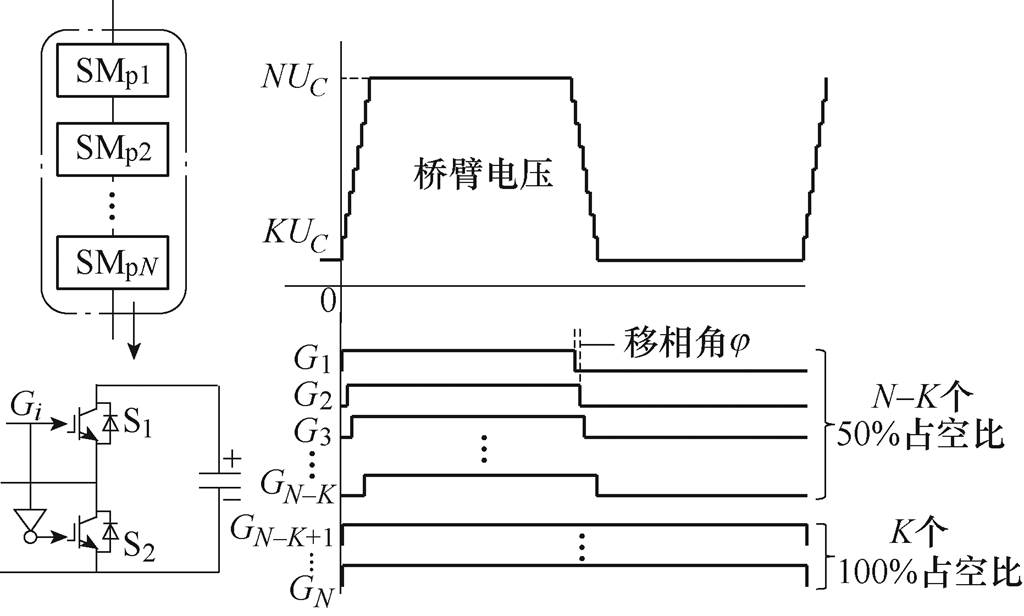
MMC单元常规的准方波调制波形如图6a所示。上、下桥臂互补输出,桥臂最大电压为直流母线电压,最小电压为0,电压调制比始终为1。为了适应宽范围输入电压调压需求,可以利用改变投入切除子模块个数调节MMC单元输出幅值。具体来说,本文通过改变一个开关周期内桥臂最少投入子模块数目来调节MMC电压调制比,其电压调制波形如图6b所示,其中有K个子模块在一个开关周期内保持投入,N-K个子模块与传统调制方法一致。
根据图6b和式(2),可以得到交流电压幅值Udc为
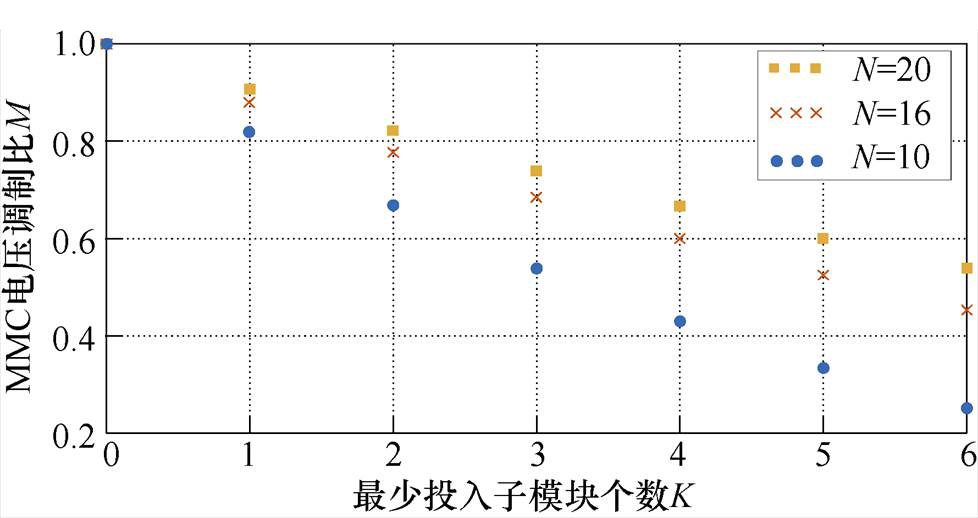
以几种不同桥臂子模块个数情况为例,MMC调制比与最少投入子模块个数K的关系在图7中绘出。可以发现,改变投切子模块个数可以有效调节MMC电压调制比。例如,N=16,K=0~6,MMC调制比可以从1调节到0.45。但是,由于投切子模块个数只能是整数,变调制比调节具有不连续性,因此无法直接应用于宽范围连续调压。
2.2 调频+变调制比自由度组合调压
结合调频控制和变调制比控制的各自优点,本文将两种控制自由度结合,以实现中压MMRC宽范围连续调压。输入到输出的电压增益表达式为
式中,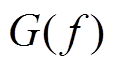 为LLC谐振腔增益;n为隔离变压器电压比。
为LLC谐振腔增益;n为隔离变压器电压比。
本文调频+变调制比结合的多自由度宽范围调压策略控制框图如图8所示,图中,前馈环根据输入电压计算所需MMC电压调制比,将宽范围输入调控成窄范围输出。反馈环再根据输出电压闭环调节开关频率,微调LLC谐振腔增益,将输出电压稳定在指令值。
为了更具体地描述该调压策略,下面以一个具体案例来进行深入分析。以输入电压8~16kV,输出375V 100kW中压MMRC为例。如果仅采用LLC调频调压方案,其设计参数见表2前两列所示。上下桥臂各需配置20个800V子模块来支撑最大输入电压。为了实现2倍的LLC增益范围调节,需要很小的励磁电感。满载下开关频率范围为5~25kHz,且轻载下的开关频率将会更高。这些缺点将对高频变压器优化设计和系统效率提升带来严峻挑战。
表2 MMRC两种调压方式设计参数对比
Tab.2 Key parameters of two voltage control methods of MMRC

参数数 值 仅调频调压多自由度调压 输入电压Uin/kV8~16 输出电压Uo/V375 功率Po/kW100 桥臂子模块数N2016 变压器电压比n181121 K0, 不变0, 1, 2, 3, 4, 5 MMC调制比M(K)11~0.523 调频调节范围G(f)0.85~1.71~1.15 谐振主频率fr/kHz1212 谐振电容Cr/nF215300 谐振电感Lr/mH800600 励磁电感Lm/mH38 开关频率范围fs/kHz5~257~12
在本文多自由度调压方法中,首先为了避免LLC轻载下调压能力差和变压器、桥臂电感高电压应力问题,将开关频率范围设计在低于主谐振频率区间,即LLC工作在增益大于1的区间。式(5)中参数N、K、n、f的具体设计原则如下:当输入电压为最低8kV时,记作Uin0,最小投入子模块个数K设为0,变压器电压比设定为12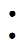 1,当开关频率等于谐振频率时,输出电压为333V。因此需要LLC调节增益为1.125,将输出升压到375V。
1,当开关频率等于谐振频率时,输出电压为333V。因此需要LLC调节增益为1.125,将输出升压到375V。
当输入电压升高到(N+1)Uin0/(N-1)时,记Uin1,最少投入子模块个数K设为1;当输入电压升高到(N+k)Uin0/(N-k)时,记Uink,最少投入子模块数K设为k;K值切换点输入电压Uink的统一表达式为
另一方面,桥臂子模块个数N的设计取决于直流输入电压和最大电容电压UC,在任一K值切换点,均须满足
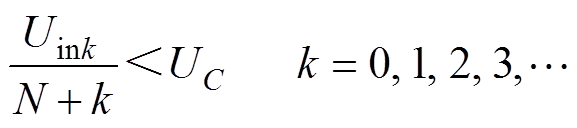 (7)
(7)
将式(6)代入式(7),得到
并且最大K值切换点输入电压需要超过直流输入最大电压Uin,max,即
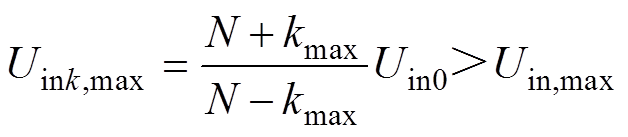 (9)
(9)
解不等式式(8)、式(9)可以得到最小N=16和最大kmax=6。
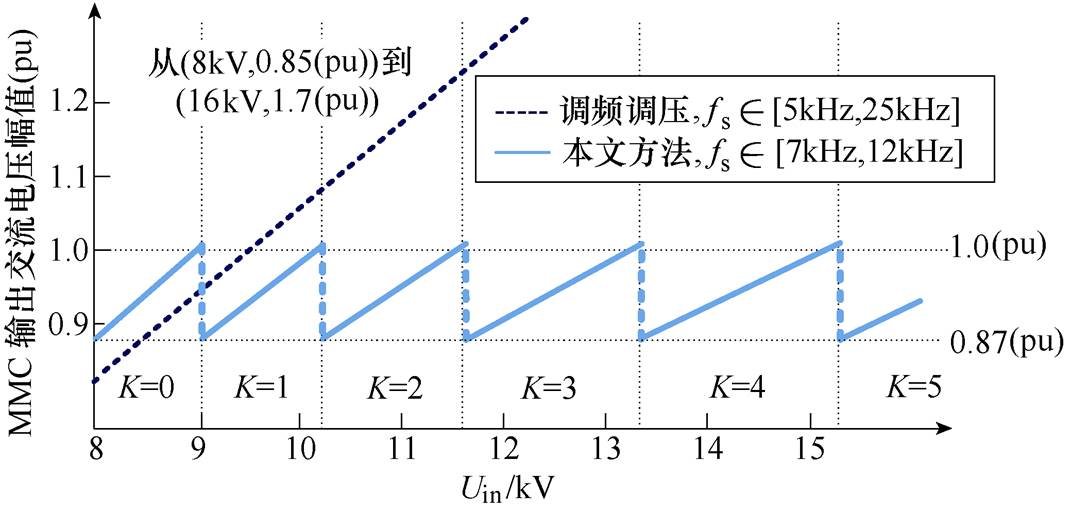
根据式(6),K值切换点和MMC输出电压幅值如图9所示,变调制比控制可将50%~100%输入电压调节在0.87~1.0(pu)范围内。
LLC谐振单元的设计原则是LLC单元可调增益需满足由于前馈控制切换K值引起的调制比阶跃变化。不难证明,在最大K值切换点kmax-1到kmax时,MMC调制比有最大阶跃。其设计参数结果在表2最后一列给出。对比的仅为LLC调频调压参数和本文的多自由度调压设计参数。本方法调频增益范围需求缩小为[1, 1.145],开关频率范围仅为[7kHz, 12kHz]。高频变压器励磁电感也从3mH增加到了8mH。
3 监督式子模块电容均压算法
3.1 子模块电容电压波动特性
采用变调制比控制下的子模块工作状态与传统调制比始终为1有所不同,这将会引起不同的电容电压波动特性。本节将重点分析采用本文所提宽范围调压方法对子模块电容电压波动特性影响,并针对性提出一种抑制子模块电容电压纹波方法。
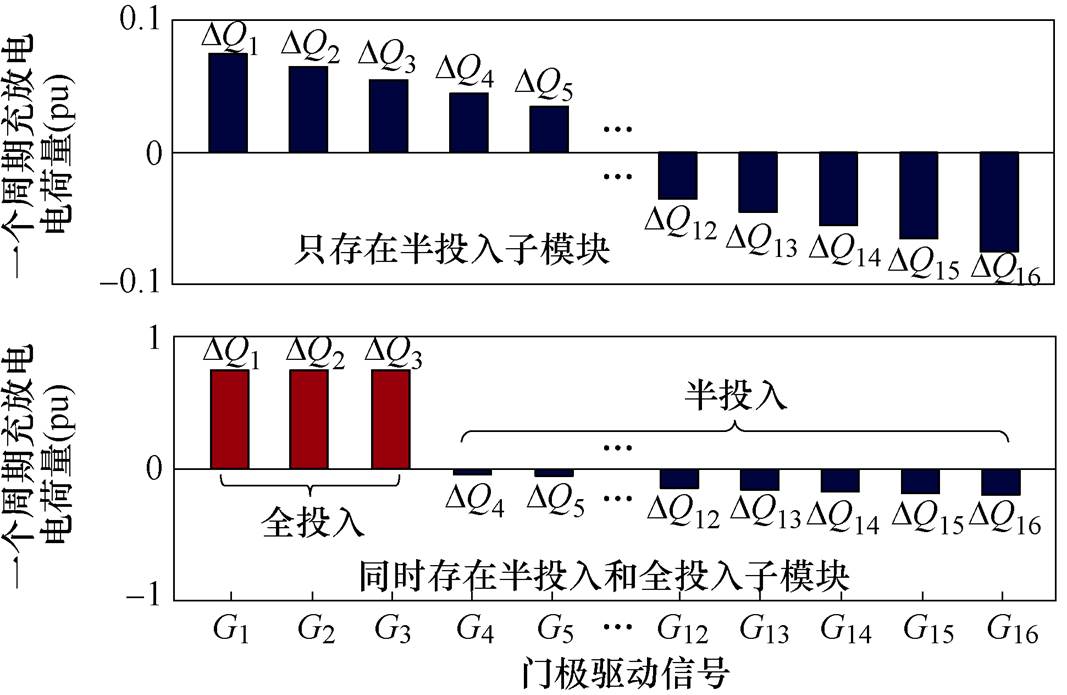
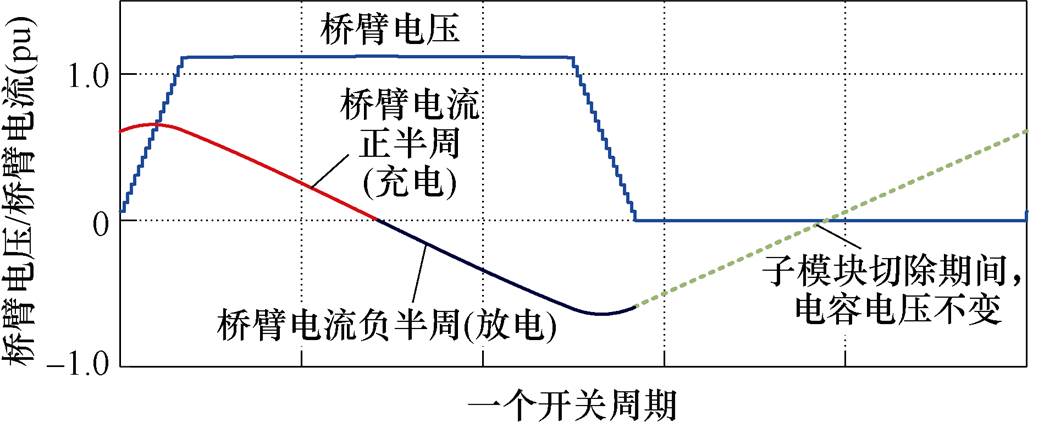
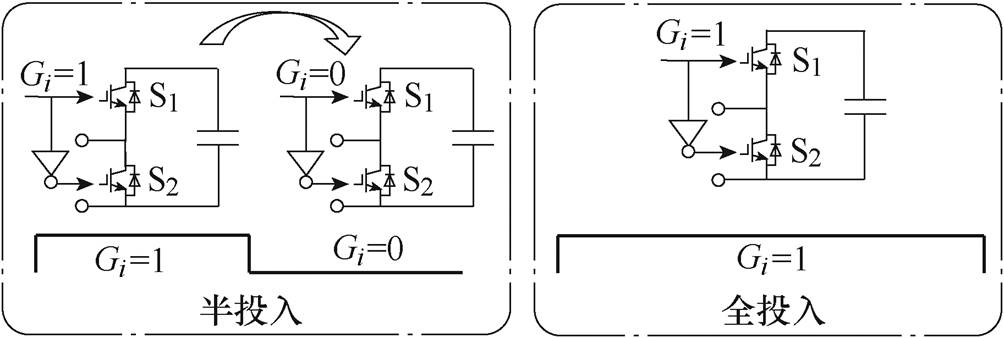
根据图10所示的桥臂电压调制方式,当MMC电压调制比小于1时,桥臂最大投入模块数为桥臂子模块个数,最小投入子模块数大于0。子模块存在两种投入模式,50%占空比投入和100%占空比投入,前者称之为“半投入”,后者称之为“全投入”。“半投入”指的是子模块电容只有一半周期处于投入状态,“全投入”指的是一个开关周期内子模块电容始终处于投入状态,子模块在一个开关周期内两种投入状态如图11所示。
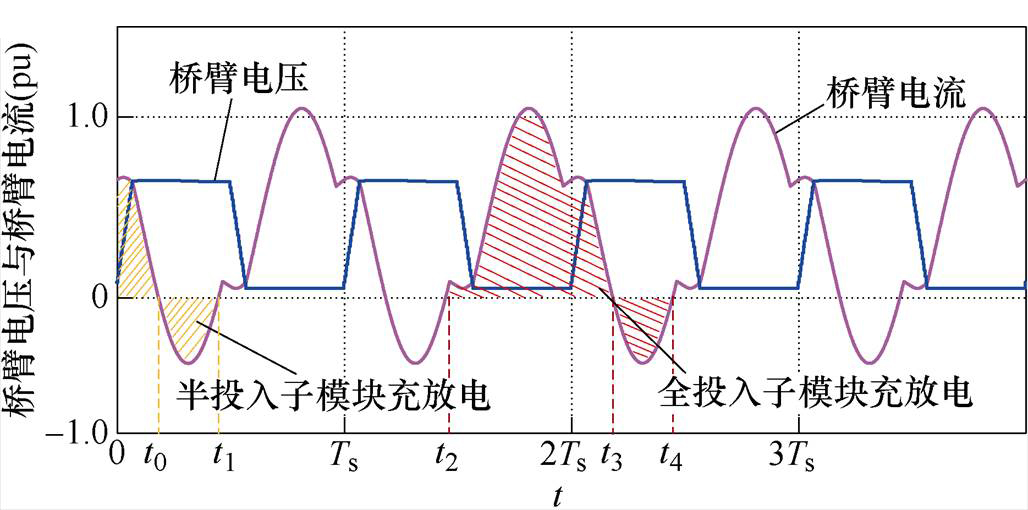
结合图12桥臂电压与桥臂电流的工作波形,可以清晰地展示“半投入”和“全投入”子模块的充放电差异,“半投入”子模块仅在0~t1区间50%周期内投入,电容先充电后放电。在调制比为1的工况下,即桥臂所有子模块均为“半投入”投切状态,“半投入”电容电压纹波大小DVhalf和一个周期电容电压变化DVhalf,Ts可通过式(10)计算,其中,C为子模块电容容值,ip为桥臂电流。忽略准方波调制中子模块间的微小移相角,所有“半投入”子模块在一个周期内电容电压变化相等且近似为0。实际中由于子模块间存在微小移相角,子模块间电容充放电存在微小差异,可以用来作为均压手段。
而对于电压调制比小于1的工况,桥臂存在一个或多个“全投入”子模块,其电容在一个开关周期内一直处于投入状态,如图12中t2~t3区间的“全投入”子模块电容被大量充电,随后t3~t4区间被放电,一个周期内电容电压变化不等于0,“全投入”电容电压纹波大小DVfull和一个周期电容电压变化DVfull,Ts可通过式(11)计算。且由于桥臂电流直流偏置的存在,重载工况下一个开关周期内“全投入”电容电压波动相比“半投入”会大很多。
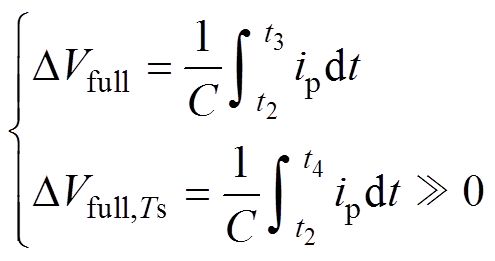 (11)
(11)
结合式(10)和式(11),40kW输出下,对于仅存在“半投入”和存在“全投入”两种工况下,一个开关周期内不同门极驱动信号对子模块电容充放电能力对比如图13所示,图中,G1~G16为图10中的门极驱动信号。对于仅存在“半投入”的工况,由于子模块间门极驱动信号的移相,一个周期内不同门极驱动信号的充放电电荷量存在微小差异,因此有文献根据该特性提前配置好门极驱动信号进行分配。但不同调制方式或负载工况下,充放电特性可能存在差异,难以有效移植该方法。对于存在“全投入”工况,“全投入”模块的充放电电荷量远大于“半投入”,且“半投入”模块的门极驱动信号均为放电状态。
文献[20-21]提出了一种不用考虑具体调制方法和工作条件的电容均压方法,通过排序电容电压和上一周期电容电压变化值,将上一周期充电能力最强的驱动信号分配给当前电容电压最低的子模块,上一周期放电能力最强的驱动信号分配给当前电容电压最高的子模块。相比一些主动轮换均压策略,该方法可以快速地平衡电容电压,实现较小的电容电压波动。
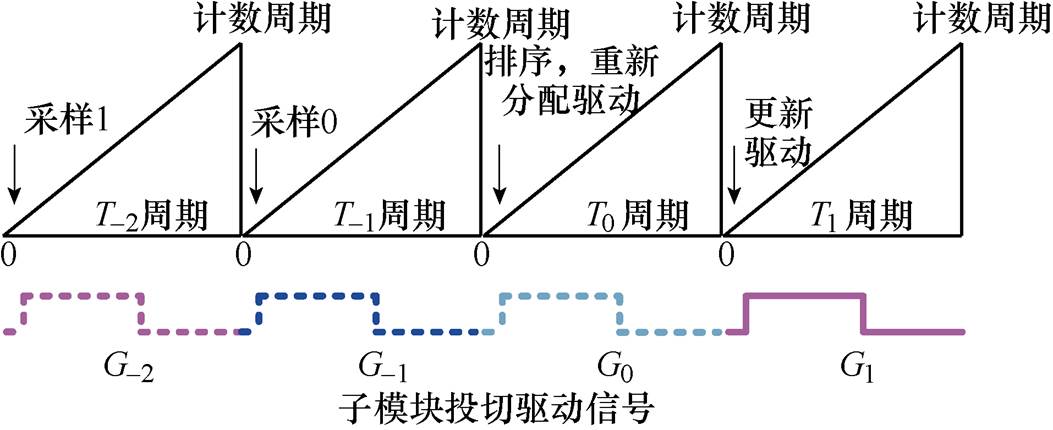
然而该均压算法并没有考虑实际应用中控制延时对电容电压波动特性和均压算法的影响,尽管该方法不会导致电容电压严重发散,但会明显增加电容电压纹波。图14所示为一种MMC DC变换器实际控制时序,控制周期与开关周期相同,受制于控制器处理速度限制,从采样到控制再到驱动信号更新有两个周期延时,不难发现,T-2周期内的电容电压变化是由G-2门极驱动信号决定,而非G-1或G0,因此,下一周期驱动信号G1应根据G-2的充放电能力进行分配,才能达到最优的均压效果。
值得一提的是,在本文采用的变调制比控制下,控制延时的存在会引发“全投入”子模块连续几个周期被过度充电,造成较大的电压波动。稳态运行下,如果不存在控制延时,某个子模块在上个周期被“全投入”后,电容电压会被充电到较高水平,本周期内电容将不会再次被“全投入”进行充电。而实际情况中,由于控制延时的存在,用来排序的电容电压是若干周期之前的,如图14所示的从采样到驱动输出的两个周期延时会引发子模块电容被连续3个周期“全投入”,相比无延迟的离线仿真,实际的电容电压纹波会是仿真的3倍。这无疑会增大电容电压应力,从而增大电容容值选型。
3.2 监督式子模块电容均压算法
为了解决变调制比调压和控制延时引起的电容电压波动大的问题,本节提出了一种基于排序预测的有监督电容均压算法。其通过电容电压排序对门极信号进行重新分配的思路与现有方法一致,但考虑了实际控制系统中的延时并加入了主动监督,对驱动信号分配结果进行二次检验,以实现最优的门极驱动信号分配,降低子模块电容电压纹波。
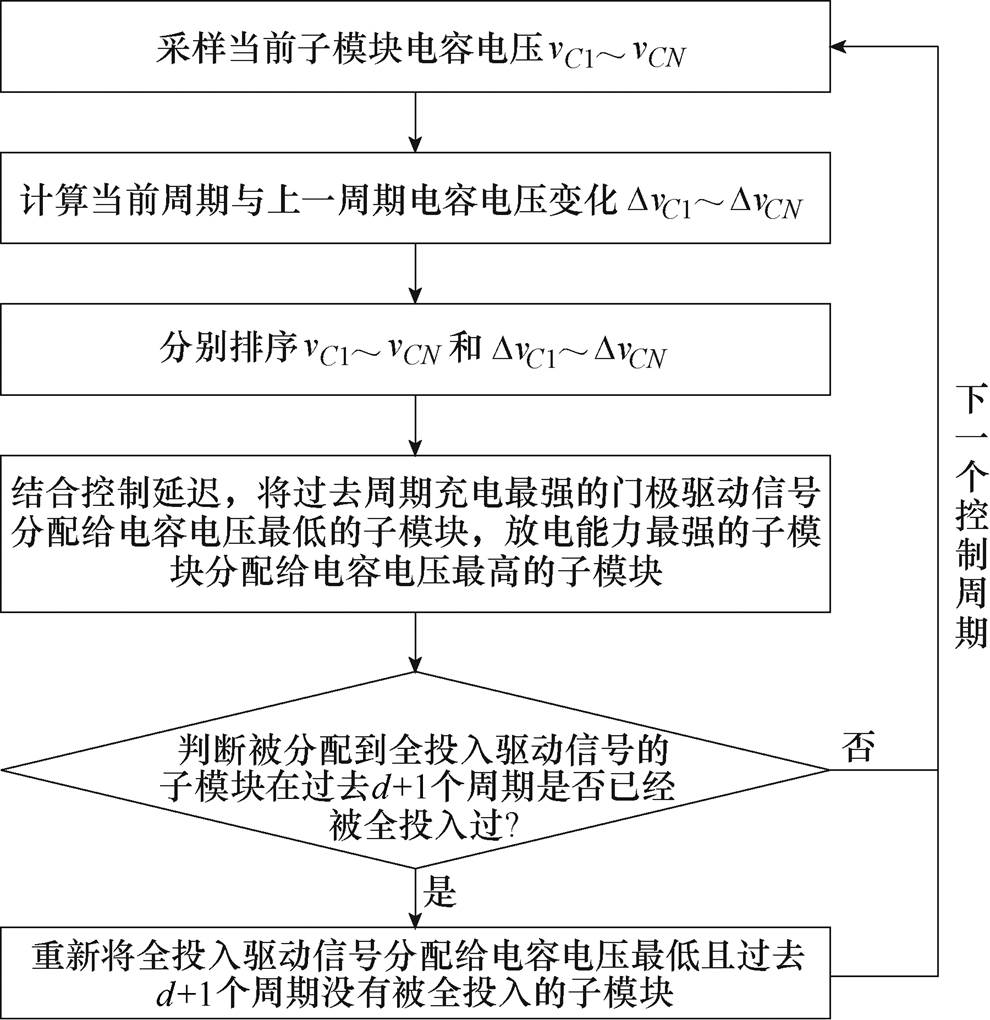
上、下桥臂内子模块均压算法相同,其具体算法框图如图15所示。
(1)子模块控制器对子模块电容电压进行采样,记作vC1~vCN,并上传到中央控制器。
(2)中央控制器计算该周期电容电压与上一周期变化值DvC1~DvCN。
(3)中央控制器对电容电压vC1~vCN和电容电压变化值DvC1~DvCN分别排序。最大的DvCi代表在两次采样间其门极信号具有最大的充电能力,最小的DvCi代表在两次采样间其门极信号具有最大的放电能力(或最小的充电能力)。
(4)根据从采样到控制输出的延迟时间,将过去充电能力最大的驱动信号重新分配给电压最低的子模块,将放电能力最大的驱动信号重新分配给电压最高的子模块。以图14所示控制时序为例,考虑到控制延时,T1周期的驱动信号应由T-2周期的驱动信号重新分配,而不是其他周期的驱动信号。
(5)对分配好的驱动信号进行监督检查,判断被分配到“全投入”信号的子模块在过去d+1个周期里是否已经分配过一次或多次“全投入”,其中,d为控制延迟周期数,如图14中d=2。如果没有,则无需调整驱动信号;如果有,则进行步骤(6)。
(6)把被分配到“全投入”且过去d+1个周期已经分配过“全投入”的子模块驱动信号重新分配给电容电压最低且过去d+1个周期都没有分配过“全投入”的子模块。
步骤(5)和步骤(6)是有别于传统无监督排序均压的显著特征。本方法也同样适用于仅有“半投入”运行工况,只不过步骤(5)和步骤(6)不会发挥作用。
该监督式子模块电容均压算法前4个步骤和现有文献均压思想相近,但考虑了控制延时去重新分配子模块驱动信号。同时通过主动监督,避免了子模块电容被连续多个周期持续被“全投入”,因此可以有效降低子模块电容电压纹波,从而减小电容容值选型,延长电容寿命。该均压算法同样兼容其他基于MMC结构的直流变换类型,如LC谐振型和双有源桥型,并适用于不同工况和不同电压调制比运行场合。
4 仿真与实验验证
4.1 仿真结果
根据表2的样机指标和设计参数,在Matlab软件中搭建仿真模型来验证所提方法的有效性。
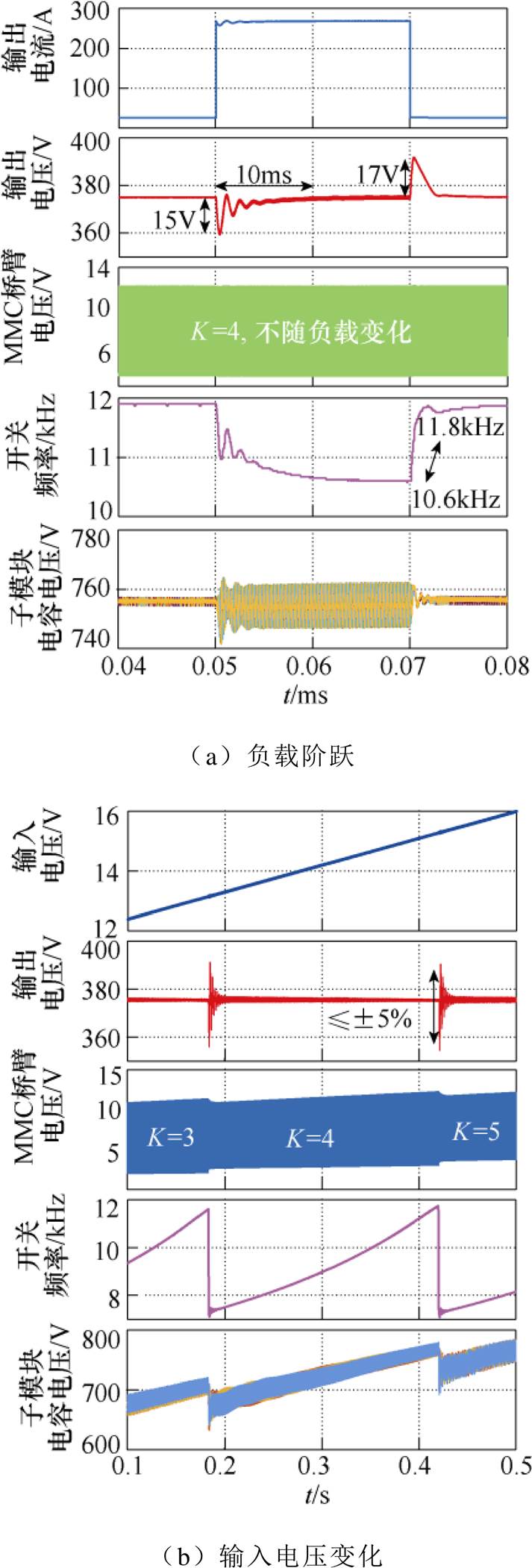
图16a给出了在输入电压Uin=15kV,切载工况下的动态波形。当输出功率由1kW突增到100kW时,输出电压瞬间跌落15V,此时仅反馈调频控制环路发挥作用,调节开关频率以提升LLC增益,MMC单元调制比保持不变,因此桥臂电压幅值也不变,输出电压稳定时间小于10ms。此外,由于输出功率的增加和开关频率的降低,子模块电容电压纹波显著增加。当输出功率由100kW骤降至1kW时,同样只有开关频率参与控制调节以保持输出电压稳定。
图16b展示了当输入电压变化时,MMRC的动态波形。其中,输出负载保持满载100kW不变,输入电压Uin在0.4s内由12kV缓慢提升至16kV,最小投入子模块数K在K值切换点由3切换至5,开关频率根据反馈控制在7.5~11.5kHz区间内调节,验证了该调控参数设计的合理性,并且K值切换期间电压波动幅度小于5%。此外,输出负载的大小不影响K值切换点的设计,但重载工况下K值切换会引起更大的电压过冲或跌落。
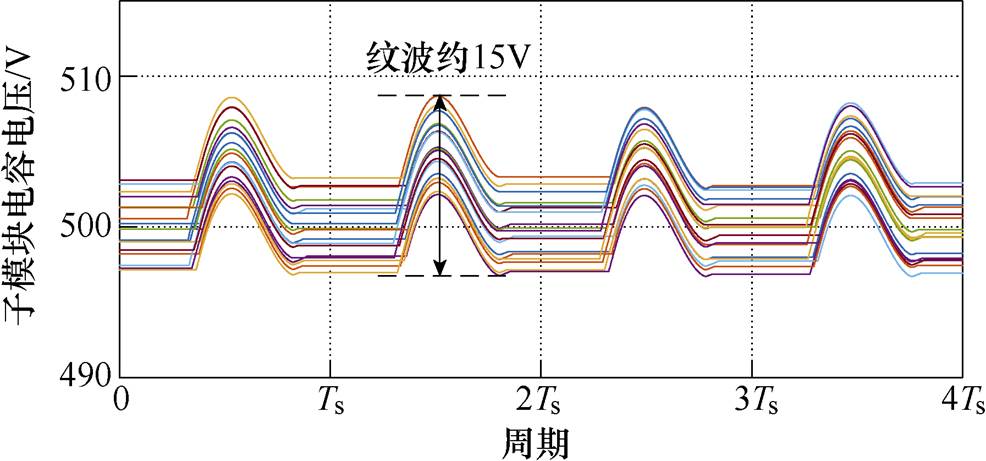
图17和图18对比了考虑控制延迟情况下,只有“半投入”状态和存在“全投入”状态的子模块电容电压仿真波形,控制延时为两个周期。两种工况子模块容值均为20mF,输出功率均为40kW。9kV输入下,只有“半投入”子模块工况下的电容纹波仅15V。
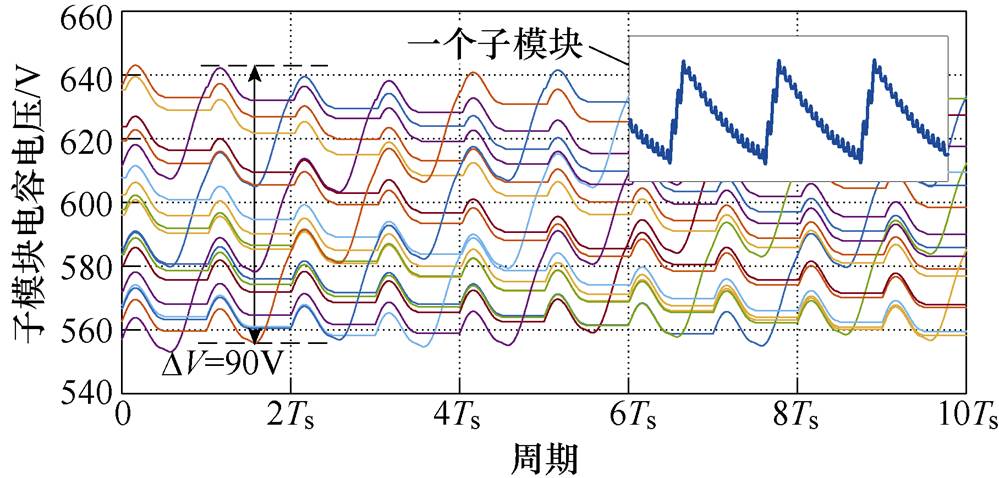
在输入电压为12kV,最少插入子模块数K值为3,存在“全投入”子模块工况下,传统均压算法尽管可以保证电容电压均衡,但40kW输出下电容电压纹波高达90V,是“半投入”的6倍。一方面是因为“全投入”子模块在一个周期内充电幅度大;另一方面控制延时会导致子模块连续3个周期被“全投入”连续充电。因此,如果不对电容电压纹波进行抑制,将会增大子模块电容选型,从而增加硬件体积和成本,同时较大的电压纹波也会降低电容寿命。
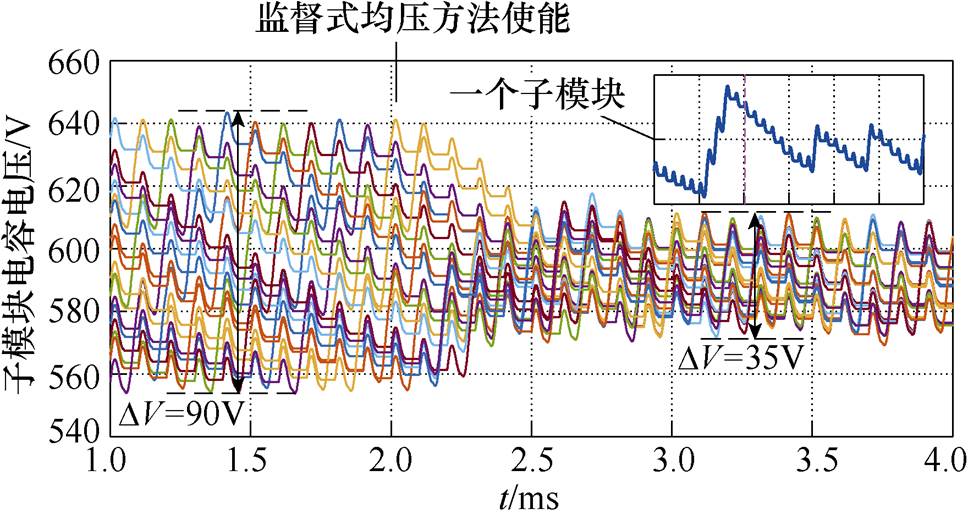
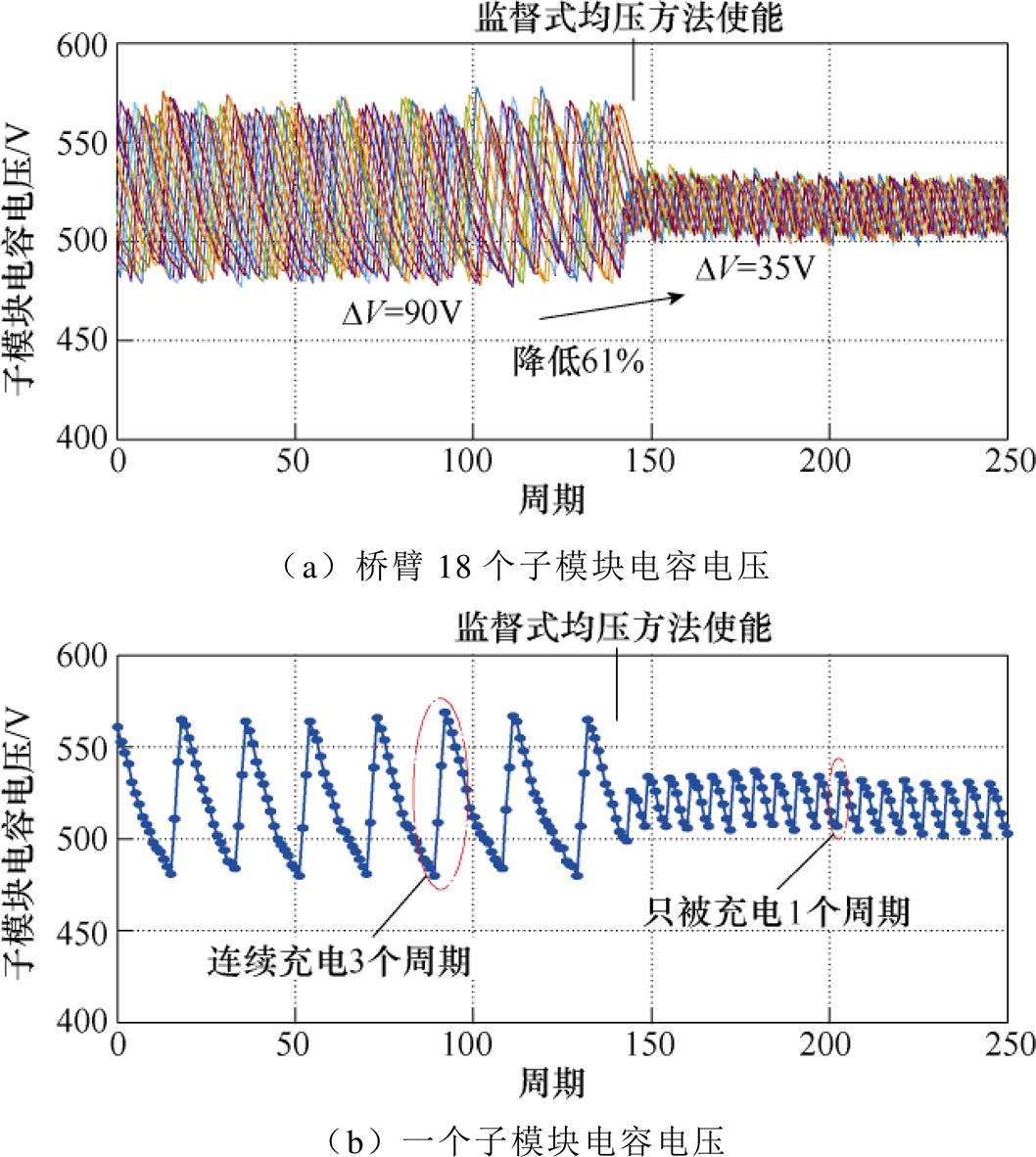
图19展示了采用传统均压算法[20-21]和本文监督式均压算法效果对比仿真波形。在使能本文监督式均压算法后,数个周期内,子模块电容电压纹波被抑制到35V左右,降幅高达61%。
4.2 实验验证
为验证MMRC拓扑在宽范围中压直流应用场景的可行性和所提出的适配宽范围输入电压的多自由度组合调压方法的有效性,研制了一台16kV/ 60kW的MMRC实验样机,如图20a所示。研制实验样机设计参数与表2设计参数一致,同时额外配置2个冗余子模块作为故障备份。中央控制器与上位机通过以太网进行信息交互,可以对系统状态和运行参数进行实时监控。
受制于实验室中压直流电源容量和低压负载容量限制,该MMRC实验样机在实验室条件下最大测试输出功率为42kW。
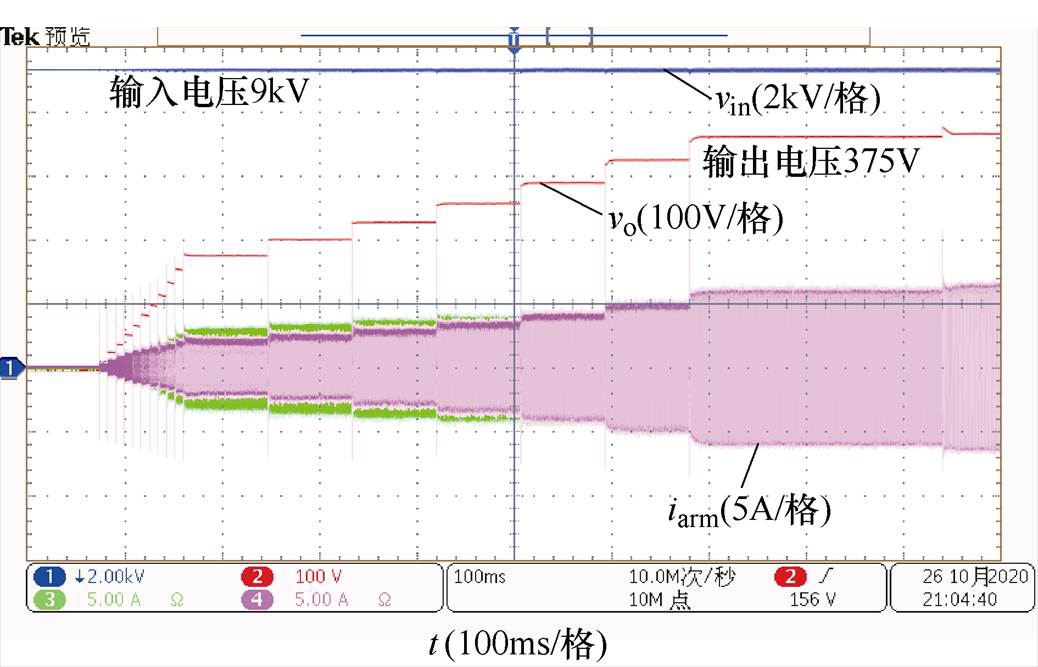
图21为研制样机软启动波形,在前100ms内,投入子模块个数K值迅速减小,输出电压快速提升以保证主控制板从输出侧可靠取电;随后K值缓慢减小直到输出电压上升至额定输出电压。该软启动策略下,输出电压、桥臂电流过冲较小,以适应带载启动场合需求。
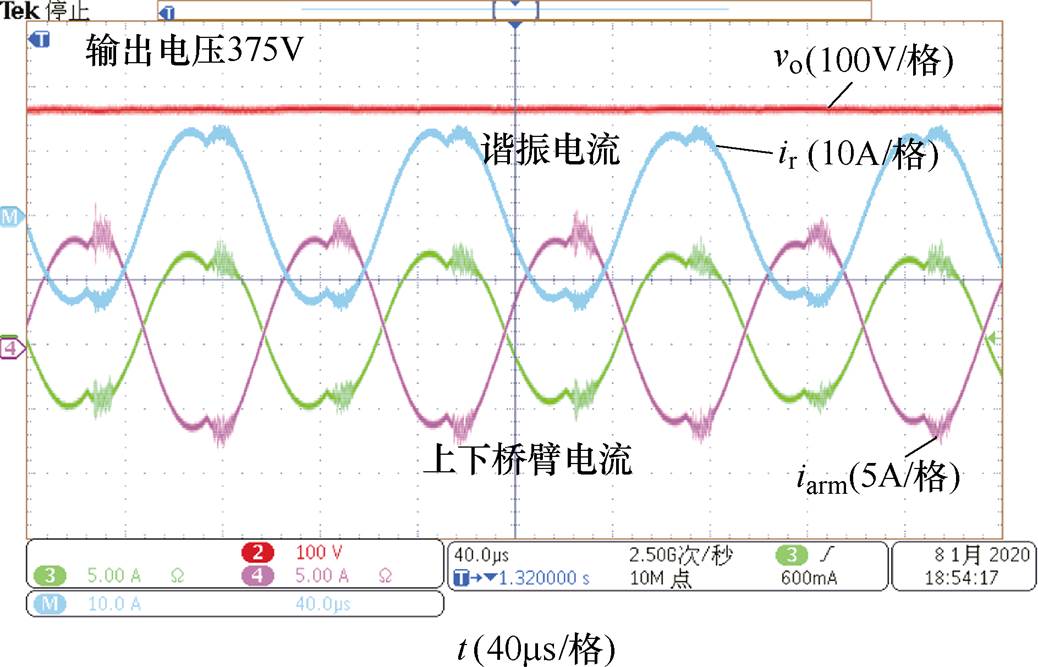
图22为研制样机在40kW工况下的稳态运行波形。桥臂电流由直流偏置电流、三角波励磁电流和正弦电流三部分组成。由于直流偏置电流和励磁电流的存在,重载工况下,在子模块投切时刻,桥臂电流较小,子模块器件可以实现近似零电流软开关。
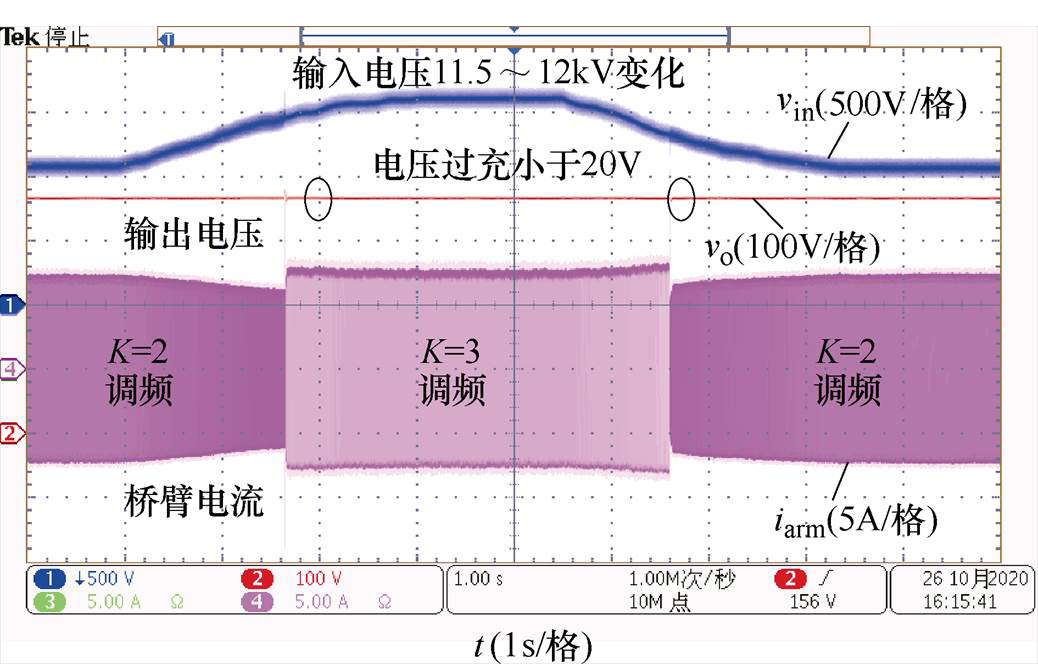
图23给出了输入电压变化时的动态波形。输出功率保持40kW,当输入电压由11.5kV缓慢上升至12.0kV,反馈环路先增加频率以降低LLC直流增益,当输入电压穿越K值切换点时,前馈控制将K值由2切换至3以降低MMC调制比,随即反馈控制降低开关频率以提升LLC直流电压增益,将输出电压稳定在375V。类似地,当输入电压由12kV降低到11.5kV时,K值由3切换回2。变调制比过程中,输出电压波动在20V以内。前馈控制采用滞回控制方式,以避免采样误差引发前馈控制环路的振荡。
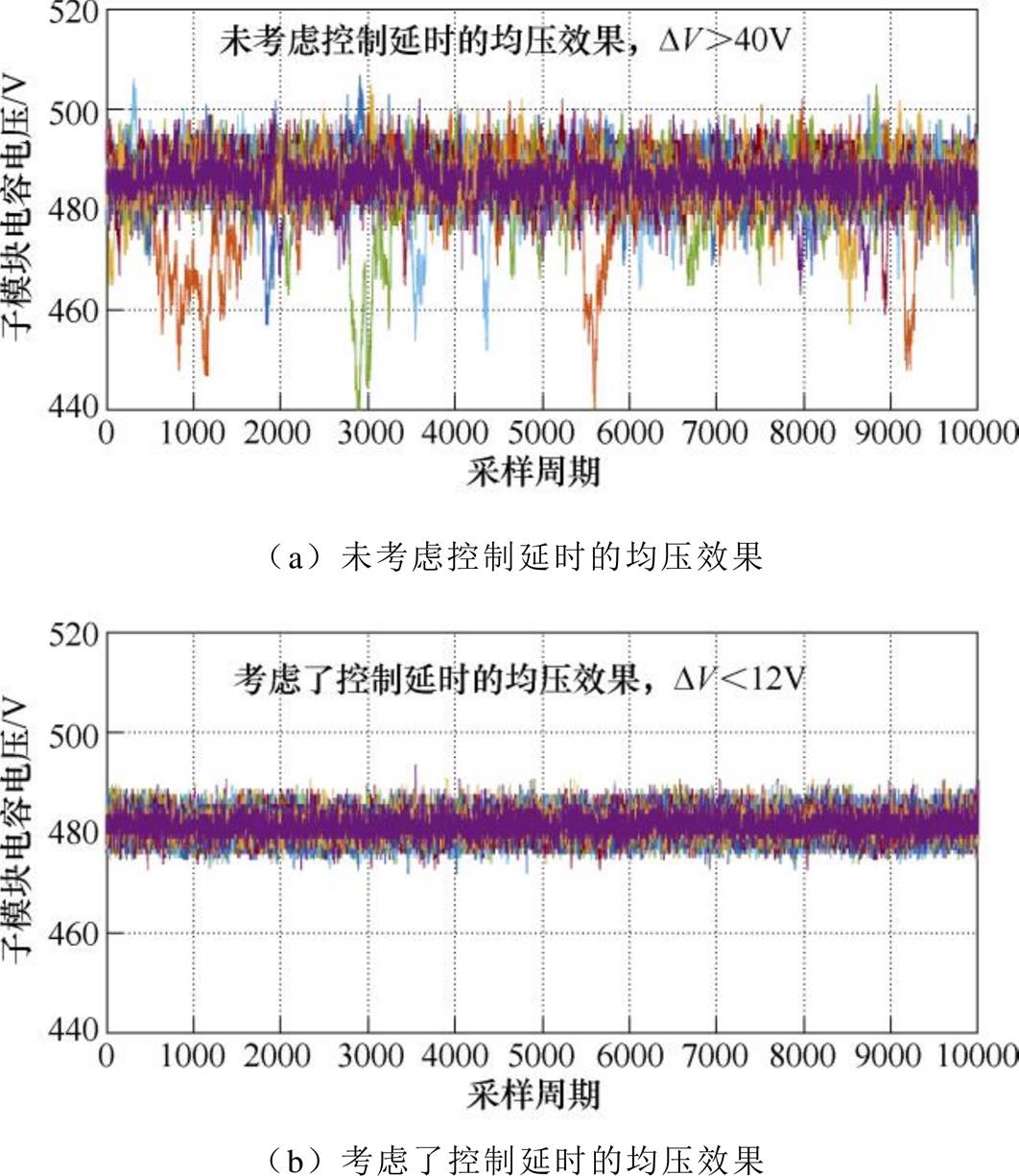
实验中子模块电容电压数据通过以太网传输给上位机,首先图24验证了控制延时对均压效果的影响。在9kV输入负载1kW工况下,传统均压算法如果未考虑控制延时对门极驱动信号进行重新分配,电容电压纹波如图24a所示,尽管电容电压不会发散,但纹波相对较大,高达40V。而本文所提均压方法考虑了控制延时,可以将电容电压纹波抑制在12V以内,如图24b所示,且均衡效果良好。
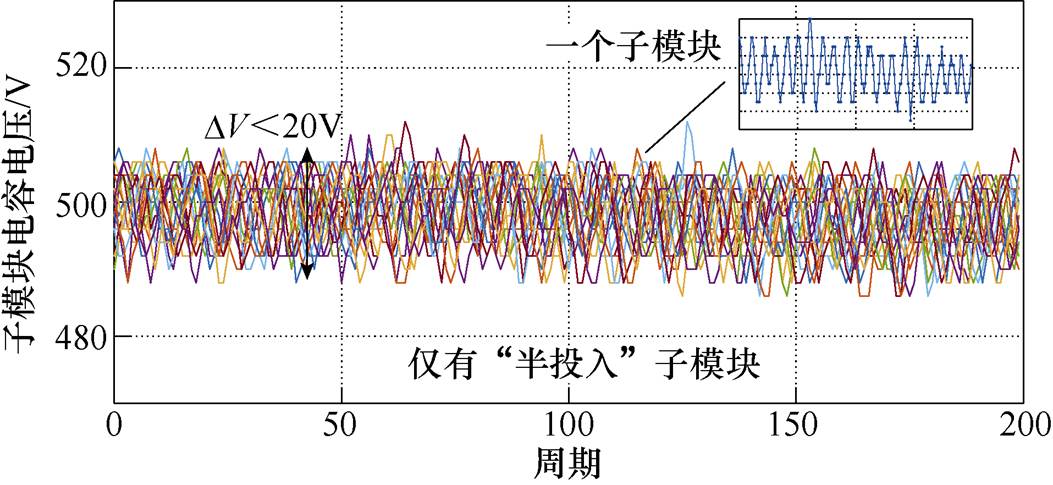
不同输入电压下满载工况的电容电压波动特性如图25和图26所示。子模块电容容值为20mF,在9.2kV输入下,MMC电压调制比为1,桥臂所有子模块均为“半投入”,40kW输出下,电容电压纹波小于20V。不存在一个周期内被大量充电的情形,控制延时对电容电压纹波影响较小,因此无监督均压算法和本文所提监督式均压方法均不会引发较大电容电压纹波。
图26给出了监督式子模块电容均压算法对电容电压纹波的抑制效果。12kV、40kW工况下,一个周期“全投入”子模块个数为3,采用传统的均压算法[20-21],电容电压纹波为90V左右,由于存在两个控制周期延时,子模块电容可能会被“全投入”连续充电3个周期。随后使能本文监督式均压算法,可以发现电容只会被“全投入”充电1个周期,随后被“半投入”进行放电若干周期,电容电压纹波幅值从90V抑制到35V,降幅高达61%,与仿真结果一致。
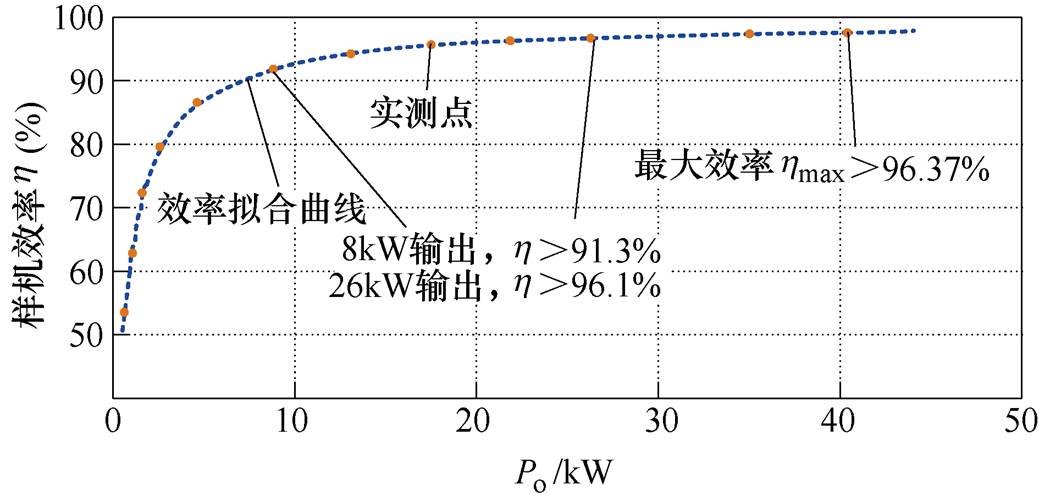
该研究对研制样机的损耗和变换效率进行了测量。图27为研制样机变换效率随输出功率Po变化的曲线,输入电压为12kV,输出功率为10kW时,样机效率为92%,当输出功率增加到30kW时,变换效率达到96%,随着输出功率的进一步增加到40kW,研制样机最大变换效率达到96.37%。
图28给出了不同输入电压Uin下的变换效率曲线。在不同输入电压下,研制样机效率基本保持一致。由于开关频率和测量误差影响,不同电压点下效率偏差在0.5%以内。实现了当输出功率为10kW时,效率可保持在92%以上,在输出功率为20kW时,效率大于94.5%,在输出功率40kW时,效率大于96%。
5 结论
针对模块化多电平谐振变换器应用于宽范围调压领域,本文提出了基于变调制比控制和调频控制相结合的多自由度调压控制策略,并详细优化设计了控制参数。相比仅采用传统LLC调频调压策略,该方法的桥臂子模块数目可减少20%,变压器励磁电流降低60%,开关频率范围缩小为原来的1/4,从而大幅降低开关器件和变压器损耗。此外,优化设计的开关频率范围可避免桥臂电感和变压器的高电压应力。本文揭示了变调制比控制下子模块电容电压纹波大的问题,提出了监督式子模块均压算法,避免了控制延迟引发的电容连续多个周期充电,电容电压纹波可降低61%,大幅降低电容容值选型。基于本文所提优化控制策略,研制了8~16kV输入,375V 60kW输出的中压实验样机,一系列实验结果验证了该调控方法的可行性和高效性,实现了宽输入范围下40kW变换效率保持在96%以上。
参考文献
[1] 贺悝, 李勇, 曹一家, 等. 考虑分布式储能参与的直流配电网电压柔性控制策略[J]. 电工技术学报, 2017, 32(10): 101-110.
He Li, Li Yong, Cao Yijia, et al. Flexible voltage control strategy of DC distribution network con- sidering distributed energy storage[J]. Transactions of China Electrotechnical Society, 2017, 32(10): 101- 110.
[2] 曾嵘, 赵宇明, 赵彪, 等. 直流配用电关键技术研究与应用展望[J]. 中国电机工程学报, 2018, 38(23): 6791-6801.
Zeng Rong, Zhao Yuming, Zhao Biao, et al. A prospective look on research and application of DC power distribution technology[J]. Proceedings of the CSEE, 2018, 38(23): 6791-6801.
[3] 韩民晓, 谢文强, 曹文远, 等. 中压直流配电网应用场景与系统设计[J]. 电力系统自动化, 2019, 43(23): 2-11.
Han Minxiao, Xie Wenqiang, Cao Wenyuan, et al. Application scenarios and system design of medium- voltage DC distribution network[J]. Automation of Electric Power Systems, 2019, 43(23): 2-11.
[4] 林霖, 裴忠晨, 蔡国伟, 等. 混合式隔离型模块化多电平变换器[J]. 电工技术学报, 2021, 36(16): 3319-3330.
Lin Lin, Pei Zhongchen, Cai Guowei, et al. Hybrid isolated modular multilevel monverter[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(16): 3319-3330.
[5] 刘建强, 赵楠, 孙帮成, 等. 基于LLC谐振变换器的电力电子牵引变压器控制策略研究[J]. 电工技术学报, 2019, 34(16): 3333-3344.
Liu Jianqiang, Zhao Nan, Sun Bangcheng, et al. Research on control strategy of power electronic traction transformer based on LLC resonant con- verter[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3333-3344.
[6] Lu Zhebie, Li Chengmin, Zhu Ankang, et al. Medium voltage soft switching DC/DC converter with series connected SiC MOSFETs[J]. IEEE Transactions on Power Electronics, 2021, 36(2): 1451-1462.
[7] 黄先进, 赵鹃, 游小杰. 一种基于输入串联输出并联移相全桥变换器的改进交错控制方法[J]. 电工技术学报, 2020, 35(增刊1): 81-90.
Huang Xianjin, Zhao Juan, You Xiaojie. An improved interlace control method based on input series output parallel phase-shifted full-bridge converter[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(S1): 81-90.
[8] 杨博, 葛琼璇, 赵鲁, 等. 基于输入串联输出并联的双向全桥串联谐振DC-DC变换器系统控制策略研究[J]. 电工技术学报, 2020, 35(12): 2574-2584.
Yang Bo, Ge Qiongxuan, Zhao Lu, et al. Control strategy of dual bridge series resonant DC-DC converter system based on input series output parallel connection[J]. Transactions of China Electrotechnical Society, 2020, 35(12): 2574-2584.
[9] 袁栋, 袁宇波, 贾勇勇, 等. 一种混合型输入串联输出并联直流变压器[J]. 电网技术, 2021, 45(1): 179-188.
Yuan Dong, Yuan Yubo, Jia Yongyong, et al. An ISOP hybrid DC transformer[J]. Power System Technology, 2021, 45(1): 179-188.
[10] 孟涛, 安彦桦, 贲洪奇. 输入串联型变换器集成变压器的分布电容影响机制与绕组布局方法[J]. 电工技术学报, 2021, 36(24): 5272-5282.
Meng Tao, An Yanhua, Ben Hongqi. Stray capaci- tances influences and windings layout of the integrated-transformer in the input-series converter[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5272-5282.
[11] Zhao Biao, Song Qiang, Li Jianguo, et al. Com- parative analysis of multilevel high frequency link and multilevel DC link DC-DC transformers based on MMC and dual-active bridge for MVDC appli- cation[J]. IEEE Transactions on Power Electronics, 2018, 33(3): 2035-2049.
[12] 王婷, 王广柱, 张勋. 基于模块化多电平矩阵变换器的电力电子变压器控制策略[J]. 电工技术学报, 2016, 31(18): 108-115.
Wang Ting, Wang Guangzhu, Zhang Xun. The control strategy of power electronic transformer based on modular multilevel matrix converters[J]. Transactions of China Electrotechnical Society, 2016, 31(18): 108-115.
[13] Xin Xiang, Zhang Xiaotian, Chaffey G P, et al. An isolated resonant mode modular converter with flexible modulation and variety of configurations for MVDC application[J]. IEEE Transactions on Power Delivery, 2018, 33(1): 508-519.
[14] 李雨岑. 谐振型中低压直流变压器的均流技术和拓扑研究[D]. 杭州: 浙江大学, 2020.
[15] Zhao Biao, Song Qiang, Li Jianguo, et al. High frequency link modulation methodology of DC-DC transformer based on modular multilevel converter for HVDC application: comprehensive analysis and experimental verification[J]. IEEE Transactions on Power Electronics, 2017, 32(5): 3413-3424.
[16] 李风华, 路艳国, 王海斌, 等. 海底观测网的研究进展与发展趋势[J]. 中国科学院院刊, 2019, 34(3): 321-330.
Li Fenghua, Lu Yanguo, Wang Haibin, et al. Research progress and development trend of seafloor obser- vation network[J]. Bulletin of Chinese Academy of Sciences, 2019, 34(3): 321-330.
[17] Lu Feng, Zhou Huaiyang, Yue Jiguang, et al. Design of an undersea power system for the East China Sea experimental cabled seafloor observatory[C]//2013 OCEANS-San Diego, San Diego, CA, USA, 2013: 1-6.
[18] Gowaid I A, Adam G P, Ahmed S, et al. Analysis and design of a modular multilevel converter with trape- zoidal modulation for medium and high voltage DC-DC transformers[J]. IEEE Transactions on Power Electronics, 2015, 30(10): 5439-5457.
[19] Zhao Biao, Song Qiang, Li Jianguo, et al. Modular multilevel high-frequency-link DC transformer based on dual active phase-shift principle for medium- voltage DC power distribution application[J]. IEEE Transactions on Power Electronics, 2017, 32(3): 1779-1791.
[20] Zhang Jianjia, Shao Shuai, Li Yucen, et al. A voltage balancing method for series-connected power devices in an LLC resonant converter[J]. IEEE Transactions on Power Electronics, 2021, 36(4): 3628-3632.
[21] Shao Shuai, Li Yucen, Sheng Jing, et al. A modular multilevel resonant DC-DC converter[J]. IEEE Transa- ctions on Power Electronics, 2020, 35(8): 7921-7932.
[22] Lu Zhongzhiguang, Lin Lei, Wang Xuehua, et al. LLC-MMC resonant DC-DC converter: modulation method and capacitor voltage balance control strategy[C]//2020 IEEE Applied Power Electronics Conference and Exposition (APEC), New Orleans, LA, USA, 2020: 2056-2061.
[23] Yeon C, Kim J, Park M, et al. Improving the light- load regulation capability of LLC series resonant converter using impedance analysis[J]. IEEE Transa- ctions on Power Electronics, 2017, 32(9): 7056-7067.
[24] 孙谦浩, 李亚楼, 孟经伟, 等. 基于移相控制的高频链模块化多电平直流变压器分布式控制管理策略及轮换电容电压平衡方法[J]. 中国电机工程学报, 2018, 38(5): 1310-1318.
Sun Qianhao, Li Yalou, Meng Jingwei, et al. Dis- tributed control strategy and alternate modulation balance algorithm of high-frequency-link modular multilevel DC transformer based on phase-shifting principle[J]. Proceedings of the CSEE, 2018, 38(5): 1310-1318.
[25] 管州, 梅军, 丁然, 等. 基于拓展移相控制的直流配电网模块化多电平直流变压器[J]. 电工技术学报, 2019, 34(13): 2770-2781.
Guan Zhou, Mei Jun, Ding Ran, et al. Modular multilevel DC transformer for DC distribution appli- cation based on extended phase-shift control[J]. Transactions of China Electrotechnical Society, 2019, 34(13): 2770-2781.
[26] 王暄, 王广柱, 孙晓伟, 等. 具有宽范围输出电压的三电平半桥LLC谐振变换器控制策略[J]. 电工技术学报, 2017, 32(21): 24-33.
Wang Xuan, Wang Guangzhu, Sun Xiaowei, et al. Control strategy of three-level half-bridge LLC resonant converter with wide output voltage range[J]. Transactions of China Electrotechnical Society, 2017, 32(21): 24-33.
Multiple-Degree-of-Freedom Control and Capacitor Voltage Balancing Method of Modular Multilevel Resonant Converter
Sheng Jing1 Chen Cong1 Xiang Xin1 Li Chushan1,2 Li Wuhua1
(1. College of Electrical Engineering Zhejiang University Hangzhou 310027 China 2. Zhejiang University-University of Illinois at Urbana-Champaign Institute Haining 314400 China)
Abstract Modular multilevel resonant converters (MMRC) have attracted many studies in the medium voltage area due to the advantages of modular multilevel topology and LLC resonant circuits. However, in the wide input range field, more in-depth research still needs to be conducted on the efficient regulation of this topology. This paper proposed a multi-degree-of-freedom (DOF) voltage regulation control method for a modular multilevel resonant converter. Firstly, the voltage regulation effects and characteristics of switching frequency and modulation index are analyzed. Then, combining both frequency regulation and modulation index control, a wide-range voltage regulation method with multi-degree-of-freedom is proposed, and the hardware parameters and control parameters are designed in detail. Moreover, a supervised capacitor voltage method for ripple suppression is proposed to reveal large capacitor ripple issue under modulation index control. Finally, the effectiveness of the proposed method is verified by a laboratory prototype with a wide input voltage of 8~16kV and an output power of 60kW. The full-load efficiency of the full input voltage range is greater than 96%, and the submodule capacitor voltage ripple is reduced by 60%.
keywords:Modular multilevel resonant converter, medium voltage wide input range, multiple degree-of-freedom control, capacitor voltage ripple suppression
DOI: 10.19595/j.cnki.1000-6753.tces.221010
中图分类号:TM46
国家重点研发计划国际合作重点专项(2022YFE0101900)、国家自然科学基金(52107214)和内蒙古自治区重大专项(2021D0026)资助项目。
收稿日期 2022-05-31
改稿日期 2022-08-05
作者简介
盛 景 男,1993年生,博士研究生,研究方向为模块化多电平变换器拓扑及其控制。E-mail: zjdxsj2013@zju.edu.cn
向 鑫 男,1990年生,研究员,博士生导师,研究方向为新能源发电并网、柔性直流输配电与大容量直流变换。E-mail: xiangxin@zju.edu.cn(通信作者)
(编辑 陈 诚)
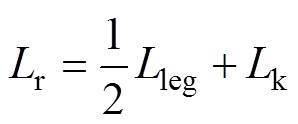 (1)
(1)
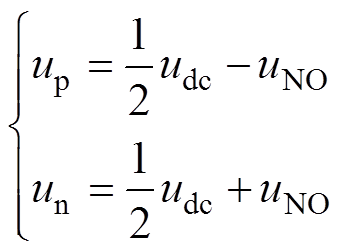 (2)
(2)
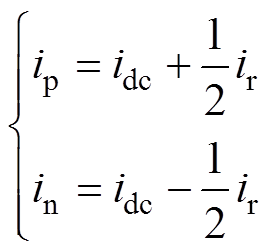 (3)
(3) 1以匹配输入输出电压,变压器二次侧接VD
1以匹配输入输出电压,变压器二次侧接VD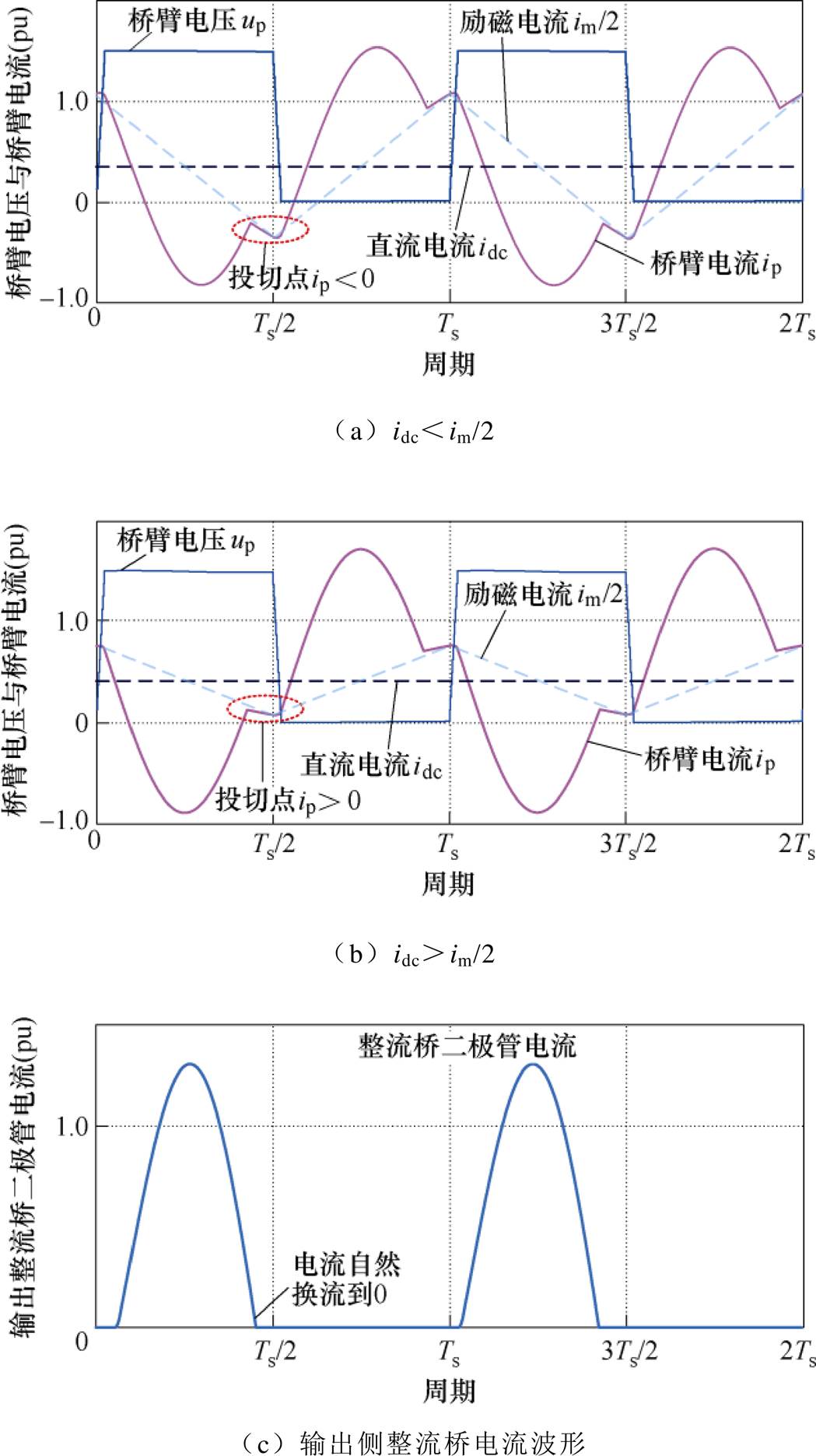


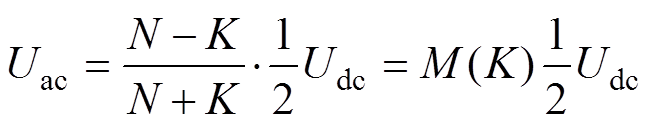 (4)
(4)

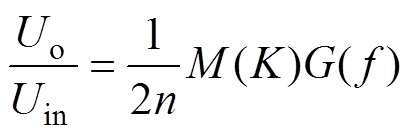 (5)
(5)
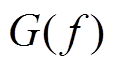 为LLC谐振腔增益;n为隔离变压器电压比。
为LLC谐振腔增益;n为隔离变压器电压比。

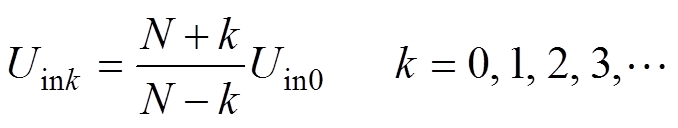 (6)
(6)
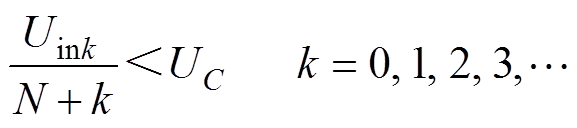 (7)
(7)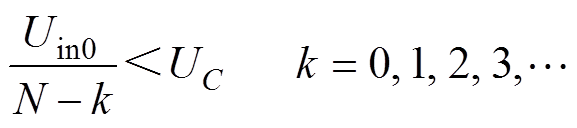 (8)
(8)
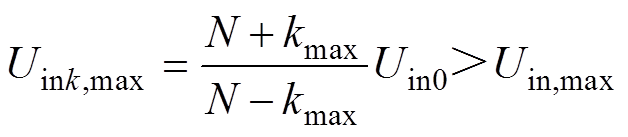 (9)
(9)
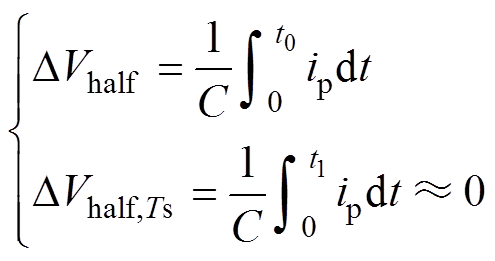 (10)
(10)
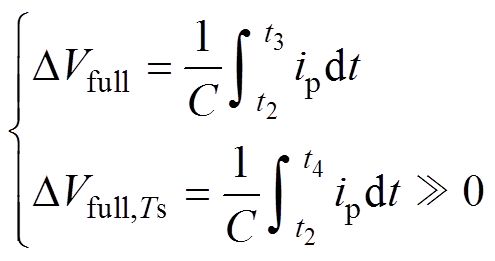 (11)
(11)