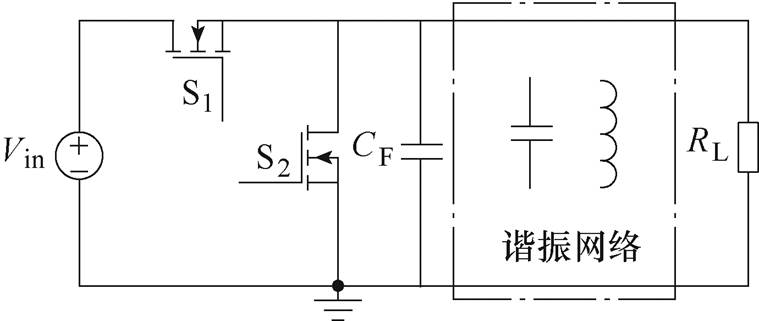
图1 半桥型Class D逆变电路拓扑结构示意图
Fig.1 Schematic diagram of the half-bridge Class D inverter circuit topology
摘要 随着电力电子技术的不断发展,超高频(30~300MHz)功率变换器逐渐成为研究热点。超高频功率变换器能有效减小系统无源元件的数值与体积,极大地提高系统的功率密度。传统的研究主要针对固定负载进行逆变器的参数设计,且基于此方法设计的变换器参数敏感度很高,然而实际场景下逆变器的负载会在一个宽范围内变化,这就对超高频变换系统的高效运行提出了挑战。该文主要针对这种宽负载超高频变换系统的谐振参数与匹配网络进行综述,介绍并比较目前超高频功率变换器的参数设计方法,同时讨论分析适用于超高频功率变换器的阻抗变换与压缩网络结构,为宽负载范围超高频功率变换器高效运行的后续研究提供理论参考。
关键词:超高频功率变换器 宽负载范围 谐振参数 匹配网络
随着小型化、轻量化需求的日益增加,超高频(30~300MHz)功率变换器近年来得以迅速发 展[1-3]。提高开关频率可以增加系统的功率密度,改善动态响应速度,有助于电力电子向模块化、集成化发展[4-5]。虽然超高频功率变换器具有如上所述优势,但极高开关频率带来的负面影响仍无法避免。首先,有源器件在开通关断瞬间由于电压电流重叠会形成较大的开关损耗,该损耗随开关频率的升高而迅速增加,因此往往需要采用具有软开关特性的谐振变换器。谐振变换器通过对由电阻、电感和电容构成的谐振网络进行优化设计来满足软开关特性需求。当变换器负载发生变化时,谐振网络的特性也随之改变,因此超高频功率变换器对负载变化十分敏感。当负载变化时,系统会偏离最优谐振工作点导致开关器件软开关特性丢失、开关管电压应力增加、系统无功电流增加等问题,进而导致系统无法高效运行甚至无法正常工作[6-7]。
越来越多的应用领域中超高频功率变换器面临负载特别是非阻性负载宽范围变化的问题。如在等离子体生成过程与晶体感应加热过程中,超高频逆变器负载的阻性分量和感性分量均大幅变化,导致超高频功率变换器性能大幅下降甚至无法正常工 作[8-9]。同时由于较高的开关频率,超高频功率变换器一般难以通过频率或占空比的调节来实现单周期闭环控制。因此如何解决宽负载范围变化条件下超高频功率变换器的高效运行问题成为了亟待突破的难点[10]。
针对上述问题,学者们主要从两个方面来实现宽负载范围高频变换器的高效运行:①优化逆变器的参数设计方法,针对宽范围负载特别是宽范围非阻性负载进行优化设计;②通过阻抗变换和压缩网络的设计,对宽范围变化的非阻性负载进行有效的压缩与调整。
本文针对宽负载范围超高频变换器的拓扑参数设计方法以及阻抗变换和压缩网络的设计进行综述。分别从逆变器拓扑与参数设计、阻抗变换与压缩网络两方面,介绍了针对阻性负载和非阻性负载的一系列逆变器设计方案,分析了其可行性及难点,并对近年来提出新型阻抗压缩网络结构进行了展望。
超高频逆变电路的研究同小功率射频电子电路的功率放大器(Power Amplifier, PA)联系较为紧密,主要采用Class D、Class E、Class F 等逆变电路 拓扑。
Class D逆变电路拓扑结构示意图如图1所示,其由半桥结构构成,通过桥臂中点后的谐振网络为开关管创造软开关条件。文献[11-12]对相关拓扑的结构和设计方法进行了深入研究,但是在超高频条件下,半桥结构上管需要采用浮地驱动,同时两开关管的驱动信号需要保证有效的死区时间防止直通,上述特性对驱动电路的设计和控制均提出了较高要求。此外,Class D电路中,零电压开通是由开关的并联寄生电容被动充放电实现的,因此在设计过程中,需要精确地把握死区时间内电容放电规律,对负载特性、寄生电容进行精确建模,在实际工作中,Class D电路的软开关往往依赖动态的死区时间控制。因此在近些年的研究中,以Class D逆变电路为代表的半桥型超高频谐振电路的工作频率还相对较低。半桥型超高频逆变电路的频率提升需依赖于包含驱动电路半桥模块的进一步发展。

图1 半桥型Class D逆变电路拓扑结构示意图
Fig.1 Schematic diagram of the half-bridge Class D inverter circuit topology
与半桥结构不同,以Class E、Class F 等拓扑为代表的单端接地型逆变电路,可有效地避免浮地驱动和开关管直通等问题,因此单端拓扑应用范围较广[13-14]。传统的Class E逆变电路和Class F 逆变电路分别如图2a和图2b所示。在Class E逆变电路中,LF为电感值极大的扼流电感,可产生近乎恒定的输入电流。CF、LS、CS构成的谐振网络为开关管营造零电压开通条件,其中谐振电容CF为开关管输出侧寄生电容和分立谐振电容并联构成的等效电容。Class F 逆变电路同Class E电路相似,其增加了由Ln和Cn构成的同开关管并联的LC支路,当该串联支路的谐振频率选取为开关频率的整数倍n时,上述基于扼流电感的Class E、Class F 逆变电路能够在一定负载条件下实现开关管的零电压以及零电压导数开通。但是上述谐振逆变电路均需要采用较大的扼流电感,不利于超高频功率变换器体积的减小与功率密度的提升。
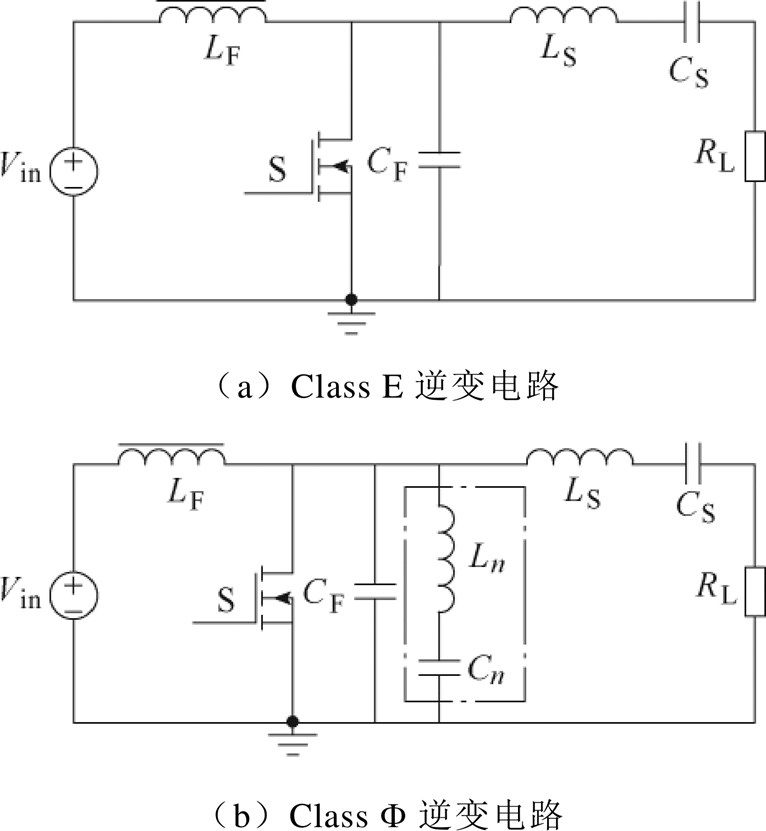
图2 单端逆变电路拓扑结构示意图
Fig.2 Schematic diagram of the a single-ended inverter
因此,近年来一些学者开始考虑能否令传统谐振网络中前端电感也参与谐振,从而减小其电感与体积。文献[15-19]提出了前端电感LF为谐振电感的拓扑结构,在后续内容中称之为全谐振电路。从拓扑结构上看,上述拓扑同传统含扼流电感的拓扑完全相同,但系统的工作状态却有较大差别。同时由于系统中各无源元件均参与谐振,其参数设计方法远比扼流电感型拓扑结构复杂。Class F2逆变器的开关漏源极等效阻抗模型如图3所示。
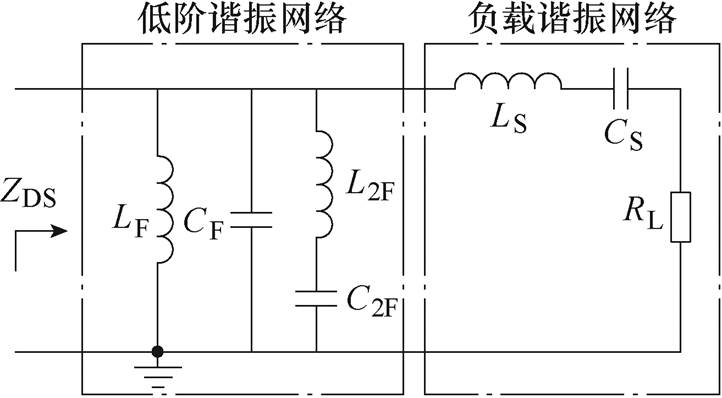
图3 Class F2逆变器的开关漏源极等效阻抗模型
Fig.3 The switch drain-to-source equivalent impedance circuit of Class F2 inverter
以全谐振的Class F2电路为例,文献[17]提出一种频域分析设计方法,将电路分为“LC负载谐振网络”和“低阶谐振网络”两部分。负载网络中的LS和CS一方面组成串联谐振腔,构造正弦输出电流;另一方面保留了一定电抗分量,用于调节输出功率。谐振网络中,将L2F和C2F的谐振频率需设定为与开关频率的2次谐波相近,使开关管漏源极两端在2次谐波频率处呈低阻抗特性,消除2次谐波,LF、CF需与L2F、C2F协同设计,使得在基波和3次谐波处,开关管漏源极两端呈高阻抗特性,以放大基波和3次谐波,达到降低开关管两端电压应力的目的。基于此方法,电路中的谐振参数表示为
 (1)
(1)
式中,fS为开关频率;LF、L2F、CF、C2F为图3中的谐振电感电容。然而,这种方法所得到的参数精度并不高,CF值的选取是基于对电路传递功率的能力和电路中环流大小的综合考虑,目前并无固定的选取标准,使用频域方法计算之后仍需要通过仿真进一步调节,且并未体现负载对于参数设计及软开关特性的影响。
为了设计更准确的电路参数,N. O. Sokal等提出了基于时域分析的参数设计方法[20]。通过分析电路工作模态,根据电路基本定理建立谐振电压、电流的表达式,以开关从开通过渡到关断状态时电流、电压连续性及零电压导通、零dv/dt导通为边界条件,通过微分方程的求解获取谐振电容、谐振电感的精准表达式。但是从建立的谐振参数表达式中可以看出,谐振参数值同负载存在正比或反比关系,意味着谐振参数受负载变化的影响较大。
上述的传统参数设计方式只能实现在特定负载下的软开关,在很多超高频逆变器的实际应用场景中,如无线电能传输、等离子体推进等领域,逆变器的等效负载随线圈位置、等离子体状态而动态变化。因此,实际应用中,希望超高频逆变器在较宽负载范围内保持稳定的输出电压和较高的效率。如文献[21-22]所述,对于依照传统方法设计的Class E电路来说,当负载变化时,开关漏源极电压波形变化过程如图4所示,Ropt为逆变器的额定负载。当负载电阻大于额定值时,开通时刻开关管两端电压将无法谐振回零,同开关管并联的谐振电容将会通过开关管放电,导致较大的开通电流尖峰;反之,当负载电阻小于额定值时,开关管两端电压会在开通时刻前提前谐振回零,在开通时刻,电流会流经开关管体二极管并产生反向导通损耗,降低系统效率。因此,基于传统设计方法的全谐振电路负载敏感度较高,负载偏离固定值时,开关器件的软开关特性极易丢失;输出电压也会随负载的变化而有所改变。
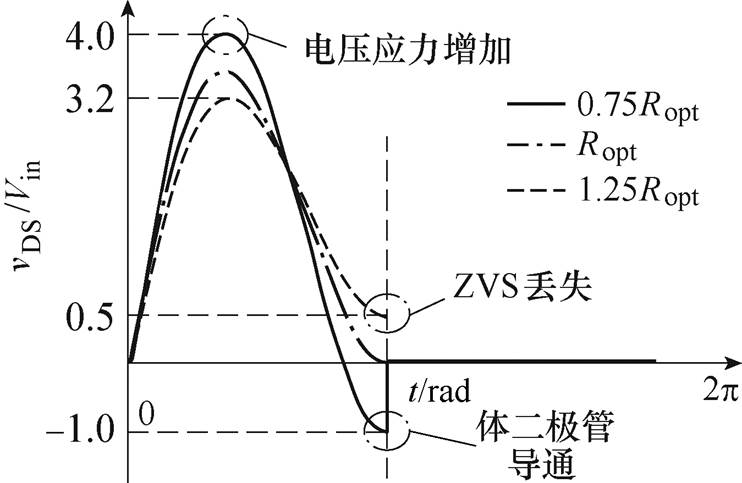
图4 当负载变化时传统E类逆变器的电压波形变化
Fig.4 Voltage waveforms of the conventional Class E inverter as the load changes
为解决上述问题,R. E. Zulinski[23]等首次提出了E类逆变器负载无关性的理论概念,表明当负载从固定电阻变为无限电阻时,E类逆变器仍可保持零电压开通(Zero Voltage Switching, ZVS)和恒定的输出电压幅值和相位,无需调谐或反馈控制,因此可以在宽负载范围内保持高效率。但该方法存在一定的局限性,如文献[23]中引入了大量的辅助参数导致计算过程较为复杂,且输入输出的电压比始终为1.45,电路只能设计为提供恒定的输出交流电压,而在某些应用中,更偏向于需要恒定的输出交流电流。该方法计算的宽负载软开关应满足如下条件
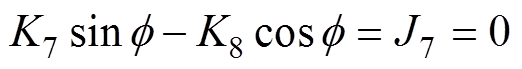 (2)
(2)
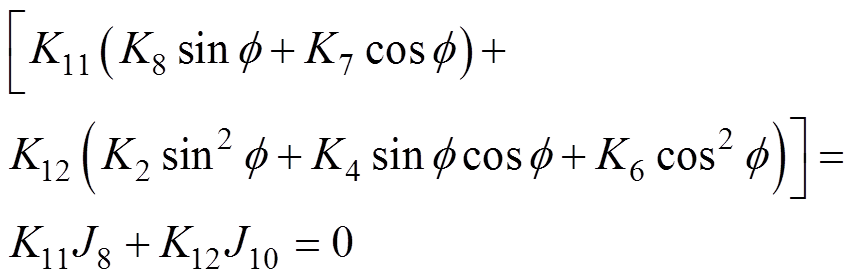 (3)
(3)
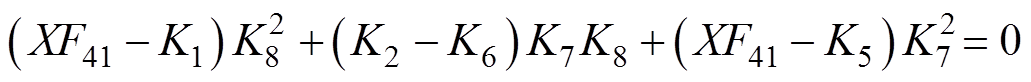 (4)
(4)
式中,X为输出端滤波器的电抗;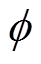 为输出电压相位;K1~K12、J7~J10、F41为与电感、电容有关的辅助参数。
为输出电压相位;K1~K12、J7~J10、F41为与电感、电容有关的辅助参数。
文献[24-25]相继对负载变化不敏感的E类逆变器设计进行了理论研究。然而这些设计方法会使系统存在较大的环流,无源元件和开关管的通态损耗增加,系统额定负载处效率下降。
在如图5所示的具有T型网络负载的推挽放大器中,文献[26]将负载无关的概念扩展到了EF级功率变换器。根据其交错并联的结构,可以将奇次谐波和偶次谐波分配给T型网络的不同支路进行分别处理。如图5所示,在奇次谐波下,每个开关的等效并联负载由差模阻抗ZD和共模电导YC共同组成,在偶次谐波下,开关等效并联阻抗仅由差模阻抗ZD构成。其独特的拓扑结构与参数设计相配合,保证了动态的阻性负载下谐振器中恒定的电流,从而使逆变器在动态负载下始终处于软开关状态。但该方法无法在负载上得到稳定的输出电流。
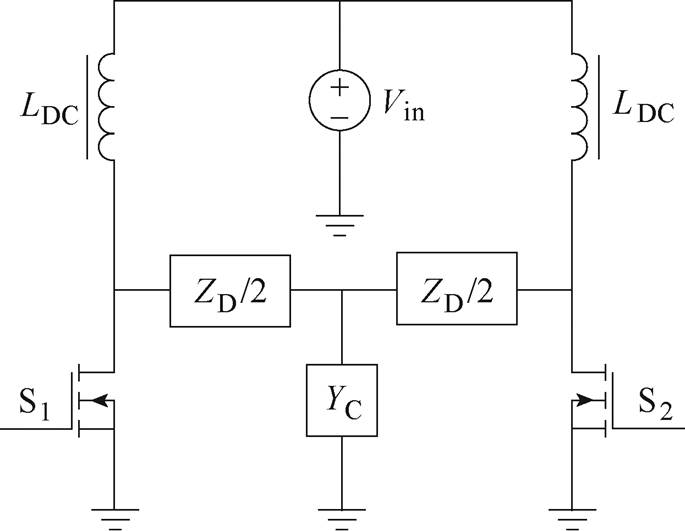
图5 文献[26]中带T型网络负载的挽式Class EF或E/F谐波调谐放大器
Fig.5 Push-pull Class EF or E/F harmonic-tuned amplifier with a T type net-work in Ref.[26]
在传统频域设计方法[17]的基础上,文献[27]对已知负载变化范围的E类逆变器电路进行负载网络拓扑的调整,通过确定电路中关键谐振网络的谐振频率和特征阻抗,调整这些参数来修改电路性能以针对大范围的负载电阻变化保持ZVS。文献[27]还提供了将其应用于Class F2甚至更高阶电路的转换方法。图6为Class F2逆变器变负载运行的转换步骤。首先根据传统频域设计方法[17]针对额定负载设计元件参数。在这种设计中,如图3所示,LS、CS构成的负载谐振网络阻抗Zload在开关频率下是感性的。因此,可以将LS、CS谐振腔分成两部分——串联谐振网络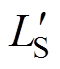 、CS和附加电感LNET。感性负载Class F2逆变电路如图6a所示。如果串联谐振网络具有足够高的品质因数,它会在开关频率下输出接近正弦的电流。在这种情况下,附加电感LNET和负载R可以用在开关频率下具有相同阻抗的并联网络(LK和RK)代替。负载并联等效电路如图6b所示。转换公式为
、CS和附加电感LNET。感性负载Class F2逆变电路如图6a所示。如果串联谐振网络具有足够高的品质因数,它会在开关频率下输出接近正弦的电流。在这种情况下,附加电感LNET和负载R可以用在开关频率下具有相同阻抗的并联网络(LK和RK)代替。负载并联等效电路如图6b所示。转换公式为
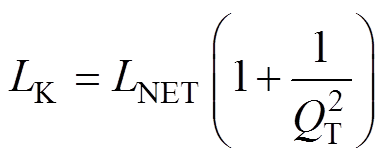 (5)
(5)
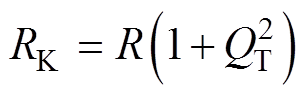 (6)
(6)
式中,LK和RK为图6b中的等效并联电感和等效负载;LNET和R为图6a中的等效附加电感及负载;QT为负载的功率因数,即
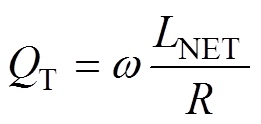 (7)
(7)
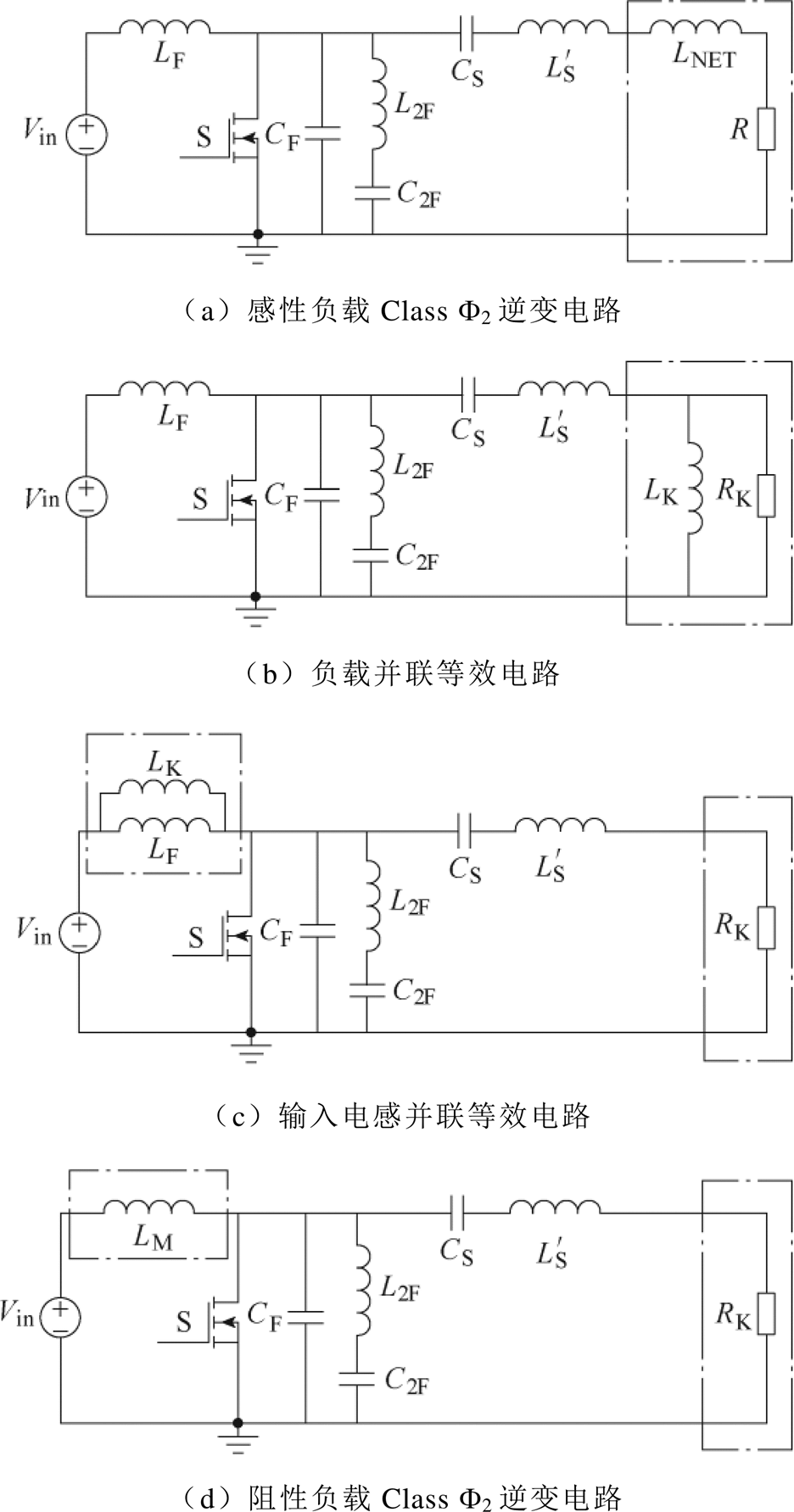
图6 文献[27]提出的Class F2逆变器变负载运行的转换步骤
Fig.6 Steps for transforming a Class F2 inverter for variable-load operation in Ref.[27]
在开关频率下,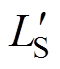 和CS处于谐振状态,因此LK实际上与输入电感LF并联,这个并联组合可用LM表示,LM=LK//LF。最终验证了转换后的参数设计可以实现从R~10R宽负载下变化的ZVS。但该电路变换仅在开关频率下严格有效,在开关频率的高次谐波下无效,且输出串联谐振回路的品质因数Q会随着逆变器负载电阻的增加而降低,逆变器输出的高次谐波含量变化明显,由于一些负载对谐波含量的作用较敏感,因而必须提供额外的滤波网络来获得正弦输出波形。
和CS处于谐振状态,因此LK实际上与输入电感LF并联,这个并联组合可用LM表示,LM=LK//LF。最终验证了转换后的参数设计可以实现从R~10R宽负载下变化的ZVS。但该电路变换仅在开关频率下严格有效,在开关频率的高次谐波下无效,且输出串联谐振回路的品质因数Q会随着逆变器负载电阻的增加而降低,逆变器输出的高次谐波含量变化明显,由于一些负载对谐波含量的作用较敏感,因而必须提供额外的滤波网络来获得正弦输出波形。
文献[21]中,P. D. Mitcheson等为与负载无关的E类逆变器提供更灵活的设计方法,并将与负载无关的概念扩展到EF类拓扑。在设计过程中,减少了对开关过程中电压、电流特性的限制,进一步放宽了软开关约束条件,不再以零电压导数开通作为边界条件。
该方法为设计对负载独立的Class E变换器,首先引入3个参数:输出电流相位j、谐振频率q和负载因数p。并在开关关断期间,列写开关电压vDS关于以上3个参数的时域方程为
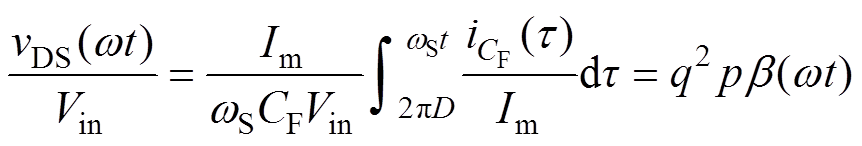 (8)
(8)
其中
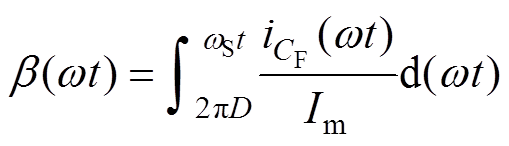 (9)
(9)
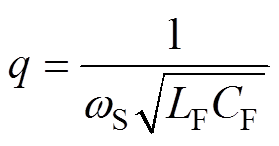 (10)
(10)
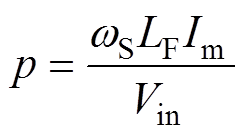 (11)
(11)
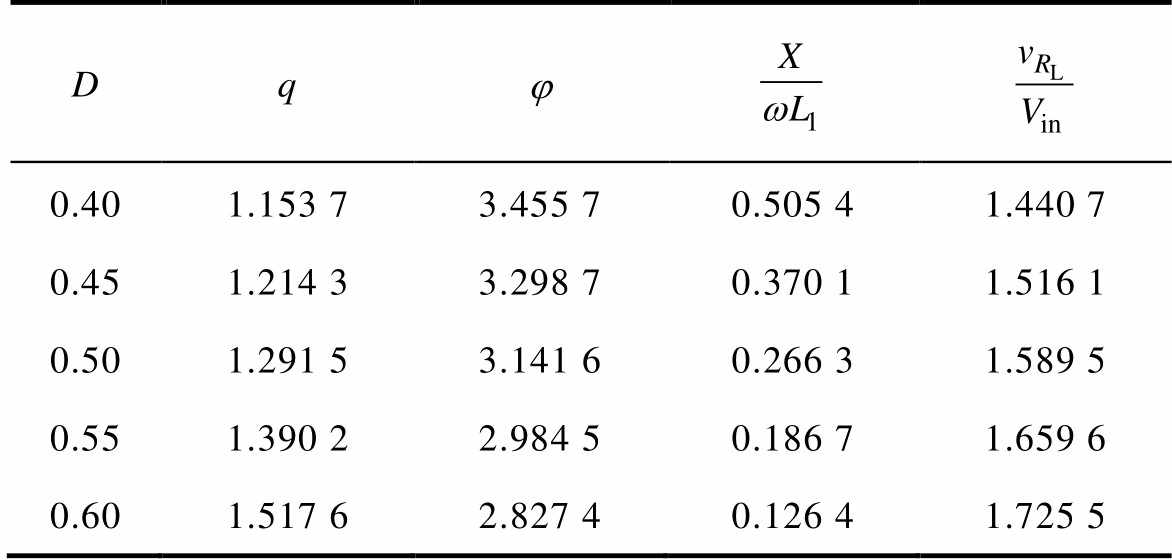
式中,Im为输出电流的幅值;Vin为输入电压的幅值;wS为逆变器的开关角频率;D为开关占空比;LF、CF、 分别为逆变器的谐振电感、电容和电容电流。为了在变化的负载下工作,电路需要满足以下两组条件:①输出电压恒定,即p在任何取值下,输出电压对p的导数为0;②软开关特性恒定,即p取任何值时软开关条件均成立。通过求解,可得到在不同占空比D下的方程解集,见表1。根据q的取值,可以计算得到LF、CF,根据附加电抗X的取值,可设计谐振腔LS、CS。最终设计得到的变换器对负载电阻不敏感,但这种方法仅针对阻性负载,当负载存在感性或容性分量时,软开关将难以保持。且基于上述设计方法的逆变电路随着负载的改变,开关管或二极管的电压应力也迅速增加。
分别为逆变器的谐振电感、电容和电容电流。为了在变化的负载下工作,电路需要满足以下两组条件:①输出电压恒定,即p在任何取值下,输出电压对p的导数为0;②软开关特性恒定,即p取任何值时软开关条件均成立。通过求解,可得到在不同占空比D下的方程解集,见表1。根据q的取值,可以计算得到LF、CF,根据附加电抗X的取值,可设计谐振腔LS、CS。最终设计得到的变换器对负载电阻不敏感,但这种方法仅针对阻性负载,当负载存在感性或容性分量时,软开关将难以保持。且基于上述设计方法的逆变电路随着负载的改变,开关管或二极管的电压应力也迅速增加。
表1 文献[21]中不同占空比下与Class E逆变器q和j的解
Tab.1 Solutions of q and j for load-independent Class E inverter at different duty cycles in Ref.[21]
Dqj 0.401.15373.455 70.505 41.440 7 0.451.21433.298 70.370 11.516 1 0.501.291 53.141 60.266 31.589 5 0.551.390 22.984 50.186 71.659 6 0.601.517 62.827 40.126 41.725 5
文献[28-29]对文献[21]中负载无关Class E逆变器的设计方法进行了更加详细的介绍,使无源元件可以更加方便地单独设计和调整,并给出了详细的设计流程。进一步地,文献[30]提出了一种在任意占空比下与负载无关的E类逆变器分析设计方法,并指出随着负载电阻的增加,无源元件的等效串联电阻和MOSFET的导通电阻与负载电阻的比值减小,这使得E类逆变器能够获得更高的功率转换效率。
在超高频功率变换器研究中一直避免半桥型拓扑的应用,主要是由于半桥结构中上管的浮地驱动难以解决,但半桥型结构一个天然的优势为其开关管两端的电压应力很低,由于其开关管与输入侧电压直接连接,所以其开关管电压应力与输入电压相同。近几年也有学者开展关于Class D逆变器宽负载运行的研究,文献[31]通过分析不同占空比(死区时间)、不同谐振频率下逆变器的工作模态,计算得到归一化频率wn下获得ZVS所需的归一化死区时间表达式为
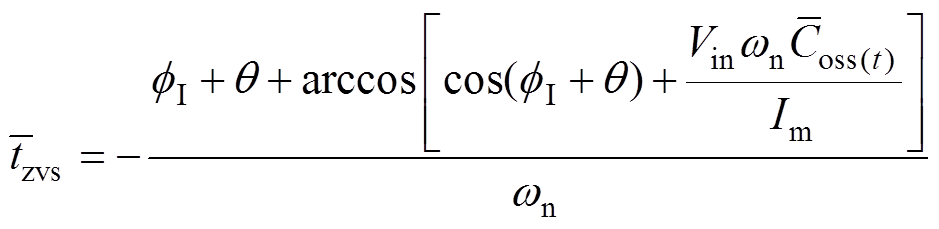 (12)
(12)
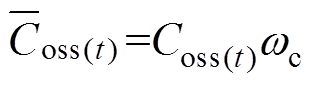 (13)
(13)
式中, 为Class D逆变器输出电流相位;q 为开关电压基波相位;wn为归一化频率,即开关频率与电感电容谐振频率wc的比值;Coss为开关并联寄生电容。
为Class D逆变器输出电流相位;q 为开关电压基波相位;wn为归一化频率,即开关频率与电感电容谐振频率wc的比值;Coss为开关并联寄生电容。
图7给出了不同负载对应的软开关区间,在两个区域重叠处,逆变器可以始终保持软开关。设计的额定负载为1 000W,电路可以在750~1 250W 的宽负载范围内保持软开关状态。
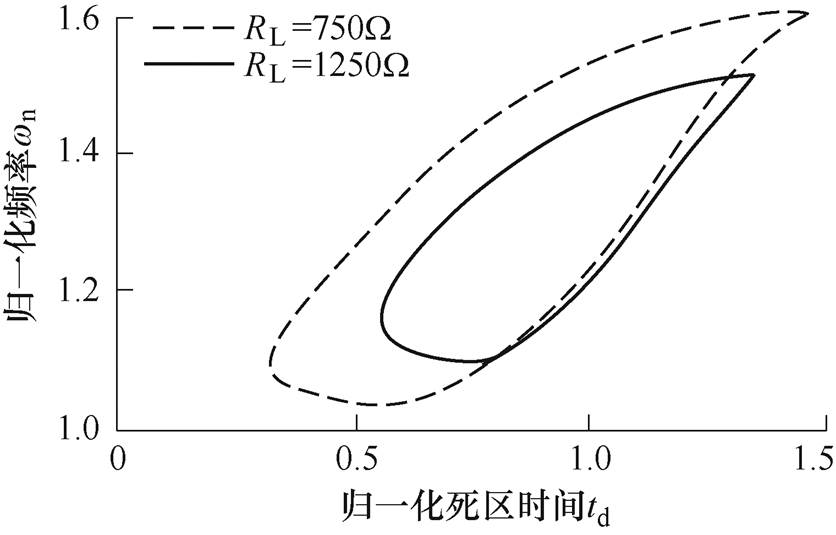
图7 文献[31]中求得可变负载下的软开关工作区
Fig.7 Soft-switch operating region under variable load in Ref.[31]
在谐振逆变电路设计过程中,逆变电路的理想负载往往同实际负载或等效负载不匹配,因此需对负载进行阻抗匹配与变换来满足逆变电路对负载的需求。此外,在实际系统中,超高频逆变器的实际负载可能从阻感性到阻容性的宽范围内变化,由此造成了极大的功率损耗,这个问题可以通过阻抗压缩的方法来解决,通过阻抗压缩网络的设计,使得每个逆变器的等效负载在一个更小的范围内变化。在超高频直流-交流或直流-直流变换器中往往采用由电感和电容构成的非隔离型阻抗变换网络对实际电路阻抗进行调整。
阻抗变换网络一般由电感、电容构成,其中结构最简单的变换网络为两元件L型网络。该网络由1个电感和1个电容构成,其电路如图8所示。其中图8a所示结构为升电阻型阻抗变换网络,即在额定点处变换时,输入侧等效负载Zin小于负载R;与之相反,图8b所示结构为降电阻型阻抗变换网络。
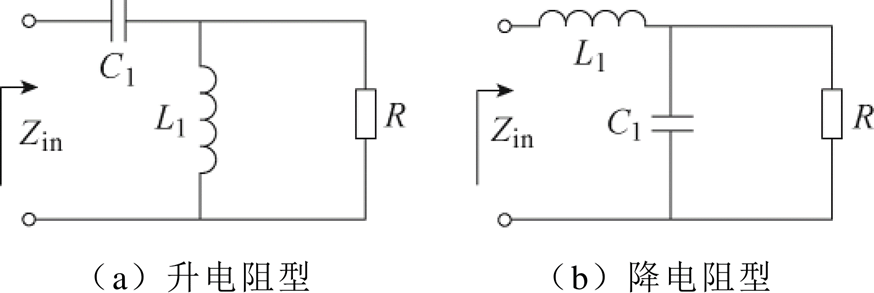
图8 L型阻抗变换网络电路
Fig.8 L-type impedance conversion network circuit diagram
在L型网络的基础上,可以用电感、电容元件以不同排列组合方式构成八种两元件网络结构,其中有三种可以实现阻抗压缩[32],压缩网络的结构如图9a~图9c中左图所示。文献[32]中具体分析了这三种网络对于阻抗的压缩效果,如图9a~图9c中右图所示,虚线表示的是压缩前负载阻抗变化轨迹,实线表示的是压缩后的等效负载变化轨迹。从图9中可见,系统特性工作状态变化时,耦合系数k变化,导致负载阻抗Z12的宽范围变化。在两元件网络的作用下,宽范围内变化的阻抗被压缩并转换到适当的窄范围,由此逆变器可以工作在理想的负载条件下,系统的输出电压、输出功率以及效率对于偏移量的敏感性降低。
然而上述的L型网络只能够在额定点处实现所期望的点对点阻性变换。当阻性负载R变化时,变换后的阻性分量也随之变化。随着负载R的增大或减小,会在输入侧阻抗Zin中引入较大的容性或感性分量,导致谐振逆变电路偏离最优工作点,造成开关器件软开关特性的丢失和系统效率的下降。因此,从压缩效果上看,L型网络只能将阻抗从一个区域大致投射到另一个区域,无法实现精准的阻抗压缩。
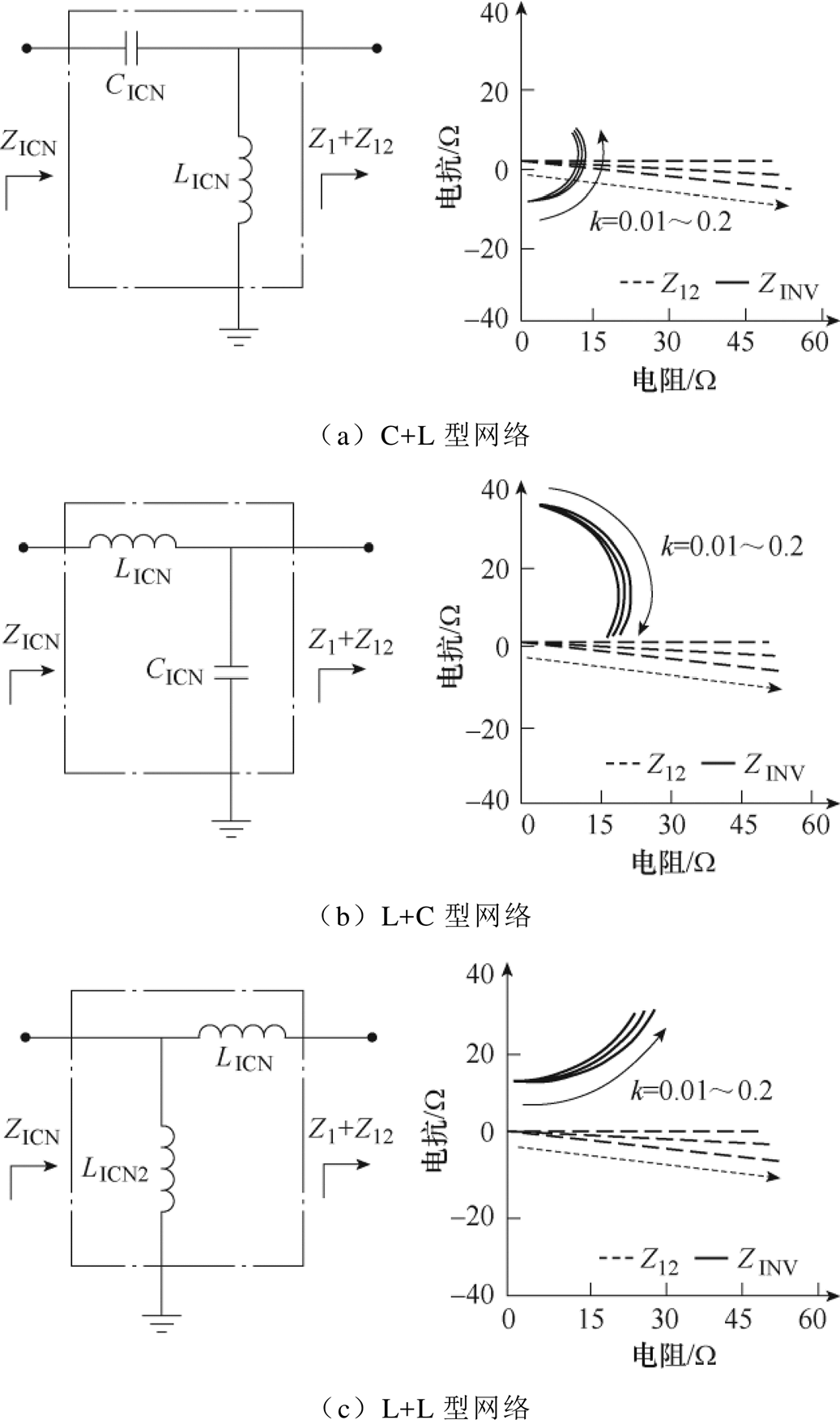
图9 文献[32]中L型阻抗变换网络电路图与压缩效果
Fig.9 L-type impedance transform network circuit diagram and compression effect in Ref.[32]
除了L型网络结构之外,文献[33]提出了另外一种两元件结构,如图10所示。由电感和电容分别构成的非对称支路被用于驱动两个同时变化的负载R,一般可令电感、电容元件的电抗等于负载变化范围的最大值与最小值的平均数。当负载R变化时,电感和电容支路分别流过不同的功率,从而补偿了负载R的偏移量,因此输入侧阻抗的变化范围被有效缩小。这种阻抗补偿方式可适用于接地型和非接地型负载,分别如图10b和图10a所示。图10a中电路的输入电阻可被表示为
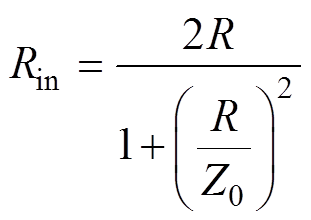 (14)
(14)
式中, ,L和C分别为电感支路和电容支路的元件值。负载阻抗的变化范围可表示为
,L和C分别为电感支路和电容支路的元件值。负载阻抗的变化范围可表示为
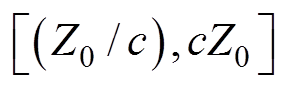 ,c为一个常数,用来表征负载阻抗的范围。在这种情况下所实现的围绕阻抗的中心值的“压缩”量见表2。
,c为一个常数,用来表征负载阻抗的范围。在这种情况下所实现的围绕阻抗的中心值的“压缩”量见表2。
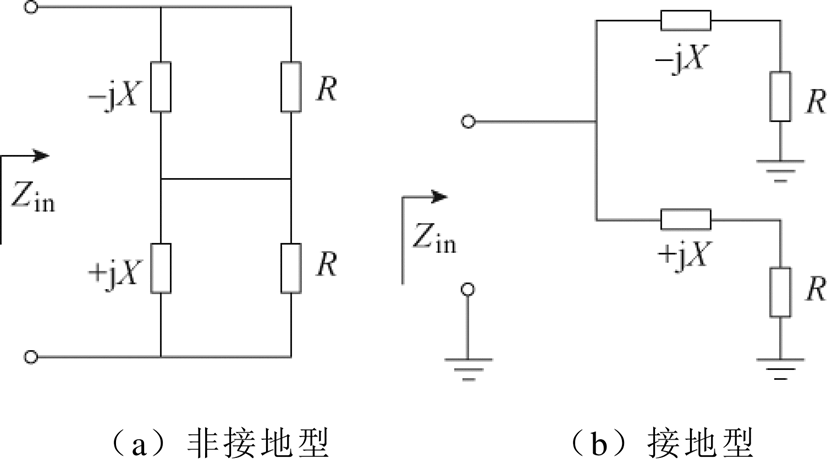
图10 两元件阻抗压缩网络电路
Fig.10 Two component impedance compression network circuit diagram
表2 文献[33]提出的两元件阻抗网络压缩效果
Tab.2 The compression effect of two-element impedance network proposed in Ref.[33]

R范围Rin范围 0.1Z0~10Z00.198Z0~Z0 0.316Z0~3.16Z00.575Z0~Z0 0.5Z0~2Z00.8Z0~Z0 0.707Z0~1.41Z00.94Z0~Z0
然而,经上述两元件压缩网络变换后的中心电阻值同电阻负载R完全相同,也就意味着上述压缩网络不能够实现电阻的变换。为了解决上述两元件结构的问题,文献[34-35]提出了由三元件构成的T型或P 型阻抗变换网络,由2个电容、1个电感或2个电感、1个电容构成,三元件阻抗变换网络电路如图11所示。与L型匹配网络不同,图11所示的任一T型或P 型匹配网络均能实现Zin<R的转换,也能实现Zin>R的转换。同时,由于增加了1个自由度,当采用T型或P 型匹配网络后,通过电容参数比值或电感参数比值的优化,可避免输出侧电阻变化所导致的输入侧容性或感性分量。但是,变换后输入侧电阻Zin的数值也会大幅变化,较大的电阻变化范围会导致开关管阻抗网络特性改变,从而导致逆变电路工作点偏移。
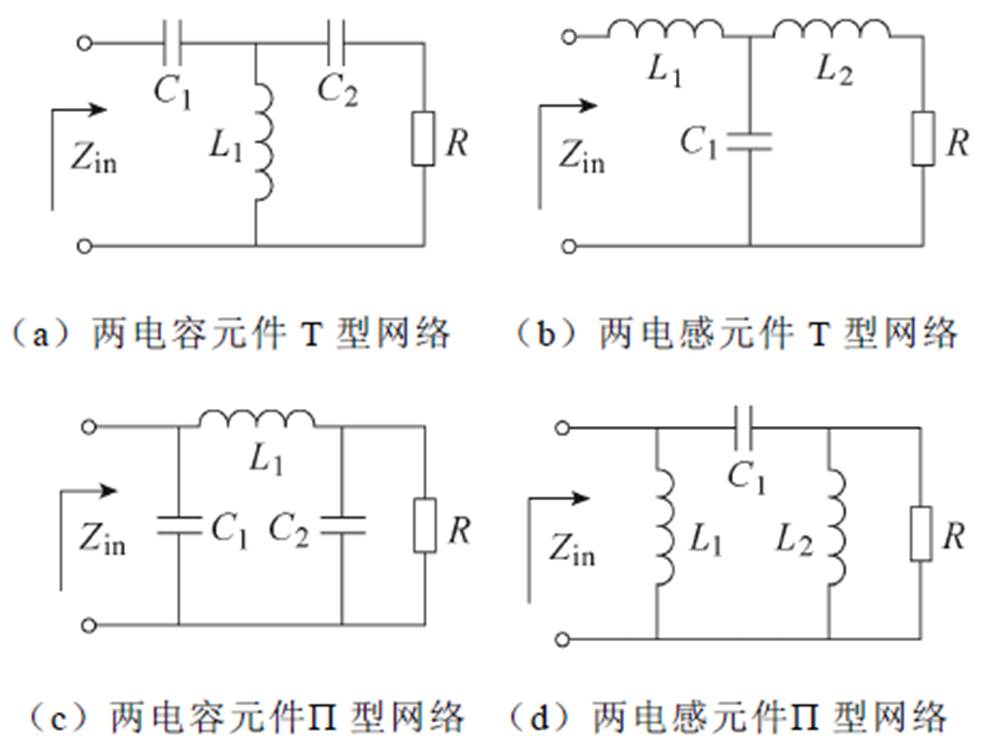
图11 三元件阻抗变换网络电路
Fig.11 Three-component impedance compression network implementation circuit diagram
文献[36]提出了一种补偿型的三元件压缩网络结构,如图12所示。其原理是将电容的投切与T型网络相结合,实现阻抗的实时控制。在此网络结构下,输入阻抗的虚部分量可以被动补偿。然而,此方案下,控制的精度受制于投切的电容数量,阻抗的控制是离散化的。
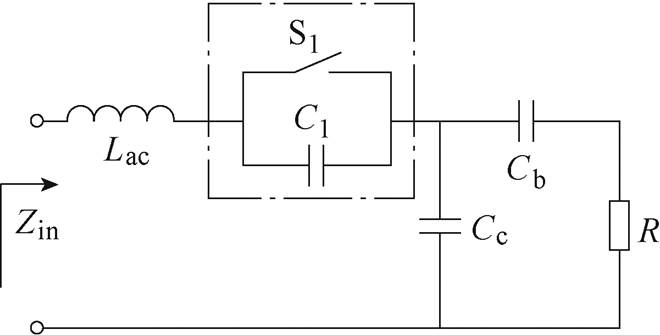
图12 补偿型三元件压缩网络电路
Fig.12 Circuit diagram of compensating three component compression network
为了提高压缩效果,文献[37]提出了一种调频式阻抗压缩方法。从自由度的角度分析,由于T型网络有3个元件,因此只有3个未知数,3个自由度,如果将一个压缩前的阻抗点完整地投射到另一个压缩后的阻抗点,压缩后负载的实部和虚部分别对应一个自由度,系统仅剩余一个自由度,因此传统的单频设计方法只能在单点匹配的基础上对阻抗范围进行优化,实际上无法精确地限制阻抗的变化范围。为了克服单频设计方法的局限性,提出了一种双频设计方法。即在两个目标频率(fA和fB)下将负载范围的两个端点(Zo,A和Zo,B)分别转换为所需的输入阻抗(Zi,A和Zi,B)转换式分别为
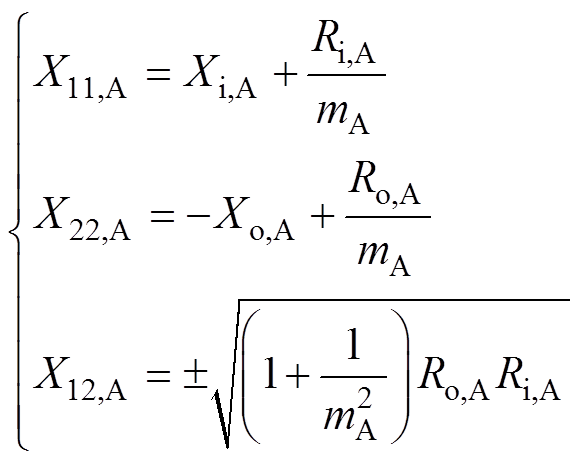 (15)
(15)
 (16)
(16)
式中,X11,A、X12,A、X22,A和X11,B、X12,B、X22,B分别为两个目标频率下二端口网络的电压电流矩阵中的参数;Ri,A、Xi,A、Ri,B、Xi,B为两个目标频率(fA和fB)下期望阻抗的电阻和电抗;同样地,Ro,A、Ro,B、Xo,A、Xo,B为两个目标频率下负载的电阻和电抗;mA、mB为自由选择的系数。通过上述参数,可以分别设计T型网络中的3个支路。当负载阻抗在Zo,A和Zo,B之间变化时,通过调节频率,可以将输入阻抗限制在更窄的范围内。
为了同时实现电阻压缩与电阻变换,图13所示的四元件压缩网络被提出[33],其在图10所示的原有结构基础上增加了1个电容和1个电感。当电抗X与电抗Y符号相同时,即两者同时为电感或同时为电容时,该网络能够在原有压缩基础上进一步减小电阻。当电抗X同电抗Y符号相反时,即两者为1个电容、1个电感,该网络能够在原有压缩基础上放大电阻。但是对于文献[33]中提出的两元件结构和四元件压缩网络,均对无源元件的电抗和负载电阻的一致性有较高的要求,当相关元件存在较大偏差时,压缩网络的压缩特性将受到极大的影响。
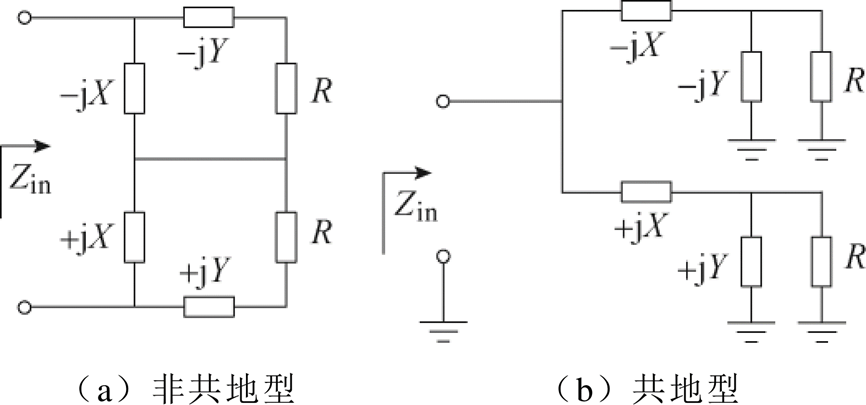
图13 四元件阻抗压缩网络电路
Fig.13 Four-component impedance compression network implementation circuit diagram
现有阻抗变换网络仅适用于阻性负载的变换与压缩,对于宽范围变化的非阻性负载实现有效的压缩与调整的相关研究较少,然而在实际条件中,系统负载往往为非阻性负载,如在等离子体生成的过程中,超高频逆变电路的负载为非阻性负载,且其电阻和电抗分量随生成进程不断变化[38]。因此,研究针对非阻性负载的阻抗压缩网络具有更普遍的适用性。
L型、T型、P 型匹配网络也能够实现非阻性负载的点对点变换,但当负载变化时,其变换后负载特性不受控,因此其依然无法应用在宽负载变化的条件下。同样,文献[35]中介绍的压缩网络也可应用于非阻性负载条件下。基于该结构阻抗变换后,输入侧负载的阻抗角将小于非阻性负载的阻抗角,能够实现相位压缩。当其非阻性负载的模值同元件电抗值相同时,输入侧负载阻抗角可压缩为零。但当上述压缩网络结构应用于非阻性负载时,其电阻/电抗的幅值压缩能力将极大退化。同时随负载阻抗模值偏离系统元件电抗,该阻抗压缩网络的相位压缩能力迅速减弱。当负载阻抗模值大于元件电抗值的4倍或小于1/4时,输入侧负载阻抗角几乎同非阻性负载阻抗角相同。
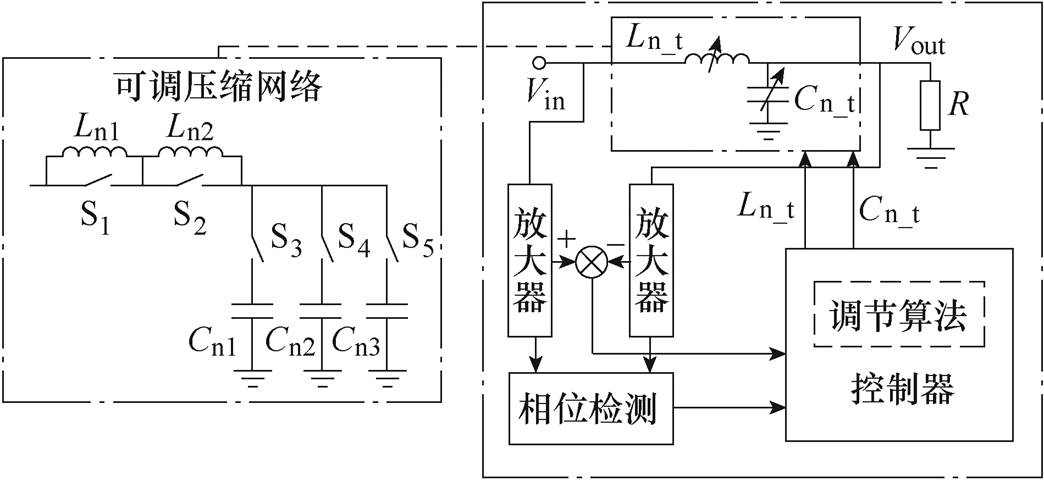
图14 可调整L型阻抗压缩网络拓扑及控制框图
Fig.14 Adjustable L-type impedance compression network topology and control block diagram
为解决非阻性负载有效压缩问题,文献[38]提出了一种基于频率调整的动态阻抗压缩网络,该方法通过调整系统的开关频率实现输入侧阻抗动态调整。但是超高频条件下工作频率的调整会直接导致系统软开关特性丢失和效率降低。同时,现有数字控制器无法实现频率的连续改变,数字控制器输出的离散频率控制信号会导致动态阻抗压缩网络无法连续调节。文献[39-40]提出了可调整L型及T型阻抗压缩网络,其中电感和电容元件可通过多个串并联的方式进行调整,该方法通过检测系统的电压比值及相位来调整控制信号,拓扑和控制方法如图14所示。该策略控制方法复杂,且采用了较多的有源及无源元件。系统状态切换过程中,系统工作在非最优工作状态下,导致逆变电路无法高效工作。综上所述,现有非阻性负载阻抗压缩网络均需要以频率调整或状态切换为代价,且难以实现连续调节。
基于现有的阻性负载压缩的相关研究,文献[41]提出了一种分别压缩幅值和相位的方法,如图15所示,电阻压缩网络(Resistance Compression Network, RCN)用来压缩阻抗幅值,相位压缩网络(Phase Compression Network, PCN)用来压缩相位,这两部分共同组成阻抗压缩网络(Impedance Compression Network, ICN),用以对非阻性负载进行变换与压缩,实现逆变器宽负载范围的高效运行。
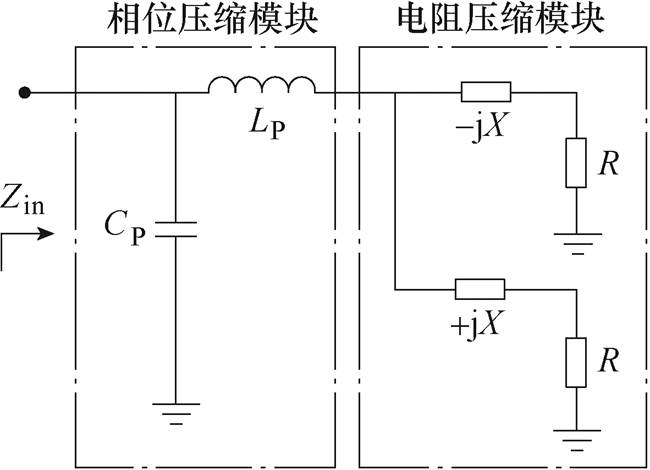
图15 分别压缩幅值与相位方法电路
Fig.15 Respectively compressed amplitude and phase method circuit diagram
在以上介绍的设计方法中,主要是通过硬件结构的设计实现阻抗的变换与压缩,可以看出,为了压缩的效果更好,实现更为精准的投射,就需要继续增加系统参数设计的自由度,传统方法只能通过增加元件个数来实现,从而增加了系统的体积、复杂度与成本。因此,未来的发展方向可以围绕多路变换器组合网络的负载阻抗压缩进行设计。通过调节各路变换器的电压幅值与相位关系,增加可调节变量的个数,从而实现更好的压缩效果。
文献[10, 42-43]中学者提出了以相位和幅值控制为基础的有源阻抗调制网络,如图16所示。图16a为两元件的电抗压缩网络,当负载电抗发生变化时,两支路中输入电压的幅值比和相位差可以被动态调节,以分别控制两支路中流过功率的比例。由此,负载的电抗可以被容性或感性支路补偿。这种网络可以将电抗分量变化较大的负载转换为纯阻性负载,当其与如图3和图5所示的宽阻性负载逆变器相配合时,逆变器可以在任意负载处工作在理想的软开关状态。在两元件网络的基础上,图16b中基于T型网络的阻抗压缩网络被提出,其原理同样是通过幅值与相位控制支路间的功率比例,与两元件网络不同的是,在该网络中,下支路的T型网络将输入电压与电流解耦,使得电阻和电抗的变化可以被同时补偿。在图16b的基础上,提出了图16c中为以L型网络为基础的阻抗压缩网络,该网络通过增加元件来提升阻抗压缩的范围,实现了将电阻、电抗两个维度同时变化的宽范围负载转换为理想的窄范围负载。
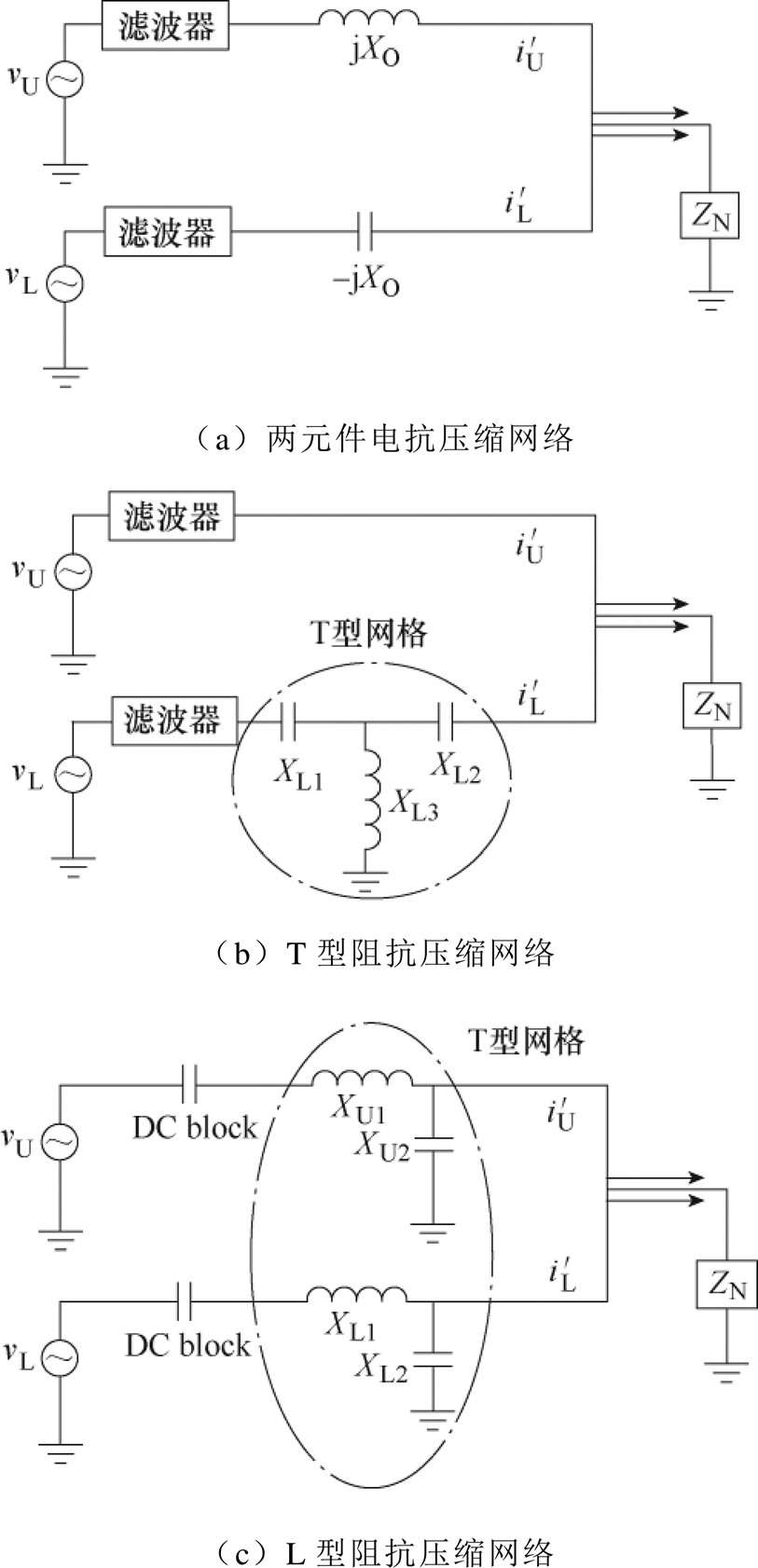
图16 双路阻抗压缩网络结构
Fig.16 Double channel impedance compression network structure
在上述网络的基础上,文献[44]中提出了“有源+无源”的两步式阻抗压缩方案,两级式阻抗压缩过程如图17所示,其中无源网络首先将负载进行阻抗匹配,并实现较小范围的压缩,三端口有源压缩网络针对性地对每个阻抗点进行进一步阻抗匹配,使在宽范围内变化的所有负载点均落入理想的区间内。在这种混合的压缩方案下,阻抗的压缩范围可以被进一步提升,进而提升了使超高频逆变器能够高效工作的负载范围。
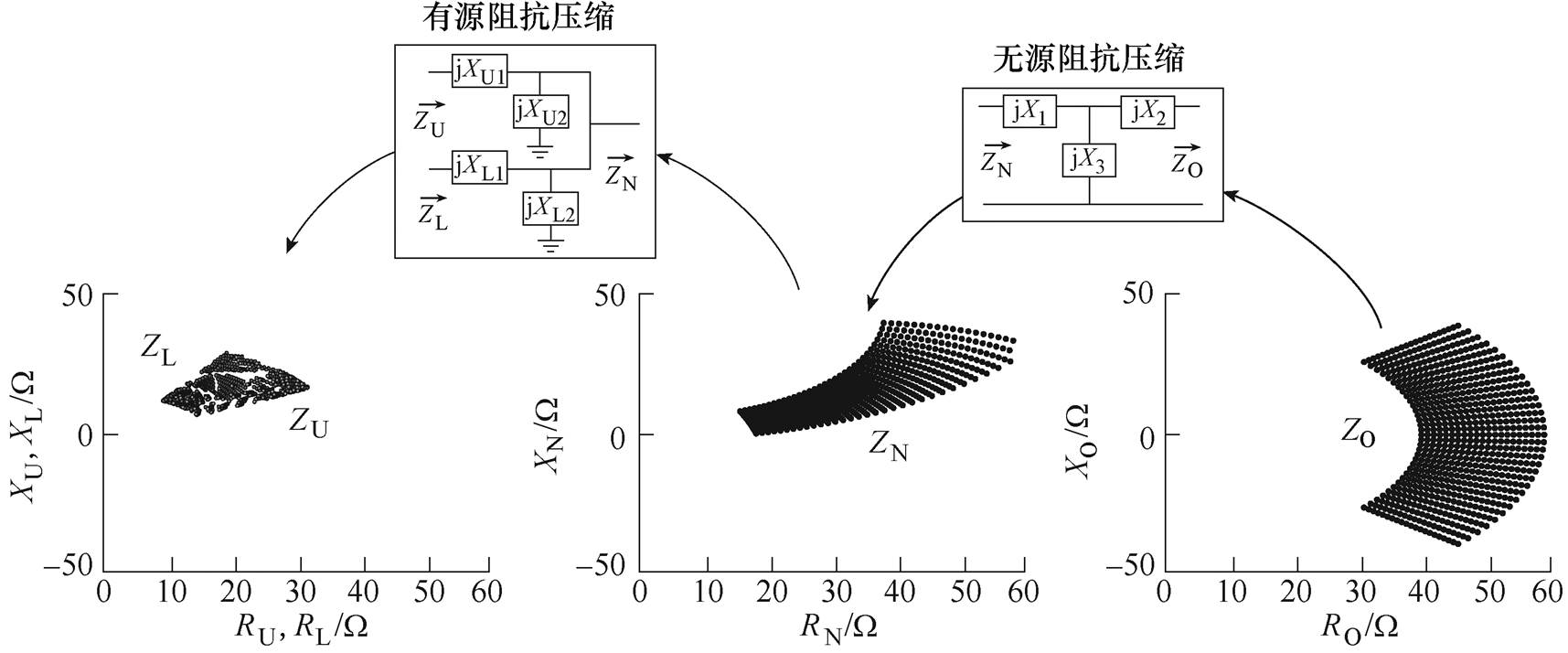
图17 两级式阻抗压缩过程
Fig.17 Impedance compression effect of a two-stage network
超高频逆变器一般由谐振逆变电路和阻抗变换网络两部分构成。实际工作场景中,超高频逆变器需要工作在宽范围变化的负载阻抗下,而谐振拓扑可实现精确软开关的负载范围较窄。本文主要针对这一矛盾对超高频变换器系统的设计方法进行了综述,分别从逆变电路和阻抗网络两方面探讨其在宽负载范围下高效工作的方法。从超高频逆变器拓扑本身角度考虑,首先从时域和频域两个角度介绍了传统的准谐振与全谐振Class E、Class F2等拓扑的参数设计方法;其次着重分析了其在变化负载下的参数优化方案;最后介绍了几种可独立于阻性负载工作的Class D、Class E、Class F2和EF逆变器。从阻抗变换与压缩网络考虑,分别从阻性负载压缩与非阻性负载压缩两方面介绍了一系列压缩网络结构。对于阻性负载,分别介绍了L型、两元件多路并联型、T型(P型)、四元件多路并联型等压缩网络结构并对比其压缩效果;对于非阻性负载,介绍了调频、电容投切、电阻相位分步压缩等压缩方案。以往的工作中,逆变器与无源压缩网络均只能使逆变系统在变化的阻性负载下工作,无法保证全负载范围内的高效工作。针对这一问题,本文介绍了一系列有源阻抗调制系统,通过幅值与相位的调节实现动态的负载阻抗的压缩,这种多路系统可以实现更宽范围的阻抗变换,将是未来超高频逆变系统的发展趋势。
参考文献
[1] 韩冲, 张波. 谐振式无线电能传输系统中高频逆变器的特性分析和参数设计[J]. 电工技术学报, 2018, 33(21): 5036-5050.
Han Chong, Zhang Bo. Characteristics analysis and parameters design of high frequency inverters in magnetic coupling resonance wireless power transfer system[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 5036-5050.
[2] 徐殿国, 管乐诗, 王懿杰, 等. 超高频功率变换器研究综述[J]. 电工技术学报, 2016, 31(19): 26-36.
Xu Dianguo, Guan Yueshi, Wang Yijie, et al. Review on very high frequency power converters[J]. Transa- ctions of China Electrotechnical Society, 2016, 31(19): 26-36.
[3] Perreault D J, Hu Jingying, Rivas J M, et al. Oppor- tunities and challenges in very high frequency power conversion[C]//2009 Twenty-Fourth Annual IEEE Applied Power Electronics Conference and Expo- sition, Washington, USA, 2009: 1:14.
[4] 王镇道, 赵亚魁, 章兢, 等. LLC半桥式谐振变换器参数模型与设计[J]. 电工技术学报, 2012, 27(12): 51-55.
Wang Zhendao, Zhao Yakui, Zhang Jing, et al. Parameter model and design for LLC resonant half-bridge converter[J]. Transactions of China Elec- trotechnical Society, 2012, 27(12): 51-55.
[5] Pilawa-Podgurski R C N, Sagneri A D, Rivas J M, et al. Very-high-frequency resonant Boost converters[J]. IEEE Transactions on Power Electronics, 2009, 24(6): 1654-1665.
[6] Rivas J M, Jackson D, Leitermann O, et al. Design considerations for very high frequency DC-DC converters[C]//2006 37th IEEE Power Electronics Specialists Conference, Jeju, Korea (South), 2006: 1-11.
[7] Hertel J C, Nour Y, Knott A. Integrated very high frequency switch mode power supplies: design considerations[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2018, 6(2): 526-538.
[8] Razzak M A, Suzuki Y, Takamura S, et al. High pressure radio frequency induction thermal plasma generation using T-LCL immittance circuit[C]//2006 37th IEEE Power Electronics Specialists Conference, Jeju, Korea (South), 2006: 1-1.
[9] Green A M. Operation of inverters supplying mutually coupled induction heating loads[C]//IEE Colloquium on Electromagnetics and Induction Heating, London, UK, 1996: 1-3.
[10] Liu Ming, Chen Minjie. Dual-band wireless power transfer with reactance steering network and reconfi- gurable receivers[J]. IEEE Transactions on Power Electronics, 2020, 35(1): 496-507.
[11] Nour Y, Knott A, Petersen L P. High frequency soft switching half bridge series-resonant DC-DC converter utilizing gallium nitride FETs[C]//2017 19th European Conference on Power Electronics and Applications (EPE'17 ECCE Europe), Warsaw, Poland, 2017: 1-7.
[12] Trung N K. 13.56MHz high power and high effici- ency inverter for dynamic EV charging systems[D]. Tokyo: Shibaura Institute of Technology, 2016.
[13] Kessler D J, Kazimierczuk M K. Power losses and efficiency of class-E power amplifier at any duty ratio[J]. IEEE Transactions on Circuits and Systems I-Regular Papers, 2004, 51(9): 1675-1689.
[14] Mediano A, Ortega-Gonzalez F J. Class-E amplifiers and applications at MF, HF, and VHF: examples and applications[J]. IEEE Microwave Magazine, 2018, 19(5): 42-53.
[15] Hu J. Design of a low-voltage low-power DC-DC HF converter[D]. Cambridge: Massachusetts Institute of Technology, 2008.
[16] Rivas J M, Leitermann O, Han Yehui, et al. A very high frequency DC-DC converter based on a Class F2 resonant inverter[J]. IEEE Transactions on Power Electronics, 2011, 26(10): 2980-2992.
[17] Rivas J M, Han Yehui, Leitermann O, et al. A high- frequency resonant inverter topology with low- voltage stress[J]. IEEE Transactions on Power Electronics, 2008, 23(4): 1759-1771.
[18] Glaser J S, Rivas J M. A 500W push-pull DC-DC power converter with a 30MHz switching frequ- ency[C]//2010 Twenty-Fifth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Palm Springs, USA, 2010: 654-661.
[19] 邹学文, 董舟, 周嫄, 等. 超高频DC-DC谐振变换器[J]. 电源学报, 2017, 15(1): 138-145.
Zou Xuewen, Dong Zhou, Zhou Yuan, et al. Very high frequency DC-DC resonant converter[J]. Journal of Power Supply, 2017, 15(1): 138-145.
[20] Grebennikov A, Sokal N O, Franco M J. Switch mode RF and microwave power amplifiers[M]. Oxford: Elsevier, 2012.
[21] Aldhaher S, Yates D C, Mitcheson P D. Load- independent class E/EF inverters and rectifiers for MHz-switching applications[J]. IEEE Transactions on Power Electronics, 2018, 33(10): 8270-8287.
[22] 张少腾, 赵晋斌, 吴月宝, 等. 基于自互感调节的无线电能传输用E类逆变器软开关技术研究[J]. 电工技术学报, 2021, 36(21): 4558-4566.
Zhang Shaoteng, Zhao Jinbin, Wu Yuebao, et al. Research on soft switching technology of class E inverter based on self mutual-inductance regulation in wireless power transfer[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4558-4566.
[23] Zulinski R E, Grady K J. Load-independent class E power inverters I. theoretical development[J]. IEEE Transactions on Circuits and Systems, 1990, 37(8): 1010-1018.
[24] Jiang Yifan, Li Heyuan, Fu Minfan. High-frequency DC/DC converter based on differential load- independent class E inverter[C]//2021 IEEE 1st International Power Electronics and Application Symposium (PEAS), Shanghai, China, 2021: 1-5.
[25] Luo Weisen, Wei Xiuqin, Sekiya H, et al. Design of load-independent class-E inverter with MOSFET parasitic capacitances[C]//2019 IEEE 62nd Inter- national Midwest Symposium on Circuits and Systems (MWSCAS), Dallas, USA, 2019: 1-4.
[26] Kee S D, Aoki I, Hajimiri A, et al. The class-E/F family of ZVS switching amplifiers[J]. IEEE Transa- ctions on Microwave Theory and Techniques, 2003, 51(6): 1677-1690.
[27] Roslaniec L, Jurkov A S, Bastami A A, et al. Design of single-switch inverters for variable resistance/load modulation operation[J]. IEEE Transactions on Power Electronics, 2015, 30(6): 3200-3214.
[28] Kaczmarczyk Z. High-efficiency class E, EF2, and E/F3 inverters[J]. IEEE Transactions on Industrial Electronics, 2006, 53(5): 1584-1593.
[29] Zhang Lujie, Ngo K. Design methodology of a ZVS class-E inverter with fixed gain[C]//2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, USA, 2019: 1-7.
[30] Obinata N, Luo Weisen, Wei Xiuqin, et al. Analysis of load-independent class-E inverter at any duty ratio[C]//45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 2019: 1-6.
[31] Dahl N J, Ammar A M, Andersen M A E. Identification of ZVS points and bounded low-loss operating regions in a class-D resonant converter[J]. IEEE Transactions on Power Electronics, 2021, 36(8): 9511-9520.
[32] Fu Wenchang, Hsieh P H. A 13.56-MHz wireless power transfer transmitter with impedance com- pression network for biomedical applications[C]// 2020 IEEE International Symposium on Circuits and Systems (ISCAS), Seville, Spain, 2020: 1-5.
[33] Han Yehui, Leitermann O, Jackson D A, et al. Resistance compression networks for radio-frequency power conversion[J]. IEEE Transactions on Power Electronics, 2007, 22(1): 41-53.
[34] Guan Yueshi, Bian Qing, Wang Yijie, et al. Analysis and design of high-frequency converter with resistive matching network and spiral inductor[J]. IEEE Transactions on Power Electronics, 2018, 33(6): 5062-5075.
[35] 范兴明, 苏斌华, 唐福鸿, 等. 基于Q值法的T型自动阻抗匹配网络的研究[J]. 电工技术学报, 2022, 37(9): 2275-2283.
Fan Xingming, Su Binhua, Tang Hongfu, et al. Research on an automatic impedance matching T- network based on Q-based design method[J]. Transactions of China Electrotechnical Society, 2022, 37(9): 2275-2283.
[36] Danilovic M, Ngo K D T, Zhang Zhemin. Com- pression of the load resistance range in constant frequency resonant inverters[C]//2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, USA, 2014: 1-8.
[37] Chung E, Ha J. Resonant network design methodo- logy based on two-port network analysis considering load impedance variation[C]//2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, USA, 2019: 1-6.
[38] Bastami A, Jurkov A, Gould P, et al. Dynamic matching system for radio-frequency plasma gener- ation[J]. IEEE Transactions on Power Electronics, 2018, 33(3): 1940-1951.
[39] Liu Shuangke, Liu Ming, Han Songyang, et al. Tunable class E2 DC-DC converter with high effici- ency and stable output power for 6.78MHz wireless power transfer[J]. IEEE Transactions on Power Electronics, 2018, 33(8): 6877-6886.
[40] 吴月宝, 赵晋斌, 张少腾, 等. 基于径向基神经网络的多负载无线电能传输系统自适应阻抗匹配方法[J]. 电工技术学报, 2021, 36(19): 3969-3977.
Wu Yuebao, Zhao Jinbin, Zhang Shaoteng, et al. An adaptive impedance matching method based on radial basis function neural network in multi-load wireless power transfer systems[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 3969-3977.
[41] Choi J, Xu Jiale, Makhoul R, et al. Implementing an impedance compression network to compensate for misalignments in a wireless power transfer system[J]. IEEE Transactions on Power Electronics, 2019, 34(5): 4173-4184.
[42] Braun W D, Perreault D J. A high-frequency inverter for variable-load operation[J]. IEEE Journal of Emerging & Selected Topics in Power Electronics, 2019, 7(2): 706-721.
[43] Liu Chang, Guan Yueshi, Wang Yijie, et al. A high performance high frequency inverter architecture with wide load range[C]//2021 IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, Canada, 2022: 1-7.
Wide Load Range Very High Frequency Power Conversion Technology: Resonant Parameter Design and Matching Network Construction
Abstract With the fast development of power electronics, very high frequency (VHF) power converters (30~300MHz) have gradually become a research focus, which can greatly reduce the value and, volume of passive components and while improving the system power density. Traditional research mainly focuses on the parameter design of the inverter with fixed load, and the designed converter based on this method has high parameter sensitivity. However, the load of the inverter varies in a wide range in the actual scene, which poses challenges to the efficient operation of the VHF conversion system. In this paper, the resonant parameters and matching network of the wide load range VHF converter are summarized, and the parameter design methods of the VHF power converter are introduced and compared. Meanwhile, the impedance conversion and compression network structure suitable for the VHF power converter are discussed and analyzed, which can provide a reference for further research of on the highly efficiency efficient operation of the VHF converter.
keywords:Very high frequency (VHF) power converter, wide load range, resonant parameter, impedance compression
DOI: 10.19595/j.cnki.1000-6753.tces.221184
中图分类号:TM46
国家自然科学基金资助项目(52007041)。
收稿日期 2022-06-21
改稿日期 2022-07-18
管乐诗 男,1990年生,副教授、博士生导师,研究方向为高频、超高频功率变换技术。E-mail: hitguanyueshi@163.com(通信作者)
刘 畅 女,1997年生,博士研究生,研究方向为超高频DC-AC变换技术。E-mail: 18800428682@163.com
(编辑 陈 诚)