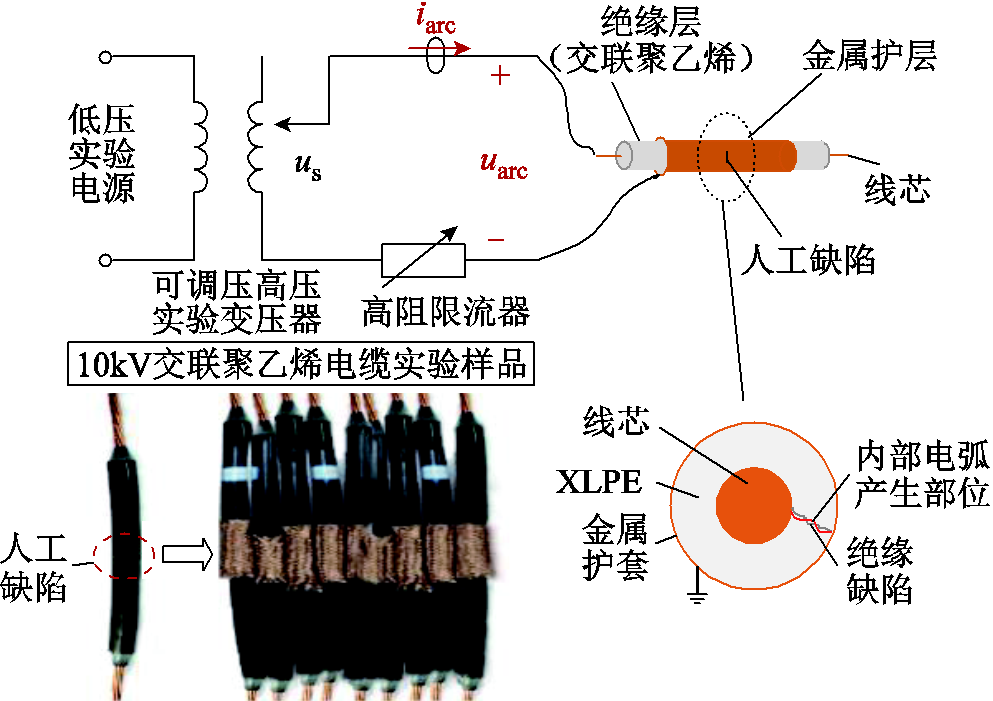
图1 电缆内部电弧高压实验原理图
Fig.1 Diagram of cable inside arc high voltage experiment
摘要 间歇性电弧是电缆故障初期发展阶段的重要过程，该文以我国配电网中广泛使用的10kV交联聚乙烯电缆为研究对象，通过实验分析发现，电缆内部电弧与常规弧光对地击穿电弧波形存在明显差异，并在其发展过程中呈现出多种波形形态。该文通过梳理总结电缆内部间歇性电弧在随机演变中的共性，将其归结出振荡间歇性电弧、稳态间歇性电弧、半稳态间歇性电弧三类主要形态。从帮助电缆故障分析的外特性重现角度，以黑箱建模思路分别基于高斯随机脉冲、弧隙能量平衡理论和占比控制，构建出三类主要电弧形态的控制模型，并根据实验样本数据统计出各模型控制参数的分布范围。所提模型利用PSCAD仿真软件得到实现，与实验波形的对比表明，该文所构建的多形态电弧模型能有效模拟出三类间歇性电弧的主要特征。该多形态间歇性电弧的发掘丰富了电缆电弧的随机多样性，为电缆初期故障分析提供了新的模型基础。
关键词：电缆内部电弧故障 电弧模型 多形态 间歇性 交联聚乙烯
10kV配电网系统中广泛使用的地下电力电缆具有金属护层的多层绝缘结构，且其金属护层通常经过接地极直接接地。当电缆出现局部绝缘缺陷时，会由线芯→主绝缘层→金属护层（地）→填充层→铠装层→外绝缘护套→敷设环境（空气/土壤）→大地的路径逐步击穿，并伴随弧光放电现象。然而，电缆的多层绝缘介质劣化并非一蹴而就，是一个逐步演变的自然过程，加之我国配电网采用小电流接地系统，故障电流大小一般仅为数安培，导致上述多层绝缘介质不容易一次性完全对地击穿[1]，因此电缆往往容易先于对地击穿前，就通过最短接地路径，即线芯至金属护层（地），长期性地形成内部间歇性电弧故障。作为介于局部放电和永久性故障之间的一种常见初期故障形态，电缆间歇性电弧具有故障电气量幅值相对较高、故障波形畸变特征明显的特点，是极具研究价值并应重点关注的一种预警性故障类别[2-3]。
当前研究中，借助电弧模型产生独特外特性故障波形是绝大部分电弧检测方法设计的关键[4-9]。电缆电弧模型历经多年发展取得了丰硕的研究进展，包括原始的方波电弧模型[10]，经典的Mayr、Cassie、Schwarz及其改进电弧模型，控制论电弧模型[11-13]，以及近年来新发展的磁流体动力学模型[14]、分段线性电弧模型[15]、复奇频电压源模型[16]等。上述模型从不同适用角度精细化了电缆电弧的模拟方式，但从各模型所模拟的结果来看，现有模型电弧波形特征均为：电弧电压以近似方波持续数个工频周期、电弧电流存在明显的周期性零休现象。该普遍存在于交流系统中的电弧波形特征在电缆弧光对地击穿电弧故障的研究中得到了广泛应用[17]，但该典型特征波形来源于主体产生在空气中的电弧[18]，而形成于电缆绝缘介质中的内部电弧是否具有与空气电弧相同的波形特征，现有文献还尚未见报道，需要展开进一步的讨论。
事实上，电缆内部电弧与弧光对地击穿电弧存在诸多不同：电缆内部电弧比弧光对地击穿电弧更早出现；燃弧路径由电缆绝缘介质所包裹，不受外界环境的影响；燃弧空间密闭、燃弧路径短。这些区别因素决定了电缆内部电弧应当具有与弧光对地击穿电弧不同的特性，同时也影响着电弧故障电压的波形形状及其相应模型的构建。
电缆电弧模型需建立于真实的电弧故障波形之上，但在实际配电网中，故障录波装置一般仅装设在变电站内，所采集到的故障波形通常已经由未知长度的线路或电力设备衰减，发生了严重的畸变，无法真实反映电弧故障的本质特征，因此通过实验获取电缆内部电弧故障波形是建模的最佳途径。
本文通过高压实验，以我国配电网中广泛使用的10kV交联聚乙烯（Cross Linked Polyethylene, XLPE）电力电缆为研究对象，模拟在电缆线芯与金属护层之间产生内部间歇性电弧故障，证实了其波形形状与弧光对地击穿电弧波形存在本质差异；基于电缆内部电弧实验波形，揭示其随机性的一般规律，根据电弧电压波形进行归类，分析总结其主要特征；并重点从故障分析重现外特性的角度，对电缆内部间歇性电弧故障分类建模，提供模型参数，为电缆初期故障分析的相关研究提供基础。
电缆内部间歇性电弧是电缆电弧的初期形态，是局部放电到对地击穿电弧或持续性电弧的过渡过程，形成于电缆线芯与金属护层之间，主要受电缆绝缘介质材料的影响。而电缆对地击穿电弧则形成于电缆线芯与大地之间，主要受外部环境（空气）、接地表面介质（土壤、树木、草皮等）的影响，因此电缆内部电弧应当具有与对地击穿电弧不同的特性。基于上述基本假设，本文以我国配电网系统中常用的10kV交联聚乙烯电缆为研究对象，模拟在电缆线芯与金属护层之间的绝缘介质内产生内部间歇性电弧，实验原理图如图1所示。
图1 电缆内部电弧高压实验原理图
Fig.1 Diagram of cable inside arc high voltage experiment
该实验电路采用可调压的高压实验变压器为电缆提供10kV配电网系统单相电压5.77kV，并在回路中串联接入高阻限流器，将故障电流限制为数安培，以模拟配电网小电流接地故障电流状态；然后将其中的单芯电缆脱去金属护层，利用小刀或打孔器在绝缘层中制造人工缺陷，再在人工缺陷表面重新覆盖金属护层，制作成电缆实验样品；最后，将制作好的电缆实验样品的线芯端与金属护层端分别接于电路中，通过反复调整人工绝缘缺陷的破坏程度，并结合持续加压，迫使在电缆线芯与金属护层间的局部绝缘缺陷发生暂态击穿，产生电缆内部间歇性电弧，利用高压探头捕获电弧电压uarc和电弧电流iarc的实验波形数据并进行分析。
通过上述实验过程，本文共采集到12组可复现的独立实验波形数据组（每组包含若干内部间歇性电弧至持续击穿的过程）。基于所采集到的实验波形数据，分析间歇性电弧的发展过程及其典型外特性。
10kV XLPE电缆内部间歇性电弧演变的实验实测电压波形如图2所示，在12组电缆内部间歇性电弧实验波形数据中，可以观测到电缆内部间歇性电弧发展的一般规律，以帮助电弧模型的构建。图2中展示了各组独立实验测量产生的电缆内部电弧电压演变所呈现的一般规律，表现为同一根电缆在持续加压后，从初步形成振荡性不稳定电弧，到最终击穿变成持续性电弧故障的全过程。在间歇性电弧波形产生期间，实验电缆外部观测不到任何弧光现象，证明该间歇性电弧的确产生于电缆内部。通过实验得到的电弧故障电压波形，可分析到如下规律：
1）电缆内部间歇性电弧的发展符合局部绝缘缺陷的劣化轨迹：随着电缆局部绝缘缺陷劣化程度的不断发展，电缆绝缘介质内的弧道环境及其恢复能力发生变化，伴随产生的电缆内部电弧波形也相应呈现出不同的形态，并在相当长的一段劣化过程中，形成反复起弧-灭弧的间歇性现象。
2）所形成的间歇性电弧集中在永久性故障前的时间段内，但其发生时刻又具有较强的随机性，体现为间歇性电弧每次重燃的频率间隔为连续发生至数十个工频周期之间不等。
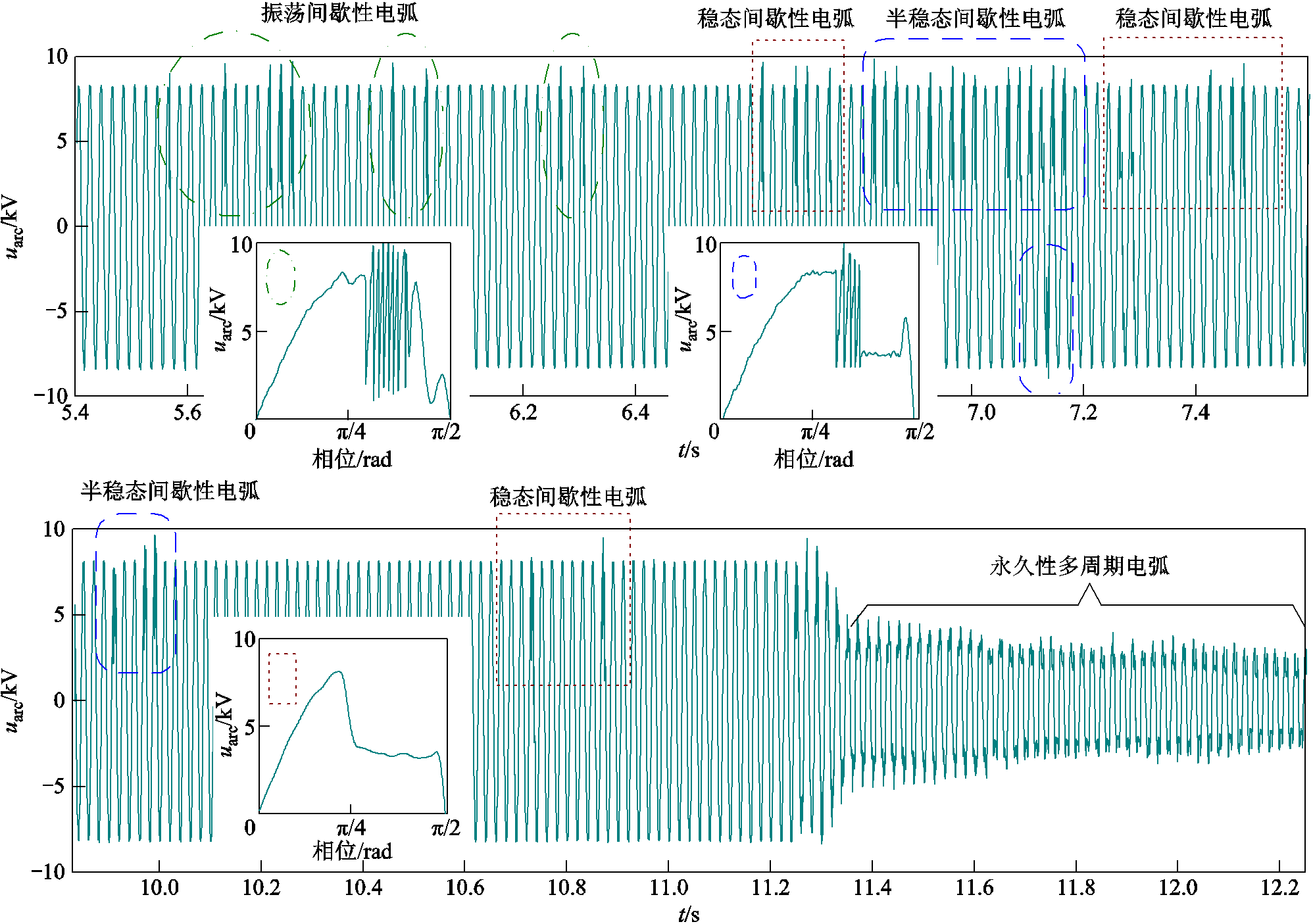
图2 10kV XLPE电缆内部间歇性电弧演变的实验实测电压波形
Fig.2 Evolution of intermittent arc voltage waveform of 10kV XLPE cable in experiment tests
3）间歇性电弧的随机性中也存在着共性特征，主要表现为：电弧电压总体上呈现出一种跌落、凹陷的波形畸变，且实验测量观测到的电缆内部电弧起弧点以相同极性电压（正弦波正半周期）峰值点为主，持续时间约为1/4工频周期。
对上述采集到的随机间歇性电弧电压外特性波形样本进行归类分析，可统计出三类主要的电弧形态样本以供建模。
1）形态一：振荡间歇性电弧
振荡间歇性电弧的电压、电流外特性波形如图3所示。振荡间歇性电弧基本集中出现在电缆内部电弧发展的初期阶段，此时电弧尚处于不稳定状态，在起弧与灭弧的状态之间来回瞬态切换，相应的电弧电压、电流呈现明显的振荡过程，持续时间少于1/4工频周期。
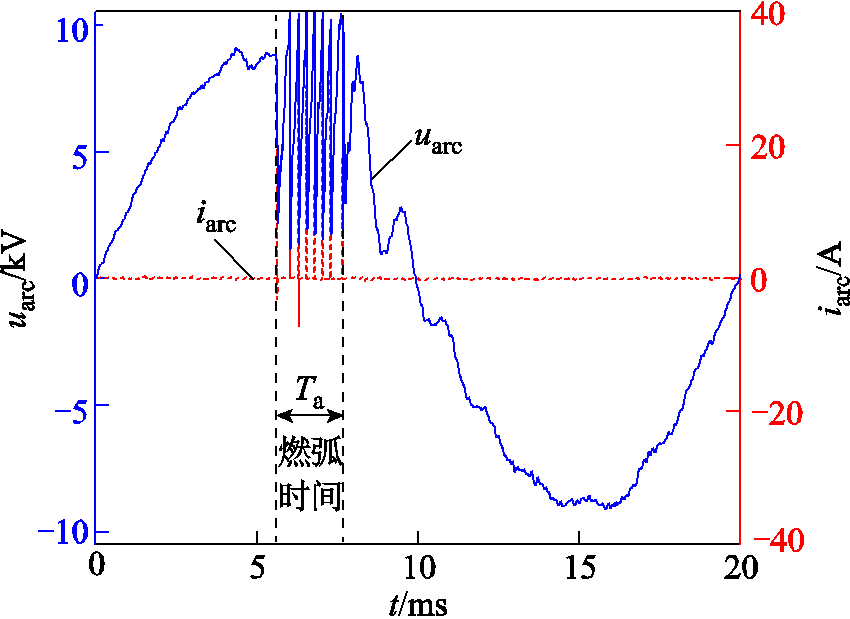
图3 振荡间歇性电弧故障外特性
Fig.3 External characteristic of oscillating intermittent arc
2）形态二：稳态间歇性电弧
稳态间歇性电弧的电压、电流外特性波形如图4所示。稳态间歇性电弧的电压、电流振荡过程完全消失，呈现稳定持续燃烧的状态，电弧电压波形较为平滑，且具有近似半弧形的独特形状。该波形随机出现在电弧发展的中期或后期，持续时间约为1/4工频周期。
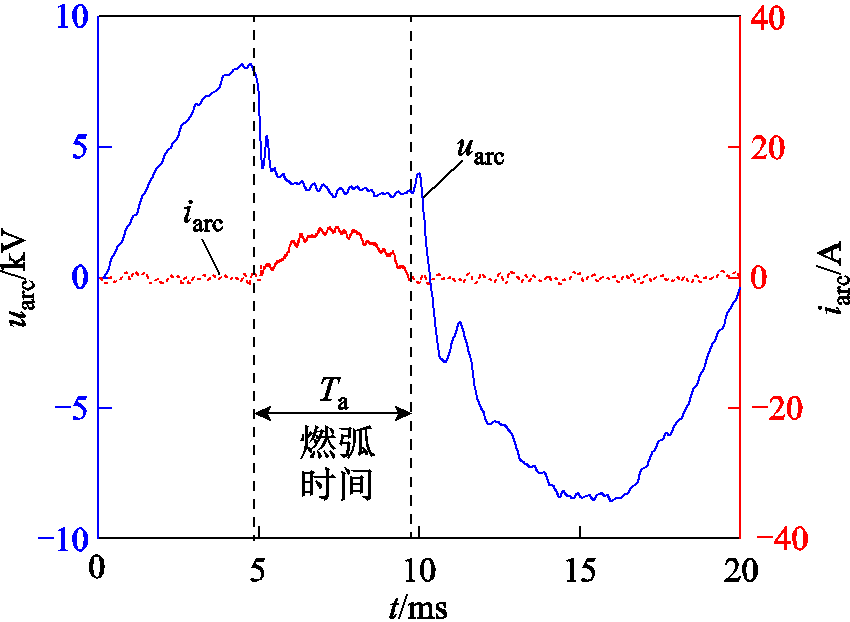
图4 稳态间歇性电弧故障外特性
Fig.4 External characteristic of steady-state intermittent arc
3）形态三：半稳态间歇性电弧
半稳态间歇性电弧的电压、电流外特性波形如图5所示。波形从不稳定的振荡间歇性波形开始，中期前后即形成稳定的燃弧过程，是介于振荡间歇性电弧与稳态间歇性电弧的中间过程，可能随机出现在电弧发展的中期或后期，持续时间约为1/4工频周期。
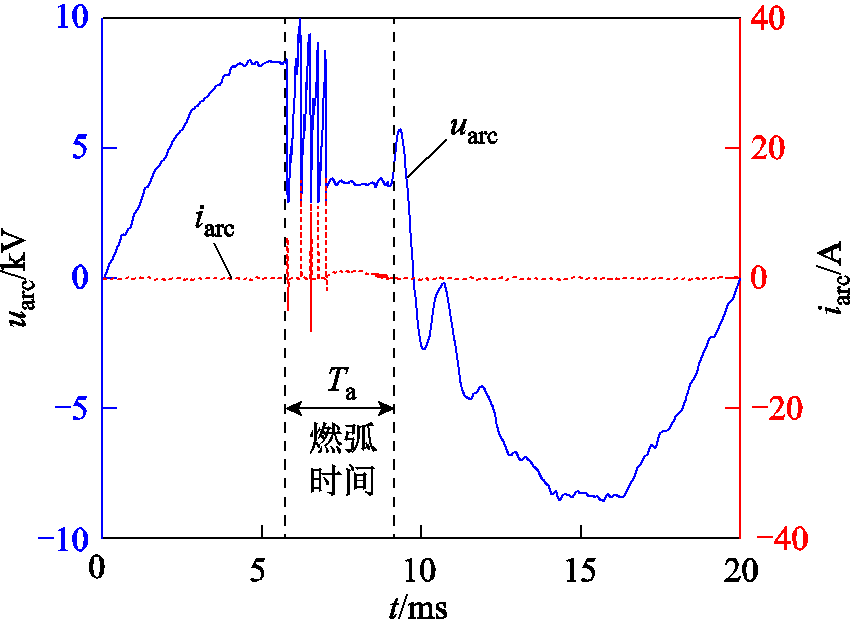
图5 半稳态间歇性电弧故障外特性
Fig.5 External characteristic of semi-steady intermittent arc
上述归结的三种典型电缆内部电弧电压、电流实验波形表明，电缆内部电弧波形会随着电弧灼烧绝缘介质的劣化程度而变化，且电缆内部电弧与弧光对地击穿电弧波形[18]的确存在本质差异，其特征对比见表1，因此有必要对电缆内部间歇性电弧建立专用故障模型。
表1 电缆内部电弧与对地击穿电弧的波形特征对比
Tab.1 Waveform characteristics comparison between arc inside cable and arc breakdown to ground
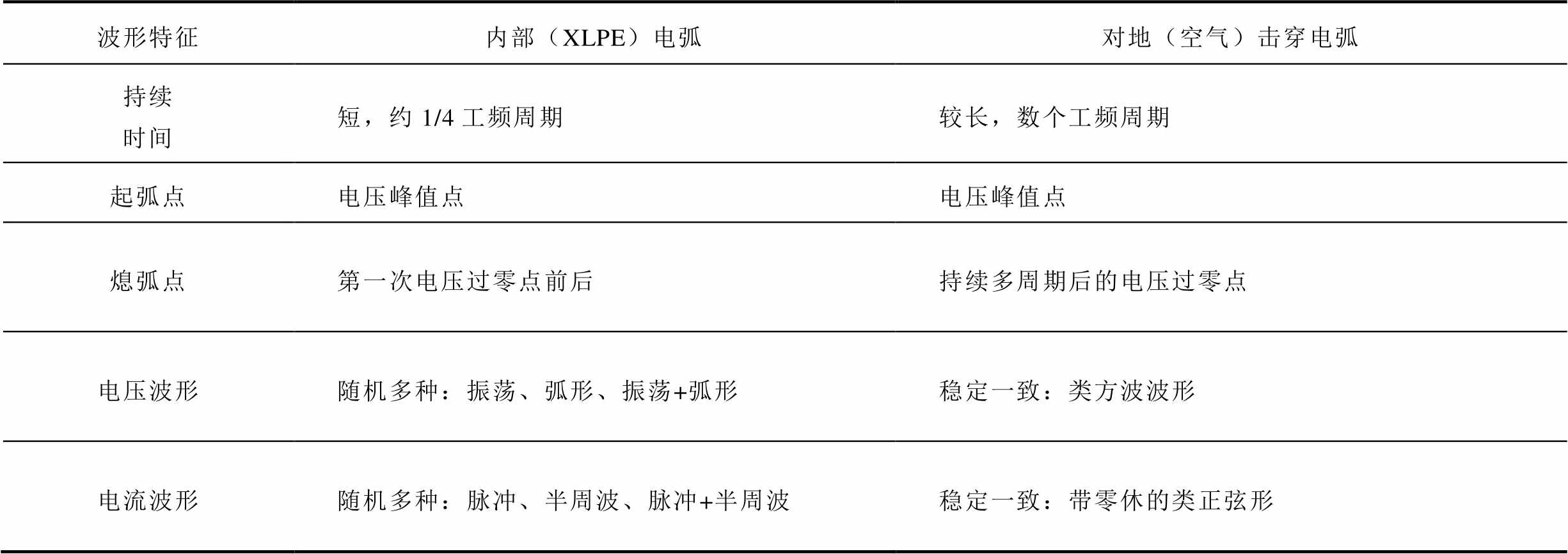
波形特征内部（XLPE）电弧对地（空气）击穿电弧 持续时间短，约1/4工频周期较长，数个工频周期 起弧点电压峰值点电压峰值点 熄弧点第一次电压过零点前后持续多周期后的电压过零点 电压波形随机多种：振荡、弧形、振荡+弧形稳定一致：类方波波形 电流波形随机多种：脉冲、半周波、脉冲+半周波稳定一致：带零休的类正弦形
间歇性电弧故障的形成本质上是电缆线芯与金属护层间短暂生成了动态畸变的非线性故障电阻（电导）。结合第2.2节分析得到的三类典型形态，本文基于黑箱建模理论，以分类模拟各电弧形态下的等效动态电弧电导来构建电弧模型。由于在配电网小电流系统中发生电缆内部电弧故障（即单相接地故障）时，故障电流增幅小，而故障电压畸变明显，因此本文构建的电弧模型以重现电弧故障电压外特性为主导，并据此重点选取电弧电压对应的波形特征点作为关键控制量来进行动态电弧电导控制函数的构建。
3.1.1 振荡电弧电导控制函数模型
从所获取的多组振荡间歇性电弧电压、电流波形样本进行分析，振荡间歇性电弧电导实测曲线如图6所示。由图6可知，当电缆电弧处于不稳定振荡阶段时，所对应的等效电弧电导将以脉冲形式在各个小区间内由最大值单调衰减至近零。因此，振荡间歇性电弧可视为分别在每个小区间内完成一次独立的起弧-灭弧过程，并由多个这样的过程组成振荡状态。
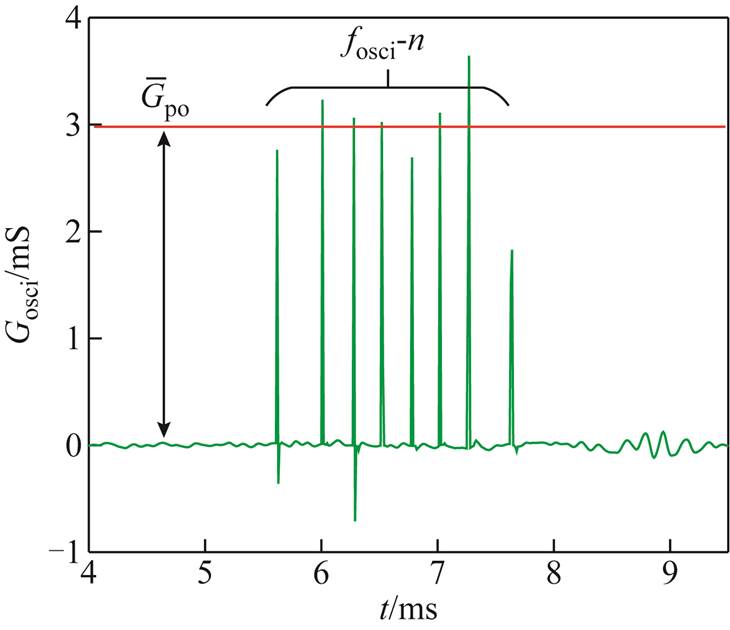
图6 振荡间歇性电弧电导实测曲线
Fig.6 Oscillating intermittent arc conductance test curve
如图6所示的电弧电导变化符合随机脉冲信号特征，本文选取高斯脉冲函数对该电弧电导的每一次独立脉冲行为进行模拟，并结合三角波函数实现振荡控制。高斯脉冲函数具有典型正态分布能量密度，是一种常用的自然脉冲模拟函数。利用高斯脉冲函数[19]、三角波周期函数构建的振荡间歇性电弧电导Gosci控制函数为
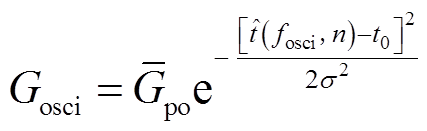（1）
式中，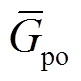
为电弧电导在振荡期间的平均峰值；t0为脉冲起始时间点；σ为时间常数，用于控制脉冲宽度；振荡控制函数
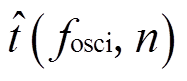为以平均频率fosci、振幅[-1/(2fosci), 1/(2fosci)]振荡n次的三角波函数，如图7所示。该函数可以控制振荡的频率和次数，对应的振荡点位于该函数过零点。
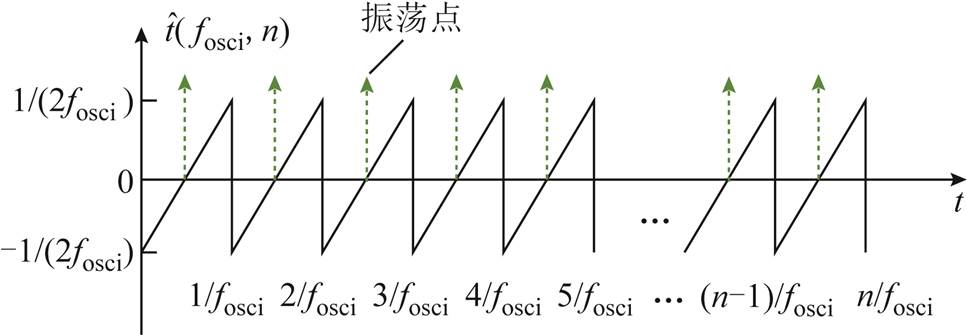
图7 振荡控制三角波函数
Fig.7 Oscillating intermittent arc conductance curve
以式（1）控制函数模拟的电弧电导理论波形如图8所示。图8中的模拟波形显示，采用本文所提出的周期性高斯脉冲函数能有效刻画振荡间歇性电弧电导的基本特征，同时该模型具有便于设置的模型控制参数。
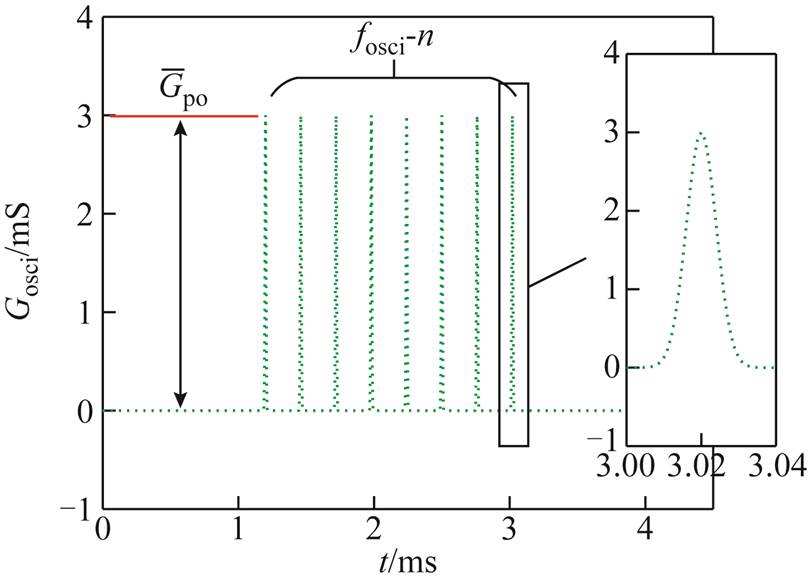
图8 周期高斯脉冲函数理论波形
Fig.8 Theoretical waveform of periodic Gaussian pulse function
3.1.2 模型控制参数计算与统计
由模型式（1）分析可知，振荡间歇性电弧电导模型包括四个控制参数：t0、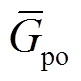、σ和联合参数fosci-n。利用实验采集到的振荡间歇性电弧数据进行统计分析，其中参数t0和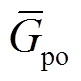呈平稳随机分布：t0以1/4工频周期（即电压正半周峰值处）为中心，在[-0.005, 0.005]工频周期内随机波动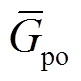；在2.2～12.6mS内随机变化。
本实验示波器采样率设置为100kHz，在电弧振荡过程中，实验观测到电压瞬时跌落的平均脉冲电流持续时间为2个采样点（0.02ms），则对应的高斯脉冲函数脉冲宽度满足
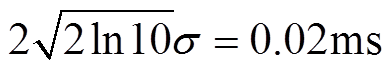（2）
则可求得式（1）中的模型时间常数σ约为0.005ms。
联合参数fosci-n则具有明显的分布趋势，其二维分布如图9所示。
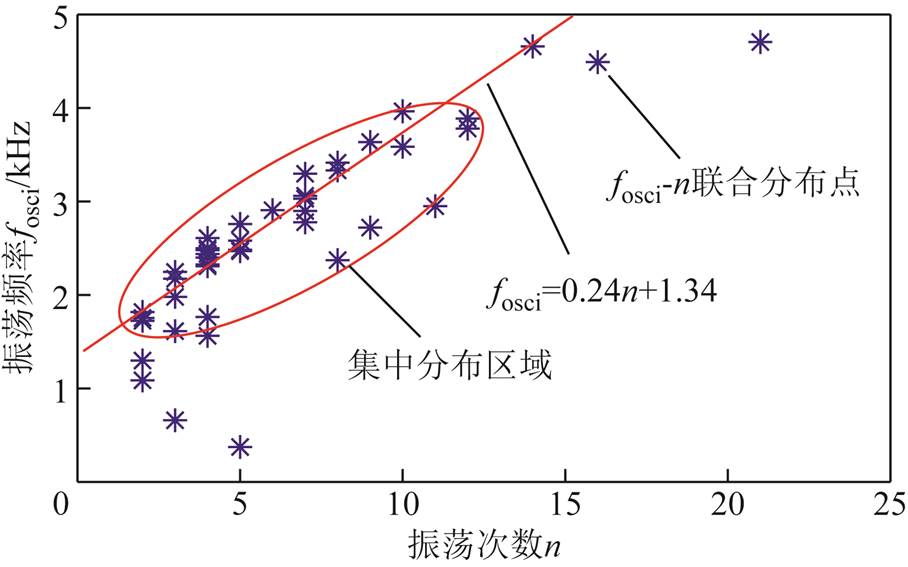
图9 联合参数fosci-n的二维分布
Fig.9 Two dimensional distribution of parameter fosci-n
观测该实验统计得到的联合参数fosci-n的分布情况可知，振荡间歇性电弧的平均振荡频率fosci集中在1.58～4.22kHz，振荡次数n集中在1～12次，且随着振荡次数的增加，对应的振荡频率变高、振荡周期变短，fosci-n在集中分布区域内呈线性相关，即
（3）
综上分析，总结各模型控制参数作用及分布范围见表2。
表2 振荡电弧电导模型控制参数
Tab.2 Control parameters of oscillating arc conductance model
参数控制作用数值 t0/工频周期起弧点0.245～0.255 /mS振荡深度2.2～12.6 σ/ms振荡脉宽0.005 fosci-n/(kHz-次)振荡频率-次数(1.58～4.22)-(1～12)
3.2.1 稳态电弧电导控制函数模型
稳态间歇性电弧波形呈现明显稳定的电弧压降，本文基于经典的弧隙能量平衡理论，结合实验所测得的独特电弧波形形状进行建模。弧隙能量平衡基本原理为电弧能量Q的变化取决于电弧注入能量与耗散能量Ploss的动态平衡，即
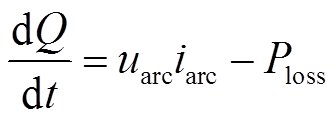（4）
在实际建模中，为便于电弧模型与电路电气量的关联与控制，一般从复现电弧外特性角度，以随电弧能量流动变化的动态电弧电导进行建模。即将电弧能量的变化率转换为等效的动态电弧电导变化率来进行计算，而电弧能量的注入与耗散则以包含电弧电压、电流的函数[20]来描述，即
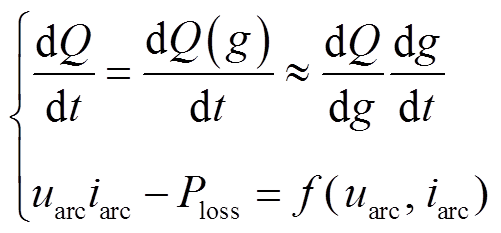（5）
式中，g为电弧电导。
联立式（4）和式（5）可推导出电弧电导建模的一般公式，即以含电弧电压或电流的函数来拟合电弧电导变化率。
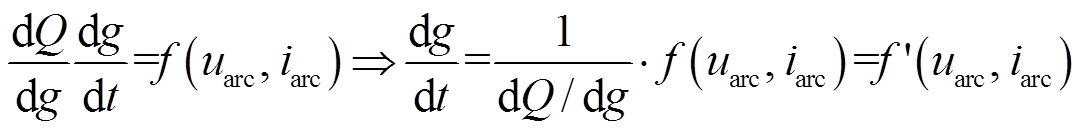（6）
根据重现电弧电压独特波形为制定电弧电导控制函数的原则，分析典型稳态间歇性电弧电压uarc、电弧电导Gstab及其一阶导数之间的对应关系，如图10所示。
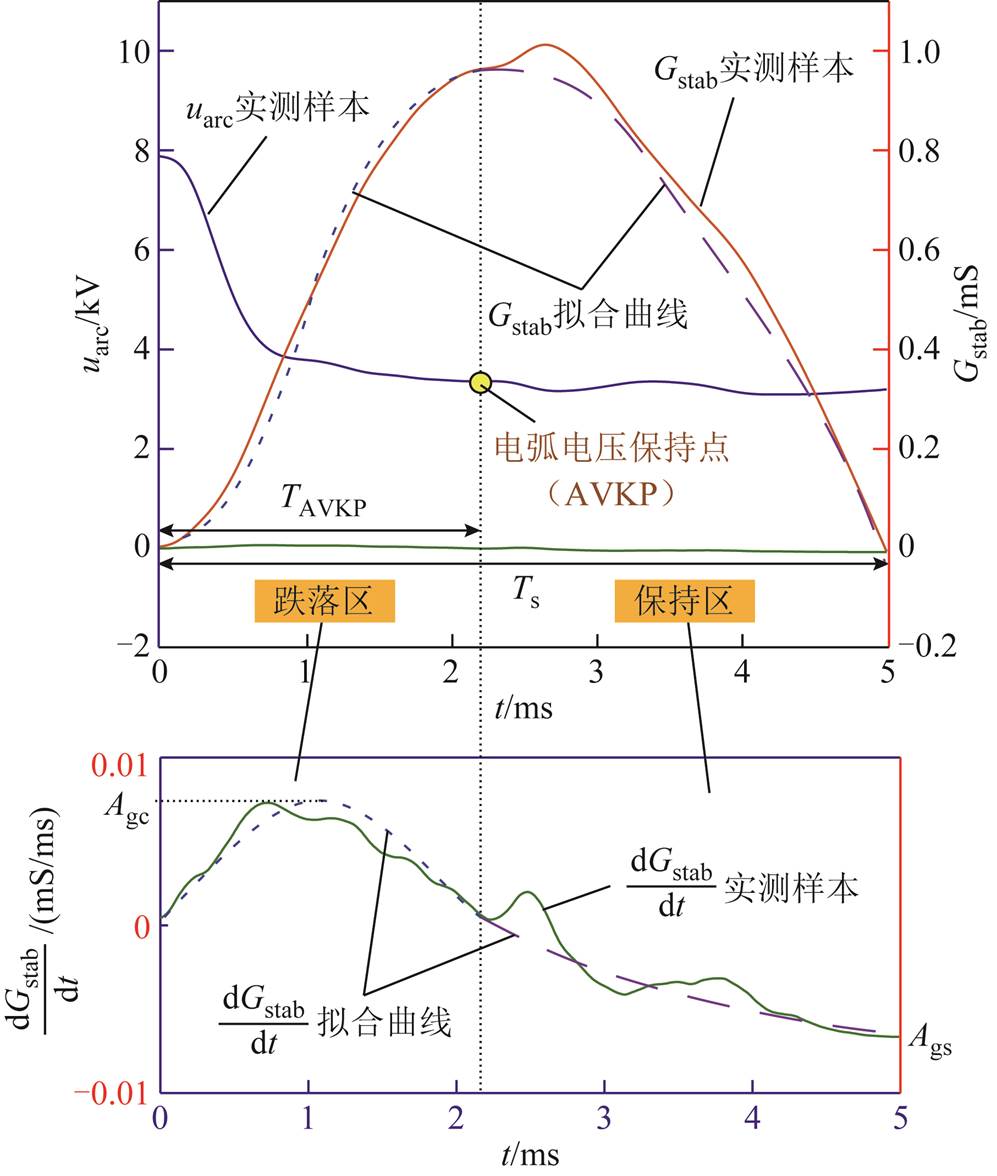
图10 稳态电弧电导与电弧电压对应关系
Fig.10 Corresponding relationship between conductance and voltage of steady-state arc
图10中稳态电弧电压uarc实测波形特性为：前半段以曲线下降，后以直线保持直至电弧熄灭。将电弧电压前后变化的分界点定义为电弧电压保持点（Arc Voltage Keeping Point, AVKP），以AVKP为界可将电弧电压的变化划分为跌落区与保持区，如图10中标示。该持续时间点相对于整个燃弧期间的占比Dc为
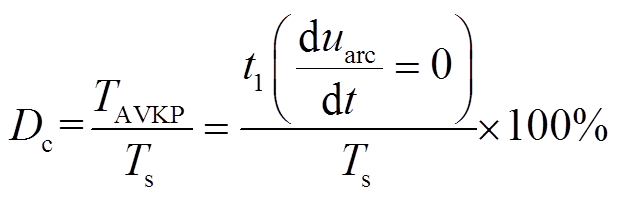（7）
式中，Ts为整个燃弧持续时间；TAVKP为电弧跌落段的持续时间，可取为电弧电压uarc一阶导数的第一次过零时间点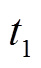
。
对应地，电弧电导Gstab也以AVKP为界，被分割为上升段和下降段。分析观察该曲线可知，Gstab并非简单的二次函数，若采用常规拟合，则至少需要6～7阶函数才能实现准确拟合。为了避免采用高阶函数进行拟合时产生拟合系数过多、物理表征不够显性的问题，本文提出1/2余弦-1/4正弦曲线近似法近似模拟该动态电弧电导的主要特征。
1/2余弦-1/4正弦曲线近似法具体为：在Gstab上升段，将电弧电导曲线近似拟合为角频率为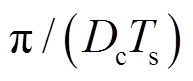
、相位在[π, 2π]区间的余弦函数，则其一阶导数为相位在[π, 2π]区间的正弦函数；在下降段内，将电弧电导曲线近似拟合为角频率为
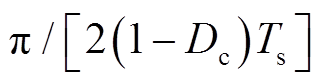、相位在[π/2, π]区间的正弦函数，其一阶导数为相位在[π/2, π]的余弦函数。则稳态电弧电导控制函数模型为
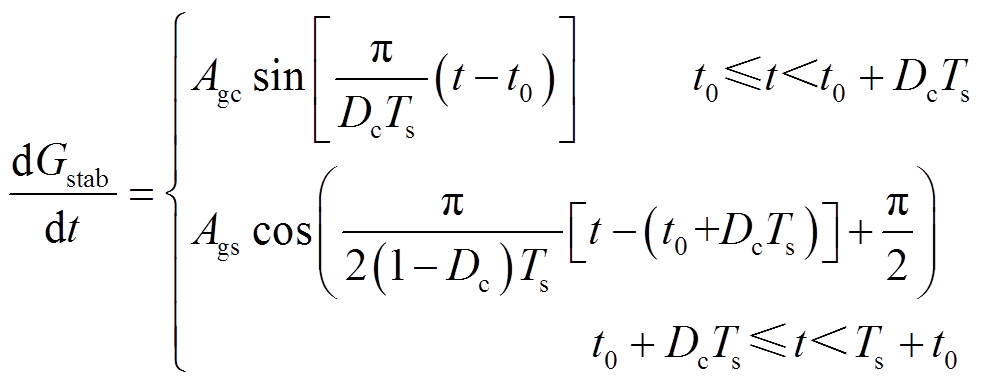（8）
式中，Agc、Ags分别为电弧电导一阶导数在跌落区和保持区的三角函数幅值，如图10中所示。
3.2.2 模型控制参数计算与统计
式（8）中的模型控制参数包括t0、Ts、Dc、Agc和Ags。其中，稳态电弧电压起弧时间t0与振荡间歇性电弧相似，均以1/4工频周期为中心，在[-0.005, 0.005]倍工频周期内随机波动；Ts基于实验波形统计，为3.1～6.7ms。
Dc可利用式（7）基于电弧电压的导数求取，其中电弧一阶导数第一次过零点t1转化为示波器离散采样点计算公式为
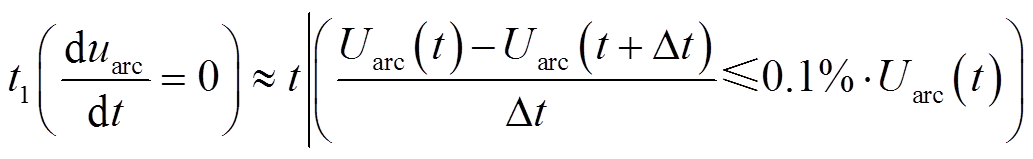（9）
式中，Δt为一个采样时间间隔；Uarc(t)为电弧电压在t时刻的离散采样点。
Agc、Ags根据实验电弧电压、电流离散采样点，利用求导运算法则分别求取，其中Agc等于电弧电导在跌落区对时间求导的最大值，Ags等于电弧电导在保持区对时间求导最小值的绝对值，即
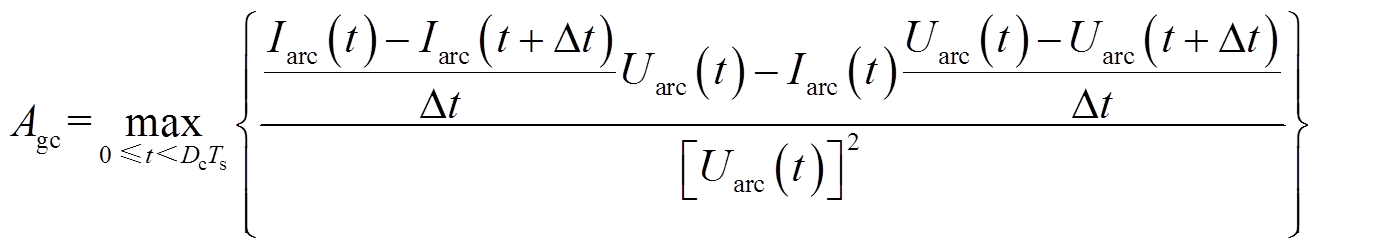（10）
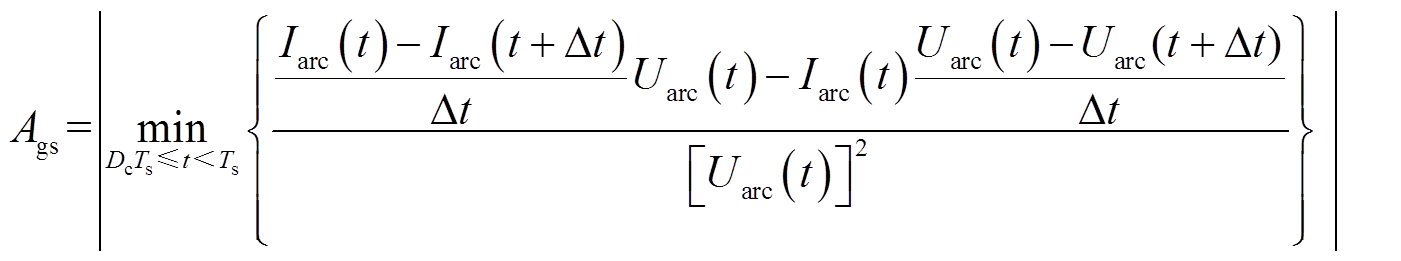（11）
式中，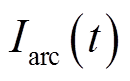
为电弧电流在t时刻的离散采样点。
利用式（7）～式（11），结合实验测量的电弧电压、电流离散采样数据，可计算统计得到各参数的分布范围，并将其控制作用总结见表3。
半稳态间歇性电弧可视为振荡电弧与稳态电弧保持区的组合，因此，可利用上述振荡电弧模型和稳态电弧保持区模型，以时间占比进行控制得到。其控制参数见表4，该模型控制函数不再赘述。
表3 稳态电弧电导模型控制参数
Tab.3 Control parameters of steady-state arc conductance model
参数控制作用数值 t0/工频周期起弧点0.245～0.255 Ts/ms持续时间3.1～6.7 Dc(%)跌落区宽23～54 Agc/(mS/ms)跌落区弧度0.004 2～0.008 2 Ags/(mS/ms)保持区平稳度0.003 6～0.007 7
表4 半稳态间歇性电弧控制参数
Tab.4 Control parameters of semi-steady intermittent arc
参数控制作用数值 Tsemi/ms总持续时间4.1～6.2 Dsemi(%)振荡阶段/稳态保持阶段占比12～52
根据上节中所构建的三类电弧电导等效模型，利用PSCAD中的CSMF模块库搭建多形态间歇性电弧控制模型。该模型由振荡间歇性电弧模块（Osci arc model）、稳态间歇性电弧模块（Stab arc model）、半稳态间歇性电弧模块（Semi arc model）组成，并通过随机切换模块（Arc select）及故障时序模块（Arc fault time）控制电弧的形态切换与起弧时刻。模型结构组成与内部控制系统在PSCAD中的实现分别如图11、图12所示。
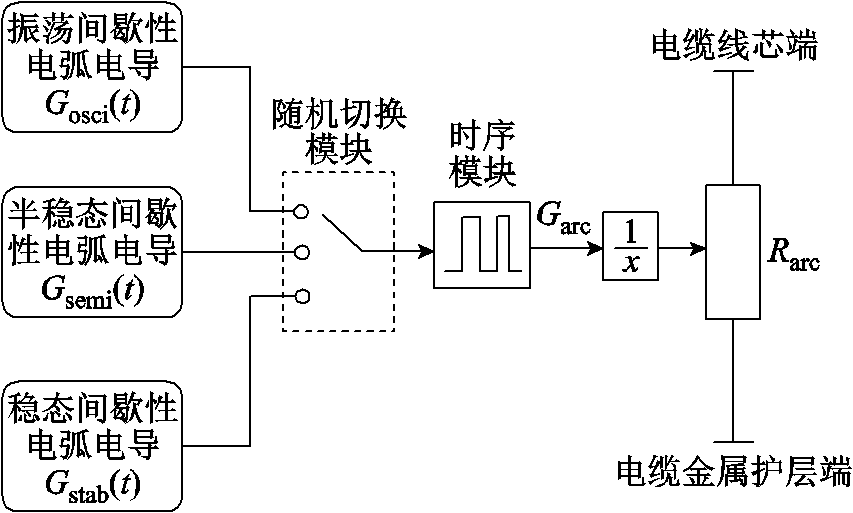
图11 多形态间歇性电弧模型的结构组成
Fig.11 Structure composition of the multi-form intermittent arc model
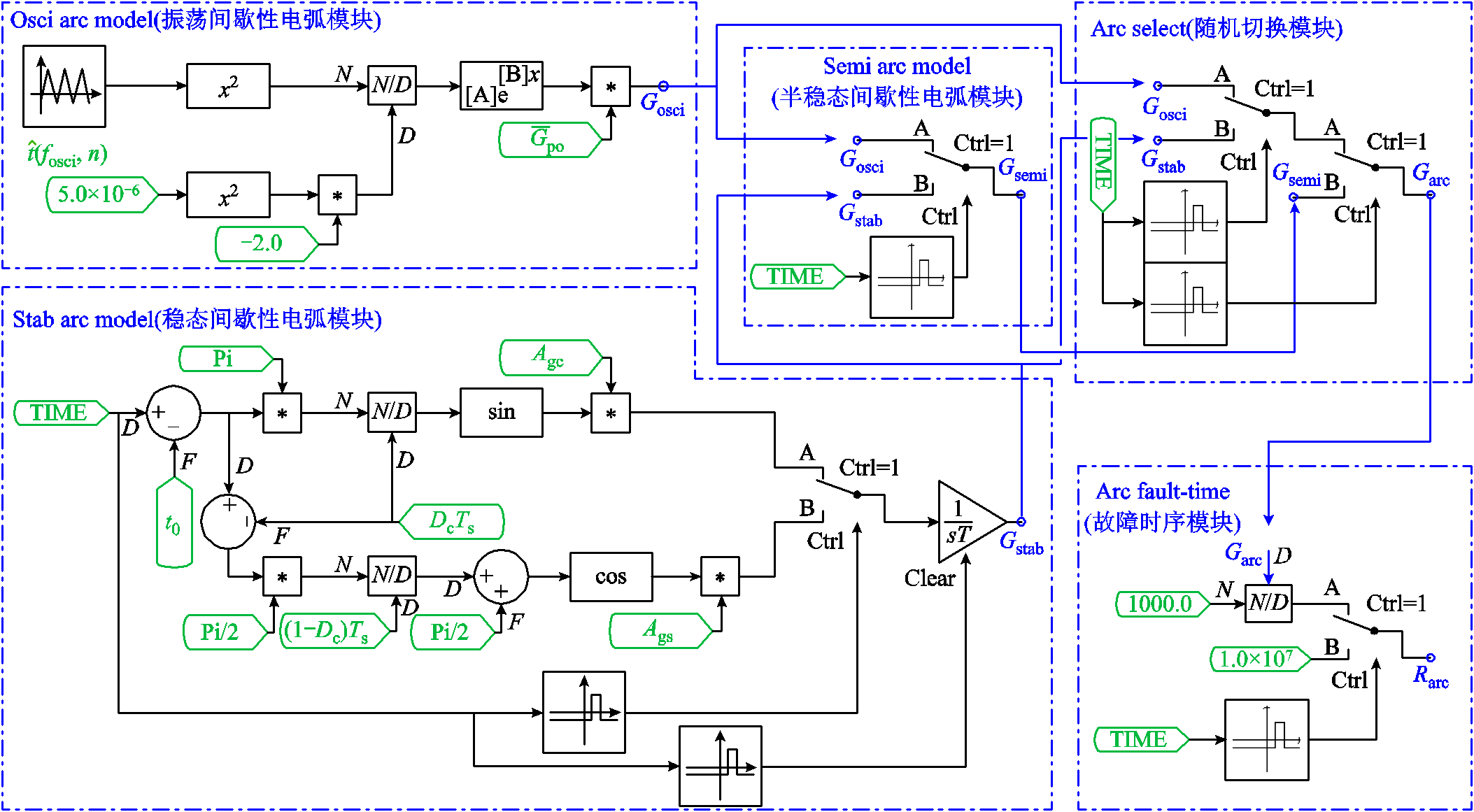
图12 多形态间歇性电弧控制模型在PSCAD中的实现
Fig.12 Realization of the multi-form intermediate arc control model in PSCAD
搭建实验主电路的等效电路如图13所示。本实验低压电源为0.22kV，电源接线端短路容量约为500kV·A，实验所采用的高压实验变压器额定参数为50kV·A/20kV/8.59%（额定容量/额定电压/阻抗电压），直接采用高压探头进行电弧故障电压测量。实验主电路等效电路中电源Us为实验变压器输出电压5.77kV/50Hz，忽略系统及变压器电阻，取电源等效电抗Ls为0.01H、变压器漏抗LT为0.602H，限流电阻Rlimit设置为1 500Ω，高压探头补偿电容Cprobe为40pF。电弧故障模型采用可控非线性时变电阻模块，其电阻值由图12中的电弧电导控制电路的最终输出Rarc所决定。
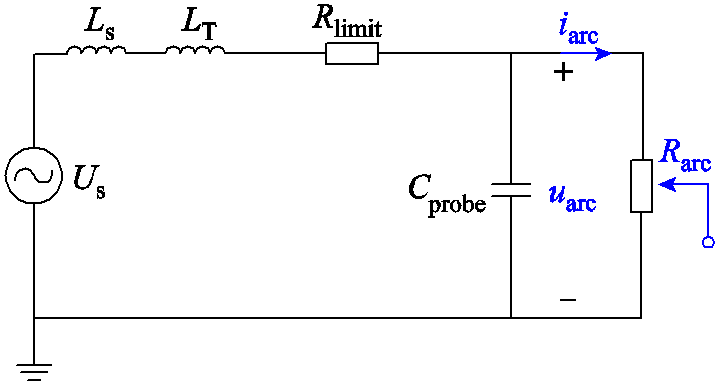
图13 实验主电路等效电路
Fig.13 Equivalent circuit of experimental main circuit
根据表2～表4的模型计算参数进行各模块设置，可得到各电弧形态的实验波形与模拟波形对比。燃弧期间电弧波形的平均模拟误差earc可用式（12）进行评估。
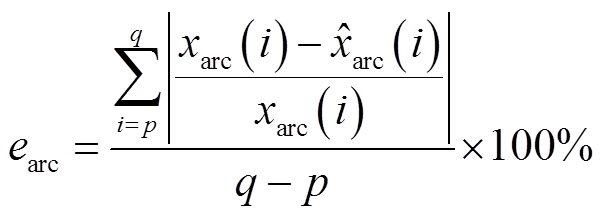（12）
式中，xarc(i)为实验电弧量的第i个离散数据点；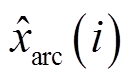
为模拟电弧量的第i个离散数据点；p、q分别为起弧点、熄弧点。
需要说明的是，对于三类电弧燃弧结束之后的电压动态恢复过程，即弧后电压波动（见下文各图中熄弧后的波形模拟结果），是由实验变压器突然空载（开路）后自身的升压特性，以及与系统等效电感、限流电阻和探头补偿电容构成的RLC二阶振荡电路放电引起。此时电弧已熄弧，电路中不存在电弧，因此该电压波动与燃弧过程本身无关，其模拟误差不作考虑，本文仅讨论燃弧期间的模拟效果。
4.3.1 振荡间歇性电弧的模拟对比
振荡间歇性电弧模拟与实验波形对比结果如图14所示。对比图14中四组实验波形与所模拟的振荡间歇性电弧波形可知，该模型在燃弧期间的冲击跌落过程与实验波形一致，跌落过程的平均模拟误差为4.1%。由于该等效模型对振荡电弧的振荡周期作了平均简化处理，导致模拟振荡间隔与实验波形存在一定差异，振荡间隔平均模拟误差为11.4%。考虑到振荡间歇性电弧的高度随机性特征，该振荡间隔的误差范围不影响其主要外特征的呈现。
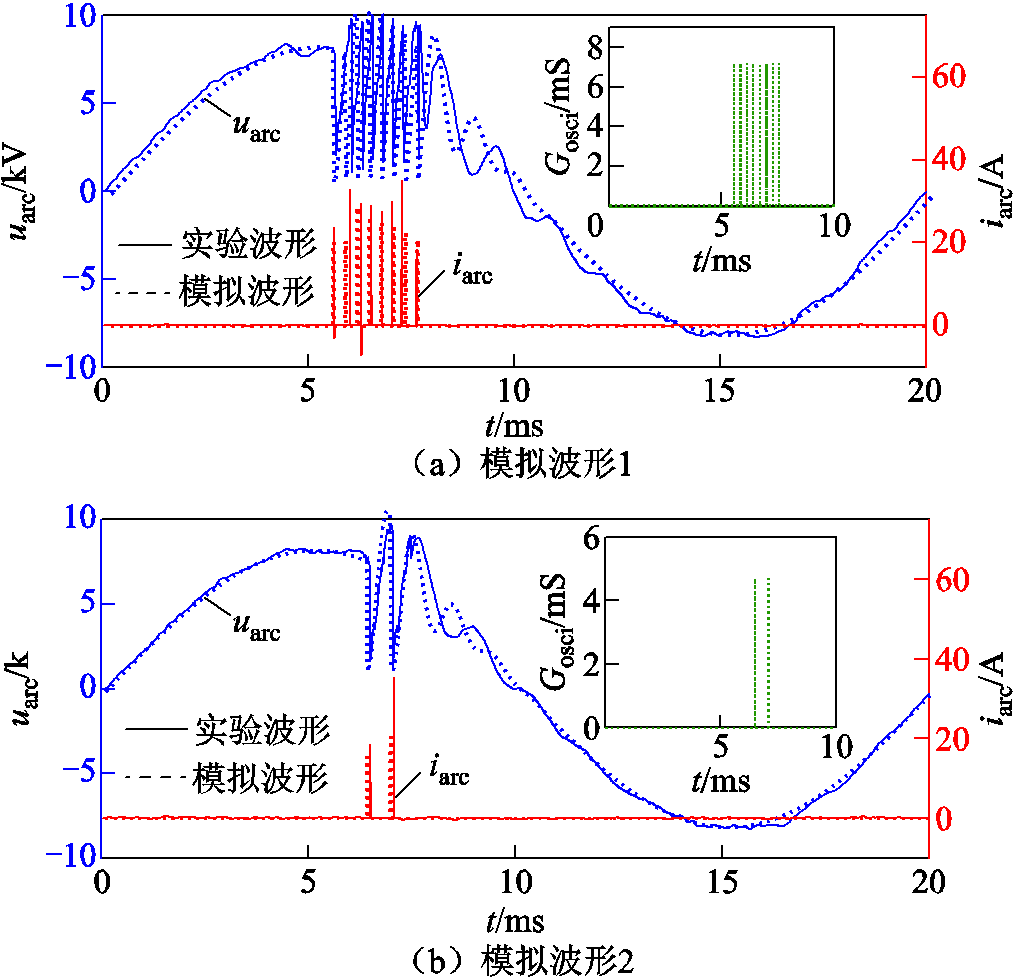
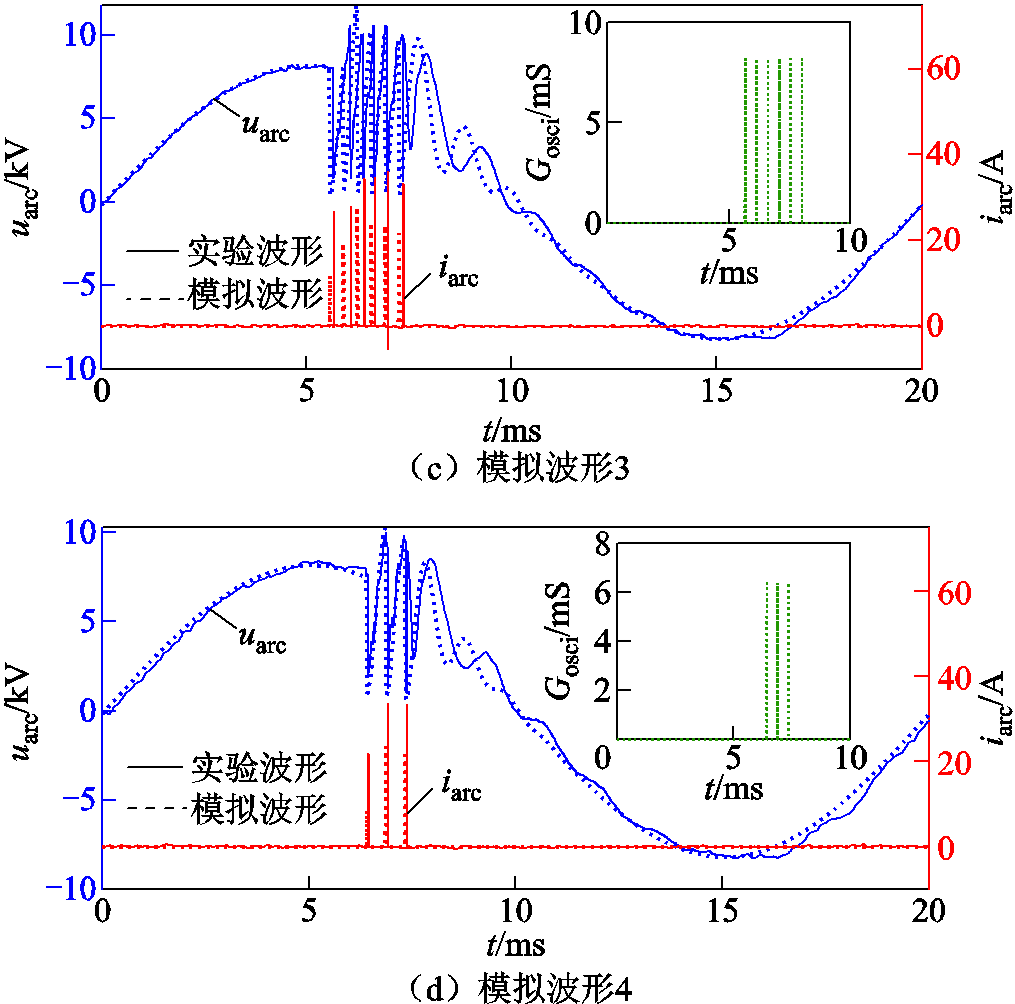
图14 振荡间歇性电弧模拟与实验波形对比
Fig.14 Comparison between simulated and experimental waveforms of oscillating intermittent arc
4.3.2 稳态间歇性电弧的模拟对比
稳态间歇性电弧模拟与实验波形对比如图15所示。图15中的四组模拟结果表明，采用本文提出的1/2余弦-1/4正弦函数近似法所模拟的稳态电弧电导，能在燃弧期间内有效还原出电弧电压的弧线形跌落和直线保持两个过程，与实验波形一致，平均模拟误差为2.3%，证明了该简化近似方法的有效性。同时注意到该控制函数中，仅有Dc、Agc、Ags三个形状控制参数，且每个参数具有明确的形状控制意义，降低了模型调节难度。
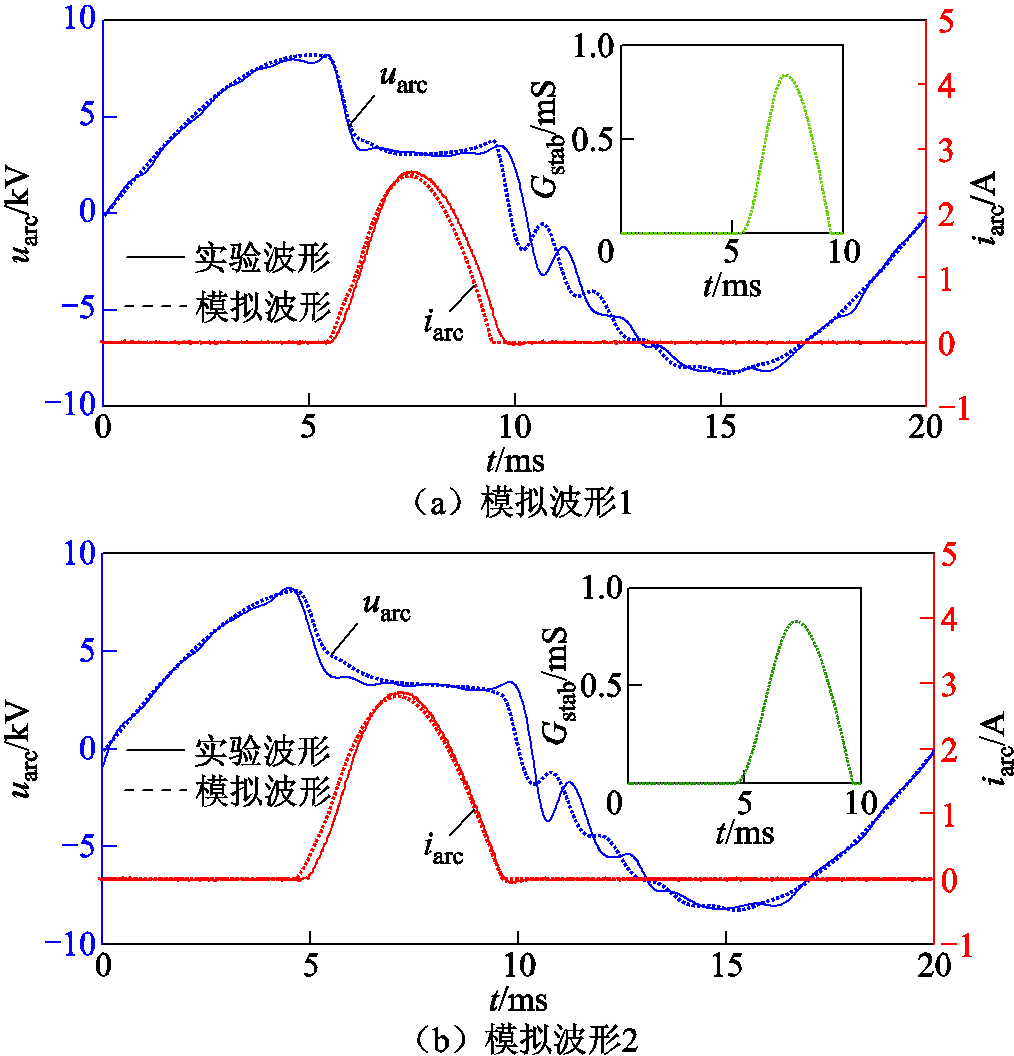
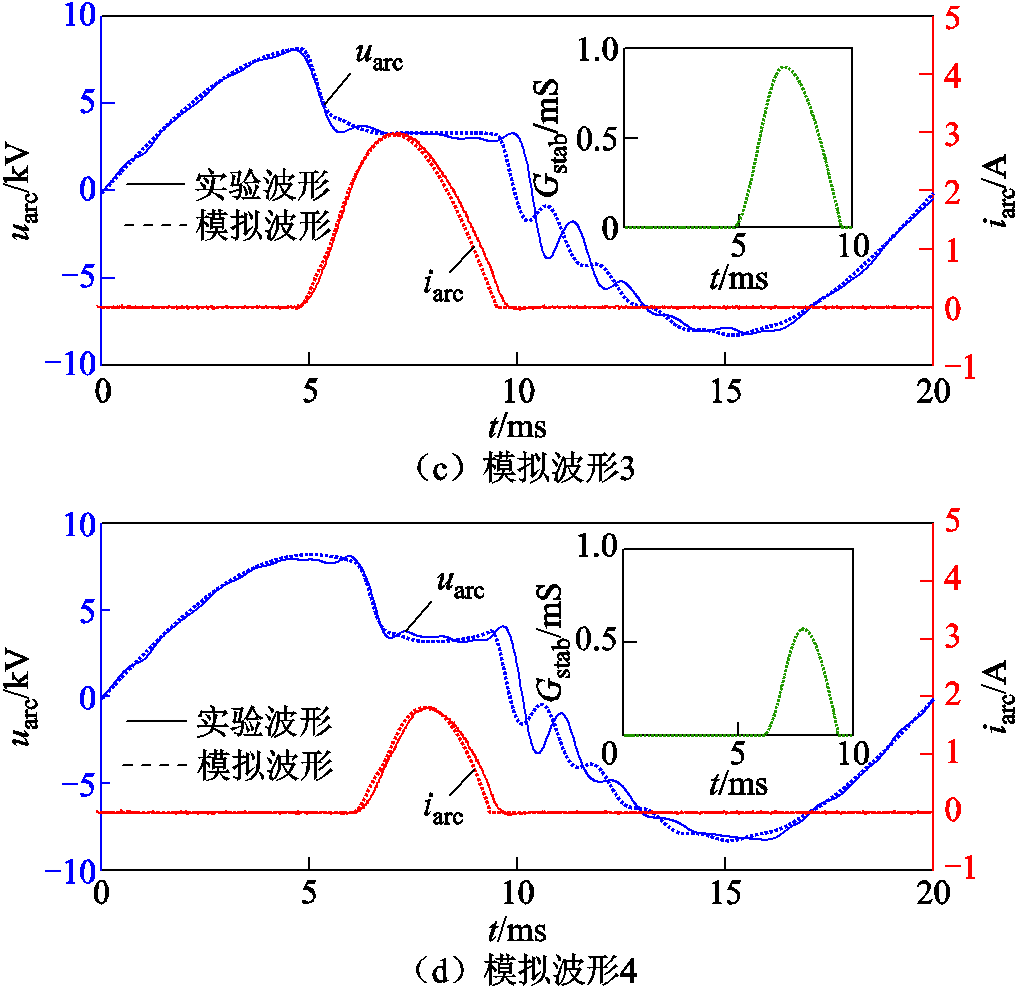
图15 稳态间歇性电弧模拟与实验波形对比
Fig.15 Comparison between simulated and experimental waveforms of steady-state intermittent arc
4.3.3 半稳态间歇性电弧的模拟对比
半稳态间歇性电弧为振荡间歇性电弧与稳态间歇性电弧的组合，上述模拟对比已充分验证了振荡电弧模型和稳态间歇性电弧模型的有效性。图16简单展示了利用图12中的占比控制模块实现半稳态间歇性电弧控制的结果，与实验波形基本一致。其中，振荡段的电压冲击跌落平均模拟误差为4.6%、振荡间隔平均模拟误差为12.8%、稳态段的模拟误差为1.6%。图16中所模拟的半稳态波形体现了电弧前半段的振荡状态以及后半段的稳定燃烧状态，证明了采用占比控制的方式能实现半稳态电弧的有效模拟。
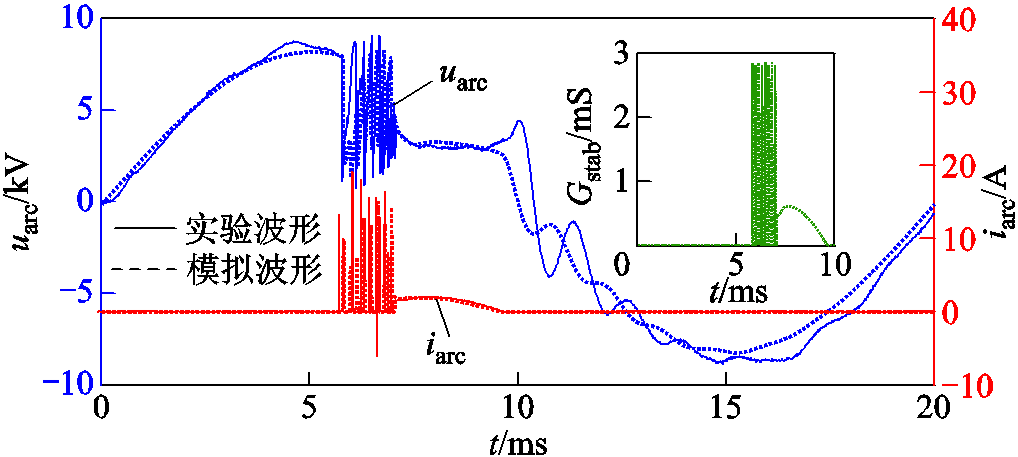
图16 半稳态间歇性电弧模拟与实验波形对比
Fig.16 Comparison between simulated and experimental waveforms of semi-steady-state intermittent arc
电缆所具有的金属护层接地结构使得电缆容易形成内部电弧故障，电缆内部电弧的燃弧路径、弧道环境与常规对地击穿电弧截然不同，因此电缆内部电弧应当具有自身独特的性质，有必要针对电缆内部电弧建立专用模型。本文通过高压电弧实验证实了这一结论，并基于电缆内部电弧实测波形特征分析，建模得到如下结论：
1）电缆内部电弧的独特波形特征为：电弧以间歇性形态在1/4工频周期附近完成一次独立起弧-灭弧过程，电弧电流不存在周期性零休现象，且故障波形随机呈现振荡、稳态、半稳态三类主要形态。
2）从重现电缆内部电弧主要外特性的角度，提出了多形态间歇性电缆电弧模型，通过仿真与实验波形对比，验证了该模型控制函数的可行性和有效性。
3）所提电弧模型模拟的电弧振荡冲击过程、稳态弧形跌落过程精确度较高，平均模拟误差小于5%；振荡间隔的平均简化处理不影响其主要外特性的呈现。
论文后续工作将针对电缆内部电弧的起弧点、持续时间、波形形态与电缆XLPE局部劣化状态的内部对应机理展开进一步研究。
参考文献
[1] Zhang Xin, Bruce A, Rowland S, et al. Modeling the development of low current arcs and arc resistance simulation[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2018, 25(6): 2049-2057.
[2] Sidhu T S, Xu Zhihan. Detection of incipient faults in distribution underground cables[J]. IEEE Transactions on Power Delivery, 2010, 25(3): 1363-1371.
[3] Jannati M, Vahidi B, Hosseinian S H. Incipient faults monitoring in underground medium voltage cables of distribution systems based on a two-step strategy[J]. IEEE Transactions on Power Delivery, 2019, 34(4): 1647-1655.
[4] 崔芮华, 佟德栓. 基于Levene检验的航空交流串联电弧故障检测[J]. 电工技术学报, 2021, 36(14): 3034-3042.
Cui Ruihua, Tong Deshuan. Aviation AC series arc fault detection based on Levene test[J]. Transactions of China Electrotechnical Society, 2021, 36(14): 3034-3042.
[5] 崔芮华, 李泽, 佟德栓. 基于三维熵距和熵空间的航空电弧故障检测与分类技术[J]. 电工技术学报, 2021, 36(4): 869-880.
Cui Ruihua, Li Ze, Tong Deshuan. Arc fault detection and classification based on three-dimensional entropy distance and entropy space in aviation power system[J]. Transactions of China Electrotechnical Society, 2021, 36(4): 869-880.
[6] 王雪菲, 李京, 陈平, 等. 基于行波波形综合相似度比较的电缆故障选线[J]. 电力系统保护与控制, 2022, 50(1): 51-59.
Wang Xuefei, Li Jing, Chen Ping, et al. Cable fault line selection based on comprehensive similarity comparison of traveling wave waveforms[J]. Power System Protection and Control, 2022, 50(1): 51-59.
[7] 邓丰, 梅龙军, 唐欣, 等. 基于时频域行波全景波形的配电网故障选线方法[J]. 电工技术学报, 2021, 36(13): 2861-2870.
Deng Feng, Mei Longjun, Tang Xin, et al. Faulty line selection method of distribution network based on time-frequency traveling wave panoramic waveform[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2861-2870.
[8] 郭凤仪, 高洪鑫, 唐爱霞, 等. 局部二值模式直方图匹配的串联故障电弧检测及选线[J]. 电工技术学报, 2020, 35(8): 1653-1661.
Guo Fengyi, Gao Hongxin, Tang Aixia, et al. Series arc fault detection and line selection based on local binary pattern histogram matching[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 1653-1661.
[9] 崔芮华, 曹欢. 基于相空间重构的航空电弧故障识别方法[J]. 电工技术学报, 2020, 35(增刊1): 243-250.
Cui Ruihua, Cao Huan. An arc fault identification method in aircraft based on phase space reconstruction[J]. Transactions of China Electrotechnical Society, 2020, 35(S1): 243-250.
[10] 刘科研, 盛万兴, 董伟杰. 配电网弧光接地故障建模仿真与实验研究综述[J]. 高电压技术, 2021, 47(1): 12-22.
Liu Keyan, Sheng Wanxing, Dong Weijie. Overview of modeling simulation and experimental research on arc grounding fault in distribution network[J]. High Voltage Engineering, 2021, 47(1): 12-22.
[11] 张姝, 林圣, 唐进, 等. 基于双层阻抗模型的三相单芯电缆自恢复故障定位[J]. 电工技术学报, 2016, 31(17): 1-10.
Zhang Shu, Lin Sheng, Tang Jin, et al. Fault location of self-clearing fault in three phase single core cables based on double impedance model[J]. Transactions of China Electrotechnical Society, 2016, 31(17): 1-10.
[12] 刘艳丽, 郭凤仪, 李磊, 等. 一种串联型故障电弧数学模型[J]. 电工技术学报, 2019, 34(14): 2901-2912.
Liu Yanli, Guo Fengyi, Li Lei, et al. A kind of series fault arc mathematical model[J]. Transactions of China Electrotechnical Society, 2019, 34(14): 2901-2912.
[13] 王宾, 崔鑫, 董新洲. 配电线路弧光高阻故障检测技术综述[J]. 中国电机工程学报, 2020, 40(1): 96-107, 377.
Wang Bin, Cui Xin, Dong Xinzhou. Overview of arc high impedance grounding fault detection technologies in distribution system[J]. Proceedings of the CSEE, 2020, 40(1): 96-107, 377.
[14] 丛子涵, 刘亚东, 严英杰, 等. 基于磁流体动力学的配电线路树-线早期故障仿真分析[J]. 电工技术学报, 2020, 35(增刊2): 562-568.
Cong Zihan, Liu Yadong, Yan Yingjie, et al. Simulation analysis of tree contact incipient fault in the distribution network based on magnetohydrodynamic[J]. Transactions of China Electrotechnical Society, 2020, 35(S2): 562-568.
[15] 王宾, 崔鑫. 中性点经消弧线圈接地配电网弧光高阻接地故障非线性建模及故障解析分析[J]. 中国电机工程学报, 2021, 41(11): 3864-3873.
Wang Bin, Cui Xin. Nonlinear modeling and analytical analysis of arc high resistance grounding fault in distribution network with neutral grounding via arc suppression coil[J]. Proceedings of the CSEE, 2021, 41(11): 3864-3873.
[16] 任伟, 薛永端, 杨帆, 等. 中性点不接地配电网电弧接地故障建模与分析[J]. 电网技术, 2021, 45(2): 705-712.
Ren Wei, Xue Yongduan, Yang Fan, et al. Modeling and analysis of arc grounding faults in isolated neutral distribution network[J]. Power System Technology, 2021, 45(2): 705-712.
[17] 郑昕, 单潇洁. 低压交流电弧电流零区电压波形特征分析与应用[J]. 电工技术学报, 2020, 35(22): 4717-4725.
Zheng Xin, Shan Xiaojie. Characteristic analysis and application research of low voltage AC arc voltage waveform at the current zero[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4717-4725.
[18] Zhang Wenhai, Xiao Xianyong, Zhou Kai, et al. Multicycle incipient fault detection and location for medium voltage underground cable[J]. IEEE Transactions on Power Delivery, 2017, 32(3): 1450-1459.
[19] 张春艳, 赵青, 刘成林, 等. 探地雷达超宽带高斯脉冲信号源的设计[J]. 强激光与粒子束, 2013, 25(3): 680-684.
Zhang Chunyan, Zhao Qing, Liu Chenglin, et al. Design of ultra-wideband Gaussian pulse source for ground penetrating radar[J]. High Power Laser and Particle Beams, 2013, 25(3): 680-684.
[20] Wei Mingjie, Liu Weisheng, Shi Fang, et al. Distortion-controllable arc modeling for high impedance arc fault in the distribution network[J]. IEEE Transactions on Power Delivery, 2021, 36(1): 52-63.
Modeling of Internal Multiform Intermittent Arc Fault for 10kV XLPE Cable
Abstract Intermittent arc is an important process in the initial development stage of cable fault. This paper takes 10kV XLPE cable widely used in China's distribution network as the research object. Through experimental analysis, it is found that there are obvious waveform differences between the arc inside the cable and the arc breakdown to the ground, and it presents a variety of waveform forms in its development process. This paper combs and summarizes the commonness in the random evolution of the intermittent cable arc, and summarizes them into three main forms: oscillating intermittent arc, steady-state intermittent arc and semi-steady-state intermittent arc. From the perspective of external characteristic reproduction to help cable fault analysis, the control models of three main arc forms are constructed based on Gaussian random pulse, arc gap energy balance theory and proportion control respectively with the idea of black box modeling. The distribution range of the control parameters of each model is calculated according to the experimental sample data. The proposed model is realized by PSCAD simulation software, and the comparison with the experimental waveform shows that the multi-form arc model constructed in this paper can effectively simulate the main characteristics of the three types of intermittent arc. The discovery of the multi-form intermittent arc enriches the random diversity of cable arc, and the arc model provides a new basis for cable incipient fault analysis.
keywords：Cable internal arc fault, arc model, multiform, intermittent, XLPE
DOI:10.19595/j.cnki.1000-6753.tces.221248
中图分类号：TM85
国家自然科学基金项目（52007079）、云南省基础研究计划（202101AU070027）和云南省人培项目（KKSY201904011）资助。
收稿日期 2022-06-27
改稿日期 2022-08-02
李露露 女，1989年生，副教授，硕士生导师，研究方向为电力扰动分析与电力电缆。E-mail：lilulu1203@foxmail.com
王开正 男，1988年生，讲师，硕士生导师，研究方向为电绝缘老化及电工绝缘材料。E-mail：wkz@kust.edu.cn（通信作者）
（编辑 李冰）