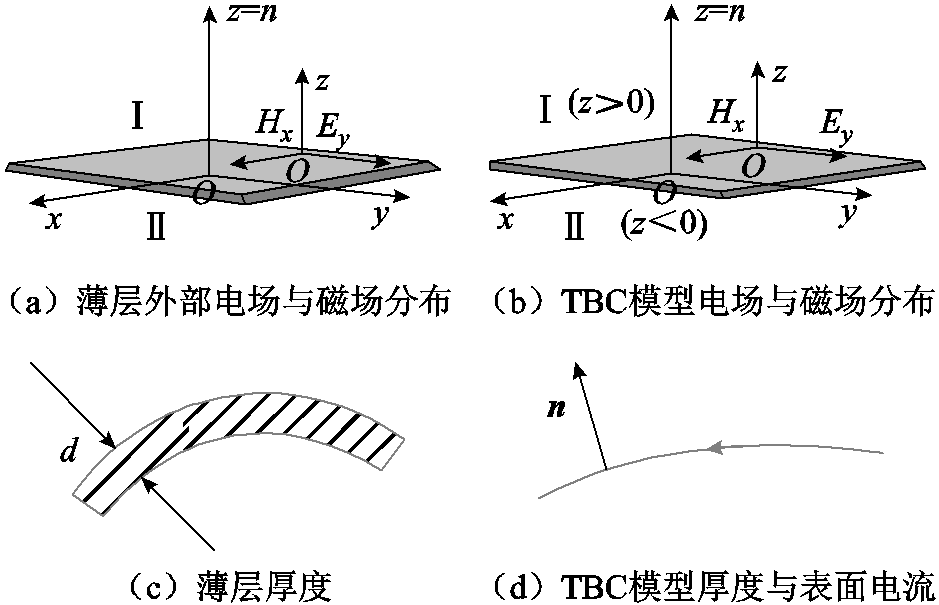
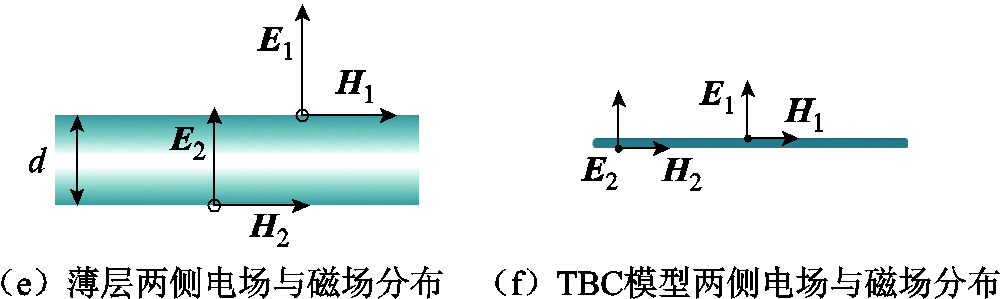
图1 纳米晶薄层屏蔽周围电场与磁场分析
Fig.1 Analysis of electric field and magnetic field around nanocrystalline thin layer
摘要 电动汽车无线充电系统中的纳米晶薄层屏蔽结构在大幅度降低耦合机构的体积与质量的同时，也为复合屏蔽的仿真计算增加了难度。该文为减小纳米晶薄层屏蔽周围磁场计算时间，结合过渡边界条件（TBC）计算方法，分析具有高磁导率的纳米晶薄层屏蔽内磁场分布，为电动汽车无线充电中纳米晶薄层屏蔽复合系统提出了无线充电薄层TBC计算模型。分别搭建无线充电系统的一般计算模型与TBC计算模型，根据趋肤深度调整计算单元，得出精确划分情况下，TBC模型与一般模型计算和实验测量结果相吻合，TBC模型计算时间最多可减小为一般模型的41.7%，大幅度加快无线充电复合屏蔽模型计算速度。
关键词：纳米晶薄层屏蔽 过渡边界条件 磁屏蔽 各向异性 计算模型
电动汽车作为绿色环保的现代交通工具受到世界各国的关注。而电动汽车的无线充电方式相对于传统充电具有防水、防尘、操作安全等优点，成为电动汽车发展的重要方向[1-6]。
作为无线充电的关键环节，电动汽车无线充电磁能耦合机构的磁屏蔽结构可通过聚集磁场提高系统传输效率、降低漏磁，减小对周围生物体与设备的影响[7-12]。国内外已有很多针对磁屏蔽的优化设计，其中新型磁性材料的引入为其研究与应用带来新的突破[13-17]。特别是多层复合纳米晶合金研制的纳米晶屏蔽薄层，电磁性能更加优异，如高饱和磁通密度和相对磁导率，可在保证屏蔽效果的基础上大幅度降低磁能耦合机构的体积与质量[18-21]，纳米晶合金的机械性能优异，强度高、延展性大且韧性好，适合移动类无线充电环境。
先进磁性材料优异的电磁性能与更薄的结构特点对分析与研究提出更高要求，特别是纳米晶屏蔽薄层较小的几何尺寸给应用带来优势的同时也给磁场的计算增加了难度。纳米晶软磁基础带材与趋肤深度基本在一个数量级，需要计算单元小于趋肤深度才能精确求解趋肤深度对磁场分布的影响，这将占用大量计算空间，增加计算时间。并且由于纳米晶薄层屏蔽中的电磁场在层厚度方向上的空间变化尺度比在它们横向方向上的尺度小三个数量级以上，应用有限元法计算时节点之间距离差距过大，容易导致矩阵方程组解的数值不稳定[22-23]。
对纳米晶薄层屏蔽分析一般引入对硅钢片叠片分析的均匀化计算方法[24-26]，以等效的具有各项异性相对磁导率与电导率的块状材料代替叠层材料，以分析叠层的涡流与磁场。文献[19]针对纳米晶薄层屏蔽中各方向磁通密度分布不均匀，考虑材料各向异性，引入等效电导率和相对磁导率表达式，分析等效均匀电导率与相对磁导率对自感、互感的影响与纳米晶薄层屏蔽中的磁通分布。文献[20]将纳米晶薄层屏蔽的等效相对磁导率与电导率定义为张量，根据磁心的等效参数求得切向趋肤深度，确定关键磁心部分的网格尺寸[27-28]。
目前虽然引入均匀化计算方法分析纳米晶薄层屏蔽，但由于趋肤深度的影响，且叠片法向与切向尺寸差距较大，将磁心均匀化后需要找寻合适的网格划分才能使模型得到精确的计算结果，网格划分工作量大。因此需要一种无线充电系统纳米晶薄层屏蔽磁场的准确快速计算方法。
本文通过分析趋肤深度对叠片中磁场分布的影响，利用传输线定理，搭建了无线充电纳米晶薄层屏蔽的过渡边界条件（Transition Boundary Condition, TBC）模型。利用有限元方法分别计算了无线充电纳米晶薄层屏蔽TBC模型与一般模型中的磁场分布，验证了模型计算的快速性。同时搭建三层屏蔽结构与实验测量设备，验证了模型计算的正确性与可行性，为加快无线充电系统中薄层屏蔽结构的磁场计算提供了新思路。
对于纳米晶薄层屏蔽周围磁场，可通过电场与磁场在层中分布情况结合边界的衔接条件进行计算，纳米晶薄层屏蔽及与其对应的TBC模型周围电场与磁场分析如图1所示。由于趋肤深度的影响，磁场在纳米晶薄层屏蔽中分布并不均匀，在无线充电环境下纳米晶薄层屏蔽的趋肤深度为(15±1)μm，而纳米晶薄层屏蔽基础带材一般为18～26μm，趋肤深度与纳米晶薄层屏蔽基础带材厚度在一个数量级，如图1所示，因此计算中需要考虑趋肤深度对磁场分布的影响，而不能简单地将其认为在切向上均匀分布或是集中在上、下表面。因此本文采用无线充电纳米晶薄层屏蔽TBC模型求解薄层周围磁场。
图1 纳米晶薄层屏蔽周围电场与磁场分析
Fig.1 Analysis of electric field and magnetic field around nanocrystalline thin layer
首先对在纳米晶薄层屏蔽内部传输的电磁波进行分析，求出TBC模型。由于纳米晶薄层屏蔽具有较高的电导率与相对磁导率，远高于周围材料，层周围的电磁波可认为是沿法向方向传输的横电磁波（Transverse Electromagnetic Wave, TEM波）[27-28]。如图1所示，将z轴与法向方向重合，由于薄层厚度较小，电场强度与磁场强度随z轴变化比其他方向快，因此层中可只考虑电场强度与磁场强度在z轴变化，表示为
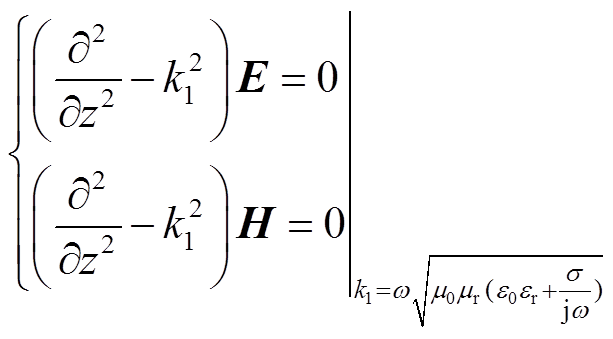（1）
式中，k1为薄层材料的传播常数；E与H分别为层内的电场强度与磁场强度；μ0和ε0分别为真空磁导率和真空的介电常数；ω为角频率；μr、σ和εr分别为薄层材料的相对磁导率、电导率和相对介电常数。
电场强度与磁场强度在层内通解形式为
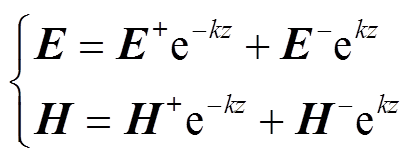（2）
式中，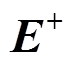
、
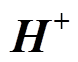为向z轴正方向传播的电场强度与磁场强度；
、
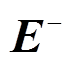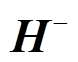为向z轴负方向传播的电场强度与磁场强度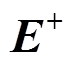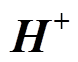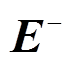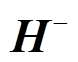；、、、均为常数，由薄层传输特性决定。
若已知层一侧表面电场强度E1与磁场强度H1，将其作为初始条件，结合传输线公式与麦克斯韦方程
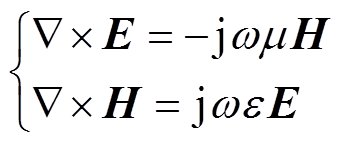（3）
可以得到层中传输方向上任一位置的电场与磁场，包括另一侧表面的电磁场。因此薄层另一侧表面的电场强度与磁场强度分别为
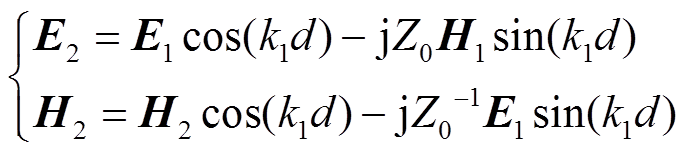（4）
式中，E1和H1分别为区域Ⅰ侧薄层表面电场强度与磁场强度，E2和H2为区域Ⅱ侧薄层表面电场强度与磁场强度，如图1所示；d为薄层厚度；Z0为薄层材料波阻抗，表示为
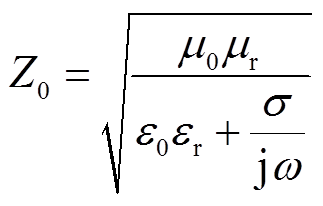（5）
因此式（4）表明薄板两侧电场强度和磁场强度的关系，通过传播常数k1、薄板厚度d与波阻抗Z0将两侧电场与磁场相关联，电磁波在薄板内传播由波阻抗表征，而不需要再对薄板内电磁波求解。
将电磁场的标量形式结合表面阻抗与传输阻抗，采用平行极化波分析，控制公式可以表示为
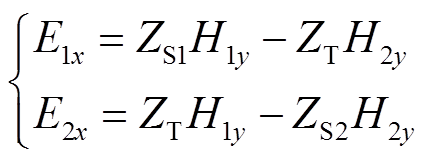（6）
式中，E1x、E2x为薄板两侧电场强度；H1y、H2y为薄板两侧磁场强度；ZS1为区域Ⅰ侧表面阻抗；ZS2为区域Ⅱ侧表面阻抗；ZT为薄板内传输阻抗。
如图1所示，区域Ⅰ、Ⅱ为薄层上侧与下侧，在薄层TBC模型下，薄层可模拟为电流薄片，不直接表示厚度，区域Ⅰ与Ⅱ可表示为z＞0与z＜0侧。
由传输线定理可以将传输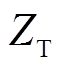阻抗
与表面阻抗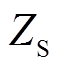
由传播常数k1与薄层厚度d表示为
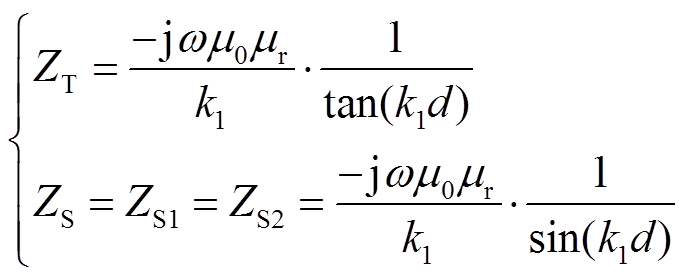（7）
可将式（6）写为简洁的对称形式，即
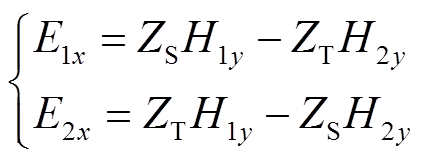（8）
通过矢量表示的TBC模型磁场强度计算公式为
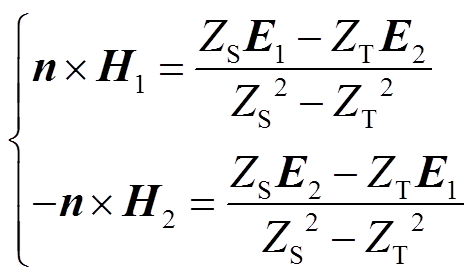（9）
TBC模型通过表面阻抗ZS与传输阻抗ZT模拟电磁波在薄层中的反射与传输，并且由于ZS和ZT与薄层厚度和薄层传播常数有关，在无线充电薄层TBC计算模型中，由传输线定理，趋肤深度对磁场分布的影响由表面阻抗与传输阻抗表示。
在导电薄层介质磁场分析中施加TBC可绕过解析薄层内部的需要。TBC模型通过对处于磁场环境下导电薄层的表面添加边界条件，以精确模拟薄层外部整个区域的场，过渡边界条件由电场和磁场之间关系来表述。因此，TBC与通过薄层精确解析计算近似的同时，可省略对薄层内部的分析。
目前针对无线充电磁屏蔽的磁场计算常采用将复合纳米晶薄层均匀化的一般计算模型，因此本文分别搭建二维无线充电复合磁屏蔽系统的一般计算模型与薄层TBC模型，对比两种模型在磁场求解时间上的差异。
复合纳米晶薄层屏蔽由多层纳米晶基础带材层叠而成，针对每层叠层建模分析会带来巨大的工作量，占用过多计算时间，实用性不强。无线充电磁屏蔽薄层仿真模型如图2所示，本文通过将复合纳米晶薄层屏蔽区域以相同体积的具有各向异性材料参数的块状区域代替[29-30]，将均匀块状纳米晶薄层屏蔽用于二维无线充电薄层TBC计算模型。
图2 无线充电磁屏蔽薄层仿真模型
Fig.2 Magnetic shield thin layer simulation model of wireless charging
等效纳米晶薄层屏蔽各方向等效电导率可表示为
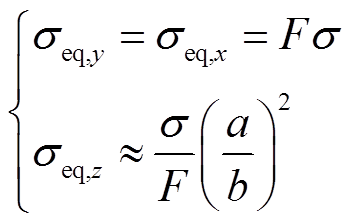（10）
式中，堆积因子F为每单位叠层厚度中的磁材料总厚度，即纳米晶带材胶合完成后表述纳米晶合金基础带材厚度占整体总厚度比例的参数；a为单层纳米晶带材厚度；b为带材整体宽度。纳米晶薄层屏蔽的等效相对磁导率可表示为
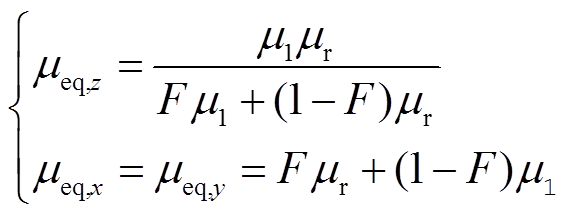（11）
式中，μ1为纳米晶薄层屏蔽单层带材间丙烯酸压敏胶（Pressure Sensitive Adhesive, PSA）的假定相对磁导率。
基础纳米晶带材相对磁导率约为30 000，电导率为106S/m，将其直接作为屏蔽应用在电动汽车无线充电系统中，会因较高的电导率产生较大涡流损耗而降低系统传输效率，因此采用一定程度碎化效果的纳米晶带材可在保证屏蔽效果的基础上减小涡流损耗。本文采用碎化后初始相对磁导率为800的纳米晶薄层作为屏蔽，当系统输入功率为11kW时，纳米晶薄层屏蔽中的磁通密度远小于纳米晶带材饱和磁通密度1.2T，因此模型中使用85kHz时纳米晶带材的初始相对磁导率，带材参数见表1。
表1 纳米晶薄层屏蔽带材基本参数
Tab.1 Nanocrystalline thin layer shielding strip basic parameters
参数数值 单层带材厚度a/μm18 整体宽度b/mm50 电阻率σ-1/(Ω·m)1.1×10-6 相对磁导率μr800 堆积因子F0.8 切向电导率σeq,x, σeq,y/(S/m)0.727×106 法向电导率σeq,z/(S/m)0.147 切向相对磁导率μeq,x, μeq,y640 法向相对磁导率μeq,zPSA假定相对磁导率μ14.9751
如图2所示，为便于观察耦合机构空间电场与磁场的分布，考虑到耦合机构的对称性，二维仿真模型选取图2的截面位置观察，即图1的xOz平面。
为确定薄层TBC计算模型的优势，将TBC计算模型与考虑趋肤深度的通过细小网格划分的一般计算模型对比求解，两种模型的网格划分如图3所示。
由于纳米晶薄层屏蔽带材法向尺寸远小于切向尺寸，为确保足够的计算精度，一般模型需考虑法向方向趋肤深度的影响，按照网格应小于计算单位一半的原则，一般模型中纳米晶薄层屏蔽网格尺寸应小于切向趋肤深度的一半，因此，仿真中一般模型在纳米晶薄层屏蔽处最大单元大小应小于等于0.1mm。
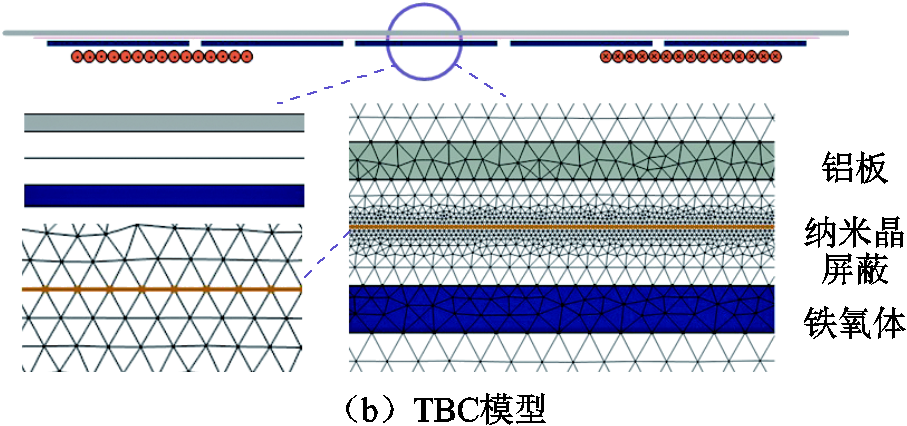
图3 二维一般模型与TBC模型网格划分
Fig.3 Meshing of 2D general model and TBC model
在TBC模型中，不需要计算电场与磁场在薄板内部的分布，且二维模型中纳米晶薄层屏蔽以带电流的线模拟，如图3b所示。因此对二维TBC模型，只需划分与一般模型中纳米晶薄层屏蔽相同元素大小的线网格。
为详细对比无线充电TBC模型与一般模型在计算时间上的差别，分别对两种模型在不同网格划分情况下计算。二维模型中采用三角形单元进行划分，由于模型因变量为1，因此自由度数为域单元的两倍，针对铁氧体、纳米晶薄层屏蔽与铝板三层屏蔽间缝隙为1mm的模型，不同网格最大单元划分精细程度下的三角形单元数量见表2。
表2 二维模型计算单元数量
Tab.2 Number of computing units of 2D model
最大网格单元/mm数量/个 一般模型TBC模型 0.0082.9×1067.5×105 0.012.4×1066.6×105 0.054.7×1053.6×105 0.14.0×1053.3×105 13.9×1053.1×105
分别对一般模型和TBC模型在不同网格划分情况下计算，两种模型仿真计算时间对比如图4所示。在一般计算模型中，网格的最大单元划分越细，模型计算自由度数越大，计算时间越长。而TBC计算模型随网格划分更精细，计算时间与自由度数增长缓慢，因此随着网格最大单元的减小，TBC模型相较于一般模型计算速度增加效果更明显。
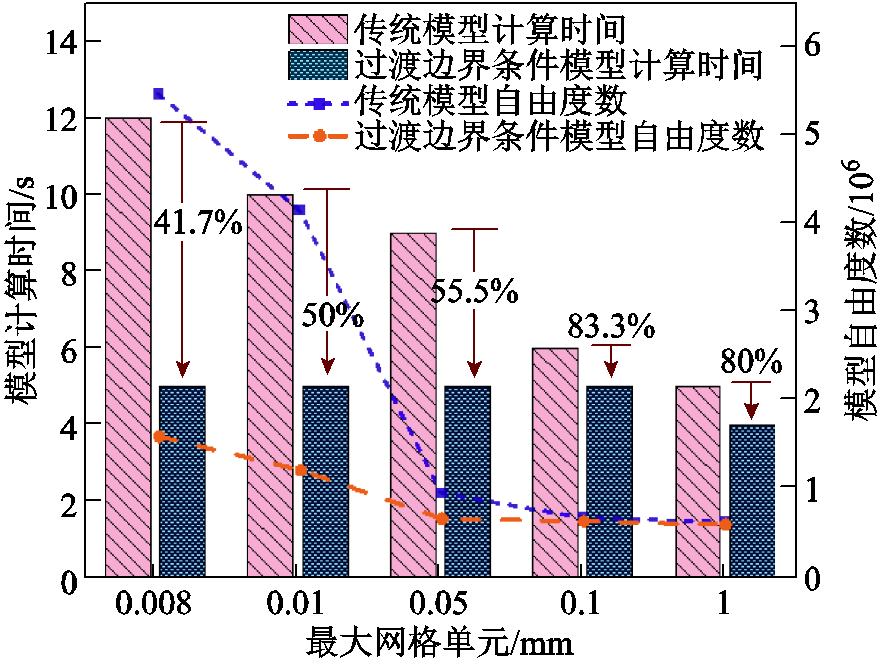
图4 一般模型与TBC模型仿真计算时间对比
Fig.4 Comparison of calculation time between general simulation and TBC simulation
在网格最大单元划分为0.008mm时，TBC模型计算时间仅为一般模型的41.7%，计算自由度数为一般模型的22.06%。验证了TBC计算模型在求解时间上具有显著的优势。
图5为二维模型下的磁场分布，一般模型仿真如图5a、图5c与图5e所示，TBC模型仿真如图5b、图5d与图5f所示。TBC模型与一般模型下整体磁通密度分布类似，如图5a与图5b所示，磁通密度主要集中在两耦合线圈之间，屏蔽层外磁通密度很小，屏蔽层边缘有一定程度漏磁现象，如图5c与图5d。
TBC模型中，磁通密度沿纳米晶薄层屏蔽法向方向分布，即磁力线垂直于纳米晶薄层屏蔽，并且以纳米晶薄层屏蔽为界限，屏蔽内铁氧体的部分漏磁经纳米晶薄层屏蔽后大幅减小。而一般模型中，由于纳米晶薄层屏蔽优良的软磁特性，磁力线也几乎垂直于纳米晶屏蔽薄层，如图5e与图5f所示，因此纳米晶薄层屏蔽附近磁场为准静态场，与TBC模型理论相符合。
图5 二维模型磁场分布
Fig.5 The magnetic flux density distribution of two-dimensional model
如图5e所示，由于纳米晶薄层屏蔽的高饱和磁通密度，一般模型中纳米晶薄层屏蔽中磁通密度模分布密集。在边缘漏磁部分，一般模型与TBC模型相似，磁力线绕过电屏蔽层铝片，而在纳米晶薄层屏蔽周围磁力线与纳米晶薄层屏蔽垂直。
搭建200W三维电磁测量实验平台如图6所示，实验平台由直流电源、耦合机构、直流负载组成，并在耦合机构两端连接逆变电路与整流电路，逆变与整流电路由信号控制系统调节。耦合机构采用串联谐振，一次线圈与二次线圈中分别通以平均值为6.65A与6.19A的交流电流。
图6 三维电磁测量实验平台
Fig.6 3D electromagnetic measurement platform
为实现对无线充电耦合机构周围磁通密度与电场强度的自动测量，搭建了三维磁场测量装置。测量装置由三维磁场测量仪、控制台、机械臂与上位机构成，可以按照控制端设置起始点与步长自动测量x、y、z轴各360mm×360mm×360mm内空间的电场强度与磁通密度，并保存数据绘制成三维电磁场分布图。
与仿真对应，制作了与仿真模型参数一致的带有屏蔽结构的耦合机构。线圈与屏蔽结构的细节如图7所示，一、二次线圈尺寸一致，匝数均为15匝，线圈间距离为120mm。铁氧体磁屏蔽、纳米晶薄层屏蔽与铝片电屏蔽结构由内向外依次放置在线圈外侧。
图7 线圈与屏蔽结构的细节
Fig.7 Details of coil and shield structure
为减小缝隙对测量结果的影响，使耦合结构中铁氧体、纳米晶薄层屏蔽与铝片屏蔽层之间缝隙相同，在缝隙为0mm与1mm的情况下分别测量空间电场强度与磁通密度，并在仿真模型中搭建屏蔽层间缝隙为0mm与1mm的耦合机构与之对应。
为充分分析屏蔽外磁场与屏蔽边缘漏磁，分别测量屏蔽的法向面与切向面的磁通密度，即xOy面与xOz面，如图8所示。缝隙为0时的测量结果如图9a和图9b所示；缝隙为1mm的测量结果如图10a和图10b所示。由图可知，屏蔽中心处磁通密度较小，越靠近屏蔽边缘漏磁越大，并且磁通密度分布具有对称性。
考虑到耦合系统屏蔽外xOz面磁通密度分布沿y轴的对称性，仿真中选取距离屏蔽10mm、30mm与100mm的切线位置，即图8中沿①②③三条曲线位置；选取距离屏蔽中心0mm、100mm与150mm的法线位置，即图8中沿④⑤⑥三条曲线位置，对比一般计算模型与薄层TBC计算模型的准确性。
图8 观察与测量位置
Fig.8 Observation and measurement position
实验测量结果与仿真求解数据对比如图9c、图9d、图10c与图10d所示。在网格划分足够精细的情况下，薄层TBC计算模型和一般模型在沿图8中六条曲线的计算结果与实验测量结果相吻合。沿①②③曲线的磁通密度先增加后减小，在屏蔽边缘处磁通密度最大，并且离屏蔽越远曲线斜率越小。沿⑤⑥曲线磁通密度随z增加而减小，而由于闭合磁力线的影响，沿曲线④磁通密度先增加后减小。误差主要来自实验平台的测量台架与其他器件对磁通密度分布的影响。
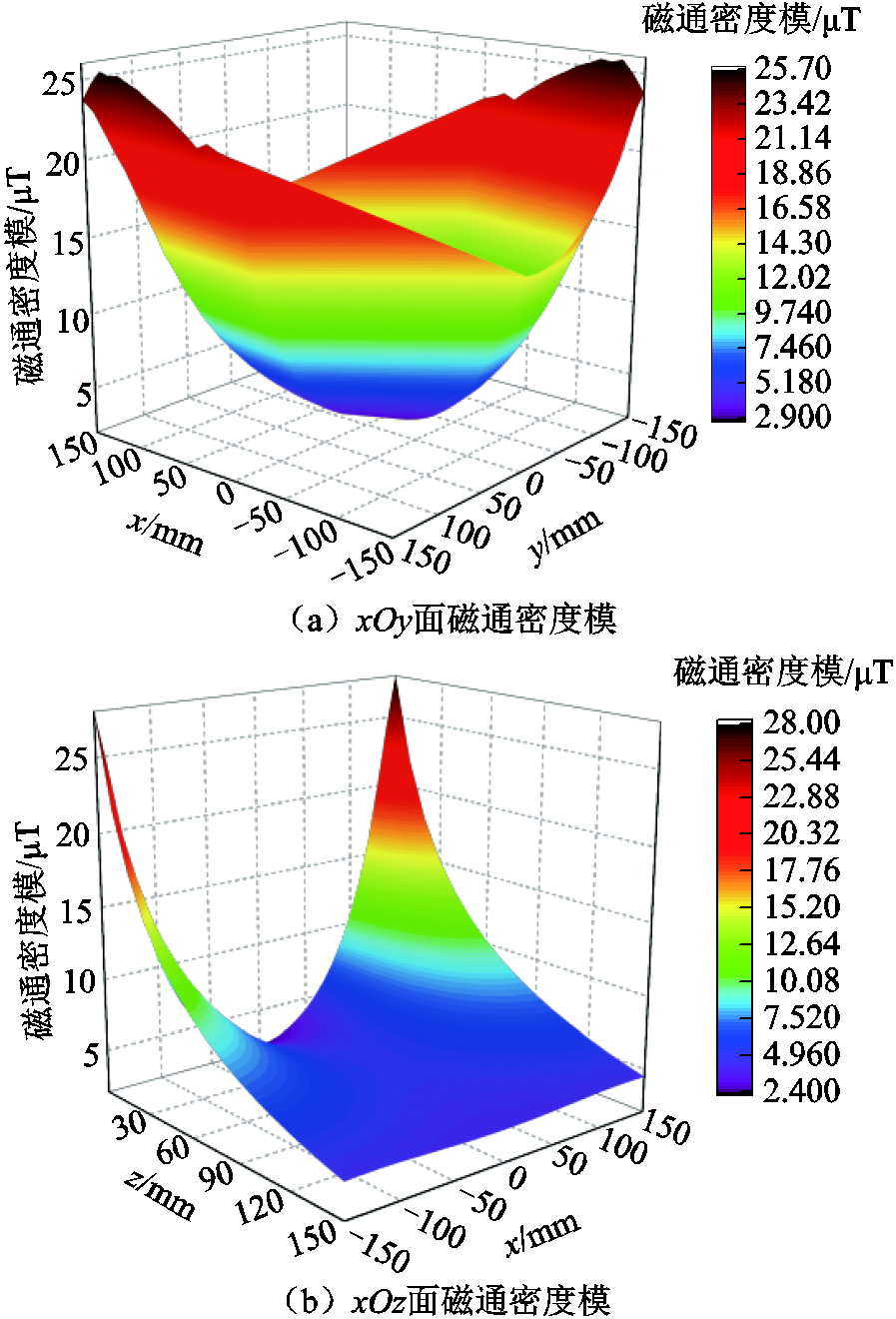
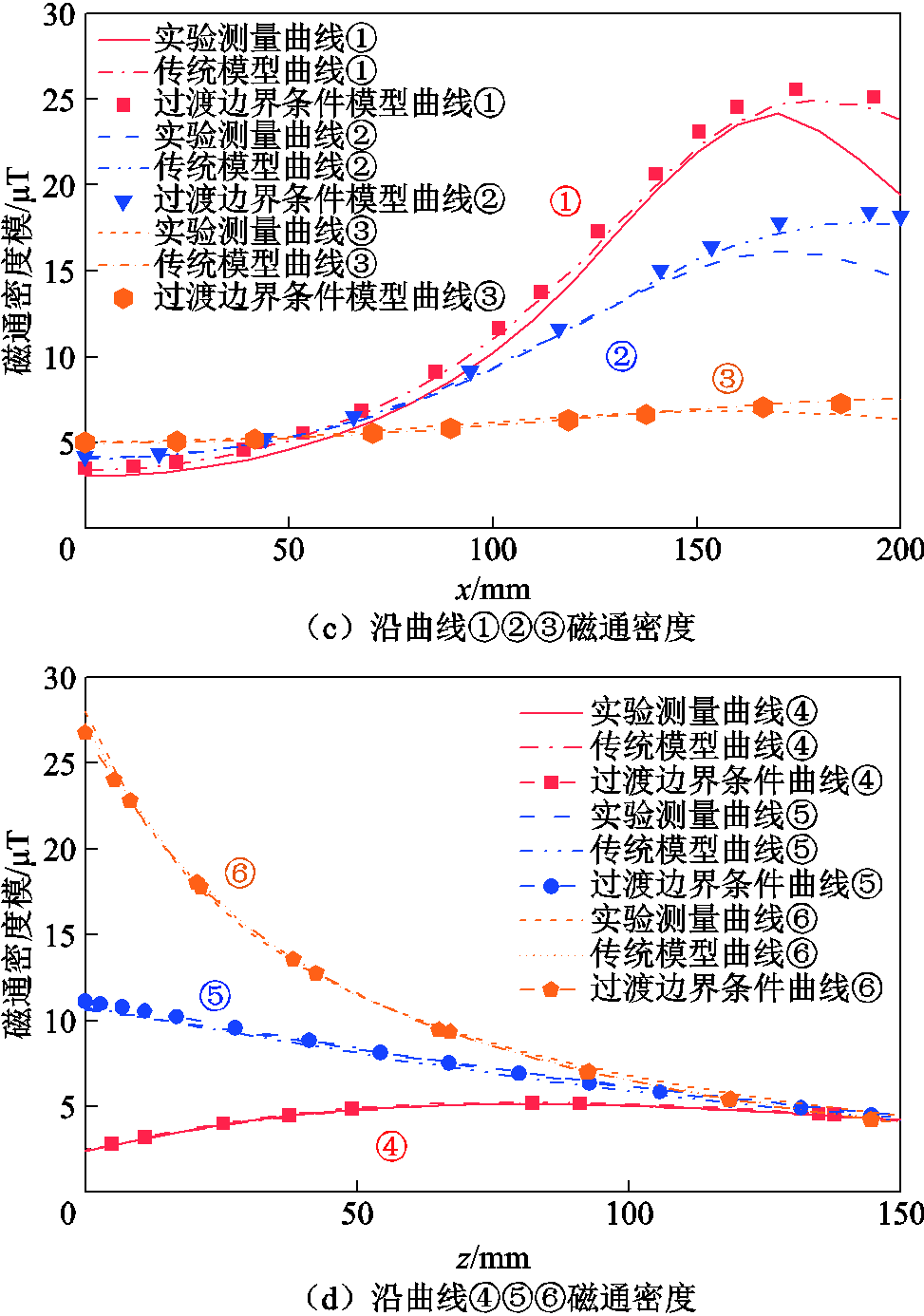
图9 缝隙为0mm时实验与仿真对比
Fig.9 Comparison between experiment and simulation when the gap is 0mm
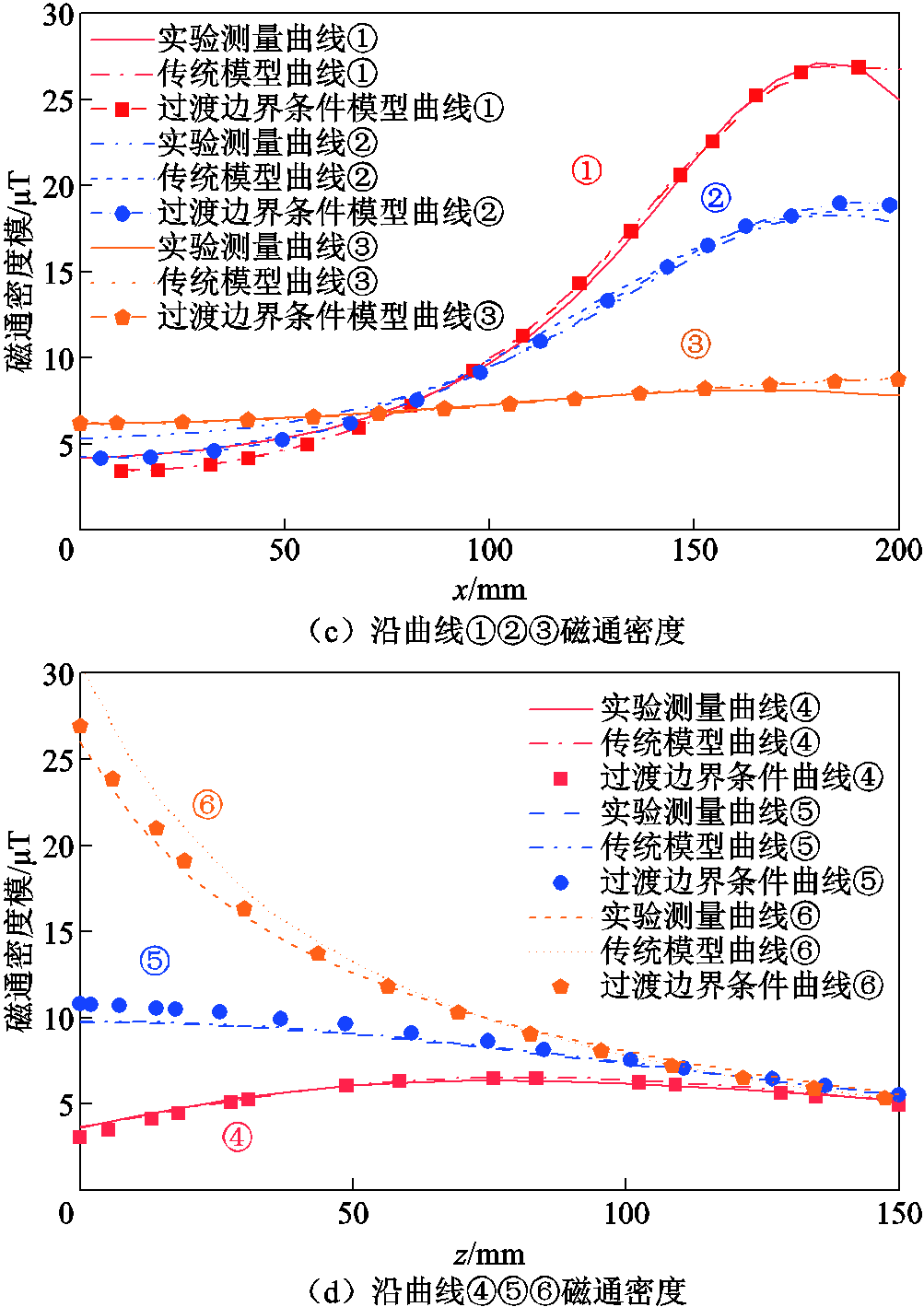
图10 缝隙为1mm时实验与仿真对比
Fig10 Comparison between experiment and simulation when the gap is 1mm
基于传输线理论，考虑趋肤深度对纳米晶薄层屏蔽磁场分布影响，提出无线充电纳米晶薄层屏蔽的TBC计算方法，得出薄层TBC模型的磁通密度求解结果与一次电流平均值为6.65A、功率为200W的实验测量结果相吻合。并且在不同网格划分情况下分别对一般模型与TBC模型求解，得出随网格划分越精细，薄层TBC模型的自由度数与计算时间增长缓慢，在最大网格划分为0.008mm时，薄层TBC模型计算时间仅为一般模型的41.7%，验证了薄层TBC模型在精确计算磁场分布的情况下能够极大地提升计算速度。本文提出的计算模型可为无线充电系统中其他新型薄层屏蔽结构的磁场计算提供新思路。
参考文献
[1] 杨庆新, 章鹏程, 祝丽花, 等. 无线电能传输技术的关键基础与技术瓶颈问题[J]. 电工技术学报, 2015, 30(5): 1-8.
Yang Qingxin, Zhang Pengcheng, Zhu Lihua, et al. Key fundamental problems and technical bottlenecks of the wireless power transmission technology[J]. Transactions of China Electrotechnical Society, 2015, 30(5): 1-8.
[2] 张献, 章鹏程, 杨庆新, 等. 基于有限元方法的电动汽车无线充电耦合机构的磁屏蔽设计与分析[J]. 电工技术学报, 2016, 31(1): 71-79.
Zhang Xian, Zhang Pengcheng, Yang Qingxin, et al. Magnetic shielding design and analysis for wireless charging coupler of electric vehicles based on finite element method[J]. Transactions of China Electrotechnical Society, 2016, 31(1): 71-79.
[3] 薛明, 杨庆新, 章鹏程, 等. 无线电能传输技术应用研究现状与关键问题[J]. 电工技术学报, 2021, 36(8): 1547-1568.
Xue Ming, Yang Qingxin, Zhang Pengcheng, et al. Application status and key issues of wireless power transmission technology[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1547-1568.
[4] 张献, 任年振, 杨庆新, 等. 电动汽车无线充电自整定控制[J]. 电工技术学报, 2020, 35(23): 4825-4834.
Zhang Xian, Ren Nianzhen, Yang Qingxin, et al. Research on self-tuning control strategy of wireless charging for electric vehicles[J]. Transactions of China Electrotechnical Society, 2020, 35(23): 4825-4834.
[5] 苏玉刚, 阳剑, 戴欣, 等. 基于TensorFlow神经网络的MCR-WPT系统负载与互感识别方法[J]. 电力系统自动化, 2021, 45(18): 162-169.
Su Yugang, Yang Jian, Dai Xin, et al. TensorFlow neural network based load and mutual inductance identification method for magnetic coupling resonant wireless power transfer system[J]. Automation of Electric Power Systems, 2021, 45(18): 162-169.
[6] 薄强, 王丽芳, 张玉旺, 等. 应用于无线充电系统的SiC MOSFET关断特性分析[J]. 电力系统自动化, 2021, 45(15): 150-157.
Bo Qiang, Wang Lifang, Zhang Yuwang, et al. Analysis of turn-off characteristics of SiC MOSFET applied to wireless charging system[J]. Automation of Electric Power Systems, 2021, 45(15): 150-157.
[7] 张献, 王朝晖, 魏斌, 等. 电动汽车无线充电系统中电屏蔽对空间磁场的影响分析[J]. 电工技术学报, 2019, 34(8): 1580-1588.
Zhang Xian, Wang Zhaohui, Wei Bin, et al. Analysis of the influence of electric shield on space magnetic field in electric vehicle wireless charging system[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1580-1588.
[8] 张献, 苑朝阳, 杨庆新, 等. 自激推挽式磁耦合无线电能传输系统磁屏蔽特性分析[J]. 中国电机工程学报, 2018, 38(2): 555-561, 686.
Zhang Xian, Yuan Zhaoyang, Yang Qingxin, et al. Analysis of the magnetic shielding characteristics of magnetic coupling resonant wireless power transmission system based on self-excited push-pull converter[J]. Proceedings of the CSEE, 2018, 38(2): 555-561, 686.
[9] 靳志芳. 磁耦合谐振式无线电能传输系统线圈的电磁分析与优化设计[D]. 北京: 北京交通大学, 2017.
[10] Cruciani S, Campi T, Maradei F, et al. Active shielding design and optimization of a wireless power transfer (WPT) system for automotive[J]. Energies, 2020, 13(21): 5575(1-12).
[11] 沈栋, 杜贵平, 丘东元, 等. 无线电能传输系统电磁兼容研究现况及发展趋势[J]. 电工技术学报, 2020, 35(13): 2855-2869.
Shen Dong, Du Guiping, Qiu Dongyuan, et al. Research status and development trend of electromagnetic compatibility of wireless power transmission system[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2855-2869.
[12] 贾金亮, 闫晓强. 磁耦合谐振式无线电能传输特性研究动态[J]. 电工技术学报, 2020, 35(20): 4217-4231.
Jia Jinliang, Yan Xiaoqiang. Research tends of magnetic coupling resonant wireless power transfer characteristics[J]. Transactions of China Electrotechnical Society, 2020, 35(20): 4217-4231.
[13] 杨庆新, 李永建. 先进电工磁性材料特性与应用发展研究综述[J]. 电工技术学报, 2016, 31(20): 1-29.
Yang Qingxin, Li Yongjian. Characteristics and developments of advanced magnetic materials in electrical engineering: a review[J]. Transactions of China Electrotechnical Society, 2016, 31(20): 1-29.
[14] 周丽波, 梁迪飞, 李维佳, 等. 无线充电用磁屏蔽材料[J]. 磁性材料及器件, 2019, 50(6): 57-63.
Zhou Libo, Liang Difei, Li Weijia, et al. Magnetic shielding material for wireless charging[J]. Journal of Magnetic Materials and Devices, 2019, 50(6): 57-63.
[15] 崔一帆, 杨庆新, 李永建. 复杂电流波形下软磁复合材料磁特性的测试[J]. 电工电能新技术, 2021, 40(7): 48-54.
Cui Yifan, Yang Qingxin, Li Yongjian. Test of magnetic properties of soft magnetic composite materials under complex current waveforms[J]. Advanced Technology of Electrical Engineering and Energy, 2021, 40(7): 48-54.
[16] 张长庚, 杨庆新, 李永建. 电工软磁材料旋转磁滞损耗测量及建模[J]. 电工技术学报, 2017, 32(11): 208-216.
Zhang Changgeng, Yang Qingxin, Li Yongjian. Measurement and modeling of rotational hysteresis loss of electric soft magnetic material[J]. Transactions of China Electrotechnical Society, 2017, 32(11): 208-216.
[17] Sun Wei, Li Qiang, Sun Le, et al. Study on magnetic shielding for performance improvement of axial-field dual-rotor segmented switched reluctance machine[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(1): 50-61.
[18] 姚可夫, 施凌翔, 陈双琴, 等. 铁基软磁非晶/纳米晶合金研究进展及应用前景[J]. 物理学报, 2018, 67(1): 8-15.
Yao Kefu, Shi Lingxiang, Chen Shuangqin, et al. Research progress and application prospect of Fe-based soft magnetic amorphous/nanocrystalline alloys[J]. Acta Physica Sinica, 2018, 67(1): 8-15.
[19] 季乐乐. 基于磁耦合谐振的电动汽车无线充电技术的研究[D]. 芜湖: 安徽工程大学, 2019.
[20] Xiong Meng, Wei Xuezhe, Huang Yonghua, et al. Research on novel flexible high-saturation nanocrystalline cores for wireless charging systems of electric vehicles[J]. IEEE Transactions on Industrial Electronics, 2021, 68(9): 8310-8320.
[21] 迟青光, 张艳丽, 陈吉超, 等. 非晶合金铁心损耗与磁致伸缩特性测量与模拟[J]. 电工技术学报, 2021, 36(18): 3876-3883.
Chi Qingguang, Zhang Yanli, Chen Jichao, et al. Measurement and modeling of lossand magnetostrictive properties for the amorphous alloy core[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3876-3883.
[22] Sarto M S. A new model for the FDTD analysis of the shielding performances of thin composite structures[J]. IEEE Transactions on Electromagnetic Compatibility, 1999, 41(4): 298-306.
[23] Sarto M S. Electromagnetic shielding of thermoformed lightweight plastic screens[J]. IEEE Transactions on Electromagnetic Compatibility, 2004, 46(4): 588-596.
[24] Wang Yiren, Calderon-Lopez G, Forsyth A J. High-frequency gap losses in nanocrystalline cores[J]. IEEE Transactions on Power Electronics, 2017, 32(6): 4683-4690.
[25] Halsáz Z, Csizmadia E, Palánki Z, et al. Homogeneity of magnetic properties within a single soft magnetic core, especially in huge cores[J]. IEEE Transactions on Magnetics, 2014, 50(4): 2004203(1-3).
[26] Dular P, Gyselinck J, Geuzaine C, et al. A 3-D magnetic vector potential formulation taking eddy currents in lamination stacks into account[J]. IEEE Transactions on Magnetics, 2003, 39(3): 1424-1427.
[27] Gaona D E, Jiang Chaoqiang, Long Teng. Highly efficient 11.1-kW wireless power transfer utilizing nanocrystalline ribbon cores[J]. IEEE Transactions on Power Electronics, 2021, 36(9): 9955-9969.
[28] Gaona D E, Ghosh S, Long Teng. Feasibility study of nanocrystalline-ribbon cores for polarized inductive power transfer pads[J]. IEEE Transactions on Power Electronics, 2020, 35(7): 6799-6809.
[29] Frljić S, Trkulja B. Two-step method for the calculation of eddy current losses in an open-core transformer[J]. IEEE Transactions on Magnetics, 2021, 57(3): 6300608(1-8).
[30] Gao Yanhui, Muramatsu K, Hatim M J, et al. The effect of laminated structure on coupled magnetic field and mechanical analyses of iron core and its homogenization technique[J]. IEEE Transactions on Magnetics, 2011, 47(5): 1358-1361.
A Calculation Method of Magnetic Field of Wireless Charging Nanocrystalline Thin Layer Shielding Based on Transition Boundary Condition
Abstract The nanocrystalline thin layer magnetic shielding structure in the wireless charging system of electric vehicle greatly reduces the volume and weight of the coupling mechanism, which increases the difficulty of the simulation calculation of the composite shielding. In order to reduce the calculation time of the magnetic field around the shield, combined with the TBC (Transition Boundary Condition) calculation method, the magnetic field distribution with high magnetic conductivity in the nanocrystalline thin layer is analyzed, and the wireless charging thin-layer TBC calculation model is designed for the nanocrystalline magnetic shielding composite system in wireless charging of electric vehicles. The general computing model and the TBC calculation model of the wireless charging system are constructed separately, and the calculation time of TBC model can be reduced to 41.7% of the general model, which speeds up the calculation speed of wireless charging composite shielding model.
Keywords：Nanocrystalline thin layer, transitional boundary conditions, magnetic shielding, anisotropy, computational model
DOI:10.19595/j.cnki.1000-6753.tces.211182
中图分类号：TM724
优秀青年科学基金（52122701）和国家自然科学基金（51977147，51807138）资助项目。
收稿日期 2021-07-30
改稿日期 2021-12-16
朱子旭 女，1998年生，硕士研究生，研究方向为无线电能传输技术。E-mail：zzxyibai@163.com
张 献 男，1983年生，教授，博士生导师，研究方向为无线电能传输技术。E-mail：zhangxian@hebut.edu.cn（通信作者）
（编辑 李冰）