
图1 实验配置方案
Fig.1 Experimental setup
摘要 电池的健康状态是电池健康管理的核心,准确的锂离子电池健康状态估计对保证电池安全、可靠、长寿命运行具有重要意义。为此,该文提出了一种基于增量容量曲线和灰色关联度分析(GRA)以及长短期记忆(LSTM)神经网络的锂离子电池健康状态估计方法。该方法通过分析电池在老化过程中的充电增量容量曲线变化模式,提取电池老化特征。为了降低计算复杂度,引入灰色关联度分析法进行特征分析与筛选,并将其作为长短时间记忆神经网络的输入,进行网络预训练进而估计电池的健康状态。最后,利用三种不同工况的电池加速老化测试数据集对所提出的健康状态估计方法进行了验证。实验结果表明,所提出的方法表现出优秀的电池健康状态估计性能,并在不同工况以及不同训练循环周期数条件下表现出良好的鲁棒性。
关键词:锂离子电池 健康状态估计 增量容量曲线 灰色关联度分析 长短期记忆神经网络
能源危机和环境污染是威胁人类健康生活和可持续发展的两大难题,大规模推广和发展新能源电动汽车是解决上述问题的有效途径之一。近年来在“碳达峰”与“碳中和”的战略目标背景下,新能源汽车技术得到了迅猛发展。在各类储能电池中,锂离子电池以其能量密度高、自放电率低、无记忆效应等优点脱颖而出,成为电动汽车首选的储能部件[1]。为满足负载的电压和功率需求,动力电池组通常由成百上千节单体电池串并成组使用。由于生产工艺、成组方式、散热条件的差异,电芯工作时的电压、电流、温度等参数存在不一致现象,进而容易引起部分单体过充、过放等问题,加速寿命衰减,影响电池组可用容量、循环寿命,甚至威胁系统安全[2]。因此,研究动力锂离子电池系统全生命周期寿命衰减机理和健康状态(State of Health, SOH)估计理论方法是推广和发展新能源电动汽车的重要基石[3]。
锂离子电池SOH的定义主要可以从电池容量衰减及内阻增加两个角度出发[4],分别映射电池放电容量的衰减及运行功率的降低。本文主要从容量衰减的角度来研究电池的SOH,并分析电池的老化模式。目前主流的SOH估计方法可以大致分为三类:基于经验/半经验公式方法、基于模型的观测器方法及基于数据驱动的方法[5]。
基于经验/半经验公式的方法通常基于电池运行的历史数据来构建电池的经验老化公式,并进一步通过数理统计的方法,如粒子滤波与高斯过程回归等[6],来分析并估计电池的老化行为。He Wei等[7]通过历史数据分析建立了基于锂离子电池退化行为的指数模型,进一步使用贝叶斯蒙特卡罗算法进行模型参数的实时更新,以预测电池的剩余放电寿命。实验结果表明,该模型可以准确地模拟电池容量衰减过程中的非线性特性,但是该方法难以描述电池搁置期间容量恢复的行为。考虑锂离子电池的非线性与非高斯容量衰减特性,Zhang Lijun等[8]提出了一种电池容量指数衰减模型,将该指数模型与粒子滤波相结合,实现了准确的锂离子电池剩余寿命估计。基于电池的老化数据及阻抗谱测试数据,A. Guha等[9]将电池的容量衰减模型与内阻增长模型相结合,提出一种基于多项式和指数函数的混合老化模型,而后利用粒子滤波算法进行电池的剩余寿命估计,并进一步探讨了模型参数变化对预测结果的影响,实验结果表明该方法的估计准确性对电池数据的依赖性较强。这一类电池SOH估计方法的精度依赖于所构建的经验/半经验老化公式的精度,并且老化经验公式的建立对电池老化数据的要求较高。
基于模型的观测器方法是通过电池的数学模型来模拟电池容量衰减的特性,进一步将模型与先进的滤波算法相结合来实现准确的SOH估计[10]。常用的电池数学模型包含等效电路模型与电化学模型,其中等效电路模型使用基础电子元器件来模拟电池的外部输出特性,而电化学模型则是通过一系列复杂的偏微分方程来描述电池内部的动力学特性[11]。等效电路模型通常使用电池内阻增长来刻画电池的SOH,如程泽等[12]将二阶等效电路模型与自适应平方根无迹卡曼滤波算法相结合,实现了电池SOH与荷电状态(State of Charge, SOC)的联合估计,但该模型无法直接刻画电池的容量衰减或内部特性的变化。电化学模型能够直接反映电池内部的老化机理,如固体电解质膜(Solid Electrolyte Interface, SEI)的增加、锂的电镀及活性材料的损失等,从电化学角度来刻画电池的老化状态[13-14]。M. T. Lawder等[15]将多孔电极伪二维模型和SEI形成副反应相结合来模拟电池内部的SEI膜生长过程,在此基础上应用伪二维模型的数学重构方法来降低模型复杂度以减少计算成本。结果证实,该方法对各种化学成分和电池类型具有较高的鲁棒性。单粒子模型是在全阶伪二维模型的基础上的简化[16],通过忽略电解质中的动力学方程并假设电解质相中锂离子浓度和电位保持不变,大大降低了计算成本。J. Li等[17]提出了一种锂离子损耗模型与单粒子模型相结合的电池老化模型,实现了随循环次数和温度变化的快速容量预测,同时还提供了SEI膜生成和扩展的量化信息,以及由此产生的电池容量衰减和功率损耗,可直接应用于电池的SOH估计。上述基于模型的方法拥有较高的精度且能够刻画电池的内外部特性,但其等效电路模型难以描述电池的容量特性,而电化学模型受限于复杂的偏微分方程和高度耦合的模型参数,使其求解变得较为困难,因此基于模型的方法难以得到实际应用。
上述方法的固有缺点是对模型精度的依赖性强,而基于数据驱动的方法是将电池实际运行的历史和实时数据与机器学习、神经网络等智能算法相结合来估计电池的SOH。与前述两类方法相比,数据驱动的方法往往具有更强的非线性逼近能力,并且对不同电池与工况具有较强的适用性[18],但其预测的精度依赖于提取的老化特征。传统的特征提取方法通常直接使用电池运行过程中电流、电压等数据作为老化特征,这类数据具有较高的测量噪声,且通常无法直接准确地表征电池的老化状态。近年来,电池的增量容量(Incremental Capacity, IC)曲线分析方法受到了广泛关注[19]。IC曲线被描述为连续电压阶跃上的增量容量,是通过将恒流充电阶段的容量增量与电压变化进行比较而获得的。研究结果表明,锂离子电池的IC曲线包含了电池老化的诸多特征,并且还可以进一步反映电池的老化机理[20]。D. Anseán等[21]将IC曲线与物理模型仿真相结合,量化分析了锂离子电池不同的老化因素,如不可逆的锂电镀及活性材料损失等,进一步拓展了IC曲线在分析电池老化机理中的应用,但受限于不同老化因素间的高度耦合与非线性关系,并未给出准确的SOH评估。M. Maures等[22]根据IC曲线峰值跟踪方法,将基于IC曲线的电池老化估计方法扩展到了电池高充电倍率条件,减少了SOH的估计时间。Li Xiaoyu等[23]将IC曲线与高斯过程回归模型相结合,使用均值和协方差函数分别预测电池的SOH及其不确定性,实现了准确鲁棒的电池SOH估计。
本文提出了一种基于数据驱动的电池SOH估计方法。该方法将电池的IC曲线与长短期记忆(Long Short-Term Memory, LSTM)神经网络相结合,通过分析电池老化过程中IC曲线变化趋势,提取老化特征进行LSTM网络的训练与估计。为了提升网络的估计精度并降低训练复杂度,引入了灰色关联度分析法(Gray Correlation Analysis, GRA)进行特征筛选。最后将该方法在三种不同循环老化工况的电池上进行了验证。实验结果表明,锂离子电池的老化有较强的工况敏感性,不同的充放电倍率对电池的老化速率有较大的影响,而所提SOH估计方法在不同的老化工况下均取得了较好的估计结果,并且针对不同比例的训练循环数表现出较好的鲁棒性。
为了分析电池老化过程中IC曲线的变化模式,并进一步验证所提GRA-LSTM电池SOH估计方法的性能,本文进行了三种不同工况的循环老化测试。实验所用电芯为力神的LR1865SZ,该款电芯的标称容量为2.5A·h,额定开路电压及充电电压分别为3.6V和4.2V,最大充放电电流倍率分别为1C和3C,工作环境温度为0~45℃。
实验配置方案如图1所示,实验装置包含用于控制充放电电流的电池测试系统(NEWARE CT—4001—5V12A)、用于控制实验环境温度的恒温箱(SUYIDA GDW—100L)及用于记录实验数据的上位机。为了分析不同的因素对电池老化的影响以及验证所提方法在不同工况下的适用性,基于上述电芯和实验装置进行了三种不同工况的循环老化测试,并构建了对应的循环老化数据集见表1。由表1可知,三款相同电芯所对应的老化工况分别为1C充电+1C放电、1C充电+2C放电及0.5C充电+2C放电,环境温度均为25℃。为了分析电池在不同老化阶段的动态特性及模拟电池容量回升现象,在电池老化循环中对电池间隔进行了标准测试,其中标准测试包含搁置、定容测试及动态测试。标准测试的间隔均为25个循环。数据集2由于实验设定误差,循环间隔产生了一定的偏差,但通过后文分析可知,容量再生现象是在循环充放电过程中引入搁置所引起。

图1 实验配置方案
Fig.1 Experimental setup
表1 循环老化实验配置
Tab.1 Battery cyele aging experiment settings

数据集充电电流放电电流工作温度/℃ 11C1C25 21C2C25 30.5C2C25
电池的增量容量描述为电池恒流充电阶段连续电压阶跃上的容量增量。如式(1)~式(3)所示,通过将充电电流转换为容量对电压的导数,可得连续的Q-V方程,即
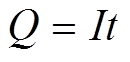 (1)
(1)
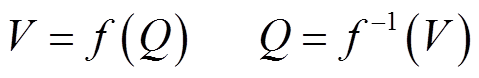 (2)
(2)
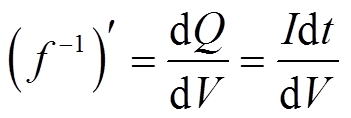 (3)
(3)
式中,Q为充电容量;I为充电电流;t为充电时间;V为电池端电压。通过式(3)可知,增量容量表达式dQ/dV可以转换为电压电流关系式,而电池的充电电压和电流信号可通过采样得到,进而可以使用差分方程描述,将连续的Q-V关系式离散化得
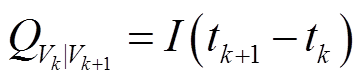 (4)
(4)
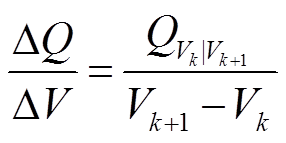 (5)
(5)
式中,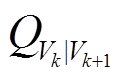 为端电压从
为端电压从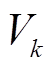 增加至
增加至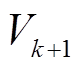 时的容量变化;k为时间步。
时的容量变化;k为时间步。
电池SOH的容量定义为电池的当前最大可用容量与初始标称容量的比值,即
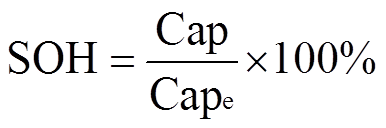 (6)
(6)
式中,Cap为电池的当前最大可用容量;Cape为电池的初始标称容量。在实际运行过程中,电池的最大可用容量通常难以直接测量。现有的研究表明,电池的IC曲线能够很好地表征电池的SOH。为了进一步分析电池老化过程中IC曲线的变化模式,基于数据集1的电芯循环老化数据,求得不同老化循环下的IC曲线,如图2所示。由图2可知,随着电池循环次数的增加,IC曲线的峰值高度及其对应的电压值发生了明显的变化。另外,从图2中可以看到,每隔25个循环的标准测试所导致的容量再生,在IC曲线上表现为曲线高度的短暂回升。由此可以看出电池的IC曲线能够很好地表征电池的SOH。
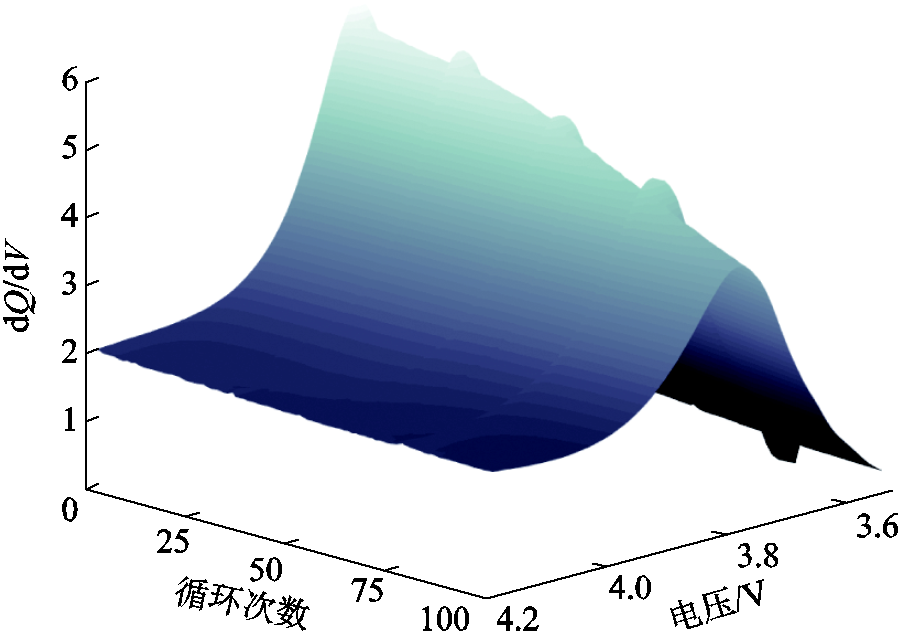
图2 IC曲线的老化分析
Fig.2 Aging analysis of IC curves
上述分析可知,IC曲线高度能够直观表征电池的SOH。因此,本文提取电池充电过程中五个电压特征点FP1~FP5所对应的IC曲线值作为电池的老化特征。五个电压特征点分别选取3.6V、3.7V、3.8V、3.9V以及4.0V。
为了降低计算复杂度,本文引入灰色关联度分析法来量化所提特征与电池SOH的关联度。
灰色关联度分析是一种基于灰色系统理论的多因素统计方法,通过分析各因素变化趋势的相似程度来判断因素之间的关联程度,进而计算关注的指标与因素之间的相关性。具体的灰色关联度分析方法为:在每个时间步k下,利用相关性公式计算不同的特征因素xi(k)与老化状态y(k)之间的关联系数,进一步求取整个时间尺度下关联系数的平均值,即可得到不同老化特征与电池SOH的关联度ri。其流程为:
(1)根据给定老化数据集,确定电池健康状态序列Y={y(k)|k=1,2, ,n},以及特征序列Xi={xi(k)|i= 1,2,
,n},以及特征序列Xi={xi(k)|i= 1,2, ,5},其中y(k)=SOH(k),xi(k)=FPi(k)。
,5},其中y(k)=SOH(k),xi(k)=FPi(k)。
(2)当k = 1, 2,…, n时,重复执行步骤(3)与步骤(4)。
(3)计算关联系数,即
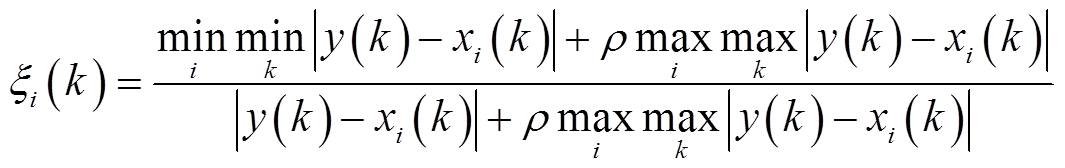 (7)
(7)
式中,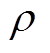 为分辨系数,
为分辨系数,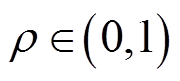 ,本文取0.6。
,本文取0.6。
(4)计算不同特征的相关性r,其定义为关联系数的均值,即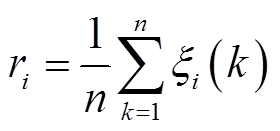 。
。
针对三种不同工况所对应的电芯,分别提取并计算五个不同特征点与电池SOH的灰色关联度,见表2,不同老化特征点与电池SOH之间的关联度各有不同,并且三种数据集对应的关联度结果也存在较大差异。最后,以灰色关联度为指标,提取关联度最大的三个老化特征作为后续神经网络的输入。
表2 灰色关联度
Tab.2 Gray correlation analysis

数据集FP1FP2FP3FP4FP5 10.590.670.920.840.84 20.520.510.770.750.76 30.560.930.800.820.82
S. Hochreiter等[24]对传统的循环神经网络进行了改进,引入了三种逻辑门结构以及记忆单元来保留历史信息,从而解决长序列训练过程中的梯度消失与梯度爆炸等问题。LSTM神经网络的单元结构如图3所示。其中,xk和hk分别表示k时间步电池老化特征序列输入及SOH估计输出。Ck为记忆单元,其存储了当前时刻神经网络的状态信息并传递给下一时刻,其计算依赖于上一时刻的网络状态信息以及当前的输入,从而保证了历史信息在长序列训练下的保留与传递。
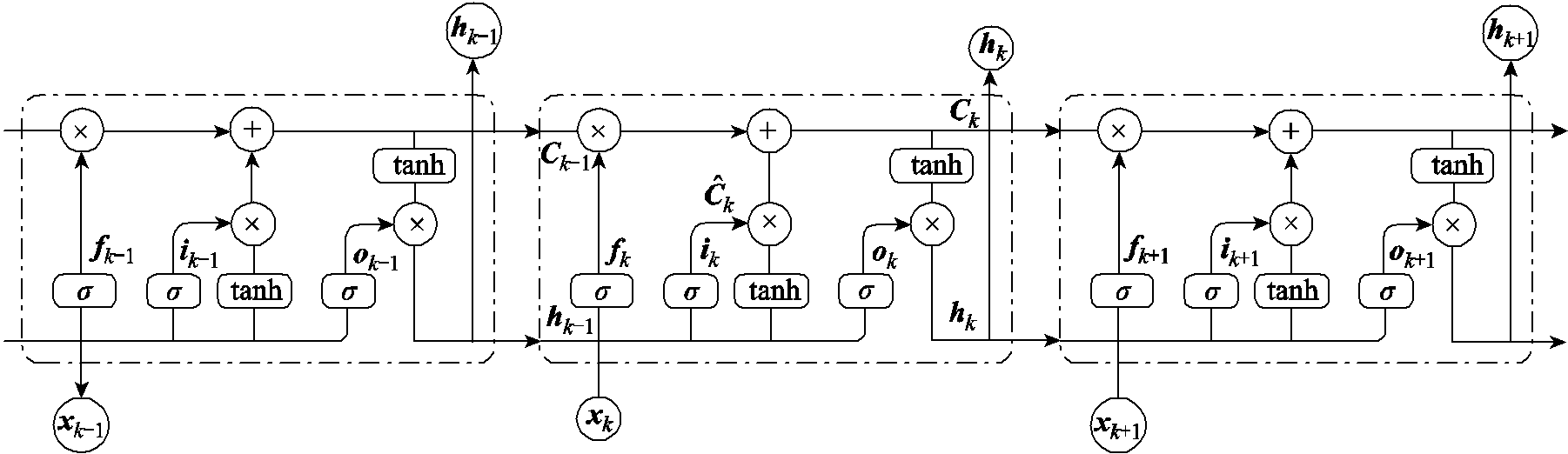
图3 LSTM神经网络框架
Fig.3 LSTM neural network framework
状态信息Ck及当前的输出hk的计算依赖于三种逻辑门,即遗忘门fk、输入门ik及输出门ok。其具体的计算公式为
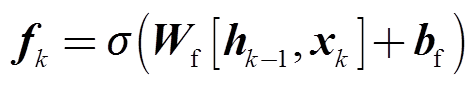 (8)
(8)
式中,Wf和bf分别为遗忘门的输入权重和偏置项;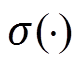 为Sigmoid函数。
为Sigmoid函数。
遗忘门用于控制上一时刻的状态信息输入保留至当前状态的比例。若fk趋近于0,则表示当前的网络状态不依赖于之前的信息;若fk趋近于1,则表示完全保留之前的状态信息。输入门ik与输出门ok的作用与遗忘门类似,分别用于控制状态更新比例以及状态输出比例。
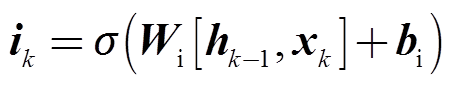 (9)
(9)
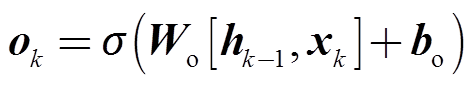 (10)
(10)
式中,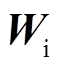 和
和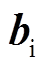 分别为输入门的输入权重和偏置项;
分别为输入门的输入权重和偏置项;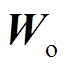 和
和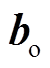 分别为输出门的输入权重和偏置项。
分别为输出门的输入权重和偏置项。
分别计算出三种逻辑门之后,进一步计算新的候选向量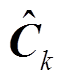 对前序状态进行更新,从而获取当前的网络状态Ck。
对前序状态进行更新,从而获取当前的网络状态Ck。
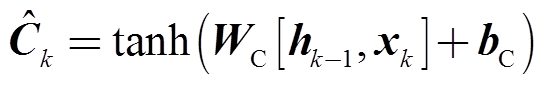 (11)
(11)
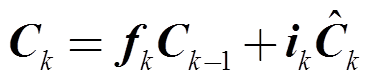 (12)
(12)
式中,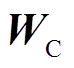 和
和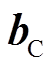 分别为
分别为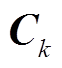 的输入权重和偏置项。
的输入权重和偏置项。
获取当前的网络状态量后,最终通过输出门计算得到当前网络的输出值,即
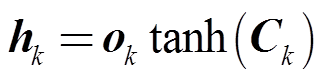 (13)
(13)
基于上述锂离子电池IC曲线的分析及LSTM神经网络的介绍,进一步构建如图4所示的GRA-LSTM框架用于实现SOH估计。整个框架大致由三个部分组成:
(1)实验数据获取。通过图1所示的实验装置进行循环老化实验,测量并记录电池运行的电流、电压及充放电容量数据。
(2)IC曲线特征提取分析。基于式(1)~式(5)及电池运行历史数据,计算不同循环下的IC曲线。为了获取平滑的曲线,引入滑动平均滤波方法对IC曲线进行处理。进一步如2.2节所述,基于所获取的IC曲线提取五个不同特征点构成不同循环下的老化特征数据集。而后,将老化特征数据集划分为测试数据集与训练数据集,并基于训练数据集和灰色关联度分析法对两种数据集进行特征分析与筛选。
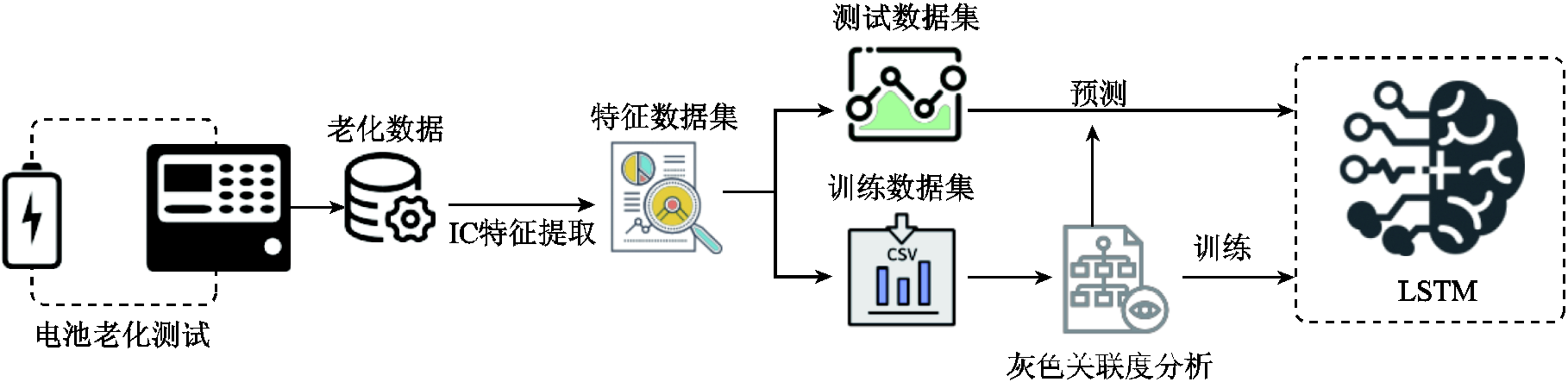
图4 GRA-LSTM电池健康状态估计框架
Fig.4 GRA-LSTM framework for battery SOH estimation
(3)LSTM网络训练与预测。根据提取的特征点数构建网络结构,基于(2)中的训练数据集对网络进行预训练。最后,基于测试数据的老化特征实现电池SOH的估计。
基于力神LR1865SZ电芯的多工况循环老化测试数据集,本节进一步分析并讨论所提GRA-LSTM电池SOH估计方法的实验结果。三种不同老化工况SOH的估计结果如图5所示。三种老化工况均以前50%的循环用于网络训练,后50%的循环用于SOH估计。从图5可以看到,所提方法的估计结果能够很好地跟踪电池真实SOH的变化。虽然随着电池循环数的增加,SOH的估计偏差会略有增加,但估计误差仍能控制在2%以内。每次搁置后,电池的容量会产生较为明显的再生,图2显示出IC曲线对电池容量再生的直观反映,而实验结果进一步验证了所提方法对电池搁置所导致的容量再生的跟随性能。虽然在每次容量再生点仍存在一定的SOH估计误差,但最大的估计误差仍被控制在5%左右。
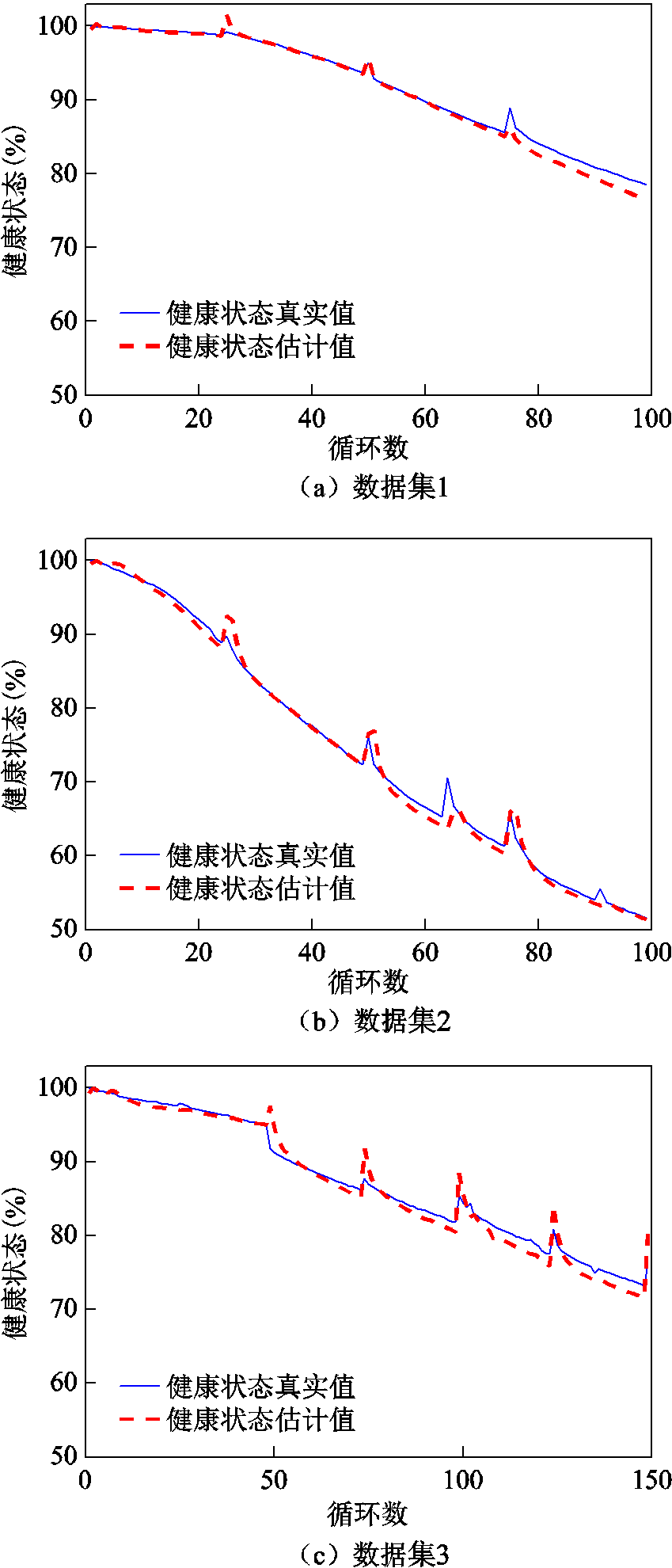
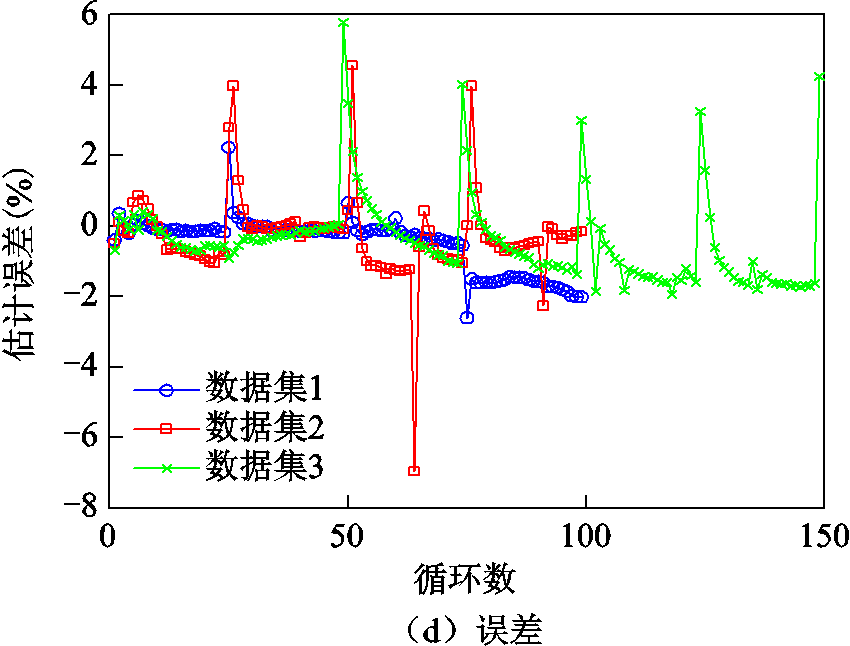
图5 针对三种不同数据集的SOH估计结果
Fig.5 Results of SOH estimation for three different datasets
为了更好地评价所提GRA-LSTM框架的SOH估计精度,引入方均根误差(Root Mean Square Error, RMSE)及绝对平均误差(Mean Absoulte Error, MAE)来度量误差大小,即
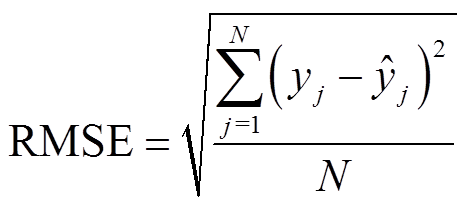 (14)
(14)
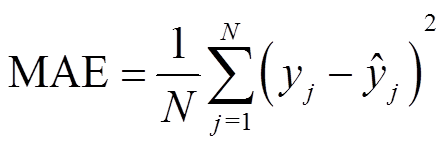 (15)
(15)
式中,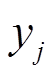 为第j个循环下的真实SOH;
为第j个循环下的真实SOH;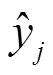 为第j个循环下的SOH估计结果;N为SOH评估的循环总次数。估计误差具体结果见表3,表中括号内的数字代表数据集中用于网络训练循环数的比例。由表3可知,三种不同工况下电池SOH估计的误差均控制在约1%,能够很好地满足实际应用的需求。
为第j个循环下的SOH估计结果;N为SOH评估的循环总次数。估计误差具体结果见表3,表中括号内的数字代表数据集中用于网络训练循环数的比例。由表3可知,三种不同工况下电池SOH估计的误差均控制在约1%,能够很好地满足实际应用的需求。
表3 GRA-LSTM健康状态估计误差
Tab.3 Errors of SOH estimation results

数据集MAE(%)RMSE(%) 1 (1/2)0.630.97 2 (1/2)0.691.20 3 (1/2)0.951.23 2 (1/3)1.882.44 2 (1/4)2.873.87
为了分析所提SOH估计方法在不同训练循环数下的鲁棒性,基于数据集2分别采用前1/2、1/3及1/4的老化循环数据对LSTM网络进行预训练,而后面的循环数据用于SOH估计。实验结果如图6所示,训练循环部分的结果表现出较好的一致性,而随着循环次数的增加,SOH估计结果开始出现较为明显的偏差。训练循环数量越少,所提方法的SOH估计结果的误差逐渐增大。误差的增加具体表现在电池老化的后半段,即伴随着循环数的增加而增加。通过表3中具体的误差数据可知,尽管减少训练循环数会降低SOH的估计精度,但即使仅用前1/4的循环数据进行网络训练,最终的平均估计误差仍能控制在4%以内。因此,所提方法对不同的训练循环数条件具有较好的鲁棒性。
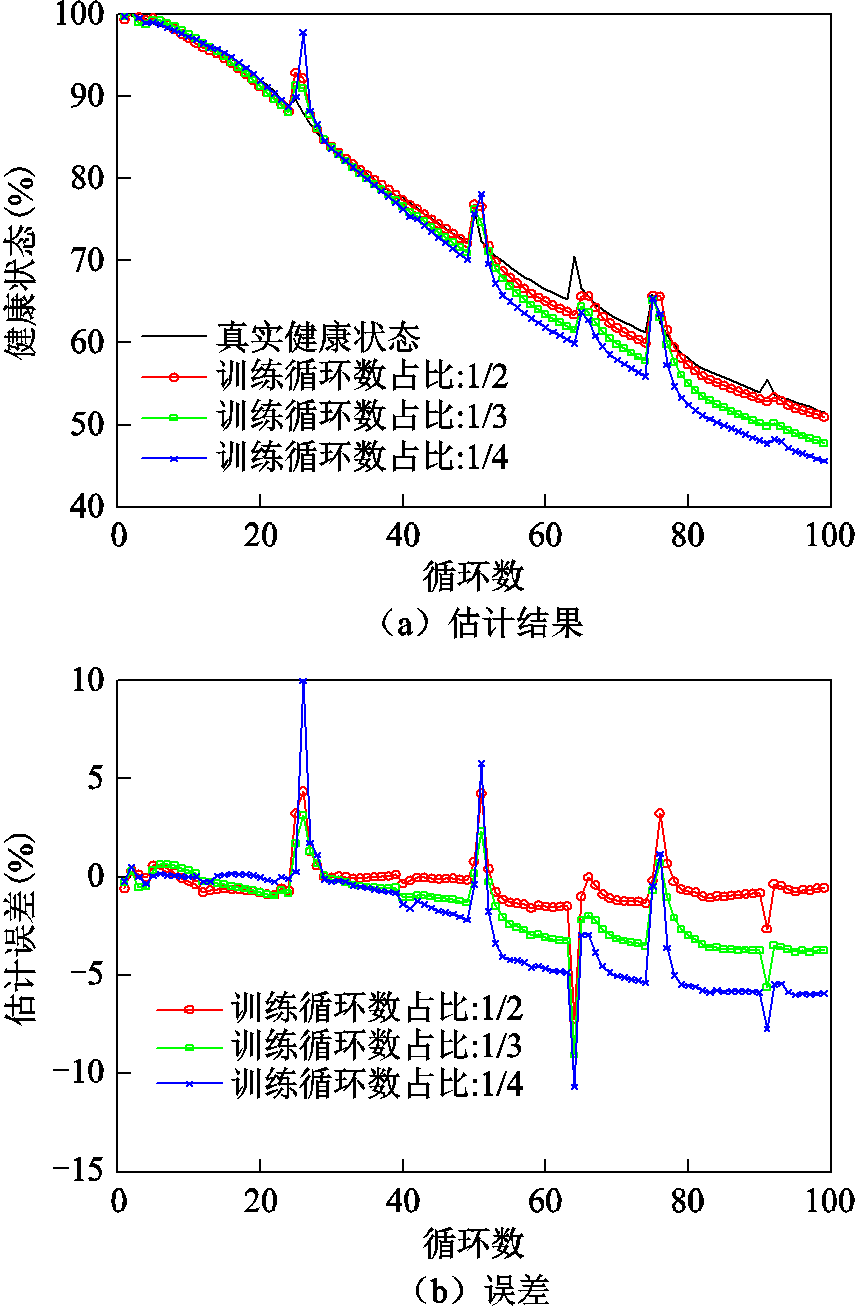
图6 不同训练循环数的实验结果
Fig.6 Results of SOH estimation with different number of training cycles
电池老化涉及较为复杂的内部电化学反应过程,其老化速率往往呈现较强的工况敏感性。进一步分析图5可以发现,相同的充电倍率下,电池的放电倍率越大,电池的老化速率越快(对比数据集1和数据集2);相同的放电倍率下,电池的充电倍率越大,电池的老化速率越快(对比数据集2和数据集3)。经过交叉对比,还可以进一步发现充电倍率对电池老化速率的影响大于放电倍率对电池老化速率的影响(对比数据集1和数据集3)。虽然不同的工况对电池的老化有较大的影响,所提SOH估计方法对不同工况仍表现出较好的估计性能,进而验证了所提方法在不同老化工况条件下的鲁棒性。
通过上述对实验结果的分析讨论可知,所提SOH估计方法具有较高的精度,并且对不同工况与训练数据量条件具有较好的鲁棒性。
准确的锂离子电池SOH估计对保障电池安全可靠运行起到关键作用。本文基于电池的充电IC曲线分析,提出了一种基于GRA-LSTM的SOH估计方法。该方法将电池IC曲线与LSTM神经网络相结合,利用电池的充电IC曲线来分析并提取电池的老化特征,进一步训练LSTM神经网络以进行SOH估计。为了提升神经网络的训练效率,进一步引入GRA方法对老化特征进行分析筛选。应用所提GRA-LSTM方法对三种不同循环老化工况的电池运行数据进行了验证分析。实验结果表明,该方法在多种不同老化工况下都取得了较好SOH估计结果,平均估计误差约为1%。并且,该方法在不同比例训练数据下也表现出了较好的鲁棒性,最大的平均误差也不超过4%。
参考文献
[1] 韩乔妮, 姜帆, 程泽. 变温度下IHF-IGPR框架的锂离子电池健康状态预测方法[J]. 电工技术学报, 2021, 36(17): 3705-3720.
Han Qiaoni, Jiang Fan, Cheng Ze. State of health estimation for lithium-ion batteries based on the framework of IHF-IGPR under variable temperature[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3705-3720.
[2] 武龙星, 庞辉, 晋佳敏, 等. 基于电化学模型的锂离子电池荷电状态估计方法综述[J]. 电工技术学报, 2022, 37(7): 1703-1725.
Wu Longxing, Pang Hui, Jin Jiamin, et al. A review of SOC estimation methods for lithium-ion batteries based on electrochemical model[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1703-1725.
[3] Wang Yujie, Tian Jiaqiang, Sun Zhendong, et al. A comprehensive review of battery modeling and state estimation approaches for advanced battery management systems[J]. Renewable and Sustainable Energy Reviews, 2020, 131: 110015.
[4] Yang Ruixin, Xiong Rui, He Hongwen, et al. A fractional-order model-based battery external short circuit fault diagnosis approach for all-climate electric vehicles application[J]. Journal of Cleaner Production, 2018, 187: 950-959.
[5] Pan Wenjie, Chen Qi, Zhu Maotao, et al. A data-driven fuzzy information granulation approach for battery state of health forecasting [J]. Journal of Power Sources, 2020, 475: 228716.
[6] Yang Duo, Zhang Xu, Pan Rui, et al. A novel Gaussian process regression model for state-of-health estimation of lithium-ion battery using charging curve[J]. Journal of Power Sources, 2018, 384: 387-395.
[7] He Wei, Williard N, Osterman M, et al. Prognostics of lithium-ion batteries based on Dempster-Shafer theory and the Bayesian Monte Carlo method[J]. Journal of Power Sources, 2011, 196(23): 10314-10321.
[8] Zhang Lijun, Mu Zhongqiang, Sun Changyan. Remaining useful life prediction for lithium-ion batteries based on exponential model and particle filter[J]. IEEE Access, 2018, 6: 17729-17740.
[9] Guha A, Patra A. State of health estimation of lithium-ion batteries using capacity fade and internal resistance growth models[J]. IEEE Transactions on Transportation Electrification, 2018, 4(1): 135-146.
[10] 郭永芳, 黄凯, 李志刚. 基于短时搁置端电压压降的快速锂离子电池健康状态预测[J]. 电工技术学报, 2019, 34(19): 3968-3978.
Guo Yongfang, Huang Kai, Li Zhigang. Fast state of health prediction of lithium-ion battery based on terminal voltage drop during rest for short time[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 3968-3978.
[11] Doyle M, Fuller T F, Newman J. Modeling of galvanostatic charge and discharge of the lithium/polymer/insertion cell[J]. Journal of the Electrochemical Society, 1993, 140(6): 1526-1533.
[12] 程泽, 杨磊, 孙幸勉. 基于自适应平方根无迹卡尔曼滤波算法的锂离子电池SOC和SOH估计[J]. 中国电机工程学报, 2018, 38(8): 2384-2393, 2548.
Cheng Ze, Yang Lei, Sun Xingmian. State of charge and state of health estimation of Li-ion batteries based on adaptive square-root unscented Kalman filters[J]. Proceedings of the CSEE, 2018, 38(8): 2384-2393, 2548.
[13] Markevich E, Salitra G, Aurbach D. Fluoroethylene carbonate as an important component for the formation of an effective solid electrolyte interphase on anodes and cathodes for advanced Li-ion batteries[J]. ACS Energy Letters, 2017, 2(6): 1337-1345.
[14] Jokar A, Rajabloo B, Désilets M, et al. Review of simplified Pseudo-two-Dimensional models of lithium-ion batteries[J]. Journal of Power Sources, 2016, 327: 44-55.
[15] Lawder M T, Northrop P W C, Subramanian V R. Model-based SEI layer growth and capacity fade analysis for EV and PHEV batteries and drive cycles[J]. Journal of the Electrochemical Society, 2014, 161(14): A2099-A2108.
[16] Tian Jiaqiang, Wang Yujie, Chen Zonghai. An improved single particle model for lithium-ion batteries based on main stress factor compensation[J]. Journal of Cleaner Production, 2021, 278: 123456.
[17] Li J, Adewuyi K, Lotfi N, et al. A single particle model with chemical/mechanical degradation physics for lithium ion battery State of Health (SOH) estimation[J]. Applied Energy, 2018, 212: 1178-1190.
[18] You G W, Park S, Oh D. Real-time state-of-health estimation for electric vehicle batteries: a data-driven approach[J]. Applied Energy, 2016, 176: 92-103.
[19] Baghdadi I, Briat O, Gyan P, et al. State of health assessment for lithium batteries based on voltage-time relaxation measure[J]. Electrochimica Acta, 2016, 194: 461-472.
[20] 姜久春, 马泽宇, 李雪, 等. 基于开路电压特性的动力电池健康状态诊断与估计[J]. 北京交通大学学报, 2016, 40(4): 92-98.
Jiang Jiuchun, Ma Zeyu, Li Xue, et al. State of health diagnosis and estimation of power lithium-ion batteries based on open circuit voltage characteristic[J]. Journal of Beijing Jiaotong University, 2016, 40(4): 92-98.
[21] Anseán D, Dubarry M, Devie A, et al. Operando lithium plating quantification and early detection of a commercial LiFePO4 cell cycled under dynamic driving schedule[J]. Journal of Power Sources, 2017, 356: 36-46.
[22] Maures M, Capitaine A, Delétage J Y, et al. Lithium-ion battery SoH estimation based on incremental capacity peak tracking at several current levels for online application[J]. Microelectronics Reliability, 2020, 114: 113798.
[23] Li Xiaoyu, Yuan Changgui, Li Xiaohui, et al. State of health estimation for Li-Ion battery using incremental capacity analysis and Gaussian process regression[J]. Energy, 2020, 190: 116467.
[24] Hochreiter S, Schmidhuber J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780.
State of Health Estimation for Lithium-Ion Battery Based on Gray Correlation Analysis and Long Short-Term Memory Neural Network
Abstract The state of health is the core of battery health management. An accurate estimation of the state of health is of great significance to ensure the safe, reliable, and long-life operation of lithium-ion batteries. To this end, this paper proposes a method for estimating the state of health of lithium-ion batteries based on incremental capacity curves and gray correlation analysis long short-term memory neural networks. This method extracts several different aging characteristics by analyzing the attenuation mode of battery charging incremental capacity curves during the aging process. In order to reduce the computational complexity, the gray correlation analysis method is introduced for features analysis and screening. Then, the extracted aging features are used as the input to train the long short-term memory network and estimate the battery health status. Finally, accelerated battery aging tests based on three different working conditions are conducted to verify the proposed method. The experimental results show that the proposed method exhibits excellent performance in estimating the state of health of the battery, and it shows good robustness under different working conditions and different number of training cycles.
keywords:Lithium-ion battery, state of health estimation, incremental capacity curve, gray correlation analysis (GRA), long short-term memory (LSTM) neural network
DOI:10.19595/j.cnki.1000-6753.tces.211366
中图分类号:TM911
国家自然科学基金项目(61803359)、安徽省高校协同创新项目(GXXT-2019-002)和中国科学技术大学“统筹推进世界一流大学和一流学科建设专项资金”(YD2350002002)资助。
收稿日期 2021-09-03
改稿日期 2022-04-15
周才杰 男,1997年生,硕士研究生,研究方向为锂电池建模、状态估计与充电优化控制。E-mail:cjzhou19@mail.ustc.edu.cn
汪玉洁 男,1990年生,博士,副研究员,研究方向为节能与新能源汽车技术,复杂系统建模、仿真与控制,燃料电池系统管理与优化控制,人工智能方法在能源系统中的应用等。E-mail: wangyujie@ustc.edu.cn(通信作者)
(编辑 李冰)