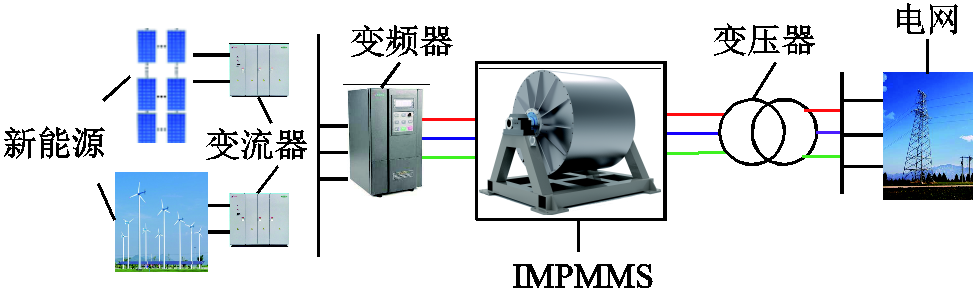
图1 永磁机组系统原理示意图
Fig.1 Schematic diagram of IMPMMS system
摘要 为解决高比例新能源微电网的短时中断问题,提出一种惯性储能永磁发电机组。该文提出的永磁机组由共外转子滚筒的永磁电动机和永磁发电机组成,具有对新能源微电网实时惯性支撑和输出电能质量高的优点。首先,从惯性储能角度出发,结合电网电能质量指标要求对永磁机组进行设计,通过有限元和场路耦合仿真验证了永磁机组设计的合理性;然后,结合永磁机组电磁-机械耦合模型,建立基于PSCAD平台的永磁机组电力系统仿真模型,仿真结果证明了在短时中断故障期间永磁机组可实现对新能源微电网的惯性支撑;最后,研制了一台55kW的缩比样机,通过实验测实验证了设计思想的正确性。
关键词:新能源微电网 惯性储能 永磁机组 惯性支撑
随着全球能源与环境问题的日益加剧,风力发电、光伏发电等新能源装机比例不断增长是未来电力系统的发展趋势。欧盟、中国和美国分别描绘出2050年高比例新能源电力系统蓝图。但新能源微电网缺乏可靠的惯性响应,且对有功功率变化和频率波动的耐受能力差,导致电网出现严重故障甚至新能源机组大规模离网,这给电力系统安全和稳定运行带来了新的挑战[1]。
为了提高新能源微电网的惯性响应能力,储能虚拟同步发电机(Virtual Synchronous Generator, VSG)技术应运而生,该技术是将同步发电机的数学模型引入新能源变流器的控制中,用于模拟同步发电机的惯性特性。文献[2]提出双馈感应发电机虚拟同步控制策略,但控制效果受到新能源出力波动性和控制系统稳定性的制约;文献[3-4]将储能VSG技术分别与永磁直驱式风机、光储相结合,提高系统所需的惯性响应;文献[5]利用在变流器直流母线所安装的储能装置快速充放电特性,实现稳定的能量输出;此外,储能VSG技术也被应用于柔性直流输电的变流器控制中,参与系统调频[6]。然而,利用VSG控制新能源发电单元参与惯性响应和一次调频,在很大程度上依赖控制参数的选取,不同回路和参数间存在强耦合,增加了响应时间,使控制系统设计更加复杂,而且过载和惯性响应能力不如真实惯量装置。
其次,新能源并网点常因电网中大功率电机起动、短路故障等产生较大的电压跌落,同时因其变流器绝缘和过电流耐受水平差,导致其故障穿越能力低。国内外学者针对不同新能源机组类型和低压穿越能力提出了相应的改进策略和方法。针对双馈风机定子直接并网电压跌落引起转子变流器过电流的问题,提出基于灭磁[7]、定子磁链动态[8]、转子动能与补偿思想[9]的控制策略,用于提升双馈风机低压穿越能力。另外一些改进的控制策略被提出以提高光伏和永磁直驱式风机的低压穿越能力[10-12]。但是随着新能源发电比例越来越高,一次故障周边残余电压从原有低于30%(pu)的区域负荷会停机到现在残余电压低于80%(pu)的区域,敏感负荷就会停机,出现了新的故障形式——短时中断。新能源机组耐受电压能力不足,如不采取相应措施会出现大范围脱网。如何实现对发生短时中断故障的新能源微电网并网点的就近补偿鲜有报道。
现有的大多数解决方法都是使变流器具备同步电机的一些优点保证电网的稳定性。然而,与真正的同步电机相比,变流器的性能并不足以满足要求。因此,文献[13]提出用于高比例新能源并网运行的电励磁发电机组,并对其输出特性[14-15]、控制策略[16-17]等进行了分析和实验验证,但内转子磁路利用不充分,材料利用率低,且同样电机外型尺寸,内转子直径比外转子小,电机自身转动惯量小,无法适应新能源场站大型惯量支撑的需要。针对这一需求,在具备文献[13]中所提出的发电机组的特性和功能的基础上,本文提出一种具有真实大惯量的可提高新能源场站抗扰动能力的惯性储能永磁发电机组,简称永磁机组(Inertia Motivity Permanent Magnet Machine Set, IMPMMS),系统原理示意图如图1所示。从图1可知,永磁机组将新能源机组和电网串联,改变了新能源通过电力电子器件直接并网的方式;永磁机组是外转子结构,当新能源并网点处发生短时中断故障时,利用其外转子机械惯量对电网进行瞬时功率补偿。

图1 永磁机组系统原理示意图
Fig.1 Schematic diagram of IMPMMS system
首先,以新能源并网点短时中断故障期间的电网特性为依据,从惯性储能角度出发设计了额定容量为1MW的永磁机组,对其进行了场路耦合分析,仿真结果验证了永磁机组输出特性满足电网电能质量要求;然后,根据永磁机组等效电路模型,列写永磁机组电气、机械方程,基于PSCAD电力系统分析平台建立永磁机组仿真模型,通过分析可知在惯性补偿期间与不串入永磁机组相比,并网点频率下降率降低1.2%、功角最大振幅下降22.5%且振荡周期缩短、电压跌落降低24.3%,证明了永磁机组在短时中断故障期间对电网具有支撑作用,可提高新能源微电网的稳定性;最后,由于机组功率、尺寸较大以及实验条件的限制,以一台缩比样机对上述所提出的机组进行实验验证,其输出特性满足设计要求,证明了设计思想的正确性。
永磁机组的惯性补偿特性表现为对电网输出电能,新能源微电网的电能质量是机组最佳设计的必要条件。目前尚未制定关于新能源微电网电能质量的具体标准,所以在设计之初,需对永磁机组输出特性即惯性补偿时间、电压质量、频率变化范围等进行约束。
目前关于新能源并网点短时中断故障还没有具体的标准说明。从电网角度,短时中断故障是一种更严重的电压暂降故障,电压暂降也可视为只是一次不完全的短时中断故障。国家电网公司在《风电并网运行反事故措施要点》中指出:风电场需具备应对电网侧出现电压暂降故障的持续运行能力,即低电压故障穿越能力。要求在并网点电压跌落2s内风电机组能不脱网连续运行,所以本文短时中断故障持续时间选为2s,即永磁机组惯性补偿时间。
值得注意的是,不同地区新能源并网点短时中断故障持续时间有差异,可根据具体情况选择惯性补偿时间。
在电力系统中电压波动表现为电压骤降和骤升,永磁机组在惯性补偿期间输出电压波动定义如图2所示。为了保证用户电器设备安全可靠运行,欧洲标准EN50160[18]定义的输出电压幅值Ud的限值为
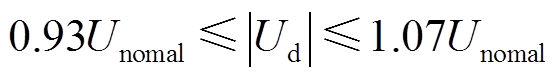 (1)
(1)
式中,Unomal为输出电压标称值。
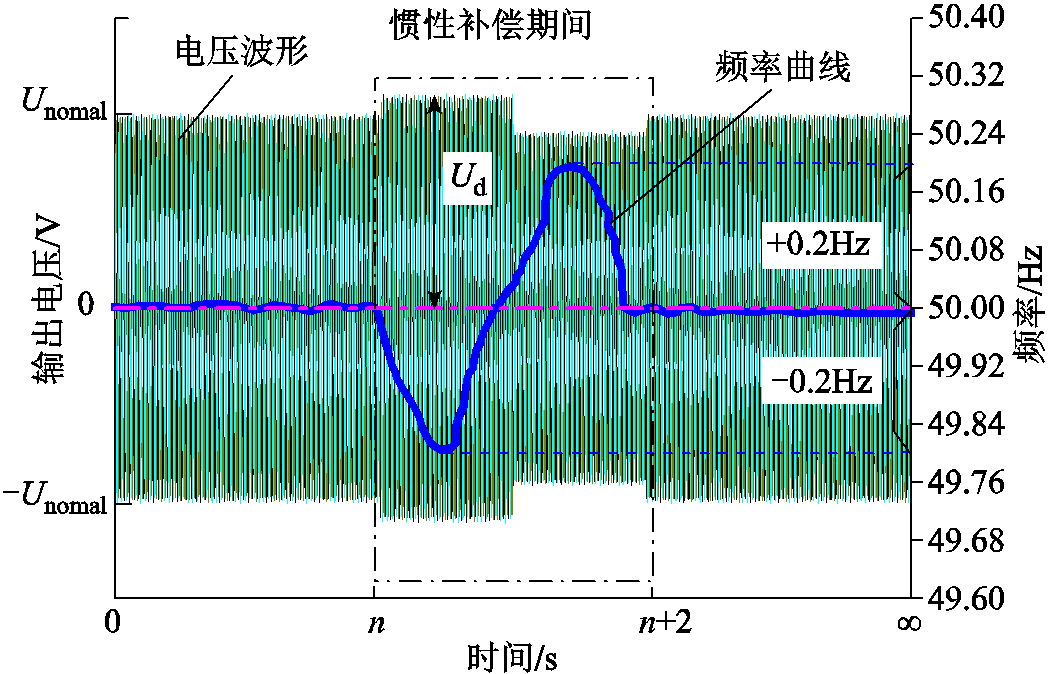
图2 永磁机组输出特性标准
Fig.2 IMPMMS output characteristic standard
由于永磁机组直接并网,输出三相电压的三相不平衡度忽略不计。
在正常运行条件下,电网的频率不会一直保持在标称值,存在一定的频率偏差。频率偏差是指系统频率的实际值与标称值之差。不同地区频率偏差的限制是不同的,例如,东北电力协调委员会(NPCC)的频率偏差为±0.5Hz,中部大陆地区电力池(MCAPP)的频率偏差为±0.3Hz,对于新能源电网频率偏差一般取±0.3Hz,本文中惯性补偿期间永磁机组受到冲击负荷作用,频率偏差规定应更加严格,故选±0.2Hz[19],如图2所示。
输出电压谐波畸变率(Total Harmonic Distortion, THD)偏高会引起电机转矩波动、高精密仪器损坏甚至烧毁,降低电压谐波畸变率可有效地解决电能质量问题。本文所考虑的电压中级标准见表1,其中IEC 61000212 2003 1 to 35kV和CENELEC EN 50160:1999 1 to 35kV是国际标准,ER G5/4:2001 6.6 to 10kV和GB/T 14549—1993是国家标准。每个标准都定义了不同阶次电压谐波限值,为了便于对比,每次谐波限值皆以其基波分量为基准值,第h次谐波电压含有率HRUh为
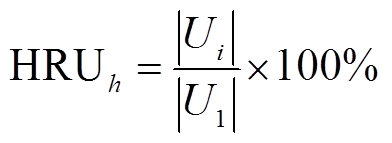 (2)
(2)
式中,Ui为第i阶电压谐波分量;U1为电压基波分量。
表1 国际和地区(国家)标准[20]
Tab.1 International and regional (national) standards [20]

电压谐波标准国际标准地区和国家标准 阶次IEC 61000 2 12 2003 1 to 35kVCENELEC EN 50160:19991 to 35kVER G5/4:2001 6.6 to 10kVGB/T14549—1993 35534 56635 75534 91.51.51.21.5 113.53.523.2 133323 150.40.50.30.5 17221.62 191.761.51.21.5 210.30.50.20.5 231.411.51.2— 251.271.50.7— 270.2—0.2— 291.06—0.63— 310.97—0.6— 330.2—0.2— 350.83—0.55— 370.77—0.53— 390.2—0.2— 410.67—0.5— 430.62—0.49— 450.2—0.2— 470.55—0.46— 490.51—0.45— THD8%50th内8%25th内4%50th内8%21th内
n阶谐波的谐波畸变率(THDn)计算公式为
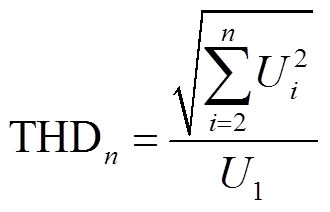 (3)
(3)
如表1所示,ER G5/4:2001 6.6 to 10kV(单元格内文字加粗)是四种标准中最严格的电压谐波电能质量标准,50次谐波以内的THD需控制在4%以内,所以选其作为本文的电压谐波电能质量标准。
永磁机组由于惯性补偿期间的瞬时工作特性,尺寸参数与其瞬时补偿功率、转动惯量有关,所以从惯性储能角度出发,确定永磁机组主要尺寸。在电网侧频率发生波动时,假设机械功率Pm不变,永磁机组运动方程为
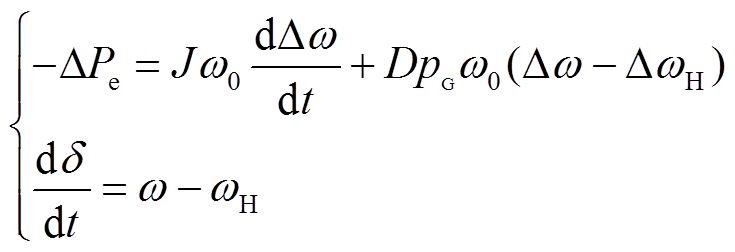 (4)
(4)
式中,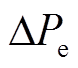 为电磁功率变化量;J为转动惯量;D为阻尼因子;ω为转子角频率;
为电磁功率变化量;J为转动惯量;D为阻尼因子;ω为转子角频率;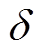 为功角;
为功角;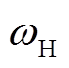 为电网侧频率;
为电网侧频率;![]() 为永磁机组额定角频率;pG为永磁机组发电机侧极对数。
为永磁机组额定角频率;pG为永磁机组发电机侧极对数。
对式(4)中第一个公式进行拉普拉斯变换得
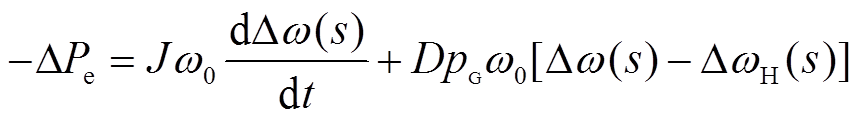 (5)
(5)
选择永磁机组端电压相量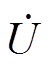 为参考相量,即令
为参考相量,即令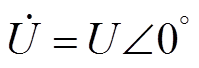 ,永磁机组输出电流为
,永磁机组输出电流为
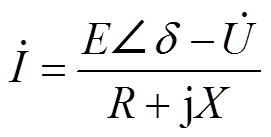 (6)
(6)
式中,E为永磁机组电动势。
结合式(6)求得永磁机组视在功率为
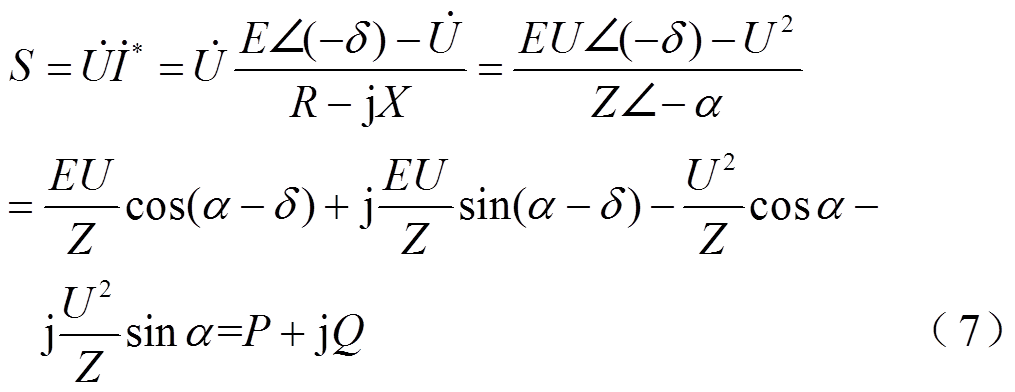
式中,P和Q分别为永磁机组的有功功率和无功功率;a为阻抗角;Z为阻抗;*表示复数运算。
永磁机组的功角和电动势表达式分别为
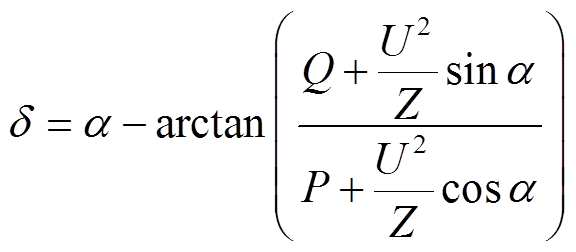 (8)
(8)
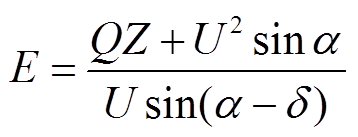 (9)
(9)
对有功功率P进行拉普拉斯变换得
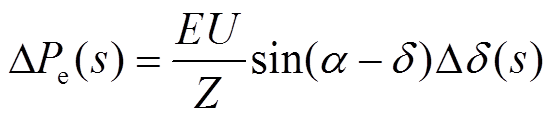 (10)
(10)
对式(4)中第二个公式进行拉普拉斯变换可得
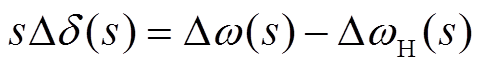 (11)
(11)
由式(4)、式(10)、式(11)可得到永磁机组输出功率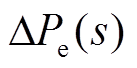 与电网侧频率
与电网侧频率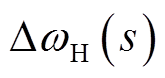 之间的关系为
之间的关系为
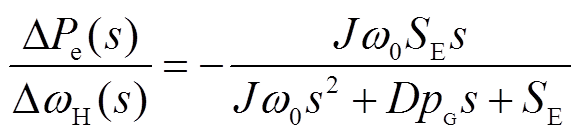 (12)
(12)
式中,SE为同步功率系数
当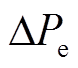 发生频率
发生频率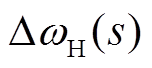 的阶跃时,根据式(12)求得此时输出功率变化量,即
的阶跃时,根据式(12)求得此时输出功率变化量,即
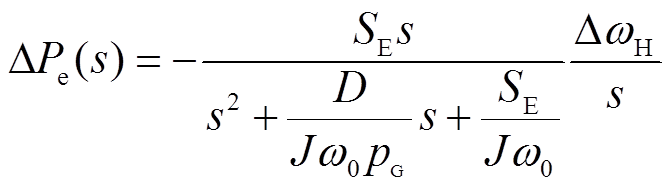 (13)
(13)
令式(13)分母为零,求得极点为
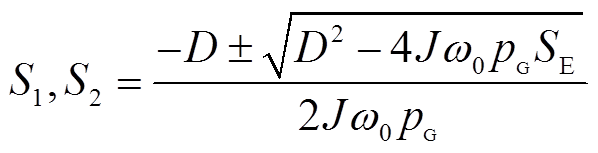
令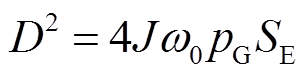 ,将
,将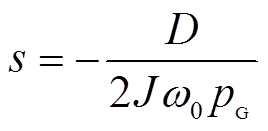 代入式(13)并进行拉普拉斯反变换得
代入式(13)并进行拉普拉斯反变换得
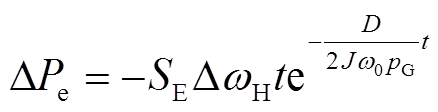 (14)
(14)
令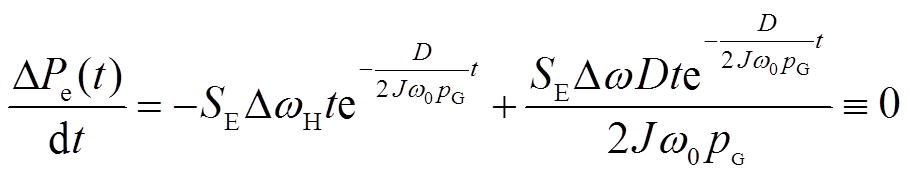 得
得
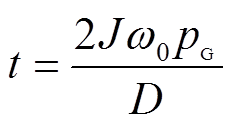 (15)
(15)
将式(15)代入式(14)求得在频率变化时,永磁机组输出功率变化量最大值与其转动惯量(即惯性补偿所需的惯量)之间的传递函数为
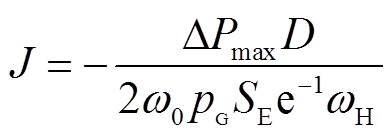 (16)
(16)
另外永磁机组转动惯量与其主要尺寸之间的关系为
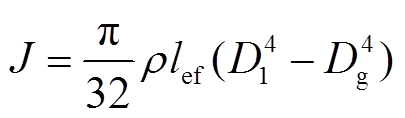 (17)
(17)
式中,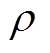 为根据永磁机组转子各部件的材料和体积估算的转子平均质量密度;lef为筒壁长度;D1为转子外径;Dg为气隙直径,一般取转子外径的0.4~0.7。
为根据永磁机组转子各部件的材料和体积估算的转子平均质量密度;lef为筒壁长度;D1为转子外径;Dg为气隙直径,一般取转子外径的0.4~0.7。
根据式(16)得到永磁机组在电网侧发生短时中断故障对其进行惯性补偿期间所需的转动惯量,通过式(17)确定永磁机组的主要尺寸,结合第1节针对机组输出特性的限定作为设计目标值和依据,设计了额定容量为1MW的永磁机组,其主要参数见表2。
表2 新型永磁机组主要参数
Tab.2 Main design parameters of novel machine set

参数数值 发电机额定功率PG/kW1 000 电动机额定功率PM/kW1 000 转动惯量J/(kg·m2)3 250 惯性补偿时间T/s2 额定电压UN/V3 300 转速n/(r/min)1 500 转子外径D1/mm1 700 筒壁长度Lef/mm1 630 筒壁厚度D/mm50 发电机极数pG4 电动机极数pM6 输出转矩Tm/(N·m)6 366 相电感/H0.002 5 相电阻/Ω0.35
永磁机组三维拓扑结构如图3所示,永磁机组由一台永磁电动机和一台永磁发电机组成。永磁电动机和永磁发电机皆采用外转子结构,两台电机转子和外转子滚筒以及两侧端盖共同构成永磁机组的旋转部件,称为一体化飞轮储能转子。永磁电动机由新能源机组驱动,新能源机组与永磁电动机一起作为原动机向永磁发电机提供机械转矩,永磁发电机将机械能变为电能后直接并入电网。在运行时,两台永磁电机转子同时、同向和同速旋转,这个转速也是电网的同步转速。
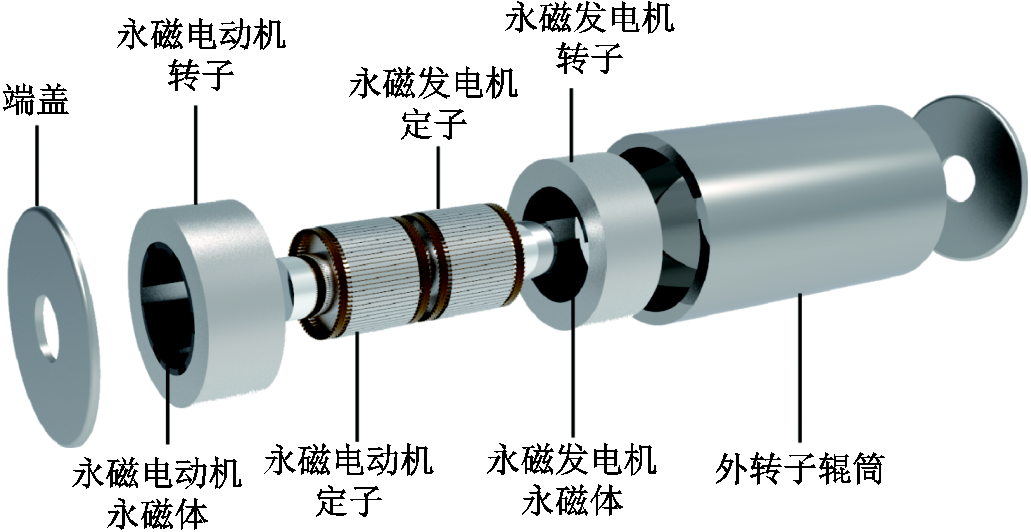
图3 永磁机组三维拓扑结构
Fig.3 Three dimensional topology of IMPMMS
当电网侧发生短时中断故障瞬间,永磁机组对电网进行惯性补偿,电网侧视为永磁机组的负载,其功率因数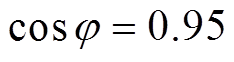 [21],等效相电阻为3.6Ω,等效相电感为0.006 3H,计算公式为
[21],等效相电阻为3.6Ω,等效相电感为0.006 3H,计算公式为
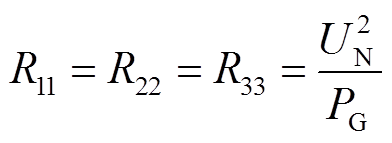 (18)
(18)
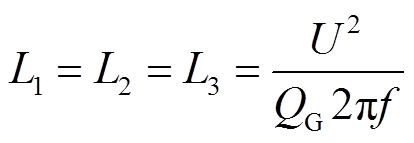 (19)
(19)
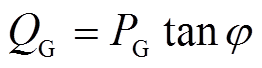 (20)
(20)
永磁机组惯性补偿外电路,如图4所示。
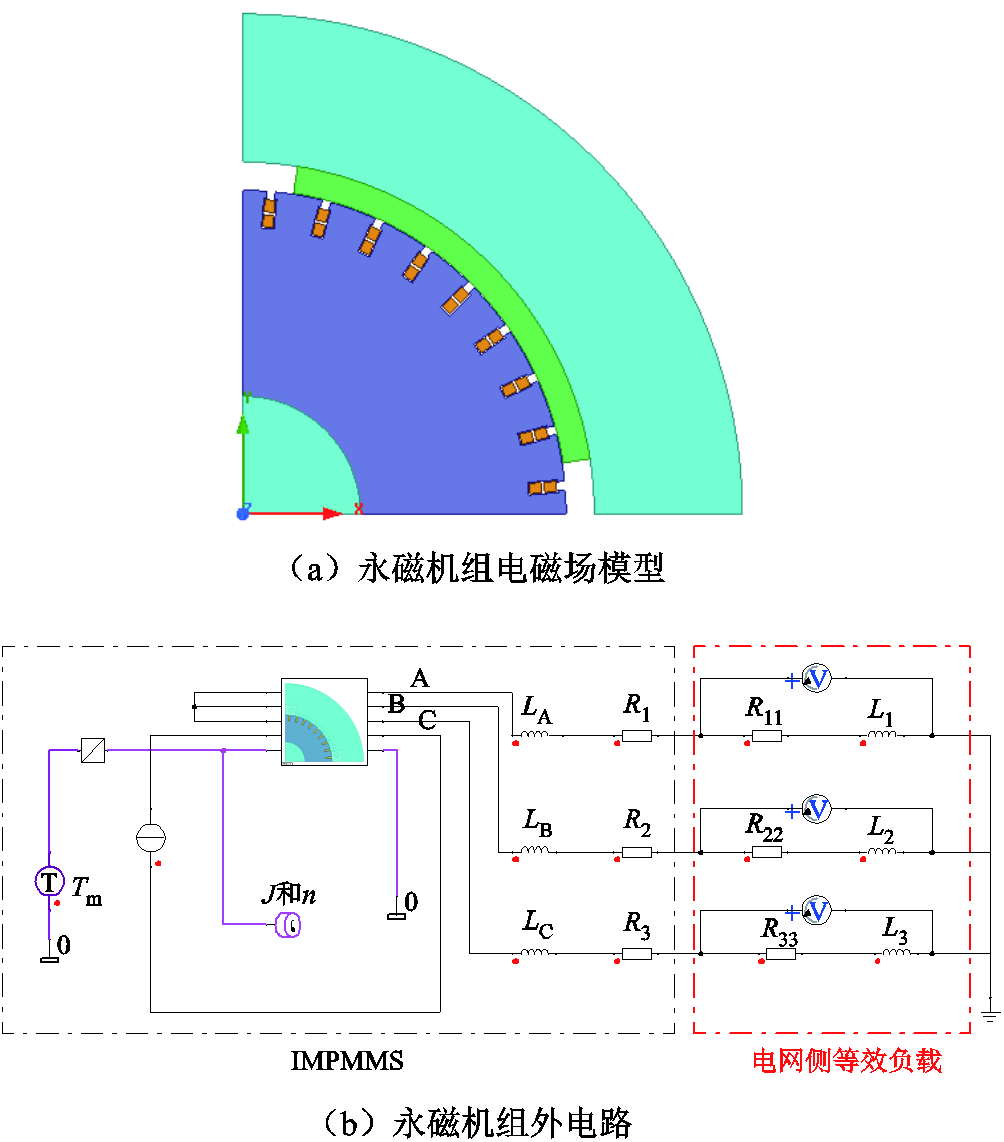
图4 永磁机组场路耦合模型
Fig.4 IMPMMS field circuit coupling model
永磁机组输出电压波形如图5所示。从图5可知,在惯性补偿过程2s内输出电压最大值UA(Max)、UB(Max)和UC(Max)三者平均值从2.415kV降至2.373kV,减小了1.74%,满足不大于7%的要求。由于在惯性补偿期间输出电压偏差很小,所以可选2s内任意一周期的电压波形进行谐波分析,时间区间为1~1.02s。

图5 永磁机组输出电压波形
Fig.5 IMPMMS output voltage waveforms
对图5中的输出电压UA进行傅里叶分解,得到永磁机组输出相电压UA各阶次谐波幅值与基波比值和THD,输出电压各次谐波值对比如图6所示。从图6可知,永磁机组相电压UA的15次谐波占基波比例0.31%,略大于ER G5/4标准的0.3%,25次、27次、33次、45次、45次和49次谐波占基波比率与ER G5/4标准相近,剩下其他次谐波皆小于ER G5/4标准要求。而且,THD值为3.35%,低于4%。
转速变化如图7所示。从图7可知,永磁机组惯性补偿过程2s内转速从1500r/min下降至 1 495.3r/min,下降率0.313%,由于永磁电机固有特性,频率变化率与转速变化率相等,即-0.157Hz,满足目标值。
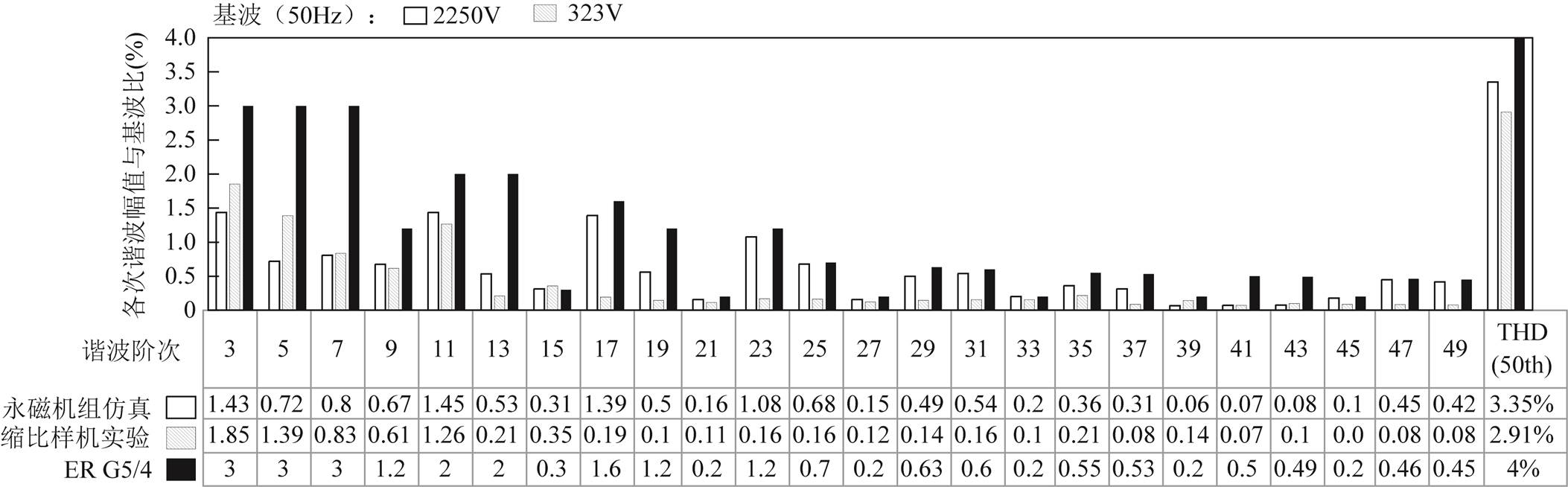
图6 输出电压各次谐波值对比
Fig.6 Comparison of harmonic values of output voltage
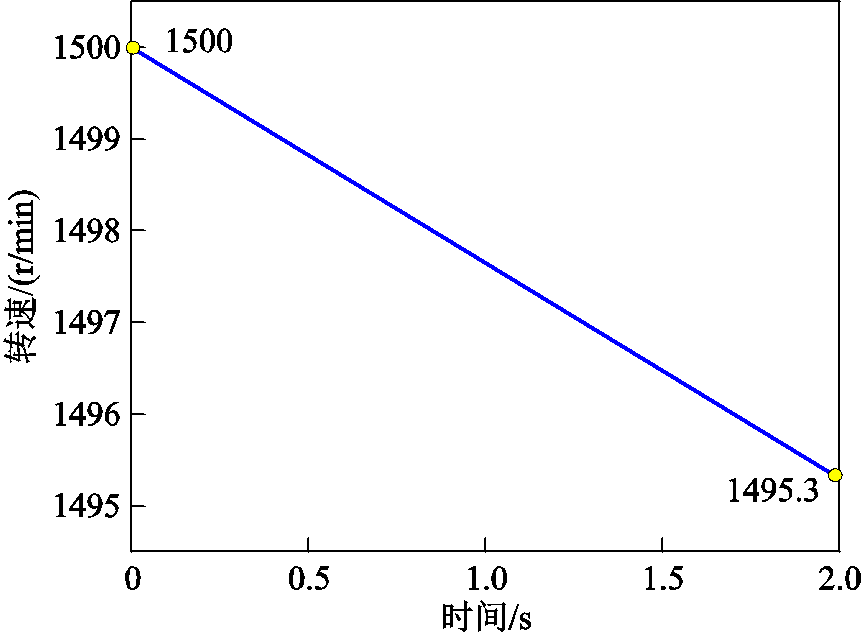
图7 转速变化
Fig.7 Speed change
永磁机组作为一种由两个永磁电机串联而成的惯性补偿设备,两侧是完全不同的交流系统,其自身特性与传统永磁电机有着显著的区别。在建立电力系统分析模型之前,需重新列写永磁机组电气和机械方程。
永磁机组中两台永磁电机转速相同,可看作对拖的连接方式,所以在建立永磁机组电气模型时,两台永磁电机的定子绕组用三相(ABC)等效绕组表示,而转子侧采用转向相反的d-q旋转坐标系表示,如图8所示。
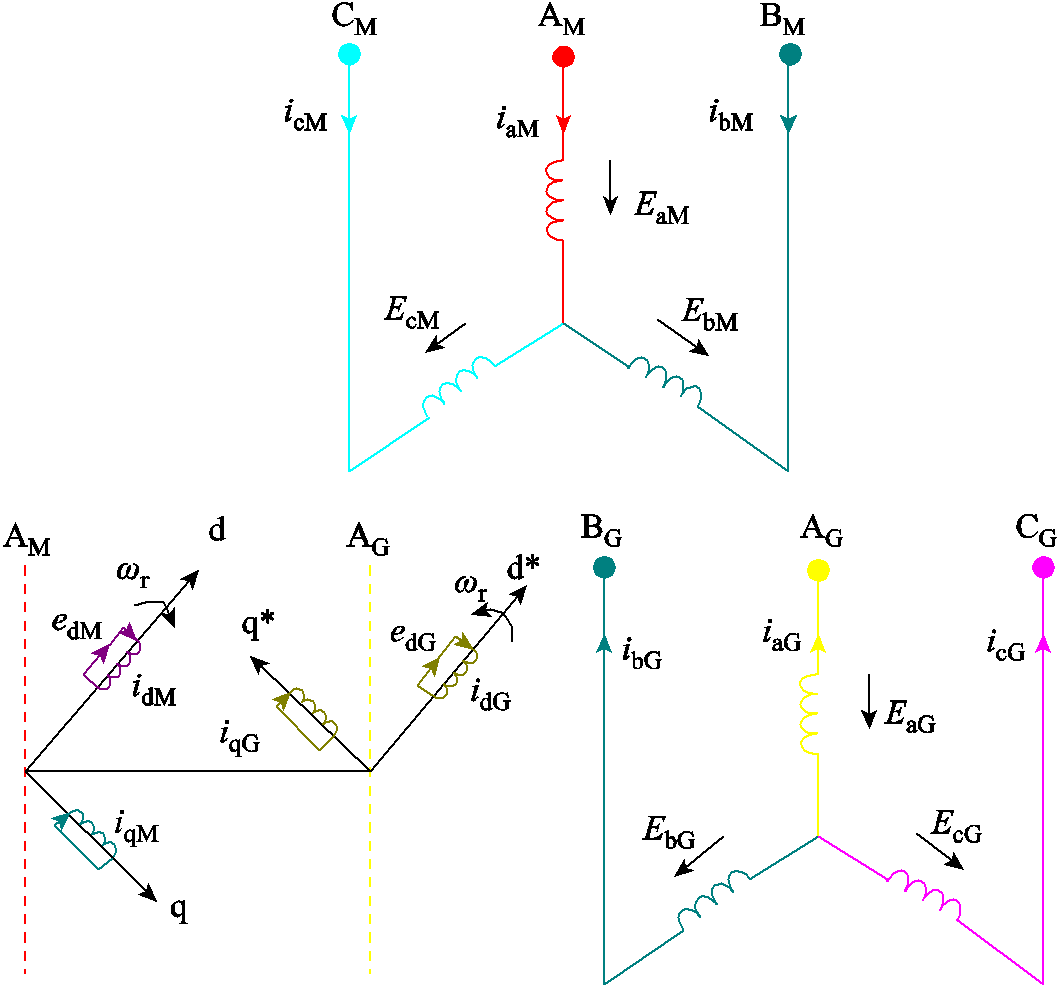
图8 永磁机组等效电路模型
Fig.8 IMPMMS equivalent circuit model
永磁电动机的电压方程为
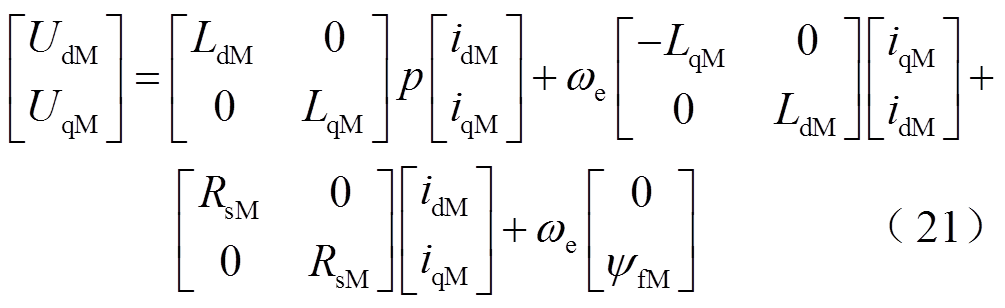
式中,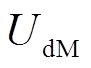 和
和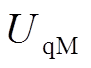 分别为永磁电动机定子d-q轴电压分量;
分别为永磁电动机定子d-q轴电压分量;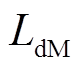 和
和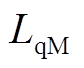 分别为永磁电动机d-q轴电感;
分别为永磁电动机d-q轴电感;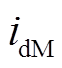 和
和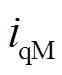 分别为永磁电动机d-q轴电流;
分别为永磁电动机d-q轴电流;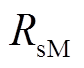 为永磁电动机相电阻;p为微分算子;
为永磁电动机相电阻;p为微分算子;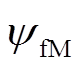 为永磁电动机永磁体磁链;
为永磁电动机永磁体磁链;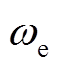 为永磁机组转子角速度;下标M、G分别表示永磁电动机和永磁发电机。
为永磁机组转子角速度;下标M、G分别表示永磁电动机和永磁发电机。
永磁发电机的电压方程为
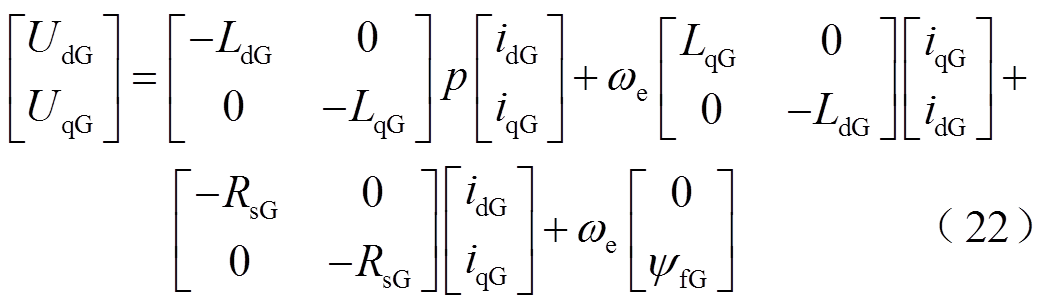
式中,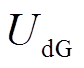 和
和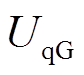 分别为永磁发电机定子d-q轴电压分量;
分别为永磁发电机定子d-q轴电压分量;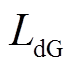 和
和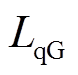 分别为永磁发电机d-q轴电感;
分别为永磁发电机d-q轴电感;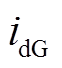 和
和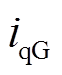 分别为永磁发电机d-q轴电流;
分别为永磁发电机d-q轴电流;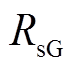 为永磁发电机相电阻;
为永磁发电机相电阻;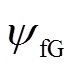 为永磁发电机永磁体磁链。
为永磁发电机永磁体磁链。
为了方便表示,将直轴、交轴电压合并成一个向量。
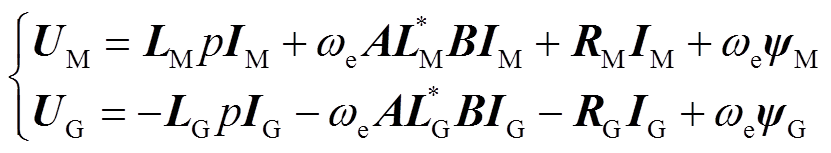 (23)
(23)
式中,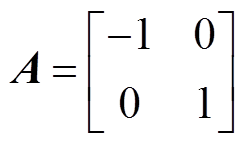 ;
;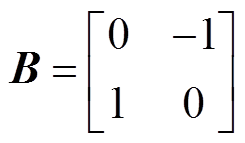 ;
;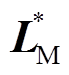 和
和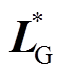 分别为矩阵
分别为矩阵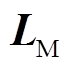 和
和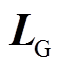 对角线互换矩阵。
对角线互换矩阵。
永磁机组电压方程为
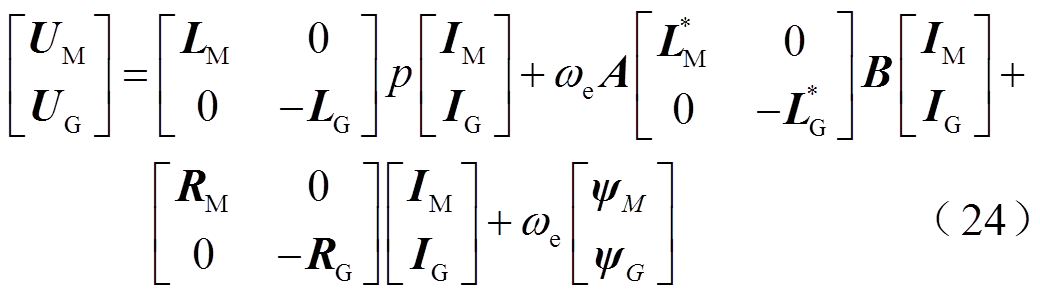
永磁机组转矩方程为
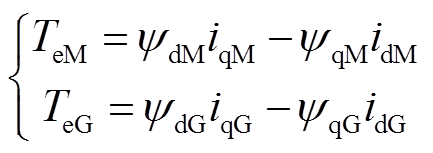 (25)
(25)
永磁机组磁链方程为
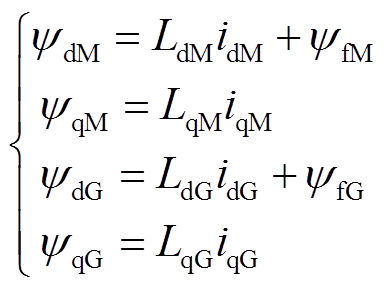 (26)
(26)
将式(26)中直、交轴电感合并成一个向量为
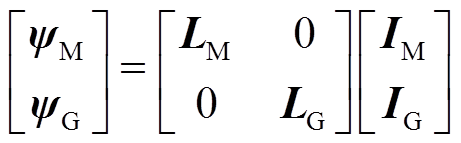 (27)
(27)
从式(24)、式(25)、式(27)的电气方程可以看到,无论是电压、转矩还是磁链方程,永磁机组中的两台电机的电气量都不存在电气上的耦合。
根据永磁电机的摇摆方程,将永磁电动机和永磁发电机的转子一阶微分方程合并得
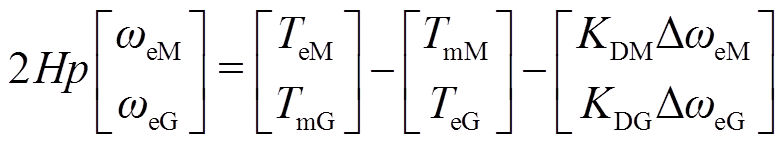 (28)
(28)
式中,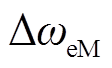 和
和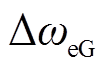 分别为永磁电动机和永磁发电机的转子角速度;H为永磁机组惯性时间常数;
分别为永磁电动机和永磁发电机的转子角速度;H为永磁机组惯性时间常数;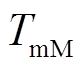 和
和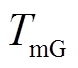 分别为永磁电动机和永磁发电机的机械转矩;
分别为永磁电动机和永磁发电机的机械转矩;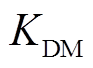 和
和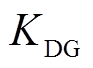 分别为永磁电动机和永磁发电机的阻尼系数。
分别为永磁电动机和永磁发电机的阻尼系数。
永磁电动机和永磁发电机功角特性可表示为
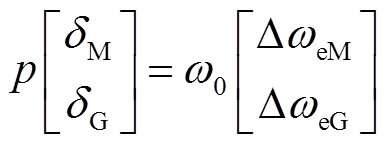 (29)
(29)
考虑网侧故障对于新能源变流器的影响是通过永磁机组与源侧和网侧之间的电磁-机械耦合作用实现的,将永磁机组的机械方程简化为
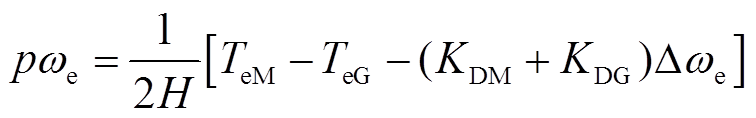 (30)
(30)
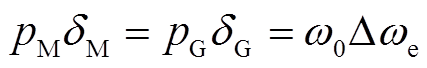 (31)
(31)
根据式(30)、式(31)得到永磁机组的机械模型框图如图9所示。
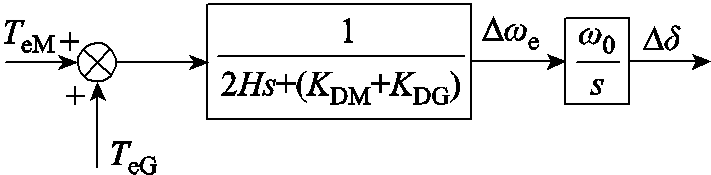
图9 永磁机组机械模型框图
Fig.9 Mechanical model block diagram of IMPMMS
结合永磁机组电压方程和机械方程,在电力系统仿真软件PSCAD中搭建永磁机组系统惯性补偿仿真模型,如图10所示。模型是一个4机2区系统,验证永磁机组对风电场的惯性补偿性能。图10中,连接母线2和4处的传统发电机被两个输出功率为1MW的风力发电机取代,且风力发电机以最大输出模型运行。在风场中一部分风力发电机以传统方式并网,另一部分串入永磁机组。
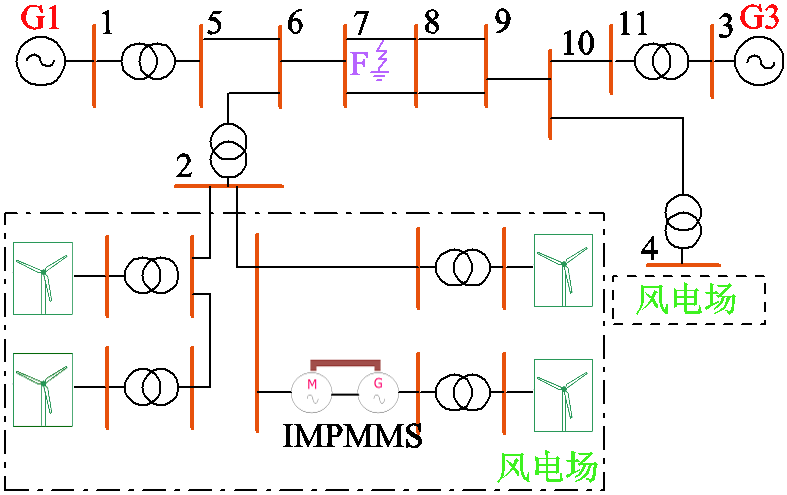
图10 基于PSCAD的永磁机组电力系统仿真模型
Fig.10 Simulation model of IMPMMS power system based on PSCAD
模型仿真时间共20s,在输电线路中的F处5s时刻发生短时中断故障,持续2s,2s后线路恢复正常。故障期间频率响应如图11所示。由于电网侧和永磁机组之间功率不平衡,电网频率会立即下降,从图11可以看出,在风机串入永磁机组后,频率最低点从0.985(pu)提高至0.997(pu),提高了1.2%,说明真实大机械惯量对频率最低点起到了支撑作用,降低了惯性响应阶段频率的变化率,提高了系统频率稳定性。在短时中断故障情况下,以最大机组功角差为指标,研究了功角稳定性,故障期间功角变化如图12所示。从图12可知,不串入永磁机组时振幅大(功角最大达到38.1°),且振荡周期长;串入永磁机组后最大功角减少至29.5°,降低22.5%,振荡趋势得到抑制。风电场并网公共耦合点母线2的电压变化如图13所示,从图13中曲线可知,在采用永磁机组并网后,故障期间电压跌落从0.78(pu)上升至0.97(pu),电压跌落率降低了24.3%,这是因为变流器电压控制器直接并网不足以支撑较短时间的电压跌落,而永磁机组具有大惯量,在短时间内可保持稳定的电压输出。
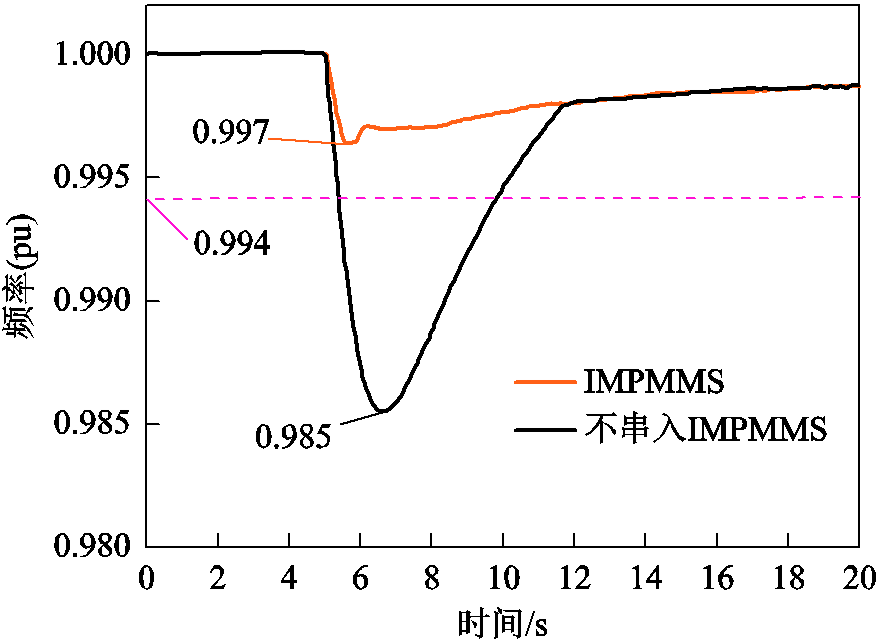
图11 故障期间频率响应
Fig.11 Frequency response during fault
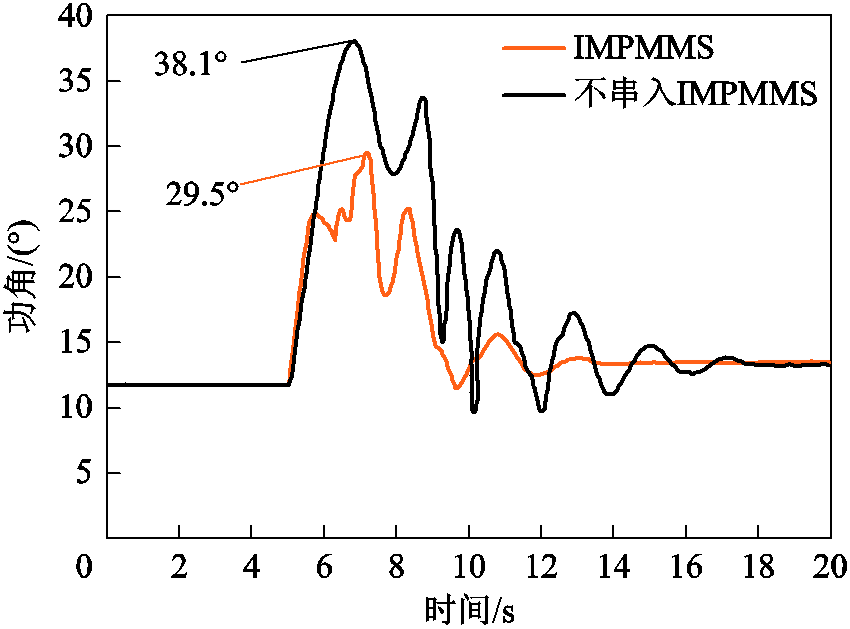
图12 故障期间功角变化
Fig.12 Power angle change during fault
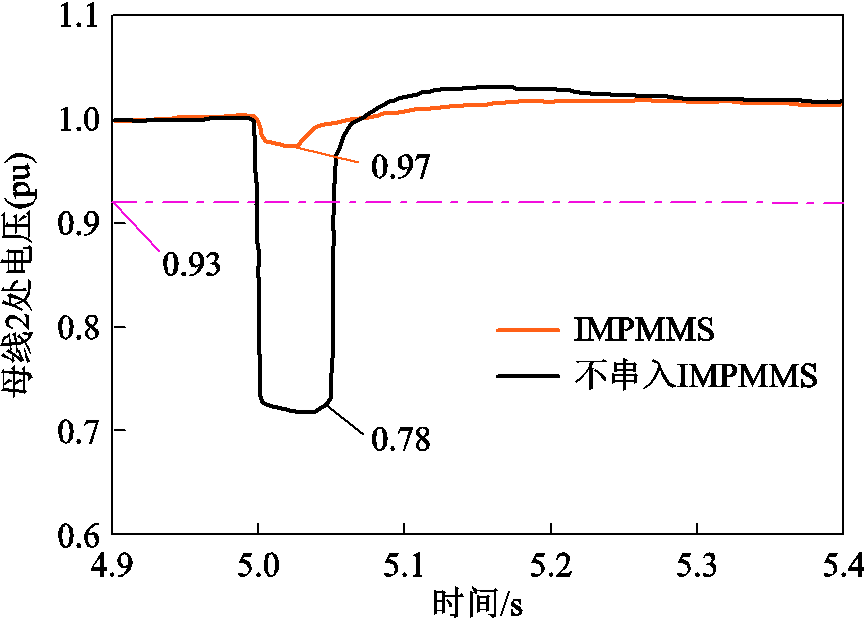
图13 故障期间母线2处电压变化
Fig.13 Voltage change at bus 2 during fault
研制了一台55kW的缩比样机,进行了实验测试。缩比样机参数见表3。由于实验条件的限制,测试的主要目的在于验证缩比样机的惯性补偿能力,并将测得的输出电压波形与电能质量标准进行对比。永磁电动机由变频器拖至额定转速后断电;发电机电枢绕组与电阻负载相连,且接有断路器,起到断电保护作用。实验的电流和电压波形是采用功率分析仪(FLUKE4000CN)测得的,相应的数据同步上传至上位机中,通过对实验数据后处理,得到输出功率曲线。缩比样机的定子和转子如图14所示,实验平台如图15所示。
表3 缩比样机参数
Tab.3 Parameters of the scaled motor prototype

参数数值 额定电压USMP/V380 额定功率PSMP/kW55 频率f/Hz50 转动惯量JSMP/(kg·m2)0.85
样机转速到达额定转速,调整负载电阻以达到55kW的额定负载后,变频器断电,样机依靠转子惯性继续旋转2s,此过程中电压波形、电流波形以及输出功率曲线如图16、图17所示。从图16可知,在惯性旋转期间,A、B、C相电流测得的有效值分别为79.5A、79.1A和79.3A,且三相平衡。从图17可知,在2s内输出电压最大值UA(Max)、UB(Max)和UC(Max)平均值从334.7V降至317.6V,减小5.1%,满足不大于7%的要求。取周期(1s, 1.02s)三相输出电压波形可以看出,电压波形正弦度较好;对缩比样机一个电周期内的输出电压UA进行傅里叶分解,结果如图6所示。从图6可知,缩比样机输出相电压UA的各次谐波皆小于ER G5/4标准要求,而且谐波畸变率为2.91%,低于标准4%要求。通过对实验测得的惯性补偿期间输出电压和输出电流波形的各时刻的数据进行处理,得到缩比样机输出功率曲线,输出功率平均值为55.3kW,与额定功率接近。由于实验条件的限制,没有搭建完整的真实并网的实验平台,这将在今后实现。总体而言,实验结果验证了本文设计思路的正确性,证明了所提出的永磁机组可实现短时的惯性补偿,且满足输出电能质量的指标要求。

图14 缩比样机
Fig.14 Scaled motor prototype

图15 实验平台
Fig.15 Experimental platform
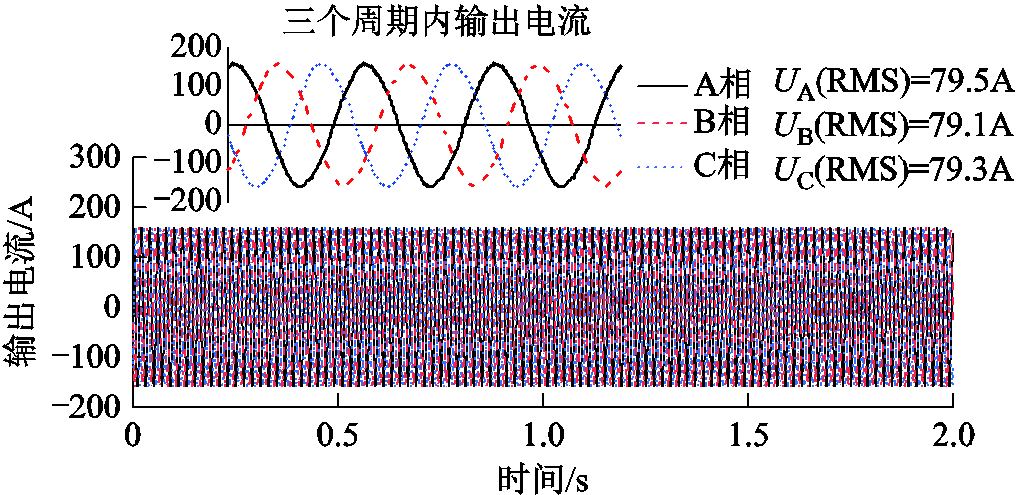
图16 输出电流实验曲线
Fig.16 Output current experimental curves
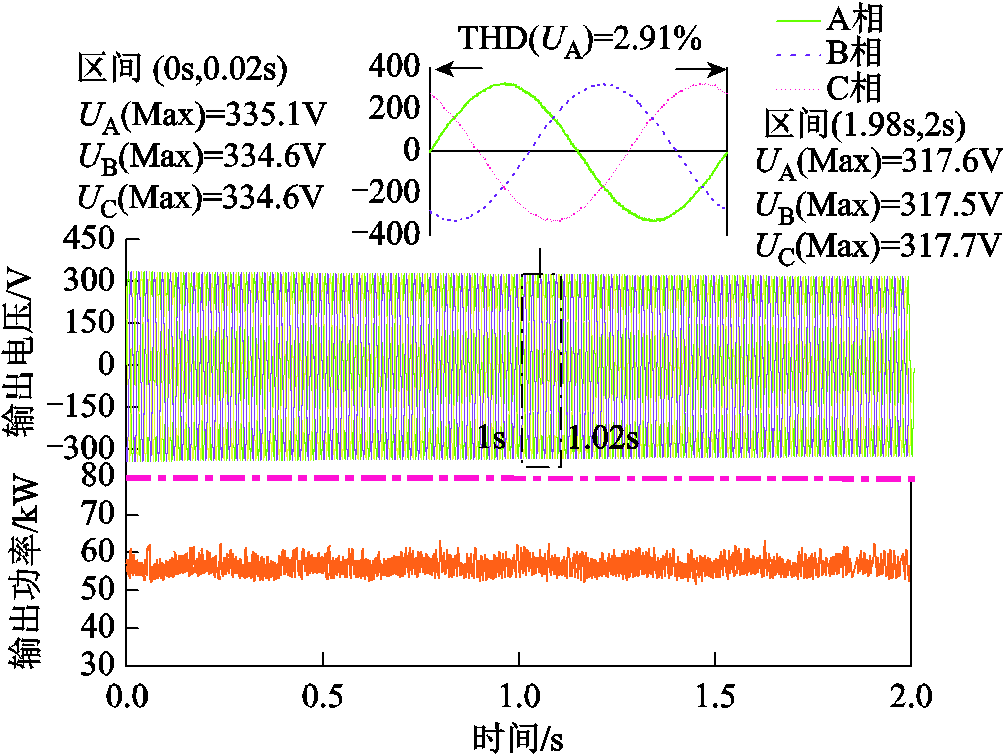
图17 输出电压和输出功率实验曲线
Fig.17 Experimental curves of output voltage and output power
本文所提出的永磁机组是电网真实转动惯量的提供者,其外转子既可以作为旋转部件又可以视为具有真实大惯量的储能飞轮。通过场路耦合和电力系统仿真分析,证明了设计思想的合理性,并研制了一台缩比样机进行了实验验证,得到结论如下:
1)本文所提出的永磁机组作为适用于新能源场站的大型同步惯量支撑设备,在新能源并网点发生短时中断故障期间,可第一时间向电网自动地提供所需的惯量支撑和高品质电能,是提高新能源微电网稳定性的一种解决方案。
2)通过场路耦合分析结果可知:在惯性补偿期间,永磁机组的输出电压波动率1.7%、各阶次谐波幅值、THD50th=3.35%皆满足标准要求。通过电力系统仿真结果可知:与不串入永磁机组相比,并网点频率下降率降低1.2%、功角最大振幅下降22.5%,且振荡周期缩短、电压跌落降低24.3%,明显提高了新能源微电网的稳定性。
3) 研制了一台额定容量为55kW的缩比样机,在机组规定的惯性运转期间,通过实验测试结果可知:输出电压波动率为5.1%,小于标准要求的7%;A相电压THD50th为2.91%,小于标准要求的4%,且各次谐波幅值也满足标准要求;输出功率平均值55.3kW与额定值基本一致,验证了本文所提出新型机组设计思想的正确性。
永磁机组是一种可有效提高高比例新能源微电网系统稳定性的技术解决方案。今后研究将集中于永磁机组的控制策略和最优化设计。
参考文献
[1] 施静容, 李勇, 贺悝, 等. 一种提升交直流混合微电网动态特性的综合惯量控制方法[J]. 电工技术学报, 2020, 35(2): 337-345.
Shi Jingrong, Li Yong, He Li, et al. A comprehensive inertia control method for improving the dynamic characteristics of hybrid AC-DC microgrid[J]. Transactions of China Electrotechnical Society, 2020, 35(2): 337-345.
[2] Wang Shuo, Hu Jiabing, Yuan Xiaoming, et al. On inertial dynamics of virtual-synchronous-controlled DFIG-based wind turbines[J]. IEEE Transactions on Energy Conversion, 2015, 30(4): 1691-1702.
[3] Xi Jiangbei, Geng Hua, Ma Shaokang, et al. Inertial response characteristics analysis and optimisation of PMSG-based VSG-controlled WECS[J]. IET Renewable Power Generation, 2018, 12(15): 1741-1747.
[4] 陶银正, 蒲道杰, 毛福斌. 虚拟同步发电机技术及其在光储微电网中的应用[J]. 电气技术, 2016, 17(11): 36-40.
Tao Yinzheng, Pu Daojie, Mao Fubin. Virtual synchronous generator technology and its application in PV-storage micro-grid[J]. Electrical Engineering, 2016, 17(11): 36-40.
[5] 张靖, 张志文, 胡斯佳, 等. 独立微电网风储协同调频的功率柔性分配策略[J].电工技术学报, 2022, DOI:10.19595/j.cnki.1000-6753.tces.211032.
Zhang Jing, Zhang Zhiwen, Hu Sijia, et al. A flexible power distribution strategy with wind turbine generator and energy storage for frequency regulation in isolated microgrid[J]. Transactions of China Electrotechnical Society, 2022, DOI:10.19595/j.cnki.1000-6753.tces.211032.
[6] 樊启高, 吕华阳, 毕恺韬, 等. 面向直流储能系统的飞跨电容三电平双向升降压变换器及其模型预测控制策略[J].电工技术学报, 2022, DOI:10.19595/j. cnki.1000-6753.tces.211127.
Fan Qigao, Lü Huayang, Bi Kaitao, et al. Flying capacitor three-level bi-directional buck-boost converter and its model predictive control strategy for DC energy storage system[J]. Transactions of China Electrotechnical Society, 2022, DOI:10.19595/j.cnki. 1000-6753.tces.211127.
[7] Morren J, de Haan S W H. Ridethrough of wind turbines with doubly-fed induction generator during a voltage dip[J]. IEEE Transactions on Energy Conversion, 2005, 20(2): 435-441.
[8] 贺益康, 胡家兵. 双馈异步风力发电机并网运行中的几个热点问题[J]. 中国电机工程学报, 2012, 32(27): 1-15.
He Yikang, Hu Jiabing. Several hot-spot issues associated with the grid-connected operations of wind-turbine driven doubly fed induction generators[J]. Proceedings of the CSEE, 2012, 32(27): 1-15.
[9] Yang Yongheng, Blaabjerg F, Wang Huai. Low voltage ride-through of single-phase transformerless photovoltaic inverters[J]. IEEE Transactions on Industry Applications, 2013, 50(3): 1942-1952.
[10] 涂春鸣, 葛钦, 肖凡, 等. 基于光伏电源支撑的多端口固态变压器故障穿越策略[J]. 电工技术学报, 2020, 35(16): 3498-3508.
Tu Chunming, Ge Qin, Xiao Fan, et al. Fault ride-through control strategy of solid state transformer with PV power generation[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3498-3508.
[11] 徐可寒, 张哲, 刘慧媛, 等. 光伏电源故障特性研究及影响因素分析[J]. 电工技术学报, 2020, 35(2): 359-371.
Xu Kehan, Zhang Zhe, Liu Huiyuan, et al. Study on fault characteristics and its related impact factors of photovoltaic generator[J]. Transactions of China Electrotechnical Society, 2020, 35(2): 359-371.
[12] Arani M F M, Mohamed Y A R I. Assessment and enhancement of a full-scale PMSG-based wind power generator performance under faults[J]. IEEE Transactions on Energy Conversion, 2016, 31(2): 728-739.
[13] Wei Siming, Zhou Yingkun, Li Song, et al. A possible configuration with motor-generator pair for renewable energy integration[J]. CSEE Journal of Power and Energy Systems, 2017, 3(1): 93-100.
[14] Zhou Yingkun, Xu Guorui, Wei Siming, et al. Experiment study on the control method of motor-generator pair system[J]. IEEE Access, 2018, 6: 925-936.
[15] Gu Yujun, Huang Yongzhang, Wu Qianyu, et al. Isolation and protection of the motor-generator pair system for fault ride-through of renewable energy generation systems[J]. IEEE Access, 8: 13251-13258.
[16] Wu Qianyu, Huang Yongzhang, Li Chenyang, et al. Small signal stability of synchronous motor-generator pair for power system with high penetration of renewable energy[J]. IEEE Access, 7: 166964-166974.
[17] Wei Siming, Zhou Yingkun, Huang Yongzhang. Synchronous motor-generator pair to enhance small signal and transient stability of power system with high penetration of renewable energy[J]. IEEE Access, 2017, 5: 11505-11512.
[18] EN 50160 Voltage characteristics in public distribution systems: voltage disturbances[S].
[19] 曹建设. GB/T 15945征求意见稿中电网频率测量时间间隔的探讨[J]. 现代建筑电气, 2010, 1(3): 57-61.
Cao Jianshe. Discussion on measuring time interval of power grid frequency in manuscript of appealing for opinions on GB/T15945[J]. Modern Architecture Electric, 2010, 1(3): 57-61.
[20] Najjar M, Moeini A, Bakhshizadeh M K, et al. Optimal selective harmonic mitigation technique on variable DC link cascaded H-bridge converter to meet power quality standards[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(3): 1107-1116.
[21] Direct acting indicating analogue electrical measuring instruments and their accessories - Part 3: Special requirements for wattmeters and varmeters: IEC 60051-3[S]. IEC, 2018.
The Inertia Motivity Permanent Magnet Machine Set for Improving the Stability of New Energy Microgrid during Short-Term Interruption
Abstract In order to solve the short-term interruption problem of high-proportion new energy microgrids, an inertia motivity permanent magnet machine set (IMPMMS) was proposed. The IMPMMS proposed in this paper is composed of a permanent magnet motor and a permanent magnet generator with a common outer rotor roller, which has the advantages of real-time inertial support for new energy microgrids and high output power quality. From the perspective of inertial energy storage, the IMPMMS was designed according to the power quality index requirements of the power grid, and the rationality of the IMPMMS design is verified by finite element method and field-circuit coupling simulation. Combined with the electromagnetic-mechanical coupling model of IMPMMS, a simulation model of IMPMMS power system based on PSCAD platform was established. The simulation results prove that IMPMMS can realize inertial support for new energy microgrids during short-term interruptions. Finally, a 55kW scaled prototype is developed, and the correctness of the design idea is verified through test.
Keywords:New energy microgrid, inertia motivity, permanent magnet machine set, inertial support
DOI:10.19595/j.cnki.1000-6753.tces.220695
中图分类号:TM351; TM712
收稿日期 2022-05-04
改稿日期 2022-06-03
郑军铭 男,1990年生,博士研究生,研究方向特种电机及其控制。E-mail:zhengjm@smail.sut.edu.cn
张炳义 男,1954年生,教授,博士生导师,研究方向为特种电机及其控制等。E-mail:zhangby@sut.edu.cn(通信作者)
(编辑 赫蕾)