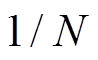 ,每条历史轨迹都记录了风电场一天内每小时的最大功率输出值。以N条风电场出力的历史轨迹作为数据集,可以估计风电场的
,每条历史轨迹都记录了风电场一天内每小时的最大功率输出值。以N条风电场出力的历史轨迹作为数据集,可以估计风电场的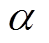 火电替代容量。
火电替代容量。摘要 风力发电具有随机性和波动性,给大规模利用风力资源造成诸多困难。通过配置储能设备可以平滑风电场功率输出,使风电场可以替代火电或供应电网负荷。首先,该文基于风资源特性定义了风电场的火电替代容量和负荷供应容量,这两个指标反映了风电场稳定输出功率或供应负荷的能力;其次,根据风资源数据和置信要求,可以通过混合整数线性规划求解火电替代容量和负荷供应容量;最后,根据风电场火电替代容量和负荷供应容量的具体需求,进一步构建了储能MW/(MW∙h)参数的优化配置方法,该方法通过计算储能参数可行域边界,再根据储能成本系数确定最优配置方案的范围。算例选用广东省风力发电历史数据,采用该文方法可以快速确定储能最优参数配置,同时兼顾配置的经济性及供电平稳性、可靠性。
关键词:风力发电 火电替代容量 负荷供应容量 储能设备 容量配置
发展可再生能源是缓解化石能源短缺和环境保护压力的重要手段,是实现我国“碳达峰,碳中和”愿景的重要途径[1]。其中,风力发电技术比较成熟,已在全球范围内广泛应用,仅在2020年,中国风力发电新增装机容量达52GW,总装机容量达288.3GW[2]。风力发电已经成为我国电力系统能源供应的重要组成部分。其中,海上风力发电拥有环境污染小、占用陆地资源少、风速稳定、容量因子高的优点。我国东部沿海地区海上风电资源丰富,具有极大的开发潜力和价值,仅在2020年,我国海上风电新增装机容量达3.06GW[2]。我国经济和负荷中心靠近东部沿海地区,有利于海上风电的输送和消纳,发展海上风电对于缓解用电紧张、实现双碳目标具有重要意义。
风力发电的大规模利用促进了电力系统低碳绿色运行进程。但是,由于风力发电具有随机性和不确定性,大规模风力发电的接入给电力系统规划配置、调度运行提出了新的要求,抑制风力发电的波动性,确保电力系统负荷供应的可靠性成为当前研究的重点[3]。储能设备具有高度灵活性,可以实现电能在时间和空间上的平移。在风力发电较多时,储能设备可以吸收多余的电量;在风力发电较少时,储能设备可以补足电量的缺额,使风电场出力平稳,可靠供应电力系统的负荷[4]。因此,储能设备对于风电场平稳运行具有关键作用,如何配置储能设备的容量和功率也是研究者关注的重点[5-6]。
针对储能设备功率和容量的配置问题,很多学者根据实际需求确定目标函数,采用多目标优化等方法获取储能设备最优参数。文献[7]研究了储能系统联合火电厂参与系统调峰时储能系统的参数配置问题,通过构建多目标优化配置储能系统最优参数。文献[8]研究了风光储系统储能容量优化配置问题,并构建双层决策模型使储能设备初始投资和联络线功率波动最小。文献[9]应用模型预测控制算法,分析了不同风电光伏配比下储能设备的参数配置。文献[10]基于主从博弈问题,研究了综合能源系统中氢储能配置问题,有效地解决了园区级综合能源系统的能量平衡问题,同时提高了系统运营商的收益。以上模型以投资方收益为关注重点,对新能源和系统的建模比较简单。同时这些方法采用少量典型场景来确定风电功率输出,具有较大的局限性,不能体现风电输出功率的不确定性。
部分文献采用聚类分析和频谱分析的方法,这类方法克服了选取典型风电功率输出场景的不足。文献[11]采用云模型理论和K-means聚类方法获取储能运行时的典型充放电曲线,以最小化风电输出功率波动为目标,建立了储能容量优化配置方法。该方法的典型场景依赖聚类数目的选择,合理的聚类数目难以事先确定。文献[12]借助离散傅里叶变换技术,对可再生能源功率输出进行频谱分解,将长周期波动/短周期波动通过反变换得到时域曲线,配置相应的储能容量。文献[13]根据响应时间将平抑风电波动所需的容量进行分类,再应用离散傅里叶变换确定风电场配套储能系统的容量需求。文献[14]采用蒙特卡洛模拟法考虑新能源出力的不确定性,对最小补偿功率进行频谱分析,确定混合储能设备的容量大小。然而按照频谱分解得出的储能容量并不一定是最优的,与如何划分高频与低频波动有关,不合理的高频和低频波动划分将影响储能参数配置的最优性。
为了更加积极地考虑风电不确定性对容量配置的影响,学者们通过引入置信水平或分布鲁棒优化,以降低优化结果的保守性。文献[15]采用变时间常数的一阶低通滤波算法,研究了用于平抑风电波动的储能设备容量配置方法,分析了不同约束条件和不同置信水平下的储能设备容量配置需求。文献[16]基于一阶巴特沃思滤波环节的平抑策略,通过引入维纳过程研究了不同时间尺度的风功率变化量的概率分布,进而提出了一种满足一定置信区间的储能装置功率和容量的配置方法。文献[17]采用分布鲁棒优化对风电不确定性进行建模,通过考虑氢储能的热平衡约束,有效提升氢储能实际可用容量,实现氢储能系统容量优化配置。文献[18]借助分布鲁棒优化,研究了考虑风电不确定性和弃电率约束的风电场配套储能设施容量规划问题。这类方法允许配置储能时在一定概率下违背部分约束条件,在较高的置信水平下能较好地兼顾储能配置的经济性和可靠性。但是,以上方法只针对固定的储能投资成本,如果储能投资成本在一定范围内变动,则需要重新求解问题。总体而言,现有方法除了上述问题,大都针对具体系统进行研究,尚且缺乏针对风力供电一般性特点的刻画与分析。
为了解决以上问题,本文从风电场置信容量出发,分别定义了风电场的火电替代容量和负荷供应容量,反映了在一定置信概率下,风电场能向外界稳定输出的功率大小和风电场能稳定供应的负荷水平。通过在储能配置问题中满足风电场火电替代容量指标和风电场负荷供应指标,能保证储能参数配置的经济性和负荷供应的可靠性。为了应对储能投资成本的可变性,本文首先求解出基于火电替代容量指标和负荷供应容量指标的储能参数配置可行域,而非一个具体的配置方案,再根据储能成本参数变化范围确定储能装置最优配置范围,给决策者提供更灵活的选择空间。
风力发电具有高度的随机性和不确定性,给电力系统的安全稳定运行带来了极大挑战。在实际运行中,风电场的功率输出受气象条件的影响,其实际最大输出功率在一定范围内波动。为了维持电力系统的稳定运行,风电场应具有向电网稳定输出功率的能力。储能装置具有良好的能量时间和空间平移能力,制定合适的储能设备的充放电策略,可以使风电场在全天范围内维持平稳的功率输出。由于储能的调节作用,风储联合系统可以长时间稳定输出功率,消除了风力发电的间歇性,在平稳输出功率、供应系统负荷上,风储联合系统发挥了与火电厂相仿的作用。本节将主要介绍风电联合系统的火电替代容量定义及其计算方法。
考虑如图1所示的风储联合系统,风电场可以向储能设备和电网输送电能,储能设备可以吸收风电场多余的功率并向电网输出功率。已知N条风电场功率输出的历史轨迹,每条历史轨迹的概率为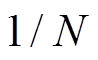 ,每条历史轨迹都记录了风电场一天内每小时的最大功率输出值。以N条风电场出力的历史轨迹作为数据集,可以估计风电场的
,每条历史轨迹都记录了风电场一天内每小时的最大功率输出值。以N条风电场出力的历史轨迹作为数据集,可以估计风电场的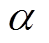 火电替代容量。
火电替代容量。
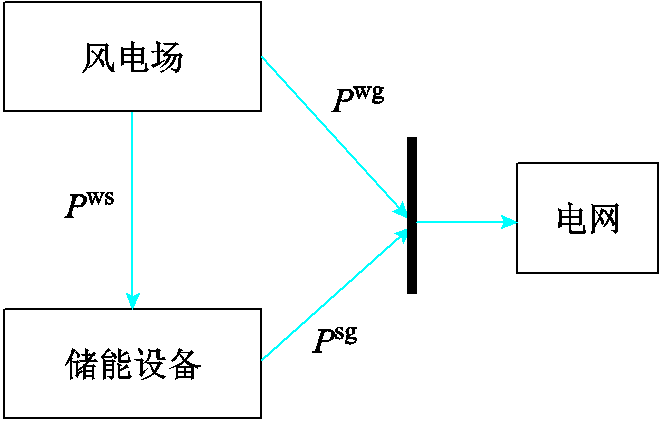
图1 风储联合结构示意图
Fig.1 Schematic of the combined wind-storage system
风电场和储能设备的参数确定。在一天内,储能设备通过制定合理的充放电策略,使风储联合系统始终能够向电网输送功率P的概率不小于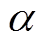 ,则称该风电场的
,则称该风电场的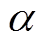 火电替代容量不小于P。满足该条件的最大功率为该风电场的
火电替代容量不小于P。满足该条件的最大功率为该风电场的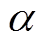 火电替代容量,即
火电替代容量,即
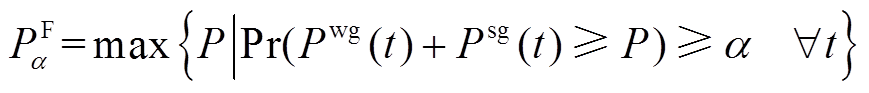 (1)
(1)
式中,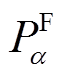 为置信概率为
为置信概率为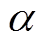 时系统的
时系统的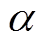 火电替代容量;
火电替代容量;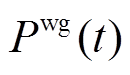 为t时刻风电场向电网输送的功率;
为t时刻风电场向电网输送的功率;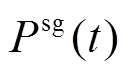 为t时刻储能设备向电网输送的功率。
为t时刻储能设备向电网输送的功率。
四条风储联合系统功率输出曲线如图2所示。假设其功率输出均经过储能设备的适当调节。以这四条曲线计算风储联合系统的火电替代容量。其中,有两天风储联合系统输出功率始终大于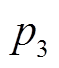 ,则
,则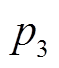 是风储联合系统的50%火电替代容量。火电替代容量反映了风储联合系统向电网稳定输出能量的能力,评估风储联合系统的火电替代容量,对风电场接入电网有重要作用。
是风储联合系统的50%火电替代容量。火电替代容量反映了风储联合系统向电网稳定输出能量的能力,评估风储联合系统的火电替代容量,对风电场接入电网有重要作用。
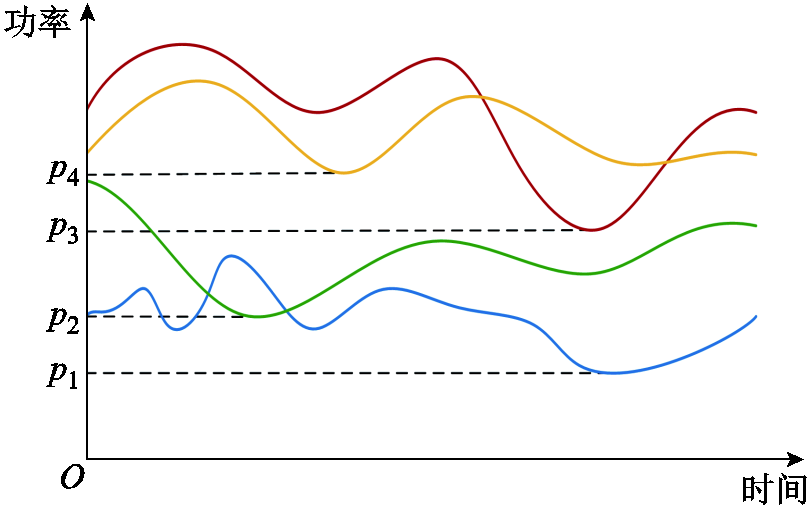
图2 单日风储联合系统功率输出
Fig.2 The power output of the combined wind-storage system in one day
根据风储系统的历史数据和储能设备参数,可以估计风储联合系统的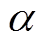 火电替代容量。首先,风储联合系统需要满足风电场运行约束条件,即
火电替代容量。首先,风储联合系统需要满足风电场运行约束条件,即
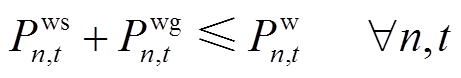 (2)
(2)
式中,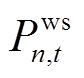 为风电场在第
为风电场在第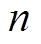 个场景
个场景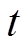 小时内向储能设备输出的功率;
小时内向储能设备输出的功率;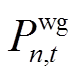 为风电场在第
为风电场在第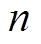 个场景
个场景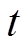 小时内向电网输出的功率;
小时内向电网输出的功率;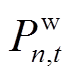 为风电场在第
为风电场在第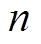 个场景
个场景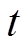 小时的最大输出功率。式(2)表示每个风电场的输出功率不超过当前场景的最大值。
小时的最大输出功率。式(2)表示每个风电场的输出功率不超过当前场景的最大值。
考虑到风储联合系统中储能设备的动态特性和安全约束,需满足
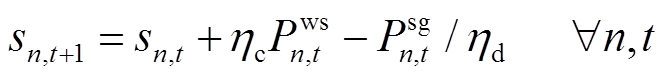 (3)
(3)
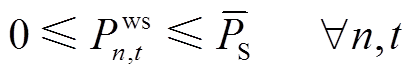 (4)
(4)
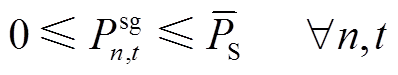 (5)
(5)
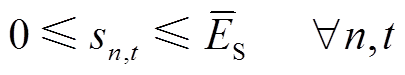 (6)
(6)
式中,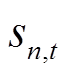 为风储联合系统储能设备在第
为风储联合系统储能设备在第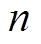 个场景第
个场景第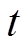 小时初存储的能量;
小时初存储的能量;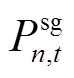 为第
为第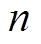 个场景第
个场景第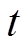 小时内储能系统向电网输出的功率;
小时内储能系统向电网输出的功率;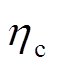 和
和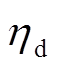 分别为储能设备的充电效率和放电效率;
分别为储能设备的充电效率和放电效率;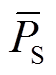 为储能设备的最大充放电功率;
为储能设备的最大充放电功率;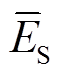 为储能设备的最大存储容量。
为储能设备的最大存储容量。
考虑到风储联合系统的输出功率的置信概率约束,风储联合功率输出应当满足
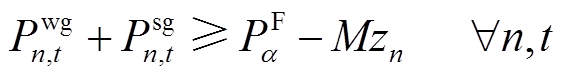 (7)
(7)
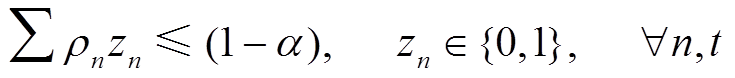 (8)
(8)
式中,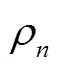 为第
为第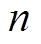 个场景发生的概率,本文中取
个场景发生的概率,本文中取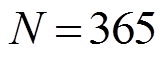 天以及
天以及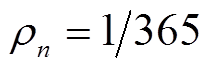 ;
;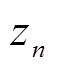 为0-1变量,
为0-1变量,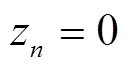 时表示要求第
时表示要求第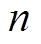 天全天风电场出力都维持在
天全天风电场出力都维持在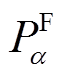 以上,
以上,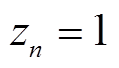 则表示对第
则表示对第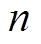 天风电场的出力大小没有要求;
天风电场的出力大小没有要求;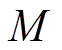 为一个很大的常数,用于配合
为一个很大的常数,用于配合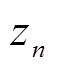 松弛约束条件,表示风电场全年中有365
松弛约束条件,表示风电场全年中有365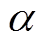 天都能保证稳定输出功率
天都能保证稳定输出功率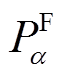 。
。
因此,在置信概率为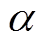 时,风储联合系统的
时,风储联合系统的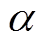 火电替代容量可通过求解混合整数线性规划式(9)获得。
火电替代容量可通过求解混合整数线性规划式(9)获得。
 (9)
(9)
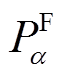 反映了在储能设备合理的调控策略下,风储联合系统能够向电网稳定供应的最大功率值。
反映了在储能设备合理的调控策略下,风储联合系统能够向电网稳定供应的最大功率值。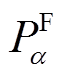 越大表明风储联合系统能替代越大的火电机组供应负荷。
越大表明风储联合系统能替代越大的火电机组供应负荷。
在风储联合系统向负荷供电时,并不需要风电场维持稳定的输出,而是需要风储系统联合火电厂跟踪负荷。因此,需要着重研究风火储联合系统能够可靠供应的负荷大小,本节首先介绍负荷供应容量的定义及其计算方法。
考虑如图3所示的风火储联合系统,风电场和火电厂均能向储能设备存储电能,风电场、火电厂和储能系统也可以直接向电网输送电能。已知N组风电场功率输出及电网负荷需求的历史轨迹,每组历史轨迹的概率为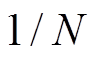 。其中,电网负荷需求历史轨迹根据电网负荷的日最大值归一化处理,反映了电网负荷的日内变化趋势。通过考虑风电场历史功率输出数据和电网负荷历史需求数据,可以估计风火储联合系统的负荷供应容量。
。其中,电网负荷需求历史轨迹根据电网负荷的日最大值归一化处理,反映了电网负荷的日内变化趋势。通过考虑风电场历史功率输出数据和电网负荷历史需求数据,可以估计风火储联合系统的负荷供应容量。
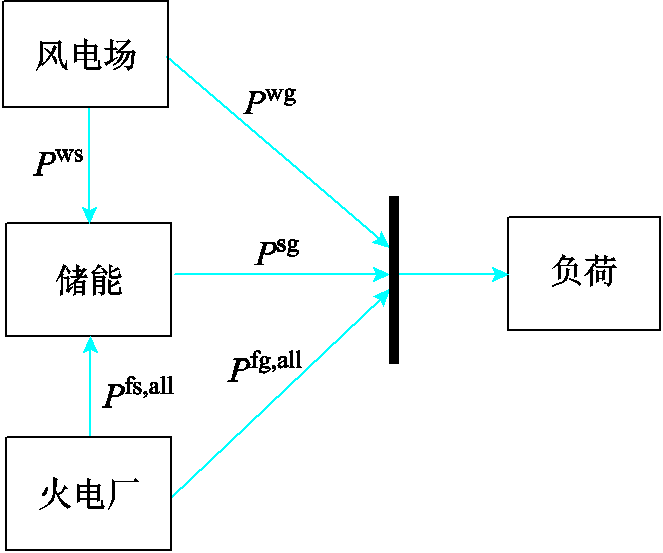
图3 风火储联合系统结构示意图
Fig.3 Schematic of the combined wind-thermal-storage system
风火储系统的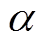 负荷供应容量定义如下:火电和储能设备的容量给定;风场容量已知;风电出力和负荷的归一化曲线已知。在一天内,储能设备和火电厂通过制定合理的调度策略,能使风火储联合系统能够满足峰值负荷为P的概率不小于
负荷供应容量定义如下:火电和储能设备的容量给定;风场容量已知;风电出力和负荷的归一化曲线已知。在一天内,储能设备和火电厂通过制定合理的调度策略,能使风火储联合系统能够满足峰值负荷为P的概率不小于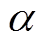 ,则称该风火储系统的
,则称该风火储系统的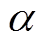 负荷供应容量不小于P。满足该条件的最大峰值负荷为该风火储系统的
负荷供应容量不小于P。满足该条件的最大峰值负荷为该风火储系统的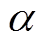 负荷供应容量,即
负荷供应容量,即
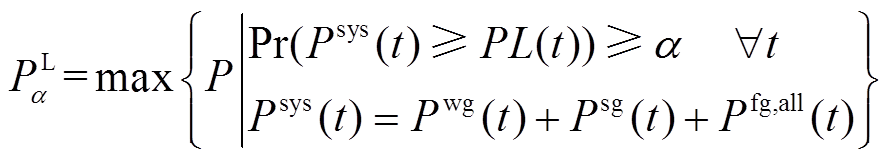 (10)
(10)
式中,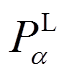 为置信概率为
为置信概率为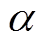 时系统的
时系统的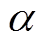 负荷供应容量;
负荷供应容量;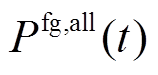 为t时刻火电厂向负荷供应的功率;
为t时刻火电厂向负荷供应的功率;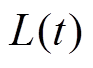 为t时刻负荷归一化数值。
为t时刻负荷归一化数值。
单日风火储系统输出功率及电网负荷需求如图4所示,彩色曲线(虚线)为风火储联合系统总出力,假设其功率输出均经过储能设备和火电厂的适当调节。黑色曲线(实线)为电网负荷需求曲线,最下方的黑色曲线(实线)为经过归一化处理后的负荷需求曲线。为了更简明地展示负荷供应容量的定义,仅在此图例中假设各个场景下电网负荷需求变化趋势一致。其余两条黑色曲线(实线)分别为最大值为 和
和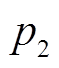 负荷需求曲线。根据
负荷需求曲线。根据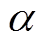 负荷供应容量定义,
负荷供应容量定义, 为风火储系统的100%负荷供应容量;
为风火储系统的100%负荷供应容量;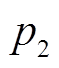 为风火储系统的50%负荷供应容量。
为风火储系统的50%负荷供应容量。
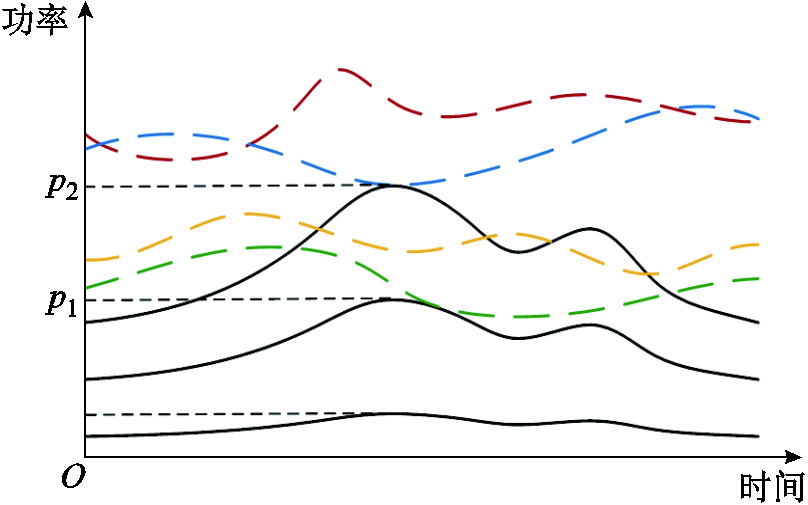
图4 单日风火储系统输出功率及电网负荷需求
Fig.4 The power output of the combined wind-thermal-storage system in one day and the power demand of the grid
根据风火储联合系统的风电场历史数据、储能设备、火电厂参数以及负荷需求历史数据,可以估计风火储联合系统的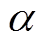 负荷供应容量。其中风电场运行约束和储能运行约束为式(2)~式(6),火电厂运行约束为
负荷供应容量。其中风电场运行约束和储能运行约束为式(2)~式(6),火电厂运行约束为
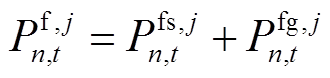 (11)
(11)
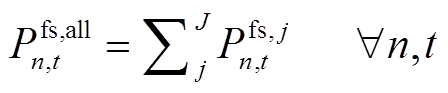 (12)
(12)
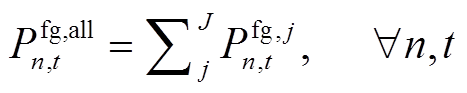 (13)
(13)
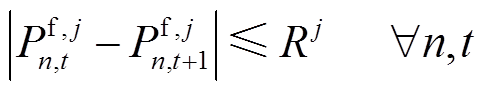 (14)
(14)
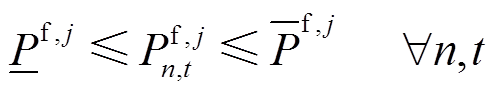 (15)
(15)
式中,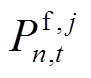 为火电厂第
为火电厂第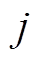 个机组在第
个机组在第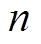 个场景
个场景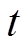 小时内输出的总功率;
小时内输出的总功率;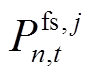 为火电厂第
为火电厂第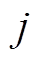 个机组在第
个机组在第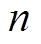 个场景
个场景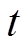 小时内向储能系统输出的功率;
小时内向储能系统输出的功率; 为火电厂第
为火电厂第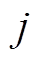 个机组在第
个机组在第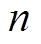 个场景
个场景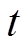 小时内向电网输出的功率;
小时内向电网输出的功率;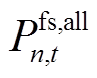 为火电厂在第
为火电厂在第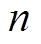 个场景
个场景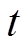 小时内向储能系统输出的总功率;
小时内向储能系统输出的总功率;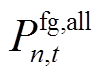 为火电厂在第
为火电厂在第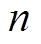 个场景
个场景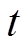 小时内向电网输出的总功率;
小时内向电网输出的总功率;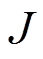 为火电厂内机组的总数;
为火电厂内机组的总数;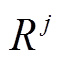 为第
为第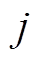 个机组的每小时上下爬坡上限;
个机组的每小时上下爬坡上限;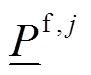 和
和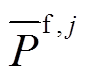 分别第
分别第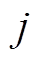 个机组的出力的下限和上限。
个机组的出力的下限和上限。
考虑到风火储联合系统的负荷供应的置信概率约束,风火储联合输出功率应当满足
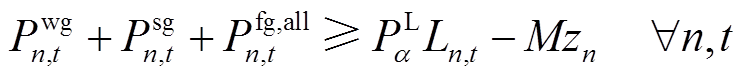 (16)
(16)
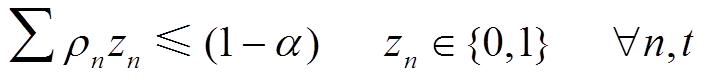 (17)
(17)
式中, 为第
为第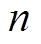 个场景
个场景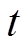 小时归一化处理后的电网负荷需求。本文中取
小时归一化处理后的电网负荷需求。本文中取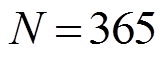 天以及
天以及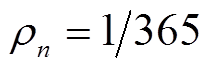 ;这些约束表示全年中有365
;这些约束表示全年中有365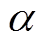 天负荷均被可靠供应。
天负荷均被可靠供应。
在置信概率为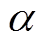 时,风火储联合系统的
时,风火储联合系统的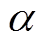 负荷供应容量可以通过求解混合整数线性规划式(18)得到。
负荷供应容量可以通过求解混合整数线性规划式(18)得到。
 (18)
(18)
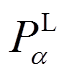 反映了在火电厂和储能系统合适的调控策略下,风火储联合系统能供应的最大电网负荷水平。
反映了在火电厂和储能系统合适的调控策略下,风火储联合系统能供应的最大电网负荷水平。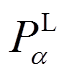 越大,表明风火储系统稳定支撑电网负荷的能力越强。
越大,表明风火储系统稳定支撑电网负荷的能力越强。
在上述火电替代容量和负荷供应容量模型中,储能设备的MW/(MW∙h)参数是给定的。在一定范围内增大储能容量,可以降低风电场弃风率,提高火电替代容量和负荷供应容量。然而储能设备成本目前仍然较高,其容量配置需要考虑逆变器(决定MW容量)和电池组(决定MW∙h容量)的成本,而成本参数往往在一定范围内变化。采用常规的优化方法只能计算某一确定成本下储能设备的最优参数配置。本文方法求解满足系统的安全运行要求,使风储系统或风火储系统满足火电替代容量或负荷供应容量要求的储能MW/(MW∙h)参数可行域,给储能设备规划和建设提供有益的参考。
针对风储联合系统,根据给定的火电替代容量指标配置储能设备参数。通过判断以下优化问题的可行性,可以确定储能设备MW/(MW∙h)参数可行域。
 (19)
(19)
式中,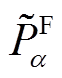 为要求风储联合系统需满足的火电替代容量指标;
为要求风储联合系统需满足的火电替代容量指标;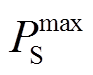 为储能设备建设的最大功率值;
为储能设备建设的最大功率值;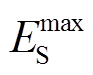 为储能设备建设的最大容量值。通过选取不同储能设备MW/(MW∙h)参数,并计算问题(19)的可行性,可获得基于火电替代容量的储能设备参数可行域边界。具体实现时,也可以求
为储能设备建设的最大容量值。通过选取不同储能设备MW/(MW∙h)参数,并计算问题(19)的可行性,可获得基于火电替代容量的储能设备参数可行域边界。具体实现时,也可以求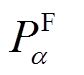 的最大值与
的最大值与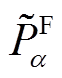 比较,若
比较,若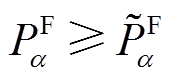 则问题(19)可行。实际上,该问题只要找到一个比
则问题(19)可行。实际上,该问题只要找到一个比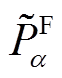 大的可行解即可断定式(19)可行;反之若将变量
大的可行解即可断定式(19)可行;反之若将变量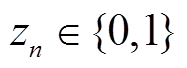 松弛为连续变量
松弛为连续变量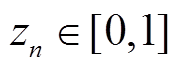 后仍然无解,则式(19)必定不可行。如此可以加速可行域的描绘过程。
后仍然无解,则式(19)必定不可行。如此可以加速可行域的描绘过程。
针对风火储联合系统,根据给定的负荷供应容量指标配置储能设备参数。储能设备MW/(MW∙h)参数可行域可通过判断以下优化问题的可行性得出
 (20)
(20)
式中,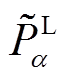 为要求风火储联合系统需满足的负荷供应容量指标。通过选取不同储能设备MW/(MW∙h)参数,并计算问题式(20)的可行性,可获得基于负荷供应容量的储能设备参数可行域边界。与式(19)同样的技巧可以应用于式(20)可行性的判断。
为要求风火储联合系统需满足的负荷供应容量指标。通过选取不同储能设备MW/(MW∙h)参数,并计算问题式(20)的可行性,可获得基于负荷供应容量的储能设备参数可行域边界。与式(19)同样的技巧可以应用于式(20)可行性的判断。
在获得满足系统火电替代容量指标和负荷供应容量指标的储能设备参数可行域后,根据储能设备的功率和容量成本,可通过线性规划的图解法直接确定储能系统的最优参数配置。已知储能设备的单位功率和容量的投资成本为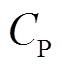 和
和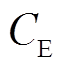 ,配置储能系统的总投资成本为
,配置储能系统的总投资成本为
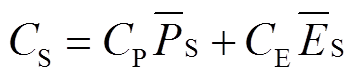 (21)
(21)
储能设备最优参数决策示意图如图5所示,蓝色曲线为储能设备MW/(MW∙h)参数可行域边界,若储能功率和容量投资成本在一定区间内,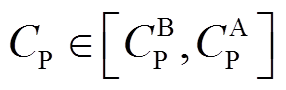 ,
,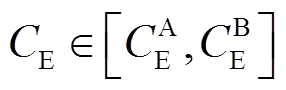 。根据成本区间计算目标函数斜率的边界值,应用线性规划图解法,参数点A和B即为最佳储能参数配置的边界点。那么,
。根据成本区间计算目标函数斜率的边界值,应用线性规划图解法,参数点A和B即为最佳储能参数配置的边界点。那么,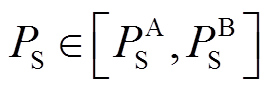 ,
, 为储能设备的最佳参数配置范围。根据风火储联合系统的实际需求,可以在此范围内选取合适的储能参数,实现储能设备的经济性配置。
为储能设备的最佳参数配置范围。根据风火储联合系统的实际需求,可以在此范围内选取合适的储能参数,实现储能设备的经济性配置。
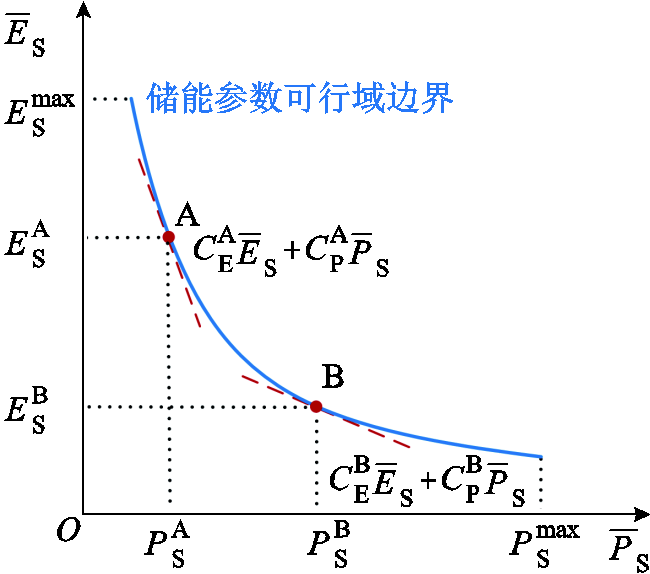
图5 储能设备最优参数决策示意图
Fig.5 Schematic of optimal parameters decision-making for energy storage equipment
针对风储联合系统,本文选用广东省风电场的全年最大理论功率输出作为风电场历史数据[19]。在该风储联合系统中,风电场总容量为100MW,储能设备的充电效率和放电效率均为0.95,储能设备建设最大功率为25MW,最大容量为150MW∙h,储能设备成本范围为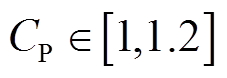 106元/MW,
106元/MW,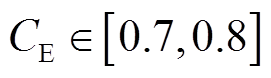 106元/(MW·h)。首先,配置不同的储能设备MW/(MW∙h)参数,计算风储联合系统的90%火电替代容量。
106元/(MW·h)。首先,配置不同的储能设备MW/(MW∙h)参数,计算风储联合系统的90%火电替代容量。
不同储能设备MW/(MW∙h)参数下,风储联合系统的90%火电替代容量如图6所示。随着储能功率和储能容量的增大,风储联合系统的火电替代容量显著的增大,这证明配置储能设备可以有效平抑风电场的功率波动,实现风电场功率的平稳输出。同时,在一定范围内,储能的功率和容量具有替代作用,减少部分储能功率可以通过增加储能容量来维持火电替代容量不变。但是火电替代容量的上限仍受风电场自身出力特性制约,当储能设备的功率和容量足够大时,风储联合系统的火电替代容量不再随储能功率和容量的增加而增大。因此,有必要从经济性的角度配置合适的储能MW/(MW∙h)参数。
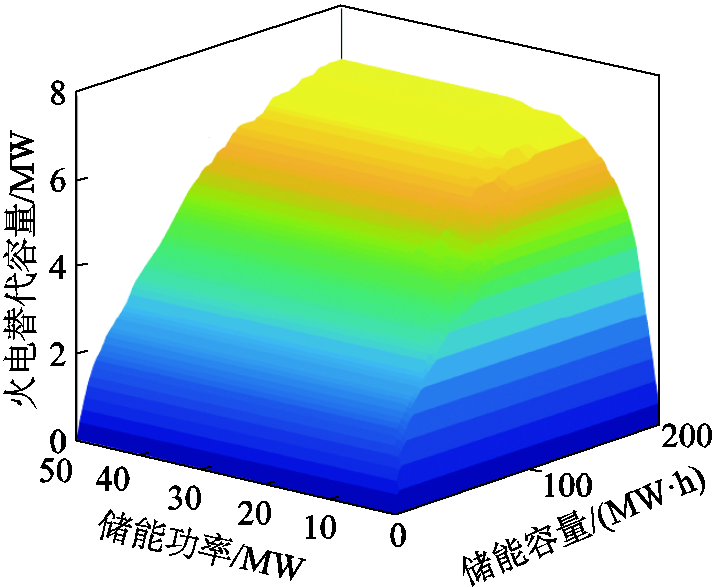
图6 风储联合系统90%火电替代容量
Fig.6 90% thermal power replacement capacity of the combined wind-storage system
在不同储能设备参数配置下,不同置信概率指标下的风储联合系统火电替代容量如图7所示。其中,火电替代容量随着置信概率的增加单调下降;在相同的置信概率下,储能设备的容量和功率越大,风储联合系统的火电替代容量越大。由于置信概率对系统火电概率影响显著,在根据该指标规划储能设备参数时,需要选取合适的置信概率,以平衡计算结果的可靠性和经济性。在图7中,在储能设备容量为20MW·h且置信概率大于0.8的条件下,储能功率为3MW、5MW、10MW时,风储联合系统火电替代容量差异较小,说明此时储能容量为火电替代容量的制约因素。综合图6来看,储能容量对火电替代容量影响更大。

图7 不同置信概率下风储联合系统火电替代容量
Fig.7 thermal power replacement capacity of the combined wind-storage system with different confidence probability
不同90%火电替代容量指标下的储能设备参数可行域如图8所示。浅色(蓝色)区域是满足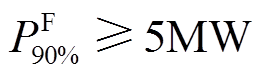 的储能设备MW/(MW∙h)参数可行域,深色(红色)区域是满足
的储能设备MW/(MW∙h)参数可行域,深色(红色)区域是满足 约束条件的储能设备MW/(MW∙h)参数可行域。图8中,蓝色区域远大于红色区域,表明越大的火电替代容量指标会导致越小的储能设备参数可行域。图8中的储能设备参数可行域边界呈现分段线性特征,当储能的MW/(MW∙h)参数经过特定数值时,参数可行域边界会发生突变。这是由式(19)混合整数线性规划的数学性质决定的,整数变量破坏了参数可行域边界的光滑性,使储能参数可行域边界会发生突变。
约束条件的储能设备MW/(MW∙h)参数可行域。图8中,蓝色区域远大于红色区域,表明越大的火电替代容量指标会导致越小的储能设备参数可行域。图8中的储能设备参数可行域边界呈现分段线性特征,当储能的MW/(MW∙h)参数经过特定数值时,参数可行域边界会发生突变。这是由式(19)混合整数线性规划的数学性质决定的,整数变量破坏了参数可行域边界的光滑性,使储能参数可行域边界会发生突变。
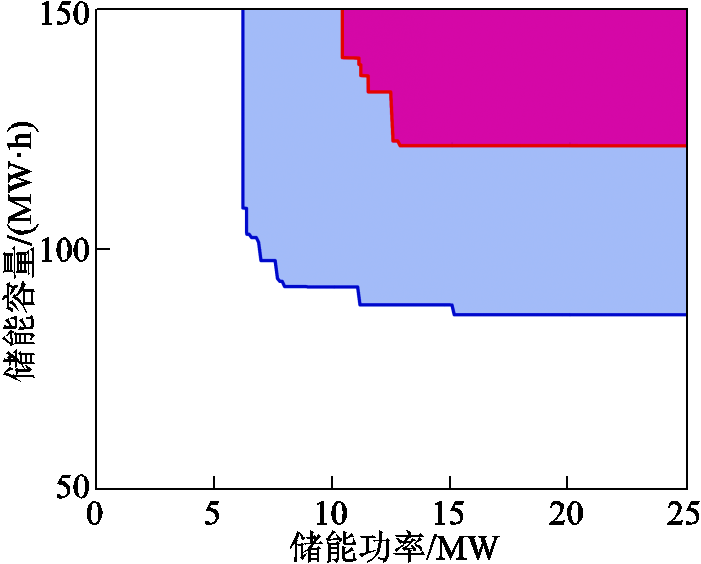
图8 90%火电替代容量指标下储能设备参数可行域
Fig.8 The parametric feasible reigon of the energy storage equipment with 90% thermal power replacement capacity
若以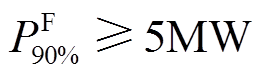 指标配置储能设备参数,根据图8中的储能设备参数可行域边界,可以得出在储能参数成本范围内,风储联合系统的最优储能配置结果,计算结果见表1,根据储能容量成本和功率成本的比值
指标配置储能设备参数,根据图8中的储能设备参数可行域边界,可以得出在储能参数成本范围内,风储联合系统的最优储能配置结果,计算结果见表1,根据储能容量成本和功率成本的比值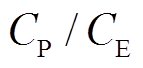 ,可以直接确定储能设备的最优参数配置结果。根据储能设备成本计算可得
,可以直接确定储能设备的最优参数配置结果。根据储能设备成本计算可得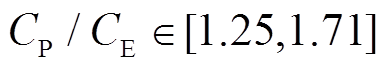 ,因此,在该储能成本价格区间内,储能设备最优参数配置为
,因此,在该储能成本价格区间内,储能设备最优参数配置为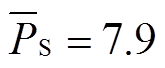 MW,
MW,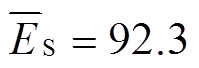 MW∙h。
MW∙h。
表1 基于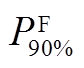 指标的储能设备最优参数配置
指标的储能设备最优参数配置
Tab. 1 The optimal parameters of the energy storage equtimenty base on the value of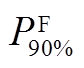

成本范围储能功率/MW储能容量/(MW∙h) 6.1108.6 6.3103.2 6.997.7 7.992.3 11.188.5 15.186.4
本节针对风火储联合系统,选用广东省风电场的全年最大理论出力作为风电历史数据,利用经过归一化处理的PJM市场负荷数据作为电网负荷需求变化曲线。其中,风电场和储能设备参数与4.1节一致。火电厂最大出力为20MW,火电厂最大爬坡速率为4MW/h。首先,通过改变火电厂和储能设备参数,研究这些参数对系统风电场负荷替代容量的影响。
不同火电厂功率和储能设备参数下的风电场90%负荷供应容量如图9所示,其中储能功率和容量始终保持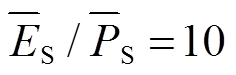 。随着火电厂功率的增大,风电厂负荷供应容量不断增大,随着储能功率的增大,风电场负荷供应容量呈现先增大后饱和的趋势。和储能设备相比,火电厂因为没有存储容量的限制,具有更大的调节潜力。但是由于储能设备的双向调节作用,配置合适的储能设备对提升风电场负荷供应容量有明显效果。
。随着火电厂功率的增大,风电厂负荷供应容量不断增大,随着储能功率的增大,风电场负荷供应容量呈现先增大后饱和的趋势。和储能设备相比,火电厂因为没有存储容量的限制,具有更大的调节潜力。但是由于储能设备的双向调节作用,配置合适的储能设备对提升风电场负荷供应容量有明显效果。
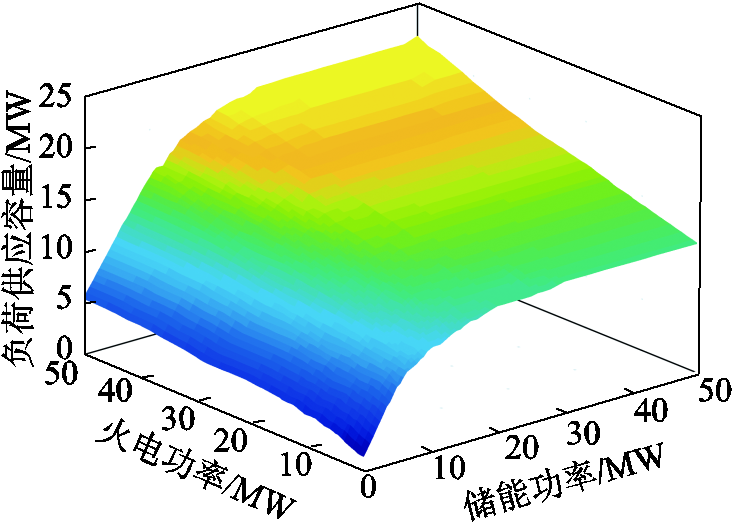
图9 不同的火电厂和储能设备参数下的风电场90%负荷供应容量
Fig.9 90% load supply capacity of the wind farm with different thermal power plant and energy storage equipment parameters
不同储能功率和容量下风电场90%负荷供应容量如图10所示,其中火电厂功率为20MW。在一定范围内,提升储能功率和容量均能增大风电场负荷供应容量。同时储能功率和容量具有替代作用,在储能功率减少时,可以通过增加储能容量来维持风电场负荷供应容量保持不变。因此,可以通过合理配置储能设备参数,实现系统的经济性配置。
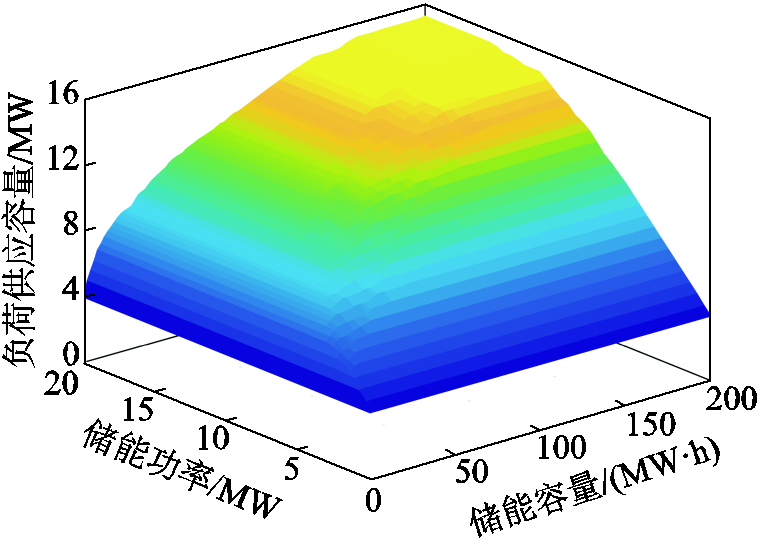
图10 不同储能设备参数下的风电场90%负荷供应容量
Fig.10 90% load supply capacity of the wind farm with different energy storage equipment parameters
不同储能参数下,不同置信概率的风电场负荷供应容量如图11所示。其中,风电场负荷供应容量随置信概率的增大单调递减。在相同置信概率下,储能设备功率和容量越大,风电场负荷供应容量越大。在图11中,当储能设备功率输出为5MW,储能设备容量分别为20MW∙h、50MW∙h、80MW∙h时,系统负荷供应容量变化不大;当储能设备容量为50MW∙h,储能设备功率为2MW、5MW、8MW时,系统负荷供应容量随储能功率增加显著提高。因此,储能功率对负荷供应容量影响更大。由于置信概率对负荷供应容量指标影响显著,在根据该指标规划储能设备参数时,应选取合适的置信概率以兼顾系统的经济性和可靠性。
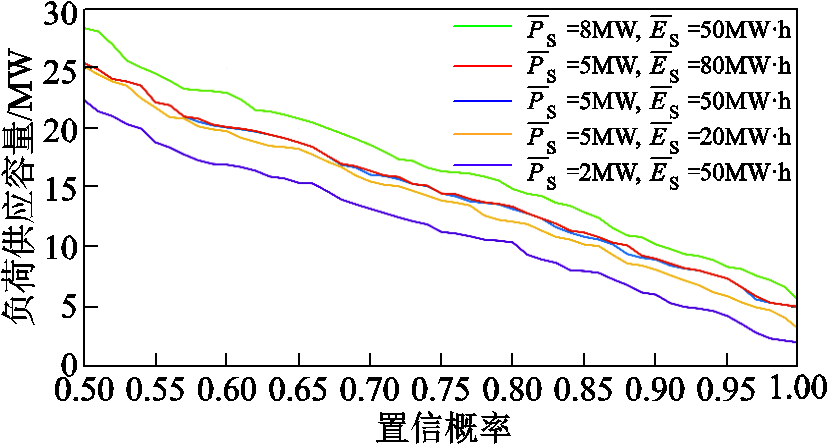
图11 不同置信概率下风电场负荷供应容量
Fig.11 Load supply replacement capacity of the wind farm with different confidence probability
90%负荷供应容量指标下储能设备参数可行域如图12所示,浅色(蓝色)区域是满足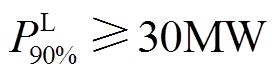 的储能设备MW/(MW∙h)参数可行域,深色(红色)区域是满足
的储能设备MW/(MW∙h)参数可行域,深色(红色)区域是满足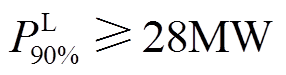 约束条件的储能设备MW/(MW∙h)参数可行域。图12中蓝色区域远大于红色区域,表明越高的负荷供应容量指标对应越小的储能设备参数可行域。同样地,由于式(20)中含有整数变量,该储能设备参数可行域呈现出突变的特征。
约束条件的储能设备MW/(MW∙h)参数可行域。图12中蓝色区域远大于红色区域,表明越高的负荷供应容量指标对应越小的储能设备参数可行域。同样地,由于式(20)中含有整数变量,该储能设备参数可行域呈现出突变的特征。
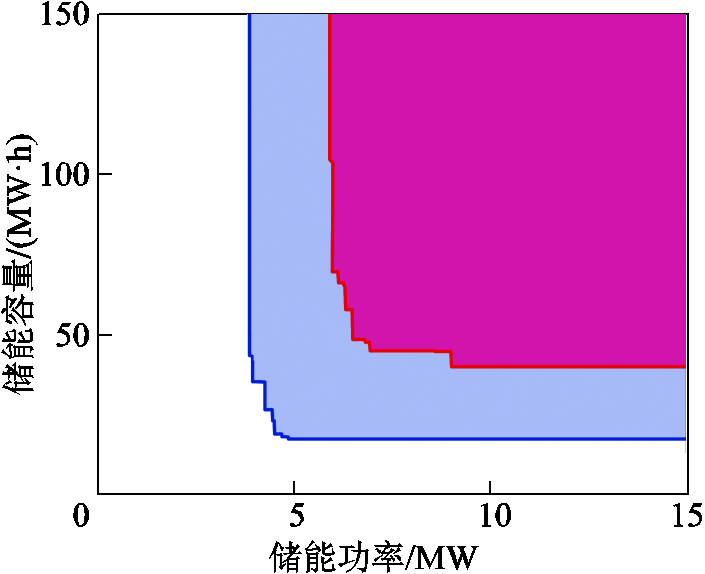
图12 90%负荷供应容量指标下储能设备参数可行域
Fig.12 The parametric feasible reigon of the energy storage equipment with 90% load supply capacity
若以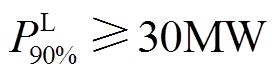 为指标配置储能设备参数,根据图12中的储能设备参数可行域边界,可以分析出储能不同参数成本范围下,风火储联合系统的最优储能参数配置结果,计算结果见表2。同样地,根据
为指标配置储能设备参数,根据图12中的储能设备参数可行域边界,可以分析出储能不同参数成本范围下,风火储联合系统的最优储能参数配置结果,计算结果见表2。同样地,根据 可以直接确定储能最优参数配置为
可以直接确定储能最优参数配置为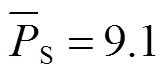 MW,
MW,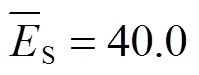 MW·h。
MW·h。
表2 基于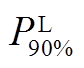 指标的储能设备最优参数配置
指标的储能设备最优参数配置
Tab.2 The optimal parameters of the energy storage equtimenty base on the value of 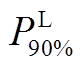

成本范围储能功率/MW储能容量/(MW∙h) 6.0104.3 6.169.5 6.648.5 7.045.0 9.140.0
为了和传统储能参数配置方法比较,本节选用文献[12]中的方法配置储能参数。此方法借助离散傅里叶变化分析风电场功率输出,将长周期和短周期功率波动解耦。将部分频段的功率输出加以补偿,可以获取经功率平抑后的风储联合系统功率输出,按照该功率和风电场功率输出差值确定储能设备应配置的最大功率,再根据仿真法确定储能设备的容量配置。
根据本文的算例数据,按照此方法应配置储能设备功率为3.21MW,储能容量为407MW∙h。与本文方法相比,该方法配置结果过于激进,因为该方法没有引入置信概率的概念,无法考虑风电场连续多日无风的场景,储能设备需要配置较大容量来实现储能设备稳定的功率输出。因此,这种方法难以有效地根据风电不确定性配置储能设备容量参数,具有一定局限性。而本文通过引入置信容量的概念,有效地避免了风电不确定性对于容量配置造成的影响,能够保证储能设备参数配置的经济性和负荷供应的可靠性。
为了平抑风电场输出功率的间歇性和随机性,需要配置储能设备以平滑风电场功率输出。本文根据风电场历史数据,分别定义了风电场火电替代容量和负荷供应容量,该指标可以考察风电场平稳输出功率的能力。通过配置储能设备,可以有效提高风电场火电替代容量和负荷供应容量,实现风电场可靠运行。根据以上指标,本文提出了储能设备最优参数配置方法,通过计算储能设备参数可行域,可以快速确定不同成本参数范围的储能设备最优参数配置。在具体的工程实践中,可以根据实际需求选取火电替代容量和负荷供应容量指标,如:可以按照电网联络线功率计划值和系统的最大负荷需求值确定指标需求。当风储联合系统需要通过联络线向电网输送功率时,需要使系统火电替代容量大于联络线功率计划值;当风火储联合系统需要稳定供应区域负荷时,需要使系统负荷供应容量大于负荷峰值。按照类似的方法选取合适的指标,可以使储能设备参数满足系统的实际运行需求,保证系统安全稳定运行。同时,本方法兼顾了储能最优参数配置的经济性和可靠性,能够有效解决储能成本在一定区间范围内变动的问题。
参考文献
[1] 周孝信, 陈树勇, 鲁宗相, 等. 能源转型中我国新一代电力系统的技术特征[J]. 中国电机工程学报, 2018, 38(7): 1893-1904, 2205.
Zhou Xiaoxin, Chen Shuyong, Lu Zongxiang, et al. Technology features of the new generation power system in China[J]. Proceedings of the CSEE, 2018, 38(7): 1893-1904, 2205.
[2] Renewable Energy Policy Network for the 21st Century.Renewables 2021 global status report[R]. 2021. https://www.ren21.net/reports/global-status-report.
[3] 康重庆, 姚良忠. 高比例可再生能源电力系统的关键科学问题与理论研究框架[J]. 电力系统自动化, 2017, 41(9): 2-11.
Kang Chongqing, Yao Liangzhong. Key scientific issues and theoretical research framework for power systems with high proportion of renewable energy[J]. Automation of Electric Power Systems, 2017, 41(9): 2-11.
[4] 朱瑛, 高云波, 臧海祥, 等. 风电机组输出功率平滑技术综述[J]. 电力系统自动化, 2018, 42(18): 182-191.
Zhu Ying, Gao Yunbo, Zang Haixiang, et al. Review of output power smoothing technologies for wind turbine[J]. Automation of Electric Power Systems, 2018, 42(18): 182-191.
[5] Zhao Haoran, Wu Qiuwei, Hu Shuju, et al. Review of energy storage system for wind power integration support[J]. Applied Energy, 2015, 137: 545-553.
[6] Yang Yuqing, Bremner S, Menictas C, et al. Battery energy storage system size determination in renewable energy systems: a review[J]. Renewable and Sustainable Energy Reviews, 2018, 91: 109-125.
[7] 李军徽, 张嘉辉, 李翠萍, 等. 参与调峰的储能系统配置方案及经济性分析[J]. 电工技术学报, 2021, 36(19): 4148-4160.
Li Junhui, Zhang Jiahui, Li Cuiping, et al. Configuration scheme and economic analysis of energy storage system participating in grid peak shaving[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4148-4160.
[8] 李建林, 郭斌琪, 牛萌, 等. 风光储系统储能容量优化配置策略[J]. 电工技术学报, 2018, 33(6): 1189-1196.
Li Jianlin, Guo Binqi, Niu Meng, et al. Optimal configuration strategy of energy storage capacity in wind/PV/storage hybrid system[J]. Transactions of China Electrotechnical Society, 2018, 33(6): 1189-1196.
[9] 陈泽西, 孙玉树, 张妍, 等. 考虑风光互补的储能优化配置研究[J]. 电工技术学报, 2021, 36(增刊1): 145-153.
Chen Zexi, Sun Yushu, Zhang Yan, et al. Research on energy storage optimal allocation considering complementarity of wind power and PV[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 145-153.
[10] 熊宇峰, 司杨, 郑天文, 等. 基于主从博弈的工业园区综合能源系统氢储能优化配置[J]. 电工技术学报, 2021, 36(3): 507-516.
Xiong Yufeng, Si Yang, Zheng Tianwen, et al. Optimal configuration of hydrogen storage in industrial park integrated energy system based on stackelberg game[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 507-516.
[11] 吴杰, 丁明, 张晶晶. 基于云模型和K-means聚类的风电场储能容量优化配置方法[J]. 电力系统自动化, 2018, 42(24): 67-73.
Wu Jie, Ding Ming, Zhang Jingjing. Capacity configuration method of energy storage system for wind farm based on cloud model and K-means clustering[J]. Automation of Electric Power Systems, 2018, 42(24): 67-73.
[12] 王成山, 于波, 肖峻, 等. 平滑可再生能源发电系统输出波动的储能系统容量优化方法[J]. 中国电机工程学报, 2012, 32(16): 1-8.
Wang Chengshan, Yu Bo, Xiao Jun, et al. Sizing of energy storage systems for output smoothing of renewable energy systems[J]. Proceedings of the CSEE, 2012, 32(16): 1-8.
[13] 李滨, 陈姝, 韦化. 风电场储能容量优化的频谱分析方法[J]. 中国电机工程学报, 2015, 35(9): 2128-2134.
Li Bin, Chen Shu, Wei Hua. Optimization of energy storage capacity based on spectral analysis for wind farm[J]. Proceedings of the CSEE, 2015, 35(9): 2128-2134.
[14] 黄金鑫, 李华强, 陆杨. 基于蒙特卡洛模拟和频谱分析法的孤岛微电网储能容量配置[J]. 电网技术, 2020, 44(5): 1622-1629.
Huang Jinxin, Li Huaqiang, Lu Yang. Energy storage capacity configuration of isolated microgrid based on Monte Carlo simulation and spectrum analysis[J]. Power System Technology, 2020, 44(5): 1622-1629.
[15] 孙玉树, 唐西胜, 孙晓哲, 等. 风电波动平抑的储能容量配置方法研究[J]. 中国电机工程学报, 2017, 37(S1): 88-97.
Sun Yushu, Tang Xisheng, Sun Xiaozhe, et al. Research on energy storage capacity allocation method for smoothing wind power fluctuations[J]. Proceedings of the CSEE, 2017, 37(S1): 88-97.
[16] 李学斌, 赵号. 基于维纳随机过程的风电场储能配置方法[J]. 电网技术, 2022, 46(9): 3437-3446.
Li Xuebin, Zhao Hao. Wind farm energy storage configuration based on Wiener stochastic process[J]. Power System Technology, 2022, 46(9): 3437-3446.
[17] 司杨, 陈来军, 陈晓弢, 等. 基于分布鲁棒的风-氢混合系统氢储能容量优化配置[J]. 电力自动化设备, 2021, 41(10): 3-10.
Si Yang, Chen Laijun, Chen Xiaotao, et al. Optimal capacity allocation of hydrogen energy storage in wind-hydrogen hybrid system based on distributionally robust[J]. Electric Power Automation Equipment, 2021, 41(10): 3-10.
[18] 杨立滨, 曹阳, 魏韡, 等. 计及风电不确定性和弃风率约束的风电场储能容量配置方法[J]. 电力系统自动化, 2020, 44(16): 45-52.
Yang Libin, Cao Yang, Wei Wei, et al. Configuration method of energy storage for wind farms considering wind power uncertainty and wind curtailment constraint[J]. Automation of Electric Power Systems, 2020, 44(16): 45-52.
[19] Pfenninger S, Staffell I. Long-term patterns of European PV output using 30 years of validated hourly reanalysis and satellite data[J]. Energy, 2016, 114: 1251-1265.
Optimal Configuration of Energy Storage Parameters Based on Confidence Capacity of Wind Farms
Abstract Wind power generation has the characteristics of random fluctuation and intermittence. The energy storage equipment can be used to smooth the output of the wind farm, which can replace thermal power plants and provide a reliable load supply for the grid. Firstly, based on the wind resource characteristics, we define the thermal power replacement capacity and load supply capacity of wind farms, which reflect the ability of wind farms to output smoothly and supply loads reliably. Given wind resource data and confidence probability requirements, thermal power replacement capacity and load supply capacity can be solved by mixed integer linear programming. According to the requirements of the thermal power replacement capacity and load supply capacity, we construct an optimal configuration method for MW/(MW·h) parameters of the energy storage. This method calculates the boundary of the parameter feasible region and then determines the range of optimal parameter configuration according to the energy storage cost coefficient. In the case study, the historical data of wind farms in Guangdong province is used. It shows that our method can determine the optimal parameter configuration of energy storage quickly, while taking into account the economy and the reliability and stability of the power supply.
keywords:Wind power generation, thermal power replacement capacity, load supply capacity, energy storage equipment, capacity configuration
DOI:10.19595/j.cnki.1000-6753.tces.220939
中图分类号:TM715
南方电网公司科技资助项目(03600KK52200049(GDKJXM20201978))。
收稿日期 2022-05-30
改稿日期 2022-09-24
陆秋瑜 女,1989年生,高级工程师,研究方向为新能源电力系统运行调控。E-mail:luqiuyu22@126.com
马千里 男,1998年生,博士,研究方向为电力系统优化调度与控制。E-mail:mql19@mails.tsinghua.edu.cn (通信作者)
(编辑 赫蕾)