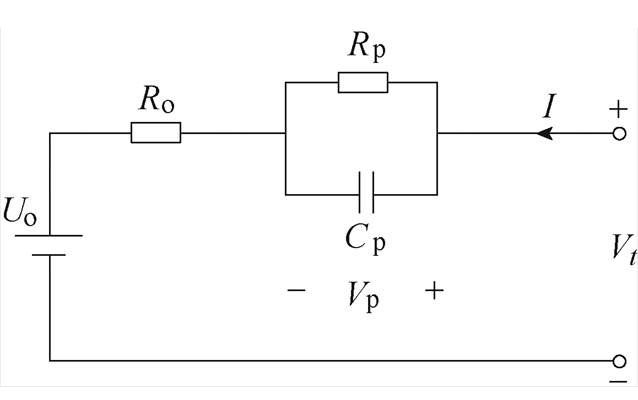
图1 Thevenin等效电路模型
Fig.1 Thevenin equivalent circuit model
摘要 在电力系统中,电池储能得到了广泛的应用,为了保证电池储能系统的运行效果,有必要对电池状态进行准确估计,电池实际可以充入的电量在一定程度上决定了电池的能量存储能力,然而仅通过电池电压、电流和温度等外部特性参数难以准确体现电池实际可充入电量状态,尤其在电池健康状态衰退的不同阶段其可充入电量估计问题一直以来都难以得到有效解决。因此,该文以Thevenin等效电路模型为基础,提出了电池可充入电量的概念,构建了可充入电量与电池开路电压(OCV)的对应关系曲线,分析了电池老化后直流内阻变化对电池可充入电量的影响,提出了基于双自适应双扩展卡尔曼滤波(ADEKF)的电池状态和模型参数联合估计方法,实现了任意老化状态电池的可充入电量在线估计。以3节不同老化程度的三元锂电池为研究对象,在联邦城市运行工况(FUDS)下验证电池状态和模型参数估计结果,在0.5C倍率恒流充电工况下验证可充入电量损失的估计结果。实验结果表明,对于新电池,FUDS工况下可充入电量估计误差小于1%,对于实验用老化电池,最大可充入电量估计误差为2.7%。通过3节不同老化程度电池在恒流0.5C倍率恒流充电下的状态估计结果比较,进一步验证了所提方法对可充入电量估计的有效性。
关键词:锂离子电池 老化 状态估计 可充入电量
电池储能系统具有配置灵活、高效稳定、响应迅速等特点,被广泛应用于电力系统的诸多领域,有效解决了发电和用电在时间和空间上的不平衡问题。国家能源局《“十四五”能源规划工作方案》中明确指出,大力发展风能和太阳能等可再生能源,而可再生能源在能量转换的连续性和稳定性方面具有不确定性,这就需要储能电池系统提供稳定可靠的能量存储,从而保证电网的稳定运行[1]。由于现有储能电池的制造工艺水平无法满足大容量、高一致性和长使用寿命的应用需求,电池经过串联或者并联构成电池模组或电池系统后,在经历长期循环充放电使用后,其电压、电量以及老化的一致性难以保障,对电池参数的辨识、优化运行调度以及均衡维护都带来了不利的影响,同时对系统级调度和安全运行也提出了新的挑战。
储能用锂离子电池老化受环境温度、正负极材料特性等诸多因素影响[2-3]。随着电池的老化,其开路电压曲线和内阻状态都会产生变化[4],导致实际可以充入的电量衰退,为了对可充入电量进行有效估计,电池参数的准确辨识是必不可少的手段。
目前,常见的电池参数辨识方法可以分为离线和在线两种类型。离线的方法主要通过混合脉冲功率测试(Hybrid Pulse Power Characteristic, HPPC)实验得到电池在脉冲电流下的电压数据,再利用得到的数据配合曲线拟合算法获取电池的模型参数。常用的曲线拟合算法有最小二乘法以及一些基于最小二乘法的改进算法[5]。文献[6]提出一种基于信息反馈粒子群优化(Feedback Particle Swarm Optimi- zation, FPSO)的参数辨识方法,旨在促进粒子局部最优位置和全局最优位置持续更新以提高寻优精度。离线方法获取的模型参数虽然准确度高,但采样点数量有限,而且模型估计精度还会受到电池温度和老化程度的影响。在线模型参数辨识方法一般会与状态估计进行联合估计,如文献[7]中利用带遗忘因子的递推最小二乘法对动态变化的模型参数进行实时在线辨识,同时采用自适应卡尔曼滤波算法对荷电状态(State of Charge, SOC)估计不断修正更新,消除系统未知噪声所引起的误差。联合估计的方式虽然提高了估计精度,但同时也加大了计算量。文献[8]根据模型参数变化较为缓慢的特点,提出了基于多尺度扩展卡尔曼滤波的电池参数及状态估计方法,保证精度的同时也降低了计算量。
电池的实际可用电量可以通过分别得到电池的SOC和健康状态(State of Health, SOH)来确定。
现有SOC估计方法可以分为基础方法、基于模型和滤波算法的方法以及基于数据驱动的方法[9-10]。估计电池SOC的基础方法主要有安时积分法[11]和开路电压法[12]。安时积分法需要准确的SOC初始值,且存在累计误差。开路电压法需要长时间静置。基于模型和滤波算法的估计方法中主要利用的滤波算法有高斯滤波(Gaussian Process, GP)[13]、粒子滤波(Particle Filter, PF)[14-15]、序列蒙特卡罗滤波(Sequential Monte Carlo Filter, SMCF)[16]和扩展卡尔曼滤波(Extended Kalman Filter, EKF)[17]等。其中,EKF的基本原理决定了其在时间域内以递推的形式实现对状态方程的“预测-修正”,在求解时无需存储大量数据,只需要根据观测的数据进行滤波处理,就可以实现状态估计,非常适合于实时处理和计算机实现,该方法被广泛应用于SOC估计。为了提高估计方法精度,在EKF算法的基础上提出了一系列的改进方法,如自适应扩展卡尔曼滤波(Adaptive Extended Kalman Filter, AEKF)[18]、自适应无迹卡尔曼滤波(Adaptive Unscented Kalman Filter, AUKF)[19]和自适应平方根无迹卡尔曼滤波(adaptive Square- Root Unscented Kalman Filter, SRUKF)[20]等。基于数据驱动的SOC估计方法主要通过大量电池的数据训练模型来获得较为准确的电池模型,以电池的电压、电流和温度等作为模型的输入,输出为电池的SOC。主要的方法包括了支持向量机方法[21-22]、神经网络方法[23]和模糊控制器方法[24]等。
现有容量估计方法可以分为数据驱动法和基于容量增量分析(Incremental Capacity Analysis, ICA)/微分电压分析(Differential Voltage Analysis, DVA)的方法。数据驱动法从电池充放电电压、电流曲线中提取与电池容量衰减相关的特征因子,利用机器学习相关的智能算法,结合大量数据训练建立估计模型。主要的方法有支持向量回归(Support Vector Regression, SVR)[25]、神经网络[23]和模糊逻辑[26]等。容量增量分析作为一种非入侵式的方法,过去被广泛用于研究锂离子电池的老化机理,而研究表明,使用ICA观察容量增量(Incremental Capacity, IC)曲线特征峰在电池寿命期间的变化,同样可以用来估计容量[27]。文献[28]利用ICA技术,将电池容量衰减与IC曲线中峰、谷及相应的电压值相关联,在不同温度下从12个度量点中提取了4个与电池老化趋势一致的度量点,利用这4个点建立电池容量的演化模型,结果显示4个模型均能准确估算电池容量。
综合现有研究,在电池实际可充入电量估计方面存在的问题如下:
(1)电池外部特性参数电压、电流和温度等难以直接表征电池当前容量和电量状态。
(2)基于数据驱动的电池状态估计方法需要大量前期实验数据作为基础数据,前期工作量巨大,而且老化轨迹具有不确定性,很难保证训练结果的普适性。
(3)现有的研究中,只能通过在线估计电池的SOC和容量,间接估计电池的实际可充入电量,这会导致估计误差叠加。
基于以上问题,本文通过建立电池Thevenin等效电路模型,利用双自适应扩展卡尔曼滤波(dual Adaptive Dual Extended Kalman Filter, ADEKF)分别实现电池模型参数的辨识和可充入电量的估计。分别利用全新电池和老化电池,采用所提出的方法进行实验验证,在对老化电池进行可充入电量估计时,只需要全新状态下单次工况测试结果就可以实现电池可充入电量与开路电压(Open Circuit Voltage, OCV)之间的对应关系的获取,并以此为输入结合ADEKF算法实现单体在全生命周期任意老化状态的可充入电量准确估计,具有工程应用价值。
电池模型的建立是电池状态估计的基础,电池模型参数辨识结果可以用于电池可充入电量的有效估计。由于等效电路模型结构简单、参数获取方便和易于实现锂电池模拟等特性被广泛应用,本文在考虑模型效果和模型复杂程度等因素后选择使用最为广泛的Thevenin等效电路模型,模型电路如图1所示。图中,Uo为电池的开路电压,开路电压可以表示为SOC的函数,Ro为电池欧姆内阻,Rp为电池极化内阻,Cp为电池极化电容,Vp为极化电压,I为电池工作电流,充电为正,Vt为t时刻电池端电压。

图1 Thevenin等效电路模型
Fig.1 Thevenin equivalent circuit model
根据基尔霍夫电压定律和基尔霍夫电流定律可以得到Thevenin等效电路模型的数学表达式为
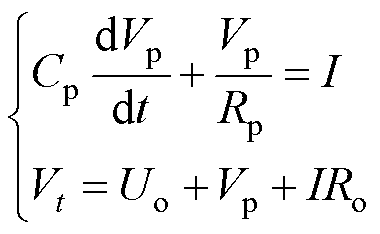 (1)
(1)
假定电池电压和电流的采样时间间隔为ts,则可以将式(1)进行离散化,有
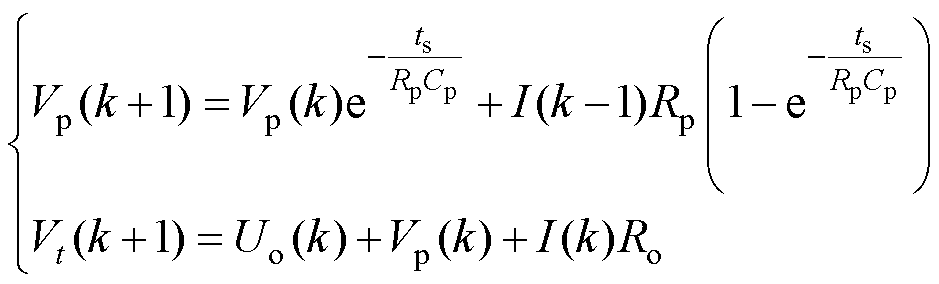 (2)
(2)
式中,k和k+1分别为k时刻和k+1时刻。
在电池等效电路模型分析的基础上,本节从老化电池实际可充入电量的角度进行分析,电池的实际可充入电量Qcha_act为
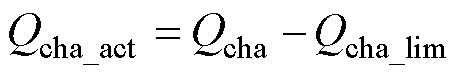 (3)
(3)
式中,Qcha为电池的理论可充入电量,即忽略内阻影响的可充入电量;Qcha_lim为电池受直流内阻影响损失的可充入电量。因此,获取电池的实际可充入电量需要先获取电池的理论可充入电量和受直流内阻影响损失的可充入电量。
电池的理论可充入电量的表达式为
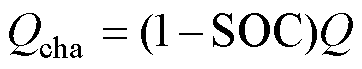 (4)
(4)
式中,Qcha为电池的理论可充入电量;SOC为电池的当前荷电状态;Q为电池实际容量。电池实际容量是表征电池能量存储能力的重要指标,一般根据出厂手册的要求进行恒流-恒压(Constant Current- Constant Voltage, CC-CV)充电,在恒流充电阶段,当达到上限截止电压时转为恒压充电模式,静置一段时间后,以恒定电流倍率放电,当达到下限截止电压时停止放电。以放出电量的安时数来表示电池的容量。CV过程在整个充电过程中的作用是通过降低充电电流使电池尽量达到充满状态,也可以通过采用极小电流1/20C倍率进行充电来尽量减小内阻对电池充入电量的影响。下文的讨论中理论可充入电量简称为可充入电量,考虑内阻影响的可充入电量简称实际可充入电量。
随着电池的循环使用,电池实际容量衰退,并伴随着电池内阻的增大。相关研究表明,金属锂在负极表面沉积形成固态电解质界面(Solid Electrolyte Interface, SEI)膜的同时阻碍锂离子的嵌入和脱出是造成电池容量衰退和内阻增大的主要原因[29]。根据图1中的电池等效电路分析可知,内阻的增大在一定程度上会加快充电时单体达到上限截止电压,从而减少可充入电量。为了得到老化电池的实际可充入电量,不仅要考虑电池自身老化对电池实际容量的影响,还需要对直流内阻影响的可充入电量损失进行计算。根据电池的Thevenin等效电路模型可得,在充电过程中,电池的端电压为
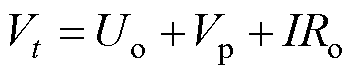 (5)
(5)
端电压的组成包含了三个部分,等式(5)右侧第一部分是电池的OCV,第二部分是电池的极化内阻产生的电压,第三部分是电池的欧姆内阻产生的电压。其中,由于充电过程的电流是恒定不变的,可以近似得到
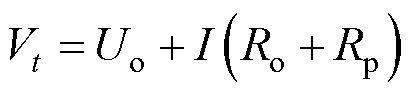 (6)
(6)
此时电池端电压只受到OCV和直流内阻产生压降的影响。在充电过程中电池的电压曲线如图2所示。
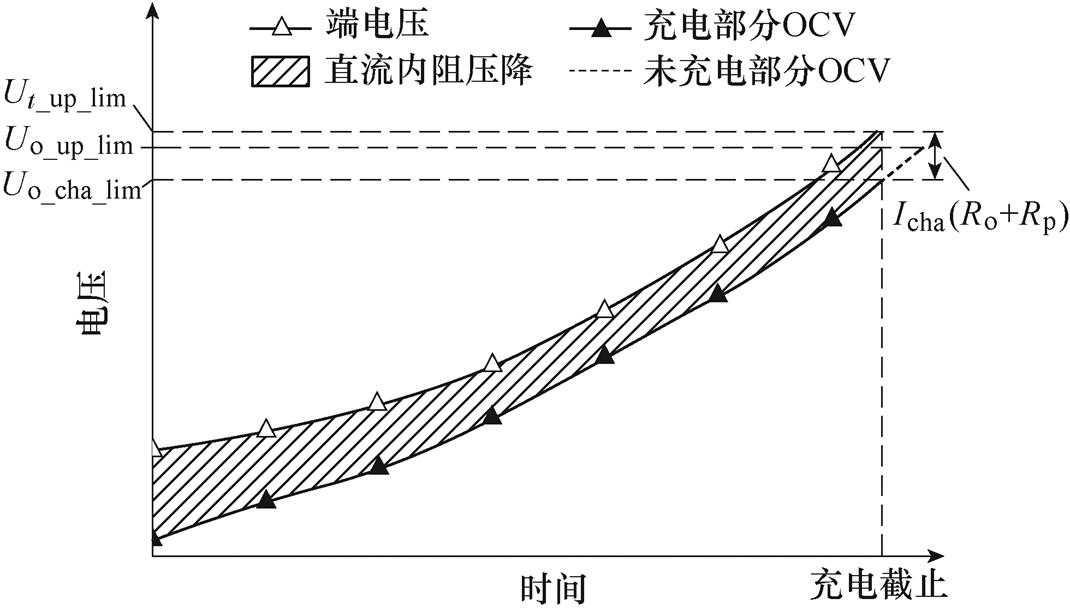
图2 充电过程中电池的电压曲线
Fig.2 The voltage curve of the battery during charging
从图2中可以看出,当电池端电压达到上限截止电压Ut_up_lim时,电池的OCV还没有达到上限值Uo_up_lim,此时理论上可充入电量不为零,但电池不能继续充电。理想情况下,忽略电池内阻的影响,电池充电过程的端电压曲线将与OCV曲线重合。实际情况下,考虑到内阻的影响,电池将提前达到上限截止电压。这部分由于电池内阻造成的可充入电量损失用Qcha_lim表示,其数值可以用端电压达到上限截止电压和OCV达到上限截止电压时刻之间充入的电量来计算。电池的充电电流Icha和端电压上限截止电压Ut_up_lim是已知的,根据式(6)可以得出电池充电时端电压的截止条件表达式为
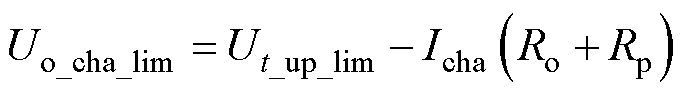 (7)
(7)
式中,Uo_cha_lim为电池充电时开路电压的上限。欧姆内阻Ro和极化内阻Rp可通过模型参数估计获得。
综合以上分析,考虑到老化电池的实际可充入电量在线估计问题,如果通过SOC和容量间接估计电池可充入电量,不仅会使估计的可充入电量误差受到SOC和容量估计误差的叠加,而且二者同时在线估计会增加计算量。因此,为了获取精确的可充入电量,本文直接将可充入电量作为估计对象,通过开路电压与SOC的对应关系得到其与可充入电量之间的对应关系。
根据电池的OCV和SOC存在单调对应关系,将电池SOC用电池的理论可充入电量和实际容量进行替换,其表达式为
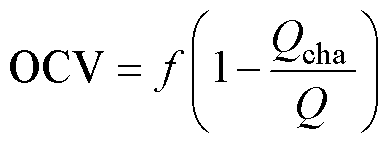 (8)
(8)
电池在正常使用情况下,容量的衰退是缓慢的,在单次循环内可以认为电池容量是不变的。根据式(8)可以得出,OCV与电池可充入电量也存在非线性对应关系。类比于OCV-SOC曲线,可以得到OCV-Qcha多项式拟合曲线。如果能够在线获得电池开路电压曲线,就可以间接获得可充入电量的估计结果。对于具有不同老化程度的电池单体,随着循环老化次数的增加,电池容量和OCV-SOC曲线会产生变化,OCV-Qcha曲线也会随之变化。如果在参数设置时以全新电池参数对电池不同老化状态的可充入电量进行估计,将会使估计误差增大。因此,在对电池可充入电量进行在线估计的同时,还需要对OCV-Qcha曲线进行实时更新来适应电池老化带来的影响。下一节将利用基于ADEKF的状态联合估计方法对老化电池可充入电量进行估计。
为了有效估计老化电池可充入电量,建立电池模型并进行状态估计是必不可少的方法。为了辨识获得电池模型参数和OCV的结果,采用ADEKF方法来实现电池状态参数和可充入电量的联合估计。
卡尔曼滤波(Kalman Filter, KF)是一种高效率的递归滤波器,它能够从一系列的不完全包含噪声的测量,估计动态线性系统的状态。为了能够将卡尔曼滤波运用到非线性系统中,采用将非线性系统进行线性化的方式对KF方法进行改进,形成了EKF。由于KF的基本方程是时间域内的递推形式,其计算过程是一个不断地“预测-修正”的过程,在求解时无需存储大量过程数据,并且一旦观测到新的数据,随即可以计算新的滤波值,因此这种滤波方法非常适合于实时处理和计算机实现。ADEKF是运用两个扩展卡尔曼滤波对系统的状态以及模型的参数进行估计,两个EKF分步运行,估计模型输出变量时将模型参数看作是常量,估计模型参数时将模型的前一步输出变量看作是常量,并通过模型的输出误差对过程激励噪声协方差和观测噪声协方差进行自适应更新,以获得更为精确的状态变量。
假定非线性离散状态空间模型为
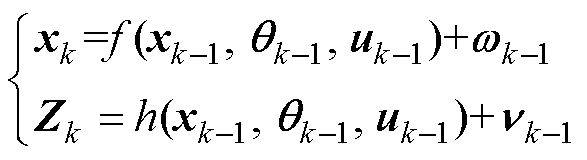 (9)
(9)
式中,xk为状态向量;f(xk-1, qk-1, uk-1)为过程方程;qk-1为模型参数向量;uk-1为输入向量;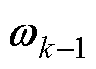 为过程激励噪声;Zk为观测向量;h(xk-1, qk-1, uk-1)为观测方程;
为过程激励噪声;Zk为观测向量;h(xk-1, qk-1, uk-1)为观测方程;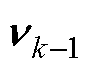 为观测噪声。ADEKF的结构框图如图3所示。
为观测噪声。ADEKF的结构框图如图3所示。
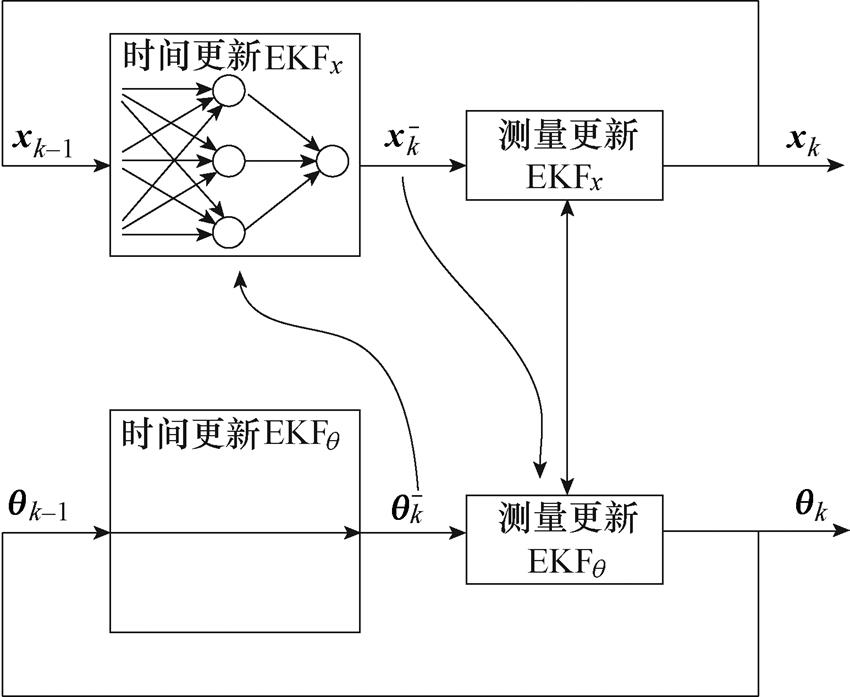
图3 ADEKF的结构框图
Fig.3 The block diagram of ADEKF
从图3中可知,ADEKF具有两个EKF,一个用于估计状态向量;另一个用于估计模型参数向量。在每个时间步长,EKFx状态滤波器都会使用当前模型参数估计值估算状态,而EKFq参数滤波器会使用当前状态估计值估算模型参数。
ADEKF的具体步骤[30]如下:
(1)向前推算参数向量为
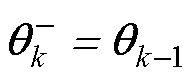 (10)
(10)
(2)向前推算参数向量误差协方差为
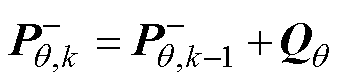 (11)
(11)
(3)向前推算状态向量为
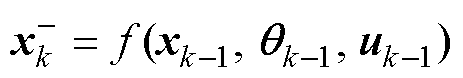 (12)
(12)
(4)向前推算状态向量误差协方差为
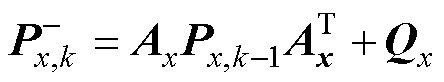 (13)
(13)
式中,Ax为系统矩阵。
(5)计算状态向量的卡尔曼增益为
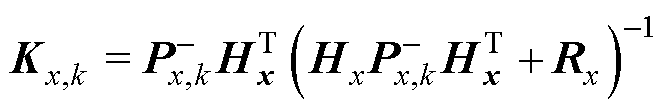 (14)
(14)
(6)由观测变量更新状态向量估计为
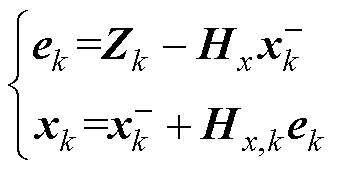 (15)
(15)
式中,Hx为观测矩阵;ek为卡尔曼滤波器中的新息残差。
(7)更新状态向量误差协方差为
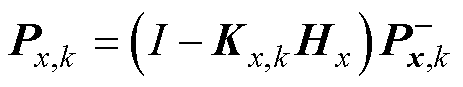 (16)
(16)
(8)更新过程激励噪声协方差和观测噪声协方差,其中,M为开窗的大小,Cx为先前残差序列的平均值导出的新息残差的协方差估计。
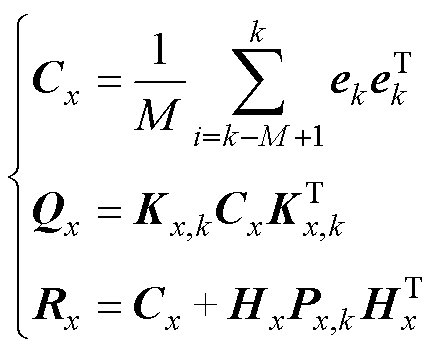 (17)
(17)
(9)计算参数向量的卡尔曼增益为
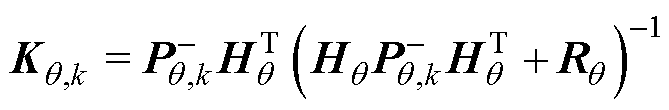 (18)
(18)
(10)由观测变量更新参数向量估计为
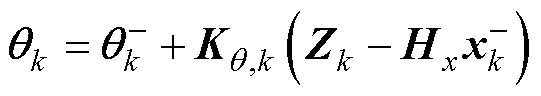 (19)
(19)
(11)更新参数向量误差协方差为
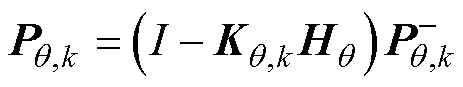 (20)
(20)
其中
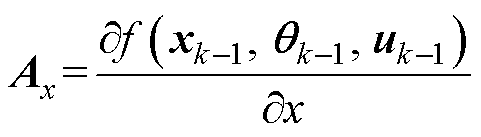 (21)
(21)
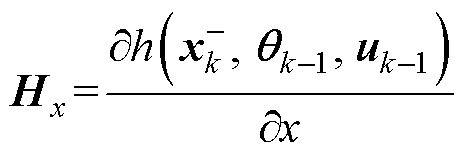 (22)
(22)
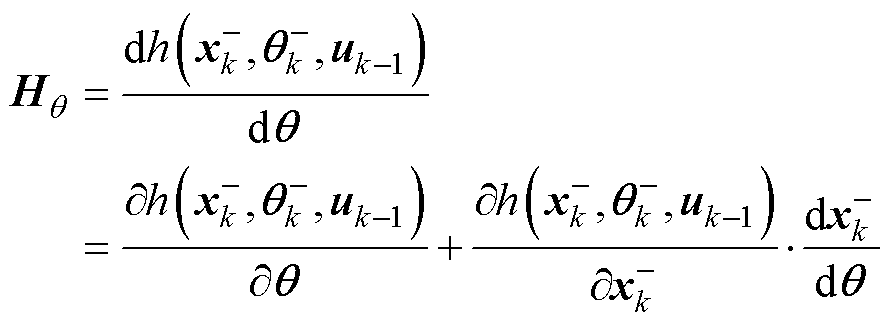 (23)
(23)
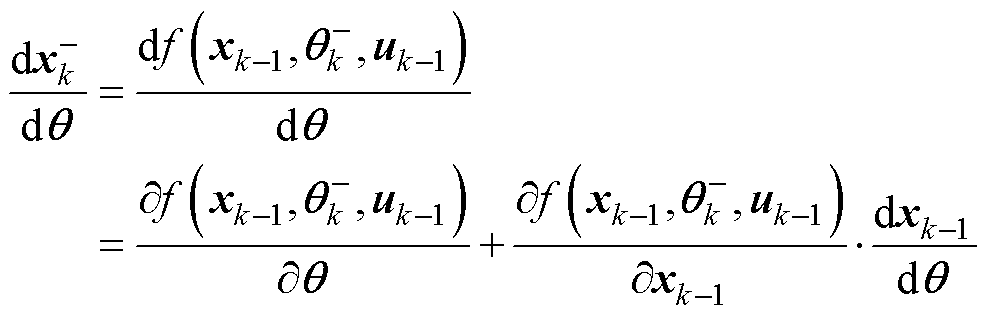 (24)
(24)
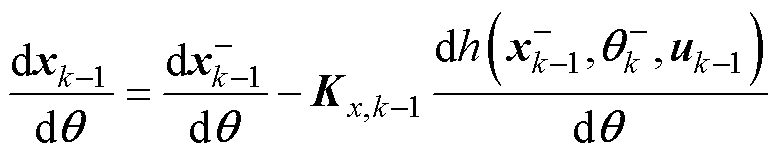 (25)
(25)
式中,Qq 为参数向量的过程激励噪声协方差矩阵;Qx为状态向量的过程激励噪声协方差矩阵;Rx为状态向量的观测噪声协方差矩阵;Rq 为参数向量的观测噪声协方差矩阵。
在老化电池的可充入电量估计问题中,电池模型参数是通过ADEKF1来实现辨识,ADEKF1的输出结果OCV作为ADEKF2的输入,进行OCV-Qcha曲线拟合参数的获取。其结构框图如图4所示。
在ADEKF1中,以电池的OCV和极化电压作为状态变量,以电池的欧姆内阻、极化内阻和极化电容作为参数变量,系统的输入为电池的负载电流,输出为模型估计得到的电池端电压。整个系统的离散状态空间模型为
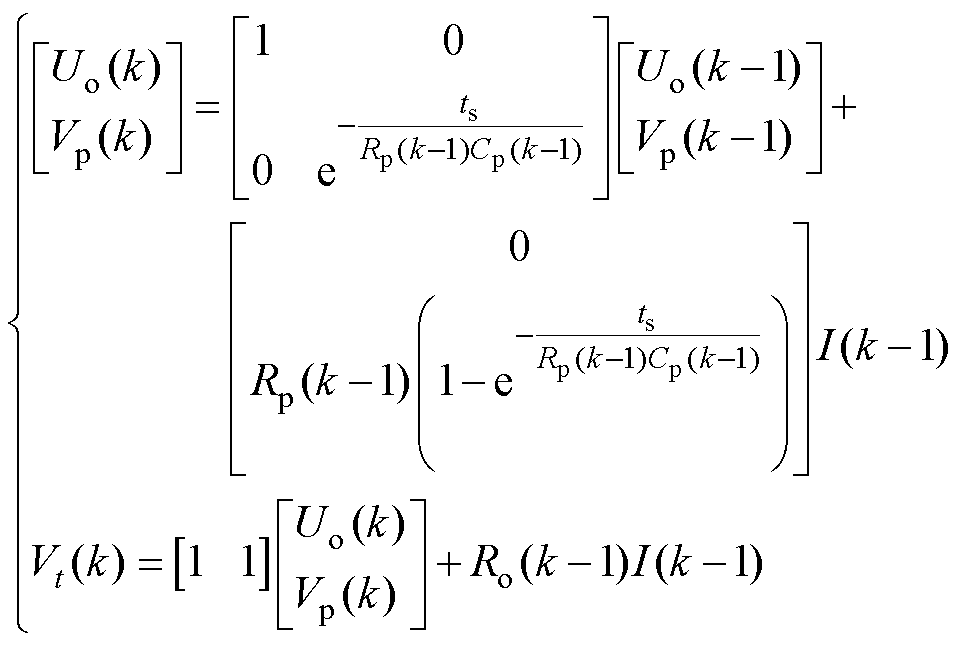 (26)
(26)
在ADEKF2中,以电池的可充入电量作为状态变量,以OCV-Qcha曲线的多项式拟合系数作为参数变量,系统的输入为电池的负载电流以及ADEKF1得到的OCV,输出为电池OCV-Qcha多项式拟合系数,整个系统的离散状态空间模型为
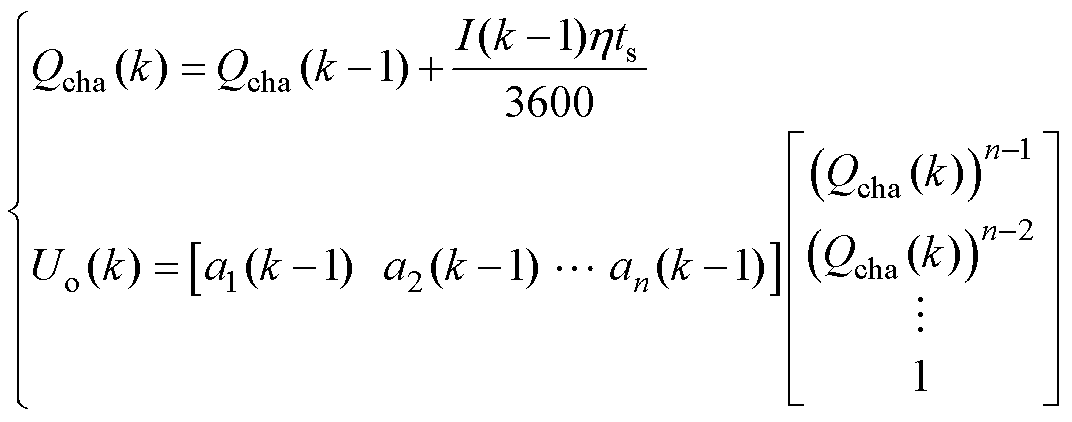 (27)
(27)
式中,[a1 a2 …an]为OCV-Qcha曲线的多项式拟合系数,n为多项式的项数;h 为库伦效率,这里取1。
综上所述,提出的基于双ADEKF的老化电池可充入电量估计方法以电池的端电压和电流作为输入,可以通过电池管理系统(Battery Management System, BMS)的实时信息采集系统定时采集,本文数据采样时间为1s/次,输出电池的OCV、可充入电量、欧姆内阻、极化内阻、极化电容和OCV-Qcha曲线的多项式拟合系数。
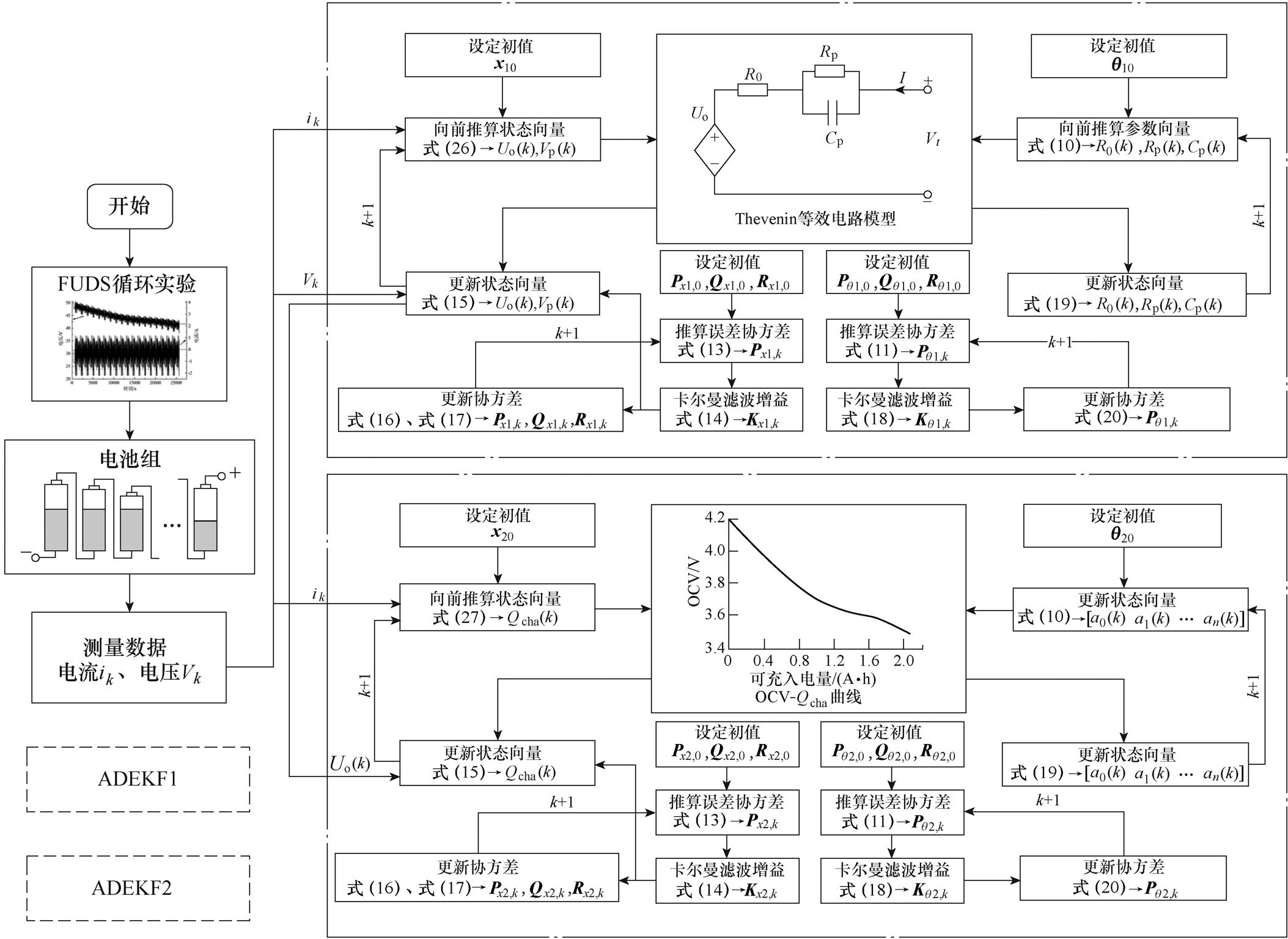
图4 基于双ADEFK的可充入电量的估计方法结构框图
Fig.4 The block diagram of the estimation method of rechargeable electric quantity based on dual ADEFK
为了验证提出的老化电池可充入电量估计方法的可行性,选取型号为ISR18650-2.2Ah的同一批次三元锂电池作为研究对象,电池参数见表1。
表1 电池参数
Tab.1 Battery parameters
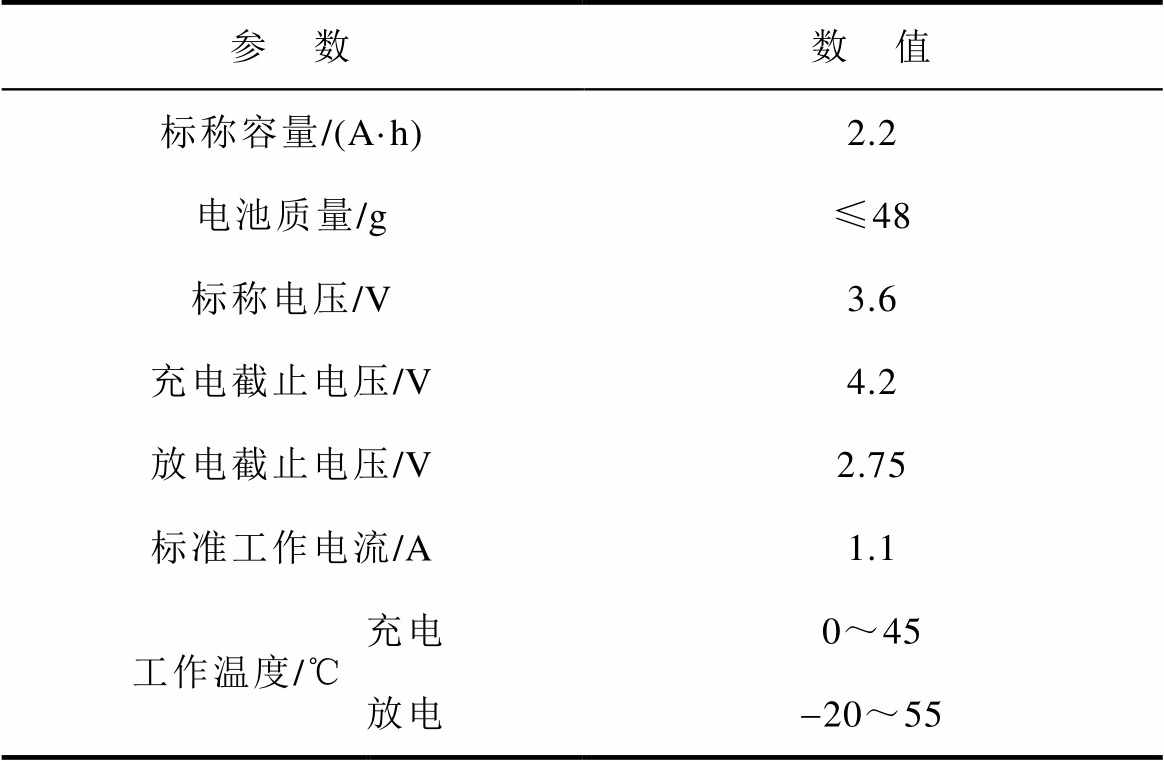
参 数数 值 标称容量/(A·h)2.2 电池质量/g≤48 标称电压/V3.6 充电截止电压/V4.2 放电截止电压/V2.75 标准工作电流/A1.1 工作温度/℃ 充电0~45 放电-20~55
实验平台如图5所示,其中包含了电池测试系统、高低温试验箱和上位机。电池测试系统的型号为Arbin BT-ML60V50A,辅助电压通道测量范围-5~5V,3个电流量程为50A/10A/1A,电压电流测量精度为±0.02%。高低温试验箱的型号为GDW-50,温度控制范围为-50~150℃,控温精度为±1℃。实验的温度设定为25℃。
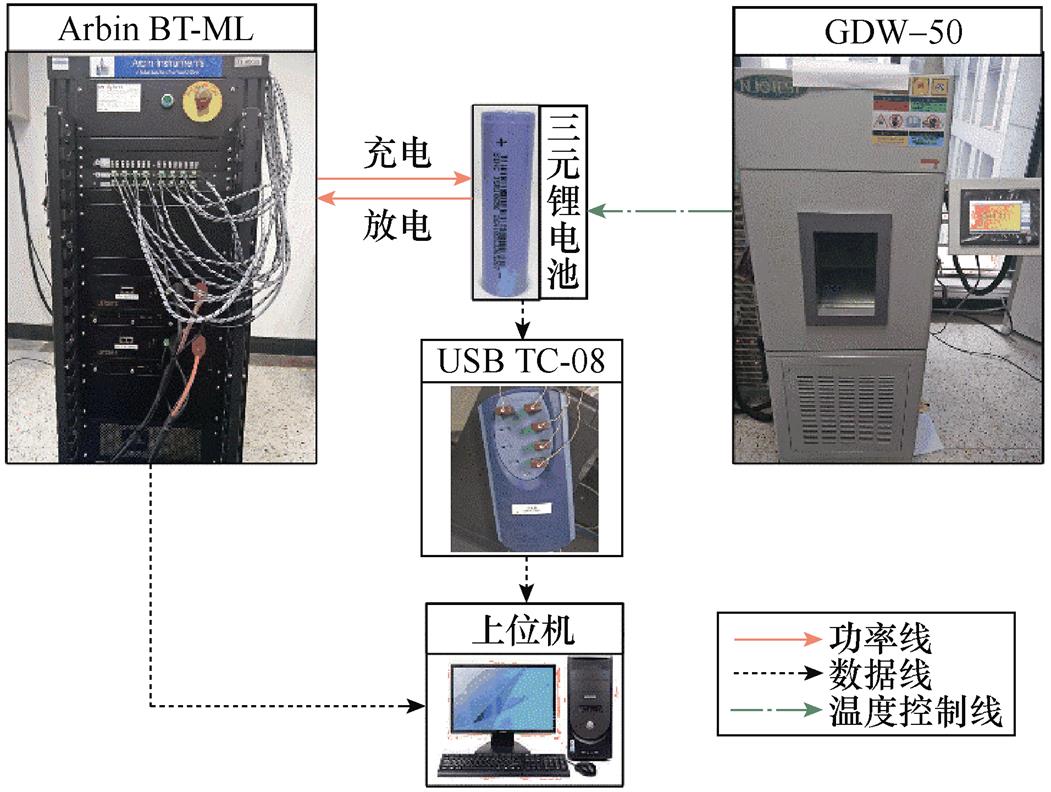
图5 实验平台
Fig.5 Experiment platform
为了验证本文提出的电池状态和参数估计方法的可行性,本文选取3节具有不同老化状态的电池作为研究对象,3节电池单体分别标记为电池1、电池2和电池3。3节电池在室温(25±2)℃以1C倍率
恒流放电容量分别为2.218A·h、1.852A·h和2.133A·h。其中,电池1为新电池,电池2和电池3分别为经过(25±2)℃ 1C恒流充放电循环老化的电池。联邦城市运行工况(Federal Urban Driving Schedule, FUDS)动态工况一个周期的电流波形如图6所示。
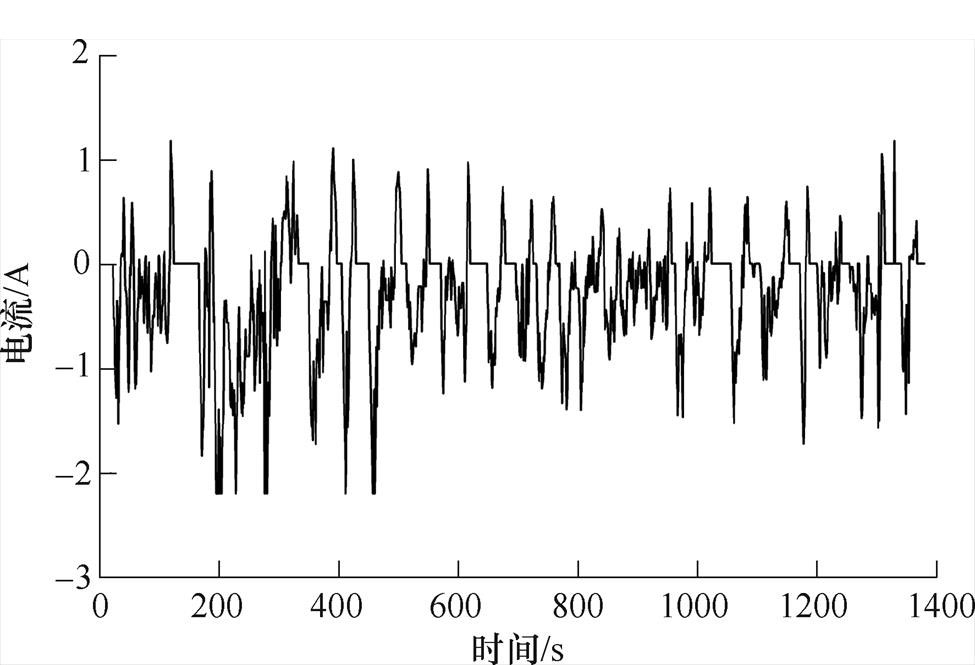
图6 FUDS动态工况一个周期的电流波形
Fig.6 The current waveform of one cycle of FUDS dynamic conditions
具体实验设计内容如下:
1)全新电池状态估计实验
(1)初值选取。OCV的初值为电池的初始端电压;可充入电量的初值为2.2A·h;欧姆内阻和极化内阻的初始值设定为0.03W 和0.02W;OCV-Qcha曲线拟合系数设定为固定值,根据1.2节所提出方法得到拟合的多项式为
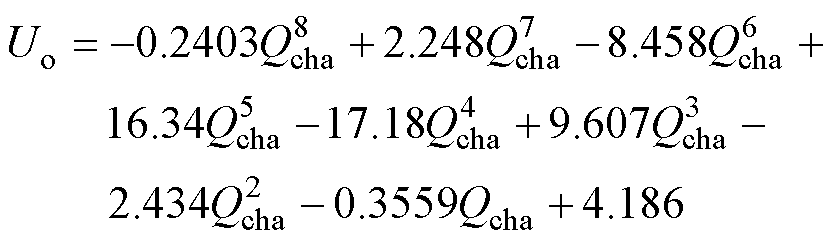 (28)
(28)
(2)FUDS工况下模型参数辨识与状态估计。利用所提出的方法对开路电压、内阻等参数进行辨识,并与HPPC实验获得的结果进行比较。
(3)恒流工况可充入电量估计结果验证。在0.5C倍率恒流充电工况下验证可充入电量估计结果。
2)老化电池状态估计实验
(1)初值选取。与全新电池初始参数相同。
(2)固定系数OCV-Qcha曲线拟合(见式(28))与自适应OCV-Qcha曲线拟合系数下的可充入电量对比分析。
3)不同老化状态单体在0.5C恒流充电工况下可充入电量估计结果验证。
1)新电池的可充入电量估计结果分析
全新电池1在FUDS工况下得到的OCV、直流内阻和可充入电量估计结果如图7所示。图7a中曲线为OCV辨识结果,黑色正三角为HPPC实验获得的OCV。可以看出,在HPPC采样点处,实验结果与辨识结果基本一致,两者之间的最大误差出现在可充入电量为2.2A·h处(放电末期),此时的误差为25mV。电池1直流内阻的估计值和实验值如图7c所示,图中的黑色方块为HPPC实验获得的直流内阻值。黑色实线为电池的欧姆内阻和极化内阻估计值的和。从图7c中可以看出,实验值与估计值的变化趋势基本保持一致,在放电时期的中间区域,直流内阻值只在小范围波动,在放电的最后阶段,直流内阻值有很大的上升趋势。电池1可充入电量的实验值和估计值以及误差值如图7b所示。图7b中,黑色实线为实验值,该实验值通过安时积分法获得,黑色虚线为估计值,从图中可以看出,实际值与估计值基本保持一致,估计效果较好。为了便于不同老化电池之间进行比较,采用绝对估计误差和相对估计误差两个参数进行比较。绝对误差为实际安时积分结果与估计结果的差值,相对误差为该差值相对于额定容量(所采用电池额定容量为2.2A·h)的比率。新电池可充入电量估计的绝对误差值范围在-0.006~0.010A·h之间,最大相对误差在1%以内。根据图4的方法步骤可知,OCV估计值用来作为ADEKF2中输出的测量值,因此OCV估计值的误差会影响可充入电量估计的准确性,可充入电量估计值的最大误差出现在初始放电阶段和最后放电阶段。初始放电阶段,模型参数的初始值存在误差,OCV的估计会存在较大误差,这会导致可充入电量的估计产生较大误差,但随着模型参数误差的减小,可充入电量的估计误差减小;最后放电阶段,电池的模型参数变化较大,导致OCV的估计误差增大,可充入电量的估计误差也增大。
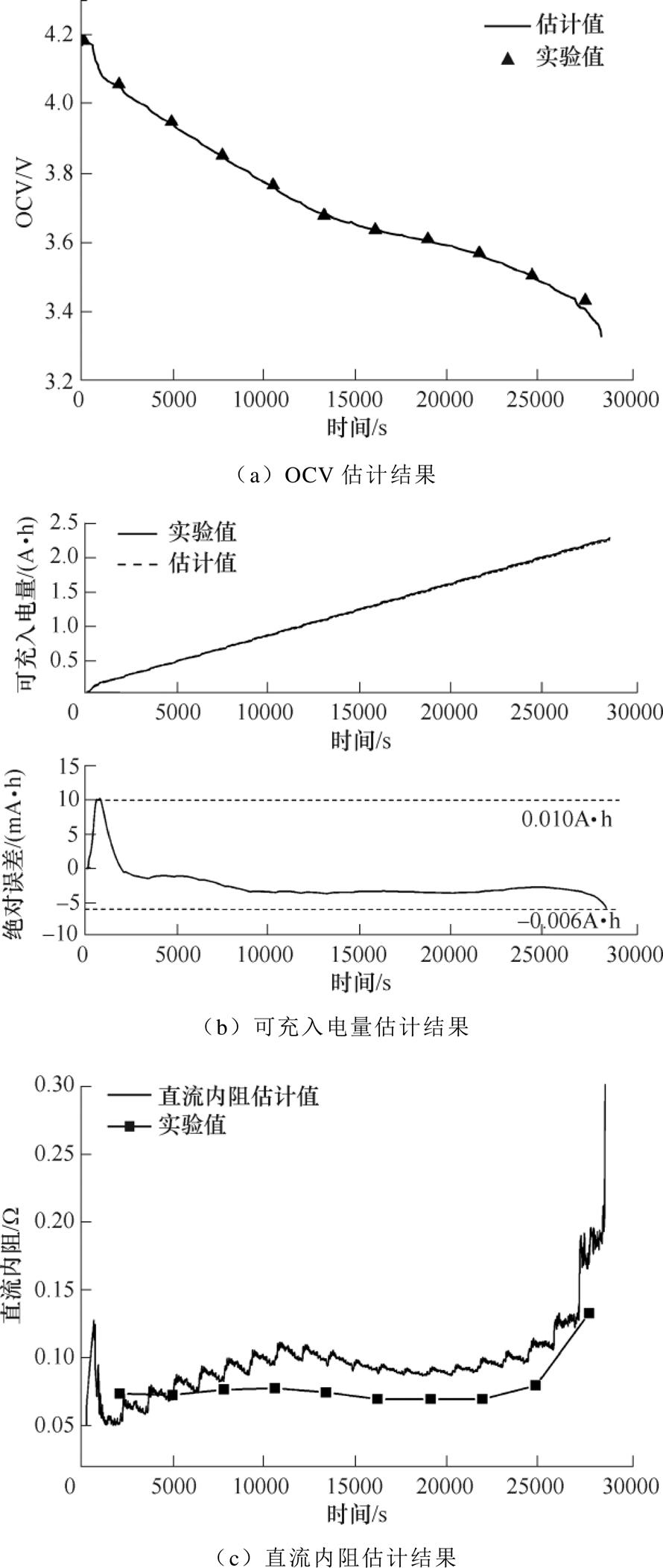
图7 电池1电池状态和模型参数估计结果
Fig.7 The results of battery state and model parameter estimation of battery 1
2)老化电池的可充入电量估计结果分析
为了验证所提出方法对老化电池可充入电量估计的有效性,分别选取电池2和电池3两节电池在FUDS运行工况下进行参数验证。首先,选取电池2分别在固定OCV-Qcha曲线拟合系数和辨识得到的曲线拟合系数条件下验证老化电池的参数辨识结果和恒流充电状态下的可充入电量估计结果。电池2电池状态和模型参数估计结果如图8所示。
电池2的OCV估计值和实验值如图8a所示,图中的黑色三角为HPPC测试得到的实验值,实线为估计值。OCV的实验值与估计值基本保持一致,两者误差最大出现在可充入电量为1.98A·h处,误差为55mV。这和电池1的情况类似,都是在可充入电量较大时,模型参数变化较快,导致OCV的估计误差变大。电池2的OCV-Qcha曲线的辨识的结果如图8c所示,图中的黑色三角为HPPC测试得到电池2的OCV实验值;实线为电池1的OCV-Qcha曲线;虚线为OCV-Qcha曲线拟合系数辨识后的曲线。对比实线和虚线可以看出,OCV-Qcha曲线在辨识修正后更加接近于实验值。电池2的直流内阻估计值如图8d所示,图中的黑色方块为电池2直流内阻的实验值;黑色实线为电池的欧姆内阻和极化内阻估计值的和。从图中可以看出,实验值与估计值的变化趋势基本保持一致,在放电的中间区域,直流内阻值只在小范围波动,在放电的最后阶段,直流内阻值有很大的上升趋势。电池2的可充入电量及误差如图8b所示。在图8b中,黑色实线为可充入电量的实验值;点线为固定OCV-Qcha曲线系数(与新电池相同)下可充入电量的估计值,最大绝对误差为0.126A·h,最大相对误差为5.7%;虚线为OCV-Qcha曲线拟合系数自适应调节情况下可充入电量的估计值,这种方法与安时积分法相比,最大绝对误差为0.059A·h,其最大相对误差为2.7%;对比图8b中点线和虚线可以看出,对OCV-Qcha曲线的在线辨识可减小由老化引起的可充入电量估计误差。
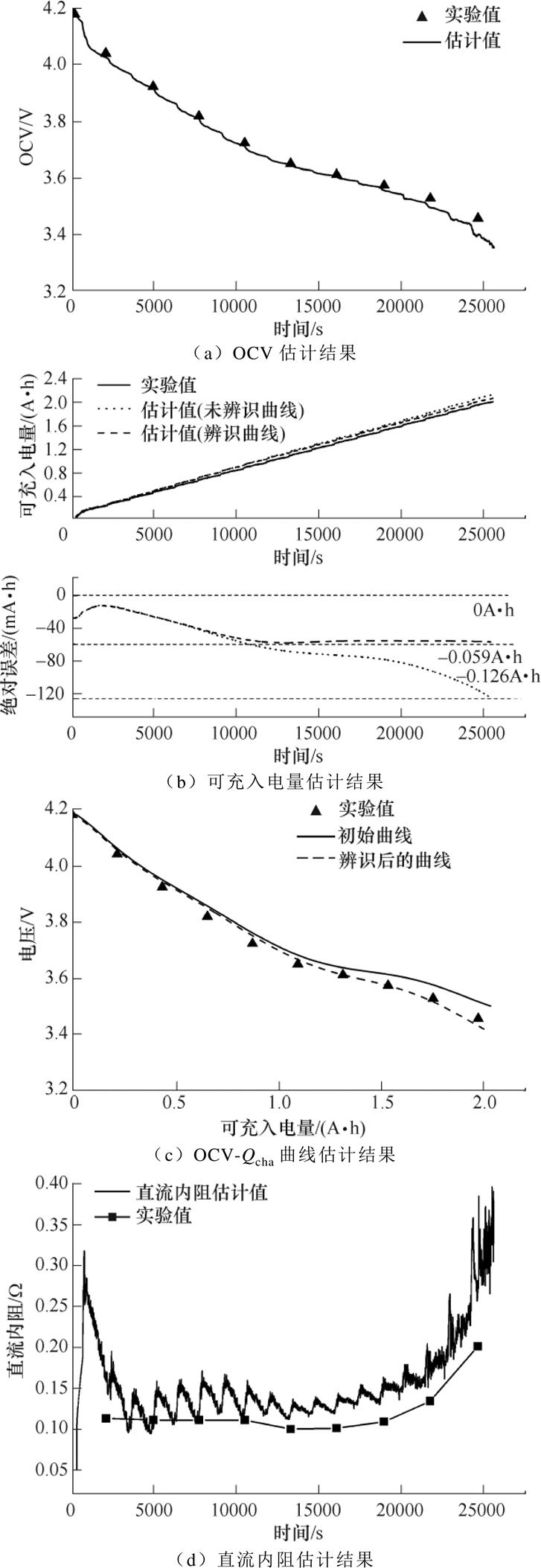
图8 电池2电池状态和模型参数估计结果
Fig.8 The results of battery state and model parameter estimation of battery 2
电池3的参数辨识和状态估计方法与电池2类似,这里不再深入讨论,其可充入电量的最大估计误差为0.015A·h。
3)0.5C倍率恒流充电工况可充入电量验证
根据FUDS工况下的参数辨识与状态估计结果,结合3节电池的内阻辨识结果就可以分别对电池1、电池2和电池3在恒流0.5C倍率条件下的充电实验结果进行验证,从而验证可充入电量的估计结果,如图9所示。其中,图9a、图9b和图9c分别为电池1、2、3的端电压估计结果。
图9中实线为电池端电压估计值,在获得OCV- Qcha曲线的基础上叠加内阻影响进行估计;虚线为估计得到的电池部分OCV-Qcha曲线;阴影区域为充电过程中估计的直流内阻的压降。从图9中可以得出,电池1以0.5C倍率充电时,全新电池1在可充入电量为0.141A·h处,端电压到达上限截止电压4.2V,受直流内阻影响损失的可充入电量为0.141A·h。电池2在可充入电量为0.280A·h处,端电压到达上限截止电压4.2V,直流内阻影响的电量为0.280A·h。电池3在可充入电量为0.200A·h处,端电压到达上限截止电压4.2V,直流内阻影响的电量为0.200A·h。3节电池受直流内阻影响损失的可充入电量的估计结果见表2,与其对比的实验值为标准CC-CV充电模式下的CV部分所充入电量。
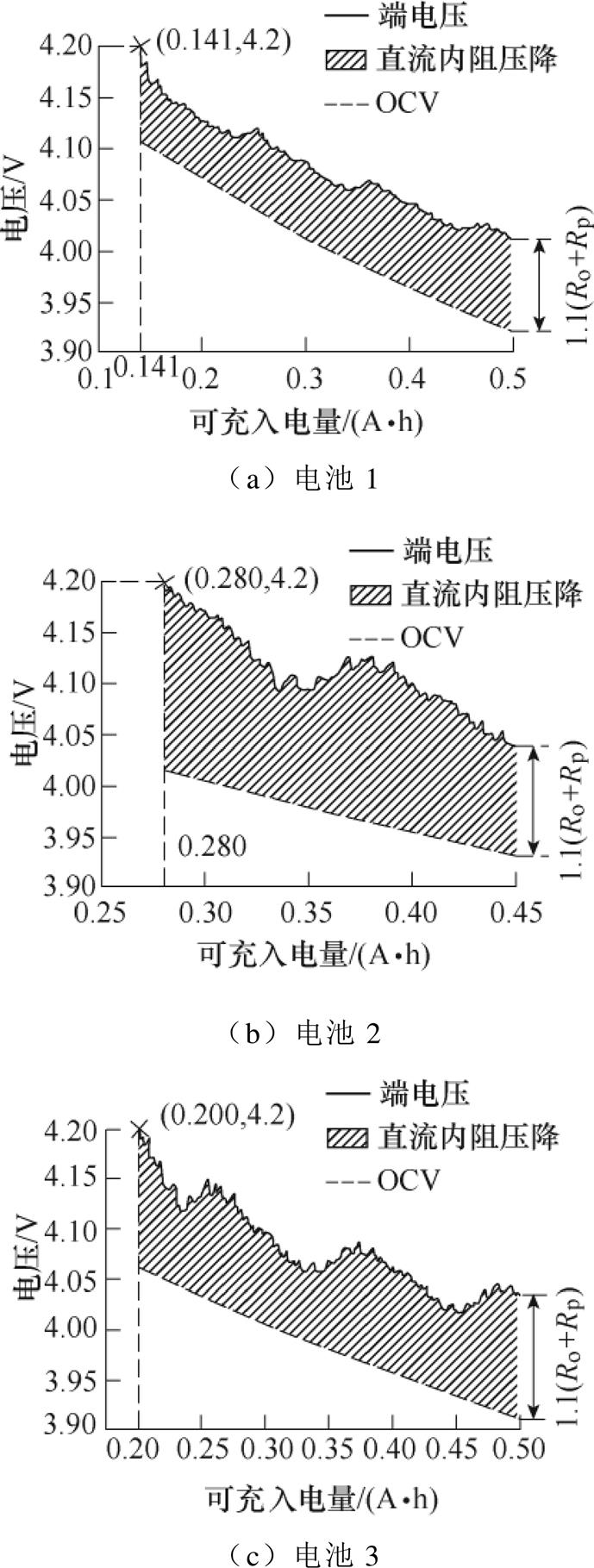
图9 三节电池1、2、3的端电压估计结果
Fig.9 The terminal voltage estimation curves of three batteries
表2 电池受直流内阻影响损失的可充入电量估计结果
Tab.2 The results of rechargeable electric quantity estimation of three batteries affected by the DC internal resistance (单位: A·h)
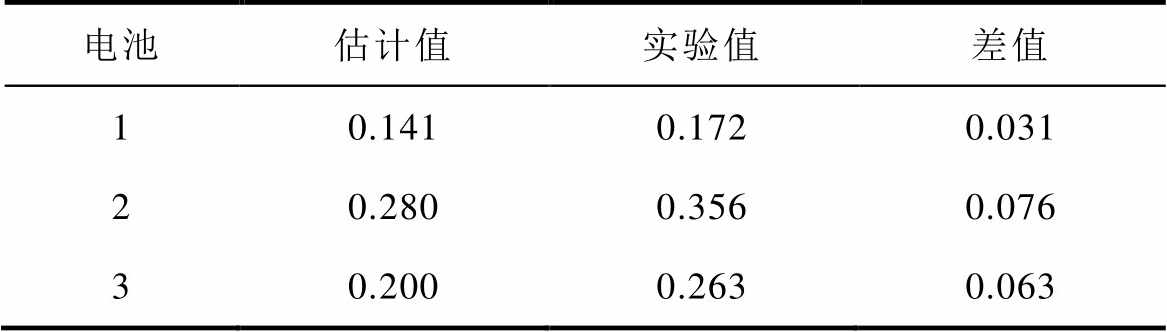
电池估计值实验值差值 10.1410.1720.031 20.2800.3560.076 30.2000.2630.063
综合上述实验结果,对于全新的电池1,由于OCV-Qcha曲线受老化影响的程度小,在估计的过程中,可以将OCV-Qcha曲线的拟合系数设定为固定值,在减少计算步骤的同时,也能保证可充入电量的估计结果有较高的精度。对于老化程度较高的电池2和电池3,OCV-Qcha曲线受老化影响的程度较大,在估计的过程中将OCV-Qcha曲线的拟合系数设定为固定值,会导致可充入电量产生较大的估计误差;对比老化电池的可充入电量估计结果可以得出,在估计的过程中对OCV-Qcha曲线拟合系数进行辨识,一方面可以有效地减小由于老化导致的可充入电量估计的误差;另一方面还能获得较为准确的OCV-Qcha曲线。通过对不同老化状态电池进行的实验验证,说明本文提出的电池状态可充入电量估计方法适用于不同老化状态电池。
通过3节不同老化状态电池在恒流0.5C倍率充电工况下的可充入电量估计结果验证可以看出,所提出的电池参数辨识和OCV-Qcha曲线拟合参数辨识结果可以有效地在充电过程中识别可充入电量的
损失。随着电池老化的加剧,通过OCV-Qcha曲线拟合参数辨识的方法可以对不同老化状态下单体OCV曲线进行修正,同时随着老化的加剧,其内阻的变化也可以通过参数辨识的方式实现更新,并综合以上两方面因素的影响,在恒流充电工况下实现可充入电量损失的有效识别。
针对储能用锂离子电池受老化影响的电池可充入电量估计问题,本文提出了一种基于双ADEKF的电池状态和模型参数联合估计方法,通过电池建模、算法分析和实验验证得出以下内容:
1)以Thevenin等效电路模型为基础,构建了可充入电量与电池OCV的关系曲线,分析了直流内阻对电池可充入电量的影响。
2)在考虑电池老化对模型参数影响的基础上,提出了基于双ADEKF的电池状态和模型参数联合估计方法。
3)以3节老化程度不同的三元锂电池为研究对象,在FUDS工况下验证电池状态和模型参数估计结果,在0.5C倍率恒流充电工况下验证可充入电量损失估计结果。实验结果表明,对于新电池,FUDS工况下可充入电量估计误差小于1%;对于老化电池,可充入电量估计误差在2.7%。通过3节不同老化程度电池恒流0.5C倍率充电结果比较,进一步验证了所提出方法对可充入电量估计的有效性。
后续将主要针对不同受温度影响的可充入电量估计方法以及OCV-SOC曲线在线修正进行进一步研究。
参考文献
[1] 桑顺, 高宁, 蔡旭, 等. 电池储能变换器弱电网运行控制与稳定性研究[J]. 中国电机工程学报, 2017, 37(1): 54-63.
Sang Shun, Gao Ning, Cai Xu, et al. Operation control and stability study of converters for battery energy storage under weak grid conditions[J]. Pro- ceedings of the CSEE, 2017, 37(1): 54-63.
[2] 王榘, 熊瑞, 穆浩. 温度和老化意识融合驱动的电动车辆锂离子动力电池电量和容量协同估计[J]. 电工技术学报, 2020, 35(23): 4980-4987.
Wang Ju, Xiong Rui, Mu Hao. Co-estimation of lithium-ion battery state-of-charge and capacity through the temperature and aging awareness model for electric vehicles[J]. Transactions of China Electro- technical Society, 2020, 35(23): 4980-4987.
[3] 陈欢, 林程, 熊瑞. 车用复合电源系统在线自适应能量管理[J]. 电工技术学报, 2020, 35(增刊2): 644- 651, 660.
Chen Huan, Lin Cheng, Xiong Rui. Online adaptive energy management strategy for a hybrid energy storage system in electric vehicles[J]. Transactions of China Electrotechnical Society, 2020, 35(S2): 644- 651, 660.
[4] 孙丙香, 任鹏博, 陈育哲, 等. 锂离子电池在不同区间下的衰退影响因素分析及任意区间的老化趋势预测[J]. 电工技术学报, 2021, 36(3): 666-674.
Sun Bingxiang, Ren Pengbo, Chen Yuzhe, et al. Analysis of influencing factors of degradation under different interval stress and prediction of aging trend in any interval for lithium-ion battery[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 666- 674.
[5] 曹铭, 张越, 黄菊花. 基于RLS法的锂离子电池离线参数辨识[J]. 电池, 2020, 50(3): 228-231.
Cao Ming, Zhang Yue, Huang Juhua. Offline para- meter identification of Li-ion battery based on RLS method[J]. Battery Bimonthly, 2020, 50(3): 228-231.
[6] 黄凯, 郭永芳, 李志刚. 基于信息反馈粒子群的高精度锂离子电池模型参数辨识[J]. 电工技术学报, 2019, 34(增刊1): 378-387.
Huang Kai, Guo Yongfang, Li Zhigang. High precision parameter identification of lithium-ion battery model based on feedback particle swarm optimization algorithm[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 378-387.
[7] 刘楠, 吕甜, 叶望博, 等. 锂离子电容在线参数辨识与SOC的联合估计[J]. 电源技术, 2020, 44(5): 736- 739, 748.
Liu Nan, Lü Tian, Ye Wangbo, et al. Online parameter identification and SOC joint estimation of lithium-ion supercapacitors[J]. Chinese Journal of Power Sources, 2020, 44(5): 736-739, 748.
[8] Xiong Rui, Sun Fengchun, Chen Zheng, et al. A data- driven multi-scale extended Kalman filtering based parameter and state estimation approach of lithium- ion polymer battery in electric vehicles[J]. Applied Energy, 2014, 113: 463-476.
[9] 李宁, 何复兴, 马文涛, 等. 基于经验模态分解的门控循环单元神经网络的锂离子电池荷电状态估计[J]. 电工技术学报, 2022, 37(17): 4528-4536.
Li Ning, He Fuxing, Ma Wentao, et al. State-of- charge estimation of lithium-ion battery based on gated recurrent unit using empirical mode decom- position[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4528-4536.
[10] 武龙星, 庞辉, 晋佳敏, 等. 基于电化学模型的锂离子电池荷电状态估计方法综述[J]. 电工技术学报, 2022, 37(7): 1703-1725.
Wu Longxing, Pang Hui, Jin Jiamin, et al. A review of SOC estimation methods for lithium-ion batteries based on electrochemical model[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1703- 1725.
[11] 林成涛, 陈全世, 王军平, 等. 用改进的安时计量法估计电动汽车动力电池SOC[J]. 清华大学学报(自然科学版), 2006, 46(2): 247-251.
Lin Chengtao, Chen Quanshi, Wang Junping, et al. Improved Ah counting method for state of charge estimation of electric vehicle batteries[J]. Journal of Tsinghua University (Science and Technology), 2006, 46(2): 247-251.
[12] He Hongwen, Xiong Rui, Guo Hongqiang. Online estimation of model parameters and state-of-charge of LiFePO4 batteries in electric vehicles[J]. Applied Energy, 2012, 89(1): 413-420.
[13] Avila L O, Errecalde M L, Serra F M, et al. State of charge monitoring of Li-ion batteries for electric vehicles using GP filtering[J]. Journal of Energy Storage, 2019, 25: 100837.
[14] Ye Min, Guo Hui, Xiong Rui, et al. A double-scale and adaptive particle filter-based online parameter and state of charge estimation method for lithium-ion batteries[J]. Energy, 2018, 144: 789-799.
[15] 刘淑杰, 郝昆昆, 王永, 等. 基于改进粒子滤波算法的动力锂离子电池荷电状态估计[J]. 大连理工大学学报, 2020, 60(4): 392-401.
Liu Shujie, Hao Kunkun, Wang Yong, et al. State of charge estimation of power lithium-ion battery based on improved particle filter algorithms[J]. Journal of Dalian University of Technology, 2020, 60(4): 392- 401.
[16] Dong Guangzhong, Chen Zonghai, Wei Jingwen. Sequential Monte Carlo filter for state-of-charge estimation of lithium-ion batteries based on auto regressive exogenous model[J]. IEEE Transactions on Industrial Electronics, 2019, 66(11): 8533-8544.
[17] 巫春玲, 胡雯博, 孟锦豪, 等. 基于最大相关熵扩展卡尔曼滤波算法的锂离子电池荷电状态估计[J]. 电工技术学报, 2021, 36(24): 5165-5175.
Wu Chunling, Hu Wenbo, Meng Jinhao, et al. State of charge estimation of lithium-ion batteries based on maximum correlation-entropy criterion extended Kalman filtering algorithm[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5165-5175.
[18] Huang Deyang, Chen Ziqiang, Zheng Changwen, et al. A model-based state-of-charge estimation method for series-connected lithium-ion battery pack considering fast-varying cell temperature[J]. Energy, 2019, 185: 847-861.
[19] 谈发明, 赵俊杰, 李秋烨. 基于简化滞回OCV模型的锂电池SOC自适应估计策略[J]. 中国电机工程学报, 2021, 41(2): 703-714.
Tan Faming, Zhao Junjie, Li Qiuye. Adaptive SOC estimation strategy for lithium battery based on simplified hysteresis OCV model[J]. Proceedings of the CSEE, 2021, 41(2): 703-714.
[20] 程泽, 杨磊, 孙幸勉. 基于自适应平方根无迹卡尔曼滤波算法的锂离子电池SOC和SOH估计[J]. 中国电机工程学报, 2018, 38(8): 2384-2393, 2548.
Cheng Ze, Yang Lei, Sun Xingmian. State of charge and state of health estimation of Li-ion batteries based on adaptive square-root unscented Kalman filters[J]. Proceedings of the CSEE, 2018, 38(8): 2384-2393, 2548.
[21] Sheng Hanmin, Xiao Jian. Electric vehicle state of charge estimation: nonlinear correlation and fuzzy support vector machine[J]. Journal of Power Sources, 2015, 281: 131-137.
[22] 徐佳宁, 倪裕隆, 朱春波. 基于改进支持向量回归的锂电池剩余寿命预测[J]. 电工技术学报, 2021, 36(17): 3693-3704.
Xu Jianing, Ni Yulong, Zhu Chunbo. Remaining useful life prediction for lithium-ion batteries based on improved support vector regression[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(17): 3693-3704.
[23] 李超然, 肖飞, 樊亚翔, 等. 基于深度学习的锂离子电池SOC和SOH联合估算[J]. 中国电机工程学报, 2021, 41(2): 681-691.
Li Chaoran, Xiao Fei, Fan Yaxiang, et al. Joint estimation of the state of charge and the state of health based on deep learning for lithium-ion batteries[J]. Proceedings of the CSEE, 2021, 41(2): 681-691.
[24] Zheng Yuejiu, Ouyang Minggao, Lu Languang, et al. On-line equalization for lithium-ion battery packs based on charging cell voltages: part 2. fuzzy logic equalization[J]. Journal of Power Sources, 2014, 247: 460-466.
[25] Weng Caihao, Cui Yujia, Sun Jing, et al. On-board state of health monitoring of lithium-ion batteries using incremental capacity analysis with support vector regression[J]. Journal of Power Sources, 2013, 235: 36-44.
[26] Zenati A, Desprez P, Razik H. Estimation of the SOC and the SOH of Li-ion batteries, by combining impedance measurements with the fuzzy logic inference[C]//IECON 2010-36th Annual Conference on IEEE Industrial Electronics Society, Glendale, AZ, USA, 2010: 1773-1778.
[27] Zheng Linfeng, Zhu Jianguo, Lu D D C, et al. Incremental capacity analysis and differential voltage analysis based state of charge and capacity estimation for lithium-ion batteries[J]. Energy, 2018, 150: 759- 769.
[28] Stroe D I, Schaltz E. Lithium-ion battery state- of-health estimation using the incremental capacity analysis technique[J]. IEEE Transactions on Industry Applications, 2020, 56(1): 678-685.
[29] 纪常伟, 潘帅, 汪硕峰, 等. 动力锂离子电池老化速率影响因素的实验研究[J]. 北京工业大学学报, 2020, 46(11): 1272-1282.
Ji Changwei, Pan Shuai, Wang Shuofeng, et al. Experimental study on effect factors of aging rate for power lithium-ion batteries[J]. Journal of Beijing University of Technology, 2020, 46(11): 1272-1282.
[30] Yang Jufeng, Xia Bing, Shang Yunlong, et al. Adaptive state-of-charge estimation based on a split battery model for electric vehicle applications[J]. IEEE Transactions on Vehicular Technology, 2017, 66(12): 10889-10898.
An Estimation Method of Rechargeable Electric Quantity for Aging Battery Based on Joint Estimation of State and Model Parameters
Abstract Battery energy storage system has been widely used in power systems. In order to ensure the operation effect of the battery energy storage system, it is important to accurately estimate the battery state. The rechargeable electric quantity of the battery determines the ability of energy storage to a certain extent. However, it is difficult to accurately reflect the actual rechargeable electric quantity of the battery only using external characteristic parameters, such as voltage, current and temperature. The problem of the rechargeable electric quantity estimation of batteries in different health states has been difficult to solve, especially in different aging states. In this paper, the concept of rechargeable electric quantity is proposed, the relationship between the rechargeable electric quantity and the open circuit voltage (OCV) is constructed, and the rechargeable electric quantity affected by DC internal resistance is analyzed based on the Thevenin equivalent circuit model. Besides, a joint estimation method of battery states and model parameters is proposed based on dual adaptive dual extended Kalman filter (ADEKF), which realizes the rechargeable electric quantity estimation of the battery in any aging state. Taking three batteries with different aging states as the research object, the battery state and model parameter estimation results are verified in the federal urban driving schedule (FUDS) operating condition, and the estimation results of the rechargeable electric quantity loss are verified at 0.5C constant current charging. The experimental results show that for the new cell, the estimation error of the rechargeable electric quantity is less than 1%, and the error affected by DC internal resistance is 0.031A·h. For the aged cell, the estimation error of the rechargeable electric quantity is 2.7%, and the error affected by DC internal resistance is 0.074A·h. The comparison of the state estimation of three batteries with different aging states at 0.5C constant current charging condition further verifies the effectiveness of the proposed method for electric quantity estimation.
Keywords:Lithium-ion battery, aging, state estimation, rechargeable electric quantity
中图分类号:TM912
DOI: 10.19595/j.cnki.1000-6753.tces.210785
国家自然科学基金项目(52007085)和黑龙江省自然科学基金重点项目(ZD2021E004)资助。
收稿日期2021-06-01
改稿日期 2021-09-10
E-mail: jinlei.sun@njust.edu.cn(通信作者)
唐传雨 男,1995年生,硕士研究生,研究方向为电池状态估计与均衡。
E-mail: tcyjay@njust.edu.cn
(编辑 崔文静)