
图1 测量平台
Fig.1 Experimental platform
摘要 变压器铁心在运行时长期承受外施应力和高频激励的影响,由此导致的振动噪声和铁损问题日益严峻。为深入研究取向硅钢片在不同频率和应力下的综合磁性能,该文搭建了软磁材料综合磁性能测量平台,首先利用单片磁特性测量装置和应力施加装置,得到了工频下拉应力和压应力对取向硅钢片磁致伸缩、磁滞回线及铁损特性的影响。进一步研究了应力和不同激励共同影响下硅钢片综合磁性能的变化趋势,得到了不同激励、应力对取向硅钢片磁特性、磁致伸缩特性及噪声特性的影响规律。测量结果及其分析表明,拉应力对硅钢片的磁性能影响相对较小,而压应力对其影响较大;在压应力作用下,随着频率的升高取向硅钢片的磁致伸缩量有所减小,但频率、谐波含量、谐波次数和压应力的增大均导致取向硅钢片噪声增大。
关键词:铁损 磁致伸缩 机械应力 振动 噪声
随着我国特高压输电的发展及应用,变压器、电抗器等高电压、大容量输电设备的振动噪声问题日益严峻[1]。柔性输电技术的成熟应用使得输变电设备在运行时承受复杂的激励,尤其是电压和电流中的高频成分,进一步加剧了设备铁心振动噪声增大,损耗明显升高等问题。变压器、电抗器等输变电设备的铁心由硅钢片叠制而成,磁致伸缩效应是造成此类设备铁心振动的主要原因[2-6]。研究表明,磁致伸缩是在外磁场作用下磁畴壁运动导致的铁磁体形变[7]。单片硅钢片在磁场的作用下每米仅有几微米的形变[8],但是由于变压器、电抗器等输变电设备铁心尺寸较大,磁致伸缩效应对其造成的影响不可小觑[9-11]。并且变压器、电抗器等输变电设备本身的构造中存在夹件、螺栓等紧固件,这使得硅钢片的工作环境中通常都有拉应力或者压应力作用。因此深入研究不同频率和不同机械应力作用下单片硅钢片的综合磁性能具有重要意义。
近年来,国内外学者对硅钢片的磁性能进行了广泛的研究。河北工业大学李永建等分析了分别对轧制方向和垂直轧制方向应用单轴应力的磁性实验结果[12]。朱立勋等提出了一种改进的模型,用以测量磁畴尺寸较大、高晶粒取向电工钢片的磁致伸缩特性[13],并将磁畴转动参数引入改进的J-A模型中,提出了准确的电工钢动态磁特性[14]。文献[15]分析了晶粒内部和晶界周围的畴壁在低拉伸应力下的特性。文献[16]模拟了矢量激励下取向硅钢片的磁致伸缩和磁化曲线,再现了因90°畴壁运动而产生的磁致伸缩。电子科技大学邱发生在应力评估中应用了磁畴动态行为特征,建立了铁磁材料微观动态和宏观磁特性之间的关系[17]。闫荣格等测量了无取向硅钢片分别沿轧制方向和垂直轧制方向的磁致伸缩,并建立了考虑各向异性的磁-机械耦合数值模型[18]。沈阳工业大学张艳丽等提出了硅钢片任意方向磁致伸缩测量的方法,构建了磁致伸缩耦合模 型[19],以及磁致伸缩数学模型,并将耦合结果与实验结果进行了对比验证[20],进一步分析了相位和振幅不同的磁场3次谐波对磁致伸缩产生的影响[21]。韩芳旭等建立了变压器三维仿真模型,采用基于磁致伸缩-热应力比拟的数值计算方法求得铁心本体的振动噪声[22]。文献[23]提出了一种快速半解析计算模型,用以分析谐波对永磁同步电机的振动和噪声影响。文献[24]基于谐波平衡法建立磁-机械耦合模型,使用频域分解算法求解耦合场,分析了变压器铁心振动特性。目前国内外研究集中于工频或谐波磁场对取向硅钢片磁性能的影响,天津工业大学祝丽花等测量了机械压应力对硅钢片磁特性的影响[25],但对不同励磁频率下硅钢片磁性能变化的研究还未重视;此外,上述对硅钢片磁性能的研究仅限于单个因素的改变产生的影响,而未分析应力和激励同时改变时取向硅钢片磁性能的变化。
本文搭建了可施加应力的单片式取向硅钢片综合磁性能测量系统,测量了不同激励、不同应力下硅钢片磁滞特性、磁致伸缩特性、噪声特性和铁损特性,分析了不同激励和应力共同作用时,取向硅钢片磁性能的变化规律。比较了拉应力和压应力对磁性能影响的差异性。
采用Brockhaus公司生产的磁致伸缩特性单片测试仪(MST500)对不同影响因素下取向硅钢片的磁致伸缩进行测量,测量平台如图1所示,测量时电源控制励磁的波形及频率,激光电源连接测量系统中的激光头,激光头发射激光以测量样片的形变,PC用以记录样片磁致伸缩及铁损数据。综合磁性能单片测量仪示意图如图2所示。

图1 测量平台
Fig.1 Experimental platform
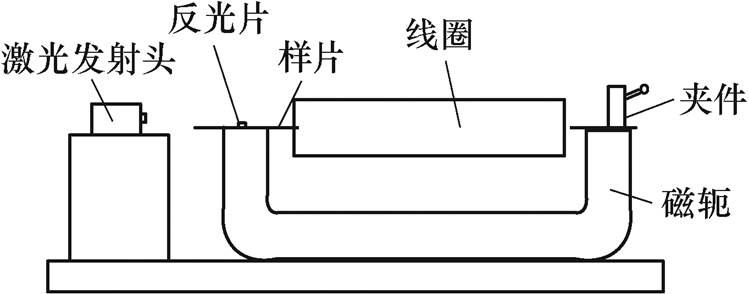
图2 综合磁性能单片测量仪示意图
Fig.2 Schematic diagram of a comprehensive single sheet tester for magnetic property
测量平台包括电源、单片测量仪以及激光发射接收器等。单片测量仪和激光发射接收器为保证不受其他因素干扰,悬浮于气垫上。单片测量仪由上下磁轭、线圈、夹件等组成。待测样片为宝钢生产型号为B30P105的取向硅钢片,尺寸为600mm× 100mm。测量时,待测样片放置于线圈内腔中,样片一端通过夹件进行固定,另一端自由伸缩并粘贴反光片。线圈中通入电流后,磁轭和样片形成闭合回路,样片在磁场作用下产生由磁致伸缩现象引发的形变,激光器发射激光后,通过检测激光头到反光片之间的距离变化,计算并记录样片的形变量,即可得到其磁致伸缩特性。
施压装置如图3所示,测量前需将样片两侧都夹紧,通过应力切换开关来控制施加压应力或者拉应力,施加方向沿硅钢片轧制方向,调节旋钮用以控制应力的大小,电子屏上显示正值代表施加拉应力,负值则代表施加压应力,后文为表述方便,以F代表施加应力。

图3 应力控制装置
Fig.3 Controlling device for externally applied stress
测量过程中,对励磁绕组施加工频正弦激励,并通过应力控制装置分别施以不同大小的应力F,获得样片的动态磁滞回线,后文简称磁滞回线。图4给出了F=0N, 100N, 200N,磁通密度峰值分别为1.2T和1.5T时的磁滞回线。
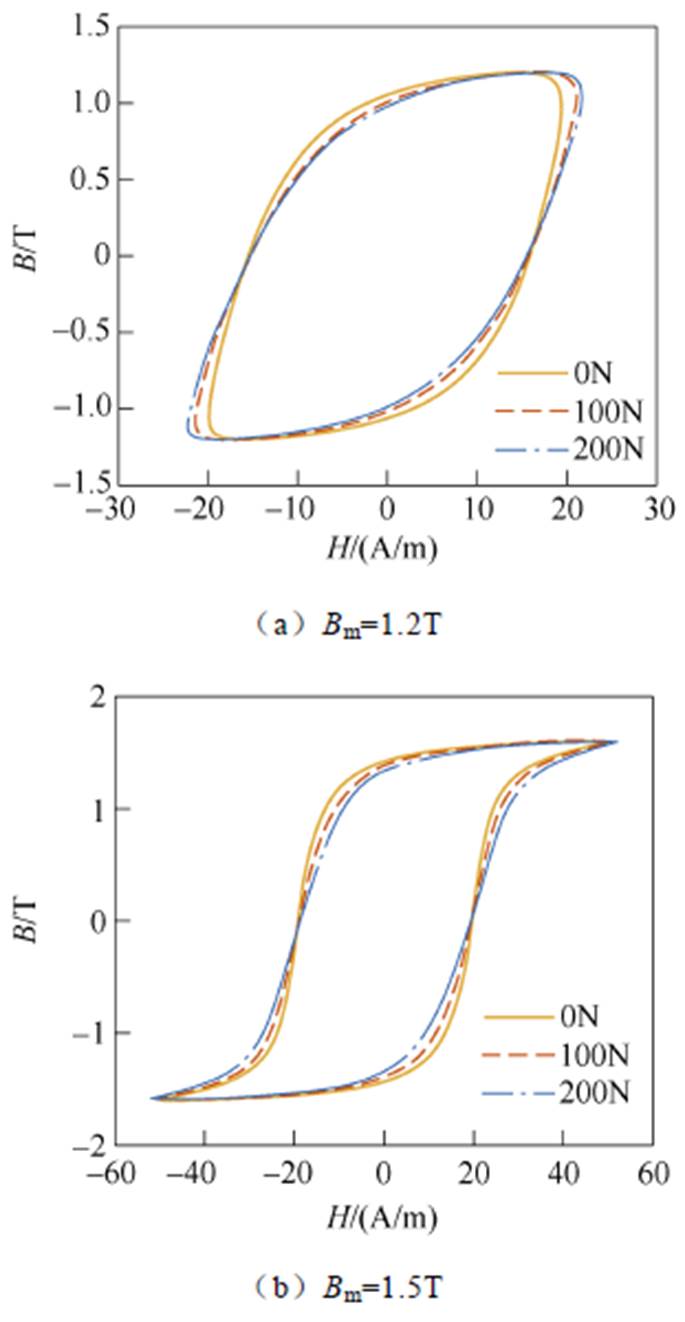
图4 不同拉应力下不同磁通密度峰值的磁滞回线
Fig.4 Hysteresis loops under different peaked flux densities as well as tensil stress
从图4中可以看出,磁滞回线中心对称,随着拉应力的改变,回线形状有一定程度的改变。在同一磁通密度下,随着拉应力的增大,磁场强度有较小幅度的增加。由此可见,拉应力对取向硅钢片磁滞回线的影响较小。
为比较拉应力和压应力对取向硅钢片磁化特性的影响是否相同,图5对比了在应力F=±200N下,磁通密度峰值Bm=1.5T时的磁滞回线。相较于拉应力,压应力作用下的磁滞回线面积迅速增大,形状的改变较为显著,表明压应力对取向硅钢片磁化特性的影响要远大于拉应力。
为此进一步深入分析工频激励下不同大小的压应力对取向硅钢片磁滞特性的影响,图6给出了F=0N, -100N, -200N,磁通密度峰值Bm=1.2T、1.5T和1.8T时的磁滞回线。
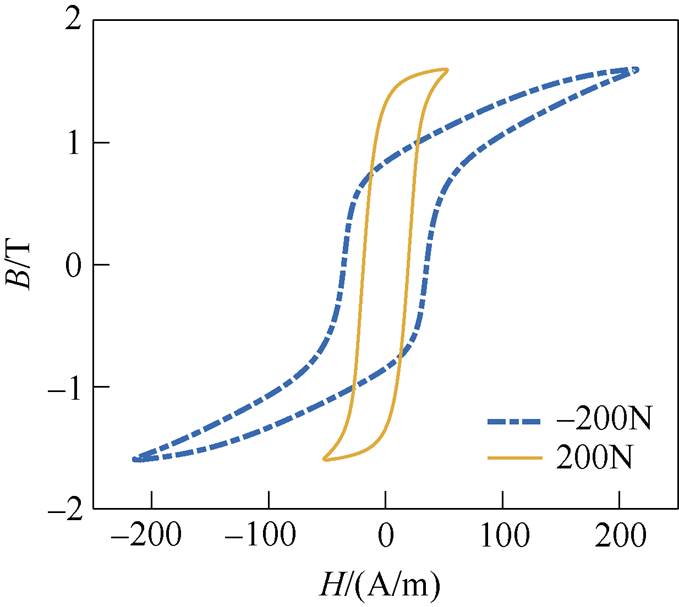
图5 F=±200N时的磁滞回线(Bm=1.5T)
Fig.5 Hysteresis loop with F=±200N (Bm=1.5T)
图6 不同压应力下不同磁通密度峰值的磁滞回线
Fig.6 Hysteresis loops under different peaked flux densities as well as compressive stress
由图6可以看出,在压应力的作用下,随着压应力的增大,磁滞回线形状、面积的改变均较为显著。特别是当磁通密度峰值Bm=1.8T、F=-200N时,磁滞回线发生一定程度的畸变。由此可见,压应力对取向硅钢片的磁滞回线影响较大。
铁损也是反映取向硅钢片磁化特性的一个重要表征,动态磁滞回线的面积在一定程度上代表了取向硅钢片的铁损,因此量化分析不同应力下取向硅钢片的铁损对深入研究取向硅钢片磁化特性随应力变化的趋势具有重要意义。对比取向硅钢片在不同应力F作用下的铁损特性,见表1,随着磁通密度峰值Bm的增大,铁损也在增大。当施加拉应力时,铁损与F=0N时相比有一定的降低,说明图4中磁滞回线的面积随拉应力的增大有一定程度的减小。而施加压应力时,取向硅钢片的铁损明显增大。
表1 不同应力下硅钢片的铁损
Tab.1 Iron loss of the grain-oriented silicon steel sheet under different stresses
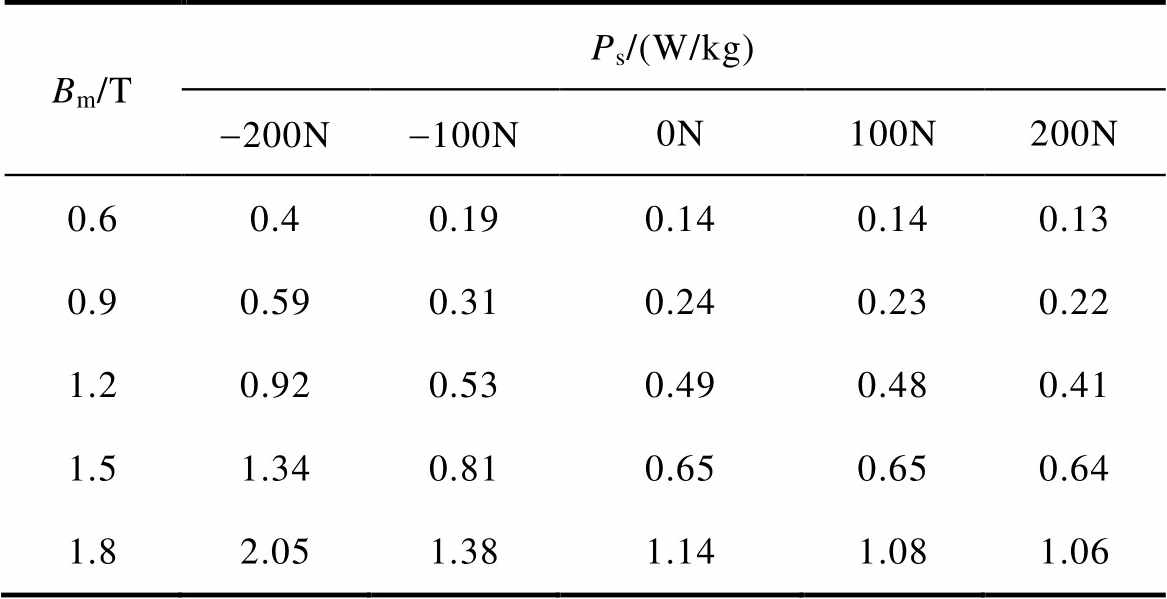
Bm/TPs/(W/kg) -200N-100N0N100N200N 0.60.40.190.140.140.13 0.90.590.310.240.230.22 1.20.920.530.490.480.41 1.51.340.810.650.650.64 1.82.051.381.141.081.06
当F=-100N和F=100N时,两种应力下铁损差异较小;但当F=-200N和F=200N时,压应力下的铁损几乎为拉应力下的两倍。说明在同一磁通密度峰值Bm下,拉应力和压应力大小相同时,压应力作用下的回线面积要比拉应力作用下的大,且应力越大,相差的倍数越大。这表明压应力对取向硅钢片的铁损有较为显著的影响,且随着压应力的增大,铁损有大幅增长的趋势。
在工频正弦激励下,测量不同磁通密度峰值Bm对应的取向硅钢片磁致伸缩应变,取得蝴蝶曲线。为分析拉应力对取向硅钢片磁致伸缩的影响,图7分别给出了F=0N、100N和200N,磁通密度峰值Bm=1.2T和1.5T时的蝴蝶曲线。
从图7中可以看出,当F=0N时,蝴蝶曲线开口向下,左右回环面积较大,取向硅钢片的形变有伸长和收缩两个方向,以收缩方向的形变为主。施加拉应力后,蝴蝶曲线整体呈“收缩”状态,形变收缩量有一定程度的增加,当磁通密度峰值Bm>1.2T时更为明显。但随着拉应力的增大,同一磁通密度峰值下取向硅钢片的形变收缩量基本保持在一定水平。
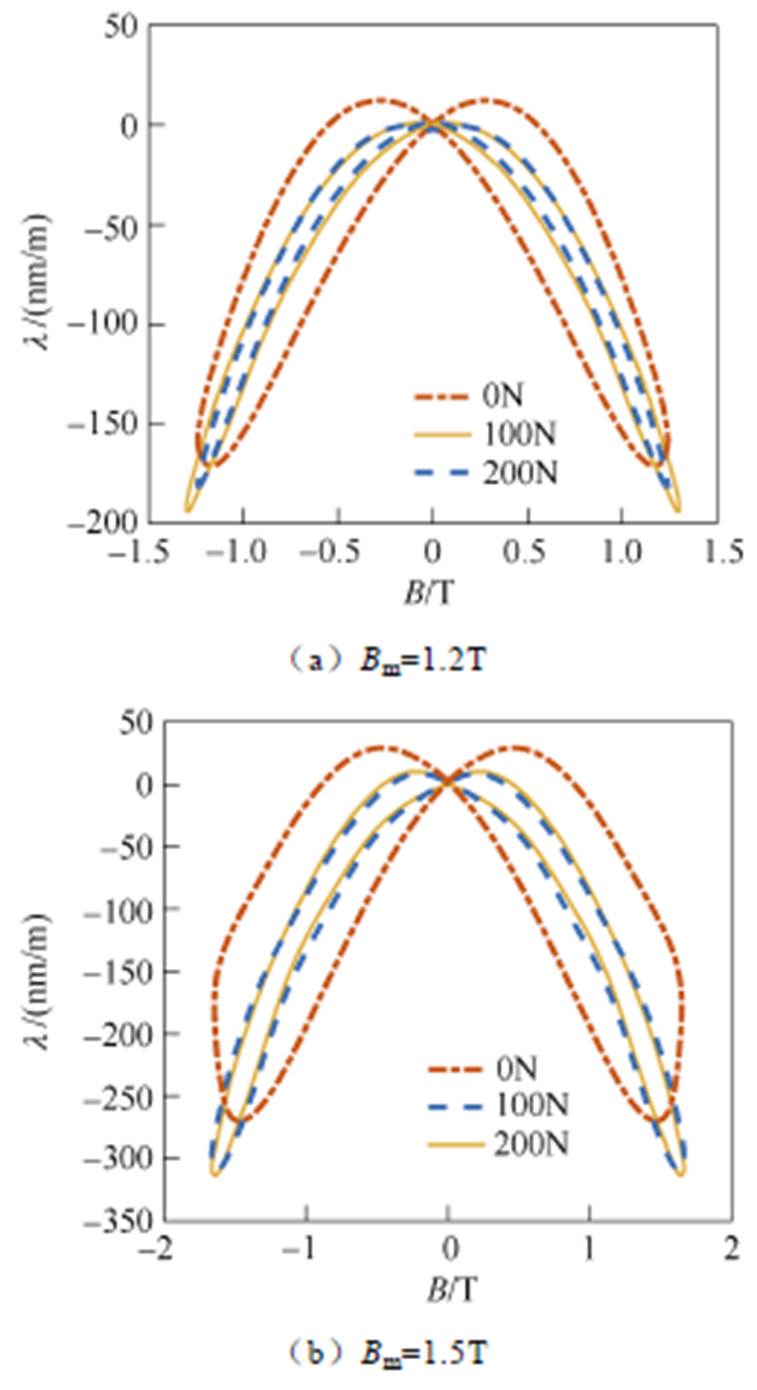
图7 不同拉应力下不同磁通密度峰值的蝴蝶曲线
Fig.7 Butterfly curves under different peaked flux densities as well as tensile stress
为进一步分析取向硅钢片的磁致伸缩在压应力下的变化情况,图8给出了磁通密度峰值Bm=1.2T和1.5T,F=0N、-100N和-200N时的蝴蝶曲线。
对比图7和图8可以看出,在压应力作用下,蝴蝶曲线开口向上,取向硅钢片有伸长和收缩两个方向的应变,以伸长方向的应变为主。当施加的压应力相同时,磁通密度幅值Bm越大,取向硅钢片形变伸长量越大;磁通密度幅值Bm相同时,随着压应力的增大,蝴蝶曲线的左右回环逐渐伸长,取向硅钢片形变伸长量逐渐加大,且两回环端部急剧“收缩”,迟滞现象有较大程度的减弱。
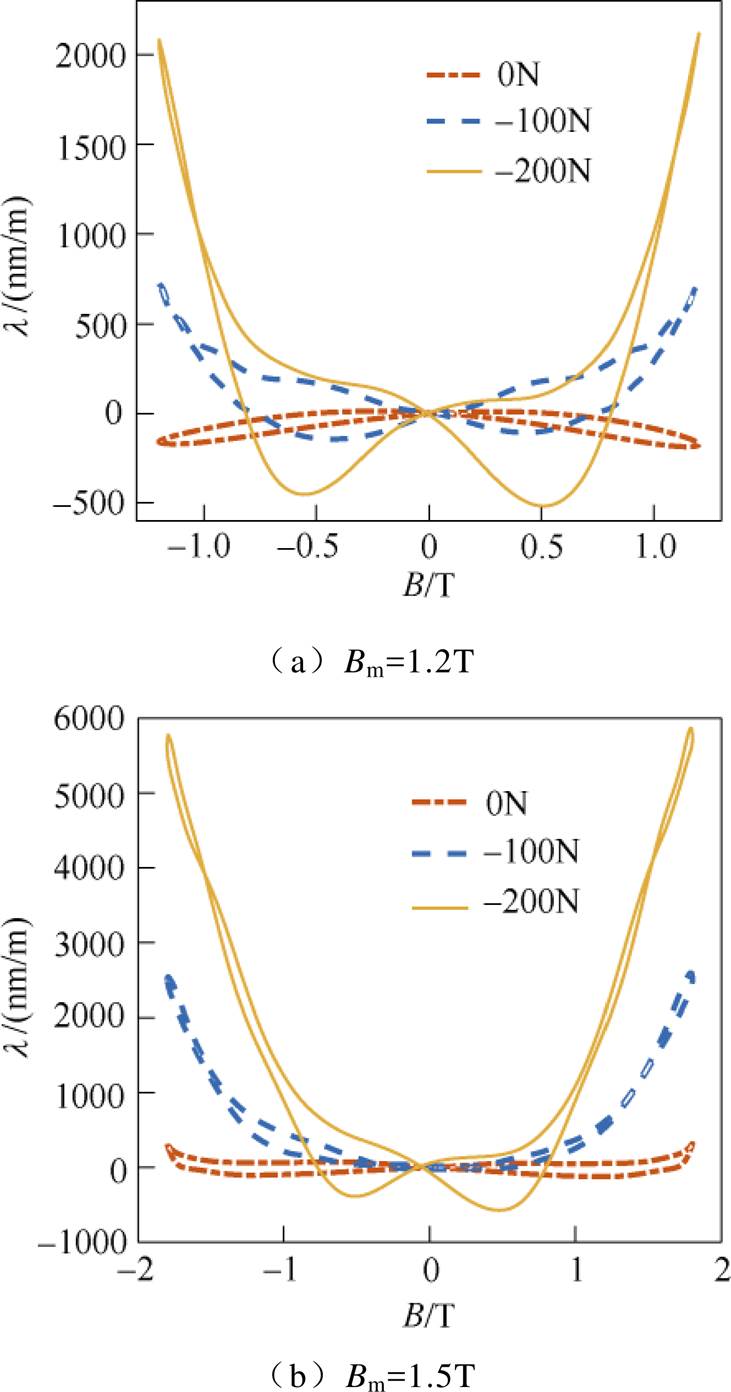
图8 不同压应力下不同磁通密度峰值的蝴蝶曲线
Fig.8 Butterfly curves under different peaked flux densities as well as compressive stress
图9给出了不同应力下的磁致伸缩峰峰值曲线,在无应力、拉应力和压应力三种情况下,磁通密度的增大都会导致磁致伸缩峰峰值lpp的增大。但是在同一磁通密度下,拉应力的增大未能引起磁致伸缩峰峰值lpp的明显改变;而随着压应力的增大,磁致伸缩峰峰值lpp迅速增大,曲线斜率也呈增大的趋势。由此可见,压应力对取向硅钢片的形变量的影响远大于拉应力对其的影响。这是因为在拉应力作用下,180°畴壁的运动占主导地位,对取向硅钢片的形变无贡献;而在压应力的作用下,90°畴壁的运动占主导地位,对取向硅钢片的形变量起正向作用[26]。
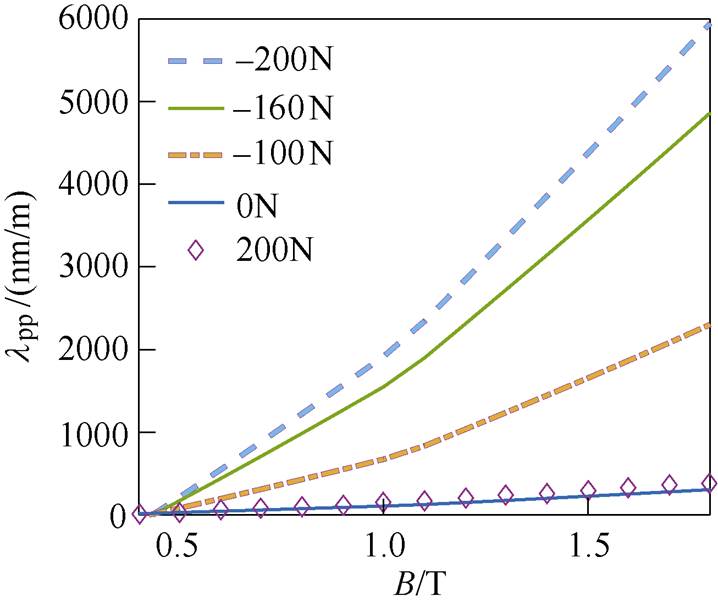
图9 不同应力下磁致伸缩峰峰值曲线
Fig.9 Peak-to-peak value curves of magnetostriction under different stress
取向硅钢片的磁致伸缩是变压器、电抗器等输变电设备在运行时所产生噪声的重要来源,深入研究分析取向硅钢片的噪声特性具有重要意义。人耳可听声音通常用A计权来表示,单片取向硅钢片换算A计权噪声的经验公式[27]为
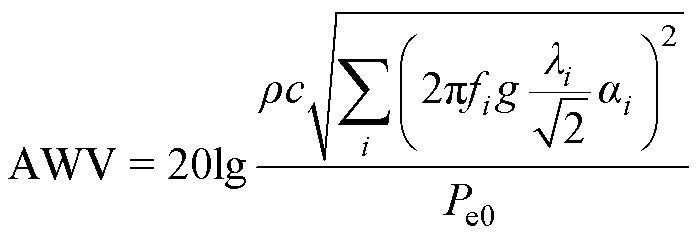 (1)
(1)
式中,AWV为A计权噪声;r 为大气密度;c为声速;fi为磁致伸缩的第i个谐波分量的频率;li为磁致伸缩第i次谐波分量的振幅;ai为不同频率下第i次谐波分量A计权系数;Pe0为基准声压值,Pe0=2× 10-5Pa。
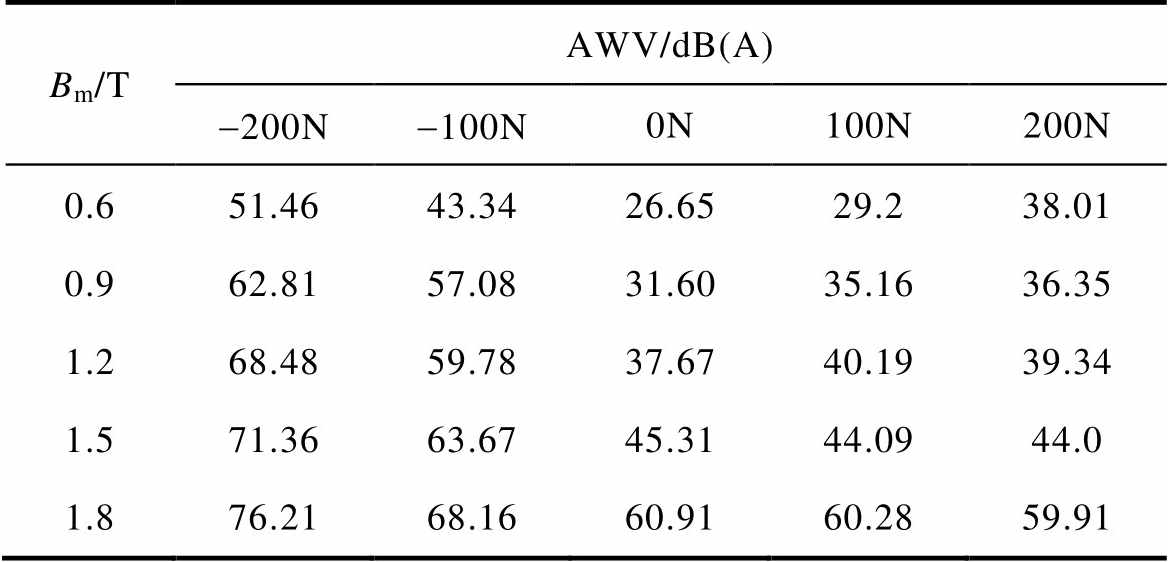
取向硅钢片的磁致伸缩频率是励磁频率的2倍,由式(1)可知,当fi相同时,取向硅钢片的AWV取决于li。对比不同应力作用下取向硅钢片的噪声特性,见表2,分别测量了F=0N、±100N和±200N时磁通密度峰值Bm从0.6~1.8T的噪声特性。以1.2T为例,在无应力和拉应力作用下,噪声均在40dB左右,上下差值较小。但是随着压应力的增大,噪声逐渐增大,特别是在F=-200N时,噪声达到近70dB,相比于F=0N时增加了近一倍,这也与前文中取向硅钢片磁致伸缩受拉应力影响较小,受压应力影响较大的规律相对应。
表2 不同应力下硅钢片的噪声特性
Tab.2 Acoustic characteristic of the grain-oriented silicon steel sheet under different stress
Bm/TAWV/dB(A) -200N-100N0N100N200N 0.651.4643.3426.6529.238.01 0.962.8157.0831.6035.1636.35 1.268.4859.7837.6740.1939.34 1.571.3663.6745.3144.0944.0 1.876.2168.1660.9160.2859.91
本节测量实验中,改变励磁频率f,并施加不同大小的应力F。图10和图11给出了f =100Hz,不同应力作用下的磁滞回线。
由图10和图11可得,频率f的增大使得磁滞回线的面积增大。频率f改变后,取向硅钢片磁滞回线在拉应力的作用下的变化仍然较小。在图6所示的磁滞回线中,当应力F=-100N时磁滞回线就已经有了较为明显的变化,而图11中应力F=-100N时与F=0N时磁滞回线无明显差异,直到应力F= -160N才开始产生变化。
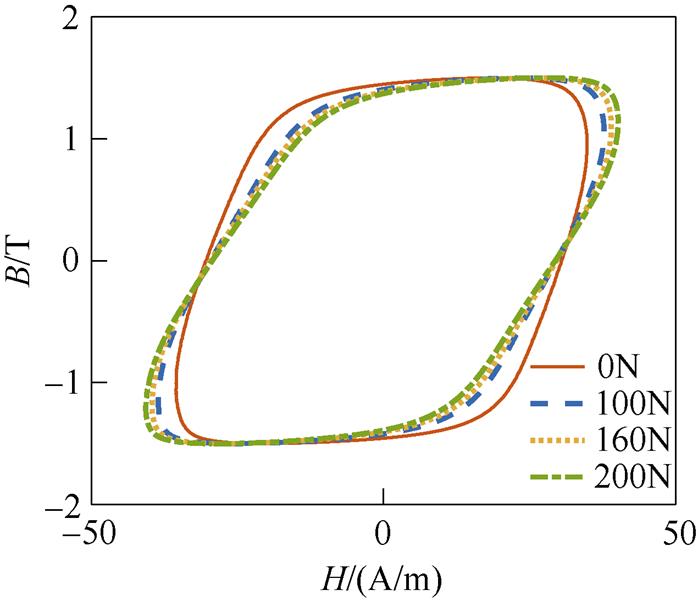
图10 不同拉应力下的磁滞回线(f =100Hz,Bm=1.5T)
Fig.10 Hysteresis loop under different tensile stress ( f =100Hz,Bm=1.5T)
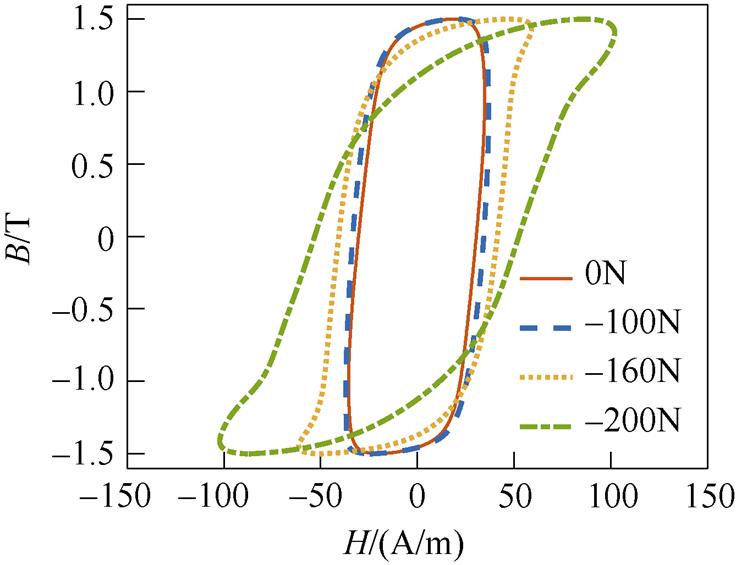
图11 不同压应力下的磁滞回线(f =100Hz,Bm=1.5T)
Fig.11 Hysteresis loop under differentcompressive stress ( f =100Hz, Bm=1.5T)
图12和图13给出了不同工况下硅钢片的铁损增长率K的变化曲线。K的表达式为
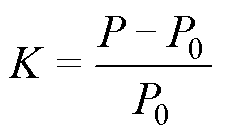 (2)
(2)
式中,K为取向硅钢片铁损增长率;P为某一应力F作用下取向硅钢片的铁损;P0为F=0N时取向硅钢片的铁损。
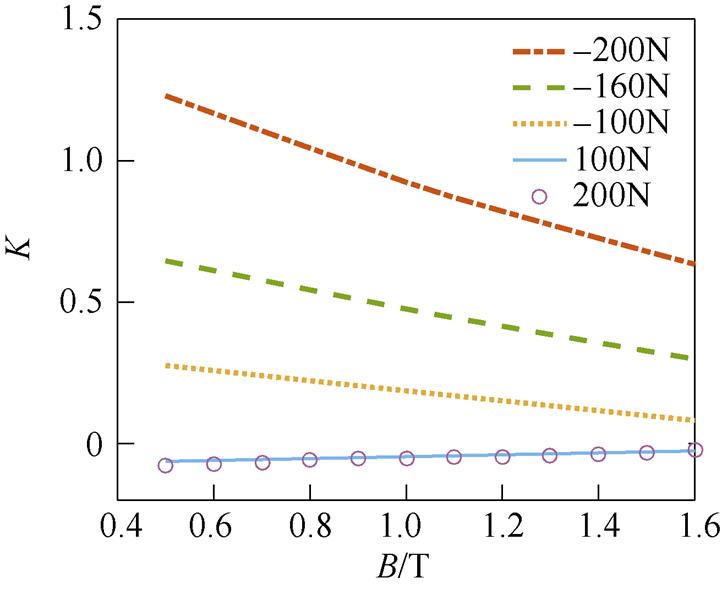
图12 不同应力下铁损增长率曲线(f =100Hz)
Fig.12 Growth rate of iron loss under different stress ( f =100Hz)
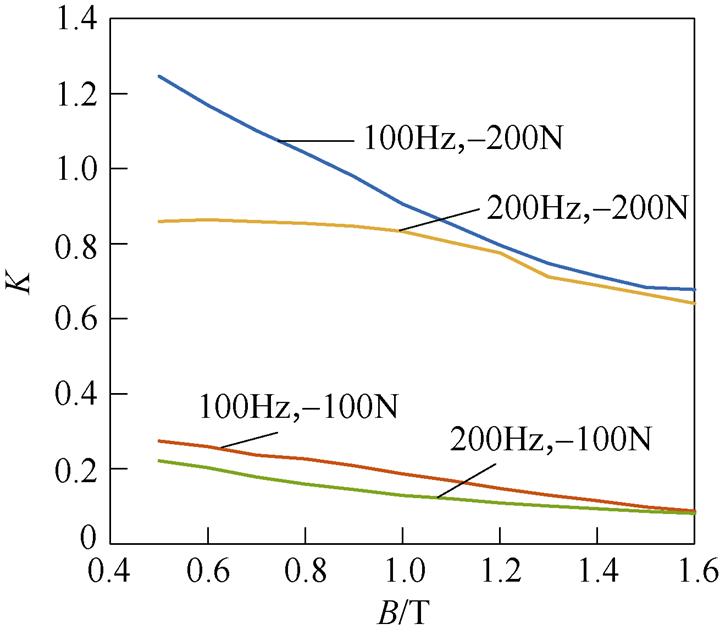
图13 频率和应力对铁损增长率的影响
Fig.13 Effect of frequency and stress on the growth rate of iron loss
从图12中可以看出,在拉应力的作用下,K一直徘徊在0值附近,拉应力的增大并没有引起铁损的增长,当磁通密度峰值Bm较小时,有负值出现,说明此时的铁损略有减小;在压应力作用下,施加压应力越大,K越大,但随着磁通密度峰值的增大,K逐渐减小,说明压应力的增大会使得取向硅钢片铁损有大幅增长,但随着取向硅钢片磁场的饱和,K呈减小趋势。
图13对比了在频率f和压应力双重影响下K的变化。由图13可得,频率f相同时,压应力的增大对K有促进作用;压应力相同时,频率f的升高对K有一定的抑制作用。且f =100Hz、F=-200N对应的曲线要远高于f =200Hz、F=-100N对应的曲线,这说明虽然压应力和频率f都会使得样片的铁损发生改变,但当两种因素共同作用时,压应力对样片铁损的影响更为显著。
图14分别给出了在F=0N, ±120N时不同频率f下的磁致伸缩蝴蝶曲线。
由图14可以看出,在无应力和压应力的作用下,随着频率f增大后,取向硅钢片的形变量逐渐减小。尤其当应力F=0N、频率f =200Hz时,蝴蝶曲线左右回环“萎缩”严重。但在拉应力的作用下,随着频率f的增大,蝴蝶曲线左右回环逐渐扩大,取向硅钢片的形变收缩量也逐步增加。
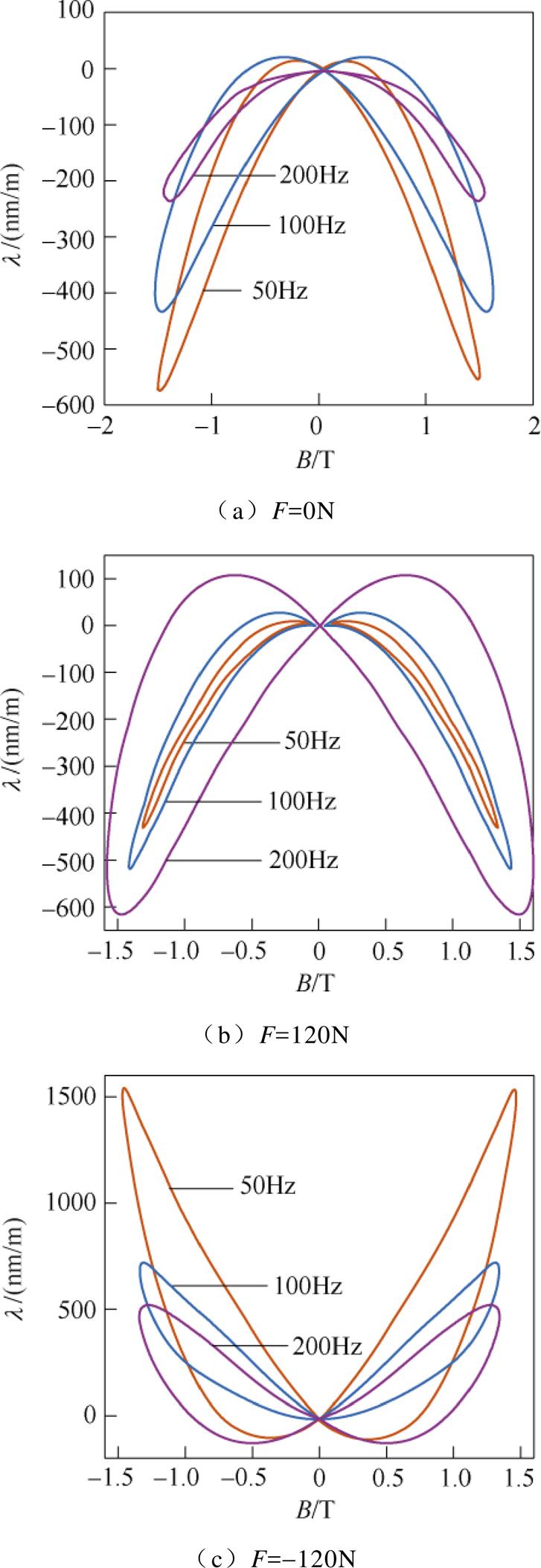
图14 不同频率下的蝴蝶曲线(Bm=1.5T)
Fig.14 Butterfly curves at different frequencies (Bm=1.5T)
图15分别给出了在F=±120N时,不同频率f下的磁致伸缩峰峰值曲线。在图15a中,当磁通密度峰值Bm相同时,频率f越高,磁致伸缩峰峰值lpp越大。如当Bm=1.6T时,f =50Hz、100Hz、150Hz、200Hz对应的lpp值分别为471.65nm/m、491.52nm/m、563.95nm/m、734.85nm/m;要达到相同大小的形变量,频率f越大,需要的磁通密度峰值越小。说明在拉应力的作用下,频率f的增加对取向硅钢片的形变量有一定的促进作用。
而在图15b中,当磁通密度峰值Bm相同时,频率f越高,磁致伸缩峰峰值lpp越小。如当Bm=1.6T时,f =50Hz、100Hz、150Hz、200Hz对应的lpp值分别为1 896.10nm/m、1 722.77nm/m、1 322.65nm/m、1 254.85nm/m。且要达到相同的形变量,频率f越大,需要的磁通密度就越大。表明在压应力的作用下,频率f的增加对取向硅钢片的形变量有一定的抑制作用。
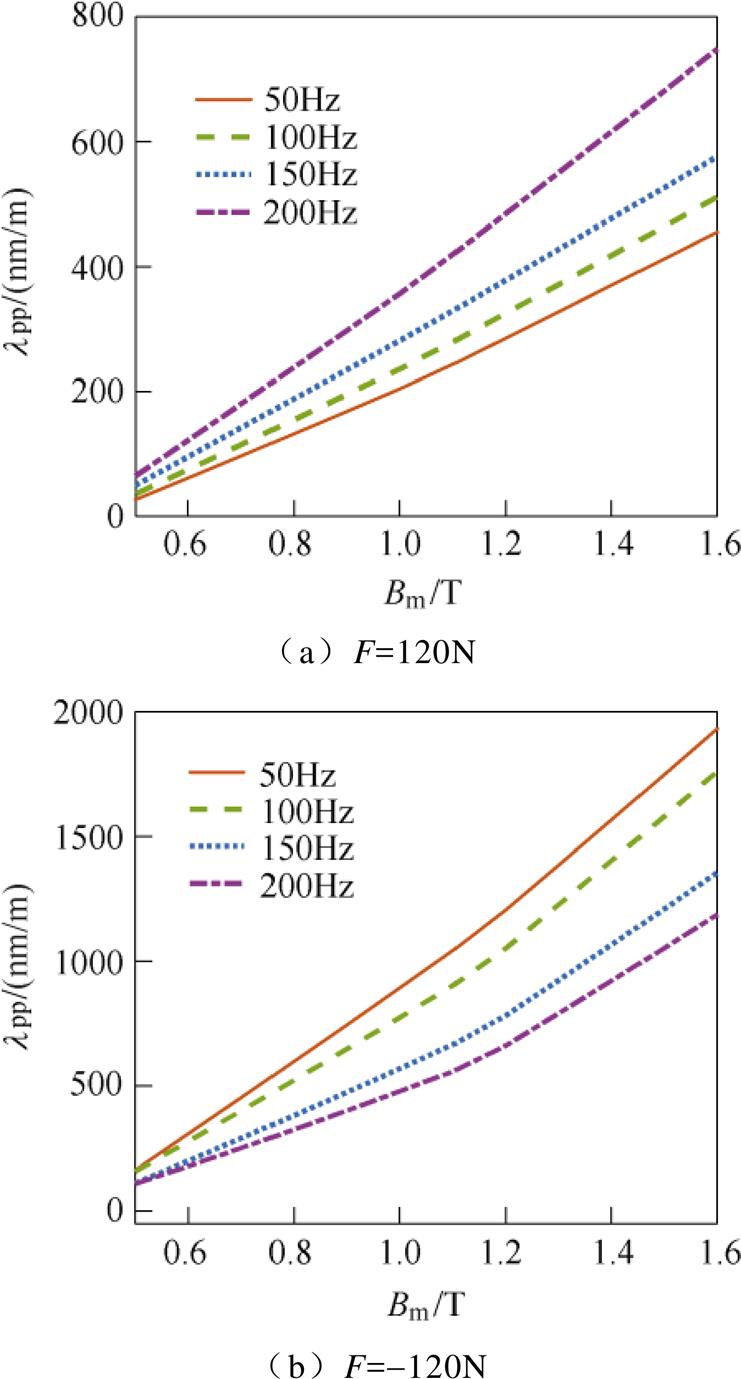
图15 不同频率下的磁致伸缩峰峰值曲线
Fig.15 Peak-to-peak value curves of magnetostriction under different frequencies
对比应力F相同、频率f不同时取向硅钢片的噪声特性,见表3和表4,无论是在拉应力还是压应力作用下,当应力F一定时,随着频率f的增加,噪声呈增大趋势。由式(1)可以看出,取向硅钢片的AWV的大小与fi和li相关,励磁频率的改变对fi和li均产生影响,但对fi的影响程度更大,这就解释了在压应力作用下,取向硅钢片的形变量随着频率的增高有一定程度的减小,但噪声依然增大的原因。但是当f增大到一定频率,如f =250Hz时,随着样片磁场的饱和,噪声也基本维持在一定水平,不再有明显增长。
表3 不同频率下硅钢片的噪声特性(F=120N)
Tab.3 Acoustic characteristic of the grain-oriented silicon steel sheet under different frequencies (F=120N)
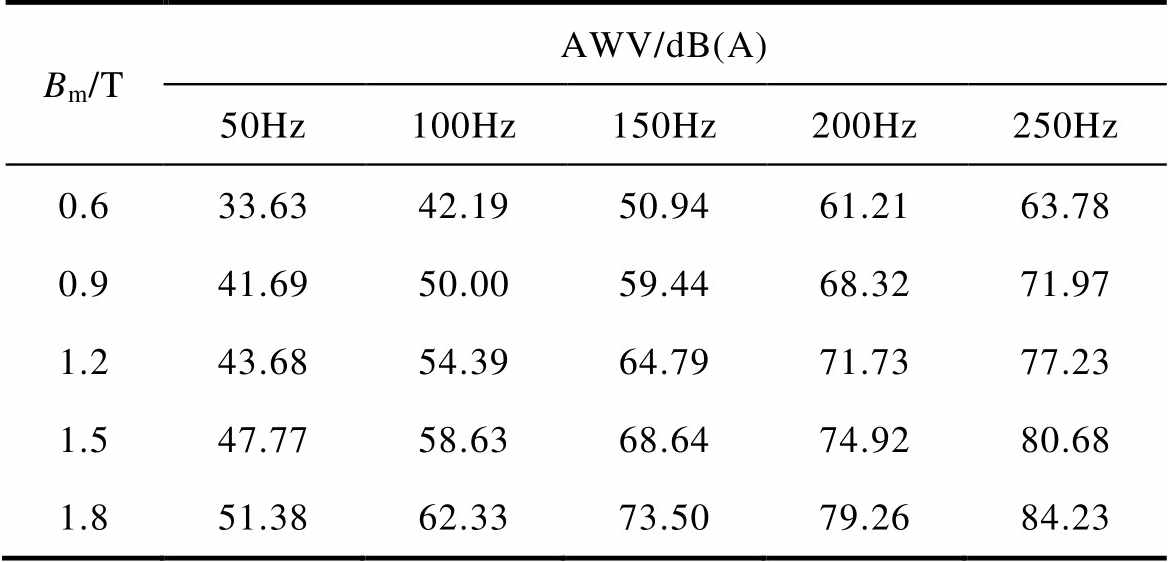
Bm/TAWV/dB(A) 50Hz100Hz150Hz200Hz250Hz 0.633.6342.1950.9461.2163.78 0.941.6950.0059.4468.3271.97 1.243.6854.3964.7971.7377.23 1.547.7758.6368.6474.9280.68 1.851.3862.3373.5079.2684.23
表4 不同频率下硅钢片的噪声特性(F=-120N)
Tab.4 Acoustic characteristic of the grain-oriented silicon steel sheet under different frequencies (F=-120N)
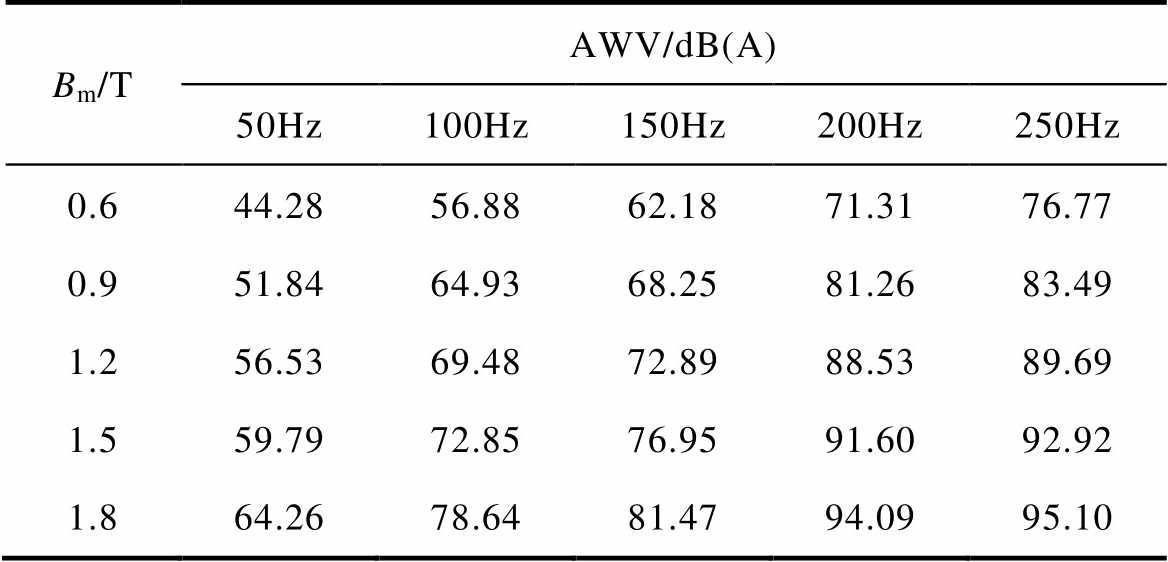
Bm/TAWV/dB(A) 50Hz100Hz150Hz200Hz250Hz 0.644.2856.8862.1871.3176.77 0.951.8464.9368.2581.2683.49 1.256.5369.4872.8988.5389.69 1.559.7972.8576.9591.6092.92 1.864.2678.6481.4794.0995.10
在实际工程中,变压器经常运行于谐波激励条件下,为此需要深入研究谐波激励下应力对取向硅钢片磁性能的影响。基于图2所示平台,施加基波与高次谐波相叠加的混合激励,即
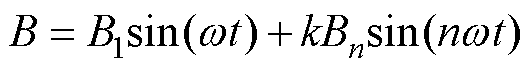 (3)
(3)
式中,w 为角频率,w=2p f,f =50Hz;n为谐波次数,n=3, 5, 7;B1为基波磁通密度幅值;Bn为n次谐波磁通密度幅值;k为n次谐波磁通密度幅值与基波磁通密度幅值之比,k =50%、100%。通过改变k、n两个参数来改变外磁场条件。
图16和图17给出了k=50%、n=3时,拉应力和压应力分别为0N、±100N、±160N、±200N时的磁滞回线。

图16 不同拉应力下的磁滞回线(k=50%, n=3, Bm=1.5T)
Fig.16 Hysteresis loop under different tensile stress (k=50%, n=3,Bm=1.5T)
对比图16和图17可得,在谐波激励下,拉应力对取向硅钢片的影响仍较小,随着压应力的增大,取向硅钢片磁滞回线的形状和面积均有较为明显的改变。
图18给出了不同压应力及不同谐波次数作用下损耗增大幅度曲线。
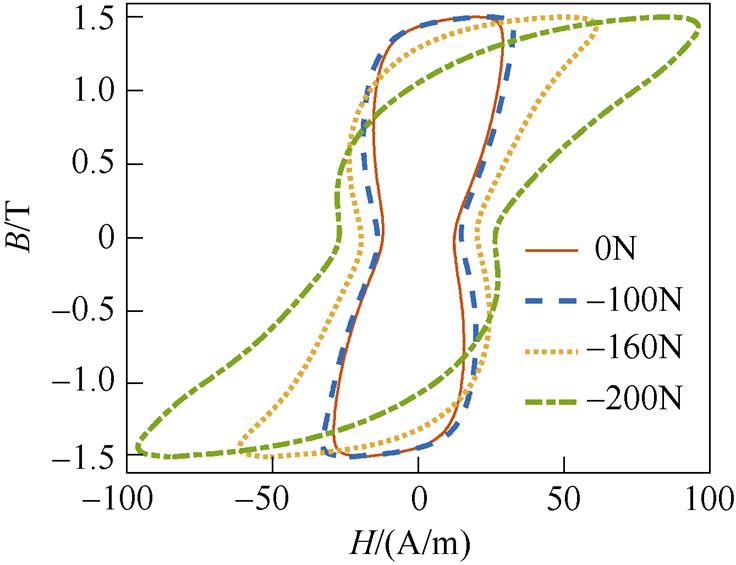
图17 不同压应力下的磁滞回线(k=50%, n=3,Bm=1.5T)
Fig.17 Hysteresis loop under differentcompressive stress (k=50%, n=3, Bm=1.5T)
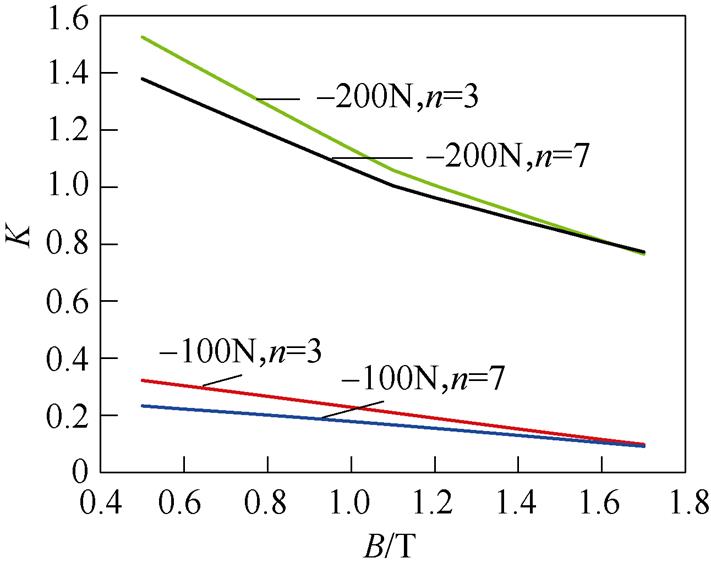
图18 谐波和应力对铁损增长率的影响
Fig.18 Effect of harmonics and stress on the growth rate of iron loss
由图18可以看出,施加压应力后,在同一应力作用下,谐波次数越高,铁损增长率越小,但随着磁通密度幅值的增大,同一应力下不同谐波次数对应的铁损增长率逐渐趋于相同;在同一谐波次数磁场激励下,压应力越大,铁损增长率越大。这说明当压应力和谐波同时作用时,压应力对样片的铁损增长率造成的影响更大;并且压应力在一定程度上会限制谐波对样片铁损造成的影响,即谐波次数越高,铁损增长率越小。
图19给出了分别施加-100N、0N、100N应力下,谐波含量为k=100%时,谐波次数n=3、5、7次时谐波励磁激励下样片的蝴蝶曲线。
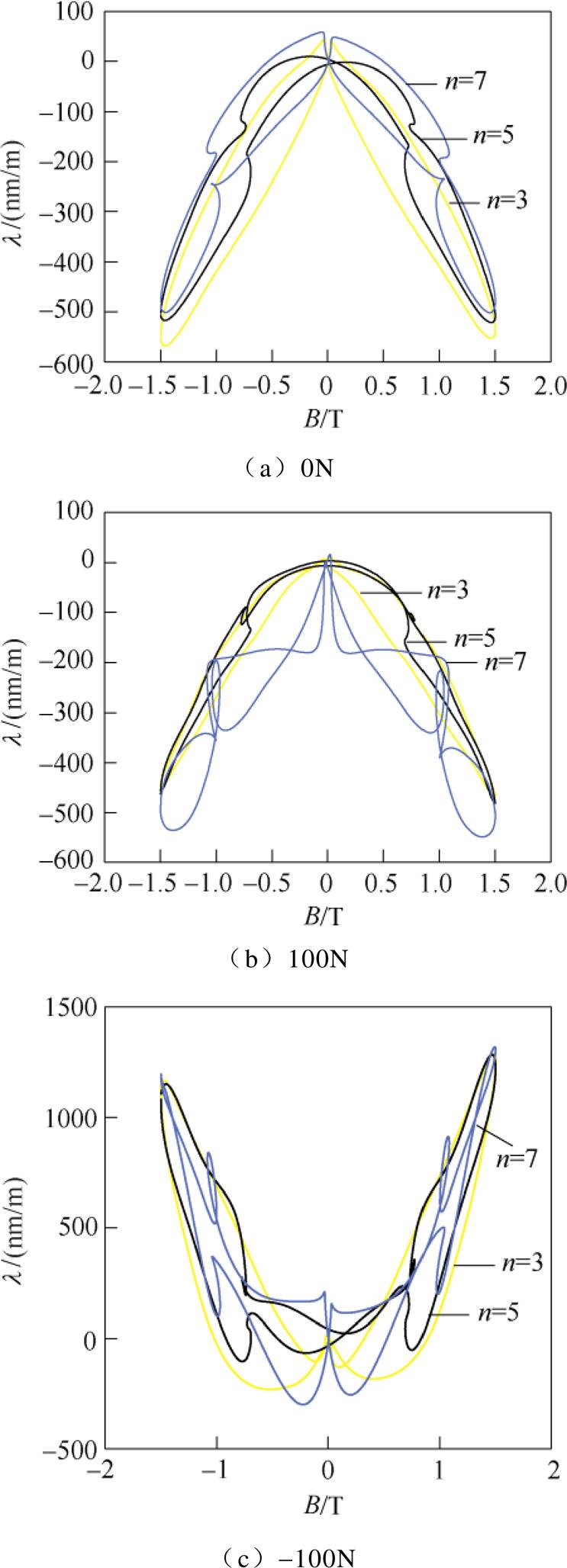
图19 应力作用下不同谐波次数的蝴蝶曲线(Bm=1.5T, k=100%)
Fig.19 Butterfly curves of different harmonic orders under stress (Bm=1.5T, k=100%)
由图19中可以看出,当无应力作用时,在高次谐波的激励下,蝴蝶曲线的左右回环都出现了弯曲,有出现小回环的趋势,且随着谐波次数的增大,取向硅钢片的磁致伸缩略有减小。在拉应力和压应力的作用下,取向硅钢片的磁致伸缩随着谐波次数的增大无明显变化。在拉应力的作用下,蝴蝶曲线左右回环弯曲更严重,且整体呈收缩状态,且此时的蝴蝶曲线出现多个小回环。而在压应力的作用下,蝴蝶曲线开口向上,样片以伸长方向的应变为主。蝴蝶曲线依然产生畸变,左右回环有多处弯曲,但没有成为多个小回环的趋势。
不同谐波激励下的硅钢片的噪声特性见表5~表7,可以看出,在同一谐波含量k下,随着谐波次数n的增大,虽然样片的磁致伸缩有微量的缩小,但噪声略有升高;当谐波次数n相同时,谐波含量越高,噪声越大。这表明当样片在不同形式的谐波激励下时,噪声的增大主要取决于样片的振动频率。且在相同数值的应力作用下,压应力下的噪声更大,说明压应力对谐波下的硅钢片噪声特性影响更大。
表5 不同谐波激励下硅钢片的噪声特性(0N)
Tab.5 Noise characteristics of silicon steel sheet under different harmonic excitations (0N)
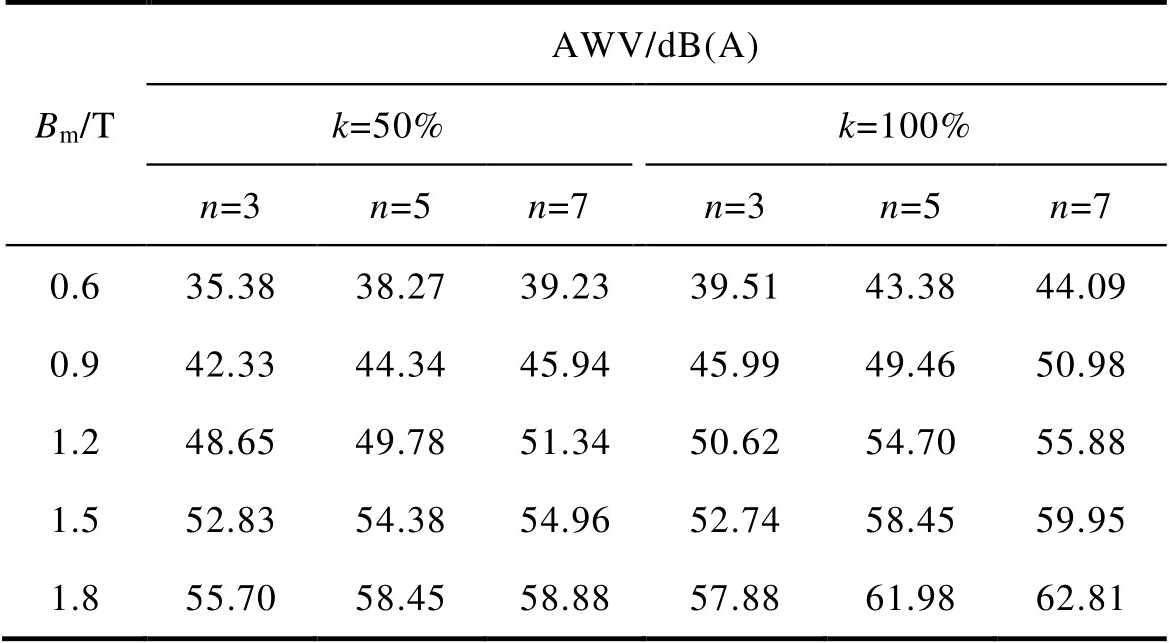
Bm/TAWV/dB(A) k=50%k=100% n=3n=5n=7n=3n=5n=7 0.635.3838.2739.2339.5143.3844.09 0.942.3344.3445.9445.9949.4650.98 1.248.6549.7851.3450.6254.7055.88 1.552.8354.3854.9652.7458.4559.95 1.855.7058.4558.8857.8861.9862.81
表6 不同谐波激励下硅钢片的噪声特性(120N)
Tab.6 Noise characteristics of silicon steel sheet under different harmonic excitations (120N)
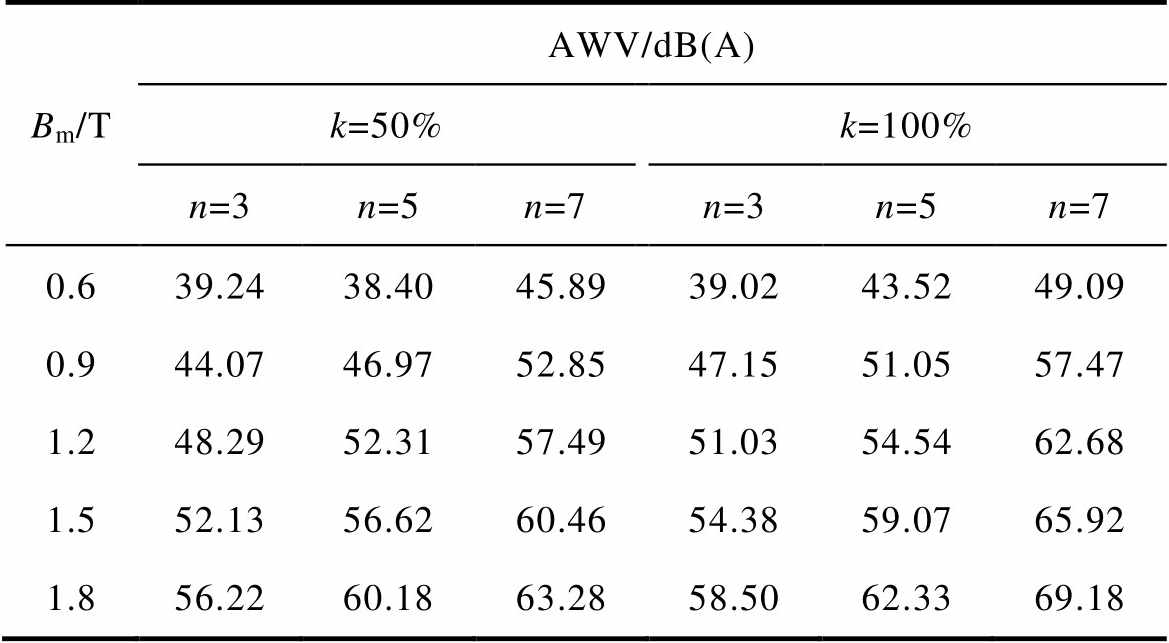
Bm/TAWV/dB(A) k=50%k=100% n=3n=5n=7n=3n=5n=7 0.639.2438.4045.8939.0243.5249.09 0.944.0746.9752.8547.1551.0557.47 1.248.2952.3157.4951.0354.5462.68 1.552.1356.6260.4654.3859.0765.92 1.856.2260.1863.2858.5062.3369.18
表7 不同谐波激励下硅钢片的噪声特性(-120N)
Tab.7 Noise characteristics of silicon steel sheet under different harmonic excitations (-120N)

Bm/TAWV/dB(A) k=50%k=100% n=3n=5n=7n=3n=5n=7 0.643.9850.7552.5347.1853.4656.67 0.953.5057.8759.8856.0661.2864.77 1.258.9963.5966.3262.3666.3371.12 1.564.4268.7771.6866.5071.1476.19 1.870.5470.7777.4772.3374.2581.97
本文重点研究了不同频率及不同应力影响下硅钢片的综合磁性能,结果表明:
1)在压应力作用下磁滞回线的形状有明显变化。取向硅钢片的铁损在同一频率下受拉应力的影响较小,受压应力的影响较大。在同一压应力下,频率的增大对铁损的增长率有一定的抑制作用。当频率和压应力同时改变时,压应力对铁损增长率的影响更加显著。
2)取向硅钢片的磁致伸缩在同一频率下受拉应力的影响较小,受压应力的影响较大。在拉应力作用下,取向硅钢片的磁致伸缩随频率的增大而增大;而在无应力和压应力作用下,频率的升高对取向硅钢片的磁致伸缩有一定的抑制作用。
3)在同一频率下,拉应力对取向硅钢片的噪声影响较小,而压应力对其影响较大;在同一应力下,取向硅钢片的噪声先随着频率的增大而增大,而后维持在一定水平,不再有明显增长。
4)谐波激励下,拉应力的增大对样片的磁性能无较大影响;压应力增大后,样片损耗的增长率呈下降趋势;谐波次数及含量越高、噪声越大。
参考文献
[1] 韩先才, 孙昕, 陈海波, 等. 中国特高压交流输电工程技术发展综述[J]. 中国电机工程学报, 2020, 40(14): 4371-4386.
Han Xiancai, Sun Xin, Chen Haibo, et al. The overview of development of UHV AC transmission technology in China[J]. Proceedings of the CSEE, 2020, 40(14): 4371-4386.
[2] 贲彤, 陈龙, 闫荣格, 等. 考虑磁化及磁致伸缩特性各向异性的感应电机铁心电磁应力分析[J]. 电工技术学报, 2019, 34(1): 66-74.
Ben Tong, Chen Long, Yan Rongge, et al. Stress analysis of induction motor core considering aniso- tropic magnetic and magnetostrictive properties[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 66-74.
[3] 张欣, 解超群, 祝丽花, 等. 考虑磁致伸缩效应的电机应力数值仿真与实验[J]. 电工技术学报, 2017, 32(增刊2): 50-55.
Zhang Xin, Xie Chaoqun, Zhu Lihua, et al. Numerical simulation and experimental research on stress of motor including magnetostriction effects[J]. Transa- ctions of China Electrotechnical Society, 2017, 32(S2): 50-55.
[4] 祝丽花, 李晶晶, 朱建国. 服役条件下取向硅钢磁致伸缩模型的研究[J]. 电工技术学报, 2020, 35(19): 4131-4138.
Zhu Lihua, Li Jingjing, Zhu Jianguo. Research on magnetostrictive model for oriented silicon steel under service conditions[J]. Transactions of China Electrotechnical Society, 2020, 35(19): 4131-4138.
[5] 陈德志, 张玉庸, 白保东, 等. 不同温度及谐波下硅钢片电磁-力特性与变频电机振动[J]. 电工技术学报, 2020, 35(22): 4647-4656.
Chen Dezhi, Zhang Yuyong, Bai Baodong, et al. Electromagnetic-forceand vibration of silicon steel sheetand variable frequency motor under different temperature and harmonic[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4647-4656.
[6] 吴胜男, 于慎波, 佟文明, 等. 磁致伸缩引起的径向磁通电机定子铁心振动精确解析模型[J]. 电工技术学报, 2019, 34(2): 226-235.
Wu Shengnan, Yu Shenbo, Tong Wenming, et al. A precise analytical model of stator core vibration due to magnetostriction for radial flux motors[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(2): 226-235.
[7] 王博文, 曹淑瑛, 黄文美. 磁致伸缩材料与器件[M]. 北京: 冶金工业出版社, 2008.
[8] 郭贻诚. 铁磁学[M]. 重排本. 北京: 北京大学出版社, 2014.
[9] Shahaj A, Garvey S D. A possible method for magnetostrictive reduction of vibration in large electrical machines[J]. IEEE Transactions on Mag- netics, 2011, 47(2): 374-385.
[10] Bartoletti C, Desiderio M, Di Carlo D, et al. Vibro- acoustic techniques to diagnose power transformers[J]. IEEE Transactions on Power Delivery, 2004, 19(1): 221-229.
[11] Kitagawa W, Ishihara Y, Todaka T, et al. Analysis of structural deformation and vibration of a transformer core by using magnetic property of magneto- striction[J]. Electrical Engineering in Japan, 2010, 172(1): 19-26.
[12] Dou Yu, Li Yongjian, Zhang Changgeng, et al. Effects of uniaxial stress along different directions on alternating magnetic properties of silicon steel sheets[J]. IEEE Transactions on Magnetics, 2020, 56(3): 1-4.
[13] Zhu Lixun, Yoon H S, Cho H J, et al. Finite-element analysis of magnetostriction force in power trans- former based on the measurement of anisotropic magnetostriction of highly grain-oriented electrical steel sheet[J]. IEEE Transactions on Magnetics, 2016, 52(3): 1-4.
[14] Zhu Lihua, Li Jingjing, Yang Qingxin, et al. An improved magnetostriction model for electrical steel sheet based on Jiles-Atherton model[J]. IEEE Transa- ctions on Magnetics, 2020, 56(3): 1-4.
[15] Liu Jia, Tian Guiyun, Gao Bin, et al. Domain wall characterization inside grain and around grain boundary under tensile stress[J]. Journal of Mag- netism and Magnetic Materials, 2019, 471: 39-48.
[16] Ito S, Mifune T, Matsuo T, et al. Energy-based magnetization and magnetostriction modeling of grain-oriented silicon steel under vectorial excita- tions[J]. IEEE Transactions on Magnetics, 2016, 52(5): 1-4.
[17] 邱发生. 基于磁畴动态行为特征的应力表征研究[D]. 成都: 电子科技大学, 2019.
[18] Ben Tong, Yang Qingxin, Yan Rongge, et al. Research on stress characteristics of shunt reactor considering magnetization and magnetostrictive anisotropy[J]. IEEE Transactions on Magnetics, 2018, 54(3): 1-4.
[19] 张艳丽, 孙小光, 谢德馨, 等. 无取向硅钢片各向异性磁致伸缩特性模拟[J]. 中国电机工程学报, 2014, 34(27): 4731-4736.
Zhang Yanli, Sun Xiaoguang, Xie Dexin, et al. Modeling of anisotropic magnetostriction property of non-oriented silicon steel sheet[J]. Proceedings of the CSEE, 2014, 34(27): 4731-4736.
[20] 张艳丽, 孙小光, 谢德馨, 等. 无取向电工钢片磁致伸缩特性测量与模拟[J]. 电工技术学报, 2013, 28(11): 176-181.
Zhang Yanli, Sun Xiaoguang, Xie Dexin, et al. Measurement and simulation of magnetostrictive properties for non-grain oriented electrical steel sheet[J]. Transactions of China Electrotechnical Society, 2013, 28(11): 176-181.
[21] Zhang Yanli, Li Qiang, Zhang Dianhai, et al. Mag- netostriction of silicon steel sheets under different magnetization conditions[J]. IEEE Transactions on Magnetics, 2016, 52(3): 1-4.
[22] 韩芳旭, 李岩, 井永腾, 等. 超高压变压器铁芯硅钢片磁致伸缩力数值计算[J]. 高电压技术, 2017, 43(3): 980-986.
Han Fangxu, Li Yan, Jing Yongteng, et al. Numerical calculation of magnetostrictive force for EHV trans- former core silicon steel[J]. High Voltage Engin- eering, 2017, 43(3): 980-986.
[23] 林福, 左曙光, 毛钰, 等. 考虑电流谐波的永磁同步电机电磁振动和噪声半解析模型[J]. 电工技术学报, 2017, 32(9): 24-31.
Lin Fu, Zuo Shuguang, Mao Yu, et al. Semi-analytical model of vibration and noise for permanent magnet synchronous motor considering current harmonics[J]. Transactions of China Electrotechnical Society, 2017, 32(9): 24-31.
[24] 赵小军, 杜雨彤, 刘洋, 等. 应用磁-机械耦合场频域解法的铁芯直流偏磁振动特性分析[J]. 高电压技术, 2020, 46(4): 1216-1225.
Zhao Xiaojun, Du Yutong, Liu Yang, et al. Vibration characteristics analysis of iron core under DC-biased condition by solving coupled magneto-mechanical field in frequency-domain[J]. High Voltage Engineering, 2020, 46(4): 1216-1225.
[25] 沙瑞, 祝丽花, 韩天衡, 等. 施加机械应力条件下硅钢片磁特性测量分析[J]. 机械设计, 2019, 36(增刊1): 51-55.
Sha Rui, Zhu Lihua, Han Tianheng, et al. Measure- ment and analysis of magnetic properties of silicon steel sheet under mechanical stress[J]. Journal of Machine Design, 2019, 36(S1): 51-55.
[26] Anderson P I, Moses A J, Stanbury H J. Assessment of the stress sensitivity of magnetostriction in grain- oriented silicon steel[J]. IEEE Transactions on Mag- netics, 2007, 43(8): 3467-3476.
[27] International Electrotechnical Commission. IEC/TR 62581 Electrical Steel-Methods of measurement of the magnetostriction characteristics by means of single sheet and Epstein test specimens[S]. Switzerland: IEC Central Office, 2010.
Experimental Study on the Effect of Mechanical Stress on the Comprehensive Magnetic Properties of the Grain-Oriented Silicon Steel
Abstract Transformer cores are subjected to external stress and high-frequency excitation for a long time during operation, which leads to increasingly severe problems of vibration, noise, and loss. To further study the comprehensive magnetic properties of the grain-oriented silicon steel sheet under different frequencies and stresses, a platform for measuring the comprehensive magnetic properties of soft magnetic material is established. Firstly, the effects of tensile and compressive stress on magnetostriction, hysteresis loop and loss characteristics of the grain-oriented silicon steel at 50Hz are obtained by using a single-sheet tester and a stress-controllable device. Furthermore, the variation of the comprehensive magnetic properties of the grain-oriented silicon steel sheet is studied, and the influence of stress and different incentives on the magnetic, magnetostrictive and acoustic characteristics is analyzed. The measured results show that compressive stress rather than tensile stress greatly influences on the magnetic properties of the grain-oriented silicon steel sheet. Furthermore, the magnetostriction decreases with the increase of frequency under compressive stress, whereas the noise increases with higher frequency, harmonic content, harmonic order, and more immense compressive stress.
Keywords:Iron loss, magnetostriction, mechanical stress, vibration, noise
中图分类号:TM41
DOI: 10.19595/j.cnki.1000-6753.tces.210703
国家自然科学基金(51777073)、北京市自然科学基金(3212036)和中央高校基本科研业务费(2019 MS078)资助项目。
收稿日期 2021-05-14
改稿日期 2021-06-11
E-mail: zxjncepu@ncepu.edu.cn(通信作者)
张凌云 女,1994年生,硕士研究生,主要研究方向为铁心本体振动噪声、多物理场耦合计算。
E-mail: zly-renew@ncepu.edu.cn
(编辑 郭丽军)