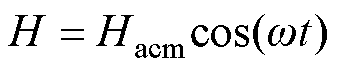 (1)
(1)
摘要 直流偏置磁场会造成磁致伸缩材料磁滞回环的畸变与不对称,影响材料的损耗数值与磁滞特性,且现有的磁能损耗模型无法对变直流偏置磁场下的损耗进行准确的表征和计算,因此有必要研究直流偏置对磁致伸缩材料磁特性的影响规律及数学表述,这对提高大功率磁致伸缩器件的输出性能具有重要意义。该文在变直流偏置激励条件下,测试了Terfenol-D样品在不同交流激励频率和磁通密度幅值下的动态磁滞回线,发现了其变化规律并提取了损耗特性和磁滞特性参数;基于Bertotti损耗分离理论和实测数据,采用Levebverg-Marquard算法,建立计及直流偏置影响的磁致伸缩材料高频损耗计算模型,该模型采用多元参数回归方法,通过引入直流偏置相关项对损耗系数进行修正;多种工况下的损耗计算值与实验值对比分析表明了计及直流偏置影响的磁致伸缩材料高频动态损耗特性模型的准确性。
关键词:Terfenol-D合金 直流偏置 高频动态磁滞特性 磁能损耗模型
超磁致伸缩材料Terfenol-D合金由于具有能量密度高(约25kJ/m3)、磁致伸缩应变大(约0.0016)响应速度快(ms级)等优点被广泛应用于制作高频换能器核心驱动元件。但高频激励下,磁致伸缩材料的巨大磁能损耗限制了磁致伸缩换能器的输出特性[1-5]。磁致伸缩换能器通常在直流偏置磁场下运行,以消除倍频效应并优化输出性能[6-7]。因此,研究磁致伸缩材料在直流偏置工况下的损耗特性和磁滞特性是高频磁致伸缩换能器结构设计与输出模型的研究基础和关键。
近年来,国内外磁能损耗的计算方法主要有两类:一是磁滞模型,主要为Jiles-Atherton模型和Preisach模型,此类模型具有较高的计算精度,但由于参数辨识过程复杂,时间复杂度较高,其工程应用较为困难[8-9];二是经验公式模型,能够简化损耗的分析处理过程,直观建立损耗、磁通密度幅值和频率的关系,通过大量的实验数据进行拟合计算识别模型参数,计算精度可以得到提高[10]。文献[11]结合静态J-A磁滞模型,通过对硅钢片进行磁性能测试获得不同频率正弦及直流偏磁工况损耗特性数据,分析了频率对磁滞特性的影响规律,提出一种可以考虑频率效应的磁滞建模方法,用于模拟不同频率正弦及偏磁工况下硅钢片的磁滞特性,但其辨识参数复杂且激励频率最大为400Hz。文献[12]以Preisach磁滞模型为基础,通过两组非对称的一阶回转曲线得到Everett函数,建立了动态损耗模型,实现交直流混合激励条件下动态磁滞特性及总损耗的预测,但该模型未通过实验对其精度进行验证。文献[13]在Steinmetz损耗模型的基础上,基于实验数据通过引入等效电导率参数提出了一种改进的考虑直流偏磁的铁损耗模型,但测试的直流偏置磁场强度较小。文献[14]在直流偏置磁场饱和效应下,基于Steinmetz Premagnetization Graph(SPG)法,通过引入考虑频率与直流偏置因素的损耗系数修正铁损模型,但该模型损耗测试的频率范围为50~500Hz且未对总损耗进行分离。文献[15]根据Bertotti损耗分离公式,在矩形激励及低直流偏置磁场(0~30A/m)工况下,通过引入直流偏磁的磁滞回环畸变形状因子建立了直流预磁化分离铁心损耗模型,该模型更适用于非正弦激励下的铁损计算,未考虑磁致伸缩材料的倍频效应影响。文献[16-18]通过搭建磁致伸缩材料Terfenol-D合金的高频损耗测试平台,根据测试的高频动态磁滞回线建立了考虑损耗系数随频率和磁通密度幅值变化的变系数磁能损耗模型,该模型可以精准预测高频下磁致伸缩材料的磁能损耗,未考虑直流偏置对Terfenol-D合金损耗及磁特性的影响。然而,实验中发现直流偏置磁场对Terfenol-D磁能损耗的影响不容忽视:当f为10kHz,交流磁通密度幅值Bacm为0.06T时,最大损耗偏差可达27.6%。
针对上述存在问题,本文搭建了考虑变直流偏置磁场的Terfenol-D高频动态磁特性实验测试平台,测试了样品在不同直流偏置Hdc、激励频率f和交流磁通密度幅值Bacm下的动态磁滞回线。基于Bertotti损耗分离理论与所测实验数据,建立了一种改进的考虑直流偏置磁场的超磁致伸缩材料高频磁能损耗分离模型。在该模型中,不仅引入直流偏置项来修正损耗系数,同时考虑了动态磁特性和趋肤效应的影响,增加了附加激励频率项和磁通密度幅值项,提高了模型精度,并对从测试的动态磁滞回线中提取偏置磁场对磁特性参数的影响因素进行详细分析。对比多组实验测试数据(频率范围为5~25kHz、磁通密度幅值范围为0.01~0.06T,直流偏置磁场强度的范围为0~5kA/m)和模型计算数据,验证了所提出的考虑变直流偏置磁场影响的磁致伸缩材料高频动态损耗模型的准确性和有效性。
磁致伸缩材料在正弦交变磁场中被磁化时,由于畴壁移动和磁畴内磁矩转向存在不可逆磁化阶段造成材料内部能量损耗,使材料内部磁感应强度始终落后于交变磁场一个相位d。在动态磁化过程中,交变磁场的简谐变化和对应的复数形式为
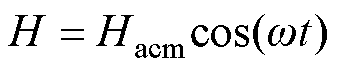 (1)
(1)
 (2)
(2)
若正弦交变磁场H较小,磁滞回线为椭圆形。磁感应强度B和H波形相同,但落后一个相位,因此B的简谐变化和对应的复数形式为
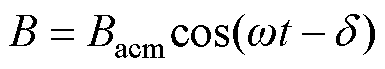 (3)
(3)
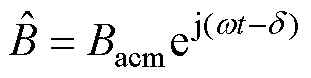 (4)
(4)
式中,Hacm为交变激励磁场的磁场强度峰值;Bacm为交流磁通密度幅值;w 为圆频率(rad/s);d 为B落后H的相位差。复数磁导率定义为
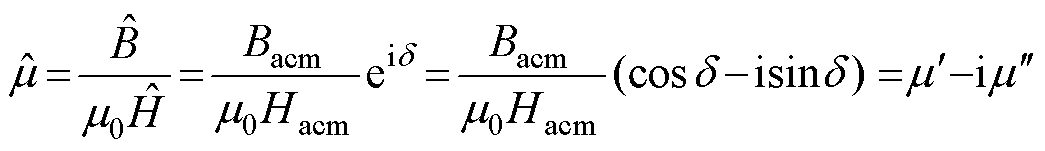 (5)
(5)
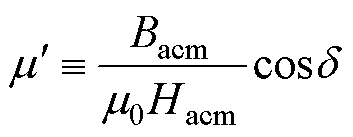 (6)
(6)
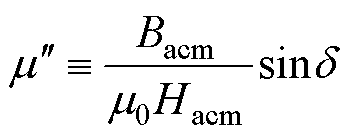 (7)
(7)
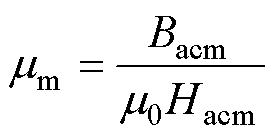 (8)
(8)
式中,m0为真空磁导率,m0=4p´10-7H/m;mm为材料的振幅磁导率,即饱和磁通密度幅值与饱和磁场的比值;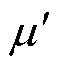 为实部磁导率,表征在动态磁化过程中材料的磁能储存;
为实部磁导率,表征在动态磁化过程中材料的磁能储存;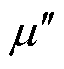 为虚部磁导率,表征在励磁磁场中材料一个周期的磁能损耗。磁致伸缩材料的等效电感和等效电阻分别为
为虚部磁导率,表征在励磁磁场中材料一个周期的磁能损耗。磁致伸缩材料的等效电感和等效电阻分别为
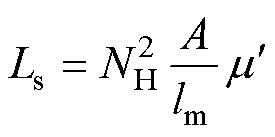 (9)
(9)
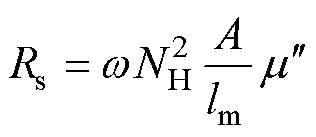 (10)
(10)
式中,A为磁致伸缩材料磁心的横截面积;lm为磁心内磁路的长度;NH为线圈匝数。
在正弦激励磁场中,介质损耗因数是材料在一个周期内磁能损耗与磁能存储的比值,表征材料在磁化过程中磁能的损耗性能。品质因数是介质损耗因数的倒数,表征材料在一个周期的磁化过程中内磁能的储存特性。材料的损耗因数和品质因数分别为
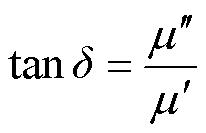 (11)
(11)
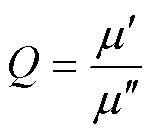 (12)
(12)
磁致伸缩材料在交变磁场中会产生形变位移,磁致伸缩效应引起的应变只与磁场的大小有关,与磁场的方向无关。因此尽管正半周和负半周的磁场方向相反,但两个半周激发的弹性波的振动方向是相同的,产生倍频现象,同时使材料的工作区域处于非线性区域。磁致伸缩材料的倍频效应如图1所示,加入直流偏置磁场后,磁致伸缩材料工作区域会偏移一个初始位移Hdc,使磁致伸缩材料工作在磁致伸缩性能良好的线性段并且消除倍频效应,增大材料输出特性。
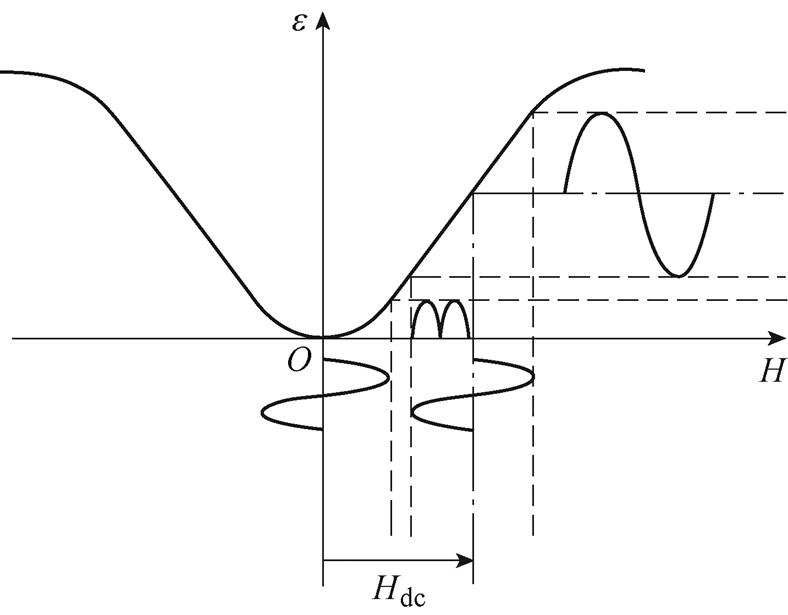
图1 磁致伸缩材料的倍频效应
Fig.1 Frequency doubling effect of the magnetostrictive materials
为获取变直流偏置下磁致伸缩材料的动态损耗及磁特性变化情况,本文根据磁特性理论搭建了直流偏置下高频动态磁特性测试系统,其原理图及实验装置图分别如图2和图3所示。
磁特性测试系统的工作原理为:由信号发生器产生正弦交变电流,通过功率放大器放大信号后经初级线圈给实验样品提供交变磁场,通过采样电阻上的电压反映磁场强度变化,并将电压变化信号录入数据采集系统。次级线圈与积分放大电路连接并通过积分放大电路中电容电压来体现实验样品磁通密度的变化。数据采集系统同时记录放大电路中电容电压信号的变化。直流电压源以第三绕组将偏置电压加载到样品中,通过调节直流电流调节偏置磁场的大小。数据采集系统记录的积分放大电路中次级线圈数据和采样电阻中初级线圈数据经计算机处理,最终得到实验样品的高频动态磁滞回线。
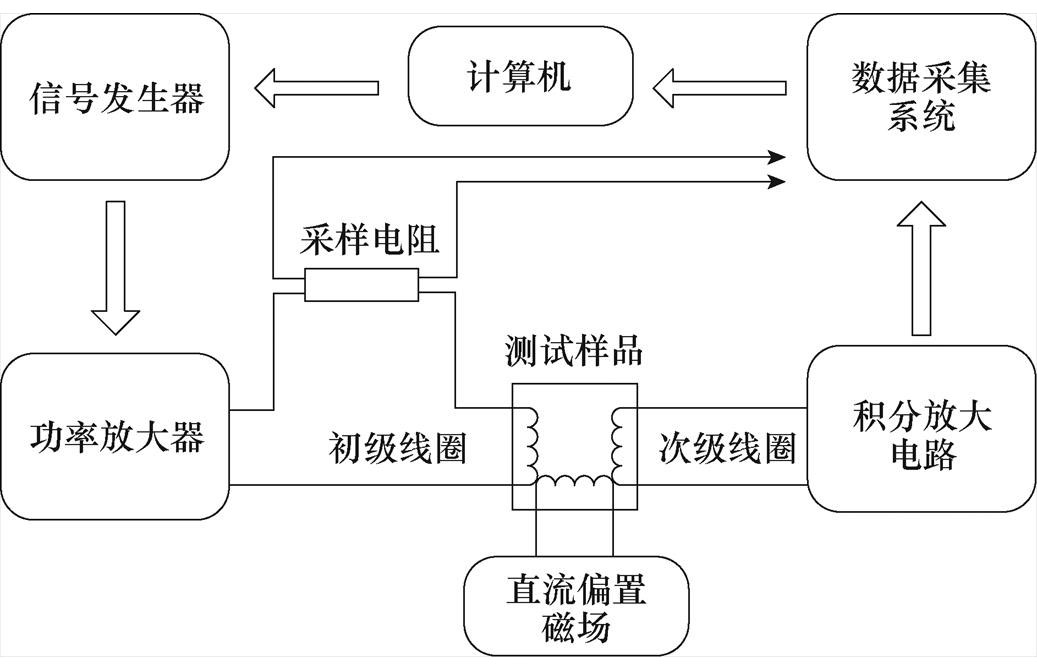
图2 直流偏置下高频动态磁特性测试系统原理图
Fig.2 Principle of dynamic magnetic characteristic testing system at DC bias

图3 高频动态磁特性测试实验装置图
Fig.3 Experiment platform of high-frequency dynamic magnetic characteristic testing system
实验样品为:Terfenol-D方环,内径9×9mm、外径15×15mm、厚度为2mm。初级线圈选用56匝、线径为0.5mm的漆包线,次级线圈选用10匝、线径为0.15mm的漆包线。直流偏置磁场第三绕组线圈选用48匝、线径为0.5mm的漆包线。
实验样品磁场强度和磁通密度的计算公式为
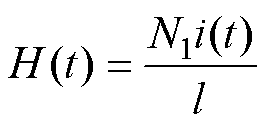 (13)
(13)
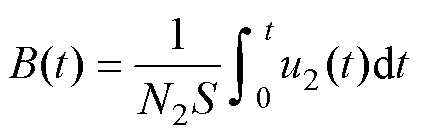 (14)
(14)
式中,N1和N2分别为初级线圈和次级线圈的匝数;S为环形样品的横截面积;l为样品的有效磁路长度;i(t)为初级线圈电流;u2(t)为次级线圈电压。根据实验测试的动态磁滞回线及磁滞回线理论可以提取实验样品的磁特性参数。
基于Bertotti损耗分离理论,Terfenol-D合金的高频磁能损耗在正弦激励下可分离为磁滞损耗、涡流损耗及剩余损耗三部分[19]。
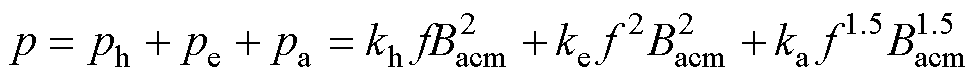 (15)
(15)
式中,f和Bacm分别为交流激励磁场频率和磁通密度幅值;kh、ke和ka分别为磁滞损耗系数、涡流损耗系数和剩余损耗系数[19]。
由于损耗产生的机理不同,磁滞损耗又称为静态损耗,涡流和异常损耗的频率依赖性敏感,通常将其统称为动态损耗[19-20],因此,高频损耗可以写成两项表达式。
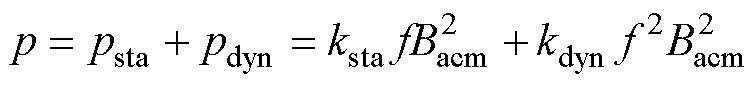 (16)
(16)
式中,ksta为静态损耗系数;kdyn为动态损耗系数。
由于Terfenol-D在高频激励下会产生涡流趋肤效应,各项损耗系数将不再是常数。根据经典的损耗分离公式,各项损耗是以磁通密度幅值与激励频率为自变量的函数,不能体现直流偏置磁场对磁能损耗的影响程度。因此,为了研究直流偏置对磁致伸缩材料的损耗及磁特性影响,探索各项损耗系数随f、Bacm、Hdc的变化规律十分必要。结合实验测试的损耗数据,本文提出的考虑直流偏磁的高频磁能损耗模型为
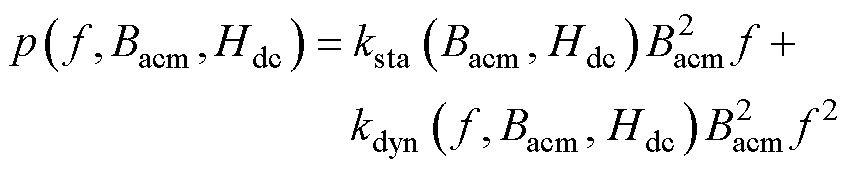 (17)
(17)
式中,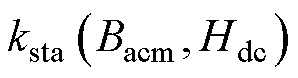 、
、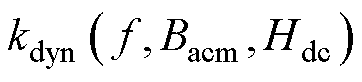 分别为考虑直流偏置磁场、激励频率、交流磁通密度幅值的改进静态损耗系数和动态损耗系数。为了对各项损耗进行分离处理,将式(17)两边同时除以f,即
分别为考虑直流偏置磁场、激励频率、交流磁通密度幅值的改进静态损耗系数和动态损耗系数。为了对各项损耗进行分离处理,将式(17)两边同时除以f,即
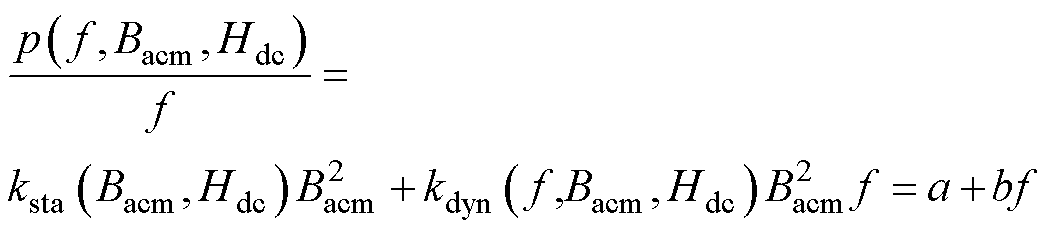 (18)
(18)
式中,a=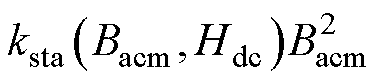 , b=
, b=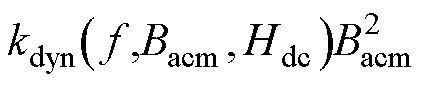 。
。
基于高频损耗实验中不同工况下实测的磁能损耗数据,静态损耗系数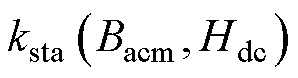 和动态损耗系数
和动态损耗系数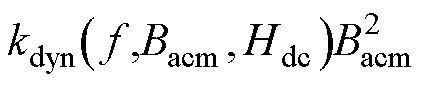 可以通过以下分离方法获得。
可以通过以下分离方法获得。
(1)当固定磁通密度幅值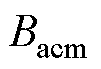 与直流偏置磁场强度Hdc时,根据式(18),可以得到测量总损耗
与直流偏置磁场强度Hdc时,根据式(18),可以得到测量总损耗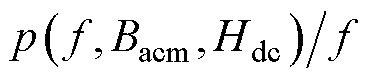 关于激励频率f的函数关系,做出
关于激励频率f的函数关系,做出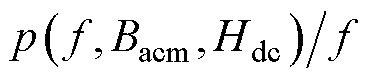 的曲线图。
的曲线图。
(2)当改变Bacm和Hdc时,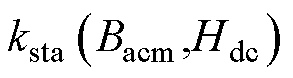 随着Bacm和Hdc的变化趋势,可以通过不同Bacm和Hdc下测量的总损耗
随着Bacm和Hdc的变化趋势,可以通过不同Bacm和Hdc下测量的总损耗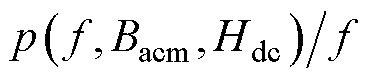 与励磁频率f的拟合曲线得到。
与励磁频率f的拟合曲线得到。
(3)将分离出的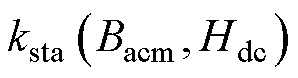 代入式(17) 中,在不同的
代入式(17) 中,在不同的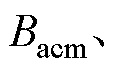
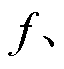
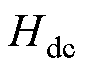 下的动态损耗
下的动态损耗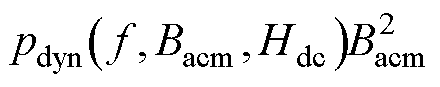 可以通过测量总损耗减去静态损耗提取。
可以通过测量总损耗减去静态损耗提取。
(4)在不同工况下的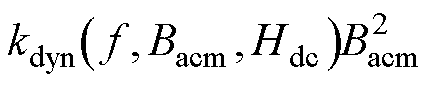 可以通过数据拟合被分离计算。
可以通过数据拟合被分离计算。
根据Levenberg-Marquardt迭代算法,通过将不同f、Bacm、Hdc下的损耗系数利用多元参数回归分析法计算,可得到考虑直流偏置磁场的损耗系数,其表达式为
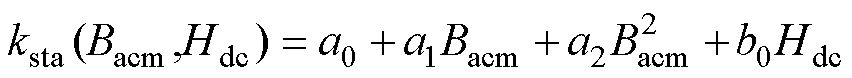 (19)
(19)
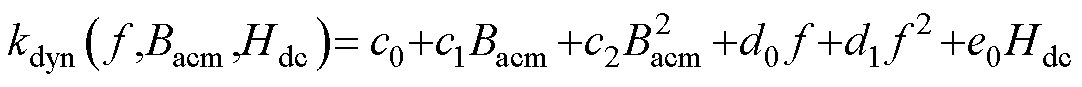 (20)
(20)
在有限测试数据基础上,将式(19)和式(20)所得损耗系数代入式(17),便可得到任意激励条件下计及直流偏置影响的磁致伸缩材料高频损耗计算值。
Terfenol-D合金样品的高频磁能损耗是激励频率f、交流磁通密度幅值Bacm、偏置磁场Hdc的三变量函数,本文采用多目标控制变量法在不同频率f、交流磁通密度幅值Bacm、偏置磁场Hdc下进行多次重复实验。结合磁致伸缩换能器在水声和超声频段的应用场合,实验测试的频率设定为5~25kHz,交流磁通密度幅值设定为0.01~0.06T;随着施加直流偏置磁场的增大和交流励磁频率的升高,由于互感等因素的影响使交流驱动磁场的增大明显受到抑制,受限于现有测试设备的交流磁场数值上限,本文测试直流偏置磁场场强Hdc设定为1 000~5 000A/m。通过变直流偏置下Terfenol-D合金在不同频率f和磁通密度幅值Bacm下的动态磁特性曲线,提取磁特性参数。
根据搭建的实验测试平台,获得Terfenol-D合金在激励磁场频率为15kHz、磁通密度幅值为0.05T时变直流偏置(0A/m,1 000A/m,3 000A/m,5 000A/m)下的动态磁滞回线,如图4所示。
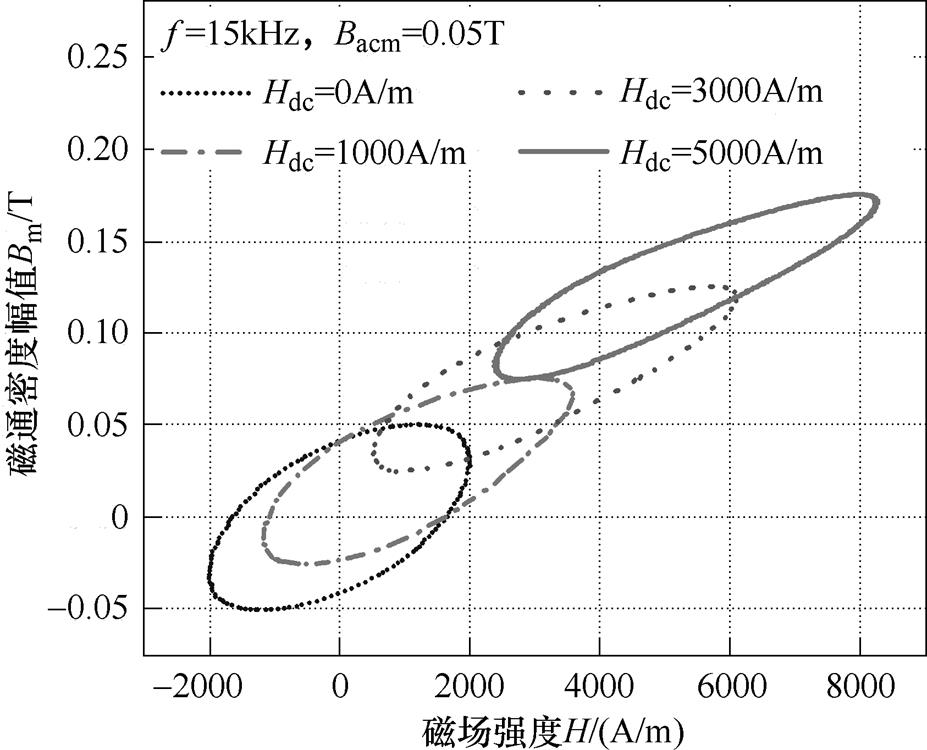
图4 不同偏置磁场下的动态磁滞回线
Fig.4 Dynamic hysteresis loops at different DC bias
图4表明,当交流磁通密度幅值和激励频率一定时,随着直流偏置磁场增加,动态磁滞回环发生上移与严重畸变,形状出现不对称,导致材料的磁滞回线发生明显变化。这是由于磁致伸缩材料在直流磁场作用下由交、直流磁通叠加,导致电流波形正负半波不对称,使材料的磁化工作点增大和相对磁导率发生变化而引起的。考虑到动态磁滞回线包围的面积在数值上等于材料磁化一周的总损耗,由此可见直流偏置磁场对实验样品内部磁畴壁移动和磁畴转动有明显影响,因此,材料磁滞特性与损耗特性也必然发生变化。
材料的磁导率是表征电工材料动态磁特性的重要参数,图5所示为Terfenol-D合金在激励磁场频率为15kHz,交流磁通密度幅值为0.05T时,振幅磁导率及实部、虚部磁导率随直流偏置磁场的变化曲线。当直流偏置磁场强度从0A/m增加到5 000A/m,实验样品的振幅磁导率与虚部磁导率随直流偏置磁场的增加而逐步减小,振幅磁导率由19.8减小到13.5,降低了31.8%,虚部磁导率由16.4减小到6.6,降低了59%,下降速率大于振幅磁导率的速率;实部磁导率呈现微小增长的趋势,由11.1增加到11.8,升高了6.3%,这是由于施加偏置外磁场后增大磁畴转向阻力造成的。
Terfenol-D合金的矫顽力代表着材料磁化过程中的不可逆程度,图6所示为实验样品在激励磁场频率为15kHz、磁通密度幅值为0.05T时,矫顽力随直流偏置磁场的变化曲线。当偏置磁场强度由0A/m增加到5 000A/m,矫顽力由1 629.7A/m减小至1 422.3A/m,降低了12.7%。当偏置磁场强度从0A/m到3 000A/m时,矫顽力减小速率逐渐变缓慢,当偏置磁场强度大于3 000A/m时,矫顽力减小速率激增,矫顽力减小。这是由于随着偏置磁场的增加,使得实验样品工作点上移,处于线性区间,降低非线性磁滞特性同时使得材料内部各向异性畴壁移动方向趋于一致,从而使矫顽力降低。该现象表明偏置磁场对于材料矫顽力有降低作用,可使磁滞回线面积变小,磁能损耗降低,揭示了随着偏置磁场增大材料不可逆磁化程度降低,抵抗退磁的能力变弱的规律,同时由于磁畴易磁化程度增大,对于磁场的响应速度增大,有利于材料输出特性的提高。
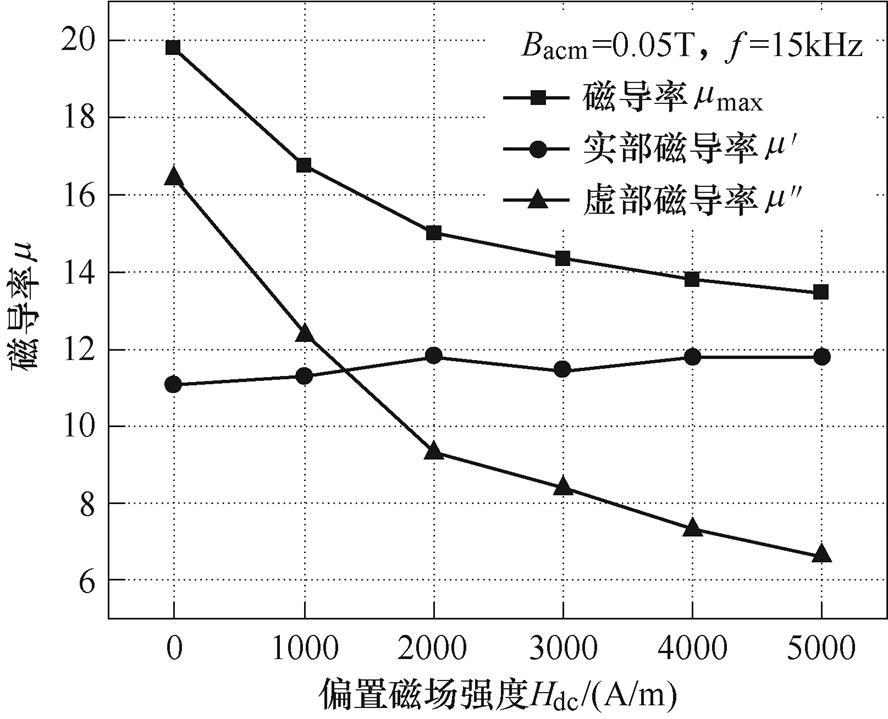
图5 振幅磁导率及实、虚部磁导率和直流偏置的关系
Fig.5 The relationship of permeability amplitude, the real and imaginary parts of the permeability vs. DC bias
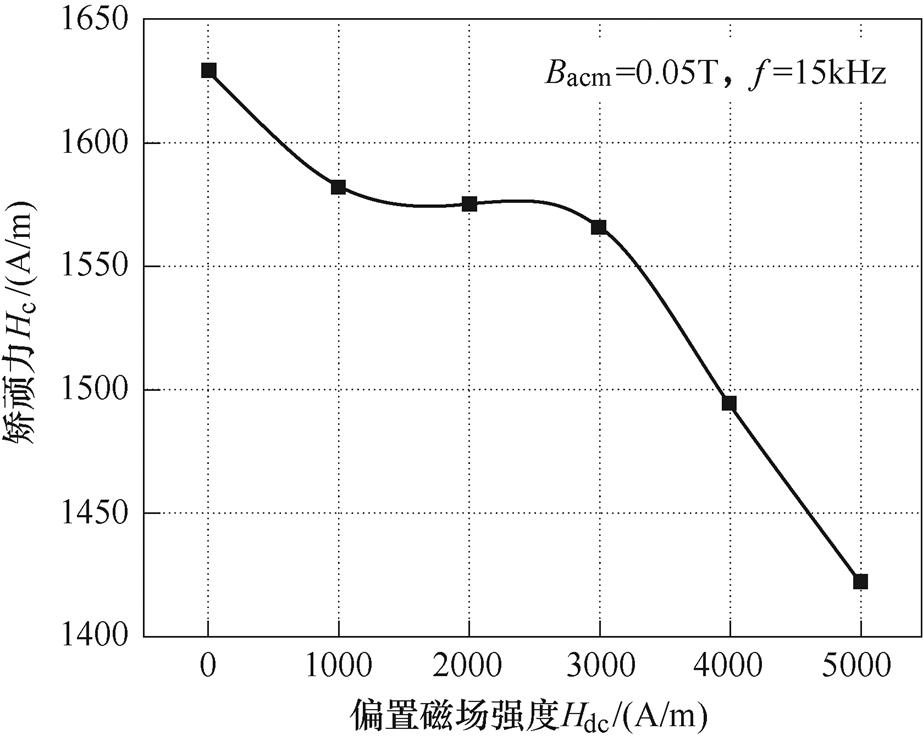
图6 矫顽力随偏置磁场的变化
Fig.6 Change of coercivity with DC bias
图7所示为Terfenol-D合金在激励磁场频率为15kHz、磁通密度幅值为0.05T时,磁能损耗随偏置磁场变化的曲线。当偏置磁场由从0A/m增加到5 000A/m,高频磁能损耗由503.74W/kg减小到419.022W/kg,降低了16.8%。根据磁致伸缩换能器的工作原理,Terfenol-D合金材料在交变电流作用下产生输出位移,施加直流偏磁场后,倍频现象消失,使实验样品工作区间线性化,磁能损耗减小。
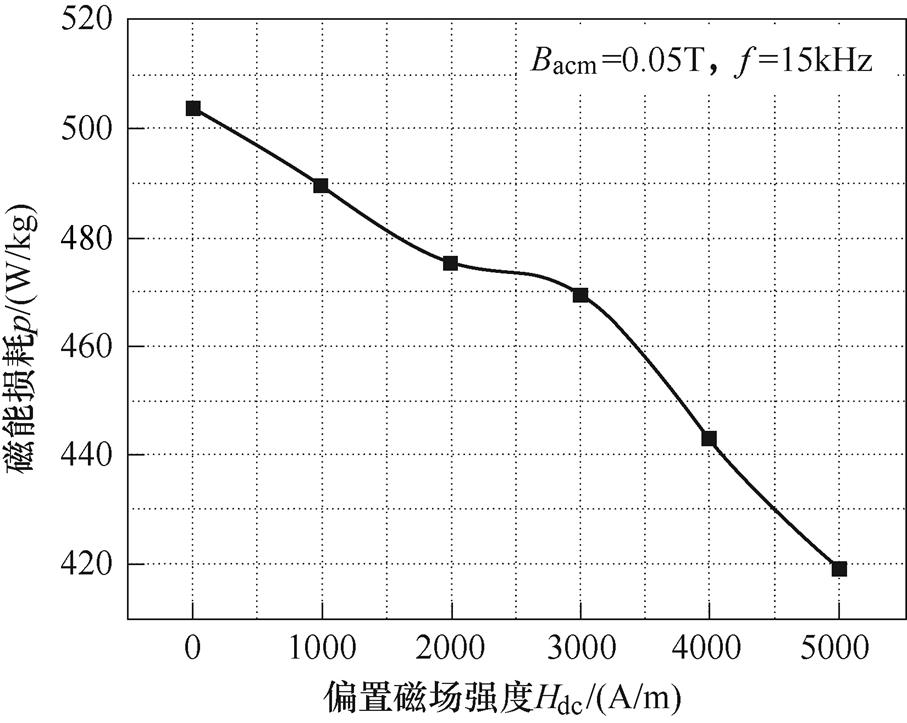
图7 磁能损耗随直流偏置的变化
Fig.7 Change of magnetic energy loss with DC bias
等效电感与等效电阻由实部磁导率和虚部磁导率计算,反映磁致伸缩材料样品在激励磁场中引起的感性与阻性。图8与图9分别为Terfenol-D合金在激励磁场频率为15kHz、磁通密度幅值为0.05T时,等效电阻和等效电感随偏置磁场的变化曲线。可以发现随着偏置磁场从0A/m增加到5 000A/m,等效电阻由989.9mW 减少至398.9mW,降低了59.7%,等效电感由7.1mH增加到7.6mH,增加了7%。表明随着直流偏置磁场的增加,实验样品在动态磁化过程中的磁能储存量增加,能量损失量减小。
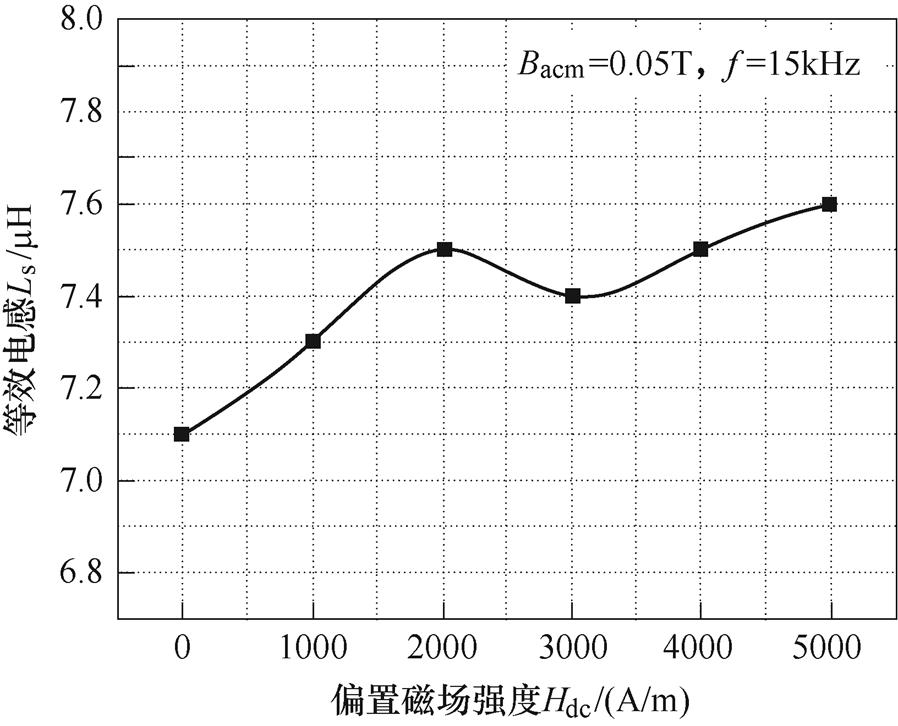
图8 等效电感随直流偏置的变化
Fig.8 Change of magnetic energy losses with DC bias
损耗因数和品质因数是衡量材料磁性的重要指标,用来描述磁性材料在一个动态磁化周期下磁能损耗和存储性能。图10为Terfenol-D合金在激励磁场频率为15kHz、磁通密度幅值为0.05T时,介质损耗因数和品质因数随直流偏置的变化曲线。可以发现,随着直流偏置增加,介质损耗因数逐渐减小,品质因数逐渐增加,结果表明随偏置磁场的增加,实验样品的高频磁能损耗逐渐减小,提高了材料的储能特性。
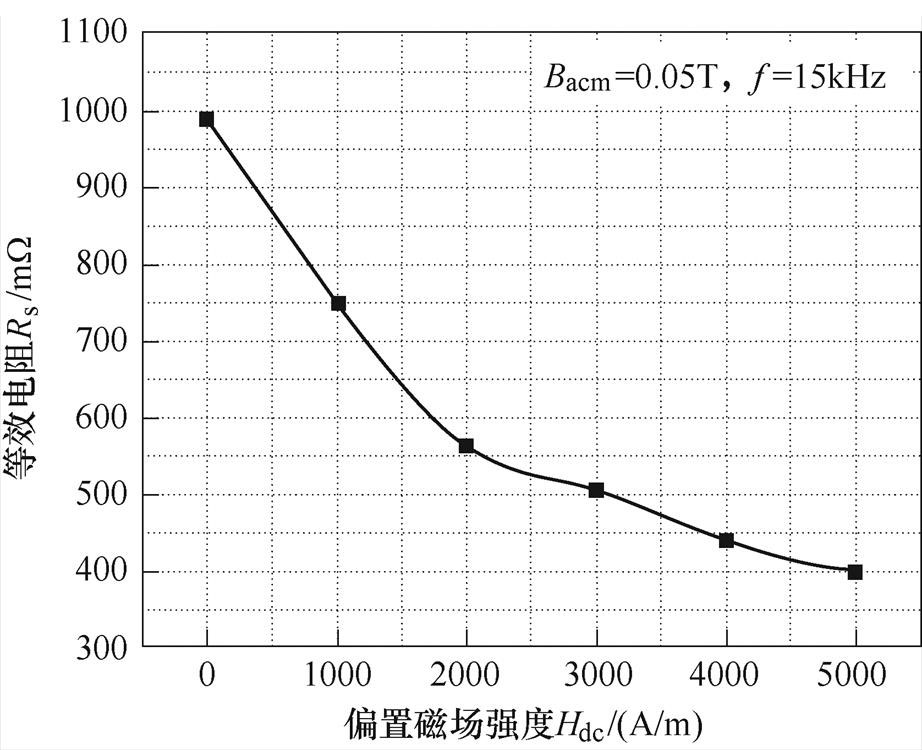
图9 等效电阻随直流偏置的变化
Fig.9 Change of magnetic energy losses with DC bias

图10 介质损耗因数和品质因数随偏置磁场的变化
Fig.10 Loss factor and quality factor change with DC
根据实验测试的Terfenol-D样品的损耗数据,提取模型的计算参数,结果见表1。
为满足材料研究的需要以及考察各部分损耗在总损耗的比率,以便根据不同情况,采取相应的措施,降低和限制损耗,本文根据所提出的模型,采用多目标控制变量法分别绘制了不同直流偏置磁场Hdc、频率f和交流磁通密度幅值Bacm下的损耗分离图,如图11~图15所示。
从图11中可以看到,随着偏置磁场的增大,总损耗呈现逐渐减小的趋势,各项损耗也随之减小。当偏置磁场由0A/m增加到5 000A/m时,总损耗由518.419W/kg减小到413.08W/kg,动态损耗值由283.64W/kg减小到269.243W/kg,占比由54.71%增加到65.12%,静态损耗由234.776W/kg减小到143.833W/kg,占比由45.29%减小到34.82%。磁致伸缩材料在交流励磁条件下会产生倍频效应,使材料的输出性能变差,电磁转换效率变低,施加直流偏磁场后,倍频现象消失,磁能损耗减小。
表1 磁能损耗计算模型参数识别
Tab.1 Parameter values of the magnetic energy loss calculation model
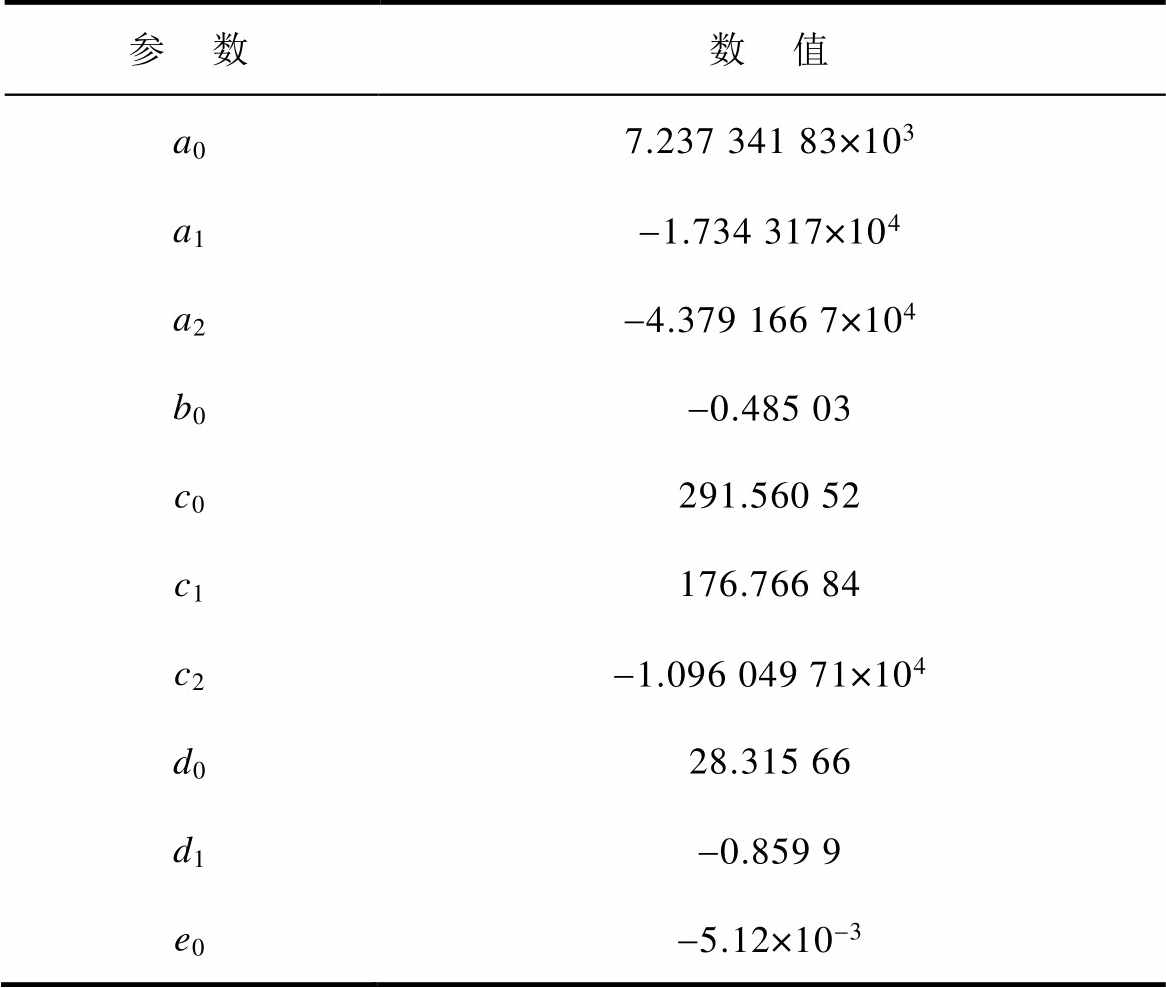
参 数数 值 a07.237 341 83×103 a1-1.734 317×104 a2-4.379 166 7×104 b0-0.485 03 c0291.560 52 c1176.766 84 c2-1.096 049 71×104 d028.315 66 d1-0.859 9 e0-5.12×10-3
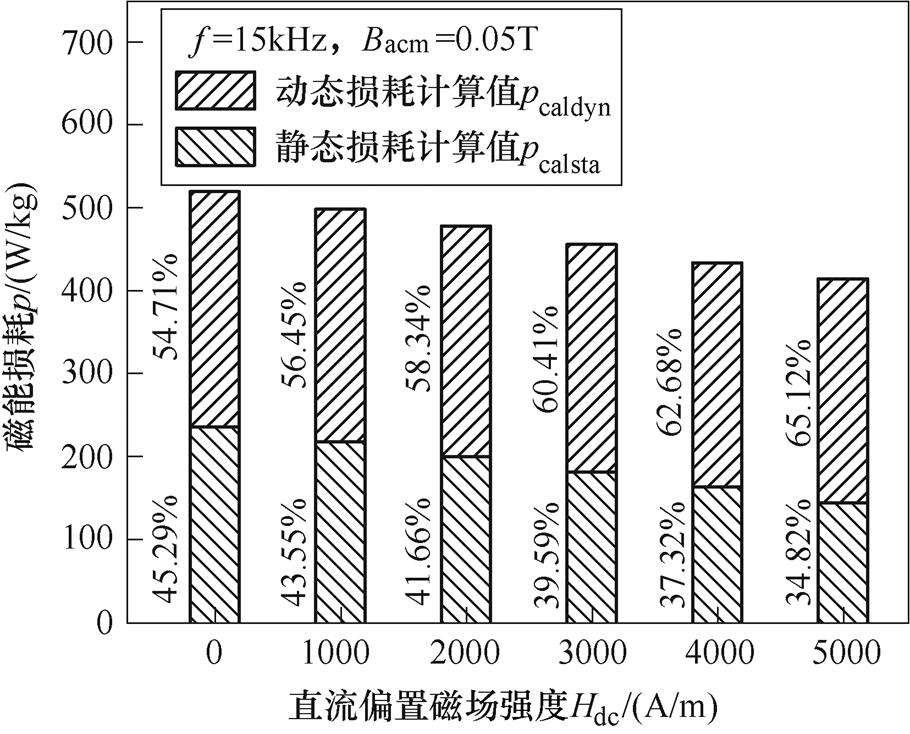
图11 各项磁能损耗随直流偏置磁场的变化
Fig.11 Change of magnetic energy losses with Hdc
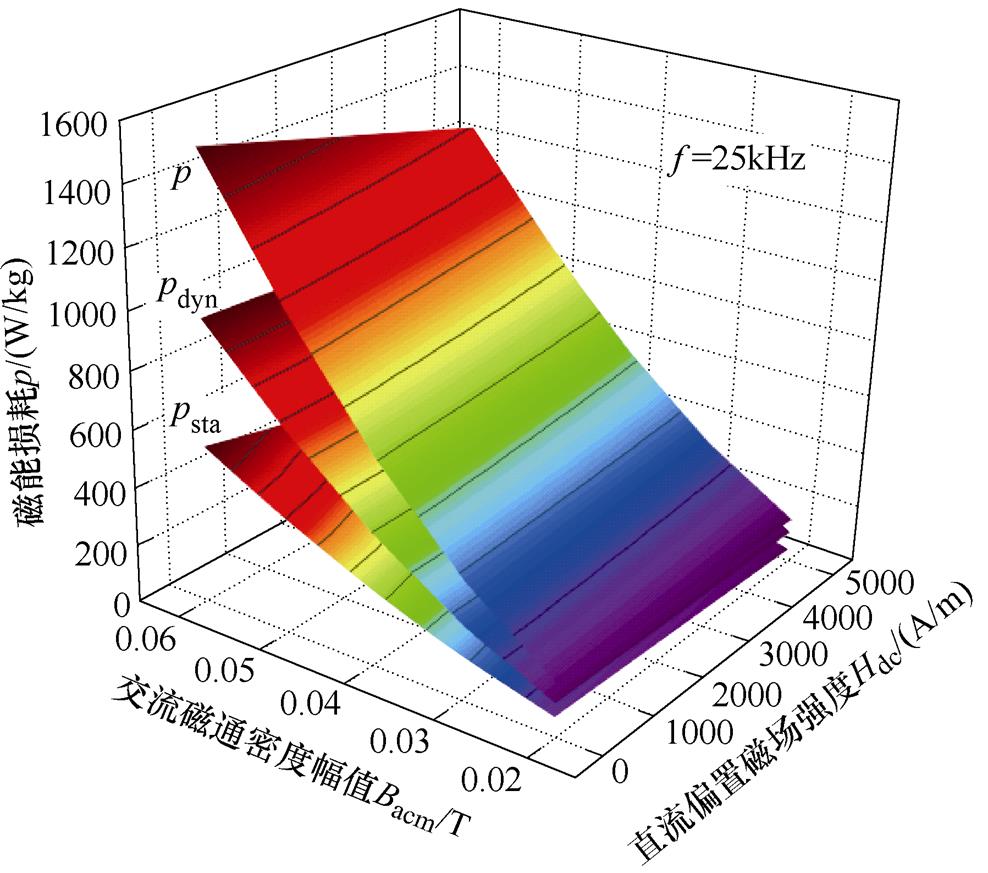
图12 损耗随偏置磁场Hdc和交流磁通密度幅值Bacm变化
Fig.12 Change of losses with Hdc and Bacm
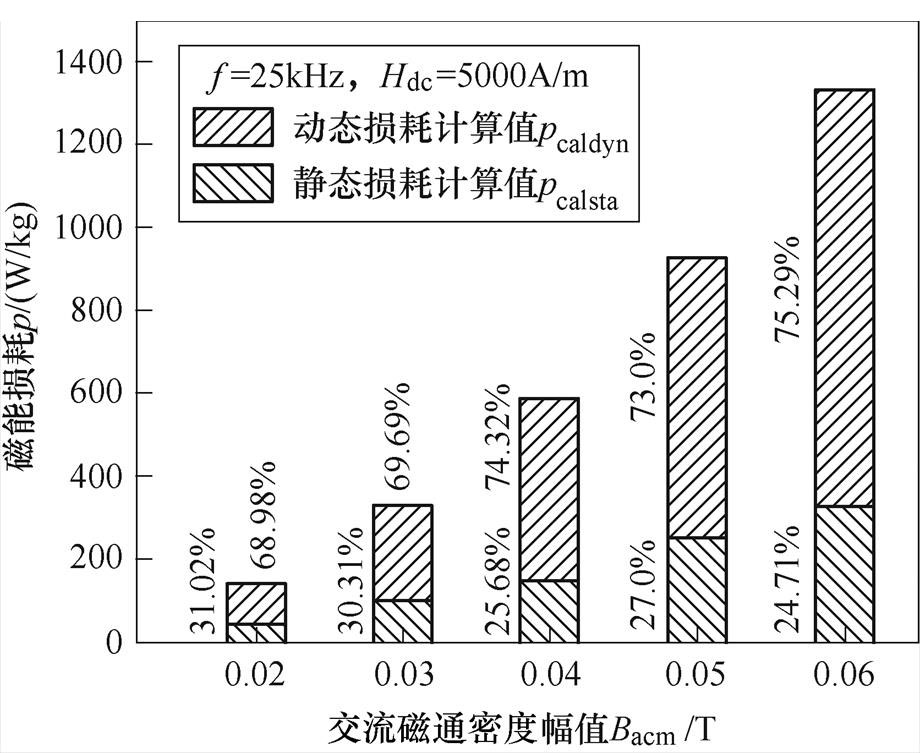
图13 各项损耗随Bacm的变化占比
Fig.13 Proportion of losses varying with Bacm
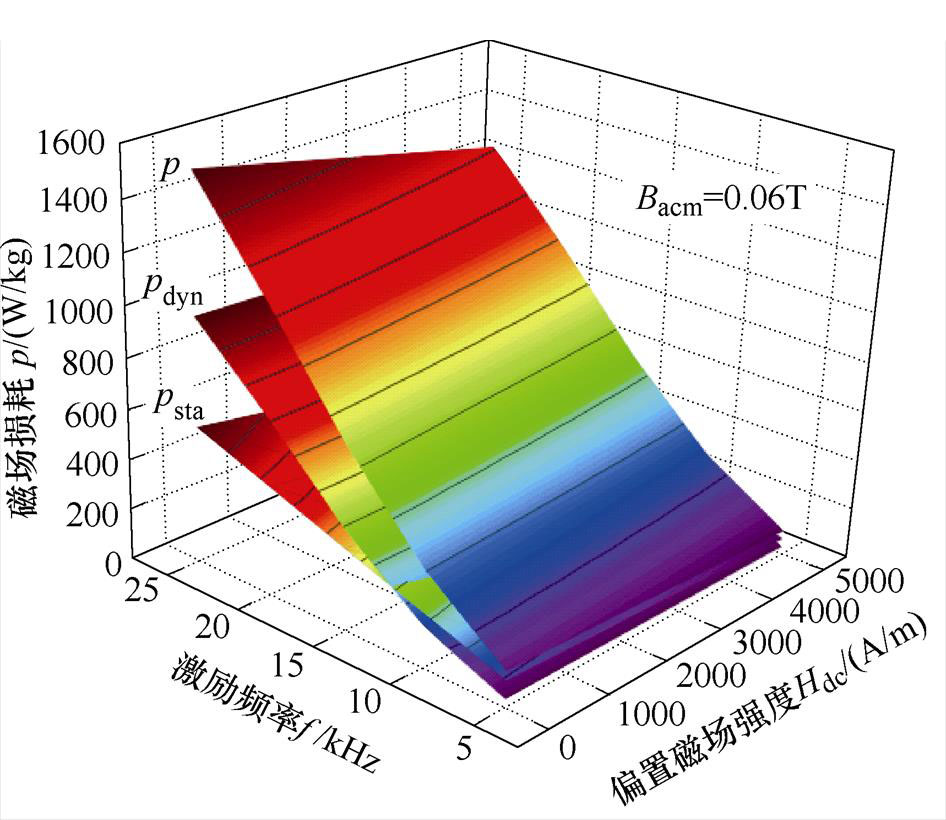
图14 总损耗随偏置磁场强度与交流磁化频率变化趋势
Fig.14 Trend of losses with Hdc and f
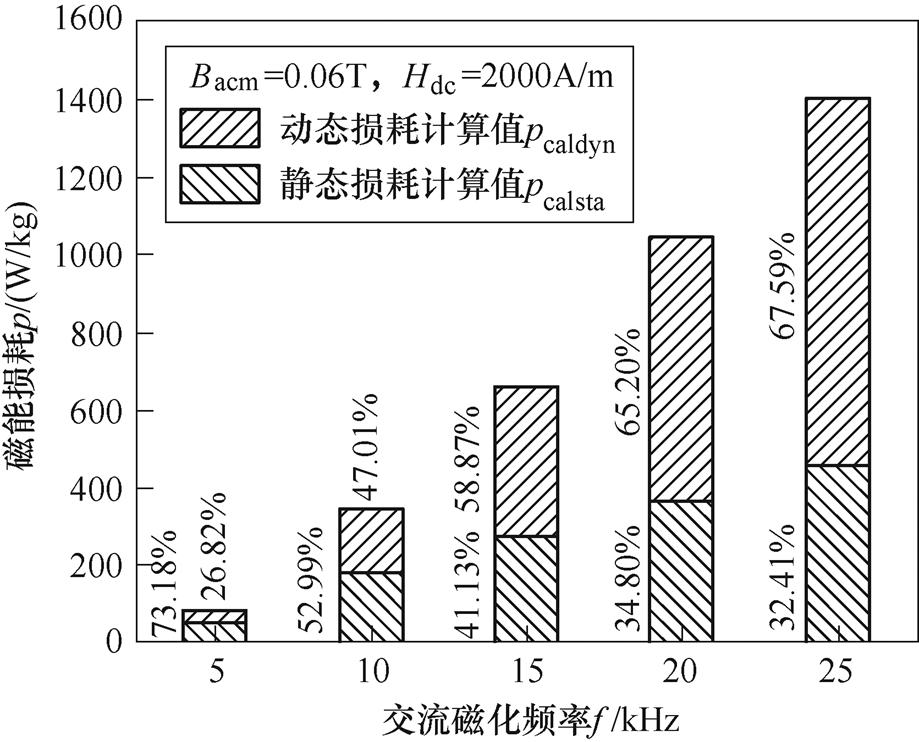
图15 各分项损耗随交流磁化频率的变化
Fig.15 Variation of losses with f
各项磁能损耗随偏置磁场强度与交流磁通密度幅值的变化趋势如图12和图13所示,由图12结果表明,当Bacm和Hdc逐渐增大时,磁能损耗呈现随着Bacm增大而增大的同时又随着Hdc增大而减小的复杂的变化趋势。图13可以看出,当激励频率为25kHz,偏置磁场为Hdc=5 000A/m时,随着交流磁通密度幅值Bacm由0.02T增加到0.06T,总损耗由153.37W/kg增加到1 242.272W/kg(8.105倍),静态损耗由44.478W/kg增加到325.256W/kg(7.312倍),占比由68.98%增加到75.29%;动态损耗由108.891W/kg增加到917.016W/kg(8.421倍),占比由31.02%降低到24.71%。结果表明随着磁通密度幅值的增大,总损耗呈现增大趋势,各项分离损耗也随之增大。这是由于当驱动磁场增大时,样品材料中的磁畴转动与畴壁移动速度加快,从而使磁能损耗不断增加。
各项磁能损耗随偏置磁场强度和交流磁化频率的变化趋势如图14和图15所示,由图14可以看出磁能损耗同时随着交流磁化频率和偏置磁场发生变化。图15表明频率增大时,总损耗呈现增大趋势,各项损耗也随之增大。当交流磁通密度幅值为0.06T,偏置磁场为2 000A/m时,随着交流磁化频率f由5kHz增加到25kHz时,总损耗由124.772W/kg到1 407.79W/kg(11.28倍),静态损耗值由91.242W/kg增加到456.213W/kg(5倍),占比由73.18%降低到32.41%;动态损耗值由33.529W/kg增加到951.576W/kg(28.28倍),占比由26.82%增加到67.59%。这是由于当激励磁场频率在高频以上阶段时,高频损耗将以磁畴进动或者共振方式出现,同时材料内部产生了垂直于磁通线的感应电流,该电流方向同外加磁场方向相反,使得材料内部的磁场减小为零,导致磁化过程中产生大量的热,进而造成损耗增加。
为了验证本文所提出的考虑变直流偏磁的变系数高频磁能损耗计算模型的准确性与可行性,计算了给定工作条件下(直流偏磁Hdc、频率f、磁通密度幅值Bacm的数值已知)磁致伸缩材料的高频磁能损耗数值,并与实验测量值进行对比分析。25kHz不同工况下的静态、动态、总损耗的计算值和实测值的对比,见表2~表4。
表2 f =25kHz下静态损耗结果对比
Tab.2 Comparison of static losses at f =25kHz
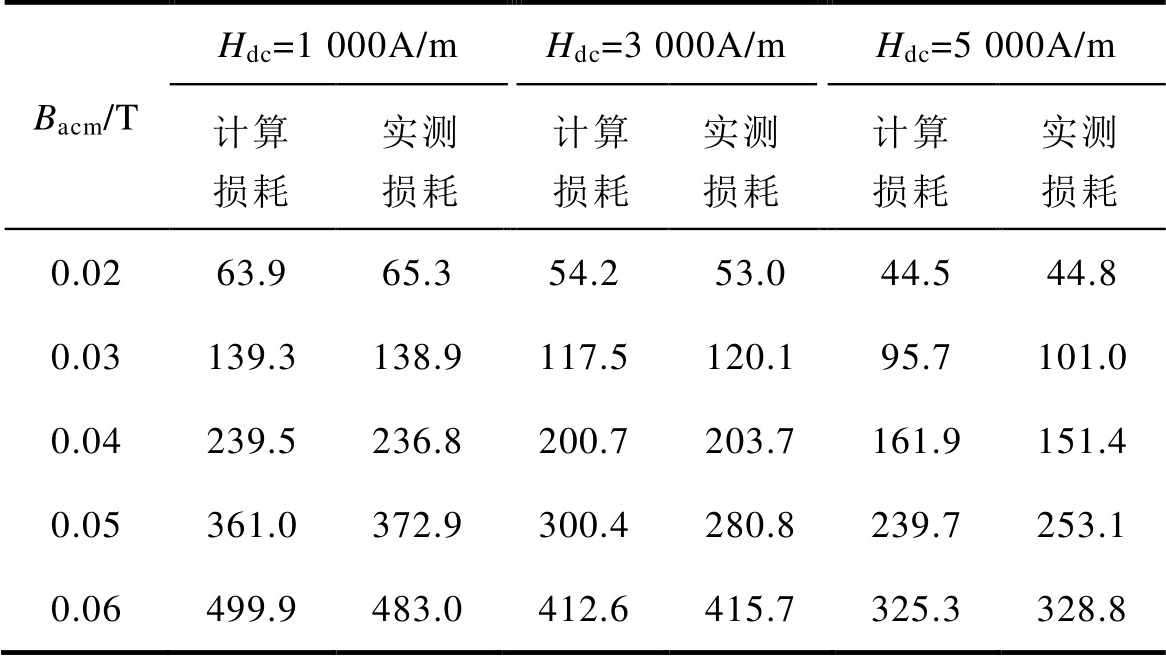
Bacm/THdc=1 000A/mHdc=3 000A/mHdc=5 000A/m 计算损耗实测损耗计算损耗实测损耗计算损耗实测损耗 0.0263.965.354.253.044.544.8 0.03139.3138.9117.5120.195.7101.0 0.04239.5236.8200.7203.7161.9151.4 0.05361.0372.9300.4280.8239.7253.1 0.06499.9483.0412.6415.7325.3328.8
表3 f =25kHz下动态损耗结果对比
Tab.3 Comparison of dynamic losses at f =25kHz
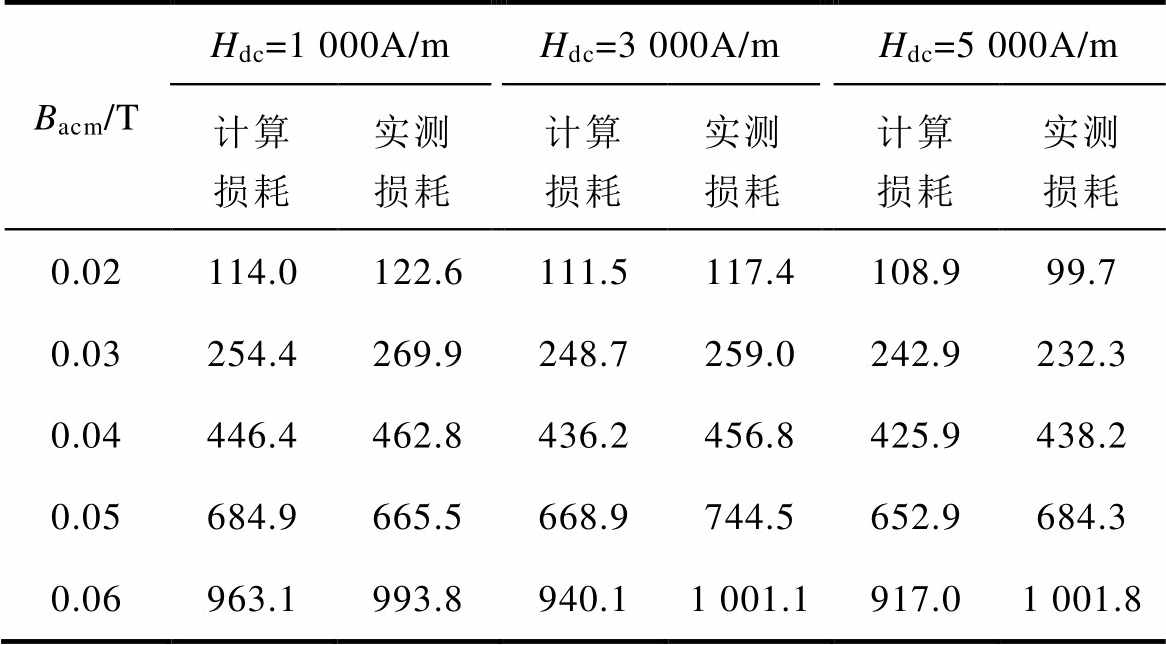
Bacm/THdc=1 000A/mHdc=3 000A/mHdc=5 000A/m 计算损耗实测损耗计算损耗实测损耗计算损耗实测损耗 0.02114.0122.6111.5117.4108.999.7 0.03254.4269.9248.7259.0242.9232.3 0.04446.4462.8436.2456.8425.9438.2 0.05684.9665.5668.9744.5652.9684.3 0.06963.1993.8940.11 001.1917.01 001.8
表4 f=25kHz下总损耗结果对比
Tab.4 Comparison of total losses at f=25kHz
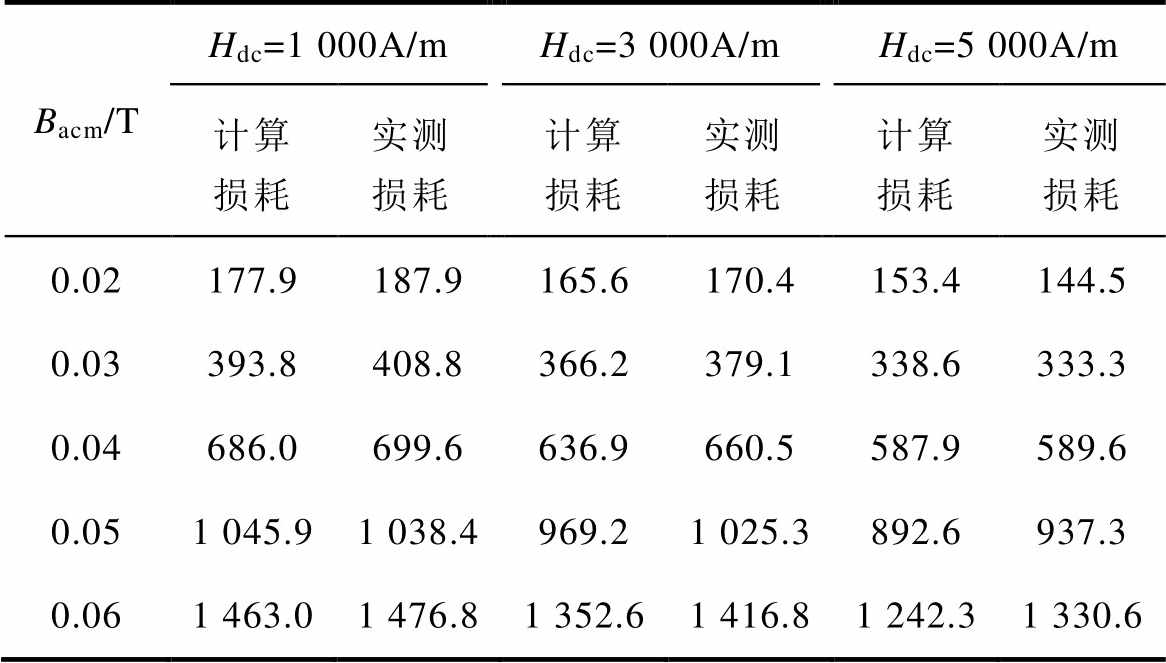
Bacm/THdc=1 000A/mHdc=3 000A/mHdc=5 000A/m 计算损耗实测损耗计算损耗实测损耗计算损耗实测损耗 0.02177.9187.9165.6170.4153.4144.5 0.03393.8408.8366.2379.1338.6333.3 0.04686.0699.6636.9660.5587.9589.6 0.051 045.91 038.4969.21 025.3892.6937.3 0.061 463.01 476.81 352.61 416.81 242.31 330.6
为使对比结果更加清晰,本文采用多目标控制变量法绘制了不同直流偏置磁场强度Hdc、频率f和磁通密度幅值Bacm下的实验结果与模型计算结果对比图,如图16~图18所示。
图16所示为在频率f为25kHz、直流偏磁分别为1 000A/m、3 000A/m、5 000A/m时,不同交流磁通密度幅值Bacm下,各项磁能损耗实验结果和模型计算结果的误差图。当磁通密度幅值Bacm由0.02T增加到0.06T,偏磁磁场为5 000A/m时,考虑变直流偏置磁场的磁能损耗模型的静态损耗、动态损耗、总损耗的最大误差分别为6.94%、9.24%、6.64%,平均误差分别为3.87%、5.93%、3.885%。
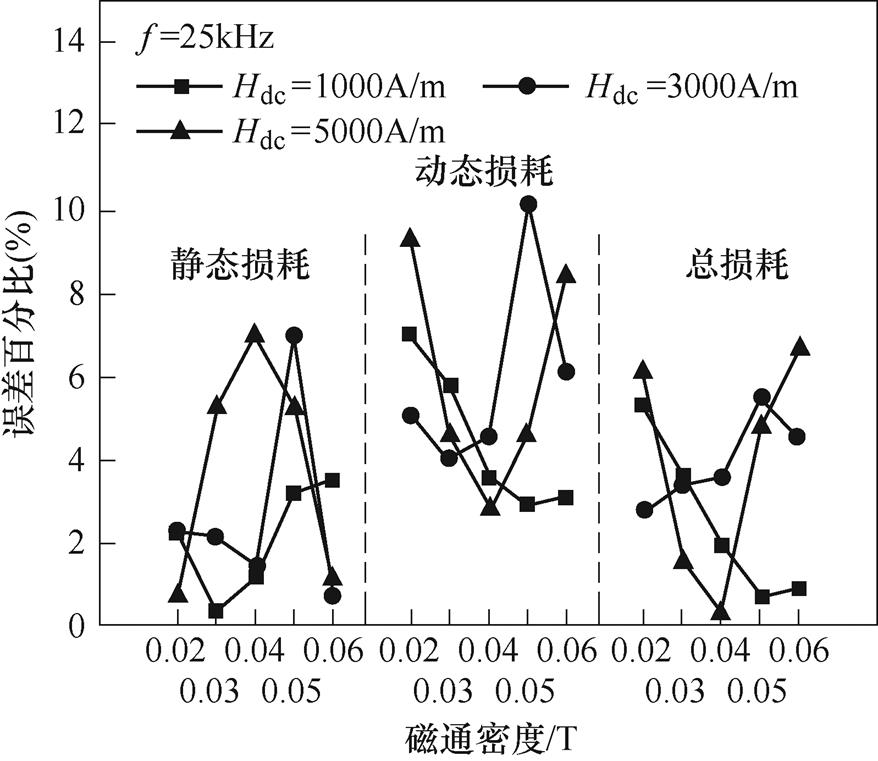
图16 各项磁能损耗随磁通密度的变化
Fig.16 Change of magnetic energy losses with Bacm
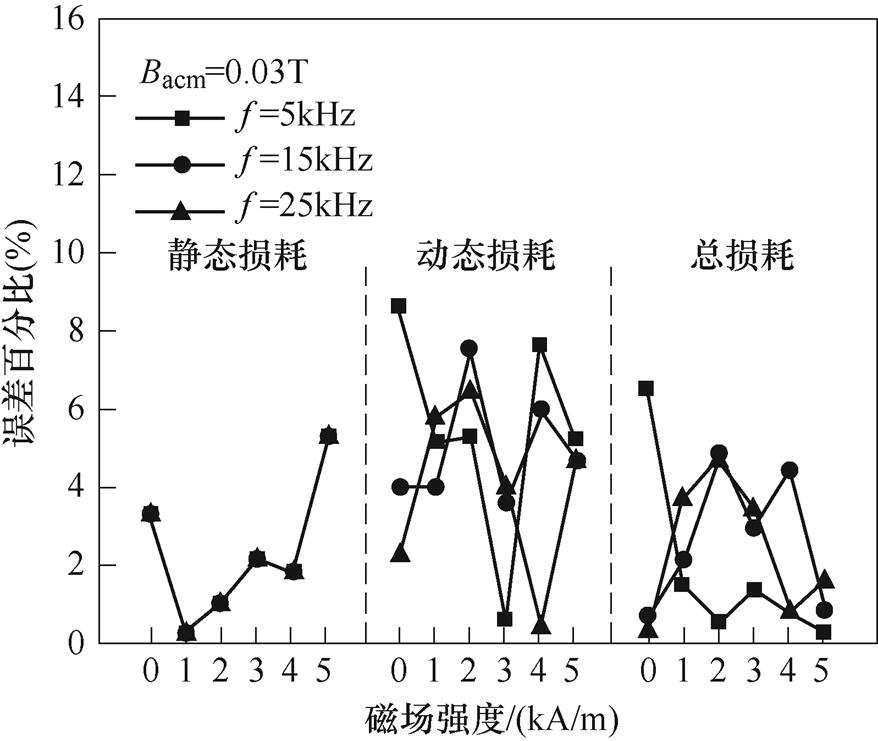
图17 各项磁能损耗随偏置磁场的变化
Fig.17 Change of magnetic energy losses with Hdc
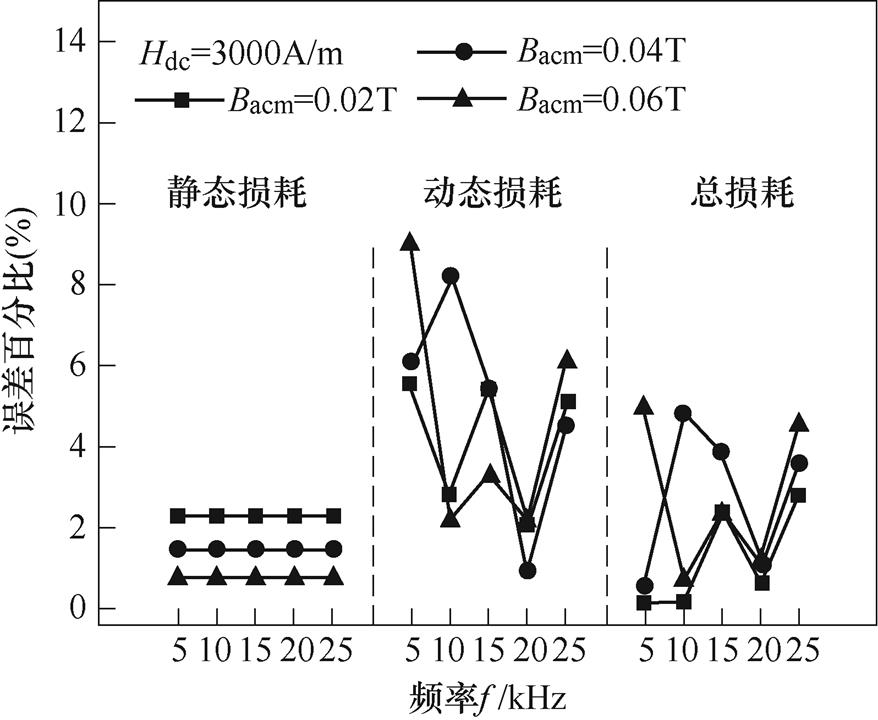
图18 各项磁能损耗随频率的变化
Fig.18 Change of magnetic energy losses with f
图17所示为在交流磁通密度幅值Bacm为0.03T、频率为5kHz、15kHz、25kHz时,不同直流偏置下,各项磁能损耗实验结果和模型计算结果的对比图。当磁通密度幅值为0.03T,激励频率为5kHz时,考虑偏置磁场的磁能损耗模型中静态损耗、动态损耗、总损耗的最大误差分别为5.28%、8.62%、6.52%,平均误差分别为2.30%、5.41%、1.83%。当磁通密度幅值为0.03T,激励频率为25kHz时,考虑偏置磁场的磁能损耗模型的静态损耗、动态损耗、总损耗的最大误差分别为5.28%、6.40%、4.68%,平均误差分别为2.30%、3.90%、2.40%。由此可以看出,考虑所提出的考虑直流偏置磁场的磁能损耗模型在激励频率为5~25kHz的范围内都具有良好的精准性。
图18为当直流偏置Hdc为3 000A/m、激励磁密为0.02T、0.04T、0.06T时,各项磁能损耗实验结果和模型计算结果的对比。当交流磁通密度幅值Bacm=0.04T,Hdc=3 000A/m时,考虑直流偏置磁场的磁能损耗模型动态损耗、静态损耗、总损耗的最大误差分别为1.43%、8.20%、4.80%,平均误差分别为1.43%、5.02%、2.77%。结果表明所提出的模型在偏置磁场一定时,可以准确地预测不同频率不同磁通密度下的磁能损耗。
本文通过搭建变直流偏置磁场下的高频磁特性测试平台,测试了不同偏置磁场条件下Terfenol-D合金样品在变激励频率和磁通密度幅值下的动态磁滞回线,建立了考虑直流偏磁影响的变系数高频磁能损耗计算模型,主要结论如下:
1)在交流磁通密度幅值Bacm为0~0.06T、激励频率f为5~25kHz的范围内时,随着直流偏置磁场强度Hdc从0A/m增加到5 000A/m时,动态磁滞回线发生上移和畸变,振幅磁导率逐步降低,矫顽力和损耗因子逐步减少。结果表明适当的直流偏置磁场可以消除磁致伸缩材料的倍频效应,降低磁致伸缩材料高频磁能损耗,有助于输出特性的提高。
2)基于多元参数回归分析的方法,提出一种改进的考虑变直流偏置磁场影响的高频磁能损耗模型,用于计算直流偏磁激励下Terfenol-D合金的损耗及各分量。该模型引入直流偏置磁场相关项对损耗系数进行修正,得到三变量(f、Bacm、Hdc)损耗系数函数表达式,从而在原有的经典磁能损耗模型的基础上建立了计及直流偏置磁场影响的变系数高频损耗计算模型。实验与计算对比结果表明所提出的模型可以准确预测不同直流偏磁下磁致伸缩材料的总损耗及各项损耗。
本研究可为超磁致伸缩器件考虑直流偏置下的高频损耗预测、发热分析以及结构优化设计提供重要的理论指导。
参考文献
[1] Rudd J, Myers O. Experimental fabrication and non- destructive testing of carbon fiber beams for delamin- ations using embedded Terfenol-D particles[J]. Journal of Intelligent Material Systems and Structures, 2018, 29(4): 600-609.
[2] Wang Wenjie, Thomas P J. Low-frequency active noise control of an underwater large-scale structure with distributed giant magnetostrictive actuators[J]. Sensors and Actuators A: Physical, 2017, 263: 113- 121.
[3] Sheykholeslami M R, Hojjat Y, Cinquemani S, et al. An approach to design and fabrication of resonant giant magnetostrictive transducer[J]. Smart Structures and Systems, 2016, 17(2): 313-325.
[4] Chakrabarti S, Dapino M J. Coupled axisymmetric finite element model of a hydraulically amplified magnetostrictive actuator for active powertrain mounts[J]. Finite Elements in Analysis and Design, 2012, 60: 25-34.
[5] Rudd J, Myers O. Experimental fabrication and nondestructive testing of carbon fiber beams for dela- minations using embedded Terfenol-D particles[J/OL]. Journal of Intelligent Material Systems and Structures, https://doi.dox.org/10.1177/1045389X17721022.
[6] Srinivasan G, de Vreugd C P, Laletin V M, et al. Resonant magnetoelectric coupling in trilayers of ferromagnetic alloys and piezoelectric lead zirconate titanate: the influence of bias magnetic field[J]. Physical Review B, 2005, 71(18): 184423.
[7] 杨蔚柠. 偏置磁场对稀土超磁致伸缩换能器性能的影响研究[D]. 湘潭: 湘潭大学, 2016.
[8] Wang Fenghua, Geng Chao, Su Lei. Parameter identification and prediction of Jiles-Atherton model for DC-biased transformer using improved shuffled frog leaping algorithm and least square support vector machine[J]. IET Electric Power Applications, 2015, 9(9): 660-669.
[9] Hovorka O, Berger A, Friedman G. Preisach model of exchange bias in antiferromagnetically coupled bilayers[J]. IEEE Transactions on Magnetics, 2006, 42(10): 3129-3131.
[10] Liu Ren, Li Lin. Calculation method of magnetic material losses under DC bias using statistical loss theory and energetic hysteresis model[J]. IEEE Transactions on Magnetics, 2019, 55(10): 1-4.
[11] 赵志刚, 马习纹, 姬俊安. 考虑频率效应的正弦及直流偏磁条件电工钢磁滞特性模拟及验证[J]. 中国电机工程学报, 2021, 41(23): 8178-8186.
Zhao Zhigang, Ma Xiwen, Ji Junan. Simulation and verification on hysteresis characteristics of electrical steel under sinusoidal and DC bias conditions considering frequency effects[J]. Proceedings of the CSEE, 2021, 41(23): 8178-8186.
[12] 赵小军, 王瑞, 杜振斌, 等. 交直流混合激励下取向硅钢片磁滞及损耗特性模拟方法[J]. 电工技术学报, 2021, 36(13): 2791-2800.
Zhao Xiaojun, Wang Rui, Du Zhenbin, et al. Hysteretic and loss modeling of grain oriented silicon steel lamination under AC-DC hybrid magnetiza- tion[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2791-2800.
[13] 孙鹤, 李永建, 刘欢, 等. 非正弦激励下纳米晶铁心损耗的计算方法与实验验证[J]. 电工技术学报, 2022, 37(4): 827-836.
Sun He, Li Yongjian, Liu Huan, et al. The calculation method of nanocrystalline core loss under non- sinusoidal excitation and experimental verification[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 827-836.
[14] Chen Wei, Huang Xiaoyan, Cao Shihou, et al. Predicting iron losses in soft magnetic materials under DC bias conditions based on steinmetz premag- netization graph[J]. IEEE Transactions on Magnetics, 2016, 52(7): 1-4.
[15] Zhou Yan, Chen Qimi, Zhang Junbo. Predicting core losses under the DC bias based on the separation model[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(2): 833-840.
[16] 翁玲, 常振, 孙英, 等. 不同磁致伸缩材料的高频磁能损耗分析与实验研究[J]. 电工技术学报, 2020, 35(10): 2079-2087.
Weng Ling, Chang Zhen, Sun Ying, et al. Analysis and experimental study on high frequency mag- netostrictive energy loss of different magnetostrictive materials[J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2079-2087.
[17] Huang Wenmei, Wu Xiaoqing, Guo Pingping. Variable coefficient magnetic energy losses calcu- lation model for giant magnetostrictive materials[J]. IEEE Transactions on Magnetics, 2021, 57(2): 1-5.
[18] 黄文美, 夏志玉, 郭萍萍, 等. 变温条件下TbDyFe合金高频磁特性和损耗特性分析[J]. 电工技术学报, 2022, 37(1): 133-140.
Huang Wenmei, Xia Zhiyu, Guo Pingping, et al. Analysis of high frequency magnetic properties and loss characteristics of TbDyFe alloy under variable temperature[J]. Transactions of China Electrotech- nical Society, 2022, 37(1): 133-140.
[19] Bertotti G. General properties of power losses in soft ferromagnetic materials[J]. IEEE Transactions on Magnetics, 1988, 24(1): 621-630.
[20] 赵志刚, 毕紫莉. 正弦及谐波激励下铁磁材料损耗模型的改进和验证[J]. 中国电机工程学报, 2022, 42(9): 3452-3459.
Zhao Zhigang, Bi Zili. Improvement and verification of ferromagnetic material loss model under sinusoidal and harmonic excitation[J]. Proceedings of the CSEE, 2022, 42(9): 3452-3459.
Impact Analysis of DC Bias on High-Frequency Dynamic Loss and Magnetic Characteristics for Magnetostrictive Materials
Abstract The DC bias magnetic field caninducedistortion and asymmetry of the hysteresis loops for magnetostrictive materials, which affects the loss values and hysteresis characteristics, and the existing magnetic energy loss models cannot accurately characterize and calculate the losses under variable DC bias magnetic fields. Therefore, it is necessary to investigate the influence and mathematical expression on the magnetic properties of magnetostrictive materials when DC bias is applied, which is of great significance to optimizing the output characteristics for high-power magnetostrictive devices. In this paper, under variable DC bias, the dynamic hysteresis loops of Terfenol-D samples at different excitation frequencies and peak magnetic density fluxes are investigated, and the variation law is found when the loss characteristics and hysteresis characteristics parameters are extracted from these hysteresis loops. Based on Bertotti's loss separation theory and measured data, the Levebverg-Marquard algorithm is induced to establish a calculation model for high-frequency losses of magnetostrictive materials under DC bias. This model uses a multiple- parameter regression method to correct the loss coefficients by introducing the DC bias-related terms. The accuracy of the proposed model is verified by comparing the calculated loss values with the experimental values under various working conditions.
Keywords:Terfenol-D alloy, DC bias, high-frequency dynamic hysteresis, magnetic energy loss model
中图分类号:TM274
DOI: 10.19595/j.cnki.1000-6753.tces.211511
国家自然科学基金资助项目(51777053, 52077052, 52130710)。
收稿日期 2021-09-23
改稿日期 2021-10-14
E-mail: huzwm@hebut.edu.cn(通信作者)
郭萍萍 女,1990年生,博士研究生,研究方向为磁性材料与器件、电机电器及控制。
E-mail: guopingpinghebut@163.com
(编辑 郭丽军)