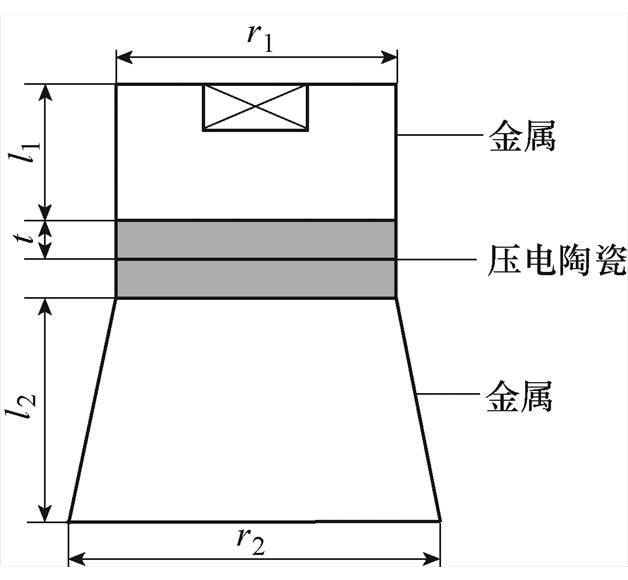
图1 Langevin夹心式定子结构示意图
Fig.1 Langevin sandwich structure
摘要 Langevin夹心式结构被广泛应用于超声波电机定子结构设计中,其压电振子工作于厚度方向振动模态,现有等效电路模型由于没有充分考虑压电振子固有损耗特性,因此无法实现对机械品质因数的准确评估。为此,该文首先建立压电振子含三类损耗的解耦机电等效电路模型,研究压电振子三类固有损耗对机械品质因数的影响规律;再进一步建立Langevin夹心式结构的机电等效电路模型,分析材料特性参数和结构参数对于共振频率、反共振频率和有效机电耦合系数等关键性能指标的影响。最后制作Langevin夹心式结构性样机,并分别对其阻抗-频率特性和振动特性进行测试,通过实验结论证实理论模型的准确性。该研究通过揭示压电振子固有损耗对其输出特性的差异性影响规律,为设计具有高机械品质因数的振子结构,并进一步开发高性能超声波电机提供理论支撑。
关键词:超声波电机 Langevin结构 机电等效电路 损耗
超声波电机是一种新型微特电机,其中Langevin换能器结构作为超声波电机定子的常用结构[1-3],具有机电转换效率高[4]、功率容量大、灵敏度高、结构简单、性能稳定[5-6]等优点。超声波电机的研究方法通常包括有限元法[7-9]、解析法[10]和等效电路 法[11-15],其中有限元法可以分析复杂的几何结构,但其使用成本高,且无法充分地描述超声波电机的电学特性;而运用解析法时,为了简化建模,通常会引入一些假设条件,导致较大的误差;相比之下,等效电路模型是利用机械振动和电路振荡的相似原理,将压电振子的机械谐振等效地转化为电路谐振,可以有效地反映出压电作动器的电学特性。文献[11-13]通过建立等效电路模型,分析几何结构对于换能器共振频率、反共振频率和有效机电耦合系数的影响;文献[14]利用等效电路法分析振动体的材料特性对振动特性的影响;文献[15]中利用等效电路法分析压电换能器结构的阻抗频率特性。上述文献在等效电路建模时仅考虑介电损耗或机械损耗,对压电损耗的考虑较少。然而,近几年已有研究表明,压电损耗在压电陶瓷的热量产生机制中具有关键的作用[16]。当前IEEE标准[17]中压电振子等效电路模型仅考虑了压电振子的机械损耗,该方法假定共振频率处的机械品质因数与反共振频率处的机械品质因数相等,但该结论与实验结果相悖。
基于此,本文提出一种充分考虑压电振子三类损耗的超声波电机解耦机电等效电路模型,分别研究三类损耗对于机械品质因数的影响规律,并进一步对Langevin夹心式定子结构进行建模,研究结构参数和材料参数对其输出特性的影响,最后,搭建实验测试平台,通过实验测试对仿真结果进行验证。
Langevin夹心式定子简化结构如图1所示,其中包括两侧的金属结构和中间两片以上叠堆的压电陶瓷振子结构。压电陶瓷振子沿厚度方向极化,两片压电陶瓷极化方向相反,中间侧接正电压,靠近金属侧接地,当向压电振子施加交流电压时,在垂直方向上产生振动,使两个金属端部产生纵向位移。
传统Langevin机电等效电路模型如图2所示,图中,V和I分别表示电气支路(即等效变压器的一次侧)的输入电压和电流。Fr1和Fr2为输出力,vr1和vr2为机械分支(即等效变压器的二次侧)中的振

图1 Langevin夹心式定子结构示意图
Fig.1 Langevin sandwich structure
动速度。Cd为压电陶瓷环的静态电容,其表达式为
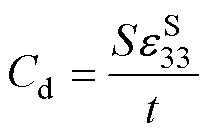 (1)
(1)
式中,S为压电陶瓷片的横截面积,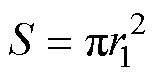 ;
;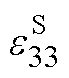 为恒应变下的介电系数分量;t为单片压电陶瓷片的 厚度。
为恒应变下的介电系数分量;t为单片压电陶瓷片的 厚度。
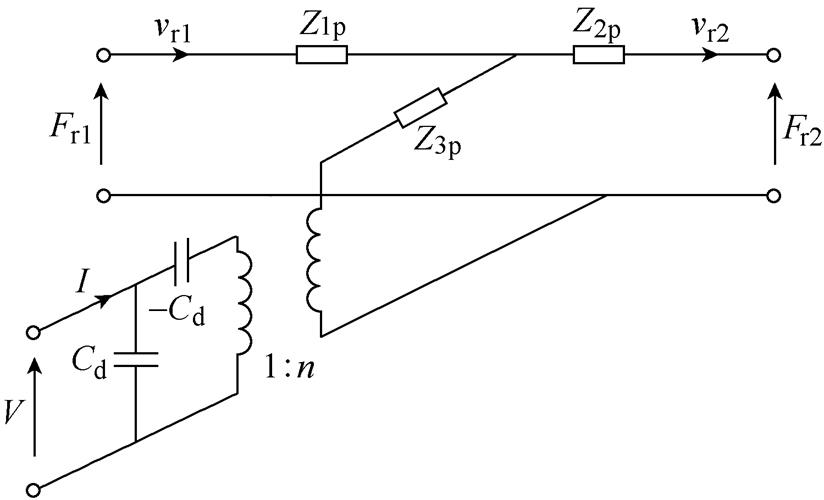
图2 传统厚度振动模态压电陶瓷机电等效电路模型
Fig.2 Conventional equivalent circuit of piezoelectrics in thickness vibration mode
n为机电耦合系数,其表达式为
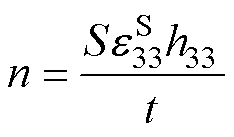 (2)
(2)
式中,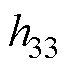 为压电系数分量。
为压电系数分量。
波速v表示为
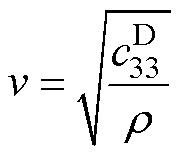 (3)
(3)
式中,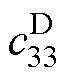 为弹性系数分量;
为弹性系数分量;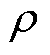 为压电材料的密度。
为压电材料的密度。
Z1p、Z2p和Z3p分别为机械分支中的阻抗,其表达式为
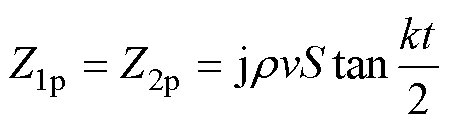 (4)
(4)
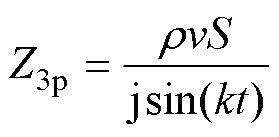 (5)
(5)
式中,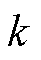 为波数,
为波数,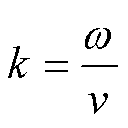 。
。
为深入研究超声波电机定子内部的发热机制,需要全面研究压电振子的损耗特性。压电振子含三类损耗:介电损耗、机械损耗和压电损耗,分别用复数表示为
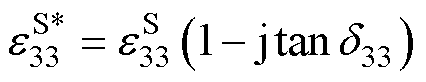 (6)
(6)
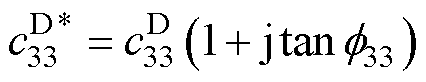 (7)
(7)
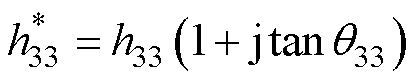 (8)
(8)
式中,j为虚数符号;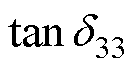 、
、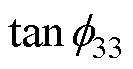 和
和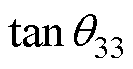 分别为介电损耗因子、机械损耗因子和压电损耗因子。由于损耗因子通常小于1%,因此在计算中可近似认为:
分别为介电损耗因子、机械损耗因子和压电损耗因子。由于损耗因子通常小于1%,因此在计算中可近似认为: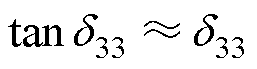 ,
,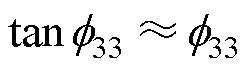 ,
,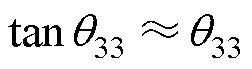 。
。
当考虑损耗时,对于机电等效电路中电学分支中的式(1)可用复数形式表示为
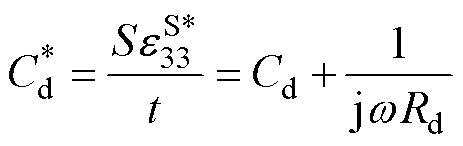 (9)
(9)
式中,Cd为存储的电能;Rd为介电损耗;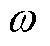 为角频率,具体表达式为
为角频率,具体表达式为
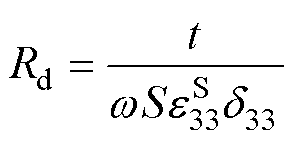 (10)
(10)
同样地,等效电路电学分支中的式(2)可用复数形式表示为
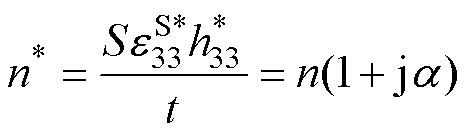 (11)
(11)
式中,n为机电转换系数;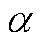 为相移,其中包含压电损耗,其表达式为
为相移,其中包含压电损耗,其表达式为
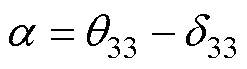 (12)
(12)
针对机电等效电路中机械侧的参数,在考虑损耗情况下的式(4)和式(5)复数表示为
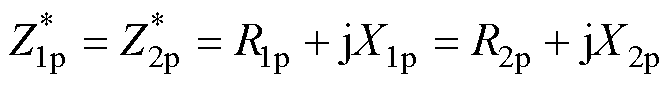 (13)
(13)
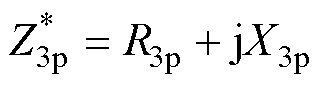 (14)
(14)
式中,R1p、R2p和R3p为机械损耗;X1p、X2p和X3p为存储的机械能量,具体表达式为
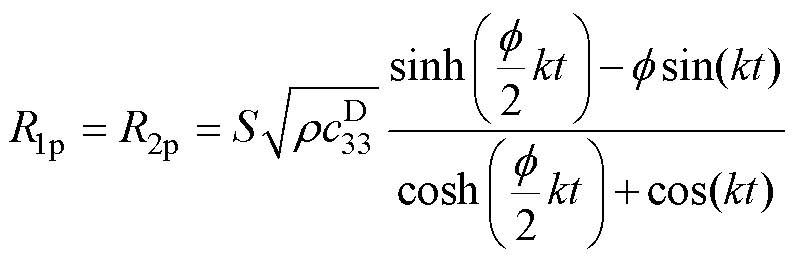 (15)
(15)
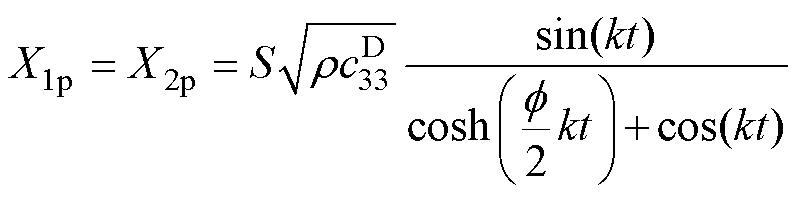 (16)
(16)
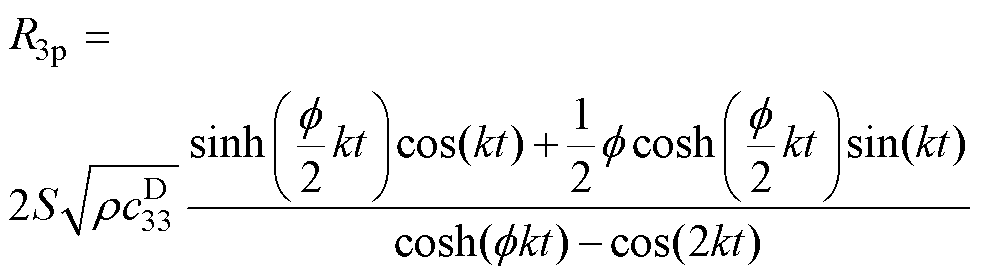 (17)
(17)
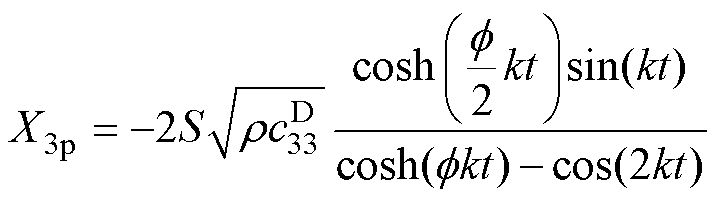 (18)
(18)
需要注意的是,X1p、X2p具有电感特性,即代表机械系统中的质量;X3p对应动态电容,即代表机械系统中的弹性。根据以上推导,新型含三类损耗的解耦机电等效电路模型如图3所示。
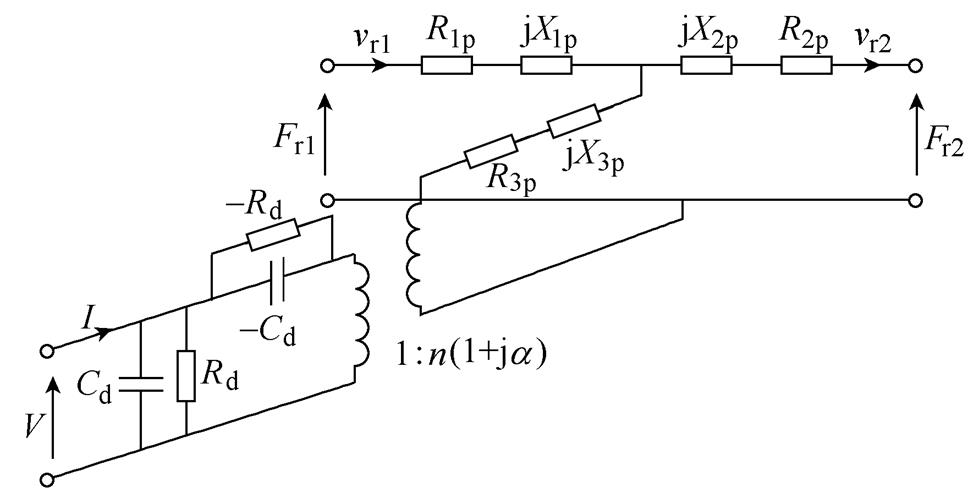
图3 新型含三类损耗的解耦机电等效电路模型
Fig.3 New decoupled electromechanical equivalent circuit with three types of losses
由于Langevin结构中的两侧金属仅具有机械特性,不具备电学特性,因此仅考虑金属的机械损耗因子,其复杨氏模量可以表示为
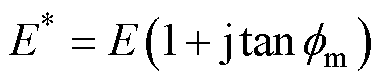 (19)
(19)
Langevin夹心式定子结构的等效电路机电模型如图4所示,其中金属结构的机械侧参数表达式为
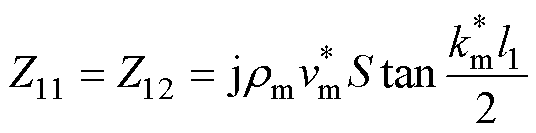 (20)
(20)
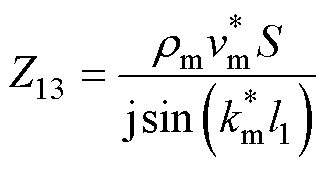 (21)
(21)
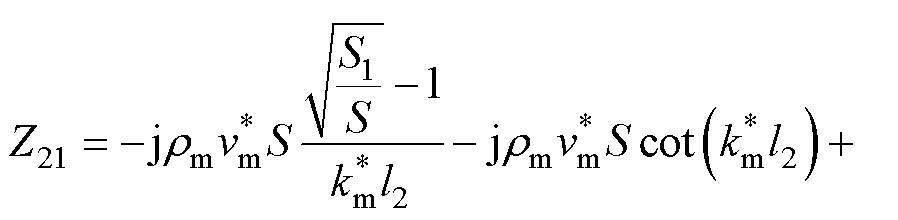
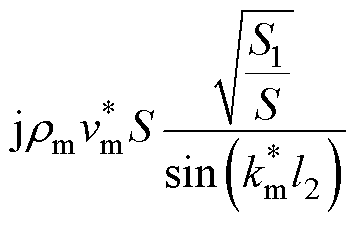 (22)
(22)
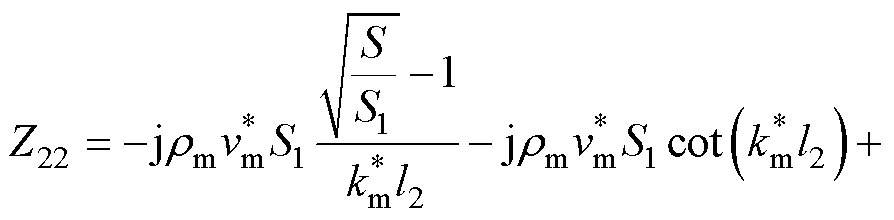
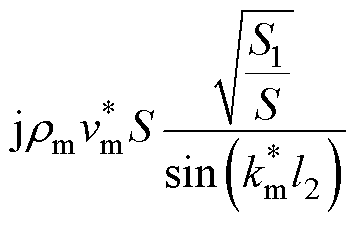 (23)
(23)
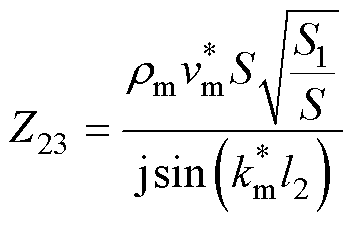 (24)
(24)
式中,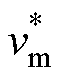 和
和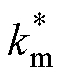 分别为机械侧波速和波数;
分别为机械侧波速和波数;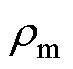 为机械侧金属的密度;
为机械侧金属的密度;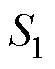 为喇叭形金属的横截面积,
为喇叭形金属的横截面积,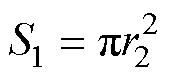 。由于金属机电等效电路中的机械侧解耦过程与压电振子相同,因此其解耦表达式不在此赘述。在分析阻抗-频率特性时,不考虑金属块两侧外加负载情况,可认为输出机械侧的边界条件为空载,即对应电学短路状态。
。由于金属机电等效电路中的机械侧解耦过程与压电振子相同,因此其解耦表达式不在此赘述。在分析阻抗-频率特性时,不考虑金属块两侧外加负载情况,可认为输出机械侧的边界条件为空载,即对应电学短路状态。
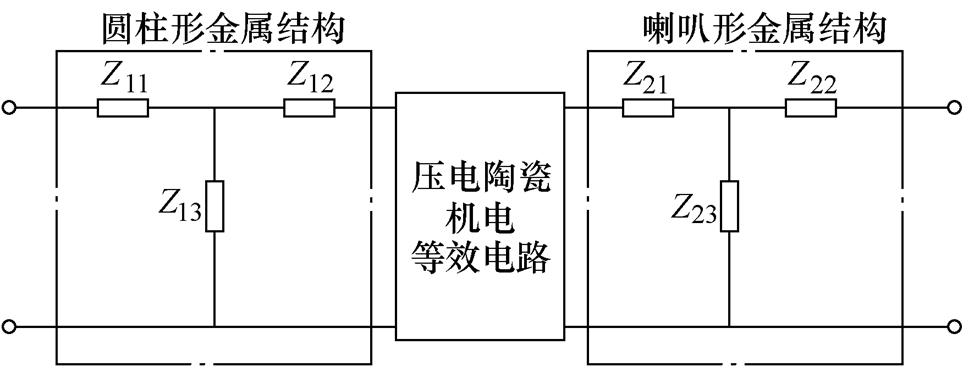
图4 Langevin夹心式定子结构机电等效电路模型
Fig.4 Electromechanical equivalent circuit model of Langevin sandwich structure
本文采用的厚度振动模态下压电振子的尺寸为:半径r1为18.5mm,单片厚度为5mm,其材料特性参数见表1。
表1 压电振子的材料特性参数
Tab.1 Materials properties of the piezoelectric ceramic

介电特性机械特性压电特性密度 材料特性 (实部)=461= N/m2=V/m= 7 600kg/m3 损耗特性(虚部)===—
利用仿真软件Matlab(版本:R2022a)对图3所示的压电振子机电等效电路模型进行仿真分析。图5为压电振子阻抗频率特性仿真结果对比,其中图5a为不含损耗与含三种损耗的阻抗频谱对比,可以看出两种情况下的共振频率和反共振频率相同,即固有损耗不影响压电振子的频率特性,而两者区别之处在于:不含损耗情况下,共振和反共振频率处均出现尖峰,因此无法计算相对应的机械品质因数;图5b为不含压电损耗与含三种损耗仿真结果对比,两者的区别在于共振频率处的3dB带宽不同,即对应的机械品质因数存在差异。在含损耗的情况下,可采用如图6所示的3dB带宽法计算共振频率fR处的机械品质因数QR和反共振频率fA处的机械品质因数QA,其表达式分别为
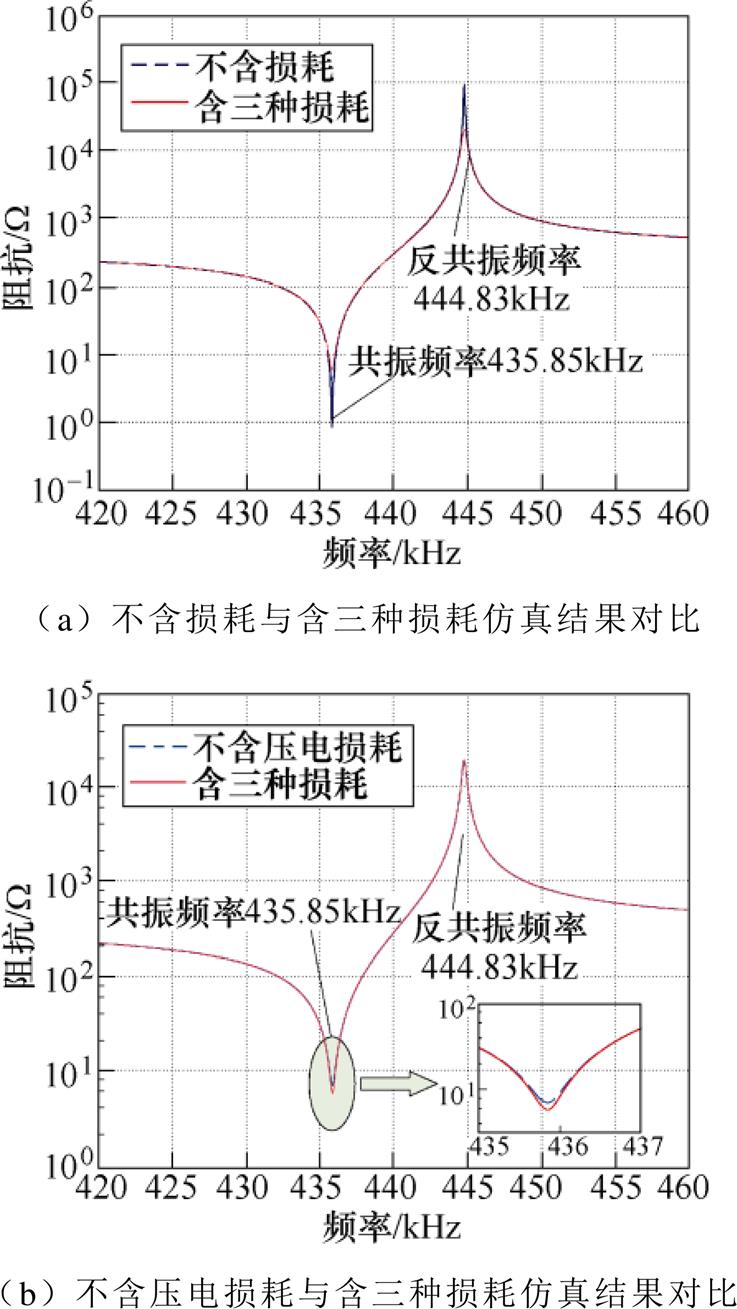
图5 压电振子阻抗频率特性仿真结果对比
Fig.5 Impedance spectrum comparison of simulation results
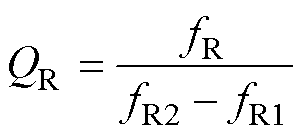 (25)
(25)
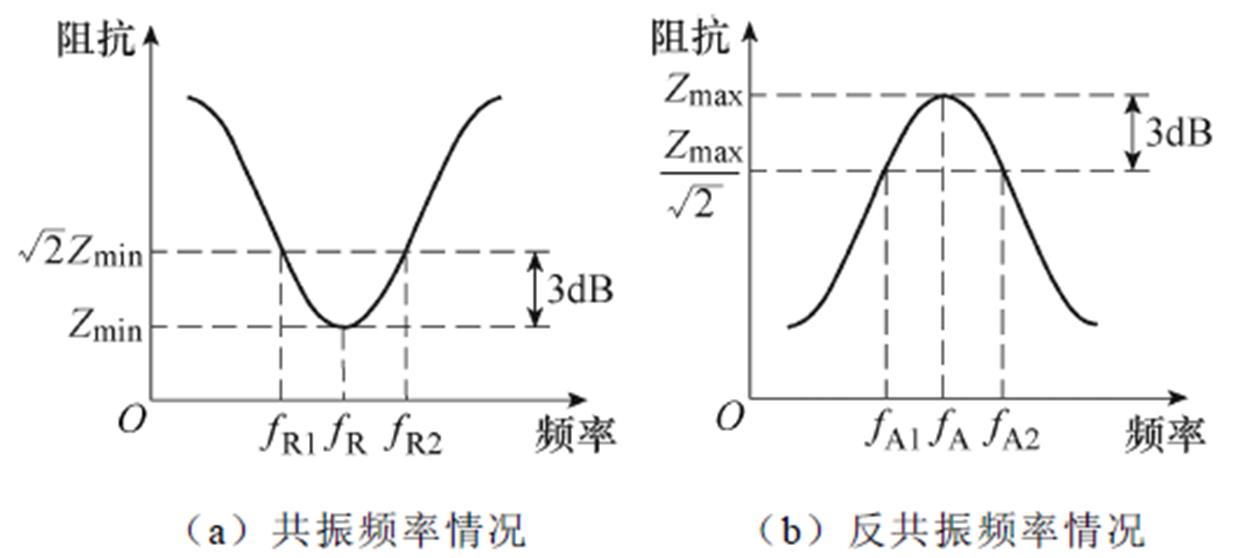
图6 3dB带宽法定义机械品质因数
Fig.6 Definitions of mechanical quality factors by 3dB bandwidth method
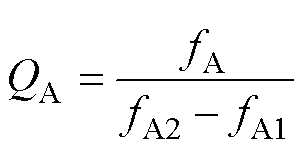 (26)
(26)
式中,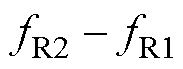 和
和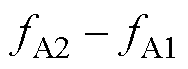 分别对应阻抗曲线中共振和反共振频率下的3dB带宽。
分别对应阻抗曲线中共振和反共振频率下的3dB带宽。
为了验证仿真结果的准确性,利用高精度阻抗特性分析仪(E4990A, Keysight Technologies, Inc., Santa Rosa, CA)对压电振子进行阻频特性实验测试,并将实验结果与仿真分析进行比较,具体结果见表2。通过对比结果可以看出,相比于不含压电损耗的仿真结果,含三类损耗的仿真结果与实验结果更为接近,其准确度的提升尤其体现在表2中加粗显示的数据,可以得出结论:压电损耗对于共振条件下的机械品质因数影响较大。
表2 含三类损耗、无压电损耗的仿真与实验结果对比
Tab.2 Results comparison of experiment, simulation with all three losses and simulation without piezoelectric loss
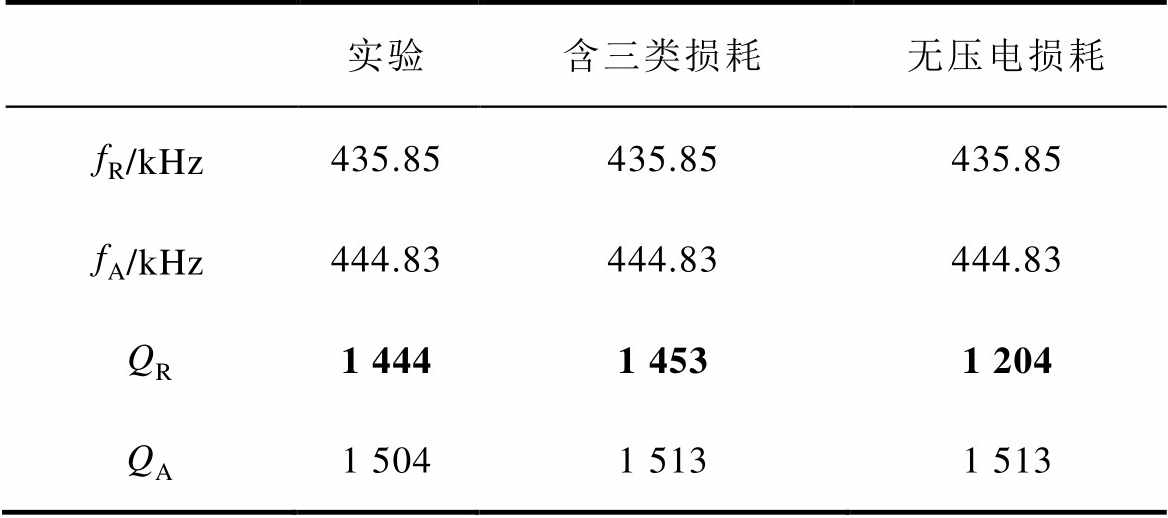
实验含三类损耗无压电损耗 fR/kHz435.85435.85435.85 fA/kHz444.83444.83444.83 QR1 4441 4531 204 QA1 5041 5131 513
图7所示为三类损耗特性对机械品质因数的影响规律,其中随着介电损耗因子和机械损耗因子增加,共振频率处的机械品质因数QR呈现下降趋势,而当压电损耗因子增加时,QR呈现升高趋势;反共振频率处的机械品质因数QA则会随着机械损耗因子的增加而减少,但不受介电损耗因子和压电损耗因子的影响。
三类材料特性对压电振子的共振频率和反共振频率的影响规律如图8所示,其中共振频率fR随着相对介电系数和压电系数的增加而降低,但随着弹性系数的增加而升高;反共振频率fA则会随着弹性系数的增加而升高,但不受相对介电系数和压电系数的影响。
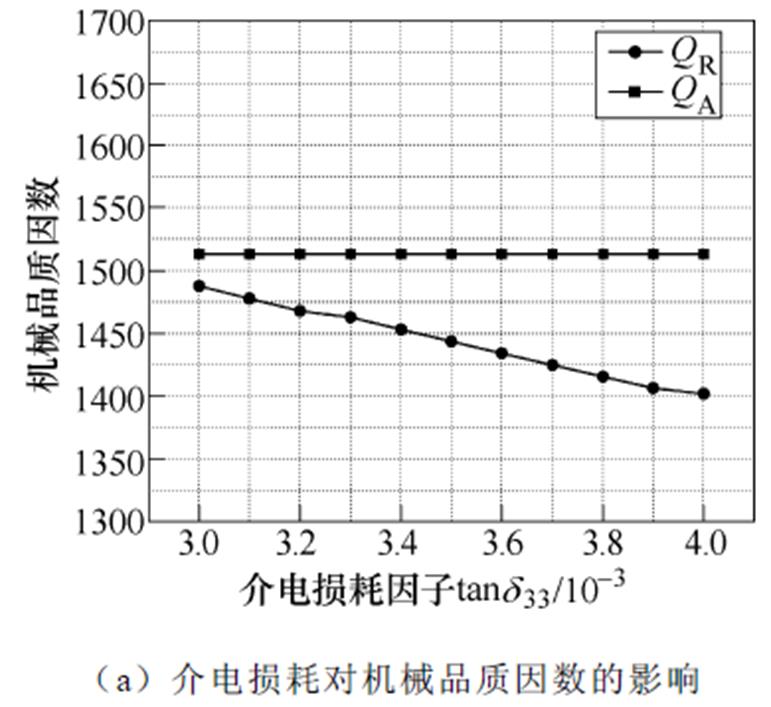
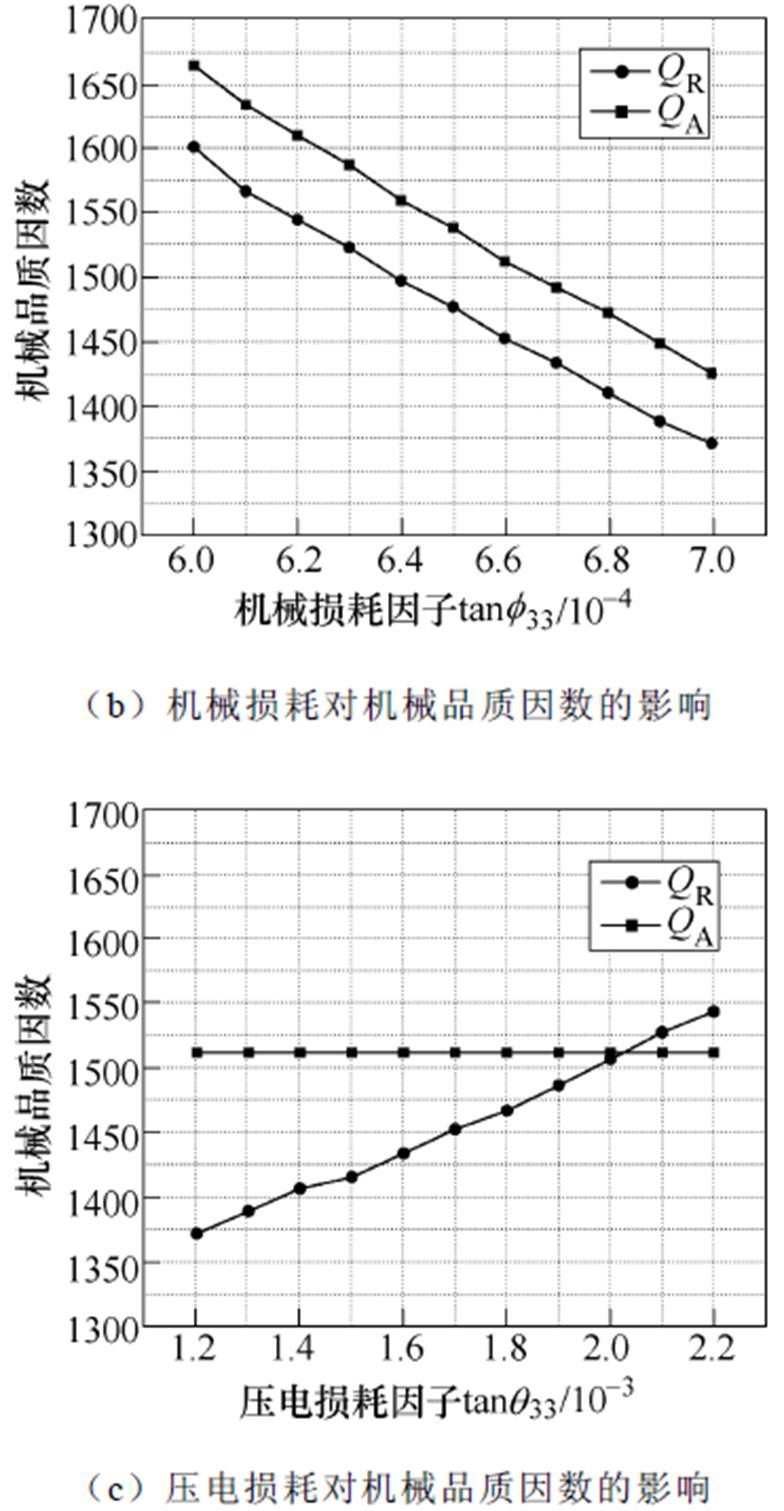
图7 三类损耗特性对机械品质因数的影响规律
Fig.7 Relationship between mechanical quality factor and three types of losses
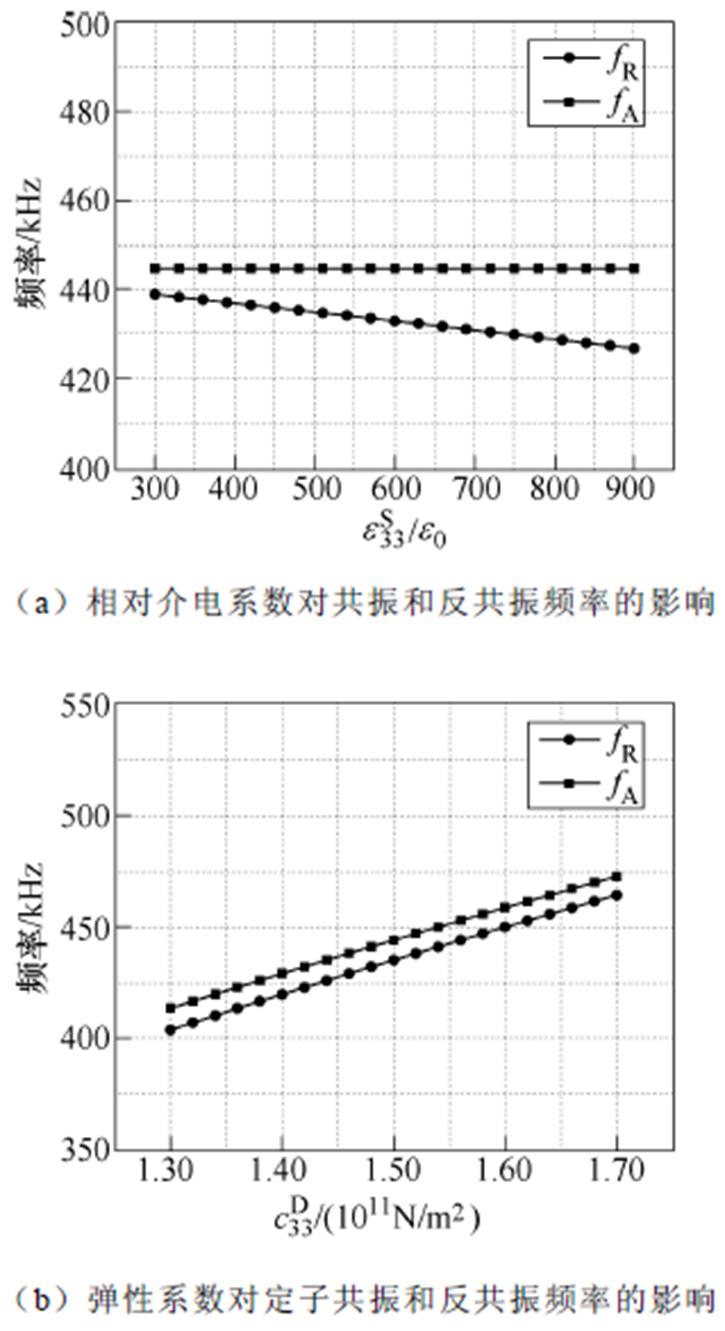
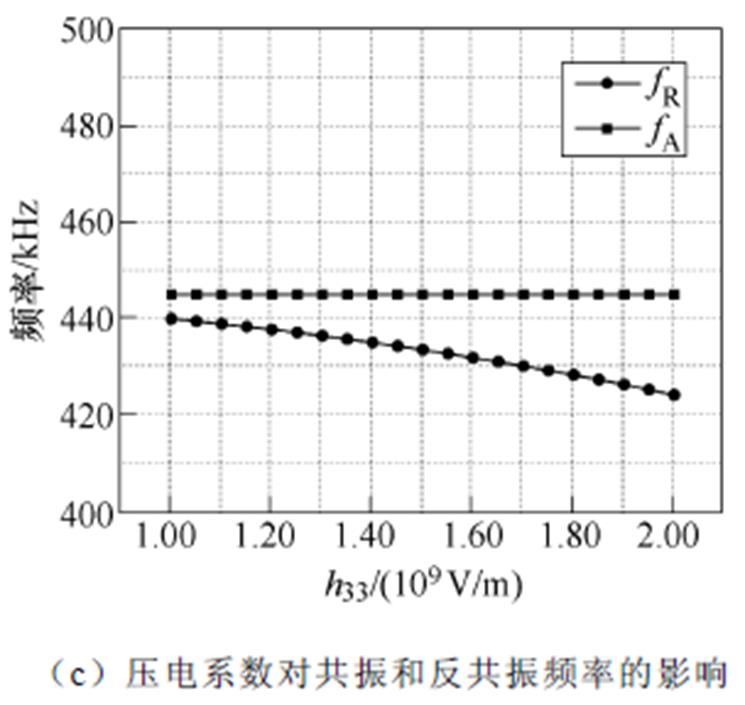
图8 材料特性对共振和反共振频率的影响规律
Fig.8 Influence of material properties on resonance and anti-resonance frequencies
有效机电耦合系数是描述电机定子机电转换效率的重要参数,可以通过如下公式求得。
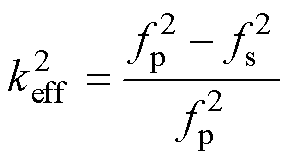 (27)
(27)
式中,fs和fp分别为压电振子的串联共振频率和并联共振频率,可分别近似于共振频率fR和反共振频率fA。图9为三类材料特性对有效机电耦合系数keff的影响规律,其中keff随着弹性系数的增大而呈现下降趋势,但随着相对介电系数和压电系数的增大而升高。
Langevin夹心式定子结构中金属的结构尺寸为:左侧圆柱体金属的厚度l1=28mm,右侧喇叭形金属的厚度l2=46mm,半径r2=29mm,材料特性为:杨氏模量E=6.92×1010N/m2,密度为2 700kg/m3。基于上述参数,对如图4所示的机电等效电路模型进行仿真,得到Langevin夹心式定子结构的共振频率为28.392kHz。
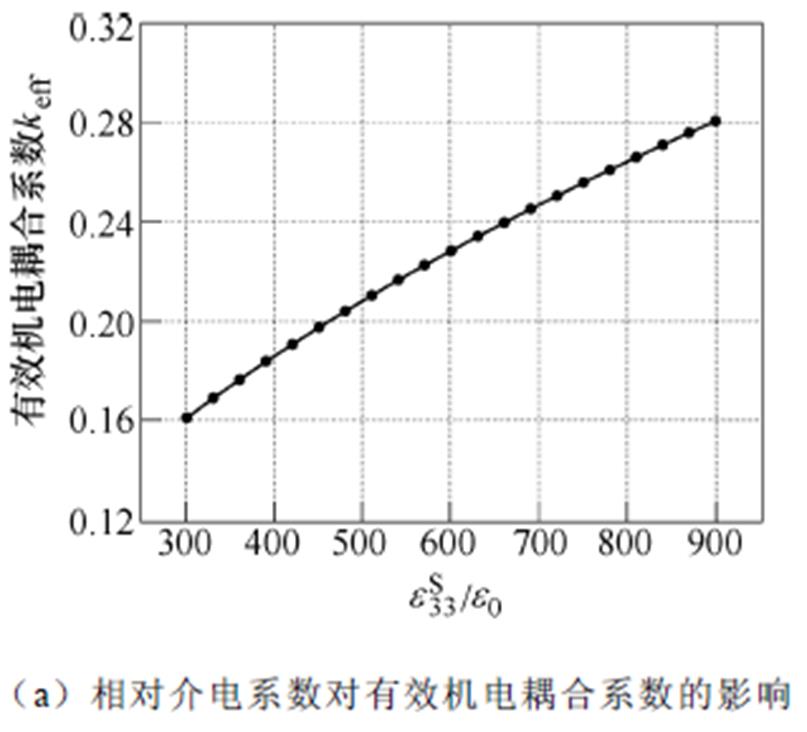
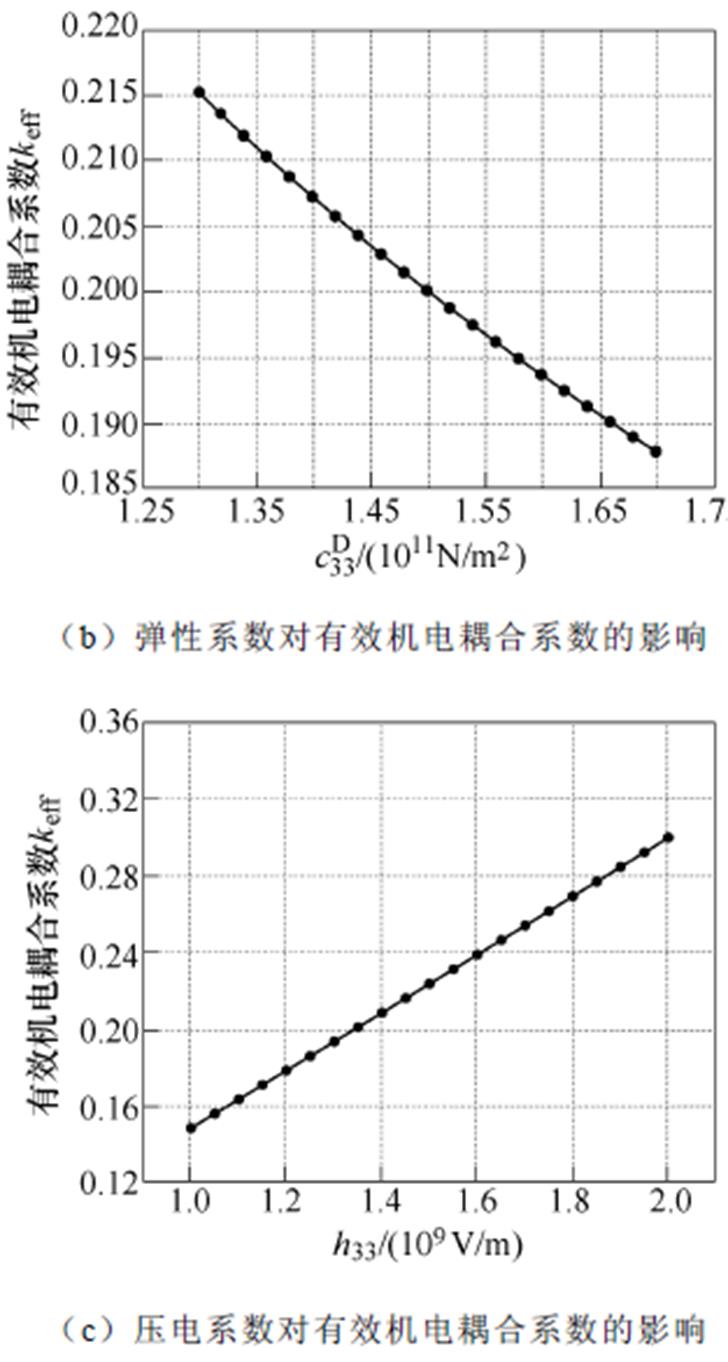
图9 材料特性对有效机电耦合系数的影响规律规律
Fig.9 Influence of material properties on effective electromechanical coupling coefficient
为了验证仿真模型结论,对Langevin夹心式定子结构采用激光测振仪(PolyTec PSV-400)进行测试。实验测试平台如图10a所示,测试时,定子结构为自由状态,将PSV-400各硬件连接成整套测试系统后,采用激光测振仪内部信号发生器产生正弦激励信号,再通过功率放大器(NF 4052)将电压信号进行放大,驱动信号通过数字示波器(Tektronix TDS 2014B)进行监控。激光测振过程采用系统自带的软件PSV8.51,依次按照如下步骤进行测试:光学设置→设置扫描点→设置参数→单点测试→扫描测量→显示数据。测试时的原始测试界面如图10b所示,由于扫描点设置和温漂现象会对频率产生一定影响,因此取5次测试结果平均值作为最终实验值,测得的共振频率为28.316kHz(最大偏差值为±0.035kHz)。考虑到建模中进行结构等效,忽略轴、螺栓和黏胶等结构引入的少量误差,可认为仿真与实验结果基本一致。
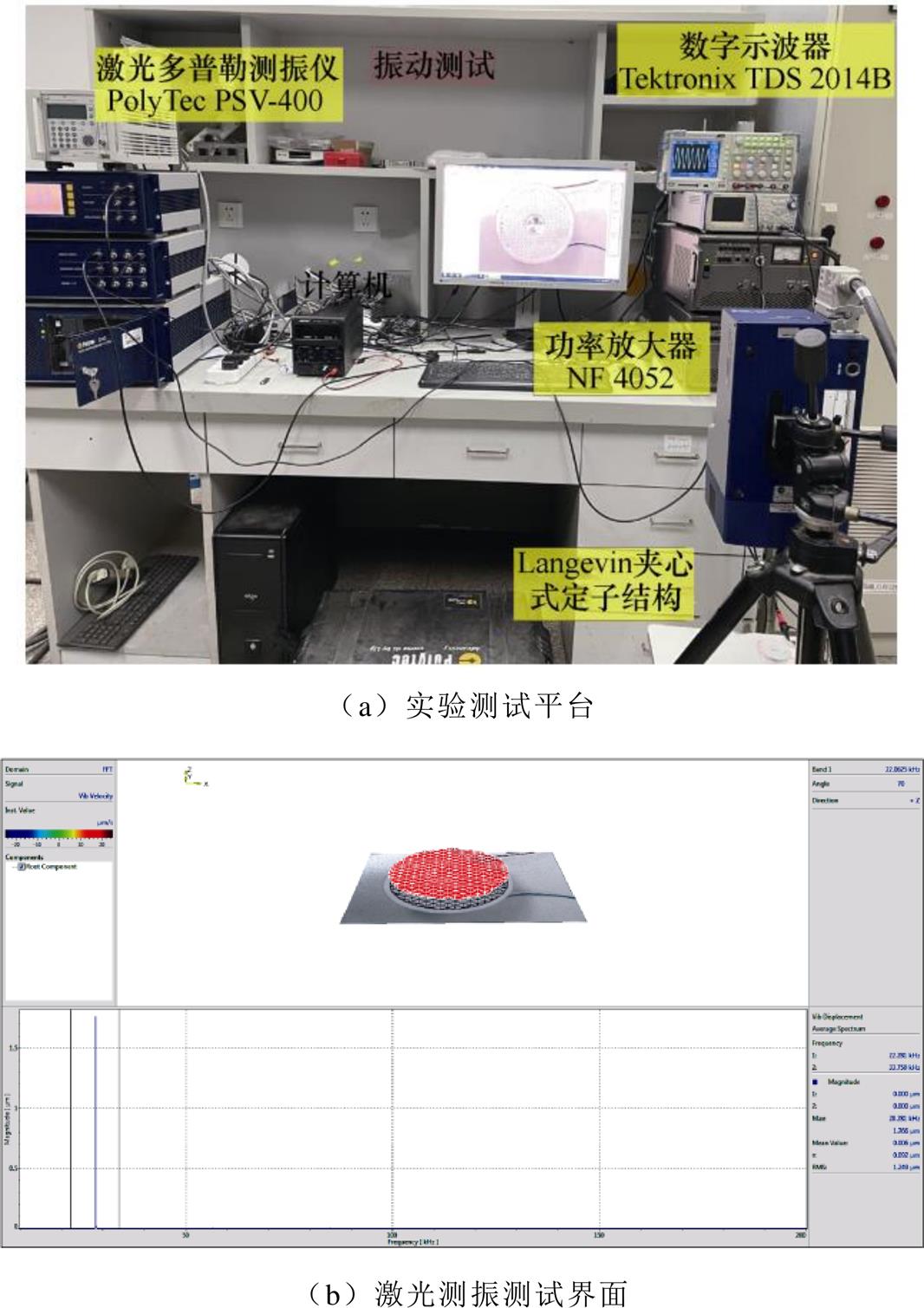
图10 Langevin夹心式定子结构激光测振实验测试
Fig.10 Laser vibration test of Langevin sandwich stator
进一步地,可以根据机电等效电路模型对Langevin夹心式定子材料和结构特性进行分析。图11为金属的杨氏模量对共振和反共振频率的影响规律,随着杨氏模量的增加,共振频率和反共振频率同时增大。图12为结构参数的变化对共振频率和反共振频率的影响规律,图中,t 为圆柱体金属的长度l1与Langevin结构总长度的比值,随着t 的增加,共振和反共振频率呈现小幅度上升趋势。相比于杨氏模量,结构参数对于频率的影响较小。图13和图14分别表示金属的杨氏模量和t 对有效机电耦合系数的影响规律。如图13和图14所示,随着杨氏模量E和结构参数t 的增加,有效机电耦合系数均呈现明显的上升趋势。该结论有助于通过合适地选取材料和设计结构来提升Langevin夹心式定子结构的机电能量转换效率。
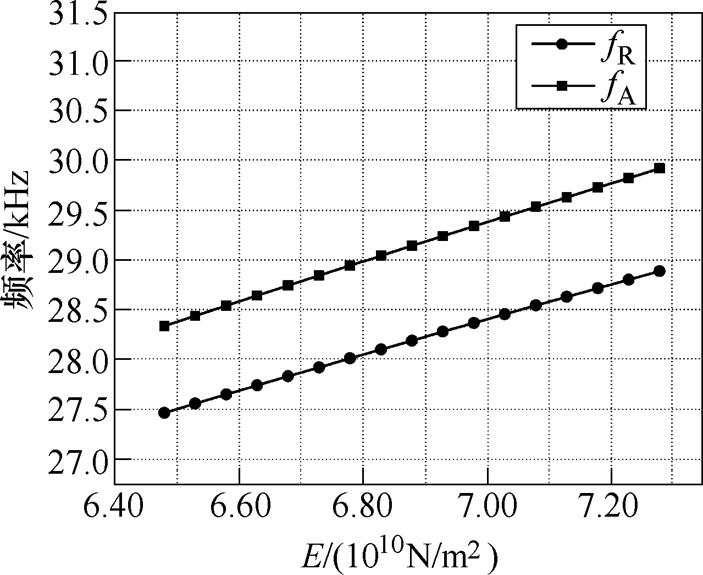
图11 杨氏模量对共振和反共振频率的影响仿真结果
Fig.11 Simulation results of the influence of Young's Modulus on resonance and anti-resonance frequencies
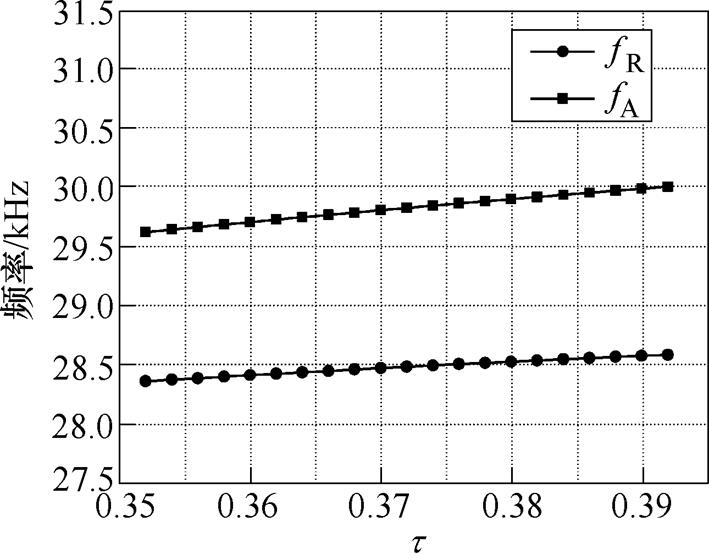
图12 t 对共振和反共振频率的影响仿真结果
Fig.12 Simulation results of influence of t on resonance and anti-resonance frequences
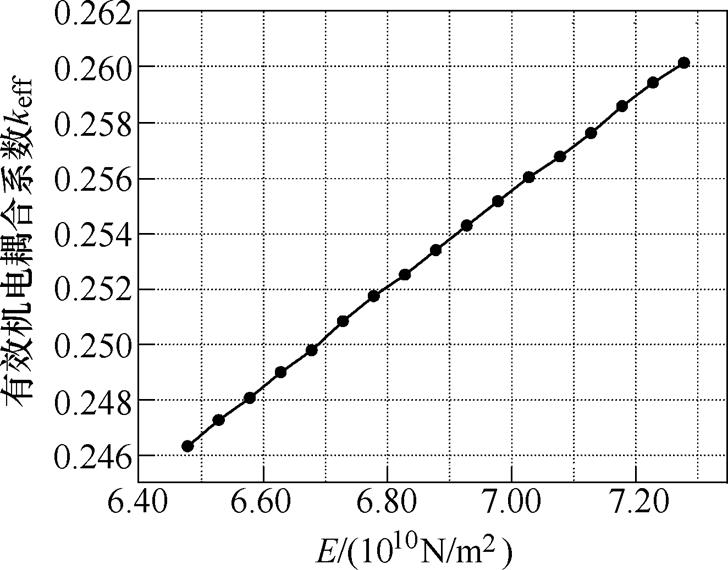
图13 杨氏模量对有效机电耦合系数的影响仿真结果
Fig.13 Simulation results of influence of Young's Modulus on effective electromechanical coupling coefficient
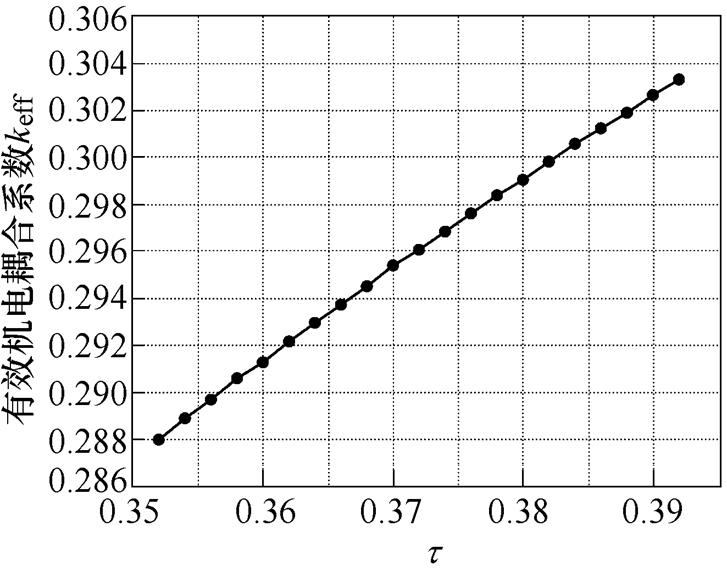
图14 t 对有效机电耦合系数的影响仿真结果
Fig.14 Simulation results of influence oft on the effective electromechanical coupling coefficient
本文建立了含损耗的Langevin夹心式定子结构解耦机电等效电路模型,通过理论模型的仿真分析可得出以下结论:
1)压电损耗对于厚度振动模态下压电振子共振频率处的机械品质因数影响较大。
2)共振频率处的机械品质因数由三类损耗共同决定,而反共振频率处的机械品质因数仅与机械损耗相关。
3)三类材料特性均对共振频率产生影响,而反共振频率仅受弹性系数影响较大。
4)材料和结构参数均对有效机电耦合系数产生较大影响。
综上所述,通过所提出的模型可为进一步设计和优化Langevin夹心式定子结构提供理论支撑。
参考文献
[1] Liu Yingxiang, Yan Jipeng, Wang Liang, et al. A two- DOF ultrasonic motor using a longitudinal-bending hybrid sandwich transducer[J]. IEEE Transactions on Industrial Electronics, 2019, 66(4): 3041-3050.
[2] Jiang Xinggang, Zhu Xianbin, Wong C Y, et al. Theory of series inductance matching to transducer at premechanical resonance zone in ultrasonic vibration cutting[J]. IEEE Transactions on Industrial Elec- tronics, 2019, 66(4): 3019-3029.
[3] Li Xuan, Stritch T, Manley K, et al. Limits and opportunities for miniaturizing ultrasonic surgical devices based on a Langevin transducer[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2021, 68(7): 2543-2553.
[4] 王天圣, 吴志军, 冯平法, 等. 压电超声换能器电负载调频特性研究[J]. 机械工程学报, 2017, 53(19): 45-51.
Wang Tiansheng, Wu Zhijun, Feng Pingfa, et al. Characteristics of piezoelectric ultrasonic transducer with electric load modifying frequency[J]. Journal of Mechanical Engineering, 2017, 53(19): 45-51.
[5] 刘继伦, 刘素贞, 金亮, 等. 用于测厚和裂纹检测的正交横波电磁超声换能器仿真分析及实验研究[J]. 电工技术学报, 2022, 37(11): 2686-2697.
Liu Jilun, Liu Suzhen, Jin Liang, et al. Simulation and experiment of orthogonal shear waves with electro- magnetic acoustic transducer for thickness measure- ment and crack detection[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2686-2697.
[6] 姚睿丰, 王妍, 高景晖, 等. 压电材料与器件在电气工程领域的应用[J]. 电工技术学报, 2021, 36(7): 1324-1337.
Yao Ruifeng, Wang Yan, Gao Jinghui, et al. Applications of piezoelectric materials and devices in electric engineering[J]. Transactions of China Elec- trotechnical Society, 2021, 36(7): 1324-1337.
[7] 韦艳飞, 杨鑫, 陈钰凯, 等. 计及损耗的超磁致伸缩材料参数提取及有限元仿真应用[J]. 电工技术学报, 2022, 37(7): 1726-1734.
Wei Yanfei, Yang Xin, Chen Yukai, et al. Parameter extraction and FEM simulation of giant mag- netostrictive transducer considering losses[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(7): 1726-1734.
[8] 王光庆, 徐文潭, 杨斌强. T型直线超声波电动机的运行机理及其特性分析[J]. 电工技术学报, 2017, 32(15): 111-119.
Wang Guangqing, Xu Wentan, Yang Binqiang. Operating mechanism and characteristics analysis of a T-shaped linear ultrasonic motor[J]. Transactions of China Electrotechnical Society, 2017, 32(15): 111- 119.
[9] 蒋春容, 董晓霄, 张津杨, 等. 径向换能型超声波电机定子振动模型[J]. 电工技术学报, 2017, 32(9): 48-55.
Jiang Chunrong, Dong Xiaoxiao, Zhang Jinyang, et al. Stator vibration model of a radial energy conversion ultrasonic motor[J]. Transactions of China Electro- technical Society, 2017, 32(9): 48-55.
[10] 王鑫, 王亮, 于鹏鹏, 等. 贴片式纵弯复合型直线超声电机的理论建模与实验研究[J]. 中国电机工程学报, 2021, 41(14): 5014-5024.
Wang Xin, Wang Liang, Yu Pengpeng, et al. Theoretical modeling and experiment studies of a bonded type longitudinal-bending hybrid linear ultrasonic motor[J]. Proceedings of the CSEE, 2021, 41(14): 5014-5024.
[11] Deng Yunyun, Zhang Guangbin, Zhang Xiaofeng. A method to depress the transmitting voltage response fluctuation of a double excitation piezoelectric transducer[J]. Applied Acoustics, 2020, 158: 107066.
[12] 陈诚, 林书玉. 基于2-2型压电复合材料的新型宽频带径向振动超声换能器[J]. 物理学报, 2021, 70(1): 341-351.
Chen Cheng, Lin Shuyu. A new broadband radial vibration ultrasonic transducer based on 2-2 pie- zoelectric composite material[J]. Acta Physica Sinica, 2021, 70(1): 341-351.
[13] Li Xiaoniu, Yao Zhiyuan, Li Rong, et al. Dynamics modeling and control of a V-shaped ultrasonic motor with two Langevin-type transducers[J]. Smart Materials and Structures, 2020, 29(2): 025018.
[14] Wu Jiang, Mizuno Y, Nakamura K. Vibration characteristics of polymer-based Langevin trans- ducers[J]. Smart Materials and Structures, 2018, 27(9): 095013.
[15] Dal Bo L, Gardonio P, Turco E. Analysis and scaling study of vibration energy harvesting with reactive electromagnetic and piezoelectric transducers[J]. Journal of Sound and Vibration, 2020, 484: 115510.
[16] Dong Xiaoxiao, Jiang Chunrong, Jin Long, et al. Inherent loss analysis of piezoelectrics in radial vibration and its application in ultrasonic motor[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2020, 67(8): 1632-1640.
[17] American National Standards Institute. An American National Standard: IEEE Standard on Piezoelectricity Standard[S]. IEEE, 1988.
Electromechanical Equivalent Model of Sandwich Stator of Ultrasonic Motors Considering Losses
Abstract The Langevin sandwich structure is widely used in the stator design of ultrasonic motors, in which the piezoelectric vibrator works in the thickness vibration mode. Because the existing equivalent circuit model does not fully consider the inherent loss characteristics of the piezoelectric vibrator, it is unable to evaluate the mechanical quality factor. In this paper, the decoupling electromechanical equivalent circuit model of a piezoelectric vibrator with three types of losses is firstly established to study the influence of three types of inherent losses of piezoelectric ceramics on the mechanical quality factor. Then, the electromechanical equivalent circuit model of the Langevin sandwich structure is established, and the influence of material and structural parameters on resonance frequency, anti-resonance frequency and electromechanical coupling coefficient is discussed. Finally, a Langevin structural prototype is fabricated, and its impedance-frequency characteristics and vibration characteristics are tested. The accuracy of the theoretical model is verified. This paper provides theoretical support for designing a vibrator structure with a high mechanical quality factor and further develops a high-performance ultrasonic motor by revealing the differential influence of the inherent loss of piezoelectric vibrators on its output characteristics.
Keywords:Ultrasonic motor, Langevin structure, electromechanical equivalent circuit, losses
中图分类号:TM35
DOI: 10.19595/j.cnki.1000-6753.tces.220994
国家自然科学基金资助项目(52107043)。
收稿日期 2022-05-13
改稿日期 2022-07-09
E-mail: dongxiaoxiao@hhu.edu.cn(通信作者)
黄肖肖 女,2000年生,硕士研究生,研究方向为微型特种电机设计及驱动控制。
E-mail: hhhuangxx@163.com
(编辑 郭丽军)