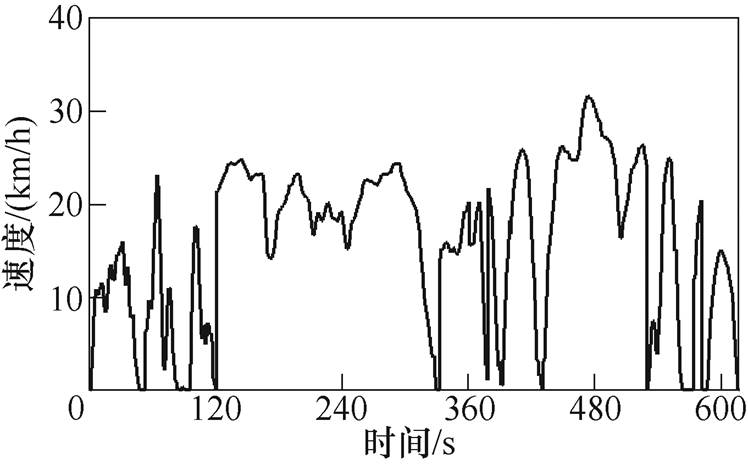
图1 运行工况曲线
Fig.1 Curve of the operation condition
摘要 双永磁游标电机基于双向磁场调制效应原理运行，在转矩密度提高的同时，存在电机损耗较大的问题。采用传统以电机额定点为优化对象的优化方法，仅能提升额定工作点的性能，难以保证电机实际运行工况下多个工作点高效运行的需求。为此，该文提出考虑运行工况的电机多工作点优化方法，设计了低损耗模块化双永磁游标电机。采用K聚类法精确提炼代表工作点及其权重，为了使优化过程更加高效化，采用灵敏度分析法将变量分区定性优化减少设计空间，结合响应面法与具有高收敛性的基于变异算子的多目标差分进化算法确定高敏参数的全局最优解，从而实现运行工况下高效准确的电机参数优化。仿真与实验结果验证了设计方法的有效性。
关键词：运行工况 差分进化算法 多目标优化 永磁游标电机
随着石油资源的日渐枯竭和环保意识的增强，汽车行业电气化进程得到持续加速和深化。电动汽车污染小且能源利用率高，是解决燃油汽车环境污染大和耗能严重问题的有效途径。良好的转矩特性与紧凑结构是车用驱动电机设计的核心指标。与常规电机相比[1-2]，磁场调制型电机具备更高的转矩密度，但大多存在结构复杂、制造难度大的问题。永磁游标电机是磁场调制型电机的典型代表，具有结构简单、转矩密度与功率密度高的优点，在电动汽车电机驱动领域受到广泛关注[3]。传统游标电机多为单边励磁结构，转矩密度的提升受磁负荷限制。为进一步提高电机转矩密度，文献[4-5]利用双边励磁产生双向磁场调制效应原理，提出了定转子上均安置永磁体的双永磁游标电机结构，有效提升了电机转矩密度，然而，双向磁场调制效应也增加了电机磁场谐波，使得铁心损耗增加，电机效率较低。
另一方面，为了满足电机性能要求，常采用电机优化设计方法对电机进行优化。电机优化设计通常需要考虑转矩密度、制造成本、损耗等多个性能指标。多目标优化通过算法可实现在多个冲突目标函数的折中优化。文献[6]选择Kriging模型为代理模型进行优化，但存在参数估计复杂、变量维数高时部分函数需人为整定的问题。文献[7-8]分别采用遗传算法与粒子群优化算法进行多目标优化。这两种算法均属于随机搜索算法，具有全局优化的优点，但收敛性较差，容易导致解集陷入局部最优。
此外，当前对于电动汽车驱动电机的优化设计往往注重于额定工作点的优化。而在实际应用中，驱动电机是在运行工况下以极为动态的转矩-速度组合运行，工作点数量众多、分布广泛且不匀，仅限于稳态性能的单一工作点优化结果，不是实际运行工况下的最优解。因此，在驱动电机的优化过程中应考虑实际运行工况。文献[9-10]根据运行工况曲线特征，简单概括出五类代表运行模式并建立相应的模式电机，根据不同模式电机设计要求确立优化目标。最后，取公共优化解集为最优参数。这种方法涉及多台电机的多个目标的优化问题，工作量大且繁琐。文献[11]进一步采用正相关性分析合并优化目标，缩减了模式电机数量，但优化效率仍然不高，且简单的模式划分无法适用于复杂多变的运行工况曲线。文献[12]将一典型运行工况下的数百个工作点按转速转矩等距划分，在各区域选取中心点作为代表工作点进行综合定量优化，但工作点分布疏密不一，划区取点无法精简提炼代表工作点，优化效率仍然不高。因此，如何在运行工况下实现高效准确的参数优化值得深入研究。
为了解决双永磁游标电机损耗大、在多工况运行下效率低的问题，本文设计了高转矩密度低铁耗的模块化双永磁游标（Modular Double Permanent- Magnet Vernier, MDPMV）电机，提出了考虑运行工况的电机多工作点优化方法。根据运行工况，采用K聚类法高效提炼有限个代表工作点作为优化对象。为了提高优化效益，采用灵敏度分析法将设计变量分区优化，结合响应面模型与具有高收敛性的基于等级的变异算子的多目标差分进化（Multi- Objective Differential Evolution with Ranking-based Mutation Operator, MODE-RMO）算法对高敏参数进行多目标优化。最后，将优化结果与传统额定点优化结果对比分析，验证考虑运行工况的电机多工作点优化设计的有效性。
汽车运行工况又称车辆测试循环，是特定交通环境下对车辆实际运行状况的定量描述，可以体现汽车道路运行的运动学特征。本文所研究的MDPMV电机是基于具有固定运行工况的轻量型校园巡逻电动车设计，对校园巡逻车的驾驶周期进行采样，通过实验数据分析建立运行工况速度-时间曲线，如图1所示。
图1 运行工况曲线
Fig.1 Curve of the operation condition
根据运行工况生成的电机工作点数量多且分布广，若采用有限元设计优化大规模工作点不仅复杂，而且费时。因此，需要引入数据分析技术，高效合理地提取代表工作点，缩小有限元优化空间。聚类分析可以通过建模把数据静态分类入不同组别，从而简化数据。其中，K聚类法作为运用最广泛的聚类分析方法之一，操作便捷，其自主学习能力能大大减少算法训练成本。此算法操作流程主要分为以下三步：
（1）输入样本数据集X与输出聚类集C，从X中选取任意k个数据组成第一代聚类中心集A。
（2）依次计算所有样本到各个聚类中心的欧式距离，并按距离最近准则将样本划入相应聚类集。具体计算公式为
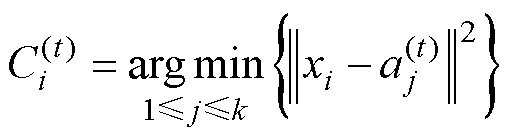（1）
式中，xi为第i个样本；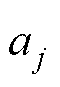
为第j个聚类中心；Ci为距离aj最近的聚类集；
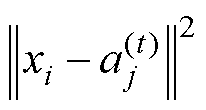为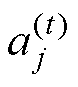
与xi之间的欧式距离函数；t为迭代次数。
（3）计算各个聚类集中样本数据的均值，作为新一代聚类中心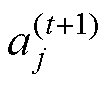
。具体计算公式为
（2）
重复迭代步骤（2）和步骤（3），直至聚类中心点变化率为零时，停止迭代并输出聚类集与聚类中心[13]。
采用K聚类法对全部工作点进行相似性划分，图2为给定运行工况下的工作点分布。根据每个聚类集中数据点的转速-转矩特性，归纳为四类运行模式：频繁起停、低速爬升、中速巡航、高速巡航。如图2所示，每一聚类的工作点的平均值即为代表工作点，每个代表工作点的转矩、转速及其权重见表1。
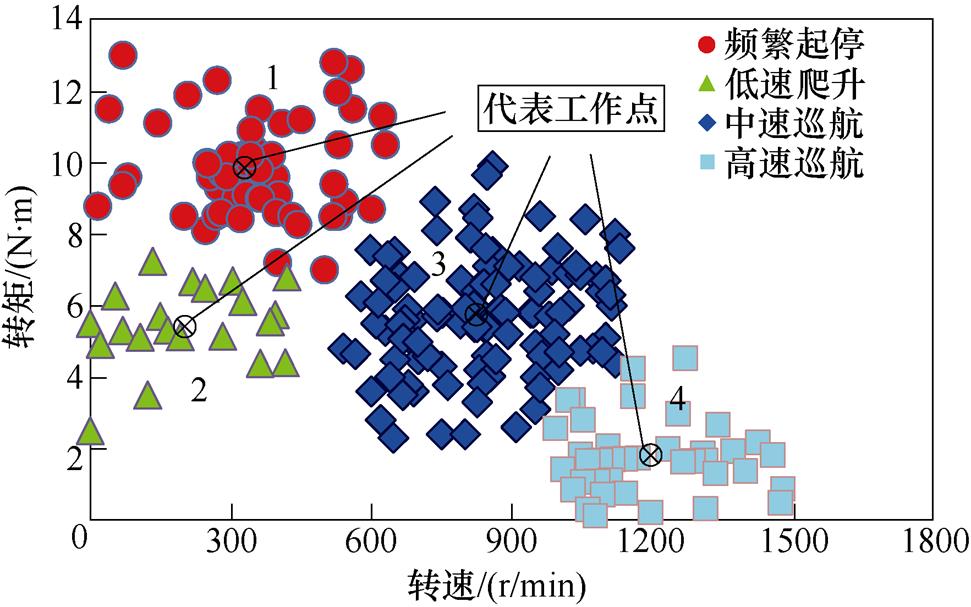
图2 工作点分布
Fig.2 Distribution of working points
表1 代表工作点转矩、转速及其权重
Tab.1 Representative working points and their weights
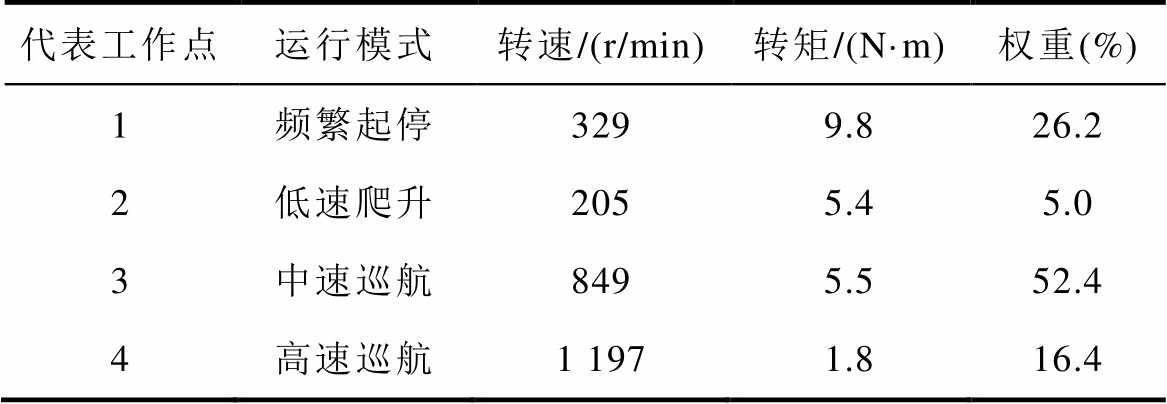
代表工作点运行模式转速/(r/min)转矩/(N·m)权重(%) 1频繁起停3299.826.2 2低速爬升2055.45.0 3中速巡航8495.552.4 4高速巡航1 1971.816.4
本文用于优化设计的模块化双永磁游标电机具有12个定子槽、12对极定子永磁体与19对极转子永磁体。电机拓扑结构如图3所示，电机主要参数见表2。与传统永磁游标电机相比，MDPMV电机定子虚齿与转子槽均内嵌永磁体，定子虚齿与转子齿均可作为调制齿参与磁场调制。双向磁场调制效应使电机定转子气隙间产生了更为丰富的谐波阶次，增加了有效工作谐波含量，提高了电机转矩密度[14]。模块化定子结构的引入改变了电机磁路，增加了低次谐波磁路磁阻，有效抑制了低次谐波含量，进一步降低了电机铁耗。同时，模块化结构使电机相间耦合度降低，具有较强的相间独立性[15]。
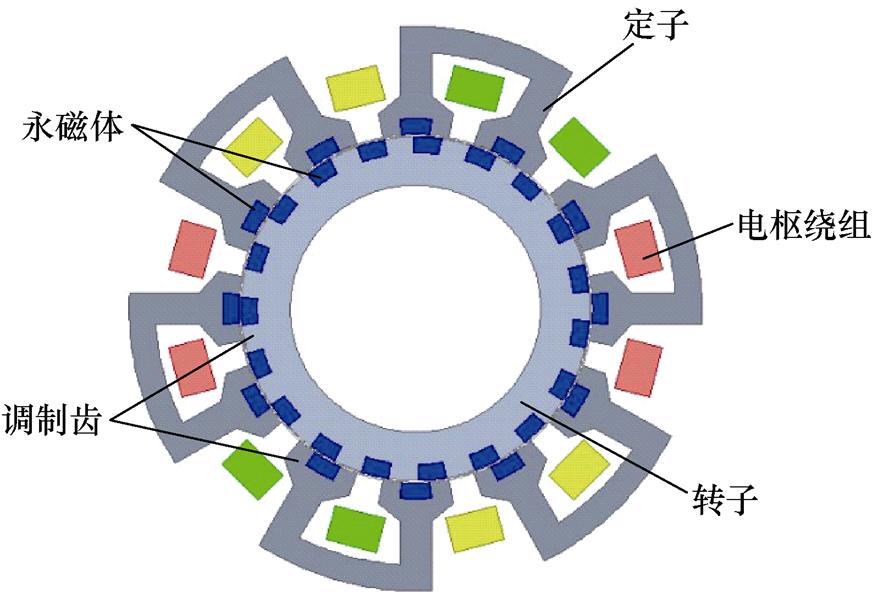
图3 电机拓扑结构
Fig.3 Topology structure of motor
表2 电机主要参数
Tab.2 Main parameters of motor
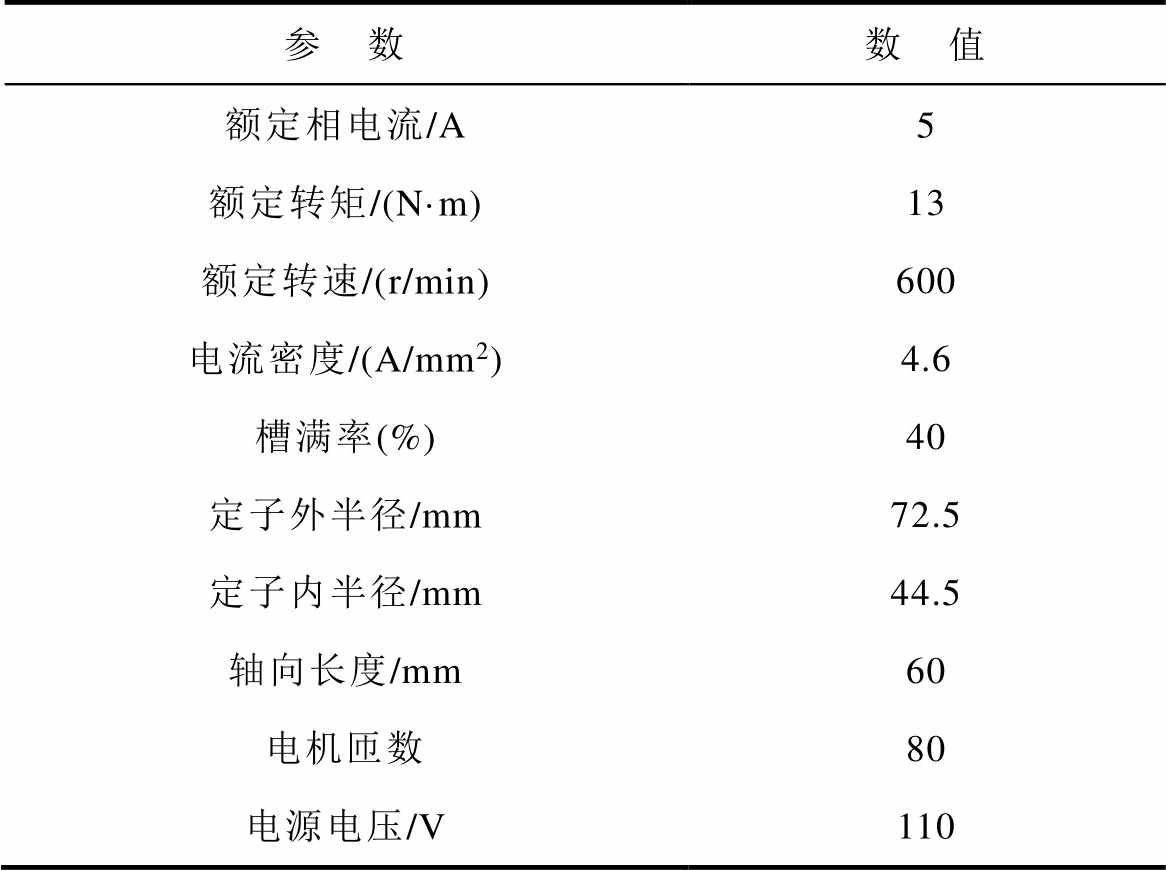
参 数数 值 额定相电流/A5 额定转矩/(N·m)13 额定转速/(r/min)600 电流密度/(A/mm2)4.6 槽满率(%)40 定子外半径/mm72.5 定子内半径/mm44.5 轴向长度/mm60 电机匝数80 电源电压/V110
MDPMV电机基于双向调制原理运行，经双向磁场调制生成的谐波阶数P可表示为
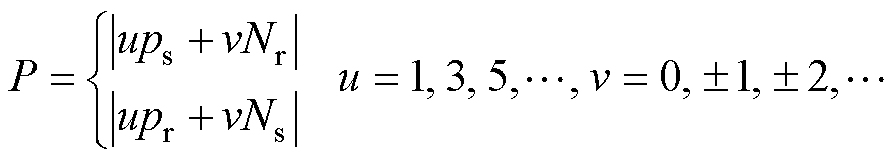（3）
式中，ps为定子永磁体极对数；pr为转子永磁体极对数；Nr为转子齿数；Ns为定子虚齿数。
根据式（3）可得，定子永磁体形成12对极、24对极永磁磁场，经19个转子齿调制分别可得7次、5次谐波磁场；转子永磁体形成19对极永磁磁场，经24个定子虚齿调制可得5对极谐波。图4为MDPMV电机气隙磁通密度。由图可知，5次、7次、19次为工作谐波，双边磁场相互叠加，工作谐波磁通密度增加。1次谐波为非工作谐波，磁通密度幅值较低。仿真结果验证了理论分析，相较传统永磁游标电机，双向调制效应增强了MDPMV电机励磁效果和工作谐波含量，提升了电机转矩密度。
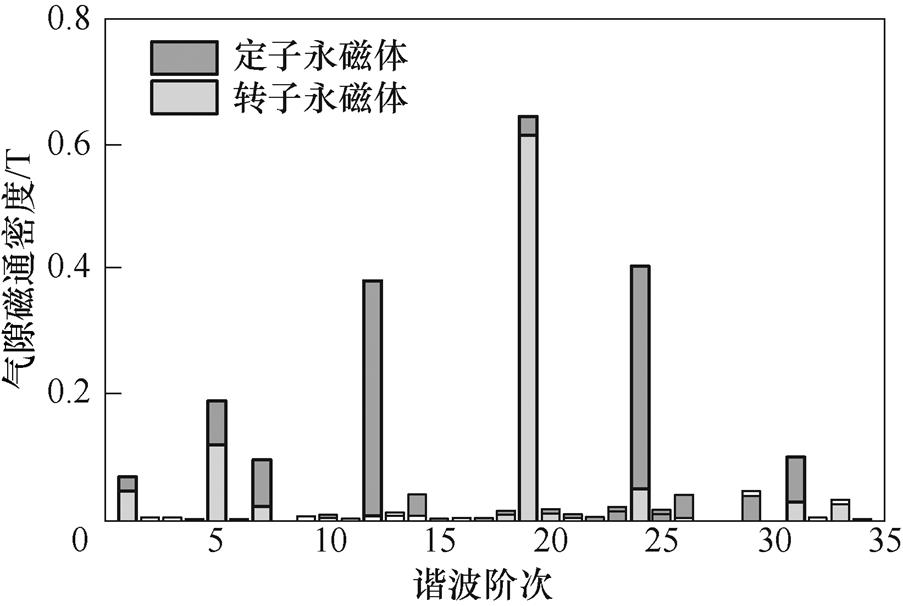
图4 MDPMV电机气隙磁通密度
Fig.4 Air gap flux density of MDPMV motor
为了保证电机在给定运行工况内有良好的工作性能，考虑运行工况的电机优化需要对多个代表工作点进行综合评估。首先，对于多目标优化中采样生成的各个样本电机，将外径、槽满率与电流密度设置为固定值，并通过调整电机轴向长度与匝数使样本电机在额定转速下获得恒定额定转矩。第p个样本电机轴向长度Lsk_p与电机匝数Np分别为
（4）
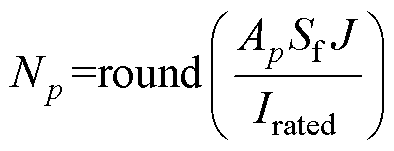（5）
式中，Lsk_0为初始电机轴向长度；Tout_0为电机额定转矩，其值为13N·m；Tout_p为第p个样本电机在额定相电流Irated下的转矩；y=round(x)为四舍五入取整函数；Ap为第p个样本电机的槽面积；Sf和J分别为槽满率和电流密度。
其次，采用响应面法拟合磁链模型，以确保模型精度的同时减少计算负担。中心复合设计（Central Composite Design, CCD）法为常用响应面试验设计之一，其设计表由立方体点、中心点和轴向点三部分组成。0为中心点，+1, -1分别为立方体点的高值和低值，a 为轴向点极值（a=2s/4，s为因素值）。Id、Iq分别为d、q轴电流，根据CCD法采样生成9组样本，拟合形成的d、q轴磁链响应面模型ld、lq如图5所示。
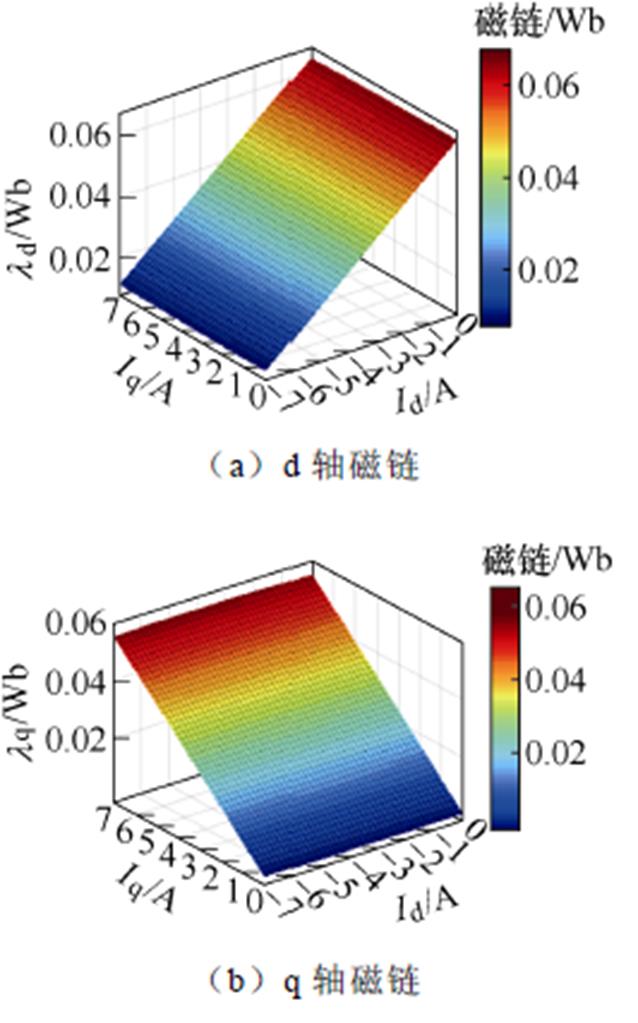
图5 磁链响应面模型
Fig.5 Response surface models of flux linkage
每个代表工作点有特定转速-转矩组合，其电枢电流计算如下。当代表工作点转速w 小于等于额定转速wbase时，电机端电压小于逆变器输出电压，电机仅受电流限制，以最大转矩电流比（Maximum Torque Per Ampere, MTPA）模式运行[16]。MTPA控制算法可视为转矩约束条件下电流幅值的最小化寻优问题，可用公式法进行描述求解，转矩Te与电流I可分别表示为
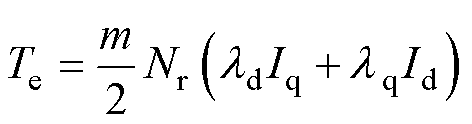（6）
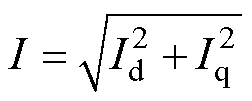（7）
式中，ld、lq分别为d、q轴磁链的多项式拟合函数；m为电机相数。
引入拉格朗日乘子q，并构建辅助函数H为
（8）
对辅助函数求极值，即分别对Id、Iq与q 求偏导并令其为零，有
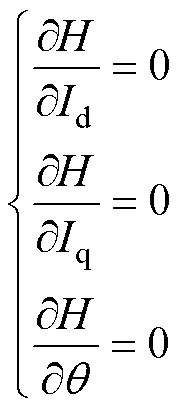（9）
联立式（6）与式（9），代入代表工作点转矩即可确定MTPA控制下的电枢电流。
当w＞wbase时，电机受电流与逆变器电压双重限制，以弱磁模式工作。在保证电压不大于额定电压下取电流幅值最小电流矢量作为电枢电流。电压限制为
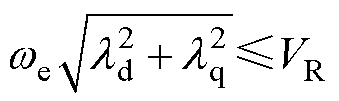（10）
式中，we为电角频率；VR为额定电压。
为了高效精准地确定运行工况下MDPMV电机参数取值，将多目标优化与运行工况分析相结合，图6为主要优化流程。第一步，根据运行工况生成工作点分布，采用K聚类法选取代表工作点；第二步，建立电机参数化模型，确定每个代表工作点的电枢电流，评估各个工作点性能；第三步，确定电机优化模型，通过灵敏度分析将设计变量分区优化。对于低灵敏区变量进行单参数优化，对于高灵敏区变量结合近似模型与MODE-RMO算法进行多目标优化。
图6 多目标优化流程
Fig.6 Flow chart of multi-objective optimization
多目标优化的首要任务为确定优化模型。为了保证最终结果比较的公平性，电机的气隙长度g、外径Rso设置为常量。为了避免优化过程产生几何冲突并且精确反映电机结构对优化目标的影响，最终选取了11个电机结构参数作为设计变量，设计变量定义如图7所示，表3列出了其初值及上下限范围。表中，bpmr为转子永磁体宽度，t 为极矩。额定点转矩脉动Trip与轴向长度Lsk设置为不等约束条件，最大值分别不超过3%和60mm；考虑到热约束和制造工艺，将电流密度J和槽满率Sf设置为等约束条件，其值分别固定为4.6A/mm2和40%。
图7 几何参数模型
Fig.7 Geometric parameter model
表3 设计变量
Tab.3 Design variables
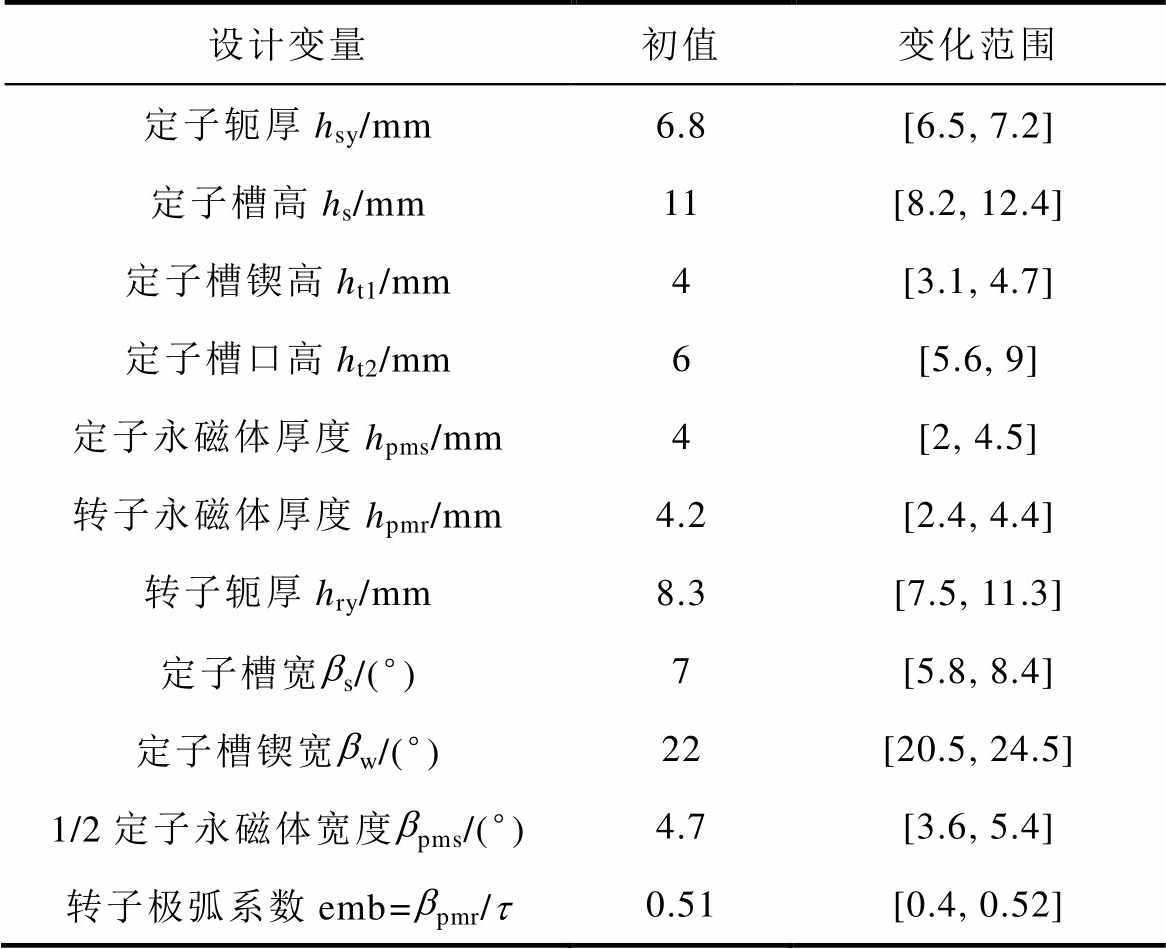
设计变量初值变化范围 定子轭厚hsy/mm6.8[6.5, 7.2] 定子槽高hs/mm11[8.2, 12.4] 定子槽锲高ht1/mm4[3.1, 4.7] 定子槽口高ht2/mm6[5.6, 9] 定子永磁体厚度hpms/mm4[2, 4.5] 转子永磁体厚度hpmr/mm4.2[2.4, 4.4] 转子轭厚hry/mm8.3[7.5, 11.3] 定子槽宽bs/(°)7[5.8, 8.4] 定子槽锲宽bw/(°)22[20.5, 24.5] 1/2定子永磁体宽度bpms/(°)4.7[3.6, 5.4] 转子极弧系数emb=bpmr/t0.51[0.4, 0.52]
根据电机使用场合和性能要求，设定以下两个优化目标：
（1）有效材料成本（Active Material Cost, AMC）。AMC由电机主部件质量与单价比加权组成，为实际成本的近似表达，方程为
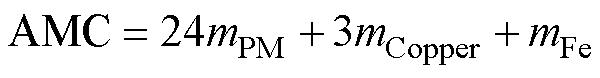（11）
式中，mPM、mCopper、mFe分别为电机永磁体、绕组、铁心的质量，三种材料单价比约为24
31。
（2）电机工况损耗。对于给定工况下的损耗计算，引入电机工况损耗Pcy进行定量优化，方程为
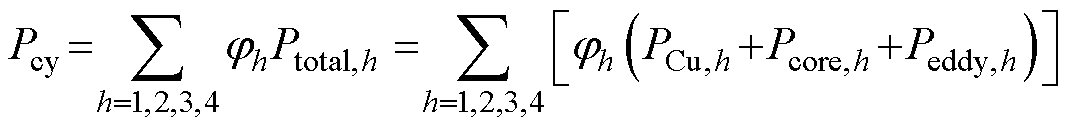（12）
式中，Ptotal,h为第h个代表工作点的总损耗，主要包括铜损PCu,h、铁心损耗Pcore,h和永磁体涡流损耗Peddy,h；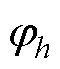
为第h个代表工作点的权重，其值见表1第5列。
多目标优化所需样本电机数目与设计变量维数呈指数正相关。MDPMV电机的初始设计变量多达11个，即使用Box-Behnken设计采样仍需188个样本。为此，引入灵敏度分析法将设计变量分区优化，将高维设计问题划分为低维子空间优化问题，降低计算成本，提高优化效率。
首先，选用试验设计法生成数据样本，计算变量灵敏度。本文采用确定性筛选设计法（Definitive Screening Design, DSD）对11个设计变量进行采样，仅需25个样本点就能快速高效地识别出对响应影响较大的因子，同时其标识非线性效应的特点避免了二阶因子与任何效应之间的混杂问题[17]。引入灵敏指标衡量设计变量对单个优化目标的灵敏程度，灵敏指标S(x)可表示为
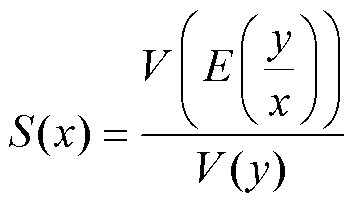（13）
式中，x、y分别为设计变量、优化目标；E( y/x)为相同x值下y的均值；S(x)为x对y的灵敏度，是E( y/x)的方差与y的方差的商，灵敏指标越高，表示设计变量的波动对优化目标的影响程度越高。
其次，通过综合灵敏度指标统筹定量分析每个设计变量对总体优化目标的灵敏程度[18-19]。综合灵敏指标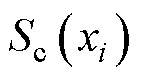
可表示为
（14）
式中，
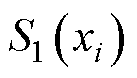与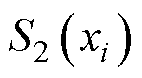
分别为第i个设计变量对有效材料成本和电机工况损耗的灵敏指标；m1和m2为权重系数，根据各个优化目标的重要性分别设置为0.4和0.6。11个设计变量的综合灵敏度指标见表4，根据综合灵敏度指标大小将设计变量依次划入高灵敏区
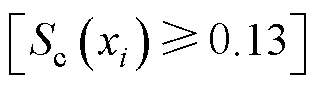与低灵敏区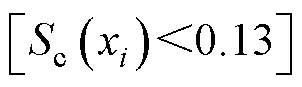
。即hs、emb、bpms划分入高灵敏设计变量，通过多目标优化方法寻最优解；hc、ht1、ht2、hpmr、hpms、hry、bs、bw划分入低灵敏设计变量，通过单参数优化方法寻最优解。
表4 综合灵敏度指标
Tab.4 Comprehensive sensitivity indexs
设计变量S1(xi)S2(xi)Sc(xi) hsy0.1070.1400.128 hs0.1640.1360.147 ht10.0920.0810.085 ht20.0960.0430.062 hpms0.1090.1380.126 hpmr0.2270.0530.123 hry0.0180.0290.025 bs0.0710.0530.060 bw0.0940.0600.074 bpms0.1480.1250.134 emb0.0960.1740.143
高敏参数的变化对优化目标影响较大，故采用响应面法与多目标算法进行参数寻优。响应面模型利用简单的多项式函数将复杂的未知函数在小区域内拟合[20-23]，与克里金模型[24-25]、神经网络模型[26]相比，具有耗时短、效率高且试验样本数少的优点。通过有限次试验建立电机代理模型，能够有效指导后续的多目标算法寻优，提高优化效益。本文使用高精度三阶多项式拟合优化目标与设计变量的响应面模型，拟合函数为
（15）
式中，n为变量总数；b为偏移系数；e 为统计误差。图8为emb和hs分别关于有效材料成本AMC、电机工况损耗Pcy的响应面模型。
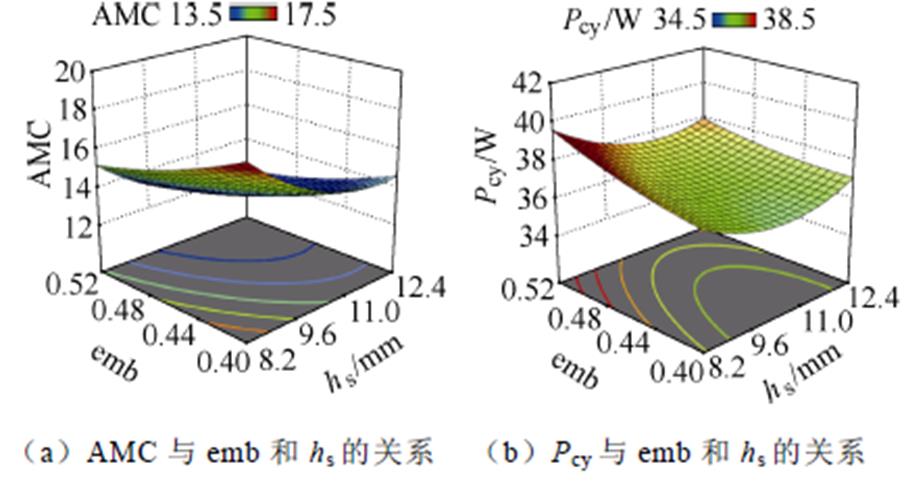
图8 响应面模型
Fig.8 Response surface models
多目标差分进化算法是应用最广泛的多目标算法之一，具有自适应性强、群体多样性丰富且收敛效率高的特点[27]。MODE算法由三种进化策略组成，分别为变异、交叉和选择。主要流程为在群体中选定变异向量，将变异向量与父代向量进行交叉处理生成试验向量，选择试验向量与父代向量中较优者进入下一层迭代，直至算法收敛。变异为MODE算法核心，可写为
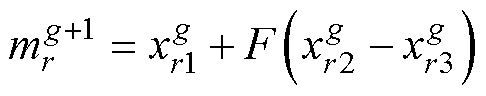（16）
式中，r1、r2、r3为3个互不相同的随机整数；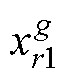
、
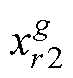与
为3个不同变异个体；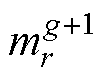
为变异向量；F为变异缩放系数，范围在0～1之间；g为迭代次数。
传统MODE算法中，3个变异个体为种群集随机选取值，MODE-RMO算法通过计算种群集各个个体的非支配前沿数和拥挤程度来确定个体等级，个体等级高者被选为变异个体的几率越大，越有利于将有用信息传递给下一代，从而加强算法搜索性能，提高算法收敛性。图9为基于MODE-RMO算法生成的帕累托解集。由于帕累托为非劣解集，为寻找最优解，定义评价函数为
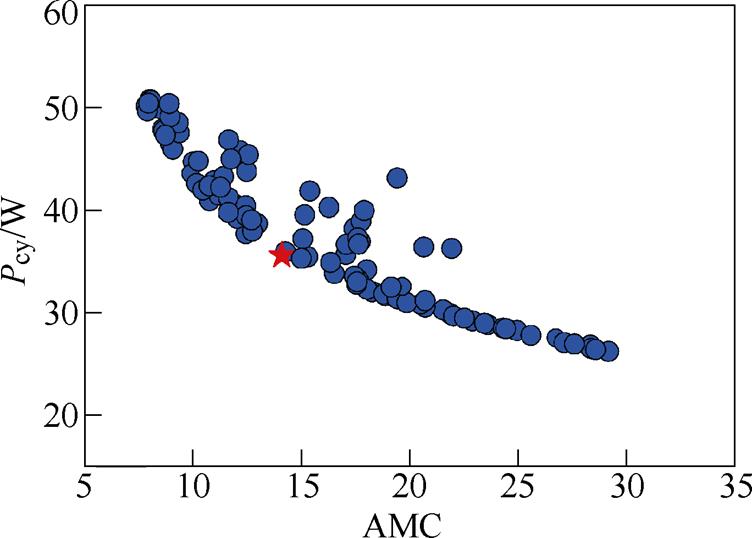
图9 MODE-RMO下的帕累托解集
Fig.9 Pareto solution set under MODE-RMO
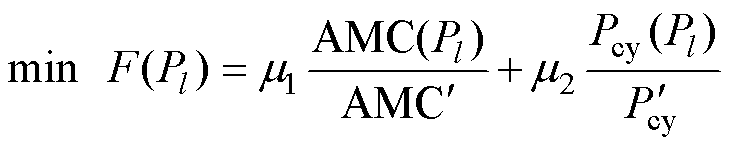（17）
式中，Pl为第l个帕累托解；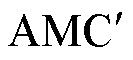
与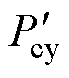
分别为初始有效材料成本、初始电机工况损耗。从预测解集中选择了最优帕累托解（图9中的五角星），其评价函数值为0.813。
本文的主要目标是根据具体运行工况来优化电机损耗与电机制造成本。为了验证考虑运行工况的电机多工作点设计的有效性，对初始电机M0、基于单一额定点优化电机M1和考虑工况的多工作点优化电机M2进行分析对比，主要参数对比见表5。
表5 主要参数对比
Tab.5 Comparison of main variables
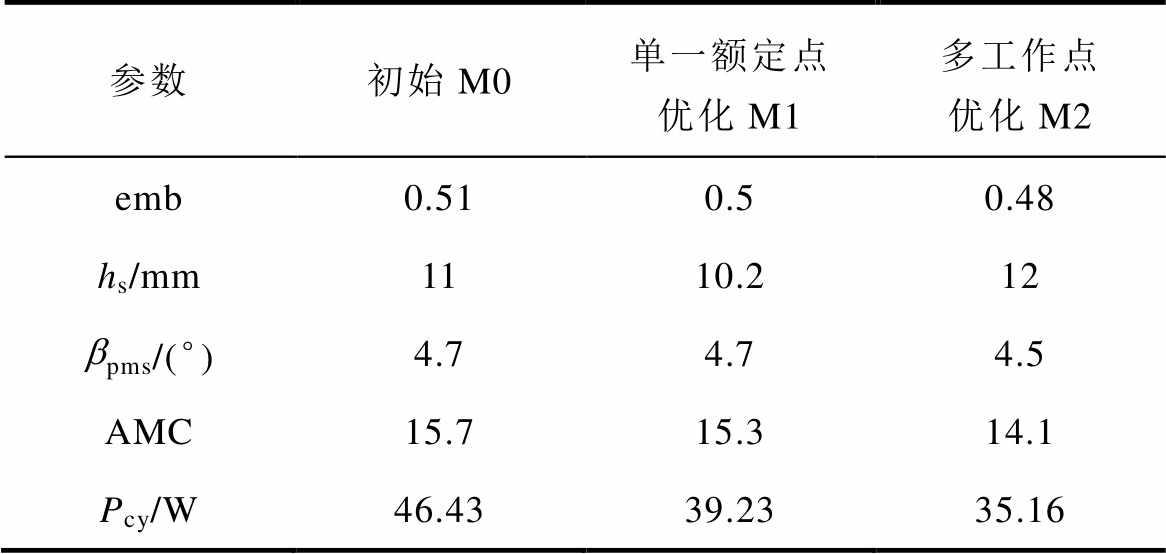
参数初始M0单一额定点优化M1多工作点优化M2 emb0.510.50.48 hs/mm1110.212 bpms/(°)4.74.74.5 AMC15.715.314.1 Pcy/W46.4339.2335.16
两种优化方式下的电机额定转矩如图10所示。由图可知，M1与M2电机的额定转矩基本相同，转矩脉动Trip分别为2.8%和2.7%，符合不等式约束条件。
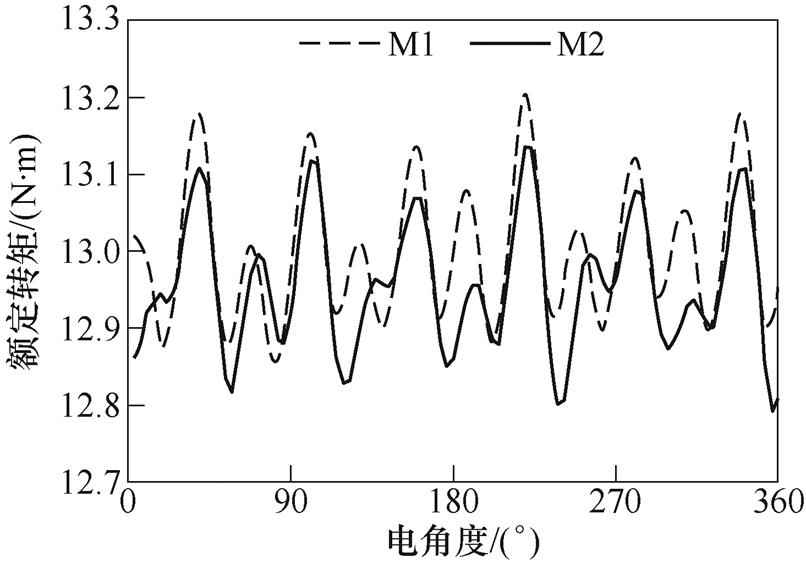
图10 额定转矩
Fig.10 Torque at rated point
优化目标对比如图11所示。图11a为电机各部件AMC分布对比情况。由图可知，电机M1与M2的AMC相较于M0分别下降了2.5%与10.2%，两种优化方式均减少了电机实际制造成本。与电机M1相比，电机M2电机槽面积增大，电机匝数随之增加，导致铜线分量稍有增加。但永磁体用量下降约为13.4%，M2电机总体有效材料成本比M1电机减少了7.8%。
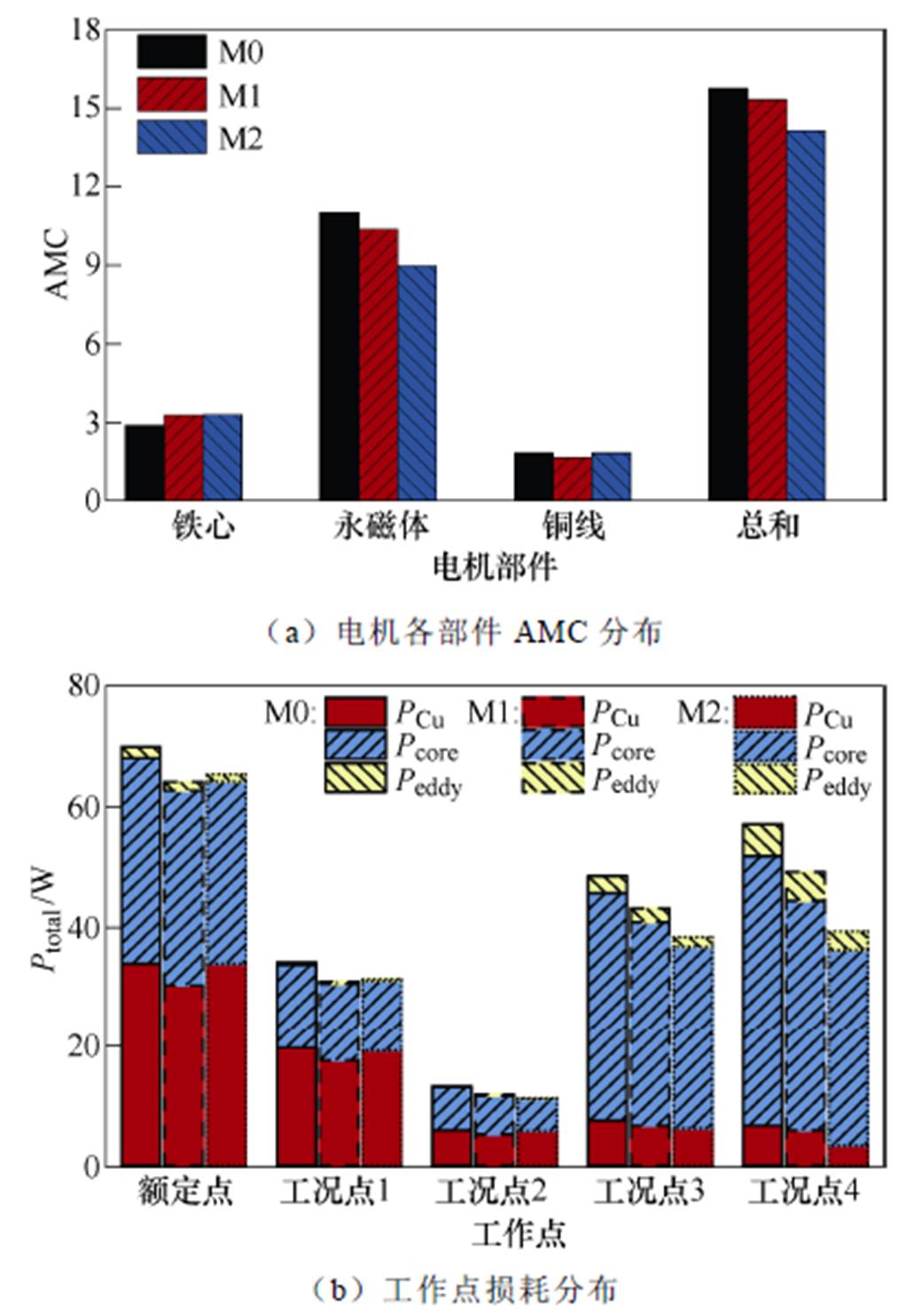
图11 优化目标对比
Fig.11 Comparison of optimization objective
图11b比较了3台电机在额定点与各个代表工作点的总损耗分量。与初始电机相比，两种优化方式下的电机损耗均有所下降。其中，M1电机以额定点为优化对象进行优化设计，额定点损耗中铜耗占比约1/2，优化主要集中于降低铜耗。M1电机通过减小定子槽面积降低电机匝数，进一步减少额定点铜耗。当电机运行于额定工作点时，电机M1额定工作点的损耗最低；M2设计以代表工作点为优化对象，对多种运行模式下电机整体损耗进行定量综合分析。工况代表点1、2位于低速区，权重值小。槽满率与电流密度恒定的情况下，M2电机相较于M1电机槽面积增大，相电阻随之增大，铜耗分量上升，低速区总损耗下降不明显。工况代表点3、4位于高速区，权重值较大。电机工作于此区域时，铁心损耗是重要组成部分，优化集中体现在降低高速运行时的铁心损耗。M2电机于工况代表点3、4的铁心损耗相较于M1电机分别下降了13.5%与14.6%。当电机运行于多个工作点时，电机M2通过定量优化各工况代表点损耗比例，整体电机工况损耗Pcy较M1电机下降10.4%，从而体现了考虑运行工况优化方式的有效性与可行性。
为了进一步验证所提出的电机及考虑运行工况的电机多工作点优化方法的有效性，制造了一台12槽19对极MDPMV电机，样机与实验平台如图12所示。图12a为模块化定子结构，图12b为转子结构，图12c为样机实验平台。图13为额定转速600r/min下的空载反电动势波形，实验值与仿真结果基本吻合。图14为转速600r/min，最大电流7A时的实验转矩与电流波形。图中，Te为输出转矩，ia、ib、ic为三相电流。输出转矩实验测量值为12.4N·m，仿真值为13N·m。由于端部效应、电机加工精度等因素影响，实测值略小于仿真值。
图12 样机及实验平台
Fig.12 Prototype machine and experimental platform
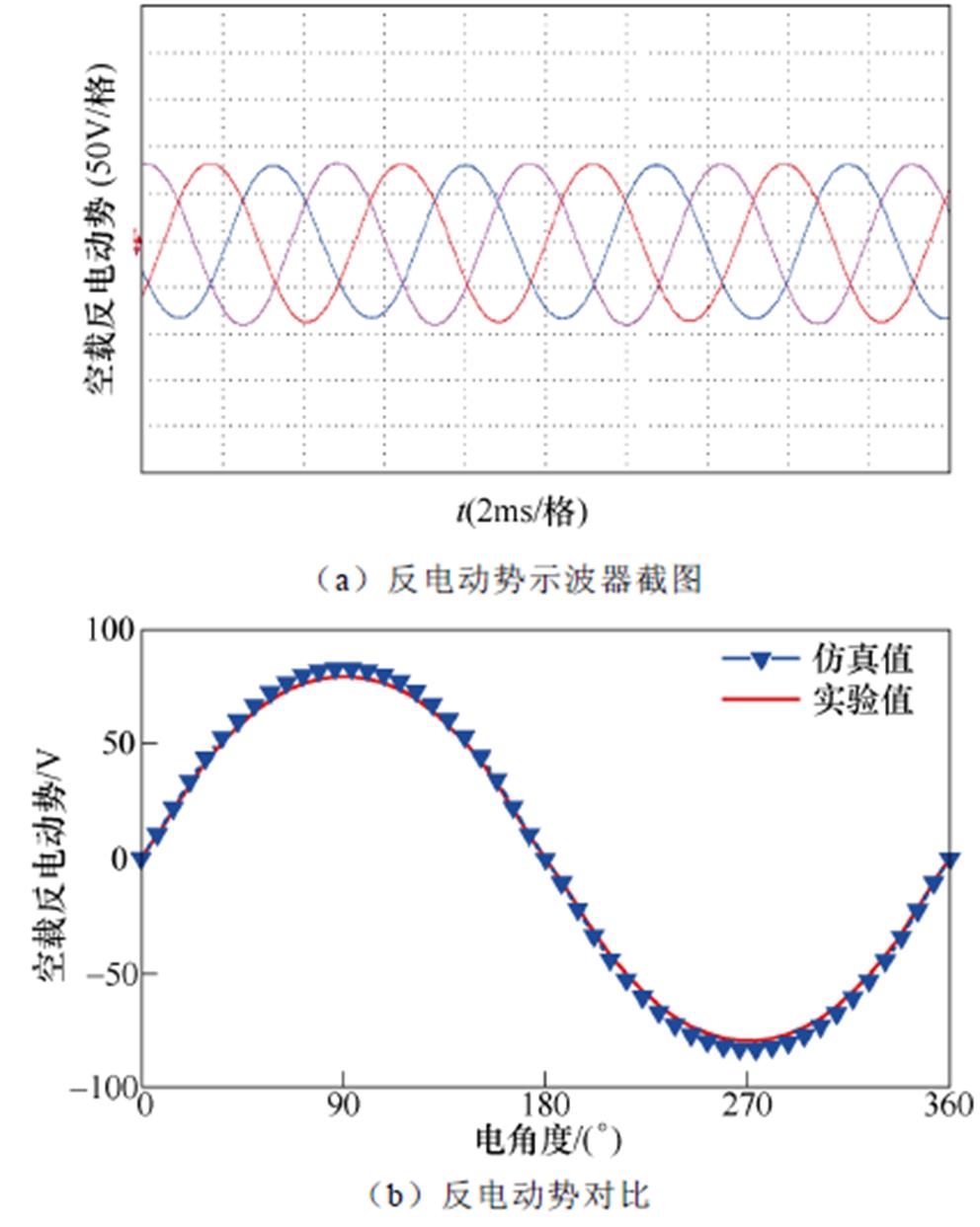
图13 空载反电动势波形
Fig.13 Waveforms of no-load back-EMF
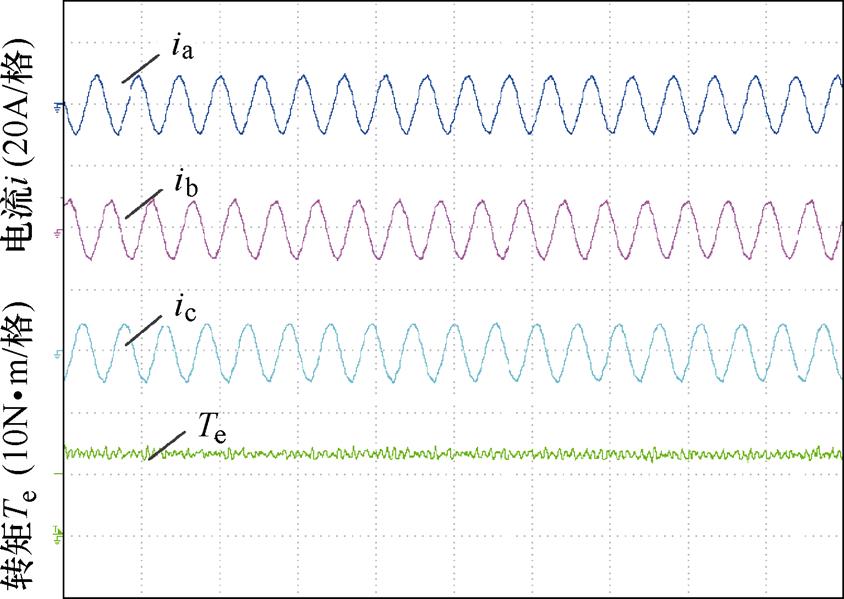
图14 实验转矩与电流波形
Fig.14 Experimental torque and current waveforms
为了满足电动汽车在具体运行工况下的性能要求，本文以MDPMV电机为例研究考虑运行工况的电机多工作点优化方法。主要研究内容和结论如下：
1）提出了一种模块化双永磁游标电机结构。双永磁结构产生的双向调制效果增加了工作谐波含量，提升了电机转矩密度。同时模块化结构设计降低了铁耗，提升了相间独立性。
2）采用K聚类技术简单高效提取代表工作点，将复杂运行工况优化精炼等效为有限个工作点的综合定量优化。通过构造磁链响应面模型并结合公式法计算各代表工作点电枢电流，显著减少有限元计算成本。
3）采用灵敏度分析法对电机结构参数分区优化，结合响应面模型和MODE-RMO算法对电机的高灵敏参数进行多目标算法寻优，高效准确地确定电机参数取值。
研究表明，考虑运行工况下的电机多工作点优化相较于额定点优化，电机具有更低的有效材料成本与工况损耗，验证了考虑运行工况优化方法的有效性与可行性。
参考文献
[1] 颜建虎, 汪盼, 费晨. 模块化开关磁阻式横向磁通电机设计与分析[J]. 中国电机工程学报, 2018, 38(22): 6723-6730.
Yan Jianhu, Wang Pan, Fei Chen. Design and analysis of modular switch reluctance transverse flux machines[J]. Proceedings of the CSEE, 2018, 38(22): 6723-6730.
[2] 张岳, 曹文平, John Morrow. 电动车用内置式永磁电机(PMSM)设计[J]. 电工技术学报, 2015, 30(14): 108-115.
Zhang Yue, Cao Wenping, Morrow J. Design of an interior permanent magnet synchronous motor (PMSM) for EV traction[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 108-115.
[3] Kwon J W, Kwon B I. Investigation of dual-stator spoke-type vernier machine for EV application[J]. IEEE Transactions on Magnetics, 2018, 54(11): 1-5.
[4] 鲍晓华, 刘佶炜, 孙跃, 等. 低速大转矩永磁直驱电机研究综述与展望[J]. 电工技术学报, 2019, 34(6): 1148-1160.
Bao Xiaohua, Liu Jiwei, Sun Yue, et al. Review and prospect of low-speed high-torque permanent magnet machines[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1148-1160.
[5] 石玉君, 程子活, 蹇林旎. 两种典型的场调制型永磁电机的对比分析[J]. 电工技术学报, 2021, 36(1): 120-130.
Shi Yujun, Cheng Zihuo, Jian Linni. Comparative analysis of two typical field modulated permanent- magnet machines[J]. Transactions of China Electro- technical Society, 2021, 36(1): 120-130.
[6] 张邦富, 程明, 王飒飒, 等. 基于改进型代理模型优化算法的磁通切换永磁直线电机优化设计[J]. 电工技术学报, 2020, 35(5): 1013-1021.
Zhang Bangfu, Cheng Ming, Wang Sasa, et al. Optimal design of flux-switching permanent magnet linear machine based on improved surrogate-based optimization algorithm[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1013-1021.
[7] Xiang Zixuan, Zhu Xiaoyong, Quan Li, et al. Multilevel design optimization and operation of a brushless double mechanical port flux-switching permanent-magnet motor[J]. IEEE Transactions on Industrial Electronics, 2016, 63(10): 6042-6054.
[8] Zhang Jingwei, Wang Honghua, Chen Ling, et al. Multi-objective optimal design of bearingless switched reluctance motor based on multi-objective genetic particle swarm optimizer[J]. IEEE Transa- ctions on Magnetics, 2018, 54(1): 1-13.
[9] Zhu Xiaoyong, Xiang Zixuan, Quan Li, et al. Multimode optimization design methodology for a flux-controllable stator permanent magnet memory motor considering driving cycles[J]. IEEE Transa- ctions on Industrial Electronics, 2018, 65(7): 5353- 5366.
[10] Zhou Xue, Zhu Xiaoyong, Wu Wenye, et al. Multi- objective optimization design of variable-saliency- ratio PM motor considering driving cycles[J]. IEEE Transactions on Industrial Electronics, 2021, 68(8): 6516-6526.
[11] Diao Kaikai, Sun Xiaodong, Lei Gang, et al. System- level robust design optimization of a switched reluctance motor drive system considering multiple driving cycles[J]. IEEE Transactions on Energy Conversion, 2021, 36(1): 348-357.
[12] Carraro E, Morandin M, Bianchi N. Traction PMASR motor optimization according to a given driving cycle[J]. IEEE Transactions on Industry Applications, 2016, 52(1): 209-216.
[13] 林俐, 潘险险, 张凌云, 等. 基于免疫离群数据和敏感初始中心的K-means算法的风电场机群划分[J]. 中国电机工程学报, 2016, 36(20): 5461-5468, 5722.
Lin Li, Pan Xianxian, Zhang Lingyun, et al. The K-means clustering algorithm for wind farm based on immune-outlier data and immune-sensitive initial center[J]. Proceedings of the CSEE, 2016, 36(20): 5461-5468, 5722.
[14] Xu Liang, Zhao Wenxiang, Wu Mengmeng, et al. Investigation of slot-pole combination of dual- permanent-magnet-excited vernier machines by using air-gap field modulation theory[J]. IEEE Transactions on Transportation Electrification, 2019, 5(4): 1360- 1369.
[15] Dajaku G, Xie Wei, Gerling D. Reduction of low space harmonics for the fractional slot concentrated windings using a novel stator design[J]. IEEE Transa- ctions on Magnetics, 2014, 50(5): 1-12.
[16] 刘永锋, 徐磊, 朱孝勇, 等. 基于多运行区域的磁场增强型内置永磁电机电流分段控制研究[J]. 中国电机工程学报, 2021, 41(10): 3611-3619, 3685.
Liu Yongfeng, Xu Lei, Zhu Xiaoyong, et al. Research on current segment control of flux-intensifying interior permanent magnet motor based on multi- operating region[J]. Proceedings of the CSEE, 2021, 41(10): 3611-3619, 3685.
[17] Zhao Wenxiang, Yao Tian, Xu Liang, et al. Multi- objective optimization design of a modular linear permanent-magnet vernier machine by combined approximation models and differential evolution[J]. IEEE Transactions on Industrial Electronics, 2021, 68(6): 4634-4645.
[18] 刘国海, 王艳阳, 陈前. 非对称V型内置式永磁同步电机的多目标优化设计[J]. 电工技术学报, 2018, 33(增刊2): 385-393.
Liu Guohai, Wang Yanyang, Chen Qian. Multi- objective optimization of an asymmetric V-shaped interior permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 385-393.
[19] Zhao Wenxiang, Ma Anqi, Ji Jinghua, et al. Multiobjective optimization of a double-side linear vernier PM motor using response surface method and differential evolution[J]. IEEE Transactions on Industrial Electronics, 2020, 67(1): 80-90.
[20] Xiang Zixuan, Pu Weiling, Zhu Xiaoyong, et al. Design and analysis of a V-shaped permanent magnet vernier motor for high torque density[J]. CES Transactions on Electrical Machines and Systems, 2022, 6(1): 20-28.
[21] 赵玫, 于帅, 邹海林, 等. 聚磁式横向磁通永磁直线电机的多目标优化[J]. 电工技术学报, 2021, 36(17): 3730-3740.
Zhao Mei, Yu Shuai, Zou Hailin, et al. Multi- objective optimization of transverse flux permanent magnet linear machine with the concentrated flux mover[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3730-3740.
[22] 罗玉涛, 卢若皓. 基于结构参数分级优化的电机电磁噪声抑制[J]. 电工技术学报, 2021, 36(14): 2957- 2970.
Luo Yutao, Lu Ruohao. Hierarchical optimization of structural parameters for motor electromagnetic noise suppression[J]. Transactions of China Electrotechnical Society, 2021, 36(14): 2957-2970.
[23] Du Longxin, Liu Xiping, Fu Jiesheng, et al. Design and optimization of reverse salient permanent magnet synchronous motor based on controllable leakage flux[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(2): 163-173.
[24] Ren Ziyan, Sun Yuan, Peng Baoyang, et al. Optimal design of electrical machines assisted by hybrid surrogate model based algorithm[J]. CES Transa- ctions on Electrical Machines and Systems, 2020, 4(1): 13-19.
[25] 李雄松, 崔鹤松, 胡纯福, 等. 平板型永磁直线同步电机推力特性的优化设计[J]. 电工技术学报, 2021, 36(5): 916-923.
Li Xiongsong, Cui Hesong, Hu Chunfu, et al. Optimal design of thrust characteristics of flat-type permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 916- 923.
[26] 张文晶, 徐衍亮, 李树才. 新型盘式横向磁通永磁无刷电机的结构原理及设计优化[J]. 电工技术学报, 2021, 36(14): 2979-2988.
Zhang Wenjing, Xu Yanliang, Li Shucai. Structure principle and optimization of a novel disk transverse flux permanent magnet brushless motor[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(14): 2979-2988.
[27] Pan Zhenbao, Fang Shuhua, Wang Hui. LightGBM technique and differential evolution algorithm-based multi-objective optimization design of DS-APMM[J]. IEEE Transactions on Energy Conversion, 2021, 36(1): 441-455.
Multi-Working Point Optimization of Modular Double Permanent-Magnet Vernier Motor Considering Operation Condition
Abstract The double permanent-magnet vernier motor operates based on the bi-directional magnetic field modulation effect principle. With the improvement of torque density, there is a problem of significant motor loss. By taking the rated point as the optimization object, the traditional optimization method can only improve the performance of the rated operating point, but has difficulty in efficiently operating multiple working points under the actual operation condition of the motor. Therefore, this paper designs a low-loss modular dual permanent-magnet vernier motor and proposes a multi-operating points optimization method considering operation condition. The representative working points and their weights are extracted using the K-clustering method. To make the optimization procedure more efficient, the sensitivity analysis method is used to qualitatively optimize the variables to reduce the design space. The optimal global solution of susceptible parameters is determined by combining the response surface method and high-convergence multi-objective differential evolution with a ranking-based mutation operator (MODE-RMO). And then, an efficient and accurate motor parameter optimization under operation condition is realized. The proposed method is verified by simulation and experiment.
Keywords：Operation condition, differential evolution algorithm, multi-objective optimization, permanent-magnet vernier motor
中图分类号：TM351
DOI: 10.19595/j.cnki.1000-6753.tces.220141
国家自然科学基金资助项目（51977099, 52177044）。
收稿日期 2022-01-28
改稿日期 2022-05-12
E-mail: jjh@ujs.edu.cn（通信作者）
沈人洁 女，1997年生，硕士研究生，研究方向为永磁电机设计。
E-mail: 2419306769@qq.com
（编辑 崔文静）