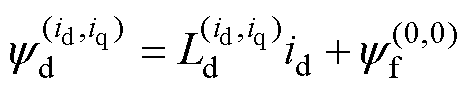 (1)
(1)
摘要 永磁同步电机通常由于安装空间和自重的限制,要求其具有较高的电、磁负荷,导致电机内部出现严重的磁路饱和,而在高磁路饱和的情况下,永磁体磁链会随电流的改变而发生非线性变化。为了准确估算电机负载状态下的永磁体磁链,该文首先描述了dq轴电流对永磁体磁链的影响,并结合定子铁心局部磁饱和特性,分析了气隙磁动势和铁心磁动势之间的比例关系,提出了基于磁链系数的永磁体磁链模型。接着根据测量的相电压以及定子铁心材料的磁导率曲线,提出了一种考虑磁路饱和的永磁体负载磁链动态估算方法。最后搭建了300kW内置式永磁同步电机实验平台,通过有限元仿真和实验验证了该文所提出的估算方法的有效性和准确性。
关键词:永磁同步电机 磁路饱和 永磁体磁链 磁链系数
近几十年来,永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)因具有高功率密度、高可靠性和高效率的特点而被广泛应用于交通、工农业生产、航空航天等对性能要求较高的领域[1-2]。在永磁同步电机高性能控制方法中,控制参数与永磁体磁链密切相关,但通常由于安装空间和自重的限制,要求电机具有较高的电、磁负荷,导致电机内部会出现严重的磁路饱和,而在高磁路饱和的情况下,永磁体磁链会随电流的改变而发生非线性变化,进而影响永磁同步电机负载时的运行性能以及系统的稳定性[3-4]。因此,为了实现高磁路饱和永磁同步电机的高性能控制,准确估算永磁体负载磁链具有重要意义。
对于饱和程度较低的永磁同步电机而言,dq轴电流对永磁体磁链的影响较小,因此通常将永磁体磁链视为静态常数或者只受温度影响而改变[5-11]。如文献[9]采用了反电动势法估算永磁体磁链,并对该方法进行了总结分析。文献[10]提出了一种测量空间矢量脉宽调制的电流响应辨识不同温度下的永磁体磁链。文献[11]建立了磁链与转速谐波之间的数学模型,提出了基于测量速度谐波的磁链在线估计方法。以上方法虽然能准确估算电机空载时的永磁体磁链,但由于没有考虑磁路饱和及电流对永磁体磁链的影响,因此并不适用于负载状态下的高磁路饱和永磁同步电机。
文献[12]采用了有限元方法获取永磁体磁链,虽然考虑了磁路饱和对永磁体磁链的影响,但对于实际工程中,同一批次的不同永磁同步电机会由于制造误差而导致参数不同,仿真结果与实际可能有较大误差。在文献[13]中提出了利用解析法估算永磁体磁链,但该方法需要详细的电机结构参数,不具备通用性。文献[14]提出用高频注入法辨识不同饱和程度下的电感参数,并利用dq轴磁链模型估算永磁体磁链,但增加了电机的转矩脉动,影响驱动系统的稳定性。此外,学者们相继提出了不同辨识算法,如文献[15]采用改进的非线性滤波器对反电动势谐波分量进行辨识,从而估算永磁体磁链。文献[16-17]分别采用了二阶和三阶广义积分通量观测器,观测永磁体磁链的变化。文献[18]中引入了基于免疫克隆的量子遗传算法,对不同负载条件下的磁链进行辨识。还有粒子群算法、神经网络算法、模型参考自适应算法[19-21]等,但这类算法普遍计算量大,难以在工程上进行实际应用。
针对在高磁路饱和永磁同步电机中,由于永磁体磁链与电流的非线性关系,导致电机负载状态下的永磁体磁链估算困难的问题。本文结合定子铁心的局部饱和特性,从磁动势(Magnetomotive Force, MMF)的角度分析了永磁体磁链的变化,建立了基于磁链系数的永磁体磁链模型,并在此基础上提出了一种考虑磁路饱和的永磁体负载磁链动态估算方法,对电机不同负载状态下的永磁体磁链进行了估算。最后,搭建了300kW内置式永磁同步电机实验平台,通过有限元仿真和实验验证了本文所提出的估算方法的有效性和准确性。
在传统考虑磁路饱和的永磁同步电机dq轴数学模型中,电感的变化取决于dq轴电流的变化,同时将永磁体磁链视为一个d轴方向上的静态常数,则考虑磁路饱和的永磁同步电机d轴磁链方程为
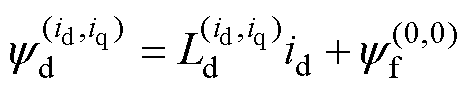 (1)
(1)
式中,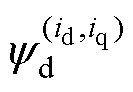 为d轴上的总磁链;
为d轴上的总磁链;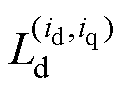 为随dq轴电流的改变而变化的d轴电感;id为d轴电流;
为随dq轴电流的改变而变化的d轴电感;id为d轴电流;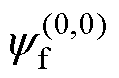 为空载时永磁体产生的磁链。
为空载时永磁体产生的磁链。
对于高磁路饱和的永磁同步电机而言,由于工作环境的要求,电机内部的磁通密度较高,导致铁心处于磁饱和状态,图1为空载时电机的磁通密度分布云图,并且随着负载增加,磁通密度逐渐增大,铁心的饱和程度也会增加。
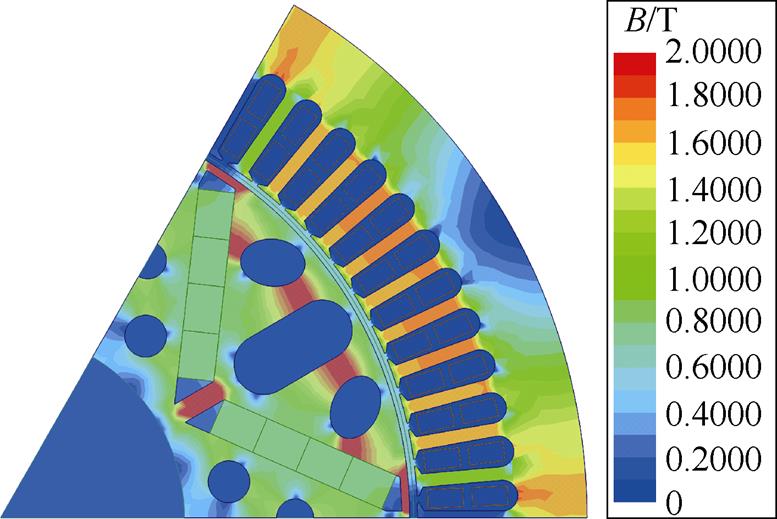
图1 空载磁通密度分布云图
Fig.1 Magnetic density distribution of motor under no load
而在高磁路饱和状态下,永磁体磁链会随dq轴电流的不同而发生改变。当id保持不变时,随着iq的增大,铁心逐渐饱和,会导致永磁体磁链非线性减小,永磁体磁链随iq的变化如图2所示。当iq保持不变时,随着id的减小,由于退磁电流的影响,d轴方向会出现退饱和现象,导致永磁体磁链非线性增大,永磁体磁链随id的变化如图3所示。
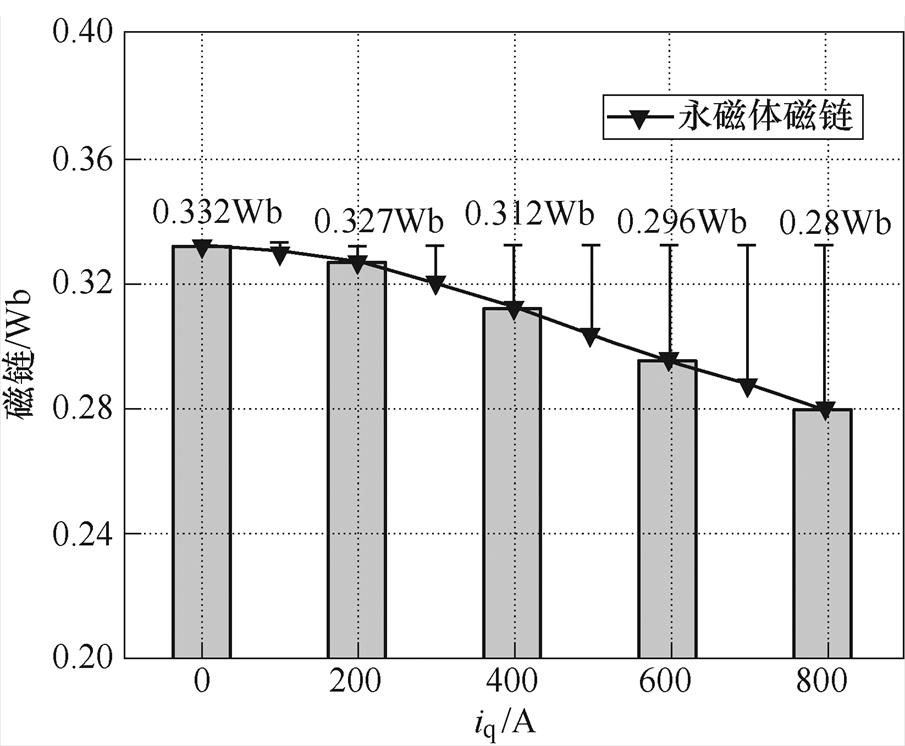
图2 永磁体磁链随iq的变化
Fig.2 Variation of permanent magnet flux linkage with the q-axis current
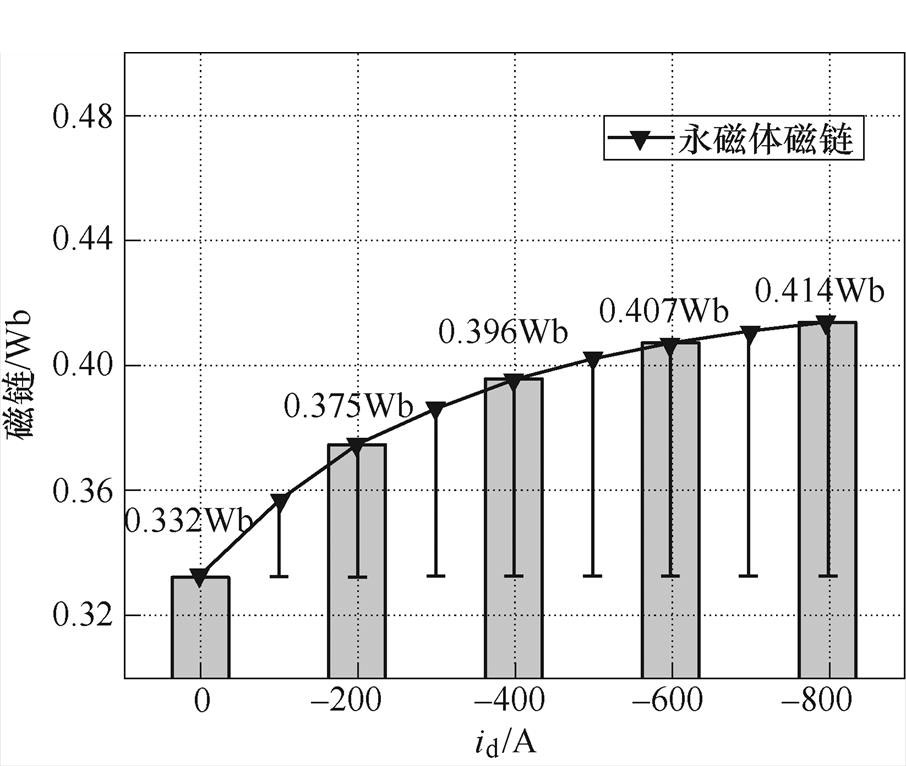
图3 永磁体磁链随id的变化
Fig.3 Variation of permanent magnet flux linkage with the d-axis current
因此,为了准确描述高磁路饱和下,永磁同步电机的参数变化,需要考虑永磁体磁链随电流的改变而发生的非线性变化,则d轴的磁链方程式(1)应改为
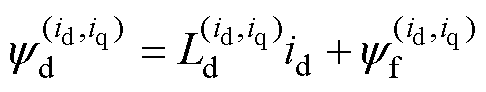 (2)
(2)
式中,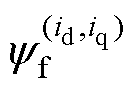 为永磁体磁链随dq轴电流变化的动态值。
为永磁体磁链随dq轴电流变化的动态值。
基于以下假设,本文对PMSM的永磁体磁链进行分析。
(1)由于磁路饱和主要集中在定子齿部,因此忽略定子轭部以及转子铁心的饱和区域。
(2)忽略定子电阻、漏抗及谐波的影响。
当id=0且不考虑磁路饱和时,将永磁体磁链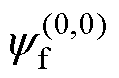 视为常数,定子磁动势沿q轴方向,转子磁动势沿d轴方向,定转子磁动势之间的电角度为dsr=90°。此时,转矩表达式[22]为
视为常数,定子磁动势沿q轴方向,转子磁动势沿d轴方向,定转子磁动势之间的电角度为dsr=90°。此时,转矩表达式[22]为
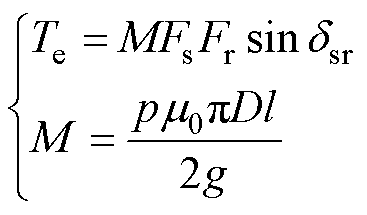 (3)
(3)
式中,l为气隙的轴向长度;D为气隙的直径;g为气隙长度;m0为空气磁导率;Fs为定子磁动势;Fr为转子磁动势;p为极对数;M为常数。
同时,将永磁体等效为励磁绕组,则转矩还可表示[22]为
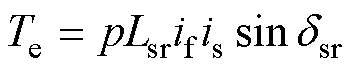 (4)
(4)
式中,Lsr为定转子之间的互感;if为永磁体等效励磁电流;is为定子绕组电流。对式(4)进行dq轴变换,即
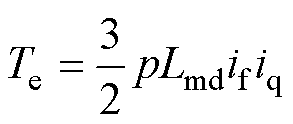 (5)
(5)
其中
Lmdif=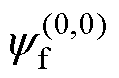
式中,Lmd为d轴等效励磁电感。结合式(3)可得,不考虑磁路饱和时,传统的转矩表达式为
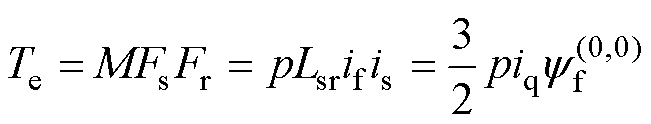 (6)
(6)
而根据图2可知,当id=0且考虑磁路饱和时,永磁体磁链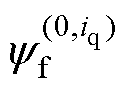 会随q轴电流发生改变。则磁动
会随q轴电流发生改变。则磁动
势可分为两部分,一部分为气隙磁动势,另一部分为铁心上的磁动势,磁动势如图4所示。
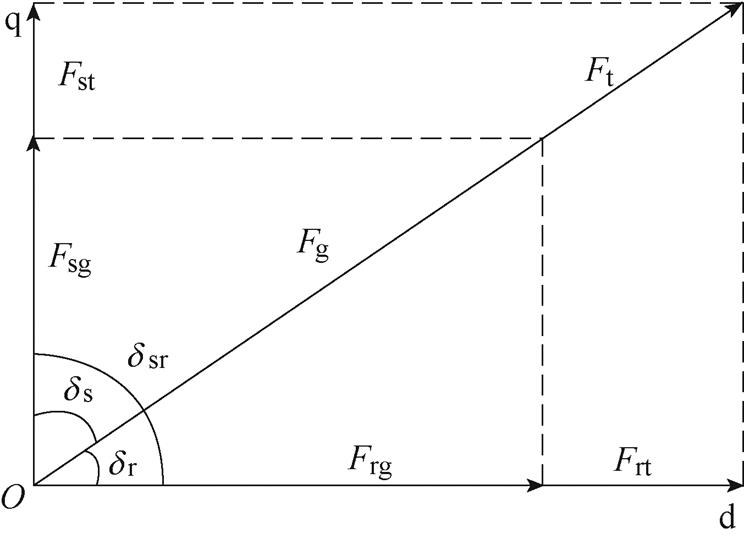
图4 磁动势
Fig.4 The MMF
此时,各部分的磁动势表示为
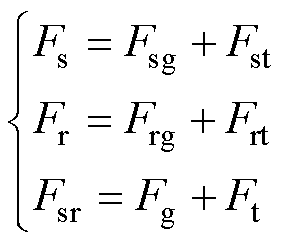 (7)
(7)
式中,Fsr为合成磁动势;Fsg和Fst分别为q轴方向上的气隙磁动势和铁心磁动势;Frg和Frt分别为d轴方向上的气隙磁动势和铁心磁动势;Fg和Ft分别为合成气隙磁动势和合成铁心磁动势。
由于在PMSM中,电能转化为机械能的过程发生在气隙磁场中,并且转矩和气隙中的定、转子磁动势成正比,则转矩表达式(3)应改写为
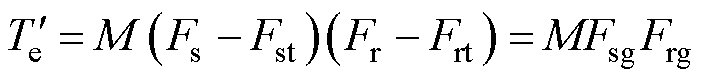 (8)
(8)
而根据式(6)可知,转矩和永磁体磁链成正比,因此,在dq轴坐标系下考虑磁饱和的转矩表达式为
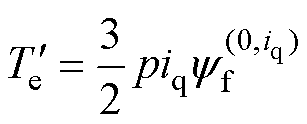 (9)
(9)
结合式(8)和式(9),即
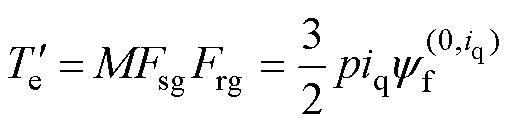 (10)
(10)
对式(6)和式(10)进行对比分析,可得
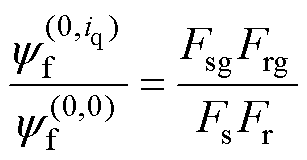 (11)
(11)
根据图4可知,合成磁动势与定、转子磁动势之间的关系为
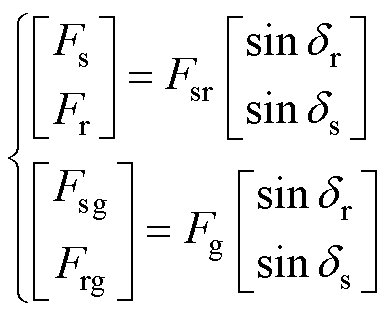 (12)
(12)
式中,dr为合成磁动势与转子磁动势之间的角度;ds为合成磁动势与定子磁动势之间的角度。将式(7)和式(12)代入到式(11)中,可得
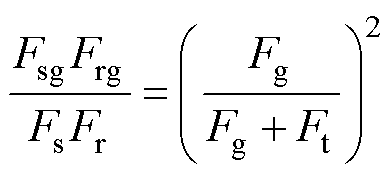 (13)
(13)
结合式(11)和式(13),本文提出了基于磁链系数K的永磁体磁链模型,即
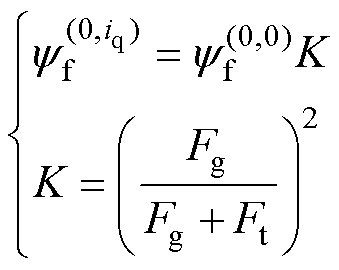 (14)
(14)
则式(9)可表示为
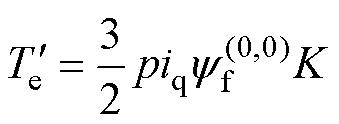 (15)
(15)
对式(14)进行分析,当忽略磁路饱和时,铁心磁动势Ft=0,磁链系数K=1;而当考虑磁路饱和时,永磁体磁链减小的程度主要取决于铁心上的磁动势和气隙磁动势之间的比例大小,随着Ft/Fg的值增大,永磁体磁链减小的程度越大,永磁体磁链和电流之间的非线性特性也就越明显。
另外从图3可知,当id<0时,由于磁路退饱和的原因,导致永磁体磁链增大,因此为了同时考虑dq轴电流对永磁体磁链的影响,将式(14)改写为
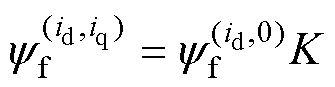 (16)
(16)
根据式(2),在忽略定子电阻的前提下,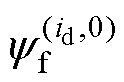 可表示为
可表示为
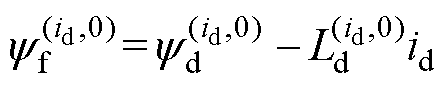 (17)
(17)
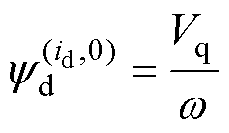 (18)
(18)
式中,Vq为q轴电压;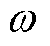 为角速度。
为角速度。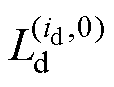 可采用高频注入法进行辨识[14]。
可采用高频注入法进行辨识[14]。
对于磁链系数K,可通过电压和磁导率计算出磁动势,即
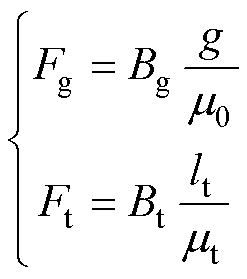 (19)
(19)
式中,Bg为气隙磁通密度;Bt为定子齿部磁通密度;mt为铁心材料的磁导率,可根据磁导率曲线获取;lt为定子齿部长度。
气隙磁通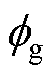 和磁通密度
和磁通密度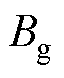 分别表示为
分别表示为
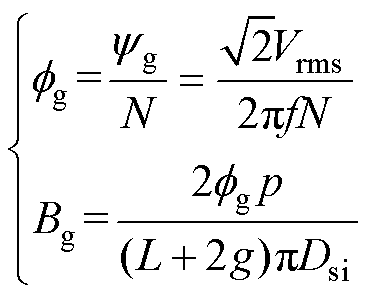 (20)
(20)
并且根据磁路法[23],气隙磁通密度和铁心磁通密度的关系为
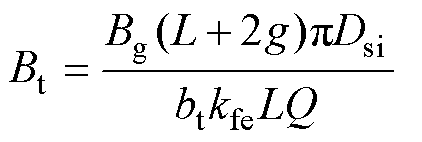 (21)
(21)
式中,Vrms为相电压有效值;N为每相串联匝数;f为频率;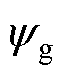 为气隙磁链;p为极对数;Dsi为气隙的平均直径;L为铁心轴向长度;L+2g为电枢计算长度;bt为定子齿宽;kfe为叠压系数;Q为定子槽数。PMSM模型的拓扑结构如图5所示。
为气隙磁链;p为极对数;Dsi为气隙的平均直径;L为铁心轴向长度;L+2g为电枢计算长度;bt为定子齿宽;kfe为叠压系数;Q为定子槽数。PMSM模型的拓扑结构如图5所示。
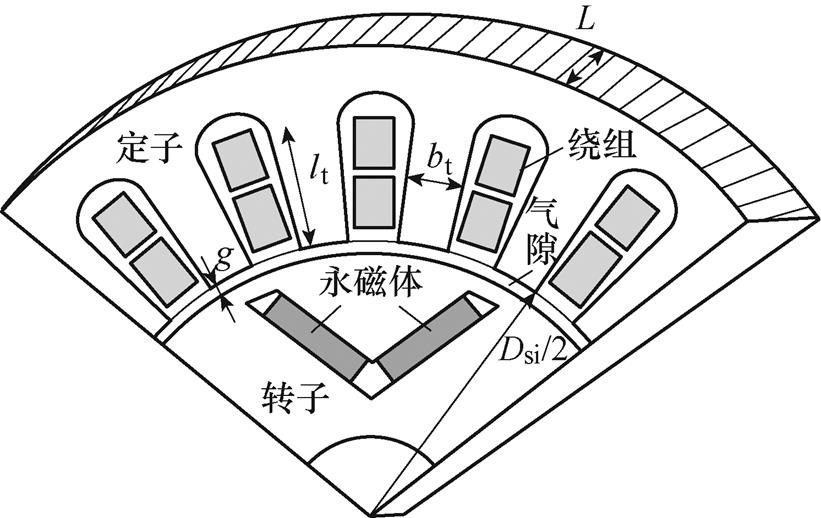
图5 PMSM 的拓扑结构
Fig.5 Topological structure of PMSM
将式(19)~式(21)代入式(14)中并化简,可得
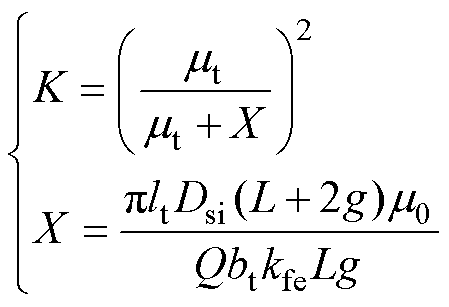 (22)
(22)
将式(20)和式(21)化简,可得
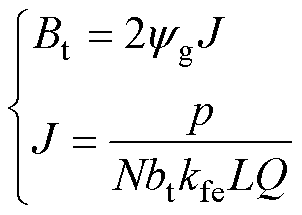 (23)
(23)
式中,J和X为结构常数。结合式(20)、式(22)和式(23),可将磁链系数K表示为
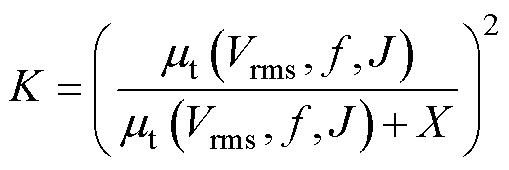 (24)
(24)
式中,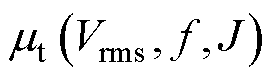 为非线性函数,可根据式(20)、式(23)以及磁导率曲线求得。
为非线性函数,可根据式(20)、式(23)以及磁导率曲线求得。
从式(24)可知,在已知J和X的前提下,估算K只需测量相电压和转速。而在一定转速下,采用id=0的控制时,求解两个未知数J和X,只需测量两组电压、电流以及转矩式(15),如图6所示。
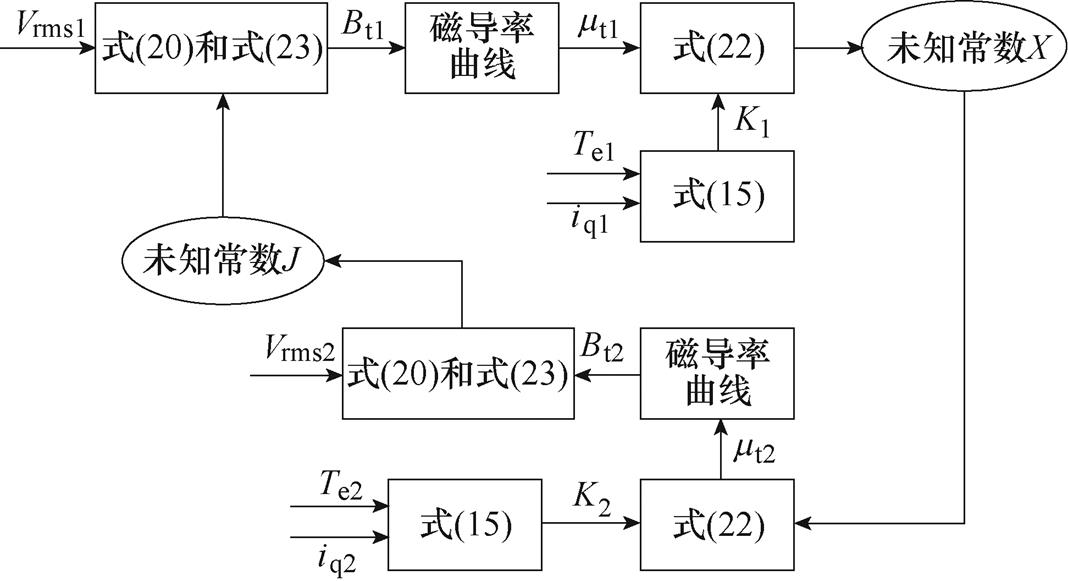
图6 求解常数J和X
Fig.6 Solving constants J and X
采用图6的方法可使本文提出的估算方法不依赖电机结构参数,同时,目前大部分铁心材料的磁导率曲线可通过文献或者仿真软件获取,因此该方法具有一定的通用性,综合以上分析,本文提出的永磁体磁链动态估算方法的具体流程如图7所示。
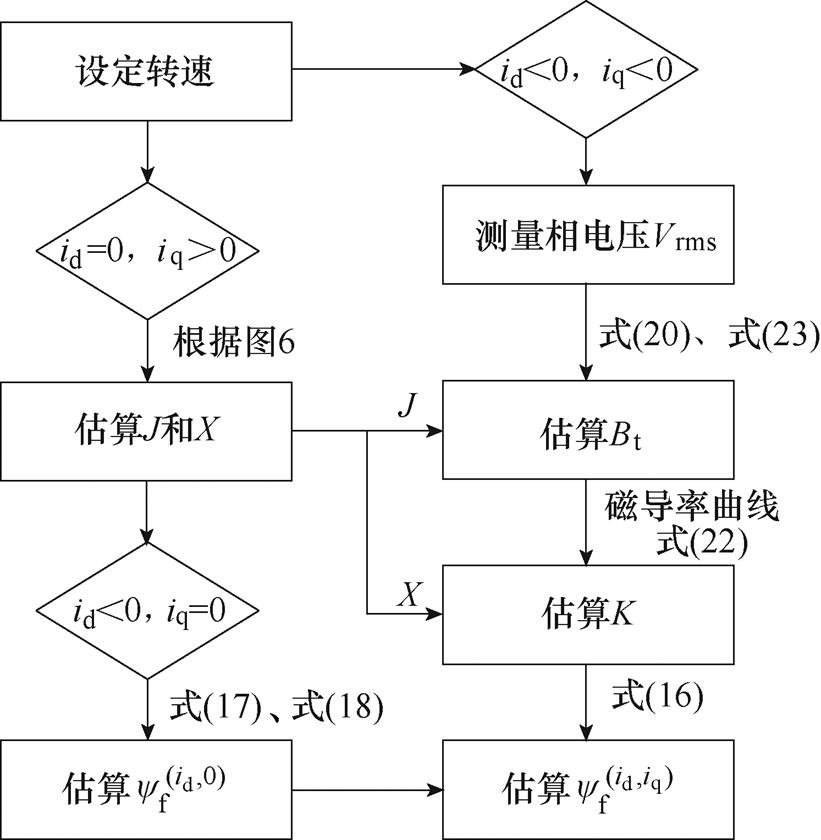
图7 永磁体磁链的估算流程
Fig.7 Estimation process of PM flux linkage
为了验证本文提出的估算方法的有效性和准确性,建立了300kW内置式PMSM的有限元法(Finite Element Method,FEM)如图1所示,并绘制了铁心材料的B-H曲线和磁导率曲线,如图8所示。
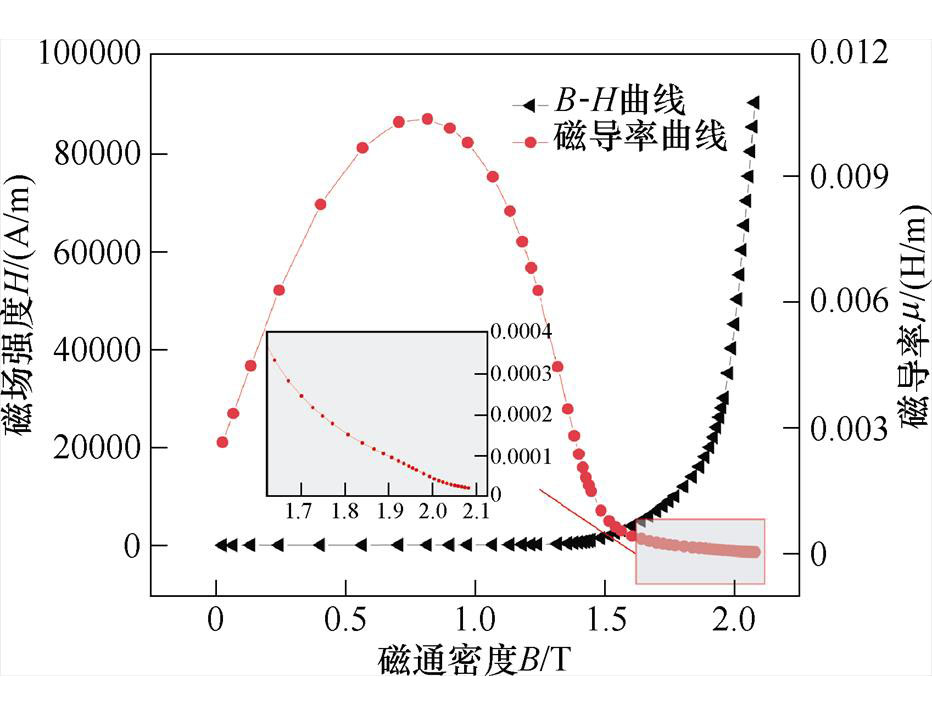
图8 B-H曲线和磁导率曲线
Fig.8 B-H curve and permeability curve
电机参数见表1。在表1上部分中列出了电机性能的主要参数,在下部分中列出了本文提到的结构参数,通过计算可得J=1.95及X=4.1×10-5,其中dq轴电感和永磁体磁链为电机空载时的值(id=0, iq=0)。
表1 电机参数
Tab.1 The parameters of the model

参 数数 值 主要参数额定功率P/kW300 额定转速n/(r/min)3 000 额定频率f/Hz150 额定转矩Te/(N·m)955 额定电流Is/A470 定子电阻Rs/W0.005 永磁体磁链/Wb0.332 d轴电感Ld/mH0.472 3 q轴电感Lq/mH1.022 8 结构参数定子内径Dsi/mm320 铁心轴向长度L/mm180 气隙g/mm3 定子齿宽bt/mm5.2 定子齿长lt/mm33.5 每相串联匝数N24 槽数Q72 极对数p3 叠压系数kfe0.95
根据内置式PMSM的运行特征(id≤0, 0≤iq),设置电机转速为额定转速3 000r/min以及电流在额定点范围内变化,即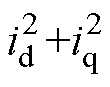 ≤6652。通过仿真可得电机不同运行工况下的相电压,如图9所示,其中空载相电压为222V。
≤6652。通过仿真可得电机不同运行工况下的相电压,如图9所示,其中空载相电压为222V。
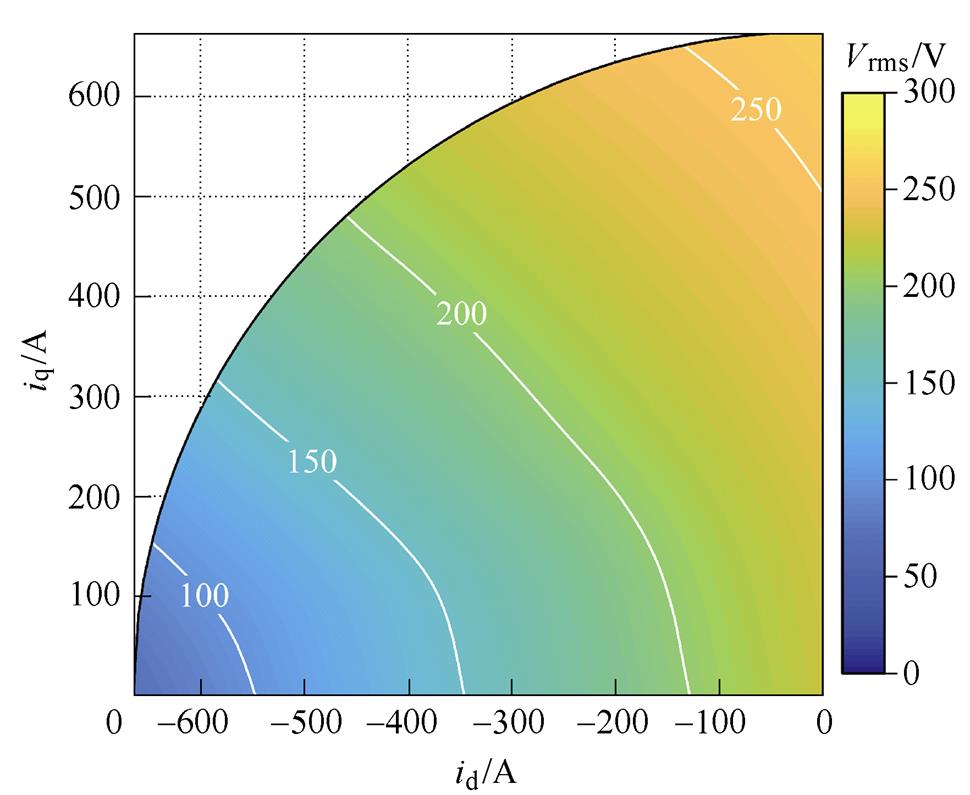
图9 仿真相电压
Fig.9 Simulation phase voltage
首先利用式(19)~式(23)估算额定电流范围内的磁链系数K,如图10所示。从图中可以看出,当id保持不变时,K随着iq的增大而减小,当iq保持不变时,K随着id的减小而增大。接着,利用式(16)和式(17)估算永磁体负载磁链,如图11所示。
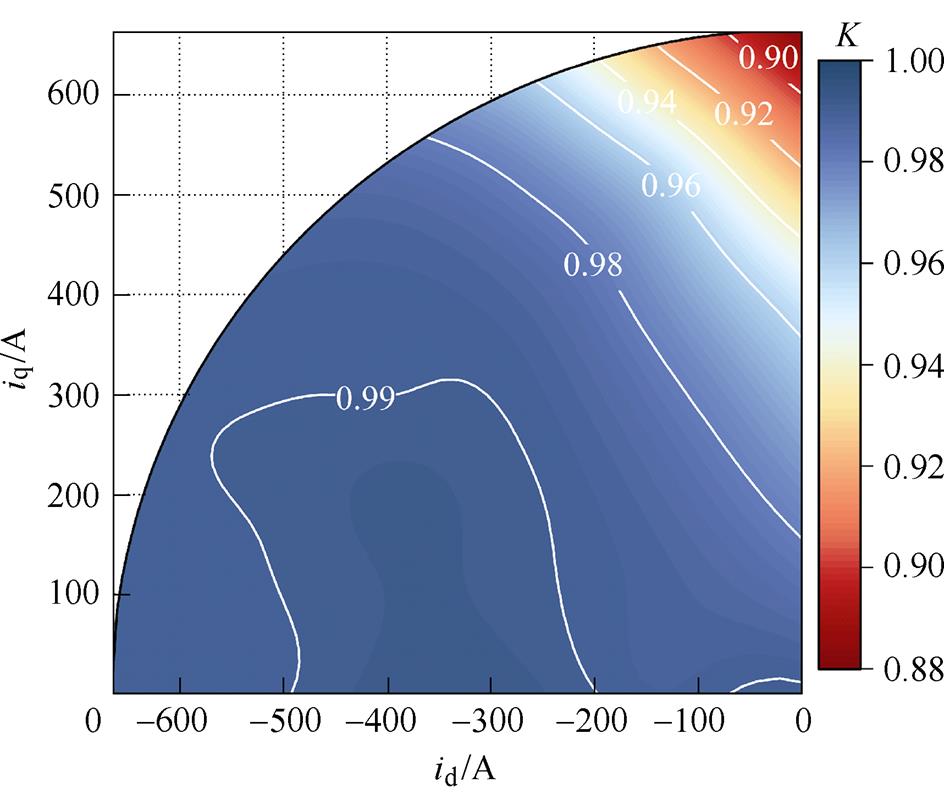
图10 磁链系数K
Fig.10 Flux linkage coefficient K
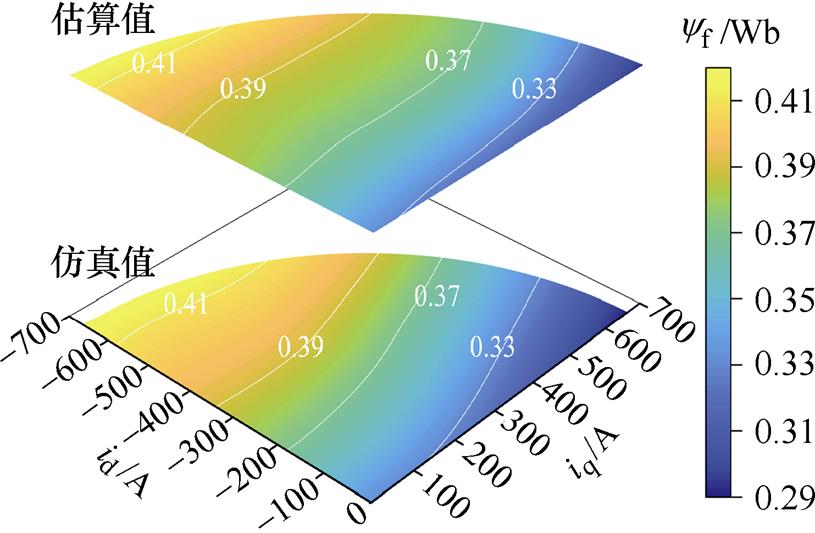
图11 永磁体磁链的估算值和仿真值
Fig.11 Estimation and simulation of permanent magnet flux linkage
最后,将估算值和仿真值进行对比,如图11所示,并采用了相对误差e 表征估算结果的准确性,有
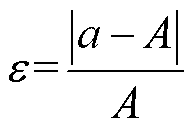 (25)
(25)
式中,a为估算值;A为仿真值。
图12为相对误差。估算值和仿真值之间的相对误差如图12a所示;而传统的估算方法将永磁体磁链视为常数,这会导致较大的误差,如图12b所示。
从图12b中可以看出,传统认为永磁体磁链为常数会导致与仿真值之间的最大相对误差超过20%,而根据磁链系数K估算的永磁体磁链与仿真值相比,最大的相对误差e 不超过3%,整体估算精度较高。验证了本文提出的估算方法的有效性和准确性,同时也说明对于高磁路饱和下的永磁同步电机来说,永磁体磁链因电流而发生非线性改变的现象不可忽视。
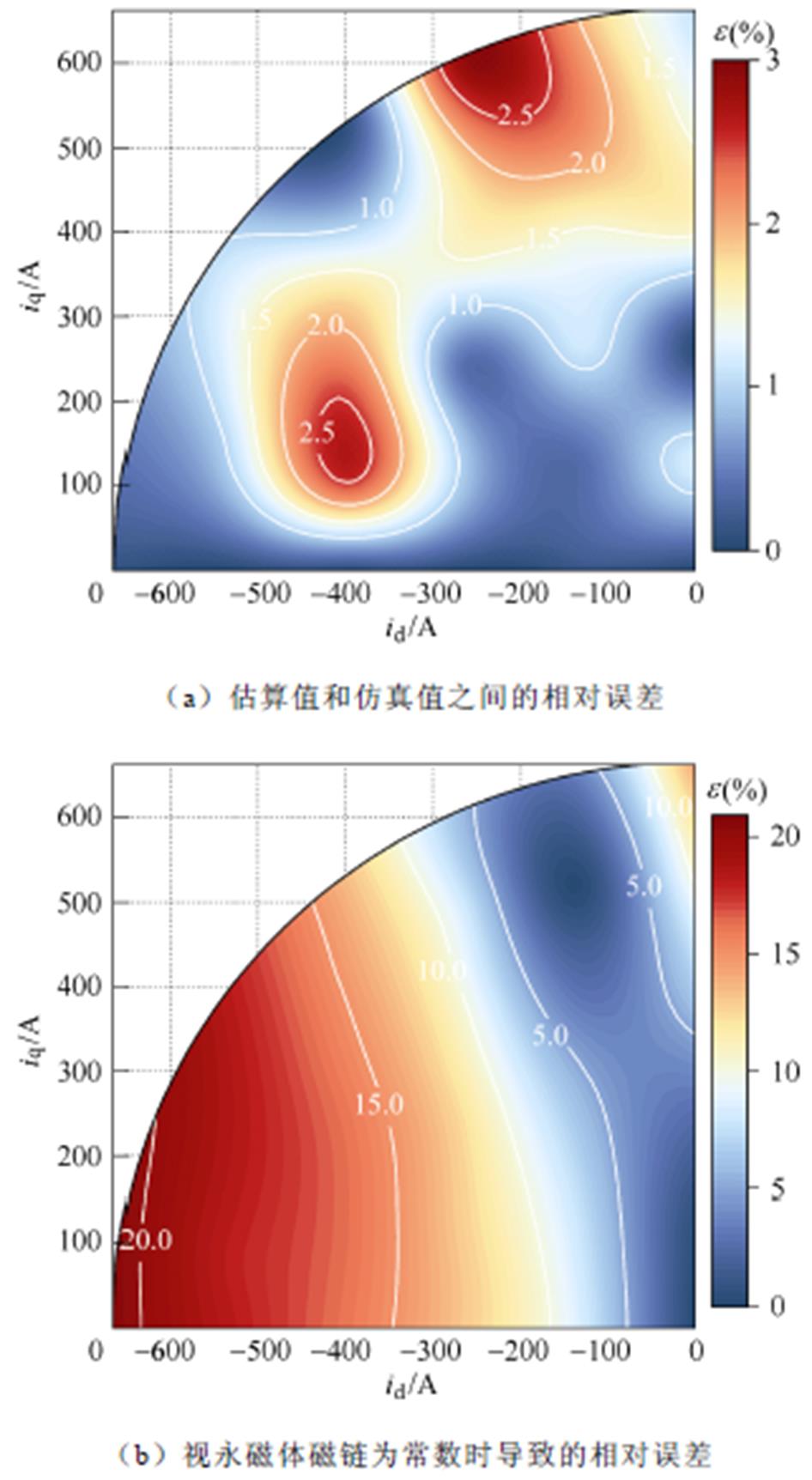
图12 相对误差
Fig.12 Relative error
为了进一步验证本文提出的估算方法,搭建了一台300kW内置式PMSM样机进行实验,其设计的模型如图1所示,参数见表1,样机由一台800kW的感应电机以额定转速(3 000r/min)拖动,运行于转矩控制模式,实现对样机的加载。同时,为了减小温度带来的影响,样机采用了水冷却方式,通入的冷却水温度为30℃,水流速为60L/min,实验平台如图13a所示。使用Hi Technologies的高速数据记录器实时观察和存储实验信息,如图13b所示,通过PC软件导出并绘制实验数据。
根据图7的估算流程,首先通过转矩仪测量id= 0,iq=600和id=0,iq=665时的转矩分别为746N·m,810N·m,通过图6的方法,计算常数J和X分别为J=1.93和X=4.23×10-5,计算结果与设计值十分接近。接着测量不同负载下的电压,具体的实验步骤为:①设定id=0,逐渐增加负载,记录负载条件下三相电压和电流;②减小id重复上述步骤,绘制额定电流范围内的相电压。其中样机在额定点运行时的三相电压和电流波形如图14所示。

图13 实验平台
Fig.13 Test platform
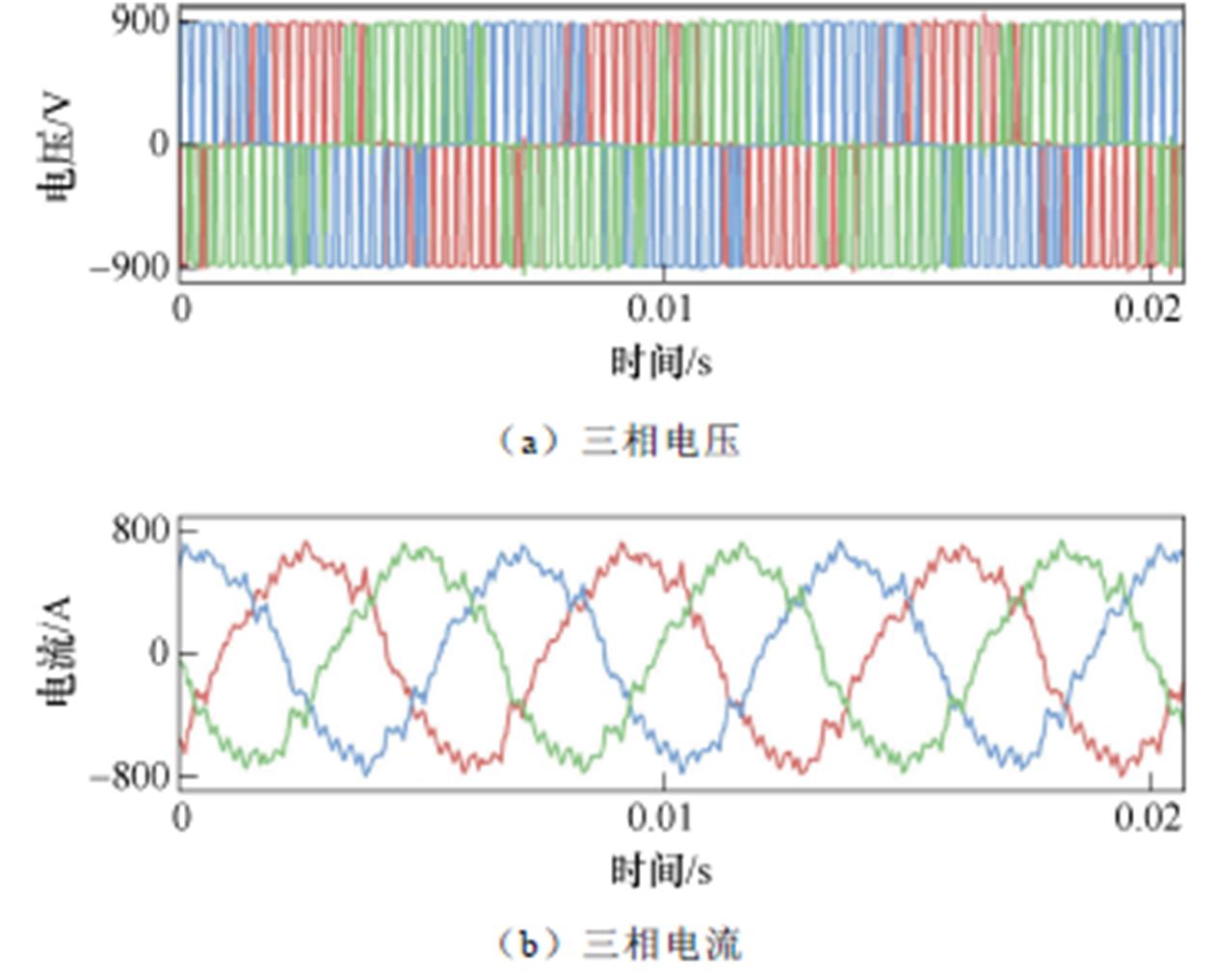
图14 额定点电压和电流波形
Fig.14 Waveforms of the experimental test at the rated conditions
由于在实验中测量的是线电压,为了便于估算,将记录的线电压数据转换为相电压,如图15所示。
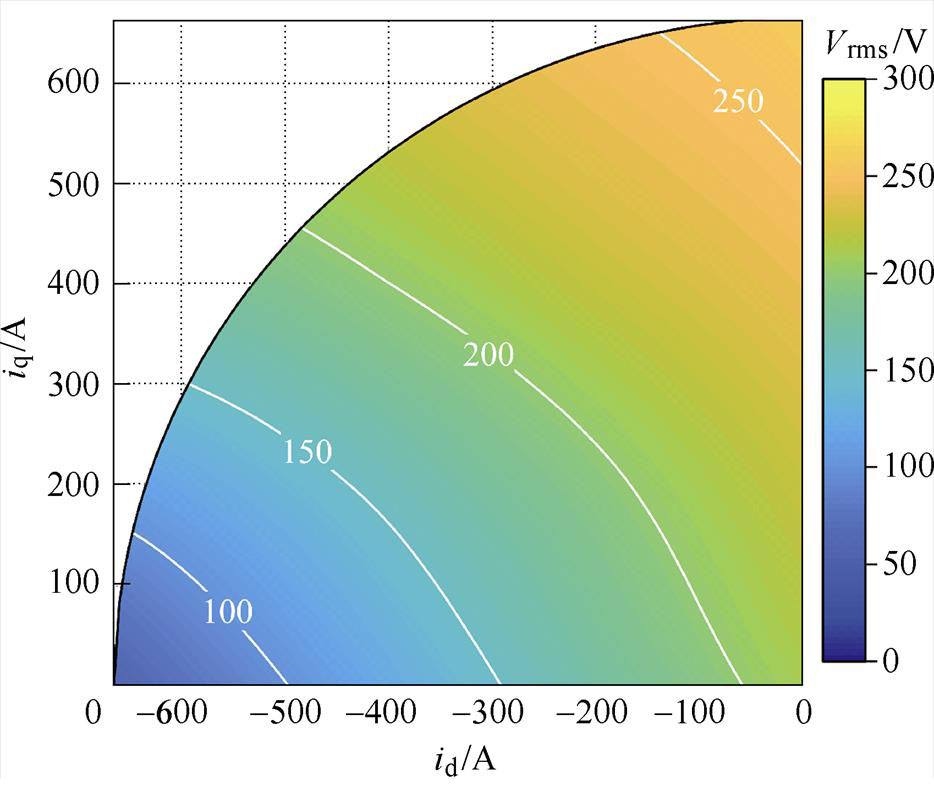
图15 测量的相电压
Fig.15 Measured phase voltage
在id=0时,根据式(14)和式(24)估算永磁体负载磁链,并根据式(15),通过测量转矩,计算永磁体磁链的实际值,将估算值和实际值对比,如图16所示。
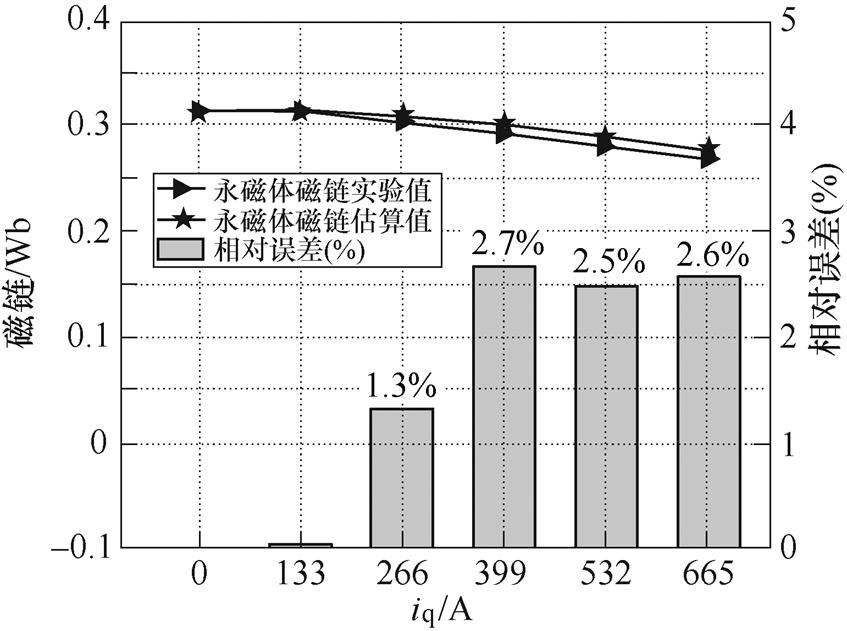
图16 实验对比
Fig.16 Experimental comparison
从图16中可以看出,在id=0时,永磁体磁链的估算值和实际值之间的相对误差仅在3%以内。为了进一步验证id<0的情况,根据式(17)和式(18)采用高频注入法估算id<0,iq=0时的永磁体磁链[14],如图17所示。
接着,根据本文提出的估算方法,估算id<0时额定电流范围内的永磁体负载磁链,同时还采用了反电动势法估算永磁体磁链,并将两种方法分别与高频注入法得到的永磁体磁链辨识值进行对比,如图18所示。
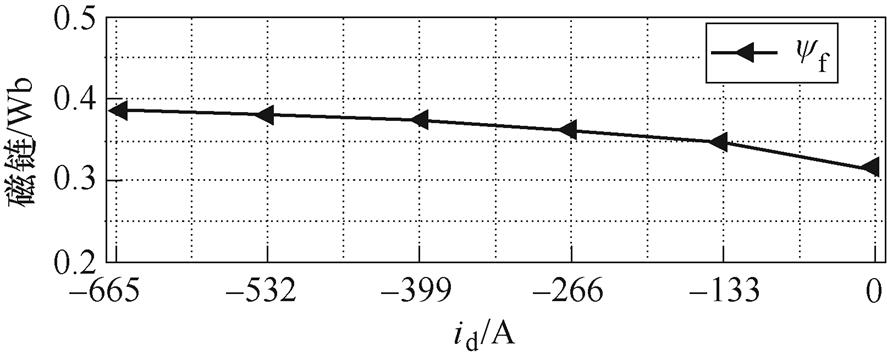
图17 永磁体磁链随id的变化
Fig.17 Variation of permanent magnet flux linkage with the d-axis current
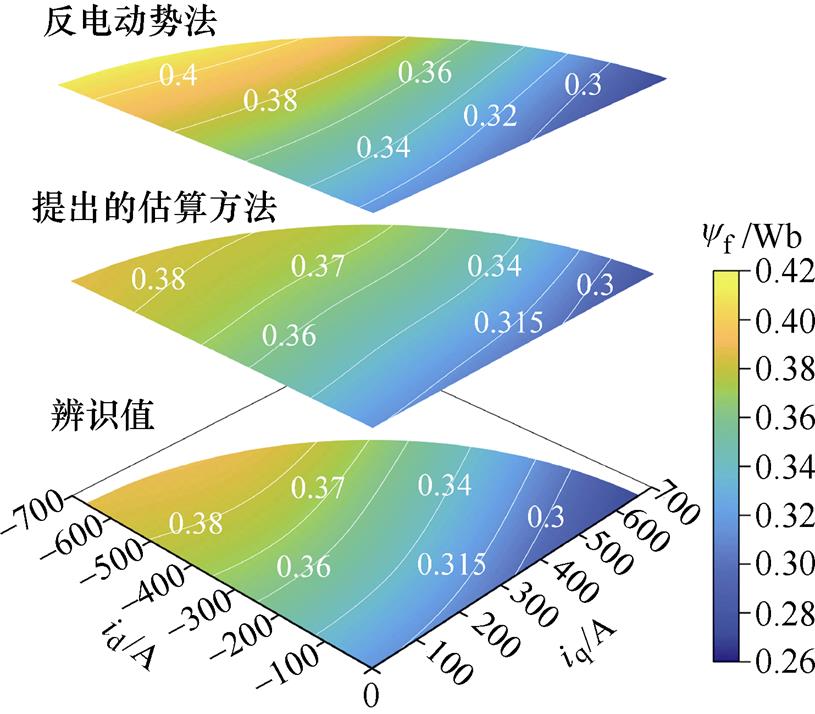
图18 实验结果
Fig.18 Experimental result
此外,为了更好地说明本文提出的估算方法的准确性,绘制了不同方法估算的永磁体磁链值与辨识值之间的相对误差,不同方法的对比如图19所示。其中,图19a为将永磁体磁链视为常数时(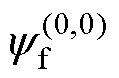 = 0.315Wb)与辨识值之间的相对误差,图19b为仿真值与辨识值之间的相对误差,其中仿真值如图11所示。图19c为采用反电动势法估算的永磁体磁链与辨识值之间的相对误差,图19d为采用本文提出的估算方法得到的永磁体磁链与辨识值之间的相对误差。最后,将不同估算方法导致的最大相对误差进行对比,见表2。
= 0.315Wb)与辨识值之间的相对误差,图19b为仿真值与辨识值之间的相对误差,其中仿真值如图11所示。图19c为采用反电动势法估算的永磁体磁链与辨识值之间的相对误差,图19d为采用本文提出的估算方法得到的永磁体磁链与辨识值之间的相对误差。最后,将不同估算方法导致的最大相对误差进行对比,见表2。
实验表明,将永磁体磁链视为静态常数会导致较大的误差,其中最大相对误差为19%。采用反电动势法导致的最大相对误差为6%,产生误差的主要原因是没有考虑磁路饱和。采用有限元仿真虽然能考虑磁路饱和,但仍然会产生7.2%的最大相对误差,主要是因为样机制造过程中存在一定的工艺和装配误差。而本文提出的估算方法仅有3.7%的最大相对误差,估算精度满足工程上的要求,验证了该方法的有效性和准确性。
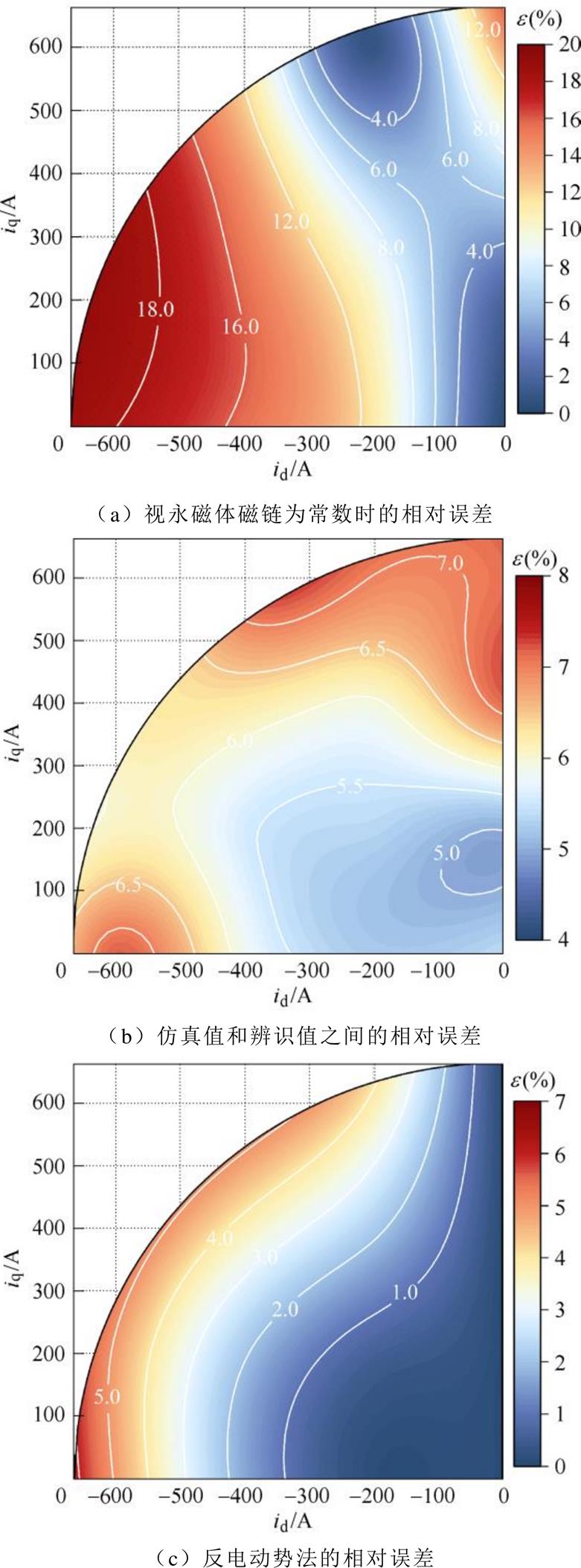
图19 不同方法的对比
Fig.19 Comparison of different methods
表2 不同估算方法对比
Tab.2 Comparison of different estimation methods

方 法最大相对误差(%) 永磁体磁链视为常数19.0 有限元仿真7.2 反电动势法6.0 提出的方法3.7
本文以高磁路饱和的永磁同步电机为研究对象,验证了电流对永磁体磁链产生的非线性影响,改进了传统的磁链模型,并提出了一种考虑磁路饱和的永磁体负载磁链动态估算方法。仿真和实验结果表明,传统的永磁体磁链估算方法会导致较大的误差,而本文提出的方法能够准确地估算电机负载状态下的永磁体磁链,同时该方法不依赖电机的结构参数,不会造成转矩脉动且易于工程实现,为今后实现高磁路饱和永磁同步电机精确控制提供了一定的参考价值。
参考文献
[1] 戴理韬, 高剑, 黄守道, 等. 变速恒频水力发电技术及其发展[J]. 电力系统自动化, 2020, 44(24): 169-177.
Dai Litao, Gao Jian, Huang Shoudao, et al. Variable- speed constant-frequency hydropower generation technology and its development[J]. Automation of Electric Power Systems, 2020, 44(24): 169-177.
[2] 姚钢, 杨浩猛, 周荔丹, 等. 大容量海上风电机组发展现状及关键技术[J]. 电力系统自动化, 2021, 45(21): 33-47.
Yao Gang, Yang Haomeng, Zhou Lidan, et al. Development status and key technologies of large- capacity offshore wind turbines[J]. Automation of Electric Power Systems, 2021, 45(21): 33-47.
[3] 黄科元, 周佳新, 刘思美, 等. 考虑逆变器非线性永磁同步电机高频注入电感辨识方法[J]. 电工技术学报, 2021, 36(8): 1607-1616.
Huang Keyuan, Zhou Jiaxin, Liu Simei, et al. Inductance identification method of permanent magnet synchronous motor considering inverter nonlinearity based on high-frequency injection[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1607-1616.
[4] 康劲松, 王硕. 基于Newton-Raphson搜索算法的永磁同步电机变电感参数最大转矩电流比控制方法[J]. 电工技术学报, 2019, 34(8): 1616-1625.
Kang Jinsong, Wang Shuo. Newton-Raphson-based searching method for variable-parameters inductance maximum torque per ampere control used for IPMSM[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1616-1625.
[5] Erazo D E G, Wallscheid O, Böcker J. Improved fusion of permanent magnet temperature estimation techniques for synchronous motors using a Kalman filter[J]. IEEE Transactions on Industrial Electronics, 2020, 67(3): 1708-1717.
[6] Jung H S, Park D, Kim H, et al. Non-invasive magnet temperature estimation of IPMSM based on high- frequency inductance with a pulsating high-frequency voltage signal injection[J]. IEEE Transactions on Industry Applications, 2019, 55(3): 3076-3086.
[7] Fernandez D, Martínez M, Diaz Reigosa D, et al. Influence of magnetoresistance and temperature on permanent magnet condition estimation methods using high-frequency signal injection[J]. IEEE Transactions on Industry Applications, 2018, 54(5): 4218-4226.
[8] Jung H S, Kim H, Sul S K, et al. Temperature estimation of IPMSM by using fundamental reactive energy considering variation of inductances[J]. IEEE Transactions on Power Electronics, 2021, 36(5): 5771-5783.
[9] Reigosa D, Fernandez D, Tanimoto T, et al. Com- parative analysis of BEMF and pulsating high- frequency current injection methods for PM tem- perature estimation in PMSMs[J]. IEEE Transa- ctions on Power Electronics, 2017, 32(5): 3691-3699.
[10] Xiao Shuai, Griffo A. PWM-based flux linkage and rotor temperature estimations for permanent magnet synchronous machines[J]. IEEE Transactions on Power Electronics, 2020, 35(6): 6061-6069.
[11] Feng Guodong, Lai Chunyan, Mukherjee K, et al. Online PMSM magnet flux-linkage estimation for rotor magnet condition monitoring using measured speed harmonics[J]. IEEE Transactions on Industry Applications, 2017, 53(3): 2786-2794.
[12] Sokolov E, Mihov M. Parameter estimation of an interior permanent magnet synchronous motor[C]// 16th Conference on Electrical Machines, Drives and Power Systems (ELMA), Varna, Bulgaria, 2019: 1-5.
[13] 佟文明, 姚颖聪, 李世奇, 等. 考虑磁桥不均匀饱和的内置式永磁同步电机等效磁网络模型[J]. 电工技术学报, 2022, 37(12): 2961-2970.
Tong Wenming, Yao Yingcong, Li Shiqi, et al. Equivalent magnetic network model for interior permanent magnet machines considering non-uniform saturation of magnetic bridges[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 2961- 2970.
[14] 李峰, 夏超英. 考虑磁路饱和的内置式永磁同步电机电感参数旋转辨识算法[J]. 电工技术学报, 2016, 31(21): 203-211.
Li Feng, Xia Chaoying. Inductance parameters identi- fication algorithms of IPMSM under rotating state taking magnetic circuit saturation into account[J]. Transactions of China Electrotechnical Society, 2016, 31(21): 203-211.
[15] Aljehaimi A M, Pillay P. Novel flux linkage esti- mation algorithm for a variable flux PMSM[J]. IEEE Transactions on Industry Applications, 2018, 54(3): 2319-2335.
[16] Xu Wei, Jiang Yajie, Mu Chaoxu, et al. Improved nonlinear flux observer-based second-order SOIFO for PMSM sensorless control[J]. IEEE Transactions on Power Electronics, 2019, 34(1): 565-579.
[17] Jiang Yajie, Xu Wei, Mu Chaoxu, et al. An improved third-order generalized integral flux observer for sensorless drive of PMSMs[J]. IEEE Transactions on Industrial Electronics, 2019, 66(12): 9149-9160.
[18] Liu Kan, Feng Jianghua, Guo Shuying, et al. Identification of flux linkage map of permanent magnet synchronous machines under uncertain circuit resistance and inverter nonlinearity[J]. IEEE Transa- ctions on Industrial Informatics, 2018, 14(2): 556- 568.
[19] 李家祥, 汪凤翔, 柯栋梁, 等. 基于粒子群算法的永磁同步电机模型预测控制权重系数设计[J]. 电工技术学报, 2021, 36(1): 50-59, 76.
Li Jiaxiang, Wang Fengxiang, Ke Dongliang, et al. Weighting factors design of model predictive control for permanent magnet synchronous machine using particle swarm optimization[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 50-59, 76.
[20] Rafaq M S, Mwasilu F, Kim J, et al. Online parameter identification for model-based sensorless control of interior permanent magnet synchronous machine[J]. IEEE Transactions on Power Electronics, 2017, 32(6): 4631-4643.
[21] Liu Zhaohua, Wei Hualiang, Li Xiaohua, et al. Global identification of electrical and mechanical parameters in PMSM drive based on dynamic self-learning PSO[J]. IEEE Transactions on Power Electronics, 2018, 33(12): 10858-10871.
[22] Umans S D. Fitzgeral & Kingslye's electric mach- inery[M]. New York: McGraw-Hill, 2013.
[23] 唐任远. 现代永磁电机理论与设计[M]. 北京: 机械工业出版社, 2016.
Dynamic Estimation of Permanent Magnet Load Flux Linkage of Permanent Magnet Synchronous Motor with High Magnetic Circuit Saturation
Abstract Due to the limitation of installation space and self-weight, a permanent magnet synchronous motor (PMSM) usually requires high electrical and magnetic loads, resulting in severe magnetic circuit saturation. Under the condition of high magnetic circuit saturation, the flux linkage of the permanent magnet (PM) changes nonlinearly with the change of current. In order to accurately estimate the PM flux linkage of the motor under load conditions, this paper first describes the influence of the dq-axis currents on the PM flux linkage. Combined with the local magnetic saturation characteristics of the stator core, the proportional relationship between the air gap magnetomotive force and the core magnetomotive force is analyzed. Then, a model of PM flux linkage based on the flux linkage coefficient is proposed. After that, according to the measured phase voltage and the permeability curve of stator core material, a dynamic estimation method of PM load flux linkage considering magnetic circuit saturation is proposed. Finally, a 300kW interior PMSM test platform is established, and the effectiveness and accuracy of the estimation method are verified by finite element simulation and tests.
Keywords:Permanent magnet synchronous motor, magnetic circuit saturation, permanent magnet flux linkage, flux linkage coefficient
中图分类号:TM351
DOI: 10.19595/j.cnki.1000-6753.tces.221002
国家自然科学基金面上资助项目(2021JJ30108)。
收稿日期 2022-06-01
改稿日期 2022-08-30
E-mail: gaojian0895@hnu.edu.cn
李承栩 男,1995年生,博士研究生,研究方向为特种电机设计与控制。
E-mail: lichengxu@hnu.edu.cn(通信作者)
(编辑 崔文静)