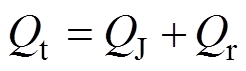 (1)
(1)
摘要 锂离子电池温度空间分布的不均匀性随着放电倍率的增大而加剧,严重影响电池寿命和安全性。针对锂离子电池放电过程中温度空间分布不均匀的情况,提出一种新的基于区域电压的不均匀发热模型,用来实时预测电池温度分布。考虑电池尺寸和热特性,将电池分为九个区域并进行开路电压测试,实时记录每个区域表面温度变化,采用每10%荷电状态(SOC)下降期间测量的表面温度和环境温度数据计算得到区域电压,根据区域电压获得电池的区域发热量,并建立三维仿真模型得到电池温度空间分布。使用该不均匀发热模型预测了放电倍率为0.5C、1C、2C、3C和4C时的电池温度空间演变,仿真结果显示该模型能捕获温度的不均匀分布,并通过实验验证,温度误差在1℃以内,相对误差在5%以内,表明该模型能够对温度分布进行有效监测。
关键词:锂离子电池 温度空间分布 区域电压 不均匀发热 温度监测
近年来,随着环境问题和能源危机的日益突出,亟需更高效、更经济和对环境更友好的能源[1]。锂离子电池具有能量密度高、循环寿命长和自放电率低等优点,被广泛应用于电动汽车和储能系统等领域[2-5]。锂离子电池的最适工作温度为15~35℃,一旦超出最适温度区域,将会加速电池性能衰退,甚至面临火灾和爆炸在内的安全问题[6-11]。然而,在复杂应用环境中,锂离子电池易发生局部温度偏高、内部温度分布不均匀等问题。
锂离子电池充放电过程中出现温度分布不均匀的热行为是由于电池内部电流密度的不均匀性、电化学反应的复杂性、生热时变性和非线性等特点导致的,这会造成电池的区域老化和荷电状态(State of Charge, SOC)分布不均匀[12-15]。严重情况下,可能会由于电池区域过度充电或过度放电而引起局部失效[16]。并且,这种不均匀温度分布在高倍率时更加显著。因此,建立识别锂离子电池温度不均匀分布的热模型至关重要。
目前的研究中,电池的热模型包括电热耦合模型和电化学热耦合模型。电热耦合模型是基于电池等效电路模型,根据过电势或电阻计算产热量,通过热方程与热模型耦合,实现温度预测。K. Onda等将电池的热量分为焦耳热和可逆热,通过内部等效电阻计算电池的产热量[17]。Xie Yi等在基础产热模型中考虑了电池集流柱产生的热量,建立了用于各种环境温度和放电倍率下的三维热模型,所提出热模型的平均统计相对误差大多数低于17% [18]。Li Junqiu等开发了一种电池过度充电时的热模型,将阻抗谱测量的电阻用于计算过充电过程中产生的热量,结果使温度估算的方均根误差减小至0.9℃以内[19]。Ding Xiaofeng等提出了一种考虑环境温度对开路电压影响的电路模型,提高了模型的精度,使电路参数识别误差小于1%[20]。刘新天等通过考虑环境温度对热模型参数的影响,建立了可变参数热模型来描述外部温度对内部热容和外部热阻的影响,模型的估计误差小于1.5℃[21]。虽然上述文献使用电热耦合模型计算出了电池的内部温度或表面温度,但其热量的计算都是采用平均发热率,并且模型的热量产生相对集中在电池的中心,而研究表明在极柱附近区域产生的热量更大[22-23]。因此,电热耦合模型不能体现电池发热的不一致性,不足以体现电池温度空间分布的不均匀性。
电化学热耦合模型通过模拟电池内部的电化学行为,实现电池温度预测。E. Hosseinzadeh等建立了锂离子电池一维电化学模型和三维热模型的耦合,表征了不同环境温度下的电池温度分布[24]。M. Mastali等在一维电化学模型的基础上,开发了软包锂离子电池的三维电化学和热耦合模型,模拟电池中的热分布,并根据实验电压和温度分布数据验证了模型的准确性[25]。虽然电化学热耦合模型可以通过不均匀的电流密度来表达温度的不均匀性,但是该方法需要许多不确定的内部参数,如正负极电势和电导率等,导致模型很难完全参数化。
针对以上问题,本文着眼于软包锂离子电池温度分布的不均匀性,提出了基于区域电压的锂离子电池不均匀发热模型,用来监测温度的不均匀分布。首先,根据电池的尺寸和热特性,将其分为九个区域,通过开路电压测试中每10%SOC放电期间九个区域的温度变化获取区域电压,即锂离子电池区域位置相对应的电压变化,基于区域电压计算电池区域产热量,用来表征不均匀发热;然后,根据电池内部热传导建立了空间热模型,得到温度空间分布;最后,通过实验验证了所构建热模型的有效性。
传统锂离子电池发热模型以电池等效电路模型为基础,将电池总热量Qt分为焦耳热QJ和可逆热Qr,即
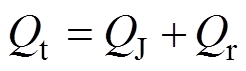 (1)
(1)
根据电池的电压或等效电阻计算总发热量,其中,焦耳热和可逆热可分别表示为
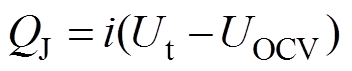 (2)
(2)
或
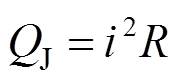 (3)
(3)
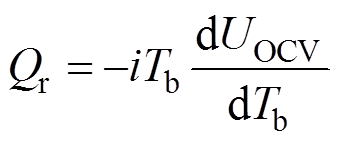 (4)
(4)
式中,i为电池的电流;Ut为电池的端电压;UOCV为电池的开路电压;R为电池的等效内阻;Tb为电池的温度;dUOCV/dT为开路电压UOCV相对于电池温度的变化(也称为熵变)。
根据该模型计算出的热量是电池总体热量,发热率为均一发热率,即电池各部分发热量相同,不能体现电池发热不均匀的现象。
本文通过将可逆热整合到焦耳热中,根据在10%SOC放电期间温度变化反向计算电压,提出基于区域电压的不均匀发热模型。
对于软包锂离子电池而言,放电过程中的热量一部分积蓄在电池的内部使电池的温度升高;一部分通过热对流与空气进行热交换。其中,使电池温度升高的能量用Q表示,表达式根据热能方程计算得到。
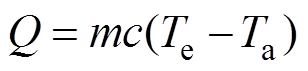 (5)
(5)
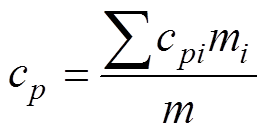 (6)
(6)
式中,m为电池的质量;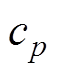 为电池的比定压热容;Te为10%SOC放电结束时测得的电池温度;Ta为环境温度;
为电池的比定压热容;Te为10%SOC放电结束时测得的电池温度;Ta为环境温度;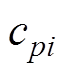 为电池每层材料的比热容;mi为电池每层材料的质量。
为电池每层材料的比热容;mi为电池每层材料的质量。
由于软包锂离子电池厚度较薄,忽略电池侧面散热量,电池上下平面与空气之间的热交换根据牛顿冷却定律可以表示为
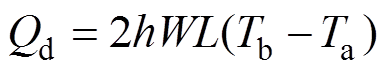 (7)
(7)
式中,Qd为热交换的能量;h为表面传热系数;W为电池宽度;L为电池长度;Tb为电池温度。
观测到的温度是电池发热和散热效果的总和,使用焦耳热公式来获取区域电压Un,将电池分为N个不同的区域,区域电压计算公式为
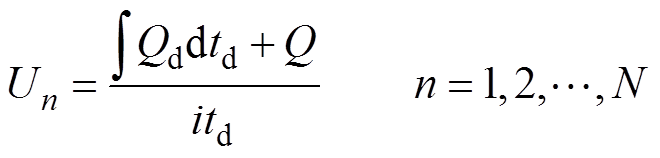 (8)
(8)
式中,td为10%SOC放电过程的持续时间。
区域电压Un是根据产生的热量计算出的电压,所以Un既包括焦耳热,又包括随SOC的熵变趋势。下标n表示在电池上的区域,每个电压对应于每个区域电池发热项的参数。使用体积平均热源,得到电池区域发热模型为
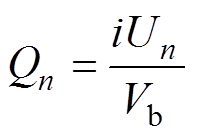 (9)
(9)
式中,Qn为区域生热率;Vb为电池的体积。电池的热量可使用式(9)的区域热量进行表征,不同区域的热量代表了电池不同的发热量。
该热模型计算出的电池热量在不同的区域具有不同的数值,反映了锂离子电池不均匀生热的现象。
锂离子电池内部的三维传热可以根据热传导定律和能量守恒方程求解,即
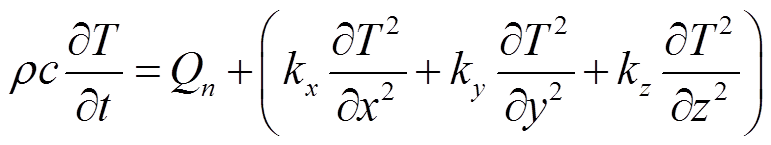 (10)
(10)
 (11)
(11)
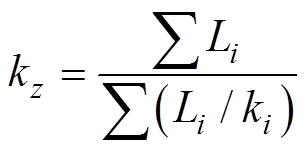 (12)
(12)
式中,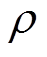 为电池的密度;t为时间;kx、ky和kz分别为电池x方向、y方向和z方向的导热系数;Li为电池第i层材料的厚度;ki为电池第i层的导热系数。
为电池的密度;t为时间;kx、ky和kz分别为电池x方向、y方向和z方向的导热系数;Li为电池第i层材料的厚度;ki为电池第i层的导热系数。
实验使用天津力神公司提供的商用SP376080SI软包钴酸锂电池为测试对象,电池额定容量为3 435mA·h,充电截止电压为4.45V,放电截止电压为3V,尺寸为78mm×59.5mm×3.4mm。实验系统如图1所示,使用NEWARE CT—4008电池测试仪对电池进行加载和采样,系统测量电压范围为0~5V,电流范围为-20~20A,误差为±0.1%。为了获得电池区域的热量变化,根据电池尺寸和热特性,将电池分为九个区域,使用2K的热敏电阻连接在每个区域的中心实时监测充/放电过程中的温度变化,热敏电阻测量范围为-30~120℃,精度为±1%,其中热敏电阻的排布如图2所示。由于软包锂离子电池卷绕结构的对称性,其两侧具有同样的温度特性,因此,只在电池一侧布置热敏电阻即可。使用装有NEWARE BTS软件的主机用来控制和记录数据,每秒记录一次电流、电压、容量和温度数据,Matlab R2019a用于数据处理。为了消除环境的不确定性,所有实验都在恒温箱中进行。将电池放置在恒温箱中,控制环境温度为25℃,恒温箱的误差范围为±1℃。实验过程中为了降低恒温箱气流对电池散热的影响,将透明的亚克力板放在通风口前5cm处,并且将电池放在远离通风口的位置。除此之外,实验过程中可能存在电噪声等随机不确定性,但在本研究中不考虑该因素。

图1 电池测试系统
Fig.1 Battery test system
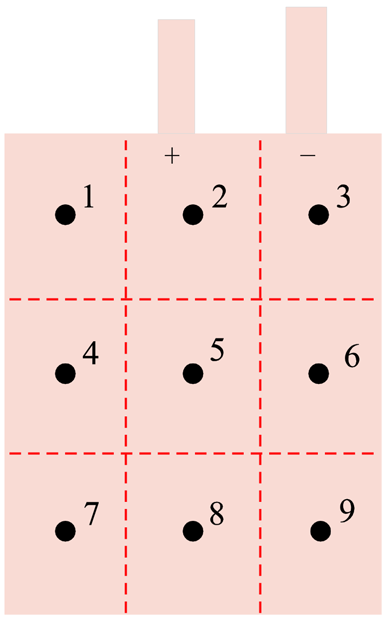
图2 热敏电阻排布
Fig.2 Arrangement of thermistors
由于电池在不同电流倍率下的可用容量不同,首先对电池进行放电容量测试。将电池充电电流统一设置为0.8C(C为标准容量),放电电流分别设置为0.5C、1C、2C、3C和4C。使用标准恒流恒压策略进行充电,即首先以0.8C的恒定电流将电池充电至4.45V的上限截止电压,然后以4.45V的恒定电压充电至电流降为0.05C(172mA),充电过程结束。电池静置1h,分别在0.5C、1C、2C、3C和4C倍率下,采用恒流方式将电池放电至下限截止电压3V,获取在不同放电倍率下的放电容量。
为了计算区域电压,对电池进行开路电压测试。将电池进行标准恒流恒压策略充电后,静置1h。分别在0.5C、1C、2C、3C和4C下采用电流脉冲方式对电池进行放电,每下降10%SOC将电池静置1h,以实现电化学和热平衡,重复该过程,直至完全放电至SOC为0。其中放电倍率为1C时的测试过程如图3a所示,图3b显示了测试过程中各区域对应的温度响应。
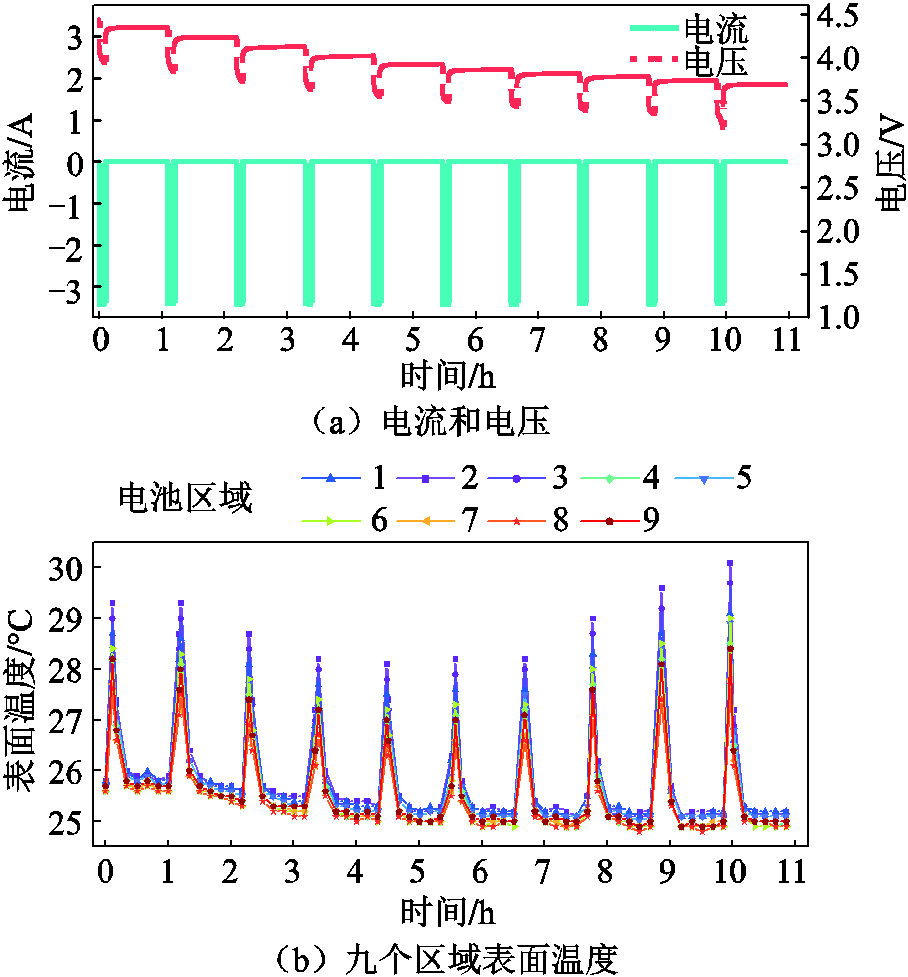
图3 开路电压测试中放电倍率为1C时的电流、电压和表面温度
Fig.3 Current, voltage and surface temperature at discharge rate of 1C in open circuit voltage test
不同放电倍率(0.5C、1C、2C、3C和4C)下电池九个区域的表面温度变化如图4所示。随着放电过程的进行和放电倍率的增大,电池的温度分布在空间上的不均匀现象愈加明显。在充/放电过程开始时电池的表面温度是均一的,随着充/放电过程的进行,电池表面温度出现不均匀现象,在整个充/放电过程中,温度最高和不均匀分布最显著时刻都是在放电结束时。
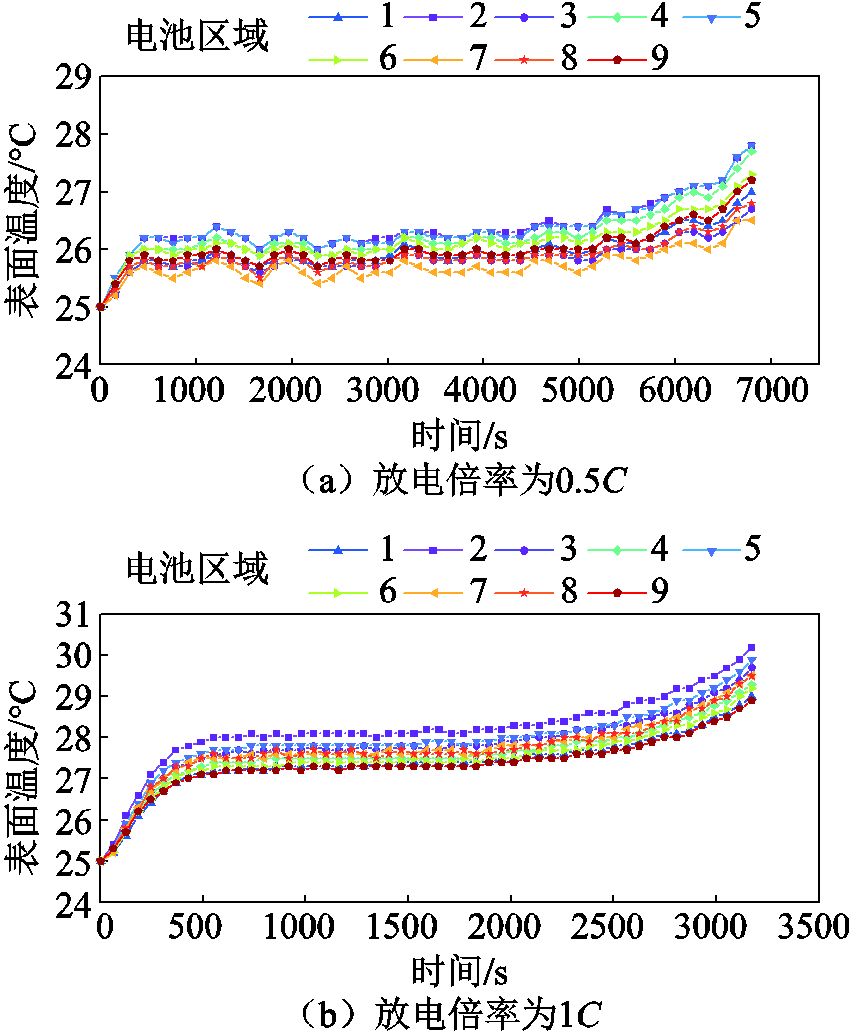
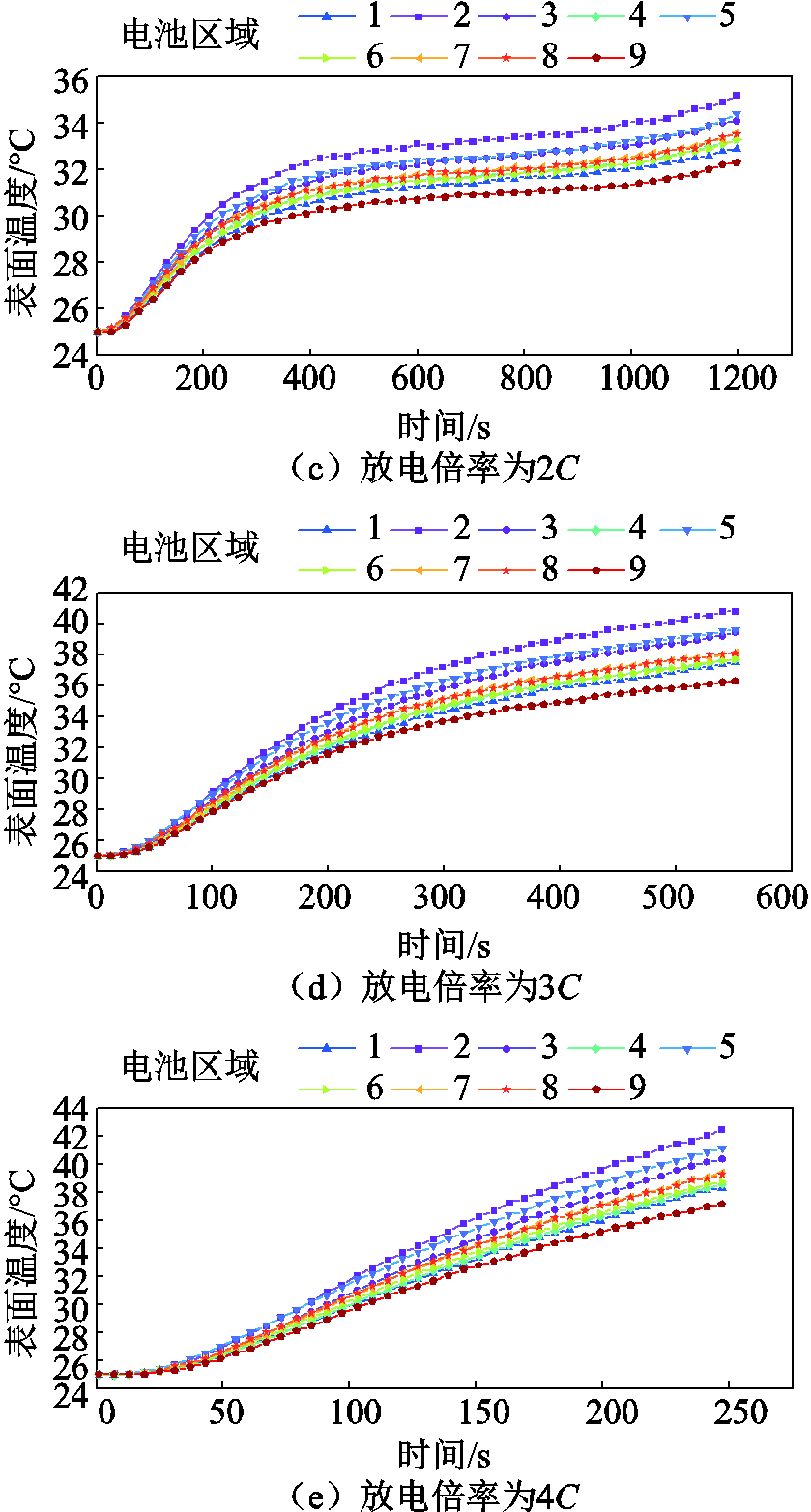
图4 不同放电倍率下表面温度
Fig.4 Surface temperature at different discharge rates
在图4中,不同放电倍率下,电池不同区域的温度分布不同。可以将其分为两组,第一组为区域2、区域3和区域5,测得较高的温度;第二组为区域1、区域4、区域6、区域7、区域8和区域9,显示出比第一组低的温度,两组的温差随着放电过程而增大。由此可见,在电池的极耳区域和中心区域可能更容易出现热老化现象。
放电过程中的电池温升可分为三个阶段,初始温度迅速升高,中间缓慢上升,最终再次迅速升高,此现象在放电倍率较低时更为明显。此三个阶段可以根据放电深度(Depth of Discharge, DOD)划分,第一阶段为DOD在0%~20%时,最初大多数的热量都存储在电池中,并且由于电池表面温度和环境温度之间差异较小而导致散热较少,进而导致温度迅速升高;第二阶段为DOD在20%~70%时,随着电池表面温度升高,向环境的散热变得更多,此外,在这个阶段热量的产生减少,导致温度缓慢上升;第三阶段为DOD在70%~100%时,电池达到放电末端,可逆热和不可逆热生成显著,引起电池的温度再次迅速上升。
在0.5C、1C、2C、3C和4C放电结束后,观察到温度最高的部位为正极柱下方(区域2),最高温度分别为28.1℃、30.6℃、35.2℃、40.9℃和42.6℃;观察到温度最低部位一般为负极柱最下端(区域9),最低温度为26.7℃、29.1℃、32.4℃、36.3℃和37.3℃;最高温度和最低温度的差值为1.4℃、1.5℃、2.8℃、4.6℃和5.3℃。由此可见,电池温度分布的不均匀性很显著,且随着放电倍率的增大而增加。
通过电池开路电压测试过程中的温度变化,根据式(8)计算区域电压,其中电池每层材料参数见表1。
表1 电池材料25℃时的计算参数
Tab.1 Calculation parameters of cell material at 25℃

电池材料质量mi/g比定压热容cpi/[J/(kg·K)]导热系数ki/[W/(m·K)] 正极钴酸锂1.13750.51.75 负极石墨0.45759.310.88 隔膜0.031 7180.22 正极集电器铝0.11897.8236.3 负极集电器铜0.23382.5394.3 外壳铝0.88897.8236.3
不同放电倍率下电池九个区域的区域电压如图5所示。对比开路电压测试过程中电池温度的变化,区域电压的变化与温度的变化趋势一致。在放电初始和末期,电池的区域电压较大,在放电中期(SOC=70%~20%),电池的区域电压较小。在不同放电倍率下,电池的区域电压变化趋势相同,数值随放电倍率的增大而增加。根据区域电压在电池上相对应的位置,锂离子电池正极柱和负极柱分别对应区域2和区域3,在开路电压测试期间,区域2和区域3产生的热量大于其他区域产生的热量;电池中间部位对应区域5,区域5的散热面积最小。因此,在区域2、区域3和区域5处获得了较高的温度和较大的区域电压。
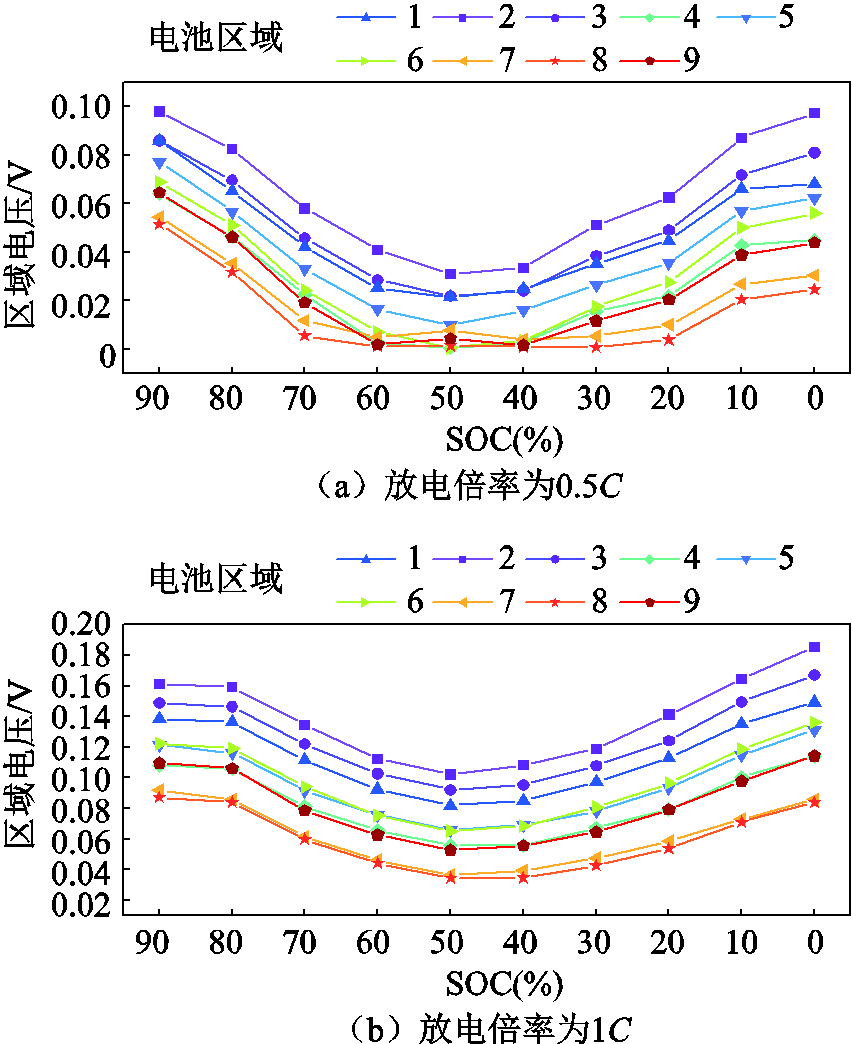
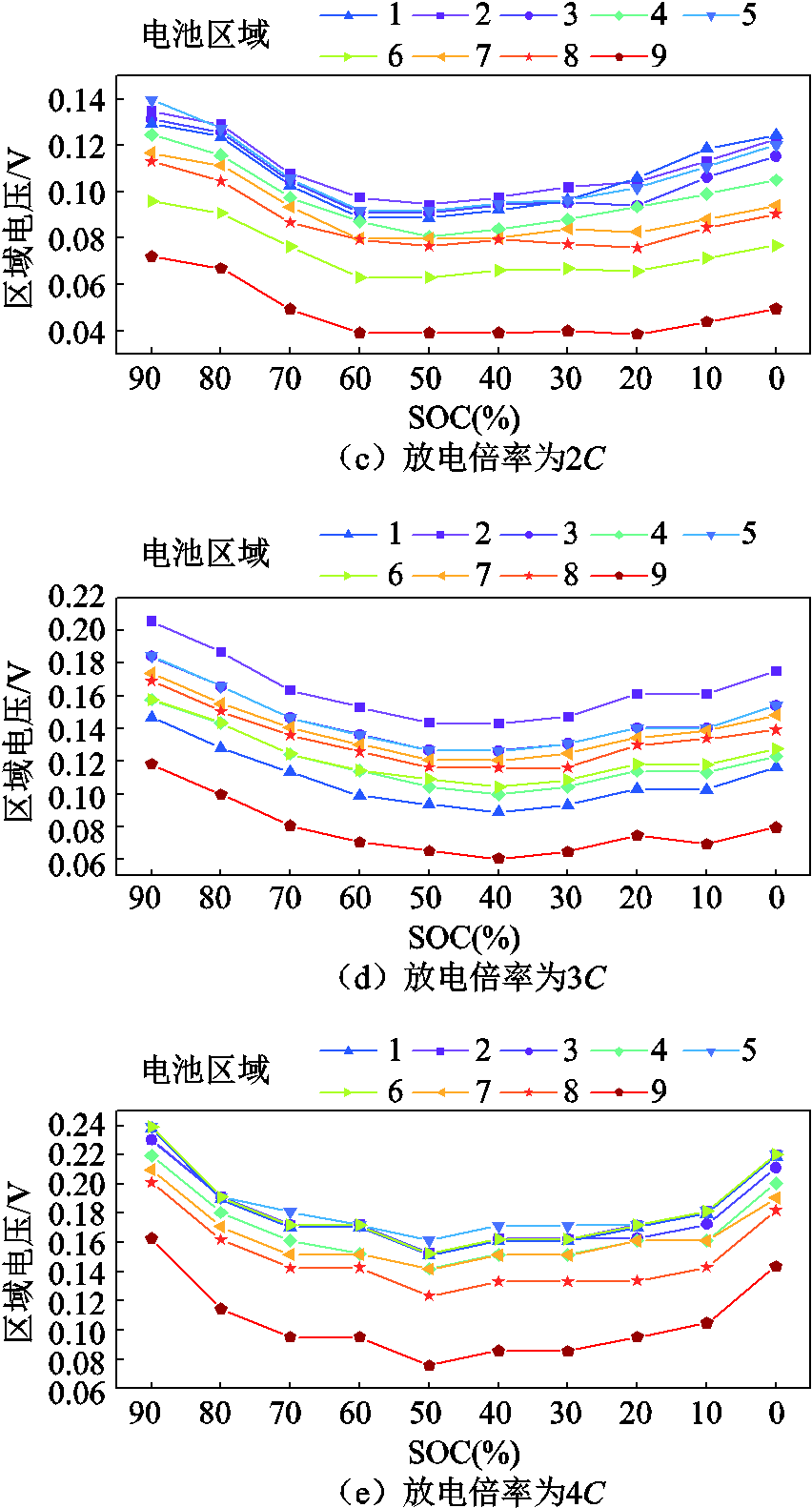
图5 不同放电倍率下区域电压
Fig.5 Regional voltage at different discharge rates
在COMSOL Multiphysics有限元分析中建立锂离子电池的三维热模型。根据区域电压的计算结果获得电池不同区域的体积平均热源,将其输入到热模型中的热源项,即可获得电池不同区域的生热率。根据电池结构和材料特性获得比热容和导热系数等热参数,结合电池内部三维传热方程,仿真获得电池的热分布。初始温度设置为25℃,在物理控制网格的序列类型和“常规”的网格尺寸类型中使用了内置的网格生成功能,使用三角形元素构建了970个域单元、780个边界元和184个边单元的完整网格。电池模型参数见表2。
表2 电池模型参数
Tab.2 Cell model parameters

参数数值 质量m/g43.05 环境温度Ta/℃25 表面传热系数h/[W/(m2·K)]9.29 宽度W/mm59.5 长度L/mm78 密度/(kg/m3)2 693.39
放电倍率为1C情况下,电池放电过程中的温度不均匀分布如图6所示。从图6中可以看出,在放电开始时,电池上端的极柱附近快速产热,随着放电过程进行热量传导到其他区域,电池中心部分聚集大量热量。在整个放电过程中,极柱附近呈现更高的温度,并且正极柱附近的温度高于负极柱附近的温度。这种现象可由以下原因解释:①极柱附近电流密度更高。在放电开始时,转移电流密度集中在极柱附近。随着放电过程的进行,电流密度的分布变得均匀,但在极柱附近仍然略高。放电结束时,极柱附近活性材料耗尽,转移电流流向电极底部。高电流密度会产生额外的焦耳热,进而加快电化学反应的速度并促进极柱附近局部热点的形成。②极柱附近生热率大。极柱附近具有相对较大的欧姆电阻和接触电阻,导致生热率的增加,造成温度的升高。③正负极集电器材料不同。由铝箔制成的正极集电器的电阻率比铜箔制成的负极集电器的电阻率大,导致正极极柱的生热率高于负极极柱的生热率。并且正极集电器铝的比热容相对负极集电器铜较高,而导热系数相对较低。比热容对温升的影响最大,而导热系数对温升变化的影响最大,导致正极的温升较大而变化较小。
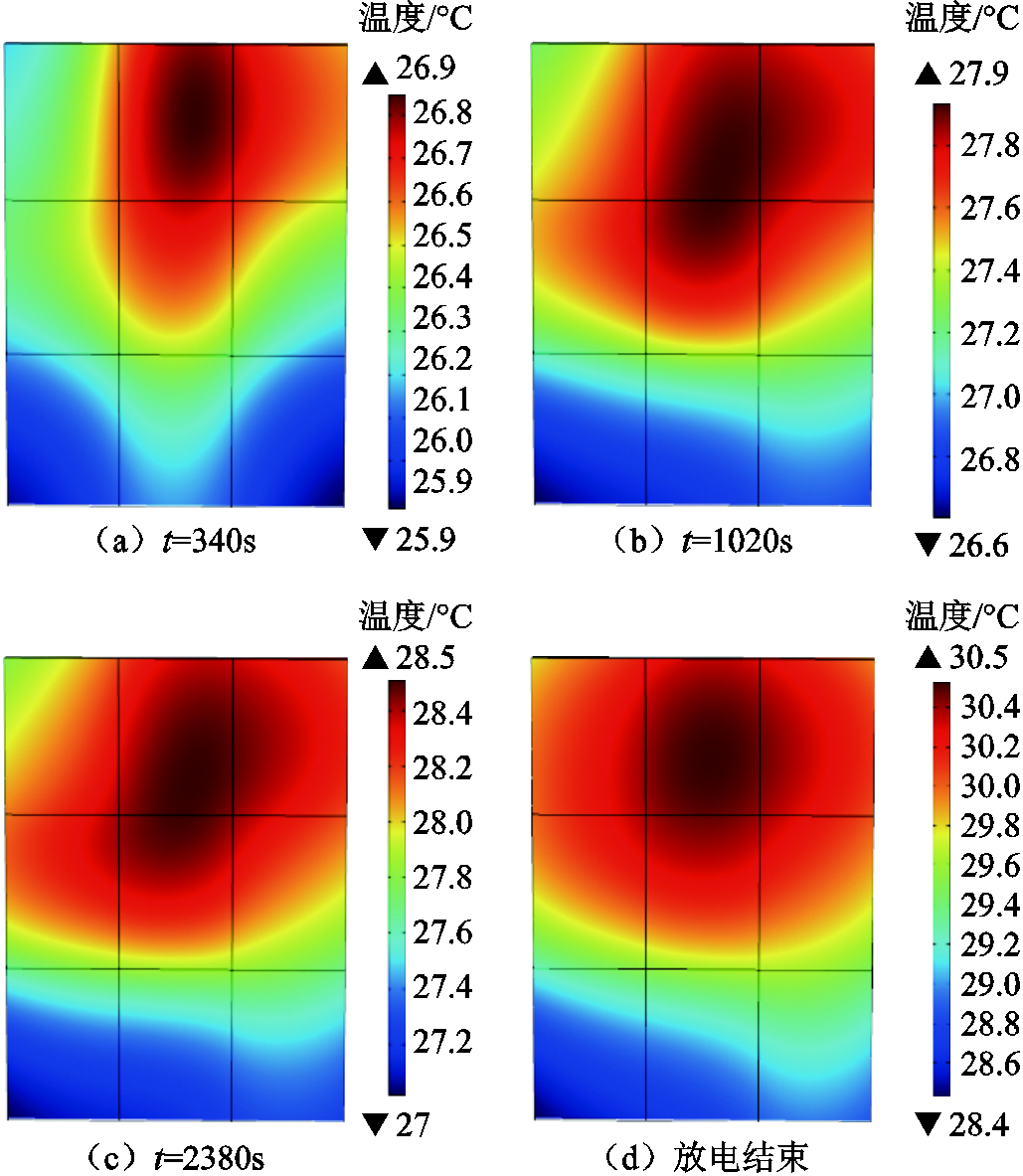
图6 1C放电过程中温度不均匀分布
Fig.6 Uneven distribution of temperature during 1C discharge
电池温度分布的不均匀性随着放电过程而加剧。仿真结果表明了所建模型能够有效模拟锂离子电池温度分布的不均匀性。
在不同放电倍率下,电池热量的产生速率不一致,为了探究不同放电倍率下热量的产生情况,选择特定SOC对电池温度进行研究。图7是SOC为50%时不同放电倍率下电池温度不均匀分布。从图7中可以看出,在不同放电倍率下,电池温度较高部分总是集中在电池极柱下方和中间区域。电池温度差和温度分布的不均匀性随着放电倍率的增加而加剧。但放电倍率为4C时,电池的最高温度和最低温度均低于放电倍率为3C时的最高温度和最低温度。根据图4放电过程中的温度变化可知,当放电倍率为3C时,在放电的前半段,温度有一个迅速升高的过程,而放电倍率为4C时,电池放电的前半段温度升高较缓慢,温度的迅速升高在放电过程的后半段。这是因为电池的热量变化与内部的化学反应和锂离子浓度梯度相关。在放电刚开始时,锂离子浓度梯度迅速增加,电池的温度较低,电池内部锂离子的扩散性和电解液的导电性等化学反应较慢。随着放电过程的进行,电解液中的锂离子浓度梯度逐渐减小,当电池极柱附近的热量经过热传导扩散到整个电池时,电解液的扩散系数和电导率整体增加,温度迅速上升。然而,对于放电速率较大的情况,特别是4C,放电时间极短,而电池内部热传导需要一定的时间,导致在放电的后期,内部所有区域的温度才获得较大的升高,电解液的扩散系数和电导率增加,反应速率加快,温度才得以迅速上升。
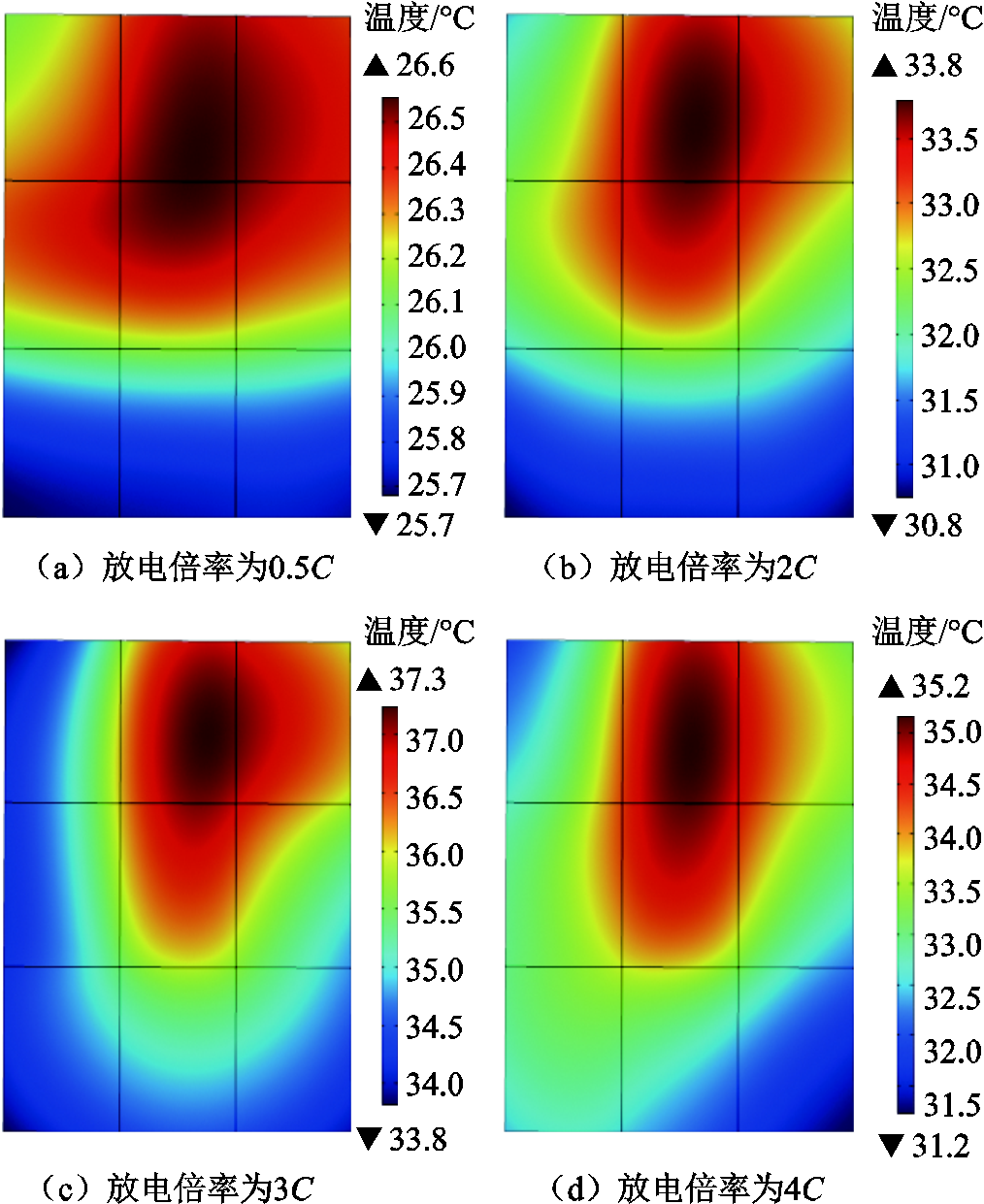
图7 不同放电倍率下内部温度不均匀分布
Fig.7 Uneven distribution of internal temperature at different discharge rates
由于实测表面温度为区域温度的平均值,因此将区域1~区域9的表面温度仿真平均值和实测温度值进行对比,来验证模型的准确性。图8比较了1C放电过程中仿真和实测的温度变化。九个区域的比较结果大致相同,仿真值能较好地与实测值吻合。在整个放电过程中,区域1~区域9的仿真值和实测值最大差值分别为0.57℃、0.69℃、0.84℃、0.37℃、0.51℃、0.37℃、0.30℃、0.89℃和0.98℃,最大误差均在1℃以内。
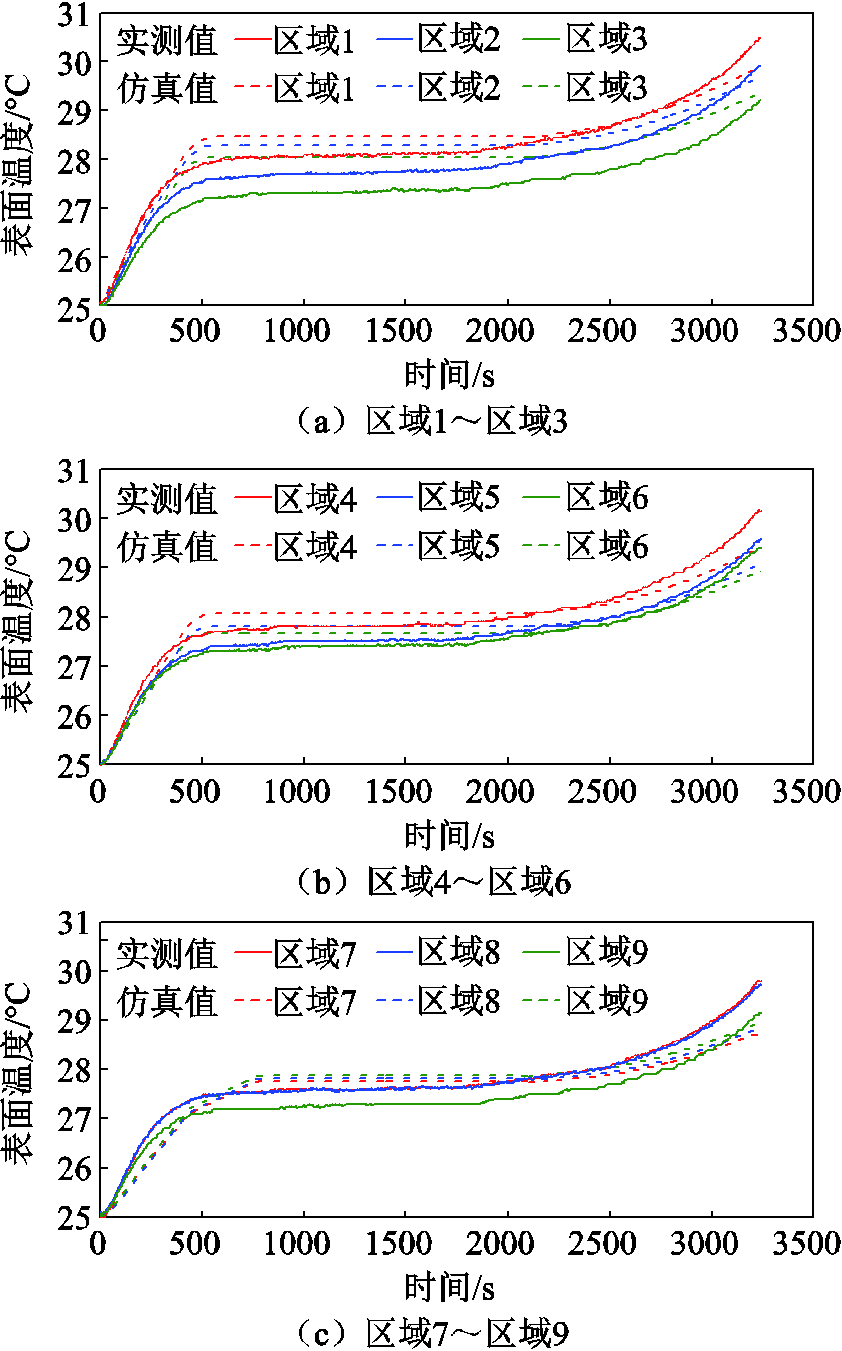
图8 1C放电过程中不同区域实测值和仿真值对比
Fig.8 Comparison of measured and simulated values in different regions during 1C discharge
对于不同放电倍率下仿真值和实测值的对比,选择固定的区域进行分析。图9是不同放电倍率下区域5的仿真值与实测值对比。在不同放电倍率下,区域5温度仿真值与实验测量值也能较好地吻合。在放电倍率为0.5C、1C、2C、3C和4C下,仿真值和实测值的最大差值分别为0.25℃、0.51℃、0.98℃、0.92℃和0.49℃。最大误差均在1℃以内,验证了模型的有效性。
为了检验模型的准确性,采用了仿真值与实测值的相对误差Re,定义为
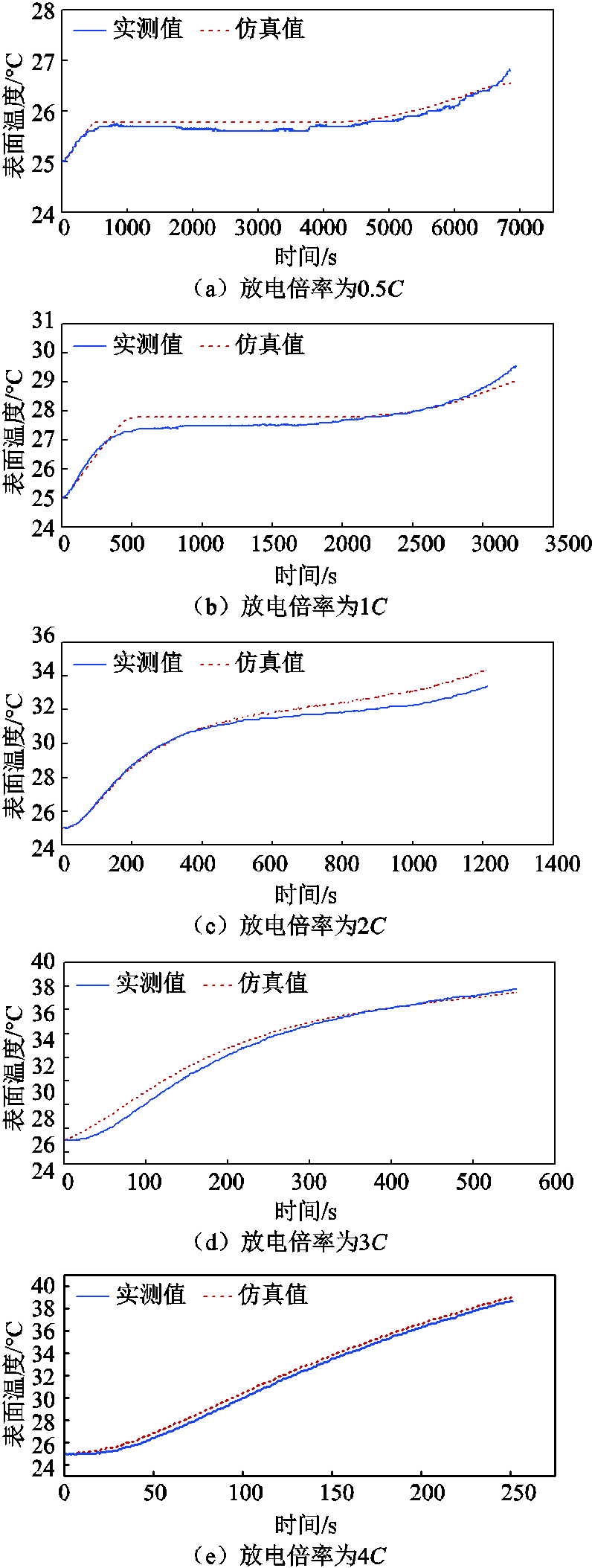
图9 不同放电倍率下区域5实测值与仿真值对比
Fig.9 Comparison of measured and simulated values in region 5 at different discharge rates
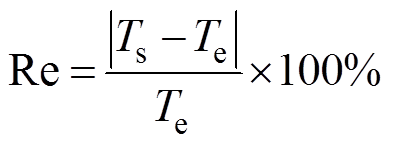 (13)
(13)
式中,Ts为仿真温度;Te为实验测得温度。
电池模型相对误差最大值见表3。在不同放电倍率下相对误差最大值分别为3.25%、3.10%、4.17%、3.58%和4.55%,均小于5%,证明模型结果在合理的误差范围内。
表3 电池模型相对误差最大值
Tab.3 Maximum relative error of cell model

区域序号最大相对误差(%) 0.5C1C2C3C4C 13.252.804.173.583.85 22.563.103.102.394.15 31.911.493.420.224.26 41.571.853.731.483.69 50.921.283.020.761.68 61.371.353.371.044.14 71.870.873.331.864.13 81.230.433.162.334.01 91.060.613.242.074.55
通过上述误差对比可知,放电倍率为1C时区域1~区域9的仿真值和实测值最大误差均在1℃以内,不同放电倍率下区域5的仿真值和实测值最大误差也在1℃以内,证明了所构建模型的有效性。不同放电倍率下的相对误差均小于5%,证明了所构建模型的准确性。
本文建立了一种基于区域电压的锂离子电池不均匀发热模型,采用开路电压测试,依据每10%SOC放电期间,电池不同区域测得的温度变化得到了区域电压,确定了电池相对位置发热量,将其代入热模型中,仿真得到电池温度空间分布。通过仿真值与实测值的对比,模型在不同区域和不同倍率下的温度预测误差都在1℃以内,相对误差在5%以内,验证了模型的有效性和准确性。本文所提出基于区域电压的电池发热模型为电池温度不均匀分布提供了一种有效的方法。
参考文献
[1] 佟明昊, 程明, 许芷源, 等. 电动汽车用车载集成式充电系统若干关键技术问题及解决方案[J]. 电工技术学报, 2021, 36(24): 5125-5142.
Tong Minghao, Cheng Ming, Xu Zhiyuan, et al. Key issues and solutions of integrated on-board chargers for electric vehicles[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5125-5142.
[2] 孙金磊, 朱春波, 李磊, 等. 电动汽车动力电池温度在线估计方法[J]. 电工技术学报, 2017, 32(7): 197-203.
Sun Jinlei, Zhu Chunbo, Li Lei, et al. Online temperature estimation method for electric vehicle power battery[J]. Transactions of China Electrotechnical Society, 2017, 32(7): 197-203.
[3] 孙丙香, 刘佳, 韩智强, 等. 不同区间衰退路径下锂离子电池的性能相关性及温度适用性分析[J]. 电工技术学报, 2020, 35(9): 2063-2073.
Sun Bingxiang, Liu Jia, Han Zhiqiang, et al. Performance correlation and temperature applicability of Li-ion batteries under different range degradation paths[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 2063-2073.
[4] Srinivasan R, Demirev P A, Carkhuff B G. Rapid monitoring of impedance phase shifts in lithium-ion batteries for hazard prevention[J]. Journal of Power Sources, 2018, 405: 30-36.
[5] 范文杰, 徐广昊, 于泊宁, 等. 基于电化学阻抗谱的锂离子电池内部温度在线估计方法研究[J]. 中国电机工程学报, 2021, 41(9): 3283-3292.
Fan Wenjie, Xu Guanghao, Yu Boning, et al. On-line estimation method for internal temperature of lithium-ion battery based on electrochemical impedance spectroscopy[J]. Proceedings of the CSEE, 2021, 41(9): 3283-3292.
[6] Raijmakers L H J, Danilov D L, Eichel R A, et al. A review on various temperature-indication methods for Li-ion batteries[J]. Applied Energy, 2019, 240: 918-945.
[7] 潘海鸿, 张沫, 王惠民, 等. 基于多影响因素建立锂离子电池充电内阻的动态模型[J]. 电工技术学报, 2021, 36(10): 2199-2206.
Pan Haihong, Zhang Mo, Wang Huimin, et al. Establishing a dynamic model of lithium-ion battery charging internal resistance based on multiple factors[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2199-2206.
[8] Ma Shuai, Jiang Modi, Tao Peng, et al. Temperature effect and thermal impact in lithium-ion batteries: a review[J]. Progress in Natural Science: Materials International, 2018, 28(6): 653-666.
[9] Nascimento M, Ferreira M S, Pinto J L. Temperature fiber sensing of Li-ion batteries under different environmental and operating conditions[J]. Applied Thermal Engineering, 2019, 149: 1236-1243.
[10] Lee C Y, Lee S J, Hung Y M, et al. Integrated microsensor for real-time microscopic monitoring of local temperature, voltage and current inside lithium ion battery[J]. Sensors and Actuators A: Physical, 2017, 253: 59-68.
[11] Wang Xueyuan, Wei Xuezhe, Chen Qijun, et al. Lithium-ion battery temperature on-line estimation based on fast impedance calculation[J]. Journal of Energy Storage, 2019, 26: 100952.
[12] Veth C, Dragicevic D, Merten C. Thermal characterizations of a large-format lithium ion cell focused on high current discharges[J]. Journal of Power Sources, 2014, 267: 760-769.
[13] 庞辉, 郭龙, 武龙星, 等. 考虑环境温度影响的锂离子电池改进双极化模型及其荷电状态估算[J]. 电工技术学报, 2021, 36(10): 2178-2189.
Pang Hui, Guo Long, Wu Longxing, et al. An improved dual polarization model of Li-ion battery and its state of charge estimation considering ambient temperature[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2178-2189.
[14] Strobridge F C, Orvananos B, Croft M, et al. Mapping the inhomogeneous electrochemical reaction through porous LiFePO4-electrodes in a standard coin cell battery[J]. Chemistry of Materials, 2015, 27(7): 2374-2386.
[15] 熊瑞, 李幸港. 基于双卡尔曼滤波算法的动力电池内部温度估计[J]. 机械工程学报, 2020, 56(14): 146-151.
Xiong Rui, Li Xinggang. Battery internal temperature estimation method through double extended Kalman filtering algorithm[J]. Journal of Mechanical Engineering, 2020, 56(14): 146-151.
[16] Han Xuebing, Ouyang Minggao, Lu Languang, et al. A comparative study of commercial lithium ion battery cycle life in electrical vehicle: aging mechanism identification[J]. Journal of Power Sources, 2014, 251: 38-54.
[17] Onda K, Ohshima T, Nakayama M, et al. Thermal behavior of small lithium-ion battery during rapid charge and discharge cycles[J]. Journal of Power Sources, 2006, 158(1): 535-542.
[18] Xie Yi, He Xiaojing, Hu Xiaosong, et al. An improved resistance-based thermal model for a pouch lithium-ion battery considering heat generation of posts[J]. Applied Thermal Engineering, 2020, 164: 114455
[19] Li Junqiu, Sun Danni, Jin Xin, et al. Lithium-ion battery overcharging thermal characteristics analysis and an impedance-based electro-thermal coupled model simulation[J]. Applied Energy, 2019, 254: 113574.
[20] Ding Xiaofeng, Zhang Donghuai, Cheng Jiawei, et al. An improved Thevenin model of lithium-ion battery with high accuracy for electric vehicles[J]. Applied Energy, 2019, 254: 113615.
[21] 刘新天, 张胜, 何耀, 等. 基于简化可变参数热模型的锂电池内部温度估计[J]. 华南理工大学学报(自然科学版), 2019, 47(4): 44-52.
Liu Xintian, Zhang Sheng, He Yao, et al. Lithium battery internal temperature estimation based on simplified variable parameter thermal model[J]. Journal of South China University of Technology (Natural Science Edition), 2019, 47(4): 44-52
[22] Jung W, Kim H K, Kim M, et al. Spatial measurement of heat generation in a pouch-type lithium-ion battery[J]. International Journal of Precision Engineering and Manufacturing, 2016, 17(8): 1085-1089.
[23] Patil M S, Seo J H, Panchal S, et al. Numerical study on sensitivity analysis of factors influencing liquid cooling with double cold-plate for lithium-ion pouch cell[J]. International Journal of Energy Research, 2021, 45(2): 2533-2559.
[24] Hosseinzadeh E, Genieser R, Worwood D, et al. A systematic approach for electrochemical-thermal modelling of a large format lithium-ion battery for electric vehicle application[J]. Journal of Power Sources, 2018, 382: 77-94.
[25] Mastali M, Foreman E, Modjtahedi A, et al. Electrochemical-thermal modeling and experimental validation of commercial graphite/LiFePO4 pouch lithium-ion batteries[J]. International Journal of Thermal Sciences, 2018, 129: 218-230.
Regional Voltage-Based Uneven Heating Model of Lithium-Ion Battery
Abstract The non-uniformity of the temperature spatial distribution of lithium-ion battery increases with the increase of the discharge rate, which seriously affects the battery life and safety. Aiming at the uneven temperature distribution during the discharge of lithium-ion battery, a new non-uniform heating model based on regional voltage is proposed to predict the battery temperature distribution in real time. Considering the battery size and thermal characteristics, the battery is divided into nine regions and the open circuit voltage test is carried out. The surface temperature change of each area is recorded in real time. Calculate the regional voltage using the surface temperature and ambient temperature data measured during every 10% of the state of charge (SOC) drops. Obtain the regional heat production of the battery according to the regional voltage, and establish a three-dimensional simulation model to obtain the spatial distribution of battery temperature. The non-uniform heating model is used to predict the spatial evolution of battery temperature when the discharge rate is 0.5C, 1C, 2C, 3C and 4C. The simulation results show that the model captures the uneven distribution of temperature. And the experimental results verify that the temperature errors are within 1℃, the relative errors are within 5%. It shows that the model can effectively monitor the temperature distribution.
keywords:Lithium-ion battery, spatial distribution of temperature, regional voltage, uneven heating, temperature monitoring
DOI:10.19595/j.cnki.1000-6753.tces.211265
中图分类号:TM911
河北省中央引导地方科技项目(216Z4406G)和清华大学电力系统国家重点实验室资助课题项目(SKLD21KZ04)资助。
收稿日期 2021-08-12
改稿日期 2021-10-28
刘素贞 女,1969年生,博士,教授,博士生导师,研究方向为工程电磁场与磁技术。E-mail:szliu@hebut.edu.cn(通信作者)
陈晶晶 女,1997年生,硕士研究生,研究方向为锂离子电池温度检测。E-mail:jingjingchen8844@foxmail.com
(编辑 李冰)