图1 几何模型
Fig.1 Geometric model
摘要 通过触头结构设计实现真空电弧有效调控是提高真空开关开断性能的重要措施之一。为提高真空灭弧室触头开断性能，该文采用SolidWorks建立了一种新型带铁心真空灭弧室3D模型，并利用三维有限元法，对触头片的开槽长度、开槽角度、工艺孔直径以及铁心个数四个参数进行单因素及正交仿真实验，选取上述四个因素作为优化对象，将电流峰值时纵向磁感应强度最大、滞后时间最小和导体电阻最低作为优化目标，得到触头参数与磁场特性的回归方程。通过对电流峰值时触头间隙中心平面纵向磁感应强度、电流过零时磁场滞后时间以及导体电阻进行多目标优化分析，得到了最优的磁场特性。结果表明，当开槽长度为25mm、开槽角度为25°、工艺孔直径为15mm、铁心个数为14时，触头的磁场特性最好。
关键词：真空灭弧室 磁场 正交实验 优化设计
真空开关由于其众多优越性在中压领域得到了广泛应用，特别是在12kV领域。如何进一步实现电弧的有效调控进而提高真空开关的开断能力和可靠性是该领域的研究热点之一[1-2]。目前，纵磁控弧技术是真空电弧常用控弧方式之一[3]，市场上利用纵磁控弧的真空灭弧室触头结构有线圈结构和杯状纵磁结构。在12kV等级真空灭弧室中，杯状纵磁结构有着比线圈结构更加广泛的应用[4-9]，而在杯状纵磁触头结构中，触头片的变化较多，对于触头间磁场分布有着较大影响。因此研究磁场特性与触头片设计参数的关系对于提高真空灭弧室的开断性能有重要意义。
针对杯状纵磁触头片的磁场特性，王仲奕、刘志远和张炫等做了大量研究，分析了触头片厚度和开槽数目对触头纵向磁场分布与磁场滞后时间的影响等结果，确定了触头片结构变化对真空灭弧室磁场分布有较大影响[10-12]。以上研究仅对径向开槽触头片作了分析，由于开槽方式也会影响触头片的涡流分布，进而影响磁场滞后时间，因此对于具有一定角度的非径向开槽触头片，也需要研究其磁场分布。为解决这一问题，庞先海对比分析了径向开槽与非径向开槽两种触头片结构的磁场特性，得出非径向开槽磁场特性优于径向开槽[13]，但其未分析不同开槽角度对磁场的影响。谢菲等在此基础上分别研究了不同开槽角度下，触头片结构变化对磁场的影响[14]。为进一步提高真空灭弧室开断电流等级，董华军等在上述研究基础上引入了铁心，分析加入铁心后，磁场分布随触头片结构参数的变化情况，并总结了磁场特性随开槽长度、开槽角度以及工艺孔直径的变化规律[15-16]。上述文献在分析过程中，往往是某一种结构变化，其他结构参数固定不变，而触头磁场分布往往是多结构参数共同影响的结果。为研究多因素变量问题，可引入正交法[17-19]，其用于研究多因素变化影响效果明显，可大大减少计算量，计算结果易于统计分析，为定量分析触头片结构参数变化对磁场特性的影响提供了参考。
基于此，本文以一种带有柱状铁心的新型杯状纵磁真空灭弧室为基础，采用Ansys Maxwell软件对上述模型进行三维瞬态磁场分析，通过设计正交实验并作回归分析，最终得到铁心式真空灭弧室磁场特性与触头片结构参数的定量关系，找出了影响真空灭弧室磁场特性的显著因素，并据此进一步对触头片进行多目标优化，使真空灭弧室磁场特性达到最好，这是以往分析单一变量所不能实现的。
本文采用有限元法对铁心式杯状纵磁触头模型进行三维瞬态磁场仿真，首先通过SolidWorks建立触头几何模型如图1所示。触头系统主要由触头杯座、柱状铁心、触头片以及电弧组成，仿真时所用电弧模型为直径与触头片直径相同、高度与最大开距相同的圆柱体[3,14-19]。随着真空灭弧室小型化的趋势，在固定触头直径的情况下，改变其他结构设计参数，对于提高灭弧室开断能力具有重要意义。本研究将触头直径设置为78mm，开距固定10mm，触头片厚度3mm，其他机构参数：杯座高度24mm，内高19mm，厚度9mm，杯指水平夹角20°，杯指高度18mm，触头片槽长20mm，开槽偏角15°。
图1 几何模型
Fig.1 Geometric model
将几何模型导入Maxwell3D中，选择瞬态磁场求解器，各零件材料设置及属性见表1。其中电工纯铁磁导率因具有饱和效应，考虑其磁化特性曲线的变化如图2所示。激励设置为电流激励，频率50Hz、有效值31.5kA，求解时间为0.02s，步长0.001s，采用软件自适应网格剖分，网格边长为5mm。
表1 各零件材料设置
Tab.1 Material settings of each part
名称材料电导率/(S/m)相对磁导率 杯座铜5.8×1071 触头片铜铬合金1.5×1071 铁心电工纯铁1.0×107B-H曲线 电弧—2 8001
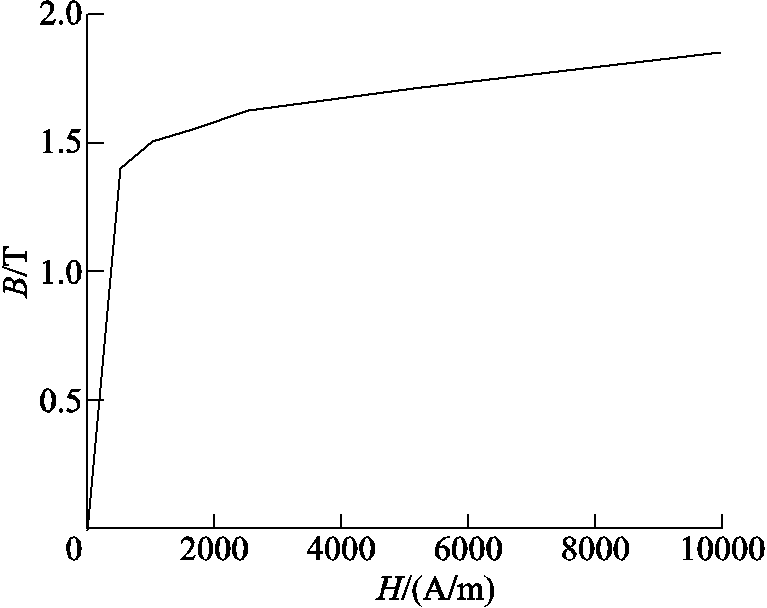
图2 电工纯铁B-H曲线
Fig 2 Electrician pure iron B-H curve
保证电弧扩散所需的临界磁感应强度值计算公式为[20]
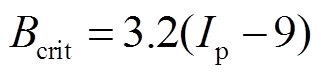（1）
式中，Bcrit为临界磁感应强度，mT；Ip为最大电流值，kA。当瞬态磁场仿真电流取31.5kA时，通过式（1）计算可得出对应的临界磁场为72mT，因此仿真所得磁感应强度值只需大于该值即可满足真空电弧扩散的需求。
为分析真空灭弧室触头片结构参数对其磁场特性的影响，现将开槽长度（A）、开槽角度（B）、工艺孔直径（C）以及铁心个数（D）作为实验因素进行有限元仿真。由于各结构设计参数取值范围不尽相同，可作归一化处理方便各参数之间的比较，因素水平编码表见表2。
表2 因素水平编码表
Tab.2 Coding of factor levels
水平A/mmB/(°)C/mmD/个 125251514 020151110 -115576
首先对0水平即开槽长度取20mm、开槽偏角取15°、工艺孔直径取11mm、铁心个数为10，进行瞬态磁场仿真。其电弧中心平面的磁感应强度分布如图3所示，最大值为0.191T，且超过临界磁场值的触头片面积占比约为88.2%，满足电弧扩散需求。从效果看，磁场在电弧中心平面上基本分布均匀，且磁感应强度最大值位于中心环状区域，这是由于杯指充当了线圈的角色，产生纵向磁场，加之铁心的束磁作用，最终呈现出环状效果。由于涡流的作用，电弧中心处磁感应强度比最大值稍小。
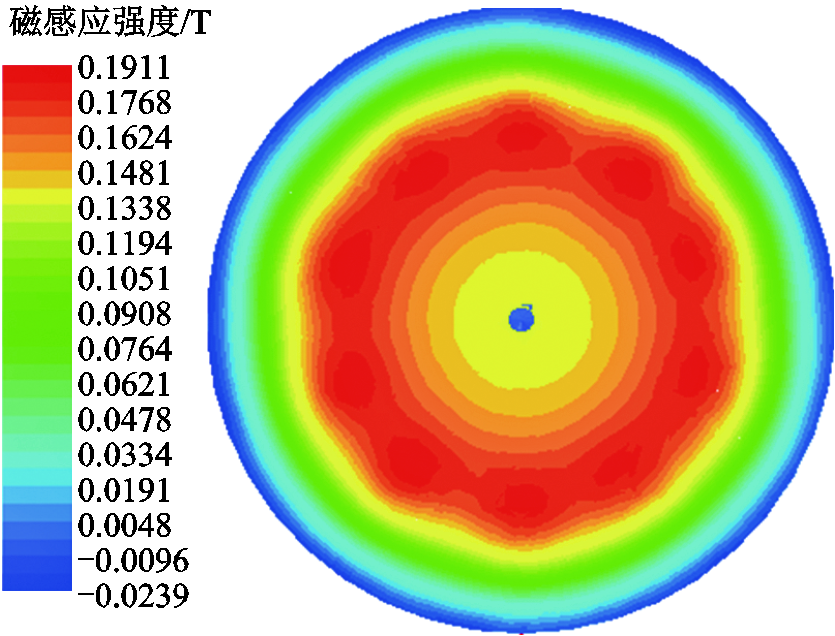
图3 电流峰值时电弧中心平面纵向磁感应强度分布
Fig.3 Distribution of longitudinal magnetic induction intensity in the arc center plane at the peak current
电弧中心平面最大纵向磁感应度值与触头片结构设计参数之间关系如图4所示，二者之间基本呈线性关系。对于开槽长度、开槽角度、工艺孔直径，纵向磁感应强度与结构参数呈正相关，即随着参数取值变大磁场增强；而铁心个数对纵向磁感应强度的影响是先变小后变大，线性关系不明显。
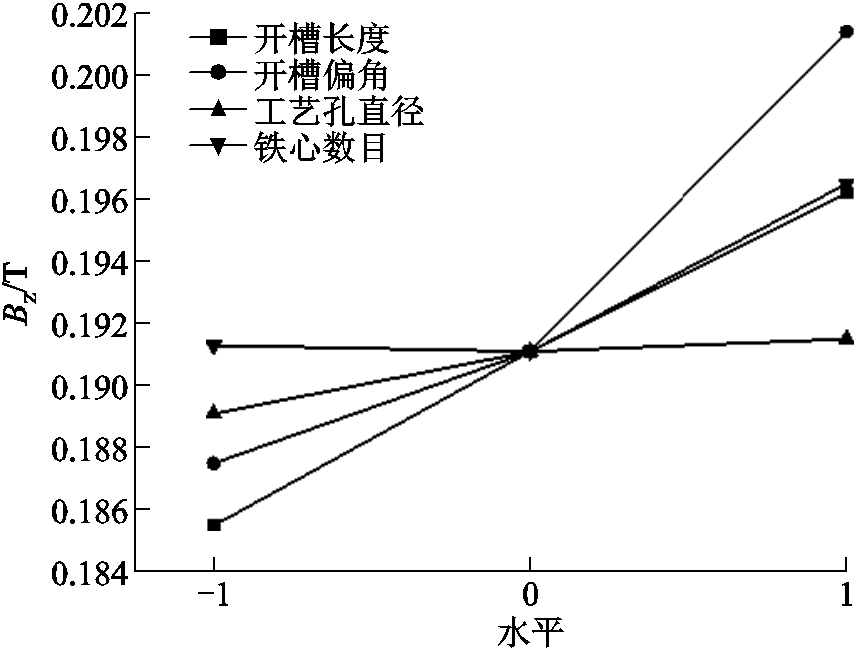
图4 电流峰值时纵向磁感应强度和触头设计参数对应关系
Fig.4 Correspondence between longitudinal magnetic induction intensity and contact design parameters at current peak
由仿真周期0.02s可知，电流在0.01s时过零，查看此时0水平下电弧中心平面磁感应强度分布，如图5所示。由图5可知，电弧中心平面在电流过零时刻纵向磁感应强度在中心处最大，最大值为0.041 3T，在电弧边缘处最小，最小值为-0.005 6T。因此，位于电弧中心的一点，其磁场滞后时间最长。磁场滞后时间是纵向磁感应强度过零时刻与电流过零时刻的差值，可通过Maxwell3D场计算器计算得到。0水平下，其磁场滞后时间为0.912 3ms，沿电弧中心平面x轴径向分布情况如图6所示。由图6可得，磁场滞后时间在x轴方向上的分布为“山峰”状，“峰顶”在原点处，“峰底”在电弧边缘处。
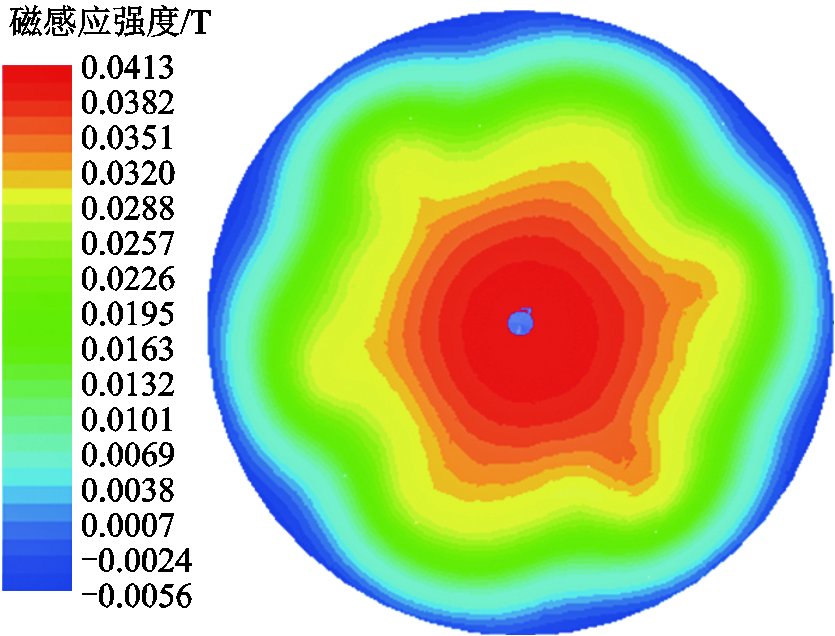
图5 电流过零时电弧中心平面纵向磁感应强度分布
Fig.5 The longitudinal magnetic induction intensity distribution in the arc center plane when the current crosses zero
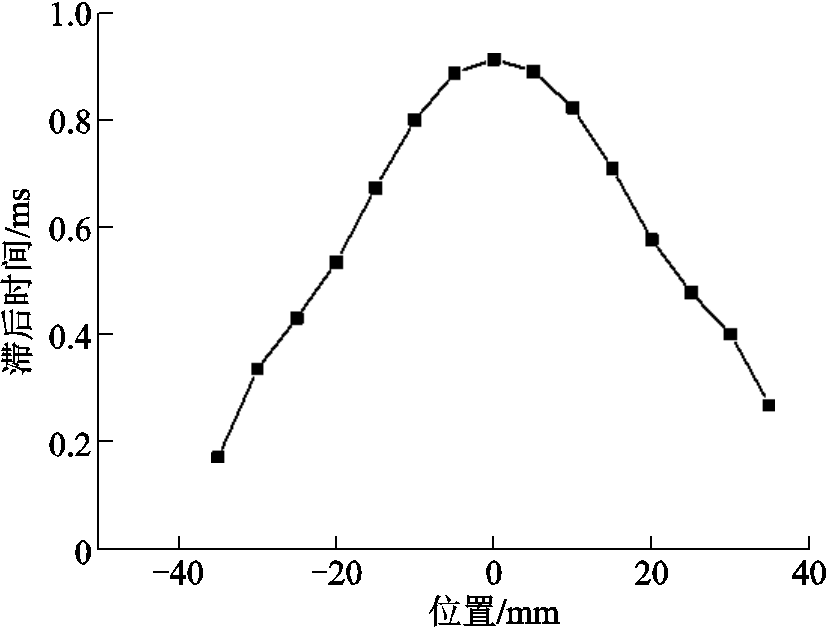
图6 磁场滞后时间沿触头开距中心平面径向分布
Fig.6 Radial distribution between the magnetic field hysteresis along the center plane of the contact distance
电弧中心点磁场滞后时间与触头片结构设计参数的关系如图7所示，对于开槽长度、工艺孔直径，电弧中心点磁场滞后时间与结构参数大致呈负相关，即磁场滞后时间随参数取值增大而减小；对于开槽角度，磁场滞后时间与结构参数呈正相关，即磁场滞后时间随参数取值增大而增大；而铁心个数对滞后时间的影响线性关系不明显。
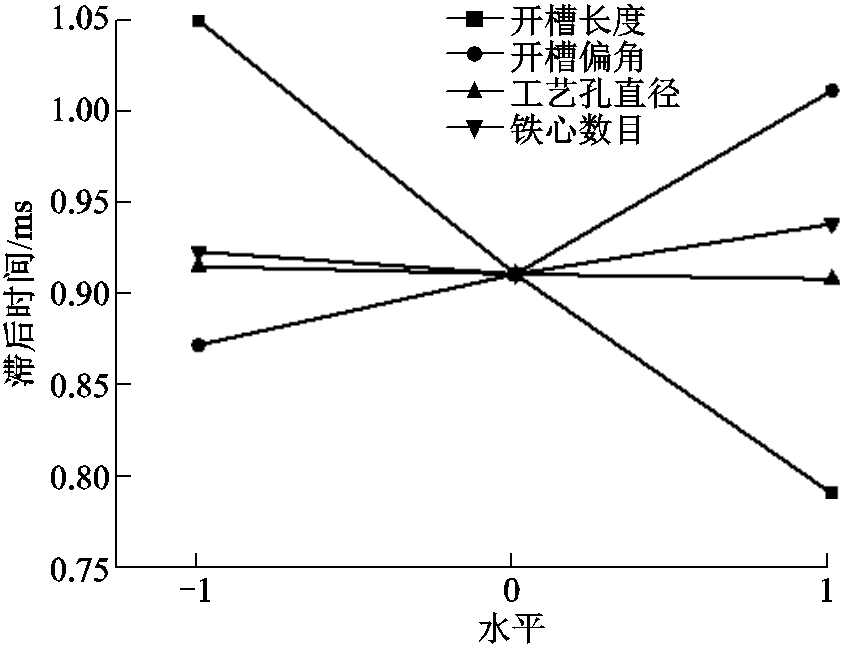
图7 磁场滞后时间和触头设计参数对应关系
Fig.7 Correspondence between magnetic field lag time and contact design parameters
触头系统电阻的大小对于真空灭弧室的温升有很大影响，并且当温升过高时，会严重影响灭弧室的电气性能。本文导体电阻指的是两个触头杯座、两个触头片以及铁心和支撑盘电阻之和，可通过场计算器计算欧姆损耗，根据电流大小，计算出导体电阻值，各因素对电阻值的影响如图8所示。
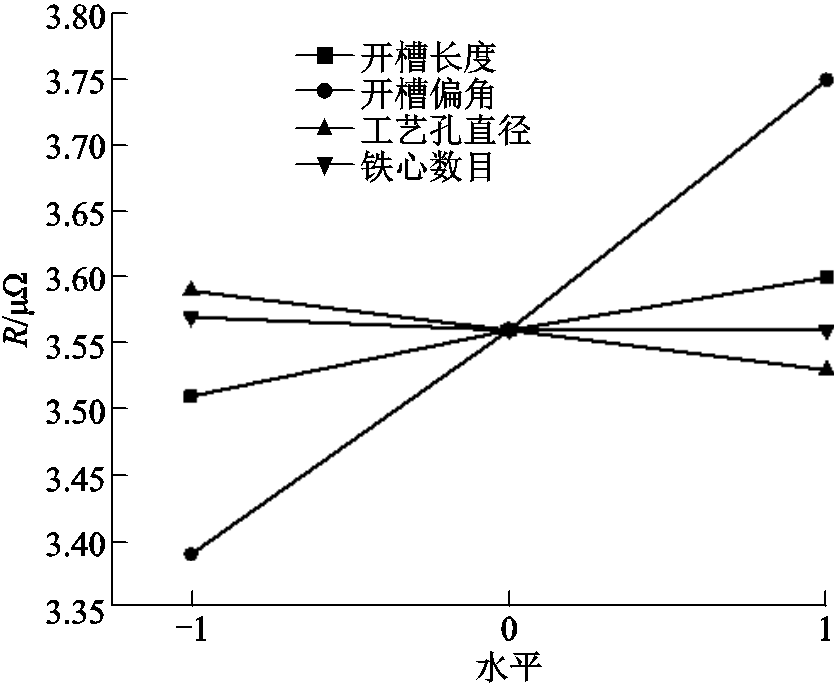
图8 导体电阻和触头设计参数对应关系
Fig.8 Correspondence between conductor resistance and contact design parameters
从图8中不难看出，导体电阻与触头片结构设计参数呈单调关系。其中，电阻随开槽角度、开槽长度增加单调递增；随杯指工艺孔直径、铁心个数单调递减。并且图8中显示，开槽偏角对导体电阻影响最大，即随着开槽长度增加，导体电阻有明显增大的趋势。
将上述四个触头结构参数作为因素设计正交实验，因素取值与水平编码参照表2，不考虑各因素之间的交互作用，参考文献[21-22]，可用L9(34)正交表进行实验分析，结果见表3，其中Bz是电弧中心点在峰值电流时刻下纵向磁感应强度值；T代表该点的磁场滞后时间；R代表导体电阻。
表3 正交实验表
Tab.3 Orthogonal experiment table
序号A/mmB/(°)C/mmD/个Bz/TT/msR/μΩ 1155760.182 61.052 73.42 2151511100.189 71.057 83.52 3152515140.186 21.130 13.60 420511140.187 20.882 93.40 520151560.190 70.913 23.53 620257100.200 71.019 43.77 725515100.180 20.720 43.37 825157140.195 00.814 43.61 925251160.199 10.868 93.78
由表3可得，触头任意两结构参数具有正交性，其中任一因素不同水平之间进行比较时，其他因素对其的影响相互抵消。此方法有效地减少了实验次数，所得数据具有典型性。
根据正交实验结果数据，现将电流峰值时刻纵向磁感应强度与各因素参数作线性回归分析，得到回归方程为
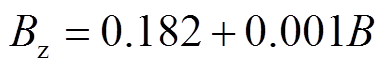（2）
通过回归分析可知，模型R2值为0.972，意味着杯指深度、杯指夹角、开槽长度以及开槽角度可解释纵向磁感应强度97.2%的变化原因。对模型进行F检验时发现F=40.198，P=0.002＜0.05，也说明上述四个因素至少有一项对纵向磁感应强度有影响。
此回归方程P值小于0.01，故可认为此方程是高度显著的，方程系数与方差分析结果见表4。
表4 电流峰值时纵向磁场强度和触头设计参数的回归方程系数及其方差分析结果
Tab.4 The regression equation coefficients and variance analysis results of the longitudinal magnetic field strength and the contact design parameters at the peak current
因素截距/mmA/mmB/(°)C/mmD/个 系数0.1820.0010.001-0.0010 P值＜0.010.1730.0190.090.696
由表4可知，开槽角度的回归系数值为0.001(P=0.019＜0.05)，意味着开槽角度会对纵向磁感应强度产生显著的正向影响关系；而开槽长度、工艺孔直径以及铁心个数，其P值均大于0.05，意味着三种因素对纵向磁感应强度影响均不显著，因此式（2）中，回归方程并没有包含开槽长度、工艺孔直径和铁心个数。
根据回归方程，开槽角度取1水平时，磁感应强度最强，最大值为0.197T；开槽角度取-1水平时，磁感应强度最弱，最小值为0.191T。
将磁场滞后时间与各因素作线性回归分析，得到回归方程为
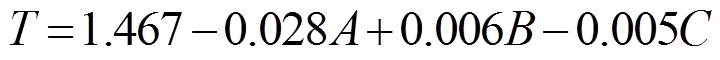（3）
通过回归分析可知，模型R2值为0.994，意味着杯指深度、杯指夹角、开槽长度以及开槽角度可以解释磁场滞后时间99.4%的变化原因。对模型进行F检验时发现F=155.295，P=0.006＜0.05，也说明上述四个因素至少有一项对磁场滞后时间有影响。
此回归方程P值小于0.01，可认为此回归方程是高度显著的。方程系数与方差分析结果见表5。
表5 磁场滞后时间和触头设计参数的回归方程系数及其方差分析结果
Tab.5 Regression equation coefficients and variance analysis results of magnetic field lag time and contact design parameters
因素截距/mmA/mmB/(°)C/mmD/个 系数1.467-0.0280.006-0.0050 P值＜0.01＜0.010.0010.0290.851
由表5可知，开槽长度的回归系数值为-0.028（P＜0.01），意味着此设计因素会对磁场滞后时间产生高度显著的负向影响关系；开槽角度的回归系数值为0.006（P=0.001＜0.01），意味着此设计因素会对磁场滞后时间产生高度显著的正向影响关系；工艺孔直径回归系数值为-0.005（P=0.029＜0.05），意味着此因素会对磁场滞后时间产生显著的负向影响关系；铁心个数的回归系数值为0（P＞0.05），意味着该设计因素对磁场滞后时间影响最不显著，因此式（3）中，回归方程并没有包含铁心个数。
根据回归方程，工艺孔直径和开槽长度取-1水平，开槽角度取1水平时，可得最大磁场滞后时间1.163ms；工艺孔直径和开槽长度取1水平，开槽角度取-1水平时，可得最小磁场滞后时间0.723ms。
根据结果数据，将导体电阻与各因素参数作线性回归分析，得到回归方程为
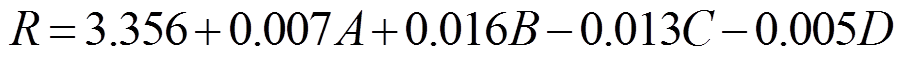（4）
通过回归分析可知，模型R2=0.994，意味着杯指深度、杯指夹角、开槽长度以及开槽角度可以解释异体电阻R的99.4%的变化原因。对模型进行F检验时发现F=154.962，P＜0.01，即说明开槽长度、开槽角度、工艺孔直径和铁心个数中至少有一项会对R产生影响关系。
此回归方程P值小于高度显著性水平0.01，故可认为此方程是高度显著的，方程系数与方差分析结果见表6。
表6 导体电阻值和触头设计参数的回归方程系数及其方差分析结果
Tab.6 The regression equation coefficients of conductor resistance and contact design parameters and the results of variance analysis
因素截距/mmA/mmB/(°)C/mmD/个 系数3.3560.0070.016-0.013-0.005 P值＜0.010.006＜0.010.0020.045
由表6可知，开槽长度的回归系数值为0.007（P=0.006＜0.01），意味着此设计因素对导体电阻产生高度显著的正向影响关系；开槽角度的回归系数值为0.016(P＜0.01)，意味着此设计因素对导体电阻产生高度显著的正向影响关系；工艺孔直径的回归系数值为-0.013(P=0.002＜0.01)，意味着此设计因素对导体电阻产生高度显著的负向影响关系；铁心个数的回归系数值为-0.005(P=0.045＜0.05)，意味着此设计因素对导体电阻产生显著的负向影响关系。
由式（4）可得，当开槽长度、开槽角度取1水平，工艺孔直径、铁心个数取-1水平时，导体电阻最大，为3.822μΩ；当开槽长度、开槽角度取-1水平，工艺孔直径、铁心个数取1水平时，导体电阻最小，为3.289μΩ。
为验证经上述分析拟合而得的回归方程的有效性，分别将单因素分析的9组实验结果与通过回归方程计算的结果相比较，计算两者之间相对误差E与平均误差Eav，计算公式为
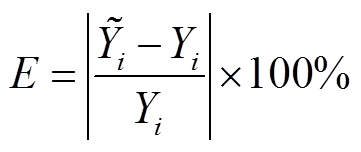（5）
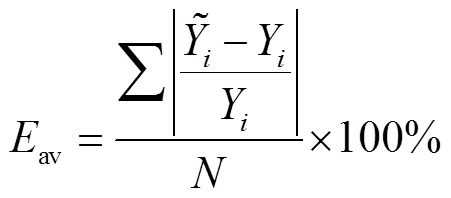（6）
式中，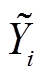
为第i号实验通过回归方程计算的结果；Yi为第i号实验的仿真结果；N为实验总数。结果见表7～表10。
表7 电流峰值时纵向磁场强度回归方程检验结果
Tab.7 Test results of regression equation of longitudinal magnetic field intensity at current peak
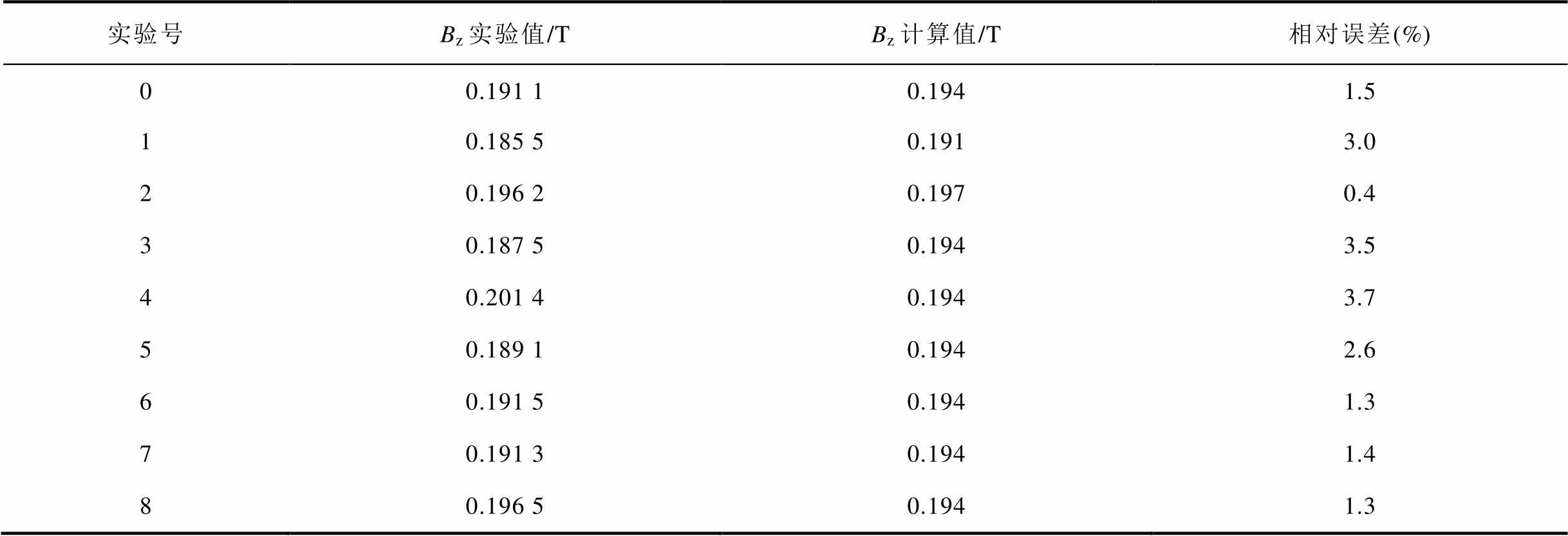
实验号Bz实验值/TBz计算值/T相对误差(%) 00.191 10.1941.5 10.185 50.1913.0 20.196 20.1970.4 30.187 50.1943.5 40.201 40.1943.7 50.189 10.1942.6 60.191 50.1941.3 70.191 30.1941.4 80.196 50.1941.3
表8 磁场滞后时间回归方程检验结果
Tab.8 Test results of the regression equation of the magnetic field lag time
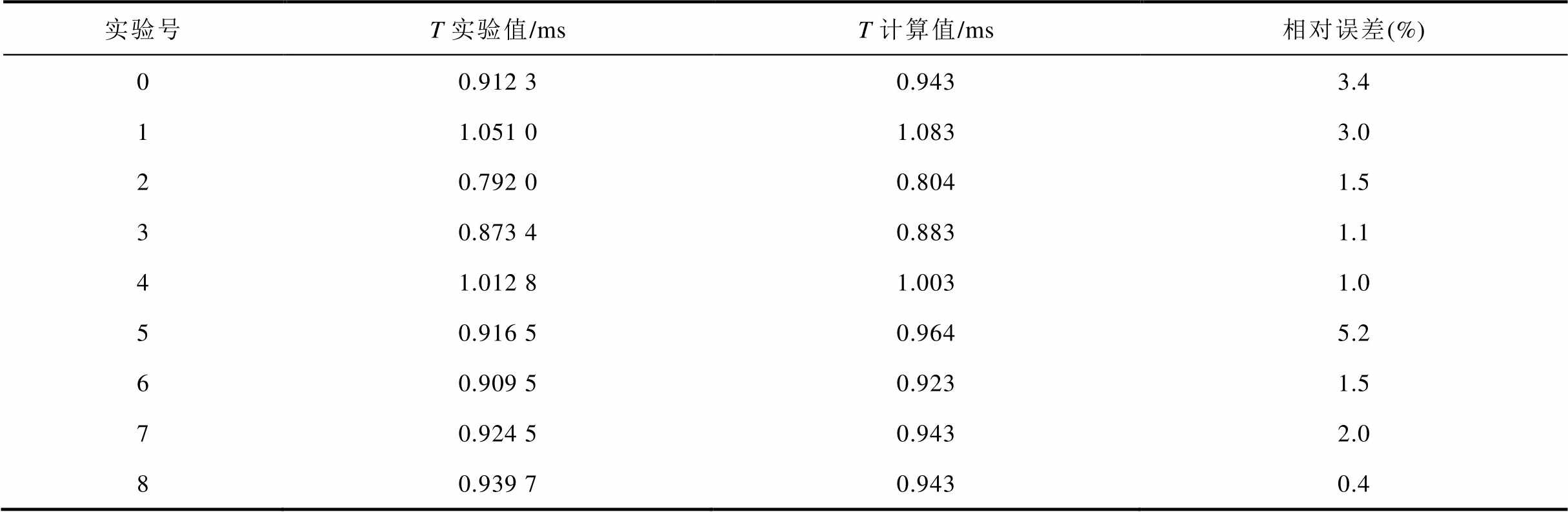
实验号T实验值/msT计算值/ms相对误差(%) 00.912 30.9433.4 11.051 01.0833.0 20.792 00.8041.5 30.873 40.8831.1 41.012 81.0031.0 50.916 50.9645.2 60.909 50.9231.5 70.924 50.9432.0 80.939 70.9430.4
表9 导体电阻值回归方程检验结果
Tab.9 Test results of conductor resistance regression equation
实验号R实验值/μΩR计算值/μΩ相对误差(%) 03.563.5560.1 13.513.5190.3 23.603.5920.2 33.393.3960.2 43.753.7160.9 53.593.6060.4 63.533.5060.7 73.573.5760.2 83.563.5360.7
表10 回归方程检验结果
Tab.10 Regression equation test results
磁场特性最大相对误差(%)平均误差(%) 峰值磁感应强度3.72.1 过零滞后时间5.22.1 导体电阻0.90.4
从表7～表10可以得出，回归方程计算结果和有限元分析结果的相对误差均在15%以内，参考文献[17-19]，在此误差范围内可以认为回归方程正确。
在提高纵向磁场极限开断能力方面，通过触头系统产生的纵向磁场越强，越有利于抑制电弧的收缩效应，将其保持在扩散态，因此，为更好地控制真空电弧，提高其纵向磁感应强度是真空灭弧室的一个优化指标；由于交流电通过导体时会产生涡流，因此电流过零时刻，触头间隙会存在剩余磁场，对于电弧扩散极为不利，若剩余磁场过强，会导致开断失败，因此，如何降低剩余磁场即如何降低磁场滞后时间也是真空灭弧室的一个优化指标；电流流过导体时，由于电阻的存在，会使导体自身温度升高，当超过导体允许的最大温升之后，就会对其机械强度以及电气性能造成影响，因此，在设计时，应尽可能减小导体电阻，这也是真空灭弧室的一个优化指标。综上所述，为提高真空灭弧室开断能力，现将电流峰值时刻纵向磁感应强度、过零时刻磁场滞后时间以及导体电阻作为优化目标。
为量化描述真空灭弧室磁场特性，用f(x)来表示，fmax、fmin为磁场特性的最大值和最小值。对于任意的f(x)归一处理。
当磁场特性与优化指标呈正相关时
（7）
当磁场特性与优化指标呈负相关时
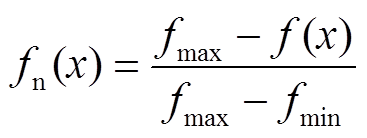（8）
按照式（7）、式（8），纵向磁感应强度与磁场特性呈正相关，磁场滞后时间与磁场特性呈负相关，可建立
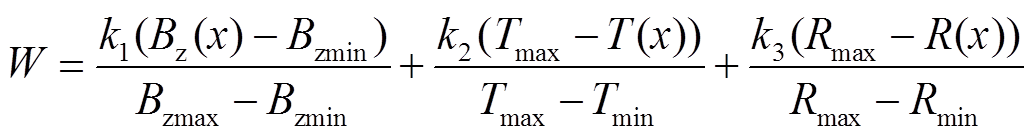（9）
式中，k1、k2、k3分别为纵向磁感应度、磁场滞后时间与导体电阻的权重，假设它们对磁场特性具有同等重要的影响，即k1= k2= k3=1/3。将第4节所得磁感应强度、滞后时间以及导体电阻的拟合公式（2）～式（4）代入，化简得
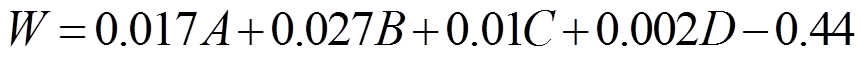（10）
由式（10）可得，当四种因素取1水平时，磁场特性最好，此时W=0.84，参考文献[17-19]，W越接近1，说明磁场特性越好。此时，纵向磁感应强度为0.207T，磁场滞后时间为0.842ms，导体电阻为3.666μΩ。
本文通过有限元仿真和正交回归分析法对一种带铁心的新型真空灭弧室触头磁场特性进行了分析与优化，在本文参数变化范围内，得出以下结论：
1）电流峰值时刻，电弧中心平面的纵向磁感应强度随开槽角度、开槽长度和工艺孔直径增大而增大。其中开槽角度对纵向磁感应强度具有显著影响。
2）电流过零时刻磁场滞后时间随开槽角度的增大而增大，随开槽长度和工艺孔直径的增大而减小。其中，开槽长度和开槽角度对磁场滞后时间的影响高度显著，工艺孔直径对其有显著影响。
3）导体电阻随开槽长度和开槽角度增大而增大，随工艺孔直径和铁心个数增大而减小。其中开槽长度、开槽角度和工艺孔直径对电阻的影响高度显著，铁心个数对电阻有显著影响。
4）通过回归分析得到了铁心式新型真空灭弧室杯状纵磁触头片结构参数影响其磁场特性的回归方程。根据回归方程，对触头结构参数进行优化，得到了磁场特性最优时的结构参数。最终优化结果：当开槽长度为25mm，开槽角度为25°，工艺孔直径为15mm，铁心个数为14时，峰值时刻纵向磁感应强度为0.207T，磁场滞后时间为0.842ms，导体电阻为3.666μΩ。
参考文献
[1] 付思, 曹云东, 李静, 等. 触头分离瞬间真空金属蒸气电弧形成过程的仿真[J]. 电工技术学报, 2020, 35(13): 2922-2931.
Fu Si, Cao Yundong, Li Jing, et al. Simulation researches on vacuum metal vapor arc formation at the initial moment of contact parting[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2922-2931.
[2] 王灿, 杜船, 徐杰雄. 中高压直流断路器拓扑综述[J]. 电力系统自动化, 2020, 44(9): 187-199.
Wang Can, Du Chuan, Xu Jiexiong. Review of topologies for medium-and high-voltage DC circuit breaker[J]. Automation of Electric Power Systems, 2020, 44(9): 187-199.
[3] 董华军, 杨海军, 郭英杰, 等. 一种具有横纵磁场的新型真空灭弧室触头三维磁场仿真[J]. 电工技术学报, 2015, 30(5): 111-118.
Dong Huajun, Yang Haijun, Guo Yingjie, et al. 3-D magnetic field simulation of a new-type contact with TMF-AMF for vacuum interrupters[J]. Transactions of China Electrotechnical Society, 2015, 30(5): 111-118.
[4] 张颖, 秦涛涛, 刘钊. 真空直流强迫过零开断中的弧后电流[J]. 电工技术学报, 2021, 36(2): 417-424.
Zhang Ying, Qin Taotao, Liu Zhao. Post arc current in vacuum DC interruption with forced current zero method[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 417-424.
[5] 王季梅, 刘志远, 修士新, 等. 国内外开发研究高压真空断路器和向超高压发展的概况[J]. 电气技术, 2006, 7(12): 5-9.
Wang Jimei, Liu Zhiyuan, Xiu Shixin, et al. Development and research of high-voltage vacuum circuit breaker at home and abroad and its development to ultra-high voltage[J]. Electrical Engineering, 2006, 7(12): 5-9.
[6] 蒋原, 李擎, 崔家瑞, 等. 纵向磁场下中频真空电弧的重燃现象分析[J]. 电工技术学报, 2020, 35(18): 3860-3868.
Jiang Yuan, Li Qing, Cui Jiarui, et al. Re-ignition of intermediate frequency vacuum arc at axial magnetic field[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3860-3868.
[7] 温伟杰, 李鹏宇, 李斌, 等. 多端口机械式直流断路器的动作策略与参数优化[J]. 电力系统自动化, 2021, 45(11): 86-94.
Wen Weijie, Li Pengyu, Li Bin, et al. Operation strategy and parameter optimization of multi-port mechanical DC circuit breaker[J]. Automation of Electric Power Systems, 2021, 45(11): 86-94.
[8] 蒋原, 李擎, 夏丽娜, 等. 中频条件下真空灭弧室的纵向磁场仿真[J]. 电工技术学报, 2021, 36(11): 2424-2432.
Jiang Yuan, Li Qing, Xia Lina, et al. Simulation of axial magnetic field in vacuum arc interrupters at intermediate frequency[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2424-2432.
[9] 李博, 包涌泉, 彭振东, 等. 基于改进型直流真空断路器弧后暂态仿真及介质恢复特性分析[J]. 电工技术学报, 2021, 36(8): 1752-1760.
Li Bo, Bao Yongquan, Peng Zhendong, et al. Post-arc transient simulation and dielectric recovery analysis based on improved DC vacuum circuit breaker[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1752-1760.
[10] 王仲奕, 刘志远, 张炫, 等. 五种纵向磁场真空灭弧室触头磁场特性分析比较[J]. 电工电能新技术, 2006, 25(1): 21-25, 67.
Wang Zhongyi, Liu Zhiyuan, Zhang Xuan, et al. Comparison of axial magnetic field characteristics of 5 axial magnetic field vacuum interrupter contacts[J]. Advanced Technology of Electrical Engineering and Energy, 2006, 25(1): 21-25, 67.
[11] 刘志远, 王仲奕, 王季梅, 等. 杯状纵磁触头纵向磁场滞后时间研究[J]. 高压电器, 2004, 40(2): 87-90.
Liu Zhiyuan, Wang Zhongyi, Wang Jimei, et al. Study on phase shift time of cup-type axial magnetic field contact[J]. High Voltage Apparatus, 2004, 40(2): 87-90.
[12] 张炫, 刘志远, 王仲奕. 杯状纵磁真空灭弧室磁场特性分析[J]. 高压电器, 2005, 41(3): 161-165, 169.
Zhang Xuan, Liu Zhiyuan, Wang Zhongyi. Analysis of axial magnetic field in vacuum interrupters with cup type axial magnetic field contacts[J]. High Voltage Apparatus, 2005, 41(3): 161-165, 169.
[13] 庞先海, 景皓, 修士新, 等. 真空灭弧室杯状纵向磁场触头的仿真分析[C]//2014年江西省电机工程学会年会论文集, 南昌, 2014: 274-279.
[14] 谢菲, 叶兆平, 修士新. 触头片开槽方式对杯状纵磁触头磁场特性的影响[C]//2010输变电年会论文集, 南京, 2010: 40-46.
[15] 杨海军, 郭英杰, 康凯, 等. 两种不同铁芯结构纵磁真空灭弧室触头三维磁场对比分析[J]. 真空, 2015, 52(2): 61-65.
Yang Haijun, Guo Yingjie, Kang Kai, et al. Comparative analysis of 3-D magnetic field for axial magnetic field vacuum interrupter contact with two different iron core structure[J]. Vacuum, 2015, 52(2): 61-65.
[16] 董华军, 司明月, 郭英杰, 等. 触头片结构对新型带铁心的杯状纵磁真空灭弧室磁场影响仿真[J]. 电工技术学报, 2018, 33(11): 2448-2455.
Dong Huajun, Si Mingyue, Guo Yingjie, et al. Influence of contact plate structure on magnetic field strength of a new type of cup-shaped axial magnetic field vacuum interrupter with iron core[J]. Transactions of China Electrotechnical Society, 2018, 33(11): 2448-2455.
[17] 韩国辉, 李昊旻, 韩桂全, 等. 126kV真空灭弧室2/3匝纵磁触头磁场分析及优化[J]. 高压电器, 2017, 53(3): 76-83.
Han Guohui, Li Haomin, Han Guiquan, et al. Analysis and optimization of axial magnetic field characteristics of a 2/3 tune coil-type contacts for 126kV vacuum interrupter[J]. High Voltage Apparatus, 2017, 53(3): 76-83.
[18] 郑跃胜, 刘志远, 王仲奕, 等. 基于正交设计的杯状纵磁真空灭弧室磁场特性分析[J]. 中国电机工程学报, 2007, 27(9): 23-27.
Zheng Yuesheng, Liu Zhiyuan, Wang Zhongyi, et al. Analysis of magnetic field characteristics of vacuum interrupters with cup-type axial magnetic field contacts based on orthogonal design[J]. Proceedings of the CSEE, 2007, 27(9): 23-27.
[19] 刘志远, 郑跃胜, 王仲奕, 等. 252kV真空灭弧室纵磁触头磁场分析及优化[J]. 中国电机工程学报, 2008, 28(15): 123-129.
Liu Zhiyuan, Zheng Yuesheng, Wang Zhongyi, et al. Analysis and optimization of axial magnetic field characteristics of 252kV vacuum interrupter contacts[J]. Proceedings of the CSEE, 2008, 28(15): 123-129.
[20] Li Dandan, Qiao Zhenyang, Yang Na, et al. Study on vector magnetic properties of magnetic materials using hybrid hysteresis model[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(3): 292-296.
[21] 李云雁, 胡传荣. 试验设计与数据处理[M]. 北京: 化学工业出版社, 2005.
[22] 刘文卿. 实验设计[M]. 北京: 清华大学出版社, 2005.
Simulation and Optimization of the Contact Magnetic Field of a New Type of Vacuum Interrupter Based on Orthogonal Experiment
Abstract The effective control of vacuum arc through the design of the contact structure is one of the important measures to improve the breaking performance of the vacuum switch. In order to improve the contact breaking performance of the vacuum interrupter, it is established a new type of 3D model of the vacuum interrupter with iron core through SolidWorks, and based on the three-dimensional finite element method, single factor and orthogonal simulation experiments are performed on the four parameters of the contact's slotting length, slotting angle, process hole diameter and the number of cores. The above 4 factors are selected as the optimization objects, then the maximum longitudinal magnetic induction intensity at the peak current, the minimum lag time and the minimum conductor resistance are the optimization objectives, and the regression equation of the contact parameters and the magnetic field characteristics is obtained. Through the multi-objective optimization analysis of the longitudinal magnetic inductance of the center plane of the contact gap when the current peaks, the magnetic field lag time when the current crosses zero, and the conductor resistance, the optimal magnetic field characteristics are obtained. The results show that when the slotting length is 25mm, the slotting angle is 25°, the process hole diameter is 15mm, and the number of iron cores is 14, the magnetic field characteristics of the contact are the best.
keywords：Vacuum interrupter, magnetic field, orthogonal experiment, optimal design
DOI:10.19595/j.cnki.1000-6753.tces.210719
中图分类号：TM561
国家自然科学基金项目（51477023）和辽宁省自然科学基金计划项目（2019-MS-036）资助。
收稿日期 2021-05-19
改稿日期 2021-08-13
董华军 男，1978年生，教授，博士生导师，研究方向为真空开关电弧基础理论、图像处理及识别。E-mail：huajundong4025@163.com（通信作者）
温超阳 男，1996年生，硕士研究生，研究方向为真空开关电磁场仿真技术。E-mail：3283995105@qq.com
（编辑 赫蕾）