高带宽数字控制LCL型并网逆变器及其提高并网系统鲁棒性的谐振抑制技术研究
沈姝衡 方天治 章益凡
(南京航空航天大学自动化学院 南京 211106)
摘要 数字控制LCL型并网逆变器的固有控制延时会影响原有谐振阻尼方案的控制特性,从而降低并网逆变器在弱电网下的鲁棒性。该文首先基于不同参数建立多机并联系统在弱电网下的多输入多输出矩阵,并推出了确保系统进网电流稳定性以及各模块交互电流稳定性的三条判据。进一步地,基于频域阻抗法分析数字控制延时在模块采用不同开关频率的情况下对系统鲁棒性的影响,进而发现在系统中引入高带宽逆变器对于抑制低频谐振的有效性。然后,分析了高频模块与低频模块之间的交互稳定性,据此选取高带宽并网逆变器的开关频率。最后,在实验室搭建了一台基于新型宽禁带器件GaN的高带宽并网逆变器原理样机,并将其并入低频模块并网系统中,通过实验验证了所提出的高带宽并网逆变器有助于提高弱电网下系统的鲁棒性,从而为提高分布式发电系统的稳定性提供了新思路。
关键词:多并网逆变器并联系统 鲁棒性 高带宽 GaN器件
0 引言
并网逆变器作为可再生能源与电网之间的能量交换接口,已成为分布式发电系统的重要组成部分[1-2]。为提高入网的电能质量,需在逆变器和电网之间加入滤波器。相对于单L滤波器,LCL滤波器具有更好的高频谐波抑制能力,且可有效减小滤波器的体积和质量。但LCL滤波器会引入固有的谐振尖峰[3-4],对之抑制的方案包括无源阻尼和有源阻尼[5-7]。其中较为行之有效的方案是电容电流比例反馈有源阻尼法,其效果相当于在滤波电容两端并联一个虚拟电阻以抑制谐振尖峰,且不会引入额外的功率损耗[8-9]。
目前并网逆变器多采用数字控制,其与模拟控制相比具有控制灵活、通用性强等优点[10]。对于数字控制LCL型并网逆变器而言,其引入的固有控制延时将导致电容电流反馈有源阻尼不再等效于并联在滤波电容两端的虚拟电阻,而是等效于一个随频率变化的虚拟阻抗[11-12],这使得采用不同电流控制方式的并网逆变器为保证系统稳定运行需满足不同的频率条件。对于单网侧电感电流反馈(Grid Current Feedback, GCF)控制方式而言,当fs/6<fr <fs/2时(fs为系统采样频率,fr为系统谐振频率),系统的相频曲线将在谐振尖峰之前的频率点提前穿越-180º,此时无需额外增加阻尼环节即可保证系统稳定[13];对于单逆变器侧电感电流反馈(Inverter Current Feedback, ICF)控制方式,当0<fr<fs/6时,并网逆变器可以稳定工作;而对于网侧电感电流反馈结合电容电流反馈有源阻尼的控制方式,此时满足fr≠ fs/6即可保证系统稳定[14]。
随着分布式电源并网功率等级的增加,越来越多的并网逆变器以并联的形式并入分布式并网发电系统中,共同向电网输送功率,这使得电网呈现出弱电网的特性。弱电网下宽范围变化的电网阻抗Zg会使得系统的谐振频率fr发生变化,由此导致不同电流控制方式下数字控制并网逆变器的特定稳定频率条件极容易不成立。综合以上分析可见,提高弱电网下数字控制并网逆变器对宽范围可变电网阻抗的鲁棒性在实际工程应用中尤为重要。
提高并网系统鲁棒性的途径之一是减小数字控制延时。由于数字控制延时中的计算延时为调制信号装载与采样的时间间隔,因此减小计算延时最直接的方法就是改变采样瞬间或调制信号装载瞬间的时序[15-17]。另一种减小数字延时的方法是通过采用适当的控制方案来补偿数字控制延时以扩大电容电流有源阻尼等效阻抗的虚拟正阻区域频率边界。文献[18]提出一种虚拟阻容阻尼器,文献[19]则提出一种相位超前单元,均有效扩大了正阻区域以补偿数字控制延时。综上可见,以上方案对提高并网系统的鲁棒性均带来了有效帮助,但由于它们都需对现有的已进行模块化设计的并网逆变器的内部结构(包括控制算法等)进行改变和重塑,故可能带来开发周期及成本的增长。
近年来电力电子装置的发展呈现高频化的趋势,在新型宽禁带器件完全取代目前的普通Si器件之前,低频与高频电力电子装置并存的局面必然存在。而探究如何有效利用高频化所带来的优势具有重大意义,其中一种效益就是生成高频电力电子模块以改善原有系统稳定性,这在直流微电网系统中已有所体现。如在文献[20]中,针对直流微电网中恒功率负载的不稳定性情况,通过储能单元和高带宽功率变换器将等效负载阻抗设定为一个自适应智能电阻,使系统本身在负载点动态地保持稳定性,同时可有效减小系统尺寸。其中的高带宽功率变换器采用了新型宽禁带器件氮化镓(GaN)来提高开关频率,以实现其高带宽特性。
然而,上述效益获取方式尚未应用于交流场合,本文即考虑将新型宽禁带器件引入交流并网场合中,得到基于GaN的高频(高带宽)并网逆变器,以抑制原有系统在弱电网下的的低频谐振。这一方案无需更改原逆变器模块的控制方式,从而为提高分布式发电系统的稳定性与鲁棒性提供新的思路。实际上,随着高频逆变模块并入电网,会形成高频与低频装置并存的局面,故有必要对多个模块并联并网系统中不同开关频率对系统在弱电网下鲁棒性的影响加以分析,而目前亦鲜有文献对基于参数不同的多机并联并网系统展开研究。
本文首先从建立多机并联并网系统在弱电网下的诺顿等效模型出发,在各模块参数不同的前提下建立多输入多输出矩阵,分析并得出系统的进网电流稳定性判据以及交互电流稳定性判据。接着从系统等效输出导纳相频特性曲线的角度入手,分析数字控制延时在模块采用不同开关频率的情况下对系统鲁棒性的影响,进而发现在系统中引入高频模块对于抑制低频谐振的有效性。进一步地,论文分析了高频模块与低频模块之间的交互稳定性,并以此作为高频并网逆变器开关频率的选择依据。最后,搭建原理样机进行了实验验证,实验结果表明,高带宽并网逆变器在保证自身稳定性的前提下,在并入并网系统中实现对低频谐振的有效抑制以提高整个系统的鲁棒性,且能以便携的“姿态”为系统注入功率。
1 弱电网下多逆变器并联并网系统的稳定性判据推导
1.1 基于不同参数的多输入多输出矩阵的构建
图1给出了弱电网下多逆变器并联并网系统的电路拓扑,其中,Vinj(j=1, 2, ,n)为各模块直流侧输入电压,vinj为各模块桥臂中点电压,L1j、Cj、L2j分别为各模块LCL型滤波器的逆变器侧滤波电感、输出滤波电容以及网侧滤波电感,iL1j、iCj、iL2j分别为各模块逆变器侧电感电流、输出滤波电容电流以及各模块的输出电流,vPCC为公共耦合点(Point of Common Coupling, PCC)电压,ig为并网电流,Yg为电网导纳,vg为交流电网电压。由于在实际应用中不能保证并入电网的所有逆变器模块的参数都是一致的,故为不失一般性,考虑系统中各逆变器模块的控制方式、参数等都不尽相同。
,n)为各模块直流侧输入电压,vinj为各模块桥臂中点电压,L1j、Cj、L2j分别为各模块LCL型滤波器的逆变器侧滤波电感、输出滤波电容以及网侧滤波电感,iL1j、iCj、iL2j分别为各模块逆变器侧电感电流、输出滤波电容电流以及各模块的输出电流,vPCC为公共耦合点(Point of Common Coupling, PCC)电压,ig为并网电流,Yg为电网导纳,vg为交流电网电压。由于在实际应用中不能保证并入电网的所有逆变器模块的参数都是一致的,故为不失一般性,考虑系统中各逆变器模块的控制方式、参数等都不尽相同。
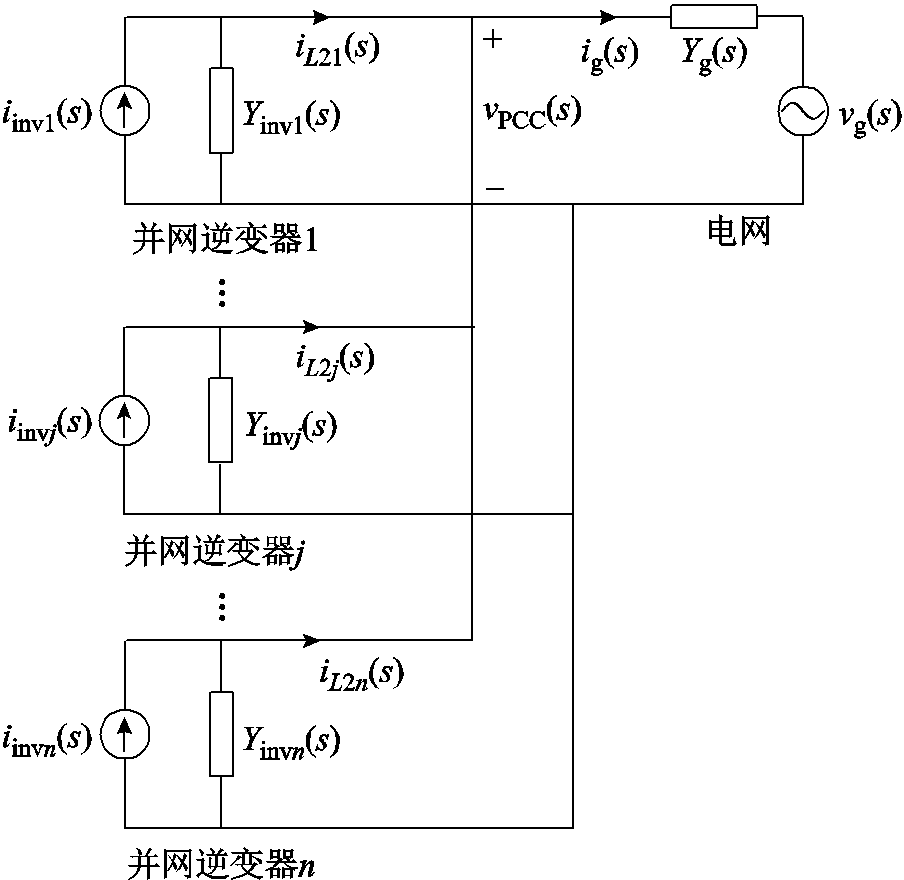
依据文献[21],可以将单台电流型控制并网逆变器等效为由一个电流源与等效输出导纳并联构成的诺顿模型。据此,可进一步得到弱电网下多逆变器并联并网系统的诺顿等效模型,如图2所示。
论文提供了关于两模块系统的推导过程,其在论文最后的附录部分给出,以此为出发点,便于进一步对本部分多模块系统的推导加深理解。而在本部分为不失一般性,仍对n模块系统进行如下分析推导。同时,亦在附录部分给出了本部分推导相应的具体过程,以使论文(即本部分)更简洁。
根据基尔霍夫电流定律,由图2可以得出逆变器模块j的输出电流表达式为
式中,iinvj(s)为逆变器模块j的等效电流源;Yinvj(s)为其等效输出导纳。
由叠加定理可以推出弱电网下公共耦合点电压vPCC(s)的表达式为
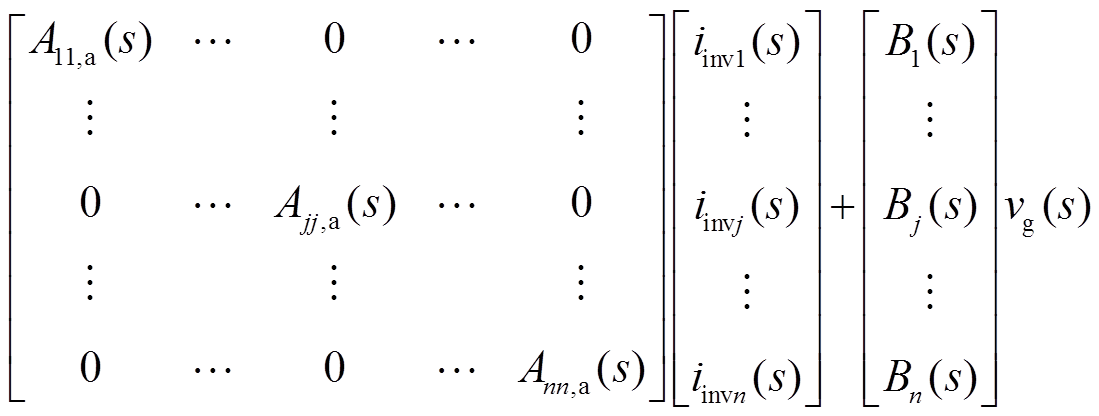
对于多逆变器并联并网系统而言,其实为多输入多输出(Multiple-Input-Multiple-Output, MIMO)系统。于是,将式(2)代入式(1),并以系统中各逆变器模块的等效输出电流源iinvj(s)以及电网电压vg(s)为输入量,各模块的输出电流iL2j(s)为输出量,则可根据式(1)构建矩阵
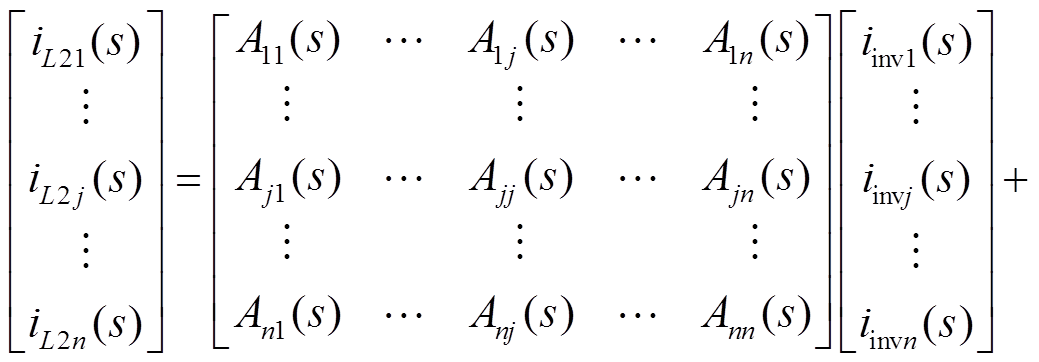
式中,An×n矩阵的对角线元素Ajj、非对角线元素Aji以及Bn×1矩阵元素Bj的表达式为
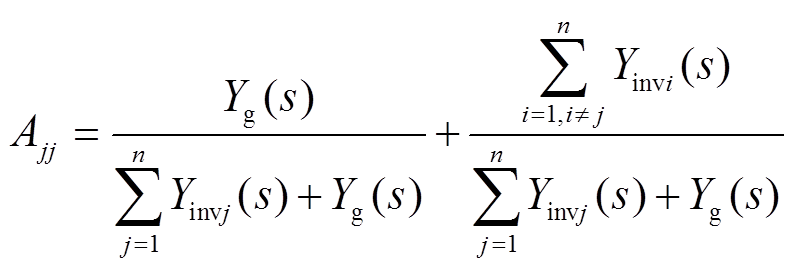 (4)
(4)
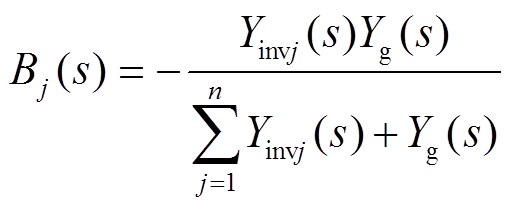 (6)
(6)
对于对角线元素Ajj,再将其分解成两项,分别为
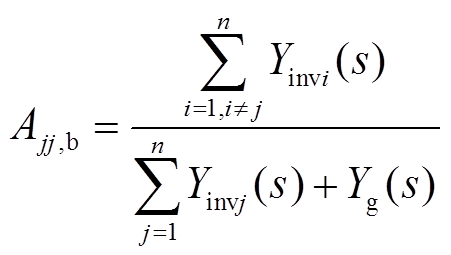 (8)
(8)
式中,Ajj,a元素仅与系统整体相关,而Ajj,b与非对角线元素Aji这两部分则体现了此逆变器模块与其他模块的耦合情况。由此可以将式(3)进一步改写为
根据式(9),可将各模块输出电流分解为模块自身送入电网的净电流分量igj(s),以及此模块与其余模块之间的交互电流分量之和,其表达式分别为
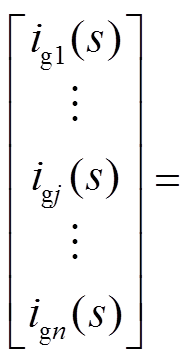

将式(4)~式(8)代入式(10)和式(11),可得其中一项的表达式为
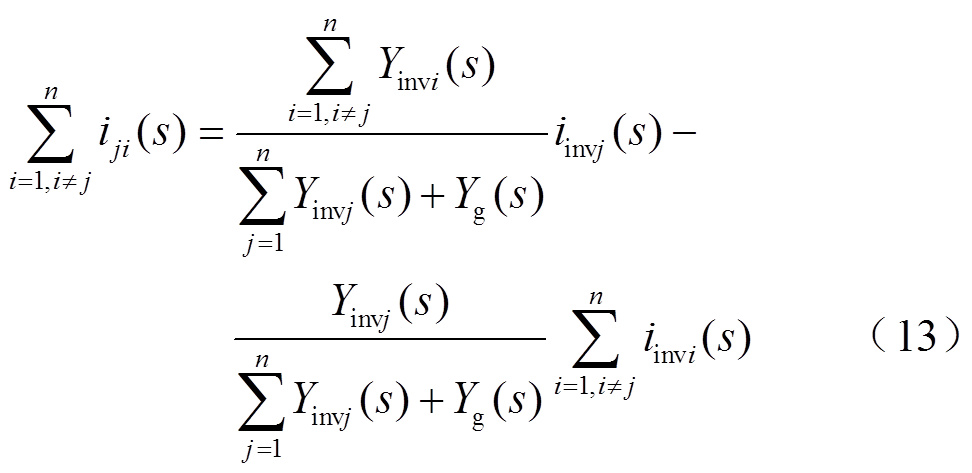
1.2 多机并联系统的进网电流稳定性判据推导
根据图2,可以得出多逆变器并联并网系统的进网总电流ig(s)为
结合式(13),可得逆变器模块j与模块i之间的交互电流iji(s)的表达式为
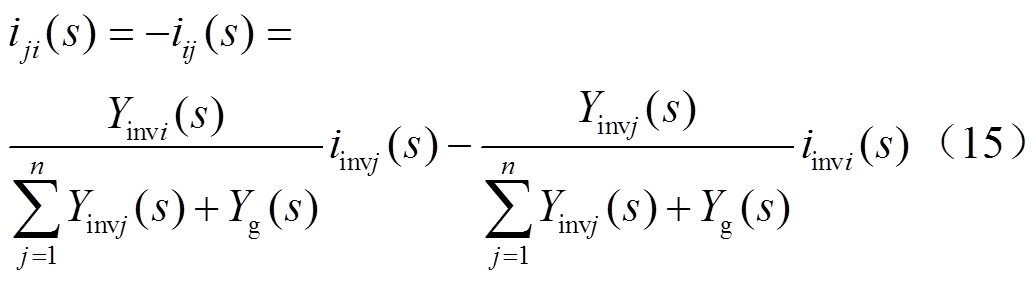
将式(14)等号右边第二项展开可得
结合式(15),可见交互电流分量总和为0。由式(14)可以发现即使各模块之间存在交互电流,但交互电流仅在模块之间流动,并不会流入电网,因此ig(s)即为各模块的并网净电流分量之和,为
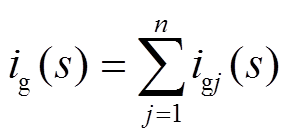 (17)
(17)
基于此,倘若各逆变器模块并网净电流是稳定的,也就可以确保多机并联系统总的进网电流的稳定性。将式(12)改写为
结合文献[21]中基于阻抗的单台并网逆变器的稳定判据,可以得出弱电网下多逆变器并联系统总的进网电流的稳定性判据:
判据一:确保系统内每个逆变器模块在不考虑电网阻抗(导纳)时可以稳定运行,即式(18)中右边括号中的式子不存在右半平面极点。
判据二:系统内所有模块等效输出导纳之和与电网导纳之比满足奈奎斯特稳定判据(即考虑式(18)左边分式乘积项)。
1.3 多机并联系统的交互电流稳定性判据推导
当系统中各逆变器模块参数一致,且不存在载波异步的情况时,模块间的交互电流为0[22]。然而在实际应用中,在公共连接点并入电网的各并网逆变器模块的功率等级、所采取的控制方式不可能完全一样,且载波同步实现起来较为困难。因此,多机并联系统中的各逆变器模块之间势必存在交互电流,故有必要对多机系统中交互电流的稳定性做进一步的分析。
在确保逆变器自身在强电网中设计为稳定的前提下,可以得到模块对应的等效电流源也是稳定的。那么由式(15)可以推出,交互电流稳定的决定性因素在于任意逆变器模块的等效输出导纳与所有模块等效输出导纳以及电网导纳之和比值的稳定性。以模块j为例,对此项决定性因素进行如下分解:
式中,M(s)为电网导纳与系统内所有模块等效输出导纳之和之比;N(s)为系统内其余模块(不包含逆变器模块j)的等效输出导纳之和与逆变器模块j的等效输出导纳之比。
对于第一个乘积项,根据线性控制理论,可以将其视为一个前向通路为1、反馈通路为M(s)系统的闭环传递函数。可以发现M(s)满足奈奎斯特稳定判据的本质与前文所推出的系统进网电流稳定的第二个条件是等价的。由于这一项的稳定性在系统进网电流稳定的基础上可以得到保证,故此处不再重复分析。
对于第二个乘积项,可以将其视为一个前向通路为1、反馈通路为N(s)系统的闭环传递函数。据此,即可得到模块间交互电流稳定的判据,也就是多逆变器并联系统的第三条判据:
判据三:系统内其余逆变器模块(不包含逆变器模块j)的等效输出导纳之和与逆变器模块j的等效输出导纳之比满足奈奎斯特稳定判据,任意模块(j = 1, 2,  , n)都需满足此条判据。
, n)都需满足此条判据。
2 基于等效输出导纳的不同开关频率模块构成的并网系统鲁棒性分析
2.1 数字控制LCL型并网逆变器等效输出导纳的频率特性
第1.2节得出了多逆变器并联系统在弱电网下关于总的进网电流的两条稳定性判据,对于判据一,对并网逆变器的LCL滤波器参数以及控制参数进行合理设计,即可确保并网逆变器在强电网下是一个稳定系统[14]。而依据经典控制理论,判据二可转换为要求所有模块等效输出导纳之和与电网导纳的幅频特性曲线不发生交截,或者在fi处交截时相位裕度PM>0,即
本文所开展的分析考虑最为恶劣的情况,忽略电网阻抗中的电阻成分,即Yg(s)=1/(sLg)。此时,Yg(s)的相位始终为-90°,由此可将判据二转化为确保所有模块等效输出导纳之和的相位小于90°。基于此,本节对数字控制LCL型并网逆变器及其并联系统等效输出导纳的频率特性展开分析。
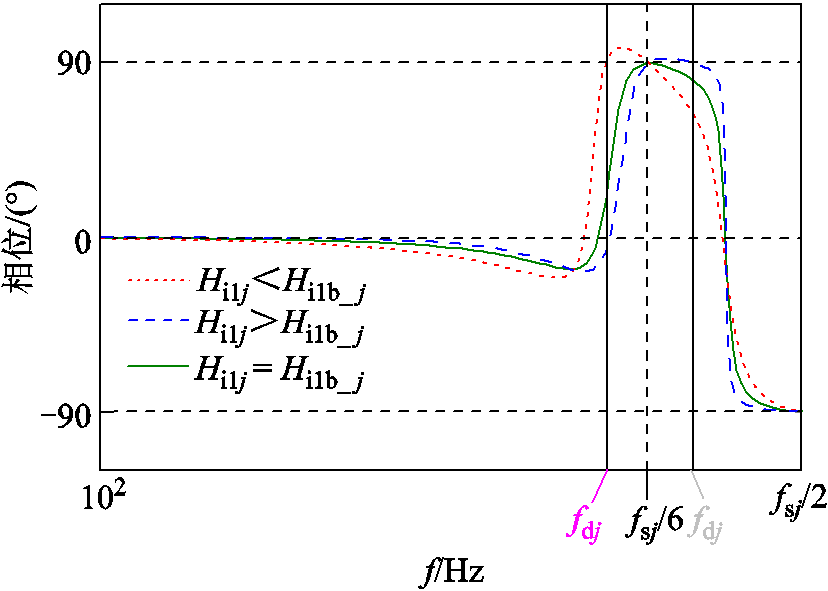
如引言部分所述,相较于GCF和ICF控制方式,在网侧电感电流反馈结合电容电流反馈有源阻尼的双环控制方式下,并网逆变器在弱电网下的稳定范围最广。图3即以双电流环控制方式为例,给出了不同电容电流采样系数下Yinvj(s)的相频特性曲线。从图3中可以看出,当Hi1j<Hi1b_ j时,Yinvj(s)在[fdj, fsj/6]范围内相位超出90°,此时对应了等效输出导纳实部Re{Yinvj(j2πfi)}<0,将其称为逆变器j的负导区域(fdj为Re{Yinvj(j2πfi)}正负的分界频率点);当Hi1j>Hi1b_ j时,Yinvj(s)在[fsj/6,fdj]范围内相位超出90°。假设Yg(s)与Yinvj(s)的幅频曲线在Yinvj(s)相位超出90°的频率区域内发生交截,显然此时系统的稳定裕度PM<0,系统无法稳定。当Hi1j= Hi1b_ j时,Yinvj(s)在fsj/6处与90°相切,PM=0°,系统仅在此频率点处无法稳定。因此将Hi1b_ j称为双电流环控制方式下的最优电容电流反馈系数,其表达式为
2.2 开关频率不同的两台并网逆变器并联系统的等效输出导纳分析
根据前文分析,可以发现每台逆变器模块至多会存在一个负导区域,此区域位于fsj/6附近。对于弱电网下n模块并网逆变器并联系统而言,考虑各模块的开关频率、LCL滤波器参数、控制参数等不一致的情况,则系统至多会存在n个不稳定的负导区域,它们在频域中“叠加”后,可能会相互抵消,或者产生新的负导区域。
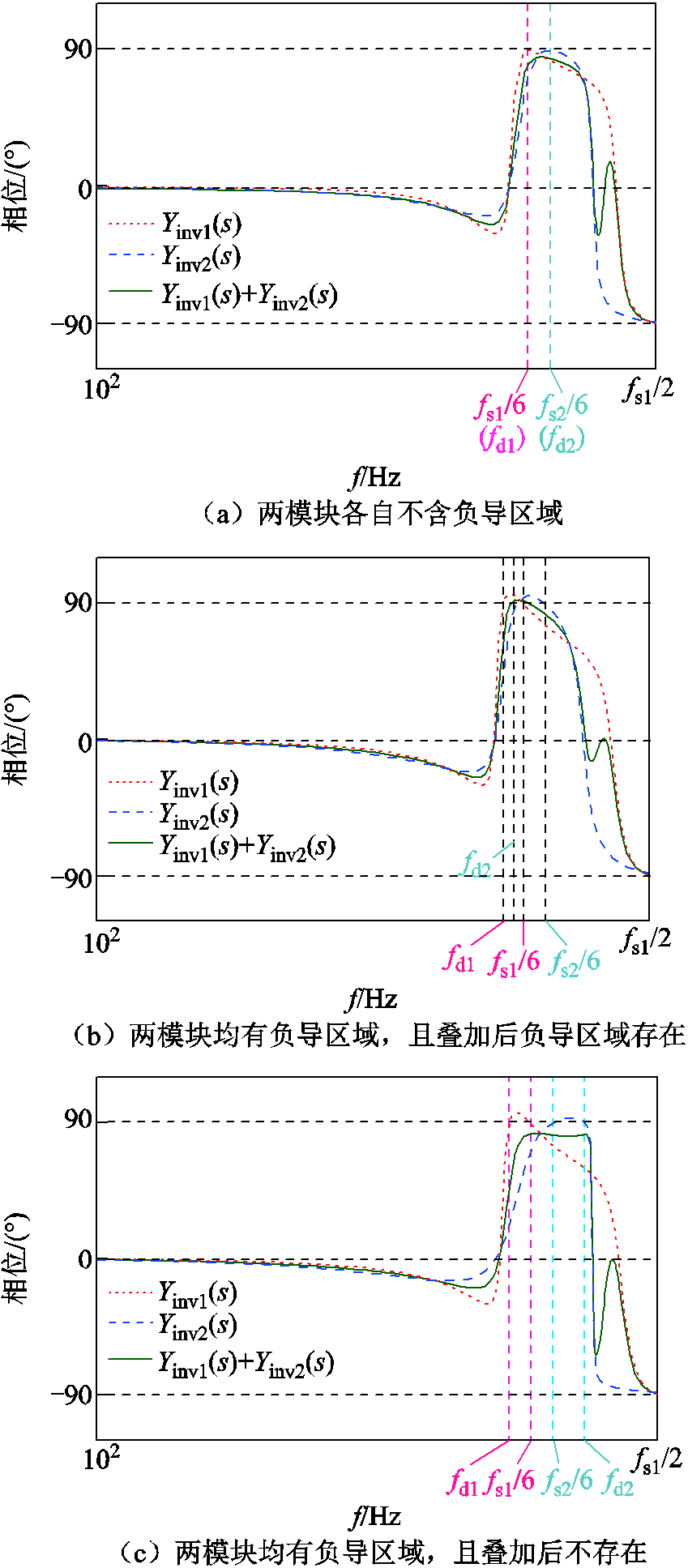
为便于展示不同负导区域在频域“叠加”后的各种情况,此处以两模块并联构成的系统为例展开讨论。图4中分别绘制了三种不同情况下Yinv1(s)、Yinv2(s)以及Yinv1(s)+Yinv2(s)的相频特性曲线。
图4a首先给出了两台逆变器模块都采用Hi1b_j(j = 1,2)时Yinv1(s)、Yinv2(s)以及Yinv1(s)+Yinv2(s)的相频特性曲线。可以发现,Yinv1(s)和Yinv2(s)的相频曲线分别在fs1/6和fs2/6处与90°相切,由于两模块的采样频率不一致,因此Yinv1(s)+Yinv2(s)的相位小于90°,系统始终满足稳定运行的相位条件。然而,在实际情况下,并网逆变器LCL滤波器的实际参数与理论中所设计的参数必然会存在一定偏差,因此负导区域依然存在,因此实际情况中并网逆变器的稳定运行条件仍较为苛刻。
对比图4b、图4c两种情况,由于两台逆变器模块均未采用Hi1b_j,因此fs1/6 ≠ fd1,fs2/6 ≠ fd2,两模块具有各自的负导区域,但两种情况下系统整体的稳定性截然不同。图4b情况下Yinv1(s)在[fd1, fs1/6]范围内相位超出90°,Yinv2(s)在[fd2, fs2/6]范围内相位超出90°,由于两个模块各自的负导区域存在一定的重合,因此两者“叠加”时负导区域无法完全消除,从图4b中可以看出系统的相频曲线仍在一定的频率范围内超出90°,此时两模块并联系统无法稳定运行,系统鲁棒性差。对于图4c情况,两模块的相频特性曲线在“叠加”后,原先各自的负导区域得到了完全的抵消,系统的相位始终小于90°,且具有一定的裕度。
综合以上三种情况可见,对于多机并联系统而言,其鲁棒性的提升具有不确定性。可以想象,随着并入系统的模块数增多,情况将越发复杂。因此仍需采取有效措施以提高其在弱电网下的鲁棒性。
3 高带宽并网逆变器抑制低频谐振的工作机理
3.1 多机并联系统中高频并网逆变器模块的引入
观察图4中两台开关频率不同的并网逆变器等效输出导纳的相频特性曲线,以开关频率低的逆变器模块为基准,另一模块的开关频率越高,数字控制引入的延时相对越短,从频域角度来看就是将等效输出导纳的相频曲线进行了右移。由此即可利用各模块等效输出导纳在同一频率处不同的相位大小,对系统等效输出导纳的相频特性曲线进行校正,保证其相位始终小于90°,满足奈奎斯特稳定判据。
为了更直观地说明上述观点,这里采用相量图法进一步加以阐释。图5即给出了图4c情况下两模块等效输出导纳的合成相量图。逆变器模块1在fs1/6附近呈现负导容性,而逆变器模块2呈现正导容性,两者相量之和呈现正导容性,使得两模块等效输出导纳之和相位小于90°,且具有一定的阻尼分量,不会与Yg(s)发生谐振。倘若进一步提高模块2的开关频率,可得到在同一频率处相角更小的等效输出导纳。在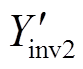 和
和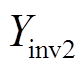 幅值相等的前提下,
幅值相等的前提下,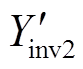 在Yinv1负导区域的相角更小,即可使得
在Yinv1负导区域的相角更小,即可使得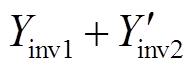 的相位裕度更大,如图5中所示。因此,对于多机并联逆变器并网系统,若提高系统中某一模块的开关频率,使其在目前低频逆变集群系统谐振频率范围内具有较强的阻尼特性,那么即可提高整个系统在弱电网下的鲁棒性。
的相位裕度更大,如图5中所示。因此,对于多机并联逆变器并网系统,若提高系统中某一模块的开关频率,使其在目前低频逆变集群系统谐振频率范围内具有较强的阻尼特性,那么即可提高整个系统在弱电网下的鲁棒性。
当下弱电网中并网逆变器集群系统与电网之间的谐振频率范围大部分集中于几百至几千Hz[23]。因此对于目前的并网逆变器集群系统,应对电力电子设备高频化的发展趋势,选择提高系统中一台逆变器模块的开关频率,若能确保其等效输出导纳在相对低频的谐振频率范围附近具有足够的阻尼外特性,即可对集群系统中的谐振进行有效抑制。相较于目前开关频率集中于10kHz~20kHz范围的低频并网逆变器而言,可以将此逆变器模块称为高频逆变器。由于对开关频率进行大幅提升的同时亦随之提高了其带宽频率,故此高频模块也具有高带宽特性,故称为高带宽并网逆变器。
结合前文所提的ICF型数字控制LCL型并网逆变器的稳定运行条件,可以发现只要通过合理设计使得LCL型滤波器的初始谐振频率小于fs/6,即可保证此高带宽并网逆变器在强电网以及弱电网下均是一个稳定系统。同样地,对等效输出导纳实部进行提取,可以推出ICF控制方式下,高频并网逆变器等效输出导纳YinvH在f<fsH/6(fsH为高频模块的采样频率)频率范围内相位始终小于90°,具有正导分量。因此对于本节所提出的高频并网逆变器,拟采用ICF(单逆变器侧电感电流反馈)型控制方式。同时,此控制方式仅需要使用一个电流霍尔传感器,有利于降低成本。
3.2 高频并网逆变器与低频并网逆变器的交互电流稳定性分析
本文所提出的高频并网逆变器在低频段的阻尼特性有利于提高系统整体的稳定性,但面对一个系统中高频与低频并网逆变器共存的局面,在保证多模块并联系统总进网电流稳定的基础上,还需对模块间的交互电流稳定性进行进一步的分析。
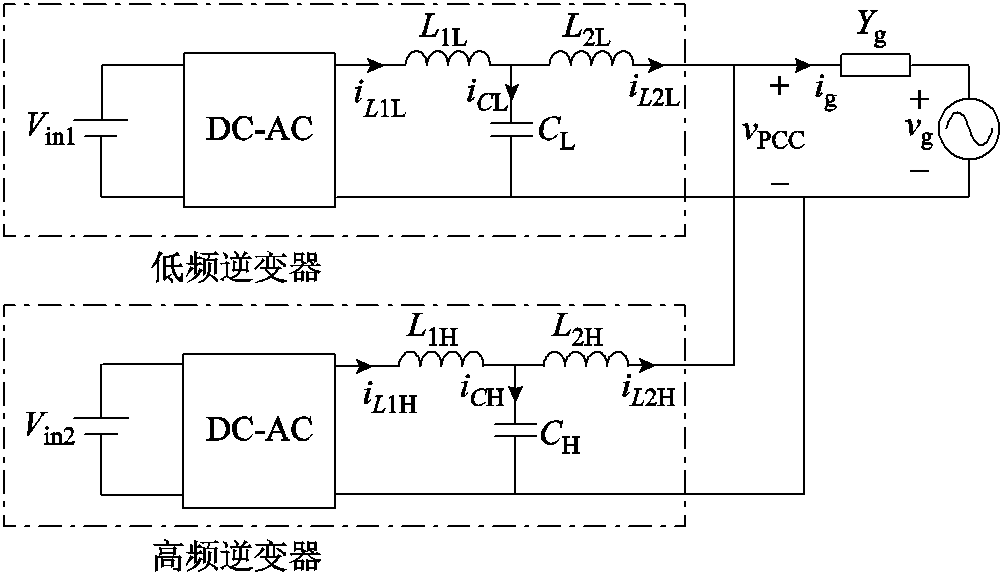
图6给出了由一台低频并网逆变器模块与一台高频逆变器模块并联构成的并网系统的电路拓扑,其中Vin1、Vin2分别为低频逆变器与高频逆变器模块的输入电压,L1L、CL、L2L分别为低频逆变器模块LCL滤波器的逆变器侧滤波电感、滤波电容、网侧滤波电感(iL1L、iCL、iL2L为对应的电流),L1H、CH、L2H分别为高频逆变器模块LCL滤波器的逆变器侧滤波电感、滤波电容、网侧滤波电感(iL1H、iCH、iL2H为对应的电流)。
第1节中将逆变器模块的输出电流分解为并网净电流以及与其余模块的交互电流,根据式(14),可得低频模块与高频模块之间的交互电流iLH(s)表达式为
结合式(15),即关于模块间交互电流稳定的第三条判据,可以得出决定iLH(s)稳定性的因素包括YinvH(s)/YinvL(s)、YinvL(s)/YinvH(s)以及Yg(s)/(YinvL(s)+ YinvH(s)),这三项均需满足奈奎斯特稳定判据。
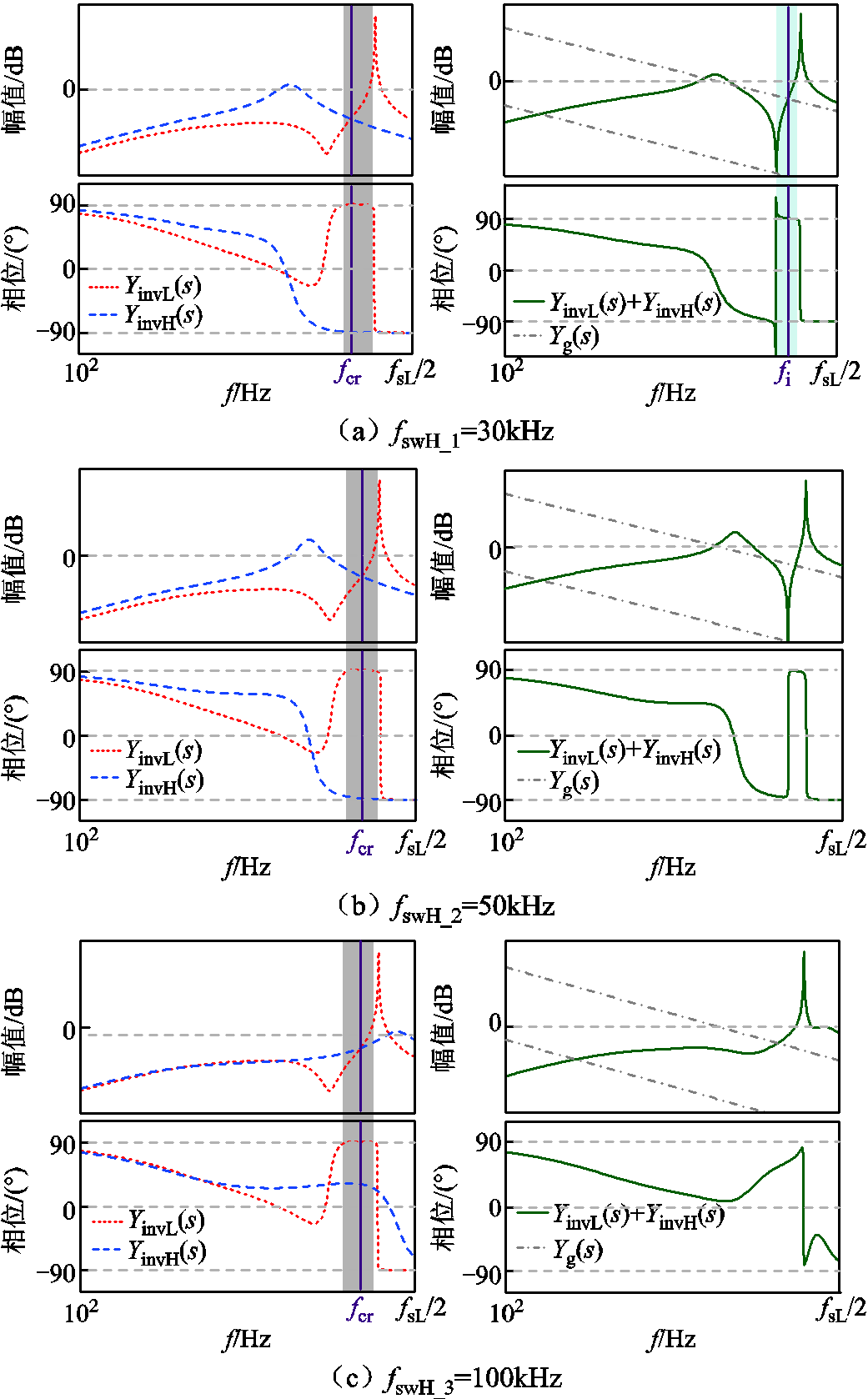
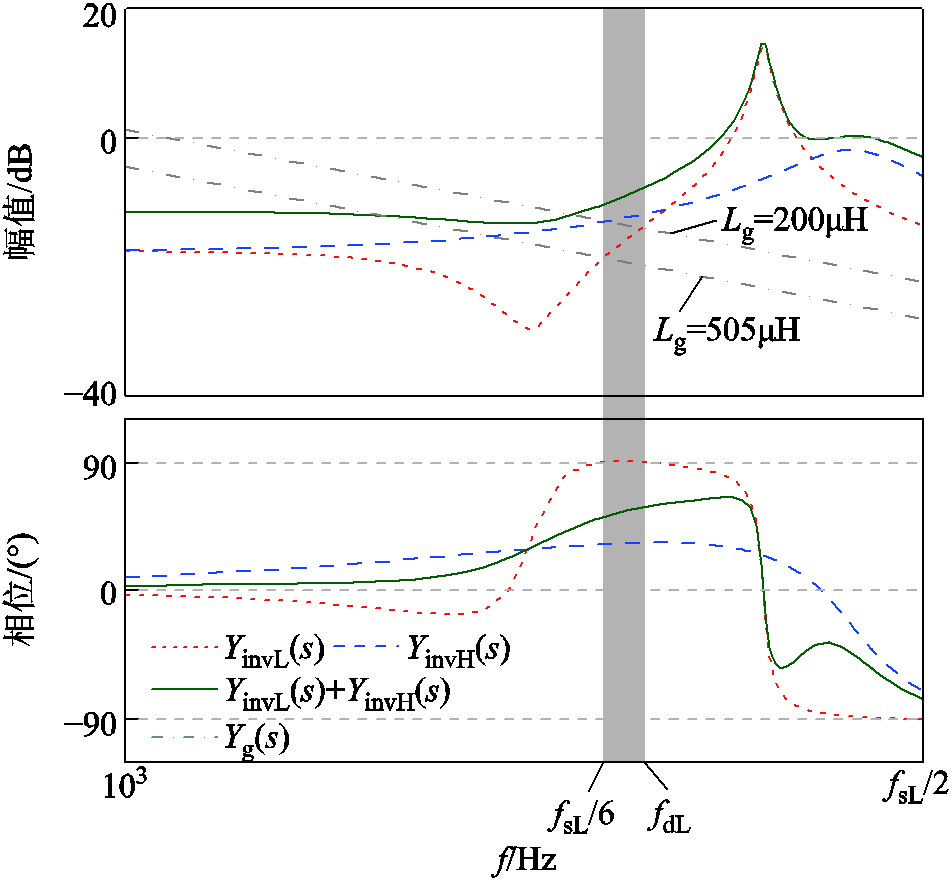
为了进一步阐释上述两模块并网系统的交互电流稳定性,图7分别给出了三种不同情况下YinvL(s)、YinvH(s)、YinvL(s)+YinvH(s)以及Yg(s)的伯德图。对于低频模块(采用网侧电感电流反馈结合电容电流有源阻尼控制方式),这里为考虑更为恶劣的情况,假设低频模块仍存在一定的负导区域,在图7中由灰色柱形区域表示。对于高频逆变器模块,确保对其开关频率的提高使得YinvH(s)的相位在低频模块的负导区域都小于90°。
在图7a所示的情况下,蓝色柱形区域表示YinvL(s)+YinvH(s)的相位大于90°,若在此频率段内YinvL(s)+YinvH(s)的幅频特性曲线与Yg(s)交截,则系统的进网电流稳定判据无法满足。显然此情况下两模块间的交互电流一定无法稳定。在图7b所示情况下,低频模块单独运行时的负导区域得到了彻底消除,YinvL(s)+YinvH(s)的相位始终小于90°,系统的进网电流稳定性得到了保证。但当YinvL(s)与YinvH(s)的幅值曲线在频率fcr处交截时,系统的相位裕度小于0°,系统对于交截频率fcr处的谐波电流抑制能力很差,易导致此交互电流出现谐振甚至失稳情况。结合上述两种情况,可以发现系统的进网电流稳定性是交互电流稳定的前提。
图7c中,将高频模块的开关频率进一步提高,此时所对应的状态即为YinvH(s)的幅值曲线与YinvL(s)的幅值曲线相交截的时候,此时两者的相位差与180°具有较大的差距,具有较好的稳定裕度,此时系统的进网电流以及模块交互电流都是稳定的。
综上,在系统中引入高频模块有助于改善原逆变器模块的鲁棒性,且使得系统进网电流能够稳定运行,但也可能造成两模块之间交互电流的谐振。因此为避免额外引入模块之间交互电流的谐振,需对此高频模块开关频率的选取作进一步探究。
3.3 高带宽并网逆变器开关频率的选取
等效输出导纳YinvH(j2πf)可视为等效电导以及等效电纳的并联形式,即
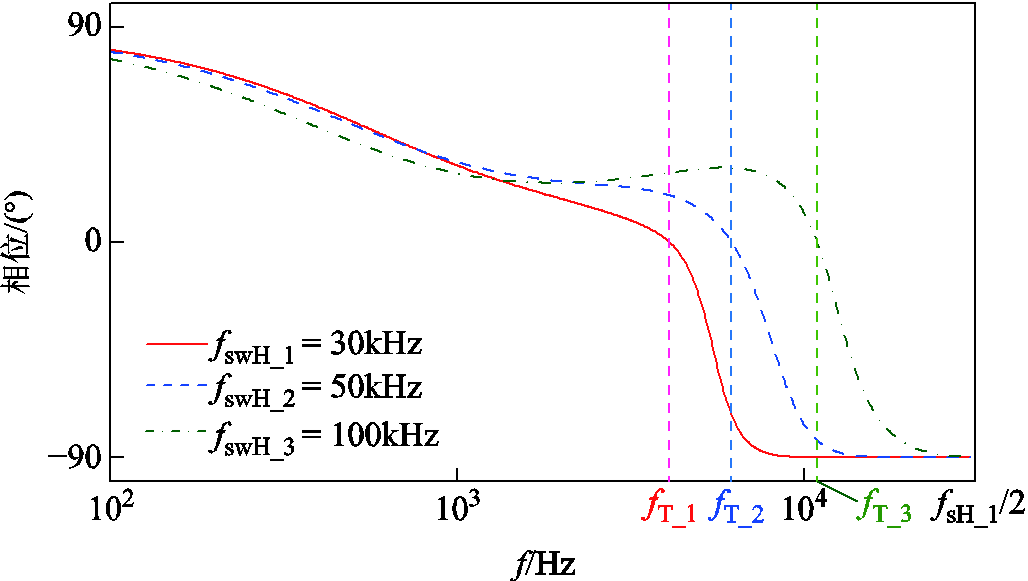
前文提出了开关频率的提高在频域中体现在相频曲线的右移,图9给出了开关频率分别为30kHz、50kHz、100kHz的并网逆变器等效输出导纳的一族相频特性曲线。可以看出随着并网逆变器开关频率的提高,相频曲线向右移动,且ICF控制方式下并网逆变器等效输出导纳的相位会在转折频率fT处发生正负改变,表现在YinvH对外呈现的是正导感性或正导容性的变化。
从图9中可以观察到,当并网逆变器的开关频率为100kHz时,参考目前的低频谐振频率范围(几百至几千Hz),其等效输出导纳的正导区域不仅涵盖了低频谐振的频率范围,且相频特性曲线的转折频率fL>10kHz,也就是可以确保在低频逆变器相位超出90°的频率范围时此高频模块仍呈现容性,也就是其相位不会接近-90°,避免了额外引入模块间交互电流谐振失稳的风险。最终本文将高频逆变器模块的开关频率选定为100kHz。
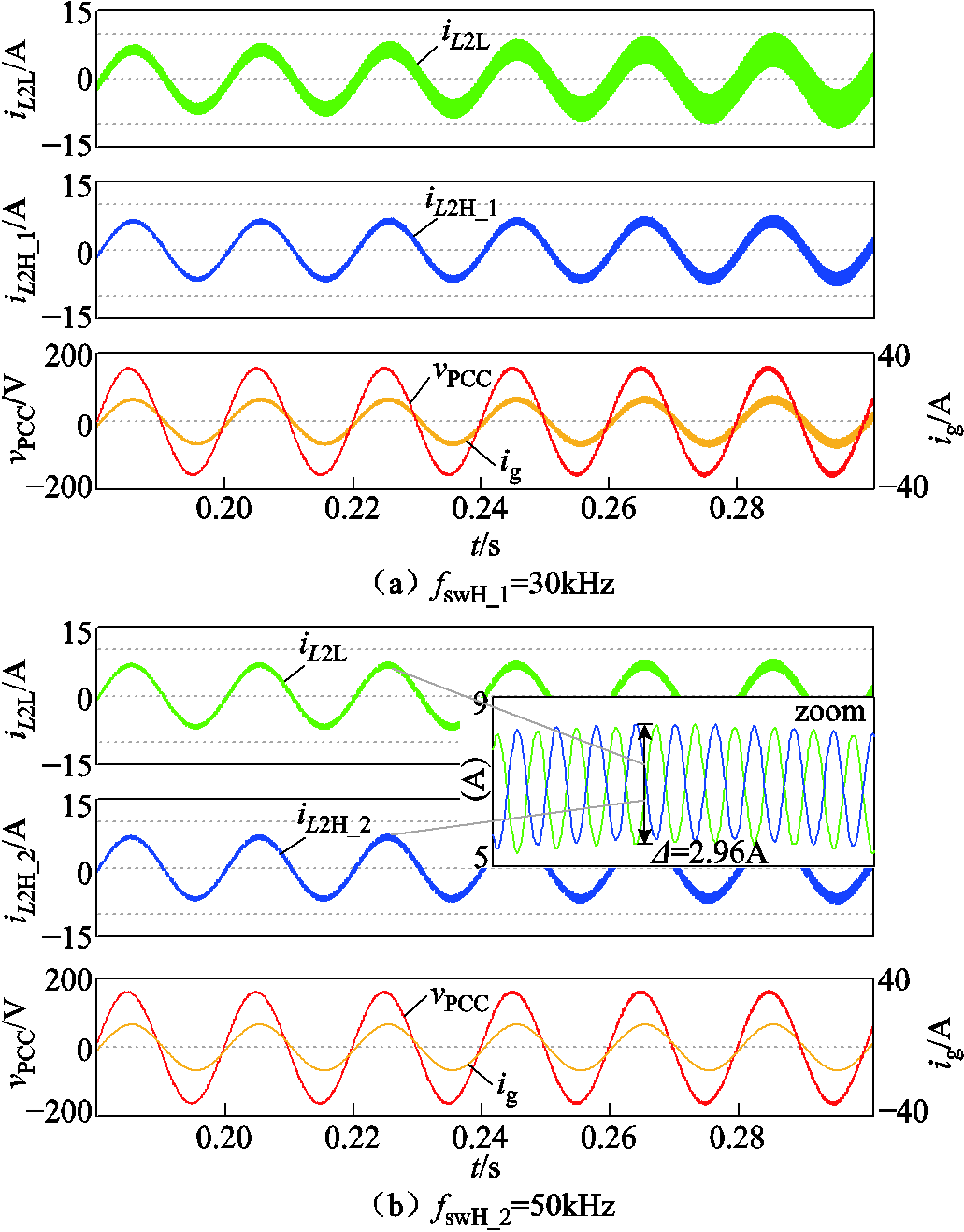
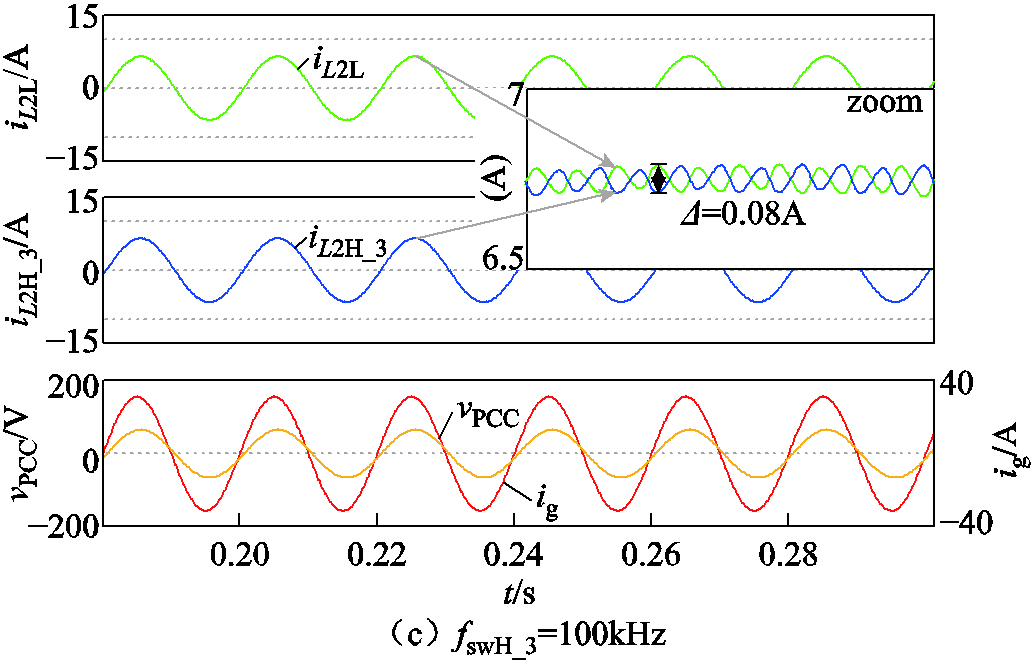
图10分别给出了三组开关频率不同的高频模块与低频模块并联运行时的仿真波形,其中iL2L为低频模块的输出电流,iL2H_j为高频模块j(j=1, 2, 3)的输出电流,ig为系统的总并网电流,vPCC为公共耦合点电压,三种情况与图7相对应。各逆变器的具体参数见表1。
由图10可见,在图10a情况下系统整体无法稳定,ig发生振荡且呈现发散的趋势。两模块之间的交互电流也无法稳定,因此iL2L和iL2H_1表现出振荡。由于两模块自身的阻尼特性不同,因此振荡幅值不同。图10b情况下系统整体稳定性得到了满足,但从iL2L和iL2H_2的波形中可以看出低频与高频模块之间的交互电流依然不稳定。图10c情况下由于两模块参数以及控制方式都有所不同,故交互电流仍然存在,但从iL2L和iL2H_3的放大图可以看出交互电流幅值非常之小,并未呈发散趋势,可见系统的进网电流稳定性以及模块间交互电流稳定性都得到了保证。
从上述三组仿真波形中可以看出,将高频模块的开关频率设定为100kHz可以确保系统的进网电流稳定性以及交互电流稳定性,验证了前文理论分析的正确性。
表1 各逆变器主要参数
Tab.1 Main parameters

参数低频模块高频模块1高频模块2高频模块3 开关频率/kHzfswL=15fswH_1=30fswH_2=50fswH_3=100 采样频率/kHzfsL=30fsH_1=60fsH_2=100fsH_3=200 输出功率/WPoL=500PoH_1=500PoH_2=500PoH_3=500 逆变器侧电感/μHL1L=550L1H_1=350L1H_2=200L1H_3=100 滤波电容/μFCL=5CH_1=30CH_2=30CH_3=4.7 网侧电感/μHL2L=75L2H_1=150L2H_2=90L2H_3=45
4 实验验证
4.1 高带宽并网逆变器的研制及自身良好并网性能的验证
为进一步验证上述理论分析的正确性,在实验室研制了一台基于GaN的高带宽数字控制并网逆变器,原理样机如图11所示,其中GaN器件选择GaN systems公司的GS66508T,DSP芯片采用Texas Instruments公司的TMS320F28069,其主要参数见表1。不难得到,这台采用ICF控制的高带宽并网逆变器的初始谐振频率为13.2kHz,低于fsH/6,满足设计要求。
图12给出了高带宽并网逆变器在强电网下的满载稳态波形,图13则给出了其在半载和满载间跳变的动态实验波形。由波形可见,所研制的高带宽并网逆变器具有良好的动静态性能。图14a和图14b分别给出了弱电网下(Lg = 400μH以及Lg = 3.2mH)的实验波形,可见所研制的高带宽并网逆变器在弱电网下具有良好的鲁棒性。上述实验结果验证了理论分析的正确性。
4.2 高带宽并网逆变器抑制低频谐振功能的验证
为验证高带宽逆变器对低频谐振进行抑制的有效性,将所研制的高带宽并网逆变器并入已有的低频模块并网系统中,低频逆变器的主要参数见表1。
为便于理解,图15给出了两台并网逆变器等效输出导纳的频率特性曲线。其中,采用双环控制的低频逆变器1在fsL/6至fdL区间内等效输出导纳YinvL的相角大于90°,在图中用灰色区域表示,由奈奎斯特稳定判据可知此时其处于不稳定状态。而YinvH的相角在此低频范围内远小于90°,从而使得YinvL+YinvH的相角始终位于小于90°的稳定范围内,可见高频逆变器的并入使得系统在奈奎斯特频段内(以fsL/2为基准)都可以保持稳定。
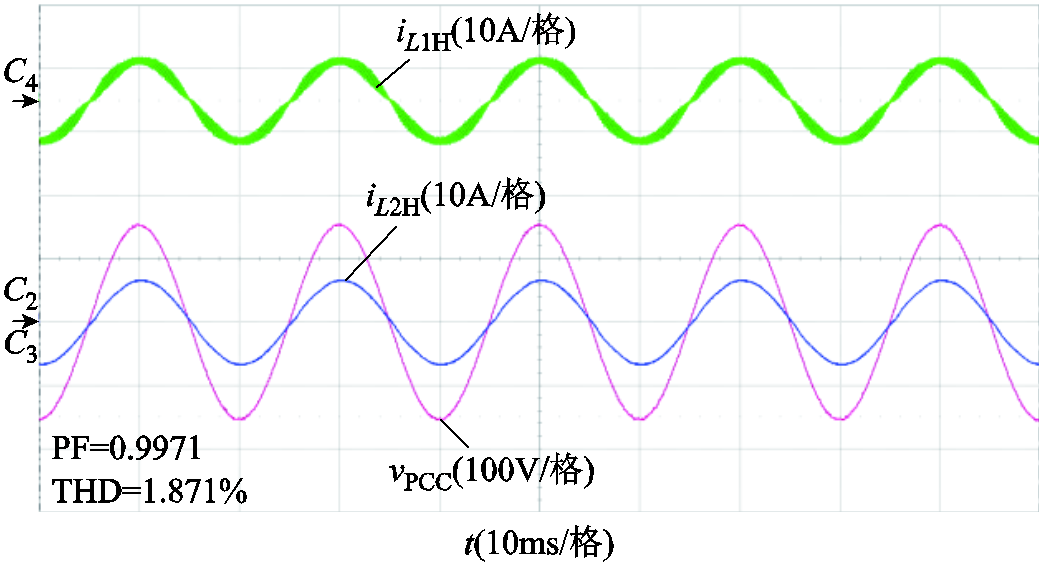
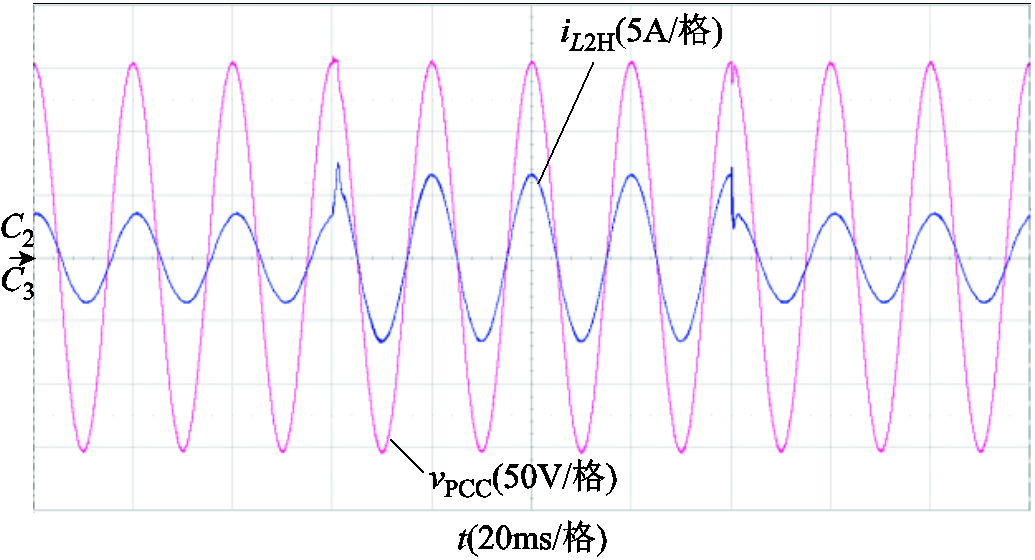
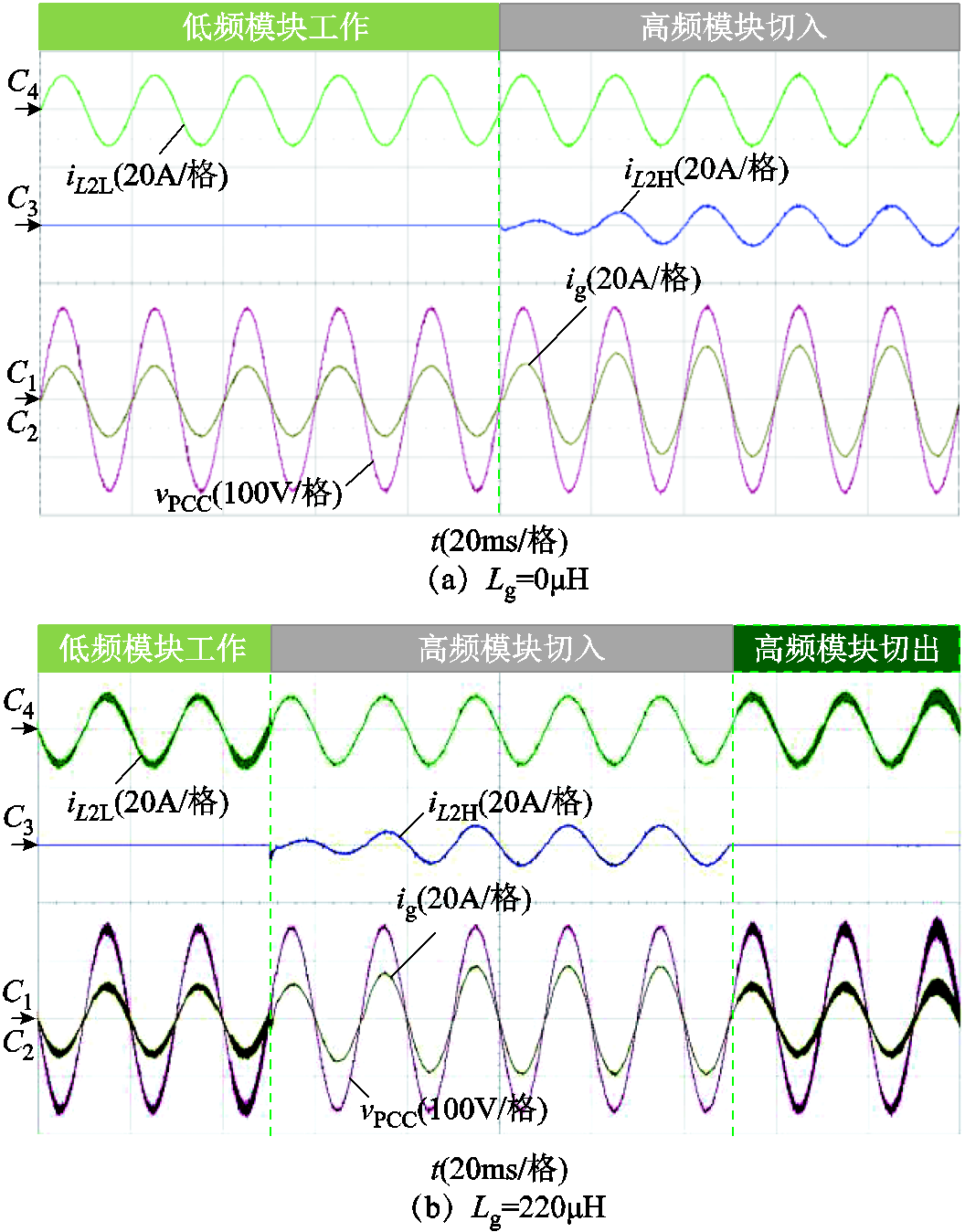
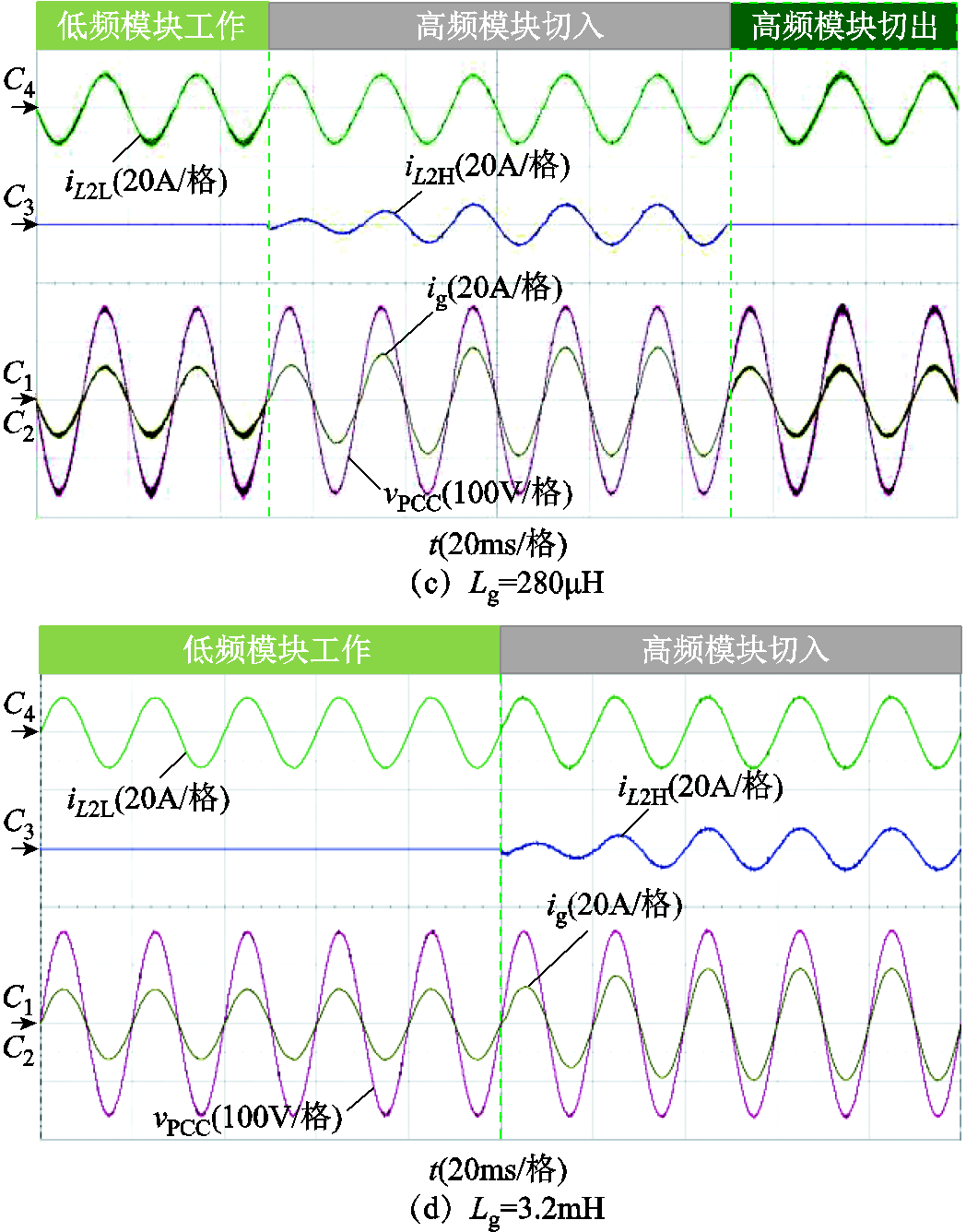
当低频模块处于强电网或者Lg = 3.2mH时,其自身可以稳定运行。当高带宽逆变器模块切入时,两者亦可共同稳定工作,波形如图16a和图16d所示。而在图16b和图16c中,即Lg = 220μH或Lg = 280μH时,原低频模块处于谐振状态。随着高频模块的并入,谐振得以有效抑制,且系统快速恢复稳定;当高频模块切出时,原低频模块又开始谐振。此外,上述各种工况下高频模块均为系统注入功率。以上实验结果验证了理论分析的正确性。
5 结论
1)本文基于各模块参数不同的前提,构建了多机并联并网系统在弱电网下的多输入多输出矩阵,并基于导纳的稳定性分析方法得出系统的进网电流及交互电流稳定性判据。
2)进一步基于频域阻抗法分析了开关频率不同对于多机并联系统在弱电网下鲁棒性的影响。结合各模块等效输出导纳的相频特性曲线,通过引入的高带宽逆变器在原低频逆变器模块谐波频率范围所具有的正导分量,以对目前弱电网下的低频谐振进行有效阻尼,为提高弱电网下并网逆变器系统的鲁棒性提供了一个新的思路。同时基于低频模块与高频模块并联系统分析了交互电流的稳定性,为高带宽逆变器开关频率的选择提供了依据。
3)采用新型宽禁带器件GaN作为开关管,选用单逆变器侧电感电流反馈(ICF)控制方式研制一台高带宽并网逆变器,确保模块自身在强电及弱电网下均具有良好的鲁棒性。进一步地,将该高带宽并网逆变器并入原有低频并网逆变器系统中,通过实验验证了高带宽逆变器的优良特性:其在低频段呈现的正阻特性能对原低频并网系统的谐振进行有效抑制,且能同时为系统注入功率。
附 录
根据图2,从整体的角度,将各逆变器模块等效的电流源以及等效输出导纳以求和的形式合并,可得附图1所示的等效模型。
附图1 图2的等效模型
App.Fig.1 Equivalent model of Fig.2
由图17通过基尔霍夫定律,可得
将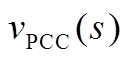 提取即可得式(2)。
提取即可得式(2)。
以逆变器模块j为例,将式(2)代入式(1),可得iL2j(s)与等效电流源以及电网电压之间的关系为
从式(A2)中可以看出模块j的输出电流不仅与自身模块的iinvj(s)以及vg(s)有关,还受到其余逆变器的影响。为了明晰各模块输出电流所受不同激励源的影响,进而分析其稳定性,本文借助MIMO矩阵,由此可将式(A2)转化为式(3)。在将激励源进行区分后,即可得式(7)。
接下来以2台并网逆变器构成的并联系统为例,对第1节中系统进网电流以及模块间交互电流的稳定性展开具体分析,由式(A2)可得
其中A11(s)、A22(s)、A12(s)、A21(s)、B1(s)、B2(s)的表达式为
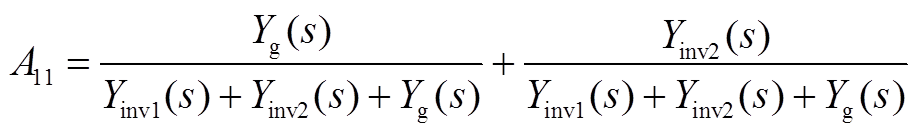 (A4)
(A4)
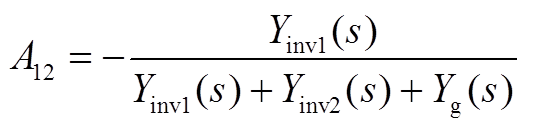 (A6)
(A6)
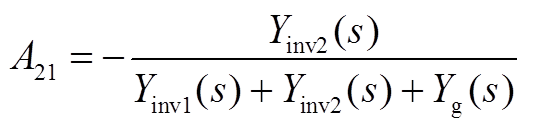 (A7)
(A7)
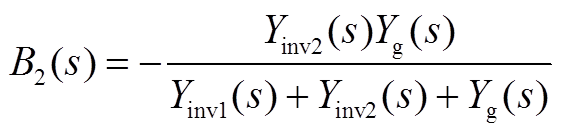 (A9)
(A9)
将式(A4)和式(A5)再分解为两项A11,a、A11,b和A22,a、A22,b分别为
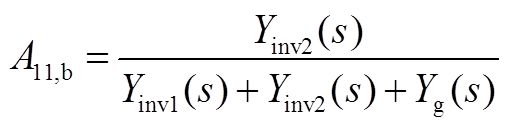 (A11)
(A11)
 (A12)
(A12)
对于逆变器1而言,A11,a元素仅与系统整体相关,而A11,b与非对角线元素A12这两部分则体现了逆变器1与逆变器2的耦合情况。在对激励源进行区分的基础上,将式(A3)改写为
结合前文分析,根据式(A13)可以写出模块1、模块2自身送入电网的净电流分量ig1(s)、ig2(s),以及两模块之间的交互电流分量i12(s)、i21(s),即
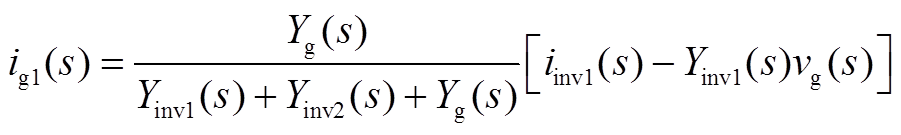 (A14)
(A14)
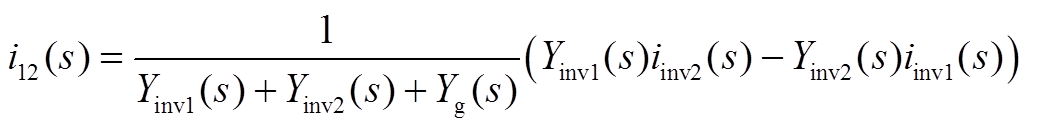 (A16)
(A16)
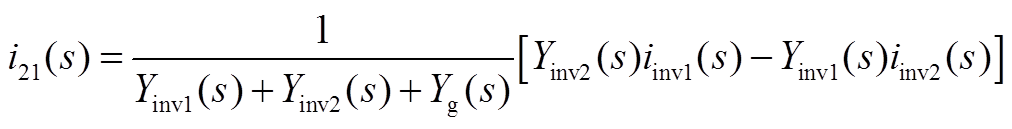 (A17)
(A17)
由此可得出2台逆变器并联并网系统的进网总电流ig(s)为
结合式(A16)和式(A17)显然可得交互电流分量总和为0,因此ig(s)即为两模块的并网净电流分量之和,即
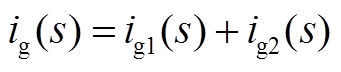 (A19)
(A19)
参考文献
[1] 郭小强, 朱铁影. 新型非隔离型三相三电平光伏并网逆变器及其漏电流抑制研究[J]. 电工技术学报, 2018, 33(1): 26-37.
Guo Xiaoqiang, Zhu Tieying. Research on leakage current suppression of novel three-phase three-level non-isolated PV inverter[J]. Transactions of China Electrotechnical Society, 2018, 33(1): 26-37.
[2] 谢志为, 陈燕东, 伍文华, 等. 弱电网下多逆变器并网系统的全局高频振荡抑制方法[J]. 电工技术学报, 2020, 35(4): 885-895.
Xie Zhiwei, Chen Yandong, Wu Wenhua, et al. A global high-frequency oscillation suppression method for multi-inverter grid-connected system in weak grid[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 885-895.
[3] 张晓, 谭力, 鲜嘉恒, 张辉. LCL并网逆变器预测电流控制算法[J].电工技术学报,2019,34(增刊1):189-201.
Zhang Xiao, Tan Li, Xian Jiaheng, et al. Predictive current control algorithm for grid-connected inverter with LCL filter[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 189-201.
[4] Li Weiwei, Ruan Xinbo, Pan Donghua, et al. Full-feedforward schemes of grid voltages for a three-phase LCL-type grid-connected inverter[J]. IEEE Transactions on Industrial Electronics, 2013, 60(6): 2237–2250.
[5] Zhang Shao, Jiang Shuai, Lu Xi, et al. Resonance issues and damping techniques for grid-connected inverters with long transmission cable[J]. IEEE Transactions on Power Electronics, 2014, 29(1): 110-120.
[6] 庄超, 叶永强, 赵强松, 等. 基于分裂电容法的LCL并网逆变器控制策略分析与改进[J].电工技术学报, 2015, 30(16): 85-93.
Zhuang Chao, Ye Yongqiang, Zhao Qiangsong, et al. Analysis and improvement of the control strategy of LCL grid-connected inverter based on split-capacitor[J].Transactions of China Electrotechnical Society, 2015, 30(16): 85-93.
[7] Jia Yaoqin, Zhao Jiqian, Fu Xiaowei. Direct grid current control of LCL-filtered grid-connected inverter mitigating grid voltage disturbance[J]. IEEE Transactions on Power Electronics, 2014, 29(3): 1532-1541.
[8] Wang Xuehua, Bao Chenlei, Ruan Xinbo, et al. Design considerations of digitally controlled LCL-filtered inverter with capacitor- current-feedback active damping[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2014, 2(4): 972-984.
[9] Bao C, Ruan X, Wang X, et al. Step-by-step controller design for LCL-type grid-connected inverter with capacitor–current-feedback active-damping [J]. IEEE Transactions on Power Electronics, 2014, 29(3): 1239-1253.
[10] 黎伟. 三相LCL型并网逆变器的数字控制技术研究[D]. 徐州: 中国矿业大学, 2017.
[11] Zou C, Liu B, Duan S, et al. Influence of delay on system stability and delay optimization of grid-connected inverters with LCL filter[J]. IEEE Transactions on Industrial Informatics, 2014, 10(3): 1775-1784.
[12] Wang Jianguo, Yan Jiu Dun, Jiang Lin, et al. Delay-dependent stability of single-loop controlled grid-connected inverters with LCL filters [J]. IEEE Transactions on Power Electronics, 2016, 31(1): 743-757.
[13] Yin Jinjun, Duan Shanxu, Liu Bangyin. Stability analysis of grid-connected inverter with LCL filter adopting a digital single-loop controller with inherent damping characteristic[J]. IEEE Transactions on Industrial Informatics, 2013, 9(2): 1104-1112.
[14] 鲍陈磊. LCL型并网逆变器的并网电流调节器和电容电流反馈有源阻尼设计[D]. 武汉: 华中科技大学, 2013.
[15] Pan Donghua, Ruan Xinbo, Bao Chenlei, et al. Capacitor-current-feedback active damping with reduced computation delay for improving robustness of LCL type grid-connected inverter[J]. IEEE Transactions Power Electronics, 2014, 29(7): 3414-3427.
[16] Chen Chen, Xiong Jian, Wan Zhiqiang, et al. A time delay compensation method based on area equivalent for active damping of an LCL-type converter [J]. IEEE Transactions on Power Electronics, 2017, 32(1): 762-772.
[17] Yang Dongsheng, Ruan Xinbo, Wu Heng. A real-time computation method with dual sampling modes to improve the current control performances of the LCL-type grid-connected inverter[J]. IEEE Transactions on Power Electronics, 2015, 62(7): 4563-4572.
[18] Wang Xiongfei, Blaabjerg F, Loh P C. Virtual RC damping of LCL-filtered voltage source converters with extended selective harmonic compensation [J]. IEEE Transactions on Industrial Electronics, 2015, 30(9): 4726-4737.
[19] 方天治, 黄淳, 陈乃铭, 等. 一种提高弱电网下LCL型并网逆变器鲁棒性的相位超前补偿策略[J]. 电工技术学报, 2018, 33(20): 4813-4822.
Fang Tianzhi, Huang Chun, Chen Naiming, et al. A phase-lead compensation strategy on enhancing robustness of LCL-type grid-tied inverters under weak grid conditions[J]. Transactions of China Electro-technical Society, 2018, 33(20): 4813-4822.
[20] Potty K A, Bauer E, Li He, et al. Smart resistor: stabilization of DC microgrids containing constant power loads using high-bandwidth power converters and energy storage [J]. IEEE Transactions on Power Electronics, 2020, 35(1): 957-967.
[21] Sun Jian. Impedance-based stability criterion for grid-connected inverters[J]. IEEE Power Electronics Letters, 2011, 26(11): 3075-3078.
[22] Yu Changzhou, Zhang Xing, Liu Fang, et al. Modeling and resonance analysis of multiparallel inverters system under asynchronous carriers conditions[J]. IEEE Transactions on Power Electronics, 2017, 32(4): 3192-3205.
[23] Harnefors L, Wang Xiongfei, Yepes A G, et al. Passivity-based stability assessment of grid-connected VSCs—an overview[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(1): 116-125.
A High-Bandwidth Digital-Control LCL-Type Grid-Tied Inverter and Resonance-Suppressing Technique for Improving the Robustness of Grid-Connected System
Shen Shuheng Fang Tianzhi Zhang Yifan
(College of Automation Engineering Nanjing University of Aeronautics and Astronautics Nanjing 211106 China)
Abstract The inherent control delay of the digital-control LCL grid-connected inverter would affect the control characteristic of the original resonance damping scheme, thereby decreasing the robustness of the system in weak grid. The multiple-input-multiple-output(MIMO) matrix of the multi-inverter parallel system based on different parameters is established firstly, and three criteria to ensure the stability of the system's grid current and interactive current is put forward. Furthermore, the influence of the digital-control-delay on the robustness of the system when the module adopts different switching frequencies is analyzed based on the frequency domain impedance method. Therefore, the introduction of a high-bandwidth inverter in the multi-inverter system is found to be effective in suppressing low-frequency resonance. Next, the interaction stability between the high-frequency module and the low-frequency module is analyzed, and the switching frequency of the high-bandwidth inverter is selected. Finally, a prototype of the high-bandwidth grid-connected inverter based on GaN was built. The effectiveness of the high-bandwidth inverter to improve the robustness of the system in weak grid is verified by experiment. This scheme provides a new idea for improving the stability of the distributed generation system.
keywords:Multiple-grid-connected-inverter parallel system, robustness, high-bandwidth, GaN device
DOI:10.19595/j.cnki.1000-6753.tces.211298
中图分类号:TM464
国家自然科学基金(52077102)和江苏省自然科学基金(BK20201299)资助项目。
收稿日期 2021-08-17
改稿日期 2022-01-29
作者简介
沈姝衡 女,1997年生,硕士研究生,研究方向为并网逆变器、电力电子系统集成。E-mail:shenshuheng0520@126.com
方天治 男,1977年生,博士,副教授,研究方向为串并联组合逆变器、并网逆变器、电力电子系统集成。E-mail:fangtianzhi@126.com(通信作者)
(编辑 郭丽军)
 ,n)为各模块直流侧输入电压,vinj为各模块桥臂中点电压,L1j、Cj、L2j分别为各模块LCL型滤波器的逆变器侧滤波电感、输出滤波电容以及网侧滤波电感,iL1j、iCj、iL2j分别为各模块逆变器侧电感电流、输出滤波电容电流以及各模块的输出电流,vPCC为公共耦合点(Point of Common Coupling, PCC)电压,ig为并网电流,Yg为电网导纳,vg为交流电网电压。由于在实际应用中不能保证并入电网的所有逆变器模块的参数都是一致的,故为不失一般性,考虑系统中各逆变器模块的控制方式、参数等都不尽相同。
,n)为各模块直流侧输入电压,vinj为各模块桥臂中点电压,L1j、Cj、L2j分别为各模块LCL型滤波器的逆变器侧滤波电感、输出滤波电容以及网侧滤波电感,iL1j、iCj、iL2j分别为各模块逆变器侧电感电流、输出滤波电容电流以及各模块的输出电流,vPCC为公共耦合点(Point of Common Coupling, PCC)电压,ig为并网电流,Yg为电网导纳,vg为交流电网电压。由于在实际应用中不能保证并入电网的所有逆变器模块的参数都是一致的,故为不失一般性,考虑系统中各逆变器模块的控制方式、参数等都不尽相同。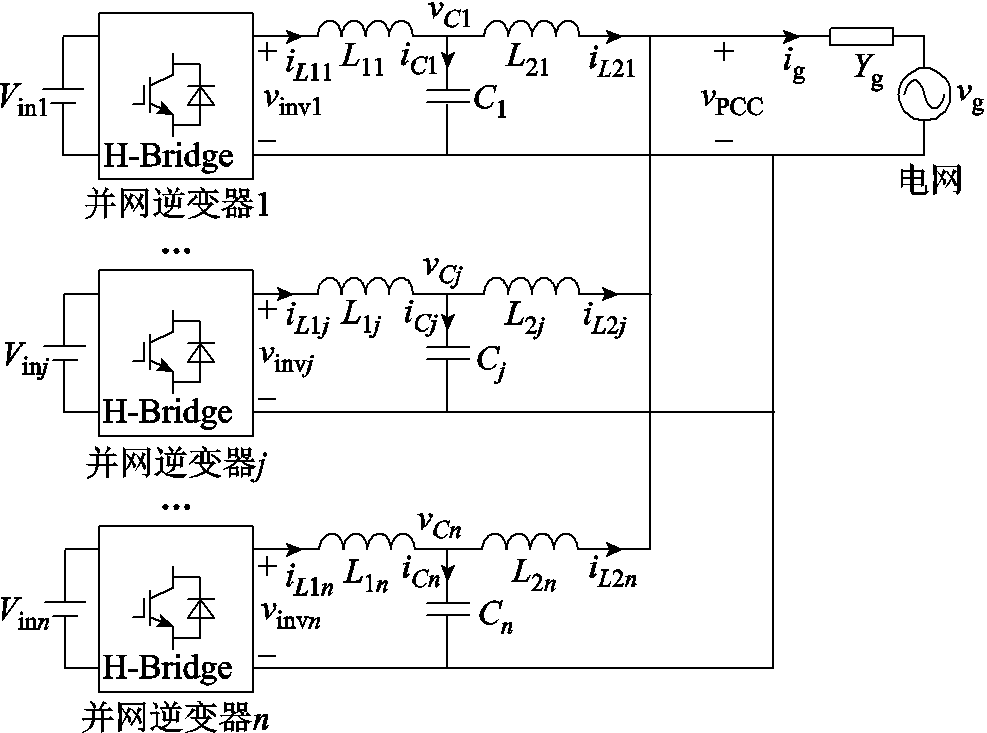
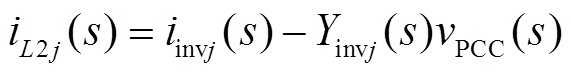 (1)
(1)
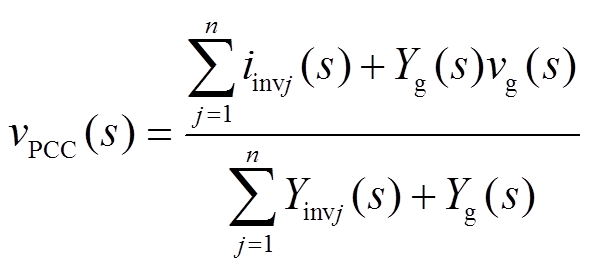 (2)
(2)

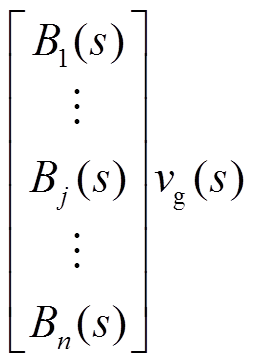 (3)
(3)
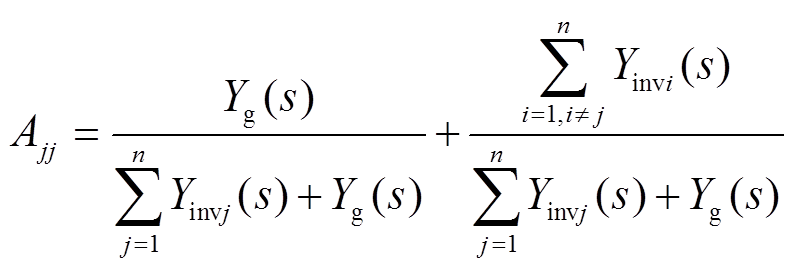 (4)
(4)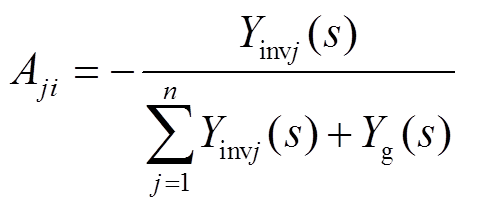 (5)
(5)
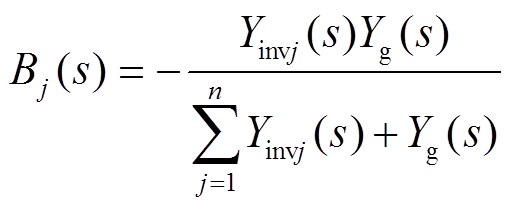 (6)
(6)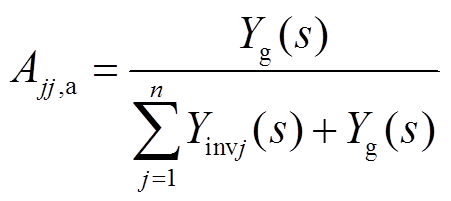 (7)
(7)
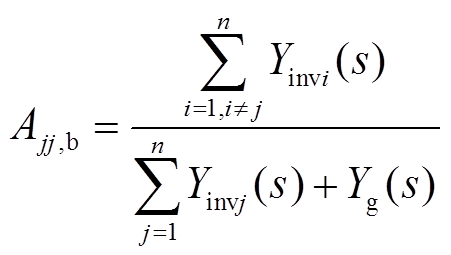 (8)
(8) (9)
(9)
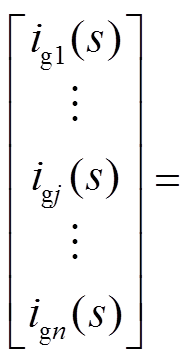
 (10)
(10)

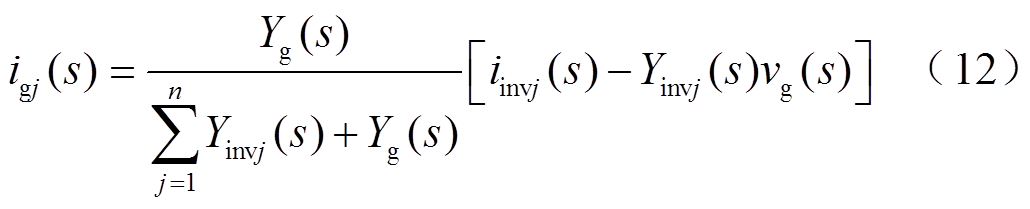
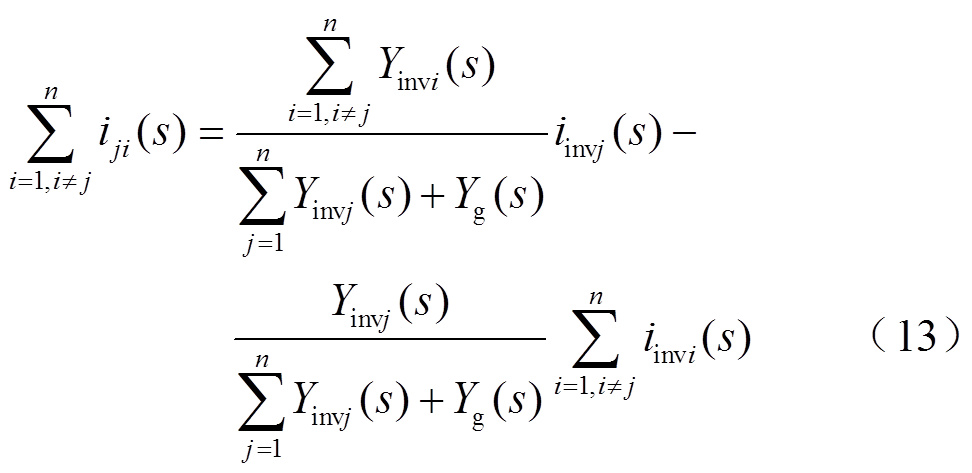
 (14)
(14)
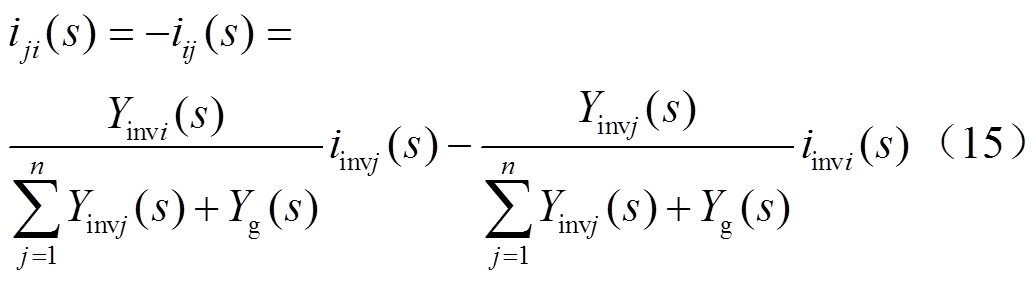

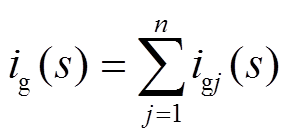 (17)
(17)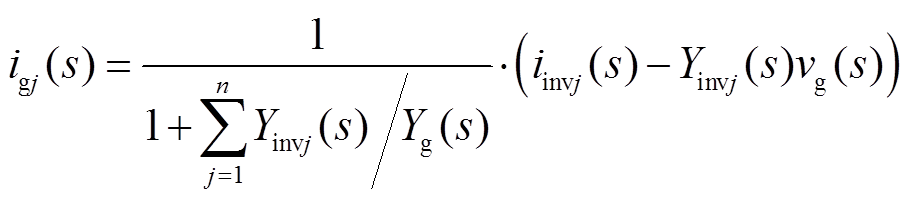 (18)
(18)
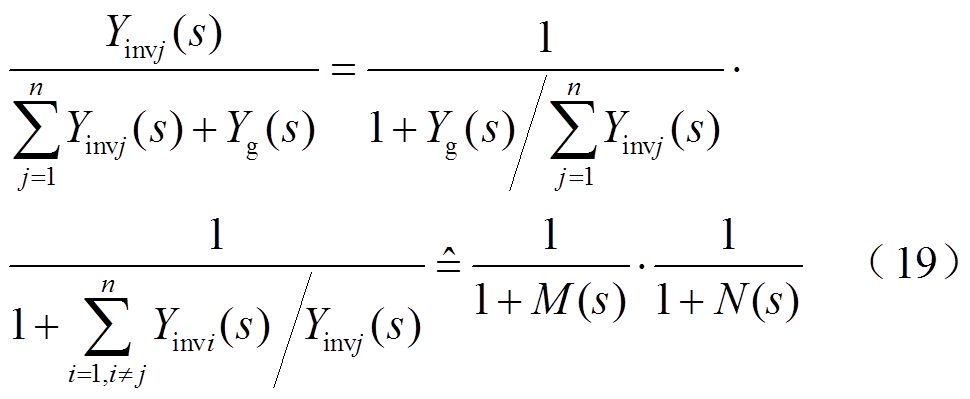
 , n)都需满足此条判据。
, n)都需满足此条判据。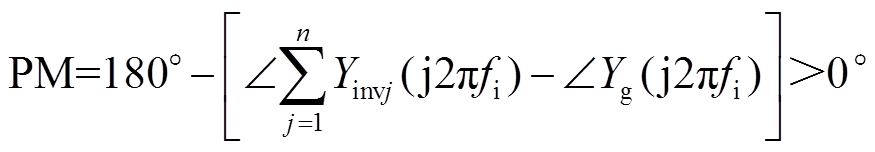 (20)
(20)
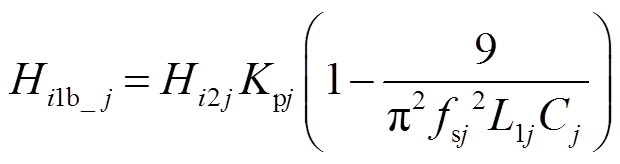 (21)
(21)
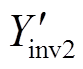 和
和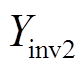 幅值相等的前提下,
幅值相等的前提下,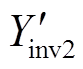 在Y
在Y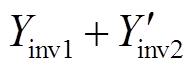 的相位裕度更大,如图5中所示。因此,对于多机并联逆变器并网系统,若提高系统中某一模块的开关频率,使其在目前低频逆变集群系统谐振频率范围内具有较强的阻尼特性,那么即可提高整个系统在弱电网下的鲁棒性。
的相位裕度更大,如图5中所示。因此,对于多机并联逆变器并网系统,若提高系统中某一模块的开关频率,使其在目前低频逆变集群系统谐振频率范围内具有较强的阻尼特性,那么即可提高整个系统在弱电网下的鲁棒性。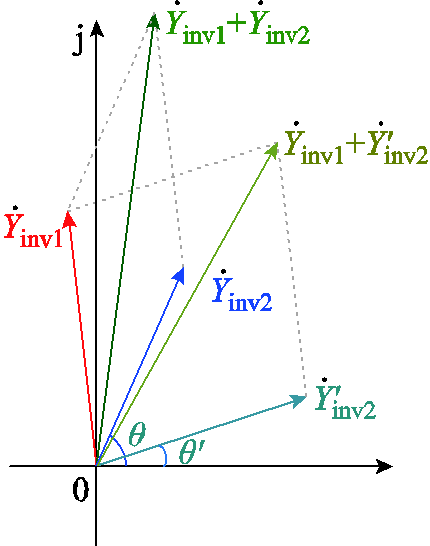
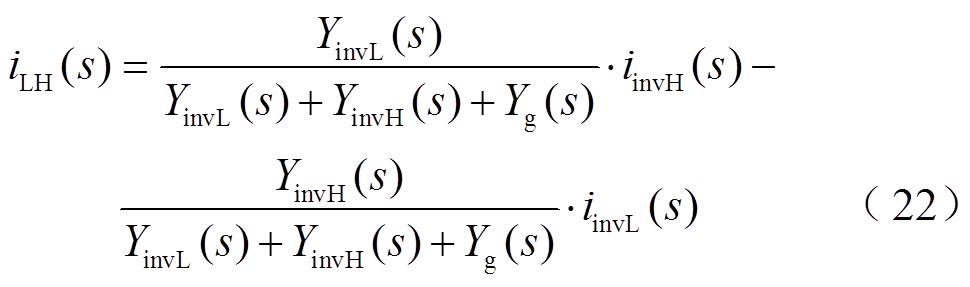
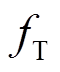 <f<
<f<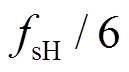 范围内,Y
范围内,Y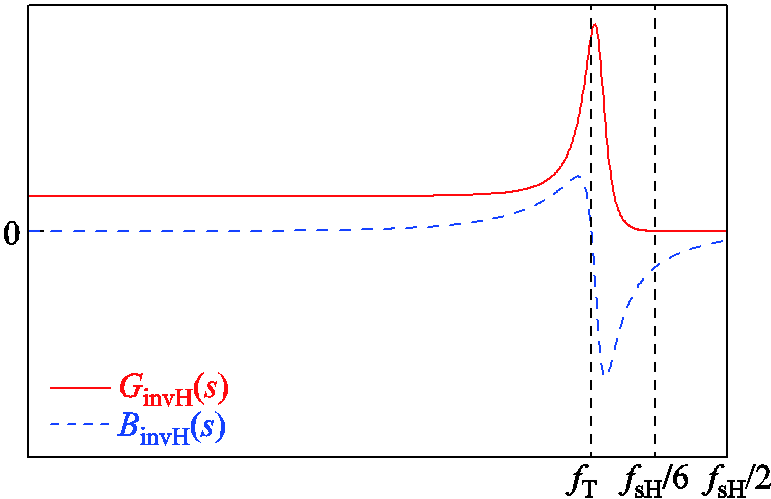



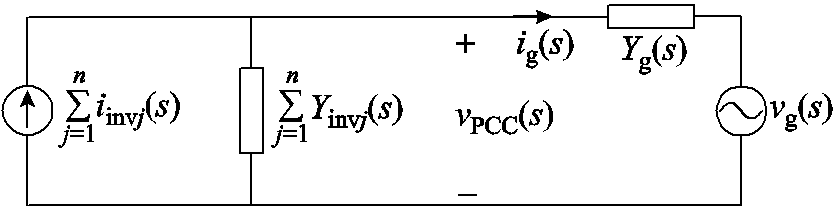
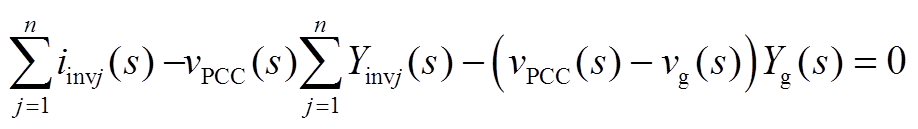 (A1)
(A1)
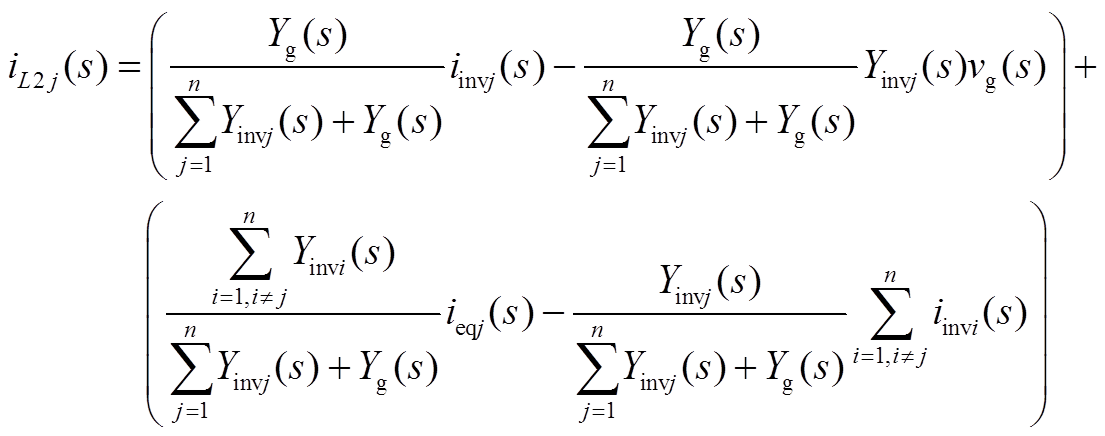 (A2)
(A2)
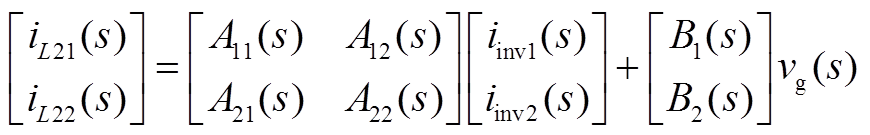 (A3)
(A3)
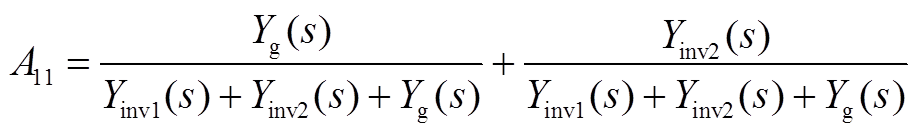 (A4)
(A4)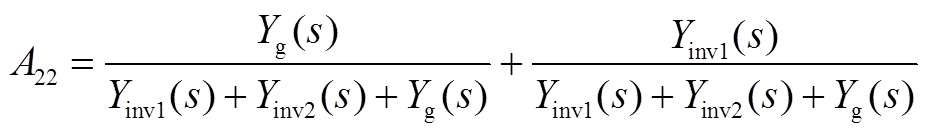 (A5)
(A5)
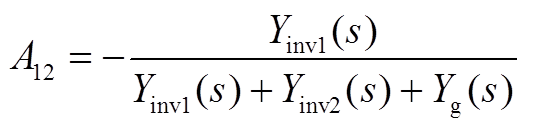 (A6)
(A6)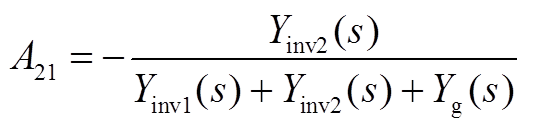 (A7)
(A7)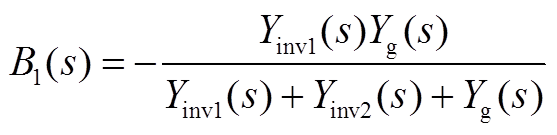 (A8)
(A8)
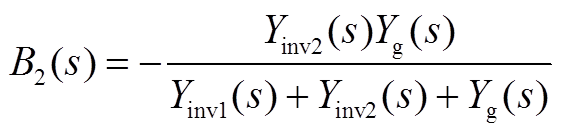 (A9)
(A9)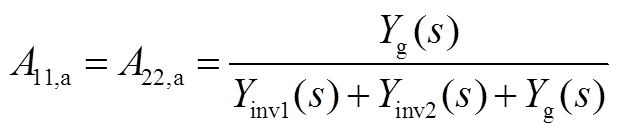 (A10)
(A10)
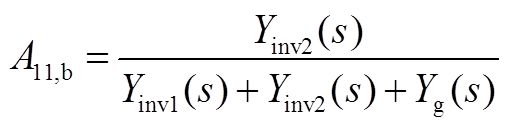 (A11)
(A11) (A12)
(A12)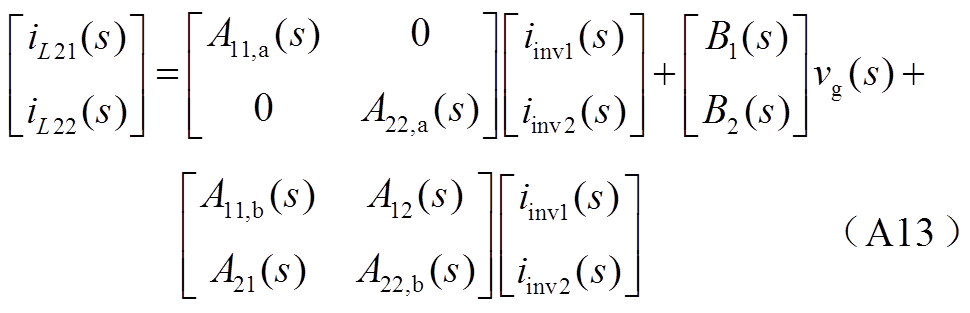
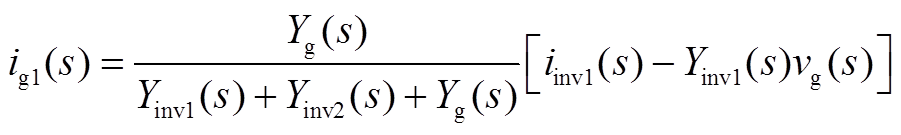 (A14)
(A14) (A15)
(A15)
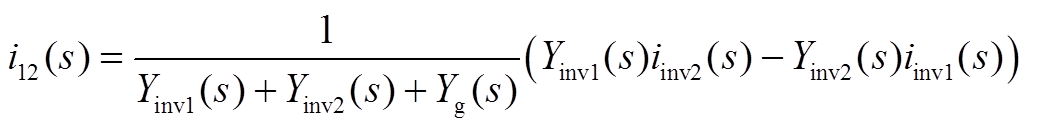 (A16)
(A16)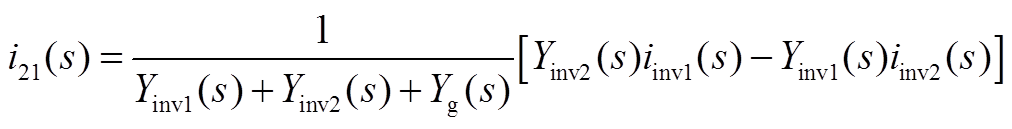 (A17)
(A17)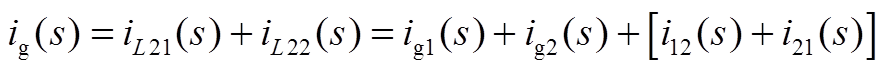 (A18)
(A18)
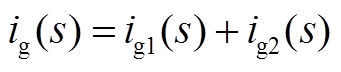 (A19)
(A19)