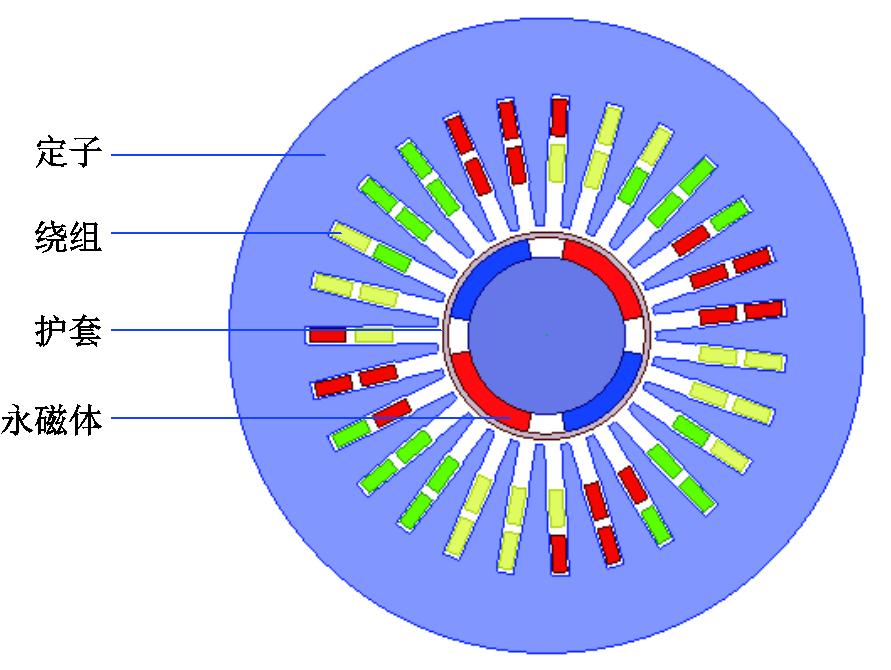
图1 HSPMM截面图
Fig.1 HSPMM cross section
摘要 高速永磁电机(HSPMM)由于具有功率密度和效率高、体积小、质量轻及动态响应快等优点受到越来越多的关注。然而,HSPMM的设计是一个典型的非线性的多物理场耦合设计过程,难以建立准确的数学模型对其进行优化设计。该文提出一种基于多物理场近似模型(MPAM)的HSPMM多目标优化设计方法。该方法采用MPAM进行多物理场的并行计算,并在优化过程中直接调用MPAM,可以有效地解决有限元模型(FEM)计算耗时的问题,同时也可以避免有限元优化过程中FEM迭代计算收敛困难的问题。最后,研制了一台1.1MW,18 000r/min的高速永磁电机,并进行了相关的实验,验证了该文所提出的HSPMM优化设计方法的可行性。
关键词:高速永磁电机 多物理场 近似模型 多目标优化
高速永磁电机(High Speed Permanent Magnet Machine, HSPMM)系统具有功率密度和效率高、体积小、质量轻以及动态响应快等显著优点[1-2],能够满足高端装备制造的特殊需求,在军工装备、能源安全及节能减排等多种高速驱动装备领域具有十分广阔的应用前景,如电动汽车、燃气轮机、空气压缩机以及飞轮储能等[3-4]。然而,由于HSPMM的“高速”与“高频”特性,使得HSPMM在设计过程中往往需要进行物理场的协同设计,主要包括电磁场、应力场、转子动力学以及温度场[5-7]。
目前HSPMM的设计方法往往是基于有限元的多物理场串行设计,即各个物理场按照顺序依次进行设计,这使得其设计过程越发耗时。此外,在进行多目标优化时,还需要多次调用有限元模型(Finite Element Method, FEM),进而容易产生优化过程中有限元迭代计算不收敛的问题。文献[8]提出一种基于FEM的多物理场优化方法,由于在优化过程中需要频繁调用FEM,因此极大地增加了优化所需的时间成本。文献[9]提出一种基于响应面(Response Surface Model, RSM)的HSPMM多目标优化设计方法,然而,RSM在处理诸如HSPMM多物理场设计之类的高度非线性问题时,将受限于多项式方法本身的不足。
近年来,近似模型(Approximate Model, AM)技术通过数学逼近的方法表示一组输入变量和输出变量之间的关系,已广泛应用于多学科设计领域[10-11]。文献[12]提出一种自适应采样的近似模型,用以减少电机多目标优化过程中的计算成本。文献[13]采用近似模型的方法对飞轮储能用高速永磁电机进行了气隙磁通密度的波形优化。综上所述,近似模型技术在电机的优化领域具有一定的可行性,而HSPMM的优化是典型的多物理场非线性设计问题,传统的FEM优化设计收敛困难且越发耗时。此外,近似模型的应用同时还将打破以往的HSPMM串行设计的桎梏,实现HSPMM多物理场的并行优化设计。
本文提出了一种基于多物理场近似模型(Multi-Physics Approximate Model, MPAM)的HSPMM多目标优化方法。首先,通过正交设计对HSPMM进行多物理场样本点采集;其次,构建本文所提出的MPAM,并对其进行误差分析,以确保构建模型的近似精度;然后,在MPAM的基础上,采用非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm, NSGA-II)对电机进行多物理场并行优化设计;最后,研制一台1.1MW的实验样机,并通过实验验证了本文所提出的基于MPAM的优化设计方法的可行性和有效性。
本文所研究的HSPMM的基本结构如图1所示,基本参数见表1。永磁体(Permanent Magnet, PM)采用NdFeB,永磁体外部采用碳纤维绑扎,永磁体与碳纤维保护套之间采用过盈配合。

图1 HSPMM截面图
Fig.1 HSPMM cross section
表1 HSPMM基本参数
Tab.1 The basic parameters of HSPMM

参数数值 额定功率/MW1.1 额定电压/V3 000 额定转速/(r/min)18 000 额定频率/Hz600 极数4 定子外径/mm550 定子内径/mm190 极弧系数0.75
由于在HSPMM设计过程中应综合考虑电磁、机械应力和转子动力学[14-15],这将大大增加设计难度。传统的设计过程通常是基于多物理场的串行设计,并且设计过程中经常需要根据设计者的经验来调整参数,这既耗时又难于找到最佳设计方案。本文提出了一种基于MPAM的HSPMM多目标优化设计方法,其流程如图2所示。
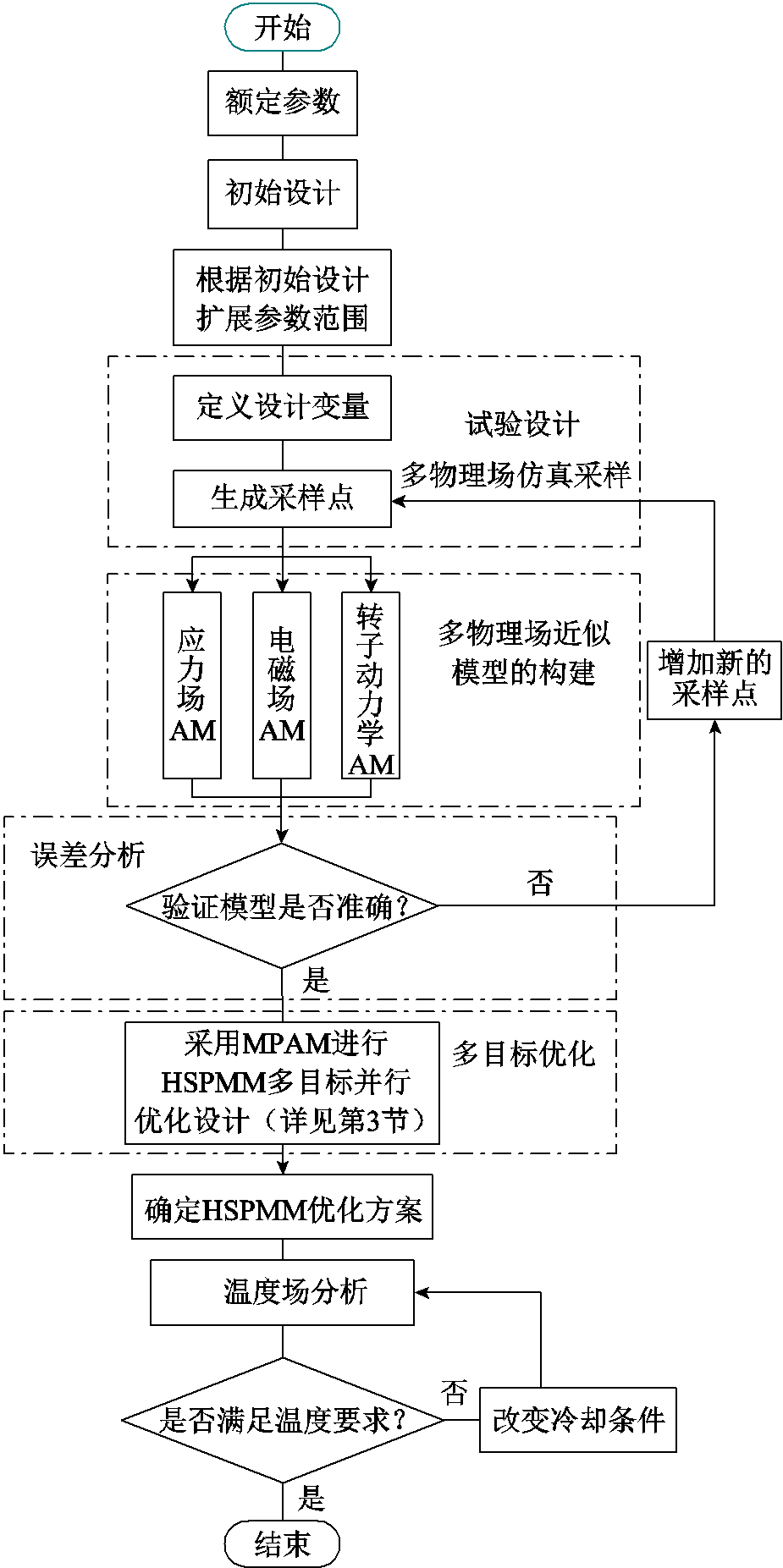
图2 基于MPAM的HSPMM多目标优化设计流程
Fig.2 Optimal design process of HSPMM based on MPAM
本文所选用HSPMM的设计变量分别是护套厚度hs,永磁体厚度hm,气隙长度δ,铁心有效长度lef和过盈量ε。设计变量的取值范围见表2,每个变量的取值范围是在满足电动机基本性能的前提下获得的。
表2 设计变量取值范围
Tab.2 The range of design variables

设计变量下限上限 护套厚度hs/mm68 永磁厚度hm/mm1618 气隙长度δ/mm24 铁心有效长度lef/mm390410 过盈量ε/mm0.050.2
在构建近似模型过程中需要事先确定优化过程中的目标/约束响应变量,综合考虑到HSPMM的多物理场特性,本文定义的目标/约束响应变量为:冷态PM的最大径向应力(σrM)、热态PM的最大切向应力(σθM(thermal))、热态护套的最大切向应力(σθS(thermal))、冷态下的最小接触应力(σc)、空载反电动势(E0)、气隙磁通密度(Bair)、输出转矩(Tout)、齿槽转矩(Tcog)以及一阶临界转速(ωn1)。
试验设计(Design of Experiment, DOE)是设计变量空间的采样计划[16-17],在近似建模的过程中,通过有效的试验设计可以在较少的样本数量条件下更有效地获取精确模型信息,从而提高构造近似模型的精度和效率。
本文采用的正交试验设计按照事先拟定好的满足正交试验条件的L64(45)正交试验表来安排样本点的采集,见表3。该正交表具有5个因子,4个水平。通过DOE设计可以清楚地看出每个设计变量对HSPMM各个物理场指标的主效应,如图3所示,其斜率越大,则表示设计变量对响应变量的主效应越明显。
表3 L64(45)正交试验表
Tab.3 L64(45) orthogonal table
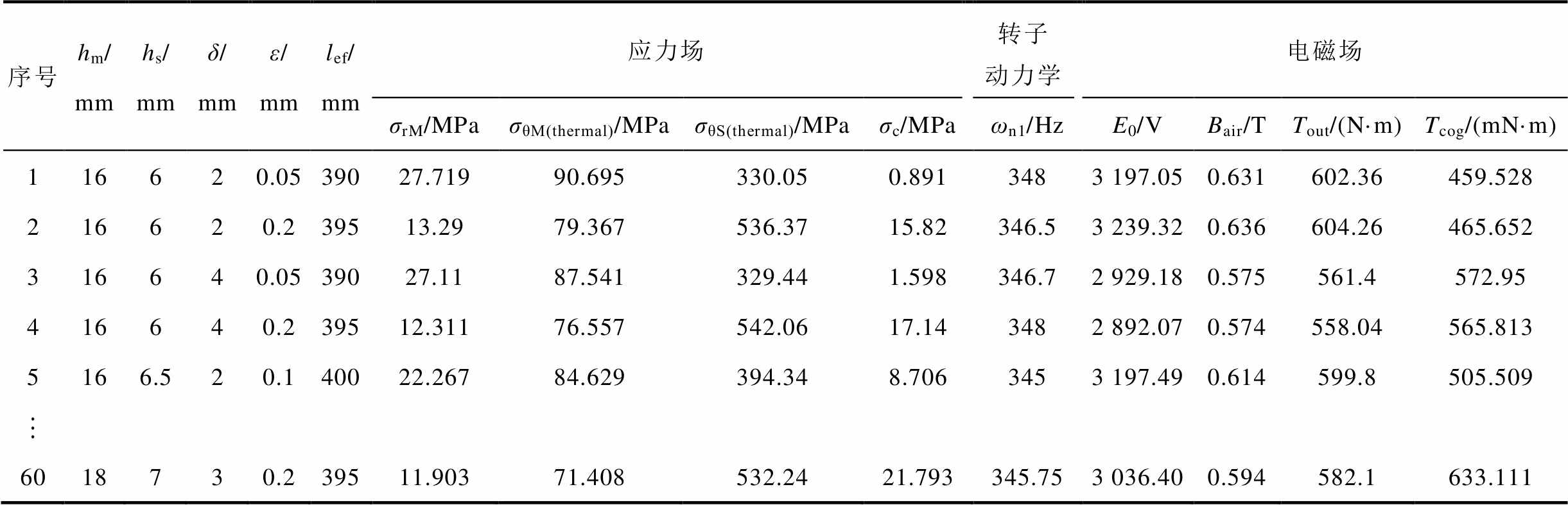
序号hm/mmhs/mmδ/mmε/mmlef/mm应力场转子动力学电磁场 σrM/MPaσθM(thermal)/MPaσθS(thermal)/MPaσc/MPaωn1/HzE0/VBair/TTout/(N·m)Tcog/(mN·m) 116620.0539027.71990.695330.050.8913483 197.050.631602.36459.528 216620.239513.2979.367536.3715.82346.53 239.320.636604.26465.652 316640.0539027.1187.541329.441.598346.72 929.180.575561.4572.95 416640.239512.31176.557542.0617.143482 892.070.574558.04565.813 5166.520.140022.26784.629394.348.7063453 197.490.614599.8505.509 6018730.239511.90371.408532.2421.793345.753 036.400.594582.1633.111
(续)
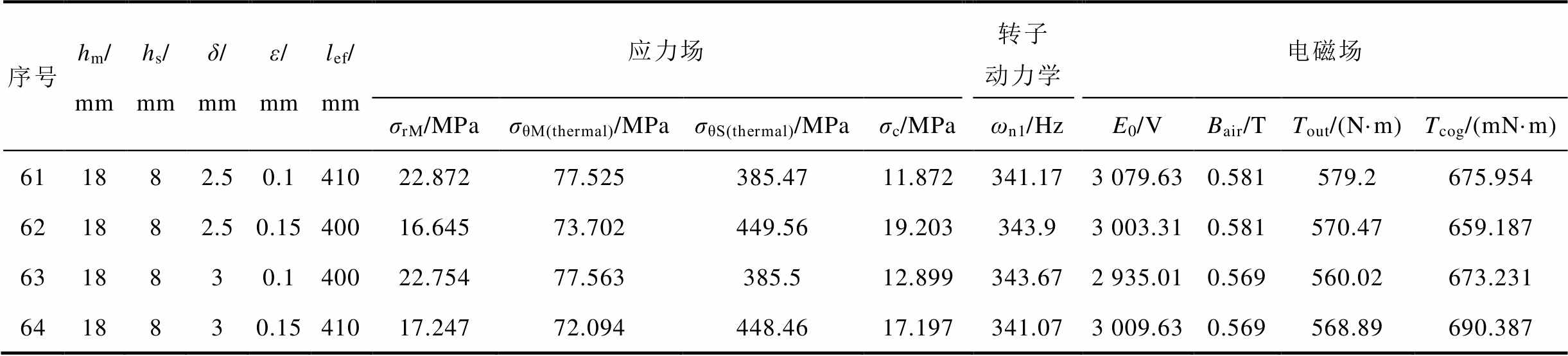
序号hm/mmhs/mmδ/mmε/mmlef/mm应力场转子动力学电磁场 σrM/MPaσθM(thermal)/MPaσθS(thermal)/MPaσc/MPaωn1/HzE0/VBair/TTout/(N·m)Tcog/(mN·m) 611882.50.141022.87277.525385.4711.872341.173 079.630.581579.2675.954 621882.50.1540016.64573.702449.5619.203343.93 003.310.581570.47659.187 6318830.140022.75477.563385.512.899343.672 935.010.569560.02673.231 6418830.1541017.24772.094448.4617.197341.073 009.630.569568.89690.387
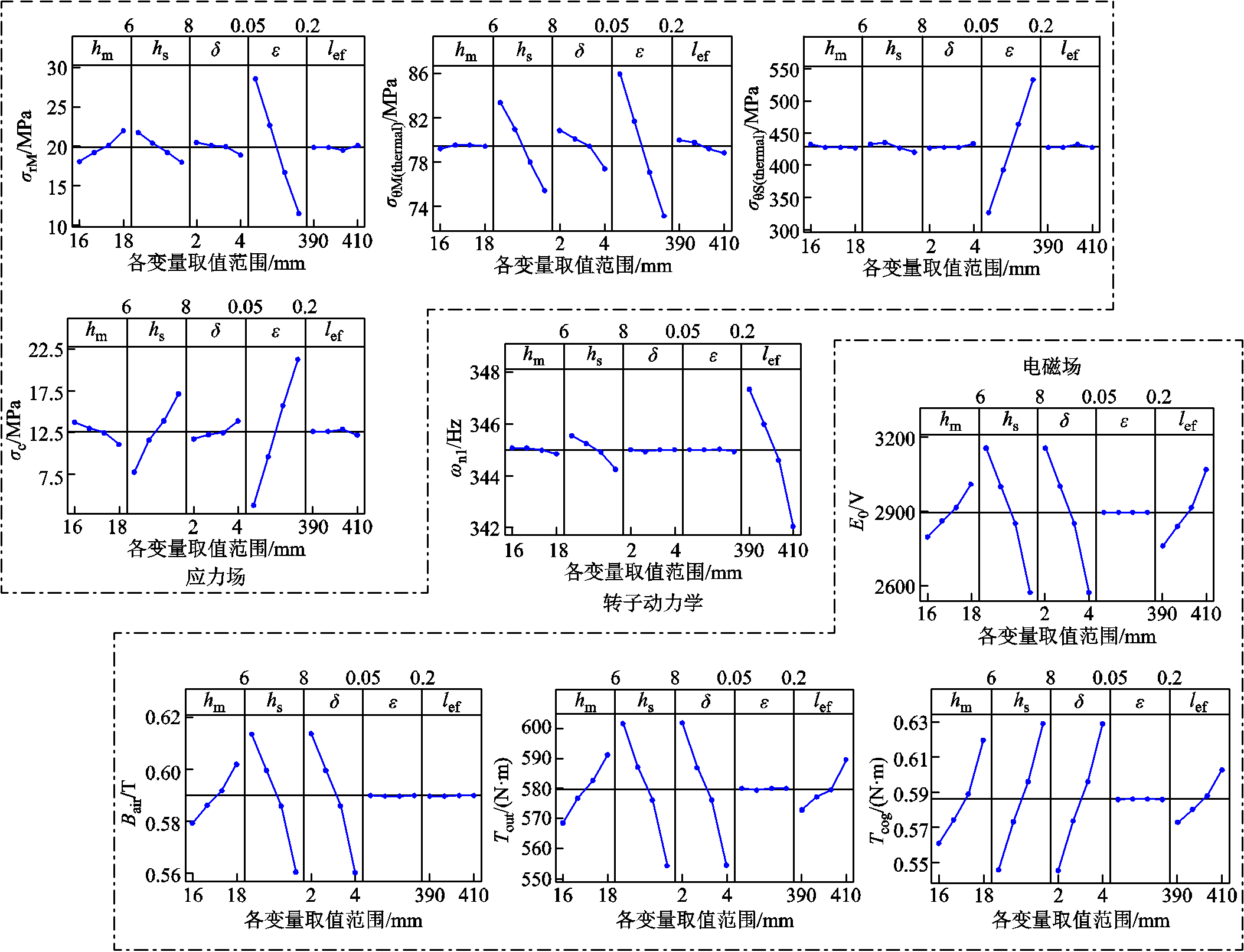
图3 各物理场主效应图
Fig.3 Main effect diagram of each physics field
多物理场近似模型构建的主要思想是数学的逼近方法,本文所构建的模型依托于Kriging模型,该模型基于变量的相关性和可变性来确定有限区域内变化的值,系统的响应值f(x)与自变量x之间的真实关系可以表示为[18]
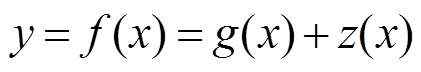 (1)
(1)
式中,g(x)为确定性部分,称为确定性漂移,通常为x的多项式;z(x)称为涨落,具有以下统计特征
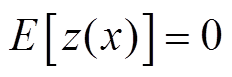 (2)
(2)
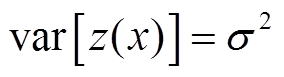 (3)
(3)
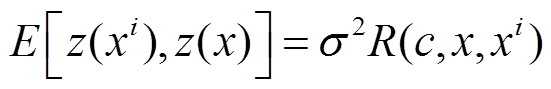 (4)
(4)
式中,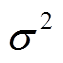 为方差;xi为第i个训练样本点的输入部分;R(c, x, xi)为一个以c为参数的相关函数。本文将指数函数作为相关函数,其可以表示为
为方差;xi为第i个训练样本点的输入部分;R(c, x, xi)为一个以c为参数的相关函数。本文将指数函数作为相关函数,其可以表示为
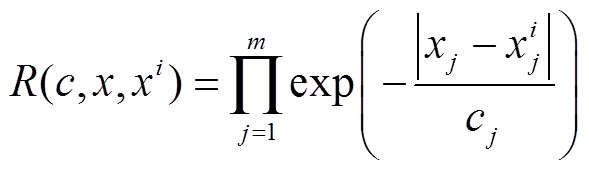 (5)
(5)
式中,cj为函数在采样点第j个方向上的常数参数;m为设计变量的维度;xj为待测点在第j个方向上的坐标;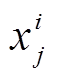 为第i个采样点在该方向的坐标。根据以上统计特征可以得到
为第i个采样点在该方向的坐标。根据以上统计特征可以得到
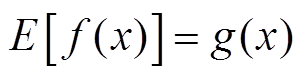 (6)
(6)
使用采样点xi的响应值yi的线性加权叠加插值计算测量点x的响应值,可以得到
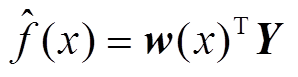 (7)
(7)
其中
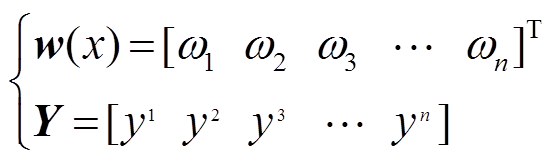 (8)
(8)
根据式(7)进行求解时,需要满足无偏条件,即
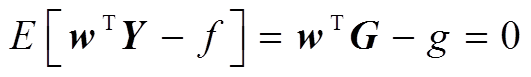 (9)
(9)
进而得到
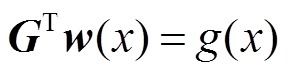 (10)
(10)
式中,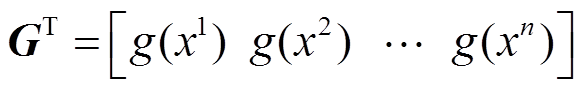 ,此时,式(7)的方差为
,此时,式(7)的方差为
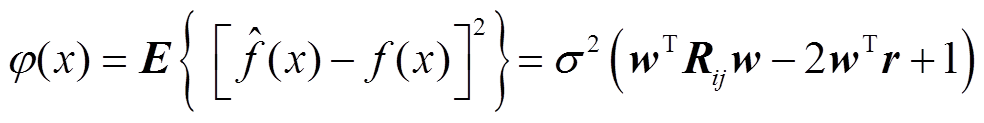 (11)
(11)
其中
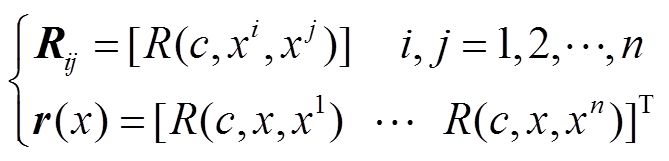 (12)
(12)
由于Kriging模型需要最小的预测方差,通过拉格朗日乘子法求解获得的最终结果为
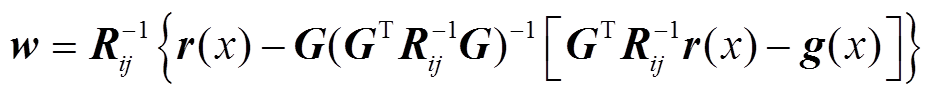 (13)
(13)
将其替换回式(7)即可得到预测值为
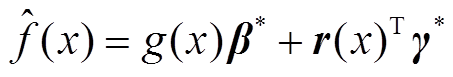 (14)
(14)
其中
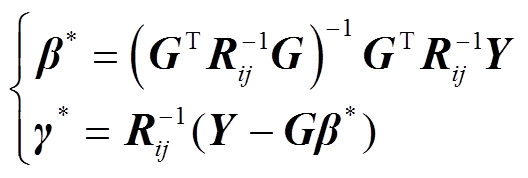 (15)
(15)
通过上述分析可以构建出各个物理场的近似模型,其预测值如图4~图6所示。图4给出了不同护套厚度hs和过盈量ε下,HSPMM所受应力的预测值。从图4中可以看出,护套厚度和过盈量的增加,有利于减小永磁体所受的径向应力和切向应力,同时也有利于增加永磁体的接触应力;然而,护套厚度的变化对护套本身所受切向应力影响很小,可以忽略不计,但是随着过盈量的增加,护套所受的切向应力将会快速增大。从应力场预测值的走势来看,与上述主效应分析一致,进而也说明了所建立应力场近似模型的可靠性。
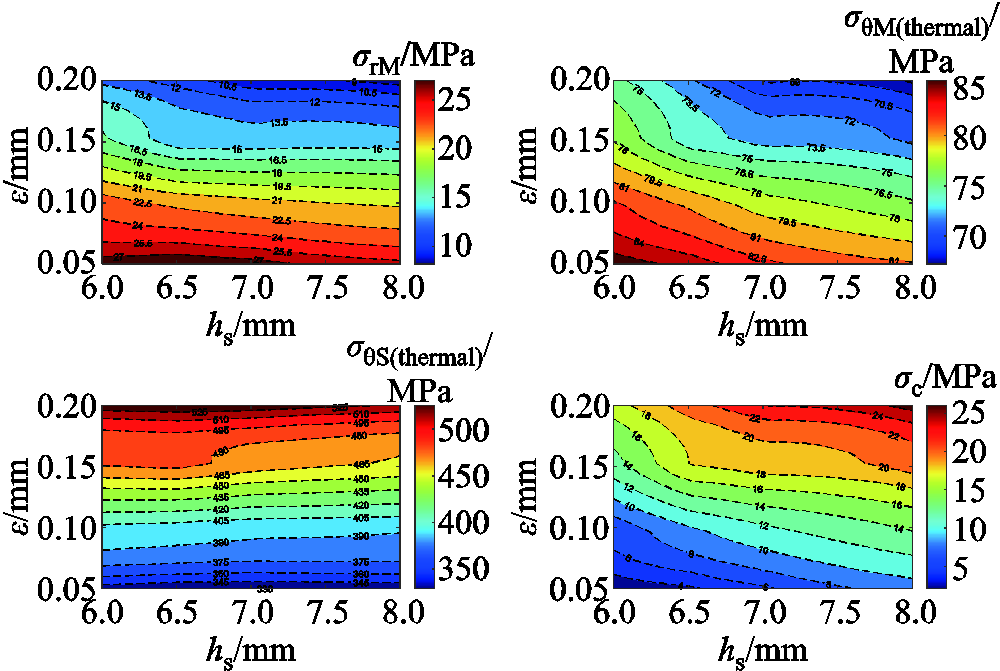
图4 应力场近似模型预测值
Fig.4 Predicted value of stress field surrogate model
图5给出了不同护套厚度hs和有效长度lef下,HSPMM的一阶固有频率。从图5中可以看出,随着护套厚度的减小,电机的一阶临界转速将增大,但是变化幅度很小,而随着轴向有效长度的减小,一阶临界转速将会逐渐增大。
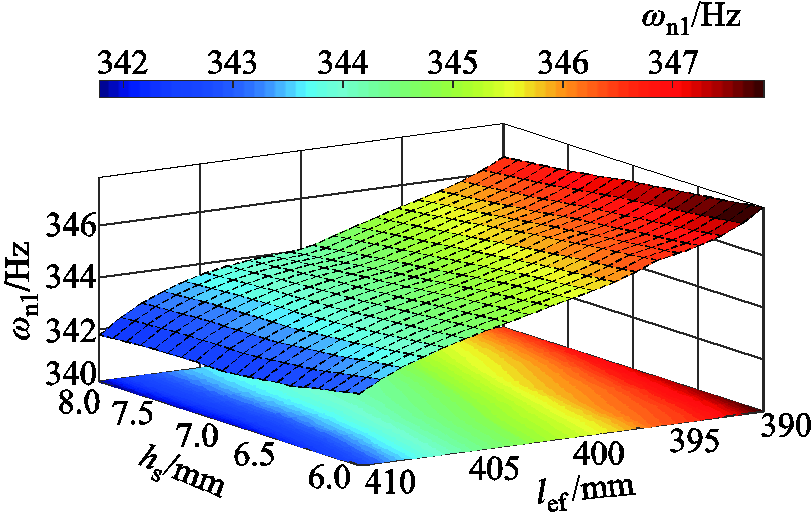
图5 转子动力学近似模型预测值
Fig.5 Predicted value of rotor dynamics surrogate model
图6以永磁厚度hm和气隙长度δ为例,对HSPMM电磁场近似模型的预测值进行说明。从图6中可以看出,随着永磁厚度hm的增加,HSPMM的空载反电动势E0、气隙磁通密度Bair、输出转矩Tout以及齿槽转矩Tcog均将随之增加;随着气隙长度的增加,HSPMM的空载反电势E0、气隙磁通密度Bair以及输出转矩Tout随之减小,但是齿槽转矩Tcog却随之增加。
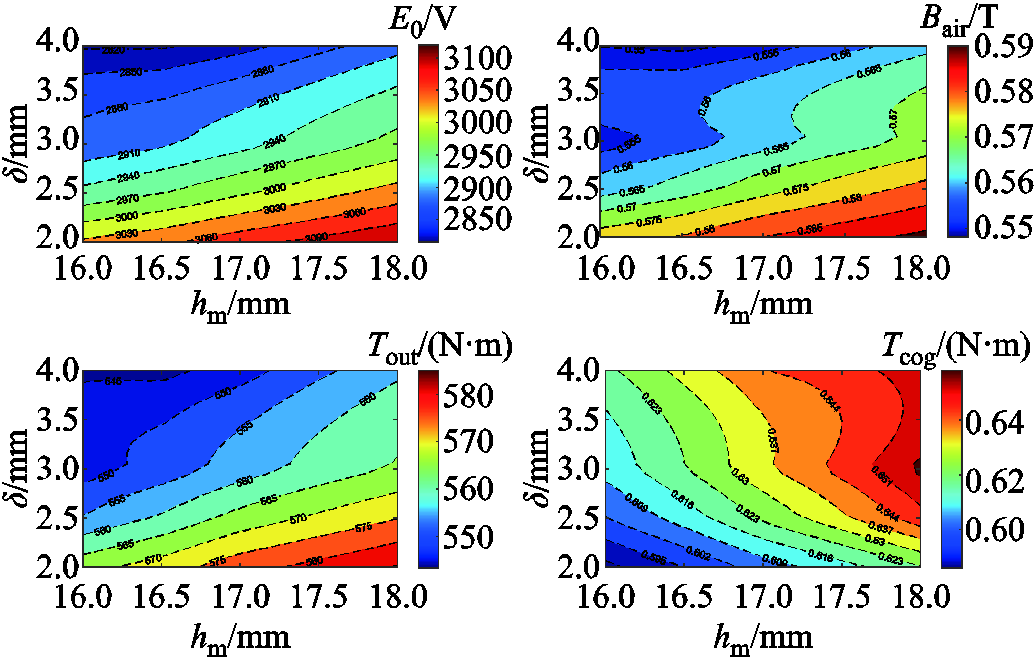
图6 电磁场近似模型预测值
Fig.6 Predicted value of electromagnetic field surrogate model
近似模型是建立在对实际的仿真计算模型进行近似的基础上,因此近似模型计算值与仿真计算实际值之间存在误差。在使用本文所建立的近似模型进行优化之前,需要对近似模型的预测精度进行误差分析和评估,以保证近似模型使用的有效性。
本文采用交叉验证(cross-validation)的方法进行误差分析。从数据样本集中随机移除10个数据点,一次移除一个,每移除一个样本点,将重新计算近似系数,并进行预测值与实际值的比较。然后将已移除的样本点放回样本集中并移除下一个样本点进行计算,依次类推。本文使用R2(R Square)作为近似模型的误差指标。R2越接近1,则替代模型越准确。为了保证模型的可靠性,本文的R2需要满足大于0.95。R2可以表示为
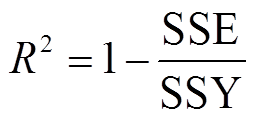 (16)
(16)
其中
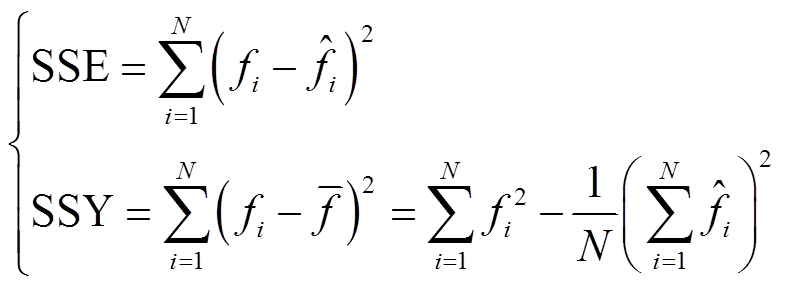 (17)
(17)
式中,N为测试集中的样本点数量;fi为FEM的计算值;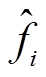 为近似模型的预测值;
为近似模型的预测值;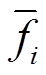 为样本点的近似平均值。
为样本点的近似平均值。
本文所选的9个响应变量的误差分析结果见表4。从表4中可以看出,响应变量的R2值均大于0.95,进而证明了本文所建立的近似模型具有高度的置信度。
表4 误差分析结果
Tab.4 The results of error analysis

响应变量R2值 σrM0.962 17 σθM(thermal)0.955 46 σθS(thermal)0.972 52 σc0.973 37 ωn10.982 25 E00.950 63 Bair0.983 31 Tout0.953 23 Tcog0.986 30
采用上述建立的多物理场代替有限元模型进行优化设计。由于高速永磁电机设计需要考虑多个目标,本文选择非支配排序遗传算法(NSGA-II)作为优化方法。在NSGA-II优化过程中,每个目标参数都需要进行单独处理,在优化过程中执行标准的遗传突变和交叉变异。选择过程基于两种主要机制,即“非支配排序”和“拥挤距离排序”[19-20]。在优化运行结束时,将构建一个Pareto集,其中每个设计都具有目标值的“最佳”组合,并且在不牺牲一个或多个其他目标的情况下,不可改善一个目标。具体优化步骤如下:
(1)初始化种群,生成父代种群Pt,其规模为N。
(2)通过非支配排序对种群Pt进行分层。
(3)对父代种群进行选择、交叉以及变异操作生成子代种群Qt。
(4)合并Pt和Qt生成新种群Mt,并进行快速非支配排序以及拥挤距离计算。
(5)使用精英策略从Mt中选取N个优良个体作为新一代的父代种群Pt+1。
(6)对新父代种群进行选择、交叉以及变异操作,生成子代种群Qt+1。
(7)判定迭代次数是否达到上限,若达到则算法结束;否则g=g+1,重复步骤(4)~步骤(7)。
根据前文的分析,HSPMM优化问题的数学模型可以描述为
 (18)
(18)
式中,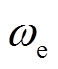 为电机的额定转速。
为电机的额定转速。
基于MPAM的多目标优化过程中的可行解与非可行解如图7所示,其中,三角代表优化过程中不可行的解,圆点代表优化过程中的可行点。从图7中可以看出,在进行多目标优化的过程中,由于各个目标之间存在冲突,在改进任何目标函数的同时,必然会削弱至少一个其他目标函数的解。最终得到的优化方案见表5,通过与初始设计相比,采用本文所提出的优化设计方法所设计的电机具有更好的性能,进而说明了本文所提出的优化设计方法的可行性。
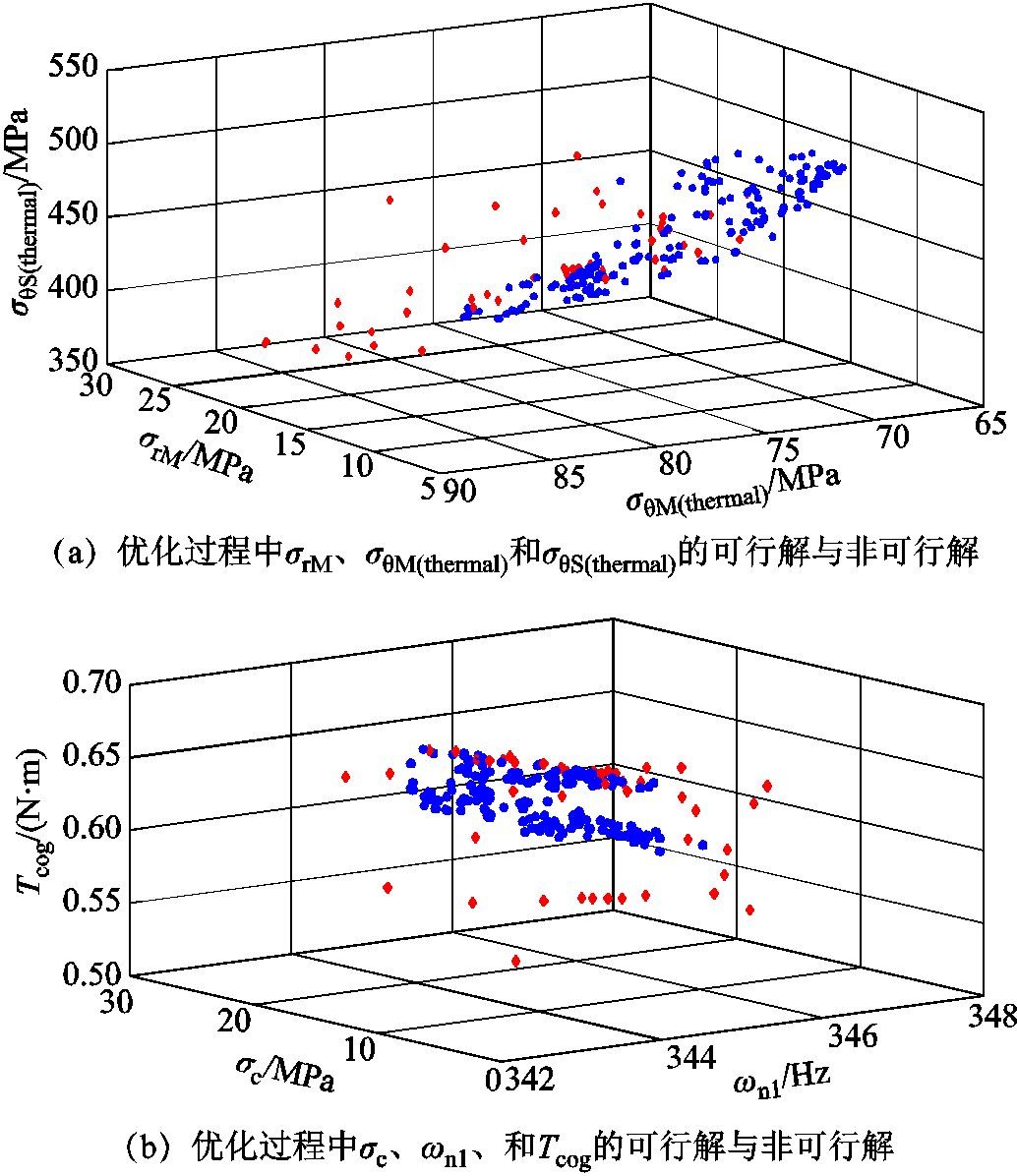
图7 基于MPAM优化的可行解与非可行解
Fig.7 Feasible and non-feasible solutions based on MPAM multi-objective optimization
表5 基于MPAM优化结果
Tab.5 Optimization Results based on MPAM

参数数值 初始设计基于MPAM优化设计 hm/mm1817 hs/mm87 δ/mm43.0 ε/mm0.10.17 lef/mm410400 σrM/MPa4.6118.62 σθM(thermal)/MPa70.877.17 σθS(thermal)/MPa449.9515.53 σc/MPa5.316.29 E0/V3 082.63 052.98 Bair/T0.530.58 Tout/(N·m)610.1610.3 Tcog/(N·m)0.710.61 ωn1/Hz345.6345.5
为了进一步验证基于MPAM优化所设计电机的准确性,本节对其进行了多物理场的性能分析以及热计算。
额定转速下转子机械应力分布情况如图8所示。从图8中可以看出,冷态下最大PM径向应力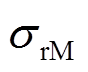 和热态下最大PM切向应力
和热态下最大PM切向应力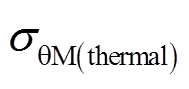 分别为18.8MPa和78MPa;热态下的最大护套切向应力
分别为18.8MPa和78MPa;热态下的最大护套切向应力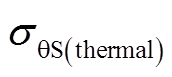 为517.8MPa;冷态下最小PM接触应力
为517.8MPa;冷态下最小PM接触应力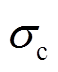 为16MPa。通过应力场FEM的分析可以看出,其值与表5中基于MPAM的优化方法所计算的值基本一致,这也证明了本文提出的优化方法在机械应力计算中的可靠性。
为16MPa。通过应力场FEM的分析可以看出,其值与表5中基于MPAM的优化方法所计算的值基本一致,这也证明了本文提出的优化方法在机械应力计算中的可靠性。
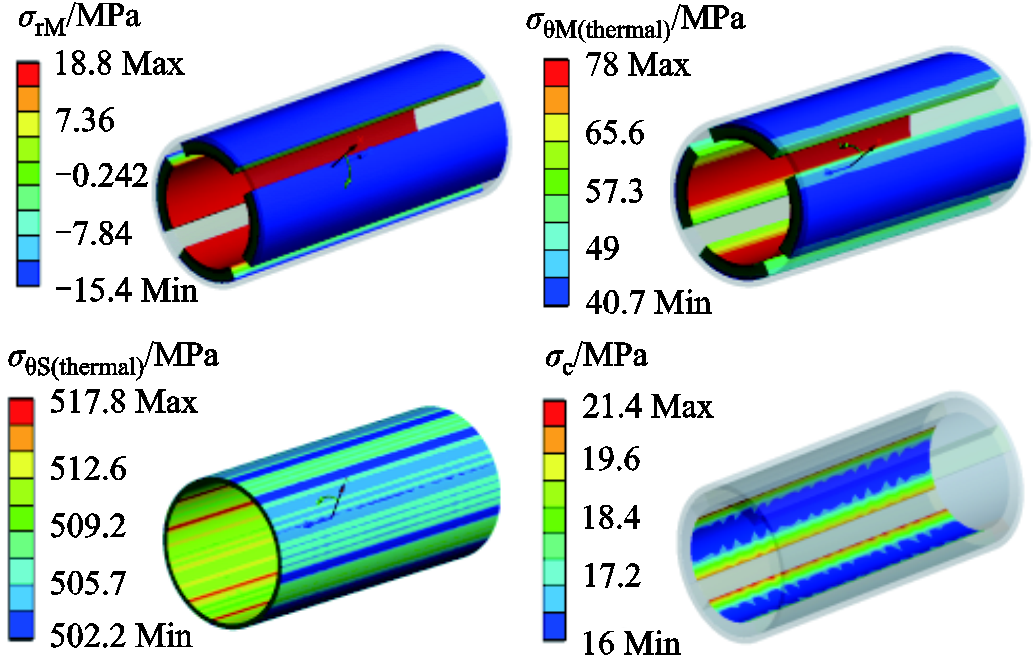
图8 转子机械应力分布
Fig.8 Rotor mechanical stress distribution
转子动力学的目的是通过预测HSPMM转子的固有频率,进而确定临界速度。对本文所设计的HSPMM进行转子动力学分析,转子动力学分析结果如图9所示。从图中可以看到,一阶临界速度约为20 735r/min,比额定速度高了15.19%,可以保证HSPMM转子的稳定运行。同时也可以看出,相应的一阶固有频率为345.58Hz,与表5中的MPAM优化设计的值(345.5Hz)基本一致。
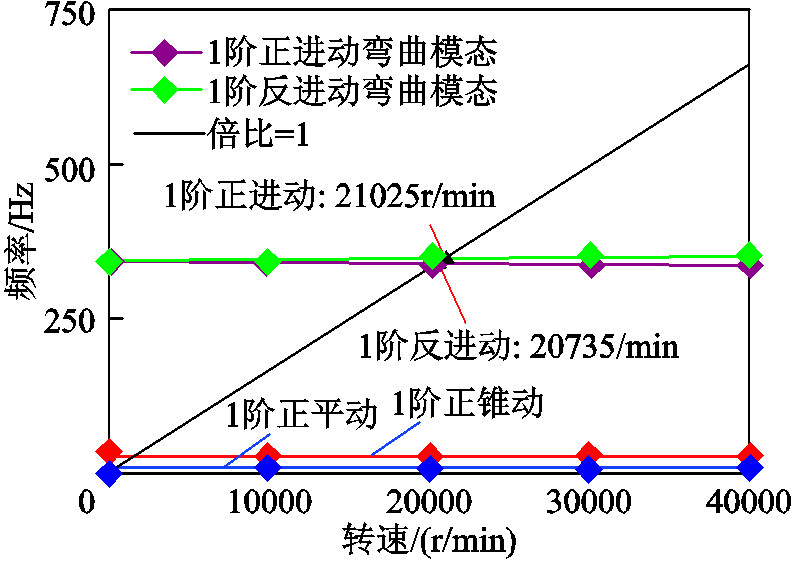
图9 转子动力学分析结果
Fig.9 The result of rotor dynamics analysis
基于多物理场近似模型优化设计所得的高速永磁电机的电磁性能如图10所示。从图中可以看出,空载反电动势有效值约为3.04kV、气隙磁通密度约为0.58T,齿槽转矩为0.6N·m,其值与表5中基于MPAM的优化方法所计算的值基本一致。
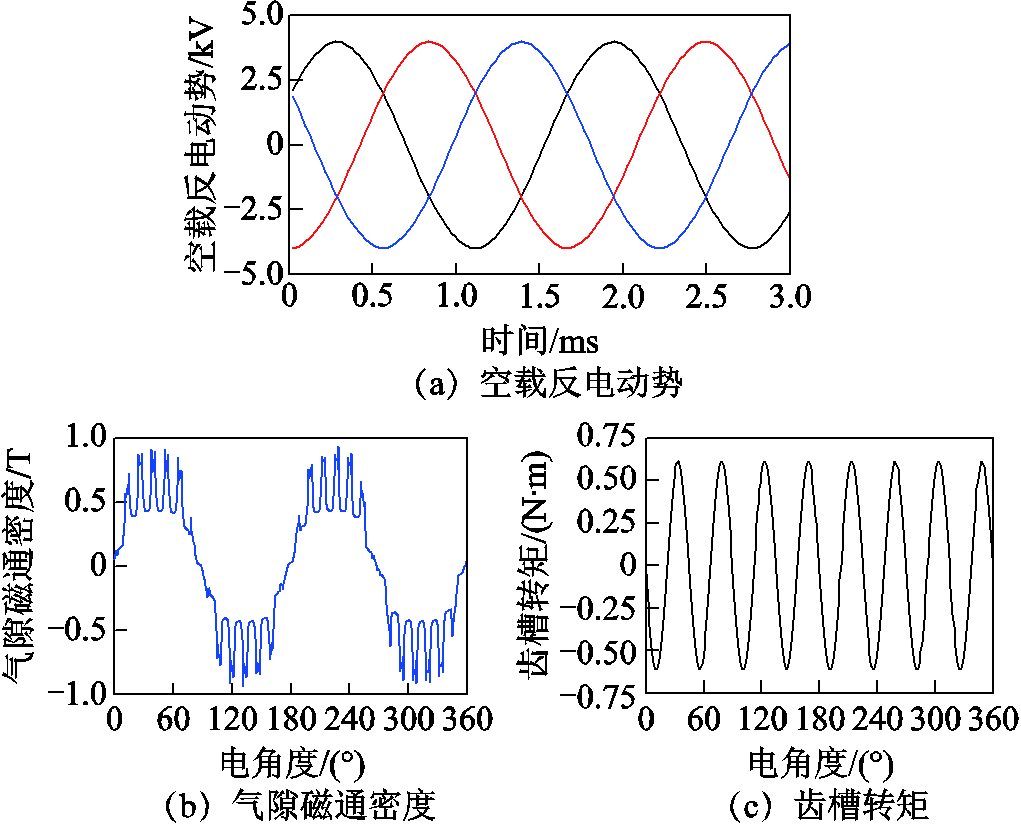
图10 HSPMM电磁性能
Fig.10 Electromagnetic performance of HSPMM
通过上述分析可以确保高速永磁电机电磁场、应力场以及转子动力学的可行性,该节将对其温度场进行验证。该电机采用机壳水冷和转子通风的混合冷却方式,本文采用流固耦合的方法对电机进行温度场计算,考虑到电机圆周方向的对称性,以定子一个槽距作为3D求解域,并作出如下假设:
(1)进风速度为15m/s,出口压力为标准大气压(0.101 325MPa)。
(2)水流道表面采用等效表面传热系数。
(3)假定进水温度为20℃,表面传热系数为2 600W/m2/K。
通过计算得到高速永磁电机的温度场分布如图11所示。从图11中可以看出,转子的最高温度为143.3℃,小于PM材料的最高工作温度,可以保障电机的可靠运行。
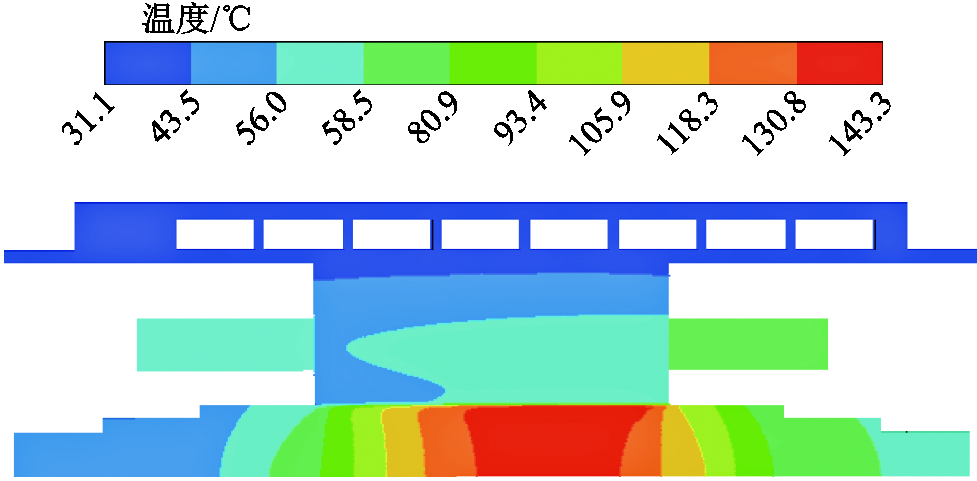
图11 温度场分析结果
Fig.11 Temperature field analysis results
通过上述分析,研制一台1.1MW,18 000r/min的实验样机,如图12所示,并对其进行了相关的研究。额定转速运行时样机的空载反电势波形以及额定负载下的电流波形如图13所示,其中空载反电势测量值约为3.1kV,额定负载时电流测量值为236A。额定转速下前后端轴承处主轴的运动轨迹如图14所示,从图14中可以看出,前端轴承在x和y方向上的峰-峰值分别为0.067 53mm和0.054 05mm;后端轴承在x和y方向上的峰-峰值分别为0.066 50mm和0.059 62mm。因此,当电动机以额定速度运行时,没有明显的振动位移。

图12 HSPMM样机
Fig.12 The prototype of HSPMM
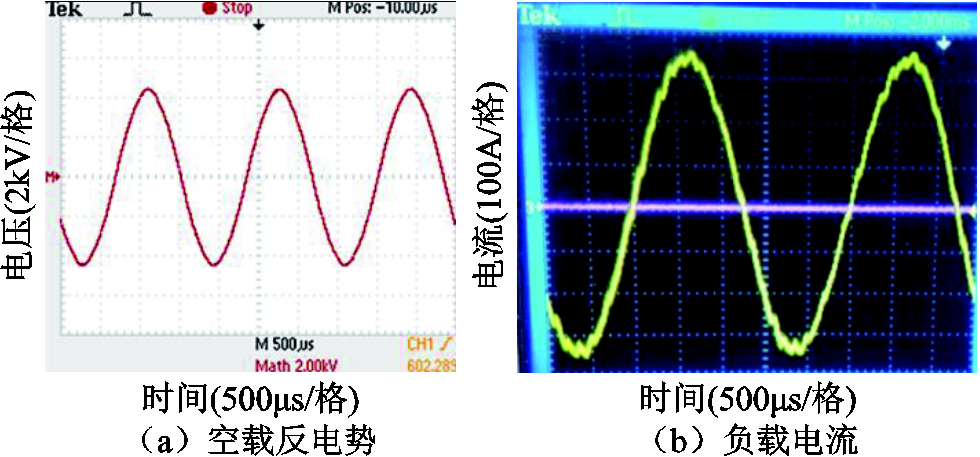
图13 实验数据
Fig.13 Experimental data

图14 额定转速下转子振动位移
Fig.14 Rotor vibration displacement at rated speed
为了对电机进行温度测试,在电机定子铁心和绕组的前后端分别布置了两个热敏电阻,对高速永磁电机12 000r/min负载持续运行3h的温度进行测试,结果见表6。从表6中可以看出,在持续运行180min时,定子绕组和铁心前后端的温度与图11中的计算结果基本吻合。
表6 电机温度实验测试结果
Tab.6 Temperature test results

时间/min定子绕组/℃定子铁心/℃ 前端后端前端后端 1042.578.532.136.6 6045.584.336.340.4 12050.487.139.843.6 18054.989.541.245.2
本文针对高速永磁电机多物理场优化问题展开研究,为有效解决传统有限元优化设计收敛困难且越发耗时的问题,提出了一种基于多物理场近似模型的高速永磁电机多目标优化设计方法,该方法通过近似模型替代传统的有限元模型实现高速永磁电机的多物理场并行优化设计。首先,通过正交试验设计对电机各物理场进行样本点数据采集;其次,构建各个物理场的近似模型并对其进行误差分析以确保模型的可靠性;然后,采用多物理场近似模型替代传统的有限元模型进行多目标优化;最后,研制了一台1.1MW实验样机,通过实验研究验证了本文所提出的基于多物理场近似模型的高速永磁电机并行优化设计方法的可行性及有效性。
参考文献
[1] 张凤阁, 杜光辉, 王天煜, 等. 高速电机发展与设计综述[J]. 电工技术学报, 2016, 31(7): 1-18.
Zhang Fengge, Du Guanghui, Wang Tianyu, et al. Review on development and design of high speed machines[J]. Transactions of China Electrotechnical Society, 2016, 31(7): 1-18.
[2] 董剑宁, 黄允凯, 金龙, 等. 高速永磁电机设计与分析技术综述[J]. 中国电机工程学报, 2014, 34(27): 4640-4653.
Dong Jianning, Huang Yunkai, Jin Long, et al. Review on high speed permanent magnet machines including design and analysis technologies[J]. Proceedings of the CSEE, 2014, 34(27): 4640-4653.
[3] Shen Jianxin, Qin Xuefei, Wang Yunchong. High-speed permanent magnet electrical machines—applications, key issues and challenges[J]. CES Transactions on Electrical Machines and Systems, 2018, 2(1): 23-33.
[4] Du Guanghui, Xu Wei, Zhu Jianguo, et al. Power loss and thermal analysis for high-power high-speed permanent magnet machines[J]. IEEE Transactions on Industrial Electronics, 2020, 67(4): 2722-2733.
[5] 沈建新, 韩婷, 尧磊, 等. 提高永磁体电阻率对降低高速永磁交流电机转子涡流损耗的有效性分析[J].电工技术学报, 2020, 35(9): 2074-2078.
Shen Jianxin, Han Ting, Yao Lei, et al. Is higher resistivity of magnet beneficial to reduce rotor eddy current loss in high-speed permanent magnets AC machines?[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 2074-2078.
[6] Du Guanghui, Huang Na, Zhao Yanyun, et al. Comprehensive sensitivity analysis and multiphysics optimization of the rotor for a high speed permanent magnet machine[J]. IEEE Transactions on Energy Conversion, 2021, 36(1): 358-367.
[7] 巩磊, 杨智, 祝长生, 等. 基于极性切换自适应陷波器的磁悬浮高速电机刚性转子自动平衡[J]. 电工技术学报, 2020, 35(7): 1410-1421.
Gong Lei, Yang Zhi, Zhu Changsheng, et al. Automatic balancing for rigid rotor of magnetically levitated high-speed motors based on adaptive Notch filter with polarity switching[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1410-1421.
[8] Huang Ziyuan, Fang Jiancheng. Multiphysics design and optimization of high-speed permanent-magnet electrical machines for air blower applications[J]. IEEE Transactions on Industrial Electronics, 2016, 63(5): 2766-2774.
[9] Du Guanghui, Zhou Qixun, Liu Shulin, et al. Multiphysics design and multiobjective optimization for high-speed permanent magnet machines[J]. IEEE Transactions on Transportation Electrification, 2020, 6(3): 1084-1092.
[10] Lee T W, Hong D K, Jung T U. High-speed, high-power motor design for a four-legged robot actuator optimized using the weighted sum and response surface methods[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(3): 224-231.
[11] 张邦富, 程明, 王飒飒, 等. 基于改进型代理模型优化算法的磁通切换永磁直线电机优化设计[J]. 电工技术学报, 2020, 35(5): 1013-1021.
Zhang Bangfu, Cheng Ming, Wang Sasa, et al. Optimal design of flux-switching permanent magnet linear machine based on improved surrogate-based optimization algorithm[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1013-1021.
[12] Son J C, Ahn J M, Lim J, et al. Optimal design of PMa-SynRM for electric vehicles exploiting adaptive-sampling kriging algorithm[J]. IEEE Access, 9: 41174-41183.
[13] Bu Jianguo, Zhou Ming, Lan Xudong, et al. Optimization for airgap flux density waveform of flywheel motor using NSGA-2 and kriging model based on MaxPro design[J]. IEEE Transactions on Magnetics, 2017, 53(8): 1-7.
[14] Uzhegov N, Kurvinen E, Nerg J, et al. Multidisciplinarydesign process of a 6-slot 2-pole high-speed permanent-magnet synchronous machine[J]. IEEE Transactions on Industrial Electronics, 2016, 63(2): 784-795.
[15] Zhang Fengge, Dai Rui, Liu Guangwei, et al. Design of HSIPMM based on multi‐physics fields[J]. IET Electric Power Applications, 2018, 12(8): 1098-1103.
[16] 李祥林, 李金阳, 杨光勇, 等. 电励磁双定子场调制电机的多目标优化设计分析[J]. 电工技术学报, 2020, 35(5): 972-982.
Li Xianglin, Li Jinyang, Yang Guangyong, et al. Multi-objective optimization analysis of electric-excitation double-stator field-modulated machine[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 972-982.
[17] 赵玫, 于帅, 邹海林, 等. 聚磁式横向磁通永磁直线电机的多目标优化[J]. 电工技术学报, 2021, 36(17): 3730-3740.
Zhao Mei, Yu Shuai, Zou Hailin, et al. Multi-objective optimization of transverse flux permanent magnet linear machine with the concentrated flux mover[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3730-3740.
[18] Parnianifard A, Azfanizam A S, Ariffin M K A, et al. Kriging-assisted robust black-box simulation optimization in direct speed control of DC motor under uncertainty[J]. IEEE Transactions on Magnetics, 2018, 54(7): 1-10.
[19] 曹永娟, 冯亮亮, 毛瑞, 等. 轴向磁场永磁记忆电机多目标分层优化设计[J]. 中国电机工程学报, 2021, 41(6): 1983-1992.
Cao Yongjuan, Feng Liangliang, Mao Rui, et al. Multi-objective stratified optimization design of axial-flux permanent magnet memory motor[J]. Proceedings of the CSEE, 2021, 41(6): 1983-1992.
[20] Wu Shaopeng, Huang Xiaojian, Tian Chenchen, et al. Multi-physical field optimization analysis of high-speed permanent magnet synchronous motor based on NSGA-II algorithm[C]//2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 2019: 1-6.
Multi-Objective Optimization Design of High-Speed Permanent Magnet Machine Based on Multi-Physics Approximate Model
Abstract High-speed permanent magnet machine (HSPMM) is attracting more attention due to its advantages of high power density and efficiency, small size, light weight and fast dynamic response. The design of HSPMM is a nonlinear, multi-physics coupled process that makes it difficult to build an accurate mathematical model to optimize design parameters. This paper presents a multi-objective optimization method based on multi-physics approximate model (MPAM). This method uses a MPAM to replace the multi-physics serial design process, and directly calls the MPAM for calculations in the optimization process, which can effectively solve the time-consuming problem and avoid the problem of non-convergence in the process of finite element model call. Finally, a 1.1MW, 18 000r/min HSPMM is produced and related experiments are carried out, the feasibility of the method proposed in this paper for HSPMM optimization is verified.
keywords:High speed permanent magnet machine, multi-physics, approximate model, multi-objective optimization
DOI:10.19595/j.cnki.1000-6753.tces.210748
中图分类号:TM355
国家自然科学基金资助项目(51920105011,52077121)。
收稿日期 2021-05-24
改稿日期 2021-12-01
戴 睿 男,1993年生,博士研究生,研究方向为高速永磁电机多物理场设计及优化。E-mail:rui_lucky@126.com
张 岳 男,1988年生,教授,博士生导师,研究方向为特种电机及其控制。E-mail:yzhang35@sdu.edu.cn(通信作者)
(编辑 赫蕾)