图1 非集成式LCC-S系统结构
Fig.1 Non-integrated LCC-S wireless power transmission system
摘要 针对无线电能传输系统在发射侧和接收侧偏移时输出功率和传输效率降低的问题,该文从共享磁通的角度提出了基于LCC拓扑的反极性同心式补偿电感集成方法,并提出了两种集成结构。建立了基于多耦合工作模式和线圈品质因数的反极性同心式无线电能传输系统输出功率和传输效率的数学模型,从数学模型上验证了集成式结构的抗偏移能力,仿真结果显示集成式结构在正对和偏移情况下,其磁通密度均优于非集成式结构。搭建了补偿电感集成式结构的实验样机,实验结果表明,补偿电感集成式结构在一定的偏移范围内能保持稳定的传输效率和输出功率,在相同输入电压和传输距离下比非集成式结构具有更高的传输效率和更大的传输功率。
关键词:共享磁通 多耦合模式 集成线圈 抗偏移 无线电能传输
磁耦合谐振式无线电能传输技术是一种新型的无接触式能量传输技术,因其相对于有线传导式传输具有安全、方便和可靠的优点[1],从而在电动汽车[2-3]和高速铁路[4-5]等领域拥有广阔的应用前景。由于无线电能传输系统的发射端和接收端之间的磁介质为空气,导致其漏感较大,同时耦合系数较低,并且在实际使用场景中,发射端和接收端多数情况下并不是工作在正对状态。因此无线电能传输系统的补偿拓扑[6]和抗偏移[7]研究尤为重要。
无线电能传输系统的补偿拓扑分为低阶拓扑、高阶拓扑[8]和混合高阶拓扑。低阶拓扑以SS型[9]为代表,高阶拓扑以LCL[10]和LCC[11]型为代表,混合高阶拓扑以LCC-S[12-13]和LCL-S[14]型为代表。由于高阶补偿拓扑和混合补偿拓扑的补偿点通常以独立电感的形式存在,因此增加了整个系统的体积。目前已经有一些研究将补偿电感和发射线圈集成起来。文献[15]针对双侧LCC型补偿结构提出一种集成结构,将两侧的补偿电感以DD型线圈的形式放在以D型线圈方式缠绕的发射线圈和接收线圈的背面,其最好效果是在偏移15cm处实现89.8%的传输效率;文献[16]将双侧LCC补偿拓扑的补偿电感以D型线圈的形式分别放置在发射线圈和接收线圈的背侧,发射线圈和接收线圈均采用DD型结构,其最好效果是在偏移15cm时实现94.8%的传输效率;文献[17]将双侧LCC补偿结构两侧的补偿电感以DD型线圈的形式嵌入到D型发射线圈和接收线圈的中孔,在偏移15cm时可以实现93%的传输效率;文献[18]则针对双侧LCL型补偿拓扑,将发射线圈和补偿电感分别作为DD型线圈的一个D型线圈进行发射端集成,接收端以同样的方式进行集成,在偏移12cm时仍能维持90%的传输效率。综上所述,可以看到目前高阶拓扑的集成方式是将补偿电感与发射线圈或接收线圈以D型或者DD型结构叠放在一起。由于DD型线圈本身就具有明显的抗偏移能力[19],因此集成后的结构也具有较强的抗偏移能力。但是当电流在集成后的DD线圈上反向流动时,势必会造成局部磁场相互抵消从而影响耦合效果,因此目前的集成方案并不利于实际应用。最新颁布的电动汽车无线充电系统国家标准[20]推荐采用D型线圈和LCC补偿拓扑,因此有必要针对LCC补偿拓扑提出新型的集成方案。
本文从单一耦合的非集成式LCC-S电路解耦分析入手,建立了非集成式LCC-S电路的数学模型,并分析了补偿电感对输出功率和传输效率的影响。从共享磁通的角度提出一种多耦合同心反极性补偿电感集成方法。从数学模型的角度揭示了在偏移状态下多耦合系数维持功率稳定的原理。在此基础上提出了补偿电感外绕式和补偿电感内绕式两种具体的集成结构。仿真和实验结果表明,本文提出的两种集成结构相比非集成式结构具有更高的磁通密度和更好的抗偏移能力,并且能够传输更高的功率。
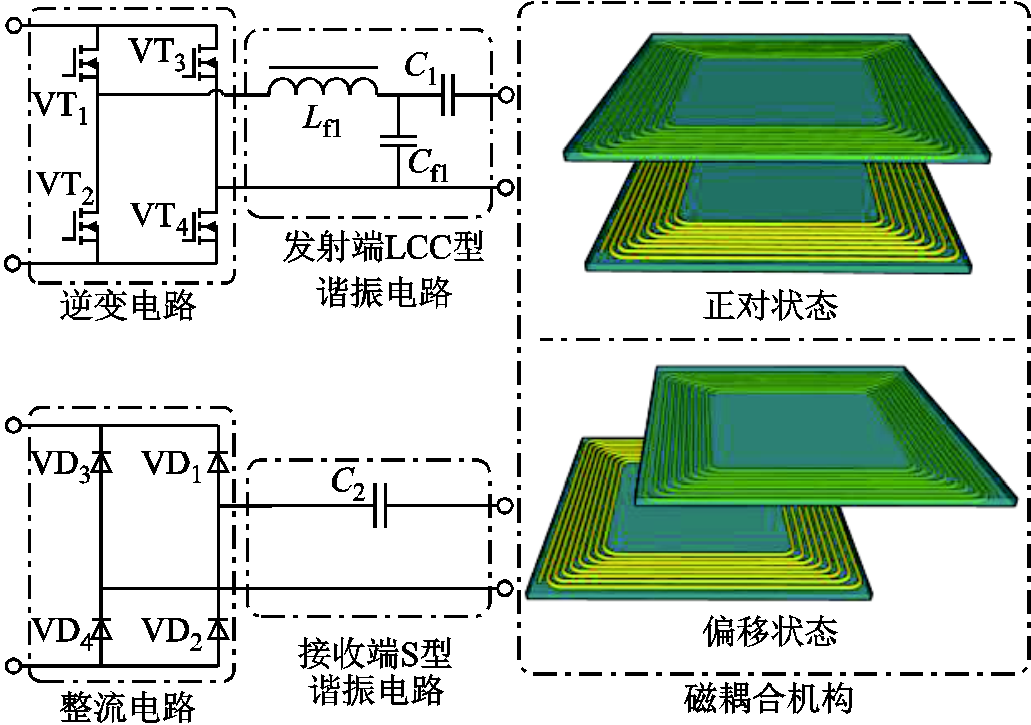
一个典型的非集成式LCC-S无线电能传输系统结构如图1所示。

图1 非集成式LCC-S系统结构
Fig.1 Non-integrated LCC-S wireless power transmission system
该系统由逆变电路、发射端谐振电路、磁耦合机构、接收端谐振电路和整流电路构成。输入直流电经过逆变电路逆变成为与系统谐振频率相同的交流电,通过谐振电路引起发射端和接收端同频率共振,将能量从发射线圈耦合到接收线圈,最终通过整流电路变为直流电供给负载。
非集成式LCC-S系统解耦电路如图2所示,定义Q1、Q2和Qf1分别为电感L1、L2和Lf1的品质因数,其表达式为Qx=ωLx/R0(x=f1,1,2),其中R0是电感的等效内阻;Rf1、R1和R2为各个电感的内阻,为简化分析过程,有R0=R1=Rf1=R2;Qn为电路等效品质因数,其表达式为Qn=ωL1/RL,RL为系统的负载电阻。由解耦电路列写回路电流方程解出回路电流,代入电路谐振条件和电感的品质因数表达式,得到非集成式LCC-S补偿拓扑工作在谐振状态时的输出功率Po和传输效率η表达式分别如式(1)和式(2)所示。
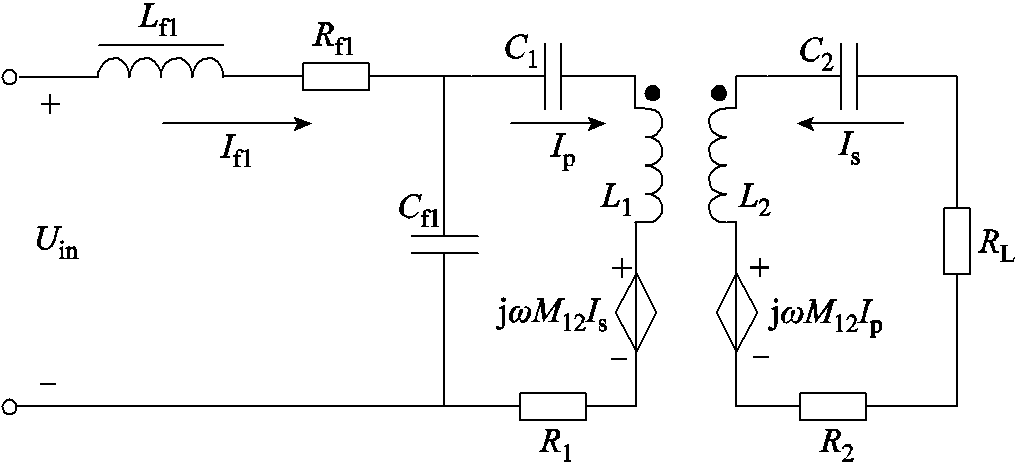
图2 非集成式LCC-S系统解耦电路
Fig.2 Non-integrated LCC-S system decoupling circuit
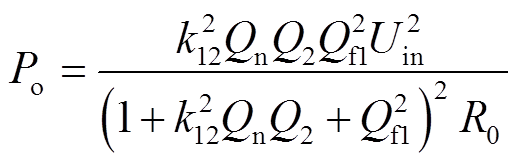 (1)
(1)
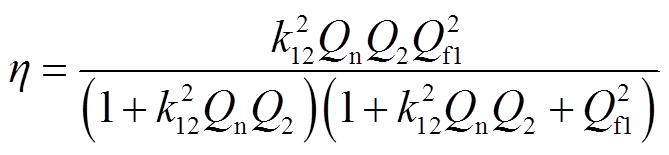 (2)
(2)
式中,k12为L1和L2之间的耦合系数。
根据式(1)和式(2)可以绘制出非集成式LCC-S结构在不同Lf1时的输出功率和传输效率随k12的变化曲线。当输入电压为100V,谐振频率为85.5kHz、R0=0.1Ω、L1=43μH、L2=65μH,Lf1分别为15μH、19μH和23μH时,非集成式LCC-S系统的输出功率和传输效率如图3所示。
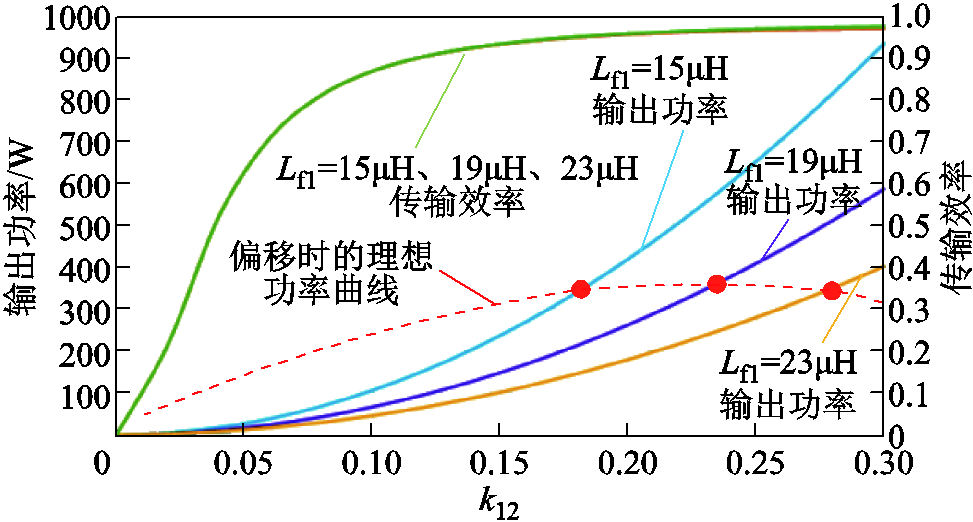
图3 Lf1不同时非集成式LCC-S系统的输出功率和传输效率
Fig.3 Output power and transmission efficiency of non-integrated LCC-S system with different Lf1
可以看出,耦合系数k12对输出功率和传输效率的影响十分明显,随着k12的降低,输出功率和传输效率均出现了明显的降低。同时可以看出不同补偿电感Lf1对传输效率的影响曲线基本重合,即不同的Lf1不会影响系统的传输效率。由输出功率曲线可以看出,Lf1越大,系统输出功率越低,因此Lf1的电感值会对系统输出功率产生重要影响。
由于补偿电感Lf1的电感值与输出功率呈现一种“负相关”的趋势,如图3中偏移时理想功率曲线所示。假如在系统发生偏移时,补偿电感Lf1的值能随耦合系数k12的降低同步减小,则在一定程度上可以维持输出功率稳定。
如1.1节所述,为了使补偿电感Lf1在系统偏移时产生减小的趋势,需要对其施加额外的耦合。
假设将两个线圈以同心圆形式嵌套在一起共同作为发射端,则其磁通的分布关系如图4所示。
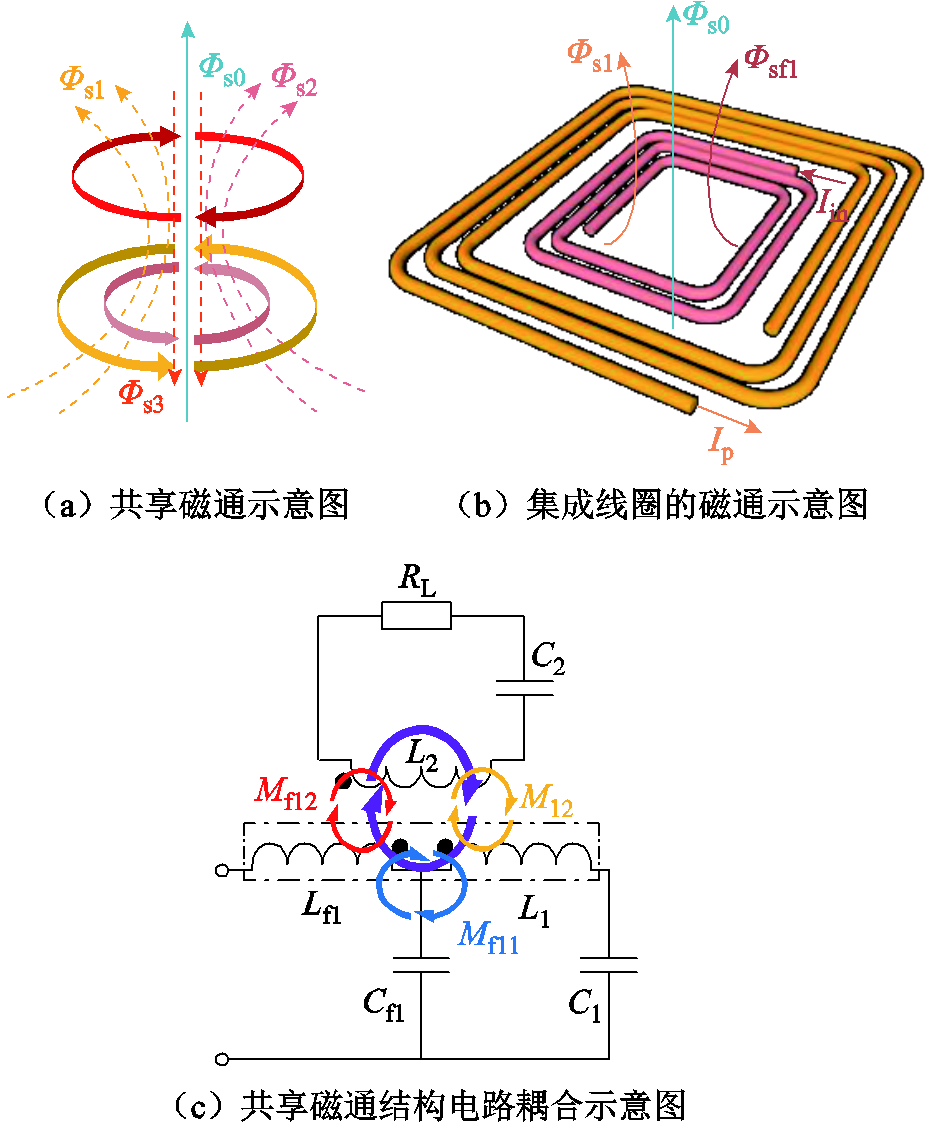
图4 LCC-S共享磁通多耦合集成发射线圈
Fig.4 LCC-S shared flux integrated firing coil
在图4a中,定义发射端和接收端互相铰链的磁通为Φs1、Φs2和Φs3,定义共享磁通为Φs0,则共享磁通Φs0的表达式为
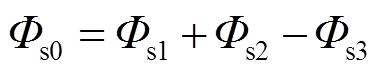 (3)
(3)
由式(3)可知,相比于没有嵌套同心圆的结构,在其他线圈参数不变的情况下,嵌套的线圈能够增强其共享磁通,进而增强其线圈电压。从增强共享磁通的角度出发,将LCC-S补偿电路的补偿电感Lf1与L1以同心形式反向极性缠绕在一起,集成后的Lf1与L1共享结构中心磁通,补偿电感Lf1以线圈形式同样参与能量传输。
如图4所示,本文所提出的新型LCC-S发射端集成结构不同于非集成式结构,其含有三个耦合关系,分别是L1和L2之间的互感M12,Lf1和L1之间的互感Mf11,Lf1和L2之间的互感Mf12。对应的三个耦合系数分别为k12、kf11和kf12,耦合系数表达式为kxy=|Mxy|/(LxLy)1/2(x=f1,1,y=1,2)。根据集成式LCC-S发射端的耦合关系,对所提结构进行解耦分析,其解耦后的电路结构如图5所示。
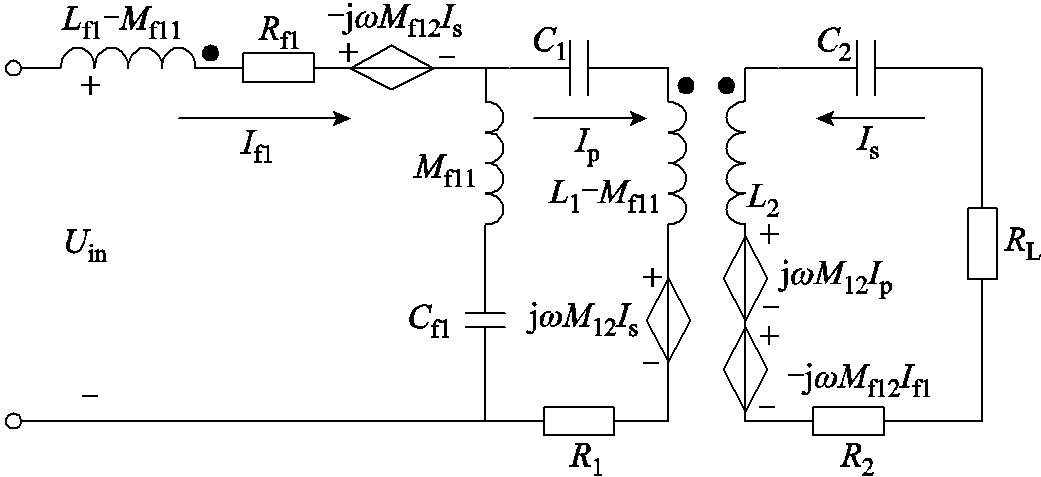
图5 集成式LCC-S解耦电路
Fig.5 Integrated LCC-S decoupling circuit
其中,由于补偿电感线圈Lf1和主发射电感线圈L1是反极性集成,Lf1和L1之间的互感Mf11使解耦后的Lf1对外的等效电感值为Lf1-Mf11,因此集成后的Lf1的电感值对外有一种减小的趋势,需要进一步建立解耦等效电路的数学模型来分析其传输功率和传输效率特性。
根据图5的集成式LCC-S发射端解耦电路,列写回路电流方程如式(4)所示。
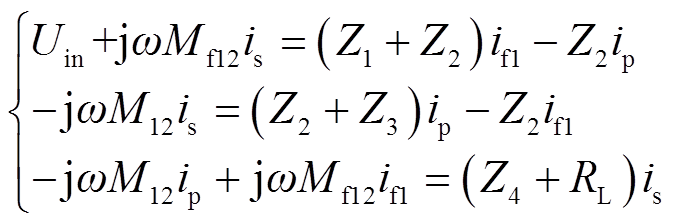 (4)
(4)
其中,Z1~Z4的表达式为
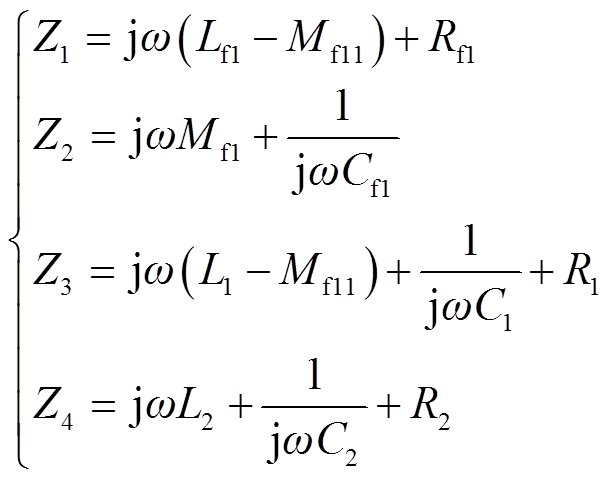 (5)
(5)
根据式(4)和式(5)解出三个回路电流的表达式,由于实际线圈的内阻很小,因此从简化分析的角度出发对电感的内阻进行等效简化,即R0=Rf1=R1=R2,LCC-S的电路谐振条件为
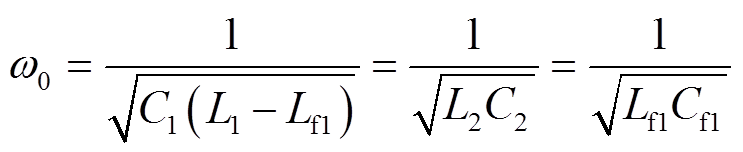 (6)
(6)
根据式(4)和式(5)解出的回路电流方程分别得到输出电压和输出电流,并根据电压和电流可求出输出功率和传输效率。将电感品质因数Qx=ωLx/R0(x=f1,1,2)、电路等效品质因数Qn=ωL1/RL和电路谐振条件式(6)代入,即可求得集成式LCC-S型发射端工作于谐振状态时的输出功率和传输效率分别为
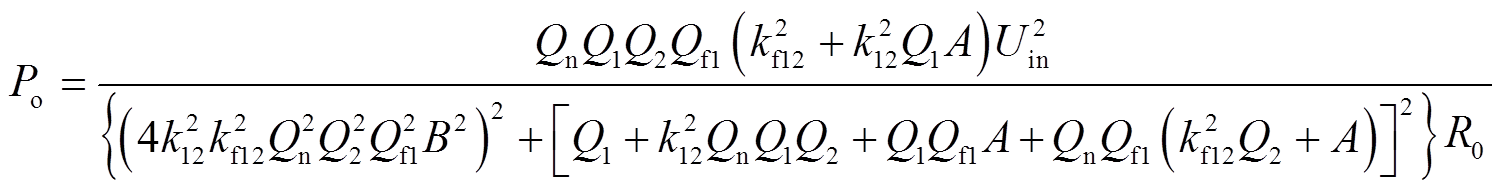 (7)
(7)
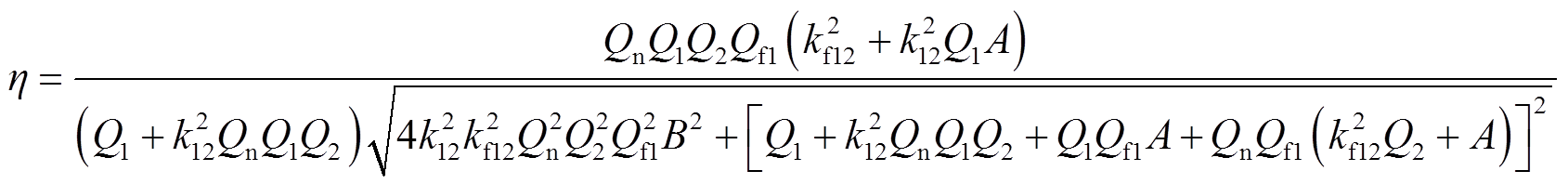 (8)
(8)
式中
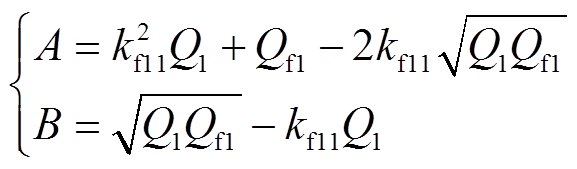 (9)
(9)
由式(7)和式(8)所示,在系统电感参数和负载确定的情况下,集成式LCC-S系统的输出功率与三个耦合系数以及输入电压有关,系统传输效率仅与三个耦合系数有关。为了更加清晰地分析三个耦合系数对系统传输功率和传输效率的影响,假设电路谐振频率为85.5kHz;L1、L2和Lf1的电感值分别为43μH、65μH和19μH;电感内阻R0为0.1Ω;负载电阻在分析时恒为12Ω;输入电压Uin为100V。通过控制变量来考察每个耦合系数对集成式LCC-S系统的输出功率和传输效率的影响趋势。
由于无线电能传输系统发射端和接收端之间的典型耦合系数在0.1~0.3之间,对于本文所提的集成式结构,k12与kf12是发射端和接收端之间的耦合系数,但由于kf11是集成式发射端内部的耦合系数,其与接收端没有耦合关系,因此在设计阶段有更广泛的调节范围。因此,本文将k12与kf12的讨论范围限定在0.1~0.3,kf11的讨论范围限定在0.1~0.9。当需要确定一个耦合系数以分析其余两个耦合系数时,令该耦合系数为0.2。
当kf11=0.2时,集成式LCC-S结构的输出功率和传输效率与k12、kf12的关系如图6所示。k12变化时不同kf12的输出功率曲线如图6a所示。由曲线可以看出,集成式LCC-S系统的输出功率随k12的增大而升高,kf12与输出功率呈现负相关的趋势,即kf12越大,输出功率越低。k12变化时不同kf12的传输效率如图6b所示。由曲线可以看出,传输效率随k12的增大出现了明显的分裂现象,并且kf12对传输效率同样呈现一种负相关的趋势,即kf12越大传输效率越低。
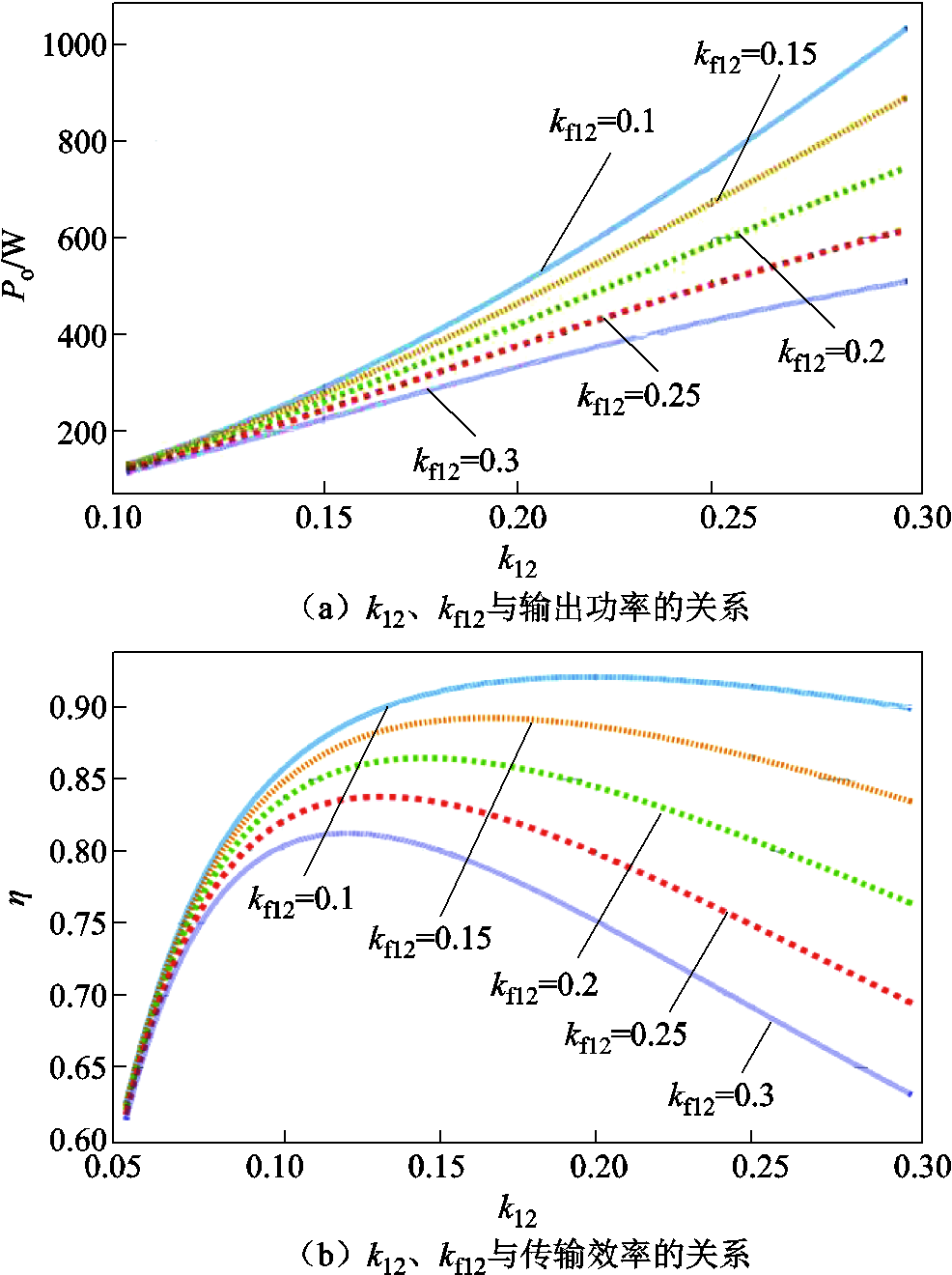
图6 k12、kf12与输出功率和传输效率的关系
Fig.6 The relationship between k12, kf12 and output power and transmission efficiency
综上所述,k12和kf12对输出功率的影响趋势是相反的,因此当发射端和接收端发生相对移动时,k12和kf12同时降低会对输出功率的变化产生一定的牵制作用,由这种牵制作用导致的输出功率曲线如图7所示,从而使集成式LCC-S结构在发生偏移时维持输出功率的相对稳定。
由于kf11是集成式发射端内部的耦合系数,不与接收端发生耦合关系,因此在发射端和接收端移动过程中认为其不发生变化。但是其作为系统耦合系数对于输出功率和传输效率仍会产生一定影响,因此需对kf11进行定性研究。
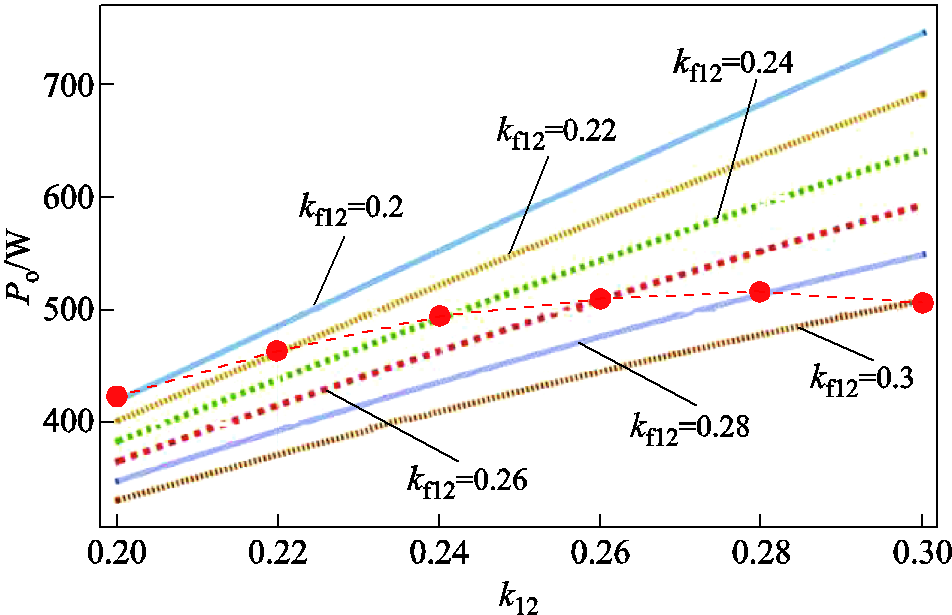
图7 k12、kf12牵制作用下的输出功率曲线
Fig.7 Output power curves under the restraint of k12 and kf12
耦合系数kf11对于系统输出功率和传输效率的影响三维图如图8所示。由图8可以看出,kf11最明显的作用是会对输出功率和传输效率产生分裂影响。图8a和图8b是kf11分别与k12和kf12对输出功率的影响,可以看出k12与输出功率仍然呈正相关趋势,但是随着kf11的增大,输出功率会逐渐增加,在出现一个明显的分裂区间后逐渐降低;kf12与输出功率呈现负相关趋势,随着kf11的增大,输出功率同样先升高,在经过一个分裂区间后逐渐降低。图8c、图8d是kf11分别与k12和kf12对传输效率的影响,可以看出k12对传输效率存在一个极大点,并且传输效率随kf11的增大逐渐降低,在经过一个分裂区间后逐渐升高;kf12与传输效率呈现负相关的趋势,随着kf11的增大传输效率同样先降低,在经过一个分裂区间后逐渐升高。综上所述,为了取得较高的传输效率,kf11在分裂区间两侧存在两个取值范围,分别是0.1~0.35的低取值区间和0.8~0.9的高取值区间。需要注意的是,由于本文所提的结构是将Lf1和L1以同心形式反极性集成,因此kf11如果位于高取值区间,会
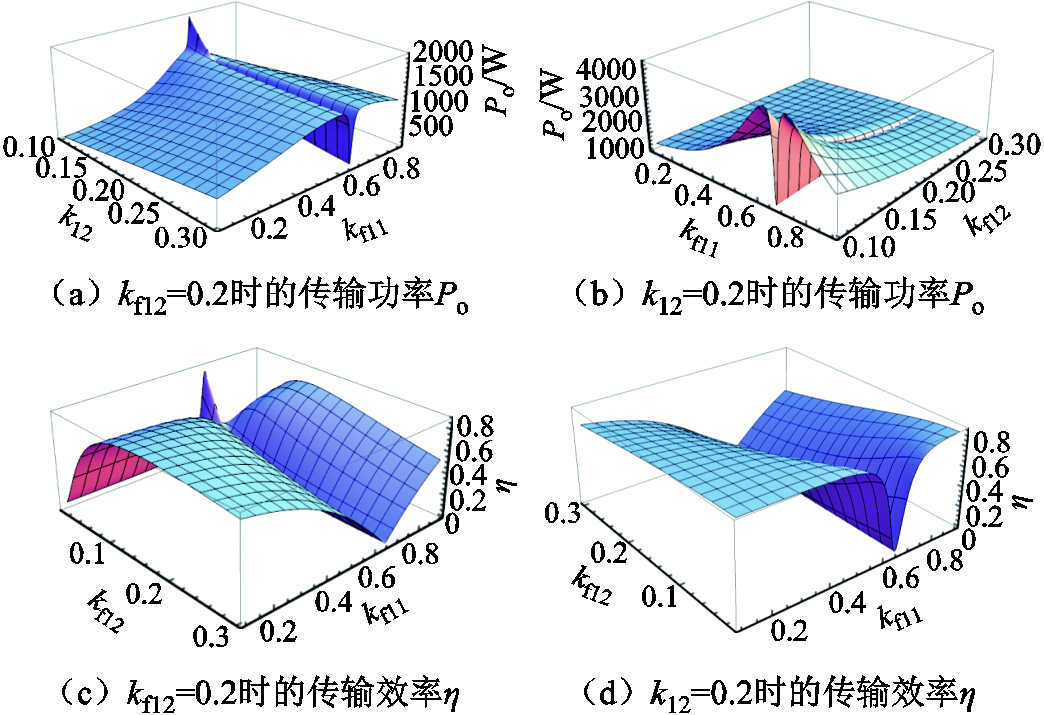
图8 kf11对输出功率和传输效率的影响
Fig.8 Effect of kf11 on output power and transmission efficiency
由于Lf1和L1之间过于紧密的耦合从而对线圈自感造成较强的影响,即为了达到设计的电感值需要过多的线圈匝数。因此,kf11不宜位于高取值区间。
综上所述,对于将LCC-S补偿拓扑的补偿电感以同心形式反极性集成的发射端,其存在三个耦合系数k12、kf11和kf12,由于k12和kf12对于输出功率的互相牵制作用,使得输出功率可以在一定的偏移范围内维持相对稳定。kf11会给系统输出功率和传输效率带来分裂现象,为了维持系统较高的输出功率和传输效率,kf11不宜过高。
在前述理论分析的基础上,本文提出两种LCC-S集成结构,分别是补偿电感内绕式结构和补偿电感外绕式结构,如图9所示。
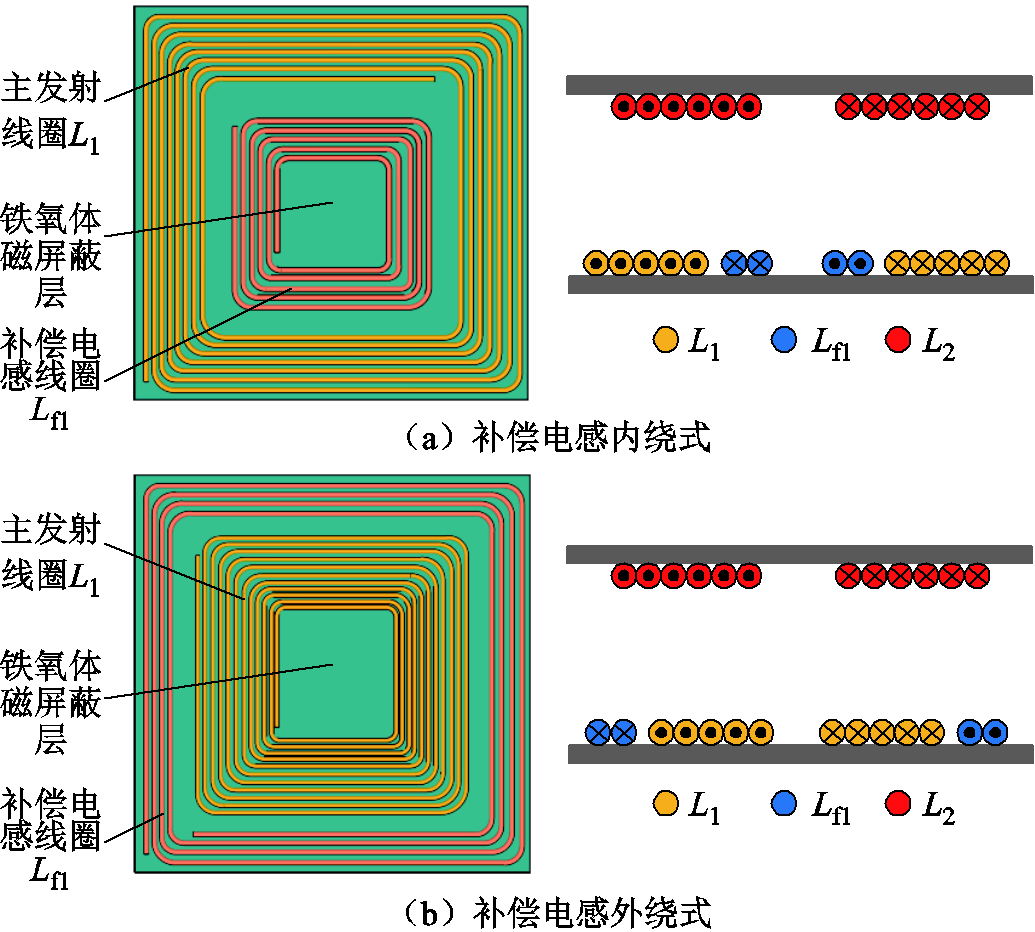
图9 LCC-S集成发射线圈结构
Fig.9 LCC-S integrated transmitting coil structure
为了分析本文所提出的集成式结构与传统非集成式结构在能量传输上的区别,搭建补偿外绕式、补偿内绕式和非集成式的多耦合仿真模型,分别在发射端与接收端正对和偏移6cm时,考察仿真模型的磁场分布情况。仿真模型的发射端和接收端距离均为12cm,仿真输入电压源电压均为100V,工作频率85.5kHz。
磁场分布仿真结果如图10所示。图10a~图10d为发射端和接收端正对时的仿真结果,可以明显地观察到在相同的传输距离和输入电压的情况下,共享磁通式集成结构相比于非集成式结构的发射端和接收端之间的磁通密度更高,集成式结构的高磁通密度宽度要大于非集成式结构的。图10e~图10h是接收端偏移6cm时的仿真结果。由仿真结果可得出,在偏移状态下,集成式结构和非集成式结构的磁通密度相比于正对状态均有所下降,但是集成式结构的磁通密度仍大于非集成式结构。因此集成式结构的磁通密度要高于非集成式结构。

图10 集成式与非集成式结构磁场分布
Fig.10 Integrated versus non-integrated simulation
为验证集成式结构的抗偏移能力,搭建实验样机。为了验证本文所提的集成式LCC-S结构在线圈偏移过程中的传输功率和传输效率的稳定性,将实验分为实验组和对照组,线圈结构如图11所示。
实验组采用本文所提出的两种新型集成式发射端结构,分别是补偿电感内绕式和补偿电感外绕式;对照组采用两种非集成式发射端结构,分别是非集成式外绕和非集成式内绕,其补偿电感以独立电感形式工作;实验组和对照组采用同一个接收端。实验组和对照组采用相同的系统参数,具体参数见表1。
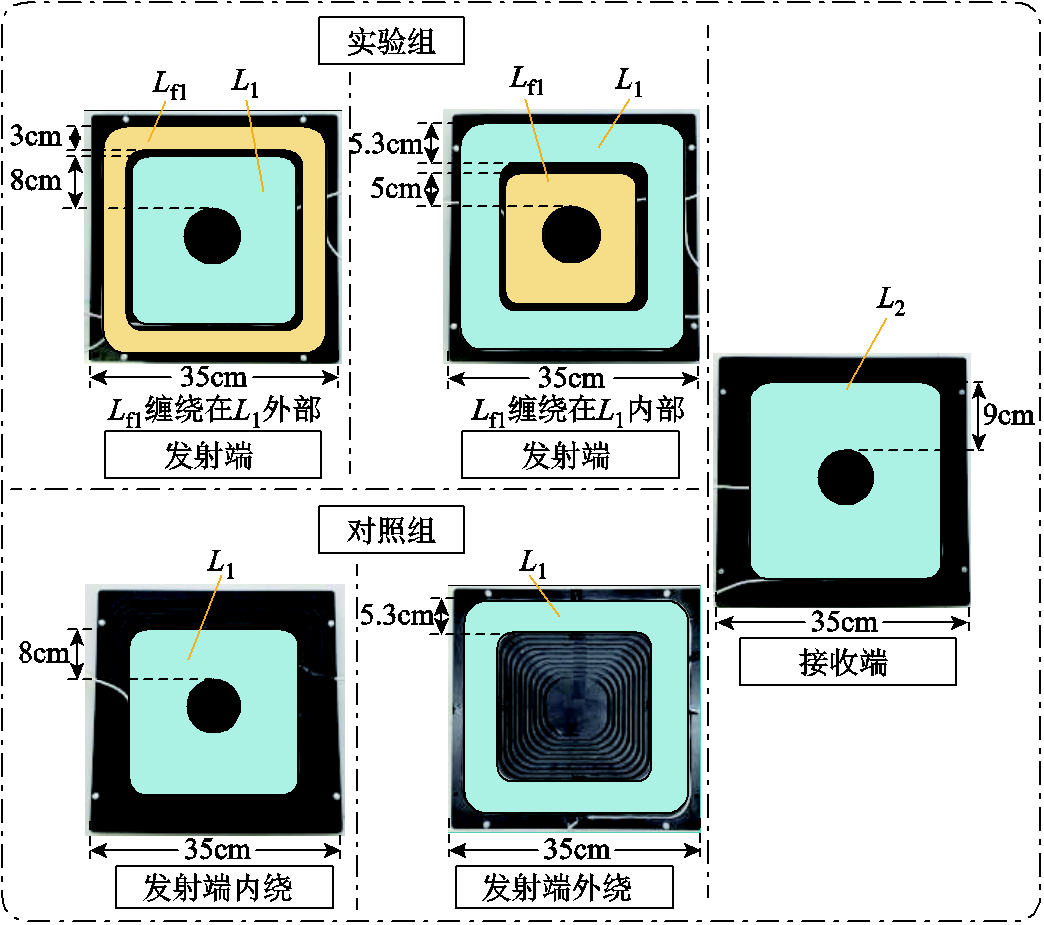
图11 实验组与对照组线圈结构
Fig.11 Coil structure of experimental group and control group
表1 实验样机参数
Tab.1 Experimental prototype parameters

参数数值 L1/μH43 L2/μH65 Lf1/μH19 C1/nF144 Cf1/nF182 C2/nF53 RL/Ω12.5 Uin/V100 f/kHz85.5
实验样机如图12所示,由直流电源、逆变电路、发射线圈、接收线圈、整流电路和负载等组成。实验时每组线圈发射端和接收端的间距均为12cm,实验最大偏移范围为零点两侧20cm。发射端和接收端正对位置为零点,通过横向移动接收端来考察不同偏移位置时的系统状态。在保持输入电压和谐振频率恒定的情况下,接收端从零点左侧偏移20cm处向右移动至零点右侧20cm处,每移动1cm测量一次DC-DC端的效率和输出功率;获得偏移过程的功率和效率曲线后,再次从零点左侧20cm处向右移动至零点右侧20cm处,每移动1cm测量一次系统的耦合系数k12、kf11和kf12,并绘制耦合系数的变化曲线。

图12 实验样机
Fig.12 Experimental prototype
实验结果如图13所示,分别从实验组与对照组的输出功率、传输效率和耦合系数进行分析。
由图13a所示,在相同输入电压、相同负载和相同传输距离的情况下,实验组的两种集成式结构在正对和相同偏移距离情况下,传输功率均远高于对照组的两种非集成式结构。集成式结构的功率曲线相比于非集成式结构出现了明显的“削顶”情况。由图13a可得,实验组补偿外绕式结构在-6cm~+6cm内输出功率标准差为19.4;补偿内绕式结构在-6cm~+6cm内输出功率标准差为19.8;对照组非集成式内绕结构在-6cm~+6cm内的输出功率标准差高达26.1;非集成式外绕结构输出功率标准差高达22.65,这意味着在一定偏移范围内集成式结构输出功率波动小于非集成结构。
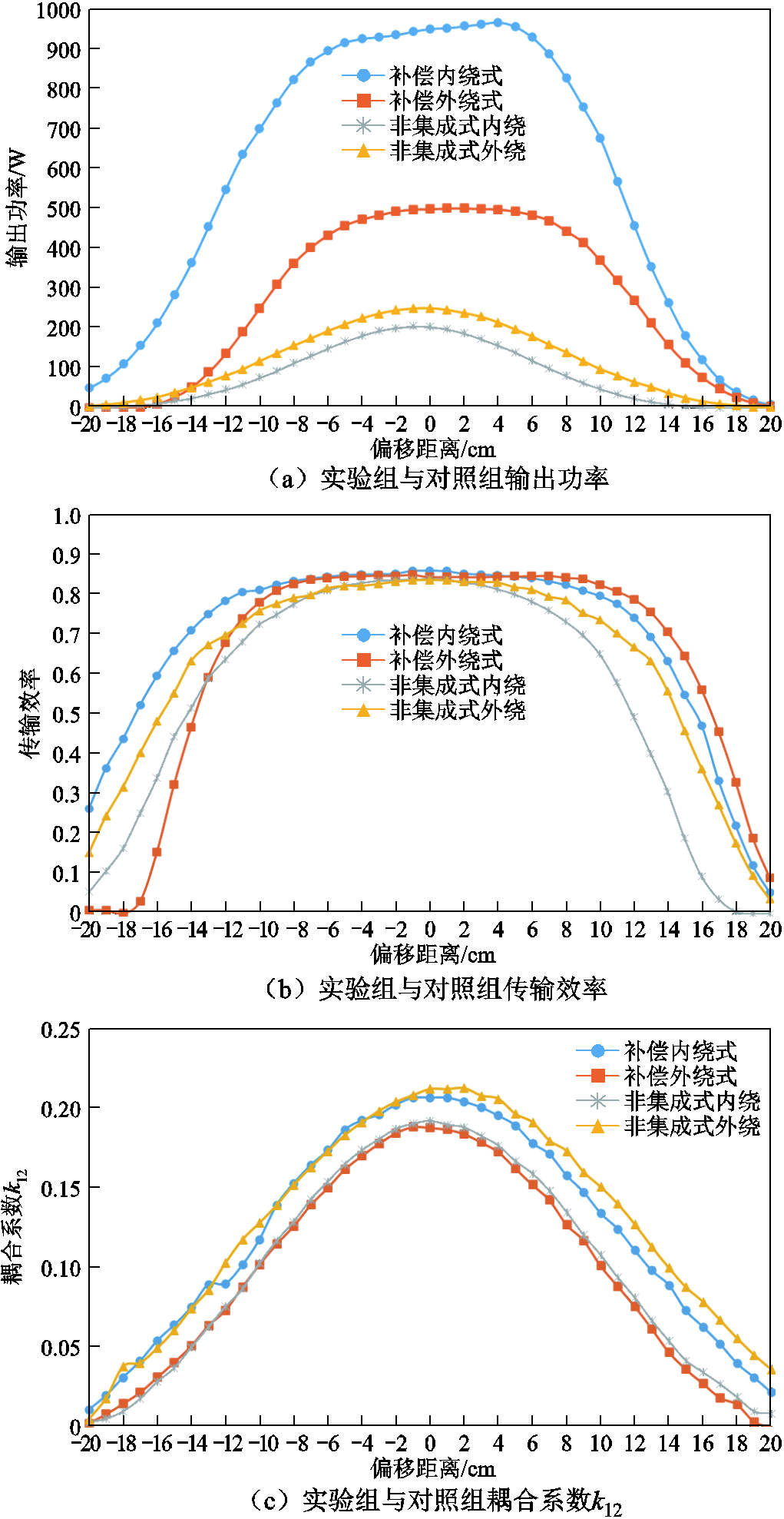
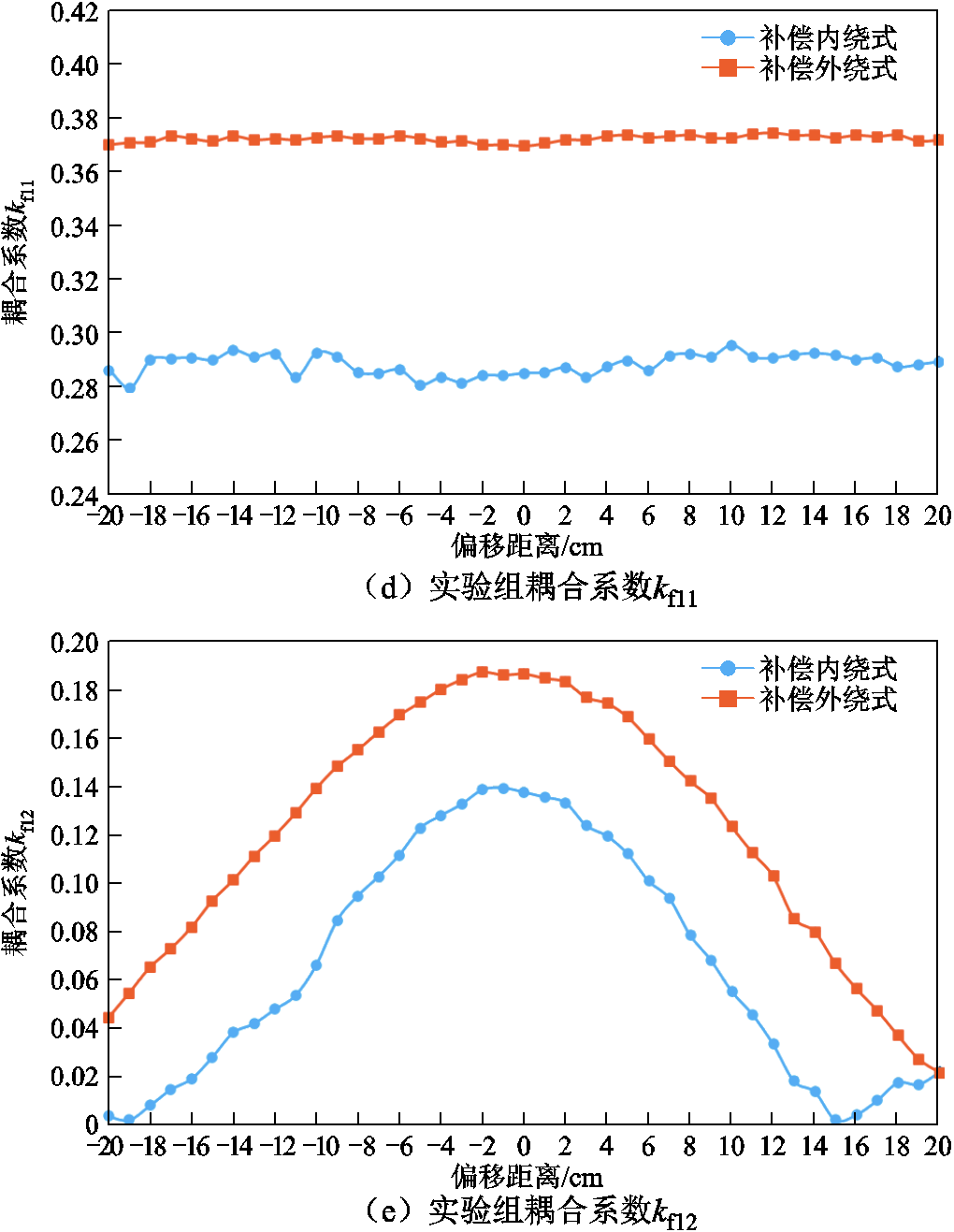
图13 实验结果
Fig.13 Experimental results
由图13c可以看出,实验组两种集成式结构和对照组两种非集成式结构的主耦合系数k12的大小基本一致;由图13d可以看出,实验组中两种集成结构的耦合系数kf11在偏移过程中基本不发生大范围波动;由图13e可以看出,补偿内绕式的耦合系数kf12小于补偿外绕式,其差值约为0.04。对比图13a两种集成结构的输出功率曲线,可以看出补偿内绕式输出功率大于补偿内绕式,验证了第1节关于kf12对输出功率的影响分析,即kf12与输出功率呈负相关趋势。
实验组和对照组在偏移6cm时的发射端补偿电路输入电压与电流,以及接收端补偿电路的输出电压与电流波形如图14所示。由图14可以看出,在相同的偏移状态下,集成式和非集成式的发射端补偿电路输入电压和电流波形均存在一定的相位差,但是非集成内绕式结构的发射端补偿电路输入电流在偏移状态下发生了明显的畸变,集成式结构的输入电流更加光滑,这意味着集成式结构在偏移状态下的电流谐波含量更小。
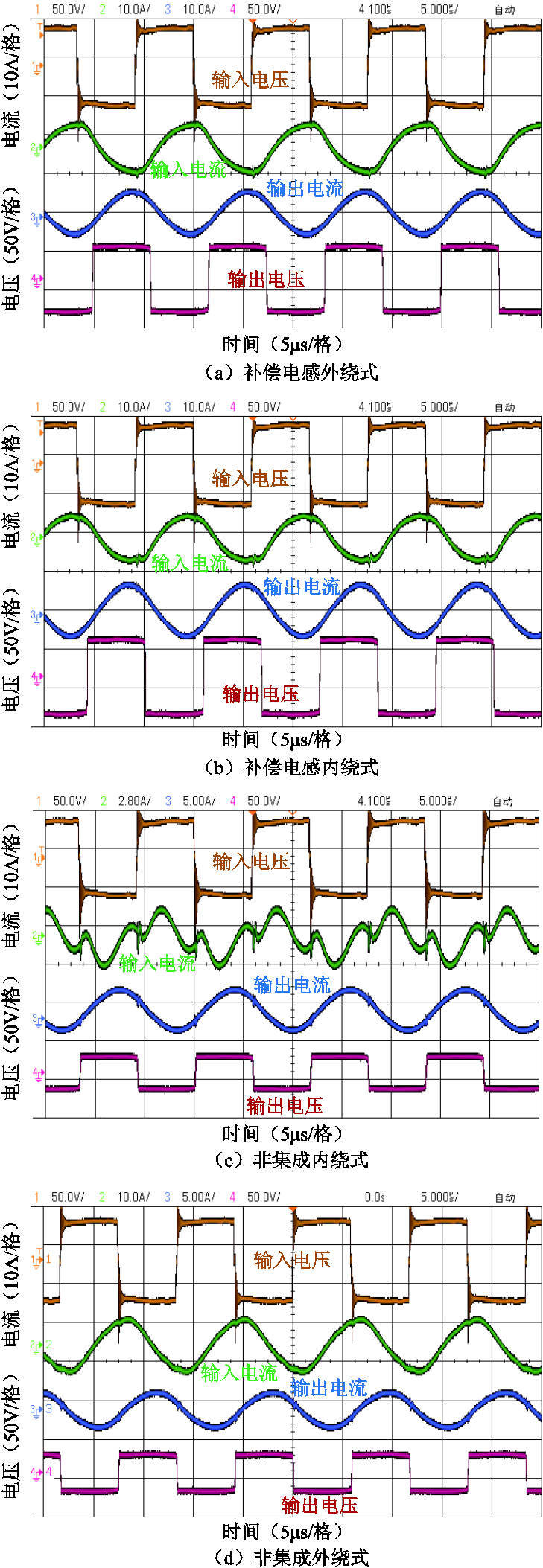
图14 实验组和对照组在偏移状态的波形
Fig.14 Waveforms of the experimental and control groups in the offset state
本文针对LCC-S型补偿拓扑的无线电能传输系统,从共享磁通的角度提出了两种补偿电感同心反极性发射端集成结构,并对其进行了多耦合工作分析,经过实验得出如下结论:
1)共享磁通式集成结构相比于非集成式结构在相同输入电压、传输距离和负载的情况下具有更强的抗偏移能力并且能够传输更高的功率。
2)共享磁通式集成结构中k12与输出功率呈正相关趋势,kf12与输出功率呈负相关趋势,在偏移发生时,由于二者的牵制使得输出功率在一定范围内保持稳定。
3)共享磁通集成式结构中kf11在偏移过程中基本不变,但是其取值对输出功率和传输效率产生分裂影响,从实际应用考虑,kf11的取值不宜过高,取值范围约为0.1~0.35。
本文所提的共享磁通式集成结构对于现有无线电能传输系统的抗偏移性能的提升具有指导意义。
参考文献
[1] 杨庆新, 章鹏程, 祝丽花, 等. 无线电能传输技术的关键基础与技术瓶颈问题[J]. 电工技术学报, 2015, 30(5): 1-8.
Yang Qingxin, Zhang Pengcheng, Zhu Lihua, et al. Key fundamental problems and technical bottlenecks of the wireless power transmission technology[J]. Transactions of China Electrotechnical Society, 2015, 30(5): 1-8.
[2] 吴理豪, 张波. 电动汽车静态无线充电技术研究综述(上篇)[J]. 电工技术学报, 2020, 35(6): 1153-1165.
Wu Lihao, Zhang Bo. Overview of static wireless charging technology for electric vehicles: part Ⅰ[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1153-1165.
[3] 张献, 王杰, 杨庆新, 等. 电动汽车动态无线供电系统电能耦合机构与切换控制研究[J]. 电工技术学报, 2019, 34(15): 3093-3101.
Zhang Xian, Wang Jie, Yang Qingxin, et al. The power coupling mechanism and switching control for dynamic wireless power supply system of electric vehicle[J]. Transactions of China Electrotechnical Society, 2019, 34(15): 3093-3101.
[4] Luo Bo, Long Tao, Guo Limou, et al. Analysis and design of inductive and capacitive hybrid wireless power transfer system for railway application[J]. IEEE Transactions on Industry Applications, 2020, 56(3): 3034-3042.
[5] 苑朝阳, 张献, 杨庆新, 等. 无线供电高铁列车非对称耦合机构[J]. 电工技术学报, 2017, 32(18): 18-25.
Yuan Zhaoyang, Zhang Xian, Yang Qingxin, et al. Asymmetric coupling mechanism of wireless power transmission system for high-speed train[J]. Transactions of China Electrotechnical Society, 2017, 32(18): 18-25.
[6] Ahmad A, Alam M S, Chabaan R. A comprehensive review of wireless charging technologies for electric vehicles[J]. IEEE Transactions on Transportation Electrification, 2018, 4(1): 38-63.
[7] Liu Daerhan, Hu Hao, Georgakopoulos S V. Misalignment sensitivity of strongly coupled wireless power transfer systems[J]. IEEE Transactions on Power Electronics, 2017, 32(7): 5509-5519.
[8] Li Weihan, Zhao Han, Deng Junjun, et al. Comparison study on SS and double-sided LCC compensation topologies for EV/PHEV wireless chargers[J]. IEEE Transactions on Vehicular Technology, 2016, 65(6): 4429-4439.
[9] Zhang Wei, Mi C C. Compensation topologies of high-power wireless power transfer systems[J]. IEEE Transactions on Vehicular Technology, 2016, 65(6): 4768-4778.
[10] Hao Hao, Covic G A, Boys J T. An approximate dynamic model of LCL-T-based inductive power transfer power supplies[J]. IEEE Transactions on Power Electronics, 2014, 29(10): 5554-5567.
[11] Li Siqi, Li Weihan, Deng Junjun, et al. A double-sided LCC compensation network and its tuning method for wireless power transfer[J]. IEEE Transactions on Vehicular Technology, 2015, 64(6): 2261-2273.
[12] Yan Zhengchao, Zhang Yiming, Zhang Kehan, et al. Fault-tolerant wireless power transfer system with a dual-coupled LCC-S topology[J]. IEEE Transactions on Vehicular Technology, 2019, 68(12): 11838-11846.
[13] 国玉刚, 崔纳新. LCC-S型无线电能传输系统优化配置及特性研究[J]. 电工技术学报, 2019, 34(18): 3723-3731.
Guo Yugang, Cui Naxin. Research on optimal configuration and characteristics based on LCC-S type wireless power transfer system[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3723-3731.
[14] 林天仁, 李勇, 麦瑞坤. 基于LCL-S拓扑的感应电能传输系统的建模与控制方法[J]. 电工技术学报, 2018, 33(1): 104-111.
Lin Tianren, Li Yong, Mai Ruikun. Modeling and control method of inductive power transfer system based on LCL-S topology[J]. Transactions of China Electrotechnical Society, 2018, 33(1): 104-111.
[15] Lu Fei, Zhang Hua, Hofmann H, et al. A dual-coupled LCC-compensated IPT system with a compact magnetic coupler[J]. IEEE Transactions on Power Electronics, 2018, 33(7): 6391-6402.
[16] Kan Tianze, Nguyen T D, White J C, et al. A new integration method for an electric vehicle wireless charging system using LCC compensation topology: analysis and design[J]. IEEE Transactions on Power Electronics, 2017, 32(2): 1638-1650.
[17] Kan Tianze, Lu Fei, Nguyen T D, et al. Integrated coil design for EV wireless charging systems using LCC compensation topology[J]. IEEE Transactions on Power Electronics, 2018, 33(11): 9231-9241.
[18] Zhao Lei, Thrimawithana D J, Madawala U K, et al. A misalignment-tolerant series-hybrid wireless EV charging system with integrated magnetics[J]. IEEE Transactions on Power Electronics, 2019, 34(2): 1276-1285.
[19] Budhia M, Boys J T, Covic G A, et al. Development of a single-sided flux magnetic coupler for electric vehicle IPT charging systems[J]. IEEE Transactions on Industrial Electronics, 2013, 60(1): 318-328.
[20] 中国电力企业联合会. GB/T 38775.3—2020 电动汽车无线充电系统第3部分:特殊要求[S]. 北京: 中国标准出版社, 2020.
An Anti-Offset Method under Flux-Sharing Multi-Coupling Mode for Wireless Power Transmission System
Abstract A method for integrating a reversed-polarity concentric compensating inductor based on the LCC topology is proposed from the perspective of shared flux, then two integrated structures are proposed. A mathematical model of the output power and transmission efficiency of the reversed-polarity concentric wireless power transmission system based on the multi-coupling mode of operation and the quality factor of the coil is developed, and the offset resistance of the integrated structure is verified from the mathematical model. The simulation results show that the integrated structure outperforms the non-integrated structure in terms of flux density in both forward and offset cases. The experimental prototype of the compensated inductor integrated structure is built. The experimental results show that the compensated inductor integrated structure can maintain stable transmission efficiency and output power within a certain offset range, and has higher transmission efficiency and higher transmission power than the non-integrated structure at the same input voltage and transmission distance.
keywords:Flux-sharing, multi-coupling mode, coil integration, anti-offset, wireless power transmission
DOI:10.19595/j.cnki.1000-6753.tces.211158
中图分类号:TM724
国家自然科学基金资助项目(51977147,51807138,52122701)。
收稿日期 2021-07-29
改稿日期 2021-12-16
张 献 男,1983年生,博士,教授,博士生导师,研究方向为无线电能传输技术,工程电磁场与磁技术等。E-mail:zxshow1983@163.com(通信作者)
韩大稳 男,1996年生,硕士研究生,研究方向为无线电能传输。E-mail:handawen@foxmail.com
(编辑 李冰)