图1 DBSRC的拓扑原理
Fig.1 The topology diagram of DBSRC
摘要 传统的基于单移相调制的双有源串联谐振变换器（DBSRC）在非单位电压增益下循环功率大，导致谐振电流幅值大。针对此问题，采用基波模型分析DBSRC在多重移相调制下的传输功率和谐振电流特性，利用拉格朗日函数对谐振电流幅值进行优化解析，得到基于谐振电流幅值优化的多重移相调制策略。理论结果表明，优化调制可以显著降低DBSRC在中轻载下的谐振电流大小。基于优化移相的调制方法，为了提高变换器对负载变化的动态响应，提出一种输出功率前馈的电压闭环控制策略。最后，通过仿真和实验验证了优化移相调制和输出功率前馈控制策略的可行性和有效性。
关键词：双有源串联谐振变换器（DBSRC） 非单位电压增益 多重移相调制 幅值优化 功率前馈控制
双有源全桥（Dual Active Bridge, DAB）直流变换器具有拓扑与控制简单、功率双向流动和自然软开关特性等优点[1-3]，带有高频化隔离变压器的特点，使其具有替代传统的含工频变压器电力电子变换系统的优势，并且适合输入或输出的串并联以构建大容量直流变换系统[4]。可应用于新能源交直流变换[5-6]、电力电子变压器[7-9]、轨道交通电力变换[10]等中大功率电力电子变换场合。
目前，对于DAB变换器已有较深入的研究[11-14]，而对于双有源串联谐振变换器（Dual active Bridge Series Resonant Converter, DBSRC）的研究较少。DBSRC是在DAB变换器的基础上在高频交流环节加入了谐振电容。与传统的DAB变换器相比，LC谐振腔可以使流过电感和高频变压器的电流正弦度更好，从而可减小磁性原件的涡流损耗[15]。谐振电容从硬件上隔离了H桥输出的直流偏置电流，从而无需较为复杂的软件控制算法来抑制直流偏磁[16]。另外，准正弦化的谐振电流使得开关器件的关断电流得以减小，从而减小了关断损耗和关断电磁干扰。
文献[17]研究了DBSRC在单移相（Single Phase Shift, SPS）调制下的稳态特性，详细分析了不同开关频率和品质因数下的传输功率、软开关范围及谐振电流电压幅值等。DBSRC在SPS调制下且在非单位电压增益模式时，越是轻载时回流功率占比越大。在同样负载下，谐振电流和谐振电压幅值会随着电压增益偏离1的大小而相应增大，这样导致系统的效率在轻载和非单位电压增益时显著降低。文献[18]利用精确的时域分析法对SPS调制下DBSRC的回流功率特性进行了分析，提出了减小回流功率的参数设计准则。总之，SPS调制方式只适合工作于直流电压增益在1左右，因此变换器的应用场合受到了一定的限制。
针对单移相调制的不足，文献[19]分析和研究了多重移相（Multi Phase Shift, MPS）调制下的稳态特性和优化的调制策略，但是缺少闭环控制策略的研究。文献[20-21]进一步研究了结合调频和移相的DBSRC调制与控制方法，但是对闭环控制方法的研究不够深入，并且在中大功率变换场合采用调频方式会带来磁性元件设计难度增加及电磁干扰抑制困难等问题。文献[22]进一步提出了一种不对称内移相角的调制策略，但是该方法使得一个桥臂上下开关管的开通时间不相等，有可能导致器件损耗不均匀。
DBSRC在优化移相（Optimized Phase Shift, OPS）调制下有3个可调节的移相角，需要根据不同电压增益的大小来动态调整。虽然目前有一定的文献对OPS调制进行了研究，但是针对基于OPS调制下的DBSRC，在电压闭环控制时负载变化下的动态性能改进鲜有文献研究，针对此现状，本文提出了一种基于OPS调制的DBSRC功率前馈电压闭环控制策略，相比无功率前馈的闭环控制方法，有功率前馈的电压闭环控制策略可以大范围提高负载突变时的输出电压动态特性，从而提高变换器输出电压在负载扰动下的跟踪能力。
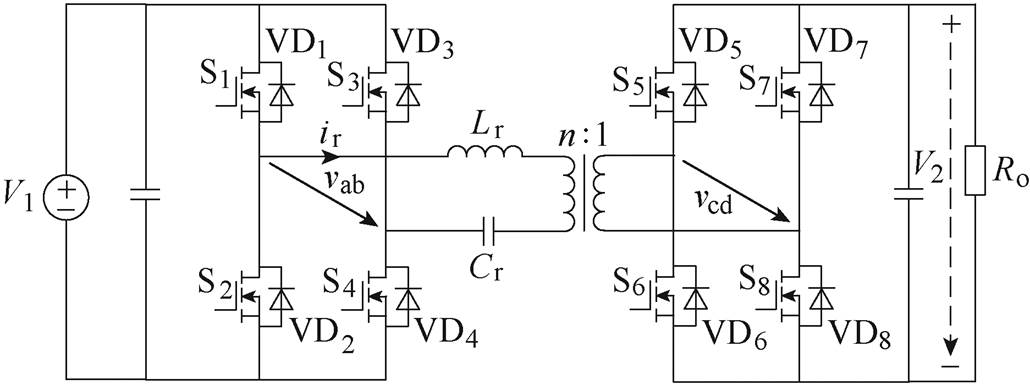
DBSRC的拓扑结构原理如图1所示，输入和输出并联容值很大的支撑电容，稳态下可以看作为电压源。V1和V2分别为输入和输出直流电压，Lr为串联电感与变压器漏感折算到一次侧总的等效谐振电感，Cr为谐振电容，n为变压器的电压比，vab为变换器输入侧H桥的输出交流电压，vcd为输出侧H桥的输出交流电压，ir为变压器的一次侧谐振电流，Ro为负载电阻或等效输出负载。S1～S8和VD1～VD8为一次、二次侧H桥的开关管及其反并联二极管。
图1 DBSRC的拓扑原理
Fig.1 The topology diagram of DBSRC
图2为DBSRC在稳态下的基波等效电路原理，图中，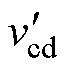
为vcd折算到变压器一次侧的电压。在稳态下，通过控制两侧H桥输出的基波电压大小或相位从而达到调节DBSRC传输功率的大小，以此实现控制变换器的输出电压。
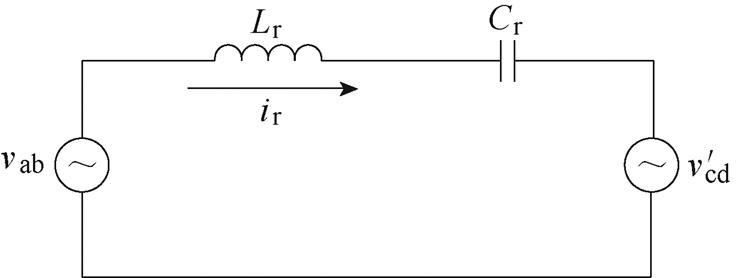
图2 DBSRC稳态运行的等效原理
Fig.2 The steady equivalent circuit of DBSRC
DBSRC在MPS调制下的中间交流环节波形示意图如图3所示，一次侧H桥输出方波电压内移相角为2a，二次侧H桥输出电压内移相角为2b，二次侧H桥输出电压相对一次电压移相角为q。
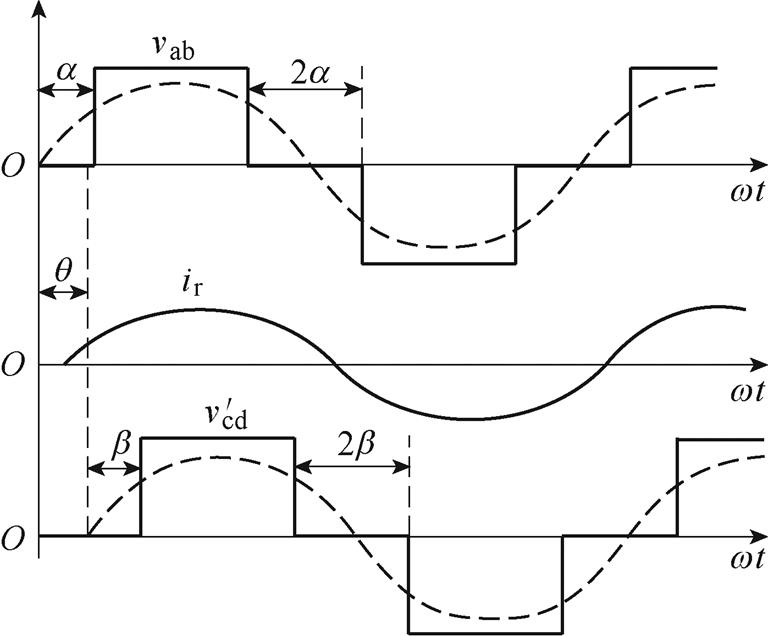
图3 MPS调制下的DBSRC波形示意图
Fig.3 Waveforms of DBSRC in MPS modulation
定义变换器的直流电压增益M为
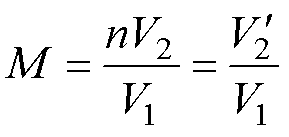（1）
谐振频率wr、频率比F、LC谐振腔交流阻抗XLC和特征阻抗Zr分别为
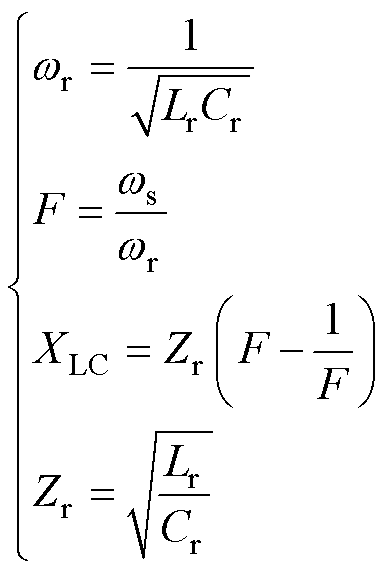（2）
LC谐振腔两侧的交流方波电压正弦基波大小为
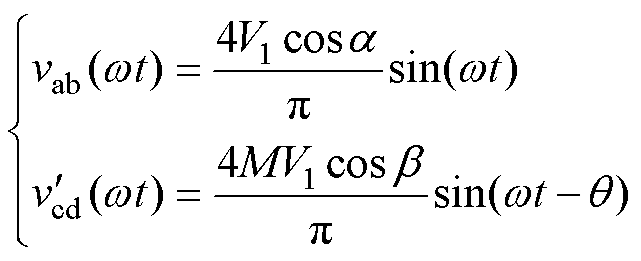（3）
谐振电流为
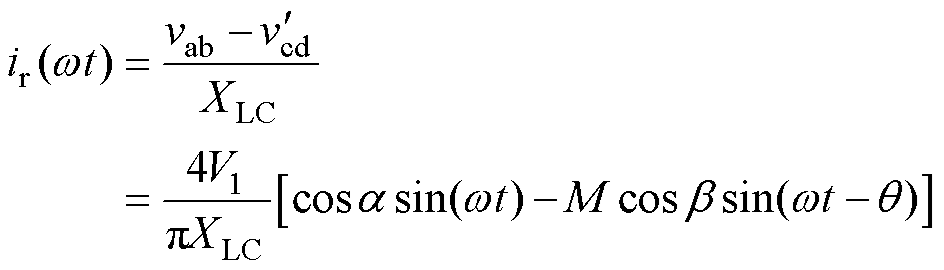（4）
忽略损耗，可得变换器的传输功率为
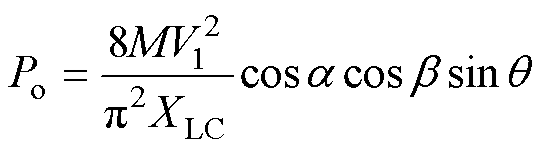（5）
有谐振回路的电感电流和电容电压幅值分别为
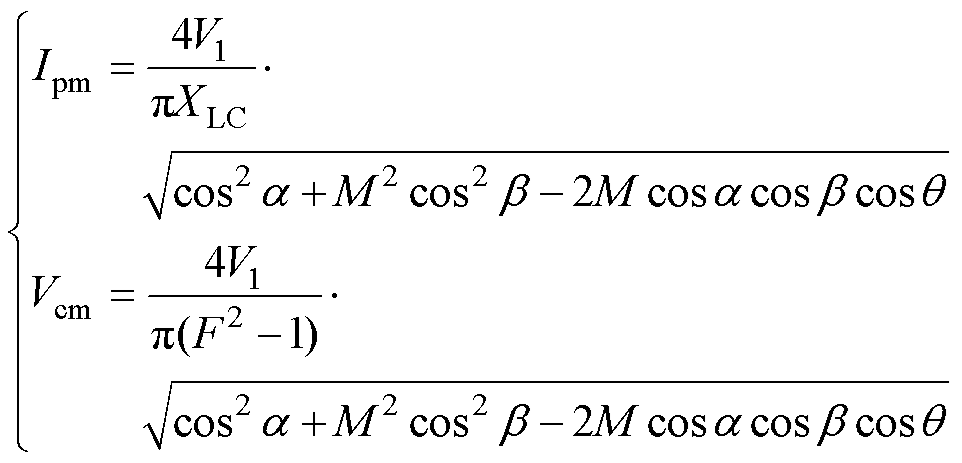（6）
采用标幺化，取电压基准为VB=V1，功率标幺值取额定功率PN。在不同直流电压增益时，SPS调制下稳态时的谐振电流幅值与传输功率关系曲线如图4所示，取F=1.2，Zr=1。可以看出，在非单位直流电压增益时，即使传输功率很小，但是谐振电流的幅值并没有同比例减小，而是保持在较大的范围附近。当直流电压增益M偏离1时，谐振环节便会产生较大的回流功率，导致谐振电流和电容电压幅值增大。从而对硬件带来较大的电流、电压应力和功率损耗。
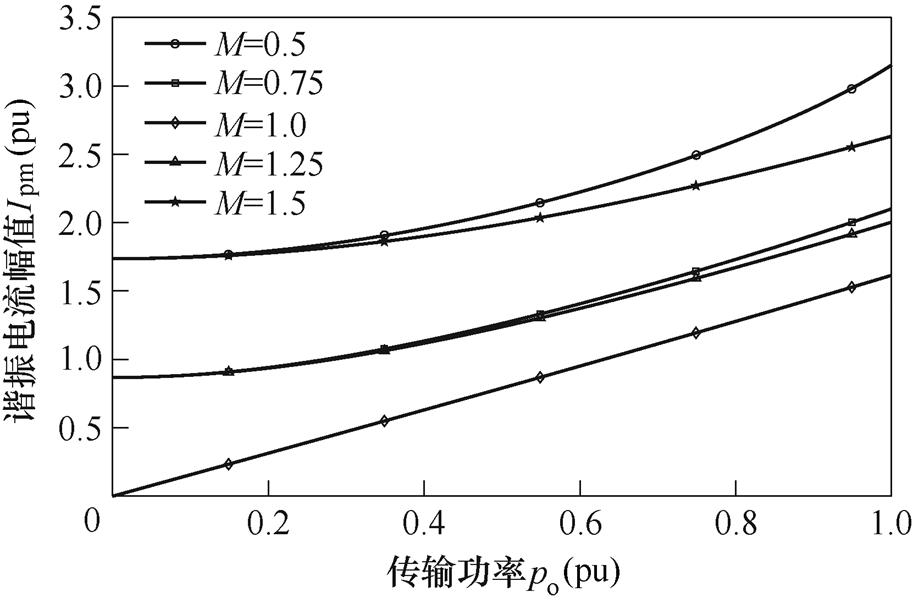
图4 SPS调制下谐振电流幅值与传输功率关系曲线（F=1.2, Zr=1）
Fig.4 The curves of the resonant current amplitude and the transmitted power in SPS modulation (F=1.2, Zr=1)
在SPS调制下，闭环控制中只有一、二次侧输出电压移相角q 这么一个控制自由度，其由电压控制器给出，受到输入、输出电压和负载大小等决定。而在MPS调制下，可以控制的量最多有3个移相角，这3个移相角同时决定传输功率的大小，因此在一定的传输功率和电压增益下，可以通过对3个角的优化从而达到减小谐振电流幅值的目的。
从式（6）中的电流幅值关系和式（5）功率约束关系，构造拉格朗日函数为
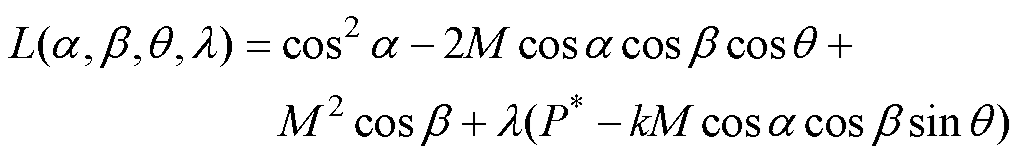（7）
其中
（8）
式中，P*为由负载和输出电压决定的功率约束。
通过解方程组
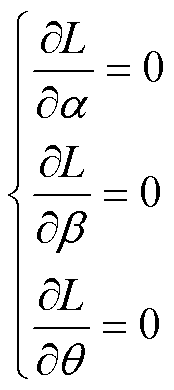（9）
可以得出最优解为
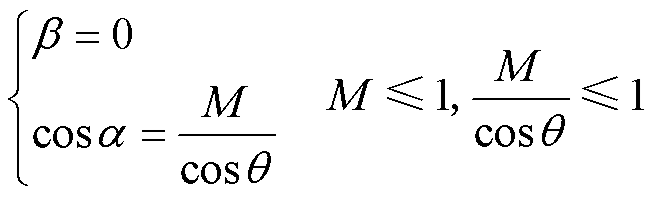（10）
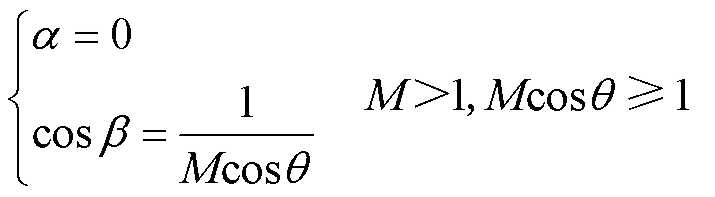（11）
可以看出，在谐振电流幅值优化且直流电压增益M和传输功率特定的情况下，一次侧或二次侧H桥有一个内移相角恒为0，并且在M接近于1时，一次侧和二次侧的H桥内移相角都为0，此时调制模式实际上变成了SPS调制。因此在一个控制周期中最多只有两个移相角需要根据功率传输大小情况进行实时计算。
从式（5）、式（10）和式（11）可以得到，在OPS调制下的变换器的传输功率大小为
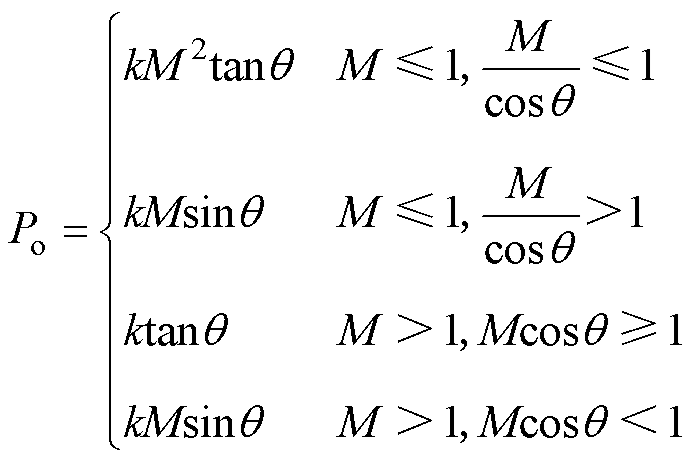（12）
如图5所示为不同直流电压增益条件下OPS调制的桥臂间移相角q 与传输功率的关系曲线。图6为OPS调制下传输功率与谐振电流幅值关系，通过OPS调制，可以减小非单位增益下的谐振电流幅值，从而减小了变换器的回流功率。
从第1节的分析可以看出，在基于电流幅值优化的调制策略下，传输功率始终与桥臂间移相角q 的正弦值成正比，因此在输出电压闭环下，电压控制器的输出可以直接作为桥臂间移相角q。图7所示为DBSRC在OPS调制下的电压闭环控制原理框图，图中，fa(M,q)和fb(M,q)由式（10）与式（11）中的关系决定，电压控制器Gvo采用PI控制器即可对直流输出电压进行无静差控制。
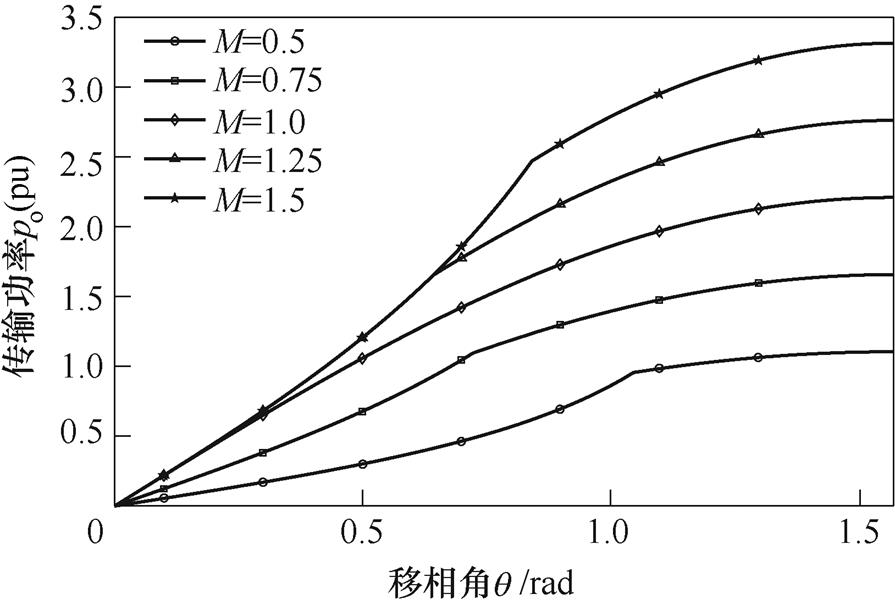
图5 OPS调制下的移相角与传输功率关系曲线
Fig.5 The curves of the phase shift angle and the transmitted power in OPS modulation
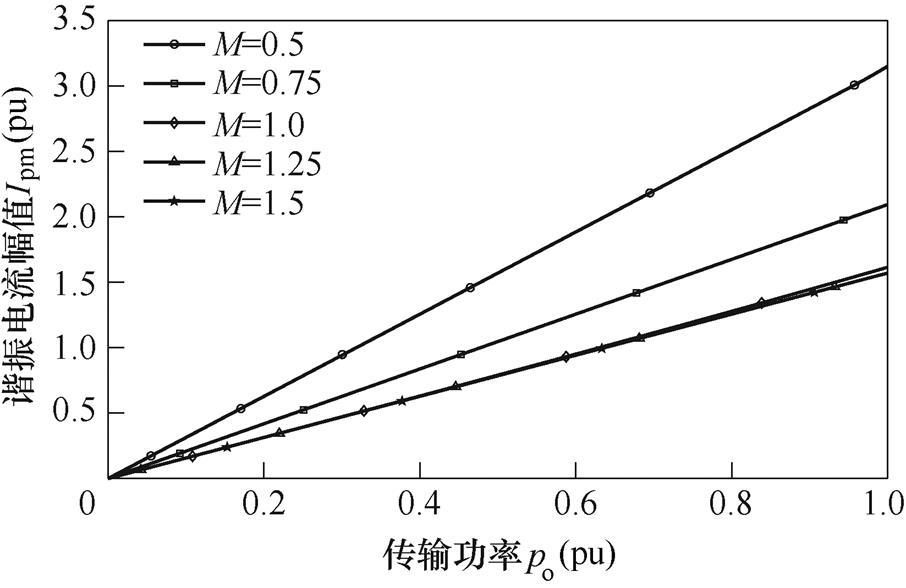
图6 OPS调制下的传输功率与谐振电流幅值关系曲线
Fig.6 The curves of the resonant current amplitude and the transmitted power in OPS modulation
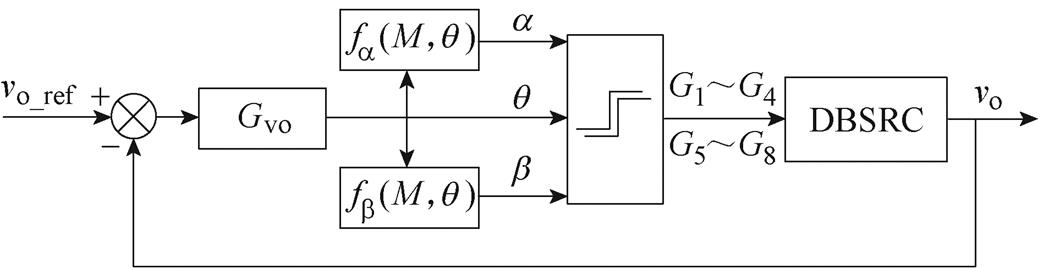
图7 OPS调制下的电压闭环控制框图
Fig.7 The diagram of the voltage closed-loop control based on OPS modulation
由于OPS调制策略是基于DBSRC的功率模型而来的，因此可以将OPS调制下的功率模型的逆模型fq (M, po)作为前馈移相角加入到图7的电压反馈闭环控制系统中。本文提出的含有输出功率前馈基于OPS调制的DBSRC的电压闭环控制策略如图8所示。
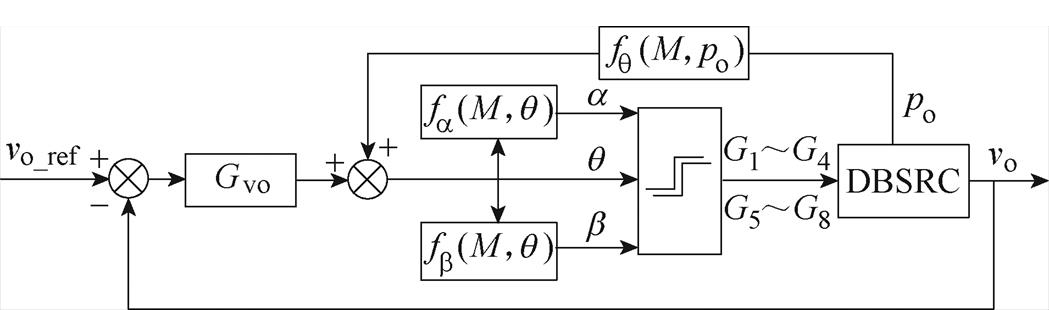
图8 OPS调制下的输出功率前馈的电压闭环控制框图
Fig.8 The diagram of the voltage closed-loop control with output power feedforward based on OPS modulation
根据式（12），可以得到在OPS下，前馈的基于输出功率模型的桥臂间移相角q 为
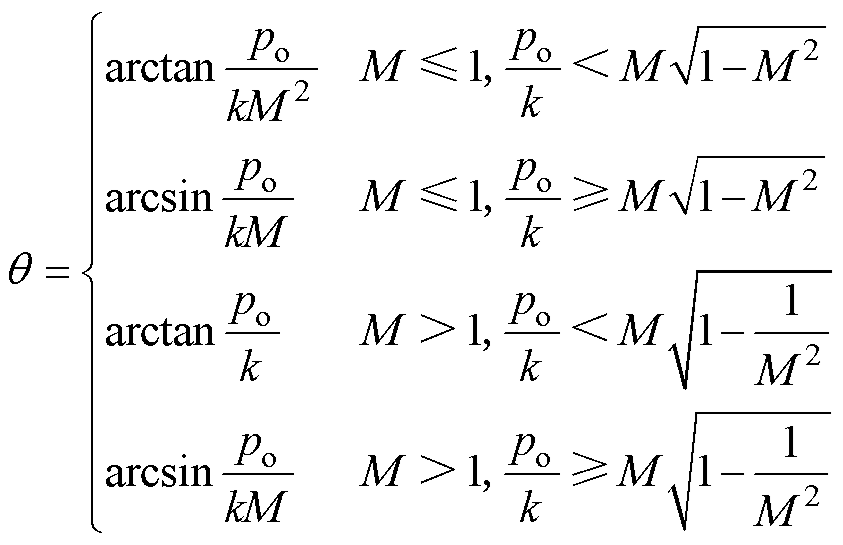（13）
第1节对DBSRC的稳态与传输功率分析只考虑到了基波成分，没有计及谐波的影响。为了验证基波分析模型的准确度，这里采用基于傅里叶级数的频域方法对传输功率做精确分析计算。
LC谐振腔两侧的电压时域级数表示为
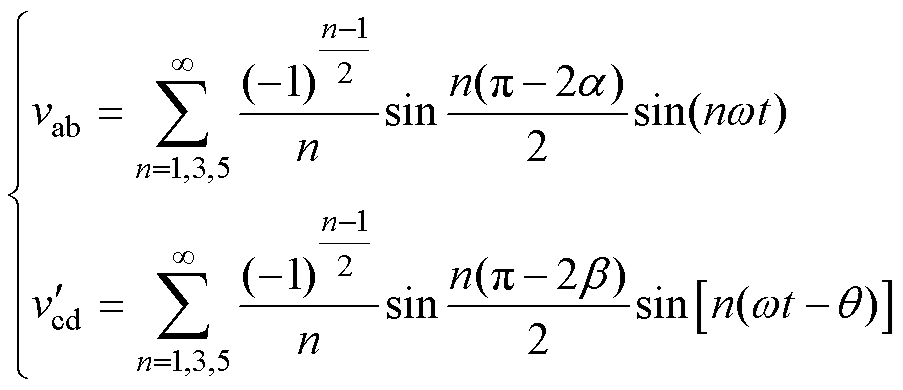（14）
总的传输功率即为各次同频率的端口电压下通过电抗传输的功率总和。因此，总的传输功率为
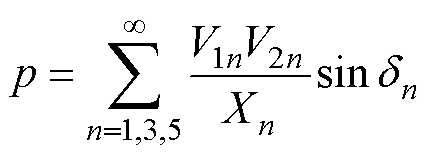（15）
其中
式中，V1n和V2n分别为vab和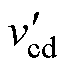
的n次谐波有效值。
图8中，控制角度的前馈量是利用基波分析法得到的前馈模型。以实际输出功率po为自变量，由式（13）可以得到相应的前馈移相角，然后再以此角度通过式（15）计算出实际前馈功率大小pt。前馈功率相对误差e定义为
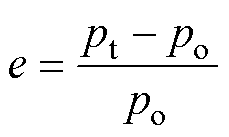（16）
前馈功率的相对误差大小如图9所示。从图9可以看出，在F=1.2、Zr=1时，基于基波分析法的变换器功率模型准确度仍然较高，相对误差e在6%以内。说明了基于该模型的前馈方法具有较高的准确度。
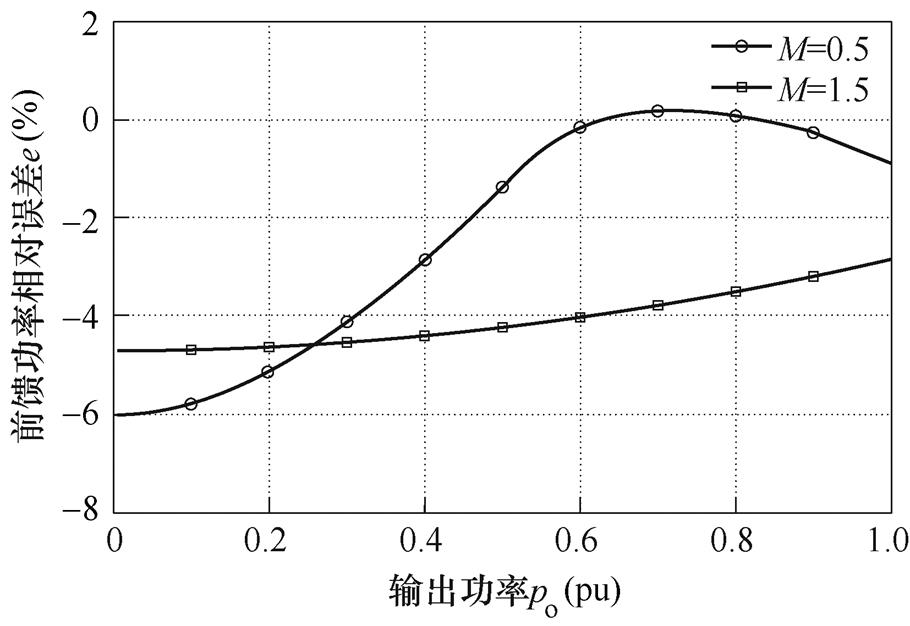
图9 前馈功率的相对误差大小
Fig.9 The relative errors of the feedforward power
利用PSIM软件，对不同工况下的DBSRC进行仿真，仿真中的主要参数见表1。
表1 仿真参数
Tab.1 The parameters of the simulation
参 数数 值 输入电压V1/V200 额定功率PN/W6 000 输出支撑电容/mF2.55 谐振电感Lr/mH32 谐振电容Cr/mF0.63 谐振频率fr/kHz35.4 电压比n11 开关频率fs/kHz42.5
分别对基于单移相调制和优化的多移相调制策略在不同直流电压增益和负载大小下进行仿真，波形结果如图10和图11所示。仿真结果表明，OPS调制下的谐振电流幅值明显低于SPS调制下的谐振电流幅值。相比SPS，OPS下的变换器的开关电流也得到了有效的减小。
图12为在不同直流电压增益下分别采用传统SPS调制与OPS调制策略的谐振电流有效值与传输功率的曲线关系对比。可以看出，OPS调制方法显著降低了中轻载下的谐振电流有效值，因此可以间接地提高中轻载负载下的变换效率。
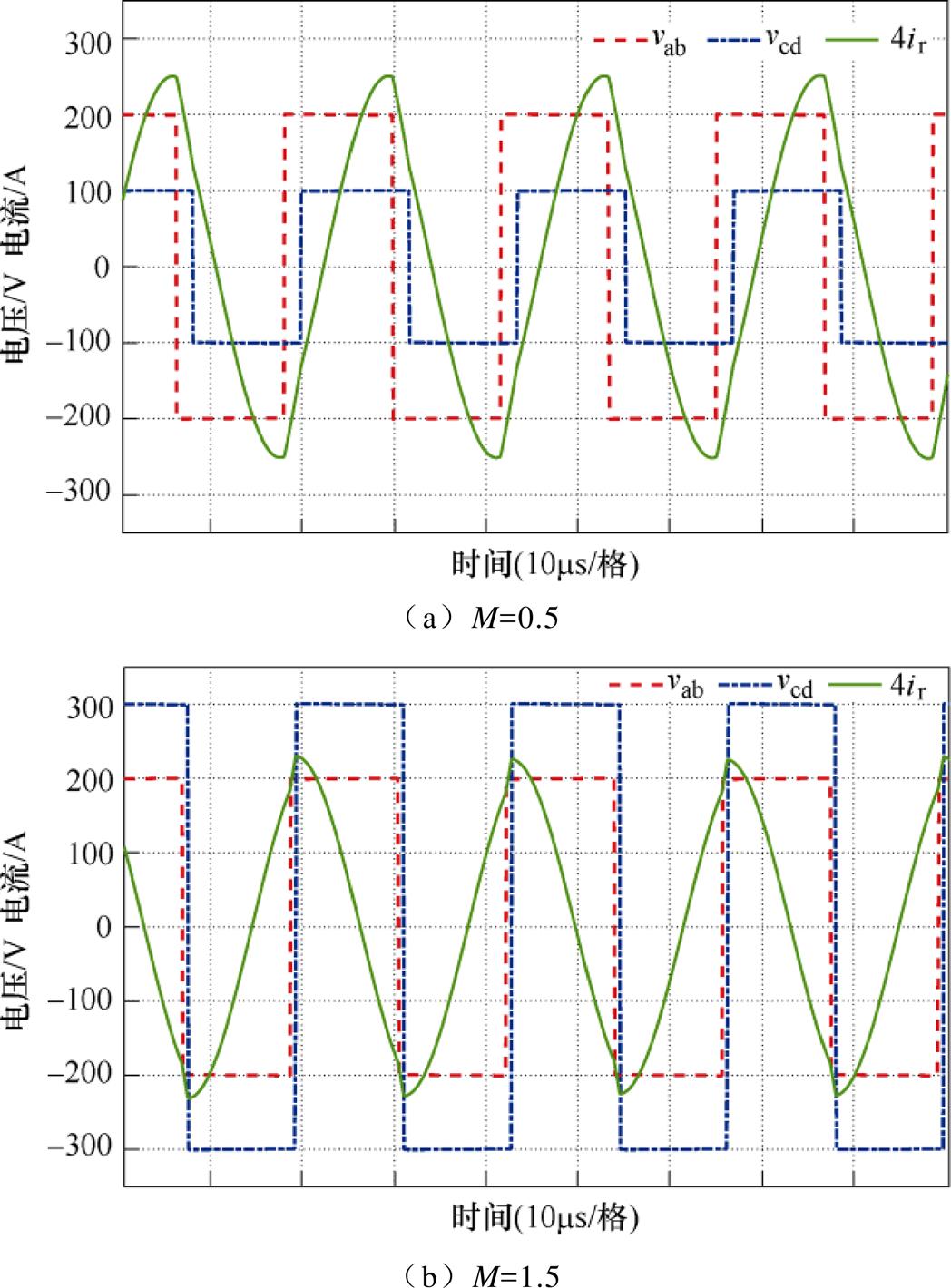
图10 DBSRC在SPS调制下的波形
Fig.10 Waveforms of DBSRC in SPS modulation
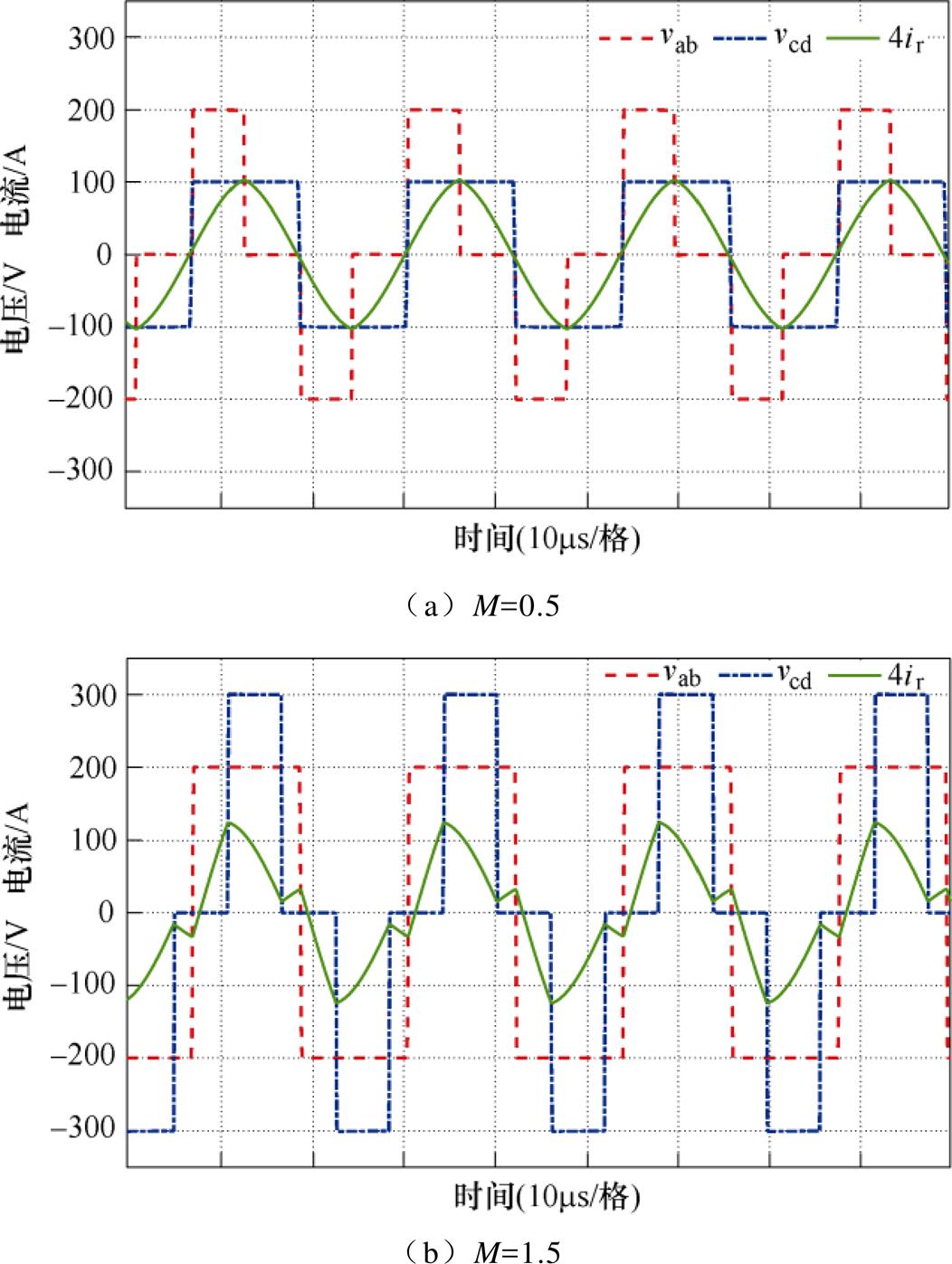
图11 DBSRC在OPS调制下的波形
Fig.11 Waveforms of DBSRC in OPS modulation
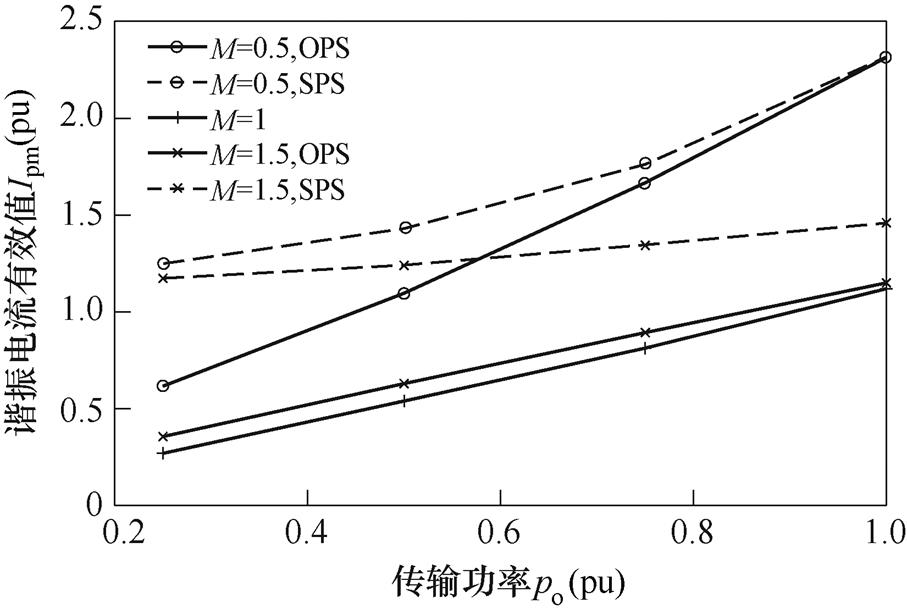
图12 不同直流增益下的谐振电流有效值与传输功率的关系曲线
Fig.12 The curves of the resonant current RMS and the transmitted power under different voltage gain
为了验证本文提出的输出功率前馈控制策略的有效性，对单电压闭环和带有输出功率前馈的两种控制策略下DBSRC的突加负载动态过程进行仿真。变换器硬件参数和表1一致。
输出电压的闭环给定值为200V，两种控制策略下电压控制器的PI参数完全相同，比例系数Kp=0.002，积分系数Ki=0.15，数字控制的控制频率为10kHz。在输入电压分别为150V和250V的两种工况下突加负载，负载电阻从24W 切换为12W，相当于输出功率从1.67kW突加到3.33kW，动态过程仿真结果如图13和图14所示，vo为输出电压，io为输出负载电流。从图13a和图14a以及图13b和图14b相互对比可以看出，有输出功率前馈时突加负载后的输出电压动态响应明显更快，输出电压跌落和恢复时间均有很大程度的减小。
在图15所示的实验样机平台上进行了实验验证，其中硬件参数和仿真部分中的表1参数相同，以TI公司的TMS320F28335为主控芯片，开关器件采用的型号为CAS300M12BM2的SiC MOSFET。
图16为基于SPS调制的DBSRC在M分别为0.5和1.5时的实验波形。较大的开关电流和母排寄生参数导致H桥输出电压存在一定的振荡。图16a为输出接3W 电阻负载的变换器波形，此时输出功率大小为3.33kW，谐振电流ir的幅值为78A。图16b为输出接24W 电阻负载的变换器波形，此时输出功率大小为3.75kW，谐振电流的幅值为72A。
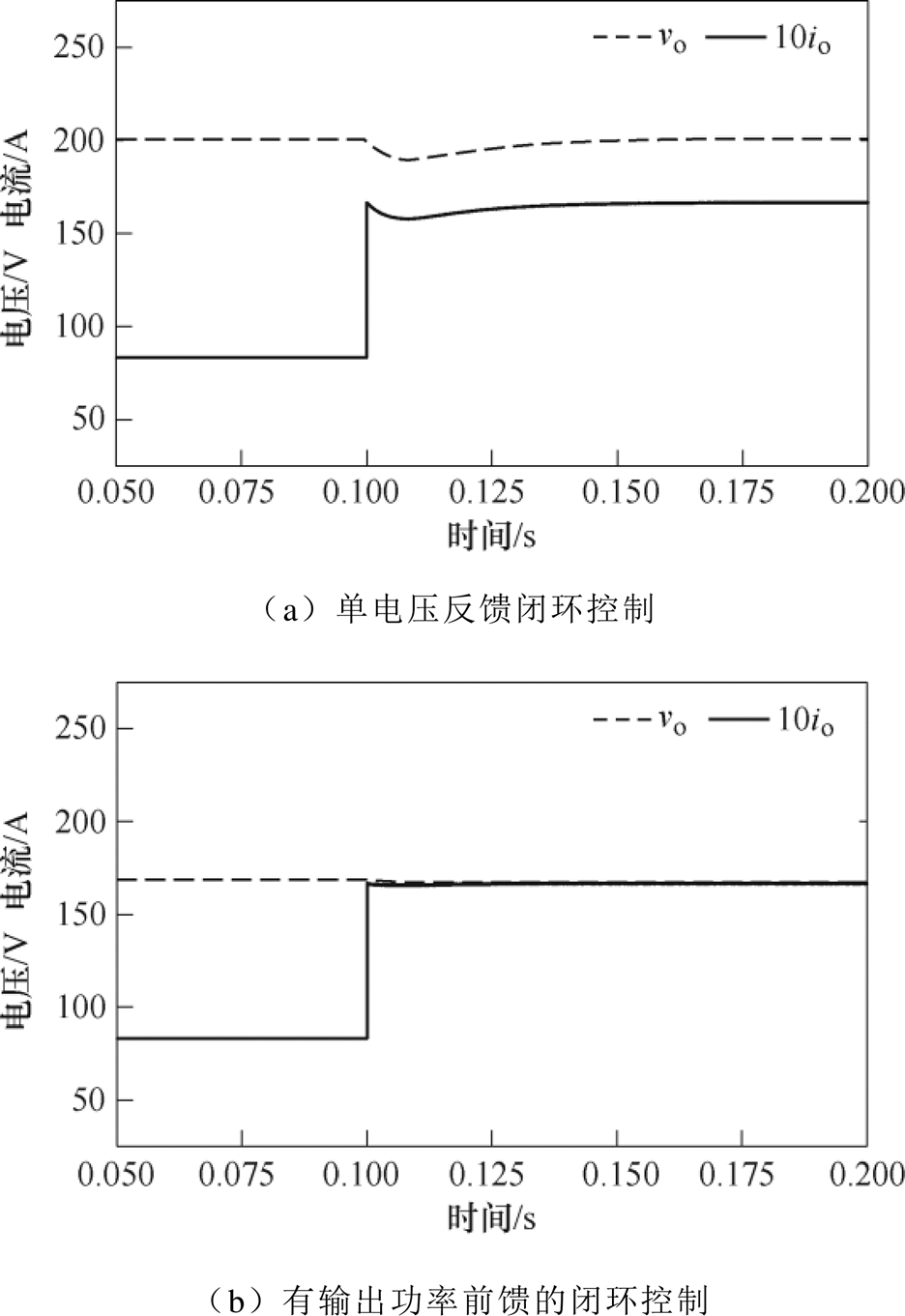
图13 M＞1时DBSRC突加负载时的动态过程波形
Fig.13 Dynamic waveforms of DBSRC under abrupt load when M＞1
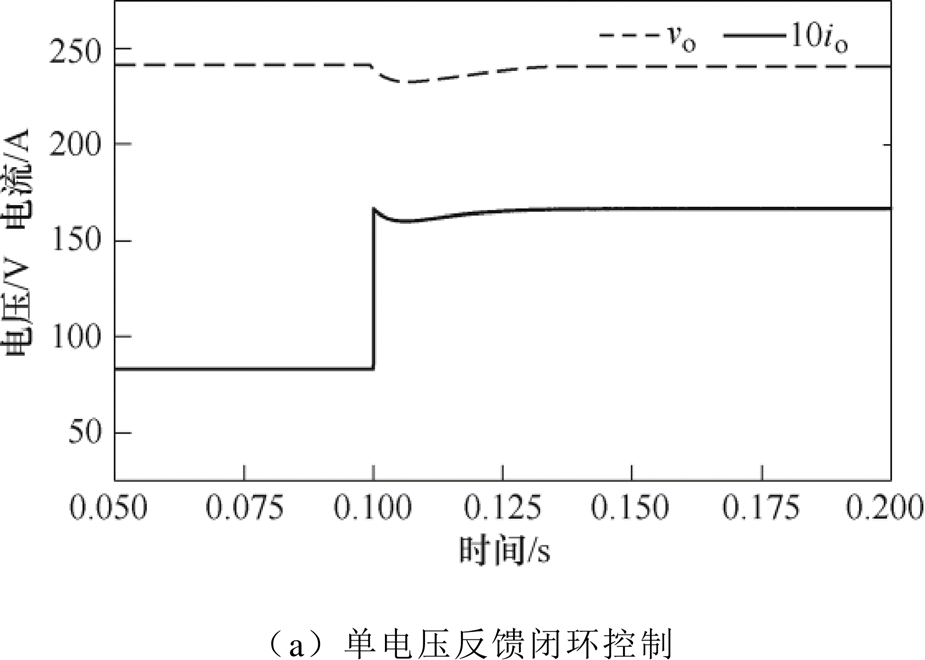
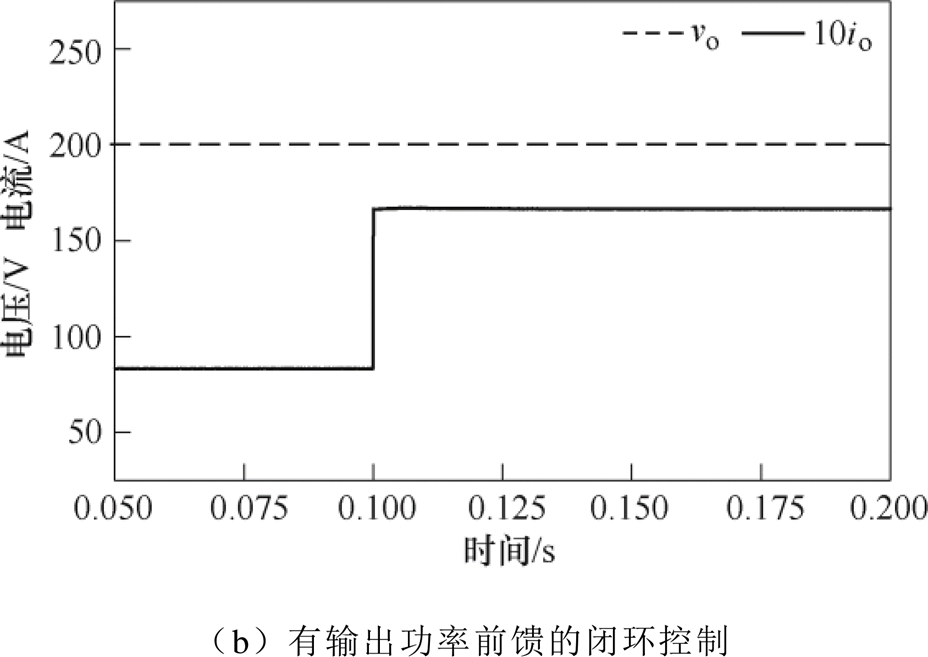
图14 M＜1时DBSRC突加负载时的动态过程波形
Fig.14 Dynamic waveforms of DBSRC under abrupt load when M＜1
图17为基于OPS调制且其他条件与图16实验相同的实验波形。在M=0.5，负载3W 时，谐振电流的幅值为59.6A。在M=1.5，负载24W 时，谐振电流的幅值为46A。
图15 实验样机平台
Fig.15 Photo of the prototype
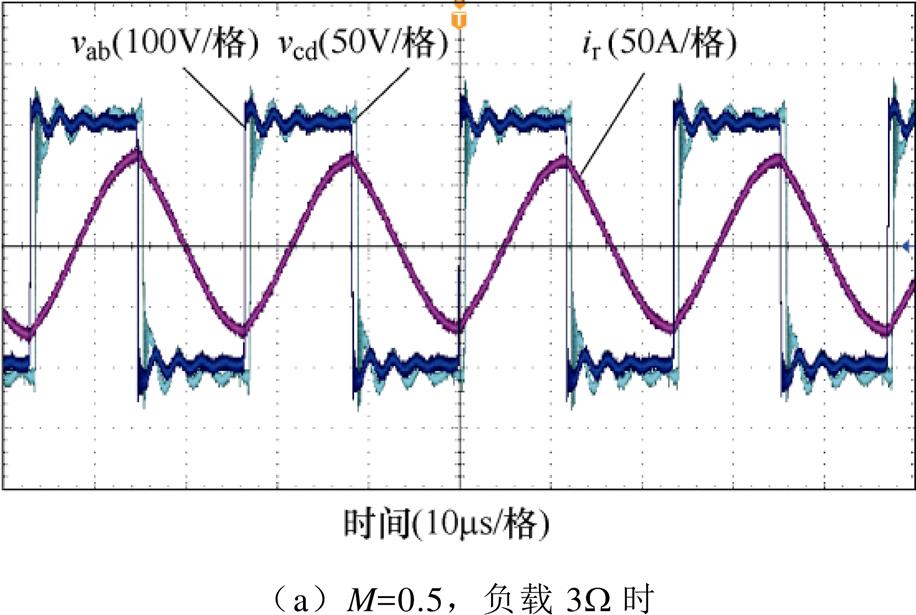
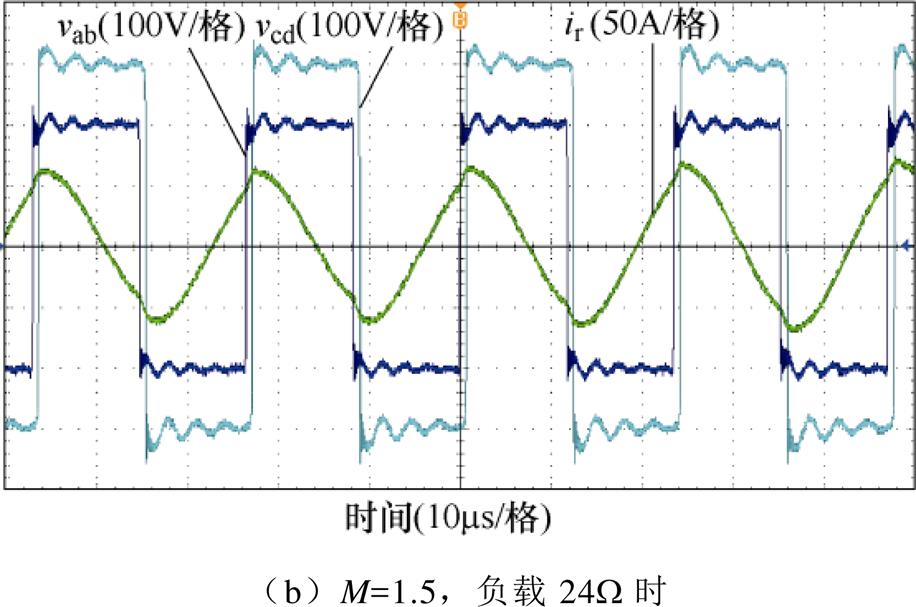
图16 SPS调制下的DBSRC实验波形
Fig.16 Experimental waveforms of DBSRC in SPS modulation
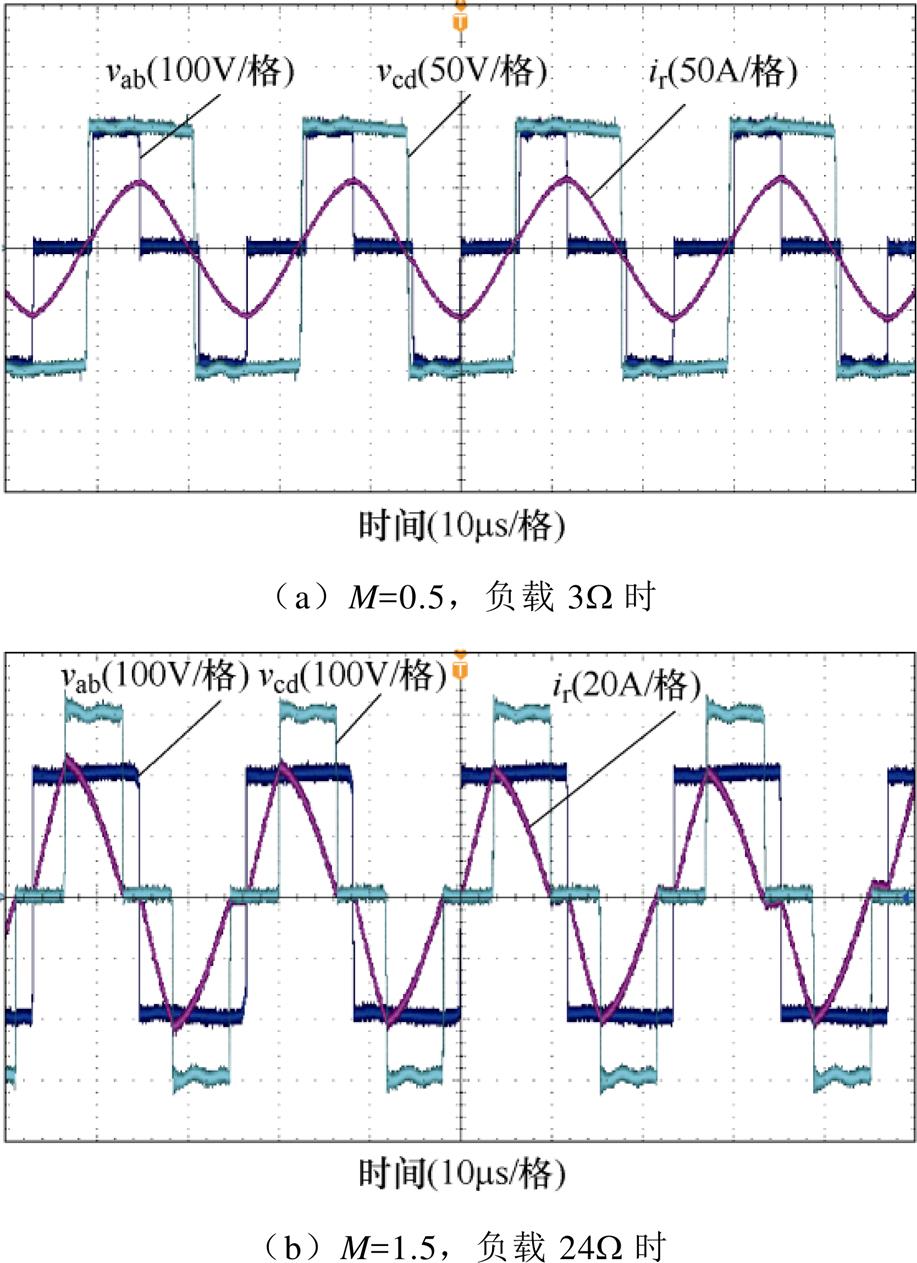
图17 基于OPS调制的交流环节波形
Fig.17 Experimental waveforms of DBSRC in OPS modulation
表2为两组不同参数下，传统单移相与优化多移相调制的谐振电流实验结果数据对比，可以看出，优化多移相调制明显降低了谐振电流的有效值和幅值，提高了变换效率。
表2 SPS与OPS调制的实验结果对比
Tab.2 The comparison of experimental results in SPS and OPS Modulation
电压增益M负载/W调制ir有效值/Air幅值/A效率(%) 0.53SPS45.77881.6 OPS36.159.690.1 1.524SPS40.17278.8 OPS24.24692.6
在实验平台上分别进行了单电压反馈闭环控制和有输出功率前馈的电压闭环控制策略实验，实验工况与仿真一致，保持输出电压闭环给定值为200V，两种控制下电压控制器的PI参数都为0.002和0.15，控制频率为10kHz。在输入电压分别为150V左右和250V左右时突加负载，负载电阻从24W 切换为12W。
图18为输入电压为150V下突加负载闭环动态波形。从图18a可以看出，在单电压反馈控制下，突加负载，即输出电流io突增后，谐振电流ir幅值增加较慢，输出电压vo有较为明显的跌落，压降约为17V，恢复时间在52ms左右。图18b显示，在有输出功率前馈的控制下突加负载后，输出电压保持恒定。
图19为输入电压为250V下突加负载闭环动态波形。在单电压反馈控制下，突加负载后，输出电压vo的跌落约为10V，恢复时间在32ms左右。图19b显示在有输出功率前馈的控制下突加负载后，输出电压基本保持恒定，变化很小。
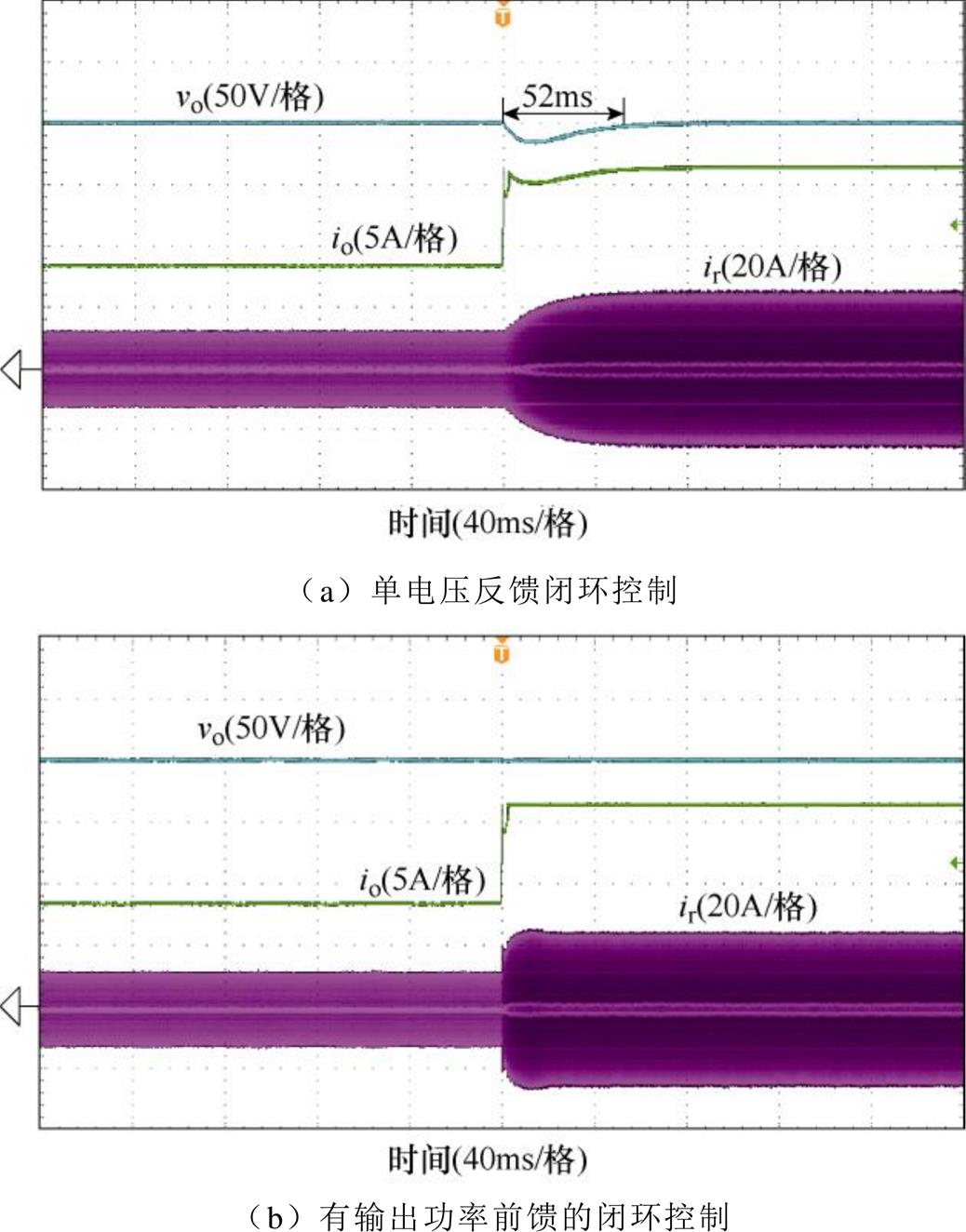
图18 M＞1时DBSRC突加负载时的实验波形
Fig.18 Experimental waveforms of DBSRC under abrupt load when M＞1
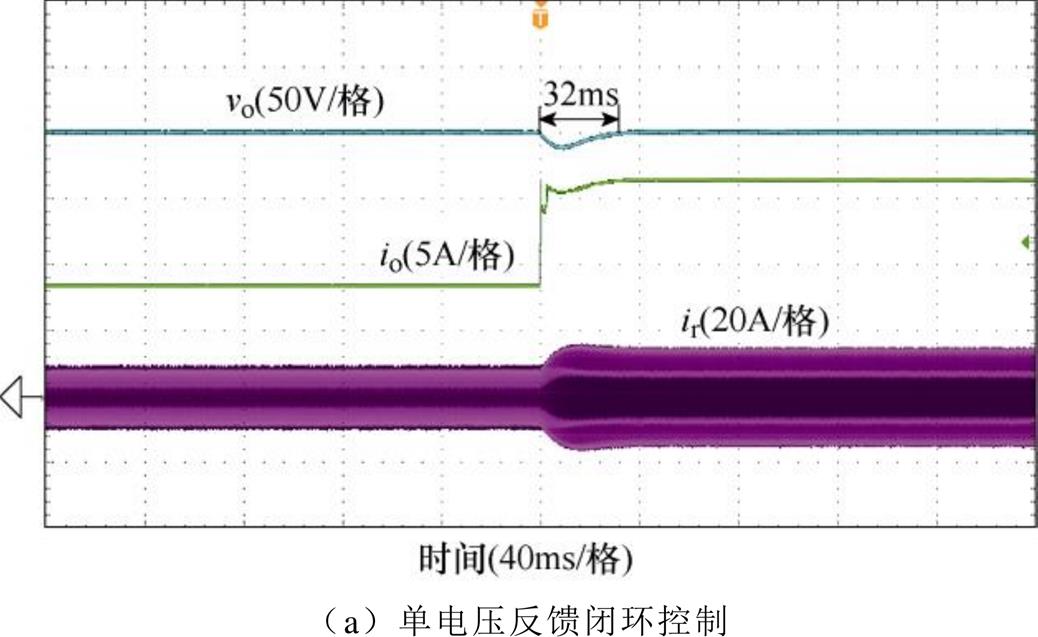
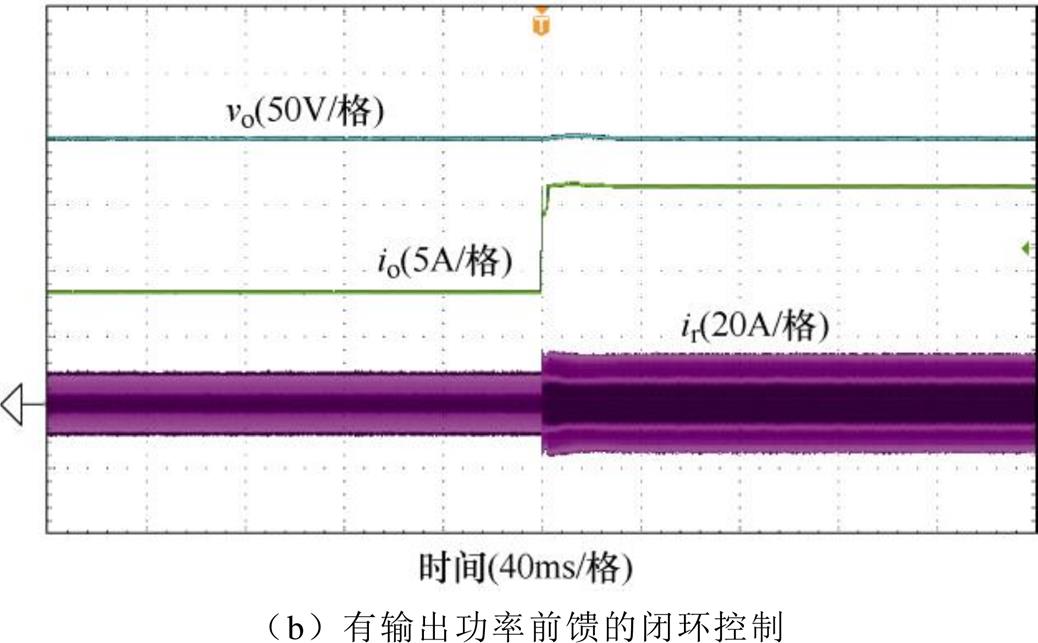
图19 M＜1时DBSRC突加负载时的动态过程波形
Fig.19 Experimental waveforms of DBSRC under abrupt load when M＜1
本文采用基波分析模型对DBSRC的MPS调制下谐振电流大小进行优化，基于OPS调制的功率模型，提出了一种输出功率前馈的电压闭环控制策略，理论分析与实验结果表明：
1）OPS调制可以减小中轻载时DBSRC谐振电流幅值与有效值，同时也有效地减小了开关电流，这有利于减小变换器的损耗，提高效率。
2）基于OPS调制的前馈功率模型具有较高的准确度。输出功率前馈的电压闭环控制可以显著地提高DBSRC在负载突变时的动态响应，相比基本单电压闭环控制，输出电压跌落大小和恢复时间都有了明显的减小。此外，本文提出的功率前馈模型简洁，易于工程实现。
参考文献
[1] Mi C, Bai H, Wang C, et al. Operation, design and control of dual H-bridge-based isolated bidirectional DC-DC converter[J]. IET Power Electronics, 2008, 1(4): 507-517.
[2] Zhao Biao, Song Qiang, Liu Wenhua, et al. Overview of dual-active-bridge isolated bidirectional DC-DC converter for high-frequency-link power-conversion system[J]. IEEE Transactions on Power Electronics, 2014, 29(8): 4091-4106.
[3] 王聪, 沙广林, 王俊, 等. 基于双重移相控制的双有源桥DC-DC变换器的软开关[J]. 电工技术学报, 2015, 30(12): 106-113.
Wang Cong, Sha Guanglin, Wang Jun, et al. The analysis of zero voltage switching dual active bridge DC-DC converters based on dual-phase-shifting con- trol[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 106-113.
[4] 孙志峰, 肖岚, 王勤. 输出并联型双有源全桥变换器控制技术研究综述[J]. 中国电机工程学报, 2021, 41(5): 1811-1830.
Sun Zhifeng, Xiao Lan, Wang Qin. Review research on control technology of output parallel dual-active- bridge-converters[J]. Proceedings of the CSEE, 2021, 41(5): 1811-1830.
[5] Choi H J, Jung J H. Enhanced power line com- munication strategy for DC microgrids using switching frequency modulation of power con- verters[J]. IEEE Transactions on Power Electronics, 2017, 32(6): 4140-4144.
[6] 涂春鸣, 孟阳, 肖凡, 等. 一种交直流混合微网能量路由器及其运行模态分析[J]. 电工技术学报, 2017, 32(22): 176-188.
Tu Chunming, Meng Yang, Xiao Fan, et al. An AC- DC hybrid microgrid energy router and operational modal analysis[J]. Transactions of China Electro- technical Society, 2017, 32(22): 176-188.
[7] 周兵凯, 杨晓峰, 张智, 等. 能量路由器中双有源桥直流变换器多目标优化控制策略[J]. 电工技术学报, 2020, 35(14): 3030-3040.
Zhou Bingkai, Yang Xiaofeng, Zhang Zhi, et al. Multi-objective optimization control strategy of dual- active-bridge DC-DC converter in electric energy router application[J]. Transactions of China Electro- technical Society, 2020, 35(14): 3030-3040.
[8] Zhao Tiefu, Wang Gangyao, Bhattacharya S, et al. Voltage and power balance control for a cascaded H-bridge converter-based solid-state transformer[J]. IEEE Transactions on Power Electronics, 2013, 28(4): 1523-1532.
[9] 赵彪, 安峰, 宋强, 等. 双有源桥式直流变压器发展与应用[J]. 中国电机工程学报, 2021, 41(1): 288-298.
Zhao Biao, An Feng, Song Qiang, et al. Development and application of DC transformer based on dual- active-bridge[J]. Proceedings of the CSEE, 2021, 41(1): 288-298.
[10] Song Wensheng, Zhong Ming, Luo Shucong, et al. Model predictive power control for bidirectional series-resonant isolated DC-DC converters with fast dynamic response in locomotive traction system[J]. IEEE Transactions on Transportation Electrification, 2020, 6(3): 1326-1337.
[11] Huang Jun, Wang Yue, Li Zhuoqiang, et al. Unified triple-phase-shift control to minimize current stress and achieve full soft-switching of isolated bidire- ctional DC-DC converter[J]. IEEE Transactions on Industrial Electronics, 2016, 63(7): 4169-4179.
[12] Shao Shuai, Jiang Mingming, Ye Weiwen, et al. Optimal phase-shift control to minimize reactive power for a dual active bridge DC-DC converter[J]. IEEE Transactions on Power Electronics, 2019, 34(10): 10193-10205.
[13] Hou Nie, Li Yunwei. Overview and comparison of modulation and control strategies for non-resonant single-phase dual-active-bridge DC-DC converter[J]. IEEE Transactions on Power Electronics, 2019, 35(3): 3148-3172.
[14] 高国庆, 雷万钧, 袁晓杰, 等. 双有源全桥变换器全状态离散迭代建模与输出电压纹波分析[J]. 电工技术学报, 2021, 36(2): 330-340.
Gao Guoqing, Lei Wanjun, Yuan Xiaojie, et al. Full- state discrete-time model and the output-voltage- ripple analysis of the dual active bridge converter[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 330-340.
[15] 武琳, 刘志刚, 洪祥. 隔离式双向全桥DC-DC变换器的功率控制特性比较与分析[J]. 电工技术学报, 2013, 28(10): 179-187.
Wu Lin, Liu Zhigang, Hong Xiang. Comparison and analysis of power control characteristic for isolated bidirectional full-bridge DC-DC converter[J]. Transa- ctions of China Electrotechnical Society, 2013, 28(10): 179-187.
[16] 余雪萍, 涂春鸣, 肖凡, 等. 三端口隔离DC-DC变换器的暂态直流偏置机理及抑制策略[J]. 电工技术学报, 2020, 35(9): 1962-1972.
Yu Xueping, Tu Chunming, Xiao Fan, et al. Transient DC bias mechanism and suppression strategy of the three-port isolated DC-DC converter[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 1962- 1972.
[17] Li Xiaodong, Bhat A K S. Analysis and design of high-frequency isolated dual-bridge series resonant DC/DC converter[J]. IEEE Transactions on Power Electronics, 2010, 25(4): 850-862.
[18] 杨博, 葛琼璇, 赵鲁, 等. 双向全桥串联谐振DC/DC变换器回流功率特性优化[J]. 中国电机工程学报, 2019, 39(23): 6990-6999, 7112.
Yang Bo, Ge Qiongxuan, Zhao Lu, et al. The backflow power optimization of dual bridge series resonant DC/DC converter[J]. Proceedings of the CSEE, 2019, 39(23): 6990-6999, 7112.
[19] Corradini L, Seltzer D, Bloomquist D, et al. Minimum current operation of bidirectional dual-bridge series resonant DC/DC converters[J]. IEEE Transactions on Power Electronics, 2012, 27(7): 3266-3276.
[20] Yaqoob M, Loo K H, Lai Y M. A four-degrees- of-freedom modulation strategy for dual-active- bridge series-resonant converter designed for total loss minimization[J]. IEEE Transactions on Power Electronics, 2019, 34(2): 1065-1081.
[21] Han Weijian, Corradini L. Wide-range ZVS control technique for bidirectional dual-bridge series- resonant DC-DC converters[J]. IEEE Transactions on Power Electronics, 2019, 34(10): 10256-10269.
[22] Hu Song, Li Xiaodong, Bhat A K S. Operation of a bidirectional series-resonant converter with mini- mized tank current and wide ZVS range[J]. IEEE Transactions on Power Electronics, 2019, 34(1): 904- 915.
Feedforward Control Strategy of Dual Active Bridge Series Resonant Converter Based on Optimized Phase Shift
Abstract The dual-active-bridge series resonant converter (DBSRC) in traditional single-phase- shift modulation under no-unit voltage gain has high backflow power, resulting in high RMS of the resonant current. For this problem, the DBSRC’s characteristics of the transmission power and the resonant current in multi-phase-shift modulation are analyzed. The multi-phase-shift modulation strategy is derived based on the optimization of the resonant current using the Lagrangian function. It is indicated that the optimized-phase-shift modulation can reduce the magnitude of the resonant current in light and medium loads. Based on optimized-phase-shift modulation method, a voltage closed-loop control strategy with output power feedforward is delivered. Finally, simulation and experimental results verify the feasibility and effectiveness of the optimized modulation and the feedforward control strategy.
keywords：Dual-active-bridge series resonant converter (DBSRC), no-unit voltage gain, multi- phase-shift modulation, magnitude optimization, power feedforward control
DOI: 10.19595/j.cnki.1000-6753.tces.211774
中图分类号：TM46
北京市自然科学基金资助项目（L201005）。
收稿日期 2021-11-05
改稿日期 2022-01-06
范恩泽 男，1994年生，博士研究生，研究方向为大功率电力电子变换器及其控制。E-mail: fanenze@mail.iee.ac.cn
赵 鲁 男，1984年生，副研究员，硕士生导师，研究方向为大功率变流器及高性能电机牵引控制技术。E-mail: zhaolu@mail.iee.ac.cn（通信作者）
（编辑 陈 诚）