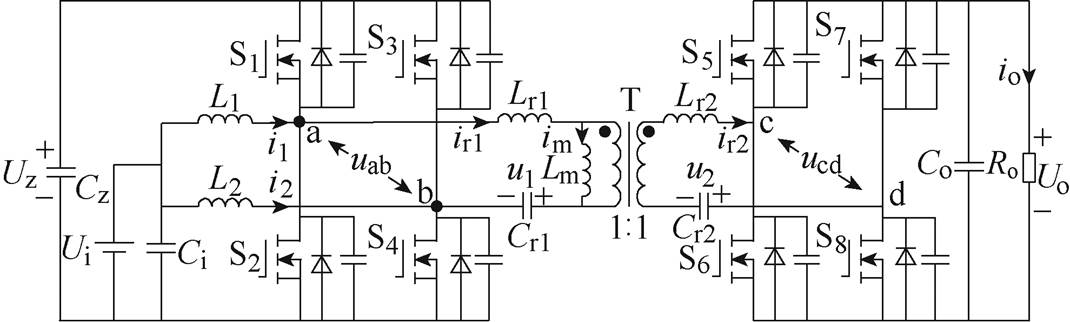
图1 交错Boost集成型CLLLC谐振变换器拓扑结构
Fig.1 Interleaved Boost integrated bidirectional CLLLC resonant converter
摘要 交错Boost集成型CLLLC谐振变换器具有高增益、高效率等优点,在使用脉宽调制时理论上可得到较宽的电压增益范围,但其在现有的定频同步PWM下会随着占空比逐渐偏离0.5而出现越来越大的电流尖峰,导致占空比调节范围受限,其电压增益范围相比于传统的谐振变换器无明显优势。为实现宽增益,该文采用双脉宽调制的方法克服了定频同步PWM的缺点,提出定频同步双脉宽调制与变频双脉宽调制两种调制方式,并通过分析,构建两种调制方式的切换点,最终形成一种宽增益控制策略。该文分析了所提出宽增益控制策略的工作原理及运行特性,并通过实验验证了该控制策略的可行性与理论分析的正确性。
关键词:交错Boost集成型CLLLC谐振变换器 定频同步双脉宽调制 变频双脉宽调制 宽电压增益
随着储能、电动汽车等领域的快速发展,作为能量转换单元的DC-DC变换器得到了广泛应用,其中隔离型双向DC-DC变换器因安全、高效、能量双向流动等特点成为当前的研究热点[1-4]。
双有源桥(Dual Active Bridge, DAB)变换器是具有代表性的隔离型双向DC-DC变换器拓扑[5-6],因其结构对称、能量双向传输、易实现软开关等优点得到广泛应用。不过随着电力电子技术的发展,高频谐振变换器凭借高效率的优势正逐渐取代DAB变换器成为隔离型双向DC-DC变换器的主要研究方向。高频谐振变换器主要有LLC变换器[7-8]、谐振型DAB变换器[9]、CLLC变换器[10]和CLLLC变换器[11-12]四种类型,它们的主要区别在于谐振回路的结构不同导致正反向运行特性存在差异,其中CLLLC变换器因具有结构对称、正反向运行特性一致、控制易实现且软开关能力强等特性,受到越来越多的关注。
CLLLC谐振变换器的常用控制方法是变频控制与移相控制,其中移相控制常被作为变频控制的补充,用于解决轻载时谐振变换器面临的输出电压失调与传输效率降低的问题[13]。但这两种调制方式下CLLLC谐振变换器的电压增益范围受负载影响,在重载时电压增益范围较窄,难以实现宽电压增益。文献[14]提出一种定频同步PWM方式,可使谐振型DAB变换器的电压增益特性不受负载影响,具有较宽的电压增益范围。文献[15]将该调制方式应用于CLLLC变换器,同样取得了良好的效果。定频同步PWM通过将CLLLC谐振变换器一侧全桥占空比固定为0.5,并调节另一侧全桥占空比的方式改变CLLLC变换器的电压增益。然而随着变压器两侧全桥占空比偏差增大,谐振回路受单侧电压影响引起的谐振电流尖峰会越来越大,容易损坏硬件电路。因此,定频同步PWM的占空比调节范围受限,电压增益范围受限。
同时,由于定频同步PWM是一种基于脉宽调制的调制方式,可考虑将使用脉宽调制的其他拓扑结构与谐振变换器集成来得到更宽的电压增益范围。文献[16-17]研究了集成型的CLLLC谐振变换器拓扑,通过双向Boost变换器与CLLLC变换器的集成得到高增益的新拓扑。其中使用定频同步PWM的交错Boost集成型CLLLC谐振变换器在实现高增益的同时具有较宽的电压增益范围和优秀的性能,不过其仍未克服定频同步PWM占空比调节范围受限的缺点,导致电压增益下限较高,不能实现真正的宽增益。
针对交错Boost集成型CLLLC谐振变换器,为提高其电压增益范围,本文提出基于双脉宽调制(Double Pulse Width Modulation, DPWM)的定频同步DPWM与变频DPWM两种调制方式,并通过分析,构建两种调制方式的切换点,最终形成一种宽增益控制策略。定频同步DPWM是在定频同步PWM的基础上,同时调节变换器中两个全桥的占空比,并保持两占空比接近,避免了谐振电流尖峰的出现,因此具有比定频同步PWM更宽的占空比调节范围与电压增益范围,可实现高增益。而变频DPWM是与传统谐振变换器的调制方式存在明显差异的调制方法,其通过降低开关频率来增加开关周期中无源谐振模态的存在时间,并利用无源谐振改变谐振回路中谐振电容的电压状态,使谐振回路在能量传递过程中对输入电压产生分压作用,以达到降低输出电压的目的,可实现低增益。本文分析了上述调制方式的工作原理以及运行特性,然后根据分析结果构建了两种调制方式的平滑切换点,提出宽增益控制策略,最后搭建实验样机验证了控制策略的可行性与理论分析的正确性。
交错Boost集成型CLLLC谐振变换器由前级交错Boost双向DC-DC变换器与后级CLLLC谐振变换器组成,其拓扑结构如图1所示。

图1 交错Boost集成型CLLLC谐振变换器拓扑结构
Fig.1 Interleaved Boost integrated bidirectional CLLLC resonant converter
图1中,Ui为电源侧输入电压;Uz为中间级电压,既是前级Boost变换器的输出电压,也是后级CLLLC变换器的输入电压;Uo为负载侧输出电压,io为负载侧输出电流;uab和ucd分别为变压器两侧的谐振槽电压;L1和L2为输入电感,流过其电流分别为i1和i2;Lm为励磁电感,流过其电流为im;Lr1和Lr2为谐振电感,流过其电流分别为ir1和ir2;Cr1和Cr2为谐振电容,其电压分别为u1和u2;Ci、Cz、Co分别为电源侧缓冲电容、中间级缓冲电容和输出侧支撑电容;为了更直观地展示变换器运行特性,变压器T的电压比n设为1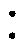 1。
1。
本文提出的定频同步DPWM是一种高增益调制方式,相比定频同步PWM能实现更高的电压增益。其工作波形如图2所示,工作频率为谐振频率,变压器两侧谐振槽电压uab和ucd基波相位相同。具体控制方式为:开关管S1、S3占空比相同,均为D1,但S1、S3的驱动信号相位差180°;开关管S5、S7占空比相同,均为D2,两者驱动信号相位同样差180°;S1、S3的驱动波形分别与S5、S7的驱动波形具有相同的基波相位;所有桥臂上管与下管互补导通。图2中,D2>D1,设D2-D1=d1。
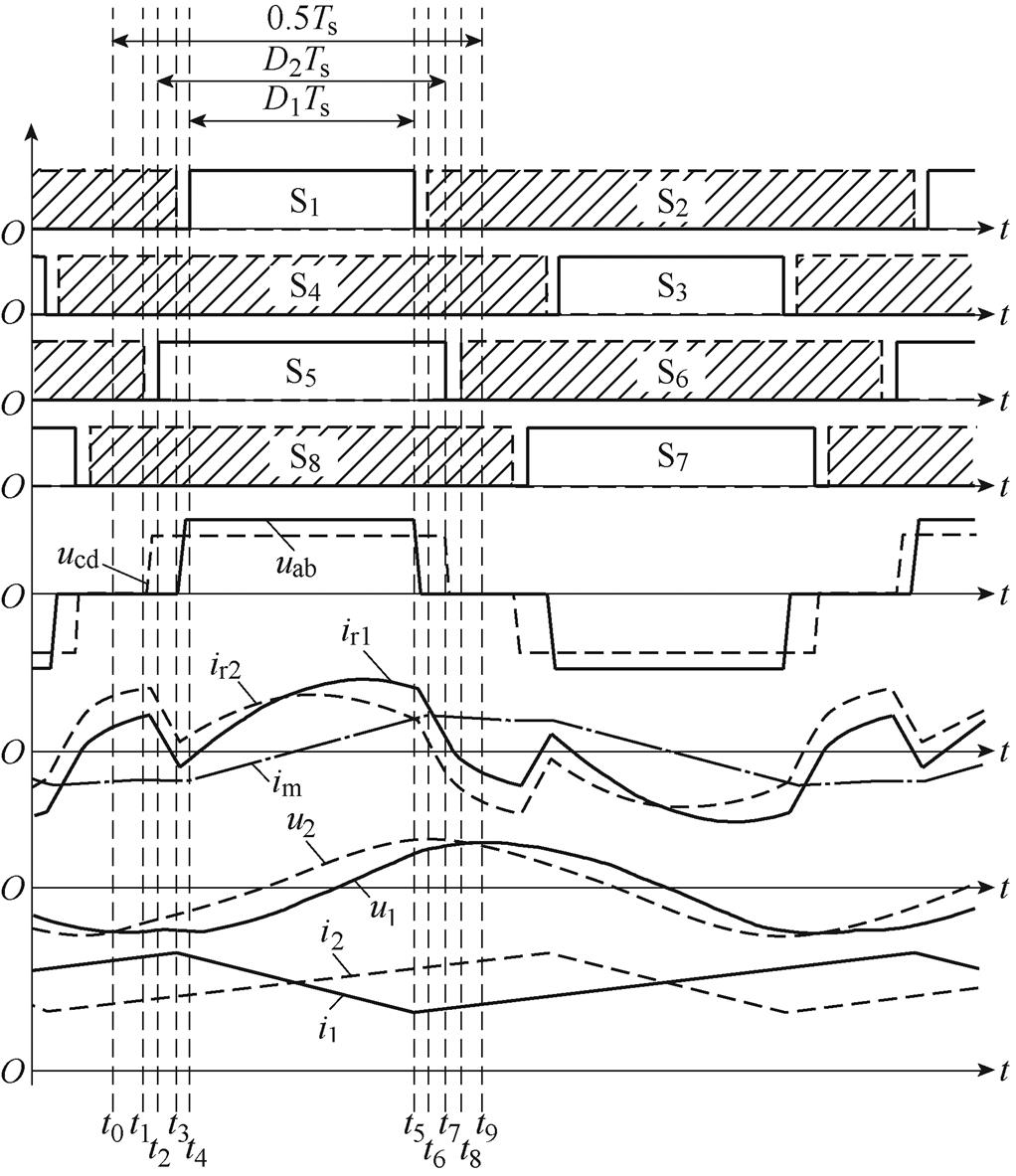
图2 定频同步DPWM控制的工作波形
Fig.2 Working waveforms of fixed-frequency synchronous DPWM control
由图2可见,定频同步DPWM与文献[13]提出的定频同步PWM相比,增加了t0~t1与t8~t9中的无源谐振模态,在定频同步PWM控制中,变换器谐振回路在t0~t3时处于uab=0,ucd=Uo的条件下,谐振回路受单侧电压作用导致谐振电感电流快速变化,出现电流尖峰。而定频同步DPWM控制减少了谐振回路受单侧电压作用的时长,变换器谐振回路在t0~t1时谐振槽电压uab=ucd=0,谐振电流缓慢变化,只要保证d1较小,就可避免谐振回路在较长时间单侧电压作用下出现较大电流尖峰。因此定频同步DPWM在占空比调节时无需考虑电流尖峰的影响,相比定频同步PWM具有更宽占空比调节范围与更高的电压增益上限。当然,上述只是(0, 0.5)占空比范围内定频同步DPWM的工作原理,在[0.5, 1]占空比范围内,定频同步DPWM的D2应大于D1,具体工作原理与(0, 0.5)占空比范围内类似,不再赘述。
变频DPWM是一种降压调制方式,其与传统变频调制最大的区别在于调节开关频率的同时分别对变压器一次侧、二次侧开关管进行占空比不同的脉宽调制,利用双脉宽调制产生的无源谐振模态改变谐振回路的电压状态,使其对输入电压进行分压,最终达到降低变换器电压增益的目的。
使用变频DPWM时变换器的工作波形如图3所示,该调制方式需要调节变压器一次侧、二次侧开关管的占空比与工作频率。具体控制方式为:开关管S1、S3占空比相同,均为D1,且两者驱动信号相位差180°;开关管S5、S7占空比相同,均为D2,且两者驱动信号相位差180°;S2、S4的驱动波形分别与S6、S8的驱动波形具有相同关断时间;所有桥臂上管与下管互补导通。此时D1>D2,设D1-D2=d2。
由图3可见,变频DPWM在t0~t2的无源谐振模态改变了谐振电容电压状态,导致t5~t6时谐振回路整体对输入电压进行分压,而在t5~t6后期虽然谐振电流开始下降,谐振电感电压反向,但此时因谐振电容电压已经上升,所以谐振回路总体还是在对输入电压进行分压,以降低变换器的电压增益。由以上分析可知,t0~t2的无源谐振模态时谐振电容电压变化越大,变频DPWM电压增益越低。而t2~t4模态主要用于快速调节谐振电流以实现软开关,这个过程中谐振电容电压变化较小。
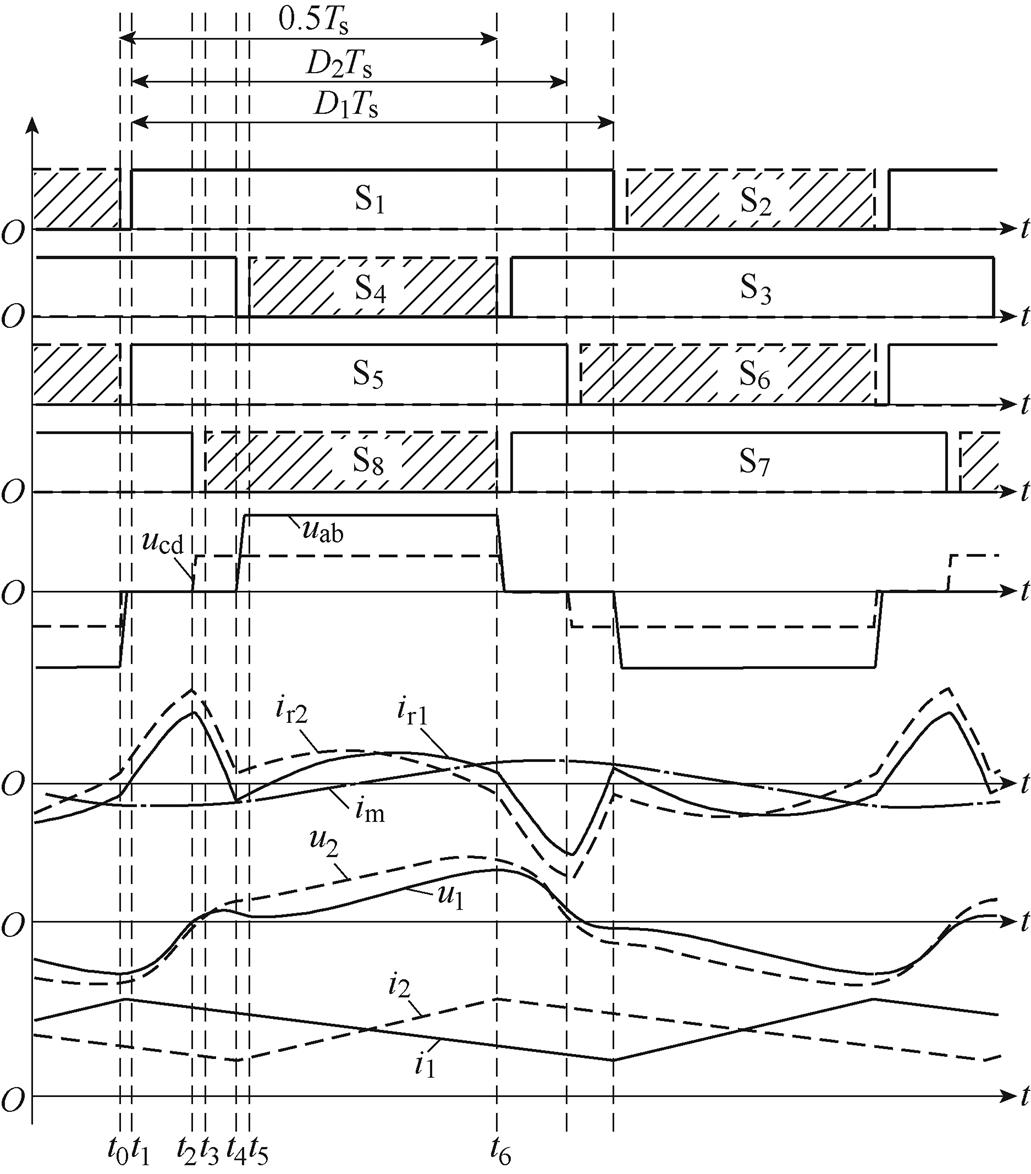
图3 变频DPWM控制的工作波形
Fig.3 Working waveforms of variable-frequency DPWM control
根据上述分析可知,变频DPWM比较复杂,为简化控制,本文将t4~t6的时长固定为半个谐振周期,保证能量传输过程中谐振电流大部分时间为正,能量由输入端向输出端传递,此时无论频率怎么变化,有源谐振模态的时间长度都维持不变。这种情况下,若开关频率为谐振频率,则t0~t4的模态不存在,整个工作波形完全由有源谐振模态构成,此时的稳态工作点亦是变频DPWM与定频同步DPWM在D1=D2=0.5时得到的公共工作点,可作为两者切换点。当开关频率fs低于谐振频率时,D1也要变化以保证t4~t6时长不变,此时fs与D1关系为
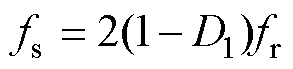 (1)
(1)
式中,fr为谐振频率。
值得注意的是,t0~t4的时长随开关频率降低而增加,当D1>0.75,fs<0.5fr时,t0~t4过程中谐振电流会经半个谐振周期开始反向流动,此时谐振电容电压反向变化,变换器电压增益不降反升,所以变频DPWM中D1的调节范围应设为[0.5, 0.75],D2的调节范围应设为[0.5, D1],同时d2应取合适值,以保证-ir1(t4)>i2(t4),变换器能实现软开关。
本节将对交错Boost集成型CLLLC谐振变换器在定频同步DPWM与变频DPWM两种调制方式下的电压增益特性展开分析,并基于两者的电压增益特性提出宽增益控制策略。
在定频同步DPWM下,因CLLLC谐振变换器工作于谐振频率,可通过基波近似法较为准确地计算出变换器的电压增益表达式。为方便后续分析,设输入电感L1=L2=L,谐振电感Lr1=Lr2=Lr,励磁电感为Lm,谐振电容Cr1=Cr2=Cr,谐振频率为fr,谐振角频率为wr,开关频率为fs,开关角频率为ws,变压器一次侧、二次侧的阻抗分别为Z1和Z2。
如图4所示是理想条件下CLLLC谐振变换器的基波等效电路。
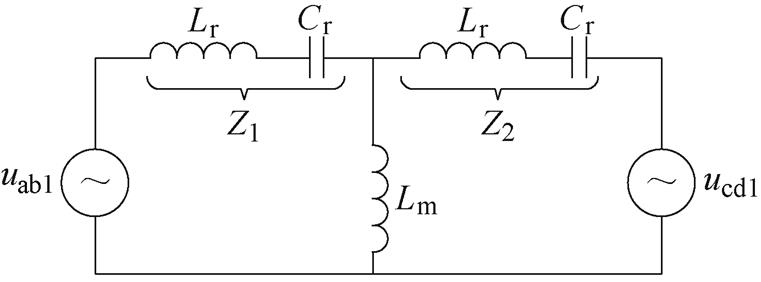
图4 基波等效电路
Fig.4 Equivalent circuit at the fundamental frequency
根据图2,谐振槽电压uab和ucd可分别展开为
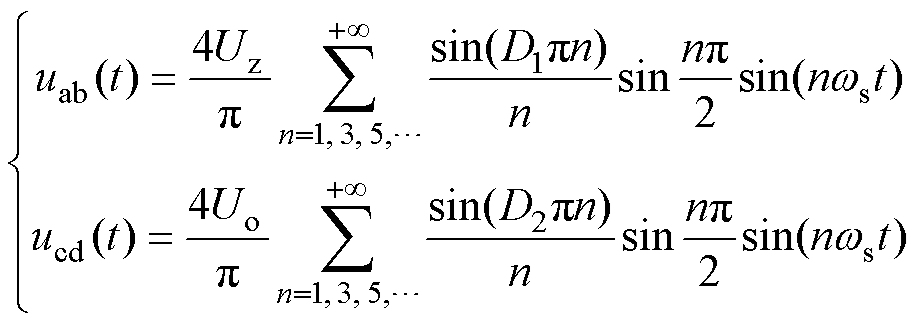 (2)
(2)
从式(2)提取基波分量uab1和ucd1可得
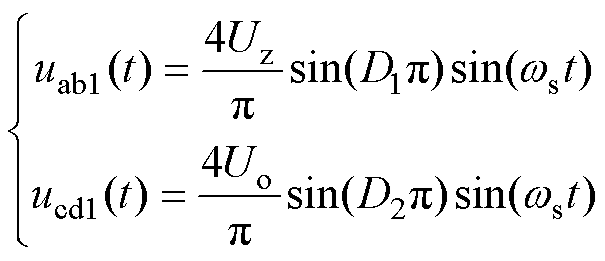 (3)
(3)
由于定频同步DPWM控制下变换器工作在谐振频率处,所以开关角频率满足
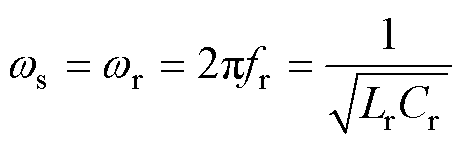 (4)
(4)
此时谐振回路的阻抗为
 (5)
(5)
因此,整个谐振网络处于准谐振状态,忽略非理想因素带来的损耗,则对电压基波分量而言,uab1=ucd1,可求得CLLLC谐振变换器的电压增益表达式为
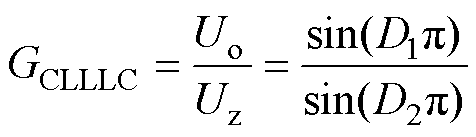 (6)
(6)
结合前级交错Boost变换器电压增益,可得交错Boost集成型CLLLC谐振变换器在定频同步DPWM控制下总电压增益表达式为
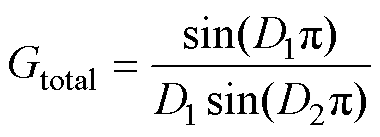 (7)
(7)
交错Boost集成型CLLLC谐振变换器在定频同步DPWM控制下,总电压增益曲线趋近于交错Boost变换器的电压增益曲线,最高可达无穷大,为方便观察非极限占空比时电压增益变化情况,这里只根据式(7)绘制[0.1, 0.9]占空比范围内的电压增益三维图,如图5所示。
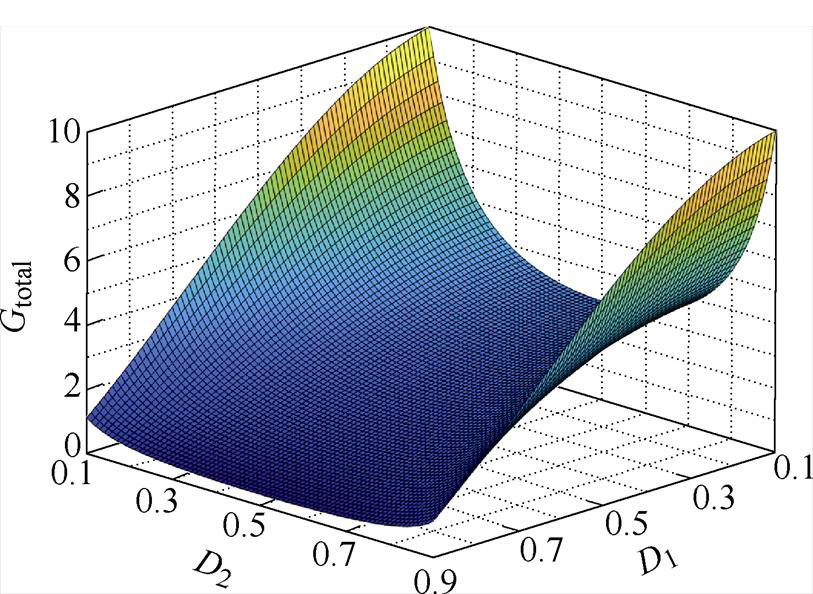
图5 电压增益Gtotal随占空比D1、D2变化三维图
Fig.5 3D diagram of voltage gain Gtotal varying with D1 and D2
由图5可见,变换器电压增益关于D2=0.5具有对称性,在D1=D2=0.1时得到最高电压增益,其值为10,当D1=0.9,D2=0.5时得到最低电压增益,其值为0.345。但正如1.2节所述,为避免出现较大电流尖峰,D1与D2需取值相近,从而结合式(7)可见,定频同步DPWM能实现的最低电压增益始终大于1,难以降压运行。
因此,为实现宽增益,本文在D1>0.5时使用变频DPWM控制。变频DPWM控制主要通过对变换器后级CLLLC进行降压来降低变换器总电压增益,因降压过程中起主要作用的并非基波,使用基波近似法进行分析会出现较大误差,因此基波近似法不适用于变频DPWM控制。若使用时域分析法,忽略死区,取ir1(t4)+ir2(t4)=ir1(t6)+ir2(t6)=0为近似条件,可以得到一个电压增益表达式,但因上述近似条件在一些情况下可能误差较大,很难保证求得的电压增益表达式在占空比调节范围内的准确性,所以时域分析法也不适用于变频DPWM。在常用数学方法难以求解准确电压增益特性的情况下,本文选择通过仿真的方式分析变频DPWM控制下变换器的电压增益特性。仿真时所用系统参数见表1。
变频DPWM下的电压增益曲线如图6所示。图6a为d2=0时,不同负载状态下变换器的电压增益变化情况;图6b为负载固定为50W,d2不同时变换器电压增益变化情况。
由图6a可见,变频DPWM控制下电压增益随占空比变化曲线是非线性的,且负载电阻越小,电压增益下降越快。由图6b可见,变频DPWM控制下电压增益曲线随d2增加而上移,其根本原因是:当d2一定时,谐振电流随负载增加而增加,输入电压一定时负载越大谐振电流值较大,可更快速地改变谐振电容电压状态,输出电压越低。当负载一定时,随d2增大,无源谐振时间减少,无源谐振过程中谐振电容电压变化量减少,对后级CLLLC变换器输入电压Uz的分压能力减弱,导致总体电压增益上升。综上所述,若占空比D1不变,则变换器电压增益随负载增加而降低,随d2增加而上升。
表1 系统参数
Tab.1 Parameters of the system

参 数数 值 输入电压Ui/V100 励磁电感Lm/mH100 谐振电感Lr1/mH5 谐振电感Lr2/mH5 输入电感L1/mH100 输入电感L2/mH100 变压器电压比11 谐振电容Cr1/nF500 谐振电容Cr2/nF500 输出电容Co/mF150 缓冲电容Cz/mF150 开关频率fs/kHz50~100 谐振频率fr/kHz100 死区时间/ns100
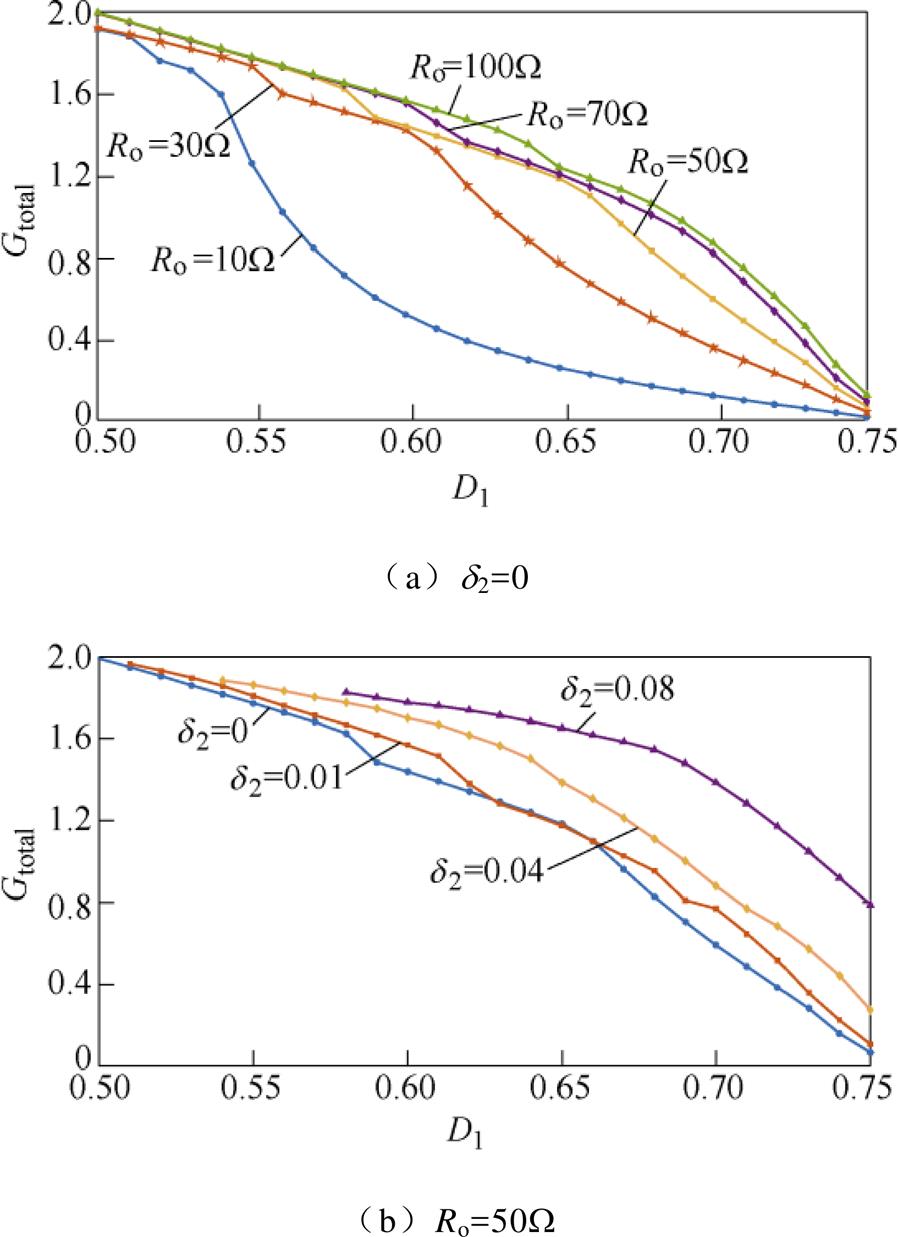
图6 变频DPWM下的电压增益曲线
Fig.6 Voltage gain curves in variable-frequency DPWM
由2.1节电压增益特性分析可以看出,本文提出的定频同步DPWM很难实现降压,而变频DPWM即为针对CLLLC谐振变换器的降压控制策略,可使变换器降到较低电压增益。1.3节提到D1=D2=0.5是定频同步DPWM与变频DPWM共有的工作点,因此可以该点作为切换点,构建一种宽增益控制策略,在(0, 0.5)占空比范围内利用定频同步DPWM的升压能力使变换器得到较高电压增益上限,在[0.5, 0.75]占空比范围内,利用变频DPWM降低变换器后级CLLLC的输出电压,使变换器总体电压增益可以达到较低水平,进而实现宽增益。
在所提出宽增益控制策略下,变换器的总体电压增益随占空比增加而下降,当两种调制方式通过切换点平滑切换时,该增益曲线连续变化,不存在间断点。为此,若0.5-d1<D1<0.5+d2,在切换点附近进行调制时,则无需维持占空比差值d1或d2,如D2上升到0.5后D1仍继续上升,则D2维持0.5不变,直到D1=D2=0.5,此时D1若继续上升,则调制方式由定频同步DPWM平滑切换到变频DPWM。关于d1与d2的取值,因d1越小,定频同步DPWM在相同D1情况下电压增益越高;d2越小,变频DPWM在相同D1情况下电压增益越低,所以为得到宽电压增益范围,d1、d2应在能实现软开关的前提下取较小值。
变换器工作在高开关频率时必须实现软开关才能有较高的工作效率,本节对所提出调制方式进行软开关特性分析,说明应该如何调节变换器中各项参数以实现软开关。
根据图2定频同步DPWM下变换器前半周期工作波形进行软开关特性分析,定义uS=u1+u2,uD=u1-u2,iS=ir1+ir2,iD=ir1-ir2,k=Lm/Lr。定频同步DPWM控制下,每个时刻为
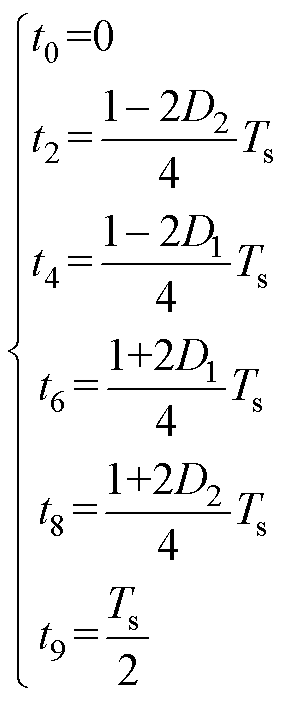 (8)
(8)
根据定频同步DPWM的工作模态可知,变压器一次侧开关管软开关实现难度比二次侧开关管软开关实现难度大,又因前级交错Boost变换器输入电流的影响,相比于CLLLC谐振变换器,交错Boost集成型CLLLC谐振变换器一次侧下管S2、S4软开关实现难度增加,上管S1、S3软开关实现难度降低。因此,以S2为例进行分析,其软开关实现条件为
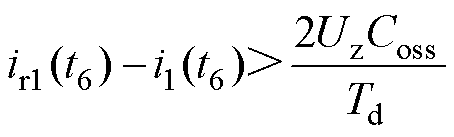 (9)
(9)
式中,Coss为开关管并联等效电容;Td为死区时间。
根据图2所示工作波形,建立各工作模态复频域下的简化等效模型,复频域简化等效模型如图7所示。图中,ir10、ir20、i10、i20、im0、u10、u20为该模态初始时刻ir1、ir2、i1、i2、im、u1、u2的值。忽略死区时间,各模态等效模型结合式(8)可以求得变量在每个模态下的时域表达式。
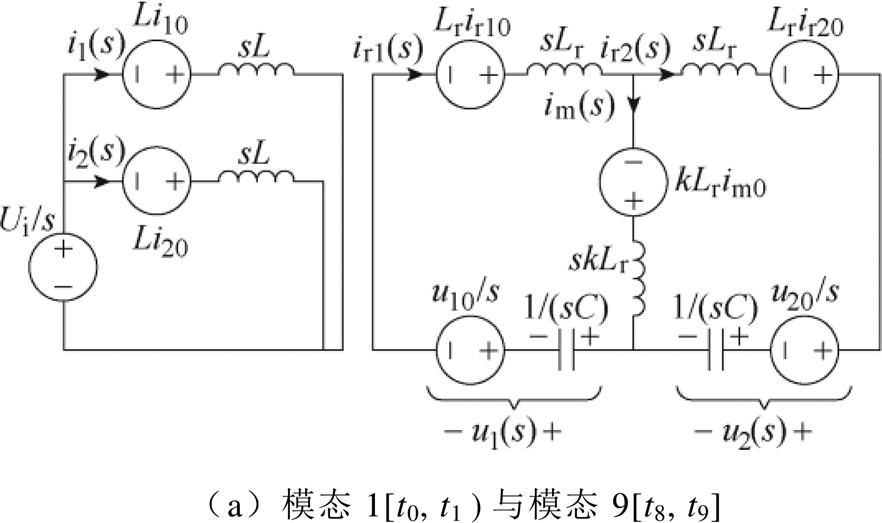
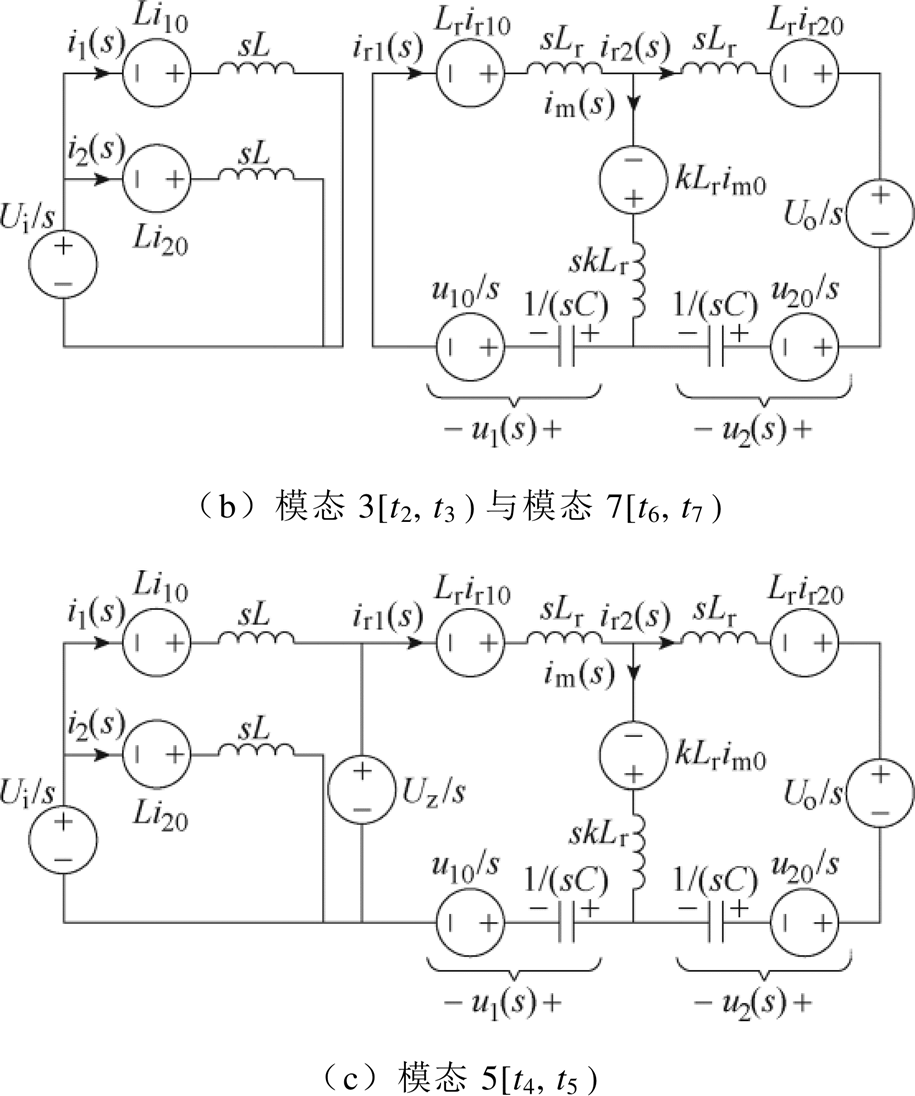
图7 复频域简化等效模型
Fig.7 Simplified equivalent circuit in frequency domain
对所求得的时域表达式进行整理,可得
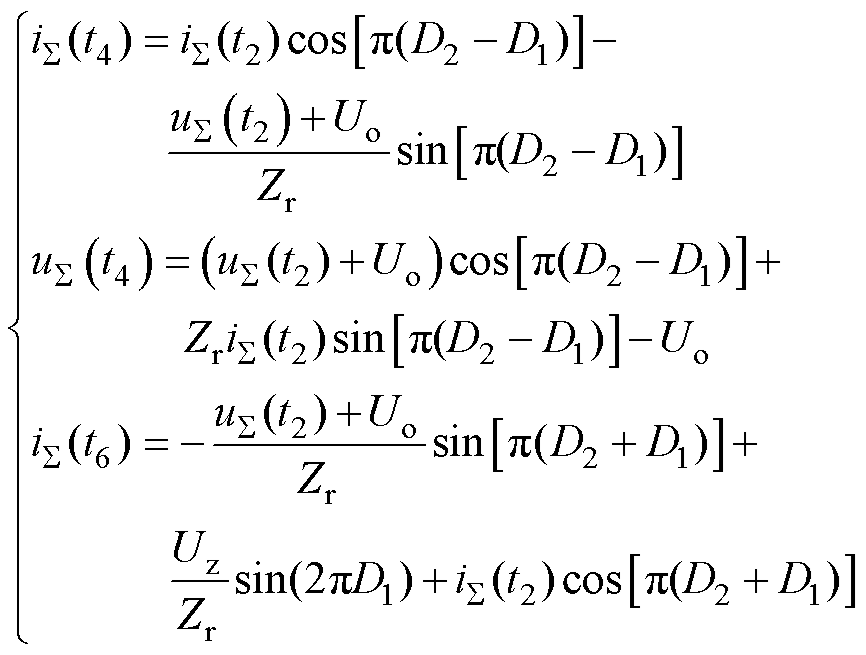 (10)
(10)
式中,Zr为谐振阻抗,Zr=(Lr/Cr)0.5。
为简化分析,并使谐振电流ir1和ir2的各时刻表达式能得到显式的解析解,建立如下假设
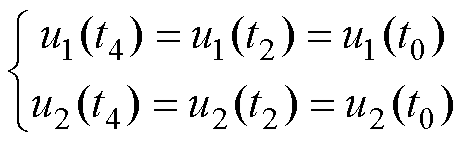 (11)
(11)
另外,根据电容安秒平衡原理可得
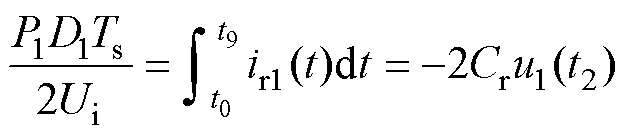 (12)
(12)
式中,P1为变换器正向工作时,输入电压源Ui的平均输入功率。由此可计算得到谐振电容Cr1在t2时刻的电压u1(t2)为
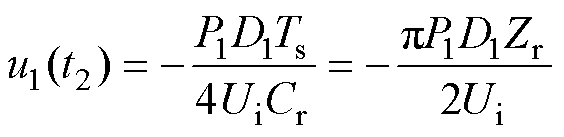 (13)
(13)
同理,谐振电容Cr2在t0时刻的电压u2(t0)为
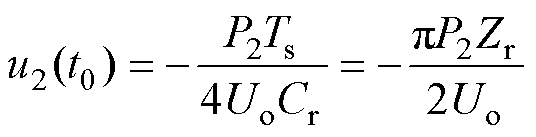 (14)
(14)
式中,P2为变换器正向工作时,输出电压Uo的平均输出功率。
将式(11)、式(13)、式(14)代入式(10)中,可得
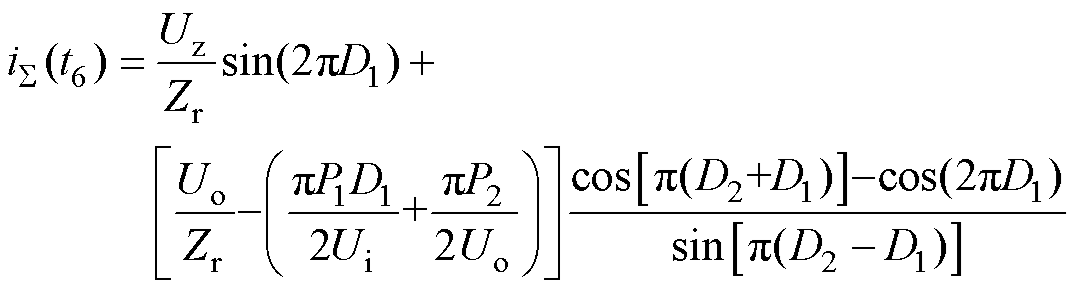 (15)
(15)
另外,由叠加定理可知
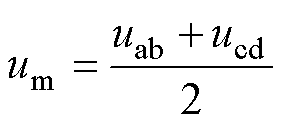 (16)
(16)
式中,um为励磁电感两端电压。在各个模态下式(16)都成立。由此,可将各模态励磁电感电流im进行线性化表示,得
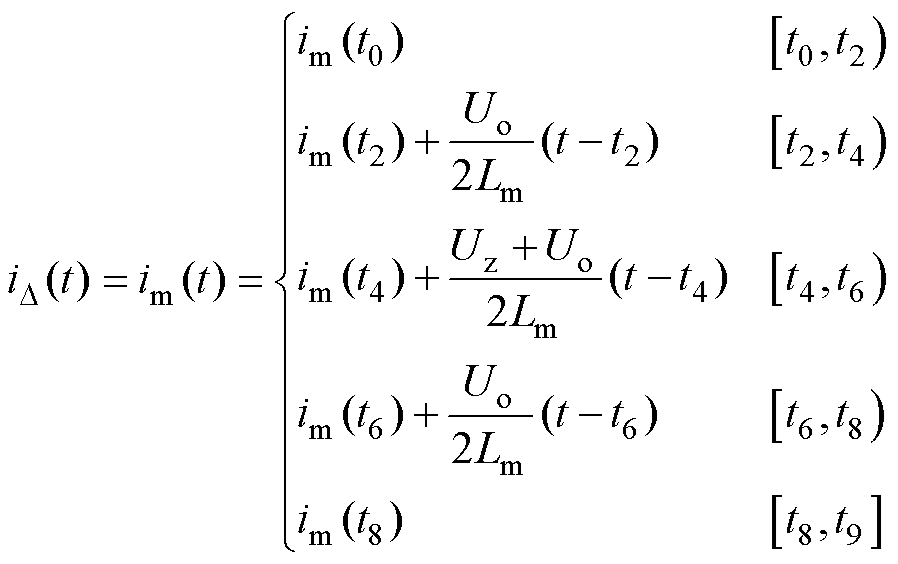 (17)
(17)
结合式(8)与工作波形的对称性关系,得励磁电感电流为
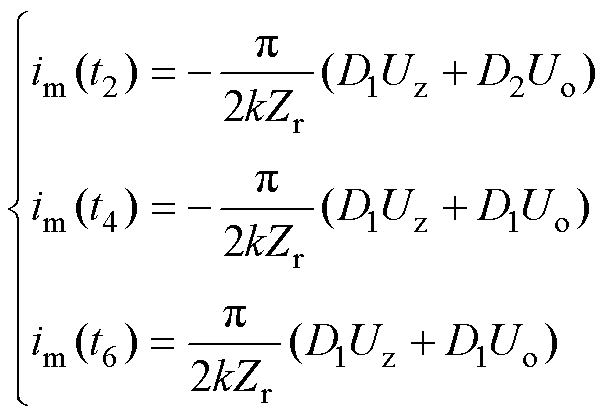 (18)
(18)
结合式(15)和式(18),可得在t6时刻谐振电流ir1的表达式为
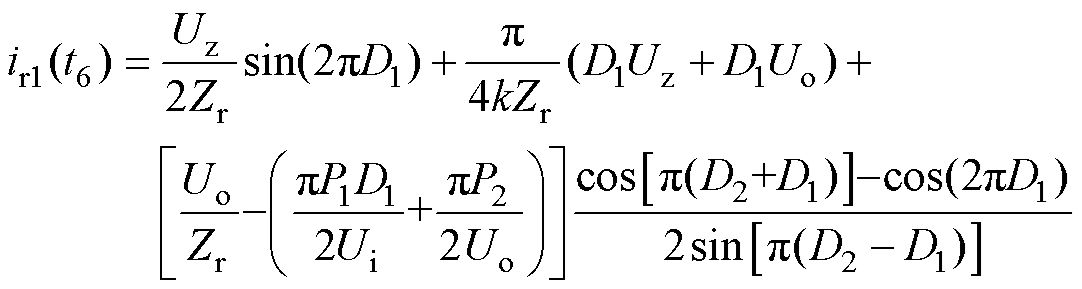 (19)
(19)
另外,结合图2中定频同步DPWM控制的工作模态可得
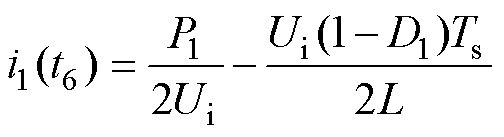 (20)
(20)
将式(19)、式(20)代入式(9)中,并结合电压增益关系,可得定频同步DPWM控制的软开关条件表达式F为
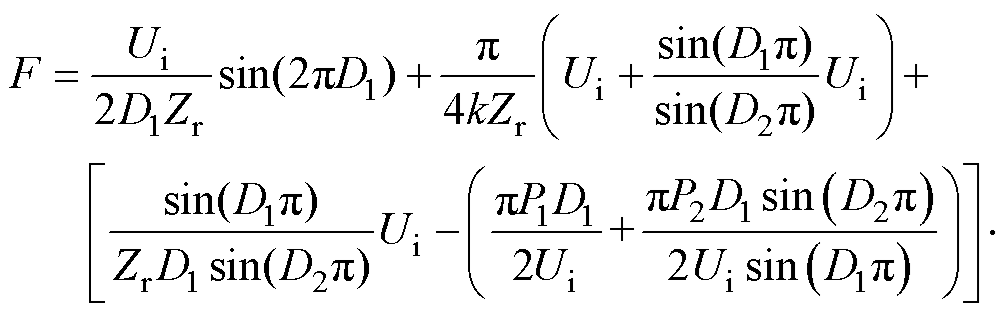
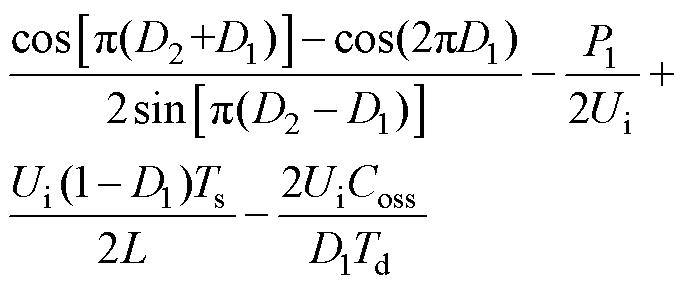 (21)
(21)
当F>0时,可实现软开关。理想条件下,设传输功率P=P1=P2,开关管并联等效电容Coss= 100pF,d1=0.02,并将表1所示参数代入式(21),可得定频同步DPWM控制下变换器主要参数与软开关范围的关系,定频同步DPWM控制软开关范围如图8所示。

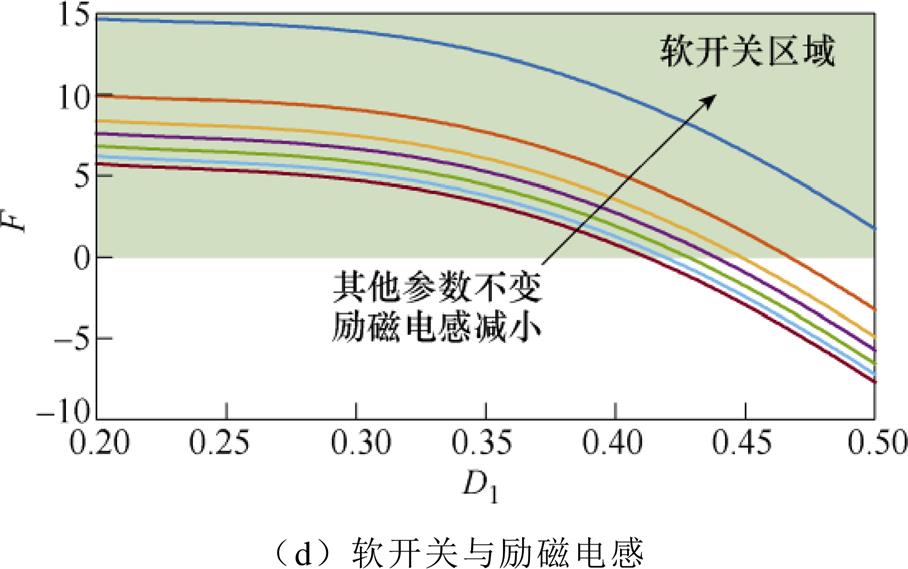
图8 定频同步DPWM控制软开关范围
Fig.8 Range of soft-switching in fixed-frequency synchronous DPWM
由图8可见:若代入式(21)中的其他参数不变,①只改变占空比D2与D1之差d1,则d1越大,软开关范围越大;②只改变传输功率P,则传输功率越小,软开关范围越大;③只改变谐振阻抗Zr,则Zr越小,软开关范围越大;④只改变励磁电感与谐振电感的比值k,则k越小,软开关范围越大。上述参数中,d1为控制时可调变量;传输功率由工况决定;谐振阻抗Zr和励磁电感的大小在参数设计中确定。
变频DPWM的软开关特性分析过程与定频同步DPWM类似,都是通过时域分析法推导软开关条件表达式,但因变频DPWM下变换器不具有如式(11)所示的近似条件,也难以找到合适的新近似条件,所以最终推导出的软开关条件表达式误差较大,难以反应实际情况,因此本文不对其展开分析。
为验证所提出宽增益控制策略的有效性,本文基于表1所示参数进行元器件选型与电路设计,搭建一台实验样机,如图9所示。样机实测参数见表2。

图9 实验样机
Fig.9 Experimental prototype
表2 样机实测参数
Tab.2 Measured parameters of the prototype
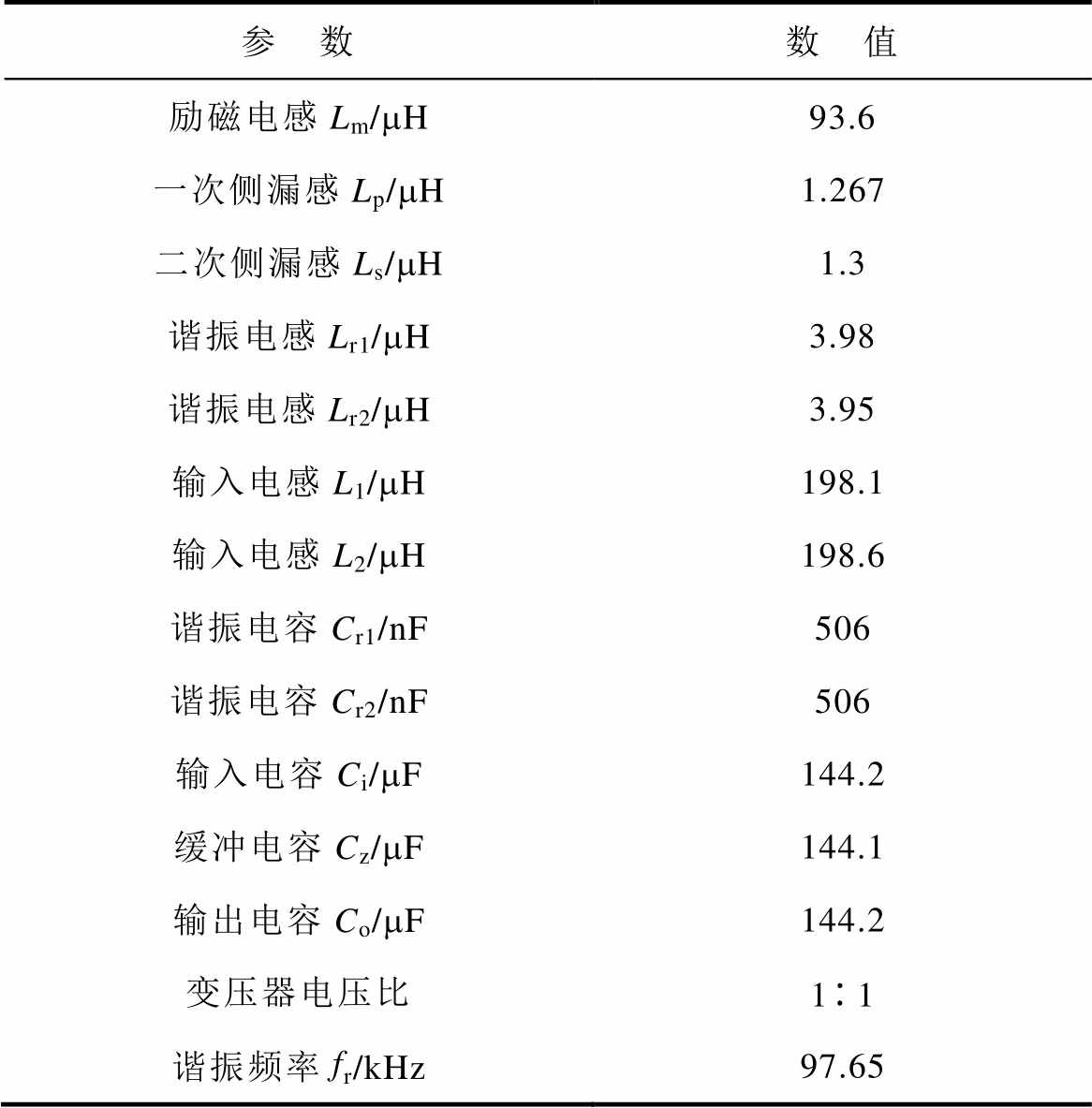
参 数数 值 励磁电感Lm/mH93.6 一次侧漏感Lp/mH1.267 二次侧漏感Ls/mH1.3 谐振电感Lr1/mH3.98 谐振电感Lr2/mH3.95 输入电感L1/mH198.1 输入电感L2/mH198.6 谐振电容Cr1/nF506 谐振电容Cr2/nF506 输入电容Ci/mF144.2 缓冲电容Cz/mF144.1 输出电容Co/mF144.2 变压器电压比11 谐振频率fr/kHz97.65
因定频同步DPWM下变压器一次侧全桥下管流过的电流峰值约为输出电流的1/D1,其余器件流过的电流峰值约为输出电流的1/2D1,考虑开关管电流应力并留有足够裕度,本文将样机的占空比调节范围设为[0.2, 0.75],本节将验证该占空比范围下变换器的电压增益范围。图10为定频同步DPWM下变换器在负载电阻50W,输入电压48.8V,开关频率100kHz,D1=0.2,D2=0.23时的实验波形,此时输出电压为204V,电压增益为4.18。
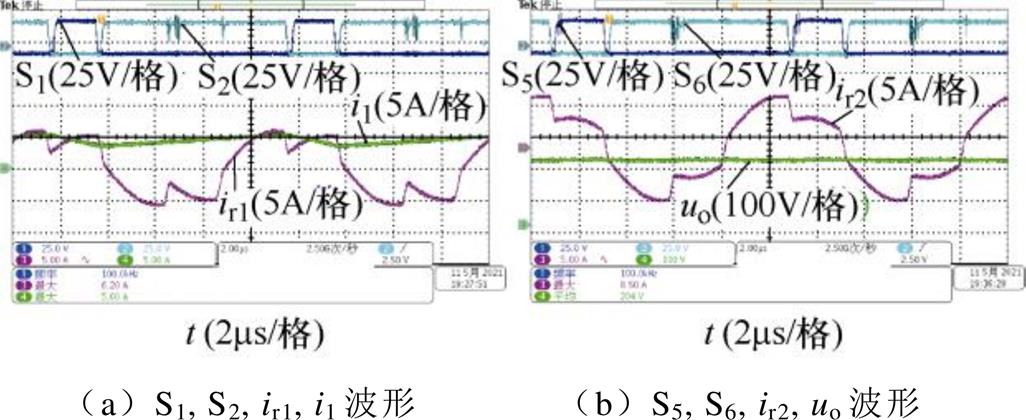
图10 D1=0.2, D2=0.23时定频同步DPWM实验波形
Fig.10 Experimental waveforms of fixed-frequency synchronous DPWM when D1=0.2, D2=0.23
图11为变频DPWM控制下变换器在负载电阻50W,输入电压50V,D1=0.75,D2=0.73时的实验波形,此时开关频率为50kHz,输出电压为10.6V,电压增益为0.212。
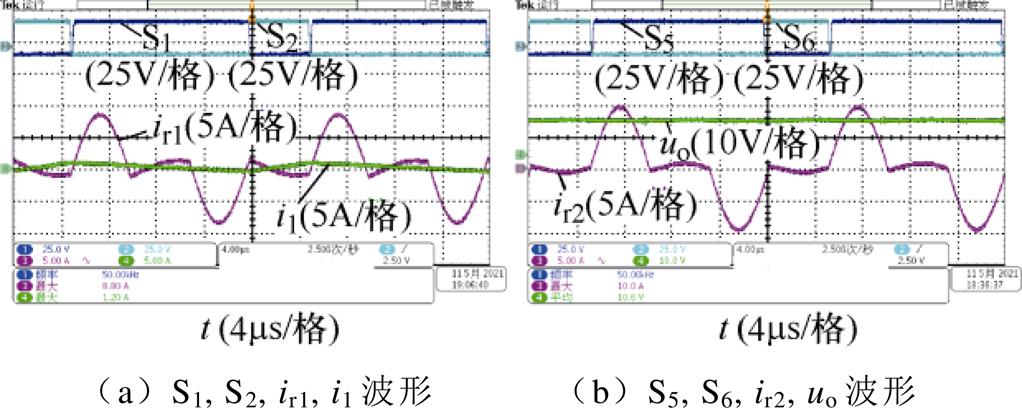
图11 D1=0.75, D2=0.73时变频DPWM实验波形
Fig.11 Experimental waveforms of variable-frequency DPWM when D1=0.75, D2=0.73
由上述可见,在实现软开关的前提下,样机在[0.2, 0.75]的占空比范围内具有[0.212, 4.18]的电压增益范围。因各种非理想因素的缘故,这一电压增益范围相比理论值略窄,但基本符合理论分析结果。
图12为定频同步DPWM下变换器在D1=0.4,D2=0.42时的实验波形,由图可见,当S1导通瞬间,i1>ir1,电流反向流过S1,S1实现零电压导通。S2导通瞬间,i1<ir1,电流反向流过S2,S2实现零电压导通。S5导通瞬间,ir2>0,电流ir2反向流过S5,S5实现零电压导通。S6导通瞬间,ir2<0,电流反向流过S6,S6实现零电压导通。又因S3、S4软开关实现原理与S1、S2基本相同,S7、S8软开关实现原理与S5、S6基本相同,可认为此时变换器所有开关管实现软开关。
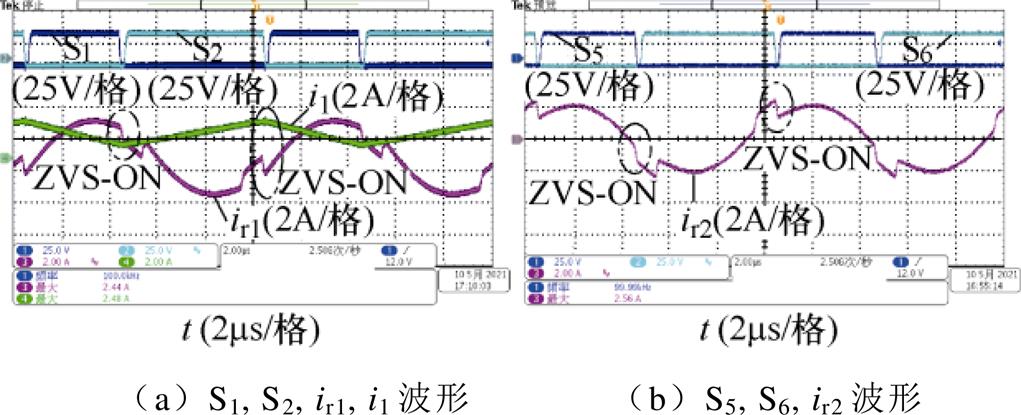
图12 D1=0.4,D2=0.42时定频同步DPWM实验波形
Fig.12 Experimental waveforms of fixed-frequency synchronous DPWM when D1=0.4, D2=0.42
图13为变频DPWM控制下变换器在D1=0.74,D2=0.71,开关频率为52kHz,负载电阻为50W 时的实验波形,由图可见,S1导通瞬间,i1>ir1,电流反向流过S1,S1实现零电压导通。S2导通瞬间,i1<ir1,电流反向流过S2,S2实现零电压导通。S5导通瞬间,ir2>0,电流反向流过S5,S5实现零电压导通。S6导通瞬间,ir2<0,电流反向流过S6,S6实现零电压导通。又因S3、S4软开关实现原理与S1、S2基本相同,S7、S8软开关实现原理与S5、S6基本相同,可认为此时变换器所有开关管实现软开关。
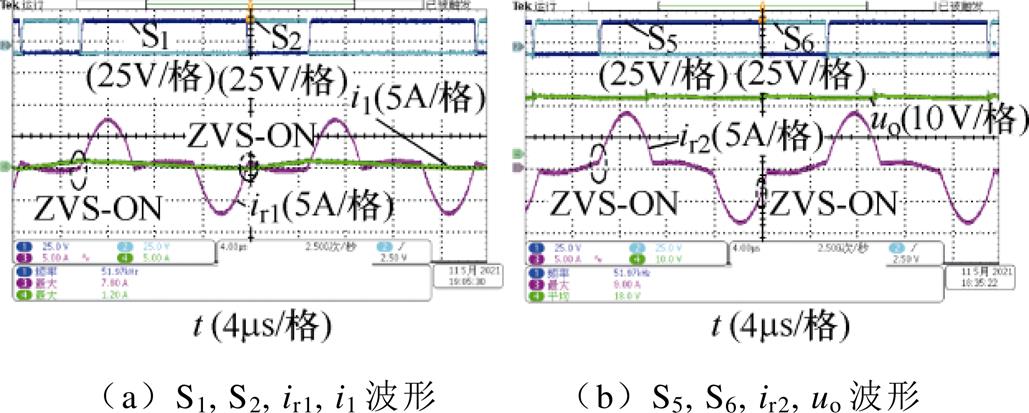
图13 D1=0.74, D2=0.71时变频DPWM实验波形
Fig.13 Experimental waveforms of variable-frequency DPWM when D1=0.74, D2=0.71
图14为变换器在D1=0.5, D2=0.5,开关频率为100kHz,负载电阻为50W 时的实验波形。该稳态工作点是定频同步DPWM与变频DPWM两种调制方式共有的稳态工作点,亦即宽增益控制策略下两者的切换点。该点的软开关实现条件与定频同步DPWM控制和变频DPWM控制一致,由图可见,此时变换器的所有开关管都实现了软开关,与理论分析一致。
图15为变换器在输入电压为50V,负载电阻为500W 时的实验波形。图15a中,D1由0.4逐渐增加至0.6,图15b中,D1由0.6逐渐减小至0.4。从图中可以看出,输出电压uo在整个过程中是平滑变化的,没有出现突变。谐振电流ir1与ir2波形因定频同步DPWM策略与变频DPWM策略工作原理不同,所以在切换点前后发生明显变化,但整个变化过程仍然是较为平滑的。
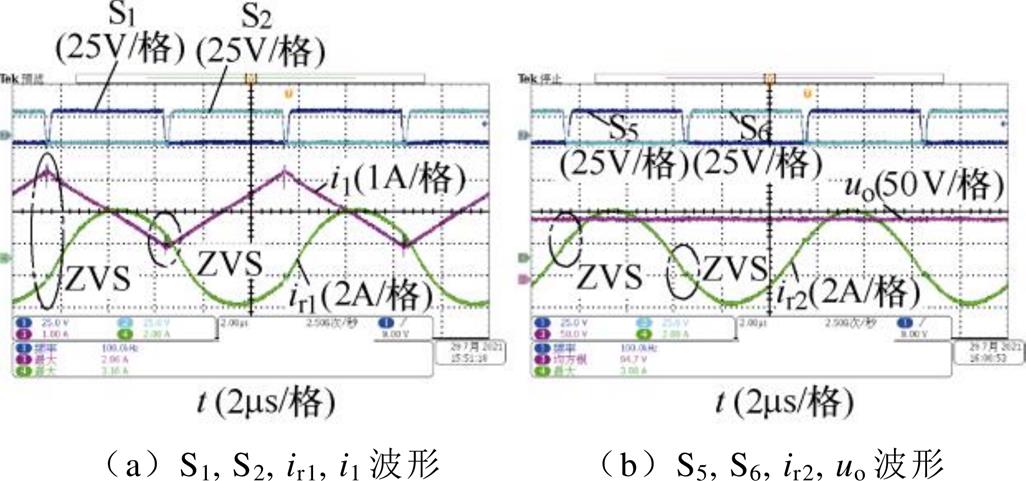
图14 D1=0.5, D2=0.5时切换点实验波形
Fig.14 Experimental waveforms at the switching point when D1=0.5, D2=0.5
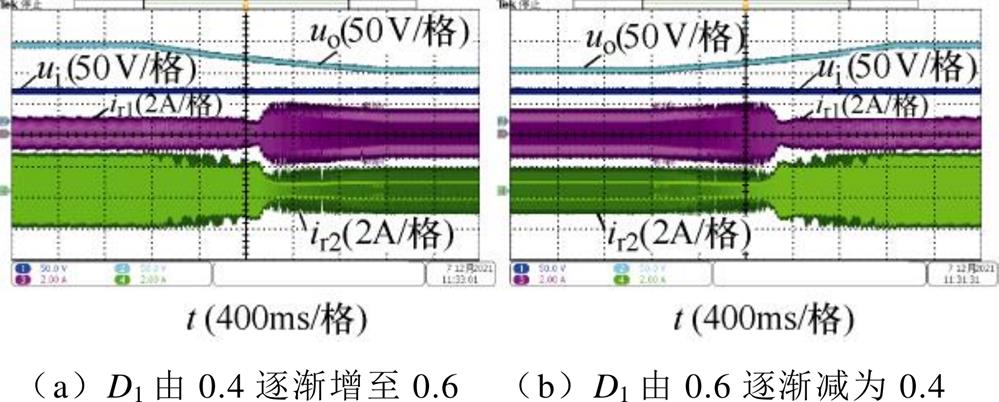
图15 平滑切换过程实验波形
Fig.15 Experimental waveforms of smooth switching process
本文提出定频同步DPWM与变频DPWM两种调制方式,并通过分析,构建两种调制方式的切换点,最终形成一种宽增益控制策略。其中,定频同步DPWM是在定频同步PWM的基础上同时调节变压器一次侧、二次侧全桥的占空比得到的,该方法避免了电流尖峰的出现,拓宽了占空比调节范围,相比传统调制方式能实现更高的电压增益。而变频DPWM通过降低开关频率,在开关周期中增加无源谐振模态的方式,改变了谐振回路的工作特性,使其在能量传输过程中可对CLLLC输入端电压进行分压,达到降低变换器整体电压增益的目的。两种调制方式优势互补,可分别实现高电压增益与低电压增益,因此由两者构建而成的控制策略可实现宽电压增益。本文介绍了上述调制方式与宽增益控制策略的工作原理,进行了相应的电压增益特性分析与软开关特性分析,最后通过实验验证了理论分析的正确性与控制策略的可行性。
参考文献
[1] Shi Zhe, Guo Yingjun, Li Pengcheng, et al. A Boost CLLC converter controlled by PWM and PFM hybrid modulation for photovoltaic power generation[J]. IEEE Access, 2020, 8: 112015-112026.
[2] 孙孝峰, 张绘欣, 张涵, 等. 一种用于电-氢多能互补型微电网的双有源桥集成Boost拓扑及其控制[J]. 电工技术学报, 2021, 36(10): 2092-2104.
Sun Xiaofeng, Zhang Huixin, Zhang Han, et al. Topology and control strategy of dual active bridge integrated Boost circuit for electro-hydrogen multi- energy complementary microgrid[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2092- 2104.
[3] Zhang Chunjiang, Li Pengcheng, Kan Zhizhong, et al. Integrated half-bridge CLLC bidirectional converter for energy storage systems[J]. IEEE Transactions on Industrial Electronics, 2018, 65(5): 3879-3889.
[4] 刘瑞欣, 王议锋, 韩富强, 等. 应用于宽输入电压范围的两模式切换型软开关谐振直流变换器[J]. 电工技术学报, 2020, 35(22): 4739-4749.
Liu Ruixin, Wang Yifeng, Han Fuqiang, et al. A two- mode soft-switching resonant DC-DC converter for wide input voltage range applications[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4739-4749.
[5] Zhao Biao, Song Qiang, Liu Wenhua, et al. Overview of dual-active-bridge isolated bidirectional DC-DC converter for high-frequency-link power-conversion system[J]. IEEE Transactions on Power Electronics, 2014, 29(8): 4091-4106.
[6] 王仁龙, 杨庆新, 操孙鹏, 等. 一种优化电流应力的双有源桥式DC-DC变换器双重移相调制策略[J]. 电工技术学报, 2021, 36(增刊1): 274-282.
Wang Renlong, Yang Qingxin, Cao Sunpeng, et al. An optimized dual phase shift modulation strategy for dual active bridge DC-DC converter[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 274- 282.
[7] 刘硕, 苏建徽, 赖纪东, 等. LLC谐振变换器PO模式增益公式与模式边界条件分析[J]. 电力系统自动化, 2020, 44(6): 164-170.
Liu Shuo, Su Jianhui, Lai Jidong, et al. Analysis on gain formula and mode boundary condition for LLC resonant converter in PO mode[J]. Automation of Electric Power Systems, 2020, 44(6): 164-170.
[8] 杨东江, 段彬, 丁文龙, 等. 一种带辅助双向开关单元的宽输入电压范围LLC谐振变换器[J]. 电工技术学报, 2020, 35(4): 775-785.
Yang Dongjiang, Duan Bin, Ding Wenlong, et al. An improved LLC resonant converter with auxiliary bi-directional switch for wide-input-voltage range applications[J]. Transactions of China Electrotech- nical Society, 2020, 35(4): 775-785.
[9] 付超, 武承杰, 孙玉巍, 等. 混合模块化直流固态变压器I: 工作原理及稳态特性分析[J]. 电工技术学报, 2019, 34(增刊1): 141-153.
Fu Chao, Wu Chengjie, Sun Yuwei, et al. Hybrid modular DC solid state transformer I: working principle and analysis of steady state characte- ristics[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 141-153.
[10] Sun Lei, Ma Yuejin, Wang Jing, et al. Analysis and design of asymmetric CLLC resonant DC-DC con- verter[J]. International Transactions on Electrical Energy Systems, 2020, 30(5): 1-11.
[11] 杨玉岗, 武艳秋, 孙晓钰, 等. 交错并联双向CLLC型谐振变换器中U+U型磁集成变压器的设计[J]. 电工技术学报, 2021, 36(2): 282-291.
Yang Yugang, Wu Yanqiu, Sun Xiaoyu, et al. Design of U+U type magnetic integrated transformer in interlaced bidirectional CLLC resonant converter[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 282-291.
[12] 陈启超, 纪延超, 王建赜, 等. MOSFET输出电容对CLLLC谐振变换器特性影响分析[J]. 电工技术学报, 2015, 30(17): 26-35.
Chen Qichao, Ji Yanchao, Wang Jianze, et al. Analysis of the influence of MOSFET output capacitance on the bidirectional CLLLC resonant converter[J]. Transactions of China Electrotechnical Society, 2015, 30(17): 26-35.
[13] Zhu Tianhua, Zhuo Fang, Zhao Fangzhou, et al. Opti- mization of extended phase-shift control for full- bridge CLLC resonant converter with improved light- load efficiency[J]. IEEE Transactions on Power Elec- tronics, 2020, 35(10): 11129-11142.
[14] Wu Hongfei, Ding Shun, Sun Kai, et al. Bidi- rectional soft-switching series-resonant converter with simple PWM control and load-independent voltage-gain characteristics for energy storage system in DC microgrids[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(3): 995-1007.
[15] 李舒成, 刘邦银, 姜庆, 等. 基于同步PWM控制的双向CLLLC谐振型直流变换器运行特性分析[J]. 电工技术学报, 2019, 34(增刊2): 543-552.
Li Shucheng, Liu Bangyin, Jiang Qing, et al. Per- formance analysis of bidirectional CLLLC resonant converter with synchronous PWM control strategy[J]. Transactions of China Electrotechnical Society, 2019, 34(S2): 543-552.
[16] 李鹏程, 张纯江, 阚志忠, 等. 软开关高增益Buck- Boost集成CLLC型直流双向变换器[J]. 中国电机工程学报, 2018, 38(11): 3295-3305.
Li Pengcheng, Zhang Chunjiang, Kan Zhizhong, et al. An integrated Buck-Boost CLLC bidirectional DC converter with high gain and soft switching[J]. Pro- ceedings of the CSEE, 2018, 38(11): 3295-3305.
[17] 李舒成. 交错Boost集成型双向CLLLC谐振变换器运行特性分析与优化设计[D]. 武汉: 华中科技大学, 2019.
Wide-Gain-Range Control Scheme for Interleaved Boost Integrated CLLLC Resonant Converter Based on Dual Pulse Width Modulation
Abstract The interleaved Boost integrated CLLLC resonant converter has the advantages of high gain and high efficiency. A wide voltage gain range can be theoretically obtained when using PWM. However, under the existing fixed-frequency synchronous PWM modulation, an increasingly large current peak appears as the duty cycle gradually deviates from 0.5, which limits the duty cycle adjustment range. Moreover, its voltage gain range has no obvious advantages compared with the traditional resonant converter. In order to achieve wide gain, this paper adopts the method of dual pulse width modulation to overcome the shortcomings of fixed-frequency synchronous PWM, and proposes two modulation methods of fixed-frequency synchronous dual pulse width modulation and variable-frequency dual pulse width modulation. The switching points of the two modulation methods are constructed, and a wide gain control strategy is formed. The working principle and operation characteristics of the proposed wide gain control strategy are analyzed. Finally, the feasibility of the proposed control strategy and the correctness of theoretical analysis are verified by experiments.
keywords:Interleaved Boost integrated CLLLC resonant converter, fixed-frequency synchronous dual pulse width modulation, variable-frequency dual pulse width modulation, wide voltage gain
DOI: 10.19595/j.cnki.1000-6753.tces.211582
中图分类号:TM46
国家自然科学基金青年科学基金(51807196)和中国博士后科学基金(2019M661983)资助项目。
收稿日期 2021-10-08
改稿日期 2022-01-04
李小强 男,1987年生,副教授,硕士生导师,研究方向为新能源发电、电力系统电力电子化稳定性、隔离型DC-DC变换器。E-mail: xiaoqiangli@cumt.edu.cn
伍小杰 男,1966年生,教授,博士生导师,研究方向为新能源并网发电、微电网稳定与控制、大功率电机传动控制。E-mail: xjwu@cumt.edu.cn(通信作者)
(编辑 陈 诚)