 (1)
(1)
摘要 针对三电平变换器,该文提出一种考虑死区电压矢量的有限集模型预测控制策略。基于死区效应,将控制集中基本矢量和对应的死区电压矢量合成虚拟矢量,并通过优化死区时间构建新的虚拟矢量控制集。为减少计算量,首先,基于无差拍预测得到参考矢量,严格证明了输出矢量和参考矢量的欧氏距离与传统价值函数中电流预测部分的等价性,从而构建新的价值函数,有效地降低了迭代计算的复杂度;其次,利用相关基本矢量来构建简化控制集,显著地缩小了寻优空间;最后,通过基于欧氏距离的价值函数从虚拟矢量控制集中选择最优虚拟矢量,实现了变死区时间模型预测控制。通过仿真和实验验证,与传统模型预测控制相比,该文提出的控制策略可使输出电流脉动减小,电流总谐波畸变率降低约40%~50%,显著地提高了变换器的控制性能。
关键词:模型预测控制 欧氏距离 死区电压矢量 无差拍预测 电流控制
随着软硬件技术的不断发展,更多的控制策略在电力电子变换器上得到了应用。模型预测控制[1]在近年来成为了一个研究热点。其中,有限集模型预测控制(Finite-Control-Set-Model Predictive Control, FCS-MPC)因具有简单的控制结构和良好的控制性能而备受关注,并成为了一种有效的电力电子变换器的控制方案[2-4],其基本原理为构建多目标优化价值函数,根据预测值和期望值的偏差来确定控制量。基于不同的控制目标,电力电子变换器中FCS-MPC的应用可以分为电流控制和直接功率控制。
在电子电力变换器运行过程中,为保证顺利完成开关状态切换,需要在切换过程中加入死区。但是,死区降低了模型的准确性,增大了变换器输出电压和电流的畸变率和纹波,影响控制性能。因此,FCS-MPC在变换器中应用时需要考虑死区问题。现有的控制策略大多采用补偿或消除[5-6]来减小死区的影响。文献[5]提出了一种结合死区消除和补偿的方法,能够有效抑制死区的影响。文献[7]通过修改电压和电流的预测模型来补偿死区效应。文献[8]首次在永磁同步电机的FCS-MPC中将死区过程的输出视为死区电压矢量,并引入“变死区时间”概念。首先通过价值函数确定最优基本矢量,再考虑优化死区时间。文献[9]进一步提出了双矢量FCS-MPC中“变死区时间”的应用。但上述采用“变死区时间”的方法在三电平变流器中应用时,最优基本矢量及对应的死区电压矢量合成得到的虚拟矢量可能并非是最优解。因此,本文提出对多个基本矢量进行分析,再基于价值函数寻优。
但是,三电平变换器中存在27个基本矢量,若逐一优化死区时间,需要进行27次迭代,导致计算量繁重。因此,需要减少迭代次数。目前为了解决FCS-MPC算法寻优复杂问题,所提出的方法主要基于以下两点:①优化矢量迭代计算的顺序,文献[10]首先计算6个正小矢量的价值函数,然后选择与最优正小矢量位于同一扇区的矢量构建简化控制集;②通过无差拍预测电流或功率得到参考矢量,文献[11]提出基于电压预测的单目标价值函数,并结合直流母线电位分布,减少了寻优次数。文献[12]根据参考矢量所在的扇区,将每次迭代计算的矢量个数从27减少到10。然而上述控制策略需要将简化控制集中的矢量逐一代入电流或功率预测模型中,仍存在较大的计算量。为解决该问题,文献[13]在电流控制中根据参考矢量所在扇区采用查表法确定简化控制集并优化价值函数,但该策略不适用于功率控制且无法拓展到多电平变换器。
基于上述讨论,本文提出考虑死区电压矢量的三电平变换器模型预测控制策略,相比于传统控制策略,具有以下特点:
(1)优化价值函数,有效降低迭代计算量:采用基本矢量和参考矢量之间的欧氏距离取代传统价值函数中电流预测偏差值,从而避免了复杂的电流预测模型计算。
(2)简化控制集,显著缩小寻优空间:根据无差拍预测电流得到参考矢量,并提出了一种通用的代数方法得到参考矢量的最近三个基本矢量及其冗余矢量,以此构建简化控制集。
(3)考虑死区效应,构建虚拟矢量控制集:逐一分析简化控制集中基本矢量对应的死区电压矢量,并优化死区时间,两者合成得到与参考矢量欧氏距离最小的虚拟矢量,从而构建虚拟矢量控 制集。
(4)实现双矢量控制,提高控制性能:基于价值函数选择最优虚拟矢量,并输出对应的控制波形。控制性能得到提高,并同时保证开关次数基本不变。
本文所提出的改进策略在保持其他性能参数基本不变的情况下,提高了三电平变换器的控制性能,减少了计算量,尤其适用于高电压大电流的工况。
三电平变换器的拓扑主要有二极管中点钳位型、飞跨电容钳位型及T型中点钳位型等。FCS- MPC策略在上述拓扑中的应用方式基本相同,不失一般性,本文对T型中点钳位型逆变器进行分析,其拓扑如图1所示。交流侧的端电压分为三类,因此共有33=27种开关状态,其对应的27个电压矢量组成的空间矢量平面如图2所示。定义开关函数为
 (1)
(1)
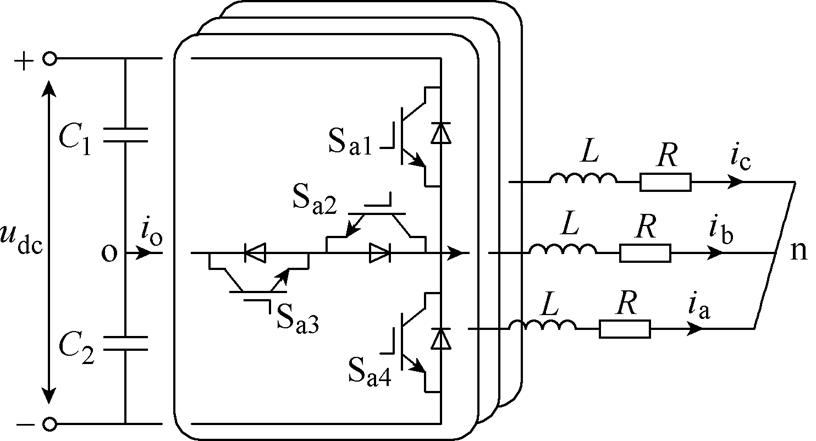
图1 T型三电平逆变器拓扑
Fig.1 The topology of three-level T-type inverter

图2 三电平逆变器空间矢量平面
Fig.2 Space vector diagram of three-level inverters
数字控制器存在一个控制周期的延迟,即第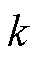 个周期计算的控制量在第
个周期计算的控制量在第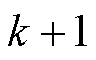 个周期进行实际控制。为了补偿一拍延迟带来的不利影响,在实际预测控制中,应结合第
个周期进行实际控制。为了补偿一拍延迟带来的不利影响,在实际预测控制中,应结合第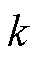 个周期的控制量来预测
个周期的控制量来预测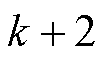 时刻的输出值[14-15],进而选择代价函数最小的电压矢量。
时刻的输出值[14-15],进而选择代价函数最小的电压矢量。
以电流控制为例,其他控制目标若仅考虑直流侧电容电压平衡,传统FCS-MPC策略的价值函数设计[15]为
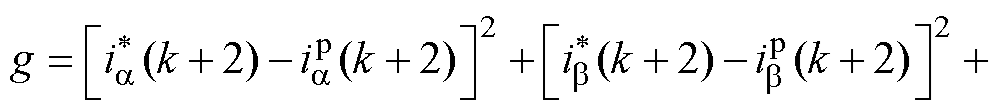
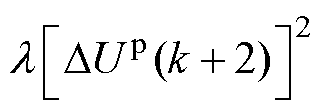 (2)
(2)
式中,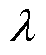 为权重因子;
为权重因子;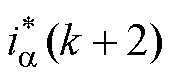 和
和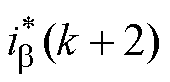 为
为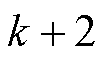 时刻
时刻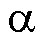 、
、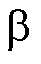 轴电流的给定值;
轴电流的给定值;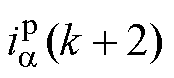 和
和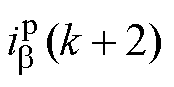 为
为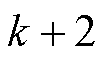 时刻的预测值;
时刻的预测值;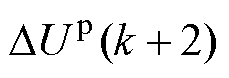 为直流侧上下电容电压差的预测值。
为直流侧上下电容电压差的预测值。
(1)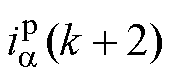 和
和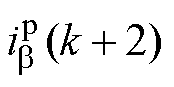 的计算方法如下:以图1中电流方向为正方向,根据基尔霍夫电压定律和Clarke变换可以得到
的计算方法如下:以图1中电流方向为正方向,根据基尔霍夫电压定律和Clarke变换可以得到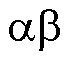 坐标系下的交流侧数学模型为
坐标系下的交流侧数学模型为
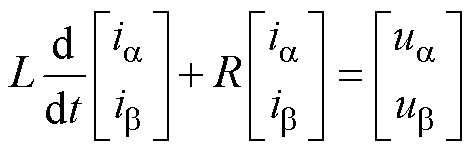 (3)
(3)
式中,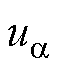 、
、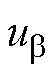 ,
, 、
、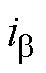 分别为输出电压、电流在
分别为输出电压、电流在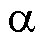 轴和
轴和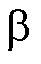 轴的分量;L为交流侧电感;R为负载。
轴的分量;L为交流侧电感;R为负载。
根据向前欧拉法,将式(3)离散化。考虑延迟补偿,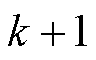 时刻的相电流估计值为
时刻的相电流估计值为
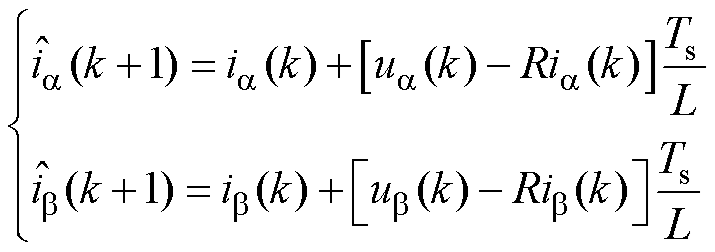 (4)
(4)
式中,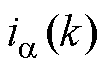 和
和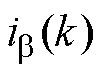 由
由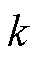 时刻的电流采样值通过Clarke变换得到;
时刻的电流采样值通过Clarke变换得到;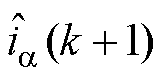 和
和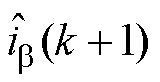 为
为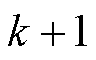 时刻输出电流的估计值;
时刻输出电流的估计值;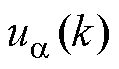 和
和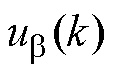 为第
为第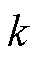 个控制周期的控制量,该电压矢量已在上一个周期得到;
个控制周期的控制量,该电压矢量已在上一个周期得到;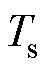 为控制周期。
为控制周期。
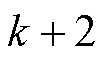 时刻,
时刻,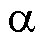 、
、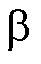 轴电流的预测值为
轴电流的预测值为
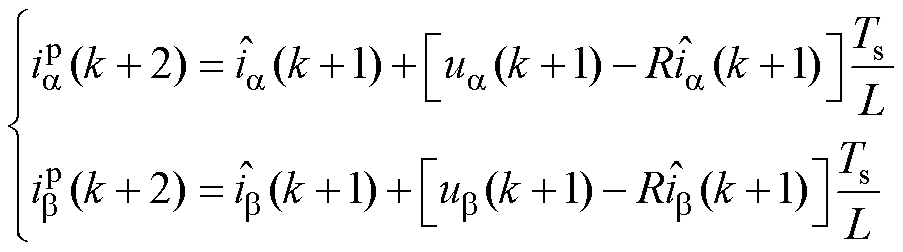 (5)
(5)
式中,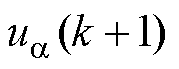 和
和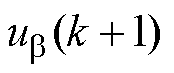 为第
为第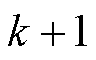 个控制周期的控制量。
个控制周期的控制量。
(2)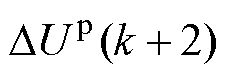 的计算方法如下:三电平逆变器在工作过程中,导致电容电压不平衡的直接原因为直流侧中点电流不为0。中点电流的表达式为
的计算方法如下:三电平逆变器在工作过程中,导致电容电压不平衡的直接原因为直流侧中点电流不为0。中点电流的表达式为
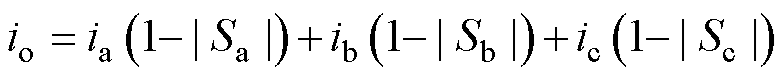 (6)
(6)
假设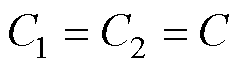 。考虑延迟补偿,
。考虑延迟补偿,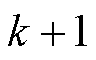 时刻的电容电压差值的估计值为
时刻的电容电压差值的估计值为
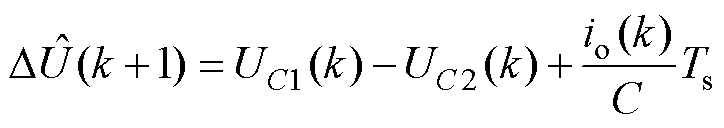 (7)
(7)
式中,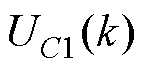 和
和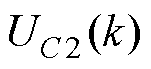 为
为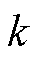 时刻的电容电压;
时刻的电容电压;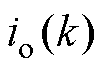 为第
为第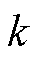 个控制周期的控制量,将其代入式(6)得到的中点电流值。
个控制周期的控制量,将其代入式(6)得到的中点电流值。
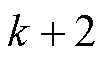 时刻的电容电压差值的预测值为
时刻的电容电压差值的预测值为
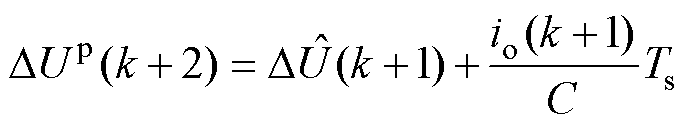 (8)
(8)
式中,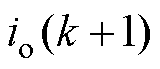 为第
为第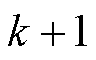 个控制周期的控制量,将其代入式(6)得到的中点电流值。
个控制周期的控制量,将其代入式(6)得到的中点电流值。
传统控制策略中,首先根据式(5)、式(8)依次计算得到27个基本矢量作为第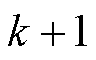 个控制周期的控制量时,
个控制周期的控制量时,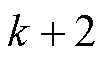 时刻系统被控量的预测值,然后通过价值函数选择最优电压矢量。
时刻系统被控量的预测值,然后通过价值函数选择最优电压矢量。
传统FCS-MPC策略中,在每个控制周期需要预测计算达27次。显然,这会导致较大的计算量。若逐一优化死区时间,会使计算量进一步增大。为对此进行优化,本节首先引入矢量欧氏距离优化价值函数,然后基于无差拍预测电流得到参考矢量,并进一步构建简化控制集。
根据无差拍预测的思想[16],假设在参考矢量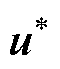 作用下,系统输出电流在一个采样周期内可以实现对给定值的无差跟踪。令
作用下,系统输出电流在一个采样周期内可以实现对给定值的无差跟踪。令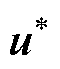 的坐标为
的坐标为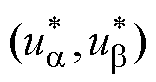 ,代入式(5)得到的电流预测值与给定值相同,即
,代入式(5)得到的电流预测值与给定值相同,即
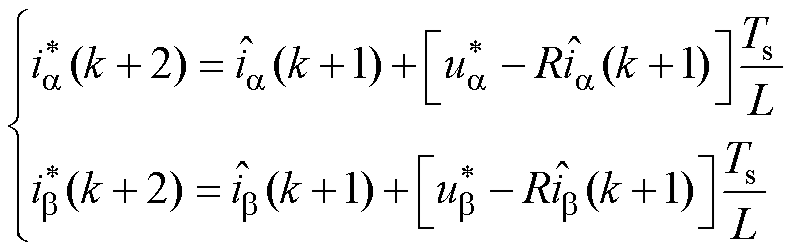 (9)
(9)
将式(5)、式(9)代入价值函数式(2)中,得到电流预测部分偏差为
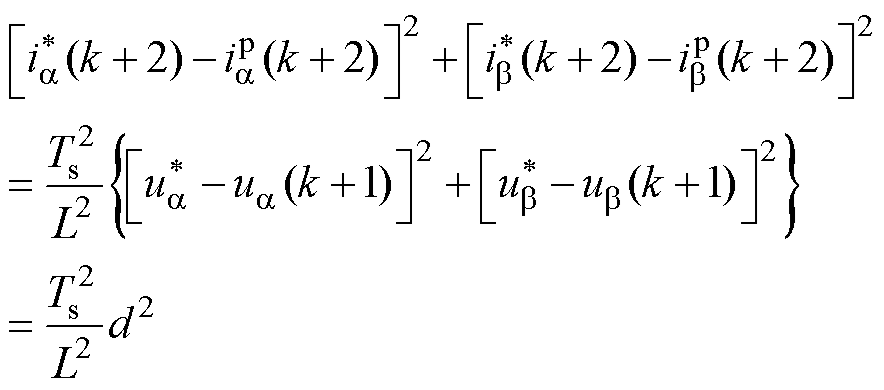 (10)
(10)
式中,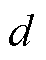 为
为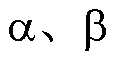 坐标系下基本矢量与参考矢量的欧氏距离。
坐标系下基本矢量与参考矢量的欧氏距离。
由式(10)可得,基本矢量和参考矢量的欧氏距离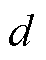 与对应的电流预测值和给定值的偏差之间存在等价性。价值函数式(2)可以改写为
与对应的电流预测值和给定值的偏差之间存在等价性。价值函数式(2)可以改写为
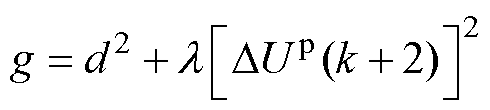 (11)
(11)
相比于传统策略,由于参考矢量获取只需计算一次电流预测模型,极大地降低了计算量。
式(10)表明空间矢量平面中,基本矢量与参考矢量的欧式距离和其电流控制效果等价。而在FCS-MPC电流控制中,相较于电容电压平衡等其他指标,电流控制在价值函数中应占最大比重。因此,距离参考矢量越近的基本矢量越可能成为最优基本矢量。
根据上述分析,基于无差拍预测电流得到参考矢量后,仅选择空间矢量平面中与参考矢量的欧氏距离最小的三个基本矢量及其冗余矢量构建简化控制集,即参考矢量所在的小三角形的顶点对应的基本矢量。当参考矢量在控制区外时,将其转化为相同相位,处于六边形边界的矢量。不失一般性,以图2中的参考矢量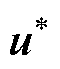 为例,简化控制集为
为例,简化控制集为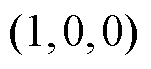 、
、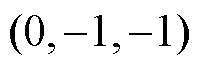 、
、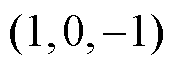 、
、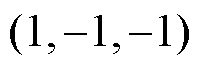 。
。
简化控制集的计算方法如下:如图2所示,任意矢量都可以用不共线的两个单位矢量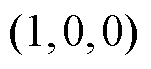 和
和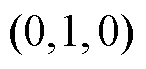 表示。
表示。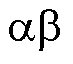 坐标系下,
坐标系下,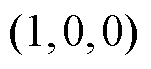 对应
对应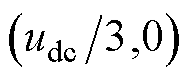 ,
,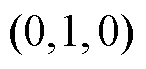 对应
对应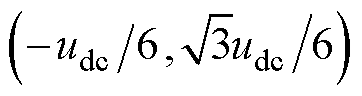 ,则任意矢量可以由
,则任意矢量可以由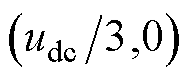 和
和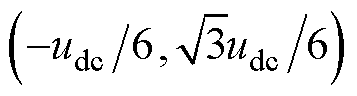 合成。对于
合成。对于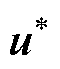 为
为
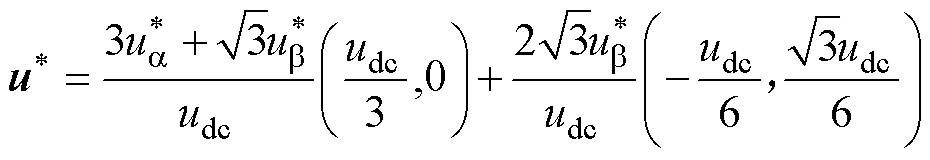 (12)
(12)
根据式(12)可以得到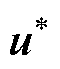 的最近三个矢量
的最近三个矢量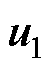 、
、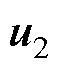 和
和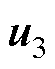 ,结果见表1,详细推导过程如附录第1节所示。
,结果见表1,详细推导过程如附录第1节所示。
表1 最近三个矢量
Tab.1 The three closest vectors
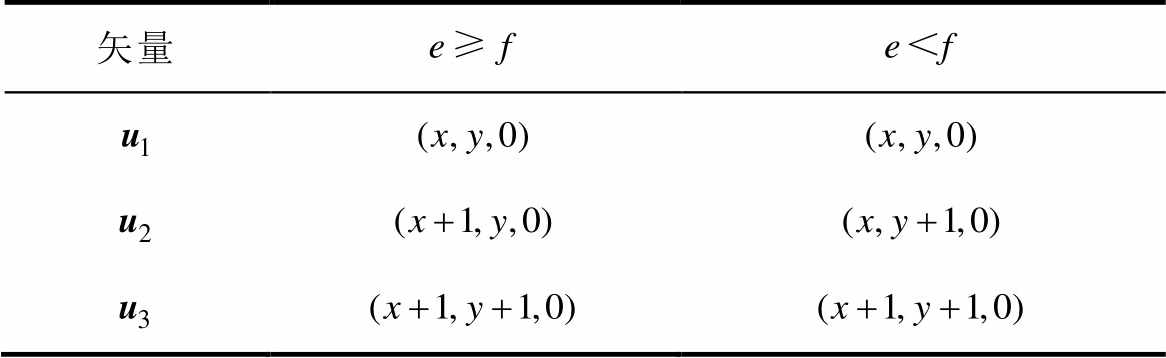
矢量
则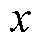 、
、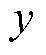 、
、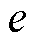 和
和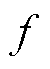 分别为
分别为
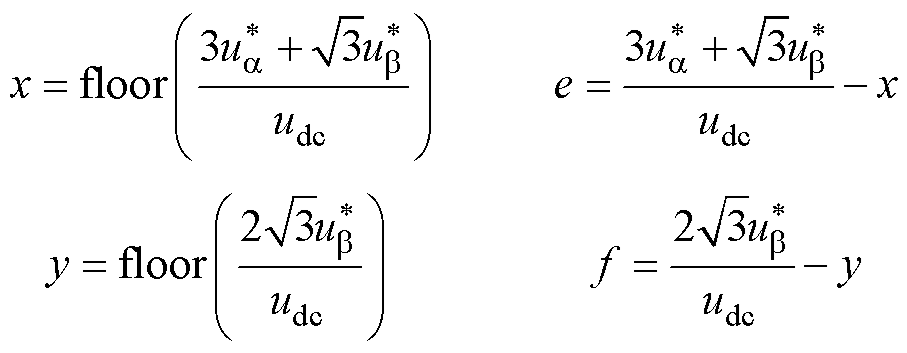
综上所述,对于任意参考矢量,计算得到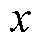 、
、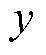 、
、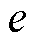 和
和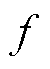 后,不需要其他复杂运算就可以确定三个矢量。然而,所得的矢量并非一定为基本矢量,且未考虑冗余矢量,因此需要进一步处理。对于表1中得到的矢量,首先对其3个元素进行排序,令最大值为max,最小值为min。当两者差值为2时,为大矢量或中矢量,没有冗余矢量,3个元素均减去min+1即可转换为基本矢量;当两者差值为1时,为小矢量,三个元素均减去min+1或min可得到两个冗余基本矢量;当两者差值为0时,为零矢量,由于零矢量对中点电位没有影响,仅采用
后,不需要其他复杂运算就可以确定三个矢量。然而,所得的矢量并非一定为基本矢量,且未考虑冗余矢量,因此需要进一步处理。对于表1中得到的矢量,首先对其3个元素进行排序,令最大值为max,最小值为min。当两者差值为2时,为大矢量或中矢量,没有冗余矢量,3个元素均减去min+1即可转换为基本矢量;当两者差值为1时,为小矢量,三个元素均减去min+1或min可得到两个冗余基本矢量;当两者差值为0时,为零矢量,由于零矢量对中点电位没有影响,仅采用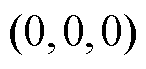 。根据图2,对于任意参考矢量,基于冗余矢量数量的不同,简化控制集中的矢量个数不多于5个。对比含有27个电压矢量的原控制集,此简化策略显著地缩小了寻优空间,降低单个控制周期的迭代次数。相比于文献[13]中提出的查表法,本节提出的控制集简化策略能够得到相同的结果。虽然计算量略微增加,但可拓展至多电平变换器且计算量不变。
。根据图2,对于任意参考矢量,基于冗余矢量数量的不同,简化控制集中的矢量个数不多于5个。对比含有27个电压矢量的原控制集,此简化策略显著地缩小了寻优空间,降低单个控制周期的迭代次数。相比于文献[13]中提出的查表法,本节提出的控制集简化策略能够得到相同的结果。虽然计算量略微增加,但可拓展至多电平变换器且计算量不变。
根据式(10)、式(11),若只考虑电流控制,传统策略选择的最优基本矢量为与参考矢量欧氏距离最小的基本矢量。以图2中的参考矢量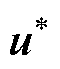 所在三角形为例,参考矢量位置与最优基本矢量的关系如图3所示,当参考矢量在该小三角形的区域①时,最近的基本矢量为
所在三角形为例,参考矢量位置与最优基本矢量的关系如图3所示,当参考矢量在该小三角形的区域①时,最近的基本矢量为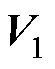 ;同理,区域②对应
;同理,区域②对应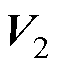 ;区域③对应
;区域③对应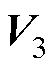 。
。
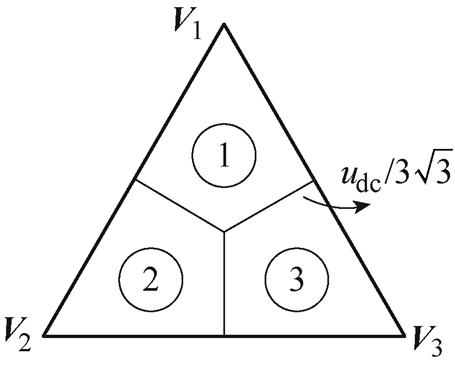
图3 参考矢量位置与最优基本矢量的关系
Fig.3 The relationship between the position of the reference vector and the optimal basic vector
稳态运行时,输出矢量和参考矢量之间的欧氏距离的最大值为定值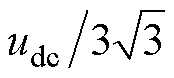 。则式(10)中,最优基本矢量对应的输出电流与参考电流的差值的最大值也为定值,与参考电流大小无关。显然,当采用双矢量[17-18]甚至三矢量[19-21]控制策略时,可以使得输出矢量和参考矢量之间的欧氏距离的最大值减小,则输出电流的脉动幅度随之降低。但是,现有的多矢量策略采用的是多个基本矢量,这导致开关次数增加。对此,本节采用死区电压矢量来实现双矢量策略,不增加开关次数并给出最优死区时间的计算方法。
。则式(10)中,最优基本矢量对应的输出电流与参考电流的差值的最大值也为定值,与参考电流大小无关。显然,当采用双矢量[17-18]甚至三矢量[19-21]控制策略时,可以使得输出矢量和参考矢量之间的欧氏距离的最大值减小,则输出电流的脉动幅度随之降低。但是,现有的多矢量策略采用的是多个基本矢量,这导致开关次数增加。对此,本节采用死区电压矢量来实现双矢量策略,不增加开关次数并给出最优死区时间的计算方法。
在T型三电平逆变器中,开关管Sz1与Sz2、Sz3与Sz4是互补导通的关系(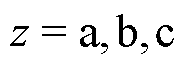 )。在一个导通的开关管没有完全关断之前,如果与之互补的开关管已经导通,则会出现直流侧电容短路的现象,因此需要加入死区。在一些情况下,尤其开关频率较高时,死区会影响输出电压的有效值。
)。在一个导通的开关管没有完全关断之前,如果与之互补的开关管已经导通,则会出现直流侧电容短路的现象,因此需要加入死区。在一些情况下,尤其开关频率较高时,死区会影响输出电压的有效值。
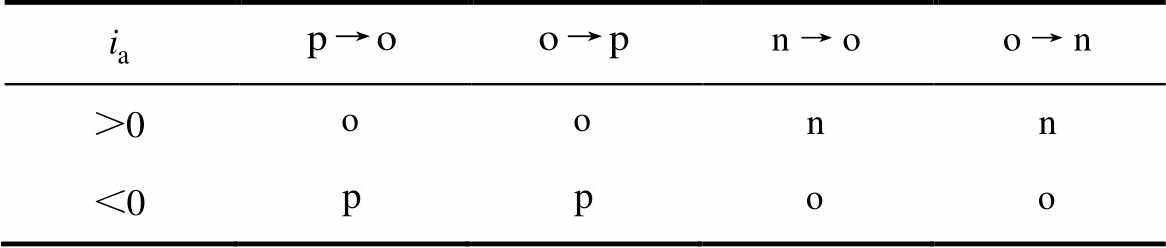
以A相输出从p电平切换到o电平为例,对死区过程的实际输出电平进行分析。Sa1关断后,不能立即导通Sa2,需要设置死区。输出电平由p电平切换到o电平的死区过程如图4所示,当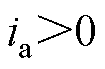 时,死区时间的输出状态为o电平;当
时,死区时间的输出状态为o电平;当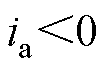 时,输出状态为p电平。同理,可以分析得到其他切换过程中死区时间的实际输出电平,见表2。
时,输出状态为p电平。同理,可以分析得到其他切换过程中死区时间的实际输出电平,见表2。
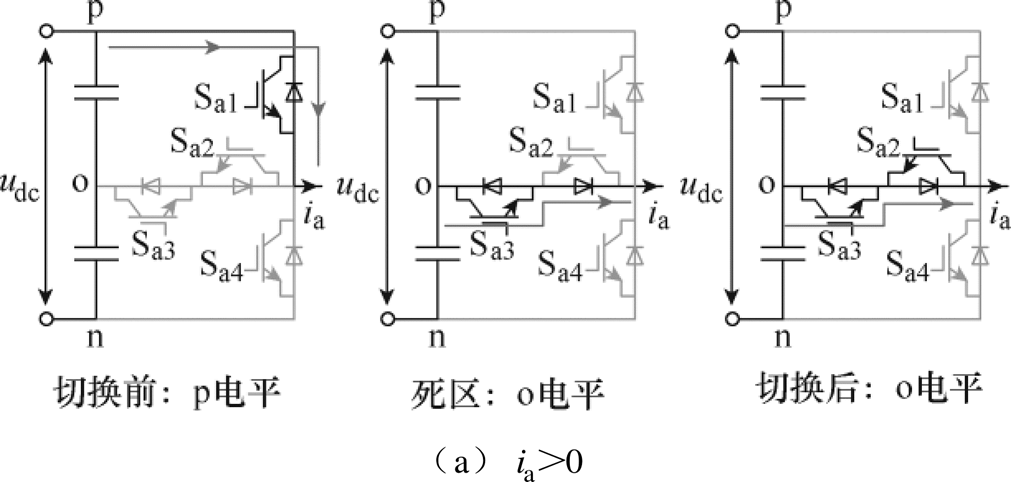
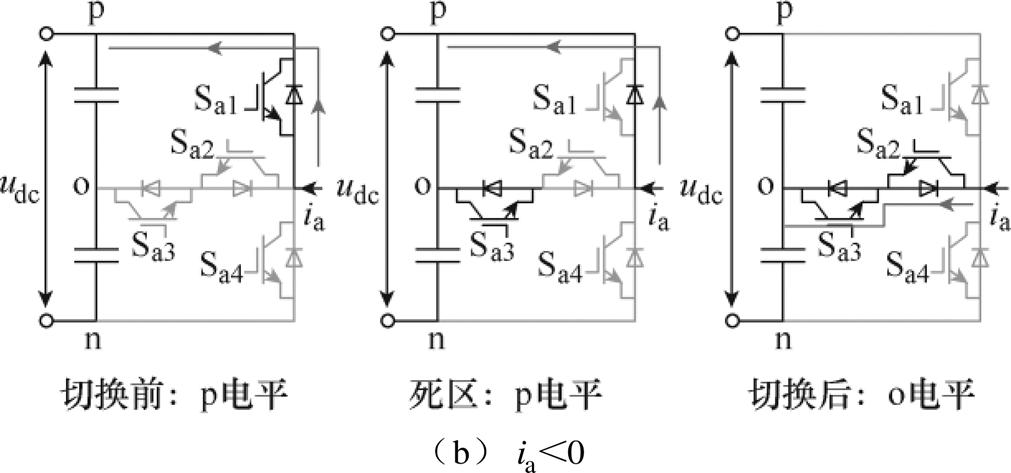
图4 输出电平由p电平切换到o电平的死区过程
Fig.4 Dead zone in which the output level is switched from p level to o level
表2 死区时间的输出电平
Tab.2 Output level of the dead-time
3.1.1 稳态性能影响分析
稳态过程中,参考矢量位于空间矢量平面内,不会出现过调制现象。不失一般性,以图2中的参考矢量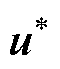 为例,设定此时
为例,设定此时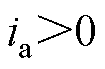 、
、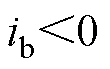 、
、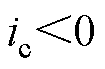 ,上一个控制周期的输出电压矢量为
,上一个控制周期的输出电压矢量为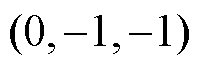 。对于2.2节中得到的简化控制集中基本矢量,根据表2得到死区时间的输出状态,即死区电压矢量。在每个周期存在两个矢量:控制集中的基本矢量
。对于2.2节中得到的简化控制集中基本矢量,根据表2得到死区时间的输出状态,即死区电压矢量。在每个周期存在两个矢量:控制集中的基本矢量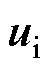 和对应的死区电压矢量
和对应的死区电压矢量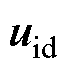 。
。
由于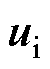 和
和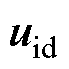 的总作用时间为固定值
的总作用时间为固定值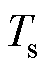 ,根据伏秒平衡公式,两者合成的虚拟矢量在它们终点的连线上。通过
,根据伏秒平衡公式,两者合成的虚拟矢量在它们终点的连线上。通过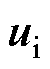 、
、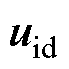 及
及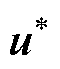 的位置关系,分析得到死区对输出性能的影响,见表3。在某些情况中,通过优化死区时间,
的位置关系,分析得到死区对输出性能的影响,见表3。在某些情况中,通过优化死区时间,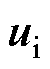 和
和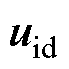 可以合成得到更靠近
可以合成得到更靠近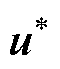 的虚拟矢量。
的虚拟矢量。
表3 死区对输出性能的影响
Tab.3 Impact of dead zone on output performance
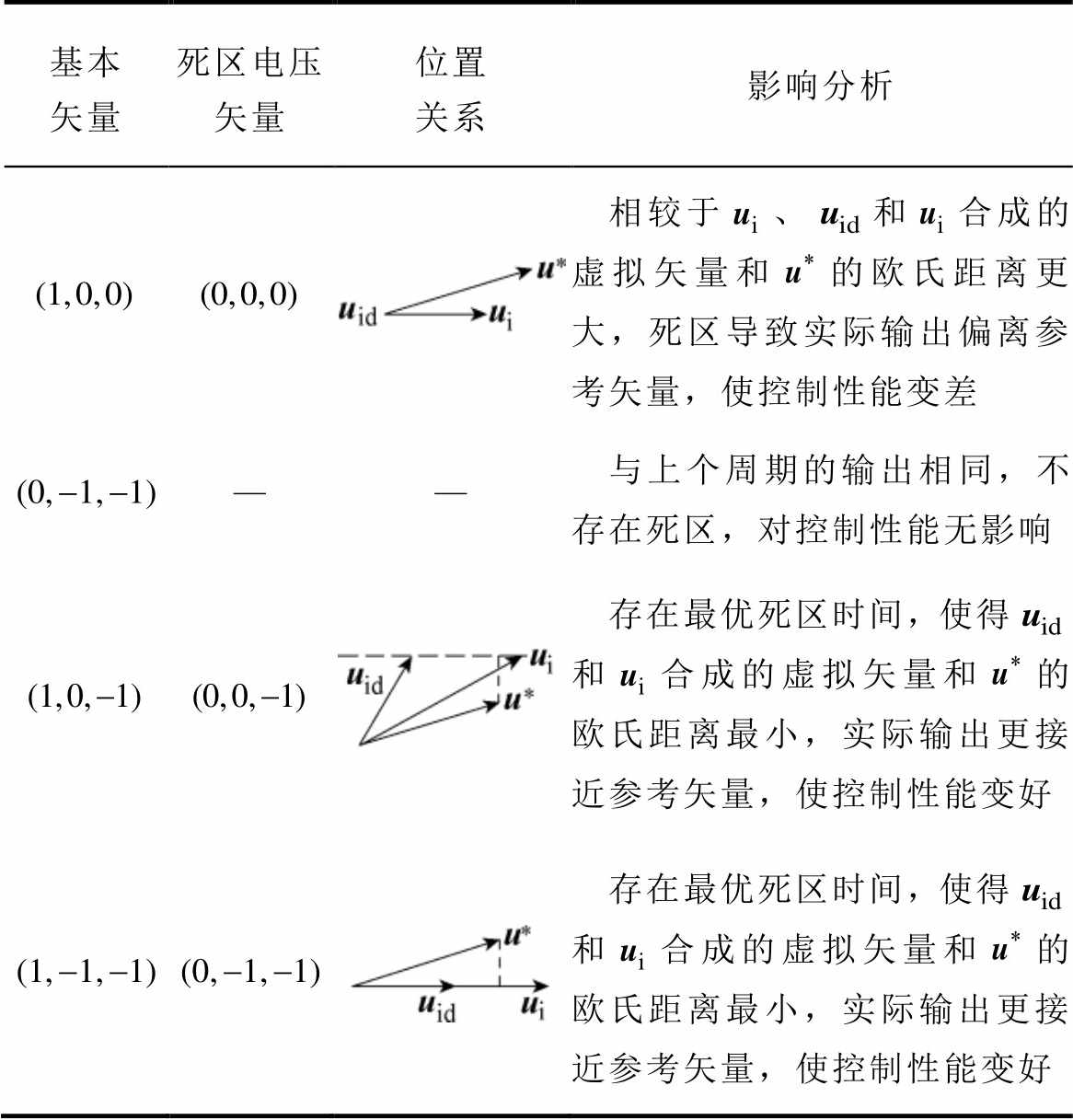
基本矢量死区电压矢量位置关系影响分析 相较于、和合成的虚拟矢量和的欧氏距离更大,死区导致实际输出偏离参考矢量,使控制性能变差 ——与上个周期的输出相同,不存在死区,对控制性能无影响 存在最优死区时间,使得和合成的虚拟矢量和的欧氏距离最小,实际输出更接近参考矢量,使控制性能变好 存在最优死区时间,使得和合成的虚拟矢量和的欧氏距离最小,实际输出更接近参考矢量,使控制性能变好
3.1.2 动态性能影响分析
动态过程中,参考矢量容易出现过调制现象。此时,相对于最靠近参考矢量的基本矢量,其对应的死区电压矢量只会导致实际输出偏离参考矢量,使控制性能变差。因此,无法通过优化死区时间来提高动态控制性能。
现有的三电平逆变器FCS-MPC策略均采用固定的死区时间。但表3的分析表明,合理地设置死区时间可以提升稳态控制性能,故在前述简化控制集的基础上,提出两步寻优的方法:①逐一分析简化控制集中基本矢量对应的死区电压矢量,并通过优化死区时间得到与参考矢量欧氏距离最小的虚拟矢量;②采用得到的若干个虚拟矢量构建虚拟矢量控制集,并基于价值函数从中选取最优虚拟矢量。
对于控制集中任意基本矢量,若存在死区过程,通过合理设置死区时间,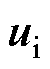 和
和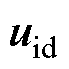 合成得到和参考矢量欧氏距离最小的虚拟矢量
合成得到和参考矢量欧氏距离最小的虚拟矢量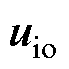 。根据
。根据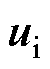 和
和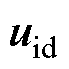 的关系,
的关系,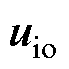 的求解可以分为两种情况(考虑
的求解可以分为两种情况(考虑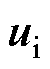 和
和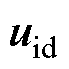 的作用时间均存在最小值
的作用时间均存在最小值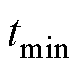 限制):
限制):
(1)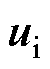 和
和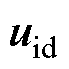 相同:虽然存在死区,但对输出没有影响。死区时间
相同:虽然存在死区,但对输出没有影响。死区时间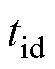 =
=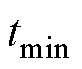 ,
,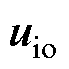 =
=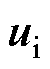 。
。
(2)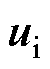 和
和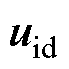 不同:
不同: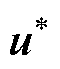 、
、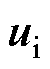 和
和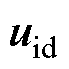 轴的相对位置关系如图5所示,
轴的相对位置关系如图5所示,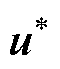 、
、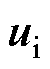 和
和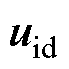 的位置关系可以分为两类:①
的位置关系可以分为两类:①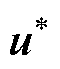 的投影在
的投影在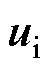 和
和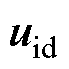 连线上;②
连线上;②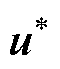 的投影在
的投影在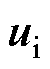 和
和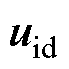 连线的延长线上。
连线的延长线上。
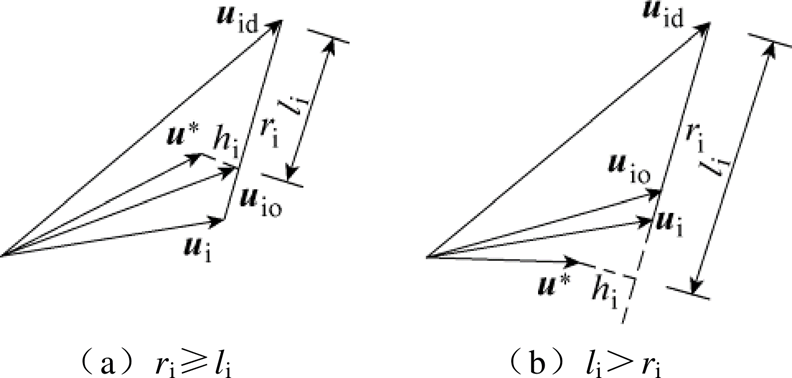
图5 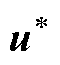 、
、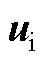 和
和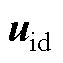 轴的相对位置关系
轴的相对位置关系
Fig.5 The relative position of 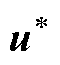 ,
, 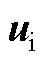 and
and 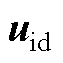
令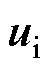 和
和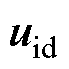 的终点之间的距离为
的终点之间的距离为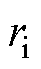 ;
;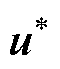 在
在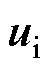 和
和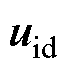 连线或延长线上的投影和
连线或延长线上的投影和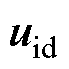 的终点之间的距离为
的终点之间的距离为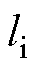 。当
。当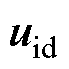 属于控制集时,三者的位置关系如图5a所示,此时
属于控制集时,三者的位置关系如图5a所示,此时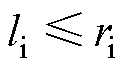 ;当
;当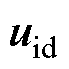 不属于控制集时,
不属于控制集时,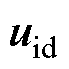 不可能比
不可能比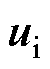 更接近
更接近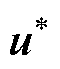 ,三者的位置关系如图5b所示,此时
,三者的位置关系如图5b所示,此时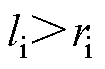 。根据
。根据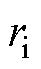 和
和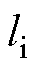 的关系,
的关系,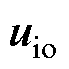 和对应的
和对应的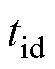 的解析解见表4,详细推导过程如附录第2节所示。
的解析解见表4,详细推导过程如附录第2节所示。
表4 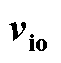 、
、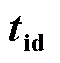 的解析解
的解析解
Tab.4 Analytical solution of 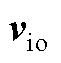 and
and 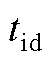
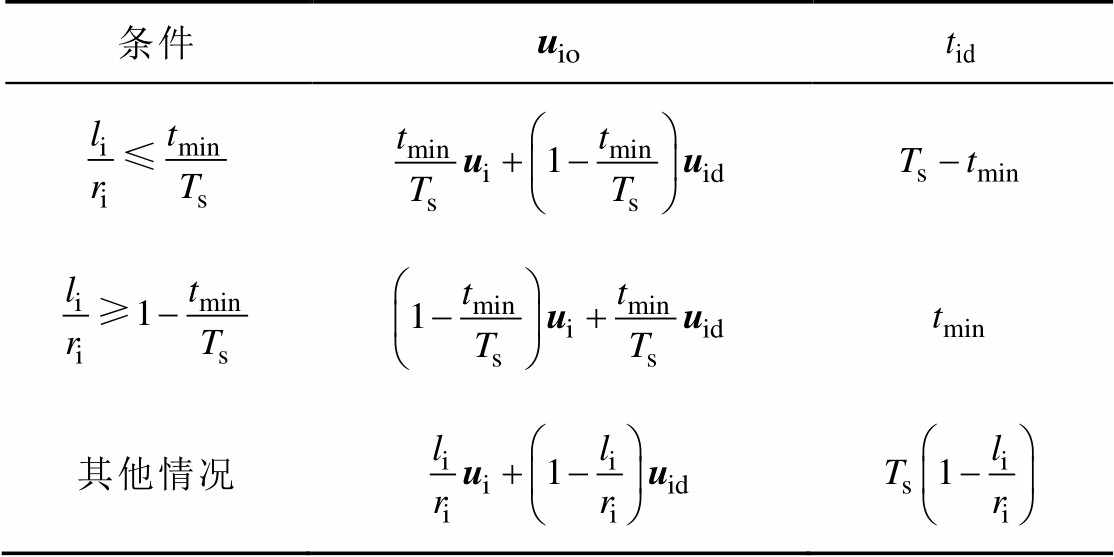
条件 其他情况
若不存在死区过程,等效于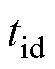 =0,
=0,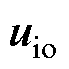 =
=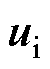 。综上所述,通过优化死区时间,将简化控制集转化为新的虚拟矢量控制集。
。综上所述,通过优化死区时间,将简化控制集转化为新的虚拟矢量控制集。
通过价值函数式(11)从虚拟矢量控制集中选取最优虚拟矢量,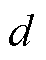 的解析式为
的解析式为
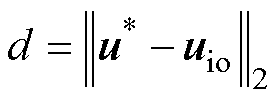 (13)
(13)
同时,价值函数中为实现直流侧电容电压平衡控制的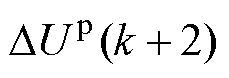 计算为
计算为
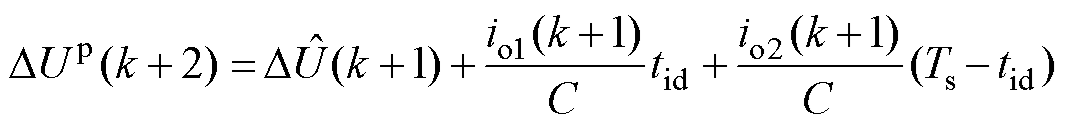 (14)
(14)
式中,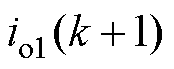 和
和 分别为将死区电压矢量和基本电压矢量代入式(6)后得到的。
分别为将死区电压矢量和基本电压矢量代入式(6)后得到的。
本文所提出的基于矢量欧氏距离的变死区时间FSC-MPC框架如图6所示,具体计算流程为:
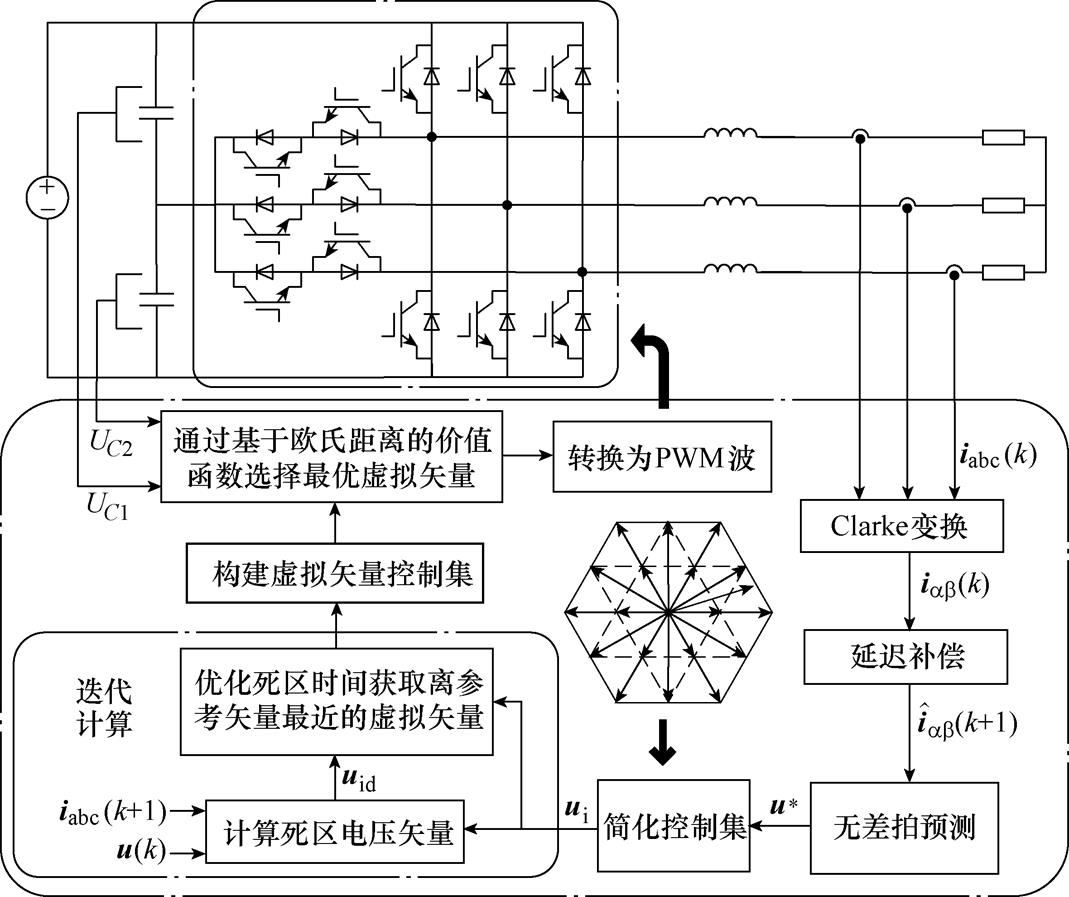
图6 考虑死区电压矢量的FCS-MPC策略框架
Fig.6 Frame of the proposed FCS-MPC strategy considering dead-zone voltage vector
(1)基于无差拍预测电流得到参考矢量。
(2)计算得到参考矢量的最近3个基本矢量及其冗余矢量,并以此作为简化控制集。
(3)以简化控制集中基本矢量和对应的死区电压矢量合成虚拟矢量,逐一优化死区时间以获取与参考矢量最近的虚拟矢量,并构建虚拟矢量控制集。
(4)针对虚拟矢量控制集,结合直流侧电容电压平衡控制,通过基于欧氏距离的价值函数选择最优虚拟矢量,并输出对应的控制波形。
为验证文中提出的优化策略的有效性,在Matlab/ Simulink仿真环境及实物平台对以下三种策略进行实验分析,具体的实验参数见表5。
表5 实验参数
Tab.5 Parameters of experimental platform

参 数数 值 直流侧电压/V100 交流侧负载/W10 交流侧电感/mH10 直流侧母线电容/mF4 000 采样频率/kHz10
(1)策略一,传统有限集模型预测控制策略。
(2)策略二,本文第2节提出的简化策略(控制效果等效于文献[13]所提出的简化策略)。
(3)策略三,本文提出的考虑死区电压矢量的模型预测控制策略。
为评估简化控制集、优化死区时间对稳态和动态性能的影响,进行仿真实验分析。0.02s时,相电流峰值的给定值由2A变为4A;0.04s时,变为2A。三种策略对应的三相相电流、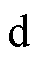 轴和
轴和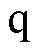 轴电流的仿真结果如图7所示。相比于传统策略,简化策略可以实现基本相同的控制效果,而控制集中基本矢量已由27个降低为不多于5个。相比之下,稳态时,本文所提出的优化策略对应的
轴电流的仿真结果如图7所示。相比于传统策略,简化策略可以实现基本相同的控制效果,而控制集中基本矢量已由27个降低为不多于5个。相比之下,稳态时,本文所提出的优化策略对应的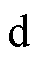 轴电流波动减少约50%,相电流波形脉动更小;动态时,均有较好的跟随效果。同时,简化策略和本文所提出的策略对应的A相相电流快速傅里叶变换(Fast Fourier Transform, FFT)的仿真实验结果如图8所示。结合死区电压矢量后,相电流的总谐波畸变率(Total Harmonic Distortion, THD)由3.02%降低为1.83%,稳态控制性能得到显著提高。
轴电流波动减少约50%,相电流波形脉动更小;动态时,均有较好的跟随效果。同时,简化策略和本文所提出的策略对应的A相相电流快速傅里叶变换(Fast Fourier Transform, FFT)的仿真实验结果如图8所示。结合死区电压矢量后,相电流的总谐波畸变率(Total Harmonic Distortion, THD)由3.02%降低为1.83%,稳态控制性能得到显著提高。
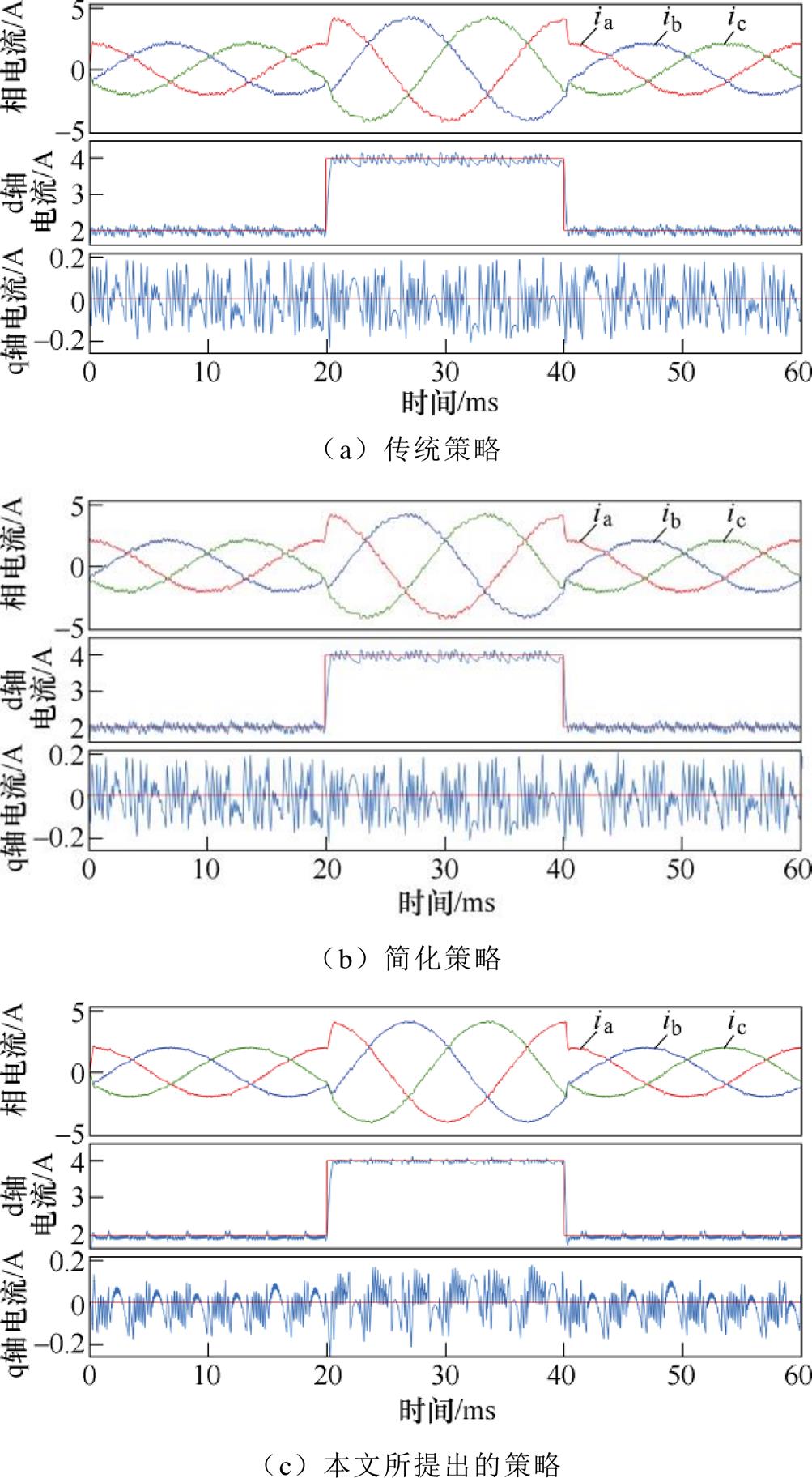
图7 三相相电流、d轴和q轴电流仿真结果
Fig.7 Three-phase current, d axis and q axis current simulation results
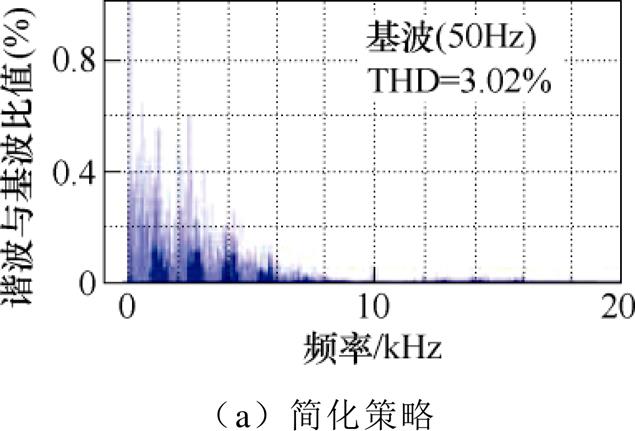
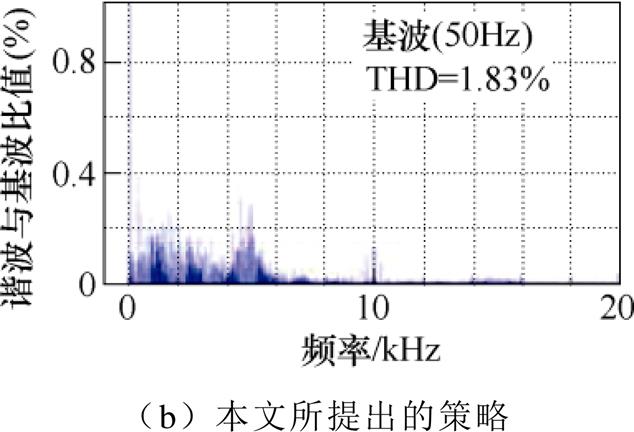
图8 A相电流FFT仿真结果
Fig.8 FFT simulation results of A phase current
为了更直观地分析死区电压矢量对逆变器实际输出的影响,分别对简化策略和本文所提出的策略在稳态运行时每个控制周期中输出的基本矢量或虚拟矢量和参考矢量的欧氏距离进行统计。相电流峰值给定为4A时,稳态运行0.05s得到的两种策略对应的欧氏距离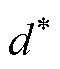 (标幺值,以小矢量的模为基准值)如图9a所示,统计结果如图9b所示。采用简化策略时,
(标幺值,以小矢量的模为基准值)如图9a所示,统计结果如图9b所示。采用简化策略时,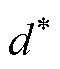 主要集中在
主要集中在 (pu)内。相比之下,采用本文所提出的策略时,
(pu)内。相比之下,采用本文所提出的策略时,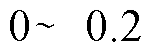 (pu)范围内所占比例明显增加,
(pu)范围内所占比例明显增加, (pu)范围内明显缩小,即输出的虚拟矢量更加接近参考矢量。
(pu)范围内明显缩小,即输出的虚拟矢量更加接近参考矢量。
三电平逆变器实验样机如图10所示,控制器采用的DSP芯片型号为TMS320F28335PGFA,FPGA芯片型号为XC6SLX9-2TQG144C。其中FPGA用于传感器信号采集与发波,并在每个发波周期结束时向DSP发送脉冲信号。DSP以此部署外部中断来运行算法,从而实现DSP的控制周期和FPGA的发波周期同步。且DSP中所计算得到的矢量在下个周期才作用在逆变器上,能够固定延迟时间,便于在控制算法中进行补偿。
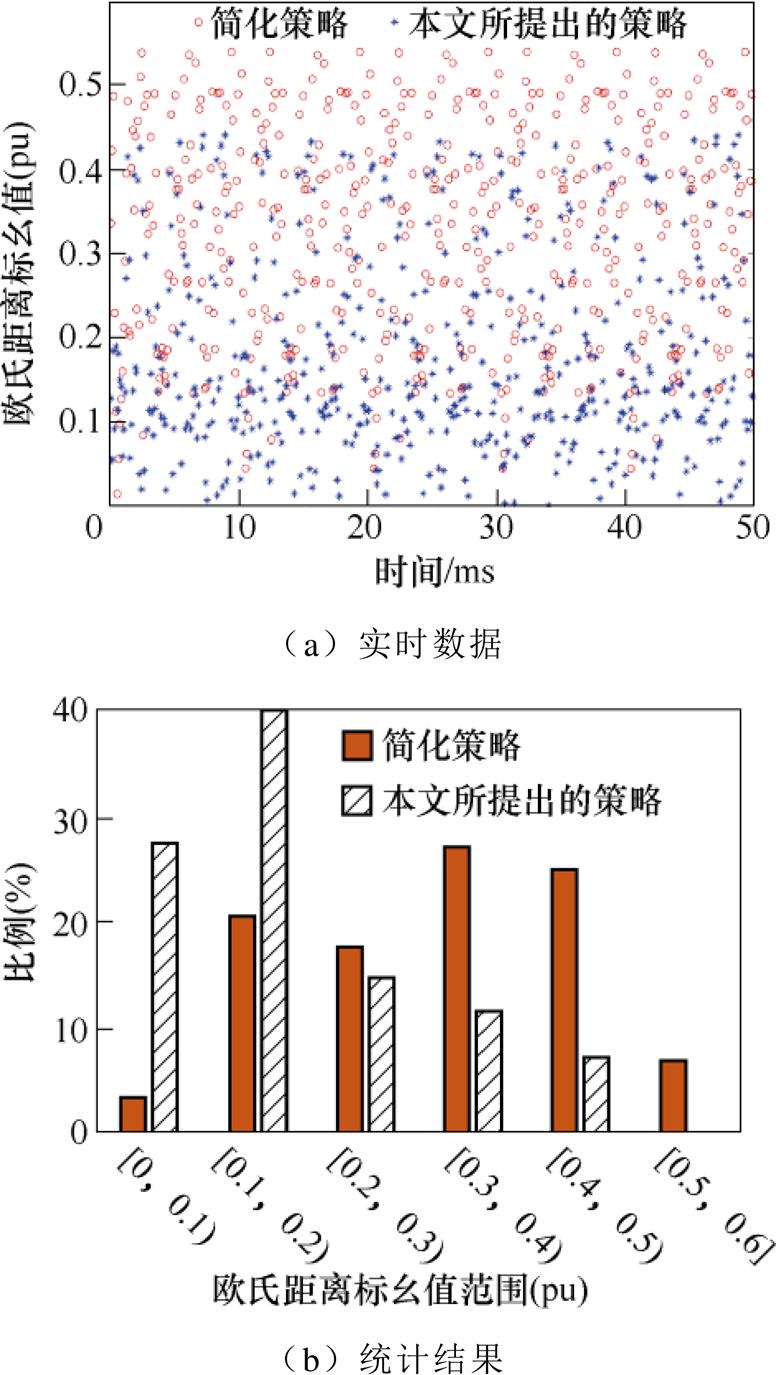
图9 输出矢量和参考矢量欧氏距离分析
Fig.9 Analysis of the Euclidean distance between the output vector and the reference vector

图10 三电平逆变器实验样机
Fig.10 Three-level inverter experimental prototype
4.2.1 计算效率分析
为了验证所提简化方法的有效性,对算法各个环节在DSP中所需要的执行时间进行记录,如图11所示。传统策略中,对27个基本矢量进行迭代计算耗时120ms;简化策略中,确定简化控制集耗时45ms,迭代计算耗时12ms,总时间为62ms;本文所提出的策略中,死区时间的优化增加了计算量,迭代计算耗时增加至34ms,总时间为84ms。当控制频率为5kHz时,传统策略与简化策略的控制效果基本相同,与仿真结果一致。由于传统策略的耗时无法满足控制频率为10kHz,且为减少篇幅,仅对简化策略和本文所提出的策略在控制频率为10kHz时的实验结果进行分析。
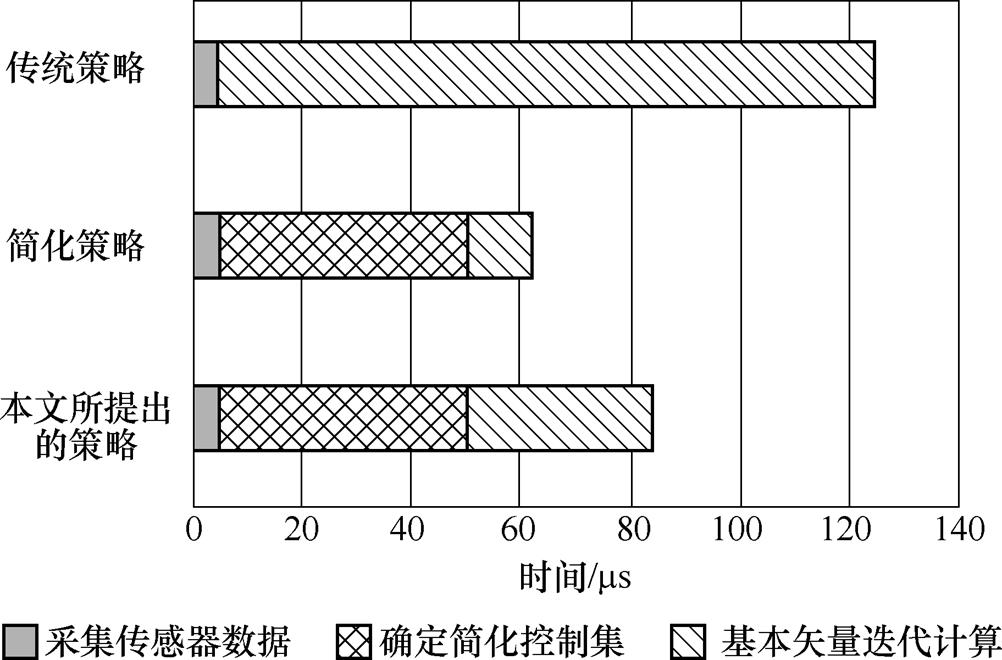
图11 DSP中程序执行时间
Fig.11 Execution time of DSP programs
4.2.2 稳态实验
当相电流峰值给定为不同值时,简化策略和本文提出的策略对应的相电流的THD值的实验结果如图12所示。当电流增大时,两种策略对应的THD值均减小;相比于简化策略,本文所提出的控制策略对应的THD值降低约40%~50%。
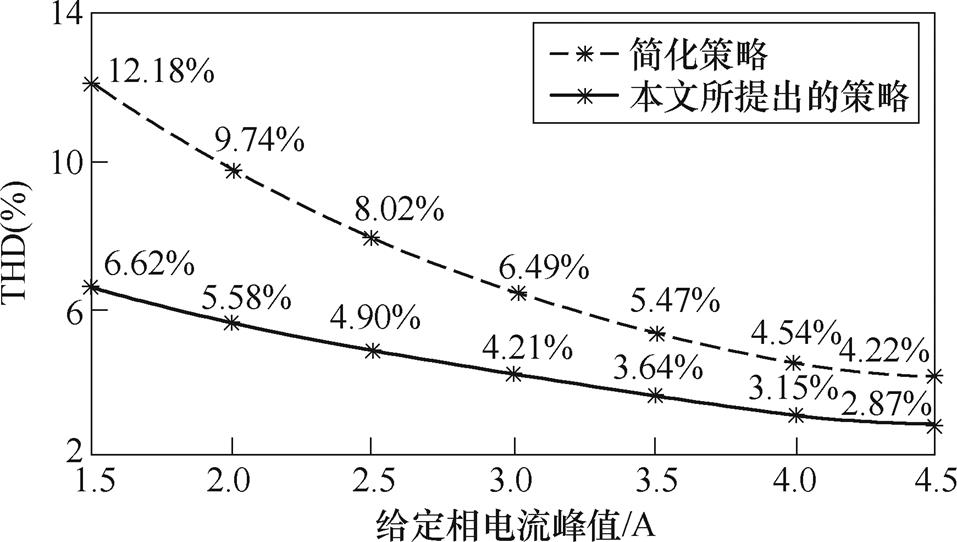
图12 不同给定电流峰值下,相电流的THD值
Fig.12 Under different given peak current, the THD value of the phase current
当相电流峰值给定为2A和4A时,三相相电流及A相相电流FFT的实验结果分别如图13和图14所示。两种策略所对应的输出电流均是较高质量的正弦电流。对于简化策略,两种情况下,相电流的脉动幅度基本相同;而本文提出的优化策略具有更好的输出电流波形,波动更小,与第3节理论分析一致。
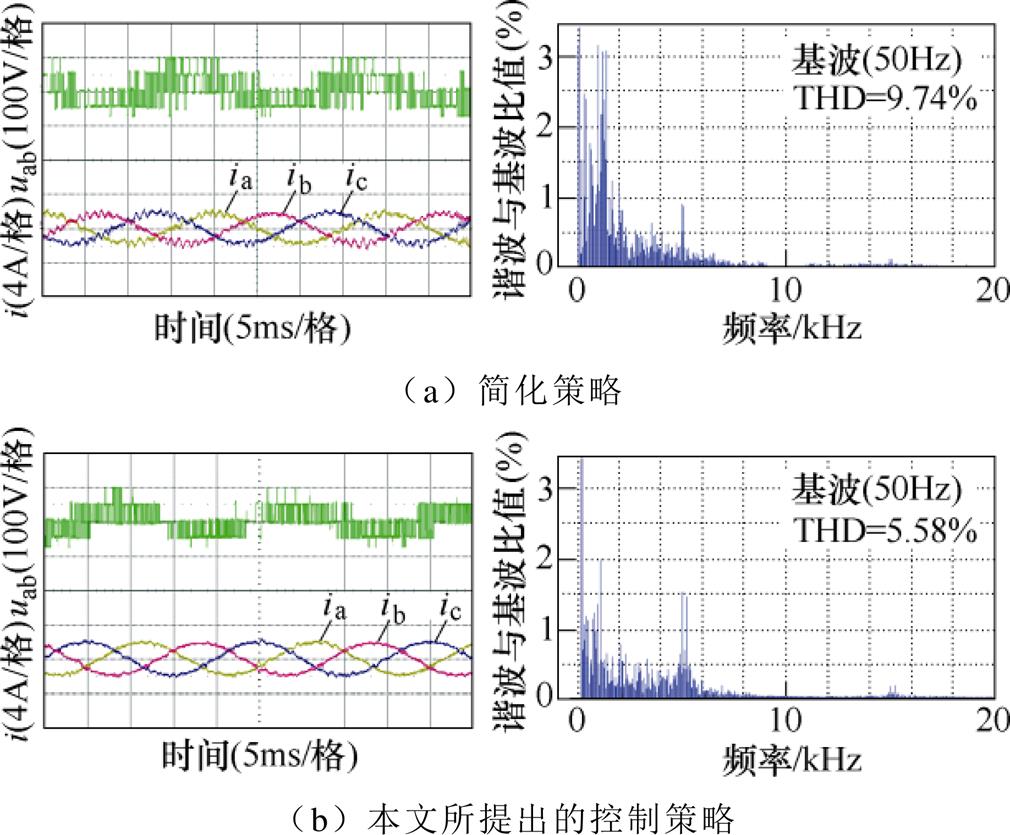
图13 相电流峰值给定为2A时稳态实验结果
Fig.13 Steady-state experimental results when the peak phase current is given as 2A
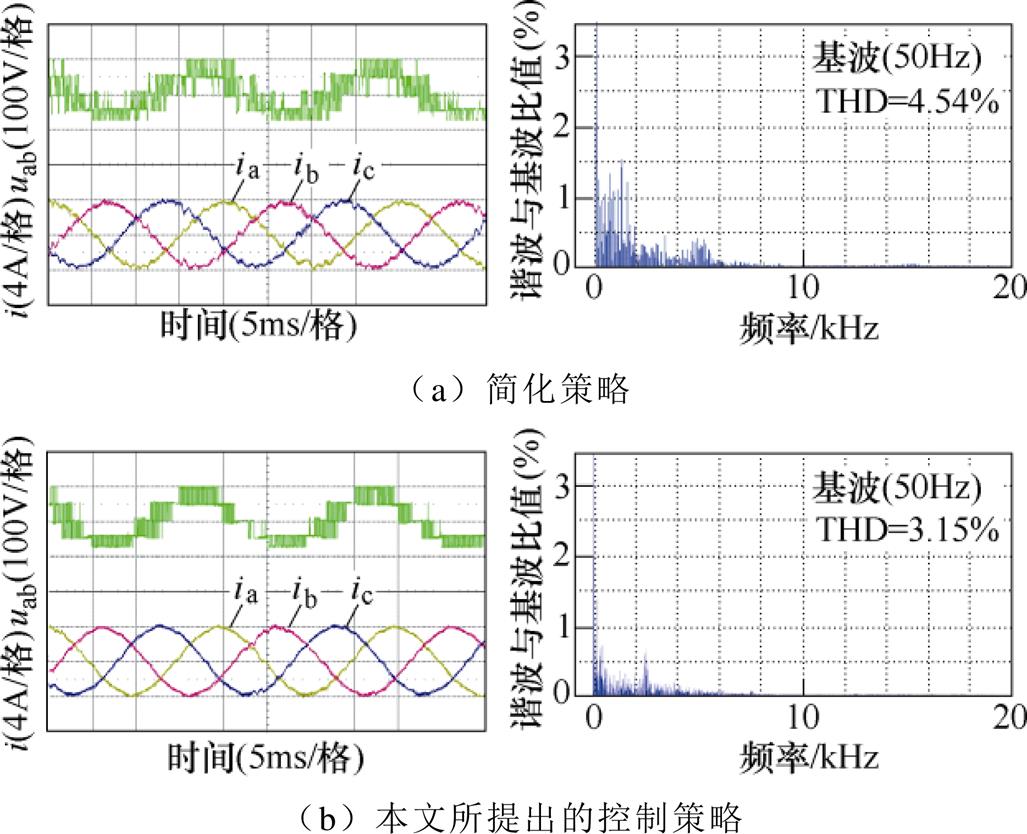
图14 相电流峰值给定为4A时稳态实验结果
Fig.14 Steady-state experimental results when the peak phase current is given as 4A
为了验证稳态时直流侧电容电压的平衡能力,在相电流峰值给定为4A时进行实验分析。直流侧电容电压值、A相电流的实验结果如图15所示。在运行过程中,直流侧电容电压能保持稳定,且两者偏差在0.5V以内。因此,这两种策略在平衡直流侧电容电压方面均具有的较好的效果。
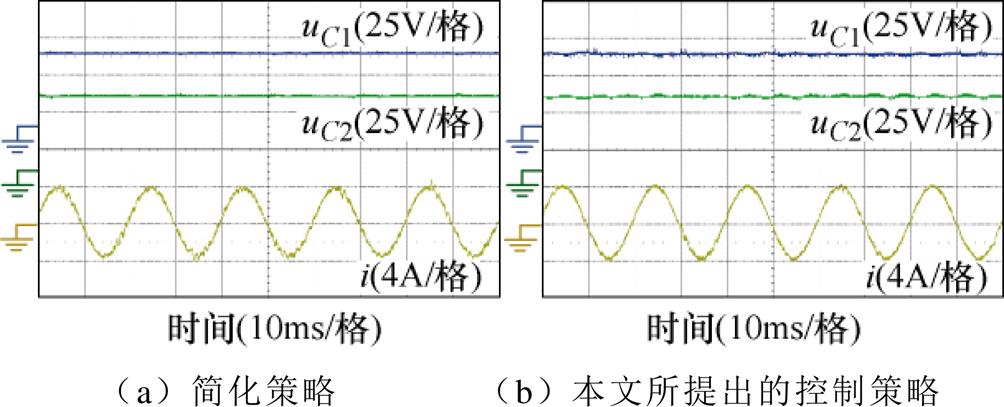
图15 直流侧电容电压值稳态实验结果
Fig.15 Steady-state experimental results of DC-link capacitor voltages
同时,在DSP程序中对稳态运行过程中的开关次数进行记录。在0.02s内,两种策略对应的开关次数均约为680。即本文所提出的策略在优化控制效果的同时并未增加开关损耗。
4.2.3 动态实验
通过使给定相电流峰值发生阶跃变化,对两种控制策略的动态性能进行分析,实验结果如图16所示。两种控制策略对应的输出电流均能较快的跟踪给定电流,耗时不到1ms,均有较好的动态性能。同时,直流侧电容电压值如图17所示,两种控制策略均能在动态过程中保证电容电压平衡。
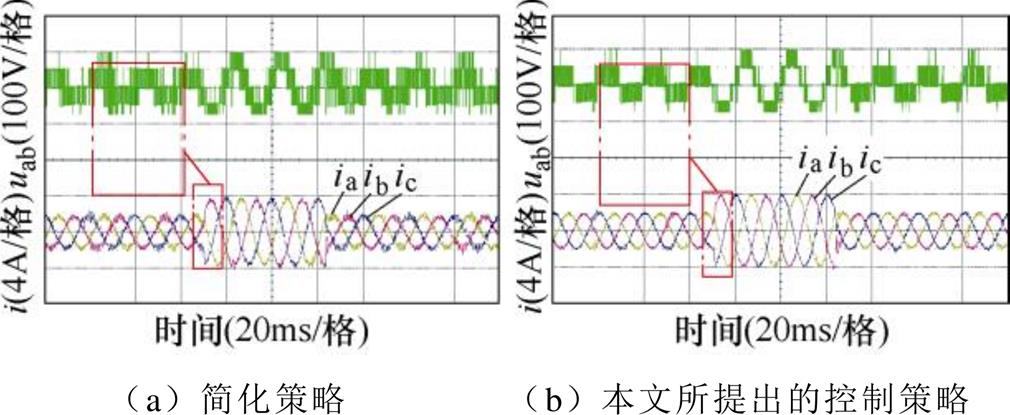
图16 输出电流动态实验结果
Fig.16 Dynamic experiment result of output current
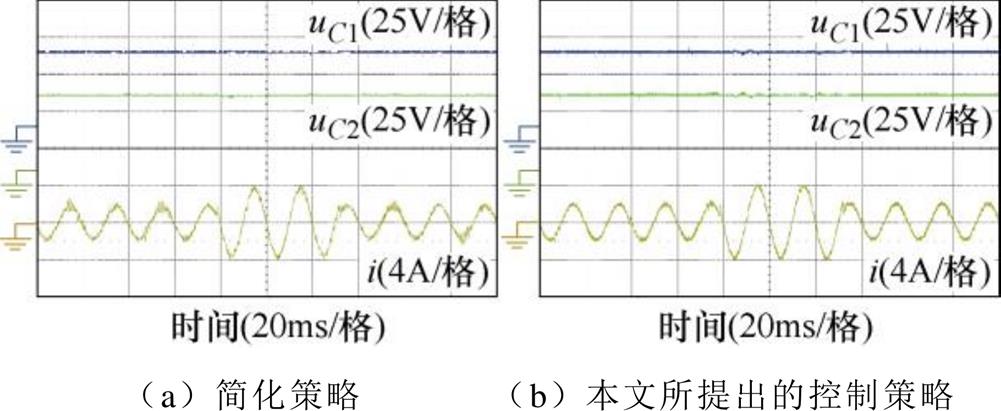
图17 直流侧电容电压值动态实验结果
Fig.17 Dynamic experimental results of DC-link capacitor voltages
本文以三电平变换器为研究对象,针对有限集模型预测控制中计算量大、死区影响的问题进行了研究和分析,提出了考虑死区电压矢量的快速FCS- MPC策略。通过理论分析和实验验证得到以下结论:
1)基于欧氏距离改进价值函数并构建简化控制集,有效地降低了计算量;通过优化死区时间,得到和参考矢量欧氏距离最小的虚拟矢量,有效地提高了控制性能。
2)由于三电平拓扑的电流、功率数学模型相同,本文所提出的策略可以应用到其他三电平拓扑中。
3)三电平变换器常用于高压大电流工况中,而本文所提出的控制策略能够提高稳态控制效果并保证开关次数基本不变,因此具有重要的实际意义。
1. 最近基本矢量及作用时间推导
定义参考矢量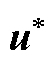 的最近三个基本矢量分别为
的最近三个基本矢量分别为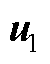 、
、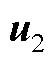 和
和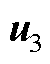 。根据伏秒平衡公式,令作用时间分别为
。根据伏秒平衡公式,令作用时间分别为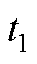 、
、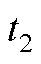 和
和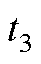 ,则存在以下关系
,则存在以下关系
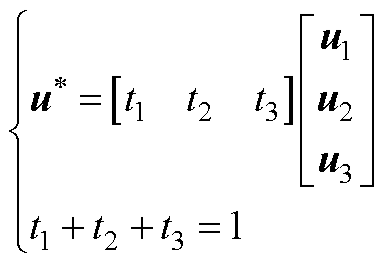 (A1)
(A1)
在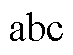 坐标系下,式(12)转化为
坐标系下,式(12)转化为
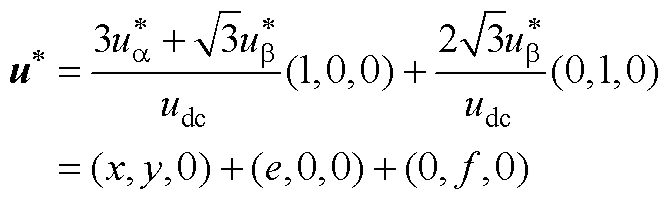 (A2)
(A2)
1)若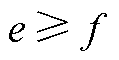 ,式(A2)转换式(A1)的形式,即
,式(A2)转换式(A1)的形式,即
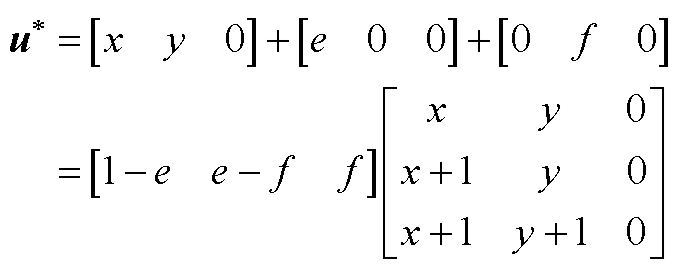 (A3)
(A3)
最近三个基本矢量分别为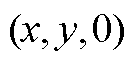 、
、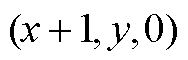 和
和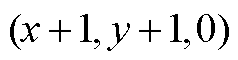 。
。
2)若 ,式(A2)转换为
,式(A2)转换为
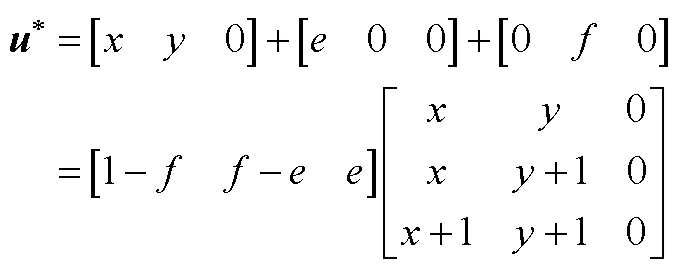 (A4)
(A4)
最近三个基本矢量分别为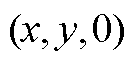 、
、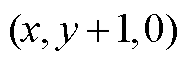 和
和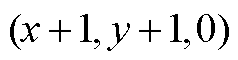 。
。
2. 最优死区时间及虚拟矢量推导
如图5所示,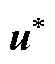 的终点到
的终点到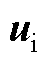 和
和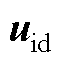 的终点连线的垂直距离
的终点连线的垂直距离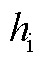 为
为
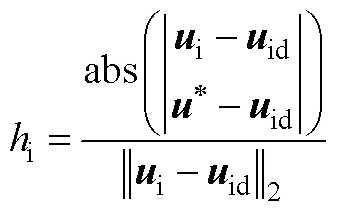 (A5)
(A5)
根据勾股定理,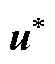 在连线上的投影和
在连线上的投影和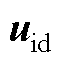 的终点之间的距离
的终点之间的距离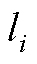 为
为
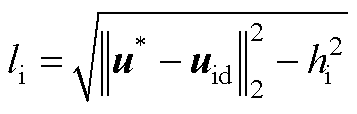 (A6)
(A6)
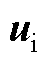 和
和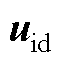 的终点之间的距离
的终点之间的距离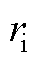 为
为
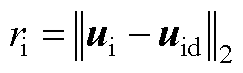 (A7)
(A7)
(1)当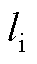 >
>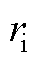 时,
时,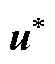 、
、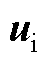 和
和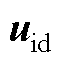 之间的位置关系如图5b所示。此时,
之间的位置关系如图5b所示。此时,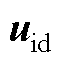 的作用时间越小,
的作用时间越小,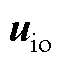 和
和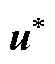 的欧氏距离越小。考虑
的欧氏距离越小。考虑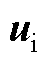 和
和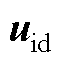 的作用时间存在最小值
的作用时间存在最小值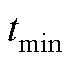 限制,
限制,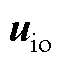 为
为
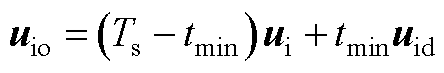 (A8)
(A8)
(2)当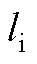 <
<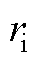 时,
时,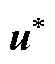 、
、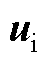 和
和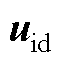 之间的位置关系如图5a所示。考虑到
之间的位置关系如图5a所示。考虑到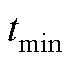 ,
,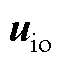 为
为
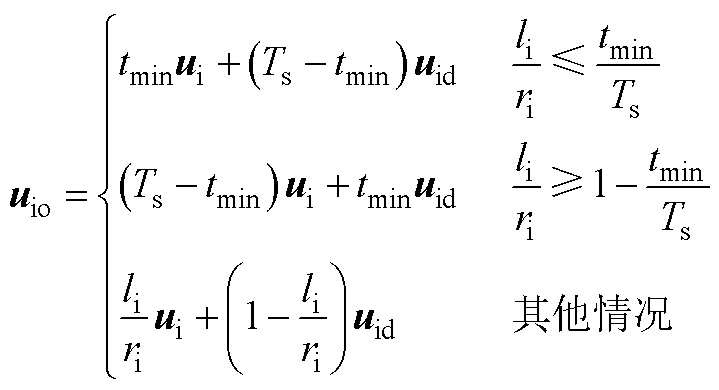 (A9)
(A9)
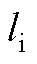 >
>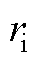 属于式(A9)中的第二种情况(
属于式(A9)中的第二种情况(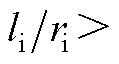
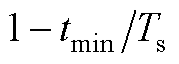 ),且式(A9)该情况中
),且式(A9)该情况中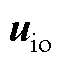 的解析式和式(A8)相同。因此,当存在死区时,
的解析式和式(A8)相同。因此,当存在死区时,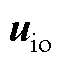 的解析式可以归纳为式(A9)。死区时间
的解析式可以归纳为式(A9)。死区时间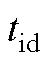 归纳为
归纳为
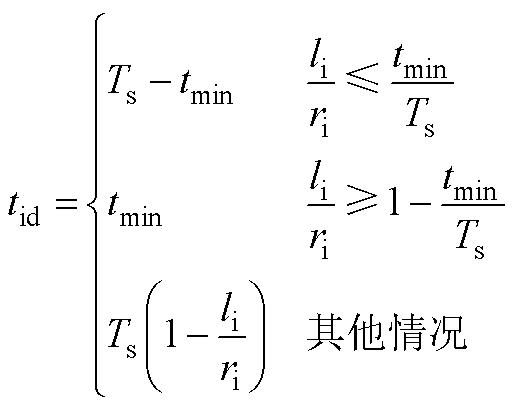 (A10)
(A10)
参考文献
[1] Quevedo D E, Aguilera R P, Geyer T. Predictive control in power electronics and drives: basic concepts, theory, and methods[C]//Advanced and Intelligent Control in Power Electronics and Drives, Springer, 2014: 181-226.
[2] Vazquez S, Rodriguez J, Rivera M, et al. Model predictive control for power converters and drives: advances and trends[J]. IEEE Transactions on Industrial Electronics, 2017, 64(2): 935-947.
[3] 李争, 安金峰, 肖宇, 等. 基于自适应观测器的永磁同步直线电机模型预测控制系统设计[J]. 电工技术学报, 2021, 36(6): 1190-1200.
Li Zheng, An Jinfeng, Xiao Yu, et al. Design of model predictive control system for permanent magnet synchronous linear motor based on adaptive observer[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1190-1200.
[4] 郭磊磊, 金楠, 李琰琰, 等. 电压源逆变器虚拟矢量模型预测共模电压抑制方法[J]. 电工技术学报, 2020, 35(4): 839-849.
Guo Leilei, Jin Nan, Li Yanyan, et al. Virtual vector based model predictive common-mode voltage redu- ction method for voltage source inverters[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(4): 839-849.
[5] 胡毕华, 康龙云, 程建材, 等. 基于死区消除与补偿的T型三电平逆变器控制策略[J]. 华南理工大学学报(自然科学版), 2018, 46(5): 109-116.
Hu Bihua, Kang Longyun, Cheng Jiancai, et al. Control strategy of T-type three-level inverter based on integrated dead-time elimination and compen- sation[J]. Journal of South China University of Technology (Natural Science Edition), 2018, 46(5): 109-116.
[6] 韩坤, 孙晓, 刘秉, 等. 一种永磁同步电机矢量控制SVPWM死区效应在线补偿方法[J]. 中国电机工程学报, 2018, 38(2): 620-627, 692.
Han Kun, Sun Xiao, Liu Bing, et al. Dead-time on- line compensation scheme of SVPWM for permanent magnet synchronous motor drive system with vector control[J]. Proceedings of the CSEE, 2018, 38(2): 620-627, 692.
[7] Ngo V Q B, Vu V H, Pham V T, et al. Lyapunov- induced model predictive power control for grid-tie three-level neutral-point-clamped inverter with dead- time compensation[J]. IEEE Access, 2019, 7: 166869- 166882.
[8] Zhang Xiaoguang, Cheng Yu, Zhao Zhihao, et al. Optimized model predictive control with dead-time voltage vector for PMSM drives[J]. IEEE Transa- ctions on Power Electronics, 2021, 36(3): 3149- 3158.
[9] Zhang Xiaoguang, Zhao Zhihao. Model predictive control for PMSM drives with variable dead-zone Time[J]. IEEE Transactions on Power Electronics, 2021, 36(9): 10514-10525.
[10] 吴琪, 胡存刚, 张云雷, 等. 三电平ANPC变换器快速模型预测控制策略研究[J]. 电力电子技术, 2020, 54(4): 103-106.
Wu Qi, Hu Cungang, Zhang Yunlei, et al. Research on fast model predictive control strategy for three-level ANPC converter[J]. Power Electronics, 2020, 54(4): 103-106.
[11] 辛业春, 王延旭, 李国庆, 等. T型三电平并网逆变器有限集模型预测控制快速寻优方法[J]. 电工技术学报, 2021, 36(8): 1681-1692.
Xin Yechun, Wang Yanxu, Li Guoqing, et al. Finite control set model predictive control method with fast optimization based on T-type three-level grid- connected inverter[J]. Transactions of China Elec- trotechnical Society, 2021, 36(8): 1681-1692.
[12] 王洋, 程志江, 李永东. 三电平并网变换器的模型预测控制[J]. 电力系统及其自动化学报, 2018, 30(10): 34-41.
Wang Yang, Cheng Zhijiang, Li Yongdong. Model predictive control of three-level grid-connected converter[J]. Proceedings of the CSU-EPSA, 2018, 30(10): 34-41.
[13] Yang Yong, Wen Huiqing, Fan Mingdi, et al. Fast finite-switching-state model predictive control method without weighting factors for T-type three-level three-phase inverters[J]. IEEE Transactions on Indu- strial Informatics, 2019, 15(3): 1298-1310.
[14] 姚绪梁, 麻宸伟, 王景芳, 等. 基于预测误差补偿的鲁棒型永磁同步电机模型预测电流控制[J]. 中国电机工程学报, 2021, 41(17): 6071-6080.
Yao Xuliang, Ma Chenwei, Wang Jingfang, et al. Robust model predictive current control for PMSM based on prediction error compensation[J]. Pro- ceedings of the CSEE, 2021, 41(17): 6071-6080.
[15] Cortes P, Rodriguez J, Silva C, et al. Delay com- pensation in model predictive current control of a three-phase inverter[J]. IEEE Transactions on Indu- strial Electronics, 2012, 59(2): 1323-1325.
[16] 尹忠刚, 白聪, 杜超, 等. 基于内模干扰观测器的永磁同步直线电机无差拍电流预测控制方法[J]. 电工技术学报, 2018, 33(24): 5741-5750.
Yin Zhonggang, Bai Cong, Du Chao, et al. Deadbeat predictive current control for permanent magnet linear synchronous motor based on internal model dis- turbance observer[J]. Transactions of China Electro- technical Society, 2018, 33(24): 5741-5750.
[17] 於锋, 朱晨光, 吴晓新, 等. 基于矢量分区的永磁同步电机三电平双矢量模型预测磁链控制[J]. 电工技术学报, 2020, 35(10): 2130-2140.
Yu Feng, Zhu Chenguang, Wu Xiaoxin, et al. Two-vector-based model predictive flux control of three-level based permanent magnet synchronous motor with sector subregion[J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2130-2140.
[18] 张晓光, 闫康, 张文涵. 开绕组永磁同步电机混合双矢量模型预测控制[J]. 电工技术学报, 2021, 36(1): 96-106.
Zhang Xiaoguang, Yan Kang, Zhang Wenhan. Hybrid double vector model predictive control for open- winding permanent magnet synchronous motor with common DC bus[J]. Transactions of China Elec- trotechnical Society, 2021, 36(1): 96-106.
[19] Dang Chaoliang, Tong Xiangqian, Song Weizhang, et al. Cost function-based modulation scheme of model predictive control for VIENNA rectifier[J]. IET Power Electronics, 2019, 12(14): 3646-3655.
[20] 王祯, 尹项根, 陈玉, 等. 基于连续控制集模型预测控制的MMC桥臂电流控制策略[J]. 电力系统自动化, 2020, 44(10): 85-91.
Wang Zhen, Yin Xianggen, Chen Yu, et al. Arm current control strategy of modular multilevel converter based on continuous control set model predictive control[J]. Automation of Electric Power Systems, 2020, 44(10): 85-91.
[21] 兰志勇, 王波, 徐琛, 等. 永磁同步电机新型三矢量模型预测电流控制[J]. 中国电机工程学报, 2018, 38(增刊1): 243-249.
Lan Zhiyong, Wang Bo, Xu Chen, et al. A novel three-vector model predictive current control for permanent magnet synchronous motor[J]. Proceedings of the CSEE, 2018, 38(S1): 243-249.
Model Predictive Control of Three-Level Converter Considering Dead-Zone Voltage Vector
Abstract Aiming at the three-level converter, this paper proposes a finite-control-set model predictive control strategy considering dead-zone voltage vector. Based on the dead-zone effect, a virtual vector is synthesized from the basic voltage vector and the corresponding dead-zone voltage vector, and a new virtual vector control set is constructed by optimizing the dead-zone time. To reduce the amount of calculation, firstly, the reference vector is obtained by the deadbeat prediction. It is strictly proved that the Euclidean distance between the output vector and the reference vector is equivalent to the current prediction of the traditional value function. Therefore, a new simplified value function is constructed, which effectively reduces the complexity of iterative calculations. Secondly, the relevant basic vector is selected to construct a simplified control set, which significantly reduces the search space. Finally, the optimal virtual vector is selected by the value function based on the Euclidean distance, and the fast model predictive control with variable dead-zone time is realized. Compared with the traditional model predictive control, the control strategy proposed in this paper can decrease the output current pulsation and reduce the total harmonic distortion of the current by about 40%~50%, which significantly improves the control performance of the converter.
keywords:Model predictive control, Euclidean distance, dead-zone voltage vector, deadbeat prediction, current control
DOI: 10.19595/j.cnki.1000-6753.tces.212128
中图分类号:TM464
国家自然科学基金项目(52177204, 51777217)、湖南省自然科学基金面上项目(2020JJ4744, 2021JJ30875)和安徽省科技重大专项项目(202003a05020019)资助。
收稿日期 2021-12-29
改稿日期 2022-04-06
周汉斌 男,1997年生,博士研究生,研究方向为多电平变流器。E-mail: amoszz@csu.edu.cn
陈晓娇 女,1989年生,副研究员,研究方向为多电平变流器。E-mail: chenxj@ipp.ac.cn(通信作者)
(编辑 陈 诚)