
图1 MMC系统失效原因分析
Fig.1 Fault analysis of MMC system
摘要 电容器作为模块化多电平换流器(MMC)系统子模块核心部件,因长期工作于交流、大功率的工作环境,使其成为最容易失效的部件之一。因此,电容器健康状态的实时监测对MMC系统可靠运行具有重要意义。该文提出一种基于Haar小波变换重构开关序列的MMC子模块电容值在线监测方法,首先,通过对MMC系统实测的电容器电压信号进行Haar小波变换重构出子模块投入与切除的开关序列;其次,基于重构的开关序列提取电容器的充电时段电压信号,并结合桥臂实测电流信号实现电容器容值在线反演计算;最后,通过MMC系统工况模拟平台验证了该文所提方法的准确性和有效性。该方法仅需控制系统原有采集的电容电压和桥臂电流信号为监测方法输入,即可实现对电容器容值的评估,去除了对开关信号的需求,极大地降低了监测的难度,为MMC系统电容器的健康状态监测和主动运维提供了方法和数据基础。
关键词:模块化多电平换流器 电容值在线监测 开关序列 小波变换
随着我国新能源的快速发展,电力系统的发电能力和容量得到极大提升[1],高压直流(High Voltage Direct Current, HVDC)输电技术被广泛应用在电力系统中,以解决能源的传输问题[2-3]。模块化多电平换流器(Modular Multilevel Converter, MMC)凭借其开关频率低、运行效率高等优点已成为直流输电系统的主流拓扑。
MMC系统中高电压、大电流、交流的运行工况都会加速电容器的老化并最终导致其失效。电容器的失效使MMC系统面临停机风险,直接影响到高压直流输电系统的运行安全[4]。统计数据表明,换流阀元件故障是造成换流阀系统故障的主要原 因[5],如图1a所示;而作为核心部件的电容器因为工作时承受着桥臂交变大电流的冲击,成为变流器中最容易发生疲劳失效的部件[6],如图1b所示。因此,检测电容器的健康状态对维持MMC系统的安全运行有着重要意义[7],影响着电力系统的可靠运行[8-10]。

图1 MMC系统失效原因分析
Fig.1 Fault analysis of MMC system
电容器老化后通常表现为电容值降低,监测容值变化可以体现电容器的实时老化状态,以确保MMC系统的稳定运行[11]。现有研究已针对MMC中的电容器提出一些状态监测方法,根据监测过程中所需的状态参量可分为基于开关序列的直接测量法和不需要开关序列的间接测量法。
直接测量法通过桥臂电流与开关信号重构得到电容电流,并利用电容电压与电流之间的关系预估电容健康状态。文献[12]通过采集电压电流波形的二倍频成分之比来求取电容值。文献[13]使用卡尔曼滤波算法构建电压和电流对应的计算模型求取容值。文献[14]提出了一种自适应算法追踪电压和电流变化来逼近电容值。文献[15]通过采集电压、电流、开关波形来提取每个周期的充电波形实现对电容值的检测。该类方法的特点在于需要采集开关序列进行计算,在实际应用中该类方法通常不直接测量开关信号而是使用控制系统的PWM信号进行计算。然而,文献[16]指出MMC系统中通常使用DSP和FPGA的复合控制,通过DSP控制FPGA产生PWM波信号实现对子模块的控制。在实际系统中仅有FPGA传输到驱动的控制信号回路,应用直接测量法监测电容时需要加设额外的数据传输回路将PWM信号从FPGA传输回DSP或上位机。在真实MMC系统中由于子模块数量众多,加设额外的传输线路会因改变系统结构而增加检测的复杂性,增加系统运行成本的同时造成一定的侵入性。
为了解决使用开关信号带来的问题,降低检测方法对原系统的侵入性,间接测量法通过电容电压和电容值之间的关系来预估电容老化状态。文献[16]基于参考电压和电流基频分量的响应关系来提取电容值。文献[17]通过对系统注入交流信号后根据其二倍频分量提取容值。文献[18]通过对工频周期内4个特殊相位点的采样电压进行计算实现容值的检测。文献[19]将启动中预充电的过程等效为充电电路,通过解析充电波形求取电容值。文献[20]为子模块电容器并联放电电阻,并在电容器关断期间进行放电后测量放电信号的波形从而提取电容器的容值。现有间接测量法不需要开关信号即可实现对电容器的健康状态监测,极大地降低了实际应用的难度和对原系统运行的侵入性。然而,现有方法仍需结合特定信息或工况(如注入电流、参考电压、相位、预充电等)才能完成状态监测,在一定程度上增加了监测系统的复杂性。
针对该问题,本文基于子模块电容电压的工作特征提出了一种基于Haar小波变换重构开关序列的无侵入性容值计算方法。当电容进入充电周期后,电压信号进行小波变换后对应的细节系数均小于0。通过追踪对应的小波变换后细节系数中低于零的成分可以有效地重构出充电周期对应的开关序列,并基于充电周期中电压电流信号实现容值的在线反演计算。本文方法对电容电压进行小波变换重构充电周期的开关序列,仅使用MMC中已有的电容电压和桥臂电流信号实现状态监测,去除了对开关信号采集的需求,相比传统方法极大地降低了容值监测的难度,并在MMC系统工况模拟平台上进行了准确性和有效性的验证。
MMC系统结构如图2所示。该系统由向三相供电的三个相单元组成,每个单元包含上、下两个桥臂,每个桥臂中由N个子模块和一个电感组成,其中每个子模块均由两个绝缘栅双极型晶体管(Insulated Gate Bipolar Transistor, IGBT)和电容器组成,通过功率模块的开关状态控制其输出状态来接入电路,相单元内接入的子模块总电压等于直流母线电压。

图2 MMC系统结构
Fig.2 Structure of MMC system
MMC子模块通过控制IGBT模块的不同状态可以工作在三个模式六种工作状态下,如图3所示。图中,虚线为IGBT模块导通控制信号,实线为关断控制信号。在投入模式下,IGBT的控制信号为上管VT1导通、下管VT2关断,子模块输出电压为电容电压uCap:子模块在状态1时投入电路进行充电,电容通过桥臂电流经由二极管上管VD1进行充电,进而引起电容电压上升,子模块在状态2时投入电路放电,电容通过IGBT上管VT1进行放电后,引起电容电压降低。子模块在切除模式下控制信号为VT1关断、VT2导通,此时电容器被旁路输出电压为0:子模块在状态3和状态4下分别通过VT2和VD2接入主电路。当控制信号均为关断时子模块进入闭锁的异常工作模式,通常发生于给电容器进行预充电或者发生故障时将电容器旁路[21-22]。对应的工作状态见表1。

图3 MMC子模块运行状态
Fig.3 Running status of the submodule in MMC system
表1 MMC系统中子模块工作状态
Tab.1 Working status of SM in MMC system
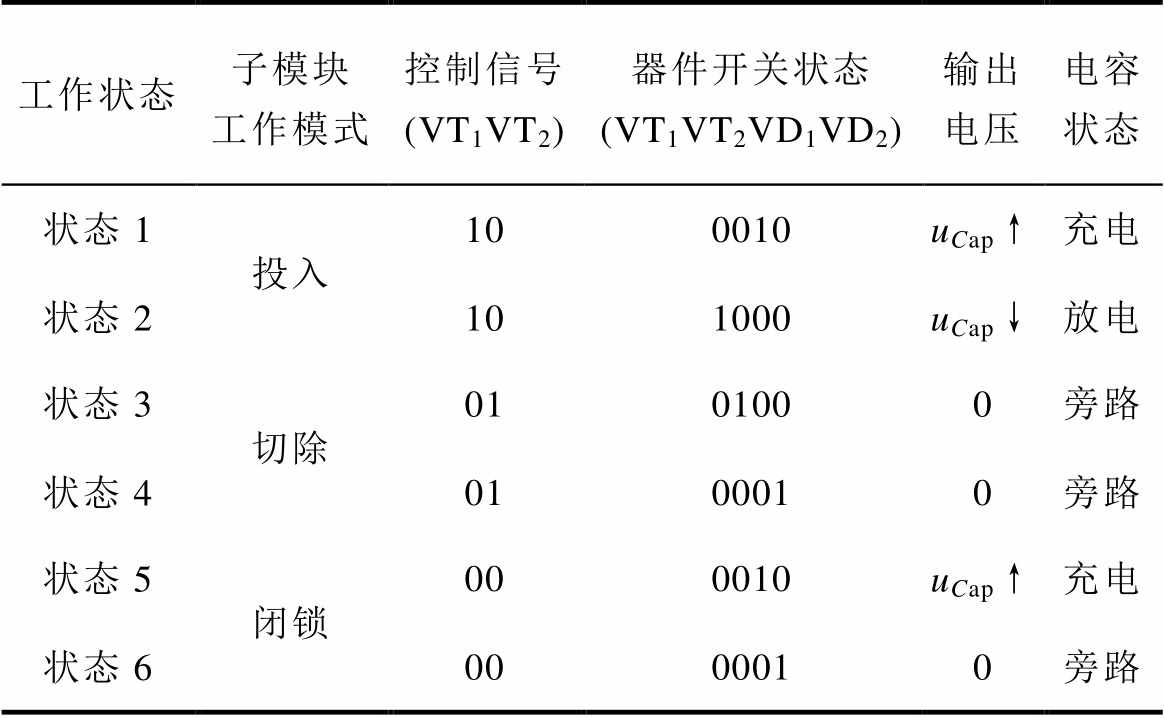
工作状态子模块工作模式控制信号(VT1VT2)器件开关状态(VT1VT2VD1VD2)输出电压电容状态 状态1投入100010uCap↑充电 状态2101000uCap↓放电 状态3切除0101000旁路 状态40100010旁路 状态5闭锁000010uCap↑充电 状态60000010旁路
在子模块电容进行充放电时,电容电压与开关信号如图4所示,图中,虚线为放电和充电的分界点。当开关信号为1时,子模块电容开始充电或者放电,电容电压开始升高或者降低;当开关信号为0时,子模块电容被切除,电容电压保持不变。

图4 子模块电容电压与开关信号
Fig.4 SM capacitance voltage and switching signal
以电容充电过程为例,放电过程的推导与充电类似。当子模块工作在状态1时对电容进行充电,电容充电电流iCap(t)受到子模块开关序列 控制,在IGBT导通时通过桥臂电流iarm(t)进行充电,即
控制,在IGBT导通时通过桥臂电流iarm(t)进行充电,即
 (1)
(1)
充电周期内的电容电压uCap(t)变化为
 (2)
(2)
式中,uCap0为初始电容电压;C为电容。
开关序列的控制与实际控制相关,当处于控制导通周期[tON_1, tOFF_1],…, [tON_n, tOFF_n]时,IGBT模块的开关信号[VT1, VT2]为[1, 0],子模块的开关序列为1;当处于切除周期时,IGBT的开关信号[VT1, VT2]为[0, 1],子模块的开关序列为0,即
 (3)
(3)
据式(1)和式(3)可知,切除状态下电容被旁路,此时电容电流和子模块输出电压均为0,因此可以将全充电周期下的电容电压变化简化为
 (4)
(4)
根据式(4)对充电周期内电流和电压进行计算提取容值,得
 (5)
(5)
式中,1~m为t~ 时刻上子模块的开通序列。
时刻上子模块的开通序列。
根据式(4)可知,开关序列是引起电容电压变化的根本原因,因此通过提取电容电压的变化特征即可提取对应的开关序列。最近电平控制(Nearest Level Control, NLC)以其开关频率低、动态性能好等优点,被广泛应用于MMC系统中[23]。由于在NLC调制策略下,子模块开关序列由当前电压排序结果决定,导致开关序列是非周期信号,不具备周期性和连续性。传统的傅里叶变换是铺满整个频域,而实际的开关过程不是周期波形,因此傅里叶变换无法有效提取开关周期的波形特征。
小波变换是一种能够实现多尺度变化的提取信号特征的方法,可以同时提取被测信号的时域和频域特征,在进行频域分析后再得到频域上的突变点对应的时域信号点,所以小波变换被广泛地应用于信号特征的提取[24-28]。电容器在充电过程中电压变化会产生突变,因此可以使用小波变换来检测突变点的变化以提取子模块的开关序列。同时,小波变换对计算力的要求极低,可以直接应用在单片机 上[29],因此在实际应用中也具备可行性。
小波变换是将非平稳时间序列的信号通过小波基函数分解为不同频域的子序列信号,其中近似系数(approximate coefficients)A是对原信号低频信号进行频率细分的结果,变化幅度小,保留基本信号特征;细节系数(detail coefficients)D是对高频信号的时间细分的结果,变化幅度大,保留信号的细节特性。对同一信号多次变换可提取多尺度下的信号特征,小波变换后信号构成如图5所示。

图5 小波变换后信号构成
Fig.5 Signal composition after wavelet transform
小波变换通过近似系数低通滤波器 和细节系数高通滤波器
和细节系数高通滤波器 将原始信号分解为不同频段的信号,分别如式(6)所示的低频近似系数A[i,t ]和式(7)所示的高频细节系数D[i,t ],i为尺度参数,t为平移参数。通过改变小波函数的尺度并对原信号进行平移处理即可求取对应的滤波后的信号。
将原始信号分解为不同频段的信号,分别如式(6)所示的低频近似系数A[i,t ]和式(7)所示的高频细节系数D[i,t ],i为尺度参数,t为平移参数。通过改变小波函数的尺度并对原信号进行平移处理即可求取对应的滤波后的信号。
 (6)
(6)
 (7)
(7)
Haar基是一种常用的小波基,定义为尺度范围内的数据为1,其他地方为0,如式(8)所示。其特点是计算简单,但是在时域上不连续。由于电容充电开始和结束时刻的电压变化并不连续,若使用连续的小波基会导致无法准确判断状态变化的分界点,所以不连续的Haar小波基对于提取充电开始和停止瞬间的跳变有更好的适应性[21]。
 (8)
(8)
将式(8)代入式(6)和式(7)得到基于Haar小波基的近似系数和细节系数的计算公式为
 (9)
(9)
 (10)
(10)
以一个运行周期内的电容波形为例,小波变换后的MMC子模块电容电压波形如图6所示。根据式(9)和式(10)分别对不同工作状态下的电容电压波形进行Haar小波变换,求取的结果如图6所示,细节系数中斜线阴影部分为充电序列,点阴影部分为切除序列,竖线阴影部分为放电序列。不同工作状态下对应的小波变换结果分析如下。
1)投入周期-充电(状态1)
在子模块进入投入周期开始充电时,桥臂电流对电容充电引起子模块电压上升,如图6中t1、t3和t5时段所示。采集到的电容电压uCap随着时间增大使得小波变换后的近似系数A>0而细节系数D<0,即
 (11)
(11)

图6 小波变换后的MMC子模块电容电压波形
Fig.6 SM capacitance voltage waveforms after wavelet transform
2)切除周期(状态3和状态4)
在子模块切除时电容被旁路,电压保持不变,采集到的电容电压与前一时刻相等,如图6中t2、t4和t6时刻的波形所示。此时小波变换后的近似系数A与上一时刻相等,而细节系数D=0,即
 (12)
(12)
3)投入周期-放电(状态2)
当子模块进入放电周期后电容电压开始降低,如图6中t7时段所示。由于采样后的电容电压随着时间降低,小波变换后的近似系数A和细节系数D均大于0,即
 (13)
(13)
在不同运行状态下对电容电压进行小波变换后的信号见表2。电容电压的近似系数A保留波形的基本信息的同时在所有运行周期内均大于0。细节系数则有效地反映出不同运行状态的变化,当子模块切除时细节系数为0,而在充电和放电状态下分别为负和正。因此,通过提取细节系数的负值部分可以获得子模块的充电序列。
表2 不同状态下小波变换后子模块电容电压信号特征
Tab.2 Signal characteristics of SM capacitance voltage after wavelet transformed in different states

投入(充电)(t1, t3, t5)投入(放电)t7切除(t2, t4, t6) 近似系数A>0>0>0 细节系数D<0>0=0
对于小于0的充电周期的细节系数序列(Dk, Dk+1,…, Dk+n),可根据小波信号的定义将其还原为原信号对应的序列,得到充电周期内的开通电压信号(u2k-1, u2k,…, u2k+2n-1, u2k+2n)。根据还原的信号可以将对应的充电周期序列(t2k-1, t2k,…, t2k+2n-1, t2k+2n)提取出来,小波信号的构成和还原如图7所示。基于提取到的充电序列根据式(5)进行电容值的计 算得
 (14)
(14)

图7 小波信号的构成和还原
Fig.7 Construction and reduction of wavelet signal
在MMC系统运行时,一个运行周期内可能存在多个充电周期,当充电时间过短时可能因为采样频率不够高导致频谱泄露而无法采集到完整的波形,使计算出的电容值不够准确。本文为保证检测结果的准确性,取单个周期内最大充电周期作为计算序列,并设置采集的最低充电时间以尽可能保证减少频谱泄露对电容测量的影响。在实际运行中,因为采样偏差,测量噪声等影响可能导致计算结果出现极值,使求取计算周期内的平均值出现较大的偏差,为减少测量的影响,本文选取1s内计算容值的中位数作为计算结果的输出容值。
基于小波变换监测容值的流程如图8所示。首先采集1s内的子模块电压电流波形,使用式(9)和式(10)对电压信号UC进行小波变换提取原始序列对应的细节系数D的序列,求取出对应的最大充电周期,并结合桥臂电流IA通过式(14)计算出各周期上对应的容值,最后输出计算容值结果的中位数。

图8 基于小波变换监测容值的流程
Fig.8 Flow chart of capacitance monitoring based on wavelet transform
本文针对NLC调制下的MMC系统,根据图2中的工作原理在Matlab/Simulink中搭建了10MW全系统仿真模型[22],模拟MMC系统的参数见表3(最低采样频率的要求见附录)。
表3 模拟MMC系统参数
Tab.3 Simulate MMC system parameters
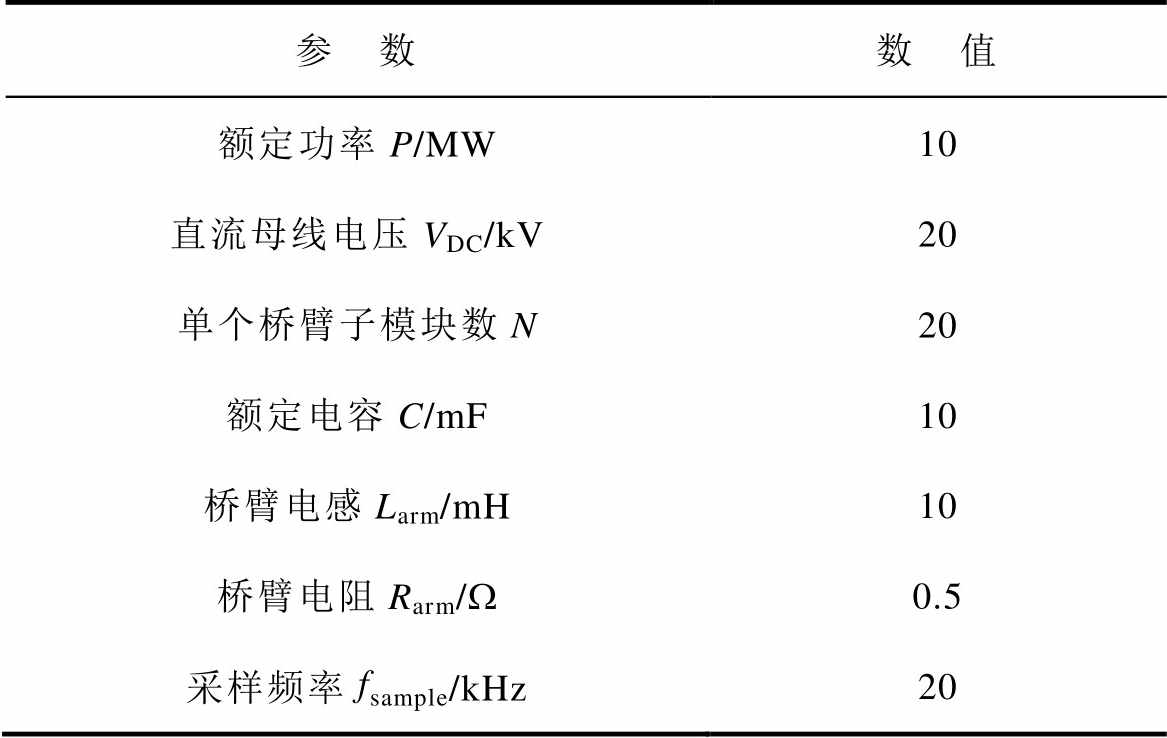
参 数数 值 额定功率P/MW10 直流母线电压VDC/kV20 单个桥臂子模块数N20 额定电容C/mF10 桥臂电感Larm/mH10 桥臂电阻Rarm/W0.5 采样频率fsample/kHz20
系统中运行到稳态后采集到1s的波形如图9a所示。以其中一个周期的波形为例,如图9b所示。对该周期的电压信号进行分解,近似系数如图9c所示,该波形为原波形的特征。细节系数如图9d所示,该周期内共有4个充电波形和1个放电波形,其中充电周期①、②和③的充电时间过短,可能会导致无法准确地提取充电信号,故以充电周期④来计算容值。真实的开关序列和还原后的开关序列对比如图9e和图9f所示,该算法有效还原了对应的开关序列。


图9 小波变换后的子模块电容电压仿真波形
Fig.9 Simulation waveforms of SM capacitor voltage after wavelet transform
计算时为避免因采样周期被截断造成计算不准确,去除第一个和最后一个运行周期后以第2~49个周期进行计算。计算出的容值如图10a所示,计算容值的中位数为10mF,计算误差由仿真系统引起,均为0.02%。为检验所提算法的运算复杂度,将采集数据延长到100s进行计算,算法的运行所需时间和计算结果如图10b所示。该算法所需运行时间约为0.7ms,对于计算要求较低即可实现对1s内的数据进行监测,能够在监测系统中实现。同时采样的数据不需要开关信号,因此可以直接将采样数据传送回上位机中进行监测。仿真结果证明,本文所提监测方法能够在很低的算法计算需求的前提下精确地监测电容器容值。

图10 全系统仿真结果
Fig.10 Results of full-system simulation
因容量、成本等限制,在实验室中难以搭建完整MMC平台[30]。因此,本文采用文献[31]中所提MMC工况模拟平台来复现完整MMC系统中单个子模块的工况。实验平台MMC系统电路结构如图11所示。

图11 实验平台MMC系统电路结构
Fig.11 Circuit structure of experimental MMC system
MMC工况模拟平台主要由主电源、全桥控制模块、被测子模块和辅助子模块构成。供电模块由全桥电路组成,全桥电路通过逆变直流电源向电路中提供桥臂电流以模拟桥臂上MMC子模块的工作电流,辅助子模块补偿被测子模块的电压直流分量从而降低直流母线电压,被测子模块和辅助子模块进行能量交换来补偿直流母线电流分量。该拓扑在降低了直流母线电压和电感需求的条件下,极大地提升了子模块上的输出电压,实现了在相同直流母线电压条件下提升电压测试的能力。
根据工况模拟平台电路结构搭建本文所用的实验测试平台,如图12a所示,电源柜为三台SP600VDC4000W可编程电源作为直流母线供电;模块柜中分别存放辅助子模块、被测子模块和电感,如图12b所示,辅助子模块使用两块IGBT模块FF1000R17IE4并联以提升辅助子模块的电流裕度,电容电压和桥臂电流分别通过差分探头DP6150A和电流探头CTB1000进行采集;控制柜主要控制模块柜中的循环水温度以及系统电源的开关;水冷箱对模块柜中的模块进行散热;实验平台测量到的桥臂电流和电容电压通过采集卡NI-6356采集后上传至上位机的Plecs软件,并通过Plecs控制DSP开发板DSP28377S实现对平台中子模块运行的调制。MMC工况模拟平台参数见表4。

图12 MMC工况模拟平台
Fig.12 MMC working condition simulation platform
表4 MMC工况模拟平台参数
Tab.4 Parameters of MMC mission profile emulator
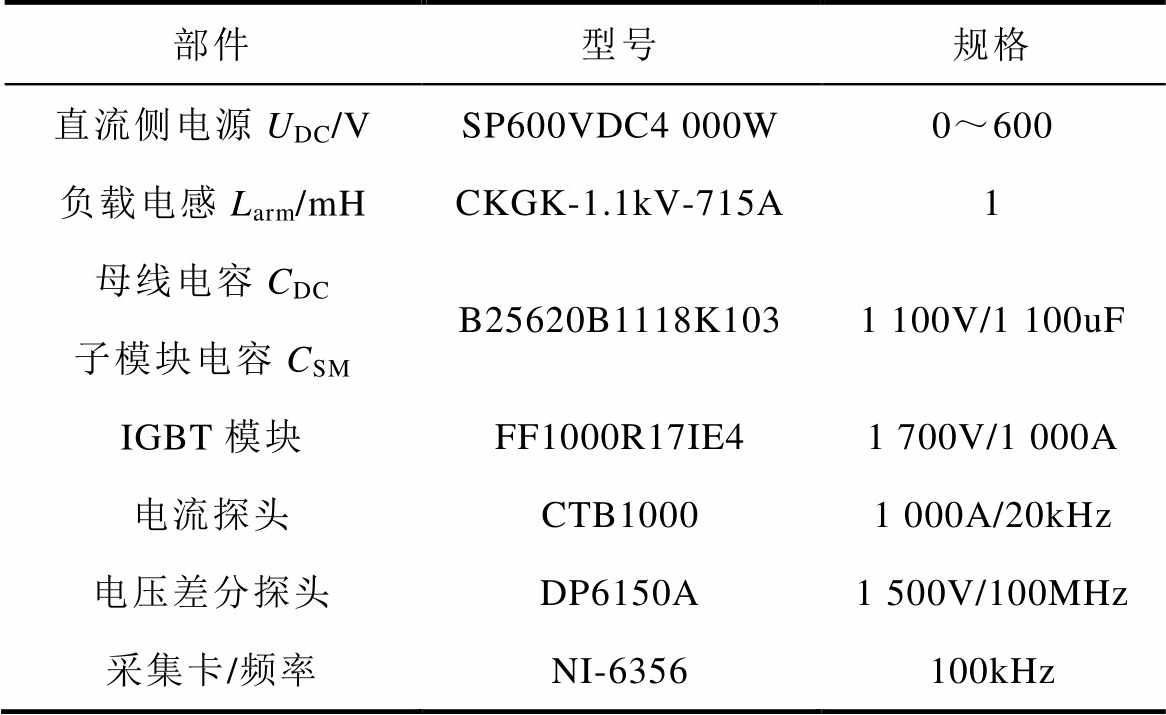
部件型号规格 直流侧电源UDC/VSP600VDC4 000W0~600 负载电感Larm/mHCKGK-1.1kV-715A1 母线电容CDCB25620B1118K1031 100V/1 100uF 子模块电容CSM IGBT模块FF1000R17IE41 700V/1 000A 电流探头CTB10001 000A/20kHz 电压差分探头DP6150A1 500V/100MHz 采集卡/频率NI-6356100kHz
被测子模块由IGBT模块FF1000R17IE4和电容器组构成。电容器组由10个1 100V/1 100mF的金属薄膜电容B25620B1118K103并联组成,采用LCR- 8110G LCR测试仪测量的容值为12.574 8mF,如图13a所示。造成该容值大于理论容值11mF的原因可能是电容母排的寄生电容、单体电容器容值分散性等因素所引起。为了模拟电容器老化,将电容器组中1个单体电容去掉以模拟容值降低,其实测值为11.493mF,如图13b所示。

图13 被测子模块实测电容值
Fig.13 Capacitance of SM under test
令MMC系统工作在最大电流为60A的工作模式下,电压电流在示波器的显示结果如图14所示,50kS/s表明测试平台可以正常运行。对该波形进行处理的结果如图15a所示,提取其中一个周期如图15b所示。将电压波形进行Haar小波变换,分解出的近似系数和细节系数分别如图15c和图15d所示。在实际采样中由于谐波和采样偏差等因素使得细节系数出现了4个充电周期,选取最大充电周期后以过滤无关信号的干扰。真实的开关序列和重构后的开关序列如图15e和图15f所示,重构序列与真实序列基本一致,但是由于采样噪声、误差等因素的干扰使得出现了多组无效的开关序列。通过选取最大的充电序列降低了无效开关序列对容值计算的 影响。

图14 测试平台示波器显示结果
Fig.14 Oscilloscope display results of test platform


图15 测试平台实验结果
Fig.15 Experimental results of test platform
为检验算法的准确性,根据本文方法对系统进行了100s内的容值测量,结果如图16a所示。对电容器组去除1个单体电容后,其测量结果如图16b所示。具体容值的在线监测结果与理论值的对比见表5。

图16 子模块电容值在线监测结果
Fig.16 Online monitoring results of SM capacitance
表5 子模块容值参考值和检测值实验结果对比
Tab.5 Comparison between reference capacitance and monitoring capacitance in experiment
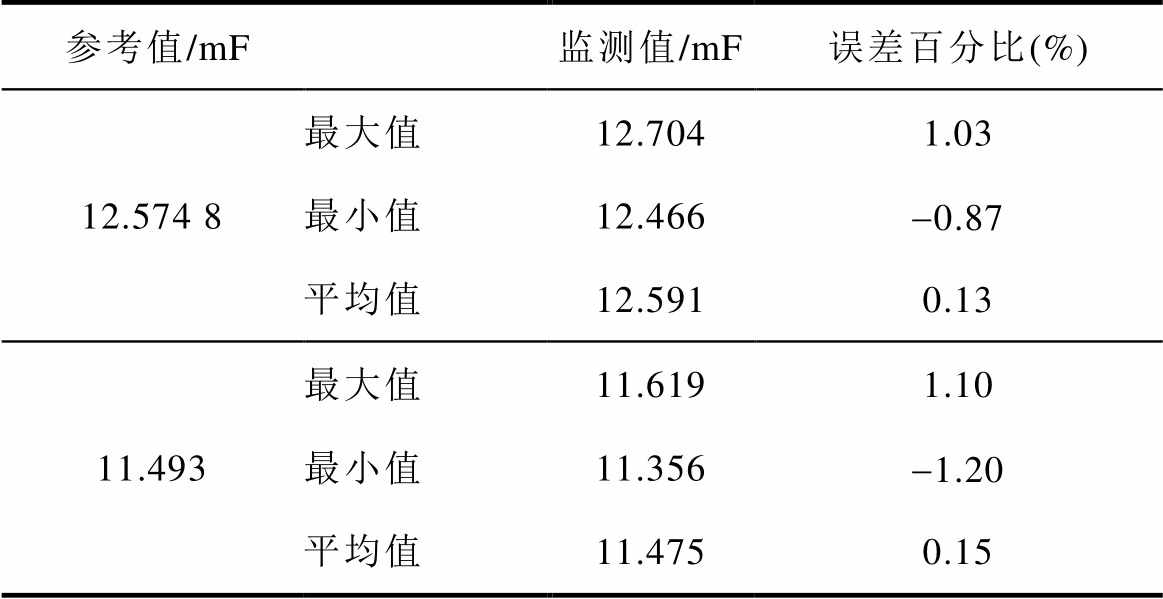
参考值/mF 监测值/mF误差百分比(%) 12.574 8最大值12.7041.03 最小值12.466-0.87 平均值12.5910.13 11.493最大值11.6191.10 最小值11.356-1.20 平均值11.4750.15
原电容器组在测量周期内的最大监测值为12.704mF,最小监测值为12.466mF,平均监测值为12.591mF,平均值误差为0.13%,误差波动范围为-0.87%~1.03%。去除1个单体电容后的电容器组在测量周期内的最大监测值为11.619mF,最小监测值为11.356mF,平均监测值为11.475mF,平均误差为0.15%,误差波动范围为-1.1%~1.2%。实验结果验证了本文所提监测方法的有效性和准确性。
本文针对模块化多电平换流器中子模块电容值监测问题,提出了一种通过Haar小波变换对子模块电压信号进行重构获取开关序列以计算容值的在线监测方法。得出了以下结论:
1)对MMC子模块电容电压进行Haar小波变换后,充电周期的细节系数为负,切除周期的细节系数为零,放电周期的细节系数为正。故根据小波变换的结果可以重构出子模块的开关序列。
2)根据本文方法利用MMC系统的子模块测量电压和桥臂电流可得电容值,实现在线对子模块电容进行状态检测。与传统方法相比,该方法可以减少对开关序列测量的需求,降低了检测的难度。其平均误差为0.15%,表明该方法具有较高准确性。
在未来的研究中计划将该方法集成于实际工程用MMC运维监控系统,为MMC系统电容器健康状态监测提供容值在线计算方法。
根据奈奎斯特采样定理最低采样频率仅需大于被测频率2倍即可满足频率不失真,但是过低的采样频率会引起待测信号的幅值失真[32]。文献[33]指出采样信号的最大幅值失真的误差为s,对应波形的采样点数的最小要求为
 (A1)
(A1)
此时采集系统的采样频率fsample和被测信号频率f0的关系需满足
 (A2)
(A2)
在计算容值时需要保证采集电流的准确性,被测信号采样点在采样周期内能够铺满充电周期,如附图1所示。
薄膜电容的失效标准为5%,故根据式(A1)可知,在保证幅值失真低于5%时的单个周期采样点数k至少为采被测频率的20倍。本文系统所用的IGBT开关频率f0= 250Hz,对应的采样频率fsample至少为5 000Hz。因此对于电压和电流的采样信号的采集频率仅需5 000Hz以上即可。采样频率越高,可以降低幅值失真的影响带来越准确的计算结果。

附图1 充电周期采样点数
App.Fig.1 Sampling points of charging cycle
参考文献
[1] Li Bo, Ma Ziming, Hidalyo-Gonzalez P, et al. Modeling the impact of EVs in the Chinese power system: pathways for implementing emissions reduction commitments in the power and trans- portation sectors[J]. Energy Policy, 2021, 149: 111962.
[2] 茆美琴, 程德健, 袁敏, 等. 基于暂态能量流的模块化多电平高压直流电网接地优化配置[J]. 电工技术学报, 2022, 37(3): 739-749.
Mao Meiqin, Cheng Dejian, Yuan Min, et al. Optimal allocation of grounding system in high voltage direct current grid with modular multi-level converters based on transient energy flow[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 739-749.
[3] 张志文, 雷诗婕, 翟承达, 等. 高压直流输电系统吸收与并联电容换相换流器特性分析[J]. 电工技术学报, 2019, 34(增刊2): 684-691.
Zhang Zhiwen, Lei Shijie, Zhai Chengda, et al. The characteristic analysis of HVDC system with absorp- tion and shunt capacitance commutated converter[J]. Transactions of China Electrotechnical Society, 2019, 34(S2): 684-691.
[4] 曹帅, 向往, 左文平, 等. 风电经柔性直流电网外送系统的交流故障诊断与穿越控制策略[J]. 中国电机工程学报, 2021, 41(4): 1295-1306.
Cao Shuai, Xiang Wang, Zuo Wenping, et al. AC fault diagnosis and ride-trough control strategy for the wind power delivery system via HVDC grid[J]. Pro- ceedings of the CSEE, 2021, 41(4): 1295-1306.
[5] 刘浔, 戴迪, 饶洪林, 等. 直流系统换流阀常见故障及处理方法[J]. 电子世界, 2015(21): 115-117.
Liu Xun, Dai Di, Rao Honglin, et al. Common faults and treatment methods of converter valve in DC system[J]. Electronics World, 2015(21): 115-117.
[6] Yang Shaoyong, Xiang Dawei, Bryant A, et al. Condition monitoring for device reliability in power electronic converters: a review[J]. IEEE Transactions on Power Electronics, 2010, 25(11): 2734-2752.
[7] 许建中, 李钰, 陆锋, 等. 降低MMC子模块电容电压纹波幅值的方法综述[J]. 中国电机工程学报, 2019, 39(2): 571-584, 654.
Xu Jianzhong, Li Yu, Lu Feng, et al. A review of suppression methods for sub-module capacitor voltage ripple amplitudes in modular multilevel converters[J]. Proceedings of the CSEE, 2019, 39(2): 571-584, 654.
[8] 贾科, 赵其娟, 冯涛, 等. 柔性直流配电系统高频突变量距离保护[J]. 电工技术学报, 2020, 35(2): 383-394.
Jia Ke, Zhao Qijuan, Feng Tao, et al. High-frequency fault component distance protection for flexible DC distribution system[J]. Transactions of China Electro- technical Society, 2020, 35(2): 383-394.
[9] 付华, 陈浩轩, 李秀菊, 等. 含边界元件的MMC- MTDC直流侧单端量故障辨识方法[J]. 电工技术学报, 2021, 36(1): 215-226.
Fu Hua, Chen Haoxuan, Li Xiuju, et al. MMC-MTDC DC side single-ended quantity fault identification method with boundary elements[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 215-226.
[10] 束洪春, 代月, 安娜, 等. 基于交叉重叠差分变换的MMC-HVDC线路故障识别方法[J]. 电工技术学报, 2021, 36(1): 203-214, 226.
Shu Hongchun, Dai Yue, An Na, et al. Fault identi- fication method of MMC-HVDC line based on sequential overlapping derivative transform[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(1): 203-214, 226.
[11] 王希平, 李志刚, 姚芳. MMC系统功率器件基频结温波动快速计算方法[J]. 中国电机工程学报, 2020, 40(18): 5805-5815.
Wang Xiping, Li Zhigang, Yao Fang. Simplified estimation of the fundamental frequency junction temperature fluctuation for IGBTs in modular multi- level converters[J]. Proceedings of the CSEE, 2020, 40(18): 5805-5815.
[12] Ronanki D, Williamson S S. Failure prediction of submodule capacitors in modular multilevel converter by monitoring the intrinsic capacitor voltage fluctu- ations[J]. IEEE Transactions on Industrial Electronics, 2020, 67(4): 2585-2594.
[13] Abushafa O, Atkinson D, Gadoue S, et al. A new scheme for monitoring submodule capacitance in modular multilevel converter[C]//8th IET Inter- national Conference on Power Electronics, Machines and Drives (PEMD 2016), Glasgow, UK, 2016: 1-6.
[14] Sun Yuting, Wang Mingyu, Ran Li. Capacitance monitoring method for metallized polypropylene film capacitor in MMC[C]//2019 IEEE Sustainable Power and Energy Conference (iSPEC), Beijing, China, 2019: 2431-2436.
[15] Deng Fujin, Qian Heng, Liu Chengkai, et al. Capa- citor ESR and C monitoring in modular multilevel converters[J]. IEEE Transactions on Power Electro- nics, 2020, 35(4): 4063-4075.
[16] Liu Chengkai, Deng Fujin, Yu Qiang, et al. Sub- module capacitance monitoring strategy for phase- shifted carrier pulse-width modulation based modular multilevel converters[J]. IEEE Transactions on Industrial Electronics, 2021, 68(9): 8753-8767.
[17] Jo Y J, Nguyen T H, Lee D C. Condition monitoring of submodule capacitors in modular multilevel con- verters[C]//Energy Conversion Congress & Exposition, Pittsburgh, PA, USA, 2014: 2121-2126.
[18] 辛熙锴, 马柯, 蔡旭. 工频周期四点电压采样的MMC子模块电容值在线监测方法[J]. 中国电机工程学报, 2021, 41(11): 3896-3903.
Xin Xikai, Ma Ke, Cai Xu. Online monitoring for sub- module capacitance in modular multilevel converter with four sampling points of capacitor voltage[J]. Proceedings of the CSEE, 2021, 41(11): 3896-3903.
[19] Wang Zhongxu, Zhang Yi, Wang Huai, et al. Capa- citor condition monitoring based on the DC-side start-up of modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2020, 35(6): 5589-5593.
[20] Wang Hanyu, Wang Huai, Wang Zhongxu, et al. Condition monitoring for submodule capacitors in modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2019, 34(11): 10403-10407.
[21] Xia Hongjian, Zhang Yi, Wang Huai, et al. Condition monitoring for capacitors in modular multilevel converter based on high-frequency transient analysis[C]// 2021 IEEE Energy Conversion Congress and Expo- sition (ECCE), Vancouver, BC, Canada, 2021: 5342- 5347.
[22] 夏宏鉴, 陈民铀, 赖伟, 等. 基于频带能量的模块化多电平换流阀中金属化薄膜电容器失效检测方法[J]. 中国电机工程学报, 2021, 41(22): 7782-7792.
Xia Hongjian, Chen Minyou, Lai Wei, et al. Failure detection method for metalized polypropylene film capacitor in modular multilevel converter based on band energy[J]. Proceedings of the CSEE, 2021, 41(22): 7782-7792.
[23] 徐政. 柔性直流输电系统[M]. 北京: 机械工业出版社, 2013.
[24] Yen G G, Lin K C. Wavelet packet feature extraction for vibration monitoring[J]. IEEE Transactions on Industrial Electronics, 2000, 47(3): 650-667.
[25] Rauber T W, de Assis Boldt F, Varejao F M. Hetero- geneous feature models and feature selection applied to bearing fault diagnosis[J]. IEEE Transactions on Industrial Electronics, 2015, 62(1): 637-646.
[26] Youssef O A S. A wavelet-based technique for discrimination between faults and magnetizing inrush currents in transformers[J]. IEEE Transactions on Power Delivery, 2003, 18(1): 170-176.
[27] 朱柏寒, 陈羽, 马金杰. 基于波前陡度的输电线路单端行波故障测距[J]. 电力系统自动化, 2021, 45(9): 130-135.
Zhu Baihan, Chen Yu, Ma Jinjie. Wavefront steepness based single-ended traveling wave fault location for transmission lines[J]. Automation of Electric Power Systems, 2021, 45(9): 130-135.
[28] 姜涛, 李孟豪, 李雪, 等. 电力系统强迫振荡源的时频域定位方法[J]. 电力系统自动化, 2021, 45(9): 98-106.
Jiang Tao, Li Menghao, Li Xue, et al. Time-frequency domain location method for forced oscillation source in power system[J]. Automation of Electric Power Systems, 2021, 45(9): 98-106.
[29] 苏燕, 徐艳华. 基于单片机的激光测距系统设计[J]. 激光杂志, 2017, 38(9): 128-131.
Su Yan, Xu Yanhua. Design of laser range system based on single chip microcomputer[J]. Laser Journal, 2017, 38(9): 128-131.
[30] 李恩溢, 马柯, 蔡旭. 模块化多电平变流器的子模块工况模拟测试方法[J]. 电力系统自动化, 2022, 46(4): 132-142.
Li Enyi, Ma Ke, Cai Xu. Operating condition simulation test method for sub-modules of modular multilevel converter[J]. Automation of Electric Power Systems, 2022, 46(4): 132-142.
[31] Tang Yuan, Ran Li, Alatise O, et al. Improved testing capability of the model-assisted testing scheme for a modular multilevel converter[J]. IEEE Transactions on Power Electronics, 2016, 31(11): 7823-7836.
[32] 王希东, 宋剑波, 任伟. 失真信号采样技术研究[J]. 电子测量与仪器学报, 2006, 20(1): 85-88.
Wang Xidong, Song Jianbo, Ren Wei. Study of the technique for acquiring the distorted signal[J]. Journal of Electronic Measurement and Instrument, 2006, 20(1): 85-88.
[33] 崔忠奎. 电测信号数据采集误差与采样频率确定[J]. 佳木斯工学院学报, 1988, 6(2): 26-30.
Cui Zhongkui. Data acquisition error and sampling frequency determination of electrical measurement signal[J]. Journal of Jiamusi University (Natural Science Edition), 1988, 6(2): 26-30.
Online Monitoring Method for Sub-Module Capacitance in Modular Multilevel Converter Based on Haar Wavelet Transform Reconstruction Switch Sequence
Abstract As the core component of the modular multilevel converter (MMC) systemsub-module (SM), the capacitoris one of the most fragile components due to its long-term working environment of high-frequency and high-power. Therefore, real-time monitoring of capacitor status is very important to ensure the reliable operation of the MMC system. In this paper, an online monitoring method for SM capacitance in MMC based on Haar wavelet transform reconstruction switch sequence is proposed. Firstly, the input and excision switch sequence of submodule is reconstructed by Haar wavelet transform on the capacitor voltage signal of the MMC system. Secondly, the voltage signal during charging period of the capacitor is selected based on the reconstructed switching sequence, and the capacitance value is monitored online combined with the bridge current signal. Finally, the accuracy and effectiveness of proposed method are verified by the MMC system working condition simulation platform. The proposed method can evaluate the capacitance through the capacitor voltage and arm current signals from the control system, which greatly reduces the difficulty of monitoring by removing the need for switching signals. It provides theoretical and method support for capacitor condition monitoring and active operation and maintenance of the MMC system.
keywords:Modular multilevel converter (MMC), capacitor online monitoring, switching sequence, wavelet transform
DOI: 10.19595/j.cnki.1000-6753.tces.220198
中图分类号:TM46
国家重点研发计划项目(2018YFB0905800)、中央高校基本科研业务费项目(2020CDJQY-A026)、国家自然科学基金资助项目(51707024)、国家自然科学基金资助项目(5200070692)和高等学校学科创新引智计划(111计划)项目(B08036)资助。
收稿日期 2022-02-15
改稿日期 2022-03-21
罗 丹 男,1991年生,博士研究生,研究方向为电力电子可靠性。E-mail: walluodan@163.com
赖 伟 男,1986年生,副教授,博士生导师,研究方向为电力电子。E-mail: laiweicqu@126.com(通信作者)
(编辑 陈 诚)