
图1 电力电子换流器建模框架
Fig.1 Modeling framework of the power converter
摘要 随着电力电子换流器的开关频率越来越高,对电力电子化系统实时仿真的精度提出更高的要求,基于电感/电容(L/C)等效的定导纳开关模型是目前的主流开关模型之一,但这种模型的开关暂态过程存在“虚拟功率损耗”问题,开关频率越高,仿真结果失真越严重。该文首先构建电力电子换流器小步长模型的离散状态空间形式,基于此,构建电力电子换流器的小步合成实时仿真模型,保留L/C模型恒导纳特性的同时有效地消除了由开关支路主导的工作模态的暂态过程,进一步分析L/C开关模型支路对电力电子换流器的工作模态的影响,通过小步合成模型消除L/C模型引入的特征值,使L/C模型更精准地模拟理想开关,同时保留系统的正常工作模态。分别构建双有源桥、三相两电平逆变器和三电平逆变器的小步合成模型并进行实时仿真,与传统实时仿真模型对比表明,所提小步合成模型在不影响仿真效率的前提下,有效地解决了L/C开关模型的“虚拟功率损耗”问题,且具有较好的通用性,无需重新设置开关参数即可适用于多种拓扑。
关键词:小步合成法 L/C模型 电力电子换流器 实时仿真 虚拟功率损耗
随着可再生能源发电、储能系统、电动汽车等电力电子设备和系统越来越广泛地接入到电力系统中[1-2],电力电子化已逐渐成为新型电力系统的重要特征,随之带来了多时间尺度电磁暂态特性的相互作用。新型电力系统逐渐形成了一套多时间尺度的仿真策略[3],对于不同的研究场景,电力电子设备及系统需要采用不同精度和效率的仿真模型。
对于电力电子器件级仿真,常采用包含多物理场、多时间尺度的精确开关物理模型[4];对于电力电子变换器级仿真,常采用可反映开关伏安特性的行为模型,一般也称为小步长模型;对于电力电子化系统级仿真,常采用平均值模型[5]、动态相量模型[6]、等效电路模型[7-8]等,可有效提高仿真效率。
在电力电子变换器级仿真中,电力电子开关模型的选择很大程度上决定了仿真的效率与精度。目前主要有两类经典模型:一类为Ron/Roff模型,又称二值电阻模型,文献[9]和Typhoon HIL将该模型用于固定拓扑的实时仿真场景中,但Ron/Roff模型在每次开关动作后都需要重新形成系统节点导纳矩阵,因而制约着仿真效率的提升;另一类为电感/电容(L/C)模型,又称恒导纳模型,因其具有开关动作前后等效导纳不变的特性,被广泛应用于电力电子系统实时仿真中,但其存在“虚拟功率损耗”的问题,严重影响仿真精度。如何同时保证电力电子开关模型的仿真效率与仿真精度是亟需解决的问题。
对于L/C模型,RTDS基于L/C模型开发了“Small_dt”电力电子元件库[10];OPAL-RT将L/C模型应用于电力电子工具包eHS中[11];ADPSS[12]和许多基于现场可编程逻辑门阵列(Field Program- mable Gate Array, FPGA)的实时仿真平台[13-15]也都采用L/C模型。但是,与理想开关相比,L/C模型在开关动作后会存在明显的暂态误差,产生严重影响仿真精度的虚拟功率损耗。为了保证L/C模型计算效率的同时有效解决“虚拟功率损耗”问题,目前主要有三类方法:
(1)设置“最优”模型参数:L/C模型的暂态过程与等效导纳参数相关,通过寻找接近理想开关特性的“最优参数”以减小“虚拟功率损耗”[16-17]。
(2)新开关模型:提出广义定导纳模型(Gen- eralized Associated Discrete Circuit model, G-ADC)[18]、改进定导纳模型[12]等。
(3)开关动作后初始化:L/C模型开关动作后的初始状态决定了开关暂态过程,通过对开关动作后的状态初始化以消除“虚拟功率损耗”[18-19]。
尽管上述方法都可以在一定程度上解决“虚拟功率损耗”问题,但它们普遍存在两个局限性:
(1)开关模型的“最优参数”与电路拓扑和运行状态相关,在复杂拓扑情况下计算过程复杂,且不一定存在“最优参数”。
(2)仿真步长越小,L/C模型虚拟功率损耗越低,但仿真步长受限于硬件计算能力,L/C模型的虚拟功率损耗目前不可忽略。
L/C模型的基本思想是将开关在导通时等效为小电感,关断时等效为小电容,开关模型的引入导致电力电子换流器模型的刚性增强,加剧了保证数值稳定性的小步长要求与保证实时仿真的计算效率要求之间的冲突[20]。本文基于同样存在明显刚性问题的运载火箭姿态运动建模[21-22],提出了一种电力电子换流器小步合成实时仿真模型。该模型使用纳秒级Dt步长进行建模以解决数值稳定性和虚拟功率损耗的问题,并使用微秒级DT步长进行仿真以满足实时仿真的计算效率要求,采用该模型仅需两个并行计算步骤即可完成单步仿真循环,电力电子换流器建模框架如图1所示。
本文以电力电子换流器为研究对象,分析开关支路采用L/C模型对整个换流器模型的影响,通过采用小步合成方法消除L/C模型所产生的虚拟功率损耗。首先基于节点分析法将电力电子换流器模型整理为离散状态空间方程的形式;然后进一步基于小步合成方法构建电力电子换流器小步合成实时仿真模型,该模型可以有效压缩由开关暂态过程主导的暂态过程,减小虚拟功率损耗,消除L/C模型对系统其余模态的影响;最后小步合成模型从电力电子换流器系统的角度出发,从根本上解决了L/C模型虚拟功率损耗问题,无需重新设置开关参数即可适用于任意拓扑结构,通过双有源桥(Dual Active Bridge, DAB)[23]、三相两电平逆变器和T型三电平逆变器的算例进行了验证。
在电磁暂态仿真中,L/C开关模型采用小电感模拟开关的导通状态,采用小电容模拟开关的关断状态,L/C模型通过离散化得到等效导纳并联历史电流源的诺顿等效电路形式[10],建模框架如图1所示。
恒导纳模型使开通和关断时的等效导纳相等,有效地避免了每次开关动作后重新构造系统的导纳矩阵造成的仿真计算量成倍增加,解决了这一问题。

图1 电力电子换流器建模框架
Fig.1 Modeling framework of the power converter
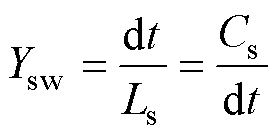 (1)
(1)
式中,Ls、Cs分别为L/C离散模型的等效电感和等效电容。
L/C离散模型的历史电流源可整理为由上一时刻的支路电压与支路电流表示,即
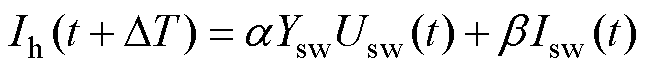 (2)
(2)
式中,a 和b 为待定系数,当采用后向欧拉法进行离散化时,可以得到
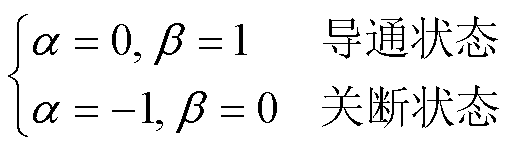 (3)
(3)
在电力电子换流器的电磁暂态仿真中,各条支路相互耦合,为了有效抑制开关动作后的暂态过程,需要对整个电力电子换流器系统进行分析。首先构建换流器整体的离散状态空间方程[24],电力电子换流器中的所有元件支路可以表示为式(2)的矩阵形式,即
 (4)
(4)
式中,Yb为支路导纳矩阵;Ub为支路电压矩阵;Ib为支路电流矩阵。当开关导通或者支路元件为电感时,b 中对应的元素为1,其余元素均为0;当开关关断或者支路元件为电容时,a 中对应的元素为-1,其余元素均为0。
1)节点电压Ub的推导
根据节点分析法,节点电压Ub可以由支路电压Un得到,即
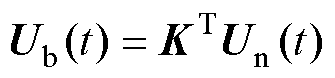 (5)
(5)
式中,K为关联矩阵。当支路j从节点i流出时,K(i, j)=1;当支路j从节点i流入时,K(i, j)=-1;当支路j从节点i无关时,K(i, j)=0。进一步分析可知,节点电压Un可以由节点电流In得到,即
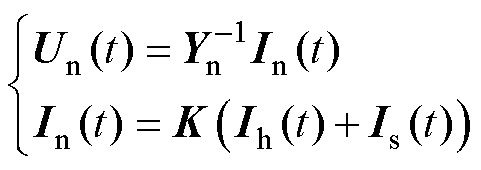 (6)
(6)
式中,Yn为节点导纳矩阵;In为节点电流,主要由历史电流Ih和外部电源诺顿等效电路的电流Is组成。根据式(5)和式(6)可以看出,支路电压Ub可以用历史电流Ih和外部注入电流Is表示。
2)支路电流Ib的推导
类似地,可以得到支路电流Ib为
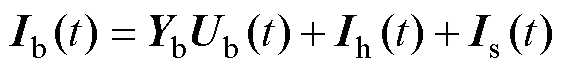 (7)
(7)
3)状态方程
将Ub和Ib的计算式(5)和式(7)代入式(4)中,以历史电流Ih为状态变量,以外部注入电流Is为输入变量,可以得到电力电子换流器的离散状态方程为
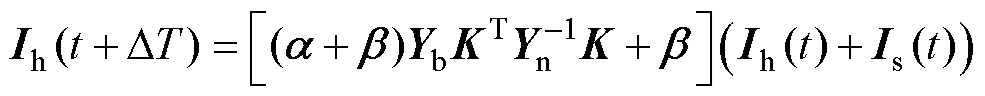 (8)
(8)
4)输出方程
选取节点电压Un与支路电流Ib为输出变量,将式(6)和式(7)合并为输出方程,可以得到
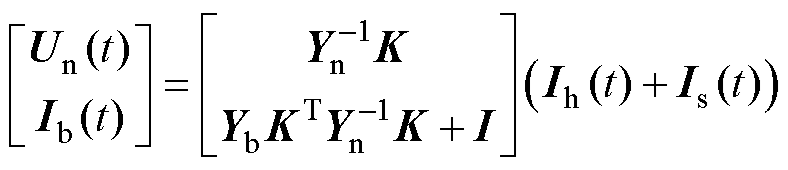 (9)
(9)
式(8)和式(9)即为电力电子换流器的离散状态空间描述形式,也可以称为电力电子换流器的离散状态空间模型,如图1所示,表示为
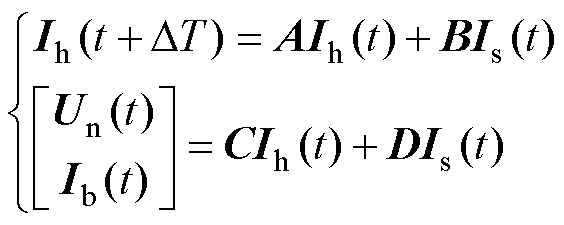 (10)
(10)
电力电子换流器的离散状态空间模型的仿真循环如图2所示。
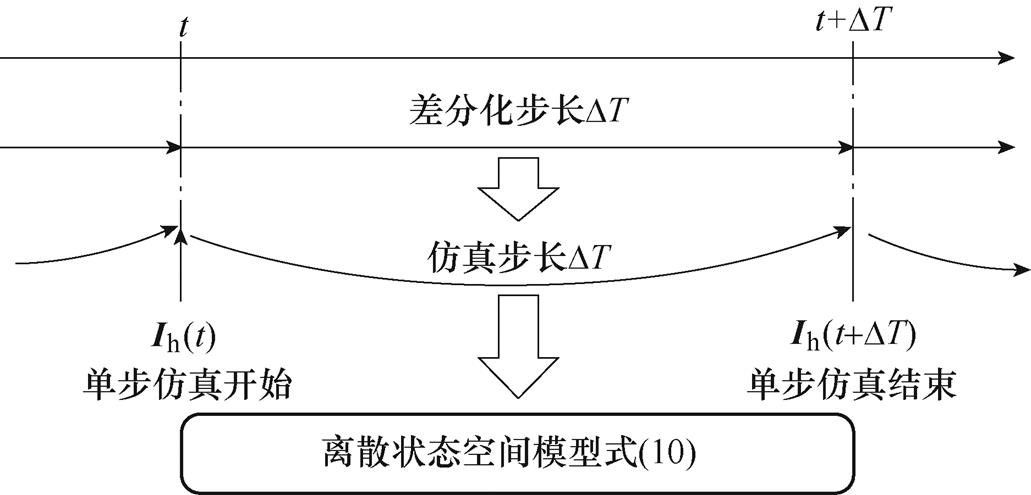
图2 离散状态空间模型的仿真循环
Fig.2 Simulation cycle of discrete state space model
在电力电子换流器系统离散状态空间模型中,仿真步长与建模差分化步长一致,均为DT。在小步合成方法中,仿真步长依旧为DT,而系统建模采用小于仿真步长的建模差分化步长Dt,小步合成模型的仿真循环如图3所示。下面基于电力电子换流器系统的离散状态空间模型构建电力电子换流器的小步合成模型。
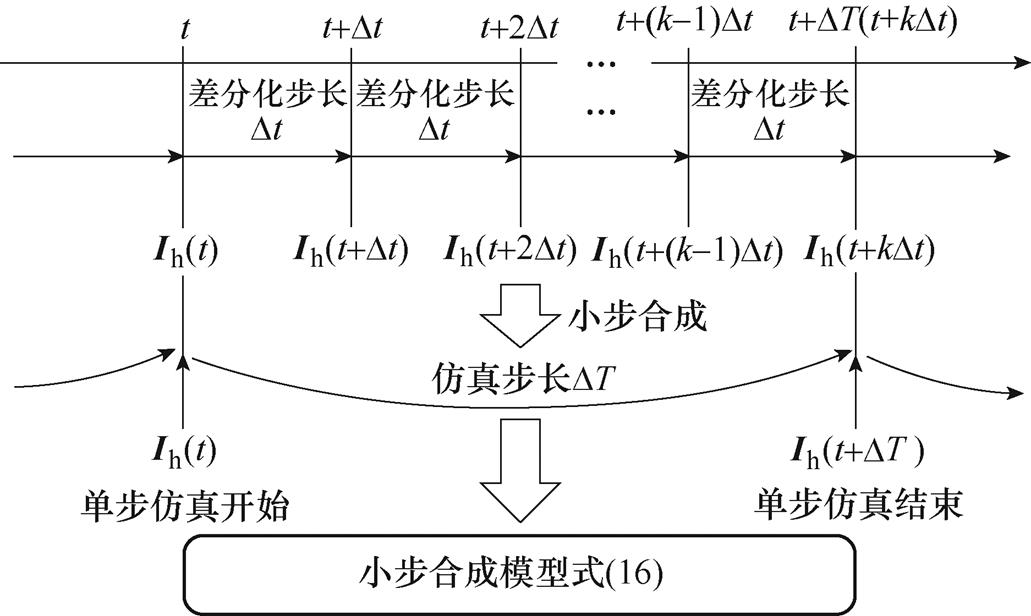
图3 小步合成模型的仿真循环
Fig.3 Simulation cycle of small-step synthesis model
以单步仿真步长DT作为整个仿真时间,采用电力电子换流器离散状态空间模型式(10)对时间[t, t+DT]内的历史电流源更新的初值问题进行分析。
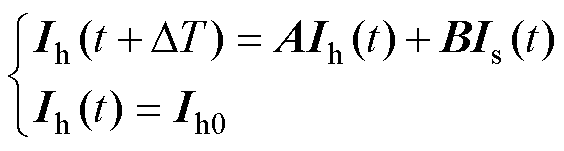 (11)
(11)
将单仿真步长区间[t, t+DT]分为k个相等的差分化步长Dt,分界点为
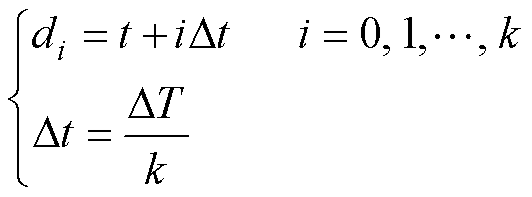 (12)
(12)
在单步仿真中,系统采用差分化步长Dt重构式(11)中的矩阵A和B,可得每一个差分化步长Dt更新历史电流源的状态方程变为
 (13)
(13)
式中,矩阵E和F均由式(10)中的状态方程采用步长Dt进行差分化得到。当按照一个仿真步长DT进行仿真时,则需要对矩阵E和F进行合成,在单仿真步长区间[t, t+DT]内进行如下迭代计算得到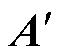 和
和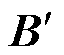 分别为
分别为
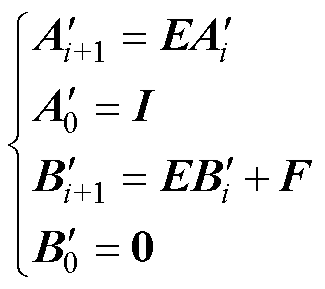 (14)
(14)
新的状态矩阵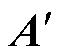 和输入矩阵
和输入矩阵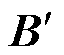 即为差分化步长为Dt、仿真步长为DT对应的矩阵,代入式(11)初值问题,可得t+DT时刻的历史电流为
即为差分化步长为Dt、仿真步长为DT对应的矩阵,代入式(11)初值问题,可得t+DT时刻的历史电流为
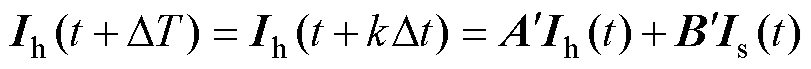 (15)
(15)
矩阵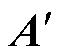 和
和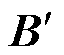 取决于仿真步长DT和差分化步长Dt,将仿真步长DT分为k个差分化步长Dt,并基于差分化步长Dt进行系统建模,再将基于差分化步长Dt计算得到的电路状态矩阵合成至仿真步长DT对应的电路状态矩阵中。从计算形式上看,小步合成方法按仿真步长DT进行仿真,但与采用差分化步长Dt进行仿真的计算结果是一致的。小步合成模型的仿真循环如图3所示。
取决于仿真步长DT和差分化步长Dt,将仿真步长DT分为k个差分化步长Dt,并基于差分化步长Dt进行系统建模,再将基于差分化步长Dt计算得到的电路状态矩阵合成至仿真步长DT对应的电路状态矩阵中。从计算形式上看,小步合成方法按仿真步长DT进行仿真,但与采用差分化步长Dt进行仿真的计算结果是一致的。小步合成模型的仿真循环如图3所示。
根据小步合成模型的推导过程,可以进一步整理,将式(10)改写为
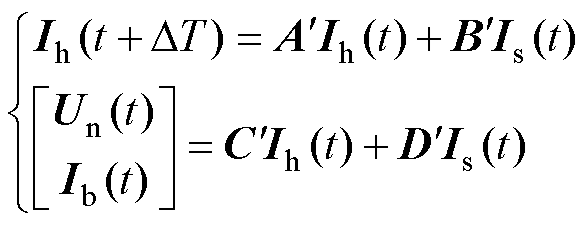 (16)
(16)
式中,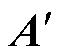 、
、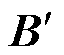 、
、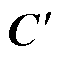 和
和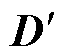 均采用差分化步长Dt并结合小步合成模型的步长合成过程式(14)计算得到,与A、B、C和D是维度一样的常系数矩阵,保留了L/C模型的恒导纳特性。
均采用差分化步长Dt并结合小步合成模型的步长合成过程式(14)计算得到,与A、B、C和D是维度一样的常系数矩阵,保留了L/C模型的恒导纳特性。
对比式(10)和式(16)的推导过程可以看出,小步合成模型对应的系数矩阵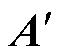 、
、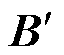 、
、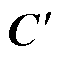 和
和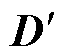 与基于传统节点分析法的电力电子换流器离散状态空间模型对应的系数矩阵A、B、C和D仅在差分化建模过程中采用的步长不同,但矩阵的维度仍保持一致,没有增加电力电子换流器的小步合成法模型的计算复杂度,仍保留了离散状态空间模型的并行计算优势。下面对电力电子换流器系统小步合成模型的根轨迹及其工作模态进行分析。
与基于传统节点分析法的电力电子换流器离散状态空间模型对应的系数矩阵A、B、C和D仅在差分化建模过程中采用的步长不同,但矩阵的维度仍保持一致,没有增加电力电子换流器的小步合成法模型的计算复杂度,仍保留了离散状态空间模型的并行计算优势。下面对电力电子换流器系统小步合成模型的根轨迹及其工作模态进行分析。
半桥电路广泛应用于电压源型三相两电平逆变器、半桥型模块化多电平换流器(Modular Multilevel Converter, MMC)等由半桥结构组成的换流器中,同样也应用于单相两电平逆变器、全桥型MMC、DAB等由全桥结构组成的换流器中,为不失一般性,选取半桥为基本结构进行模态分析。
在半桥子模块中,仅考虑两种工作模态:①开关S1导通、开关S2关断;②开关S1关断、开关S2导通。由于上下开关对称,在本文中仅分析第①种工作模态,采用后向欧拉法对半桥电路中的每个元件支路均进行离散化,得到图4所示的离散系统,图中,YC为电容的等效导纳,YL为电感的等效导纳,Ysw为开关的等效导纳。
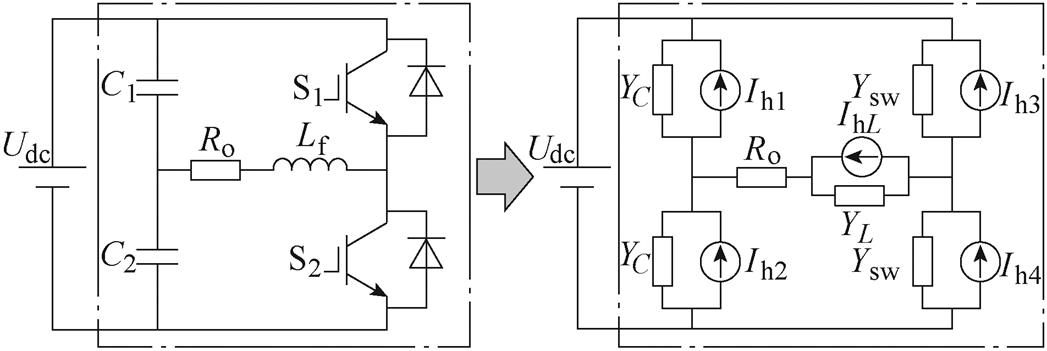
图4 半桥电路离散化
Fig.4 Discretization of half-bridge converter
选取各个元件支路的历史电流源Ih为状态变量,直流电压Udc为输入变量,构建其离散状态方程为
 (17)
(17)
式中,A为状态矩阵;B为系数矩阵,具体表达式见附录;选取直流电压Udc=100V,仿真步长为1ms,开关等效导纳Ysw=1S,电感等效导纳YL=0.001S,电容等效导纳YC=100S,负载电阻为1W,可以得到其状态矩阵A为
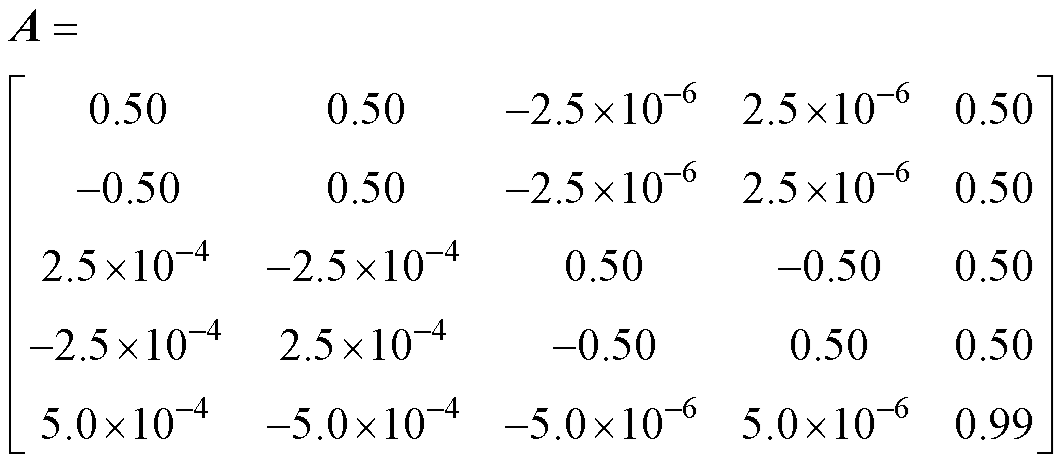 (18)
(18)
根据离散时间系统稳定性理论,离散状态矩阵A的特征值决定了系统的暂态响应特性。通过对半桥系统特征矩阵A的计算,可以得到其特征值为
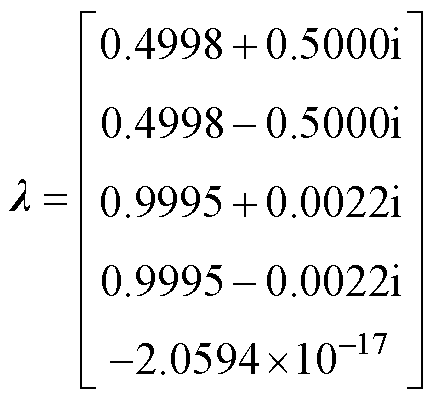 (19)
(19)
根据特征值可以看出,l1和l2对应于一个振荡频率较高的振荡模态,l3和l4对应于一个振荡频率接近于0的模态,l5可近似认为等于0,对应于一个非振荡稳定模态。
一般情况下,每一个特征值均对应一个系统模态,由于各支路之间相互耦合,每一条支路状态变量Ih都与系统的模态相关联。为了确定每一个状态变量Ih和模态之间的关系,通过计算参与矩阵P,度量状态变量Ih和模态之间关联程度。
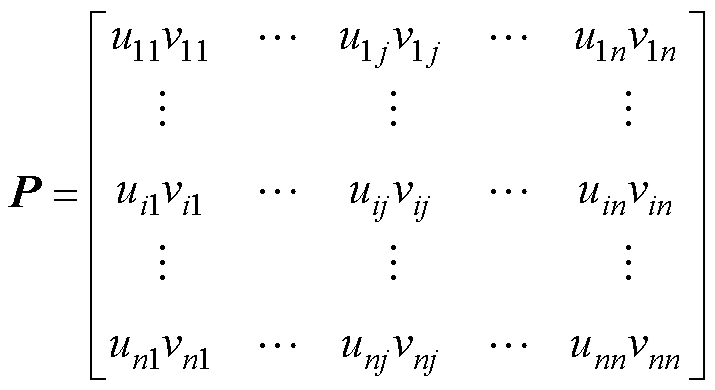 (20)
(20)
式中,Pij=uijvij为参与因子,通过参与因子的相对大小可以判断出来第i个状态变量和第j个系统模态的相互参与程度;uij为状态矩阵A对应的右特征值向量中的元素;vij为状态矩阵A对应的左特征值向量中的元素。
对于半桥系统,可以得到状态矩阵A对应的参与矩阵P为
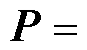
 (21)
(21)
根据半桥系统的参与矩阵P可以看出,特征值l1和l2受开关支路的历史电流的影响最大,该模态对应于开关动作后的明显暂态过程,也是造成L/C模型虚拟功率损耗的根本原因;特征值l3和l4主要受电容支路和电感支路的影响,该模态的阻尼很大,在一个仿真步长中可以认为该模态对应的状态变量Ih保持不变,因此一般在对小步长开关分析时可以将电容等效为电压源,电感等效为电流源;特征值l5主要受电容支路的影响,该非振荡模态可以认为对系统的影响微乎其微。
为了消除特征值l1和l2对应的模态所造成的开关暂态误差,一般采用减小步长的方法。随着仿真步长从10ms减小至10ns,半桥电路离散状态空间模型的特征值如图5所示。
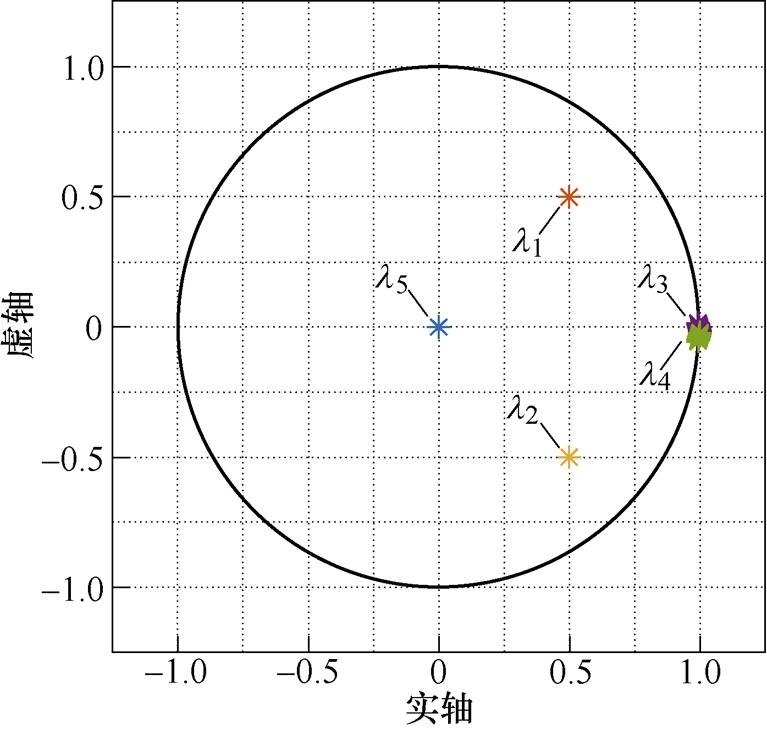
图5 半桥电路离散状态空间模型的特征值
Fig.5 Eigenvalues of discrete state space model of half-bridge converter
图5中,随着仿真步长的减小,系统特征值l1~l5均没有明显变化,L/C开关模型支路主导的特征值l1和l2仍会导致开关动作后产生明显暂态过程,虚拟功率损耗问题不能得到有效解决。目前大多数实时仿真器难以完成100ns步长及以下的实时仿真,因此减小仿真步长不是解决虚拟功率损耗问题的根本办法。小步合成法为这一问题提供了新的解决思路,可以在保持系统原有特征值l3、l4和l5对应的工作模态的前提下,消除L/C开关模型主导的特征值l1和l2所引入的振荡工作模态,有效抑制开关动作后的暂态过程,解决虚拟功率损耗问题。
从3.1节中的分析可知,单纯减小仿真步长Dt不能有效解决“虚拟功率损耗”问题,如何在不影响电路正常工作模态的情况下,有效消除由L/C模型引入的特征值,即可消除“虚拟功率损耗”问题。在本节中对半桥模块构建小步合成模型,并进行根轨迹及模态分析。选择仿真步长为1ms,仿真步长DT与差分化步长Dt之比k为变量,得到半桥系统小步合成模型的根轨迹,如图6所示。
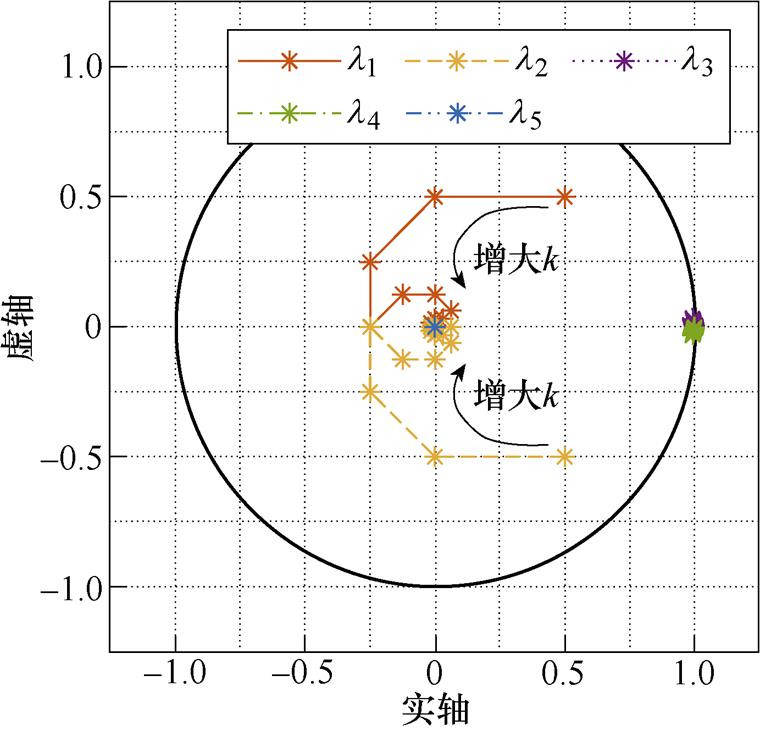
图6 半桥电路小步合成模型的根轨迹
Fig.6 Eigenvalues of small-step synthesis model of half-bridge converter
从图6中可以看出,随着仿真步长与差分化步长之比k的增大,由开关支路主导的特征值l1和l2逐渐趋向原点,表明L/C开关模型引入的振荡工作模态逐渐消失,开关动作后的暂态过程逐渐消失,L/C模型越来越趋近于理想开关,“虚拟功率损耗”问题也随之解决。而由电路其他元件支路主导的特征值l3、l4和l5仍基本保持不变,保留了半桥模块原有的工作模态。对比电力电子换流器离散状态空间模型和小步合成模型的特征值的模,如图7所示。
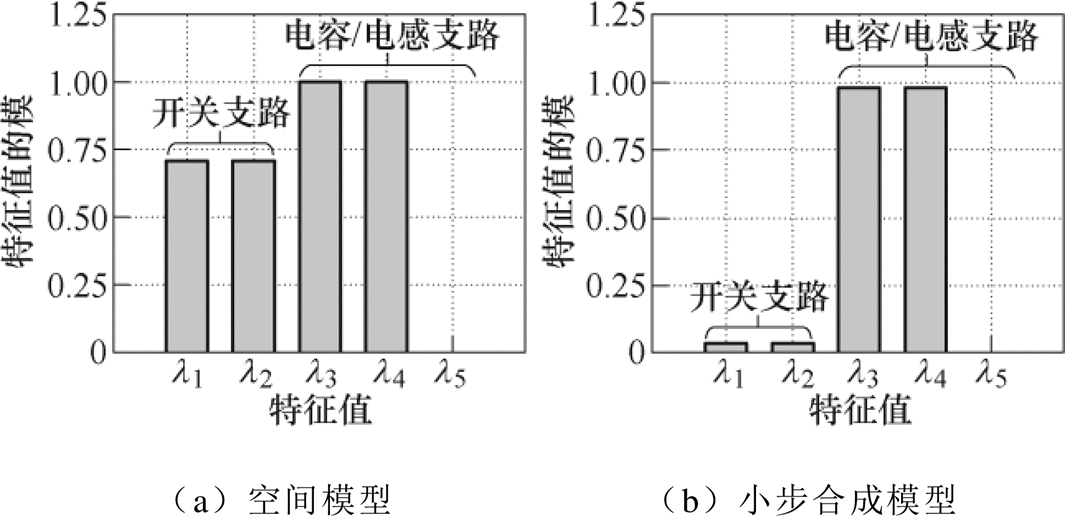
图7 半桥电路的离散状态空间模型和小步合成模型特征值对比
Fig.7 Comparison of eigenvalues of discrete state space model and small-step synthesis model
从图7中可以看出,小步合成模型有效消除了由L/C模型引入的特征值所造成的影响,同时又保留换流器的正常工作模态,针对性地解决了L/C模型引入的虚拟功率损耗问题。一般情况下,L/C小步长开关模型选取的电容/电感值都远小于电路其余支路,因此开关支路相对于系统来说动态过程很慢,由于开关支路主导的特征值基本不受其他支路的干扰,因此小步合成模型可以有效抑制L/C开关模型引入的局部振荡模态。
为了验证小步合成模型的有效性,本文基于NI-PXI系统的CPU-FPGA实时仿真平台[13]开展实验验证。其中CPU控制器为NI PXIe-8135(含Intel i7-3610QE处理器),FPGA模块为NI PXIe-7975R(含Xilinx K7系列FPGA),仿真步长为250ns,L/C模型等效导纳为1S。本文采用DAB作为实时仿真算例。电路参数为:直流电压源400V;变压器漏感160mH;输出电容200mF;负载电阻50W;开关频率10~40kHz;采用输出电压控制,输出电压为200V。分别采用以下三种模型对DAB进行建模与实时仿真。图8a为PLECS离线仿真波形,作为基准仿真结果,其中开关采用理想开关模型;图8b采用DAB的小步合成模型进行实时仿真波形,其中开关采用L/C开关模型,数值积分方法采用后向欧拉法,仿真步长DT与建模步长Dt之比k=30;图8c采用DAB的离散状态空间模型(非合成的小步长模型)进行实时仿真测试,其中开关采用L/C开关模型,数值积分方法采用后向欧拉法。

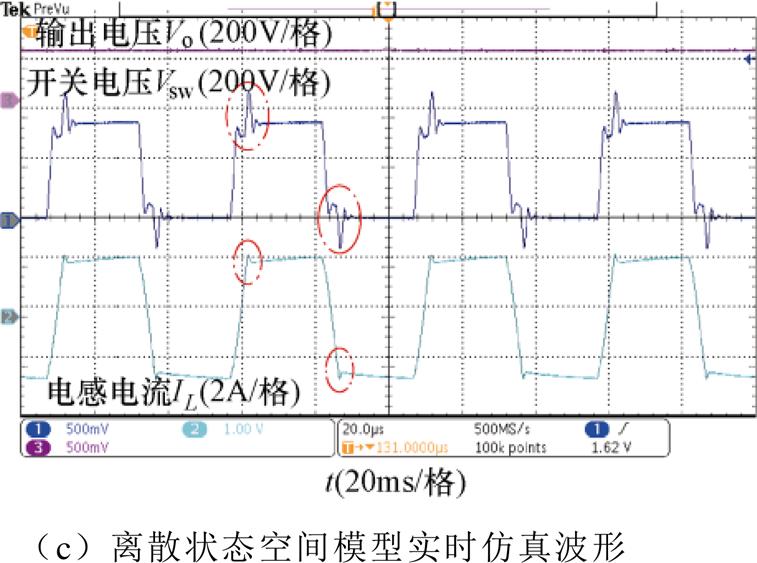
图8 DAB的开关电压、电感电流和输出电压的仿真结果对比
Fig.8 Comparison of simulation results of DAB switch voltage, inductor current and output voltage
图8a为在PLECS离线仿真中DAB的输入侧开关S的电压、流过开关S的电流(变压器一次侧漏感的电流)和输出电压的波形,图8b为采用小步合成模型进行实时仿真的DAB的输入侧开关S的电压、流过开关S的电流(变压器一次侧漏感的电流)和输出电压的波形,图8c为采用离散状态空间模型进行实时仿真的DAB的输入侧开关S的电压、流过开关S的电流(流过变压器一次侧漏感的电流)和输出电压的波形。对比三组仿真结果可以看出,采用离散状态空间模型进行仿真,在开关动作后存在明显的暂态过程,与理想开关存在明显差别;而小步合成模型不仅稳态结果与PLECS一致,同时可以消除开关动作后的暂态过程,有效解决虚拟功率损耗问题。
电力电子换流器小步合成模型主要解决L/C开关模型引入的虚拟功率损耗问题,但虚拟功率损耗往往因开关频率或换流器拓扑的变化而改变,为了验证小步合成模型的精确性和通用性,本节针对不同开关频率和不同换流器拓扑,测试采用不同模型进行仿真所产生的虚拟功率损耗。考虑电路中其他元件均为理想元件,因此定义输入功率Pin与输出功率Pout之差为虚拟功率损耗Ploss。
4.2.1 不同开关频率下的虚拟功率损耗
图9展示了开关频率分别为10kHz和40kHz时的开关电压波形,保持输出功率恒定。从图9a中可以看出,采用离散状态空间模型,开关在动作后会存在持续10ms的明显暂态过程,而小步合成模型则可以使开关动作后快速收敛至稳态。从图9b中可以看出,在40kHz的开关频率下,L/C模型在开关动作后的暂态过程占整个开关周期的56%。随着开关频率的增加,开关动作后的暂态过程占据开关周期的比例增加,因而导致虚拟功率损耗随之增加;而小步合成模型不受开关频率的影响,开关波形均接近理想开关。
表1展示了在不同开关频率下的虚拟功率损耗占输入功率的比例,可以看出,开关频率在10kHz以上时,离散状态空间模型所造成的虚拟功率损耗已经严重影响了仿真结果的准确性,而小步合成模型可以在宽载波频率范围内均实现低虚拟功率损耗,使仿真结果更精确。
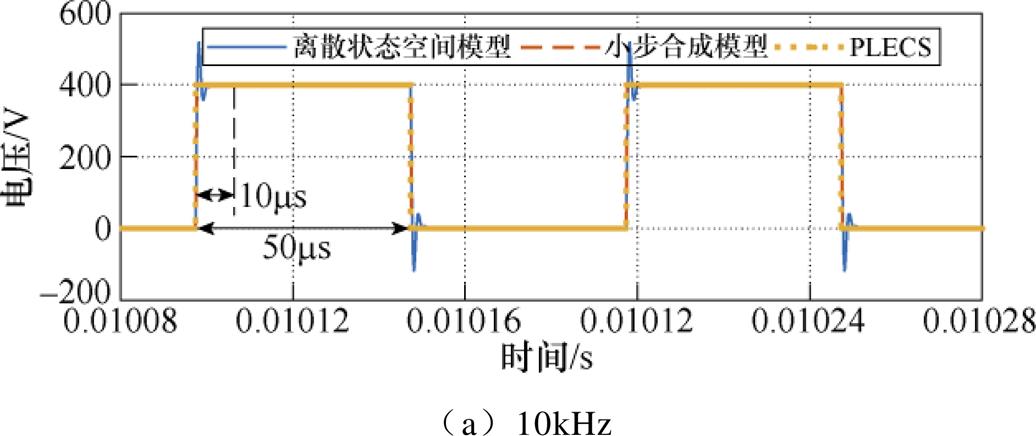

图9 不同开关频率下DAB开关电压对比
Fig.9 Comparison of DAB switch voltage under different carrier frequencies
表1 不同开关频率下的虚拟功率损耗占输入功率的比例
Tab.1 Virtual power loss ratio under different switching frequencies

模 型虚拟功率损耗/输入功率(%) 10kHz20kHz40kHz DAB离散状态空间模型(非合成的小步长模型)7.7215.3631.52 DAB小步合成模型0.170.381.1
4.2.2 不同换流器拓扑的虚拟功率损耗
传统解决虚拟功率损耗的方法一般需要根据不同的拓扑重新设计L/C开关模型参数,而小步合成模型无需重新设计开关参数即可实现任意拓扑下的低虚拟功率损耗。本节中分别将小步合成方法应用于两电平逆变器和T型三电平逆变器中,分别测试其在不同开关频率下的虚拟功率损耗,如图10所示。
从图10中可以看出,采用离散状态空间模型,两电平逆变器和三电平逆变器的虚拟功率损耗随开关频率的变化而明显变化,均严重影响仿真精度;而采用小步合成模型,无需针对拓扑重新设计开关等效导纳参数,均可实现有效减小虚拟功率损耗,验证了小步合成模型的有效性与通用性。
4.2.3 不同等效导纳参数下的虚拟功率损耗
根据参考文献[16-17],L/C开关模型的等效导纳会影响开关动作后的暂态过程,一般情况下,等效导纳设置为0.001~10S的区间范围内。当系统参数保持不变时,选择不同的开关等效导纳参数,DAB和两电平逆变器的虚拟功率损耗对比如图11所示。
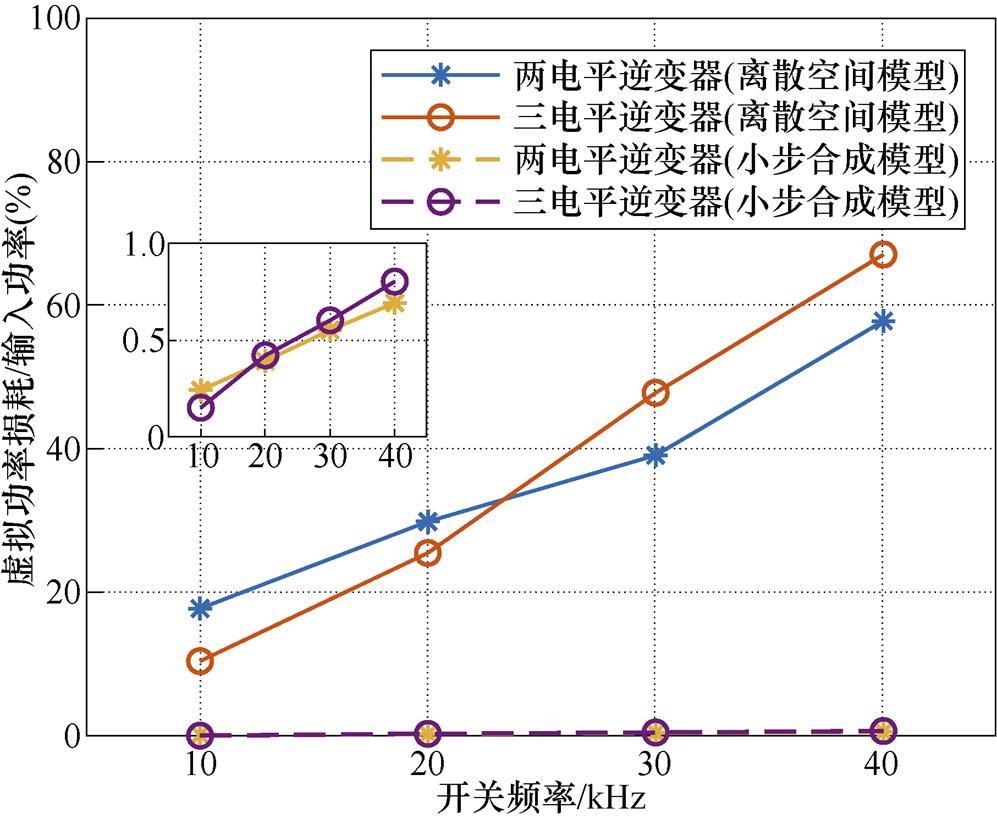
图10 不同拓扑下的虚拟功率损耗对比
Fig.10 Comparison of virtual power loss of different topologies
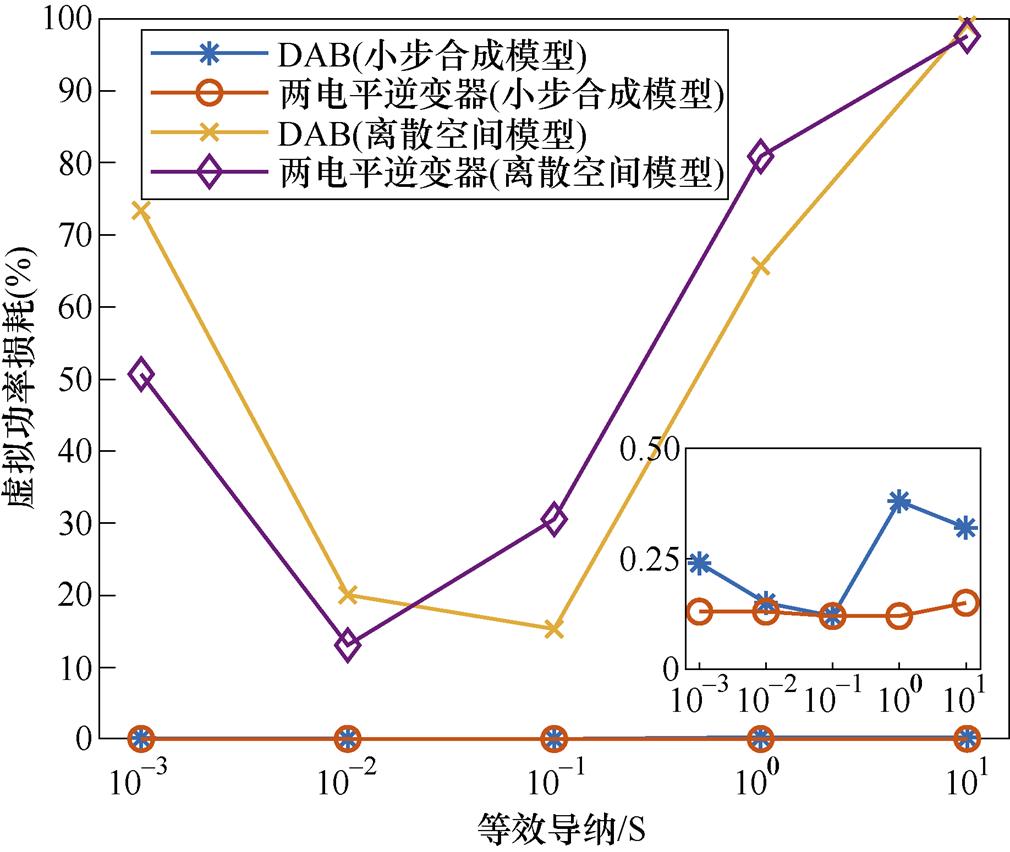
图11 不同等效导纳参数下的虚拟功率损耗对比
Fig.11 Comparison of virtual power loss of different equivalent admittances
从图11中可以看出,使用基于传统节点分析法法的离散状态空间模型,开关等效导纳参数的选择严重影响虚拟功率损耗,只有当开关等效导纳参数达到某一特定值(最优值)的时候,虚拟功率损耗最低,对应于开关参数的寻优过程。然而根据这一寻优过程往往又与拓扑相关,因此每一个拓扑对应的最优参数均不相同。相比之下,使用小步合成法进行实时仿真时,在较宽的开关等效导纳范围内的虚拟功率损耗均可忽略不计,同时无需根据拓扑重新设计L/C开关模型等效导纳参数。
本文提出了一种适用于电力电子换流器的小步合成实时仿真模型。电力电子换流器采用不同的步长分别进行建模与仿真,保留系统原有工作模态的同时压缩由开关暂态过程主导的模态,有效解决L/C模型的虚拟功率损耗问题,并满足实时性要求。在算例分析中,将小步合成模型与基于传统节点分析法的离散状态空间模型以及PLECS模型的仿真结果进行了对比。仿真结果表明,小步合成模型在不同拓扑和开关频率下,无需重新设置参数即可实现L/C模型的低虚拟功率损耗。综上所述,小步合成模型为解决虚拟功率损耗问题提供了新的思路,在仿真精度和模型通用性方面都更加适用于电力电子换流器实时仿真。
以下给出第3节中半桥电路的状态矩阵和输入矩阵,式(17)中的状态矩阵A可以表示为
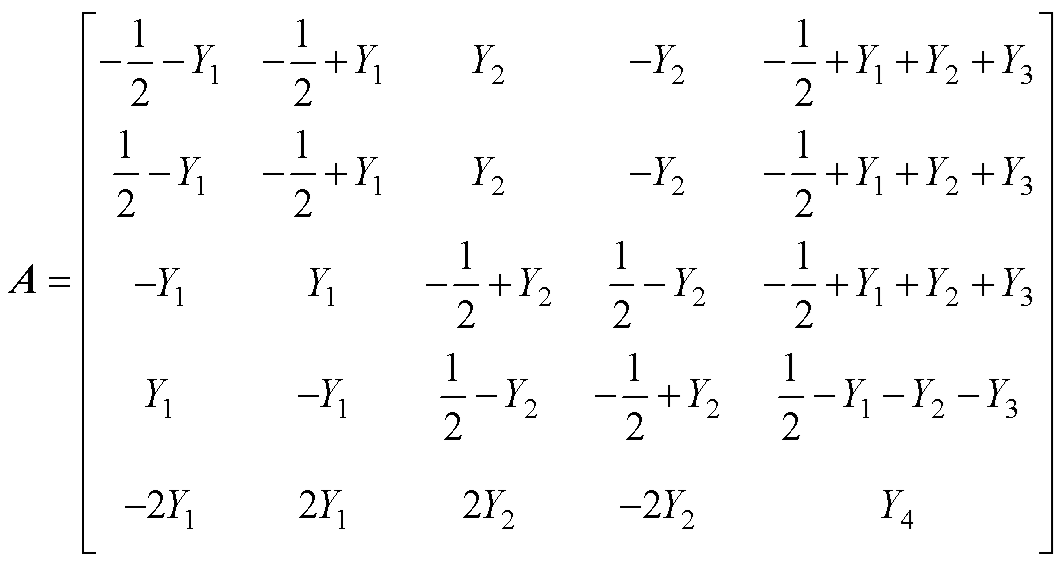 (A1)
(A1)
其中
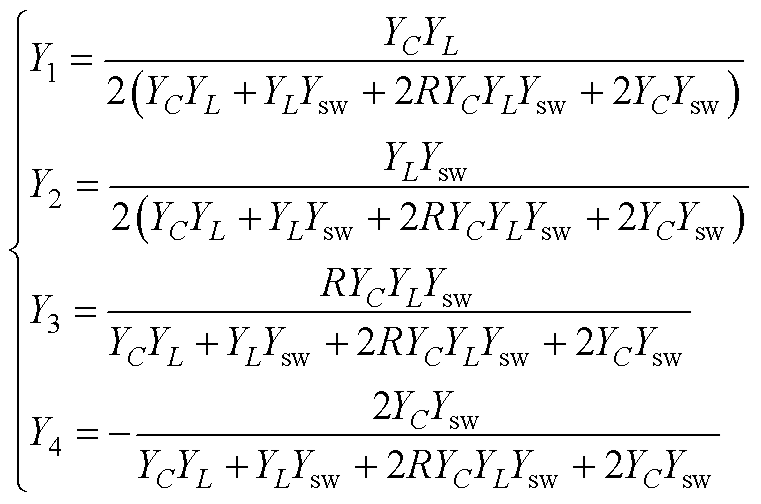 (A2)
(A2)
式(17)中的输入矩阵B可以表示为
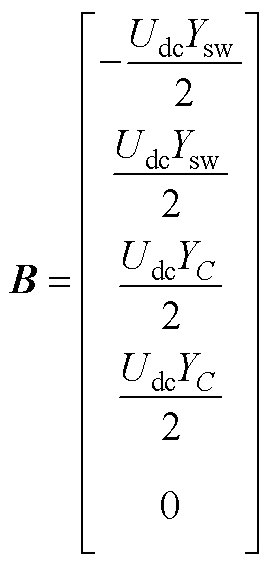 (A3)
(A3)
根据式(A2)可以得到式(18),进而分析半桥电路的特征值。
以下给出仿真步长DT与差分化步长Dt之比k的求解方法与常用范围。
根据式(14)和解线性方程组的迭代法,定义渐近收敛速度为
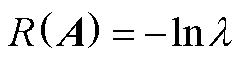 (A4)
(A4)
可以反映k趋于无穷时系统特征值的渐进性质,其中l 为状态矩阵A中LC开关模型对应的特征值。当特征值越小时,开关的暂态过程越短,LC模型越接近理想开关。根据式(A5)和式(A6)可以估计所需要的迭代次数k,即仿真步长DT与建模步长Dt之比k。
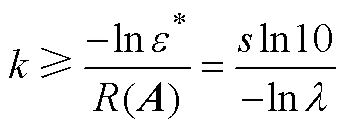 (A5)
(A5)
式中,e*为迭代n个步长后系统的误差向量en的范数与初始误差向量e0的范数的比值,一般情况下,令
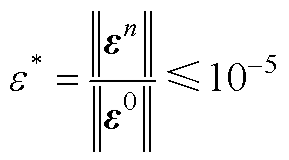 (A6)
(A6)
一般来说,k≥30即可满足特征值l 趋近于0的要求,保证L/C模型在开关动作后的一个仿真步长DT内即可达到稳态。若k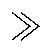 30,则会增加矩阵
30,则会增加矩阵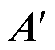 、
、 、
、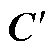 和
和 在预计算过程中的计算负担。
在预计算过程中的计算负担。
同时,根据参考文献[18]中整理得到的两电平换流器对应的状态矩阵和三电平换流器对应的状态矩阵采用小步合成方法,同样可以验证,当k=30时,即可满足L/C模型主导的特征值l 趋近于0的要求。因此在选择k时,可以通过上述渐近收敛速度进行验证。
参考文献
[1] 熊家祚, 张能, 翟党国, 等. 大规模电力电子设备接入的电力系统混合仿真接口技术综述[J]. 电力系统保护与控制, 2018, 46(10): 152-161.
Xiong Jiazuo, Zhang Neng, Zhai Dangguo, et al. Review of hybrid simulation interface technology for power system of large-scale power electronic equipment access[J]. Power System Protection and Control, 2018, 46(10): 152-161.
[2] Li Zirun, Xu Jin, Wang Keyou, et al. FPGA-based real-time simulation for EV station with multiple high-frequency chargers based on C-EMTP algo- rithm[J]. Protection and Control of Modern Power Systems, 2020, 5(1): 1-11.
[3] 徐晋, 汪可友, 李国杰. 电力电子设备及含电力电子设备电力系统实时仿真研究综述[J]. 电力系统自动化, 2022, 46(10): 8-22.
Xu Jin, Wang Keyou, Li Guojie. Review of real-time simulation of power electronic devices and power system integrated with power electronic devices[J]. Automation of Electric Power Systems. 2022, 46(10): 8-22.
[4] 黄华震, 仝涵, 王宁燕, 等. 考虑寄生振荡的IGBT分段暂态模型对电磁干扰预测的影响分析[J]. 电工技术学报, 2021, 36(12): 2434-2445.
Huang Huazhen, Tong Han, Wang Ningyan, et al. Analysis of the influence of IGBT segmented transient model with parasitic oscillation on electro- magnetic interference prediction[J]. Transactions of China Electrotechnical Society, 2021, 36(12): 2434- 2445.
[5] Liu Hong, Deng Zhanfeng, Li Xialin, et al. The averaged-value model of a flexible power electronics based substation in hybrid AC/DC distribution systems[J]. CSEE Journal of Power and Energy Systems, 2020, 8(2): 452-464.
[6] 解润生, 张国荣, 高凯, 等. 适用于频变输电线的动态相量谐波分析建模与仿真[J]. 电工技术学报, 2021, 36(15): 3200-3210.
Xie Runsheng, Zhang Guorong, Gao Kai, et al. Modeling and simulation of dynamic phasor harmonic analysis for frequency-dependent transmission line[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3200-3210.
[7] 许建中, 高晨祥, 丁江萍, 等. 高频隔离型电力电子变压器电磁暂态加速仿真方法与展望[J]. 中国电机工程学报, 2021, 41(10): 3466-3479.
Xu Jianzhong, Gao Chenxiang, Ding Jiangping, et al. Electromagnetic transient acceleration simulation methods and prospects of high-frequency isolated power electronic transformer[J]. Proceedings of the CSEE, 2021, 41(10): 3466-3479.
[8] 王洁聪, 刘崇茹, 徐东旭, 等. 基于实时数字仿真器的模块化多电平换流器内部故障混合仿真模型[J]. 电工技术学报, 2019, 34(18): 3831-3842.
Wang Jiecong, Liu Chongru, Xu Dongxu, et al. Hybrid simulation model of modular multilevel converter internal fault based on real-time digital simulator[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3831-3842.
[9] Maguire T, Elimban S, Tara E, et al. Predicting switch ON/OFF statuses in real time electromagnetic tran- sients simulations with voltage source converters[C]// 2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 2018: 1-7.
[10] Qi Li, Woodruff S, Steurer M. Study of power loss of small time-step VSC model in RTDS[C]//2007 IEEE Power Engineering Society General Meeting, Tampa, FL, 2007: 1-7.
[11] 孙鹏琨, 葛琼璇, 王晓新, 等. 基于硬件在环实时仿真平台的高速磁悬浮列车牵引控制策略[J]. 电工技术学报, 2020, 35(16): 3426-3435.
Sun Pengkun, Ge Qiongxuan, Wang Xiaoxin, et al. Traction control strategy of high-speed maglev train based on hardware-in-the-loop real-time simulation platform[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3426-3435.
[12] Mu Qing, Liang Jun, Zhou Xiaoxin, et al. Improved ADC model of voltage-source converters in DC grids[J]. IEEE Transactions on Power Electronics, 2014, 29(11): 5738-5748.
[13] 吴盼, 汪可友, 徐晋, 等. 基于CPU-FPGA异构平台的虚拟同步并网逆变器实时仿真算法设计[J]. 电力系统保护与控制, 2020, 48(14): 85-94.
Wu Pan, Wang Keyou, Xu Jin, et al. Real-time simulation algorithm design of a virtual synchronous grid-connected inverter system based on a CPU- FPGA heterogeneous platform[J]. Power System Protection and Control, 2020, 48(14): 85-94.
[14] Huang Zhen, Dinavahi V. A fast and stable method for modeling generalized nonlinearities in power elec- tronic circuit simulation and its real-time imple- mentation[J]. IEEE Transactions on Power Elec- tronics, 2019, 34(4): 3124-3138.
[15] 李鹏, 王智颖, 王成山, 等. 基于多FPGA的有源配电网实时仿真器并行架构设计[J]. 电力系统自动化, 2019, 43(8): 174-187.
Li Peng, Wang Zhiying, Wang Chengshan, et al. Design of parallel architecture for multi-FPGA based real-time simulator of active distribution network[J]. Automation of Electric Power Systems, 2019, 43(8): 174-187.
[16] 穆清, 周孝信, 王祥旭, 等. 面向实时仿真的小步长开关误差分析和参数设置[J]. 中国电机工程学报, 2013, 33(31): 120-129, 15.
Mu Qing, Zhou Xiaoxin, Wang Xiangxu, et al. Error analysis and parameters of switches in small step simulation for real-time simulation[J]. Proceedings of the CSEE, 2013, 33(31): 120-129, 15.
[17] 徐晋, 汪可友, 李国杰, 等. 基于参数化历史电流源的广义小步长开关模型[J]. 中国电机工程学报, 2018, 38(6): 1647-1654, 1901.
Xu Jin, Wang Keyou, Li Guojie, et al. A general small time-step model based on the parameterized history current sources[J]. Proceedings of the CSEE, 2018, 38(6): 1647-1654, 1901.
[18] Wang Keyou, Xu Jin, Li Guojie, et al. A generalized associated discrete circuit model of power converters in real-time simulation[J]. IEEE Transactions on Power Electronics, 2019, 34(3): 2220-2233.
[19] 曹阳, 顾伟, 柳伟, 等. 基于交叉初始化的换流器参数化恒导纳模型[J]. 中国电机工程学报, 2021, 41(10): 3518-3527.
Cao Yang, Gu Wei, Liu Wei, et al. A parameterized fixed-admittance model of converters based on cross initialization[J]. Proceedings of the CSEE, 2021, 41(10): 3518-3527.
[20] 檀添, 赵争鸣, 李帛洋, 等. 基于离散状态事件驱动的电力电子瞬态过程仿真方法[J]. 电工技术学报, 2017, 32(13): 41-50.
Tan Tian, Zhao Zhengming, Li Boyang, et al. Discrete state event driven based methods for transient simulation of power electronic converters[J]. Transa- ctions of China Electrotechnical Society, 2017, 32(13): 41-50.
[21] 费景高. 运载火箭姿态运动实时仿真建模的小步合成方法[J]. 导弹与航天运载技术, 1996(3): 26-33.
Fei Jinggao. The small step synthesis method for modelling for real-time digital simulation of the attitude motion of a launch vehicle[J]. Missiles and Space Vehicles, 1996(3): 26-33.
[22] 费景高. 计算机仿真建模方法(三)[J]. 计算机仿真, 1996, 13(2): 53-58.
Fei Jinggao. Lectures in modelling methods for computer simulation(3)[J]. Computer Simulation, 1996, 13(2): 53-58.
[23] Tong Anping, Hang Lijun, Chung H S H, et al. Using sampled- data modeling method to derive equivalent circuit and linearized control method for dual- active-bridge converter[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(2): 1361-1374.
[24] 韩应生, 孙海顺, 穆清, 等. 一种基于元件离散模型的系统状态空间构成新方法[J]. 中国电机工程学报, 2020, 40(20): 6569-6577.
Han Yingsheng, Sun Haishun, Mu Qing, et al. A novel approach to construct the power system state space based on the discrete-time state space model of the component[J]. Proceedings of the CSEE, 2020, 40(20): 6569-6577.
A Discrete Small-Step Synthesis Real-Time Simulation Model for Power Converters
Abstract L/C-based fixed admittance switch model is widely used in the system-level real-time simulation of power electronic systems. However, this model has the problem of “virtual power loss”, which seriously affects the simulation accuracy. The higher the switching frequency, the more distorted the simulation results are. In this paper, the discrete state space model of the power converter is firstly built. Based on this model, the small-step synthesis model is built, which can retain the constant admittance characteristics of the L/C model and effectively eliminate the transient process after the switching action. Further, this paper analyzes the influence of L/C model branches on operating modes of the converter, and eliminates the eigenvalues introduced by the L/C model. Thus, the L/C model can simulate the ideal switch more accurately, while retaining the normal operating mode of the system. Small-step synthesis models of half-bridge, dual active bridge and two-level converter are built and simulated. The simulation results show that the small-step synthesis model can be applied to a variety of topologies without complicated parameter settings while ensuring real-time performance, which effectively solves the virtual power loss problem.
keywords:Small-step synthesis method, L/C model, power converter, real-time simulation, virtual power loss
DOI: 10.19595/j.cnki.1000-6753.tces.211908
中图分类号:TM743
国家重点研发计划(2022YFE0105200)和国家自然科学基金(52107113, 51877133)资助项目。
收稿日期 2021-11-16
改稿日期 2022-04-11
李子润 男,1996年生,博士研究生,主要研究方向为新能源接入与分析、电力电子化系统建模与仿真等。E-mail: lzr9602@sjtu.edu.cn
徐 晋 男,1991年生,博士,助理教授,主要研究方向为电力系统分析、新能源接入、实时仿真与建模等。E-mail: xujin20506@sjtu.edu.cn(通信作者)
(编辑 陈 诚)