图1 ICR-DCB基础电路拓扑
Fig.1 Fundamental circuit topology of ICR-DCB
摘要 为满足分布式储能系统中蓄电池组与直流母线互联时对DC-DC变换器的高效率、高功率密度、宽电压调节范围的要求，该文提出一种中间电容谐振型级联双向DC-DC变换器。该级联变换器的低压侧采用改进的谐振型双有源桥（DAB），与传统DAB不同，该结构利用DAB高频变压器漏感与级联拓扑的中间直流母线电容进行谐振，工作频率在2倍谐振频率且在最高效率点运行；高压侧采用传统双向Buck-Boost拓扑，以提升电路的整体电压调节范围。该级联变换器具有中间直流母线电容小、电压调节范围宽、控制复杂度低、效率高、功率密度高的优点。该文首先，分析了变换器的拓扑结构、工作原理和控制策略；其次，推导了关键状态变量和电压增益；然后，建立了变换器的损耗模型，并据此进行谐振参数设计；最后，搭建了一台额定功率7.5kW的样机，其功率密度为1.15W/cm3，满载效率为95.9%，实验验证了该级联变换器高效率、高功率密度和宽电压调节范围的特性。
关键词：双有源桥（DAB）变换器 宽电压调节范围 损耗模型 谐振参数设计
具有宽电压调节范围、高升压比、高效率高功率密度的隔离双向DC-DC变换器是分布式储能系统中蓄电池组与直流母线互联的关键设备[1]，此外，还在电动汽车、轨道交通、智能电网、数据中心等领域得到了广泛应用[2]。目前应用于大功率隔离双向DC-DC变换器的拓扑普遍采用双有源桥（Dual Active Bridge, DAB），根据有无储能电感，可分为电压型DAB（Voltage-Fed DAB, VF-DAB）、电流型DAB（Current-Fed DAB, CF-DAB），根据是否谐振，又可分为非谐振型DAB和谐振型DAB。非谐振VF-DAB具有控制简便、易于进行模块并联的特点，但由于其关断损耗较大，限制了效率的提升[3-4]。针对效率的优化如最小回流功率优化[5]、电流应力优化[6]、电流有效值优化等，虽提高了效率但提升空间有限，且增加了控制复杂度。谐振型VF-DAB普遍采用串联谐振和LLC谐振，采用变频控制，具有软开关范围宽、关断电流小的特点[7]，但变频控制使大功率变压器磁心元件设计困难，同时能量双向流动切换速度较慢，变换器电流不可控，限制了模块并联和大功率场合的应用[8]。由于CF-DAB的直流端口侧串入一个较大的储能电感，抑制电流纹波，进而降低了高频变压器匝数比[9]，但由于变压器漏感的存在，当储能大电感与漏感串联时，由于两个电感上的电流不相等，有可能在开关管寄生电容上产生极高的电压尖峰而导致开关器件损坏[10]。
针对以上两种DAB的特点，文献[11]在LLC谐振型DAB的基础上增加了一种工作模态。文献[12]在LLC型的基础上增加辅助半桥支路，通过控制全桥和辅助半桥的驱动信号占空比，实现了固定开关频率下的宽电压范围调节，但文献[11]的二次侧开关管没有完全工作在同步整流中。文献[13]提出了输入电流型谐振单元，并扩展到谐振型DAB，通过储能电感和H桥之间的电容与变压器漏感进行谐振，抑制电压尖峰的同时可以实现零电压软开关（Zero Voltage Switching, ZVS）开通和准零电流软开关（Zero Current Switching, ZCS）关断，但缺少对其工作特性的详细分析。文献[14]通过在DAB一次侧增加两个电感支路，构成交错并联Buck-Boost的结构，使变压器漏感电流近似梯形波，降低电流应力的同时增大了电压调节范围，但导致关断电流较大。综上所述，通过拓扑的改进可以将谐振型VF-DAB与CF-DAB的特点相结合，通过谐振实现软开关，通过CF-DAB的储能电感降低电流应力。本文提出的拓扑将谐振电容移到全桥和储能电感之间，既实现软开关，又保留了CF-DAB的特点，同时抑制了传统CF-DAB可能出现的电压尖峰。
以上分析均为单级变换器，在宽电压调节范围、高效率高功率密度应用场合，如分布式储能系统中蓄电池组与直流母线互联时，单级谐振型DAB频率变化范围较大，不利于谐振参数优化，提高了对变压器磁心的设计难度，降低了效率和功率密度[15]。为了适应高效高功率密度、宽电压调节范围应用场合，通常采用级联结构，对于谐振型DAB，一般与Buck-Boost变换器构成级联结构。文献[16]提出DAB变换器与Buck-Boost变换器级联拓扑，其中DAB为采用频率跟踪控制的串联谐振结构，实现了谐振回路的低环流、开关的ZVS开通和低电流关断，但调频控制存在的固有不足无法避免。文献[15]提出一种高频变压器一次侧串联LLC与交错并联Buck-Boost的级联变换器以满足宽电压调节范围、低压大电流的应用，但为了实现前后两级解耦，需要较大的中间直流电容。文献[17]采用了LLC谐振型DAB变换器与Buck-Boost变换器级联实现峰值效率94.9%的宽范围输出，同样为了稳定中间直流母线电压，采用了较大的中间电容，降低了功率密度。文献[9]提出电流型DAB变换器与Buck-Boost变换器级联实现了50～150V/200V，但对于电流型DAB可能出现的电压尖峰问题没有进行改进，降低了变换器稳定性。综上所述，目前的级联变换器的拓扑存在中间直流电容较大、中间电感可能引起电压尖峰的问题。
为了在实现宽电压调节范围的同时，保证变换器的高效和高功率密度，本文提出一种中间电容谐振型DAB级联Buck-Boost变换器（Intermediate Capacitor Resonant DAB Cascaded Buck-Boost, ICR- DCB）。本文首先介绍ICR-DCB的拓扑结构和工作原理；其次建立谐振电路模型，推导谐振电感电流和谐振电容电压的表达式；然后建立ICR-DCB的损耗模型，提出谐振网络参数的优化设计方法，求取ICR-DCB的效率最高工作点；最后搭建一台额定功率7.5kW、额定电压60V/750V的ICR-DCB样机，验证上述分析的有效性。
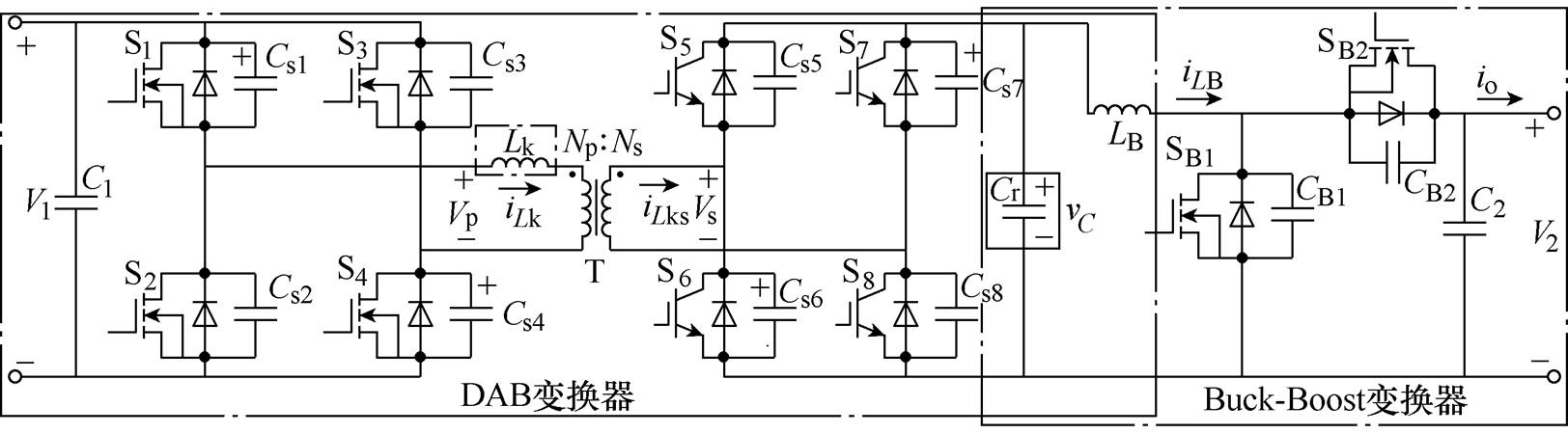
本文所提ICR-DCB的基础电路拓扑如图1所示。
图1 ICR-DCB基础电路拓扑
Fig.1 Fundamental circuit topology of ICR-DCB
图1中，V1为低压侧电压，vC为中间直流电容电压，V2为高压侧电压，Vp为变压器一次侧端电压，Vs为变压器二次侧端电压，变压器电压比N为Np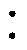
Ns，S1～S4与S5～S8分别构成两个全桥，Lk为高频变压器漏感，Cr为中间直流电容，SB1、SB2为Buck-Boost开关管，LB为Buck-Boost变换器的储能电感，C1为低压侧滤波电容，C2为高压侧滤波电容。iLk为变压器一次侧漏感电流，iLks为折算到二次侧的漏感电流，iLB为Buck-Boost变换器的电流，io为负载电流。
ICR-DCB在结构上与传统级联方法类似，可分为DAB变换器和Buck-Boost变换器两部分，二者通过中间直流电容Cr相连。不同之处在于，ICR- DCB的中间直流电容Cr与DAB变换器中的变压器漏感Lk工作在谐振状态，避免了传统级联方案需要较大的中间直流电容来实现直流母线电压稳定，降低了变换器体积，提高了功率密度。同时，谐振状态的工作使得ICR-DCB工作在软开关状态，提升了工作效率。同时，两部分之间的储能电感和中间电容对于DAB变换器起到降低电流应力的作用，对于Buck-Boost变换器起到升降压和滤波的作用，实现了储能电感和中间电容的复用。
本文所提变换器的前级采用开环控制，响应速度快，当遇到突加或突减负载时，能量的变化直接由电感Lr和LB承担，而中间母线电压的波动维持在较小的可控范围内，保证变换器快速可靠的动态特性。因此，在控制策略上，ICR-DCB的DAB变换器可以采用最优谐振频率开环控制以提高效率，Buck-Boost变换器则采用功率控制或输出电压控制以实现能量的双向流动，无需变频控制，既简化了控制复杂度又降低了磁性元件的设计难度，同时满足宽电压调节范围、大升压电压比的应用需要。在本文中Buck-Boost变换器采用电压外环、电流内环的双闭环控制。
ICR-DCB变换器的特点在于中间直流电容Cr与DAB变换器中的变压器漏感Lk工作在谐振状态，本节对此进行详细分析，Buck-Boost变换器的工作原理可参考文献[9]。
定义能量从低压侧流向高压侧表示正向工作，ICR-DCB的稳态工作时序如图2所示。
图2中，实线和虚线分别为正向和反向工作状态下ICR-DCB变换器的时序。Vg1为前级DAB的驱动信号，Vg2为后级Buck-Boost的驱动信号，fD为DAB变换器的开关频率，对应的周期为TD，D为开关管S1的占空比。Buck-Boost变换器的开关频率fB为DAB变换器开关频率fD的2倍，对应的周期为TB，d为SB2的导通占空比。[t0, tb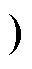
为Buck-Boost变换器的SB2导通时段，此时能量流向电容C2，流过电感LB的电流下降；[tb, t6]为SB1导通时段，此时能量由电容Cr流向电感LB，流过电感LB的电流上升。
以正向工作为例，前级DAB变换器在一个周期内存在6个工作模态，因前、后半个周期的工作模态对称，图3给出了前半个周期的3个工作模态示意图。
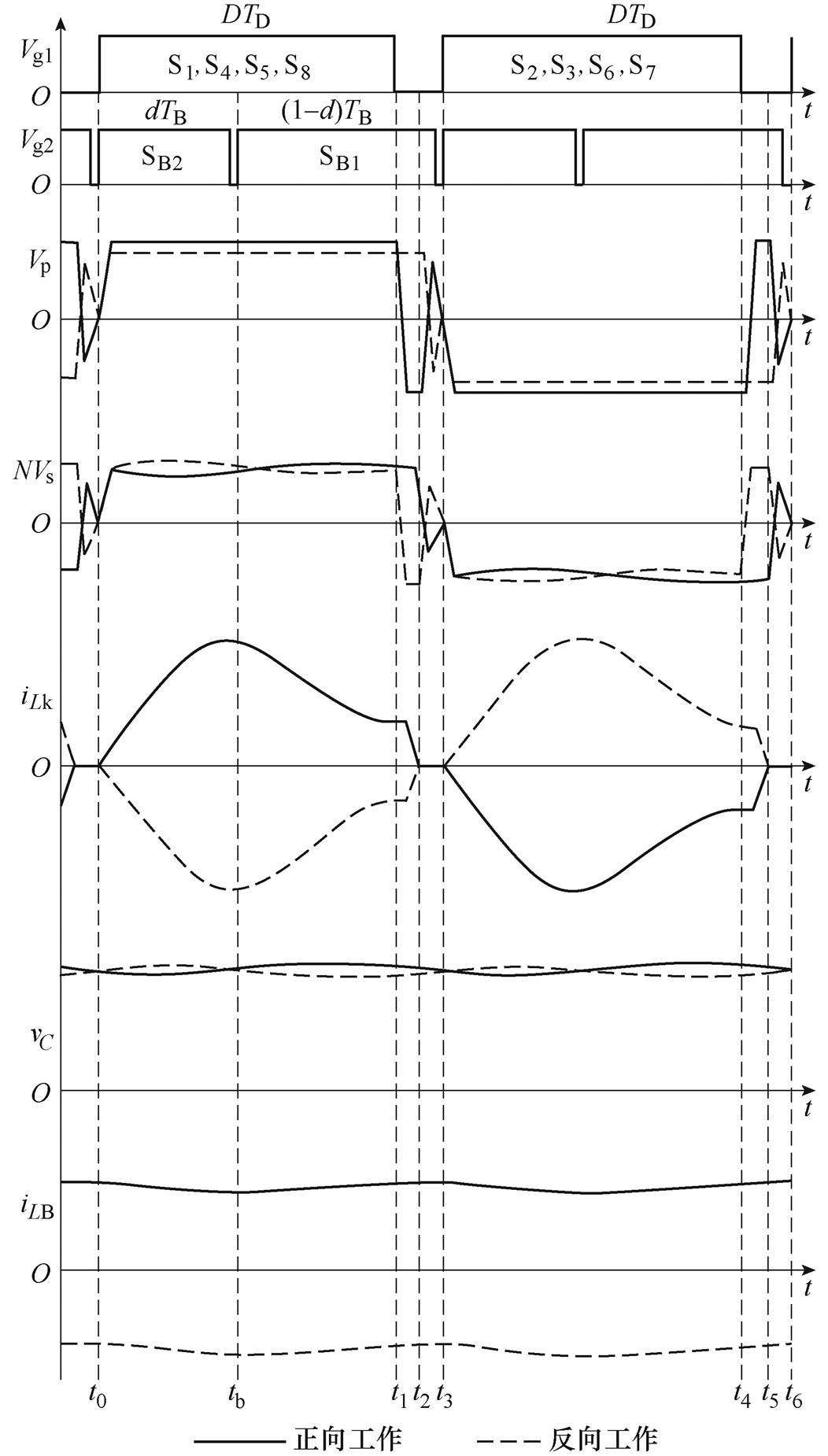
图2 工作时序
Fig.2 Working timing
工作模态1[t0, t1
：如图3a所示，t0时刻，开关管S1、S4的寄生电容向S2、S3的寄生电容充电结束，S1、S4两端电压降到0，此时开通S1和S4，实现ZVS开通，同理，开关管S5、S8的寄生电容向S6、S7的寄生电容充电结束，S5、S8两端电压降到0，实现S5、S8的ZVS开通。[t0, t1阶段，Lk和Cr谐振，漏感电流iLk在t0时刻从0开始谐振增大，等效电路如图4所示。图中，Cs6、Cs7分别为S6、S7寄生电容，两者相等；Rs为电源内阻与开关管导通电阻之和；Req为等效负载。该模态下的数学模型可以表示为
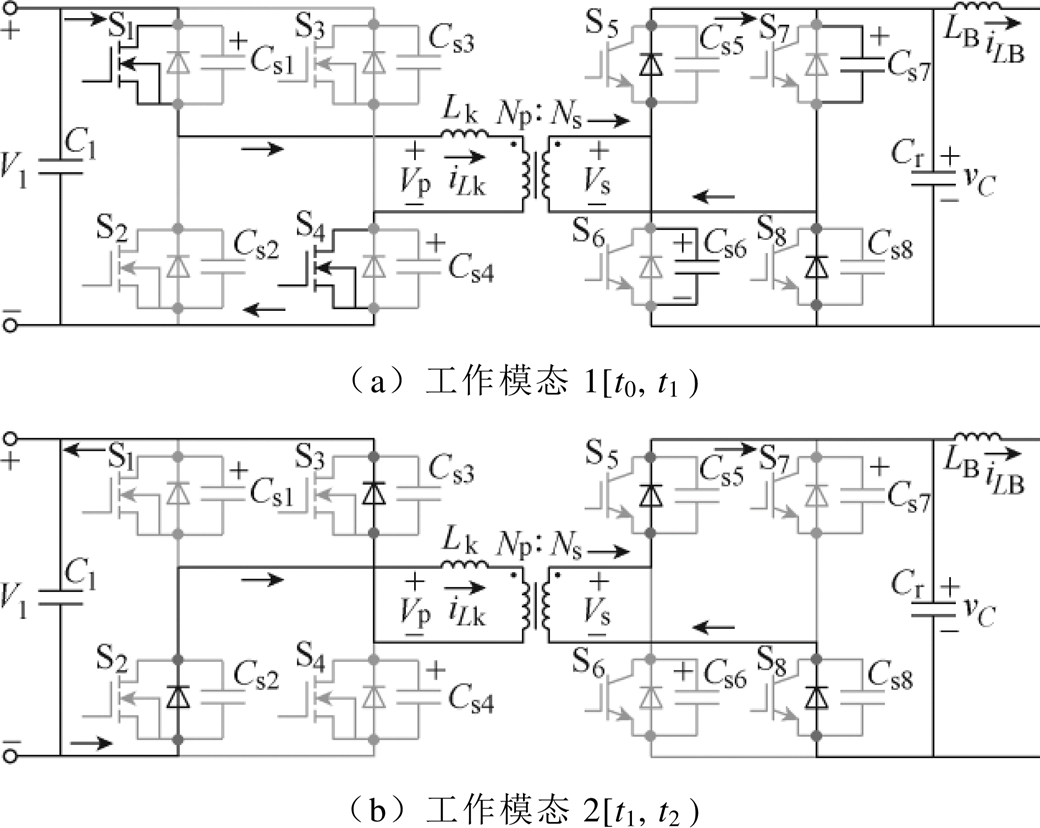
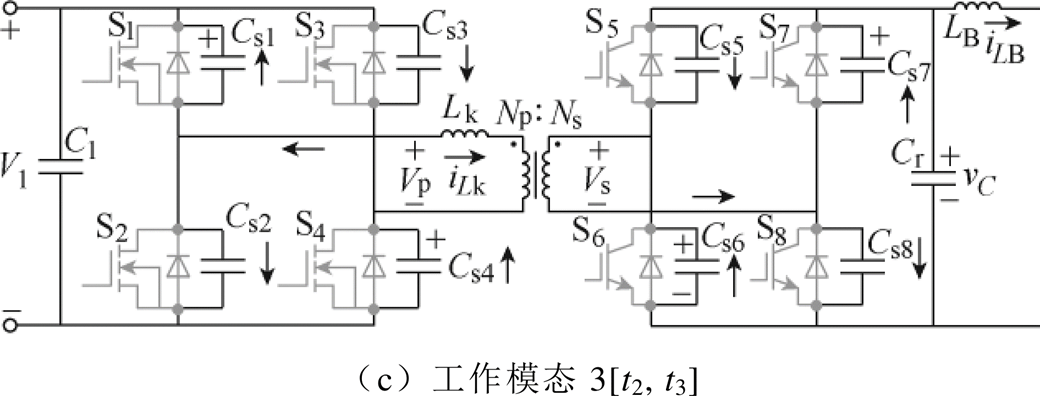
图3 前半个周期的工作模态
Fig.3 Operating modes of the first half cycle
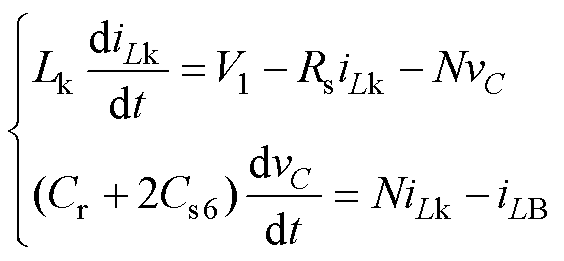（1）
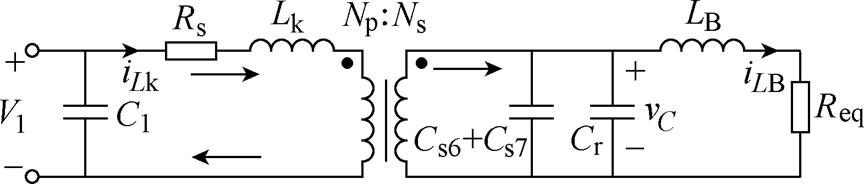
图4 工作模态1下的等效谐振电路
Fig.4 The equivalent resonant circuit under operating mode 1
工作模态2[t1, t2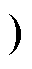：如图3b所示，t1时刻，谐振电流振荡到最低点，此时关断S1和S4，近似实现ZCS关断，同理，二次侧开关管的电流为谐振电流与励磁电流的差值，关断电流接近0，S5和S8也实现ZCS关断。[t1, t2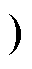阶段，S1和S4关断之后，首先由S2和S3的寄生电容Cs2和Cs3向S1和S4的寄生电容充电，充电结束之后，S2、S3的反向并联二极管续流，电感电流满足
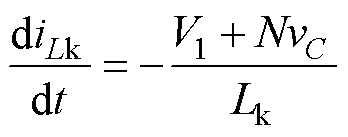（2）
工作模态3[t2, t3]：如图3c所示，t2时刻，电感电流降到0，续流二极管关断，变压器两侧开关管的寄生电容重复充放电，直到变压器一次侧端电压为0，此模态下变压器漏感电流处于振荡衰减状态。由于中间直流电容Cr远大于寄生电容，可假设vC在该过程保持不变。振荡最初，寄生电容Cs1、Cs4向Cs2、Cs3充电；寄生电容Cs6、Cs7向Cs5、Cs8充电，电感电流反向增大，满足
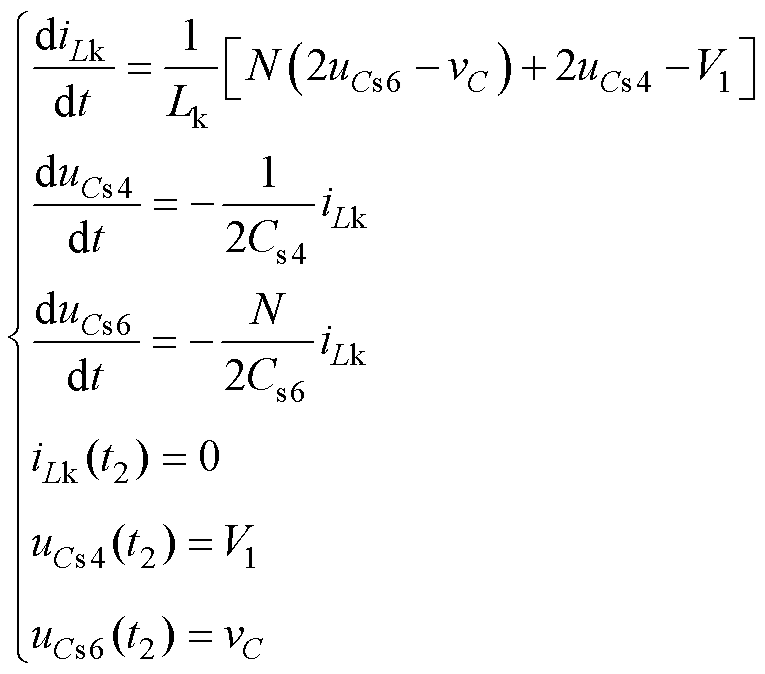（3）
t3时刻，电感电流振荡衰减到0，S2、S3实现ZVS开通，变换器进入后半个开关周期，其工作模态与前半个周期对称。在反向工作模式下，能量从V2侧向V1侧传输，同样地，一个完整开关周期可划分为6个工作模态，时序波形与正向工作时对称，因此不再一一赘述。此外，对于高频变压器的磁复位问题，结合图2分析可知，变换器在稳态运行时，由于一个周期内的前后半个周期工作模态对称，中间直流电容电压vC在前后半个周期的波形相等，如图2所示，Cr加在变压器励磁电感上的电压在前后半个周期是大小相等、方向相反的。在前半周，Cr为励磁电感提供正向伏秒；在后半周，Cr为励磁电感提供负向伏秒，两者相等，实现变压器的磁复位，保证变换器长时间稳定运行。
由于Buck-Boost变换器的电感LB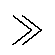
Lk，在稳态下，其流过的电感电流近似不变。因此在[t0, t1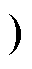时段内，Buck-Boost变换器可等效为电流源，S1、S4导通时的等效简化电路如图5所示。
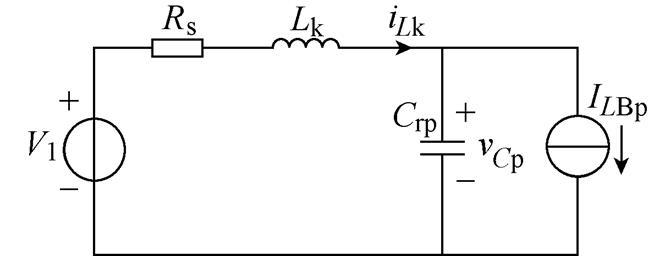
图5 模态1的等效简化电路
Fig.5 Equivalent simplified circuit of mode 1
图5中，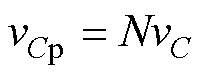
，
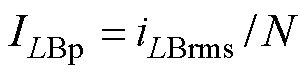，iLBrms为Buck- Boost变换器电感电流得有效值，
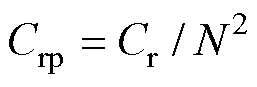，谐振电感电流和电容电压满足
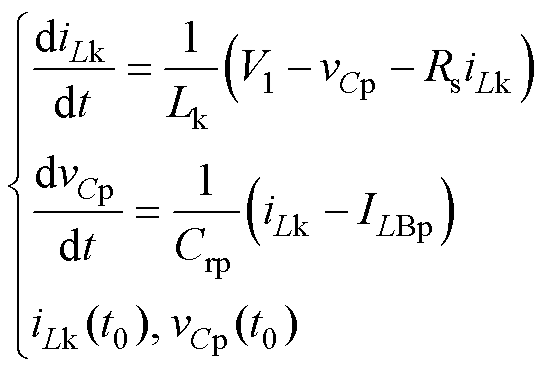（4）
可得[t0, t1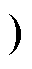时，谐振电感电流iLk为
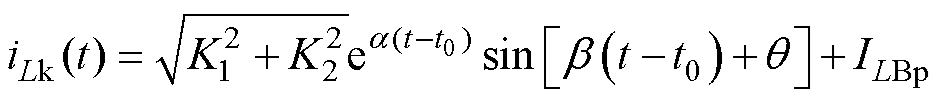
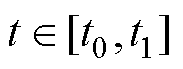（5）
其中
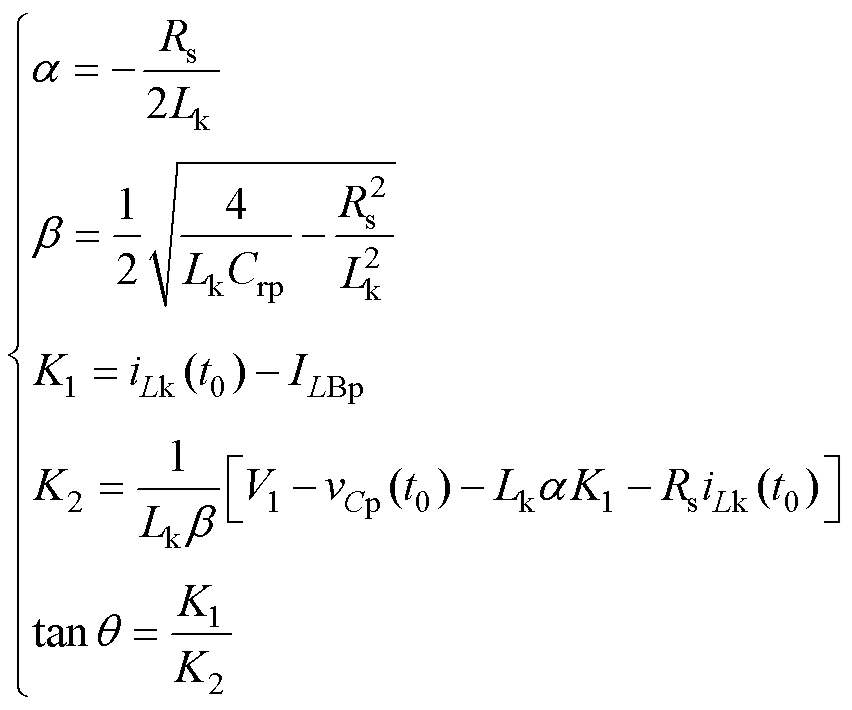（6）
由式（6）可得简化的谐振频率fr表达式为
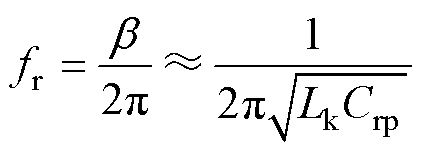（7）
折算到一次侧的中间直流电容电压vCp为
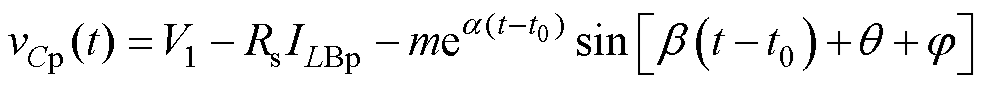（8）
其中
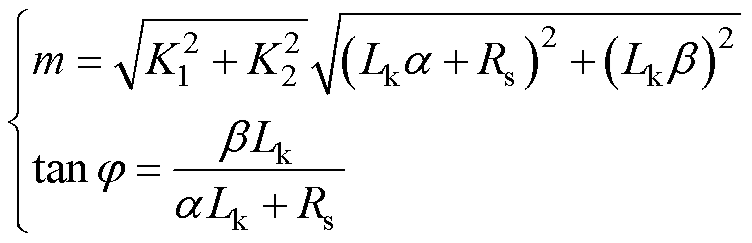（9）
由式（5）可得t1时刻的关断电流表达式为
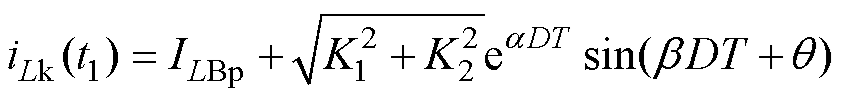（10）
设定初值为
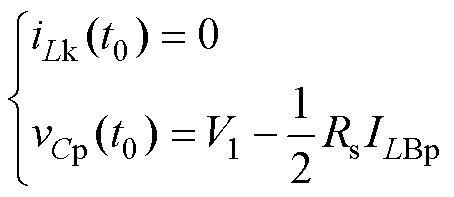（11）
结合式（6）、式（11）可得
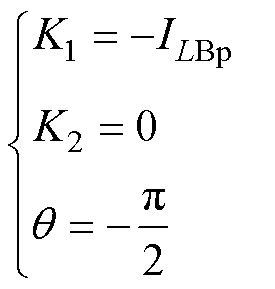（12）
结合式（7）、式（10）、式（12），推出关断电流表达式为
（13）
改变Cr、fr时，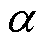
、K1为常数，关断电流iLk(DT)在
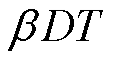为
时取得极小值，即
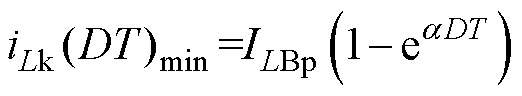（14）
若占空比D趋近0.5，此时fr/fD分别为2, 4，可知对应的关断损耗同样取得极小值。同时fr/fD≈3时的关断电流值偏高，结合式（5），这是由于关断电流中除了直流分量，还有叠加的正向正弦分量，因此fr/fD≈3的设计会导致较大的开关损耗。而 fr/fD≈2, 4时，关断电流中除了直流分量，还有叠加的反向正弦分量，因此关断电流要小于fr/fD≈3的情况。
由式（5）、式（6）分析可得，随着中间直流电容Cr的增大，电感电流振荡的幅值呈先减小再增大再减小的趋势；而由式（6）、式（8）、式（9）可知，随着中间直流电容Cr的减小，电容电压振荡的幅值随之增大，导致输出电压不稳定。
DAB变换器输出电压即中间直流电容电压vC经Buck-Boost变换器到负载，Buck-Boost变换器采用电压外环电流内环的双闭环控制输出电压稳定。考虑到vC的波动将影响Buck-Boost变换器的闭环控制稳定性，下面对Buck-Boost变换器进行分析。
Buck-Boost变换器的两个开关管SB1、SB2采用互补PWM信号驱动，本文中Buck-Boost变换器开关频率fB=2fD，以减小LB的大小，提高功率密度。
设SB2的驱动信号占空比为d，则Buck-Boost变换器在一个开关周期内，流过电感LB的电流为
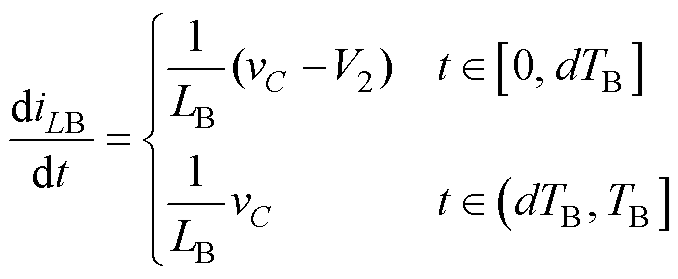（15）
式中，vC=vCp(t)/N。将式（8）代入（15）可得iLB为
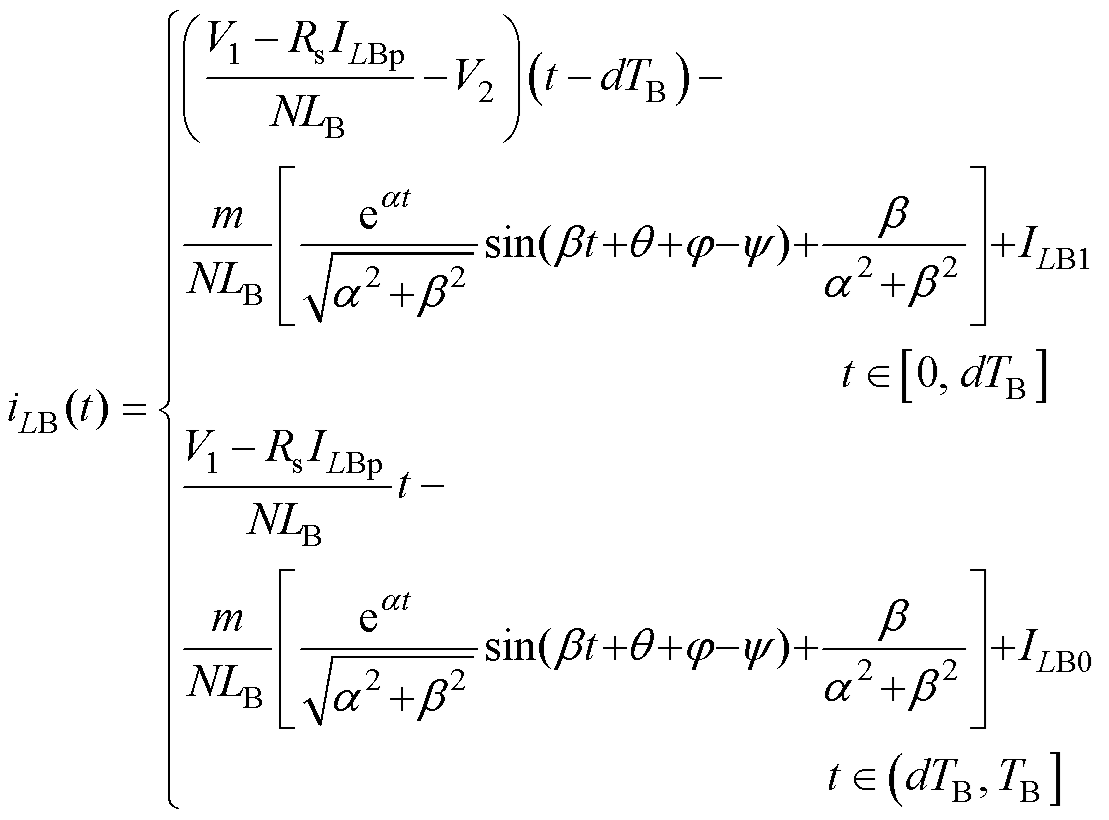（16）
式中，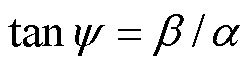
；ILB0、ILB1分别为两个时间段对应的电感电流初值，满足
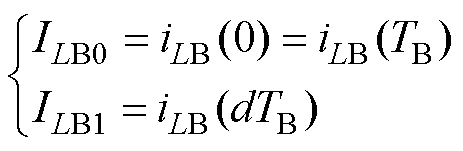（17）
假设初值ILB0=ILBrms=NPo/V1，Po为负载功率。由式（16）可看出，由于中间直流母线电容谐振引起的电压波动，在电感电流上将出现最大振幅为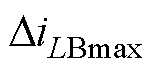
的衰减正弦波动，
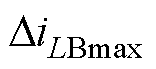可表示为
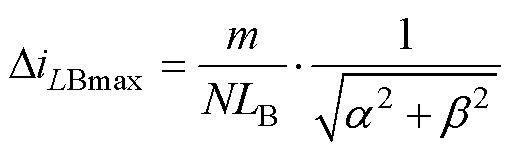（18）
将式（6）、式（11）、式（12）代入式（18）得
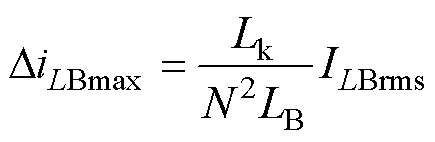（19）
式中，变压器漏感Lk为nH级，LB为mH级。分析可得，中间母线电容电压波动引起的电感电流波动的最大振幅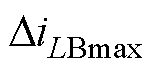
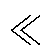ILBrms，表明中间母线电容电压波动不会对Buck-Boost变换器的闭环控制稳定性造成影响。同时，在对电感设计时，将中间母线电压视为恒值，不会影响电流纹波的抑制比，设计方法与传统方法相同。
对于前级DAB变换器，借鉴文献[13]对电流源型谐振腔的电气特性的分析，得出电流源型谐振腔具有单位增益特性，下面结合图5所示的简化等效电流源型谐振腔模型和电容电压表达式（8），从时域的角度，分析前级DAB变换器的单位电压增益特性。
为方便计算，对高压侧电压基准值Vb，电流基准值Ib进行以下假设
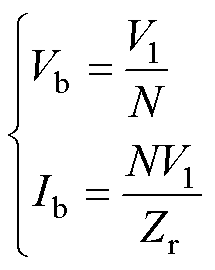（20）
式中，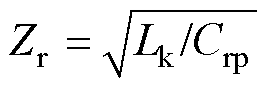
为谐振腔的特征电阻。基于变换器前后半个周期运行的对称性，在稳态情况下的半个周期内，vC(t)的初值和终值应相等，满足
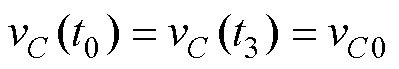（21）
在电流初值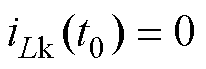
的情况下，通过对vC(t)的时域分析，前级DAB变换器的压增益MD可表示为
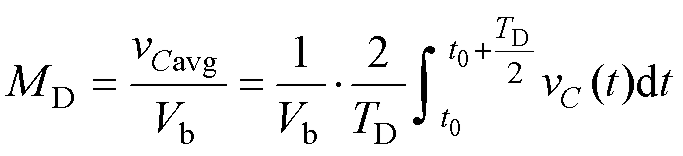（22）
式中，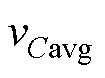
为电容电压vC的平均值。
结合式（8）、式（9）、式（21）、式（22），并忽略死区时间，可推出电压增益MD的表达式为
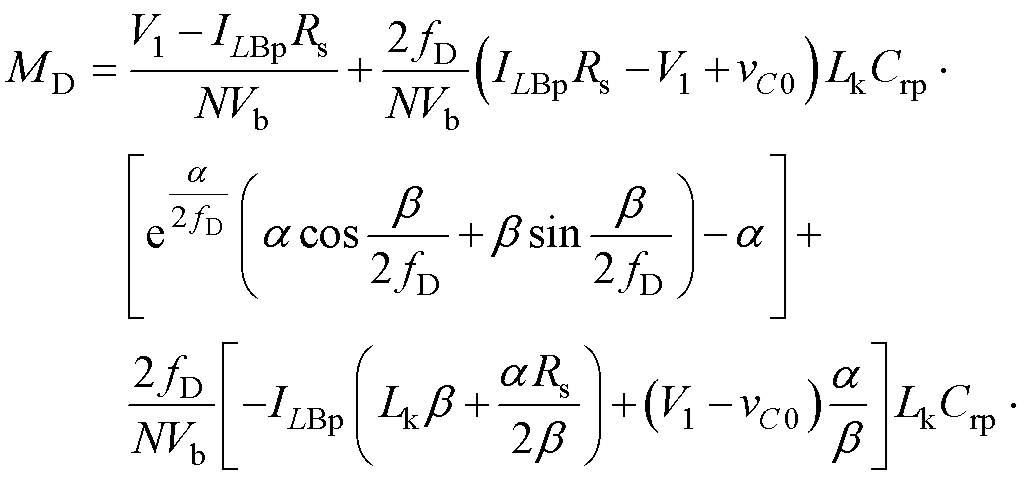
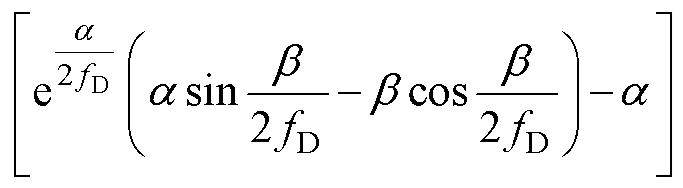（23）
通过对式（23）的数值求解，可以绘制出不同参数下的电压增益MD与开关频率的关系曲线。设ki=NILBp/Ib，kf =fD/fr。不同ki的情况下，MD随kf的变化曲线如图6所示。注意到MD的变化范围在0.9～1之间，若忽略内阻的影响，电压增益将在1附近变化，表明该变换器的前级DAB变换器具有单位增益特性。由图6可以看出，kf =0.5对应MD的极大值点，此时谐振电感电流iLk在第一个谐振周期的最低点关断；kf =0.35对应MD的极小值点，此时谐振电感电流iLk在第二个谐振周期的最高点关断。kf ＞0.5后，随着kf的增加，MD下降。同时，由于变换器内阻的影响，随着ki的增加，内阻上的压降增大，MD曲线整体下移。
对于后级Buck-Boost变换器，两个开关管SB1和SB2互补导通，SB2的占空比为d，根据电感LB的伏秒平衡，可得后级电压增益MB的表达式为
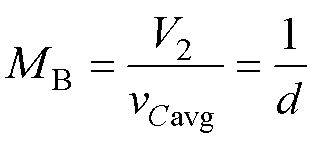（24）
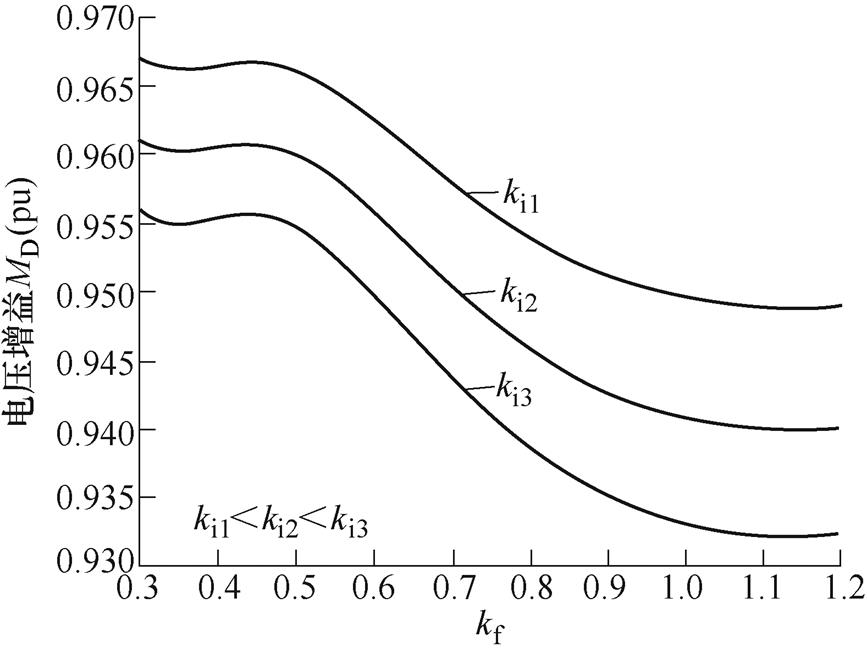
图6 不同ki对应的电压增益MD
Fig.6 Voltage gain MD corresponding to different ki
综合分析，本文提出的级联变换器的前级DAB变换器具有单位增益特性，采用固定开关频率开环工作，负责不同电压等级间的电气隔离及高效率功率变换；后级Buck-Boost通过双闭环控制调节占空比，具有较高的电压增益和较宽的调压范围。
由式（4）～式（9）的推导发现，通过改变中间直流电容Cr，漏感电流交流分量的幅值和频率随之改变，进而影响开关管的损耗大小。为进一步提高变换器的效率，下面对变换器各器件的主要损耗以及谐振参数对各损耗的影响进行分析。
在本文的电路拓扑中，主要有两种器件损耗：①主功率开关管损耗；②磁性元件的损耗，包括高频变压器、电感。除此之外，影响效率的还有辅助单元的损耗，如驱动损耗、有源散热损耗，但由于其值不随工况的改变而变化，基本恒定。下面主要对开关管和磁性元件的损耗进行详细分析。
1）导通损耗
变换器开关管总的导通损耗如式（25）所示，DAB变换器由于S1、S4同时导通，S5、S8同时导通，因此导通电阻为单管的2倍。
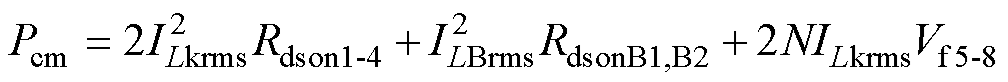（25）
式中，Rdson1-4为DAB变换器MOSFET S1～S4的通态电阻；RdsonB1,B2为Buck-Boost变换器的MOSFET SB1、SB2的通态电阻；Vf5-8为DAB变换器二次侧IGBT的导通压降，上述参数均可由Datasheet表获得。
2）开关损耗
为简化损耗模型，通过线性化开关等效模型计算开关损耗。对于MOSFET的开通和关断时间的近似计算如式（26）、式（27）所示，开通时间可分为电流上升时间tri和电压下降时间tfu，计算公式为
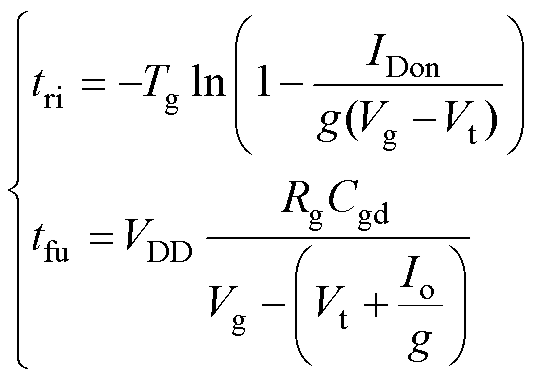（26）
式中，VDD为电源电压；IDon为导通电流；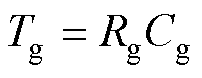
，Rg为驱动电阻，Cg为开关管输入电容，Cg=Ciss；g为跨导；Vg为驱动电压；Vt为米勒平台电压；Cgd为反向传输电容，Cgd=Crss；以上数据均可由器件数据表得到。
同理，关断时间可分为电压上升时间tru和电流下降时间tfi，计算公式分别为
（27）
式中，IDoff为关断电流。
IGBT的开通和关断时间可根据其Datasheet表获得，并近似为恒定，在损耗模型精度要求较低的场合，MOSFET的开关时间变化可以忽略，同样可以由其Datasheet表获得。
不考虑寄生电容影响下，由式（26）、式（27）可得开通和关断损耗分别为
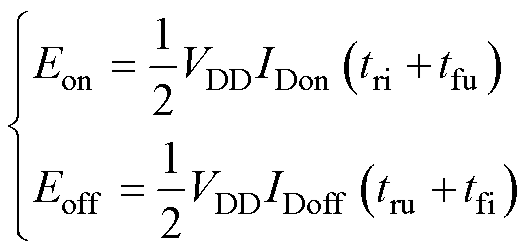（28）
考虑反并联二极管的反向恢复损耗EonD为
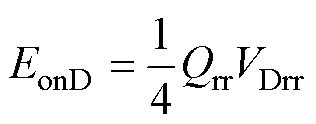（29）
式中，Qrr为反向恢复的充电电荷；VDrr为反向恢复过程时二极管电压，近似看作VDD。
DAB变换器开关管工作在ZVS开通，开关损耗为
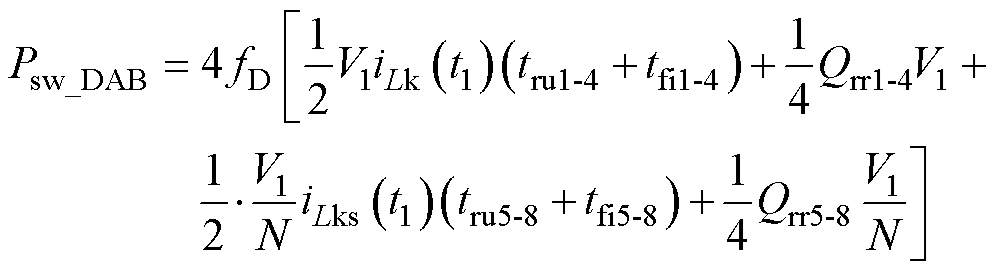（30）
式中，tru1-4、tfi1-4为MOSFET S1～S4的电压上升和电流下降的关断时间；tru5-8、tfi5-8为IGBT S5～S8的关断时间；iLks为折算到高压侧的谐振电感电流。
Buck-Boost变换器SB1和SB2开关能量分别为
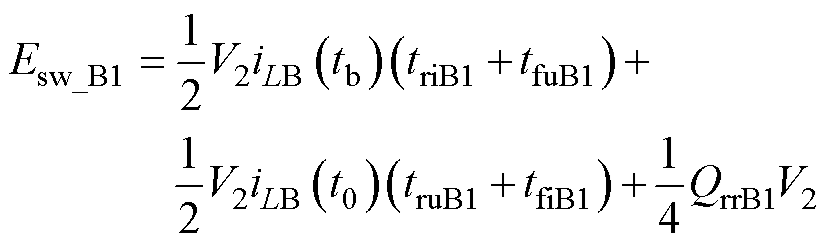（31）
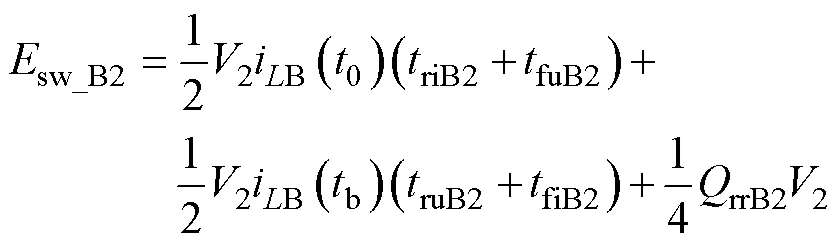（32）
Buck-Boost变换器总的开关损耗为
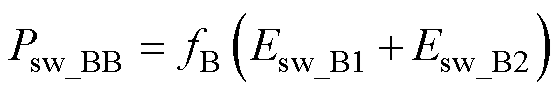（33）
综上所述，Psw_DAB大小主要由关断损耗决定，即由关断电流iLk(t1)决定。而Buck-Boost变换器iLB只与负载电流有关，与谐振状态无关，Psw_BB近似不变。因此要选择合适的谐振参数，使得iLk(t1)尽可能地小，以减小Psw_DAB。结合式（10）～式（14），fr/fD取2, 4时，关断电流取得极小值，关断损耗最小，近似ZCS关断。
高频变压器损耗包括铜耗和磁心损耗，对于T型等效电路，由于励磁支路的电流较小，可忽略励磁支路的损耗。假设一次、二次绕组的内阻分别为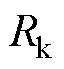
、
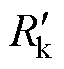，铜耗计算公式为
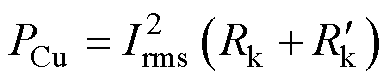（34）
式中，Irms为流经变压器的电流有效值。
对于磁心损耗，常用Steinmetz公式计算，计算公式为
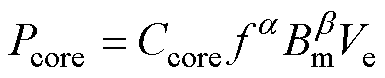（35）
式中，Ccore为磁心的损耗系数；Bm为磁通密度，可以通过法拉第电磁感应定律计算；Ve为磁心体积；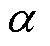
和
均为常数系数，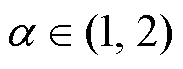
，
。
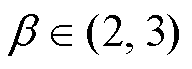电感损耗：由于利用变压器的漏感作为该变换器的谐振电感，无需额外的谐振电感，电感损耗仅包括Buck-Boost变换器的滤波电感。与变压器类似，电感损耗包括铜耗和磁心损耗，计算公式与式（34）、式（35）相同，不再赘述。
基于式（4）～式（35）理论推导和损耗计算模型，并结合具体型号谐振电容的容值建立变换器仿真模型，进而得到谐振参数与效率的关系曲线，最终确定谐振网络的参数。
结合式（5）和式（30）～式（33）可知，谐振网络的参数对ICR-DCB变换器的效率有直接影响，有必要对谐振参数进行优化，以实现变换器效率最优的目的。结合低压储能端60V直流母线和750V直流母线互联互通的应用场景，本节以7.5kW ICR- DCB变换器为例，对谐振参数进行优化设计，变换器其他参数见表1。
表1 ICR-DCB实验样机参数
Table1 ICR-DCB experimental prototype parameters
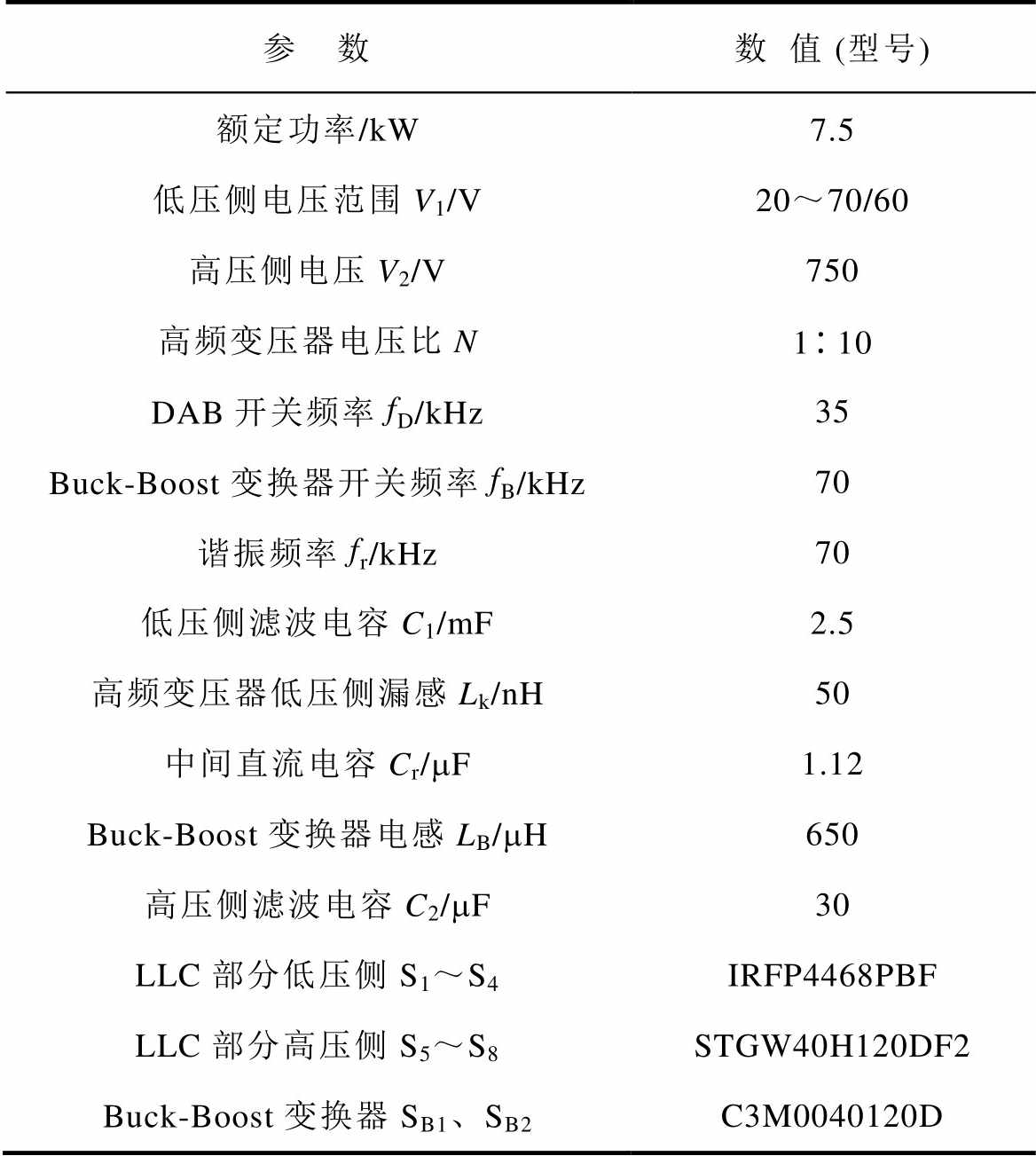
参 数数值 (型号) 额定功率/kW7.5 低压侧电压范围V1/V20～70/60 高压侧电压V2/V750 高频变压器电压比N110 DAB开关频率fD/kHz35 Buck-Boost变换器开关频率fB/kHz70 谐振频率fr/kHz70 低压侧滤波电容C1/mF2.5 高频变压器低压侧漏感Lk/nH50 中间直流电容Cr/mF1.12 Buck-Boost变换器电感LB/mH650 高压侧滤波电容C2/mF30 LLC部分低压侧S1～S4IRFP4468PBF LLC部分高压侧S5～S8STGW40H120DF2 Buck-Boost变换器SB1、SB2C3M0040120D
在仿真软件中搭建如图1所示ICR-DCB变换器模型。前级DAB采用开环运行，开关频率为35kHz，固定占空比0.45；后级Buck-Boost变换器闭环控制实现输出电压稳定，开关频率为70kHz，输出功率7.5kW，固定变换器开关频率以排除开关频率变化对开关损耗的影响。通过改变中间直流电容Cr的大小来改变谐振频率，得到不同谐振频率fr（2fD, 2.5fD, 3fD, 3.5fD, 4fD）下变压器二次侧的漏感电流iLks、中间直流电容电压vC，Buck-Boost变换器的电感电流iLB和输出电压V2仿真波形如图7所示，图中数值均以式（20）的Vb、Ib作为基准值，注意驱动信号数值仅表示开关状态。
从图7可知，在相同开关频率下，随着fr的增大，iLks振荡幅值呈先增大再减小再增大的趋势，vC的振荡幅值逐渐增大，与式（5）、式（8）相符。同时，在关断时刻的漏感电流值呈先增大后降低的现象，说明不同谐振网络参数下ICR-DCB变换器的关断损耗差异较大，且存在局部最优的情况，与式（13）相符。另外，不同fr对应的Buck-Boost变换器的电感电流iLB和输出电压V2波形基本重合，由谐振电压vC波动引起的iLB波动非常小，与式（19）相符，而电感LB的充放电纹波主要由Buck-Boost两端的电压平均值和开关管的占空比决定。
图7 仿真波形
Fig.7 Simulation waveforms
当fr/fD=2时，将表1所示参数代入式（5）、式（6）可知，关断处的电感电流相位与开通处的相位差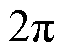
，即完成了一个完整周期的谐振，这也是本拓扑与串联谐振SRC、LLC在半个周期内仅仅完成半个谐振周期的不同之处。因此，仅从开关损耗考虑，fr/fD=2, 4时对应的电流关断点最低，相应的关断损耗最小。但是fr/fD=4时，iLks、vC的波动都较大，交变功率分量较大，因此初步选定fr/fD=2为稳态工作最优点。下面通过分析fr/fD对变换器整体损耗的影响来进一步证明该结论。
输入60V、输出750V、负载7.5kW时，ICR-DCB变换器各部分损耗与谐振频率的关系如图8所示，Pcm为变换器的总导通损耗，纵轴损耗以Po作为标幺基准值。
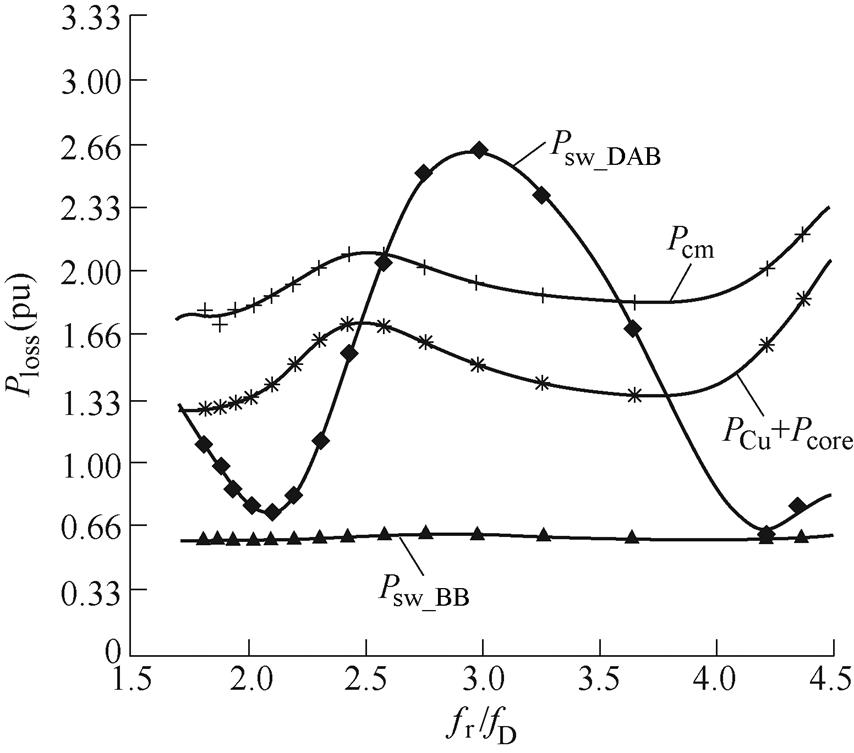
图8 各器件损耗随fr/fD变化的曲线
Fig.8 The curves of each device loss with fr/fD
从图8可知，谐振频率对Psw_DAB的影响最大，结合图7与式（13）可知，这是由于不同谐振频率下，关断电流大小不同造成的，且在fr/fD=2, 4附近时，Psw_DAB最小，与式（13）的分析一致。同时可以发现，在fr/fD=2, 4附近，总导通损耗Pcm和磁性元件损耗PCu+Pcore也处于较低的位置，而Buck- Boost变换器的开关损耗近似保持恒定。
图9给出了谐振频率变化时，输入60V，负载分别为5kW、7.5kW时，fr/fD与传输效率的变化曲线。从图9可以看出，与图7、图8相对应，效率最高点出现在低压侧关断损耗较低处，此时fr/fD在2, 4附近，负载为7.5kW时对应的最大效率分别为95.07%、94.77%。而fr/fD增大到4之后，若再进一步降低中间直流电容，谐振频率大大增加，漏感电流将在前半周期过0，出现回流功率，使效率明显下降。结合图7～图9可知，谐振参数的选择应该使得fr/fD=2, 4，能实现较大转换效率。
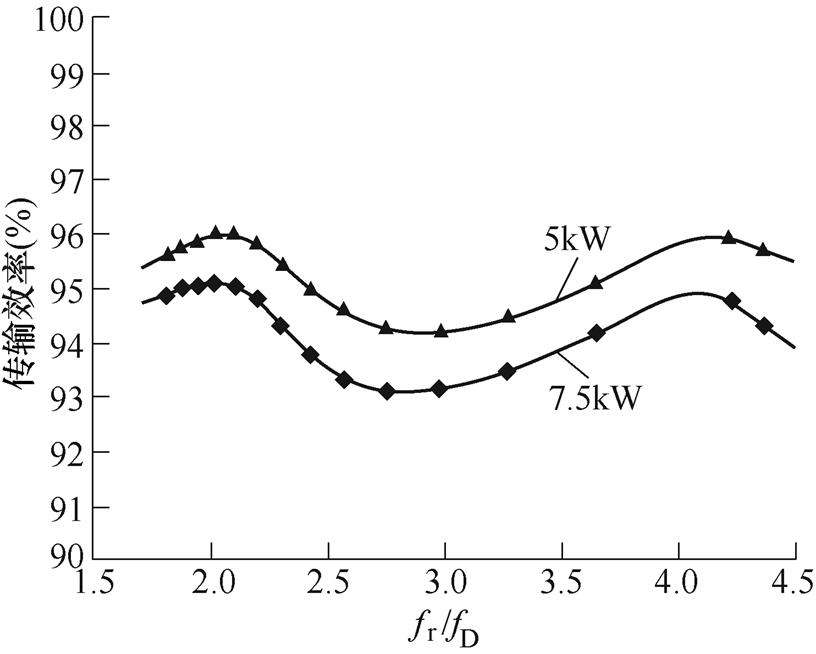
图9 传输效率随fr/fD变化的曲线
Fig.9 The curves of transmission efficiency varying with fr/fD
从图9可以看出，fr/fD=2时的电流应力和电压应力要远小于fr/fD=4时的值。综上可知，fr/fD=2是谐振网络优化的优选值，据此可以计算得到7.5kW ICR-DCB变换器的谐振参数。以fD=35kHz为例，若Lk=50nH，N=1/10，由式（36）可计算出Cr=1.03mF，本文选择耐压1 000V的0.224mF通过5个电容并联来满足电容参数要求。
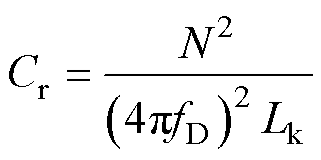（36）
为了验证第1～4节分析的有效性，本文搭建了一台7.5kW ICR-DCB变换器样机，如图10所示，样机功率密度为1.15W/cm3，样机主要参数见表1。
图10 ICR-DCB变换器实验样机
Fig.10 Experimental prototype of ICR-DCB converter
图10中，DAB变换器的每个低压侧开关管由5个Si MOSFET（型号IRFP4468PBF）并联组成，考虑到MOSFET的成本，高压侧开关管用IGBT，每个高压侧开关管由2个IGBT（型号STGW40H120DF2）并联组成；Buck-Boost变换器的每个开关管由2个SiC MOSFET（型号C3M0040120D）并联组成。
图11为变换器在正向工作和反向工作的稳态电压、电流波形，包括S1的栅源电压Ugs1、漏源电压Uds1，S6的漏源电压Uds6，变压器高压侧漏感电流iLks，中间直流电容电压vC，Buck-Boost变换器的开关管SB2的漏源电压UdsB2、储能电感电流iLB和正向输出电压V2，反向输出电压V1。额定状态下低压侧电压60V，高压侧电压750V，负载7.5kW，fr/fD=2。考虑到低压侧最大电流的保护，当低压侧电压较小时，变换器不再满功率运行。
图11中前级双有源全桥的开关管的漏源电压表明稳态情况下两侧开关管均工作在ZVS开通，高压侧开关管近似ZCS关断。经过储能电感后，电感电流近似为三角波，纹波低于10%，中间电容电压波动对Buck-Boost的影响可以忽略，验证了式（19）、图7的理论推导和仿真的正确性。图11a～图11c给出了正向工作时，低压侧输入电压在20～70V之间变化时相应的工作波形，可以发现，低压侧电压变化时，输出电压恒定在750V，同时，随着低压侧电压的升高，开关管SB2的导通占空比降低。图11d、图11f给出了反向工作时，低压侧输出电压在30～70V之间变化时相应的工作波形，此时高压侧输入电压为750V，可以发现，变换器可以实现低压侧30～70V的稳定输出。
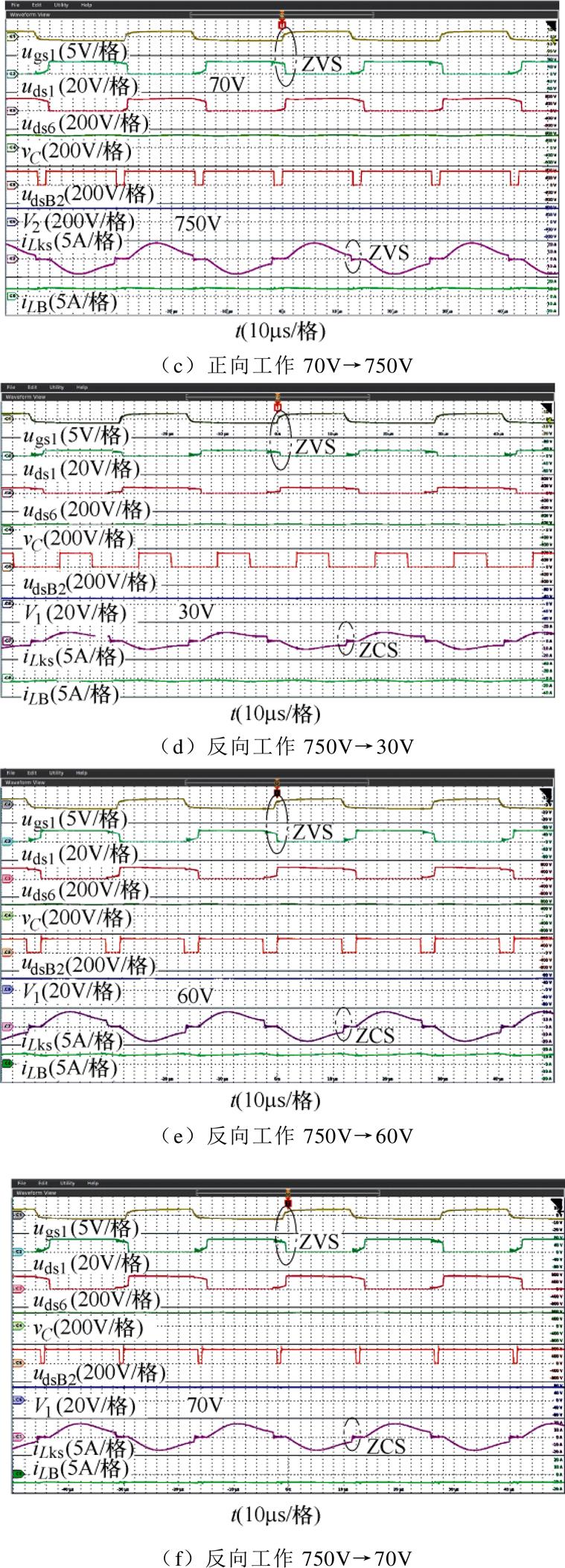
图11 正反向工作下的稳态电压、电流波形
Fig.11 Steady-state voltage and current waveforms under forward and reverse operation
图12为ICR-DCB变换器在正向工作的情况下，输入电压60V，输出电压750V时，突加负载时的动态过程，此时负载由2kW突加到4kW。可以看出，当负载突变时，输出电压波动极小，谐振电流也在3ms内重新达到稳定状态，证明了变换器的动态响应的稳定性。结合前面的分析可知，这是由于变换器的前级采用开环控制，响应速度快，当遇到突加或突减负载时，能量的变化直接由电感Lr和LB承担，而中间母线电压的波动维持在较小的可控范围内，保证变换器快速可靠的动态特性。
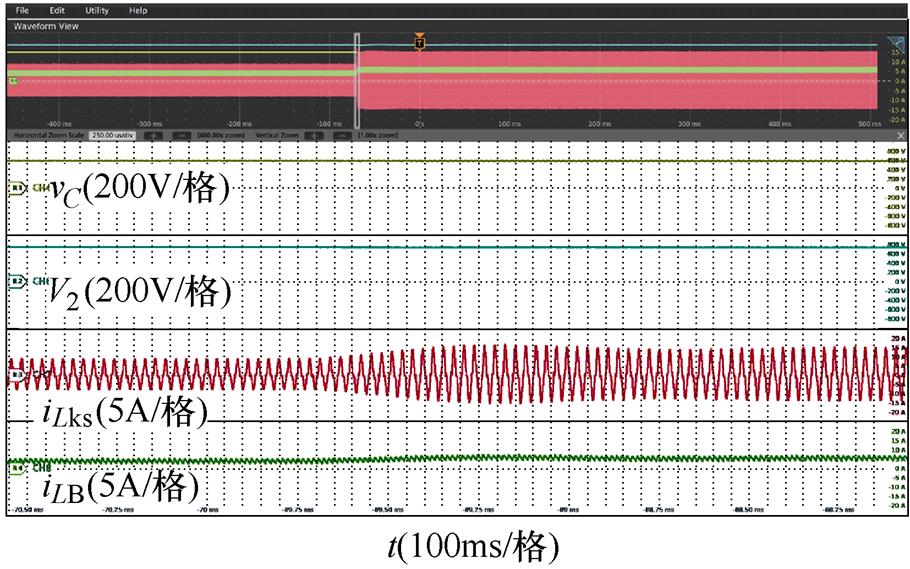
图12 ICR-DCB变换器的动态过程
Fig.12 Dynamic process of ICR-DCB converter
图13为fr/fD=2时，正向工作输入电压分别为50V、60V、70V和反向工作输入电压750V，输出电压分别为50V、60V、70V下的全功率效率曲线。图13a可以看出，正向工作时，输入电压60V对应的满载效率为95.27%，在额定功率0.3(pu)处峰值效率为95.85%。图13b可以看出，反向工作时，输出电压60V对应的满载效率为95.9%，在额定功率0.3(pu)处峰值效率为96.06%。结合图13a和图13b可以发现，该变换器的满载效率与峰值效率接近，保证了变换器在满载工作时的高效性。
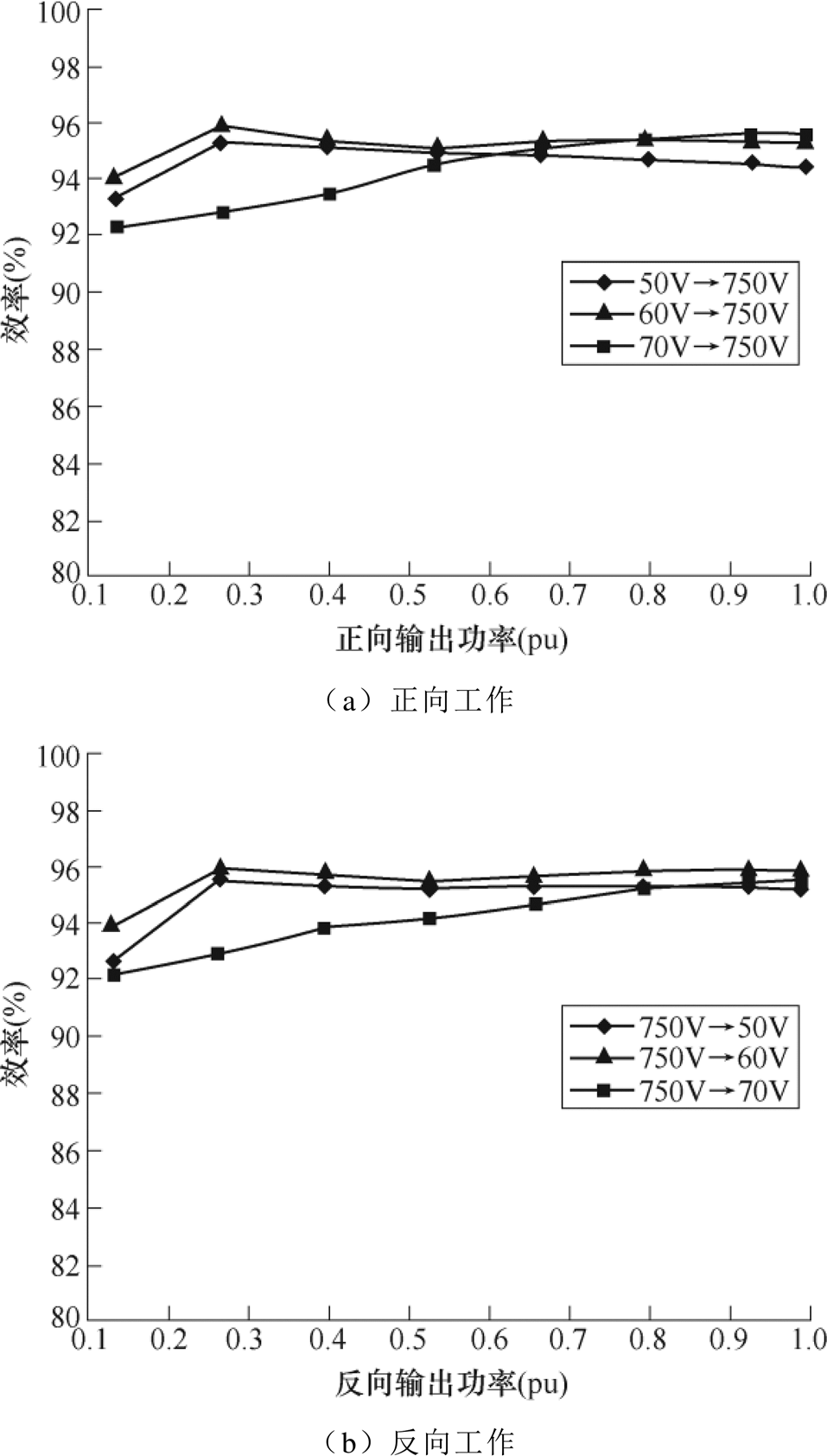
图13 不同电压下的全功率效率曲线
Fig.13 Full power efficiency curves under different voltages
本文提出的拓扑与双向Buck-Boost级联电流型DAB（Bidirectional Boost-Buck Current-Fed Isolated DC-DC Converter, B3CFIDC）[9]、CLTC谐振型DAB[18]、VF-DAB[9]、CF-DAB[10]的效率对比如图14所示，横坐标负载功率均以各自的额定负载功率作为标幺基准值。本文提出的拓扑与CLTC谐振型DAB相比，负载低于额定功率时，效率较低，原因在于本文提出的级联拓扑的Buck-Boost变换器的开关管和电感增大了总损耗。但在满载运行的情况下，本文拓扑在效率上具有明显优势，同时本文拓扑的控制相比CLTC谐振型的变频控制，由于固定频率工作在1/2谐振频率处，大大降低了磁性元件的设计难度和控制复杂度。本文拓扑与B3CFIDC、CF-DAB相比，通过中间直流母线电容和变压器漏感的谐振，实现软开关技术，降低关断电流，使效率明显提升；与VF-DAB相比，储能电感的存在使电流应力降低，导通损耗更小，因此效率高于VF-DAB。
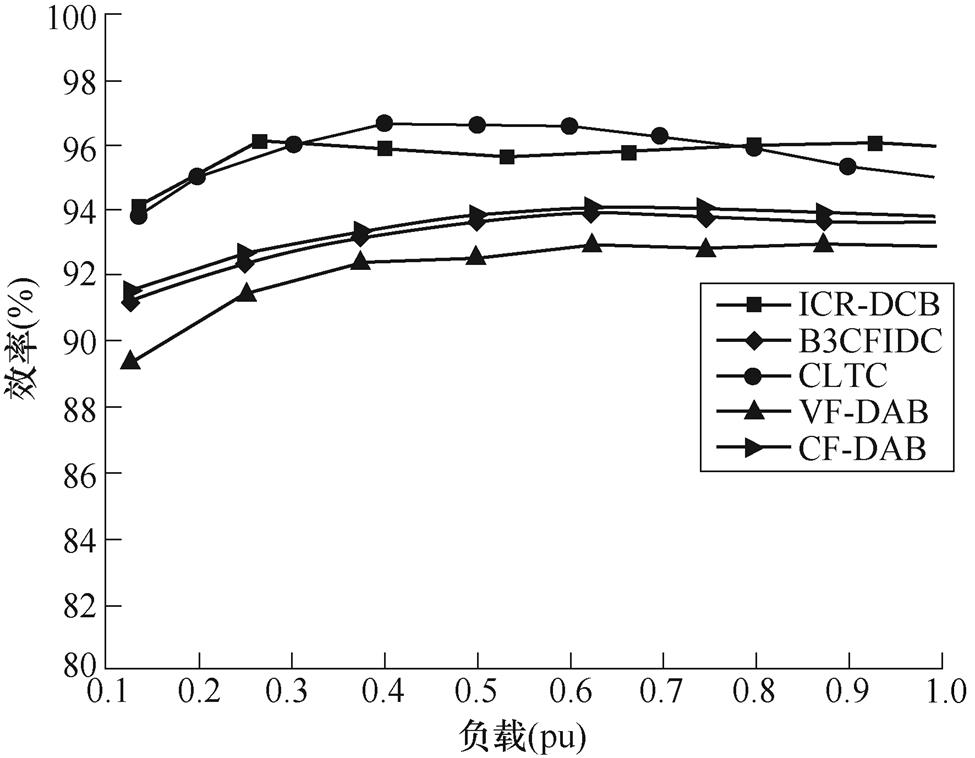
图14 五种隔离双向DC-DC变换器的效率
Fig.14 Efficiency of five isolated bidirectional DC-DC converter
本文提出的拓扑通过DAB与Buck-Boost级联实现宽电压调节范围；通过中间直流电容与变压器漏感的谐振实现了软开关；储能电感对于DAB变换器达到了降低电流应力的目的，对于Buck-Boost变换器达到了升降压和滤波的目的，实现了储能电感的复用，提高了效率和功率密度。但Buck-Boost变换器的开关管工作在硬开关状态，占总损耗的较大一部分，影响了负载较小时的效率。通过与其他谐振变换器和级联变换器对比发现，本文变换器在满功率运行下，效率具有明显优势，轻载下略有不足，下一步将对变换器的控制和参数作相应的改进，实现全范围软开关，进一步提高效率。
针对现有DC-DC变换器的电压调节范围窄、控制复杂度高、中间直流母线电容较大的问题，本文提出一种中间电容谐振型级联双向DC-DC变换器ICR-DCB。理论分析与实验结果表明：
1）本文提出的ICR-DCB变换器与传统串联谐振和LLC谐振电路相比，电压调节范围更宽，无需额外增加谐振电容，无需过于复杂的控制方式；与现有级联DC-DC变换器相比，中间直流母线电容更小。
2）通过对ICR-DCB谐振参数设计，分析了fr/fD变化和变换器各部分损耗以及传输效率的关系，确定了fr/fD=2时的谐振参数为最优参数。
3）经7.5kW实验样机验证，谐振参数优化后，ICR-DCB样机的功率密度达1.15W/cm3，峰值效率为96.06%，满载时效率可达到95.9%。对比分析表明，ICR-DCB经谐振参数优化后，在效率和电流应力上具有优势，同时具有较宽的电压调节范围。
参考文献
[1] 雷志方, 汪飞, 高艳霞, 等. 面向直流微网的双向DC-DC变换器研究现状和应用分析[J]. 电工技术学报, 2016, 31(22): 137-147.
Lei Zhifang, Wang Fei, Gao Yanxia, et al. Research status and application analysis of bidirectional DC-DC converters in DC micro-grids[J]. Transactions of China Electrotechnical Society, 2016, 31(22): 137-147.
[2] 肖智明, 陈启宏, 张立炎. 电动汽车双向DC-DC变换器约束模型预测控制研究[J]. 电工技术学报, 2018, 33(增刊2): 489-498.
Xiao Zhiming, Chen Qihong, Zhang Liyan. Con- strained model predictive control for bidirectional DC-DC converter of electric vehicles[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 489-498.
[3] 曾进辉, 孙志峰, 雷敏, 等. 双重移相控制的双主动全桥变换器全局电流应力分析及优化控制策略[J]. 电工技术学报, 2019, 34(12): 2507-2518.
Zeng Jinhui, Sun Zhifeng, Lei Min, et al. Global current stress analysis and optimal control strategy of dual active full bridge converter based on dual phase shift control[J]. Transactions of China Electro- technical Society, 2019, 34(12): 2507-2518.
[4] Wu Fengjiang, Feng Fan, Gooi H B. Cooperative triple-phase-shift control for isolated DAB DC-DC converter to improve current characteristics[J]. IEEE Transactions on Industrial Electronics, 2019, 66(9): 7022-7031.
[5] 杨向真, 孔令浩, 杜燕, 等. 基于动态矩阵控制的DAB变换器电流应力与回流功率优化方法[J]. 电力系统自动化, 2021, 45(17): 153-160.
Yang Xiangzhen, Kong Linghao, Du Yan, et al. Optimization method of current stress and backflow power of DAB converter based on dynamic matrix control[J]. Automation of Electric Power Systems, 2021, 45(17): 153-160.
[6] 胡燕, 张宇, 张天晖, 等. 考虑不同软开关模式的双有源桥变换器电流应力优化方法[J]. 电力系统自动化, 2019, 43(23): 58-64.
Hu Yan, Zhang Yu, Zhang Tianhui, et al. Optimization method of current stress for dual active bridge converter considering different soft switching modes[J]. Automation of Electric Power Systems, 2019, 43(23): 58-64.
[7] 李浩昱, 李振伟, 赵雷, 等. 宽输入LLC谐振变换器多电平控制策略[J]. 电工技术学报, 2017, 32(4): 48-57.
Li Haoyu, Li Zhenwei, Zhao Lei, et al. Multi-level control strategy of wide input LLC resonant converter[J]. Transactions of China Electrotechnical Society, 2017, 32(4): 48-57.
[8] 杨博, 葛琼璇, 赵鲁, 等. 双向全桥串联谐振DC/DC变换器回流功率特性优化[J]. 中国电机工程学报, 2019, 39(23): 6990-6999, 7112.
Yang Bo, Ge Qiongxuan, Zhao Lu, et al. The backflow power optimization of dual bridge series resonant DC/DC converter[J]. Proceedings of the CSEE, 2019, 39(23): 6990-6999, 7112.
[9] Wu Fengjiang, Fan Shuai, Li Xiaoguang, et al. Bidirectional Buck-Boost current-fed isolated DC-DC converter and its modulation[J]. IEEE Transactions on Power Electronics, 2020, 35(5): 5506-5516.
[10] Pan Xuewei, Rathore A K. Novel bidirectional snubberless naturally commutated soft-switching current-fed full-bridge isolated DC/DC converter for fuel cell vehicles[J]. IEEE Transactions on Industrial Electronics, 2014, 61(5): 2307-2315.
[11] Zhao Xiaonan, Zhang Lanhua, Born R, et al. A high-efficiency hybrid resonant converter with wide- input regulation for photovoltaic applications[J]. IEEE Transactions on Industrial Electronics, 2017, 64(5): 3684-3695.
[12] Sun Xiaofeng, Li Xiaohua, Shen Yanfeng, et al. Dual-bridge LLC resonant converter with fixed- frequency PWM control for wide input applications[J]. IEEE Transactions on Power Electronics, 2017, 32(1): 69-80.
[13] Qin Wei, Wu Xinke, Zhang Junming. A family of DC transformer (DCX) topologies based on new ZVZCS cells with DC resonant capacitance[J]. IEEE Transa- ctions on Power Electronics, 2017, 32(4): 2822-2834.
[14] Sha Deshang, Zhang Jiankun, Liu Ke. Leakage inductor current peak optimization for dual- transformer current-fed dual active bridge DC-DC converter with wide input and output voltage range[J]. IEEE Transactions on Power Electronics, 2020, 35(6): 6012-6024.
[15] 石健将, 章江铭, 龙江涛, 等. 高频变压器一次侧串联LLC+输出端并联Buck级联直流变换器[J]. 电工技术学报, 2015, 30(24): 93-102.
Shi Jianjiang, Zhang Jiangming, Long Jiangtao, et al. A cascaded DC converter with primary series transformer LLC and output interleaved Buck[J]. Transactions of China Electrotechnical Society, 2015, 30(24): 93-102.
[16] 黄启程, 贾晓宇, 陈敏, 等. 谐振双向DC/DC变换器频率跟踪控制[J]. 电源学报, 2014, 12(3): 64-69.
Huang Qicheng, Jia Xiaoyu, Chen Min, et al. Resonantbi-directional DC/DC converter with frequency tracking control[J]. Journal of Power Supply, 2014, 12(3): 64-69.
[17] 张东, 王一军. 一种两级式隔离型双向DC/DC变换器的分析与设计[J]. 电源学报, 2016, 14(3): 75-82.
Zhang Dong, Wang Yijun. Analysis and design of two-stage isolated bi-directional DC/DC converter[J]. Journal of Power Supply, 2016, 14(3): 75-82.
[18] Wang Chengshan, Zhang Shuhuai, Wang Yifeng, et al. A 5kW isolated high voltage conversion ratio bidi- rectional CLTC resonant DC-DC converter with wide gain range and high efficiency[J]. IEEE Transactions on Power Electronics, 2019, 34(1): 340-355.
A Cascaded Bidirectional DC-DC Converter with Intermediate Capacitor Resonance
Abstract In order to meet the requirements of high efficiency, high power density and wide voltage regulation range of DC-DC converters for the interconnection between battery banks and DC bus in the distributed energy storage system, a cascaded bidirectional DC-DC converter with intermediate capacitor resonance is proposed. The proposed converter adopts a modified resonant dual active bridge (DAB) on the low-voltage side. Different from the conventional DAB, it uses the leakage inductance of the high-frequency transformer to resonate with the intermediate DC bus capacitor. The modified DAB runs in open-loop mode to operate at the highest efficiency point. On the low-voltage side, a conventional bidirectional Buck-Boost topology is used to extend the voltage regulation range of the cascaded converter. This proposed cascaded converter has the advantages of small intermediate DC bus capacitance, wide voltage regulation range, low control complexity, high efficiency, and high-power density. Firstly, the topology, operating principle and control strategy of the converter are analyzed. Secondly, the key state variables and voltage-gain expression are derived. Thirdly, the loss model of the converter is established, and the resonant parameters are designed accordingly. Finally, a prototype with rated power of 7.5kW is built with the power density of 1.15W/cm3 and the full load efficiency of 95.9%, which verifies the characteristics of the converter with high efficiency, high power density and wide voltage regulation range.
keywords：Dual active bridge (DAB) converter, wide voltage regulation range, loss model, resonant parameters design
DOI: 10.19595/j.cnki.1000-6753.tces.211966
中图分类号：TM46
山东省自然科学基金项目（ZR2021ME249）、中国科学院前沿重点项目（QYZDB-SSW-JSC024）、中国科学院先导A课题项目（XDA21050100）和国家科技部重点研发专项项目（2017YFB0903300）资助。
收稿日期 2021-12-01
改稿日期 2022-01-29
李 福 男，2000年生，硕士研究生，研究方向为电力电子变换器。E-mail: lfxwj@mail.iee.ac.cn
张国驹 男，1984年生，博士，研究方向为分布式发电与电网技术、电力电子技术。E-mail: zhangguoju@mail.iee.ac.cn（通信作者）
（编辑 陈 诚）