基于开关电容与双降压变换器的三相AC-AC变换器
王汝田 李 辉 刘 闯 裴忠晨 孔令国
(东北电力大学电气工程学院 吉林 132012)
摘要 针对配电网中传统自耦变压器铁心体积大、电压调控难等问题,该文提出一种基于开关电容(SC)与双降压变换器(DBC)的三相AC-AC变换器进行替代。该拓扑采用双级式功率变换结构,具有高降压比、电压连续可调、易于模块化拓展等特性,能够满足配电网电压变换需求。首先,详细介绍所提变换器的拓扑结构及工作原理,通过双级式功率变换与无死区控制的设计与应用,实现输出电压柔性调节;其次,推导三相AC-AC变换器输出增益表达式与等效电路模型并设计简单的电压闭环控制策略,探讨三相AC-AC变换器关键参数设计方法,通过与几种结构对比清晰地反映变换器特点;最后,搭建一台3.5kW实验样机,验证了所提拓扑结构的正确性和可行性。
关键词:配电网 开关电容 双降压变换器 三相 交-交变换器
0 引言
自耦变压器作为电网与负载之间电能调节的设备被广泛应用于工业和商业领域[1],其铁心体积大、功率密度低,并且难以维持负载电能质量。为解决这些问题,通常采用电力电子装置替代传统自耦变压器。非隔离型AC-AC变换器是其主要候选方案,已经开展大量研究。
传统的脉冲宽度调制(Pulse Width Modulation, PWM)型AC-AC变换器中诸如矩阵变换器、混合矩阵变换器、带有中间直流链的AC-DC-AC变换器等结构,具有变频、调压等多种功能,但是这些拓扑结构与控制策略较为复杂[2-3]。此外,基于Buck或Boost等变换器演变的AC-AC变换器[4-5]只改变电压幅值,结构简单,但受电感纹波及开关管电压应力等条件限制,难以适应大功率高电压比的应用场景。这类变换器通常采用双向开关管,并采用复杂的调制策略或钳位电路抑制双向开关管换流暂态过程产生的电压振荡或尖峰问题。
AC-AC型开关电容变换器(Switched-Capacitor Converter, SCC)具有高升/降压比、电压自均衡、结构简单等优点,并且不含磁性元件,因此,相比上述结构,其具有更高的功率密度及转换效率。文献[6]首次将SC原理引入AC-AC变换领域,提出一种差分型单相SCC拓扑结构,该结构由两个SC模块差分连接构成,允许直流分量引入各电容,避免了电容负电压,因此电路中功率开关管全部采用两象限开关管(Two-Quadrant Switches, TQS)。文献[7]提出了无差分连接的单相SCC,该结构仅由一个SC模块组成,结构简单,同时保证了输入输出共地,但却采用双向开关管。文献[8-9]分别将无差分和有差分连接的单相SCC拓展到三相系统,提出的两种SCC均具有良好的输出特性。其中,无差分连接的SCC接线方式更加灵活,但电路开关管数量较多,而采用差分连接的三相SCC采用TQS,显著地减少了功率开关管的使用,提高了变换器运行的可靠性。
然而,差分型SCC与其他纯SCC相同,存在电压增益固定的弊端,只能开环运行,因此限制了应用范围。目前针对AC-AC型SCC输出电压调节的研究较少,但借鉴其他类型SCC研究经验可知,为解决这一问题,通常要将SC模块与传统变换器相结合,充分发挥两部分电路优势[10-13],或者在原有SCC中嵌入谐振电感,保证开关器件软开关的同时,通过移相、调频等方法实现输出电压调节[14-16],但这种方法调压范围较窄且非线性的调压方式增加了系统控制的复杂性。
本文提出一种SC与双降压变换器(Dual-Buck Converter, DBC)[17-18]组合的三相AC- AC变换器,解决了差分型三相SCC调压问题。该变换器利用两部分电路工作特性进行组合,继承了SCC高降压比和易于模块化拓展等优点,并且利用后级电路实现了输出电压线性调节;能够采用简单的控制策略保证三相输出电压稳定,无需引入锁相环。同时两部分功率开关管均为TQS,减少了电路开关管数量且不存在换流问题。本文详细介绍了变换器的结构组成及工作原理,推导了变换器等效模型并给出其控制策略,探讨了变换器参数设计方法,通过与其他结构类比更清晰地反映其结构特点,最后通过实验验证所提拓扑结构的正确性和有效性。
1 基于SC与DBC的三相AC-AC变换器
1.1 拓扑结构
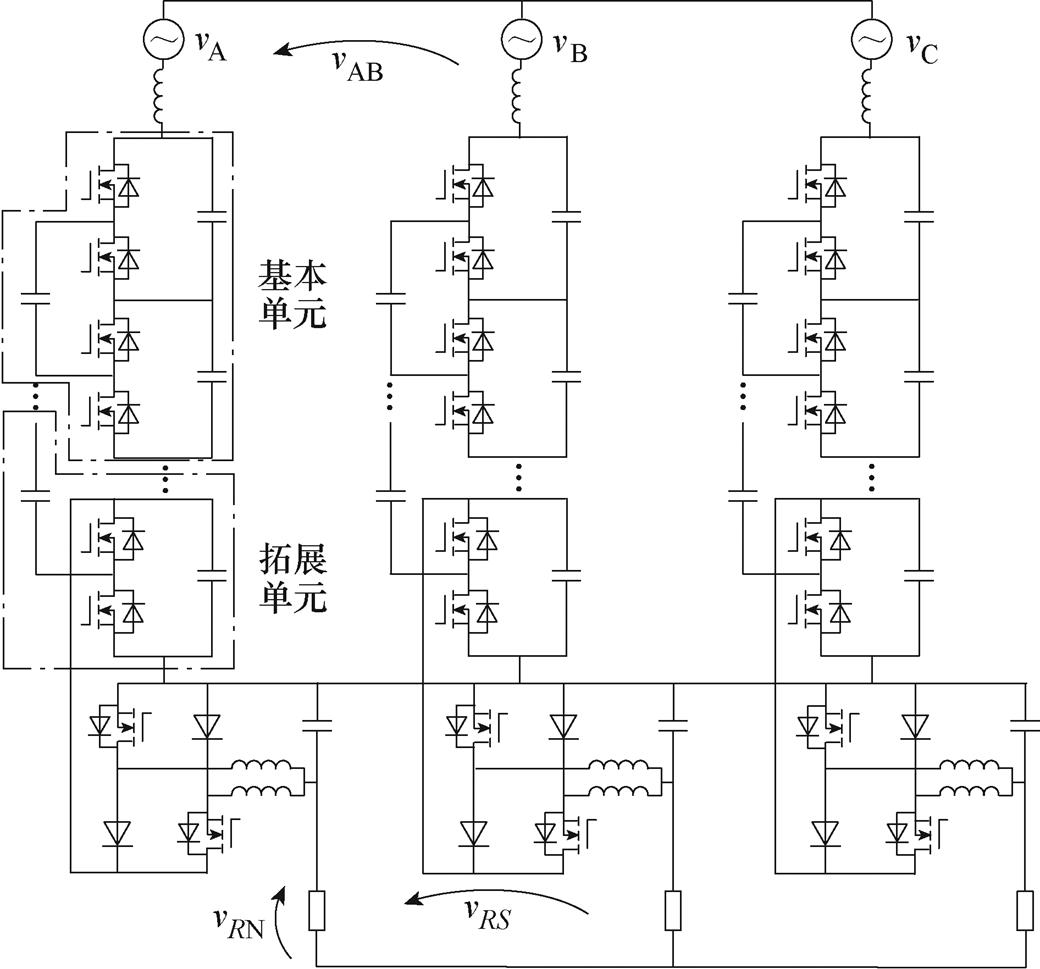
本文提出的基于SC与DBC的三相AC-AC变换器拓扑结构如图1所示,该变换器三相具备相同的结构,每相由前级SC模块与后级DBC两部分组成。其中,A相SC模块结构如图1上部分点画线框所示,由4个TQS(S1~S4)、2个均压电容(C2、C3)和一个开关电容(C1)构成。3个SC模块末端星形联结,中性点为 ,构成三相SCC,首端则经小电感分别与三相输入电源相连。A相DBC结构如图1下部分点画线框所示,由基本的开关模块P-cell、N-cell组成,包括2个功率开关管(Sp1、Sn1)、2个二极管(VDp1、VDn1)、2个分裂电感(L1、L2)及输出滤波电容(Coa)。DBC分别与各相SC模块后级均压电容(C3、C6、C9)并联,用以实现输出电压线性调节。三相负载为差分连接(类似于H桥、三相三臂的电压源逆变器负载连接方式),因此允许将直流分量引入各电容,而后在三相负载中抵消。值得注意的是,负载中性点N点不能与
,构成三相SCC,首端则经小电感分别与三相输入电源相连。A相DBC结构如图1下部分点画线框所示,由基本的开关模块P-cell、N-cell组成,包括2个功率开关管(Sp1、Sn1)、2个二极管(VDp1、VDn1)、2个分裂电感(L1、L2)及输出滤波电容(Coa)。DBC分别与各相SC模块后级均压电容(C3、C6、C9)并联,用以实现输出电压线性调节。三相负载为差分连接(类似于H桥、三相三臂的电压源逆变器负载连接方式),因此允许将直流分量引入各电容,而后在三相负载中抵消。值得注意的是,负载中性点N点不能与 点以及电网中点O点相连,因为变换器差分特性将会消失,导致变换器不能工作。
点以及电网中点O点相连,因为变换器差分特性将会消失,导致变换器不能工作。
变换器为双级式功率变换结构,两部分电路能够结合取决于各部分电路工作特性。首先,前级SCC在运行初始时刻引入直流分量,是后级DBC能够并联于SC模块最后一级均压电容的前提;此外,后级DBC无死区控制是两部分电路实现组合的又一重要因素。以下对这两部分电路工作原理进行论述。
1.2 开关电容变换器
如图1所示,变换器前级的SCC由3个相同的SC模块末端星形联结构成,共包含12个TQS,编号分别为S1~S12。下标为奇数的开关管S2n-1(n∈{1, 2, 3, 4, 5, 6})与下标为偶数的开关管S2n互补导通,作用时间分别为D1Ts1和D2Ts1(D1、D2分别为两部分开关占空比,Ts1为开关周期),中间加入死区时间td,以避免桥臂直通。通常,当开关占空比D1、D2接近50%时,SCC获得最高效率以及静态电压增益[19]。
SCC具有电压自均衡特性,其通过开关电容与均压电容交替并联实现各电容之间的电压均衡。三相具有相同的工作模式,当不考虑开关管及电容寄生电阻时,对于A相SC模块,下标为奇数的开关导通时,开关电容C1与均压电容C2并联,此时电容电压vC1=vC2;下标为偶数的开关导通时,开关电容C1与另一均压电容C3并联,此时电容电压vC1=vC3。若开关频率足够高,则vC1=vC2=vC3,即实现了A相均压电容之间的电压平衡。同样地,B、C相分别通过开关电容C4与C7保证了均压电容C5、C6以及C8、C9之间的电压平衡。因此点2、3之间电压,点5、6之间电压,点8、9之间电压分别为点1、3,点4、6,点7、9之间电压值的一半。
前级SCC具有电压自均衡特性,即后级电路能量输出造成均压电容的电压降低以及能量反馈造成均压电容的电压升高,能通过开关电容实时补偿。因此,分析前级电路时可忽略后级电路的影响。在运行初始时刻,三相对称交流电源vA、vB、vC作用于SCC,此时将有两相输入电压为正而一相输入电压为负,若认为此时B相为负,则该相模块中功率开关管的反并联二极管将全部正向偏置,电路状态如图2a所示。此时为不控整流阶段,A相、C相模块电容开始充电,O点与 点间电压逐渐上升。当电流
点间电压逐渐上升。当电流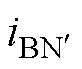 为零时,O、
为零时,O、 间电压达到输入相电压峰值Vpk,B相模块中功率开关管的反并联二级管反向偏置,电路进入稳态,此时状态如图2b所示。由于初始暂态过程,使得各电容中产生了直流分量,大小为Vpk/2。
间电压达到输入相电压峰值Vpk,B相模块中功率开关管的反并联二级管反向偏置,电路进入稳态,此时状态如图2b所示。由于初始暂态过程,使得各电容中产生了直流分量,大小为Vpk/2。
SCC在运行初始时刻直流分量自然产生,因此,在稳态运行时各相模块电容电压均含有交流分量以及直流分量。A相模块电容C1、C2、C3电压交流分量大小为vA/2,且与A相电源电压同相,直流分量大小为Vpk/2。B相、C相模块电容电压与A相相似,只是交流分量相位相差-120°与120°。
SCC中各电容承受最高电压为Vpk,各功率开关管由相应的电容进行钳位,因此最大电压应力也为Vpk。
1.3 双降压变换器
DBC由两种基本的开关单元并联组成,这两种基本开关单元与DBC电路如图3所示。每个开关单元均由一个功率开关管以及二极管构成,并且包含3个端口,其中 端口与电压源或者电容正极相连,
端口与电压源或者电容正极相连, 端口与电压源或者电容负极相连,公共端口连接限流电感,“→、←”表示公共端口电流方向。P-cell电流只流出公共端口,N-cell电流只流入公共端口。P-cell与N-cell并行组合,使得DBC具有双向电流能力,通常用于实现逆变功能。
端口与电压源或者电容负极相连,公共端口连接限流电感,“→、←”表示公共端口电流方向。P-cell电流只流出公共端口,N-cell电流只流入公共端口。P-cell与N-cell并行组合,使得DBC具有双向电流能力,通常用于实现逆变功能。
由图3c中输出滤波连接方式可知,本文的DBC为直流斩波变换器而非逆变器。与其他直流斩波变换器不同的是,虽然文中DBC的输入与输出电压均为含有直流与交流分量的直流电压,但是由于负载的差分连接,使得流过两电感交点端口的电流为交流。DBC具有桥臂电流选择特性,P-cell和N-cell能够在电流正负半周分别承担斩波功能。为保证斩波作用相同,需要设置P-cell和N-cell开关管占空比之和等于1。DBC由于限流电感的存在而无需设置死区时间,因此避免了死区时间电流通路问题,使得上述条件易于满足。
考虑到DBC结构特点,在保证P-cell和N-cell斩波作用相同的条件下,能够通过交错开关调制策略提高变换器等效开关频率,进而降低滤波尺寸以及开关频率要求[20]。将直流调制信号D分别与两个相位互差180°的三角载波Ca1、Ca2相比较分别获得各相P桥臂开关管Sp1~Sp3驱动信号以及N桥臂功率开关管Sn1~Sn3驱动信号的互补信号。该调制策略为全周期调制,无需判断电流方向,因此不存在过零畸变问题。
文中后级DBC应用具有特殊性,为了更好地说明变换器工作特点,以下介绍采用交错开关调制时后级电路的工作过程。变换器三相具有相同的工作状态,这里以A相为例进行详细分析。由于端口只输出正向电压,因此根据电流ieqa方向可将DBC工作模式分为能量传输与能量反馈两种。在电流ieqa正半周,均压电容C3通过分裂电感L1向负载传输能量,此时由P桥臂实现斩波功能,而N桥臂开关管则提供续流回路。电流ieqa正半周DBC详细的运行模式如图4所示,四种运行模式与开关管Sp1、Sn1状态直接相关。当占空比D=0.5时,电路在模式2与模式3交替工作;当D>0.5时,电路共有三种运行模式(模式1、模式2、模式3),并按模式1、模式2、模式1、模式3的顺序交替工作;当D<0.5时,电路同样存在三种运行模式(模式2、模式3、模式4),并按模式4、模式2、模式4、模式3的顺序交替工作。由于续流回路的存在,使得电流ieqa纹波频率提高为实际开关频率的2倍,尤其当D=0.5时,即使任一分裂电感电流纹波达到最大值,电流ieqa纹波仍为零。由于等效开关频率提高,滤波电感的尺寸能够相应减小。而在电流ieqa负半周期,负载能量通过电感L2向均压电容C3反馈,此时由N桥臂实现斩波功能,P桥臂开关管则提供续流回路,详细的工作模式与正半周类似,这里不再赘述。
2 等效模型与控制策略
2.1 理想电压增益
SC模块实现2倍降压,后级DBC与均压电容相连,对其进行斩波,因此A相输出滤波电容电压可以表示为
B、C相输出滤波电容电压与A相相似,只是交流分量互差-120°与120°。三相输出经过差分连接,直流分量相互抵消,只留下对称的交流分量。于是,A相负载相电压与线电压分别为
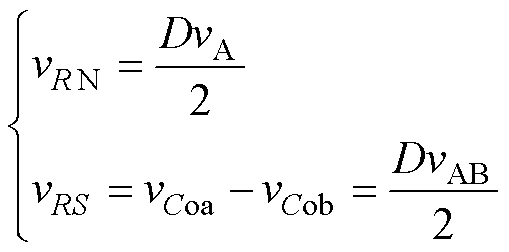 (2)
(2)
因此,该变换器理想电压增益可以表示为
输出电压与占空比D呈线性关系,且0≤D≤1,因此电压增益在[0, 0.5]范围可调。
2.2 等效模型
2.2.1 后级电路等效模型
考虑后级电路采用交错开关调制,工作模式较多且与占空比D相关,列写状态方程求取等效模型较为复杂。本文采用戴维南等效电路求取后级等效模型。
以A相为例对变换器后级电路进行分析,SCC开关高频动作以及均压电容较高的容值使得均压电容电压纹波很小,可以忽略。假设其输入电压为
式中,w 为输入电源角频率。将主动管Sp1、Sn1开关模式用开关函数分别表示为
 (5)
(5)
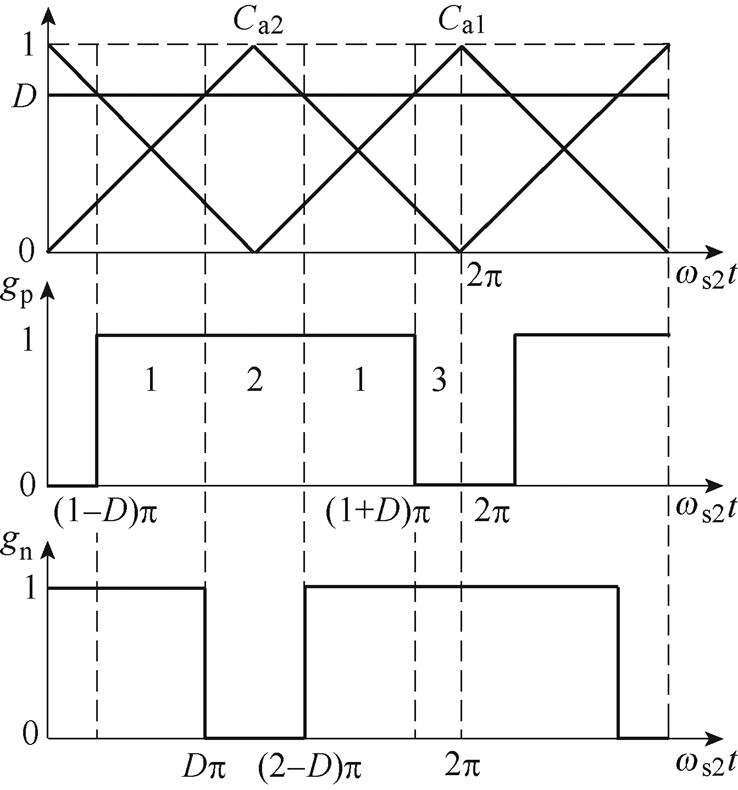
此外,两开关管开关函数与占空比D之间的关系如图5所示。
通过傅里叶级数将两开关函数展开,表达式为
式中,ws2为DBC开关角频率。根据开关函数,列出P-cell公共点电压vp与N-cell公共点电压vn为
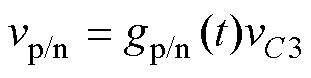 (7)
(7)
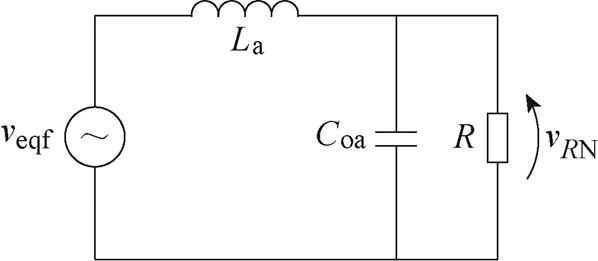
vp与vn标于图3c中。已知vp与vn,则可列出由滤波电容看入DBC的二端等效电路。其中,等效滤波电感La为分裂电感值的一半;开路电压,即滤波前电压veq为
将式(4)、式(6)、式(7)代入式(8),并进行化简,可得
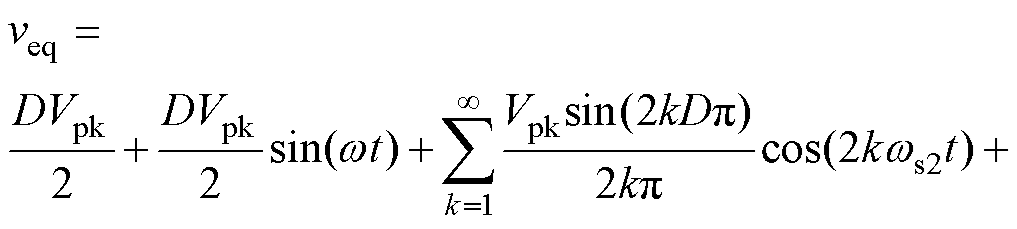
图6中,veqf为veq中的基频分量,其有效值与占空比D成正比,因此通过改变后级电路开关占空比便能实现输出电压的线性调节。此外,等效电路与传统交流斩波电路相同,即本文后级结构通过引入直流分量,采用单向结构实现了交流斩波功能。
2.2.2 变换器等效模型
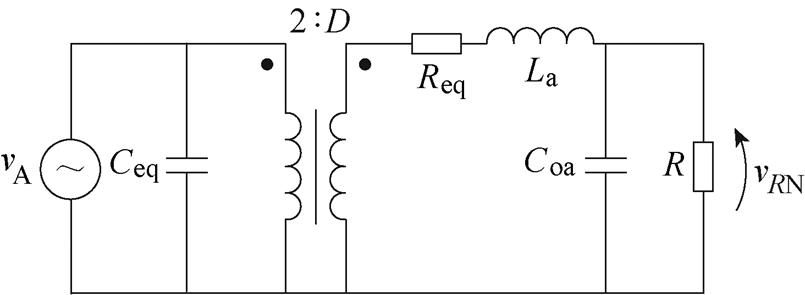
考虑前级SCC的影响,变换器单相等效电路如图7所示。
图7中,Ceq为变换器高压侧看进去的等效电容,Req为变换器等效内阻,以下对各分量详细说明。
由于开关电容C1与均压电容C2、C3依次并联,作用时间分别为D1Ts1和D2Ts1,因此可以表示为容值为D1C1与D2C1的两个电容分别与C2、C3并联[6]。当D1=D2=0.5时,等效电容Ceq大小可表示为
式中,Csc为开关电容(C1、C4、C7);Cd为均压电容(C2、C3、C5、C6、C8、C9)。
SCC具有电压自均衡特性,但是由于电容之间充放电引起的损耗,导致各电容电压无法实现完全平衡,该损耗可由变换器等效内阻Req表示,其值通过计算为
式中,t 为开关电容充放电时间常数;RDS(on)为MOSFET的漏-源极通态电阻;RSE为开关电容的串联等效电阻。这里,Req的表达式与DC-DC型SCC[21]类似,是因为变换器在任一瞬时工作过程与DC-DC型SCC相同,并且均压电容一直与输入电源相连且具有较高的电容值,可以认为在SCC的一个开关周期(Ts1)内,均压电容电压为定值,因此能够将开关电容充放电回路简化为一阶RC电路,满足DC-DC型SCC等效内阻假设条件。不同之处在于,式(11)中,Req表达式分子多了D2的关系,这是由于后级电路的引入改变了开关电容电流与输出电流之间的关系。而当D固定,D1=D2=0.5时,Req取最小值,因此,本文中前级SCC设置占空比D1=D2≈0.5且固定不变。
2.3 控制策略
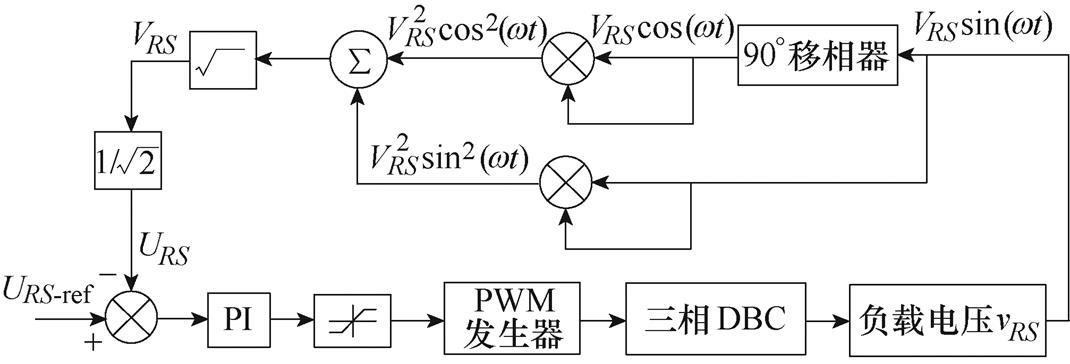
该变换器为双级式功率变换结构,前级SCC只能开环运行,设置占空比D1、D2固定并接近0.5,以获得最高效率和静态电压增益。通过对后级电路独立控制,实现输出电压柔性调节。由于后级电路与传统交流斩波电路的等效电路相同,因此两者控制策略也并无本质区别[22],文中变换器闭环控制框图如图8所示。本文以一相输出线电压作为控制目标,实现三相输出电压调节。这是因为SCC具有电压自均衡特性,当三相DBC给定相同占空比情况下,无论负载类型如何,变换器输出线电压能够一直保持平衡。
对输出线电压vRS实时检测并计算其有效值URS,与线电压给定值URS-ref相比较,差值信号通过PI控制器,生成三相DBC开关占空比D,并利用PWM模块形成高频动作信号,作用于后级电路开关管,从而实现输出电压调节。
3 参数设计
变换器参数设计规格:输入相电压有效值Uin= 220V(50Hz),额定输出功率Po=3.5kW,输出线电压有效值150V,输入功率因数PF=0.96(容性),占空比D1=D2≈0.5,D∈[0, 1]。
3.1 前级参数设计
3.1.1 电容设计
由于变换器前级SCC中的无功功率通常远大于滤波电路中的无功功率。根据变换器等效电路,可计算该变换器中的无功功率Qi为
式中,fin为输入电压频率。可以看出,Qi与负载类型无关,类似于传统电磁式变压器中由于励磁电感引起的无功功率。因此通过电路中指定的无功功率或者功率因数可以确定最大等效电容值。认为输出为纯电阻负载并忽略电路中的损耗,最大等效电容值Ceq_max为
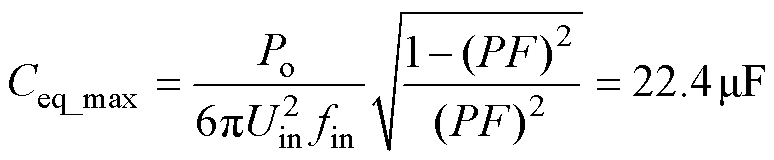 (13)
(13)
因此每相均压电容选择20mF/600V的薄膜电容,开关电容选择2个20mF/600V的薄膜电容并联,此时Ceq=20mF。
3.1.2 开关及其频率选择
SCC根据电路时间常数和开关周期的关系可以将工作模式分为不充电(No Charge, NC)、部分充电(Partial Charge, PC)和完全充电(Complete Charge, CC)三种模式[7],其中,最佳工作模式是PC模式和NC模式,而NC模式通常要求极高的开关频率和极高的电容值,并且其优势相比于PC模式并不明显,因此,通常将SCC工作模式设置为PC模式。
由于电容在经过5t 后,充放电过程结束,为保证SCC工作于PC模式,开关电容充放电时间应小于5t,因此最大开关周期Ts1m与充放电时间常数的关系可以表示为
考虑D1=D2=0.5,PC模式最小开关频率fs1与时间常数关系可表示为
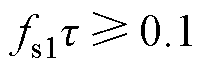 (15)
(15)
此外,相比于MOSFET的漏-源极通态电阻RDS(on),开关电容的串联等效电阻RSE很小,可以忽略不计。此时,电路时间常数t =2RDS(on)Csc。工作于PC模式,RDS(on)是影响SCC效率的主要因素,减小RDS(on)可以显著提高变换器效率[23]。选择IPW65R041CFD型号Cool MOSFET,在25℃时RDS(on)=41mW,100℃时为67mW。SCC部分开关频率选择为50kHz,此时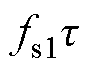 =0.268,SCC工作于PC模式,满足设计要求。
=0.268,SCC工作于PC模式,满足设计要求。
3.1.3 模块数设计
SCC为阶梯型结构,易于实现模块化拓展。通过拓展能够降低变换器电压增益以及各元件电压应力,进而提升输入电压等级,满足配电网各种电压等级变换需求。为了便于区分,定义图1上部分点画线框中的SC模块为基本单元,在其基础上增加的单元为拓展单元。变换器模块化拓展拓扑结构如图9所示,并在图9中标出了基本单元与拓展单元。其中,拓展单元由2个功率开关管、1个均压电容以及1个开关电容组成。根据其数量n,则能够确定变换器各元件最大电压应力为2Vpk/(2+n),以选择合适的功率开关管。此时变换器理想电压为
3.2 后级参数设计
由于与SCC后级均压电容相连,DBC中的4个开关管承受最大电压应力相等且等于Vpk,忽略变换器内部损耗,以A相为例,流过每个开关管的电流有效值IS为
式中,URN、IRN分别为A相负载电压与电流有效值。因此,选择IPW65R041CFD/650V型号Cool MOSFET,以及IDW40G65C5B/650V型号二极管;开关频率选择为25kHz,此时DBC等效开关频率为50kHz。后级采用交错开关调制策略,当占空比D不同时,电流ieqa纹波表达式也不相同,可分为D>0.5、D<0.5、D=0.5三种状态,即
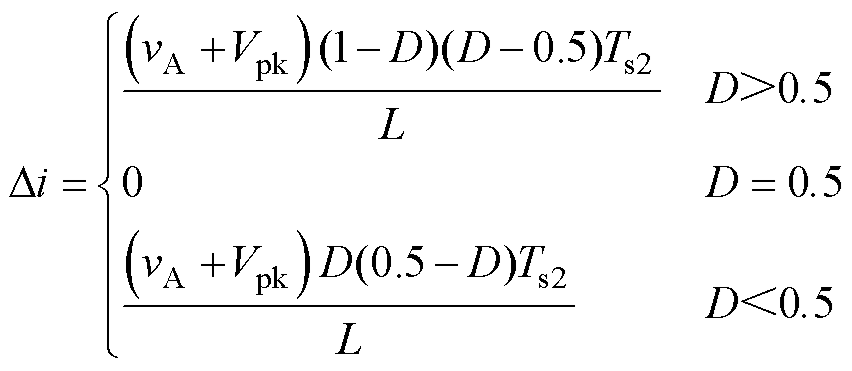 (18)
(18)
当占空比D=0.5时,即使任一电感电流纹波值最大,电流ieqa纹波仍为0。当D=0.25,0.75时,电流ieqa纹波在输入电压峰值时达到最大值,为保证电流ieqa纹波值不超过输出电流最大值的10%,计算得电感最小值为0.8mH,因此选择1mH的电感作为DBC的分裂电感,输出滤波电容选用2mF薄膜电容,此时L/2-C滤波截止频率为5.03kHz,约为等效开关频率的10%。
4 拓扑结构比较
将文中所提结构与差分型三相SCC[9]、三相Buck变换器[5]、电压直流链的背靠背变换器(Back- to-Back Converter with Voltage bus, V-BBC)以及传统矩阵变换器(Conventional Matrix Converter, CMC)[2]这几种典型的AC-AC变换器进行比较,以更好地说明所提变换器结构特点,所提结构与其他四种结构对比结果见表1。
表1 所提结构与其他四种AC-AC变换器对比
Tab.1 Comparison between of the proposed converter and other four AC-AC converters
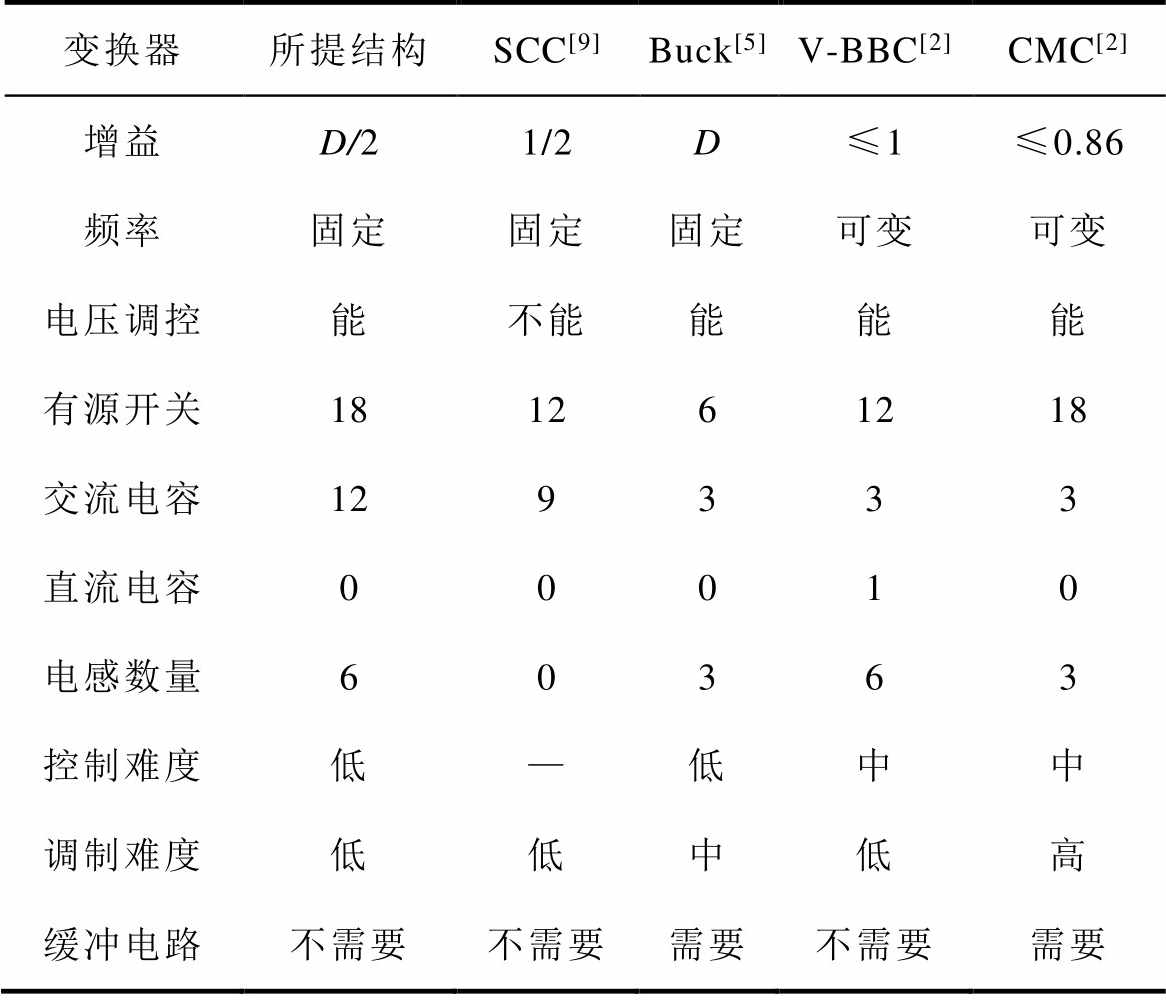
变换器所提结构SCC[9]Buck[5]V-BBC[2]CMC[2] 增益D/21/2D≤1≤0.86 频率固定固定固定可变可变 电压调控能不能能能能 有源开关181261218 交流电容129333 直流电容00010 电感数量60363 控制难度低—低中中 调制难度低低中低高 缓冲电路不需要不需要需要不需要需要
三相Buck变换器为直接式PWM型AC-AC变换器,结构最为简单,开关数量以及无源器件的使用最少,但是存在输入电流离散、换流等固有问题。此外,三相Buck变换器降压比相比于文中结构低两倍。要实现相同的降压效果,三相Buck变换器需要工作在更低的占空比状态,这导致该结构效率无法得到保证。文中结构为SCC与斩波电路的组合结构,单独与其中一种结构相比都相当于增加了元器件,因此其经济性降低。但分别克服两种结构的固有弊端(开关电容结构调压问题以及交流斩波电路降压比、换流等问题),所提变换器前级电路实现高效降压,后级电路对输出电压管控且不会引入波形畸变或增加调制难度。
V-BBC与CMC是两种能够同时改变输出电压幅值与频率的PWM型AC-AC变换器。其中,V-BBC的主要缺点是存在中间直流链的大电容,增加了系统体积及维护负担,并且为维持直流链电压,增加控制难度。而文中结构同样为双级式功率变换结构,却不存在明显的中间级,结构紧凑,并且由于SCC具有电压自均衡特性,也无需对各电容电压进行控制;CMC同样取消了中间级具有功率密度高的优点,且本身为降压结构。但是其开关状态的改变必须考虑输入电压以及输出电流情况,致使调控难度提高。
总的来说,几种变换器各有特点,在配电网具有不同的应用场景。直接式AC-AC变换器多用于调压场合[22];以固定频率降压为目标时,本文结构及调控简单,易于实现应优先考虑;而应用于变频领域,矩阵变换器更具优势[24]。
5 实验结果分析
基于第3节给出的变换器参数设计规格,搭建了输入线电压380V/50Hz,输出功率3.5kW的实验样机,验证所提变换器结构的正确性。实验样机如图10所示,包括功率板、驱动板、采样板、控制板四部分。其中,控制板由DSP TMS320F28335与AD7606芯片组成,实现闭环运算并产生两组调制信号,分别为前级的互补信号和后级的交错信号,分配到各开关管的驱动电路;功率板由前级与后级两部分组成,连接方式如图1所示;三相电源侧串入的小电感为130mH,以滤除输入电流的高频谐波分量,SCC部分和DBC部分实验所用参数及规格见表2。
表2 实验参数
Tab.2 Experimental parameters
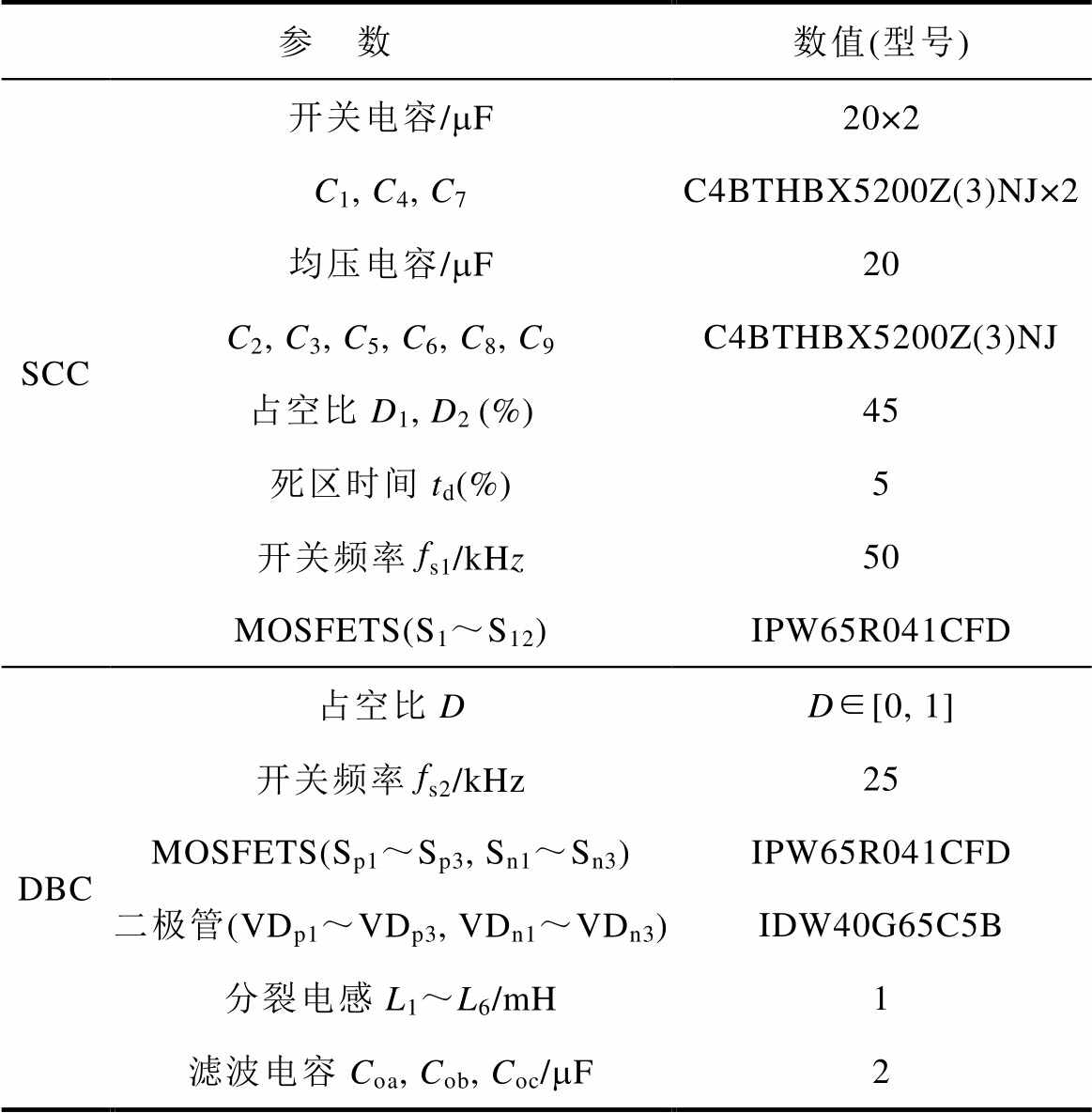
参 数数值(型号) SCC开关电容/mFC1, C4, C720×2 C4BTHBX5200Z(3)NJ×2 均压电容/mFC2, C3, C5, C6, C8, C920 C4BTHBX5200Z(3)NJ 占空比D1, D2 (%)45 死区时间td(%)5 开关频率fs1/kHz50 MOSFETS(S1~S12)IPW65R041CFD DBC占空比DD∈[0, 1] 开关频率fs2/kHz25 MOSFETS(Sp1~Sp3, Sn1~Sn3)IPW65R041CFD 二极管(VDp1~VDp3, VDn1~VDn3)IDW40G65C5B 分裂电感L1~L6/mH1 滤波电容Coa, Cob, Coc/mF2
以下实验结果分为开环与闭环运行两部分。其中开环包括轻载、额定负载以及不平衡负载运行工况下的波形,该部分设置占空比D=0.8;闭环实验则设置线电压参考值为100V。
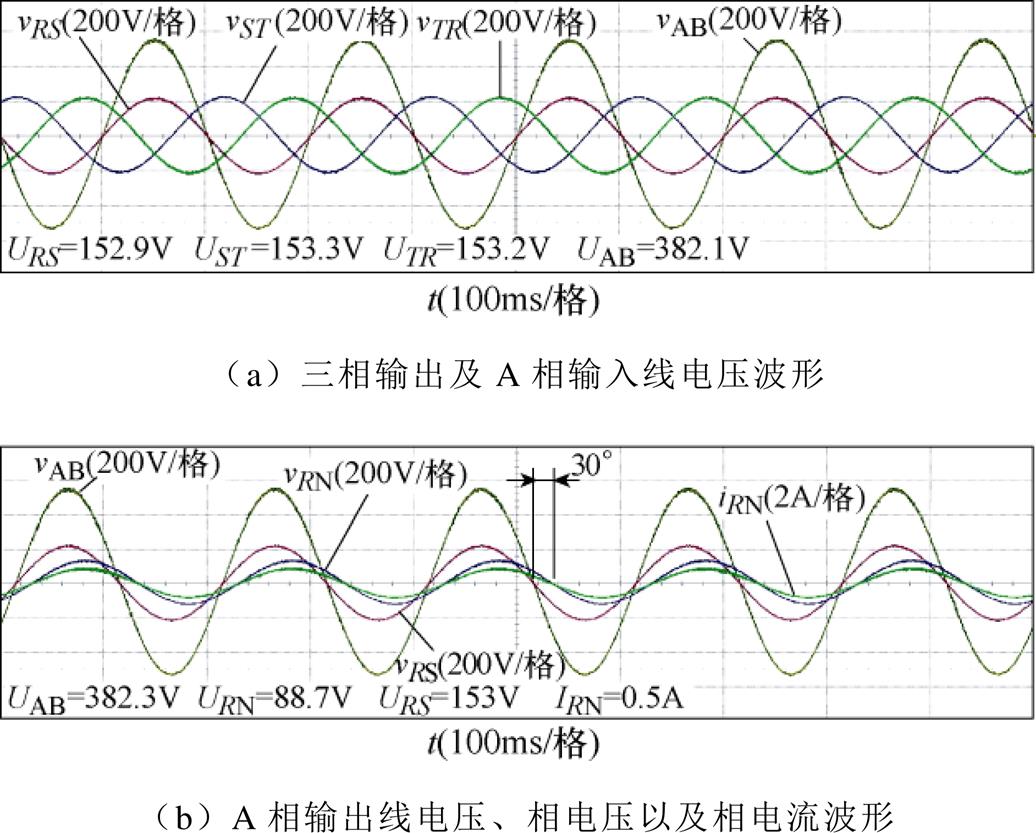
变换器轻载运行输入输出实验波形如图11所示,此时为后级DBC占空比D=0.8、三相负载160W 工作时的输入输出波形。如图11a所示,输出电压仅改变了电压幅值,且大小与理论分析值(DvAB/2)一致。此外,输出电压THD=0.83%,说明后级变换器不会引入波形畸变;如图11b所示,A相输出线电压与输入线电压保持同相位,并且由于负载为纯阻性,输出线电压超前输出相电压30°,证明变换器轻载运行时具有良好的输出特性。
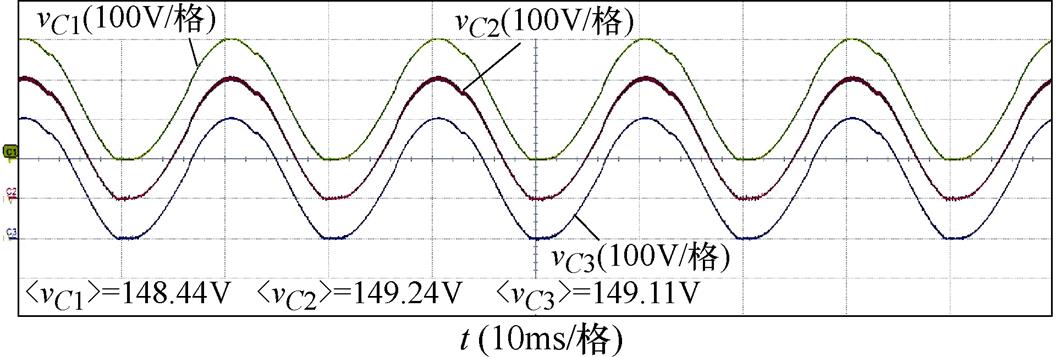
变换器A相开关电容模块电容电压实验波形如图12所示,各电容电压均包含直流及交流分量,并且电压保持相等,证明了SCC电压自均衡特性。电容中直流分量大小即为电容电压平均值,其值低于理论值,这是由于直流分量在变换器运行初始时刻产生,在每个电网周期,电容对变换器内部杂散电阻放电,导致电压降低;而当电容电压降为零时,对应侧二极管正向偏置,电路进入暂态;当直流电压恢复至相电压峰值时,电路将再次回归稳态。
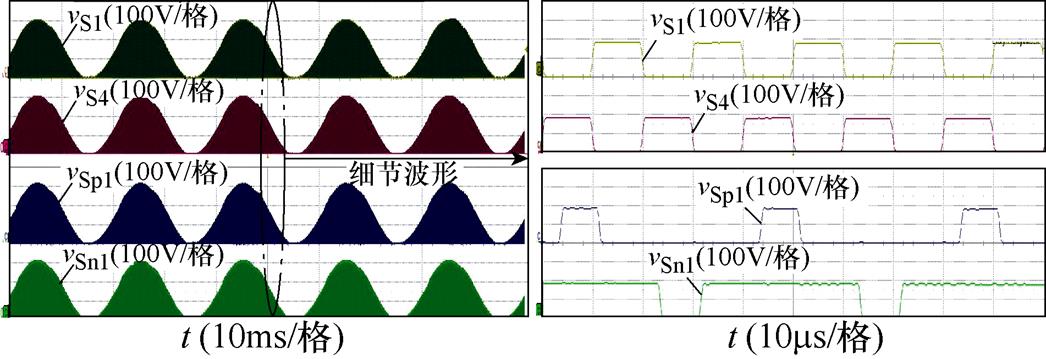
变换器A相功率开关管两端电压实验波形如图13所示,可以看出,各开关管具有相同的电压应力,其包络线为该模块电容电压。此外,细节波形可以反映前级SCC奇数开关S1与偶数开关S4互补导通,占空比约为0.5;而后级P-cell开关管Sp1占空比约为0.8,N-cell开关管Sn1占空比约为0.2,并且为交错导通。
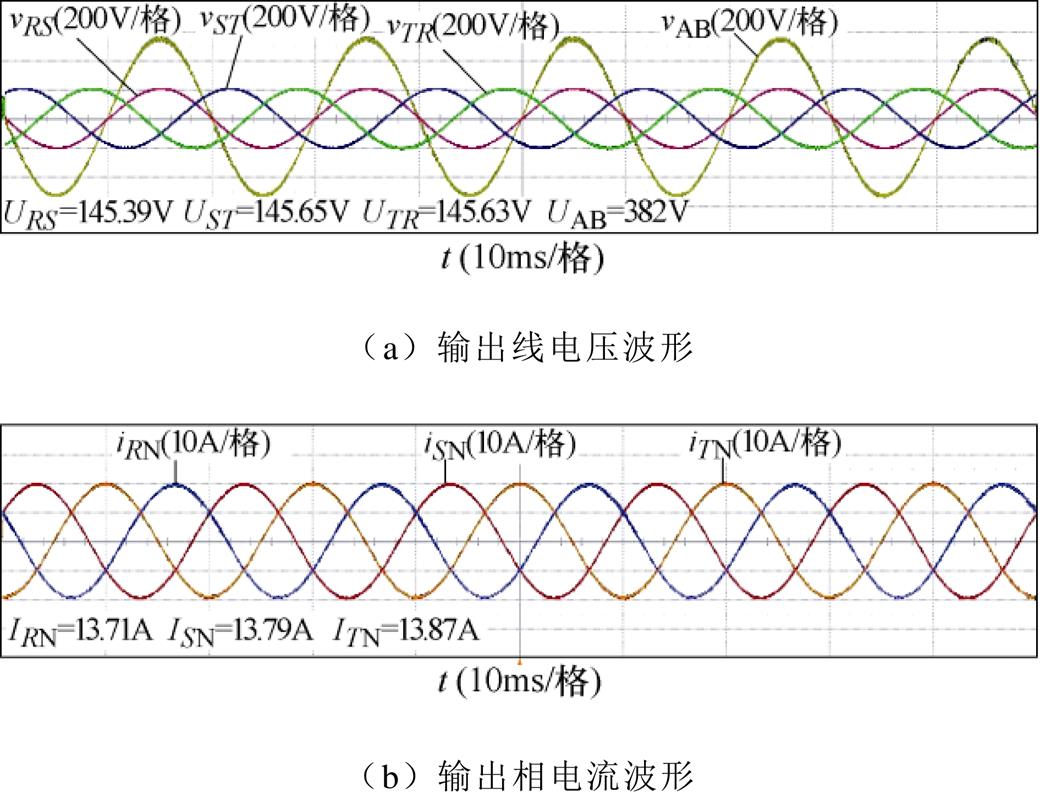
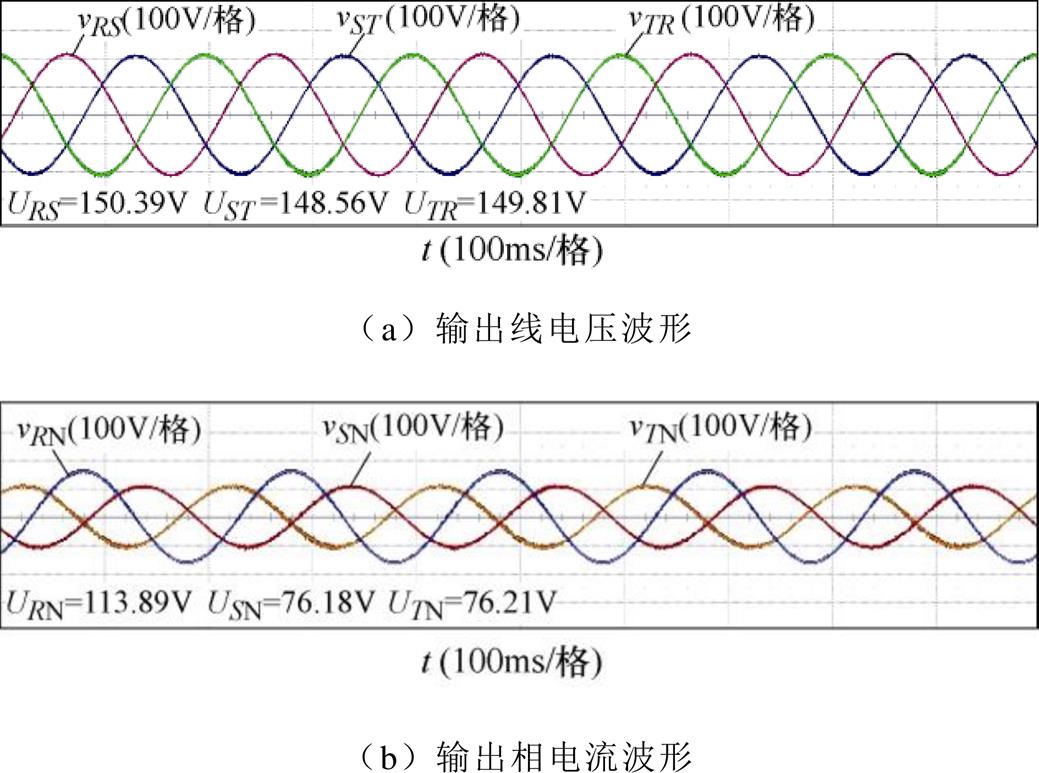
变换器在额定负载运行输出电压电流实验波形如图14所示。此时三相输出线电压约为理论分析值(DvAB/2)的95.7%,4.3%的电压降落主要是由变换器等效内阻引起的。
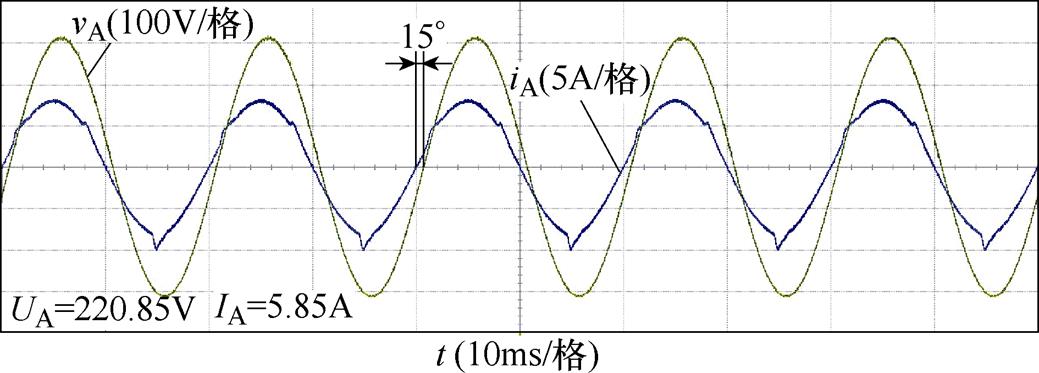
变换器额定负载运行A相输入电压与电流波形如图15所示。变换器呈容性,电流超前电压15°,输入功率因数为0.966,与理论分析值一致。而输入电流存在畸变,THD=6.06%,这是由于SC模块电容电压直流分量衰减导致电压提前过零,变换器进入暂态引起的。为改善上述现象,应考虑精细化布板,降低实验电路板以及连接导线等因素的影响。
变换器三相不对称负载运行输出电压实验波形如图16所示,此时为后级DBC占空比D=0.8,A相输出功率384W,B、C相输出功率573W时的输出电压波形。可以看到,三相输出相电压由于在中性点电压偏移而产生不对称,但三相输出线电压仍基本保持平衡,证明变换器带不对称负载能力。
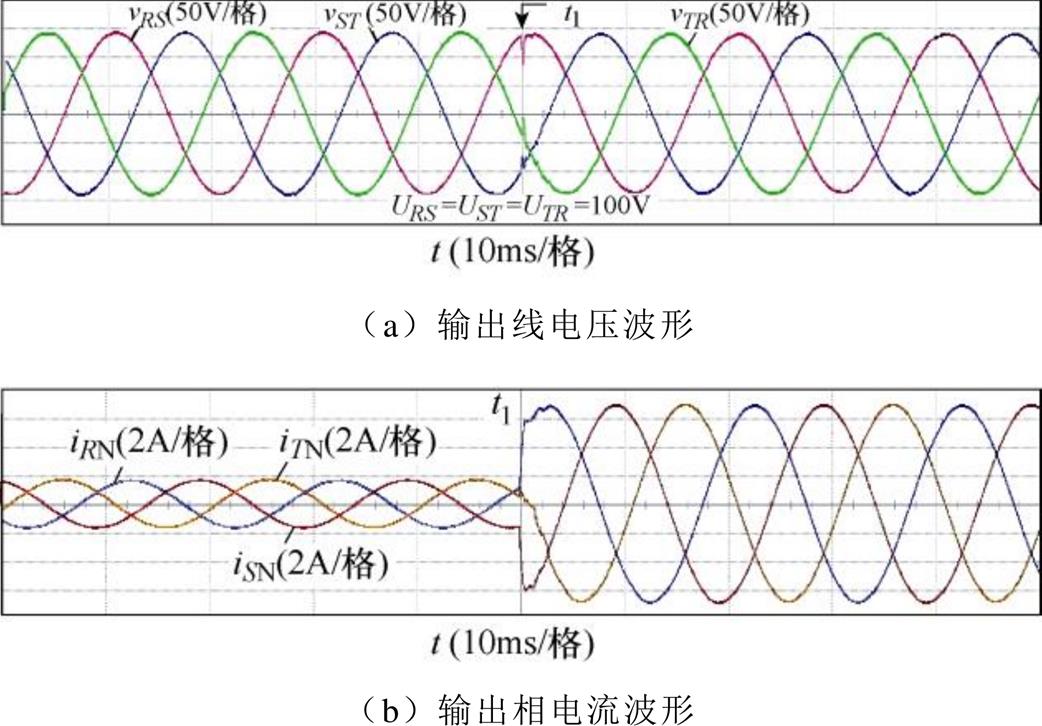
变换器闭环运行输出电压电流实验波形如图17所示。此时,给定线电压参考值100V,t1时刻负载功率由每相78W阶跃为每相306W,可以看出,输出相电流由1.34A阶跃为5.3A,但输出线电压仍保持100V不变,证明了所提控制策略的有效性。
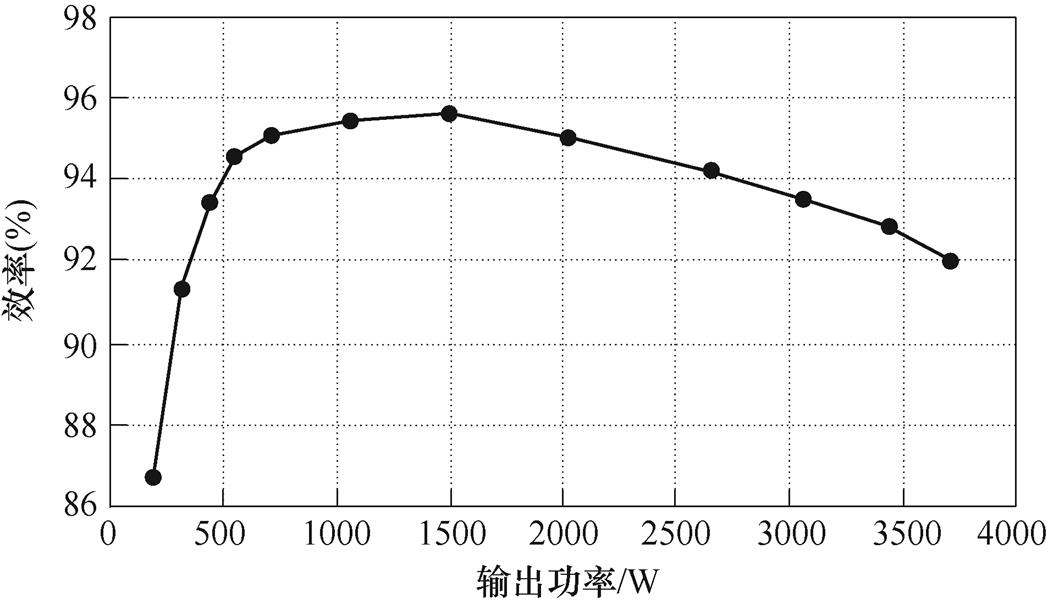
后级DBC保持占空比为0.8,通过改变负载测得变换器效率曲线,如图18所示。在满载时变换器效率为92.9%,而效率最高值在输出功率为1 500W左右出现为95.8%。
6 结论
本文提出一种基于SC与DBC的三相AC-AC变换器拓扑结构替代传统自耦变压器,该变换器利用前级电场能量转换和后级斩波电路联合降压,减少了稀有金属铜的用量;继承了原SCC调制简单、易于模块化拓展等优点,并且解决了其输出电压无法调节的难题,采用简单控制策略便能保证输出电压稳定;同时采用TQS实现交-交变换,减少了电路开关数量,避免了换流难题。文中详细介绍了变换器的结构组成及工作原理,给出了变换器的等效模型及控制策略,探讨了变换器参数设计方法,通过结构对比清晰地反映了变换器特点,最后搭建3.5kW实验样机进行验证,结果表明:
1)前级电路无需附加控制便能实现电容电压 均衡。
2)变换器在轻载、额定负载以及不对称负载情况下,均具有良好的输出波形质量。
3)闭环运行状态下,负载阶跃时能够保证输出电压稳定。
参考文献
[1] Eguchi K, Asadi F, Ishibashi T, et al. Design of an inductor-less step-down AC/AC converter combined with a symmetrical-type converter and ladder-type converters[C]//3rd International Conference on Power and Energy Applications, Busan, 2020: 89-93.
[2] Kolar J W, Friedli T, Rodriguez J, et al. Review of three-phase PWM AC-AC converter topologies[J]. IEEE Transactions on Industrial Electronics, 2011, 58(11): 4988-5006.
[3] 王文杰, 杨益平, 杭丽君, 等. 应用于交-交变换的M3C矩阵变换器系统控制策略[J]. 电力系统自动化, 2020, 44(12): 186-192.
Wang Wenjie, Yang Yiping, Hang Lijun, et al. Control strategy of M3C matrix converter system applied to AC-AC transformation[J]. Automation of Electric Power Systems, 2020, 44(12): 186-192.
[4] 杨君东, 李磊. Buck-Boost式三电平单级AC/AC变换器[J]. 电工技术学报, 2010, 25(2): 107-113.
Yang Jundong, Li Lei. A Buck-Boost mode three- level single-stage AC/AC converter[J]. Transactions of China Electrotechnical Society, 2010, 25(2): 107- 113.
[5] Rosas-Caro J C, Mancilla-David F, Gonzalez-Lopez J M, et al. A review of AC choppers[C]//20th Inter- national Conference on Electronics Communications and Computers, Cholula, 2010: 252-259.
[6] Lazzarin T B, Andersen R L, Martins G B, et al. A 600W switched-capacitor AC-AC converter for 220V/ 110V and 110V/220V applications[J]. IEEE Transa- ctions on Power Electronics, 2012, 27(12): 4821- 4826.
[7] Andersen R L, Lazzarin T B, Barbi I. A 1kW step- up/step-down switched-capacitor AC-AC converter[J]. IEEE Transactions on Power Electronics, 2013, 28(7): 3329-3340.
[8] Lazzarin T B, Andersen R L, Barbi I. A switched- capacitor three-phase AC-AC converter[J]. IEEE Transactions on Industrial Electronics, 2015, 62(2): 735-745.
[9] de Silva R L, Lazzarin T B, Barbi I. Reduced switch count step-up/step-down switched-capacitor three- phase AC-AC converter[J]. IEEE Transactions on Industrial Electronics, 2018, 65(11): 8422-8432.
[10] 王立乔, 韩胥静, 李占一, 等. 一种新型飞跨电容型Zeta多电平逆变器[J]. 电工技术学报, 2022, 37(1): 254-265.
Wang Liqiao, Han Xujing, Li Zhanyi, et al. A novel flying-capacitor Zeta multi-level inverter[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(1): 254-265.
[11] Silva G V, de Andrade J M, Coelho R F, et al. Switched-capacitor differential Boost inverter: design, modeling, and control[J]. IEEE Transactions on Industrial Electronics, 2020, 67(7): 5421-5431.
[12] 丁杰, 高双, 赵世伟, 等. 基于耦合电感的对称式交错并联低输入电流纹波高增益DC-DC变换器[J].电工技术学报, 2021, 36(7): 1507-1515.
Ding Jie, Gao Shuang, Zhao Shiwei, et al. Sym- metrical interleaved low input current ripple high step-up DC-DC converter based on coupled indu- ctor[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1507-1515.
[13] 王要强, 张亨泰, 赖锦木, 等. 低应力高电平开关电容逆变器及其调制策略[J]. 电工技术学报, 2021, 36(20): 4237-4248.
Wang Yaoqiang, Zhang Hengtai, Lai Jinmu, et al. Topology and modulation strategy for switched capacitor inverter with low voltage stress and high level[J]. Transactions of China Electrotechnical Society, 2021, 36(20): 4237-4248.
[14] 刘妍, 杨晓峰, 闫成章, 等. 考虑寄生电感的谐振开关电容变换器电压尖峰抑制[J]. 电工技术学报, 2021, 36(12): 2627-2639.
Liu Yan, Yang Xiaofeng, Yan Chengzhang, et al. Suppression of voltage spike in resonant switched capacitor converter considering parasitic indu- ctance[J]. Transactions of China Electrotechnical Society, 2021, 36(12): 2627-2639.
[15] 闫成章, 杨晓峰, 刘妍, 等. 基于移相控制的谐振开关电容变换器占空比优化策略[J]. 电工技术学报, 2021, 36(增刊2): 676-687.
Yan Chengzhang, Yang Xiaofeng, Liu Yan, et al. Duty cycle optimization of phase shift control based on resonant switched capacitor converter[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(S2): 676-687.
[16] He Liangzong, Zeng Tao, Zhang Jianhuan. The regulation characteristics of bridge modular switched- capacitor AC-AC converter[J]. IEEE Access, 2019, 7: 147683-147693.
[17] Sun Pengwei, Liu Chuang, Lai J S, et al. Three-phase dual-Buck inverter with unified pulse width modu- lation[J]. IEEE Transactions on Power Electronics, 2012, 27(3): 1159-1167.
[18] Liu Chuang, Wang Yixu, Cui Jianfeng, et al. Trans- formerless photovoltaic inverter based on interleaving high-frequency legs having bidirectional capability[J]. IEEE Transactions on Power Electronics, 2016, 31(2): 1131-1142.
[19] 蔡慧, 包莅庭, 张子省, 等. 变比为2的升压型开关电容变换器研究[J]. 中国电机工程学报, 2017, 37(10): 2963-2970.
Cai Hui, Bao Liting, Zhang Zixing, et al. Research on a step-up switched-capacitor converter with a con- version gain of 2[J]. Proceedings of the CSEE, 2017, 37(10): 2963-2970.
[20] 王议锋, 程鹏宇, 马小勇, 等. 基于SiC的交错并联型Buck变换器的参数综合设计方法[J/OL]. 电工技术学报: 1-10[2022-03-24]. https://kns.cnki.net/kcms/ detail/11.2188.TM.20211274.0904.001.html.
Wang Yifeng, Cheng Pengyu, Ma Xiaoyong, et al. The parameter synthesis design method of staggered parallel buck converter based on SiC[J/OL]. Transa- ctions of China Electrotechnical Society: 1-10 [2022- 03-24]. https://kns.cnki.net/kcms/detail/11.2188.TM. 20211274.0904.001.html.
[21] Evzelman M, Ben-Yaakov S. Average-current-based conduction losses model of switched capacitor con- verters[J]. IEEE Transactions on Power Electronics, 2012, 28(7): 3341-3352.
[22] 王艺博, 蔡国伟, 刘闯, 等. 基于双极性直接式AC/AC变换的单相动态电压恢复器[J]. 电力系统自动化, 2020, 44(6): 171-177.
Wang Yibo, Cai Guowei, Liu Chuang, et al. Single- phase dynamic voltage restorer based on bipolar direct AC/AC conversion[J]. Automation of Electric Power Systems, 2020, 44(6): 171-177.
[23] Cheung C K, Tan S C, Tse C K, et al. On energy efficiency of switched-capacitor converters[J]. IEEE Transactions on Power Electronics, 2013, 28(2): 862-876.
[24] Dan Hanbing, Zeng Peng, Xiong Wenjing, et al. Model predictive control-based direct torque control for matrix converter-fed induction motor with reduced torque ripple[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(2): 90-99.
A Three-Phase AC-AC Converter Based on Switched-Capacitor and Dual-Buck Converter
Wang Rutian Li Hui Liu Chuang Pei Zhongchen Kong Lingguo
(School of Electrical Engineering Northeast Electric Power University Jilin 132012 China)
Abstract The traditional auto-transformer in distribution network suffers from problems such as heavy magnetic core and difficult voltage regulation. To overcome these problems, a three-phase AC-AC converter based on switched-capacitor (SC) and dual-Buck converter (DBC) is proposed in this paper. The topology adopts a two-stage power conversion structure with high step-down ratio, continuously adjustable voltage and easy modular expansion, which can meet the requirements of voltage level transformation in distribution network. Firstly, the structure and operation principle of the converter were presented in detail, and the flexible regulation of output voltage was realized through the design and application of two-stage power conversion and dead-zone-free control. Secondly, the output gain expression and the equivalent circuit model of the converter were derived, and a simple voltage closed-loop control strategy was designed. Then the design method of key parameters was given, and the characteristics of the converter were reflected clearly by comparing with several structures. Finally, a 3.5kW experimental prototype was built to verify the correctness and feasibility of the proposed topology.
keywords:Distribution network, switched-capacitor, dual-Buck converter, three-phase, AC-AC conversion
DOI: 10.19595/j.cnki.1000-6753.tces.220150
国家自然科学基金资助项目(51877035)。
中图分类号:TM46
收稿日期 2022-01-28
改稿日期 2022-03-20
作者简介
王汝田 男,1979年生,教授,硕士生导师,研究方向为变换器拓扑与控制、新能源发电并网控制技术。E-mail: wrtmail@163.com
刘 闯 男,1985年生,教授,博士生导师,研究方向为能源互联网与柔性电网络中高效高可靠电力电子功率变换的基础理论与技术。E-mail: victorliuchuang@163.com(通信作者)
(编辑 陈 诚)
 ,构成三相SCC,首端则经小电感分别与三相输入电源相连。A相DBC结构如图1下部分点画线框所示,由基本的开关模块P-cell、N-cell组成,包括2个功率开关管(Sp1、Sn1)、2个二极管(VDp1、VDn1)、2个分裂电感(L1、L2)及输出滤波电容(Coa)。DBC分别与各相SC模块后级均压电容(C3、C6、C9)并联,用以实现输出电压线性调节。三相负载为差分连接(类似于H桥、三相三臂的电压源逆变器负载连接方式),因此允许将直流分量引入各电容,而后在三相负载中抵消。值得注意的是,负载中性点N点不能与
,构成三相SCC,首端则经小电感分别与三相输入电源相连。A相DBC结构如图1下部分点画线框所示,由基本的开关模块P-cell、N-cell组成,包括2个功率开关管(Sp1、Sn1)、2个二极管(VDp1、VDn1)、2个分裂电感(L1、L2)及输出滤波电容(Coa)。DBC分别与各相SC模块后级均压电容(C3、C6、C9)并联,用以实现输出电压线性调节。三相负载为差分连接(类似于H桥、三相三臂的电压源逆变器负载连接方式),因此允许将直流分量引入各电容,而后在三相负载中抵消。值得注意的是,负载中性点N点不能与 点以及电网中点O点相连,因为变换器差分特性将会消失,导致变换器不能工作。
点以及电网中点O点相连,因为变换器差分特性将会消失,导致变换器不能工作。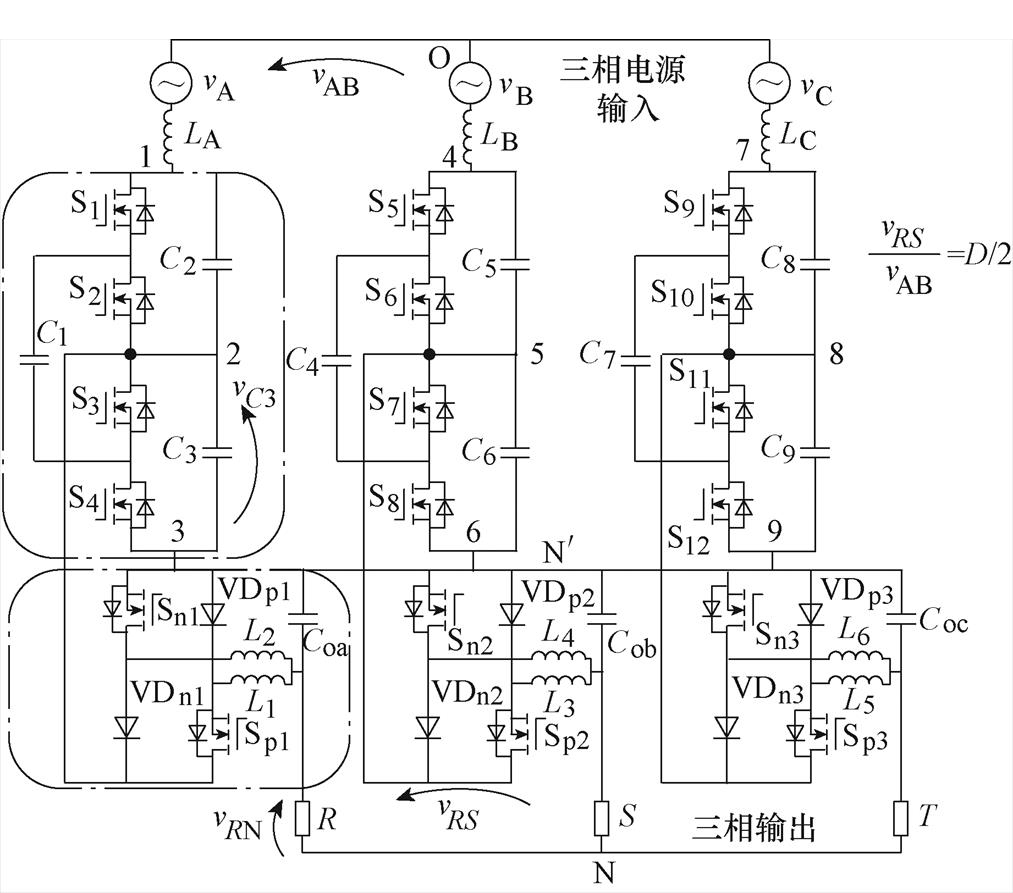
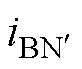 为零时,O、
为零时,O、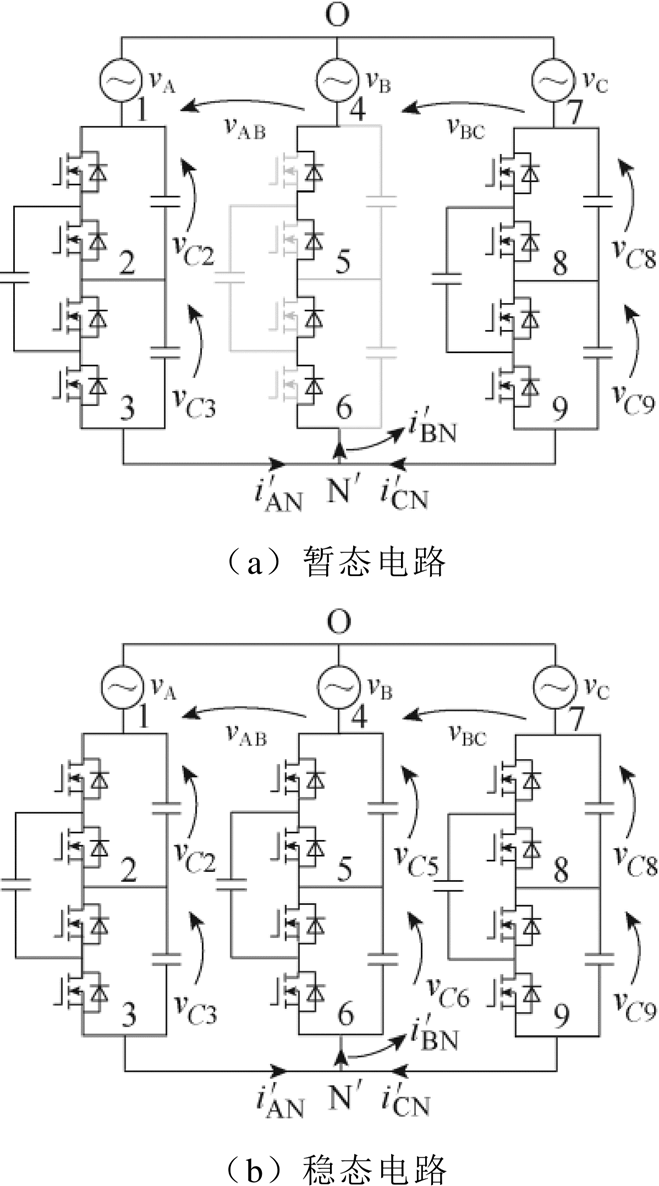
 端口与电压源或者电容正极相连,
端口与电压源或者电容正极相连, 端口与电压源或者电容负极相连,公共端口连接限流电感,“→、←”表示公共端口电流方向。P-cell电流只流出公共端口,N-cell电流只流入公共端口。P-cell与N-cell并行组合,使得DBC具有双向电流能力,通常用于实现逆变功能。
端口与电压源或者电容负极相连,公共端口连接限流电感,“→、←”表示公共端口电流方向。P-cell电流只流出公共端口,N-cell电流只流入公共端口。P-cell与N-cell并行组合,使得DBC具有双向电流能力,通常用于实现逆变功能。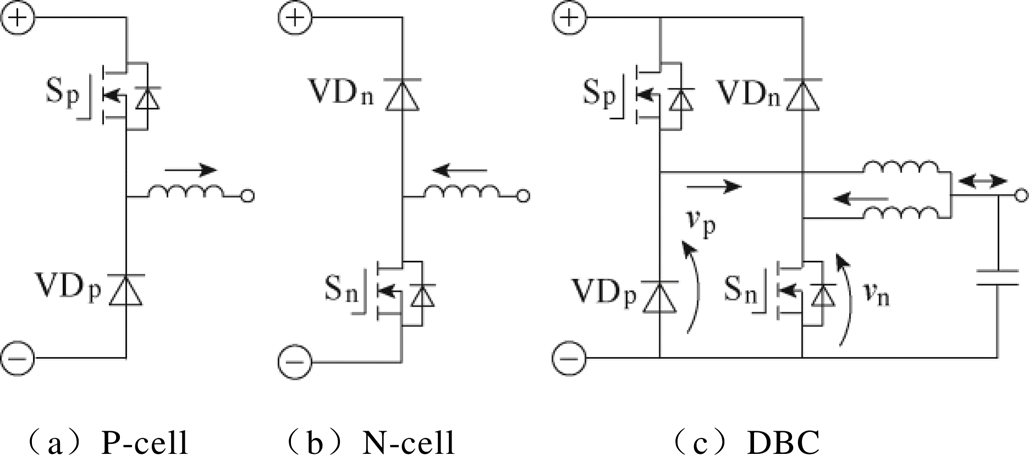

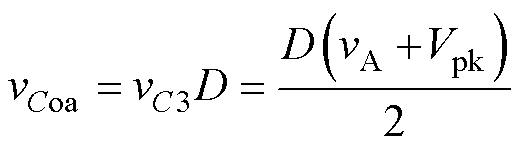 (1)
(1)
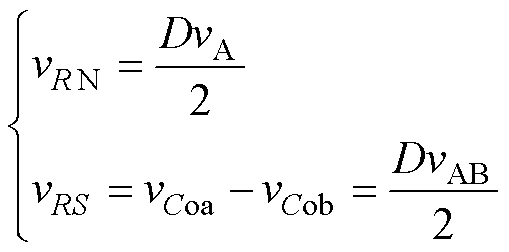 (2)
(2)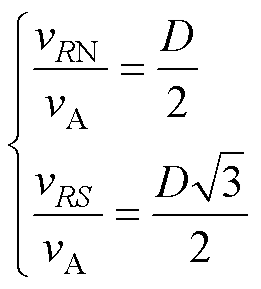 (3)
(3)
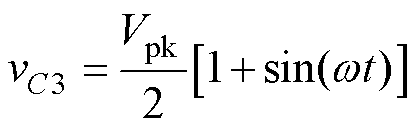 (4)
(4)
 (5)
(5)
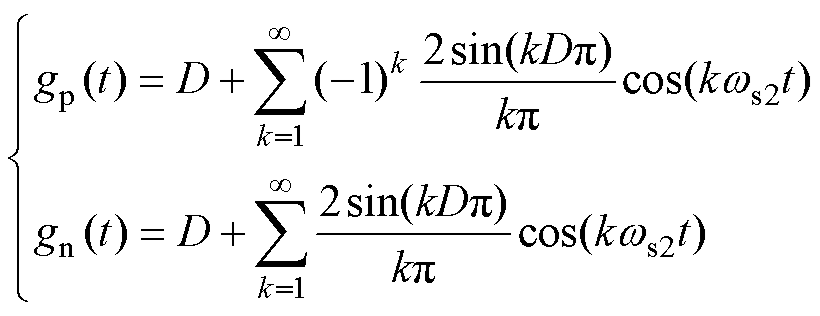 (6)
(6)
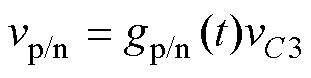 (7)
(7)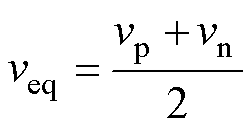 (8)
(8)
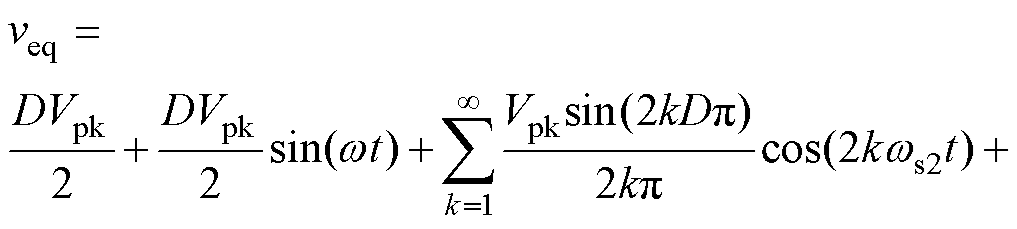
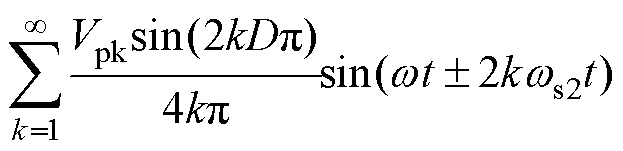 (9)
(9)
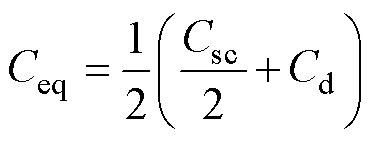 (10)
(10)
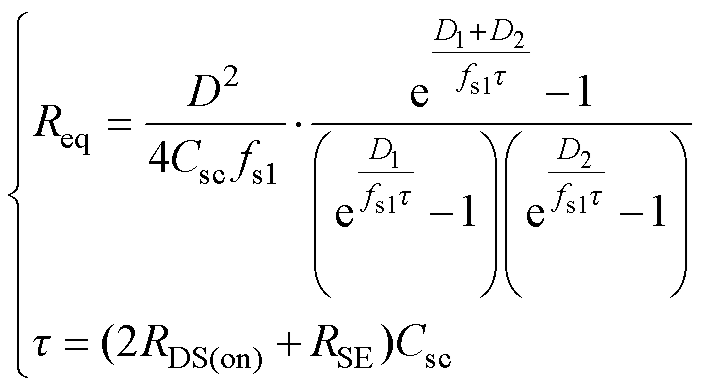 (11)
(11)
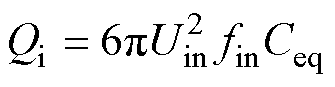 (12)
(12)
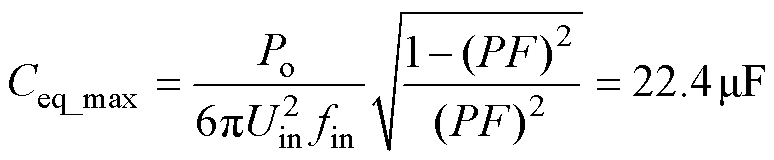 (13)
(13)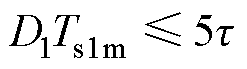 (14)
(14)
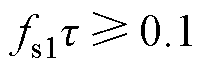 (15)
(15)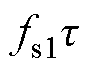 =0.268,SCC工作于PC模式,满足设计要求。
=0.268,SCC工作于PC模式,满足设计要求。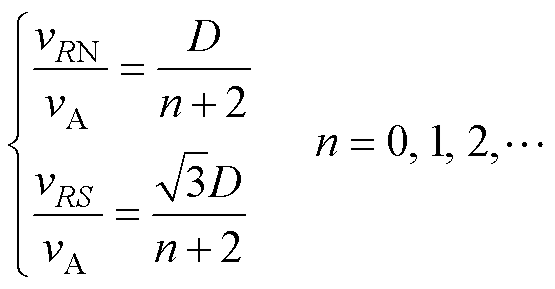 (16)
(16)
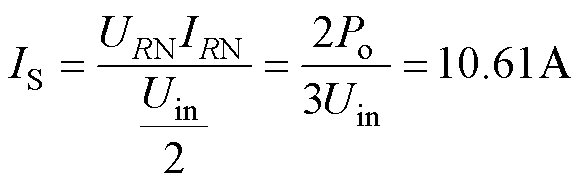 (17)
(17)
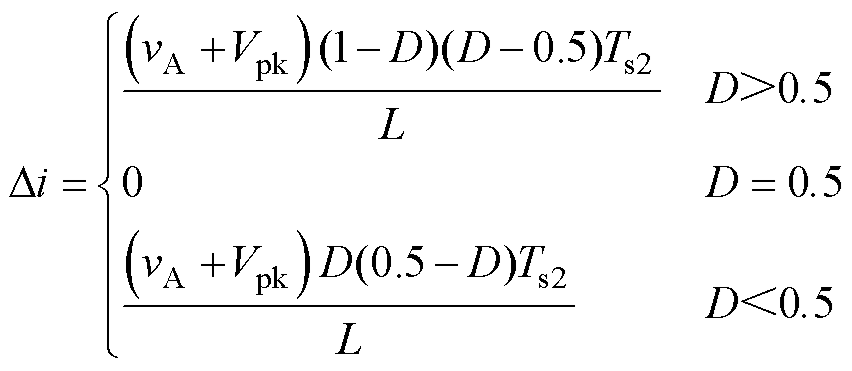 (18)
(18)