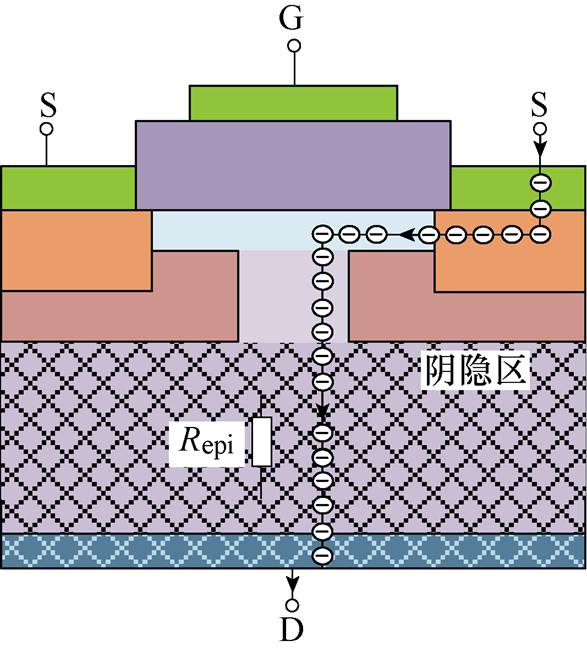
图1 传统的SiC MOSFET静态模型
Fig.1 Traditional static model of the SiC MOSFET
摘要 碳化硅（SiC）材料因其在禁带宽度、击穿电场、电子饱和速度等方面的优势，使得SiC MOSFET具有高频、高压以及高温等优势。然而SiC MOSFET的特殊材料、结构以及高开关速度使得开关瞬态过程中器件内部的物理机理更为复杂。传统的SiC MOSFET模型沿用了部分硅（Si）器件的建模方法，难以准确评估器件在装置中的动静态特性。为此，该文提出一种基于物理的SiC MOSFET改进电路模型。基于器件的工作机理，分析传统SiC MOSFET模型的不足，并针对不足进行改进建模。电流扩散方式是影响SiC MOSFET静态特性的重要因素，由于器件N-漂移区较窄，导致漂移区电流扩散呈梯形，进而对漂移区电阻进行改进建模。SiC MOSFET开关瞬态模型刻画了器件的高频应用特性，基于突变结、穿通特性以及负电压关断分别对器件结电容进行改进建模。最后基于CREE 1 200V/325A的SiC MOSFET器件进行实验，仿真与实验具有较好的一致性，验证了改进模型的准确性。
关键词：SiC MOSFET 电路模型 静态特性 瞬态特性
目前的主流硅（Si）功率半导体器件受限于材料的物性极限，难以满足未来电力电子系统中大容量电能变换装置高速、高频和高温等极端工作条件要求。而以碳化硅（SiC）器件为代表的宽禁带半导体器件由于在禁带宽度、击穿电场、电子饱和速度、热导率等方面较Si具有明显优势[1-2]，使器件工作温度、开关频率、损耗等性能得到大幅提升，由此带来装置滤波电路体积、冷却系统体积等的大幅减小，进而可以大幅提升装置的功率密度、工作效率以及工作频率。然而，更高的开关速度使得SiC功率器件开关瞬态呈现更为复杂的工作过程，精确特性表征的难度较传统Si器件更大，封装技术较传统Si器件更苛刻[3-4]。因此，为指导SiC器件在电力电子装置中的应用及优化设计，需要一个能够准确表征SiC MOSFET静态和瞬态特性的仿真模型。
在SiC MOSFET器件建模研究方面，目前国内外研究主要分为行为模型、物理模型、数值模型以及混合模型（半物理模型）。行为模型[5-7]因其不能够描述器件内部特性，对器件的应用指导作用较弱；如英国P. Alexakis等建立了SiC MOSFET行为模 型[5]，该模型由漏源电压控制电流源和定电容构成，考虑了封装寄生电感的影响，对SiC MOSFET开关瞬态特性进行了仿真分析；V. Talesara等通过拟合多项式函数方法对器件动态特性进行了行为建 模[6-7]，该方法通过数据优化的方式达到了较高的精度。文献[8]采用神经网络学习的方法建立了SiC MOSFET模型，该模型实质上仍是通过数据拟合得到的行为模型。
针对数值模型，美国B. N. Pushpakaran等借助SILVACO ATLAS软件建立了有限元模型[9]，可模拟复合效应、禁带变窄、碰撞电离和晶格加热等效应。数值模型是一种较为精确的建模方法，适用于元胞和芯片级别的仿真设计及优化。
物理模型是基于器件内部载流子变化的物理机理来表征器件特性的一种模型，它利用半导体数学方程来描述器件内部载流子的变化规律，通过对这些方程的求解来表征器件的端口电气特性。物理模型不仅能够准确表征器件的工作特性，同时又能反映器件内部载流子变化的物理过程，因此更加适合用于指导器件在装置中的应用。美国Fu Ruiyun等建立了SiC MOSFET物理模型[10]，通过非线性电压源和电阻网络模拟了JFET区电流分布不均的特点，采用一组函数实现器件线性区和饱和区的静态特性表征。罗马尼亚G. Chindris等提出了一种基于PSpice的SiC MOSFET物理模型[11]，从器件内部机理映射至外部特性，在软件自带MOSFET内核的基础上进行了改进；瑞士G. Kampitsis等在Simulink环境建立了SiC MOSFET模型[12]，其实质也是基于自带MOSFET模型构建外围补偿电路。文献[13]的SiC MOSFET建模也是基于PSpice自带的MOSFET模型进行改进建模。此外，SiC MOSFET开关瞬态分段线性模型也是经典模型之一[14]，该类模型通过分段线性假设来简化器件的开关瞬态，实现SiC MOSFET开关过程解耦及建模。
综上所述，SiC MOSFET虽然结构较为简单，但由于其材料特性及结构不同使其工作特性较Si MOSFET有较大差别，使得Si器件的特性分析与建模原理及方法并不完全适用于SiC器件[15-16]。而目前的SiC MOSFET模型大部分是基于传统Si MOSFET模型发展得到，大部分模型仅仅是修改了材料特性参数及结构参数；并且由于器件的逐步更新迭代，传统建模方法已经较难对现有器件进行准确表征[17-18]，尤其是开关瞬态特性，因此需要对传统模型进行改进。
本文首先对传统SiC MOSFET物理模型的不足进行了分析，传统模型未考虑SiC MOSFET基区宽度较窄以及突变结等结构特点，针对上述不足对动静态特性的影响进行研究。基于SiC MOSFET器件工作机理建立了改进的动静态模型，然后在PSpice仿真平台中构建了等效电路模型。最后采用CREE 1 200V/325A SiC MOSFET模块进行了仿真与实验验证。
SiC MOSFET传统模型中，其通态电流和电阻的计算采用的均是全扩散模型。传统的SiC MOSFET静态模型如图1所示，图中阴影部分表示载流子在基区的扩散，这类扩散在Si器件中最为常见，这是由于Si器件具有较宽的基区以及较高的载流子迁移率。然而SiC MOSFET与Si器件材料特性以及结构具有较大的不同：SiC材料的临界电场要远远大于Si器件，使得其采用较小的基区宽度就能够达到较高的击穿电压。而导通压降与基区宽度近似成正比，因此器件厂商在设计SiC MOSFET器件时，为了实现低导通压降，一般采用较小的基区宽度以及较高的掺杂浓度。此外，SiC材料的迁移率低于传统的Si材料，导致正向导通过程中SiC MOSFET载流子扩散方式与传统的Si器件不再相同，因此采用传统Si器件建模方法得到的SiC MOSFET静态模型的导通压降相比实际器件的导通压降偏小。
图1 传统的SiC MOSFET静态模型
Fig.1 Traditional static model of the SiC MOSFET
SiC MOSFET瞬态特性主要由3个结电容CGS、CDS和CGD决定，这些结电容具有非线性特征，它们对器件的开关速度和振荡特性有很大的影响，因此3个结电容的准确建模对于器件特性表征，尤其是高频振荡特性的准确表征具有重要意义。然而传统的SiC MOSFET模型中，结电容建模要么是采用Si器件的建模方法，要么采用函数拟合以及定电容。这些模型针对单一工况下的SiC MOSFET瞬态特性仿真较为准确，但是针对多工况下的器件瞬态特性表征会带来较大的影响。
针对SiC MOSFET栅漏极电容CGD，在传统模型中，CGD建模仍采用的是Si MOSFET建模方法。然而，SiC MOSFET的基区宽度比普通Si器件要小得多。在SiC MOSFET关断过程中，当电压施加到漏源极两端时，反偏结将产生较宽的耗尽层，所加电压越大，耗尽层越宽。由于P+基区是高掺杂区，N-漂移区是轻掺杂区，所以耗尽层随着电压的增加在漂移区内拓展。过去，SiC MOSFET的电压等级一般低于600V，此电压等级的器件关断过程中耗尽层一般不会穿通器件基区。然而，目前商用最高电压等级已经达到了1 700V，远大于Si器件。对于这些中高压等级器件，一般采用的是穿通型设计，由此达到低导通电阻的目的[18]。当耗尽层穿通N-区域以后，由于N+区域掺杂浓度较高，耗尽层宽度基本不再增加，即栅漏极电容将保持不变。而传统模型未考虑这一点则会使得穿通工况下器件的电容表征产生较大偏差。
针对漏源级电容CDS建模，传统物理模型中一般是采用一个二级管与结电容并联来模拟漏源极电容正向导通与阻断之间变化。在CDS建模过程中，可以近似将该结电容当作PN结进行建模，但是传统模型未考虑SiC材料与Si材料的不同：在Si器件中，为了实现器件的软恢复，现有的制造工艺一般采用先扩散后进行局部离子注入的方式进行PN结制造，因此Si器件中PN结一般为缓变结。而由于SiC材料的特殊性，无论是采用外延、扩散或者离子注入工艺，其掺杂离子生长速率以及深度较传统Si材料均较小，因此最终形成PN结的掺杂过渡属于突变型[18]。传统SiC MOSFET模型采用缓变结建模方法将对结电容表征产生较大影响。
针对CGS建模，现有的SiC MOSFET模型中采用的仍是普通Si器件建模方法：Si MOSFET采用正电压开通、零电压关断，此过程可将CGS近似看作恒定值。但是由于SiC材料的特殊性，一般采用的是负电压关断，这样可减小器件的漏极电流，使器件更可靠的关断。当栅源电压为负时，此时在源极N+区域会形成耗尽层，这将导致栅源极电容增大，而传统模型中没有考虑到这一点，则会导致较大的误差。
图2所示为完整的SiC MOSFET物理模型组成。主要包括静态模型和开关瞬态模型。静态模型包括通态电流模型和通态电阻模型。传统建模文献[6, 13]中一般关注器件导通V-I特性曲线的电流模型，忽略了器件通态电阻的建模研究，通常采用等效电阻模型。实际上，通态电阻除了影响线性区电压对电流的变化率，其对于瞬态特性也具有较大影响，更直接影响开关瞬态特性中高频振荡衰减的幅度，因此需要针对通态电阻模型进行研究。
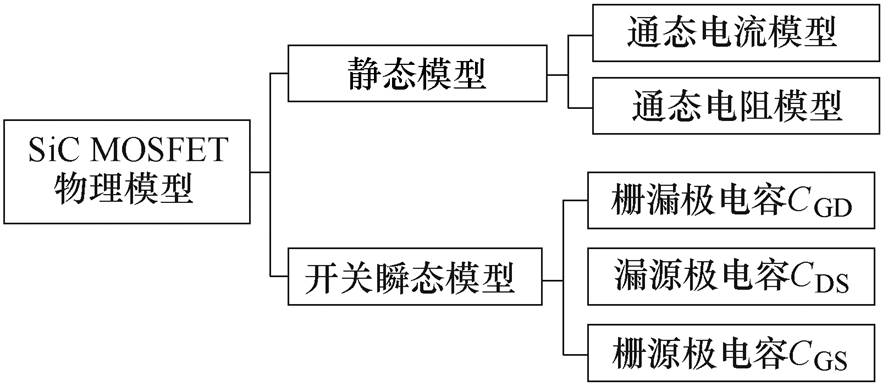
图2 SiC MOSFET动静态模型组成
Fig.2 Composition of SiC MOSFET dynamic and static models
图3所示为SiC MOSFET正向导通时等效电路，当栅源极电压VGS≤Vth（阈值电压）时，MOS结构的金属和SiC半导体之间存在能带差，电子不能够在沟道中聚集，即使漏源极电压VDS＞0，MOS沟道中没有输运电子流过，因此器件电流iD=0。
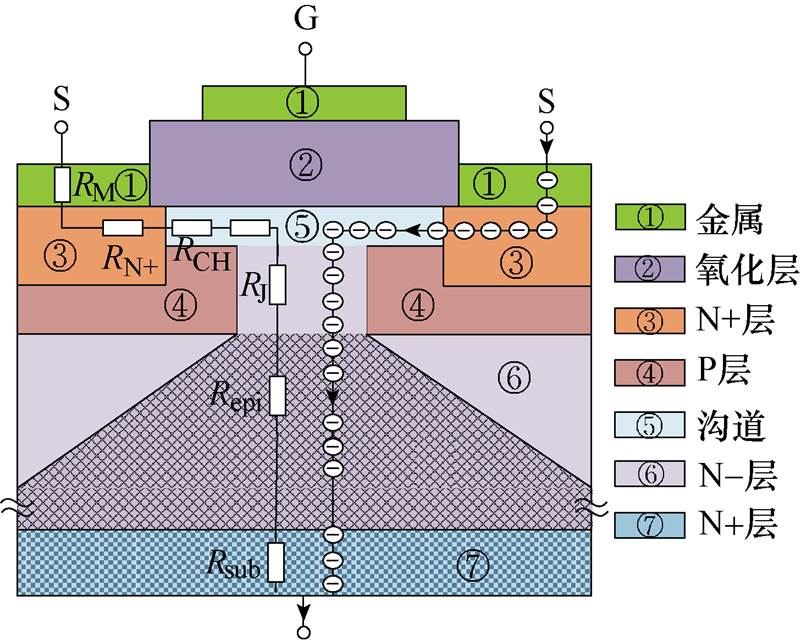
图3 SiC MOSFET静态模型
Fig.3 Static model of the SiC MOSFET
随着栅极电压逐渐增加：当VGS＞Vth时，栅极电压越界，根据金属和半导体接触特性，将会形成一条反型层沟道，沟道的垂直扩展只有几纳米，此时由源极注入的电子在反型层沟道传输。随着VDS增大，沟道电流进一步增加，但是沟道两侧的电压降V(y)也将增加，这意味着远离源极的电压降将减少，将使得沟道变窄。单位长度的沟道电阻表示为
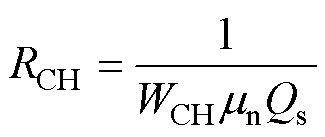（1）
式中，WCH为垂直于横截面的沟道宽度；mn为SiC材料中电子迁移率；Qs为沟道电荷。沿着沟道长度为y的区域，存在电荷Q( y)=Qs。因此可以得到对于长度y的沟道电阻和电荷关系表示为
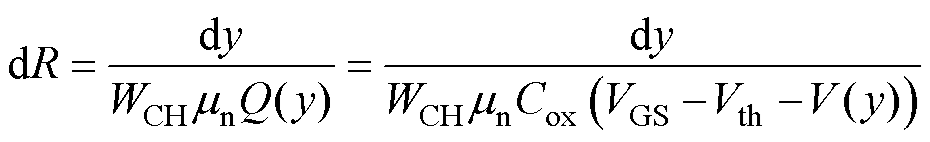（2）
式中，Vth为阈值电压；Cox为栅氧层电容；V(y)为沿着沟道电压降。此时在单位电阻dR上的电压降为
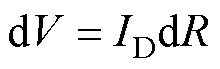（3）
将式（2）代入式（3）并整理可以得到
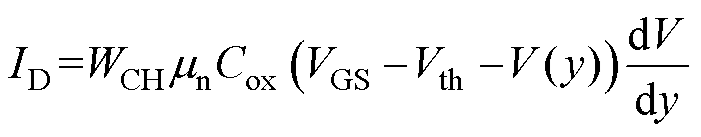（4）
沿沟道位置y =0到y =LCH（LCH为沟道长度）进行积分可得
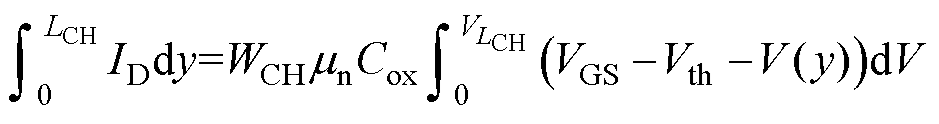（5）
对于VCH＜VGS-Vth的情形，积分式（5）可以得到
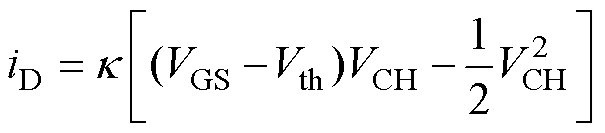（6）
其中
式中，VCH为沟道压降。SiC MOSFET工作在线性区（欧姆区），电流随着VCH的增加而逐渐增大，若此时VCH较小，式（6）可以化简为
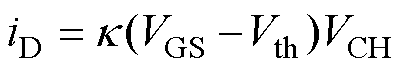（7）
此时沟道电阻可以近似表示为
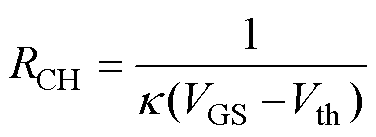（8）
当VCH=VGS-Vth时，此时电流流过沟道产生的电压与VGS-Vth相等，意味着MOS沟道其中一端开始关断，即此时为线性区与饱和区的分界点。
随着VCH继续增加，VCH＞VGS-Vth，理论上沟道端点电压会继续增加，但是由于沟道电压是由电流决定的，此时沟道已经逐渐关断，电流也会逐渐趋于不变，两者达到一个平衡。因此，可以将VCH=VGS-Vth代入式（6）并化简可得
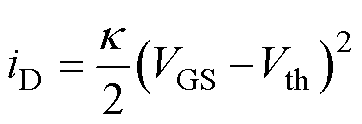（9）
此外，考虑到SiC MOSFET沟道长度调制效应，需在上述模型基础上添加1+lVCH进行拟合，l 为沟道长度调制系数[6]。综上所述，即为SiC MOSFET通态电流模型。
评估SiC MOSFET导通性能的另一个重要因素是通态电阻，如图3所示器件内部通态电阻分布。传统的SiC MOSFET模型通常只针对沟道电阻进行建模，而把其他部分的电阻当作寄生电阻对待。这在一定工况下是可行的，但是对于多工况仿真则会引入较大的误差。
SiC MOSFET通态电阻由多个电阻共同组成，不同工况下其导通电阻分别由不同部分的电阻占主导。在栅极电压较大时，沟道电阻以及积累区域电阻较小，漂移区电阻占比较大。但是随着栅极电压的逐渐降低，沟道电阻以及积累区电阻相对总导通电阻的占比逐渐增加；当栅极电压降低至8V时，沟道电阻以及积累区电阻相对总导通电阻占比相对较大，而漂移区电阻占比相对较小。也正是由于此原因，在栅压逐渐降低过程中，器件V-I曲线的非线性逐渐增加。因此，传统模型只采用一个沟道电阻进行拟合，通常情况下很难对不同工况的器件特性进行准确表征。如图3所示，通态电阻Ron主要由6个电阻串联组成，即
（10）
式中，Repi为漂移区电阻；RM为源接触电阻；RN+为源区电阻；RCH为沟道电阻；RJ为积累区与JFET区总电阻；Rsub为N+衬底电阻。
针对小功率SiC MOSFET器件的导通电阻，如电压等级在50V以下的器件，在额定栅压（20V）下，其线性区静态导通电阻RCH、RJ、Repi各占总电阻25%左右；但是针对中等功率以上的SiC MOSFET，如600V以上的功率SiC MOSFET，在额定栅压下，Repi占线性区总电阻97%以上[18]，在此工况下建模可主要针对Reqi分电阻开展。考虑到SiC相比Si材料具有较高的临界电场，因此其基区宽度要窄得多，使得正向导通情况下基区的电流扩散为梯形，基于该特性对Repi进行了改进建模。
1）漂移区电阻Repi
SiC MOSFET正向导通N-区域电流扩散如图4所示。漂移区电阻Repi指的是电流由JFET区域扩展到漂移区这一部分的电阻，如图4所示N-区域中的阴影部分。在传统的SiC MOSFET模型中，阴影区域覆盖了整个N-区域，如图1所示。由于器件导通电阻与电流扩散面积成反比，因此采用传统全扩散的方式计算得到的导通电阻要比实际更小。而在实际SiC MOSFET导通过程中，该阴影区域是从宽度为a的JFET区域逐渐扩散至衬底区。这是由于SiC MOSFET具有高掺杂及高击穿电场的优势，且SiC MOSFET基区宽度相比传统Si器件基区宽度更窄，使得电流扩散途径主要为梯形。N-基区的电阻包括两部分：第一部分为电流扩散面积随着扩散深度逐渐增加；第二部分为均匀的长方形电流横截面。
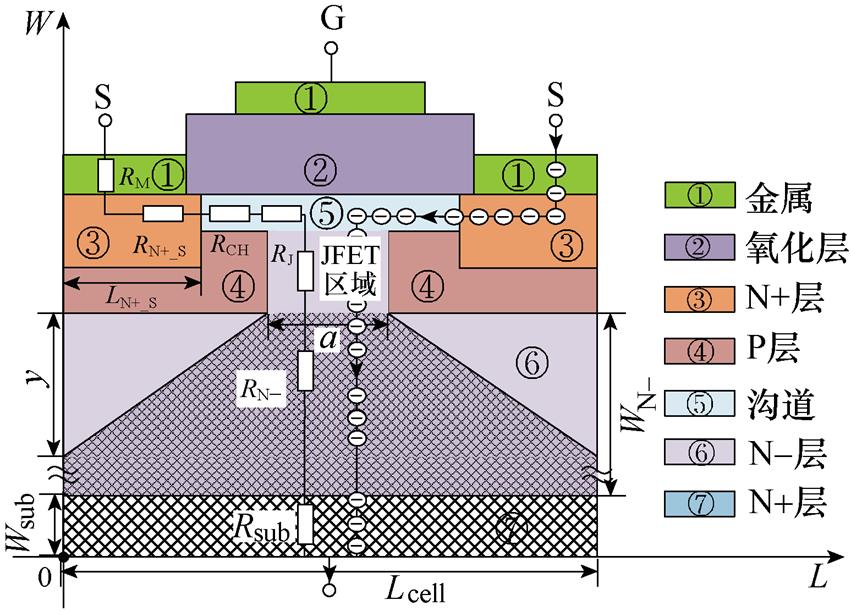
图4 SiC MOSFET正向导通N-区域电流扩散
Fig.4 Current diffusion in the N- region during the SiC MOSFET forward conduction
在图4所示的电流模式中，假设第一部分电流的横截面为从JFET区域以45°角向基区扩散，此时JFET下方深度为y处的电流横截面宽度为
XD=a+2y （11）
式中，a为JEFT区域的宽度；JFET区域下方深度dy的微分电阻为
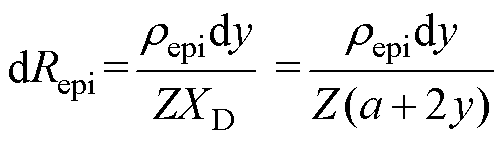（12）
式中，Z为垂直于横截面区域的深度；ρepi为漂移区的电阻率，可以表示为
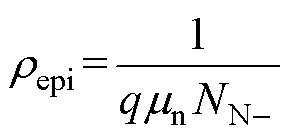（13）
式中，q为元电荷量；NN-为基区掺杂浓度。对式（13）从y =0到y =(Lcell-a)/2进行积分可以得到漂移区第一部分的电阻表示为
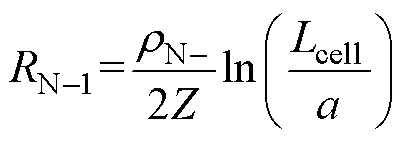（14）
式中，Lcell为元胞长度。当电流扩散至全基区以后，将以长方形进行扩散，可认为电流流过的区域是一个均匀的横截面，该部分的电阻可表示为
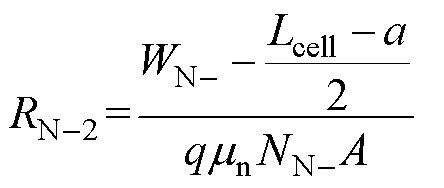（15）
式中，WN-为N-区域的宽度；A为芯片面积；漂移区总电阻Repi为RN-1和RN-2两个电阻之和。
2）源接触电阻RM
源接触电阻为源电极与N+源区之间的金属接触电阻，可以通过均分接触特征电阻
除以接触面积得到。接触特征电阻由接触金属的功函数和源极N+区域掺杂浓度来确定，可以得到
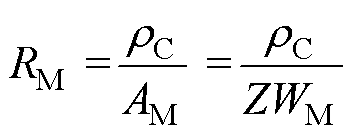（16）
式中，AM为源电极与N+源区之间的金属接触面积；WM为源极接触区域的宽度。
3）源区电阻RN+
电流从接触点进入N+源区以后，在到达沟道之前必须从源区通过，该部分的电阻值可以由源极N+区域的宽度WN+_S及其长度LN+_S计算为
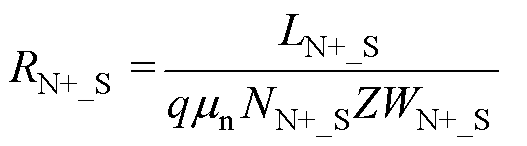（17）
4）沟道电阻RCH
由通态电流线性区模型可以近似得到沟道电阻表示为
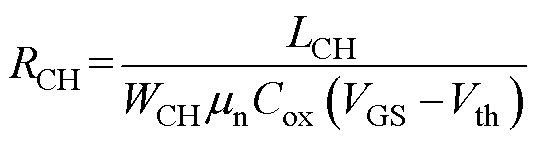（18）
5）积累区与JFET区总电阻RJ
在正向导通过程中，由于电场的作用，电子会在栅氧层下方形成积累层，该区域指的是电流通过反型层沟道后进一步到达JFET区域之间的扩散区。积累层电阻为通过P型区域边缘处到栅中心处的电流产生的电阻。此部分电流流动方式与沟道电流类似，因此电阻计算方式与沟道电阻相同，即
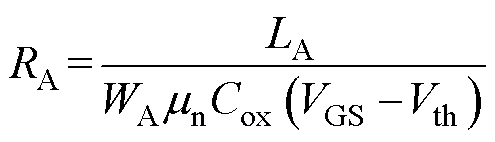（19）
式中，WA为积累层的宽度；LA为电流运输到积累层的距离。
在SiC MOSFET中，由于P型区域是平面形状，因此可以假设JEFT区域的宽度基本不变。如图4所示，假设电流在宽度为a的均匀横截面积内流动，流动距离为WJ，其电阻可以表示为
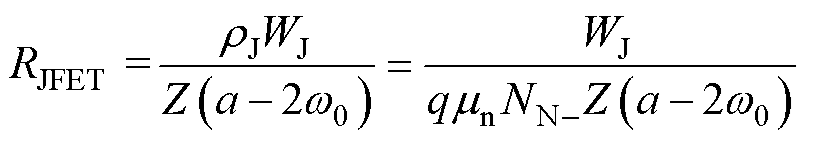（20）
式中，ω0为零偏置条件下JFET区域的耗尽层宽度，可以表示为
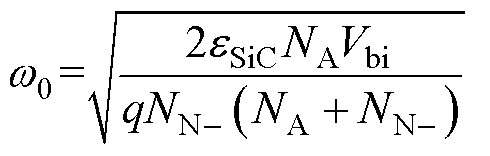（21）
式中，eSiC为SiC MOSFET的介电常数；NA为P+区域的掺杂浓度；Vbi为PN结阈值电压。因此，可以得到积累区和JFET区总电阻表示为
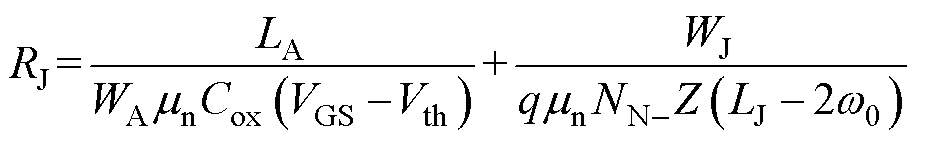（22）
6）N+衬底电阻Rsub
当电流到达底部区域时，会非常迅速地扩散到整个重掺杂的N+衬底。因此，可以假设电流通过衬底为一个均匀的横截面区域，在此条件下，N+衬底的电阻可以表示为
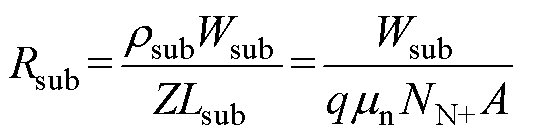（23）
式中，Lsub为N+型衬底x轴方向的长度（见图4）；Wsub为N+型衬底y轴方向的长度；NN+为N+区的掺杂浓度。
综上即为SiC MOSFET正向导通静态模型。在参数提取部分，只针对基区电阻Repi的相关参数进行了提取。对于其他的电阻模型，如沟道电阻RCH以及积累区与JFET区的电阻RJ模型，这一部分电阻涉及到芯片的非常细节的微观结构，难以进行直接观测或实验提取，因此，本文采用典型值进行仿真。
SiC MOSFET高频特性主要体现在瞬态特性的表征上，器件动态响应主要由栅源极电容CGS、漏源极电容CDS和栅漏极电容CGD决定，这些电容具有非线性特性，它们对器件开关速度和损耗有很大影响。如图5所示为SiC MOSFET开关瞬态特性模型，图中分别表示了3个结电容的形成位置。
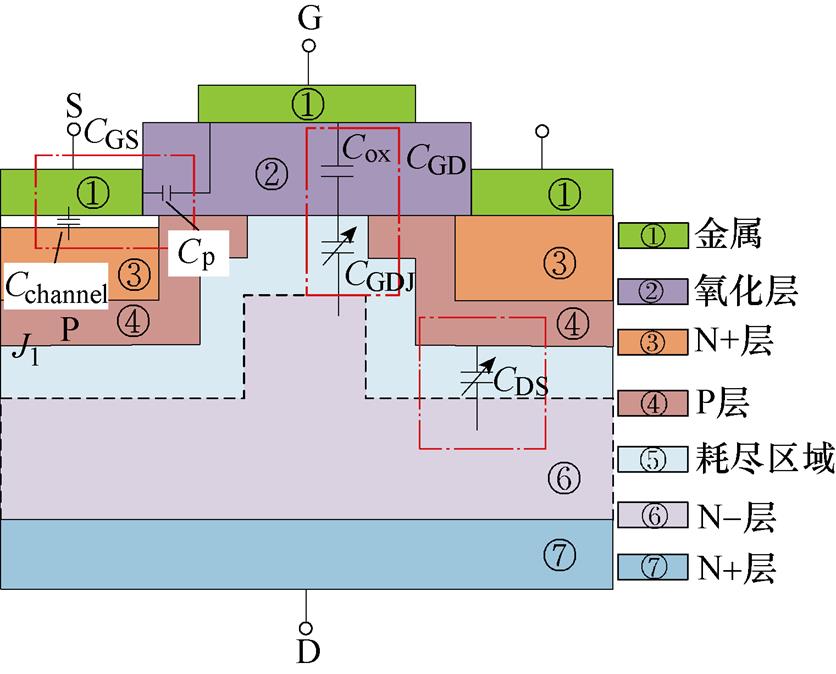
图5 SiC MOSFET瞬态特性模型
Fig.5 Transient model of the SiC MOSFET
SiC MOSFET 3个结电容对开关瞬态特性的影响由大到小排序为：CGD＞CDS＞CGS。在静态模型的基础上，SiC MOSFET开关瞬态过程可等效为3个电容的充放电过程。由于SiC材料及制造工艺的特殊性（掺杂较难扩散），使得其PN结属于突变 结[18]。另外，针对中高压等级的SiC MOSFET，一般采用的是穿通型设计，由此达到低导通电阻的目的。最后，与Si MOSFET器件采用零电压关断不同，SiC MOSFET一般采用的是负电压关断，这样可减小器件的漏极电流，使器件更可靠的关断。综上所述，需要分别根据穿通工况、突变结以及负电压关断特性对传统电容模型进行改进建模。
栅漏极电容CGD又称米勒电容，存在于栅极和漏极之间，作为负反馈阻碍SiC MOSFET栅极开关瞬态切换[18]。因此，CGD为影响器件开关瞬态的关键电容。CGD随栅漏极电压的变化而变化，由于其复杂的物理机制，目前诸多建模工作都集中在该电容上。针对栅漏极电容CGD，它是由Cox（氧化层电容）和CGDJ（MOS分界面耗尽层电容）串联组成，因此CGD可以表示为
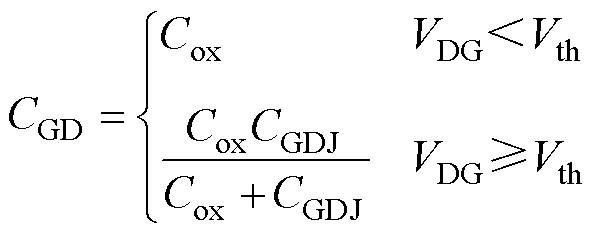（24）
氧化层电容Cox可以表示为
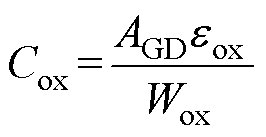（25）
式中，AGD为栅漏极交叠面积；eox为氧化层介电常数；VDG为栅漏极电压；Wox为氧化层厚度。上述模型与传统模型相同。
MOS分界面耗尽层电容对于栅漏极电压具有极强的依赖性，当电压VDG上升时，CGDJ将迅速下降，可以表示为
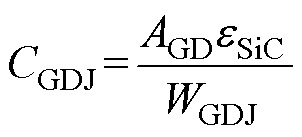（26）
其中
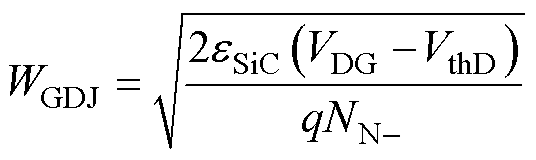（27）
式中，VthD为栅漏极阈值电压。
然而，为了获取较低的导通电阻Ron，SiC MOSFET漂移区宽度相比Si器件要薄得多（见图5），因此耗尽层随着外加电压的逐渐增加容易穿通进入N+区域。当耗尽层穿通以后，耗尽层宽度基本不再增加，即结电容基本保持不变。因此，可以推导得到耗尽层宽度如式（28）所示，进而可以由式（24）～式（26）计算得到CGD。
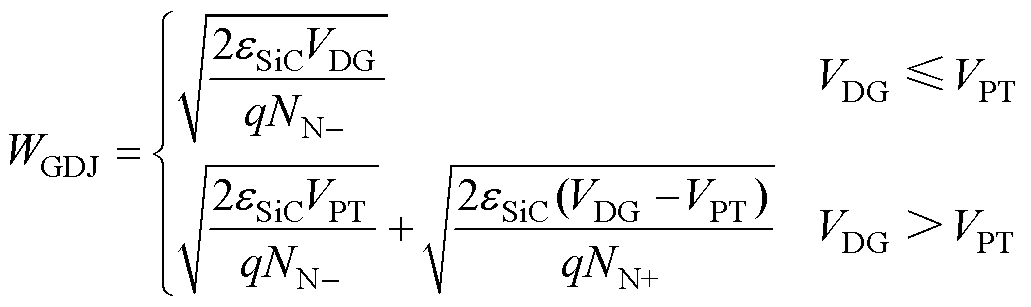（28）
式中，VPT为穿通电压。如图6所示为栅漏极电容CGD改进模型、传统模型和数据表的对比。随着VDS的增加，电容CGD逐渐减小。当VDS电压增加到600V左右时，结电容有个明显的转折点，而后即使电压继续升高，电容也基本保持不变。这是由于在电压达到600V时，此时耗尽层将穿通N-区，而后耗尽层变化很小，因此结电容基本保持不变。而传统模型由于没有考虑穿通条件，所以电容在600V后会继续下降。因此，传统模型与数据表之间的误差会随着电压的增大而增大。通过比较，本文提出的CGD模型与数据表具有较好的一致性，验证了CGD模型的有效性和准确性。
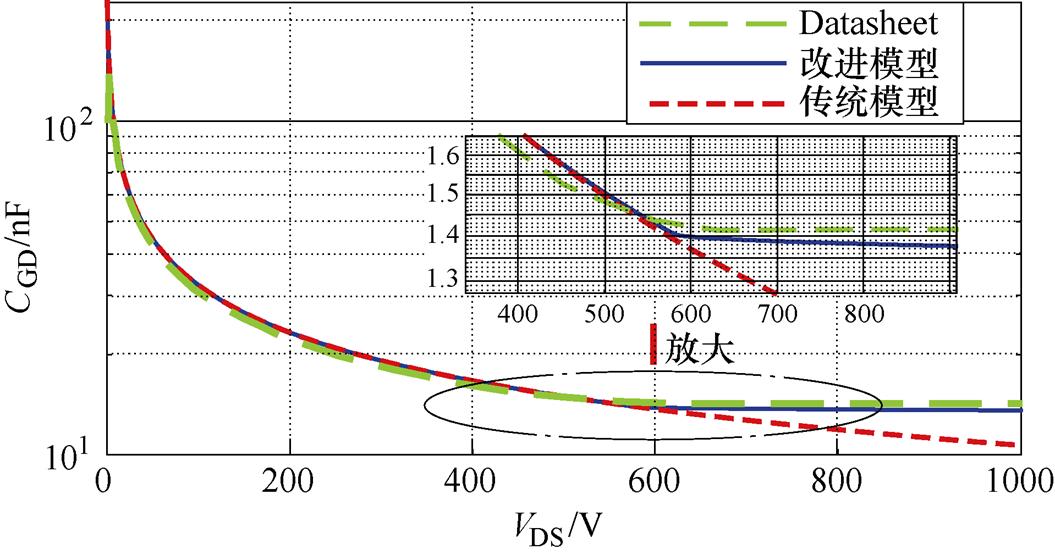
图6 栅漏极电容CGD随VDS变化
Fig.6 Gate-drain capacitance CGD varies with VDS
漏源极电容CDS为SiC MOSFET反向阻断以后在P+层与N-层之间形成的结电容，可以等效为一个PN结电容。在反向偏置的PN结中，每单位面积的电容被定义为
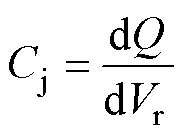（29）
式中，dQ为每单位面积电荷的变化量，它是由电压的增量dVr引起；Vr为PN结两端的电压。
由于SiC器件的材料及生产工艺与Si器件具有较大不同，其PN结属于非常突变的结构，因此PN结处的掺杂浓度具有较大的变化。传统模型中使用dQ=qNN-dW来近似表征P+N-结处耗尽层电荷将会带来较大的误差，由此计算得到的漏源极电容相比实际数值偏大，在小电流条件下尤为明显，因此需要对其进行分析改进。突变结处空间电荷区中同一符号的电荷可通过对空间电荷密度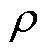
进行积分得到，即
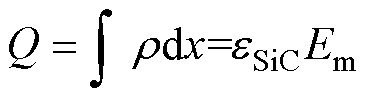（30）
式中，Em为空间电荷区最大电场强度[18]，表示为
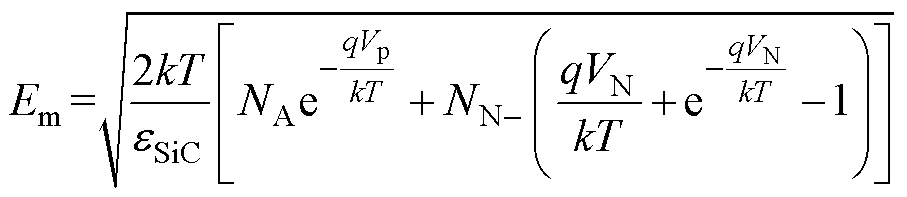（31）
其中
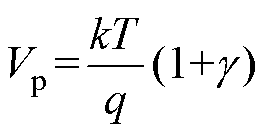
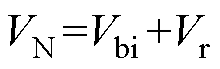
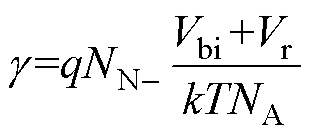
式中，k为玻耳兹曼常数；T为热力学温度。由于NN-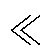
NA，且(Vbi+Vr)/(kT)
1，将式（31）代入式（30），可化简得到单位面积电容为
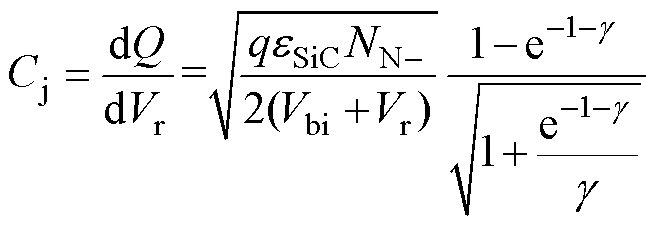（32）
图7所示为源漏极电容CDS随VDS变化曲线。通过对比可以发现，本文模型与数据表结果具有较好的一致性，也验证了CDS模型的有效性，为瞬态特性仿真提供了理论验证支撑。
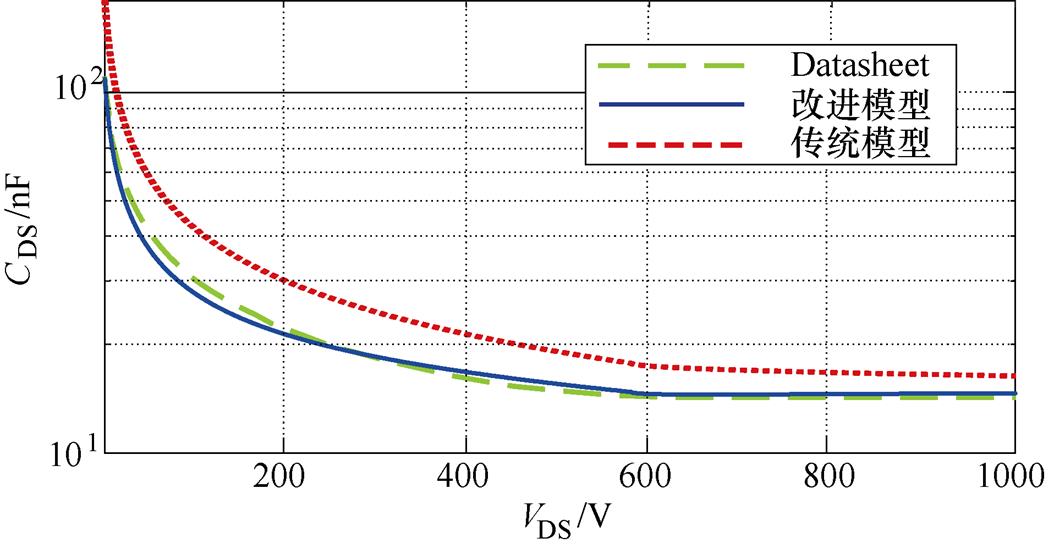
图7 源漏极电容CDS随VDS变化
Fig.7 Souce-drain capacitance CDS varies with VDS
如图5所示，CGS被分为性质不同的两部分：第一部分是沟道区域的栅极氧化层电容，表示为Cchannel，由于栅极氧化物的厚度很薄，Cchannel相对较大；第二部分是Cpp，它源于器件表面栅极和源极的平行布置结构，但是由于栅极和源极之间的绝缘层相对栅极氧化物较厚，导致Cpp比Cchannel要小得多，CGS由这两部分电容并联而成，因此栅源极电容可以近似表示为CGS=Cchannel。
SiC MOSFET一般采用的是负电压关断。当栅源电压为负时，此时在源极N+区域将会形成耗尽层，这将导致栅源极电容增加，增加后的电容为CGS_off，因此可得栅源极电容CGS表示为
（33）
由于栅源极电容CGS相比其他电容对于器件的瞬态特性影响偏小，且涉及许多工艺参数，通常情况下为了提升仿真收敛性，一般使用典型值代替。
基于物理的SiC MOSFET电路模型不仅可以更好地了解器件的工作机理，并可以较好地预测不同工况下SiC MOSFET的静态和瞬态特性。但是，它的使用也伴随着一些挑战，如模型参数提取。本文将模型的参数提取分为两个步骤：
（1）参数初步提取，主要包括半导体物理参数、器件结构参数、寄生电路参数。在物理模型的发展过程中，由于模型仿真的需要，一些文献提出了一系列模型参数提取方法[19-20]。通过这些方法可以对参数进行初步评估。
（2）利用文献[21]中提出的基于软件的模型参数优化工具，对（1）中提取的参数进行优化，进一步提高物理模型的精度。本文模型使用的主要模型参数见表1，其余参数如栅源极结电容等典型值由数据手册给出。
表1 SiC MOSFET模型物理参数
Tab.1 Physical parameters for the SiC MOSFET model
参 数数 值 芯片有效面积A/cm21.8 基区宽度WN-/mm128 基区掺杂浓度NN-/cm-33.93×1015 栅漏极交叠面积AGD/cm20.33 氧化层厚度Wox/nm28 N+衬底宽度WN+/mm55 N+衬底掺杂浓度NN+/cm-31×1017 P区掺杂浓度NA/cm-31×1018
所建立的SiC MOSFET电路模型已在PSpice仿真软件中采用等效电路的形式进行了搭建，并通过用户定义的模型库进行了调用。图8所示为SiC MOSFET模型主要部分的等效电路，静态模型主要通过受控电流源以及等效电阻构成。瞬态模型部分主要针对非线性电容进行了搭建：通过固定电容与受控电流源并联实现了可变电容。
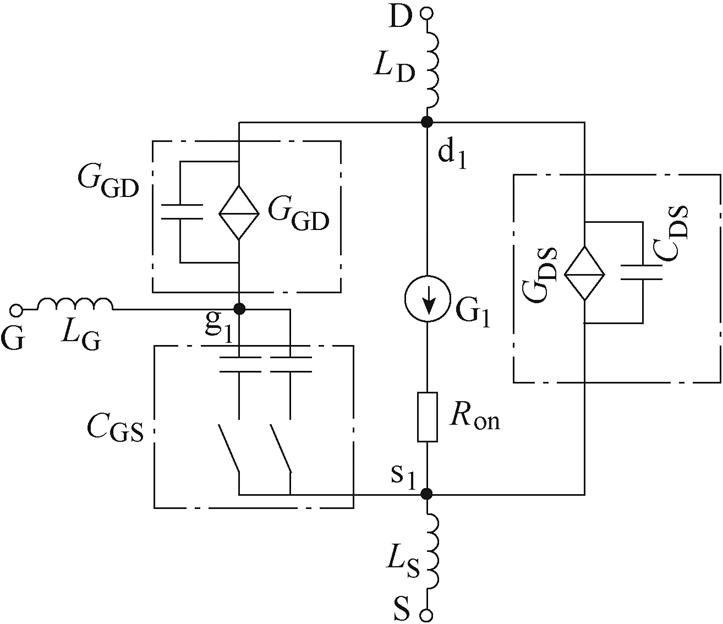
图8 SiC MOSFET改进模型等效电路
Fig.8 Equivalent circuit diagram of the improved SiC MOSFET model
首先，利用PSpice的DC分析得到改进模型与传统模型在不同栅极电压下的静态特性。图9所示为CREE 1 200V/325A SiC MOSFET模块（CAS325M12HM2），将仿真得到的静态特性与模块数据手册中的静态特性曲线进行了对比。SiC MOSFET静态特性仿真与实验对比如图10所示，在不同栅极电压下，相比传统模型，改进模型与实验的一致性更高。改进模型考虑了N-基区电流梯形的扩散方式，与器件实际工作机理相符；而传统模型采用的全扩散模型，其载流子流通的路径要大于改进模型，导致通态电阻更小，因此传统模型通态压降小于改进模型压降。图11为改进模型与传统模型导通压降仿真误差对比，在栅压为16V和12V时，传统模型的误差总体在15%以内；在栅压为20V和8V时，部分工况误差稍大，总体在20%左右。在工程应用中，20%的误差能够满足装置级以及系统级的仿真要求。本文的模型在传统模型的基础上考虑了载流子扩散呈梯形的特点，将传统模型的精度进一步提升至10%以内，使之能够满足器件级的电路仿真，为器件的动静态特性提供更加准确的表征，仿真和实验较好的一致性验证了改进模型的准确性。
图9 测试模块及其等效电路
Fig.9 Test module and its equivalent circuit diagram
图10 SiC MOSFET静态特性仿真与实验对比
Fig.10 Simulation and experimental comparison of the SiC MOSFET static characteristics
图11 改进模型与传统模型V-I特性仿真误差对比
Fig.11 Comparison of V-I curves errors of the improved and traditional models
双脉冲测试平台如图12所示，SiC MOSFET瞬态特性仿真与实验采用双脉冲测试电路。考虑到器件具有极快的开关速度，因此需要控制测试回路杂散电感，于是设计了双脉冲测试母排，并将测试模块靠近直流电容进行连接，直流电容采用低感薄膜电容。
图13所示为SiC MOSFET驱动控制连接，驱动与控制板之间通过差分转换器连接，目的是进一步高低压隔离，确保控制板的可靠性。测试设备需要满足SiC MOSFET极快开关速度的要求，表2为实验平台所用的各型设备、元器件及测量工具参数及型号。
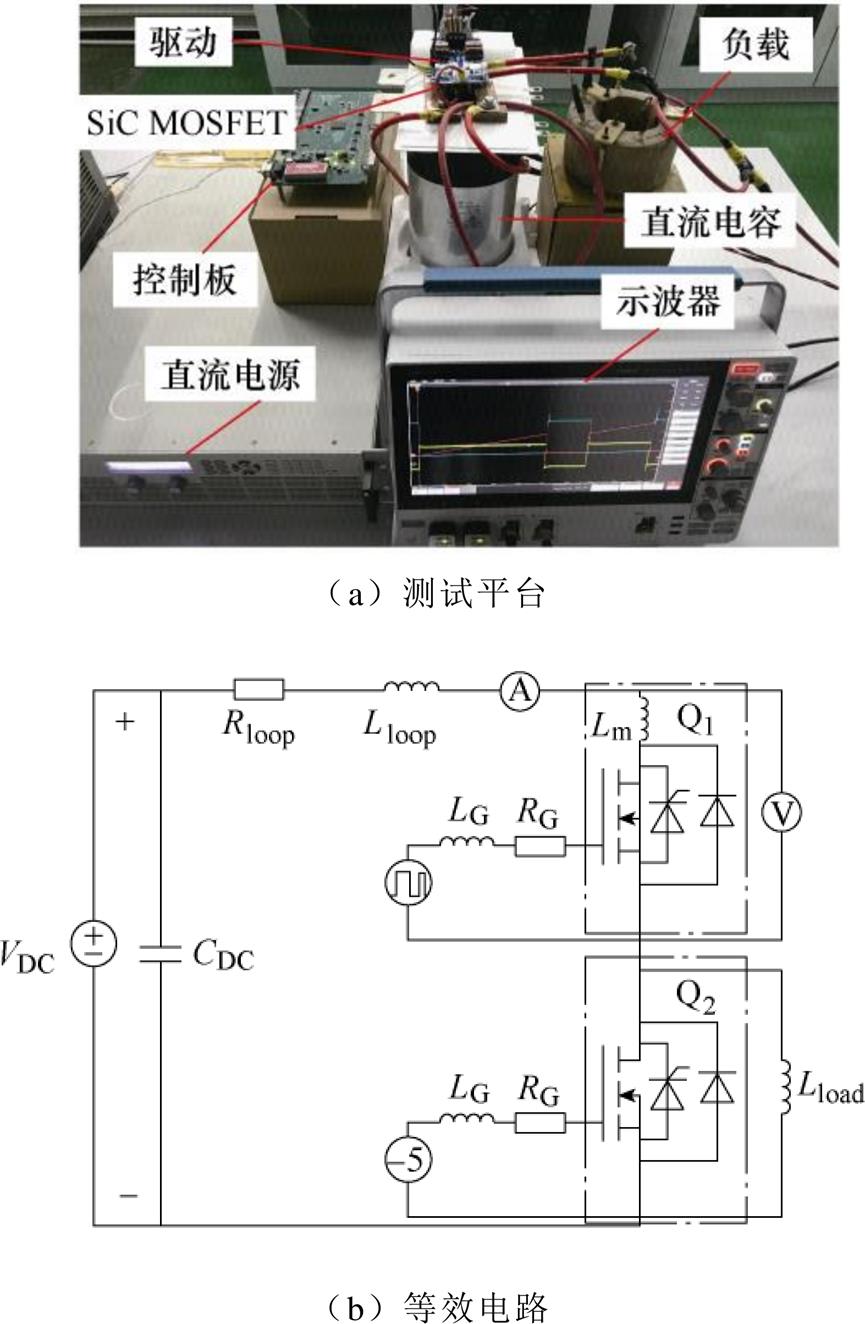
图12 双脉冲测试平台
Fig.12 Double pulse test platform
图13 驱动控制示意图
Fig.13 Schematic diagram of driver control
表2 实验平台设备参数
Tab.2 Types and parameters of experiment instruments
设备参数数 值型 号 直流源/V0～1 500KEYSIGHTN8957A 电容/mF2 000FARATRONIC 示波器/GHz1DPO5104B 电压传感器/V0～1 500THDP0200 电流传感器/A0～1 200CWTMini50HF FPGA控制板—Altera Cyclone IV
SiC MOSFET具有极快的开关速度，其瞬态特性对于杂散电感极为敏感[22]，包括器件封装以及工作回路的寄生电感。SiC MOSFET在开关瞬态过程中，其电容和回路电感很容易通过相互作用产生RLC高频振荡和电压峰值，振荡及产生的尖峰电压对于器件的损耗及可靠性评估较为重要。因此，为了对器件进行准确表征，需要对寄生电感进行提取。
通过阻抗测试可以得到模块寄生电感，如本文用于实验的SiC MOSFET器件，模块功率回路的寄生电感约为9.5nH。在器件开关瞬态过程中，模块寄生电感与回路杂散电感一起，对瞬态特性造成影响，因此需要针对总的杂散电感进行了提取。
本文采取了实验方法对回路杂散电感进行提取，实验法通过双脉冲电路对器件电流和尖峰电压进行测量，其原理是电流变化率在杂散电感上会产生电压，根据Dv=Ldi/dt可以计算得到杂散电感。相比有限元提取方法以及阻抗分析仪测试方法，实验方法具有效率高以及便捷的优势。本文采用积分 法[23]针对实验电路的杂散电感进行了提取，相比传统的微分法，积分法可以降低偶然性以及测量误差带来的影响。如图12所示，将各个部分的杂散电感进行等效：Leq=Lloop+Lm。表3为不同工况下提取得到的杂散电感。最终计算得到杂散电感约为80nH，将提取得到的杂散电感代入仿真电路进行仿真。
表3 回路电感提取
Tab.3 Inductance extraction of the loop circuit
电压/V电流/A电感Leq/mH 20820.085 333 30940.083 797 301260.084 363 401220.082 605 401660.082 609 501540.080 444 502060.077 018 601840.079 828
为了验证所提出的SiC MOSFET模型的准确性，对不同电压和电流下的仿真与实验进行了比较，如图14所示。改进模型仿真与实验的电压vDS波形以及电流iD波形具有较好的一致性。在图14a中，SiC MOSFET开通过程中主要为电流高频振荡，在电流上升斜率、电流振荡频率以及电流尖峰等关键特性中，模型仿真与实验结果均较为一致。传统模型只能够仿真第一个波形，而不能够准确仿真多个振荡波形。本文模型考虑了器件物理机理，对于器件的非线性结电容进行了准确的描述，因此能够准确地仿真包括高频振荡特性在内的开通瞬态特性。
图14 SiC MOSFET瞬态特性仿真与实验对比
Fig.14 Simulation and experimental comparisons of the SiC MOSFET transient characteristics
针对SiC MOSFET器件的关断瞬态：如图14b所示，由于高频振荡的发生，使得vDS波形有两个主要的斜率，第一段斜率是器件本身开关特性决定；当高频振荡发生以后，器件关断过程中的电压变化率dv/dt受到高频振荡特性的影响而微降低。仿真波形中：第一段斜率dvDS/dt约为1.7kV/ms，实验波形中第一段斜率dvDS/dt约为1.65kV/ms。第二段dvDS/dt的仿真与实验波形斜率分别为1.5kV/ms以及1.55kV/ms，可以看出，仿真与实验在dv/dt表征上具有较好的一致性，误差保持在5%以内。针对SiC MOSFET高频振荡特性，所提出的模型也能够较好地进行模拟，在600V/100A以及500V/80A工况下实验振荡频率分别为12.5MHz及12MHz，而模型仿真振荡频率分别为12.8MHz及12.4MHz，误差维持在5%以内，验证了杂散参数提取以及模型的准确性。
此外，为了更直观地验证所提模型的准确性，还将仿真与实验的电压、电流峰值、上升和下降时间以及振荡频率进行了比较，结果对比见表4。与实验结果相比，模型仿真的振荡频率误差小于5%，电压和电流峰值误差均小于8%，漏极电流上升和下降时间误差小于10%。对仿真时间误差偏大的原因进行了分析：由于存在测量偏置、参数提取误差以及模型本身误差，导致仿真与实验的时间存在几ns的误差；而SiC MOSFET开关时间极快，只有几十ns，相比之下，计算得到的误差偏大。
表4 SiC MOSFET开关瞬态性能仿真与实验对比
Tab.4 Simulation and experimental comparisons of the SiC MOSFET transient characteristics
电压/V电流/A特性实验仿真误差(%) 50080开通电流尖峰/A1501406.7 开通时间/ns60558.3 振荡频率/MHz1212.43.3 关断尖峰电压/V5655741.6 尖峰电流/A-14-157.1 关断时间/ns42.438.39.7 振荡频率/MHz1212.43.3 650100开通电流尖峰/A1791733.4 开通时间/ns66.460.49.0 振荡频率/MHz12.512.82.4 关断尖峰电压/V781.57901.1 尖峰电流/A-22-20.66.4 关断时间/ns3633.27.8 振荡频率/MHz12.512.82.4
SiC MOSFET所有的开关瞬态特性仿真与实验对比结果表明，本文模型与实测结果吻合较好，验证了所提模型具有较好的准确性和精度。
本文的SiC MOSFET模型暂未考虑结温变化对于器件特性影响。实际上，器件工作过程中产生的损耗会使得结温变化，进而对SiC MOSFET动静态特性产生影响。为了提高模型在不同工作温度下的适用性，应给出模型参数的温度模型，该部分工作涉及电热联合仿真部分内容，有待后续完善。
本文针对SiC MOSFET动静态模型进行了改进建模，静态模型主要针对导通电阻进行理论推导及改进建模。由于SiC MOSFET为单极性器件，与双极性半导体器件（如IGBT）导通机理存在较多不同，因此静态模型建模过程中形成的建模方法只能用于单极性器件建模。瞬态模型由非线性结电容模型组成，在非线性电容建模（CGD和CDS）过程的形成方法及步骤不具有限定性，可以将其应用至SiC其他器件，如SiC MPS二极管以及未来可能商业化的SiC IGBT。
本文建模主要针对的是单个器件或者单个模块进行，部分模型参数采用的集总参数，能够在精度和效率之间达到一个较好的平衡。仿真与实验误差小于10%，达到了器件级模型仿真的要求。本文模型主要适用于单个器件（分立式或模块式）动静态特性仿真模拟，评估单器件的工作区间，为器件在装置中的应用提供参考。
本文基于SiC MOSFET工作机理及结构特点，提出了一种基于物理的SiC MOSFET改进电路模型。针对静态特性，由于SiC MOSFET中N-漂移区较窄，导致漂移区电流扩散呈梯形，对静态模型进行了改进建模。针对影响器件高频应用的瞬态特性，根据目前SiC MOSFET的工艺结构特点，基于突变结、穿通特性以及负电压关断分别对SiC MOSFET结电容进行了改进建模。改进模型的正确性和仿真精度通过CREE 1 200V/325A模块进行验证，仿真模型能够准确地模拟SiC MOSFET动静态特性，误差小于10%，验证了本文理论分析和仿真模型的正确性。
参考文献
[1] 林弘毅, 伍梁, 郭潇, 等. 高功率密度SiC静止无功补偿器强迫风冷散热综合建模及优化设计方法[J]. 电工技术学报, 2021, 36(16): 3446-3456.
Lin Hongyi, Wu Liang, Guo Xiao, et al. A com- prehensive model of forced air cooling and optimal design method of high power density SiC-static var generator[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3446-3456.
[2] Wang Yijie, Lucia O, Zhang Zhe, et al. A review of high frequency power converters and related technologies[J]. IEEE Open Journal of the Industrial Electronics Society, 2020, 1: 247-260.
[3] 盛况, 董泽政, 吴新科. 碳化硅功率器件封装关键技术综述及展望[J]. 中国电机工程学报, 2019, 39(19): 5576-5584, 5885.
Sheng Kuang, Dong Zezheng, Wu Xinke. Review and prospect of key packaging technologies for silicon carbide power devices[J]. Proceedings of the CSEE, 2019, 39(19): 5576-5584, 5885.
[4] 王征, 刘文, 梅云辉, 等. 宽禁带电力电子器件关键封装材料研究进展[J]. 电力电子技术, 2017, 51(8): 82-85.
Wang Zheng, Liu Wen, Mei Yunhui, et al. Review on of key packaging materials for wide-band-gap power semiconductors[J]. Power Electronics Technology, 2017, 51(8): 82-85.
[5] Alexakis P, Alatise O, Li Ran, et al. Modeling power converters using hard switched silicon carbide MOSFETs and Schottky barrier diodes[C]//European Conference on Power Electronics and Applications, Lille, France, 2013: 1-9.
[6] Talesara V, Xing Diang, Fang Xiangxiang, et al. Dynamic switching of SiC power MOSFETs based on analytical subcircuit model[J]. IEEE Transactions on Power Electronics, 2020, 35(9): 9682-9691.
[7] 周林, 李寒江, 解宝, 等. SiC MOSFET的Saber建模及其在光伏并网逆变器中的应用和分析[J]. 电工技术学报, 2019, 34(20): 4251-4263.
Zhou Lin, Li Hanjiang, Xie Bao, et al. Saber modeling of SiC MOSFET and its application and analysis in photovoltaic grid-connected inverter[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4251-4263.
[8] 李玉豪. SiC MOSFET神经网络模型及应用研究[D]. 天津: 天津工业大学, 2020.
[9] Pushpakaran B N, Bayne S B, Ogunniyi A A. Electro-thermal transient simulation of silicon carbide power MOSFET[C]//IEEE Pulsed Power Conference (PPC), San Francisco, CA, USA, 2013: 1-6.
[10] Fu Ruiyun, Grekov A, Hudgins J, et al. Power SiC DMOSFET model accounting for nonuniform current distribution in JFET region[J]. IEEE Transactions on Industry Applications, 2012, 48(1): 181-190.
[11] Chindris G, Pop O, Alin G, et al. New PSPICE model for power MOSFET devices[C]//International Spring Seminar on Electronics Technology, Calimanesti- Caciulata, Romania, 2001: 158-162.
[12] Kampitsis G, Antivachis M, Kokosis S, et al. An accurate Matlab/Simulink based SiC MOSFET model for power converter applications[C]//IEEE Applied Power Electronics Conference and Exposition, Charlotte, NC, USA, 2015: 1058-1064.
[13] 庞一华. 大功率碳化硅模块的建模与特性研究[D]. 成都: 西南交通大学, 2019.
[14] 朱义诚, 赵争鸣, 王旭东, 等. SiC MOSFET与SiC SBD换流单元瞬态模型[J]. 电工技术学报, 2017, 32(12): 58-69.
Zhu Yicheng, Zhao Zhengming, Wang Xudong, et al. Analytical transient model of commutation units with SiC MOSFET and SiC SBD pair[J]. Transactions of China Electrotechnical Society, 2017, 32(12): 58-69.
[15] 盛况, 任娜, 徐弘毅. 碳化硅功率器件技术综述与展望[J]. 中国电机工程学报, 2020, 40(6): 1741- 1752.
Sheng Kuang, Ren Na, Xu Hongyi. A recent review on silicon carbide power devices technologies[J]. Proceedings of the CSEE, 2020, 40(6): 1741-1752.
[16] 薄强, 王丽芳, 张玉旺, 等. 应用于无线充电系统的SiC MOSFET关断特性分析[J]. 电力系统自动化, 2021, 45(15): 150-157.
Bo Qiang, Wang Lifang, Zhang Yuwang, et al. Analysis of turn-off characteristics of SiC MOSFET applied to wireless charging system[J]. Automation of Electric Power Systems, 2021, 45(15): 150-157.
[17] Baliga B J. Fundamentals of power semiconductor devices[M]. New York, USA: Springer, 2008.
[18] Lutz J. Semiconductor power devices: physics, characteristics, reliability[M]. Heidelberg, Germany: Springer, 2011.
[19] Hasanuzzaman M. MOSFET modeling, simulation and parameter extraction in 4H-and 6H-silicon carbide[D]. Knoxville, USA: University of Tennessee, 2005.
[20] 刘博, 刘伟志, 董侃, 等. 基于全碳化硅功率组件的变流器母排杂散电感解析计算方法[J]. 电工技术学报, 2021, 36(10): 2105-2114.
Liu Bo, Liu Weizhi, Dong Kan, et al. Analytical calculation method for stray inductance of converter busbar based on full silicon carbide power module[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2105-2114.
[21] McNutt T R, Hefner A R, Mantooth H A, et al. Silicon carbide power MOSFET model and parameter extraction sequence[J]. IEEE Transactions on Power Electronics, 2007, 22(2): 353-363.
[22] 王莉娜, 马浩博, 袁恺, 等. SiC MOSFET半桥电路开关瞬态过电流、过电压建模与影响因素分析[J]. 电工技术学报, 2020, 35(17): 3652-3665.
Wang Lina, Ma Haobo, Yuan Kai, et al. Modeling and influencing factor analysis of SiC MOSFET half- bridge circuit switching transient overcurrent and overvoltage[J]. Transactions of China Electro- technical Society, 2020, 35(17): 3652-3665.
[23] 谢宗奎, 柯俊吉, 赵志斌, 等. 碳化硅MOSFET换流回路杂散电感提取方法的优化[J]. 电工技术学报, 2018, 33(21): 4919-4927.
Xie Zongkui, Ke Junji, Zhao Zhibin, et al. Optimized extraction method of stray inductance in commutation path for silicon carbide MOSFET[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 4919- 4927.
An Improved Physics-Based Circuit Model for SiC MOSFET
Abstract SiC MOSFET has advantages of high frequency, high voltage and high temperature due to its material advantages in bandgap width, breakdown electric field and electron saturation speed. However, the special material, structure and high-switching speed of SiC MOSFET make the internal physical mechanism of the device more complicated during the switching transient. The traditional SiC MOSFET model adopted the modeling methods of some Si devices, and it is difficult to accurately evaluate the dynamic and static characteristics of the device. Therefore, an improved physics-based SiC MOSFET circuit model is proposed in this paper. Firstly, the shortcomings of the traditional SiC MOSFET model are analyzed and improved based on the operation principles of the device. The mode of current diffusion is an important factor affecting the static characteristics of the SiC MOSFET. The current diffusion in the N- region are trapezoid due to the narrow N- drift region. Hence, the drift region resistance model is improved. The transient model of the SiC MOSFET describes the high-frequency application characteristics of the device. Then junction capacitance models of the SiC MOSFET are improved based on the abrupt junction, punch-through condition and negative-voltage turn-off characteristics. Finally, experiments are carried out on a CREE SiC MOSFET (1 200V/325A). Simulation and experiment are in a good agreement, which verifies the effectiveness and accuracy of the improved model.
keywords：SiC MOSFET, circuit model, static characteristics, dynamic characteristics
DOI: 10.19595/j.cnki.1000-6753.tces.210225
中图分类号：TN312.4
JCJQ计划（2020-JCJQ-ZD-105）和国家重点研发计划（2019YFC0119101）资助项目。
收稿日期 2021-03-21
改稿日期 2021-05-26
李 鑫 男，1993年生，博士研究生，研究方向电力电子与电力传动。E-mail: l.x04@mail.scut.edu.cn
史泽南 男，1996年生，博士研究生，研究方向电力电子与电力传动。E-mail: 2060049908@qq.com（通信作者）
（编辑 陈 诚）