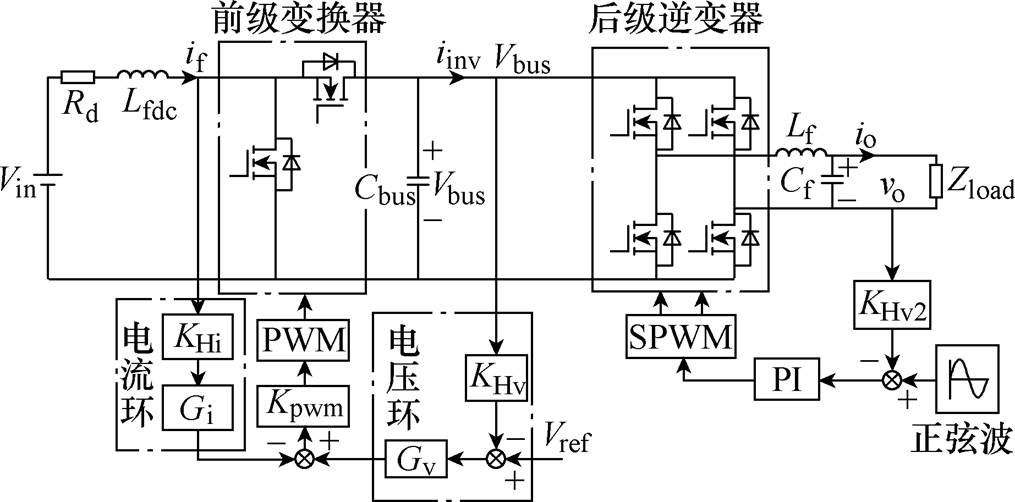
图1 储能系统结构及控制电路
Fig.1 Structure and control circuit diagram of energy storage system
摘要 直流微电网中储能系统直流侧的电感电流含有2次谐波分量,将会增大变换器中开关管的电流应力和通态损耗。该文首先通过分析得到,传统的双闭环控制方法对2次谐波电流的抑制效果不明显,且使得系统在负载跳变时的动态特性变差。针对这两个问题,提出一种引入陷波器(NF)、准比例谐振器(QPR)及负载功率前馈(LPF)的双闭环控制方法,在不降低电压调节器的幅频增益以及不改变等效阻抗的频率适应性的条件下,该方法可以增加直流侧电感支路的等效阻抗在2倍输出频率处的幅值,对2次谐波电流有很好的抑制效果,同时使得直流侧电感支路等效阻抗在2倍输出频率外的幅值降低,改善了系统的抗负载突变能力。最后,通过实验验证了所提控制方法的有效性。
关键词:直流微电网 储能系统 2次谐波电流 陷波器 准比例谐振器 负载功率前馈
微电网作为新型电力系统的重要组成部分,对实现能源可持续发展、助力实现“双碳”目标具有重要意义[1-4]。储能系统通常用来平抑新能源产生的功率波动,以此保障直流微电网的稳定运行[5-8]。受储能系统交流侧正弦输出电压和电流的影响,后级逆变器瞬时输出功率以2倍输出频率脉动,使得直流侧电感电流含有大量的2次谐波分量[9-10],该2次谐波电流将导致电流有效值升高,增大前级变换器中开关管的电流应力、通态损耗以及磁性元件的损耗[11-12],当前级变换器采用软开关技术时会减小开关管的软开关范围,降低变换器的效率[13-14],严重时还会影响蓄电池及电力电子设备的寿命[15-16]。
为了减小储能系统直流侧电感上的2次谐波电流,常通过引入新元件构成辅助电路来吸收2次谐波电流。文献[17]通过在直流侧加入LC滤波器的方法来吸收2次谐波电流,但该方法使得系统的体积和质量难以优化。文献[18-19]提出通过构建一个基于有源电容器的纹波吸收电路来吸收2次谐波电流,该方法能有效地抑制2次谐波电流,但引入的吸收电路将使系统结构及控制变得复杂。文献[20-21]通过在中间母线上引入双向变换器为后级逆变器提供脉动功率的方法来减小直流侧电感电流中的2次谐波含量,但引入双向变换器使得系统的效率降低。
除此之外,还有一类无需引入新元件的方法,即通过控制的方法来减小2次谐波电流。文献 [22-23]提出了电压电流双闭环的控制方法,通过增大储能系统直流侧变换器在输出电压全频段的闭环输出阻抗,抑制了2次谐波电流,但该方法要求电压外环截止频率较低,导致系统抗负载突变能力变差。文献[24]提出了一种通过注入其他次谐波电流来使得原始的2阶振荡功率转移至4阶或6阶甚至任意高阶的方法,较高频率的电流具有较低的振荡能量,因此可以很容易地被过滤掉,对2次谐波电流有较好的抑制效果,但该方法在抑制2次谐波电流的同时引入了其他次谐波电流。文献[25-26]采用开关器件的复用技术来抑制2次谐波电流,但其抑制能力取决于直流母线电容的大小。综上所述,目前关于减小储能系统直流侧电感上的2次谐波电流的研究现状存在系统体积过大、结构复杂、系统效率降低、系统动态特性较差、易引入其他次谐波电流以及抑制能力取决于系统参数等问题。
因此,针对直流微电网的储能系统,提出一种引入陷波器(Notch Filter, NF)+准比例谐振器(Quasi- Proportional Resonant, QPR)+负载功率前馈(Load Power Feedforward, LPF)的双闭环控制方法,既没有引入多余的器件,也解决了传统电压电流双闭环控制中因限制外环电压截止频率而引起的系统动态特性变差的问题,同时可以在不影响储能系统直流侧电感支路等效阻抗的频率适应性的条件下进一步增强对2次谐波的抑制效果,主要工作如下:
(1)介绍储能系统直流侧2次谐波电流的产生机理,同时分析传统的电压电流双闭环控制方法下对2次谐波电流的抑制效果及其在负载突变时的动态特性。
(2)为既能增强对2次谐波电流的抑制效果,又能改善系统抗负载突变能力,提出引入NF+QPR+ LPF的双闭环控制方法,并对NF、QPR以及LPF的原理进行分析。
(3)对所提的引入NF+QPR+LPF的双闭环控制方法下2次谐波电流的抑制效果以及抗负载突变能力进行分析,最后对所提的控制方法进行实验验证。
储能系统结构及控制电路如图1所示。图中,Lfdc为前级变换器的滤波电感,Rd为滤波电感Lfdc的等效串联电阻,Cbus为前级变换器的滤波电容,Lf为后级逆变器输出滤波电感,Cf为后级逆变器输出滤波电容,Zload为后级逆变器所带负载,if为滤波电感Lfdc上电感支路电流,iinv为后级逆变器输入电流。在不失通用性的情况下,采用图1所示的储能系统结构来说明其产生2次谐波电流的机理。

图1 储能系统结构及控制电路
Fig.1 Structure and control circuit diagram of energy storage system
假设后级逆变器输出电压波形为标准正弦波且转换效率为100%,直流母线电容容值足够大,此时可忽略直流母线上的电压纹波,将直流母线电压视为恒定值Vbus,可推导出后级逆变器的输入电流为
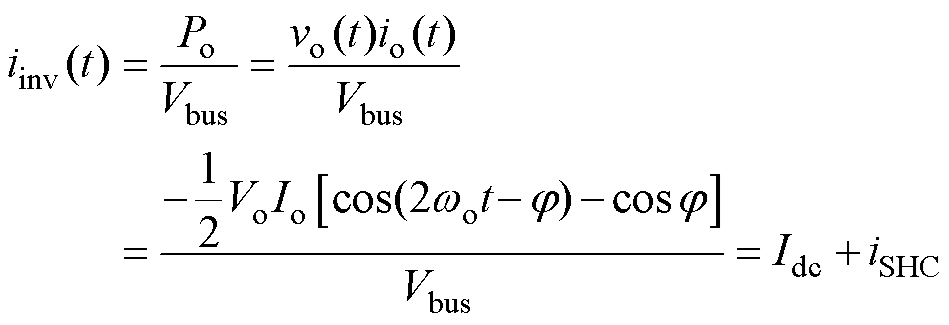 (1)
(1)
式中,Vo和Io为后级逆变器输出电压和输出电流的幅值;wo为角频率;j 为负载阻抗角。后级逆变器的输入电流包含两个部分:一个是直流量Idc;另一个是二倍频的交流输入量iSHC。
当二倍频交流输入量由电感支路提供时,会增大前级变换器开关管的电流应力和通态损耗,降低前级变换器的效率。同时,由于电池与电感支路直接相连,电池端同样会有明显的2次谐波电流,严重影响电池的寿命。
储能系统的前级变换器采用电压电流双闭环控制方法,如图1所示,图中,KHv为直流母线电容电压采样系数,KHi为电感电流采样系数,Kpwm为调制器增益,Gv(s)和Gi(s)分别为电压调节器和电流调节器,两者均采用PI控制器。
由图1推导得到,传统双闭环控制下的系统环路增益Av_s(s)表达式为
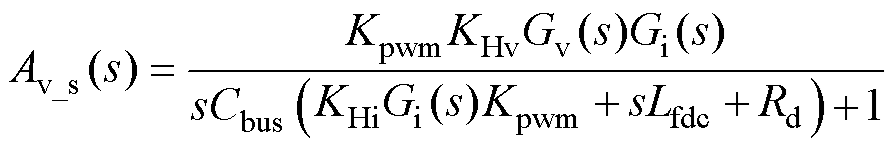 (2)
(2)
电感支路等效阻抗ZL1(s)的表达式为
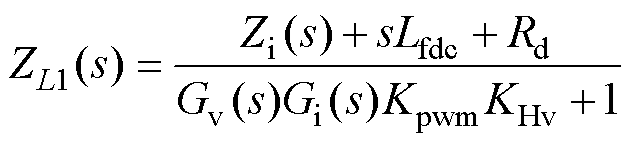 (3)
(3)
式中,Zi(s)为虚拟阻抗,Zi(s)=KHiGi(s)Kpwm。
采用传统双闭环控制下的闭环输出阻抗由两部分阻抗并联构成:直流母线电容阻抗和电感支路等效阻抗ZL1(s)。当直流母线电容支路的阻抗一定时,电感支路等效阻抗越大,该支路的分流系数就越小,即2次谐波电流含量越少。
串联虚拟阻抗Zi(s)和电感支路固有阻抗的幅频特性比较结果如图2所示。由于2次谐波频率远远小于电流环截止频率,导致2次谐波频率处串联虚拟阻抗的幅值远远大于电感支路固有阻抗的幅值,即传统的双闭环控制下输入侧的2次谐波电流含量主要由串联虚拟阻抗的幅值决定。
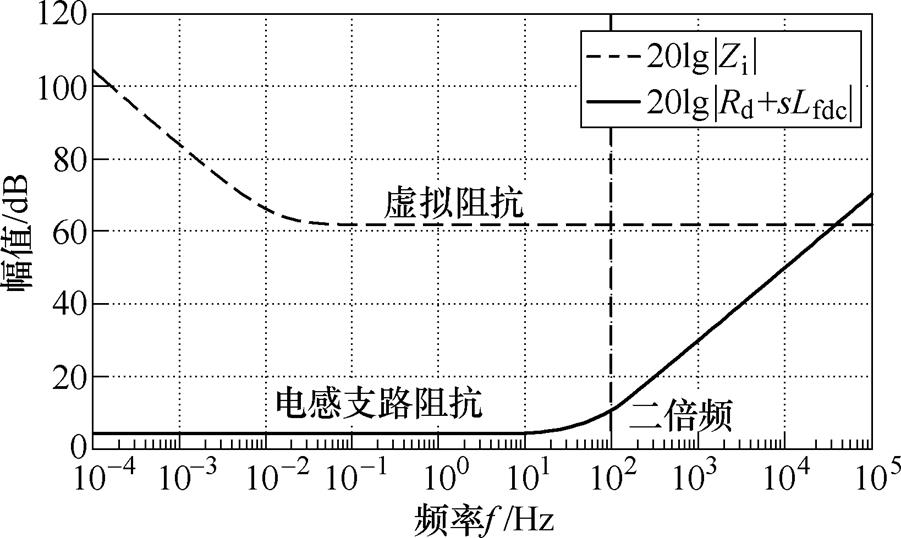
图2 阻抗幅频特性比较
Fig.2 Comparison diagram of amplitude frequency characteristics of the impedances
由式(3)推导出的电感支路等效阻抗ZL1(s)可知,降低电压调节器Gv(s)的增益|Gv(s)|可使电感支路在2次谐波频率处的等效阻抗幅值增加,电感支路中流过的2次谐波电流含量便会降低。然而,由式(2)推导出的环路增益Av_s(s)可知,降低电压调节器Gv(s)的增益|Gv(s)|会导致环路增益|Av_s(s)|减小,使得电压外环截止频率fc降低,从而使得系统的抗负载变化能力劣化。因此需要寻找一种方法,在提高2次谐波频率处的电感支路等效阻抗的同时不影响系统的抗负载突变能力。
为改善传统双闭环控制方法的2次谐波电流抑制能力和提高系统抗负载突变能力,提出一种NF+QPR+LPF的双闭环控制方法,其控制电路及框图分别如图3和图4所示,其在电压环中引入NF,在电流环中引入QPR,同时引入负载功率前馈LPF,接下来对各新增环节的原理进行论述。
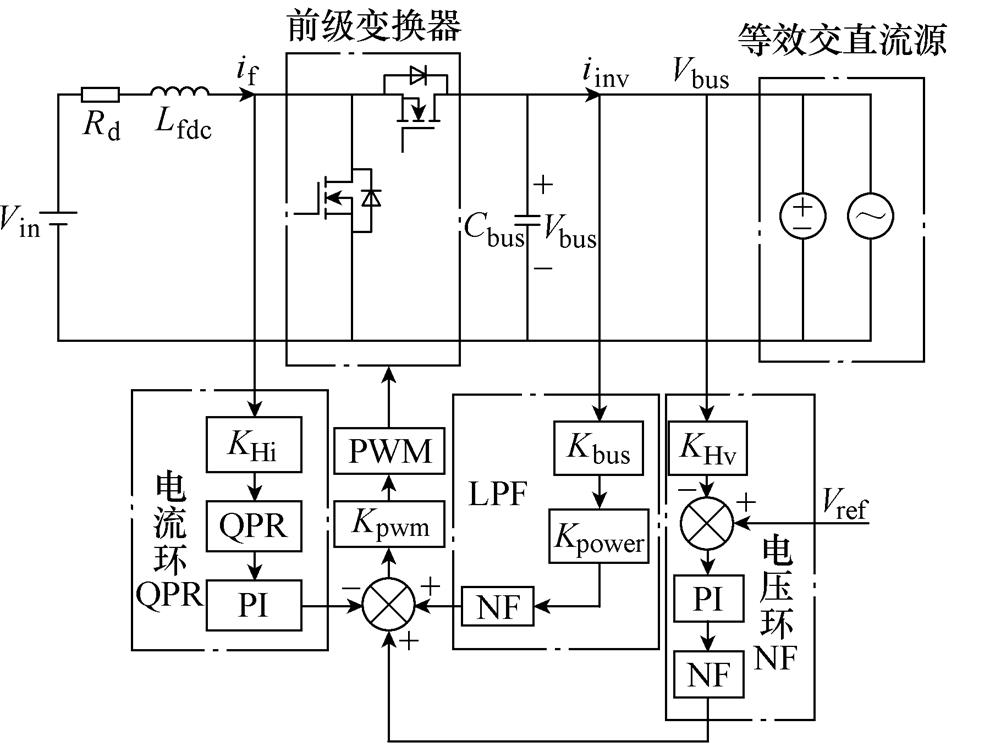
图3 引入NF+QPR+LPF的双闭环控制电路
Fig.3 Control circuit diagram of dual-loop control with NF+QPR+LPF
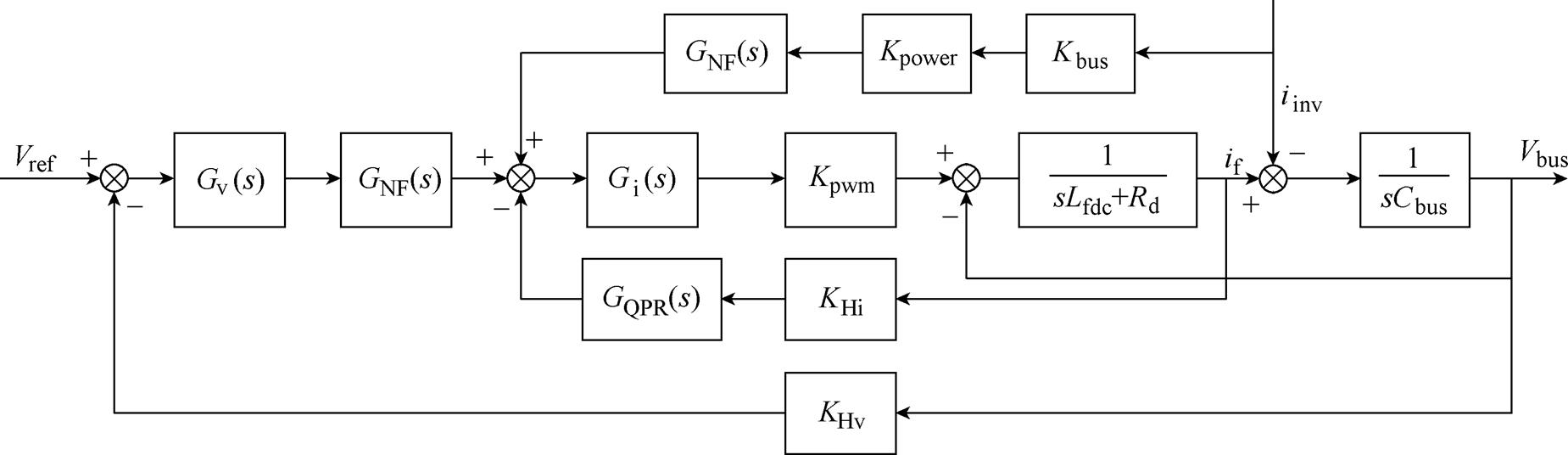
图4 引入NF+QPR+LPF的双闭环控制框图
Fig.4 Control block diagram of dual-loop control with NF+QPR+LPF
在传统双闭环控制中,调低电压调节器Gv(s)的增益|Gv(s)|,将使得电感支路阻抗在全频段的幅值得到提升,以达到抑制电感支路2次谐波电流的目的。但是这种做法会使得负载突变时系统的动态响应特性严重劣化。因此,提出一种在传统双闭环控制的基础上在电压环中串联NF的控制方法,以实现在只增大2次谐波频率处电感支路等效阻抗幅值的情况下又不影响系统的抗负载突变能力。
NF传递函数的表达式为
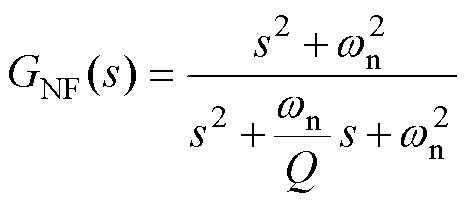 (4)
(4)
式中,Q为品质因数,可以改变谐振峰值和频率适应性;wn为特征角频率,与2次谐波角频率保持一致。
NF的伯德图如图5所示,NF特征频率fN=100Hz,其幅值增益在2次谐波频率处达到最小值,而在其他频段会迅速衰减为0dB。因此可利用NF的特性来增大电感支路阻抗在2次谐波频率处的幅值,而不影响其他频段的幅值。

图5 NF的伯德图
Fig.5 Bode diagram of NF
图4中,仅考虑将NF串联至电压调节器Gv(s)的输出端时,参照传统双闭环控制下的电感支路等效阻抗的求取思路,将NF的传递函数引入电压环中,得到引入NF后的电感支路等效阻抗ZL2(s),其表达式为
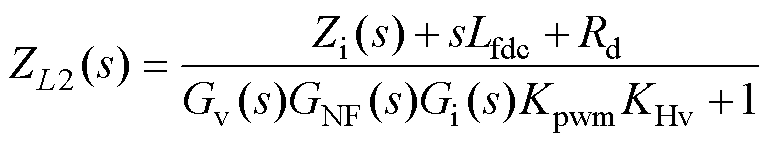 (5)
(5)
引入NF的双闭环控制的电感支路等效阻抗变化效果如图6所示,图6a和图6b分别为在低增益和高增益电压调节器的条件下引入NF前后对比,低增益下Gv(s)=10+200/s,高增益下Gv(s)=40+6 600/s。由图6可知,低增益下引入NF前后电感支路等效阻抗幅值在2次谐波频率处由28dB升高至64.3dB,而高增益下由-4.08dB升高至61.5dB,即在低增益和高增益电压调节器下NF均可使得电感支路等效阻抗幅值在2次谐波频率处大幅增加,并且两者2次谐波频率处幅值相差无几。因此引入NF的双闭环控制可保证电压调节器为高增益的同时使系统具有对2次谐波电流良好的抑制效果。

图6 引入NF和传统双闭环控制的电感支路等效阻抗变化效果
Fig.6 Effect diagram of inductance branch equivalent impedance with NF and traditional dual-loop control
值得注意的是,为了进一步改善2次谐波电流的抑制效果,可以通过降低品质因数,使NF在特征频率处的幅值增益减小,进而提高电感支路等效阻抗在2次谐波频率处的幅值。但结合图5可知,这将影响非2次谐波频率处的电感支路等效阻抗。
要增大加入NF后的2次谐波频率处的电感支路等效阻抗,就需要增大NF的谐振峰值,即减小品质因数Q,但是这会使得频率适应性增强,影响非2次谐波频率处的电感支路等效阻抗,导致系统动态响应特性变差。又因2次谐波电流含量主要由串联虚拟阻抗的幅值决定,因此可通过增大电感支路上串联虚拟阻抗Zi(s)增益,从而增大电感支路等效阻抗,以此增强2次谐波电流的抑制效果。
为此,在2.2节所提方法的基础上,提出一种在电流内环中串联QPR的控制方法,可以在不改变电感支路等效阻抗的频率适应性的条件下增大其在2次谐波频率处的幅值。
QPR传递函数的表达式为
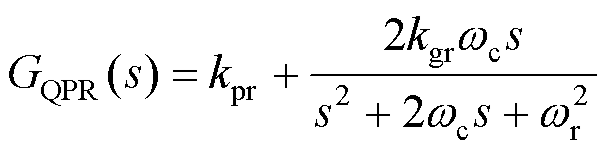 (6)
(6)
式中,wr为谐振角频率;wc为带宽角频率;kgr为谐振增益系数;kpr为谐振比例系数。
QPR的伯德图如图7所示,QPR谐振频率fr= 100Hz,其幅值增益在2次谐波频率处达到最大值,在其他频段会迅速衰减至0dB。谐振比例系数kpr的功能为改变全频段幅频;谐振增益系数kgr的功能为调节频率适应性,增大其值,频率适应性增强,并伴随着小幅度的谐振峰值变化;带宽角频率wc的功能为改变谐振峰值,增大其值,谐振峰值大幅增加。
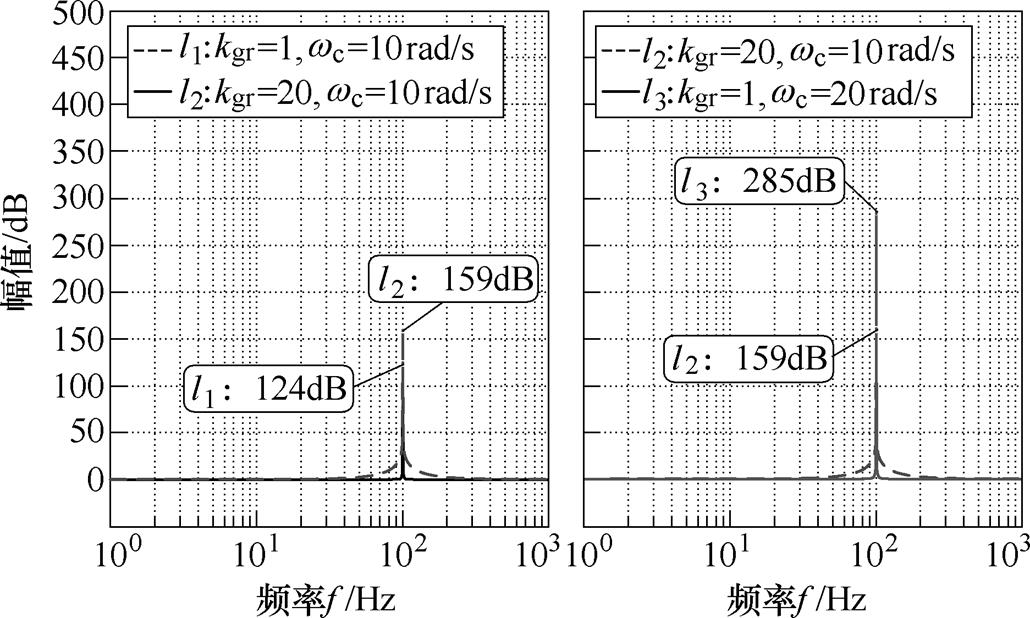
图7 QPR的伯德图
Fig.7 Bode diagram of QPR
仅考虑在电流反馈环中电流采样系数KHi的输出端串联QPR,同时电压环中NF保持不变时,可得电感支路等效阻抗ZL3(s)的表达式为
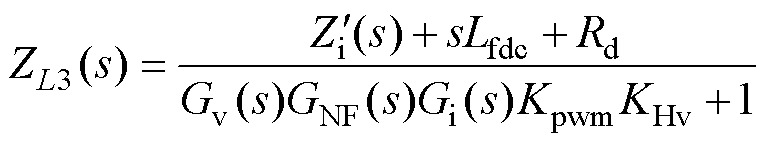 (7)
(7)
式中,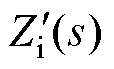 =KHiGQPR(s)Gi(s)Kpwm。
=KHiGQPR(s)Gi(s)Kpwm。
由式(7)可知,引入NF+QPR的双闭环控制能保证在NF的品质因数取值较大时,仍然可以增大电感支路等效阻抗在2次谐波频率处的幅值,达到在不改变电感支路等效阻抗的频率适应性的条件下抑制电感支路2次谐波电流的目的。
为优化负载跳变时前级变换器的动态响应,可以引入LPF,其本质为减小电感支路等效阻抗幅值,以此改善系统动态特性。而减小电感支路等效阻抗幅值,又与2.3节分析的为抑制2次谐波电流而增大电感支路等效阻抗幅值的方法背道而驰。
为了避免引入LPF后导致2次谐波电流增大,不妨在LPF上再串联NF,即在2次谐波频率处不改变电感支路等效阻抗,以避免2次谐波电流的含量增大,而在非2次谐波频率处减小电感支路等效阻抗,以此改善系统抗负载突变能力。
引入NF+QPR+LPF的双闭环控制框图如图4所示,其中,Kbus和Kpower为前馈调节系数,其电感支路等效阻抗ZL4(s)为
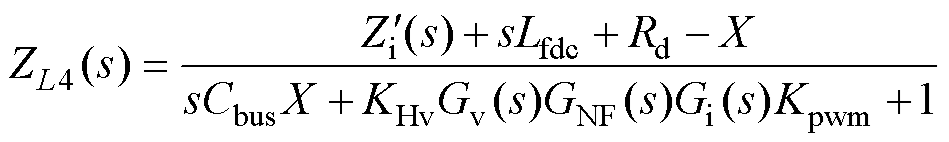 (8)
(8)
式中,X=KbusKpowerGNF(s)Gi(s)Kpwm。
由式(8)可知,X作为ZL4(s)分子的减数,由于引入了NF,在2次谐波频率处的幅值较小,可忽略不计,而在非2次谐波频率处幅值较大,起到减小电感支路等效阻抗的作用。因此,该方法可以达到在尽可能使得2次谐波频率处的电感支路阻抗幅值保持不变的情况下,削减其他频段处电感支路阻抗的幅值的目的,既能保持2次谐波电流有很好的抑制效果,也能改善系统抗负载突变能力。
传统、引入NF、引入NF+QPR和引入NF+QPR+ LPF的双闭环控制下电感支路等效阻抗幅值对比,如图8所示,这四种控制方法下均采用高增益电压调节器。在传统的双闭环控制下电感支路等效阻抗的幅值在2次谐波频率处为-4.35dB,只引入NF和NF+QPR的双闭环控制下电感支路等效阻抗的幅值在该频率处得到明显提高,分别增大至88.9dB和188dB。引入NF+QPR+LPF的双闭环控制下,2次谐波频率处的幅值为187dB。由此可知,在这四种控制方法中,引入NF+QPR和引入NF+QPR+LPF的双闭环控制方法抑制电感支路2次谐波电流的效果最好。
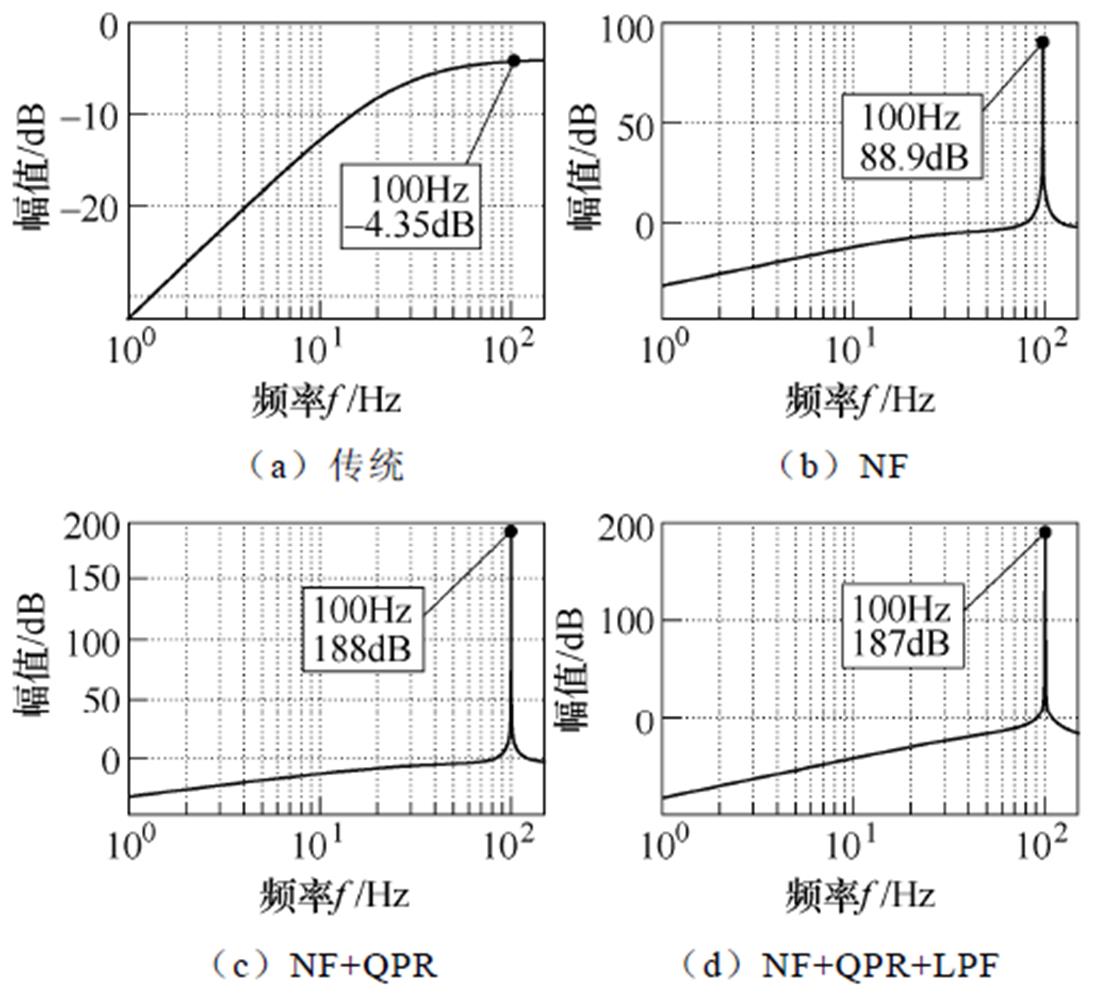
图8 不同情况下电感支路等效阻抗幅值的对比
Fig.8 Comparison diagram of inductance equivalent impedance amplitude under different conditions
进一步地,分析四种控制方法对系统动态性的影响。在系统控制框图中,逆变器输入电流iinv作为扰动,则扰动传递函数Ge(s)=Vbus/iinv可以表示母线电压Vbus随扰动iinv变化的幅度,换句话说,即扰动增益|Ge(s)|越大,同等级别的扰动电流iinv为母线电压带来的跳动越大,系统的动态性能越差;而扰动增益|Ge(s)|越小,系统的动态性能越好。在四种控制方法下,计算得到扰动传递函数的表达式分别为
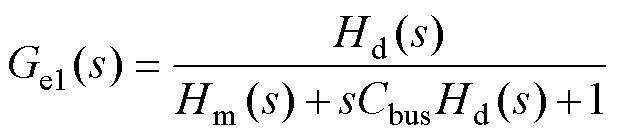 (9)
(9)
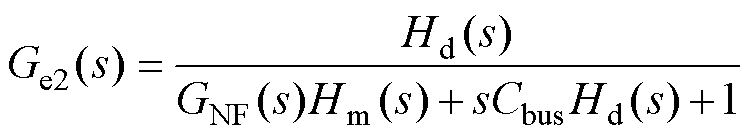 (10)
(10)
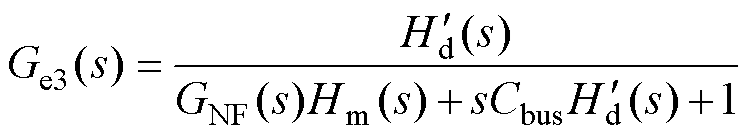 (11)
(11)
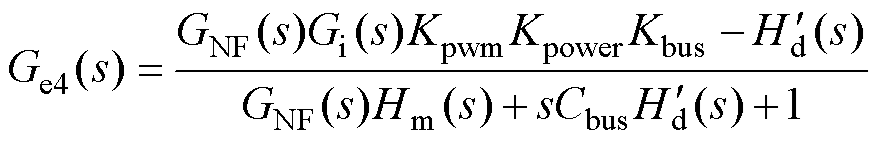 (12)
(12)
式中,Hd(s)=Zi(s)+sLfdc+Rd;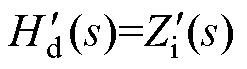 +sLfdc+Rd;Hm(s)=Gv(s)Gi(s)KpwmKHv。
+sLfdc+Rd;Hm(s)=Gv(s)Gi(s)KpwmKHv。
在四种控制方法下扰动传递函数伯德图如图9所示。由图9可知,前三种方法下扰动增益基本一致,系统的动态性能几乎无变化,甚至在20~100Hz频率之间,引入NF和引入NF+QPR的双闭环控制方法的扰动增益要比传统双闭环控制方法的更高,系统的动态性能变差。但是引入NF+QPR+LPF的双闭环控制下扰动增益相比前三种方法,除尖峰处比传统方法稍高外,在其余频段都有所降低,系统动态性得到大幅的改善。
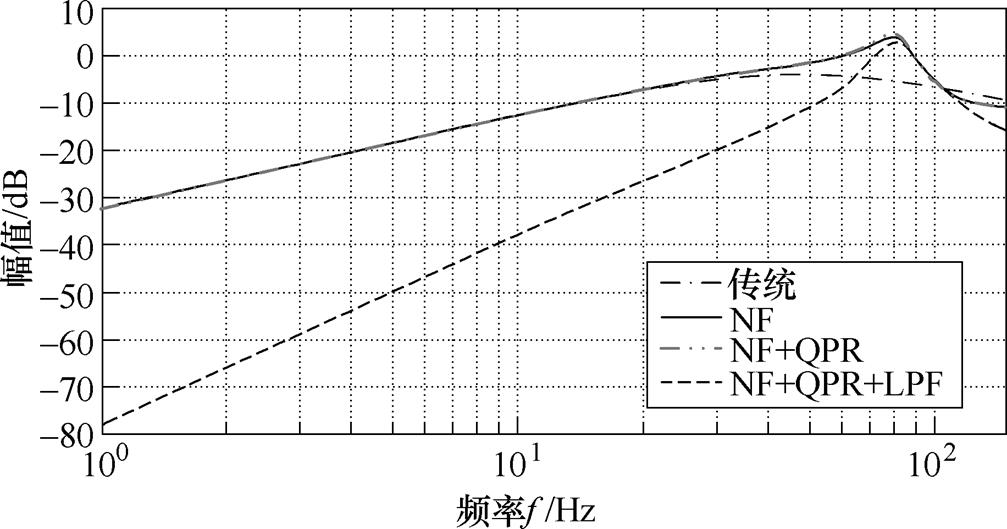
图9 四种控制方法下扰动传递函数伯德图
Fig.9 The Bode diagrams of the perturbation function under four control methods
为了验证第2节理论分析的正确性,观察采用所提控制方法后系统的稳定性和动态性,在RT-Lab OP5600半实物仿真平台上进行实验验证,在上位机中建立主电路模型,并将主电路模型装载到实时仿真器OP5600中。当模型运行时,OP5600通过I/O端口实时发送模拟信号到实时仿真控制器上位机,上位机对数据处理后将数字控制信号实时传输到OP5600中,数据可以实时交互,保证系统正常运行,系统主要参数见表1,硬件如图10所示。
针对传统、引入NF、引入NF+QPR及引入NF+ QPR+LPF这四种双闭环控制方法,改变每种方法下的控制参数进行稳态和负载响应动态特性实验,其实验结果见表2。
表1 系统主要参数
Tab.1 Main system parameters
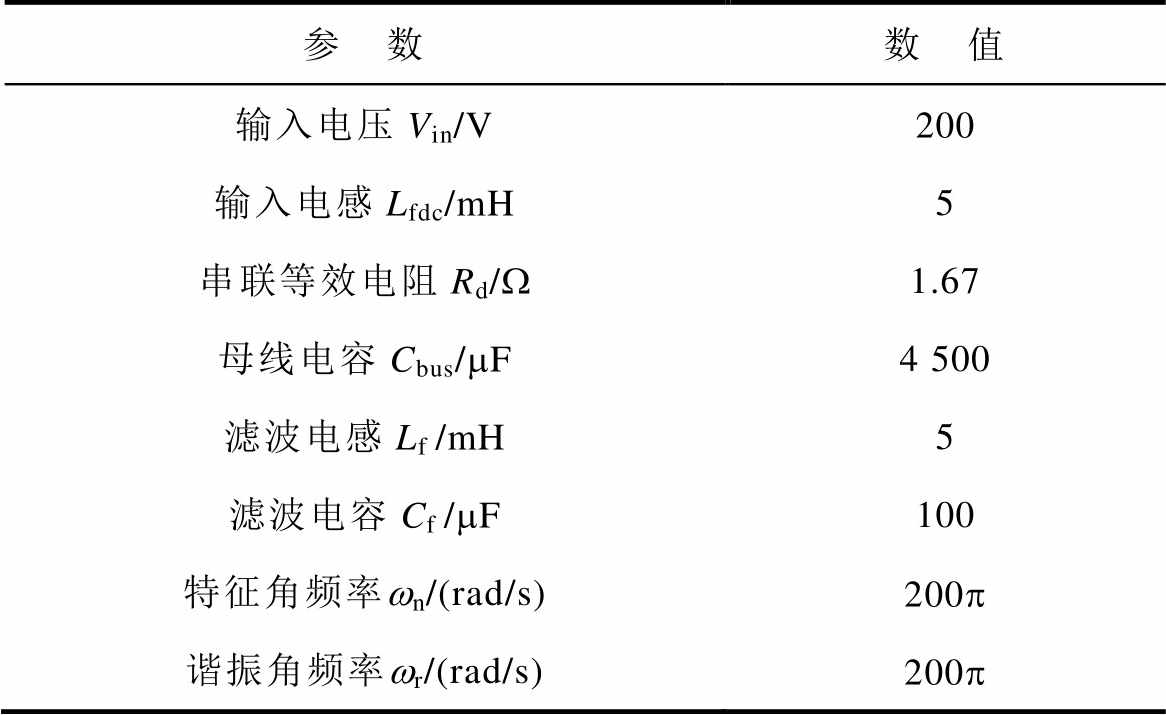
参 数数 值 输入电压Vin/V200 输入电感Lfdc/mH5 串联等效电阻Rd/W1.67 母线电容Cbus/mF4 500 滤波电感Lf /mH5 滤波电容Cf /mF100 特征角频率wn/(rad/s)200p 谐振角频率wr/(rad/s)200p

图10 硬件展示
Fig.10 Hardware display
表2 谐波抑制效果及抗负载突变能力的实验结果
Tab.2 Experimental results of harmonic suppression effect and anti load mutation ability
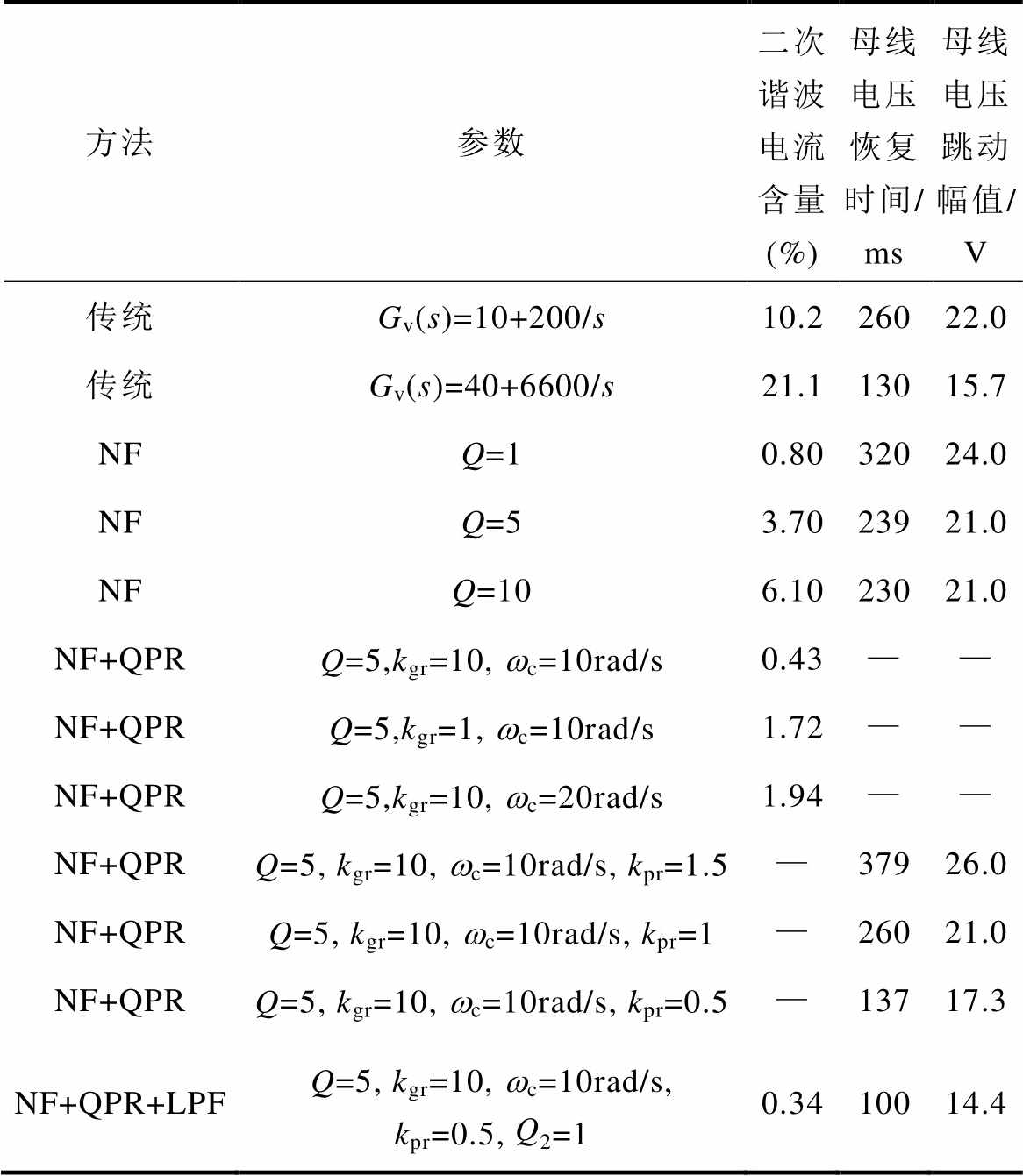
方法参数二次谐波电流含量 (%)母线电压恢复时间/ ms母线电压跳动幅值/ V 传统Gv(s)=10+200/s10.226022.0 传统Gv(s)=40+6600/s21.113015.7 NFQ=10.8032024.0 NFQ=53.7023921.0 NFQ=106.1023021.0 NF+QPRQ=5,kgr=10, wc=10rad/s0.43—— NF+QPRQ=5,kgr=1, wc=10rad/s1.72—— NF+QPRQ=5,kgr=10, wc=20rad/s1.94—— NF+QPRQ=5, kgr=10, wc=10rad/s, kpr=1.5—37926.0 NF+QPRQ=5, kgr=10, wc=10rad/s, kpr=1—26021.0 NF+QPRQ=5, kgr=10, wc=10rad/s, kpr=0.5—13717.3 NF+QPR+LPFQ=5, kgr=10, wc=10rad/s, kpr=0.5, Q2=10.3410014.4
传统的双闭环控制下,高/低增益电压调节器的稳态和负载响应动态特性实验结果分别如图11和图12所示。由图11和表2可知,低增益和高增益电压调节器下2次谐波电流含量分别为10.2%、21.1%,由此可知,低增益电压调节器下2次谐波电流抑制效果更好。但由图12和表2可知,高增益电压调节器下母线电压恢复时间和跳变幅值均小于低增益电压调节器,其动态响应特性更好。为了保证系统的抗负载跳变能力,故选取高增益电压调节器。
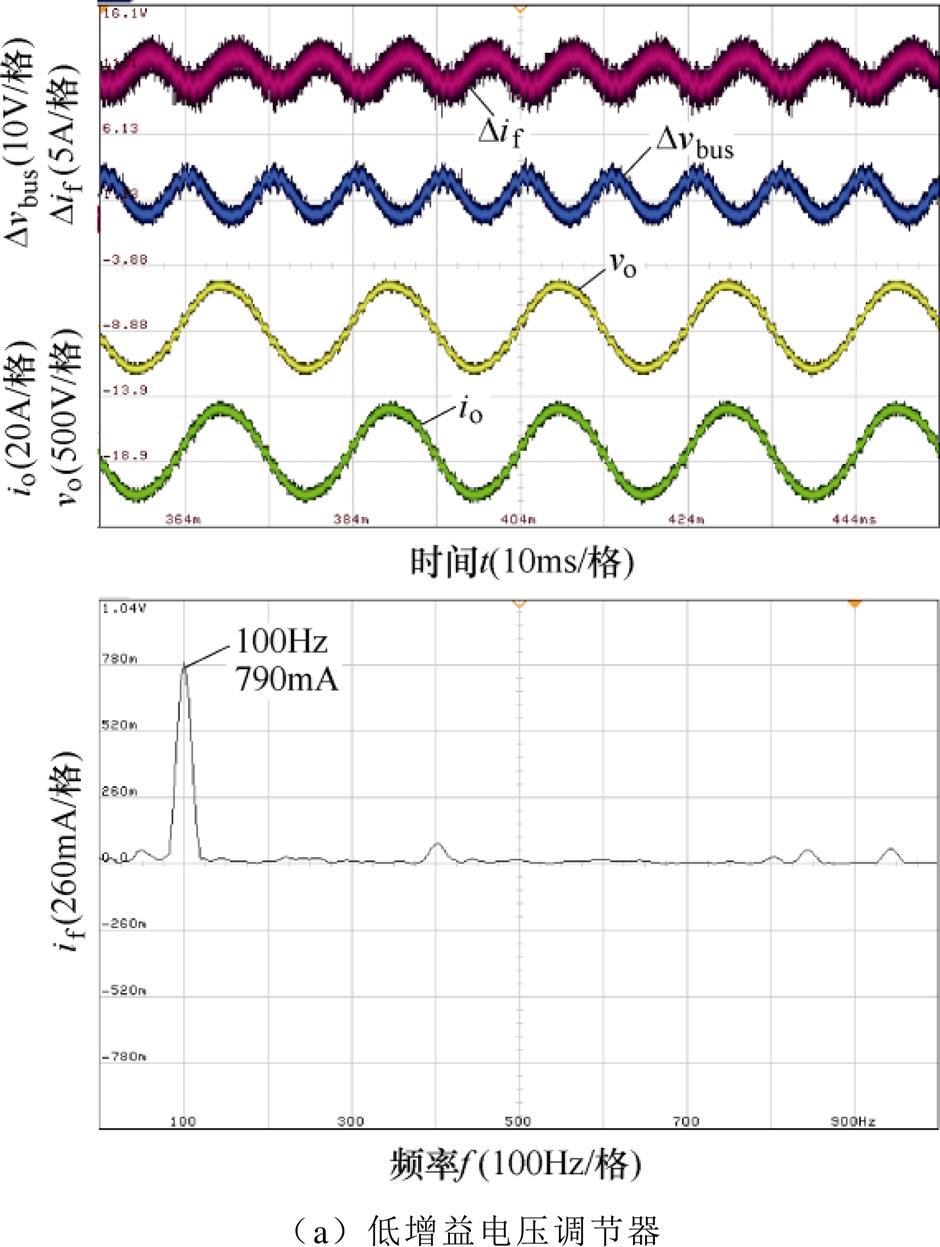
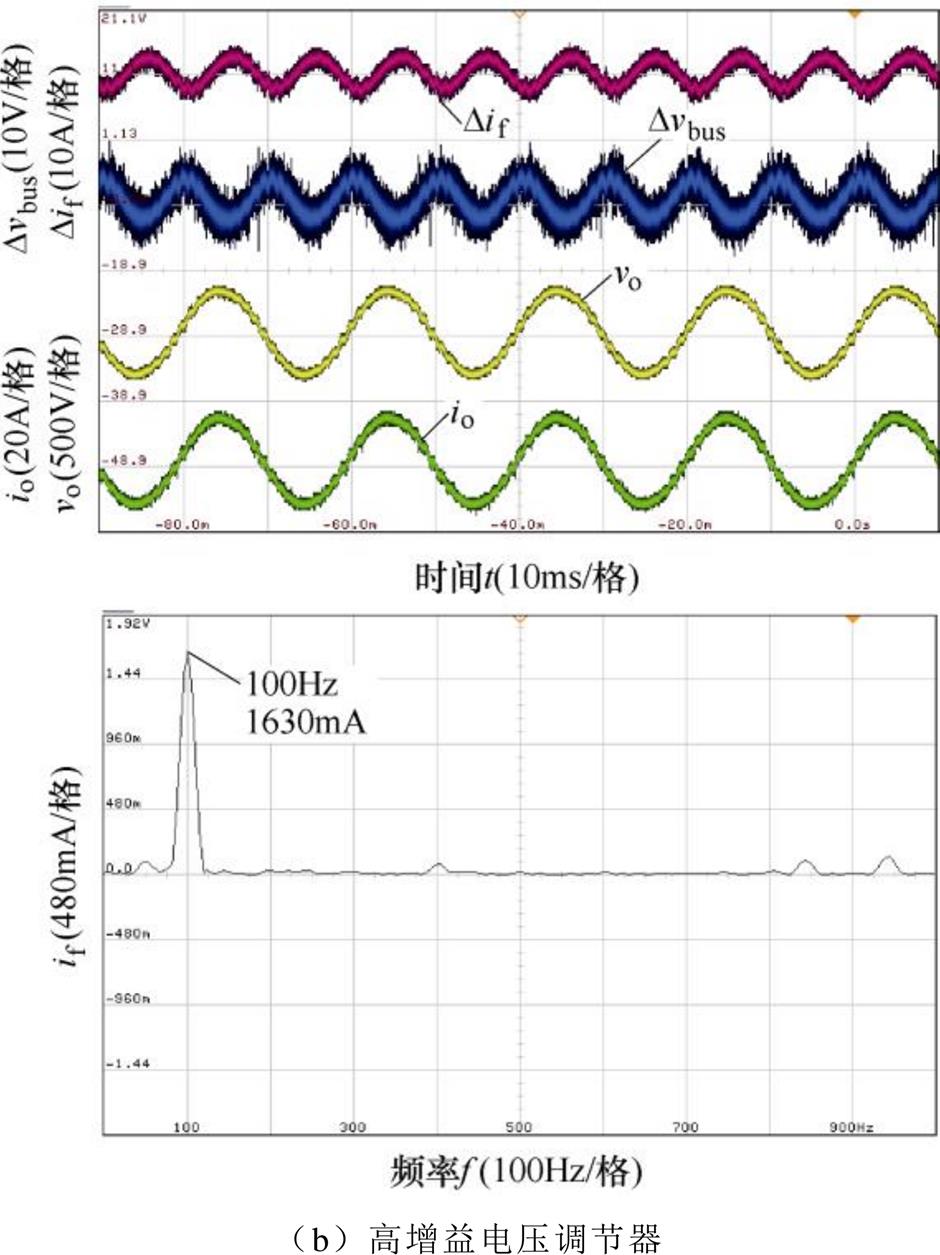
图11 传统的双闭环控制下稳态实验结果
Fig.11 Steady-state experimental results of traditional dual-loop control
在选取高增益电压调节器的基础上,引入NF的双闭环控制的稳态和负载响应动态特性实验结果分别如图13和图14所示。由图13和表2可知,品质因数Q分别为1、5和10时,电感支路2次谐波电流含量分别为0.80%、3.70%和6.10%。这是由于增大品质因数,NF的谐振峰值将会减小,从而使得电感支路等效阻抗在2次谐波频率处的幅值下降,对2次谐波电流的抑制能力降低。由图14和表2可知,品质因数Q分别为1、5和10时,负载突变后恢复时间分别为320ms、239ms和230ms,品质因数Q越大,恢复时间越短,即抗负载跳变能力越强。这是由于品质因数越大,对2次谐波频率以外的幅频特性影响越小。
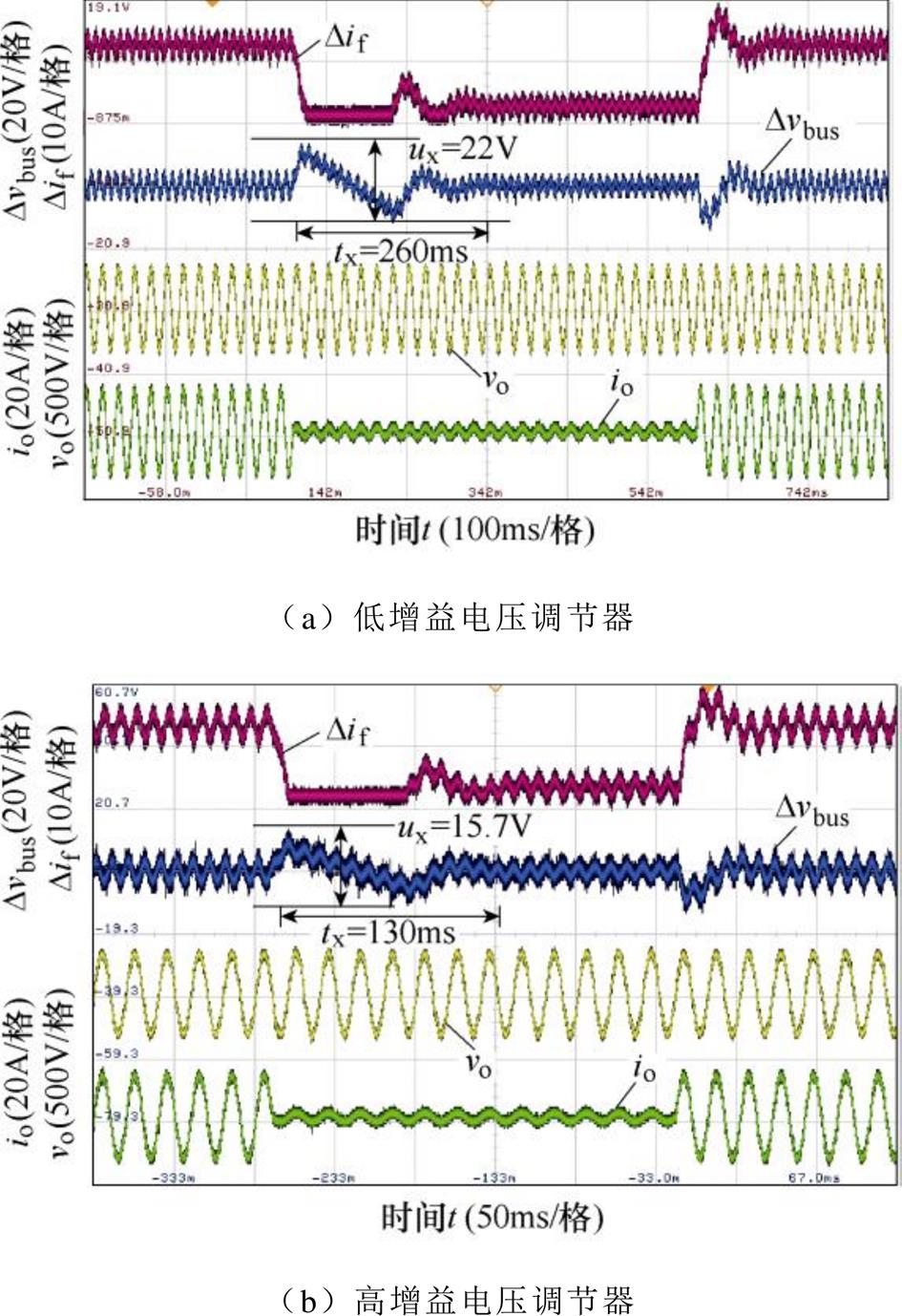
图12 传统的双闭环控制下负载响应动态特性
Fig.12 Dynamic characteristics of load response of traditional dual-loop control
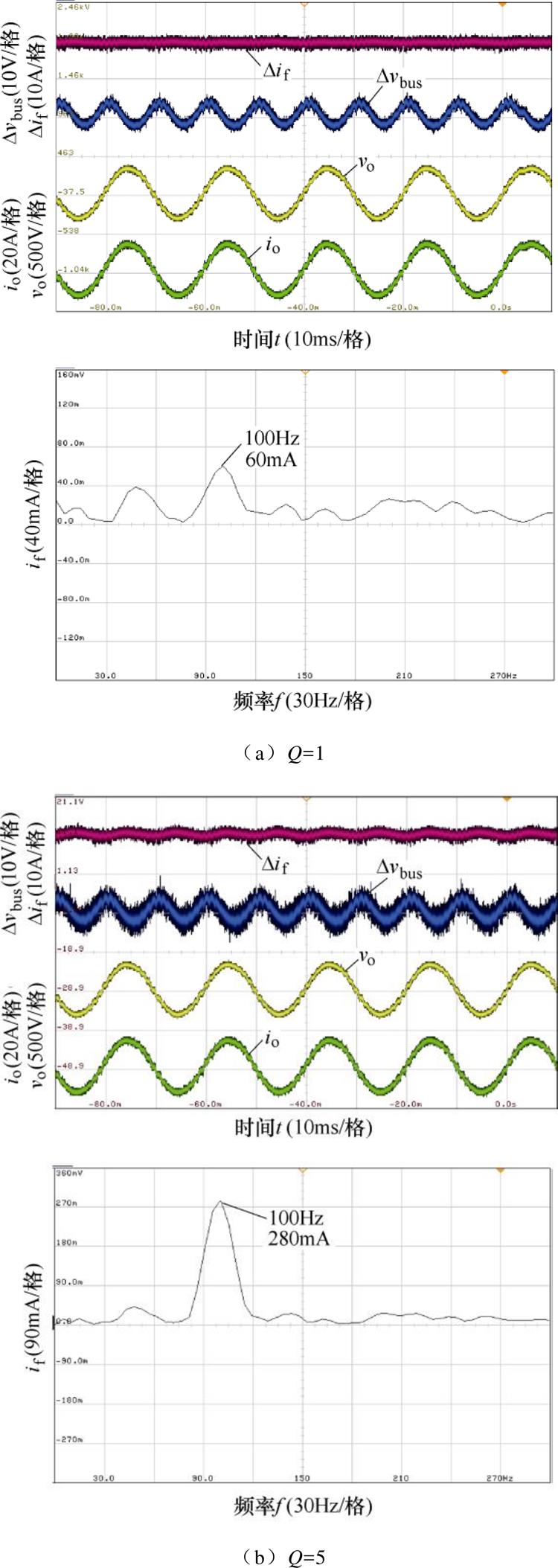
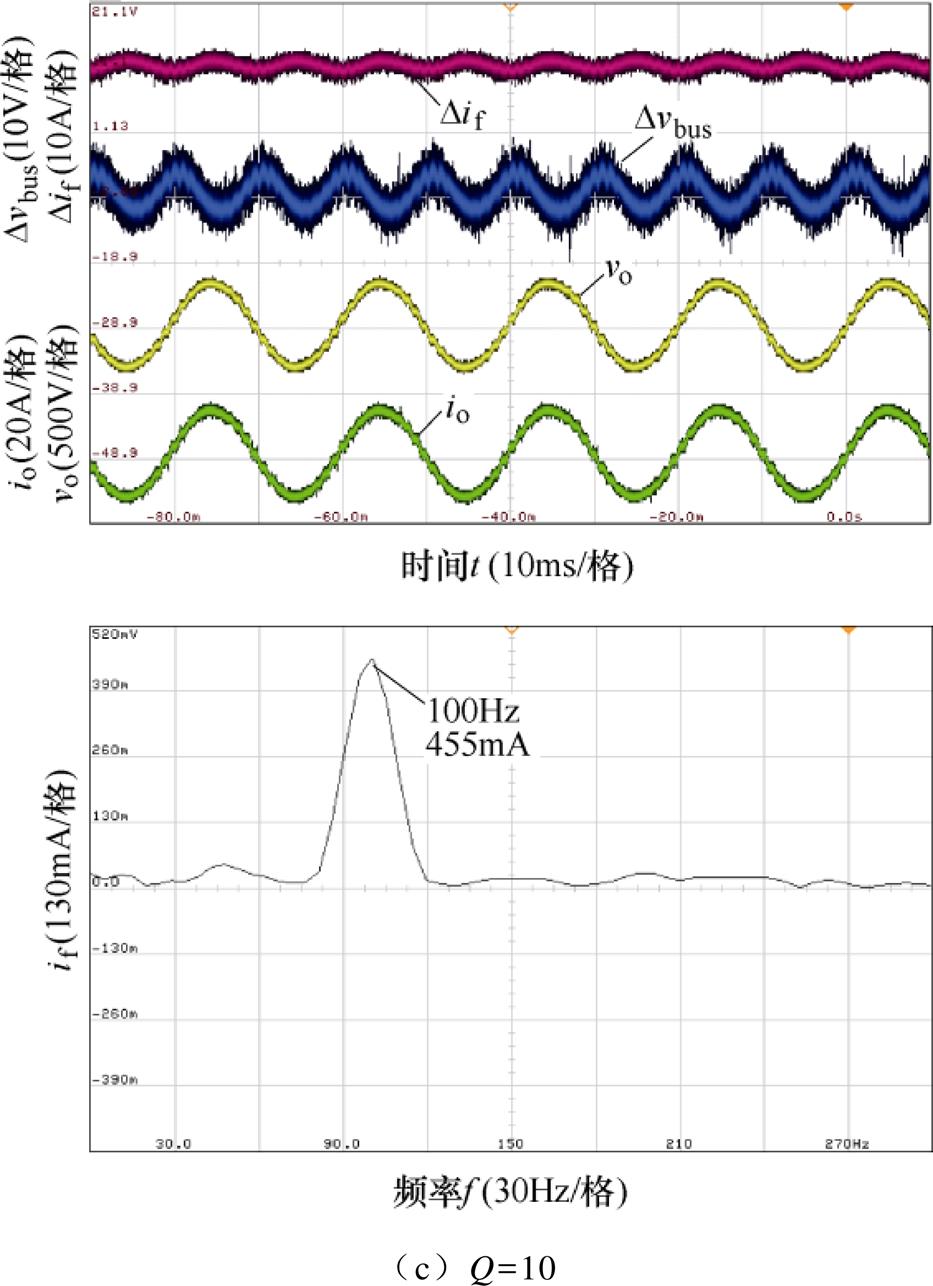
图13 引入NF的双闭环控制下稳态实验结果
Fig.13 Steady-state experimental result of dual-loop control with NF
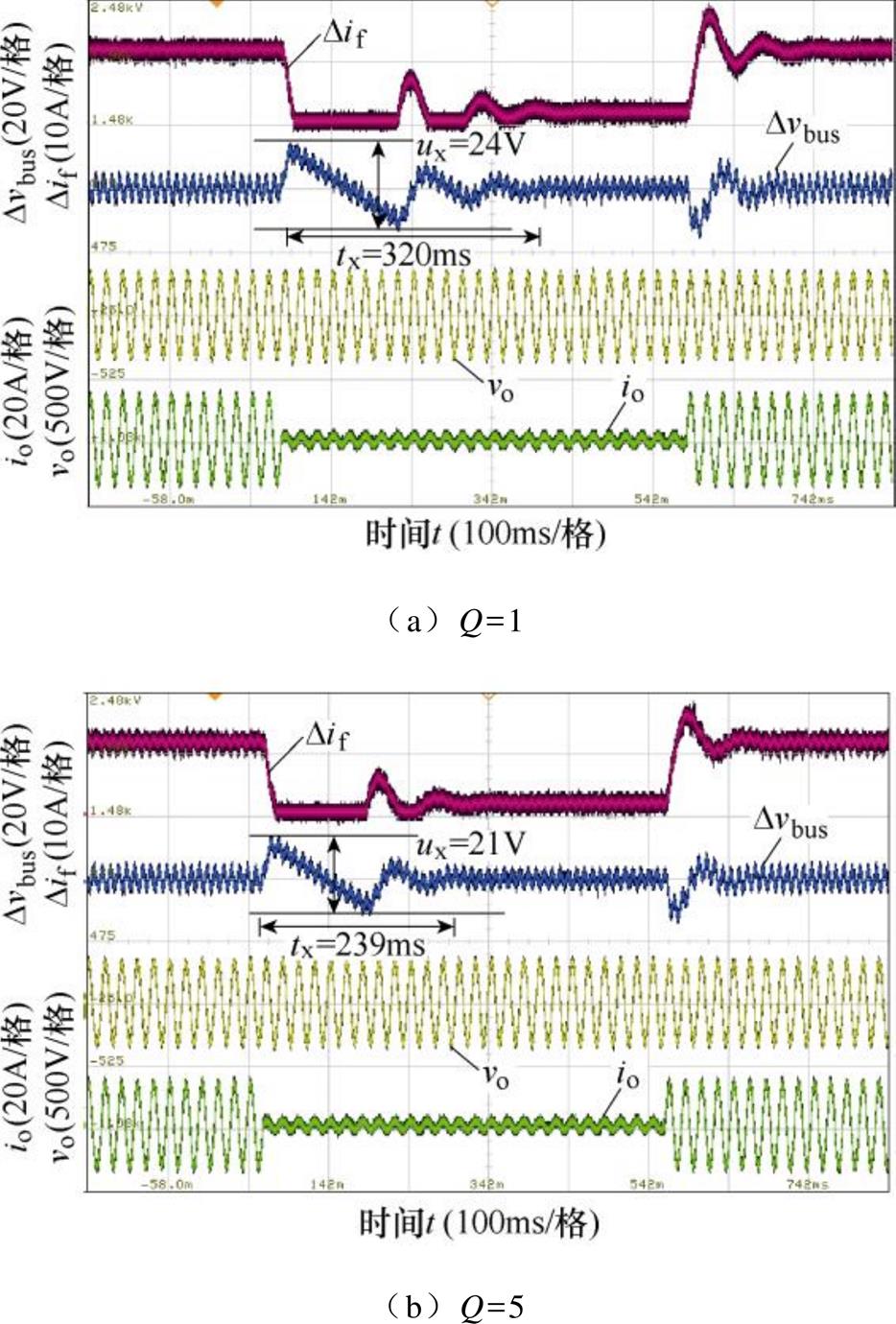
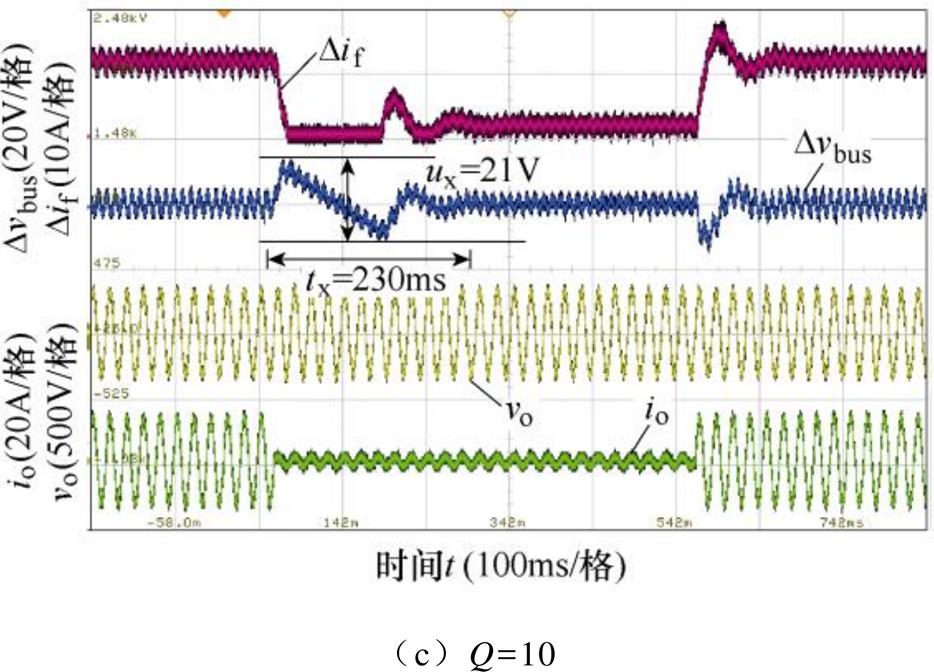
图14 引入NF的双闭环控制下负载响应动态特性
Fig.14 Dynamic characteristics of load response of dual-loop control with NF
因此,在引入NF的双闭环控制下,减小品质因数,可以使得NF的谐振峰值增大,减小2次谐波电流含量,但品质因数过低会降低其他频段的等效阻抗,从而使得动态响应特性下降。综合考虑2次谐波电流抑制效果和负载响应动态特性,选取品质因数Q=5。
在Q=5的基础上,引入NF+QPR的双闭环控制下稳态实验结果如图15所示,图15a~图15c对应的谐振增益参数分别为kgr=10,wc=10rad/s;kgr=1,wc=10和kgr=10,wc=20rad/s。在这三组不同参数下2次谐波电流含量分别为0.43%、1.72%和1.94%,由此说明,增大谐振增益系数kgr和减小带宽角频率wc可以减小2次谐波电流含量。这是由于按照上述情况改变这两个参数会增大QPR的谐振幅值,使得电感支路等效阻抗在2次谐波频率处增大,从而增强2次谐波电流抑制能力。同时,与引入NF的双闭环控制对比分析,该方法下电感支路的2次谐波电流含量更少。
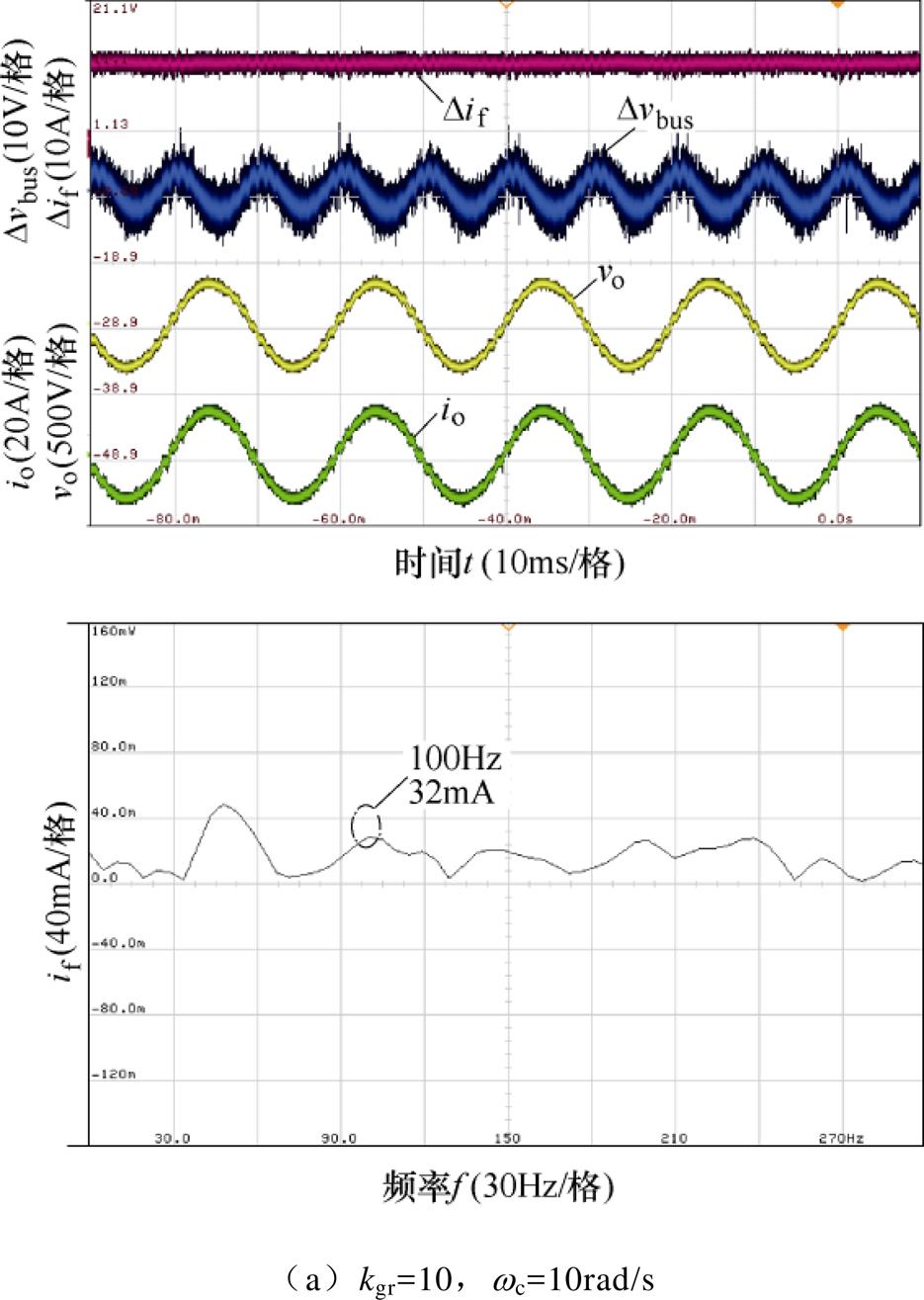
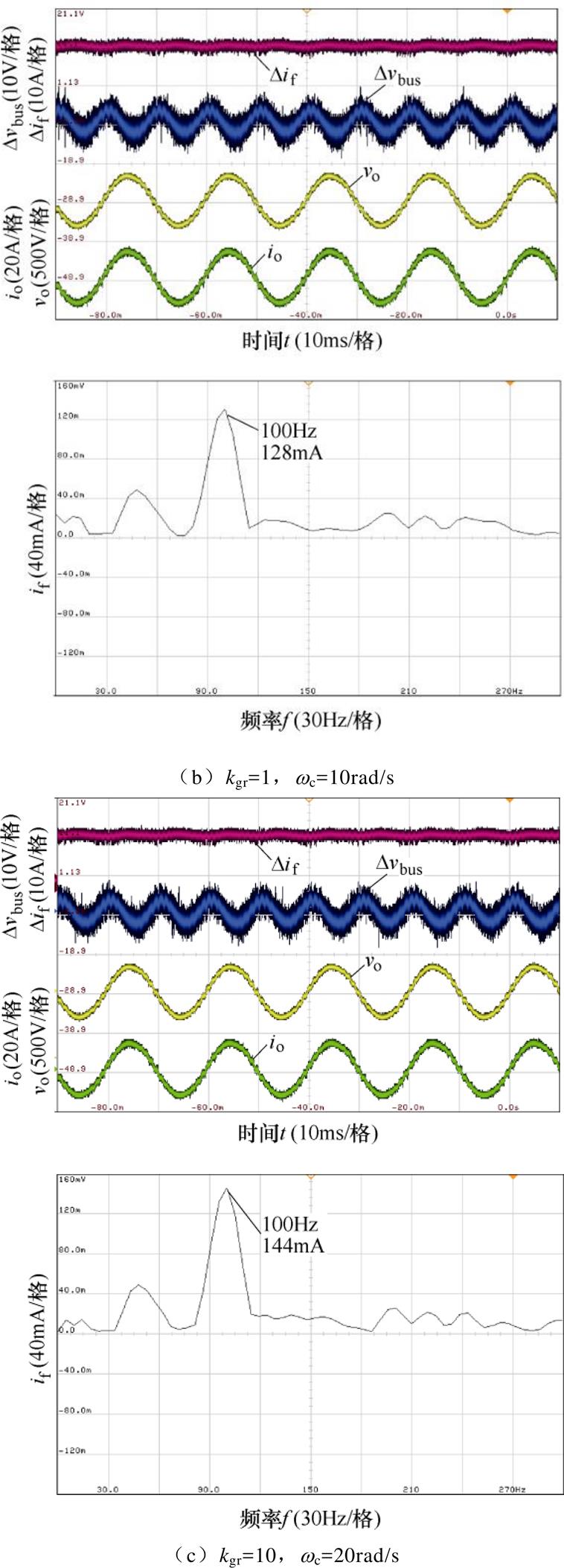
图15 引入NF+QPR的双闭环控制下稳态实验结果
Fig.15 Steady-state experimental results of dual-loop control with NF+QPR
考虑到2次谐波电流抑制效果,选择kgr=10,wc=10rad/s继续进行负载响应动态特性实验,实验结果如图16所示,图16a~图16c对应的谐振比例系数分别为kpr=1.5、kpr=1和kpr=0.5,负载突变后恢复时间分别为379ms、260ms和137ms,减小谐振比例系数kpr可以减小负载突变后的母线电压恢复时间,即改善系统负载响应动态特性。这是由于减小谐振比例系数kpr,使得QPR全频段幅值减小,从而减小非2次谐波频率处电感支路等效阻抗,优化系统的负载响应动态特性,而且由于QPR的谐振峰值较大,降低QPR的全频段幅值对2次谐波频率处的电感支路等效阻抗的影响较小,因此对2次谐波电流抑制效果的影响不大。

图16 引入NF+QPR的双闭环控制下负载响应动态特性
Fig.16 Dynamic characteristics of load response of dual-loop control with NF+QPR
在4.3节基础上,引入NF+QPR+LPF的双闭环控制稳态和负载响应动态特性实验结果分别如图17和图18所示。相比于引入NF、NF+QPR的双闭环控制方法,引入NF+QPR+LPF的双闭环控制下谐波含量有所降低,虽幅度不大,趋势仍为下降,2次谐波电流抑制效果略微提高。但值得注意的是,直流母线电压跳动幅值减小至14.4V,系统恢复时间降低至约为100ms,系统抗负载突变能力得到大幅改善。
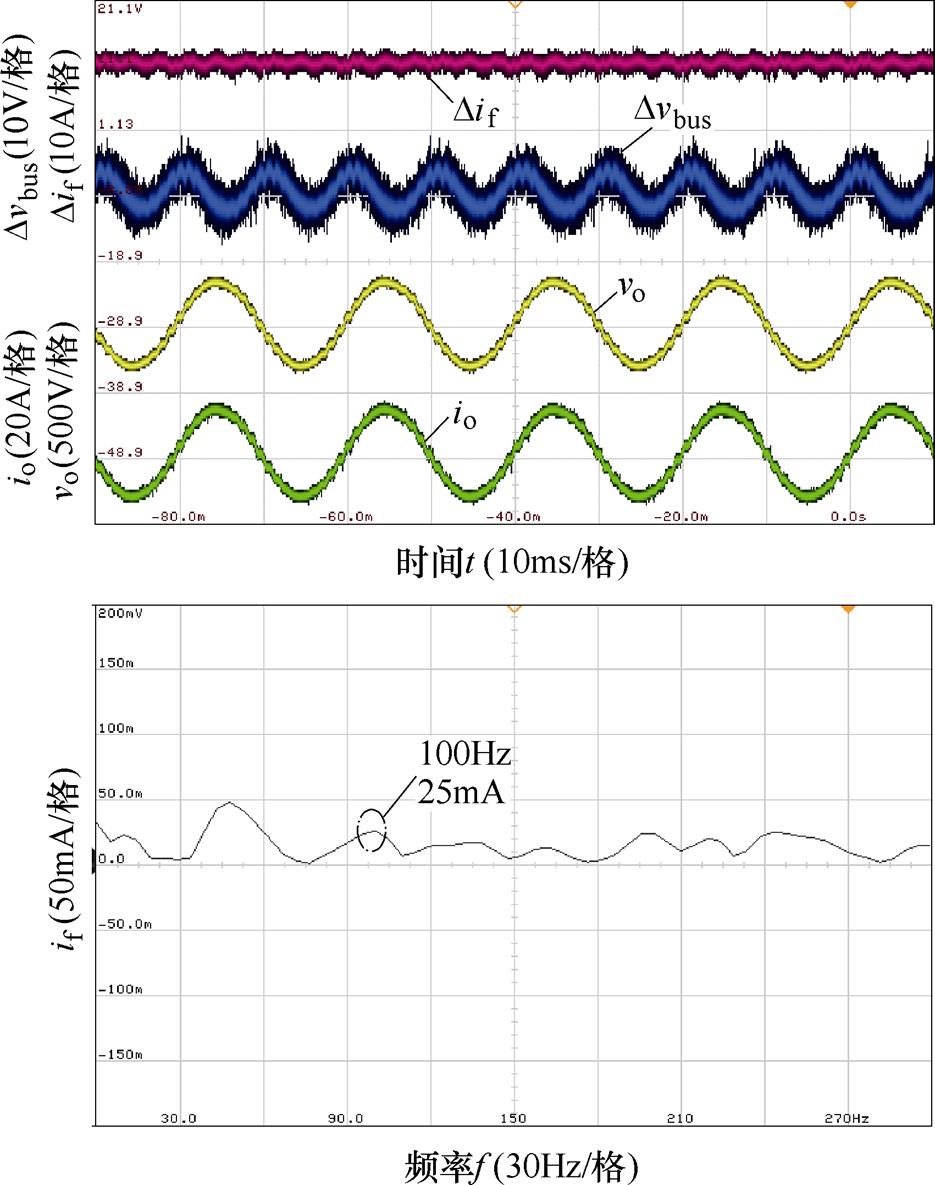
图17 引入NF+QPR+LPF双闭环控制下稳态实验结果
Fig.17 Steady-state experimental results of dual-loop control with NF+QPR+LPF
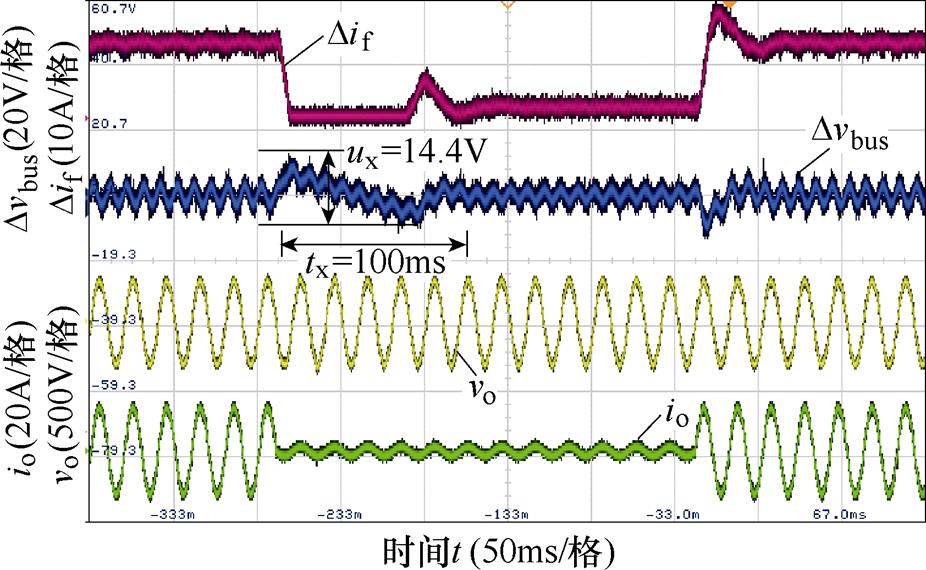
图18 引入NF+QPR+LPF的双闭环控制下负载响应动态特性
Fig.18 Dynamic characteristics of load response of dual-loop control with NF+QPR+LPF
因此,综合考虑2次谐波电流抑制效果和抗负载突变能力两个因素,相比于传统、引入NF、引入NF+QPR及引入NF+QPR+LPF的双闭环控制,引入NF+QPR+LPF的双闭环控制可以兼顾这两个因素,该方法能有效抑制电感中的2次谐波电流,同时减小负载跳变时直流母线电压的波动,保证较好的动态特性,确定为最优方案。
本文提出一种引入NF+QPR+LPF的双闭环控制方法,并得出如下结论:
1)减小品质因数Q,可以使得NF的谐振峰值增大,减小2次谐波电流含量,但品质因数过低会降低其他频段的等效阻抗,从而使得动态响应特性下降。
2)增大谐振增益系数kgr和减小带宽角频率wc会增大QPR的谐振幅值,减小2次谐波电流含量;减小谐振比例系数kpr可以减小负载突变后的母线电压恢复时间。
3)在LPF环节上串联NF,使得电感支路等效阻抗的幅值在非2次谐波频率处减小,降低了负载跳变时直流母线电压的波动,改善了系统的抗负载突变能力。
参考文献
[1] Alshareef M, Lin Zhengyu, Li Fulong, et al. A grid interface current control strategy for DC micro- grids[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(3): 249-256.
[2] 孙孝峰, 张绘欣, 张涵, 等. 一种用于电-氢多能互补型微电网的双有源桥集成Boost拓扑及其控制[J]. 电工技术学报, 2021, 36(10): 2092-2104.
Sun Xiaofeng, Zhang Huixin, Zhang Han, et al. Topology and control strategy of dual active bridge integrated Boost circuit for electro-hydrogen multi- energy complementary microgrid[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2092- 2104.
[3] 刘彦呈, 庄绪州, 张勤进, 等. 基于虚拟频率的直流微电网下垂控制策略[J]. 电工技术学报, 2021, 36(8): 1693-1702.
Liu Yancheng, Zhuang Xuzhou, Zhang Qinjin, et al. A virtual current-frequency droop control in DC microgrid[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1693-1702.
[4] 刘津铭, 陈燕东, 伍文华, 等. 孤岛微电网序阻抗建模与高频振荡抑制[J]. 电工技术学报, 2020, 35(7): 1538-1552.
Liu Jinming, Chen Yandong, Wu Wenhua, et al. Sequence impedance modeling and high-frequency oscillation suppression method for island microgrid[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1538-1552.
[5] 年珩, 叶余桦. 三端口隔离双向DC-DC变换器模型预测控制技术[J]. 电工技术学报, 2020, 35(16): 3478-3488.
Nian Heng, Ye Yuhua. Model predictive control of three-port isolated bidirectional DC-DC converter[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3478-3488.
[6] 周京华, 翁志鹏, 宋晓通. 兼顾可靠性与经济性的孤岛型光储微电网容量配置方法[J]. 电力系统自动化, 2021, 45(8): 166-174.
Zhou Jinghua, Weng Zhipeng, Song Xiaotong. Capacity configuration method of islanded microgrid with photovoltaic and energy storage system con- sidering reliability and economy[J]. Automation of Electric Power Systems, 2021, 45(8): 166-174.
[7] Iovine A, Carrizosa M J, Damm G, et al. Nonlinear control for DC microgrids enabling efficient rene- wable power integration and ancillary services for AC grids[J]. IEEE Transactions on Power Systems, 2019, 34(6): 5136-5146.
[8] 余雪萍, 涂春鸣, 肖凡, 等. 三端口隔离DC-DC变换器软开关特性[J]. 电工技术学报, 2021, 36(23): 5014-5026.
Yu Xueping, Tu Chunming, Xiao Fan, et al. Soft switching characteristics of the three-port isolated DC-DC converter[J]. Transactions of China Electro- technical Society, 2021, 36(23): 5014-5026.
[9] 邓翔, 韦徵, 龚春英, 等. 一种新颖的抑制两级式直交逆变器输入电流低频脉动的方法[J]. 中国电机工程学报, 2011, 31(30): 24-29.
Deng Xiang, Wei Zheng, Gong Chunying, et al. A novel technique for low frequency input current ripple reduction in two-stage DC-AC inverter[J]. Pro- ceedings of the CSEE, 2011, 31(30): 24-29.
[10] 王旭东, 张方华, 肖旭, 等. 带双Buck逆变器的DC/DC变换器低频电流纹波抑制[J]. 电力电子技术, 2013, 47(5): 35-37, 58.
Wang Xudong, Zhang Fanghua, Xiao Xu, et al. Low frequency current ripple rejection of a DC/DC converter with dual-Buck inverter load[J]. Power Electronics, 2013, 47(5): 35-37, 58.
[11] 徐辰华, 伍建松, 刘斌, 等. 直流侧电压高二次纹波率条件下的单相逆变器谐波削弱调制[J]. 电力系统自动化, 2020, 44(3): 176-184.
Xu Chenhua, Wu Jiansong, Liu Bin, et al. Harmonic reduction modulation strategy of single-phase inverter with high second-order ripple rate of voltage on DC side[J]. Automation of Electric Power Systems, 2020, 44(3): 176-184.
[12] 姚陶, 马超, 孙辰军, 等. 两级式单相逆变器输入谐波特性分析及抑制[J]. 电力电子技术, 2021, 55(7): 68-71.
Yao Tao, Ma Chao, Sun Chenjun, et al. Analysis and suppression of input harmonic current in the two- stage single-phase inverter[J]. Power Electronics, 2021, 55(7): 68-71.
[13] 祝国平, 阮新波, 王学华, 等. 两级式单相逆变器二次纹波电流的抑制与动态特性的改善[J]. 中国电机工程学报, 2013, 33(12): 72-80, 188.
Zhu Guoping, Ruan Xinbo, Wang Xuehua, et al. Suppression of the second harmonic current and improvement of the dynamic performance for two- stage single-phase inverters[J]. Proceedings of the CSEE, 2013, 33(12): 72-80, 188.
[14] 张力, 阮新波, 任小永. 两级式逆变器中前级直流变换器的控制方法[J]. 中国电机工程学报, 2015, 35(3): 660-670.
Zhang Li, Ruan Xinbo, Ren Xiaoyong. Control schemes for the front-end DC-DC converter in the two-stage inverter[J]. Proceedings of the CSEE, 2015, 35(3): 660-670.
[15] 章勇高, 付伟东, 刘鹏, 等. 一种新型逆变器交流侧功率解耦电路及其控制策略[J]. 中国电机工程学报, 2020, 40(22): 7440-7451.
Zhang Yonggao, Fu Weidong, Liu Peng, et al. Study on a novel AC-side power decoupling circuit of inverter and its control strategy[J]. Proceedings of the CSEE, 2020, 40(22): 7440-7451.
[16] Guo Xiaoqiang, Yang Yong, Wang Xuehui. Optimal space vector modulation of current-source converter for DC-link current ripple reduction[J]. IEEE Transa- ctions on Industrial Electronics, 2019, 66(3): 1671- 1680.
[17] Fukushima K, Norigoe I, Shoyama M, et al. Input current-ripple consideration for the pulse-link DC-AC converter for fuel cells by small series LC circuit[C]// IEEE Applied Power Electronics Conference and Exposition (APEC), Washington, DC, 2009: 447-451.
[18] Wang Haoran, Liu Yang, Wang Huai. On the practical design of a two-terminal active capacitor[J]. IEEE Transactions on Power Electronics, 2019, 34(10): 10006-10020.
[19] 林智乐, 何良宗, 周鸿彦. 基于有源负电容的电压源型逆变器直流母线二次功率脉动的抑制方法[J]. 中国电机工程学报, 2021, 41(22): 7772-7781.
Lin Zhile, He Liangzong, Zhou Hongyan. Suppressing secondary power pulsation method for DC bus of voltage source inverter based on active negative capacitor[J]. Proceedings of the CSEE, 2021, 41(22): 7772-7781.
[20] Kyritsis A C, Papanikolaou N P, Tatakis E C. A novel parallel active filter for current pulsation smoothing on single stage grid-connected AC-PV modules[C]// 2007 European Conference on Power Electronics and Applications, Aalborg, 2007: 1-10.
[21] Wai R J, Lin Chunyu. Dual active low-frequency ripple control for clean-energy power-conditioning mechanism[J]. IEEE Transactions on Industrial Elec- tronics, 2011, 58(11): 5172-5185.
[22] Itoh J I, Hayashi F. Ripple current reduction of a fuel cell for a single-phase isolated converter using a DC active filter with a center tap[J]. IEEE Transactions on Power Electronics, 2010, 25(3): 550-556.
[23] Liu Changrong, Lai J S. Low frequency current ripple reduction technique with active control in a fuel cell power system with inverter load[J]. IEEE Transa- ctions on Power Electronics, 2007, 22(4): 1429-1436.
[24] Li Zhongxi, Lizana R, Lukic S M, et al. Current injection methods for ripple-current suppression in delta-configured split-battery energy storage[J]. IEEE Transactions on Power Electronics, 2019, 34(8): 7411-7421.
[25] 史尤杰, 刘邦银, 段善旭. 单级式单相逆变器及其低频输入电流纹波抑制[J]. 高电压技术, 2019, 45(1): 259-268.
Shi Youjie, Liu Bangyin, Duan Shanxu. Single-stage single-phase inverter and its low-frequency input current ripple reduction[J]. High Voltage Engineering, 2019, 45(1): 259-268.
[26] Kan Jiarong, Xie Shaojun, Wu Yunya, et al. Single- stage and Boost-voltage grid-connected inverter for fuel-cell generation system[J]. IEEE Transactions on Industrial Electronics, 2015, 62(9): 5480-5490.
NF+QPR+LPF Dual-Loop Secondary Harmonic Current Suppression Method for Energy Storage System in DC Microgrid
Abstract The current on inductive branch on the DC side of the energy storage system in the DC microgrid contains a secondary harmonic component, which will increase the current stress and through-state loss of the switching tube in the converter. The traditional dual-loop control method shows that the secondary harmonic current is not suppressed obviously and the dynamic characteristics of the system is inferior during load hopping. Aiming at these two problems, a control method of introducing notch filter (NF), quasi-proportional resonator (QPR) and load power feedforward (LPF) based on dual-loop control is proposed. The method increases the amplitude of the equivalent impedance of the DC-side inductance branch at twice the output frequency without reducing the amplitude-frequency gain of the voltage regulator or changing the frequency adaptability of the equivalent impedance, and has a excellent suppression effect of the second harmonic current. Meanwhile, the equivalent impedance of the DC side inductance branch outside the double output frequency amplitude is reduced under this control method, which improves the system's ability to resist sudden changes in load. Finally, the experimental results demonstrate the effectiveness of the proposed control method.
keywords:DC microgrid, energy storage system, secondary harmonic current, notch filter, quasi-proportional resonator, load power feedforward
DOI: 10.19595/j.cnki.1000-6753.tces.212064
中图分类号:TM46
国家自然科学基金(52107185)和广东省基础与应用基础研究基金(2019A1515110768)资助项目。
收稿日期 2021-12-21
改稿日期 2022-02-08
徐卿瀚 男,2001年生,本科,研究方向为直流微电网运行与控制。E-mail: 1425962791@qq.com
杨 苓 女,1992年生,讲师,博士研究生,研究方向为可再生能源发电及其电能质量控制技术、并网变换器建模与稳定性分析。E-mail: 1650148795@qq.com(通信作者)
(编辑 陈 诚)