
图1 分布式IDR信息流示意图
Fig.1 Information flow diagram of distributed IDR
摘要 针对目前集中式、集中-分布式综合需求响应(IDR)方法的实现依赖于园区层能量管理系统的问题,研究一种基于改进一致性算法的工业园区分布式IDR方法。首先,设计工业园区的分布式信息交互机制;其次,提出一种在均衡状态下能使用户个体最优与园区整体最优的IDR方案相一致的工业园区IDR市场机制;然后,基于一致性算法和工业园区集中式IDR模型,提出分布式IDR模型;最后,为提升模型实际适用性,对一致性算法进行改进,通过使全局偏差达成一致,并利用分布式的排队法提升收敛性,建立最终的工业园区分布式IDR模型。算例结果表明,所提分布式IDR方法可在不依赖于园区层能量管理系统及减少用户对外提供信息的同时得到与集中式IDR一致的IDR方案,并且用户可获得比各自独立参与IDR更高的收益。
关键词:分布式综合需求响应 一致性算法 排队法 工业园区 市场机制
近年来,构建综合能源系统(Integrated Energy System, IES),实现电、热、冷、气等各种能源的耦合互补已经成为能源领域发展的主要方向[1]。传统的电力需求响应(Demand Response, DR)正逐步扩展为综合需求响应(Integrated Demand Response, IDR)[2]。
目前,关于IDR的研究大多是考虑单一主体或对工商业园区进行集中式、集中-分布式的优化调度,而对于完全分布式IDR的研究较少。文献[3]考虑工业园区中电池储能和冰蓄冷设备的协同运行,建立了响应分时电价的IDR模型。文献[4]提出通过刺激工业园区用户的用热需求,使得园区内的热电联供系统在多产热的同时发出更多电能,达到DR的效果。文献[5]采用分段线性函数表示负荷削减量与其成本的关系,进而根据各种能源的边际成本确定DR价格。文献[6]基于差异化弹性系数矩阵和激励型DR补偿模型建立了微电网优化调度模型,上述文献所提出的模型适用于集中式IDR。文献[7]提出了一种集中-分布式IDR方法,园区能量管理系统(Energy Management System, EMS)作为集中节点,以园区整体IDR成本最低为目标调节IDR补偿价格,用户各自优化意愿提供的IDR容量,相比集中式IDR能够减少用户需要对外提供的信息。
集中式IDR和集中-分布式IDR的实现需要依赖于园区层EMS,无法适用于不存在园区层EMS的场景。此外,在优化程序实现方面对于新参与用户的扩展性较差,本文采用一致性算法实现无园区层EMS下的分布式IDR。一致性算法被广泛应用于电力系统分布式调控研究中,具有计算效率高、保护用户隐私性等优点[8-9],非常适合用于分布式IDR。
在上述背景下,本文以工业园区为研究对象,提出一种基于改进一致性算法的分布式IDR方法。首先,结合现行市场机制设计了适用于工业园区分布式IDR的调峰需求响应市场机制,在该机制引导下,用户个体最优与园区整体最优的IDR方案相一致。然后,提出基于一致性算法的分布式IDR模型,但在实际应用中存在困难。最后,对一致性算法进行改进,使全局偏差达成一致,并利用分布式的排队法,建立适用于实际的工业园区分布式IDR模型。在分布式迭代计算过程中无需依赖于园区EMS,同时用户需要对外提供的信息仅为IDR边际成本和容量迭代值,能够较好地保护其信息私密性。
与园区EMS进行集中式或集中-分布式的优化管理不同,在分布式IDR机制中工业用户是通过多次相互之间的消息传递,最终对IDR方案达成共识,其中各用户以自身利益最大化为目标进行用能优化。以包含5个用户的工业园区为例,用户之间的通信网络以及多方主体之间传递的信息如图1所示。图1中,li,k为第i个用户在第k次消息传递中发出的信息,本文中该消息包括IDR边际成本、IDR容量以及IDR容量的变化量。

图1 分布式IDR信息流示意图
Fig.1 Information flow diagram of distributed IDR
在图1园区中实施分布式IDR的具体流程为:首先,工业用户考虑生产过程的多能协同,对分时电价做出响应,进行IDR用能优化,并向上级电网发送用能计划。本文以15min为最小时间单位,建立工业用户同时响应分时电价和调峰需求的模型[10-11]。考虑用户工厂IES中包含电、气、热、冷四种能源形式,其主要设备和能流结构如附图1所示。IES设备模型在现有文献中已有较多研究,附图1中各种设备模型采用与文献[7]相同的模型。附录给出了工业用户个体的IDR优化模型,同时也是园区集中式IDR模型,用以与分布式IDR进行结果对比。
对上级电网进行系统安全性评估,若不能通过安全校核,则向用户下发调峰需求[7]。最后,在设计的工业园区IDR市场机制下,基于一致性算法,用户之间通过多次相互传递IDR边际成本、IDR容量以及IDR容量的变化量信息得到IDR方案。每次消息传递后,用户根据邻近用户的IDR边际成本和IDR容量更新自身的IDR边际成本值,并发送给邻近用户,并且以最小化自身运行成本为目标更新意愿提供的调峰容量,其中邻近用户是指存在通信信道相连的用户。最终各用户的IDR边际成本趋于一致,将其确定为IDR市场的出清价格,同时得到各用户的调峰量,上报上级电网。
通过优化方法求取园区IDR方案时,为了使响应成本最小,各用户会优先使用较为廉价的可调节资源,因此IDR边际成本具有递增的特点。当所有用户的总运行成本最低时,各用户的IDR边际成本将趋于一致[12],即对于仍有可调节能力的用户,其IDR边际成本为一相同值,而IDR边际成本低于上述值的用户已提供其最大响应容量。一致量的存在使得园区IDR问题适合采用一致性算法进行分布式计算。
上述分布式IDR互动机制中工业用户无需对外提供生产和具体设备用能等信息,具有与集中-分布式IDR相同的优势,有利于保护用户的信息安全。
工业园区分布式IDR的目的是在减少用户对外提供信息的同时尽可能达到与集中式IDR相同的响应效果,即令园区整体运行成本最小。但是各工业用户是独立的利益主体,为了使他们在追求自身成本最小的同时能共同实现园区整体运行目标,需要设计合理的IDR市场机制加以引导。
本文在工业园区的IDR市场中采用统一价格机制,各用户之间通过相互传递IDR边际成本信息确定市场出清价格。在1.1节所述的分布式IDR互动机制下,各用户的IDR边际成本最终趋于一致,各中标用户均存在收益。由于调峰容量是在园区各用户之间分配,用户间为非合作博弈关系,因此可避免用户通过保留容量抬升价格。
当前国内对工业用户大多实施两部制电价,即按照电量电价和基本电价两部分计算电费。在基本电价中已包含了容量费用,因此用户在参与IDR后削减或增加的容量均应得到电网的补偿。为了促进并规范园区用户参与需求响应,本文从激励和惩罚两方面设置IDR市场机制。
1)激励机制
按照统一价格机制得到最终的IDR市场出清结果后,各工业用户获得的收益为
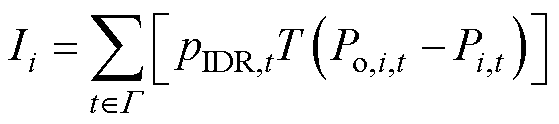 (1)
(1)
式中,Ii为第i个用户在园区IDR市场中获得的收益;pIDR,t为IDR市场出清价格;T为单位时段时长;Pi,t为参于IDR后第i个用户在时段t的购电功率;Po,i,t为用户初始计划购电功率。
若电网调用工业园区用户进行调峰,则需按照不低于pIDR,t的价格对园区用户进行补偿。假定发电侧在时段t提供调峰容量为Pd,t时的边际成本为pmax,t,若有pIDR,t>pmax,t,则电网将选择采用发电侧进行调峰以降低成本;若pIDR,t≤pmax,t,则园区用户将被选择参与调峰。为激励用户参与IDR,电网按照发电侧和用户侧二者调峰边际成本区间中的价格0.05pmax,t+0.95pIDR,t对园区进行补偿。由于通信链接较多的用户在分布式IDR中通信量较大,通信设备成本及功耗较高,将电网额外激励的部分补偿按通信链接数量分配至各用户,即
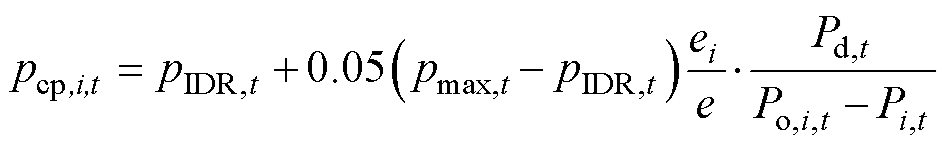 (2)
(2)
式中,pcp,i,t为电网对用户参与调峰需求响应的补偿价格;ei为通信网络中第i个用户节点的度;e为通信网络的总度数。
则各用户在参与IDR后最终获得的收益为
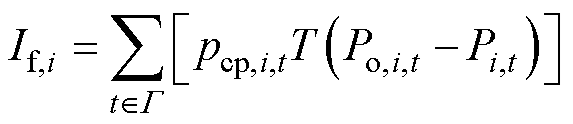 (3)
(3)
式中,If,i为第i个用户参与IDR后最终获得的收益。
2)惩罚机制
在上述激励机制中,电网以用户自行申报的用能计划为负荷基准,确定对用户的补偿量。在这种情况下,用户可能会申报虚假的用电计划,以套取调峰收益。为了限制用户的投机行为,本文借鉴新加坡电力市场的需求响应机制[13]设计工业园区IDR市场的惩罚机制。当上级电网不存在调峰需求或用户的IDR容量没有中标时,用户应严格执行其事先申报的用能计划。考虑到负荷预测存在误差,当用户实际用电量与申报负荷量的偏差超过5%时,对用户进行惩罚,总惩罚量为
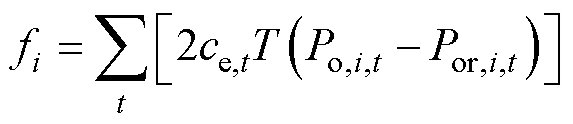 (4)
(4)
式中,fi为第i个用户由于用能偏差受到的惩罚量;Por,i,t为电网不存在调峰需求或用户的IDR容量未中标时用户i的实际购电功率;ce,t为时段t的电价。
上述对用电偏差量的惩罚价格为分时电价的2倍,该严格的惩罚机制能够促使园区用户申报真实的负荷需求,从而有效限制用户的投机行为。同时,由于用户的基准负荷是由其自行申报,这对用户的负荷预测精度提出了较高的要求。如果用户无法较为准确地预测实际负荷,则在上述市场机制下将会受到较大的惩罚。工业用户的负荷自动化水平较高,负荷量与生产计划有较强的相关性,相较于居民和商业用户其负荷预测精度通常更高,因此选用工业用户实施IDR,能够较好地适应上述市场机制。
在上述IDR市场机制下,IDR容量按照统一价格结算,各用户的最优策略是使其IDR边际成本等于结算价格[12],即各用户均有意愿使各自的IDR边际成本趋于一致,因此该机制能够实现园区整体运行成本最小化,第1.1节中将IDR边际成本作为用户间传递的消息使其最终趋于一致是合理的。
图1工业园区中工业用户之间的信息传递过程可通过无向图G=(V, E)表示,V中的元素vi为顶点,由用户组成,E中的元素eij为边,顶点i和j间存在信息传递通道时,称i和j两点相邻。
定义A为图G的邻接矩阵,D为图G的度矩阵。其中,A矩阵的对角元素为零,非对角元素aij为0~1变量,顶点i和j之间连接则为1;否则为零。D(G)=diag(d1,d2,…,dn)为对角矩阵[14-15],对角元素为对应顶点的相邻顶点数,即矩阵A的行元素之和。图G的拉普拉斯矩阵定义为L=D-A,矩阵L反映了图1的动态特性以及一致性算法的收敛性[16-17]。
一致性算法是指通信网络中的各节点通过与各自的邻接节点进行信息交互,不断更新本地的状态变量,最终使网络中各节点的状态变量趋于一 致[18]。如第1节所述,在园区IDR问题的最优解处,各用户的IDR边际成本趋于相同的值,因而适合采用一致性算法分布式求解。与分布式梯度下降算法相比,一致性算法的收敛性和鲁棒性较优。另外在常用的交替方向乘子算法中,对偶变量的更新需要集中协调节点,与一致性算法相比并非严格意义的完全分布式算法。目前,在电力系统分布式经济调度问题中,一致性算法相比其他分布式算法应用更为广泛[19]。连续一阶一致性算法的动态表达式为
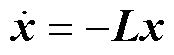 (5)
(5)
式中,x为由各节点的状态变量组成的向量;L为通信网络拓扑的拉普拉斯矩阵。
在实际系统中,状态变量的变化和传播是离散的。离散一致性算法的迭代表达式为
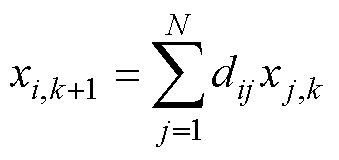 (6)
(6)
式中,xj,k为经过k次迭代后第j个节点的状态变量值;dij为与邻接矩阵对应的非负行随机矩阵的第i行第j列元素,其可按式(7)取值[20],即
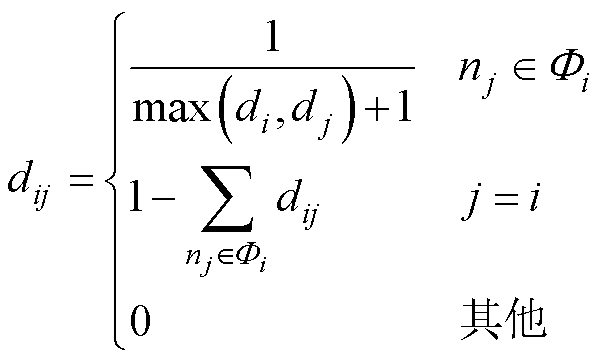 (7)
(7)
式中,nj为工业园区中的第j个用户;Fi为通信网络中第i个用户的邻近用户集合;di为通信网络中第i个用户的邻近用户数量,即度矩阵D的对角元素。
在上述一致性算法中,本地状态变量的更新利用了邻接节点的状态变量信息,使得各节点的状态变量趋于一致。文献[18-21]中本地节点的状态变量均是一维的。文献[22]提出可将一致性算法推广到多维的情形。如本节所述,在本文IDR市场机制下,当所有用户的IDR边际成本趋于一致时,园区整体运行成本最小,并且用户个体达到均衡状态下的最优。因此,可将IDR边际成本作为一致性算法中的状态变量。
若优化问题中存在全局性的约束,如所有用户的IDR总容量等于电网调峰需求的约束,则需要在一致性算法的状态变量迭代公式(6)中增加与全局约束相关的项[21]。对于工业园区分布式IDR问题,基于一致性算法的状态变量迭代表达式为
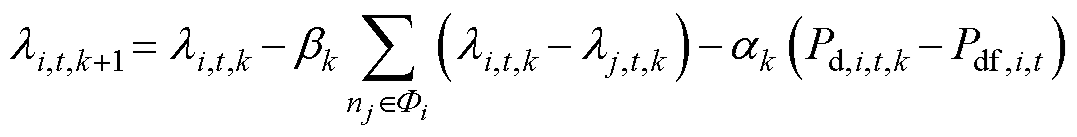
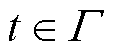 (8)
(8)
式中,li,t,k为第k次消息传递后第i个用户更新的时段t的IDR边际成本值;bk和ak为权重系数;Pdf,i,t为第i个用户对自身最终提供IDR容量的估计值;Pd,i,t,k为第k次迭代后用户意愿提供的IDR容量,计算为
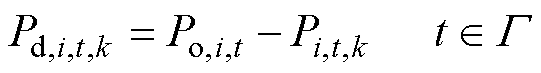 (9)
(9)
式中,Pi,t,k为第k次迭代后t时段用户的购电功率。
各用户对自身最终提供IDR容量的估计值需要满足约束为
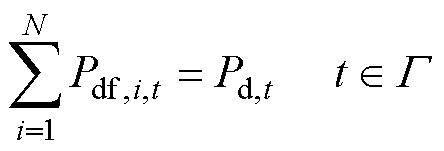 (10)
(10)
实际在分布式IDR中,各用户可能并无足够信息对自身最终提供的IDR容量进行准确预测,为满足式(10)所示约束,可取
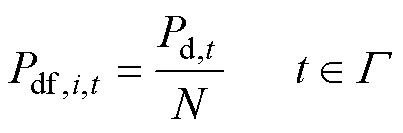 (11)
(11)
式(8)中包含bk的表达式称为“一致项”,该项使得不同节点的状态变量趋于一致;包含ak的表达式称为“创新项”,该项基于本地节点的IDR容量和电网的调峰需求量对状态变量进行修正,使得式(A3)所示的全局约束最终得到满足。
上述一致性算法收敛的必要条件[21]如下:
(1)通信网络的拓扑图是连通的。
(2)权重系数数列{bk}和{ak}是单调递减的,并且当k→∞时,满足bk→0和ak→0。
(3)数列{bk}和{ak}的级数发散,即
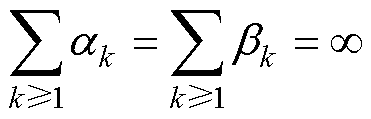 (12)
(12)
(4)当k→∞时,bk/ak→∞。
在分布式IDR中,不要求工业用户两两之间建立通信,每个用户可仅与邻近的用户进行通信,使上述条件(1)中通信网络的连通性得到满足。
在实际应用中,上述一致性算法的权重系数bk和ak选择较为困难,算法的收敛性能无法得到保证,并且在工业园区每次进行分布式IDR时,由于电网调峰需求和用户用能计划均不同,可能需要重新确定权重系数以提升收敛速度。此外,在上述一致性算法中通过引入“创新项”以使全局性的约束得到满足,其中包含了用户对自身最终提供IDR容量的估计量Pdf,i,t。由于在分布式IDR中各用户可获取的信息较少,通常仅能按式(11),即采用调峰需求量的平均值为Pdf,i,t赋值。当各用户IDR边际成本趋于一致时,若不同用户的IDR容量相差较大,则Pd,i,t,k-Pdf,i,t也将始终为一较大的值,这将对算法的收敛性能造成不利影响。
基于上述不足,本文在一致性算法的计算过程中,通过使各用户对IDR总量与电网需求量的偏差这一全局量达成一致,从而提升算法的收敛性。首先基于一致性算法分布式地计算各用户IDR容量的平均值[23],迭代表达式为
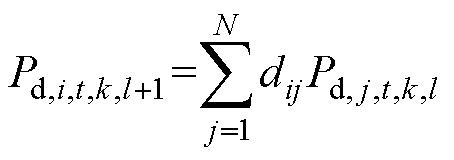 (13)
(13)
式中,Pd,i,t,k,l为第l次迭代后第i个用户对IDR容量平均值的估计,初值Pd,i,t,k,0=Pd,i,t,k。
当满足如下条件时,迭代计算完成。
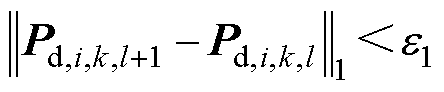 (14)
(14)
式中,e1为给定的计算精度要求;Pd,i,k,l为第l次迭代后在调峰时段用户计算所得Pd,i,t,k,l构成的向量。
园区IDR总量与电网调峰需求量的偏差为
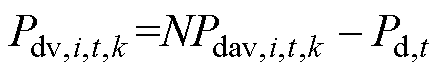 (15)
(15)
式中,Pdv,i,t,k为园区IDR总量与电网需求量的偏差;Pdav,i,t,k为第i个用户得到的IDR容量平均值。
进而利用园区IDR总量与电网需求量的偏差这一信息,对式(8)进行修正,得
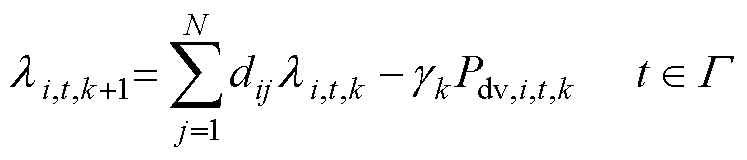 (16)
(16)
式中,gk为权重系数,其取值满足
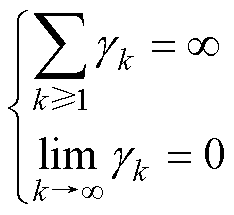 (17)
(17)
由于Pdv,1,t,k=Pdv,2,t,k=…=Pdv,N,t,k,因此通过式(16)的迭代,最终用户的IDR边际成本值仍趋于一致。
现有基于一致性算法的分布式优化调度研究中,所讨论各智能体的目标函数大多为二次函数[21, 24],这对于算法的收敛是一种较好的函数形式。而在分布式IDR问题中,由于各用户会优先利用较为廉价的资源进行调节,各用户的IDR成本与IDR容量之间的关系具有分段函数的特征,其中部分分段可能接近于一次函数,例如,利用电池储能[25-26]进行调节所产生的运行维护成本。具有分段特征的IDR成本函数对应的边际成本示意图如图2所示。
实际上,若多智能体优化的目标函数具有接近一次函数的特征,则一致性算法的收敛性能将会变差。如图2所示,当迭代计算过程中边际成本在pmgc附近变化时,用户意愿提供的IDR容量会发生突变,变化量达到|Pdg,2-Pdg,1|。若在最优结果中,各用户的IDR边际成本接近于pmgc,则一致性算法将难以收敛。针对这种情况,本文设置一致性算法迭代计算的终止条件为
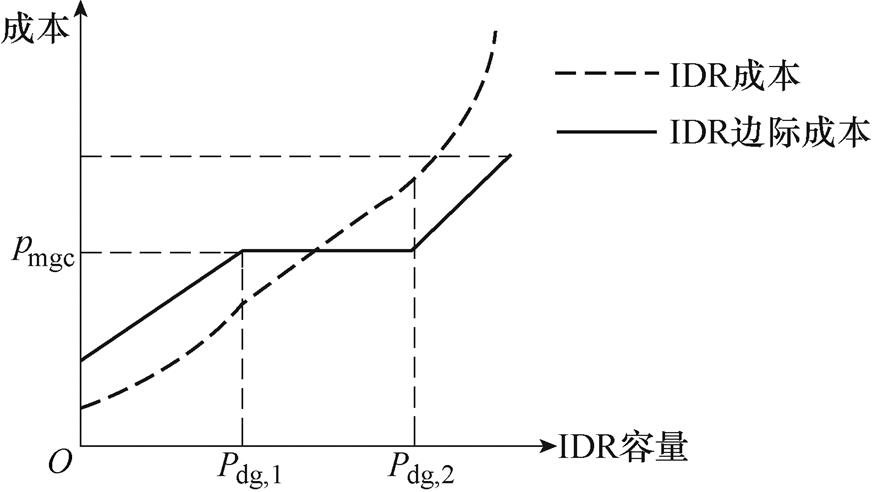
图2 IDR边际成本示意图
Fig.2 Diagram of IDR marginal cost
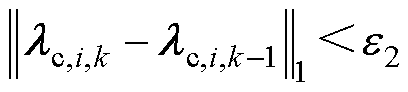 (18)
(18)
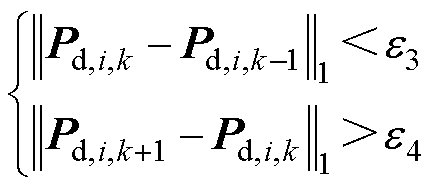 (19)
(19)
式中,e2、e3和e4为给定的计算精度要求,e3<e4;lc,i,k为第k次迭代后在调峰时段用户的IDR边际成本构成的向量;Pd,i,k为第k次迭代后在调峰时段用户的IDR容量构成的向量。
式(19)即为对应上述在最优结果附近IDR容量存在突变情况下的收敛条件,收敛后取最后一次园区IDR总量大于电网需求量的计算结果。当算法在式(19)所示条件下收敛时,园区IDR总量可能与电网需求量不平衡。对此本文采用分布式的排队法,确定各个用户最终提供的IDR容量。在收敛时IDR容量变化量较大的用户,其IDR边际成本关于IDR容量变化较为不敏感,应优先减少这类用户的IDR容量。利用分布式的排队法对用户最大IDR容量变化量进行排序,迭代表达式为
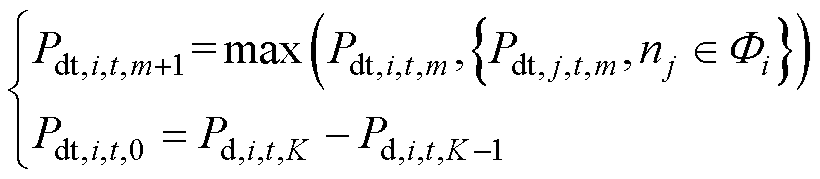 (20)
(20)
式中,Pd,i,t,K为用户意愿提供的IDR容量迭代结果;Pdt,i,t,m为第m次迭代后第i个用户得到的用户最大IDR容量变化量。
上述迭代计算的收敛条件为Pdt,i,t,m=Pdt,i,t,m-1,设此时得到IDR容量变化量最大为第v个用户,将该用户加入到集合Y 中。若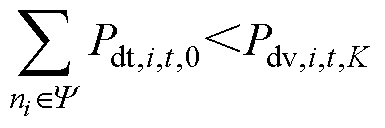 ,则第v个用户将其IDR容量变化量置为0,继续进行式(20)所示的迭代计算;若
,则第v个用户将其IDR容量变化量置为0,继续进行式(20)所示的迭代计算;若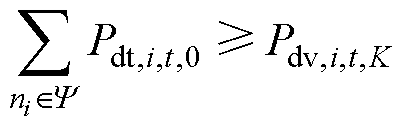 ,则迭代计算完成,第v个用户提供的IDR容量相比其期望提供的容量减少
,则迭代计算完成,第v个用户提供的IDR容量相比其期望提供的容量减少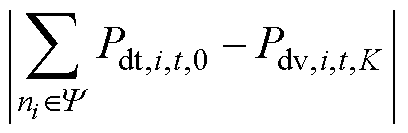 ,集合Y中其他用户提供的IDR容量减少Pdt,i,t,0。
,集合Y中其他用户提供的IDR容量减少Pdt,i,t,0。
每次完成式(16)的迭代计算后,用户期望提供的IDR容量Pd,i,t,k需要随着IDR边际成本的变化进行更新,以实现用户自身成本的最小化。文献[18, 21-22]中均假设优化问题的目标函数为二次函数,并且约束条件为变量上下限值约束等较为简单的约束,利用KKT(Karush-Kuhn-Tucker)条件即可得到优化问题的最优解,从而对全局约束变量进行更新。但本文所讨论的IDR问题和数学模型较为复杂,对于附录中的工业园区集中式IDR模型,难以直接求出其最优解的显式表达式。为此需要采用不同的方法求出与li,t,k对应的用户IDR容量。本文通过求解如下的优化问题对用户的IDR容量进行更新。
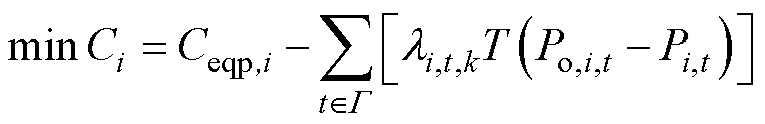 (21)
(21)
式中,Ci为第i个工业用户根据本地的IDR边际成本值预计的其参与IDR后的总成本。
约束条件为设备运行约束[7]和如式(A4)~式(A7)所示。根据KKT条件,在该约束条件下,当用户的用能成本Ceqp,i关于Pi,tT的边际成本与li,t,k尽可能接近时,用户的总成本最小,即在上述优化问题的最优解处,用户的IDR边际成本将趋于li,t,k。因此,可将求得的Pi,t最优值作为Pi,t,k的更新值,进而利用式(9)对Pd,i,t,k进行更新。
上述优化问题和式(13)、式(16)、式(20)所示的迭代表达式仅涉及用户本地和相邻用户的一致性变量信息,可以分布式地进行计算。最终得到的IDR方案使得各用户的IDR边际成本趋于一致,并且满足式(A3)所示的全局约束。
在集中式IDR中用户需要向园区提供可调节设备参数、设备运行状态、生产用能计划、新能源出力预测结果等大量信息,可能涉及用户隐私。而在上述分布式IDR中,用户仅需要对外提供IDR边际成本和容量信息,不涉及工厂内部运行情况和具体设备信息,提高了用户的信息安全性。
本文以广州某电压等级为35kV的工业园区为例分析所提的分布式IDR方法。在该园区中共有5个用户参与IDR,符合典型园区的用户数量[27]。用户之间的通信网络如图1所示,各用户的工厂IES中配置的设备种类和数量见附表1,可中断负荷的参数见附表2。各类设备参数、分时电价、热蒸汽和天然气的价格与文献[7]相同。工厂日内优化运行考虑的时段为8 00~24
00~24 00。以15min为最小IDR调节周期,将8
00。以15min为最小IDR调节周期,将8 00~24
00~24 00划分为64个时段。各用户的电、热、冷负荷以及光伏预测出力如附图2~附图5所示。计算精度要求为e1=0.1kW,e2=0.001元/(kW·h),e3= 5kW·h,e4=10kW·h。
00划分为64个时段。各用户的电、热、冷负荷以及光伏预测出力如附图2~附图5所示。计算精度要求为e1=0.1kW,e2=0.001元/(kW·h),e3= 5kW·h,e4=10kW·h。
根据第2节所述IDR机制,用户首先对分时电价做出响应,向上级电网发送用能计划。各用户以式(A2)最小化为目标,以设备运行约束和式(A4)~式(A7)为约束条件建立响应分时电价的IDR模型,优化得到初始计划购电功率。5个用户的用能成本分别为71 789元、61 898元、38 557元、33 312元和44 313元。上级电网得到工业用户的初始购电计划后,通过评估电力系统整体用能情况的安全性,向园区下发调峰需求:在11 15~12
15~12 15的4个时段,调峰需求分别为5.54MW、4.83MW、4.90MW和4.99MW。
15的4个时段,调峰需求分别为5.54MW、4.83MW、4.90MW和4.99MW。
采用CPLEX优化软件求解工业园区集中式IDR模型,4.2节中更新用户IDR容量的优化问题。
根据附录中的集中式IDR模型,计算得到各用户的调峰容量见表1,各用户在参与集中式IDR后的用能成本分别为72 078元、62 151元、38 648元、33 344元和44 345元。
表1 集中式IDR后各用户的调峰容量
Tab.1 IDR capacity of each user after centralized IDR
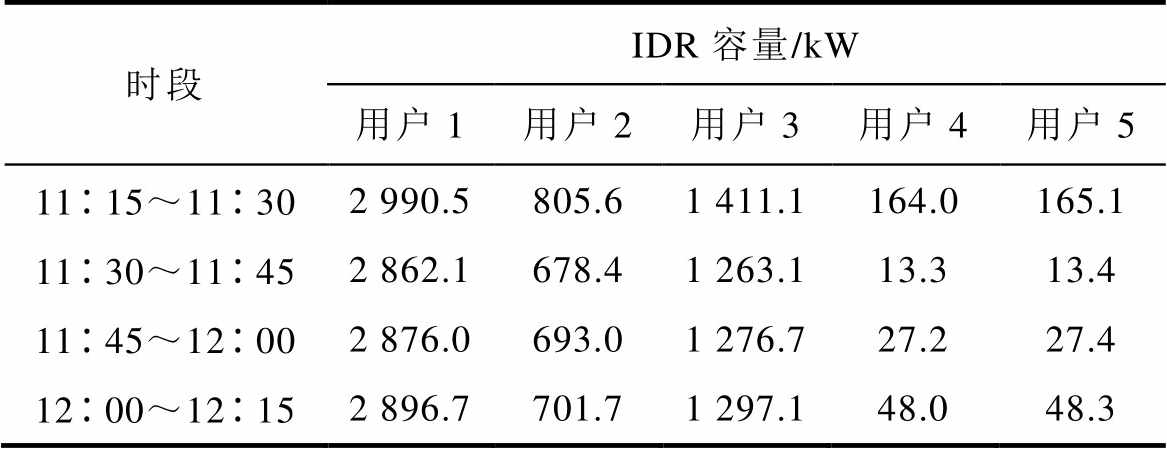
时段IDR容量/kW 用户1用户2用户3用户4用户5 1115~11302 990.5805.61 411.1164.0165.1 1130~11452 862.1678.41 263.113.313.4 1145~12002 876.0693.01 276.727.227.4 1200~12152 896.7701.71 297.148.048.3
结合附表1,可以看出能源设备种类、数量较多,多能耦合更为紧密的用户具有更强的IDR能力和更低的响应成本,因此在集中式IDR方案中其所提供的削峰容量也较多。在表1所示的削峰容量下,各用户在4个调峰时段的IDR边际成本分别为0.511 6元/(kW·h)、0.507 0元/(kW·h)、0.507 4元/(kW·h)、0.508 1元/(kW·h),各用户的IDR边际成本一致。
本节利用基于改进一致性算法的分布式IDR模型计算工业园区的调峰需求响应方案。5个用户设置本地的IDR边际成本初始值分别为0.84元/(kW·h)、0.58元/(kW·h)、0.75元/(kW·h)、0.42元/(kW·h)、0.66元/(kW·h),进行第4节所述的分布式IDR响应过程。
与图1所示通信网络的邻接矩阵对应的非负行随机矩阵取值为
 (22)
(22)
式中,d为图1所示网络对应的非负行随机矩阵。
式(16)中的权重系数gk取值需要满足式(17),可采用p级数[28]对应的数列为其赋值,即
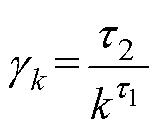 (23)
(23)
式中,t1和t2为正常数。
根据p级数的性质,当式(23)中0<t1≤1时,{gk}的级数发散,可满足式(17)。t1可选取接近于0的数,使得全局偏差量的修正作用随迭代次数缓慢减弱。t2的选取与式(16)中跟权值系数相乘的因子大小有关,应避免使迭代过程中状态变量的变化超出其合理取值范围,本算例中使迭代过程中IDR边际成本的变化量在1元/(kW·h)以内。通过实验选取权重系数t1=0.1,t2=1×10-5。
每次进行式(16)所示的迭代计算前,根据式(13)分布式地计算各用户IDR容量的平均值,进而利用式(15)计算园区IDR总量与电网调峰需求量的偏差,用以对IDR边际成本进行修正。
经过26次迭代后计算收敛,最终得到各用户的调峰容量,见表2,5个用户的用能成本分别为72 082元、62 155元、38 647元、33 335元和44 347元。
表2 分布式IDR后各用户的调峰容量
Tab.2 IDR capacity of each user after distributed IDR
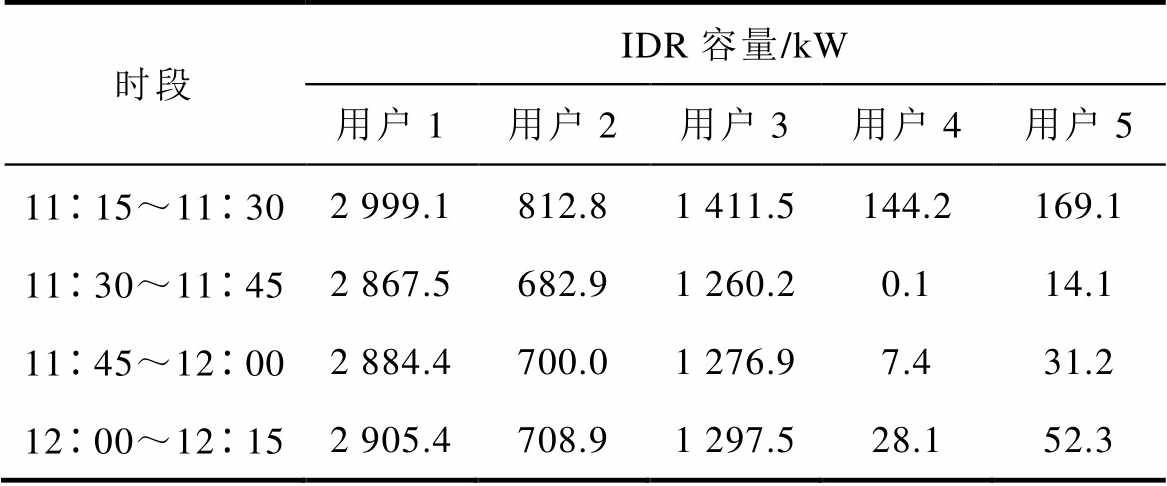
时段IDR容量/kW 用户1用户2用户3用户4用户5 1115~11302 999.1812.81 411.5144.2169.1 1130~11452 867.5682.91 260.20.114.1 1145~12002 884.4700.01 276.97.431.2 1200~12152 905.4708.91 297.528.152.3
对比表1和表2,可以看出采用第3节的分布式IDR模型得到的IDR方案与集中式IDR接近。若期望得到更精确的结果,可以通过减小计算精度要求e1、e2实现,但同时也需要更多的迭代次数。
在分布式IDR迭代过程中,各用户在时段11 15~11
15~11 30的IDR边际成本变化如图3所示。
30的IDR边际成本变化如图3所示。
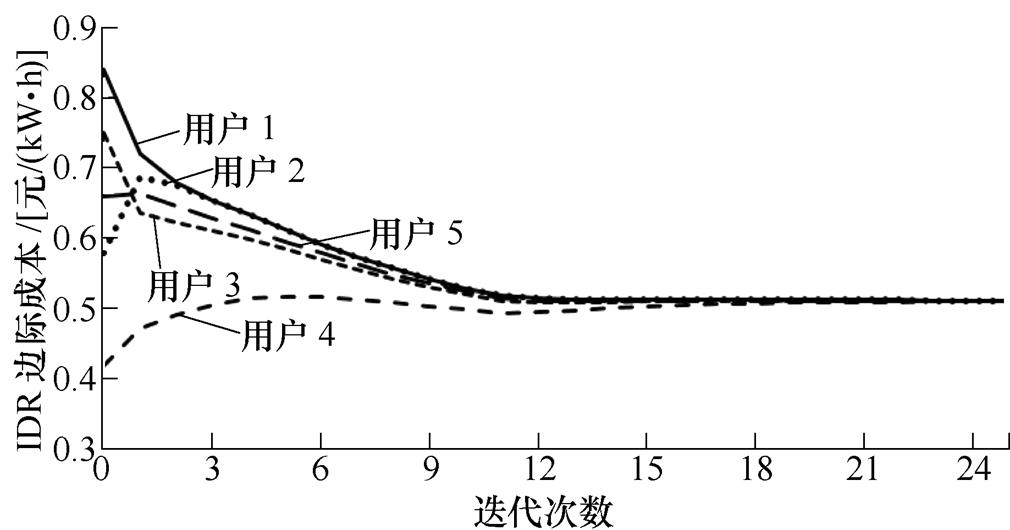
图3 IDR边际成本的变化
Fig.3 Change of IDR marginal cost
当迭代结束时,各用户在4个调峰时段的IDR边际成本见表3。
表3 各用户的IDR边际成本
Tab.3 IDR marginal cost of each user

时段IDR边际成本/[元/(kW·h)] 用户1用户2用户3用户4用户5 1115~11300.511 860.511 860.511 610.510 990.511 72 1130~11450.507 170.507 170.506 920.506 300.507 03 1145~12000.507 690.507 690.507 430.506 820.507 54 1200~12150.508 320.508 320.508 070.507 460.508 18
从图3和表3可以看出,随着用户之间的消息传递和迭代计算的进行,各用户的IDR边际成本逐渐趋于一致,并且与集中式IDR得到的结果接近。
与文献[7]的集中-分布式IDR方法相比,上述分布式IDR方法得到的结果与其接近,而计算过程不依赖于园区EMS,可适用于不存在园区EMS的工业园区。此外,若有新参与的用户,在分布式IDR中对于原有优化程序仅需要修改其中的矩阵d,而在集中-分布式IDR中则需要对园区EMS即集中节点的优化程序整体进行修改,因此本文分布式IDR优化程序在有新用户参与时扩展更为方便。
采用第3节的基于一致性算法的分布式IDR模型计算工业园区的调峰需求响应方案。式(8)中的权重系数bk和ak的取值需要满足第2节的条件(2)~条件(4),同样可采用p级数对应的数列为其赋值,即
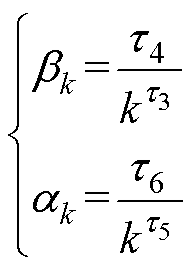 (24)
(24)
式中,t3、t4、t5和t6为正常数。
由条件(4)可知,随着迭代的进行,一致项将对状态变量的变化起主导作用,因此t3<t5,通常可将t3取为0.001,t5在10-1数量级范围内调节。t4和t6的选取应避免使迭代过程中状态变量的变化超出其合理取值范围。通过实验选取权重系数为
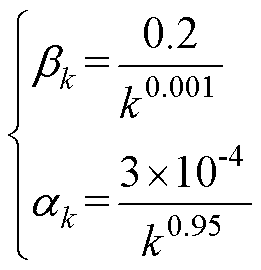 (25)
(25)
以式(18)作为迭代计算的收敛条件,经过128次迭代后计算收敛,各用户在时段11 15~11
15~11 30的IDR一致性算法的收敛情况如图4所示。
30的IDR一致性算法的收敛情况如图4所示。
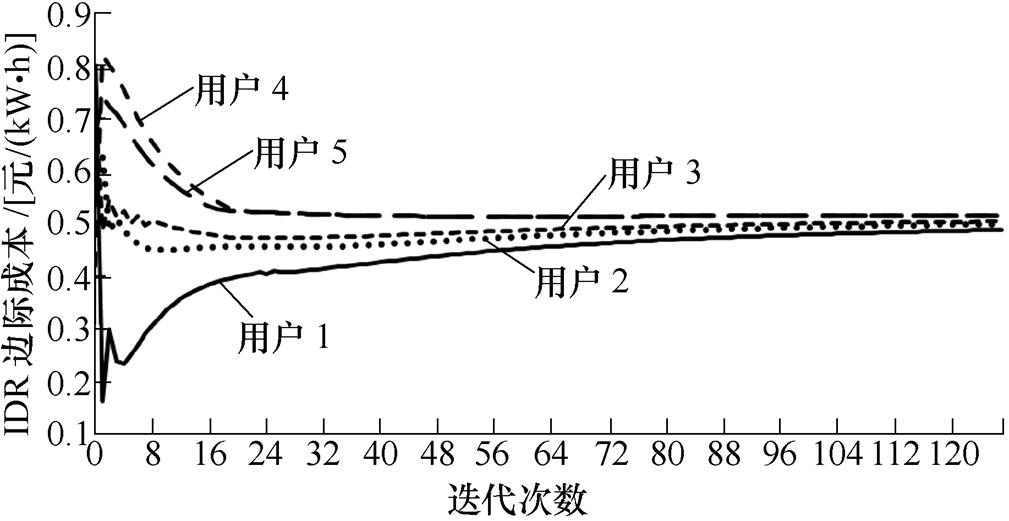
图4 IDR一致性算法的收敛情况
Fig.4 Convergence of the consensus algorithm
对比图3和图4,可以看出相比本文方法,一致性算法收敛的迭代次数较多,并且在计算收敛时各用户的IDR边际成本仍存在较大差异。图5对比了集中式IDR、本文方法和一致性算法所得在时段11 15~11
15~11 30各用户的IDR容量。
30各用户的IDR容量。
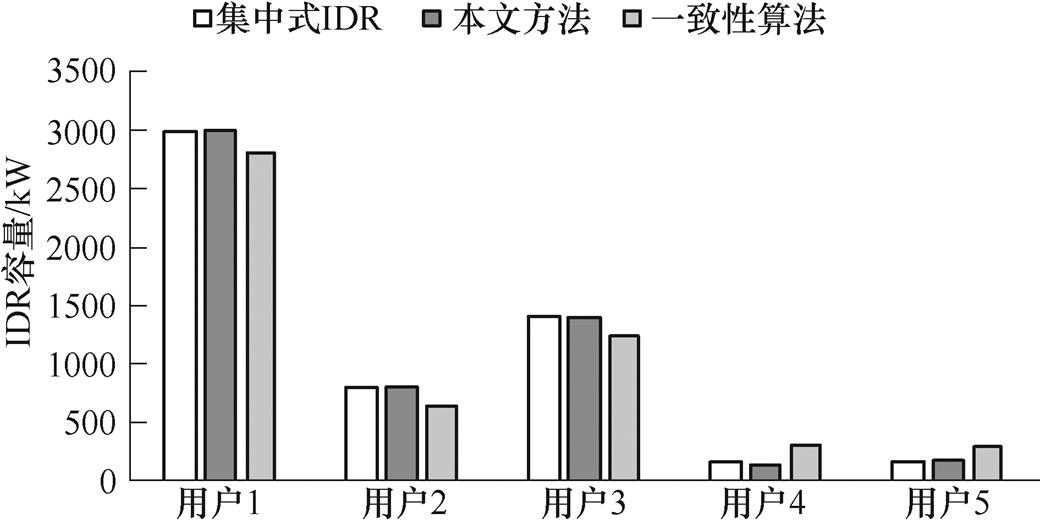
图5 不同IDR算法计算结果
Fig.5 Calculation results of different IDR algorithms
由图5可以看出,本文方法得到的IDR方案与集中式IDR十分接近。在一致性算法中,由于用户1的最优IDR容量远大于创新项中的估计值1 385kW,用户4和用户5的最优IDR容量远小于创新项中的估计值,因此在迭代过程中用户1的IDR边际成本偏小,而用户4和用户5的IDR边际成本偏大。随着迭代的进行,一致项将对状态变量的变化起主导作用,由于用户2的一致项受用户1的影响较大,因此其IDR边际成本也偏小。上述原因导致一致性算法无法收敛至优化问题的最优解。
采用一致性算法最终得到的IDR方案中,各用户在4个调峰时段提供的调峰容量和IDR边际成本见附表3,结合表1~表3,可以看出基于一致性算法的分布式IDR结果与本文方法及集中式IDR存在较大偏差,并未收敛至最优解,本文对一致性算法改进后提升了其收敛性能。
在上述调峰时段,发电侧的调峰价格为0.550元/(kW·h),根据2.2节所述的工业园区IDR市场机制确定各用户参与IDR的收益分别为1 484.1元、371.5元、671.2元、24.0元和35.1元。各用户在参与分布式IDR后的总成本分别为70 598元、61 784元、37 976元、33 311元和44 312元。园区用户缴纳的基本电费所对应的容量分别9MW、5.7MW、3.8MW、3.6MW和4.2MW,当各用户独立参与IDR时,用户间不进行信息交互,直接根据以上容量按比例分配调峰量,并按照分布式IDR中得到的价格0.05pmax,t+0.95pIDR,t对用户进行补偿。各用户在响应分时电价后的初始计划用能成本、集中式IDR后的成本、分布式IDR后的成本和各自独立参与IDR的成本见表4。
表4 各用户的成本
Tab.4 Cost of each user(单位: 元)
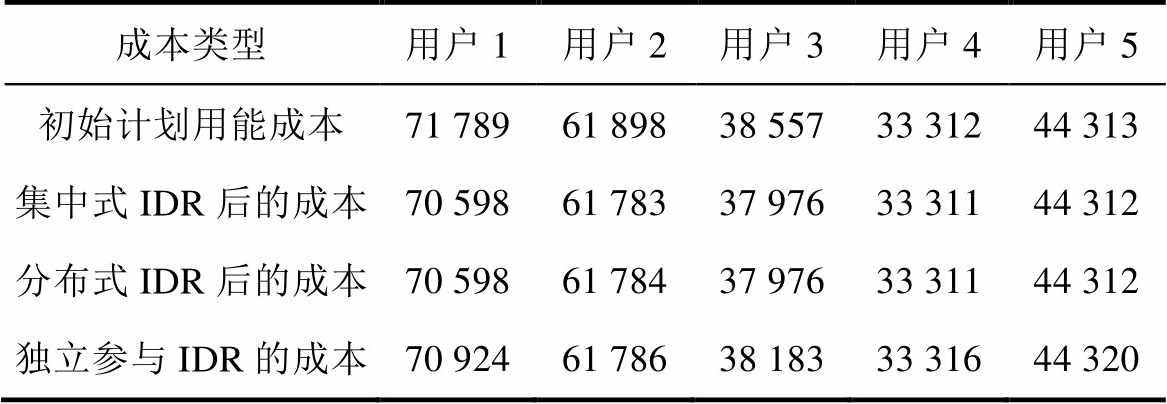
成本类型用户1用户2用户3用户4用户5 初始计划用能成本71 78961 89838 55733 31244 313 集中式IDR后的成本70 59861 78337 97633 31144 312 分布式IDR后的成本70 59861 78437 97633 31144 312 独立参与IDR的成本70 92461 78638 18333 31644 320
由表4可知,相比于初始计划用能的成本,各用户按本文IDR机制参与调峰需求响应后的总成本更低,该机制可使用户具有参与IDR的意愿。采用第3节所述的分布式IDR得到的用户成本与集中式IDR结果接近。此外,若园区用户各自独立地参与IDR,则无法实现用户之间IDR资源的协调,每个用户的成本相比采用本文IDR机制均有所提高。同时由于各用户的IDR边际成本并未趋于一致,上述价格补偿小于用户1、用户4和用户5的调节成本,此时这些用户将无参与IDR的意愿。
通过上述分析可以得出,本文的工业园区IDR市场机制能够有效地配置园区内IDR资源。在调峰需求量一定的约束下,可使得各用户参与IDR的成本达到最低或使收益达到最大。同时,分布式的迭代计算结果使各用户的IDR边际成本尽可能地趋于一致,因此园区整体的IDR成本也达到最小。
本文提出了一种基于改进一致性算法的工业园区分布式IDR方法,其特点如下:
1)与集中式IDR相比,在本文分布式信息交互机制下用户需要对外提供的信息较少,有利于保护其信息安全性和控制自主性。
2)与集中式-分布式IDR相比,本文分布式IDR无需依赖于园区层EMS,能够适用于不存在园区层EMS的工业园区,并且在IDR优化程序实现方面对于新参与用户的扩展性较好。
3)设计了工业园区分布式IDR机制,在该机制引导下园区分布式IDR的优化结果可使园区整体IDR成本达到最小。
4)通过使各用户对园区IDR总量与电网调峰需求量的偏差达成一致,并利用分布式的排队法对一致性算法进行改进,提升了算法的收敛性。进一步提升分布式IDR算法的收敛性,并考虑通信网络状态变化和通信时延对分布式IDR迭代计算的影响,是本文后续的研究方向。
工厂IES能流结构如附图1所示。附图1中,箭头表示能量流方向,其中电池储能与工厂IES间的能量流可为双向。
工业园区集中式IDR的目标是使参与IDR后园区整体的用能成本最小,目标函数为
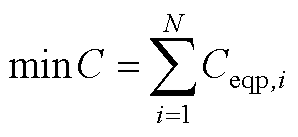 (A1)
(A1)
式中,C为工业园区的总用能成本;Ceqp,i为第i个工业用户的用能成本;N为工业园区的用户数量。
式(A1)中工业用户的用能成本为

附图1 工厂IES能流结构
App.Fig.1 Energy flow structure of IES in a plant
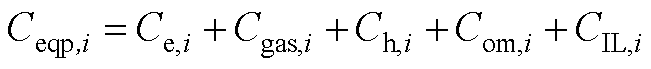 (A2)
(A2)
式中,Ce,i、Cgas,i和Ch,i分别为第i个工业用户的购电、购气和购热成本;Com,i为设备运行维护成本;CIL,i为中断负荷引起的损失成本。
式(A2)中各项成本的计算与文献[7]相同。式(A1)体现了园区对分时电价的响应,本文的IDR还考虑园区对上级电网调峰需求的响应,即
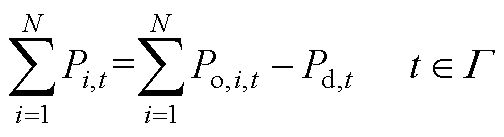 (A3)
(A3)
式中,t为日内的时段编号;Pi,t为参与IDR后第i个用户在时段t的购电功率;Po,i,t为用户初始计划购电功率;Pd,t为电网在时段t的调峰需求容量;G 为需调峰的时段集合。
工厂IES的运行需满足电、热、冷功率平衡,即
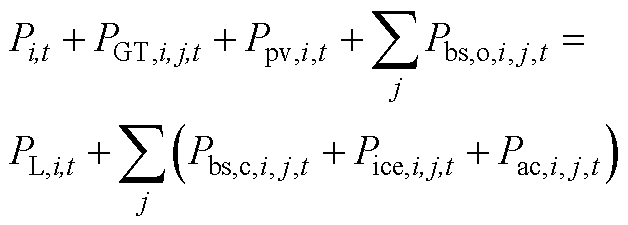 (A4)
(A4)
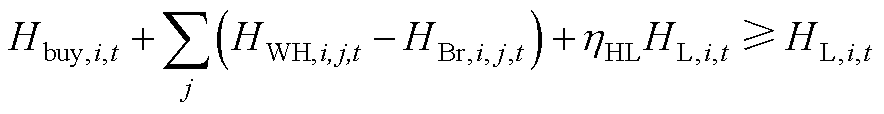 (A5)
(A5)
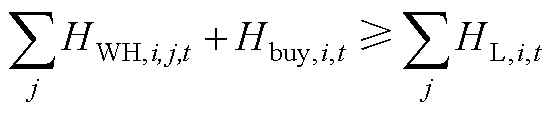 (A6)
(A6)
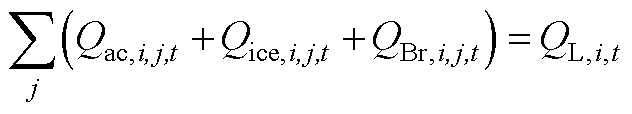 (A7)
(A7)
式中,PGT,i,j,t为第j台燃气轮机在时段t的产电功率;Ppv,i,t为光伏出力;Pbs,c,i,j,t和Pbs,o,i,j,t分别为第j个电池储能在时段t的充电功率和放电功率;Pice,i,j,t和Qice,i,j,t分别为冰蓄冷装置的耗电功率和制冷功率;Pac,i,j,t和Qac,i,j,t分别为第j台中央空调的耗电功率和制冷功率;PL,i,t、HL,i,t和QL,i,t分别为电负荷、热负荷和冷负荷;Hbuy,t为购热功率;HWH,i,j,t为从第j台燃气轮机回收生产的热功率;HBr,i,j,t和QBr,i,j,t分别为吸收式制冷机的耗热功率和制冷功率;ηHL为热负荷的热回收效率。式(A5)为热能总供应量不小于总需求量,式(A6)为中品位热供应量不小于中品位热需求量,保证热能的品位对口和梯级利用。
各用户的设备见附表1。可中断负荷参数见附表2。
附表1 各用户的设备
App.Tab.1 Equipments of each user
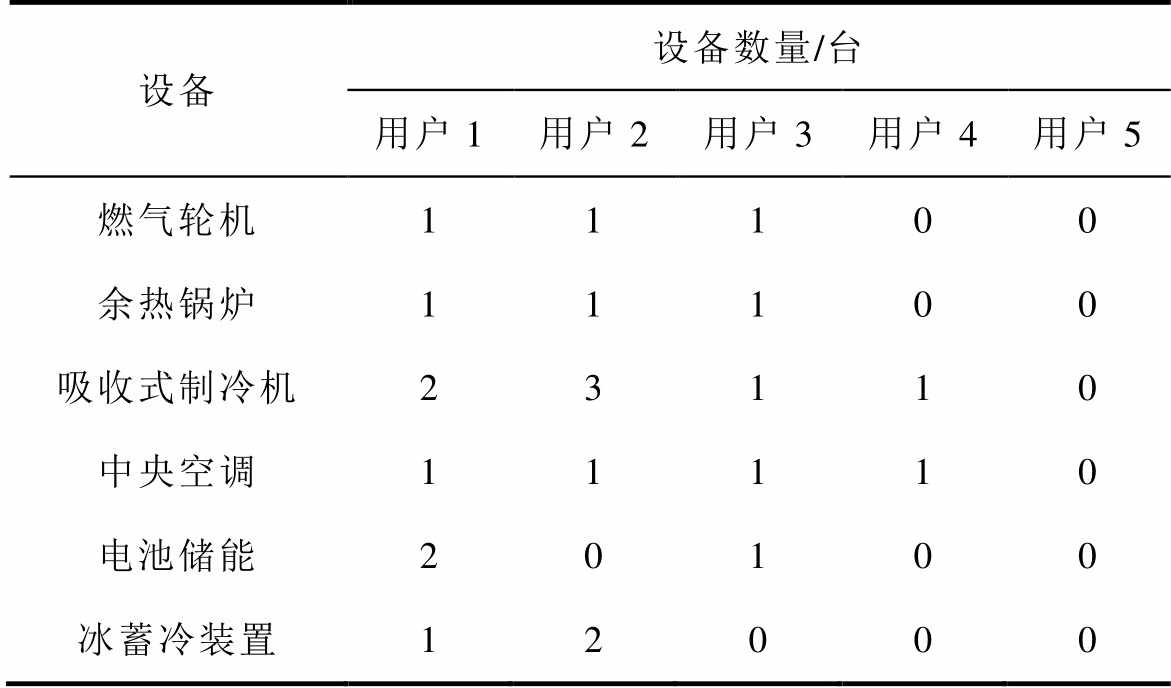
设备设备数量/台 用户1用户2用户3用户4用户5 燃气轮机11100 余热锅炉11100 吸收式制冷机23110 中央空调11110 电池储能20100 冰蓄冷装置12000
附表2 可中断负荷参数
App.Tab.2 Interruptible load parameters
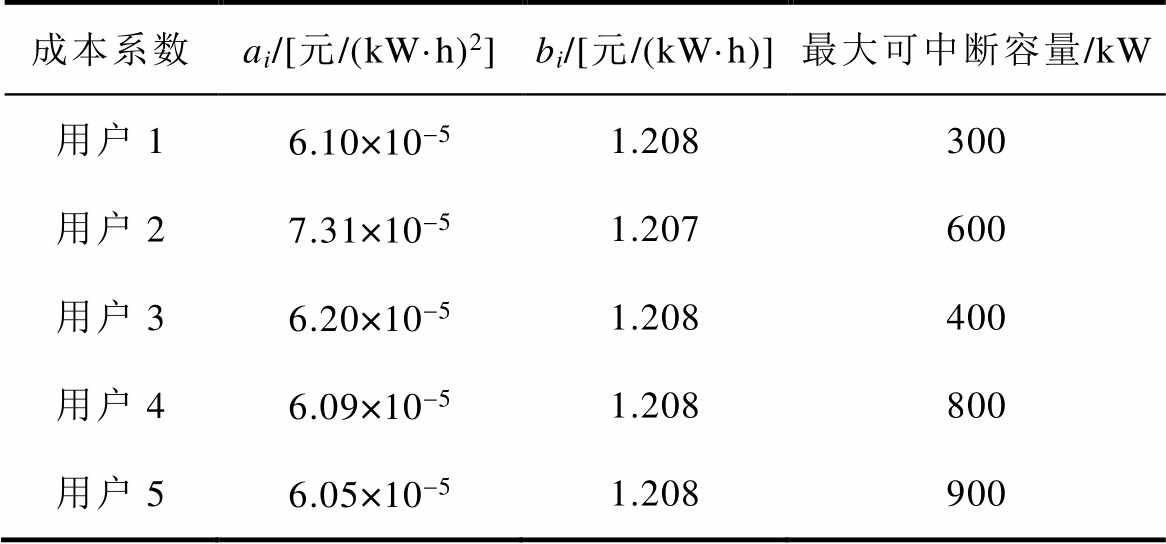
成本系数ai/[元/(kW·h)2]bi/[元/(kW·h)]最大可中断容量/kW 用户16.10×10-51.208300 用户27.31×10-51.207600 用户36.20×10-51.208400 用户46.09×10-51.208800 用户56.05×10-51.208900
电负荷如附图2所示。热负荷如附图3所示。冷负荷如附图4所示。光伏出力如附图5所示。基于一致性算法的分布式IDR结果见附表3。
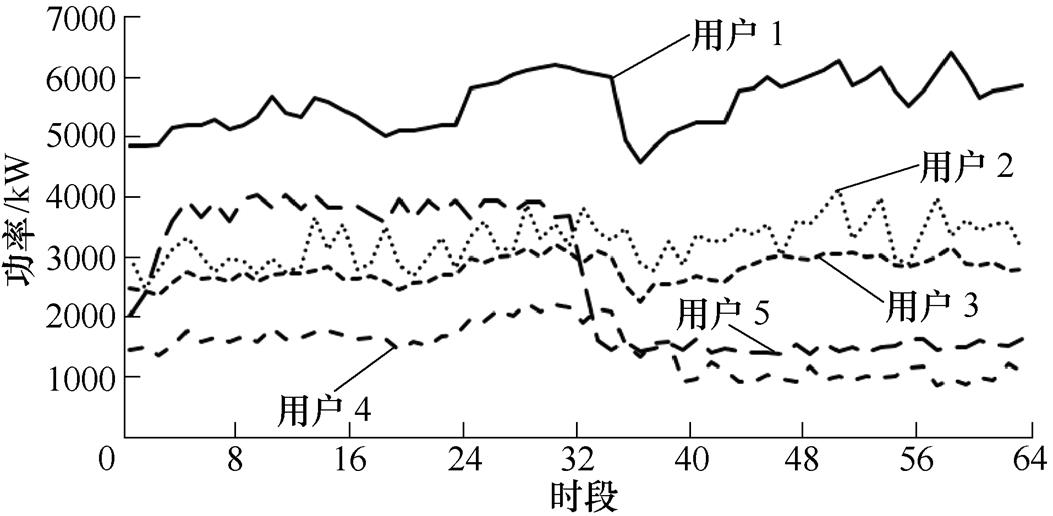
附图2 电负荷
App.Fig.2 Electrical load
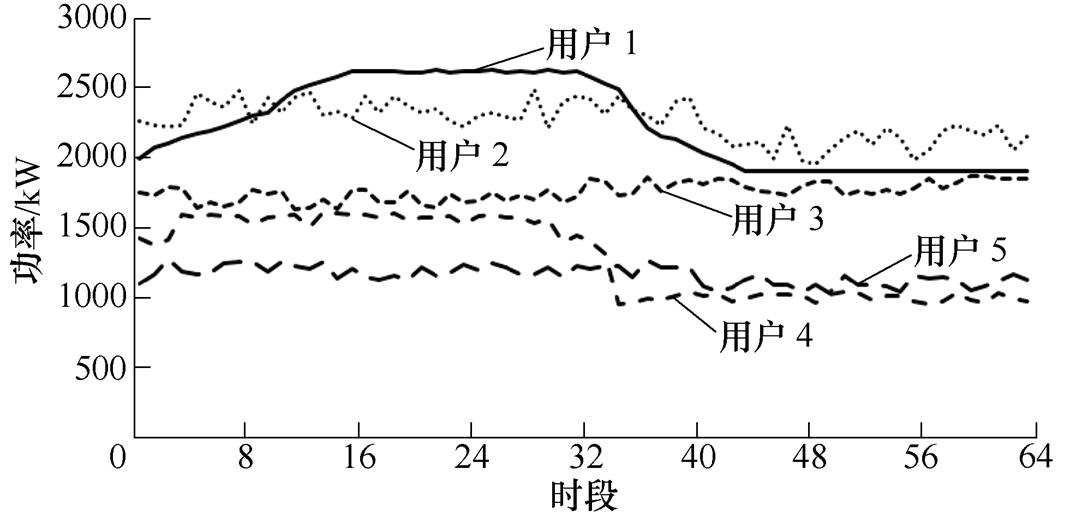
附图3 热负荷
App.Fig.3 Hot-water load
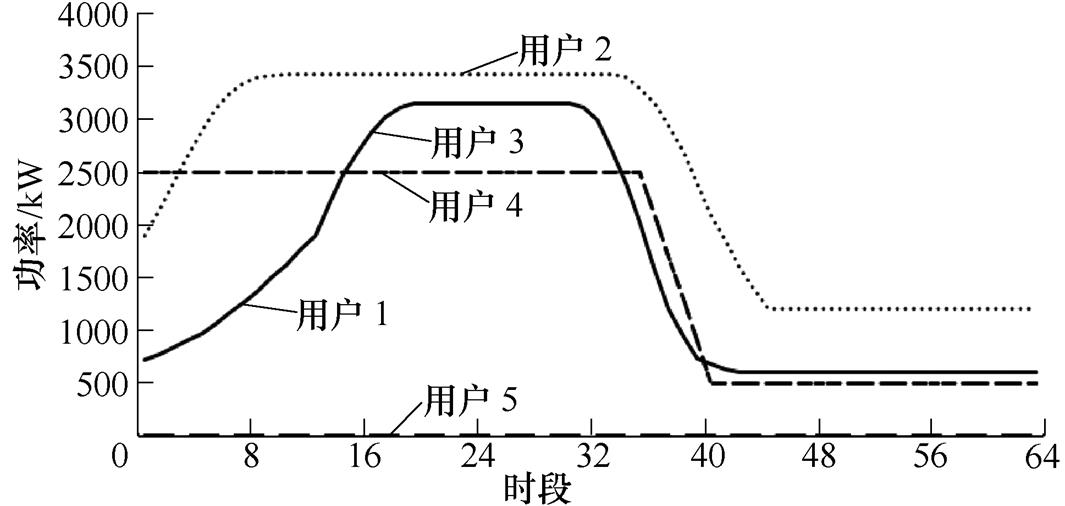
附图4 冷负荷
App.Fig.4 Cooling load
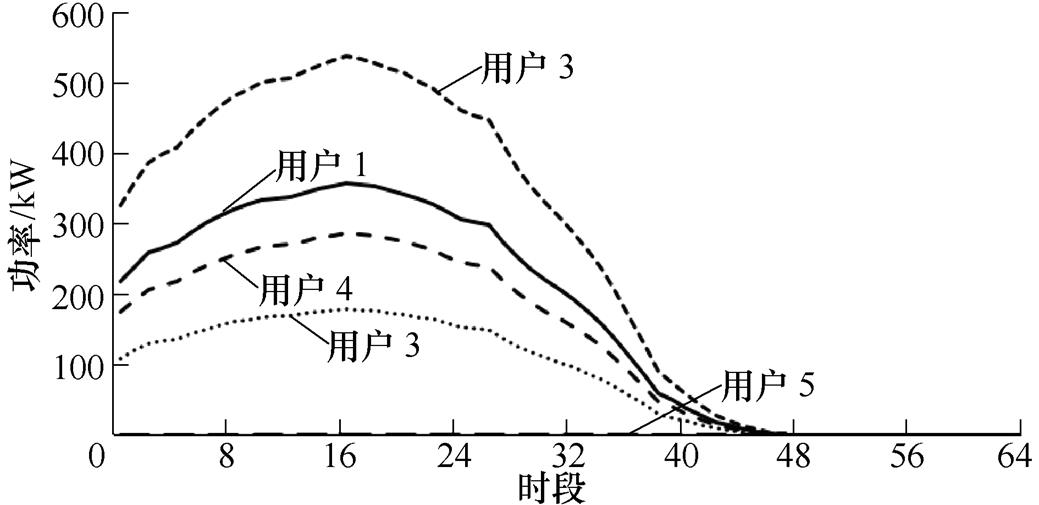
附图5 光伏出力
App.Fig.5 Photovoltaic output power
附表3 基于一致性算法的分布式IDR结果
App.Tab.3 IDR results based on the consensus algorithm

时段IDR容量/kW 用户1用户2用户3用户4用户5 1115~11302 826.7641.61 250.0308.1309.5 1130~11452 848.8640.01 250.00.00.0 1145~12002 848.8643.01 250.00.00.0 1200~12152 848.8634.41 250.00.00.0 时段IDR边际成本/[元/(kW·h)] 用户1用户2用户3用户4用户5 1115~11300.488 320.488 320.488 320.488 320.488 32 1130~11450.450 340.450 340.450 340.450 340.450 34 1145~12000.457 880.457 880.457 880.457 880.457 88 1200~12150.468 610.468 610.468 610.468 610.468 61
参考文献
[1] 崔全胜, 白晓民, 董伟杰, 等. 用户侧综合能源系统规划运行联合优化[J]. 中国电机工程学报, 2019, 39(17): 4967-4981, 5279.
Cui Quansheng, Bai Xiaomin, Dong Weijie, et al. Joint optimization of planning and operation in user- side multi-energy systems[J]. Proceedings of the CSEE, 2019, 39(17): 4967-4981, 5279.
[2] Chen Zhengqi, Sun Yingyun, Ai Xin, et al. Integrated demand response characteristics of industrial park: a review[J]. Journal of Modern Power Systems and Clean Energy, 2020, 8(1): 15-26.
[3] 何仲潇, 徐成司, 刘育权, 等. 考虑多能协同的工厂综合需求侧响应模型[J]. 电力自动化设备, 2017, 37(6): 69-74.
He Zhongxiao, Xu Chengsi, Liu Yuquan, et al. Industrial park IDR model considering multi-energy cooperation[J]. Electric Power Automation Equipment, 2017, 37(6): 69-74.
[4] 徐航, 董树锋, 何仲潇, 等. 基于多能互补的电/热综合需求响应[J]. 电网技术, 2019, 43(2): 480-487.
Xu Hang, Dong Shufeng, He Zhongxiao, et al. Electro- thermal comprehensive demand response based on multi-energy complementarity[J]. Power System Tech- nology, 2019, 43(2): 480-487.
[5] Zhang Xiaping, Shahidehpour M, Alabdulwahab A, et al. Hourly electricity demand response in the stochastic day-ahead scheduling of coordinated electricity and natural gas networks[J]. IEEE Transactions on Power Systems, 2016, 31(1): 592-601.
[6] 彭春华, 张金克, 陈露, 等. 计及差异化需求响应的微电网源荷储协调优化调度[J]. 电力自动化设备, 2020, 40(3): 1-7.
Peng Chunhua, Zhang Jinke, Chen Lu, et al. Source- load-storage coordinated optimal scheduling of micro- grid considering differential demand response[J]. Electric Power Automation Equipment, 2020, 40(3): 1-7.
[7] 徐成司, 董树锋, 张舒鹏, 等. 面向工业园区的集中-分布式综合需求响应方法[J]. 电网技术, 2021, 45(2): 489-497.
Xu Chengsi, Dong Shufeng, Zhang Shupeng, et al. Centralized-distributed integrated demand response method for industrial park[J]. Power System Tech- nology, 2021, 45(2): 489-497.
[8] 边晓燕, 孙明琦, 赵健, 等. 基于一致性算法的源-荷协同分布式优化调控策略[J]. 中国电机工程学报, 2021, 41(4): 1334-1347, 1540.
Bian Xiaoyan, Sun Mingqi, Zhao Jian, et al. Dis- tributed coordinative optimal dispatch and control of source and load based on consensus algorithm[J]. Proceedings of the CSEE, 2021, 41(4): 1334-1347, 1540.
[9] 蒲天骄, 刘威, 陈乃仕, 等. 基于一致性算法的主动配电网分布式优化调度[J]. 中国电机工程学报, 2017, 37(6): 1579-1589.
Pu Tianjiao, Liu Wei, Chen Naishi, et al. Distributed optimal dispatching of active distribution network based on consensus algorithm[J]. Proceedings of the CSEE, 2017, 37(6): 1579-1589.
[10] 李翔宇, 赵冬梅. 基于模糊-概率策略实时反馈的虚拟电厂多时间尺度优化调度[J]. 电工技术学报, 2021, 36(7): 1446-1455.
Li Xiangyu, Zhao Dongmei. Research on multi-time scale optimal scheduling of virtual power plant based on real-time feedback of fuzzy-probability strategy[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1446-1455.
[11] 王昀, 谢海鹏, 孙啸天, 等. 计及激励型综合需求响应的电-热综合能源系统日前经济调度[J]. 电工技术学报, 2021, 36(9): 1926-1934.
Wang Yun, Xie Haipeng, Sun Xiaotian, et al. Day- ahead economic dispatch for electricity-heating integrated energy system considering incentive inte- grated demand response[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1926-1934.
[12] 甘德强, 杨莉, 冯冬涵. 电力经济与电力市场[M]. 北京: 机械工业出版社, 2010.
[13] 张兰, 张经纬, 肖云鹏, 等. 新加坡电力市场需求响应机制及对中国电力市场建设的启示[J]. 中国电力, 2020, 53(9): 98-106.
Zhang Lan, Zhang Jingwei, Xiao Yunpeng, et al. Demand response mechanism in singapore electricity market and its enlightenment to China's power market construction[J]. Electric Power, 2020, 53(9): 98-106.
[14] Olfati-Saber R, Fax J A, Murray R M. Consensus and cooperation in networked multi-agent systems[J]. Proceedings of the IEEE, 2007, 95(1): 215-233.
[15] 吕振宇, 吴在军, 窦晓波, 等. 基于离散一致性的孤立直流微网自适应下垂控制[J]. 中国电机工程学报, 2015, 35(17): 4397-4407.
Lü Zhenyu, Wu Zaijun, Dou Xiaobo, et al. An adaptive droop control for the islanded DC microgrid based on discrete consensus algorithm[J]. Pro- ceedings of the CSEE, 2015, 35(17): 4397-4407.
[16] 张孝顺, 余涛. 互联电网AGC功率动态分配的虚拟发电部落协同一致性算法[J]. 中国电机工程学报, 2015, 35(15): 3750-3759.
Zhang Xiaoshun, Yu Tao. Virtual generation tribe based collaborative consensus algorithm for dynamic generation dispatch of AGC in interconnected power grids[J]. Proceedings of the CSEE, 2015, 35(15): 3750-3759.
[17] Ren Wei, Beard R W. Consensus seeking in multiagent systems under dynamically changing interaction topo- logies[J]. IEEE Transactions on Automatic Control, 2005, 50(5): 655-661.
[18] Zhang Ziang, Chow M Y. Convergence analysis of the incremental cost consensus algorithm under different communication network topologies in a smart grid[J]. IEEE Transactions on Power Systems, 2012, 27(4): 1761-1768.
[19] 杨珺, 侯俊浩, 刘亚威, 等. 分布式协同控制方法及在电力系统中的应用综述[J]. 电工技术学报, 2021, 36(19): 4035-4049.
Yang Jun, Hou Junhao, Liu Yawei, et al. Distributed cooperative control method and application in power system[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4035-4049.
[20] 刘忠, 杨陈, 蒋玮, 等. 基于一致性算法的直流微电网储能系统功率分配技术[J]. 电力系统自动化, 2020, 44(7): 61-69.
Liu Zhong, Yang Chen, Jiang Wei, et al. Consensus algorithm based power distribution technology for energy storage system in DC microgrid[J]. Auto- mation of Electric Power Systems, 2020, 44(7): 61-69.
[21] Kar S, Hug G. Distributed robust economic dispatch in power systems: a consensus+innovations approach[C]// 2012 IEEE Power and Energy Society General Meeting, San Diego, USA, 2012: 1-8.
[22] Hug G, Kar S, Wu Chenye. Consensus+innovations approach for distributed multiagent coordination in a microgrid[J]. IEEE Transactions on Smart Grid, 2015, 6(4): 1893-1903.
[23] Xin Huanhai, Liu Yun, Qu Zhihua, et al. Distributed control and generation estimation method for inte- grating high-density photovoltaic systems[J]. IEEE Transactions on Energy Conversion, 2014, 29(4): 988-996.
[24] 吕朋蓬, 赵晋泉, 苏大威, 等. 基于一致性理论的独立微电网分布式动态经济调度[J]. 电力系统自动化, 2019, 43(5): 22-44.
Lü Pengpeng, Zhao Jinquan, Su Dawei, et al. Consensus- based distributed dynamic economic dispatching for islanded microgrids[J]. Automation of Electric Power Systems, 2019, 43(5): 22-44.
[25] 熊宇峰, 司杨, 郑天文, 等. 基于主从博弈的工业园区综合能源系统氢储能优化配置[J]. 电工技术学报, 2021, 36(3): 507-516.
Xiong Yufeng, Si Yang, Zheng Tianwen, et al. Optimal configuration of hydrogen storage in indu- strial park integrated energy system based on stackelberg game[J]. Transactions of China Electro- technical Society, 2021, 36(3): 507-516.
[26] 肖静, 吴宁, 冯玉斌, 等. 计及需求侧响应的用户侧储能最优运行决策分析[J]. 电气技术, 2021, 22(3): 20-25.
Xiao Jing, Wu Ning, Feng Yubin, et al. Decision analysis for optimal operation of user-side energy storage considering demand-side response[J]. Elec- trical Engineering, 2021, 22(3): 20-25.
[27] 吴界辰, 艾欣, 胡俊杰, 等. 面向智能园区多产消者能量管理的对等模型(P2P)建模与优化运行[J]. 电网技术, 2020, 44(1): 52-60.
Wu Jiechen, Ai Xin, Hu Junjie, et al. Peer-to-peer modeling and optimal operation for prosumer energy management in intelligent community[J]. Power System Technology, 2020, 44(1): 52-60.
[28] 苏德矿. 微积分(下)[M]. 北京: 高等教育出版社, 2001.
Distributed Integrated Demand Response of Industrial Park Based on Improved Consensus Algorithm
Abstract In view of the problem that the implementation of centralized and centralized- distributed integrated demand response (IDR) methods depends on the park level energy management system, this paper proposes a distributed IDR method for the industrial park based on the improved consensus algorithm. Firstly, a distributed information interaction mechanism of industrial park is designed. Then, an IDR market mechanism within the park is proposed, which can make the optimal IDR scheme of individual users consistent with that of the whole park. Furthermore, based on the consensus algorithm and the centralized IDR model of industrial park, a distributed IDR model is proposed. Finally, in order to improve the practical applicability of the model, the consensus algorithm is improved by making the global deviation consistent and using the distributed merit-order method to improve the convergence. The final distributed IDR model of industrial park is established. Simulation results show that the proposed distributed IDR method can get an IDR scheme consistent with the centralized IDR without relying on the park level energy management system and reducing the information provided by users, and users can get higher benefits than participating in IDR independently.
keywords:Distributed integrated demand response, consensus algorithm, merit-order method, industrial park, market mechanism
DOI: 10.19595/j.cnki.1000-6753.tces.211896
中图分类号:TM73
国家自然科学基金资助项目(52077193)。
收稿日期 2021-11-19
改稿日期 2022-03-21
徐成司 男,1995年生,硕士,研究方向为综合需求响应。E-mail: 3140103128@zju.edu.cn
董树锋 男,1982年生,副教授,博士生导师,研究方向为综合能源系统与微电网优化运行。E-mail: dongshufeng@zju.edu.cn(通信作者)
(编辑 陈 诚)