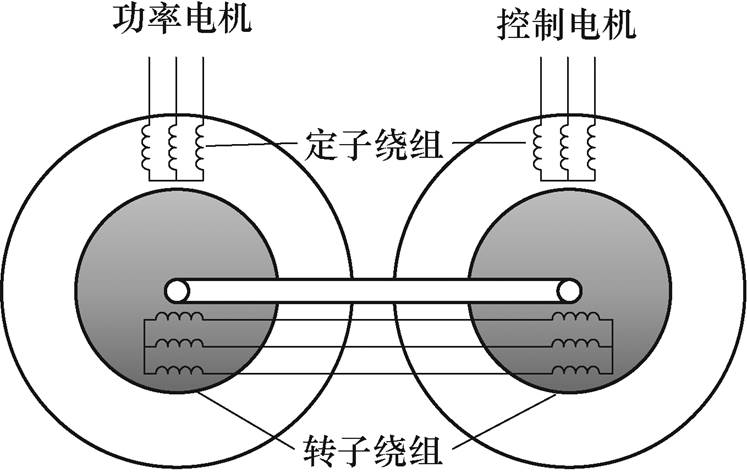
图1 级联式无刷双馈电机的结构
Fig.1 Structure of the CBDFIG
摘要 该文主要研究了级联式无刷双馈电机的矢量控制以及功率流。首先建立了其动态和稳态模型,对网侧变换器使用电网电压定向矢量控制,对机侧变换器使用定子磁链定向矢量控制,以实现无刷双馈电机的变速恒频运行以及有功与无功功率的解耦控制。同时背靠背变换器的矢量控制可实现功率的双向流动。然后进行了功率流分析,探究了其有功功率分配和不同转速下功率绕组和控制绕组的功率状态,揭示了考虑铜耗下控制侧功率流的变化趋势。通过仿真和实验,验证了矢量控制的有效性以及功率流分析的正确性。
关键词:级联式无刷双馈电机 矢量控制 网侧变换器 机侧变换器 功率流
为了缓解越来越严重的能源危机以及环境污染问题,必须发展可再生能源。风力发电在可再生能源发电中技术最成熟,大功率变速风力发电系统发展迅速[1-4]。无刷双馈电机(Brushless Doubly-Fed Machine, BDFM)保留了双馈电机所需功率变换器容量小的优点,同时兼具可靠性高和维护成本低[5-8]的优势,因此BDFM在变速风力发电领域潜力巨大。
本文以级联式无刷双馈感应电机(Cascaded Brushless Doubly-Fed Induction Generator, CBDFIG)为研究对象,其由两台绕线转子感应电机同轴连接而成[9],结构如图1所示,两台电机转子机械耦合,转子绕组正相序相连,这两台电机分别称为功率电机和控制电机,其定子绕组分别为功率绕组(Power Winding, PW)和控制绕组(Control Winding, CW)。该电机优点在于PW和CW可以在各自的电机空间中产生独立的旋转磁场,减少了气隙中磁场的谐波含量。

图1 级联式无刷双馈电机的结构
Fig.1 Structure of the CBDFIG
在无刷双馈风力发电系统中,为控制方便,多采用三相不控整流(或直流电源)获得直流电压,将直流电压逆变成可变频率的交流电压,再实现对电机的控制[10-11],这与无刷双馈风力发电系统的实际运行模式不符,无法实现控制侧功率的双向流动,尤其当电机运行于超同步速时,无法将回馈的能量输送到电网。采用背靠背变换器,当电机运行在超同步速时,网侧变换器(Grid Side Converter, GSC)在维持直流母线电压稳定的同时,可将回馈的能量输送到交流侧电网,实现了能量的双向流动,提高了发电效率[12],本文将搭建采用背靠背变换器的无刷双馈风力发电系统实验平台。
BDFM功率流的研究中常忽略铜耗[13-16],这将导致功率分析出现误差,最大风能跟踪控制中无法计算出精确的参考功率[16],从而影响转速跟踪的效果。本文将考虑定、转子铜耗,对CBDFIG进行功率流分析,以探究铜耗对控制侧功率流的影响。
首先基于矢量控制技术,通过背靠背变换器实现了对CBDFIG的功率控制。针对级联式无刷双馈电机的功率流,分析了其有功功率分配和不同转速下功率和控制绕组的功率状态,揭示了考虑铜耗下控制侧功率流的变化趋势,并通过仿真和实验验证了功率流分析的正确性。
图2所示为无刷双馈风力发电系统拓扑[17],包含两套定子绕组,功率绕组直接连接电网,控制绕组则连接背靠背变换器,此时变换器只需部分额定功率(约30%),大大降低了变换器的容量和成本。背靠背变换器包括机侧变换器(Machine Side Con- verter, MSC)和网侧变换器,PW和CW通过转子绕组实现了间接耦合。
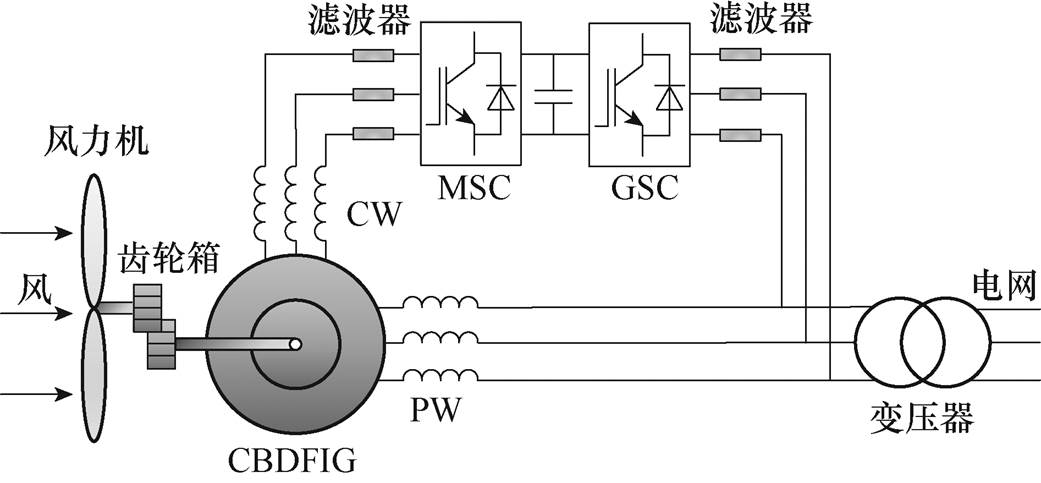
图2 无刷双馈风力发电系统拓扑
Fig.2 Topology of the brushless doubly fed wind power generation system
为简化分析,作如下假设:①气隙中磁通正弦分布;②运行中定、转子电阻恒定,损耗只考虑铜耗;③励磁电流线性变化,即忽略饱和、磁滞效应;④三相绕组电压、电流对称,只考虑电压和电流的基波分量。
根据异步电机的数学模型和两台电机的转子绕组联结方式,可以得到级联式无刷双馈电机的数学模型,将同步速坐标系的d轴定向到PW的定子磁链,则CBDFIG在同步坐标系下的数学模型[11, 15, 18]如下所述。
电压方程为
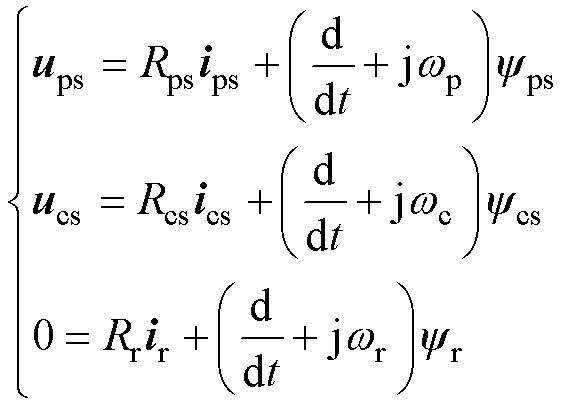 (1)
(1)
式中,u为电压矢量;i为电流矢量;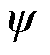 为磁链矢量;R为单相电阻;下标ps、r和cs为功率绕组、转子和控制绕组;wp为PW电角频率;wr为转差角频率;wc为CW电角频率,其定义为
为磁链矢量;R为单相电阻;下标ps、r和cs为功率绕组、转子和控制绕组;wp为PW电角频率;wr为转差角频率;wc为CW电角频率,其定义为
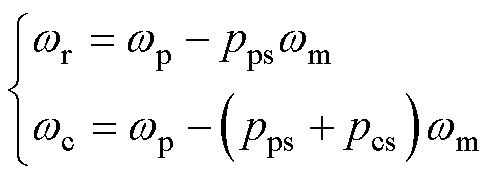 (2)
(2)
式中,pps和pcs分别为功率绕组、控制绕组的极对数;wm为转子的机械角速度。当CW电角频率wc为零时,无刷双馈电机的转速为同步速wN,其表达式为
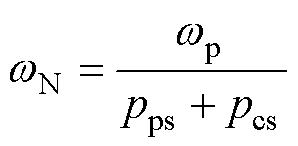 (3)
(3)
磁链方程为
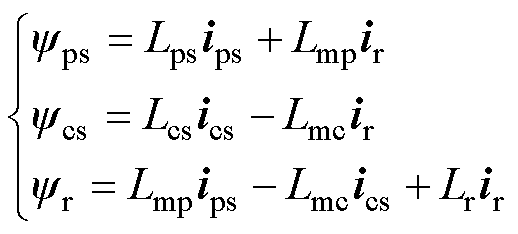 (4)
(4)
式中,L为电感,下标m代表励磁电感,其他为自感。
电磁转矩方程为
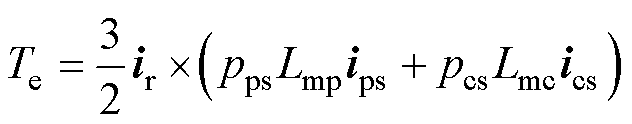 (5)
(5)
运动方程为
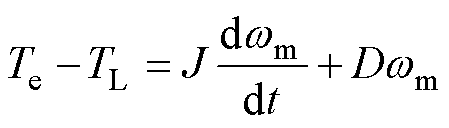 (6)
(6)
式中,TL为负载转矩;J为机组的转动惯量;D为转矩阻尼系数。
CBDFIG的稳态模型由电压和电流相量表示,用正弦相量替代式(1)和式(4)动态模型中的空间矢量,可以推导出电机的稳态模型[18-19],其表达式为
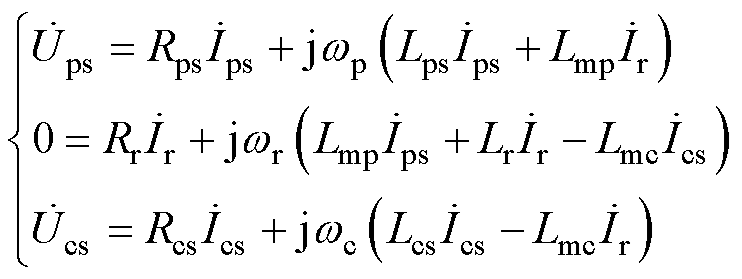 (7)
(7)
为了推导CBDFIG的单相等效电路,需要将式(7)中的角频率均转换为wp。定义功率绕组转差率sp、控制绕组转差率sc以及等效转差率s,其表达式分别为
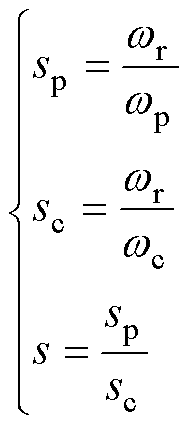 (8)
(8)
则根据式(7)和式(8)可得
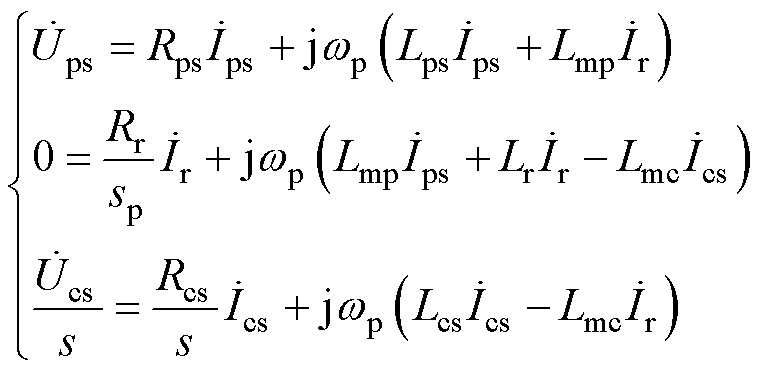 (9)
(9)
式(9)即为CBDFIG归算到功率侧的稳态模型,图3为其单相等效电路,图中,Ls 为漏感。
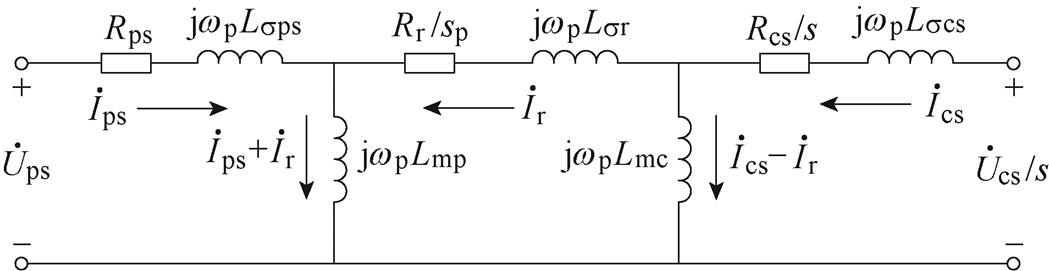
图3 CBDFIG单相等效电路
Fig.3 The single-phase equivalent circuit of CBDFIG
本节主要介绍通过控制背靠背变换器来实现无刷双馈风力发电系统的矢量控制[20-21]:通过网侧变换器,采用以电压矢量定向的矢量控制技术实现对直流母线电压的调节;基于CBDFIG的数学模型,通过机侧变换器实现对CBDFIG的定子磁链定向矢量控制。
通过网侧变换器调节直流母线电压,不仅可以保证背靠背变换器正常的直流电压支撑,还能保证变换器有功功率的安全传输[22-23]。电网电压定向控制策略将变量从abc坐标系变换到dq同步旋转坐标系,电压、电流稳态时在dq坐标系下为直流量,便于网侧变换器的控制。
基于dq坐标系下网侧变换器的数学模型[23],采用基于PI调节器的网侧变换器控制器,其表达式为
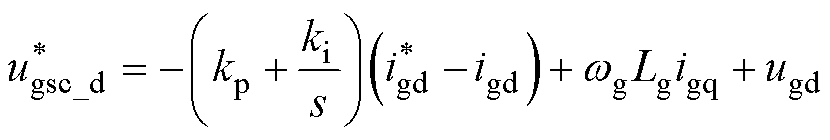 (10)
(10)
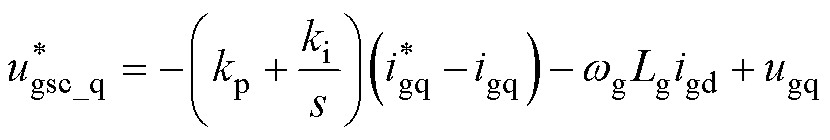 (11)
(11)
式中,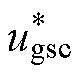 为网侧电压指令;ug为网侧电压实际值;
为网侧电压指令;ug为网侧电压实际值;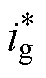 为网侧电流指令;ig为网侧电流实际值;wg为电网的电角频率;Lg为网侧变换器电感;下标d、q则分别为d、q轴;kp和ki分别为比例、积分系数。
为网侧电流指令;ig为网侧电流实际值;wg为电网的电角频率;Lg为网侧变换器电感;下标d、q则分别为d、q轴;kp和ki分别为比例、积分系数。
由式(10)和式(11)可得如图4所示的网侧变换器控制系统,图中,公式下标ab 表示ab 静止坐标系,qg为电网电角度。该系统采用双闭环控制:一个电压外环,两个电流内环,均基于PI调节器进行控制。电压外环用于调节直流母线电压Udc,电压外环的输出和无功功率的给定作为电流内环的参考值输入;然后通过电流内环控制d、q轴电流igd、igq跟随参考值,并将电流内环的输出作为整个系统控制电压的参考值;之后产生PWM信号,用于控制网侧变换器。
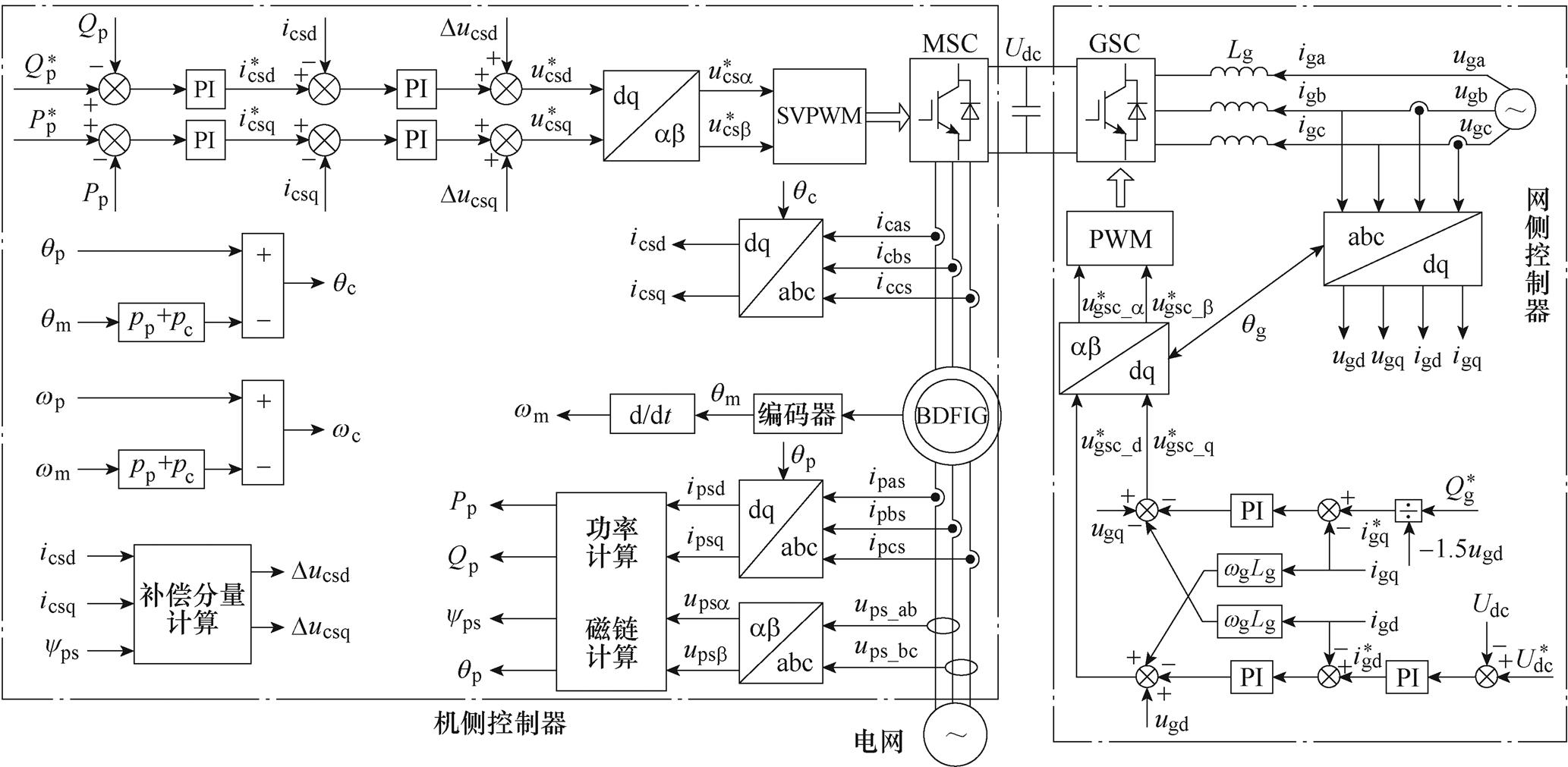
图4 CBDFIG的矢量控制系统结构
Fig.4 The structure diagram of CBDFIG vector control system
定子磁链定向矢量控制中,同步坐标系的d轴定向于PW的磁链矢量yps,两者相对静止,都以同步速旋转。当忽略PW电阻Rps,电压矢量ups超前磁链矢量yps 90°,即位于q轴方向,则磁链、电压矢量的dq轴分量分别为
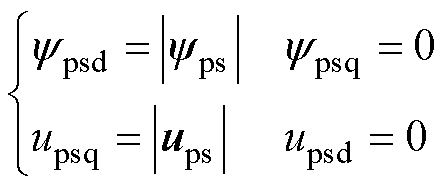 (12)
(12)
根据瞬时功率理论和式(12),CBDFIG功率绕组的有功功率Pp和无功功率Qp的表达式为
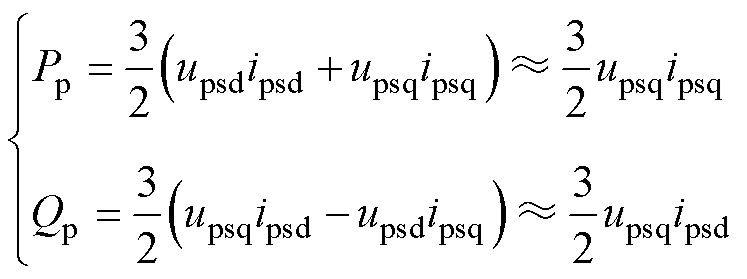 (13)
(13)
因此该矢量控制中PW的有功和无功功率可以通过控制PW的q轴、d轴电流来调节,而由于PW直接连接电网,PW电流不能直接调节,可以通过控制CW电流以间接调节PW电流。
基于式(1)和式(4)所述的CBDFIG数学模型,可得CW控制电压参考值为
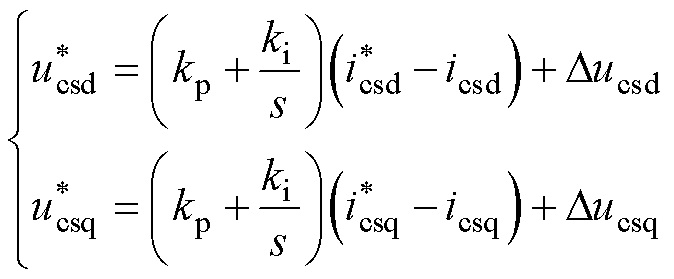 (14)
(14)
其中
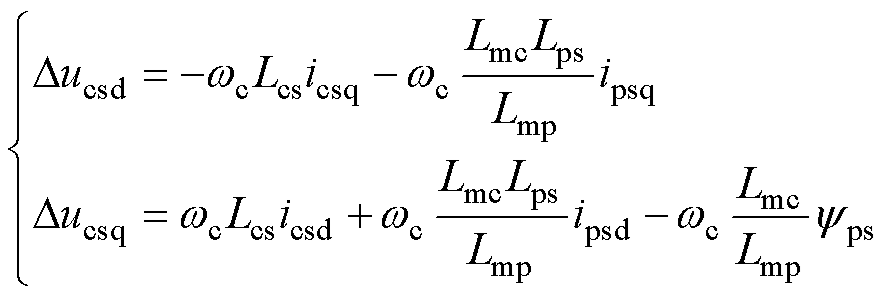 (15)
(15)
式中,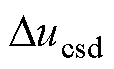 和
和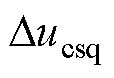 分别为消除CW中d、q轴交叉耦合的补偿分量。
分别为消除CW中d、q轴交叉耦合的补偿分量。
定子磁链定向矢量控制策略的原理框图如图4所示,qp为PW电角度,qc为CW电角度,qm为转子的机械角度。整个系统采用双闭环控制结构,外环为功率环,内环为电流环。功率指令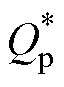 、
、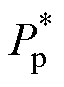 与功率反馈值Qp、Pp比较后送入PI调节器,输出CW电流指令
与功率反馈值Qp、Pp比较后送入PI调节器,输出CW电流指令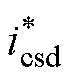 和
和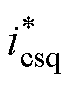 ,其与电流反馈值icsd和icsq比较后送入PI调节器,加上电压补偿分量后,可获得电压指令值
,其与电流反馈值icsd和icsq比较后送入PI调节器,加上电压补偿分量后,可获得电压指令值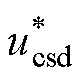 和
和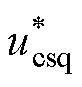 ,最后根据电压指令产生PWM信号,以实现CBDFIG的变速恒频运行以及有功与无功功率的解耦控制。
,最后根据电压指令产生PWM信号,以实现CBDFIG的变速恒频运行以及有功与无功功率的解耦控制。
为优化对CBDFIG的控制,本文对CBDFIG进行了功率流分析,研究了其有功功率分配,在不同转速下功率和控制绕组的功率状态以及考虑铜耗后控制侧功率流的变化趋势。
根据式(7)中的稳态模型,可更清楚地了解无刷双馈电机的功率分配关系[20]。将式(7)中的第一行乘以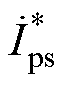 ,取实数部分得到
,取实数部分得到
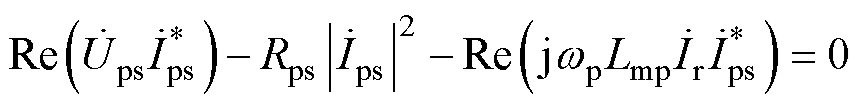 (16)
(16)
式中,各项分别为功率绕组有功功率、铜耗、气隙有功功率。
将式(7)中的第二行乘以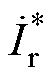 ,取实数部分得到
,取实数部分得到
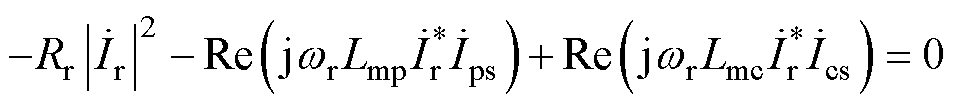 (17)
(17)
使用式(8)中的转差关系,并求共轭,可得
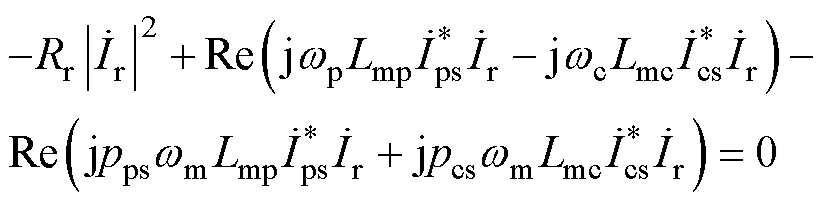 (18)
(18)
式中,各项分别为转子铜耗、功率绕组与控制绕组的气隙功率、转子机械功率。
将式(7)中的第三行乘以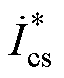 ,取实部得到
,取实部得到
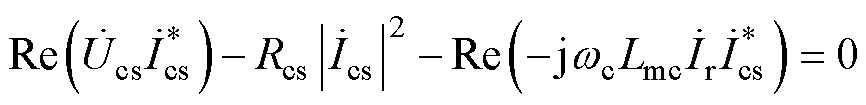 (19)
(19)
式中,各项分别为控制绕组有功功率、铜耗、气隙有功功率。
输入到转子的功率Prin是功率绕组Pgp和控制绕组Pgc的气隙功率之和,即
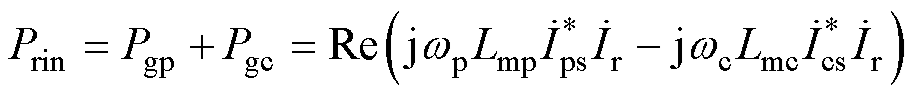 (20)
(20)
总机械功率Pmec与功率绕组和控制绕组气隙功率的关系为
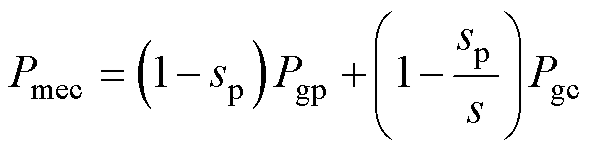 (21)
(21)
在无刷双馈电机中,spPgp的部分功率损失,成为转子铜耗,剩余部分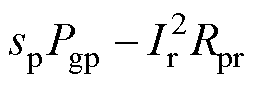 通过转子传输,以增加控制绕组处理的功率,其中,Rpr为功率电机转子绕组电阻。综合式(16)~式(21),可得无刷双馈电机的有功功率分配,如图5所示。
通过转子传输,以增加控制绕组处理的功率,其中,Rpr为功率电机转子绕组电阻。综合式(16)~式(21),可得无刷双馈电机的有功功率分配,如图5所示。
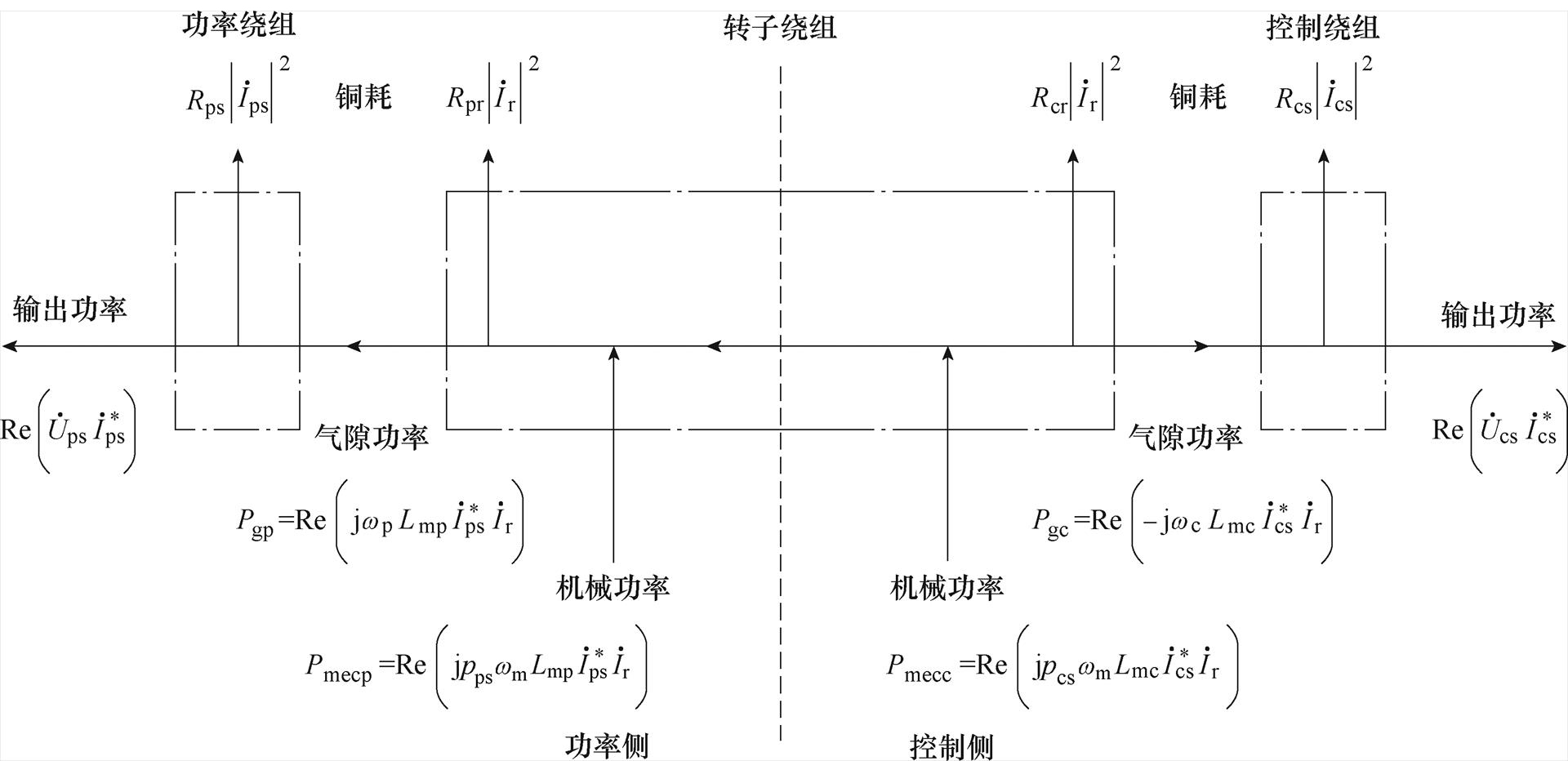
图5 有功功率分配
Fig.5 The distribution diagram of active power
功率绕组的功率方程为
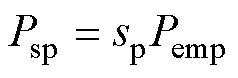 (22)
(22)
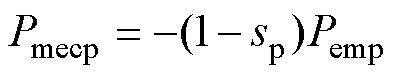 (23)
(23)
式中,Psp为功率绕组转差功率;Pemp为功率绕组的电磁功率;Pmecp为功率绕组机械功率。
控制绕组的功率方程为
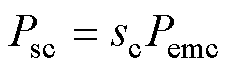 (24)
(24)
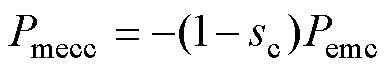 (25)
(25)
式中,Psc为控制绕组转差功率;Pemc为控制绕组电磁功率;Pmecc为控制绕组机械功率。
转子回路的功率平衡方程[13]为
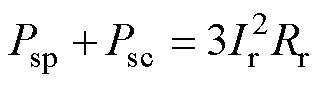 (26)
(26)
式中,PCuR为转子铜耗,PCuR=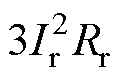 ;Ir为转子每相电流的有效值。
;Ir为转子每相电流的有效值。
由式(24)和式(26),控制绕组电磁功率Pemc可用功率绕组电磁功率Pemp表示,即
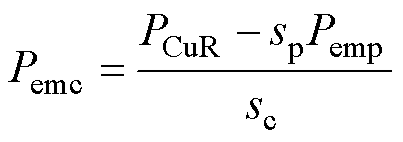 (27)
(27)
本文主要分析发电状态下级联式无刷双馈电机的功率流,该电机在发电状态下亚同步速、同步速以及超同步速时功率和控制绕组的功率状态如下所述。
4.2.1 亚同步速发电状态
当CBDFIG运行在亚同步速状态时,结合式(8),其转差为
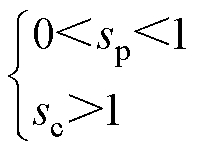 (28)
(28)
由式(22)、式(23)和式(28)可知,功率绕组的功率状态为
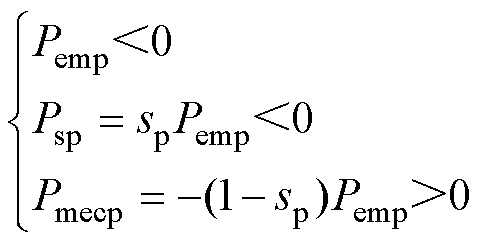 (29)
(29)
同理由式(25)~式(28),可得控制绕组的状态关系为
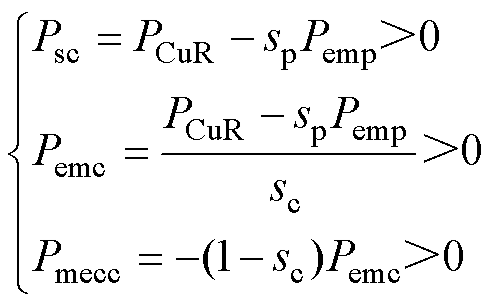 (30)
(30)
由式(29)和式(30)可知,控制绕组将从电网吸收功率Pemc,转轴吸收机械功率Pmecc以转差功率形式传递给功率绕组转子回路,功率绕组则吸收转差功率和机械功率Pmecp,发出电功率Pemp。
4.2.2 同步速和超同步速发电状态
当CBDFIG运行在同步速状态时,结合式(8),可知其转差为
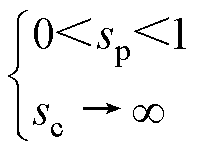 (31)
(31)
而当CBDFIG运行在超同步速状态且转速不超过功率电机同步速(60fp/pps)时,其转差为
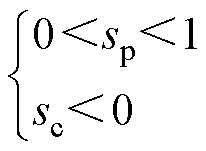 (32)
(32)
由式(28)~式(32),可得在不同转速下CBDFIG功率绕组和控制绕组的功率状态,见表1。由表1可知,同步速时控制绕组将吸收的机械功率Pmecc以转差功率形式传递给功率绕组,而超同步速时控制绕组将吸收的机械功率Pmecc一部分以电磁功率Pemc形式输送到电网,另一部分以转差功率形式传递给功率绕组。
表1 不同转速下功率和控制绕组的功率状态
Tab.1 The power state between PW and CW under different speeds

亚同步速同步速超同步速 功率绕组sp—(0, 1)— Pemp—<0— Psp—<0— Pmecp—>0— 控制绕组sc>1→∞<0 Psc>0>0>0 Pemc>0=0<0 Pmecc>0>0>0
结合表1可得不同转速下功率和控制绕组的功率状态,如图6所示,图中,①状态代表亚同步速,②状态代表同步速,③状态代表超同步速。
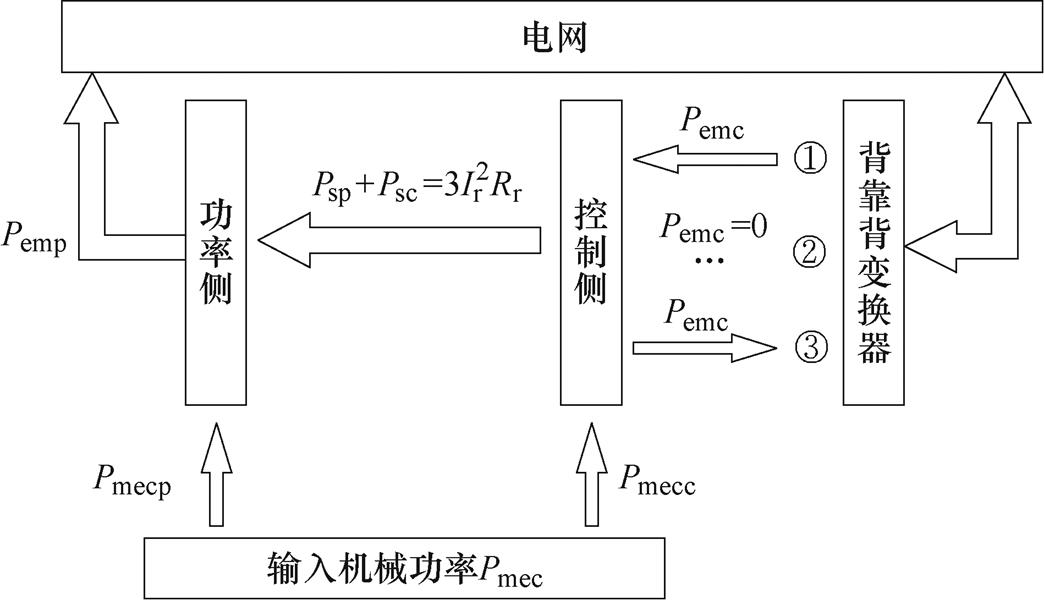
图6 不同转速下功率和控制绕组的功率状态
Fig.6 The power state of PW and CW under different speeds
4.2节中,式(27)仅描述了控制绕组电磁功率和功率绕组电磁功率间的关系,为了获得控制侧输出有功Pc和功率侧输出有功Pp的关系,还需利用电磁功率和输出功率的关系,即
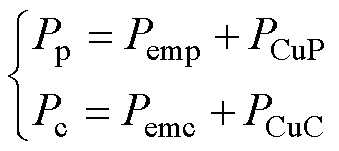 (33)
(33)
其中
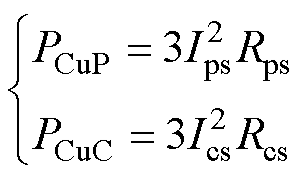 (34)
(34)
式中,PCuP为功率绕组铜耗;PCuC为控制绕组铜耗;Ips、Ics分别为功率、控制绕组单相电流的有效值。则控制侧有功Pc可用功率侧有功Pp表示为
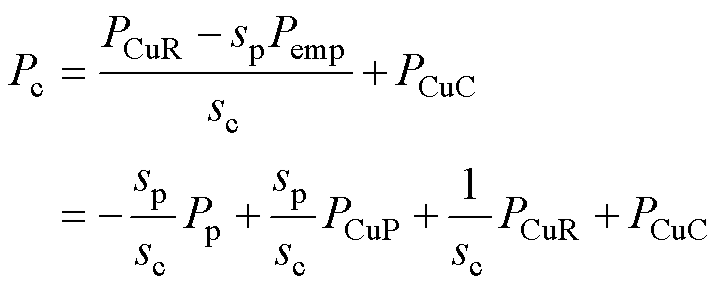 (35)
(35)
由表1和式(35)可知,与不考虑铜耗时相比,考虑铜耗后,控制侧的功率流将发生变化。亚同步速时,式(35)中第一项为正,后三项也为正,即亚同步速时考虑铜耗后控制侧吸收有功功率将增加;同步速时,式(35)中前三项为零,最后一项为正,即同步速时考虑铜耗后控制侧将吸收有功功率;超同步速时,式(35)中第一项为负,后三项为正,总和为负,即超同步速时考虑铜耗后控制侧发出的有功功率将减少。
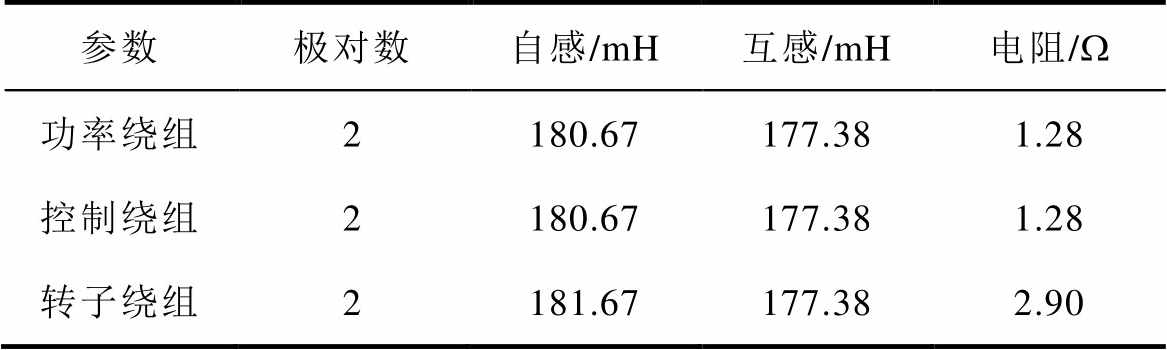
基于Matlab/Simulink,搭建无刷双馈风力发电系统仿真模型。选用CBDFIG参数见表2。
表2 CBDFIG参数
Tab.2 Parameters of CBDFIG
参数极对数自感/mH互感/mH电阻/W 功率绕组2180.67177.381.28 控制绕组2180.67177.381.28 转子绕组2181.67177.382.90
转速变化时矢量控制的仿真结果如图7所示,其展示了在有功功率Pp为-600W,无功功率Qp为0var,转速从600r/min逐渐增加到900r/min的变化过程中,CBDFIG的PW电流、CW电流、实际功率跟随参考功率的仿真波形。从图中可以看出,当转速变化时,控制绕组电流的频率发生改变,这是因为实现变速恒频发电必须根据转速的变化实时改变控制绕组电流的频率,以维持功率绕组的电流频率恒定,这说明定子磁链定向矢量控制系统能够实现CBDFIG的变速恒频发电。
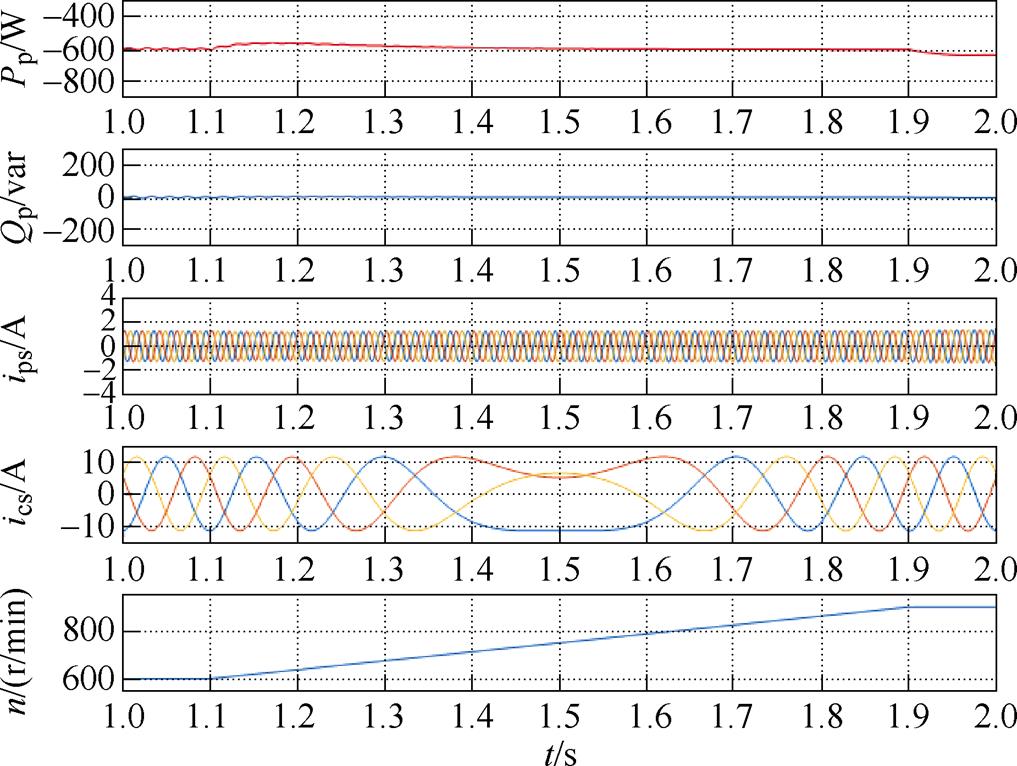
图7 转速变化时矢量控制的仿真结果
Fig.7 Simulation results of vector control when speed changes
基于矢量控制进行了如图8所示的CBDFIG功率流仿真。图8在Pp为-600W,转速变化(600r/min→750r/min→900r/min)的情况下记录了控制侧有功功率,以研究在不同转速下控制侧功率流的变化规律。

图8 转速变化时控制侧功率流的变化规律
Fig.8 The change rule of CW power flow during the speed variation
当忽略定、转子铜耗时,由式(29)和图8可知,当电机处于亚同步状态(600r/min)时,控制绕组吸收有功功率(100W);在同步状态(750r/min)时控制绕组与电网无能量传输,控制绕组有功为0W;在超同步状态(900r/min)时控制绕组发出有功功率(-100W)。考虑定、转子铜耗后,控制侧的功率流发生变化。当电机为亚同步速,控制绕组吸收的有功功率为220W,与不考虑铜耗时相比,控制侧吸收的有功功率增加了120W;同步速时,控制绕组吸收的有功功率为84W,增加了84W;超同步速时,控制绕组发出的有功功率为-79W,减少了21W。因此为正确分析CBDFIG的功率流,必须考虑电机的定、转子铜耗。
为验证矢量控制的有效性以及CBDFIG功率流分析的正确性,进行了实验研究。图9展示了CBDFIG系统的实验配置:使用异步电机作为原动机,以模拟风力机[24],使用dSAPCE 1103控制器生成PWM信号,驱动背靠背变换器调节控制侧电压,实现电机的变速恒频运行以及有功与无功功率的解耦控制。

图9 CBDFIG系统的实验配置
Fig.9 Experimental configuration of the CBDFIG system
单变流器控制中当电机运行于超同步速时,机侧变换器将能量回馈至直流母线端,由于网侧为不控整流电路,无法将能量输送到电网,这将造成直流母线电压持续上升,直至损坏器件。为防止这种情况发生,一般在直流母线上设置制动斩波器,通过电阻来消耗回馈的能量。而采用背靠背变换器,超同步速时不仅可维持母线电压稳定,还能将回馈的能量输送到交流侧电网,实现了对能量的充分利用。
两种方法的直流母线电压比较结果如图10所示,CBDFIG均运行于超同步速(900r/min),电机的输出功率为1kW。采用单变流器时,机侧变换器回馈的能量导致直流母线电压持续上升,启动制动斩波器后母线电压逐渐趋于稳定;采用背靠背变换器时,直流母线电压稳定在400V,回馈到直流母线的功率被输送至电网。在超同步速(900r/min)功率侧输出有功功率为1kW时,由于背靠背变流器回收了控制侧的有功功率,与单变流器控制相比,采用背靠背变流器后总输出功率提升了约15.9%。
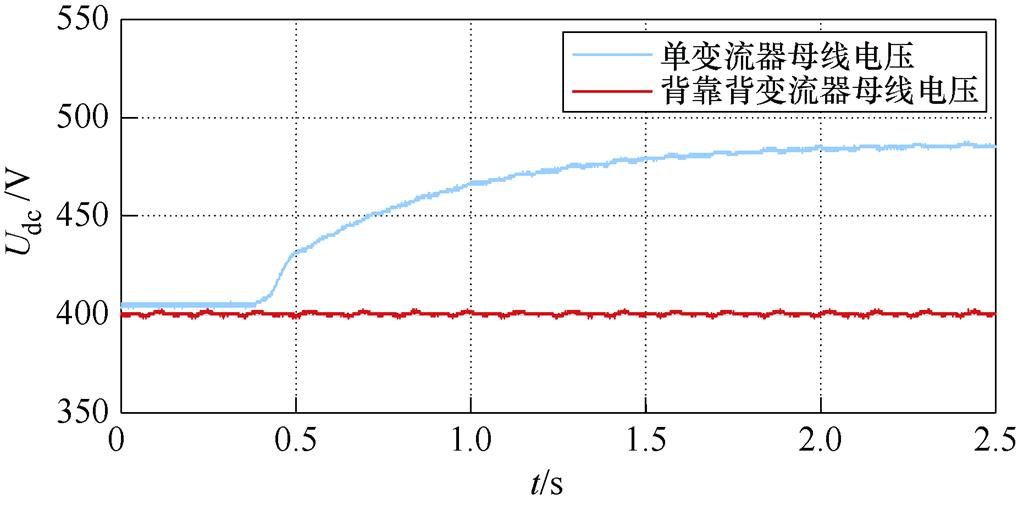
图10 超同步速时两种方法直流母线电压的比较
Fig.10 Comparison of the DC link voltage of two methods at super-synchronous speed
图11为CBDFIG在亚同步速(600r/min),有功功率阶跃时矢量控制的实验结果,功率侧有功功率Pp从-600W阶跃变化至-900W,再阶跃变化至-750W。图12则为CBDFIG在亚同步速(600r/min),无功功率阶跃时矢量控制的实验波形,功率侧无功功率Qp从-600var阶跃变化至0var,再阶跃变化至-300var。从实验中可以看出,定子磁链定向矢量控制可以实现有功功率和无功功率的解耦控制。
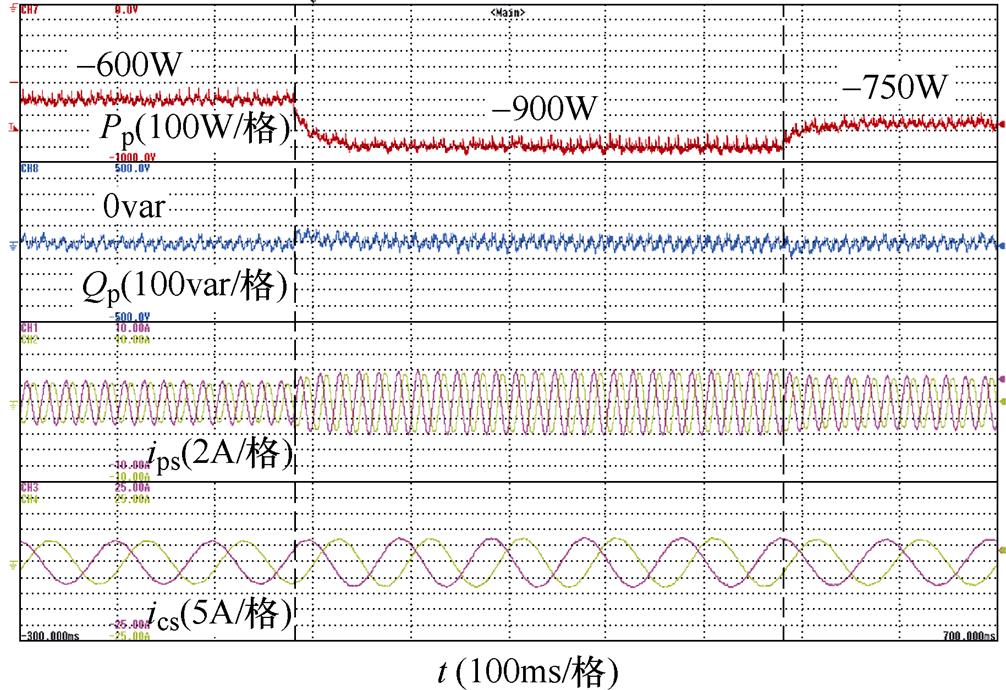
图11 亚同步速有功功率阶跃下矢量控制的实验结果
Fig.11 Experimental results of vector control during active power step at the sub-synchronous speed
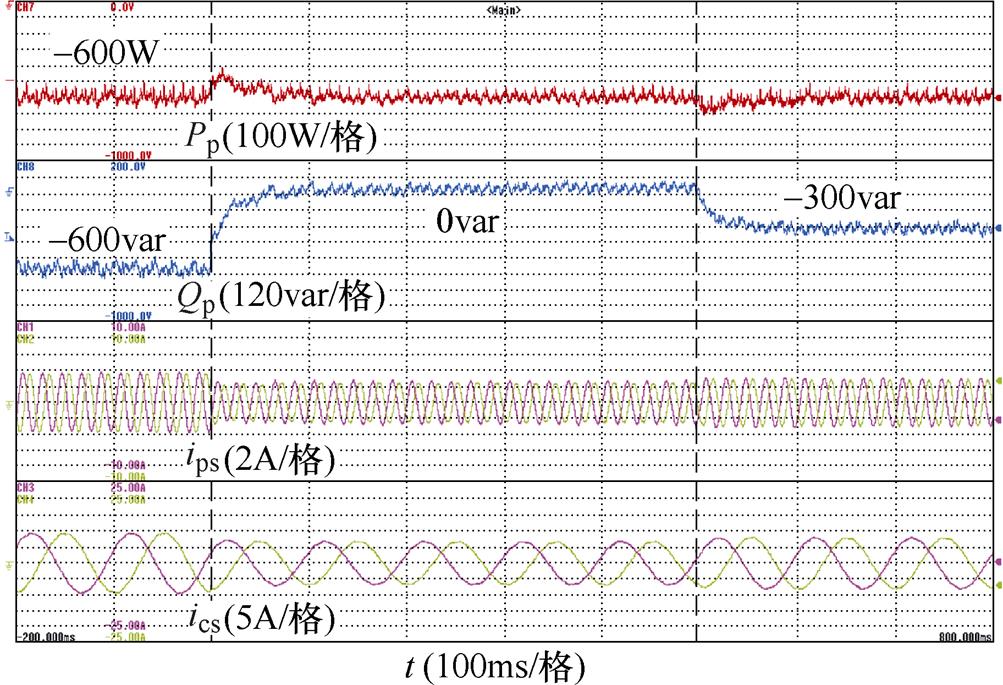
图12 亚同步速无功功率阶跃下矢量控制的实验结果
Fig.12 Experimental results of vector control during reactive power step at the sub-synchronous speed
为分析考虑铜耗后控制侧功率流的变换规律(即控制侧有功功率Pc随转速和功率侧有功功率Pp变化的规律),基于矢量控制在功率阶跃以及转速变化的情况下记录了控制侧有功功率。图13~图15分别展示了在亚同步速(600r/min)、同步速(750r/min)和超同步速(900r/min)Pp阶跃(-500W→-800W→ -400W)时Pc的变化规律。而图16展示了Pp为-500W,转速线性增加(600r/min→900r/min)时Pc的变化规律。为了更清楚地了解Pp和Pc的数量关系,在Pp为-500W不同转速下铜耗和Pc的值见表3,表3中不考虑和考虑铜耗后Pc预测值是根据当前Pp值和铜耗使用式(35)计算出来的,而Pc实际值则为实测值。
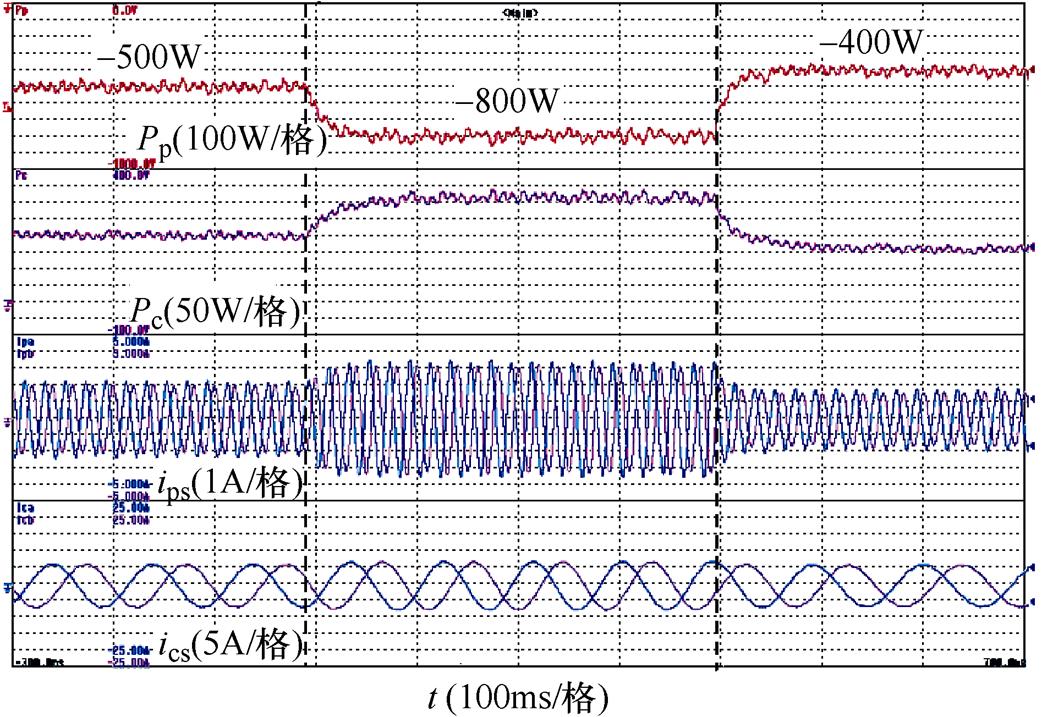
图13 亚同步速(600r/min)Pp阶跃时Pc的变化规律
Fig.13 The change rule of Pc during Pp step at the sub-synchronous speed (600r/min)
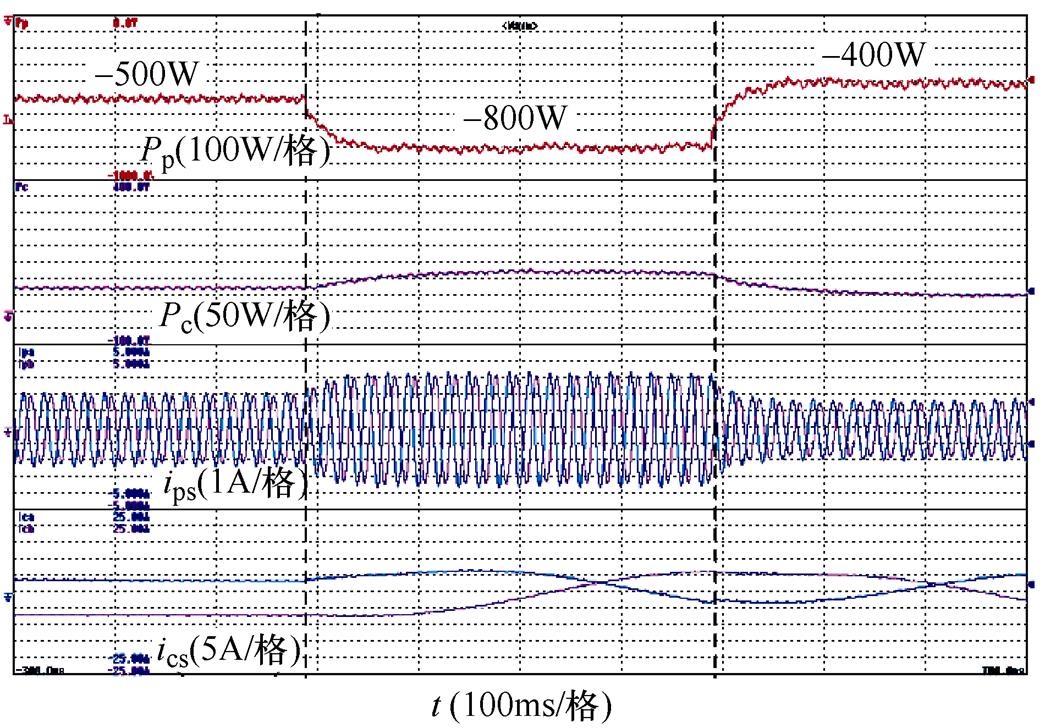
图14 同步速(750r/min)Pp阶跃时Pc的变化趋势
Fig.14 The change rule of Pc during Pp step at the synchronous speed (750r/min)

图15 超同步速(900r/min)Pp阶跃时Pc的变化规律
Fig.15 The change rule of Pc during Pp step at the super-synchronous speed (900r/min)
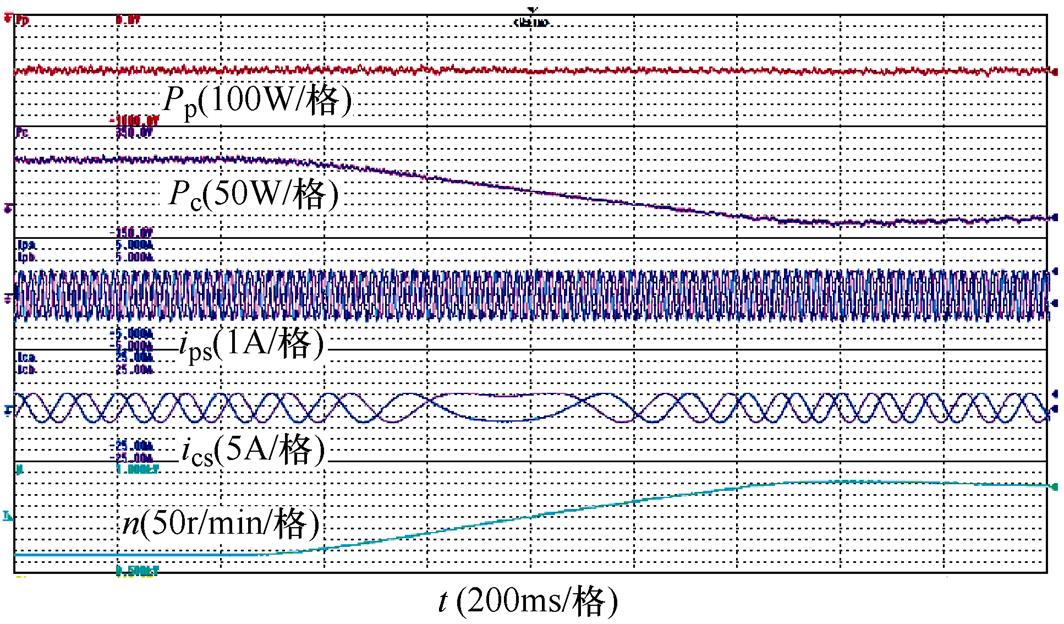
图16 Pp=-500W转速变化时Pc的变化规律
Fig.16 The change rule of Pc during speedvariation when Pp equals to -500W
表3 Pp为-500W不同转速下铜耗和Pc的值
Tab.3 Copper loss and Pc values when Pp equals to -500W under different speeds
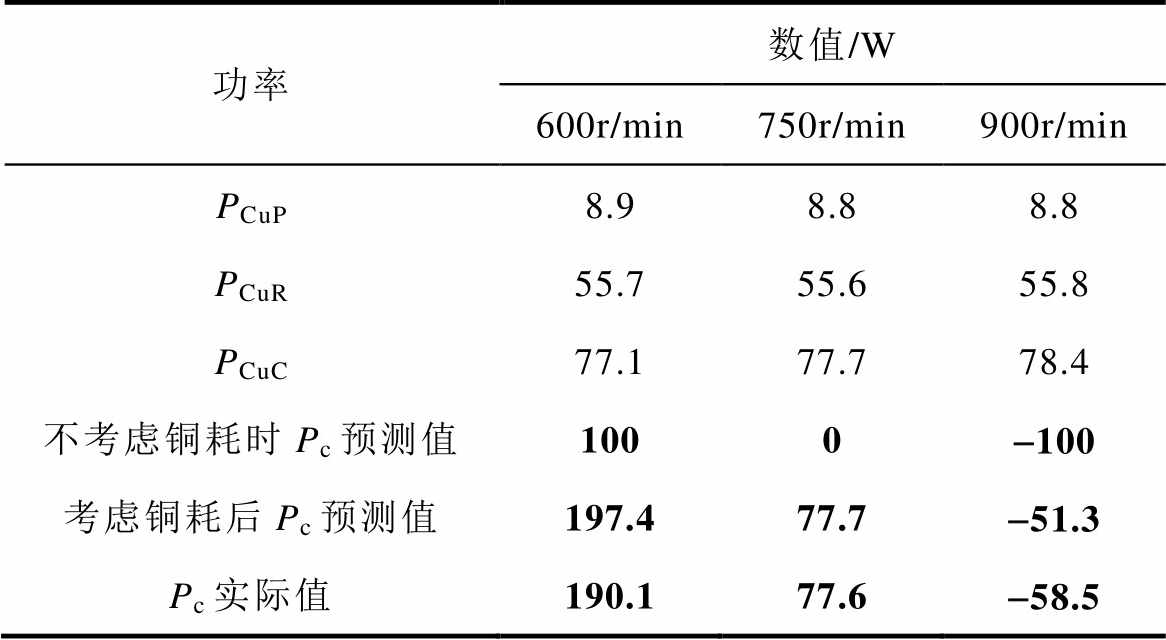
功率数值/W 600r/min750r/min900r/min PCuP8.98.88.8 PCuR55.755.655.8 PCuC77.177.778.4 不考虑铜耗时Pc预测值1000-100 考虑铜耗后Pc预测值197.477.7-51.3 Pc实际值190.177.6-58.5
考虑铜耗后,根据图13可知,当电机为亚同步速时,CW吸收有功功率,且Pc随着Pp的增大而增加;由图14可知,同步速状态时,CW吸收有功功率,且当PW发出有功越大,CW吸收的有功功率也越多;由图15可知,当电机处于超同步速时,CW发出有功功率,且随着Pp的增大而增加;由图16可知,当转速从亚同步速增加到超同步速时,CW由吸收有功功率逐渐变为发出有功。另外根据表3可知,考虑铜耗后Pc预测值与实际值接近,这验证了式(35)描述的控制侧有功与功率侧有功关系的正确性。与不考虑铜耗时相比,考虑铜耗后当电机处于亚同步状态时,控制绕组吸收的有功功率增多,在同步状态时控制绕组吸收有功功率,在超同步状态时控制绕组发出的有功减少。
综上所述,控制侧的功率流不仅与功率侧有功功率、转速相关,还受到定、转子铜耗的影响。考虑铜耗后便于正确分析电机功率流,有利于提高电机控制的准确性[25]。
本文针对级联式无刷双馈电机,研究了其动态和稳态模型,采用矢量控制技术控制背靠背变换器,实现CBDFIG的变速恒频运行以及有功与无功功率的解耦控制。然后进行了功率流分析,研究了不同转速下功率和控制绕组的功率状态,揭示了考虑铜耗下控制侧功率流的变化趋势。为验证矢量控制的有效性以及功率流分析的正确性,对CBDFIG系统实施了仿真和实验。研究表明,采用背靠背变换器的矢量控制实现了功率的双向流动,超同步速时可增加输出功率;考虑定、转子铜耗后,控制侧的功率流发生了变化,与不考虑铜耗时相比,当电机为亚同步速,控制绕组吸收的有功功率增加;同步速时,控制绕组吸收有功功率;超同步速时,控制绕组发出的有功功率减少。
参考文献
[1] Cheng Ming, Zhu Ying. The state of the art of wind energy conversion systems and technologies: a review[J]. Energy Conversion and Management, 2014, 88: 332- 347.
[2] Cheng Ming, Han Peng, Buja G, et al. Emerging multiport electrical machines and systems: past deve- lopments, current challenges, and future prospects[J]. IEEE Transactions on Industrial Electronics, 2018, 65(7): 5422-5435.
[3] 王涛, 诸自强, 年珩. 非理想电网下双馈风力发电系统运行技术综述[J]. 电工技术学报, 2020, 35(3): 455-471.
Wang Tao, Zhu Ziqiang, Nian Heng. Review of operation technology of doubly-fed induction generator- based wind power system under nonideal grid conditions[J]. Transactions of China Electrotechnical Society, 2020, 35(3): 455-471.
[4] 边春元, 邢海洋, 李晓霞, 等. 基于速度变化率的无位置传感器无刷直流电机风力发电系统换相误差补偿策略[J]. 电工技术学报, 2021, 36(11): 2374- 2382.
Bian Chunyuan, Xing Haiyang, Li Xiaoxia, et al. Compensation strategy for commutation error of sensorless brushless DC motor wind power generation system based on speed change rate[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2374- 2382.
[5] 兰志勇, 沈凡享, 李理, 等. 级联式无刷双馈风力发电机功率绕组电流检测系统容错控制研究[J]. 电工技术学报, 2020, 35(13): 2901-2912.
Lan Zhiyong, Shen Fanxiang, Li Li, et al. Research on fault-tolerant control of cascade brushless doubly-fed wind generator power winding current detection system[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2901-2912.
[6] Han Peng, Cheng Ming, Zhu Xinkai, et al. Analytical analysis and performance characterization of brush- less doubly fed induction machines based on general air-gap field modulation theory[J]. Chinese Journal of Electrical Engineering, 2021, 7(3): 4-19.
[7] Zhang Fengge, Yu Siyang, Wang Hao, et al. Over- view of research and development status of brushless doubly-fed machine system[J]. Chinese Journal of Electrical Engineering, 2016, 2(2): 1-13.
[8] Xu Litong, Cheng Ming, Wei Xinchi, et al. Dual synchronous rotating frame current control of brushless doubly fed induction generator under unbalanced network[J]. IEEE Transactions on Power Electronics, 2021, 36(6): 6712-6724.
[9] Protsenko K, Xu Dewei. Modeling and control of brushless doubly-fed induction generators in wind energy applications[J]. IEEE Transactions on Power Electronics, 2008, 23(3): 1191-1197.
[10] Shao Shiyi, Abdi E, Barati F, et al. Stator-flux- oriented vector control for brushless doubly fed induction generator[J]. IEEE Transactions on Indu- strial Electronics, 2009, 56(10): 4220-4228.
[11] Barati F, Shao Shiyi, Abdi E, et al. Generalized vector model for the brushless doubly-fed machine with a nested-loop rotor[J]. IEEE Transactions on Industrial Electronics, 2011, 58(6): 2313-2321.
[12] Hu Jiabing, Xu Hailiang, He Yikang. Coordinated control of DFIG's RSC and GSC under generalized unbalanced and distorted grid voltage conditions[J]. IEEE Transactions on Industrial Electronics, 2013, 60(7): 2808-2819.
[13] 邓先明. 无刷双馈电机的电磁分析与设计应用[M]. 北京: 机械工业出版社, 2009.
[14] Zhang Fengge, Zhu Liancheng, Jin Shi, et al. Controller strategy for open-winding brushless doubly fed wind power generator with common mode voltage elimination[J]. IEEE Transactions on Industrial Electronics, 2019, 66(2): 1098-1107.
[15] Shao Shiyi, Long Teng, Abdi E, et al. Dynamic control of the brushless doubly fed induction gener- ator under unbalanced operation[J]. IEEE Transa- ctions on Industrial Electronics, 2013, 60(6): 2465- 2476.
[16] 许利通, 程明, 魏新迟, 等. 考虑损耗的无刷双馈风力发电系统功率反馈法最大功率点跟踪控制[J]. 电工技术学报, 2020, 35(3): 472-480.
Xu Litong, Cheng Ming, Wei Xinchi, et al. Power signal feedback control of maximum power point tracking control for brushless doubly-fed wind power generation system considering loss[J]. Transactions of China Electrotechnical Society, 2020, 35(3): 472-480.
[17] 韩鹏. 双定子无刷双馈电机设计与驱动控制[D]. 南京: 东南大学, 2017.
[18] 魏新迟. 双定子无刷双馈风力发电系统的控制技术研究[D]. 南京: 东南大学, 2018.
[19] Roberts P C, McMahon R A, Tavner P J, et al. Equivalent circuit for the brushless doubly fed machine (BDFM) including parameter estimation and experimental verification[J]. IEE Proceedings-Electric Power Applications, 2005, 152(4): 933.
[20] Chen Jiansheng, Zhang Wei, Chen Bojian, et al. Improved vector control of brushless doubly fed induction generator under unbalanced grid conditions for offshore wind power generation[J]. IEEE Transa- ctions on Energy Conversion, 2016, 31(1): 293-302.
[21] Pena R, Clare J C, Asher G M. Doubly fed induction generator using back-to-back PWM converters and its application tovariable-speed wind-energy gener- ation[J]. IEE Proceedings-Electric Power Appli- cations, 1996, 143(3): 231.
[22] 张兴, 张崇巍. PWM整流器及其控制[M]. 北京: 机械工业出版社, 2012.
[23] Boardman G. Modelling and performance analysis of the doubly fed twin stator induction machine[D]. Sydney: University of Technology, 2003.
[24] 王超, 黄文新, 王前双. 基于异步电机的风力机特性模拟[J]. 电力电子技术, 2010, 44(6): 7-9.
Wang Chao, Huang Wenxin, Wang Qianshuang. Imitation of the characteristic of wind turbine based on induction motor[J]. Power Electronics, 2010, 44(6): 7-9.
[25] 程明, 文宏辉, 曾煜, 等. 电机气隙磁场调制行为及其转矩分析[J]. 电工技术学报, 2020, 35(5): 921- 930.
Cheng Ming, Wen Honghui, Zeng Yu, et al. Analysis of airgap field modulation behavior and torque component in electric machines[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 921- 930.
Study on Vector Control System and Power Flow of Cascaded Brushless Doubly-Fed Induction Generator
Abstract The vector control and power flow of the cascaded brushless doubly-fed induction generator (CBDFIG) are studied in this paper. Firstly, the dynamic model and steady-state equation are established. The grid-side converter is controlled by the grid voltage-oriented vector control and the machine-side converter is controlled by the stator flux-oriented vector control to realize the variable- speed constant-frequency operation of CBDFIG and the decoupling control of active and reactive power. Meanwhile, the vector control of the back-to-back converter can realize the bidirectional flow of power. Then, the power flow analysis is carried out. The active power distribution and the power state of power winding and control winding at different speeds are explored, and the changing trend of the power flow on the control side is revealed under consideration of copper loss. Through simulation and experiment, the effectiveness of the vector control and the correctness of the power flow analysis are verified.
keywords:Cascaded brushless doubly-fed induction generator, vector control, grid side converter, machine side converter, power flow
DOI: 10.19595/j.cnki.1000-6753.tces.210767
中图分类号:TM315
国家自然科学基金资助项目(61973073)。
收稿日期 2021-05-27
改稿日期 2021-06-28
程 明 男,1960年生,教授,博士生导师,主要研究方向为电动车驱动控制技术、新能源发电技术、微特电机及测控系统等。E-mail: mcheng@seu.edu.cn(通信作者)
许利通 男,1994年生,硕士研究生,研究方向为无刷双馈电机的驱动与控制。E-mail: xulitong_ee@163.com
(编辑 崔文静)