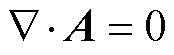），建立关于矢量磁位A的瞬态磁场边值问题[29]为摘要 随着远距离风电外送系统并网引起的次同步振荡现象和风险的增加，电力变压器经常会运行在含次同步分量的条件下，其铁心的非对称偏置磁化会导致谐波畸变和无功功率增加。含次同步分量下电力变压器铁心无功功率分析属于时-频域混合计算问题。针对该问题，首先，在时域下建立基于定点法的三维场路耦合有限元模型并编写计算程序，以求取不同次同步分量注入时变压器的励磁电流；其次，提出通过最大基波无功和平均基波无功的变压器基波无功特性分析方法，以及基于多重矢量功率理论的变压器频域无功特性分析方法；再次，通过一台物理变压器模型的空载实验，验证该文提出的时域场路耦合模型能够准确模拟变压器励磁电流中显著分量的频谱特性；最后，通过对该模型的仿真，分别对变压器的基波无功特性和多频率无功特性进行计算，并对计算结果进行分析讨论。
关键词：次同步频率分量 变压器偏置磁化 三维场路耦合有限元 无功功率 多重矢量功率理论
随着远距离风电外送系统的大规模并网，系统次同步振荡的现象和风险也不断增加。自2009年美国德克萨斯州风电场次同步振荡事故[1]以来，我国的华北沽源[2]、东北通榆[3]和新疆哈密[4]等地都曾出现过不同程度次同步振荡现象，因而引起国内外学者对该现象的广泛关注，并提出了各类串并联抑制策略以防止次同步振荡事故的扩散。然而无论是系统自发产生的次同步振荡现象，还是为抑制该现象接入的抑制装置，都不可避免地会使变压器中流过不同的次同步分量。在频率上，次同步振荡可涵盖4～35Hz内的多种频率[5-6]；在幅值上，可检测到主变压器上感应的次同步电压分量最高达基波分量的5.5%[7]。次同步分量注入变压器会导致铁心出现非对称偏置磁化现象，造成铁心饱和[8]、变压器损耗和温升增 大[9]、谐波畸变和无功功率增加[10]、振动和噪声加 剧[11]等问题，影响变压器的正常工作。在系统运行中，谐波和无功功率的波动会导致无功补偿装置非正常运行而跳闸，进而造成输电线路和变压器过载，并最终引发整个电网继电保护跳闸的联锁反应[12]；次同步电压施加在具有非线性特性的变压器铁心，还会产生大量间谐波分量并以畸变无功形式向电网扩散，此类分量也是引起主变压器保护和线路保护误动的重要原因之一[13]。综上所述，对不同次同步分量注入下变压器铁心无功功率的研究十分重要。
针对变压器在不同饱和条件下的励磁电流和无功功率关系，V. D. Albertson等通过对实测励磁电流进行傅里叶分解，提出变压器出现半波饱和现象时，畸变的励磁电流中含有大量谐波，该部分谐波是变压器无功功率增加的主要原因[14]；曹建春等通过对饱和变压器使用实时数字模拟系统（Real Time Digital Simulator, RTDS）仿真，提出变压器饱和时的励磁电流叠加至一次电流，会导致一次电流在峰值处出现明显畸变[15]，是变压器铁心饱和影响系统运行工况的重要佐证；D. H. Boteler等通过电磁暂态程序（Electro-Magnetic Transient Program, EMTP）对变压器励磁电流进行仿真，提出计算无功功率时还应考虑变压器的电压谐波[16]。基于励磁电流的分析方法仅适用于基波无功的计算，为更精确地探究变压器饱和时的无功特性，P. R. Price等建立耦合磁路模型，分析地磁感应电流注入时变压器的磁通和电流波形[17]；刘连光等利用模型进一步提出基于K值法的变压器GIC-Q计算方法[18]；R. Langella等建立不同铁心结构的电路-磁路耦合模型，对不同次同步电压分量激励下的励磁电流进行分析，并提出等效磁通系数，认为励磁电流峰值和有效值与等效磁通系数相关[19-20]。以上基于耦合磁路法的模型均建立在变压器的电感特性或F -i曲线上，仅可作为局部结构磁特性的近似均一化处理，不能考虑变压器铁心中磁通密度分布的非均匀性，对此，王帅兵等提出2D的场路耦合时间周期有限元模型计算变压器的稳态励磁电流[21]，王泽忠等提出基于变压器互感电路模型的间接耦合方法分析变压器动态电感特性[22]，但并未直接对无功功率进行分析。
在直流偏磁的条件下，变压器铁心各周期的饱和情况相同，且不考虑一次侧交流电压的畸变情况，因此大多只针对基波无功特性进行研究；但次同步分量注入会导致系统电压在各基波周期下的偏磁情况不同，且电流中出现大量间谐波分量，因此不能只考虑基波情况下的无功。针对非正弦情况的无功计算，C. Budeanu通过电压和电流的频域分解，将有功功率和无功功率分别定义为各频率下有功功率和无功功率之和，并引入失真功率以满足功率矢量多边形条件[23]，但其无功功率和失真功率缺乏明确物理意义；L. S. Czarnecki等将电流分解为一系列相互正交的分量，并对应不同的物理现象，提出了电流物理分量（Currents’ Physical Components, CPC）理论[24]，但各功率分量的结果仅仅是一个数值，不能描述电路能量流的本质及负载属性；A. Menti等学者将非正弦电路中电压与电流转化到矢量空间，基于几何代数（Geometric Algebra, GA）理论提出多重矢量功率定义[25]，并随后由H. Lev-Ari等扩展至三相多谐波系统[26]，可以准确地描述功率分量且遵循电路基本定理。但现有多重矢量功率理论都是在假设电压谐波工况下，针对理想RL电路模型进行功率解析的计算，而实际系统中的电压和负载的工况更为复杂且具有时变特性，且未有考虑次同步分量等间谐波引起的功率现象。
次同步分量注入将导致铁心在不同周期下的偏置磁化情况各不相同，因此以基波为计算周期的频域法不再适用，还须通过时域法对各个时刻的磁化特性进行模拟；而无功功率计算则通常借助傅里叶分解，以电压和电流的频域分量进行计算。且由于次同步分量注入导致谐波畸变程度增加，以及电流中次同步和超同步间谐波的出现，仅计算基波无功不能准确体现铁心的无功功率特性。因此，含次同步分量下电力变压器的无功功率研究是一类时-频域混合计算问题。一方面，针对变压器的时域稳态磁特性模拟，本文建立三维场路耦合时域有限元模型并编写计算程序，以获得不同次同步分量注入时变压器的励磁电流；另一方面，针对变压器的无功功率，本文提出考虑次同步分量注入的变压器基波无功功率分析方法和频域下的功率多重矢量分析方法。最后设计并制造一台三相物理变压器验证本文场路耦合模型有效性，并对变压器在不同次同步分量注入下的无功特性进行研究。
针对磁性材料的空间场模拟，有学者提出利用2D有限元模型对叠片铁心的磁场进行计算[21, 27]，但2D模型只能对中间平面局部磁场作近似处理，不能考虑铁心在叠片厚度方向的空间结构特性，特别是在三相铁心出现非对称偏置磁化时，各相饱和程度不同，仍对各铁心区域采用均一化等效厚度进行计算，会使结果存在较大误差。3D模型可直接根据完整铁心结构描述各区域及方向的饱和磁化特 性[28]，因此，本文建立3D场路耦合有限元模型，进行变压器铁心时域空间漏磁场计算。首先，考虑库仑规范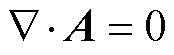（），建立关于矢量磁位A的瞬态磁场边值问题[29]为
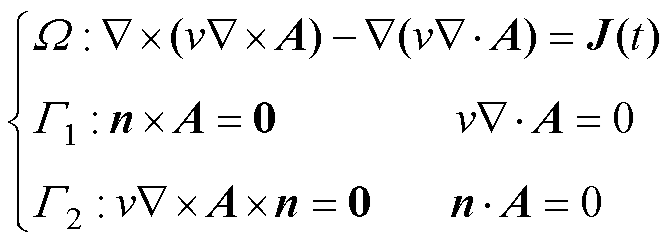（1）
式中，J(t)为绕组区域流过的电流密度矢量函数；v为材料磁阻率；W 为整个空间磁场求解区域；G1为法向磁感应强度为0的计算边界；G2为切向磁场强度为0的计算边界；n为边界法向量。
在包含铁磁媒质的非线性磁场中，引入定点磁阻率vf，磁场场量[30]满足
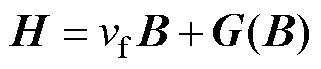（2）
其中
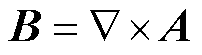
式中，H为磁场强度矢量；B为磁感应强度矢量；G为类磁化强度矢量。此时，域内微分方程可以写为
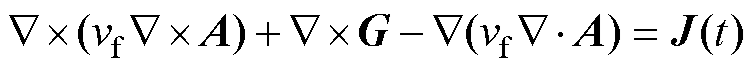（3）
电力变压器运行时，绕组通常接励磁电压源或负载，根据法拉第电磁感应定律建立电路方程为
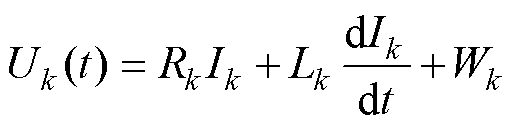
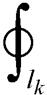
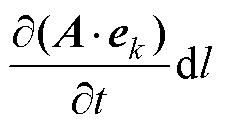
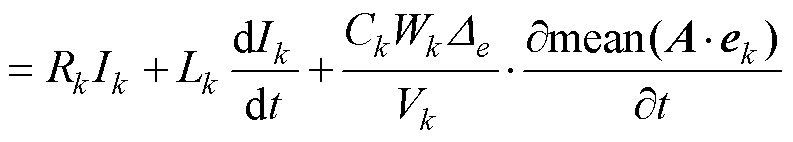（4）
式中，Uk(t)为施加在绕组k上的电压函数；Ik为施加在绕组k上的电流；Rk和Lk分别为外电路等效串联电阻和串联电感；Wk为绕组匝数；lk为绕组k区域中一条包围铁心的闭合曲线；Ck为单匝绕组的周长；D e为单元e的体积；Vk为绕组k在场域中所占总体积；mean(A·ek)为求单元内各节点矢量磁位在绕组方向投影均值的函数。
采用四面体网格划分求解区域，并利用线性基函数对域内进行插值，根据伽辽金有限元法，建立场路耦合计算的微分方程为
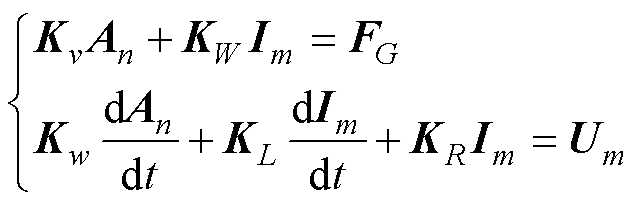（5）
式中，An和Im分别为由n个节点矢量磁位待求量和m个绕组支路电流待求量形成的计算列向量；Kv、KW和FG分别为与定点磁阻率v、绕组匝数W和类磁化强度矢量G相关的计算矩阵及列向量；Kw、KR、KL和Um分别为与场域绕组分布、电路电阻R、电感L和m个支路电源相关的计算矩阵及列向量。
由于次同步分量的存在，变压器各基波周期的饱和情况各不相同，因此计算周期不能取基波周期，而应取基波周期和次同步分量周期的最小公倍数，有
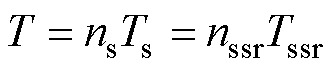（6）
式中，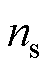
、
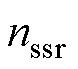为互质的两个整数；
、
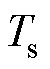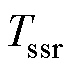分别为基波周期和次同步分量的周期。
若对式（5）所示的方程以时步法进行迭代，则该场路耦合模型的计算达到稳态时，应满足周期性条件为
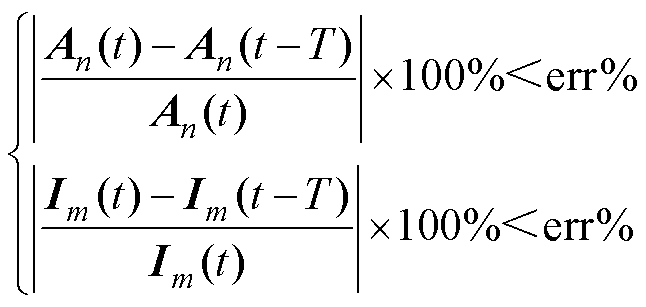（7）
式中，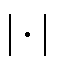
为求计算向量中各参数点相对误差矢量的绝对值；err%为周期性条件的各点相对误差限值。
变压器铁心无功功率需通过励磁电流IT和感应电压UT进行计算，根据所得稳态的计算结果，感应电压可由式（4）中法拉第电磁感应定律的部分公式得出，同时变压器的励磁电流为
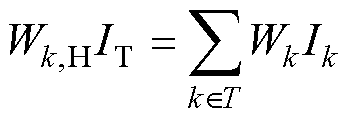（8）
式中，Wk,H为变压器高压侧绕组匝数；k为包围变压器铁心的所有绕组。
根据我国沽源、通榆等风电网的运行实例[15]，在多数次同步振荡事件中，一次电流中出现了次同步和超同步频率的异常分量，以及高次谐波的显著增加，主变压器感应电压中出现畸变和以次同步频率的波动。根据法拉第电磁感应定律，单一频率正弦感应电压有效值E对应磁通峰值F 的关系为E= 4.44NfF，即F =E/(4.44Nf)，交流励磁电压产生的磁通与次同步频率成反比，与电压幅值成正比，因此电压中的高次谐波产生的谐波磁通分量较低，而低频次同步电压分量在铁心中会产生较大的次同步磁通分量[31]。以5%的电压分量为例，若该分量对应5Hz的次同步频率，其次同步磁通峰值可达基波磁通峰值的50%（50Hz/5Hz×5%）；若该分量对应3次谐波，则其谐波磁通分量为基波磁通的1.67%（1/3×5%），随电压谐波次数增加，其产生的谐波磁通分量会更低。因此，当次同步分量注入变压器时，可以认为铁心中仅含基波和次同步分量两项主要磁通分量，因此，总铁心磁通为
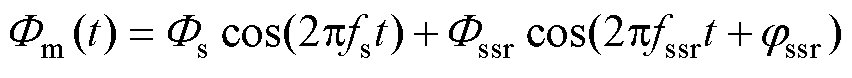（9）
式中，Fm(t)为铁心磁通函数；Fs和Fssr分别为基波磁通和次同步磁通分量的峰值；fs和fssr分别为基波和次同步分量的频率；jssr为次同步磁通分量相位。
为了充分利用硅钢片导磁性能，变压器铁心正常工作时，额定工况下的铁心峰值磁通应在膝点附近且小于膝点磁通。在膝点磁通以下，铁心磁导率远大于空气磁导率；在膝点磁通以上，铁心微分磁导率迅速下降，接近空气磁导率。当铁心注入次同步分量时，该次同步磁通与铁心基波磁通叠加为总交流磁通，总交流磁通峰值最大值将超过膝点磁通，使铁心饱和，导致励磁电流峰值迅速增加，此时铁心F-i曲线工作情况如图1所示。
图1 含次同步分量磁通流入时铁心F -i曲线工作情况
Fig.1 Working condition of F-i curves with subsynchronous component magnetic flux injection
变压器铁心注入次同步分量后，根据式（9），当基波磁通与次同步磁通峰值时刻重合时，最大磁通峰值为Fs+Fssr。以5Hz、5%的次同步电压分量为例，其次同步磁通峰值可达基波磁通峰值的50%，使总磁通峰值达到额定工况下的1.5倍，远超膝点磁通，将极大地增加一个周期下的最大基波无功[32]。根据有限元模型得出的稳态计算结果，取区间为基波周期Ts的时间窗，可以得到最大基波无功计算式为
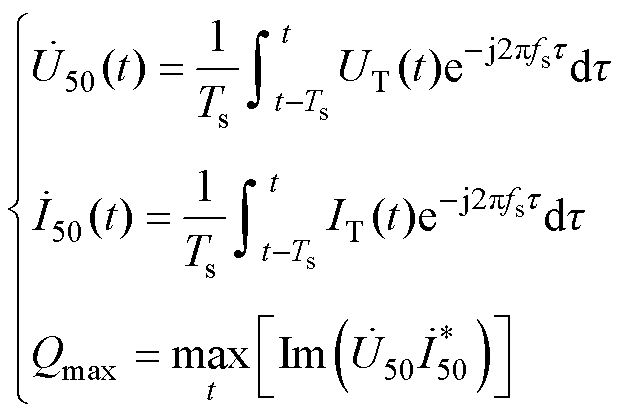（10）
式中，
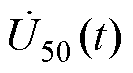和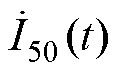
分别为感应电压UT和励磁电流IT的时变基波相量；Qmax为最大基波无功；
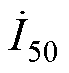为复数/相量的共轭计算；Im( )为取虚部函数；上标*为对复数/相量的共轭计算。
然而，最大基波无功仅表征铁心饱和最严重一个周期下的无功功率，由式（6）可知，含次同步分量时，变压器的稳态周期为ns个基波周期，为获得变压器的稳态基波无功特性，还应对整个计算周期下的感应电压和励磁电流进行傅里叶分解，并通过其中50Hz频率分量，计算平均基波无功。以整个计算周期T为时间窗，可以得到平均基波无功计算式为
（11）
式中，
和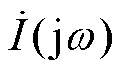
分别为以T为计算周期的傅里叶变换结果；Qmean为整个稳态计算周期下的平均基波无功。
与直流偏磁不同的是，次同步分量的注入导致变压器运行时引入了新的频率分量，次同步磁通分量施加在非线性铁心中还会导致各次谐波附近出现khfs±fssr（kh为谐波次数）的间谐波，仅计算各相基波无功不足以描述总铁心无功功率，因此变压器在次同步分量注入下的无功功率研究是一类非正弦条件下的功率分析问题，选择适当的工具能够更全面地探究相移、谐波/间谐波、三相不平衡等引起的功率现象。对于此类问题，C. Budeanu提出的功率定义所能表现的功率信息很少，且不满足功率守恒；L. S. Czarnecki提出的电流物理分量法依赖系统电压的不变性，不适合用于频率和幅值可变的含次同步分量系统分析，且各功率分量的计算结果仅仅是一个没有符号的值（体现功率大小），不能体现能量流的关系；基于几何代数的功率理论的功率分析方法，功率计算、对比均在矢量空间内进行，并可以通过选择合适的矢量工具进行功率流的分析或获得不同功率现象。因此，本文以基于几何代数的多重矢量功率理论为基础，提出适用于变压器铁心多频率工况的无功功率分析方法，以准确分析变压器的全频域无功特性。
2.2.1 考虑间谐波的多重矢量功率理论
文献[25]中证明了应用几何代数法进行电路的功率分析，并且可以对含有不同电气元件和电路结构功率现象进行准确描述，但仅限于单相系统的应用。文献[26]提出了几何代数法在多相正弦系统中的应用，并类比正弦系统将其推广至多谐波系统，但其仅形式化地提出一种在多重矢量功率的计算形式，且没有结合实际应用场景进行分析。
设一个节点处的电压和电流表示为
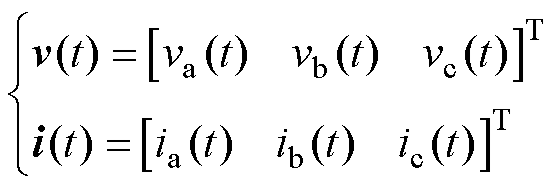（12）
式中，v和i分别为三相时域电压和电流函数组成的列向量；vabc为三相电压；iabc为三相电流。
当考虑变压器直流偏磁以及换流变压器的多谐波工况时，其傅里叶分解的计算周期仍为工频基波周期；有理次次同步分量注入后，各电气分量仍满足周期性条件，但傅里叶分解应以式（6）形成的计算周期T下进行计算，此时工频基波分量和次同步分量则分别对应该计算周期的ns和nssr次计算谐波。为分析含次同步分量后的系统全频域功率特性，将式（12）中的时域电气量按频率分解为
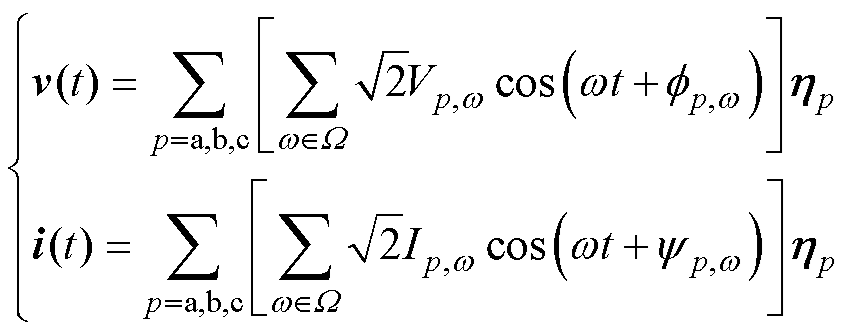（13）
式中，p为三相标识；W为计算中需考虑的角频率集合；Vp,w和fp,w分别为p相中对应角频率w 的电压分量有效值和相位；Ip,w和yp,w分别为p相中对应角频率w 的电流分量有效值和相位；hp为3维列向量，p=a, b, c时对应向量中第1, 2, 3项为1，其余为0。
为便于区分，以双下标表示基矢量，选取电压原基矢量e和扩展基矢量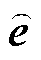
分别为
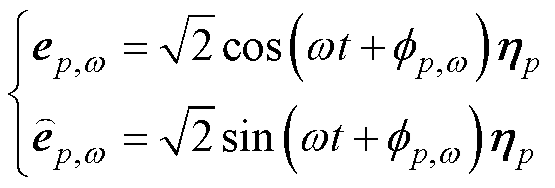（14）
如式（14）所示，根据正余弦函数间的正交关系，同相但不同角频率间的基矢量以及同一角频率的原基矢量与扩展基矢量，均为相互正交关系；不同相的基矢量也不会产生有功功率（即a相电压与b、c相电流之间不产生有功功率，其余同理），因此也可认为相互正交。则根据式（13）中对电压和电流的频域分解结果，可以在几何代数空间下，将电压和电流分别以矢量形式表示为
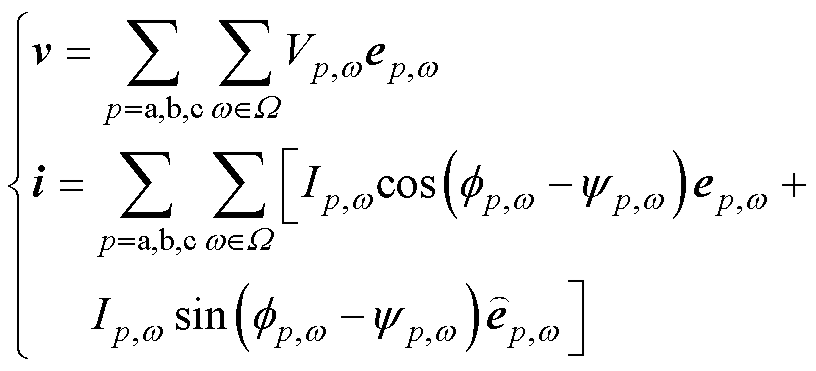（15）
则多重矢量功率为电压与电流矢量的几何积为
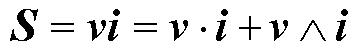（16）
式中，S为多重矢量功率；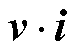
为电压和电流矢量的内积，表示系统的有功功率；
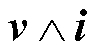为电压和电流矢量的外积，包含所有的无功功率。
将式（15）代入式（16），则可根据所含基向量得到多重矢量功率计算公式及其成分划分为
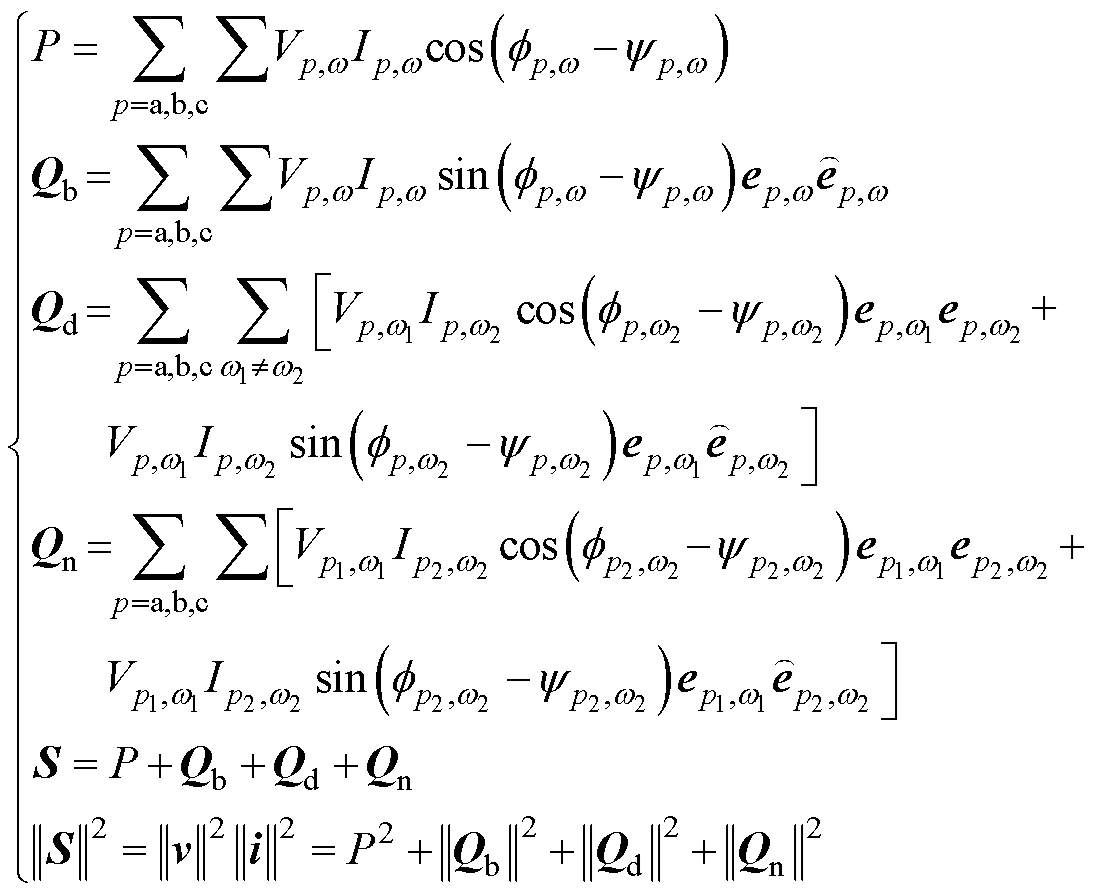（17）
式中，P为系统传输的总有功功率；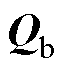
为各相在各频率下的Bedeanu无功功率；
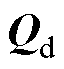为各相电压和电流谐波引起的畸变无功功率；
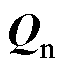为三相负载不平衡引起的相间传输无功功率；S等于以上各无功分量的矢量和；||·||为求矢量及多重矢量的模。
由式（16）和式（17）可知，通过将电压和电流的几何积定义为多重矢量功率，解决了多频率下无功功率计算的问题；且通过基矢量对功率成分进行划分，使各功率分量相互正交且可以描述不同的功率现象。
2.2.2 含次同步分量下变压器多频率无功功率分析
由式（14）可知，对应每个频率需要6个基矢量，当考虑最大谐波次数为N时，电压矢量的维度为3N，电流矢量的维度为6N，在对实际电力系统中的电压与电流信号进行计算时，理论上存在无穷多种频率的谐波和间谐波，由此将导致需要的电压和电流矢量的维度也是无穷大的。但次同步振荡发生期间，变压器上的感应电压中主要含有基波和次同步两种频率[15]，而励磁电流则以基波、奇次谐波、次同步分量以及频率为khfs±fssr（kh≥1为谐波次数）的间谐波为主要分量[19]。因此，进行含次同步分量下的变压器多频率无功功率分析时，对电压只需考虑两种频率，对电流需建立如下相-频双指标集合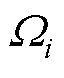
为
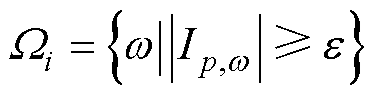（18）
式中，e 为在计算中考虑的谐波/间谐波电流有效值下限。
在不考虑铁心磁滞和涡流损耗效应时，由感应电压和励磁电流计算出的功率多重矢量中有功功率P=0，因此多重矢量功率仅由各无功成分组成。
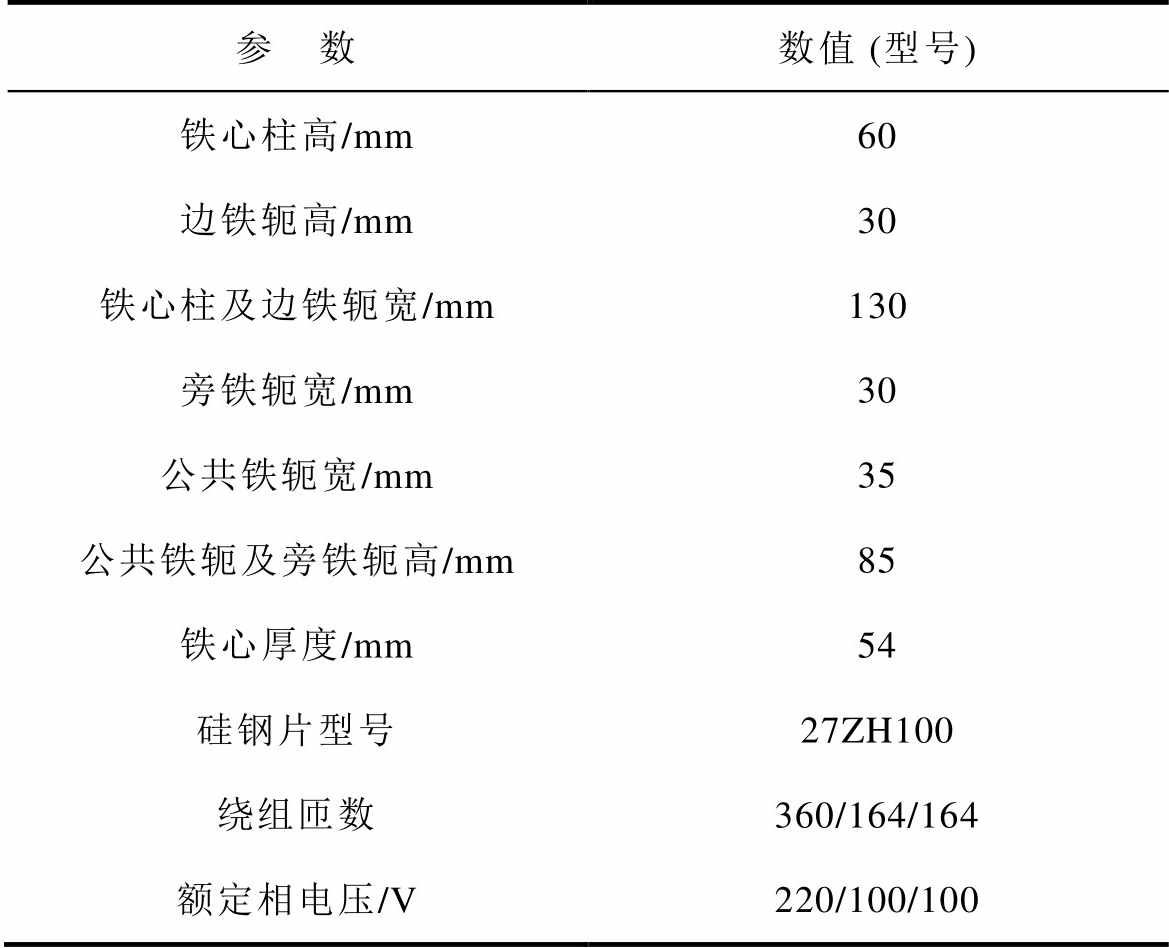
为探究次同步分量注入时变压器的铁心基波无功和频域无功功率特性，本节针对一台额定电压为380V的三相壳式变压器模型进行不同次同步分量下的仿真计算，并与实验结果进行对比。实验电压源由可编程电源CSW5550提供，并可利用其内置波形采集装置测量并导出电流和电压实验结果，对于1kHz频率以下的分量，其电压分辨率/精度为0.25V/0.1%，电流精度为0.1%。对变压器进行空载实验，空载条件下所测绕组电流即为变压器励磁电流。其中物理实验变压器结构参数见表1。
表1 实验变压器结构参数
Tab.1 Parameters of transformer
参 数数值 (型号) 铁心柱高/mm60 边铁轭高/mm30 铁心柱及边铁轭宽/mm130 旁铁轭宽/mm30 公共铁轭宽/mm35 公共铁轭及旁铁轭高/mm85 铁心厚度/mm54 硅钢片型号27ZH100 绕组匝数360/164/164 额定相电压/V220/100/100
经短路实验测得基波下电源内阻为(1+j0.02)W，变压器高压侧总等效短路电抗为j0.64W，忽略偏磁条件下变压器漏感变化[33]，并考虑到空载条件下励磁电感远大于漏感，取变压器高压侧单侧漏感为L=1.02mH（对应基波电抗j0.32W）。
根据我国电网运行历史，2010～2014年华北沽源出现多次频率在10Hz以下的次同步振荡现象[2]，并在事故发生过程中检测到主变压器高中压侧的次同步电压分量为0.9%～5.5%[7]；2015年新疆哈密地区出现频率在17～23Hz范围内变化的次同步振荡现象，平均振荡频率为19.2Hz，持续时间达3.4h[5]；2016年吉林通榆地区相继出现频率为5.33Hz和4.85Hz的两次次同步振荡现象[3]。综合电网次同步振荡情况和实验条件，分别向变压器施加频率为5Hz和15Hz，幅值占比5%的次同步电压分量进行实验，根据式（6），对每个算例取10个工频基波周期（0.2s），对比A相励磁电流结果如图2所示。
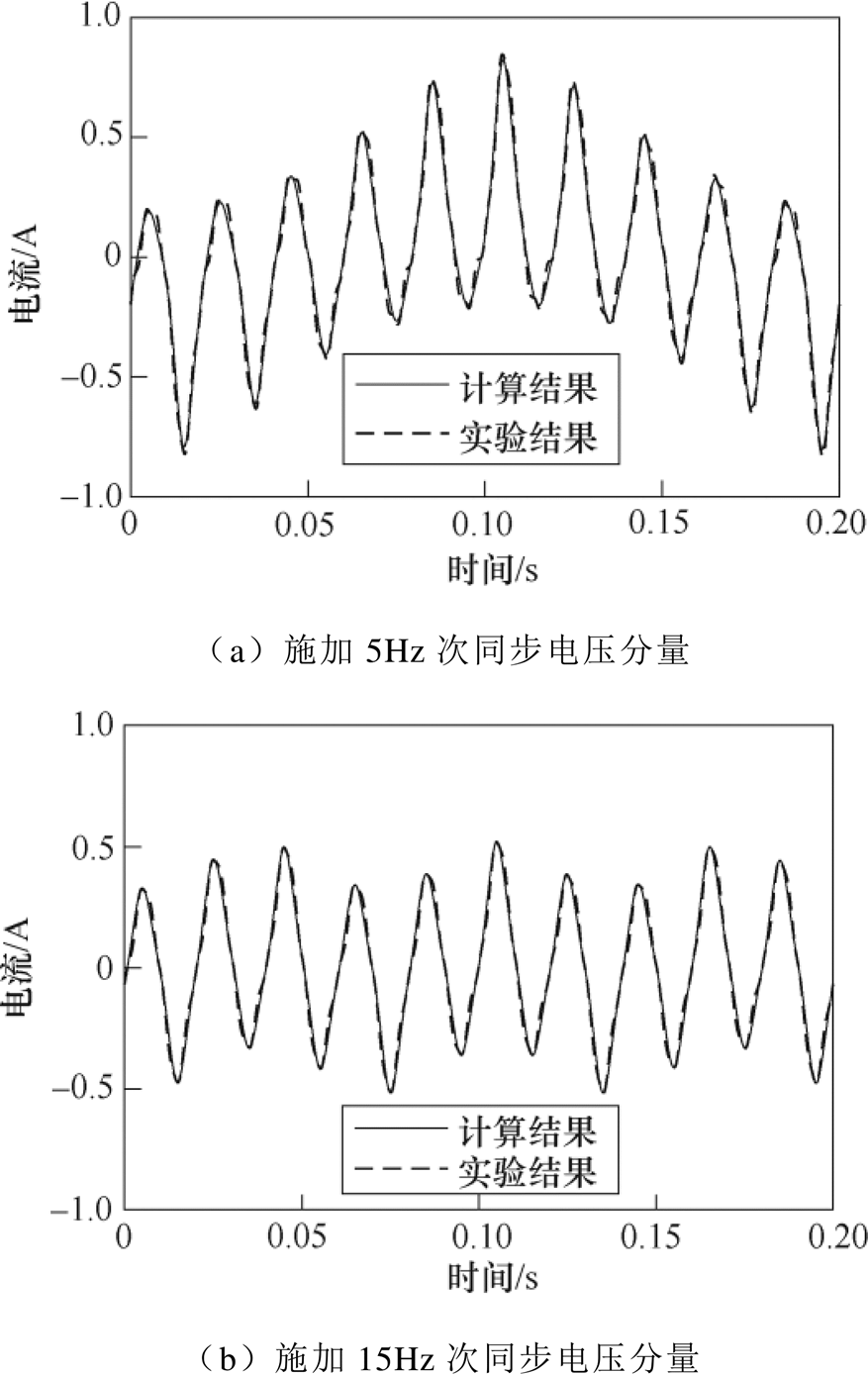
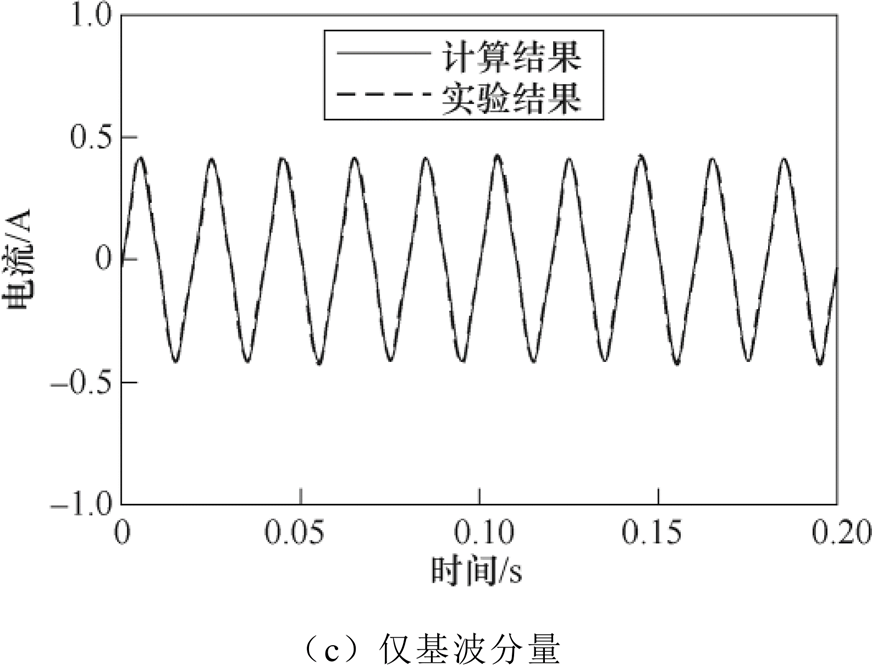
图2 含不同频率次同步分量条件下励磁电流仿真结果
Fig.2 The simulation results of magnetizing current with sub-synchronous components
由图2可知，本文算法的仿真结果与实验结果一致；施加次同步电压分量后，励磁电流峰值呈周期性振荡，振荡频率与次同步分量频率一致；次同步电压分量的频率越低，励磁电流峰值所在基波周期的偏移情况越大，表示铁心饱和情况越严重。为进行变压器无功分析，对图2所示励磁电流进行傅里叶分解，得到其谐波及间谐波的有效值频谱如图3所示。
如图3所示，在各类次同步分量算例下，励磁电流频谱计算结果中显著分量（有效值大于0.01A的谐波及间谐波分量）的相对误差在5.98%以内，因此认为本文算法能够准确模拟变压器励磁电流的频谱特性。对比基波和谐波幅值可知，对于相同占比的次同步电压分量，频率越低，基波和谐波电流越大，铁心饱和程度越高。对比频率成分可知，在无次同步分量的额定基波条件下，变压器励磁电流中只有奇次谐波；在施加15Hz次同步分量后，励磁电流中仍不存在偶次谐波，但在2次谐波频率附近（100Hz±fssr）出现了显著间谐波分量；随次同步分量频率降低，饱和程度提高，出现显著间谐波分量的频率点个数也会增加，即施加5Hz次同步分量后又导致在3次和4次谐波频率附近（200Hz±fssr）都检测到显著间谐波分量。
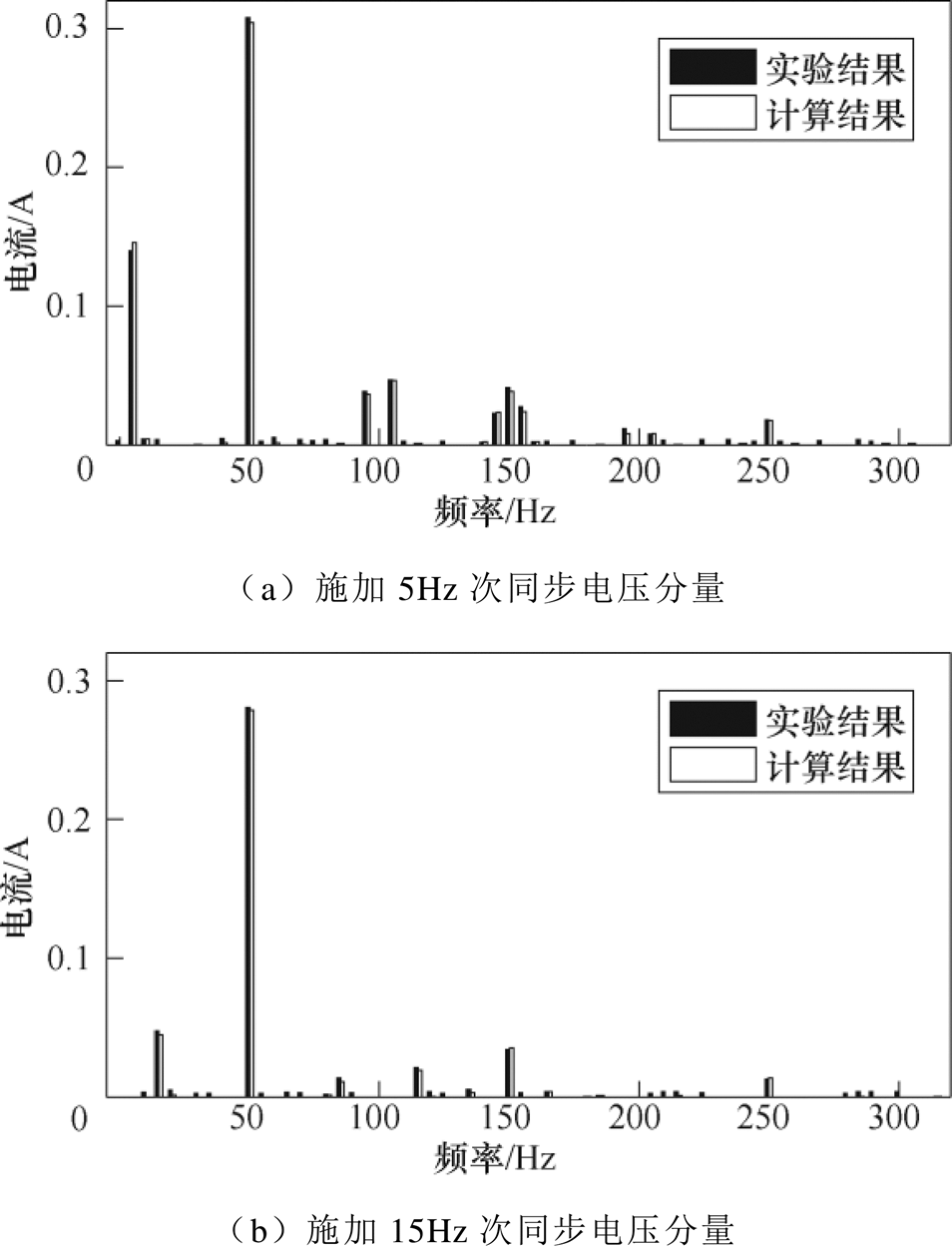
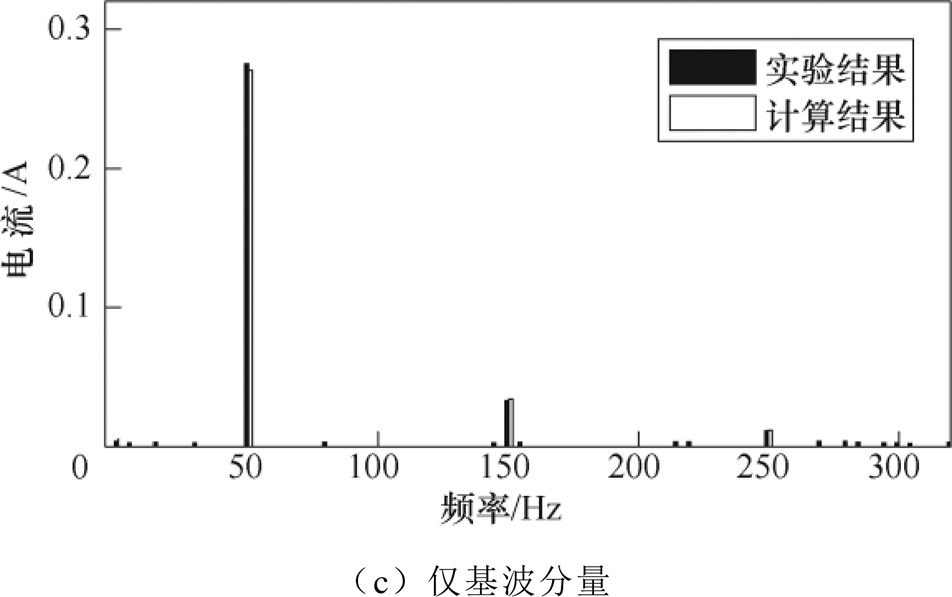
图3 含不同频率次同步分量条件下励磁电流各谐波/间谐波分量方均根值
Fig.3 The root mean square value of harmonic and inter-harmonic components of the magnetizing current with sub-synchronous components
考虑实际电力系统运行情况，设置频率为4～25Hz，占比1%～5%的次同步电压分量，以A相为例，对比励磁电流基波有效值、最大峰值、总谐波/间谐波畸变率（除基波外其他各分量总方均根值与基波有效值之比），以及整体铁心最大局部磁通密度如图4所示。
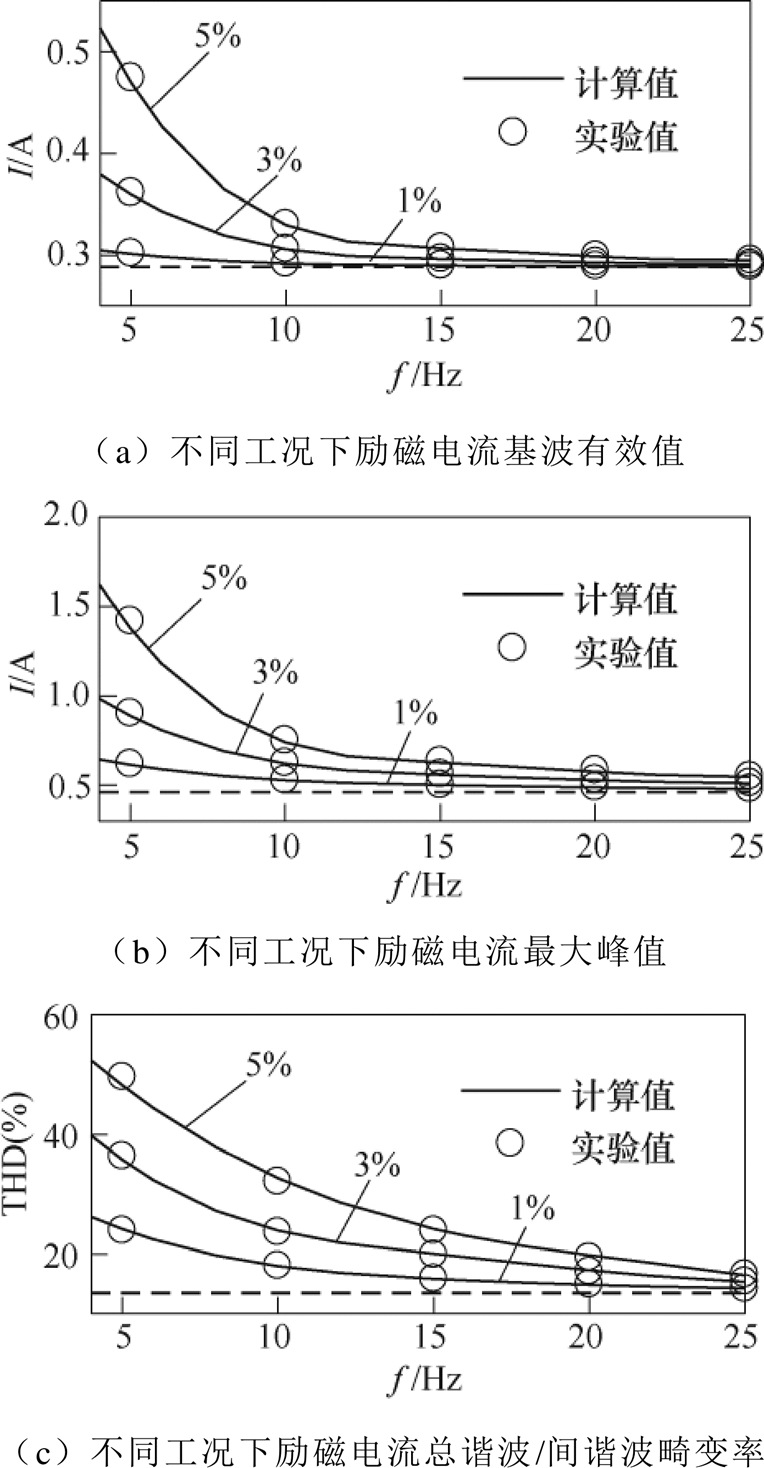
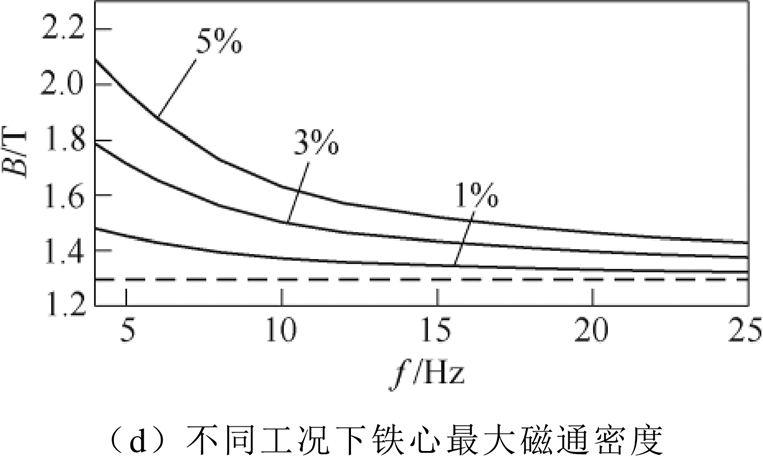
图4 不同次同步分量工况下算例对比
Fig.4 Comparison of calculation cases under different sub-synchronous components
由图4可知，本计算模型可以准确模拟变压器各次同步分量工况下的场路耦合特性；且幅值越大、频率越低的次同步分量对变压器运行影响越大，在施加频率为4Hz，占比为5%的次同步分量电压时，励磁电流基波有效值和最大峰值分别较额定工况增加了81%和253%，将极大地增加变压器消耗的无功功率。此外，励磁电流的总谐波畸变率增大至52.4%，铁心局部最大磁通密度增大至2.07T，对变压器的其他运行状态也将造成显著影响。
根据2.1节的相关分析，铁心磁通变化还会受次同步分量初始相位影响，以频率为5Hz，占比为5%的次同步分量为例，对比不同初始相位下，励磁电流峰值与铁心最大磁通密度结果如图5所示。
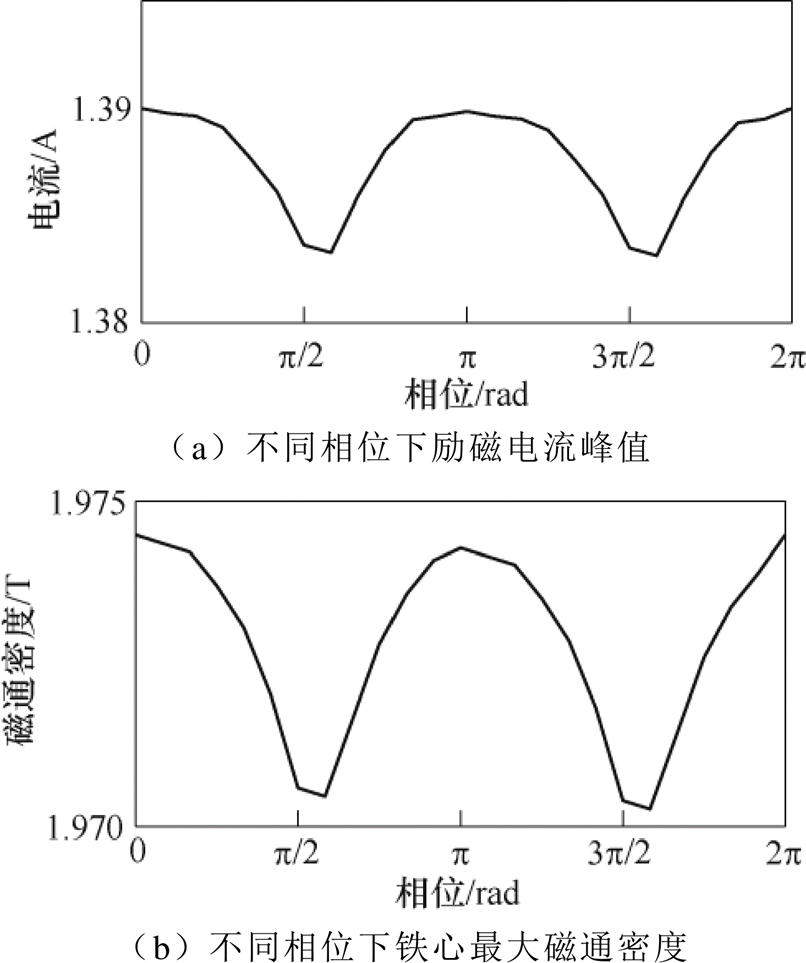
图5 不同次同步分量初始相位下算例对比
Fig.5 Comparison of calculation cases under different sub-synchronous component phases
由图5可知，次同步分量初始相位对变压器的影响呈以p 周期的波动曲线，且初始相位为0或p 时，分别对应次同步磁通与基波磁通的峰值或谷值时刻重合，此时励磁电流峰值和铁心最大磁通密度均为极大值；但不同初始相位下，对励磁电流峰值的波动仅有0.495%，铁心最大磁通密度的波动仅有0.213%，因此为避免结果偏于保守，在后续无功功率计算中可直接取次同步分量初始相位为0，并忽略实验及计算中初始相位对变压器运行的影响。
根据2.1节的相关分析，次同步分量注入后各基波周期下的变压器偏置磁化程度各不相同，因此不同周期下的基波无功功率也不相同，本文仍取频率5Hz，占比5%的次同步电压分量的条件，得到不同周期下铁心基波无功以及稳态周期下的平均基波无功如图6所示。
如图6所示，次同步分量注入会导致铁心无功功率增加。由图6a可知，铁心在额定工况下三相无功各周期保持不变，但施加次同步分量后，各时刻基波无功有显著波动，部分基波周期下无功小于额定工况，而最大基波无功显著增加，并且三相无功峰值时刻及无功峰值也存在较大差异；由图6b可知，次同步分量注入导致稳态周期下的基波无功也显著增加，但三相基本相等，最大与最小相无功功率差值小于2.2var（相对差值小于3%）。
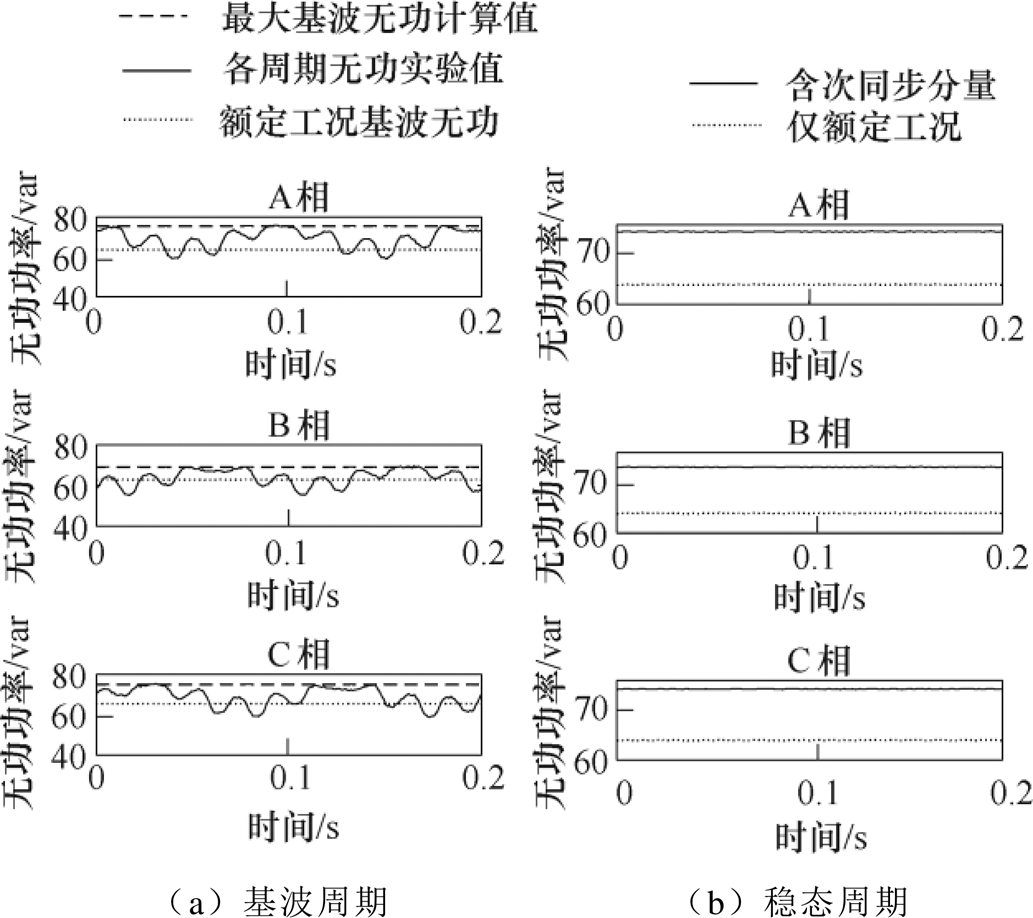
图6 变压器铁心基波无功功率实验
Fig.6 Fundamental frequency reactive power experiments for transformer
向变压器施加4～25Hz的不同频率次同步分量，对各相的最大单周期无功功率及完整计算周期下的三相平均基波无功之和进行计算，对比结果如图7所示。
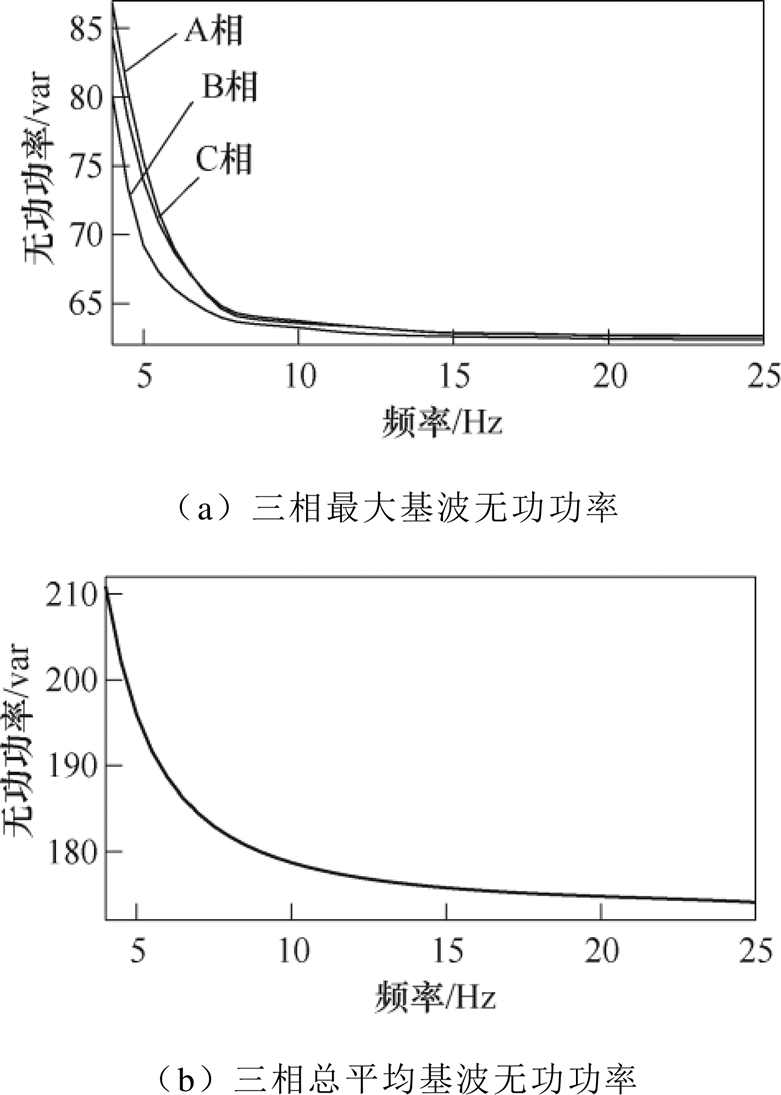
图7 不同次同步分量下变压器铁心基波无功功率
Fig.7 Fundamental frequency reactive power of transformer under different sub-synchronous components
由图7a可知，在施加15Hz以上的次同步分量导致变压器铁心饱和程度较低时，三相最大基波无功的相对偏差在0.32%以内，表明三相铁心的磁路基本对称；随频率降低，饱和程度增大时，对于处于中间相的B相，其主磁通可经两个边相（A、C相）的铁心闭合，而边相的主磁通主要经中间B相铁心闭合，只有少量磁通流经另一边相铁心，因此B相等效磁路长度较A、C相磁路较短，无功的增长量也更小，因此B相与其他两相最大基波无功的相对偏差最大达到8.31%；而A、C相磁路完全对称，该两相最大基波无功的相对偏差都在0.63%以内，此无功的差异主要源自网格划分不对称引起的计算误差。由图7b可知，由于变压器各基波周期的饱和程度不同，三相总平均基波无功曲线小于三项最大无功功率之和，且三相平均无功随频率的变化曲线较三相最大基波无功曲线更为平缓。
次同步分量注入会向变压器感应电压中引入新的频率分量，并导致励磁电流中出现次同步频率电流分量以及频率为kh fs±fssr的各间谐波分量，因此只考虑基波无功并不能完全体现变压器铁心的无功效应。本文利用多重矢量功率理论对3.1节的三种工况下变压器铁心的频域无功功率进行对比。
在多重矢量功率计算中，考虑以下假设：①由于次同步及谐波频率下的铁心感抗远大于电源内阻及变压器漏抗，因此感应电压中除基波和次同步分量外的频率分量极小，可只取该两个频率分量建立电压矢量；②由于铁心非线性效应，理论上电流中会存在各种频率分量，但含量极小的频率分量并不影响总体无功计算精度，因此电流矢量建立中仅考虑有效值大于0.01A的显著分量；③由于场路耦合计算中不考虑铁心磁滞效应，因此对铁心损耗的计算中不存在有功损耗；④由于施加次同步分量后各算例主要频率分量的个数及频率不同，因此对各详细谐波/间谐波的无功对比无实际意义，因此省略对算例中功率多矢量的展开计算过程，只表示式（17）中各功率分量的模。根据以上设置，得到多重矢量功率计算结果见表2。
对比表2中基波平均无功占比可知，额定条件下，基波无功的占比为99.3%，而在高饱和情况下，基波无功只占全部功率多重矢量的88.8%，因此只考虑基波无功已不能完全反映变压器铁心的无功功率；对比各功率分量可知，高饱和及低饱和算例中变压器总无功功率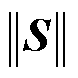
分别增长3.86%和37.29%，而畸变无功
分别增长了111.24%和429.12%，因此谐波/间谐波畸变无功是变压器无功功率增加的最显著成分。
表2 基于多重矢量功率的变压器无功功率计算
Tab.2 Transformer reactive power calculation by multivector power theory
算例基波平均功率代数和Q1/var,多重矢量功率/(V·A)基波无功占比(%) 仅基波Q1=176.17=101.70=12.19=144.86=177.4199.3 低饱和-15Hz次同步分量Q1=178.78=103.22=25.75=150.43=184.2597.0 高饱和-5Hz次同步分量Q1=216.35=124.97=64.50=198.87=243.5688.8
考虑4～25Hz不同频率的次同步分量，计算各功率分量模并与实验结果对比，结果如图8所示。
如图8所示，由于3.1节所得各主要谐波/间谐波分量的误差很小，因此对各无功分量也可准确模拟。由图8可知，由于各功率分量体现的负载特性不同，因此随次同步频率的变化趋势也有差异；由图8a、图8d和图8e可知，虽然三相视在功率中三相基波无功代数和的占比有所降低，但对于以工频分量为主的电力系统，矢量Bedeanu无功功率和三相总视在功率中仍以三相基波无功为主要分量，因此有相似的相对变化趋势；图8b表明，对于25Hz以下的频率分量，随次同步分量频率降低，铁心饱和程度增加，虽然谐波/间谐波畸变无功的增长率高，但增长速度基本一致，整体曲线走势较为平缓；图8c表明，当注入较低频率次同步分量导致铁心饱和程度较高时，铁心磁路的三相不平衡度增加，因此施加9Hz以下的次同步分量后，不平衡无功的变化曲线明显变陡。
图8 变压器频域无功功率分量对比
Fig.8 Components of transformer reactive power in frequency domain
1）为模拟变压器的时域稳态磁特性，本文引入定点法处理考虑库仑规范的磁场方程。通过伽辽金有限元法和电磁感应定律建立场路耦合求解模型，并编写计算程序求取不同次同步分量注入时变压器的励磁电流。
2）由于次同步分量注入导致变压器各周期的偏磁情况并不相同，本文提出分别通过三相最大单周期无功和完整计算周期下的平均无功对变压器基波无功特性进行分析；由于次同步分量注入导致谐波畸变和大量间谐波的出现，仅靠基波分量不能完全体现铁心损耗特性，因此提出基于多重矢量功率理论的无功功率分析方法计算变压器的多频率无功功率。
3）设计并制造了一台物理变压器模型，并通过变压器空载实验表明，本文提出的时域场路耦合模型能够准确地模拟变压器励磁电流中显著分量的频谱特性，随次同步分量频率降低变压器饱和程度会增加，使其中显著间谐波分量的频率个数及幅值均会增加。由于变压器三相磁路不同，饱和时边相最大单周期无功功率大于中间相最大单周期无功功率，且三相平均无功功率随频率的变化曲线与各单相最大单周期无功功率曲线相比较平缓。随变压器饱和程度增加，谐波/间谐波畸变无功功率是变压器总无功功率增加最显著的成分，因此只考虑基波无功功率并不能完全反映变压器铁心的无功功率；且由于不同功率分量体现的负载特性不同，各功率分量随次同步频率的变化趋势也各不相同。
参考文献
[1] Gross L. Sub-synchronous grid conditions: new event new problem and new solutions[C]//37th Annual Western Protective Relay Conference (WPRC), Spokane, Washington, 2010: 1-19.
[2] 董晓亮, 田旭, 张勇, 等. 沽源风电场串补输电系统次同步谐振典型事件及影响因素分析[J]. 高电压技术, 2017, 43(1): 321-328.
Dong Xiaoliang, Tian Xu, Zhang Yong, et al. Practical SSR incidence and influencing factor analysis of DFIG-based series-compensated trans- mission system in Guyuan farms[J]. High Voltage Engineering, 2017, 43(1): 321-328.
[3] 王春华, 宋晓喆, 高培生, 等. 吉林通榆风电基地次同步振荡现象研究[J]. 电气自动化, 2017, 39(4): 88-91.
Wang Chunhua, Song Xiaozhe, Gao Peisheng, et al. A research on sub-synchronous oscillation at Tongyu wind power base in Jilin[J]. Electrical Automation, 2017, 39(4): 88-91.
[4] 郑彬, 印永华, 班连庚, 等. 新疆与西北主网联网第二通道工程系统调试[J]. 电网技术, 2014, 38(4): 980-986.
Zheng Bin, Yin Yonghua, Ban Liangeng, et al. System commissioning for the second transmission channel project interconnecting Xinjiang grid with northwest China main grid[J]. Power System Tech- nology, 2014, 38(4): 980-986.
[5] 李明节, 于钊, 许涛, 等. 新能源并网系统引发的复杂振荡问题及其对策研究[J]. 电网技术, 2017, 41(4): 1035-1042.
Li Mingjie, Yu Zhao, Xu Tao, et al. Study of complex oscillation caused by renewable energy integration and its solution[J]. Power System Technology, 2017, 41(4): 1035-1042.
[6] 曹建春, 项祖涛, 燕翚, 等. 抑制双馈风电场次同步谐振的STATCOM研究[J]. 电网技术, 2019, 43(3): 895-902.
Cao Jianchun, Xiang Zutao, Yan Hui, et al. Research on mitigating DFIG wind farm SSR with STATCOM[J]. Power System Technology, 2019, 43(3): 895-902.
[7] 曹建春. 抑制双馈风电场次同步谐振的STATCOM研究[D]. 北京: 中国电力科学研究院, 2018.
[8] 孙佳安, 李琳. 含次同步分量下变压器时间周期有限元的Parareal求解模型[J]. 中国电机工程学报, 2020, 40(13): 4348-4357.
Sun Jiaan, Li Lin. Time-periodic FEM using Parareal for transformer electromagnetic characteristics analysis with sub-synchronous components[J]. Proceedings of the CSEE, 2020, 40(13): 4348-4357.
[9] 王泽忠, 李明洋, 宣梦真, 等. 单相四柱式变压器直流偏磁下的温升试验及仿真分析[J]. 电工技术学报, 2021, 36(5): 1006-1013.
Wang Zezhong, Li Mingyang, Xuan Mengzhen, et al. Temperature rise test and simulation of single-phase four-column transformer under DC-bias[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(5): 1006-1013.
[10] 黄天超, 王泽忠. 特高压换流变压器拉板损耗的频率特性分析[J]. 电工技术学报, 2021, 36(19): 4132- 4139.
Huang Tianchao, Wang Zezhong. Frequency characte- ristic analysis of flitch plate losses in UHV converter transformer[J]. Transactions of China Electrote- chnical Society, 2021, 36(19): 4132-4139.
[11] 李冰, 王泽忠, 刘海波, 等. 直流偏磁下500kV单相变压器振动噪声的试验研究[J]. 电工技术学报, 2021, 36(13): 2801-2811.
Li Bing, Wang Zezhong, Liu Haibo, et al. Experiment on vibro-acoustic characteristic of 500kV single- phase transformer under DC-bias[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2801- 2811.
[12] 刘教民, 朱溪, 刘洪正, 等. 电力变压器的GIC-Q损耗算法的研究综述[J]. 高电压技术, 2018, 44(7): 2284-2291.
Liu Jiaomin, Zhu Xi, Liu Hongzheng, et al. Calcu- lation methods for reactive power loss of transformers due to geomagnetically induced current[J]. High Voltage Engineering, 2018, 44(7): 2284-2291.
[13] 武骁. 交直流混联系统输电线路继电保护关键问题研究[D]. 成都: 西南交通大学, 2015.
[14] Albertson V D, Kappenman J G, Mohan N, et al. Load-flow studies in the presence of geomagnetically- induced currents[J]. IEEE Transactions on Power Apparatus and Systems, 1981, PAS-100(2): 594-607.
[15] 曹建春, 项祖涛, 武丹, 等. 风电次同步谐振对主变偏磁的影响机理[J]. 电网技术, 2019, 43(6): 2080- 2086.
Cao Jianchun, Xiang Zutao, Wu Dan, et al. Influence mechanism of wind farm subsynchronous resonance on magnetic bias of transformer[J]. Power System Technology, 2019, 43(6): 2080-2086.
[16] Boteler D H, Shier R M, Watanabe T, et al. Effects of geomagnetically induced currents in the BC hydro 500kV system[J]. IEEE Transactions on Power Deli- very, 1989, 4(1): 818-823.
[17] Price P R. Geomagnetically induced current effects on transformers[J]. IEEE Transactions on Power Delivery, 2002, 17(4): 1002-1008.
[18] 刘连光, 钱晨, 朱溪, 等. 应用K值算法的甘肃电网GIC-Q扰动计算[J]. 电网技术, 2016, 40(8): 2370-2375.
Liu Lianguang, Qian Chen, Zhu Xi, et al. Calculation of geomagnetically induced currents reactive power loss disturbance in Gansu grid with parameter K[J]. Power System Technology, 2016, 40(8): 2370-2375.
[19] Langella R, Testa A, Emanuel A E. On the effects of subsynchronous interharmonic voltages on power transformers: single phase units[J]. IEEE transactions on power delivery, 2008, 23(4): 2480-2487.
[20] Langella R, Testa A, Emanuel A E. On the effects of subsynchronous interharmonic voltages on power transformers: three phase units[J]. IEEE Transactions on Power Delivery, 2008, 23(4): 2461-2471.
[21] 王帅兵, 李琳, 赵小军, 等. 定点时间周期有限元法及其在变压器直流偏磁特性分析中的应用[J]. 中国电机工程学报, 2017, 37(17): 5198-5205, 5240.
Wang Shuaibing, Li Lin, Zhao Xiaojun, et al. Fixed- point time-periodic finite element method and its application for DC bias characteristics of trans- former[J]. Proceedings of the CSEE, 2017, 37(17): 5198-5205, 5240.
[22] 王泽忠, 潘超, 周盛, 等. 基于棱边有限元的变压器场路耦合瞬态模型[J]. 电工技术学报, 2012, 27(9): 146-152.
Wang Zezhong, Pan Chao, Zhou Sheng, et al. Transient magnetic-circuit coupled model of trans- former based on edge finite element method[J]. Transactions of China Electrotechnical Society, 2012, 27(9): 146-152.
[23] Budeanu C. Puissances réactives et fictives[M]. Paris: Institut National Roumain pour L’Étude de L’Aménagement et de l’utilisation des sourcesd’Énergie, 1927.
[24] Czarnecki L S, Haley P M. Unbalanced power in four-wire systems and its reactive compensation[J]. IEEE Transactions on Power Delivery, 2015, 30(1): 53-63.
[25] Menti A, Zacharias T, Milias-Argitis J. Geometric algebra: a powerful tool for representing power under nonsinusoidal conditions[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2007, 54(3): 601-609.
[26] Lev-Ari H, Stanković A M. A geometric algebra approach to decomposition of apparent power in general polyphase networks[C]//IEEE 41st North American Power Symposium, Starkville, MS, USA, 2009: 1-6.
[27] 赵小军, 李琳, 程志光, 等. 定点谐波平衡有限元法与叠片铁心直流偏磁磁化特性研究[J]. 中国电机工程学报, 2011, 31(9): 126-132.
Zhao Xiaojun, Li Lin, Cheng Zhiguang, et al. Fixed-point harmonic-balanced finite element method and DC-biasing magnetizing characteristics of laminated core[J]. Proceedings of the CSEE, 2011, 31(9): 126-132.
[28] 金亮, 李育增, 杨庆新, 等. 大规模工程电磁场的亿自由度可扩展并行计算方法[J]. 电工技术学报, 2022, 37(3): 589-598.
Jin Liang, Li Yuzeng, Yang Qingxin, et al. Extensible parallel computing method with hundreds of millions of freedoms for large-scale engineering electro- magnetic field[J]. Transactions of China Electro- technical Society, 2022, 37(3): 589-598.
[29] Biro O, Preis K. On the use of the magnetic vector potential in the finite-element analysis of three- dimensional eddy currents[J]. IEEE Transactions on Magnetics, 1989, 25(4): 3145-3159.
[30] Dlala E, Arkkio A. Analysis of the convergence of the fixed-point method used for solving nonlinear rota- tional magnetic field problems[J]. IEEE Transactions on Magnetics, 2008, 44(4): 473-478.
[31] 孙佳安, 李琳. 考虑次同步分量下时间周期问题的三维定点有限元法及变压器电磁特性分析[J]. 电工技术学报, 2022, 37(14): 3475-3486.
Sun Jiaan, Li Lin. 3-D fixed-point finite element method for time periodic problems with subsyn- chronous components and analysis of transformer electromagnetic characteristics[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3475- 3486.
[32] 王泽忠, 黄天超. 变压器地磁感应电流-无功功率动态关系分析[J]. 电工技术学报, 2021, 36(9): 1948- 1955.
Wang Zezhong, Huang Tianchao. Analysis of geo- magnetically induction current-reactive power dynamic relationship of transformer[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1948-1955.
[33] 潘超, 王泽忠, 李海龙, 等. 基于瞬态场路耦合模型的变压器直流偏磁计算[J]. 电工技术学报, 2013, 28(5): 174-181.
Pan Chao, Wang Zezhong, Li Hailong, et al. DC-bias calculation for single phase transformers based on transient field-circuit coupled model[J]. Transactions of China Electrotechnical Society, 2013, 28(5): 174- 181.
Analysis of Reactive Power of Transformer Core with Subsynchronous Components
Abstract With the increase of subsynchronous oscillation phenomena and risks caused by long-distance wind power transmission systems, power transformers often operate with subsynchronous components, which causes asymmetrical bias magnetization of the core and leads to harmonic distortion and increase in reactive power. Aiming at this mixed time-frequency domain problem of power transformer reactive power with subsynchronous components, firstly, this paper established a 3D field-circuit coupling finite element model based on the fixed-point method to solve the magnetizing current. Secondly, the analysis method of transformer fundamental reactive power characteristics based on the maximum fundamental reactive power and average fundamental reactive power, and a transformer multi-frequency reactive characteristics analysis method based on the multivector power theory are proposed. Thirdly, the no-load experiment of a physical transformer model shows that the time-domain field-circuit coupling model proposed in this paper can accurately simulate the spectral characteristics of the significant components in the magnetizing current. Finally, through the simulation of this transformer, the fundamental reactive power characteristics and multi-frequency reactive power characteristics of the transformer are calculated and analyzed.
keywords：Subsynchronous frequency components, asymmetric bias, 3D field-circuit coupling finite element, reactive power, multivector power theory
DOI: 10.19595/j.cnki.1000-6753.tces.211986
中图分类号：TM41
国家重点研发计划课题（2021YFB2401703）和国家自然科学基金（52177005）资助项目。
收稿日期 2021-12-07
改稿日期 2022-01-17
孙佳安 男，1994年生，博士研究生，研究方向为电磁场数值计算与变压器暂态建模。E-mail: 1182101023@ncepu.edu.cn
李 琳 男，1962年生，教授，博士生导师，研究方向为电磁场理论及应用与电力系统电磁兼容。E-mail: lilin@ncepu.edu.cn（通信作者）
（编辑 崔文静）