变厚板塑性形变超声非线性响应及其实验
赵国梁1,2 刘素贞1,2 张 闯1,2 金 亮1,2 杨庆新1
(1. 省部共建电工装备可靠性与智能化国家重点实验室(河北工业大学) 天津 300130 2. 河北工业大学河北省电磁场与电器可靠性重点实验室 天津 300130)
摘要 超声波在变厚板中的传播特性尚不明确,构建高精度超声非线性响应模型是将超声非线性技术用于变厚板早期损伤检测的关键。基于金属塑性形变的本构关系,推导单轴拉伸下变厚板塑性应变的分布方程,将表征变厚板塑性应变分布的函数与超声波波动方程结合,构建变厚板超声非线性响应模型。由构建模型可知:二次谐波幅值(A2)与基波幅值(A1)二次方的比值(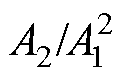 )随传播距离及波数均呈“二次方”增长;相同传播距离,
)随传播距离及波数均呈“二次方”增长;相同传播距离,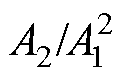 与总体塑性形变呈正相关,
与总体塑性形变呈正相关,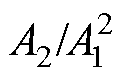 携带了变厚板塑性形变信息。在COMSOL中构建铝合金变厚板弹塑性模型,验证了利用线性方程描述变厚板塑性应变分布的合理性;构建电磁超声系统,验证了超声非线性响应模型的有效性。制备不同塑性形变的变厚板试件,研究电磁超声表面波在其中的传播规律。实验结果表明,构建的超声非线性响应模型能够精确描述变厚板中超声波的传播行为。该文为利用超声非线性技术实现变厚板塑性损伤的量化检测提供理论基础,为超声非线性技术在异形结构上的应用提供了研究思路。
携带了变厚板塑性形变信息。在COMSOL中构建铝合金变厚板弹塑性模型,验证了利用线性方程描述变厚板塑性应变分布的合理性;构建电磁超声系统,验证了超声非线性响应模型的有效性。制备不同塑性形变的变厚板试件,研究电磁超声表面波在其中的传播规律。实验结果表明,构建的超声非线性响应模型能够精确描述变厚板中超声波的传播行为。该文为利用超声非线性技术实现变厚板塑性损伤的量化检测提供理论基础,为超声非线性技术在异形结构上的应用提供了研究思路。
关键词:电磁超声换能器 变厚板 超声非线性 塑性形变
0 引言
在工业界追求节能环保和轻量化的大背景下,铝合金材质以较低的密度和良好的可塑性等诸多优点,获得了日益广泛的应用[1]。在工程中,很多关键部位的铝合金结构承受着拉伸载荷,由于塑性损伤的累积而导致的突然失效,往往会引起重大安全事故[2]。研究表明,微观损伤(如位错、滑移等)占材料疲劳寿命的80%~90%,因而在宏观损伤(如裂纹和断裂等)出现之前,对结构的健康状态或剩余服役寿命给出精确可靠的评估意义重大[3]。
常规超声检测的理论极限为超声波波长的1/2,对微纳级别的缺陷几乎没有检出能力[4]。扫描电镜和透射电镜能够精确追踪材料微观组织的演化过程,但需要从被测结构上取样,这在工业应用中通常不被允许[5]。研究表明,微观损伤会引起材料的非线性变化,超声波在其中传播时,会发生畸变并产生各次谐波[6]。由于超声非线性对材料的微观损伤极为敏感,在材料早期损伤检测方面,超声非线性技术越来越受到学者们关注[7]。
利用超声非线性技术对材料的微观损伤进行检测,始于20世纪60年代,1965年A. Hikata等对铝单晶介质施加拉力,并向其中注入了一列超声波,在静态拉应力从0增长到106dyn/cm2的过程中,二次谐波的幅值显著增加,A. Hikata等认为二次谐波的幅值同静态应力值以及位错环长度有关[8]。W. J. N. de Lima等求解了超声波波动方程,并分析了和频波、差频波及二次谐波的产生机理[9]。J. Y. Kim和J. H. Cantrell等分别研究了微观缺陷对材料非线性系数b 的影响,并分别提出了b 的计算方法[10-11]。C. Pruell和C. Bermesa等基于Lamb波对铝合金板进行了超声非线性检测,结果显示,当塑性应变小于12%时,b 随塑性形变的增加几乎呈线性增长[12-13]。S. Choi等利用线阵激光束诱发了表面波,并对发生塑性形变的铝合金板进行了检测,结果显示,b 与试件损伤程度呈正相关[14]。文献[15]利用电磁超声对铝合金试件进行了超声检测,结果显示,当塑性应变小于7%时,b 随塑性形变的增加近似呈线性增加。
目前,超声非线性技术在金属材料塑性形变的量化检测方面已经取得了一定成果,但已有研究大多针对等厚板进行。变厚板作为一种常用结构,其设计初衷是实现结构减重且不影响性能,如飞机襟翼和风电叶片等。由于实际工况的复杂性,变厚板结构往往承受多种非预期载荷,且变厚板的结构特点会增强这些载荷的破坏性,如风轮流场扰动和风剪效应等会导致叶片不均匀振动进而引起疲劳损 伤[16-17]。工业界对变厚板结构的早期损伤评估有很大需求,而相关的研究很少[18]。M. E. C. El-Kettani等利用数值仿真研究了Lamb波在变厚板中传播时其速度和频率的变化规律[19]。P. Marical等基于有限元方法研究了Lamb波在变厚板中传播时的模态转换[20]。尚世同等研究了Lamb波截止频率与变厚板厚度变化的关系[21]。上述文献大多利用Lamb波的频散效应对变厚板结构进行检测,但存在以下两个问题:①检测目标仅限于结构表面缺陷,对内部损伤不敏感;②检测结果在一定程度上反映了变厚板结构的外观变化,而不能对材料的微观损伤状态做出评估。
考虑到成本、敏感性及技术积累,超声非线性仍是变厚板早期损伤检测的最佳手段之一[18]。由于变厚板的横截面积沿轴向均匀变化,相同载荷下,其损伤分布和等厚板并不一致,因而基于等厚板得到的超声非线性检测方法并不能直接应用于变厚板。塑性形变是一种典型的损伤模式,本文基于材料塑性形变的本构方程,推导单轴拉伸下变厚板塑性应变分布,并将表征变厚板塑性分布规律的非线性系数函数引入超声波波动方程,利用微扰法推导塑性形变下变厚板的超声非线性响应模型。利用COMSOL软件构建变厚板弹塑性力模型和电磁超声系统,分别对塑性应变分布规律和超声非线性响应进行有限元验证,最后搭建电磁超声非线性检测平台,对超声非线性响应模型进行实验验证。
1 变厚板塑性形变的超声非线性响应模型
1.1 变厚板塑性应变分布
金属塑性形变阶段的非线性应力应变本构关系可由Hollomon模型描述,图1为合金塑性阶段应力应变示意图。图1中,sb为材料抗拉强度,ss为材料屈服强度。在该阶段,应力 表示为
表示为
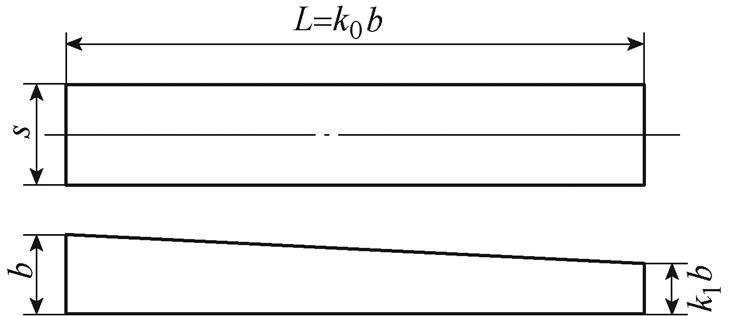
图2为变厚板尺寸示意图,其厚端厚度为b,薄端厚度为k1b,长度为L(L=k0b),宽度为s,角度为arctan[(b-k1b)/L]。工程中常见变厚板结构的角度通常小于3°[18],即1-k1≤0.052k0。
设y轴平行于变厚板轴线,起始点与变厚板厚端平齐,当变厚板在轴向拉力F的作用下发生塑性形变时,根据式(1),沿变厚板轴向的塑性应变为
对式(2)进行积分,可得变厚板沿拉伸方向的总体塑性形变。设总体塑性形变D,表示为
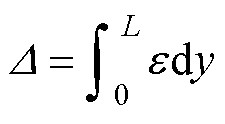 (3)
(3)
计算可得
将式(4)代入式(2)可以得到变厚板的塑性应变分布为
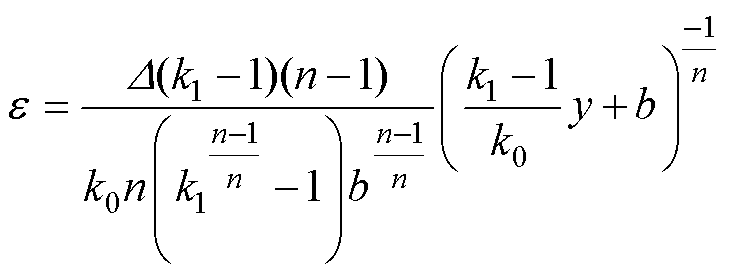 (5)
(5)
变厚板不发生颈缩的条件是薄端的应力小于抗拉极限,将式(5)代入式(1),可以得到以塑性形变为参考的颈缩临界点,即
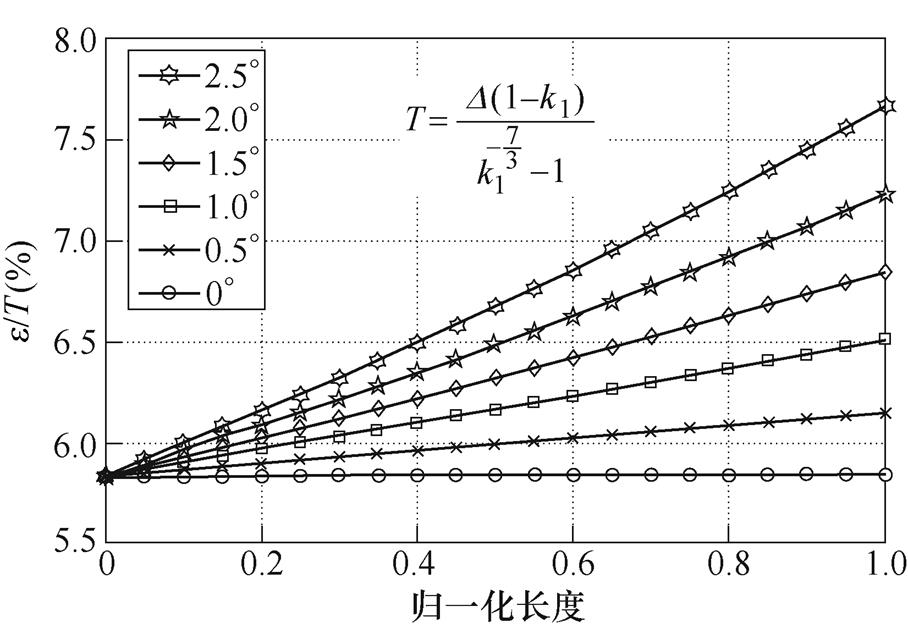
合金的硬化指数n通常在0.2~0.5之间,为量化观察变厚板塑性应变分布,这里取n=0.3。以美国国家可再生能源实验室(National Renewable Energy Laboratory, NREL)的5MW风电机组叶片为参考,其变厚度部分长度约40m,厚端厚度约2m,即b=2m,k0=20。根据式(5),在不同塑性形变下,当变厚板角度分别为0°、0.5°、1°、1.5°、2°和2.5°时,根据式(5),其塑性应变沿轴向的分布如图3所示。
图3中,k1的取值由变厚板角度决定,为了使结果更具一般性,未对塑性形变D 进行赋值。T的数值由k1和D 决定,其计算公式已在图3中给出,图3的纵坐标与T相关。由图3可知,当角度为0°时,沿轴向各处的塑性应变相等,此时变厚板实际上为等厚板;当角度大于0°时,变厚板各处的塑性应变不再相等,呈现出厚端塑性应变小而薄端塑性应变大的规律,且随着角度的增大,这个规律越发明显。总体而言,变厚板塑性应变沿轴向近似呈线性分布。
1.2 变厚板塑性形变的超声非线性响应
一维条件下超声波波动方程可以表示[22-24]为
式中,u为质点位移;c为超声波传播速度;t和x分别为时间和传播距离。当材料发生微小损伤时,其应力s-应变e 本构关系将以非线性形式出现,即
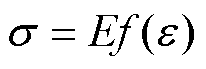 (8)
(8)
式中,E为弹性模量。将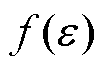 以泰勒级数形式展 开为
以泰勒级数形式展 开为
式中,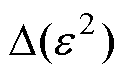 为e 的高阶无穷小。式(7)~式(9)为广泛使用的超声波波动方程,在此基础上,结合1.1节中变厚板近似线性的损伤分布,利用材料非线性系数的函数来表征其损伤分布规律,建立超声非线性响应模型,为研究超声波在变厚板中的传播规律建立理论基础。
为e 的高阶无穷小。式(7)~式(9)为广泛使用的超声波波动方程,在此基础上,结合1.1节中变厚板近似线性的损伤分布,利用材料非线性系数的函数来表征其损伤分布规律,建立超声非线性响应模型,为研究超声波在变厚板中的传播规律建立理论基础。
文献[12]从理论上推导了材料非线性系数与塑性应变的线性关系。文献[13-15]表明,对于铝合金,这种线性关系在一定塑性应变范围内十分明显。据此,变厚板塑性形变沿轴向的近似线性分布,可以用材料非线性系数的一次函数来表征,即
式中,Q为塑性形变参数,变厚板总塑性形变越大,Q值越大。将式(9)、式(10)代入式(7),超声波在变厚板中的波动方程可以表示为
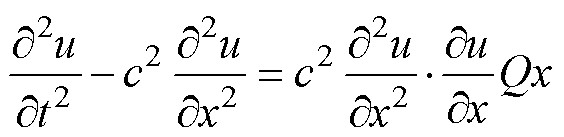 (11)
(11)
在等厚度结构中构建超声波非线性波动方程时,材料非线性系数为常数,而变厚板结构中材料非线性系数为超声波传播距离的函数,这导致式(11)为非典型偏微分方程,因而无法得到其精确解。基于微扰理论,对初始系统赋值,并计算与之匹配的微扰项,从而求出待求系统的近似解。设式(11)的解可以展开为
式中,u0(x, t)为一列振幅为A1、角频率为ω、波数为k的正弦波,即
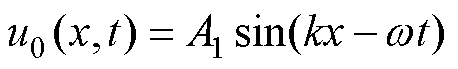 (13)
(13)
根据微扰动理论,首先将式(13)代入式(11)的右端得
设与式(14)相匹配的u1(x, t)为
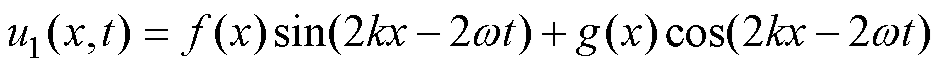 (15)
(15)
式中,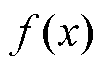 和
和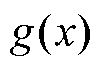 为构造函数。将式(15)代入式(14)的左端得
为构造函数。将式(15)代入式(14)的左端得
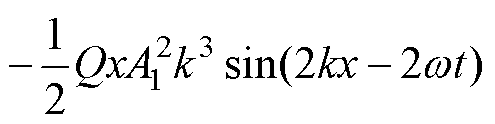 (16)
(16)
式中,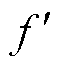 和
和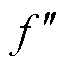 分别为
分别为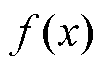 的一阶和二阶导数;
的一阶和二阶导数;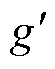 和
和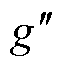 分别为g(x)的一阶和二阶导数。由式(16)可知
分别为g(x)的一阶和二阶导数。由式(16)可知
对式(17)进行整理,可得
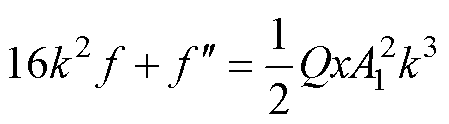 (18)
(18)
根据二阶线性微分方程的解法,式(18)的解为
将式(19)代入式(17),可得到g(x)的解为
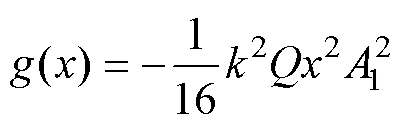 (20)
(20)
将式(19)和式(20)代入式(15),可得
式中,N和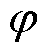 分别为简化u1(x, t)的表达式而构建的变量,即
分别为简化u1(x, t)的表达式而构建的变量,即
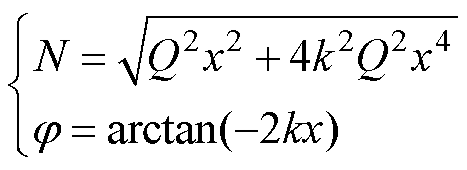 (22)
(22)
在超声非线性检测中,激励波的频率通常高于1MHz,声波在固体中的传播速度在103m/s这一量级,由此可知,波数k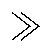 1。因而,式(21)可以简化为
1。因而,式(21)可以简化为
二次谐波的幅值A2为
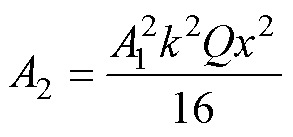 (24)
(24)
由上述推导过程可知,当一列正弦波在发生塑性形变的变厚板中传播时,将激发二次谐波,且二次谐波的幅值A2是基波幅值A1、传播距离x、波数k以及塑性形变参数Q的函数。由式(24)可得
至此得到了变厚板超声非线性响应模型。超声非线性响应模型的建立,为变厚板塑性形变的量化检测提供了理论基础。
2 变厚板塑性形变有限元分析
2.1 变厚板轴向拉伸仿真设置
塑性应变的线性分布是超声非线性响应模型的建立基础,利用仿真研究轴向拉伸下变厚板塑性应变分布规律。在COMSOL固体力学模块中建立变厚板的三维几何仿真模型。变厚板长度226mm,宽度40mm,厚度由5mm均匀减少至4.8mm。在材料库中选取铝合金材料参数并导入仿真模型,铝合金材料参数见表1。
表1 铝合金材料参数
Tab.1 Material parameters of aluminum alloy

参 数数 值 密度/(kg/m3)2 700 泊松比0.33 弹性模量/GPa70 电导率/(S/m)3.5×10-7 相对磁导率1
在固体力学模块的塑性接口下导入AA6061-T6铝合金的实测应力应变曲线,网格剖分选择“超细”规格。将变厚板的右端面设置为固定约束,在左端面施加拉伸载荷,研究总体塑性形变为5mm、10mm、15mm、20mm、24mm和28mm时塑性应变分布情况。对仿真得到的塑性应变分布和根据式(5)计算得到的塑性应变分布进行对比分析。通过AA6061-T6的实测应力应变曲线可知,其材料参数K约为166MPa,硬化指数n约为0.25,抗拉强度sb=282MPa,屈服强度ss=180MPa。变厚板模型厚端厚度b=0.005m,k0=45.2,k1=0.98。
2.2 变厚板轴向拉伸仿真结果
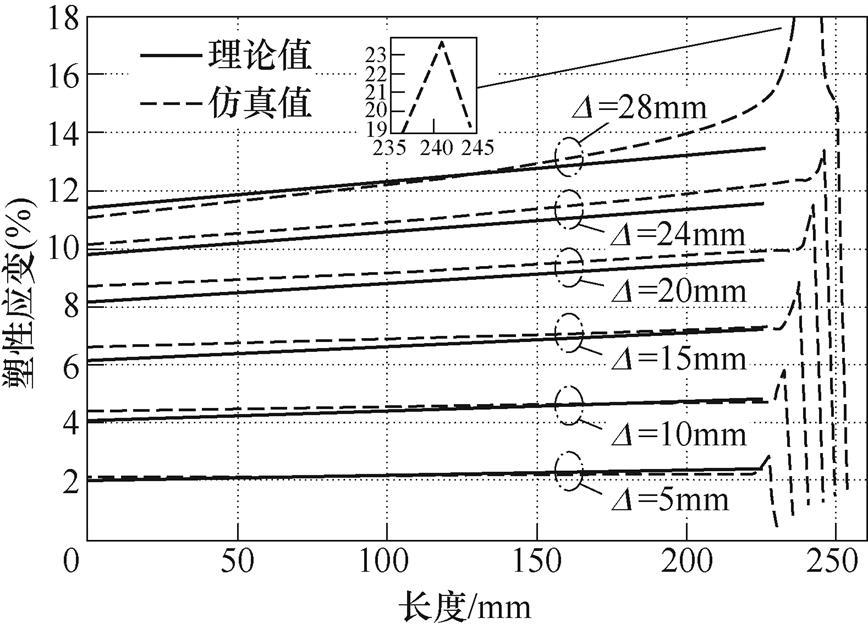
图4为塑性形变分别为5mm、10mm、15mm、20mm、24mm和28mm时变厚板塑性应变仿真值与根据式(5)计算得到的理论值。仿真结果表明,当塑性形变分别为5mm、10mm、15mm、20mm和24mm时,塑性应变沿变厚板轴向由厚端至薄端逐渐增大,近似呈线性增长,理论值与仿真值的吻合度较好。在仿真曲线的右端,均有一个尖峰,随后快速下降,这是将变厚板右侧端面设置为固定约束导致的。当塑性形变为28mm时,仿真曲线右端的尖峰(该尖峰的位置和大小如图4中小窗所示)远高于其他曲线的尖峰。这表明此时变厚板右端发生了颈缩。根据式(6),仿真中变厚板模型发生颈缩的理论临界塑性形变为30.9mm,理论临界值与仿真临界值相差约10%。仿真结果表明,式(5)能够准确描述变厚板的塑性应变分布。
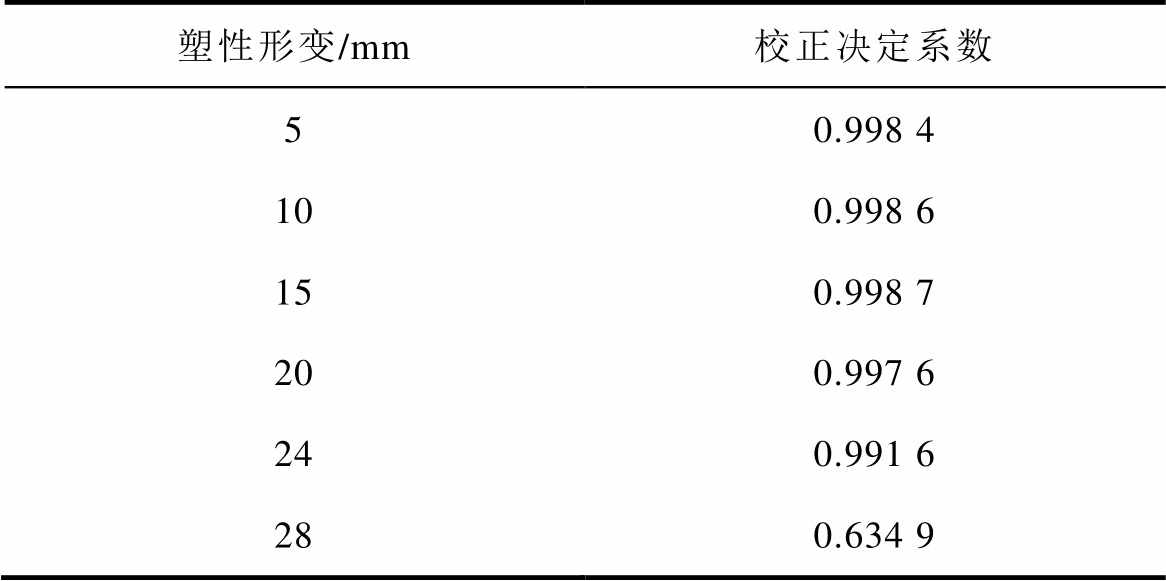
为验证变厚板塑性应变分布线性表征的合理性,对仿真结果进行了线性拟合,线性拟合的校正决定系数(Adjusted R-Square, ARS)见表2。在数据分析中,校正决定系数用来评价回归方程的优劣,其取值范围为[0, 1],校正决定系数越大,表明拟合越优。由表2可知,当变厚板的塑性形变分别为5mm、10mm、15mm、20mm和24mm时,其塑性应变线性拟合的校正决定系数十分接近1,这表明塑性应变由厚端至薄端几乎呈线性增长,利用线性方程描述变厚板的塑性应变具有可行性。当变厚板塑性形变为28mm时,其薄端发生了颈缩,因而仿真值和理论值出现了较大偏离。由于颈缩已经超出了材料早期塑性损伤阶段,因而不属于本文研究范畴。
表2 仿真结果线性拟合的校正决定系数
Tab.2 Adjusted R-square of linear fitting on simulation results
塑性形变/mm校正决定系数 50.998 4 100.998 6 150.998 7 200.997 6 240.991 6 280.634 9
3 超声非线性响应模型有限元分析
为了验证1.2节中超声非线性响应模型的正确性,利用COMSOL软件的多物理场耦合功能,模拟电磁超声表面波在非线性参数沿轴向线性变化的介质中的传播。通过控制变量,分别研究超声非线性响应随波数k、塑性形变参数Q以及传播距离x的变化规律。
3.1 超声非线性响应仿真设置
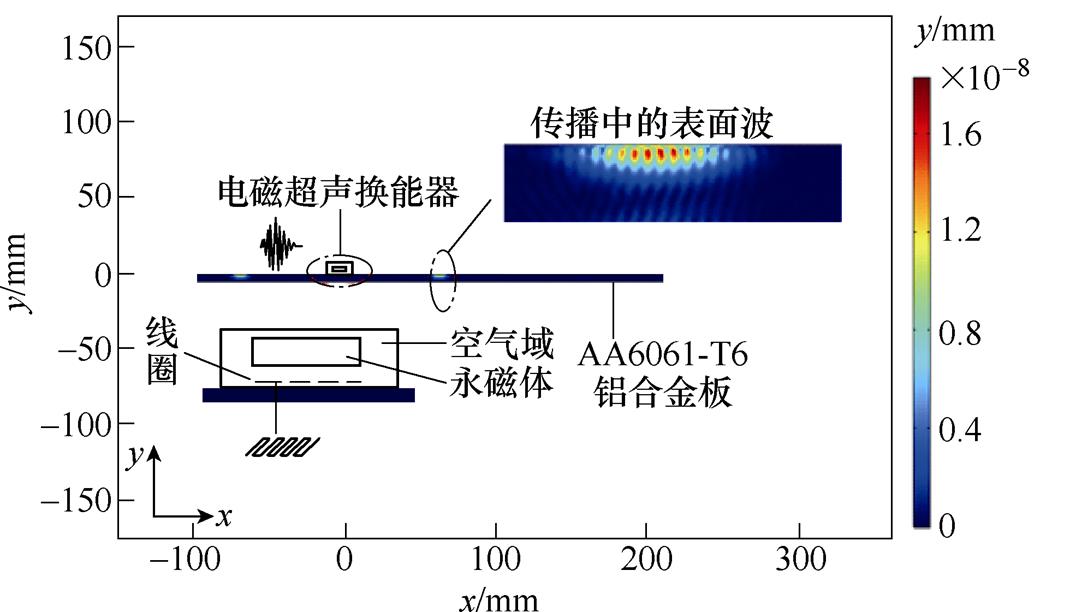
在二维空间构建仿真系统,电磁超声非线性系统仿真模型如图5所示。仿真的设置主要包括:AA6061-T6铝合金变厚板,在0~226mm范围内,变厚板厚度由5mm均匀减至4.8mm,变厚板的相关参数见表1;空气域,参数由软件材料库直接导入;永磁体,材质为钕铁硼,剩余磁通密度1.2T;线圈参数见表3。图5右侧的图例为质点在y方向的位移。
表3 线圈参数
Tab.3 Parameters of coil

参 数数 值 电导率/(S/m)2.67×10-7 磁导率/(H/m)4p×10-7 导线截面长/mm0.2 导线截面宽/mm0.05
仿真中,线圈距离变厚板0.2mm,线圈中施加5个周期经汉宁窗调制的tone-burst激励电流。为减少计算,将板左右两侧面和下表面设置为低反射边界。变厚板的下表面对应的纵坐标为y=-5mm,电磁超声换能器的右端面对应的横坐标为x=0。表面波每传播30mm设置一个检测点,共设置7个检测点,检测点距离变厚板上表面0.05mm,7个检测点的坐标分别为(30, -0.077)mm、(60, -0.103)mm、(90, -0.130)mm、(120, -0.156)mm、(150, -0.183)mm、(180, -0.209)mm和(210, -0.236)mm,检测参数为质点在垂直于波传播方向上的位移。仿真中,Q的设置值为0.15、0.30、0.45、0.60和0.75,f的设置值为1.0MHz、1.3MHz、1.6MHz、1.9MHz和2.2MHz,x的范围为0~210mm。
3.2 仿真结果分析
激励波波数与频率成正比,通过改变激励波频率,可以间接研究波数对超声非线性响应的影响,归一化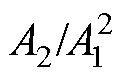 随激励波频率的变化如图6所示,归一化
随激励波频率的变化如图6所示,归一化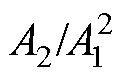 随塑性形变参数的变化如图7所示。
随塑性形变参数的变化如图7所示。
图6a为激励波取不同频率时,第4个检测点(120, -0.156)mm接收信号的频谱。此时表面波的传播距离为120mm。为了更加清楚地展示二次谐波幅值,图6a采用了对数形式的纵坐标。图6a显示,随着激励波频率的增加,基波幅值变化不大,2次谐波幅值逐渐增长。以激励波频率为1.0MHz时的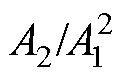 为基准,计算5个频率下归一化
为基准,计算5个频率下归一化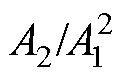 的理论值和仿真值,结果如图6b所示。根据式(25),
的理论值和仿真值,结果如图6b所示。根据式(25),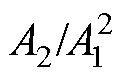 与k2成正比,5个频率下,归一化
与k2成正比,5个频率下,归一化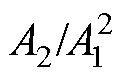 的理论值分别为1、1.69、2.56、3.61和4.84。归一化
的理论值分别为1、1.69、2.56、3.61和4.84。归一化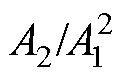 的仿真值分别为1、1.60、2.49、3.50和4.75。仿真值与理论值最大相差5.3%,平均相差2.58%,两者具有较好的吻合度。
的仿真值分别为1、1.60、2.49、3.50和4.75。仿真值与理论值最大相差5.3%,平均相差2.58%,两者具有较好的吻合度。
通过改变塑性形变参数Q,研究其对超声非线性响应的影响。图7a为Q取不同值时,第4个检测点(120, -0.05)mm接收信号的频谱。为了更加清楚地展示二次谐波幅值,图7a采用了对数形式的纵坐标。
图7a显示,随着Q值的增长,基波幅值几乎没有变化,而二次谐波幅值的增长比较明显。以Q= 0.15时的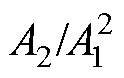 为基准,计算归一化
为基准,计算归一化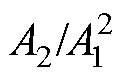 的理论值和仿真值,结果如图7b所示。根据式(25),
的理论值和仿真值,结果如图7b所示。根据式(25),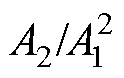 与Q成正比,五种情况下,归一化
与Q成正比,五种情况下,归一化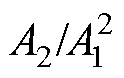 的理论值分别为1、2、3、4和5。归一化
的理论值分别为1、2、3、4和5。归一化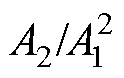 的仿真值分别为1、2.05、3.11、4.16和5.19。仿真值与理论值最大相差4.0%,平均相差2.8%,两者具有较好的吻合度。归一化
的仿真值分别为1、2.05、3.11、4.16和5.19。仿真值与理论值最大相差4.0%,平均相差2.8%,两者具有较好的吻合度。归一化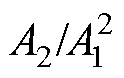 随传播距离的变化如图8所示。
随传播距离的变化如图8所示。
图8a为7个检测点接收信号的频谱。为了更加清楚地展示二次谐波幅值,图8a采用了对数形式的纵坐标。图8a显示,随着传播距离的增加,基波幅值逐渐降低,降低幅度很小,二次谐波幅值逐渐增长。以传播距离为30mm时的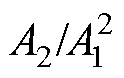 为基准,计算7个检测点归一化
为基准,计算7个检测点归一化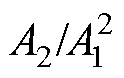 的理论值和仿真值,结果如图8b所示。根据式(25),
的理论值和仿真值,结果如图8b所示。根据式(25),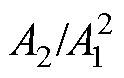 与x2成正比,7个检测点归一化
与x2成正比,7个检测点归一化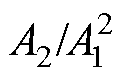 的理论值分别为1、4、9、16、25、36和49。归一化
的理论值分别为1、4、9、16、25、36和49。归一化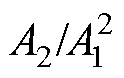 的仿真值分别为1、4.13、9.21、16.74、26.15、36.98和50.12。仿真值与理论值最大相差4.6%,平均相差2.8%,两者具有较好的吻合度。
的仿真值分别为1、4.13、9.21、16.74、26.15、36.98和50.12。仿真值与理论值最大相差4.6%,平均相差2.8%,两者具有较好的吻合度。
仿真结果表明,本文所构建的变厚板超声非线性响应模型能够精确描述超声波在发生塑性形变的变厚板中的传播行为,可以为变厚板塑性损伤的量化检测提供理论支持。
4 电磁超声非线性检测实验结果与分析
4.1 试件制备与实验平台搭建
为了更深入地研究变厚板的超声非线性响应,搭建电磁超声非线性检测平台并进行实验研究。
实验需要4块变厚板(记为1~4号),为确保材料性能和机械性能一致,4块变厚板取自同一块AA6061-T6板材,并在室温下由数控机床加工至图9所示变厚板尺寸。变厚板总长496mm,变厚度部分长226mm,在变厚度部分,厚度由5mm均匀减至4.8mm。1号试件保持完好,不进行任何加载。利用WDW3100电子万能试验机对2~4号试件实施拉伸加载,直至变厚度部分分别出现约10mm、15mm和20mm的塑性形变。
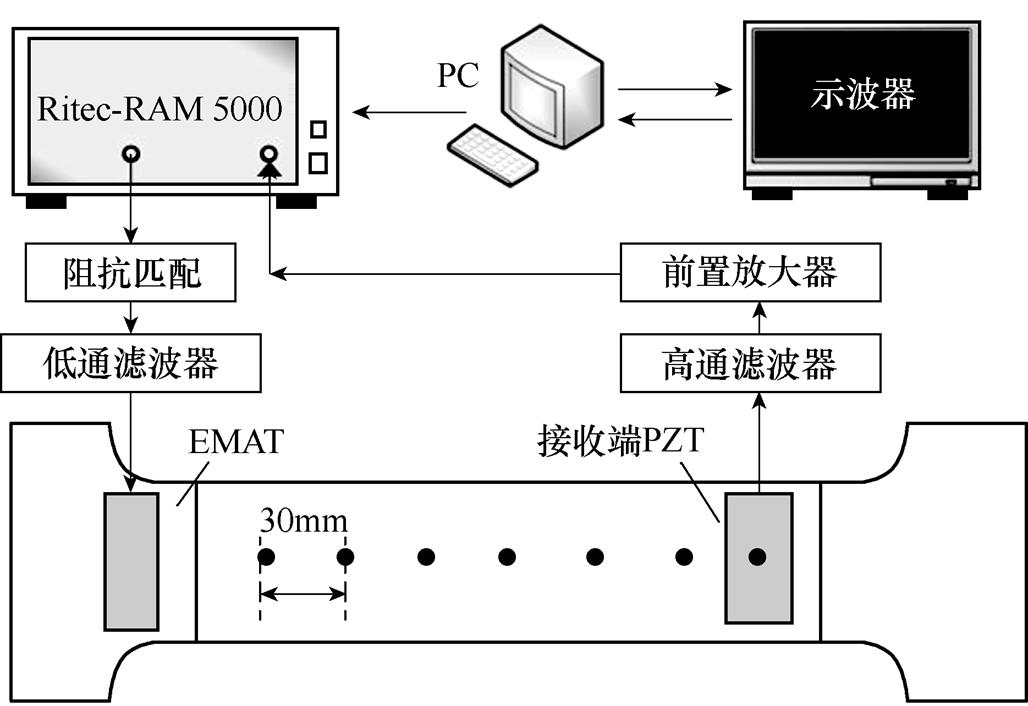
电磁超声非线性检测平台如图10所示,主要包括电磁超声换能器(Electromagnetic Acoustic Transducer, EMAT)、压电传感器(Piezoelectricity, PZT)接收探头、滤波器、匹配阻抗和前置放大器。
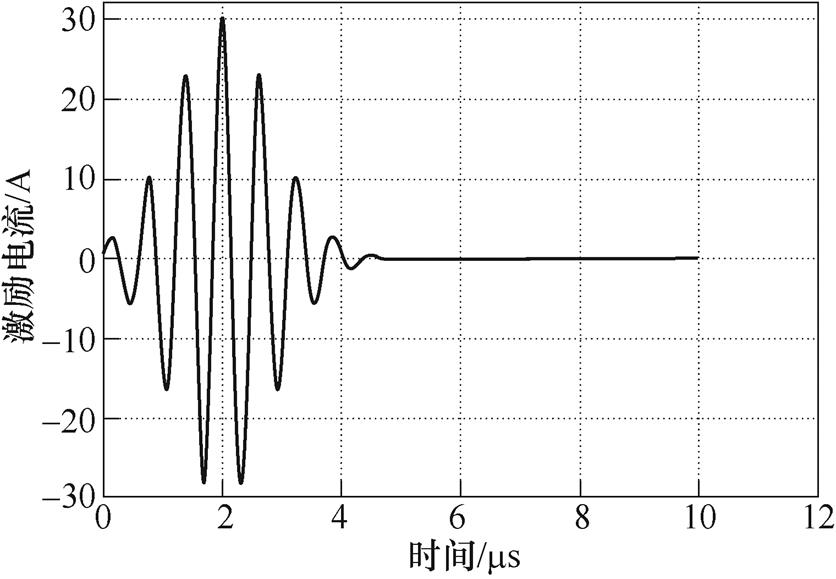
实验中,利用Ritec-RAM 5000系统输出频率为1.6MHz,经汉宁窗调制的5个周期tone-burst激励电流至EMAT,激励电流信号如图11所示。EMAT在变厚板厚端激发表面波,表面波向薄端传播。沿变厚板轴向每隔30mm设置一个检测点,共7个检测点,如图10中变厚板上的圆形所示。在检测点处利用压电探头接收信号并通过FFT获得基波和二次谐波幅值。实验进行3次,实验结果取平均值。
4.2 实验结果及分析
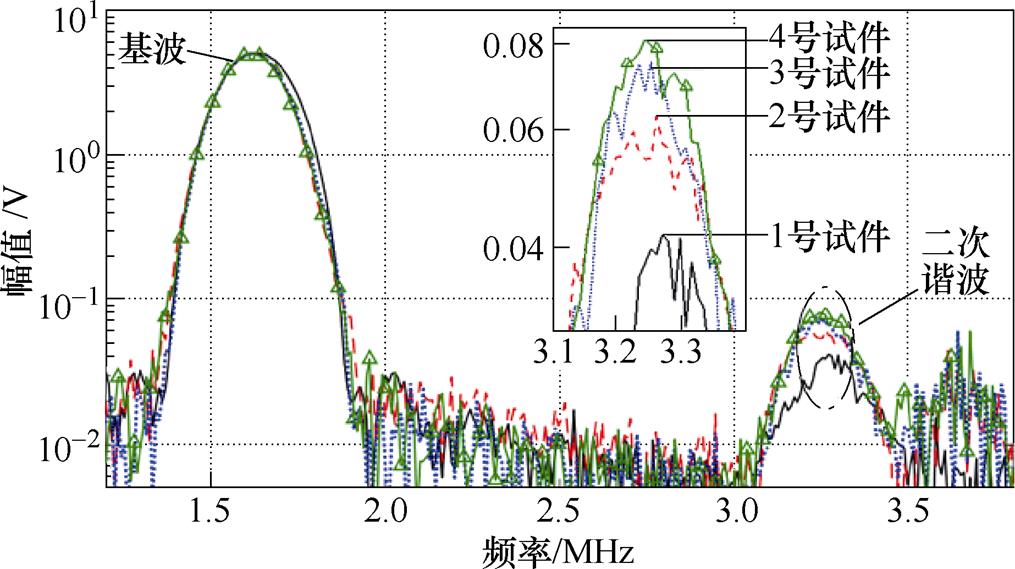
第1个测试点上的检测结果如图12所示,此时表面波传播了30mm。图12中,在4个试件上均检测到了二次谐波成分,为了更加清楚地展示二次谐波幅值,对二次谐波进行了局部放大。由图12可知,1号试件上二次谐波幅值较小,2~4号试件上的二次谐波幅值较大。
通过提取基波幅值A1与二次谐波幅值A2,获得了7个测试点上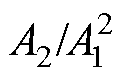 的值,如图13所示。图13中,1号试件上的
的值,如图13所示。图13中,1号试件上的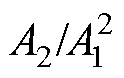 较小,约为1.6×10-3V-1,且随传播距离的增加未出现明显变化。相比1号试件,2~4号试件上的
较小,约为1.6×10-3V-1,且随传播距离的增加未出现明显变化。相比1号试件,2~4号试件上的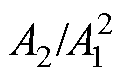 显著提高,且随传播距离的增加而增加。这表明超声非线性对变厚板的塑性形变十分敏感。图13中,在相同检测点,均为4号试件上的
显著提高,且随传播距离的增加而增加。这表明超声非线性对变厚板的塑性形变十分敏感。图13中,在相同检测点,均为4号试件上的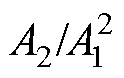 最大,3号试件次之,2号试件最小。这表明当励波波数k和传播距离x恒定时,
最大,3号试件次之,2号试件最小。这表明当励波波数k和传播距离x恒定时,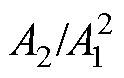 与Q呈正相关,实验结果与变厚板超声非线性响应模型分析相一致。
与Q呈正相关,实验结果与变厚板超声非线性响应模型分析相一致。
图13中,2号、3号和4号试件的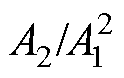 曲线均在第4个检测点上发生了较为显著的转折,这是由于实际拉伸中变厚板塑性形变的不均匀增长造成的。金属塑性形变是位错滑移的宏观表现,由于位错结构的运动是依次进行的,维持位错运动的力小于致使位错源开动的力,因而,金属材料在从弹性阶段进入塑性阶段时,应力会波动或者下降,这在应力应变上表现为曲线在屈服点附近的振荡。图14为实测的准静态拉伸下AA6061-T6铝合金材料的应力应变曲线,图中在应变约为4%时,应力出现了较为明显的振荡。在拉力作用下,变厚板会从薄端到厚端次第进入塑性形变阶段,即弹性阶段和塑性阶段的转换点会随着拉伸逐渐移动。随着拉力的不断增大,当转换点恰好到达第4个和第5个检测点之间时,由于薄端横截面面积小于厚端,且塑性形变进一步使薄端横截面面积减小,薄端开始加速塑性形变。塑性形变增速差异的分界线落在了第4个和第5个检测点之间。材料非线性系数与塑性应变呈正相关,因而在分界线的右侧,谐波的激发量明显提升。
曲线均在第4个检测点上发生了较为显著的转折,这是由于实际拉伸中变厚板塑性形变的不均匀增长造成的。金属塑性形变是位错滑移的宏观表现,由于位错结构的运动是依次进行的,维持位错运动的力小于致使位错源开动的力,因而,金属材料在从弹性阶段进入塑性阶段时,应力会波动或者下降,这在应力应变上表现为曲线在屈服点附近的振荡。图14为实测的准静态拉伸下AA6061-T6铝合金材料的应力应变曲线,图中在应变约为4%时,应力出现了较为明显的振荡。在拉力作用下,变厚板会从薄端到厚端次第进入塑性形变阶段,即弹性阶段和塑性阶段的转换点会随着拉伸逐渐移动。随着拉力的不断增大,当转换点恰好到达第4个和第5个检测点之间时,由于薄端横截面面积小于厚端,且塑性形变进一步使薄端横截面面积减小,薄端开始加速塑性形变。塑性形变增速差异的分界线落在了第4个和第5个检测点之间。材料非线性系数与塑性应变呈正相关,因而在分界线的右侧,谐波的激发量明显提升。
研究表明,材料发生塑性形变时,其内部的位错会被第二相粒子等钉扎,形成类似弦的弓出,弓出的弦状结构称为位错弦。当超声波作用在位错弦上时,位错弦就会产生受迫振动,使入射波发生波形畸变,产生谐波,材料显现出非线性特征[25]。文献[26-27]表明,由材料位错结构引起的非线性系数bd正比于位错单极子密度。在一定范围内,位错单极子密度正比于材料塑性形变量[28]。可知由位错引起的材料非线性与塑性形变量呈正相关。实验中,4号试件塑性形变量最大,因而由位错引起的超声非线性参数最大,3号试件次之,2号试件最小,3个试件相同传播距离上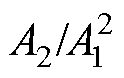 大小关系与之相应,这表明变厚板超声非线性响应模型能够准确反映塑性形变对超声非线性的影响。
大小关系与之相应,这表明变厚板超声非线性响应模型能够准确反映塑性形变对超声非线性的影响。
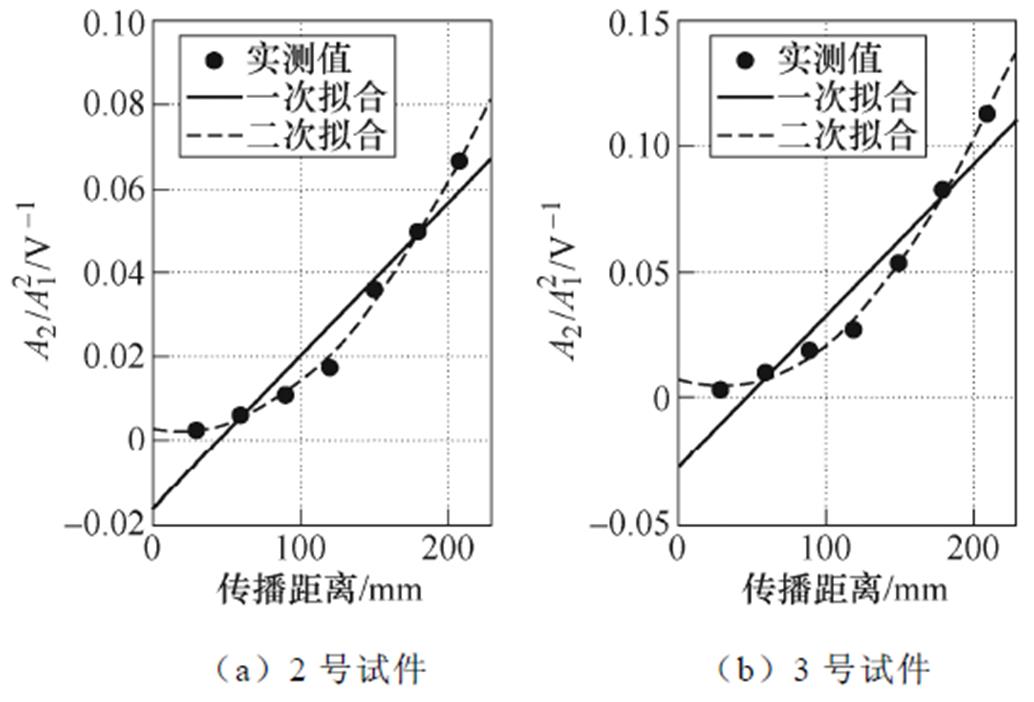
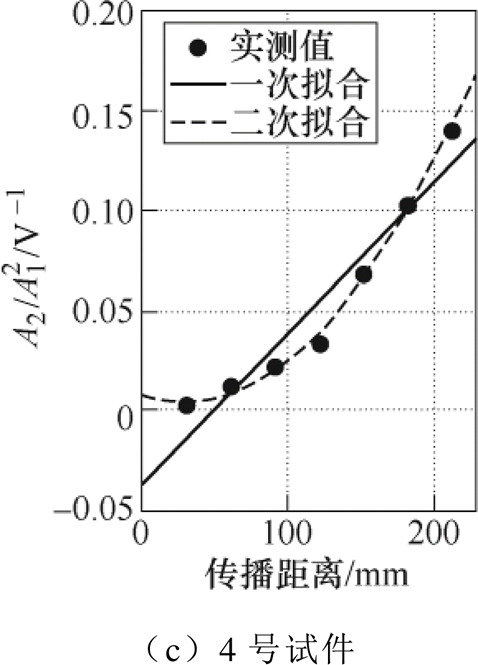
分别对2~4号试件的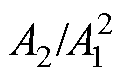 与传播距离x进行线性、二阶和三阶拟合,残差模见表4。表4中,相比线性拟合,二阶拟合的残差模大幅下降,三阶及更高阶次的拟合,其残差模的降幅很小,且拟合曲线的不稳定性显著增加,因而认为二阶拟合为最佳。图15为2~4号试件上测试数据的一次和二次拟合,结果表明,实验中
与传播距离x进行线性、二阶和三阶拟合,残差模见表4。表4中,相比线性拟合,二阶拟合的残差模大幅下降,三阶及更高阶次的拟合,其残差模的降幅很小,且拟合曲线的不稳定性显著增加,因而认为二阶拟合为最佳。图15为2~4号试件上测试数据的一次和二次拟合,结果表明,实验中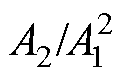 随传播距离基本呈“二次方”式增长。实验结果与变厚板超声非线性响应模型的分析一致。
随传播距离基本呈“二次方”式增长。实验结果与变厚板超声非线性响应模型的分析一致。
表4 各阶拟合的残差模
Tab.4 Residual error of each order fitting
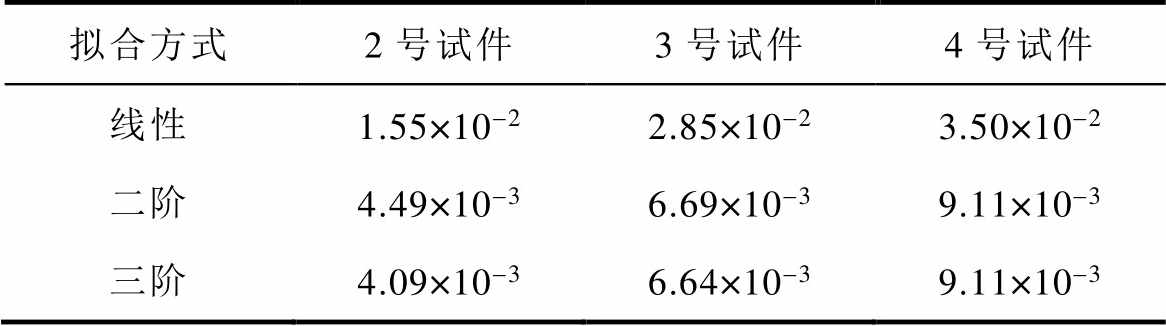
拟合方式2号试件3号试件4号试件 线性1.55×10-22.85×10-23.50×10-2 二阶4.49×10-36.69×10-39.11×10-3 三阶4.09×10-36.64×10-39.11×10-3
文献[12-15]研究结果表明,位错引起的材料非线性与塑性形变量呈正相关。对于变厚板而言,几何特征导致其塑性形变沿轴向线性分布,相应地,bd亦会沿轴向线性分布。bd的大小代表激发谐波能力的强弱。在变厚板塑性形变的线性分布特征和累积效应的共同作用下,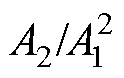 的增长总是在初期比较平缓,而后变得迅速,整体呈“二次方”趋势,实验结果与超声非线性响应模型高度吻合。
的增长总是在初期比较平缓,而后变得迅速,整体呈“二次方”趋势,实验结果与超声非线性响应模型高度吻合。
综上所述,变厚板塑性分布方程能够准确反映单轴拉伸下变厚板塑性损伤的分布规律,超声非线性响应模型能够精准地描述微观层面超声波与位错等组织相互作用后的畸变规律。仿真和实验结果表明,超声非线性响应模型在变厚板特殊的损伤分布和超声非线性响应之间搭建了精确的数学关系,为变厚板塑性形变的量化检测建立了理论基础,为超声非线性技术在异形结构上的量化检测提供了研究思路。
5 结论
本文推导了单轴拉伸下变厚板塑性形变的分布方程,并将超声波波动方程和变厚板塑性损伤相结合,分析了变厚板的超声非线性响应,主要结论如下:
1)单轴拉伸下变厚板的塑性形变分布不均匀,塑性应变沿轴向由厚端至薄端呈直线增长,变厚板总体塑性形变量越大,同一位置处的塑性应变越大。
2)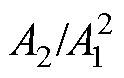 携带了变厚板塑性形变信息,超声波在塑性形变的变厚板中传播时,受累积效应和塑性损伤线性分布的共同影响,
携带了变厚板塑性形变信息,超声波在塑性形变的变厚板中传播时,受累积效应和塑性损伤线性分布的共同影响,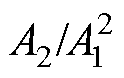 随传播距离呈二次方增长。在相同传播距离上,变厚板塑性形变越大,
随传播距离呈二次方增长。在相同传播距离上,变厚板塑性形变越大,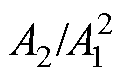 越大。
越大。
3)变厚板超声非线性响应模型能够精确描述超声波传播行为,可以据此探索变厚板塑性形变的量化检测。
参考文献
[1] 孙文秀, 刘国强, 夏慧, 等. 非铁磁材料的电磁超声接收过程数值模拟及实验研究[J]. 电工技术学报, 2018, 33(19): 4443-4449.
Sun Wenxiu, Liu Guoqiang, Xia Hui, et al. Numerical simulation and experimental study of electromagnetic acoustic transducer receiving process in nonferro- magnetic material[J]. Transactions of China Electro- technical Society, 2018, 33(19): 4443-4449.
[2] 门平, 董世运, 康学良, 等. 材料早期损伤的非线性超声诊断[J]. 仪器仪表学报, 2017, 38(5): 1101- 1118.
Men Ping, Dong Shiyun, Kang Xueliang, et al. Material early damage diagnosis with nonlinear ultrasound[J]. Chinese Journal of Scientific Instru- ment, 2017, 38(5): 1101-1118.
[3] 敦怡, 师小红, 王广龙, 等. 微纳米级裂纹的非线性超声检测[J]. 光学精密工程, 2011, 19(1): 132-137.
Dun Yi, Shi Xiaohong, Wang Guanglong, et al. Nonlinear ultrasonic test of micro-nano crack[J]. Optics and Precision Engineering, 2011, 19(1): 132- 137.
[4] 张剑锋, 轩福贞, 项延训. 材料损伤的非线性超声评价研究进展[J]. 科学通报, 2016, 61(14): 1536- 1550.
Zhang Jianfeng, Xuan Fuzhen, Xiang Yanxun. Evaluation of material damage using nonlinear ultrasonic wave[J]. Chinese Science Bulletin, 2016, 61(14): 1536-1550.
[5] Shintani T, Murata Y. Evaluation of the dislocation density and dislocation character in cold rolled type 304 steel determined by profile analysis of X-ray diffraction[J]. Acta Materialia, 2011, 59(11): 4314- 4322.
[6] 刘素贞, 杨圣哲, 袁路航, 等. 含微裂纹铝材的电磁超声Lamb波混频非线性检测及量化分析[J]. 电工技术学报, 2021, 36(17): 3639-3648.
Liu Suzhen, Yang Shengzhe, Yuan Luhang, et al. Nonlinear detection and quantitative analysis of electromagnetic ultrasonic Lamb wave mixing for aluminum with micro crack[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3639-3648.
[7] Cai Zhichao, Cheng Hao, Liu Chengcheng. Nonlinear electromagnetic acoustic testing method for tensile damage evaluation[J]. Journal of Sensors, 2018, 4: 1745257.
[8] Hikata A, Chick B B, Elbaum C, et al. Dislocation contribution to the second harmonic generation of ultrasonic waves[J]. Journal of Applied Physics, 1965, 36(1): 229-236.
[9] de Lima W J N, Hamilton M F. Finite-amplitude waves in isotropic elastic plates[J]. Journal of Sound and Vibration, 2003, 265(4): 819-839.
[10] Kim J Y, Qu Jianmin, Jacobs L J, et al. Acoustic nonlinearity parameter due to microplasticity[J]. Journal of Nondestructive Evaluation, 2006, 25(1): 28-36.
[11] Cantrell J H, Yost W T. Nonlinear ultrasonic characterization of fatigue microstructures[J]. Inter- national Journal of Fatigue, 2001, 23: 487-490.
[12] Pruell C, Kim J Y, Qu J, et al. Evaluation of fatigue damage using nonlinear guided waves[J]. Smart Materials and Structures, 2009, 18(3): 035003.
[13] Bermes C, Kim J Y, Qu Jianmin, et al. Nonlinear lamb waves for the detection of material non- linearity[J]. Mechanical Systems and Signal Pro- cessing, 2008, 22(3): 638-646.
[14] Choi S, Seo H, Jhang K Y. Noncontact evaluation of acoustic nonlinearity of a laser-generated surface wave in a plastically deformed aluminum alloy[J]. Research in Nondestructive Evaluation, 2015, 26(1): 13-22.
[15] 刘素贞, 田钰霖, 张闯, 等. 铝合金拉伸塑性变形的非线性电磁超声检测[J]. 电工技术学报, 2020, 35(15): 3153-3160.
Liu Suzhen, Tian Yulin, Zhang Chuang, et al. Nonlinear electromagnetic acoustic detection of aluminum alloys with tensile plastic deformation[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3153-3160.
[16] 张立军, 米玉霞, 赵昕辉, 等. 计及风剪效应的垂直轴风力机叶片倾角优化[J]. 中国石油大学学报(自然科学版), 2018, 42(5): 135-140.
Zhang Lijun, Mi Yuxia, Zhao Xinhui, et al. Optimization of blade dip angle for vertical axis wind turbine considering wind shear effect[J]. Journal of China University of Petroleum (Edition of Natural Science), 2018, 42(5): 135-140.
[17] 方玉财, 高志鹰, 闫萌萌, 等. 叶片挥舞振动后风轮流场特性[J]. 排灌机械工程学报, 2020, 38(4): 390-395.
Fang Yucai, Gao Zhiying, Yan Mengmeng, et al. Characteristics of wind turbine flow field after blade vibration[J]. Journal of Drainage and Irrigation Machinery Engineering, 2020, 38(4): 390-395.
[18] 李喜朋. 变厚度板超声导波检测理论与技术[D]. 北京: 北京理工大学, 2014.
[19] El-Kettani M E C, Luppé F, Guillet A. Guided waves in a plate with linearly varying thickness: experi- mental and numerical results[J]. Ultrasonics, 2004, 42(1-9): 807-812.
[20] Marical P, El-Kettani M E C, Predoi M V. Guided waves in elastic plates with Gaussian section variation: experimental and numerical results[J]. Ultrasonics, 2007, 47(1-4): 1-9.
[21] 尚世同, 尚瑜娟. 超声板波法在变厚度板检测中的应用[J]. 无损检测, 1998, 20(3): 80-82, 85.
Shang Shitong, Shang Yujuan. Application of ultrasonic plate wave method to inspecting the plates with varied thicknesses[J]. Nondestructive Testing, 1998, 20(3): 80-82, 85.
[22] 张闯, 李雪霏, 刘素贞, 等. 单向载荷下铝板电磁超声兰姆波的波速响应特性[J]. 电工技术学报, 2021, 36(8): 1579-1586.
Zhang Chuang, Li Xuefei, Liu Suzhen, et al. Wave velocity response characteristics of electromagnetic ultrasonic Lamb wave of aluminum plate under unidirectional load[J]. Transactions of China Electro- technical Society, 2021, 36(8): 1579-1586.
[23] Bender F A, Kim J Y, Jacobs L J, et al. The gen- eration of second harmonic waves in an isotropic solid with quadratic nonlinearity under the presence of a stress-free boundary[J]. Wave Motion, 2013, 50(2): 146-161.
[24] Van Den Abeele K E A. Elastic pulsed wave propagation in media with second-or higher-order nonlinearity. Part I. Theoretical framework[J]. The Journal of the Acoustical Society of America, 1996, 99(6): 3334-3345.
[25] Rao V V S J, Kannan E, Prakash R V, et al. Observation of two stage dislocation dynamics from nonlinear ultrasonic response during the plastic deformation of AA7175-T7351 aluminum alloy[J]. Materials Science and Engineering: A, 2009, 512(1-2): 92-99.
[26] Mondal C, Mukhopadhyay A, Sarkar R. A study on precipitation characteristics induced strength variation by nonlinear ultrasonic parameter[J]. Journal of Applied Physics, 2010, 108(12): 1617.
[27] Zhang Jianfeng, Xuan Fuzhen, Xiang Yanxun, et al. Non-linear ultrasonic response of plastically defor- med aluminium alloy AA 7009[J]. Materials Science and Technology, 2013, 29(11): 1304-1309.
[28] Zhang Jianfeng, Li Shenyu, Xuan Fuzhen, et al. Effect of plastic deformation on nonlinear ultrasonic response of austenitic stainless steel[J]. Materials Science and Engineering: A, 2015, 622: 146-152.
Ultrasonic Nonlinear Response of Plate with Varying Thickness in Plastic Deformation and Experiment
Zhao Guoliang1,2 Liu Suzhen1,2 Zhang Chuang1,2 Jin Liang1,2 Yang Qingxin1
(1. State Key Laboratory of Reliability and Intelligence of Electrical Equipment Hebei University of Technology Tianjin 300130 China 2. Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability of Hebei Province Hebei University of Technology Tianjin 300130 China)
Abstract Since the propagation characteristics of ultrasound in plate with varying thickness (PWVT) are not clear, it is important to construct high-precision model of ultrasonic nonlinear response (UNR) to detect early damage on PWVT by ultrasonic nonlinearity. Based on the constitutive relationship of metal with plastic deformation, the distribution equation of plastic strain in PWVT under uniaxial tension is deduced. The model of UNR in PWVT is obtained by combining the distribution equation and the wave equation of ultrasound. The model shows that the ratio of A2 (the second harmonic amplitude) to 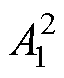 (square of the fundamental wave amplitude),
(square of the fundamental wave amplitude), 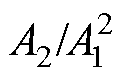 , increases “quadratically” with the propagation distance and wave number, and
, increases “quadratically” with the propagation distance and wave number, and 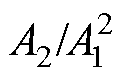 is positively correlated with the plastic deformation at constant distance, namely,
is positively correlated with the plastic deformation at constant distance, namely, 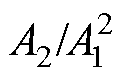 carries the information of plastic deformation in PWVT. The elastic-plastic model of aluminum alloy PWVT is constructed in COMSOL, which verifies the rationality of the linear equation in describing the distribution of PWVT’s plastic strain. The electromagnetic acoustic system is constructed and the effectiveness of the model of UNR is verified. In experiment, the PWVT specimens with different plastic deformation are prepared, and their propagation behaviors of ultrasound are studied by electromagnetic ultrasonic surface waves. The experimental results show that the model of UNR can describe the propagation behavior of ultrasound in PWVT accurately. This paper provides a theoretical basis for quantitative detection of plastic damage in PWVT by ultrasonic nonlinearity and a research idea for the application of ultrasonic nonlinearity to special-shaped structures.
carries the information of plastic deformation in PWVT. The elastic-plastic model of aluminum alloy PWVT is constructed in COMSOL, which verifies the rationality of the linear equation in describing the distribution of PWVT’s plastic strain. The electromagnetic acoustic system is constructed and the effectiveness of the model of UNR is verified. In experiment, the PWVT specimens with different plastic deformation are prepared, and their propagation behaviors of ultrasound are studied by electromagnetic ultrasonic surface waves. The experimental results show that the model of UNR can describe the propagation behavior of ultrasound in PWVT accurately. This paper provides a theoretical basis for quantitative detection of plastic damage in PWVT by ultrasonic nonlinearity and a research idea for the application of ultrasonic nonlinearity to special-shaped structures.
keywords:Electromagnetic acoustic transducer, plate with varying thickness, ultrasonic nonlinearity, plastic deformation
DOI: 10.19595/j.cnki.1000-6753.tces.220060
中图分类号:TM15
国家自然科学基金资助项目(51777052, 51977058)。
收稿日期 2022-01-12
改稿日期 2022-04-07
作者简介
赵国梁 男,1988年生,博士研究生,研究方向为电磁无损检测技术。E-mail: 942322551@qq.com
刘素贞 女,1969年生,博士,教授,博士生导师,研究方向为工程电磁场与磁技术。E-mail: szliu@hebut.edu.cn(通信作者)
(编辑 陈 诚)
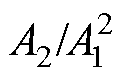 )随传播距离及波数均呈“二次方”增长;相同传播距离,
)随传播距离及波数均呈“二次方”增长;相同传播距离,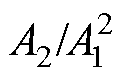 与总体塑性形变呈正相关,
与总体塑性形变呈正相关,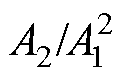 携带了变厚板塑性形变信息。在COMSOL中构建铝合金变厚板弹塑性模型,验证了利用线性方程描述变厚板塑性应变分布的合理性;构建电磁超声系统,验证了超声非线性响应模型的有效性。制备不同塑性形变的变厚板试件,研究电磁超声表面波在其中的传播规律。实验结果表明,构建的超声非线性响应模型能够精确描述变厚板中超声波的传播行为。该文为利用超声非线性技术实现变厚板塑性损伤的量化检测提供理论基础,为超声非线性技术在异形结构上的应用提供了研究思路。
携带了变厚板塑性形变信息。在COMSOL中构建铝合金变厚板弹塑性模型,验证了利用线性方程描述变厚板塑性应变分布的合理性;构建电磁超声系统,验证了超声非线性响应模型的有效性。制备不同塑性形变的变厚板试件,研究电磁超声表面波在其中的传播规律。实验结果表明,构建的超声非线性响应模型能够精确描述变厚板中超声波的传播行为。该文为利用超声非线性技术实现变厚板塑性损伤的量化检测提供理论基础,为超声非线性技术在异形结构上的应用提供了研究思路。 表示为
表示为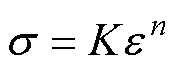 (1)
(1)
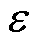 为应变;K和n为材料参数(n亦被称为硬化指数)。
为应变;K和n为材料参数(n亦被称为硬化指数)。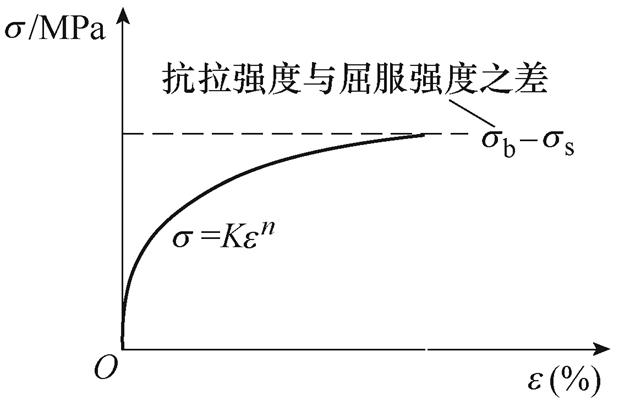
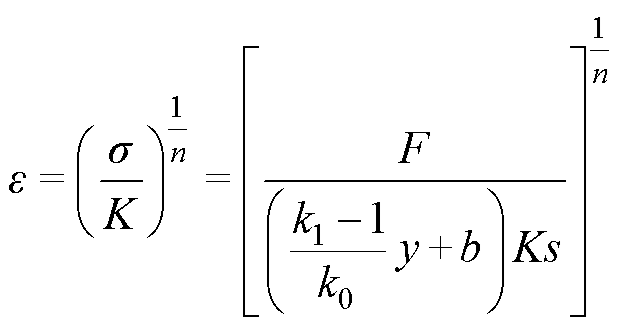 (2)
(2)
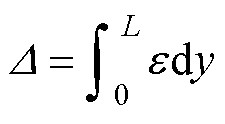 (3)
(3)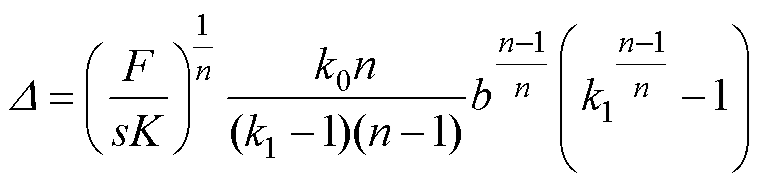 (4)
(4)
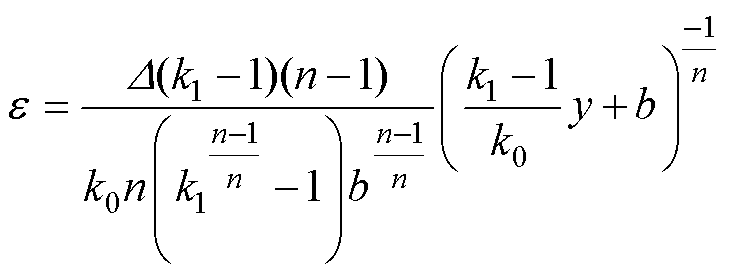 (5)
(5)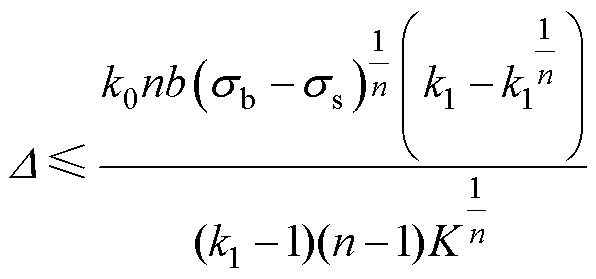 (6)
(6)
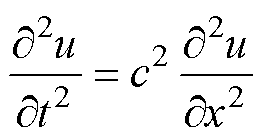 (7)
(7)
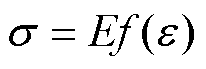 (8)
(8)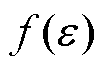 以泰勒级数形式展 开为
以泰勒级数形式展 开为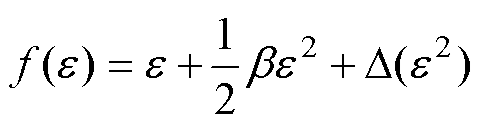 (9)
(9)
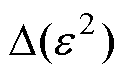 为
为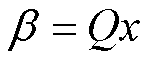 (10)
(10)
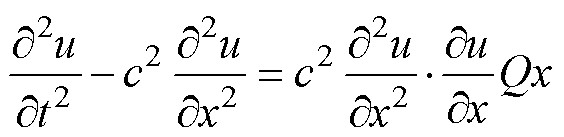 (11)
(11)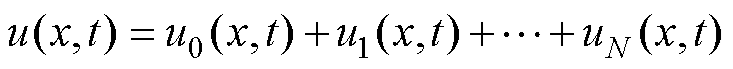 (12)
(12)
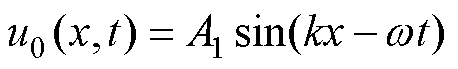 (13)
(13)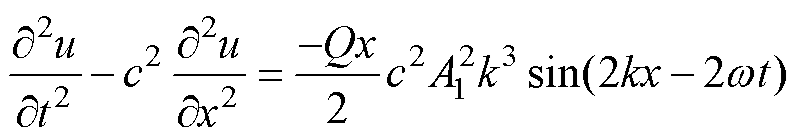 (14)
(14)
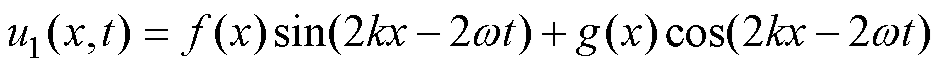 (15)
(15)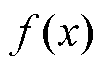 和
和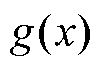 为构造函数。将式(15)代入式(14)的左端得
为构造函数。将式(15)代入式(14)的左端得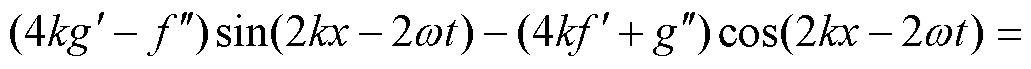
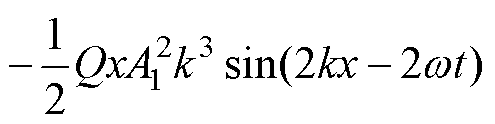 (16)
(16)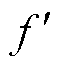 和
和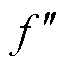 分别为
分别为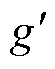 和
和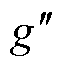 分别为g(x)的一阶和二阶导数。由式(16)可知
分别为g(x)的一阶和二阶导数。由式(16)可知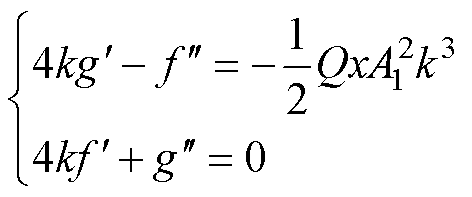 (17)
(17)
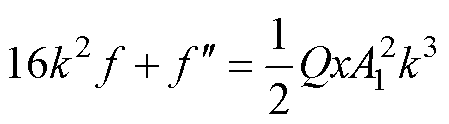 (18)
(18)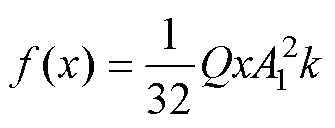 (19)
(19)
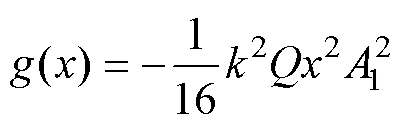 (20)
(20)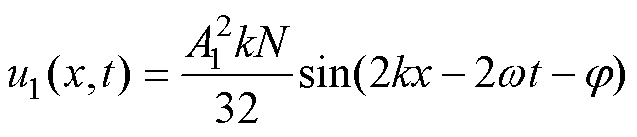 (21)
(21)
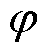 分别为简化u
分别为简化u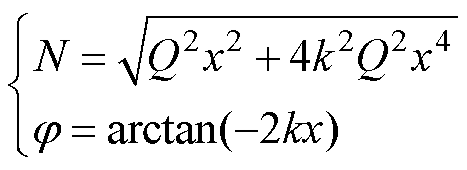 (22)
(22)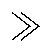 1。因而,式(21)可以简化为
1。因而,式(21)可以简化为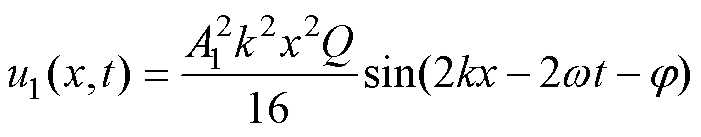 (23)
(23)
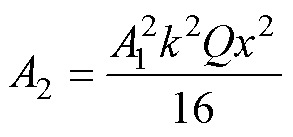 (24)
(24)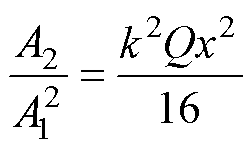 (25)
(25)



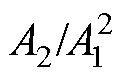 随激励波频率的变化如图6所示,归一化
随激励波频率的变化如图6所示,归一化
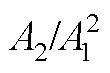 随激励波频率的变化
随激励波频率的变化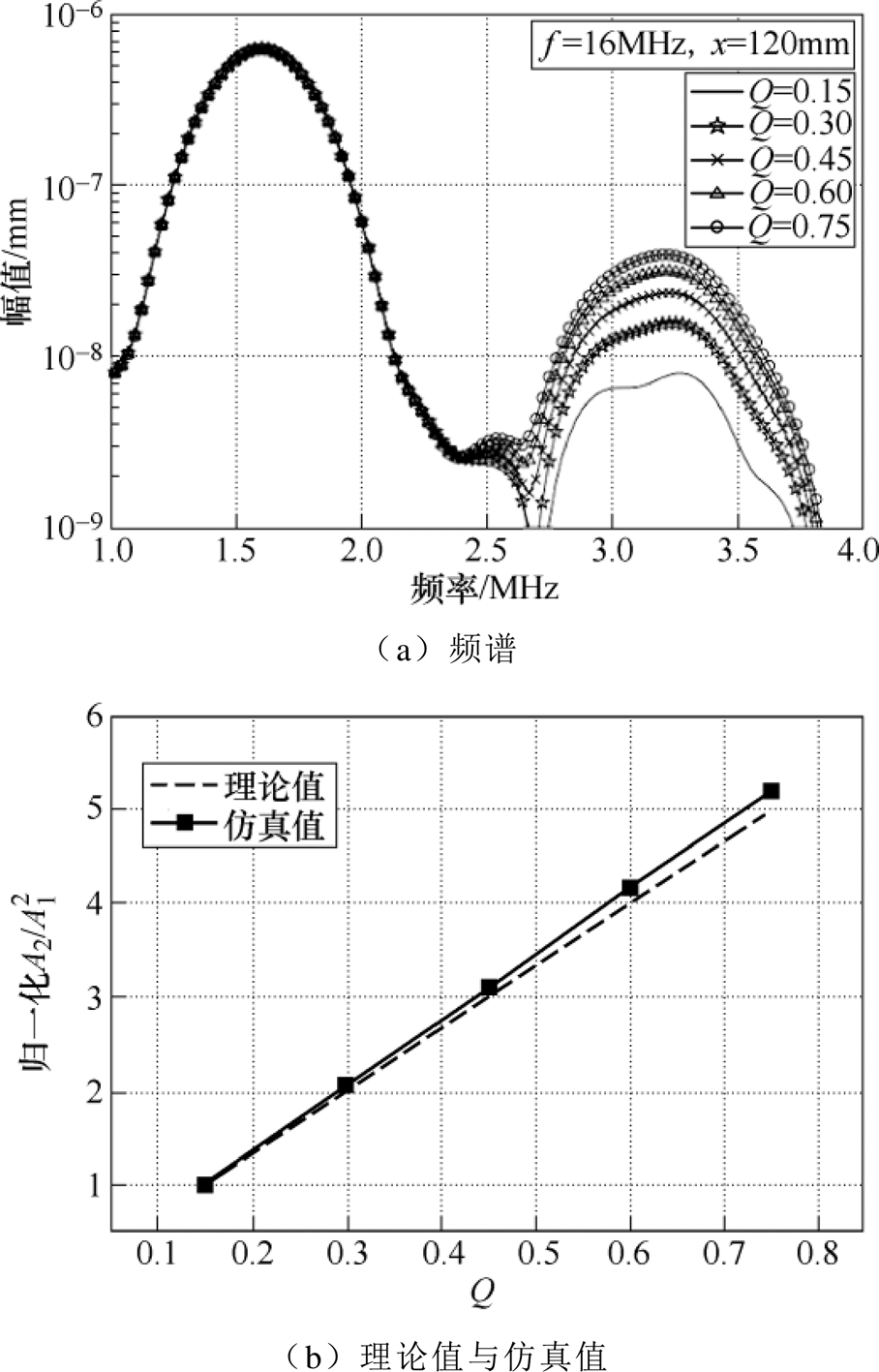
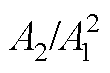 随塑性形变参数的变化
随塑性形变参数的变化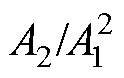 为基准,计算归一化
为基准,计算归一化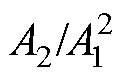 的理论值和仿真值,结果如图7b所示。根据式(25),
的理论值和仿真值,结果如图7b所示。根据式(25),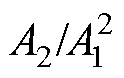 与Q成正比,五种情况下,归一化
与Q成正比,五种情况下,归一化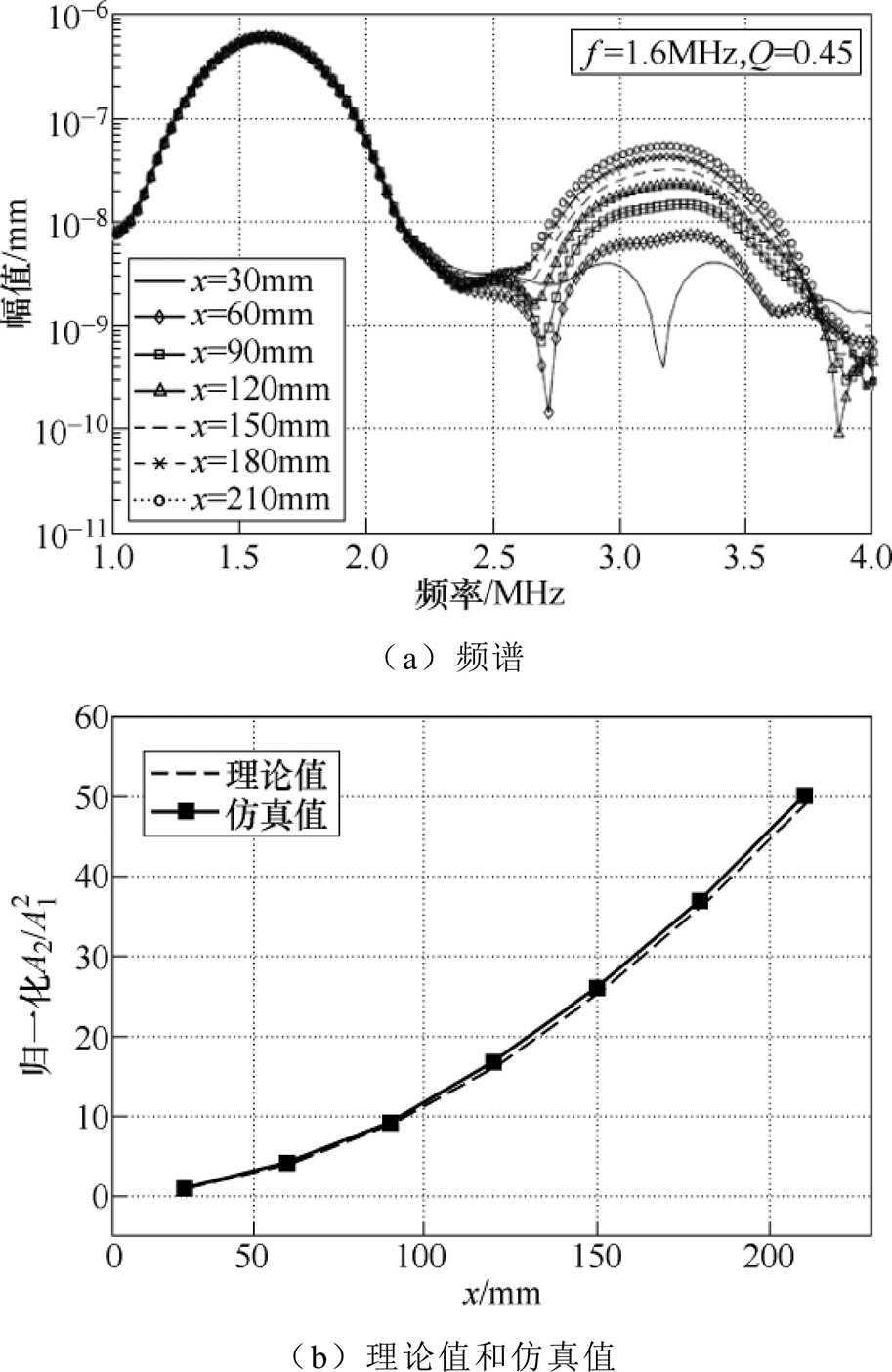
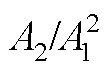 随传播距离的变化
随传播距离的变化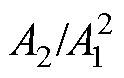 与x
与x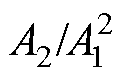 的理论值分别为1、4、9、16、25、36和49。归一化
的理论值分别为1、4、9、16、25、36和49。归一化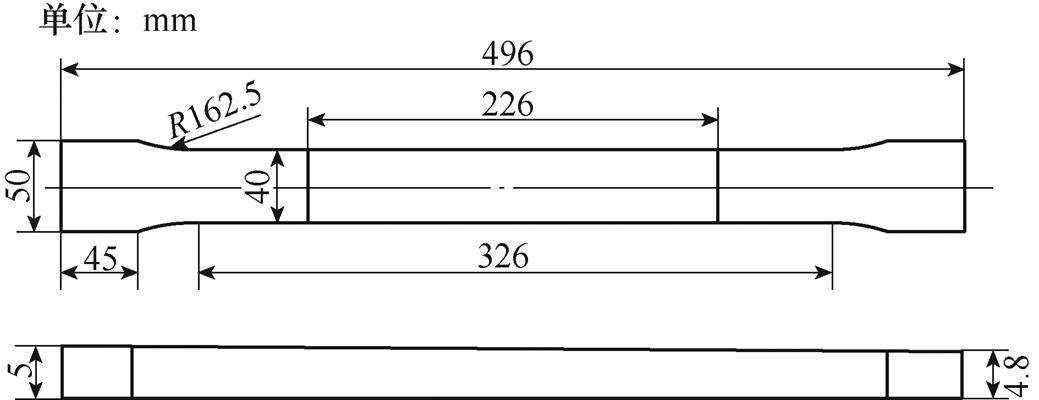
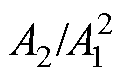 显著提高,且随传播距离的增加而增加。这表明超声非线性对变厚板的塑性形变十分敏感。图13中,在相同检测点,均为4号试件上的
显著提高,且随传播距离的增加而增加。这表明超声非线性对变厚板的塑性形变十分敏感。图13中,在相同检测点,均为4号试件上的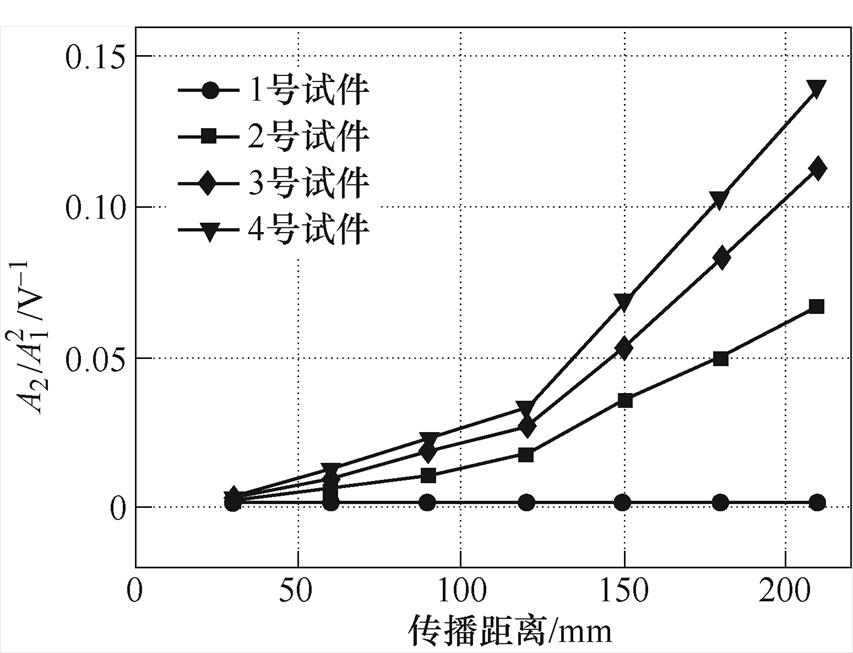
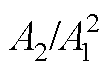 at 7 test points
at 7 test points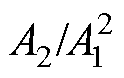 曲线均在第4个检测点上发生了较为显著的转折,这是由于实际拉伸中变厚板塑性形变的不均匀增长造成的。金属塑性形变是位错滑移的宏观表现,由于位错结构的运动是依次进行的,维持位错运动的力小于致使位错源开动的力,因而,金属材料在从弹性阶段进入塑性阶段时,应力会波动或者下降,这在应力应变上表现为曲线在屈服点附近的振荡。图14为实测的准静态拉伸下AA6061-T6铝合金材料的应力应变曲线,图中在应变约为4%时,应力出现了较为明显的振荡。在拉力作用下,变厚板会从薄端到厚端次第进入塑性形变阶段,即弹性阶段和塑性阶段的转换点会随着拉伸逐渐移动。随着拉力的不断增大,当转换点恰好到达第4个和第5个检测点之间时,由于薄端横截面面积小于厚端,且塑性形变进一步使薄端横截面面积减小,薄端开始加速塑性形变。塑性形变增速差异的分界线落在了第4个和第5个检测点之间。材料非线性系数与塑性应变呈正相关,因而在分界线的右侧,谐波的激发量明显提升。
曲线均在第4个检测点上发生了较为显著的转折,这是由于实际拉伸中变厚板塑性形变的不均匀增长造成的。金属塑性形变是位错滑移的宏观表现,由于位错结构的运动是依次进行的,维持位错运动的力小于致使位错源开动的力,因而,金属材料在从弹性阶段进入塑性阶段时,应力会波动或者下降,这在应力应变上表现为曲线在屈服点附近的振荡。图14为实测的准静态拉伸下AA6061-T6铝合金材料的应力应变曲线,图中在应变约为4%时,应力出现了较为明显的振荡。在拉力作用下,变厚板会从薄端到厚端次第进入塑性形变阶段,即弹性阶段和塑性阶段的转换点会随着拉伸逐渐移动。随着拉力的不断增大,当转换点恰好到达第4个和第5个检测点之间时,由于薄端横截面面积小于厚端,且塑性形变进一步使薄端横截面面积减小,薄端开始加速塑性形变。塑性形变增速差异的分界线落在了第4个和第5个检测点之间。材料非线性系数与塑性应变呈正相关,因而在分界线的右侧,谐波的激发量明显提升。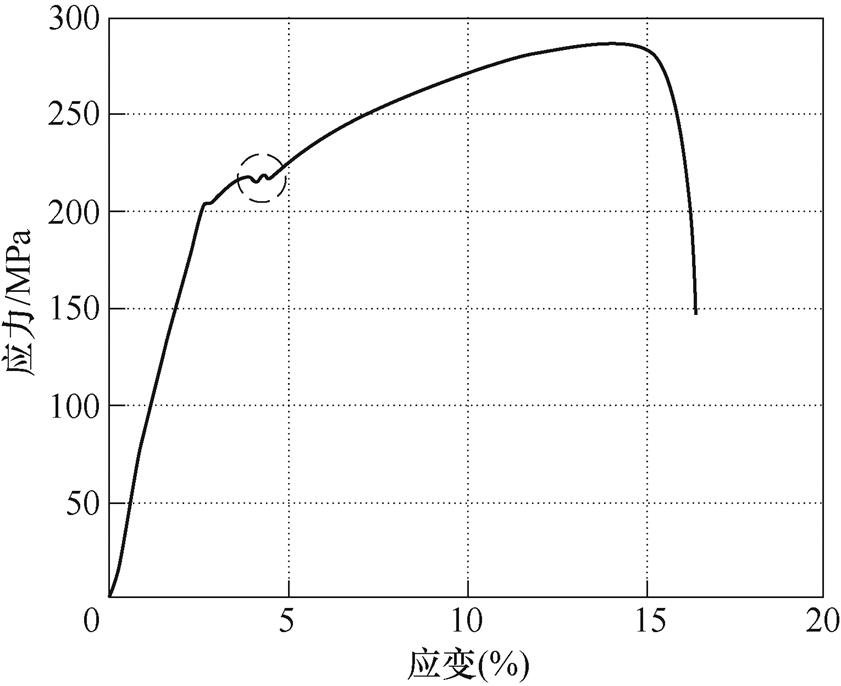
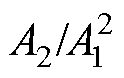 大小关系与之相应,这表明变厚板超声非线性响应模型能够准确反映塑性形变对超声非线性的影响。
大小关系与之相应,这表明变厚板超声非线性响应模型能够准确反映塑性形变对超声非线性的影响。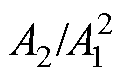 与传播距离x进行线性、二阶和三阶拟合,残差模见表4。表4中,相比线性拟合,二阶拟合的残差模大幅下降,三阶及更高阶次的拟合,其残差模的降幅很小,且拟合曲线的不稳定性显著增加,因而认为二阶拟合为最佳。图15为2~4号试件上测试数据的一次和二次拟合,结果表明,实验中
与传播距离x进行线性、二阶和三阶拟合,残差模见表4。表4中,相比线性拟合,二阶拟合的残差模大幅下降,三阶及更高阶次的拟合,其残差模的降幅很小,且拟合曲线的不稳定性显著增加,因而认为二阶拟合为最佳。图15为2~4号试件上测试数据的一次和二次拟合,结果表明,实验中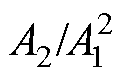 随传播距离基本呈“二次方”式增长。实验结果与变厚板超声非线性响应模型的分析一致。
随传播距离基本呈“二次方”式增长。实验结果与变厚板超声非线性响应模型的分析一致。
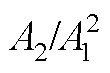 and their primary and secondary fitting
and their primary and secondary fitting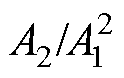 随传播距离呈二次方增长。在相同传播距离上,变厚板塑性形变越大,
随传播距离呈二次方增长。在相同传播距离上,变厚板塑性形变越大,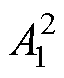 (square of the fundamental wave amplitude),
(square of the fundamental wave amplitude),