图1 漏电断路器的中间环节
Fig.1 Leakage circuit breaker intermediate link diagram
摘要 对高可靠性、长寿命的电子式漏电断路器建立基于Wiener过程的剩余寿命预测模型并对其进行可靠性预测。首先对电子式漏电断路器进行以温度为加速应力、剩余动作电流值为退化特征量的恒定应力加速退化试验，根据试验数据描述其性能退化轨迹，分析性能退化规律；然后对加速退化试验数据进行正态分布检验，验证其符合Wiener过程，利用极大似然估计的方法，对剩余寿命预测模型进行参数估计，预测出漏电断路器的剩余寿命；将漏电断路器初始时刻的剩余寿命作为伪失效寿命，外推出漏电断路器在正常应力下的使用寿命大约为2 085天。
关键词：性能退化 Wiener过程 恒定应力加速退化试验 剩余寿命预测
漏电断路器是电力系统中重要的低压保护电器，广泛应用于低压配电系统的终端保护中，在防止漏电事故、保护用电人员的生命财产安全上发挥着重大作用。但是随着使用时间的增加，漏电断路器疲劳老化不断积累，漏电断路器的性能逐渐降低，最终会对人民生命财产造成重大损失。目前，国内所应用的漏电断路器中电子式漏电断路器因其制造成本及制造工艺比电磁式漏电断路器更具优势，市场占用率近似达到90%。因此，对电子式漏电断路器的性能退化进行分析并对剩余寿命进行剩余预测，对保障低压配电系统的安全稳定运行和其他电力设备的正常工作意义重大[1-2]。
目前，剩余寿命预测广泛应用于低压电器等各个行业，寿命预测以及可靠性评估得到了广泛应 用[3-6]。李华等以超程时间为继电器的退化特征量，将超程时间的参数值融入回归模型当中，对继电器的寿命进行预测[7]；李志刚等同样将超程时间作为继电器的退化特征量，对小波包变换进行改进，并和径向基函数（Radial Basis Function, RBF）神经网络模型结合预测继电器的寿命[8]；李奎等以交流接触器的触头质量损耗为性能退化参数，并利用统计回归方法和非线性Wiener退化模型对交流接触器触头质量损耗建立预测模型，从而预测出交流接触器剩余寿命[9]；段宇等以电弧侵蚀量作为交流接触器的性能退化参数，并将累积电弧侵蚀量进行分段处理，建立Wiener退化模型预测交流接触器的剩余寿命[10]。上述论文的研究对象属于频繁动作的控制类电器，它们可以找到像接触电阻、触头电弧侵蚀量以及超程时间等标志性退化特征量。漏电断路器属于不频繁动作的保护类电器，正常情况下只有出现漏电故障时，才会发生动作。漏电断路器的工作特点使得漏电断路器没有明显的性能退化特征量。
本文首先根据预试验确定了剩余动作电流作为漏电断路器的退化特征量；其次进行以温度为加速变量的恒定应力加速退化试验，建立Wiener退化模型并利用极大似然估计法对模型参数进行估计，预测其在加速应力下的剩余寿命；最后通过Arrhenius加速模型外推出漏电断路器在正常应力下的使用寿命。
漏电断路器主要由四大部分组成，包括检测元件、中间环节、执行机构和试验装置。电子式漏电断路器的中间环节由印制电路板（Printed Circuit Board, PCB）、电容、晶闸管等电子元器件组成，如图1所示。漏电断路器对漏电信号进行的整流、放大和传递的处理由中间环节完成，中间环节组成元器件性能的好坏直接影响漏电断路器的剩余电流保护特性。通过对电容、PCB、晶闸管等电子元器件进行温度环境试验，国内外相关学者发现，温度是影响电子元器件性能改变甚至损坏失效的重要因 素[11-12]。长期温度作用下，电子式漏电断路器内部电容、电阻、晶闸管等电子元器件，同样可能发生性能改变甚至损坏，进而对漏电断路器动作特性产生影响，从而导致漏电断路器故障[13]，故选取温度作为加速变量。
图1 漏电断路器的中间环节
Fig.1 Leakage circuit breaker intermediate link diagram
确定漏电断路器的退化特征量是进行加速退化试验和可靠性预测的前提。在退化试验中，退化特征量是用来表征产品性能是否发生退化的物理量，当退化特征量不断退化并超过指定的阈值时，产品就会发生退化型失效。
设置前期预试验，以温度为加速变量来检验在长期温度作用过程中，漏电断路器动作特性参数剩余动作电流值和分断时间的变化情况。GB/Z 6829- 2008《剩余电流动作保护电器的一般要求》中规定，漏电断路器在储存、安装和运输过程中应保持的温度范围是-35～60℃，同时参照GB/T 2423-2008《电工电子产品环境试验标准》，将前期预试验中漏电断路器的试验温度定为55℃。随机抽取5只额定剩余动作电流In=0.03A电子式漏电断路器进行试验，试验一共进行10个周期，每一周期温度设置为：在25℃下保持2h，然后通过调温调湿箱控制温度在2h内升高至55℃并保持72h，时间到达后再控制温度在2h内降低至25℃并保持2h，一周期末尾检测数据[14]。用拟合法对剩余动作电流值和分断时间数据进行处理，其结果如图2和图3所示。
图2 剩余动作电流值变化情况
Fig.2 Change of residual operating current
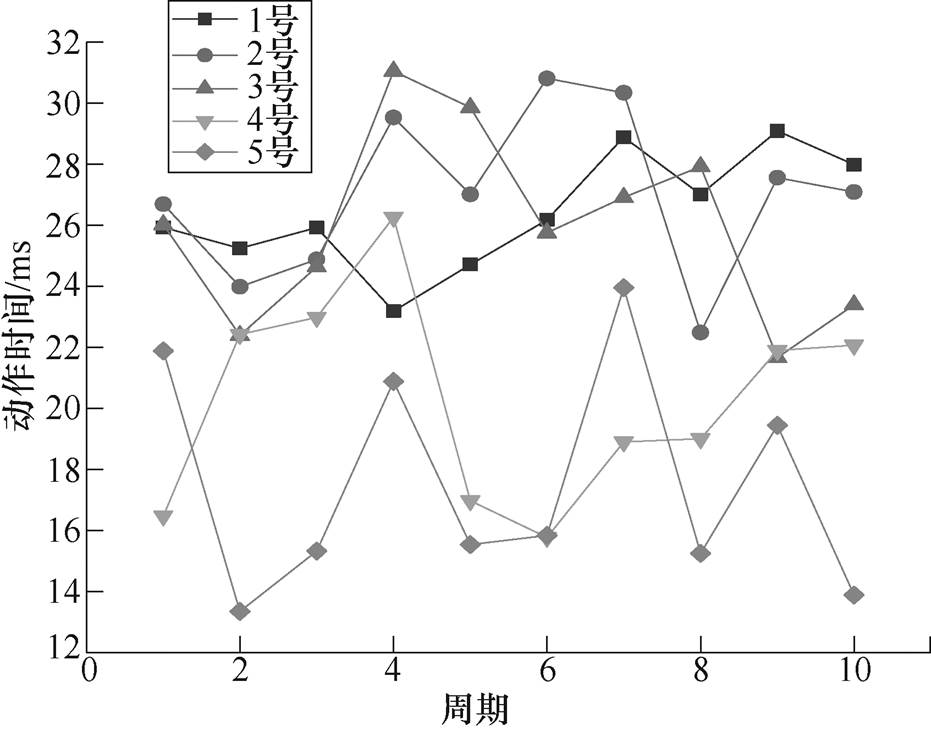
图3 分断时间变化情况
Fig.3 Change of break-time
通过图2可知，随着试验周期的延长，在长时间周期性温度的作用下，漏电断路器的剩余动作电流值个别周期略有波动，总体上呈线性降低趋势。由图3可知，漏电断路器的分断时间变化较为随机，没有明显确定的规律可循。根据产品退化特征量的选取条件，选择漏电断路器的剩余动作电流值作为其性能退化的退化特征量。
恒定应力加速退化试验可以得到产品在各个应力水平下加速退化数据，从而使得其可靠性评估的精度较高，同时恒定应力加速退化试验的试验分析方法更加成熟、完善，寿命预测的线性回归效果较为显著，因此，采用以温度为加速应力的恒定应力加速退化试验来获取漏电断路器的加速退化数据。最低加速应力水平T1应略高于产品最高工作温度，选择为50℃。最高加速应力水平T4应不改变产品的失效机理，漏电断路器外壳在95℃以上高温会发生软化，因而，T4选定为85℃。T2、T3选取中间水平60℃、70℃。参考现行国家标准GB 2689.1-1981《恒定应力寿命试验和加速寿命试验方法总则》中有关试验样品数量的规定：每个应力水平下的样品数量不少于10只，特殊产品不少于5只，综合试验周期和试验成本等因素，选择每个应力水平下在同一批产品中随机抽取5只漏电断路器作为试验 样品。
漏电断路器加速退化试验步骤如下：
（1）从同一批电子式漏电断路器中随机抽取20个试品，每个温度下5个试品，在4个温度应力下（T1=50℃，T2=60℃，T3=70℃，T4=85℃）依次进行加速试验。
（2）首先在常温25℃下测量20个漏电断路器剩余动作电流的初始值，然后在每个周期的末尾时段检测数据，一周期24h，每个应力下的试验时间为28个周期。
对每一温度应力下漏电断路器的剩余动作电流的退化数据进行处理。同一加速应力下5个漏电断路器试品退化趋势一致，且平均退化速率差异性较小，因此，取50℃-A1、60℃-B1、70℃-C1、85℃-D1 4个试品为例，做出其剩余动作电流随时间的变化情况，如图4所示。
图4 剩余动作电流变化情况
Fig.4 Change of residual operating current value
由图4可以看出，随着试验时间的增长，4组温度应力下的剩余动作电流基本呈线性下降趋势，且不同温度应力下的漏电断路器剩余动作电流下降速率不同，温度应力越高下降速度越快，这说明高温使得漏电断路器性能退化加剧，将温度作为加速应力进行恒定应力加速退化试验得到的数据是有效的。
根据试验数据建立Wiener退化模型是以退化量数据为特征来分析产品的性能退化过程的，同一加速应力下5个漏电断路器试品退化趋势一致[15-17]，且平均退化速率差异性较小，以60℃-B1试品为例，做出其剩余动作电流累积退化量的退化轨迹模型，如图5所示。并对漏电断路器剩余动作电流值退化量进行分段，每个周期为一段，每段的退化量记为DX，其分段的剩余动作电流退化量如图6所示。
图5 剩余动作电流累积退化量
Fig.5 Cumulative degradation of residual operating current
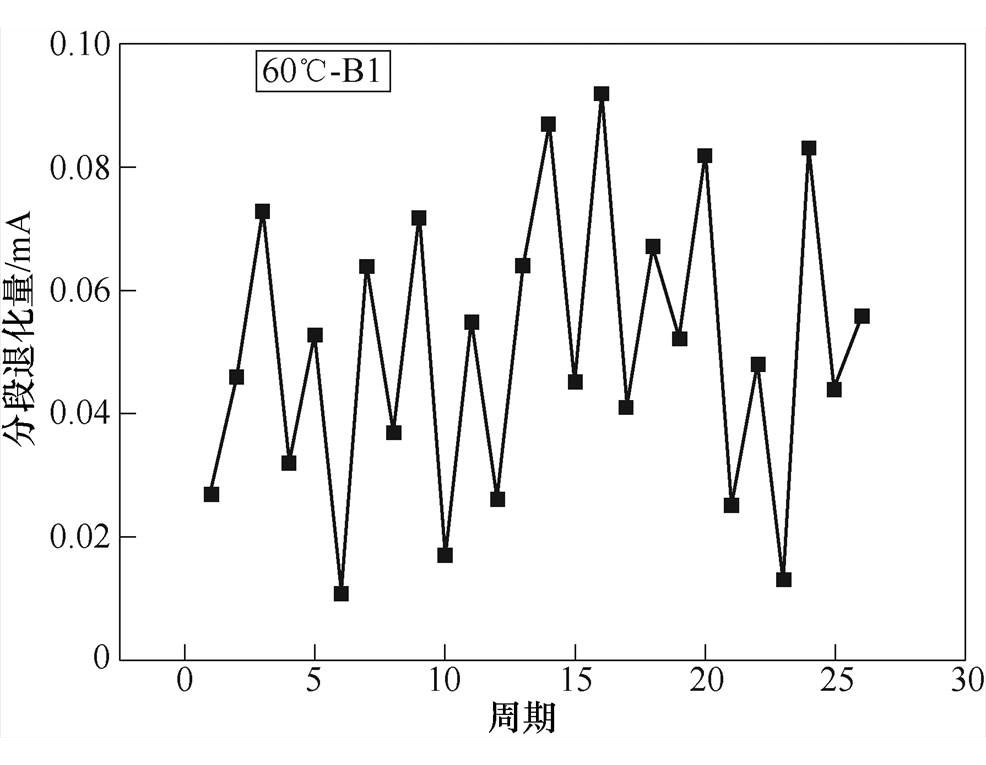
图6 剩余动作电流分段退化量
Fig.6 Segmental degradation of residual operating current
从图5可以得出，漏电断路器剩余动作电流退化量基本呈线性增长的趋势，与时间周期近似为线性关系。随着试验时间的增长，漏电断路器的剩余动作电流退化量不断累积增长。漏电断路器剩余动作电流退化量如果符合正态分布，则可以通过一元线性Wiener过程对漏电断路器进行退化建模，为了验证剩余动作电流退化量是否符合Wiener过程，以60℃下的5个试品为例进行分析，图7为置信水平为95%时正态分布检验结果。
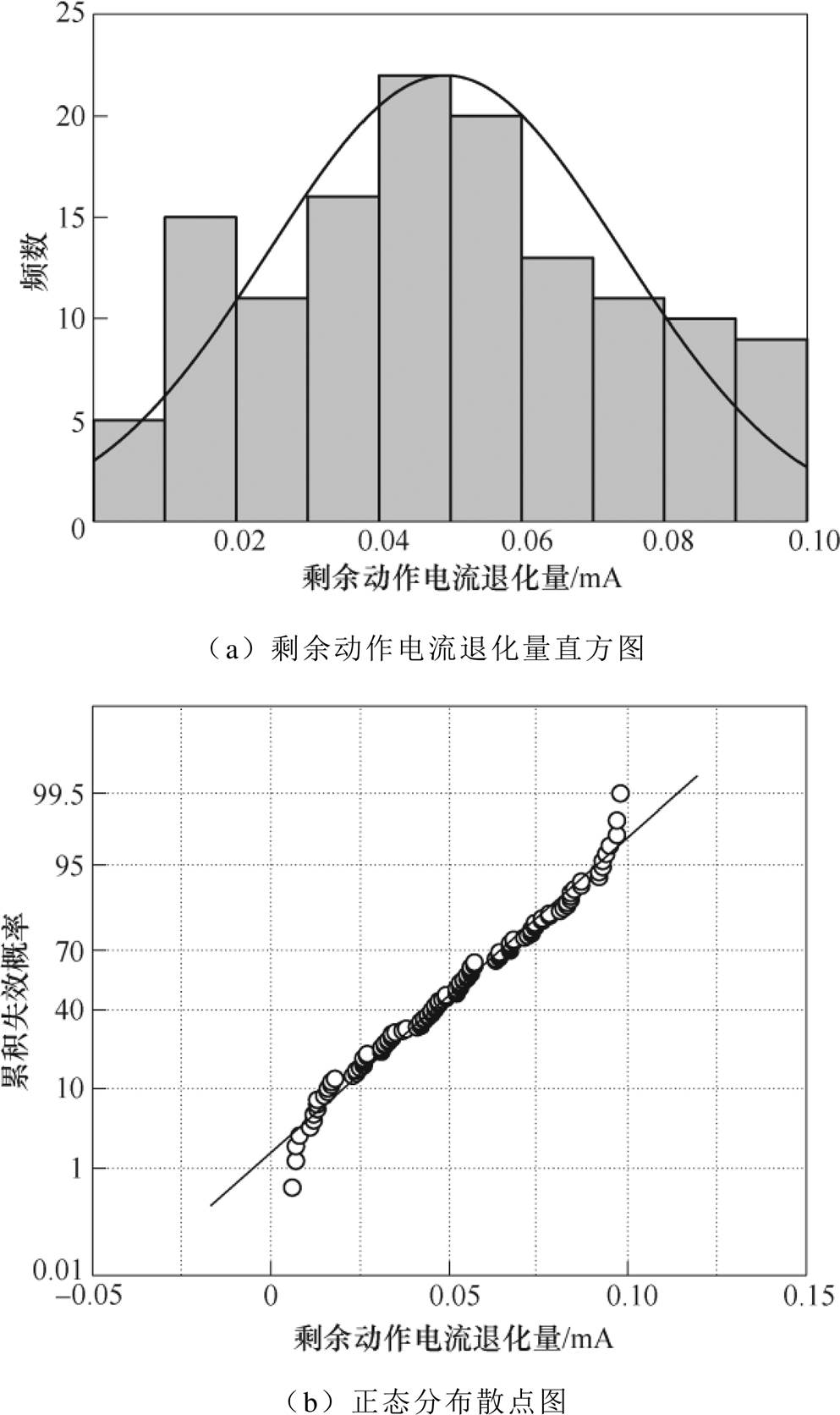
图7 剩余动作电流退化量正态分布检验
Fig.7 Normal distribution of residual operating current
由图7a中可以看出，剩余动作电流退化量大多集中在（0.03, 0.06）mA范围内。图7b中的数据点绝大多数分布在直线上，只有几个数据点落在直线外，利用概率统计学的知识判断，可以认为漏电断路器剩余动作电流的分段退化量符合正态分布，可以使用Wiener退化模型对漏电断路器剩余动作电流建模，实现剩余寿命预测。其他漏电断路器试品可以用同样的正态分布检验方法验证符合Wiener过程。
Wiener过程作为寿命预测方法中应用较为广泛的概率统计模型，既可以给出预测的点估计值，又可以给出预测结果的概率密度函数和可靠度函数，能够较好地描述非单调的性能退化过程。以剩余动作电流值作为漏电断路器性能退化特征量，根据时间进行分段以及统计回归，建立带漂移的一元线性Wiener退化模型[18-20]为
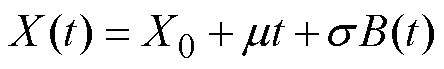（1）式中，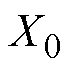
为初始时刻的剩余动作电流退化量；t为漏电断路器时间分段个数；X(t)为剩余动作电流值的累计退化量，
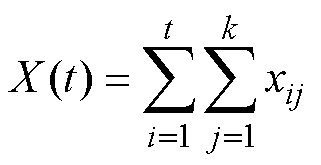服从正态分布
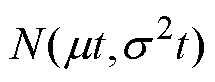，xij为第i段第j个时间区间内剩余动作电流的退化增量；
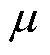为漂移系数；
为扩散系数；B(t)为标准布朗运动。
当漏电断路器的性能退化过程可以用一元线性Wiener过程来表示时，可以用Ti作为漏电断路器在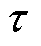
时刻的剩余寿命，且其运行到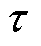时刻仍未失效。则有
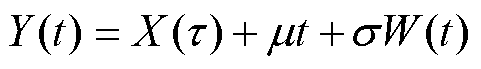
（2）式中，漏电断路器在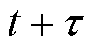
时刻的退化量为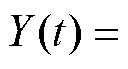
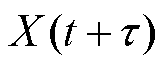，漏电断路器在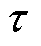时刻的退化量为
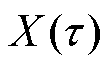，且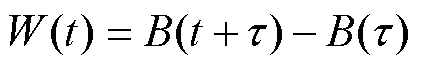
。
根据Wiener过程独立增量性质和齐次马尔科夫性，漏电断路器在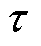时刻的剩余寿命可以表示为
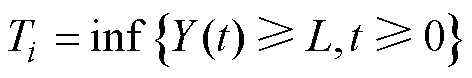
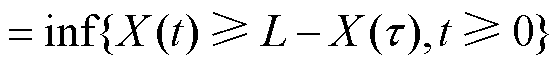（3）式中，L为漏电断路器失效阈值。
由式（2）和式（3）可以得到漏电断路器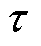时刻剩余寿命Ti的概率密度函数，即
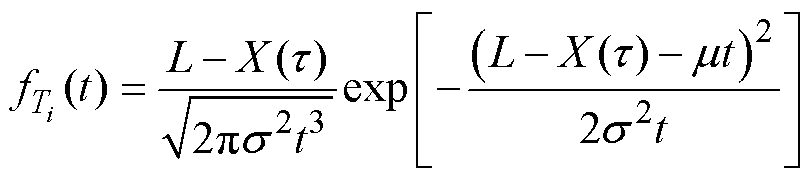（4）与之相对应的可靠度函数为
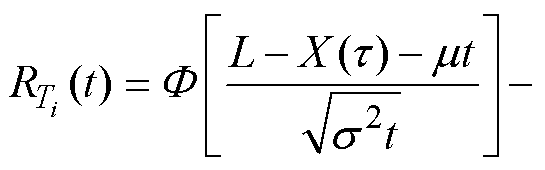
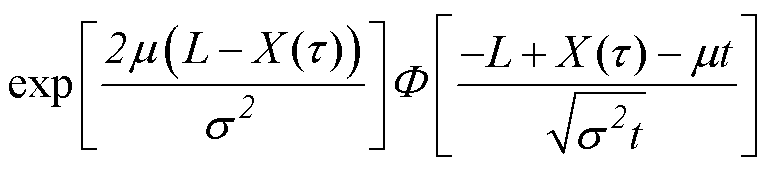（5）通过漏电断路器性能退化数据估计退化模型的参数m 和s，得到m、s2的极大似然估计值为
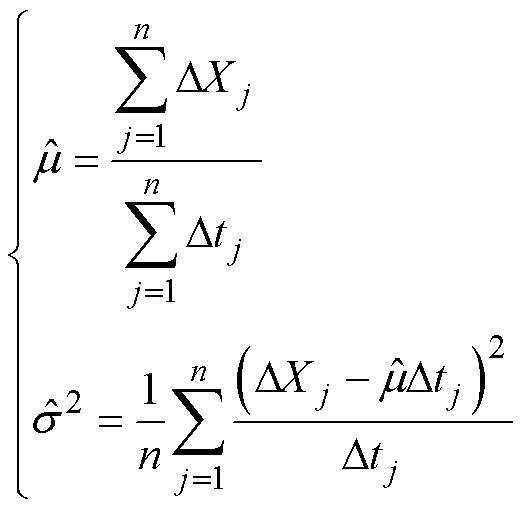（6）
式中，DXj=Xj-X(j-1)为漏电断路器在时刻t(j-1)～tj之间的性能退化量。
根据60℃加速应力下B1试品的加速退化试验数据建立漏电断路器的性能退化模型，根据式（6）可以求出参数m =0.050 5，参数s =0.023 1。漏电断路器失效阈值L=(27.67-15)mA=12.67mA。将m、s 失效阈值等参数代入式（4）和式（5）可以得到漏电断路器的可靠度和剩余寿命概率密度曲线，如图8和图9所示。
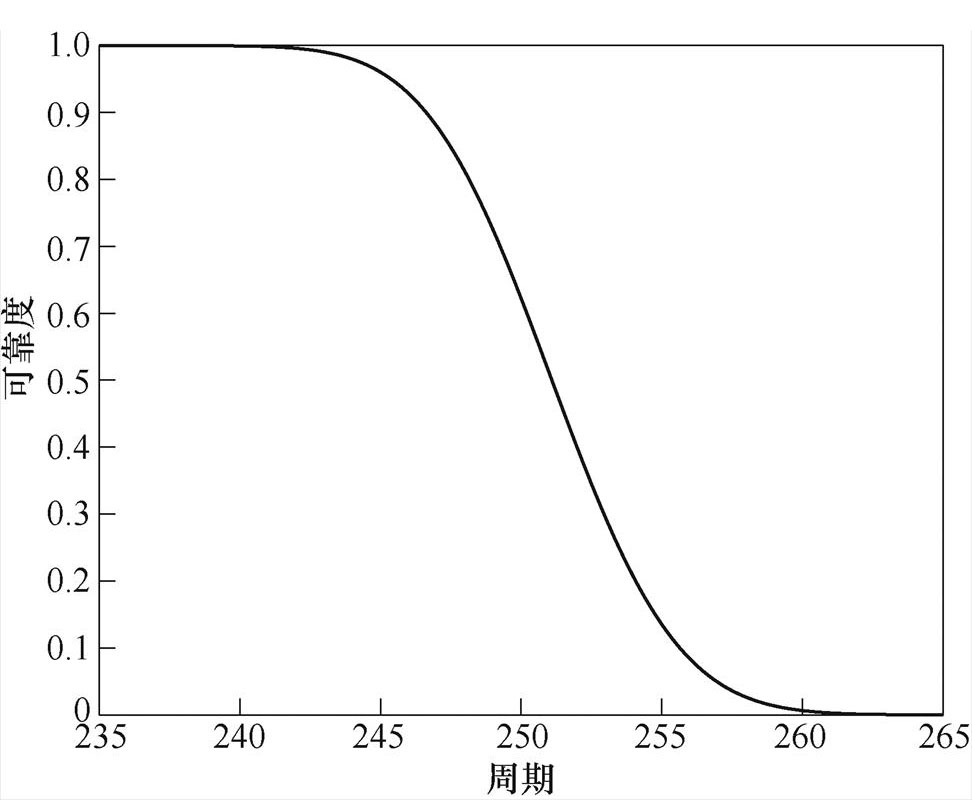
图8 漏电断路器可靠度
Fig.8 Reliability of earth leakage circuit breaker
从图8可以看出，当试验周期达到240时，漏电断路器的可靠度开始显著降低，当可靠度降低到0.5时，试验周期达到251。结合图9漏电断路器剩余寿命的概率密度曲线和图8可靠度曲线，把可靠度为0.5时对应的周期，当作B1试品初始时刻的剩余寿命。
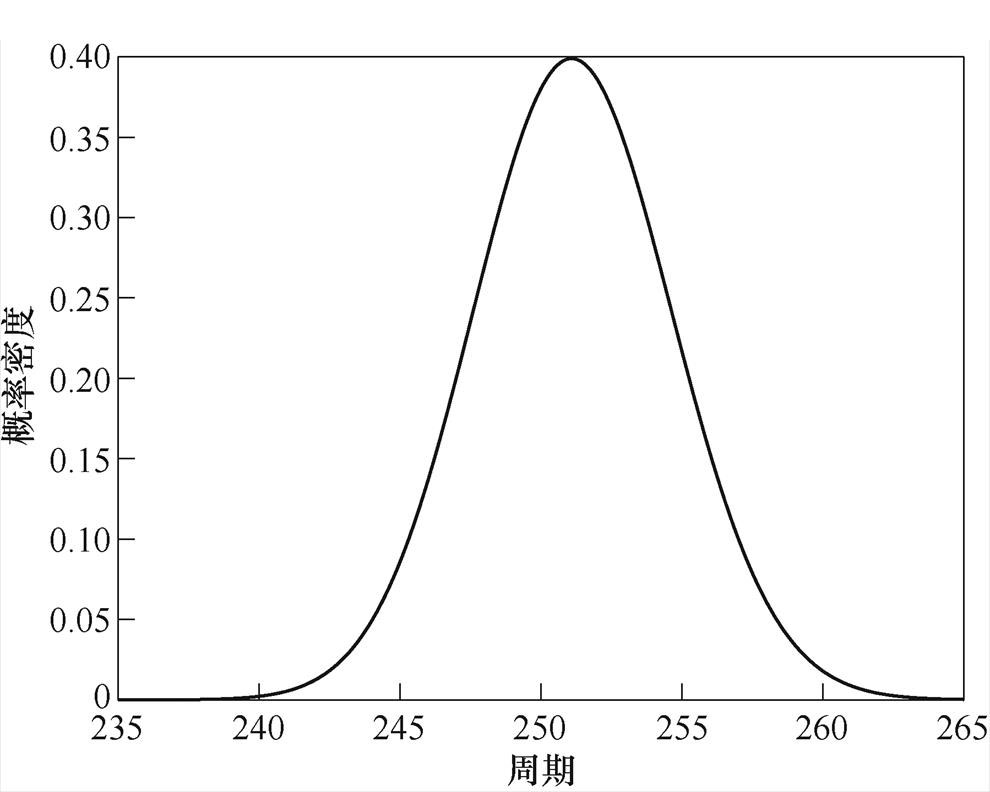
图9 剩余寿命概率密度
Fig.9 Residual life probability density
通过Wiener退化模型可以预测出各加速应力下漏电断路器初始时刻的剩余寿命，即从试验开始到达失效阈值所需要的试验时间，而其恰恰符合伪失效寿命的定义。因此，本文将漏电断路器初始时刻的剩余寿命作为漏电断路器的伪失效寿命。各加速应力下漏电断路器的伪失效寿命见表1。
表1 漏电断路器的伪失效寿命
Tab.1 False failure life of earth leakage circuit breaker
序号温度/℃编号伪失效寿命/天 150A1542 A2502.6 A3483.2 A4480.6 A5514.2 260B1251 B2230.6 B3239 B4246.5 B5260.2 370C1171.8 C2143.8 C3148.4 C4153.6 C5154.1 485D1129.3 D2103 D3114 D4109 D5104
将表1中各加速应力下的5个伪失效寿命数据作为子样，对漏电断路器的伪失效寿命做出正态分布的估计。由于子样数据个数较少，利用S-W检验法对各加速应力下的伪失效寿命数据进行正态分布检验。检验统计量见表2。
表2 检验统计量
Tab.2 Test statistics
温度/℃统计量 500.922 600.996 700.884 850.873
经查表可知，当置信水平为95%，数据个数n=5时，S-W检验统计量为0.762，表中各应力下伪失效寿命数据检验统计量均大于0.762，因此，可近似认为漏电断路器的伪失效寿命服从正态分布。利用极大似然估计法由式（6）可以得到伪失效寿命的参数估计值，见表3。
表3 漏电断路器参数估计值
Tab.3 Estimated values of leakage circuit breaker parameters
序号温度/℃m/天s/天 150504.5225.143 8 260245.4811.321 5 370154.3410.628 2 485111.0410.764 2
利用Arrhenius模型来外推漏电断路器的寿命。Arrhenius模型作为一种技术非常成熟的经验模型，应用范围非常广泛，它描述产品退化速率与激活能的指数成反比、与温度倒数的指数成正比。其表达式为
（7）式中，R为反应速度；K为绝对温度；k 为玻耳兹曼常数；Ea为激活能；a为一常量。
令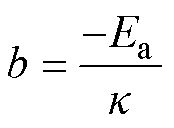
，对等式两边积分（从0积到t）可得
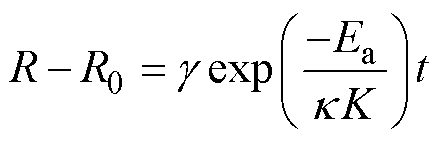（8）令DR=R-R0，对等式两边取对数，可得
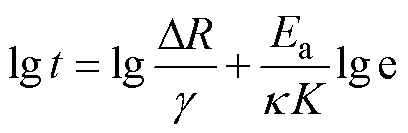（9）
令
，则式（9）可写为
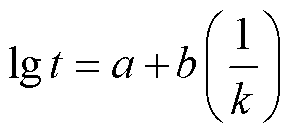（10）式中，t为产品的寿命，且产品寿命t的对数与温度K的倒数呈线性关系。将表3中m 的参数估计值代入式（10），利用最小二乘法求解式（10）中参数a和b，最小二乘法拟合结果如图10所示。
从图10中可以得到常数项a和回归系数b，相关系数r以及残差二次方和RSS，其中，相关系数r＞r0.02=0.980 0，且残差二次方和RSS极为接近于0，所以可以认为，线性回归效果是显著的。将a、b代入式（10）中，可得
（11）根据式（11）可以预测出漏电断路器在常温时的寿命，计算可得寿命的点估计值为2 085天。
图10 最小二乘法拟合结果
Fig.10 Least squares fitting results
在实际使用中，并未对漏电断路器规定使用年限。本文通过加速方程外推出漏电断路器的寿命。漏电断路器的剩余动作电流逐渐下降，预测大约在使用5～6年后，即使电路中的漏电电流不大于额定剩余不动作电流，漏电断路器也会发生误动作，切断供电电源，不能保证可靠用电。
分析漏电断路器的失效原因，随使用时间增加，漏电断路器内部元件老化，性能参数会发生变化，如零序电流互感器铁心的磁导率以及晶闸管的触发电压与触发电流会下降。元器件的参数变化对剩余动作电流的影响互相牵制。电流互感器铁心的磁导率下降导致剩余动作电流增加，晶闸管的触发电压与触发电流下降致使剩余动作电流降低。然而电流互感器铁心材料具有较好的抗老化性能，磁导率下降较小，对剩余动作电流值的影响较小，晶闸管的参数变化成为引起漏电断路器剩余动作电流变化的主要因素。改善晶闸管抗老化性或寻求元件间最优匹配可以提高产品寿命和可靠性。
本文通过试验确定以剩余动作电流值作为漏电断路器的特征退化量，以剩余动作电流退化量首次达到失效阈值作为失效判据，建立了基于Wiener过程的漏电断路器剩余寿命预测模型。得到的主要结论如下：
1）根据加速退化试验数据，建立各加速应力下 剩余动作电流退化量的退化轨迹，得出高温应力会使漏电断路器的性能退化加剧。
2）以单个周期作为时间分段，根据中心极限定理，以及分段退化量的正态分布检验图，可以验证每个周期漏电断路器剩余动作电流分段退化量服从正态分布，从而验证符合Wiener过程。
3）利用概率统计的方法推导出其剩余寿命概率密度函数和可靠度函数；采用极大似然估计的方法，得到m、s 的估计值；建立漏电断路器剩余寿命预测模型，预测出漏电断路器在加速应力初始时刻的剩余寿命。
将漏电断路器初始时刻的剩余寿命作为该加速应力下的伪失效寿命，通过Arrhenius加速模型，基于最小二乘法对参数进行估计，最终预测出漏电断路器在常温下的寿命为2 085天。
参考文献
[1] 郑荣进, 丁柯婷, 黄晓生, 等. 剩余电流保护断路器动作特性自动测试系统设计[J]. 福建工程学院学报, 2018, 16(4): 381-385.
Zheng Rongjin, Ding Keting, Huang Xiaosheng, et al. An action characteristic automatic test system design of residual current protection circuit breaker[J]. Journal of Fujian University of Technology, 2018, 16(4): 381-385.
[2] 李奎, 陆俭国, 武一, 等. 自适应漏电保护技术及其应用[J]. 电工技术学报, 2008, 23(10): 53-57.
Li Kui, Lu Jianguo, Wu Yi, et al. Adaptive leakage protection technology and its application[J]. Transa- ctions of China Electrotechnical Society, 2008, 23(10): 53-57.
[3] 韦海燕, 陈静, 王惠民, 等. 新陈代谢灰色粒子滤波实现电池剩余寿命预测[J]. 电工技术学报, 2020, 35(6): 1181-1188.
Wei Haiyan, Chen Jing, Wang Huimin, et al. Remaining useful life prediction of battery using metabolic grey particle filter[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1181- 1188.
[4] 陈琳, 陈静, 王惠民, 等. 基于小波包能量熵的电池剩余寿命预测[J]. 电工技术学报, 2020, 35(8): 1827-1835.
Chen Lin, Chen Jing, Wang Huimin, et al. Prediction of battery useful life based on wavelet packet energy entropy[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 1827-1835.
[5] 孙曙光, 王锐雄, 杜太行, 等. 基于粗糙集与证据理论的交流接触器预期电寿命预测[J]. 电工技术学报, 2020, 35(10): 2158-2169.
Sun Shuguang, Wang Ruixiong, Du Taihang, et al. Expected electrical life prediction of AC contactor based on rough set and evidence theory[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(10): 2158-2169.
[6] 高俊国, 孟睿潇, 胡海涛, 等. 电机定子绝缘老化寿命预测研究进展[J]. 电工技术学报, 2020, 35(14): 3065-3074.
Gao Junguo, Meng Ruixiao, Hu Haitao, et al. Research process on prediction of aging life of motor stator insulation[J]. Transactions of China Electro- technical Society, 2020, 35(14): 3065-3074.
[7] 李华, 孙东旺, 贺鹏举, 等. 基于超程时间回归模型的继电器寿命预测方法[J]. 电工技术学报, 2013, 28(增刊2): 414-417.
Li Hua, Sun Dongwang, He Pengju, et al. The method of relay life prediction based on the regression model of super-path time[J]. Transactions of China Elec- trotechnical Society, 2013, 28(S2): 414-417.
[8] 李志刚, 刘伯颖, 李玲玲, 等. 基于小波包变换及RBF神经网络的继电器寿命预测[J]. 电工技术学报, 2015, 30(14): 233-240.
Li Zhigang, Liu Boying, Li Lingling, et al. Relay life prediction based on wavelet packet transform and RBF neural network[J]. Transactions of China Elec- trotechnical Society, 2015, 30(14): 233-240.
[9] 李奎, 高志成, 武一, 等. 基于统计回归和非线性Wiener过程的交流接触器剩余寿命预测[J]. 电工技术学报, 2019, 34(19): 4058-4070.
Li Kui, Gao Zhicheng, Wu Yi, et al. Remaining life prediction of AC contactors based on statistical regression and nonlinear Wiener process[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(19): 4058-4070.
[10] 李奎, 段宇, 黄少坡, 等. 基于Wiener过程的交流接触器剩余电寿命预测[J]. 中国电机工程学报, 2018, 38(13): 3978-3986, 4039.
Li Kui, Duan Yu, Huang Shaopo, et al. Remaining electric life prediction of AC contactors based on Wiener process[J]. Proceedings of the CSEE, 2018, 38(13): 3978-3986, 4039.
[11] Lakshminarayanan V, Sriraam N. The effect of tem- perature on the reliability of electronic compo- nents[C]//IEEE International Conference on Electro- nics, Computing and Communication Technologies, Bangalore, 2014: 1-6.
[12] 雷芸, 邱云峰. 基于温度变化的电子元器件参数响应研究[J]. 计算机与数字工程, 2015, 43(1): 155-158.
Lei Yun, Qiu Yunfeng. Research on parameter response of electronic components based on tem- perature change[J]. Computer and Digital Engin- eering, 2015, 43(1): 155-158.
[13] 刘帼巾, 边鑫磊, 马晓燕, 等. 漏电断路器动作特性检测装置的研究[J]. 电测与仪表, 2018, 55(8): 113-118.
Liu Guojin, Bian Xinlei, Ma Xiaoyan, et al. Research on the detection device for the operating charac- teristics of leakage circuit breakers[J]. Electrical Measurement and Instrumentation, 2018, 55(8): 113-118.
[14] 边鑫磊. 温湿度对电子式漏电断路器性能影响的研究[D]. 天津: 河北工业大学, 2017.
[15] Peng C Y, Tseng S T. Mis-specification analysis of linear degradation models[J]. IEEE Transactions on Reliability, 2009, 58(3): 444-455.
[16] Tang Shengjin, Guo Xiaosong, et al. Real time remaining useful life prediction based on nonlinear Wiener based degradation processes with measure- ment errors[J]. Journal of Central South University, 2014, 12(21): 4509-4517.
[17] 朱磊, 左洪福, 蔡景. 基于Wiener过程的民用航空发动机性能可靠性预测[J]. 航空动力学报, 2013, 28(5): 1006-1012.
Zhu Lei, Zuo Hongfu, Cai Jing. Reliability prediction of civil aviation engine performance based on Wiener process[J]. Aerodynamics News, 2013, 28(5): 1006- 1012.
[18] 胡姚刚, 李辉, 廖兴林, 等. 风电轴承性能退化建模及其实时剩余寿命预测[J]. 中国电机工程学报, 2016, 36(6): 1643-1649.
Hu Yaogang, Li Hui, Liao Xinglin, et al. Wind turbine bearing performance degradation modeling and real-time remaining life prediction[J]. Pro- ceedings of the CSEE, 2016, 36(6): 1643-1649.
[19] 刘建强, 陈爱峰, 闫一凡, 等. 高速列车电磁接触器可靠性评估方法[J]. 电工技术学报, 2018, 33(增刊2): 461-471.
Liu Jianqiang, Chen Aifeng, Yan Yifan, et al. Reliability evaluation method of electromagnetic contactor used in high-speed train[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 461- 471.
[20] Zhang Xiang, Gockenbach E, Liu Zhaolin, et al. Reliability estimation of high voltage SF6 circuit breakers by statistical analysis on the basis of the field data[J]. Electric Power Systems Research, 2013, 103: 105-113.
Remaining Life Prediction of Electronic Residual Current Circuit Breaker Based on Wiener Process
Abstract For high-reliability, long-life electronic leakage circuit breakers, a residual life prediction model based on Wiener process is established to predict its reliability. First, the constant stress accelerated degradation test is carried out for the electronic leakage circuit breaker, with temperature as the accelerated stress and residual operating current as the degradation characteristic quantity. According to test data, its performance degradation trajectory is described, and the performance degradation rules are analyzed. Then, the test data of the accelerated degradation are checked by normal distribution to verify that it conforms to the Wiener process. The maximum likelihood estimation method is used to estimate the parameters of the residual life prediction model and predict the residual life of the leakage circuit breaker. Taking the remaining life of the circuit breaker at the initial moment as the pseudo-failure life, it is extrapolated that the life under normal stress is about 2 085 days.
Keywords：Performance degradation, Wiener process, constant stress accelerated degradation test, remaining life prediction
中图分类号：TM506
DOI: 10.19595/j.cnki.1000-6753.tces.200837
河北省自然科学基金项目（E2020202221）和河北省高等学校科学技术研究项目（ZD2019041）资助。
收稿日期 2020-07-09
改稿日期 2020-11-20
E-mail: liuguojin72@163.com（通信作者）
李 想 女，1995年生，硕士研究生，研究方向为电器可靠性及检测技术。
E-mail: li1995X@126.com
（编辑 崔文静）