
图1 交流接触器结构
Fig.1 Structure diagram of AC Contactor
摘要 交流接触器是一种频繁操作的开关电器,其运动过程中的吸反力配合直接影响可靠性和性能指标,良好的吸反力配合能减少触头弹跳、提高分断特性。在此过程中,交流接触器的弹簧系统发挥着关键作用。针对交流接触器弹簧系统的多目标优化问题,提出一种动态过程的电磁-机械耦合仿真方法和弹簧实体仿真方法,在此基础上引入基于灰色关联法和响应曲面法的综合优化方法,建立触头弹跳时间、触头刚分速度、触头闭合速度、铁心闭合速度与触头弹簧自由高度、触头弹簧有效圈数、反力弹簧自由高度和反力弹簧有效圈数的二阶预测模型,对弹簧系统进行优化设计。实验结果表明,该优化方法获得的弹簧系统参数能有效减小触头弹跳时间,降低触头及铁心的闭合时间,提高触头分断速度,对于提高交流接触器的工作性能具有积极意义。
关键词:交流接触器 响应面法 触头弹跳 弹簧系统 多目标优化
交流接触器是一种应用广泛的控制电器,其工作可靠性和各项性能指标直接影响系统的运行情况[1]。吸力与反力特性的合理配合是保证交流接触器可靠性及工作性能的关键。研究人员提出了许多交流接触器电磁机构的优化方法以改善吸力特性[2]。但是单纯优化吸力特性是不全面的,还应考虑弹簧系统的优化设计。交流接触器常使用圆柱螺旋弹簧和截锥螺旋弹簧配合构成反力系统,其设计参数多,且力学特性非线性,因此,需要重点研究如何设计一个合理的弹簧系统。
虚拟样机技术能够有效提高设计效率,文献[3-5]采用等效磁路模型计算电磁机构动态特性。等效磁路法有着计算快、建模方便等优点,但误差较大,且涉及一些重要参数难以精确计算。文献[6-8]将有限元理论引入电磁机构的计算中,利用电磁有限元软件计算电磁机构的动态过程。有限元法考虑了电磁机构内磁场的分布情况,比等效磁路法更接近实际工作情况。以上文献未考虑触头系统及其他部件,只对电磁系统建模计算。文献[9-11]采用实验方法对接触器和继电器的触头弹跳影响因素进行探究,分析触头闭合瞬时速度、弹簧刚度、触头规格等因素对弹跳振动的影响。文献[12]建立真空断路器触头合闸弹跳的动力学理论模型,分析触头弹跳影响因素,但该模型将机构等效为质点和理想杆件,进行较大的简化和理想化处理,不适用于定量计算。文献[13-16]通过机械动力学软件建立含触头系统的接触器模型,引入触头系统和电磁系统的碰撞弹跳。碰撞弹跳计算需要确定接触刚度系数等关键参数,但文献并未给出这些参数的确定方法。为了获得最优设计参数,在虚拟样机的基础上,研究人员通过优化算法对接触器进行优化。文献[17-18]建立电磁机构有限元模型,对分磁环结构进行分析和优化。文献[19]采用遗传算法和模拟退火算法对永磁接触器的永磁体进行优化。文献[20]采用径向基函数(Radial Basis Function, RBF)神经网络和粒子群算法对螺管式接触器进行结构优化。上述文献仅从静态特性角度进行优化。
本文提出一种电磁-机械耦合仿真方法和基于梁单元的实体弹簧仿真方法,实现交流接触器电磁场与机械动作过程的耦合仿真和圆柱螺旋弹簧、截锥螺旋弹簧力学特性的计算。在动态仿真方法的基础上,首次在交流接触器弹簧系统的优化设计中引入基于灰色关联系数和响应曲面法的综合优化方法,从动态特性角度对弹簧系统进行优化设计。通过中心复合试验,以最少的试验次数为响应曲面优化提供足够的数据。通过灰色关联系数,将多目标问题转化为单目标决策问题。最后采用响应曲面法对交流接触器的弹簧系统进行了优化设计。
交流接触器结构如图1所示,其线圈额定电压220V。线圈通电后,电磁机构被磁化,产生电磁吸力,克服反力弹簧作用驱动动铁心运动,动铁心通过支架带动触头系统运动。当动静触头接触,碰撞瞬间产生接触力,导致动触头弹跳。动铁心继续运动,压缩触头弹簧。动静铁心碰撞后,动铁心弹跳。由于缓冲件的存在,动静铁心在其作用下做阻尼振动,抑制铁心弹跳,进而避免触头二次弹跳。线圈断电后,磁场快速消失,电磁吸力降至小于反力以后,动铁心在反力的作用下,推动触头分断。

图1 交流接触器结构
Fig.1 Structure diagram of AC Contactor
接触器工作过程中,各部件之间存在着相对运动、非线性接触碰撞及摩擦现象。对于约束机械系统,系统动力学模型的一般形式可以表示为
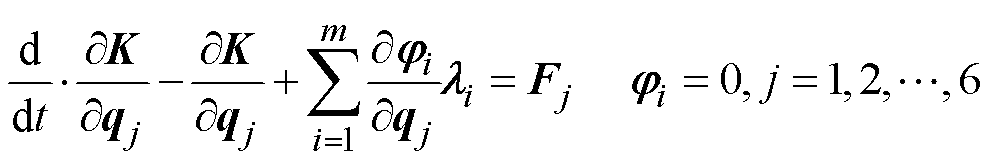 (1)
(1)式中,K为动能;qj为欧几里得空间的广义坐标向量;ji为系统约束方程;m为约束方程总数;i为第i个约束方程;Fj为广义坐标方向上的力;li为拉格朗日乘子;j为刚体自由度。每一个刚体都可以用6个拉格朗日方程和相应的约束方程表示。
交流接触器动作过程中,动静触头、动静铁心及支架等部件之间存在动态接触。其特点是作用时间短、瞬间作用力大、非线性、不连续。采用连续接触力法求解碰撞接触。法向接触力为
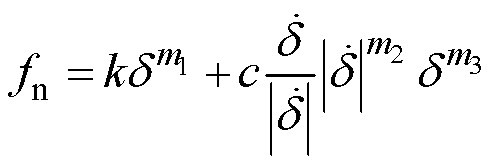 (2)
(2)式中,k为接触刚度系数;c为阻尼系数;d 为接触穿透深度;![]() 为接触物体的相对速度;m1、m2、m3分别为刚度指数、阻尼指数、凹痕指数,这些指数与接触部件的弹性模量、泊松比以及形状有关。
为接触物体的相对速度;m1、m2、m3分别为刚度指数、阻尼指数、凹痕指数,这些指数与接触部件的弹性模量、泊松比以及形状有关。
以往的模型多是通过经验或实验求取接触刚度系数k值。由于k与接触物体的形状、材料、运动情况有关,上述方法的通用性较差。本文对大量文献及接触力学理论进行考证和推算,引入Hertz弹性接触理论计算动态接触刚度系数[21]。经典的Hertz接触理论假设接触区域发生微小形变、接触面呈椭圆形、接触物体材料各向同性,其计算式为
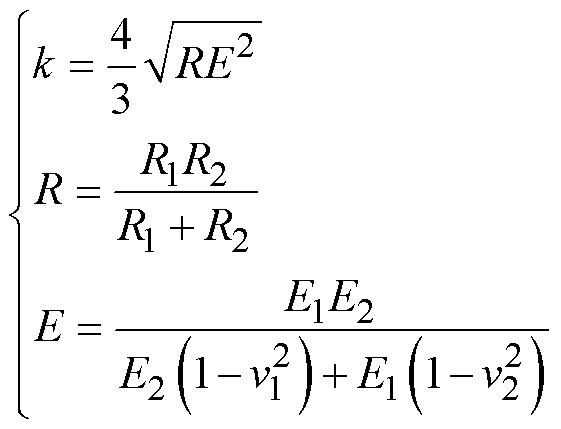 (3)
(3)式中,R1、R2为接触物体的曲率半径;E1、E2为接触物体的弹性模量;v1、v2为接触物体的泊松比。
研究对象的动静触头、支架及动静铁心等接触区域皆为矩形平面,如图2所示。对于矩形接触区域,式(3)中的R1和R2趋近于无穷大。为了使式(3)适用于研究对象,必须对Hertz公式进行变形。
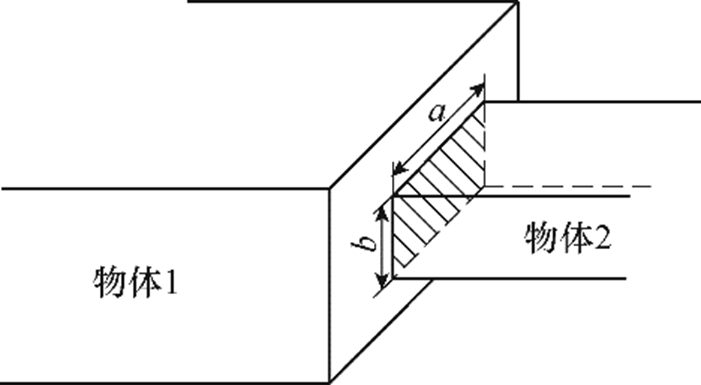
图2 矩形平面接触示意图
Fig.2 Diagram of rectangular area contact
根据文献[21],接触力f均匀作用于矩形接触区域时,物体的平均接触穿透深度为
 (4)
(4)式中,![]() 为修正系数;S为接触面积;v为泊松比;E为杨氏模量;a为矩形长边长度;b为矩形短边长度。不同边长比下的
为修正系数;S为接触面积;v为泊松比;E为杨氏模量;a为矩形长边长度;b为矩形短边长度。不同边长比下的![]() 值见表1[21]。
值见表1[21]。
表1 不同边长比下的s 值
Tab.1 The value of s in different side ratios

a/bs 1.00.95 1.50.94 2.00.92 3.00.88 5.00.82 10.00.71
两个物体接触时,接触总穿透深度d 为
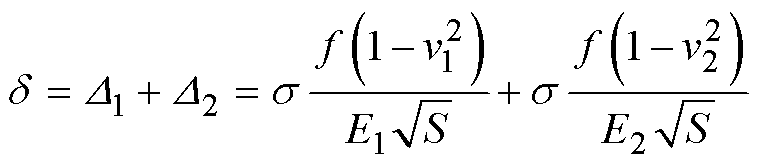 (5)
(5)式中,![]() 、
、![]() 分别为两个接触物体穿透深度。
分别为两个接触物体穿透深度。
根据稳定接触时的接触力
可以进一步推导出矩形平面接触区域的接触刚度系数为
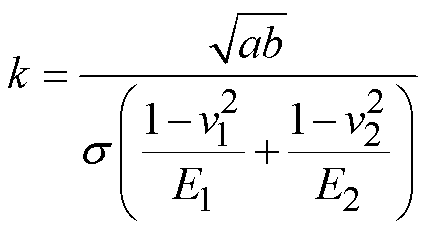 (7)
(7)
接触阻尼系数c工程上一般取为接触刚度系数的0.1%~1%[22],金属-金属接触及钢铁-塑料接触一般取0.1%[21, 23]。
接触器工作中存在磁场和机械的动态过程,因此求解电磁系统的动态吸力及动态吸力与机械过程的耦合是计算接触器动态过程的关键。耦合仿真模型由三部分组成:①电磁方程求解;②运动学和接触方程求解;③电路求解。电磁-机械耦合求解的流程如图3所示。
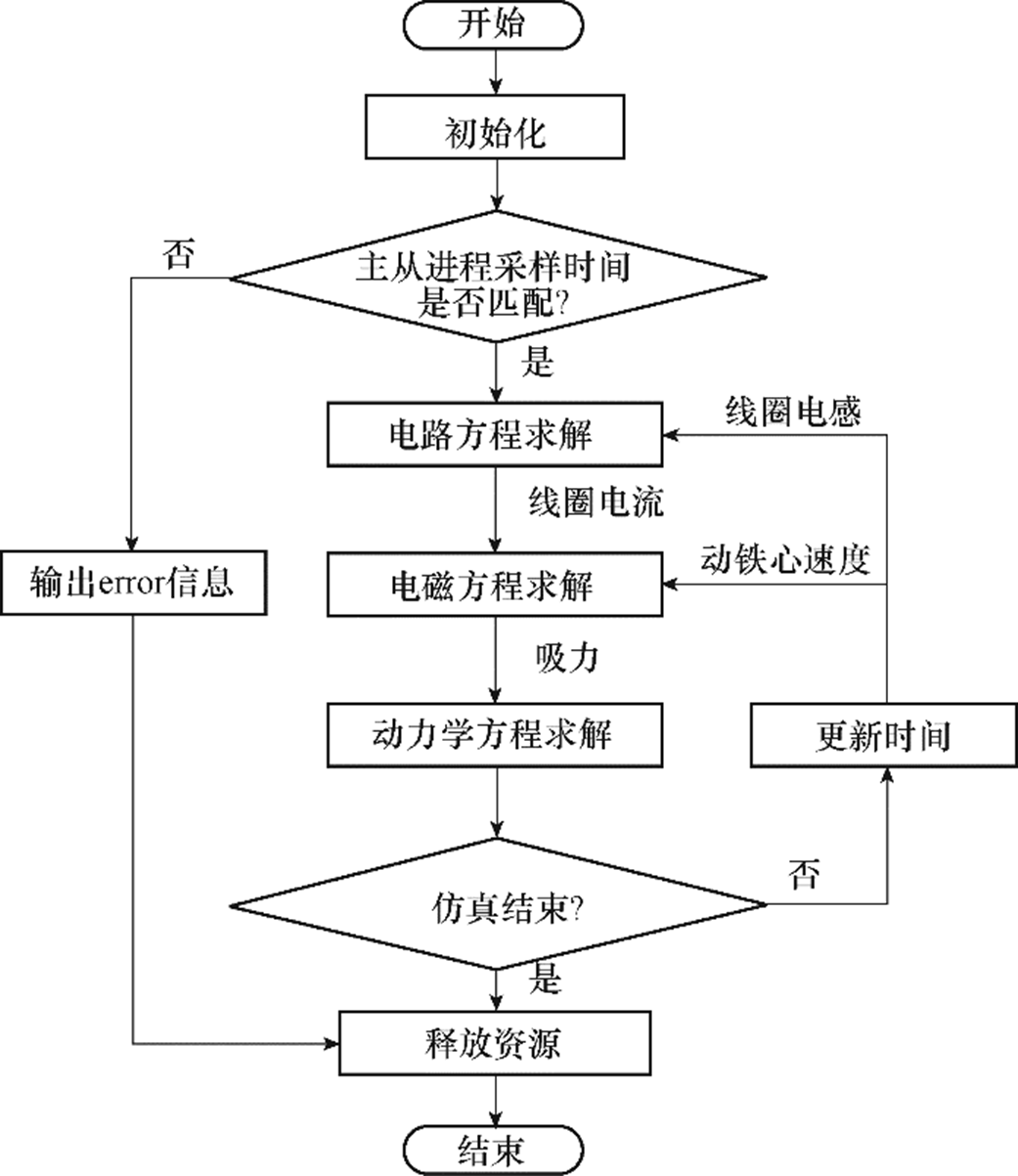
图3 耦合过程示意图
Fig.3 Diagram of coupling process
接触器弹簧系统由触头弹簧和反力弹簧组成。触头弹簧常为圆柱螺旋弹簧,反力弹簧常为截锥螺旋弹簧。圆柱螺旋弹簧具有良好的线性度,刚度系数较稳定;截锥螺旋弹簧是非线性弹簧,刚度系数随压缩量变化而变化。截锥弹簧具有自振频率不固定的优点,常用于减振的场合,用作反力弹簧,可降低接触器吸合时弹簧的晃动,保持弹簧稳定。
对于螺旋弹簧,弹簧圈的任意一段簧丝剖面上受到切向力F和转矩T的作用,因此,可以将每一段簧丝视为曲梁(curved beam),将弹簧实体离散为多段簧丝,通过梁单元理论计算各段簧丝两端的力学特性[24-25],相邻的簧丝截面由beam力连接。簧丝间自接触可由式(3)确定。beam力为
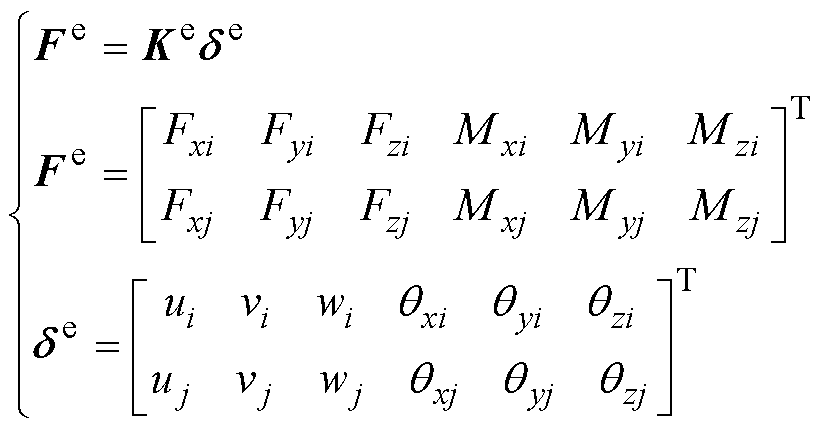 (8)
(8)式中,![]() 为节点力矩阵;Fxi、Fyi、Fzi、Fxj、Fyj、Fzj分别为梁单元i端点和j端点在x、y、z 3个方向的节点剪力;Txi、Tyi、Tzi、Txj、Tyj、Tzj分别为梁单元i端点和j端点在x、y、z 3个方向的弯矩;Ke为刚度矩阵;de为梁单元两端节点位移矩阵。
为节点力矩阵;Fxi、Fyi、Fzi、Fxj、Fyj、Fzj分别为梁单元i端点和j端点在x、y、z 3个方向的节点剪力;Txi、Tyi、Tzi、Txj、Tyj、Tzj分别为梁单元i端点和j端点在x、y、z 3个方向的弯矩;Ke为刚度矩阵;de为梁单元两端节点位移矩阵。
图4a和图4b分别为圆柱状的触头弹簧和截锥状的反力弹簧的实体模型。其中,触头弹簧自由高度为11.8mm,有效圈数为6;反力弹簧自由高度为27mm,有效圈数为4。在弹簧上、下两端分别设置一个顶板和一个底板。底板作为弹簧的固定板,约束弹簧的横向运动和转动。顶板作为弹簧的受力板,以一个恒定速度沿着垂直方向压缩弹簧,检测弹簧与顶板的接触力,即可获得弹簧的力学特性。
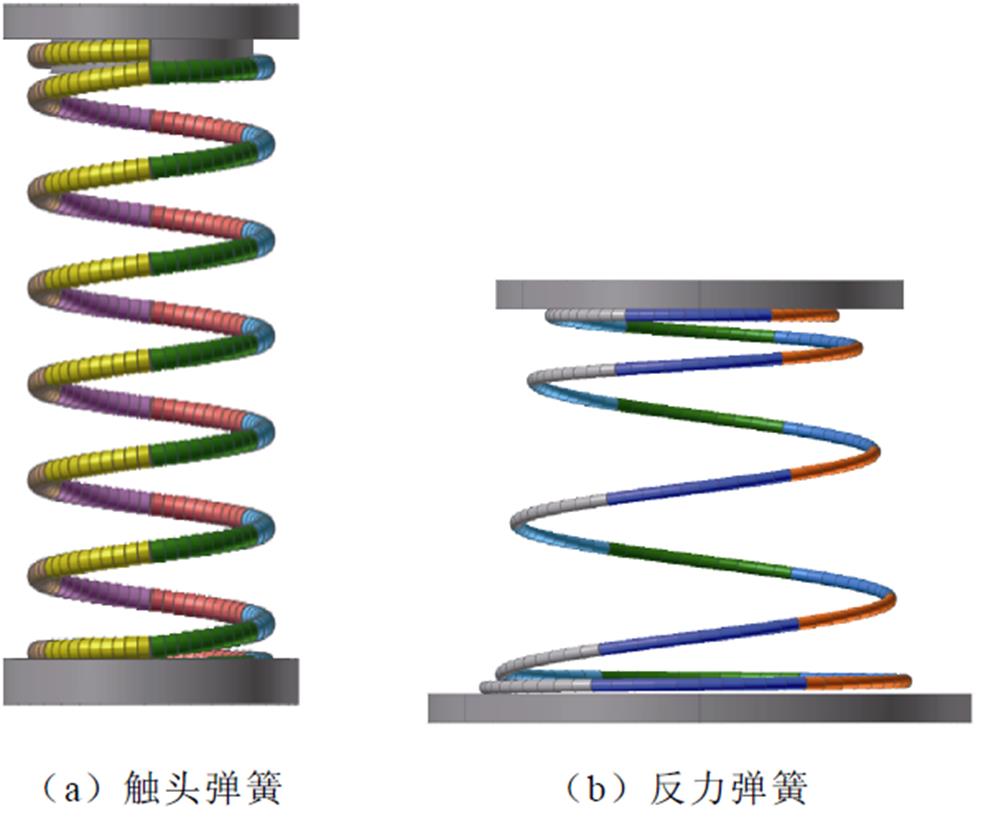
图4 触头弹簧与反力弹簧模型
Fig.4 Contact spring and return spring model
搭建“接触器动态特性测试系统”测量研究对象的动态特性。动态特性测试系统主要由“选相合闸与分闸控制电路”和“KEYENCE LK-G5000”激光位移传感器组成。通过“选相合闸与分闸控制电路”控制线圈的合闸相位,实现交流接触器在设定相位下吸合;激光位移传感器通过非接触方式测量动铁心的位移。触头弹跳信号通过主回路外接3V直流源测量。当动静触头接触,主回路接通,弹跳信号为高电平;动静触头分开,主回路电路断开,信号转变为低电平。实验现场如图5a所示。弹簧的力学特性通过“艾普”弹簧压力测试机进行测量。实验现场如图5b所示。
动态特性对比如图6和图7所示。图6为励磁电压220V,频率50Hz,0°线圈合闸相位下动铁心位移曲线、线圈电流曲线以及触头碰撞弹跳信号的仿真与实验对比结果。从图可知,吸合过程仿真曲线与实验吻合度较好。动静铁心在0.02s左右闭合,铁心碰撞瞬间挤压橡胶缓冲件,动铁心位移有一个振荡过程。本文为了提高计算效率,对橡胶缓冲件进行了简化,导致动铁心位移在0.02s处存在一定误差。图7为分闸过程动铁心位移及线圈电压的仿真与实验对比结果。从图可知,分断过程仿真曲线与实验基本吻合。

图5 实验现场
Fig.5 Experimental spot
表2为0°~150°不同吸合相位下交流接触器吸合时间和触头弹跳时间的仿真与实验值对比。由表2可知,仿真结果与实测数据基本吻合,误差在15%以内,说明模型能够反映样机的各参量的动态变化趋势,验证了交流接触器动态模型的正确性。

图6 吸合动态特性仿真实验对比
Fig.6 Simulation and experiment comparison of closing dynamic characteristics
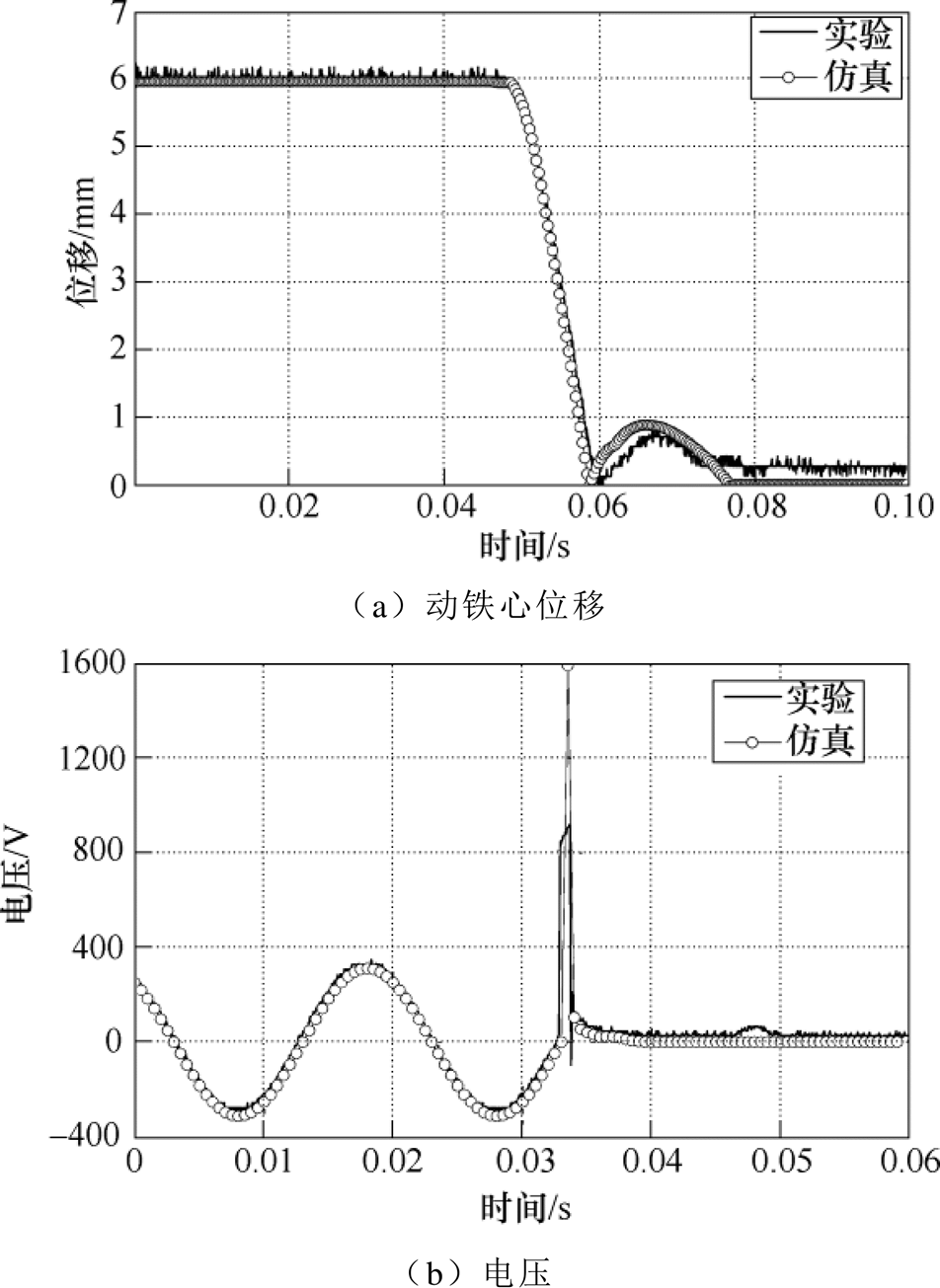
图7 分断动态特性仿真实验对比
Fig.7 Simulation and experiment comparison of breaking dynamic characteristics
表2 动态特性验证
Tab.2 Dynamic performance verification

相位/(°)吸合时间/ms弹跳时间/ms 仿真实验仿真实验 018.2619.342.252.2 3017.9218.712.82.68 6023.8724.143.624 9027.1827.792.22.4 12023.9924.572.352.54 15021.4121.672.172.3
通过1.4节提出的弹簧仿真模型计算触头弹簧和反力弹簧的力学特性。图8a和图8b分别为触头弹簧和反力弹簧仿真得到的位移-力特性曲线与实验结果的对比。从图中可知,仿真所得的位移-力特性曲线与实验结果基本一致,因此,仿真模型可以反映交流接触器触头弹簧和反力弹簧的力学特性。

图8 弹簧系统仿真实验对比
Fig.8 Simulation and experiment comparison of springs
反力特性是接触器设计的基础,反力特性与吸力特性的合理配合是保证交流接触器可靠工作以及提高其工作性能和经济指标的重要环节。
考虑到实际的加工工艺和弹簧在样机中的装配条件,仅对触头弹簧和反力弹簧的自由高度和有效圈数进行分析。
3.1.1 触头弹簧
图9为不同自由高度下圆柱螺旋弹簧的刚度。从图中可见,自由高度对弹簧刚度没有影响。因此,可以通过调整自由高度来调整触头弹簧的初压力。
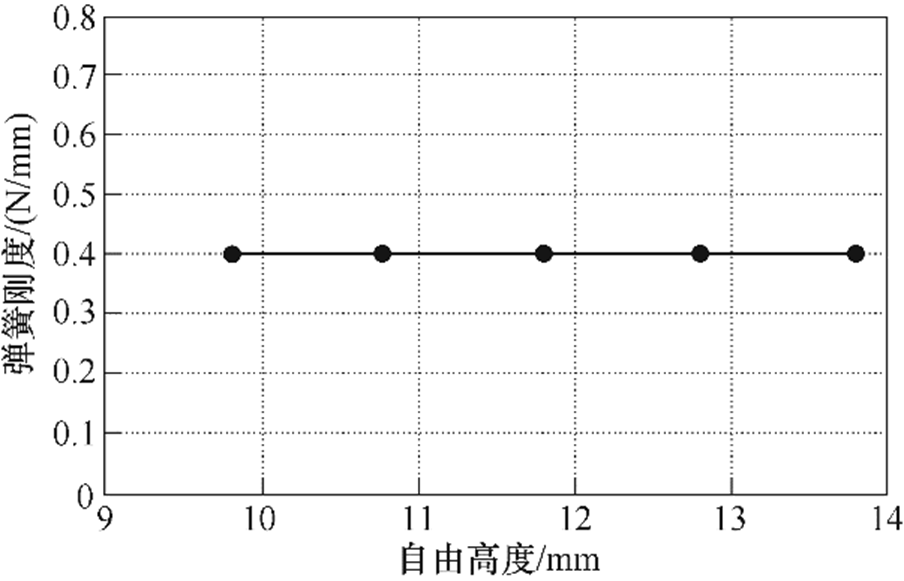
图9 不同自由高度弹簧刚度
Fig.9 Spring stiffness of different free height
图10为不同有效圈数下圆柱螺旋弹簧的刚度。从图中可见,有效圈数及弹簧中径与刚度之间呈负相关关系,即有效圈数或弹簧中径越大,弹簧刚度越大。
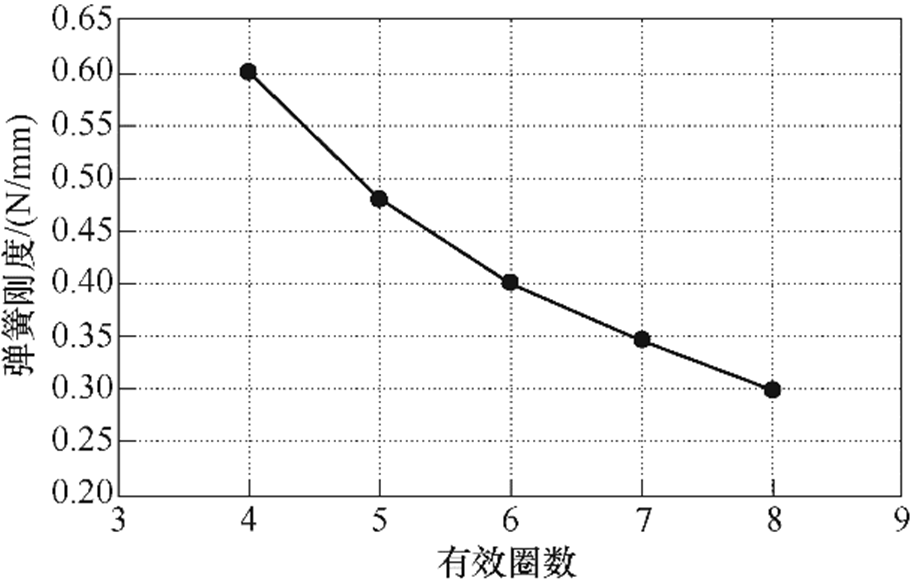
图10 不同有效圈数弹簧刚度
Fig.10 Spring stiffness of different working coil
3.1.2 反力弹簧
图11为不同自由高度下截锥螺旋弹簧的力学特性曲线。在其线性区域,弹簧刚度不随自由高度变化。进入非线性段后,自由高度小的截锥弹簧的力学特性曲线更加陡峭,刚度更大。此外,自由高度越小的弹簧进入非线性段所需的压缩量越小。
图12为不同有效圈数下截锥螺旋弹簧的力学特性曲线。从图中可见,截锥螺旋弹簧的刚度与有效圈数呈负相关关系。

图11 不同自由高度弹簧力特性
Fig.11 Force characteristic of different free height
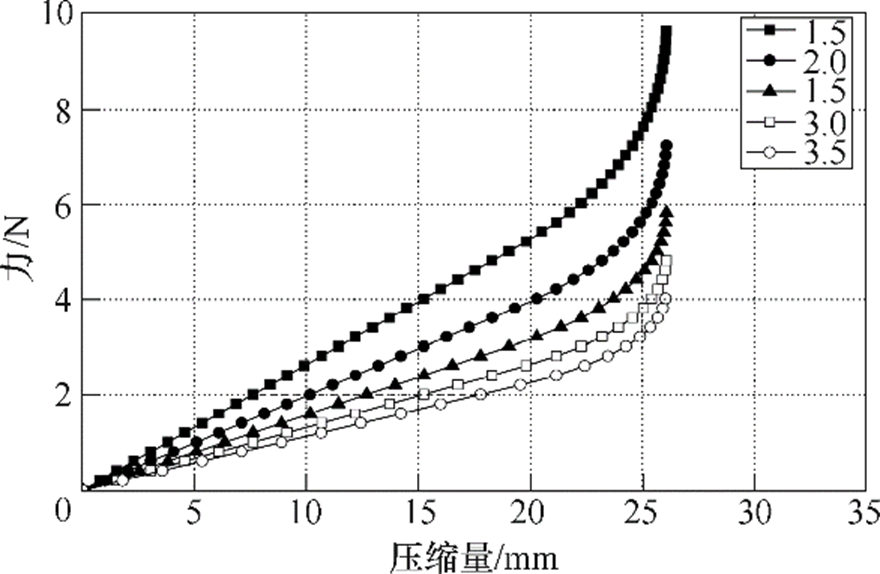
图12 不同有效圈数弹簧力特性
Fig.12 Force characteristic of different working coil
采用灰色关联度和响应曲面综合优化方法对弹簧系统进行优化,步骤如下:①设计中心复合试验;②求试验组灰色关联度;③拟合响应与设计变量的回归方程;④寻找弹簧参数的最优匹配。
3.2.1 试验设计与计算结果
考虑到实际工艺和装配条件,以触头弹簧自由高度lc、触头弹簧有效圈数nc、反力弹簧自由高度lf、反力弹簧有效圈数nf为优化变量,以触头闭合时间tc、触头弹跳时间tb、铁心闭合时间tt、铁心闭合速度vt、触头刚分速度vb及85%UN下能否吸合为优化目标。由于设计变量较多,若采用全因子试验需要625次试验,试验次数多,计算时间长,本文选用四因子五水平的中心复合试验方法(Central Composite Design, CCD)进行试验设计,以最少的试验次数建立二阶响应曲面模型。表3为CCD因子水平,CCD试验设计表及仿真结果见附表1。
3.2.2 灰色关联系数计算
在多目标优化过程中,多个目标之间可能会出现相互矛盾的情况,需要对多个目标进行归一化综合处理,将多目标问题转化为单目标问题。本文采用灰色关联法(Grey Relational Analysis, GRA),建立交流接触器弹簧系统的多维灰色关联度模型。
表3 CCD因子水平
Tab.3 Horizontal table of CCD

水平因子 lc/mmnclf/mmnf -29.83251.5 -110.84262 011.85272.5 112.86283 213.87293.5
灰色关联分析法是一种多因素统计分析方法,它以各因素的样本数据为基础,通过灰色关联度来描述各因素的强度、大小和顺序。灰色关联分析的基本思想是根据序列的曲线集合形状的相似性来确定它们之间的关系是否密切。曲线越相似,对应序列之间的相关性越大。
设性能指标的参考序列为
式中,n为设计变量个数;m为评价方案个数。
灰色关联系数(Grey Relational Coefficient, GRC)的计算公式为
式中,r 为分辨系数,取值范围0~1,通常取0.5。
设计目标中,触头闭合时间tc、触头弹跳时间tb、铁心闭合时间tt和铁心闭合速度vt为望小特性,触头刚分速度vb为望大特性。根据试验结果,基准矢量序列X0={16.54, 0.9, 18.49, 1.185, 0.81}。
灰色关联度(Grey Relational Degree, GRD)是灰色关联系数的加权和,其表达式为
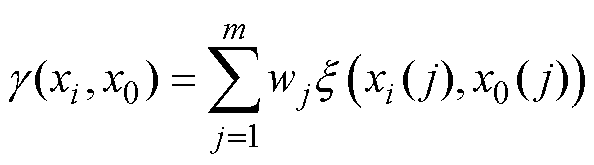 (11)
(11)式中,wj为第j个指标的权重系数。
权重系数wj通过熵权法确定。熵权法是一种依据各指标所含信息量的多少来确定指标权重的客观赋权法。某个指标的熵值越小,说明该指标的变异程度越大,所提供的信息量也就越多,在综合评价中起的作用越大,则该指标的权重也应越大。
对于m个评价方案,n项指标构成的评价矩阵R=(rij)m´n,可以将指标标准化为
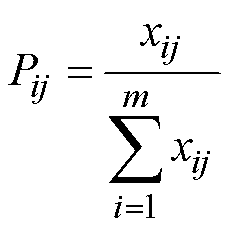 (12)
(12)式中,Pij为标准化的指标数据。
评价指标的熵值和权重分别为
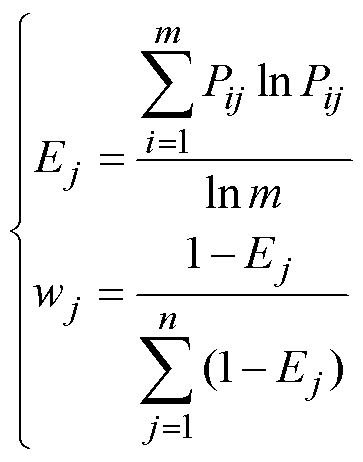 (13)
(13)式中,Ej为第j项评价指标的熵值;wj为第j项评价指标的权重,∑wj=1。
根据式(13)与式(14)可以求得触头闭合时间tc、触头弹跳时间tb、铁心闭合时间tt、铁心闭合速度vt、及触头刚分速度vb的权重分别为8.43%、72.36%、8.41%、5.84%及4.94%。弹簧系统的综合评价公式为
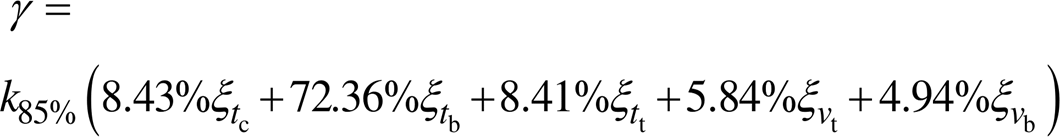 (14)
(14)式中,k85%为85%的额定电压下交流接触器能否吸合,若能够稳定吸合,则k85%=1,若无法吸合,则k85%=0;![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 分别为触头闭合时间tc、触头弹跳时间tb、铁心闭合时间tt、铁心闭合速度vt及触头刚分速度vb的灰色关联系数。
分别为触头闭合时间tc、触头弹跳时间tb、铁心闭合时间tt、铁心闭合速度vt及触头刚分速度vb的灰色关联系数。
根据上述理论计算灰色关联系数和灰色关联度。弹簧系统的灰色关联系数见附表2。
3.2.3 基于响应曲面法的弹簧系统优化设计
为了实现对交流接触器弹簧系统的优化设计,必须建立交流接触器的性能指标与弹簧系统设计变量之间的映射关系[26]。通常,响应面法中的二阶数学回归模型用于确定响应与设计变量之间的关系。二阶回归方程为
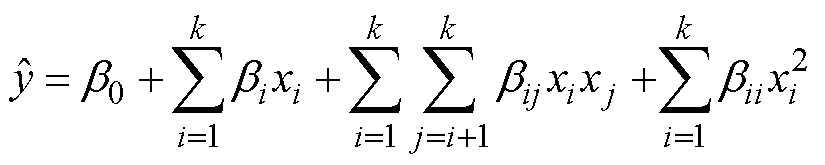 (15)
(15)式中,xi为弹簧系统的4个结构参数;![]() 为GRG估计值;b 为二次回归系数;第二项表示线性效应;第三项表示交互效应;第四项表示二次效应。
为GRG估计值;b 为二次回归系数;第二项表示线性效应;第三项表示交互效应;第四项表示二次效应。
通过坐标变换法寻找最优参数[27]。将式(15)用矩阵形式表示为
在设计空间中随机选择一组起始点x0,按Bayesian D最优性准则[28]对单个因子求局部最优点xs。通过式(17)将式(16)变换到以xs为中心的新坐标系中。
![]() (17)
(17)
以xs为起始点更换因子重复上述过程直到完成所有因子的优化。对所有因子多次重复该算法以接近全局最优设计。
对附表2的结果进行回归分析,建立交流接触器弹簧系统的灰色关联度预测模型,可表示为
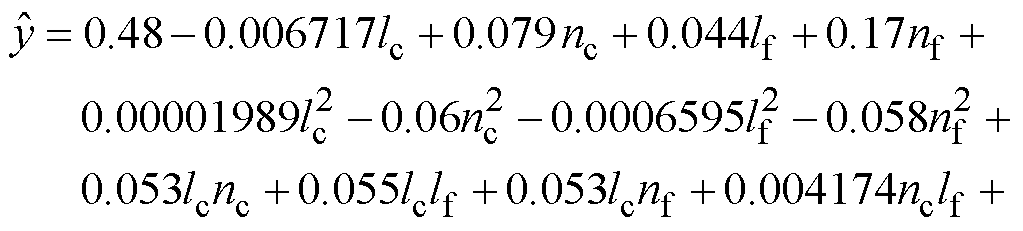
![]() (18)
(18)
图13为预测模型的残差,图中,残差均分布在零附近,均低于0.05。评价指标复相关系数R2为0.897 9,![]() 为0.802 5。R2和
为0.802 5。R2和![]() 越大,表明回归模型的拟合程度越好,该回归模型的拟合程度达89.79%,表明模型的准确性和可靠性。
越大,表明回归模型的拟合程度越好,该回归模型的拟合程度达89.79%,表明模型的准确性和可靠性。

图13 预测模型残差
Fig.13 Prediction model residuals
根据灰色关联理论[29-30],灰色关联度越大,相应的目标响应越好。优化获得最佳参数匹配为:触头弹簧自由高度为12.78mm、有效圈数为5.2,反力弹簧自由高度为29.99mm、有效圈数为2.99,其灰色关联度的预测值为1.011。考虑到实际工艺,选取了两组优化结果进行比较。优化1:触头弹簧自由高度为12.8mm、有效圈数为5,反力弹簧自由高度为30mm、有效圈数为3,灰色关联度预测值为1.007;优化2:触头弹簧自由高度为12.8mm、有效圈数为5.5,反力弹簧自由高度为30mm、有效圈数为3,灰色关联度预测值为1.003。优化1灰色关联度更高,认为优化1的性能指标更好。
图14为两组优化与原样机的反力对比。优化前后性能指标对比如图15~图19所示,性能指标中位数见表4,其中,原样机各性能指标为实验结果,优化组的性能指标为仿真结果。由图15和图17可知,优化组的触头闭合时间和铁心闭合时间均低于原样机;优化1和优化2的触头弹跳时间远低于原样机,中位数分别为1.33ms和1.7ms,原样机为2.47ms。优化1和优化2的铁心闭合速度低于原样机,中位数分别为1.21m/s和1.25m/s,原样机为1.4m/s;优化1和优化2的触头刚分速度高于原样机,中位数分别为0.67m/s和0.66m/s,原样机为0.65m/s。
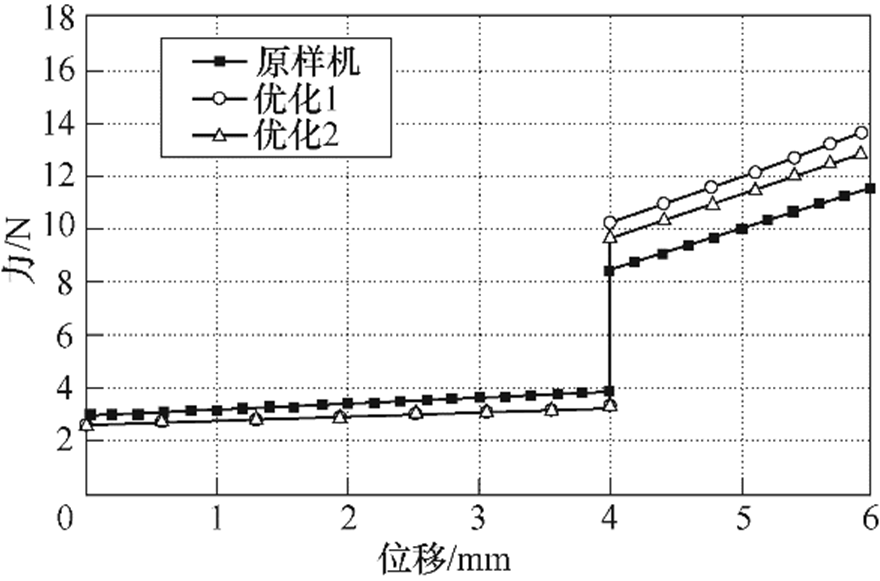
图14 优化反力与原样机反力对比
Fig.14 Optimized and original reaction force comparation
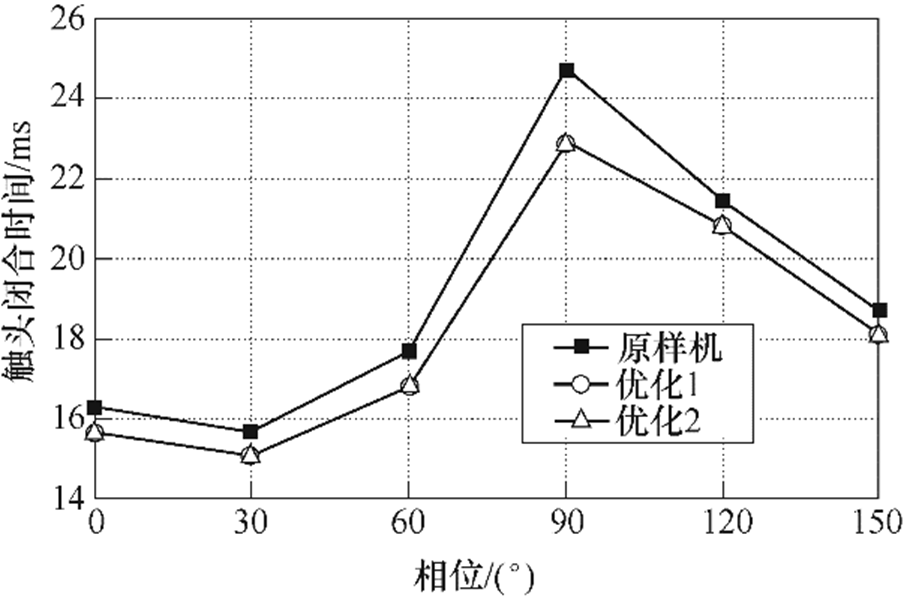
图15 触头闭合时间
Fig.15 Contact closing time
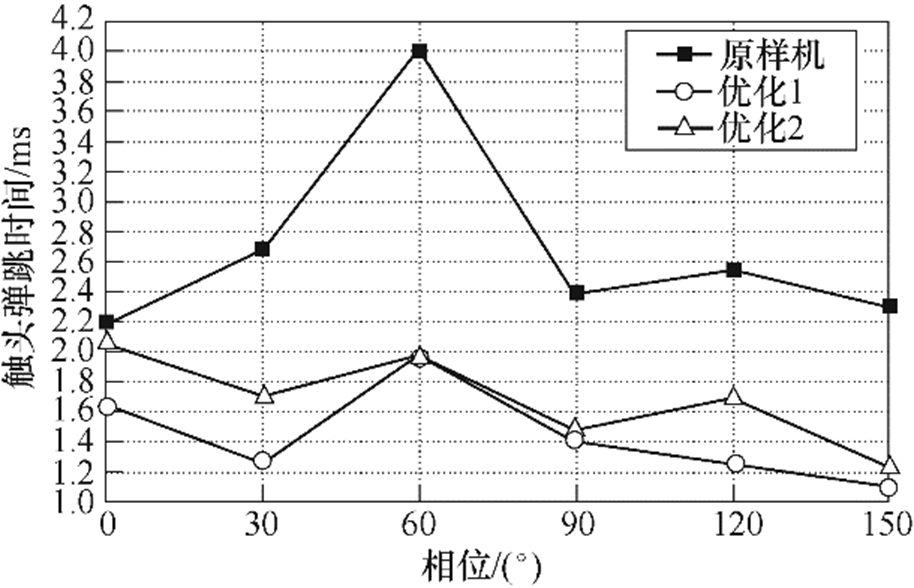
图16 触头弹跳时间
Fig.16 Contact bounce time

图17 铁心闭合时间
Fig.17 Iron core closing time
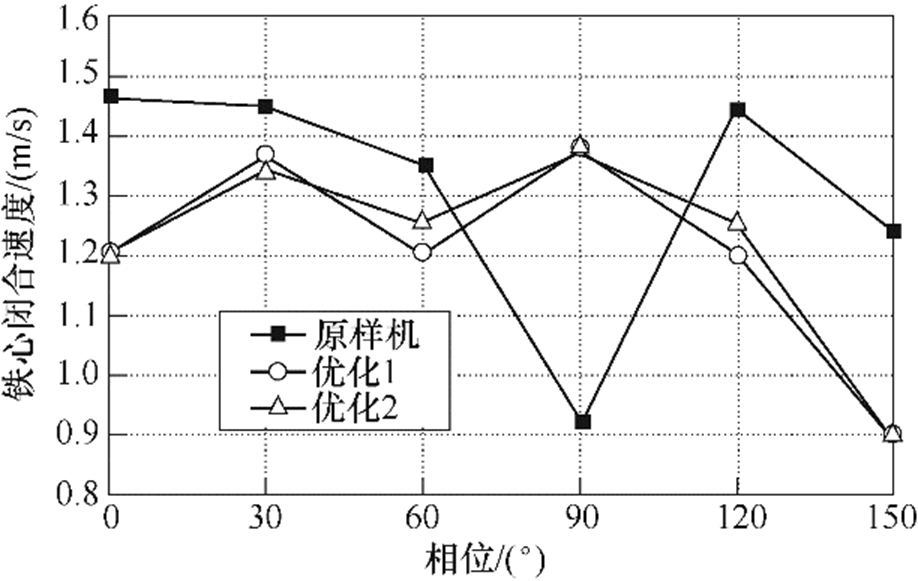
图18 铁心闭合速度
Fig.18 Iron core closing velocity
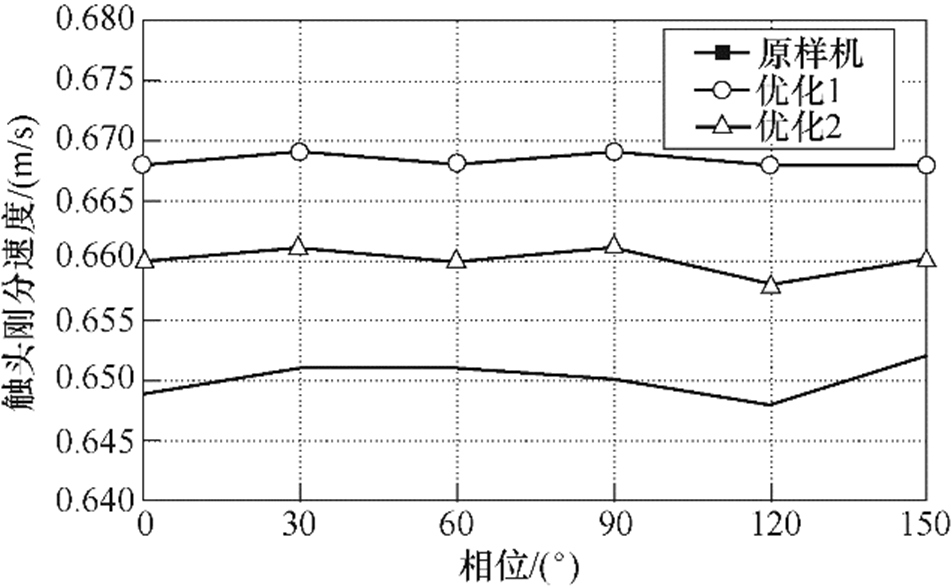
图19 触头刚分速度
Fig.19 Contact breaking velocity
表4 优化指标中位数
Tab.4 Median of optimizing index

指标原样机优化1优化2 tc/ms18.1617.4217.42 tb/ms2.471.331.7 tt/ms22.919.4319.73 vt/(m/s)1.41.211.25 vb/(m/s)0.650.670.66
综合考虑各项性能指标,优化1>优化2>原样机。因此,选取触头弹簧自由高度为12.8mm,触头弹簧有效圈数为5,反力弹簧自由高度为30mm,反力弹簧有效圈数为3为优化后的反力系统。
根据第3.2节分析,最优弹簧组合为:触头弹簧自由高度为12.8mm,触头弹簧有效圈数为5,反力弹簧自由高度为30mm,反力弹簧有效圈数为3。为了验证优化结果的准确性,采用上述参数组合加工了触头弹簧和反力弹簧,利用“接触器动态特性测试系统”测量交流接触器的触头闭合时间tc、触头弹跳时间tb、铁心闭合时间tt、铁心闭合速度vt和触头刚分速度vb 5个指标,图20为90°合闸相位的吸合曲线,可以看到,优化后的闭合时间、触头弹跳等指标都得到改善。优化后各指标值见表5。与原样机各指标对比,优化后样机触头闭合时间缩短了4.5%,触头弹跳时间缩短了31.1%,铁心闭合时间缩短了16.2%,铁心闭合速度减小了19.9%,触头刚分速度提高了4.6%,因此,该优化方法能有效提高交流接触器的吸合分断特性。
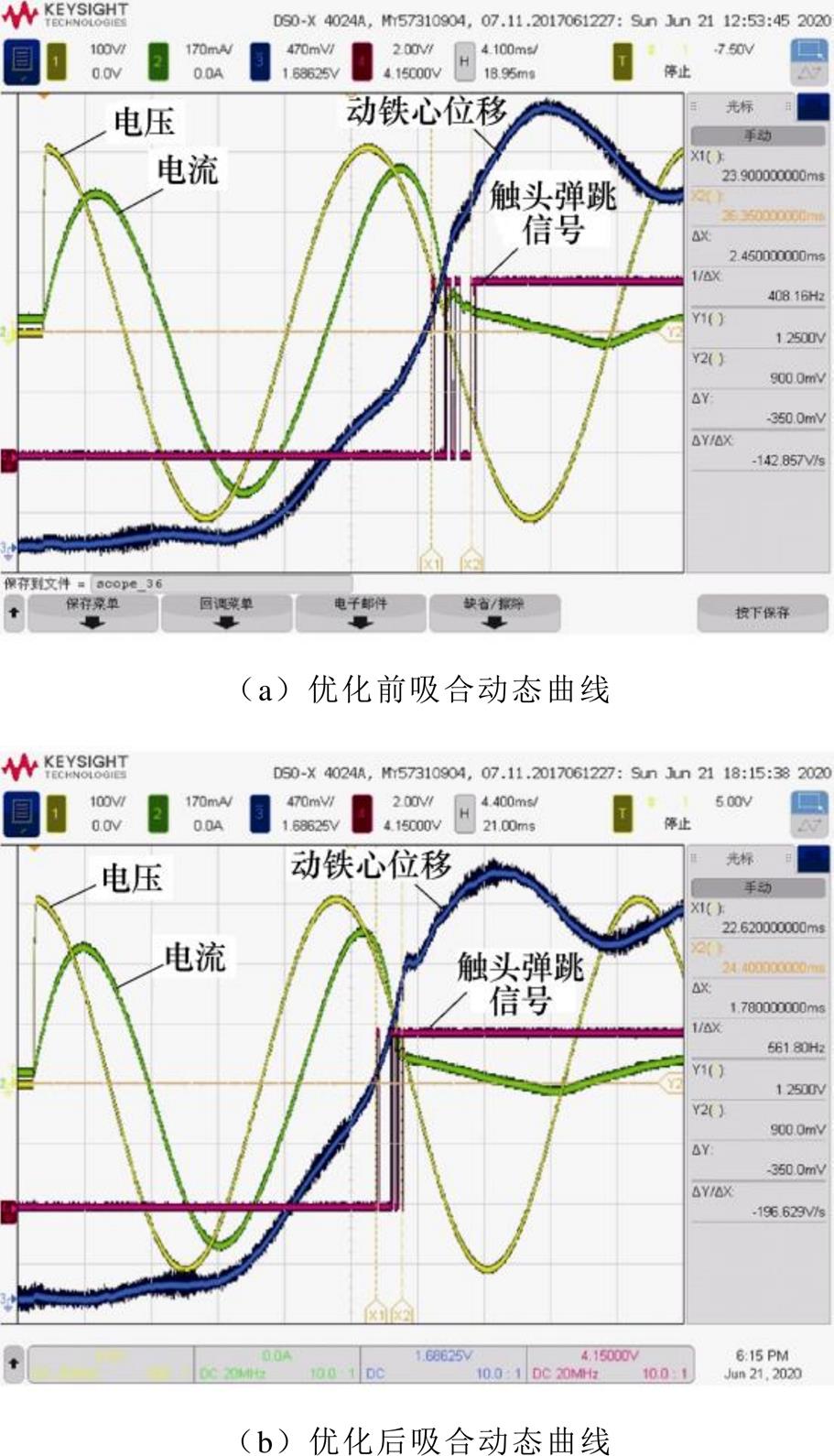
图20 优化前后90°吸合动态过程
Fig.20 90°dynamic process before and after optimization
表5 优化后的指标值
Tab.5 Optimized index values

相位/(°)指 标 tc/mstb/mstt/msvt/(m/s)vb/(m/s) 015.631.6518.11.180.68 30151.35171.320.681 6016.72.2618.41.220.68 9023.371.7523.91.360.68 12020.81.3722.31.20.679 150181.02200.880.68
1)提出一种电磁-机械耦合的交流接触器仿真方法,引入赫兹弹性接触理论确定各部件之间的接触参数,能考虑交流接触器铁心、触头等部件之间的多体作用,模拟交流接触器工作全过程电磁过程、运动过程耦合计算。
2)建立了圆柱螺旋弹簧和截锥螺旋弹簧的实体模型,分析了不同自由高度和有效圈数下圆柱螺旋弹簧的刚度系数变化情况以及截锥螺旋弹簧非线性力学特性的变化情况。对于圆柱螺旋状的触头弹簧,弹簧自由高度对弹簧刚度系数没有影响,可以通过调整自由高度调整初压力;圆柱螺旋弹簧的刚度系数与有效圈数呈负相关。对于截锥螺旋状的反力弹簧,其刚度是非线性的。在线性区域,刚度系数不受自由高度影响,进入非线性段后,自由高度小的截锥螺旋弹簧的力学特性曲线更加陡峭;截锥螺旋弹簧的刚度系数与有效圈数呈负相关。
3)设计中心复合试验,计算不同结构弹簧系统下交流接触器的吸合与分断动态特性,采用灰色关联分析法和响应面法对弹簧系统进行多目标优化,得到触头弹簧自由高度、触头弹簧有效圈数、反力弹簧自由高度和反力弹簧有效圈数的最优匹配,使得触头吸合时间缩短4.5%,触头弹跳时间缩短31.1%,铁心闭合时间缩短16.2%,铁心闭合速度减小19.9%,触头刚分速度提高4.6%,有助于提高交流接触器的速动性,减小触头弹跳引起的触头烧蚀,对触头的电寿命具有积极意义。
附 录
附表1 CCD试验表与结果
App.Tab.1 CCD test table and results

水平因 子 lc/mmnclf/mmnftc/mstb/mstt/msvt/(m/s)85%UNvb/(m/s) 112.8628317.421.8619.41.7310.67 210.8628221.672.9723.691.46500.65 39.85272.518.193.2220.3351.7310.59 411.85272.518.191.9320.421.6910.68 510.8426219.731.9122.4751.50510.7 610.8626219.732.9922.391.5410.63 711.85272.518.191.9320.421.6910.68 811.85272.518.191.9320.421.6910.68 913.85272.518.191.0820.541.6610.76 1011.85272.518.191.9320.421.6910.68 1111.85292.518.962.121.6551.62510.69 1212.8626316.951.918.891.7110.66 1310.8428221.67223.7251.4300.72 1411.83272.518.191.1220.6151.63500.7 1511.85252.517.551.8919.541.7110.67 1611.85272.518.191.920.421.6910.68 1712.8628221.671.8623.731.42500.72 1811.85272.518.191.920.421.6910.68 1912.8428317.421.0319.461.710.77 2011.85273.516.54218.491.8510.64 2112.8426219.730.9922.6551.4500.8 2212.8626219.731.9122.7251.50510.71 2310.8628317.422.9419.361.7610.59 2412.8426316.941.1518.941.6810.68 2510.8426316.952.0418.881.70510.65 2611.87272.518.192.8620.3651.7210.62 2711.85271.526.741.9830.191.18500.76 2812.8428221.670.923.7951.3700.81 2910.8428317.421.9919.391.7310.66 3010.8626316.952.8118.851.74510.57
附表2 灰色关联系数
App.Tab.2 Grey relational coefficient table

试验GRCGRD tc/mstb/mstt/msvt/(m/s)vb/(m/s) 10.8990.8910.8960.9350.9820.899 20.6040.3660.5220.9650.9800.464 30.8260.3700.6730.9350.9730.497
(续)

试验GRCGRD tc/mstb/mstt/msvt/(m/s)vb/(m/s) 40.8260.3490.6680.9390.9840.482 50.7100.3480.5690.9610.9860.465 60.7100.3660.5720.9570.9780.477 70.8260.3490.6680.9390.9840.482 80.8260.3490.6680.9390.9840.482 90.8260.3360.6620.9430.9940.473 100.8260.3490.6680.9390.9840.482 110.7640.3510.6050.9470.9850.474 120.9500.3480.7690.9370.9810.500 130.6040.3500.5210.9700.9890.453 140.8260.3360.6570.9460.9860.472 150.8860.3480.7230.9370.9820.491 160.8260.3480.6680.9390.9840.481 170.6040.3480.5210.9700.9890.452 180.8260.3480.6680.9390.9840.481 190.8990.3350.7280.9380.9950.484 201.0000.3500.8000.9220.9790.507 210.7100.3350.5610.9670.9990.455 220.7100.3480.5580.9610.9870.464 230.8990.3650.7350.9320.9730.504 2440.9510.3370.7650.9400.9840.492 250.9500.3500.7700.9380.9800.502 260.8260.3640.6720.9360.9760.492 270.4340.3490.3641.0000.9940.428 280.6040.3330.5190.9771.0000.442 290.8990.3500.7330.9350.9810.494 300.9500.3630.7720.9330.9700.510
参考文献
[1] 许志红. 电器理论基础[M]. 北京: 机械工业出版社, 2014.
[2] 张冠生. 电磁铁与自动电磁元件[M]. 北京: 机械工业出版社, 1982.
[3] 林抒毅, 许志红. 晃电故障下交流接触器的工作特性分析[J]. 中国电机工程学报, 2011, 31(24): 131-137.
Lin Shuyi, Xu Zhihong. Performance characteristics of AC contactor during voltage sag[J]. Proceedings of the CSEE, 2011, 31(24): 131-137.
[4] Kanokbannakorn W, Saengsuwan T, Sirisukprasert S. A novel simulation of AC magnetic contactor based on electromagnetic transients program[J]. IEEJ Transa- ctions on Electrical & Electronic Engineering, 2014, 9(2): 144-150.
[5] Jordi-Roger R R, Antonio G E, Luis R. A computer model for teaching the dynamic behavior of AC contactors[J]. IEEE Transactions on Education, 2010, 53(2): 248-256.
[6] 杨帆, 辜承林, 王晨卉, 等. 永磁双稳态电磁离合器磁场分析及优化设计[J]. 电工技术学报, 2018, 33(增刊1): 71-78.
Yang Fan, Gu Chenglin, Wang Chenhui, et al. Magnetic field analysis and optimal design of a permanent magnet bistable electromagnetic clutch[J]. Transactions of China Electrotechnical Society, 2018, 33(S1): 71-78.
[7] Gollee R, Gerlach G. An FEM-based method for analysis of the dynamic behavior of AC contactors[J]. IEEE Transactions on Magnetics, 2000, 36(4): 1337- 1340.
[8] 赵升, 舒亮, 吴自然, 等. 电磁-永磁复合型接触器数值仿真与控制方法[J]. 电工技术学报, 2020, 35(5): 1083-1092.
Zhao Sheng, Shu Liang, Wu Ziran, et al. Numerical simulation and control method of electromagnetic- permanent composite contactor[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1083- 1092.
[9] 熊军, 何俊佳, 臧春艳. 直流继电器触头弹跳影响因素的实验研究[J]. 低压电器, 2008(13): 1-3,19.
Xiong Jun, He Junjia, Zang Chunyan. An experi- mental investigation of influencing factors on contact bounce of DC relay[J]. Low Voltage Apparatus, 2008(13): 1-3, 19.
[10] 李俊峰, 苏秀苹, 郑新芳, 等. 基于触头动态接触压力的触头弹跳分析[J]. 电工技术学报, 2015, 30(9): 138-144.
Li Junfeng, Su Xiuping, Zheng Xinfang, et al. Analysis of the contact bounce based on dynamic contact pressure[J]. Transactions of China Electro- technical Society, 2015, 30(9): 138-144.
[11] 熊军, 何俊佳, 臧春艳. 基于正交实验的航天继电器触头弹跳的多因素分析[J]. 电工技术学报, 2009, 24(2): 60-66.
Xiong Jun, He Junjia, Zang Chunyan. Multifactor analysis on contact bounce of aerospace relay based on orthogonal experiments[J]. Transactions of China Electrotechnical Society, 2009, 24(2): 60-66.
[12] 吴伟光, 马履中. 真空断路器触头合闸弹跳特性的研究[J]. 江苏理工大学学报(自然科学版), 2000, 21(3): 58-61.
Wu Weiguang, Ma Lüzhong. A study on characteri- stics of the contact bounce of vacuum circuit breakers in switching-on[J]. Journal of Jiangsu University (Natural Science Edition), 2000, 21(3): 58-61.
[13] 付饶, 梁慧敏, 叶雪荣, 等. 接触器触点超程分析及其退化状态的诊断[J]. 电工技术学报, 2020, 35(1): 125-133.
Fu Rao, Liang Huimin, Ye Xuerong, et al. Analysis of the contact overtravel of contactor and its degra- dation state evaluation[J]. Transactions of China Electrotechnical Society, 2020, 35(1): 125-133.
[14] 杨文英, 刘兰香, 翟国富. 热场影响下新能源用接触器弹跳特性研究[J]. 电工技术学报, 2019, 34(22): 4687-4698.
Yang Wenying, Liu Lanxiang, Zhai Guofu. The bounce characteristics of contactors for new energy under the influence of thermal field[J]. Transactions of China Electrotechnical Society, 2019, 34(22): 4687-4698.
[15] 张高廷, 曹云东, 刘炜. 簧片式继电器固有振动特性研究[J]. 电工技术学报, 2020, 35(2): 292-299.
Zhang Gaoting, Cao Yundong, Liu Wei. The natural vibration characteristics of reed relay[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(2): 292-299.
[16] Shu Liang, Wu Lang, Wu Guichu, et al. A fully coupled framework of predicting the dynamic characteristics of permanent magnet contactor[J]. IEEE Transactions on Magnetics, 2016, 52(8): 1-7.
[17] Schmidt E, Degwerth A. Comparison of shading ring arrangements of low voltage AC contactors[C]// Australasian Universities Power Engineering Con- ference, Perth, 2007: 1-6.
[18] Schmidt E, Degwerth A. Design optimization studies on low voltage contactors by using voltage driven transient finite element analyses[C]//2007 Inter- national Conference on Electrical Machines and Systems, Seoul, 2007: 1450-1454.
[19] Lin Heyun, Wang Xianbing, Fang Shuhua, et al. Design, optimization, and intelligent control of permanent-magnet contactor[J]. IEEE Transactions on Industrial Electronics, 2013, 60(11): 5148-5159.
[20] Yang Wenying, Guo Jiuwei, Liu Yang. Multi- objective optimization of contactor’s characteristics based on RBF neural networks and hybrid method[J]. IEEE Transactions on Magnetics, 2019, 55(6): 1-4.
[21] Hamid L. Canonical equations of motion and estimation of parameters in the analysis of impact problems[D]. Arizona: The University of Arizona, 1988.
[22] Shimizu N. RecurDyn for beginners innovation for design & analysis with multibody dynamics[M]. Korea: FunctionBay, 2015.
[23] 石远豪. 结合面接触阻尼和接触刚度的实验检测研究[D]. 广州: 广东工业大学工学, 2016.
[24] 王黎钦, 陈铁鸣. 机械设计[M]. 哈尔滨: 哈尔滨工业大学出版社, 2003.
[25] 张健, 齐朝晖, 卓英鹏, 等. 基于精确几何模型梁单元的螺旋弹簧刚度分析[J]. 工程力学, 2020, 37(2): 16-22, 80.
Zhang Jian, Qi Zhaohui, Zhuo Yingpeng, et al. Stiffness analysis of helix spring using exact geo- metric beam element[J]. Engineering Mechanics, 2020, 37(2): 16-22, 80.
[26] 李祥林, 李金阳, 杨光勇, 等. 电励磁双定子场调制电机的多目标优化设计分析[J]. 电工技术学报, 2020, 35(5): 972-982.
Li Xianglin, Li Jinyang, Yang Guangyong, et al. Multi-objective optimization analysis of electric- excitation double-stator field-modulated machine[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 972-982.
[27] Meyer R K, Nachtsheim C J. The coordinate exchange algorithm for constructing exact optimal designs[J]. Technometrics, 1995, 37(1): 60-69.
[28] Jones B, Lin D K J, Nachtsheim C J. Bayesian D-optimal supersaturated designs[J]. Journal of Statistical Planning and Inference, 2008, 138(1): 86-92.
[29] 李鹏. 直觉模糊信息决策方法研究: 基于灰色关联和证据推理的方法[M]. 镇江: 江苏大学出版社, 2014.
[30] 时珉, 许可, 王珏, 等. 基于灰色关联分析和GeoMAN模型的光伏发电功率短期预测[J]. 电工技术学报, 2021, 36(11): 2298-2305.
Shi Min, Xu Ke, Wang Jue, et al. Short-term photovoltaic power forecast based on grey relational analysis and GeoMAN model[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2298- 2305.
Optimal Design Method for AC Contactor Spring System Based on Response Surface Method
Abstract AC contactor is a frequently operated switching device, and its match of the magnetic force and reaction force during movement directly affects the reliability and performance. A good force match can reduce contact bounce and improve breaking performance. In the process, the spring system plays a key role. For the multi-objective optimization of the spring system, an electromagnetic-mechanical coupling simulation framework and an entity simulation method for springs are presented. A comprehensive optimization method based on grey relational method and response surface method is introduced. The second-order prediction model is established that describes the influence of contact spring free height, contact spring effective coil number, reaction spring free height and reaction spring effective coil number on bounce time, contact breaking velocity, contact closing velocity and iron core closing velocity. Accordingly, the reaction system parameters are optimized. The experimental results show that the optimal reaction system parameters can effectively reduce the bounce time and the closing time of the contact and the iron core, and increase the contact breaking velocity, which is helpful to improve the working performance of AC contactors.
Keywords:AC contactor, response surface method, contact bounce, spring system, multi-objective optimization
中图分类号:TM572.6
DOI: 10.19595/j.cnki.1000-6753.tces.200735
福建省2018科技创新领军人才资助项目。
收稿日期 2020-06-28
改稿日期 2020-07-29
E-mail: 353453798@qq.com
许志红 女,1963年生,教授,博士生导师,研究方向为电器及其智能化技术。
E-mail: 641936593@qq.com(通信作者)
(编辑 崔文静)