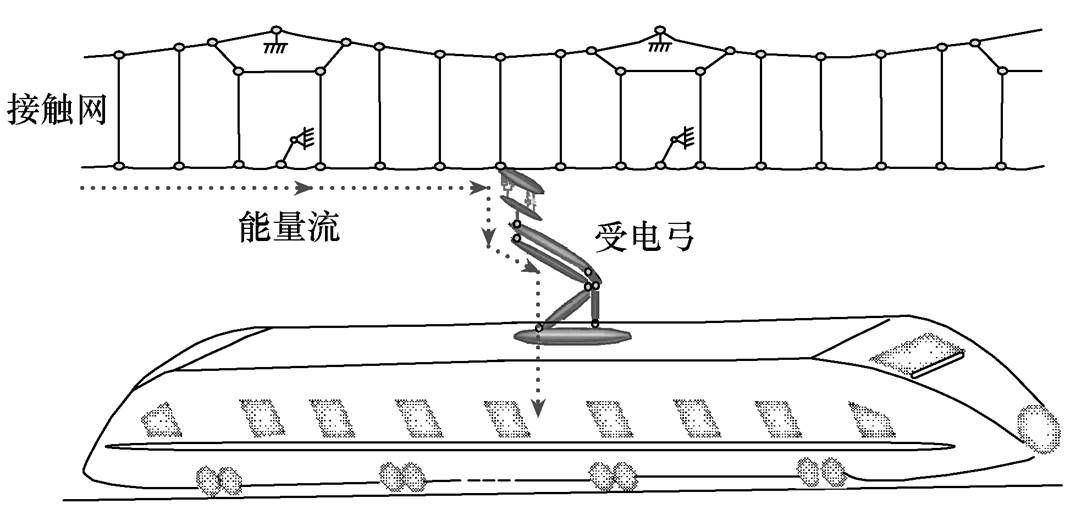
图1 受电弓与接触网模型
Fig.1 The pantograph and catenary system
摘要 随着列车运行速度的提高,受电弓与接触网系统之间的耦合振动加剧,导致接触力波动加大,恶化高速列车的受流质量,影响了高速列车的安全稳定运行。受电弓的主动控制能够降低接触力的波动,保证高速列车的稳定受流,但在受电弓主动控制中,存在作动器时滞的问题。针对该问题,提出一种考虑作动器时滞的控制策略来降低接触力的波动。采用鲁棒自适应无迹卡尔曼滤波的估计方法,获取噪声时变环境下的受电弓状态信息;将弓网接触力、受电弓弓头加速度和弓头位移作为测量状态,构建控制性能输出函数;引入估计器,分析作动器时滞问题,设计最优控制器;采用非线性受电弓-接触网模型,验证了控制器的有效性和受电弓参数摄动下的鲁棒性。研究结果表明,即使受电弓存在作动器时滞问题,设计的控制器也能显著降低接触力的波动;并且在受电弓参数摄动的影响下,控制器能够保证良好的鲁棒性。
关键词:高速铁路受电弓 主动控制 时滞 状态估计 测量状态
高速铁路采用电力牵引的方式进行供能,受电弓与接触网(简称弓网)系统在供能过程中扮演着非常重要的角色。受电弓与接触网为两个独立的机电系统,二者通过弓网接触力耦合在一起,相互接触,为电流传输提供通道,其模型如图1所示。弓网接触力是判断列车受流质量的一个重要指标[1]。随着列车运行速度的不断提升,外界环境的影响逐渐增大,弓网耦合系统之间的振动不断加剧,导致弓网系统之间的接触力波动增大,恶化高速列车受流质量,不利于高速列车的安全平稳运行。因此,降低弓网耦合系统之间的振动对高速铁路安全运营具有重要的意义。

图1 受电弓与接触网模型
Fig.1 The pantograph and catenary system
为了降低接接触力的波动,文献[2-3]研究了弓网结构特性,但是这种方法不仅受到材料的限制,还需要巨大的成本,而受电弓的主动控制能够在不改变原有受电弓的结构和既有线路的基础上降低接触力的波动。近年来,许多控制策略被应用到受电弓的主动控制,包括比例-积分-微分(Proportion- Integration-Differentiation, PID)控制[4]、模型预测控制[5]、滑模控制[6-7]、最优控制[8]、反馈控制[9]以及鲁棒控制[10]等。虽然这些控制策略在受电弓主动控制方面取得了一些进步,但还存在一些问题:
(1)接触力作为评价指标和反馈信号,分析其特性是非常必要的。但现有控制策略的控制目标中,往往忽略了接触力的特性。本文通过对接触力的分析,采用弓网接触力、受电弓弓头加速度和受电弓弓头位移构建性能输出函数。
(2)受电弓的状态信息作为反馈信号,可以提高控制器的性能[11]。当列车高速运行时,每一个状态量对控制器设计都是至关重要的。由于弓网系统运行环境复杂,存在电磁干扰和环境干扰,会使获得的状态信息存在误差,而估计器能够减小外界的干扰得到准确的状态信息[12]。基于卡尔曼滤波的估计器得到大量的研究和优化,如扩展卡尔曼滤波[13-16]、容积卡尔曼滤波[17-18]、无迹卡尔曼滤波[19-20]。鲁棒自适应无迹卡尔曼滤波(Robust Adaptive Unscented Kalman Filter, RAUKF)能在噪声时变的环境下精确地获得受电弓的状态信息,并能够保证鲁棒性。
(3)控制系统中存在作动器的时滞难题,它会影响控制器的有效性。考虑作动器时滞的控制策略已被成功应用于其他领域,如航天器的容错采样控制[21]、悬架系统的鲁棒非脆弱静态输出反馈控制[22]、非线性系统的反馈控制[23]等。本文基于最优控制,解决受电弓主动控制器的时滞难题。
(4)采用非线性弓网系统模型,验证控制器的有效性是非常重要的。文献[9]采用简化的弓网线性模型验证控制器,但是简化模型只能表达部分动态性能。相比简化的线性模型,弓网非线性系统模型更能表达弓网系统的动态性能。
基于上述分析,本文提出了一种考虑作动器时滞的控制策略来降低接触力的波动。首先,分析接触力的特性,确定性能输出函数和控制目标;其次,在弓网系统运行环境噪声时变的影响下,采用鲁棒自适应无迹卡尔曼滤波方法,设计估计器得到受电弓的状态信息;最后,根据最优控制和测量状态信息设计考虑时滞的控制器,并结合估计器,在非线性弓网系统模型上,验证控制器的有效性和鲁棒性。主要内容及关系如图2所示。
受电弓与接触网模型是研究受电弓主动控制的基础。受电弓模型通常采用三质量块模型[10],如图3所示,它可以有效地表达受电弓的动态性能。其中,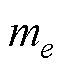 (e=1, 2, 3)为受电弓弓头、上框架以及下框架的质量;
(e=1, 2, 3)为受电弓弓头、上框架以及下框架的质量; 为等效阻尼;
为等效阻尼;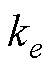 为受电弓弓头、上框架和下框架之间的等效刚度;u为主动控制力。
为受电弓弓头、上框架和下框架之间的等效刚度;u为主动控制力。
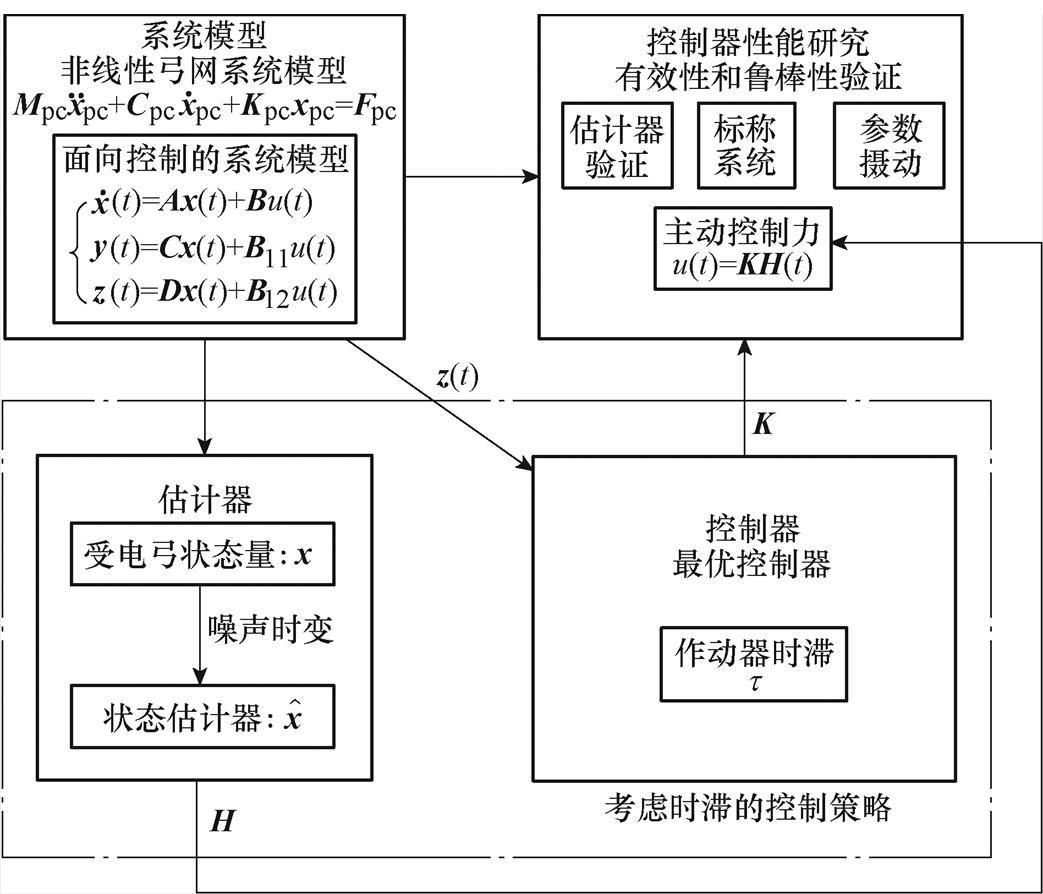
图2 主要内容及关系
Fig.2 Main contents and relations
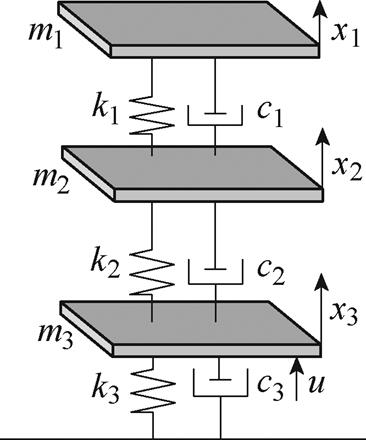
图3 受电弓三质量块模型
Fig.3 The three-level lumped-mass model of pantograph
受电弓的运动方程可以描述为
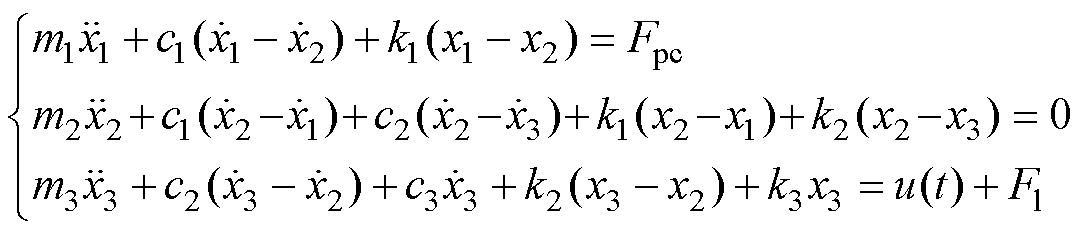 (1)
(1)式中, 、
、 和
和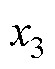 为每个质量块的位移;
为每个质量块的位移;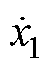 、
、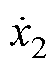 和
和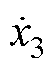 为每个质量块的速度;
为每个质量块的速度;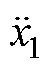 、
、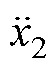 和
和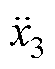 为每个质量块的加速度;
为每个质量块的加速度;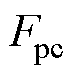 和
和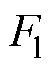 分别为弓网接触力和静态抬升力。
分别为弓网接触力和静态抬升力。
接触网是沿着轨道上空呈“之”字形架设的,为列车运行提供电能的高压输电线,主要包括接触悬挂、支持装置、定位装置支柱与基础等。采用有限元方法,建立接触网的模型;采用非线性索单元,建立接触线或承力索模型;采用非线性杆单元,建立吊弦的模型,得到接触网的动态方程为
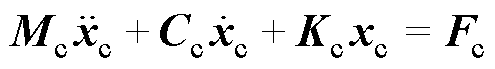 (2)
(2)式中,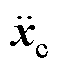 、
、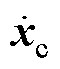 、
、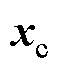 分别为加速度、速度和位移向量;
分别为加速度、速度和位移向量;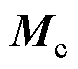 、
、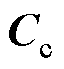 、
、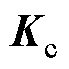 分别为质量、阻尼和刚度矩阵;
分别为质量、阻尼和刚度矩阵;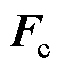 为力。
为力。
根据式(1)和式(2)推导,可得受电弓和接触网系统的运行方程为
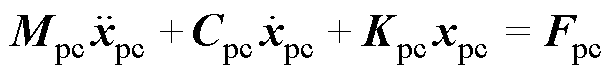 (3)
(3)其中
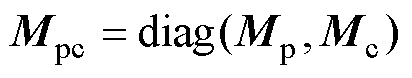
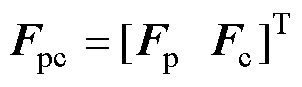
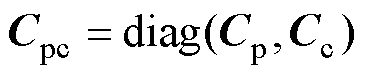
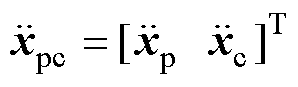
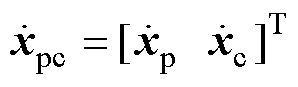
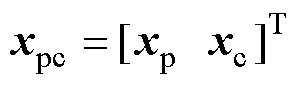
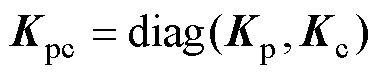
文献[24]验证了受电弓与接触网系统模型建模方法的有效性,计算结果符合欧洲标准EN50318。
在以往的研究中,控制策略直接降低接触力的波动,忽视了对接触力的特性分析。本文通过对接触力的分析,提出一种降低接触力波动的方法。由式(1)可得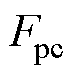 的表达式,采用受电弓DSA380的参数,见表1。
的表达式,采用受电弓DSA380的参数,见表1。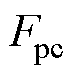 的表达式中,
的表达式中,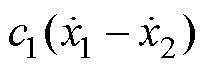 非常小,可以忽略。因此,
非常小,可以忽略。因此,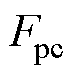 可以简化为
可以简化为
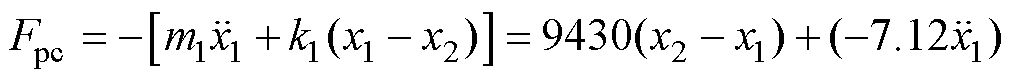 (4)
(4)其中
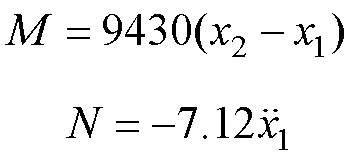
表1 受电弓DSA380的参数及参数摄动
Tab.1 Parameters and parameter perturbation of the pantograph DSA380
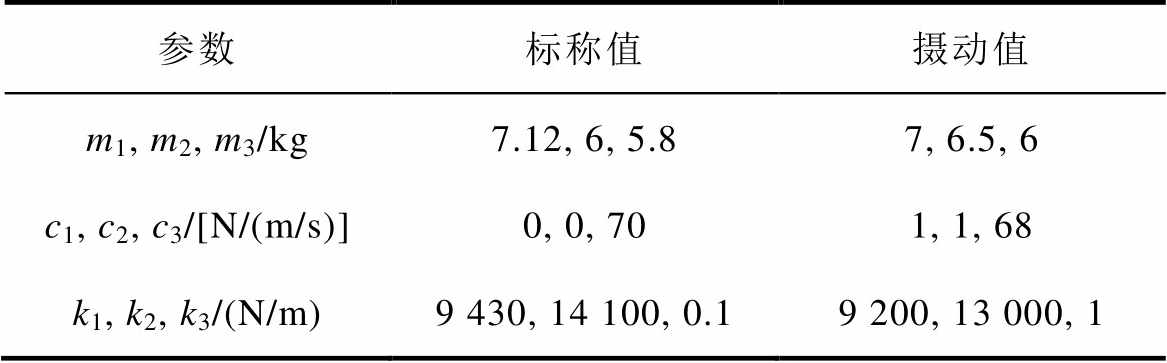
参数标称值摄动值 m1, m2, m3/kg7.12, 6, 5.87, 6.5, 6 c1, c2, c3/[N/(m/s)]0, 0, 701, 1, 68 k1, k2, k3/(N/m)9 430, 14 100, 0.19 200, 13 000, 1
当列车速度为360km/h时,可以得到弓网接触力的波形。由式(4)可知,接触力等效为M与N之和。如图4所示,M和接触力有着大致相同的趋势,但是N在剧烈地变化。因此,通过抑制N,即受电弓弓头加速度来降低接触力的波动。
基于以上的分析,本文所提出的控制策略目标函数主要包括以下几个方面:
(1)减小接触力的波动是受电弓主动控制策略的基本要求,可以描述为
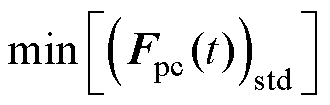
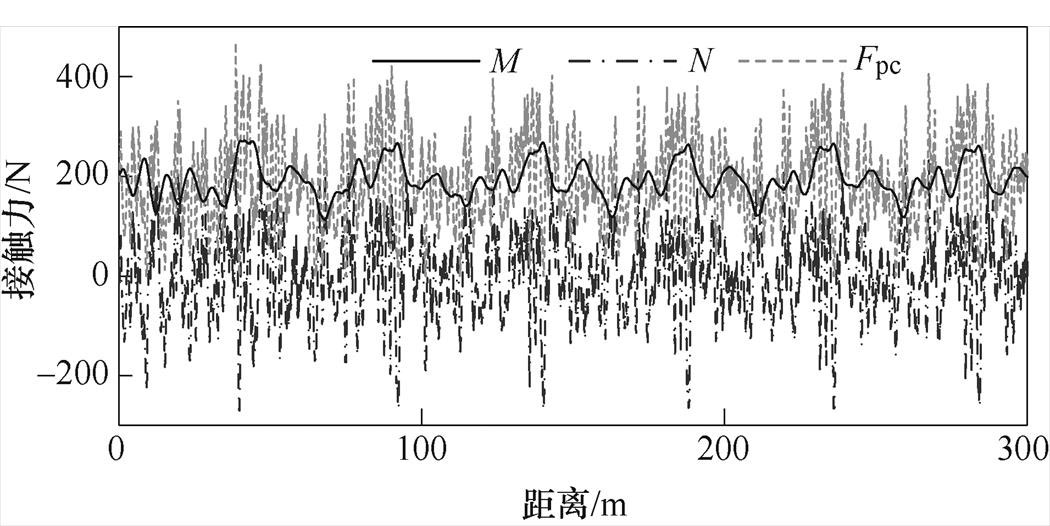
图4 速度360km/h接触力的波形
Fig.4 The waveforms of the contact force at 360km/h
(2)最小化受电弓弓头的加速度:减小接触力的波动可以抑制其成分变化剧烈的物理量,表示为
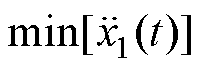
(3)限制受电弓弓头的抬升:为了保证受电弓安全稳定地运行,限制弓头抬升是有必要的,根据文献[25]设置受电弓抬升最大值为0.1m。
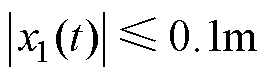
(4)限制主动控制力:为了保证作动器能在一个稳定的区间内工作,其输出需要限制在合理的范围。
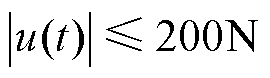
(5)考虑到受电弓的测量状态信息:列车在运行时,接触力、受电弓弓头加速度及受电弓弓头抬升可以作为性能输出函数。
基于有限元方法建立的系统模型十分复杂而不适用于设计控制器,本文采用面向控制的系统模型,进行控制器的设计,采用有限元方法建立非线性系统模型,完成控制器的有效性和鲁棒性的验证。面向控制的弓网系统模型主要是对接触网模型的简化,准确表示出接触网的静态刚度是简化模型的关键。根据非线性系统模型,接触网的静态刚度为
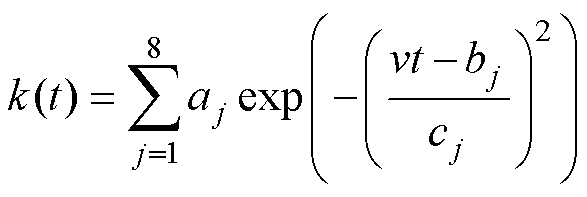 (5)
(5)式中,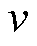 和
和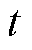 分别为运行速度和时间;
分别为运行速度和时间;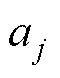 、
、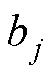 、
、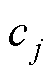 为拟合系数。
为拟合系数。
因此,接触力可以表示为
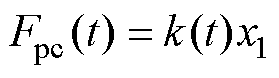 (6)
(6)由式(1)、式(5)和式(6),若状态变量为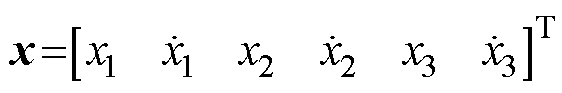 ,系统的输出变量为
,系统的输出变量为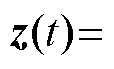
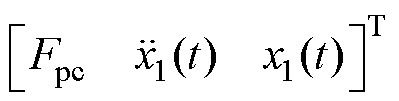 ,相应的弓网系统空间方程为
,相应的弓网系统空间方程为
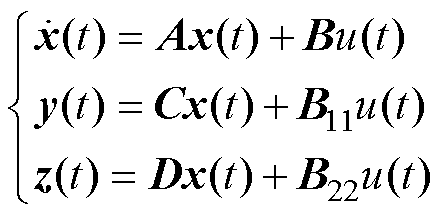 (7)
(7)
其中
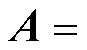
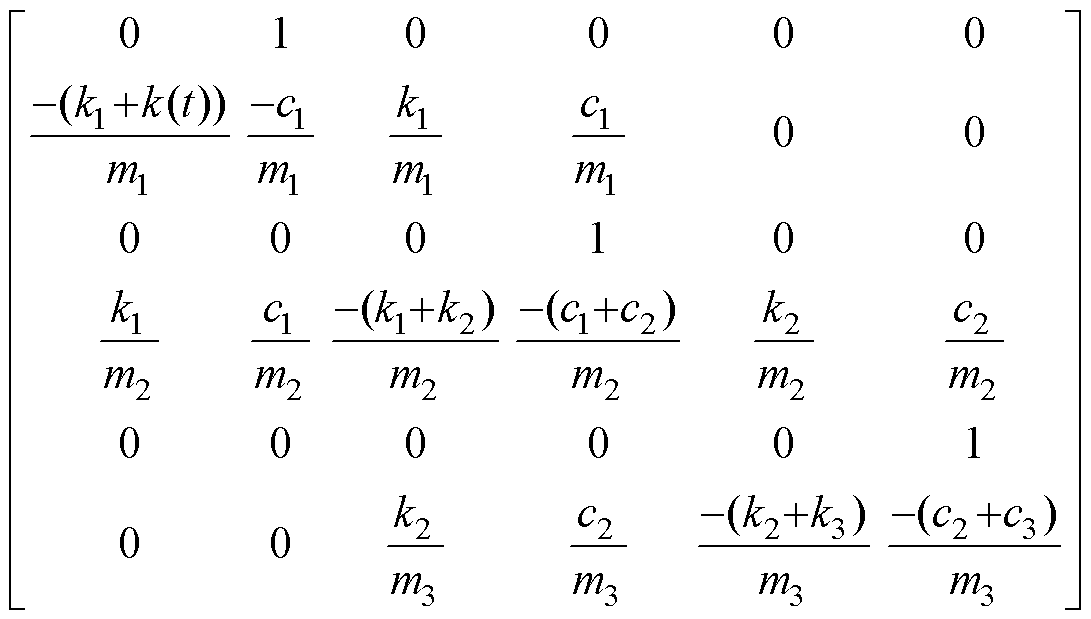
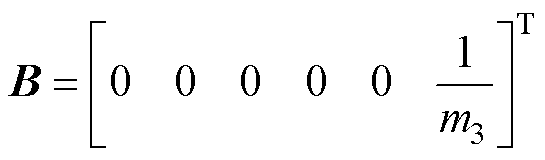
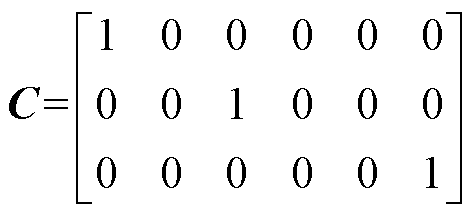
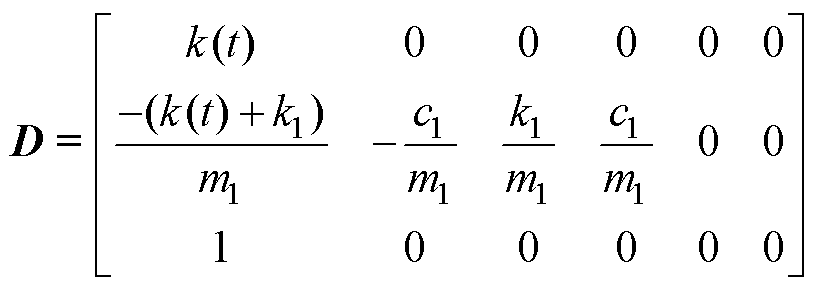
根据式(7)可知,需要求出6个受电弓的状态信息。由于弓网系统复杂的工作环境,存在电磁干扰和环境干扰,不能准确地获取状态量。因此,采用状态估计器,可以得到受电弓的状态量。弓网系统离散的状态空间方程为
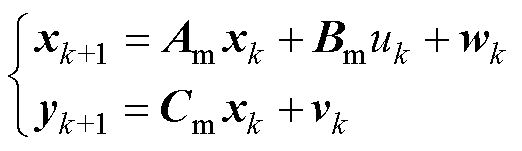 (8)
(8)式中,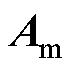 、
、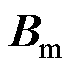 、
、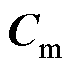 为系数矩阵;
为系数矩阵;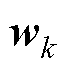 、
、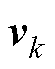 (k=1,2,…,n)分别为过程噪声和测量噪声,满足零均值高斯白噪声;uk为主动控制力。
(k=1,2,…,n)分别为过程噪声和测量噪声,满足零均值高斯白噪声;uk为主动控制力。
RAUKF估计算法[26-27]为
(1)计算Sigma采样点和权重值
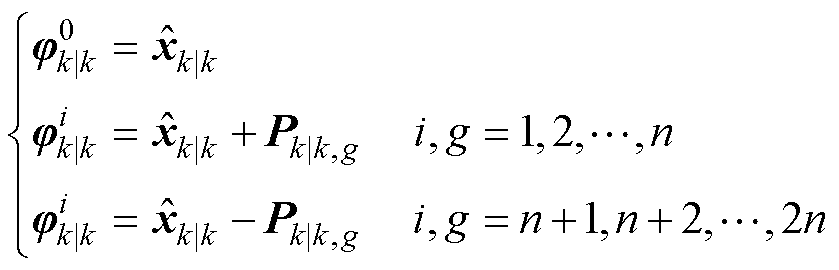 (9)
(9)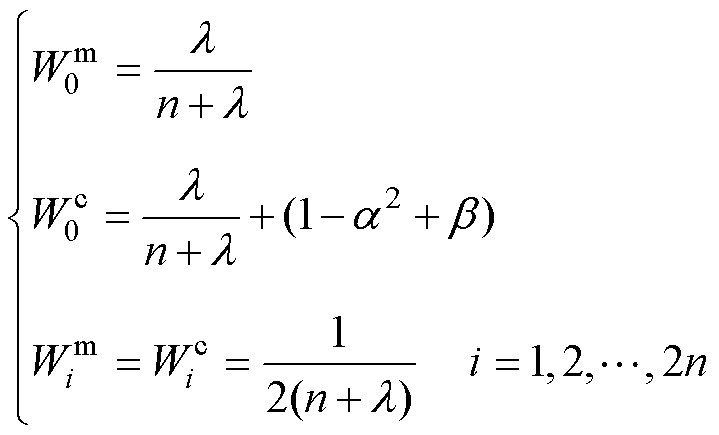 (10)
(10)
式中,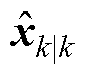 为k时刻的估计值;
为k时刻的估计值;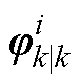 为根据k-1时刻的估计值得到的第i个Sigma点;
为根据k-1时刻的估计值得到的第i个Sigma点;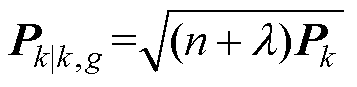 ,
,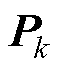 为协方差矩阵;
为协方差矩阵;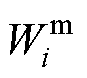 、
、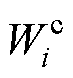 分别为计算权重的均值和方差;
分别为计算权重的均值和方差;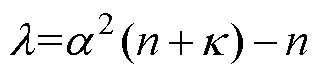 为微调参数,
为微调参数,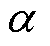 为比例修
为比例修
正因子,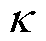 为次级采样因子,
为次级采样因子,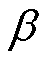 用来提高协方差精度,n为状态向量的维数。
用来提高协方差精度,n为状态向量的维数。
(2)计算传播后的Sigma点集的均值和协方差
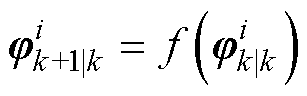 (11)
(11)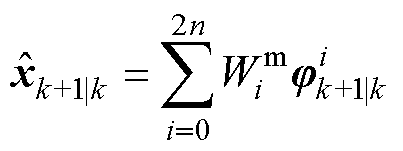 (12)
(12)
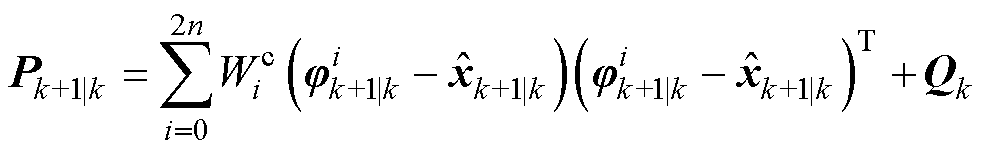 (13)
(13)
(3)计算量测均值和协方差矩阵
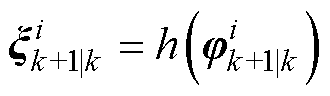 (14)
(14)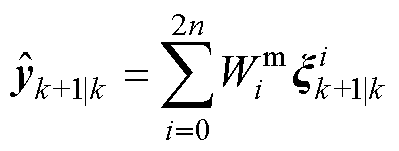 (15)
(15)
(4)计算协方差矩阵和增益
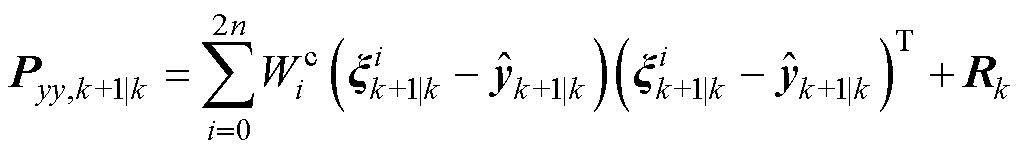 (16)
(16)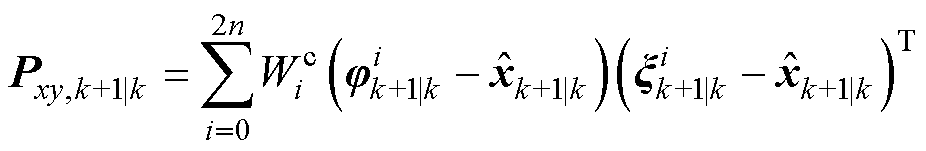 (17)
(17)
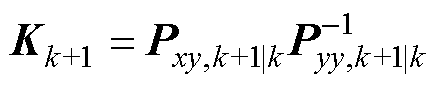 (18)
(18)
(5)计算估计值和协方差矩阵
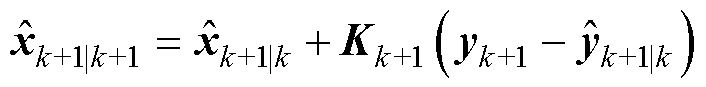 (19)
(19)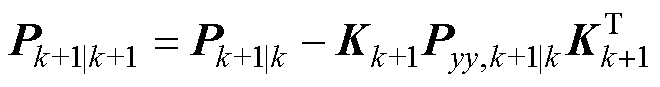 (20)
(20)
(6)更新过程噪声和测量噪声
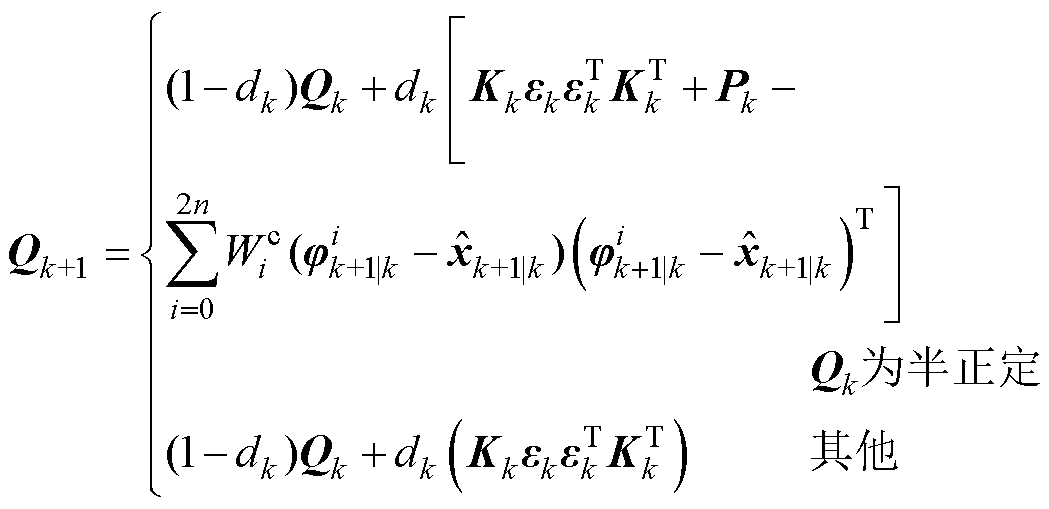 (21)
(21)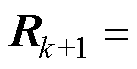
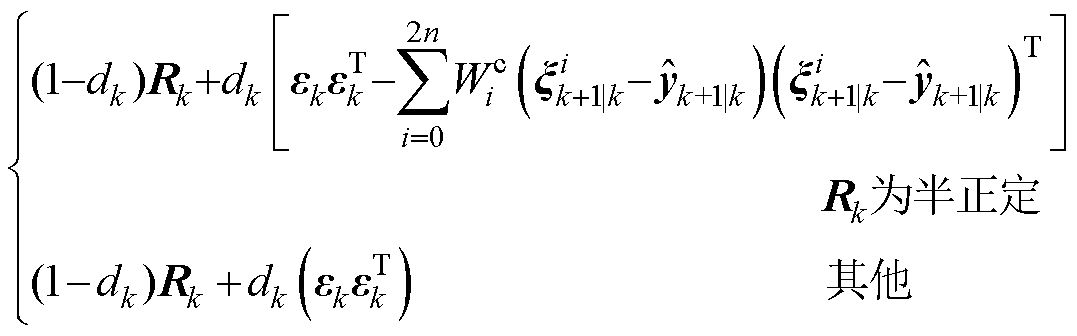 (22)
(22)
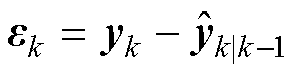 (23)
(23)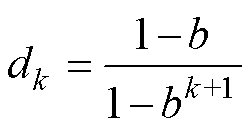 (24)
(24)
式中,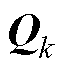 、
、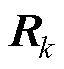 分别为
分别为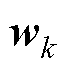 、
、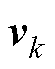 协方差矩阵,两者互不相关;
协方差矩阵,两者互不相关;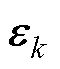 为k时刻测量值与估计值的误差;b为遗忘因子。
为k时刻测量值与估计值的误差;b为遗忘因子。
考虑作动器的时滞,式(7)可以转换为
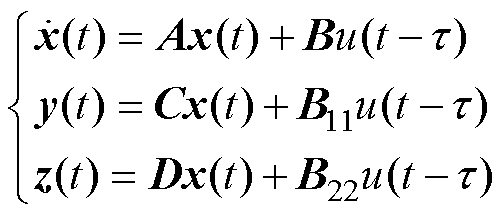 (25)
(25)式中,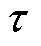 为作动器时滞。
为作动器时滞。
由状态转换可以得到系统方程为
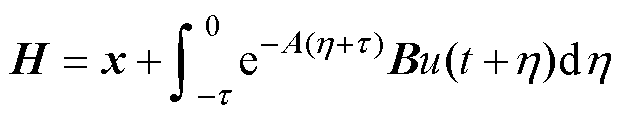 (26)
(26)由式(26)可以得到
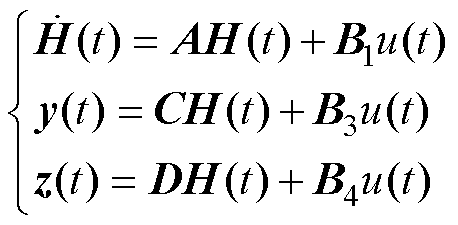 (27)
(27)
其中
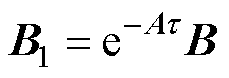
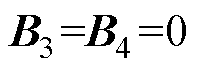
从式(26)可以看出,控制器包含作动器时滞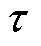 和积分项
和积分项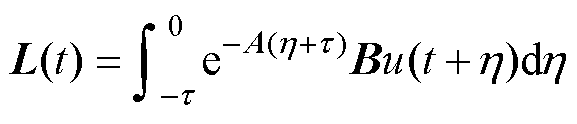 ,积分项可以通过数值计算来得到。
,积分项可以通过数值计算来得到。
对于任何的时滞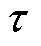 ,可以描述为
,可以描述为
 (28)
(28)式中,T为采样周期;l为一个正整数;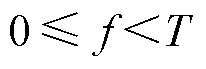 。通过数值计算,
。通过数值计算,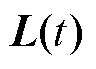 可以转换为
可以转换为
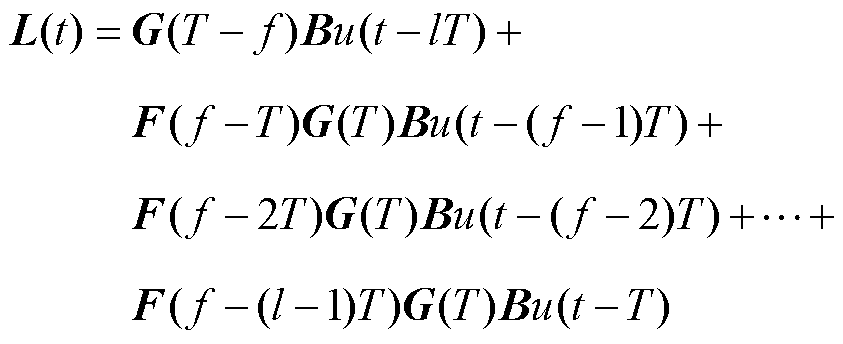 (29)
(29)其中
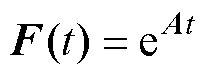
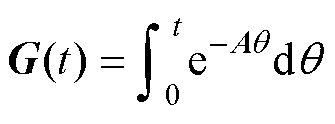
积分项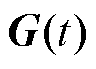 为
为
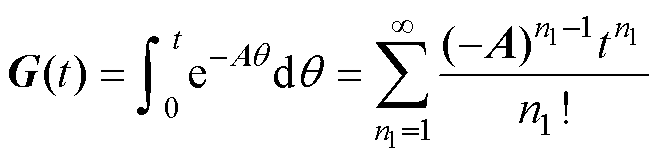 (30)
(30)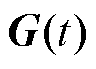 通过有限次迭代计算可以收敛到一个常数矩阵。
通过有限次迭代计算可以收敛到一个常数矩阵。
基于性能输出函数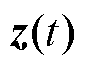 ,可以得到最优控制的性能指标为
,可以得到最优控制的性能指标为
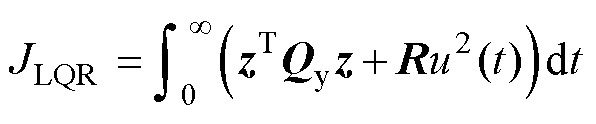 (31)
(31)
式中,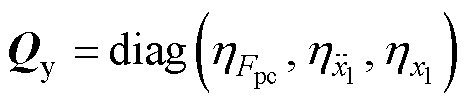 为正定的,并且可以通过数值最优得到,可以表示为
为正定的,并且可以通过数值最优得到,可以表示为
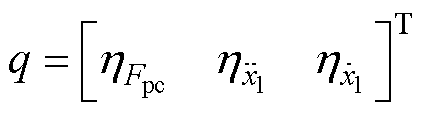 (32)
(32)由控制目标得到代价函数为
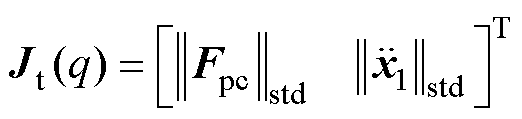 (33)
(33)
根据上述分析,代价函数可以转换为多目标最优问题为
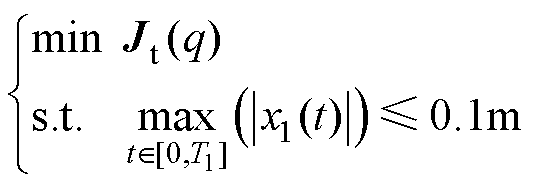 (34)
(34)式中,T1为仿真时间。
采用多目标基因遗传算法,求解受电弓多目标控制策略最优问题。
结合估计器,状态反馈为
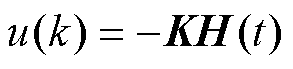 (35)
(35)式中,K为最优控制求出的增益矩阵。
采用DSA380受电弓和京津线接触网的结构参数,验证在不同运行速度下受电弓控制策略的有效性和鲁棒性,具体参数见表1和表2。
表2 京津线接触网结构参数
Tab.2 Structural parameters of the catenary of the Beijing-Tianjin railway line
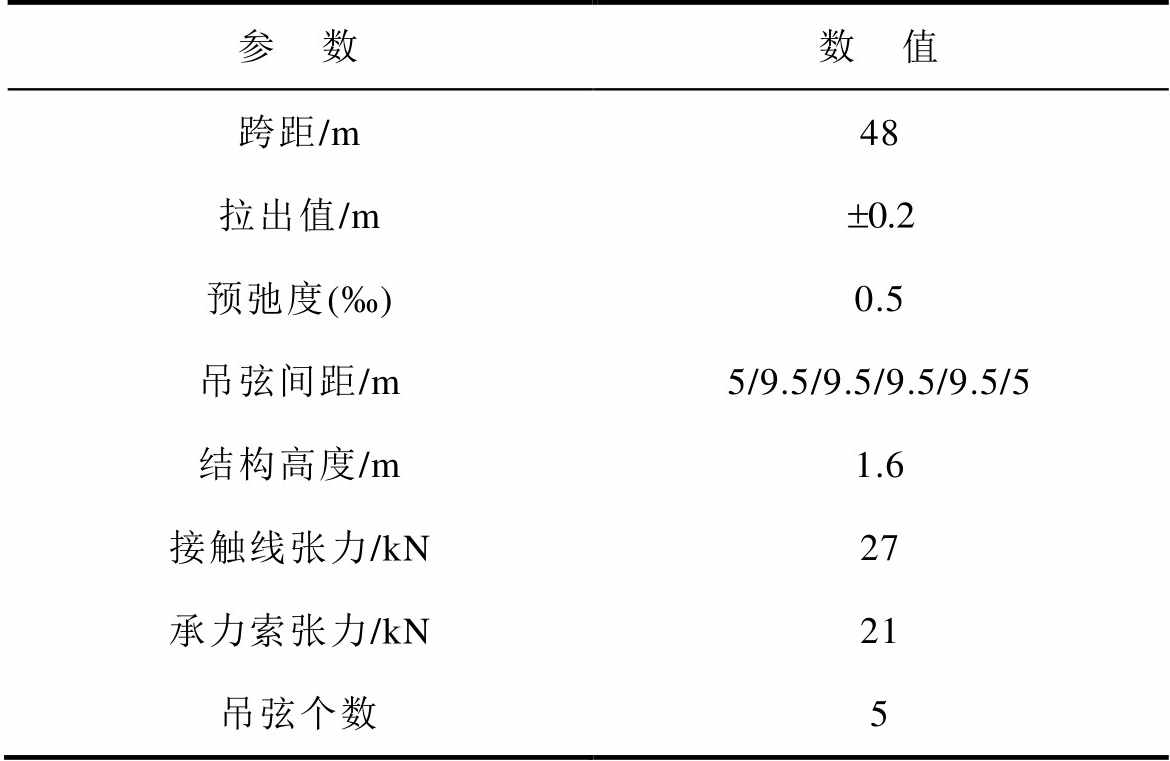
参 数数 值 跨距/m48 拉出值/m 预弛度(‰)0.5 吊弦间距/m5/9.5/9.5/9.5/9.5/5 结构高度/m1.6 接触线张力/kN27 承力索张力/kN21 吊弦个数5
采用非线性弓网系统模型,验证了估计器的性能。由于弓网系统工作环境的复杂性,噪声干扰是时变的,测量噪声为均根误差可知,估计算法即使在噪声时变的情况下,也能够保证估计的精确性。
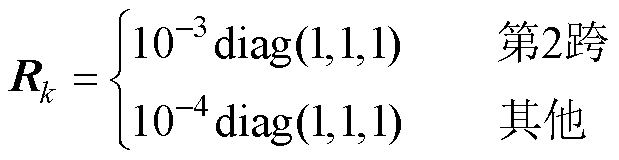
有
P0|0=10-6eye(6) Q=10-6eye(6) 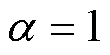
 v=360km/h
v=360km/h基于每个质量块位移的测量值得到受电弓的状态量,图5为质量块位移的估计值、仿真值和观测值,图6为质量块速度的估计值和仿真值。
图5a~图5c为质量块1~3的垂直位移,图6a~图6c为质量块1~3的速度。受电弓状态量的方均根误差分别为0.001 3,0.006 6,0.001 3,0.004 8,0.001 3,0.004 1。分析受电弓状态量的方
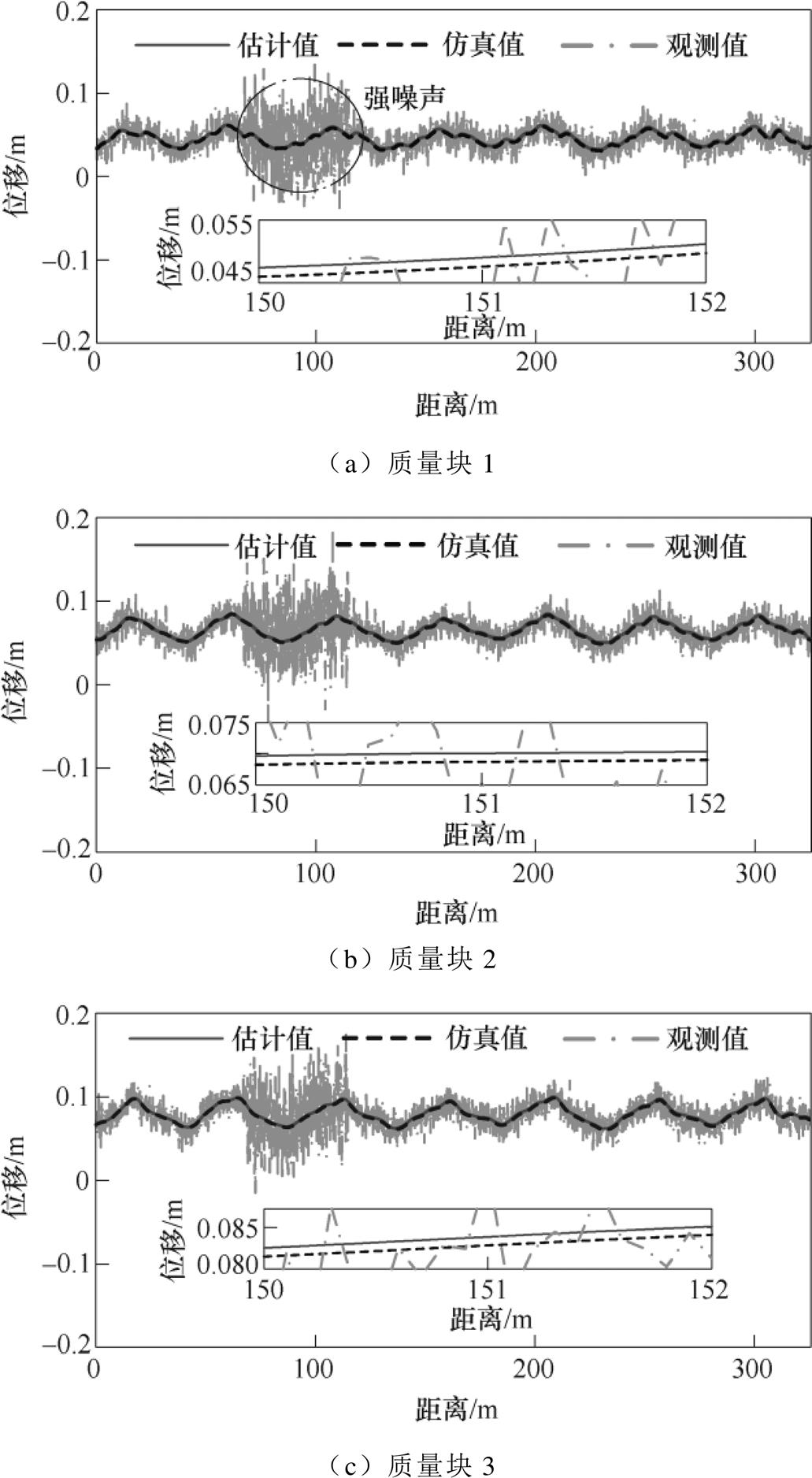
图5 质量块位移的估计值、仿真值和观测值
Fig.5 The estimated states, simulation states and measured states of the mass displacement
采用非线性系统弓网模型,验证了控制器的性能。基于表1和表2的数据,考虑时滞为40ms,可以计算出控制增益矩阵为
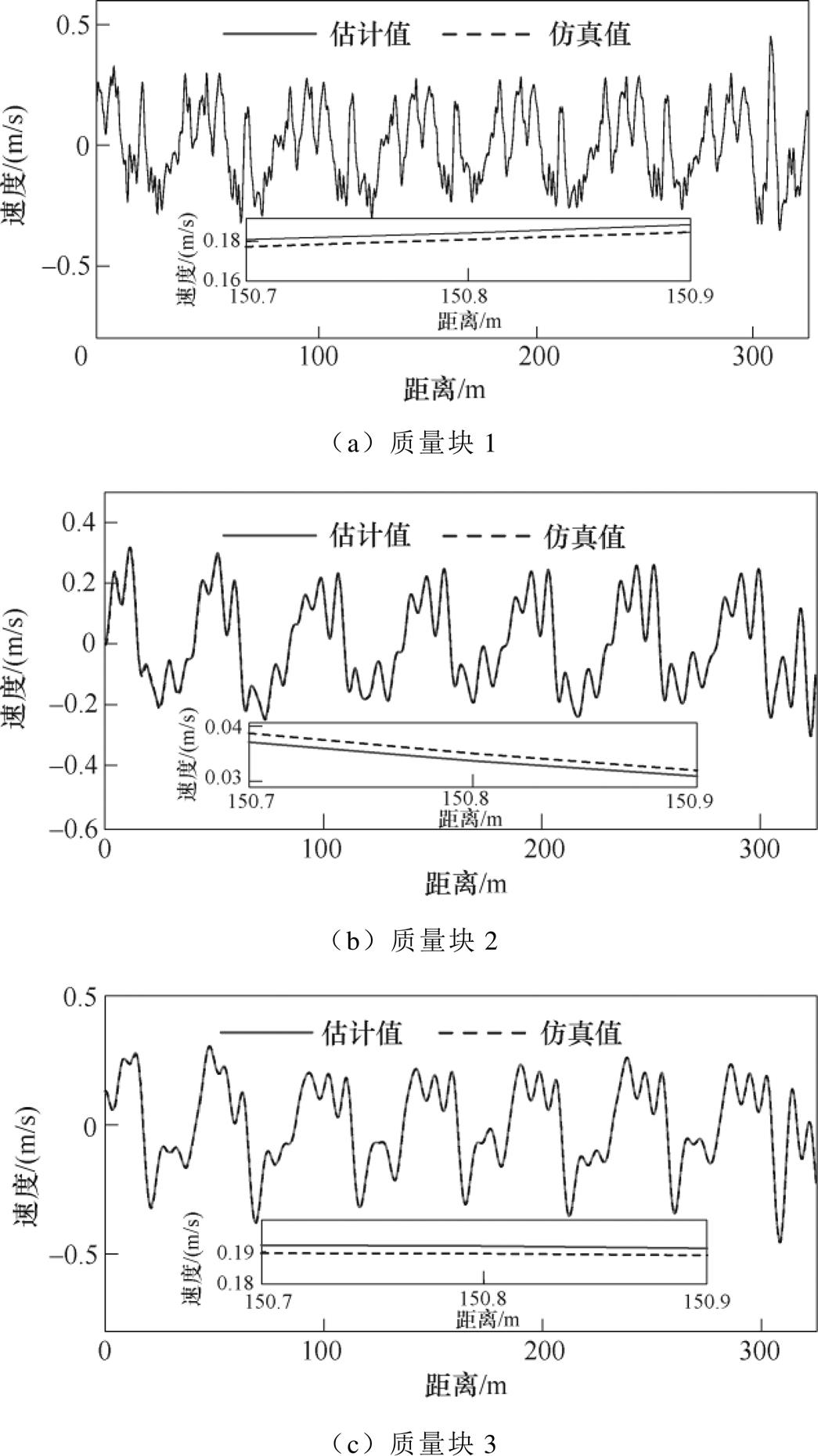
图6 质量块速度的估计值和仿真值
Fig.6 The estimated states and simulation states of the mass speed
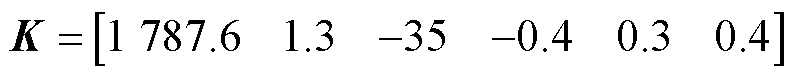
当列车运行速度300km/h和360km/h时,弓网接触力控制前后的波形如图7所示,受电弓弓头位移控制前后的波形如图8所示。
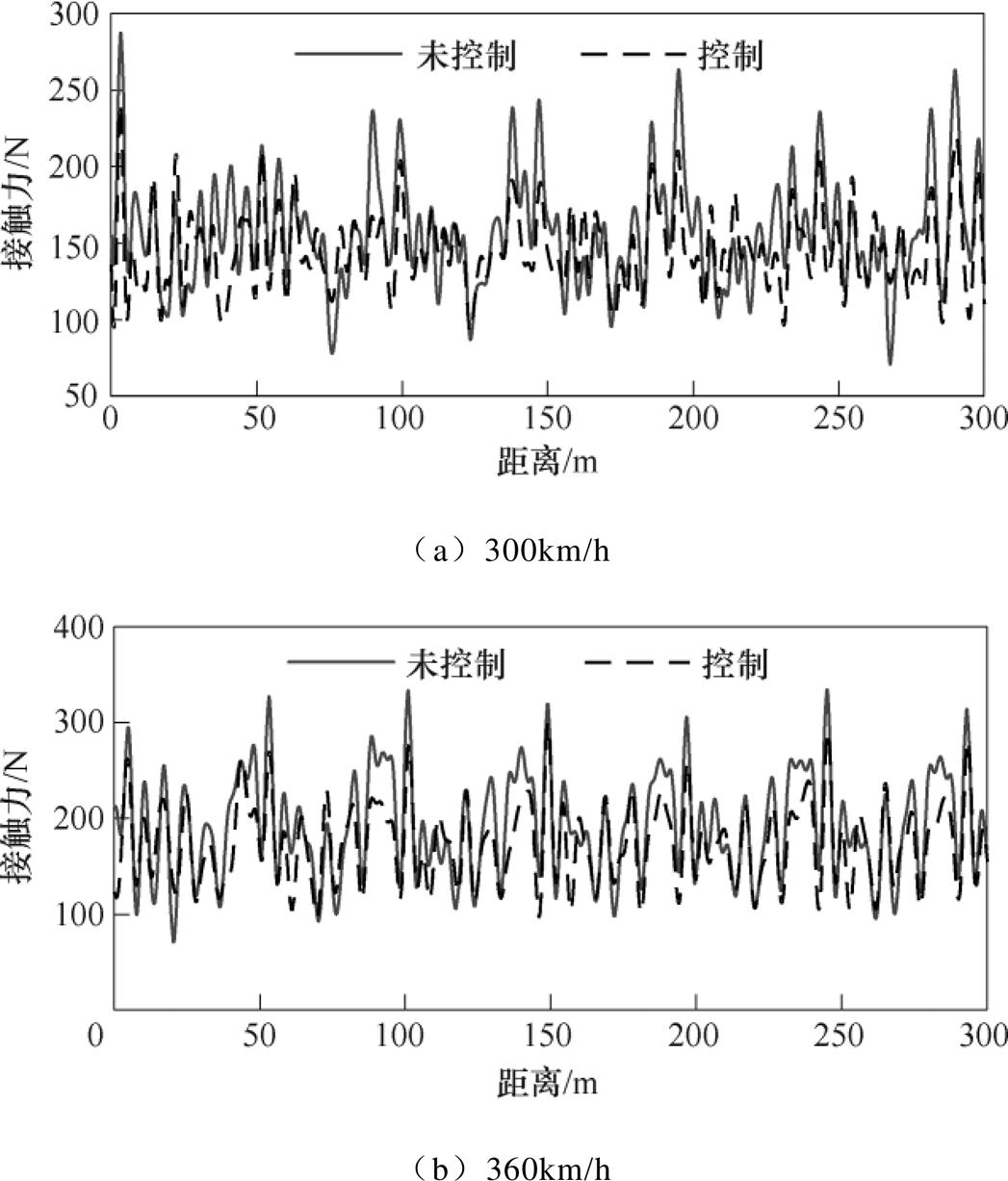
图7 接触力的波形
Fig.7 The waveforms of contact force
由接触力曲线和计算数据分析可得,控制后接触力极大值减小,接触力的标准差分别降低27.14%和22.45%。随着高速列车的速度提高,控制器的性能逐渐减弱,但从接触力的标准差可以看出,控制器仍能有效降低接触力波动。受电弓弓头位移都有一定程度的减小,更重要的是受电弓弓头位移小于控制目标的限定值0.1m。
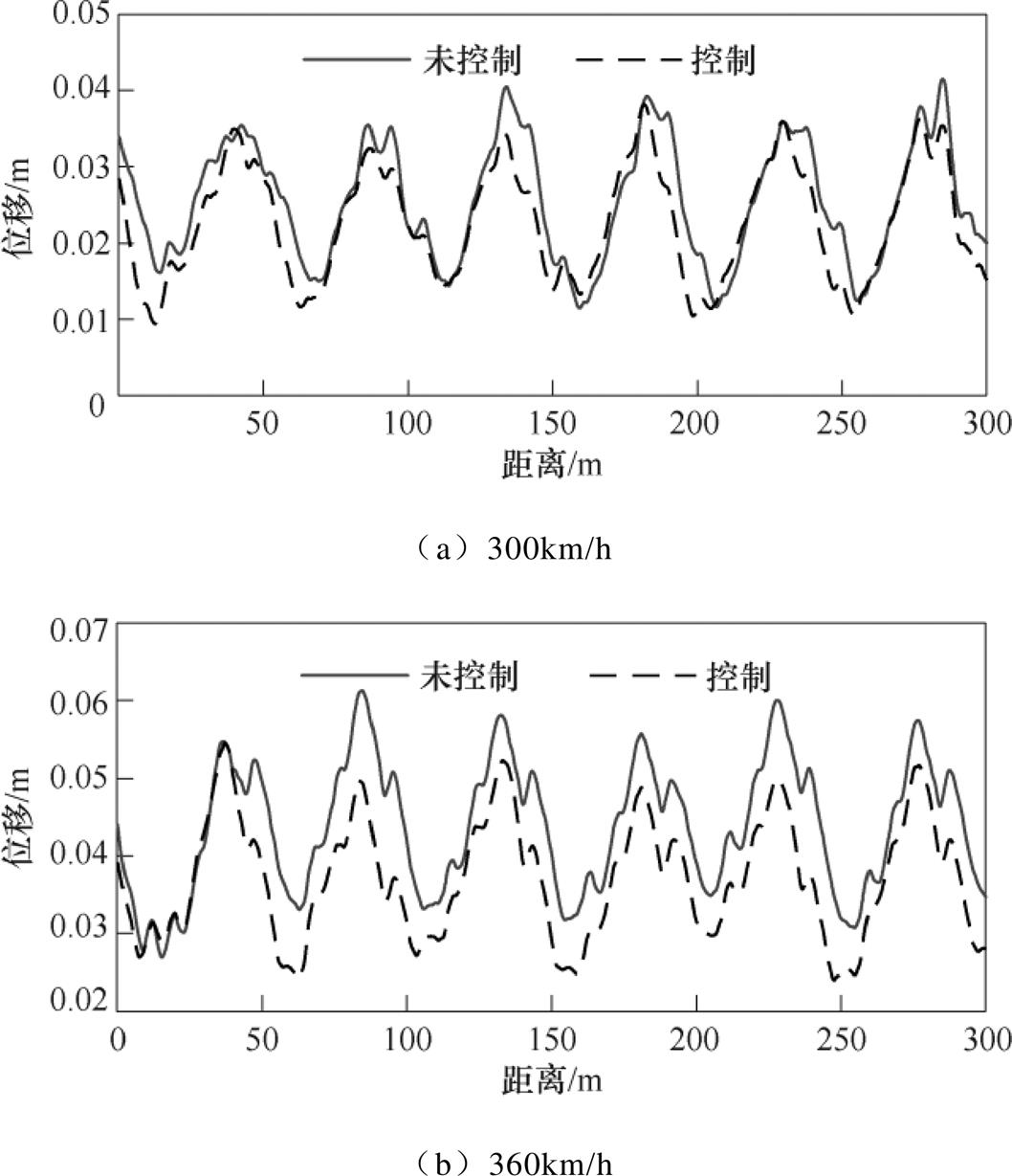
图8 受电弓弓头的波形
Fig.8 The waveforms of collector displacement
由于模型参数摄动会影响控制器性能,因此,在受电弓参数摄动的影响下验证控制器的鲁棒性。DSA380型受电弓参数摄动值见表1。图9为在列车运行速度300km/h下,受电弓参数摄动的控制效果。
图9a~图9c分别为改变受电弓等效质量、等效阻尼和等效刚度的控制效果,图9d为三者参数同时摄动的控制效果,控制后有效地降低了接触力的峰值,并且接触力的标准差分别降低27.72%、26.84%、28.32%和25.76%,结果表明,控制器在受电弓参数摄动的情况下也能保证良好的性能。
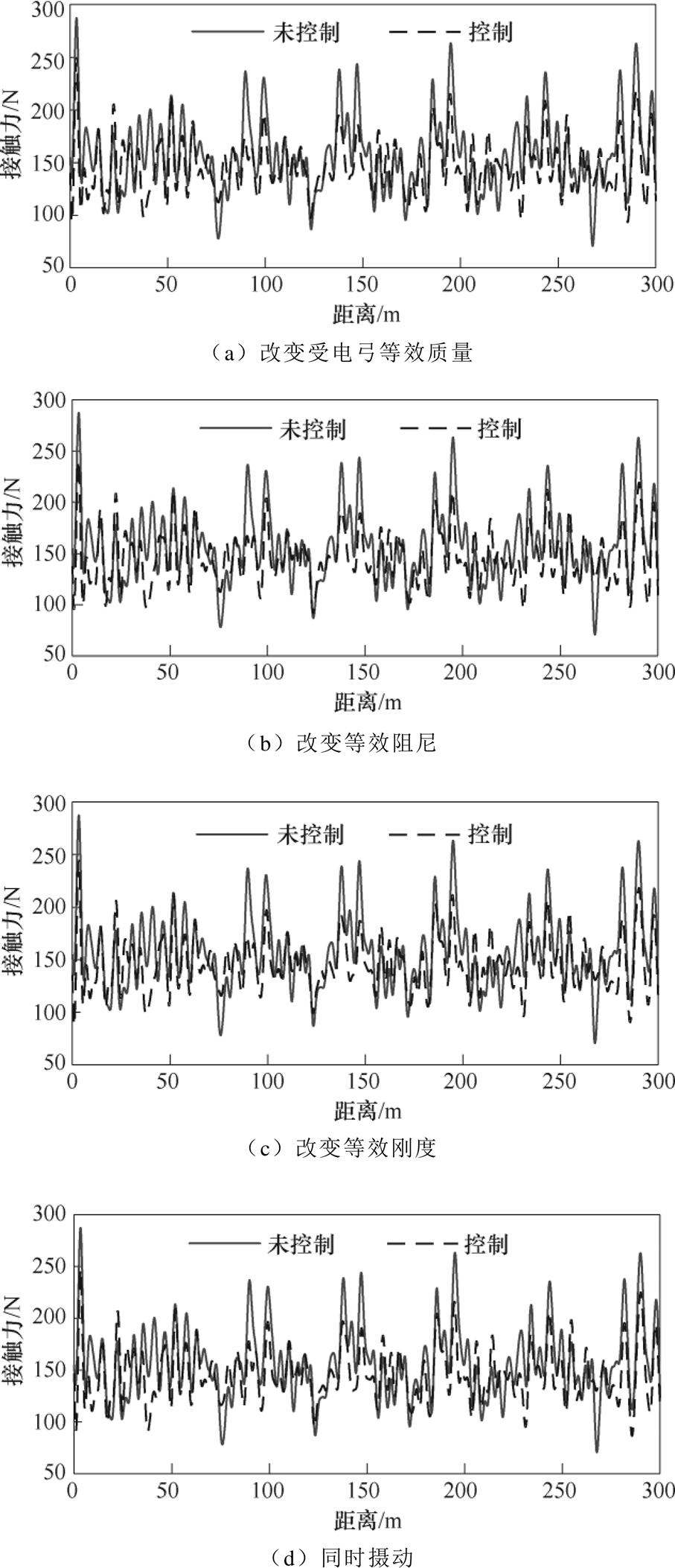
图9 速度为300km/h参数摄动下的控制性能
Fig.9 Control performance under parameter perturbation at 300km/h
本文针对受电弓主动控制中存在作动器时滞的问题,提出了一种基于作动器时滞的受电弓主动控制方法。通过弓网接触力分析,以降低接触力的波动为目的,确定控制策略的控制目标,构建性能输出函数。为了在噪声时变的环境下准确获得受电弓的状态信息,采用鲁棒自适应无迹卡尔曼滤波估计受电弓的状态量,即使在噪声干扰的情况下,受电弓状态估计量的方均根误差分别为0.001 3、0.006 6、0.001 3、0.004 8、0.001 3、0.004 1,验证了估计器的有效性。在时滞为40ms情况下,以非线性弓网模型为基础,接触力的标准差在列车速度为300km/h和360km/h时分别降低27.14%和22.45%,受电弓弓头的抬升始终小于0.1m。考虑受电弓参数的摄动问题,在列车运行速度为300km/h时,接触力的标准差在不同参数摄动的情况下分别降低27.72%、26.84%、28.32%和25.76%。结果表明,控制器能显著降低接触力的波动,提高受流质量,同时在受电弓参数摄动下,控制器也具有良好的鲁棒性。
参考文献
[1] Wang Hongrui, Liu Zhigang, Song Yang, et al. Detection of contact wire irregularities using a quadratic time-frequency representation of the pantograph-catenary contact force[J]. IEEE Transa- ctions on Instrumentation and Measurement, 2016, 65(6): 1385-1397.
[2] 时光, 陈忠华, 郭凤仪, 等. 波动载荷下弓网接触电阻特性及建模研究[J]. 电工技术学报, 2019, 34(11): 2287-2295.
Shi Guang, Chen Zhonghua, Guo Fengyi, et al. Research on characteristic of the contact resistance of pantograph-catenary under load fluctuation[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(11): 2287-2295.
[3] Chen Liming, Peng Peihuo, He Fan. Fatigue life analysis of dropper used in pantograph-catenary system of high-speed railway[J]. Advances in Mechanical Engineering, 2018, 10(5): 1-10.
[4] Song Yang, Ouyang Huajiang, Liu Zhigang, et al. Active control of contact force for high-speed railway pantograph-catenary based on multi-body pantograph model[J]. Mechanism and Machine Theory, 2017, 115: 35-59.
[5] Schirrer A, Aschauer G, Talic E, et al. Catenary emulation for hardware-in-the-loop pantograph testing with a model predictive energy-conserving control algorithm[J]. Mechatronics, 2017, 41: 17-28.
[6] Song Yang, Liu Zhigang, Ouyang Huajiang, et al. Sliding mode control with PD sliding surface for high-speed railway pantograph-catenary contact force under strong stochastic wind field[J]. Shock and Vibration, 2017: 48953211-489532116.
[7] 时光, 陈忠华, 郭凤仪, 等. 基于最优载荷的受电弓自适应终端滑模控制[J]. 电工技术学报, 2017, 32(4): 140-146.
Shi Guang, Chen Zhonghua, Guo Fengyi, et al. Adaptive terminal sliding mode control of pantograph based on optimal load[J]. Transactions of China Electrotechnical Society, 2017, 32(4): 140-146.
[8] 时光, 陈忠华, 刘健辰, 等. 基于伺服模型的受电弓LQR控制[J]. 电子测量与仪器学报, 2016, 30(7): 1120-1126.
Shi Guang, Chen Zhonghua, Liu Jianchen, et al. Research of LQR control of pantograph based on servo model[J]. Journal of Electronic Measurement and Instrumentation, 2016, 30(7): 1120-1126.
[9] Chater E, Ghani D, Giri F, et al. Output feedback control of pantograph-catenary system with adaptive estimation of catenary parameters[J]. Journal of Modern Transportation, 2015, 23(4): 252-261.
[10] Lu Xiaobing, Liu Zhigang, Song Yang, et al. Estimator-based multi-objective robust control strategy for an active pantograph in high-speed railways[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2018, 232(4): 1064-1077.
[11] Liu Zhi, Liu Yicheng, Zhou Ning, et al. Backstepping controller design for pantograph-catenary system[C]// IOP Conference Series: Materials Science and Engineering, Chengdu, China, 2018: 12-45.
[12] Wang Yanbo, Chen Zhe, Wang Xiongfei, et al. An estimator-based distributed voltage-predictive control strategy for AC islanded microgrids[J]. IEEE Transa- ctions on Power Electronics, 2015, 30(7): 3934-3951.
[13] 谷苗, 夏超英, 田聪颖. 基于综合型卡尔曼滤波的锂离子电池荷电状态估算[J]. 电工技术学报, 2019, 34(2): 419-426.
Gu Miao, Xia Chaoying, Tian Congying. Li-ion battery state of charge estimation based on com- prehensive Kalman filter[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 419-426.
[14] 刘芳, 马杰, 苏卫星, 等. 基于自适应回归扩展卡尔曼滤波的电动汽车动力电池全生命周期的荷电状态估算方法[J]. 电工技术学报, 2020, 35(4): 698-707.
Liu Fang, Ma Jie, Su Weixing, et al. State of charge estimation method of electric vehicle power battery life cycle based on auto regress extended kalman filter[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 698-707.
[15] 王大方, 李琪, 张鹏, 等. 带有相电压补偿基于EKF的无传感器感应电机转速估计[J]. 电机与控制学报, 2019, 23(1): 35-44.
Wang Dafang, Li Qi, Zhang Peng, et al. Speed estimation method based on extended Kalman filter with phase voltage compensation for sensorless ACIM drives[J]. Electric Machines and Control, 2019, 23(1): 35-44.
[16] Yin Zhonggang, Gao Fengtao, Zhang Yanqing, et al. A review of nonlinear Kalman filter appling to sensorless control for AC motor drives[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(4): 351-362.
[17] 李扬, 李京, 陈亮, 等. 复杂噪声条件下基于抗差容积卡尔曼滤波的发电机动态状态估计[J]. 电工技术学报, 2019, 34(17): 3651-3660.
Li Yang, Li Jing, Chen Liang, et al. Dynamic state estimation of synchronous machines based on robust cubature Kalman filter under complex measurement noise conditions[J]. Transactions of China Electro- technical Society, 2019, 34(17): 3651-3660.
[18] 丁家琳, 肖建, 赵涛. 自适应CKF强跟踪滤波器及其应用[J]. 电机与控制学报, 2015, 19(11): 111-120.
Ding Jialin, Xiao Jian, Zhao Tao. Adaptive CKF strong tracking filter and application[J]. Electric Machines and Control, 2015, 19(11): 111-120.
[19] 颜湘武, 邓浩然, 郭琪, 等. 基于自适应无迹卡尔曼滤波的动力电池健康状态检测及梯次利用研究[J]. 电工技术学报, 2019, 34(18): 3937-3948.
Yan Xiangwu, Deng Haoran, Guo Qi, et al. Study on the state of health detection of power batteries based on adaptive unscented Kalman filters and the battery echelon utilization[J]. Transactions of China Electro- technical Society, 2019, 34(18): 3937-3948.
[20] 曲正伟, 董一兵, 王云静, 等. 用于电力系统动态状态估计的改进鲁棒无迹卡尔曼滤波算法[J]. 电力系统自动化, 2018, 42(10): 87-92.
Qu Zhengwei, Dong Yibing, Wang Yunjing, et al. Improved robust unscented Kalman filtering algorithm for dynamic state estimation of power systems[J]. Automation of Electric Power Syetems, 2018, 42(10): 87-92.
[21] Sakthivel R, Selvi S, Mathiyalagan K. Fault-tolerant sampled-data control of flexible spacecraft with probabilistic time delays[J]. Nonlinear Dynamics, 2015, 79(3): 1835-1846.
[22] Wang Gang, Chen Changzheng, Yu Shenbo. Robust non-fragile finite-frequency H∞ static output- feedback control for active suspension systems[J]. Mechanical Systems and Signal Processing, 2017, 91: 41-56.
[23] Kamalapurkar R, Fischer N, Obuz S, et al. Time- varying input and state delay compensation for uncertain nonlinear systems[J]. IEEE Transactions on Automatic Control, 2016, 61(3): 834-839.
[24] Song Yang, Liu Zhigang, Wang Hongrui, et al. Nonlinear modelling of high-speed catenary based on analytical expressions of cable and truss elements[J]. Vehicle System Dynamics, 2015, 53(10): 1455-1479.
[25] Kiessling F, Puschmann R, Schmieder A, et al. Contact lines for electric railways, planning, design, implementation, maintenance[M]. Erlangen: Publicis Publishing, 2009.
[26] Afshari H H, Gadsden S A, Habibi S. Gaussian filters for parameter and state estimation: a general review of theory and recent trends[J]. Signal Processing, 2017, 135: 218-238.
[27] Ali Mehrjouyan, Alireza Alfi. Robust adaptive unscented Kalman filter for bearings-only tracking in three dimensional case[J]. Applied Ocean Research, 2019, 87: 223-232.
Optimal Control of Pantograph for High-Speed Railway Considering Actuator Time Delay
Abstract With the increasing speed of the high-speed train, the coupling vibration between the pantograph and catenary aggravates the fluctuation of the contact force, and deteriorates the current flow quality, which brings challenges to the safety and stability of the high-speed train. The active control of the pantograph can reduce the fluctuation of contact force and ensure the stable current flow of the high-speed train. However, there is the problem of actuator time-delay in the active control. To solve this problem, a control strategy considering actuator time delay was proposed. Based on the robust adaptive unscented Kalman filter, the estimation method was adopted to obtain the state information of pantograph in the time-varying noise environment. The contact force, collector acceleration and collector uplift were used as the measurement states to construct the design control performance output function. Considering the actuator time-delay, the optimal controller combined with the estimator was designed. With the parameter perturbation of the pantograph, the effectiveness and the robustness of the controller were verified by the nonlinear pantograph-catenary system model. The simulation results show that the controller can significantly reduce the fluctuation of the contact force even if the actuator time delay exists. In addition, the controller can guarantee the robustness under the influence of the pantograph parameters perturbation.
Keywords:High-speed railway pantograph, active control, time delay, state estimation, measured state
中图分类号:TM571
DOI: 10.19595/j.cnki.1000-6753.tces.200867
国家自然科学基金资助项目(U1734202, 51405401)。
收稿日期 2020-07-17
改稿日期 2020-11-09
E-mail: xiesldl@163.com
张 静 女,1979年生,副教授,硕士生导师,研究方向为高速铁路受电弓主动控制和高速弓网受流特性。
E-mail: sdzj2006@126.com(通信作者)
(编辑 崔文静)