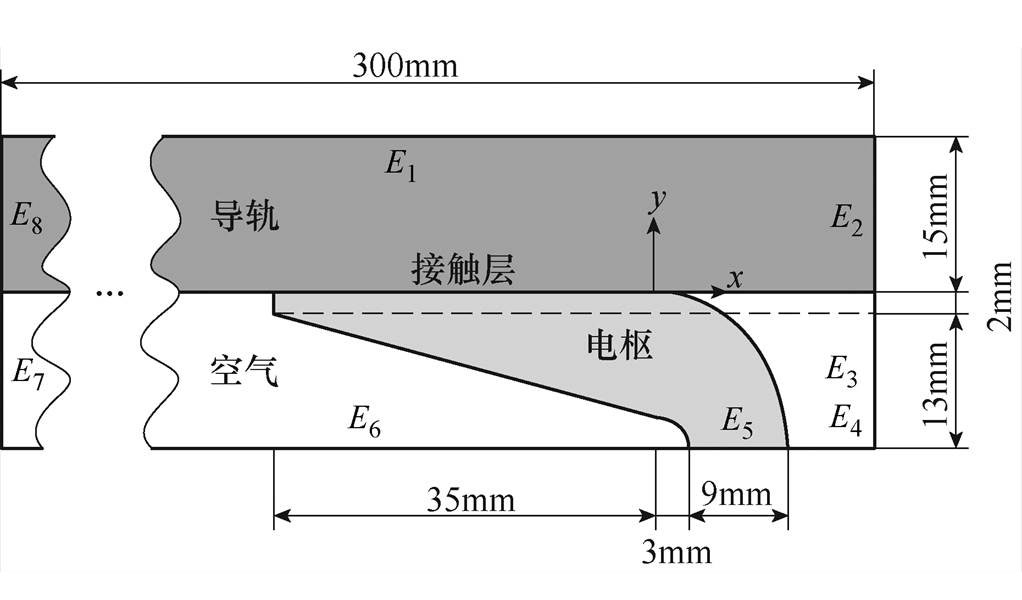
图1 仿真几何模型
Fig.1 Analysis geometric model
摘要 该文提出一种考虑初始接触压力的磁扩散模型分析电磁轨道发射装置中的磁感应强度、电流密度、焦耳热、电磁力分布、趋肤深度随时间的演变。该模型分析枢轨接触状态对接触面导电特性造成的差异，从而得到不规则电枢形状、驱动电流波形条件下的多场分布。计算结果表明，过盈量为1mm时，实际接触区域处于理论接触区域的中段，而电流初始聚集在实际接触区域的枢尾一端，随后向电枢头部移动。分析其他四种接触电导分布情况发现，在实际接触区域由压力造成的导电性能差异不会主导电流的分布。电流由于趋肤效应，在轴向距离电枢越近的导轨趋肤深度越浅，模型计算结果与理论公式比较误差较小，且斜坡电流的趋肤效应比阶跃电流更明显。该研究可以为电枢转捩、趋肤效应、电枢结构优化提供研究方向，为三维多场计算奠定基础。
关键词：电磁轨道发射装置 过盈接触 磁扩散模型 趋肤效应
电磁轨道发射装置是一种将脉冲功率电源电磁能转化为弹丸动能的武器，相比于传统火炮，电磁炮具有发射速度高、启动时间短、发射动能大、负载可变、可靠性高、可维护性好等优点[1]。针对电磁发射各分系统，国内外学者进行了许多研究[2-5]。
在使用固体电枢的轨道炮中，电枢在两导轨间受到电磁力向前滑动并推动弹丸加速，由于其高速、大电流、大应变的极端瞬态工况，电流在电枢导轨上的流动是不均匀的。时变电流在导体上流动聚集在表面的现象叫做趋肤效应，文献[5]给出了正弦交变电流在导体上传导时，趋肤深度与频率、导体特性关系的公式。文献[6]给出了趋肤深度与导通时间的关系。电流在导轨和电枢上不均匀分布，在接触界面集中分布的位置产生更高的焦耳热，极大影响电磁发射的状态。而轨道电磁发射系统中，金属轨道和电枢是将电源电能转化为弹丸动能的关键部件，其性能的好坏直接决定了系统的发射能力[7]。热量的集中使局部材料相变随电枢移动丢失，导致枢轨的接触失效进而产生转捩，影响轨道炮的使用寿命，研究接触界面的电流、热量分布十分有必要。
前人利用磁扩散方程进行了一系列有关热、电分布的问题研究。文献[8]给出了具有涂层条件下的磁扩散模型方程。杨玉东、Li Xin、殷强等使用磁扩散模型进行了细致的研究。文献[9]用有限差分法对磁扩散模型进行了计算，验证了用此方法进行电流分析的可行性。文献[10]对该方法使用的数值计算方法进行优化使之易于收敛。文献[11]将磁扩散模型扩展到三维进行磁、电、热分布分析，这些文献中使用的电枢尾部都是规则矩形，便于用有限差分法计算结果。文献[12]使用不规则形状电枢，利用有限元分析，用该模型计算电流密度，并以此结合毕奥－萨伐尔定律进一步计算电枢前方炮膛的磁感应强度，其考虑了接触压力不均匀对枢轨接触造成的影响，但使用的是电流峰值时加载了电磁力的接触状态。
文献[13]通过仿真证明初始接触的压力分布是不均匀的，甚至理论接触面与实际接触面有明显的差异。文献[14]通过试验证明电枢熔蚀发生在初始接触压力最大的区域附近。初始接触压力对滑动电接触界面的磁扩散过程具有重要影响，但尚未发现有国内外学者从事此方面的研究。本文提出的模型利用磁扩散方程计算电流、热量分布，重点考虑了发射初始接触面压力差异造成的影响，可以较大程度地完善滑动电接触的磁扩散模型。
用于仿真计算的几何模型如图1所示。导轨高15mm，长300mm；半个电枢高15mm，长47mm，其中，在电枢与导轨的接触面上假设深度为0.1mm的区域作为接触层，以理论接触面最右端点为几何坐标（0, 0），垂直xy平面向内为z轴正方向。
图1 仿真几何模型
Fig.1 Analysis geometric model
假设电枢和导轨在z方向上足够厚，则该二维平面就可以忽略磁感应强度在x、y方向上的分量，电流在z方向的分量。通过Maxwell方程推导得到二维磁扩散模型方程[8]为
（1）式中，Bz为B在z方向上的分量，B为磁感应强度矢量（T）；vx为速度v（m/s）在x方向上的分量；t为时间（s）；m 为磁导率（H/m），分析域均取4p×10-7H/m；s 为电导率（S/m）。分析中将电枢作为参考系，即计算中电枢的vx为0。
忽略材料温度特性和摩擦热的热传导方程[8]为
（2）式中，T为温度（K）；r 为材料密度（kg/m3）；k为热导率（W/(m·K)）；cp为比定压热容（J/(kg·K)），忽略边界的热通量。材料特性参数见表1。
由于假设了电枢、导轨足够厚，电流密度j只有在x、y方向上的分量，计算jx和jy分别为
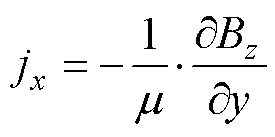（3）表1 材料特性参数
Tab.1 Material parameters
参 数电枢(Al)导轨(Cu) 电导率s/(S/m)3.77×1075.99×107 热导率k/[W/(m·K)]238400 比定压热容cp/[J/(kg·K)]900385 密度r/(kg/m3)2 7008 960 杨氏模量E/Pa7×10101.1×1011 泊松比0.330.35
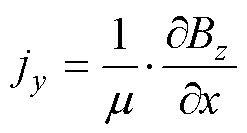（4）仿真中边界条件如下：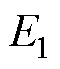
～
：
；
：
；
：
；
, 
：
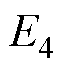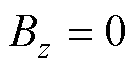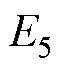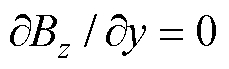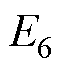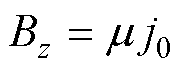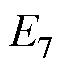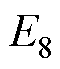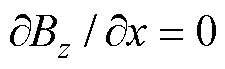。其中，j0为激励电流线密度。初始值Bz0=0，T0=288K。
电磁力大小为
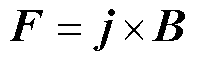（5）利用式（1）～式（5）可得图1截面上磁感应强度、电流密度、焦耳热、电磁力等物理量的分布及随时间演变的情况。
本文采用电枢尾翼向外张开的过盈结构，过盈量1mm。在仿真模型中利用接触层的物理特性来表征接触状态。
为了表征预应力对电枢的影响，本文首先对电枢与导轨单独进行了结构力学分析，初始接触压力与接触电导率如图2所示，距离电枢尾部端点0～35mm是理论接触位置，其中，距离3～24mm的区域是实际接触位置，其分布特性、量级与文献[13]的分析结果具有相同的趋势，压力集中在理论接触面的中段，并分别向前、向后逐渐衰减为0，即不接触。
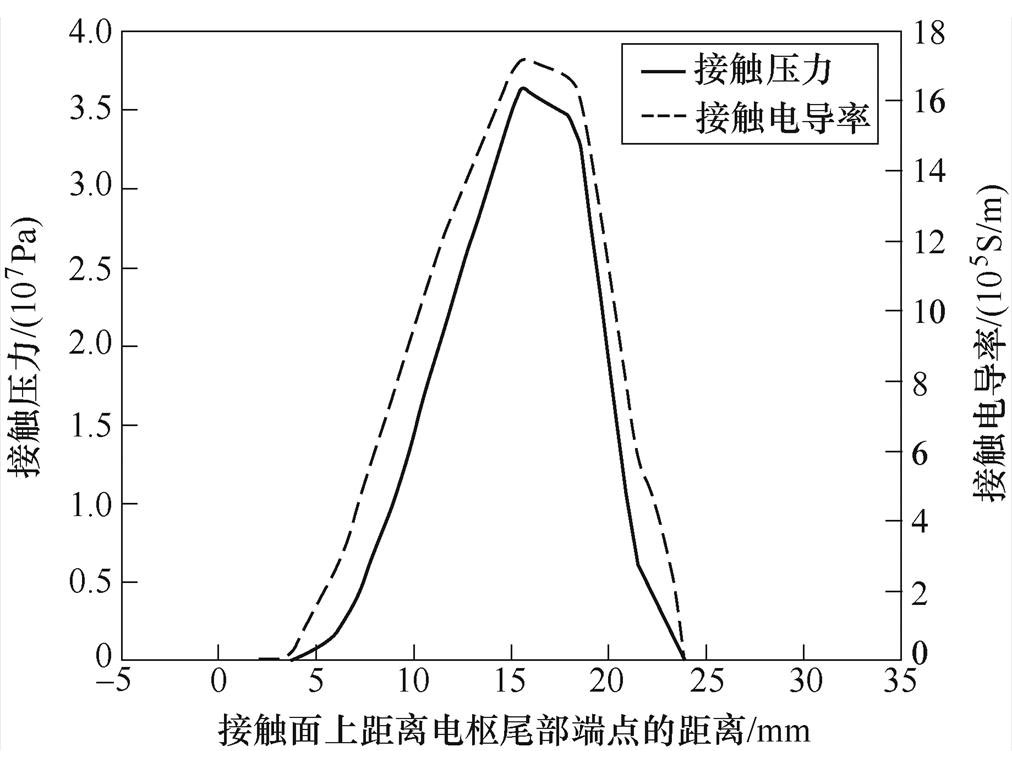
图2 初始接触压力与接触电导率
Fig.2 Initial contact pressure and conductivity
接触压力的差异对接触界面导电性能的影响采用CLM（contact layer model）模型[15-16]表征，CLM模型用于计算接触电导h1（S/m），即
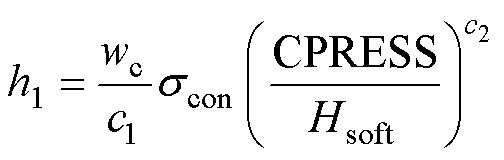（6）式中，wc为接触层厚度（m）；scon为两种接触材料电导率的算术平均数（S/m）；CPRESS为接触压力（Pa）；Hsoft为接触对中较软材料的硬度（Pa），本模型取600MPa；c1、c2与接触对特性有关，本文分别取9.45×10-4、0.63。
计算得到接触电导值如图2所示，与压力呈相同的变化趋势。当压力为0时，意味着不接触，为了计算收敛，将空气域电导率和不接触部分的收缩电导率都设置为1S/m。
本文分别计算了不考虑接触压力的理想情况与考虑接触压力的非理想情况的结果。
对于理想接触，即不考虑接触层的特殊性，模型将接触层与电枢视为一体，使用同样的材料参数进行计算。计算条件相对移动速度v=0，激励电流线密度j0=2.4×107A/m，t =0.1ms时刻的磁场分布状况如图3所示，图中省略了空气域；图4给出了接触层上的电流密度与电枢尾端距离的关系曲线。
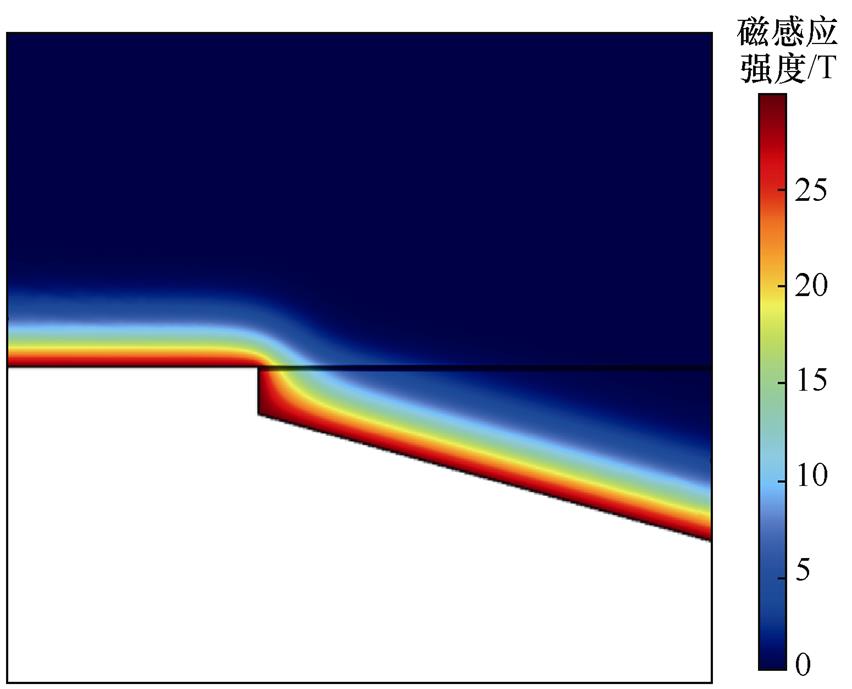
图3 不考虑接触压力的磁场分布
Fig.3 Magnetic field without considering contact pressure
观察可知，在假设压力均匀分布的情况下，实际接触面与理论接触面完全重合，电流从枢尾顶端穿过理论接触界面。分析温度可知，其在枢尾顶端最大，约为1 165K，远超铝的熔点，足以使电枢熔化。但此点向周围方向的温度梯度较高，0.2mm范围内即降到800K左右。可以预见，在尾部材料受热熔化后失去接触，电流会不断向电枢头部方向移动，这是符合传统的熔化波模型对于枢轨接触情况演变描述的[17]。
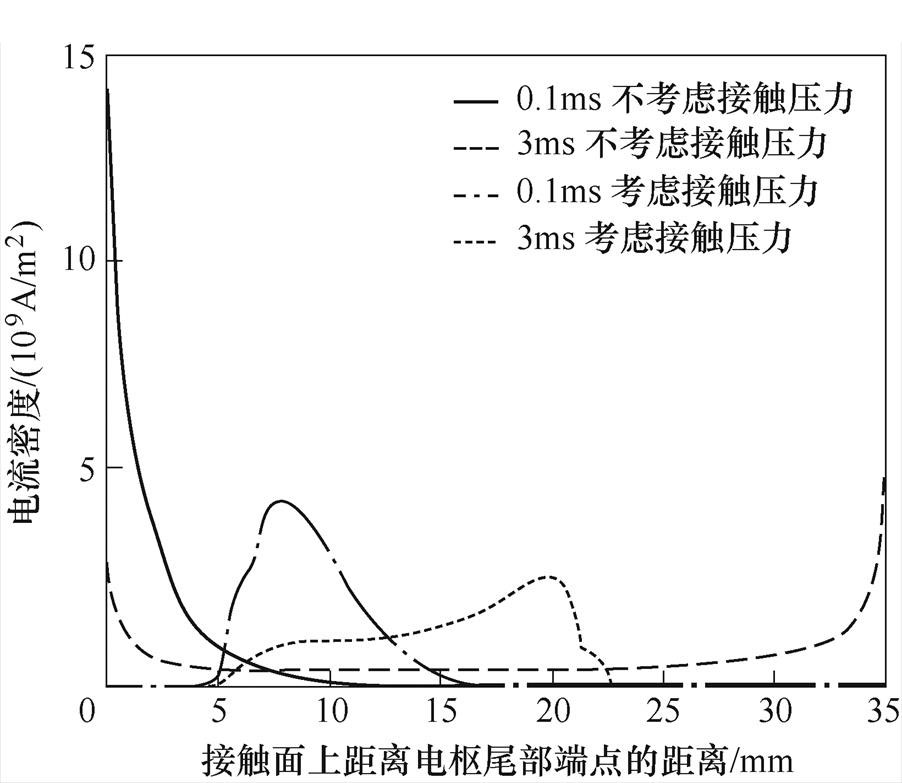
图4 接触层上电流密度
Fig.4 Current density along the contact layer
对于非理想接触，模型按照1.2节过盈1mm情况的接触参数计算，与2.1节相同激励条件的电流密度分布如图4所示，t =0.1ms磁场分布如图5所示。
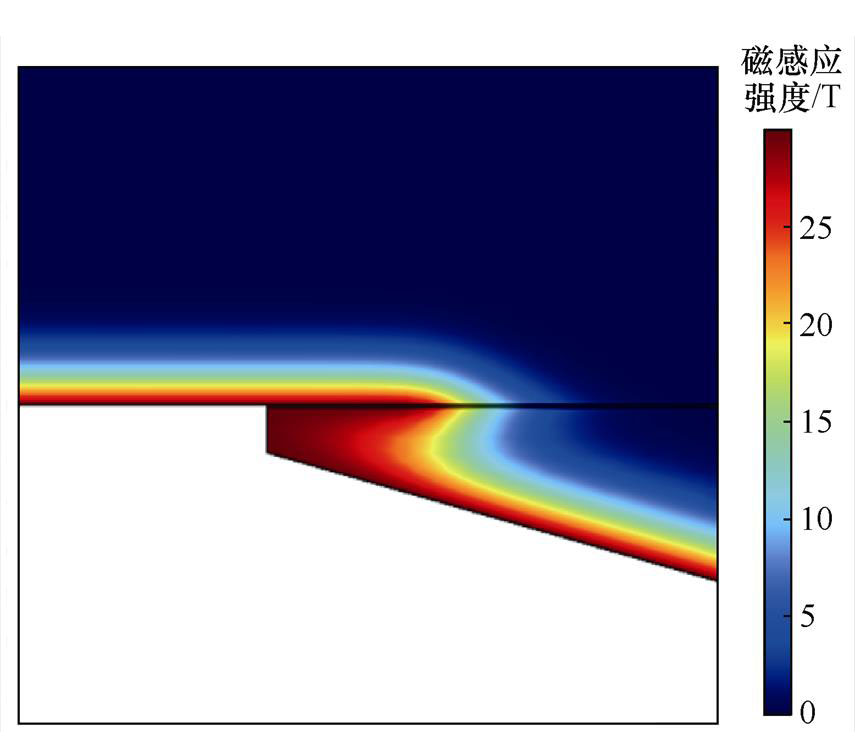
图5 考虑接触压力CLM模型磁场分布
Fig.5 Magnetic field with considering contact pressure in CLM model
由分布云图可知，其扩散规律与2.1节的理想接触模型基本一致。但电流穿过理想接触界面的区域在距离电枢尾部5～15mm位置处，处于实际接触区域中靠近枢尾的位置，即电流从实际接触的后缘穿越枢轨接触面，这是符合电枢最末端与导轨无接触所以不导通电流的实际情况的。由于趋肤效应，电流在电枢表面聚集。该时刻，温度最高点944K出现在电枢喉部，而枢轨接触面最高温度约为613K，与接触面最大电流密度点在同一位置。
在1.2节给定的压力分布下，实际接触区域内的电流密度并未发现与压力大小有明显相关性；考虑接触压力的模型，电流最大值约为不考虑情况的1/3。
可见，考虑实际接触压力的模型可以更贴合实际的电流在接触面的流动状况。在t =3ms，磁扩散过程已经稳定，接触层电流密度不再变化，如图4所示，电流密度最大值分布在接触界面的右侧，也就是头部端，和文献[18]吻合，这是由于导轨电导率高于电枢，平行路径下电流趋向于在电导较高的材料中流动，此时，趋肤效应与电导分流效应相比，在决定电流路径上已无优势。
故可以在前人有关熔化波模型的基础上得出结论：熔化波并不是从电枢的实际尾部开始，而是从枢轨实际接触的尾部位置开始，并不断向前移动。
可以沿路径积分计算任意两点的电势差DU和电场强度大小E，有
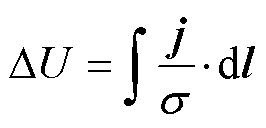（7）
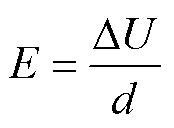（8）
式中，l为积分路径矢量；d为积分路径起终点距 离。枢尾端由于预应力影响分离，计算电枢尾翼最末端和导轨距离其最近点的电势差与电场强度，得到DU=1.76V，E=2 514.29V/m。一般情况下，空气击穿场强为3MV/m，故该条件不会导致枢尾电弧 击穿。
为了研究不同接触特性对于电流分布的影响，本文给出其他四种不同的接触电导分布情况：
情况A：基于1.1节给出的枢轨几何模型，过盈量为0.8mm的接触电导率h2。
情况B：基于1.1节给出的枢轨几何模型，过盈量为1.2mm的接触电导率h3。
情况C：在假设的实际接触区域设定正弦函数变化规律的接触电导率h4，解析表达式如式（9）所示。
情况D：在假设的实际接触区域设定线性函数变化规律的接触电导率h5，解析表达式如式（10）所示。
各种情况下的接触层上接触电导率，0.1ms和3ms下的接触层电流密度如图6所示。
（9）
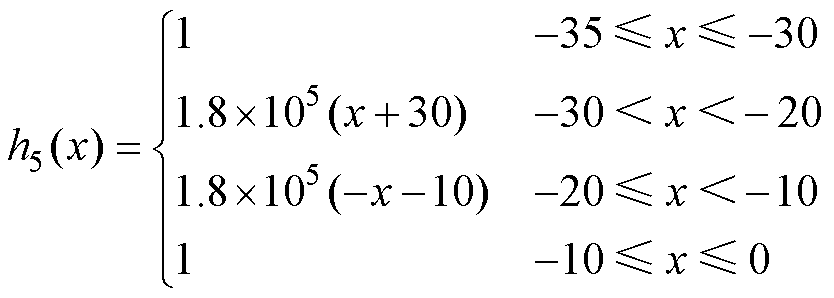（10）
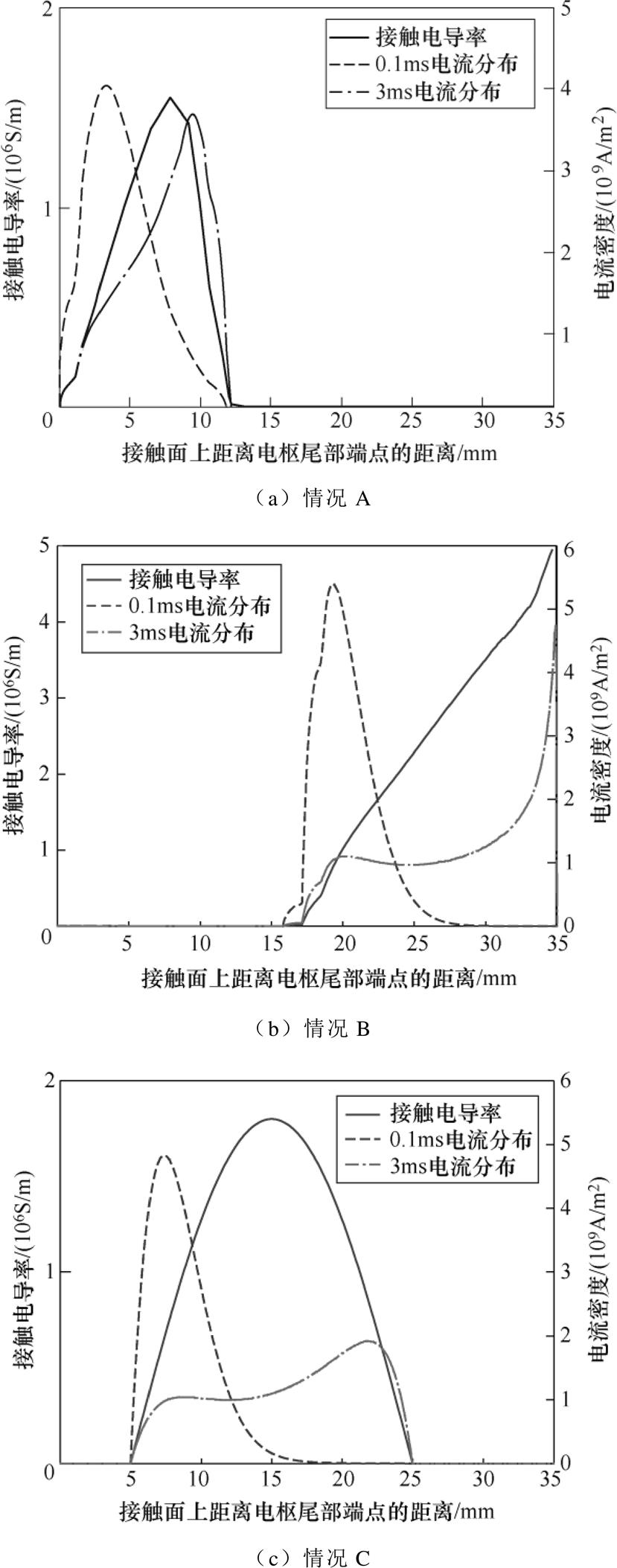
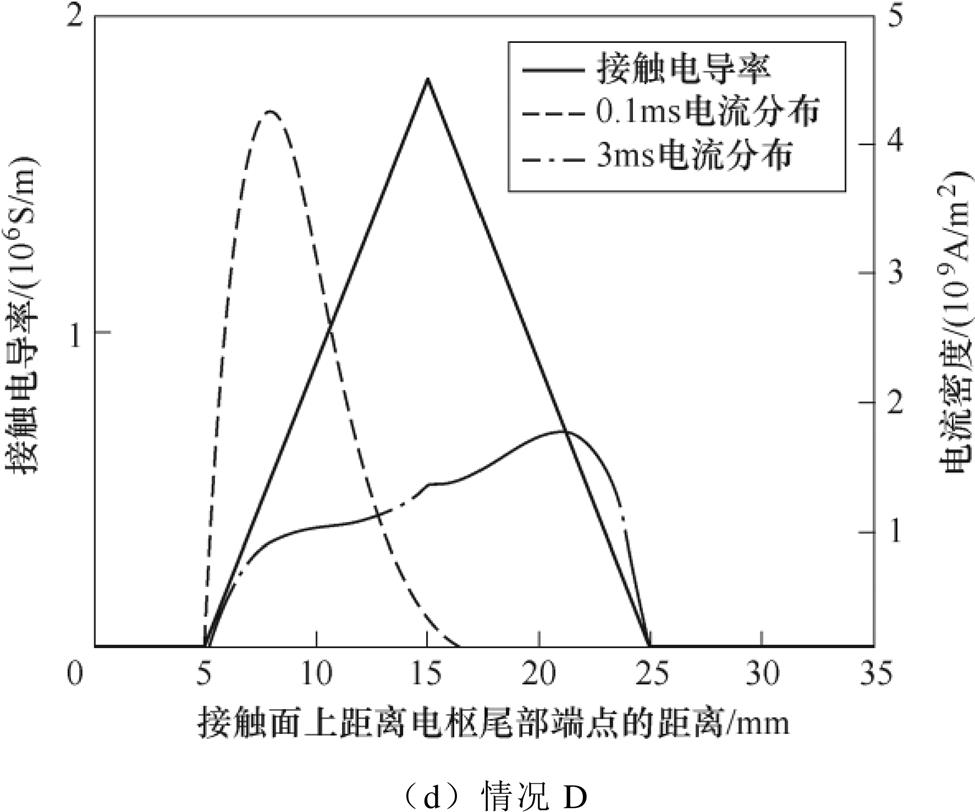
图6 不同情况下接触电导率，0.1ms和3ms电流密度
Fig.6 Current density at 0.1ms & 3ms and conductivity under different situations
可以发现，各种情况下，在初始时刻（t =0.1ms），电流最大密度点都在实际接触面的左端（枢尾端），并在接近稳态的时刻（t =3ms）转移到实际接触面右端（枢头端），电流不会在实际接触面之外穿过接触层。但两个时刻的最大电流密度点与对应的最大压力接触点没有明显的相关关系，只有线性接触电导分布情况下，3ms时在最大压力接触点有一些扬起，但最大电流密度点依然在头部。这说明电枢发射时，理论接触面上的电流聚集点主要受实际接触面的最靠电枢尾端的位置以及导通的时长决定，实际接触区域的接触压力差异不产生实际的影响。
该模型不仅可以计算磁感应强度、电流密度、焦耳热、电磁力的分布，还可以通过简单的换算，计算不同电流波形下导轨内的电流趋肤深度。本文主要计算四种情况，详细描述如下：
情况a：阶跃电流，设置仿真条件v=200m/s，j0=2.4×10-7A/m。
情况b：阶跃电流，在A的基础上提高脉冲，设置仿真条件v=200m/s，j0=4.8×107A/m。
情况c：斜坡电流，与实际工况较为接近，设置仿真条件v=200m/s，j0=2.4×106 t A/m。
情况d：斜坡电流，在C的基础上增加电流斜率，设置仿真条件v=200m/s，j0=4.8×106t A/m。
设导轨上坐标（x, y）点的电流密度为j(x, y)，则点（xm, yn）的相对电流密度大小为j(xm, yn)/ max[ j(xm, y)]，而由磁扩散模型特性，max[ j(xm, y)]必然在导轨内侧表面，即max[j(xm, y)]= j(xm, 0)。
图7给出情况a下，导轨上几何坐标x= -30mm、-35mm、-40mm、-45mm、-225mm上导轨内的相对电流密度分布曲线，可以发现，电流在向导体内部渗透时，表面的电流密度最大，越向内部，电流密度越低。
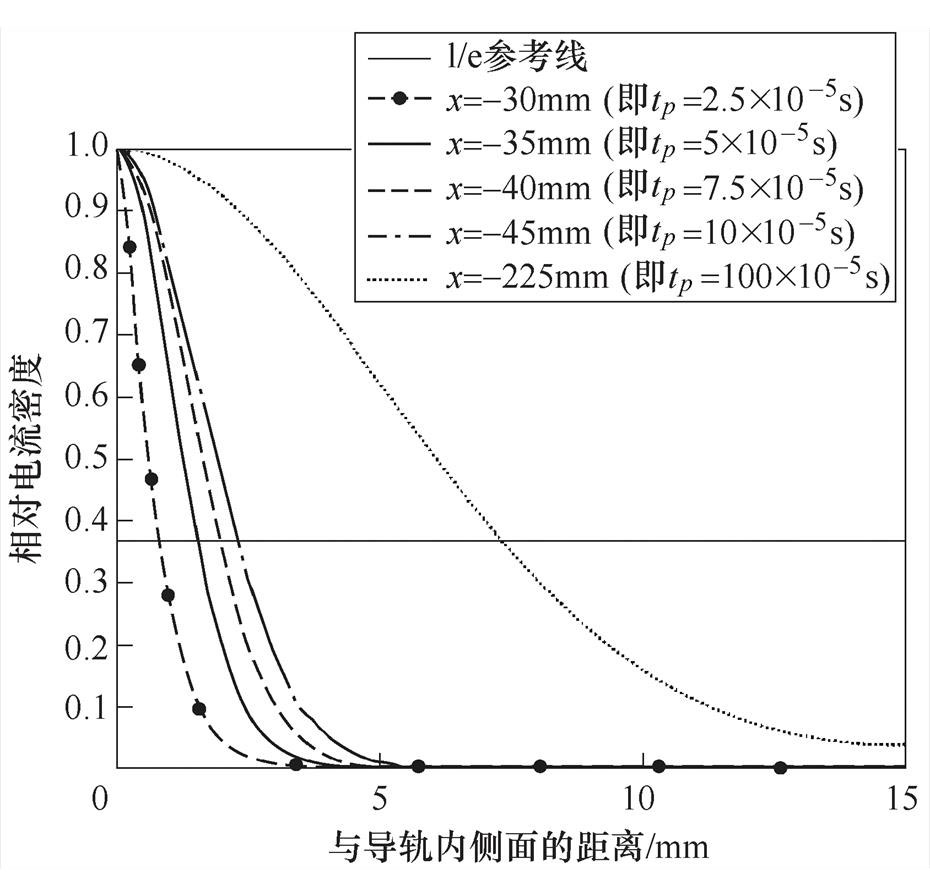
图7 情况a下不同位置的相对电流密度曲线
Fig.7 Relative current density under situation a
本文依据传统定义对趋肤深度进行计算。导体内某一截面深度为d的电流密度为表面电流密度的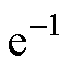
倍时，则称d 为该位置的趋肤深度。本模型中，该截面与电流流入枢轨界面的距离p可以换算成已导通电流的时间tp，有
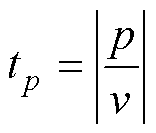（11）本文以2.2节的接触情况为研究对象，并假设电流从几何坐标x=-25mm的位置流入接触面。
由图7可知，x=-30mm、-35mm、-40mm、-45mm、-225mm处，其位置逐渐远离电枢的过程中，趋肤深度在非线性地增长，其增长速度随与电枢的距离增长而逐渐衰减。
关于趋肤深度的计算公式[6, 12]为
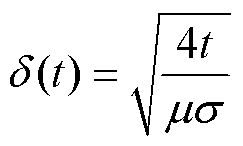（12）
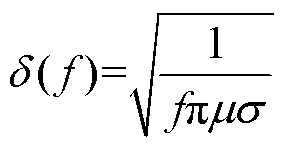（13）
式中，f为频率（Hz）。式（13）用于计算导体中稳定正弦电流的趋肤深度，而本文讨论的趋肤深度与导通时间密切相关，故采用式（12）与数值计算进行对照。
记d0为式（12）的计算结果，d1为情况a的计算结果，d2为情况b的计算结果，d3为情况c的计算结果，d4为情况d的计算结果，趋肤深度计算结果见表2。
表2 趋肤深度计算结果
Tab.2 Results of skin depth
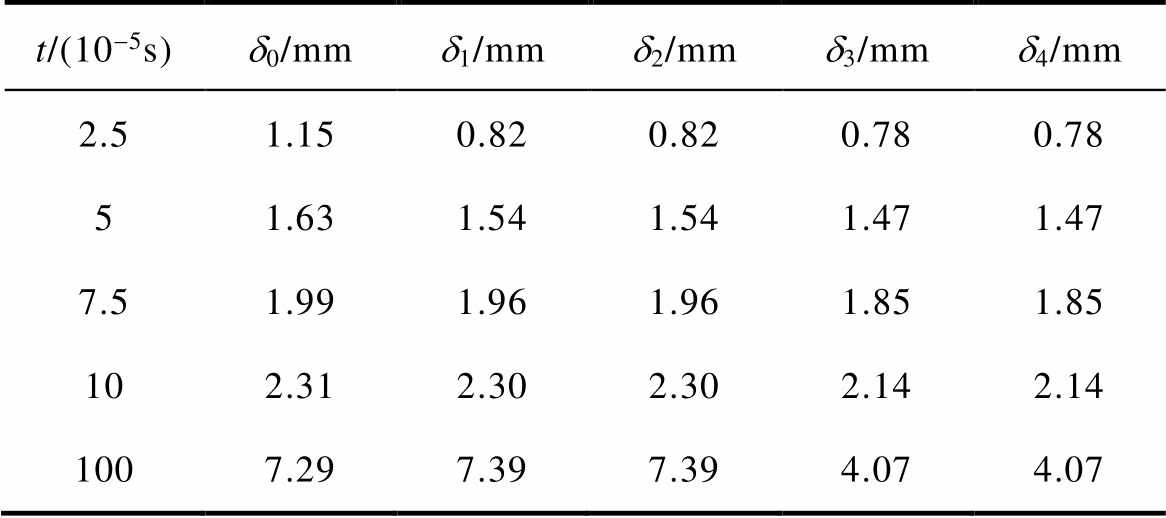
t/(10-5s)d0/mmd1/mmd2/mmd3/mmd4/mm 2.51.150.820.820.780.78 51.631.541.541.471.47 7.51.991.961.961.851.85 102.312.302.302.142.14 1007.297.397.394.074.07
可以发现，d1与d2结果一致，d3与d4结果一致，说明趋肤深度不因电流的幅值或斜率而改变；与解析计算值d0相比，阶跃电流与斜坡电流的趋肤深度在t =2.5×10-5s极短时间尺度的误差都较大，这可能是由于时间太短，电流从整个面穿过枢轨接触界面，导致无法准确确定电流流入点的位置造成的，但阶跃电流在之后的结果几乎与解析解一致。同时刻的斜坡电流与阶跃电流的趋肤深度相比要更浅，这说明电流的波形可以一定程度地影响趋肤深度，斜坡电流产生的趋肤效应更明显，电流聚集情况更剧烈。
本文提出一个使用过盈电枢考虑预应力作用下实际接触情况的磁扩散模型，通过CLM模型，可在不同电流波形情况下计算电枢导轨的电磁、热、力场的结果，并得到以下结论：
1）计算结果表明，过盈量为1mm时，实际接触区域处于理论接触区域的中段，而接触界面上电流聚集在实际接触区域的枢尾端，熔化波并不是从电枢的尾部开始，而是从枢轨实际接触的尾部位置开始，并不断向前移动，直到受热失去所有金属接触，发生转捩。该仿真条件下，电枢尾部端点与导轨的电压差不足以产生电弧击穿；并且压力造成的实际接触区域上的导电性能的差异不会主导影响电流的分布。随时间发展，最大电流密度点向电枢头部方向移动，峰值下降。
2）该模型使用阶跃电流波形计算趋肤深度与解析解拟合度高，而实际发射情况多为斜坡电流波形，电流聚集情况更为强烈，利用本模型计算趋肤深度可以获得更精确的结果。
本文建立的模型可以较好地分析初始接触状态对滑动电接触电流分布的影响，从理论上指导电枢的设计，避免实际接触靠近电枢头部造成过早转捩，趋肤深度的计算可以更好地指导计算轨道焦耳热。但模型没有考虑材料相变损失导致枢轨实际接触区域变化后对枢轨磁扩散的影响，下一步将从此角度深入研究。
参考文献
[1] 马伟明, 鲁军勇. 电磁发射技术[J]. 国防科技大学学报, 2016, 38(6): 1-5.
Ma Weiming, Lu Junyong. Electromagnetic launch technology[J]. Journal of National University of Defense Technology, 2016, 38(6): 1-5.
[2] 李白, 鲁军勇, 谭赛, 等. 滑动电接触界面粗糙度对电枢熔化特性的影响[J]. 电工技术学报, 2018, 33(7): 1607-1615.
Li Bai, Lu Junyong, Tan Sai, et al. Effect of interfacial roughness of sliding electrical contact on the melting characteristics of armature[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(7): 1607-1615.
[3] 杜佩佩, 鲁军勇, 冯军红, 等. 电磁轨道发射器电磁结构耦合动态发射过程数值模拟[J]. 电工技术学报, 2020, 35(18): 3802-3810.
Du Peipei, Lu Junyong, Feng Junhong, et al. Numeri- cal simulation of dynamic launching process of electromagnetic rail launcher with electromagnetic and structural coupling[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3802-3810.
[4] 朱博峰, 鲁军勇, 张晓, 等. 大容量脉冲电容器放电起始阶段晶闸管电压高频振荡机理研究[J]. 电工技术学报, 2020, 35(6): 1272-1278.
Zhu Bofeng, Lu Junyong, Zhang Xiao, et al. Study on the high frequency voltage oscillation of thyristor during the initial stage of pulse capacitor discharge[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1272-1278.
[5] 阮景煇, 陈立学, 夏胜国, 等. 电磁轨道炮电流分布特性研究综述[J]. 电工技术学报, 2020, 35(21): 161-169.
Ruan Jinghui, Chen Lixue, Xia Shengguo, et al. A review of current distribution in electromagnetic railguns[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 161-169.
[6] Nearing J C, Huerta M A. Skin and heating effects of railgun current[J]. IEEE Transactions on Magnetics, 1989, 25(1): 381-386.
[7] 肖铮. 电枢—轨道载流滑动接触面摩擦磨损研究[D]. 武汉: 华中科技大学, 2012.
[8] Ghassemi M, Barsi Y M. Effect of liquid film (indium) on thermal and electromagnetic distribution of an electromagnetic launcher with new armature[C]// IEEE 2004 12th Symposium on Electromagnetic Launch Technology, Snowbird, UT, USA, 2004: 386- 392.
[9] 杨玉东, 王建新, 薛文. 轨道炮速度趋肤效应的分析与仿真[J]. 强激光与粒子束, 2011, 23(7): 1965- 1968.
Yang Yudong, Wang Jianxin, Xue Wen. Simulation and analysis of velocity skin effect of railgun[J]. High Power Laser and Particle Beams, 2011, 23(7): 1965- 1968.
[10] 杨玉东, 付成芳, 薛文, 等. 轨道与电枢间运动电磁场分布的数值计算[J]. 火炮发射与控制学报, 2014, 35(3): 1-5.
Yang Yudong, Fu Chengfang, Xue Wen, et al. Numerical calculation of movement electromagnetic field distribution between rail and armature[J]. Journal of Gun Launch & Control, 2014, 35(3): 1-5.
[11] Li Xin, Weng Chunsheng. Three-dimensional investi- gation of velocity skin effect in U-shaped solid armature[J]. Progress in Natural Science, 2008(12): 1565-1569.
[12] 殷强, 张合, 李豪杰, 等. 考虑电枢与导轨实际接触状态的电磁轨道炮膛内磁场分析[J]. 兵工学报, 2019, 40(3): 464-472.
Yin Qiang, Zhang He, Li Haojie, et al. Analysis of in-bore magnetic field in electromagnetic railgun considering the realistic armature-rail contact status[J]. Acta Armamentarii, 2019, 40(3): 464-472.
[13] 冯登, 夏胜国, 陈立学, 等. 轨道电磁发射装置中电枢装配接触压力分布的不均匀特性[J]. 高电压技术, 2015, 41(6): 1873-1878.
Feng Deng, Xia Shengguo, Chen Lixue, et al. Non- uniformity of contact pressure distribution in armature assembly for railguns[J]. High Voltage Engineering, 2015, 41(6): 1873-1878.
[14] 胡宇阳. 电磁发射小口径电枢电流熔蚀特性研究[D]. 武汉: 华中科技大学, 2017.
[15] Xia Shengguo, Chen Lixue, Xiao Zheng, et al. Effects of contact pressure concentrations in rail/armature surface at startup of a railgun launch[C]//IEEE 2012 16th International Symposium on Electromagnetic Launch Technology, Beijing, 2012: 1-5.
[16] Hsieh K T, Satapathy S, Hsieh M T. Effects of pressure-dependent contact resistivity on contact interfacial conditions[J]. IEEE Transactions on Mag- netics, 2008, 45(1): 313-318.
[17] Paul B P. Current melt-wave model for transitioning solid armature[J]. Journal of Applied Physics, 1990, 67(7): 3511-3516.
[18] Li Chengxian, Xia Shengguo, Chen Lixue, et al. Simulations on current distribution in railgun under imperfect contact conditions[J]. IEEE Transactions on Plasma Science, 2019, 47(5): 2264-2268.
A Magnetic Diffusion Model of Electromagnetic Launcher Considering Initial Contact Pressure
Abstract This paper proposed an optimized magnetic diffusion model to analyze magnetic flux density, current density, Joule heat, electromagnetic force and current skin depth in different time and position of an electromagnetic launcher. The model concerned on the difference caused by the contact state, so that the multi-field distribution under the conditions of irregular armature shape, driving current waveform can be obtained. The result shows that when the interference is 1mm, the actual contact area is in the middle of the theoretical contact area, and the current concentrates at the rear end of the actual contact area and then moves ahead. It is found that the difference in electrical conductivity of the actual contact area would not affect the current distribution after the other four typical contact states were analyzed. Due to the skin effect, the skin depth close to the armature is shallow, and the ramp current has more obvious skin effect than the step current. The results deduced by this model are consistent with the theoretical formula. This study can provide an approach to observe transition, skin effect and armature structure optimization, laying a foundation for 3D field calculation.
Keywords：Electromagnetic rail launcher, interference contact, magnetic diffusion model, skin effect
中图分类号：TM359.4
DOI: 10.19595/j.cnki.1000-6753.tces.L90227
国家自然科学基金（51925704, 51877214, 51907203）、湖北省自然科学基金（2019CFB371, 2019CFB373, 2020CFB341）和中国博士后特别基金（2019T120972）资助项目。
收稿日期 2020-07-04
改稿日期 2020-10-27
E-mail: nue9595@163.com
鲁军勇 男，1978年生，教授，博士生导师，研究方向为电磁发射技术。
E-mail: jylu2019@163.com（通信作者）
（编辑 崔文静）