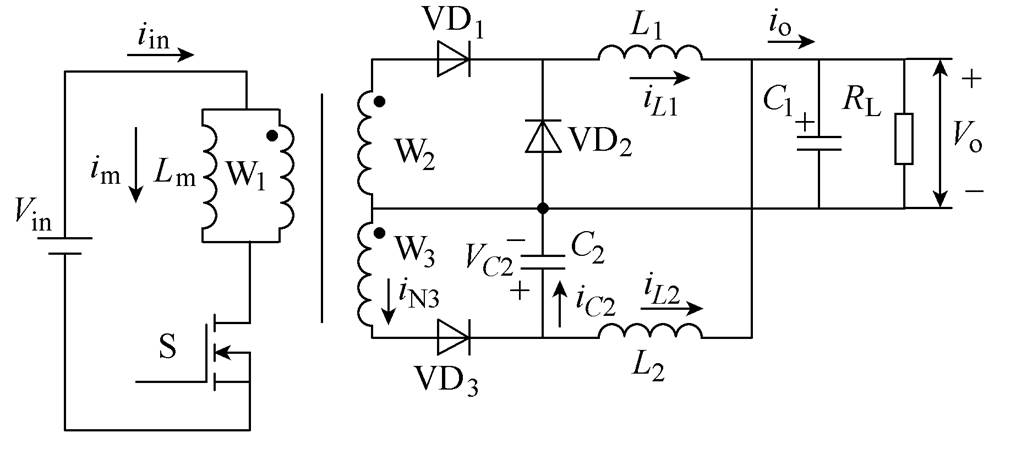
图1 附加LC的正反激组合变换器拓扑
Fig.1 The forward-flyback converter topology with additional LC
摘要 为减小正反激组合变换器的输出电压纹波,提出一种附加LC的正反激组合变换器。依据附加LC的电压电流波形,分析所提出正反激组合变换器的工作原理及能量传输过程,得出使得辅助电感电流不发生倒流且确保正激电感和辅助电感的叠加电流纹波最小的最佳工作模态。分析工作于最佳工作模态下的输出纹波电压,指出其随辅助电感的减小而减小;在给定输入电压和负载变化范围内,推导出正激电感分别工作于连续导电模式(CCM)和不连续导电模式(DCM)时使得辅助电感电流不发生倒流的临界条件,据此提出一种辅助电感和电容的优化设计方法。实例及实验结果验证了理论分析的正确性及所提出优化设计方法的可行性。
关键词:正反激 输出纹波电压 工作模式 优化设计
正反激组合变换器与反激变换器相比可获得更高的输出功率和效率[1-2],与正激变换器相比可将励磁能量传输到负载,提高变压器的转换效率[3-5],改善电路的工作特性[6-7],因此,得到了广泛的关注和应用。但其功率分配影响变换器效率及其他性能,且输出电流脉动及纹波电压较大[8-9],降低了输出电能质量[10]。为此,本文提出一种附加LC的正反激组合变换器,对于降低其输出纹波以及推广正反激组合变换器的应用具有重要意义。
文献[11]研究了一种双管双变压器正-反激组合变换器,通过改变匝比来灵活分配两变压器功率,但两变压器匝比不等时,输出纹波电流较大;匝比相等时,输出纹波电流小但正激传输的功率较少,效率低。文献[12]提出了一种变压器二次侧4个二极管结构的正反激组合变换器,其结构简单,变压器转换效率高,但正激部分只能工作于断续,输出电流脉动较大,且变压器一般需增加气隙,不适合大功率输出。文献[13]提出了一种励磁能量可回收的交错正激变换器,其工作原理类似两个并联的正激变换器,减小了输出纹波,但此变换器包含两个变压器和两个开关管,且额外增加两个二极管来保证励磁能量反馈至电源侧,使得电路结构复杂。文献[14]提出一种双变压器的正反激组合结构,有效地解决了反激变换器输出电流纹波大、功率小等缺点,省去了二次侧滤波电感,但变压器数量增加,设计难度较大。为提高正反激组合变换器的输出功率和效率,减小输出纹波,文献[15-18]也提出了针对性的解决方案,但同样带来了一些新的问题。
本文基于传统正反激变换器拓扑进行改进,提出一种附加LC的正反激组合变换器,有效地减小了输出电流脉动及纹波电压。首先,分析改进的正反激组合变换器的工作原理,指出变换器的最佳工作模式并分析最大输出纹波电压;其次,在此基础上,提出附加LC的优化设计方法;最后,通过实验验证理论分析的正确性。
附加LC的正反激组合变换器主电路拓扑如图1所示,图1中,Lm为变压器的等效励磁电感,W1为一次绕组,S为开关管。由正激绕组W2、整流二极管VD1、正激储能电感L1、续流二极管VD2及输出滤波电容C1构成正激电路;由反激绕组W3、二极管VD3、附加电容C2及电感L2构成反激电路。iN3、iL1、iL2、iC2和io为相应支路电流,im为变压器励磁电流,VC2为电容C2电压。

图1 附加LC的正反激组合变换器拓扑
Fig.1 The forward-flyback converter topology with additional LC
开关导通期间,变换器工作于正激状态,通过变压器将一部分能量直接传递到负载,另一部分能量转化为磁场能存储在正激电感L1中,同时,上一周期存储于电容C2的励磁能量经辅助电感L2与正激电感L1并联共同为负载提供能量;开关关断期间,变换器工作于反激状态,励磁能量耦合至反激绕组W3,经VD3存储于电容C2并通过辅助电感L2将励磁能量传递至负载侧直至变压器完成磁复位,且正激电感L1通过VD2续流。
根据正激电感L1和反激绕组W3上的电流是否连续,变换器存在三种工作模式:正激连续导电模式(Continuous Conduction Mode, CCM)/反激不连续导电模式(Discontinuous Conduction Mode, DCM)、正激DCM/反激DCM和正激DCM/反激CCM。在设计过程中,为提高变换器输出功率和效率,选择变换器工作于正激CCM/反激DCM。为便于分析其工作原理,首先做如下说明:
(1)所有功率器件、电感及电容均为理想元器件。
(2)除特殊说明外,输出滤波电容视为足够大,输出纹波电压相对输出电压可忽略不计。
(3)辅助电感L2的电流单向流动,无倒流现象。
当正激CCM/反激DCM时,变换器进入稳态后,一个开关周期可分为四种工作模态,各模态等效电路模型和主要工作波形分别如图2和图3所示。
(1)模态1 [t0, t1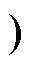 :开关管S导通、二极管VD1导通,VD3和VD2截止。输入电能一部分通过变压器传递给负载,一部分转换为磁场能存储于L1和Lm中,励磁电流从零线性上升;C2经L2对负载放电。此阶段iL2的升降取决于VC2,在t0~
:开关管S导通、二极管VD1导通,VD3和VD2截止。输入电能一部分通过变压器传递给负载,一部分转换为磁场能存储于L1和Lm中,励磁电流从零线性上升;C2经L2对负载放电。此阶段iL2的升降取决于VC2,在t0~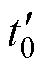 时间段,VC2>Vo,iL2递增;
时间段,VC2>Vo,iL2递增;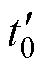 ~t1时间段,VC2<Vo,iL2递减。t1时刻,VC2降至最小值,iL1达到最大值IL1P。
~t1时间段,VC2<Vo,iL2递减。t1时刻,VC2降至最小值,iL1达到最大值IL1P。
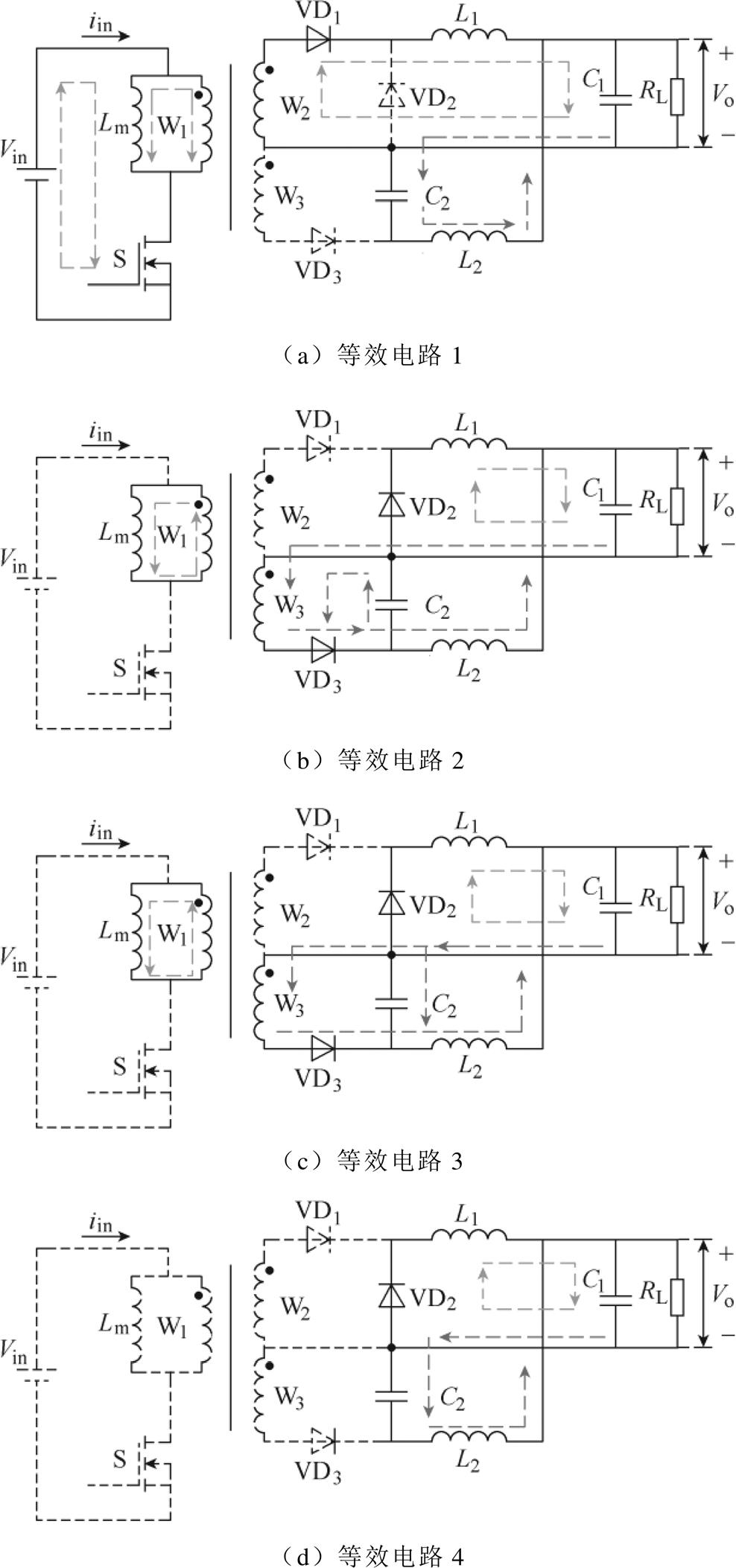
图2 各工作模态等效电路
Fig.2 Equivalent circuit in different operating modes
(2)模态2 [t1, t2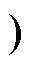 :t1时刻开关管S关断,二极管VD1截止,VD2和VD3导通,反向电压n2VC2加在励磁电感上使变压器磁复位。励磁能量耦合到反激绕组W3,一部分通过二极管VD3给电容C2充电,另一部分经辅助电感L2传输至负载,其中iL2的升降同样取决于VC2。同时,L1通过VD2续流,电流iL1线性下降。此模态一直持续到C2充电结束的t2时刻,电流iC2降至零,VC2达到最大值。
:t1时刻开关管S关断,二极管VD1截止,VD2和VD3导通,反向电压n2VC2加在励磁电感上使变压器磁复位。励磁能量耦合到反激绕组W3,一部分通过二极管VD3给电容C2充电,另一部分经辅助电感L2传输至负载,其中iL2的升降同样取决于VC2。同时,L1通过VD2续流,电流iL1线性下降。此模态一直持续到C2充电结束的t2时刻,电流iC2降至零,VC2达到最大值。
(3)模态3 [t2, t3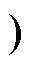 :t2时刻后,iC2开始反向增加,电容C2通过电感L2放电,其两端电压VC2逐渐减小,C2中的电场能一部分转化为磁场能存储在电感L2中,一部分转化为电能传递给负载,且同样存在VC2>Vo时,iL2递增;VC2<Vo时,iL2递减。同时,正激电感L1继续通过二极管VD2续流。此模态一直持续到-iC2=iL2时刻,此时电容C2的放电电流等于流进电感L2的电流且iN3=0,二极管VD3自然关断,变压器完成磁复位。
:t2时刻后,iC2开始反向增加,电容C2通过电感L2放电,其两端电压VC2逐渐减小,C2中的电场能一部分转化为磁场能存储在电感L2中,一部分转化为电能传递给负载,且同样存在VC2>Vo时,iL2递增;VC2<Vo时,iL2递减。同时,正激电感L1继续通过二极管VD2续流。此模态一直持续到-iC2=iL2时刻,此时电容C2的放电电流等于流进电感L2的电流且iN3=0,二极管VD3自然关断,变压器完成磁复位。
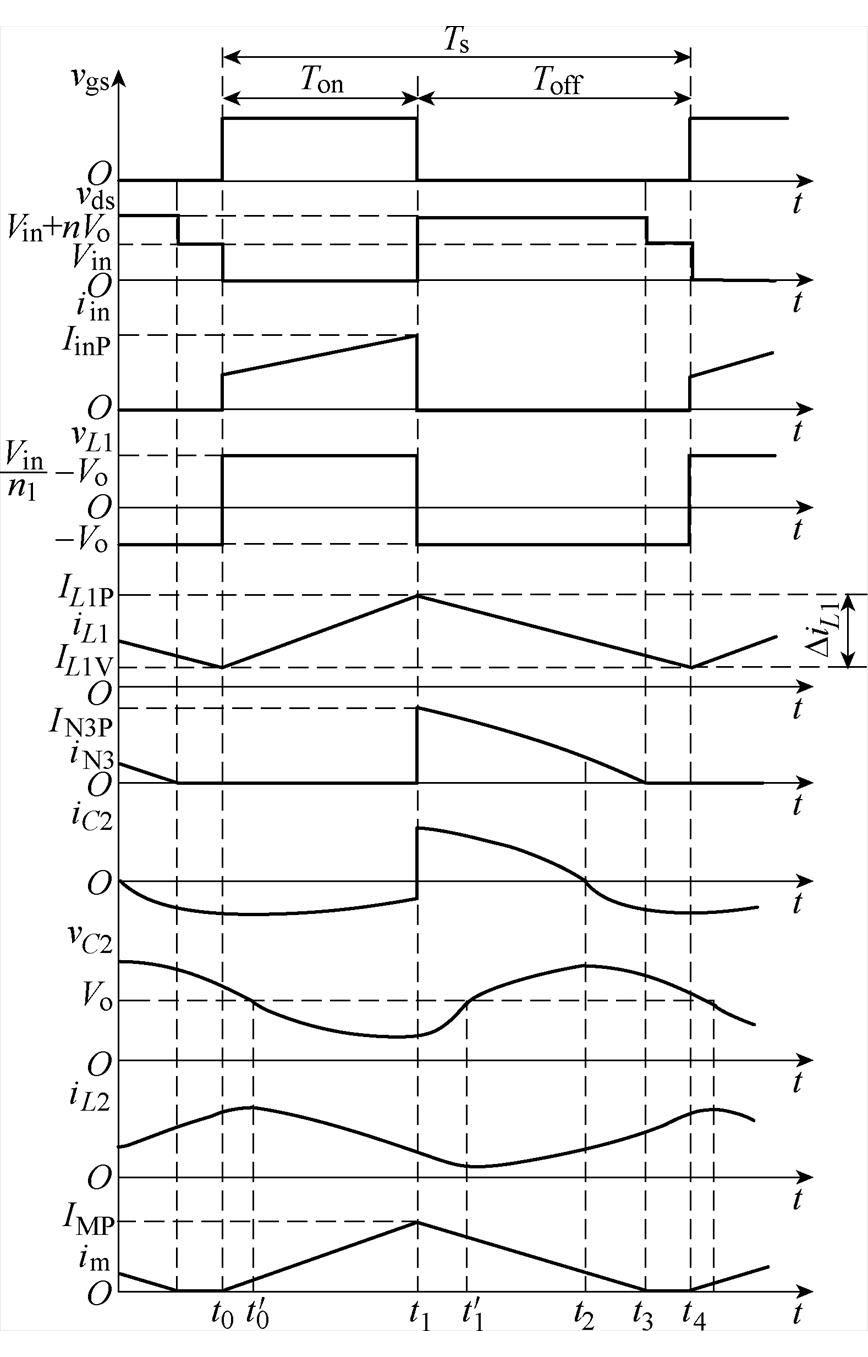
图3 变换器主要工作波形
Fig.3 Main working waveforms of converter
(4)模态4 [t3, t4]:t3时刻后,电容C2继续通过L2向负载供能,同样存在VC2>Vo时,iL2递增;VC2<Vo时,iL2递减。同时,正激电感L1继续通过二极管VD2续流。直到下一个开关周期到来时刻,此模态结束。
为确定辅助电感L2的最佳工作模态,对电感电流iL1、iL2与输出电流Io的关系进行分析。由于L2两端电压为VC2-Vo,因此,根据不同时刻VC2与Vo的大小关系,得到如图4所示的辅助电感电流变化波形。图中,辅助电感L2的电流实际是按照平滑的曲线变化的,为便于分析,图中iL2以直线代替曲线;Q1为iL1>Io期间产生的电荷量;同时,在iL1>Io期间,iL2产生的电荷量为Q2。
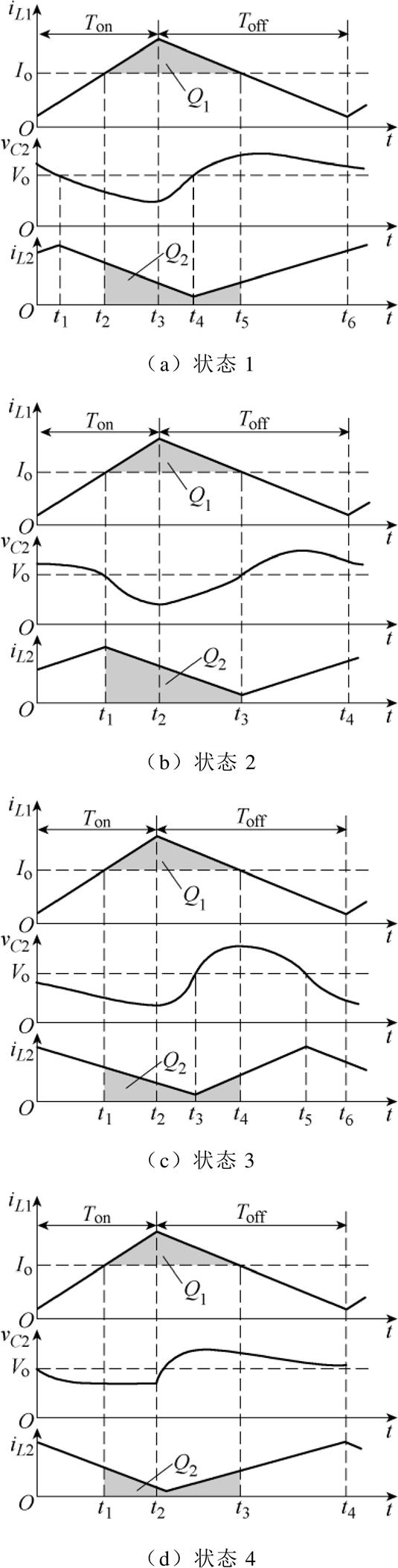
图4 iL1、iL2与输出电流Io的关系
Fig.4 Relationship between iL1、iL2 and output current Io
状态1:开关导通瞬间VC2>Vo,L2两端电压为正,iL2逐渐增大,当C2放电至VC2<Vo时,L2两端电压变为负,iL2逐渐减小;当开关关断时,耦合到反激绕组W3的励磁电流从某一最大初始值递减为C2充电,VC2在较短时间内达到Vo,iL2开始逐渐增大,一直持续到下一个导通期间VC2=Vo时刻,在此期间,C2会经历充电和放电两个阶段。
状态2:在iL1>Io时,VC2<Vo,电流iL2逐渐减小;在iL1<Io时,VC2>Vo,电流iL2逐渐增大。
状态3:开关导通瞬间VC2<Vo,C2经电感L2放电,开关导通期间iL2始终递减;开关关断后同模态1类似,不同的是,在开关关断期间VC2会提前降到Vo,iL2在开关关断期间会由递增变为递减。
状态4:开关导通期间VC2<Vo,辅助电感电流iL2下降,正激电感电流iL1增加;关断期间VC2>Vo,辅助电感电流iL2上升,正激电感电流iL1下降,两者电流变化趋势相反。
结合图4显然可知,状态2对输出电容充电的电荷量(Q1与Q2之和)最大,状态1和状态3次之,状态4最小。因此,辅助电感的工作状态4为最佳工作模态,此时对应的输出电压纹波最小。
为减小输出纹波电压,提高输出电能质量且增加变换器的可靠性,辅助电感应工作于最佳模态,即状态4。根据文献[19]并结合此附加LC的正反激组合变换器可知,在给定的输入电压和负载变化范围内,最大的输出纹波电压Vpp,max就等于其工作于正激CCM时的最大输出纹波电压。因此,基于最佳的工作模式,对变换器的输出纹波电压进行分析,其中,附加LC的正反激组合变换器输出纹波电流及电压波形如图5所示。
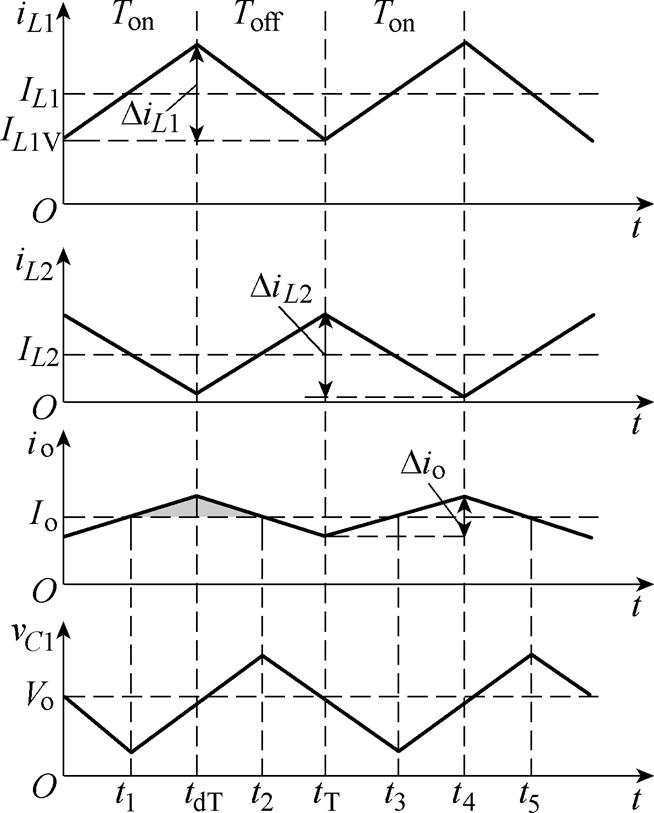
图5 最佳工作模态下的输出纹波电流及电压波形
Fig.5 Output ripple current and voltage waveforms in the best operating mode
输出电流Io为正激电感电流IL1与辅助电感电流IL2之和,满足Io=IL1+IL2,当iL1+iL2<Io时,电容C1、电感L1与L2同时给负载供能,C1处于放电状态,输出电压减小;当iL1+iL2>Io时,电感L1与L2给负载RL和电容C1供能,C1处于充电状态,输出电压增加,即Q1与Q2之和越大,变换器的输出纹波电压越大。电容电压变化量DV与电容量C和电荷量Q的关系为DV=Q/C,根据图4中电流与时间轴围成的面积可将变换器的输出纹波电压Vpp表示为
 (1)
(1)由式(1)可知,Q1和Q2之和越小,变换器的纹波电压越小。当辅助电感L2工作于最佳工作模态时,Q1与Q2之和最小,使输出电流和电压纹波达到最小,其具体性能与附加LC参数相关,变换器的输出纹波电压随L2与C2的减小而减小,随输入电压的增大而增大。
辅助电感L2的设计与电容C2密切相关,在优化设计过程中:首先,兼顾开关管电压应力和输出纹波电压要求,选取电容C2的最优值;其次,在电感L2工作于状态4情况下,设计出辅助电感电流不发生倒流的最优电感值。据此,给出综合考虑开关管电压应力、变换器输出电压纹波及辅助电感电流不发生倒流的最优L2、C2参数设计方法。
由于电容C2的平均电压等于输出电压Vo,若C2取值较小,将会导致开关管的电压应力较高,且辅助电感较大,实际设计中,可根据其电压纹波系数γ来选取C2。可令励磁能量全部存储于电容C2,其电压变化量DVC2为
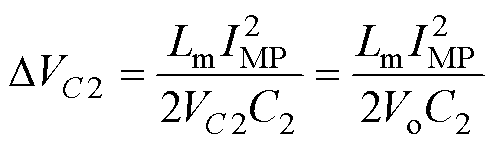 (2)
(2)则其电压纹波系数为
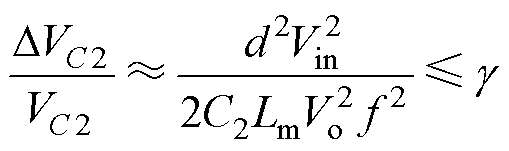 (3)
(3)
式中,d为占空比;f为开关频率。
考虑输入电压范围,可得电容C2的最优取值为
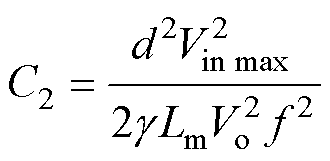 (4)
(4)为了减小开关管的电压应力,取g=10%。
4.2.1 正激电感CCM时的临界辅助电感L2C
为了得到临界电感L2C,令L2电流最小值为IL2,MV,同时,基于最佳工作状态4可知,L2在开关导通期间的平均电压绝对值为DVC2/4,因此,其电流最小值IL2,MV为
 (5)
(5)令IL2,MV=0,并消去占空比d可知,正激电感L1工作于CCM时,辅助电感L2的临界值为
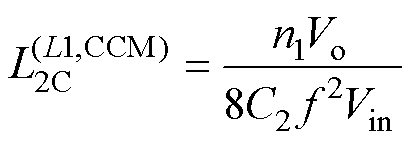 (6)
(6)
可知,在正激电感CCM时,临界辅助电感L2C随输入电压和电容C2的增大而减小,且与负载电阻无关。根据L2优化设计的原则,在动态范围下,L2选取最大值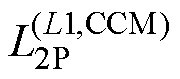 ,满足
,满足
 (7)
(7)4.2.2 正激电感DCM时的临界辅助电感L2C
正激电感L1工作于DCM时,电感L1的峰值电流IL1P为
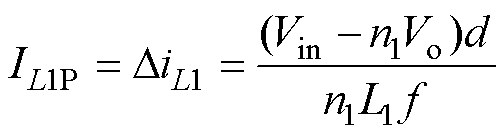 (8)
(8)令开关导通期间正激电感L1存储的能量为E1,开关导通期间存储在Lm中的励磁能量为E2,一个开关周期内通过变压器从源侧传到负载侧的能量为E3,负载吸收的总能量为EA,根据能量守恒可知
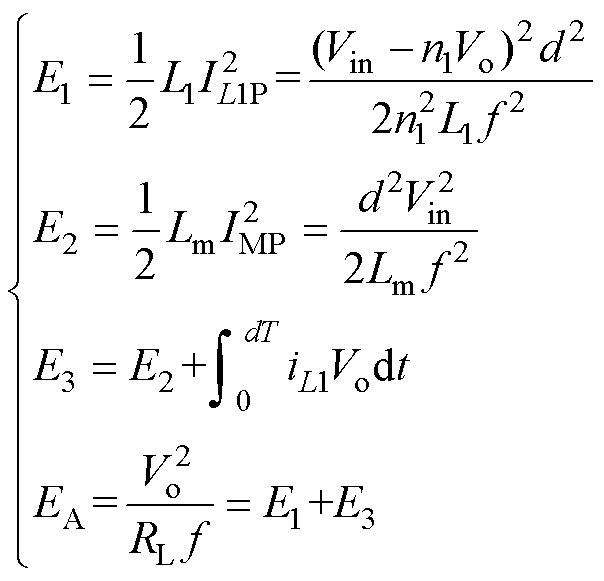 (9)
(9)
式中,IMP为变压器励磁电流最大值;iL1为正激电感电流,表示为
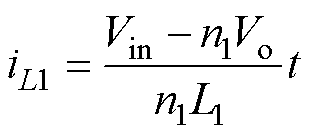 (10)
(10)联立式(8)~式(10)可得,正激电感DCM时,变换器的占空比d为
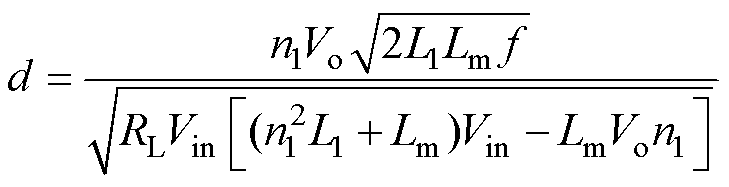 (11)
(11)
同理,令辅助电感L2的电流最小值为零可得,正激电感工作于DCM时,L2的临界值为
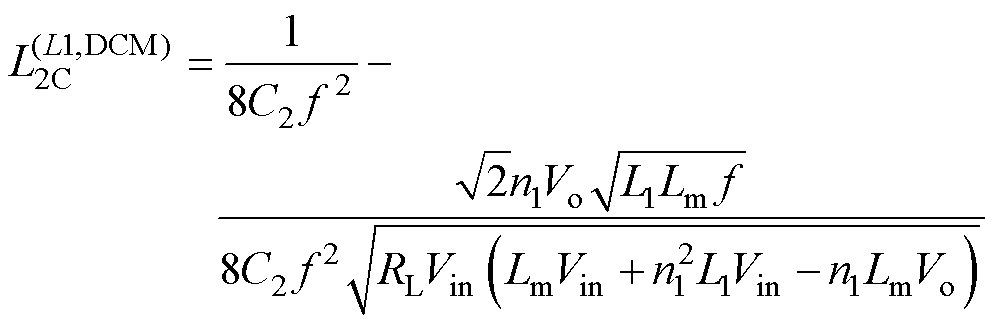 (12)
(12)可知,正激电感工作于DCM时,临界电感L2C随负载电阻和输入电压的增大而增大,随辅助电容C2的增大而减小。因此,根据L2优化设计的原则,L2选取最大值 ,满足
,满足
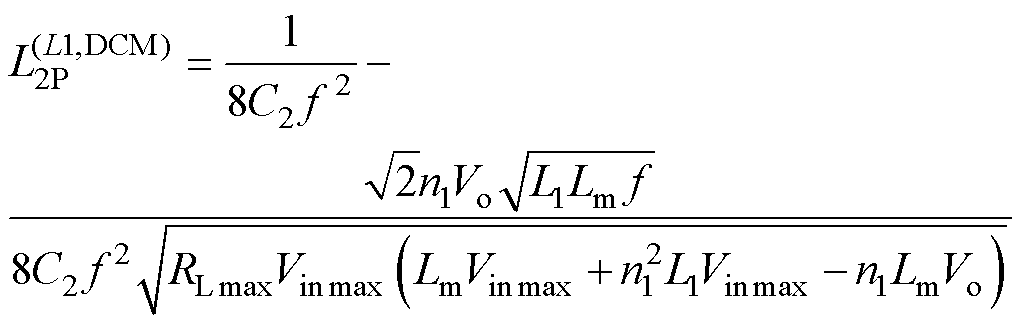 (13)
(13)
式中,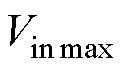 为输入电压最大值;
为输入电压最大值;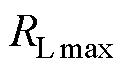 为负载最大值。
为负载最大值。
根据以上分析,在给定的输入电压和负载变化范围内,结合L2的优化设计原则,为减小输出纹波电压且避免无功损耗,辅助电感L2的最优取值应根据式(7)和式(13)选择两者中的较大值。
为了验证理论分析的正确性,研制了一台输入电压范围AC 165V~AC 250V,输出电压48V,负载电阻变化范围4.8~48W,最大输出功率480W的实验样机,如图6所示。变换器主要参数:开关频率为100kHz,变压器匝比N1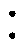 N2
N2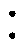 N3=26
N3=26 14
14 7,励磁电感Lm=2.3mH,正激电感L1=140mH,辅助电感L2= 10mH,辅助电容C2=0.68mF,输出滤波电容C1= 470mF。
7,励磁电感Lm=2.3mH,正激电感L1=140mH,辅助电感L2= 10mH,辅助电容C2=0.68mF,输出滤波电容C1= 470mF。

图6 实验样机
Fig.6 The experimental prototype
在输入电压为AC 200V,负载约为1.1A时,正激电感L1进入临界连续导电模式,变换器主要的电量波形如图7所示。
图7 正激电感L1临界模式时的主要电量波形
Fig.7 The main waveforms in boundary conduction mode of forward inductance L1
由图7可知,开关频率约为100kHz;电容C2电压变化范围约为47~52V,其电压纹波系数为10.4%;开关导通期间,流过电感L2的电流iL2递减,开关关断期间,电流iL2递增,其电流变化趋势与正激电感电流iL1变化趋势相反,工作于所设计的状态4,且无反向倒流,与理论分析相同。
为验证变换器辅助电感最佳工作模态下的输出纹波电压与辅助电感L2及输入电压Vin之间的关系,电感L2分别取10mH和18mH,且输入电压分别为AC 180V和AC 250V时,对样机辅助电感电流iL2及输出纹波电压VPP进行测试,实验波形如图8所示。
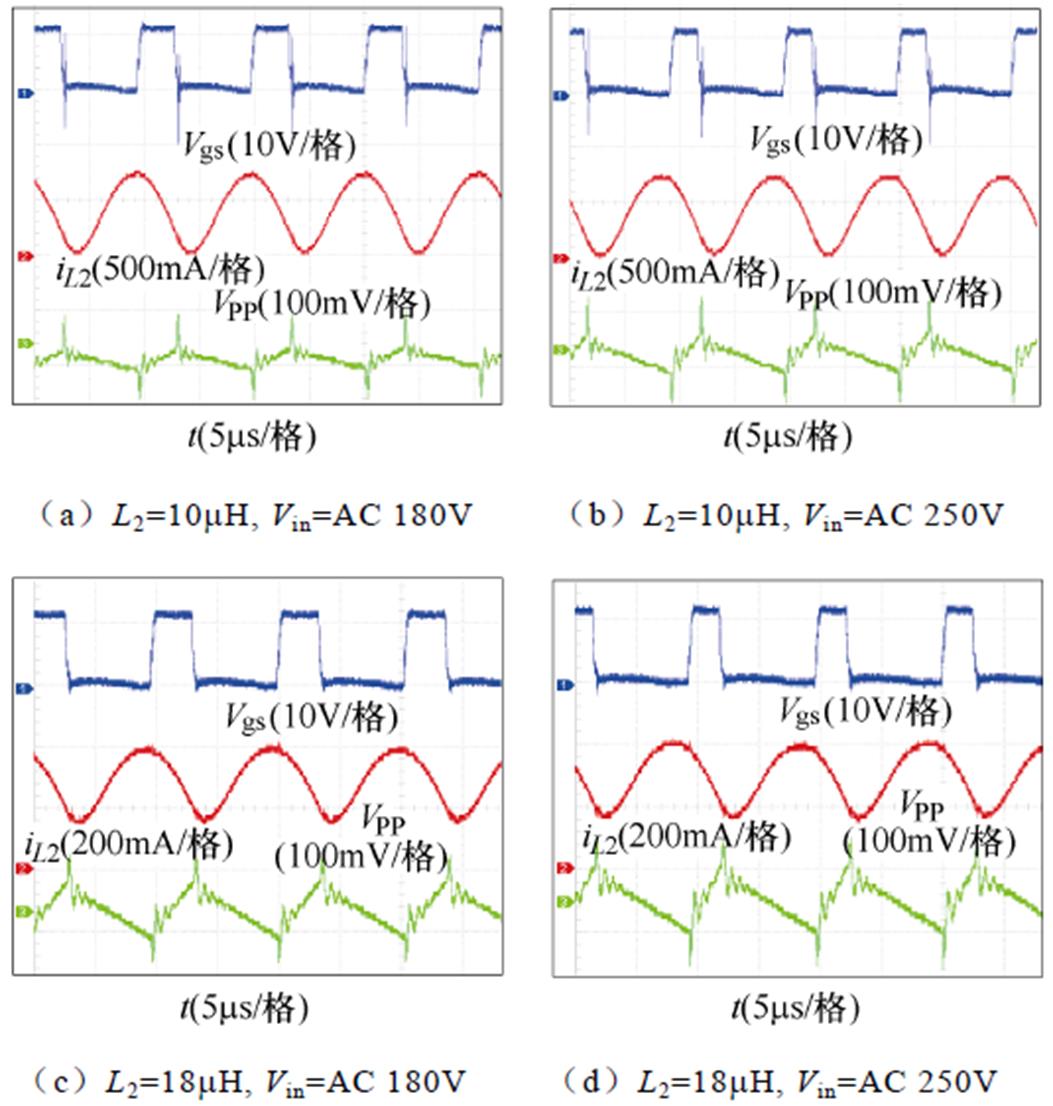
图8 不同L2和Vin下的iL2和VPP实验波形
Fig.8 iL2 and VPP experimental waveforms under different L2 and Vin
由图8可知,当辅助电感L2及输入电压Vin不同时,L2的电流变化量及变换器的输出纹波电压不同。分别对比图8a和图8b,图8c和图8d可以发现,输出纹波电压VPP随辅助电感L2和输入电压Vin增大而增大,当电感L2依据优化原则及临界电感表达式(7)和式(13)取10mH时,其电流临界连续,且输出纹波电压最小,与理论分析一致。
本文提出了一种附加LC的正反激组合变换器,并对其工作原理及能量传输过程进行了深入研究,结合变换器的特性,指出了辅助电感最佳工作模态并分析了输出电压纹波,推导得出辅助电感临界值,同时,提出了一种对附加LC参数优化设计的方法,实验结果验证了理论分析与设计方法的正确性,对设计高性能的正反激组合变换器具有重要的指导意义。得到主要结论如下:
1)依据附加LC的电压电流波形,分析了所提出正反激组合变换器的工作原理及能量传输过程,指出辅助电感L2工作于状态4为变换器的最佳工作模式。
2)当变换器辅助电感工作于最佳工作模态时更适合大功率输出,避免了传统正反激组合变换器输出电流脉动较大的缺点,有效地减小了输出纹波电压,仅需较小的输出滤波电容就可满足纹波电压要求,有利于变换器的小型化。
3)分别详细推导了正激电感工作于CCM和DCM时的临界辅助电感L2C,得出,当正激电感工作于CCM时,L2C随输入电压和电容C2的增大而减小,且与负载电阻无关;正激电感工作于DCM时,L2C随输入电压和负载电阻的增大而增大,随电容C2的增大而减小。根据L2的优化设计方法,在输入电压和负载变化范围内,较大的临界值即为L2最优的参数设计。
参考文献
[1] 彭祥宇, 李佳晨, 吕征宇. 高增益软开关Forward- Flyback变换器[J]. 电力电子技术, 2018, 52(11): 57-59.
Peng Xiangyu, Li Jiachen, Lü Zhengyu. High step-up soft-switching Forward-Flyback converter[J]. Power Electronics, 2018, 52(11): 57-59.
[2] Alireza, Lahooti, Eshkevari, et al. Design, modelling, and implementation of a modified double-switch flyback-forward converter for low power appli- cations[J]. IET Power Electronics, 2019, 12(4): 739- 748.
[3] 谢小高, 赵晨, 郑凌蔚, 等. 有源钳位正反激变流器的第三绕组与电流型混合同步整流驱动方案[J]. 中国电机工程学报, 2012, 32(33): 31-36, 172.
Xie Xiaogao, Zhao Chen, Zheng Lingwei, et al. A third-winding and current-driven hybrid driving scheme for SRs of active-clamped forward-flyback converters[J]. Proceedings of the CSEE, 2012, 32(33): 31-36, 172.
[4] 吴琨, 钱挺, 王浩. 一种开关频率固定的输出可调型有源钳位正激双向谐振变换器[J]. 电工技术学报, 2018, 33(20): 4771-4779.
Wu Kun, Qian Ting, Wang Hao. A novel fixed switching frequency active-clamp forward dual resonant converter with regulation capability of output voltage[J]. Transactions of China Electro- technical Society, 2018, 33(20): 4771-4779.
[5] 胡海兵, 吴红飞, 刘薇, 等. 一族有源钳位正激变换器[J]. 电工技术学报, 2013, 28(12): 245-250, 261.
Hu Haibing, Wu Hongfei, Liu Wei, et al. A family of active clamp forward converter[J]. Transactions of China Electrotechnical Society, 2013, 28(12): 245- 250, 261.
[6] Qian Ting, Wu Qichen. A scheme of resonant Forward-Flyback converter with suppressed frequency variation[J]. IEEE Transactions on Power Electronics, 2018, 33(5): 3711-3716.
[7] 黄峰, 陈剑, 刘俊峰, 等. 正反激倍压DC-DC变换器机理分析与仿真[J]. 东北电力大学学报, 2018, 38(4): 35-39.
Huang Feng, Chen Jian, Liu Junfeng, et al. Mechanism analysis and simulation of forward and flyback DC-DC converter[J]. Journal of Northeast Electric Power University, 2018, 38(4): 35-39.
[8] Quan Chao, Geng Yuchuan, Chen Qianhong, et al. Analysis, design and control of a resonant forward- flyback converter[C]//2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, 2018: 2275-2280.
[9] Lee H, Choe H, Ham S, et al. High-efficiency asymmetric Forward-Flyback converter for wide output power ranger[J]. IEEE Transactions on Power Electronics, 2017: 433-440.
[10] Chen F, Amirahmadi A, Batarseh I. Zero voltage switching Forward-Flyback converter with efficient active LC snubber circuit[C]//Applied Power Elec- tronics Conference & Exposition, Fort Worth, 2014: 2041-2047.
[11] 李晓高, 洪峰. 双管双变压器正-反激组合变换器研究[J]. 电力电子技术, 2007(11): 26-28.
Li Xiaogao, Hong Feng. Analysis of a forward- flyback converter employing two switches and two transformers[J]. Power Electronics, 2007(11): 26-28.
[12] 刘树林, 曹剑, 胡传义, 等. 正-反激组合变换器的能量传输模式及输出纹波电压分析[J]. 电工技术学报, 2019, 34(8): 1647-1656.
Liu Shulin, Cao Jian, Hu Chuanyi, et al. Energy transmission modes and output ripple voltage of forward-flyback converter[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1647-1656.
[13] Ke C, Liang T, Tseng W, et al. Design and implementation of an interleaved forward converter with magnetizing energy recycled[C]//2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, 2019: 5949-5953.
[14] 王星星, 嵇保健, 洪峰, 等. 一种改进的正反激并网微型逆变器[J]. 电工技术学报, 2017, 32(18): 202-210.
Wang Xingxing, Ji Baojian, Hong Feng, et al. An improved forward-flyback grid-connected micro- inverter[J]. Transactions of China Electrotechnical Society, 2017, 32(18): 202-210.
[15] Murthy-Bellur D, Kazimierczuk M K. Two-switch Flyback-Forward PWM DC-DC converter with reduced switch voltage stress[C]//Proceedings of 2010 IEEE International Symposium on Circuits and Systems, Paris, 2010: 3705-3708.
[16] Jaeil Baek, Han-Shin Youn. Full-bridge active-clamp Forward-Flyback converter with an integrated trans- former for high-performance and low cost low- voltage DC converter of vehicle applications[J]. Energies, 2020, 13(4): 863.
[17] Dobakhshari S S, Taheri M, Banaiemoghadam A, et al. A new integrated high step-up quasi-resonant flyback- forward converter[J]. International Journal of Circuit Theory and Applications, 2018, 46(10): 1899-1916.
[18] Young-Tae Jeon, Joung-Hu Park. Frequency-PWM hybrid controller of single-switch forward-flyback converter for DC-link regulation of 27-level cascaded H-bridge inverter[J]. IEICE Electronics Express, 2017, 14(13): 20170492.
[19] 刘树林, 刘健著. 开关变换器分析与设计[M]. 北京:机械工业出版社, 2010.
Analysis of the Optimal Operating Mode of Auxiliary Inductance and LC Parameter Optimization Design of Forward-Flyback Converter with Additional LC
Abstract In order to reduce the output voltage ripple of the forward-flyback converter, a forward-flyback converter with additional LC was proposed. According to the voltage and current waveforms of the additional LC, the working principle and energy transmission process of the proposed forward-flyback converter were analyzed, and the optimal operation mode was obtained to ensure that the current of the auxiliary inductor is not reversed while the superimposed current ripple of the forward inductor and the auxiliary inductor is minimized. The output ripple voltage in this mode decreased with the decrease of the auxiliary inductor. Within a given range of input voltage and load variation, the critical conditions for the auxiliary inductor current not to reverse when the forward inductor work in continuous conduction mode (CCM) and discontinuous conduction mode (DCM) were derived respectively. Thus, an optimal design method of auxiliary inductors and capacitors was proposed. Examples and experimental results verify the correctness of the theoretical analysis and the feasibility of the proposed optimization design method.
Keywords:Forward-flyback converter, output ripple voltage, operating mode, optimized design
中图分类号:TM46
DOI: 10.19595/j.cnki.1000-6753.tces.L90394
国家自然科学基金资助项目(51777167, 51604217)。
收稿日期 2020-07-11
改稿日期 2020-11-24
E-mail: lsigma@163.com
王航杰 男,1996年生,硕士研究生,研究方向为电力电子与电力传动。
E-mail: 467955483@qq.com(通信作者)
(编辑 陈 诚)